Abstract
Unconventional superconductors often feature competing orders, small superfluid density, and nodal electronic pairing. While unusual superconductivity has been proposed in the kagome metals AV3Sb5, key spectroscopic evidence has remained elusive. Here we utilize pressure-tuned and ultra-low temperature muon spin spectroscopy to uncover the unconventional nature of superconductivity in RbV3Sb5 and KV3Sb5. At ambient pressure, we observed time-reversal symmetry breaking charge order below 110 K in RbV3Sb5 with an additional transition at 50 K. Remarkably, the superconducting state displays a nodal energy gap and a reduced superfluid density, which can be attributed to the competition with the charge order. Upon applying pressure, the charge-order transitions are suppressed, the superfluid density increases, and the superconducting state progressively evolves from nodal to nodeless. Once optimal superconductivity is achieved, we find a superconducting pairing state that is not only fully gapped, but also spontaneously breaks time-reversal symmetry. Our results point to unprecedented tunable nodal kagome superconductivity competing with time-reversal symmetry-breaking charge order and offer unique insights into the nature of the pairing state.
Subject terms: Superconducting properties and materials, Electronic properties and materials
The nature of the superconductivity in the kagome metals AV3Sb5 (A = K, Rb, Cs) remains under debate. Here, using muon spin spectroscopy, the authors find that the superconductivity in RbV3Sb5 and KV3Sb5 evolves from nodal to nodeless with increasing pressure and the superconducting state breaks time-reversal symmetry after suppression of the charge order.
Introduction
Due to their inherent geometric frustration and unique band structure, kagome materials1 represent an excellent platform for discovering, classifying and understanding correlated electronic phases of quantum matter2–6. The novel family of kagome metals AV3Sb5 (A = K, Rb, Cs)7–11 exhibit an array of interesting effects such as giant anomalous Hall conductivity12,13, charge order11,14–23, orbital order24, and possible unconventional superconductivity7,8,10. An important feature of the charge order, which onsets at temperatures Tco ~ 100 K at ambient pressure, is the breaking of time-reversal symmetry, as reported by scanning tunneling microscopy (STM) measurements11,14,15,17 in (K,Rb,Cs)V3Sb5, by muon spin relaxation (μSR) in KV3Sb525 and CsV3Sb526,27, and by Kerr effect measurements in CsV3Sb528. This implies that the charge-ordered state displays not only bond distortions, but also orbital current loops (see Fig. 1a)29–32.
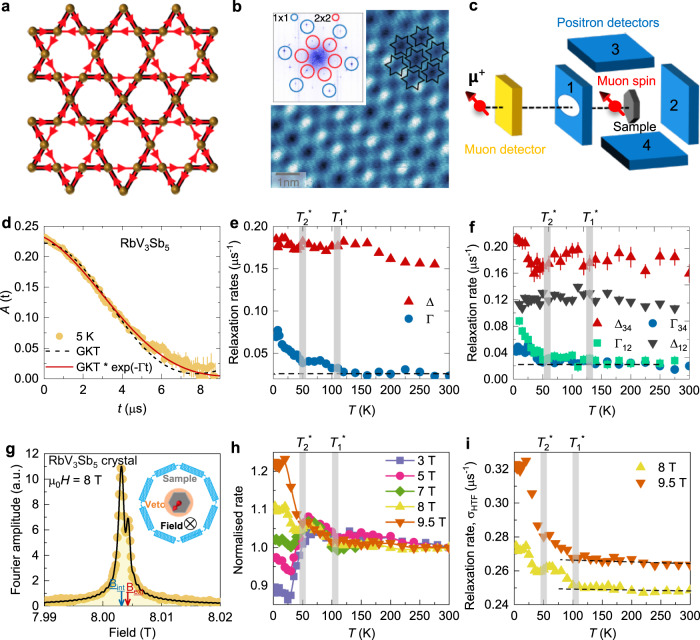
Fig. 1. Time-reversal symmetry-breaking charge order in RbV3Sb5.
a Schematic example of an orbital current state (red arrows) in the kagome lattice. b Scanning tunneling microscopy of the Sb surface showing 2 × 2 charge order as illustrated by black lines. The inset is the Fourier transform of this image, displaying 1 × 1 lattice Bragg peaks (blue circles) and 2 × 2 charge-order peaks (red circles). The latter have different intensities, suggesting a chirality of the charge order. c A schematic overview of the experimental set-up (see the “Methods” section). d The ZF μSR time spectra for the polycrystalline sample of RbV3Sb5, obtained at T = 5 K. The dashed and solid curves represent fits using the Gaussian Kubo–Toyabe (GKT) function without (black) and with (red) a multiplied exponential term, respectively. Error bars are the standard error of the mean (s.e.m.) in about 106 events. The temperature dependences of the relaxation rates Δ and Γ, which can be related to the nuclear and electronic contributions respectively, are shown in a wide temperature range for the polycrystalline (e) and the single crystal samples (f) of RbV3Sb5. f presents Γ obtained from two sets of detectors. The error bars represent the standard deviation of the fit parameters. g Fourier transform of the μSR asymmetry spectra for the single crystal of RbV3Sb5 at 3 K in the presence of an applied field of μ0H = 8T. The black solid line is a two-component signal fit. The peaks marked by the arrows denote the external and internal fields, determined as the mean values of the field distribution from the silver sample holder (mostly) and from the sample, respectively. Inset shows the schematic high-field μSR experimental set-up (see the “Methods” section). h The temperature dependence of the high transverse field muon spin relaxation rate σHTF for the single crystal of RbV3Sb5, normalized to the value at 300 K, measured under different c-axis magnetic fields. i The temperature dependence of the relaxation rate, measured under magnetic field values of μ0H = 8 and 9.5 T.
Similarly to charge order, superconductivity, with transition temperature Tc ~ 1 K at ambient pressure, was also reported to display intriguing features, such as multiple gaps in (K,Cs)V3Sb533–36, diminished superfluid density in KV3Sb525, and double-dome structures in the pressure phase diagrams of all three compounds37–39. However, no consensus on the superconducting gap structure has been reached yet25,33–35,40–43, partly due to the challenges of performing spectroscopic studies under extreme conditions including ultra low temperatures and large pressures. Moreover, the role of the unconventional charge order in the emergence of these unusual superconducting features remains unclear, since the former onsets at a much higher temperature than the latter. In this regard, the sensitivity of both Tc and Tco on the applied pressure37–39 offers a rare setting to study the interplay between these two orders with a disorder-free tuning knob.
Here, we tackle these issues by employing zero-field and high-field muon spin relaxation experiments to directly probe the interplay between charge order and superconductivity across the temperature-pressure phase diagram of RbV3Sb5. This allows us to assess not only the time-reversal symmetry-breaking nature of these two states, but also the evolution of the low-energy superconducting excitations as Tco is suppressed and Tc is enhanced. The latter measurements unearth a remarkable pressure induced crossover from nodal pairing, when superconductivity coexists with charge order, to nodeless pairing, when optimal superconductivity is achieved near the critical pressure for charge order. They also reveal distinct relationships between Tc and the superfluid density in these two regimes. The same behaviors are also observed in KV3Sb5, attesting to the robustness of our conclusions for the understanding of the pairing mechanism in the AV3Sb5 family. We discuss different scenarios for the symmetries of both the superconductivity and charge order states that may account for the unusual nodal-to-nodeless transition.
Results and discussion
Probing spontaneous time-reversal symmetry breaking
Scanning tunneling microscopy observes 2 × 2 charge order in RbV3Sb5 (Fig. 1b and ref. 14) with an unusual magnetic field response14, suggestive of time-reversal symmetry-breaking charge order. To directly probe signatures of time-reversal symmetry-breaking, we carried out zero field (ZF) μSR experiments (see Fig. 1c) on both single crystal and polycrystalline samples of RbV3Sb5 above and below Tco. The ZF-μSR spectra (see Fig. 1d) were fitted using the Gaussian Kubo–Toyabe (GKT) depolarization function44 multiplied with an exponential decay function25:
| 1 |
here, Δ/γμ is the width of the local field distribution due to the nuclear moments and γμ = 0.085 μs−1 G−1 is the muon gyromagnetic ratio. A GKT shape is expected due to the presence of the dense system of nuclear moments with large values of nuclear spins (I = 3/2 for 39K, I = 7/2 for 51V, and I = 5/2 for 121Sb) in KV3Sb5 and a high natural abundance. The exponential relaxation rate Γ is mostly sensitive to the temperature dependence of the electronic contribution to the muon spin relaxation, as we discussed previously in our work that reported time-reversal symmetry-breaking in KV3Sb525. Because the zero-field relaxation is decoupled by the application of a small external magnetic field applied in a direction longitudinal to the muon spin polarization, BLF = 50 G (see Supplementary Note 4 and Supplementary Fig. 4), the relaxation is, therefore, due to spontaneous fields that are static at the microsecond timescale45. In Fig. 1e, the temperature dependence of the Gaussian and exponential relaxation rates Δ and Γ for the polycrystalline sample of RbV3Sb5 are shown over a broad temperature range. The main observation is the two-step increase of the relaxation rate Γ, consisting of a noticeable enhancement at 110 K, which corresponds approximately to the charge-order transition temperature Tco, and a stronger increase below 50 K. To substantiate this result, data from the single crystals are presented in Fig. 1f. The data from the up–down (34) and forward–backward (12) sets of detectors not only confirm the increase of Γ, but also shed more light into the origin of the two-step behavior. In particular, while Γ34 is enhanced mostly below 50 K, Γ12 also features a mild initial increase right below 110 K. Since the enhanced electronic relaxation rate below is seen mostly in Γ12, it indicates that the local field at the muon site lies mostly within the ab-plane of the crystal. Below , the internal field also acquires an out-of-plane component, as manifested by the enhancement of both Γ12 and Γ34. The increase of the electronic contribution to the internal field width is also accompanied by maxima and minima in the temperature dependence of the nuclear contribution to the internal field width Δ/γμ, particularly for the up–down set of detectors (Fig. 1e, f).
The increase in the exponential relaxation of RbV3Sb5 between and 2 K is about 0.05 μs−1, which can be interpreted as a characteristic field strength Γ12/γμ ≃ 0.6 G. While these ZF-μSR results are consistent with the onset of time-reversal symmetry-breaking at Tco, high-field μSR experiments, illustrated in the inset of Fig. 1g, are essential to confirm this effect. As we discussed previously25, the onset of charge order might also alter the electric field gradient experienced by the nuclei and correspondingly the magnetic dipolar coupling of the muon to the nuclei. This can induce a change in the nuclear dipole contribution to the zero-field μSR signal. In a high magnetic field, the direction of the applied field defines the quantization axis for the nuclear moments, so that the effect of the charge order on the electric field gradient at the nuclear sites is irrelevant. Figure 1g shows the probability distribution of the magnetic field measured at 3 K for the single-crystal samples of RbV3Sb5 in the presence of a c-axis magnetic field of 8 T (see “Methods” for the details of the analysis, see also Supplementary Note 5 and Supplementary Fig. 5). The contribution from the internal field is clearly identified. Figure 1h shows the corresponding temperature-dependent relaxation rate σHTF for different values of the external c-axis field. For 3 T, it displays a non-monotonic behavior, staying nearly constant across and then decreasing to a minimum before increasing again at low temperatures. Upon increasing the external field, the relaxation rate not only shows an increase right at 110 K, but its temperature dependence below is reversed from being reduced to being enhanced upon lowering the temperature. Thus, as shown in Fig. 1, the relaxation rate extracted from the high-field μSR data shows a qualitatively similar two-step increase as the ZF data at the same characteristic temperatures 110 K and 50 K—although the features are more pronounced at high fields. Because the temperature dependence of the nuclear contribution to the relaxation cannot be changed by an external field, we conclude that the two-step increase in the relaxation rate is driven by the electronic/magnetic contribution.
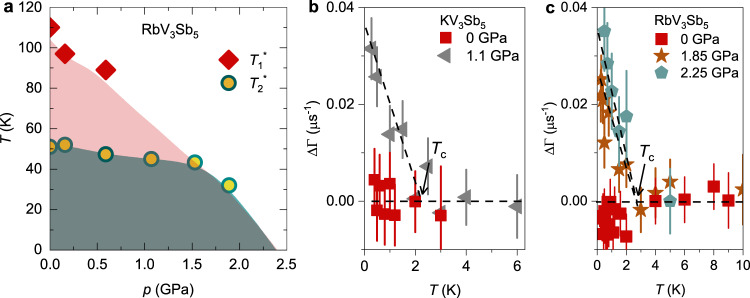
Therefore, the combination of ZF-μSR and high-field μSR results on RbV3Sb5 provide direct evidence for time-reversal symmetry-breaking below the onset of charge order, which approximately coincides with 110 K. It is important to note that the entire sample volume experiences an increase in the relaxation rate, indicating the bulk nature of the transition below . As we previously discussed for KV3Sb525, one plausible scenario to explain this effect is that loop currents along the kagome bonds are generated by a complex charge order parameter16,22,23. Within this framework, muons can couple to the fields generated by these loop currents via their spin, resulting in an enhanced internal field width sensed by the muon ensemble (see also Supplementary Information). The lower-temperature increase of the relaxation rate at 50 K is suggestive of another ordered state that modifies such loop currents. An obvious candidate is a secondary charge-ordered state onsetting at . Indeed, experimentally, it has been reported that RbV3Sb5 and CsV3Sb5 kagome metals may display two charge-order transitions19–21. Theoretically, different charge-order instabilities have been found in close proximity18. Because time-reversal symmetry is already broken at , it is not possible to distinguish, with our μSR data, whether this secondary charge-order state would break time-reversal symmetry on its own, or whether it is a more standard type of bond-charge-order. The two transitions in the relaxation rate observed in RbV3Sb5 is different from KV3Sb5, where only one transition is observed. This suggests the presence of only one type of TRSB charge order in KV3Sb5, while multiple nearby magnetic-charge order instabilities seem to be present in RbV3Sb5. Therefore, the TRSB effects in RbV3Sb5 are clearly different that those in KV3Sb525. Furthermore, we followed these two transitions in RbV3Sb5 as a function of pressure (see the details in the Supplementary Note 7 and the Supplementary Fig. 7). As shown in Fig. 2a, both and are suppressed by hydrostatic pressure. More specifically, the two-step charge-order transition becomes a single time-reversal symmetry-breaking charge-order transition at ~1.5 GPa, above which = shows a faster suppression (see the “Methods” section for details).
Fig. 2. Time-reversal symmetry-breaking charge order and superconductivity in (K,Rb)V3Sb5 under pressure.
a The pressure dependences of the transition temperatures and . Temperature dependence of the absolute change of the electronic relaxation rate ΔΓ = Γ(T) − Γ(T > Tc) for KV3Sb5 (b) and RbV3Sb5 (c) in the temperature range across Tc, measured at ambient pressure and above the critical pressure at which Tc is maximum. The error bars represent the standard deviation of the fit parameters.
The same ZF-μSR analysis can also be employed to probe whether there is time-reversal symmetry-breaking inside the superconducting state. Because charge order already breaks time-reversal symmetry at Tco ≫ Tc, it is necessary to suppress Tco, which can be accomplished with pressure. Pressure of 1.85 GPa allows to enter the optimal Tc region of the phase diagram (see Fig. 3a) in RbV3Sb5 at which only a single time-reversal symmetry-breaking charge order transition is observed (see Fig. 2a). The maximum pressure we could apply (2.25 GPa) is enough to completely suppress the charge-order in RbV3Sb5. The pressure value of p > 0.5 GPa is large enough to assess the pure superconducting state of the related compound KV3Sb5. In Fig. 2b, we show the behavior of the internal field width Γ, extracted from the ZF-μSR data, across the superconducting transition of KV3Sb5 measured both at ambient pressure (red, where charge-order is present) and at 1.1 GPa (gray, where charge-order is absent). While at ambient pressure Γ is little affected by superconductivity, at the higher pressure there is a significant enhancement of Γ, comparable to what has been observed in superconductors that are believed to spontaneously break time-reversal symmetry, such as SrRu2O446. The similar enhancement of Γ below Tc ~ 3 K is observed for RbV3Sb5 at p = 1.85 and 2.25 GPa, as shown in Fig. 2c. This provides strong evidence for time-reversal symmetry-breaking superconducting states in KV3Sb5 and RbV3Sb5, indicative of an unconventional pairing state.
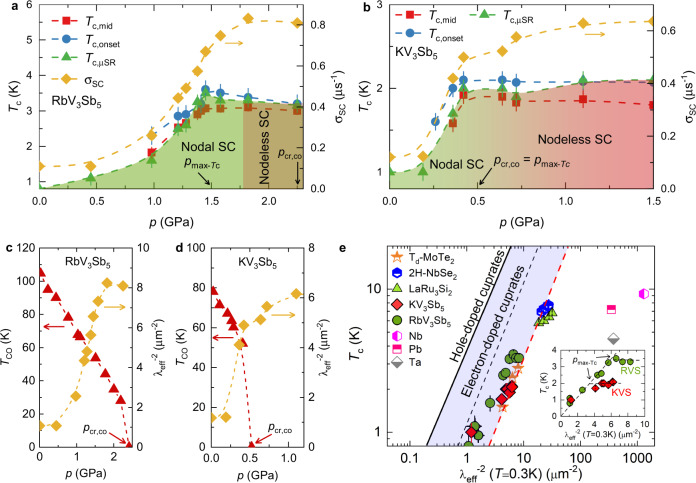
Fig. 3. Coupled charge order and nodal superconductivity in kagome lattice.
Pressure dependence of the superconducting transition temperature (left axis) and of the base-T value of σsc (right axis) for the polycrystalline samples of RbV3Sb5 (a) and KV3Sb5 (b). Here, Tc,ons and Tc,mid were obtained from AC measurements and Tc,μSR, from μSR. Pressure dependence of and charge order temperature Tco (ref. 38) for RbV3Sb5 (c) and KV3Sb5 (ref. 39) (d). The arrows mark the critical pressure pcr,co at which charge order is suppressed and the pressure at which Tc reaches its maximum value. e Plot of Tc versus in logarithmic scale obtained from our μSR experiments in KV3Sb5 and RbV3Sb5. Inset shows the plot in a linear scale. The dashed red line represents the relationship obtained for the kagome superconductor LaRu3Si2 as well as for the layered transition metal dichalcogenide superconductors Td-MoTe2 and 2H-NbSe251,52. The relationship observed for cuprates is also shown50, as are the points for various conventional superconductors. The error bars represent the standard deviation of the fit parameters.
Superfluid density as a function of pressure
An additional property of the superconducting state that can be directly measured with μSR is the superfluid density. This is accomplished by extracting the second moment of the field distribution from the muon spin depolarization rate σsc, which is related to the superconducting magnetic penetration depth λ as (see the “Methods” section). Because λ−2 is proportional to the superfluid density, so is σsc. Figures 3 and 4 summarize the pressure and temperature dependences of σsc (measured in an applied magnetic field of μ0H = 5 mT) in the superconducting states of RbV3Sb5 and KV3Sb5. As the temperature is decreased below Tc, the depolarization rate σsc starts to increase from zero due to the formation of the flux-line lattice (see Fig. 4a). As the pressure is increased, not only Tc (as determined from AC susceptibility and μSR experiments), but also the low-temperature value of σsc (measured at the baseline of 0.25 K) show a substantial increase for both compounds, as shown in Fig. 3a, b. In both cases, Tc,ons first quickly reaches a maximum at a characteristic pressure , namely, 3.5 K at 1.5 GPa for the Rb compound and ≃2.1 K at 0.5 GPa for the K compound. Beyond those pressure values, the transition temperature remains nearly unchanged. The superfluid density σsc (0.25 K) also increases significantly from its ambient-pressure value upon approaching , by a factor of approximately 7 for the Rb compound and 5 for the K system. In both cases, σsc (0.25 K) continues increasing beyond , although at a lower rate that may indicate approach to saturation.
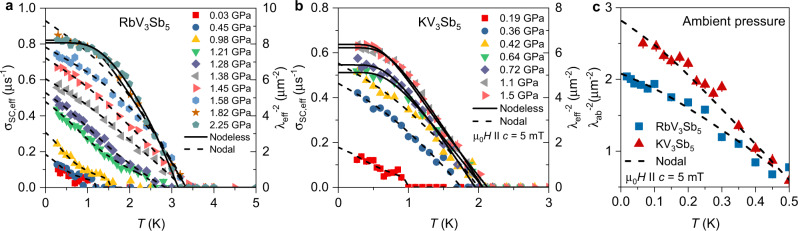
Fig. 4. Tunable nodal kagome superconductivity.
The temperature dependence of the superconducting muon spin depolarization rates σsc for RbV3Sb5 (a) and KV3Sb5 (b), measured in an applied magnetic field of μ0H = 5 mT at ambient and various applied hydrostatic pressures. The error bars represent the standard deviations of the fit parameters. The solid (dashed) lines correspond to a fit using a model with nodeless (nodal) two-gap superconductivity. c The inverse squared penetration depth for the single crystals of KV3Sb5 and RbV3Sb5 as a function of temperature at ambient pressure.
These behaviors are consistent with competition between charge order and superconductivity. Indeed, as shown in Fig. 3c, d, the increase in the superfluid density is correlated with the decrease in the charge ordering temperature Tco. More specifically, the pressure values for which Tc is maximum are close to the critical pressures pcr,co beyond which charge order is completely suppressed. In fact, as displayed in Fig. 3b, pcr,co essentially coincides with for KV3Sb5. Since both superconductivity and charge order occurs in the entire sample volume, there is no volume wise competition of these orders in real space. They rather compete for the same electronic states in reciprocal space. In this case, competition with charge order could naturally account for the suppression of the superfluid density towards the low-pressure region of the phase diagram, where Tco is the largest. Since charge order partially gaps the Fermi surface, as recently seen by quantum oscillation47 and ARPES17,34 studies, the electronic states available for the superconducting state are suppressed, thus decreasing the superfluid density48,49.
Next, it is important to note some differences in the temperature-pressure phase diagrams of RbV3Sb5 (Fig. 3a) and KV3Sb5 (Fig. 3b). For RbV3Sb5, Tc as well as σsc shows a smooth increase with increasing pressure until it reaches a maximum value at 1.5 GPa. In contrast, in KV3Sb5, both Tc and σsc show a sharp increase upon approaching 0.5 GPa. This suggests that the transition from the charge ordered state to optimal superconducting state is more likely first-order in KV3Sb5 and second-order in RbV3Sb5. Another difference is that for the RbV3Sb5, 1.5 GPa is lower than the critical pressure pcr ≃ 2.2 GPa38, while in KV3Sb5 these two pressures coincide 0.5 GPa.
Having extracted σsc, we can directly obtain the magnetic penetration depth λ (see “Methods”). For polycrystalline samples, this gives an effective penetration depth λeff, whereas for single crystals, it gives the in-plane λab. It is instructive to plot the low-temperature penetration depth not as a function of pressure, but as a function of Tc50. As shown in Fig. 3e, the ratio for unpressurized RbV3Sb5 is ~0.7 K μm−2, similar to the one previously reported for KV3Sb525. This ratio value is significantly larger from that of conventional BCS superconductors, indicative of a much smaller superfluid density. Moreover, we also find an unusual relationship between and Tc in these two kagome superconductors, which is not expected for conventional superconductivity. This is presented in the inset of Fig. 3e: below , the superfluid density (which is proportional to ) depends linearly on Tc, whereas above , Tc barely changes for increasing . Historically, a linear increase of Tc with has been observed only in the underdoped region of the phase diagram of unconventional superconductors. Deviations from linear behavior were previously found in an optimally doped cuprate51, in some Fe-based superconductors52, and in the charge-ordered superconductor 2H-NbSe2 under pressure51. Therefore, in RbV3Sb5 and KV3Sb5, it is tempting to attribute this deviation to the suppression of the competing charge ordered state by the applied pressure. More broadly, these two different dependences of Tc with indicate superconducting states with different properties below and above .
To further probe this scenario, we quantitatively analyze the temperature dependence of the penetration depth λ(T)53 for both compounds as a function of pressure, see Fig. 4a, b. Quite generally, upon decreasing the temperature towards zero, a power-law dependence of is indicative of the presence of nodal quasiparticles, whereas an exponential saturation-like behavior is a signature of a fully gapped spectrum. The low-T behavior of for single crystals of RbV3Sb5 and KV3Sb5, measured down to 18 mK and shown in Fig. 4c, displays a linear-in-T behavior, consistent with the presence of gap nodes. Quantitatively, the curve is well described by a phenomenological two-gap model, where one of the gaps has nodes and the other does not (see “Methods”). Such a linear-in-T increase of upon approaching T = 0 is also seen in polycrystalline samples for pressures up to . In the case of RbV3Sb5 (Fig. 4a), for two pressure values available above GPa, the penetration depth curves seem to be better fitted by a model with a nodeless gap (see the Supplementary Note 13 and Supplementary Figs. 11 and 13). This conclusion is supported by a -comparison, revealing a value of reduced at p = 1.85 GPa and p = 2.25 GPa for the nodal gap model that is higher by factor of ~3.9 than the one for the nodeless gap model. The analysis clearly shows that at least ten points below 2 K do not follow a linear temperature dependence. This is also clear in the case of KV3Sb5 (Fig. 4b): above GPa, displays a saturation-like behavior that is well captured quantitatively by a model with a nodeless gap (see Supplementary Figs. 12 and 13). Since is close to pco,cr, especially for the K compound, these results show that charge order strongly influences the superconducting gap structure in (Rb,K)V3Sb5, inducing nodes in an otherwise fully gapped pairing state. To the best of our knowledge this is the first direct experimental demonstration of a plausible pressure-induced change in the superconducting gap structure from nodal to nodeless in these kagome superconductors.
One possible explanation for these results is on the changes that the emergence of charge order causes on the Fermi surface. First-principle calculations on AV3Sb5 compounds indicate the existence of multiple Fermi pockets in the absence of charge order47. The simplest fully-gapped pairing state is an s-wave one consisting of different nodeless gaps (with potentially different signs) around each pocket. The onset of long-range charge order further breaks up these pockets into additional smaller pockets. Depending on the relative sign between the original gaps and on the details of the reconstructed Fermi pockets, accidental nodes could emerge. Such a scenario was proposed in the case of competing s+−-wave superconductivity and spin-density wave in iron-pnictide superconductors54.
The main drawback of this scenario is that it does not account for the time-reversal symmetry-breaking of the “pure" superconducting state. In this regard, a fully gapped pairing state that also breaks time-reversal symmetry is the chiral state55,56. As long as the charge ordered state preserves the point-group symmetry of the disordered state, the chiral pairing symmetry is expected to be retained below Tco, suggesting a nodeless superconducting state. However, if the charge-ordered state breaks the threefold rotational symmetry of the lattice, as proposed experimentally57 and theoretically18,22 for certain AV3Sb5 compounds, a nodal gap is stabilized for a sufficiently large charge order parameter, as we show in the Supplementary Fig. 14 (see the Supplementary Note 14). In this case, the nodal-to-nodeless transition does not coincide with the full suppression of charge order, unless the transition from the charge-ordered superconducting state to the “pure" superconducting state is first-order. We note that the same conclusions would also apply for the triplet chiral px + ipy state. As it was mentioned above, our phase diagrams suggest that the transition from the charge ordered superconducting state to optimal superconducting state in KV3Sb5 is more likely first-order and second-order in RbV3Sb5. Within the framework of our theoretical model, we expect the crossover from nodal to nodeless pairing to start at a lower pressure than pcr in RbV3Sb5 and at pcr in KV3Sb5. This is in excellent qualitative agreement with the experimental results.
In conclusion, our results provide direct evidence for unconventional superconductivity in (Rb,K)V3Sb5, by combining the observations of nodal superconducting pairing and a small superfluid density at ambient pressure, which in turn displays an unconventional dependence on the superconducting critical temperature. Moreover, we find that the hydrostatic pressure induces a change from a nodal superconducting gap structure at low pressure to a nodeless, time-reversal symmetry-breaking superconducting gap structure at high pressure. The crossover from nodal to nodeless pairing is correlated with the establishment of the optimal superconducting region of the phase diagram, which corresponds to full suppression of charge order in KV3Sb5 and partial suppression of charge order in RbV3Sb5. Our results point to the rich interplay and accessible tunability between nodal unconventional superconductivity and time-reversal symmetry-breaking charge orders in the correlated kagome lattice, offering new insights into the microscopic mechanisms involved in both orders.
Methods
Experimental details
ZF and transverse field (TF) μSR experiments at ambient pressure on the single crystalline and polycrystalline samples of RbV3Sb5 and KV3Sb5 were performed on the GPS instrument and high-field HAL-9500 instrument, equipped with BlueFors vacuum-loaded cryogen-free dilution refrigerator (DR), at the Swiss Muon Source (SμS) at the Paul Scherrer Institut, in Villigen, Switzerland. μSR experiments under pressure were performed at the μE1 beamline of the Paul Scherrer Institute (Villigen, Switzerland using the instrument GPD, where an intense high-energy (pμ = 100 MeV c−1) beam of muons is implanted in the sample through the pressure cell. The 4He cryostats equipped with the 3He insets (base temperature ≃ 0.25 K) were used. A mosaic of several crystals stacked on top of each other was used for these measurements. The magnetic field was applied both in-plane (along the ab-plane) and out-of-plane (along the crystallographic c-axis). A schematic overview of the experimental setup for zero-field and low transverse field measurements is shown in Fig. 1c. The crystal was mounted such that the c-axis of it is parallel to the muon beam. Using the ”spin rotator” at the πM3 beamline, muon spin was rotated (from its natural orientation, which is antiparallel to the momentum of the muon) by 44.5(3)° with respect to the c-axis of the crystal. So, the sample orientation is fixed but the muon spin was rotated. The rotation angel can be precisely estimated to be 44.5(3)° by measurements in weak magnetic field, applied transverse to the muon spin polarization. The sample was surrounded by four detectors: Forward (1), Backward (2), Up (3) and Down (4). A schematic overview of the experimental setup for high-field μSR instrument is shown in the inset of Fig. 1g. The muon spin forms 90° with respect to the c-axis of the crystal. The sample was surrounded by 2 times 8 positron detectors, arranged in rings. The specimen was mounted in a He gas-flow cryostat with the largest face perpendicular to the muon beam direction, along which the external field was applied. Zero field and high transverse field μSR data analysis on single crystals of RbV3Sb5 were performed using both the so-called asymmetry and single-histogram modes45.
Sample growth
Single crystals of RbV3Sb5 were synthesized by Rb ingot (purity 99.9%), V powder (purity 99.9%), and Sb grains (purity 99.999%) using the self-flux method10. Magnetization experiments reveal two characteristic temperatures of 110 K and 50 K (see Supplementary Note 3 and Supplementary Fig. 3).
μSR experiment
In a μSR experiment58, nearly 100% spin-polarized muons μ+ are implanted into the sample one at a time. The positively charged μ+ thermalize at interstitial lattice sites, where they act as magnetic microprobes. In a magnetic material, the muon spin precesses in the local field Bμ at the muon site with the Larmor frequency νμ = γμ/(2π)Bμ (muon gyromagnetic ratio γμ/(2π) = 135.5 MHz T−1). Using the μSR technique, important length scales of superconductors can be measured, namely, the magnetic penetration depth λ and the coherence length ξ. If a type II superconductor is cooled below Tc in an applied magnetic field ranging between the lower (Hc1) and the upper (Hc2) critical fields, a vortex lattice is formed which in general is incommensurate with the crystal lattice, with vortex cores separated by much larger distances than those of the crystallographic unit cell. Because the implanted muons stop at given crystallographic sites, they will randomly probe the field distribution of the vortex lattice. Such measurements need to be performed in a field applied perpendicular to the initial muon spin polarization (so-called TF configuration).
The magnetic penetration depth λ(T) is related to the superconducting muon spin depolarization rate σSC(T) in the presence of a triangular (or hexagonal) vortex lattice by the equation58:
| 2 |
where γμ is the gyromagnetic ratio of the muon and Φ0 is the magnetic-flux quantum. Since the applied field is a factor of ~30 times smaller than the second critical magnetic fields in RbV3Sb5, this equation is valid to estimate the λ.
Pressure cell
Pressures up to 1.9 GPa were generated in a double wall piston-cylinder type cell made of CuBe/MP35N, specially designed to perform μSR experiments under pressure59. A fully assembled typical double-wall pressure cell is presented and discussed in Supplementary Fig. 1 and Supplementary Note 1. The body of the pressure cell consists of two parts: the inner and the outer cylinders which are shrink fitted into each other. Outer body of the cell is made out of MP35N alloy. Inner body of the cell is made out of CuBe alloy. Other components of the cell are: pistons, mushroom, seals, locking nuts, and spacers. The mushroom pieces and sealing rings were made out of non hardened Copper Beryllium. With both pistons completely inserted, the maximum sample height is 12 mm. As a pressure transmitting medium Daphne oil was used. The pressure was measured by tracking the superconducting transition of a very small indium plate by AC susceptibility. The filling factor of the pressure cell was maximized. The fraction of the muons stopping in the sample was approximately 40%.
Crystal structure of RbV3Sb5
Additional characterization information is provided here on the kagome superconductor RbV3Sb5 which crystallizes in the novel AV3Sb5-type structure (space group P6/mmm, where A = K, Rb, Cs). The crystallographic structure of prototype compound RbV3Sb5 shown in panel (a) of Supplementary Fig. 2 (see Supplementary Note 2) illustrates how the V atoms form a kagome lattice (medium beige circles) intertwined with a hexagonal lattice of Sb atoms (small red circles). The Rb atoms (large purple circles) occupy the interstitial sites between the two parallel kagome planes. In panel (b) the vanadium kagome net has been emphasized, with the interpenetrating antimony lattice included to highlight the unit cell (see dashed lines). Supplementary Fig. 2c shows an optical microscope image of several single crystals of RbV3Sb5 on millimeter paper. The Laue X-ray diffraction image (see Supplementary Fig. 2d) demonstrates the single crystallinity of the samples used for μSR experiments.
Analysis of high-field TF-μSR data
Figure 1g shows the probability field distribution, measured at 3 K for the single-crystal samples of RbV3Sb5 in the c-axis magnetic field of 8 T. In the whole investigated temperature range, two-component signals were observed: a signal with fast relaxation (low frequency) and another one with a slow relaxation (high frequency). The narrow signal arises mostly from the muons stopping in the silver sample holder and its position is a precise measure of the value of the applied magnetic field. The width and the position of the narrow signal is assumed to be temperature independent and thus they were kept constant in the analysis. The relative fraction of the muons stopping in the sample was fixed to the value obtained at the base-T and kept temperature independent. The signal with the fast relaxation, which is shifted towards the lower field from the applied one, arises from the muons stopping in the sample and it takes a major fraction (80%) of the μSR signal. This points to the fact that the sample response arises from the bulk of the sample. We note that in high magnetic fields we cannot systematically discriminate between the nuclear and the electronic contribution to the relaxation rate and thus we show the total high-field muon spin relaxation rate σHTF in Fig. 1i.
Analysis of ZF-μSR data under pressure
As an example, in Supplementary Fig. 6 (see Supplementary Note 6) is displaying the zero-field μSR spectra, recorded at p = 1.07 GPa for various temperatures. The experimental data were analyzed by separating the μSR signal on the sample (s) and the pressure cell (pc) contributions51:
| 3 |
Here A0 is the initial asymmetry of the muon-spin ensemble, and As (Apc) and Ps(t) [Ppc(t)] are the asymmetry and the time evolution of the muon-spin polarization for muons stopped inside the sample (pressure cell), respectively. The response of the pressure cell [Ppc(t)] was studied in separate set of experiments.
The sample contribution includes both, the nuclear moment and an additional exponential relaxation Γ caused by appearance of spontaneous magnetic fields:
| 4 |
Here is the GKT relaxation function (see Eq. (1)) describing the magnetic field distribution created by the nuclear magnetic moments44. Fits of Eq. (3) to the ZF-μSR pressure data were performed globally. The ZF-μSR time-spectra taken at each particular pressure (p = 0.16, 0.59, 1.07, 1.53, and 1.89 GPa) were fitted simultaneously with As, Apc, and σGKT as common parameters, and λ an individual parameter for each particular data set. The fits were limited to T ≃ 150 K, i.e., up to the temperature where the nuclear contribution of RbV3Sb5 remains constant (σGKT ≃ const, see Fig. 1e).
Macroscopic superconducting properties under pressure
The temperature dependence of the AC-susceptibility χAC for various pressures for the polycrystalline samples of RbV3Sb5 and KV3Sb5 are shown in Supplementary Fig. 8a, b (see Supplementary Note 8). We kept the position of the AC coil, mounted on the pressure cell, the same for the measurements at various applied pressures in order to be able to directly compare the superconducting responses at various applied pressures in both RbV3Sb5 and KV3Sb5. Moreover, we used the same amount of RbV3Sb5 and KV3Sb5 samples. The data for RbV3Sb5 at the pressure 1.45 GPa, where Tc reaches the maximum shows sharp superconducting transition with saturated full superconducting screening. We used the maximum value of the diamagnetic susceptibility at 1.45 GPa and normalize the rest of the data by that. Our results indicate a strong diamagnetic response and sharp superconducting transitions in both samples. This points to the high quality of the samples and providing evidence for bulk superconductivity in these polycrystalline samples.
Analysis of λ(T)
λ(T) was calculated within the local (London) approximation (λ ≫ ξ) by the following expression60 (see Supplementary Notes 9 and 10 and Supplementary Fig. 9):
| 5 |
where is the Fermi function, φ is the angle along the Fermi surface, and Δi(T, φ) = Δ0,iΓ(T/Tc)g(φ) (Δ0,i is the maximum gap value at T = 0). The temperature dependence of the gap is approximated by the expression ,61 while g(φ) describes the angular dependence of the gap and it is replaced by 1 for both an s-wave and an s+s-wave gap, for a d-wave gap, and for a f-wave gap.
For RbV3Sb5 and KV3Sb5, the λ−2(T) data above are analyzed using two s-wave gaps. At pressure below , the combination of dominant nodal -gap and one s-wave gap is used.
Analysis of the temperature dependence of the penetration depth for the single crystals RbV3Sb5 and KV3Sb5 at ambient pressure
at ambient pressure were analyzed within the framework of quasi-classical Eilenberger weak-coupling formalism, where the temperature dependence of the gaps was obtained by solving self-consistent coupled gap equations rather than using the phenomenological α-model, where the latter considers a similar BCS-type temperature dependence for both gaps (see Supplementary Note 10 and Supplementary Fig. 10). This method is described in details elsewhere62–64, including in our recent paper on KV3Sb525. The temperature dependence of down to 18 mK in the applied field of 5 mT is shown in Supplementary Fig. 9 for RbV3Sb5 along with the KV3Sb5 data. A well-pronounced two-step behavior is observed in RbV3Sb5, similar to KV3Sb525. Our numerical analysis allows to determine the interband coupling and the superconducting gap values. The analysis reveals that the two step transition in σsc(T) at 5 mT requires the interband coupling constant to be small, 0.001. The small values of interband coupling constants imply that the band(s), where the large and the small superconducting energy gaps are open, become only weakly coupled. One important point is that if we assume the maximum gap-to-Tc ratio to be 3.75 (BCS value), then one can not reproduce the sharp step-like feature in σsc(T). The data are well explained by a large value of 2Δ/kBTc ≃ 7. Our observation of two step behavior of penetration depth in the system KV3Sb5 with single Tc is consistent with two gap superconductivity with very weak interband coupling and large value of 2Δ/kBTc ≃ 7. The interband coupling is extremely small which is sufficient to have same values of Tc for different bands but still shows the two step temperature behavior of the penetration depth65. The for both (Rb,K)V3Sb5 are well described by one constant gap and one dominant angle-dependent -gap, indicating the presence of gap nodes. Upon increasing pressure two step behavior gets smoothed out, but angle-dependent gap becomes more dominant and persists all the way up to 1.5 and 0.5 GPa for RbV3Sb5 and KV3Sb5, respectively. At pressures above , the λ−2(T) is described by constant gaps.
Analysis of TF-μSR data under pressure
The TF μSR data were analyzed by using the following functional form60:
| 6 |
here As and Apc denote the initial asymmetries of the sample and the pressure cell, respectively. φ is the initial phase of the muon-spin ensemble and Bint represents the internal magnetic field at the muon site. The relaxation rates σsc and σnm characterize the damping due to the formation of the FLL in the superconducting state and of the nuclear magnetic dipolar contribution, respectively. In the analysis σnm was assumed to be constant over the entire temperature range and was fixed to the value obtained above Tc where only nuclear magnetic moments contribute to the muon depolarization rate σ. The Gaussian relaxation rate, σpc, reflects the depolarization due to the nuclear moments of the pressure cell. The width of the pressure cell signal increases below Tc (see Supplementary Note 12 and Supplementary Fig. 10). This is due to the influence of the diamagnetic moment of the superconducting sample on the pressure cell, leading to the temperature dependent σpc below Tc. In order to consider this influence we assume the linear coupling between σpc and the field shift of the internal magnetic field in the superconducting state:
| 7 |
where σpc(T > Tc) = 0.25 μs−1 is the temperature-independent Gaussian relaxation rate. μ0Hint,NS and μ0Hint,SC are the internal magnetic fields measured in the normal and in the superconducting state, respectively. As indicated by the solid lines in Supplementary Fig. 10a–d, the μSR data are well described by Eqs. (6) and (7).
Supplementary information
Acknowledgements
The μSR experiments were carried out at the Swiss Muon Source (SμS) Paul Scherrer Institute, Villigen, Switzerland. M.H.C. was supported by the Carlsberg foundation. M.Z.H. acknowledges visiting scientist support from IQIM at the California Institute of Technology. Experimental work at Princeton University was supported by the Gordon and Betty Moore Foundation (GBMF4547 and GBMF9461; M.Z.H.) and the material characterization is supported by the US Department of Energy under the Basic Energy Sciences program (grant no. DOE/BES DE-FG-02-05ER46200). Y.S. acknowledges the National Natural Science Foundation of China (U2032204) and the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (No. XDB33000000). H.C.L. was supported by Ministry of Science and Technology of China (Grant No. 2018YFE0202600), Beijing Natural Science Foundation (Grant No. Z200005). The work of R.G. was supported by the Swiss National Science Foundation (SNF-Grant No. 200021-175935). R.M.F (phenomenological modeling) was supported by the Air Force Office of Scientific Research under award number FA9550-21-1-0423. P.D. at Rice is supported by U.S. DOE BES DE-SC0012311. Z.G. acknowledges useful discussions with Dr. Robert Johann Scheuermann.
Author contributions
Z.G. conceived and supervised the project. Growth and characterization of single crystalline and polycrystalline samples of RbV3Sb5: Q.Y., Z.T., C.G., and H.C.L..; growth of single crystalline and polycrystalline samples of KV3Sb5: H. Liu and Y.S.; μSR experiments and corresponding discussions: Z.G., R.K., C.M.III., D.D., R.G., H. Luetkens, M.E., T.G., J.-X.Y., N.S., M.Z.H., P.D., M.H.C., R.M.F., A.A.; μSR data analysis: Z.G. with contributions from R.K., C.M.III., D.D., and H. Luetkens; STM experiment and corresponding discussions: J.-X.Y., N.S., M.S.H., Z.G., and M.Z.H.; theoretical calculations: R.M.F. and M.H.C.; all authors discussed the results, interpretation, and conclusion. Figure development and writing the paper: Z.G. with contributions from R.M.F. and all other authors.
Peer review
Peer review information
Nature Communications thanks Guo-qing Zheng and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Data availability
All relevant data are available from the authors. Alternatively, the data can be accessed through the database at the following link http://musruser.psi.ch/cgi-bin/SearchDB.cgi.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Z. Guguchia, Email: zurab.guguchia@psi.ch
H. Luetkens, Email: hubertus.luetkens@psi.ch
R. Khasanov, Email: rustem.khasanov@psi.ch
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-022-35718-z.
References
- 1.Syôzi I. Statistics of Kagome lattice. Prog. Theor. Phys. 1951;6:306. doi: 10.1143/ptp/6.3.306. [DOI] [Google Scholar]
- 2.Zhou Y, Kanoda K, Ng T-K. Quantum spin liquid states. Rev. Mod. Phys. 2017;89:025003. doi: 10.1103/RevModPhys.89.025003. [DOI] [Google Scholar]
- 3.Guguchia Z, et al. Tunable anomalous Hall conductivity through volume-wise magnetic competition in a topological kagome magnet. Nat. Commun. 2020;11:559. doi: 10.1038/s41467-020-14325-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yin J-X, Pan SH, Hasan MZ. Probing topological quantum matter with scanning tunneling microscopy. Nat. Rev. Phys. 2021;3:249–263. doi: 10.1038/s42254-021-00293-7. [DOI] [Google Scholar]
- 5.Mielke III C, et al. Nodeless kagome superconductivity in LaRu3Si2. Phys. Rev. Mater. 2021;5:034803. doi: 10.1103/PhysRevMaterials.5.034803. [DOI] [Google Scholar]
- 6.Yin J-X. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature. 2020;583:533–536. doi: 10.1038/s41586-020-2482-7. [DOI] [PubMed] [Google Scholar]
- 7.Ortiz B, et al. CsV3Sb5: a Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 2020;125:247002. doi: 10.1103/PhysRevLett.125.247002. [DOI] [PubMed] [Google Scholar]
- 8.Jiang, K. et al. Kagome superconductors AV3Sb5 (A=K, Rb, Cs). Natl Sci. Rev. nwac199 (2021). [DOI] [PMC free article] [PubMed]
- 9.Neupert T, Denner MM, Yin J-X, Thomale R, Hasan MZ. Charge order and superconductivity in kagome materials. Nat. Phys. 2022;18:137–143. doi: 10.1038/s41567-021-01404-y. [DOI] [Google Scholar]
- 10.Yin Q, et al. Superconductivity and normal-state properties of kagome metal RbV3Sb5 single crystals. Chin. Phys. Lett. 2021;38:037403. doi: 10.1088/0256-307X/38/3/037403. [DOI] [Google Scholar]
- 11.Jiang Y-X, et al. Discovery of topological charge order in kagome superconductor KV3Sb5. Nat. Mater. 2021;20:1353–1357. doi: 10.1038/s41563-021-01034-y. [DOI] [PubMed] [Google Scholar]
- 12.Yang S, et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 2020;6:1–7s. doi: 10.1126/sciadv.abb6003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Yu F, et al. Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal. Phys. Rev. B. 2021;104:041103. doi: 10.1103/PhysRevB.104.L041103. [DOI] [Google Scholar]
- 14.Shumiya N, et al. Tunable chiral charge order in kagome superconductor RbV3Sb5. Phys. Rev. B. 2021;104:035131. doi: 10.1103/PhysRevB.104.035131. [DOI] [PubMed] [Google Scholar]
- 15.Wang Z, et al. Electronic nature of chiral charge order in the kagome superconductor CsV3Sb5. Phys. Rev. B. 2021;104:075148. doi: 10.1103/PhysRevB.104.075148. [DOI] [Google Scholar]
- 16.Denner M, Thomale R, Neupert T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs) Phys. Rev. Lett. 2021;127:217601. doi: 10.1103/PhysRevLett.127.217601. [DOI] [PubMed] [Google Scholar]
- 17.Kang M, et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. 2022;18:301–308. doi: 10.1038/s41567-021-01451-5. [DOI] [Google Scholar]
- 18.Christensen MH, Birol T, Andersen BM, Fernandes RM. Theory of the charge-density wave in AV3Sb5 kagome metals. Phys. Rev. B. 2021;104:214513. doi: 10.1103/PhysRevB.104.214513. [DOI] [Google Scholar]
- 19.Wenzel, M. et al. Optical study of RbV3Sb5: multiple density-wave gaps and phonon anomalies. Phys. Rev. B105, 245123 (2022).
- 20.Hu, Y. et al. Coexistence of tri-hexagonal and star-of-David pattern in the charge density wave of the kagome superconductor AV3Sb5. Phys. Rev. B106, L241106 (2022).
- 21.Luo J, et al. Possible star-of-David pattern charge density wave with additional modulation in the kagome superconductor CsV3Sb5. npj Quantum Mater. 2022;7:30. doi: 10.1038/s41535-022-00437-7. [DOI] [Google Scholar]
- 22.Park T, Ye M, Balents L. Electronic instabilities of kagome metals: saddle points and Landau theory. Phys. Rev. B. 2021;104:035142. doi: 10.1103/PhysRevB.104.035142. [DOI] [Google Scholar]
- 23.Lin Y-P, Nandkishore RM. Complex charge density waves at Van Hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in the kagome metals AV3Sb5. Phys. Rev. B. 2021;104:045122. doi: 10.1103/PhysRevB.104.045122. [DOI] [Google Scholar]
- 24.Song D, et al. Orbital ordering and fluctuations in a kagome superconductor CsV3Sb5. Sci. China Phys. Mech. Astron. 2022;65:247462. doi: 10.1007/s11433-021-1826-1. [DOI] [Google Scholar]
- 25.Mielke III C, et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature. 2022;602:245–250. doi: 10.1038/s41586-021-04327-z. [DOI] [PubMed] [Google Scholar]
- 26.Rustem K, et al. Time-reversal symmetry broken by charge order in CsV3Sb5. Phys. Rev. Research. 2022;4:023244. doi: 10.1103/PhysRevResearch.4.023244. [DOI] [Google Scholar]
- 27.Yu L, et al. Simultaneous formation of two-fold rotation symmetry with charge order in the kagome superconductor CsV3Sb5 by optical polarization rotation measurement. Phys. Rev. B. 2022;106:205109. doi: 10.1103/PhysRevB.106.205109. [DOI] [Google Scholar]
- 28.Wu, Q. et al. The large static and pump-probe Kerr effect with two-fold rotation symmetry in Kagome metal CsV3Sb5. Preprint at https://arxiv.org/abs/2110.11306v2 (2021).
- 29.Haldane FDM. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the parity anomaly. Phys. Rev. Lett. 1988;61:2015–2018. doi: 10.1103/PhysRevLett.61.2015. [DOI] [PubMed] [Google Scholar]
- 30.Varma CM. Non-Fermi-liquid states and pairing instability of a general model of copper oxide metals. Phys. Rev. B. 1997;55:14554–14580. doi: 10.1103/PhysRevB.55.14554. [DOI] [Google Scholar]
- 31.Nersesyan AA, Japaridze GI, Kimeridze IG. Low-temperature magnetic properties of a two-dimensional spin nematic state. J . Phys. Condens. Matter. 1991;3:3353–3366. doi: 10.1088/0953-8984/3/19/014. [DOI] [Google Scholar]
- 32.Fittipaldi R, et al. Unveiling unconventional magnetism at the surface of Sr2RuO4. Nat. Commun. 2021;12:5792. doi: 10.1038/s41467-021-26020-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Xu H-S, et al. Multiband superconductivity with sign-preserving order parameter in kagome superconductor CsV3Sb5. Phys. Rev. Lett. 2021;127:187004. doi: 10.1103/PhysRevLett.127.187004. [DOI] [PubMed] [Google Scholar]
- 34.Nakayama K, et al. Multiple energy scales and anisotropic energy gap in the charge-densitywave phase of the kagome superconductor CsV3Sb5. Phys. Rev. B. 2021;104:L161112. doi: 10.1103/PhysRevB.104.L161112. [DOI] [Google Scholar]
- 35.Gupta R, et al. Microscopic evidence for anisotropic multigap superconductivity in the CsV3Sb5 kagome superconductor. npj Quantum Mater. 2022;7:49. doi: 10.1038/s41535-022-00453-7. [DOI] [Google Scholar]
- 36.Duan W, et al. Nodeless superconductivity in the kagome metal CsV3Sb5. Sci. China Phys. Mech. Astron. 2021;64:107462. doi: 10.1007/s11433-021-1747-7. [DOI] [Google Scholar]
- 37.Chen K, et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 2021;126:247001. doi: 10.1103/PhysRevLett.126.247001. [DOI] [PubMed] [Google Scholar]
- 38.Wang NN, et al. Competition between charge-density-wave and superconductivity in the kagome metal RbV3Sb5. Phys. Rev. Res. 2021;3:043018. doi: 10.1103/PhysRevResearch.3.043018. [DOI] [Google Scholar]
- 39.Du F, et al. Pressure-induced double superconducting domes and charge instability in the kagome metal KV3Sb5. Phys. Rev. B. 2021;103:L220504. doi: 10.1103/PhysRevB.103.L220504. [DOI] [Google Scholar]
- 40.Gu Y, et al. Gapless excitations inside the fully gapped kagome superconductors AV3Sb5. Phys. Rev. B. 2022;105:L100502. doi: 10.1103/PhysRevB.105.L100502. [DOI] [Google Scholar]
- 41.Wang, Y. et al. Proximity-induced spin-triplet superconductivity and edge super-current in the topological Kagome metal, KV1−xSb5. Preprint at https://arxiv.org/abs/2012.05898 (2021).
- 42.Chen H, et al. Roton pair density wave and unconventional strong-coupling superconductivity in a topological kagome metal. Nature. 2021;559:222. doi: 10.1038/s41586-021-03983-5. [DOI] [PubMed] [Google Scholar]
- 43.Zhao, C. et al. Nodal superconductivity and superconducting domes in the topological Kagome metal CsV3Sb5. Preprint at https://arxiv.org/abs/2102.08356v1 (2021).
- 44.Kubo, R. & Toyabe, T. Magnetic Resonance and Relaxation (Elsevier, 1967).
- 45.Yaouanc, A. & Dalmas de Reotier, P. Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter (Oxford University Press, 2011).
- 46.Luke GM, et al. Time-reversal symmetry-breaking superconductivity in Sr2RuO4. Nature. 1998;394:559. doi: 10.1038/29038. [DOI] [Google Scholar]
- 47.Ortiz BR, et al. Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5. Phys. Rev. X. 2021;11:041030. [Google Scholar]
- 48.Fernandes RM, Schmalian J. Transfer of optical spectral weight in magnetically ordered superconductors. Phys. Rev. B. 2010;82:014520. doi: 10.1103/PhysRevB.82.014520. [DOI] [Google Scholar]
- 49.Machida K. Charge density wave and superconductivity in anisotropic materials. J. Phys. Soc. Jpn. 1984;53:712. doi: 10.1143/JPSJ.53.712. [DOI] [Google Scholar]
- 50.Uemura, Y. J. et al. Universal correlations between Tc and ns/m (carrier density over effective mass) in high-Tc cuprate superconductors. Phys. Rev. Lett. 62, 2317–2320 (1989). [DOI] [PubMed]
- 51.Von Rohr FO, et al. Unconventional scaling of the superfluid density with the critical temperature in transition metal dichalcogenides. Sci. Adv. 2019;5:eaav8465. doi: 10.1126/sciadv.aav8465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Guguchia Z, et al. Direct evidence for the emergence of a pressure induced nodal superconducting gap in the iron-based superconductor Ba0.65Rb0.35Fe2As2. Nat. Commun. 2015;6:8863. doi: 10.1038/ncomms9863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Guguchia Z, et al. Signatures of the topological s+− superconducting order parameter in the type-II Weyl semimetal Td-MoTe2. Nat. Commun. 2017;8:1082. doi: 10.1038/s41467-017-01066-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Maiti S, Fernandes RM, Chubukov AV. Gap nodes induced by coexistence with antiferromagnetism in iron-based superconductors. Phys. Rev. B. 2012;85:144527. doi: 10.1103/PhysRevB.85.144527. [DOI] [Google Scholar]
- 55.Wu X, et al. Nature of unconventional pairing in the kagome superconductors AV3Sb5. Phys. Rev. Lett. 2021;127:177001. doi: 10.1103/PhysRevLett.127.177001. [DOI] [PubMed] [Google Scholar]
- 56.Kiesel ML, Thomale R. Sublattice interference in the kagome Hubbard model. Phys. Rev. B. 2012;86:121105. doi: 10.1103/PhysRevB.86.121105. [DOI] [Google Scholar]
- 57.Xiang Y, et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 2021;12:6727. doi: 10.1038/s41467-021-27084-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sonier JE, Brewer JH, Kiefl RF. μSR studies of the vortex state in type-II superconductors. Rev. Mod. Phys. 2000;72:769. doi: 10.1103/RevModPhys.72.769. [DOI] [Google Scholar]
- 59.Khasanov R, et al. High pressure research using muons at the Paul Scherrer Institute. High Pressure Res. 2016;36:140–166. doi: 10.1080/08957959.2016.1173690. [DOI] [Google Scholar]
- 60.Suter, A. & Wojek, B. M. Musrfit: a free platform-independent framework for μSR data analysis. Phys.Proc.30, 69–73 (2012).
- 61.Carrington A, Manzano F. Magnetic penetration depth of MgB2. Phys. C. 2003;385:205. doi: 10.1016/S0921-4534(02)02319-5. [DOI] [Google Scholar]
- 62.Prozorov R, Giannetta RW. Magnetic penetration depth in unconventional superconductors. Supercond. Sci. Technol. 2006;19:R41. doi: 10.1088/0953-2048/19/8/R01. [DOI] [Google Scholar]
- 63.Khasanov R, et al. SrPt3P: a two-band single-gap superconductor. Phys. Rev. B. 2014;90:140507(R). doi: 10.1103/PhysRevB.90.140507. [DOI] [Google Scholar]
- 64.Kogan VG. London approach to anisotropic type-II superconductors. Phys. Rev. B. 1981;24:1572. doi: 10.1103/PhysRevB.24.1572. [DOI] [Google Scholar]
- 65.Kogan, V. G., Martin, C. & Prozorov, R. Superfluid density and specific heat within a self-consistent scheme for a two-band superconductor. Phys. Rev. B80, 014507 (2009).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All relevant data are available from the authors. Alternatively, the data can be accessed through the database at the following link http://musruser.psi.ch/cgi-bin/SearchDB.cgi.