SEMIPARAMETRIC DOSE FINDING METHODS FOR PARTIALLY ORDERED DRUG COMBINATIONS

Abstract

We investigate a statistical framework for Phase I clinical trials that test the safety of two or more agents in combination. For such studies, the traditional assumption of a simple monotonic relation between dose and the probability of an adverse event no longer holds. Nonetheless, the dose toxicity (adverse event) relationship will obey an assumption of partial ordering in that there will be pairs of combinations for which the ordering of the toxicity probabilities is known. Some authors have considered how to best estimate the maximum tolerated dose (a dose providing a rate of toxicity as close as possible to some target rate) in this setting. A related, and equally interesting, problem is to partition the 2-dimensional dose space into two sub-regions: doses with probabilities of toxicity lower and greater than the target. We carry out a detailed investigation of this problem. The theoretical framework for this is the recently presented semiparametric dose finding method. This results in a number of proposals one of which can be viewed as an extension of the Product of Independent beta Priors Escalation method (PIPE). We derive useful asymptotic properties which also apply to the PIPE method when seen as a special case of the more general method given here. Simulation studies provide added confidence concerning the good behaviour of the operating characteristics.

1. Introduction

The importance of multi-agent Phase I trials in drug development has grown in recent years. The practical benefits of drug combinations are numerous: several modes of action can be combined or the negative side effects of one drug can potentially be attenuated by the presence of a second compound. The aim of Phase I oncology trials is to find one or more maximum tolerated dose (MTD) combinations having probability of toxicity as close as possible to some threshold α, specified in advance by clinicians (common values are 20%, 25% and 33%). Algorithmic designs remain a popular approach to the identification of the MTD within a discrete set of levels, both for single-agent trials (Storer, 1989), as well as for dual-agent trials (Huang, 2007). These designs make no appeal to any model, and the escalation/de-escalation rules are determined as a function of the most recent set of observations. The simplicity of these methods leads to their frequent implementation in practice. Algorithmic designs have a Markov property, sometimes referred to in this context as a lack-of-memory property. These methods are not efficient and lack desirable statistical properties, such as almost sure convergence. Many model-based designs have been suggested, but their widespread adoption in practice remains an unaccomplished goal. This is even more the case with dual-agent trials because of the complexity and lack of interpretability of some of the proposed models, as well as operational difficulties that can discourage clinical investigators. Model based designs come under two headings: parametrics and non-parametric.

The design and analysis of dual-agent trials can be carried out using Wages, Conaway and O’Quigley (2011), the partial ordering continual reassessment method (CRM) and Wang and Ivanova (2005) with extensions of the CRM; Thall (2003) with a six-parameter logistic-type model and Braun and Wang (2010) with the use of beta distributions and log-linear models. The second one is the class of non-parametric models. For dual-agent trials, we have Mander and Sweeting (2015) with the product of independent beta probabilities escalation design (PIPE) and the Bayesian Optimal Interval (2d-BOIN) method of Lin and Yin (2016). The primary focus of many methods for dual-agent trials has been to find a single MTD for recommendation in phase II studies. However, an arguably more relevant task is centered around the idea that, for combination studies, multiple, essentially, equivalent MTDs may exist. The collection of these MTDs form a maximum tolerated contour (MTC) in two-dimensional space. In this case, the primary objective of the study may be to identify multiple MTD’s for further testing, and investigators may desire a trial designed to meet this objective. This is all the more so as it is becoming common to study more than a single dose in the subsequent dose expansion cohorts (Iasonos and O’Quigley, 2016, DEC).

Our motivation here is to describe a journey that starts with estimation of the MTD and ends with estimation of the MTC. Our signposts are built from illustrations and our ultimate purpose is to allow deeper study of the problem of early phase dose finding for combinations of treatments. We set out on our journey (Section 2) via a look at the landscape, a look at the context in which these problems arise and, specifically, an actual trial carried out at the University of Virginia School of Medicine, and a particular hypothesized set of rates of DLT. Next stop (Section 3) outlines the tools that we will be using in the more usual setting of an MTD target, while Section 4 - our destination is in sight - spells out, step by step, the way in which to solve MTC estimation. Dose finding in two dimensions is necessarily more complex and Section 4.2 examines how actual experimentation can be implemented. Although typically sample sizes will not be large, large sample theory is helpful in providing some confidence in how well the designs should work in practice (Section 5). In particular, Theorem 1 shows that, for all the methods, the almost sure convergence to the MTD is equivalent to the almost sure convergence to the MTC. We have arrived at our destination and Section 6 makes use of what we have learned to carry out a simulated comparison with an available method (PIPE) while Section 7 returns to our original illustration (Section 2) and studies it more deeply.

In addition, the Appendix contains several documents to enable deeper understanding of this work. We include a table that summarizes all of the notation, we look closely at the dose allocation strategie, how to calibrate the methods, numerical experiments in the MTC setting, as well as proofs of theorems and other properties.

2. Context and motivation

We describe a Phase 1 clinical trial on drug combinations that was carried out at the University of Virginia School of Medicine. The trial involved C6 Ceramide NanoLiposome (CNL) and Vinblastine in patients with relapsed/refractory acute myeloid leukemia and patients with untreated acute myeloid leukemia. A grid of 5 by 4 dose-combinations is considered: 5 levels for CNL (from 54 to 215 mg/m²) and 4 levels for Vinblastine (from 0.375 to 2.25 mg/m²). The target rate α was taken to be 20% and the maximum sample size was fixed at 60 patients. This particular real application provides us with the opportunity to illustrate the workings of such a Phase I drug combinations design as well as providing a means to introduce some of the essential ideas developed in this article. In Table 1, a hypothesized dose toxicity function, called Scenario T, is described.

Table 1:

Scenario T corresponds to a hypothetical pattern of toxicity probability in a study of Vinblastine and C6 Ceramide NanoLiposome (CNL). The 5×4 grid of dose combinations is fixed and chosen by the investigator. Dose combinations from the minimal set are shown in bold (see Definition 2).

Toxicity probabilities (%) of dose combinations		Scenario T Drug A1: CNL
Drug A2: Vinblastine	Level (mg/m2)	54	81	122	183	215
	2.25	24	29	34	59	70
	1.5	13	18	22	49	53
	0.75	7	9	16	35	42
	0.375	2	5	9	21	30

Let the dose d = (i, j) represents the combination of the i-th dose of an agent A1 and the j-th dose of an agent A2, with i ∈ {1, …, I} and j ∈ {1, …, J}. In Scenario T, I and J are respectively equal to 5 and 4 and dose (2, 3) corresponds to 81 mg/m² of CNL and 1.5 mg/m² of Vinblastine. Let D be the set of all dose combinations: D = {1, …, I} × {1, …, J}. The sequence ${\left(X_n,Y_n\right)}_{n\in \mathbb{N}}$ is a sample of observations. At step n, corresponding to the n-th patient enrolled in the trial, the variable X_n is the dose selected among the I × J combinations; and the variable Y_n is the observed binary response at this dose taking values {0, 1}; 1 for a dose limiting toxicity (DLT) and 0 otherwise. Each combination of drug d is associated with a toxicity probability noted P_d.

Assumption 1. $\forall n\in \mathbb{N},\mathbb{P}\left(Y_n=1\mid X_n=d\right)=P_d$.

In Scenario T, P_(2,3) is equal to 0.18. Note that the ranges {1, …, I} and {1, …, J} are ordered in terms of the probability of toxic response. Such an assumption is common in Phase I trials for cytotoxic agents. The ordering of the marginal doses induces a partial ordering on the full range of doses D. Sign < or ≤ will be used for the total ordering on $ℝ$ and the partial ordering on the set of doses D: (i, j) ≤ (r, s) if and only if i ≤ r and j ≤ s.

Assumption 2. $(i,j)<(r,s)\Rightarrow P_{(i,j)}<P_{(r,s)}$.

In Scenario T, dose (2, 3) is ordered with dose (3, 3), as are their respective toxicity probabilities: 18% and 22%. The ordering assumption is fundamental to extract information on a dose d from observations on neighboring doses. In particular, given any dose d, the partial ordering allows a decomposition of the set D into four subsets: D = {d} ∪ 𝒜_d ∪ ℬ_d ∪ 𝒞_d, where 𝒜_d = {d′ ∈ D : d′ > d}, ℬ_d = {d′ ∈ D : d′ < d} and 𝒞_d = D \ (𝒜_d ∪ ℬ_d). Those combinations where d belongs to the set 𝒜_d, are associated with toxicity probabilities higher than P_d. The set ℬ_d contains those combinations of doses below d which are associated with toxicity probabilities lower than P_d. The dose combinations in 𝒞_d are not ordered with dose d which means that no prior assumption of order exists between their respective probabilities of toxicity. In Scenario T, the set 𝒞_(2,3) contains doses associated to toxicity probabilities below or above P_(2,3) = 0.18 : e.g. P_(3,1) = 0.09 and P_(1,4) = 0.24. Not unlike the single-agent setting, the primary objective of a Phase I combination study is often to identify a single MTD for further testing in the Phase II setting.

Numerous existing designs try to determine which combination d* among those available in D has a probability of toxicity closest to the target toxicity rate α so that d* = arginf_d∈D |P_d − α|. For Scenario T, the MTD, dose (4, 1), is associated with a toxicity probability 0.21, just above the threshold, α = 0.2, fixed by the investigators. However, in the context of dual-agent dose-finding, the notion of a single MTD is less clear cut. Indeed, aiming for the MTD is justified by an assumption of an ordering on the probabilities of efficacy, corresponding to an analogous ordering of the doses. For a single agent (full ordering), choosing the MTD amounts to maximizing the efficacy probability (probability of observing a sufficient therapeutic effect) under the constraint of being close to some chosen threshold of toxicity. This is no longer true in the dual-agent setting. Indeed, there exist situations in which a particular combination, less toxic than the MTD, may be more efficacious overall (Harrington et al., 2012). In Scenario T, let the efficacy probabilities of doses (4, 1) and (2, 3) be equal to 0.10 and 0.90, respectively. Such a situation is coherent with the partial ordering on D, as dose (2, 3) belongs to 𝒞_(4,1). In this case, the MTD (4, 1) is not particularly advantageous. As a result, a dual-agent trial may aim to locate more than a single MTD, forming an MTC (a cut or a contour) across the dose surface comprised of multiple combinations with similar acceptable toxicity profiles. The objective of the trial then becomes one of determining an MTD curve c* consisting of a set of combinations with toxicity probabilities close to α. In Scenario T, the MTD contour is represented by the line splitting the set of doses in two parts: the dose combinations associated to toxicity probabilities below the target α and those associated to toxicity probabilities above α. The minimal set related to this specific contour contains the closest doses from the line according to the partial ordering (see doses with bold toxicity probabilities in Table 1). This set is defined more formally in Section 4.

However, a design aiming for a single MTD will be of interest in some situations. This is the case if we have too small a number of patients available in order to determine a complete contour of the MTD (20 or 30 patients in a grid of 5 by 4), or if the investigators have some strong prior assumptions or requirements on the set of potential outcomes. We present an example of such an assumption. In the context of CNL and Vinblastine combinations, the investigators may want to reach a dose combination with a level of Vinblastine at least equal to 1.5mg/m², because this agent has previously shown positive results in term of efficacy at this level. The general structure of the semiparametric class of dose finding methods is described by a hierarchical model where the first level deals with the goal of the study - the doses themselves - and the second level is devoted to the dose-response curve. Here, the goal of the study is to find a single MTD. The first level of our model is then a distribution Π on the MTD itself. This distribution is updated in the Bayesian setting after each patient (see Section 3 for further details). In Figure 1, the posterior distribution on the MTD at the end of the trial is summarized by a histogram. Throughout the trial, the next dose combination is selected as the one maximizing the posterior Π according to the observations. The prior distribution on the range of doses D is a matrix of positive weights summing up to 1. It can easily be tuned to allow a progressive exploration in the range of doses or to correspond to expert knowledge: here, if possible, the investigators prefer to increase the level of vinblastine until 1.5 mg/m² (see Section E.2 for the exact prior distribution). This is what is done in the trial. At the beginning, the method recommends increasing the dose levels of vinblastine while keeping the CNL level at 54 mg/m². After 15 patients, the method stays at dose (2, 3). This dose is the one recommended at the end of the trial: 9 patients among 48 treated at this dose experienced a DLT (rate= 18.75%) and the posterior distribution puts its mass at 33.5% on it. According to the posterior distribution, the two other most probable dose combinations are (1, 4) and (3, 3) which, respectively, account for 13.4% and 13.7% of the posterior mass. Note that semiparametric methods can be easily adjusted either to meet a specific criteria or to work under general conditions with uninformative priors. For readers interested in having a rapid overview, the analysis based on semiparametric methods for scenario T continues at the end of the article (Section 7).

Figure 1:

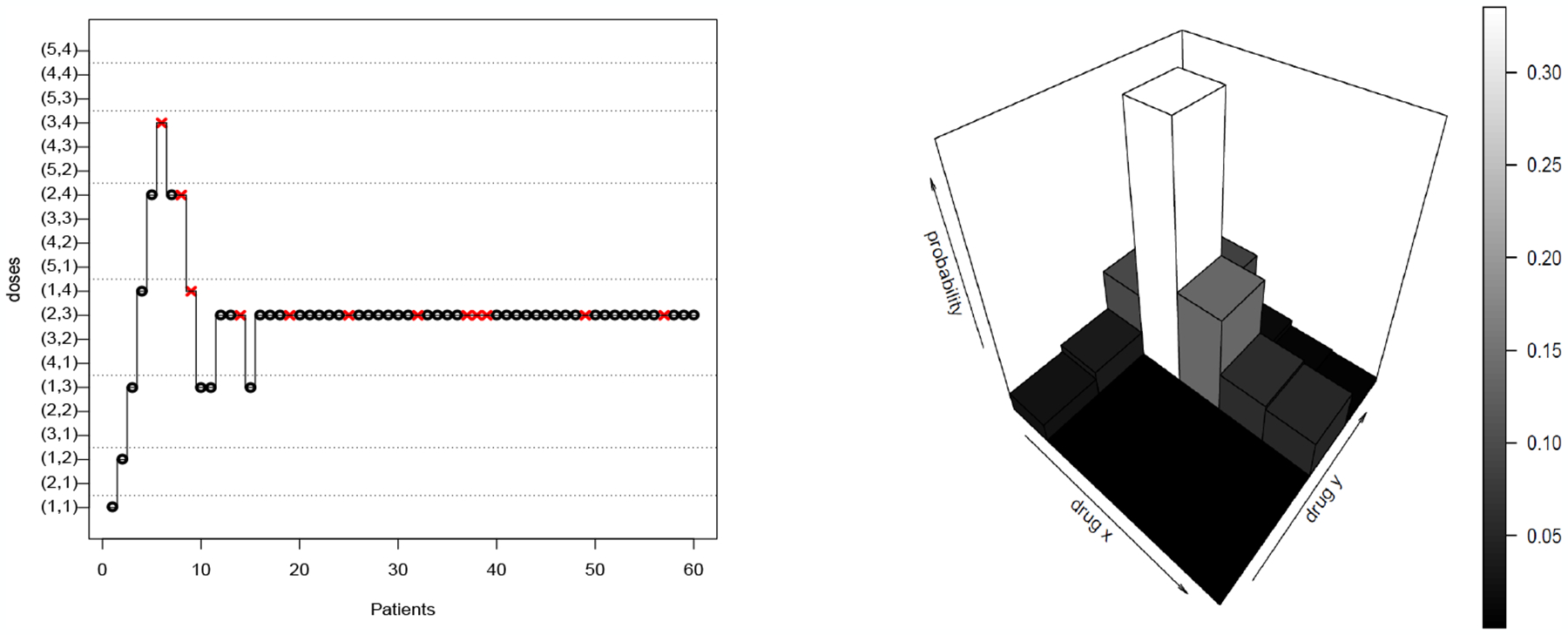
A simulated trial under scenario T using poSPM and the final posterior Π₆₀, which means the probabilties of each dose combination for being the MTD conditionnaly to observation on 60 patients. Red cross: Dose Limiting Toxicity; black circle: no toxicity response.

The illustrated trial of Figure 1 shows classical behaviour for a model-based design, as we tend to converge to a single MTD (Bayesian model in Section 3). However, a more useful goal may be to explore the MTD curve in order to determine multiple safe dose combinations associated with potentially different probabilities of efficacy (Section 4).

3. Semiparametric methods and a single MTD target

We briefly recall the semiparametric dose finding method introduced in (Clertant and O’Quigley, 2017, SPM) and then indicate how we can exploit these same ideas to tackle the problem of partial ordering. We refer to this as poSPM. The way in which we achieve an extension of the simpler to the more complex situation is to build a model around the non-ordered dose combinations. This extension corresponds to a non-informative prior which is structured in such a way that no distinction can be made between two doses d₁ and d₂ on the basis of observations on a dose d₃ that is not ordered with respect to d₁ and $d_2:d_3\in {𝒞}_{d_1}$ and $d_3\in {𝒞}_{d_2}$.

Consider the set S ⊂ [0, 1]^D, having elements $P={\left(P_d\right)}_{d\in D}$. Then, P_d provides the probability of toxicity for scenario P at dose d. The set S is partitioned according to the different values (dose levels) that θ can assume.

$$S=\underset{\theta \in D}{\cup }{S}_{\theta }\text{, where }{S}_{\theta }\subset \left\{P\in S|\forall d\in D,|P_{\theta }-\alpha |\le |P_d-\alpha \mid \right\}\text{.}$$

S breaks down into I × J classes indexed by θ, where every scenario from the same class has the same MTD. Any P belonging to S_θ associates the MTD at dose θ. For more discussion on this topic, we refer the reader to (Clertant and O’Quigley, 2017, section 4). The definition of S_θ used in practice is expressed via Assumption 3 below. For a fixed P ∈ S, the likelihood that we can associate with the history $\left(X_1^n,Y_1^n\right)={\left(X_k,Y_k\right)}_{1\le k\le n}$ is:

$$ℒ\left(P,X_1^n,Y_1^n\right)=\prod _{k=1}^n{\left(P_{X_k}\right)}^{Y_k}{\left(1-P_{X_k}\right)}^{1-Y_k}=\prod _{d\in D}{P}_d^{n_d^1}{\left(1-P_d\right)}^{n_d^0},$$ (3.1)

where $n_d^1$ represents the number of DLTs occurring at dose d, and $n_d=n_d^1+n_d^0$ the number of patients that are treated at dose d. Let Π be the prior for the parameter θ. Then Π is a probability measure on the discrete space D, i.e. a matrix of positive numbers with I rows and J columns summing up to 1. Each class S_θ is endowed with a prior noted Λ_θ = Λ(.|θ). The family of distributions (Λ_θ)_θ∈D and Π defines a prior on the whole set of scenarios. This prior can be updated sequentially as observations are made. The posterior Π_n on the parameter of the MTD, θ, is obtained by integration over the support S_θ of the scenarios associated with this dose.

$${\Pi }_n(\theta )=\Pi \left(\theta \mid X_1^n,Y_1^n\right)\propto {\int }_{S_{\theta }}ℒ\left(P,X_1^n,Y_1^n\right){\Lambda }_{\theta }(dP)\Pi (\theta ).$$ (3.2)

The family of distributions (Λ_θ)_θ∈D plays a predictive role and provides the basis that underlies the practical implementation of the adaptive process. We call this the prior model. In the sequential study, the next patient or cohort of patients is allocated to the dose having the highest probability of being the MTD according to the posterior Π_n. The MTD and the probability of toxicity at any dose d, P_d, are estimated sequentially by:

$${\widehat{\theta }}_n=\underset{\theta \in D}{\text{argmax}}{\Pi }_n(\theta )\text{ and }{\widehat{P}}_d^{(n)}={\mathbb{E}}_{{(\Lambda \otimes \Pi )}_n}\left[P_d\right]=\sum _{\theta \in D}\left[\int P_d{\Lambda }_{\theta ,n}\left(d{P}_d\right)\right]{\Pi }_n(\theta )\text{. }$$ (3.3)

The prior model is a family of I × J distributions on the set of scenarios. Moreover, each scenario can be viewed as a matrix with I rows and J columns having elements P_d, the toxicity probability at dose d. The following assumption expresses a simple structure for the prior Λ_θ. For this purpose the Bernoulli parameter space is broken down into three sets. The high and low toxicity probabilities belong to A = [α + ϵ, 1] and B = [0, α − ϵ], respectively. The probabilities of toxicity in the neighborhood of the target α lie in the centered Interval I = [α − ϵ, α + ϵ]. This interval results from our choice of and can be made arbitrarily small. Indeed it can be reduced to a single point, α by choosing ϵ equal to 0. From the point of view of the MTD parameter θ, the marginal ${\Lambda }_{\theta }^d$ distributes its probability mass according to the relative position of the doses d. The prior Λ_θ weights only those scenarios in which the MTD is θ. Given θ, ${\Lambda }_{\theta }^d$ is the prior of toxicity probability at dose d itself. The position of d relative to θ, summarized in the following assumption, indicates that: (i) if d = θ, as θ is the parameter indicating the MTD, the marginal weights are on the centered interval I, (ii) if d > θ (i.e. d ∈ 𝒜_θ), then ${\Lambda }_{\theta }^d$ puts its mass on the highest probability interval A, (iii) if d < θ (i.e d ∈ ℬ_θ), then ${\Lambda }_{\theta }^d$ puts its mass on the lowest probability interval B, (iv) if the dose d is non-ordered with θ (i.e. d ∈ 𝒞_θ), the marginal ${\Lambda }_{\theta }^d$ is uninformative and the weights are on the whole interval [0,1].

Assumption 3. Λ_θ is a product of unidimensionnal distribution, i.e.

$${\Lambda }_{\theta }(dP)=\prod _{d\in D}{\Lambda }_{\theta }^d\left(d{P}_d\right),$$

and the support $S_{\theta }^d$ of the distribution ${\Lambda }_{\theta }^d\left(d{P}_d\right)$ satisfies: $d\in {𝒜}_{\theta }\Rightarrow S_{\theta }^d=A$; $d\in {ℬ}_{\theta }\Rightarrow S_{\theta }^d=B$; $d\in {𝒞}_{\theta }\Rightarrow S_{\theta }^d=[0,1]$; $d=\theta \Rightarrow S_{\theta }^d=I$.

The probabilities of toxicity in each set 𝒜_θ, ℬ_θ and 𝒞_θ are conditionally independent once we have fixed S_θ. Marginally, of course, they are not independent so that any independency assumption fails to be valid when considering the whole model {(Λ_θ)_θ∈D, Π}. This is intuitively clear when a stochastic order is chosen for the marginal ${\left({\Lambda }_{\theta }^d\right)}_{\theta \in D}$, at a certain dose $r:\forall r,d<d^{\prime }\Rightarrow {\Lambda }_{d^{\prime },n}^r⪯{\Lambda }_{d^{\prime },n}^r$. The coherence principle introduced by Cheung (2005) can be extended to the case of partial ordering.

Definition 1 (Partial ordering coherence). A method ℳ is coherent if the sequence of selected doses satisfies: (X_n, Y_n) = (d, 0) ⇒ X_n+1 ∈ D\ℬ_d and (X_n, Y_n) = (d, 1) ⇒ X_n+1 ∈ D \ 𝒜_d.

This definition matches the one of Cheung (2005) in the case of a single-agent trial, and can be seen to be a logical extension of this criteria in the case of partial ordering. Note that the stochastic ordering implies that the poSPM is coherent.

Proposition 1. Under Assumptions 3 and 6 (appendix), the poSPM is coherent.

Working with a simple product of the marginals allows us to choose conjugate priors for the likelihood, in particular Beta distributions of which the uniform is a special case.

4. Identifying the Maximum Tolerated Contour (MTC)

4.1. Semiparametric Model

In the setting of partially ordered doses, the semiparametric class of methods on the contour (poSPMc) takes its inspiration from the PIPE model (Mander and Sweeting, 2015) and a method for single agents (Clertant and O’Quigley, 2018).

The set of dose combinations D can be naturally partitioned into two subsets defined by the toxicity target α. The partition includes one set of dose combinations that are associated with toxicity probabilities below α : D⁻ = {d ∈ D : P_d < α}, and a set of dose combinations associated with toxicity probabilities above α : D⁺ = {d ∈ D : P_d > α}. We have: D = D⁻ ∪ D⁺. The maximum tolerated contour, also called the MTC curve, is a line separating the set D⁻ and D⁺ (see Figure 2). The goal of poSPMc is to allocate patients at acceptable doses around the contour in order to better study dose combinations close to the toxicity threshold. If these dose combinations are not ordered, then they do not share information in terms of the probability of efficacy. In general a contour c is a line which separates the set of dose combinations into two ordered sets of doses: one set of dose combinations above the contour, 𝒜_c, and another set of dose combination below the contour, ℬ_c. For any given contour c, we note that:

$$d\in {𝒜}_c\text{ and }{d}^{\prime }\in {ℬ}_c\Rightarrow d>d^{\prime }\text{ or }d\text{ and }{d}^{\prime }\text{ non-ordered}$$

In Figure 2, we can describe any contour as a polygonal chain tracing out a path from (0.5, J + 0.5) to (I + 0.5, 0.5) with steps of size 1 along the abscissa and of size −1 on the ordinate axis. Only rightward and downward steps are permitted. As a result, for the range D containing I × J dose combinations, there exist $\left(\begin{array}{c}I+J\\ I\end{array}\right)$ possible contours c. Let C be the set of these contours and c^⋆ the maximum tolerated contour (MTC) defined by the true, unknown, toxicity probabilities at each dose combination. Estimating the MTC may appear to be a considerable challenge as the number of contours increases exponentially with the number of doses: 70 possible contours for a 4 × 4 grid and 962 for a 6 × 6 grid. Fortunately, each contour c is associated with a minimal set ℳ_c of dose combinations on which we need to have observations in order, with probability one, to confirm or disprove that this contour can be identified as the MTC. The dose combinations belonging to ℳ_c are the closest doses of the contour in our partially ordered set of doses D (see Figure 2). In the following definition, the minimum and maximum operators are applied to partially ordered sets.

Figure 2:

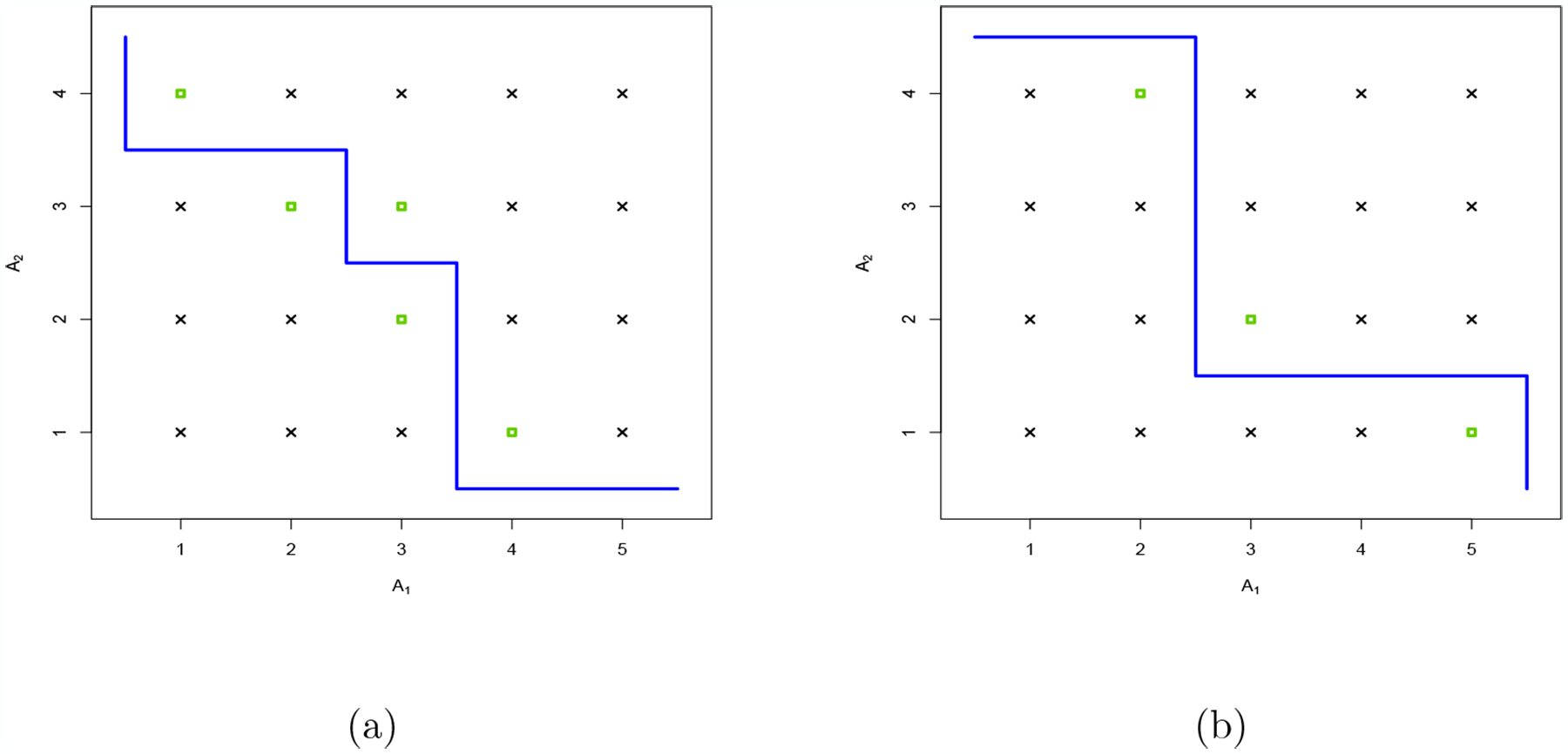
Two contours called (a) and (b): the green squares represent the dose combinations belonging to the minimal set. Contour (a) corresponds to the one of Scenario T (Table 1)

Definition 2. The minimal set of dose combinations, ℳ_c, associated with the contour c is: ℳ_c = min 𝒜_c ∪ max ℬ_c.

For a grid with I doses for agent A₁ and J doses for agent A₂, the number of dose combinations belonging to a minimal set varies between 1 and 2 × min(I, J), except in the case I = J where the maximum is equal to 2I − 1. The average number of combinations inside a minimal set is equal to 2IJ/(I+J). If a minimal set contains only one dose combination, all of the toxicity probabilities (P_d)_d∈D are on the same side of the target, either below or above. If a minimal set contains only two doses, it corresponds to a vertical or a horizontal contour.

Let ${ℳ}_{c^{\star }}$ be the minimal set associated with the MTC. Dose combinations in ${ℳ}_{c^{\star }}$ are not necessarly the ones closest to α in term of toxicity probabilities. However, ${ℳ}_{c^{\star }}$ satisfies the following properties which justify that a model for a dose combination study focuses on the contour or the associated minimal set.

Proposition 2. 1) For all dose combinations $d\notin {ℳ}_{c^{\star }}$, there exists a dose $d^{\prime }\in {ℳ}_{c^{\star }}$ ordered with d such that: |P_d − α| > |P_d′ − α|.

2) The MTD belongs to the minimal set associated with the $MTC:d^{\star }\in {ℳ}_{c^{\star }}$.

The proof is immediate by using Definition 2. The proposed model takes place in the setting of SPM; γ is the parameter of interest, the MTC itself. As in Section 3, S is a broad set of scenarios and P = (P_d)_d∈D is an element of S with P_d the toxicity probability of the scenario P at dose d. The set S is partitioned according to $\gamma :S={\cup }_{\gamma \in C}{S}_{\gamma }$, where S_γ = {P ∈ [0, 1]^D : d ∈ 𝒜_γ ⇒ P_d > α and d ∈ ℬ_γ ⇒ P_d < α}. S is partitioned into $\left(\begin{array}{c}I+J\\ I\end{array}\right)$ classes indexed by γ, where every scenario of the same class has the same MTC.

Let Π be the prior for the parameter γ, which means that Π is a probability measure on the discrete space C. Each class S_γ is endowed with a prior noted Λ_γ = Λ(.|γ), and the family (Λ_γ)_γ∈C is called the prior model. This family can be easily shaped by the following assumption and the use of truncated beta distributions for each marginal.

Assumption 4. Λ_γ is a product of one-dimensional distributions, i.e.

$${\Lambda }_{\gamma }=\prod _{d\in D}{\Lambda }_{\gamma }^d,$$

where ${\Lambda }_{\gamma }^d$ is a prior for P_d, the toxicity probability at dose d. The support $S_{\gamma }^d$ of the distribution ${\Lambda }_{\gamma }^d$ satisfies: $d\in {𝒜}_{\gamma }\Rightarrow S_{\gamma }^d=[\alpha ,1]$; $d\in {ℬ}_{\gamma }\Rightarrow S_{\gamma }^d=[0,\alpha ]$.

In Figure 3, the distribution Λ_γ is illustrated when γ represents the two contours in Figure 2. The parameters of these two distributions are the ones used in the numerical experiments. Note that, in Figure 3 (d) marginal prior model Λ_(a) is steepest than Λ_(b); the dose (2,3) and (3,3) are in the minimal set for contour (a) but not for contour (b).

Figure 3:

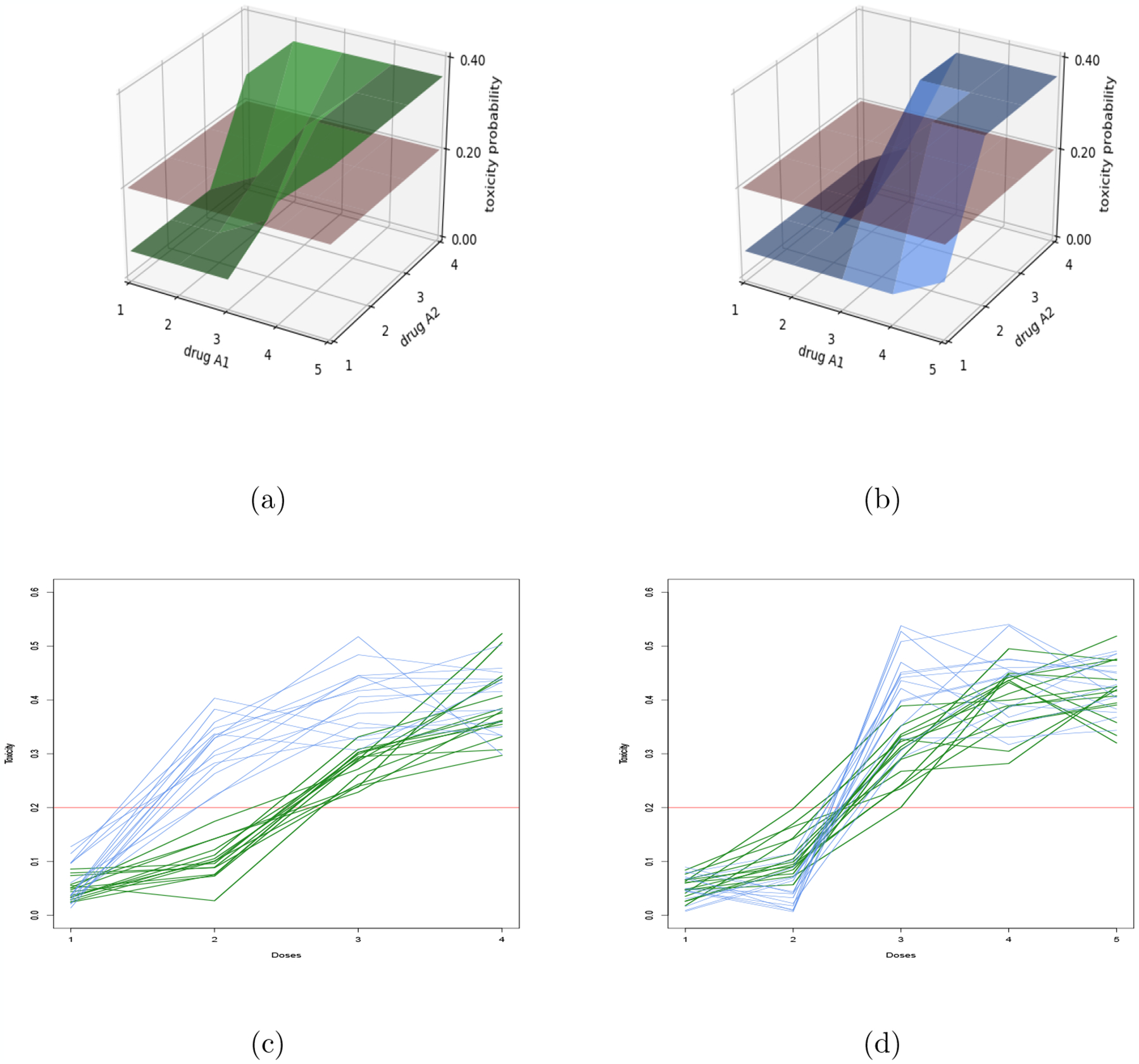
Model of two competitive contours: The blue and green models corresponds to contours (a) and (b) (Figure 2). Figures (a) and (b) show the modes of ${\Lambda }_{(a)}^d$ and ${\Lambda }_{(b)}^d$ for each dose d in comparison to the target α = 0.20. Figures (c) and (d) represent sampling of marginal scenarios under these models when agent A1 (respectively A2) is fixed at dose level 3.

The family of distributions (Λ_γ)_γ∈C and Π define a prior on the whole set of scenarios S. The posterior Π_n on the parameter of the MTC given the data $\left(X_1^n,Y_1^n\right)$ is:

$${\Pi }_n(\gamma )\propto {\int }_{S_{\gamma }}ℒ\left(P,X_1^n,Y_1^n\right){\Lambda }_{\gamma }(dP)\Pi (\gamma ).$$ (4.4)

The current estimate of the contour is.

$${\widehat{\gamma }}_n=\underset{\gamma \in D}{\text{argmax }}{\Pi }_n(\gamma ).$$ (4.5)

The algorithm for allocating the patient (or the next cohort of patients) during the trial is based on the following two steps: (i) the prior Π_n is updated and the most probable contour ${\widehat{\gamma }}_n$ is selected; (ii) the dose where the next patient will be treated is selected by an allocation strategy in the most probable minimal set according to our posterior: $X_{n+1}\in {ℳ}_{c^{\star }}$. Such an allocation strategy spreading the observations inside the estimated minimal set is developped in Section 4.2.

The PIPE method (Mander and Sweeting, 2015) might be seen as the first example using a semiparametric method on the contour. However, it has some strong limitations in term of calibration as it does not clearly specify priors on the MTC and the space family (S_γ)_γ∈C. For this method, the toxicity probability at each dose d is modelled by a weak beta prior with parameter a_d and b_d. For each contour, a posterior probability is obtained by multiplying the posterior of the interval [0, α] for every dose below the contour and the posterior of the interval [α, 1] for those doses above the contour. Let B_I(a, b) be the truncated beta distribution with parameter a and b on the interval I and B(x, a, b) be the incomplete beta function. In the setting of SPM, the PIPE model is defined by:

$$\{\begin{array}{ll}{\Lambda }_c\hfill & ~\prod _{d\in {ℬ}_c}{B}_{[0,\alpha ]}\left(a_d,b_d\right)\times \prod _{d\in {𝒜}_c}{B}_{[\alpha ,1]}\left(a_d,b_d\right)\hfill \\ \Pi (c)\hfill & \propto \prod _{d\in {ℬ}_c}B\left(\alpha ;a_d,b_d\right)\times \prod _{d\in {𝒜}_c}\left(1-B\left(\alpha ;a_d,b_d\right)\right).\hfill \end{array}$$

Note that, for the PIPE method, the prior model (Λ_c)_c∈C and the prior on the contour Π are defined by the I × J prior of the toxicity probabilities at each dose combination. The indirect calibration of the prior model and the prior on the set of contours can undermine the performance of this method. In particular, the prior Π defined through the PIPE model is not chosen for allowing a progressive exploration of the range of doses but is dependent on the target toxicity probability α.

4.2. Allocation strategy

In a minimal set, many of the doses are not ordered and the question of allocation within this set needs to be addressed. This is not straightforward and we do not exhaust all possibilities here. Several allocation strategies can be made available and any particular choice will result in some particular trial behaviour. The allocation strategy introduced hereafter is a compromise between one that spreads experimentation ‘equally’ against one that tests those doses that will, in expectation, bring more information into the study. We also need restrict experimentation to an area of the minimal set considered to be safe. After n observations, the next dose X_n+1 is:

$$X_{n+1}=\underset{d\in {ℳ}_{{\widehat{\gamma }}_n}\backslash T_n}{\text{min}}\frac{1}{k_d}\left\{\left(\sum _{j\in {ℬ}_d\cup \left\{d\right\}}{n}_j^0\right)\times H(\alpha \mid 0)+\left(\sum _{j\in {𝒜}_d\cup \left\{d\right\}}{n}_j^1\right)\times H(\alpha \mid 1)\right\},$$ (4.6)

where H(p|q) is the entropy of p relative to q : H(p|q) = −q × log(p) − (1 − q) log(1 − p), with the convention log(0) = −∞ and 0 × (−∞) = 0, and k_d = #𝒜_d+#ℬ_d+1. In Equation 4.6, the relative entropy, which corresponds to a quantity of information, is counter-balanced by k_d, the number of dose combinations ordered with d, in other words, the number of dose combinations on which we aim to learn something subsequent to an observation on d.

The next dose X_n+1 is selected among the safe dose combinations in the estimated minimal set: ${ℳ}_{{\widehat{\gamma }}_n}\backslash T_n$. the set of dose combinations on which we already have some evidence of overly toxicity is denoted T_n. It is estimated by using local Bayesian tests at each of the doses and the assumption of partial ordering. A dose d₀ is excluded from the study if:

$$d_0\in T_n=\left\{d\in D:\exists d^{\prime }\in H_n,d\ge d^{\prime }\right\},$$

with $H_n=\left\{d\in D:{\mathbb{P}}_{𝒰}\left[P_d>{\theta }_T\mid \left(n_d,n_d^1\right)\right]>{\delta }_T\right\}$, and 𝒰 is the uniform prior on the parameter space [0, 1].

This allocation strategy spreads the observations along the estimated contour and tests slightly more often the doses in the middle of the grid. Since a DLT corresponds to a greater quantity of information, those doses with a smaller number of toxicities are tried more often (for α = 0.25 : H(α|1)/H(α|0) = log(α)/log(1 − α) ≈ 4.82). A longer description of this allocation strategy can be found in Section C

5. Large sample theory

Two distinct and complementary asymptotic behaviors are described here. The first kind of large sample behavior is that of ϵ-sensitivity, introduced by Cheung (2011). This corresponds to the almost sure convergence to a dose combination for which the true probability of toxicity lies inside the interval [α − ϵ; α + ϵ].

Definition 3. Let ε ≥ 0 and I = [α−ε; α+ε]. We consider the set ℰ(I, P) of the collection of dose combinations associated with a toxicity probability belonging to I, i.e. ℰ(I, P) = {d ∈ D : P_d ∈ I}. A method is ε-sensitive if for all scenarios P = (P_d)_d∈D such that ℰ(I, P) ≠ ∅, we have:

$$\mathbb{P}\left[\exists N,\forall n>N:X_n\in ℰ(I,P)\right]=1.$$

The ε-sensitivity corresponds to strong consistency for a single dose associated with a toxicity rate close to the threshold α. This dose is not necessarily the MTD if there exist two or more doses in the interval I. The almost sure convergence to the MTD is obtained if the MTD is a unique dose in ℰ(I, P). Such an assumption on the scenario is necessary in the light of the impossibility theorem of Azriel (2011). The particularity of our semiparametric method for a single MTD (poSPM) is that the interval I is a parameter which can be directly calibrated. This requires us to choose a small interval I which could potentially fail to contain any of the toxicity probabilities associated with the given doses. For this reason, the complementary behavior of the ϵ-sensitivity introduced by Clertant and O’Quigley (2017) is extended to the case of partial ordering. We define as balanced behavior the almost sure convergence to a set of doses. More S precisely, a sequence ${\left(X_n\right)}_{n\in \mathbb{N}}$ converges to a set B, denoted by $X_n\stackrel{S}{\to }B$, when:

$$\underset{x\in B}{\text{max }}\left(\underset{n\to }{\text{lim}}\underset{+\infty }{\text{inf}}\delta \left(X_n,x\right)\right)=0,$$

and where δ(., .) is Euclidean distance. In the case of a complete ordering, the sequence ${\left(X_n\right)}_{n\in \mathbb{N}}$ converges to the set consisting of the two consecutive doses on either side of the target α. This set of two doses corresponds to the definition of the minimal set for the maximum tolerated contour (see definition 2): ${ℳ}_{c^{\star }}=\text{max}{D}^{-}\cup \text{min}{D}^{+}$.

Definition 4. Let D be a range of doses. A method is balanced, if for all scenarios, we have:

$$X_n\stackrel{S}{\to }{ℳ}_{c^{\star }},a\text{.}s\text{. }$$

The doses recommended infinitely often by the current estimator of a balanced method are all the doses in $M_{c^{\star }}$ and only these doses. The following theorem completes in a natural way the impossibility theorem formulated by Azriel (2011).

Theorem 1. For any allocation method, the three following statements are equivalent :

1. For all scenarios, there exists a statistic F on the sample $\left(X_1^n,Y_1^n\right)$ such that $F\left(X_1^n,Y_1^n\right)\to d^{\star },a\text{.}s\text{.}$

2. For all scenarios, there exists a statistic F on the sample $\left(X_1^n,Y_1^n\right)$ such that $F\left(X_1^n,Y_1^n\right)\to c^{\star },a\text{.}s\text{.}$.

3. For all scenarios, there exists a set of dose combinations D′ with $M_{c^{\star }}\subset D^{\prime }$ such that the sequence of recommended doses satisfies:

   $$X_n\stackrel{S}{\to }{D}^{\prime },a\text{.}s\text{.}$$

In particular, this basic theorem expresses a necessary condition for any method: the minimal set $M_{c^{\star }}$ is the smallest set of dose combinations on which we need to have observations in order to find almost surely the MTD and the MTC under general circumstances. Some assumptions are needed on our models in order to obtain the desired asymptotic behavior. The regularity assumptions (7, Appendix) on the prior model of the poSPM and the poSPMc are readily met. An other assumption concerns the allocation strategy.

Assumption 5. (a) The next dose combination X_n+1 is selected from ${ℳ}_{{\widehat{\gamma }}_n}$.

(b) All the doses in the limit supremum of ${\left({ℳ}_{{\widehat{\gamma }}_n}\right)}_{n\in \mathbb{N}}$ are selected infinitely often:

$$\forall d\in \underset{n\ge 1}{\cap }\underset{k\ge n}{\cup }{ℳ}_{{\widehat{\gamma }}_k},\left\{\sum _{i=1}^n{\mathbb{1}}_{\left\{X_n=d\right\}}\underset{n\to \infty }{\to }\infty \right\}\text{, }a\text{.}s\text{.}$$

Assumption 5 (b) means that if a contour is selected infinitely often by ${\widehat{\gamma }}_n$, all the doses in the minimal set associated to this contour would be explored infinitely often (a.s). This is a necessary conditions to obtain a balanced behavior (simple consequence of Theorem 1’s proof). This constructive assumption is satisfied by the allocation strategy defined in Section 4.2.

Theorem 2. (a) Suppose that P^T is the true scenario. Under assumptions 3 and 7, we have: if ϵ > 0 and ℰ(I, P^T) contains no couple of ordered doses then the poSPM is ε-sensitive; when ϵ = 0 then poSPM is balanced.

(b) Under assumptions 4, 5 and 7, poSPMc is balanced.

When ϵ = 0, the poSPM is balanced which means that the method explores all the dose combinations included in ${ℳ}_{c^{\star }}$ when the sample size becomes large enough. However, this only describes asymptotic behavior and, at finite sample sizes, the simulations will often converge to a single dose identified as the MTD (see Figure 1). Conversely, the balanced behavior of poSPMc at a finite sample size can be observed in Figure 4.

Figure 4:

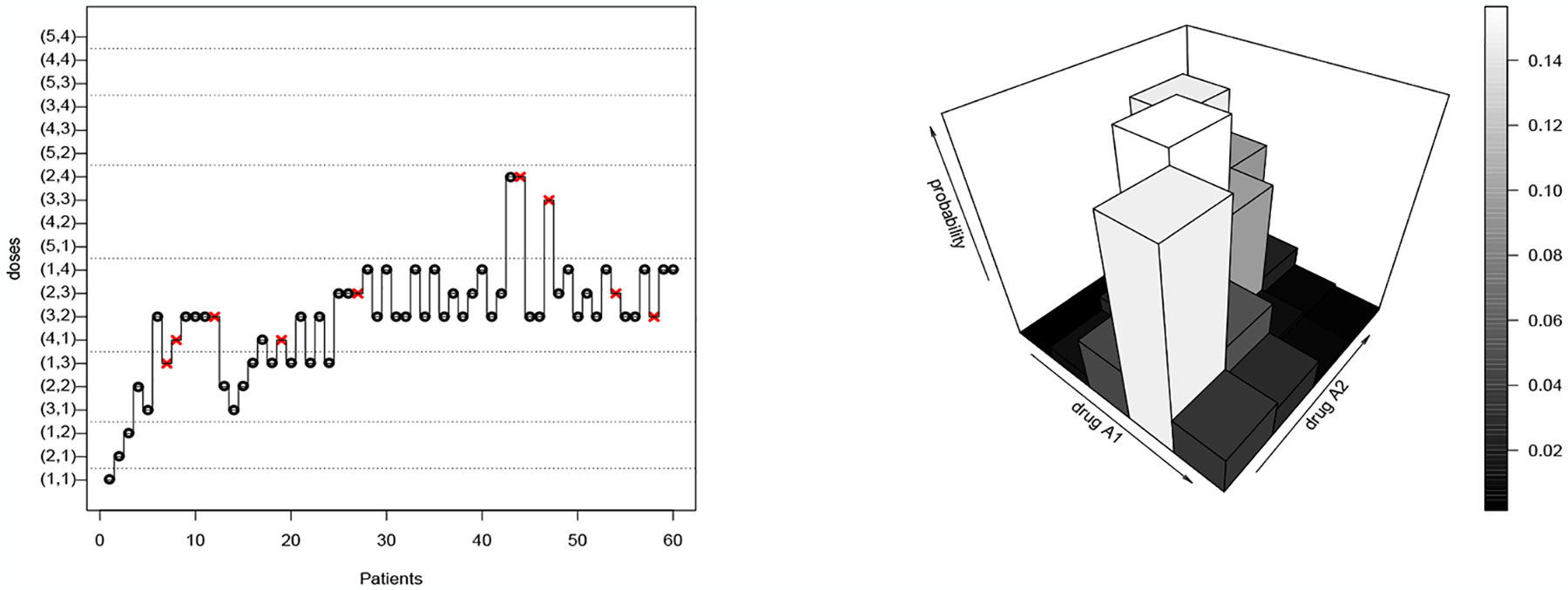
A simulated Trial under scenario T using poSPMc and the final posterior ${\tilde{\Pi }}_{60}$.on the dose combinations. Red cross: Dose Limiting Toxicity; black circle: no toxicity response.

6. Numerical experiments: MTC setting

In the MTC setting, we compared the poSPM to the PIPE design in terms of each method’s ability to identify and treat patients along a target MTC. Each trial targets a toxicity level of α = 0.20, with a total sample size of 50 and 1 patient per cohort. The calibration of the two methods is fully described in appendix E.1 and E.3. Table 2 shows the operating characteristics of the 2 methods under the 4 scenarios shown in Table 5. As in the MTD setting, for each scenario, we report the percentage of patient allocation (experimentation %) and percentage of MTD selection (recommendation %) for doses contained within five different ranges of true toxicity probabilities. Since α = 0.20, the target interval containing the true MTD is [0.15, 0.25]. In Scenarios 1 and 4, the poSPM and PIPE method have very similar operating characteristics with regards to recommending and experimenting at combinations in the target interval. The difference in the methods in Scenarios 1 and 4 can be observed in the intervals outside the target range. In both scenarios, when outside the target interval, the poSPM allocates to combinations below the target range, whereas the PIPE method tends to be more aggressive. This has an impact on the accuracy index (see Equation D.10) for experimentation in Scenario 4, with poSPM yielding a larger value: 0.67 vs. 0.55. For both of these scenarios, PIPE induces a higher overall percentage of DLT’s, on average.

Table 2:

Experimentation and recommendation percentages for the poSPM and the PIPE design. Column containing the MTD in bold. Scenarios 1 to 4 correspond to scenarios A, C, E, G in Mander and Sweeting (2015). they can be found in Appendix A.

Scenario	Method	Experimentation %					Acc	%DLTs
		[0, 0.10)	[0.10, 0.15)	[0.15, 0.25]	(0.25, 0.30]	(0.30, 1]
1	poSPM	9.0	25.8	56.9	7.7	0.4	0.35	16.9
	PIPE	2.8	7.5	59.4	26.1	4.2	0.39	22.0
2	poSPM	0.0	26.4	45.0	9.4	19.1	0.88	23.5
	PIPE	0.0	6.2	21.2	11.5	61.0	0.63	36.0
3	poSPM	12.2	27.0	36.1	22.8	1.9	0.38	18.0
	PIPE	0.0	6.6	21.8	11.5	60.2	0.33	35.9
4	poSPM	31.2	19.4	32.4	13.7	3.2	0.67	14.2
	PIPE	12.3	14.0	34.0	26.0	13.4	0.55	22.1
		Recommendation %					Acc	${\overline{N}}_{MTD}$
		[0, 0.10)	[0.10, 0.15)	[0.15, 0.25]	(0.25, 0.30]	(0.30, 1]
1	poSPM	2.0	19.9	71.6	6.3	0.0	0.63	3.73
	PIPE	0.3	5.2	70.3	23.7	0.4	0.64	2.23
2	poSPM	0.0	17.8	54.3	12.8	15.0	0.92	2.60
	PIPE	0.0	8.8	38.4	17.4	35.3	0.84	1.44
3	poSPM	3.8	29.1	36.6	29.5	0.9	0.44	3.18
	PIPE	0.0	9.8	37.7	17.5	35.0	0.28	1.44
4	poSPM	20.1	22.6	39.1	16.8	1.2	0.77	4.2
	PIPE	17.4	23.5	38.0	19.1	2.0	0.77	2.77

In Scenario 2, poSPM is the best performing method by all metrics. It demonstrates better performance from the viewpoints of experimentation (45.0% vs. 21.2%) and recommendation (54.3% vs. 38.4%) percentages in the target interval. PIPE again tends to be more agressive, allocating 61% of patients to combinations with toxicity probabilities in the interval (0.30, 1.00]. The improvement of poSPM over the PIPE is also reflected in the accuracy indices in Scenario 2. In Scenario 3, the methods have similar operating characteristics in terms of recommendation percentage in the target interval (36.6% vs. 37.7%), although the poSPM maintains an advantage when considering experimentation and accuracy. Similarly to Scenario 2, PIPE allocates 60.2% of patients to combinations with toxicity probabilities in the interval (0.30, 1.00]. The more aggressive behavior of PIPE is further indicated in the overall percentage of DLT’s observed, as this value is both higher than the corresponding value for poSPM, as well as larger than the target α = 0.20 in all scenarios. Considering the average performance over the four scenarios the poSPMc is the best method by all the metrics. In particular the poSPMc recommends a larger number of doses (3.43 doses vs. 1.97) yet maintaining greater accuracy than the PIPE method (0.69 of accuracy recommendation vs. 0.63).

7. CNL and vinblastine combination, a study of Scenario T

Three versions of our semiparametric class of methods are compared on Scenario T introduced in Table 1 in the context of CNL and vinblastine combination:

• poSPMc is the semiparametric method targeting the MTD contour (or the associated minimal set); the calibration is the same as in Section 6,

• poSPM1 is the semiparametric method targeting a single MTD, without including expert knowledge (uninformative prior); the calibration is the same as in Appendix D,

• poSPM2 is the semiparametric method targeting a single MTD which is calibrated in line with expert knowledge as described in Section 2 (‘if possible, the investigators prefer to increase the level of vinblastine until 1.5 mg/m²’), the calibration is the same as in Appendix D except that the mass of the prior Π on doses (i, j) ∈ {2, …, 5} × {1, 2} is divided by two.

In Table 3, the three methods are compared on Scenario T. The target α is 20% and 60 patients are to be enrolled in the study. 10 000 trials are simulated for each method. Cheung’s accuracy metric is defined in Section D. The metric ${\overline{N}}_{MTD}$ is the average number of dose combinations recommended at the end of the trial: 4.31 for poSPMc (less than the number of doses in the minimal set of Scenario T), 1 for the other methods. Regarding the final recommendation percentages in interval [0.15, 0.25], poSPM1 obtains better performance than poSPM2 and poSPMc. For poSPM2, this is due to the steep toxicity profile around the MTDs in the middle of the grid rather than around the dose (1, 4), which is then more difficult to locate. The difference between poSPMc and poSPM1 in terms of allocation and recommendation percentage in interval [0.15, 0.25] is due both to the exploration behavior of poSPMc and the multiple recommendation at the end of the trial (It is more difficult to recommend 4 dose combinations in interval [0.15, 0.25] than 1). However, the percentage of dose combinations recommended by poSPMc which are inside the interval [0.15, 0.25] is still satisfactory (60.7%).

Table 3:

Experimentation and recommendation percentages for poSPMc, poSPM1 and poSPM2 on Scenario T. Column containing the MTD in bold.

Method	Experimentation %					Acc	%DLTs
	[0, 0.10)	[0.10, 0.15)	[0.15, 0.25]	(0.25, 0.30]	(0.30, 1]
poSPMc	27.5	8.8	47.3	8.9	7.4	0.52	18.1
poSPM1	14.7	19.4	55.7	8.7	18.7	0.48	22.2
poSPM2	10.7	20.1	42.9	14.1	11.9	0.48	21.6
	Recommendation %					Acc	${\overline{N}}_{MTD}$
	[0, 0.10)	[0.10, 0.15)	[0.15, 0.25]	(0.25, 0.30]	(0.30,1]
poSPMc	13.9	8.4	60.7	11.5	5.4	0.63	4.31
poSPM1	5.4	2.2	73.0	9.1	10.1	0.67	1
poSPM2	1.7	18.2	62.9	11.5	5.6	0.65	1

In order to show the benefits of targeting the MTD curve (poSPMc), four hypotheses concerning the efficacy profile of CNL and vinblastine are considered. The minimal set of Scenario T contains dose combinations (1,4), (2,3), (3,2), (3,3) and (4,1). Note that the true MTD always belongs to the minimal set; for Scenario T, this is (4, 1). The hypotheses lean on the set of doses with sufficient efficacy probabilities in the minimal set. In the four hypotheses, the only dose combinations which are sufficiently efficacious and not associated with overly toxicity probabilities belong to set H₁ = {(2, 3), (3, 3)}, H₂ = {(3, 2), (3, 3)}, H₃ = {(4, 1)} and H₄ = {(1, 4)}, respectively. These four hypotheses are coherent with the partial order applied to the efficacy probabilities. They represent 4 possible profiles of efficacy. Note that a dose combination of CNL and Vinblastine is considered to have a sufficient efficacy profile if its efficacy rate exceeds that associated with competitive therapies. The aim of the Phase I design is to then recommend such a dose combination for further exploration in Phase II. In Table 4, the percentage of trials (among the 10 000) which recommend a dose in the set H1, H2, H3 and H4 are detailed for each of the three methods. The advantage of the method targeting the MTD curve over methods aiming for a single MTD is a significant one. For poSPMc, the percentage of trials in which at least one dose with a sufficient efficacy profile is recommended is between 60 and 75% for all the hypotheses. The same metric goes from 2 to 45% for poSPM1 and poSPM2. This does not mean that the two methods are not accurate, but they are not equipped to deal with this situation.

Table 4:

Experimentation and percentage of trials recommending at least a dose in sets H₁ = {(2, 3), (3, 3)}, H₂ = {(3, 2),(3, 3)}, H₃ = {(4, 1)} and H₄ = {(1, 4)} for poSPMc, poSPM1 and poSPM2. Each of this set may be the only one containing dose combitions sufficiently efficacious and not associated with overly toxicity probabilities.

		Experimentation %
Scenario T	Method	H 1	H 2	H 3	H 4
	poSPMc	18.8	16.7	10.6	8.0
	poSPM1	32.6	37.2	4.3	2.9
	poSPM2	12.6	24.5	0.1	17.8
		% of trials Recommendation
Scenario T	Method	H 1	H 2	H 3	H 4
	poSPMc	65.2	74.3	64.8	62.8
	poSPM1	44.9	43.6	6.5	3.75
	poSPM2	21.3	41.3	0.2	20.2

Balanced behavior of poSPMc is outlined via a trial presented in Figure 4. At the beginning of the trial, the method explores each of the dose combinations of the progressive inverted diagonals (e.g. (1,2) and (2,1)) until a first DLT is observed. Following the twentieth patient, almost all the recommended dose combinations are in the minimal set of Scenario T.

Note that poSPMc updates a distribution Π on the possible maximum tolerated contour. The method does not immediately lead to a posterior distribution on the MTD. However, as the model (Λ, Π) is a distribution on the range of scenarios, one can still calculate a distribution $\tilde{\Pi }$ on the MTD parameter by integrating out the toxicity probabilities conditional upon each possible value that could be assumed by the MTD. Instead of doing this complex calculation, we can use the following formula which holds for all n :

$$\forall c\in C,\forall d\in D,{\tilde{\Pi }}_n\propto \frac{1}{\overline{{𝒱}_d}}\sum _{c\in {𝒱}_d}{\Pi }_n(c),$$ (7.7)

where 𝒱_d is a neighborhood in terms of contours for dose combination d : 𝒱_d = {c ∈ C: d ∈ ℳ_c}, and $\overline{{𝒱}_d}$ its cardinality. The following proposition shows that ${\tilde{\Pi }}_n$ is the desired result by considering a poSPM model $(\tilde{\Lambda },\tilde{\Pi })$ for which the updating process is conjugate with the one of the poSPMc model.

Proposition 3. For all $n\in \mathbb{N}$, the probability ${\tilde{\Pi }}_n$ defined by Equation 7.7 is the posterior on the set of dose combinations from the poSPM model $(\tilde{\Lambda },\tilde{\Pi })$ where:

$$\tilde{\Pi }(d)\propto \frac{1}{{\overline{𝒱}}_d}\sum _{c\in {𝒱}_d}\Pi (c)\text{ and }{\tilde{\Lambda }}_d=\sum _{c\in {𝒱}_d}{r}_c^d{\Lambda }_c\text{ with }{r}_c^d=\frac{\Pi (c)}{\sum _{c\in {𝒱}_d}\Pi (c)}\text{.}$$ (7.8)

Thus, there always exists a model $(\tilde{\Lambda },\tilde{\Pi })$ of poSPM such that, for all $n\in \mathbb{N}$, the distributions ${\tilde{\Pi }}_n$ can be seen to correspond to the posterior of $\tilde{\Pi }$. This conjugacy property associates, with every poSPMc model on the MTD curve, a poSPM model for a single MTD. However, this association is not trivial and appealing to an allocation strategy for poSPMc allows the design to explore the full MTD curve. At the end of a trial with poSPMc, the final recommendation can rely on the posterior ${\tilde{\Pi }}_n$. In Figure 4, more than 60% of the posterior mass of $\tilde{\Pi }$ is on the minimal set of Scenario T.

Appendix

A. Scenarios for the MTC setting

Table 5:

Toxicity scenarios 1–4 for the two-drug combinations. Dose combinations in the minimal set are in bold. Doses associated to a toxicity probability equal to 0.20 belong to D⁻ and D⁺ (see Section 4); they are always in the minimal set.

	Dose	Drug A2
	Level	1	2	3	4	1	2	3	4
	Scenario 1					Scenario 2
	4	22	26	30	34	55	65	75	85
	3	16	20	24	28	40	50	60	70
	2	10	14	18	22	25	35	45	55
	1	4	8	12	16	10	20	30	40
Drug
A1	Scenario 3					Scenario 4
	4	11	21	31	41	10	30	50	80
	3	10	20	30	31	6	15	30	45
	2	9	19	29	30	4	10	15	20
	1	8	18	28	29	1	2	3	4

B. Notations

Table 6:

Important notations

Notation	Description
d or X	a dose combination
Y	response in term of toxicity
D	set of dose combinations
I and J	number of doses for agent 1 and 2
𝒜d, ℬd and 𝒞d	set of doses above, below and non-ordered with d
P	a scenario, i.e a I × J matrix of bernoulli parameters
c and ℳc	a contour and a minimal set associated to this contour
𝒜c and ℬc	set of dose combinations above and below c
C	set of possible contour in the range of dose combinations
d*	true Maximum Tolerated Dose (MTD)
c*	true Maximum Tolerated Contour (MTC)
Π	distribution on the MTD or the MTC parameter
θ	MTD parameter
γ	MTC parameter
Λ = (Λθ)θ∈D	distributions on the scenarios conditioned by the MTD parameter
Λ = (Λγ)γ∈C	distributions on the scenarios conditioned by the MTC parameter
S, Sθ, Sγ	support of Λ, Λθ and Λγ
${\Lambda }_{\theta }^d$ (or ${\Lambda }_{\gamma }^d$)	marginal at dose combination d

C. Allocation strategy

In a minimal set, many of the doses are not ordered and the question of allocation within this set needs to be addressed. This is not straightforward and we do not exhaust all possibilities here. Several allocation strategies can be made available and any particular choice will result in some particular trial behaviour. The allocation strategy introduced hereafter is a compromise between one that spreads experimentation ‘equally’ against one that tests those doses that will, in expectation, bring more information into the study. We also need for experimentation to be restricted to an area of the minimal set considered to be safe.

While allocating patients within the estimated minimal set, we want to do our best to avoid the selection of dose combinations which are already associated with having an unacceptably high toxicity probability. We can address this issue by making use of a Bayesian test based on a uniform prior 𝒰 on the space of Bernoulli parameters. The set H_n describes those dose combinations indicated as being too toxic following these local Bayesian tests at each of the doses.

$$H_n=\left\{d\in D:{\mathbb{P}}_{𝒰}\left[P_d>{\theta }_T\mid \left(n_d,n_d^1\right)\right]>{\delta }_T\right\}.$$

We are then in a position to use the partial ordering in D to extend these exclusions to other doses that are unfavourably ordered with the doses belonging to this set, e.g. a dose d′ in 𝒜_d with d belonging to H_n.

Exclusion rule:

A dose d₀ is excluded from the study if:

$$d_0\in T_n=\left\{d\in D:\exists d^{\prime }\in H_n,d\ge d^{\prime }\right\},$$

where T_n is the set of dose combinations considered as overly toxic. A dose combination of the estimated minimal set ${ℳ}_{{\widehat{\gamma }}_n}$ will not be tested if it belongs to T_n. Note that this exclusion rule corresponds also to a stopping rule when the evidence of unacceptably high toxicity is associated with the lowest dose. This rule is an extension in the context of partial ordering to rules introduced by Ji et al (2010).

The approach based on a compromise between spreading the observations along the contour as opposed to making observations on those doses that we estimate would bring more information into the study leans on two quantities: (i) the number of doses which will potentially benefit from the next observation through the partial ordering structure and (ii) the amount of information already collected. Each dose d, can be associated with a value k_d corresponding to the number of dose combinations ordered with d plus one: k_d = # 𝒜_d + # ℬ_d + 1, where the cardinality of a set E is noted $\overline{E}$. The value k_d corresponds to the number of dose combinations on which we aim to learn something subsequent to an observation on d. Observing a DLT at dose d implies that the patient would have experienced a DLT for all the doses in 𝒜_d, and conversely, all the doses in ℬ_d would have been safe for a patient who does not experience a DLT at dose d. This structure is naturally taken into account by our model. When the objective is to optimize the quantity of information obtained during the trial, those doses associated with the highest value k_d are, in expectation, those that provide the most information. Note that these doses are located along the diagonal going from the combination (1, 1) to (I, J). The notion of entropy is our second tool. It corresponds to a quantity of information per unit of data, in our case the observation related to a single patient. As the goal of the study is to determine doses that are close to α in term of toxicity probability, we will use the concept of relative entropy between each observation and the target α. If p and q denotes two Bernoulli distributions and their parameters, the entropy of p relative to q is: H(p|q) = −q × log(p)−(1−q)log(1−p), with the convention log(0) = −∞ and 0×(−∞) = 0. Thus, n×H(α|1) is the quantity of information relative to the target alpha which is brought by n DLT (H(α|0) for the non toxic observations). It corresponds to the log-likelihood in α. After n observations, the next dose X_n+1 is:

$$X_{n+1}=\underset{d\in {ℳ}_{{\widehat{\gamma }}_n}\setminus T_n}{\text{min}}\frac{1}{k_d}\left\{\left(\sum _{j\in {ℬ}_d\cup \left\{d\right\}}{n}_j^0\right)\times H(\alpha \mid 0)+\left(\sum _{j\in {𝒜}_d\cup \left\{d\right\}}{n}_j^1\right)\times H(\alpha \mid 1)\right\}.$$ (C.9)

This allocation strategy spreads the observations along the estimated contour and tests slightly more often the doses in the middle of the grid. Since a DLT corresponds to a greater quantity of information those doses with a smaller number of toxicities are tried more often (for α = 0.25: H(α|1)/H(α|0) = log(α)/log(1 − α) ≈ 4.82).

D. Numerical experiments: MTD setting

We evaluate the operating characteristics of poSPM and compared them to the 2d-BOIN method (Lin et al., 2016) and the poCRM (Wages, Conaway and O’Quigley, 2011). Performance evaluation was based on several metrics under 4 toxicity scenarios. Our goal is to evaluate: (1) how well each method provides a recommendation of sets of doses at and around the target rate (i.e. acceptable MTD’s), and (2) how well each method allocates patients to acceptable MTD’s. While traditional evaluation measures, such as the percentage of recommendation and allocation to the true MTD’s are useful in assessing performance, it is also beneficial to consider the entire distribution of selected dose combination, as it provides more detailed information as to what combinations are being recommended. For evaluating recommendation, Cheung (2011) proposes to use the accuracy index so that, after n patients, he defines,

$$A_n=1-I\times J\times \frac{\sum _{i=1}^I\sum _{j=1}^J{\left(P_d-\alpha \right)}^2\times {\rho }_d}{\sum _{i=1}^I\sum _{j=1}^J{\left(P_d-\alpha \right)}^2},$$ (D.10)

where P_d is the true toxicity probability at dose combination d = (i, j), ρ_d is the percentage of trials in which combination d = (i, j) was selected as the MTD, and n is the total sample size. For experimentation, the same formula can be used with ρ_d representing the percentage of patients treated at combination d = (i, j). The maximum value of A_n is 1 with larger values (close to 1) indicating that the method has high accuracy. For each method, we simulated 10,000 trials under the 4 different sets of assumed DLT probabilities in a 6×6 grid of combinations with varying positions and number of true MTD’s, as shown in Table 7. The target toxicity rate is α = 0.25 and the total sample size for each simulated study is 40 patients. For each method, a cohort of size 1 is used. The calibration of the three methods is fully described in Appendix E.1 and E.2.

Table 8 shows the operating characteristics of the 3 methods under 10 000 trials for the 4 scenarios considered. For each scenario, we report the percentage of patient allocation (experimentation %) and percentage of MTD selection (recommendation %) for doses contained within five different ranges of the true toxicity probabilities. Since α = 0.25, the target interval containing the true MTD is [0.20, 0.30]. In Scenarios 1 and 2, the poSPM and poCRM have very comparable performance, with each method outperforming 2d-BOIN in terms of experimentation %, recommendation %, as well as accuracy of experimentation and recommendation. For both of these scenarios, 2d-BOIN induces a higher percentage of DLT’s, on average. In Scenario 3, the 2d-BOIN exhibits the best performance when considering experimentation and recommendation percentages in the target interval. The accuracy of recommendation of the poSPM is very close to that of the 2d-BOIN due to the higher recommendation percentage for 2d-BOIN on the toxicity probability interval [0, 0.10). In the final scenario, poSPM is the best performing method according to all metrics.

Table 7:

True toxicity probabilities for the four scenarios of a 6 × 6 grid, with maximum tolerated doses shown in bold

	Dose	Drug A1
	Level	1	2	3	4	5	6	1	2	3	4	5	6
	Scenario 1							Scenario 2
	6	20	29	31	43	47	50	37	45	51	54	55	58
	5	18	20	29	34	41	48	30	38	41	43	46	47
	4	16	19	21	32	36	42	23	25	35	36	40	42
	3	10	15	20	25	30	37	19	20	26	33	35	39
	2	3	9	16	19	21	32	15	17	21	24	31	33
	1	2	5	10	17	21	30	5	10	16	20	25	28
Drug
A2	Scenario 3							Scenario 4
	6	11	13	15	17	25	33	65	70	76	80	84	90
	5	9	11	13	15	16	25	55	63	69	77	80	85
	4	7	9	11	14	15	17	45	56	60	72	76	79
	3	5	8	10	11	13	15	35	42	52	65	70	73
	2	3	6	7	9	12	13	25	34	46	54	60	64
	1	1	3	5	7	9	11	15	25	36	43	49	55

We anticipate that there will always be certain scenarios in which some methods perform better than others. A useful tool in this regard for comparing dose-finding designs can be average performance over a range of scenarios. Across the 4 scenarios, the poSPM method, the 2d-BOIN design and poCRM methods demonstrated averages of 46.7%, 42.5%, and 43.3% recommendation percentages for combinations in the true target interval [0.20, 0.30], respectively. The overall percentage of observed toxicities of the poSPM method, the 2d-BOIN design, and poCRM methods were on average; 24.1%, 27.3%, and 23.1%, respectively. It is desirable for the value to be as close as possible to the target rate α. This is achieved by the poSPM. The average percentage of patients allocated to a dose combination in the target interval of the poSPM method, the 2d-BOIN design, and poCRM methods were 34.13%, 30.75%, and 31.75%, respectively. Based on the accuracy index for recommendation, the poSPM yielded an average value of 0.77, the 2d-BOIN method produced an average value of 0.73, and the poCRM design resulted in an average value of 0.71. For accuracy of experimentation, the average index values over the four scenarios were 0.54, 0.48, and 0.52 for the poSPM, 2d-BOIN, and poCRM, respectively.

Table 8:

Experimentation and recommendation percentages for the poSPM, the BOIN design and the poCRM in four scenarios of a 6 × 6 grid of true toxicity probabilities. Column containing the MTD in bold.

Scenario	Method	Experimentation %					A 40	%DLTs
		[0, 0.10)	[0.10, 0.20)	[0.20, 0.30]	(0.30, 0.40]	(0.40, 1]
1	poSPM	11.1	18.7	42.3	22.3	6.6	0.35	23.9
	BOIN	8.6	16.2	32.0	23.9	19.3	0.34	27.5
	poCRM	11.0	26.0	43.0	17.0	4.0	0.37	22.2
2	poSPM	4.6	18.5	44.0	26.6	6.4	0.54	25.8
	BOIN	4.3	15.3	40.0	31.2	18.2	0.26	29.3
	poCRM	4.0	22.0	47.0	24.0	4.0	0.64	25.1
3	poSPM	14.6	52.6	17.7	15.1	0.0	0.38	17.5
	BOIN	14.3	38.7	25.1	21.8	0.0	0.48	20.0
	poCRM	25.0	57.0	10.0	9.0	0.0	0.20	14.6
4	poSPM	0.0	24.2	32.5	25.5	17.8	0.90	29.2
	BOIN	0.0	18.4	25.9	24.4	28.9	0.83	32.3
	poCRM	0.0	18.0	27.0	29.0	26.0	0.86	32.3
		Recommendation %					A 40
		[0, 0.10)	[0.10, 0.20)	[0.20, 0.30]	(0.30, 0.40]	(0.40, 1]
1	poSPM	0.4	16.0	54.2	25.1	4.3	0.68
	BOIN	1.2	16.9	46.6	27.4	7.45	0.65
	poCRM	1.0	24.0	56.0	16.0	3.0	0.68
2	poSPM	0.1	10.1	56.5	29.6	3.7	0.74
	BOIN	0.1	13.69	44.5	33.5	8.1	0.63
	poCRM	0.0	15.0	59.0	25.0	3.0	0.76
3	poSPM	0.6	47.0	30.6	21.8	0.0	0.71
	BOIN	2.5	44.3	37.4	15.8	0.0	0.72
	poCRM	12.0	63.0	18.0	8.0	0.0	0.46
4	poSPM	0.0	17.5	45.5	28.7	8.2	0.95
	BOIN	0.0	11.5	41.4	30.7	13.3	0.93
	poCRM	0.0	12.0	40.0	35.0	11.0	0.94

E. Calibration

E.1. poCRM, 2d-BOIN and PIPE methods

For poCRM, we utilized six possible orderings in all scenarios, arranging the combinations across rows, up columns, and up or down any diagonal as suggested by Wages and Conaway (2013). A uniform prior was placed on the orderings. The skeleton values for poCRM were generated according to the algorithm of Lee and Cheung (2009) using the getprior function in R package dfcrm. Specifically, we used getprior(0.035,0.25,12,36), and all simulation results were generated using the functions of the R package poCRM.

For the BOIN method, we used the default cutoff values α₁ = 0.6α and α₂ = 1.4α and a Beta(0.5, 0.5) prior for the toxicity probability at each combination. The boundaries for the optimal interval for the BOIN method are (0.197, 0.298).

The prior distributions for PIPE are set to be the true DLT probabilities taken from Scenario 1 in Table 5. PIPE uses a neighbourhood dose-skipping constraint, as well as the closest doses chosen from the admissible dose set. The dose escalation algorithm employs the smallest sample size strategy, and a weak prior distribution (1/16) is specified.

E.2. poSPM

The marginals of the prior model are beta distributions truncated according to their support (Assumption 3). Let B_I(a, b) be the truncated beta distribution with parameters a and b and let B_I(m, T) be an alternative parametrization of this distribution such that: B_I(m, T) = B(m × T + 1,(1 − m) × T + 1). Then, m is the mode of the beta distribution and T is a dispersion parameter.

The family of I × J matrix (m_θ)_θ∈D is associated with the prior model (Λ_θ)_θ∈D. The element of the matrix m_θ in position d, noted $m_{\theta }^d$, is the mode of the marginal ${\Lambda }_{\theta }^d$. The value T₁ and T₂ are the dispersion parameters used on the different marginals. In the Bayesian setting, they can be equated to a number of pseudo observations providing toxicities and non-toxicities. The rank of a dose combination θ = (i, j), noted $\overline{\theta }$, is equal to i+j. All the doses on the same diagonal have the same rank. Let r₁ and r₂ be two positive values used for the calibration of the prior Π. The poSPM model used in the simulations can be summarized by:

$$\{\begin{array}{ll}{\Lambda }_{\theta }\hfill & ~\prod _{d\in {ℬ}_{\theta }}{\text{B}}_B\left(m_{\theta }^d,T_1\right)\times \prod _{d\in {𝒜}_{\theta }}{\text{B}}_A\left(m_{\theta }^d,T_1\right)\times \prod _{d\in {𝒞}_{\theta }}{\text{B}}_{[0,1]}\left(m_{\theta }^d,T_2\right)\times {\text{B}}_I\left(m_{\theta }^{\theta },T_1\right)\hfill \\ \Pi (\theta )\hfill & \propto r_1^{\overline{\theta }-2}\times r_2^{\overline{\theta }-3},\hfill \end{array}$$

We set: ${𝒜}_{\theta }^{\prime }=\{d\in 𝒜:\overline{\theta }+1<\overline{d}\}$ and ${ℬ}_{\theta }^{\prime }=\{d\in ℬ:\overline{\theta }>\overline{d}+1\}$. The parameters of the prior model are: $m_{\theta }^d=\alpha \left(1+{0.4\mathbb{1}}_{{𝒜}_{\theta }}\left(d\right)+{0.2\mathbb{1}}_{{𝒜}_{\theta }^{\prime }}\left(d\right)-{0.4\mathbb{1}}_{{ℬ}_{\theta }}\left(d\right)-{0.2\mathbb{1}}_{{ℬ}_{\theta }^{\prime }}\left(d\right)\right)$, T₁ = 40 and T₂ = 10. The parameters r₁ and r₂ are chosen to produce a progressive allocation in the range of doses. The goal is to obtain a prior Π that is non-informative with the purpose of compensating the weight given to the highest dose combinations by the first non-toxic observations. For α = 0.25, we choose: r₁ = 0.942724 and r₂ = 0.95566. In order to explore the diagonal going from (1, 1) to (I, J) before a DLT is observed, a very small weight (10⁻⁵) is added to these doses. Thus, the poSPM follows the sequence of dose combinations (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), … until a first DLT is observed. After N observations, the final recommendation is made by using our current estimator ${\widehat{\theta }}_N$, which corresponds to the most probable MTD according to the posterior Π_N.

E.3. poSPMc

We use the same notation as for the poSPM calibration. The poSPMc model fulfills Assumption 4. The allocation strategy defined by Equation (4.6) is used. The family of I × J matrix (m_γ)_γ∈C is associated with the prior model (Λ_γ)_γ∈C. The rank of a contour γ, noted $\overline{\gamma }$, is the number of dose combination in ℬ_γ. T is the dispersion parameter of the truncated beta distributions, r₁ and r₂ are two positive values used for the calibration of the prior Π.

$$\{\begin{array}{ll}{\Lambda }_{\gamma }\hfill & ~\prod _{d\in {ℬ}_{\gamma }}{\text{B}}_{[0,\alpha ]}\left(m_{\gamma }^d,T\right)\times \prod _{d\in {𝒜}_{\gamma }}{\text{B}}_{[\alpha ,1]}\left(m_{\gamma }^d,T_1\right),\hfill \\ \Pi (\gamma )\hfill & \propto r_1^{\overline{\gamma }-2}\times r_2^{\overline{\gamma }-3},\hfill \end{array}$$

The parameters of the prior model are: $m_{\gamma }^d=\alpha (1+{0.5\mathbb{1}}_{{𝒜}_{\gamma }}(d)+{0.25\mathbb{1}}_{{𝒜}_{\gamma }\setminus {ℳ}_{\gamma }}(d)-{0.4\mathbb{1}}_{{ℬ}_{\gamma }}(d)-{0.2\mathbb{1}}_{{ℬ}_{\gamma }\setminus {ℳ}_{\gamma }}(d))$ and T = 25. The parameters r₁ and r₂ are chosen to produce a progressive allocation in the range of dose combinations. The goal is to obtain a prior Π that is non informative with the idea of compensating the weight given to the highest contour in term of rank by the the first non-toxic observations. For α = 0.2, we choose r₁ = 0.8739592 and r₂ = 0.9749345 and for α = 0.3, we choose r₁ = 0.8117365 and r₂ = 0.950334. For the exclusion rules (End of section 4.2), we choose to exclude a dose when the probability of our posterior on the upper interval attains 95%: δ = 0.95. An ϵ = 10⁻⁵ is added to the part multiplying 1/k_d such that the value k_d drives the allocation between dose combinations for which we do not yet posses any observations. After N observations, we recommend all the dose combinations in the estimated minimal set ${ℳ}_{{\widehat{\gamma }}_N}$, except the doses for which we have less than 2 observations and the doses in $H_n^{\prime }$ which are considered as toxic:

$$H_n^{\prime }=\left\{d\in D:{\mathbb{P}}_{𝒰}\left[P_d>\alpha +0.05\mid \left(n_d,n_d^1\right)\right]>0.9\right\}.$$

F. Computation of minimal set

In the two dimensional case, I and J are the number of doses for each of the agents. The set of contours could be described as all the polygonal chains tracing out a path from (0.5, J + 0.5) to (I + 0.5, 0.5) with steps of size 1 along the abscissae and of size −1 on the ordinate axis. Only rightward and downward steps are permitted. This set is also equivalent to all the combinations of I among I + J which could be generated with the R function combn of package combinat. From there, it is easy to obtain matrices indicating which dose combinations are below or above the contour c that correponds to the sets 𝒜_c and ℬ_c.

Computing the minimal set is equivalent to computing min 𝒜_c and max ℬ_c. For the general problem “computing the maximum of a partially ordered set” the greatest calculation burden is 𝒪(n²): in a set where no element are a priori ordered, all the elements have to be compared to solve the problem. In the case of two drugs, the structure of ${\mathbb{N}}^2$ leads to a time complexity 𝒪(n). Let ${\text{mat}}_{{ℬ}_c}$ be a I × J matrix of 0 and 1 indicating the dose combinations in ℬ_c. From row N to 1:

1. Select the last element equal to 1 of the row in ${\text{mat}}_{{ℬ}_c}$, if it exists. Otherwise, go to next row.

2. Compare the selected element to the previous one. Keep it, if they are notordered. Otherwise, delete it.

Finally, the selected elements are the maximum set of ℬ_c.

Note that in order to save time, all the arrays containing the minimal set associated to each contour can be saved for use in simulations. If we do so, the 𝒪(n²) solution (exhaustive comparison two by two) could be used as it is only applied one time.

G. Proofs of two properties and a general theorem

G.1. Coherence

When there is no confusion, we write Λ_θ(dP_r) for ${\Lambda }_{\theta }^r\left(d{P}_r\right)$, with r ∈ D We then state a stochastic partial ordering assumption on the prior-model.

Assumption 6. Let d and d^′ be two doses such that d < d′. For all marginal r ∈ D, the posterior ${\Lambda }_{d,n}^r$ is stochastically greater than ${\Lambda }_{d^{\prime },n}^r$:

$${\Lambda }_{d,n}^r([0,x])\le {\Lambda }_{d^{\prime },n}^r([0,x])\forall x\in [0,1].$$

This assumption is satisfied by the calibration of poSPM presented in Section E.2.

Proposition 1. Under Assumptions 3 and 6 (appendix), the poSPM is coherent.

Proof. Suppose that Y_n+1 = 1. The case Y_n+1 = 0 can be solved in the same way. By construction, we have

$${\Pi }_{n+1}(\theta )\propto \left[\int P{\Lambda }_{\theta ,n}(dP)\right]{\Pi }_n(\theta ).$$

Furthermore,

$$\begin{gathered} \int P_r{\Lambda }_{\theta ,n}(dP)=\int \left[\int {\mathbb{1}}_{\left\{0\le x\le P_r\right\}}\mu (dx)\right]{\Lambda }_{\theta ,n}\left(d{P}_r\right) \\ =\int {\Lambda }_{\theta ,n}^r(]x,1])\mu (dx). \end{gathered}$$

If ${\widehat{\theta }}_n=r$, then for all θ ∈ D, Π_n(θ) ≤ Π_n(r). Let t > r. According to Assumption 6, we know that ${\Lambda }_{r,n}^r(.)$ is stochastically greater than ${\Lambda }_{t,n}^t(.)$, i.e.

$$\int {\Lambda }_{r,n}^r(]x,1])\mu (dx)\ge \int {\Lambda }_{t,n}^r(]x,1])\mu (dx),$$

that is

$$\int P_r{\Lambda }_{r,n}(dP)\ge \int P_r{\Lambda }_{t,n}(dP).$$

Finally Π_n+1(r) ≥ Π_n+1(t), which ends the proof. □

G.2. Conjugacy property

Proposition 3. For all $n\in \mathbb{N}$, the probability ${\tilde{\Pi }}_n$ defined by Equation 7.7 is the posterior on the set of dose combinations from the poSPM model $(\tilde{\Lambda },\tilde{\Pi })$ where:

$$\tilde{\Pi }(d)\propto \frac{1}{\overline{{𝒱}_d}}\sum _{c\in {𝒱}_d}\Pi (c)and{\tilde{\Lambda }}_d=\sum _{c\in {𝒱}_d}{r}_c^d{\Lambda }_c\text{with}{r}_c^d=\frac{\Pi (c)}{\sum _{c\in {𝒱}_d}\Pi (c)}\text{.}$$

Proof. We have the following proportionnality relations:

$$\begin{gathered} {\tilde{\Pi }}_n(d)\propto \frac{1}{\overline{{𝒱}_d}}\sum _{c\in {𝒱}_d}{\Pi }_n(c)\propto \frac{1}{\overline{{𝒱}_d}}\sum _{c\in {𝒱}_d}\left[\int L_n(P){\Lambda }_c(dP)\right]\times \frac{\Pi (c)}{\sum _{c\in {𝒱}_d}\Pi (c)}\times \sum _{c\in {𝒱}_d}\Pi (c) \\ \propto \left[\int L_n(P)\sum _{c\in {𝒱}_d}{r}_c^d\times {\Lambda }_c(dP)\right]\times \left(\frac{1}{{\overline{𝒱}}_d}\sum _{c\in {𝒱}_d}\Pi (c)\right)\propto \left[\int L_n(P){\tilde{\Lambda }}_d(dP)\right]\times \tilde{\Pi }(d). \end{gathered}$$

□

G.3. Proof of Theorem 1

Proof. The proof is made by showing that the two first statements are equivalent to the third one. As the proofs of these two equivalences are very similar, we focus on: (i) ⇔ (iii). The implication (i) ⇐ (iii) is immediate by using the Law of Large Number for the frequentist estimators $n_d^1/n_d$ at each dose of the minimal set. We show (i) ⇒ (iii) by using a reductio ad absurdum argument.

T is a scenario whose the maximum tolerated dose is MTD_T and the maximum tolerated contour is MTC_T. We choose this scenario T and a dose d₀ ∈ MTC_T such that there exists a set of sequences of our sample, $A=\left\{a=\left(x_1^{\infty },y_1^{\infty }\right)\right\}$ satisfying: (1) $\forall a=\left(x_1^{\infty },y_1^{\infty }\right)\in A$, $F\left(x_1^n,y_1^n\right)\to MT{D}_T$, (2) ${\mathbb{P}}_T(A)>0$, (3) $\forall a\in A,d_0\notin \underset{N=1}{\overset{\infty }{\cap }}\underset{n=N}{\overset{\infty }{\cup }}\left\{x_n\right\}$. This is possible as the absence of (3) for any dose contradicts the negation of (iii) and the absence of (1) and (2) together contradicts (i). The point (3) implies that there exists $N_0\in \mathbb{N}$ such that:

$${\mathbb{P}}_T\left(B=\left\{s\in A:\nexists n>N_0,x_n=d_0\right\}\right)>0.$$

We introduce the two following sets: $B^{\prime }=\{\omega \in \Omega :\exists a=\left(x_1^{\infty },y_1^{\infty }\right)\in A$, $\left(X_{N_0}^{\infty },Y_{N_0}^{\infty }\right)(\omega )=\left(x_{N_0}^{\infty },x_{N_0}^{\infty }\right)\}$ and $B^{″}=\{\omega \in \Omega :\exists a=\left(x_1^{\infty },y_1^{\infty }\right)\in A$, $\left(X_1^{N_0},Y_1^{N_0}\right)(\omega )=\left(x_1^{N_0},x_1^{N_0}\right)\}$. We have: ${\mathbb{P}}_T(B)={\mathbb{P}}_T\left(B^{\prime }\mid B^{″}\right)\times {\mathbb{P}}_T\left(B^{″}\right)$ and then ${\mathbb{P}}_T\left(B^{\prime }\mid B^{″}\right)>0$. Let T′ be a scenario such that, for all d ∈ D \ {d₀}, P_T′(Y = 1|X = d) = P_T(Y = 1|X = d) and MTD_T′ = d₀. We then have: ${\mathbb{P}}_{T^{\prime }}\left(B^{\prime }\mid B^{″}\right)>0$, as the same method chooses the next dose being used for the two scenarios and the dose is not tried after N₀ for any sequence of B. Moreover, $B^{″}=\underset{\left(x_1^{\infty },y_1^{\infty }\right)\in A}{\cup }\{\omega \in \Omega :\left(X_1^{N_0},Y_1^{N_0}\right)(\omega )=\left(x_1^{N_0},x_1^{N_0}\right)\}$ with:

$${\mathbb{P}}_{T^{\prime }}\left(\left\{\omega \in \Omega :\left(X_1^{N_0},Y_1^{N_0}\right)(\omega )=\left(x_1^{N_0},x_1^{N_0}\right)\right\}\right),$$

as the constraints are on the first N₀ terms. Thus, ${\mathbb{P}}_{T^{\prime }}(B)>0$ and on this set of sequences of the sample the statistic F converges to MTD_T ≠ d₀ = MTD_T′.□

H. Proof of asymptotic results for poSPM

H.1. Proof of Theorem 2 (a)

This assumption leans upon the regularity of the prior model.

Assumption 7. The following conditions are valid except when ${\Lambda }_{\theta }^{\theta }$ is a Dirac measure.

1. For all d ∈ D, the marginal distribution ${\Lambda }_{\theta }^d$ is absolutely continuous with respect to the Lebesgue measure and ${\lambda }_{\theta }^d$ denotes its density function.

2. There exist two numbers s and S in ${ℝ}_{+}^{*}$, such that, for all θ and d in D, we have:

   $$\forall P_d\in S_{\theta }^d,s<{\lambda }_{\theta }^d\left(P_d\right)<S.$$

Note that this assumption can be used for the poSPMc by replacing θ by γ, the parameter of the contour.

The second point is only useful for the sake of the demonstration when some β_(i,j) are equal to 0 or 1. In order to establish asymptotic properties for the poSPM, we introduce the set $\tilde{D}$ to indicate those doses that are observed infinitely often:

$$d\in \tilde{D}\iff n_d\underset{n\to \infty }{\to }\infty .$$

Proof. Let us start with the proof of ε-sensitivity. In this proof, we are interested in the asymptotic behavior of poSPM, that is why we are able to ignore those doses tested only a finite number of times and we can reason as though they had never been used. Specifically, the doses in this proof are always considered to be in $\tilde{D}$. We assume that ℰ(I, P^T) is not empty (P^T denotes the true scenario). Let $r\in \tilde{D}\setminus ℰ\left(I,P^T\right)$. We can distinguish two cases. The first case is the existence of a dose d ∈ ℰ(I, P^T) such that d is ordered with r. We are then reduced to the SPM in the case of total ordering and the proof can be found in Clertant and O’Quigley (2017).

The second case is where there exists no dose in ℰ(I, P^T) ordered with r. So there exists a dose d ∈ ℰ(I, P^T) not ordered with r, because we assume that ℰ(I, P^T) is not empty. We want now to compare the integrals I_n,r and I_n,d, where g(p, n, m) = pⁿ(1 − p)^m.

$$\frac{I_{n,r}}{I_{n,d}}=\prod _{k\in \tilde{D}}\frac{M_{n,r}^k}{M_{n,d}^k}=\prod _{k\in \tilde{D}}\frac{{\int }_{S_r^k}g\left(P_k,n_k^1,n_k^0\right){\Lambda }_r\left(d{P}_k\right)}{{\int }_{S_d^k}g\left(P_k,n_k^1,n_k^0\right){\Lambda }_d\left(d{P}_k\right)}$$ (H.11)

$$=\prod _{k\in \tilde{D}}\frac{{\int }_{S_r^k}g\left(P_k,n_k^1,n_k^0\right){\lambda }_r\left(P_k\right)d{P}_k}{{\int }_{S_d^k}g\left(P_k,n_k^1,n_k^0\right){\lambda }_d\left(P_k\right)d{P}_k}$$ (H.12)

$$\le \frac{S}{s}\prod _{k\in \tilde{D}}\frac{{\int }_{S_r^k}g\left(P_k,n_k^1,n_k^0\right)d{P}_k}{{\int }_{S_d^k}g\left(P_k,n_k^1,n_k^0\right)d{P}_k},$$ (H.13)

where Equation (H.11) follows from Assumption 3, Equation (H.12) from Assumption 7 (a) and Inequation (H.13) from Assumption 7 (b). We are able to state the following property. For all functions f that are continuous on [0, 1], we have

$$\int f\left(P_k\right)\frac{g\left(P_k,n_k^1,n_k^0\right)}{\text{Beta}\left(n_k^1+1,n_k^0+1\right)}d{P}_k\underset{n_k\to \infty }{\to }\int f\left(P_k\right){\mathbb{1}}_{\left\{P_k\right\}}\left(P_k\right)\gamma \left(d{P}_k\right)=f\left(P_k\right),$$ (H.14)

where Beta(.) denotes the Beta function and γ the counting measure. Let then $k\in \tilde{D}$. We are looking for the behavior, when n_k increases without bound, of

$$R_k=\frac{{\int }_{S_r^k}g\left(P_k,n_k^1,n_k^0\right)d{P}_k}{{\int }_{S_d^k}g\left(P_k,n_k^1,n_k^0\right)d{P}_k}.$$

The case $S_r^k=S_d^k$ is straightforward. For the other cases, we use the convergence expressed in Equation (H.14). As d is not ordered with r, with Assumption 3, we have six cases left to deal with.

• $S_r^k=A$ or B or I and $S_d^k=[0,1]$. Then $R_k\underset{n_k\to \infty }{\to }{\mathbb{1}}_A\left(P_k^T\right)$ or ${\mathbb{1}}_B\left(P_k^T\right)$ or 0. This last result is due to the fact that r ∉ ℰ(I, P^T).

• $S_r^k=[0,1]$ and $S_d^k=I$. Then $R_k\underset{n_k\to \infty }{\to }1$, because d ∈ ℰ(I, P^T).

• $S_r^k=[0,1]$ and $S_d^k=A$. Then $R_k\underset{n_k\to \infty }{\to }1/{\mathbb{1}}_A\left(P_k^T\right)=1$. As there is no couple of ordered dose in ℰ(I, P^T), $P_k^T$ belongs to A.

• $S_r^k=[0,1]$ and $S_d^k=B$. With the same argument as the previous case, we have $R_k\underset{n_k\to \infty }{\to }1$.

Finally, going back to Inequality (H.13), we conclude that I_n,r/I_n,d tends to 0 when n increases without bound. This leads to a contradiction because, as $r\in \tilde{D}$, this ratio is greater than 1 infinitely often. So $\tilde{D}\subset ℰ(I,P)$, that is, the poSPM is ε-sensitive.

We prove now that poSPM is also balanced. Assumption 3 allows us to focus on the marginal ratio

$$\frac{M_{n,r}^k}{M_{n,t}^k}=\frac{\int g\left(P_j,n_k^1,n_k^0\right){\Lambda }_r^k\left(d{P}_k\right)}{\int g\left(P_k,n_k^1,n_k^0\right){\Lambda }_t^k\left(d{P}_k\right)}\hspace{1em}\text{and}\hspace{1em}\frac{I_{n,r}}{I_{n,t}}=\prod _{k\in D}\frac{M_{n,r}^k}{M_{n,t^k}}\text{.}$$

Assumption 7 involves:

$$d\left(P_k^T,S_r^k\right)=d\left(P_k^T,S_t^k\right)\Rightarrow 0<\underset{n\to \infty }{\text{lim inf}}\frac{M_{n,r}^k}{M_{n,t}^k}\le \underset{n\to \infty }{\text{lim sup}}\frac{M_{n,r}^k}{M_{n,t}^k}<+\infty ,a\text{.}s\text{.}$$ (H.15)

The ε-balanced behavior corresponds to the case where, forall k ∈ D, $P_k^T\notin I$. We show that

$$r\notin {ℳ}_{c^{\star }}\Rightarrow \mathbb{P}\left(\left\{n_r\to \infty \right\}\right)=0$$ (H.16)

By symmetry we can choose r ∈ D⁻. The set ${ℳ}_{c^{\star }}\cap D^{-}\cap {𝒜}_r$ is not empty. Let t be a dose in ${ℳ}_{c^{\star }}\cap D^{-}\cap {𝒜}_r$. By using Equation (H.15), as 𝒜_t ⊂ 𝒜_r and $S_t^k=[0,1]$ when k ∈ 𝒞_t, we have

$$\forall k\in A_t\cup C_t,\mathbb{P}\left(\underset{n\to \infty }{\text{lim sup}}\frac{M_{n,r}^k}{M_{n,t}^k}<\infty \mid n_k\to \infty \right)=1.$$

If k ∈ (ℬ_r ∪ 𝒞_r) ∩ ℬ_t then $P_k^T\in B$ and we obtain the same result

$$\mathbb{P}\left(\underset{n\to \infty }{\text{lim sup}}\frac{M_{n,r}^k}{M_{n,t}^k}<\infty \mid n_k\to \infty \right)=1.$$

We consider now the ratios $M_{n,r}^k/M_{n,t}^k$ when k ∈ (ℬ_t ∩ 𝒜_r)∪{t, r}. In that case, we have $P_k^T\in B$, $S_t^k=B$ and $S_r^k$ equals to I or A. By using Proposition 4, we have

$$\forall k\in \left({ℬ}_t\cap {𝒜}_r\right)\cup \left\{t,r\right\},\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{M_{n,r}^k}{M_{n,t}^k}=0\mid n_k\to \infty \right)=1.$$

We then have

$$\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{I_{n,r}}{I_{n,t}}=0\mid n_r\to \infty \right)=1\text{ and }\mathbb{P}\left(\left\{\underset{n\to \infty }{\text{lim}}\frac{I_{n,r}}{I_{n,t}}=0\right\}\cap \left\{n_r\to \infty \right\}\right)=0,$$

which proves Equation (H.16). We achieve the proof of the ε-balanced property by showing that

$$t\in {ℳ}_{c^{\star }}\Rightarrow \mathbb{P}\left(n_t\to \infty \right)=1$$ (H.17)

By using Equation (H.16), we have, for all r and t in ${ℳ}_{c^{\star }}$

$$\forall k\in D,k\ne r\text{ and }k\ne t,\mathbb{P}\left(\underset{n\to \infty }{\text{lim sup}}\frac{M_{n,r}^k}{M_{n,t}^k}<\infty \right)=1.$$

Moreover, for all $r\in {ℳ}_{c^{\star }}$, $P_r^T$ is included in $S_t^r$. As $P_r^T\notin I=S_r^r$, we have

$$\forall r\in {ℳ}_{c^{\star }},\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{M_{n,r}^r}{M_{n,t}^r}=0\mid n_r\to \infty \right)=1.$$

Let E_r be the event {n_r → ∞} ∩ {n_t → ∞}^c. Then,

$$\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{I_{n,r}}{I_{n,t}}=0\mid E_r\right)=1\text{ and }\mathbb{P}\left(\left\{\underset{n\to \infty }{\text{lim}}\frac{I_{n,r}}{I_{n,t}}=0\right\}\cap E_r\right)=0\text{,}$$

As $\mathbb{P}\left({\sum }_{{ℳ}_{c^{\star }}}{n}_k\to +\infty \right)=1$, we have $\mathbb{P}\left({\cup }_{{ℳ}_{c^{\star }}}{E}_r\right)=1$, which proves Equation (H.17) and ends the demonstration of the poSPM ε-balanced behavior. □

H.2. Proof of Theorem 2 (b)

Proof. We set:

$$I_{n,c}=\prod _{k\in \tilde{D}}{M}_{n,c}^k=\prod _{k\in \tilde{D}}{\int }_{S_c^k}g\left(P_k,n_k^1,n_k^0\right){\Lambda }_c\left(d{P}_k\right)$$

We note that the regularity assumption 7 involves:

$$\delta \left(P_k^T,S_r^k\right)=\delta \left(P_k^T,S_t^k\right)\Rightarrow 0<\underset{n\to \infty }{\text{lim inf}}\frac{M_{n,r}^k}{M_{n,t}^k}\le \underset{n\to \infty }{\text{lim sup}}\frac{M_{n,r}^k}{M_{n,t}^k}<\infty ,a\text{.}s\text{.}$$

We will show the following assertion

$$c\in C\backslash c^{*}\Rightarrow \mathbb{P}\left(n_c\to \infty \right)=0$$ (H.18)

As c ≠ c*, we have ${ℳ}_c\ne {ℳ}_{c^{\star }}$ and there exists k ∈ ℳ_c such that $P_k^T$ is included in $S_{c^{*}}^k$ and not in $S_c^k$. By using Proposition 4, we have

$$\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{M_{n,c}^k}{M_{n,c^{*}}^k}=0\mid n_c\to \infty \right)=\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{M_{n,c}^k}{M_{n,c^{*}}^k}=0\mid n_k\to \infty \right)=1,$$

where the first equality arises from Assumption 5(b). For all doses d ∈ D, the distribution Λ_c* models correctly the probability of toxicity, in other words $P_d^T\in S_{{𝒞}^{*}}$. We then have

$$\mathbb{P}\left(\underset{n\to \infty }{\text{lim}}\frac{I_{n,c}}{I_{n,c^{*}}}=0\mid n_c\to \infty \right)=1\text{ and }\mathbb{P}\left(\left\{\underset{n\to \infty }{\text{lim}}\frac{I_{n,c}}{I_{n,c^{*}}}=0\right\}\cap \left\{n_c\to \infty \right\}\right)=0,$$

which ends the proof. (H.18). □

I. A general bayesian property

The following property is used in the proof of asymptotic results. It has already been proved in (Clertant and O’Quigley, 2018). Here, for the convenience of the reader, we reproduce this property without its proof.

The couple (Ω, 𝒜) denotes an abstract space endowed with its σ-field. We denote by I a finite set and by ${\left(X_k\right)}_{k\in \mathbb{N}}$ a sequence of independent random variables taking their values in I. Let F be the set of functions from I to the segment [0, 1]. For any element q ∈ F, q_i denotes its value at i ∈ I. Let $S=\left\{q\in F:{\sum }_{i\in I}{q}_i=1\right\}$ be the probability space on which we want to work. We say that a random variable X follows the distribution q if $\mathbb{P}\left\{X=i\right\}=q_i$, for all i ∈ I. Let Λ₁ and Λ₂ be two probabilities on the Borel σ-field ℬ of S. Let S₁ and S₂ be the topological supports of Λ₁ and Λ₂ respectively. We would like to know the asymptotic behavior of the ratio of the expected likelihood under Λ₁ on the one under Λ₂. We define the operator r as follows

$$r\left({\Lambda }_1,{\Lambda }_2,n\right)=\frac{\int \prod _{k=1}^n{q}_{X_k}{\Lambda }_1(dq)}{\int \prod _{k=1}^n{q}_{X_k}{\Lambda }_2(dq)}=\frac{\int \prod _{i\in I}{q}_i^{n_i}{\Lambda }_1(dq)}{\int \prod _{i\in I}{q}_i^{n_i}{\Lambda }_2(dq)},$$

Where $n_i={\sum }_{k=1}^n{\mathbb{1}}_{\left\{X_k=i\right\}}$, for i ∈ I We assume that, under the true probability β, the random variables X_k, $k\in \mathbb{N}$ are identically distributed. The convergence of r(Λ₁, Λ₂, n) depends mainly on the localization of β compared to the supports S₁ and S₂. To deal with this problem, we make use of the usual concept of entropy. The entropy of q relative to p is $H(q\mid p)=-{\sum }_{i\in I}{p}_i\log q_i$, with the conventions log 0 = −∞ and 0 × −∞ = 0. We suppose that β is closer to S₁ than S₂ in terms of entropy.

Assumption 8. Let V be a subspace of S₂ satisfying Λ₂(V) > 0. There exists δ > 0 such that

$$\underset{q\in S_1}{\text{inf}}H(q\mid \beta )-\underset{q\in V}{\sup }H(q\mid \beta )>4\delta \text{.}$$

This leads to a simple characterisation of the behavior of r(Λ₁, Λ₂, n).

Proposition 4. Under Assumption 8, we have $r\left({\Lambda }_1,{\Lambda }_2,n\right)\underset{n\to \infty }{\to }0$.