Abstract
Timescales characterize the pace of change for many dynamic processes in nature. Timescales are usually estimated by fitting the exponential decay of data autocorrelation in the time or frequency domain. Here we show that this standard procedure often fails to recover the correct timescales due to a statistical bias arising from the finite sample size. We develop an alternative approach which estimates timescales by fitting the sample autocorrelation or power spectrum with a generative model based on a mixture of Ornstein-Uhlenbeck (OU) processes using adaptive approximate Bayesian computations (aABC). Our method accounts for finite sample size and noise in data and returns a posterior distribution of timescales that quantifies the estimation uncertainty and can be used for model selection. We demonstrate the accuracy of our method on synthetic data and illustrate its application to recordings from primate cortex. We provide a customizable Python package implementing our framework with different generative models suitable for diverse applications.
1. Introduction
Dynamic changes in many stochastic processes occur over typical periods known as timescales. Accurate measurements of timescales from experimental data are necessary to uncover mechanisms controlling the dynamics of underlying processes and reveal their function [1–5]. The timescales of a stochastic process are defined by the exponential decay rates of its autocorrelation function. Accordingly, timescales are usually estimated by fitting the autocorrelation of a sample time-series with exponential decay functions [1,5–15] or fitting the shape of the sample power spectral density (PSD) with a Lorentzian function [3,16].
However, the values of sample autocorrelation computed from a finite time-series systematically deviate from the true autocorrelation [17–22]. This bias is exacerbated by the lack of independence between the samples, especially when the timescales are large and time-series are short [23–25]. Generally, the magnitude of bias depends on the length of the sample time-series, but also on the value of the true autocorrelation at each time-lag. The expected value and variance of the autocorrelation bias can be derived analytically in simple cases (e.g., singletimescale Markov process) [17, 20], but become intractable for more general processes with multiple timescales or additional temporal structure. Moreover, since the bias depends on the true autocorrelation itself, which is unknown, it cannot be easily corrected.
The statistical bias deforms the shape of empirical autocorrelations and, according to the Wiener–Khinchin theorem [26], PSDs and hence can affect the timescales estimated by direct fitting methods. Indeed, fitting the sample autocorrelation of an Ornstein-Uhlenbeck (OU) process with an exponential decay function results in systematic errors in the estimated timescale and confidence interval [27]. To avoid these errors, it is possible to fit the time-series directly with an autoregressive model, without using autocorrelation or PSD [27,28]. However, the advantage of autocorrelation is that factors unrelated to the dynamics of the processes under study (e.g., slow activity drifts) can be efficiently removed with resampling methods [29–32]. In contrast, accounting for irrelevant factors in the autoregressive model requires adding components which all must be fitted to the data. Thus, fitting the summary statistic such as autocorrelation or PSD is attractive, but how the statistical bias affects the estimated timescales was not studied systematically.
We show that large systematic errors in estimated timescales arise from the statistical bias due to a finite sample size. To correct for the bias, we develop a flexible computational framework based on adaptive approximate Bayesian computations (aABC) that estimates timescales by fitting the autocorrelation or PSD with a generative model. The aABC algorithm approximates the multivariate posterior distribution of parameters of a generative model using population Monte-Carlo sampling [33]. The posterior distributions can be used for quantifying the estimation uncertainty and model selection. Our computational framework can be adapted to various types of data and can find broad applications in neuroscience, physics and other fields.
2. Results
2.1. Bias in timescales estimated by direct fitting
Timescales of a stochastic process are defined by the exponential decay rates of its autocorrelation function, i.e. correlation between values of the process at time points separated by a time lag t. For stationary processes, the autocorrelation function only depends on the time lag:
| (1) |
Here μ and σ2 are, respectively, the mean and variance of the process, and is the expectation over . For empirical data, the true values of μ and σ are unknown. Hence, several estimators of the sample autocorrelation were proposed, which use different estimators for the sample mean and sample variance (Methods 4.1) [17,18]. The sample autocorrelation can also be computed as the inverse Fourier transform of PSD, based on the Wiener–Khinchin theorem [26]. However, for any of these methods, the sample autocorrelation is a biased estimator: for a finite-length time-series the values of the sample autocorrelation systematically deviate from the ground-truth autocorrelation [17–22] (Fig. 1, Supplementary Figure 1). This statistical bias deforms the shape of the sample autocorrelation or PSD and may affect the estimation of timescales by direct fitting of the shape.
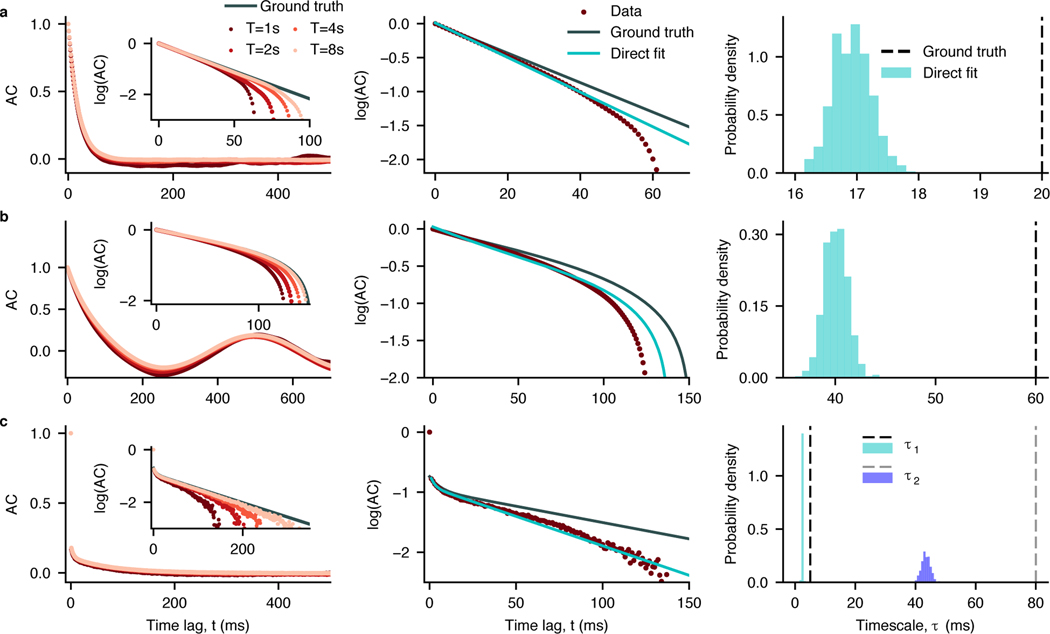
Fig. 1. Bias in sample autocorrelations and timescales estimated by direct exponential fitting.
a, Data are generated from an OU process with the timescale τ = 20 ms. Left: Sample autocorrelation (colored dots) systematically deviates from the ground-truth autocorrelation (gray line). The shape of sample autocorrelation depends on the time-series duration (T) approaching the ground truth with increasing T (inset: close up in logarithmic-linear scale). Middle: Direct fitting of the analytical autocorrelation function (cyan) to sample autocorrelation (brown, T = 1 s) does not recover the ground-truth autocorrelation shape (gray). Right: The ground-truth timescales largely deviate from the distribution of timescales estimated by direct exponential fitting across 500 independent realizations of the same process. b, same as (a) for data from a linear mixture of an OU process with the timescale τ = 60 ms and an oscillation with frequency f = 2 Hz. c, same as (a) for data from an inhomogeneous Poisson process with the instantaneous rate generated from a linear mixture of two OU processes with timescales τ1 = 5 ms and τ2 = 80 ms. All simulation parameters are provided in Supplementary Table 1.
To investigate the impact of autocorrelation bias on the timescales estimated by direct exponential fitting, we tested how accurately this procedure recovers the correct timescales on synthetic data with known ground truth. We generated synthetic data from several stochastic processes for which the autocorrelation function can be computed analytically (Methods 4.2). The exponential decay rates of the analytical autocorrelation provide the ground-truth timescales. We considered three ground-truth processes which differed in the number of timescales, additional temporal structure and noise: (i) an OU process (Fig. 1a), (ii) a linear mixture of an OU process and oscillatory component (Fig. 1b, resembling the firing rate of a neuron modulated by a slow oscillation [34,35]), and (iii) an inhomogeneous Poisson process (often used to model spiking activity of neurons [36]) with the instantaneous rate modeled as a linear mixture of two OU processes with different timescales (Fig. 1c).
For all three processes, the sample autocorrelation exhibits a negative bias: the values of the sample autocorrelation are systematically below the ground-truth autocorrelation function (Fig. 1, left). This bias is clearly visible in the logarithmic-linear scale, where the ground-truth exponential decay turns into a straight line. The sample autocorrelation deviates from the straight line and even becomes systematically negative at intermediate lags (hence not visible on the logarithmic scale) for processes with a strictly positive ground-truth autocorrelation (Fig. 1a,c). The deviations from the ground truth are larger when the timescales are longer or when multiple timescales are involved. The negative bias decreases for longer trial durations (Fig. 1, left inset), but it is still substantial for realistic trial durations such as in neuroscience data.
Due to the negative bias, a direct fit of the sample autocorrelation with the correct analytical function cannot recover the ground-truth timescales (Fig. 1, middle, right, Supplementary Figure 2, 3). When increasing the duration of each trial, the timescales obtained from the direct fits become closer to the ground-truth values (Supplementary Figure 4). This observation indicates that timescales estimated from datasets with different trial durations cannot be directly compared, as differences in the estimation bias may result in misleading interpretations. Thus, direct fitting of a sample autocorrelation, even with a known correct analytical form, is not a reliable method for measuring timescales in experimental data. Bias-correction methods based on parametric bootstrapping can mitigate the estimation bias of timescales from direct fits [37]. However, since the amount of bias depends on the ground-truth timescales, such corrections cannot guarantee accurate estimates in all cases (Supplementary Figure 5).
Alternatively, we can estimate timescales in the frequency domain by fitting the PSD shape with a Lorentzian function, equation (5), which is the ground-truth PSD for a stochastic process with an exponentially decaying autocorrelation [3,16]. Comparison of the ground-truth PSD with the sample PSD of an OU process with finite duration reveals that the statistical bias also persists in the frequency domain (Supplementary Figure 6a). Due to this bias, the estimated timescale deviates from the ground truth by the amount that depends on the fitted frequency range. Although careful choice of the fitted frequency range can improve the estimation accuracy (Supplementary Figure 6b), without knowing the ground-truth timescale, there is no principled way to choose the correct range for all cases. Slightly changing the fitted frequency range can produce large errors in estimated timescale, especially in the presence of additional noise, e.g., spiking activity.
2.2. Estimating timescales by fitting generative models with aABC
Since direct fitting cannot estimate timescales reliably, we developed an alternative computational framework based on fitting the sample autocorrelation (or PSD) with a generative model. Using a model with known ground-truth timescales, we can generate synthetic data matching the essential statistics of the observed data, i.e. with the same duration and number of trials, mean and variance. Hence the sample autocorrelations (or PSDs) of the synthetic and observed data will be affected by a similar statistical bias when their shapes match. As a generative model, we chose a linear mixture of OU processes—one for each estimated timescale—which if necessary can be augmented with additional temporal structure (e.g., oscillations) and noise. The advantage of using a mixture of OU processes is that the analytical autocorrelation function of this mixture explicitly defines the timescales. We set the number of components in the generative model according to our hypothesis about the autocorrelation in the data, e.g., the number of timescales, additional temporal structure, and noise (Methods 4.2). Then, we optimize parameters of the generative model to match the shape of the autocorrelation (or PSD) between the synthetic and observed data. The timescales of the optimized generative model provide an unbiased estimation of timescales in the data.
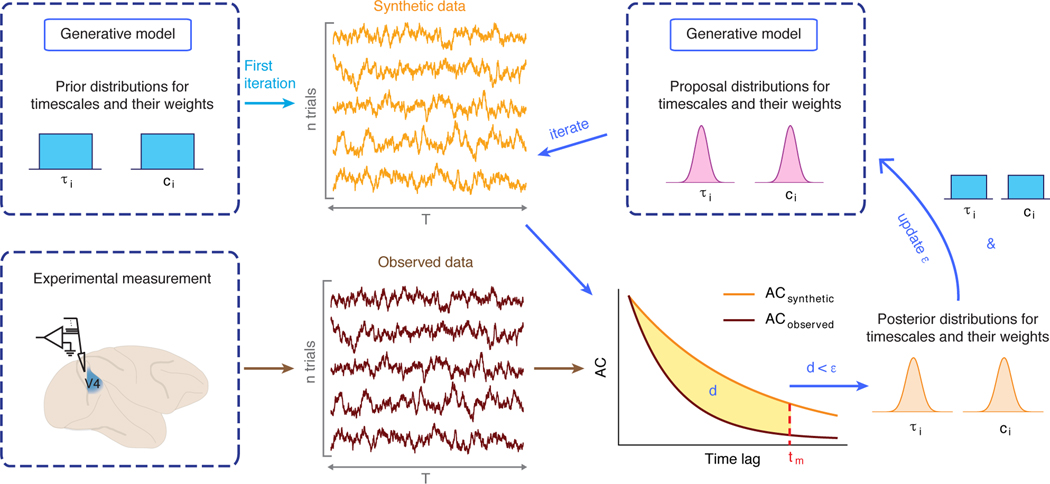
For complex generative models, calculating the likelihood can be computationally expensive or even intractable. Therefore, we optimize the generative model parameters using aABC (Fig. 2) [33]. aABC is an iterative algorithm that minimizes the distance between the summary statistic of synthetic and observed data (Fig. 2, Methods 4.3). Depending on the application, we can choose a summary statistic in time (autocorrelation) or frequency (PSD) domain. On each iteration, we draw a set of parameters of the generative model either from a prior distribution (first iteration) or a proposal distribution and generate synthetic data using these parameter samples. The sampled parameters are accepted if the distance d between the summary statistic of the observed and synthetic data is smaller than a selected error threshold ε. The last set of accepted parameter samples provides an approximation of the posterior distribution. The joint posterior distribution quantifies the estimation uncertainty taking into account the stochasticity of the observed data (Supplementary Figure 7). We implemented this algorithm in the abcTau Python package including different types of summary statistics and generative models (Methods 4.5). To visualize the posterior distribution of a parameter (e.g., a timescale), we marginalize the multivariate posterior distribution over all other parameters of the generative model.
Fig. 2. Estimation of timescales with adaptive approximate Bayesian computations.
aABC estimates timescales by fitting the sample autocorrelation of observed data with a generative model. At the first iteration of the algorithm, parameters of the generative model are drawn from the multivariate prior distribution, e.g., a uniform distribution (upper left). Synthetic data are generated from the generative model with these parameters. If the distance d between the autocorrelations of synthetic and observed data is smaller than a specific error threshold ε, these parameters are added to the multivariate posterior distribution (lower right). In the subsequent iterations, new parameters are drawn from a proposal distribution which is computed based on the posterior distribution of the previous iteration and the initial prior distribution (upper right, see Methods 4.3 and 4.5).
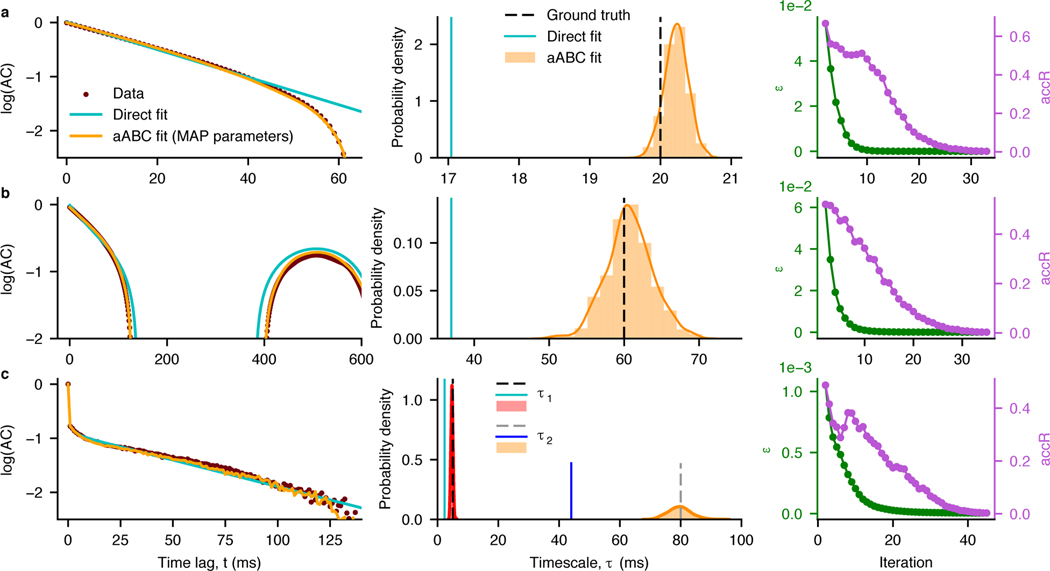
We illustrate our method on synthetic data from the processes described in the previous section, using the autocorrelation as the summary statistic (Fig. 3 cf. Fig. 1). For all three processes, the shape of the sample autocorrelation of the observed data is accurately reproduced by the autocorrelation of synthetic data generated using the maximum a posteriori (MAP) estimate of parameters from the joint multivariate posterior distribution (Fig. 3, left). The posterior distributions inferred by aABC include the ground-truth timescales (Fig. 3, middle). The posterior variance quantifies the estimation uncertainty. In our simulations, the number of trials controls the signal-to-noise ratio in sample autocorrelation, and consequently the width of the posteriors (Supplementary Figure 8).
Fig. 3. Accurate estimation of timescales and uncertainty quantification with aABC algorithm.
The same synthetic data as in Fig. 1 for T = 1 s. a, Data are generated from an OU process with the timescale τ = 20 ms. Left: The shape of the data autocorrelation (brown) is accurately reproduced by the autocorrelation of synthetic data from the generative model with the MAP estimate parameters (orange, τMAP = 20.2 ms), but it cannot be captured by the direct exponential fit (cyan). Middle: The marginal posterior distributions (histograms overlaid with Gaussian kernel smoothing) include the ground-truth timescales, while direct exponential fits (cyan) underestimate the ground-truth timescales. The width of the posteriors indicates the estimation uncertainty. Right: The convergence of the aABC algorithm is defined based on the acceptance rate accR (purple), which decreases together with the error threshold ε (green) over the iterations of the algorithm. Data are plotted from the second iteration. Initial error threshold for all fits was set to 1. b, same as (a) for data from a linear mixture of an OU process with the timescale τ = 20 ms and an oscillation with frequency f = 2 Hz. τMAP = 60.5 ms. c, same as (a) for data from an inhomogeneous Poisson process with two timescales τ1 = 5 ms and τ2 = 80 ms. τ1,MAP = 4.7 ms, τ2,MAP = 80 ms. Other parameters are provided in Supplementary Tables 1,2.
The aABC method also recovers the ground-truth timescales by fitting the sample PSD without tuning the frequency range, even in the presence of multiple timescales and additional spiking noise (Supplementary Figure 9) or multiple oscillatory components (Supplementary Figure 10). Moreover, aABC method can uncover slow oscillations in signals that do not exhibit clear peaks in PSD due to the short duration of time-series and the low frequency resolution (Supplementary Figure 9c). The aABC method can be used in combination with any method for computing the PSD (e.g., any window functions for removing the spectral leakage), since the exact same method applied to synthetic data would alter their sample PSD in the same way.
Different summary statistics and fitting ranges may be preferred depending on the application. For example, autocorrelations allow for using additional correction methods such as jittering [31], whereas PSD estimation can be improved with filtering or multitapers [38]. Furthermore, selecting a smaller maximum time-lag when fitting autocorrelations prevents overfitting to noise in the autocorrelation tail. The choice of summary statistic (metric and fitting range) can influence the shape of the approximated posterior (e.g., posterior width), but the posteriors peak close to the ground-truth timescales as long as the same summary statistic is used for observed and synthetic data (Supplementary Figure 11). The advantage of such behavior is particularly visible when changing the range over which we compute the summary statistics (e.g., minimum and maximum frequency in PSD), which affects direct fit but not aABC estimates (Supplementary Figure 6).
In the aABC algorithm, we set a multivariate uniform prior distribution over the parameters of the generative model. The ranges of uniform prior should be broad enough to include the ground-truth values. Selecting broader priors does not affect the shape of posteriors and only slows down the fitting procedure (Supplementary Figure 12). Hence, we can set wide prior distributions when a reasonable range of parameters is unknown. Timescales estimated from the direct exponential fits can be used as a potential lower bound for the priors.
We evaluated the reliability of the aABC method on a wide range of timescales and trial durations and compared the results to direct fitting (Supplementary Figure 13). The estimation error of direct fitting increases when trial durations become short relative to the timescale, whereas the aABC method always returns reliable estimates. However, the estimation of the full posterior comes at a price of higher computational costs (Supplementary Table 3) compared to point estimates. Thus, the direct fit of the sample autocorrelation may be preferred when the long time-series data are available so that statistical bias does not corrupt the results. To empirically verify whether this is the case, we implemented a pre-processing algorithm in our Python package that uses parametric bootstrapping to return an approximate error bound of the direct fit estimates (Methods 4.5.1, Supplementary Figure 14).
Fitting generative models with the aABC method provides a principled framework for estimating timescales that can be used with different metrics in time or frequency domain. Furthermore, joint posterior distribution of the inferred parameters allows us to examine correlations between different parameters, find manifolds of possible solutions, and identify a potential degeneracy in the parameter space (Supplementary Figure 15).
2.3. Estimating the timescale of activity in a branching network
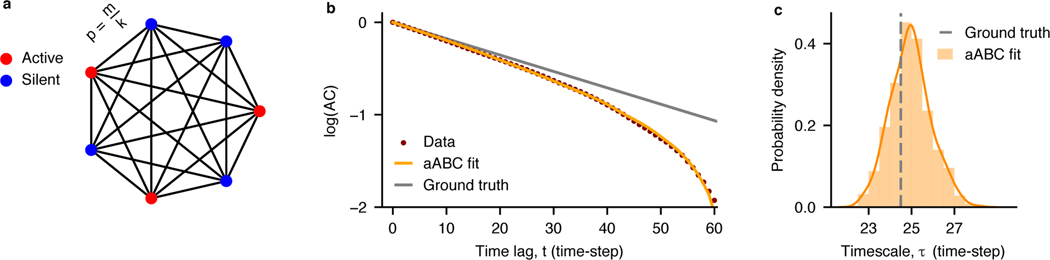
So far, we demonstrated that our aABC method accurately recovers the ground-truth timescales when the generative model and the process that produced the observed data are the same. However, the timescale inference based on OU processes is broadly applicable when the mechanism that generated the exponential decay of autocorrelation in the data is not an OU process. As an example, we tested our method on discrete-time data from an integer-valued autoregressive model with a known ground-truth autocorrelation function. Specifically, we applied our method to estimate the timescale of the global activity in a branching network model, which is often used to study the operating regime of dynamics in neuronal networks (Fig. 4a) [39–41]. We simulated the network model to generate the time-series data of the global activity. We then used aABC to fit the sample autocorrelation of these data with a one-timescale OU process as a generative model. The inferred posterior is centered on the theoretically predicted timescale of the branching network, and the MAP estimate parameter accurately reproduces the shape of the sample autocorrelation of the network activity (Fig. 4b,c). These results show that our framework can be used to estimate timescales in diverse types of data.
Fig. 4. aABC inference with a generative model based on the OU process in a branching network.
a, A schematic of a fully connected branching network with binary neurons. Branching parameter (m = 0.96) and number of neurons (k = 104) define the probability of activity propagation (p). Each neuron receives an external input with probability h = 10−3. b, The shape of the sample autocorrelation of simulated activity in the branching network (brown) deviates from the ground truth (gray), but is accurately reproduced by the autocorrelation of synthetic data generated from a one-timescale OU process with the MAP estimate timescale from the aABC method. τMAP = 24.9. The data contained 100 trials of 500 time-steps. c, The aABC posterior distribution includes the ground-truth timescale. τground truth = 24.5, τaABC = 24.9 ± 0.9 (mean ± std). Fitting parameters are provided in Supplementary Table 2
2.4. Model selection with ABC
For experimental data, the correct generative model (e.g., number of timescales) is usually unknown. Thus, we need a procedure to select between alternative hypotheses. Assuming that the autocorrelation or PSD is a sufficient summary statistic for estimating timescales, we can use ABC to approximate the Bayes factor for selecting between alternative models [42–44]. Model selection based on ABC can produce inconsistent results when the summary statistic is insufficient [45], but whether this is likely the case can be verified empirically [44]. Specifically, the summary statistic can be used for model selection with ABC if its mathematical expectation is significantly different for the two models.
Based on this empirical procedure [44], we developed a method for selecting between two alternative models M1 and M2 using their aABC fits (Methods 4.4). We compare models using a goodness of fit measure computed as the distance d between the summary statistic of synthetic and observed data. For selecting between M1 and M2, we estimate the Bayes factor, which is the ratio of marginal likelihoods of the two models and accounts for the model complexity [46]. Assuming both models are a priori equally probable, the Bayes factor can be approximated as the ratio between the cumulative distribution functions (CDFs) of distances d for two models at different error thresholds .
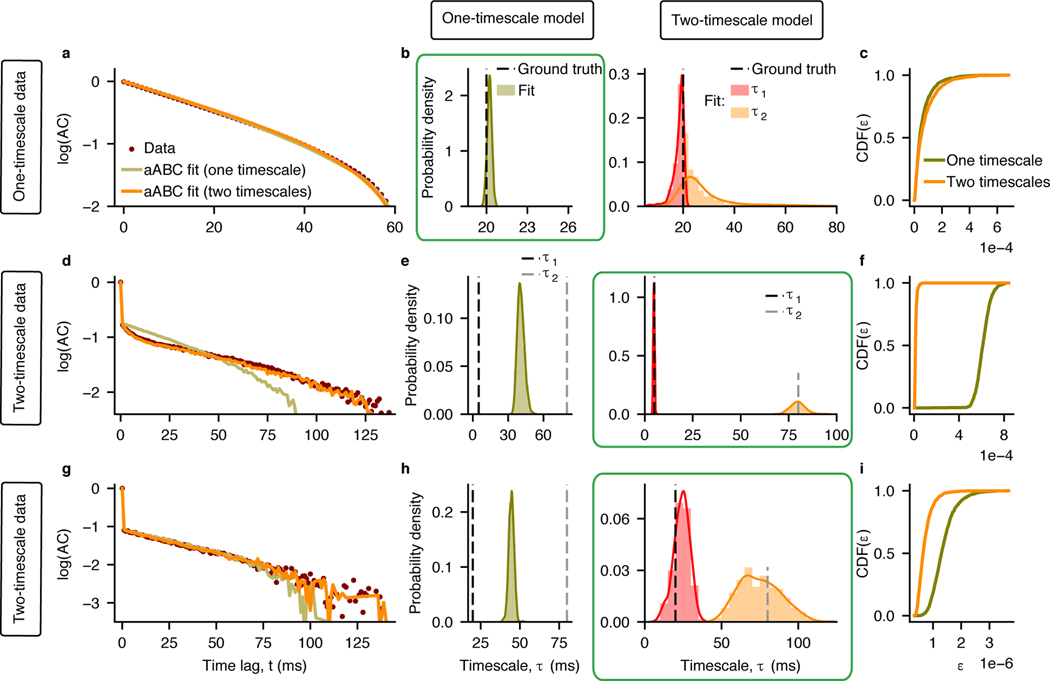
We evaluated our model selection method using synthetic data from three example processes with known ground truth, so that the correct number of timescales is known. We used an OU process with a single timescale (Fig. 5a) and two different examples of an inhomogeneous Poisson process with two timescales: one with well separated ground-truth timescales, such that multiple timescales are evident in the autocorrelation shape (Fig. 5d), and another with similar ground-truth timescales, such that the autocorrelation shape does not clearly suggest the number of timescales in the underlying process (Fig. 5g). For all three example processes, we fitted the data with one-timescale (M1) and two-timescale (M2) generative models using aABC and selected between these models by computing the Bayes factors. The one- and two-timescale models were based on a single OU process or a linear mixture of two OU processes, respectively. For the data from inhomogeneous Poisson processes, the generative model also incorporated an inhomogeneous Poisson noise.
Fig. 5. Model selection with ABC.
a-c, Data are generated from a one-timescale OU process with τ = 20 ms. a, The data autocorrelation (brown) is fitted with a one-timescale (olive, M1) and two-timescale (orange, M2) generative models (sample autocorrelations for MAP estimate parameters are shown). b, Marginal posterior distribution of the timescale estimated using the one-timescale model includes the ground truth and has small variance (left). Marginal posterior distributions of two timescales estimated using the two-timescale model heavily overlap and have large variance (right). c, Cumulative distributions of distances d for two models, . Since M1 resulted in smaller distances (P = 0.002, CL = 0.54) and for all ε, the one-timescale model is selected (green box in b). d-f, Data are generated from an inhomogeneous Poisson process with two timescales: τ1 = 5 ms, τ2 = 80 ms. d, Same format as (a). e, Marginal posterior distributions for two timescales estimated by the two-timescale model include the ground truth (right). Marginal posterior distributions for the timescale estimated by the one-timescale model falls in between the ground-truth timescales (left). f, Cumulative distributions of distances d for two models. Since M2 resulted in smaller distances (P < 10−10, CL = 1) and for all ε, the two-timescale model is selected (green box in e). g-i, Same as (d-f), but for τ1 = 20 ms, τ2 = 80 ms (P < 10−10, CL = 0.93). For all fits, are computed from n1 = n2 = 1000 samples. P-values and effect sizes (CL) are computed from the two-sided Wilcoxon rank-sum test. Simulation and fitting parameters are provided in Supplementary Tables 1,2.
For the example OU process with a single timescale, the one- and two-timescale models fitted the shape of the data autocorrelation almost equally well (Fig. 5a). The marginal posterior distributions of two timescales estimated by the two-timescale model heavily overlap around their peak values (Fig. 5b), which indicates that the one-timescale model possibly better describes the data. For the two-timescale model we enforce the ordering τ1 < τ2, which generates the difference between their distributions. To select between two models, we compare the CDFs of distances (Fig. 5c). Although the two-timescale model has more parameters, it has significantly larger distances than the one-timescale model (Wilcoxon rank-sum test, P = 0.002, mean dM1 = 6 × 10−5, mean dM2 = 8 × 10−5). The two-timescale model has a larger average distance because its posterior distribution has larger variance leading to a higher possibility to sample a combination of parameters with a larger distance. Since (i.e. ) for all ε, the one-timescale model is preferred over the two-timescale model, in agreement with the ground-truth generative process.
For both example inhomogeneous Poisson processes with two timescales, the shape of the data autocorrelation is better matched by the two-timescale than by the one-timescale model (the difference is subtle for the second example, Fig. 5d,g). The marginal posterior distributions of two timescales estimated by the two-timescale model are clearly separated and include the ground-truth values, whereas the timescale estimated by the one-timescale model is in between the two ground-truth values (Fig. 5e,h). The two-timescale model has significantly smaller distances (Wilcoxon rank-sum test, Fig. 5f: P < 10−10, mean dM1 = 6 × 10−4, mean dM2 = 1.5 × 10−5; Fig. 5i: P < 10−10, mean dM1 = 10−6, mean dM2 = 7 × 10−7). Since (i.e. ) for all ε, the two-timescale model provides a better description of the data for both examples, in agreement with the ground truth. Thus, our method selects the correct generative model even for a challenging case where the shape of the data autocorrelation does not suggest the existence of multiple timescales. Our method can be used to discriminate between a broad class of models, e.g., slow periodic (e.g., oscillation) versus aperiodic (e.g., exponential decay) components in the time-series (Supplementary Figure 16).
2.5. Estimating timescales of ongoing neural activity
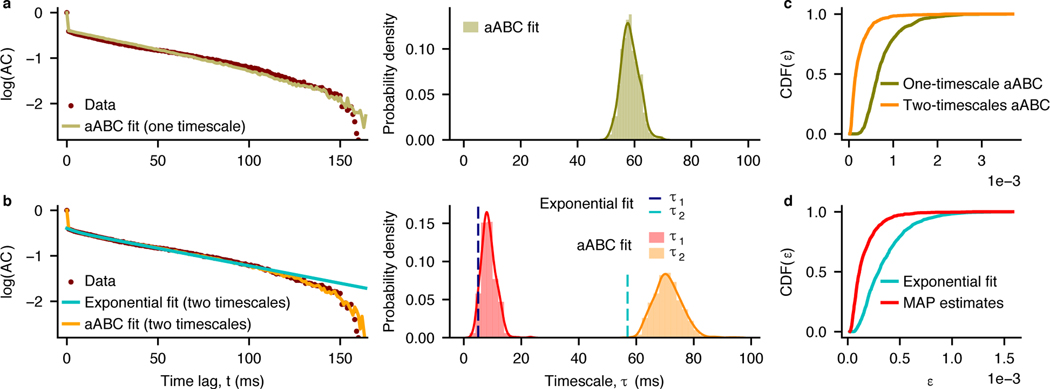
To illustrate an application of our framework to experimental data, we estimated the timescales of ongoing spiking activity in the primate visual cortex during fixation on a blank screen [47]. We computed the autocorrelation of the population spiking activity pooled across 16 recording channels (Methods 4.7). Previously, the autocorrelation of neural activity in several brain regions was modeled as an exponential decay with a single timescale [1]. To determine whether a single timescale is sufficient to describe the temporal dynamics of neural activity in our data, we fitted the one-timescale (M1) and two-timescale (M2) models using aABC and selected the model that better described the data (Fig. 6a-c). As a generative model, we used a doubly-stochastic process [36,48], where spike-counts in each time-bin are generated from an instantaneous firing rate modeled as one OU process (M1) or a mixture of two OU processes (M2). To account for the non-Poisson statistics of the spike-generation process [49], we sampled spike-counts from a gamma distribution (Methods 4.2.3). The two-timescale model provided a better description of the data, since it had smaller distances and for all error thresholds (Fig. 6c, Wilcoxon rank-sum test, P < 10−10, mean dM1 = 8 × 10−4, mean dM2 = 2 × 10−4).
Fig. 6. Estimating timescales of ongoing neural activity and comparing hypotheses about their number with aABC.
a, Left: The autocorrelation of neural spike-counts (brown) is fitted with a one-timescale doubly-stochastic model using aABC (olive, sample autocorrelation for MAP estimate parameters). Right: Posterior distribution of the timescale. τMAP = 58 ms. b, Left: Same data as in (a) is fitted directly with a double exponential function (cyan) and with a two-timescale doubly-stochastic model using aABC (orange, sample autocorrelation for MAP estimate parameters). Right: Timescales estimated by the direct exponential fit (τ1 - blue, τ2 - cyan) and marginal posterior distributions of timescales inferred with aABC (τ1 - red, τ2 - orange). τ1,exp = 5 ms, τ2,exp = 57 ms, τ1,MAP = 8 ms, τ2,MAP = 70 ms. c, Cumulative distribution of distances d for one-timescale (M1) and two-timescale (M2) models. Since M2 resulted in smaller distances (P < 10−10, CL = 0.92, n1 = n2 = 1000) and for all ε, the two-timescale model is selected. d, Cumulative distributions of distances d between the autocorrelation of neural data and synthetic data from the two-timescale doubly-stochastic model with parameters either from the direct fit (cyan) or MAP estimate with aABC (red). The MAP parameters have smaller distances (P < 10−10, CL = 0.82, n1 = n2 = 1000), i.e. describe the autocorrelation of neural data more accurately than the direct fit. P-values and effect sizes (CL) are computed from the two-sided Wilcoxon rank-sum test. Fitting parameters are provided in Supplementary Table 2.
We further compared our method with a direct exponential fit of the sample autocorrelation which is usually employed to infer the timescales of neural activity [1,5–12]. We fitted the sample autocorrelation with a double exponential function and compared the result with the two-timescale aABC fit (Fig. 6b). Similar to synthetic examples, the direct fit produced timescales systematically smaller than the MAP estimates from aABC. Since the ground-truth timescales are not available for biological data, we used a sampling procedure to evaluate whether the data were better described by the timescales from the direct fit or from the MAP estimates (Fig. 6d, Methods 4.7). The results indicate that MAP estimates better capture the shape of neural data autocorrelation (Wilcoxon rank-sum test, P < 10−10, mean distance of MAP parameters 10−4, mean distance of exponential fit parameters 3 × 10−4). Thus, our method estimates the timescales of neural activity more accurately than a direct exponential fit and allows for comparing alternative hypotheses about the underlying dynamics.
3. Discussion
Direct fitting the shape of sample autocorrelation or PSD often fails to recover the correct timescales. While previous work [27] attributed errors in the estimated timescales to fitting noise in the tail of autocorrelation, we find that the main source of error is the statistical bias in the sample autocorrelation due to finite sample size. This bias arises primarily due to the deviation of the sample mean from the ground-truth mean. If the ground-truth mean of the process is known, using the true mean for computing the autocorrelation largely eliminates the bias. When the true mean is unknown but assumed to be the same across all trials, the bias is reduced by estimating a single sample mean from the whole dataset instead of estimating a separate mean for each trial. However, this assumption does not always hold. For example, the mean neural activity can change across trials because of changes in animal’s behavioral state. If the assumption of a constant mean is violated in the data, estimating the sample mean from the whole dataset leads to strong distortions of the autocorrelation shape introducing additional slow timescales [50]. Since the bias depends on the duration of time-series, comparing timescales estimated from direct fits of experimental data with different duration can produce misleading interpretations.
We focused on exponentially decaying autocorrelations, which correspond to Lorentzian PSD with the 1/f power-law exponent of 2. The definition of timescales based on the exponential decay rates of autocorrelation is widely used in the literature [1,5–15] and has a clear interpretation as a timescale of a generative dynamical system. Many types of data exhibit PSD with 1/f exponents deviating from 2 [3,16,51,52], but there is no universally accepted answer to what is the definition of timescale for these types of data and what is the nature of processes generating this behavior. Indeed, a prominent hypothesis is that the 1/f PSD arises from a mixture of many processes with exponential autocorrelations and different timescales [51,52], which can be modeled as a mixture of OU processes. For example, a combination of excitatory and inhibitory synaptic currents with distinct timescales was suggested as a potential mechanism for creating different 1/f exponents in neural data [51]. However, sometimes we are interested in separating a process with a well-defined timescale from 1/f background. To handle such cases, we introduced an augmented generative model (Methods 4.2.4) which can be used to estimate timescales in the presence of a background process with an arbitrary PSD shape (e.g., 1/f exponents other than 2). This generative model is agnostic to the nature of the process generating the background activity and directly models the desired PSD shape. We can use this model to simultaneously estimate the 1/f exponent and exponential decay timescales (Supplementary Figure 17).
The general framework of inferring timescales with aABC using OU processes can be adapted to various data types, different generative models and summary statistics using our Python package. It provides an unbiased estimation of timescales and returns a posterior distribution that quantifies the estimation uncertainty and can be used for hypothesis testing. Since estimating the full posterior is computationally expensive, we included a pre-possessing algorithm that verifies whether direct-fit estimates are sufficiently reliable for given data and thus may be preferred due to lower computational costs. In addition, for processes with complex temporal dynamics, finding a plausible generative model that captures all aspects of the data might be challenging. Some of the challenges can be mitigated by including background processes with an arbitrary PSD shape in the generative model (Methods 4.2.4). Our method can select the best model from a proposed set of plausible models. However, when the data amount is very limited, the model selection may fail to detect the optimal model, producing an inconclusive result. This limitation can be addressed by collecting a larger dataset. The modular implementation of our Python package allows users to easily incorporate additional types of dynamics and non-stationarities into customized generative models, or use other types of summary statistic which can be added directly to the package. Our approach is particularly favorable for data organized in short trials or trials of different durations, when direct fitting is unreliable.
4. Methods
4.1. Computing sample autocorrelation
In experiments or simulations, the autocorrelation needs to be estimated from a finite sample of empirical data. A data sample from the process constitutes a finite time-series measured at discrete times (, where N is the length of the time-series). For example, the sample time-series can be spike-counts of a neuron in discrete time bins, or a continuous voltage signal measured at a specific sampling rate. Accordingly, the sample autocorrelation is defined for a discrete set of time lags tj. Several estimators of the sample autocorrelation were proposed, using different estimators for the sample mean and sample variance [17,18]. One possible choice is:
| (2) |
with the sample variance and two different sample means , . Different normalizations of autocorrelation are used in literature, but our results do not depend on a specific choice of normalization.
4.2. Generative models
We used several generative models based on a linear mixture of OU processes—one for each estimated timescale—sometimes augmented with additional temporal structure (e.g., oscillations) and noise.
4.2.1. Ornstein–Uhlenbeck process with multiple timescales
An Ornstein–Uhlenbeck (OU) process is defined as
| (3) |
where is a Gaussian white noise with zero mean, and the diffusion parameter D sets the variance [53,54]. The autocorrelation of the OU process is an exponential decay function [55]
| (4) |
Accordingly, the parameter τ provides the ground-truth timescale. The PSD of the OU process is a Lorentzian function
| (5) |
Here f is the frequency and is the normalization constant. From the knee frequency fk, we can compute the timescale as .
We define an OU process with multiple timescales as a linear mixture of OU processes with timescales τk, , zero mean and unit variance:
| (6) |
Here n is the number of timescales in the mixture and ck are the mixing coefficients that set the relative weights of components without changing the total variance of the process. We simulate each OU process Ak by iterating its time-discrete version using the Euler scheme [55]
| (7) |
where is the discretization time-step and is a random number generated from a normal distribution. We set the unit variance for each OU process by fixing . The parameter-vector θ for a linear mixture of n OU processes consists of 2n − 1 values: n timescales τk and n − 1 coefficients ck in equation (6).
We match the mean and variance of the multi-timescale OU process to the sample mean and sample variance of the observed data using a linear transformation:
| (8) |
We use the process as a generative model for data fitting and hypothesis testing (Methods 4.3).
4.2.2. Multi-timescale Ornstein–Uhlenbeck process with oscillations
To obtain a generative model with an oscillation, we add an oscillatory component with the weight ck+1 to a multi-timescale OU process, equation (6):
| (9) |
For each trial, we draw the phase independently from a uniform distribution on [0,2π]. We use the linear transformation in equation (8) to match the mean and variance of this generative process to the observed data.
The autocorrelation of this process with a single timescale τ is given by
| (10) |
hence, the ground-truth timescale is defined by the OU parameter τ.
For the analysis in Fig. 1b and in Fig. 3b, we assumed that the frequency f is known and only fitted the weight ck+1 to show that the bias of the direct fit persists even if we know the correct frequency of oscillation. The frequency f can be fitted with aABC as an additional free parameter (Supplementary Figure 9,10).
4.2.3. Doubly stochastic process with multiple timescales
The doubly stochastic process with multiple timescales is generated in two steps: first generating time-varying rate and then generating event-counts from this rate. To generate the time-varying rate, we scale, shift and rectify a multi-timescale OU process, equation (6), using the transformation
| (11) |
The resulting rate is non-negative and for it has the mean and variance . We then draw event-counts s for each time-bin from an event-count distribution , where is the mean event-count and is the bin size (in our simulations ). A frequent choice of is a Poisson distribution
| (12) |
which results in an inhomogeneous Poisson process.
To match the mean μ and variance σ2 of the doubly stochastic process to the observed data, we need to estimate parameters of generative model , , and the variance of the event-count distribution . According to the law of total expectation, the mean rate , where is the sample mean of the observed event-counts. According to the law of total variance [48], the total variance of event-counts σ2 arises from two contributions: the variance of the rate and the variance of the event-count distribution
| (13) |
For the Poisson distribution, the variance of the event-count distribution is equal to its mean: . However, the condition of equal mean and variance does not always hold in experimental data [49]. Therefore, we also use other event-count distributions, in particular a Gaussian and gamma distribution. We define α as the variance over mean ratio of the event-count distribution . For the Poisson distribution, α = 1 always holds. For other distributions, we assume that α is constant (i.e. does not depend on the rate). With this assumption, the law of total variance, equation (13), becomes
| (14) |
where is the mean rate. From equation (14) we find the rate variance
| (15) |
where is the sample variance of event-counts in the observed data. We find that with the correct values of , and α, both the Gaussian and gamma distributions of event-counts produce comparable estimates of timescales (Supplementary Figure 18).
To calculate with equation (15), we first need to estimate α from the observed data. We estimate α from the drop of autocorrelation of event-counts between the time-lags t0 and t1. Since event-counts in different time-bins are drawn independently, this drop mainly reflects the difference between the total variance of event-counts and variance of the rate (equation (13), we neglect a small decrease of the rate autocorrelation between t0 and t1) and does not depend on timescales. Thus, we find α with a grid search that minimizes the distance between the autocorrelation at t1 of the observed and synthetic data from the generative model with fixed timescales. Alternatively, α can be fitted together with all other parameters of the generative model using aABC. We find that since α is almost independent from other parameters, aABC finds the correct value of α first and then fits the rest of parameters. The MAP estimate of α converges to the same value as estimated by the grid search, but aABC requires more iterations to get posterior distributions for estimated timescales with a similar variance (Supplementary Figure 19). Therefore, grid-search method is preferred when moderate errors in α are acceptable and approximate range of ground-truth timescales are known, but for more accurate results it is better to fit α by aABC together with other parameters.
For a doubly stochastic process, we can compute the autocorrelation function analytically based on the autocorrelation of its underlying time-varying rate and the mean and variance of the doubly stochastic process. For the the two-timescale inhomogeneous Poisson process (Fig. 1c) the autocorrelation is given by:
| (16) |
Here τ1 and τ2 are the ground-truth timescales defined by the parameters of two OU processes, c1 is the mixing coefficient, and μ and σ2 are the mean and variance of the event-counts, respectively. The drop of autocorrelation between t0 and t1 mainly reflects the Poisson-process variance. To estimate the timescales with direct exponential fits (Fig. 1c), we assumed that the mean and variance of the event-counts are known and only estimated τ1, τ2 and the coefficient c1 by fitting equation (16) to the sample autocorrelation starting from the lag t1. Later, when we estimate the timescales from the data, we need as a first step to find the correct μ and σ2.
4.2.4. Modeling background processes with an arbitrary PSD shape
We can generate random time-series with any desired shape of the PSD. First, we convert the power spectrum PSD(f) to amplitudes . Then, we draw random phases from a uniform distribution on [0, 2π] and construct a frequency domain signal . We transform this signal to the time domain by applying the inverse Fast Fourier Transform (iFFT) and z-score the time-series to obtain zero mean and unit variance.
For example, a common class of background processes exhibit power-law decay in PSD [3,16, 51,52]. We model this PSD shape as PSD , where is the frequency range and χ is the power-law exponent. We can set the lower frequency cut-off at fmin = 1 Hz and the upper frequency cut-off fmax is defined by the Nyquist frequency (i.e. half of the desired sampling rate). We can combine this process with time-series generated from an OU process with the timescale τ to obtain a PSD shape with both 1/f and Lorentzian components (Supplementary Figure 17). We sum the two time-series with the coefficients c and 1 − c and rescale using the linear transformation in equation (8) to match the mean and variance to the observed data. This generative process can be used when the 1/f exponent in the data PSD deviates from 2 (i.e. Lorentzian shape). This method can be applied to generate background processes with arbitrary desired PSD shapes and estimate the relevant parameters.
4.2.5. Generating synthetic data for direct fitting
Each synthetic dataset consisted of 500 independent realizations of the process (i.e. trials) with a fixed duration. Such trial-based data are typical in neuroscience but usually with a smaller number of trials. We computed the sample autocorrelation for each trial using equation (2), averaged them to reduce the noise, and then fitted the average autocorrelation with the correct analytical functional form to estimate the timescale parameters. We repeated the entire procedure 500 times to obtain a distribution with multiple independent samples of timescales estimated by direct fit (i.e. we simulated 500 × 500 trials for each distribution).
4.3. Optimizing generative model parameters with aABC
We optimize parameters of generative models with adaptive approximate Bayesian computations (aABC) following the algorithm from Ref. [33]. aABC is an iterative algorithm to approximate the multivariate posterior distribution of model parameters. It uses population Monte-Carlo sampling to minimize the distance between the summary statistic of the observed and synthetic data from the generative model.
We can use autocorrelations as the summary statistic and define the suitable distance d between the autocorrelations of synthetic and observed data, e.g., as
| (17) |
where tm is the maximum time-lag considered in computing the distance. Alternatively, we can compute distances between the PSDs of synthetic and observed data:
| (18) |
where fn and fn+m define the frequency range for computing the distance. Distances can also be computed on logarithmic scale. For the figures in the main text we used the autocorrelation as the summary statistic and compute distances in linear scale.
First, we choose a multivariate prior distribution over the parameters of the generative model and set an initial error threshold ε at a rather large value. On the first iteration of the algorithm, the parameters of the generative model are drawn from the prior distribution. We use a multidimensional uniform prior distribution π(θ) over fitted parameters (e.g., timescales and their weights). The domain of prior distribution for the timescales is chosen to include a broad range below and above the timescales estimated by the direct exponential fits of data autocorrelation (Table 2). For the weights of timescales ck, we use uniform prior distributions on [0,1]. The model with parameters is used to generate synthetic time-series with the same duration and number of trials as in the observed data. Next, we compute the distance d between the summary statistics of the synthetic and observed data. If d is smaller than the error threshold ε (initially set to 1), the parameters are accepted and added to the multivariate posterior distribution. Each iteration of the algorithm is repeated until 500 parameters samples are accepted.
On subsequent iterations, the same steps are repeated but with parameters drawn from a proposal distribution and with an updated error threshold. On each iteration, the error threshold is set at the first quartile of the accepted sample distances from the previous iteration. The proposal distribution is computed for each iteration as a mixture of Gaussian distributions based on the prior distribution and the accepted samples , from the previous iteration:
| (19) |
Here is the importance weight of the accepted sample from the previous iteration
| (20) |
is the random walk kernel for the population Monte Carlo algorithm, which is a multivariate Gaussian with the mean and the covariance equal to twice the covariance of all accepted samples from the previous iteration :
| (21) |
Here κ is the number of fitted parameters, and is the determinant of Σ.
In the regular ABC algorithm [56], the error threshold is fixed and parameters are sampled from the prior distribution (same as in the first step of aABC). Updating the error threshold and proposal distribution in successive iterations of aABC allows for a more efficient fitting procedure especially when setting wide prior distributions [33].
The convergence of the algorithm is defined based on the acceptance rate accR, which is the number of accepted samples divided by the total number of drawn samples on each iteration. The algorithm terminates when the acceptance rate reaches accRmin, which is set to accRmin = 0.003 in our simulations. Smaller accRmin leads to a smaller final error threshold (Fig. 3, right) and a better approximation of the posterior distributions, but requires longer fitting time. To find the MAP estimates, we smooth the final joint posterior distribution with a multivariate Gaussian kernel and find its maximum with a grid search.
4.4. Model selection and Bayes factor approximation with ABC
We compare the two alternative models M1 and M2 using a goodness of fit measure that describes how well each model fits the data. The goodness of fit can be measured by the distance d between the summary statistic (e.g., autocorrelation or PSD) of synthetic and observed data, i.e. residual errors, equation (17), (18). For a fair comparison, the same summary-statistics and fitting range should be used for fitting both models. Since d is a noisy measure because of the finite sample size and uncertainty in the model parameters, we compare the distributions of distances generated by two models with parameters sampled from their posterior distributions. To approximate the distributions of distances, we generate multiple samples of synthetic data from each model with parameters drawn from its posterior distribution and compute the distance d for each sample. If the distributions of distances are significantly different (i.e. expectations of the summary statistic for two models are significantly different [44]), then we continue with the model selection, otherwise the summary statistic is insufficient to distinguish these models.
Using the distributions of distances we estimate the Bayes factor to select between the two models. Bayes factor is the ratio of marginal likelihoods of the two models and accounts for the model complexity [46]. Assuming both models are a priori equally probable , the Bayes factor can be approximated using the models’ acceptance rates for a specific error threshold ε [42,45,57]
| (22) |
indicates that the model M2 is more likely to explain the observed data and vice versa. To eliminate the dependence on a specific error threshold, we compute the acceptance rates and the Bayes factor with a varying error threshold. For each error threshold ε, the acceptance rate is given by the cumulative distribution function of the distances . Hence, the ratio between CDFs of two models gives the value of the Bayes factor for every error threshold . We select the model M2 if , i.e. if for all ε, and vice versa. For experimental data, it is often reasonable to put an upper bound on ε for computing the Bayes factor (e.g., largest median(ε) between the two models), since only small values of ε indicate a well-fitted model.
4.5. abcTau Python package
We developed the abcTau Python package implementing our aABC framework for estimation of timescales from autocorrelations or PSDs of various types of experimental data, and the Bayesian model comparison to select between different hypotheses [58]. We also provided tutorials as Jupyter Notebooks and example Python scripts to make our framework easily accessible for researchers in different fields.
The minimal requirements for using this package are Python 3.7.1, Numpy 1.15.4 and Scipy 1.1.0. For visualization, Matplotlib >= 3.0.2 and Seaborn >= 0.9.0 are required. The basis of aABC algorithm in the package is adopted from a previous implementation originally developed in Python 2 (https://github.com/rcmorehead/simpleabc). Since all parameters of our generative models are positive and sometimes subject to additional conditions (e.g., τ2 > τ1), we introduced constraints on sampling from proposal distributions. Moreover, we enhanced the algorithm for parallel processing required for analyzing large datasets.
The abcTau package includes various types of generative models that are relevant for different types data and various methods for computing the autocorrelation or PSD. Using this functionality, users can apply our framework to their time-series data, supplied in a Numpy array structured as trials times time-points. The object oriented implementation of the package allows users to easily replace any function, including generative models, summary statistic computations, distance functions, etc., with their customized functions to better describe statistics of the data. Users can also add their customized generative models directly to the package to create a larger database of generative models available for different applications.
The package also includes a module for Bayesian model selection. This module computes the cumulative distribution of distances from estimated posterior distributions (i.e., Bayes factor for different error thresholds), runs the statistical tests and suggests the best hypothesis describing the underlying processes in data.
4.5.1. Pre-processing for evaluating quality of direct fit
Since Bayesian inference of a full posterior distribution can be computationally expensive, we implemented a fast pre-processing function that uses parametric bootstrapping to determine whether the direct exponential fit provides satisfactory estimates of timescales (Supplementary Figure 14). In this function, a generative model (e.g., based on a mixture of OU processes) with parameters obtained from the direct exponential fit can be used to generate multiple synthetic datasets, each with the same amount of data as in the original data. For each synthetic dataset, timescales are estimated by direct exponential fitting. The obtained distribution of timescales from this bootstrapping procedure can be compared to the initial direct-fit estimate from the original data. The error between the mean of bootstrapping distribution and the initial direct fit is used to approximately evaluate the direct fit quality. If the error is small enough, the direct exponential fit may be sufficiently accurate. The accuracy of timescale estimates with the direct fit can be further improved by empirical bias-correction using the measured deviation between the mean of the parametric bootstrap distribution and the direct-fit estimates (Supplementary Figure 5). However, this method does not guarantee an accurate bias correction since the deviation of the direct fit from the ground truth can be larger than the observed deviation between the bootstrap and direct fit. Hence, we recommend users to be conservative with the decision to rely on the direct-fit estimates if accurate estimates of timescales are desired.
4.6. Branching network model
A branching network consists of k interconnected binary neurons, each described by the state variable , where xi = 1 indicates that neuron i is active, and 0 that it is silent. We considered a fully-connected network. Each active neuron can activate other neurons with the probability p = m/k and then, if not activated by other neurons, it becomes inactive again in the next time-step. Additionally, at every time-step, each neuron can be activated with a probability h by an external input. For a small input strength h, the state of the network’s dynamics is governed by a branching parameter m (m = 1 corresponds to the critical state). The autocorrelation function of the global activity in this network is known analytically [5]. Thus the ground-truth timescale of this activity is given by .
4.7. Neural recordings and analysis
Experimental procedures and data pre-processing were described previously [47]. Experimental procedures were in accordance with NIH Guide for the Care and Use of Laboratory Animals, the Society for Neuroscience Guidelines and Policies, and Stanford University Animal Care and Use Committee.
In brief, a monkey was trained to fixate a central dot on a blank screen for 3 s on each trial. Spiking activity was recorded with a 16-channel micro-electrode array inserted perpendicularly to the cortical surface to record from all layers in the visual area V4. For fitting, we used a recording session with 81 trials. We pooled the activity across all channels and calculated the population spike-counts in bins of 1 ms. First, we subtracted the trail-averaged activity (PSTH) from spike-counts to remove the slow trends locked to the trial onset [1]. Then, we computed the autocorrelation of spike-counts using equation (2) the autocorrelation across all trials.
To estimate the timescales from direct fitting, we fitted the average autocorrelation of spike counts with a double exponential function
| (23) |
up to the same tm = 150 ms as used for the aABC fit. Including all the time lags in exponential fitting results in a larger bias in estimated timescales. To compare the goodness of direct-fit estimates with the MAP estimates from the aABC fit we used a sampling method based on parametric bootstrapping. We generated multiple samples of synthetic data using the two-timescale doubly-stochastic generative model with parameters from either the direct fit or MAP estimates from aABC. For each sample, we measured the distance between the autocorrelation of synthetic and neural data to obtain the distribution of distances for both types of fits. Then, we used two-sided Wilcoxon rank-sum test to compare the distributions.
4.8. Parameters of simulations and aABC fits in figures
For all fits, the initial error threshold was set to ε = 1. The aABC iterations continued until accR ⩽ 0.003 was reached. All datasets (except for the branching network) consisted of 500 trials each of 1 s duration. The dataset for the branching network (Fig. 4) consisted of 100 trials with 500 time-steps. The parameters for simulations and aABC fits are given in Supplementary Tables 1 and 2, respectively.
4.9. Statistics and reproducibility
As the first step of the model selection with ABC, we used two-sided Wilcoxon rank-sum test (also known as Mann–Whitney U test) to compare the distribution of distances of the two models. For this non-parametric test, we can compute the common language effect size [59] CL = U/(n1n2) using U statistics from the rank-sum test and number of samples n1 and n2 from the two models. For computing the effect size, we took the model with the larger average distance as the reference point. Hence, CL = 1 is the largest effect size. We truncated P-values smaller than 10−10 and rounded the remaining P-values to the third decimal place. We rounded the effect size values to the second decimal place.
For all model comparisons performed in this paper, there were always a significant difference between the distances of the two models (i.e. P < 0.05). The detailed results of the statistical analysis can be found in the captions of Fig. 5 and Fig. 6. We reported P-values, effect sizes and sample sizes (test statistic U can be computed directly from the effect size and sample sizes as U = CL · n1 · n2).
Supplementary Material
Acknowledgments
This work was supported by a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation, endowed by the Federal Ministry of Education and Research (RZ, AL), SMARTSTART2 program provided by Bernstein Center for Computational Neuroscience and Volkswagen Foundation (RZ), NIH grant R01 EB026949 (TAE), the Pershing Square Foundation (TAE), and Alfred P. Sloan Foundation Research Fellowship (TAE). We acknowledge the support from the BMBF through the Tübingen AI Center (FKZ: 01IS18039B) and International Max Planck Research School for the Mechanisms of Mental Function and Dysfunction (IMPRS-MMFD). We thank N. A. Steinmetz and T. Moore for sharing the electrophysiological data [47].
Footnotes
Code availability
The abcTau Python package together with tutorials and Jupyter Notebooks for reproducing figures are available on GitHub at: https://github.com/roxana-zeraati/abcTau and on Zenodo at https://doi.org/10.5281/zenodo.5949117 [58].
Competing interests statement
The authors declare no competing interests.
Data availability
Electrophysiogical recordings from primate area V4 were performed at Stanford University and presented in Ref. [47]. The raw electrophysiogical data (session 2013–06-18, blank screen condition) are available on Fighshare at https://doi.org/10.6084/m9.figshare.19077875.v1 [60]. Processed data and data from example aABC fits and model selections are available on GitHub at https://github.com/roxana-zeraati/abcTau and on Zenodo at https://doi.org/10.5281/zenodo.5949117 [58]. Source data for Figures 1, 3-6 are available with this paper.
References
- [1].Murray JD et al. A hierarchy of intrinsic timescales across primate cortex. Nature Neuroscience 17, 1661 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Watanabe T, Rees G. & Masuda N. Atypical intrinsic neural timescale in autism. eLife 8, e42256 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Gao R, van den Brink RL, Pfeffer T. & Voytek B. Neuronal timescales are functionally dynamic and shaped by cortical microarchitecture. eLife 9, e61277 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Zeraati R. et al. Attentional modulation of intrinsic timescales in visual cortex and spatial networks. bioRxiv (2021). URL https://www.biorxiv.org/content/10.1101/2021.05.17.444537v1.
- [5].Wilting J. & Priesemann V. Inferring collective dynamical states from widely unobserved systems. Nature Communications 9, 1–7 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Cavanagh SE, Wallis JD, Kennerley SW & Hunt LT Autocorrelation structure at rest predicts value correlates of single neurons during reward-guided choice. eLife 5, e18937 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Siegle JH et al. Survey of spiking in the mouse visual system reveals functional hierarchy. Nature 592, 86–92 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Stringer C. et al. Inhibitory control of correlated intrinsic variability in cortical networks. eLife 5, e19695 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Fascianelli V, Tsujimoto S, Marcos E. & Genovesio A. Autocorrelation structure in the macaque dorsolateral, but not orbital or polar, prefrontal cortex predicts response-coding strength in a visually cued strategy task. Cerebral Cortex 29, 230–241 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].MacDowell CJ & Buschman TJ Low-dimensional spatiotemporal dynamics underlie cortex-wide neural activity. Current Biology (2020). [DOI] [PMC free article] [PubMed]
- [11].Kim R. & Sejnowski TJ Strong inhibitory signaling underlies stable temporal dynamics and working memory in spiking neural networks. Nature Neuroscience 24, 129–139 (2021). [DOI] [PubMed] [Google Scholar]
- [12].Ito T, Hearne LJ & Cole MW A cortical hierarchy of localized and distributed processes revealed via dissociation of task activations, connectivity changes, and intrinsic timescales. NeuroImage 221, 117141 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Strey H, Peterson M. & Sackmann E. Measurement of erythrocyte membrane elasticity by flicker eigenmode decomposition. Biophysical Journal 69, 478–488 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Rohrbach A, Meyer T, Stelzer EH & Kress H. Measuring stepwise binding of thermally fluctuating particles to cell membranes without fluorescence. Biophysical Journal (2020). [DOI] [PMC free article] [PubMed]
- [15].Liu K. et al. Hydrodynamics of transient cell-cell contact: The role of membrane permeability and active protrusion length. PLoS Computational Biology 15, e1006352 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Donoghue T. et al. Parameterizing neural power spectra into periodic and aperiodic components. Nature Neuroscience 23, 1655–1665 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Marriott F. & Pope J. Bias in the estimation of autocorrelations. Biometrika 41, 390–402 (1954). [Google Scholar]
- [18].Sastry ASR Bias in estimation of serial correlation coefficients. Sankhy¯a: The Indian Journal of Statistics 281–296 (1951).
- [19].Huitema BE & McKean JW Autocorrelation estimation and inference with small samples. Psychological Bulletin 110, 291 (1991). [Google Scholar]
- [20].White JS Asymptotic expansions for the mean and variance of the serial correlation coefficient. Biometrika 48, 85–94 (1961). [Google Scholar]
- [21].Lomnicki Z. & Zaremba S. On the estimation of autocorrelation in time series. The Annals of Mathematical Statistics 28, 140–158 (1957). [Google Scholar]
- [22].Kendall MG Note on bias in the estimation of autocorrelation. Biometrika 41, 403–404 (1954). [Google Scholar]
- [23].Afyouni S, Smith SM & Nichols TE Effective degrees of freedom of the pearson’s correlation coefficient under autocorrelation. NeuroImage 199, 609–625 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Bartlett MS On the theoretical specification and sampling properties of autocorrelated time-series. Supplement to the Journal of the Royal Statistical Society 8, 27–41 (1946). [Google Scholar]
- [25].Cliff OM, Novelli L, Fulcher BD, Shine JM & Lizier JT Assessing the significance of directed and multivariate measures of linear dependence between time series. Physical Review Research 3, 013145 (2021). [Google Scholar]
- [26].Khintchine A. Korrelationstheorie der stationären stochastischen prozesse. Mathematische Annalen 109, 604–615 (1934). [Google Scholar]
- [27].Strey HH Estimation of parameters from time traces originating from an Ornstein-uhlenbeck process. Physical Review E 100, 062142 (2019). [DOI] [PubMed] [Google Scholar]
- [28].Spitmaan MM, Seo H, Lee D. & Soltani A. Multiple timescales of neural dynamics and integration of task-relevant signals across cortex. Proceedings of the National Academy of Sciences (2020). [DOI] [PMC free article] [PubMed]
- [29].Brody CD Slow covariations in neuronal resting potentials can lead to artefactually fast cross-correlations in their spike trains. Journal of Neurophysiology 80, 3345–3351 (1998). [DOI] [PubMed] [Google Scholar]
- [30].Ventura V, Cai C. & Kass RE Trial-to-trial variability and its effect on time-varying dependency between two neurons. Journal of Neurophysiology 94, 2928–2939 (2005). [DOI] [PubMed] [Google Scholar]
- [31].Amarasingham A, Harrison MT, Hatsopoulos NG & Geman S. Conditional modeling and the jitter method of spike resampling. Journal of Neurophysiology 107, 517–531 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Cohen MR & Kohn A. Measuring and interpreting neuronal correlations. Nature Neuroscience 14, 811 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Beaumont MA, Cornuet J-M, Marin J-M & Robert CP Adaptive approximate bayesian computation. Biometrika 96, 983–990 (2009). [Google Scholar]
- [34].Kelly RC, Smith MA, Kass RE & Lee TS Local field potentials indicate network state and account for neuronal response variability. Journal of Computational Neuroscience 29, 567–579 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Ecker AS et al. State dependence of noise correlations in macaque primary visual cortex. Neuron 82, 235–248 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Genkin M. & Engel TA Moving beyond generalization to accurate interpretation of flexible models. Nature Machine Intelligence 2, 674–683 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Neophytou D, Arribas D, Levy R, Park IM & Oviedo HV Recurrent connectivity underlies lateralized temporal processing differences in auditory cortex. bioRxiv (2021). [DOI] [PMC free article] [PubMed]
- [38].Babadi B. & Brown EN A review of multitaper spectral analysis. IEEE Transactions on Biomedical Engineering 61, 1555–1564 (2014). [DOI] [PubMed] [Google Scholar]
- [39].Haldeman C. & Beggs JM Critical branching captures activity in living neural networks and maximizes the number of metastable states. Physical Review Letters 94, 058101 (2005). [DOI] [PubMed] [Google Scholar]
- [40].Zierenberg J, Wilting J, Priesemann V. & Levina A. Description of spreading dynamics by microscopic network models and macroscopic branching processes can differ due to coalescence. Physical Review E 101, 022301 (2020). [DOI] [PubMed] [Google Scholar]
- [41].Zierenberg J, Wilting J, Priesemann V. & Levina A. Tailored ensembles of neural networks optimize sensitivity to stimulus statistics. Physical Review Research 2, 013115 (2020). [Google Scholar]
- [42].Grelaud A. et al. Abc likelihood-free methods for model choice in gibbs random fields. Bayesian Analysis 4, 317–335 (2009). [Google Scholar]
- [43].Didelot X, Everitt RG, Johansen AM, Lawson DJ et al. Likelihood-free estimation of model evidence. Bayesian Analysis 6, 49–76 (2011). [Google Scholar]
- [44].Marin J-M, Pillai NS, Robert CP & Rousseau J. Relevant statistics for bayesian model choice. Journal of the Royal Statistical Society: Series B: Statistical Methodology 833–859 (2014).
- [45].Robert CP, Cornuet J-M, Marin J-M & Pillai NS Lack of confidence in approximate bayesian computation model choice. Proceedings of the National Academy of Sciences 108, 15112–15117 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Bishop CM Pattern recognition and machine learning (Springer, 2006). [Google Scholar]
- [47].Engel TA et al. Selective modulation of cortical state during spatial attention. Science 354, 1140–1144 (2016). [DOI] [PubMed] [Google Scholar]
- [48].Churchland AK et al. Variance as a signature of neural computations during decision making. Neuron 69, 818–831 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Goris RL, Movshon JA & Simoncelli EP Partitioning neuronal variability. Nature Neuroscience 17, 858 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Brody CD Correlations without synchrony. Neural Computation 11, 1537–1551 (1999). [DOI] [PubMed] [Google Scholar]
- [51].Gao R, Peterson EJ & Voytek B. Inferring synaptic excitation/inhibition balance from field potentials. Neuroimage 158, 70–78 (2017). [DOI] [PubMed] [Google Scholar]
- [52].Wagenmakers E-J, Farrell S. & Ratcliff R. Estimation and interpretation of 1/f α noise in human cognition. Psychonomic bulletin & review 11, 579–615 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Uhlenbeck GE & Ornstein LS On the theory of the brownian motion. Physical Review 36, 823 (1930). [Google Scholar]
- [54].Risken H. Fokker-planck equation. In The Fokker-Planck Equation, 63–95 (Springer, 1996). [Google Scholar]
- [55].Lindner B. A brief introduction to some simple stochastic processes. Stochastic Methods in Neuroscience 1 (2009). [Google Scholar]
- [56].Sunnåker M. et al. Approximate bayesian computation. PLoS Computational Biology 9 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Toni T. & Stumpf MP Simulation-based model selection for dynamical systems in systems and population biology. Bioinformatics 26, 104–110 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Zeraati R, Engel TA & Levina A. roxana-zeraati/abcTau: a flexible Bayesian framework for unbiased estimation of timescales (2022). URL 10.5281/zenodo.5949117. [DOI] [PMC free article] [PubMed]
- [59].McGraw KO & Wong SP A common language effect size statistic. Psychological bulletin 111, 361 (1992). [Google Scholar]
- [60].Steinmetz N. & Moore T. Dataset of linear-array recordings from macaque V4 during a fixation task (2022). URL 10.6084/m9.figshare.19077875.v1. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Electrophysiogical recordings from primate area V4 were performed at Stanford University and presented in Ref. [47]. The raw electrophysiogical data (session 2013–06-18, blank screen condition) are available on Fighshare at https://doi.org/10.6084/m9.figshare.19077875.v1 [60]. Processed data and data from example aABC fits and model selections are available on GitHub at https://github.com/roxana-zeraati/abcTau and on Zenodo at https://doi.org/10.5281/zenodo.5949117 [58]. Source data for Figures 1, 3-6 are available with this paper.