Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Dec 27;8(1):1146–1153. doi: 10.1021/acsomega.2c06602

Estimation of Adsorbed Amounts in Organoclay by Machine Learning

Hayato Shobuke 1, Takumi Matsumoto 1, Fumiya Hirosawa 1, Masaya Miyagawa 1, Hiromitsu Takaba 1,*
PMCID: PMC9835538  PMID: 36643430

Abstract

graphic file with name ao2c06602_0009.jpg

Adsorption properties of organoclay have been investigated for decades focusing on the morphology and physicochemical properties of two-dimensional interlayers. Experimental studies have previously revealed that the adsorption mechanisms depend on the molecular species of the organocation and adsorbate, making it difficult to estimate the adsorbed amount without experiments. Considering that the adsorption of aromatic compounds has been reported by using various clays, organocations, and adsorbates, machine learning is a promising method to overcome the difficulty. In the present study, we collected adsorption data from the literature and constructed models to estimate the adsorbed amount of the organoclay by random forest regression. The composition of the clay, molecular descriptors of the organocation and adsorbate obtained by the RDKit, and experimental conditions were used as the explanatory variables. Simple model construction by using all the experimental data resulted in low R2 and a mean absolute error. This problem was solved by the correction of the adsorbed amount data by the Langmuir or Freundlich equation and the following model construction at various equilibrium concentrations. The plots of the adsorbed amount estimated by the latter model were located close to the corresponding adsorption isotherm, while that by the former was not. Thus, it was revealed that the adsorbed amount was estimated quantitatively without understanding the adsorption mechanisms individually. Feature importance analysis also revealed that the combination of the organocation and adsorbate is important at high equilibrium concentrations, while the clay should be selected carefully as the concentration gets lower. Our results give an insight into the rational design of the organoclay including the synthesis and adsorption properties.

1. Introduction

Estimation of adsorption properties including the maximum adsorption amount and selectivity is significant in materials design. Two- or three-dimensional inorganic materials such as layered clay mineral, zeolite, and metal–organic frameworks have extensively been developed due to their robustness and adsorption selectivity.1−3 Numerous adsorption experiments have revealed that the morphology of the host material and its molecular modification are keys to improving the adsorption properties.4−11 For example, the pore size is definitely important in zeolite and metal–organic frameworks from a viewpoint of adsorption selectivity. The modification by amine is effective for CO2 adsorption because both chemisorption and physisorption take place. In the adsorption property, the adsorbed amount is one of the simplest parameters and can be measured experimentally. However, it is difficult to estimate the adsorbed amount theoretically on the basis of the composition of the composite.

Layered clay minerals, especially smectites, are representative adsorbents because of their natural abundance.8,12,13 Montmorillonite is a well-known natural and commercially available smectite, which consists of negatively charged aluminosilicate layers and interlayer cations such as Na+ and K+ for charge compensation. The negative charge of the layer generally originates from isomorphous substitution of Si4+ or Al3+ to Al3+, Mg2+, or Fe2+. Because the interlayer cation is exchangeable, its amount is equal to the cation exchange capacity (CEC, hereafter). For application to the adsorption material, the interlayer is often modified by exchange of the interlayer cation with an organocation, which endows the interlayer with hydrophobicity. In this exchange reaction, quaternary ammonium ions such as trimethylphenylammonium ion and hexadecyltrimethylammonium ion are often introduced into the interlayer. The obtained nanocomposite is called organoclay and adsorbs aromatic compounds from water.14−33 Because the adsorption properties of the organoclay depend on the interlayer environment, various host clays with different compositions and CEC have hitherto been used as well as the organocation.5,14,16,25

Comparison of adsorption isotherms has suggested that the adsorbed amount in the organoclay is determined by the following three structural or physicochemical characteristics:14,19,22,27,34−36 the first is the interaction between the adsorbate and the clay layer or organocation because the adsorbate is supposed to be stabilized by attractive interactions in the interlayer. Spectroscopy is a promising method to investigate the interaction, but in situ measurement of the interlayer has not been accomplished with sufficient special resolution. In addition, water is also intercalated in liquid-state adsorption, making the structural analysis more difficult. The second is the solubility of the adsorbate in water. The hydrophobic adsorbate is adsorbed in the organoclay more easily than the hydrophilic adsorbate because the introduction of the organocation makes the interlayer of the organoclay hydrophobic. The last is the gallery height of the organoclay. The adsorbate is believed not to be intercalated if the gallery height is not sufficiently large by the pre-intercalation of the small or planar organocation. However, similar to the interaction in the interlayer, it is difficult to determine the gallery height of the organoclay immersed in water by the conventional experimental technique. The swelled gallery height has recently been measured by transmission X-ray diffraction, but few cases have ever been reported.19,37

Because it is difficult to quantify the above three characteristics and numerous combinations of the host clay, organocation, and adsorbate are possible, constructing a theoretical model to estimate the adsorbed amount in the organoclay is unrealistic. In contrast, machine learning is a promising approach, where the value of the objective variable is expected to be estimated by that of explanatory variables in the dataset.38−41 In other words, the adsorbed amount is estimated from the experimental condition such as the compositions of the host clay and the molecular species of the organocation and adsorbate. Such an estimation will lead to a cost-effective design of the organoclay with superior adsorption properties.

In the present study, we constructed estimation models of the adsorbed amount by collecting adsorption isotherm data of the organoclay from the literature. Correction of the adsorbed amount data by the Langmuir or Freundlich equation and the following construction of the models at various equilibrium concentrations by random forest regression resulted in good consistency of the estimated adsorbed amount with the test data. Feature importance analysis suggested that the composition of the host clay should be carefully considered when the equilibrium concentration is low, while the organocation becomes significant at high concentrations.

2. Method

2.1. Dataset

Eighty adsorption isotherms containing 573 adsorbed amount data were collected from the literature by using SciFinder.14,16,19−29 The value of the adsorbed amount and the corresponding equilibrium concentration were obtained by Engauge Digitizer.42 The dataset contains information of the host clay, organocation, adsorbate, and experimental conditions. A set of data was not included in the dataset if any of the following data cannot be derived from the literature. In the dataset of the host clay, the composition of the tetrahedral and octahedral moieties, CEC, and Li substitution ratio are included. For the organocation, simplified molecular input line entry system (SMILES), dipole moment, the number of atoms, and the exchange amount in meq/100 g clay are included in the dataset. For the adsorbate, the SMILES, dipole moment, logP, the number of atoms, the adsorbed amount, and the corresponding equilibrium concentration are included in the dataset. For other experimental conditions, the temperature and exchange ratio (i.e., exchange amount/CEC) are included. All the data in the dataset were obtained from the corresponding literature except the values of logP and dipole moment. The value of logP was cited from the database in SciFinder. The value of the dipole moment of the organocation and adsorbate was calculated by quantum chemical calculation, where the geometry is optimized at the DFT/GGA-PBE level by using the DMol3 package (BIOVIA, Inc.).43 In the 573 adsorbed amount data in the dataset, 16 host clays with the different CEC, 18 organocations, and 15 adsorbates are included.

2.2. Model Construction

The 80 adsorption isotherm data in the dataset were divided into two groups at a ratio of 7:1. The adsorbed amount data in the 70 isotherms were used as the training data for the model construction, while the rest was used as the test data to evaluate the predictive ability of the model. The organocation and adsorbate expressed by the SMILES were converted into molecular descriptors by using RDKit (version: 2021.03.5) with Python (version: 3.6.13).45,46 The adsorbed amount was used as the objective variable (y). To determine the explanatory variables, the standard deviation of the RDKit descriptors was examined. The descriptors were excluded from the explanatory variables if their standard deviation is zero. The rest and other parameters of the host clay and others described above were used as explanatory variables. The total number of explanatory variables was 250. The explanatory variables are schematically illustrated in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Schematic illustration of the explanatory variables.

In the model construction, random forest regression was applied to the training data, where the feature importance of the model is also obtained, enabling us to discuss the significance of each component shown in Figure 1. The hyperparameters were determined by fivefold cross-validation with Optuna,44 and their combination was determined by the R2 value. The optimized hyperparameters and their ranges are listed in Table S1. In the present study, the models were constructed by two different approaches. One is called the raw approach, where the adsorbed amounts obtained from the literature were used as the training data without further modifications. In this approach, the number of training data was 504. The other is called the correction approach, where the raw data were preliminarily fitted by the Langmuir or Freundlich equation:

2.2. 1
2.2. 2

where W, WS, a, and C in eqs 1 and 2 represent the adsorption amount, saturated adsorption amount, adsorption equilibrium constant, and equilibrium concentration, respectively. KF and n in eq 2 represent adsorption constants. The equation with a higher R2 value was used in each adsorption isotherm, and the adsorbed amount, W, at the equilibrium concentrations of 1, 10, 25, 50, 75, and 100 mg L–1 was calculated by using the values of a and Ws or KF and n. Of the 80 adsorption isotherms, the 46 isotherms were fitted by the Langmuir equation, while the rest were fitted by the Freundlich equation. This fitting process is also supposed to be effective to minimize the error of the experimental value. Finally, the models were constructed at each equilibrium concentration. Thus, the number of the training data was 70. We note that the explanatory variables do not include the equilibrium concentration in the model construction by the correction approach. The models constructed by the raw and correction approaches were examined on the basis of R2 and mean absolute error (MAE).

3. Results and Discussion

3.1. Validity of Models Constructed by Two Approaches

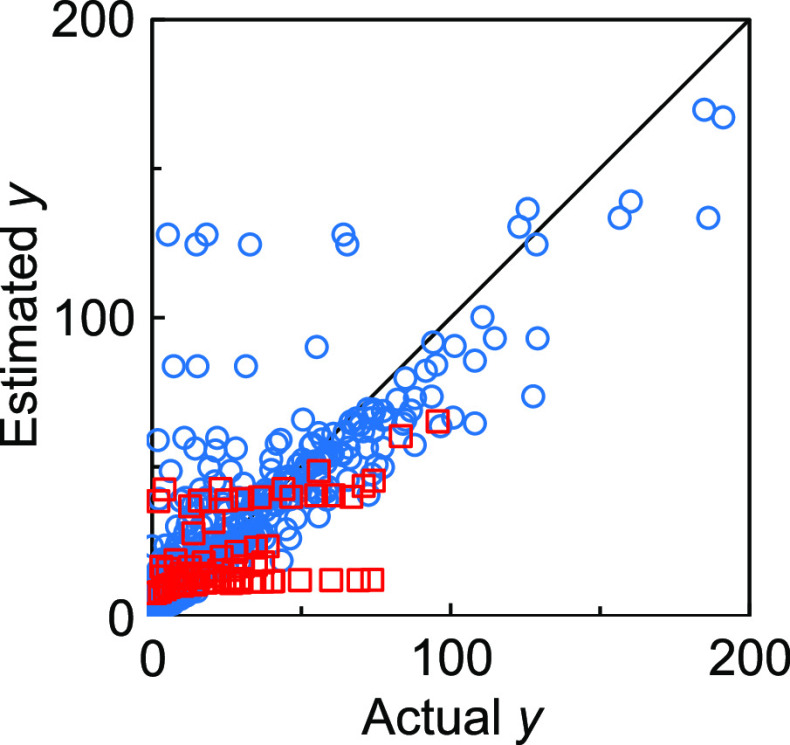
Figure 2 shows the estimation results of the training and test data with the model constructed by the raw approach. The R2 and MAE values are listed in Table 1. The test plots are mostly located below the diagonal line, indicating that the absorbed amount is poorly estimated by the raw approach. This result may be ascribed to the similarity of the training data: when more than one adsorbed amount data are collected in the same adsorption isotherm, their explanatory variables are almost the same because the same host clay, organocation, and adsorbate are used in the adsorption experiment as well as the experimental conditions such as temperature. In other words, the only difference in the explanatory variables is the equilibrium concentration. Consequently, it is difficult to estimate the adsorbed amount with high accuracy. Comparison of the estimated y with the corresponding adsorption isotherm will be demonstrated in the next section.

Figure 2.

Figure 2

Open in a new tab

Correlation between the actual y values and the estimated y values in the model constructed by the raw approach. Blue circles and red squares represent the training and test data, respectively.

Table 1. R2 and MAE Values in Models Developed by the Raw and Correction Approaches.

    R2
 MAE
approach equilibrium concentration/mg L–1 training test training test
raw   0.788 0.184 10.152 14.913
correction 1 0.965 0.384 0.825 2.076
10 0.943 0.138 2.093 7.416
25 0.899 0.480 3.837 9.831
50 0.863 0.674 6.995 10.687
75 0.902 0.725 9.493 10.351
100 0.904 0.683 12.996 11.710
Open in a new tab

Figure 3 shows the estimation results of the training and test data with the models constructed by the correction approach. Compared to the results of the raw approach shown in Figure 2, the plots of the test data are mainly located on or close to the diagonal line, suggesting that the adsorbed amount is estimated well. The R2 and MAE values in the correction approach are summarized in Table 1. In all the equilibrium concentration models, the MAE value of the test data is smaller than that by the raw approach. The R2 value is also improved in the 1, 25, 50, 75, and 100 mg L–1 models. It is true that the R2 value in the 10 mg L–1 model is comparable to that obtained by the raw approach, but the MAE value is significantly lowered. In addition, the abovementioned similarity in the raw approach is excluded in the correction approach by constructing the models at each equilibrium concentration. Thus, it is concluded that the correction approach is better to estimate the adsorbed amount of the organoclay than the raw approach.

Figure 3.

Figure 3

Open in a new tab

Correlation between the actual y values and the estimated y values in the models of (a) 1, (b) 10, (c) 25, (d) 50, (e) 75, and (f) 100 mg L–1 constructed by the correction approach, respectively. Blue circles and red squares represent the training and test data, respectively.

In the dataset, 84% of the host clay is montmorillonite with the different CEC, and 86% of the adsorbate is the quaternary ammonium ion containing the linear alkyl or phenyl group. All the adsorbates in the dataset are substituted benzenes or heterocyclic compounds. Thus, it is suggested that our model should be applicable to the adsorption of simple aromatic compounds by the organoclay composed of montmorillonite and the quaternary ammonium ion. The reliability of the model will be discussed in the next section by comparison of the estimated adsorbed amount with the experimental data corrected by the fitting analysis.

3.2. Consistency of the Estimated Adsorbed Amount with the Experimental Data

Figures 4 and 5 show estimation results of the test data with the models by the raw and correction approaches, respectively. In Figure 4a,b, the positive correlation is not reproduced between the equilibrium concentration and the adsorbed amount. The estimated value is lower than the experimental value and does not change significantly as the equilibrium concentration is increased due to the similarity of the input data. In contrast, the positive correlation is observed by the correction approach, as shown in Figure 5a,b, where the plots of the estimated adsorption amount are located close to the corresponding Langmuir or Freundlich adsorption isotherms obtained by the fitting analysis of the raw adsorbed amount data. The difference is within the MAE value. In other words, the adsorbed amounts are sufficiently estimated at each equilibrium concentration by the correction approach.

Figure 4.

Figure 4

Open in a new tab

Estimation of the adsorbed amount of organic molecules in the organoclay by the raw approach: (a) toluene in trimethylphenylammmonium-modified montmorillonite with 90 meq/100 g CEC, (b) buthylbenzene in trimethylphenylammmonium-modified Li+-containing montmorillonite with 130 meq/100 g CEC, (c) caffeine in benzylammonium-modified montmorillonite with 119 meq/100 g CEC, and (d) alachlor in benzyltriethylammonium-modified montmorillonite with 80 meq/100 g CEC. The red circle and black square represent the adsorbed amounts estimated by the random forest and observed experimentally. Detailed experimental conditions are written in ref (14) for (a) and (b), 19 for (c), and 22 for (d).

Figure 5.

Figure 5

Open in a new tab

Estimation of the adsorbed amount of organic molecules in organoclay by the correction approach: (a) toluene in trimethylphenylammmonium-modified montmorillonite with 90 meq/100 g CEC, (b) buthylbenzene in trimethylphenylammmonium-modified Li+-containing montmorillonite with 130 meq/100 g CEC, (c) caffeine in benzylammonium-modified montmorillonite with 119 meq/100 g CEC, and (d) alachlor in benzyltriethylammonium-modified montmorillonite with 80 meq/100 g CEC. The red circle and black dotted line represent the adsorbed amounts estimated by the random forest and the adsorption isotherm of the test data, respectively. Detailed experimental conditions are written in ref (14) for (a) and (b), 19 for (c), and 22 for (d).

Because the estimation plots shown in Figure 5 well reproduce the corresponding adsorption isotherm within the MAE values, usage of the RDKit descriptors is found to be effective to represent the organocation and adsorbate. Our model is also applicable to the reduced-charge host clay shown in Figure 5b, whose CEC is reduced by introduction of Li+ into the clay layer. Furthermore, it is notable that the adsorbed amounts are well estimated despite different adsorption mechanisms. In the adsorption isotherm shown in Figure 5a, the siloxane surface of montmorillonite serves as the adsorption site of toluene, while trimethylphenylammmonium ions indirectly affect the adsorption and are pillars to provide enough gallery height for the intercalation.14,27 The same mechanism is proposed in the adsorption of butylbenzene shown in Figure 5b. In the adsorption of caffeine and alachlor shown in Figure 5c,d, the adsorption mechanisms are different from those of toluene and butylbenzene described above as well as the type of the adsorption isotherm: Caffeine is adsorbed effectively due to the interaction both with benzylammonium ions and siloxane surface, while the interaction with the siloxane surface, π–π interaction, and hydrogen bonding with benzyltriethylammonium ions are thought to induce the adsorption of alachlor, where the size and shape of the organocation are also not negligible.19,22 Summarizing these results, it is revealed that the adsorbed amount in the organoclay is estimated on the basis of its composition.

Our results demonstrate that understanding of neither the detailed interlayer morphology nor the adsorption mechanism in the individual adsorption system is necessary to estimate the adsorbed amount. This fact is beneficial because it is difficult experimentally to elucidate the nanostructure and interaction in the organoclay swelled by water. It is true that the molecular dynamics method may be a promising approach to investigate the nanoscopic morphology,47 but the water content in the organoclay cannot be determined without thermal gravimetry analysis (TGA) data, as pointed out previously.48 The TGA data are available in some organoclay such as montmorillonite modified with trimethylammonium ions and hexadecyltrimethylammonium ions, but hugely limited.35,49 In the present study, however, the adsorbed amount is estimated by the information of the host clay, organocation, adsorbate, and experimental conditions, which is easily derived from the literature. Therefore, it is concluded that machine learning is a superior method to estimate the adsorbed amount in the organoclay.

3.3. Feature Importance and Relation with Each Concentration Model

Figure 6 shows the top 10 feature importances in each model. In the models of ≤50 mg L–1, the organocation exchange amount/CEC, Li substitution of the clay, CEC of the clay, and the exchange amount of the organocation are listed, indicating that the adsorbed amount is significantly affected by the composition of the organoclay. In contrast, these explanatory variables are not listed in the models of 75 and 100 mg L–1, and the molecular descriptors obtained by the RDKit appear. Because only the top 10 features are listed among the 250 explanatory variables, it is unclear how much each component shown in Figure 1 affects the adsorbed amount in each equilibrium concentration model. Thus, the significances of the clay, organocation, adsorbate, and others are evaluated by adding the values of the feature importance individually.

Figure 6.

Figure 6

Open in a new tab

Top 10 feature importance in each model: (a) 1, (b) 10, (c) 25, (d) 50, (e) 75, and (f) 100 mg L–1, respectively. Labels in gray, green, blue, and black represent the clay, organocation, adsorbate, and others, respectively. Definition of the listed variables is explained in ref (45).

Figure 7 shows the correlation between the feature importances of the clay, organocation, adsorbate and others and the equilibrium concentration of the model. In the models of ≥50 mg L–1, the adsorbed amount is found to be determined mostly by the organocation and adsorbate, suggesting that their combination is highly important to improve the adsorption property of the organoclay. This result is consistent with the well-known fact that the organocation should be carefully selected in the design of the organoclay. For example, the effect of the organocation on the adsorbed amounts of phenol and chlorophenols is reported previously in bentonite modified with hexadecyltrimethylammonium ions, hexadecylpyridinium ions, trimethylphenylammmonium ions, and tetramethylammonium ions.36 In contrast, the ratio of the clay is relatively large in the models of ≤25 mg L–1, while that of the organocation gets small correspondingly. This result suggests that the composition of the host clay should be paid attention to when the equilibrium concentration is low. The effect of the CEC of the host clay on the adsorbed amount is often investigated focusing on the pore volume of the interlayer:19,25,28 Neostigmine-modified saponite with the CEC of 71 meq/100 g adsorbs caffeine, while montmorillonite with the CEC of 119 meq/100 g does not. A similar result is also reported in the adsorption of 2,4-dichlorophenol, where methylviologen is used as the organocation. The introduction of Li+ into the host clay is also known to greatly increase the adsorbed amount of the aromatic hydrocarbons, especially at the low equilibrium concentration because the CEC is lowered by the decrease in the layer charge.14 Our result that the host clay is relatively important at the low equilibrium concentration is consistent with the abovementioned experimental findings. Therefore, it is concluded that the organocation is generally important to maximize the adsorbed amount, and the composition of the host clay is also paid attention to when the equilibrium concentration is low.

Figure 7.

Figure 7

Open in a new tab

Correlation between the feature importance and equilibrium concentration of the model. Gray, green, blue, and black bars represent the clay, organocation, adsorbate, and others, respectively.

4. Conclusions

In the present study, we demonstrated that the adsorbed amount in the organoclay is predictable by constructing the estimation model by the random forest regression. The model constructed by using the raw adsorption data was simple but not suitable. The R2 and MAE values were insufficient, and the changes in the adsorbed amount by the equilibrium concentration were not reproduced due to the similarity of the input data. This problem was solved by the model construction at the individual equilibrium concentration after the correction of the adsorbed amount by the Langmuir or Freundlich equation. The adsorbed amount was estimated within the MAE value by the correction approach in various organoclay adsorption systems despite different adsorption mechanisms. In other words, the estimation was achieved without physicochemical understanding of the organoclay including the nanostructure and molecular interaction. According to the feature importance analysis, the significance of the clay, organocation, adsorbate, and other experimental conditions is dependent on the equilibrium concentration. When the equilibrium concentration is relatively high, the adsorbed amount is determined mainly by the combination of the organocation and adsorbate while the clay is becoming important as the concentration is low. Therefore, it was concluded that machine learning is a promising method to estimate the adsorbed amount in the organoclay and also suggests a rational strategy for optimization of the materials design without performing experiments.

Acknowledgments

The authors appreciate the support from JSPS KAKENHI grant number 21K14705.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c06602.

  • Optimized hyperparameters for the model construction (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

Supplementary Material

ao2c06602_si_001.pdf (62.1KB, pdf)

References

  1. Okada T.; Ide Y.; Ogawa M. Organic-inorganic hybrids based on ultrathin oxide layers: Designed nanostructures for molecular. Chem. – Asian J. 2012, 7, 1980–1992. 10.1002/asia.201101015. [DOI] [PubMed] [Google Scholar]
  2. Li J.-R.; Kuppler R. J.; Zhou H.-C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. 10.1039/b802426j. [DOI] [PubMed] [Google Scholar]
  3. Li Y.; Li L.; Yu J. Applications of Zeolites in Sustainable Chemistry. Chem 2017, 3, 928–949. 10.1016/j.chempr.2017.10.009. [DOI] [Google Scholar]
  4. Zahir R.; Najwa N. Characteristics of phenol and chlorinated phenols sorption onto surfactant-modified bentonite. J. Colloid Interface Sci. 2006, 298, 39–49. 10.1016/j.jcis.2005.11.063. [DOI] [PubMed] [Google Scholar]
  5. Phuekphong A. (. F.).; Imwiset K. (. J.).; Ogawa M. Designing nanoarchitecture for environmental remediation based on the clay minerals as building block. J. Hazard. Mater. 2020, 399, 122888 10.1016/j.jhazmat.2020.122888. [DOI] [PubMed] [Google Scholar]
  6. Jesse R.; Omar Y. Strategies for Hydrogen Storage in Metal–Organic Frameworks. Angew. Chem., Int. Ed. 2005, 44, 4670–4679. 10.1002/anie.200462786. [DOI] [PubMed] [Google Scholar]
  7. Wang S.; Peng Y. Natural zeolites as effective adsorbents in water and wastewater treatment. Chem. Eng. J. 2010, 156, 11–24. 10.1016/j.cej.2009.10.029. [DOI] [Google Scholar]
  8. Ogawa M.; Kuroda K. Preparation of Inorganic-Organic Nanocomposites through Intercalation of Organoammonium Ion into Layered Silicates. Bull. Chem. Soc. Jpn. 1997, 70, 2593–2618. 10.1246/bcsj.70.2593. [DOI] [Google Scholar]
  9. Ding M.; Cai X.; Jiang H.-J. Improving MOF stability: approaches and applications. Chem. Sci. 2019, 10, 10209–10230. 10.1039/C9SC03916C. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Zhao M. M.; Hassan M. K.; Khraisheh M.; Al-Maadeed M. A. A.; Nazarenko S. A review on recent advances in CO2 separation using zeolite and zeolite-like materials as adsorbents and fillers in mixed matrix membranes (MMMs). Chem. Eng. J. Adv. 2021, 6, 100091 10.1016/j.ceja.2021.100091. [DOI] [Google Scholar]
  11. Jadhav P. D.; Chatti R. V.; Biniwale R. B.; Labhsetwar N. K.; Devotta S.; Rayalu S. S. Monoethanol Amine Modified Zeolite 13X for CO2 Adsorption at Different Temperatures. Energy Fuels 2007, 21, 3555–3559. 10.1021/ef070038y. [DOI] [Google Scholar]
  12. Nakato T.; Kawamata J.; Takagi S.. Inorganic Nanosheets and Nanosheet-Based MAterials, 1st ed.; Springer, 2017. [Google Scholar]
  13. Régis G. Organoclay applications and limits in the environment. C. R. Chem. 2019, 22, 132–141. 10.1016/j.crci.2018.09.004. [DOI] [Google Scholar]
  14. Jaynes W. F.; Boyd S. A. Hydrophobicity of Siloxane Surfaces in Smectites as Revealed by Aromatic Hydrocarbon Adsorption from Water. Clays Clay Miner. 1991, 39, 428–436. 10.1346/CCMN.1991.0390412. [DOI] [Google Scholar]
  15. Burstein F.; Borisover M.; Lapides I.; Yariv S. Secondary Adsorption Of Nitrobenzene ANDm-Nitrophenol By Hexadecyltrimethylammonium-Montmorillonite Thermo-XRD-analysis. J. Therm. Anal. Calorim. 2008, 92, 35–42. 10.1007/s10973-007-8732-1. [DOI] [Google Scholar]
  16. Okada T.; Matsutomo T.; Ogawa M. Nanospace Engineering of Methylviologen Modified Hectorite-Like Layered Silicates with Varied Layer Charge Density for the Adsorbents Design. J. Phys. Chem. C 2010, 114, 539–545. 10.1021/jp9089886. [DOI] [Google Scholar]
  17. Liu S.; Wu P.; Yu L.; Li L.; Gong B.; Zhu N.; Dang Z.; Yang C. Preparation and characterization of organo-vermiculite based on phosphatidylcholine and adsorption of two typical antibiotics. Appl. Clay Sci. 2017, 137, 160–167. 10.1016/j.clay.2016.12.002. [DOI] [Google Scholar]
  18. Phuekphong A. (. F.).; Imwiset K.; Ogawa M. Adsorption of Triclosan onto Organically Modified-Magadiite and Bentonite. J. Inorg. Organomet. Polym. Mater. 2021, 31, 1902–1911. 10.1007/s10904-021-01919-0. [DOI] [Google Scholar]
  19. Okada T.; Oguchi J.; Yamamoto K.; Shiono T.; Fujita M.; Iiyama T. Organoclays in Water Cause Expansion That Facilitates Caffeine Adsorption. Langmuir 2015, 31, 180–187. 10.1021/la503708t. [DOI] [PubMed] [Google Scholar]
  20. Okada T.; Morita T.; Ogawa M. Adsorption Behavior of Phenol for mono, bis and tris(2,2’-bipyridine)nickel(II)- and tris(ethylenediamine)nickel(II)-Sapontte Intercalation Compounds From Aqueous Solution. Clay Sci. 2004, 12, 277–284. 10.11362/jcssjclayscience1960.12.277. [DOI] [Google Scholar]
  21. Okada T.; Morita T.; Ogawa M. Tris(2,2V-bipyridine)ruthenium(II)-clays as adsorbents for phenol and chlorinated phenols from aqueous solution. Appl. Clay Sci. 2005, 29, 45–53. 10.1016/j.clay.2004.09.004. [DOI] [Google Scholar]
  22. El-Nahhal Y.; Nir S.; Polubesova T.; Margulies L.; Rubin B. Leaching, Phytotoxicity, and Weed Control of New Formulations of Alachlor. J. Agric. Food Chem. 1998, 46, 3305–3313. 10.1021/jf971062k. [DOI] [Google Scholar]
  23. Polubesova T.; Nir S.; Rabinovitz O.; Rubin B. Mepiquat–acetochlor formulations: sorption and leaching. Appl. Clay Sci. 2001, 18, 299–307. 10.1016/S0169-1317(01)00034-5. [DOI] [Google Scholar]
  24. El-Nahhal Y.; Nir S.; Serban C.; Rabinovitch O.; Rubin B. Montmorillonite-Phenyltrimethylammonium Yields Environmentally Improved Formulations of Hydrophobic Herbicides. J. Agric. Food Chem. 2000, 48, 4791–4801. 10.1021/jf000327j. [DOI] [PubMed] [Google Scholar]
  25. Okada T.; Ogawa M. 1,1A-Dimethyl-4,4A-bipyridinium-smectites as a novel adsorbent of phenols from water through charge-transfer interactions. Chem. Commun. 2003, 1378–1379. 10.1039/B302144K. [DOI] [PubMed] [Google Scholar]
  26. Okada T.; Ogawa M. p-Phenylenediammonium-Smectites as Adsorbents with Colorimetric Detection Ability for Phenols in Water. Bull. Chem. Soc. Jpn. 2004, 77, 1165–1170. 10.1246/bcsj.77.1165. [DOI] [Google Scholar]
  27. Jaynes W. F.; Boyd S. A. Trimethylphenylammonium-Smectite as an Effective Adsorbent of Water Soluble Aromatic Hydrocarbons. J. Air Waste Manage. Assoc. 1990, 40, 1649–1653. 10.1080/10473289.1990.10466811. [DOI] [PubMed] [Google Scholar]
  28. Seki Y.; Ogawa M. The Removal of 2-Phenylphenol from Aqueous Solution by Adsorption onto Organoclays. Bull. Chem. Soc. Jpn. 2010, 83, 712–715. 10.1246/bcsj.20090191. [DOI] [Google Scholar]
  29. Chun Y.; Sheng G.; Boyd S. A. Sorptive Characteristics Of Tetraalkylammonium-Exchanged Smectite Clays. Clays Clay Miner. 2003, 51, 415–420. 10.1346/CCMN.2003.0510407. [DOI] [Google Scholar]
  30. Zhang L.; Zhang B.; Wu T.; Sun D.; Li Y. Adsorption behavior and mechanism of chlorophenols ontoorganoclays in aqueous solution. Colloids Surf. A Physicochem. Eng. Asp. 2015, 484, 118–129. 10.1016/j.colsurfa.2015.07.055. [DOI] [Google Scholar]
  31. Nafees M.; Waseem A. Organoclays as Sorbent Material for Phenolic Compounds: A Review. Clean – Soil, Air, Water 2014, 42, 1500–1508. 10.1002/clen.201300312. [DOI] [Google Scholar]
  32. Sharmasarkar S.; Jaynes W. F.; Vance G. F. BTEX sorption by montmorillonite organo-clays: TMPA, ADAM, HDTMA. Water, Air, Soil Pollut. 2000, 119, 257–273. 10.1023/A:1005167524630. [DOI] [Google Scholar]
  33. Marcal L.; Faria E. H.; Nassar E. J.; Trujillano R.; Martín N.; Vincente M. G.; Rives V.; Gil A.; Korili S. A.; Ciuffi K. J. Organically Modified Saponites: SAXS Study of Swelling and Application in Caffeine Removal. ACS Appl. Mater. Interfaces 2015, 7, 10853–10862. 10.1021/acsami.5b01894. [DOI] [PubMed] [Google Scholar]
  34. Shen Y.-H. Phenol sorption by organoclays having different charge characteristics. Colloids Surf., A: Physicochem. Eng. Asp. 2004, 232, 143–149. 10.1016/j.colsurfa.2003.10.014. [DOI] [Google Scholar]
  35. Abbas A.; Sallam A. S.; Usman A. R. A.; Al-Wabel M. I. Organoclay-based nanoparticles from montmorillonite and natural clay deposits: Synthesis, characteristics, and application for MTBE removal. Appl. Clay Sci. 2017, 142, 21–29. 10.1016/j.clay.2016.11.028. [DOI] [Google Scholar]
  36. Mortland M. M.; Shaobai S.; Boyd S. A. Clay-Organic Complexes As Adsorbents For Phenol And Chlorophenols. Clays Clay Miner. 1986, 34, 581–585. 10.1346/CCMN.1986.0340512. [DOI] [Google Scholar]
  37. Okada T.; Yoshida T.; Iiyama T. Kinetics of Interlayer Expansion of a Layered Silicate Driven by Caffeine Intercalation in the Water Phase Using Transmission X-ray Diffraction. J. Phys. Chem. B 2017, 121, 6919–6925. 10.1021/acs.jpcb.7b03200. [DOI] [PubMed] [Google Scholar]
  38. Yuyama S.; Kaneko H. Correlation between the Metal and Organic Components, Structure Property, and Gas-Adsorption Capacity of Metal–Organic Frameworks. J. Chem. Inf. Model. 2021, 61, 5785–5792. 10.1021/acs.jcim.1c01205. [DOI] [PubMed] [Google Scholar]
  39. Wang M.; Xu Q.; Tang H.; Jiang J. Machine Learning-Enabled Prediction and High-Throughput Screening of Polymer Membranes for Pervaporation Separation. ACS Appl. Mater. Interfaces 2022, 14, 8427–8436. 10.1021/acsami.1c22886. [DOI] [PubMed] [Google Scholar]
  40. Pardakhti M.; Moharreri E.; Wanik D.; Suib S. L.; Srivastava R. Machine Learning Using Combined Structural and Chemical Descriptors for Prediction of Methane Adsorption Performance of Metal Organic Frameworks (MOFs). ACS Comb. Sci. 2017, 19, 640–645. 10.1021/acscombsci.7b00056. [DOI] [PubMed] [Google Scholar]
  41. Zhu X.; Wan Z.; Tsang D. C. W.; He M.; Hou D.; Su Z.; Shang J. Machine learning for the selection of carbon-based materials for tetracycline and sulfamethoxazole adsorption. Chem. Eng. J. 2021, 406, 126782 10.1016/j.cej.2020.126782. [DOI] [Google Scholar]
  42. Mitchell M.; Muftakhidinov B.; Winchen T.; Wilms A.; Schaik B.. Engauge Digitizer Software. http://markummitchell.github.io/engauge-digitizer, Last Accessed: June 2, 2022.
  43. Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  44. Akiba T.; Sano S.; Yanase T.; Ohta T.; Koyama M.. Optuna: A Next-generation Hyperparameter Optimization Framework. In KDD.
  45. Landrum G.RDKit: Open-Source Cheminformatics Software. https://www.rdkit.org/.
  46. https://www.rdkit.org/docs/source/rdkit.Chem.Descriptors.html#rdkit.Chem.Descriptors.ExactMolWt (accessed October 12, 2022).
  47. Zhao Q.; Burns S. E. Modeling Sorption and Diffusion of Organic Sorbate in Hexadecyltrimethylammonium-Modified Clay Nanopores – A Molecular Dynamics Simulation Study. Environ. Sci. Technol. 2013, 47, 2769–2776. 10.1021/es3045482. [DOI] [PubMed] [Google Scholar]
  48. Zhou Q.; Shen W.; Zhu J.; Zhu R.; He H.; Zhou J.; Yuan P. Structure and dynamic properties of water saturated CTMA-montmorillonite: molecular dynamics simulations. Appl. Clay Sci. 2014, 97-98, 62–71. 10.1016/j.clay.2014.05.029. [DOI] [Google Scholar]
  49. Aguiar K. L. N. P.; Pereira K. A. B.; Mendes M. S. L.; Pedroni L. G.; Oliveira P. F.; Mansur C. R. E. Study of the modification of bentonite for the formation of nanocomposite hydrogels with potential applicability in conformance control. J. Pet. Sci. Eng. 2020, 195, 107600 10.1016/j.petrol.2020.107600. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c06602_si_001.pdf (62.1KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES