Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Dec 30;39(1):119–128. doi: 10.1021/acs.langmuir.2c02281

A Systematic Search for the Adsorption Motif of All Stereoisomers of Propylene Glycol on a Palladium(111) Surface for Fuel Cell Applications

Michael Gonzalez 1, Michael N Groves 1,*
PMCID: PMC9835992  PMID: 36583559

Abstract

graphic file with name la2c02281_0007.jpg

Small organic molecules have been shown to produce sufficient power densities allowing them to be environmentally friendly renewable fuel sources and an important part of fuel cell research. Affiliated experimental work found propylene glycol, as a source of renewable fuel, produces viable power densities when utilized with an alkaline-acid fuel cell and a Pd(111) catalyst. There is limited theoretical work on propylene glycol’s energy reaction pathway. Thus, the first step in understanding how propylene glycol reacts with the Pd(111) slab is understanding its adsorption. In this paper, we present the investigation of adsorption potential energies (APE) of propylene glycol stereoisomers (S)-propane-1,2-diol (1,2PGS), (R)-propane-1,2-diol (1,2PGR), and propane-1,3-diol (1,3PG) on Pd(111). The isomers are systematically scanned through different configurations to analyze the preferred stable orientation and positional motifs. Density functional theory (DFT) is used to optimize the molecular geometries and surface relaxations. The most stable configuration of the 1,2PG stereoisomers resulted in an APE of −0.97 eV. The most stable configuration of the 1,3PG resulted in an APE of −1.19 eV. Both the 1,2PG(S/R) and 1,3PG isomers favor a motif in which at least one hydroxyl oxygen atom interacts with the surface of the Pd(111) catalyst. The 1,2PG carbon backbone prefers to have the center carbon positioned away from the slab, while the 1,3PG prefers to have the center carbon positioned closer to the slab. The most stable 1,3PG differs from other reported 1,3PG and 1,2PG relaxed configurations in that both of the hydroxyl oxygen atoms interact with the Pd(111) surface. These results show more favorable APEs than previously reported calculations. This paper will discuss in detail the differences between the hydroxyl group motifs and their role in affecting adsorption.

Introduction

Due to global warming and its environmental dangers,1 efforts to mediate our carbon footprint have become a central scientific issue. Fossil fuels have been the primary focus of regulation, and mediation efforts to combat the hazardous effects of greenhouse gases, such as CO2, are beginning to come into effect. For example, some sustainability efforts focus on creating efficient methods to increase the capture and conversion of CO2 emissions.2,3 Other approaches focus on systematically decreasing the consumption of alternative fossil-fuel-dependent energy resources, such as hydrogen and ammonia.4 In comparison to coal, natural gas does work as a more sustainable source of energy but still produces moderate greenhouse gas emissions and is expensive to produce.5 As sustainability efforts in how fossil fuels are obtained and captured diversify, efforts to develop sustainable fuel resources that can replace fossil fuels have as well. As a promising sustainable method of producing energy, fuel cells have been growing in interest. This is because fuel cells, utilizing metal-catalysis, can produce consistent energy with very low greenhouse gas emissions. Fuel cells also allow for the utilization of diverse metal-catalyst materials and fuel sources. Despite this diversity and to make fuel cells practical, more research into metal-catalysts and environmentally friendly fuel sources is required to increase energy transfer and storage.6−12

Research into small organic molecules as a sustainable source of fuel cell energy has been growing in interest.13 Methanol, an extensively researched alcohol, has been shown to produce power densities of 135.1 mW cm–2 at 80 °C with Pd–Ag supported on carbon nanotubes, 31 mW cm–2 at 90 °C with alkaline-doped polybenzimidazole membrane direct methanol fuel cells (APM-DMFC), and 5.5 mW cm–2 at 50 °C with anion exchange membrane–direct methanol fuel cells (AEM-DMFC).14,15 The two-carbon alcohol ethanol showed power densities of 60 mW cm–2 at 90 °C with direct ethanol fuel cells (DEFC) and 202.3 mW cm–2 at 80 °C with Pd–Ag supported on carbon nanotubes.14,16 Although methanol and ethanol show viable applications as small renewable energy molecules, they both contain corresponding challenges. Methanol is toxic, volatile, and highly flammable.17 Ethanol’s carbon–carbon bonds become challenging to break at low temperatures and produce low electron transfer rates as well as suffering from a low oxidation reaction rate. Both of these problems affect efficiency.15,16 On the basis of these issues, interest in longer chain polyalcohols has been increasing as they are found to produce viable power densities, have higher boiling points and high specific energy, and can be manufactured using environmentally safe and renewable methods.18,19

Cellulose, located in plant cell walls, is renewable biomass that has been used to synthesize ethylene glycol as well as other polyalcohols.20 Ethylene glycol utilized in anion-exchange membrane direct ethylene glycol fuel cells (AEM-DEGFC) has been shown to produce maximum power densities of 67 mW cm–2 at 60 °C.15 Other research shows ethylene glycol in an APM-DEGFC reaches power density peaks of 80 mW cm–2 at 60 °C, 112 mW cm–2 at 90 °C, and 245.2 mW cm–2 80 °C when catalyzed with Pd–Ag carbon nanotubes.14,16,21 Glycerol is a byproduct of biodiesel production that could potentially be used as a renewable fuel source.22 Glycerol has shown power densities of 276.2 mW cm–2 at 80 °C with Pd–Ag carbon nanotubes and 275 mW cm–2 at 60 °C with direct liquid fuel cells.16,21 The extent of potential biofuels is not limited to those we have described thus far. However, it is important to exemplify the potential benefits of diversifying our options for renewable fuels. This field of research would accelerate if the reaction pathways were better understood. Adsorption of these organic molecules onto the catalyst would be an important first step in understanding the reaction pathway.

Propylene glycol (PG) or propanediol is a renewable biofuel that has received increased interest. The central carbon of propane-1,2-diol (1,2PG) is chiral with two enantiomers: (S)-propane-1,2-diol (1,2PGS) and (R)-propane-1,2-diol (1,2PGR). Additionally, the central OH group can also be on the 3 carbon position, resulting in a third stereoisomer propane-1,3-diol (1,3PG). For example, the use of 1,2PG in a Pd-CeO2/C direct polyalcohol fuel cell (DPFC) at 60 °C produced a power density of 45.2 mW cm–2.18 More recent experimental data by Haan et al. show the 1,2PGS and 1,2PGR enantiomers produce similar power densities of 64 mW cm–2 at 60 °C with a Pd black cathode. Although the 1,2PGS and 1,2PGR showed to produce similar power densities, the 1,3PG produced a higher power density of 103 mW cm–2 under the same conditions.21 The difference in power densities on the Pd anode catalysts demonstrates that there is a clear distinction between the 1,3PG and 1,2PG(R/S) isomers in terms of efficiency. Thus, investigating how propylene glycol theoretically adsorbs onto a catalyst could help us better understand its reaction pathway and the interactions of other renewable biofuels.

A density functional theory (DFT) investigation by Garcia-Muelas et al. sought to understand the relationship between several polyalcohols and their adsorption to Pd(111) and Pt(111) slabs to create a multifactorial linear-scaling relationship. Within their systematic investigation, they reported absorbance potential energies (APE) for both the 1,2PGS (−0.711 eV) and 1,3PG (−0.851 eV) on a Pd(111) surface.23 Previously we discussed how the experimental data by Chinoet al. revealed the 1,3PG to produce a higher power density than the 1,2PG. This higher power density could be linked to the increased APE of the 1,3PG, similar to how volcano plots24−28 based on the Brønsted–Evans–Polanyi principle29,30 have linked the APE of one of the reaction intermediates to the catalytic activity of a given process. The Garcia-Muelas et al. 1,3PG and 1,2PG display very similar geometric configurations in which the hydroxyl functional groups follow very similar adsorption motifs yet have distinct APEs. It could be assumed that similar molecules with very similar adsorption motifs would produce similar APEs and, via the previously stated Brønsted–Evans–Polanyi principle, produce the same catalytic activity. Garcia-Muelas et al. explain this by suggesting the carbon backbone’s van der Waals (VdW) interactions influence the adsorption geometry for the PG isomers affecting the overall APE. Although literature supports this claim, later discussed in more detail, the similarities between the Garcia-Muelas et al. 1,3PG and 1,2PG adsorption geometries and vdW effects could be further investigated to better understand why there is a distinct difference in APE. Furthermore, the Garcia-Muelas et al. investigation explored the (S) 1,2PG stereoisomer only and not the (R) stereoisomer, justifying a PG-specific systematic inquiry into the adsorption potential energies and adsorption geometries of the 1,3PG and both 1,2PG stereoisomers on a Pd(111) surface.

In this paper, we present the results of a systematic DFT search of the adsorption potential energies with respect to heterogeneous catalysis between Pd(111) and the three stereoisomers of PG: (S)-propane-1,2-diol, (R)-propane-1,2-diol, and propane-1,3-diol. Our search has revealed a new adsorption geometry for all three stereoisomers, which is more favorable than previously published results. We present important distances between the PG molecule and Pd(111) catalyst as well as present an electron density difference plot (EDDP) to interpret our results. Understanding how polyalcohols adsorb on catalyst surfaces is an important first step in explaining electrochemical experimental data for PG as well as other polyalcohols.

Methods

Density Functional Theory (DFT)

DFT calculations were used to scan all three PG stereoisomers over a Pd(111) slab and optimize the geometries identified as potential energy surface minima. GPAW, an open source, real space, Python-based DFT code,31,32 was used for all calculations and was supported by the atomic simulation environment (ASE).33 The PBE exchange-correlation functional34 was used, and the Tkatchenko–Scheffler surface van der Waals correction35,36 was utilized to calculate the missing van der Waals interactions. The finite difference mode was used to decide arrangements for the Laplacian operator in the Kohn–Sham and Poisson equations, and the grid spacing in all three directions was less than 0.1740 Å. All 1,2PG and 1,3PG configurations were initially scanned over a 4 × 4 × 2 Pd(111) slabs using only the gamma point for 4 steps. Potential energy minima identified from these initial scans were then relaxed to a maximum force cutoff of 0.05 eV/Å. An energy cutoff of 0.15 eV from the most stable configuration of each isomer was used to select preliminary relaxed configurations to be relaxed with the final calculation parameters. The final calculations presented in this work were relaxed on 4 × 4 × 4 Pd slabs with the bottom layer held fixed to bulk positions using a 2 × 2 × 1 k-point mesh on a Monkhorst–Pack grid with an energy cutoff of 0.02 eV/Å. All atom bond distances are relative to the nearest palladium atom (Å).

Adsorption potential energies (APE) will be expressed in eV and are calculated via the formula

graphic file with name la2c02281_m001.jpg 1

When comparing our calculated results with those from the literature, all literature APE data were converted to eV and made negative to be consistent with eq 1.

Molecular Configuration

1,2PG

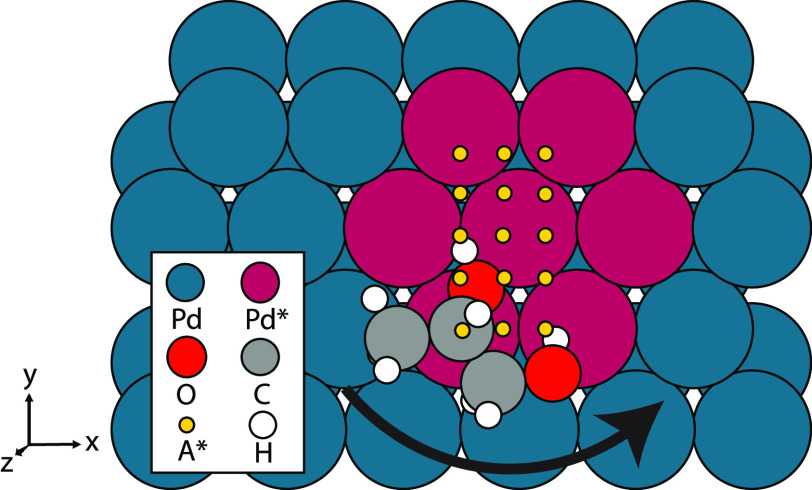
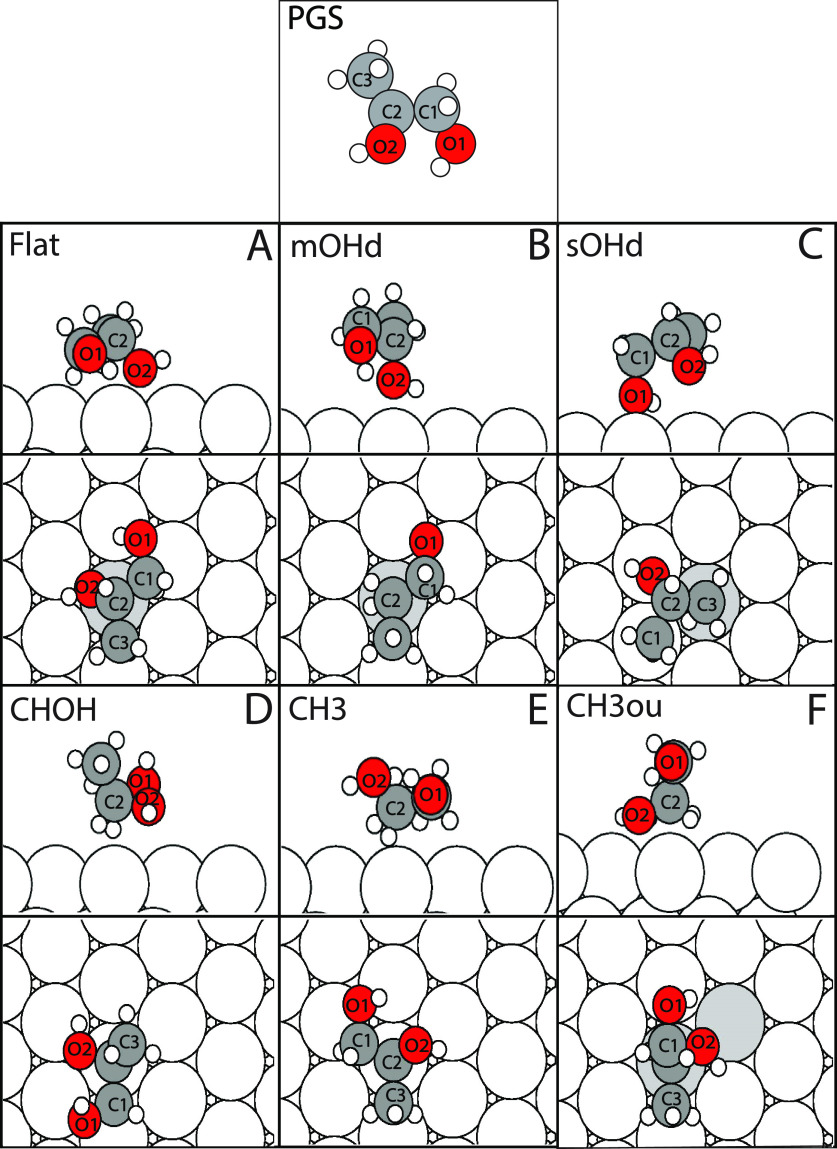
The three PG molecules are scanned across several positions along the slab (Figure 1) and oriented in several different configurations (Figures 2 and 3). These configurations are categorized via their common prerelaxation orientations and thereafter are allowed to relax freely. The 1,2PG stereoisomers are set on the slab in six different configurations, as observed in Figure 2. Atoms in Figure 2 are labeled beginning from the terminal hydroxyl group (C1, O1, and H1) and ending with the methyl group (C3). During these six configurations, the O2–C2–C1–O1 dihedral angle (also depicted in Figure 2) was rotated 0°, 90°, 180°, and 270°. The molecule was also translated vertically to the next equivalent Pd atom using five steps, translated horizontally to the next equivalent Pd atom using three steps, and turned counterclockwise at angles 0°, 20°, and 40° parallel to the slab, using C2 as the reference of movement (Figure 1). After the scan was complete, a numerical first derivative test was performed on every degree of freedom for each configuration. If the first-derivative test concluded that every degree of freedom was a minimum, then the configuration was deemed to be a minimum in the potential energy surface and was fully relaxed using the parameters above.

Figure 1.

Figure 1

Open in a new tab

Representation of molecule movement (yellow circles) along the Pd(111) slab (blue). Representative area of movement (purple). Molecules are rotated 0°, 20°, and 40° counterclockwise around the z-axis (out of the page) at every position. Pd atoms are represented in blue, Pd atoms in the area of movement are in purple, C atoms are gray, O atoms are red, and H atoms are white.

Figure 2.

Figure 2

Open in a new tab

Six different initial template adsorption geometries used for 1,2PG. These molecules were translated and rotated around the surface of the slab. The O2–C2–C1–O1 dihedral angle was rotated at angles 0°, 90°, 180°, and 270°.

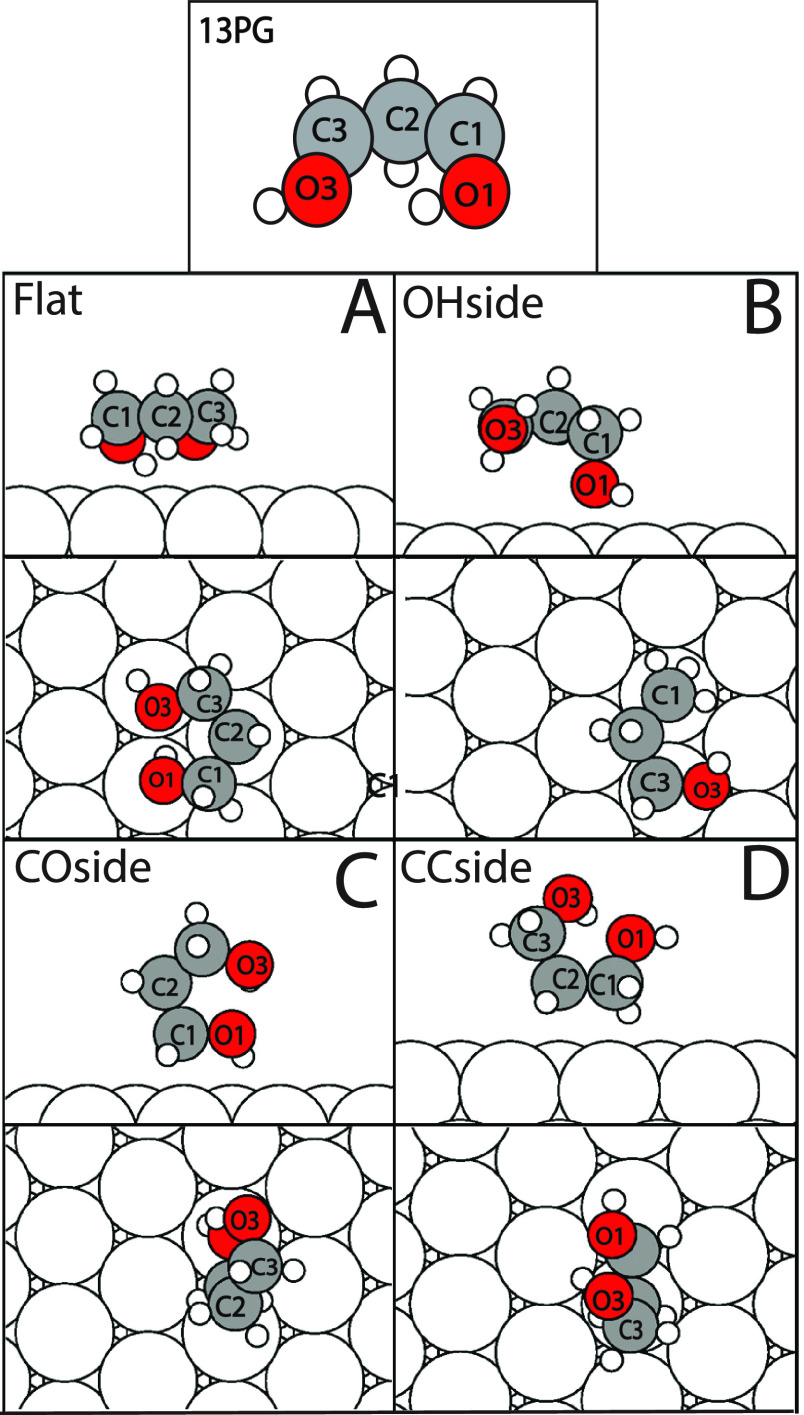
Figure 3.

Figure 3

Open in a new tab

Four different initial template adsorption geometries used for 1,3PG. These molecules were translated and rotated around the surfaces of the slab. O3–C3–C2–C1 and O1–C1–C2–C3 dihedral angles were rotated at angles 0°, 90°, 180°, and 270°. The closest oxygen atom is depicted as O1, and the remaining atoms are respective to it.

The first configuration for the 1,2PG stereoisomers is the flat orientation in which the carbon backbone is parallel with the slab (Figure 2A). When creating the mOHd configurations for the scan described above, the center chiral carbon hydroxyl group (atom O2) is initially oriented toward the Pd slab (Figure 2B). When creating the sOHd configurations, the side carbon with the hydroxyl group (atom O1) is initially oriented toward the Pd slab (Figure 2C) as the molecule is modified and translated according to the description of the scan. When creating the CHOH configurations, the C–O bond (atoms C2–O2) is initially oriented such that it are parallel with the Pd slab (Figure 2D). For the CH3 configurations the bond between atoms C2–C3 is initially oriented so that it are parallel with the Pd slab while the molecule is rotated and translated across the surface (Figure 2E). Finally, for the CH3ou configuration, the bond between the central carbon (C2) and hydroxyl carbon (C1) is initially oriented to be perpendicular to the Pd slab (Figure 2F) while the molecule is changed according to the scan rules presented previously.

1,3PG

The 1,3PG utilized four different configurations to strategically optimize the molecules as depicted in Figure 3. Because the 1,3PG is symmetric, the oxygen atom that is closest to a Pd(111) atom is defined as O1 while the further oxygen atom is defined as O3. During these 4 configurations the O3–C3–C2–C1 dihedral angle was rotated 0°, 90°, 180°, and 270°, and a second O1–C1–C2–C3 dihedral angle was rotated 0°, 90°, 180°, and 270°. The molecule is also translated to the next equivalent Pd atom vertically using five steps, translated to the next equivalent Pd atom horizontally using three steps, and turned counterclockwise at angles 0°, 20°, and 40° parallel to the slab using C2 as a reference of movement.

The first 1,3PG configuration has the carbon backbone set parallel with the slab (Figure 3A). The OHdown configuration mimicked the Flat configuration, except one of the hydroxyl groups (C1–O1) is initially oriented to be set perpendicular to the slab (Figure 3B). The COside configuration sets the carbon–oxygen bond (C1–O1) to be initially parallel with the slab (Figure 3C) while the molecule is translated and rotated and the dihedral angles are rotated. Finally, the CCside configuration has one carbon–carbon bond (C2–C1) parallel with the slab (Figure 3D) while the molecule is modified according to the strategy outlined above.

Results and Discussion

1,2PG

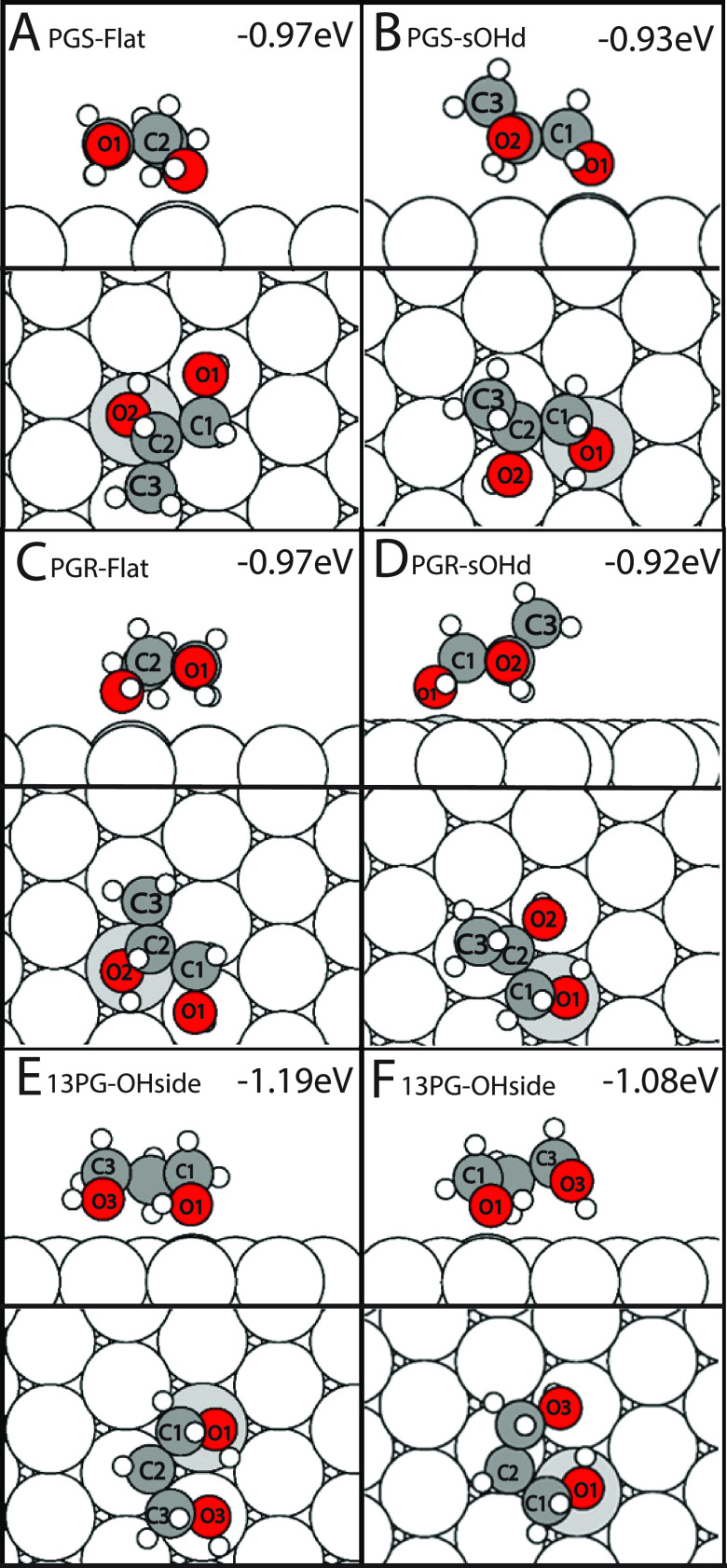
The most favorable configuration for both the PGS and PGR stereoisomers is the Flat configuration in which the carbon backbone is parallel to the slab. The two stereoisomers, illustrated in Figure 4A,C, are shown to be exact mirror images of each other with the hydroxyl groups oriented closer to the slab than the carbon backbone. These leading PGS and PGR configurations show that the hydroxyl group (O2–H2) bound to the chiral carbon (C2) prefers to be closer to the slab (2.322 and 2.328 Å, respectively) than the terminal hydroxyl group (O1) (3.247 and 3.251 Å, respectively). These and other distances between the nearest Pd atom and the specified atoms in the leading 1,2PG can be found in Table 1. The relaxed 1,2PG isomers also exhibit motifs in which the oxygen atom bound to the chiral carbon atom (O2) is positioned on top of a Pd(111) atom, and the hydroxyl bond (O2–H2) is oriented parallel to the slab and toward the direction of the terminal hydroxyl oxygen atom (O1). The terminal hydroxyl group (O1–H1) is oriented so that H1 (2.379 and 2.37 Å, S/R respectively) is closer to the slab than H2 (2.614 and 2.624 Å, S/R respectively) of the hydroxyl group bound to the chiral carbon atom (C2). The PGS resulted in an APE of −0.97 eV, while the PGR enantiomer resulted in an APE of −0.967 eV. The next PGS and PGR configurations (Figures 4B and 4D) are shown to follow similar hydroxyl group motifs as the leading 1,2PG; however, the roles of the hydroxyl groups are reversed. The terminal hydroxyl group (O1–H1) is closer, parallel to the slab, and oriented toward the oxygen atom bound to the chiral carbon atom (O2–H2). The hydroxyl group bound to the chiral carbon atom is now oriented, so its hydrogen bond (O2–H2) is toward the nearest Pd(111) atom. This configuration also positions the hydroxyl groups to be on top of the nearest Pd(111) atom, as the leading 1,2PG did. More importantly, compared to the Flat orientation, the carbon backbone is oriented to have C3 raised away from the slab. These PGS and PGR configurations resulted in an APE of −0.928 and −0.92 eV, respectively.

Figure 4.

Figure 4

Open in a new tab

Most favorable binding energies for PGS (A, B), PGR (C, D), and 1,3PG (E, F) calculated in this work.

Table 1. Distances between the Nearest Pd Atom and the Specified Atoms in 1,2PG and 1,3PG Both from This Work and Atoms from the Configurations Reported by Garcia-Muelas et al.23 Relaxed in Our Environment.

  atom–Pd bond distances (Å)
molecule 1,3PG (lead) 1,3PG (second) Garcia-Muelas23 1,3PG
C1 3.368 3.284 3.261
C2 3.261 3.267 3.41
lowest H on C2 2.172 2.213 2.377
C3 3.519 3.823 3.861
O1 2.368 2.291 2.276
H on O1 2.659 2.708 2.681
O3 2.577 3.209 3.272
H on O3 2.773 2.43 2.417
  atom–Pd bond distances (Å)
molecule PGS (lead) PGR (lead) Garcia-Muelas23 1,2PG
C1 3.522 3.523 4.118
C2 3.384 3.372 3.207
H on C2 4.283 4.28 2.171
C3 3.389 3.344 3.768
O1 3.247 3.251 3.301
H on O1 2.379 2.36 2.658
O2 2.322 2.328 2.34
H on O2 2.614 2.624 2.658
Open in a new tab

1,3PG

The most favorable configuration of the 1,3PG isomer has an APE of −1.19 eV and is illustrated in Figure 4E. Illustrated in the side view of Figure 4E, the molecule’s orientation positions both O1 (2.368 Å) and O3 (2.577 Å) closer to the slab while the carbon backbone (C1: 3.368 Å; C2: 3.261 Å; C3: 3.519 Å) is further away. Both hydroxyl groups also follow a motif in which the oxygen atom is positioned on top of the Pd(111) atom and oriented, so the hydrogen bond is parallel to the slab. These and other distances between the nearest Pd atom and the specified atoms in 1,3PG can be found in Table 1. The carbon backbone is tilted so that the center carbon (C2) is slightly lower than the other adjacent carbons. The second leading 1,3PG configuration, with an APE of −1.08 eV, had the O1–H1 hydroxyl group (2.291 Å) positioned on top and closer to the slab than the hydroxyl group O3–H3 oxygen atom (2.43 Å) and oriented the hydrogen bond toward the O3–H3 hydroxyl group. The O3–H3 hydroxyl group oriented its hydrogen bond toward the nearest Pd(111), similarly to the 1,2PG. This configuration’s carbon backbone is tilted so that C3 (3.823 Å) is farther from the slab than the leading configuration, with a 0.304 Å difference.

Existing adsorption research demonstrates that different characteristics influence how a molecule adsorbs onto a catalyst surface, such as van der Waals forces, molecular tilting, molecule–slab distance, molecular geometry, and interacting functional groups.37−43 From these characteristics, theoretical van der Waals and functional group–slab interactions have been shown to be important in producing more accurate DFT calculations. This becomes more prevalent when calculating the adsorption of the conjugated, extended carbon chain, or conjugated and extended carbon chain systems. The exclusion or inclusion of van der Waals interactions has shown even to change whether a molecule chemisorbs (chemical bond) or physisorbs (intermolecular forces).44 For example, DFT adsorption research (with and without van der Waals corrections) of increasing carbon length alkanethiols on Au(111) showed to calculate more stable APEs when van der Waals corrections are included in the optimizations, and as the number of carbons in the alkanethiol molecule increased, the APE would also increase. The research also sought to compare the differences between the physisorption of the intermolecular forces and the chemisorption of the thiol group. These results showed the alkanethiol preferred to chemisorb via the sulfur–Au(111) interaction, but its intermolecular forces are responsible for the molecule’s flat configuration to the slab.45 The results shown in this example reflect a common motif found in the adsorption of many other molecules on the metal catalyst. More related to our research, the adsorption of different larger conjugated and aromatic alcohols on Pd(111) catalysts also show to chemisorb via the hydroxyl oxygen atom and are influenced by van der Waals forces that promote larger molecule–slab surface attractions. Guaiacol and phenol are aromatic alcohols that show to adsorb similarly on Pd(111) surfaces. The research found that both molecules would primarily chemisorb on Pd(111) via their hydroxyl group, but van der Waals interactions were responsible for their flat configuration, similar to the alkanethiols.46,47 These examples help illustrate how various characteristics allow for complex adsorption motifs and impact theoretical optimizations. A better understanding of how these molecules adsorb could allude to how the full reaction pathway occurs and help guide further research, improving our use of renewable biofuels.48

As stated previously, methanol is an extensively researched alcohol for renewable biofuel. As the smallest alcohol, methanol is calculated to have an APE ranging from −0.3 to −0.472 eV depending on the computational model and metal utilized.23,49−52 As another potential renewable biofuel, ethanol is calculated to have an APE of −0.507 and −0.563 eV depending on the computational model and metal utilized.23,53 In approaching similarities to PG, ethylene glycol (EG) contains one fewer carbon than PG but has the same number of hydroxyl groups. Adsorption research on EG found that when bound to Pd(111), the adsorption energy was −0.528 eV.52 The previously discussed guaiacol and phenols showed to be highly influenced due to the conjugation, but small carbon chain alcohols do not have the same extended systems. Thus, as the ratio of hydroxyl groups to carbon chain length shifts, it becomes less apparent which forces have a stronger influence. Although van der Waals forces still have an influence on the adsorption of small alcohols, research shows that hydroxyl groups prioritize hydroxyl–slab bonding. As the smallest possible alcohol, methanol adsorbs on top of a Pd(111) via the oxygen lone pair and orients its hydrogen bond to be parallel to the surface. This preference of the hydroxyl group forces the adjacent methyl group to be oriented farther away from the surface but shows to interact, albeit very weak.52,54 Ethanol adsorption on Pd(111) continues to follow similar motifs as methanol. The adsorption prioritizes the hydroxyl oxygen atom to be on top of the Pd(111) atom while the carbon chain is forced to adjust further away from the slab. The hydrogen bond of the hydroxyl group is oriented to be parallel to the slab.53,55,56 Ethylene glycol, containing two hydroxyl groups, showed to adsorb similarly to methanol and ethanol on Pd(111) via one of the hydroxyl oxygen atoms. However, the other hydroxyl group showed to adsorb with its hydrogen bond toward the nearest Pd(111) and with the carbon chain weakly interacting.23,56 These examples reflect a common motif for small alcohols that prioritizes the adsorption of one or more hydroxyl groups than the intermolecular forces of the carbon backbone.23,57,58 Complexities such as chiral centers59 and distances between one hydroxyl group to the next hydroxyl group further complicate how alcohols adsorb. Despite these complications, they still show similar adsorption motifs as seen with propylene glycol’s three isomers.23,60

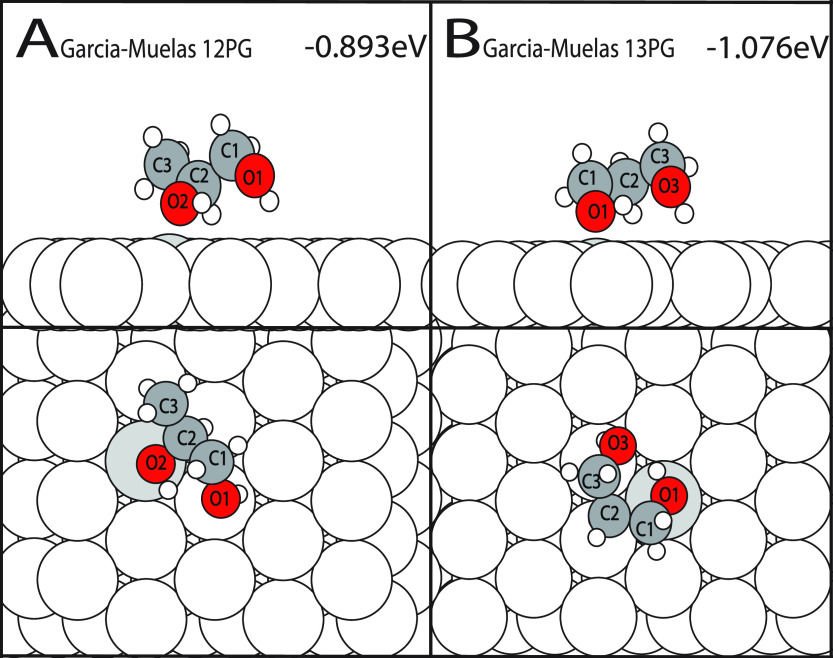
Computational work by Garcia-Muelas et al. investigated the adsorption PG on Pd(111) utilizing the B3LYP exchange-correlation functional and 6-311++g (2d,2p) basis set for molecule gas-phase optimizations. After the gas-phase optimizations, the PBE exchange-correlation functional and Grimme’s DFT-D2 van der Waals correction were used for surface relaxations and APE calculations. Their investigation found that 1,2PG exhibits an APE of −0.73 eV while the 1,3PG exhibits an APE of −0.875 eV.23 To make a direct comparison between their results and the results presented in this work, the 1,2PG and 1,3PG configurations from their paper were replicated and calculated in our environment. The resulting APE was −0.893 eV for the 1,2PG and −1.076 eV for the 1,3PG. These replicated configurations resulted in a 0.077 eV (S/R 1,2-PG) and 0.114 eV (1,3PG) less stable APE than our most favorable configurations (shown in Figure 5A,B). This indicates that the scan conducted as a part of this work has potentially identified a more stable adsorption motif for 1,2PG and 1,3PG that, to the author’s knowledge, has yet to be reported.

Figure 5.

Figure 5

Open in a new tab

APE from the Garcia-Muelas et al. 1,2PG and 1,3PG configurations calculated in this work’s environment. (A) illustrates the fully relaxed 1,2PG, while (B) illustrates the fully relaxed 1,3PG.

Garcia-Muelas et al. also utilized experimentally determined temperature-programmed desorption (TPD)61 data to calculate approximate experimental APEs via the Redhead equation.62 For 1,2PG, they reported an APE based on TPD data of −0.861 eV. A 0.131 eV difference between their computational results and the TPD determined results is remarkable. Our DFT determined result is more favorable than the TPD derived value by 0.109 eV, which also suggests that our result for 1,2PG is consistent with experiment.

1,2PG Motif

Our results showed very common motifs among all three stereoisomers in how the hydroxyl groups are positioned and oriented relative to the slab. Notably, because the 1,2PG(s) and 1,2PG(R) showed to adsorb the same and produce the same APE, they will be termed 1,2PG. The first and second most stable 1,2PG illustrated in Figure 4A,B shows the hydroxyl group closest to the slab is positioned on top of a Pd(111) atom and the O–H bond is oriented away toward the other corresponding group. That same corresponding hydroxyl group orients its hydrogen bond toward the nearest Pd(111) atom. Although both the first and second most stable 1,2PG molecules share similar hydroxyl adsorption motifs, their carbon backbones are oriented differently and could be the reason for the difference in overall APE. The leading 1,2PG’s Flat configuration allowed the chiral hydroxyl group to adsorb the closest, while the sOHd configuration resulted in the terminal hydroxyl being the closest interacting group. The previously mentioned Garcia-Muelas et al. PG adsorption study maintains similar hydroxyl group motifs as our leading 1,2PG configurations,23 adsorbing via the chiral hydroxyl group. Although the hydroxyl groups contained similar motifs, our 1,2PG configurations showed the previously mentioned 0.077 eV difference in APE. In order to understand the 0.077 eV difference, we investigated the distances between individual atoms in our leading 1,2PG configurations and those of Garcia-Muelas et al. It is important to reiterate that the Garcia-Muelas et al. configuration’s original APEs and atom to Pd(111) distances were calculated via the PBE functional and Grimme’s DFT-D2 vdW correction. Thus, the difference in their original APEs for 1,2PG (−0.73 eV) and 1,3PG (−0.875 eV) could be due to different VdW corrections. This difference in method is why we relaxed the Garcia-Muelas et al. 1,2PG and 1,3PG configurations in our environment. Figure 4B illustrates an example where the second leading 1,2PG chiral hydrogen (H2) is positioned close to the slab. The carbon backbone is oriented to accommodate the adsorption of both hydroxyl groups, resulting in having C3 further away from the slab. In Garcia-Muelas et al.’s 1,2PG, the same characteristic results in positioning C1 and C3 further away from the slab, imitating a “V”-like shape. Our leading 1,2PG configuration (Figure 4A) instead has the chiral hydrogen (H2) away from the surface and results in a configuration in which the carbon backbone is parallel to the surface. Despite containing different carbon backbone adsorption orientations and APEs, the leading configurations of our 1,2PG and those of Garcia-Muelas show the hydroxyl groups are primarily responsible for the adsorption to the Pd(111) surface. These differences in APEs could then be attributed to the carbon backbone-dependent van der Waals interactions with the Pd(111) surface.

1,3PG Motif

The hydroxyl group O1 of the second most stable 1,3PG configuration reflects the same motif as our previously mentioned 1,2PG (Figure 4F). Because of the 1,3PG’s symmetry, it is inferred the other hydroxyl group (O3) has the same APE capabilities as the O1 hydroxyl group. Our second leading 1,3PG (−1.08 eV) and Garcia-Muelas et al.’s leading 1,3PG (−1.076 eV) showed to have very similar adsorption motifs. In both configurations, the hydroxyl oxygen (O1) closest to the slab adsorbs on top of a Pd(111) atom while the further hydroxyl oxygen (O3) orients its hydrogen bond toward the nearest Pd(111) atom. Although our second most stable 1,3PG found similarities with the Garcia-Muelas et al. 1,3PG configuration, our most stable 1,3PG and most stable overall configuration showed a different hydroxyl group motif and a 0.11 eV more stable APE. The O1 and O3 of the leading 1,3PG maintain an average 0.302 Å distance closer to the nearest Pd atom than O1 and O3 of the Garcia-Muelas et al. 1,3PG. Illustrated in Figure 4E, O1 and O3 are both shown to interact with a Pd(111) atom via their oxygen atoms on top and their hydrogen bonds parallel with the slab. This contrasts with the second most stable 1,3PG (Figure 4F) and the Garcia-Muelas leading 1,3PG (Figure 5B) in which only O1 appears to interact with a Pd(111) atom in this manner. The leading 1,3PG has both O1 and O3 hydroxyl groups oriented in the same direction, as illustrated in Figure 4E. A common characteristic that occurs in all 1,2PG and 1,3PG leading configurations is that the hydroxyl groups are placed over the Pd(111) atom, as shown in all of Figures 4 and 5. The most significant finding of both our and Garcia-Muelas’ investigations is that 1,3PG adsorbs more strongly to Pd(111) when compared to the 1,2PG isomer. The difference in APE between our leading 1,3PG and 1,2PG is 0.22 eV, while in Garcia-Muelas it is 0.18 eV. Garcia-Muelas suggests that the distance between one hydroxyl group and the next impedes on its adsorption due to geometric strain. For example, ethylene glycol and 1,2PG contain hydroxyl groups via neighboring carbons, while 1,3PG contains hydroxyl groups separated via a single carbon atom (C2). Because these compounds are shown to primarily absorb via the hydroxyl group and experience geometric strain, the carbon backbone is not going to interact with the surface as strongly. It is due to these effects that our leading 1,3PG shows to bind stronger to the surface than all other PG configurations discussed thus far. Our leading 1,3PG hydroxyl to hydroxyl distance allows the compound to be geometrically favorable to adsorb both hydroxyl oxygen atoms and can maximize van der Waals interactions, leading to a higher APE.

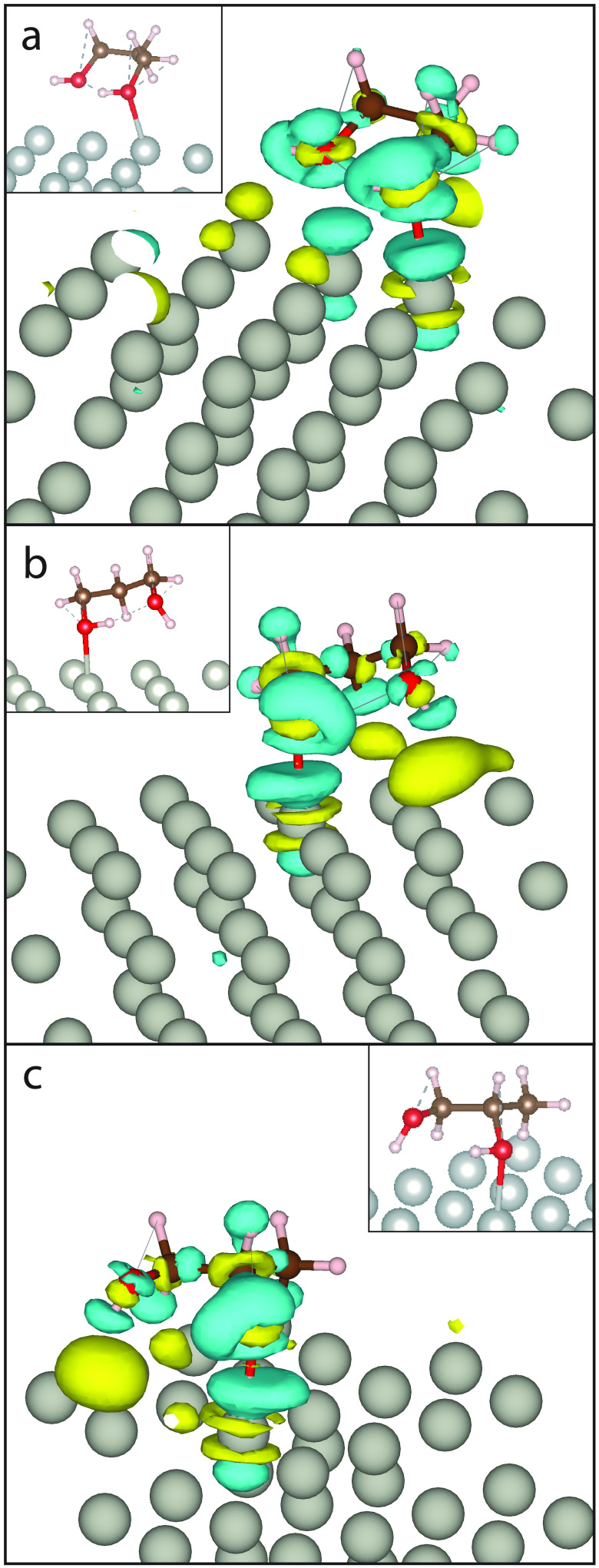
Electron Density Difference of PG

In both our model and that of Garcia-Muelas et al., the 1,3PG shows to be more strongly binding than the 1,2PG. Previous adsorption research shows methanol adsorbs to metal surfaces via oxygen’s lone pair.49,51 This could help explain why both our leading 1,2PG and 1,3PG configurations show to prioritize hydroxyl oxygen interaction with the Pd catalyst. In order to quantify the effect of oxygen–Pd interactions on the APE, we calculated the electron density difference of the leading 1,3PG, second leading 1,3PG, and 1,2PG (Figure 6) motifs with the Pd(111) surface. The EDDP of the 1,2PG in Figure 6c visually shows a stronger interaction of O2 with the corresponding Pd atom than O1 does with its corresponding Pd atom. The interacting O2 atom shows to donate electron density to the Pd atom, shown in blue. O1 of the 1,2PG does not show the same strong interaction due to the hydrogen atoms presence and its lack of donating electron density to the Pd atom. Our second leading 1,3PG (Figure 6b) shows to have a similar EDDP as the leading 1,2PG via how only one hydroxyl group donates electron density to the Pd slab. Our leading configuration (Figure 6a) shows both oxygen atoms contribute electron density to the Pd atom, which can be indicative to why it has a higher APE than the second leading 1,3PG and 1,2PG previously described. The APE and the EDDP of the 1,3PG, in comparison to the 1,2PG, shows that stereochemistry does seem to take a role in the adsorption of PG. The 1,2PG chiral center restricts the geometry of the molecule and thus limits the interaction with the slab. We previously described an example in Garcia-Muela’s chiral hydrogen (C–H2) and how its configuration affects the interaction. The 1,3PG’s geometry allows the oxygen atoms to interact with less restriction. Because 1,3PG’s symmetry allows for the oxygen atoms to orient indiscriminately, the probability of interacting in the same manner as our leading configuration is higher.

Figure 6.

Figure 6

Open in a new tab

Energy difference plot of leading configurations: (a) most stable 1,3PG, (b) second most stable 1,3PG, and (c) 1,2PG(S).

Conclusion

Our investigation revealed a new configuration for the adsorption of 1,2PG and 1,3PG on Pd(111). For the 1,2PG, both R and S stereoisomers showed to adsorb with an APE of −0.97 eV while the 1,3PG showed to adsorb via a APE of −1.19 eV. The adsorption of these alcohols and those found in the literature are shown to primarily adsorb via the hydroxyl functional group, as observed by the adsorption motifs and electron density difference plot. Geometric strain limits the 1,2PG’s ability to use both OH groups to bind to the surface while 1,3PG can better maximize molecule–surface interactions. The van der Waals forces have a secondary role in PG’s adsorbance and is affected by the geometric strain. Our results help give more theoretical insight as to why research shows the 1,3PG produces a higher power density than the 1,2PG.

Acknowledgments

The authors thank the Center for Computational and Applied Mathematics at California State University - Fullerton for providing the computational resources used in this project.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.langmuir.2c02281.

  • Atomic configurations of all reported structures (PDF)

  • Crystallographic data (ZIP)

The authors declare no competing financial interest.

Supplementary Material

la2c02281_si_002.pdf (102KB, pdf)
la2c02281_si_001.zip (16.1KB, zip)

References

  1. Gulland F. M.; Baker J. D.; Howe M.; LaBrecque E.; Leach L.; Moore S. E.; Reeves R. R.; Thomas P. O. A review of climate change effects on marine mammals in United States waters: Past predictions, observed impacts, current research and conservation imperatives. Clim. Change Eco. 2022, 3, 100054. 10.1016/j.ecochg.2022.100054. [DOI] [Google Scholar]
  2. Nagy T.; Mizsey P. Effect of Fossil Fuels on the Parameters of CO2 Capture. Environ. Sci. Technol. 2013, 47, 8948–8954. [DOI] [PubMed] [Google Scholar]
  3. Ma Z.; Legrand U.; Pahija E.; Tavares J. R.; Boffito D. C. From CO2 to Formic Acid Fuel Cells. Ind. Eng. Chem. Res. 2021, 60, 803–815. 10.1021/acs.iecr.0c04711. [DOI] [Google Scholar]
  4. Logan B. E. Ending Our Hydrogen and Ammonia Addiction to Fossil Fuels. Environ. Sci. Technol. Lett. 2019, 6, 257–258. 10.1021/acs.estlett.9b00188. [DOI] [Google Scholar]
  5. McKellar J. M.; Bergerson J. A.; MacLean H. L. Replacing Natural Gas in Alberta’s Oil Sands: Trade-Offs Associated with Alternative Fossil Fuels. Energy Fuels 2010, 24, 1687–1695. 10.1021/ef901036q. [DOI] [Google Scholar]
  6. Staff J. C. E. Batteries and fuel cells. J. Chem. Educ. 1978, 55, 399. 10.1021/ed055p399. [DOI] [Google Scholar]
  7. Föger K.; Ahmed K. Catalysis in High-Temperature Fuel Cells. J. Phys. Chem. B 2005, 109, 2149–2154. 10.1021/jp0490507. [DOI] [PubMed] [Google Scholar]
  8. Lomneth R.; Taylor C.; Wood-Black F.. Perspectives on Biofuels: Potential Benefits and Possible Pitfalls; Chapter 1, pp 1–8. [Google Scholar]
  9. Kaker B.; Hribernik S.; Mohan T.; Kargl R.; Stana Kleinschek K.; Pavlica E.; Kreta A.; Bratina G.; Lue S. J.; Božič M. Novel Chitosan–Mg(OH)2-Based Nanocomposite Membranes for Direct Alkaline Ethanol Fuel Cells. ACS Sustainable Chem. Eng. 2019, 7, 19356–19368. 10.1021/acssuschemeng.9b02888. [DOI] [Google Scholar]
  10. Huang L.; Zaman S.; Tian X.; Wang Z.; Fang W.; Xia B. Y. Advanced Platinum-Based Oxygen Reduction Electrocatalysts for Fuel Cells. Acc. Chem. Res. 2021, 54, 311–322. 10.1021/acs.accounts.0c00488. [DOI] [PubMed] [Google Scholar]
  11. Rabis A.; Rodriguez P.; Schmidt T. J. Electrocatalysis for Polymer Electrolyte Fuel Cells: Recent Achievements and Future Challenges. ACS Catal. 2012, 2, 864–890. 10.1021/cs3000864. [DOI] [Google Scholar]
  12. Wang Y.; Chu F.; Zeng J.; Wang Q.; Naren T.; Li Y.; Cheng Y.; Lei Y.; Wu F. Single Atom Catalysts for Fuel Cells and Rechargeable Batteries: Principles, Advances, and Opportunities. ACS Nano 2021, 15, 210–239. 10.1021/acsnano.0c08652. [DOI] [PubMed] [Google Scholar]
  13. Huang D.; Zhou H.; Lin L. Biodiesel: an Alternative to Conventional Fuel. Energy Procedia 2012, 16, 1874–1885. 10.1016/j.egypro.2012.01.287. [DOI] [Google Scholar]
  14. An L.; Zeng L.; Zhao T. An alkaline direct ethylene glycol fuel cell with an alkali-doped polybenzimidazole membrane. Int. J. Hydrogen Energy 2013, 38, 10602–10606. 10.1016/j.ijhydene.2013.06.042. [DOI] [Google Scholar]
  15. An L.; Zhao T.; Shen S.; Wu Q.; Chen R. Performance of a direct ethylene glycol fuel cell with an anion-exchange membrane. Int. J. Hydrogen Energy 2010, 35, 4329–4335. 10.1016/j.ijhydene.2010.02.009. [DOI] [Google Scholar]
  16. Qi J.; Benipal N.; Liang C.; Li W. PdAg/CNT catalyzed alcohol oxidation reaction for high-performance anion exchange membrane direct alcohol fuel cell (alcohol = methanol, ethanol, ethylene glycol and glycerol). Appl. Catal. B: Environ. 2016, 199, 494–503. 10.1016/j.apcatb.2016.06.055. [DOI] [Google Scholar]
  17. Munoz F.; Hua C.; Kwong T.; Tran L.; Nguyen T. Q.; Haan J. L. Palladium–copper electrocatalyst for the promotion of the electrochemical oxidation of polyalcohol fuels in the alkaline direct alcohol fuel cell. Appl. Catal. B: Environ. 2015, 174–175, 323–328. 10.1016/j.apcatb.2015.03.027. [DOI] [Google Scholar]
  18. Lenarda A.; Bellini M.; Marchionni A.; Miller H.; Montini T.; Melchionna M.; Vizza F.; Prato M.; Fornasiero P. Nanostructured carbon supported Pd-ceria as anode catalysts for anion exchange membrane fuel cells fed with polyalcohols. Angew. Chem., Int. Ed. 2018, 470, 213–220. 10.1016/j.ica.2017.05.020. [DOI] [Google Scholar]; Special Volume: Protagonists in Chemistry Dedicated to Professor Carlo Mealli.
  19. Catal T.; Xu S.; Li K.; Bermek H.; Liu H. Electricity generation from polyalcohols in single-chamber microbial fuel cells. Biosens. Bioelectron. 2008, 24, 849–854. 10.1016/j.bios.2008.07.015. [DOI] [PubMed] [Google Scholar]
  20. Cao Y.; Wang J.; Kang M.; Zhu Y. Efficient synthesis of ethylene glycol from cellulose over Ni-WO3/SBA-15 catalysts. J. Mol. Catal. A 2014, 381, 46–53. 10.1016/j.molcata.2013.10.002. [DOI] [Google Scholar]
  21. Chino I.; Vega L.; Keramati A.; Hendrix K.; Haan J. L. A direct liquid fuel cell powered by 1,3- or 1,2-propanediol. Appl. Energy 2020, 262, 114564. 10.1016/j.apenergy.2020.114564. [DOI] [Google Scholar]
  22. Yu E. H.; Krewer U.; Scott K. Principles and Materials Aspects of Direct Alkaline Alcohol Fuel Cells. Energies 2010, 3, 1499–1528. 10.3390/en3081499. [DOI] [Google Scholar]
  23. García-Muelas R.; López N. Collective Descriptors for the Adsorption of Sugar Alcohols on Pt and Pd(111). J. Phys. Chem. C 2014, 118, 17531–17537. 10.1021/jp502819s. [DOI] [Google Scholar]
  24. Logadottir A.; Rod T.; Nørskov J.; Hammer B.; Dahl S.; Jacobsen C. The Brønsted–Evans–Polanyi Relation and the Volcano Plot for Ammonia Synthesis over Transition Metal Catalysts. J. Catal. 2001, 197, 229–231. 10.1006/jcat.2000.3087. [DOI] [Google Scholar]
  25. Cheng J.; Hu P.; Ellis P.; French S.; Kelly G.; Lok C. M. Brønsted-Evans-Polanyi Relation of Multistep Reactions and Volcano Curve in Heterogeneous Catalysis. J. Phys. Chem. C 2008, 112, 1308–1311. 10.1021/jp711191j. [DOI] [Google Scholar]
  26. Saidi W. A. Emergence of local scaling relations in adsorption energies on high-entropy alloys. npj Comput. Mater. 2022, 8, 86. 10.1038/s41524-022-00766-y. [DOI] [Google Scholar]
  27. Huang Y.; Lu H.-L.; Chen Z.-X. DFT and microkinetic study of acetylene transformation on Pd(111), M(111) and PdM(111) surfaces (M = Cu, Ag, Au). Phys. Chem. Chem. Phys. 2022, 24, 3182–3190. 10.1039/D1CP05353A. [DOI] [PubMed] [Google Scholar]
  28. Chen J.; Zhang R. Volcano Plots of Reaction Yields in Cross-Coupling Catalysis. J. Phys. Chem. Lett. 2022, 13, 520–526. 10.1021/acs.jpclett.1c04099. [DOI] [PubMed] [Google Scholar]
  29. Bronsted J. N. Acid and Basic Catalysis. Chem. Rev. 1928, 5, 231–338. 10.1021/cr60019a001. [DOI] [Google Scholar]
  30. Evans M. G.; Polanyi M. Inertia and driving force of chemical reactions. Trans. Faraday Soc. 1938, 34, 11–24. 10.1039/tf9383400011. [DOI] [Google Scholar]
  31. Mortensen J. J.; Hansen L. B.; Jacobsen K. W. Real-space grid implementation of the projector augmented wave method. Phys. Rev. B 2005, 71, 035109. 10.1103/PhysRevB.71.035109. [DOI] [Google Scholar]
  32. Enkovaara J.; et al. Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method. J. Phys.: Condens. Matter 2010, 22, 253202. 10.1088/0953-8984/22/25/253202. [DOI] [PubMed] [Google Scholar]
  33. Larsen A. H.; et al. The atomic simulation environment—a Python library for working with atoms. J. Phys.: Condens. Matter 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  34. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  35. Tkatchenko A.; Scheffler M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. 10.1103/PhysRevLett.102.073005. [DOI] [PubMed] [Google Scholar]
  36. Ruiz V. G.; Liu W.; Zojer E.; Scheffler M.; Tkatchenko A. Density-Functional Theory with Screened van der Waals Interactions for the Modeling of Hybrid Inorganic-Organic Systems. Phys. Rev. Lett. 2012, 108, 146103. 10.1103/PhysRevLett.108.146103. [DOI] [PubMed] [Google Scholar]
  37. Yildirim H.; Kara A. Effect of van der Waals Interactions on the Adsorption of Olympicene Radical on Cu(111): Characteristics of Weak Physisorption versus Strong Chemisorption. J. Phys. Chem. C 2013, 117, 2893–2902. 10.1021/jp311361e. [DOI] [Google Scholar]
  38. Ohmann R.; Levita G.; Vitali L.; De Vita A.; Kern K. Influence of Subsurface Layers on the Adsorption of Large Organic Molecules on Close-Packed Metal Surfaces. ACS Nano 2011, 5, 1360–1365. 10.1021/nn103058e. [DOI] [PubMed] [Google Scholar]
  39. Liu W.; Tkatchenko A.; Scheffler M. Modeling Adsorption and Reactions of Organic Molecules at Metal Surfaces. Acc. Chem. Res. 2014, 47, 3369–3377. 10.1021/ar500118y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Dostert K.-H.; O’Brien C. P.; Riedel W.; Savara A.; Liu W.; Oehzelt M.; Tkatchenko A.; Schauermann S. Interaction of Isophorone with Pd(111): A Combination of Infrared Reflection–Absorption Spectroscopy, Near-Edge X-ray Absorption Fine Structure, and Density Functional Theory Studies. J. Phys. Chem. C 2014, 118, 27833–27842. 10.1021/jp506637v. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Malone W.; Matos J.; Kara A. Adsorption of thiophene on transition metal surfaces with the inclusion of van der Waals effects. Surf. Sci. 2018, 669, 121–129. 10.1016/j.susc.2017.11.013. [DOI] [Google Scholar]
  42. Pang S. H.; Medlin J. W. Adsorption and Reaction of Furfural and Furfuryl Alcohol on Pd(111): Unique Reaction Pathways for Multifunctional Reagents. ACS Catal. 2011, 1, 1272–1283. 10.1021/cs200226h. [DOI] [Google Scholar]
  43. Wang Y.; Li C.; Xu B. Adsorption of Formic Acid on Pd(111) Catalyst in the Gas Phase. Prog. React. Kinet. Mech. 2017, 42, 30–35. 10.3184/146867816X14696270772589. [DOI] [Google Scholar]
  44. Su G.; Yang S.; Jiang Y.; Li J.; Li S.; Ren J.-C.; Liu W. Modeling chemical reactions on surfaces: The roles of chemical bonding and van der Waals interactions. Prog. Surf. Sci. 2019, 94, 100561. 10.1016/j.progsurf.2019.100561. [DOI] [Google Scholar]
  45. Mete E.; Yortanli M.; Danişman M. F. A van der Waals DFT study of chain length dependence of alkanethiol adsorption on Au(111): physisorption vs. chemisorption. Phys. Chem. Chem. Phys. 2017, 19, 13756–13766. 10.1039/C7CP01653K. [DOI] [PubMed] [Google Scholar]
  46. Hensley A. J.; Wang Y.; McEwen J.-S. Adsorption of guaiacol on Fe (110) and Pd (111) from first principles. Surf. Sci. 2016, 648, 227–235. 10.1016/j.susc.2015.10.030. [DOI] [Google Scholar]; Special issue dedicated to Gabor Somorjai’s 80th birthday.
  47. Hensley A. J.; Wang Y.; McEwen J.-S. Adsorption of phenol on Fe (110) and Pd (111) from first principles. Surf. Sci. 2014, 630, 244–253. 10.1016/j.susc.2014.08.003. [DOI] [Google Scholar]
  48. Delmonde M. V. F.; Sallum L. F.; Perini N.; Gonzalez E. R.; Schlögl R.; Varela H. Electrocatalytic Efficiency of the Oxidation of Small Organic Molecules under Oscillatory Regime. J. Phys. Chem. C 2016, 120, 22365–22374. 10.1021/acs.jpcc.6b06692. [DOI] [Google Scholar]
  49. Jiang R.; Guo W.; Li M.; Fu D.; Shan H. Density Functional Investigation of Methanol Dehydrogenation on Pd(111). J. Phys. Chem. C 2009, 113, 4188–4197. 10.1021/jp810811b. [DOI] [Google Scholar]
  50. Desai S. K.; Neurock M.; Kourtakis K. A Periodic Density Functional Theory Study of the Dehydrogenation of Methanol over Pt(111). J. Phys. Chem. B 2002, 106, 2559–2568. 10.1021/jp0132984. [DOI] [Google Scholar]
  51. Huang Y.; Chen Z.-X. Density Functional Investigations of Methanol Dehydrogenation on Pd-Zn Surface Alloy. Langmuir 2010, 26, 10796–10802. 10.1021/la100619q. [DOI] [PubMed] [Google Scholar]
  52. Cortese R.; Schimmenti R.; Armata N.; Ferrante F.; Prestianni A.; Duca D.; Murzin D. Y. Investigation of Polyol Adsorption on Ru, Pd, and Re Using vdW Density Functionals. J. Phys. Chem. C 2015, 119, 17182–17192. 10.1021/acs.jpcc.5b04007. [DOI] [Google Scholar]
  53. Li M.; Guo W.; Jiang R.; Zhao L.; Shan H. Decomposition of Ethanol on Pd(111): A Density Functional Theory Study. Langmuir 2010, 26, 1879–1888. 10.1021/la902641t. [DOI] [PubMed] [Google Scholar]
  54. Peng X.-Y.; Feng S.-L. Adsorption and Dissociation of Methanol on Pd(111), Pd/Au(111) and Pd/Rh(111) Surfaces. Chin. J. Struct. Chem. 2019, 38, 2057–2069. [Google Scholar]
  55. Tereshchuk P.; Da Silva J. Ethanol and Water Adsorption on Close-Packed 3d, 4d, and 5d Transition-Metal Surfaces: A Density Functional Theory Investigation with van der Waals Correction. J. Phys. Chem. C 2012, 116, 24695–24705. 10.1021/jp308870d. [DOI] [PubMed] [Google Scholar]
  56. Bezerra R. C.; Mendonça J. P. A. d.; Mendes P. C. D.; Passos R. R.; Da Silva J. L. F. Role of the OH-group in the adsorption properties of methanol, ethanol, and ethylene glycol on 15-atom 3d, 4d, and 5d transition-metal clusters. Phys. Chem. Chem. Phys. 2021, 23, 17553–17566. 10.1039/D1CP01806J. [DOI] [PubMed] [Google Scholar]
  57. Liu B.; Greeley J. A density functional theory analysis of trends in glycerol decomposition on close-packed transition metal surfaces. Phys. Chem. Chem. Phys. 2013, 15, 6475–6485. 10.1039/c3cp44088e. [DOI] [PubMed] [Google Scholar]
  58. Liu B.; Greeley J. Decomposition Pathways of Glycerol via C-H, O-H, and C-C Bond Scission on Pt(111): A Density Functional Theory Study. J. Phys. Chem. C 2011, 115, 19702–19709. 10.1021/jp202923w. [DOI] [Google Scholar]
  59. Liriano M. L.; Carrasco J.; Lewis E. A.; Murphy C. J.; Lawton T. J.; Marcinkowski M. D.; Therrien A. J.; Michaelides A.; Sykes E. C. H. The interplay of covalency, hydrogen bonding, and dispersion leads to a long range chiral network: The example of 2-butanol. J. Chem. Phys. 2016, 144, 094703. 10.1063/1.4941560. [DOI] [PubMed] [Google Scholar]
  60. Mendes P. C. D.; Costa-Amaral R.; Gomes J. F.; Da Silva J. L. F. The influence of hydroxy groups on the adsorption of three-carbon alcohols on Ni(111), Pd(111) and Pt(111) surfaces: a density functional theory study within the D3 dispersion correction. Phys. Chem. Chem. Phys. 2019, 21, 8434–8444. 10.1039/C9CP00752K. [DOI] [PubMed] [Google Scholar]
  61. Griffin M. B.; Jorgensen E. L.; Medlin J. W. The adsorption and reaction of ethylene glycol and 1,2-propanediol on Pd(111): A TPD and HREELS study. Surf. Sci. 2010, 604, 1558–1564. 10.1016/j.susc.2010.05.025. [DOI] [Google Scholar]
  62. Redhead P. Thermal desorption of gases. Vacuum 1962, 12, 203–211. 10.1016/0042-207X(62)90978-8. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la2c02281_si_002.pdf (102KB, pdf)
la2c02281_si_001.zip (16.1KB, zip)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES