On the interplay of hierarchies, conflicts, and cooperation: An experimental approach

Abstract

Previous research suggests that it is difficult to maintain cooperation in a large society when there is a strong hierarchical structure. In this study, we implement online human experiments to study the effects of exogenous variation in a particular notion of hierarchy on cooperation and conflict within groups. We demonstrate how cooperation can be maintained when collective action is accompanied by dyadic conflicts whose outcome feeds back on the hierarchical rank of the contestants. We find that the majority of individuals take part in conflicts and that highly ranked individuals mostly cooperate and engage in conflicts as a way to punish noncooperators. As a consequence, stable hierarchical groups can arise and maintain high levels of cooperation. Our results are in agreement with the prediction of earlier theoretical models on hierarchical societies and are relevant to understanding the interplay of hierarchy, cooperation, and conflict.

Significance Statement.

Studies of primate groups and human societies show that cooperation is often hindered by hierarchical societal structures. We implemented experiments to check whether conflicts between individuals affecting their social ranking can support cooperative, hierarchical societies. Our results show that such feedback between hierarchy and conflict can induce highly ranked individuals to be more cooperative, thus perpetuating and possibly transmitting their prosocial position. We have also observed that attacks are used as a deterrent to punish noncooperators, further increasing cooperation. Our study thus supports the spontaneous emergence of cooperative, hierarchical societies.

Hierarchical structures exist in many social animals (1–6), where the most common structure is a linear hierarchy: the classic pecking order (7). Two main hypotheses have been proposed to explain those structures, namely that they are due to intrinsic attributes of the subjects (8), or that they arise from social dynamics (9). Alternatively, competition with others in a group can also lead to dominance hierarchies. Indeed, mathematical models (10–13) suggest that hierarchies could result from a self-organizing process: winners increase their probability of winning, and losers reinforce theirs of losing. Agent-based models (14, 15) also show that such reinforcement mechanisms may transform an egalitarian society into a hierarchical one. This mechanism is not universal; for instance, some animals make transitive inferences about dominance rank, deferring to an opponent who they saw defeat someone who defeated them (16). Ethologists have also demonstrated that hyenas, baboons, mice, etc. have cognitive representations of the dominance hierarchies in their group, meaning that they understand the dominance relations among others rather than only changing their aggression based on previous experience (17, 18). In this study, we focus on the feedback loop between conflicts, ranking, and cooperation among human beings interacting through a controlled experimental platform. Our work may be relevant to a large, but not universal subset of hierarchical species, although we expect that our insights may be extended to other social contexts.

The existence of a hierarchical structure in a group may have a strong impact on the cooperation behavior of its individuals (19–24). Here, cooperation is understood as a collective effort to achieve a common goal, not necessarily restricted to social dilemma situations. Large-scale cooperation is often found in insect societies (1), while in primates, the situation is much more diverse. Thus, chimpanzees, living in a linear hierarchy, show little cooperation (21, 25), while cottontop tamarins are much more cooperative (20, 21, 23). On the other hand, the connection between hierarchical structure and cooperative behavior in humans is much less understood. Some experimental evidence suggests that steep hierarchies lead to low cooperation (26) and less steep hierarchies preserve it (27). Other theoretical analyses show that leaders can act seemingly altruistically in between-group conflicts, i.e., making larger efforts and having lower reproductive success than their subordinate groupmates (28, 29).

In this paper, we study experimentally how individuals in a hierarchical setting behave in a cooperation dilemma when dyadic conflicts are possible. Our starting point is a recent agent-based model (30) that considers individuals, characterized by their rank, taking part in a collective action problem. Individuals can attack others for the resources they obtained from the common pool; individuals with a higher rank have more probabilities of winning and ranks are readjusted according to the outcome of the competition. The model suggests that a hierarchy can spontaneously arise in a cooperative society. Therefore, we run several controlled experiments to check the insights from the model. Specific hypotheses were preregistered at the Open Science Foundation (OSF) (31) addressing questions about both individual and collective behavior.

At the individual level, a key ingredient of the model is the possibility to attack other individuals to steal their profit from cooperation. If individuals do not use this possibility in the experiment, the whole model would become void. On the other hand, it is to be expected that there are individuals more inclined to attack others and others that are less so inclined. Thus, our first hypothesis is the following: In a context where it is possible to attack other subjects for their share of resources, two behavioral types will emerge and will be distributed in a bimodal way: subjects who attack very often and subjects who do not (hereafter, for brevity, existence of aggressor types). Assuming that attacks do take place, we then ask whether it is possible that individual cooperativeness affects subjects’ conflict behavior. Our agent-based model suggests that subjects that contributed to the common pool are less likely to attack others (peaceful cooperators) and are less likely to be chosen to be in a conflict against (pacifism towards cooperators). The other interplay we are interested in is that of hierarchy and attacking behavior. Given the advantage high-ranked individuals have in our definition of conflict, they may be more prone to steal resources by attacking low-ranked individuals. Therefore, we hypothesize that subjects with high ranks attack more often (high-ranked aggressors). On the other hand, high-ranked individuals may feel that their rank protects them from attacks so they cooperate to get the reward (and keep it), and hence, we conjecture that high-ranked individuals cooperate more often than subjects with low ranks (high-ranked cooperators).

Looking now at the collective level, and guided again by our model, we hypothesize that cooperation is higher in hierarchical settings as compared to a standard public goods game (PGG) without conflicts (hierarchy-supported cooperation). As to the relationship between conflicts and cooperation, our conjecture is that cooperation is higher when there is feedback between hierarchy and conflicts compared to a PGG with conflicts that do not affect ranks (rank-supported cooperation). Lastly, we want to assess to what extent the group size has any effect on the stability of the hierarchy. Our hypothesis is that hierarchies are more stable in larger groups, i.e., individual ranks do not oscillate as much as in smaller groups (large hierarchy stability).

Experimental Setup

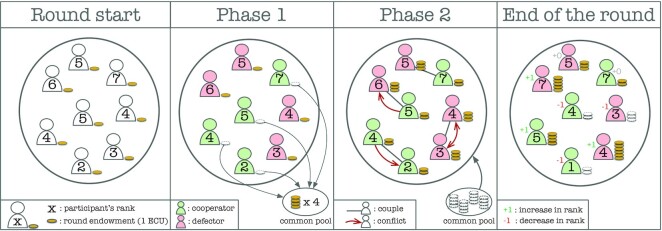
The overall structure of the experiment resembles the theoretical model presented in ref. (30). Three treatments were implemented: egalitarian group, small hierarchy, and large hierarchy, which we describe in detail below. Each treatment included seven independent groups for a total of 224 involved subjects. In Fig. 1, we report a graphical representation of the experiment. In the hierarchical treatments, each participant is assigned a rank that represents the participant’s level within the group. This number is an integer value between one and the group size n. At the beginning of the experiment, all participants start in the middle of the hierarchy by setting their initial rank to ⌊n/2⌋. We implemented a level-based hierarchy, i.e., participants may share the same rank, instead of a linear one, i.e., each participant has a different rank. The difference between small group and large group treatments is the group size n, and the values we considered were n = 8 and n = 16, the same as in refs. (30, 32). On the other hand, in the egalitarian group treatment, which represents our baseline scenario, there is no ranking.

Fig. 1.

Experimental setup. In each treatment, participants went through 60 rounds including two phases. In the first phase, they take part in a PGG with a multiplication factor set to be half of the group size. In the second phase, they could engage into conflict against their coupled participant to steal from them their round earnings. In the egalitarian group treatment, ranks were not present and conflicts were randomly decided with 50% probability of winning for both participants. In the Hierarchical (small hierarchy and large hierarchy) treatments, ranks changed after each engaged conflict and winning probabilities were rank-dependent. See the main text and the Supplementary Information (SI) Appendix for more details on the experiment.

Experiments for the baseline scenario were carried out only for n = 8. Thus, this design only allows us to identify the effect of hierarchy between small group treatments and the effect of size between hierarchical treatments. This design choice prevents us from getting both the combined effect of size and hierarchy. While this is an interesting question, it is somewhat beyond the scope of this work. We may not exclude that this choice might miss the impact of group size on the level of cooperation or possible interactions of the cooperation level with conflict decisions. Indeed, the size of the matching group may matter in pairwise interactions with stranger matching (33). Nonetheless, we believe that at the scale we are discussing here, these effects should not be very important. In any event, to be consistent with our design choice, we will discuss our results by comparing the egalitarian and the hierarchical small groups, and the two hierarchical treatments with each other.

At each round, participants go through two phases for a total of 60 rounds, although this exact number was unknown to them; participants were only told that they would play for a number of rounds between 50 and 70. In the first phase, subjects play a PGG with a multiplication factor of m: participants may choose to contribute, i.e., spending their entire round endowment to a common pool, or not, i.e., keeping it. The round endowment was set to be one point, while m was set to be half of the group size to make proper comparisons between different group sizes (m = 4 for the egalitarian group and the small hierarchical treatments, m = 8 for the large hierarchy one). Contributions were added up and then shared equally among all group members after being multiplied by m. In the second phase, participants were randomly and anonymously coupled with another participant of the same group and each of them had the opportunity to engage into a conflict over the round earnings the other individual obtained in the previous phase: the round endowment, in the case it was saved, and the earnings obtained from the common pool. Pairings were arranged in a way that each participant was only present in one pairing per round. At the beginning of this phase, participants were asked if they wanted to engage into a conflict with the other participant. In hierarchical treatments, the information on the rank of the other participant and the contribution decision taken in the previous phase was common knowledge to both participants. In the egalitarian group treatment, which we use as baseline, only the contribution decision was shown. No additional information such as numbers or letters to infer participants’ identity was included. In hierarchical treatments, in the case that at least one of the two participants of the couple decided to engage into the conflict a winner and a loser were chosen in a random, but hierarchy-based, manner: the higher the rank, the more probable was that a participant won the conflict. The intuition behind this feature is that individuals who lose conflicts (and hence are low-ranked) lose their share of the resource, so they are weaker than higher-ranked ones. Alternatively, one could think of higher-ranked individuals recruiting allies more easily in view of the fact that they have more resources available to share with friends. In particular, the winning probability of participant i against participant j was computed as P(i, j) = r_i/(r_i + r_j), where r_i and r_j are the corresponding participants’ ranks. Thus, the outcome in a conflict where participants had the same rank was 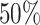for both of them, as it was for all conflicts in the egalitarian group treatment. Participants who win the conflict increase their ranks by one, while those who lose it decrease them by the same unit. In all cases, the maximum achievable rank was set to be as the size of the group n, while the minimum to one.

Results

Evolution of Cooperation and Hierarchy Stability

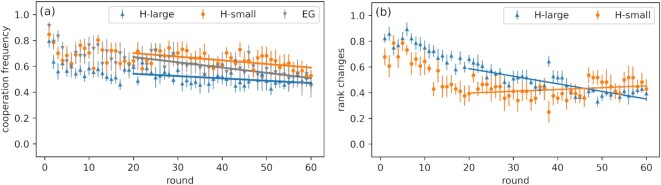
We look at the existence of global cooperation by looking at cooperation frequencies by round in Fig. 2a. We first observe that cooperation in all treatments is generally higher with respect to previous experimental studies that do not include conflicts and/or hierarchies but having similar group sizes and PGG multiplication factors, e.g., see ref. (34) for classical experimental results with similar multiplication factors showing a rapid decay of the contributions. However, we cannot fully confirm that hierarchy supports cooperation, since our participant sample, the experimental setup, and other minor details may significantly differ from previous studies and further treatments should be implemented to confirm this hypothesis. Nevertheless, although cooperation level decay seems to be slower than those observed in standard PGGs, the overall trend in all treatments appears to be decreasing as the number of rounds increases. We find that cooperation frequency results to be more stable in the large hierarchy treatment, i.e., having a less pronounced decreasing pattern, while cooperation in the small hierarchy treatment decreases faster although achieving higher frequencies. The egalitarian group treatment, instead, lies in between the two lines (OLS model from round 20 onwards; small hierarchy: β = −0.0028, ϵ = 0.76, P*** < 0.001; large hierarchy: β = −0.0018, ϵ = 0.58, P** = 0.0015; egalitarian group: β = −0.0041, ϵ = 0.75, P*** < 0.001).

Fig. 2.

Cooperation frequency and rank changes by round and treatment. (a) Observed cooperation levels are higher and more stable with respect to previous PGG that did not include conflicts and/or hierarchical structures. (b) The larger the number of rank changes is, the less the established hierarchy can be considered as stable. As the number of rank changes decreases with time, we find that hierarchies are more stable in larger groups than in smaller ones. Error bars represent the Standard Error of the Mean (SEM) considering each group as an independent observation.

Finally, we looked at how many times participants changed rank in hierarchical treatments as a proxy for measuring the stability of the established hierarchy, if any. The number of rank changes in Fig. 2b starts around 70 to 80% for both hierarchical treatments and, after the first 20 rounds, hierarchy stability in the large hierarchy treatment still increases as the number of rank changes decreases. Smaller groups, on the contrary, result to be less stable as the number of rounds goes by (OLS model from round 20 onwards; small hierarchy: β = 0.0014, ϵ = 0.37, P = 0.096; large hierarchy: β = −0.0059, ϵ = 0.7, P*** < 0.001). Although further experimental evidence is required, these results are in agreement with the hypothesis that larger groups build more stable hierarchies. In fact, belonging to a larger group means that a highly ranked individual can be separated by many hierarchical levels from a lowly ranked one. Since conflicts become more deterministic in favor to highly ranked individuals when rank differences increases, rank changes are more difficult to occur when a hierarchy is polarized and composed by more layers.

In the SI Appendix, we also report additional results on individual cooperation frequency (Figs. S2 to S4), the evolution of Gini indices calculated using cumulated payoffs (Fig. S11) or ranks (Fig. S12) as measures for wealth inequality in the three treatments, as well as simulation results using the model in ref. (30) with suitable parameters to represent our experimental setup (see SI Appendix for more details).

Conflict/Attack Frequencies

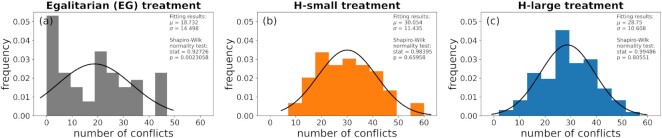
In order to verify our first hypothesis, existence of aggressor types, we analyzed the conflict and attack frequency within the three treatments. In qualitative agreement with our hypothesis, the distribution of conflict choices in Fig. 3a does not follow a normal distribution (Shapiro–Wilk test: W = 0.9273, P** = 0.0023) but rather a bimodal or even multimodal one: most of the individuals are involved in conflicts very few times whereas less individuals are involved in more frequently. In contrast, looking at behaviors observed in hierarchical treatments of Fig. 3b and c, their corresponding conflict frequencies follow normal distributions (small hierarchy: W = 0.9840, P = 0.6596; large hierarchy: W = 0.9949, P = 0.8055). Both distributions have means very close to the half of the number of rounds, i.e., 30, in stark contrast with the mean of the baseline treatment, i.e., less than a third of the number of rounds. These results show the significant impact of including hierarchies in increasing the average number of conflicts and in affecting their distribution. However, the histogram of attacks (SI Appendix, Fig. S6) for the baseline treatment is much more similar to a normal distribution, suggesting that there are more conflicts initiated bilaterally in the egalitarian treatment (thus flattening the histogram) than in the hierarchical ones.

Fig. 3.

Participants’ conflict frequency distribution by treatment. Participants are involved in a conflict more often in hierarchical treatments with respect to the egalitarian group treatment. Furthermore, conflict frequencies follow normal distributions for both hierarchical treatments.

We then analyze the attack choices as a function of participants’ contribution decisions (i.e., hypotheses about peaceful cooperators and pacifism towards cooperators). In Fig. 4, we report how individuals identified by their contribution decision in the first phase of a given round behaved in terms of their conflict decision in the second phase of the same round. First of all, we observe that in the egalitarian group treatment, cooperators attacked defectors more often while defectors had no bias on the contribution decision of their conflict opponent [Mann–Whitney (MW) test; egalitarian group cooperator frequencies: W = 1, P** = 0.0012; egalitarian group defector frequencies: W = 27, P = 0.8048].

Fig. 4.

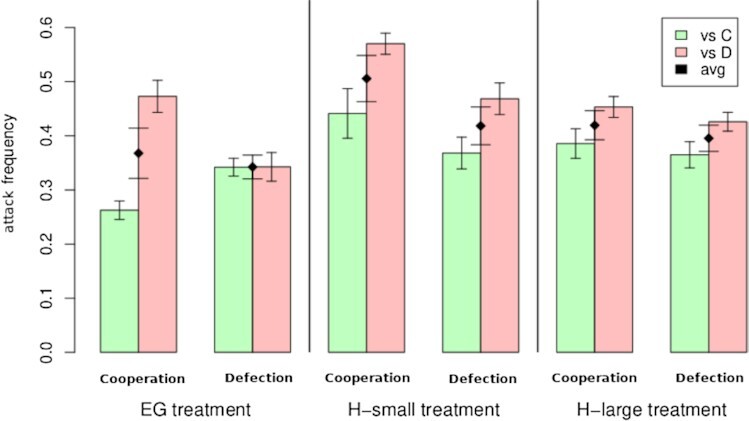
Attack frequency by treatment and contribution decisions. Participants who contributed in the first phase, i.e., cooperators, are more willing to engage into a conflict against defectors, i.e., not contributors, especially in the egalitarian group treatment. Defectors, instead, do not discriminate between defectors and cooperators in the egalitarian group treatment, while they do in hierarchical treatments.

The trend, although less pronounced, is also observed in hierarchical treatments for conflict behavior of participants who cooperated (MW test; small hierarchy cooperation frequencies: W = 9, P = 0.0530; large hierarchy cooperation frequencies: W = 10, P = 0.0728). On the other hand, participants who defected decided to engage into conflicts more often against other defectors than cooperators (MW test; small hierarchy defection frequencies: W = 9.5, P = 0.0636; large hierarchy defection frequencies: W = 12, P = 0.1282). There is also significant difference on the averages of the attack frequency between small and large hierarchies, as individuals are more conflict-driven in smaller groups (MW test; small hierarchy vs. large hierarchy total frequencies: W = 516, P* = 0.0430); possibly due to a higher chance of increasing their rank. The fact that cooperators are attacked less is thus confirmed for both small and large groups, especially in egalitarian groups. In contrast, in small hierarchy, cooperators are seen to attack more, contrary to our hypothesis: When we compare the average attack frequencies of cooperators and defectors in small hierarchical groups, we observe an opposite behavior from the one we expected, finding a significant difference in favor of cooperators (MW test; small hierarchy cooperation vs. defection total frequencies: W = 144, P* = 0.0365). Other treatment comparisons do not show significant differences between cooperation and defection average attack frequencies (MW test, egalitarian group cooperator vs. defector frequencies: W = 100, P = 0.9459; large hierarchy cooperation vs. defection total frequencies: W = 110, P = 0.6027). Furthermore, we report in the SI Appendix, Fig. S5, the round conflict frequency by treatment finding in the long run, i.e., after 20 rounds, stable conflict frequency patterns with minor oscillations for all treatments.

Cooperative Behavior and Attacks by Rank

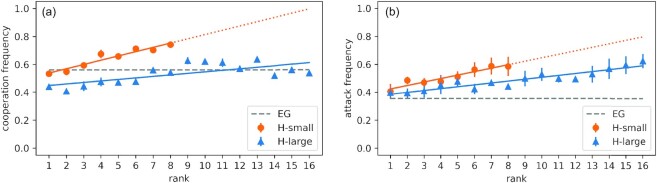
To study our hypotheses on high-ranked aggressors and cooperators, we looked at participants’ cooperation and attack frequencies as a function of their rank position. From Fig. 5(a), one can see that the egalitarian group treatment has an overall cooperation frequency around 0.56, while small hierarchy and large hierarchical treatments have rather heterogeneous frequencies for different ranks. For both hierarchical treatments, we find statistically significant linear fits with participants’ contribution behavior: the higher the rank, the more an individual cooperates (OLS model; small hierarchy: β = 0.031, ϵ = 0.51, P** = 0.0021; large hierarchy: β = 0.011, ϵ = 0.44, P*** < 0.001). The principal differences between hierarchical treatments are that cooperation frequency is higher for lower ranks of the small hierarchy treatment and that its increase as a function of the rank is larger with respect to what we observe in the large hierarchy treatment. Therefore, our hypothesis is correct and highly ranked participants cooperate more often than low-ranked ones. This may be due by the fact that highly ranked individuals quickly understood that the strategy of cooperating and then engaging into conflicts gives them more points in the long run. Focusing instead on Fig. 5b, we can find a similar relationship in agreement with Fig. 5a: the higher the rank, the more individuals choose to engage into conflicts. Again, this correlation is stronger in the small hierarchy treatment (OLS model; small hierarchy: β = 0.025, ϵ = 0.4, P*** < 0.001; large hierarchy: β = 0.008, ϵ = 0.44, P*** < 0.001). Although it is true that higher ranks provide more possibilities of winning points through conflicts instead than defecting, with this last result, we can also confirm that high-ranked individuals attack more often (see also Figs. S7 to S9 of the SI Appendix, for attack frequencies by coupled ranks and Fig. S10 for the rank evolution by group). As previously observed, the attack frequency is smaller in the egalitarian group treatment, i.e., around 0.36.

Fig. 5.

Cooperation and attack frequencies by rank position and treatment. Highly ranked participants cooperate and engage into conflicts more often than lowly ranked ones for both hierarchical treatments. Both frequencies follow linear fits. For comparison purposes with large hierarchy treatment results, we report dashed lines for the small hierarchy treatment as projected frequencies for ranks that are not reachable in small groups. Cooperation and attack frequencies of the egalitarian group treatment are reported as the average value observed in the entire treatment. Error bars represent the SEM considering each individual decision as an independent observation.

We also investigated correlations between cooperative and attack behavior finding no significant patterns. We assume that these behavioral types cannot be detected since ranks largely influence participants’ decisions to engage into a conflict (see SI Appendix, Figs. S13 and S14).

Discussion

In this study, we have carried out several experiments to study the interplay of conflicts, hierarchies, and cooperation. This research question was inspired by a model (30), which included as its key feature the possibility of fights for the resources between agents. Our experiments show that actual people do use this possibility and actually attack others to reap their benefits from cooperation. We have observed that this is the case both in environments with and without a social ranking or hierarchy. We have also found that there are no separate types of individuals, meaning that the distribution of the number of attacks by the same individual is approximately normal. In the experiment, stable hierarchies arise when individuals can compete for resources, leading to results compatible with the predictions of our model. One important result is that hierarchies established from conflicts exhibit higher levels of cooperation than their egalitarian counterparts. Interestingly, higher-ranked individuals cooperate more often than low-ranked ones, but also attack more often. The fact that highly ranked individuals cooperate more aligns with the predictions in ref. (35) reporting a model with no conflicts but with inter-group competition. We have also shown that individuals discriminate between cooperators and defectors, attacking more often those who do not cooperate. This suggests that conflicts can act as an indirect punishment against free-riders (34, 36).

Our experimental results allow us to present a picture of how conflicts, hierarchy, and cooperation affect each other. To begin with, our data show that highly ranked individuals choose to attack more often. Then, because their probability of winning is higher, they accumulate more resources, which helps them keep their social status. This agrees with the results in ref. (37), where institutionalized hierarchy emerges from egalitarian societies when there are persistent and/or heritable differences in resources. Our results are also aligned with the models in  refs. (38, 39), where it has been suggested that complex societies exhibiting high levels of cooperation evolved as a results of intense competition, in particular (but not only) warfare. Also, recent models and experiments (40) showed that when subjects know their ability to win conflicts, those with higher abilities—i.e., higher ranking in our model—attack more frequently than low-ranked individuals. At the same time, even if low-ranked individuals would not be in a position to compete, they will still choose cooperation often hoping not to be involved in any conflict. Crucially, if they do not cooperate, they will most likely end up receiving nothing because their chances to attack others and win are very low. On the other hand, our study shows once again that humans recognize cooperation and punish defection using the tools at their disposal—institutional punishment, direct punishment, or, as in this case, indirect punishment through individual attacks. This is in contrast with previous research (41), where it was shown that when retaliation to punishment was possible, cooperation unraveled. In our setup, we do have the possibility to retaliate in later stages of the game, but cooperation persisted, suggesting new ways to look as punishment as a way to support cooperation. Our results thus suggest a mechanism explaining how hierarchies can arise from egalitarian societies, while keeping high levels of cooperation.

As stated in the Introduction, our results are a first step in the experimental study of how hierarchy and cooperation can coexist, as it is linked to a specific form of feedback between hierarchy and conflict. This raises the question as to whether situations in which more complex cognitive processes are involved (16–18) could also be understood by means of experiments. We believe that such an extension of our setup might be possible by providing more info to the participants, including the results of conflicts among other subjects. This implies moving away from anonymous interaction, which would be a more faithful representation of a complex society. Such an experimental setup would also allow to address other hierarchy-forming mechanisms for which the coexistence with cooperation has not been addressed, e.g., conflicts between pairs in a group where the other individuals choose sides to determine the winner (42). Interestingly, in this scenario, hierarchies could arise from subjects consistently supporting the same people, but this was not observed. It would then be possible that a cooperative interaction could catalyze the formation of a hierarchy. We hope that our work inspires further research along these lines.

Material and Methods

We programmed the online experiment in oTree (v1.3) (43) and recruited participants using the IBSEN platform (44). Before the beginning of a session, subjects were randomly assigned to one of the three treatments. Five sessions were implemented between October and December, 2020. Experimental points were converted to real money with an exchange rate of 20 points = 1 EUR. Participants received an average payment of 11.6 EUR (13.7 USD), also including a participation fee to complete the entire experiment of 2 EUR. Participants read detailed instructions about the experiment for a maximum of 10 minutes. Participants who were missing, i.e., not shown online at the beginning of the experiment, or dropped out during the experiment, i.e., missing more than two decisions, were not paid and automatic decisions, i.e., randomly sampled decisions from other active participants belonging to the same session, were implemented at their place. All sessions lasted a maximum of 50 minutes. The SI Appendix includes participant demographics (Section 1) and the experimental instructions and screenshots (Fig. S1, Section 2). In Section 3, we report additional results while statistical analysis on implemented tests can be found in Section 3.2 for OLS models, see Tables S1 to S9, and in Section 3.3 for GLS models, see Tables S10 to S13. Finally, we compare our experimental results with the model in ref. (30) in Section 4, see Fig. S15.

Notes

Competing Interest: The authors declare no competing interest.

Ethics Approval Statement

All our experiments were approved by the ethical committee at the Universidad Carlos III de Madrid. Informed consent was obtained from all participants involved in our study, in strict compliance with the principles expressed in the Declaration of Helsinki.

Funding

This research has been partially funded by grant PGC2018-098186-B-I00 (BASIC) funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. A.A. acknowledges the financial support of the Spanish Ministry of Science and Innovation under grant no. IJC2019-040967-I.

Authors' Contributions

All authors conceived the experimental setting. P.L. and A.A. ran online experiments and performed the data analysis. All authors discussed the results, drew conclusions, and wrote the manuscript.

Data Availability

Experimental data and files to generate the figures are available at https://zenodo.org/record/5718702. Experimental instructions are included in the SI Appendix.