Abstract
We investigate the effect of subway system openings on urban air pollution. On average, particulate concentrations are unchanged by subway openings. For cities with higher initial pollution levels, subway openings reduce particulates by 4 percent in the area surrounding a city center. The effect decays with distance to city center and persists over the longest time horizon that we can measure with our data, about four years. For highly polluted cities, we estimate that a new subway system provides an external mortality benefit of about $1 billion per year. For less polluted cities, the effect is indistinguishable from zero. Back of the envelope cost estimates suggest that reduced mortality due to lower air pollution offsets a substantial share of the construction costs of subways.
Traffic congestion is a serious issue in many cities around the world, in part because of its impact on air pollution and human health. One proposed solution is subways and other public transit infrastructure. These are costly up-front investments, and there is little evidence about whether they are worth it. In this paper, we investigate the effect of subway openings on urban air pollution. We rely on two principal data sources. The first describes the universe of world subway systems. The second is a remotely sensed measure of particulates, Aerosol Optical Depth (AOD), recorded by the Moderate Resolution Imaging Spectroradiometer (MODIS) aboard the Terra and Aqua earth observing satellites between February 2000 and December 2017. These data allow us to measure airborne particulates everywhere in the world, monthly, with an approximately 3 kilometer (km) spatial resolution. Our strategy for establishing the causal effect of subways on AOD relies on a comparison of changes in particulates within a city around the time of a new subway system opening. We consider multiple geographies, but our preferred outcome variable is air pollution in a 10-km disk with centroid in the city center.
For an average opening, the data indicate that subways result in a tiny decrease in AOD during the 18 post opening months but this decrease cannot be distinguished from zero. This average effect, however, conceals considerable heterogeneity across cities. Our main analysis focuses on the 58 subway openings that occurred between August 2001 and July of 2016. Of these, our event study research design indicates that 20 openings increased AOD and 12 had no measurable effect. In the remaining 26 cities, not quite half the sample, AOD fell after the subway opened.
Our investigations fail to find measurable relationships between estimated subway effects and initial city or subway characteristics, save one. The 23 cities where subways reduced AOD are overwhelmingly among those whose initial level of AOD was above median. For the set of cities in the top half of the initial AOD distribution, with above 0.36 AOD (approximately 28 μg/m3 pm2.5) on average in 2000, AOD levels fell by about 4 percent after the opening of the subway. This effect is robust to a variety of regression specifications and to changes in the details of how we calculate city average AOD levels. The effect is larger near the center of cities where subway service is usually concentrated and we cease to find significant pollution effects beyond 25 km from the city center. Data limitations hinder our ability to estimate the effects of subways over longer time horizons. However, the available data suggest the 4 percent decline in AOD experienced by an average high AOD city persists for at least four years.
As a complementary analysis, we provide evidence that subway ridership is a key correlate of AOD reductions, that is, cities where AOD fell significantly are also those in which ridership—and hence automobile substitution—is largest. Finally, we also investigate the effect of subway expansions1 beyond the inaugural lines and find small effects, both for the average city and high AOD cities.
Our findings are important for three reasons. Subways are often proposed as a policy response to urban air pollution. For example, Vollmer Associates et al. (2011) list air pollution reduction as an objective for New York City’s second avenue subway expansion. Our analysis provides a basis for assessing their cost effectiveness relative to other remediation policies. Apart from this paper, we are aware of only one study, Chen and Whalley (2012), that measures the effect of subways on air pollution. Like the present investigation, Chen and Whalley (2012) use an event study research design. Unlike the present study, Chen and Whalley (2012) study the opening of a single subway. In contrast, we study all of the 58 subway openings and 143 expansions that occurred anywhere in the world between August 2001 and July 2016. Thus, we dramatically improve on our ability to assess whether subway openings, in fact, reduce urban air pollution.
Second, our estimates of the reduction in pollution following subway openings and expansions, together with existing estimates of the health implications of particulates, allow us to calculate the value of averted mortality that follows from subway openings. We estimate that, for an average city initially in the top half of the AOD distribution, a subway opening prevents 22.5 infant and 500 total deaths per year. Using standard income-adjusted life values, this averted mortality is worth about $43 million and $1 billion per year, respectively. These estimates do not include the effects of particulate reduction on morbidity or on productivity and so probably understate actual health benefits. Although available subway capital cost estimates are crude, the estimated external health effects represent a significant fraction of construction costs, particularly for subway systems with costs at the low end of the observed range. Note that these estimates apply only to cities that are initially in the upper half of our AOD distribution. For cities in the lower half of the AOD distribution, the effect of subway openings is small and not distinguishable from zero.
Finally, little is known about transportation behavior in developing countries, and we shed indirect light on this important topic. First, and interestingly, we find no evidence that developing world and developed world cities respond differently to subways. This supports the idea that, at least in this regard, the two classes of cities are similar. Second, a back of the envelope calculation suggests that subways typically account for between 1.5–10 percent of trips within a few years of their opening. Given what is known about the relationship between subway ridership and traffic, and between traffic and particulate matter pm10, this level of ridership can plausibly account for the observed 4 percent reduction in particulates that follows a subway opening only if subways divert trips that would otherwise have occurred in particularly dirty vehicles or at particularly congested times. This is consistent with evidence that public transit serves the poor and that subways are much more heavily used at peak times for vehicle traffic.
I. Data
To investigate the effect of subways on urban air pollution we require data for a panel of cities describing subways, air pollution, and control variables. Our air pollution data are based on remotely sensed measures of suspended particulates. Our subways data are the result of primary data collection. We describe these data and their construction below, before turning to a description of control variables.
A. Subways
We use the same subways data as Gonzalez-Navarro and Turner (2019) organized into a monthly panel and updated to December 2017.2 These data define a “subway” as an electric-powered urban rail system isolated from interactions with automobile traffic and pedestrians. This excludes most streetcars because they interact with vehicle and pedestrian traffic at stoplights and crossings, but underground streetcar segments are counted as subways. The data do not distinguish between surface, underground, or aboveground subway lines as long as the exclusive right of way condition is satisfied. To focus on intra-urban subway transportation systems, the data exclude heavy rail commuter lines (which tend not to be electric powered). For the most part, these data describe public transit systems that would ordinarily be described as “subways,” e.g., the Paris metro and the New York city subway, and only such systems. As with any such definition, the inclusion or exclusion of particular marginal cases may be controversial.
On the basis of this definition, the data report the latitude, longitude, and date of opening of every subway station in the world. We originally compiled these data manually between January 2012 and February 2014 and updated them during 2020, using the following process. First, using online sources such as UrbanRail (2020) and links therein, together with links on Wikipedia (2020), we compiled a list of all subway stations worldwide. Next, for each station on our list, we recorded opening date, station name, line name, terminal station indicator, transfer station indicator, city and country. We obtain latitude and longitude for each station from Google maps 2020. We use the subways data to construct a monthly panel describing the count of operational stations in each subway city between February 2000 and December 2017, the time period for which our air pollution data are available.
Our analysis hinges on the ability to observe a subway city for some time before and after an opening. Thus, we face a trade-off between sample size, the length of time we observe cities, and maintaining a constant sample of cities. While we experiment with other study windows, our primary econometric exercise considers the change in AOD in the period extending from 18 months before until 18 months after a subway opening. Since the AOD data cover February 2000 to December 2017, to base this exercise on a constant sample of cities, we restrict our attention to subways that open between August 2001 and July 2016. Online Appendix Table A.7 lists the 58 subway system openings taking place in this time period, by date of opening, together with basic information about the cities where they are located. Subways opened fairly uniformly throughout the period and the average opening date is June 2010.3
For 42 of these 58 cities we are able to gather ridership data describing unlinked trips, mostly from annual reports, statistical agencies, or industry associations.4 Ridership is reported at the monthly level for around half of these 42 cities. For the rest, we interpolate to calculate monthly ridership from quarterly or yearly data. Online Appendix Table A.7 also reports mean daily ridership for each city where data are available, 18 months after the system’s inauguration. For the average city in our sample, 130,000 people rode the subway on an average day in the eighteenth month of the system’s operation.
Figure 1 shows the evolution of ridership as a function of time from opening for the first five years of system operation. The horizontal axis in this figure is months from the opening date. The vertical axis is mean daily ridership per 1,000 of city population. We see that ridership about triples over the first three years of operation, from about 20 to 60 riders per thousand of population. The rate of increase begins to slow about three years after opening.
Figure 1. Daily Ridership Per Capita.
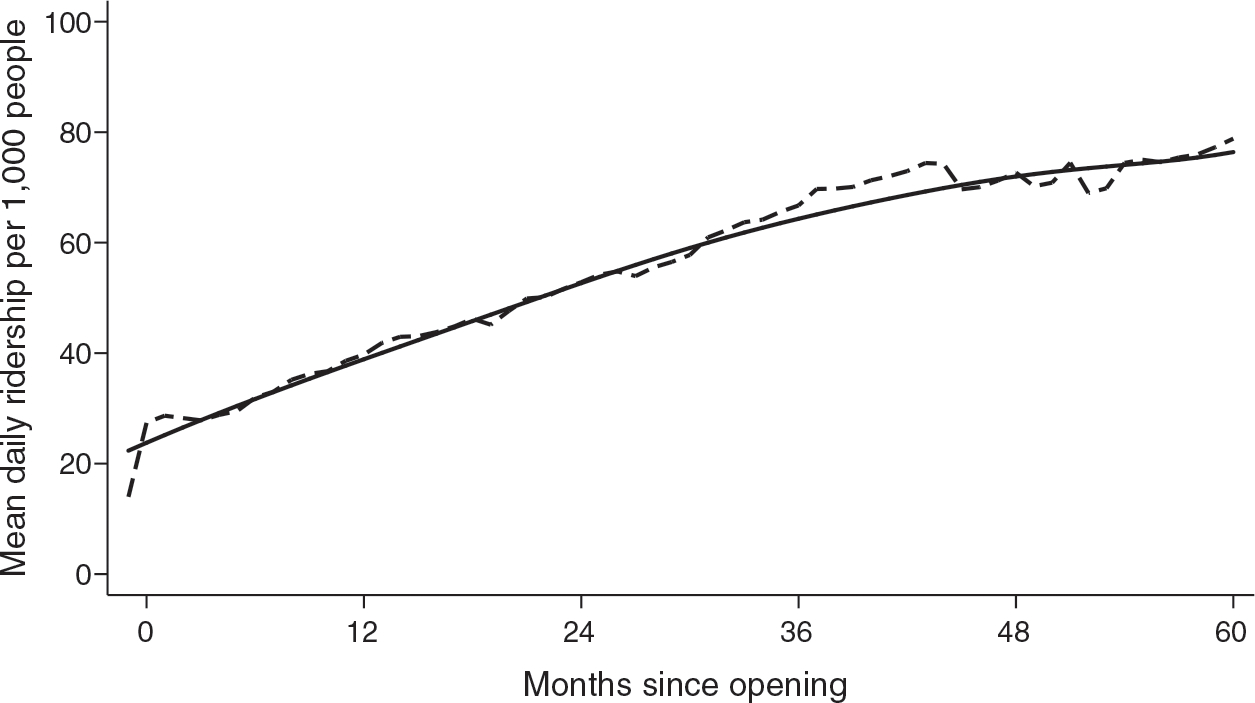
Note: This graph depicts average daily passengers on subway per 1,000 people in metropolitan area, as well as a locally weighted regression of the series.
Finally, we determine the date when construction began for each subway opening in our sample. On average, construction begins 77 months prior to opening and shows high variance.
B. Satellite-based Pollution
The Moderate Resolution Imaging Spectroradiometers aboard the Terra and Aqua earth-observing satellites provide daily measures of the aerosol optical depth of the atmosphere at a 3-km spatial resolution everywhere in the world (Levy and Hsu 2015). Remer, Levy, and Munchak (2013) provide a description of how the AOD measure is constructed. Loosely, these instruments operate by comparing reflectance intensity in a particular band against a reference value and attributing the discrepancy to particulates in the air column.5 Data are available in “granules,” which describe five minutes of satellite time. These granules are available, more or less continuously, from February 24, 2000 until December 31, 2017 for the Terra satellite, and from July 4, 2002 until December 31, 2017, for Aqua. During September 2018, we downloaded all available granules and subsequently consolidated them into daily rasters describing global AOD. Each of these daily aggregates describes about 86 million pixels covering the earth in a regular grid of 3-km cells.
Figure 2 presents a map showing AOD for December 1, 2017, and for average AOD during all of 2017, both from the Terra satellite. Darker shades indicate higher AOD readings. Unsurprisingly, the figures show high AOD in India and China. Myhre et al. (2008) attribute high AOD over Central and Western Africa to anthropogenic biomass burning in the region. White areas indicate missing data. Because they are highly reflective, the algorithm for recovering AOD from reflectance values performs poorly over light surfaces, so missing data are common in desert regions and over snow (Levy et al. 2013).
Figure 2. Worldwide AOD: Terra Satellite.

Notes: Darker colors indicate higher levels of AOD. White is missing.
The MODIS instrumentation can only record AOD on cloud-free days. In the December 1, 2017 image, much of the missing data reflect cloud cover, though some reflect the fact that Terra’s polar orbit brings it over most, but not all of the earth’s surface each day. Because AOD reporting is sensitive to cloud cover and light surfaces, there is seasonality in the MODIS data. We see more missing data in the Northern Hemisphere in the winter than in the summer. The countercyclical Southern Hemisphere phenomena is less dramatic.
Figure 3, panel A illustrates the AOD data for Palma, Spain in June 2017. To show scale, the large circle in this image is 25 km in radius. Panel B provides the corresponding image for December 2017. The small white circles represent subway stations at the end of the sample.
Figure 3. Seasonality in AOD, Influence Area Disks, and City Footprints for Palma, Spain.
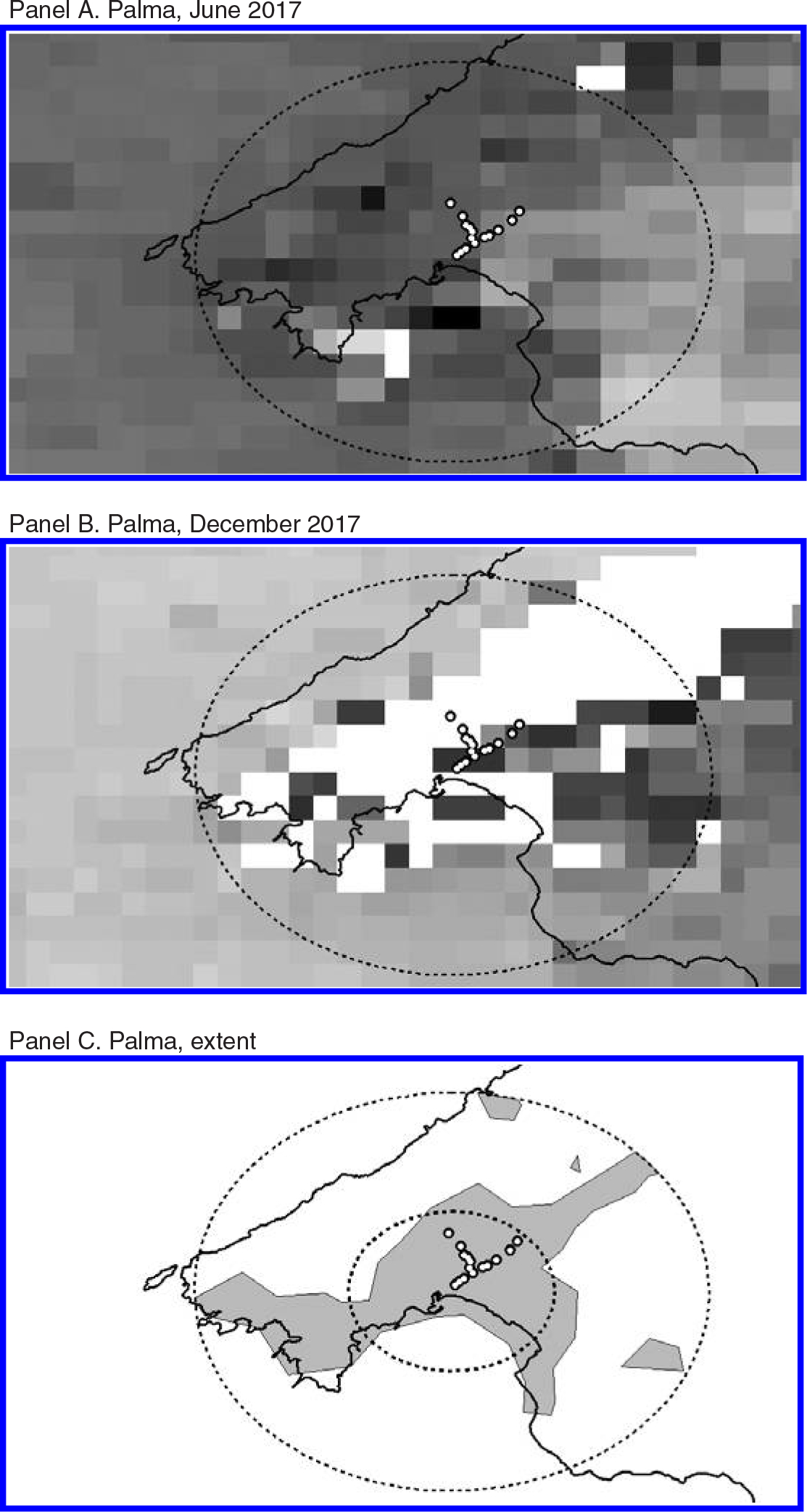
Notes: Terra AOD for Palma, Spain in June 2017 presented in panel A, and December 2017 presented in panel B. Darker pixels indicate areas where AOD is higher, and white pixels indicate missing values. The large circle in each image has a radius of 25 km and is centered on the central business district as reported in UN Department of Economic and Social Affairs (2018). Panel C illustrates the 25 km disk from above, the 10 km disk on which our analysis usually relies, and the lights at nightbased city footprint. Subway stations as of December 2017 are shown as small white circles.
While it is straightforward to calculate average AOD for any given area, we must choose the area over which to average. Panel C illustrates the geographies that we consider as the basis of this study. They are the 10-km and 25-km radius rings illustrated in panel C, and the intersection of these rings with a city footprint formed by tracing around the area that is sufficiently brightly lit at night to be considered part of the urban area. Panel C illustrates this footprint as the gray polygons.
In online Appendix C, we check that AOD is highly predictive of ground-measured pm10 and pm2.5. In addition, we find that the relationship between ground-based and remotely sensed particulates is not sensitive to the exact region we use to calculate city average AOD. That is, AOD is about equally good at explaining ground based measures if we evaluate AOD over a 10-km disk centered on the city, a 25-km disk centered on the city, or the corresponding city footprints derived from lights at night data. Given this, our analysis relies primarily on AOD averages calculated over 10-km disks. Finally, we note that in our preferred specification, one unit of remotely sensed AOD is associated with about 114 μg/m3 of pm10 measured by a ground-based instrument.
With daily images in hand, it is straightforward to construct monthly averages. To calculate our city-level monthly AOD measure, we average over the whole disk centered on the city for each day, and then average these city-day measures, weighting by the number of pixels observed in each day. Thus, our measure of AOD within 10 km of the center of a city is an average of all pixel-days of AOD readings that fall in this region during the month. We calculate this average for both satellites using disks of radius r ∈ {10km, 25km, 50km} as well as the intersection of these disks with city footprints for all cities in our sample.
Table 1 provides worldwide and continental summary statistics. In 2017, the average AOD reading within 10 km of a city center from the Aqua satellite was 0.40. It was higher in Asian cities, 0.50, and dramatically lower in European and North American cities. The corresponding reading from Terra is slightly higher. The top panel of Table 1 also reports AOD measurements based on disks with 25 km radius centered on each city. Unsurprisingly, these larger disks have slightly lower AOD levels than the smaller and more central 10-km disks. As for the 10-km disks, AOD measures based on Terra are slightly higher than those for Aqua, and Asian cities are more polluted than non-Asian cities. Table 1 also reports mean AOD over the more carefully drawn city footprints illustrated in panel C of Figure 3. Interestingly, these values barely differ from the corresponding values calculated on the basis of the comparable disk. Online Appendix Table A.7 reports the mean and standard deviation of AOD for each of our sample subway cities using the Terra satellite.
Table 1—
Mean AOD and Mean Pixel Counts for New Subway Cities
| World | Africa | Asia | Europe | N. America | S. America | |
|---|---|---|---|---|---|---|
|
| ||||||
| New subway cities | 58 | 1 | 39 | 9 | 3 | 6 |
| 2017 | ||||||
| AOD, Aqua, 10-km disk | 0.40 | 0.19 | 0.50 | 0.17 | 0.22 | 0.26 |
| AOD, Terra, 10-km disk | 0.41 | 0.20 | 0.50 | 0.18 | 0.20 | 0.24 |
| # pixels, Aqua, 10-km disk | 86.95 | 206.20 | 81.74 | 136.68 | 38.93 | 50.27 |
| # pixels, Terra, 10-km disk | 100.77 | 216.66 | 97.68 | 153.22 | 47.01 | 44.82 |
| AOD, Aqua, 25-km disk | 0.39 | 0.18 | 0.49 | 0.15 | 0.17 | 0.21 |
| AOD, Terra, 25-km disk | 0.39 | 0.19 | 0.49 | 0.17 | 0.18 | 0.23 |
| # pixels, Aqua, 25-km disk | 782.62 | 1,905.79 | 691.68 | 1,236.55 | 614.42 | 597.95 |
| # pixels, Terra, 25-km disk | 849.67 | 1,899.85 | 791.80 | 1,310.07 | 548.60 | 512.17 |
| AOD, Terra, 10-km footprint | 0.41 | 0.20 | 0.51 | 0.18 | 0.23 | 0.22 |
| # pixels, Terra, 10-km footprint | 87.02 | 150.77 | 87.24 | 129.28 | 38.02 | 29.49 |
| AOD, Terra, 25-km footprint | 0.42 | 0.20 | 0.51 | 0.17 | 0.20 | 0.26 |
| # pixels, Terra, 25-km footprint | 371.72 | 846.38 | 368.19 | 585.83 | 154.85 | 102.84 |
| 2000 | ||||||
| AOD, Terra, 10-km disk | 0.42 | 0.24 | 0.51 | 0.25 | 0.23 | 0.26 |
| AOD, Terra, 25-km disk | 0.41 | 0.23 | 0.51 | 0.23 | 0.19 | 0.24 |
| AOD, Terra, 10-km footprint | 0.43 | 0.23 | 0.52 | 0.25 | 0.27 | 0.27 |
| AOD, Terra, 25-km footprint | 0.43 | 0.21 | 0.52 | 0.23 | 0.21 | 0.27 |
In an average month, the AOD reading for an average 10-km city disk is based on 89 pixel-days for Aqua and 104 for Terra. Since the pixels are nominally 3 km, if all possible pixel-days in a 10 km disk were recorded over a month, we would expect about (365/12) × π × (10km/3km)2 = 1,061 pixels. Thus, conditional on observing one or more pixel-days, our city-month AOD values are based on measurements of about 10 percent of possible pixel-days. About 4 percent of city-months contain zero pixel-day observations and do not appear in our sample.
Table 1 also reports pixel counts for the two footprint measures. The count of pixels in the 10 km disk and 10 km footprint means are quite close. This is consistent with what we see in Figure 3. The lights based city footprint typically almost completely includes the 10 km disk centered on the city. In contrast, the 25 km footprint measure contains many fewer pixels than does the 25 km disk. This is also consistent with what we see in Figure 3.
The second panel of Table 1 presents AOD averages for 2000 for 10 km disks. Because only the Terra satellite was in operation in 2000, the second panel presents only these measures. Comparing across years, we see that variation across years is small compared to the level and compared to variation across continents. Table 1 suggests a slight downward trend in European AOD, and no obvious trend for the other continents or for the 58 cities as a whole.
We observe a strong seasonal pattern in AOD. This reflects seasonal variation in cloud cover and motivates our use of city-by-calendar month indicators as controls in our regressions. Together the two panels of online Appendix Figure A.1 suggest that a relationship exists between the extent of AOD data availability and the level of AOD. In fact, a regression of average AOD in a city-month disk on the count of pixel-days used to calculate that average reveals a slightly positive relationship. We conjecture that this reflects the fact that the air is cleaner in rainy places where cloud cover is more common. Regardless of the reason, we experiment broadly with sampling rules that reduce the importance of city-months with sparse AOD data and with controlling for the count of pixel-days used to construct each city-month average, and we find no qualitative changes in our results. In most of our regression results we control for the number of pixel-days used to construct each city-month AOD observation.
C. Other Control Variables
Consistent with the large related literature that we describe in online Appendix C, we find that local weather conditions are important determinants of remotely sensed AOD. Given this, we construct several controls for city-month weather conditions. The CRU gridded dataset from Harris et al. (2014) provides high resolution monthly climatic data describing cloud cover percentage, frost day frequency, mean temperature, precipitation, and vapor pressure. We use these data to calculate monthly and annual averages of these variables over disks centered on each city. Together with AOD pixel count these are our “climate controls.”
We also include city population and country GDP per capita to characterize the level of economic activity of each city. Our city population data come from the United Nation’s World Urbanization Prospects data (UN Department of Economic and Social Affairs 2018). These data describe annual population counts for the universe urban agglomerations with populations exceeding 300,000 in 2018. We use these data in three main ways. First, they provide coordinates for the centers of all of the cities they describe. With a few exceptions that we adjusted by hand on the basis of lights at night data, we use these coordinates for the centers of all of our cities. Second, we rely on these data as source of city level population data. Third, in some of our regressions, we expand our sample to include non-subway cities as a way to increase the precision with which we estimate control variables effects. In these regressions, we include all of the 461 non-subway cities in our sample.
We use the Penn World Tables to obtain annual measures of country GDP (Feenstra, Inklaar, and Timmer 2015) for all cities in our sample. Online Appendix Table A.7 reports population and country level GDP per capita for each city in our estimating sample at the time of subway system opening. Cities that opened subways in recent years are large, their average population is 4.0 million when their subways open, and they tend to be in middle or high-income countries.
II. Conceptual Framework
The logic of a relationship between subways and air pollution rests on two hypotheses about the relationships between subways, travel behavior, and pollution. First, that internal combustion engines contribute to air pollution. Second, that subway trips reduce motor vehicle trips, at least at certain times and places in a city. We discuss both below, along with other factors that have the potential to amplify or attenuate these relationships in different urban settings.
The relationship between automobile traffic and pollution is much studied. Chen et al. (2016) uses variation in Beijing traffic caused by a license plate restriction and widespread superstitious avoidance of licence plates ending in “4” to provide convincing causal estimates of a negative relationship between a traffic congestion index and an air quality index. Friedman et al. (2001) examine changes in traffic and changes in pm10 in Atlanta around the 1996 Summer Olympics. During this time, the city imposed restrictions on driving and saw traffic fall by about 2.8 percent over a 17-day period. During the same period, pm10 fell by 16.1 percent. That is, each 1 percent reduction in driving was associated with about a 5 percent reduction in pm10. In a related exercise, Gibson and Carnovale (2015) examine the effect of a change in Milan’s congestion pricing program on both traffic and pm10. Their estimates allow us to calculate that a 4 percent reduction in traffic caused about a 1 percent pm10 reduction.6 The variation in these point estimates foreshadows the variance we will find in the effects of subways on AOD, and it is natural to suspect that physical geography may be partly responsible for this variation. Unlike the studies described above, our sample is large enough to allow us to explore whether wind patterns and city topography are relevant determinants of heterogeneous effects of subway systems, by allowing pollutants to be easily dispersed or entrapped, respectively.
The literature also investigates the relationship between subways and vehicle traffic in large cities. Anderson (2014) examines changes in Los Angeles traffic congestion during a 35-day transit strike in 2003. During the strike, delay per mile increases by about half during peak hours on highways serving the same region as LA’s subway lines. The effect on delay at other times and places is approximately zero. In a sample of 42 Chinese cities, Gu et al. (2020) examine changes in a cell phone-based measure of street-segment-by-hour traffic speed for segments near newly opened subway lines. They find a measurable increase in traffic speed for 48 weeks (the extent of their data) following the opening of a subway line. Both results are consistent with subway openings causing a reduction in driving.
Together, these results suggest subways affect pollution by reducing traffic. Chen and Whalley (2012) tests this relationship directly by comparing air pollution in central Taipei during the year before and after the opening of the Taipei subway in March of 1996. Comparing hourly pollution measurements from measuring stations in central Taipei to hourly ridership data, they estimate a 5–15 percent reduction in carbon monoxide following the subway opening, about the same effect on nitrous oxides, but little effect on either ozone or particulates.
This evidence in hand, we note its limits. The results above describe time periods measured in weeks and are restricted to routes that compete with the subway. Given the generational planning horizon for subway systems, extending these results to a longer time horizon is important. Over a longer time horizon, other responses to subway availability may offset short-run reductions in traffic and pollution. Foremost is the possibility that decreases in traffic caused by the subway will be short-lived as drivers eventually exploit the newly available road capacity. Duranton and Turner (2011) provide indirect evidence for such an effect. Comparing total vehicle miles driven in US metropolitan areas to total lane miles of highways over a ten-year period, they find that a 1 percent increase in highways causes a 1 percent increase in total driving.7 Although Duranton and Turner (2011) studies highway expansions, the logic of their finding suggests that a reduction in traffic due to increased subway ridership, like other capacity expansions, should cause an offsetting increase in the demand for automobile and truck travel. If so, subways will not reduce traffic and pollution in metropolitan areas over a decennial time scale. We will show well-identified, short-term effects as well as evidence from longer time horizons to shed some light on the issue of temporal decay.
To the extent that subways reduce the cost of urban mobility we should also expect changes in the spatial organization of economic activity. This is the most basic prediction of theoretical models of cities (Duranton and Puga 2015) and the evidence that transportation infrastructure in general, and subways in particular, lead to a reorganization of cities is compelling. Baum-Snow (2007) finds that the interstate highway system played an important role in the decentralization of US cities from 1950 to 1990. Baum-Snow et al. (2017) confirm that Chinese highways have much the same effect on Chinese cities. For subways, in a sample of 161 subway cities between 1950 and 2010, Gonzalez-Navarro and Turner (2018) find that subway networks tend to favor movement in and out of the downtown core, and that they cause cities to become more decentralized. Heblich, Redding, and Sturm (2020) refines this conclusion and shows that the opening of the London underground led to a concentration of employment in the center and increased separation of workplace and residence.
In short, subways reduce the cost to move people. In response, cities reorganize in ways that require greater mobility: they spread out and the separation of workplace and residence increases. In the analysis that follows, we will investigate the spatial extent of the effect of subways on air pollution. In particular, we will be interested in estimating pollution impacts at different distances from the downtown of a city. Because subways tend to serve central cities, substitution of automobile trips should confer larger pollution reductions in areas closer to downtowns and decay as distance from the downtown increases.
Finally, a central prediction of most theoretical models is that reductions in transportation costs will draw more people and economic activity into a city (e.g., Duranton and Puga 2015). Therefore, to the extent that pollution and economic activity are complementary, subways should increase pollution levels.8
Summing up, the available evidence supports the idea that subways reduce traffic and hence pollution during (about) the year after the subway opens. This evidence, however, is pieced together from studies of small numbers of cities, and it is natural to wonder whether this chain of causation leads to the same outcome for all new subways.
Back-of-the-envelope calculations of the sensitivity of automobile travel to subway openings suggest that subways can reasonably provide between about 1.5 percent and 10 percent of trips in a city.9 For the sake of illustration, suppose a 1 percent reduction in traffic results in a 1 percent reduction in pm10 and that there is no demand response for car travel as drivers shift trips to the subway. In this case, a subway reduces pm10 by between 1.5 percent and 10 percent. This brackets our estimated 4 percent reduction in high AOD cities.
This example highlights two points. First, the logic of induced demand will mean that each 1 percent of trips diverted to the subway will elicit additional automobile trips. Moreover, a 1 percent reduction in automobile trips will generally result in a less than 1 percent reduction in pollution. Therefore, given the back-of-the-envelope calculations described above, if subway openings result in meaningful reduction in AOD, it will be because they are displacing trips that are particularly dirty, either because they involve particularly dirty vehicles or trips that make large contributions to congestion.
Second, the range of effects suggested by our back-of-the-envelope calculations suggests that the way cities respond to subways is likely to be heterogeneous. Indeed, in our sample, ridership varies from a low of 4,000 passengers per day to a maximum of over 400,000 passengers per day 18 months after opening. Understanding this heterogeneity will be an important part of our analysis. If subways are to play a role in improving urban air quality, it is important to learn where we should expect larger effects. On the basis of the discussion above, our investigation of city heterogeneity implicitly involves looking for cities where subways draw a lot of riders, where induced demand is relatively small, and where car trips are relatively polluting.
More specifically, we investigate how the effect of subways on AOD varies with the following classes of city attributes. Cities that already enjoy clean air have less potential to improve, while windy cities, and those with flat geography should be better able to disperse pollution. Poor countries may benefit more from subway construction given that their vehicle fleets tend to be more polluting. City size may explain heterogeneous effects because traffic congestion is most relevant in cities experiencing large or increasing levels of population. Thus, we investigate heterogeneous effects by city population density, city size, city growth, and whether the subway system at opening is relatively large or small.
III. Results
A. Econometric Framework
In our primary econometric exercise, we examine changes in AOD using an event study design that exploits the high-frequency air pollution data as well as the sharp starting date of subway systems.
Let i = 1, …, I index cities and t index months. Let AODit denote AOD in city i at time t. We usually observe a city twice in each month, once with each of the two satellites, but suppress the satellite subscript for legibility.
If city i opens its subway in month t′, then define τit = t − t′. That is, τit is “months since the subway opened,” with months before the opening taking negative values. Let k describe the window over which we analyze AOD, i.e., τit ∈ {−k, …, 0, …, k}. We will most often be interested in the case of k = 18, that is, the 37-month period extending from 18 months before until 18 months after a subway opening. Now define the following families of indicator variables,
| (1) |
| (2) |
Equation (1) describes indicators for sets of city-months that are the same number of months away from the month when the subway system opens. Equation (2) describes indicators for a set of step functions beginning in j and ending j′ months from the subway opening month.
To estimate the effect of subway system opening on urban air pollution, we use the following event study specification:
| (3) |
where βi is a city fixed effect and Dit(j) is a dummy indicating observations j months from a subway opening in city i. The reference category excluded from the regression is Dit(−6). Note, αj are the coefficients of interest, which will be negative after opening (j > 0) if subways improve air quality. We are also interested in verifying that the estimated coefficients corresponding to months before subway opening (j < 0) are not statistically different from zero, as this provides evidence of a lack of preexisting trends in pollution before treatment. We can also bin the data in a more aggregated manner so that the coefficient αj can correspond to a series of three- or six-month bins in equation (3). When we do this, the reference period becomes the bin containing month six before a subway opens.
We also include the following control variables: a satellite indicator to account for slightly different AOD measurements from each satellite, year-by-continent indicators to flexibly account for regional trends in AOD, and city-by-calendar month (1–12) indicators to capture seasonality in pollution patterns that repeat annually but are idiosyncratic to each city. We control for linear and quadratic terms in monthly city-specific climate variables (cloud cover percentage, frost day frequency, mean temperature, precipitation, and vapor pressure). Finally, we also control for the count of AOD pixel-days used to calculate the city-month AOD measure.
For most of our analysis, we use a 37-month study window, running from 18 months before, to 18 months after each city’s subway opening. This window length strikes a balance between maintaining the set of cities from which we identify our coefficient of interest and having a long analysis window. Here and throughout, we cluster errors at the city level.
We also allow for a city specific pretreatment and posttreatment window by including city-specific dummies 1it(τ < −k), 1it (τ > k), and Dit(0) as part of our control set. This allows us to use all city-months in our sample to estimate city-by-calendar month indicators, continent-by-year indicators, and climate variables, while only using AOD variation near the subway opening date to estimate the effect of subways on AOD. Month of opening τ = 0 is “partially treated” depending on the exact day subway system started making it harder to interpret.10
In addition to the event study graph, we also present regression results in table format. Here, instead of estimating a series of coefficients around subways introduction, we compare AOD in the 18-month period before the subway to the 18-month period after it starts. More specifically, these regressions take the form
| (4) |
This is a regression of AOD on an indicator for post-opening and controls, keeping everything else unchanged from the event study specification. The coefficient of interest is α1, the difference in conditional mean AOD between city-months with τit ∈ {−18, …, −1} and those with τit ∈ {1, …, 18}.
B. Average Effect
We present our estimates of the average effect of subways on air quality in Figure 4. The figure displays estimated coefficients αj around subway opening from equation (3) as well as 95 percent confidence intervals. The vertical axis is AOD units. Panel A shows three-month bin estimates, while panel B presents results using six-month bins, where the indexing of αj runs over these sets of bins. As explained above, the bin containing month −6 is set as the reference period, and the point estimate is depicted in the middle of the bin. For example, in the 3-month bin specification shown in panel A, the reference bin refers to months −4, −5, and −6 and the point estimate is shown in the middle month of the bin (τ = −5 ). Both figures display a lack of pretreatment trends as well as a slight reduction in AOD that is not statistically different from zero. This figure suggests that for the average city in the sample, we cannot reject that the effect of subways on urban air pollution is nil. Note that mean AOD in our sample is about 0.46, so monthly variation in point estimates is small relative to the mean level.
Figure 4. Event Study.
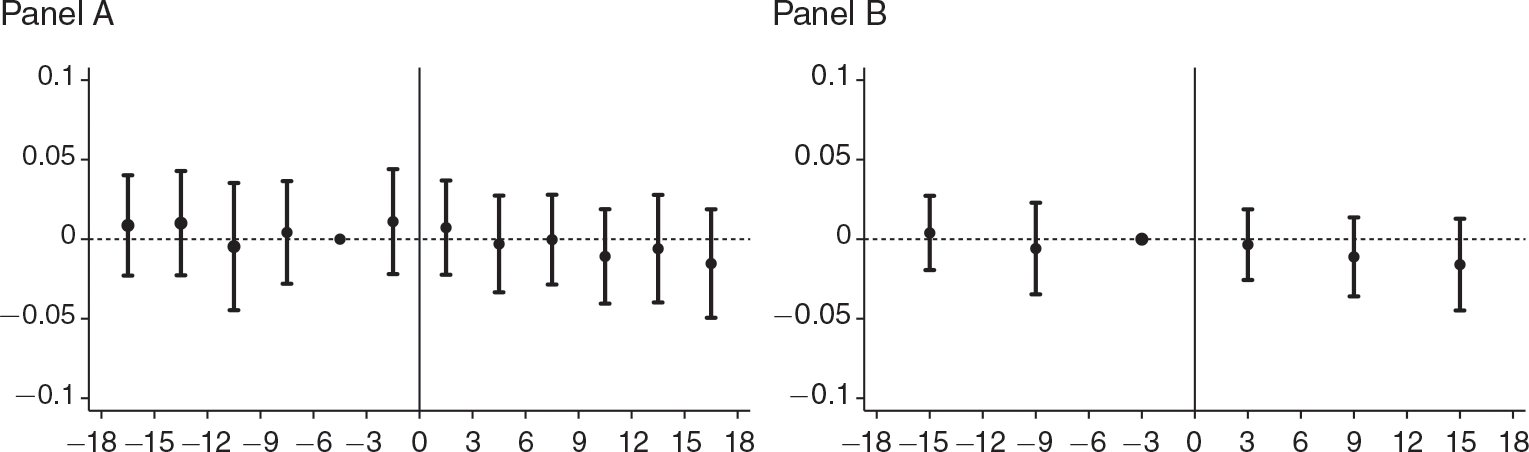
Notes: This figure shows event study coefficients of AOD around the time of subway opening and confidence intervals based on standard errors clustered at the city level. The vertical line at x = 0 indicates the month of subway opening. Panel A shows coefficients estimated using three-month bins (reference bin is months τ = {−6, −5, −4}). Panel B shows coefficients using six-month bins (reference bin is months τ = {−6, −5, −4, −3, −2, −1}). Coefficient estimates are shown in the graph at the midpoint of the bin. Controls are as in column 5 of Table 2.
Table 2 shows results using specification (4). Moving across the columns of the table, we add progressively more controls. Column 1 estimates a version of specification 4 with a minimal set of controls.11 Column 2 adds satellite and continent-by-year dummies, column 3 adds city-by-calendar month dummies, column 4 adds climate controls, while column 5 instead uses climate-by-continent controls. In all cases we estimate a treatment effect of about −0.01. This is small relative to the 0.46 sample mean AOD and is not distinguishable from zero at conventional levels of significance. Column 6 adds observations from all cities in the UN cities database to estimate more precisely common controls such as continent by year and climate, and we find virtually the same result.
Table 2—
Average Effect of Subway Openings
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
|
| |||||||
| Post | −0.0128 (0.0115) | −0.0081 (0.0123) | −0.0088 (0.0089) | −0.0094 (0.0090) | −0.0094 (0.0090) | −0.0092 (0.0079) | 0.0021 (0.0151) |
| Post × t | −0.0012 (0.0014) | ||||||
| Satellite | N | Y | Y | Y | Y | Y | Y |
| Cont. × year | N | Y | Y | Y | Y | Y | Y |
| City × cal. mo. | N | N | Y | Y | Y | Y | Y |
| Climate | N | N | N | Y | N | N | N |
| Climate × cont. | N | N | N | N | Y | Y | Y |
| City trend | N | N | N | N | N | N | Y |
| Mean AOD | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.42 | 0.46 |
| R 2 | 0.61 | 0.62 | 0.80 | 0.80 | 0.80 | 0.76 | 0.80 |
| Number of events | 58 | 58 | 58 | 58 | 58 | 58 | 58 |
| Number of cities | 58 | 58 | 58 | 58 | 58 | 519 | 58 |
| Observations | 21,806 | 21,806 | 21,806 | 21,806 | 21,806 | 194,458 | 21,806 |
Notes: Dependent variable is mean AOD in a 10-km disk with centroid in the city center. Column 6 adds all non-subway cities. All specifications control for city fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure, and frost days. Standard errors clustered at the city level are in parentheses.
Column 7 investigates whether we observe a change in the time trend of AOD with subways using the main estimating sample of 58 cities and allowing for city specific time trends in AOD. The regressor of interest is now an 18-month post-subway dummy as well as the interaction with time. Again, while the point estimate on the AOD trend post-subway-opening is negative, the estimate is not sufficiently large to differentiate it from zero.
First, note that to the extent that subways decrease pollution for an average system opening in this sample, this effect is small. Second, the controls matter in the way we would hope. As we move from column 1 to column 5, the coefficient of interest is steady, while R2 values increase and standard errors decrease or stay constant. Third, when we control for trends in column 7, the level effect of subways shrinks and becomes slightly positive. That the trend variable is slightly negative suggests that the slight negative effect we see in the first five columns is captured by the trend variables.
Online Appendix Table A.3 reports robustness checks for the regression reported in column 5 of Table 2. In particular, we repeat this specification but we (i) weight observations by the count of observed AOD pixels that make up each city-month AOD measurement count, (ii) drop observations with low pixel count, and (iii) calculate city-month AOD on the basis of three different city footprints. Online Appendix Table A.4 repeats the specification of Table 2, column 5 for a variety different windows of analysis (k = 6 months, 12 months, 24 months, and 36 months). All of these alternative specifications confirm the conclusion suggested by Table 2: the average effect of subways on AOD is consistently negative and not distinguishable from zero at conventional levels of significance.
Following Andrews (1993, 2003) and Hansen (2000), we checked for a structural break in the level and trend of AOD around the time of system opening by estimating a series of regressions of AOD on a step function or spline, as we allow the timing of the step or spline to traverse the study period. The details of these tests are presented in online Appendix F. These tests do not support the hypothesis that there is a break in the level or trend of AOD around the time of an average subway opening.
We also note that in theory, our research design could confound the effects of system openings with those of expansions that occur soon afterward. Among the 58 cities that make up our main sample, 19 experienced an expansion of their subway systems within 18 months of the system opening. We also experiment with dropping cities that experience an expansion soon after an opening from our sample. Our results are robust to such changes.
C. Heterogeneous Effects
We estimate a version of equation (4) where we allow the effect of subways to be different in every city. When we do this, we find evidence of substantial heterogeneity of impacts. There are 20 cities where subway openings appear to cause statistically significant increases in AOD, 26 where they appear to cause a decrease, and 12 where the effect is, like the average, indistinguishable from zero.
We now turn to an investigation of the reasons for such dramatically heterogeneous responses. Table 3 investigates whether subways have different effects on different types of cities. In this table, we replicate the results of column 5 of Table 2, but add an interaction between the post-subway indicator and a particular city characteristic.
Table 3—
Heterogeneous Treatment Effects
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Post | −0.0178 (0.0102) | −0.0087 (0.0088) | −0.0020 (0.0075) | −0.0102 (0.0087) | −0.0160 (0.0136) | −0.0081 (0.0143) | 0.0032 (0.0145) | 0.0126 (0.0083) |
| Post × x | 0.0169 (0.0164) | −0.0014 (0.0173) | −0.0140 (0.0162) | 0.0016 (0.0167) | 0.0128 (0.0157) | −0.0026 (0.0160) | −0.0243 (0.0168) | −0.0403 (0.0148) |
| Satellite | Y | Y | Y | Y | Y | Y | Y | Y |
| Cont. × year | Y | Y | Y | Y | Y | Y | Y | Y |
| City × cal. mo. | Y | Y | Y | Y | Y | Y | Y | Y |
| Climate × cont. | Y | Y | Y | Y | Y | Y | Y | Y |
| Mean AOD | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 |
| R 2 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 | 0.80 |
| Number of events | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 |
| Number of cities | 58 | 58 | 58 | 58 | 58 | 58 | 58 | 58 |
| Observations | 21,806 | 21,806 | 21,806 | 21,806 | 21,806 | 21,806 | 21,806 | 21,806 |
Notes: Dependent variable is mean AOD in a 10-km disk with centroid in the city center. Each column uses the same specification as in column 5 of Table 2, with the addition of an interaction term. Interaction terms x are as follows: column 1, above median city population in 2000; column 2, above median density in 2000; column 3, above median population growth, 1990–2000; column 4, below median country GDP per capita in 2000; column 5, above median elevation range in a 25 km disk centered around the city center; column 6, above median wind speed in 2000; column 7, above median number of stations per capita at opening; column 8, above median AOD in 2000. Standard errors clustered at the city level are in parentheses.
We choose interaction effects to investigate on the basis of the discussion in Section II. We are interested in whether and how the effect of subways on AOD varies with the overall level of hydrocarbon powered travel or the characteristics of the vehicle fleet, with the extent to which such traffic is congested, with the extent or importance of the subway, and with physical geography related to pollution dispersion.
In the first three columns of Table 3, we rely on indicator variables describing basic city characteristics; (1) above median city population in 2000; (2) above median density in 2000,12 and (3) above median population growth, 1990–2000. Column 4 explores heterogeneity by median country GDP per capita in 2000. Columns 5 and 6 investigate the role of geographical features. Column 5 explores heterogeneity by city relief and column 6 by wind speed.13 Column 7 investigates heterogeneity by the size of the subway supply shock as measured by an indicator of whether the number of stations per capita is above the median in the sample.
Column 1 suggests that subways have a larger effect on AOD in smaller cities, while column 3 suggests that subways may have a larger effect in faster growing cities. Smaller cities tend to grow faster, so these results, although statistically insignificant, seem to be consistent with each other. We do not find heterogeneous effects by city density in column 2. We also do not find meaningful heterogeneous effects by country income. Column 5 includes an indicator for above median elevation range in a 25 km disk centered around the city center and column 6 includes an indicator for above median wind speed in 2000. Neither effect is distinguishable from zero. Column 7 includes an indicator for above median number of stations per capita at opening. This effect, also, is not distinguishable from zero.
Finally, column 8 considers above cities with above median AOD in 2000. This effect is large and highly significant. Subways have a much larger effect on AOD in more polluted cities. To help understand this heterogeneity in more detail, Figure 5 presents two funnel plots summarizing the 58 city-specific estimates of the effect of a subway opening on AOD. The top figure shows estimates among cities with above median AOD levels at baseline, while the bottom figure shows estimates for cities with below median AOD levels at baseline. The horizontal axis displays the coefficient estimate of the subway effect for each city. The vertical axis displays the corresponding standard error. Shaded regions indicate statistical significance at usual confidence levels. For example, the white area in the center indicates estimates that are not distinguishable from zero. The large extreme left and extreme right, light gray shaded areas indicate coefficient estimates that are significant at least at the 1 percent level. In both figures, the large triangle indicates the average effect that we estimated in Table 2, column 5 for the overall sample. The distribution of subway effects in the top figure for high AOD cities clearly lies to the left of those in the bottom figure with the less polluted cities in the sample.
Figure 5. Heterogeneous Treatment Effects by High and Low Baseline AOD Levels.
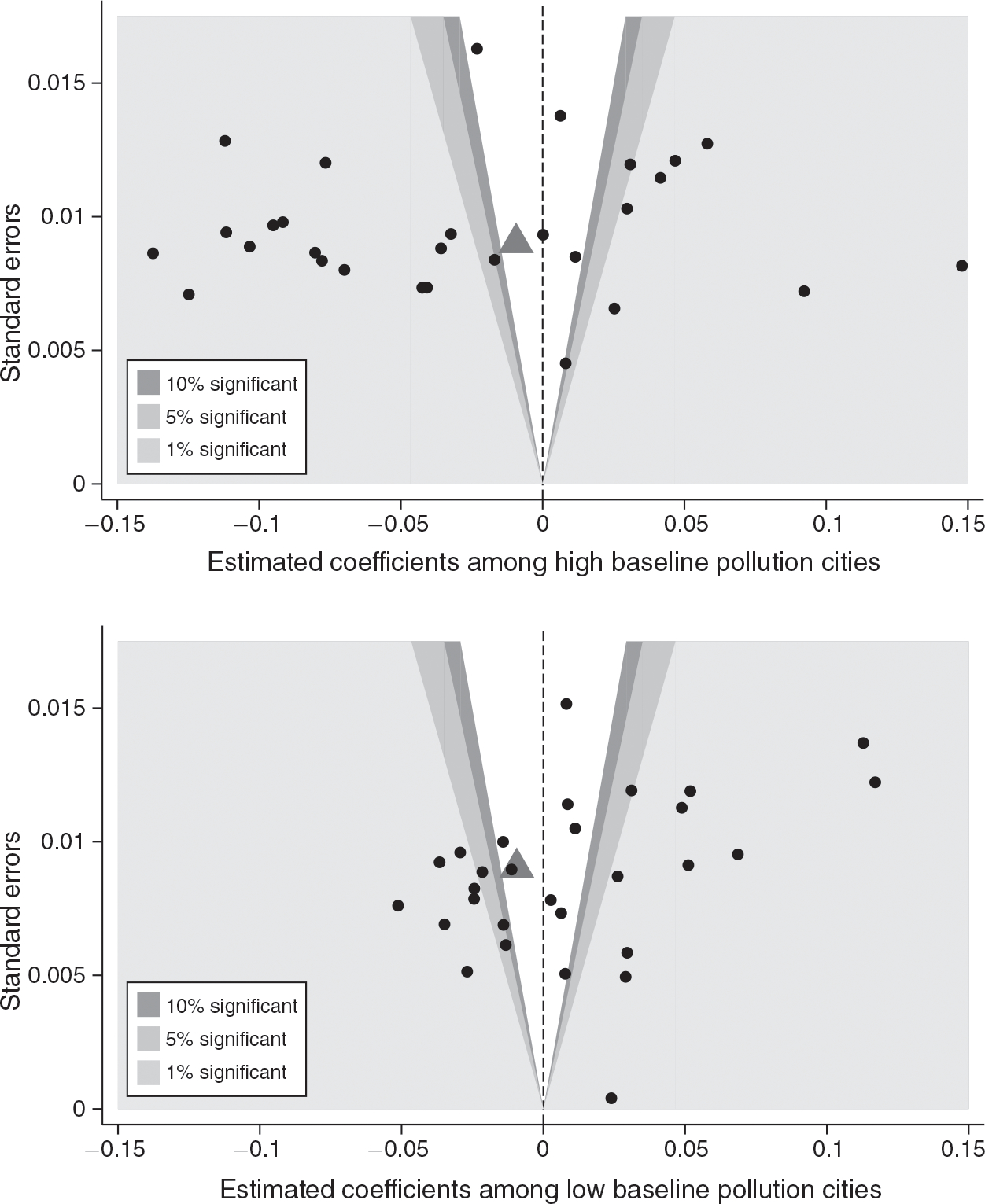
Notes: These funnel graphs show the 58 city-specific subway effects as small circles based on equation (4), where the coefficient α is allowed to vary by city. The x-axis shows coefficient estimates, the y-axis shows standard errors. The region in white contains estimates that are not significantly different from zero. Dark, medium, and light gray regions are different from zero at 10 percent, 5 percent, and 1 percent in two-sided tests, respectively. The top (bottom) panel shows estimates for cities with above (below) median AOD levels at baseline. In both figures, the large triangle indicates the overall sample mean effect estimated in Table 2, column 5. Controls are as in column 5 of Table 2. Standard errors are clustered at the city level.
Figure 6 goes further in showing the heterogeneity by initial level of AOD by presenting coefficient estimates for every city against average AOD level in 2000 on the x-axis. In the figure, dark dots are significant at the 5 percent level and the solid line shows a linear fit of the coefficient estimates. As can be seen, subway openings reduce air pollution more in initially more polluted cities. The dots to the right of the vertical dashed line correspond to the top graph in Figure 5. While clearly more negative on average, the figure also indicates a pattern of higher variance in the coefficient estimates among highly polluted cities.
Figure 6. Treatment Effects and Initial AOD Levels.
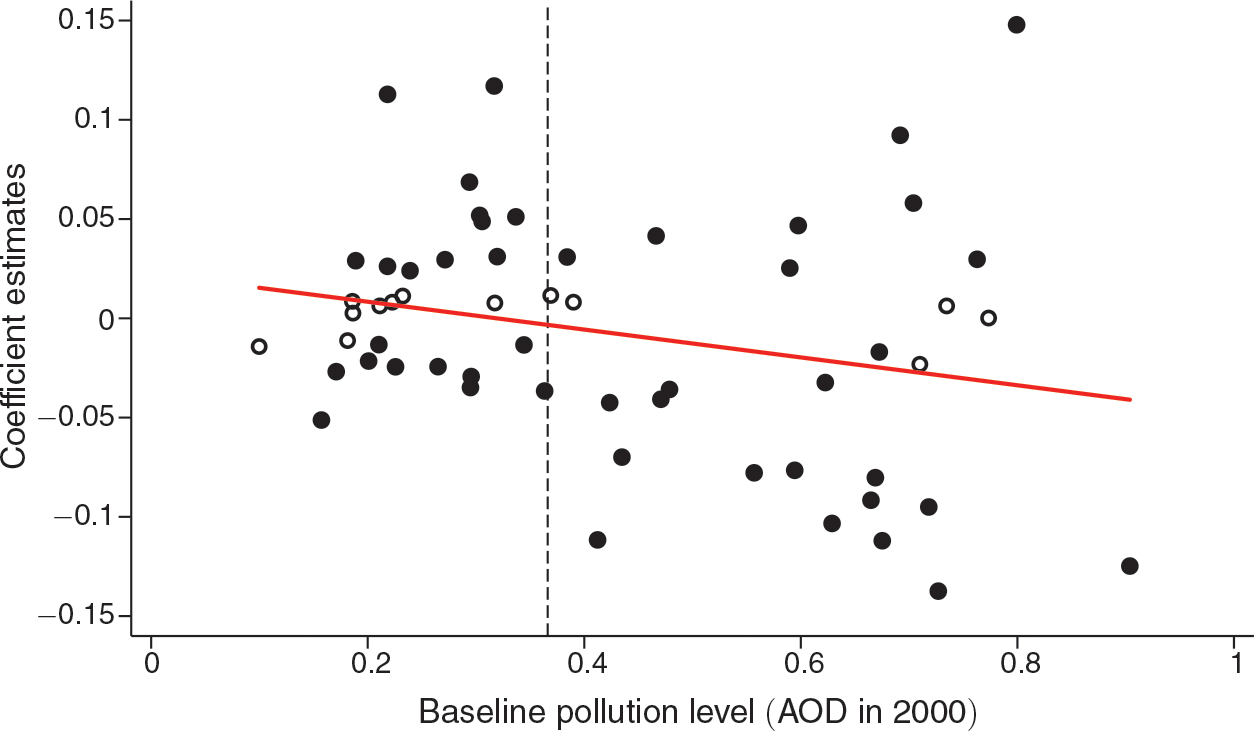
Notes: This figure shows the 58 city-specific subway effects as small circles based on equation (4) where the coefficient α is allowed to vary by city. Dark dots are significant at the 5 percent level. The x-axis shows initial AOD level in 2000, the y-axis shows coefficient estimates. The solid line shows a linear fit of the dots and the vertical dashed line shows the partition of the sample into below and above median initial AOD level. Standard errors are clustered at the city level.
To test the robustness of the effect of subways on pollution among high AOD cities, Table 4 replicates specifications 1–6 from Table 2 on the high AOD subset of cities. We see that the estimated effect of subways on AOD in this sample is about −0.03. This is the difference between the main effect and the interaction effect in column 8 of Table 3. This magnitude is consistent across specifications and is distinguishable from zero (as opposed to the mean for less polluted cities) at low levels of significance in columns 4 and 5, where we include our most exhaustive sets of controls. In an effort to improve the precision of our estimates, in column 6 we expand our sample to include 461 cities without subways in the final year of our sample. Since these cities do not experience subway openings they do not contribute to the estimate of the treatment effect directly. However, they do increase the precision with which we are able to estimate continent level and climate related controls. In column 6 of Table 4, we see that this strategy gives a more precise estimate of the subway effect, although the magnitude of the coefficient is essentially unchanged.
Table 4—
Effect of Subway Openings in High AOD Cities
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Post | −0.0290 (0.0207) | −0.0246 (0.0212) | −0.0246 (0.0147) | −0.0272 (0.0146) | −0.0270 (0.0147) | −0.0284 (0.0130) |
| Satellite | N | Y | Y | Y | Y | Y |
| Cont. × year | N | Y | Y | Y | Y | Y |
| City × cal. mo. | N | N | Y | Y | Y | Y |
| Climate × cont. | N | N | N | N | Y | Y |
| Mean AOD | 0.66 | 0.66 | 0.66 | 0.66 | 0.66 | 0.43 |
| Bootstrap p-value | 0.174 | 0.252 | 0.111 | 0.078 | 0.083 | 0.049 |
| R 2 | 0.34 | 0.35 | 0.65 | 0.66 | 0.66 | 0.75 |
| Number of events | 29 | 29 | 29 | 29 | 29 | 29 |
| Number of cities | 29 | 29 | 29 | 29 | 29 | 490 |
| Observations | 10,896 | 10,896 | 10,896 | 10,896 | 10,896 | 183,548 |
Notes: Dependent variable is mean AOD in a 10km disk with centroid in the city center. Column 6 includes all non-subway cities. All specifications control for city fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure, and frost days. Standard errors clustered at the city level are in parentheses.
For the 10,896 city months in high AOD cities, AOD averages 0.66. From Table 4, the subway effect is about −0.028. Thus, our benchmark estimate for the effect of subways on AOD in polluted cities is about a 4 percent decline.
Cameron, Gelbach, and Miller (2008) find that asymptotic standard errors may not approximate exact finite sample standard errors in samples containing 30 or fewer clusters. Given this, we implement the wild-cluster bootstrap procedure recommended in Cameron et al. (2008) and report wild cluster bootstrap p-values for the treatment effect based on 300 bootstrap replications in the lower part of the table. This turns out not to have much effect on the estimated precision of our results.
As a further test of the robustness of the effect of subways on AOD in high AOD cities, online Appendix Table A.6 repeats the specifications 5 and 6 from Table 4 using treatment and control windows of 6, 12, 24, and 36 months. Effects are generally negative but are statistically distinguishable from zero only for the 36-month pre/post window and the specification of column 6 of Table 4, that is at windows of analysis of ±18 months or ±36 months.
Table 4 and online Appendix Table A.5 indicate a robust and fairly precise estimate of the treatment effect. Online Appendix Table A.6 suggests more caution. With this said, we note three reasons to discount the evidence in online Appendix Table A.6. First, the AOD process is clearly a noisy one, so we should not be surprised to see precision increase as we increase window width. Second, Figure 1 suggests that it may take some time before subways achieve their equilibrium usage, and so a smaller effect over short windows may actually reflect how subways work over shorter time horizons. Table 8, which uses the ridership data, will provide some support for this idea. Third, when we consider a longer treatment window, we must exclude almost a quarter of the high AOD cities. Given the cross-city heterogeneity on display in Figure 5, we should not be surprised that the average effect is sensitive to sampling.
Table 8—
Ridership
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
|
| ||||
| Post | 36.8857 (5.3940) | −0.0182 (0.0094) | 0.0043 (0.0112) | 0.0033 (0.0089) |
| Post × x | −0.0439 (0.0163) | −0.0411 (0.0164) | ||
| Satellite | Y | Y | Y | |
| Cont. × year | Y | Y | Y | |
| City × cal. mo. | Y | Y | Y | |
| Climate × cont. | Y | Y | Y | |
| Mean AOD | 0.46 | 0.46 | 0.46 | |
| R 2 | 0.85 | 0.81 | 0.81 | 0.81 |
| Number of events | 42 | 42 | 42 | 42 |
| Number of cities | 42 | 42 | 42 | 42 |
| Observations | 8,415 | 15,863 | 15,863 | 15,863 |
Notes: column 1: Dependent variable is ridership per 1,000 people. Column 2: Dependent variable is mean AOD in a 10 km disk with centroid in the city center. Controls are as in Table 2 column 5, but restricted to sample with ridership data. Column 3: Same as column 2 but includes interaction of treatment with indicator for above median ridership per 1,000 people 12 m after opening. Column 4: Same as column 2 but includes interaction of treatment with indicator for above median ridership 12 m after opening. All specifications control for city fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure, and frost days. Standard errors clustered at the city level are in parentheses.
D. Longer Run Effects in High AOD Cities
Subways are durable and their effects probably extend over decades. Hence, it is of interest to extend our estimates of the effects of subways to the longest possible horizon that our data permit. Unfortunately, considering a longer treatment period requires that we degrade our research design in one of two ways. As we consider longer treatment periods, we must either allow later posttreatment effects to reflect a decreasing set of cities, opening the door to confounding composition with subway effects, or else restrict attention to progressively smaller samples of cities, reducing precision and raising questions of external validity. In spite of this, the importance of obtaining estimates over a time horizon that more nearly approximates the planning horizon suggests that such estimates will be useful, even though we have less confidence in them.
In Table 5 we continue to consider a pretreatment period beginning 18 months before an opening, but consider longer post-treatment periods. Panel A on top reports effects by year to assess dynamics, while panel B below reports average effects over the post-treatment period. In columns 1 and 2 we consider two years after an opening using a specification that is otherwise the same as in Table 2 columns 5 and 6. We see that the one year effect is about −0.02, slightly smaller, but statistically indistinguishable from our estimate of the 18 month effect in Table 2. Point estimates of the second year effect are about the same and are estimated with slightly higher precision than the 1 year effect. We can reject neither the hypothesis that the second year effect is zero nor that it is the same as the one year effect. Panel B estimates the average subway effect over the two year post-period considered in the first two columns. Unsurprisingly, this average effect is statistically different from zero, but not from −0.03. We also provide wild-cluster bootstrap p-values for the average effect. Bootstrapped p-values do not indicate a level of precision that is dramatically different from conventional estimates based on asymptotics.
Table 5—
Long Run Effects of Subway Openings in High AOD Cities
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Panel A | ||||||
| 1–12 months post | −0.0177 (0.0163) | −0.0208 (0.0153) | −0.0227 (0.0160) | −0.0236 (0.0160) | −0.0304 (0.0158) | −0.0306 (0.0168) |
| 13–24 months post | −0.0184 (0.0153) | −0.0224 (0.0130) | −0.0253 (0.0169) | −0.0279 (0.0141) | −0.0209 (0.0167) | −0.0242 (0.0150) |
| 25–36 months post | −0.0429 (0.0161) | −0.0441 (0.0125) | −0.0405 (0.0152) | −0.0437 (0.0132) | ||
| 37–48 months post | −0.0333 (0.0195) | −0.0416 (0.0167) | ||||
| Satellite | Y | Y | Y | Y | Y | Y |
| Cont. × year | Y | Y | Y | Y | Y | Y |
| City × cal. mo. | Y | Y | Y | Y | Y | Y |
| Climate × cont. | Y | Y | Y | Y | Y | Y |
| Mean AOD | 0.64 | 0.42 | 0.64 | 0.42 | 0.60 | 0.42 |
| R 2 | 0.70 | 0.75 | 0.70 | 0.75 | 0.73 | 0.75 |
| Number of events | 27 | 27 | 24 | 24 | 21 | 21 |
| Number of cities | 27 | 488 | 24 | 485 | 21 | 482 |
| Observations | 10,169 | 18,2821 | 8,993 | 181,645 | 7,840 | 180,492 |
| Panel B | ||||||
| Average post | −0.0180 (0.0139) | −0.0216 (0.0122) | −0.0295 (0.0132) | −0.0319 (0.0106) | −0.0306 (0.0125) | −0.0350 (0.0116) |
| Bootstrap p-value | 0.213 | 0.095 | 0.030 | 0.008 | 0.025 | 0.008 |
Notes: Dependent variable is mean AOD in a 10km disk with centroid in the city center. Even-numbered columns include all non-subway cities. All specifications control for city fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure, and frost days. Standard errors clustered at the city level are in parentheses.
In columns 3 and 4 of Table 5, we extend the post-treatment period to 36 months. Each of the three post treatment years are negative and indistinguishable from 0.03. The second and third year effects are estimated with about the same precision as the one year effect but because they are larger, can be distinguished from zero. Panel B of Table 5 estimates the average subway effect over the three year post-period considered in columns 3 and 4. This average is about −0.03 and different from zero. The bootstrapped p-value is consistent with asymptotic standard errors. In order to accommodate the longer time horizon, we need to drop 3 cities from our sample of 27 high AOD cities, so some of the difference between columns 1–2 and 3–4 may reflect this change in sample.
Finally, columns 5 and 6 extend our analysis to four years post opening. Here we see larger effects that are distinguishable from zero in three of four years. The average effect over all years is −0.035. This effect is different from zero, but not different from 0.03. Again, extending our treatment period requires dropping an additional three high AOD cities that open their systems between three and four years of the end of our sample.
Inspection of these results reveals two patterns. First, across specifications, point estimates are within 1.64 standard errors of the 18 month effect of −0.03 in almost all cases. Second, in most specifications, coefficient magnitudes increase with time from opening, while standard errors stay about constant with time from opening. These results are consistent with a persistent AOD decrease of about 0.03 following subway openings in high AOD cities that lasts at least four years.
E. Spatial Scale of Effect in High AOD Cities
Subways overwhelmingly serve the areas close to the most central part of a city. Gonzalez-Navarro and Turner (2018) document that about 40 percent of all subway stations in existing subway systems lie within 5 km of the center and another 30 percent within 10 km of the center. Thus, we expect larger effects on AOD nearer to the centers of high AOD cities than further away
Table 6 documents precisely this phenomenon. For reference, the first two columns of this table reproduce the first two columns of Table 4, which use a 10-km disk around the city center to measure air pollution. Columns 3 and 4 are identical to columns 1 and 2, except that the dependent variable is mean monthly AOD in a donut between 10 km and 25 km of the center rather than within 10 km. Columns 5 and 6 examine AOD in the donut between 25 km and 50 km. As expected, the effect of subways on AOD decreases with distance from the city center in our sample of high AOD cities. In particular, the estimated improvements in air quality among high AOD cities are no longer statistically different from zero beyond 25 km from the center.
Table 6—
Spatial Decay of Effects of Subway Openings in High AOD Cities
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Post | −0.0270 (0.0147) | −0.0284 (0.0130) | −0.0219 (0.0141) | −0.0272 (0.0110) | −0.0137 (0.0151) | −0.0172 (0.0111) |
| Satellite | Y | Y | Y | Y | Y | Y |
| Cont. × year | Y | Y | Y | Y | Y | Y |
| City × cal. mo. | Y | Y | Y | Y | Y | Y |
| Climate × cont. | Y | Y | Y | Y | Y | Y |
| Mean AOD | 0.66 | 0.43 | 0.64 | 0.40 | 0.59 | 0.38 |
| Bootstrap p-value | 0.083 | 0.049 | 0.136 | 0.026 | 0.364 | 0.143 |
| R 2 | 0.66 | 0.75 | 0.73 | 0.81 | 0.73 | 0.81 |
| Number of events | 29 | 29 | 29 | 29 | 29 | 29 |
| Number of cities | 29 | 490 | 29 | 490 | 29 | 490 |
| Observations | 10,896 | 183,548 | 10,896 | 183,446 | 10,893 | 183,427 |
Notes: Dependent variable is mean AOD. Columns 1 and 2 replicate columns 5 and 6 from Table 4 for reference. Dependent variable in columns 3 and 4 is AOD in a donut 10–25km from the city center. Columns 5 and 6 use AOD in a donut 25–50km from the city center. All specifications control for city fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure, and frost days. Standard errors clustered at the city level are in parentheses.
F. Further Results
Expansions versus Openings:
Our investigation has focused on the effects of the initial opening of a subway. We now turn to an investigation of expansions, that is, the addition of subway lines after the system has entered service.
In column 1 of Table 7 we consider all subway expansions that occur during the study period examined by Table 2. This sample includes all expansions, including those that occur in cities that open their systems prior to the beginning of our study period, and may include more than one expansion for some cities. This leaves us with a sample of 70 cities and 143 expansions. We conduct a regression like that described in equation (4), but our “event” is an expansion rather than an opening. The estimated effect of expansions is tiny (−0.004) and indistinguishable from zero.14 In the second column of Table 7, we restrict attention to all expansions that occur in one of the 58 cities that are part of our main sample. Of these 58, we observe expansions in 20. For this sample we observe a negative effect that is just distinguishable from zero. In columns 3 and 4 we repeat the first two columns, but also interact the treatment with an indicator for a high AOD city, much as in Table 3. We see that the effects of expansions are larger in high AOD cities, but this change is not distinguishable from zero.15 In sum, this table provides suggestive evidence that subway expansions are on average less important than openings.
Table 7—
Expansions
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
|
| ||||
| Post | −0.0044 (0.0039) | −0.0154 (0.0091) | −0.0002 (0.0031) | −0.0046 (0.0102) |
| Post × x | −0.0076 (0.0072) | −0.0134 (0.0141) | ||
| Satellite | Y | Y | Y | Y |
| Cont. × year | Y | Y | Y | Y |
| City × cal. mo. | Y | Y | Y | Y |
| Climate × cont. | Y | Y | Y | Y |
| Mean AOD | 0.44 | 0.63 | 0.44 | 0.63 |
| R 2 | 0.78 | 0.73 | 0.78 | 0.73 |
| Number of events | 143 | 42 | 143 | 42 |
| Number of cities | 70 | 20 | 70 | 20 |
| Observations | 52,268 | 15,595 | 52,268 | 15,595 |
Notes: Dependent variable is mean AOD in a 10km disk with centroid in the city center. Column 1 includes all expansions anywhere in the world (includes old subway cities outside of our main sample). Column 2 includes expansions restricted to the set of new subway cities used in Table 2. Column 3 is the same as 1 but includes the interaction of treatment with indicator for AOD in 2000 above 0.36 (median AOD in 2000 in the sample of new subway cities used in Table 2). Column 4 is the same as 2 but includes the interaction of treatment with indicator for AOD in 2000 above.36 (median AOD in 2000 in the sample of new subway cities used in Table 2). All specifications control for event fixed effects, event-specific pre-window indicators, event-specific post-window indicators, and event-specific period-0 indicators. Climate controls are pixel count and linear and quadratic terms in temperature, precipitation, cloud cover, vapor pressure and frost days. Standard errors clustered at the event level are in parentheses.
Just as for openings, our data permit us to estimate the effect of every single subway expansion on AOD. Online Appendix Figure A.5 presents all 70 such estimates that are possible using the sample of column 1 of Table 7. This figure is analogous to Figure 5; coefficient estimates are on the x-axis and standard errors are on the y-axis. Expansion effects are statistically different from zero with progressively higher levels of significance as they lie in darker regions of the figure. This figure looks much like the corresponding figure for subway openings, although, if anything, there is even more variation in the effects of expansions than openings. Unlike openings, however, expansions in high AOD cities are not measurably different from those in low AOD cities.
Ridership:
Table 8 examines the effects of subway openings and expansions on subway ridership and investigates the relationship between ridership and AOD. All four regressions examine changes around the opening of the subway using regressions like equation (4) and we restrict attention to the 42 out of 58 cities that opened a subway during our study period for which we could assemble ridership data.
In column 1, we document average daily ridership per 1,000 people in the 18 month period after system opening. In line with Figure 1, we see that an average system carries about 36 riders per thousand of population in its first year and a half of operation.
In column 2 we replicate column 5 of Table 2 and predict the change in AOD during the 18 months post opening. We see that, in this set of 42 cities with ridership data, subway openings decrease AOD by about 0.018 units and that the mean AOD in this sample is about as high as in the high AOD city sample. Thus, the 42 cities where ridership data are available have higher air pollution levels and, on average, have effects of subway openings on AOD that are more responsive to subways than the 17 cities where ridership data are not available.
In column 3 we repeat column 2, but we add an interaction between the treatment indicator and an indicator for above median ridership per 1,000 people. We see that the interaction effect is strongly negative. This suggests that the reduction in average AOD is driven by effects among cities where subways are used intensively. Column 4 is like column 3, but we measure subway usage with an indicator for above median level of subway ridership. This estimate is very close to that of column 3. Because ridership could be endogenous in this regression specification, some caution is required in interpreting these results. With that said, these estimates suggest that subways affect AOD by attracting riders and diverting automobile trips.
IV. Value of AOD Reductions Following Subway Openings in High AOD Cities
A. Value of Health Benefits from Estimates in the Economics Literature
Arceo, Hanna, and Oliva (2016) use data describing Mexico City between 1997 and 2006 to estimate a weekly infant death rate of 0.24 per 100,000 per μg/m3 of pm10. Thus, of 100,000 births, a 1 μg/m3 decrease in ambient pm10 averts about 12.5 infant deaths.16 Knittel, Miller, and Sanders (2016) use data from California between 2002 and 2007 to estimate a weekly infant death rate of 0.19 per 100,000 births per μg/m3 of pm10. This estimate implies that of 100,000 births, a 1 μg/m3 decrease in ambient pm10 averts 9.9 infant deaths. Chay and Greenstone (2003) consider data describing infant deaths in about 1,000 US counties between 1978 and 1984 and estimate that a one unit μg/m3 decrease in ambient total suspended particles (TSP) averts about 5.2 infant deaths per 100,000 births. Converting from TSP to pm10 is nontrivial, however pm10 = 0.55 × TSP is a sometimes used rule of thumb (World Bank Group, United Nations Environment Programme, and the United Nations Industrial Development Organization 1999). Rescaling the estimate from Chay and Greenstone (2003) implies that a one μg/m3 decrease in ambient pm10 averts about 9.5 infant deaths per 100,000 births. In sum, these studies suggest that a one μg/m3 decline in pm10 averts about 10 infant deaths per 100,000 births.17
That none of these estimates can be distinguished from the others despite a range of mean pm10 from about 28 μg/m3 for Knittel, Miller, and Sanders (2016) to about 67 μg/m3 for Arceo, Hanna, and Oliva (2016) suggests that the infant mortality response is approximately linear in pm10 (as Arceo, Hanna, and Oliva 2016 observe). Burnett et al. (2014) confirms the approximately linear dose-response relationship suggested by Arceo, Hanna, and Oliva (2016). More specifically, Burnett et al. (2014) surveys the large public health literature on the health consequences of pm10 and finds that responses are approximately linear in the range from 5–100 μg/m3, although they find nonlinearities outside of this range.
Online Appendix Figure A.2(b) shows that most of our city-months fall in this 5–100 μg/m3 range. Therefore, in light of the results described above, we can reasonably assume a linear dose-response relationship in our sample.
These results, together with our estimates, allow us to estimate annual infant deaths averted by a subway opening for an average high-AOD city. From Table 4, subway openings cause about a 0.028 unit decrease in AOD. Using column 2 of online Appendix Table A.2 to convert from AOD to pm10 gives about 3.2 μg/m3 of pm10. At 10 infant deaths per 100,000 births per μg/m3 of pm10, the number of averted deaths due to a subway opening in city i is given by
An average city in our high AOD subset sample has a population of about 5.3 million in the year before its subway opens. With a 2 percent birthrate, a subway opening in this city averts about 34 infant deaths per year.18
With country-level birthrate data from the World Health Organization (2016b) and our population data, we can make this calculation somewhat more precisely. Specifically, imputing country-level birth rates to cities, calculating the implied number of averted infant deaths for each city, and averaging over cities, we find that the average subway opening in high AOD cities averts 22.5 infant deaths per year.
To monetize this benefit, we use country-adjusted values of a statistical life (VSL) to value averted infant deaths in each city.19 Averaging over all high AOD cities, the value of averted infant deaths is $43.0 million per year. Our estimates do not allow us to conclude that subways continue to affect air quality beyond five years after their opening date. With a 5 percent discount rate, the present discounted value of this amount over five years is about $195.5 million. If the effect is permanent, the corresponding present value is $903 million.
B. Value of Health Benefits from the Global Burden of Disease Methodology
To extend our mortality calculations over the entire age distribution, we apply the methodology employed by Global Burden of Disease project (WHO 2016a). This methodology is complicated and is described in detail in online Appendix D.
We obtain integrated risk functions from Burnett et al. (2014) for five causes of mortality. These functions summarize the results of several epidemiological cohort studies, and consist of nonlinear maps between pm2.5 concentrations and mortality risk ratios. We quantify the contribution of air pollution to age and disease-specific mortality by computing the population attributable fraction. This is the percentage mortality reduction that would occur if pm2.5 concentrations were reduced to a counterfactual exposure level. We proceed in three steps. First, using coefficients in column 8 of online Appendix Table A.2 (Terra), we predict city-level pm2.5 concentrations during the 12 months preceding the opening of a subway. Second, applying the integrated risk functions, we calculate the population attributable fractions associated with a 1.7 μg/m3 pm2.5 decrease from the predicted pre-subway exposure level.20 Third, using city population and country-level death rates from the World Health Organization (WHO 2016b), we construct city-specific mortality for each disease and age class. The total number of avoided deaths in each city is obtained by applying the population attributable fractions to the mortality rates, summing over every disease. Averaging over all high AOD cities, the 0.028 unit decrease in AOD that follows a subway opening saves about 500 lives per year.
Valuing these lives, as before, with country-adjusted values of a statistical life, the value of averted deaths is $1 billion per year. With a 5 percent discount rate, the present discounted value of this amount over five years is about $4.54 billion. If the effect is permanent, the corresponding present value is $21 billion.
C. Discussion
These benefit calculations are obviously crude. They do not account for morbidity, for possible effects on labor productivity, nor for the fact that subways may reduce pollutants other than particulates. While the magnitudes of these effects remain uncertain, they are almost surely positive, and possibly large, e.g., Chang et al. (2016) or Forouzanfar et al. (2016). Thus, we might reasonably expect that a complete accounting for the health and productivity related benefits of subway-induced improvements in air quality would lead to a much larger value than we describe above.
The mean length of track for a newly opened subway system in our study period is 19.2 km. Baum-Snow, Kahn, and Snow (2005) examine 16 US subway systems and estimate constructions costs ranging between $25 million and $287 million per mile. Using this range of cost estimates, the cost of construction for an average subway system in our sample ranges from $298 million to about $3.4 billion. Our estimates of the present value of avoided infant mortality in an average subway city range between $195.5 million and $903 million, depending on whether the subway effect on pollution lasts for five years or is permanent. Our estimates of the present value of avoided all-age mortality in an average subway city range between $4.54 billion and $21 billion, again depending on whether the subway effect on pollution lasts for five years or is permanent. Comparing these magnitudes suggests that the value of subway-induced improvements to air quality account for at least a substantial fraction of subway construction costs in cities with poor baseline air quality (above 0.36 AOD on average in a year or approximately 28 μg/m3 pm2.5).
V. Conclusion
Our results indicate that for the 58 cities that opened a subway system between August 2001 and July of 2016, the average effect of subway system openings on AOD was slightly negative and indistinguishable from zero at ordinary levels of significance. This average conceals dramatic heterogeneity. Estimating a subway effect for each city individually, we find that in 20 cities subways appear to have caused an increase in AOD, in 12 the effect is about zero, while in the remaining 26 the effect is negative.
We find a clear pattern to this heterogeneity. Cities with initial AOD levels in the top half of our sample, that is above 0.36 in 2000 on average, see AOD levels decrease by about 0.028 after their subways open. Since the mean AOD in this sample of cities is about 0.66, this is about a 4 percent decline. This effect is not sensitive to the inclusion or exclusion of a range of control variables in our regression, nor to the exact geography we use to measure each city’s AOD. As might be expected, subways have a larger effect on AOD nearer the city center than further away, and the effect is strongly increasing with ridership. Our ability to extend our estimates to time periods far in the future of subway opening is limited by data availability and our event study research design. With this said, subways appear to have a constant or increasing effect on AOD over the first four years of their operation. In all, the data seem to provide considerable support for the hypothesis that subways cause a modest, persistent reduction in AOD levels for cities in the top half of the initial AOD distribution, and no effect otherwise. We note that our estimates are somewhat sensitive to the duration of treatment and control periods. We suspect that this sensitivity reflects the intrinsic noisiness of the AOD process and sampling issues that inevitably follow changes in the duration of these periods.
Our 0.028 estimated subway effect in high AOD cities is only about 4 percent of the level, but it is large compared to world trends. Comparing AOD levels across continents in Table 1, we see that the difference between Europe and North America in 2017 is about 0.05, one and a half subway effects, and between Europe and Asia the difference is 0.33, about 11 subway effects. In all, this suggests that subways may play a moderately important role in explaining time series and cross-sectional patterns in urban AOD.
The effects of subway expansions seem to be smaller than those of subway openings, although, like openings, there is dramatic heterogeneity in these effects. Unlike openings, however, we cannot discern a pattern on the heterogeneity of the effects of expansions. In particular, subway expansions in high AOD cities are not more likely to reduce AOD than they are in low AOD cities. To the extent that public policy encourages subway construction, this suggests that openings are relatively more important than expansions. We note that the decreasing marginal effect of subway expansion seems to be broadly consistent with the slight decreasing returns in the effects of metropolitan road networks observed in Couture, Duranton, and Turner (2018).
Extant estimates of the effects of particulates on mortality suggest that they are sufficiently poisonous that, for high AOD cities, the small nominal reductions from subway openings are economically important. In particular, they appear to be large enough to justify at least moderate subsidies for subway construction. As we should expect, our results suggest that subway openings affect AOD through their effect on ridership. This, in turn, suggests that they reduce AOD by reducing the use of competing modes of transportation. This conclusion is broadly consistent with other results in the literature.
Supplementary Material
Acknowledgments
This paper was first developed when Gendron-Carrier, Gonzalez-Navarro, and Turner were at University of Toronto. We are grateful to Christopher Balette, Jessica Burley, Alejandra Hernandez, Tasnia Hussain, Andy Liu, Fern Ramoutar, Mahdy Saddradini, Mohamed Salat, David Valdes, Farhan Yahya, and Guan Yi for research assistance. Assistance from Lynn Carlson and Yi Qi with the MODIS data and from Windsor Jarrod with computing is gratefully acknowledged, as are helpful conversations with Ken Chay and Michelle Marcus, and comments from Leah Brooks, Gabriel Kreindler, Remi Jedwab, and many seminar participants. This paper is part of a Global Research Program on Spatial Development of Cities, funded by the Multi-Donor Trust Fund on Sustainable Urbanization by the World Bank and supported by the UK Department for International Development. The project was made possible through financial support from SSHRC under grant #224995, the International Growth Center under grant #89337, the Connaught Fund, and the Ontario Work-Study program
Footnotes
We define expansions as the opening of new subway lines beyond the inaugural lines. This definition excludes a common expansion type in which one or more subway stations are added to an existing subway line.
Data available for download at Gonzalez-Navarro and Turner (2019).
There are 11 cities where the subway system opening occurs within 18 months of the beginning or end of the available pollution data, which are excluded from the table since they are excluded from our main estimation sample.
Online Appendix Table A.1 reports data sources for ridership data.
That is, it is a measure of the fraction of incoming light reflected by the air column before reaching the ground. Since at least zero light is reflected by the atmosphere, AOD must be positive and increasing in the share of reflected light (Jacob 1999, 105). The nominal scale of AOD reported by MODIS is 0–5,000, although we have rescaled to 0–5 for legibility, as is common in the literature. The MODIS data are available for download at ftp://ladsweb.nascom.nasa.gov/allData/6/.
From Gibson and Carnovale (2015), from table 6, treatment increased log pm10 by 0.0404 and, from Table 2, traffic by 26,725 cars. From Table 2, mean traffic and pm10 are 169,744 and 47.66. Using these values to calculate percentage changes we arrive at a 16 percent change in traffic and 4 percent change in pm10.
Hsu and Zhang (2014) replicate Duranton and Turner (2011) for Japan; Garcia-Lopez, Pasidis, and Viladecans-Marsal (2017) for Europe; and Chen and Klaiber (2020) for China.
We note, however, Gonzalez-Navarro and Turner (2018) provide contrary evidence. They examine the relationship between subway system extent and population in a sample of 161 subway cities over decennial time scales and find no relationship.
On the basis of travel survey data described in Akbar and Duranton (2017), residents of Bogota take about 2.69 trips per day and of these 19.3 percent, or 0.52 trips per day, are by private car or taxi. From online Appendix Table A.7, in the year of a subway opening, an average city in our sample has a population of about 4.0 million. Multiplying per capita trips by this population, if people drive at the same rate as does the population of Bogota, then an average city in our sample generates about 2 million trips by car or taxi per day. From Figure 1, in the second year of its operation an average subway in our data provides about 50 rides per 1,000 of population. Applying this rate to a city of 4.0 million, an average subway system provides about 200,000 rides per day. If all subway rides replace car or taxi rides, this is about 10 percent of all rides in our hypothetical city. We can perform a similar calculation on the basis of US national averages. An average US household took 3.8 trips per day (2009 National Household Transportation Survey, nhts.ornl.gov/2009/pub/stt.pdf, Table 3), about 90 percent by car (Duranton and Turner 2018). If everyone in a city of 4.0m takes as many trips as an average American, then the city generates about 13m trips by car per day. If the subway system provides the same 200,000 rides per day and if all subway rides replace car or taxi rides, then the subway opening should reduce car trips by about 1.5 percent.
In an earlier version of this paper, we used common pre- and post-indicators. These coefficients reflect sample mean pre- and post-period AOD averages. This is problematic conceptually because these variables could, in theory, also measure treatment effects. It is problematic in practice because these pre- and post-period AOD averages sometimes change across samples and (slightly) affect estimates of treatment effects. The more flexible specification resolves this problem.
City fixed effects, city-specific pre-window indicators, city-specific post-window indicators, and city-specific period-0 indicators.
The density measure is the elasticity of lights at night to distance from the city center and is taken from Gonzalez-Navarro and Turner (2018).
City relief is from Gonzalez-Navarro and Turner (2018) and wind speed is from Wentz et al. (2015).
In a handful of cases, expansions occur within 36 months of each other or of an opening. In this case, control months for one event are treatment months for another. We experimented with dropping these events, and it does not qualitatively affect our results.
To be consistent with the definition used up until Table 7, we define “high AOD cities” as those with average AOD levels in 2000 at or above the median in our main sample of 58 cities with openings between August 2001 and July 2016. The median AOD level in 2000 in our sample of 58 is 0.366.
An infant survives its first year if it survives 52 weeks. Thus, a weekly death rate of 0.24 × 10−5 gives [1 − (1 − (0.24 × 10−5))52] 105 = 12.47 infant deaths per 100,000 births.
Currie and Neidell (2005) use data describing pm10 and infant mortality in California between 1989 and 2000 and conclude that pm10 has no measurable effect on infant mortality. Knittel, Miller, and Sanders (2016) and Arceo, Hanna, and Oliva (2016) both replicate the Currie and Neidell (2005) research design and find much smaller effects than the IV estimates reported above. We note that Jayachandran (2009) and Gutierrez (2010) also estimate the effects of particulates on infant mortality. We do not discuss their estimates because they do not present their results in a way that permits a conversion to mortality rates per μg/m3 of pm10.
The World Bank reports that the world average crude birth rate is 19.5/1,000 (http://data.worldbank.org/indicator/SP.DYN.CBRT.IN, accessed April 2017).
Specifically, we take Viscusi and Aldy’s (2003) 0.6 elasticity of VSL with respect to income, and impute a country’s VSL from the US value of $6 million.
From column 8 of online Appendix Table A.2, a 0.028 unit decrease in AOD converts to a 0.028 × 60.57 = 1.696 μg/m3 decrease in pm2.5.
Go to https://doi.org/10.1257/app.20180168 to visit the article page for additional materials and author disclosure statement(s) or to comment in the online discussion forum.
Contributor Information
Nicolas Gendron-Carrier, Department of Economics, McGill University, CIRANO, and CIREQ.
Marco Gonzalez-Navarro, Agricultural and Resource Economics Department, UC-Berkeley, JPAL, CEGA and BREAD.
Stefano Polloni, Mapdwell.
Matthew A. Turner, Department of Economics, Brown University, PERC, IGC, NBER, PSTC, and S4.
REFERENCES
- Akbar Prottoy, and Duranton Gilles. 2017. “Measuring the Cost of Congestion in a Highly Congested City: Bogota.” https://faculty.wharton.upenn.edu/wp-content/uploads/2017/05/Estimating-the-cost-of-congestion-Gilles-1.pdf.
- ▶Anderson Michael L. 2014. “Subways, Strikes, and Slowdowns: The Impacts of Public Transit on Traffic Congestion.” American Economic Review 104 (9): 2763–96. [Google Scholar]
- ▶Andrews Donald W.K. 1993. “Tests for Parameter Instability and Structural Change with Unknown Change Point.” Econometrica 61 (4): 821–56. [Google Scholar]
- ▶Andrews Donald W.K. 2003. “Tests for Parameter Instability and Structural Change with Unknown Change Point: A Corrigendum.” Econometrica 71 (1): 395–97. [Google Scholar]
- ▶Arceo Eva, Hanna Rema, and Oliva Paulina. 2016. “Does the Effect of Pollution on Infant Mortality Differ between Developing and Developed Countries? Evidence from Mexico City.” Economic Journal 126 (591): 257–80. [Google Scholar]
- ▶Baum-Snow Nathaniel. 2007. “Did Highways Cause Suburbanization?” Quarterly Journal of Economics 122 (2): 775–805. [Google Scholar]
- Baum-Snow Nathaniel, Kahn Matthew E., and Voith Richard. 2005. “Effects of Urban Rail Transit Expansions: Evidence from Sixteen Cities, 1970–2000.” Brookings-Wharton Papers on Urban Affairs 1 (4): 147–97. [Google Scholar]
- ▶Baum-Snow Nathaniel, Brandt Loren, Henderson J. Vernon, Turner Matthew A., and Qinghua Zhang. 2017. “Roads, Railroads, and Decentralization of Chinese Cities.” Review of Economics and Statistics 99 (3): 435–48. [Google Scholar]
- ▶Burnett Richard T., Pope C. Arden 3rd, Majid Ezzati, Casey Olives, Lim Stephen S., Sumi Mehta, Shin Hwashin H., et al. 2014. “An Integrated Risk Function for Estimating the Global Burden of Disease Attributable to Ambient Fine Particulate Matter Exposure.” Environmental Health Perspectives 122 (4): 397–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ▶Cameron A. Colin, Gelbach Jonah B., and Miller Douglas L.. 2008. “Bootstrap-Based Improvements for Inference with Clustered Errors.” Review of Economics and Statistics 90 (3): 414–27. [Google Scholar]
- ▶Chang Tom, Joshua Graff Zivin Tal Gross, and Neidell Matthew. 2016. “Particulate Pollution and the Productivity of Pear Packers.” American Economic Journal: Economic Policy 8 (3): 141–69. [Google Scholar]
- ▶Chay Kenneth Y., and Greenstone Michael. 2003. “The Impact of Air Pollution on Infant Mortality.” Quarterly Journal of Economics 118 (3): 1121–67. [Google Scholar]
- Chen Shuai, Yang Jun, Qin Ping, and Xu Jintao. 2016. “Truth behind Chinese Superstition: Non-linear Effects of Vehicle Traffic on Urban Air Quality in Beijing.” Environment for Development (EfD) Discussion Paper 16–16. [Google Scholar]
- ▶Chen Wei, and Klaiber H. Allen. 2020. “Does Road Expansion Induce Traffic? An Evaluation of Vehicle-Kilometers Traveled in China.” Journal of Environmental Economics and Management 104: 102387. [Google Scholar]
- ▶Chen Yihsu, and Whalley Alexander. 2012. “Green Infrastructure: The Effects of Urban Rail Transit on Air Quality.” American Economic Journal: Economic Policy 4 (1): 58–97. [Google Scholar]
- ▶Couture Victor, Duranton Gilles, and Turner Matthew A.. 2018. “Speed.” Review of Economics and Statistics 100 (4): 725–39. [Google Scholar]
- ▶Currie Janet, and Neidell Matthew. 2005. “Air Pollution and Infant Health: What Can We Learn from California’s Recent Experience?” Quarterly Journal of Economics 120 (3): 1003–30. [Google Scholar]
- Duranton Gilles, and Puga Diego. 2015. “Chapter 8—Urban Land Use.” In Handbook of Regional and Urban Economics, Vol. 5, edited by Gilles Duranton, Henderson J. Vernon, and Strange William C., 467–560. Amsterdam: North-Holland. [Google Scholar]
- ▶Duranton Gilles, and Turner Matthew A.. 2011. “The Fundamental Law of Road Congestion: Evidence from US Cities.” American Economic Review 101 (6): 2616–52. [Google Scholar]
- ▶Duranton Gilles, and Turner Matthew A.. 2018. “Urban Form and Driving: Evidence from US Cities.” Journal of Urban Economics 108: 170–91. [Google Scholar]
- ▶Feenstra Robert C., Inklaar Robert, and Timmer Marcel P.. 2015. “The Next Generation of the Penn World Table.” American Economic Review 105 (10): 3150–3182. [Google Scholar]
- Forouzanfar Mohammad H., Afshin Ashkan, Alexander Lily T., Anderson H. Ross, Bhutta Zulfiqar A., Stan Biryukov, Michael Brauer, et al. 2016. “Global, Regional, and National Comparative Risk Assessment of 79 Behavioural, Environmental and Occupational, and Metabolic Risks or Clusters of Risks, 1990–2015.” Lancet 388 (10053): 1659–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ▶Friedman Michael S., Powell Kenneth E., Hutwagner Lori, Graham LeRoy M., and Teague W. Gerald. 2001. “Impact of Changes in Transportation and Commuting Behaviors during the 1996 Summer Olympic Games in Atlanta on Air Quality and Childhood Asthma.” JAMA 285 (7): 897–905. [DOI] [PubMed] [Google Scholar]
- Garcia-Lopez Miquel-Angel, Pasidis Ilias, and Elisabet Viladecans-Marsal. Forthcoming. “Congestion in Highways when Tolls and Railroads Matter: Evidence from European Cities.” Journal of Economic Geography. [Google Scholar]
- Gendron-Carrier Nicolas, Marco Gonzalez-Navarro Stefano Polloni, and Turner Matthew A.. 2022. “Replication data for: Subways and Urban Air Pollution.” American Economic Association [publisher], Inter-university Consortium for Political and Social Research [distributor]. 10.3886/E126401V1. [DOI] [Google Scholar]
- ▶Gibson Matthew, and Carnovale Maria. 2015. “The Effects of Road Pricing on Driver Behavior and Air Pollution.” Journal of Urban Economics 89: 62–73. [Google Scholar]
- ▶Gonzalez-Navarro Marco, and Turner Matthew A.. 2018. “Subways and Urban Growth: Evidence from Earth.” Journal of Urban Economics 108: 85–106. [Google Scholar]
- Gonzalez-Navarro Marco, and Turner Matthew A.. 2019. “Replication Data for: Subways and Urban Growth: Evidence from Earth.” Harvard Database. 10.7910/DVN/VHPRTA. [DOI] [Google Scholar]
- Google. 2020. “Google Maps.” https://www.google.com/maps (accessed February 2020).
- ▶Gu Yizhen, Jiang Chang, Zhang Junfu, and Zou Ben. 2021. “Subways and Road Congestion.” American Economic Journal: Applied Economics 13 (2): 83–115. [Google Scholar]
- ▶Gutierrez Emilio. 2010. “Using Satellite Imagery to Measure the Relationship between Air Quality and Infant Mortality: An Empirical Study for Mexico.” Population and Environment 31: 203–22. [Google Scholar]
- ▶Hansen Bruce E. 2000. “Testing for Structural Change in Conditional Models.” Journal of Econometrics 97 (1): 93–115. [Google Scholar]
- Harris I, Jones PD, Osborn TJ, and Lister DH. 2014. “Updated High-Resolution Grids of Monthly Climatic Observations—CRU TS3.26 Dataset.” International Journal of Climatology. https://crudata.uea.ac.uk/cru/data/hrg/ (accessed October 28, 2018). [Google Scholar]
- ▶Heblich Stephan, Redding Stephen J., and Sturm Daniel M.. 2020. “The Making of the Modern Metropolis: Evidence from London.” Quarterly Journal of Economics 135 (4): 2059–2133. [Google Scholar]
- ▶Hsu Wen-Tai, and Zhang Hongliang. 2014. “The Fundamental Law of Highway Congestion Revisited: Evidence from National Expressways in Japan.” Journal of Urban Economics 81: 65–76. [Google Scholar]
- Jacob Daniel J. 1999. Introduction to Atmospheric Chemistry. Princeton: Princeton University Press. [Google Scholar]
- ▶Jayachandran Seema. 2009. “Air Quality and Early-Life Mortality—Evidence from Indonesia’s Wildfires.” Journal of Human Resources 44 (4): 916–54. [Google Scholar]
- ▶Knittel Christopher R., Miller Douglas L., and Sanders Nicholas J.. 2016. “Caution, Drivers! Children Present: Traffic, Pollution, and Infant Health.” Review of Economics and Statistics 98 (2): 350–66. [Google Scholar]
- Levy Rob, and Hsu Christina. 2015. “MODIS Atmosphere L2 Aerosol Product.” USA: NASA MODIS Adaptive Processing System, Goddard Space Flight Center. 10.5067/MODIS/MYD04_L2.006 (accessed November 2018). [DOI] [Google Scholar]
- ▶Levy RC, Mattoo S, Munchak LA, Remer LA, Sayer AM, Patadia F, and Hsu NC. 2013. “The Collection 6 MODIS Aerosol Products over Land and Ocean.” Atmospheric Measurement Techniques 6 (11): 2989–3034. [Google Scholar]
- Remer LA, Mattoo S, Levy RC, and Munchak LA. 2013. “MODIS 3 km Aerosol Product: Algorithm and Global Perspective.” Atmospheric Measurement Techniques 6: 69–112. [Google Scholar]
- UN Department of Economic and Social Affairs. 2018. “World Urbanization Prospects: The 2018 Revision.” UN. https://esa.un.org/unpd/wup/ (accessed February 2020). [Google Scholar]
- UrbanRail. 2020. UrbanRail.Net. http://urbanrail.net/ (accessed February 2020).
- ▶Viscusi W. Kip, and Aldy Joseph E.. 2003. “The Value of a Statistical Life: A Critical Review of Market Estimates throughout the World.” Journal of Risk and Uncertainty 27: 5–76. [Google Scholar]
- Vollmer Associates, LLP, SYSTRA Consulting, Inc., and Allee King Rosen and Fleming, Inc. 2011. Manhattan East Side Transit Alternatives (MESA)/Second Avenue Subway Summary Report. New York: MTA New York City Transit. [Google Scholar]
- Wentz FJ, Scott J, Hoffman R, Leidner M, Atlas R, and Ardizzone J. 2015. “Remote Sensing Systems Cross-Calibrated Multi-platform (CCMP) 6-Hourly Ocean Vector Wind Analysis Product on 0.25 deg Grid, Version 2.0.” Remote Sensing Systems, Santa Rosa, CA. www.remss.com/measurements/ccmp (accessed October 28, 2019). [Google Scholar]
- Wikipedia. 2020. “Wikipedia.” www.wikipedia.org (accessed February 2020).
- World Bank Group, United Nations Environment Programme, and the United Nations Industrial Development Organization. 1999. Pollution Prevention and Abatement Handbook, 1998—Toward Cleaner Production. Washington, DC: World Bank. [Google Scholar]
- World Health Organization (WHO). 2016a. Ambient Air Pollution: A Global Assessment of Exposure and Burden of Disease. Geneva: WHO. [Google Scholar]
- World Health Organization (WHO). 2016b. “Global Health Estimates 2015: Deaths by Cause, Age, Sex, by Country and by Region, 2000–2015.” Geneva: WHO. https://www.who.int/healthinfo/global_burden_disease/estimates_regional_2000_2015/en/. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


