Variable selection with multiply-imputed datasets: choosing between stacked and grouped methods

Abstract

Penalized regression methods are used in many biomedical applications for variable selection and simultaneous coefficient estimation. However, missing data complicates the implementation of these methods, particularly when missingness is handled using multiple imputation. Applying a variable selection algorithm on each imputed dataset will likely lead to different sets of selected predictors. This paper considers a general class of penalized objective functions which, by construction, force selection of the same variables across imputed datasets. By pooling objective functions across imputations, optimization is then performed jointly over all imputed datasets rather than separately for each dataset. We consider two objective function formulations that exist in the literature, which we will refer to as “stacked” and “grouped” objective functions. Building on existing work, we (a) derive and implement efficient cyclic coordinate descent and majorization-minimization optimization algorithms for continuous and binary outcome data, (b) incorporate adaptive shrinkage penalties, (c) compare these methods through simulation, and (d) develop an R package miselect. Simulations demonstrate that the “stacked” approaches are more computationally efficient and have better estimation and selection properties. We apply these methods to data from the University of Michigan ALS Patients Biorepository aiming to identify the association between environmental pollutants and ALS risk. Supplementary materials are available online.

1. Introduction

Variable selection in the presence of missing data is a common problem in applied statistics. Existing statistical methods (Table S1) to deal with both missing data and variable selection fall into two broad classes depending on whether the missing data is handled prior to or at the same time as variable selection. While one can, in principle, handle missingness and selection simultaneously (Yang et al., 2005; Garcia et al., 2010; Johnson et al., 2008), in this paper we focus on a different scenario, where missing data have already been handled via multiple imputation and we wish to do variable selection post-imputation. In practice, we often find ourselves in the latter scenario for many reasons. Some examples include: (i) existing data sources or analytical pipelines provide the analyst with already imputed datasets (Schafer, 2001), (ii) data privacy settings where the missingness mechanism depends on sensitive information that is not needed for downstream analyses, and (iii) practical situations where the analyst wants to use an existing imputation software package to generate the multiply imputed datasets to be used across various analyses. That is, in this article we assume that the imputation model is correctly specified, imputed datasets are given to us, and we focus purely on variable selection techniques post-imputation. In particular, the challenge is to guarantee uniform selection of variables across multiply imputed datasets and to generate point estimates for the regression coefficients corresponding to the selected variables.

To address this issue, there are some existing methods in the literature proposed for variable selection post-imputation. The most common approach is to define an ad-hoc rule for harmonizing selection across imputed datasets (Wood et al., 2008; Lachenbruch, 2011; Ghosh et al., 2015). Wood et al. (2008) outlined three rules for finalizing selection after identifying the active set of predictors in each imputed dataset. These rules consider a variable to be selected if it is selected in at least one imputed dataset, if it is selected in all imputed datasets, or if it is selected in at least half of the imputed datasets. Another related approach is to apply variable selection methods on bootstrapped datasets (Heymans et al., 2007; Long and Johnson, 2015; Liu et al., 2016). One such method, proposed by Long and Johnson (2015), imputes missing values in the bootstrapped samples from the original data and then applies penalized regression on each bootstrapped imputed dataset. Proportions of each covariate being selected over all bootstrap imputed datasets are provided and the final active set is determined by thresholding the proportions. The challenge with such thresholding approaches is that there are no clear guidelines on how to choose the threshold. An alternative class of methods are penalized regression estimators whose objective functions involve a joint optimization over all imputed datasets. Wan et al. (2015) proposed a penalized regression estimator which is equivalent to fitting the penalized regression model on the stacked imputed datasets. The stacked method can also be interpreted in terms of maximizing an objective function pooled over imputed datasets, where regression coefficients are assumed to be the same across datasets. Chen and Wang (2013) proposed the multiple imputation-least absolute shrinkage and selection operator (MI-LASSO) which utilizes a group LASSO penalty to group regression coefficients of the same variable across imputed datasets together, thus arriving at uniform variable selection across imputed datasets. This grouped approach is less restrictive than the stacked approach, in that the parameter values are allowed to differ across imputed datasets. The stacked and grouped approaches are appealing because they handle variable selection and regression coefficient estimation simultaneously, and no ad hoc rules are required to determine the final active set.

Despite the advantages of the stacked and grouped approaches, automated implementation of these two methods (Wan et al., 2015; Chen and Wang, 2013) has been limited in practice. There is a lack of easy-to-use software for both approaches, and for variable selection with multiple imputed datasets in general. More specifically, off-the-shelf R packages such as glmnet (Hastie and Qian, 2014) and gcdnet (Yang et al., 2017) are inadequate for optimizing the stacked objective function proposed in Wan et al. (2015). Namely, the R package glmnet does not exclusively apply adaptive weights to the L₁ penalty, as in adaptive elastic net, and the gcdnet package does not implement observation weights. As for the grouped approach with the group LASSO penalty function, gglasso (Yang and Zou, 2015) cannot be directly used without changing the data structure. The dimension of the new design matrix scales linearly with the number of imputed datasets and introduces many zero entries, which is computationally inefficient. Furthermore, existing approaches are targeted towards continuous outcomes and have not been extended to discrete/categorical outcomes that are abundant in practice. Even for continuous outcomes, the algorithm for MI-LASSO in Chen and Wang (2013) has an important limitation. Specifically, the existing MI-LASSO implementation is an optimization procedure that relies on a local quadratic approximation to the L₁ penalty, which converts the penalized objective function into multiple ridge regressions. Coefficient estimates are always non-zero, requiring a manual threshold for setting small coefficient estimates exactly to zero.

To address the aforementioned limitations, we extend existing work on the stacked and grouped approaches for handling variable selection with multiple imputed datasets to incorporate binary outcomes and adaptive penalties (Section 2). We derive cyclic coordinate descent algorithms for optimizing the pooled objective functions from the stacked approach and majorization-minimization (MM) algorithms coupled with block coordinate descent updates to obtain optimizers of the pooled objective functions from the grouped approach (Section 3). Unlike the optimization routine in Chen and Wang (2013), our proposed methods provide exact shrinkage to zero without any ad hoc thresholding. We provide an R package miselect available on the Comprehensive R Archive Network (CRAN), allowing users to easily implement the proposed methods. In our motivating example, we apply these methods to identify persistent organic pollutants (POPs) associated with Amyotrophic Lateral Sclerosis (ALS) susceptibility using data collected from the University of Michigan ALS Patients Biorepository (Section 4). Seventeen of the 23 POPs have between 10% to 60% below their respective detection limits, making complete-case analysis infeasible. Finally, through a simulation study, we compare the performance of the proposed methods in terms of variable selection and estimation accuracy (Section 5).

2. Methods

We will first review and illustrate the issues with identifying an active set of predictors when fitting separate penalized regressions on each individual imputed dataset. We will then present the stacked and grouped approaches for uniform variable selection with imputed datasets. Let X_d denote the n × p matrix of predictor variables and Y_d be the n × 1 vector of responses for the d-th imputed dataset (d = 1, … D). Let X_d,i indicate the p × 1 covariate vector for the i-th observation in the d-th imputed dataset, Y_d,i be the response for the i-th observation in the d-th imputed dataset, and X_d,ij, denote the j-th covariate for the i-th observation in the d-th imputed dataset.

2.1. Penalized regression on individual datasets

A common approach in practice is to use ad hoc rules for determining the final set of selected variables. Often this proceeds by fitting a penalized regression procedure on each imputed dataset separately:

$${\widehat{\mathit{\theta }}}_d=\underset{{\mathit{\theta }}_d}{\mathrm{argmin}}\left\{-\frac{1}{n}\sum _{i=1}^n\log L\left({\mathit{\theta }}_d\mid Y_{d,i},{\mathit{X}}_{d,i}\right)+\lambda P_{\alpha }\left({\mathit{\beta }}_d\right)\right\}$$ (1)

for d = 1, …, D where log L is the log-likelihood function, β_d is the p × 1 vector of regression coefficients for the d-th dataset, and θ_d = (μ_d, β_d) is the vector of regression parameters including the intercept and coefficients for the d-th imputed dataset. P_α(β_d) is the penalty function parameterized by α and λ ∈ (0, ∞) which are tuning parameters that control the relative contribution of the penalty to the overall optimization problem.

In this paper, we will focus on four penalty functions: LASSO (Tibshirani, 1996), adaptive LASSO (aLASSO) (Zou, 2006), elastic net (ENET) (Zou and Hastie, 2005) and adaptive elastic net (aENET) (Zou and Zhang, 2009). The penalty functions can be expressed as:

1. LASSO: $P_{\alpha }\left({\mathit{\beta }}_d\right)={\sum }_{j=1}^p\left|{\beta }_{d,j}\right|$

2. aLASSO : $P_{\alpha }\left({\mathit{\beta }}_d\right)={\sum }_{j=1}^p{\widehat{a}}_{d,j}\left|{\beta }_{d,j}\right|$

3. ENET: $P_{\alpha }\left({\mathit{\beta }}_d\right)=\alpha {\sum }_{j=1}^p\left|{\beta }_{d,j}\right|+(1-\alpha ){\sum }_{j=1}^p{\beta }_{d,j}^2$

4. aENET: $P_{\alpha }\left({\mathit{\beta }}_d\right)=\alpha {\sum }_{j=1}^p{\widehat{a}}_{d,j}\left|{\beta }_{d,j}\right|+(1-\alpha ){\sum }_{j=1}^p{\beta }_{d,j}^2$

β_d,j is the coefficient for the j-th covariate in the d-th dataset. The intuitive appeal of adaptive weights is that they allow differential penalization of each covariate based on an initial estimate of the regression coefficient vector ${\widehat{\mathit{\beta }}}_d^0$ (smaller ${\widehat{\beta }}_{d,j}^0$ implies a harsher penalty on β_d,j). Moreover, adaptive penalties are known to address estimation and selection consistency issues that have been observed for non-adaptive penalties (Zou, 2006; Zou and Zhang, 2009). Here, the adaptive weight ${\widehat{a}}_{d,j}={\left(\left|{\widehat{\beta }}_{d,j}^0\right|+1/n\right)}^{-\gamma }$ for some γ > 0, where ${\widehat{\beta }}_{d,j}^0$ is an initial estimate of β_d,j, is often determined from ordinary least squares (OLS) or maximum likelihood estimation when p is smaller than n. If p is larger than n, ${\widehat{\beta }}_{d,j}^0$ can be obtained using LASSO or ENET depending on the correlation structure of the predictors. For the purposes of this paper, we use ENET initial values to calculate the adaptive weights for both aLASSO and aENET. To avoid tuning on γ, we follow Zou and Zhang (2009), which fixes γ = ⌈2v/1 − v⌉ + 1 where $v=\log (p)/\log (n)$. The 1/n term prevents division by zero for initial regression coefficient estimates that are exactly equal to zero.

For illustrative purposes, suppose that there are three imputed datasets and that LASSO is fit separately on each imputed dataset. Furthermore, assume that X_d is an n × 2 matrix for all d = 1, 2, 3, i.e., we are applying LASSO shrinkage to coefficients of only two covariates. Figure 1 visualizes the geometry of the constrained region in this hypothetical scenario. As shown in the figure, the maximum likelihood estimates for each of the imputed datasets are slightly different and, when shrunk to the constrained region, lead to two cases: (i) ${\widehat{\beta }}_{d,1}=0$ and ${\widehat{\beta }}_{d,2}\ne 0$ and (ii) ${\widehat{\beta }}_{d,1}\ne 0$ and ${\widehat{\beta }}_{d,2}=0$. This toy example illustrates the fundamental problem of trying to harmonize variable selection across imputed datasets without borrowing information across imputed datasets.

Figure 1:

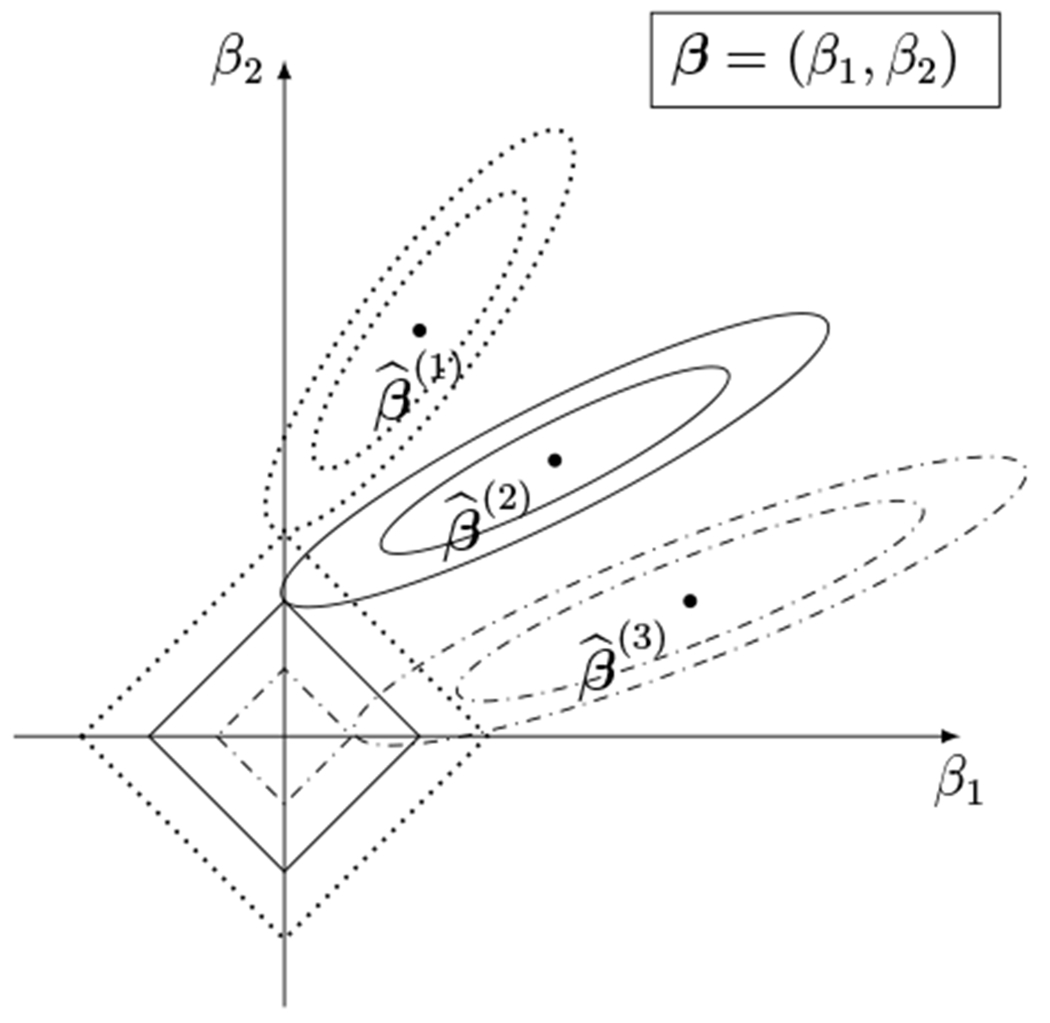
Example of LASSO fit separately on each imputed dataset with two predictor variables. β₁ and β₂ represent the first and second coefficient, respectively. ${\widehat{\mathit{\beta }}}^{(d)}$ denotes the maximum likelihood estimate in the d-th imputed dataset without the constraint (d = 1, 2, 3). The diamond-shaped areas around the origin represent the resulting constrained regions for the imputed datasets. The contours surrounding the maximum likelihood estimates represent the loss function.

2.2. Stacked objective functions

In a stacked objective function, we sum the loss functions for each of the imputed datasets together and jointly optimize the collective objective function:

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\mathrm{argmin}}\left\{-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n\log L\left(\mathit{\theta }\mid Y_{d,i},{\mathit{X}}_{d,i}\right)+\lambda P_{\alpha }(\mathit{\beta })\right\}$$ (2)

Note that θ is not indexed by d. This implies that optimizing the pooled objective function will result in one estimated parameter vector $\widehat{\mathit{\theta }}$, thereby enforcing uniform selection across all imputed datasets.

A nice feature of the stacked objective function is that optimization is straightforward. Namely, optimization of the stacked objective function is equivalent to stacking the imputed datasets and fitting the desired penalized regression algorithm on the stacked imputed datasets with existing software. Therefore, the stacked objective function provides a framework for pooling penalized regression estimates across imputed datasets for a general class of objective functions. However, stacking all imputed datasets can be viewed as artificially increasing the sample size. A common way to address this is to add an observation weight, o_i = 1/D, so that the total weight for each subject in the stacked dataset sums up to one. An alternative observational weight specification, proposed in Wan et al. (2015), is o_i = f_i/D, where f_i is the number of observed predictors out of the total number of predictors for subject i, which accounts for varying degrees of missing information for each subject. That being said, upweighting subjects with less missingness and downweighting subjects with more missingness can, in some sense, be viewed as making the optimization more like complete-case analysis, which might be problematic for Missing at Random (MAR) and Missing not at Random (MNAR) scenarios. Going forward, we consider both equal weights (o_i = 1/D) and the observation weights proposed in Wan et al. (2015) (o_i = f_i/D). The weighted stacked objective function can be written as:

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\mathrm{argmin}}\left\{-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i\log L\left(\mathit{\theta }\mid Y_{d,i},{\mathit{X}}_{d,i}\right)+\lambda P_{\alpha }(\mathit{\beta })\right\}$$ (3)

In (3), we directly sum the log-likelihoods ignoring the correlation for the same observation across all imputed datasets. This is not a problem for point estimation. Averaging over the number of imputed datasets D can be viewed as obtaining the expected log-likelihood conditional on the observed data and then subsequently averaging over all n observations leads to the conditional log-likelihood given the observed data. This strategy of defining an objective function summed across correlated imputed datasets is well-founded in the statistical literature on missing data (Wang and Robins, 1998; Robins and Wang, 2000). Ignoring the dependence between these datasets will have an impact on estimation of standard errors, but the coefficient estimator will still be consistent (Wang and Robins, 1998; Robins and Wang, 2000).

From this stacked approach, we extend the penalty functions to LASSO, aLASSO, ENET and aENET. When equal weights are used, the names for different versions of the stacked methods are as follows:

1. Stacked LASSO (SLASSO): $P_{\alpha }\left(\mathit{\beta }\right)={\sum }_{j=1}^p\left|{\beta }_j\right|$

2. Stacked adaptive LASSO (SaLASSO): $P_{\alpha }\left(\mathit{\beta }\right)={\sum }_{j=1}^p{\widehat{a}}_j\left|{\beta }_j\right|$

3. Stacked elastic net (SENET): $P_{\alpha }\left(\mathit{\beta }\right)=\alpha {\sum }_{j=1}^p\left|{\beta }_j\right|+(1-\alpha ){\sum }_{j=1}^p{\beta }_j^2$

4. Stacked adaptive elastic net (SaENET): $P_{\alpha }\left(\mathit{\beta }\right)=\alpha {\sum }_{j=1}^p{\widehat{a}}_j\left|{\beta }_j\right|+(1-\alpha ){\sum }_{j=1}^p{\beta }_j^2$

where ${\widehat{a}}_j={\left(\left|{\widehat{\beta }}_j\right|+1/(nD)\right)}^{-\gamma }$ and ${\widehat{\beta }}_j$ is estimated through SENET. Following Zou and Zhang (2009), γ is fixed to be $\lceil 2v/1-v\rceil +1$, where v = log(p)/log(nD).

When o_i = f_i/D, the penalized methods are named SLASSO(w), SaLASSO(w), SENET(w) and SaENET(w), respectively. Adaptive weights for the stacked approach with the observation weights are calculated using SENET(w).

2.3. Grouped objective functions

An alternative to the stacked objective function is the grouped objective function. This method imposes uniform variable selection across imputed datasets by adding a group LASSO penalty across imputed datasets (Chen and Wang, 2013; Geronimi and Saporta, 2017; Yuan and Lin, 2006). The optimizer of the grouped objective function can be mathematically expressed as:

$$\left({\widehat{\mathit{\theta }}}_1,\dots ,{\widehat{\mathit{\theta }}}_D\right)=\underset{{\mathit{\theta }}_1,\dots ,{\mathit{\theta }}_D}{\mathrm{argmin}}\left\{-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n\log L\left({\mathit{\theta }}_d\mid Y_{d,i},{\mathit{X}}_{d,i}\right)+\lambda P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)\right\}$$ (4)

where λ ∈ (0, ∞) is a tuning parameter. Chen et al. (2013) originally formulated a special case of the grouped objective function known as MI-LASSO, where the penalty function is:

$$P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)=\sum _{j=1}^p\sqrt{\sum _{d=1}^D{\beta }_{d,j}^2}$$

In the grouped objective function, the parameter vector is now indexed by d, meaning that θ₁ ≠ … ≠ θ_D. Although the θ_d’s are not identical, for any fixed j, the group LASSO penalty jointly shrink all β_d,j’s to zero, i.e. ${\beta }_{1,j}=\dots ={\beta }_{D,j}=0$. This allows for uniform selection across imputed datasets but also allows for variability in the non-zero estimated coefficients across imputed datasets. Based on Chen et al. (2013), we consider the following penalties:

1. Group LASSO (GLASSO): $P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)={\sum }_{j=1}^p\sqrt{{\sum }_{d=1}^D{\beta }_{d,j}^2}$

2. Group adaptive LASSO (GaLASSO): $P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)={{\sum }_{j=1}^p\widehat{a}}_j\sqrt{{\sum }_{d=1}^D{\beta }_{d,j}^2}$

where ${\widehat{a}}_j={\left(\sqrt{{\sum }_{d=1}^D{\widehat{\beta }}_{d,j}^2}+1/(nD)\right)}^{-\gamma }\cdot {\widehat{\beta }}_{d,j}$ is estimated from GLASSO, γ = ⌈2v/1 − v⌉ + 1, and $v=\log (pD)/\log (nD)$ (Zou and Zhang, 2009).

Remark:

We do not extend the grouped LASSO based approaches to grouped ENET based approaches because grouping itself provides constraints similar to the ENET penalty. How to effectively account for correlations among predictors using the grouped penalty remains an open question.

3. Optimization

In this section, we outline the optimization routines for SaENET(w) and GaLASSO with binary outcomes. To optimize the SaENET(w) objective function, we use local quadratic approximation coupled with a cyclic coordinate descent algorithm (Friedman et al., 2010). To obtain an optimizer of the GaLASSO objective function, we use a MM algorithm combined with block coordinate descent updates to handle the group LASSO component of the penalty function. The other objective functions listed in Section 2 are special cases of SaENET(w) and GaLASSO, and therefore can be optimized with minor simplifications (see Figure 2). Namely, when α = 1, SaENET(w) reduces to SaLASSO(w), and SENET(w) reduces to SLASSO(w). Furthermore, when ${\widehat{a}}_j=1$ for j = 1, 2, .., p, SaENET(w) reduces to SENET(w) and GaLASSO reduces to GLASSO. Optimizing the stacked objective function with equal weights can be achieved by setting o_i = 1/D.

Figure 2:

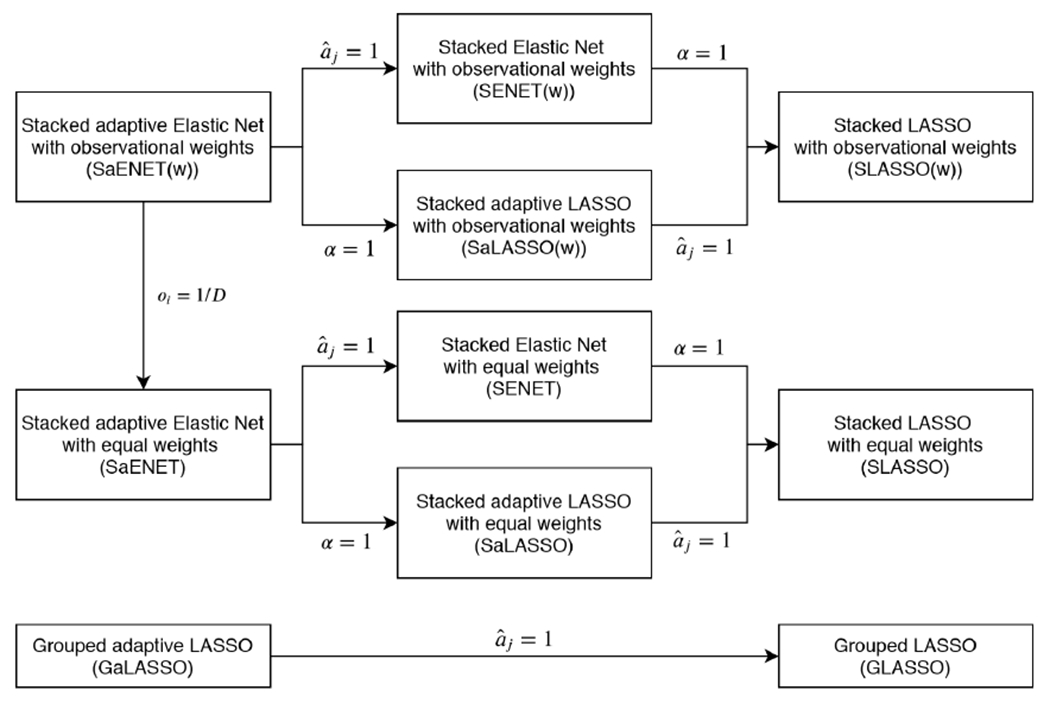
Illustration of how to obtain penalized pooled objective function methods, which are special cases of SaENET(w) and GaLASSO.

3.1. Optimization of SaENET(w)

Without loss of generality, suppose that the variables in the design matrix are standardized after stacking all the imputed datasets. That is, ${\sum }_{d=1}^D{\sum }_{i=1}^n{x}_{d,ij}=0$, $\frac{1}{n}{\sum }_{d=1}^D{\sum }_{i=1}^n{x}_{d,ij}^2=1$ , for j = 1, 2, …, p. Let $\mathit{\eta }={\left({\mathit{\eta }}_1^T,{\mathit{\eta }}_2^T,\dots ,{\mathit{\eta }}_D^T\right)}^T$ be the linear predictor based on $\mathit{\theta }={\left(\mu ,{\mathit{\beta }}^T\right)}^T$ such that ${\eta }_{d,i}=\mu +x_{d,i}^T\mathit{\beta }$. Then the sum of the weighted loss functions can be expressed as:

$$L(\mathit{\eta })=\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i\left\{-y_{d,i}{\eta }_{d,i}+\log \left(1+\exp \left({\eta }_{d,i}\right)\right)\right\}.$$

Let η^(t) denote the linear predictor at the t-th iteration. Following Friedman et al. (2010), we use a Taylor expansion at η^(t) to construct a quadratic approximation to the loss function:

$$L_Q\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)=\frac{1}{2n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}{\left({\tilde{y}}_{d,i}-\mu -x_{d,i}^T\mathit{\beta }\right)}^2+C{\left({\mathit{\eta }}^{(t)}\right)}^2,$$

where

$${\tilde{y}}_{d,i}={\mu }^{(t)}+x_{d,i}^T{\mathit{\beta }}^{(t)}+\frac{y_{d,i}-\tilde{p}\left(x_{d,i}\right)}{\tilde{p}\left(x_{d,i}\right)\left(1-\tilde{p}\left(x_{d,i}\right)\right)}$$ (5)

is the working response, $w_{d,i}=\tilde{p}\left(x_{d,i}\right)\left(1-\tilde{p}\left(x_{d,i}\right)\right)$ is a subject weight that is specific to each imputed dataset, and

$$\tilde{p}\left(x_{d,i}\right)=P\left(Y_{d,i}=1\mid X_{d,i}=x_{d,i}\right)={\left(1+\exp \left(-\left({\mu }^{(t)}+x_{d,i}^T{\mathit{\beta }}^{(t)}\right)\right)\right)}^{-1}.$$

Going forward we will use, $O_Q=L_Q\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)+\lambda P_{\alpha }(\mathit{\beta })$, as shorthand notation for the objective function after quadratic approximation. We then use coordinate descent to solve:

$$\underset{\mathit{\theta }}{\mathrm{argmin}}{O}_Q=\underset{\mathit{\theta }}{\mathrm{argmin}}\left\{L_Q\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)+\lambda P_{\mathit{\alpha }}(\mathit{\beta })\right\}$$

The derivative of the approximate objective function with respect to the intercept parameter is:

$$\frac{\partial O_Q}{\partial \mu }=-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}\left({\tilde{y}}_{d,i}-\mu -x_{d,i}^T\mathit{\beta }\right)=-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}\left({\tilde{y}}_{d,i}-x_{d,i}^T\mathit{\beta }\right)+\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}\mu .$$

Let $z_0={\sum }_{d=1}^D{\sum }_{i=1}^n{o}_i{w}_{d,i}\left({\tilde{y}}_{d,i}-x_{d,i}^T\mathit{\beta }\right)$. Then μ can be updated as:

$${\mu }^{(t+1)}\leftarrow \frac{z_0}{{\sum }_{d=1}^D{\sum }_{i=1}^n{o}_i{w}_{d,i}}$$ (6)

If β_j > 0,

$$\frac{\partial O_Q}{\partial {\beta }_j}=-\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}\left({\tilde{y}}_{d,i}-\mu -x_{d,i(-j)}^T{\mathit{\beta }}_{(-j)}\right)+\frac{1}{n}\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}^2{\beta }_j+\lambda \alpha {\widehat{a}}_j+2\lambda (1-\alpha ){\beta }_j$$

where x_d,i(−j) refers to the value of the covariate vector for the i-th observation in the d-th imputed dataset after removing the j-th covariate, and β_(−j) refers to the regression coefficient vector β without the j-th entry. If β_j < 0 then the derivative of O_Q with respect to β_j is the same as the derivative when β_j > 0, the only exception being that the $\lambda \alpha {\widehat{a}}_j$ term becomes $-\lambda \alpha {\widehat{a}}_j$. Setting $z_j={\sum }_{d=1}^D{\sum }_{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}\left({\tilde{y}}_{d,i}-\mu -x_{d,i(-j)}^T{\mathit{\beta }}_{(-j)}\right)$, then β_j can be updated as:

$${\beta }_j^{(t+1)}\leftarrow \frac{S\left(\frac{1}{n}{z}_j,\lambda \alpha {\widehat{a}}_j\right)}{\frac{1}{n}{\sum }_{d=1}^D{\sum }_{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}^2+2\lambda (1-\alpha )}$$ (7)

where S(z, λ) is the soft-thresholding operator:

$$S(z,\lambda )=\{\begin{array}{ll}0& \mathrm{if}\left|z\right|\le \lambda \\ z-\lambda & \mathrm{if}z>\lambda \\ z+\lambda & \mathrm{if}z<-\lambda \end{array}$$

A summary of the optimization routine for SaENET(w) is presented in Algorithm 1. One thing to note is that we never directly compute z_j after each update of β_j. A more computationally efficient approach is to update z_j through the residual $r_{d,i}={\tilde{y}}_{d,i}-\mu -x_{d,i}^T\mathit{\beta }$. Specifically,

$$\begin{array}{c}{z}_j\leftarrow \sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}{r}_{d,i}+\sum _{d=1}^D\sum _{i=1}^n{o}_i{w}_{d,i}{x}_{d,ij}^2{\beta }_j^{(t)}\\ r_{d,i}\leftarrow r_{d,i}^{\prime }-x_{d,ij}\left({\beta }_j^{(t)}-{\beta }_j^{(t+1)}\right)\end{array}$$ (8)

where $r_{d,i}^{\prime }$ indicates the previous estimate of r_d,i (we do not use the (t) superscript notation here because r_d,i is updated multiple times within the same iteration). Updating the intercept parameter μ is similar, in that we assign $r_{d,i}\leftarrow r_{d,i}^{\prime }-\left({\mu }^{(t)}-{\mu }^{(t+1)}\right)$ and update z₀ accordingly. Once a coefficient is shrunk to zero, it will stay at zero for the remaining iterations.

3.2. Optimization of GaLASSO

Although Chen and Wang (2013) initially proposed the idea of grouped objective functions, their optimization procedure relies on a local quadratic approximation argument to rewrite the grouped objective function as the sum of D separate ridge regressions. Because the ridge penalty does not shrink regression coefficient estimates all the way to zero, the user is then forced to threshold the resulting regression coefficient estimates in an ad hoc manner. Another limitation of the algorithm proposed in Chen and Wang (2013) is that they only consider continuous outcome variables. In many biomedical applications, including our motivating example, the outcome is a binary indicator of disease status. To address both of these concerns, we developed a MM algorithm for GaLASSO with binary outcome data. The primary computational advantage of the MM-Algorithm is that it allows us to transform the optimization of a non-linear loss function into an optimization of a linear function, called the majorizing function. Block coordinate descent can then be applied to optimize the linear majorizing function, where the blocks correspond to regression coefficient estimates for each covariate across all imputed datasets, i.e., (β_1,j, β_2,j, …, β_D,j) for the j-th covariate.

Without loss of generality, we standardize the data by letting ${\sum }_{i=1}^n{x}_{d,ij}=0,n^{-1}{\sum }_{i=1}^n{x}_{d,ij}^2=1$, for j = 1, 2, …, p and d = 1, 2, …, D. Let $\mathit{\eta }={\left({\mathit{\eta }}_1^T,{\mathit{\eta }}_2^T,\dots ,{\mathit{\eta }}_D^T\right)}^T$ be the linear predictor based on (θ₁, θ₂, …, θ_D), where ${\mathit{\theta }}_d={\left({\mu }_d,{\mathit{\beta }}_d^T\right)}^T$, ${\mathit{\eta }}_d={\left({\eta }_{d,1},{\eta }_{d,2},\dots ,{\eta }_{d,n}\right)}^T$ and ${\eta }_{d,i}={\mu }_d+{\beta }_{d,1}{x}_{d,i1}+\dots +{\beta }_{d,p}{x}_{d,ip}$. For binary outcome data, the sum of loss functions in (4) can be written as:

$$L(\mathit{\eta })=\sum _{d=1}^D\sum _{i=1}^n\left\{-y_{d,i}{\eta }_{d,i}+\log \left(1+\exp \left({\eta }_{d,i}\right)\right)\right\}$$

Let ${\mathit{\eta }}^{(t)}$ be the linear predictor at the t-th iteration, $L({\mathit{\eta }}^{(t)})$ be the loss function given η^(t), and $\tilde{L}\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)$ be the majorizing function of $L({\mathit{\eta }}^{(t)})$ (Breheny and Huang, 2015), which can be expressed as:

$$\tilde{L}\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)=L\left({\mathit{\eta }}^{(t)}\right)+{\left(\mathit{\eta }-{\mathit{\eta }}^{(t)}\right)}^T\nabla L\left({\mathit{\eta }}^{(t)}\right)+\frac{v}{2}{\left(\mathit{\eta }-{\mathit{\eta }}^{(t)}\right)}^T\left(\mathit{\eta }-{\mathit{\eta }}^{(t)}\right).$$

Here, $v={\mathit{max}}_d{\mathit{max}}_i{\mathit{sup}}_{\eta }\left\{{\nabla }^2{L}_{d,i}(\eta )\right\}=0.25$ (Breheny and Huang, 2015). Ignoring constants not involving $\mathit{\eta }$, $\tilde{L}\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)$ can be written in terms of (θ₁, θ₂, …, θ_D):

$$\tilde{L}\left(\mathit{\eta }\mid {\mathit{\eta }}^{(t)}\right)=\tilde{L}\left({\mathit{\theta }}_1,{\mathit{\theta }}_2,\dots ,{\mathit{\theta }}_D\right)\propto \frac{v}{2n}\sum _{d=1}^D\sum _{i=1}^n{\left({\tilde{y}}_{d,i}-{\mu }_d-x_{d,i}^T{\mathit{\beta }}_d\right)}^2$$

where

$${\tilde{y}}_{d,i}={\mu }_d^{(t)}+x_{d,i}^T{\mathit{\beta }}_d^{(t)}+\frac{y_{d,i}-\tilde{p}\left(x_{d,i}\right)}{v}$$ (9)

is the working response and

$$\tilde{p}\left(x_{d,i}\right)=P\left(Y_{d,i}=1\mid X_{d,i}=x_{d,i}\right)={\left(1+\exp \left(-\left({\mu }_d^{(t)}+x_{d,i}^T{\mathit{\beta }}_d^{(t)}\right)\right)\right)}^{-1}.$$

Going forward, let $M_Q=\tilde{L}\left({\mathit{\theta }}_1,{\mathit{\theta }}_2,\dots ,{\mathit{\theta }}_D\right)+\lambda P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)$ denote the penalized majorizing function, which we want to optimize:

$$\underset{{\mathit{\theta }}_1,{\mathit{\theta }}_2,\dots ,{\mathit{\theta }}_D}{\mathrm{argmin}}{M}_Q=\underset{{\mathit{\theta }}_1,{\mathit{\theta }}_2,{\dots }_{,}{\mathit{\theta }}_D}{\mathrm{argmin}}\left\{\tilde{L}\left({\mathit{\theta }}_1,{\mathit{\theta }}_2,\dots ,{\mathit{\theta }}_D\right)+\lambda P\left({\mathit{\beta }}_1,{\mathit{\beta }}_2,\dots ,{\mathit{\beta }}_D\right)\right\}$$

To derive the block coordinate descent updates for the majorizing function optimization, we first need to introduce some new notation to distinguish coefficients within an imputed dataset from those across the imputed datasets. Let $\mathit{\mu }={({\mu }_1,{\mu }_2,\dots ,{\mu }_D)}^T$ be the vector of all intercept parameters across the imputed datasets, let ${\mathit{\beta }}_{·,j}={({\beta }_{1,j},{\beta }_{2,j},\dots ,{\beta }_{D,j})}^T$, for j = 1, 2, …, p denote the vector of the j-th regression coefficients across all imputed datasets, and let ${\mathit{\beta }}_{d,·}={({\beta }_{d,1},{\beta }_{d,2},\dots ,{\beta }_{d,p})}^T$ for d = 1, 2, …, D indicate the regression coefficients for the d-th imputed dataset. If we take the subdifferential of M_Q with respect to μ, we get:

$$\frac{\partial M_Q}{\partial \mathit{\mu }}=-\frac{v}{n}{\mathit{z}}_0+v\mathit{\mu }$$

where

$${\mathit{z}}_0=\left[\begin{array}{c}{\sum }_{i=1}^n\left({\tilde{y}}_{1,i}-x_{1,i}^T{\mathit{\beta }}_{1,·}\right)\\ {\sum }_{i=1}^n\left({\tilde{y}}_{2,i}-x_{2,i}^T{\mathit{\beta }}_{2,·}\right)\\ ⋮\\ {\sum }_{i=1}^n\left({\tilde{y}}_{D,i}-x_{D,i}^T{\mathit{\beta }}_{D,·}\right)\end{array}\right]$$

Since x_d,ij, have been centered, the intercept can be updated as:

$${\mathit{\mu }}^{(t+1)}\leftarrow \left[\begin{array}{c}\frac{1}{n}{\sum }_{i=1}^n{\tilde{y}}_{1,i}\\ \frac{1}{n}{\sum }_{i=1}^n{\tilde{y}}_{2,i}\\ ⋮\\ \frac{1}{n}{\sum }_{i=1}^n{\tilde{y}}_{D,i}\end{array}\right]$$ (10)

We now derive the update for the block of coefficients β_·,j, j = 1, …, p. If β_·,j ≠ 0, the subdifferential of M_Q with respect to β_·,j is:

$$\frac{\partial M_Q}{\partial {\mathit{\beta }}_{\cdot ,j}}=-\frac{v}{n}{\mathit{z}}_j+v{\mathit{\beta }}_{\cdot ,j}+\lambda {\widehat{a}}_j\frac{{\mathit{\beta }}_{\cdot ,j}}{\Vert {\mathit{\beta }}_{\cdot ,j}\Vert }$$

where

$${\mathit{z}}_j=\left[\begin{array}{c}{\sum }_{i=1}^n{x}_{1,ij}\left({\tilde{y}}_{1,i}-{\mu }_1-x_{1,i(-j)}^T{\mathit{\beta }}_{1,(-j)}\right)\\ {\sum }_{i=1}^n{x}_{2,ij}\left({\tilde{y}}_{2,i}-{\mu }_2-x_{2,i(-j)}^T{\mathit{\beta }}_{2,(-j)}\right)\\ ⋮\\ {\sum }_{i=1}^n{x}_{D,ij}\left({\tilde{y}}_{D,i}-{\mu }_D-x_{D,i(-j)}^T{\mathit{\beta }}_{D,(-j)}\right)\end{array}\right]$$

Here, x_d,i(−j) is the vector of covariates for the i-th observation in the d-th dataset after removing x_d,ij, and β_d,(−j) is the corresponding vector of regression coefficients. The form of the partial derivative with respect to β_·,j indicates that the β_·,j update must lie on the line segment joining the zero vector, 0, and z_j. Therefore, β_·,j can be updated as:

$${\mathit{\beta }}_{.,j}^{(t+1)}\leftarrow \frac{1}{v}S\left(\frac{v}{n}\Vert {\mathit{z}}_j\Vert ,\lambda {\widehat{a}}_j\right)\frac{{\mathit{z}}_j}{\Vert {\mathit{z}}_j\Vert }$$ (11)

As with SaENET(w), we do not directly calculate z_j but use the residual r_d,i to update z_j. Let $r_{d,i}={\tilde{y}}_{d,i}-{\mu }_d-x_{d,i}^T{\mathit{\beta }}_{d,\cdot }$. Then

$${\mathit{z}}_j\leftarrow \left[\begin{array}{c}{z}_{1,j}\\ z_{2,j}\\ ⋮\\ z_{D,j}\end{array}\right]=\left[\begin{array}{c}{\sum }_{i=1}^n{x}_{1,ij}{r}_{1,i}+n{\beta }_{1,j}^{(t)}\\ {\sum }_{i=1}^n{x}_{2,ij}{r}_{2,i}+n{\beta }_{2,j}^{(t)}\\ ⋮\\ {\sum }_{i=1}^n{x}_{D,ij}{r}_{D,i}+n{\beta }_{D,j}^{(t)}\end{array}\right]$$ (12)

$$r_{d,i}\leftarrow r_{d,i}^{\prime }-x_{d,ij}\left({\beta }_{d,j}^{(t)}-{\beta }_{d,j}^{(t+1)}\right)$$

Updating the intercept parameter μ is similar, in that we assign $r_{d,i}\leftarrow r_{d,i}^{\prime }-\left({\mu }_d^{(t)}-{\mu }_d^{(t+1)}\right)$ and update z₀ accordingly. Once the block of regression coefficients corresponding to the j-th covariate is shrunk to zero, it will stay at zero for the remaining iterations. A summary of the optimization routine is described in Algorithm 2.

3.3. Tuning parameters

The implementation of SaENET(w) and GaLASSO in the miselect package sets tuning parameter values based on a 5-fold cross-validation routine combined with a “one-standard-error” rule (Hastie et al., 2009, 2015). More specifically, GaLASSO chooses the largest λ, such that the cross-validation error is within one standard error of the minimum cross-validation error. SaENET(w) selects an (α, λ) pair by first identifying all dyads whose cross-validation errors are within one standard error of the minimum cross-validation error, and then picking the (α, λ) pair with the largest L₁ penalty, i.e, λα. For both GaLASSO and SaENET(w), the default sequence for λ ranges from λ_min to λ_max on the log scale where λ_max is chosen to be the smallest value where all the coefficients are shrunk to zero, and λ_min = 10⁻⁶λ_max. Since α ∈ [0, 1], then for SaENET(w) we can choose a sequence of values, say (0.2, 0.4, …, 0.8, 1), to fully explore the tradeoff between L₁ and L₂ shrinkage. When the non-adaptive methods are used, i.e. GLASSO, SENET(w), SLASSO(w), we set λ_min = 10⁻³λ_max. The reason that λ_min is smaller for the adaptive methods is to prevent large adaptive weights from overwhelming the overall shrinkage.

One caveat with cross-validation to select tuning parameters for the stacked objective function approach is that, by stacking the imputed datasets on top of one another, there are now D rows corresponding to the same subject. Therefore, if the D rows corresponding to the same subject are distributed across the validation folds, then we are prone to overfitting. To prevent this issue, we restrict the fold assignment such that all of the rows corresponding to the same subject are assigned to a single validation fold.

4. Data example

Our motivating example is derived from data in the University of Michigan ALS Patient Biorepository which aims to identify environmental risk factors associated with ALS (Su et al., 2016; Goutman et al., 2019; Yu et al., 2014). ALS is progressive disease primarily involving motor neuron cells in the brain and spinal cord leading to weakness of voluntary muscles and death within 2-4 years due to respiratory failure (Goutman, 2017). ALS has a complex etiology driven by the combination of genetic susceptibility and environmental exposures (Paez-Colasante et al., 2015; Goutman et al., 2018; Al-Chalabi and Hardiman, 2013). In this particular study we are interested in characterizing the relationship between persistent organic pollutant (POP) exposure and ALS susceptibility. In total, 167 ALS cases and 99 healthy controls were recruited between 2011 and 2014. All participants provided written informed consent and the study was IRB approved (Su et al., 2016; Goutman et al., 2019). Participants provided their weight and height measurements at the time of study enrollment and 5 years prior to enrollment and their educational attainment. Plasma samples were collected from each study participant to measure 122 potentially neurotoxic POPs, which can be broadly partitioned into three chemical classes: organochlorine pesticides, polychlorinated biphenyls (PCBs), and polybrominated diphenyl ethers (PBDEs). Of the 122 POPs, a subset of 23 POPs with less than 60% non-detects were used for further analysis. More information regarding data collection and study protocols can be found in (Su et al., 2016; Goutman et al., 2019).

From a statistical perspective, the target model of interest is a penalized logistic regression model, where the outcome is ALS case/control status and the design matrix of predictors and covariates contains the 23 log-transformed POPs, age, sex, body mass index (BMI), rate of BMI change over the five years prior to survey consent, and education. The confounders are selected based on existing ALS literature (Chio et al., 2009). Elastic net regularization is of particular interest here, because many of the POPs have medium pairwise correlations with one another (Figure S1) (Goutman et al., 2019). We only penalize regression coefficients corresponding to POPs to ensure that adjustment covariates are retained in the final model. If we look at the percent missingness (Table S2), we observe that 9 of the 23 variables have more than 30% below the detection limit and 24.4% of subjects have incomplete BMI. Complete-case analysis in this context is infeasible, as every control is missing at least one covariate or has at least one measured POP below its respective detection limit. POP concentrations below their respective detection limits were imputed 10 or 50 times conditional on case/control status following the censored likelihood multiple imputation strategy outlined in Boss et al. (2019). After imputing the exposure non-detects, multiple imputation by chained equations (mice) was used to impute the missing adjustment covariates (Van Buuren and Groothuis-Oudshoorn, 2011).

To illustrate the problem with fitting separate penalized regression routines, we first apply LASSO, aLASSO, ENET, and aENET to each imputed dataset and calculate the proportion of imputed datasets in which each variable is selected. In Table 1, we summarize the results for scenarios with 10 and 50 imputed datasets. The final active set for each method is determined using the ad hoc rules outlined in Wood et al. (2008), namely (i) a variable is considered selected if it is selected in all imputed datasets, (ii) a variable is considered selected if it is selected in at least one imputed dataset, (iii) a variable is considered selected if it is selected in at least half of the imputed datasets. Note that depending on whether we use (i), (ii), or (iii), the number of selected POPs changes, especially when D = 50. For example, if ad hoc combining rule (i) is used, then ENET selects PBDE 153, pentachlorobenzene (PeCB), trans-chlordane, cis-nonachlor, and PCB 151. However, ad hoc combining rule (ii) additionally selects PBDE 28, PBDE 99, PCB 110, PCB 174, and PCB 180. As expected, the final active set determined by aLASSO and aENET is much more sparse than their non-adaptive counterparts; if ad hoc combining rule (iii) is used then aLASSO and aENET only select PeCB and cis-nonachlor.

Table 1:

The proportion of imputed datasets in which each POP is selected. Note that only 10 out of the 23 POPs are listed because the other 13 POPs were never selected by LASSO, aLASSO, ENET, or aENET. Bolded entries indicate a selection proportion over 0.50 and dashes denote a selection proportion of zero. D is the number of imputed datasets. The total number of POPs in the final active set, as determined by three ad hoc combining rules, are presented in the rows titled, Union (in at least one dataset), 50%-cutoff (in over 50% datasets), and Intersection (in all datasets).

POPs	LASSO		aLASSO		ENET		aENET
	D=10	D=50	D=10	D=50	D=10	D=50	D=10	D=50
PBDE28	-	-	-	-	0.1	0.1	-	-
PBDE99	-	-	-	-	-	0.04	-	-
PBDE153	1	1	-	0.02	1	1	-	0.02
PeCB	1	1	1	1	1	1	1	1
trans-chlordane	0.9	0.94	0.1	0.08	1	1	0.1	0.08
cis-nonachlor	1	1	1	1	1	1	1	1
PCB 110	-	0.02	-	-	-	0.06	-	-
PCB 151	0.9	0.96	-	0.04	1	1	-	0.06
PCB 174	-	0.02	-	-	0.1	0.08	-	-
PCB 180	-	-	-	-	-	0.02	-	-
Union	5	7	3	5	7	10	3	5
50%-cutoff	5	5	2	2	5	5	2	2
Intersection	3	3	2	2	5	5	2	2

A more subtle point that deserves further comment is that non-uniform POPs selection across imputed datasets makes it difficult to obtain final regression coefficient estimates. For example, consider aLASSO when D = 50, which selects PeCB in all 50 imputed datasets. Although PeCB is always selected, the interpretation of the regression coefficient for PeCB is conditional on the other selected exposures. That is, although PeCB is selected for all imputed datasets, the PeCB regression coefficient estimates are not necessarily comparable across imputed datasets because they condition on different sets of selected exposures.

The regression coefficient estimates obtained from the stacked and grouped objective function methods with 50 imputed datasets are in Table 2 and with 10 imputed datasets are in Table S3. Because the grouped methods produce different regression coefficient estimates across imputed datasets, the final estimates are the average of the regression coefficient estimates across imputed datasets. All coefficient estimates are positive, which is consistent with the hypothesis that higher POP exposure positively associates with a higher ALS risk. All of the non-adaptive methods select PBDE 153, PeCB, trans-chlordane, cis-nonachlor, and PCB 151. Similarly, the adaptive methods all select PeCB and cis-nonachlor, however the equally weighted stacked objective functions additionally select PCB 151 while the stacked objective functions with observational weights additionally select PBDE 153, trans-chlordane and PCB 151. Since all methods select PeCB and cis-nonachlor, we conclude that further studies should be conducted to assess the PeCB and cis-nonachlor neurotoxicity.

Table 2:

Regression coefficient estimates for five POPs collected as part of the University of Michigan ALS Patients Biorepository case-control study (167 ALS cases and 99 healthy controls). Results are based on 50 imputed datasets. Only five of the 23 POPs are displayed because the other 18 POPs were not selected by any method.

POPs	SLASSO	SaLASSO	SENET	SaENET	SLASSO (w)	SaLASSO (w)	SENET (w)	SaENET (w)	GLASSO	GaLASSO
PBDE 153	0.083	-	0.092	-	0.086	-	0.095	-	0.075	-
PeCB	0.331	0.744	0.367	0.715	0.284	0.670	0.322	0.657	0.299	0.968
trans-chlordane	0.074	-	0.109	-	0.073	0.034	0.109	0.036	0.044	-
cis-nonachlor	0.247	0.576	0.303	0.558	0.253	0.615	0.309	0.601	0.198	0.191
PCB151	0.080	0.156	0.128	0.151	0.057	0.189	0.111	0.184	0.038	-
# selected	5	3	5	3	5	4	5	4	5	2
# removed	18	20	18	20	18	19	18	19	18	21

5. Simulation

We now evaluate the performance of the stacked methods and the grouped methods mentioned in Section 2, including SLASSO, SaLASSO, SENET, SaENET, SLASSO(w), SaLASSO(w), SENET(w), SaENET(w), GLASSO, and GaLASSO.

5.1. Simulation setting

We simulate 1000 datasets of size n containing outcome Y and p covariates X under 4 different cases. For Cases 1 and 2 we take n = 500 and p = 20, and for Cases 3 and 4 we take n = 1000 and p = 100. In all cases, covariates are generated from a multivariate normal distribution with zero mean and unit variance. The correlation structure of the covariates is block-diagonal, in order to mimic the correlation structure of the POPs. A more comprehensive breakdown of the correlation structure is detailed in Table 3.

Table 3:

Data generation details for all simulation settings. In the correlation structure column, covariates within the same parentheses have an exchangeable pairwise correlation structure with one another, but are independent from all other covariates. For Case 1 and Case 2, n = 500, p = 20, approximately 25% subjects are missing {X₁, …, X₅}, 35% are missing {X₆, …, X₁₃}, 45% are missing {X₁₄, …, X₁₇}, and 55% are missing {X₁₈, X₁₉}. For Case 3 and Case 4, n = 1000, p = 100, about 25% subjects are missing {X₁, …, X₃₀}, 35% are missing {X₃₁, …, X₆₀}, 45% are missing {X₆₁, …, X₈₂}, 55% are missing {X₈₃, …, X₉₅}, and 60% are missing {X₉₆, …, X₉₉}. The No. Signals (%) column refers to the number of covariates that have non-null coefficients and the corresponding relative percentage.

	Correlation structure	Signal structure	No. Signals (%)	Signals
Case 1	(X1, X2, X3) as 0.9 (X6, X7, X8) as 0.5 (X11, X12, X13) as 0.3	Concentrated	5 (25%)	β1 = 2, β4 = 1.5, β7 = 1.5, β11 = 1, β14 = 1;
Case 2	(X1, X2, X3) as 0.9 (X6, X7, X8) as 0.5 (X11, X12, X13) as 0.3	Distributed	5 (25%)	β1 = 2, β2 = 1, β4 = 2, β7 =1, β11 = 1
Case 3	(X1, …, X6) as 0.9 (X11, …, X16) as 0.5 (X21, …, X26) as 0.3	Concentrated	10 (10%)	β2 = 2, β7 = 0.8, β9 = 0.8, β12 = 0.5, β17 = 1.5, β27 = 1, β37 = 0.8, β47 = 0.4, β48 = 1, β49 = 1;
Case 4	(X1, …, X6) as 0.9 (X11, …, X16) as 0.5 (X21, …, X26) as 0.3	Distributed	10 (10%)	β1 = 1.2, β2 = 0.8, β3 = 0.4, β4 = 0.4, β12 = 1.2, β13 = 1 β17 = 1.2, β27 = 1, β37=1, β47 = 1;

Given X, we generate a binary Y from

$$logit(P(Y=1\mid X))={\beta }_0+{\beta }_1{X}_1+\dots +{\beta }_p{X}_p$$

The true value of β is specified according to different simulation cases, where Cases 1 and 3 correspond to concentrated signals and Cases 2 and 4 correspond to distributed signals. Here, signals are concentrated if there is only one non-null coefficient in a group, and signals are distributed if there is more than one non-null coefficient in a group. Regression coefficient magnitudes are set to fix the prevalence of Y = 1 at about 50% and maintain the Cox-Snell pseudo-R² at approximately 0.5. The four simulation settings are summarized in Table 3.

Missing values are generated under the Missing at Random (MAR) assumption (Little and Rubin, 2019). In all cases the outcome and the last covariate X_p are fully observed and the missingness indicator M_j for covariate X_j is generated from the logistic regression model

$$logit\left(Pr\left(M_j=1\right)\right)={\alpha }_{0j}+{\alpha }_{1j}{X}_p+{\alpha }_{2j}Y$$

where R_j = 1 indicates that covariate X_j is missing, and α_0j, α_1j and α_2j are chosen to control the percentage of missingness for X_j. For Case 1 and Case 2, about 25% of subjects are missing {X₁, …, X₅}, 35% are missing {X₆, …, X₁₃}, 45% are missing {X₁₄, …, X₁₇} and 55% are missing {X₁₈, X₁₉}. For Case 3 and Case 4, about 25% of subjects are missing {X₁, …, X₃₀}, 35% are missing {X₃₁, …, X₆₀}, 45% are missing {X₆₁, …, X₈₂}, 55% are missing {X₈₃, …, X₉₅}, and 60% are missing {X₉₆, …, X₉₉}. In total, less than 5% of subjects have complete data, and about 13% of subjects have more than 90% data for all covariates. R package mice (Van Buuren and Groothuis-Oudshoorn, 2011) is used to multiply impute the missing data using predictive mean matching. Each simulated dataset is imputed 10 or 50 times. To obtain independent imputed values, we set the number of iterations to 30 in mice. The stacked and grouped methods are then applied to perform variable selection and parameter estimation.

5.2. Simulation results

We evaluate simulation results in terms of the following four metrics. In the following definitions, T and F are the number of non-null and null coefficients in the data generating model, respectively, R is the total number of simulation runs, ${\widehat{\beta }}_j^r$ is the coefficient estimate for β_j in the r-th run. Since the estimates for the j-th coefficient by GLASSO and GaLASSO are different across imputed datasets, the mean $\frac{1}{D}{\sum }_{d=1}^D{\widehat{\beta }}_{d,j}^r$ is used to approximate ${\widehat{\beta }}_j^r$ .

• $\text{Sensitivity}(\text{SENS})=\frac{1}{RT}{\sum }_{r=1}^R\left(\#\mathit{of\; selected\; non}-\mathit{null\; coefficients\; in\; the}{r}_{\mathit{th}}\mathit{run}\right)$

• $\text{Specificity}(\text{SPEC})=\frac{1}{RF}{\sum }_{r=1}^R(\#\mathit{of\; selected\; null\; coefficients\; in\; the}{r}_{\mathit{th}}\mathit{run})$

• Mean squared error for non-null coefficients $\left({\text{MSE}}_{\text{non-null}}\right)=\frac{1}{R}{\sum }_{r=1}^R{\sum }_{j=1}^p{\left({\widehat{\beta }}_j^r-{\beta }_j\right)}^{2}I\left({\beta }_j\ne 0\right)$

• Mean squared error for null coefficients $\left({\text{MSE}}_{\text{null}}\right)=\frac{1}{R}{\sum }_{r=1}^R{\sum }_{j=1}^p{\left({\widehat{\beta }}_j^r-{\beta }_j\right)}^{2}I\left({\beta }_j=0\right)$

Sensitivity and specificity capture the accuracy of variable selection and vary between 0 and 1, with larger values indicating better performance. The MSEs quantify the estimation accuracy with smaller values being preferred.

Figure 3–4 and Table S4 present sensitivity, specificity, MSE for non-null coefficients, and MSE for null coefficients for all four cases with 50 imputed datasets. Using SLASSO as the benchmark, the ratio to SLASSO for each measure is presented in Table S5. Overall, compared to the corresponding non-adaptive methods, the adaptive methods perform better with respect to estimation and selection. Specifically, the adaptive methods have similar sensitivity but considerably higher specificity, and considerably smaller MSE for non-null coefficients, except for GaLASSO under Case 4. For null coefficients, the adaptive methods have similar MSE to those of non-adaptive methods under Cases 1 and 2, and noticeably larger MSE under Cases 3 and 4, except for GaLASSO under Cases 3 and 4. Adaptive methods have high sensitivity across all cases and high specificity under Cases 1 and 2. Under Cases 3 and 4, GaLASSO has the highest specificity, followed by SaLASSO(w) and SaENET(w). The stacked methods with adaptive weights have smaller MSE for non-null coefficients than the grouped method with adaptive weights under all 4 cases. On the other hand, under Case 4, GaLASSO has the largest MSE for non-null coefficients and the smallest MSE for null coefficients, which is due to relatively low sensitivity and high specificity compared to other adaptive methods. In addition, the stacked approach performs better than the grouped approach in terms of estimation and selecting important variables. Compared to SLASSO, GLASSO has slightly lower sensitivity in all four cases, but has noticeably lower specificity in Cases 3 and 4. The MSE for non-null coefficients is larger for GLASSO than SLASSO in all four cases, in addition to the MSE for null coefficients in Cases 3 and 4, due to large variability in the coefficient estimates.

Figure 3:

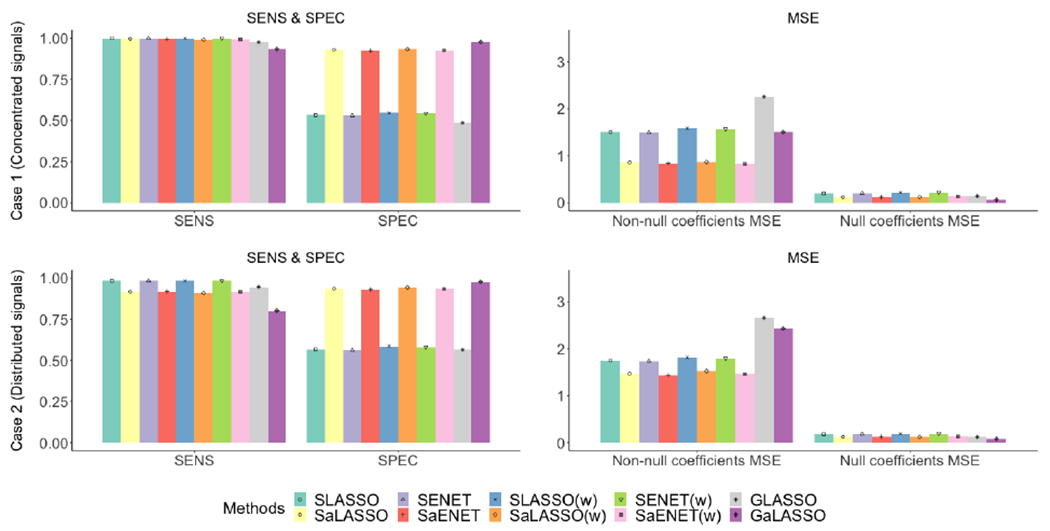
Simulation results for Case 1 (top panel) and Case 2 (bottom panel) where n=500 and p=20 for 50 imputed datasets. Sensitivity (SENS) and specificity (SPEC) are on the left and MSE for non-null and null coefficients are on the right.

Figure 4:

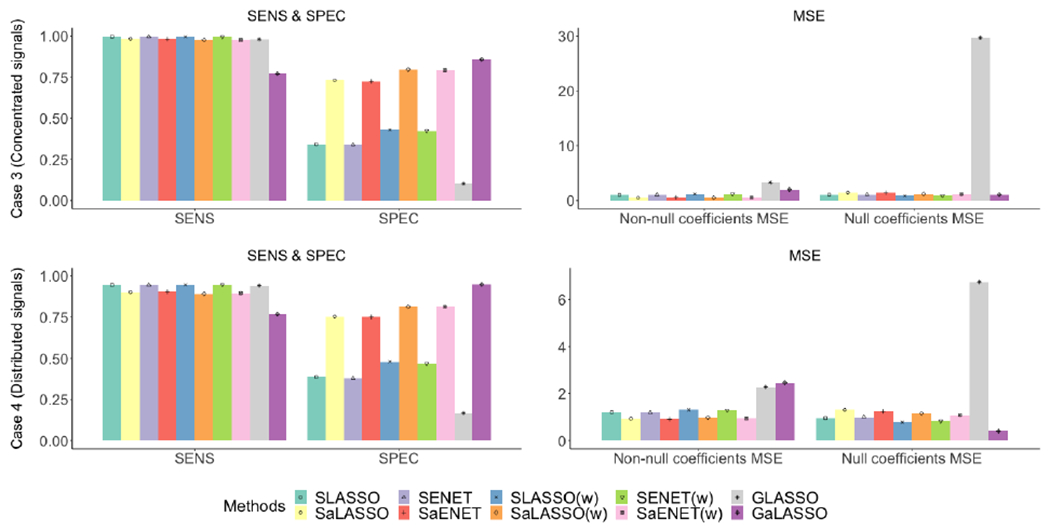
Simulation results for Case 3 (top panel) and Case 4 (bottom panel) where n=1000 and p=100 for 50 imputed datasets. Sensitivity (SENS) and specificity (SPEC) are on the left and MSE for non-null and null coefficients are on the right.

The average runtime for each method is presented in Table 4. Compared to the grouped methods, the stacked methods are faster in all cases. SLASSO is 5.7 times faster than GLASSO in Case 1 when the sample size is small. When the sample size is large, i.e. Case 3, SLASSO is 8.9 times faster than GLASSO. The adaptive methods have longer average runtimes than the non-adaptive methods because the adaptive methods require an elastic net initialization step to construct the adaptive weights.

Table 4:

Average runtime (in minutes) of each method for 4 simulation cases with 10 imputed datasets (1000 replications). Case 1 and Case 2 have 500 observations and 20 covariates. Case 3 and Case 4 have 1000 observations and 100 covariates.

	SLASSO	SaLASSO	SENET	SaENET	SLASSO (w)	SaLASSO (w)	SENET (w)	SaENET (w)	GLASSO	GaLASSO
Case 1	12.8	56.7	51.3	77.1	12.7	52.4	47.7	69.1	73.1	86.1
Case 2	15.6	65.7	57.8	94.4	16.3	62.3	55.1	85.8	106.0	126.7
Case 3	127.0	585.0	557.8	704.5	129.6	549.2	527.9	638.2	1129.1	1182.8
Case 4	219.9	830.5	769.3	1086.5	194.7	736.4	686.3	931.4	1417.5	1467.0

To understand how the performance of these methods is affected by the number of imputed datasets, we provide simulation results for a smaller number of 10 imputed datasets in the supplementary materials and compare sensitivity, specificity, MSE for nonnull coefficients, and MSE for null coefficients (Figure S2–S3, Table S6–S7). Overall, increasing the number of imputed datasets improves the MSE for both non-null and null coefficients, but has little impact on sensitivity and specificity, especially when p is large. The improvement coming from an increased number of imputed datasets is more significant for the grouped methods than the stacked methods. For example, in Case 3, the MSE for non-null and null coefficients for SLASSO with 10 imputed datasets are 1.07 and 1.22, respectively, and with 50 imputed datasets are 1.04 and 1.08, respectively. While for GLASSO, the MSE for non-null and null coefficients with 10 imputed datasets are 4.09 and 42.27, respectively, and with 50 imputed datasets are 3.30 and 29.70, respectively.

6. Discussion

In this paper, we elucidated the difference between stacked and grouped pooled objective functions, which are both designed to achieve uniform variable selection across multiple imputed datasets. The stacked pooled objective function assumes that the underlying true signals are the same across imputed datasets, including the signal magnitude, while the grouped pooled objective function assumes uniform signal selection but allows for different active signal magnitudes across imputed datasets. We extended existing methods to handle binary outcomes, developed a MM algorithm combined with block coordinate descent updates to optimize grouped pooled objective functions for LASSO and aLASSO regularization, and derived cyclic coordinate descent algorithm for the stacked pooled objective functions with ENET and aENET regularization. Algorithms for implementing the stacked and grouped approaches outlined in Section 2, for both continuous and binary outcomes, are available in the miselect R package on CRAN.

From a practical perspective, there are several reasons that one might prefer stacked over grouped objective functions. Based on our simulations, the overall MSE for estimates generated by optimizing stacked objective functions was either smaller than or equal to the estimates generated by optimizing the grouped objective function, provided that adaptive weighting is used. We also observed that the total runtime for optimizing stacked pooled objective functions is noticeably lower compared to the grouped objective function optimization routine. An additional practical consideration is that the stacked objective functions are much easier to extend beyond ENET penalization. For example, if one wanted to use a hierarchical interaction detection penalty, such as hierNet (Bien et al., 2013), one would only need to download the hierNet package from CRAN, and use the existing hierNet implementation on the stacked imputed datasets. Conversely, grouped methods would necessitate the development of additional algorithms to optimize an objective function with both a group LASSO penalty and a hierarchical interaction detection penalty. Lastly, although we did not observe a substantial difference between equal weights and the observational weights proposed by Wan et al. (2015), there are still conceptual concerns with having the observational weights depend on the fraction of missingness. As we mentioned earlier, upweighting observations with more data artificially moves the analysis in the direction of complete-case analysis, which is known to be biased under MAR and MNAR missing data mechanisms.

The positive ALS-POPs associations identified in the data example add to a growing body of literature on environmental risk factors for ALS (Kamel et al., 2012; McGuire et al., 1997; Sutedja et al., 2008). A major advantage of the data collected in this study is that POP concentrations were measured in plasma samples, rather than through surveys. Since ALS results from the complex interplay of multiple risks combined with neurotoxic environmental exposures (the gene-time-environment hypothesis), we contend that additional work is needed to more fully understand gene and pesticide exposure interaction (Paez-Colasante et al., 2015; Goutman et al., 2018; Al-Chalabi and Hardiman, 2013).