Creation of Neuronal Ensembles and Cell-Specific Homeostatic Plasticity through Chronic Sparse Optogenetic Stimulation

Abstract

Cortical computations emerge from the dynamics of neurons embedded in complex cortical circuits. Within these circuits, neuronal ensembles, which represent subnetworks with shared functional connectivity, emerge in an experience-dependent manner. Here we induced ensembles in ex vivo cortical circuits from mice of either sex by differentially activating subpopulations through chronic optogenetic stimulation. We observed a decrease in voltage correlation, and importantly a synaptic decoupling between the stimulated and nonstimulated populations. We also observed a decrease in firing rate during Up-states in the stimulated population. These ensemble-specific changes were accompanied by decreases in intrinsic excitability in the stimulated population, and a decrease in connectivity between stimulated and nonstimulated pyramidal neurons. By incorporating the empirically observed changes in intrinsic excitability and connectivity into a spiking neural network model, we were able to demonstrate that changes in both intrinsic excitability and connectivity accounted for the decreased firing rate, but only changes in connectivity accounted for the observed decorrelation. Our findings help ascertain the mechanisms underlying the ability of chronic patterned stimulation to create ensembles within cortical circuits and, importantly, show that while Up-states are a global network-wide phenomenon, functionally distinct ensembles can preserve their identity during Up-states through differential firing rates and correlations.

SIGNIFICANCE STATEMENT The connectivity and activity patterns of local cortical circuits are shaped by experience. This experience-dependent reorganization of cortical circuits is driven by complex interactions between different local learning rules, external input, and reciprocal feedback between many distinct brain areas. Here we used an ex vivo approach to demonstrate how simple forms of chronic external stimulation can shape local cortical circuits in terms of their correlated activity and functional connectivity. The absence of feedback between different brain areas and full control of external input allowed for a tractable system to study the underlying mechanisms and development of a computational model. Results show that differential stimulation of subpopulations of neurons significantly reshapes cortical circuits and forms subnetworks referred to as neuronal ensembles.

Introduction

Cortical computations rely on the neural dynamics that emerge from local cortical microcircuits (Douglas et al., 1995; Yuste, 2015; Barack and Krakauer, 2021). While it is not known how the appropriate connectivity between the tens of thousands of neurons within local circuits emerges through development, it is known that experience and patterned activity shape cortical circuits into functional neuronal ensembles (Hebb, 1949; Gerstein et al., 1989; Buzsáki, 2010; Carrillo-Reid and Yuste, 2020). Neuronal ensembles are often defined as subgroups of coactive and interconnected neurons that underlie numerous neural computations, from encoding memories to guiding behavior (Cossart et al., 2003; Stringer et al., 2019; Perez-Ortega et al., 2021). It has been shown that patterned stimulation of subpopulations of neurons alters the functional connectivity of local microcircuits and leads to the formation of neuronal ensembles (Johansen et al., 2010; Carrillo-Reid et al., 2016; Kim et al., 2016; Mendez et al., 2018; Sadeh and Clopath, 2021).

Neuronal ensembles are often identified based on high degrees of correlated activity between neurons within an ensemble, and decorrelated activity between ensembles. This neural signature, however, appears to be at odds with other dynamic regimes, which are characterized by network-wide or global patterns of activity. The best-studied example of such global activity regimes is Up-states, in which highly correlated transitions from a quiescent state to a depolarized state occur simultaneously in all neurons within a local microcircuit (Sanchez-Vives and McCormick, 2000; Neske et al., 2015; Bartram et al., 2017). Up-states seem to comprise a fundamental and intrinsic cortical dynamic regime because they are observed during anesthesia, slow-wave sleep, quiet wakefulness (Steriade et al., 1993; Timofeev et al., 2000; Beltramo et al., 2013; Hromádka et al., 2013), as well as in acute slices (Sanchez-Vives and McCormick, 2000; Shu et al., 2003; Fanselow and Connors, 2010; Sippy and Yuste, 2013; Xu et al., 2013; Sadovsky and MacLean, 2014; Neske et al., 2015; Bartram et al., 2017). Indeed, Up-states even emerge over the course of ex vivo development (Plenz and Kitai, 1998; Seamans et al., 2003; Johnson and Buonomano, 2007; Kroener et al., 2009; Motanis and Buonomano, 2020). While Up-states have been reported to have some spatiotemporal structure (MacLean et al., 2005; Sadovsky and MacLean, 2014; Motanis and Buonomano, 2020), a defining property of Up-states is that they are characterized by a global shift in activity, in which virtually all excitatory and inhibitory neurons become depolarized and increase their firing rate simultaneously. The global nature of Up-states poses a paradox regarding how distinct functional connections within ensembles of neurons are maintained and whether the identity of the ensembles can be preserved during Up-states. Here we examined both the ability for patterned stimulation to shape local microcircuits and induce ensembles, as well as whether the induced ensemble identities are preserved during network-wide Up-states.

Our approach was to chronically optogenetically stimulate sparse populations of pyramidal neurons and record spontaneous Up-states. The use of ex vivo cortical cultures allowed us to preserve the defining microcircuitry of local cortical networks while unambiguously ascertaining that the observed dynamics emerge locally within the circuit being studied (i.e., in the absence of influences from downstream or upstream circuits). This approach also allowed us to develop a spike-based computational model of network dynamics that captures the “stand-alone” results of an isolated cortical circuit.

We first show that, consistent with previous results, chronic global stimulation induces a dramatic homeostatic decrease in Up-state frequency (Motanis and Buonomano, 2015). In contrast, the same amount of optical stimulation to a sparse subpopulation of neurons did not abolish spontaneous Up-states, but induced intrinsic homeostatic plasticity of the optogenetically stimulated neurons. Critically, these units formed a local ensemble, and during Up-states the identity of this ensemble was preserved through differences in firing rate and pairwise correlations. Mechanistically, these alterations were associated with subpopulation-specific changes in connectivity and intrinsic excitability. When incorporated into a spiking neural network model, these mechanistic changes were able to account for the differential ensemble activity during simulated Up-states.

Materials and Methods

Organotypic cultures

Cortical organotypic slices were prepared and transduced as described previously (Motanis and Buonomano, 2015; Goel and Buonomano, 2016). Slices were obtained from postnatal day 6-7 WT FVB mice of either sex. Organotypic cultures were prepared using the interface method (Stoppini et al., 1991). Coronal slices (400 µm thickness) containing primary somatosensory and auditory cortex were sliced using a vibratome (Leica VT1200) and bisected before being placed on filters (Millipore) with 1 ml of culture media. Culture media was changed at 1 and 24 h after cutting and every 2-3 d thereafter. Cutting media consisted of MEM (Corning 15-010-CV) plus (final concentration in mm): MgCl₂, 3; glucose, 10; HEPES, 25; and Tris-base, 10. Culture media consisted of MEM (Corning 15-010-CV) plus (final concentration in mm): glutamine, 1; CaCl₂, 2.6; MgSO₄, 2.6; glucose, 30; HEPES, 30; ascorbic acid, 0.5; 20% horse serum, 10 units/L penicillin, and 10 μg/L streptomycin. Slices were incubated in 5% CO₂ at 35°C.

Viral transduction

For the dense transduction optogenetic experiments, slices were transduced with AAV9-CaMKIIα-hChR2(H134R)-mCherry [1 × 10¹³], whereas for the sparse experiments, slices were transduced with diluted AAV9-CaMKIIα-Cre [1 × 10⁹] and nondiluted AAV9-DIO-ChR2-mCherry [5 × 10¹²]. Each slice received a total of 1 μl of viral solution gently delivered via a sterilized pipette above the cortex. All viral transductions were performed at DIV 7 and recordings were performed between DIV 21-30 to allow sufficient time for viral expression.

Chronic optogenetic stimulation

To reduce variability, experiments relied on “sister” slices; that is, experimental groups were derived from the same batch of animals (littermates), maintained with the same culture medium and serum, placed in the same incubator, and virally transduced in the same session. For the fully transduced slices, both stimulated and unstimulated sister slices were simultaneously placed into the stimulation incubator to ensure identical culture environments and experimental conditions. The optical stimulation protocol consisted of 50 ms pulses of blue light (465 nm) delivered every 5 s for either 24 or 48 h. The sparsely transduced slices underwent an identical stimulation protocol for 48 h.

Electrophysiology

Culture filters were transferred to the recording rig and perfused with oxygenated ACSF composed of the following (in mm): 125 NaCl, 5 KCl, 2.5 MgSO₄, 25 NaHCO₃, 1 NaH₂PO₄, 25 glucose, 2.5 CaCl₂ (ACSF was formulated to match the standard culture media). Temperature was maintained at 32°C-33°C and perfused at 5 ml/min. Whole-cell solution was be composed of the following (in mm): 100 K-gluconate, 20 KCl, 4 ATP-Mg, 10 phosphocreatine, 0.3 GTP, 10 HEPES (adjusted to pH 7.3 and 300 mOsm). For the dense transduction experiments, whole-cell current-clamp recordings were performed on pyramidal neurons in both stimulated and nonstimulated slices. For the sparse transfection experiments, simultaneous whole-cell current-clamp recordings were performed on one ChR^– and one ChR⁺ pyramidal neuron or two ChR^– neurons. In both paradigms, transduced cells were identified by the presence of mCherry expression and additionally confirmed by the presence of a direct light-evoked response.

Intrinsic excitability was measured as the number of action potentials evoked during a 250 ms current step at intensities of (0.05, 0.1, 0.15, 0.2, 0.25, 0.3 nA). For each neuron, a minimum of 5 min of spontaneous activity was recorded. Connectivity between stimulated and nonstimulated pyramidal neurons was assessed through simultaneous current-clamp recordings where alternating trains of current were applied to each cell. A connection was considered to exist if the average EPSP amplitude was at least 3 times the baseline SD.

In the sparse transduction experiments, we fit the mean spike frequency × intensity (F-I) curve to a threshold-linear activation function.

Up-state quantification/analysis

A minimum of 5 min of spontaneous activity was recorded for each neuron. Recordings were sampled at 10 kHz. Spontaneous network events and Up-states were quantified based on previously defined criteria (Johnson and Buonomano, 2007; Goel and Buonomano, 2013). The first criterion for Up-states was voltage deflections of 5 mV above the resting membrane potential. However, during network events, the membrane potential would often make multiple crossings above and below the 5 mV threshold before returning to the resting potential. Thus, we defined Up-states as events that remained above threshold for at least 500 ms, allowing for drops below threshold that lasted <100 ms. We also calculated the SD of the voltage during spontaneous activity to provide an assumption-independent measure of overall spontaneous activity.

Up-state pairwise correlations were calculated with median-filtered traces (25 ms window) to remove the spikes during Up-states. For each Up-state, the median-filtered voltage was taken from 50 ms after its detected onset to 50 ms before its detected offset to exclude the transitions between Down- and Up-states. The set of resulting Up-state voltage segments (representing the same time indices in each cell's recording) were then concatenated for each cell in a paired recording, and the two concatenated voltage time series were correlated to yield a single correlation coefficient for each simultaneously recorded pair of cells, either (ChR^–/ChR^–) or (ChR⁺/ChR^–).

Statistics

Comparisons between stimulated and unstimulated slices were performed with unpaired two-tailed t tests; comparisons that used paired recordings of ChR⁺ and ChR^– cells in the same slice were performed with paired two-tailed t tests. To compare the F-I curve results, we used a two-way repeated-measures ANOVA with factors of Cell (ChR^–, ChR⁺) and Intensity (0.05, 0.1, 0.15, 0.2, 0.25, 0.3 nA). Mann–Whitney tests were used to compare the experimental Up-state voltage correlations, EPSP amplitudes, and EPSP slopes because the data were not normally distributed. To compare the proportion of connected versus unconnected pairs of pyramidal neurons, a χ² test was used. Wilcoxon signed-rank tests were used to compare the model units' mean pairwise Up-state voltage correlations across simulations.

Computational model

Elaborating on previous work (Jercog et al., 2017), we modeled a network of 2000 units (1600 Ex and 400 Inh) that were sparsely connected (25%) by current-based synapses. Units in the model were leaky integrate-and-fire neurons with an adaptation current whose membrane potential was governed by the following equations:

$$C_m\frac{dV(t)}{dt}=g_L\left(E_L-V(t)\right)+I^{Syn}(t)-I^{Ad}(t)+\sigma \sqrt{{\tau }_m}\eta (t)$$

$$\frac{d{I}^{Ad}(t)}{dt}=\frac{-I^{Ad}(t)}{{\tau }_{Ad}}$$

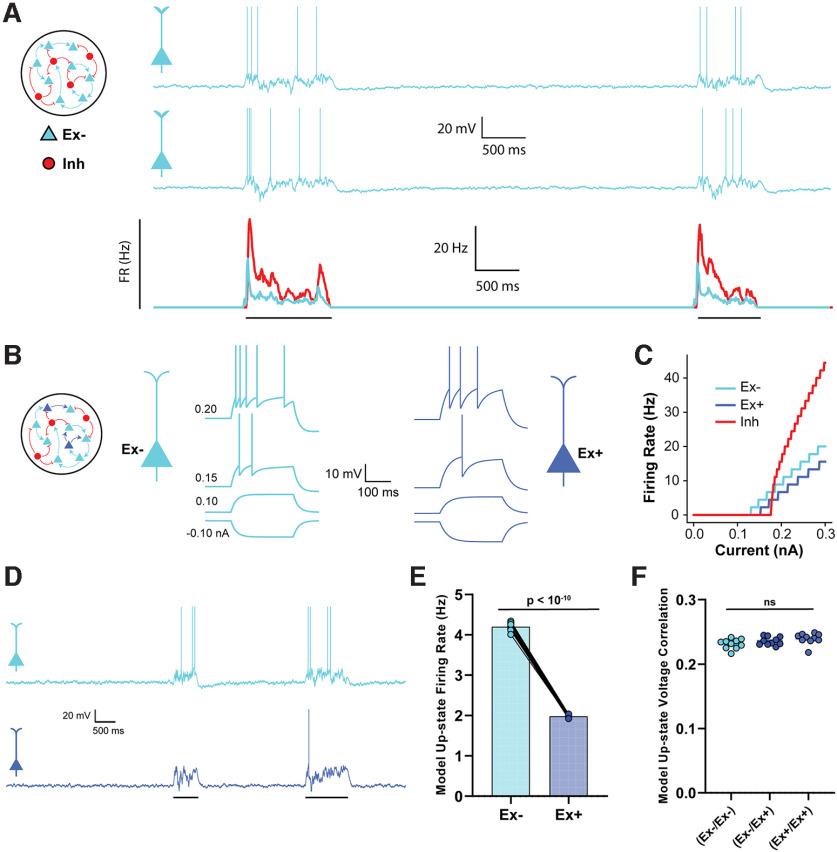
The noise term $\sigma \sqrt{{\tau }_m}\eta (t)$ represents an Ornstein–Uhlenbeck process with zero mean, SD $\sigma$, and a time constant equal to the membrane time constant ${\tau }_m=C_m/g_L$. When $V(t)\ge V_{thresh}$, the unit emitted a spike, its voltage was reset to $V_{reset}$, and its adaptation current $I^{Ad}$ was incremented by $\beta /{\tau }_{Ad}$. After spiking, the unit entered an absolute refractory period ${\tau }_{refractory}$, during which time it could not emit spikes. In some simulations (see Fig. 5), the unit parameters for 200 of the 1600 Ex units were modified based on empirical observations to create a subpopulation we refer to as Ex⁺. Default values for unit parameters based on their type can be found in Table 1.

Figure 5.

Empirically observed changes in intrinsic excitability is sufficient to account for cluster-specific changes in firing rate. A, The neural network model was composed of 2000 adaptive integrate-and-fire units (1600 Ex, 400 Inh). Traces represent two example Up-states in two sample Ex units in the baseline model. Average firing rate of all excitatory and inhibitory neurons during an Up-state is shown below. B, In the experimental network, there were two populations of Ex units (Ex⁺ and Ex^–) with different intrinsic excitability. Spike threshold, leak conductance, and membrane capacitance parameters differed between the Ex^– and Ex⁺ units. Traces represent the response to 250 ms square waves of injected current. C, F-I curves comparing the spiking output of the Ex⁺, Ex^–, and Inh units. The difference in spike threshold and slope for the Ex^– and Ex⁺ units qualitatively match empirical findings. D, Sample Up-states in the experimental neural network. E, Average firing rates of Ex^– and Ex⁺ units during Up-states were significantly different. F, The mean pairwise correlations between the Ex^–/Ex^–, Ex^–/Ex⁺, and Ex⁺/Ex⁺ pairs were not significantly different (data from 10 simulations).

Table 1.

Unit parameters

Cell parameter	Symbol	Ex–	Ex+	Inh	Unit
Resting potential	EL	−65	−65	−65	mV
Reset potential	V reset	−58	−58	−58	mV
Spike threshold	V thresh	−52	−46	−43	mV
Refractory period	τrefractory	2.5	2.5	1	ms
Membrane capacitance	Cm	200	240	120	pF
Leak conductance	gL	10	8	8	nS
Membrane time constant	τ	20	30	15	ms
Adaptation strength	β	10	10	1	nA·ms
Adaptation time constant	τa	500	500	500	ms
Noise SD	σ	1	1	1	mV

Total synaptic current $I_{syn}\left(t\right)$ was summed across each unit's incoming synapses with distinct synaptic weights determined by matrices J^EE, J^EI, J^IE, and J^II. Thus, for example, the total synaptic current to the i^th excitatory unit was given by the following:

$$I_i^{Syn}\left(t\right)={\displaystyle \sum }_{j=1}^{N_{exc}}{J}_{ij}^{EE}{s}_{ij}\left(t\right)+{\displaystyle \sum }_{j=1}^{N_{inh}}{J}_{ij}^{EI}{s}_{ij}\left(t\right),i\in N_{exc}$$

We use “post-pre” notation for the weight matrices $J^{XY}$ such that the weights from presynaptic population Y onto postsynaptic population X. The kinetics of synaptic currents were determined by the function $s_{syn}\left(x,y,t\right)$ for each presynaptic unit y and postsynaptic unit x. When a presynaptic spike occurred in unit y at time $t^{*}$, $s_{syn}\left(x,y,t\right)$ was incremented by an amount described by a delayed difference of exponentials equation (Brunel and Wang, 2003) as follows:

$$\text{Δ}{s}_{ij}\left(t\right)=\frac{{\tau }_m}{{\tau }_d-{\tau }_r}\left[\exp \left(-\frac{t-{\tau }_l-t^{*}}{{\tau }_d}\right)-\exp \left(-\frac{t-{\tau }_l-t^{*}}{{\tau }_r}\right)\right]$$

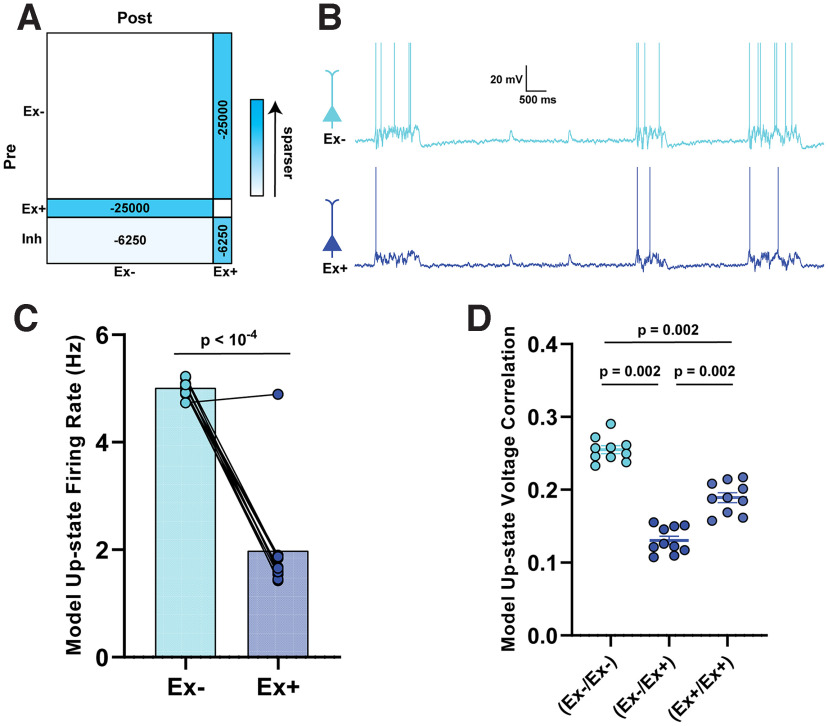
where ${\tau }_m$ indicated the postsynaptic membrane time constant. Thus, the temporal envelope of a synaptic current was determined by the synaptic delay ${\tau }_l$, the synaptic rise time ${\tau }_r$, and the synaptic decay time ${\tau }_d$, which differed for excitatory and inhibitory synapses (Table 2). Normalization constants were chosen so that varying synaptic time constants would not affect the time integral of the synaptic current. The synaptic delay ${\tau }_l$ was uniformly distributed between 0 and 1 ms (0 and 0.5 ms) across all excitatory (inhibitory) synapses. Default values for synaptic parameters can be found in Table 2. Weight matrices J^EE, J^EI, J^IE, and J^II were predefined to contain normally distributed weights that were capable of supporting stable Up-states with empirically observed firing rates (Soldado-Magraner et al., 2022). The average value of the non-zero elements of J^EE, J^EI, J^IE, and J^II are shown in Table 2. Neither J^EE nor J^II had non-zero diagonal elements; in other words, there were no autapses (self-connections). In some simulations (see Fig. 6), the weight matrix J^EE was modified based on empirical observations. Specifically, E units were first divided into two populations (Ex^– and Ex⁺) consisting of 1400 and 200 units, respectively, and 50% of the mutual connections between the Ex^– and Ex⁺ units were randomly deleted, which reduced the probability of connection between the Ex^– and Ex⁺ populations from 25% to 12.5%. In order to prevent a large imbalance of excitation and inhibition from causing spurious model behavior, J^EI was also modified by deleting a number of inhibitory connections equivalent to the deleted excitatory connections of that same postsynaptic population.

Table 2.

Synaptic parameters

Synaptic parameter	Value	Unit
Average E-to-E weight	252	pA
Average E-to-I weight	264	pA
Average I-to-E weight	308	pA
Average I-to-I weight	282	pA
Excitatory rise time	8	ms
Excitatory fall time	23	ms
Inhibitory rise time	1	ms
Inhibitory fall time	1	ms
Mean excitatory synaptic delay	1	ms
Mean inhibitory synaptic delay	0.5	ms

Figure 6.

Empirically observed changes in probability of connection are sufficient to account for cluster-specific differences in firing rates and correlations. A, Schematic of the changes made to the weight matrix compared with the baseline network in Figure 5A. B, Sample Up-states following manipulation of the synaptic coupling between Ex⁺ and Ex^– populations. C, Average firing rates of Ex^– and Ex⁺ units during Up-states were significantly different. D, There was a significant decrease in the mean pairwise Ex^–/Ex⁺ correlations compared with the Ex^–/Ex^– and Ex⁺/Ex⁺ correlations, as well as a weaker correlation in the Ex⁺/Ex⁺ compared with Ex^–/Ex^– pairs. Because the correlations are bounded between −1 and 1, we are using nonparametric sign-rank statistics; thus, all p values can be the same despite the differences in the group values.

In order to model the stochastic process by which Up-states are initiated, we simulated 60 s trials in which external “kicks” (DeWeese and Zador, 2006; Jercog et al., 2017) were applied to a subpopulation of 100 Ex units (these units were always Ex^– units for simulations with subpopulations of Ex⁺ units). To do so, we first defined kick times by randomly generating a Poisson process with the mean parameter $\lambda =$ 0.2 Hz over the 60 s trial period. At each kick time, the subpopulation of 100 kicked Ex units each received a large excitatory synaptic current with an equivalent synaptic weight of 960 pA, which typically caused exactly one spike. Spike times of all Inh units were used to construct a poststimulus time histogram with a bin size of 10 ms. Up-states were detected as contiguous periods of time in which the population FR of inhibitory neurons exceeded 0.2 Hz for at least 500 ms, and fluctuations beneath the 0.2 Hz threshold that were <100 ms were considered interruptions of an Up-state. For each Up-state, the FR of each unit was calculated as the number of spikes it fired during that Up-state divided by that Up-state's duration. Each unit's average FR during the Up-state was then calculated as the mean FR across all Up-states in the 60 s trial, yielding distinct values for each unit. Up-state voltage correlation among all pairwise units was calculated using identical methodology to what was used for the experimental data. Pairwise correlations between units in different populations were then separated. A total of ten 60 s simulations were run for each manipulation (control, intrinsic excitability, or connectivity) where the initial weight matrix would undergo a random shuffling of weights within each weight class. The average Up-state firing rate of each population per simulation was used as the unit of observation for analyses in Figures 5E and 6C. The average pairwise Up-state voltage correlation within each population of neurons per simulation was used as the unit of observation for analyses in Figures 5F and 6D.

Simulations were implemented in the Brian 2 library (Stimberg et al., 2019) on Python 3.7 using forward Euler integration with a time step of 0.1 ms. Code is available at https://github.com/BuonoLab/spiking-upstates/tree/liu-et-al.

Results

Homeostatic regulation of Up-states following chronic optical stimulation

To confirm the effectiveness of chronic optogenetic stimulation ex vivo, we first densely expressed channelrhodopsin-2 (ChR) using AAV9-CaMKIIα-ChR2-mCherry in excitatory neurons of mouse cortical organotypic slices. We stimulated the transduced slices at 0.2 Hz with 50 ms pulses of 465 nm blue light in the incubator for 24 or 48 h (Fig. 1A). Using whole-cell patch-clamp recordings, we confirmed that each 50 ms pulse of light was sufficient to elicit 1 or 2 action potentials in ChR⁺ pyramidal neurons, and consistent with previous results observed that optical stimulation often triggered Up-states. We quantified spontaneous Up-state activity using three measures: SD of the membrane potential (STD_Vm), Up-state frequency, and Up-state duration (Fig. 1B; see Materials and Methods). There was a significant decrease in both STD_Vm (Fig. 1C) at 24 h (t₍₇₀₎ = 5.6, p < 10⁻⁴, unpaired t test) and 48 h (t₍₇₈₎ = 5.9, p < 10⁻⁴). We also observed a decrease in spontaneous Up-state frequency following both 24 h (t₍₆₉₎ = 5.8, p < 10⁻⁴) and 48 h (t₍₇₇₎ = 6.6, p < 10⁻⁴) of light stimulation (Fig. 1D). There was no change in the observed Up-state duration (Fig. 1E).

Figure 1.

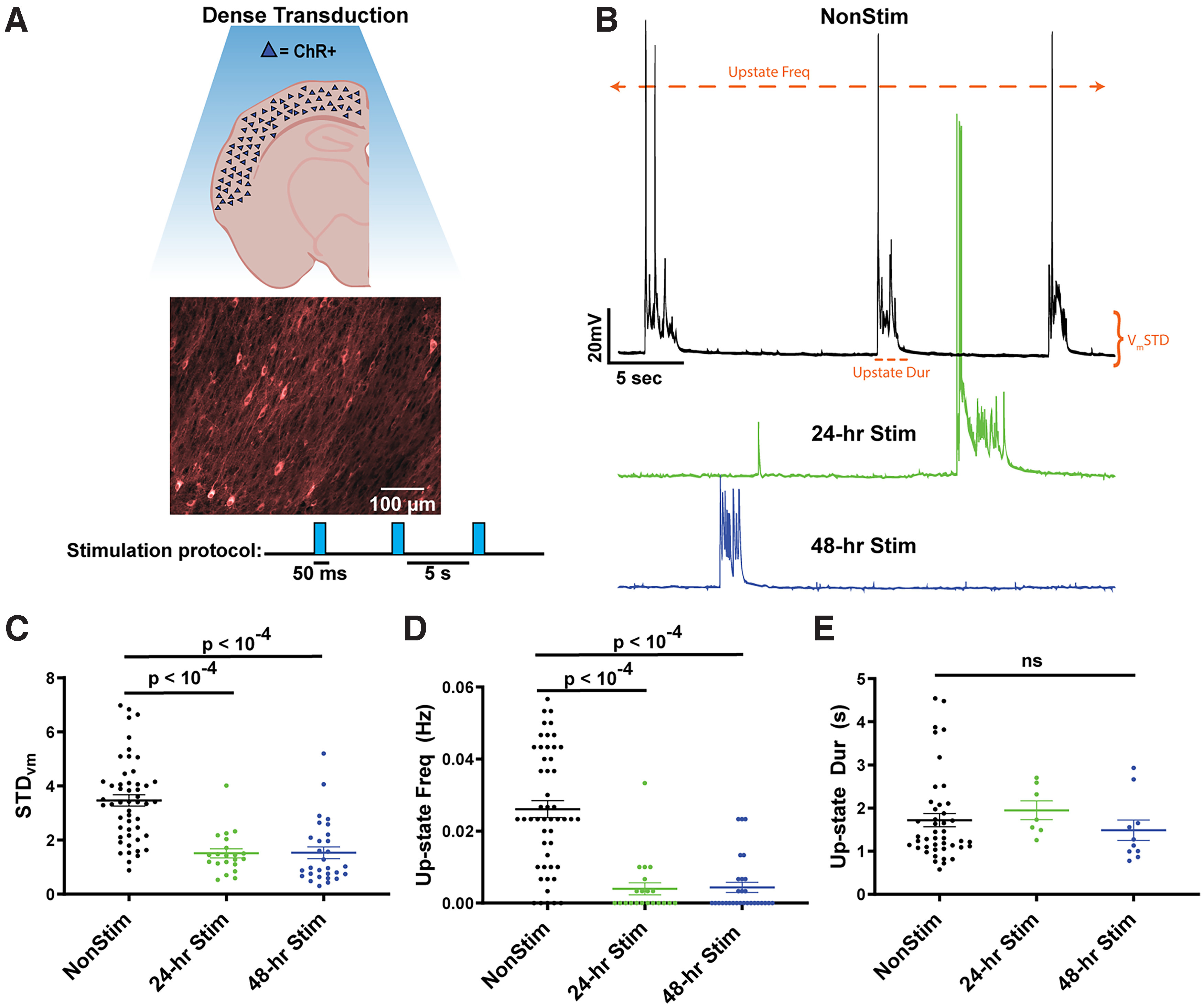
Spontaneous Up-state frequency is reduced in densely transduced cortical slices following 24 or 48 h of stimulation. A, Schematic of densely transduced cortical circuits in organotypic slice cultures (top) and image from auditory cortex densely transduced with AAV9-CaMKIIα-hChR2(H134R)-mCherry and chronic optogenetic stimulation paradigm (bottom). B, Example traces of spontaneous Up-states in Pyramidal neurons from unstimulated (black), 24 h stimulated (green), and 48 h stimulated (blue) slices. Up-states were rarely observed in the 24 and 48 h stimulated slices. Orange annotations represent the three quantitative measures of spontaneous activity shown in C–E. C, The SD of membrane voltage was significantly decreased by both 24 and 48 h of stimulation. STD_Vm was calculated over a 5 min period of spontaneous activity in Pyr neurons. D, Spontaneous Up-state frequency was significantly decreased by both 24 and 48 h of stimulation. E, Although Up-state frequency was decreased by stimulation, when Up-states occurred, on average, they were of the same duration.

These data demonstrate that chronic stimulation of excitatory neurons produced a pronounced homeostatic downregulation of Up-states, consistent with the notion that neural circuits seek out “setpoint” levels of activity (Turrigiano, 2008, 2012; Slomowitz et al., 2015; Hengen et al., 2016), which in control slices are achieved through internally generated spontaneous Up-states. But in the stimulated slices, these setpoints are achieved through external inputs, resulting in the internal activity being downregulated.

Chronic stimulation of a sparse subpopulation of pyramidal neurons generates a decorrelation of activity between stimulated and nonstimulated populations

To determine whether we could induce distinct ensembles or “clustering” through differential stimulation of neurons, we next expressed ChR in a sparse population of pyramidal neurons using a Cre-dependent ChR and a diluted Cre expressing AAV (see Materials and Methods). This approach led to sparse (∼10%) transduction of cortical pyramidal neurons (Fig. 2A). We next used the same 48 h chronic stimulation protocol used above. In contrast to the effect of stimulation on densely transduced circuits, robust spontaneous Up-states were present in the sparsely transduced slices.

Figure 2.

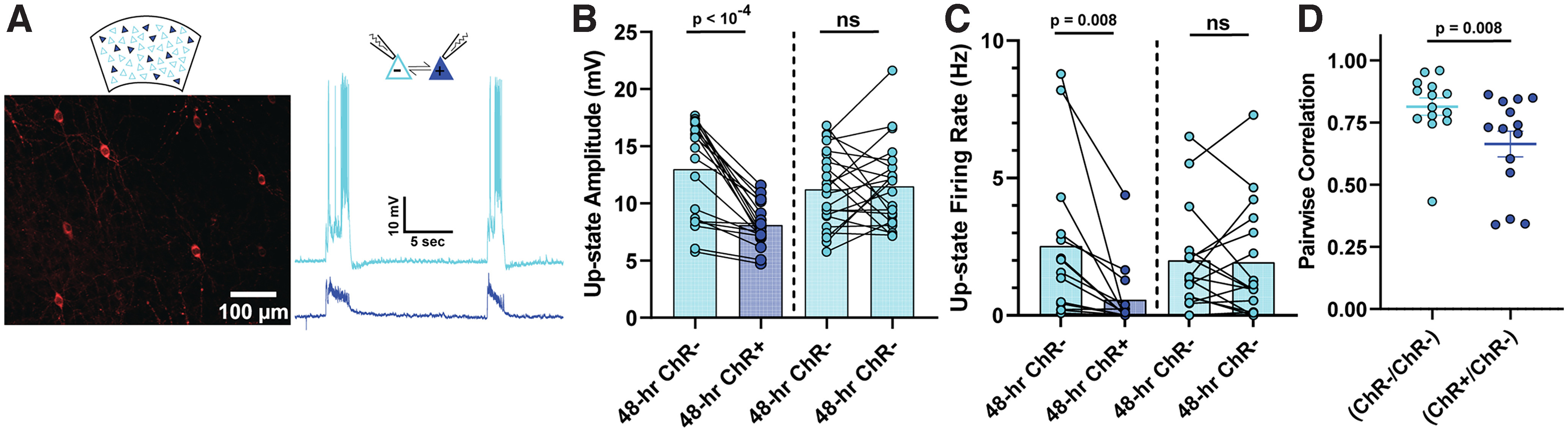
Pairwise differences in Up-state amplitude, firing rate, and voltage correlation between stimulated and nonstimulated pyramidal neurons in sparsely transduced slices. A, Example of cortical pyramidal neurons sparsely transduced with AAV9-CaMKIIα-Cre and EF1a-DIO-hChR2(H134R)-mCherry (left), and sample paired recordings of ChR⁺ and ChR^– neurons (right). B, Spontaneous Up-state amplitude was significantly reduced in ChR⁺ compared with ChR^– pyramidal neurons. Up-state amplitude was not significantly different between simultaneously recorded ChR⁺ pyramidal neurons grouped according to their resting membrane potential (ChR^– pyramidal neurons with the lower resting membrane potential of the pair was plotted on the left). C, Spontaneous Up-state firing rate was significantly reduced in ChR⁺ versus ChR^– pyramidal neurons. Up-state firing rate was not significantly different between simultaneously recorded ChR^– pyramidal neurons grouped according to their resting membrane potential. D, The correlation between the Up-state voltage dynamics of ChR⁺ and ChR^– neurons was significantly less than ChR^– and ChR^– pairs, indicating a decorrelation between the shared inputs to the ChR⁺ and ChR^– subpopulations.

Up-states correspond to global changes in network activity which are believed to recruit all excitatory neurons in a circuit. Thus, as expected, there was no difference in Up-state frequency between ChR⁺ and ChR^– subpopulations. Interestingly, however, there were differences in the voltage dynamics during the Up-state between the ChR⁺ and ChR^– subpopulations. First, the amplitude of Up-states was significantly reduced (t₍₁₈₎ = 6.3, p < 10⁻⁴, paired t test) in the ChR⁺ compared with the ChR^– neurons (Fig. 2B). To control for the possibility that the amplitude differences could be driven by the changes in the intrinsic properties of ChR⁺ and ChR^– neurons (see below), such as resting membrane potential, we also compared Up-state amplitude of simultaneously recorded ChR^– pairs grouped by lowest and highest membrane potential. These analyses revealed that Up-state amplitude was not affected by baseline V_m (Fig. 2B, right). The average firing rate during Up-states was also significantly lower (t₍₁₃₎ = 3.1, p = 0.008, paired t test) in ChR⁺ neurons (Fig. 2C), although there was no difference in the firing rate between ChR^– pairs with low and high membrane potential (t₍₁₅₎ = 0.2, p = 0.85). Importantly, the pairwise correlation of Up-state activity between simultaneously recorded ChR^–/ChR^– pairs was significantly greater (U = 41, n₁ = n₂ = 14, p = 0.008, Mann–Whitney test) than in ChR⁺/ChR^– pairs (Fig. 2D). These findings suggest that chronic patterned stimulation of a sparse population of pyramidal neurons in a cortical network led to the formation of distinct clusters or neuronal ensembles, whereby the ChR⁺ is decoupled from ChR^– subpopulation as indicated by the differences in firing rate and correlations during Up-states.

Differential input–output functions between stimulated and nonstimulated neurons

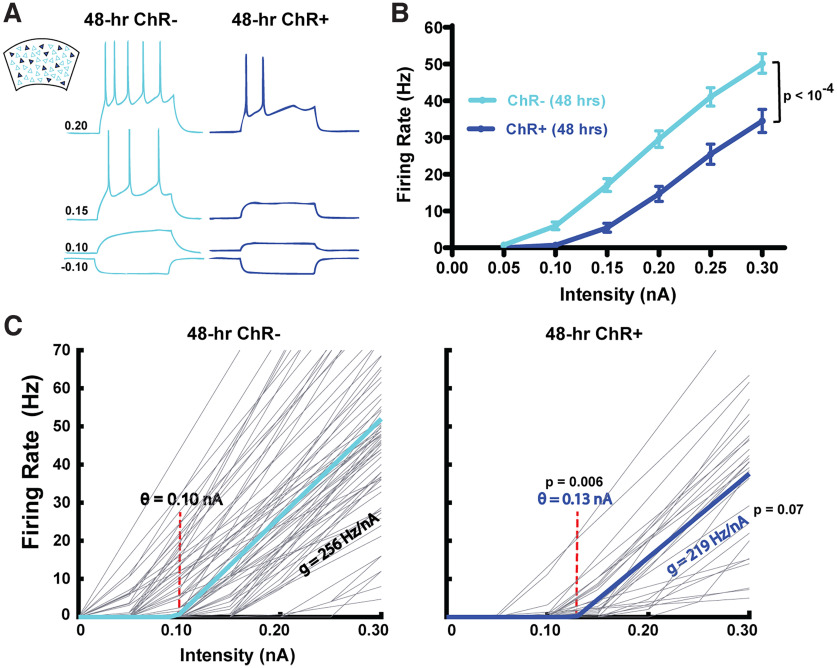
The differential activity during Up-states is somewhat surprising given that Up-states are a global network-wide phenomenon. To begin to understand whether this decoupling may be accounted for by intrinsic and/or network properties, we analyzed the intrinsic neuronal properties of the ChR⁺ and ChR^– subpopulations, including the F-I curve (i.e., the input–output function as defined by the relationship between spike frequency and injected current; Fig. 3A). Consistent with previous studies of intrinsic homeostatic plasticity (Desai et al., 1999; Karmarkar and Buonomano, 2006), chronic stimulation of the ChR⁺ neurons resulted in significantly different F-I curves (F_(1,86) = 20.5, p < 10⁻⁴; Fig. 3B). To quantify the source of these differences, and to incorporate the differences in intrinsic excitability in a neurocomputational model (see below), we fit the F-I curve of each neuron to a rectified linear function defined by a threshold and gain (Romero-Sosa et al., 2021). Results revealed that the differences in F-I curve could be accounted for by a significant increase (t₍₁₀₉₎ = 2.8, p = 0.006, paired t test) in the threshold from θ = 0.10 ± 0.06 nA in the ChR^– population to θ = 0.13 ± 0.04 nA in ChR⁺ neurons (Fig. 3C). There was also a trend (t₍₁₀₉₎ = 1.8, p = 0.07) for an accompanying decrease in the gain (the slope of the F-I curve) in the ChR⁺ subpopulation. Additionally, there was a small difference in resting V_m between ChR⁺ and ChR^– cells (−65.6 ± 5.3 and −67.5 ± 3.2 mV, respectively; p = 0.05), and input resistance (236 ± 54 and 202 ± 63 mΩ, respectively; p = 0.01). Overall, these results establish that there are significant changes in intrinsic excitability that could contribute to the subpopulation differences. Specifically, the intrinsic plasticity may account for the observed decrease in Up-state firing rate observed in the ChR⁺ neurons (Fig. 2C); however, it is less clear whether the changes in intrinsic excitability could account for the decoupling of the correlation in activity (Fig. 2D).

Figure 3.

Cell-autonomous decreases in the intrinsic input–output function of ChR⁺ compared with ChR^– pyramidal neurons in sparsely transduced slices. A, Sample intrinsic excitability traces simultaneously recorded from ChR^– and ChR⁺ pyramidal neurons from sparsely transduced cortical circuits stimulated for 48 h (250 ms current steps ranged from −0.10 to 0.3 nA). B, F-I curves of the average input–output functions from ChR^– and ChR⁺ pyramidal neurons from sparsely transduced cortical slices stimulated for 48 h. C, Threshold-linear fits of the F-I curves of the ChR^– and ChR⁺ populations. Light gray lines indicate the fits of the F-I curves of individual neurons. Solid cyan or blue lines indicate the mean threshold-linear fit. The threshold (θ = 0.10 nA) of the ChR^– Pyr neurons was significantly lower than the ChR⁺ Pyr neurons (θ = 0.13 nA).

Synaptic decoupling between stimulated and nonstimulated pyramidal neurons

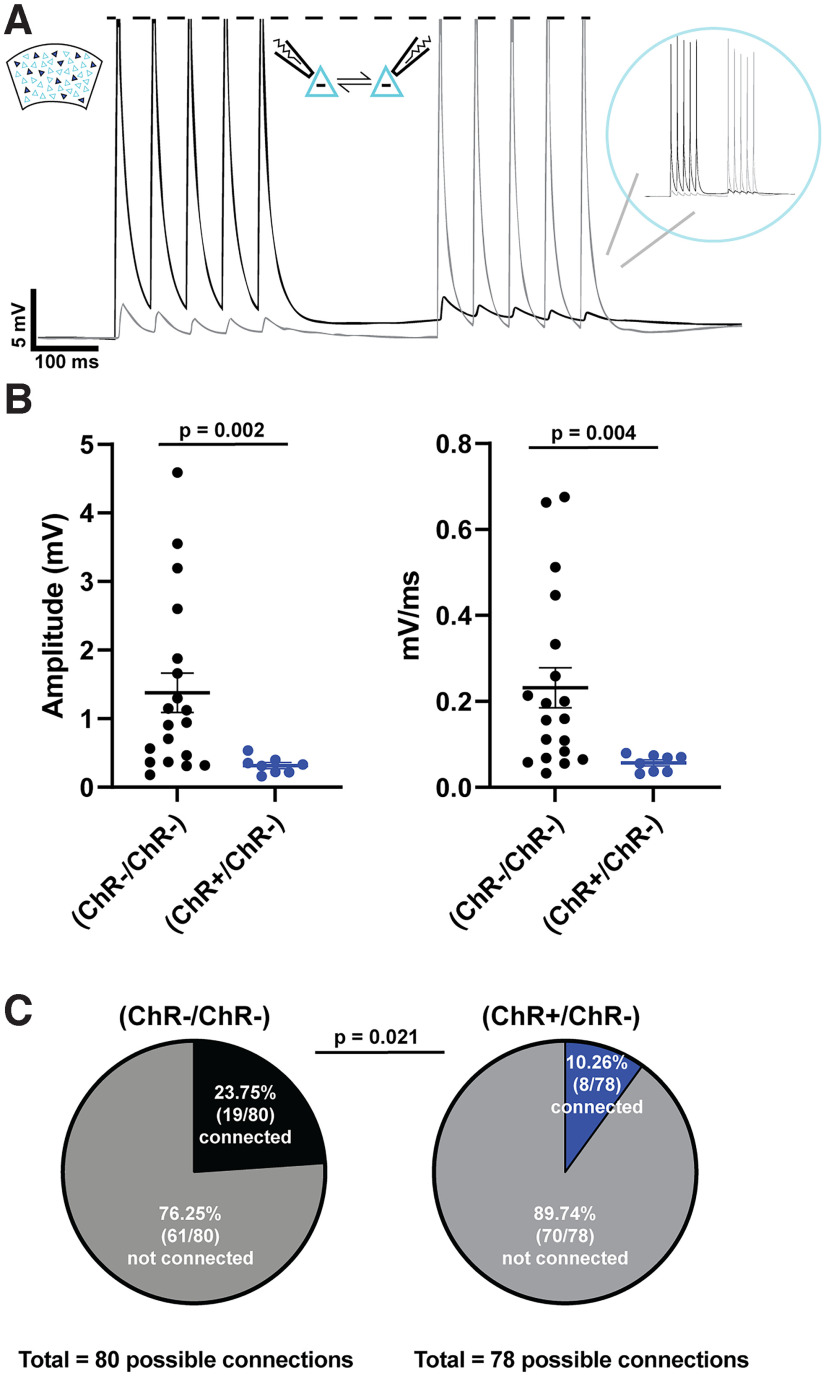
To examine whether network-level changes contribute to the observed differential effects in firing rate and activity correlation, we next asked whether there is a synaptic decoupling between the ChR⁺ and ChR^– subpopulations. We assessed the connection probability and strength of the connections between ChR⁺ and ChR^–. Connectivity between nearby pyramidal neurons (<50 μm) was measured through paired whole-cell current-clamp recordings. Trains of action potentials were alternatively elicited in one cell while measuring any corresponding EPSPs in the other (Fig. 4A). We recorded from ChR⁺/ChR^– and ChR^–/ChR^– pairs. Because of the sparseness of the ChR expression, it was not feasible to record from nearby ChR⁺/ChR⁺ pairs, and recording from distant pairs dramatically decreased the connectivity likelihood.

Figure 4.

Synaptic decoupling between ChR⁺ and ChR^– pyramidal neurons. A, Example traces of a paired recording between reciprocally connected ChR^– and ChR^– pyramidal neurons (<50 μm apart). B, EPSP amplitude and slope were significantly reduced between connected pairs of ChR⁺ and ChR^– pyramidal neurons compared with connected pairs of ChR^– pyramidal neurons following 48 h of stimulation. C, Connectivity ratio was higher between pairs of ChR^– pyramidal neurons compared with pairs of ChR⁺ and ChR^– pyramidal neurons.

Among the connected pairs both the unitary EPSP amplitudes (U = 20, n₁ = 8, n₂ = 19, p < 0.002, Mann–Whitney test) and slopes (U = 24, n₁ = 8, n₂ = 19, p < 0.004) were dramatically smaller in ChR⁺/ChR^– compared with ChR^–/ChR^– pairs (Fig. 4B). In addition to weaker synaptic connections between the subpopulations, there was a significant difference in connection probability (${\chi }_{1,158}^2=5.1$, p = 0.02, χ²) between pairs of ChR^–/ChR^– (0.24) compared with ChR⁺/ChR^– (0.10) (Fig. 4C). There was not a significant difference in the likelihood in the proportion of reciprocal connections (${\chi }_{1,21}^2=1.1$, p = 0.31) between the ChR^–/ChR^– (4 of 15 pairs) and the ChR⁺/ChR^– (3 of 6 pairs), nor was there any detectable asymmetry in the direction of the ChR⁺ ↔ ChR^– connections. Together, these results establish that chronic stimulation of sparsely transduced pyramidal neurons resulted in a rewiring of the local cortical circuit in the form of a synaptic decoupling between ChR⁺ and ChR^– subpopulations.

Synaptic decoupling between subpopulations accounts for the experimental observations

In order to determine whether either, or both, the empirically observed changes in intrinsic excitability and synaptic decoupling, could account for the observed changes in Up-state firing rate, we next implemented an empirically informed spike-based computational model of Up-states (see Materials and Methods). Previous computational and mathematical models of Up-states and inhibition-stabilized networks have carefully characterized the constraints that must be met in order for networks to exhibit transiently stable Up- and Down-states (Tsodyks et al., 1997; Destexhe, 2009; Ozeki et al., 2009; Jercog et al., 2017; Maes et al., 2020). Key among these is the appropriate balance of excitation and inhibition in both the excitatory and inhibitory populations. The model was composed of 1600 excitatory (Ex) and 400 inhibitory (Inh) integrate-and-fire units. We first established that in the baseline network, in which all Ex units had the same input–output function and a uniform connection probability, the network exhibited global transitions between a quiescent Down-state and depolarized Up-states (Fig. 5A). This provided the opportunity to directly model and evaluate the influence of the empirically observed cell-specific and connectivity changes to account for the observed changes in firing rates during Up-states. Our approach allowed us to independently adjust both the input–output function as well as the connection probability between populations in the spiking neural network model to approximately match the empirically observed changes following chronic optogenetic stimulation.

We first created two subpopulations of excitatory units (Ex⁺ and Ex^–), as defined by the F-I curves of the ChR⁺ and ChR^– neurons (Fig. 3), respectively. Simply adjusting the input–output function of the Ex⁺ population to match the empirically derived F-I curves was sufficient to account for the population-specific changes in Up-state firing rate (Fig. 5B-E). Specifically, we modified the intrinsic parameters of 200 (12.5%) Ex units so that they had a higher spike threshold and lower gain (Ex⁺) while leaving the intrinsic parameters of the remaining 1400 Ex units untouched (Ex^–). We then ran ten 60 s simulations with the manipulated intrinsic parameters and shuffled the weights within each weight class for each simulation. Across simulations, the Up-state median firing rate of the Ex⁺ population was significantly reduced to 1.9 Hz compared with the Ex^– population's median of 4.2 Hz (t₍₉₎ = 100.2, p < 10⁻¹⁰). To determine whether changes in intrinsic excitability could account for the decrease in voltage correlation during Up-states between the ChR⁺ and ChR^– populations (Fig. 2D), we also measured the pairwise correlation of model units' voltage during Up-states using the same methodology used to quantify the experimental data. We found that, across simulations, there was no significant difference in the median pairwise correlations during Up-states between or within ChR⁺ and ChR^– populations (Fig. 5F): (Ex^–/Ex^–) versus (Ex^–/Ex⁺) (n = 10, W = 29, p = 0.16), (Ex^–/Ex⁺) versus (Ex⁺/Ex⁺) (n = 10, W = 33, p = 0.10), (Ex^–/Ex^–) versus (Ex⁺/Ex⁺) (n = 10, W = 35, p = 0.08).

We next modified the model to incorporate only the empirically observed changes in connectivity, while leaving the intrinsic excitability unchanged (i.e., as in the baseline model, all Ex units in this simulation have the same input–output function) (Fig. 6). According to our observation that the connection probability between ChR⁺ and ChR^– neurons decreased (symmetrically) from 24% to 10% (Fig. 4C), we deleted half of the connections between Ex⁺ (200 units) and Ex^– (1400 units) populations (reciprocally), decreasing their probability of connection from 25% to 12.5%. However, because of the model's sensitivity to the balance of excitation and inhibition, we found that deleting a portion of excitatory connections without an accompanying decrease in inhibition resulted in unbalanced dynamics and implausible behavior in the model. We thus made an additional assumption that there was an excitatory/inhibitory rebalancing, implemented by decreasing the inhibitory connections onto each of the two populations (Fig. 6A). Across simulations, the Up-state median firing rate of the Ex⁺ population was significantly reduced compared with the Ex^– population (Fig. 6B; t₍₉₎ = 8.5, p < 10⁻⁴). Importantly, we also observed a marked decrease in the voltage correlation between Ex⁺/Ex^– pairs during Up-states (Fig. 6C), compared with the Ex^–/Ex^– (n = 10, W = 55, p = 0.002) and the Ex⁺/Ex⁺ populations (n = 10, W = 55, p = 0.002).

These findings indicate that either decreases in the intrinsic excitability of the ChR⁺ subpopulation or synaptic decoupling of the ChR⁺ and ChR^– subpopulations can account for the observed decreases in firing rate during Up-states, but only the manipulation of synaptic connectivity accounted for the decrease in Up-state voltage correlations. Our results are consistent with the hypothesis that parallel forms of plasticity cooperate in a synergistic and redundant manner to implement homeostatic adjustments and experience-dependent neuronal ensembles, and that each plasticity locus can produce distinct or shared phenotypes (Burrone et al., 2002; Maffei and Turrigiano, 2008; Tetzlaff et al., 2011; Turrigiano, 2012; Slomowitz et al., 2015; Wefelmeyer et al., 2016; Gainey and Feldman, 2017).

Discussion

Cortical circuits must carefully balance opposing neuronal and circuit properties, including the balance of excitation and inhibition (Froemke, 2015; Hennequin et al., 2017), and overall levels of neuronal activity so that cells are neither underactive nor overactive (Turrigiano, 2008; Goold and Nicoll, 2010; Pozo and Goda, 2010). Additionally, cortical circuits must balance the degree to which interconnected neurons function as independent groups or as globally coactive networks. On one hand, distinct neuronal ensembles must operate independently during cortical processing, but also remain a part of a larger network during global dynamic regimes, including Up-states and sleep states. Here we have begun to address this balance between local versus global dynamic regimes by showing that, while chronic stimulation of subsets of neurons induces a decoupling from other neurons in the circuit, it remains the case that both populations of neurons participate in global Up-state dynamics. Critically, however, in contrast to the prevailing view in computational models of Up-states in which all neurons participate equally in Up-state dynamics (Destexhe, 2009; Jercog et al., 2017), we observed that functionally distinct ensembles can preserve their identity during Up-states through differential firing rates and decreased cross-ensemble correlations.

Homeostatic plasticity of Up-states

Up-states have been proposed to have multiple functional roles, including memory consolidation and synaptic homeostasis (Tononi and Cirelli, 2003; Sirota and Buzsáki, 2005; Marshall et al., 2006; Vyazovskiy et al., 2008; Diekelmann and Born, 2010). Consistent with previous studies, our results suggest that Up-states also play a role in the homeostatic regulation of neural activity (Goel and Buonomano, 2013; Motanis and Buonomano, 2015). Specifically, in densely transduced cortical circuits, chronic optical stimulation dramatically reduced the frequency of spontaneous Up-states: in many cases, no Up-states were observed in stimulated slices, suggesting that, in the presence of an external source of neural activity, networks downregulated spontaneous network-wide Up-states to adjust their activity setpoints. We note that, while the concept of an activity setpoint is generally interpreted as an ontogenetically determined target level of activity as measured by the mean levels of Ca²⁺, the existence and potential mechanisms of these hypothesized setpoints remain an open question (Turrigiano, 2008; Pozo and Goda, 2010; Trojanowski et al., 2021).

In sparsely transduced slices, network-wide Up-states were observed in both ChR^– and ChR⁺ neurons; however, the firing rate during Up-states was significantly reduced in the directly stimulated population. This indicates that all neurons participated in Up-states at the same time, but that ChR⁺ neurons downregulated their spiking, again consistent with the notion that they reached their activity setpoints through direct optical stimulation and downregulated their activity during Up-states to achieve activity homeostasis. To the best of our knowledge, this is the first result suggesting that, based on activation history, different subpopulations of the same neuron class may have distinct activity signatures during Up-states.

Ensembles maintain identity within Up-states

It is widely accepted that the formation of functionally distinct subcircuits embedded within larger local cortical networks is of fundamental importance to cortical computations (Hebb, 1949; Yuste, 2015; Carrillo-Reid and Yuste, 2020; Sadeh and Clopath, 2021). This functional specialization has been observed in many in vivo and in vitro studies (Dechery and MacLean, 2017; Carrillo-Reid et al., 2019; DeNardo et al., 2019; Marshel et al., 2019; Sugden et al., 2020). Furthermore, in vivo studies have shown that it is possible to artificially induce the formation of ensembles by direct coactivation of cortical neurons (Carrillo-Reid et al., 2016; Kim et al., 2016), consistent with the theory that Hebbian plasticity contributes to this functional specialization. Here, we demonstrate that the coactivation of a subset of pyramidal neurons also reconfigures cortical circuits ex vivo, resulting in a synaptic decoupling between directly activated ChR⁺ neurons and the ChR^– subpopulation, and the formation of neuronal ensembles.

One might have predicted that our stimulation protocol would have resulted in ChR⁺ neurons becoming hubs of a rich-club network architecture, in which ChR⁺ neurons asymmetrically drive ChR^– neurons, a prediction that might be expected based on STDP or reports of rich-club networks in the cortex (Nigam et al., 2016). We did not observe any enhanced connectivity from ChR⁺ to ChR^– neurons; however, given the relatively low interpopulation connectivity, it is possible that a small degree of ChR⁺ ↔ ChR^– asymmetry could have been missed. Nevertheless, our results suggest that the differential stimulation of different subpopulations of neurons favors the formation of neural ensembles rather than rich-club networks.

While neuronal ensembles refer to functionally interconnected subpopulations of neurons, it is recognized that they are not fully isolated functional units. Ensembles are composed of overlapping subpopulations of neurons; but during some cortical regimes most, if not all, neurons within a local circuit undergo synchronous shifts between inactive Down-states to depolarized Up-states. This tension between compartmentalized and global activity regimes raises the question of if and how ensemble identity is maintained during Up-states. Here we show that ensemble identity is preserved during Up-states. Specifically, in addition to the lower firing rates during Up-states, the cross-ensemble correlations are weaker. At the mechanistic level, this is likely to be a result of the decreased cross-ensemble connectivity.

Mechanisms underlying the formation of neuronal ensembles and homeostasis

The experience-dependent reconfiguration of cortical subnetworks observed here must be mediated through specific learning rules and plasticity mechanisms. Part of the observed changes are attributed to well-defined homeostatic mechanisms: activity-dependent upregulation and downregulation of intrinsic excitability (Desai et al., 1999; Maffei et al., 2004; Karmarkar and Buonomano, 2006; Grubb and Burrone, 2010; Wefelmeyer et al., 2016; Debanne et al., 2019). Homeostatic plasticity by itself, however, cannot fully account for our results as it would not account for the selective decrease in cross-ensemble connectivity (e.g., the decrease in ChR⁺ to ChR^– connectivity). Thus, associative Hebbian mechanisms that capture the correlational structure of neuron pairs are likely to operate in parallel with homeostatic plasticity (Watt and Desai, 2010; Turrigiano, 2011; Walcott et al., 2011; Zbili et al., 2021).

A limitation of our study was that we were not able to specifically contrast the connectivity between ChR⁺ pairs and ChR^– pairs because of the challenges in performing paired ChR⁺ recordings in sparsely transduced slices in which the ChR⁺ neurons were distant from each other. Thus, future studies should specifically determine whether the connectivity within ChR⁺ pairs is the same, or perhaps higher, than between ChR^– pairs. However, our computational model allowed us to demonstrate that synaptic decoupling was sufficient to account for the observed cross-ensemble decreases in correlations, as well as for the lower firing rates in ChR⁺ neurons. Overall, our experimental and computational results support the notion that the nervous system engages multiple synergistically operating plasticity loci in parallel to robustly implement experience-dependent cortical reorganization.