Abstract
Identifying the functional specialization of the brain has moved from using cognitive tasks and resting state to using ecological relevant, naturalistic movies. We leveraged a large-scale neuroimaging dataset to directly investigate the hierarchical reorganization of functional brain activity when watching naturalistic films compared to performing seven cognitive tasks and resting. A thermodynamics-inspired whole-brain model paradigm revealed the generative underlying mechanisms for changing the balance in causal interactions between brain regions in different conditions. Paradoxically, the hierarchy is flatter for movie-watching, and the level of nonreversibility is significantly smaller in comparison to both rest and tasks, where the latter in turn have the highest levels of hierarchy and nonreversibility. The underlying mechanisms were revealed by the model-based generative effective connectivity (GEC). Naturalistic films could therefore provide a fast and convenient way to measure important changes in GEC (integrating functional and anatomical connectivity) found in, for example, neuropsychiatric disorders. Overall, this study demonstrates the benefits of moving toward a more naturalistic neuroscience.
Thermodynamics-inspired framework reveal mechanisms of flattened brain hierarchy in movie-watching compared to rest and task.
INTRODUCTION
“Cinema is the most beautiful fraud in the world” - Jean-Luc Godard.
Watching a movie is a favorite pastime for billions of people, with the moving images and sound making us feel and think in often transformative ways. Most, if not all, would agree that the subjective experience of watching naturalistic, multimodal dynamics of film is highly motivating, soothing, and entirely different from our usual everyday resting experience of mind-wandering (1, 2). Movie-watching also feels very different and more relaxing than our often stressful experience of working and having to solve problems. These subjective experiences of different workload in different states must be associated with changes in brain dynamics, and the study of naturalistic films has already yielded interesting findings (3–8). Yet, the underlying brain mechanisms responsible for the change in computations associated with watching naturalistic stimuli are not well understood.
Traditionally, in cognitive neuroscience, neuroimaging studies of the human brain initially focused on measuring localized activity evoked during relatively simple parametric tasks using tightly controlled abstract stimuli. These “localizationist” frameworks were designed to assign specific cognitive processes to discrete brain regions (9, 10). This has led to a deeper understanding of how the brain solves complex psychological tasks such as, for example, working memory (11) and reward (12), but at the same time, this also led to the accidental discovery of a network of regions that are more active during rest than during task (13, 14). Over time, this has grown into a burgeoning field, which has provided new insights into how spontaneous resting state activity recapitulates task activity (15–22). However, it has also become clear that the field needs more realistic real-life stimuli where the brain is forced to integrate complex multimodal stimuli over longer time spans. Proposals have been made to create a naturalistic neuroscience dedicated to measuring how the brain reacts to ecologically valid stimuli such as moving images, speech, and music (3, 6, 23).
Hence, over the past decades, the use of naturalistic films has emerged as a promising tool for investigating brain function (4, 5, 24). While the earliest studies date back to 1954 where researchers recorded electroencephalography (EEG) from human participants watching a movie (25), this provided little in terms of spatiotemporal dynamics. A turning point in cognitive neuroscience came in 2004 with two pioneering papers investigating the spatiotemporal brain activity linked to films (4, 5). One of these studies used Sergio Leone’s classic film “The Good, the Bad and the Ugly” to elucidate the intersubject synchronization of cortical activity (4). Speaking to the importance of using complex stimuli for understanding brain function, Sonkusare and colleagues (3) made the argument that naturalistic movies mimic experiences from everyday life. Other exciting approaches have used an intersubject phase synchronization approach to reveal brain networks synchronizing to various features of a task, which not always predicted by the temporal structure of this task (26, 27).
As such, movies provide an alternative to resting state functional magnetic resonance imaging (fMRI) and exceed them in some respects, such as higher test-retest reliability and acceptability in younger and clinical populations (23), although please note that the umbrella term “naturalistic” can be misleading when referring to media stimuli, given that films are carefully crafted for form and function (28).
Naturalistic movies with fast perceptual information embedded in slower narrative contexts provide an obvious route to identifying one of the key organizational objectives of the brain, namely, to capture the complex, multiscale dynamics of natural stimuli (29). To reveal these objectives, it is important to understand how the computational demands for brain changes, when resting or when solving problems, where the brain must reconfigure the communication channels between specialized brain regions. For example, when trying to extract moving features from a visual scene, the specialized middle temporal visual area region of the brain must be engaged and communicate differently with the relevant networks (30). Equally, solving problems requires the prefrontal cortex to engage according to the difficulty of the task (11, 12, 31–35). Hence, it has been proposed that the brain is hierarchically organized such that a group of brain regions, often called the global workspace, collaborate to orchestrate optimal brain communication and computation (36–38). Different conditions have been shown to reconfigure the functional hierarchy of different states, with the prefrontal cortex temporarily overriding the global workspace to solve specific difficult problems (31, 35). However, it is not clear how watching naturalistic movies reorganizes the functional hierarchy compared to rest or when solving cognitive tasks.
To directly solve this problem, we created the GCAT (generative connectivity of the arrow of time) framework, allowing us to infer the causal mechanisms underlying changes in the hierarchy of the causal interactions between brain regions across the whole brain. This generative model uses the previously described INSIDEOUT framework for determining the model-free changes in hierarchy in a given condition (39). The INSIDEOUT framework was inspired by the ideas put forward by Buzsáki (40), who proposed that self-organized dynamics of the brain constrains how the brain acts on the world rather than being solely driven by sensations. In other words, the “inside-out” balance of intrinsic and extrinsic brain dynamics could serve as a distinguishing signature of a brain state. The INSIDEOUT framework also provides a faster and more flexible way to quantifying causal brain interactions instead of the more complex and computationally demanding measures of Granger causality (41) or the more general measures of transfer entropy (38, 42, 43). This thermodynamics-inspired framework estimates pairwise interactions between regions and is based on insights from thermodynamics (44, 45), showing that it is possible to capture the asymmetry in causal interactions by estimating the level of nonreversibility (NR). A convenient way of capturing NR between pairs of regions is through the comparison of not only the forward time series of signals but also the backward reversed time series of these signals. Specifically, the GCAT framework computes the time-shifted correlations between (i) the forward time series of the two regions and (ii) the time-shifted correlations of the reversed time series. Comparing these two time-shifted correlations provides a reliable quantification of the asymmetry in the interactions between pairs of regions, which, in turn, quantifies the extent to which one region is driving another.
Another way to describe GCAT framework is to use the language of thermodynamics, where the breaking of the detailed balance is said to be reflected in the level of NR, i.e., the arrow of time (39, 44, 46–49). The resulting model-free measure is directly related to production entropy (46, 49) but much simpler to directly estimate from the empirical neuroimaging data.
Crucially, here, we use this model-free quantification of the level of NR fitted to a causal mechanistic whole-brain model. This provides the generative effective connectivity (GEC), which is the effective weighting of the existing anatomical connectivity. Note that this is an extension of the classic concept of effective connectivity (50): (i) GEC is generative using the whole-brain model to adapt the strength of existing anatomical connectivity (i.e., the effective conductive values of each fiber), and (ii) the optimization target for GEC is the NR INSIDEOUT matrix. In other words, creating a whole-brain model of the arrow of time in the empirical neuroimaging data provides direct access to determining the generative mechanisms creating the hierarchy in any condition and therefore provides a direct measure of the hierarchical reconfiguration between conditions.
Specifically, we use the notion of hierarchy to describe the asymmetry in the directionality of information flow. In physics and systems biology, creating this asymmetry is usually referred to as “breaking the detailed balance.” Hence, a flat hierarchy is characterized by a low level of directionality of information flow, i.e., what is called the detailed balance. When the detailed balance is broken, i.e., when there is an increase in the directionality of information flow, this results in a high level of hierarchical reorganization. This notion of thermodynamic hierarchy allows for the determination of asymmetry in space (given by the information flow interactions), which gives rise to asymmetry in time (measured as the arrow of time, or NR) (39). At different scales, this gives rise to different spatial and temporal hierarchies (51–53).
The hierarchy across the whole brain can thus be estimated by using this framework for all pairs of regions in the brain, describing the breaking of the detailed balance in movie-watching, rest, or cognitive tasks. This is consistent with other examples of proposed hierarchical organization of brain states that include core synaptic hierarchy (54), global workspace (36, 37), and core periphery (51).
Here, we applied the GCAT framework to the large-scale Human Connectome Project (HCP) neuroimaging data of the 176 individuals watching movies and resting (scanned with 7 T) and performing seven cognitive tasks and resting (scanned with 3 T). The model-free results showed that global levels of NR in the empirical brain signals are significantly lower in naturalistic movie-watching than in both resting and tasks (with the highest levels for the latter). The lower levels of NR in movie-watching directly reflect a more flattened hierarchy. We then built a whole-brain model where the resulting GEC allowed us to identify the underlying causal mechanisms generating the flattening of hierarchy appearing when watching naturalistic films compared to rest and tasks. Overall, the findings provide insights into functional hierarchical reorganization in movie-watching and more generally the GCAT framework provides the means to harvest the full potential of moving to a more naturalistic neuroscience.
RESULTS
The move toward a more naturalistic neuroscience requires new advanced methods and our overall aim was to assess the GCAT framework for quantifying the functional hierarchical changes in the brain. This is achieved by using a model-free measure of the NR capturing the breaking of the detailed balance, combined with a model-based approach, which can identify the causal mechanisms underlying specific changes in brain state. Specifically, we applied the GCAT framework to large-scale neuroimaging data of human participants watching a naturalistic movie, resting, or solving cognitive tasks.
Description of GCAT framework
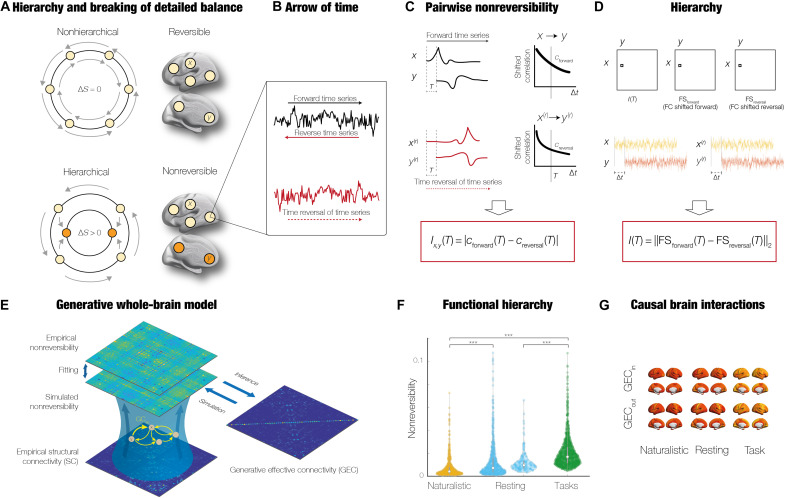
Figure 1 summarizes the overall framework based on the thermodynamics notion of NR, which can be used to quantify the breaking of detailed balance of a hierarchical system. In particular, the upper panel of the figure shows a nonhierarchical system, which is in detailed balance and therefore fully reversible over time. In thermodynamics, this means that the production entropy, S, over time is equal to zero. The production entropy is quantified as the Kullback-Leibler distance between the forward and backward transition probabilities of the dynamical evolution of a system and therefore a measure of NR (46, 49).
Fig. 1. GCAT framework for discovering underlying causal mechanisms of hierarchical organization.
(A) Level of hierarchy is given by the level of asymmetry of causal interactions between brain regions arising from the breaking of the detailed balance. The upper subpanel shows a nonhierarchical system in full detailed balance and thus fully reversible over time, i.e., no change in production entropy, S. In contrast, the bottom subpanel shows a change in production entropy, reflecting the asymmetry of the underlying causal interactions. (B) Estimating the arrow of time requires the forward time series of each region (in black) and the time-reversed time series (in red). (C) Basic principle of how the level of NR can be computed through the pairwise level of asymmetry using a time-shifted measure of the correlations between the forward (x, y) (top row) and the reversed [x(r), y(r)] time series (bottom row). The difference between these time-shifted correlations provides a quantification of the asymmetry in the interactions between pairs of regions (for a given shift ∆t = T). (D) Hierarchy is computed through the generalization of the pairwise NR for the whole brain, i.e., as a matrix involving all pairs. The hierarchy is given by the NR matrix, which is the difference between the two time-shifted correlation matrices for the forward and reversed time series (at a given shift time point ∆t = T; see Methods). (E) NR matrix is used to fit a whole-brain model creating the GEC, which provides the underlying causal mechanisms (see Methods). (F) Average of the NR matrix provides a model-free estimate of the hierarchy that can be contrasted over conditions. (G) Further mechanistic insights into hierarchy can be provided by rendering the in and out degree of the GEC matrix.
In a hierarchical system without detailed balance, the production entropy is always larger than zero (shown in the bottom subpanel of Fig. 1A). Hence, this is a measure of the asymmetry of the underlying causal interactions, i.e., measuring the breaking of the detailed balance. In other words, the hierarchy of a system can be quantified directly by assessing NR.
In addition to production entropy, Jarzynski et al. (44, 45) proposed to measure the level of NR by estimating the arrow of time in the underlying signals of a dynamical system. Specifically, their method requires both the forward time series of each region and the time reversed time series (generated by flipping the time ordering from the empirical time series; see Fig. 1B and Methods). Their method then uses machine learning to classify whether these two time series are distinguishable. If they are not distinguishable, then there is no arrow time and the system is fully reversible and vice versa.
Here, we propose a variation on this time-consuming machine learning process. We simply measure the pairwise level of temporal asymmetry by computing a time-shifted measure of correlation between the two time series. Figure 1C shows how to compute the pairwise NR as the absolute value of the difference between these time-shifted correlations of the forward and reversed time series. In other words, this quantifies the extent to which one region is driving another by providing the level of asymmetry in the interactions between pairs of regions (for a given shift ∆t = T; see Methods).
This allows us to compute the brain hierarchy as the generalization of the pairwise NR to a matrix involving all pairs, i.e., covering all regions of the brain. Figure 1D shows how the hierarchy is simply given by the NR matrix, which is the difference between the two time-shifted correlation matrices for the forward and reversed time series (at a given shift time point ∆t = T; see Methods).
To gain a deeper understanding of the generative principles of functional hierarchy, we then modeled these empirical, model-free measures. Figure 1E shows how a whole-brain model can be fitted to the empirical NR matrix by iteratively estimating the GEC with a pseudo-gradient algorithm (see Methods). The underlying changes in model-free functional hierarchy (shown in Fig. 1F) can be directly quantified by the model-based GEC matrix, which provides direct insights into the information flow involved in the breaking of the detailed balance (Fig. 1G).
Empirical, model-free changes in functional hierarchy for movies, rest, and tasks
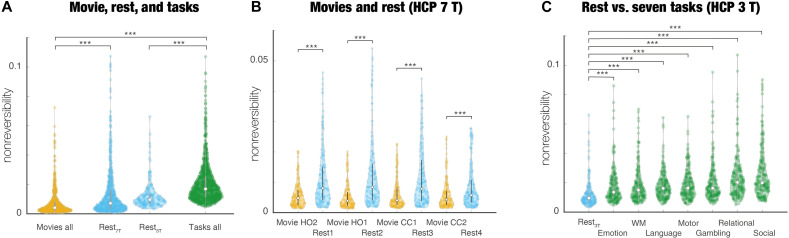
We assessed the overall significant changes in functional hierarchy for movies, rest, and tasks. As can be seen in Fig. 2A, a direct comparison of hierarchy shows that movie-watching (averaged over all sessions) has a significantly more flattened hierarchy (lower NR) compared to both rest (P < 0.001, Wilcoxon) and tasks (average over all seven tasks, P < 0.001, Wilcoxon). Even the differences between rest and cognitive tasks are highly significant (P < 0.001, Wilcoxon) with resting less nonreversible than cognitive tasks. These results show that the level of NR in movie-watching is similar to anesthesia and deep sleep (as quantified in recent papers) (39, 49) than rest and task. This flattening of the hierarchy is suggestive of a less active dynamical repertoire than when resting, which, in turn, most likely reflects less computation. In other words, the flattened hierarchy reflects less asymmetric interactions between brain region and the decrease of NR in anesthesia, and deep sleep reflects less directed information flow in the underlying substrate, associated with much less computational demand. It has been found that the lack of dynamical flexibility found in unconscious states (such as deep sleep and anesthesia) is also reflected in a stronger correlation between the functional and anatomical connectivity (55, 56). In other words, the unconscious brain activity is more driven by the underlying anatomical backbone of connectivity. This is also the case when movie-watching, where the correlation between the average FCallmovies and structural connectivity (SC) is 0.40, while the correlation between the average functional connectivity (FC)allrest and SC is 0.37.
Fig. 2. Different functional hierarchies for movies, rest, and tasks.
We estimated the functional hierarchy as characterized by the levels of NR. (A) Direct comparison of hierarchy in naturalistic movie, rest, and tasks shows that movie-watching (averaged over all sessions) has a significantly more flattened hierarchy (i.e., lower NR) compared to both rest and tasks (average over all seven tasks). Rest is less nonreversible than movie-watching but significantly less than task. (B) Each session of movie-watching (measured with 7-T fMRI) is significantly less nonreversible than rest. (C) Equally, all seven cognitive tasks (measured with 3-T fMRI) are significantly more hierarchically (i.e., nonreversible) than rest, suggesting the importance of hierarchy for computation.
Further analyses of each session of movie-watching whether watching Hollywood or Creative Commons (CC) movies (compared with rest) showed significantly different levels of hierarchy (P < 0.001, Wilcoxon; see Fig. 2B). Equally, Fig. 2C shows that each of the seven cognitive tasks (measured with 3-T fMRI) is significantly more nonreversible than resting state (P < 0.001, Wilcoxon). This increase in the hierarchy during cognitive tasks is suggestive of the specific computational demands, which is reflected in specific asymmetric, causal interactions between regions in cognition.
Whole-brain modeling of hierarchical changes: GEC
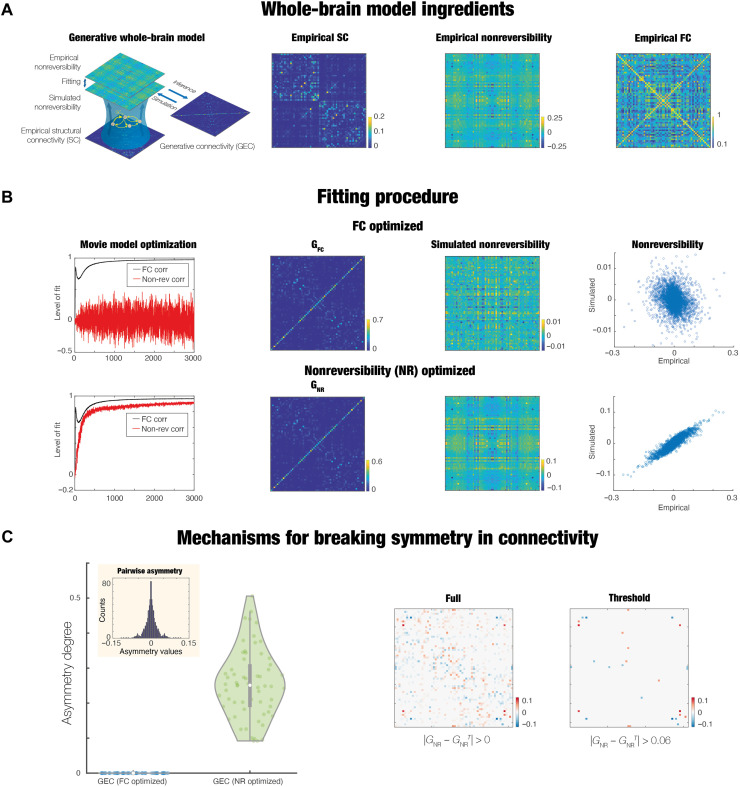
We went beyond the empirical, model-free measures of NR by constructing a generative whole-brain model, allowing us to infer the underlying causal mechanisms for hierarchical changes in movies, rest, and tasks. The whole-brain model combines the anatomical connectivity with the local dynamics to fit the empirical functional data (57–59). The models come in many flavors (e.g., spiking, dynamical mean field, and Hopf) and can fit many different empirical observables (FC and dynamic FC]. Here, crucially, we use a Hopf model (since this has been shown to provide the best fit) and the model-free observable of NR identifying the hierarchical organization. More specifically, Fig. 3A shows the procedure for fitting a whole-brain model, initially using the anatomical connectivity and then iteratively adjusting a GEC, which are the weights of the existing anatomical connections. To study the influence of the previously unknown observable, we first carried out this fitting procedure using the traditional approach of fitting only the empirical FC, which resulted in the GEC matrix, GFC. Second, we also fitted the whole-brain model both to the FC and the NR matrices, which produced the GEC matrix, GNR (see Methods).
Fig. 3. Whole-brain model provides causal insights into the functional hierarchy of movie-watching.
The figure shows how to identify the underlying causal mechanisms resulting in the different levels of hierarchy (i.e., NR) when movie-watching. (A) Procedure starts with fitting a whole-brain model, initially using the anatomical connectivity and then iteratively adjusting a GEC according to either fitting this to the empirical FC alone (GFC) or including the NR (GNR) matrices. (B) Upper row shows the optimization of the whole-brain model based on optimizing only with FC, while the lower row shows the same but including the optimization with NR. As can be seen in the leftmost panels, the evolution of learning improves the level of fit to FC (correlation between empirical and simulated matrices, black curves) in both cases but only fitting the FC does not give a good fit to the empirical NR (see red curves). The second column of panels show the optimized GEC matrices (GFC and GNR). While difficult to discern, the former is symmetrical, while the latter is asymmetrical, as quantified below. The third column of panels shows the simulated NR matrices, and the level of fit to the empirical NR is shown in the scatterplot in the fourth column of panels. It is very clear that only the GNR optimization is able to capture the level of empirical NR and consequently, the hierarchy. (C) Leftmost figure is quantifying the level of asymmetry of the GNR. As can be seen in the boxplot, there is no asymmetry for GFC, but strong asymmetry for GNR. This is further explored in the inset, which shows that there are many asymmetric pairs of brain regions. Last, we visualize these asymmetries with the full and thresholded matrices.
Figure 3B shows that only fitting to the NR matrices generated an acceptable fit to the empirical levels of NR (compare upper row with lower row). Specifically, the leftmost graphs show the evolution of the level of fit over time when fitted to the FC (upper) and when fitted to FC and NR (lower). The correlation between the empirical and simulated matrices are represented by black (FC) and red (NR) curves. In both cases, we found good levels of the model fit to FC (black curves). However, only when fitting the model using both FC and NR, we obtained a good level of fit to the empirical NR (see the convergence of red curve in the lower graph and nonconvergence in the upper graph). This nontrivial finding shows that the whole-brain model needs to explicitly fit the empirical levels of NR to be able to account for this observable and consequently capture the mechanisms underlying the functional hierarchy.
The importance of this result can also be seen when inspecting the results of the fitting procedure, in the second column of panels showing the optimized GEC matrices (GFC and GNR). Equally, the third column of panels shows the simulated NR matrices, while the levels of fit to the empirical NR are shown in the scatterplots in the fourth column of panels. As can be appreciated, only the GNR optimization is able to capture the level of empirical NR and, consequently, the hierarchy.
The figure shows the reason why the whole-brain model can capture the hierarchy, namely, due to the underlying asymmetry found in the GEC matrix GNR. Figure 3C shows a boxplot demonstrating the lack of asymmetry for GFC but strong asymmetry for GNR. The inset shows that there are many asymmetric pairs of brain regions, which are visualized through renderings of the full and thresholded matrix differences (rightmost panels; see Methods).
Discovering the underlying regions involved in hierarchical changes in movies, rest, and tasks
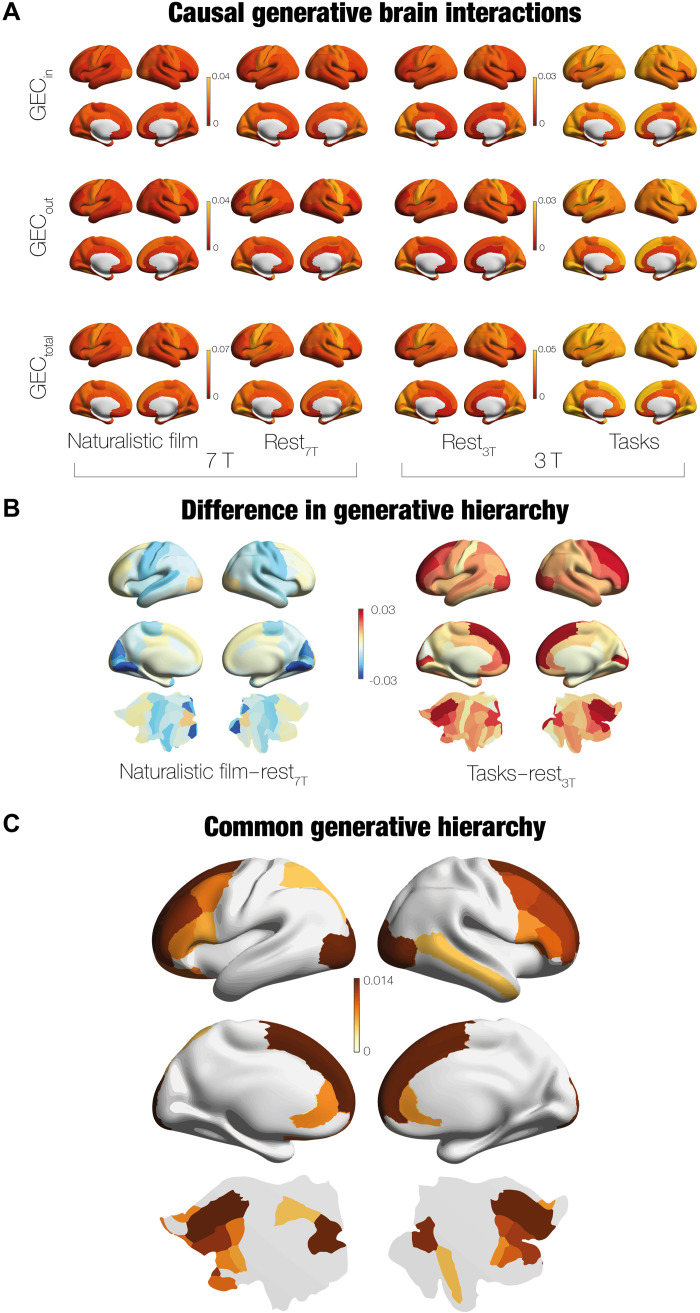
The information flow between different brain regions is captured by the GEC matrix resulting from fitting the whole-brain model to the empirical FC and NR data. This, in turn, provides a precise description of the regions serving as drivers and receivers under different conditions. More specifically, these can be identified from the GEC matrix. The receivers can be determined as the incoming information, Gin, given by the in-degree of the GEC matrix, while the drivers can be found as the outgoing information, Gout, from the out-degree of the GEC matrix. Similarly, a measure of orchestration is given by the sum of ingoing and outgoing information, Gtotal = Gin + Gout.
For all conditions, Fig. 4A shows a rendering of the receivers (incoming Gin), drivers (outgoing Gout), and the sum of them (Gtotal). The figure shows the significantly flattened hierarchy in movie-watching (deeper red) compared to both rest (more orange) and task (strongest yellow). This expands on the model-free results reported above, which found differences between the average total for the conditions. Here, using the GEC, we were able to pinpoint the regional, topological differences driving the changes in hierarchy. These results further strengthen the interpretation that the brain is performing less computation in movie-watching compared to both rest and when performing tasks.
Fig. 4. Identifying the underlying causal drivers of hierarchy changes in movies, rest and tasks.
We can determine the information flow in terms of drivers and receivers by using the matrices of the GEC, obtained through using a whole-brain model for movies, rest, and tasks (fitted to both the model-free measures of NR and FC). This provides direct measures of the underlying brain hierarchy. (A) For all conditions, the figures show the receivers (incoming, Gin), drivers (outgoing, Gout), and their sum (Gtotal). The hierarchy is given by the gradations in color and, as can be seen movie, has a significantly lower hierarchy (deeper red) than both rest (orange) and task (strongest yellow). (B) Decrease in hierarchy in movies versus rest can be explicit shown by rendering the difference between their respective Gtotal. As can be seen from the colormap, where negative values are more blue and positive values are more yellow, only prefrontal and some visual regions are stronger for movies than rest. In other words, while the general hierarchy is flattened in movies, the prefrontal and visual regions are more nonreversible for movies, suggesting that the computation performed by these regions drives the breaking of the detailed balance when movie-watching. In contrast, when comparing the Gtotal for the average over all tasks versus rest, the general hierarchy is significantly larger for tasks and the main drivers of the computation is again found primarily in the prefrontal regions. (C) Confirming the role of prefrontal cortex in driving the breaking of the detailed balance, we computed the intersection of the top 50% regions of the contrasts shown in (B). This showed that primarily prefrontal regions (as well as some parietal, visual, and temporal) are the common drivers orchestrating computation in the brain.
The significant topological differences between movie-watching and rest as well as the differences between cognitive tasks and rest are further quantified in Fig. 4B. There is a significant decrease in hierarchy in movies compared to rest, which is explicitly shown by rendering the difference between their respective Gtotal. As can be seen from the colormap in the left, movie-watching is more balanced than resting, except in prefrontal and visual regions. This demonstrates the counterintuitive finding that resting involves more computation than movie-watching, which is perhaps driving our desire for watching movies. However, the prefrontal cortices are still more nonreversible than in rest, reflecting that breaking of the detailed balance is being orchestrated by these prefrontal regions. This finding is reinforced by the finding (shown in right of Fig. 4B) that the general hierarchy is significantly larger for tasks than rest, where the main drivers of the breaking of the detailed balance is once again found primarily in the prefrontal regions.
Figure 4C quantifies this important finding of the role of the prefrontal cortex in computation and driving the breaking of the detailed balance. To identify the common drivers across movie-watching and cognitive tasks, we selected the top 50% regions of the contrasts in Fig. 4B and computed the intersection of the two contrasts. We found that primarily prefrontal regions [bilateral superior frontal, rostral middle frontal, inferior frontal gyrus (pars triangularis), caudal middle frontal cortices, and left lateral orbitofrontal cortices] as well as right rostral anterior cingulate, left superior parietal, right middle temporal, and lateral occipital cortices are the main drivers orchestrating computation in the brain.
GEC matrix is significantly better for classification
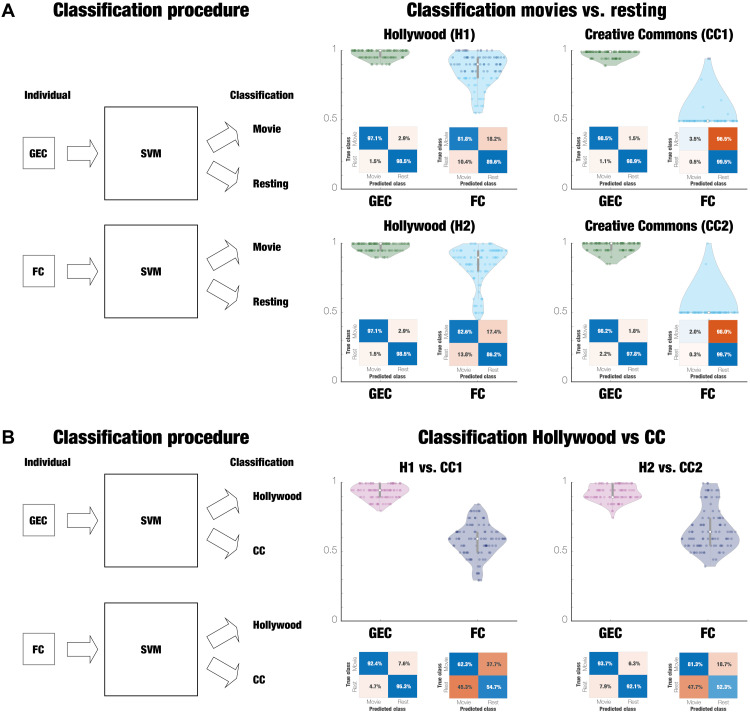
The GEC matrix provides the causal mechanistic principles for a given condition and can therefore be used for revealing the main drivers of computation. It should therefore be excellent for classification of a given condition. To test this, we used machine learning [with an support vector machine (SVM) classifier] using either GEC or FC to classify movie-watching compared to rest and comparing between different kind of movies (Hollywood or CC license on Vimeo). Figure 5A shows the boxplots of the classification performance (across 100-fold) and the associated average confusion matrix (see Methods). The results show that the classification is much better when using GEC than when using FC. In each case, the performance numbers are shown on the figure. This improvement is caused by the fact that the GEC matrix is a generative measure capturing the asymmetry of causal interactions, while the FC matrix is symmetric, capturing functional correlations.
Fig. 5. GEC is excellent for classification of movie-watching.
We used machine learning to classify movie-watching compared to rest and between different movies using either GEC or FC. (A) Figure shows the boxplots of the classification performance (across 100-fold) and the associated average confusion matrix. As can be seen, the classification is much better when using GEC than using FC (with the performance numbers shown on the figure). (B) Similarly, the classification of specific movie extracts (Hollywood or CC license on Vimeo) is also much better when using GEC than using FC. Here, using classification with GEC is significantly better than using FC. As can be seen, the average performance for GEC is 93.4%, while the average performance using FC is closer to chance levels (62.7%). Overall, the GEC provides the causal mechanistic principles for a given condition and therefore is excellent for classification of that condition.
Equally, as shown in Fig. 5B, the GEC matrix is much better than the FC matrix for classifying specific movie extracts. The average performance for GEC is 93.4%, while the average performance using FC is closer to chance levels (62.7%).
DISCUSSION
Over the past century, neuroscience has started to reveal much about the functional specialization of the brain, yet we are only beginning to identify the overall whole-brain hierarchical organization needed for orchestrating brain computation. Over time, focus has shifted from using relatively simple parametric cognitive tasks to using more ecologically valid naturalistic stimuli such as movies. Here, we used a thermodynamics-inspired GCAT framework to directly determine the brain hierarchy involved in the computation evoked by naturalistic movies compared to rest and parametric cognitive tasks in a large-scale neuroimaging dataset. This framework directly measured the hierarchy in the empirical data in a model-free and model-based manner through assessing the level of NR, i.e., the arrow of time. The model-free results showed that the hierarchy is significantly flatter for naturalistic movies compared to both rest and cognitive tasks. Equally, the model-free results also showed that cognitive tasks involve more computation with significantly higher levels of hierarchy than both resting and movie-watching.
The model-based findings were entirely consistent with the model-free results in revealing a flattened hierarchy for movie-watching compared to cognitive tasks and rest. Crucially, however, the GEC matrix obtained by the whole-brain modeling (fitted to the model-free measure of NR) revealed the causal interactions that give rise to the empirical hierarchy, i.e., the level of NR. In particular, we were able to identify the common drivers across movie-watching and cognitive tasks, which were found to be mainly prefrontal regions (bilateral superior frontal, rostral middle frontal, inferior frontal gyrus pars triangularis, caudal middle frontal cortices, and left lateral orbitofrontal cortices). This provides causal insights into the large literature on the prefrontal regions, which shows that the prefrontal cortex is crucial for flexible computation needed for complex problems (11, 12, 31–35). This also fits well with the extensive literature on mind-wandering and spontaneous thought, where a very influential review by Christoff et al. (60) pointed to role of DMN centered on the medial prefrontal cortex as a main driver of mind-wandering. In addition, it is of significant interest that the orbitofrontal cortex is a driving region for both movie-watching and solving cognitive tasks, given its role in the hedonic processing and motivation (12).
In addition, we were also able to show that the asymmetric, generative GEC matrix is much better than the correlative FC matrix for the classification of condition. In particular, the GEC matrix was much better for classifying different conditions (movie-watching and resting) and between movie conditions (Hollywood versus CC).
Using thermodynamics framework to infer generative hierarchy
The findings reported here provide evidence for the generative hierarchy of brain function and thus significantly expanding on the research carried out over the past hundred years of neuroscience. Previous research has convincingly demonstrated that the anatomy of the brain is hierarchically organized across scales, from single units to the larger circuits (54, 61–66). It has also become clear that this fixed anatomy is reflected in the functional organization of the brain leading to a clear topographic organization of the brain with some functional specialization (67). Yet, finding the true richness of the functional hierarchical organization requires advanced methods for estimating the flow of information between brain regions, which provides the scaffold for the necessary orchestration of computation performed by the brain.
Previously, in terms of going beyond the anatomical restrictions to describe the richness of functional activity, Marsel Mesulam was one of the first to propose how the anatomical connectivity can lead to brain processing shaped by a hierarchy of distinct unimodal areas orchestrated by integrative transmodal areas (54). Recently, this idea has been further extended with functional neuroimaging by researchers such as Margulies et al. (68) providing a gradiental perspective on hierarchical processing and Atasoy et al. (69, 70) providing a more generalized perspective based on the ubiquitous idea of harmonic modes found everywhere in Nature. Equally, Northoff et al. (51, 71–73) have proposed a similar hierarchical core-periphery principle. This led them to the demonstration of a convergence of temporal and spatial hierarchy during rest which changes compared to task (51, 71–73), consistent with the findings presented here.
Yet, even stronger evidence of the functional hierarchical brain organization can only come from methods directly estimating the causal interactions between brain regions using versions of transfer entropy and Granger causality (38, 74–76). Using a version of normalized directed transfer entropy (NDTE) has been key to quantify the notion of a “global workspace” orchestrating brain function and where information is integrated in a small group of brain regions before being broadcast to many other regions across the whole brain (36, 37). Hence, the global workspace can be thought of as prototypical example of a hierarchical system, akin to a small core assembly of people in charge of a large organization. Such larger brain network organization has been shown to be efficient, robust, and largely fault tolerant (63, 77, 78).
Using the NDTE framework allowed for the identification of global workspace used for the orchestration of the functional hierarchical organization (38), which included the left precuneus, left nucleus accumbens, left putamen, left posterior cingulate cortex, right hippocampus, right amygdala, and left and right isthmus cingulate. Lesioning of these regions in a whole-brain model destroys the functional hierarchical organization.
Nevertheless, the computation of the direct causal interactions using NDTE and other related methods is a time-consuming process and depends on having large datasets. Here, we improved on the state of the art by using an efficient and robust thermodynamics-inspired GCAT framework providing two complementary quantifications of hierarchy: A model-free, indirect measure of hierarchy (as the level of NR), which in turn provides the observable for a model-based, direct quantification of the causal interactions giving rise to the hierarchical organization.
Thus, by its very nature, the GCAT framework developed here provides measures of the NR of the brain during different conditions and allows for a precise identification of the brain regions involved in breaking the balance and net fluxes between the underlying networks. The INSIDEOUT method used here can used to reveal the hierarchical organization of brain states, and it has been demonstrated to capture the causality of time series found [as shown in figure S4 in the paper of Deco et al. (39)]. Causal measures of time series have a long history with considerable arguments in the literature as to the appropriateness of using these on blood oxygenation dependent level (BOLD) time series due to the potential impact of the variability of the hemodynamic response across brain regions (79–81). At the same time, it has also been shown that causal time series methods perform much better with sufficiently fast sampling and low measurement noise (82). Here, we use state-of-the-art HCP data with a fast repetition time (TR) of 0.78 s (for the 3-T data) and 1.0 s (for the 7-T data), providing excellent subsampling of the hemodynamic response function. This lessens any potential problems with poor subsampling with long TR that can lead to problems with spurious and undetectable causality as well as distortion of relative strengths.
Intuitively, it might seem that movie-watching would involve more computation than when resting and therefore would involve a steeper hierarchical organization. However, the empirical analysis carried out here show that this is not the case. Instead, we found a flattening of the brain hierarchy in movie-watching, which is perhaps one of the reasons why watching films is a preferred relaxing pastime for many people. Perhaps surprisingly, resting is not particularly desirable with Killingsworth and Gilbert (83) showing that the introspection and mind-wandering state rarely leads to a happy mind, probably since resting leads to thinking about what is not happening, which involves significant, and often undesirable, computation. In contrast, movie-watching provides a desirable audio-visual narrative where the necessary computation is minimal. Hence, naturalistic films may be a better alternative compared to resting when investigating younger and clinical populations, especially given that naturalistic films also have higher test-retest reliability (23).
Overall, the proposed framework provides important model-free and model-based insights into the causal mechanisms underlying complex changes in brain hierarchy under different conditions. This provides much needed tools for leveraging the move toward a more naturalistic neuroscience, which, in turn, will benefit our understanding of how the brain operates in its natural ecological context.
METHODS
Ethics
The Washington University–University of Minnesota (WU-Minn HCP) Consortium obtained full informed consent from all participants, and research procedures and ethical guidelines were followed in accordance with Washington University Institutional Review Board (IRB) approval (Mapping the Human Connectome: Structure, Function, and Heritability; IRB #201204036).
Participants
All data were extracted from the HCP using the same 176 participants with complete data of movie-watching and rest (in 7 T) and seven tasks and rest (in 3 T), which were a subset of approximately 1200 participants scanned at 3 T. Note that the dataset includes many sets of siblings and twins (whether mono- and dizygotic), and ultimately, the data derive from 90 unique families. All participants (106 females and 70 males) were generally healthy young adults between 22 and 36 years old (mean age = 29.4 and SD = 3.3).
Experimental paradigms
The experimental paradigms performed in the scanner included movie-watching, rest, and seven cognitive tasks as described in detail in the following.
Movie-watching and rest in 7-T scanner
Participants passively viewed a series of audiovisual movie clips in four functional runs (of approximately 15 min each) consisting of four or five clips of varying length from 1:03 to 4:19 min:s. In between each clip there was 20-s period of rest. The first and third runs contained clips from independent films (both fiction and documentary) made freely available under CC license on Vimeo, while the second and fourth runs contained clips from Hollywood films prepared by Cutting et al. (84, 85). For a brief description of each clip, see (86). The movies were presented in a full-screen mode (size, 21.8° width × 15.7° height) and audio was delivered via Sensimetrics earbuds.
The same participants underwent four resting state scans (of approximately 16 min each), where the participants were instructed to keep their eyes open and maintain relaxed fixation on a bright cross-hair on a dark background in a darkened room. Given that the direction of phase encoding alternated between posterior to anterior and anterior to posterior across runs, we included all four scans.
Seven cognitive tasks and rest in 3-T scanner
We chose the same 176 participants who also performed seven tasks contained in the HCP task battery (39, 87), which were designed to cover a broad range of human cognitive abilities in seven major domains that sample the diversity of neural systems (i) visual, motion, somatosensory, and motor systems; (ii) working memory, decision-making, and cognitive control systems; (iii) category-specific representations; (iv) language processing; (v) relational processing; (vi) social cognition; and (vii) emotion processing.
The participants also underwent four resting state scans (of approximately 15 min), where the participants were instructed to keep their eyes open and maintain relaxed fixation on a bright cross-hair on a dark background in a darkened room. Unlike the 7-T data, the direction of phase encoding was the same across the four scans and so we only used the first resting scan.
Neuroimaging data
The HCP website (http://humanconnectome.org/) provides the full details of participants, the acquisition protocol and preprocessing of the data. Below, we have briefly summarized this information.
3-T structural data
The HCP structural data were acquired using a customized 3-T Siemens Connectom Skyra scanner with a standard Siemens 32-channel radio frequency (RF)–receive head coil. For each participant, at least one three-dimensional (3D) T1w MPRAGE image and one 3D T2w SPACE image were collected at 0.7-mm isotropic resolution.
3-T diffusion MRI
To reconstruct a high-quality SC matrix, we obtained multishell diffusion-weighted imaging data from 32 participants from the HCP database (scanned for approximately 89 min). The acquisition parameters are described in detail on the HCP website (88). This is used for constructing the whole-brain model as the first estimate of the GEC, which is then iteratively improved to fit the functional data (see below).
3-T functional data
Briefly, the HCP 3-T fMRI data were acquired using a customized 3-T Siemens Connectom Skyra scanner with a standard Siemens 32-channel RF receive head coil, with the following parameters: 2.0-mm isotropic voxels, TR = 720 ms, echo time (TE) = 33.1 ms, flip angle = 52°, field of view (FOV) = 208 × 180 mm, 72 slices, and multiband factor = 8. For full details of the task scans, see http://protocols.humanconnectome.org/HCP/3T/imaging-protocols.html.
7-T functional data
For each participant, HCP fMRI data were acquired using a 7-T Siemens Magnetom scanner with a Nova32 32-channel RF receive head coil, using the following parameters: 1.6-mm isotropic voxels, TR = 1000 ms, TE = 22.2 ms, flip angle = 45°, matrix = 130 × 130, FOV = 208 × 208 mm, 85 slices, multiband factor = 5, image acceleration factor = 2, partial Fourier sampling = 7/8, echo spacing = 0.64 ms, and bandwidth = 1924 Hz/Piels. The direction of phase encoding alternated between posterior to anterior and anterior to posterior across runs. For full details, see http://protocols.humanconnectome.org/HCP/7T/.
Neuroimaging preprocessing for fMRI HCP
The preprocessing of the HCP resting state and task datasets is described in detail on the HCP website. Using an existing pipeline (39), the data are preprocessed using the HCP pipeline, which is using standardized methods using FSL (FMRIB Software Library), FreeSurfer, and the Connectome Workbench software (89, 90). This standard preprocessing included correction for spatial and gradient distortions and head motion, intensity normalization and bias field removal, registration to the T1 weighted structural image, transformation to the 2-mm Montreal Neurological Institute space, and using the FIX artefact removal procedure (90, 91). The head motion parameters were regressed out and structured artefacts were removed by ICA + FIX processing [independent component analysis followed by FMRIB’s ICA-based X-noiseifier (92, 93)]. Preprocessed time series of all grayordinates are in HCP Connectivity Informatics Technology Initiative (CIFTI) grayordinates standard space and available in the surface-based CIFTI file for each participants for resting state and each of the seven tasks.
We used a custom-made MATLAB script using the ft_read_cifti function [FieldTrip toolbox (94)] to extract the average time series of all the grayordinates in each region of the Mindboggle-modified Desikan-Killiany parcellation (95) with a total of 62 cortical regions (31 regions per hemisphere) (96), which are defined in the HCP CIFTI grayordinates standard space. The BOLD time series were filtered using a second-order Butterworth filter in the range of 0.008 to 0.08 Hz.
GCAT framework and associated methods
The thermodynamics-inspired GCAT framework is a general method, which allows us to infer the causal interactions between brain regions through the level of NR across the whole brain. This allows us to build a causal mechanistic whole-brain model, which creates the GEC, as the effective weighting of the existing anatomical connectivity, giving rise to the observed level of NR.
Empirical FC
The empirical FC, , is a matrix of Pearson correlations across the fMRI BOLD time series activity between brain regions, i and j, in the different conditions (naturalistic films, rest, and tasks).
Method for quantifying causal interactions through the levels of NR
Rather than using direct causal measures such as transfer entropy, we estimate the pairwise interactions between regions by computing the time-shifted correlations between both the forward and the reversed fMRI BOLD time series of any two brain regions (39). This provides a reliable quantification of asymmetry in the interactions between pairs of regions, which, in turn, quantifies how one region is driving another. This is inspired by thermodynamics, where the breaking of the detailed balance is quantified by the level of NR, i.e., the arrow of time. Following procedures previously described in (39), we capture the level of NR precisely as the difference in the time-shifted correlations between forward and reverse time series. Using this empirical framework on all pairs of regions in the brain provides a quantification of the hierarchy in a given condition (movie-watching, rest, or tasks).
Specifically, let us consider first the detection of the level of NR (i.e., the arrow of time) between two time series x(t) and y(t). The causal dependency between the time series x(t) and y(t) is measured through the time-shifted correlation. For the forward evolution the time-shifted correlation is given by
| (1) |
Equally, we create the reversed backward version of x(t) [or y(t)] that we call x(r)(t) [or y(r)(t)], which is obtained by flipping the time ordering, i.e., by ordering the time evolution of x(r)(t) [or y(r)(t)] as the inverted sequence. Thus, the time-shifted correlation of the reversal evolution is given by
| (2) |
The pairwise level of NR, i.e., the degree of temporal asymmetry capturing the arrow of time, is consequently given by the absolute difference between the causal relationship between these two time series in the forward and reversed backward evolution at a given shift Δt = T, i.e.
| (3) |
We selected the optimal T (for the 7- and 3-T scans) using a two-step procedure, where we first compute the averaged autocorrelation over all signals and identified the approximate value of T, where the autocorrelation has sufficiently decayed. For the 7-T data (movie-watching and rest), we selected the optimal T7T = 2 TRs, i.e., 2 s. We then optimize around this value to find the most significant results. Similarly, for the 3-T data (rest and seven cognitive tasks), we selected the optimal T3T = 3 TRs, i.e., 2.16 s.
To compute the whole-brain level of NR, we define the forward and reversal matrices of time-shifted correlations for the forward version, xi(t), and respective reversed backward version, , of a multidimensional time series, where the subindex i denotes the different brain regions. The forward and reversal matrices expressing the functional causal dependencies between the different variables for the forward and artificially generated reversed backward version of a multidimensional system are given by
| (4) |
| (5) |
respectively. The FS functional causal dependencies matrices are expressed as the mutual information based on the respective time-shifted correlations. The level of NR is given by the quadratic distance between the forward and reversal time-shifted matrices at a given shift Δt = T. In other words, the level of NR in the multidimensional case is given by
| (6) |
Where the notation ‖Q‖2 is defined as the mean value of the absolute squares of the elements of the matrix Q. In other words, if we define a difference matrix FSdiff in the following way
| (7) |
The matrix FSdiff is thus a matrix whose elements are the squared of the elements of the matrix [FSforward(T) − FSreversal(T)], where for each pair, the level of NR is as measured by the squared difference. Thus, the level of NR, I, is the mean value of the elements of FSdiff.
Whole-brain model of NR
To reveal the causal mechanisms underlying the hierarchy as measured by the NR in each condition, we created a whole-brain model fitting the empirical NR measures by creating the GEC.
Hopf whole-brain model
Similar to our previous papers (57, 97), we fit the empirical BOLD activity at the whole-brain level by using a Hopf whole-brain model (98), which captures the dynamics emerging from the mutual interactions between brain regions connected using the anatomical SC and weighted by the GEC. The model consists of 62 coupled dynamical regions from the Mindboggle-modified Desikan-Killiany parcellation (95) with a total of 62 cortical regions (31 regions per hemisphere) (96).
The local dynamics of each brain region is described by the normal form of a supercritical Hopf bifurcation, also called a Landau-Stuart oscillator, which is the canonical model for studying the transition from noisy to oscillatory dynamics (99). When coupled together using brain network architecture, the complex interactions between Hopf oscillators have been shown to successfully replicate features of brain dynamics observed in electrophysiology (100, 101), magnetoencephalogram (102), and fMRI (98, 103–105).
The dynamics of an uncoupled node n is given by the following set of coupled dynamical equations, which describes the normal form of a supercritical Hopf bifurcation in Cartesian coordinates
| (8) |
| (9) |
with additive Gaussian noise, ηn(t), with SD β. This normal form has a supercritical bifurcation an = 0, so that if an > 0, then the system engages in a stable limit cycle with frequency fn = ωn/2π. In contrast, for an < 0, the local dynamics are in a stable fixed point representing a low activity noisy state. Within this model, the intrinsic frequency ωn of each node is in the 0.008- to 0.08-Hz band (n = 1, …, 62). The intrinsic frequencies were estimated from the data, as given by the averaged peak frequency of the narrowband BOLD signals of each brain region. Similar to previous findings (98), the best fit was obtained with an = − 0.02.
Modeling the whole-brain dynamics requires modeling the coupling, which we include by adding a diffusive coupling term representing the input received in region n from every other region p, which is weighted by the corresponding GEC, Gnp. This input was modeled using the common difference coupling, which approximates the simplest (linear) part of a general coupling function. Thus, the whole-brain dynamics was defined by the following set of coupled equations
| (10) |
| (11) |
where the noise SD is set to β = 0.01.
Methods for updating GEC
We optimized GEC between brain regions by comparing the output of the model with the empirical measures of forward and reversed time-shifted correlations and the empirical FC. Using a heuristic gradient algorithm, we proceed to update the GEC such that the fit is optimized. To work only positive values for the algorithm, all values are transformed into a mutual information measure (assuming Gaussianity).
More specifically, the updating uses the following form
| (12) |
Where the FSij is based on the nonshifted FCij as the mutual information measure obtained by
| (13) |
The model was run repeatedly with the updated GEC until the fit converges toward a stable value.
We initialized using the anatomical connectivity (obtained with probabilistic tractography from dMRI) and only update known existing connections from this matrix (in either hemisphere). However, there is one exception to this rule, which is that the algorithm also updates homolog connections between the same regions in either hemisphere, given that tractography is known to be less accurate when accounting for this connectivity. We used ε = 0.0005 and ε′ = 0.0001 and continue until the algorithm converges. For each iteration, we compute the model results as the average over as many simulations as there are participants.
Functional hierarchical organization
Using the GEC matrix, we can establish and study the functional organization of the brain, where the different levels of information flow to and from a given brain region i are given Gin(i), Gout(i), and Gtotal(i). The functional relevance and hierarchy can be obtained from the averaged information flow, Gij, across all participants. For each brain region i, we define the incoming level of information flow (i.e., the degree of being a receiver) by Gin(i) = ∑jGij. Similarly, for each brain region i, the outgoing level of information flow (i.e., the degree of being a driving region) by Gout(i) = ∑jGji. The total level of functional interaction for each brain region i is given by Gtotal(i) = Gin(i) + Gout(i).
Measuring asymmetry of differently optimized GEC matrices for movie
We measured the asymmetry of the two optimized GEC matrices [using either only FC (GFC) or both FC and NR (GNR)], where the matrices were computed as the average over all four movie sessions. Specifically, the asymmetry was captured as ∑j∣Gij − Gji∣, i.e., the sum of the difference between the matrix and its transposed and show the boxplots for them in Fig. 5C. We also show the pairwise asymmetry of GNR as the histogram of pairwise differences, not including symmetric values (see inset in Fig. 5C).
SVM used for condition classification
We used a SVM with polynomial kernels as implemented in the MATLAB function fitcecoc. The function returns a fully trained, multiclass, error-correcting output codes model. This is achieved using the predictors in the input with class labels. The SVM used inputs of the 62 × 62 matrices of either empirical FC or model GEC, while the output was two classes corresponding to the conditions (rest versus all movies or Hollywood movies versus CC movies). We used the output from all 176 HCP participants used for generalization, subdivided into 90% training and 10% validation, repeated, and shuffled 100 times.
Acknowledgments
Funding: G.D. is supported by the Human Brain Project Specific Grant Agreement 3 Grant agreement no. 945539 and by the Spanish Research Project AWAKENING: Using whole-brain models perturbational approaches for predicting external stimulation to force transitions between different brain states, ref. PID2019-105772GB-I00/AEI/10.13039/501100011033, financed by the Spanish Ministry of Science, Innovation and Universities (MCIU), State Research Agency (AEI). Y.S.P. is supported by European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant 896354. E.T. is supported by grants PICT-2018-03103 and PICT-2019-02294 funded by Agencia I+D+I (Argentina) and by a Mercator fellowship granted by the German Research Foundation. M.L.K. is supported by the Centre for Eudaimonia and Human Flourishing (funded by the Pettit and Carlsberg Foundations) and Center for Music in the Brain (funded by the Danish National Research Foundation, DNRF117).
Author contributions: All the authors designed the study, developed the methods, performed the analyses, and wrote and edited the manuscript. All the authors edited the manuscript.
Competing interests: The authors declare that they have no competing interests.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. The Human Connectome Project dataset used in this study is publicly available by the WU-Minn Consortium in ConnectomeDB (https://humanconnectome.org/). The code used to analyze the data is available in DOI (10.5281/zenodo.7233436) and in the GitHub repository (https://github.com/decolab/gec).
REFERENCES AND NOTES
- 1.J. R. Andrews-Hanna, J. Smallwood, R. N. Spreng, The default network and self-generated thought: Component processes, dynamic control, and clinical relevance. Ann. N. Y. Acad. Sci. 1316, 29–52 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.J. R. Andrews-Hanna, The brain's default network and its adaptive role in internal mentation. Neuroscientist 18, 251–270 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.S. Sonkusare, M. Breakspear, C. Guo, Naturalistic stimuli in neuroscience: Critically acclaimed. Trends Cogn. Sci. 23, 699–714 (2019). [DOI] [PubMed] [Google Scholar]
- 4.U. Hasson, Y. Nir, I. Levy, G. Fuhrmann, R. Malach, Intersubject synchronization of cortical activity during natural vision. Science 303, 1634–1640 (2004). [DOI] [PubMed] [Google Scholar]
- 5.A. Bartels, S. Zeki, Functional brain mapping during free viewing of natural scenes. Hum. Brain Mapp. 21, 75–85 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Y. Yeshurun, M. Nguyen, U. Hasson, The default mode network: Where the idiosyncratic self meets the shared social world. Nat. Rev. Neurosci. 22, 181–192 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.E. S. Finn, Is it time to put rest to rest? Trends Cogn. Sci. 25, 1021–1032 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.E. S. Finn, E. Glerean, U. Hasson, T. Vanderwal, Naturalistic imaging: The use of ecologically valid conditions to study brain function. Neuroimage 247, 118776 (2022). [DOI] [PubMed] [Google Scholar]
- 9.T. S. Coalson, D. C. Van Essen, M. F. Glasser, The impact of traditional neuroimaging methods on the spatial localization of cortical areas. Proc. Natl. Acad. Sci. U.S.A. 115, E6356–E6365 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.R. Cabeza, L. Nyberg, Imaging cognition II: An empirical review of 275 PET and fMRI studies. J. Cogn. Neurosci. 12, 1–47 (2000). [DOI] [PubMed] [Google Scholar]
- 11.V. Menon, M. D'Esposito, The role of PFC networks in cognitive control and executive function. Neuropsychopharmacology 47, 90–103 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.M. L. Kringelbach, The human orbitofrontal cortex: Linking reward to hedonic experience. Nat. Rev. Neurosci. 6, 691–702 (2005). [DOI] [PubMed] [Google Scholar]
- 13.G. L. Shulman, M. Corbetta, J. A. Fiez, R. L. Buckner, F. M. Miezin, M. E. Raichle, S. E. Petersen, Searching for activations that generalize over tasks. Hum. Brain Mapp. 5, 317–322 (1997). [DOI] [PubMed] [Google Scholar]
- 14.M. E. Raichle, A. M. MacLeod, A. Z. Snyder, W. J. Powers, D. A. Gusnard, G. L. Shulman, A default mode of brain function. Proc. Natl. Acad. Sci. U.S.A. 98, 676–682 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.R. L. Buckner, F. M. Krienen, B. T. T. Yeo, Opportunities and limitations of intrinsic functional connectivity MRI. Nat. Neurosci. 16, 832–837 (2013). [DOI] [PubMed] [Google Scholar]
- 16.M. W. Cole, D. S. Bassett, J. D. Power, T. S. Braver, S. E. Petersen, Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.I. Tavor, O. Parker Jones, R. B. Mars, S. M. Smith, T. E. Behrens, S. Jbabdi, Task-free MRI predicts individual differences in brain activity during task performance. Science 352, 216–220 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.G. Northoff, P. Qin, T. Nakao, Rest-stimulus interaction in the brain: A review. Trends Neurosci. 33, 277–284 (2010). [DOI] [PubMed] [Google Scholar]
- 19.S. Wainio-Theberge, A. Wolff, G. Northoff, Dynamic relationships between spontaneous and evoked electrophysiological activity. Commun. Biol. 4, 741 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Z. Huang, J. Zhang, A. Longtin, G. Dumont, N. W. Duncan, J. Pokorny, P. Qin, R. Dai, F. Ferri, X. Weng, G. Northoff, Is there a nonadditive interaction between spontaneous and evoked activity? Phase-dependence and its relation to the temporal structure of scale-free brain activity. Cereb. Cortex 27, 1037–1059 (2017). [DOI] [PubMed] [Google Scholar]
- 21.A. Wolff, S. de la Salle, A. Sorgini, E. Lynn, P. Blier, V. Knott, G. Northoff, Atypical temporal dynamics of resting state shapes stimulus-evoked activity in depression-an EEG study on rest-stimulus interaction. Front. Psych. 10, 719 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.A. Wolff, J. Gomez-Pilar, J. Zhang, J. Choueiry, S. de la Salle, V. Knott, G. Northoff, It's in the timing: Reduced temporal precision in neural activity of schizophrenia. Cereb. Cortex 32, 3441–3456 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.T. Vanderwal, J. Eilbott, F. X. Castellanos, Movies in the magnet: Naturalistic paradigms in developmental functional neuroimaging. Dev. Cogn. Neurosci. 36, 100600 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.L. Naci, R. Cusack, M. Anello, A. M. Owen, A common neural code for similar conscious experiences in different individuals. Proc. Natl. Acad. Sci. U.S.A. 111, 14277–14282 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.H. J. Gastaut, J. Bert, EEG changes during cinematographic presentation; moving picture activation of the EEG. Electroencephalogr. Clin. Neurophysiol. 6, 433–444 (1954). [DOI] [PubMed] [Google Scholar]
- 26.T. Bolt, J. S. Nomi, S. G. Vij, C. Chang, L. Q. Uddin, Inter-subject phase synchronization for exploratory analysis of task-fMRI. Neuroimage 176, 477–488 (2018). [DOI] [PubMed] [Google Scholar]
- 27.L. Xu, T. Bolt, J. S. Nomi, J. Li, X. Zheng, M. Fu, K. M. Kendrick, B. Becker, L. Q. Uddin, Inter-subject phase synchronization differentiates neural networks underlying physical pain empathy. Soc. Cogn. Affect. Neurosci. 15, 225–233 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.C. Grall, E. S. Finn, Leveraging the power of media to drive cognition: A media-informed approach to naturalistic neuroscience. Soc. Cogn. Affect. Neurosci. 17, 598–608 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.L. L. Gollo, A. Zalesky, R. M. Hutchison, M. van den Heuvel, M. Breakspear, Dwelling quietly in the rich club: Brain network determinants of slow cortical fluctuations. Philos. Trans. R. Soc. Lond. B Biol. Sci. 370, 20140165 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.S. Zeki, The response properties of cells in the middle temporal area (area MT) of owl monkey visual cortex. Proc. R. Soc. Lond. B Biol. Sci. 207, 239–248 (1980). [DOI] [PubMed] [Google Scholar]
- 31.J. M. Fuster, The Prefrontal Cortex (5th ed.) (Academic Press, London, ed. 3, 2015). [Google Scholar]
- 32.S. N. Haber, H. Liu, J. Seidlitz, E. Bullmore, Prefrontal connectomics: From anatomy to human imaging. Neuropsychopharmacology 47, 20–40 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.S. M. Kolk, P. Rakic, Development of prefrontal cortex. Neuropsychopharmacology 47, 41–57 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.N. P. Friedman, T. W. Robbins, The role of prefrontal cortex in cognitive control and executive function. Neuropsychopharmacology 47, 72–89 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.J. M. Fuster, Cognitive networks (Cognits) process and maintain working memory. Front. Neural Circuits 15, 790691 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.B. J. Baars, A Cognitive Theory of Consciousness (Cambridge Univ. Press, 1989). [Google Scholar]
- 37.S. Dehaene, M. Kerszberg, J. P. Changeux, A neuronal model of a global workspace in effortful cognitive tasks. Proc. Natl. Acad. Sci. U.S.A. 95, 14529–14534 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.G. Deco, D. Vidaurre, M. L. Kringelbach, Revisiting the Global Workspace orchestrating the hierarchical organization of the human brain. Nat. Human Behav. 5, 497–511 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.G. Deco, Y. Sanz Perl, E. Tagliazucchi, M. L. Kringelbach, The INSIDEOUT framework provides precise signatures of the balance of intrinsic and extrinsic dynamics in brain states. Commun. Biol. 5, 572 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.G. Buzsáki, The Brain from Inside Out (Oxford Univ. Press, 2019). [Google Scholar]
- 41.C. W. J. Granger, Investigating causal relations by econometric models and cross-spectral methods. Econometrica 37, 424–438 (1969). [Google Scholar]
- 42.A. Brovelli, D. Chicharro, J. M. Badier, H. Wang, V. Jirsa, Characterization of cortical networks and corticocortical functional connectivity mediating arbitrary visuomotor mapping. J. Neurosci. 35, 12643–12658 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.L. Barnett, A. K. Seth, The MVGC multivariate Granger causality toolbox: A new approach to Granger-causal inference. J. Neurosci. Methods 223, 50–68 (2014). [DOI] [PubMed] [Google Scholar]
- 44.A. Seif, M. Hafezi, C. Jarzynski, Machine learning the thermodynamic arrow of time. Nat. Phys. 17, 105–113 (2021). [Google Scholar]
- 45.C. Jarzynski, Equalities and inequalities: Irreversibility and the second law of thermodynamics at the nanoscale. Annu. Rev. Condens. Matter Phys. 2, 329–351 (2011). [Google Scholar]
- 46.C. W. Lynn, E. J. Cornblath, L. Papadopoulos, M. A. Bertolero, D. S. Bassett, Broken detailed balance and entropy production in the human brain. Proc. Natl. Acad. Sci. U.S.A. 118, e2109889118 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.L. de la Fuente, F. Zamberlan, H. Bocaccio, M. Kringelbach, G. Deco, Y. Sanz Perl, E. Tagliazucchi, Temporal irreversibility of neural dynamics as a signature of consciousness. Cereb. Cortex , bhac177 10.1093/cercor/bhac177 (2022). [DOI] [PubMed] [Google Scholar]
- 48.A. S. Eddington, The Nature of the Physical World (Macmillan, 1928). [Google Scholar]
- 49.Y. Sanz Perl, H. Bocaccio, I. Perez-Ipiña, S. Laureys, H. Laufs, M. Kringelbach, G. Deco, E. Tagliazucchi, Nonequilibrium brain dynamics as a signature of consciousness. Phys. Rev. E 104, 014411 (2021). [DOI] [PubMed] [Google Scholar]
- 50.K. J. Friston, L. Harrison, W. Penny, Dynamic causal modelling. Neuroimage 19, 1273–1302 (2003). [DOI] [PubMed] [Google Scholar]
- 51.M. Golesorkhi, J. Gomez-Pilar, F. Zilio, N. Berberian, A. Wolff, M. C. E. Yagoub, G. Northoff, The brain and its time: Intrinsic neural timescales are key for input processing. Commun. Biol. 4, 970 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.G. Deco, J. Cruzat, M. L. Kringelbach, Brain songs framework used for discovering the relevant timescale of the human brain. Nat. Commun. 10, 583 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.X. Kobeleva, A. López-González, M. L. Kringelbach, G. Deco, Revealing the relevant spatiotemporal scale underlying whole-brain dynamics. Front. Neurosci. 15, 715861 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.M. M. Mesulam, From sensation to cognition. Brain 121, 1013–1052 (1998). [DOI] [PubMed] [Google Scholar]
- 55.P. Barttfeld, L. Uhrig, J. D. Sitt, M. Sigman, B. Jarraya, S. Dehaene, Signature of consciousness in the dynamics of resting-state brain activity. Proc. Natl. Acad. Sci. U.S.A. 112, 887–892 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.E. Tagliazucchi, D. R. Chialvo, M. Siniatchkin, E. Amico, J.-F. Brichant, V. Bonhomme, Q. Noirhomme, H. Laufs, S. Laureys, Large-scale signatures of unconsciousness are consistent with a departure from critical dynamics. J. R. Soc. Interface 13, 20151027 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.M. L. Kringelbach, G. Deco, Brain states and transitions: Insights from computational neuroscience. Cell Rep. 32, 108128 (2020). [DOI] [PubMed] [Google Scholar]
- 58.M. Breakspear, Dynamic models of large-scale brain activity. Nat. Neurosci. 20, 340–352 (2017). [DOI] [PubMed] [Google Scholar]
- 59.G. Deco, M. L. Kringelbach, Great expectations: Using whole-brain computational connectomics for understanding neuropsychiatric disorders. Neuron 84, 892–905 (2014). [DOI] [PubMed] [Google Scholar]
- 60.K. Christoff, Z. C. Irving, K. C. Fox, R. N. Spreng, J. R. Andrews-Hanna, Mind-wandering as spontaneous thought: A dynamic framework. Nat. Rev. Neurosci. 17, 718–731 (2016). [DOI] [PubMed] [Google Scholar]
- 61.D. J. Felleman, D. C. Van Essen, Distributed hierarchical processing in the primate cerebral cortex. Cereb. Cortex 1, 1–47 (1991). [DOI] [PubMed] [Google Scholar]
- 62.N. T. Markov, J. Vezoli, P. Chameau, A. Falchier, R. Quilodran, C. Huissoud, C. Lamy, P. Misery, P. Giroud, S. Ullman, P. Barone, C. Dehay, K. Knoblauch, H. Kennedy, Anatomy of hierarchy: Feedforward and feedback pathways in macaque visual cortex. J. Comp. Neurol. 522, 225–259 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.E. Bullmore, O. Sporns, The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349 (2012). [DOI] [PubMed] [Google Scholar]
- 64.M. P. van den Heuvel, O. Sporns, Rich-club organization of the human connectome. J. Neurosci. 31, 15775–15786 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.P. Hagmann, L. Cammoun, X. Gigandet, R. Meuli, C. J. Honey, V. J. Wedeen, O. Sporns, Mapping the structural core of human cerebral cortex. PLOS Biol. 6, e159 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.G. Zamora-López, C. Zhou, J. Kürths, Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Front. Neuroinform. 4, 1 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.S. B. Eickhoff, R. T. Constable, B. T. T. Yeo, Topographic organization of the cerebral cortex and brain cartography. Neuroimage 170, 332–347 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.D. S. Margulies, S. S. Ghosh, A. Goulas, M. Falkiewicz, J. M. Huntenburg, G. Langs, G. Bezgin, S. B. Eickhoff, F. X. Castellanos, M. Petrides, E. Jefferies, J. Smallwood, Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci. U.S.A. 113, 12574–12579 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.K. Glomb, M. L. Kringelbach, G. Deco, P. Hagmann, J. Pearson, S. Atasoy, Functional harmonics reveal multi-dimensional basis functions underlying cortical organization. Cell Rep. 36, 109554 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.S. Atasoy, I. Donnelly, J. Pearson, Human brain networks function in connectome-specific harmonic waves. Nat. Commun. 7, 10340 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.A. Wolff, N. Berberian, M. Golesorkhi, J. Gomez-Pilar, F. Zilio, G. Northoff, Intrinsic neural timescales: Temporal integration and segregation. Trends Cogn. Sci. 26, 159–173 (2022). [DOI] [PubMed] [Google Scholar]
- 72.M. Golesorkhi, J. Gomez-Pilar, Y. Çatal, S. Tumati, M. C. E. Yagoub, E. A. Stamatakis, G. Northoff, From temporal to spatial topography: Hierarchy of neural dynamics in higher- and lower-order networks shapes their complexity. Cereb. Cortex 32, 5637–5653 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.M. Golesorkhi, J. Gomez-Pilar, S. Tumati, M. Fraser, G. Northoff, Temporal hierarchy of intrinsic neural timescales converges with spatial core-periphery organization. Commun. Biol. 4, 277 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.M. Lobier, F. Siebenhühner, S. Palva, J. M. Palva, Phase transfer entropy: A novel phase-based measure for directed connectivity in networks coupled by oscillatory interactions. Neuroimage 85 (Pt. 2), 853–872 (2014). [DOI] [PubMed] [Google Scholar]
- 75.A. Hillebrand, P. Tewarie, E. van Dellen, M. Yu, E. W. Carbo, L. Douw, A. A. Gouw, E. C. van Straaten, C. J. Stam, Direction of information flow in large-scale resting-state networks is frequency-dependent. Proc. Natl. Acad. Sci. U.S.A. 113, 3867–3872 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.L. Barnett, S. D. Muthukumaraswamy, R. L. Carhart-Harris, A. K. Seth, Decreased directed functional connectivity in the psychedelic state. Neuroimage 209, 116462 (2020). [DOI] [PubMed] [Google Scholar]
- 77.C. J. Honey, O. Sporns, Dynamical consequences of lesions in cortical networks. Hum. Brain Mapp. 29, 802–809 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.J. Alstott, M. Breakspear, P. Hagmann, L. Cammoun, O. Sporns, Modeling the impact of lesions in the human brain. PLOS Comput. Biol. 5, e1000408 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.O. David, I. Guillemain, S. Saillet, S. Reyt, C. Deransart, C. Segebarth, A. Depaulis, Identifying neural drivers with functional MRI: An electrophysiological validation. PLOS Biol. 6, 2683–2697 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.K. Friston, Causal modelling and brain connectivity in functional magnetic resonance imaging. PLOS Biol. 7, e33 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.S. M. Smith, K. L. Miller, G. Salimi-Khorshidi, M. Webster, C. F. Beckmann, T. E. Nichols, J. D. Ramsey, M. W. Woolrich, Network modelling methods for FMRI. Neuroimage 54, 875–891 (2011). [DOI] [PubMed] [Google Scholar]
- 82.A. K. Seth, P. Chorley, L. C. Barnett, Granger causality analysis of fMRI BOLD signals is invariant to hemodynamic convolution but not downsampling. Neuroimage 65, 540–555 (2013). [DOI] [PubMed] [Google Scholar]
- 83.M. A. Killingsworth, D. T. Gilbert, A wandering mind is an unhappy mind. Science 330, 932 (2010). [DOI] [PubMed] [Google Scholar]
- 84.J. E. Cutting, K. L. Brunick, A. Candan, Perceiving event dynamics and parsing Hollywood films. J. Exp. Psychol. Hum. Percept. Perform. 38, 1476–1490 (2012). [DOI] [PubMed] [Google Scholar]
- 85.R. Rajimehr, H. Xu, A. Farahani, S. Kornblith, J. Duncan, R. Desimone, Functional architecture of cerebral cortex during naturalistic movie-watching. bioRxiv, 2022.2003.2014.483878 (2022).
- 86.E. S. Finn, P. A. Bandettini, Movie-watching outperforms rest for functional connectivity-based prediction of behavior. Neuroimage 235, 117963 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.D. M. Barch, G. C. Burgess, M. P. Harms, S. E. Petersen, B. L. Schlaggar, M. Corbetta, M. F. Glasser, S. Curtiss, S. Dixit, C. Feldt, D. Nolan, E. Bryant, T. Hartley, O. Footer, J. M. Bjork, R. Poldrack, S. Smith, H. Johansen-Berg, A. Z. Snyder, D. C. Van Essen; WU-Minn HCP Consortium , Function in the human connectome: Task-fMRI and individual differences in behavior. Neuroimage 80, 169–189 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.K. Setsompop, R. Kimmlingen, E. Eberlein, T. Witzel, J. Cohen-Adad, J. A. McNab, B. Keil, M. D. Tisdall, P. Hoecht, P. Dietz, S. F. Cauley, V. Tountcheva, V. Matschl, V. H. Lenz, K. Heberlein, A. Potthast, H. Thein, J. Van Horn, A. Toga, F. Schmitt, D. Lehne, B. R. Rosen, V. Wedeen, L. L. Wald, Pushing the limits of in vivo diffusion MRI for the human connectome project. Neuroimage 80, 220–233 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.M. F. Glasser, S. N. Sotiropoulos, J. A. Wilson, T. S. Coalson, B. Fischl, J. L. Andersson, J. Xu, S. Jbabdi, M. Webster, J. R. Polimeni, D. C. Van Essen, M. Jenkinson; WU-Minn HCP Consortium , The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.S. M. Smith, C. F. Beckmann, J. Andersson, E. J. Auerbach, J. Bijsterbosch, G. Douaud, E. Duff, D. A. Feinberg, L. Griffanti, M. P. Harms, M. Kelly, T. Laumann, K. L. Miller, S. Moeller, S. Petersen, J. Power, G. Salimi-Khorshidi, A. Z. Snyder, A. T. Vu, M. W. Woolrich, J. Xu, E. Yacoub, K. Uğurbil, D. C. Van Essen, M. F. Glasser; WU-Minn HCP Consortium , Resting-state fMRI in the Human Connectome Project. Neuroimage 80, 144–168 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.T. Navarro Schroder, K. V. Haak, N. I. Zaragoza Jimenez, C. F. Beckmann, C. F. Doeller, Functional topography of the human entorhinal cortex. eLife 4, e06738 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.G. Salimi-Khorshidi, G. Douaud, C. F. Beckmann, M. F. Glasser, L. Griffanti, S. M. Smith, Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.L. Griffanti, G. Salimi-Khorshidi, C. F. Beckmann, E. J. Auerbach, G. Douaud, C. E. Sexton, E. Zsoldos, K. P. Ebmeier, N. Filippini, C. E. Mackay, S. Moeller, J. Xu, E. Yacoub, G. Baselli, K. Ugurbil, K. L. Miller, S. M. Smith, ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. Neuroimage 95, 232–247 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.R. Oostenveld, P. Fries, E. Maris, J.-M. Schoffelen, FieldTrip: Open source software for advanced analysis of MEG, EEG, and invasive electrophysiological data. Comput. Intell. Neurosci. 2011, 156869 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.R. S. Desikan, F. Ségonne, B. Fischl, B. T. Quinn, B. C. Dickerson, D. Blacker, R. L. Buckner, A. M. Dale, R. P. Maguire, B. T. Hyman, M. S. Albert, R. J. Killiany, An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980 (2006). [DOI] [PubMed] [Google Scholar]
- 96.A. Klein, J. Tourville, 101 labeled brain images and a consistent human cortical labeling protocol. Front. Neurosci. 6, 171 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.G. Deco, J. Cruzat, J. Cabral, E. Tagliazucchi, H. Laufs, N. K. Logothetis, M. L. Kringelbach, Awakening: Predicting external stimulation to force transitions between different brain states. Proc. Natl .Acad. Sci. U.S.A. 116, 18088–18097 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.G. Deco, M. L. Kringelbach, V. Jirsa, P. Ritter, The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Sci. Rep. 7, 3095 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Y. A. Kuznetsov, Elements of applied bifurcation theory (Springer, 1998). [Google Scholar]
- 100.F. Freyer, J. A. Roberts, R. Becker, P. A. Robinson, P. Ritter, M. Breakspear, Biophysical mechanisms of multistability in resting-state cortical rhythms. J. Neurosci. 31, 6353–6361 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.F. Freyer, J. A. Roberts, P. Ritter, M. Breakspear, A canonical model of multistability and scale-invariance in biological systems. PLOS Comput. Biol. 8, e1002634 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.G. Deco, J. Cabral, M. W. Woolrich, A. B. A. Stevner, T. J. van Hartevelt, M. L. Kringelbach, Single or multiple frequency generators in on-going brain activity: A mechanistic whole-brain model of empirical MEG data. Neuroimage 152, 538–550 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.M. L. Kringelbach, A. R. McIntosh, P. Ritter, V. K. Jirsa, G. Deco, The rediscovery of slowness: Exploring the timing of cognition. Trends Cogn. Sci. 19, 616–628 (2015). [DOI] [PubMed] [Google Scholar]
- 104.G. Deco, M. L. Kringelbach, Turbulent-like dynamics in the human brain. Cell Rep. 33, 108471 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.G. Deco, Y. Sanz Perl, P. Vuust, E. Tagliazucchi, H. Kennedy, M. L. Kringelbach, Rare long-range cortical connections enhance human information processing. Curr. Biol. 31, 4436–4448.e5 (2021). [DOI] [PubMed] [Google Scholar]