Abstract
We use mental models of the world – cognitive maps - to guide behavior. The lateral orbitofrontal cortex (lOFC) is typically thought to support behavior by deploying these maps to simulate outcomes, but recent evidence suggests that it may instead support behavior by supporting map creation. We tested between these two alternatives using outcome-specific devaluation and a high-potency chemogenetic approach. Selectively inactivating lOFC principal neurons when male rats learned distinct cue-outcome associations, but prior to outcome devaluation, disrupted subsequent inference, confirming a role for the lOFC in creating new maps. However, lOFC inactivation surprisingly led to generalized devaluation, a result inconsistent with a complete mapping failure. Using a novel reinforcement learning framework, we show that this effect is best explained by a circumscribed deficit in credit assignment precision during map construction, suggesting that lOFC plays a selective role in defining the specificity of associations that comprise cognitive maps.
Editor summary:
Animals form cognitive maps of the world to guide behavior. This study shows that the lateral orbitofrontal cortex is essential for creating precise, outcome-specific cognitive maps during initial learning, but not for general map creation in itself.
Introduction
Animals behave in ways that suggest that the brain can build, store, and use internal representations that account for the predictive relationships between elements in the external world. Also called associative models or cognitive maps, these mental constructs are thought to be especially important for adaptive behavior under new or changed conditions1. The inability to use such models properly is thought to be a key feature of mental illnesses such as schizophrenia2, substance use disorder3, and obsessive compulsive disorder4. However, despite their importance, we are only beginning to understand the informational structure of cognitive maps and how the brain creates, stores, and uses them.
In this regard, the lateral orbitofrontal cortex (lOFC) has been extensively implicated in model-based behaviors5–7. However, its exact contributions to defining or using the cognitive maps that support these behaviors are still controversial. One influential idea is that the lOFC represents the current task space to allow mental simulation of likely outcomes at the time a decision is made8–10. While broadly consistent with the literature, this view is most strongly supported by devaluation experiments in which pairing a given outcome with illness (or satiety) leads to reduced conditioned responding to a cue predicting that outcome in a probe test. This effect has been shown repeatedly and across species to require the lOFC at the time of the probe 11–15, a result generally interpreted as showing a necessity for lOFC in using the map formed earlier in training. Compromising the lOFC disrupts this usage, resulting in supposedly “model-free” or habit-like behavior. By this account, the lOFC offers a form of specialized working memory required for mental simulation using established models.
However, recent studies suggest that the lOFC might instead serve as the cognitive “cartographer”, playing a critical role not in using maps but rather in creating and modifying them16. Studies across different tasks17–19, including economic choice20, sensory pre-conditioning21, and Pavlovian to instrumental transfer (PIT)22, show that the lOFC or its projections to other regions are required for acquiring or updating mental models during task performance. According to this view, lOFC manipulations in devaluation probe tests could affect behavior not because lOFC is required for mental simulation but rather because the probe test requires changes to, or recombinations of, existing cognitive maps.
A logical, but untested, corollary of this alternative proposal is that the lOFC should also be necessary during initial conditioning in the reinforcement devaluation task, when a major part of the cognitive map used in the later probe is created. On the other hand, if the classic view is correct – that, at the time of decision-making, the lOFC just uses maps made and maintained elsewhere – then this region should not be necessary during the conditioning phase. This prediction allows for an acid test to differentiate whether the lOFC is a reader or a cartographer of cognitive maps. Here, we performed this test using a within-subject outcome-specific devaluation task and high-potency chemogenetics to inactivate lOFC transiently when maps were first being formed.
Results
lOFC is needed for normal map creation
Food restricted male rats, transfected with either hM4d (inhibitory DREADD receptor, n=15) or only mCherry (control; n=13) in the lOFC (Figure 1), served as experimental subjects. The lack of female rats, due to pandemic-related logistical issues, is a potential limitation of this study. That said, we have not found sex differences in overall performance or in the effects of lOFC inactivation in previous work 21. Rats underwent conditioning in which two different auditory cues (A and B) predicted the delivery of either banana- or bacon-flavored pellets (Figure 2A). Before each session, rats were injected with JHU37160 dihydrochloride (JH60; i.p. 0.2 mg/kg), a high-potency DREADD agonist 23, to inactivate lOFC principal neurons in hM4d-transfected rats both transiently and selectively, as validated previously 24. The use of this new generation compound avoids several confounds associated with other DREADD agonists 23,25.
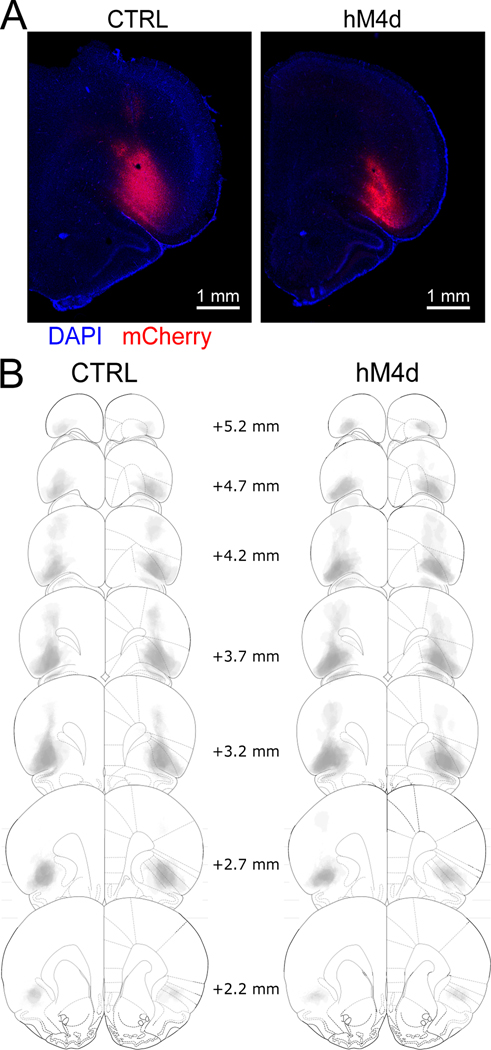
Figure 1. Chemogenetic strategy for determining the role of lOFC in cognitive map creation.
(A): Representative photomicrographs of viral transfection in one control and one hM4d rat. (B): Reconstruction of viral expression patterns in the lOFC across the control and hM4d groups. Viral spread was mostly contained withing lOFC and was similar for control and hM4d subjects. CTRL n=13 and hM4d n=15 biologically independent animals.
Figure 2. Chemogenetic inactivation of lOFC during conditioning abolishes subsequent sensory-specific responses to devalued cues.
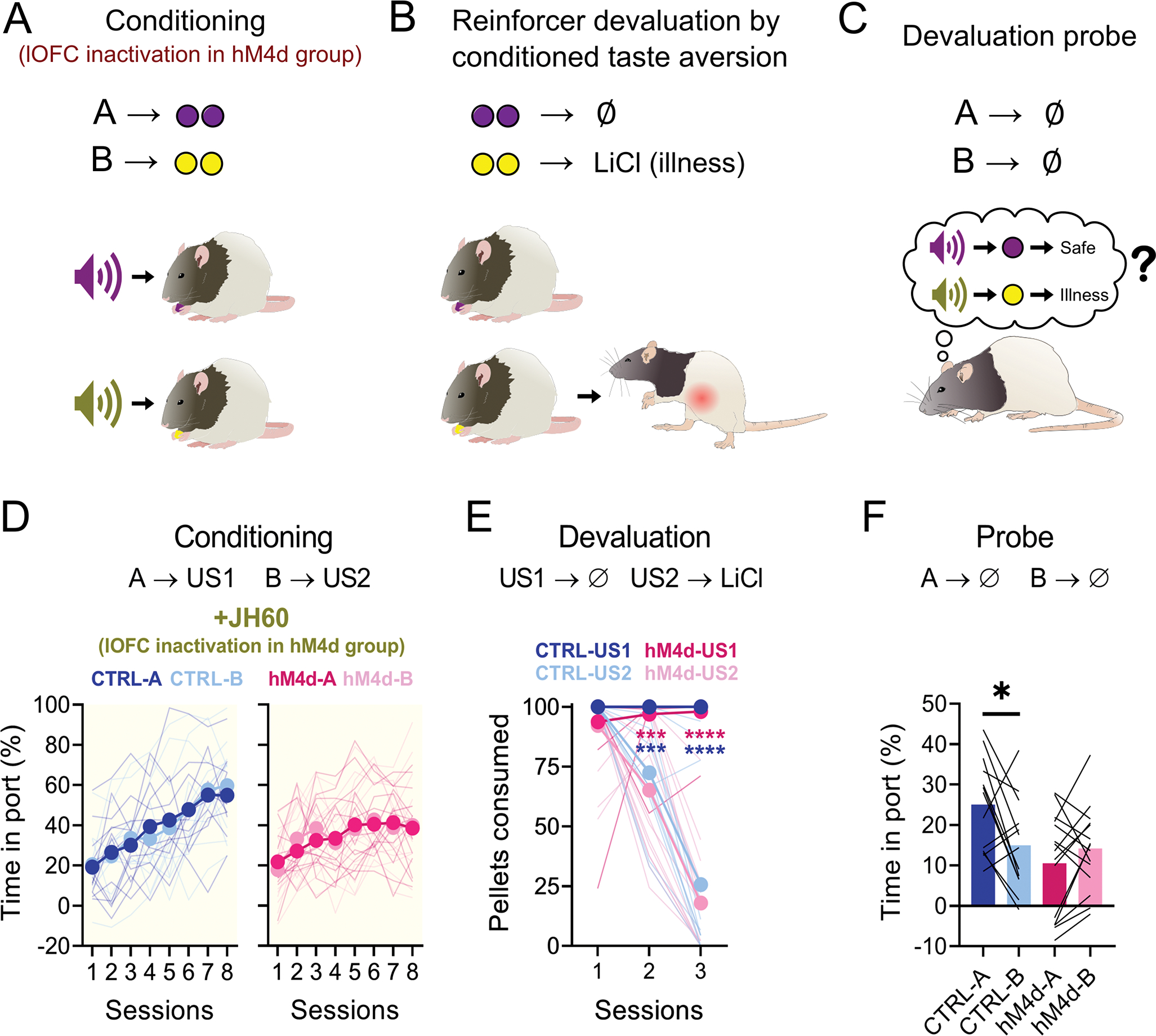
(A-C): Schematic of the behavioral procedures. (A): Rats were conditioned to two cues, A and B, which lead to different rewards. The lOFC was inactivated in the hM4d group. (B): Later, one of the rewards was paired with LiCl injections. (C): Finally, rats were re-exposed to the conditioned cues, testing if a model-based association had been established between them and the rewards. (D): Food cup responding during conditioning. There was no isolated or interaction effect of cue identity (3-way ANOVA; A vs B F(1,26) = 0.021, P = 0.886; sessions vs cue: F(7,182) = 1.353, P = 0.897; sessions vs cue vs group: F(7,182) = 0.066, P = 0.936;), nor an isolated group effect (F(1,26) = 0.717, P = 0.405), and rats of both groups increased responding as sessions progressed (F(7,182) = 26.74, P < 0.0001****). However, there was a significant interaction between group and session progression (F(7,182) = 4.672, P<0.0001****), visible in the last two sessions. (E): Pellet consumption during CTA. Rats from both groups consumed nearly all pellets in the first CTA session and consumed less of the devalued pellet type as sessions progressed (3-way ANOVA; session effect: F(2,52) = 64.18, P<0.0001****; session vs pellet type: F(2,52) = 83.36, P<0.0001****; all other comparisons: F < 3, P > 0.099). (F): Food cup responding during probe. There was a significant effect of group (2-way ANOVA; F(1,26) = 4.34, P=0.047*), and the interaction of the group with the cues (F(1,26) = 8.013, P=0.009**), as control rats responded more to A than to B, while hM4d rats responded equally to both cues (all other comparisons: F < 3.5, P > 0.089). Asterisks in graphs indicate post-hoc multiple comparison test results. See Supplementary Table 1 for more detailed statistics. Data are represented as mean ± SEM. CTRL n= 13 and hM4d n=15 biologically independent animals. *P<0.05; ***P<0.001; ****P<0.0001.
Despite inactivation, rats in both groups progressively increased responding to the food cup during presentation of either cue (Figure 2D). Initial acquisition rates were similar, although rats in the hM4d group responded slightly less during the last two sessions of conditioning, in agreement with recent work showing that transient lOFC inactivation can reduce asymptotic conditioned responding in some settings26.
After conditioning, rats were subjected to conditioned taste aversion (CTA) training, in which one of the rewards (the one associated with B), was paired with LiCl injections, inducing nausea (Figure 2B). Rats initially preferred both rewards equally, but quickly and selectively reduced consumption of the pellet type paired with LiCl (Figure 2E).
Finally, after CTA training, rats were given a probe test, in which the cues were presented as during conditioning but without reward (Figure 2C). As expected, control rats responded more to cue A (paired with the non-devalued pellet) than to cue B (paired with the devalued pellet), indicating they had learned the specific cue-reward and reward-illness associations and were able to integrate them in the probe test to infer that B might lead to devalued reward (Figure 2F). By contrast, rats in the hM4d group responded equally to both cues (Figure 2F). This result is inconsistent with the hypothesis that lOFC’s main function is to use mental maps to support model-based behaviors at the time a decision is made, and instead supports the alternative hypothesis that lOFC plays a critical role in drawing (or redrawing) those maps16.
That said, while this result supports this alternative hypothesis, rats in the hM4d group did not simply lack the devaluation effect, as would be expected if acquisition of the initial model were entirely dependent on OFC, but rather they appeared to generalize the devaluation effect across cues, both as a group (Figure 2F) and at the individual level (Figure 3A). This generalization effect was evident even if responses during the probe were normalized to the end of conditioning, indicating that the effect was not related to the modest reduction in asymptotic conditioned responding caused by OFC inactivation (Figure 3B). Indeed, that these two effects were orthogonal to each other is further supported by the lack of correlation between responding at the end of conditioning and the effect of devaluation (Figure 3C). Generalization in the hM4d group was also independent of extinction dynamics, which were similar in the two groups (Figure 3D), ruling out weaker learning or retention; nor was it related to differences in CTA retention as preference tests revealed that CTA effects were similar in the two groups after the probe test (Figure 3E).
Figure 3. lOFC inactivation during initial learning leads to generalized devaluation.
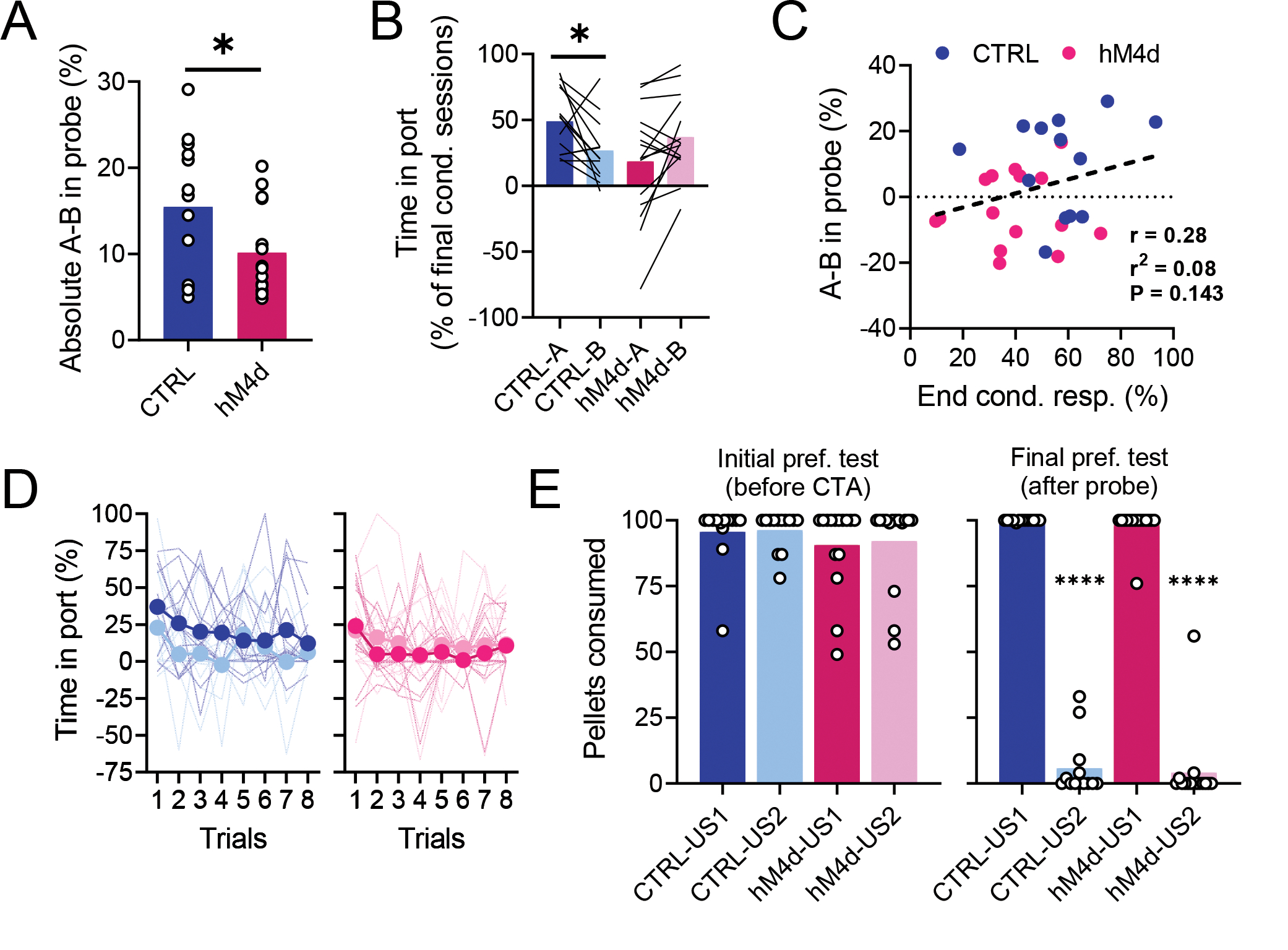
(A): Absolute difference in responding to cues A and B in the probe. Rats in the hM4d group were more similar in their responding to cues A and B (two-tailed unpaired t-test, P = 0.0436*), which strengthens the interpretation of generalized learning. (B): Food port responding in the final probe session but normalized to the last two sessions of conditioning. Normalization did not abolish the observed generalization effect. There was a significant interaction effect of the group with the cues (2-way ANOVA, P = 0.002**; all other comparisons: F < 0.95, P > 0.348), as well as only a significant difference between A and B in the control group in the post-hoc test. (C): Differential responding to valued and devalued cues (mean responding to A – mean responding to B) was not correlated (linear regression; r2=0.28, P=0.143)to the conditioned responding at the end of initial learning (average of % time in port for both cues in the last two sessions of conditioning). (D): Trial-by-trial responding behavior during the probe test. Analyses (3-way ANOVA) showed a main effect of trial progression, i.e., extinction learning (F7,182 = 4.14, P = 0.0003***), and an interaction effect of cue and group (F1,26 = 4.76, P = 0.038*), but no other effect (all other comparisons, F < 3.12, P > 0.09), suggesting that the observed differences in overall responding between groups cannot be ascribed to different extinction dynamics. (E): Consumption of pellets during preference tests for CTRL (blue and light blue) and hM4d (red and pink) rats. Rats from both groups consumed all pellets similarly during the first preference test (2-way ANOVA; ND × D: F1,26 = 0.12, P = 0.7318; CTRL vs hM4d: F1,26 = 1.235, P = 0.2766; interaction: F1,26 = 0.0171, P = 0.8969) and both groups equally consumed significantly less of the devalued pellet type (the one previously associated with cue B and paired with LiCl during CTA) in the second preference test (2-way ANOVA; ND vs D: F1,26 = 1364, P < 0.0001****; CTRL vs hM4d: F1,26 = 0.3519, P = 0.5582; interaction: F1,26 = 0.0005, P = 0.9825). See Supplementary Table 1 for more detailed statistics. Asterisks in the graphs indicate results of post-hoc multiple comparison tests. Data are represented as mean ± SEM. CTRL n= 13 and hM4d n=15 biologically independent animals. *P<0.05; ****P<0.0001.
Generalization of devaluation also could not be accounted for by gross effects of lOFC inactivation on perception or memory. To show this, we tested a subset of these rats in an object recognition task 27. lOFC was inactivated prior to the sample phase of the task, while the rats first explored two identical objects (Figure 4A). Over the next 2 days, the rats were brought back to the same arena for two recognition tests in which novel objects were substituted for the objects introduced in the sample phase (Figure 4B–C). If lOFC inactivation in these rats induced perceptual confusion, accelerated forgetting, or context-dependent learning, then inactivation in the sample phase of this task should have disrupted object discrimination in the first but not the second recognition test, yet we found no such effect (Figure 4D–I).
Figure 4. lOFC inactivation does not affect object recognition.
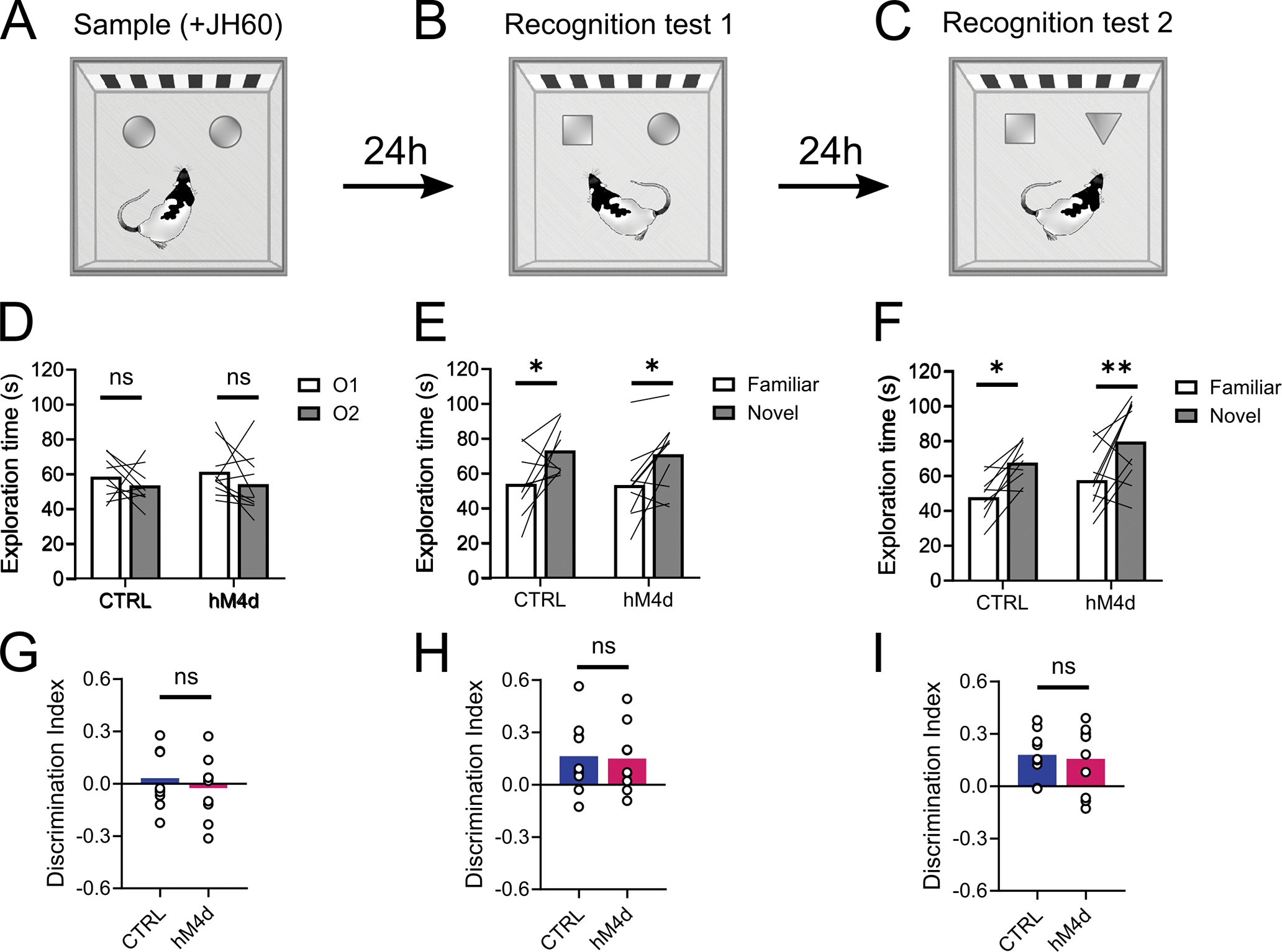
(A): Sample phase, where rats explored two identical objects and received JH60 injections. (B): First recognition test, where one familiar object was replaced by a novel one. (C):Second recognition test, where the previous familiar object was substituted by yet another novel object. (D and G): Rats in both groups explored the two objects for the same amount of time during sample (2-way ANOVA; O1 × O2: F1,17 = 1.833, P = 0.193; CTRL vs hM4d: F1,17 = 0.14, P = 0.712; interaction: F1,26 = 0.059, P = 0.809)(D) which was evident in the discrimination index (two-tailed unpaired t-test, P = 0.634)(G), demonstrating that lOFC inactivation does not affect exploratory behavior in this task. (E and H): Rats from both groups showed equally robust object recognition learning, evident in the increased exploration of the novel object (2-way ANOVA; Familiar × Novel: F1,17 = 13.53, P = 0.002**; CTRL vs hM4d: F1,17 = 0.045, P = 0.835; interaction: F1,26 = 0.025, P = 0.876) (E) and an increase in the discrimination index, which was identical between groups (two-tailed unpaired t-test; P = 0.882) (H), indicating that lOFC inactivation in sample did not affect recognition learning or memory retention, nor did it induce some form of context-dependent learning. (F and I): Again, rats in both the control and hM4d groups showed a similar level of preference for the novel object (2-way ANOVA; Familiar × Novel: F1,17 = 18.13, P = 0.0005***; CTRL vs hM4d: F1,17 = 3.085, P = 0.097; interaction: F1,26 = 0.053, P = 0.82) (F), as confirmed in the discrimination index (two-tailed unpaired t-test; P = 0.775)(I), confirming that learning under the effects of JH60 injections was similar to when no drug was injected. Asterisks in E and F indicate results of post-hoc multiple comparison tests. Data are represented as mean ± SEM. CTRL n= 9 and hM4d n=10 biologically independent animals. *P<0.05, **P<0.01.
lOFC determines cognitive map precision
The generalization of devaluation in the lOFC inactivated group was unexpected and intriguing, since model-based learning is traditionally treated as an all-or-none phenomenon. A complete failure of model-based control would leave only devaluation-insensitive, model-free behavior intact, resulting in high responding to both cues. It has been proposed that associative learning may operate as a dynamic mixture of model-based and model-free learning28, and that the lOFC may mediate this process29. Therefore, we considered whether our results could be explained by a change in the balance between model-based to model-free learning under lOFC inactivation. This explanation has some intrinsic disadvantages, as it requires at least two parallel learning systems and a third process to integrate their outputs, i.e., it is complex, with many free parameters. We found that it was possible to reproduce our results with this approach provided we also added a forgetting parameter (Extended Data Figure 1). However, the resultant fits were hard to reconcile with the general understanding of lOFC function, as they did not produce a decrease in model-based learning with lOFC inactivation, but rather an increase in model-free learning rates (Extended Data Figure 1C). This suggests a form of structural over-fitting, consistent with the observation that the fitted parameters could not be reliably recovered from simulated data (Extended Data Figure 1D). Thus, a complete or partial shift from model-based to model-free control seemed not to offer a good explanation for the experimental results.
A more promising way to account for the results is to consider the possibility that the hM4d subjects are still building, and then using, a cognitive map, but that the map is different – perhaps less precise – without the contribution of lOFC during its initial formation. This idea would be consistent with recent arguments against pure model-free processing 30, evidence that the lOFC is particularly important for sculpting representations of various aspects of tasks9, and findings in lOFC-lesioned macaques of impaired credit assignment 31. Translating this idea to the current task, we hypothesized that the lOFC might be particularly important for segregating and separately updating each unique cue-outcome pair, which were of uncertain importance in initial conditioning.
We tested this proposal by fitting our data with a novel model-based reinforcement learning algorithm trained on the same sequence of trials as in the task28,32 (Figure 5). The effect of lOFC inactivation on learning during initial conditioning was captured by introducing an “imprecision” parameter (χ) that defined how credit assignment spread – i.e., whether updates were selective for each cue-outcome pair during the conditioning phase of the task (Figure 5A). Thus, receiving a banana-flavored pellet after cue A updates the association between the alternative cue B and the banana-flavored pellet by an amount proportional to χ. Only if χ = 0, would the update be confined exclusively to cue A. A model with a high χ value would therefore be able to learn that auditory cues predict sucrose pellets but would have trouble differentiating which pellet flavor (e.g., banana) is associated with which cue (A or B). Substantial confusion during conditioning (high χ) would cause the loss of value imposed by the following CTA training (Figure 5B) to be at least partially generalized to both cues A and B, due to the imprecision of specific state predictions and subsequent inference (Figure 5C), noting that the rats remained well aware of the separate values of the pellet types after the probe test (Figure 3E).
Figure 5. A model-based reinforcement learning algorithm that simulates imprecise state identity credit assignment.
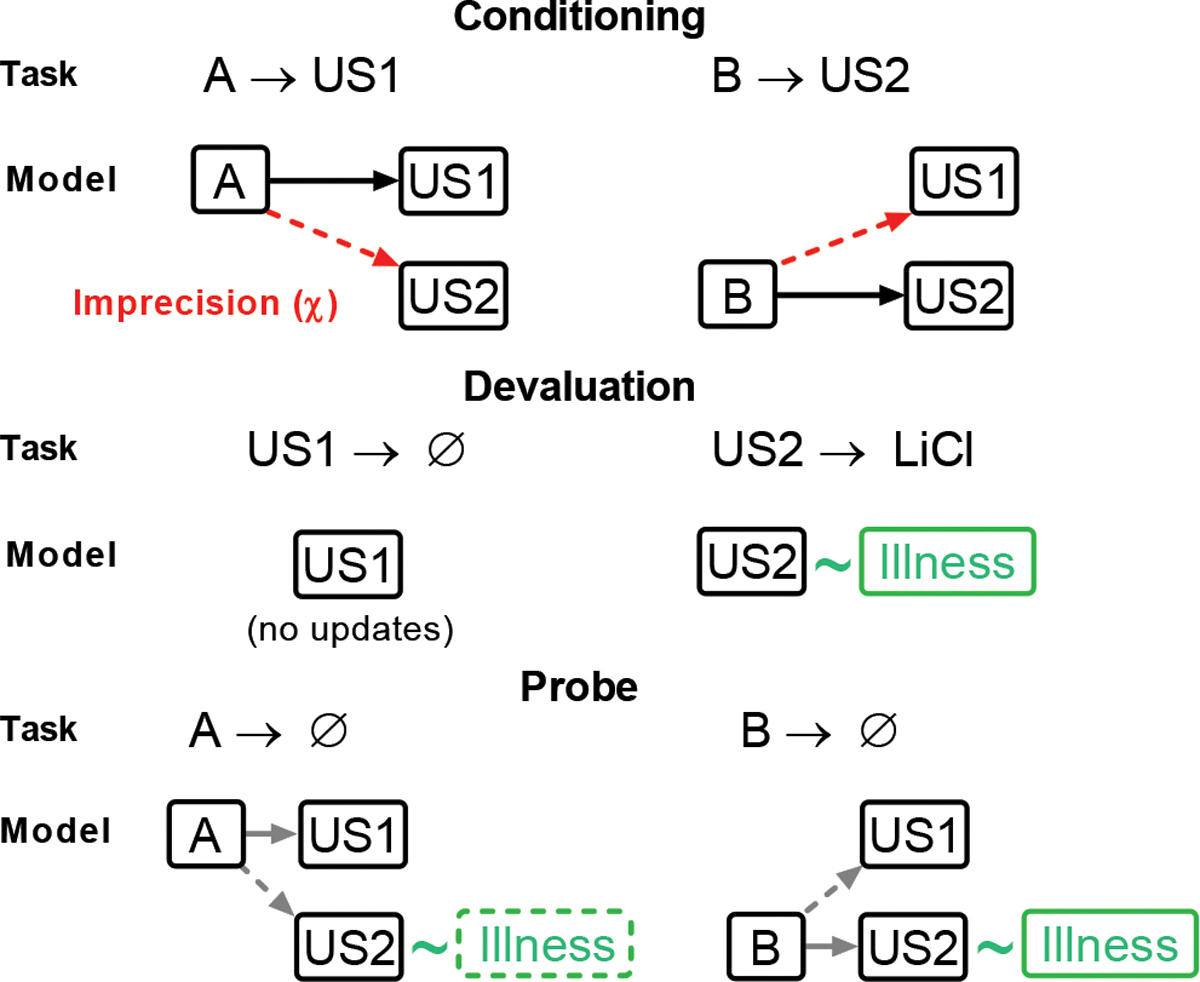
(A): During initial conditioning, the value and state transition matrices are updated according to the task contingencies (A-US1, B-US2; solid black arrows). In parallel, a separate update of the opposite association (A-US2, B-US1) occurs proportionately to the imprecision term χ (dashed red arrows). (B): During the CTA devaluation procedure, state values are updated in line with task contingencies, leading to no changes in the value estimate for US1, but to a reduced value estimate for US2, as it is now associated with illness (green box). (C) During the probe, the value of cue states is inferred (grey arrows) from the state transition matrices (learned during conditioning) and value estimates of US1 and US2 (updated during CTA). In case of a high χ during conditioning this leads to imprecise value estimates for A and B, as each cue is associated with both outcomes.
We found that this “imprecision” model fit our behavioral results well (Figure 6A), reproducing the normal behavior in the control group and all effects of lOFC inactivation, including both the apparent generalization of devaluation in the probe test (Figure 6B–C) as well as the lower asymptotic performance in conditioning (Figure 6E–F). Critical parameters in the model, particularly χ, were recoverable from simulated data (Extended Data Figure 2)33. Model fits to data from control and hM4d groups differed in their imprecision term χ, which was significantly higher in hM4d models (Figure 6B and Supplementary Table 2). Furthermore, χ was highly correlated with the difference in responding to the valued (A) versus devalued (B) cues during probe (Figure 6C), even though this parameter only affected learning during conditioning (Figure 5A). Notably, this effect was not due to an effect of χ on the strength of conditioning, as these were uncorrelated (Figure 6D).
Figure 6. lOFC inactivation effects on reinforcer devaluation are explained by a deficit in differentiating specific cue-outcome associations.
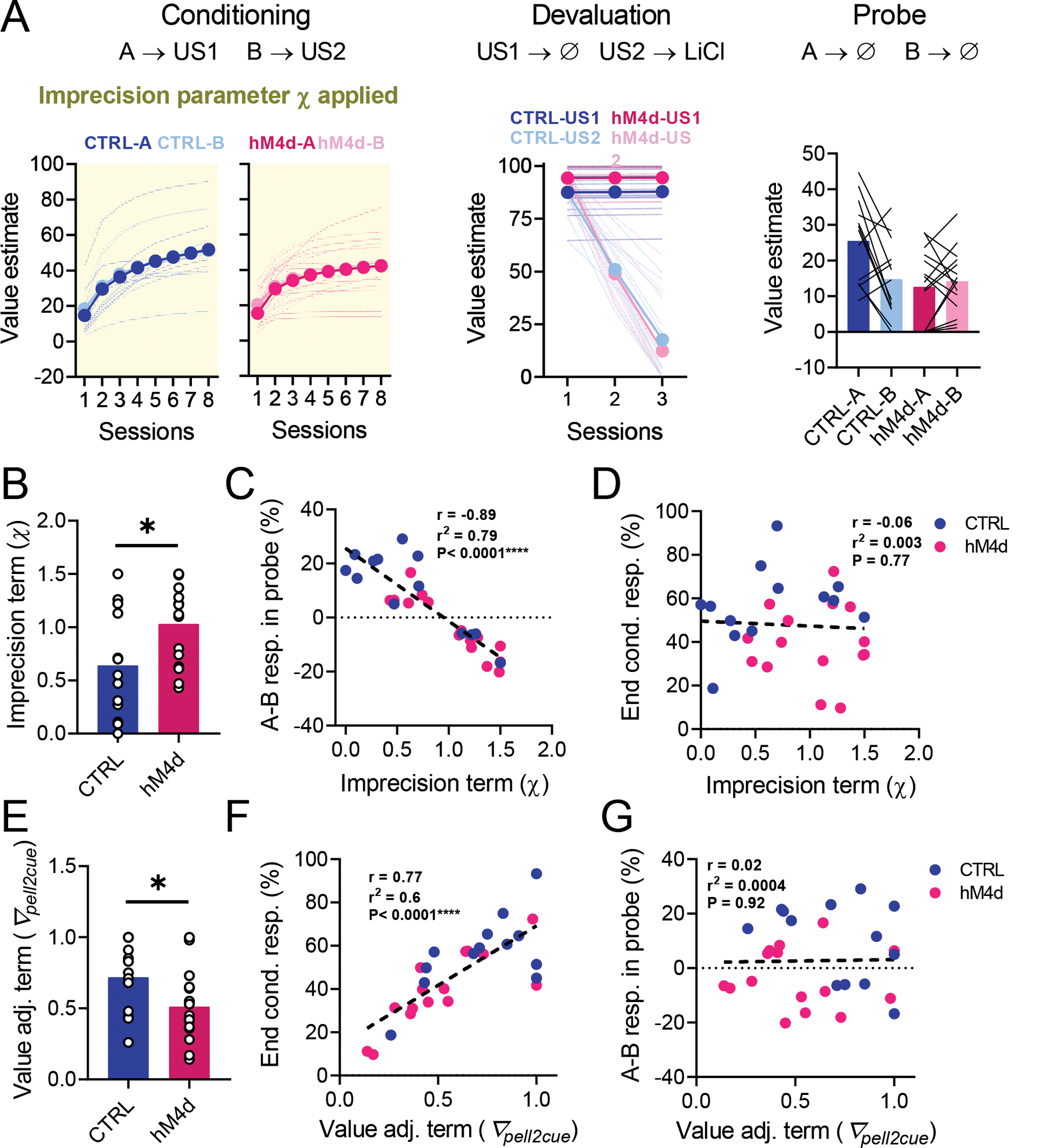
. (A): Model fit results for our model-based reinforcement learning model with potential outcome identity confusion. (B): The imprecision term χ was significantly higher in models fitted to hM4d behavioral data in relation to controls (two-tailed unpaired t-test; P=0.027*). (C): χ was negatively correlated with the differential responding to cues in the probe session (linear regression; r2=0.79, P<0.0001****). (D): χ was not correlated with the average responding to cues at the end of conditioning (linear regression; r2=0.003, P=0.77). (E): The value adjustment term ∇pell2cue was significantly lower in hM4d models (two-tailed unpaired t-test; P = 0.04*). (F):∇pell2cue was positively correlated with average cue responding at the end of conditioning (linear regression; r2=0.6, P<0.0001****). (G):∇pell2cue was uncorrelated with differential responding to cues in the probe session (linear regression; r2=0.0004, P=0.92). See Supplementary Table 2 and Extended Data Figure 2 for detailed parameter comparisons. Data are represented as mean ± SEM. CTRL n= 13 and hM4d n=15 fits of data from biologically independent animals. *P<0.05.
Our model also recapitulated other aspects of the results, specifically by having a value adjustment parameter (∇pell2cue) that captured the asymptotic performance during conditioning. The value of this parameter differed between fits for control and hM4d subjects (Figure 6E), accounting for the reduced responding of hM4d rats at the end of conditioning (Figure 2D, 3C and 6F). Importantly, ∇pell2cue did not correlate with the difference in cue responses during the probe (Figure 6G). These results confirm that the effects of lOFC inactivation during model creation on subsequent model-based decision making are not related to the concurrent effects on asymptotic value estimation. The latter may be related to the known role of lOFC in representing and updating outcome value10.
Finally, to validate that our model can reproduce results in other behavioral contexts, we retrieved the empirical data from one of the few previous studies linking lOFC function to outcome-specific Pavlovian conditioning 22. In this experiment, conducted by an independent laboratory, inactivation of lOFC terminals in the basolateral amygdala of rats during conditioning prevented the subsequent use of the learned information in a specific PIT test. Though these data are consistent with a complete failure to acquire the Pavlovian associations, they were also fully reproduced by fitting a larger χ parameter to the inactivated group in our imprecision model (Extended Data Figure 3).
Discussion
Our study demonstrates first that lOFC is necessary for the construction of a normal cognitive map and second that the lOFC appears to play a circumscribed role in this construction process. In our task, map-making did not cease when lOFC was inactivated, but the created map was degraded and less specific about which cues led to which outcomes. This was modeled as a lack of precision in credit assignment, but a failure to create appropriately “granular”34,35 internal representations of these external events would produce the same result and seems more likely than a direct control of lOFC over error signal assignment.
As an intuitive example of the utility of setting this granularity properly, a child may learn that McDonald’s™ serves Happy Meals™ while Burger King™ serves King Jr™ meals, each with different toys, while their parent may only recall that fast food restaurants serve kids’ meals. Both cognitive maps lead to food, but only one will help you collect all the Disney™ dragons! Whether to keep or discard the information related to which restaurant serves which kids’ meal with which toy is a question of how to segregate the states during learning34,35; it is this process that we propose lOFC controls or contributes to during cognitive mapping 16. This example also illustrates the fact that the generalization afforded by discarding information is not automatically incorrect – it should respond to the exigencies of the circumstance.
We argue that the lOFC is making critical contributions to this process of separating or collapsing states during the initial conditioning in our task. Importantly, this is not merely a sensory deficit; previous work has demonstrated that lOFC lesions or inactivation does not impair sensory processing generally, or auditory discrimination in particular, in either Pavlovian and instrumental tasks36–38. Indeed, in the current study, lOFC inactivation had no effect on novel object recognition learning, indicating that inactivation did not induce a general disruption in perception, memory formation and retention, or state-dependent learning. Instead, we would speculate that lOFC’s particular contribution is in determining whether to maintain or collapse separation between states that have uncertain, or perhaps only potential, biological significance.
Maps formed with too little separation due to hypofunction in lOFC would tend to underrepresent potential or hidden associations and meaning and be unable to link to and infer relationships with other maps, as we have seen here. A similar deficit is also evident in substance use disorder39, neurodegenerative diseases40, and advanced aging41, in which lOFC function is compromised39–42, and in children and adolescents43, which have immature frontal cortices. Conversely, maps formed with too much separation due to an over-exuberant lOFC would tend to instill meaning where it does not exist; such an effect is arguably evident in obsessive compulsive disorder and paranoid psychosis, which involve hyperfunction in the lOFC and related areas42,44,45. Notably this proposal fits well with recent demonstrations that OFC activity causes learning-dependent changes in the specificity or precision of representations in some sensory regions, including primary auditory cortex 46,47.
The proposal that the lOFC plays a critical role in defining the states that form the basis of cognitive maps is congruent with much existing data17–19,21,48. This includes classic findings based on manipulations in the probe phase of reinforcer devaluation experiments11–15, since the probe phase confounds the integration of established maps with their first time use. That is, the function proposed here would be invoked in the probe test in devaluation by the need to recognize the common reward state in the maps created during the conditioning and devaluation phases. Similar conclusions apply to other cardinal studies that have implicated the lOFC in model-based behaviors, since these also normally involve integrating or remodeling task maps37,49. This more limited role for lOFC also explains better why this area is especially important in behavioral settings where normal behavior depends upon recognizing states that are somewhat ambiguously defined with regard to biological value, including for instance the differential outcomes effect38, sensory pre-conditioning21,37, latent inhibition24, and specific PIT22,50, and why lOFC seems to be less important in settings like reversal learning or economic choice once maps are well-established16,48,51,52.
Particularly relevant to this idea are two recent studies showing that manipulations affecting lOFC can selectively impact conditioning in a manner consistent with a disruption of model-based learning. For example, inactivation of lOFC during stimulus-stimulus learning in the first phase of a sensory preconditioning task impairs subsequent differential responding to the preconditioned cues in the final probe test 21. Likewise, inactivation of lOFC terminals in basolateral amygdala during Pavlovian conditioning has a similar effect on later assessment of specific PIT, a finding which can be recapitulated with our modelling strategy22. While such results can be interpreted as a loss of model-based learning, they are also consistent with the selective effect on the precision of such learning, as demonstrated here.
Because our proposal integrates devaluation mechanisms and appropriate credit assignment, it is important to acknowledge that recent work in monkeys, using probabilistic choice tasks, has distinguished the function of credit assignment, narrowly defined, from processes underlying devaluation. While the latter have been consistently associated with areas 11 and 13 and associated agranular regions, areas likely homologous with the rat lOFC targeted here, the former functions have most recently been reassigned to ventrolateral prefrontal cortex53–56 While the current data implicating rat lOFC in both processes may seem at odds with these findings, it could be that species differences can account for any lack of alignment. These functions may be differentially distributed across frontal cortical areas in rats, as there is some evidence that the rat medial prefrontal cortex is also involved in processes related to state credit assignment 57,58. However, another explanation for the apparent conflict may be that the learning impaired here differs from that in these primate studies in that it is purely Pavlovian (i.e. there is no choice or item selected), and it does not depend on differences in outcome value. The lack of value differences may be particularly important for critically engaging lOFC since it makes the need to maintain separate states for each and assign credit for them differentially during learning of uncertain or hidden significance. In fact, we predict that if the outcomes were of markedly different value, or perhaps even if they were trained in advance to differentiate the outcomes59, then inactivation of lOFC might no longer affect learning. In this regard, as alluded to at the start of this discussion, the actual implementation of the “imprecision” of credit assignment underlying the deficit explored in this study may be quite different from the credit assignment at play during value-based choice.
Finally, perhaps the most intriguing implication of our finding that lOFC inactivation fails to reveal model-free learning is the speculative possibility that most learning is, to some degree, model-based, but that mental representations or cognitive maps can be formed with different degrees of granularity or specificity. This may be defined by the circuits that are engaged in the learning process, including the lOFC and other prefrontal areas. In the absence of experimental interventions, illness, or lesions, it could be that the main determinant of the resolution of a cognitive map would be task requirements and learning context. This would mean that perhaps there is a unified learning process that can be more or less complex depending on the contribution of specific circuits or environmental demands.
Methods
Experimental Model and Subject Details
All experiments were performed in accordance with NIH guidelines determined by the NIDA IRP Animal Care and Use Committee (protocol #20-CNRB-108). Experiments were performed on 32 male Long-Evans rats (n=16 for each group, >3 months of age at the start of the experiment (Charles River Laboratories and NIDA IRP Breeding Facility) housed on a 12-hr. light/dark cycle at 25 °C. Whether there are potential sex differences in the effects reported in this paper is a question ripe for further investigation. These rats were food restricted to ~85% of their original weight for the duration of the experiments. All rats had ad libitum access to water during the experiment and were fed 16–20 g of food per day, including rat chow and pellets consumed during the behavioral task. Behavior was performed during the light phase of the light/dark schedule. The number of rats used was determined based on previous publications from the lab using Pavlovian conditioning tasks. Prior to surgery, rats were handled every other day for 5–10 minutes for one week. Handling procedures included the performance of mock i.p. injections (rats were scruffed and the experimenter gently poked their abdomen with his finger or the end of a syringe with no needle attached) to prepare the subjects for future real injections. These rats were also used in another study 24. One rat in each group was excluded due to incorrect anatomical placement, and two rats were excluded from the control group due to a hardware malfunction during one of the behavioral sessions, leading to n=13 for the control group and n=15 for the hM4d group.
Surgical procedures
Rats were anesthetized with 1–2% isoflurane and received either AAV8-CaMKIIa-hM4d-mCherry (a Gi-coupled designer receptor exclusively activated by designer drugs (DREADD)) or AAV8-hSyn-mCherry (control), both purchased from Adgene (Cambridge, MA), bilaterally into the lOFC (AP −3.0 mm, ML ± 3.2 mm, and DV −4.4 and −4.5 mm from the brain surface) 24. A total 0.5 μL was delivered in each site at 0.1 μL/min via an infusion pump.
Sensory-specific conditioning
Rats were trained and tested at least eight weeks after the surgeries in standard behavioral boxes (12” × 10” × 12,” Coulbourn Instruments, Holliston, MA). Each box was equipped with a food cup, a pellet dispenser and two wall speakers. Head entries into the food cup was measured based on breaks of an infra-red beam.
Rats were conditioned for eight sessions. Prior to each session, each rat received an i.p. injection of JH60 (0.2 mg/kg, dissolved in 0.9% NaCl) and was left in their home cage for at least 15 minutes before the start of the session, to allow for the DREADD agonist to effectively inhibit transfected lOFC neurons in the hM4d group 23,24.
In every session, rats were exposed to two auditory stimuli, A and B (siren or white noise, counterbalanced across rats); each cue was presented for 10 seconds, immediately followed by the delivery of two bacon- or banana-flavored pellets (TestDiet; counterbalanced pairing). Each pairing was presented eight times per session with an average ITI of 2.5 minutes and the order of presentation was randomized and counterbalanced. Group allocation was also randomized and counterbalanced.
Behavioral responses were quantified as the percentage of time that each rat spent in the food cup during the last 5 seconds of each CS, subtracted by the time they spent in the food cup 5 seconds before CS onset.
Reward preference tests
Prior to the devaluation procedure, rats were given a preference test comparing consumption of the two pellet-types. Rats were provided 100 pellets of each type, placed in two ceramic bowls for 30 minutes with the location of the bowls reversed every 5 minutes. The remaining pellets were counted after the 30-minute period. This procedure was repeated after the devaluation probe to confirm the permanence of conditioned taste aversion.
Reinforcer devaluation via conditioned taste aversion with LiCl
For outcome-specific reinforcer devaluation, we paired the reward associated with cue B with LiCl, while the reward associated with cue A was not paired with anything. This devaluation procedure lasted a total of six days. On days 1, 3 and 5, rats were given 30 minutes of access to the devalued pellet, followed immediately by an i.p. injection of 0.3 M LiCl, then returned to their home cages 48. On alternate days (2, 4 and 6), rats were given 30 minutes of access to the non-devalued pellet and then returned to their home cages. All preference and consumption tests were performed in clean home cages.
Devaluation probe
The devaluation probe was performed and analyzed exactly like one of the conditioning sessions, except that no reinforcer was delivered, and the rats did not receive an injection.
Object recognition task
A subset of 10 rats from each group of the previous experiment was randomly selected for this procedure. One of the control rats was the one excluded due to incorrect anatomical placement, leading to n=9 for the control group and n=10 for the hM4d group for this experiment.
One square arena (60 × 60 cm) made of brown plexiglass with a striped black and white rectangular spatial cue was placed in a dimly (~3 lumens) red-light illuminated room. A video camera was mounted above the arenas, and activity during test sessions was digitized with a high-definition webcam (C920S PRO HD, Logitech, Suzhou, China). The objects to be discriminated were white glass bulbs, transparent glass jars, cylindrical amber glass bottles and trapezoidal white plastic bottles. All objects were glued to heavy metal disks to prevent them from being displaced by the rats and positioned at the back corners of the arena (10 cm from walls). To avoid olfactory cues, the arena and objects were thoroughly cleaned with 0.1% acetic acid after each trial.
For habituation, the rats were positioned into the open-field arena without any objects for 10 min the day before the start of the experiment. Throughout the experiment, the position of the objects was constant, but the objects used and their relative positions were counterbalanced for every animal. In the sample phase, rats were placed in the arena facing the wall opposite the objects and were allowed to freely explore two identical objects (either two light bulbs or two jars) for 10 min. Prior to the sampling session, each rat received an i.p. injection of JH60 (0.2 mg/kg, dissolved in 0.9% NaCl) and was left in their home cage for at least 20 minutes before the start of the session. This period was given to allow for the DREADD agonist to reach the brain and effectively inhibit transfected lOFC neurons in the hM4d group. After 24 h, on memory test 1, rats were allowed to explore freely one copy of the previously presented object (familiar) together with a new one (novel) for 10 min. A second memory test was performed 24 h after the first test. During the second memory test, the object that was introduced in the previous memory test was kept in place (so now it was the familiar object), and the previous familiar object was replaced by a novel object (either amber or white bottles), and rats explored freely for 10 min.
As previously described27, exploration was defined as pointing the nose toward to an object at a distance of less than 1 cm and/or touching it with the nose. Turning around or sitting on the objects was not considered as exploratory behavior. A Discrimination Index (DI) was calculated, where DI = difference between exploration of the novel and familiar objects / total object exploration time during each memory test, such as that a DI of 0 indicates equal preference for both objects, a DI of 1 indicates exclusive exploration of the novel object, and a DI of −1 indicates exclusive exploration of the familiar object. This measure was also calculated using only the first 5 min of each test, but results were similar to when the whole test period was used (data not shown). Video recordings were scored automatically using TopScan Suite (Clever Sys, Reston, VA). Exploration times were verified manually by a trained rater blinded to treatment and objects identities using BORIS software (Version 7.9.19, University of Torino, Italy).
Histological procedures
After completion of the experiment, rats were perfused with chilled phosphate buffer saline (PBS) followed by 4% paraformaldehyde in PBS. The brains were then immersed in 18% sucrose in PBS for at least 24 hours and frozen. The brains were sliced at 40 μm and stained with DAPI (Vectashield-DAPI, Vector Lab, Burlingame, CA). Fluorescent microscopy images of the slides were acquired with a BZ-X800 Keyence microscope. Expression patterns were extracted from the images and then superimposed on anatomical templates 24.
Statistics and Reproducibility
Data were analyzed using GraphPad Prism (GraphPad Software, San Diego, CA). Error bars in figures denote the standard error of the mean. Effects of experimental treatments on behavioral or model variables were examined with two-tailed unpaired t-tests (in the case of single factor comparisons), or repeated-measures 2-way and 3-way ANOVAs (in the case of multiple factor comparisons) combined with Sidak’s or Tukey’s post-hoc tests, respectively. Correlations between variables were analyzed with linear regression analyses. Statistical significance threshold for all tests was set at P<0.05. No statistical method was used to predetermine sample size. Three rats were excluded due to technical issues, as described previously. Experiments were conducted in one cohort of animals. Counterbalancing and group allocation was pseudorandomized. The investigators were not blinded to allocation during experiments and outcome assessment, except during the scoring of the novel object learning task, which was conducted by a fully blinded investigator. Data distribution was assumed to be normal but this was not formally tested.
Reinforcement learning modelling
Background
We modelled the five stages of the experiment in chronological order: Conditioning (COND), Preference Test 1 (PRFT1), Devaluation (DEV), Preference Test 2 (PRFT2) and finally Probe testing (PROBE). For COND and PROBE, the Port Stay Probability (PSP) upon cue presentation was quantified. In PRFT1, DEV and PRFT2, the percentage of pellets eaten (PPE) was quantified. Two pellets of a single type were delivered in each case.
On each trial, an internal value estimate () was calculated based on contributions from a model based (MB) system (and, for the alternative hypothesis of a loss of MB learning, in combination with a model free, MF, system). This value estimate was then transformed to the behavioral measurement that was appropriate to the experimental stage. In keeping with standard practice, we described the Pavlovian connection between cue and outcome as being associations; however, in keeping with the temporal evolution of the task, we actually model them as transitions from cue to outcome. MB (and MF) systems were updated using the state transitions that were observed (e.g., A→ValuedOutcome) and the rewards that were received.
The main hypothesis (we call this Ha) that we tested was that the lOFC enables precise credit assignment through separation of specific cue-outcome relations (i.e., that sound A predicts banana flavored pallets) and when deactivated, only the general relation (that any auditory cue predicts delivery of food) can be learned. However, we also tested a model (Hb) which could potentially characterize a more conventional view of lOFC deactivation, namely that it would suppress MB over MF control. Since Hb mostly nests Ha, we provide a partly integrated discussion.
Formal model
S = {s1,...,sn} is the set of states. Each state is typically associated with the presentation of a cue or an outcome that can be rewarded or devalued, i.e., S ∼ {A,B, ValuedOutcome, DevaluedOutcome}.
In order to be able to characterize MB and MF systems fairly, we considered forms of both that represent the uncertainty in their predictions of rewards and values. However, we adopt a heuristic Bayesian scheme, with observation rates (the equivalent of learning rates) that are parameters (rather than pure conjugate distributional updates).
Following Dearden et al.32, normal-gamma distributions are used to characterize this uncertainty (since, following Daw et al. 28, MB and MF systems share the characterization of the values of the final outcomes, albeit potentially with different parameters, and with only the MB system being subject to the effects of devaluation).
We write this down in terms of the value of state s. The normal-gamma distribution for the value Vs and the precision is written as . According to this, the conditional distribution of Vs given is a normal distribution
| (1) |
and the precision has an unconditional gamma distribution
| (2) |
in terms of our problem, we interpret the parameters as follows:
ms is the mean reward across the previous iterations
λs is the number of outcomes seen (this also includes the cases when no reward (r = 0) is delivered in this state)
αs describes the total opportunity for learning about the precision; assuming that we initialize alpha to:, then it holds that at all times αs = 0.5 * λs.
βs describes the scale of the precision across previous seen rewards implying that the marginal mean and variance of Vs are:
| (3) |
For MB computations, we also need an internal model of the state graph. We use T to describe the distribution of transition probabilities from all to all states. Programmatically, T can be described by a matrix where each row contains ϕ’s that are parameters for the multinomial distribution that characterizes the transition probabilities from a “source” state s to any of the other states (including the source state itself):
This will only be interpretable for non-terminal “source” states s, as the trial ends afterwards and no information about consecutive states can be collected. The terminal states are thus absorbing. The sum of probabilities for a fixed source state to all possible target states is 1 (see model-based value calculation).
Initialization
We initialize all ϕ’s in T to 11. This implies a moderately strong prior that the transition probabilities are uniform across all states:
| (4) |
We initialize the distribution describing the value distribution parameters to:
| (5) |
The rationale for these values is that to ensure Vs has a finite marginal variance. The value of was chosen to be 0 as animals start out with no value expectation. was set to , as this ratio is also maintained by the updates. was set to 1.5 in order to set the starting marginal variance to . However, we confirmed that our results are stable to quite a wide range of initialization values, provided that the variance is well-defined (αs > 1).
During the conditioning stage, rValuedOutcome = rDevaluedOutcome = 2 (for the number of pellets provided). The reward of the DevaluedOutcome changes during the devaluation period to NegRew < 0, which is a parameter that captures the strength of the devaluation effect for each animal.
Model updates and value calculation
The normal-gamma distribution characterizing the value Vs of a state s updates according to each observation. For a terminal state s, given an observation , writing for the updated distribution at s, we update the parameters as:
| (6) |
where η is called an observation rate and stands in for the number of subjective observations associated with each experience – it need only be positive and is not constrained to be less than 1.
For the MB system, writing , the update happens using and observation rate η = ηmb.
For the transition matrix, if the state s(t) is a non-terminal state that is followed by state s(t + 1), the parameters of the transition probability distribution Ts(t). are updated using a notional transition observation rate ηt as:
| (7) |
The MB system combines its knowledge of transitions and immediate rewards by applying the Bellman equation, which, in this case is very straightforward, since there are only two steps. Ignoring any posterior correlation between T and μ, σ, this implies that:
The expected value for the next state is discounted by γmb, which normally is close to 1. The expected value for the transition probability from state s(t) to state s(t + 1) can be calculated using: .
The approximate variance can be calculated from the Bellman equation (again ignoring correlations).
Transformation of Estimated Values to Behavioral Measures
Having generated a prediction from the MB system, it is necessary to convert it into the different experimental measures used in the various stages of the experimental paradigm. To do this, the combined value is normalized by the standard scalar reward received (2, for the number of pellets), and thresholded at 0 in order to avoid negative percentages when calculating the behavioral measures:
| (8) |
This normalized value can then be transformed to the respective behavioral measures for each stage, each given as percentages in the range [0,100]:
| (9) |
| (10) |
| (11) |
∇pell2cue accounts for the difference in the impact of a secondary predictor versus a primary reinforcer, and ∇cp may account for the forgetting of cue values from COND to the PROBE phase. Both factors are in the range [0,1]. An additional factor for the calculation of was not necessary. and are calculated the same way as .
Ha: Outcome-specific encoding deficit
In this version, only the MB system is used, and we assume no forgetting happens from COND to PROBE so ∇cp is fixed to 1.
We model the inactivation of lOFC as implying that the representation of the relevant cues (here, A and B) is potentially only partially distinct. Thus, if, for instance s(t) = A is presented, then writing as the ‘other’ cue, we imagine a spillover or fuzziness factor χ is introduced that is taken into consideration when doing the updates so that, along with equation 7, we have
| (12) |
If χ = 0, nothing is learned for the opposite state, if χ = 1, then exactly the same transition information is learned for both states, and if χ > 1, then more is learned for the opposite/unseen state. Note that we continue to consider the outcome pellets to be perfectly distinguishable.
The free parameters used for model fitting are: NegRew, ∇pell2cue, ηmb, ηt, χ.
Model Fitting
Separate sets of parameters were fit for each animal using scipy.optimize.least_squares, optimizing the mean squared error (MSE) between the real behavioral recordings and the model “behavior” outputs based on the current set of parameters. A weighted MSE was used in order to increase the contribution of the PROBE trials as behavioral differences across groups (control/lOFC deactivation) were most apparent here, and the number of trials comparably few (there is 8x more condition trials, so PROBE trials have an 8x higher weight). The following bounds for the parameter fitting were defined as follows:
| Param | NegRew | ∇ pell2cue | η mb | η t | χ |
| Min | −90 | 0 | 0 | 0 | 0 |
| Max | 0 | 1 | 40 | 40 | 1.5 |
Individual parameter estimates for either of the models were then compared across groups using two-tailed t-tests and Bonferroni-corrected for multiple comparisons.
Parameter Recovery
In order to ensure that recovered parameter values are meaningful in case of the model fits, we checked parameter recoverability. Here, we use known parameter values along with realistic noise to generate synthetic data, and then assess if we can recover from these data values of the parameters that are close to the original generating levels. In order to stay close to the real data, we used the parameters recovered for each animal individually to generate one synthetic dataset/behavioral trace per animal. The noise was generated using individual variability estimates of per trial behavioral measures for each experiment stage (COND, DEV, PROBE). This yields 28 pairs (one pair per animal) of real and estimated parameter values for each of the model’s parameters. Good parameter recoverability is when real and estimated parameter values are well correlated.
Recovery of most of the parameters was good (rNegRew = 0.9, , , and rχ = 0.7); only the recovery of the state transition observation rate ηt was slightly less faithful (), and so should be interpreted cautiously.
Repeating the recovery procedure multiple times produced comparable results. We also used a synthetic generative procedure to assess the posterior correlations between recovered parameter values, something that matters for prediction, albeit less for the overall interpretation of the model. We started out with the median parameter values across animals to generate synthetic data, with noise generated based on the variability of behavioral measures per experiment stage, this time on the group level, and recovered those parameter values from these data. We did this 30 times and assessed the correlations between all pairs of inferred parameters. We found that most of the correlations were mild – although the highest correlations between ∇pell2cue and ηt (r = −0.57), were quite substantial. This is not unexpected, as in effect ∇pell2cue accounts for the difference between the asymptotic performance at the end of conditioning, which is in turn set by the observation rates.
Hypothesis Hb. MB deficit
Hb parameterizes a more conventional view of the effect of lOFC inactivation, allowing for a combination between MF and MB learning and control, with the possibility that this combination is disturbed by inactivation.
As hypothesis Hb makes use of both model free and model-based value systems, it employs two sets of value distributions:, and ,. MB learning and inference happens as for hypothesis Ha, except that the imprecision parameter χ is not part of Hb. Following Dearden et al. (18), the MF value system uses normal-gamma distributions for characterizing the values of all states s, both terminal (with rewards) and non-terminal (with cues).
For the MF system, each time the animal passes through state s, the value distribution at this state is updated according to either a scalar estimate of the long-run reward from that state s for the MF system, or the immediate reward r using an observation rate ηmf.
Updating the MF values of terminal states is the same as for the MB system (using equation 6) with and an observation rate η = ηmf. Updating the values of non-terminal (cue) states also follows analogously but now taking into the long-run reward instead, with , as the reward directly received at non-terminal states is always 0. The full update formula is described in Dearden et al.32.
Generally, the estimated value of the model free system is and the estimated variance is given by the expression in equation 3.
According to Hb, both MB and MF contribute to the value of a cue, according to a convex combination parameter wmf, which is in range [0,1] with 0 meaning only the model-based system is used and 1 that only the model free system is used:
| (13) |
This then generates the normalized value
| (14) |
which leads to behavioral measures as in equations (9)–(11).
For convenience of fitting, the observation rate for the transition matrix was fixed to the one for the model-based value distributions ηt = ηmb, and γmf and γmb were set to 1. The free parameters used for model fitting were therefore: NegRew, ∇pell2cue, ∇cp, ηmf, ηmb and wmf. As an important simplification, we fixed wmf to have the same value for COND and PROBE, even in the inactivation case, as if this had been stamped in during COND, for instance because of heightened MB uncertainty. If wmf was lower in PROBE then, we would not have expected such equivalent decreased responding to both cues. An alternative possibility we did not explore is that inactivation would leave the MB system with impaired learning in COND, even at asymptote for both cues; and that if wmf was indeed lower in PROBE, reduced responding would come from averaging a persistent value from the MF system with the decreased output of the MB system. This would be an alternative to making parameter ∇cp small.
The same constraints as above were used for fitting the MB system (albeit with χ effectively clamped at 0). Additionally, we had
| Param | ∇ cp | η mf | w mf |
| Min | 0 | 0 | 0 |
| Max | 1 | 40 | 1 |
Parameter recovery of the observation rate parameters were the least faithful ( and ), while the estimated values of the other parameters were closer to real ones (rNegRew = 0.9, ). Thus, when interpreting this model, less emphasis should be placed on the first three parameters. Correlations in the recovered values of the parameters were mild – with the highest correlation being between ∇pell2cue and wmf (r = −0.54).
Adaption of the Ha model to the experiment of Sias et al.22
We adapted the model from Ha (“Outcome-specific encoding deficit”) to the experimental conditions of Sias et al22, who studied the effects on stimulus-outcomes encoding of inactivation of lOFC terminals in basolateral amygdala during Pavlovian conditioning. Sias et al22 used an outcome-selective form of Pavlovian to Instrumental Transfer (PIT) as a key behavioral paradigm. We modeled the animal behavior data available from the online version of their manuscript (Figure 4 – source data 1).
The procedure in Sias et al22 comprises three main stages: Pavlovian Conditioning (“PC”, which is akin to the Conditioning stage of our experiment), followed by Instrumental Conditioning (“IC”) and lastly a Pavlovian-to-instrumental transfer (PIT) test. During PC, the associations between auditory cues (conditioned stimuli CS1 and CS2; presented for epochs of 2 mins) and rewarding outcomes (O1 and O2 delivered intermittently at a rate of one per 30s on average) were learned. 8 sessions of PC were conducted, each of which contained 4 presentations of each cue-outcome pair (CS1-O1 and CS2-O2). The IC stage involved 11 separate sessions for each of two levers (A1 and A2), with pressing leading to the delivery of a specific outcome (O1 or O2 respectively). A session was terminated once the respective outcome had been delivered 30 times or after a maximum duration of 45 mins. In the initial IC sessions, the outcomes were always delivered, but the probability of outcome delivery decreased in later sessions. For simplicity, in the modelling we keep this probability constant at 100%, and ignored the instrumentality, just assuming that each animal would press the lever 30 times per session, and thus see 30 action-outcome contingencies.
After IC, the animals experienced a single extinction session in which both levers were persistently available. Animals could press at will, but with no reward. This session was not included in the modelling. This was followed by a single main PIT session, again with both levers being available, and in extinction. Over the course of this session, each of the two Pavlovian cues was presented 4 times for two minutes. Lever presses in the presence and absence of each cue were recorded.
We adapted the “imprecision” model from Ha (“Outcome-specific encoding deficit”) to characterize this experiment. Six main states can be identified in the experiment, thus S = {CS1, CS2, O1, O2, A1, A2}. There are two outcome states that are perceived as rewarding (rO1 = rO2 = 2). The distributions describing the values of each of the six states (Vs and ) and the matrix describing the transition probabilities between those states (T) are initialized and updated in the same way as described above (abstracting the intermittent delivery in Sias et al22 as the same sort of discrete trials of our main experiment). Given the format of the available behavioral data points (as maximal elevation of lever presses during CS presentation versus pre-CS baseline), the formulas determining the behavioral output measures for both PC (RESP_PC) and IC (RESP_IC) were chosen as follows:
| (15) |
where the division by two reflects the delivery of two pellets. Both RESPPC and RESPIC make use of a new hyperparameter maxelev that describes the maximal elevation of lever presses from baseline (bound between 0 and 1). The behavioral measure for the PIT is more complex: First, a weight (actw) for each of the two actions is calculated as the sum of the expected transition probability for the current state (in the PIT, only CS1 or CS2 are presented) to each next state (with O1 and O2 being the only likely candidates) multiplicated by the relative transition probability from that next state to the respective action. For the latter we assume that the associations learned during IC are symmetric (that is A1-O1 equals O1-A1) and use the entry from the matrix corresponding to the transitions from action to outcomes (learned during IC). The final measure for PIT was modeled as the propensity/weight of the animal to pick the “correct” action (i.e. the action that leads to the outcome, whose availability is singled out by the CS) in relation to that of picking the other action.
| (16) |
| (17) |
The behavioral measures are aggregated across all trials of the same type for each session to enable the fit to the available animal data. The ∇pell2cue and the NegRew hyperparameters were not necessary anymore and thus dropped, leaving a total of 4 hyperparameters for the final modified model: maxelev, ηmb, ηt, χ.
Extended Data
Extended Data Fig. 1. Data fitting with a reinforcement learning model that allows for a shift between model-based (MB) and model-free (MF) learning.
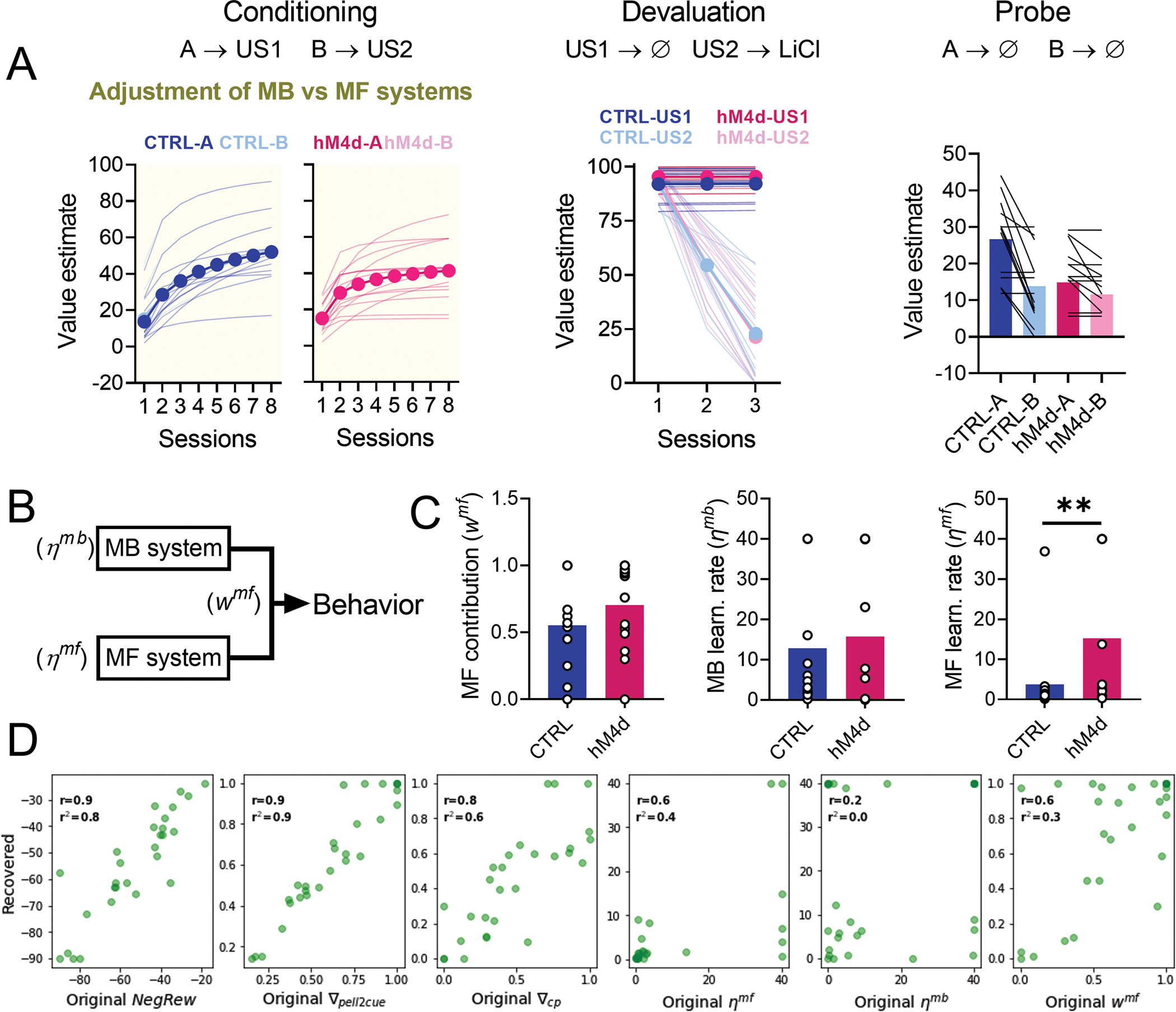
(A) Model fit results for our MB vs MF reinforcement learning model. Note that it can also replicate our behavioral results well. (B) Schematic of the critical aspect of the model and the expected result: the observation rate for both the MB and MF systems, as well as the potential contribution of each to behavior, were free parameters, and we expected that the contribution of the MB system would be diminished, either by a reduced MB observation rate or an increase in the MF contribution. (C) Values of the critical observation rate-related parameters, namely the proportion of contribution of the MF (wmf) system, the MF observation rate (ηmf), and the MB observation rate (ηmb) for both control and hM4d model fits (two-tailed unpaired t-test; P=0.007**). Note that instead of a reduction in MB learning or proportional contribution, only the MF observation rate was significantly higher in the hM4d group. See Supplementary Table 2 for detailed parameter comparisons. (D) Correlations between estimated and original parameters for the MB vs MF model. Note that parameter recovery of all critical observation rate-related parameters was not very faithful (linear regression; r < 0.7). Data are represented as mean ± SEM. CTRL n= 13 and hM4d n=15 fits of data from biologically independent animals. **P<0.01.
Extended Data Fig. 2: Parameter recovery and correlations for the reinforcement learning model with association specificity deficit.
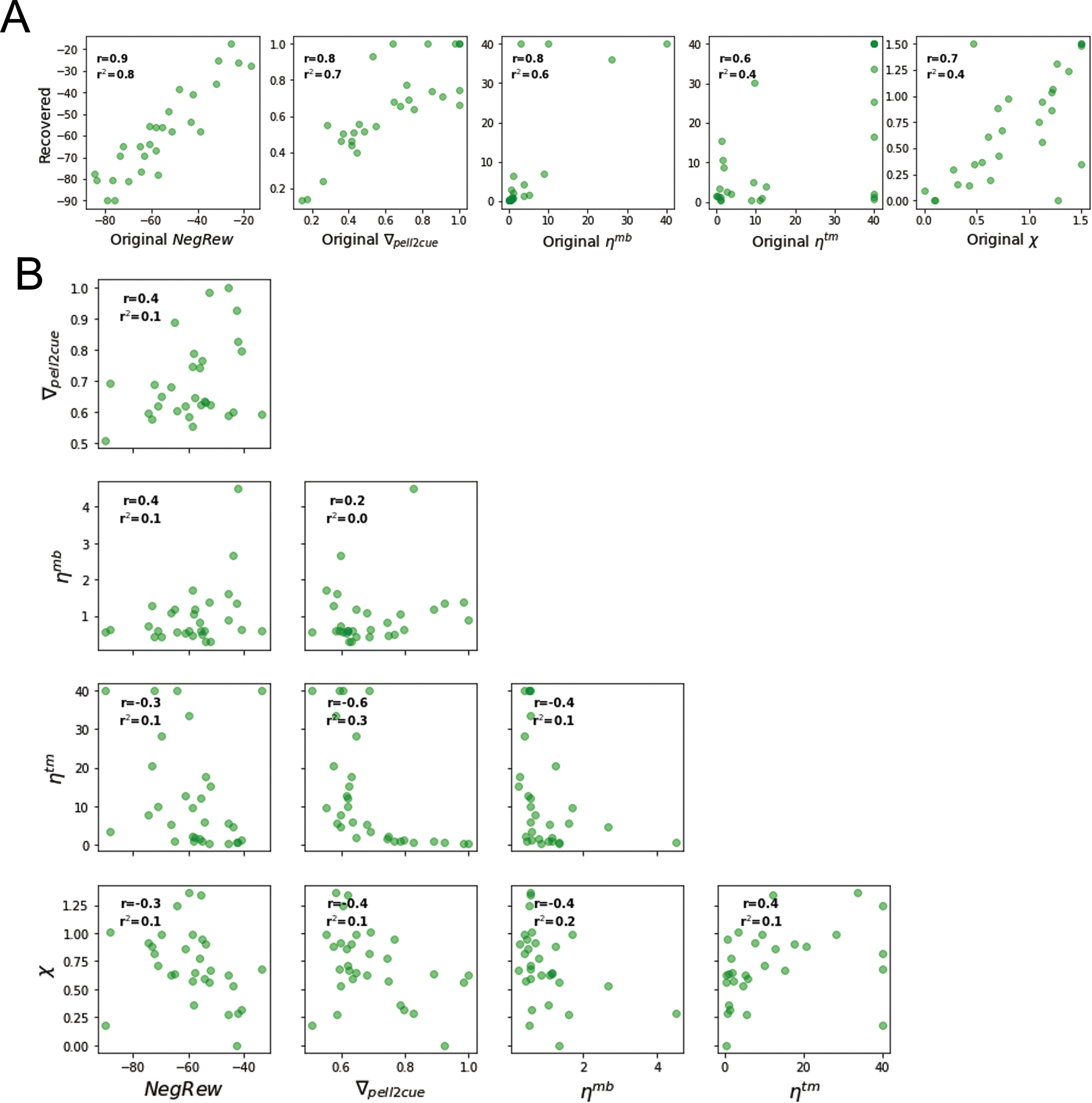
A) Correlations (linear regression) between estimated and original parameters. Note that most parameters were recovered with r>0.7, with the least faithfully recovered parameter being the state transition observation rate ηtm with r < 0.6. (B) Correlations between fitted parameters (linear regression). Note that only correlations between ∇pell2cue and wmf (r = −0.54) in HB and between ∇pell2cue and ηtm (r = −0.57) are substantial. CTRL n= 13 and hM4d n=15 fits of data from biologically independent animals.
Extended Data Fig. 3. Replication of the results of Sias et al.22 with the imprecision model.
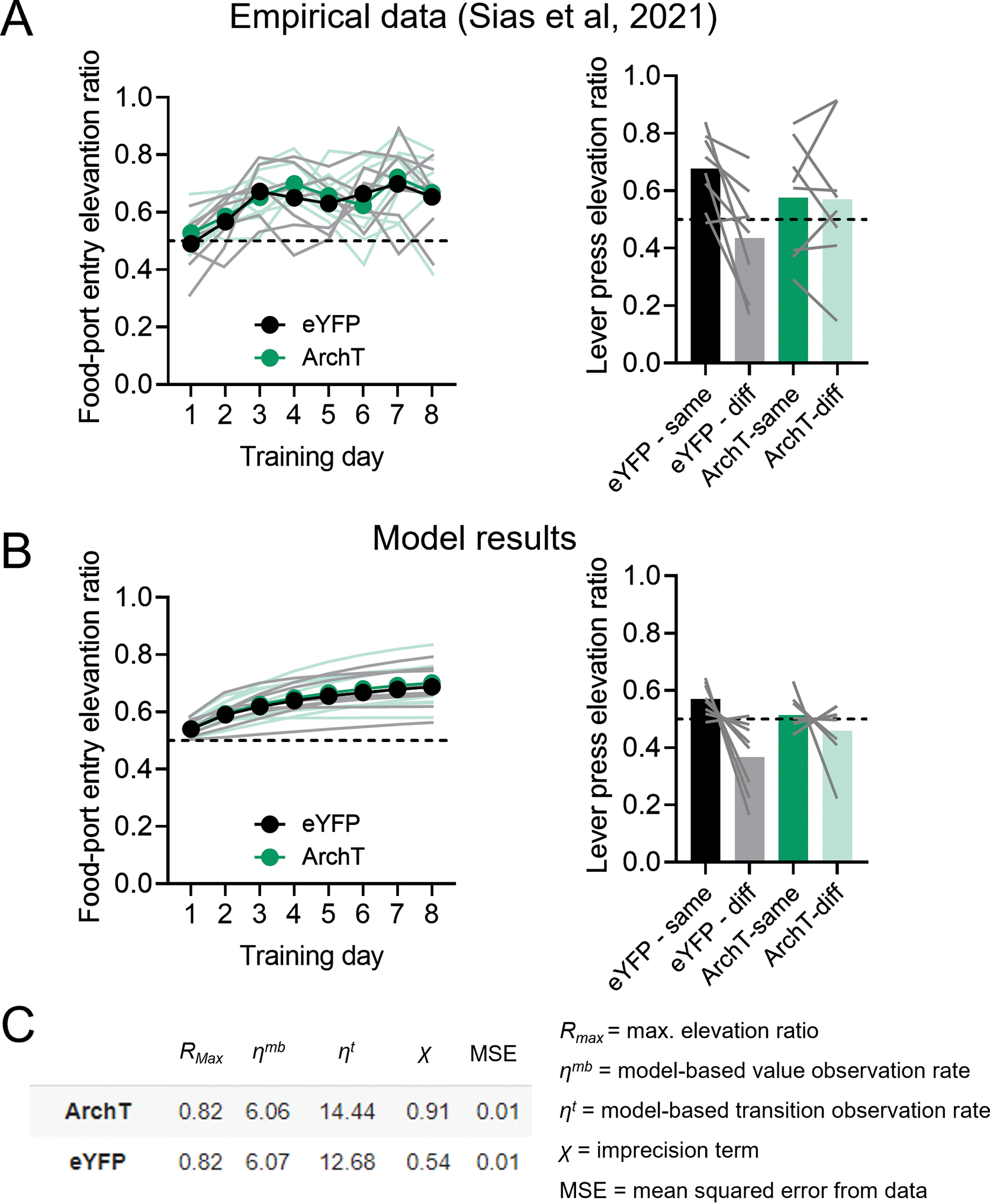
(A) Plots of the empirical data retrieved from the study by Sias et al.22 (Figure 4 of that paper), where it was shown that inactivation of lOFC terminals in basolateral amygdala (ArchT group) during outcome-specific Pavlovian training did not impair Pavlovian acquisition (left panel) but did prevent subsequent PIT effects on the elevation ratio of lever pressing for congruent rewards (right panel), in relation to controls (eYFP group). (B) Modeling of the empirical results in A with the imprecision model. Note that the model fully recapitulates the observed effects. (C) average values of the model parameters and their definitions. Note that the imprecision term χ was increased by ~60% in the model fits for the behavior of ArchT rats in comparison to eYFP controls. CTRL n= 13 and hM4d n=15 fits of data from biologically independent animals. eYFP and Arch T n= 8 fits of data from biologically independent animals.
Supplementary Material
Acknowledgments
We thank Jordi Bonaventura for guidance on chemogenetic methods, Nishika Raheja and Savana Agyemang for technical assistance, as well as Marios Panayi, Evan Hart, Peter Rudebeck, and Peter Holland for stimulating discussions. The opinions expressed in this article are the authors’ own and do not reflect the view of the NIH/DHHS. This work was funded by the Intramural Research Program at the National Institute on Drug Abuse (KMC, MG, GS), the Max Planck Society (RS, KL, PD), the German Federal Ministry of Education and Research (RS), the Humboldt Foundation (PD), and the German Research Foundation grant MA 8509/1–1 (KMC).
Footnotes
Competing interests statement
Authors declare that they have no competing interests.
Code availability
All code and data used in this study are available on https://colab.research.google.com/drive/1VYRAnvAO8OmzQpVaJe5radKIZnpEn638?usp=sharing and https://colab.research.google.com/drive/1ORP8Q9ceLBXlupvrCDh7HLAhQKsjQswr?usp=sharing.
Supplementary Information:
Supplementary tables 1–2; Extended Data Figure legends 1–3.
Data availability
All code and data used in this study are available on https://colab.research.google.com/drive/1VYRAnvAO8OmzQpVaJe5radKIZnpEn638?usp=sharing and https://colab.research.google.com/drive/1ORP8Q9ceLBXlupvrCDh7HLAhQKsjQswr?usp=sharing. Additional information on materials and protocols are available upon request to the corresponding authors.
References
- 1.Behrens TEJ et al. What Is a Cognitive Map? Organizing Knowledge for Flexible Behavior. Neuron 100, 490–509 (2018). [DOI] [PubMed] [Google Scholar]
- 2.Titone D, Ditman T, Holzman PS, Eichenbaum H & Levy DL Transitive inference in schizophrenia: impairments in relational memory organization. Schizophr. Res. 68, 235–247 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Schoenbaum G, Chang CY, Lucantonio F & Takahashi YK Thinking Outside the Box: Orbitofrontal Cortex, Imagination, and How We Can Treat Addiction. Neuropsychopharmacology vol. 41 2966–2976 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sharp PB, Dolan RJ & Eldar E Disrupted state transition learning as a computational marker of compulsivity. (2020) doi: 10.31234/OSF.IO/X29JQ. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wallis JD Cross-species studies of orbitofrontal cortex and value-based decision-making. Nat. Neurosci. 2011 151 15, 13–19 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rudebeck PH & Rich EL Orbitofrontal cortex. Curr. Biol. 28, R1083–R1088 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rudebeck PH & Murray EA The Orbitofrontal Oracle: Cortical Mechanisms for the Prediction and Evaluation of Specific Behavioral Outcomes. Neuron 84, 1143–1156 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wilson RC, Takahashi YK, Schoenbaum G & Niv Y Orbitofrontal cortex as a cognitive map of task space. Neuron 81, 267–279 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schuck NW, Cai MB, Wilson RC & Niv Y Human Orbitofrontal Cortex Represents a Cognitive Map of State Space. Neuron 91, 1402–1412 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rustichini A & Padoa-Schioppa C A neuro-computational model of economic decisions. J. Neurophysiol. 114, 1382–1398 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gallagher M, McMahan RW & Schoenbaum G Orbitofrontal Cortex and Representation of Incentive Value in Associative Learning. J. Neurosci. 19, 6610–6614 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Izquierdo A, Suda RK & Murray EA Bilateral Orbital Prefrontal Cortex Lesions in Rhesus Monkeys Disrupt Choices Guided by Both Reward Value and Reward Contingency. J. Neurosci. 24, 7540–7548 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Howard JD et al. Targeted Stimulation of Human Orbitofrontal Networks Disrupts Outcome-Guided Behavior. Curr. Biol. 30, 490–498.e4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.West EA, DesJardin JT, Gale K & Malkova L Transient Inactivation of Orbitofrontal Cortex Blocks Reinforcer Devaluation in Macaques. J. Neurosci. 31, 15128–15135 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rudebeck PH, Saunders RC, Prescott AT, Chau LS & Murray EA Prefrontal mechanisms of behavioral flexibility, emotion regulation and value updating. Nat. Neurosci. 16, 1140–1145 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gardner MPH & Schoenbaum G The orbitofrontal cartographer. Behav. Neurosci. 135, 267–276 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Miller KJ, Botvinick MM & Brody CD Value Representations in the Rodent Orbitofrontal Cortex Drive Learning, not Choice. bioRxiv 245720 (2022) doi: 10.1101/245720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Malvaez M, Shieh C, Murphy MD, Greenfield VY & Wassum KM Distinct cortical–amygdala projections drive reward value encoding and retrieval. Nat. Neurosci. 2019 225 22, 762–769 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Baltz ET, Yalcinbas EA, Renteria R & Gremel CM Orbital frontal cortex updates state-induced value change for decision-making. Elife 7, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gardner MPH et al. Processing in Lateral Orbitofrontal Cortex Is Required to Estimate Subjective Preference during Initial, but Not Established, Economic Choice. Neuron 108, 526–537.e4 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hart EE, Sharpe MJ, Gardner MP & Schoenbaum G Responding to preconditioned cues is devaluation sensitive and requires orbitofrontal cortex during cue-cue learning. Elife 9, (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sias AC et al. A bidirectional corticoamygdala circuit for the encoding and retrieval of detailed reward memories. Elife 10, (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bonaventura J et al. High-potency ligands for DREADD imaging and activation in rodents and monkeys. Nat. Commun. 10, 1–12 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Costa KM, Sengupta A & Schoenbaum G The orbitofrontal cortex is necessary for learning to ignore. Curr. Biol. 31, 2652–2657.e3 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gomez JL et al. Chemogenetics revealed: DREADD occupancy and activation via converted clozapine. Science (80-.). 357, 503–507 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Panayi MC & Killcross S The Role of the Rodent Lateral Orbitofrontal Cortex in Simple Pavlovian Cue-Outcome Learning Depends on Training Experience. 2, 1–14 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Weiler M et al. Effects of repetitive Transcranial Magnetic Stimulation in aged rats depend on pre-treatment cognitive status: Toward individualized intervention for successful cognitive aging. Brain Stimul. Basic, Transl. Clin. Res. Neuromodulation 14, 1219–1225 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Daw ND, Niv Y & Dayan P Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci. 2005 812 8, 1704–1711 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Panayi MC, Khamassi M & Killcross S The rodent lateral orbitofrontal cortex as an arbitrator selecting between model-based and model-free learning systems. Behav. Neurosci. 135, 226–244 (2021). [DOI] [PubMed] [Google Scholar]
- 30.Miller KJ, Shenhav A & Ludvig EA Habits without values. Psychol. Rev. 126, 292–311 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Walton ME, Behrens TEJ, Buckley MJ, Rudebeck PH & Rushworth MFS Separable Learning Systems in the Macaque Brain and the Role of Orbitofrontal Cortex in Contingent Learning. Neuron 65, 927–939 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dearden R, Dearden R, Friedman N & Russell S Bayesian Q-learning. IN AAAI/IAAI 761–768 (1998). [Google Scholar]
- 33.Wilson RC & Collins AGE Ten simple rules for the computational modeling of behavioral data. Elife 8, (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dezfouli A & Balleine BW Learning the structure of the world: The adaptive nature of state-space and action representations in multi-stage decision-making. PLOS Comput. Biol. 15, e1007334 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gershman SJ & Niv Y Learning latent structure: carving nature at its joints. Curr. Opin. Neurobiol. 20, 251–256 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Panayi MC & Killcross S Functional heterogeneity within the rodent lateral orbitofrontal cortex dissociates outcome devaluation and reversal learning deficits. Elife 7, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jones JL et al. Orbitofrontal cortex supports behavior and learning using inferred but not cached values. Science (80-.). 338, 953–956 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McDannald MA, Saddoris MP, Gallagher M & Holland PC Lesions of Orbitofrontal Cortex Impair Rats’ Differential Outcome Expectancy Learning But Not Conditioned Stimulus-Potentiated Feeding. J. Neurosci. 25, 4626–4632 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Volkow ND & Fowler JS Addiction, a Disease of Compulsion and Drive: Involvement of the Orbitofrontal Cortex. Cereb. Cortex 10, 318–325 (2000). [DOI] [PubMed] [Google Scholar]
- 40.Van Hoesen GW, Parvizi J & Chu CC Orbitofrontal Cortex Pathology in Alzheimer’s Disease. Cereb. Cortex 10, 243–251 (2000). [DOI] [PubMed] [Google Scholar]
- 41.Denburg NL et al. The Orbitofrontal Cortex, Real-World Decision Making, and Normal Aging. Ann. N. Y. Acad. Sci. 1121, 480 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jackowski AP et al. The involvement of the orbitofrontal cortex in psychiatric disorders: an update of neuroimaging findings. Brazilian J. Psychiatry 34, 207–212 (2012). [DOI] [PubMed] [Google Scholar]
- 43.Decker JH, Otto AR, Daw ND & Hartley CA From Creatures of Habit to Goal-Directed Learners: Tracking the Developmental Emergence of Model-Based Reinforcement Learning. Psychol. Sci. 27, 848–858 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rauch SL et al. Functional Magnetic Resonance Imaging Study of Regional Brain Activation During Implicit Sequence Learning in Obsessive–Compulsive Disorder. Biol. Psychiatry 61, 330–336 (2007). [DOI] [PubMed] [Google Scholar]
- 45.Walther S et al. Limbic links to paranoia: increased resting-state functional connectivity between amygdala, hippocampus and orbitofrontal cortex in schizophrenia patients with paranoia. Eur. Arch. Psychiatry Clin. Neurosci. 1, 1–12 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Winkowski DE et al. Orbitofrontal Cortex Neurons Respond to Sound and Activate Primary Auditory Cortex Neurons. Cereb. Cortex 28, 868–879 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Banerjee A et al. Value-guided remapping of sensory cortex by lateral orbitofrontal cortex. Nat. 2020 5857824 585, 245–250 (2020). [DOI] [PubMed] [Google Scholar]
- 48.Gardner MPH, Conroy JS, Shaham MH, Styer CV & Schoenbaum G Lateral Orbitofrontal Inactivation Dissociates Devaluation-Sensitive Behavior and Economic Choice. Neuron 96, 1192–1203.e4 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Takahashi YK et al. The Orbitofrontal Cortex and Ventral Tegmental Area Are Necessary for Learning from Unexpected Outcomes. Neuron 62, 269–280 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ostlund SB & Balleine BW Orbitofrontal Cortex Mediates Outcome Encoding in Pavlovian But Not Instrumental Conditioning. J. Neurosci. 27, 4819–4825 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Schoenbaum G, Nugent SL, Saddoris MP & Setlow B Orbitofrontal lesions in rats impair reversal but not acquisition of go, no-go odor discriminations. Neuroreport 13, 885–890 (2002). [DOI] [PubMed] [Google Scholar]
- 52.Dias R, Robbins TW & Roberts AC Dissociable Forms of Inhibitory Control within Prefrontal Cortex with an Analog of the Wisconsin Card Sort Test: Restriction to Novel Situations and Independence from “On-Line” Processing. J. Neurosci. 17, 9285–9297 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Murray EA, Moylan EJ, Saleem KS, Basile BM & Turchi J Specialized areas for value updating and goal selection in the primate orbitofrontal cortex. Elife 4, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Murray EA & Rudebeck PH Specializations for reward-guided decision-making in the primate ventral prefrontal cortex. Nat. Rev. Neurosci. 2018 197 19, 404–417 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Folloni D et al. Ultrasound modulation of macaque prefrontal cortex selectively alters credit assignment-related activity and behavior. Sci. Adv. 7, 7700 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rudebeck PH, Saunders RC, Lundgren DA & Murray EA Specialized Representations of Value in the Orbital and Ventrolateral Prefrontal Cortex: Desirability versus Availability of Outcomes. Neuron 95, 1208–1220.e5 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Iordanova MD, Killcross AS & Honey RC Role of the Medial Prefrontal Cortex in Acquired Distinctiveness and Equivalence of Cues. Behav. Neurosci. 121, 1431–1436 (2007). [DOI] [PubMed] [Google Scholar]
- 58.West EA et al. Noninvasive Brain Stimulation Rescues Cocaine-Induced Prefrontal Hypoactivity and Restores Flexible Behavior. Biol. Psychiatry 89, 1001–1011 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Blair CAJ, Blundell P, Galtress T, Hall G & Killcross S Discrimination between outcomes in instrumental learning: effects of preexposure to the reinforcers. Q. J. Exp. Psychol. B. 56, 253–265 (2003). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All code and data used in this study are available on https://colab.research.google.com/drive/1VYRAnvAO8OmzQpVaJe5radKIZnpEn638?usp=sharing and https://colab.research.google.com/drive/1ORP8Q9ceLBXlupvrCDh7HLAhQKsjQswr?usp=sharing. Additional information on materials and protocols are available upon request to the corresponding authors.