Supervised chemical graph mining improves drug-induced liver injury prediction

Summary

Drug-induced liver injury (DILI) is the main cause of drug failure in clinical trials. The characterization of toxic compounds in terms of chemical structure is important because compounds can be metabolized to toxic substances in the liver. Traditional machine learning approaches have had limited success in predicting DILI, and emerging deep graph neural network (GNN) models are yet powerful enough to predict DILI. In this study, we developed a completely different approach, supervised subgraph mining (SSM), a strategy to mine explicit subgraph features by iteratively updating individual graph transitions to maximize DILI fidelity. Our method outperformed previous methods including state-of-the-art GNN tools in classifying DILI on two different datasets: DILIst and TDC-benchmark. We also combined the subgraph features by using SMARTS-based frequent structural pattern matching and associated them with drugs’ ATC code.

Graphical abstract

Highlights

• •Supervised subgraph mining (SSM) constructs subgraph-level features
• •Subgraph-level features over-represented in DILI-positive compounds
• •SSM outperformed existing methods in experiments with two benchmark data sets
• •ATC code-specific discriminative sets of multiple subgraph features are suggested

Drugs; Computational chemistry; Artificial intelligence.

Introduction

Drug-induced liver injury (DILI) has been the leading cause of drug withdrawal or the discontinuation of newly approved drugs from the market in the US since 1970.^1,2 Only 4.7$\%$ of drug candidates progress from preclinical trials to the clinical stage due to safety concerns.^1,2,3 Thus, DILI is a major hurdle in drug development. While direct DILI can be detected in preclinical/clinical studies in a dose-related manner, idiosyncratic DILI is detected only at an incidence rate of 0.1% or below during clinical studies.^2,4,5,6 What makes DILI identification even more difficult in clinical trials is the low concordance between DILI outcomes in animal and human models, with 63% and 43% in non-rodents and rodents, respectively.^2,7,8,9 Thus, a number of research projects have been launched to characterize DILI from multiple perspectives.

Evaluating DILI directly from small-molecule drugs in terms of clinical outcomes is very difficult, and it was necessary to design new approaches to fill in a large gap in how chemical structures translate to hepatotoxic risk in humans.¹⁰ Thus, additional biochemical experiments are performed to explore the mechanism of DILI using high-throughput screening or pharmacogenomics^11,12 in projects designed to bridge the gap between structural information and the DILI outcome. Tox21 is a seminal project to broadly define the chemical toxicity of more than 10,000 chemical compounds.^13,14 Tox21 includes 14 major projects designed to improve our understanding of how chemical drugs reflect biochemical mechanisms and affect downstream pathways, and Tox21 data have been used for further investigation. Wu et al.¹⁵ divided drug modes of action into 17 different assays to investigate whether a drug affects individual targets. This approach demonstrated how to integrate assay data into DILI prediction to improve our knowledge of the mechanistic details of DILI. Follow-up methods adopted a similar strategy by leveraging deep learning (DL) architecture¹⁶ or gene expression profiles¹⁷ to bridge the gap between chemical structure and DILI outcome using biological/biochemical measurements.

On the other hand, we also need to understand the toxicity of small-molecule drugs directly from the chemical structure perspective because projects such as Tox21 require careful experimental design and expert knowledge on how to integrate and interpret the vast amount of experimental data, which is expensive and time consuming. For more than 90% of orally administered drugs, the liver is the main site of structure-dependent metabolism. Thus, the detection of DILI at the compound structure level requires the identification of substructures of toxic drugs. A structural alert (SA) is a substructure of a compound that contributes to a specific chemical property and determines the metabolic process of a compound. Examples of SAs include functional groups such as aromatic amines, carboxylic acids, and benzene moieties. Some chemical moieties are reported to be related to chemical toxicity, such as arylacetic acid, 2-aminothiazole, furan, aniline, and iodobenzene.^18,19,20 Although several SAs for DILI have been reported and reviewed, they have not yet been extensively utilized in machine learning (ML) models.²⁰ In recent articles, SAs were compiled for target organs based on the assumption that hepatotoxicity stems from a specific structure in the compound.^21,22,23

Research problem and motivation

Research problem

In this study, we aim to develop a prediction method for DILI using compound structure information only. In addition, we wish to discover potential SAs or substructures of drugs in terms of DILI. For this goal, the main challenge is obtaining sufficient data. Hepatotoxicity results are empirically obtained over a long period of time at the clinical or commercial stage. Thus, the amount of hepatotoxicity data is very small (only 1,279 drugs by the US FDA in Thakkar et al.²⁴) In addition, computational methods need to identify relevant features for DILI prediction. However, structural features for DILI are not well known as of now. Thus, the prediction method needs to overcome these challenges, i.e., small amounts of data for training prediction methods and feature identification for DILI.

Limitations of existing DILI prediction methods

Traditional approaches to DILI prediction mostly rely on pre-computed molecular descriptors or fingerprints.²⁵ These fingerprints are designed to describe general chemical compounds; thus, they are not tailored to predict DILI. Because of the weak expressiveness of fingerprints, neither shallow nor deep ML techniques performed well for DILI prediction (see Section: results and Vall et al.²⁵).

Limitations of deep or graph learning methods

Compounds can be viewed as graphs where atoms are nodes and bonds are edges. Thus, emerging graph learning methods are well suited for this task. We tested state-of-the-art graph learning methods for use in DILI prediction: MolHGCN, GraphLOG, and benchmark Graph Isomorphism Network (GIN) approaches.^26,27,28 MolHGCN alleviates oversmoothing and overfitting problems by flexible modeling of the complex relationships between the atoms in molecular structures as hypergraphs. GraphLOG is a pre-training method that uses self-supervised learning to simultaneously reflect the local information of the graph and the hierarchical and global information between the graphs. GIN is one of the most expressive graph neural network (GNN) architectures which is well suited for pre-training chemical graphs.²⁸ These methods were comparable to the previous DILI prediction methods at maximum 0.672 in AUC (see Section: results). Thus, the current graph learning algorithms are not powerful enough to overcome the challenges of the limited data for training prediction methods and feature identification for DILI. In fact, this result is consistent with the findings in a recent study that graph learning methodologies are not powerful enough to address chemical graphs.²⁹

Our subgraph mining approach

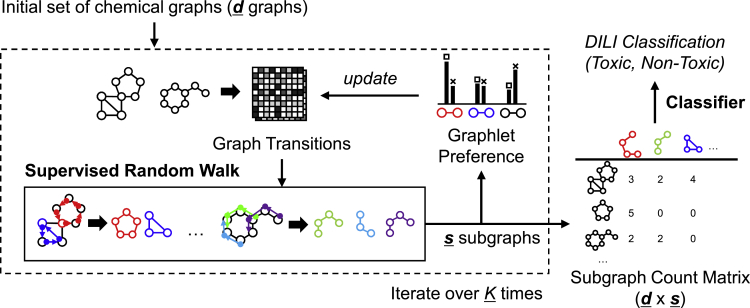
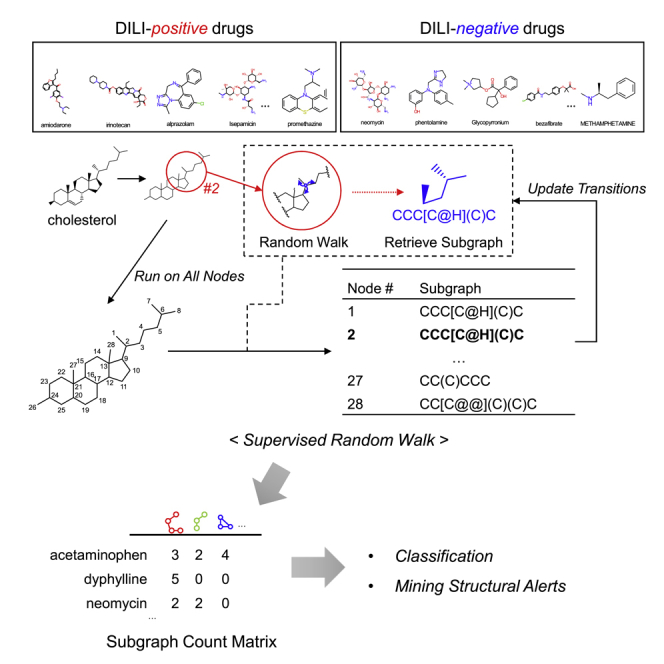
We propose a completely different approach, a supervised subgraph mining (SSM) framework (Figure 1) where subgraph features are learned by iteratively generating subgraphs for DILI prediction (Figure 2). Our method achieved improved performance up to 0.720 in AUC compared to the previous state-of-the-art ML methods including GNNs. In addition, our method is designed to produce subgraph patterns that are overrepresented in either DILI-positive or DILI-negative chemical drugs and thus can provide structural insights on drug design.

Figure 1.

Overview of the proposed method

A set of drugs is transformed into graphs and transitions are prepared. SSM produces subgraphs in a supervised manner with optimization in terms of DILI labels. Doublet preference is used to supervise the whole process by redefining graph transitions. The final subgraph counts are then used for the classification of DILI. The proposed pipeline is evaluated on two independent DILI datasets: DILIst and TDC-benchmark (See Section: STAR Methods).

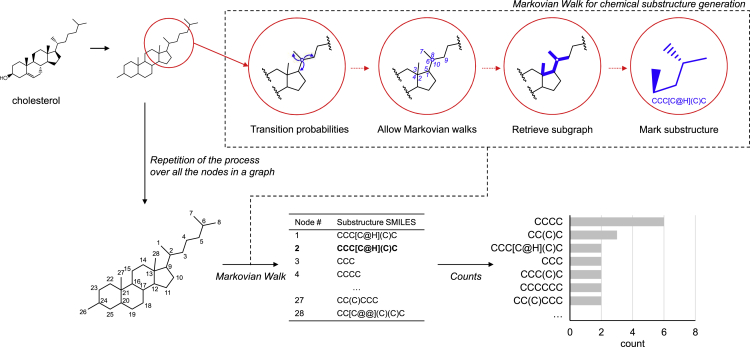
Figure 2.

Subgraph generation on chemical graphs is illustrated using cholesterol as an example

First, cholesterol compound is represented as a plain graph. For each node, transition probability is assigned and a random walker starts to traverse on the graph in a Markov chain. Subgraph is retrieved out of the visited nodes and edges. This process is run over all the nodes in the graph to generate the set of subgraphs. Then, unique subgraph counts are returned for cholesterol compound.

Subgraph generation is done by using the random walk (RW) approach, which has been successfully used in many fields of ML for graph learning.^30,31,32,33 Basically, performing RW on a graph to generate subgraphs is highly dependent on the edge weights. To increase the discrimination power of RW, a supervised version of RW (supervised random walk; SRW) was introduced for link prediction³⁴ and for identifying significant mutational clusters to classify cancer types.³⁵ We extended SRW methods to handle a set of chemical drugs. The novelty of our approach is to iteratively update edge weights on a set of chemical graphs in a supervised way in the framework of generating, testing, and refining subgraphs.

Results

Performance was evaluated using two independent datasets: DILIst and TDC datasets (see Section: liver toxicity chemical data).

Liver toxicity chemical data

The DILI datasets used in this study are listed in Table 1. The datasets were retrieved from Thakkar et al. and²⁴ Xu et al.³⁷ and used as the same in this study including the data splits provided from the original literature—temporal split (before and after 1997) for DILIst and scaffold split for TDC. To consider a drug as a graph, a chemical drug was represented in SMILES and converted to rdkit mol and networkx graph objects by setting heavy atoms as nodes and bonds as undirected edges. When there were multiple graphs clustered with ionic bonds, the largest connected component (a structure composed of only covalent bonds) was selected as the compound graph. Salts and ions were removed using rdkit SaltRemover. Thus, the numbers in the datasets are different from the numbers in the references due to the applicability of our analysis framework.

Table 1.

DILI datasets used in this study

Source	Label	Training	Validation	Test	Total
DILIst	Pa N	455 293		148 98	603 391
TDC	P N	175 150	11 43	50 46	236 239

The DILIst dataset was retrieved from Thakkar et al.²⁴ and the TDC benchmark DILI dataset was retrieved from Huang et al.³⁶

^aP: DILI-Positive, N: DILI-Negative.

The two datasets are well balanced in DILI class labels with positive vs. negative ratios. The ratio values of DILIst dataset were 1.55:1 and 1.51:1 for training and validation datasets, respectively, while 1.17:1, 0.26:1, and 1.09:1 in TDC training, validation, and test datasets, respectively.

Performance evaluation for DILI classification

In the DILIst and TDC-benchmark datasets, SSM generated 10,459 and 9,683 subgraph features, respectively. Our model was compared to three types of existing works: previously reported DILI prediction tools, state-of-the-art DNN methods, and random forest (RF) on molecular fingerprints.

Comparison to previous DILI prediction tools

As shown in Table 2, SSM achieved the best DILI prediction performance at 0.691, 0.784, and 0.338 in AUC, F1-score, and MCC, respectively, outperforming ML methods on Mold2 descriptors as well as state-of-the-art GNN methods. For both AUC and F1-score, SSM-RF outperformed with significant margins of 0.032 and 0.029 (more than twice greater than the error values - 0.011 for AUC and 0.008 for F1-score), respectively. The only previously reported approach evaluated on the same dataset was DeepDILI,³⁸ where the performance was 0.659 in AUC. They used an ensemble learning approach on the set of base classifiers (logistic regression, K-nearest neighbors, XGBoost, random forests, and support vector machine) to improve the prediction power. They compared three different descriptors: Mold2, Mol2vec, and MACCS. DeepDILI developed on Mold2 descriptor was reported to perform the best on DILIst dataset. Though Mold2 descriptor was developed to describe general aspects of chemical compounds as a 777-long descriptor,³⁹ it was not sufficient for the descriptor to be used for DILI classification. In the literature, as the other descriptors also showed comparable performance (Mol2vec: 0.654 and MACCS: 0.640 in AUC), this reassures that our approach was effective in generating data-specific features.

Table 2.

Performance comparison of SSM to previous studies on DILIst dataset was retrieved from²⁴

Model	AUC	F1-score	MCC	Accuracy
SSM
SSM - RF (margin to DeepDILI)	0.691 $\pm$ 0.011 (+0.032)	0.784 $\pm$ 0.008 (+0.029)	0.338 $\pm$ 0.030 (+0.007)	0.687 $\pm$ 0.005 (−)
SSM - MLP	0.654 $\pm$ 0.008	0.752 $\pm$ 0.007	0.240 $\pm$ 0.019	0.639 $\pm$ 0.006
SSM - soft voting: RF & MLP	0.664 $\pm$ 0.008	0.760 $\pm$ 0.007	0.264 $\pm$ 0.020	0.683 $\pm$ 0.004
Mold2 descriptor
DeepDILI	0.659	0.755	0.331	0.687
XGBoost	0.651 0.015	0.732 $\pm$ 0.012	0.219 $\pm$ 0.037	0.642 $\pm$ 0.016
RF	0.658 $\pm$ 0.012	0.736 $\pm$ 0.009	0.225 $\pm$ 0.030	0.645 $\pm$ 0.013
SVM	0.645 $\pm$ 0.009	0.752 $\pm$ 0.008	0.220 $\pm$ 0.035	0.646 $\pm$ 0.013
KNN	0.580 $\pm$ 0.021	0.657 $\pm$ 0.020	0.125 $\pm$ 0.038	0.582 $\pm$ 0.019
LR	0.628 $\pm$ 0.009	0.744 $\pm$ 0.007	0.130 $\pm$ 0.038	0.617 $\pm$ 0.011
Deep graph neural network methods
InfoMax	0.624 $\pm$ 0.009	0.687 $\pm$ 0.007	0.226 $\pm$ 0.027	0.627 $\pm$ 0.011
ContextPred	0.628 $\pm$ 0.009	0.687 $\pm$ 0.030	0.242 $\pm$ 0.029	0.632 $\pm$ 0.018
EdgePred	0.642 $\pm$ 0.010	0.690 $\pm$ 0.021	0.261 $\pm$ 0.025	0.639 $\pm$ 0.015
AttrMask	0.608 $\pm$ 0.009	0.653 $\pm$ 0.032	0.203 $\pm$ 0.032	0.606 $\pm$ 0.022
MolHGCN	0.541 $\pm$ 0.024	0.669 $\pm$ 0.023	0.087 $\pm$ 0.051	0.576 $\pm$ 0.025
GraphLOG	0.577 $\pm$ 0.017	0.751	0.000	0.602

Standard error of DeepDILI was not provided from the original article.

Performance without errors in GraphLOG indicates that all predicted values were DILI-positive.

The performance values of the previous models on DILIst data were built on Mold2 descriptor. Performance comparison on TDC-benchmark DILI dataset³⁶ is provided in Table S1.

We also achieved the best AUC at 0.923 using random forest classifier for the TDC dataset (Table S1). However, the performance of previous models reached 0.919 in AUC at best by AttrMask, as reported in the official TDC publication.³⁶ To provide more concrete comparison, we measure different metrics such as F1-score, MCC, and accuracy (Table S1). As a result, our SSM model outperformed the other methods in AUC, MCC, and accuracy values. Among the graph learning methods run in this study, EdgePred was the most effective in all the performance metrics. We note here that our algorithm was superior to the previous models when training on DILIst to test on TDC and vice versa (Table S5). For individual prediction results, see Table S6.

Comparison to graph learning methods

As our method uses subgraphs as features, a natural question would be how well the two state-of-the-art deep graph learning methods perform in DILI prediction. Thus, we compared our model with pre-trained GINs and two deep graph learning methods, MolHGCN and GraphLOG.^26,27,28 Surprisingly, the performance of graph learning methods is similar to that of traditional methods. Among the GNN methods compared here, GIN-EdgePred was the best performed model at 0.642. We note here that even the best-performing GNN model (GIN-EdgePred) showed less predictive power than both unsupervised SSM (AUC: 0.686) and supervised SSM (AUC: 0.691) at the margins of 0.044 and 0.047, respectively.

GraphLOG and MolHGCN achieved 0.577 and in AUC, respectively. Their performance was far behind even to non-DL methods such as DeepDILI and our unsupervised version. We note here that GraphLOG predictions were all DILI positive. The two GNN models (GraphLOG and MolHGCN) were also run and compared on TDC-benchmark dataset. Their performance (GraphLOG: 0.723 and MolHGCN: 0.707) was far behind even to the best-performed model of our investigation: AttrMask. The main reason why such powerful graph learning technology does not work for DILI prediction is because the graph learning methods are not yet powerful enough to handle subgraphs as features and to be trained with insufficient data. This result is consistent with the findings in a recent research work.²⁹

Comparison to molecular fingerprints

We further checked the prediction power of the refined subgraphs as follows. We first investigated whether replacing the subgraphs from SSM with widely used molecular fingerprints was effective in DILI prediction. Most of the existing widely used molecular fingerprints were not effective in DILI prediction with the highest AUC of 0.631 on DILIst dataset using Avalon⁴⁰ fingerprints and 0.895 on TDC-benchmark dataset using klekota-roth⁴¹ fingerprints (Table S2). Other fingerprints, such as Morgan,⁴² Pubchem,⁴³ MACCS,⁴⁴ and daylight,⁴⁵ were also ineffective in DILI prediction. As mentioned in Section: research problem and motivation, such fingerprints are not powerful enough to describe chemical structures although they are known to be effective for capturing general chemical features. Overall, it is evident that our strategy was successful in mining subgraph features for liver toxicity and consequently increased the prediction power of our algorithm.

Performance evaluation of experimental settings and predictions of SSM

Various parameter combinations were tested for performance optimization, such as the length of random walks $\left(l\right)$, augmentation level $\left(h\right)$, and the rate of updating graph transitions $\left(\alpha \right)$. The number of allowed random walks $\left(l\right)$ varied from 1 to 10 to investigate to how much extent subgraph mining is needed. Applying $l=1$ is equivalent to mining only doublets as subgraphs, where the best model AUC is 0.635. Allowing higher $l$ gradually improved the performance until $l=7$, while there was a decreasing trend afterward (Table S3). This is because larger subgraphs tend to occur in a smaller number of times, thus increasing the sparsity (see Section: discussion). To reduce the sparsity of the subgraph count matrix, we applied augmented random walk that independently generates more subgraphs on each of the nodes in a graph. As a result, generating more subgraphs was effective than generating single subgraphs for each node when comparing $h=1$ and $h=3$ (Table S4). However, increasing the level of augmentation resulted in a steady decrease in performance. Varying $\alpha$ did not show a significant difference in performance. Testing on both the $\alpha =0.1$ and $\alpha =0.5$, the AUC values were 0.684 and 0.690, respectively.

Doublet preference: Indicators to reflect the difference in DILI labels

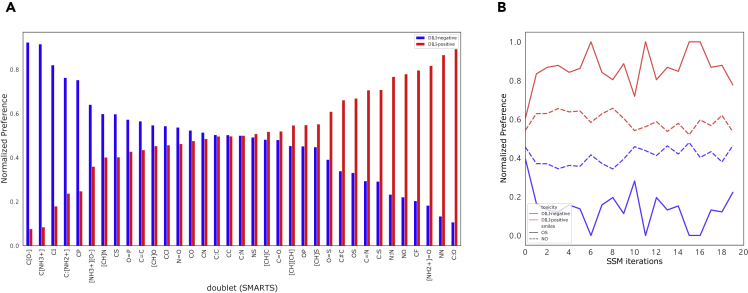
As doublets are the most basic unit to build chemistry, doublet preference was first explored for DILI-positive/negative drugs. The spectrum of the doublet preference is shown in Figure 3A. Aromatic bonds (C:O and C:S) are found to be more preferred by DILI-positive drugs to DILI-negative drugs (89.3% and 70.8% DILI-positive preference, respectively). It was also interesting that C-F bond is prevalent in subgraph features of DILI-positive drugs, while C-Cl bond is the opposite even though both F and Cl are in the same halogens. When the halogen is changed to iodine, DILI-negative compounds are found to be prevalent at 82.0%. Thus, it is found that the larger the halogen element bonded to aliphatic carbon (C-F $>$ C-Cl $>$ C-I), the less liver toxicity is likely to be found in chemical compounds. We note here that N-N and O=S bonds are also found to be strong toxic alert candidates in the previous literature.⁴⁶

Figure 3.

Doublet preference used from mined subgraph features

(A) Spectrum of commonly present doublets with probability of each class label.

(B) Doublet preference over iteration of OS and NO. At the initial state (unsupervised), the difference between DILI-positive and DILI-negative drugs to use of the two bonds was marginal. However, after several steps, the preference was reinforced to favor the either of the DILI labels.

To investigate how doublet preference changes over iterations, both OS and NO were chosen as examples (Figure 3B). Both of the doublets are more frequently found and used by DILI-positive drugs at the first step (SSM without supervision). As supervision applied, the preference of both doublets to DILI-positive drugs increased.

Convergence of transitions

We first investigated how fast each of the transition matrices converges over iterations. Figure S2 shows the convergence of the drugs in DILIst dataset. All the transition matrices converge dramatically at the beginning of the iteration. After several iterations, there are subtle fluctuations at later iterations. The top 3 convergent drugs are AMANTADINE (CID: 2130), TERBUTALINE (CID: 5403), and PROPOFOL (CID: 4943) and the least 3 convergent drugs are FOSFOMYCIN (CID: 446987), CID: 16682735, and CID: 5255827.

When we ranked the drugs in terms of the convergence rate of the corresponding transition matrix, there was a no statistically significant difference in the rate of convergence between DILI-positive and DILI-negative drugs as shown in Figure S3 ($p$ = 0.3148; Kolmogorov-Smirnov test). To investigate whether such difference was not correlated with chemical properties, the convergence rank was compared with molecular weight, logP, the number of rings, and the number of aromatic rings (Figure S4). No significant correlation was observed between the convergence rate and either of molecular weight and logP. However, there was a slight correlation between convergence and the number of ring systems. There was a steady decrease in convergence as the number of rings starts from 0 to 6 (third panel of Figure S4). However, gradual increase in the convergence rate was observed in growing number of aromatic rings (fourth panel of Figure S4).

Discussion

To train ML models from data, features need to be well defined, and the amount of data needs to be sufficient. Often, both data and features are well defined in ML model development. However, the amount of data in the case of DILI prediction is very small (Table 1). Widely used features such as molecular fingerprints have limitations in discovering important features of chemical compounds for DILI (Table S2). In addition, it is important that DILI features are constructed in a way that allows chemical interpretation. Thus, we used subgraphs as DILI features. A natural question arises here—what subgraphs are important in terms of DILI? Thus, we discuss our results in terms of the enrichment of the subgraphs for DILI.

Evaluation of SA potentials of single subgraphs

Doublets are too small in size to reflect the mechanistic diversity in chemistry of various sizes and compositions. In fact, DILI prediction using $l$ = 1 (using doublets as features) had 0.667 in AUC at best, far behind the optimized performance (Table S3). Thus, we tried to represent important features using subgraphs. To understand the behavior of our model on the chemistry side, the SA potentials of single subgraphs were investigated using the feature importance of the trained RF model. For DILIst dataset, our model generated 10,459 subgraphs, of which 5,233, 2,736, and 2,490 subgraphs were present in DILI-positive-only, both, and DILI-negative-only drugs, respectively.

The 762 subgraphs were considered important with entropy $<$ 0.5 and feature importance $>$ 0.0001 in classifying DILI compounds (Table S7). Entropy was measured on each subgraph by comparing the support between DILI-positive and DILI-negative drugs. Feature importance was calculated from random forests classifier. Among the subgraphs, 29 subgraphs of greater support in DILI-positive drugs than in DILI-negative drugs with more than 1% support in DILI-positive drugs were considered as single-subgraph SAs in this study (Table 3). Among them, sixteen subgraphs (red-colored in Table 3) showed high fidelity to DILI-positive drugs in both training and test datasets. For example, cNc(c)c was exclusively present in 1.98% of DILI-positive drugs. This pattern was similarly observed in the test data with 2.03% coverage for DILI-positive drugs. For selected subgraphs (cNc(c)c, cSccc, NNC=O, cccBr, ccCNCCNC, and CCC=CN), matched drugs are displayed in Figure 4. We were able to observe that there are commonly present substructures within the subgraph-matched drugs of each panel in Figure 4. For example, in case of cNc(c)c (Figure 4A), seven out of nine drugs (piperacetazine, chlorpromazine, cyamemazine, perphenazine, trimeprezine, phenothiazine, and promethazine) share phenothiazine moiety as common backbone structure. They are all categorized as tricyclic antidepressants. This was also the case in cSccc-matched drugs (Figure 4B) as nine out of eleven drugs are of phenothiazine-based tricyclic antidepressants. We note that none of the subgraphs displayed in Figures 4A–2F were found in DILI-negative drugs. Thus, we were able to observe that these subgraphs are single-subgraph SAs.

Table 3.

Twenty-nine subgraphs with feature importance $>$ 0.001 and entropy $<$ 0.5

SMILES	Support (Train)		Support (Valid)		Importance x (1e-2)
	F_NT	F_T	F_NT	F_T
CCNN	0.34	2.86	1.02	–	0.094
C[C@](C)(C)C	0.34	3.08	–	–	0.064
cNc(c)c	–	1.98	–	2.03	0.057
C[C@H](C)CO	–	2.20	4.08	0.68	0.048
nncS	–	1.76	–	–	0.044
cSccc	–	2.42	–	0.68	0.042
NNC=O	–	2.20	–	1.35	0.042
cScc	0.34	2.86	–	0.68	0.040
cncc[nH]	–	1.54	–	0.68	0.030
CCOCn	–	1.10	2.04	–	0.022
CC(=C)N	–	1.98	1.02	0.68	0.021
cc(c)o	–	1.76	–	1.35	0.020
C=CN	–	1.31	2.04	0.68	0.019
CCC=CN	–	1.10	–	0.68	0.018
cccBr	–	1.54	–	1.35	0.018
ccScc	–	1.76	–	1.35	0.018
ccCNCCNC	–	1.32	–	1.35	0.017
cccCNCCCC	–	1.10	1.02	2.03	0.017
CC(N)=CC	–	1.32	1.02	–	0.016
Coc	–	1.10	–	0.68	0.011
cc(N)cS	–	1.32	–	–	0.011
cCNCC = O	–	1.10	1.02	–	0.011
C[C@@H](C)CO	–	1.98	4.08	2.70	0.011
C/C(c)=N	–	1.10	–	0.68	0.010
C=C[C@H](C)C	–	1.10	–	–	0.010
C1=CCCCC1	–	1.10	1.02	0.68	0.010
C=C/CO	–	1.54	3.06	–	0.010
NC=CCS	–	1.10	–	–	0.010
C[C@@H](C)CCCC	–	1.10	–	1.35	0.010
CNCC=O	–	1.10	–	0.68	0.010
cccSC	–	1.10	–	0.68	0.010

Figure 4.

Examples of single SA identification

(A) cNc(c)c, (B) cSccc, (C) NNC=O, (D) cccBr, (E) ccCNCCNC, and (F) CCC=CN. For each SA, matched patterns in each of the drugs are highlighted. All the drugs here are labeled as DILI-positive.

Discriminative subgraph combinations of DILI with respect to the drugs’ ATC code

A set of subgraphs is mixed up in a single compound, and they co-occur at different positions with varying inter-distances. We want to discover a set of subgraphs that are overrepresented in DILI-positive/negative compounds. Thus, a set of these subgraphs is referred to as discriminative subgraph combinations (DiSC) and further considered as potential SAs for DILI-positive drugs. We used SMILES arbitrary target specification (SMARTS) language⁴⁷ to combine individual subgraphs where “.” notation denotes a combined string representation of subgraphs. There are 500 and 368 subgraphs for DiSC identification in DILIst and TDC-benchmark datasets, respectively. We experimented on 2-subgraph and 3-subgraph combinations in this study. Detailed methods are described in Discriminative Subgraph Combinations.

We investigate whether subgraph combinations are enriched according to Anatomical Therapeutic Chemical Classification System (ATC) code of the matched drugs (See Discriminative Subgraph Combinations and Table 4). There are 68 and 44 DiSCs of 2-subgraph and 3-subgraph combinations in DILIst dataset, respectively. (Table 4).

Table 4.

DiSCs enriched to ATC code

ATC	Description	DiSC	Total Drugs		Matched Drugs		$p$-value	Coverage
			DILIp	DILIn	DILIp	DILIn
2-subgraph DiSCs
A03	Drugs for functional gastrointestinal disorders	C=O.COccO	5	4	0	1	7.72e-3	0.11
A10	Drugs used in diabetes	CCCCCCNC.CCc	1	11	0	3	9.78e03	0.25
C01	Cardiac therapy	cCCN.cO	9	10	5	1	1.77e-3	0.32
C03	Diuretics	CCC.ccccS	4	8	2	1	8.04e-3	0.25
C07	Beta blocking agents	CCCNC.cc(c)C=O	7	6	0	3	3.80e-3	0.23
C08	Calcium channel blockers	CCC.cC(C)CC	4	10	2	2	6.85e-3	0.29
C09	Agents acting on the renin–angiotensin system	CCCCCCNC.CCc	2	12	0	4	7.31e-3	0.29
C10	Lipid modifying agents	cC=O.cOCC	2	9	1	1	6.14e-3	0.18
J01	Antibacterials for systemic use	Cccc.O=CCNC=O	11	39	5	16	4.21e-5	0.42
J05	Antivirals for systemic use	CCC.cc(n)N	4	7	2	0	5.01e-3	0.18
L01	Antineoplastic agents	CN.cCCO	11	29	6	6	6.18e-6	0.30
M01	Anti-inflammatory and antirheumatic products	Ccc.cc(c)c	2	11	1	2	5.30e-3	0.23
M03	Muscle relaxants, directly acting agents	C=O.CC[N&+](C)C	5	7	3	0	5.57e-3	0.25
N01	Anesthetics	C1CCNCC1.Cc(c)ccc	5	7	2	1	8.94e-3	0.25
N02	Analgesics	CC.cC(C)CC	13	6	9	0	7.61e-3	0.47
N03	Antiepileptics	CN.cC(C)CC	2	10	1	2	9.05e-3	0.25
N05	Psycholeptics	CCC.ccccS	18	28	2	8	9.98e-8	0.22
N06	Psychoanaleptics	ccccN.cn	5	22	0	4	9.74e-6	0.15
P01	Antiprotozoals	C1CCNCC1.Cc(c)ccc	3	8	0	2	6.71e-3	0.18
R06	Antihistamines for systemic use	CO.C1CCNCC1	8	6	3	1	7.35e-3	0.29
3-subgraph DiSCs
A03	Drugs for functional gastrointestinal disorders	C=O.COccO.CNCC	5	4	0	1	7.72e-3	0.11
A10	Drugs used in diabetes	ccC.cccCCN.CC	1	11	0	2	4.17e-3	0.17
C01	Cardiac therapy	ccO.cCCN.cO	9	10	5	0	6.39e-4	0.26
C07	Beta blocking agents	CC(C)N.cOC.CCCcc	7	6	3	0	4.29e-3	0.23
C08	Calcium channel blockers	CC.cC(C)CC.CCN(C)CC	4	10	0	2	1.37e-3	0.14
C09	Agents acting on the renin–angiotensin system	cCC.ccCCCN.CC	2	12	1	3	7.41e-3	0.29
C10	Lipid modifying agents	cC.ccc(c)c.c1ccccc1	2	9	0	2	6.94e-3	0.18
J01	Antibacterials for systemic use	Cccc.CCSCC.O=CCNC=O	11	39	4	15	1.21e-5	0.38
J05	Antivirals for systemic use	CCC.cc(n)N.cn	4	7	2	0	5.01e-3	0.18
L01	Antineoplastic agents	CCC.cCCO.cO	11	29	5	4	6.63e-7	0.23
M03	Muscle relaxants, directly acting agents	CCC.OccO.C=O	5	7	2	1	8.94e-3	0.25
N01	Anesthetics	C=O.C1CCNCC1.Cc(c)ccc	5	7	2	1	8.94e-3	0.25
N02	Analgesics	CCCO.cCCN.Cccccc	13	6	9	0	7.61e-3	0.47
N05	Psycholeptics	cccN.cccS.CCN(C)C	18	28	2	7	4.70e-8	0.20
N06	Psychoanaleptics	CC.COccO.CNCC	5	22	2	7	4.06e-6	0.11
P01	Antiprotozoals	cc.cccccc.Cc(c)ccc	3	8	0	2	6.71e-3	0.18
R06	Antihistamines for systemic use	CO.C1CCNCC1.Cc1ccccc1	8	6	3	1	7.35e-3	0.29

The subgraph patterns were retrieved for those of $p$-value less than 0.01 and the coverage on the corresponding ATC code more than 10%. In this table, only 20 and 17 representative patterns with the maximum coverage for each ATC code are displayed for 2-subgraph and 3-subgraph patterns, respectively. ATC code (level 2) was matched to each drug for upon availability. Full list of DiSCs, matched CIDs, and SMILES information is provided in Table S8. ($p$-values were calculated by chi-square test).

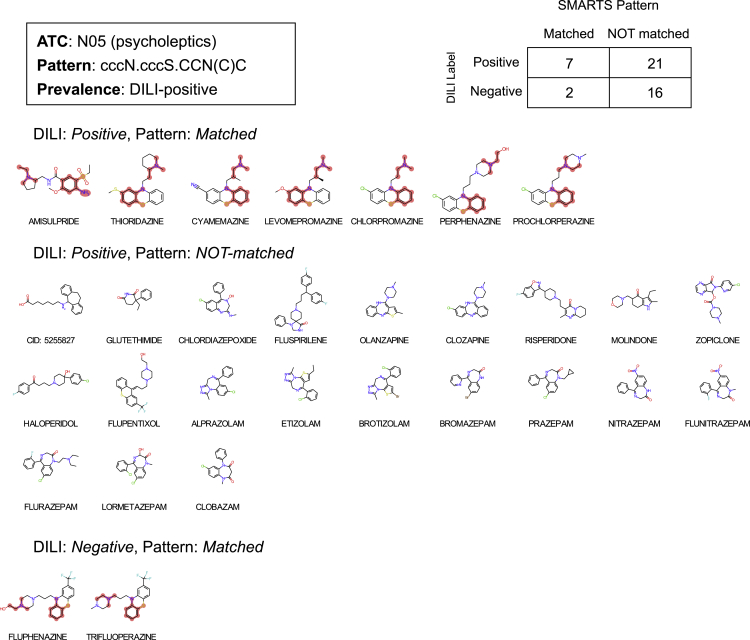
Among the 2-subgraph DiSCs, drugs with “ccccN.cn” on ATC:N06 (psychoanaleptics) and “Cccc.O=CCNC=O” on ATC:J01 (antibacterials for systemic use) are displayed in Figures 5 and 6, respectively. Drugs matched with “ccccN.cn” on ATC:N06 were mirtazapine, tacrine, nefazodone, and trazodone. Both nefazodone and trazodone share the common backbone structure that is not found in any of DILI-positive drugs without the pattern. There are 16 out of 39 DILI-positive drugs matched with “Cccc.O=CCNC=O” on ATC:J01 drugs (Figure 6). Among the 3-subgraph DiSCs, drugs with “cccN.cccS.CCN(C)C” on ATC:N05 (psycholeptics) and “CC.cC(C)CC.CCN(C)CC” on ATC:C08 (calcium channel blockers) are displayed in Figures 7 and 8.

Figure 5.

“ccccN.cn” enriched to ATC code: N06 (Psychoanaleptics)

The matched drugs are displayed along with subgraph pattern as highlighted.

Figure 6.

“Cccc.C=CCNC=O” enriched to ATC code: J01 (Antibacterials for systemic use)

The matched drugs are displayed along with subgraph pattern as highlighted.

Figure 7.

“cccN.cccS.CCN(C)C” enriched to ATC code: N05 (Psycholeptics)

The matched drugs are displayed along with subgraph pattern as highlighted.

Figure 8.

“CC.cC(C)CC.CCN(C)CC” enriched to ATC code: C08 (Calcium channel blockers)

The matched drugs are displayed along with subgraph pattern as highlighted.

Limitations of the study

There are two limitations when using individual subgraphs as SA candidates. First, there is a trade-off between coverage and specificity. A small-sized subgraph is likely to be found in a significant number of drugs, resulting in many false positives. In contrast, with a large subgraph, the coverage for DILI-positive/negative drugs is decreased. Among the exclusively present SAs, only six (C[C@](C)(C)C, CCNN, cScc, cSccc, NNC=O, and C[C@H](C)CO) exceeded 2% fidelity to DILI-positive drugs in the training data. Second, single subgraphs cannot account for the variations derived from bioisosteres.⁴⁸ Partial modifications outside the core structure of the toxic motifs can lead to similar toxicity mechanisms.⁴⁹ Thus, we extended our approach to “structured SAs” to suggest extended SAs with both specific and meaningful coverage against DILI-positive drugs.

Besides, as mentioned in Results that DL methods suffer from the lack of data in DILI classification, our method can also be improved by incorporating more DILI information. Recent studies in graph learning extensively use pre-training strategies using a large-scale non-labeled chemical database (e.g. Zinc lead compounds) to build an embedding of chemical compounds with rich structural diversity. Future methods can be directed to leverage non-labeled chemical structures in building subgraph features.

Finally, potential SAs need to be experimentally verified, which is costly and time consuming. An effective strategy would be to prospectively examine the presence of these DILI-alert and DILI-safe subgraphs in newly reported toxic drugs. On the computational side, our algorithm does not guarantee the discovery of all subgraphs overrepresented in toxic drugs. The main reason is that subgraph generation using SRW does not enumerate all possible subgraph set, although the iterated supervision on doublet probabilities has shown good convergence behavior. Another important graph mining issue is that subgraphs from DILI datasets may not be sufficient to estimate the true distribution of chemical compound space in terms of DILI. DL-based link prediction methods can be extended for this purpose, but the technology is not yet powerful enough to overcome problems of insufficient data.

Conclusion

Our work explicitly uses subgraphs as features to classify the liver toxicity of chemical drugs. To the best of our knowledge, our approach is the first subgraph mining approach for DILI prediction. Our contributions can be summarized as follows. First, the prediction accuracy of chemical toxicity outperforms the previous tools and state-of-the-art GNN methods. Second, subgraphs with high/extreme fidelity to DILI were extensively searched for by iterative supervision on graph transitions. Thus, the subgraph population can be directly used to catalog structural characteristics and to infer mechanism of DILI. We compiled 762 potential single SAs and 68 DiSCs enriched to either DILI label. Finally, our report can be extended as a computational guidance to structure-based drug design, as both DILI-alert and DILI-safe subgraph sets are prepared against many disease targets (ATC codes).

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
DILIst dataset	Li et al., 202038	https://pubs.acs.org/doi/suppl/10.1021/acs.chemrestox.0c00374/suppl_file/tx0c00374_si_004.xlsx
Therapeutics Data Commons (TDC) - DILI dataset	Huang et al., 202136	https://tdcommons.ai/single_pred_tasks/tox/#dili-drug-induced-liver-injury
Software and algorithms
Supervised Subgraph Mining (SSM)	This study	https://github.com/sslim0814/SSM
DeepDILI	Li et al., 202038	https://github.com/TingLi2016/DeepDILI
GIN - InfoMax/ContextPred/EdgePred/AttrMask	Hu et al., 202028	https://github.com/snap-stanford/pretrain-gnns
MolHGCN	Chen et al., 202226	https://github.com/fychen32/MolHGCN
GraphLOG	Xu et al., 202127	https://github.com/DeepGraphLearning/GraphLoG

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Sun Kim (sunkim.bioinfo@snu.ac.kr).

Materials availability

This study did not generate new unique reagents.

Method details

An overview of the proposed method is illustrated in Figure 1. Each part is explained in detail as follows.

• •Preliminaries
• •Generate candidate subgraphs by supervised random walks
• •Updating Graph Transitions
• •Experiments for Performance Evaluation
• •Structural Alert Mining from Subgraph Features

Preliminaries

A chemical compound is transformed into an undirected and unweighted graph $g=⟨V\left(g\right),E\left(g\right)⟩$ that consists of a set $V\left(g\right)$ of nodes (heavy atoms) and a set $E\left(g\right)$ of edges (bonds). The degree and adjacency matrices of $g$ are denoted as $D_g$ and $A_g$, respectively. The transition matrix of $g$ is defined as $T_g=D_g^{-1}{A}_g$. For a set $S$ of graphs that are labeled DILI-positive or DILI-negative, the doublet preference $F_S$ denotes the frequency table with counts of both labels for each distinct doublet found in $S$ (Figure S1). In addition, $\alpha$ is a hyperparameter for updating graph transition matrix $T_g$; $k$ denotes the number of iterations; $l$ is the number of allowed walks; $h$ is the number of subgraphs for the augmentation.

Supervised subgraph mining algorithm

The workflow of our subgraph mining algorithm is illustrated in Figure 1 and Algorithm 1. Subgraphs are generated using a supervised RW-based approach so that subgraphs are overrepresented in either DILI-positive or DILI-negative class labels, not both. The final subgraphs set $S$ is stored and used for the next iteration. This process is iteratively executed by updating the graph transitions $\left(T_g\right)$ of each chemical graph $g$ using the doublet preference $\left(F_S\right)$. From the subgraph sets stored as a result of each iteration, the subgraph set with the highest accuracy is selected as the final feature for the DILI prediction model. The whole procedure is described more formally in Algorithm 1.

Algorithm 1.

Overall procedure of supervised subgraph mining

Generate candidate subgraphs by supervised random walks

As in Algorithm 1, subgraphs are generated for each of the nodes in a chemical graph $\left(g\right)$. For each node in $V\left(g\right)$, a random walker selects one of its direct neighbors based on transition probabilities in $T_g$. The selection of nodes and edges by the walker is recorded for a preset number of random walks $\left(l\right)$ in a Markov chain model. Then, the final sets of two node and edge lists are used to mine a subgraph. We allowed multiple subgraphs to be generated from each node by setting up $h$ augmentation so that they independently traverse the compound graph, generating $h{\sum }_g\left|V\left(g\right)\right|$ subgraphs. The final subgraph information of $g$ is then translated into a frequency table.

As an example, in Figure 2, cholesterol is transformed into an undirected and unweighted graph where the nodes are heavy atoms and the edges are bonds between the atoms. Then, for carbon numbered 2, a walker traverses the cholesterol graph with ten walks allowed ($l$ = 10) producing the list of visited nodes (blue-colored numbers from 1 to 10). The subgraph retrieved using the graph traversal information is CCC[C@H](C)C (in SMARTS). This process is applied to all the nodes in the cholesterol graph to generate subgraphs. There are 28 subgraphs with $h=1$. The subgraphs are summarized by which and how many subgraphs are generated. Thus, the final frequency table of cholesterol is {CCCC:6, CC(C)C:3, CCC[C@H](C)C: 2, …}.

Updating graph transitions

Subgraphs set $S$ as a result of each iteration is used to update the graph transitions for the next iteration. For this process, all subgraphs in $S$ are decomposed into doublets, and the doublets are counted for each class of origin. This means that the subgraph outcome is translated into a doublet-based class preference regarding how many time doublets are used in both class labels. The counts are then normalized to probabilities for each doublet to calculate the doublet preference $\left(F_S\right)$. In Figure S1, there are selected subgraphs from two example drugs from both class labels. These subgraphs are decomposed into doublets, resulting in 13 unique doublets as a union set. Then, subgraphs are counted for each class of origin. There are 2 and 1 C-C subgraphs in the DILI-positive and DILI-negative classes, corresponding to 0.67 and 0.33 probability values, respectively.

Finally, the transition matrix $T_g$ of each compound graph $g$ is updated using the doublet preference $F_S$ depending on the given class label of a compound. Given an adjacency matrix $A_g$ = $\left[a_{ij}\right]$ and a doublet preference $F_S$ of a compound graph, the temporary transition matrix is built as $T_g^{\prime }=\left[t_{ij}^{\prime }\right]$, where $t_{ij}^{\prime }=Su{p}_{ij}^P/\left(Su{p}_{ij}^P+Su{p}_{ij}^N\right)$ if $a_{ij}=1$ and the doublet consisting of vertices (=heavy atoms) i, j and their connecting edge (=bond) exists in $F_S$; otherwise, $t_{ij}^{\prime }=0$. $Su{p}_{ij}^P$ and $Su{p}_{ij}^N$ are the DILI-positive and DILI-negative frequencies of the doublet in $F_S$, respectively. Subsequently, $T_g^{\prime }$ is row-wise normalized (${\sum }_j{t}_{ij}$ = 1). As there are $k$ iterations, $T_g^k$ is updated using $T_g^{\prime }$ at iteration $k$ with parameter $\alpha$ to calculate $T_g^{k+1}$, where varying the hyperparameter $\alpha$ controls the rate of supervision (Equation 1).

$$T_g^{k+1}=\alpha T_g^k+\left(1-\alpha \right){T^{\prime }}_g^k$$ (Equation 1)

Experiments for performance evaluation

DILI prediction was performed by the ensemble of both random forest (RF) and multi-layer perceptron (MLP) classifiers of the sklearn library (version 0.23.2) of Python 3.7.7 on the subgraph count matrix from SSM. We chose the best performed model by combining both of the classifiers. For the RF classifier, the number of base trees was 100. For the MLP classifier, two layers were stacked with 1024 and 128 neurons for the first and second layer, respectively. Other parameters were set default unless mentioned elsewhere. Area under the ROC Curve (ROC-AUC) was used as a metric of performance. The results from the previous DILI prediction tools were retrieved from^37,38 and directly compared in this study. Also, selected state-of-the-art GNN methods (GraphLOG,²⁷ MolHGCN and GIN³⁶) are directly run on the same DILI data sets in this study. For supervised subgraph generation, we tested all parameter combinations for $l=\left\{\mathrm{1,2,3,4,5,6,7,8,9,10}\right\}$, $\alpha =\left\{\mathrm{0.1,0.5}\right\}$, and $h=\left\{\mathrm{1,3,5,10,20}\right\}$.

Structural alert mining from subgraph features

Single-subgraph SAs

Subgraphs that are mined by our SSM algorithm are overrepresented in either DILI-positive or DILI-negative drugs. In addition, individual subgraphs are tested for their predictive power for DILI with independent data sets. We chose important subgraphs with feature importance $>$ 0.0001 (greater than random importance) from the random forests model and entropy $<$ 0.5 at the individual subgraph level as single-subgraph SAs.

Discriminative subgraph combinations

A potential SA is a set of subgraphs that co-occur in many toxic compounds but not necessarily at consecutive positions of a compound. Thus, we name this set of subgraphs as Discriminative Subgraph Combinations (DiSCs).

However, there are two major challenges for mining potential SAs by combining subgraphs. First, there are small subgraphs with many overlapping parts due to their similar chemical composition: as we can see in the DILIst data that the average numbers of nodes and edges in the subgraphs are 6.11 $\pm$ 1.25 and 5.16 $\pm$ 1.27, respectively. Thus, we need to effectively combine them to increase the coverage of subgraphs in toxic drugs. Second, it is computationally infeasible to enumerate all possible subgraph combinations. Our SSM produced 10,459 subgraphs (see Section: results). Combining two of the 10,459 subgraphs from SSM requires to consider $\left(\begin{array}{c}\mathrm{10,459}\\ 2\end{array}\right)$ = 54,690,111 combinations. In general, these would require considering ${\sum }_{k=2}^{\mathrm{10,459}}\left(\begin{array}{c}\mathrm{10,459}\\ k\end{array}\right)$ combinations. Thus, a strategy to combine all subgraphs would result in many false-positive SAs, although we did investigate whether subgraph combinations are overrepresented in toxic compounds.

We tackle the problem of characterizing DiSCs as follows: (1) mining non-overlapping subgraphs by utilizing SMARTS based pattern matching (2) iterative extension upon promising DiSC candidates. To cope with the exponentially large search space, we utilized a branch-and-bound like search tree pruning.

In this study, we restricted the template subgraphs to be combined into SMARTS pattern at 2% minimum support against the whole data drugs. This is because the individual subgraphs are sufficiently large enough to be matched against compound graphs, thus, combining more than three subgraphs hardly produces informative SAs, rather produces highly sparse SAs. Moreover, considering all possible $N$ combinations of subgraphs requires exponential computational cost, which is not feasible. As we have selected the individual subgraphs for DiSC as those with more than 2% support, there are 500 and 368 subgraphs used for DILIst and TDC-benchmark data sets, respectively.

• 1.Among the found subgraphs $s\in S$, those with support less than 2% are dropped. For the remaining ones, if $s$ and $s^{\prime }$ have same support (occurs in the same set of compounds) while $s^{\prime }$ is a subgraph of $s$, $s^{\prime }$ is again dropped.
• 2.Remaining subgraphs are considered as 1-mer SAs $\left(C_1\right)$; we repeat the following step to find $k$-mer SAs $\left(C_k\right)$ for 1$k>$.
• (a)For $c\in C_{k-1}$ and subgraph $s\in S-C_{k-1}$, we generate the SMARTS pattern for $c^{\prime }=c\cup \left\{s\right\}$ to $C_{k-1}$ by using grouping operator ‘.’.
• (b)Match the generated pattern to the set of compounds to find support on DILI-positive $\left(Su{p}^P\right)$ and support on DILI-negative $\left(Su{p}^N\right)$ drugs, and compute entropy-based significance score of the support values to see whether this $k$-mer is a potential SA. The significance is computed as:

$$1-\text{Entropy}\left(Su{p}^P,Su{p}^N\right)$$

• (c)If the significance or support is below the predefined criteria (resp. 0.1 and 0.02), we define this to be (resp.) insignificant/infrequent and discard from further enumeration. Otherwise, we add $c^{\prime }$ to $C_k$.

As the potential SA pattern grows in size, support does monotonically decrease, but in general entropy does not. Nevertheless, to explore the vast search space effectively, our approach can be interpreted as growing the promising SAs. We note that for initial $C_1$, entropy cutoff is not applied, due to small generic backbone subgraphs such as short carbon chains appearing universally among both toxic and nontoxic compounds. Application of entropy cutoff to $C_1$ can lead to a premature termination of the search, ignoring meaningful combination of small motifs that can be informative in identifying toxic compounds.

To make our results interesting, DiSCs were investigated against ATC code of the data set drugs.

Published: January 20, 2023

Supplemental information

Table S6. Individual prediction results from the SSM, related to Section

Performance Evaluation for DILI Classification. A DILIst test data, B TDC benchmark test data, Please refer to the excel file (file name: SSM_extended_supplementary_tables.xlsx) attached to the Supplementary File. See STAR Methods for experimental details.

Table S7. Important subgraphs in classifying DILI. There are 762 subgraphs, related to Section

Evaluation of SA Potentials of Single Subgraphs. Please refer to the excel file (file name: SSM_extended_supplementary_tables.xlsx) attached to the Supplementary File. See STAR Methods for experimental details.

Table S8. Table of ATC-enriched SMARTS patterns and the list of matched drugs, related to Table 4

Please refer to the excel file (file name: SSM_extended_supplementary_tables.xlsx) attached to the Supplementary File. See STAR Methods for experimental details.

Data and code availability

• •DILIst data set can be found in Li et al.³⁸ and TDC benchmark data set can be found in https://tdcommons.ai/single_pred_tasks/tox/#dili-drug-induced-liver-injury.
• •All original code has been deposited at GitHub and is publicly available as of the date of publication. The DOI is listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.