Who should bear the burden of COVID-19 related fiscal pressure? An optimal income taxation perspective

Abstract

The COVID-19 pandemic has led to an increase in public debt in most countries, and the Ukraine war is likely to have similar effects. This will increase fiscal pressure in the future. We study how the shape of the optimal nonlinear income tax schedule is affected by this increase. We calibrate the workhorse optimal income tax model to five European countries: France, Germany, Italy, Spain and the UK. Applying an inverse-optimum approach to the pre COVID-19 economies we obtain the Pareto weights implicitly applied by the different countries. We then ask how the schedule of marginal and average tax rates should be optimally adjusted to the increase in fiscal pressure. For all countries, we find that the increase in fiscal pressure leads to a less progressive optimal tax schedule both in terms of marginal and average tax rates.

1. Introduction

The COVID-19 pandemic will leave us with a considerable stock of additional government debt. Further, the economic fallout of the Ukraine war will lead to an additional burden on public finances, as spending on defense, energy security and help for refugees surges. Servicing this debt will limit the fiscal leeway in the future and force governments to spend less or raise more revenue, probably both. The view is widespread that it is important to distribute the burden of servicing the additional debt fairly, suggesting that taxes should become more progressive.1 For instance, in a recent paper on tax policy, the IMF argues that “countries have multiple options to enhance the effective progressivity of their tax systems” (de Mooij et al., 2020 p. 1) and adds that “options include more progressive personal income tax systems” (de Mooij et al., 2020 p. 3). However, the paper also reminds policymakers that “the optimal degree of progressivity should strike a balance between equity and efficiency.” (de Mooij et al., 2020 p. 4).

How does the optimal degree of income tax progression change if governments need to raise more revenue? Somewhat surprisingly, this issue has received rather little attention in the optimal income tax literature à la Mirrlees. An exception is a recent paper by Heathcote and Tsujiyama (2021b) who elaborate the role of fiscal pressure for the optimal shape of marginal tax rates.2 For the U.S., they find that an increase in fiscal pressure pushes the optimal tax schedule from a progressive shape of marginal tax rates, first to a flat and then to a U-shaped schedule of optimal marginal tax rates. This analysis helps to reconcile different quantitative findings in the literature, e.g. the fact that Saez (2001) found very high marginal tax rates at the bottom compared to Heathcote and Tsujiyama (2021b).

In this paper, we take the workhorse optimal income taxation model to ask how the optimal progressivity of the tax-transfer system changes due to a COVID-19 related increase in fiscal pressure. We study five European countries: France, Germany, Italy, Spain and the UK. For all these countries, we find that marginal and average tax rates should increase in particular for lower incomes. This implies that the tax schedule should become less progressive. Nevertheless, in terms of absolute tax payments, higher incomes will bear a larger burden.

Why does optimal progressivity fall in response to higher revenue requirements? We show that considering Laffer bounds on marginal tax rates helps to understand the implications of fiscal pressure. We find that the additional leeway governments have for rising marginal tax rates is significantly higher for low incomes: the difference between Laffer bounds for marginal tax rates and actual marginal tax rates is highest for low incomes.

Our simulations for different European countries show that the change in optimal tax progressivity depends on country-specific properties of the tax-transfer system, though it is quantitatively significant for all countries. Importantly, we do not rely on a particular social welfare function that may imply different preferences for redistribution than those of current governments. Instead, we use an inverse-optimum approach (Bourguignon and Spadaro, 2012). We calibrate the Pareto weights for which the pre-pandemic tax-transfer systems are optimal. Then we ask how the optimal progressivity of the tax-transfer system should change due to COVID-19 induced fiscal pressure given these welfare weights.

We start the paper with a refresher about optimal nonlinear income taxation. First, we consider a simple benchmark without income effects and exogenous marginal social welfare weights. In this case, an increase in fiscal pressure does not affect the progressivity of marginal tax rates. It solely results in a decrease in the lump-sum transfer and hence, the schedule of average taxes becomes less progressive.

This ‘irrelevance result’ for marginal tax rates can be overcome by either one normative or one positive feature. The normative feature is to endogenize marginal social welfare weights which can be achieved e.g. by a classical Utilitarian objective and decreasing marginal utility of consumption. This implies that the desire to redistribute between two individuals does not only depend on the difference in their consumption but also on the level. The positive feature is to account for income effects: a decrease in the lump-sum transfer leads to an increase in labor supply of individuals if leisure is assumed to be a normal good, ceteris paribus. This induces a change in the income distribution and thus, optimal marginal tax rates adjust.

We calibrate the model with income effects and endogenous welfare weights to the pre-pandemic situation in five European countries. We account for the whole tax-transfer system including income taxes, social insurance contributions, and income transfer payments as well as the phasing out of these transfers (everything based on the micro-simulation model EUROMOD). We calibrate the income distributions based on EU-SILC data. This allows us to ‘invert’ the optimal income tax approach, and ask for which Pareto weights the pre-pandemic tax-transfer systems were optimal.

In a next step, we calibrate the implied fiscal pressure due to COVID-19 debt, and consider two different repayment scenarios. We then ask how the optimal schedule of marginal and average tax rates changes due to this increase in fiscal pressure. For all countries, we find that the schedule of marginal tax rates is pushed upwards in a U-shaped fashion. Marginal tax rates should particularly increase for low incomes. For average tax rates, we find that the increase in average tax rates is highest for low incomes and then strictly declines in income.

Our results indicate that the lump-sum transfers should be decreased substantially. However, we also inspect the possibility of a constitutional or political constraint that prohibits governments from decreasing transfers. In this case, we find an even more regressive change of marginal tax rates. However, the change of average tax rates is less regressive. Yet, the overall conclusion is very similar.

Related literature.

The optimal income tax problem (Mirrlees, 1971, Diamond, 1998, Saez, 2001) has been extended in many directions, such as to account for different labor supply margins (Kleven and Kreiner, 2006, Jacquet et al., 2013), taxation of couples (Kleven et al., 2009) and general equilibrium effects (Rothschild and Scheuer, 2013, Sachs et al., 2020). Heathcote and Tsujiyama (2021b) is the first paper to thoroughly elaborate the role of fiscal pressure in a Mirrleesian framework. They find that fiscal pressure has a strong influence on the shape of the optimal tax schedule. Governments facing a low level of fiscal pressure will set an optimal tax schedule with increasing marginal tax rates. Higher marginal tax rates at low incomes lead only to small redistributive gains as lump-sum transfers are already relatively high. Increasing fiscal pressure first flattens the optimal tax schedule and then leads to a U-shape pattern. Optimal lump-sum transfers get smaller and redistributive gains at low incomes are larger. Thus, higher marginal tax rates at low income levels are optimal.  Heathcote et al. (2017) investigate the relationship between an increase in government consumption and the progressivity of the tax system as well, but consider a parametric tax function with a constant rate of progressivity in a richer equilibrium model. They find that both, theoretically and numerically, an increase in government consumption leads to a less progressive tax system.

We provide an applied contribution to this literature by elaborating the implications of COVID-19 related fiscal pressure using an inverse-optimum approach. For this purpose, we deploy Laffer bounds of marginal tax rates as defined in Lorenz and Sachs (2016). We show that Laffer bounds provide a straightforward way to interpret the implications of fiscal pressure as they reflect the leeway for increasing marginal tax rates for different income levels. Further, Laffer bounds are easy to implement as they are expressed in closed form. We show that the increase in marginal tax rates follows closely the difference in the Laffer bounds of marginal tax rates and current marginal tax rates. Finally, we generalize the approach of the literature and consider the case where governments cannot adjust the lump-sum element. Once the lump-sum transfer is not allowed to be changed, the incidence of fiscal pressure is less regressive.

2. The workhorse model of optimal income taxation

We briefly review the workhorse model of nonlinear income taxation and discuss how the optimality conditions are affected by fiscal pressure. We start with a pedagogical irrelevance benchmark: without income effects on labor supply and with constant marginal utility, optimal marginal tax rates are independent of fiscal pressure. We then introduce two relaxations: decreasing marginal utility and income effects on labor supply.

2.1. Irrelevance benchmark – no income effects and exogenous welfare weights

We first consider iso-elastic preferences of the form: $u(c,l)=c-\frac{l^{1+\frac{1}{\varepsilon }}}{1+\frac{1}{\varepsilon }}$, where $c$ is consumption, $l$ is labor supply and $\varepsilon$ is the elasticity of labor supply. Denote productivity by $w$, the cumulative distribution function by $F\left(w\right)$ and the density by $f\left(w\right)$. The income of an individual is the product of her labor supply and her productivity, $y=lw$. The government maximizes the weighted utilitarian welfare function with type-specific Pareto weights3 which is given by:

$$W={\int }_{\underset{\_}{w}}^{\overline{w}}u(c\left(w\right),l\left(w\right))s\left(w\right)f\left(w\right)dw,$$

where we normalize the Pareto weights $s\left(w\right)$ such that ${\int }_{\underset{\_}{w}}^{\overline{w}}s\left(w\right)f\left(w\right)dw=1$. To obtain a desire for redistribution, we need $s^{\prime }\left(w\right)<0$. The important aspect of this welfare function is that the marginal social welfare weights are independent of consumption.

Government problem.

The government chooses a nonlinear tax-transfer system $T\left(\cdot \right)$. The government’s problem reads as:

$$\underset{T\left(\cdot \right)}{max}{\int }_{\underset{\_}{w}}^{\overline{w}}u\text{(}(l\left(w\right)w-T\left(l\left(w\right)w\right),l\left(w\right))s\left(w\right)f\left(w\right)dw$$

subject to individual optimality

$$l\left(w\right)=\underset{l}{arg\; max}u\text{(}(l\left(w\right)w-T\left(l\left(w\right)w\right),l\left(w\right))$$

and budget feasibility

$${\int }_{\underset{\_}{w}}^{\overline{w}}T\left(l\left(w\right)w\right)f\left(w\right)dw\ge E,$$

where $E$ is the exogenous revenue requirement.

It is a standard exercise to show that the formula for optimal marginal tax rates reads as:

$$\frac{T^{\prime }\left(y\left(w\right)\right)}{1-T^{\prime }\left(y\left(w\right)\right)}=\left(1+\frac{1}{\varepsilon }\right)\frac{{\int }_w^{\overline{w}}\left(1-s\left(x\right)\right)f\left(x\right)dx}{f\left(w\right)w}.$$ (1)

where $y\left(w\right)$ is the income of an individual with productivity $w$ who maximizes her utility. That is, $y\left(w\right)=l\left(w\right)w$.

Note that this expression provides a closed form for the optimal marginal tax rate for a given productivity level $w$. The respective lump-sum element $T\left(0\right)$ then follows from budget feasibility. A change in fiscal pressure which is captured by an increase in the revenue requirement $E$ only affects the lump-sum element $T\left(0\right)$ and nothing else. The schedule of optimal marginal tax rates is unaffected by fiscal pressure: both the RHS of (1) and the income levels $y\left(w\right)$ are exogenous with respect to the lump-sum element.

2.2. Endogenous welfare weights

Now, we consider the same economy as before, but the utility function reads as

$$u(c,l)=U\left(c-\frac{l^{1+\frac{1}{\varepsilon }}}{1+\frac{1}{\varepsilon }}\right),$$

where $U^{\prime }>0,U^{\prime \prime }<0$. This utility function still abstracts from income effects but implies decreasing marginal utility of consumption.

For ease of notation, let $u\left(w\right)$ to denote the utility of an individual with productivity $w$ who maximizes her utility. That is, $u\left(w\right)=u(c\left(w\right),l\left(w\right))$. Then, it is simple to show that the formula for the optimal marginal income tax rate reads as

$$\frac{T^{\prime }\left(y\left(w\right)\right)}{1-T^{\prime }\left(y\left(w\right)\right)}=\left(1+\frac{1}{\varepsilon }\right)\frac{{\int }_w^{\overline{w}}\left(1-\frac{u_c\left(x\right)s\left(x\right)}{\lambda }\right)f\left(x\right)dx}{f\left(w\right)w}$$

where the marginal value of public funds, $\lambda$, is given by

$$\lambda ={\int }_{\underset{\_}{w}}^{\overline{w}}{u}_c\left(z\right)s\left(z\right)f\left(z\right)dz.$$

which follows from the transversality condition.

It is almost equivalent to (1), only the element which captures the desire to redistribute is now endogenous with respect to the revenue requirement:

$${\int }_w^{\overline{w}}\left(1-\frac{u_c\left(x\right)s\left(x\right)}{{\int }_{\underset{\_}{w}}^{\overline{w}}{u}_c\left(z\right)s\left(z\right)f\left(z\right)dz}\right)f\left(x\right)dx.$$

Note that this element captures how much the social planner wants to redistribute from those with income higher than $y\left(w\right)$ to those with income lower than $y\left(w\right)$. This depends on the ratios of marginal utilities and is endogenous with respect to the lump-sum transfer. A decrease in the lump-sum element increases the desire to redistribute from above $y\left(w\right)$ to below $y\left(w\right)$. This role of fiscal pressure is discussed in detail in Section 5.2 of Heathcote and Tsujiyama (2021b).

2.3. Income effects

With income effects, fiscal pressure influences optimal tax progressivity beyond the endogenous welfare weights channel: as soon as the lump-sum element gets adjusted, labor supply of individuals adjusts. If leisure is a normal good, individuals will ceteris paribus work more due to fiscal pressure.

Formally, consider the widely used preferences:

$$u(c,l)=\frac{c^{1-\gamma }}{1-\gamma }-\frac{l^{1+\frac{1}{\varepsilon }}}{1+\frac{1}{\varepsilon }},$$

where $\gamma$ is the constant relative risk aversion and $\varepsilon$ captures the Frisch elasticity of labor supply.

It is simple to show that in this case the optimal tax schedule is characterized by:

$$\frac{T^{\prime }\left(y\left(w\right)\right)}{1-T^{\prime }\left(y\left(w\right)\right)}=\left(1+\frac{1}{\varepsilon }\right)\frac{{\int }_w^{\overline{w}}\left(1-\frac{u_c\left(x\right)s\left(x\right)}{\tilde{\lambda }}+\eta \left(x\right)T^{\prime }\left(y\left(x\right)\right)\right)f\left(x\right)dx}{f\left(w\right)w},$$ (2)

where $\eta \left(w\right)=\frac{\partial y\left(w\right)}{\partial T\left(0\right)}$ is the income effect parameter which captures the absolute change in income if the lump-sum element of the tax schedule is increased by one unit.4 Further, we have to scale the marginal value of public funds to account for income effects.

$$\tilde{\lambda }=\frac{{\int }_{\underset{\_}{w}}^{\overline{w}}{u}_c\left(z\right)s\left(z\right)f\left(z\right)dz}{1+{\int }_{\underset{\_}{w}}^{\overline{w}}{T}^{\prime }\left(y\left(z\right)\right)\eta \left(z\right)f\left(z\right)dz}.$$

Obtaining comparative statics for how fiscal pressure affects optimal tax progressivity is challenging. Even if one finds assumptions for which the behavior of certain elements of the RHS of (2) can be described, one cannot conclude anything on the adjustment of marginal tax rates immediately since the optimal marginal tax rates are a nonlinear transformation of the RHS of (2). Therefore, a computational analysis is required. Before we move to the quantification of the model, we introduce the concept of Laffer bounds in this environment, which turn out to be helpful to understand the quantitative results below.

Laffer bounds.

If the government increases marginal tax rates to deal with fiscal pressure, it is constrained by the Laffer bound on marginal tax rates. Those are e.g. defined in Lorenz and Sachs (2016) or Bierbrauer et al. (2021) and are given by:

$$\frac{T_{\text{Laffer}}^{\prime }\left(y\left(w\right)\right)}{1-T_{\text{Laffer}}^{\prime }\left(y\left(w\right)\right)}=\left(1+\frac{1}{\varepsilon }\right)\frac{{\int }_w^{\overline{w}}\left(1+\eta \left(x\right)T^{\prime }\left(y\left(x\right)\right)\right)f\left(x\right)dx}{f\left(w\right)w}.$$ (3)

Note that we set welfare weights above $w$ to zero. Hence, this is the marginal tax rate that a social planner would obtain – holding marginal tax rates fixed at other levels – if the goal was to raise as much tax revenue as possible from individuals with income above $y\left(w\right)$. As we show below, these Laffer bounds are a useful benchmark to understand the implications of fiscal pressure. They show how much leeway a government still has in increasing marginal tax rates for certain income levels.

3. Calibration

We calibrate the model with income effects and endogenous welfare weights to match five European countries: France, Germany, Italy, Spain and the UK. In a first step, we calibrate the income distributions based on EU-SILC data. Then, we calibrate the tax-transfer systems by using the tax–benefit microsimulation model EUROMOD. Based on the assumed utility function, we then calibrate the skill distributions as in Saez (2001). Finally, we calibrate our measure for COVID-19 induced fiscal pressure based on OECD data and the IMF World Economic Outlook.

Income distributions.

To obtain country-specific income distributions we use data on annual incomes from the 2018 cross-sectional European Union Statistics on Income and Living Conditions (EU-SILC). EU-SILC contains annual income data in a harmonized framework which allows for cross-country comparisons. Annual incomes are reported for the previous year of the survey leading to 2017 as the reference year for the income distribution. To calibrate the country-specific distributions, we apply a standard kernel density estimation to get a smooth distribution. For incomes above €150,000, we append a Pareto distribution where the Pareto parameter decreases linearly between €150,000 and €250,000.5 The Pareto parameter at the income threshold of €150,000 is chosen such that the ratio $\frac{f\left(y\right)y}{1-F\left(y\right)}$ is continuous as in Sachs et al. (2020). For incomes above €250,000, we leave the Pareto parameter constant at the country-specific values from Atkinson et al. (2011). Finally, we smooth the resulting distributions to ensure differentiability of the hazard ratios at €150,000 and €250,000. We assume that a fixed mass of the population earns an income of zero. The fixed shares are chosen to match the country-specific shares of recipients of disability benefits as in Mankiw et al. (2009).6 Table 1 contains the country-specific values used in the calibration of the income distributions.7 Fig. 6 in Appendix A.1.2 illustrates the country-specific income distributions.

Table 1.

Parameters for calibration.

	France	Germany	Italy	Spain	UK
Calibration
Pareto Threshold Start	€150,000	€150,000	€150,000	€150,000	€150,000
Pareto Threshold Constant	€250,000	€250,000	€250,000	€250,000	€250,000
Pareto Parameter Start	2.8	2.95	2.56	2.21	2.34
Pareto Parameter Constant	2.20	1.67	2.22	2.11	1.78
Mass of People with Zero Earnings	5.6%	4.4%	3.2%	3.8%	7.0%
Lump-Sum Transfer	€13,347	€20,763	€2,540	€6,991	€15,037
Measure of Fiscal Pressure
5-year Payback	2.65%	2.96%	3.52%	3.58%	4.90%
10-year Payback	1.32%	1.48%	1.76%	1.79%	2.45%

Notes: The constant threshold of €250,000 is chosen based on the estimation by Jenkins (2017). The starting Pareto parameter at the income threshold of €150,000 is chosen such that the hazard rate $\frac{f\left(y\right)y}{1-F\left(y\right)}$ is continuous as in Sachs et al. (2020). The values of the constant Pareto parameters are from Atkinson et al. (2011). The mass of people with zero earnings matches the shares of recipients of disability benefits reported by OECD (2009). For France, we use the average across OECD countries. The values of the lump-sum transfer match the average minimum income protection from the 2017 Social Assistance and Minimum Income Protection Interim Dataset and are converted into Euro. The 5-year (10-year) payback measure denotes a scenario where governments are required to pay back the additional stock of debt in five (ten) years. Both measures for fiscal pressure are expressed as a percentage of GDP.

Fig. 6.

Country-specific income distributions.

Note: The probability density functions (pdf) are based on a standard kernel density estimation and add a Pareto distribution for incomes above €150,000, where the Pareto parameter decreases linearly between €150,000 and €250,000. All income-distributions involve a fixed mass of individuals with an income of zero. The underlying income data originate from the 2018 EU-SILC.

Current tax-transfer systems.

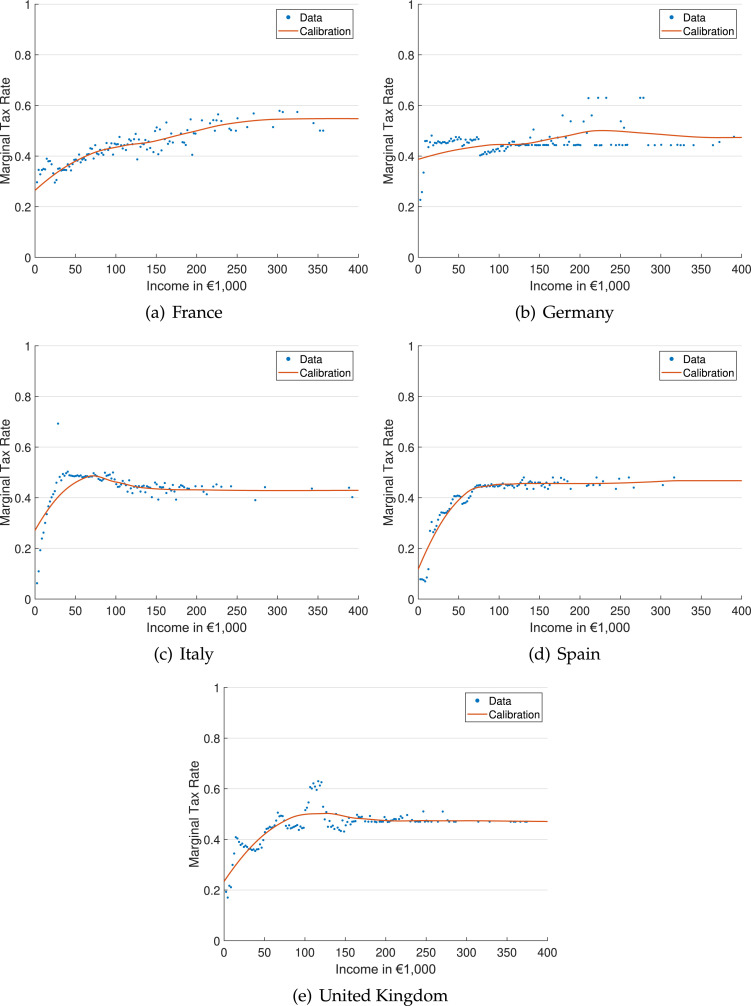
We approximate the current income tax systems with the tax–benefit microsimulation model EUROMOD and EU-SILC as the underlying input data.8 First, we simulate effective marginal tax rates based on the 2017 tax-transfer system and calculate average marginal tax rates for income bins with a size of €5,000. The simulated effective marginal tax rates include taxes, means-tested benefits, pension and social insurance contributions. To smooth the average marginal tax rates, we perform a second-order local weighted regression (LOESS) with a constant extrapolation for income values outside the covered income range of EU-SILC data. Afterwards, we employ a constrained quadratic B-spline to overcome the kink at the income level where the extrapolation starts.9 The simulated and smoothed marginal tax rates are illustrated in Fig. 7 in Appendix A.1.3.

Fig. 7.

Simulated average and smoothed marginal tax rates with EUROMOD.

Note: The blue dots illustrate the simulated marginal tax rates with EUROMOD. The red line illustrates the current schedule of marginal tax rates calibrated by a second-order local weighted regression (LOESS) with a constant extrapolation based on a EUROMOD simulation of effective marginal tax rates.

Skill distributions.

We infer the skill distributions from the income distributions and the simulated effective marginal tax rates by inverting the individual labor supply first-order condition as in Saez (2001). We assume that all countries have the same Frisch elasticity of labor supply of $\varepsilon =0.2$.10 For the utility function, we adopt the specification of preferences with income effects of Section 2.3, i.e. $u(c,l)=\frac{c^{1-\gamma }}{1-\gamma }-\frac{l^{1+\frac{1}{\varepsilon }}}{1+\frac{1}{\varepsilon }}$, with $\gamma =1$.11 The first-order condition also depends on the individual’s consumption, which is calculated as the difference between income and paid taxes plus a lump-sum transfer. The lump-sum transfers are set to match the average minimum income protection in each country.12 Table 1 contains details on the used country-specific values of the lump-sum transfer in the simulations.

Fiscal pressure.

To simulate the fiscal pressure governments face as a result of the COVID-19 pandemic, we use the following approach. First, we compute the total additional amount of debt governments accumulated and are expected to accumulate between 2020 and 2022 compared to the average deficit levels before COVID-19. For these calculations, we rely on actual government data from the OECD (OECD, 2019) as well as forecast data from the IMF World Economic Outlook (IMF, 2021), see Appendix A.1.4 for details. Then, we assume that governments are required to pay back this additional stock of debt in varying periods, namely five and ten years. This means we abstract from additional spending needs caused by the Ukraine war. We do so for two reasons. First, the size of this burden is still uncertain. Second, our assumptions for the payback period of five and ten years for COVID-19 related debt are already quite restrictive.

Table 1 shows the fiscal pressure that governments face. As expected, paying back the additional debt in five years puts a significant strain on government expenditure. It ranges from 2% of GDP for France to 4.90% of GDP for the UK. Paying back the debt in ten years halves the fiscal pressure. Lastly, the expenditure forecast in 2023 shows that the expenditure numbers will be similar to the two hypothetical fiscal pressure specifications, except for France and the UK.

In a low interest rate environment, an additional stock of debt does not really hurt the balance between expenditures and revenue in governments’ budget. However, with higher interest rates an additional stock of debt matters for the balance between expenditures and revenues. Therefore, we think that our scenarios for fiscal pressure are an interesting benchmark, even if the magnitude is debatable.

Inverse-optimum weights.

Maximizing the welfare of an economy requires the definition of welfare weights for different levels of skills. Instead of imposing exogenous welfare weights, we employ an inverse optimum approach (Bourguignon and Spadaro, 2012, Lockwood and Weinzierl, 2016, Jacobs et al., 2017): we invert the optimal tax formula to calibrate the Pareto weights that governments were implicitly using before the pandemic. In particular, we calibrate the endogenous welfare weights such that our simulated marginal tax rates by EUROMOD are optimal given the income distributions and the assumed utility function. Fig. 1(a) shows the endogenous welfare weights $U^{\prime }\left(w\right)\frac{s\left(w\right)}{\lambda }$ as a function of income. First, note that our calibrated weights increase for low incomes. A similar finding has been shown by Jacobs et al. (2017) in the Dutch context and has described the fact that middle incomes have higher weights than low incomes as the tyranny of the middle class. At around €50,000 all weights start to decrease before they start to increase for incomes above €150,000 again. The reason for this increase is our calibration of the income distribution. Revenue maximizing tax rates remain constant for incomes above €200,000 and are significantly lower at around €140,000. This contrasts with real world tax schedules, where marginal tax rates do not quickly increase between €140,000 and €200,000. Finally, note that our weights show small kinks and discontinuities. This is due to the fact that our calibrated tax functions are not as smooth as the calibrated income distributions.

Fig. 1.

Calibrated welfare weights.

Note: The left panel shows the calibrated endogenous welfare weights $U^{\prime }\left(\omega \right)\frac{s\left(\omega \right)}{\lambda }$ and the right panel shows the Pareto weights $s\left(\omega \right)$ as a function of income.

Fig. 1(b) shows the implied Pareto weights $s\left(w\right)$ which depend on the curvature of the underlying utility function. Overall, these weights increase in income which implies that governments have a smaller desire for redistribution than a classical Utilitarian planner under the same utility function.

4. Quantitative results

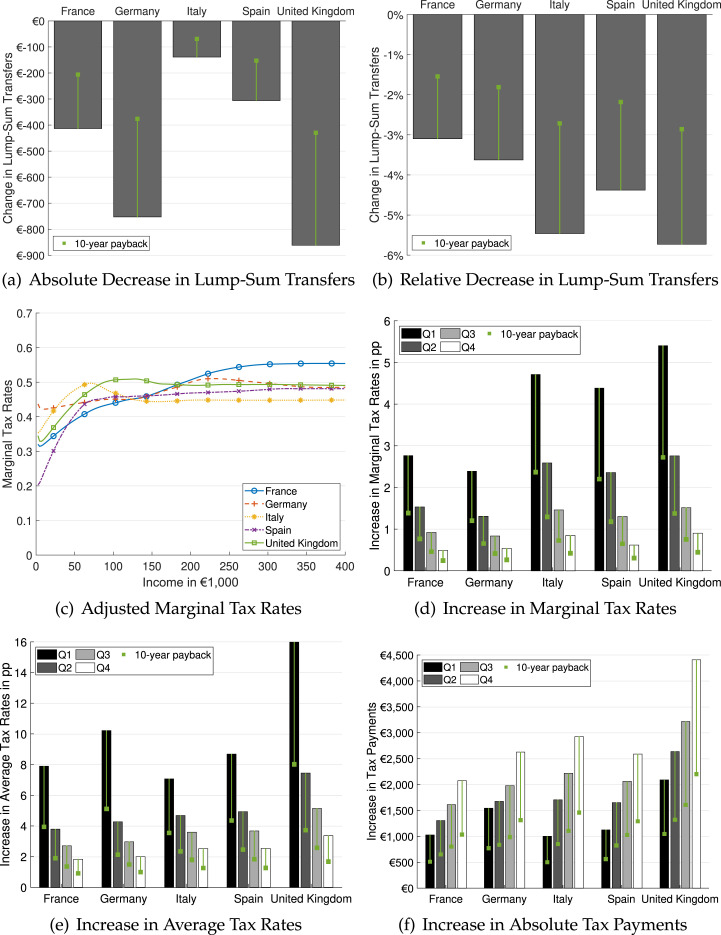
We now present our quantitative results for how the different countries should adjust their tax systems as a response to the increase in fiscal pressure.13 We first consider the adjustment of lump-sum transfers, then the adjustment of marginal tax rates and finally the resulting changes in average tax rates and absolute tax payments. For illustrative purposes, we focus on the case with strong fiscal pressure where the governments repay the additional debt within five years. The other case of ten-year repayment is discussed in Appendix A.2.

To better understand the cross-country differences, we also construct a scenario where all countries face the same increase in fiscal pressure measured as a share of GDP. We choose 5% for the harmonized value.

4.1. Adjustment of lump-sum transfers

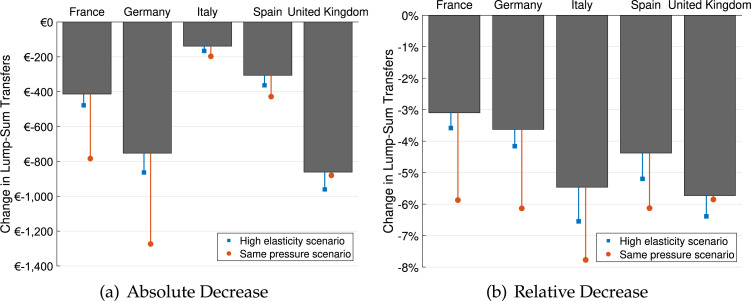
Fig. 2 shows how much the lump-sum elements should change. The relative decrease of the lump-sum elements in Fig. 2(b) mirrors the increase in fiscal pressure: in percentage terms, the lump-sum element decreases more strongly in countries with a higher increase in fiscal pressure. Italy is an exception. This is a consequence of the lower baseline value of the lump-sum transfer in Italy. The red circles in Fig. 2 show our results for the case of harmonized fiscal pressure. There we find that the relative decrease of the lump-sum transfer is very similar across the countries. Italy is again a slight outlier: the relative decrease in the lump-sum element is larger, which reflects again the low baseline value of the lump-sum transfer.

Fig. 2.

Decrease in lump-sum transfers for 5-year repayment scenario.

Note: The left panel shows the change in the lump-sum transfer due to fiscal pressure in absolute values and the right panel shows the change as a percentage of the initial transfer. The red circles correspond to a scenario where all countries face the same increase in fiscal pressure of 5% and the blue squares correspond to a scenario where the Frisch elasticity of labor supply takes a value of $\varepsilon =0.54$ (Chetty et al., 2011). See Section 5 for a discussion of the latter.

4.2. Adjustment of marginal tax rates

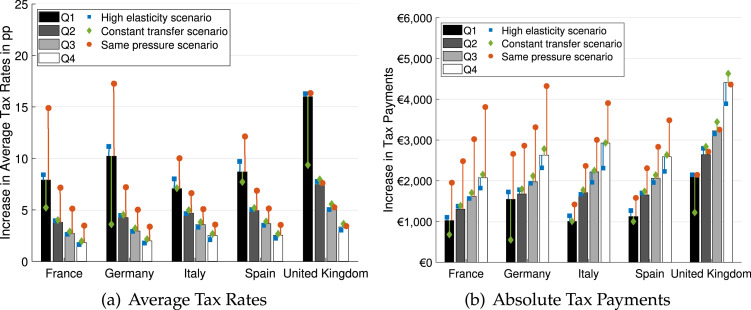
The increase in marginal tax rates is illustrated in Fig. 3. In the left panel, we can see that the increase in marginal tax rates follows a U-shape pattern with high increases at low incomes. The tax rate changes are significant. For instance, for the lowest income quartile in the UK, the marginal tax rate increases from 29% to 35%. The increase for the top quartile is much smaller. In the right panel, we illustrate the average increases for different quartiles of the income distribution. Here, the U-shape cannot be seen since the increasing part of the U is already in the top quartile for all countries.

Fig. 3.

Tncrease in marginal tax rates for 5-year payback scenario.

Note: The left panel shows the change in the optimal marginal tax rates in percentage points due to fiscal pressure up to an income level of €400,000. The right panel shows the average change in the optimal marginal tax rates in percentage points for all quartiles of the income distribution. The red circles correspond to a scenario where all countries face the same increase in fiscal pressure of 5%, the blue squares correspond to a scenario where the Frisch elasticity of labor supply takes a value of $\varepsilon =0.54$ (Chetty et al., 2011) and the green diamonds correspond to a situation where lump-sum transfers remain constant. See Section 5 for a discussion of the latter two.

To understand the intuition behind the result, recall the discussion in Section 2.2: lower lump-sum payments increase the marginal value from redistribution and hence, optimal marginal tax rates increase. Further, the additional leeway for increasing marginal tax rates differs along the income distribution. In Fig. 4, we illustrate the Laffer bounds for marginal tax rates as defined in Section 2.3. The Laffer bounds have the typical U-shape which reflects well-understood properties of income distributions (Saez, 2001). The leeway to further increase marginal tax rates is then given by the difference in the Laffer values of marginal tax rates and the current marginal tax rates. This explains the U-shape of the increase in marginal tax rates.

Fig. 4.

Laffer bounds and current tax schedules.

Note: The yellow dotted curves illustrate the Laffer bounds as defined in (3). The blue bold curves illustrate the current schedule of marginal tax rates calibrated by a second-order local weighted regression (LOESS) with a constant extrapolation based on a EUROMOD simulation of effective marginal tax rates and the red curves illustrate the for fiscal pressure adjusted optimal marginal tax rates. See Section 3 for a detailed explanation of the tax system calibration.

Another way of interpreting this regressive increase is through the lens of the social objective. An increase in revenue requirement decreases consumption of all individuals. In particular, it increases the share of low income individuals to high income individuals. Since we have a weighted utilitarian welfare function with type-specific weights, this means that relative social weights of low incomes will increase. Effectively, the social objective will get closer to a Rawlsian objective with higher welfare weight for low incomes. As Saez (2001) shows, the optimal marginal tax rates should be more regressive for a Rawlsian welfare objective than a utilitarian welfare objective.

Despite these similarities, there are some differences between the countries. For example, the U-shape is much more pronounced for the UK and Spain. This can be well understood by the fact that baseline marginal tax rates for low incomes are lower in these countries (see Fig. 4). Once we harmonize fiscal pressure, our results are very similar again, see the yellow circles in Fig. 3(b). The increase in marginal tax rates is regressive and marginal tax rates for the lowest quartile increase by 4–7 percentage points whereas they only increase by about 1 percentage point or less for the highest quartile.

4.3. Adjustment of average tax rates and tax payments

Combining the changes in the lump-sum transfers and the marginal tax rates, we can also calculate the implied change in average tax rates. Fig. 5(a) shows the implied change in average tax rates. The decrease in the lump-sum transfers and the regressive increase in marginal tax rates both imply a regressive increase in average tax rates. For the 5-year payback scenario that we consider here, the increases are substantial and up to 16 percentage points, whereas it is only 3 percentage points for the highest quartile.14 Considering the normalized fiscal pressure scenario, we see that average taxes for the lowest quartile increase 2–5 times as much as average taxes for the highest quartile. The increase in average tax rates is more regressive in France, Germany and the UK as compared to Italy and Spain. The reason is that lump-sum elements are lower in the latter two countries and therefore the absolute adjustments are smaller.

Fig. 5.

Increase in average tax rates and absolute tax payments for 5-year payback scenario.

Note: The left panel shows the average change in the optimal average tax rates in percentage points due to fiscal pressure for all quartiles of the income distribution and the right panel shows the change in the absolute tax payments. The red circles correspond to a scenario where all countries face the same increase in fiscal pressure by 5%, the blue squares correspond to a scenario where the Frisch elasticity of labor supply takes a value of $\varepsilon =0.54$ (Chetty et al., 2011) and the green diamonds correspond to a situation where lump-sum transfers remain constant. See Section 5 for a discussion of the latter two.

Fig. 5(b) shows how this translates into an increase in absolute tax payments. The additional tax burden increases in income even though the increase in average tax rates is stronger for lower incomes. The top quartile has to pay around twice as much as the bottom quartile.

5. Robustness

Now, we explore the sensitivity of our results to alternative specifications of the model.

5.1. Constant lump-sum transfers

So far, governments could respond to fiscal pressure along two margins. First, by adjusting the lump-sum transfer and second, by adjusting marginal tax rates. Now, we consider a scenario where governments can only modify marginal tax rates. Such a setting corresponds to situations where constitutional or political restrictions do not allow for changing lump-sum transfers. For example, countries are compelled to guarantee a minimum subsistence level.

In Fig. 3, Fig. 5 the green diamonds show the changes in optimal marginal tax rates, average tax rates and absolute tax payments triggered by fiscal pressure. With only one adjustment margin, the change in marginal tax rates is larger and more regressive compared to the baseline setting with two adjustment margins. However, the increase in average taxes and the amount of paid taxes is more progressive as compared to the case with variable lump-sum elements.

5.2. Elasticity

Now, we increase the Frisch elasticity of labor supply to $\varepsilon =0.54$ following Chetty et al. (2011). Note that with a higher elasticity, the increase in labor supply induced by income effects is also larger. The blue squares in Fig. 2, Fig. 3, Fig. 5 show the change in the lump-sum transfer, marginal tax rates, average tax rates and absolute tax payments triggered by fiscal pressure. Optimal lump-sum transfers are decreased by a larger extent compared to the baseline simulation. Further, governments should increase optimal marginal tax rates to a smaller extent. Taken together, this implies that the increase in marginal, average and absolute taxes is more regressive than in the benchmark scenario with a lower elasticity.

5.3. Wealth distribution shocks

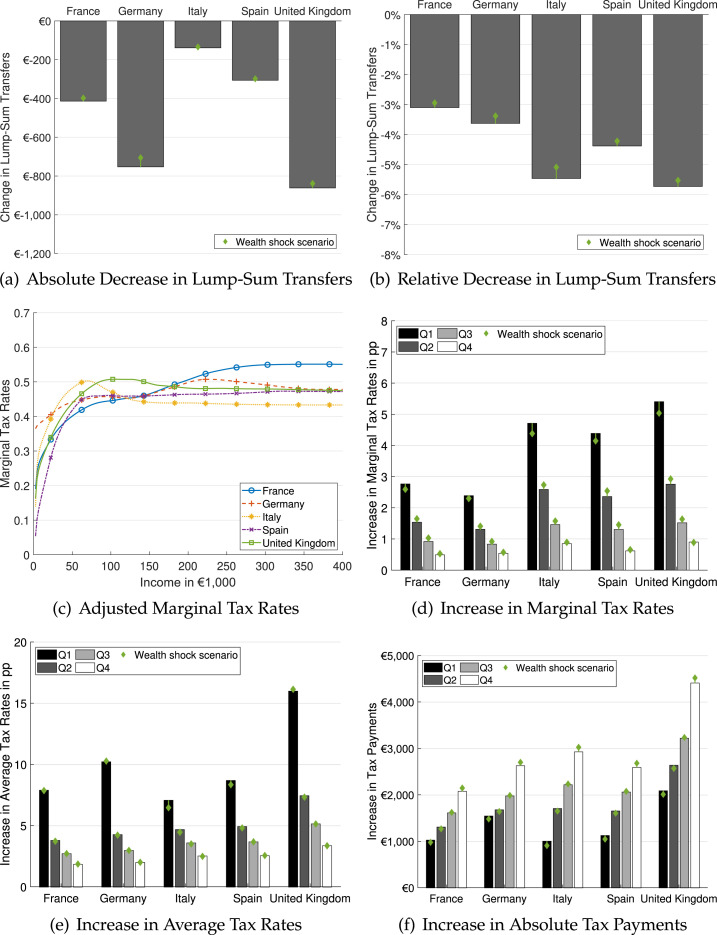
Angelopoulos et al. (2022) show that COVID-19 led to an uneven change of the wealth distribution in the UK. In particular, individuals with an income above the median experienced a persistent increase in wealth, while individuals with an income below the median experienced a persistent decrease in wealth. Now, we integrate the increase in wealth inequality to our analysis.

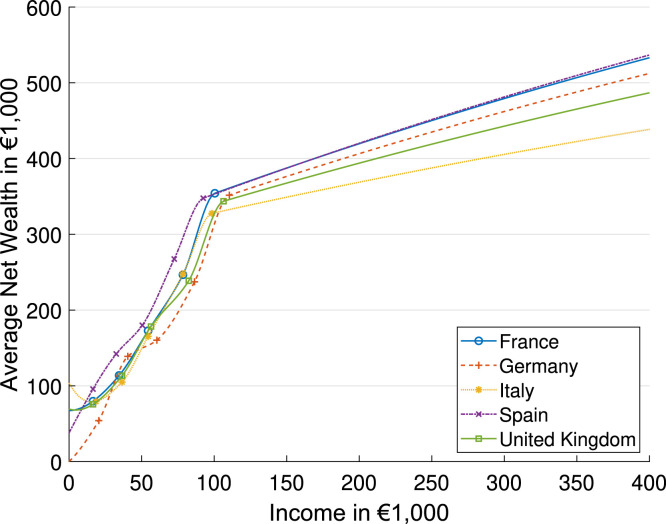
To calibrate the level of net wealth across the income distribution, we use data on the average net wealth for six points of the income distribution from the 2017 Household Finance and Consumption Survey together with a shape-preserving piece-wise cubic interpolation. This gives us country-specific distributions of wealth conditional on income.15 Fig. 10 in Appendix A.3 shows the calibrated average net wealth levels across the income distribution. To get an approximation for the change in the wealth distribution induced by COVID-19, we use the simulation results of the dynamic evaluation of the wealth distribution for the UK from Angelopoulos et al. (2022).16 To the best of our knowledge, there exists no detailed evidence for France, Germany, Italy and Spain. Thus, we assume that the change of the wealth distribution in these countries is the same as in the UK. Fig. 11 in Appendix A.3 shows the expected percentage change in wealth in 2023 induced by the outbreak of COVID-19.

Fig. 10.

Average net wealth across the income distribution.

Note: The six markers illustrate the average net wealth for six points of the income distribution taken from Table A4 from the Statistical Tables of the 2017 Household Finance and Consumption Survey. The curves fit these values based on a shape-preserving piece-wise cubic interpolation. In Germany, the average net wealth of the lowest income is set to zero. For the UK we use the average of the Euro area countries as the UK is not included in the Household Finance and Consumption Survey.

Fig. 11.

Expected percentage change in wealth.

Note: The shown values are taken from Figure 4 in Angelopoulos et al. (2022).

Given that we consider a static model, it is not obvious how to incorporate the changes in wealth inequality in our analysis. Our approach is to assume that individuals either save a part of their income to restore their wealth before the pandemic or consume the extra wealth that is accumulated during the pandemic. To be consistent with our assumption regarding the fiscal pressure, we assume that this saving or dissaving process also takes 5 years. In essence, the inclusion of the wealth shock implies an increase in consumption inequality. This is because lower income households are negatively effected by the wealth shock and have to save a part of their income to restore their wealth, whereas higher income households are able to consume more thanks to their positive wealth shock.

To focus on the implied increase in consumption inequality, we consider a utility specification without income effects for this robustness exercise.17 As in the main specification in Section 3, we then calibrate the skill distributions using EUROMOD data, and calculate the inverse-optimum Pareto weights. Then, to model the effects of the COVID-19, we add the wealth shocks together with the fiscal pressure shock that is also present in our baseline analysis.

Fig. 12 in Appendix A.3 shows how lump-sum transfers and optimal marginal tax rates adjust if one takes into account the increase in wealth inequality. The fact that lower income households are affected negatively by the wealth shock limits governments’ ability to conduct a regressive tax reform to finance the extra debt caused by COVID-19. This results in smaller decreases in transfers and less regressive increases in marginal tax rates. As a result, tax payments of higher income households increase more compared to our baseline scenario.

Fig. 12.

Change in tax rates and tax payments with wealth shocks.

Note: The figure compares the change in lump-sum transfers, marginal tax rates, average tax rates and absolute tax payments due to fiscal pressure from our simulations without income effects to another scenario where individuals are affected by the wealth shock due to COVID-19. The bars correspond to the simulations without wealth the shock. The green squares correspond to a scenario, where individuals are affected by the wealth shock and required to restore their old wealth level by saving or dissaving. There are no income effects in both scenarios.

5.4. Further robustness

We document various further robustness checks in Appendix A.4 and show that the main message barely changes.

Utility function.

First, we increase the risk-aversion of individuals by setting $\gamma =1.5$. s, we consider a different utility function with the following form $u(c,l)={\left(\frac{c^{1-\gamma }}{1-\gamma }-\frac{l^{1+\frac{1}{\varepsilon }}}{1+\frac{1}{\varepsilon }}\right)}^{\xi }$, where $\xi$ describes the overall concavity of the utility function. This parameter alters the risk-aversion of individuals but does not affect their labor supply behavior. Another way to interpret the same parameter is through the overall welfare. Instead of thinking $\xi$ as a parameter of individual utility, we can think of it as a parameter of the social welfare. For example, $\xi =1$ corresponds to a weighted utilitarian welfare and decreasing $\xi$ puts more relative weight on lower incomes. We can slightly relax our assumption of linear welfare function with type-specific weights by applying a non-linear transformation to individual utilities. We try $\xi =0.5$ and $\xi =2$. For both alternative specifications, our main results are very similar. Fiscal pressure leads now to a slightly smaller decrease in lump-sum transfers and a slightly larger change in optimal marginal tax rates in first case and in the second case with higher $\xi$, and vice versa with lower $\xi$.

Initial lump-sum transfer.

Instead of matching the initial lump-sum transfer to the average minimum income protection in each country, we assume that the lump-sum transfer takes a value of €10,000 in all countries. Now, an increase in fiscal pressure leads to a similar proportional adjustment of lump-sum transfers across countries.

Mass of people with zero earnings.

Instead of calibrating the mass of people with zero earnings to match the country-specific shares of disability benefit recipients, we assume that in each country 5% of the population always earns an income with zero earnings. Our results are not sensitive to this assumption.

6. Conclusion

This paper investigates how an increase in the tax revenue requirement due to COVID-19 affects the optimal progressivity of the income tax system for five European countries. We apply an inverse-optimum approach and find that optimal progressivity declines. There is a trade-off between the objectives of raising revenue and redistributing through the tax system by making it more progressive. This suggests that governments may face difficult choices when it comes to financing the burden of the additional debt incurred as a result of the COVID-19 pandemic. To what extent the policy implications will be amplified by the ongoing war in Ukraine is still unclear because the size of the additional burden is uncertain at the moment.

Our approach was welfarist and based on the inverse-optimum approach. Alternative approaches would, for example, be to follow an equal-sacrifice approach (Weinzierl, 2014) or fairness approaches (Fleurbaey and Maniquet, 2006).

Of course, our analysis has focused on the income tax only. In the debate on who bears the cost of the crisis, other taxes also play a role, in particular wealth taxes, inheritance taxes and taxes paid by multinational firms. Whether it is optimal to increase income taxes or make wealth and inheritance taxes more progressive is beyond the analysis in this paper.

Appendix.

A.1. Details on calibration

A.1.1. Data

For the calibration of the country-specific income distributions, we utilize data on labor income restricted to individuals in the working age (18–65) with positive income from the 2018 European Union Statistics on Income and Living Conditions (EU-SILC). Gross labor income is calculated as the sum of employment and self-employment income. Annual incomes are reported for the previous year of the survey leading to 2017 as the reference year of all country-specific income distributions. See Atkinson et al. (2017) for details.

A.1.2. Kernel density estimation

We employ a standard kernel density estimation based on a normal kernel function to smooth the country-specific income distributions obtained from the EU-SILC. For all countries, we use an evenly spaced income grid with 1000 nodes that are spaced between €2,500 and €2,000,000. We use a large bandwidth of €30,000 as the number of observations is rather small in EU-SILC data. Lockwood (2020) and Choné and Laroque (2010) note that a large bandwidth is useful for obtaining smooth income distributions. Fig. 6 shows the country-specific income distributions.

A.1.3. Current tax-transfer system

See Fig. 7.

A.1.4. Fiscal pressure

We use government spending data and forecasts from the OECD (2019) and the IMF (2021) to simulate the fiscal pressure faced by governments due to the COVID-19 pandemic.

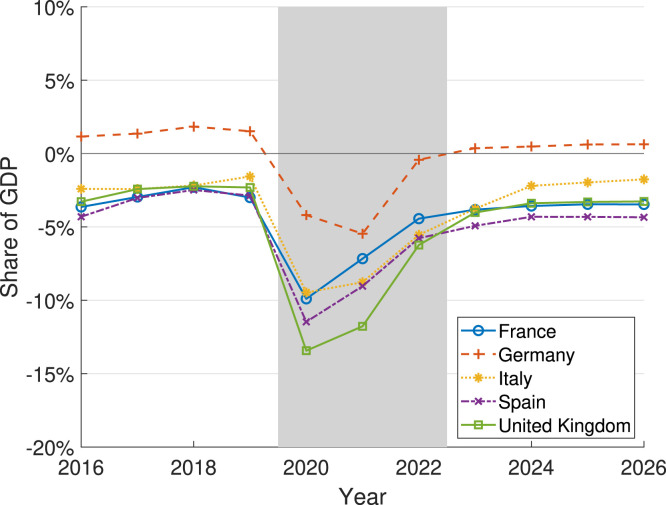
Fig. 8 shows the net government lending or borrowing from 2016 until 2026. The gray area marks the pandemic time period. It is clear that all governments have had already and are expected to have significantly higher budget deficits during the pandemic period compared to before.

Fig. 8.

Net government lending/borrowing.

Note: For years until 2020, we use the actual data from the OECD’s Government at a Glance. For years from 2021, we use the forecast data from the IMF World Economic Outlook. The gray area denotes the pandemic time period.

A.2. Different repayment scenarios

See Fig. 9.

Fig. 9.

Change in tax rates and tax payments for different measures of fiscal pressure.

Note: The figure compares the average change in lump-sum transfers, marginal tax rates, average tax rates and absolute tax payments due to fiscal pressure from the baseline simulation to another measure of fiscal pressure. The bars correspond to the baseline simulation where governments are required to pay back the additional stock of debt in five years. The green squares correspond to a scenario where governments are required to pay back the additional stock in ten years.

A.3. Wealth distribution shocks

See Fig. 10, Fig. 11, Fig. 12 and Table 2.

Table 2.

Net wealth means across the income distribution.

	All	Bottom 20%	20–40%	40–60%	60–80%	80–90%	90-100%
Euro Area	229.1	75.6	113.4	178.3	238.7	343.7	736.1
Belgium	366.2	121.7	254.8	399.5	410.4	522.3	773
Germany	232.8	54.1	138.9	160.3	237.3	351.7	798.1
Estonia	111.9	39	59.2	73.7	130.8	136.7	377.7
Ireland	365.5	176.4	210.6	273.9	380.3	632.2	944.2
Greece	93.9	39.9	58.4	96.5	101.9	140.2	206.3
Spain	257.8	95.7	142.1	179.9	267.4	347.7	862.7
France	242	79.7	113.7	172.7	246.6	354.2	840.8
Croatia	106.6	109.8	64	69.8	98.7	118.6	264.6
Italy	214.3	79.3	105	165.3	247.5	327.6	621.6
Cyprus	499.7	137.4	243.3	304.7	481.1	676.9	1998.4
Latvia	43	11.4	28.5	27.5	47.1	58	144.1
Lithuania	84.3	62.8	57.9	83.1	95	102.1	145.3
Luxembourg	897.9	305.8	530.1	626.2	924.4	1438.2	2784.9
Hungary	73	32.1	43.9	61.4	71.7	93.6	218.7
Malta	400.7	211.4	316.7	265.3	427.7	462.5	1117.7
Netherlands	186	75.6	98.6	138.8	178.6	314.9	563
Austria	250.3	67.5	113	178.8	260.8	332.1	932.3
Poland	95.5	42.2	60.1	85.7	102.6	138.5	236.3
Portugal	162.3	63.6	79.2	103.8	151.6	194.5	632.4
Slovenia	144.3	77.2	96.3	128.4	147	202	344.4
Slovakia	103.5	48.3	76.7	83.4	107.8	156.6	247
Finland	206.6	63	111.3	170.9	214.5	281.8	665.2

Notes: The table is taken from the Statistical Tables of the 2017 Household Finance and Consumption Survey from the European Central Bank (2017) (Table A4).

A.4. Further robustness

See Fig. 13.

Fig. 13.

Change in tax rates and tax payments for different scenarios.

Note: The figure compares the average change in lump-sum transfers, marginal tax rates, average tax rates and absolute tax payments due to fiscal pressure from the baseline simulation to different measures of fiscal pressures. The bars correspond to the baseline simulation. The blue squares correspond to a scenario where individuals are more risk averse, the green diamonds correspond to a scenario where all countries have the same level of transfers initially and the red circles correspond to a scenario where all countries have the same share of individuals with zero income.