View-sharing for 4D magnetic resonance imaging with randomized projection-encoding enables improvements of respiratory motion imaging for treatment planning in abdominothoracic radiotherapy

Highlights

• •The acquisition of respiratory phase-resolved 4D magnetic resonance imaging (MRI) with sufficiently high spatiotemporal resolution and coverage remains challenging.
• •This work demonstrates a 4D-MRI technique for improving the spatiotemporal resolution of respiratory motion imaging.
• •The method defines a sampling function based on projection-encoding and peripheral k-space view-sharing.
• •The respiratory signal is used to optimize spatial resolution and minimize temporal blurring by limiting the extent of data sharing in the Fourier domain.

Abstract

Background and Purpose

The accuracy and precision of radiation therapy are dependent on the characterization of organ-at-risk and target motion. This work aims to demonstrate a 4D magnetic resonance imaging (MRI) method for improving spatial and temporal resolution in respiratory motion imaging for treatment planning in abdominothoracic radiotherapy.

Materials and Methods

The spatial and temporal resolution of phase-resolved respiratory imaging is improved by considering a novel sampling function based on quasi-random projection-encoding and peripheral k-space view-sharing. The respiratory signal is determined directly from k-space, obviating the need for an external surrogate marker. The average breathing curve is used to optimize spatial resolution and temporal blurring by limiting the extent of data sharing in the Fourier domain. Improvements in image quality are characterized by evaluating changes in signal-to-noise ratio (SNR), resolution, target detection, and level of artifact. The method is validated in simulations, in a dynamic phantom, and in-vivo imaging.

Results

Sharing of high-frequency k-space data, driven by the average breathing curve, improves spatial resolution and reduces artifacts. Although equal sharing of k-space data improves resolution and SNR in stationary features, phases with large temporal changes accumulate significant artifacts due to averaging of high frequency features. In the absence of view-sharing, no averaging and detection artifacts are observed while spatial resolution is degraded.

Conclusions

The use of a quasi-random sampling function, with view-sharing driven by the average breathing curve, provides a feasible method for self-navigated 4D-MRI at improved spatial resolution.

1. Introduction

The accuracy and precision of radiation therapy are dependent on the characterization of target motion [1]. Respiration-induced tumor and organ-at-risk (OAR) displacements are of concern primarily for lung and upper abdominal malignancies. In these anatomical sites, a typical workflow for treatment planning employs an estimate of target and OAR motion in order to determine safety margins. Four-dimensional X-ray computed tomography (4D-CT) is currently the most widely adopted modality for estimating the displacement of abdominothoracic targets. The electromechanical design of CT scanners limits the sampling pattern to axial or helical line-integrals and often leads to re-sampling artifacts. For organs in the abdomen, lesion detection is further challenged by the lack of inherent CT contrast between tumors and the surrounding parenchyma. In this context, the main advantage of magnetic resonance imaging (MRI) is the simplicity with which the sampling function can be designed and the wide range of inherent MRI contrast mechanisms. These advantages can be exploited in the investigation of novel acquisition and reconstruction methods for improved image quality and target detection in treatment planning [2], [3], [4], [5], [6], [7], [8], [9], [10]. The increased quality of planning images will directly impact the accuracy of manual or automatic contouring.

Respiratory motion may be estimated with 2D, 3D, or 4D imaging: phase navigators [11], time-resolved tomographic or projection imaging [12], and time-resolved or respiratory phase-resolved volumetric imaging [13] represent respective acquisitions from each approach. While recent technical advances in MRI hardware and software are encouraging, the acquisition of time-resolved 3D datasets with sufficiently high spatiotemporal resolution and coverage remains challenging. The alternative strategy, respiratory phase-resolved 4D imaging, is based on prospective or retrospective sorting of projections into a predefined number of breathing phases.

Phase-resolved imaging relies on the measurement of a breathing signal. The estimation of the amplitude and period of breathing motion guides image sorting into respective respiratory phases. The signal may be determined from the displacement of an external device placed on the patient surface, from image-based respiratory surrogate metrics, or from projection data in the Fourier domain [7], [11], [14], [15], [16], [17], [18], [19], [20], [21]. An image for each respiratory phase is then reconstructed from the raw data that has been assigned to that motion state.

MRI pulse sequences that rely on non-Cartesian sampling provide advantages in several clinical applications [22]. Projection-encoding, or radial sampling, refers to the acquisition of the MR signal along rays (spokes, views) traversing the center of k-space. This imaging technique can generate inherently volumetric measurements, has reduced sensitivity to flow and motion artifacts, and allows for shorter echo times as compared to traditional Cartesian methods [23]. The raw data in k-space have the additional advantage of providing an estimate for the respiratory signal without the need for an external tracking device [20]. When the number of rays in radial imaging is chosen to satisfy the Nyquist criterion at the periphery of k-space, the sampling function is redundant towards the center of k-space [24]. The redundancy can be exploited in methods of projection-encoding with view-sharing (PEVS) which attempt to improve spatiotemporal resolution and coverage based on the premise that the periphery of k-space, where high-frequency features are encoded, does not need to be updated as often as the center [25], [26], [27].

The primary aim of this study is to demonstrate a 4D-MRI technique for improving the spatiotemporal resolution of phase-resolved respiratory motion imaging by considering a novel sampling function based on quasi-random projection-encoding and peripheral k-space view-sharing. The average breathing curve is used to optimize spatial resolution and temporal blurring by limiting the extent of view-sharing in the Fourier domain. The method further exploits the property of the center of k-space to estimate the breathing signal, obviating the need for an external surrogate marker.

2. Materials and methods

2.1. Sampling and reconstruction technique

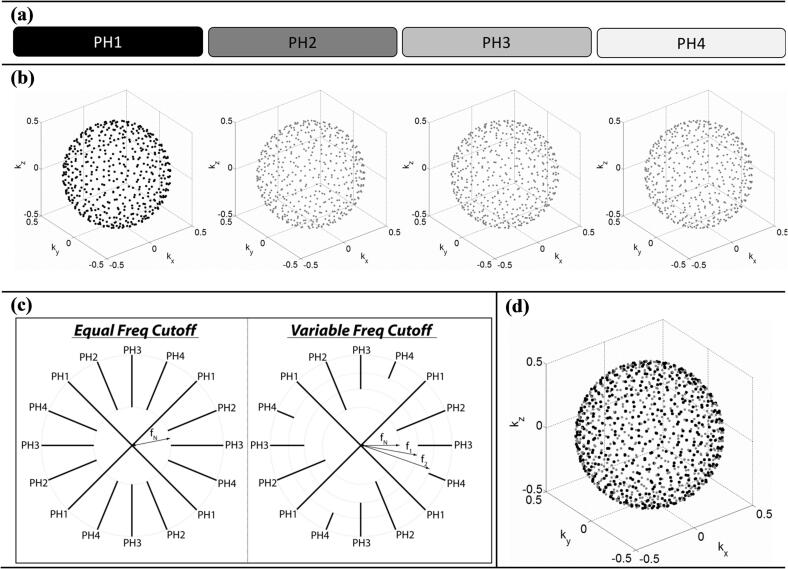
We hypothesize that 4D-PEVS, with the degree of view-sharing guided by the average breathing curve, improves the quality of respiratory motion imaging. Fig. 1 shows an overview of the sampling and reconstruction strategy. For simplicity, assume the respiratory cycle is divided into four phases, as depicted in Fig. 1(a). A three-dimensional radial function with a quasi-random distribution of polar/azimuthal k-space angles can be designed such that it provides efficient sampling of each respiratory phase while simultaneously sampling the entire k-space with non-overlapping points, as shown in Fig. 1(b). In this work, we consider radial sampling with the multidimensional golden means [28] and the stack-of-stars trajectories [29]. The multidimensional golden means trajectory provides radial sampling in all three dimensions while the stack-of-stars trajectory provides radial sampling in two dimensions and Cartesian in the third one. These functions allow for randomized acquisitions that enable efficient k-space sampling for each respiratory phase, and the methods are becoming readily available for routine clinical use in most diagnostic scanners.

Fig. 1.

Sampling and reconstruction strategy for respiratory imaging with 4D-PEVS. (a) In this diagram, k-space data for each respiratory phase (PH) are represented by a rectangle (for clarity, respiratory cycle hypothetically divided into four phases). Grayscale intensity (black = all, white = none) illustrates the amount of respective k-space data used to reconstruct phase 1. (b) k-space sampling functions (for clarity, only end-point of radial spokes shown). MR data for each phase are acquired in a quasi-random distribution of non-overlapping k-space points. (c) An overview of PEVS filters (2D k-space shown). The periphery of k-space data from all phases may contribute equally to the reconstruction of phase 1 (equal frequency cutoff) or the contribution of k-space from neighboring phases can be reduced by varying the cutoff frequency (variable frequency cutoff). f_N represents the radial distance in k-space below which the sampling rate is higher than that required by the Nyquist criterion. (d) Sampling function for reconstruction of phase 1; black represents the sampling points for phase 1 while gray represents the sampling points from all other phases.

The amount of data sharing can be controlled by a k-space filtering method, conceptually described in Fig. 1(c). For the sampling function of a given respiratory phase, we define f_N to be the radial distance below which the sampling rate is equal to or higher than that required by the Nyquist criterion. When reconstructing the image from this phase (phase 1 in the example in Fig. 1), peripheral k-space data from the remaining respiratory phases can be added in varying degrees by increasing the cutoff sampling frequency above f_N. The cutoff frequency can be global, as in the case of the equal frequency cutoff approach, or respiratory phase dependent, as shown for the general case of the varying frequency cutoff approach in Fig. 1(c).

For the reconstruction of a given respiratory phase, the k-space frequency cutoff can be written as:

$$f_i=f_N+{\delta }_i\ast \left(k_{\mathit{max}}-f_N\right)$$ (1)

where the index i references the k-space data of the respective respiratory phase, the parameter ${\delta }_i$ controls the amount of view-sharing, and k_max is the maximum k-space coordinate that defines the spatial resolution being reconstructed. We consider the following PEVS strategies:

$$\begin{gathered} {\delta }_i=1,\forall i:noview-sharing\left(NVS\right) \\ {\delta }_i=0,\forall i:equalsharingfromallphases\mathit{\left(}ESP\mathit{\right)} \\ {\delta }_i=\overline{\mathrm{\Delta }{s}_n}:view-sharingdrivenbyrespiratorysignal\left(RSGR\right) \end{gathered}$$ (2)

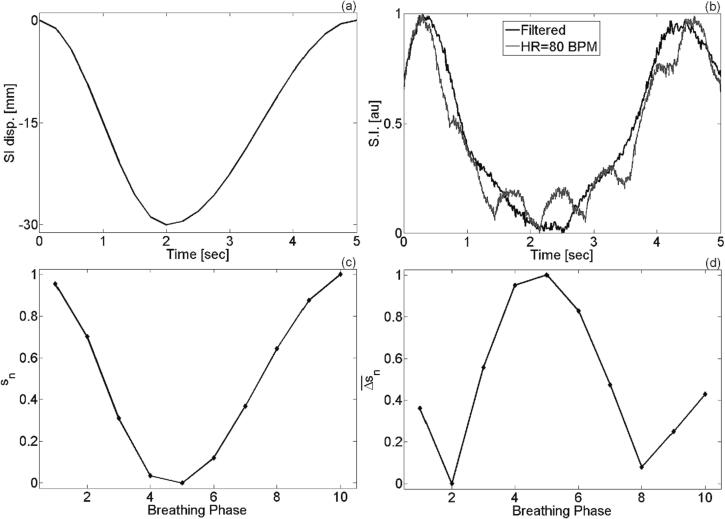
where $\overline{{\mathrm{\Delta }s}_n}$ is the normalized change in the average breathing signal (s_n). The average breathing signal is estimated from all cycles in the dataset while the difference is with respect to the phase being reconstructed, as depicted in Fig. 2. The method of view-sharing driven by the average breathing signal will be referred as respiratory signal-guided reconstruction (RSGR). In this technique, ${\delta }_i$ defines the fractional change in the average breathing curve. PEVS with RSGR relies on the premise that the average breathing signal is a measure of spatial changes across respiratory phases and accordingly adapts the amount of data sharing to minimize spatiotemporal blurring.

Fig. 2.

(a) Input curve for diaphragm motion and (b) respiratory signal extracted from the center of k-space. If the cardiac signal is superimposed on the breathing signal, its effect on retrospective sorting can be discarded by applying a band-pass filter. In this example, a type II Chebyshev filter has been applied. (c) Averaged and normalized breathing signal used to derive $\overline{{\mathrm{\Delta }s}_n}$. (d) Example of RSGR filter used for reconstruction of phase 2.

2.2. XCAT digital phantom simulations

The proposed sampling and reconstruction strategies were validated in the 4D extended cardiac torso (XCAT) digital phantom [30], [31]. The 4D-XCAT phantom was used to simulate the abdominothoracic anatomy of the adult male with the parameters listed in Supplementary Materials S1. Noise was modeled with a Gaussian distribution of SNR = 15 [32]. The MR signal was simulated by sampling the Fourier transform of the XCAT phantom along the points defined by the three radial trajectories described above. The breathing signal was estimated from the DC-component of k-space or from principal component analysis of projections along the z-direction [7]. The signal was retrospectively sorted into ten equal respiratory phases based on phase angle. Gridding reconstruction was implemented with a modified Kaiser-Bessel kernel [33] and iterative density compensation factors [34], [35].

2.3. Phantom experiments

The method was validated experimentally using a 4D phantom consisting of a 2 mm inner diameter polyethylene tube placed over another tube with an inner diameter of 15 mm. Both tubes were filled with a 5 mM CuSO₄ solution and oriented such that their long axes were on orthogonal planes. The phantom was connected to a linear actuator (Dynamic Phantom, CIRC, Norfolk, VA) able to generate a user-selected trajectory. The phantom motion and imaging parameters are listed in Supplementary Materials S2. The motion trajectory was confirmed with cine-MRI and compared to that estimated from the reconstruction with 4D-PEVS.

2.4. In vivo experiments

The feasibility of the proposed technique was tested in free-breathing lung and abdominal imaging in human volunteers. The study was approved by the Institutional Review Board and informed consent was obtained prior to data acquisition. The experiments were performed in MRI scanners from two vendors using the imaging parameters listed in Supplementary Materials S3.

2.5. Image quality assessment

The effect of view-sharing on image quality was assessed quantitatively by considering three features: resolution, target detection, and noise. Spatial resolution was estimated using the reconstruction edge-spread function (rESF). Adjacent line profiles were measured in a region-of-interest (ROI) at the lung-liver interface and rESF was computed as the mean of the spatial derivative (i.e., image gradient) in the ROI. In this framework, higher values of rESF imply a sharper edge, hence higher spatial resolution. Improvements in resolution are assessed by separately considering features that have minimal motion and features with large temporal changes during the respiratory cycle.

Target detection was estimated by analyzing the location of the lesion center-of-mass, lesion circularity and solidity, and lesion volume as a function of respiratory phase. Circularity and solidity were included as metrics for assessing target shape changes with respect to simulated spherical target. The mean value of the image quality metrics across breathing phases was compared using one-way ANOVA with repeated measures. Pairs of reconstruction techniques were analyzed with the paired-sample t-test. Statistical significance was determined based on a P-level less than 0.05.

The impact of the technique on signal-to-noise ratio (SNR) was evaluated by examining the noise floor. The noise floor was estimated by the standard deviation of signal intensity in a large background region devoid of streaking artifacts or NMR signal [32].

3. Results

3.1. XCAT digital phantom simulations

Fig. 2 demonstrates the properties of the center of k-space in the context of monitoring respiratory motion and provides an example of the normalized change in the average breathing signal used for 4D-PEVS with RSGR. Panels 2(a) and 2(b) compare the input respiratory signal and the k-0 signal from the simulation of the XCAT phantom. Although the cardiac signal may be superimposed on the breathing signal, its effect on retrospective sorting can be discarded by applying a band-pass filter. The breathing signal averaged over all phases is shown in Fig. 2(c). This function is used to derive $\overline{{\mathrm{\Delta }s}_n}$, plotted in Fig. 2(d). A montage of all phases reconstructed using RSGR-PEVS is provided in Supplementary Figure. S2.

Fig. 3 presents a comparison of the reconstruction techniques for the stack-of-stars sampling trajectory. Improvements in spatial resolution are quantified by the line profiles through the simulated stationary pulmonary vessels, as shown in Fig. 3(b). Given the size of the vessels, the ratio of the peak-to-peak amplitude of the line profiles can serve as a surrogate measure for the modulation transfer function. Under this assumption, when compared to reconstruction without view-sharing, RSGR-PEVS and ESP-PEVS respectively improve spatial resolution by approximately 65 % and 70 %.

Fig. 3.

Comparison of reconstruction techniques demonstrating spatial resolution improvements in features with minimal motion during the respiratory cycle. (a) Top and bottom row are chosen in locations representative of stationary features in the spinal canal and pulmonary vessels. From left to right: XCAT phantom, NVS-PEVS, ESP-PEVS, RSGR-PEVS. Arrows point to regions that demonstrate improvements in spatial resolution. (b) Line profiles through pulmonary vessels (arrow in panel (a), bottom row). The effect of view-sharing is shown for the stack-of-stars trajectory. See Supplementary Figure S4 for the multidimensional golden means trajectory.

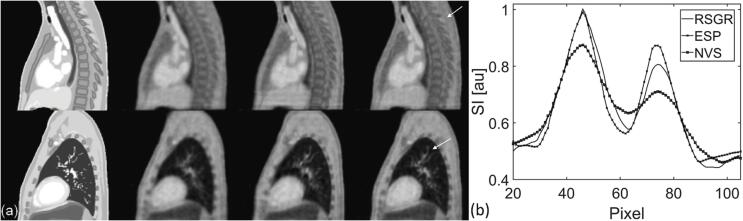
Fig. 4 illustrates spatial resolution improvements in features with large temporal changes during the respiratory cycle. Spatial resolution was evaluated using the reconstruction edge-spread function estimated at the lung-liver interface, highlighted in panel 4(a). Mean rESF was significantly different across reconstruction techniques (p-value≪0.05); RSGR-PEVS outperforms NVS-PEVS which in turn outperforms ESP-PEVS. This result demonstrates how reconstruction with equal data sharing degrades spatial resolution by approximately 10 % in regions with rapid motion. In these regions, ESP-PEVS leads to an overlay of moving edges which in turn causes spatial blurring. Spatial resolution also varies across breathing phases, as shown in Supplementary Figure S3. RSGR-PEVS optimizes spatial resolution and minimizes temporal blurring by limiting the extent of data sharing in the Fourier domain. Although edges are blurred, RSGR-PEVS and NVS-PEVS can determine the location of the lung-liver interface with comparable accuracy, while ESP-PEVS underestimates overall displacement, as shown in Fig. 4(c).

Fig. 4.

Comparison of the effect of view-sharing reconstruction techniques in regions with large temporal changes (a) Dashed box highlights lung-liver interface where the average rESF was estimated. (b) Mean rESF across breathing phases as a function of reconstruction technique. Normalized value of unity refers to highest spatial resolution. In regions with large temporal changes, RSGR-PEVS provides a significant improvement in spatial resolution while ESP-PEVS degrades spatial resolution. Bar-plots depict average ± standard error of mean. (c) Displacement of lung-liver interface determined from ten line profiles at the region highlighted in panel (a). The effect of view-sharing is shown for the stack-of-stars trajectory. See Supplementary Figure S5 for the multidimensional golden means trajectory.

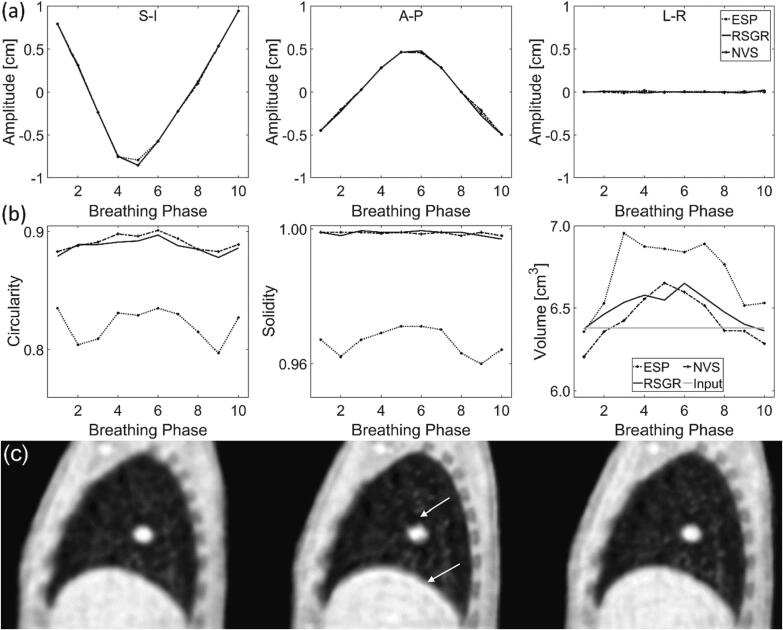
Lesion detection is characterized in Fig. 5. No significant difference was found when comparing the coordinates of the lesion center-of-mass, as shown in panel 5(a) (p-value = 0.32, p-value = 0.45, p-value = 0.76 for SI, AP, LR, respectively). Distortions estimated by lesion circularity, solidity, and volume are examined in Fig. 5(b). Lesion distortion is not significantly different in images reconstructed with RSGR-PEVS and NVS-PEVS (for circularity, solidity, and volume: p-value = 0.77). Lesion circularity and solidity is significantly lower in images reconstructed with ESP-PEVS while lesion volume is significantly higher (p-value≪0.05). In these images, circularity is approximately 9 % lower and solidity is approximately 3 % lower. Again, ESP-PEVS leads to an overlay of moving edges which in turn causes significant lesion distortions. This can be appreciated in Fig. 5(c) where the truncation artifact can be observed at the lesion boundary. The artifact is caused by the k-space discontinuity of ESP-PEVS.

Fig. 5.

Characterization of lesion detection as a function of reconstruction method. (a) Displacement of lesion center-of-mass in (left) superior-inferior (center) anterior-posterior and (right) left–right direction. (b) Shape metrics as a function of respiratory phase: (left) circularity, (center) solidity, and (right) volume of lesion. (c) Sagittal view at respiratory phase 3 for reconstructions with (left) NVS-PEVS, (center) ESP-PEVS, and (right) RSGR-PEVS. Notice truncation artifact and intensity ripples (arrows) caused by the sharp discontinuity in k-space sampling with ESP-PEVS. The effect of view-sharing is shown for the stack-of-stars trajectory. See Supplementary Figure S6 for the multidimensional golden means trajectory.

3.2. In vivo experiments

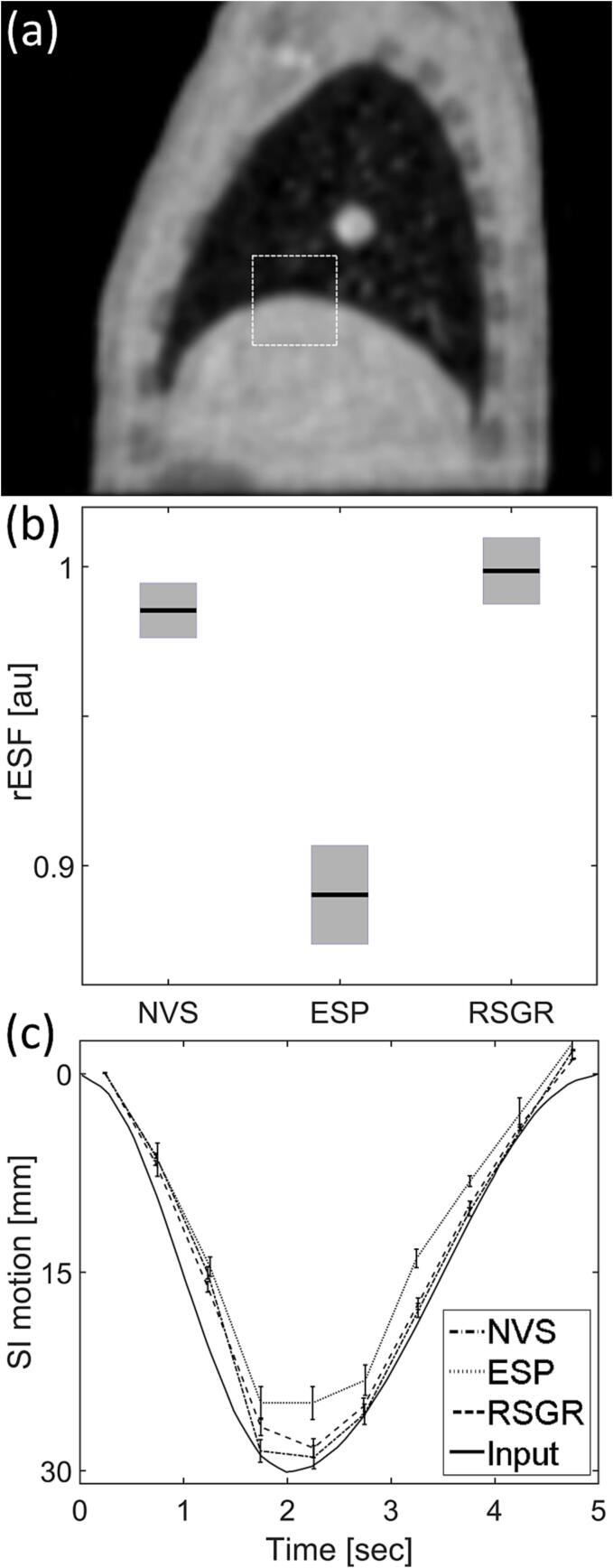
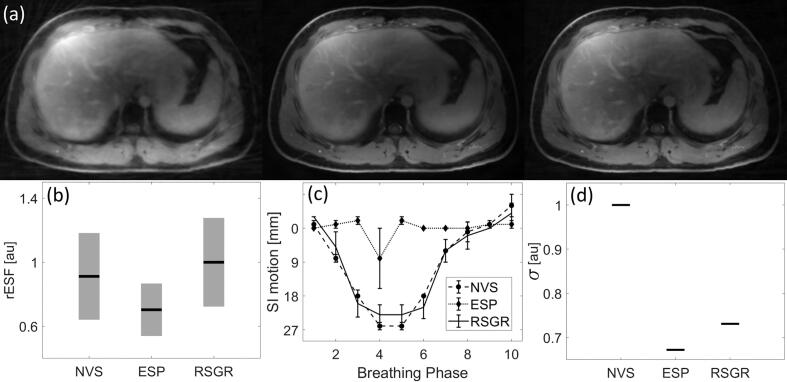
Fig. 6 demonstrates improvements in image quality in a volunteer study using the 3D radial stack-of-stars trajectory. The effects of reconstruction on resolution, detection, and SNR are analyzed in an approach analogous to the one used in the digital XCAT phantom. The mean rESF across breathing phases reveals that the degree of blurring in moving edges reconstructed with RSGR-PEVS is comparable to that found in images reconstructed without view-sharing, as seen in panel 6(b). Reconstruction with equal data sharing degrades spatial resolution by approximately 26 % in regions with rapid motion. Panel 6(c) compares the detection of the location of the lung-liver interface. This example demonstrates that equal sharing of the data at the periphery of k-space leads to temporal blurring that results in a lung-liver interface that may appear as stationary. Finally, a comparison of the noise floor reveals that while ESP-PEVS provides the largest improvement in SNR (decrease of noise floor by approximately 32 %), RSGR-PEVS also provides an improvement in SNR (decrease of noise floor by approximately 28 %), as shown in Fig. 6(d).

Fig. 6.

Image quality as a function of reconstruction method in a volunteer study. (a) Axial slice for (left) NVS-PEVS, (center) ESP-PEVS, and (right) RSGR-PEVS. Images normalized by maximum value of reconstructed intensity and displayed using equal window/level settings. (b) Mean rESF across breathing phases at lung-liver interface as a function of reconstruction technique. In regions with large temporal changes RSGR-PEVS provides a significant improvement in spatial resolution while ESP-PEVS does not improve resolution. Bar-plots depict average ± standard error of mean. (c) Displacement of lung-liver interface as a function of breathing phase. (d) Effect of reconstruction technique on noise. The noise floor (σ) is estimated by the standard deviation of signal intensity (across phases) in a large background region with no NMR signal.

4. Discussion

This proof-of-principle study develops and validates a method for improving the spatiotemporal resolution of respiratory motion with 4D-MRI. The technique defines a novel sampling function based on quasi-random projection-encoding and peripheral k-space view-sharing. The respiratory signal is determined from k-space data, obviating the need for an external surrogate marker. The average breathing curve is used to optimize spatial resolution and minimize temporal blurring by limiting the extent of data sharing in the Fourier domain. It is shown that the proposed technique can measure respiratory-induced motion with improved spatial resolution. These findings complement research in methods for improved respiratory imaging with novel sampling and reconstruction techniques [4], [7], [36]. Note that when compared to compressed sensing methods that rely on sparsity for improvements in spatiotemporal resolution [7], in this study we explicitly define how the data is shared. This allows us to improve image quality using a fast reconstruction method, such as re-gridding. The addition of compressed sensing reconstruction will likely provide further enhancements in image quality.

PEVS exploits the redundancy of the 3D radial sampling function towards the center of k-space. In this framework, the raw MR data for each respiratory phase is acquired using a limited number of k-space views by implementing a randomized sampling function. The amount of data sharing at the periphery of k-space can be guided by the breathing signal based on the hypothesis that the average signal is a measure of spatial changes across respiratory phases. Under such conditions, the requirements on temporal resolution may be relaxed at the benefit of improved spatial resolution and coverage. We validate this assumption and demonstrate the advantages of the method in developing a 4D-MRI protocol for respiratory motion imaging. Note that our work uses re-gridding as part of reconstruction and does not evaluate iterative or artificial-intelligence based reconstructions which may provide further improvements when combined with PEVS. Furthermore, RSGR-PEVS requires the breathing signal to be known for the entire acquisition (in order to compute the average breathing signal) and will currently work only for retrospective sorting.

Spatial resolution improvements with RSGR-PEVS are location and respiratory-phase dependent. In regions with rapid temporal changes the effects of the reconstruction technique are not trivial, as shown in Supplementary Figure S3. This is a consequence of variable data sharing. Alternatively, equal sharing of the periphery of k-space would result in blurring, distortion, and truncation artifacts, as seen in Fig. 4 and Fig. 5. RSGR-PEVS leads to selective improvements in spatial resolution while balancing the effects of temporal blurring. The simulations in the digital phantom reveal that the choice of the sampling function may have a limited effect on image quality. When comparing the multidimensional golden means trajectory (radial sampling in all three dimensions) and the stack-of-stars trajectory (radial sampling in two dimensions and Cartesian sampling in the third one) the results are generally the same. The similarity in spatial resolution is primarily due to the use of isotropic voxels for simulations. While a typical stack-of-stars acquisition has a larger voxel size in the Cartesian dimension (to improve coverage), we chose isotropic voxels to avoid confounding factors from volume averaging. The main difference between these trajectories arises for reconstructions with equal sharing of the periphery of k-space, as can be seen when comparing the results for circularity and solidity for ESP-PEVS. Overall, circularity and solidity are lower for the stack-of-stars trajectory with ESP-PEVS which may be due to the effect of inter-stack temporal blurring, in addition to temporal blurring from equal sharing at the periphery of k-space. Note that these results may also be dependent on spatial resolution as circularity and solidity are metrics that rely on thresholding. Finally, the degree of improvement in all metrics used to quantify image quality will depend on the sampling function, patient breathing signal, and sequence parameters. A specific implementation of the method may benefit from a similar analysis presented here.

The use of k-space data as a surrogate for sorting projections into respective respiratory phases has been previously demonstrated for sampling functions other than view-sharing. RSGR-PEVS can be implemented with an average breathing signal estimated with any of the techniques already mentioned, such as from the displacement of an external device placed on the patient surface, from image-based respiratory surrogate metrics, or from projection data in the Fourier domain [7], [11], [14], [15], [16], [17], [18], [19], [20], [21]. However, the challenges in the physical design of the MRI scanner and limitations of the external respiratory surrogates [37] reinforce the need for marker-less and self-sorted methods, an example of which is presented in this work.

In conclusion, this work demonstrates a 4D-MRI technique for improving the spatiotemporal resolution of respiratory motion imaging using a novel sampling function based on quasi-random projection-encoding and peripheral k-space view-sharing. The respiratory signal is used to optimize spatial resolution and minimize temporal blurring by limiting the extent of data sharing in the Fourier domain.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: