Network-based approaches for modeling disease regulation and progression

Abstract

Molecular interaction networks lay the foundation for studying how biological functions are controlled by the complex interplay of genes and proteins. Investigating perturbed processes using biological networks has been instrumental in uncovering mechanisms that underlie complex disease phenotypes. Rapid advances in omics technologies have prompted the generation of high-throughput datasets, enabling large-scale, network-based analyses. Consequently, various modeling techniques, including network enrichment, differential network extraction, and network inference, have proven to be useful for gaining new mechanistic insights. We provide an overview of recent network-based methods and their core ideas to facilitate the discovery of disease modules or candidate mechanisms. Knowledge generated from these computational efforts will benefit biomedical research, especially drug development and precision medicine. We further discuss current challenges and provide perspectives in the field, highlighting the need for more integrative and dynamic network approaches to model disease development and progression.

Graphical Abstract

1. Introduction

Various biomolecular components of a cell work together to carry out fundamental molecular processes and functions and ultimately influence clinical phenotypes and complex traits. Most diseases do not arise from a single gene mutation, but their etiology could be driven by multiple genes or perturbations that accumulate over time through interacting molecular components [1], [2]. Complex biological systems can be represented in the form of networks or graphs, in which nodes represent molecules (e.g. genes or proteins) and edges indicate physical or functional relationships. Examples of biological networks include protein-protein interaction (PPI) [1], [2], co-expression [3], metabolic [4], signaling [5], [6], and gene regulatory networks (GRNs) [7]. A major challenge in biomedical research is to extract meaningful and interpretable knowledge from molecular profiling (omics) data [8]. Consequently, the field of systems medicine, which deals with network-based modeling of biological systems, has led to deeper and even mechanistic insights from the accumulating wealth of omics data (see Fig. 1 for an overview of these techniques). In particular, network-based approaches to study diverse disease contexts have important clinical and biomedical applications, including hypothesis generation, biomarker discovery, disease classification, target prioritization, and drug repurposing [9]. We review recent network-based approaches used to study diseases, focusing on methods proposed in the last five years and some classical methods, and offer perspectives in the field. First, we discuss de novo network enrichment, which overlays molecular profiles onto a biological network to obtain new candidate disease mechanisms. Next, we discuss gene regulatory network inference, which aims to recover the set of gene-gene relationships from high-throughput data. We further discuss the emerging areas of differential co-expression networks and sample-specific networks.

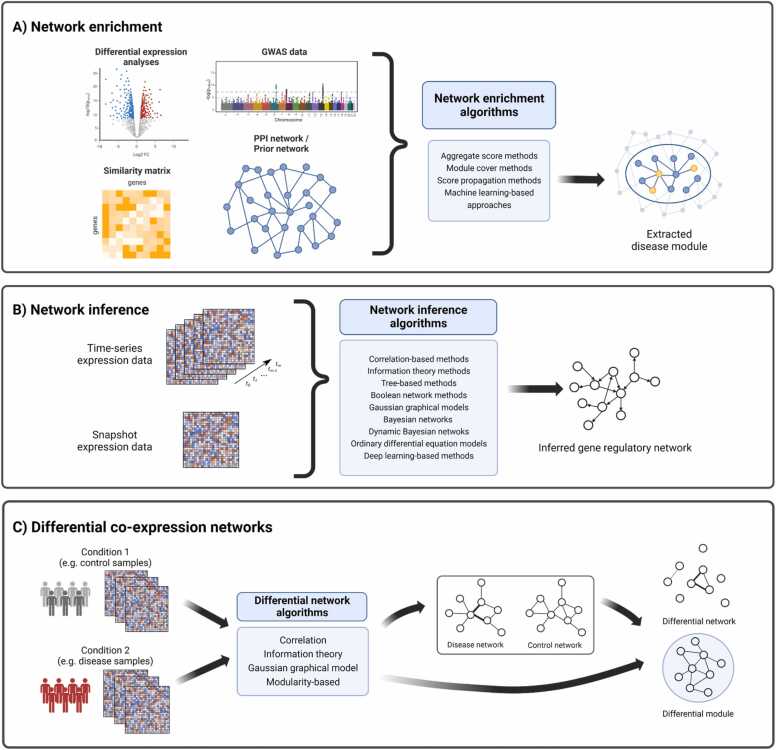
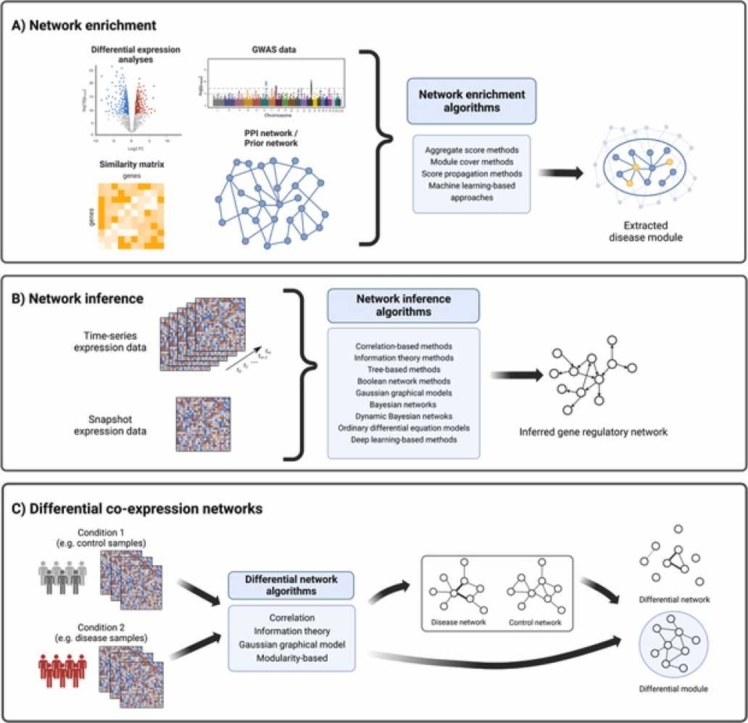
Fig. 1.

Overview of main network-based techniques for modeling human diseases. A) Network enrichment aims to find active subnetworks associated with a specific disease state from arbitrary networks. B) Gene regulatory network inference methods infer relationships between a regulator and its target gene by using snapshot data (condition-specific) and/or time-series omics data. C) Differential network analysis identifies interactions that are rewired between two conditions. Created with BioRender.com.

2. De novo network enrichment

De novo network enrichment methods (DNE), also referred to as active module identification methods, can be used to identify a disease module, i.e. a connected subnetwork of the human interactome that can be linked to a disease of interest [10]. The concept of disease modules is based on the observation that disease genes are not scattered randomly, but, due to their functional association, tend to be highly connected among themselves or in the same neighborhood in the interactome [11], [12]. The accurate identification of disease modules can help to identify new disease genes and pathways and aid rational drug target identification [13], [14].

In contrast to classical enrichment analysis, i.e. using Fisher’s exact test or gene set enrichment analysis [15], [16], DNE extracts condition-specific subnetworks in a more data-driven manner. Rather than relying on predefined pathways or curated gene sets [17], which are unlikely to reveal new mechanisms underlying diseases, DNE methods construct “active” subnetworks by projecting experimental data (mostly transcriptomic or genomic profiles) onto a molecular interaction network. Candidate subnetworks are then scored by an objective function and heuristics are implemented to identify locally optimal solutions efficiently. Batra et al. compared seven state-of-the-art DNE tools and concluded that the optimal subnetwork identification strategy depends on the specific application [17]. Expanding on the categories suggested by Batra et al., we review some of the recently published DNE methods (Table 1).

Table 1.

Recently developed network enrichment tools categorized by algorithm type. Links to code/tools are provided in Supplementary Table 1.

Tool	Input data type (s)	Algorithm Type	Example application	Reference
SigMod	GWAS	Aggregate score	Identify functionally and biologically relevant genes in childhood-onset asthma[18]	[18]
IODNE	Gene expression	Aggregate score	Identify potentially novel target genes for drug selection in triple-negative breast cancer[19]	[19]
PCSF	Multi-omics data (gene expression, mutation profiles, or copy number)	Aggregate score	Extract subnetworks of enriched metabolite interactions in multiple sclerosis[36]	[20]
Omics Integrator	Gene expression	Aggregate score	Link α-synuclein to multiple parkinsonism genes and druggable targets[37]	[21]
MuST	Disease-associated genes (derived from GWAS or DEG analyses)	Aggregate score	Investigation of coagulation pathway in COVID-19[38]	[22]
ROBUST	Disease-associated genes (derived from GWAS or DEG analyses)	Aggregate score	Identify an oxidative stress module in multiple sclerosis[23]	[23]
DOMINO	Disease-associated genes (derived from GWAS or DEG analyses)	Aggregate score	Integrated as the downstream analysis step in a splicing-aware framework for time course data analysis[39]	[24]
KeyPathwayMiner	Gene expression / multi-omics data	Module cover	Reveal epigenetic targets in SARS-CoV-2 infection, used together with gene co-expression networks[40]	[25]
ModuleDiscoverer	Gene expression	Module cover	Identify regulatory modules of the response to mesenchymal stromal cells treatment for mitigating liver damage[41]	[26]
NoMAS	Mutation profiles	Module cover	Identify subnetworks with strong association to survival in different cancer types[27]	[27]
nCOP	Mutation profiles	Module cover	Identify cancer genes including those with low mutation frequencies across 24 different cancer types[28]	[28]
NetDecoder	Gene expression; mutation profiles	Score propagation	Studying mechanism of CCN1-associated resistance to HSV-1-derived oncolytic immunovirotherapies for glioblastomas[42]	[29]
HotNet2	Mutation profiles	Score propagation	Identify mutated subnetworks in a genome-scale interaction network used for subtyping pancreatic cancer[43]	[30]
Hierarchical HotNet	Mutation profiles	Score propagation	Detect functional interactions that connect the cellular targets of viral proteins with the downstream changes in SARS-CoV and SARS-CoV2[44]	[31]
Grand Forest	Gene expression / methylation data	Machine learning	Stratify lung cancer patients into clinically relevant molecular subgroups[32]	[32]
N2V-HC	GWAS	Machine learning	Discover biologically meaningful modules related to pathways underlying Parkinson's disease and Alzheimer's diseases[33]	[33]
BiCoN	Gene expression / methylation data	Machine learning	Applied to TCGA breast cancer data for subtyping[34]	[34]
TiCoNE	Time-series expression data	Machine learning	Analysis of time-series lipidomics dataset of human mesenchymal stem cells after drug treatment[45]	[35]

Aggregate score methods compute a summary score for a candidate subnetwork based on the assigned scores to individual genes. Scores are typically calculated using fold changes or P-values derived from differential expression analyses. SigMod takes gene-level P-values from genome-wide association studies (GWAS) and a network as input and implements a min-cut algorithm to identify optimally enriched disease modules [18]. Based on Kruskal’s algorithm for obtaining a minimum spanning tree, IODNE scores nodes and edges based on differential expression and the topology of the PPI network [19]. Alternatively, several tools extract subnetworks by solving the prize-collecting Steiner forest (PCSF) problem. PCSF maximizes an objective function in which node scores (here called prizes) count positively, whereas edge weights, reflecting the confidence of an interaction, are counted negatively. In the R package PCSF, differential expression, mutation status, or copy number data can be used [20]. Similarly, the Omics Integrator package solves a variation of the PCSF problem with support for other omics types [21]. Menche et al. demonstrated that pairwise shortest paths of known disease genes show a significant left shift in their distribution compared to the random expectation [12]. Therefore, Minimum-weight Steiner trees (MWSTs), that can be viewed as generalizations of shortest paths with more than two endpoints (terminals), are a good choice to cover a large fraction of the disease-relevant molecular pathways. Using known disease genes as seeds (terminals), MuST identifies a disease module by aggregating several approximations of Steiner trees into a single subnetwork [22]. ROBUST is another method using MWST which offers improved robustness compared to MuST by enumerating pairwise diverse rather than pairwise non-identical disease modules [23]. Levi et al. demonstrated that most DNE methods using gene expression data do not fully exploit the information contained in this data [24]. They tried to address this issue in DOMINO by aiming to find disjoint connected Steiner trees in which the active genes (seeds) are over-represented [24].

Module cover approaches either accept a user-provided list of relevant (active) genes for a specific condition (e.g. the result of differential gene expression analysis) or implement a separate preprocessing step to determine such genes. These tools then extract subnetworks that “cover” a large number of the pre-selected active genes. For instance, KeyPathwayMiner expects molecular profiles encoded as binary indicator matrices as input to solve a variant of the maximal connected subnetwork problem [25]. ModuleDiscoverer identifies subnetworks based on the maximum clique enumeration problem. Starting from random seed proteins, the algorithm iteratively extends cliques of size 3, selects cliques that are significantly enriched in differentially expressed genes, and assembles them into regulatory modules [26]. NoMAS operates on mutation profiles and finds subnetworks that are enriched in mutations associated with survival time by solving the maximal connected k-set log-rank problem [27]. A related tool is nCOP, which utilizes individual mutation profiles based on the minimum connected set cover problem and finds a connected subnetwork that covers as many patients as possible who collectively harbor alterations in genes involved in pathways [28].

Score propagation methods assign initial scores to the nodes and propagate them through the network before extracting high-scoring subnetworks. NetDecoder extracts sparse subnetworks as directed graphs using information flow between sources and sinks that act as regulators. It first creates a weighted interactome by integrating a PPI network with a co-expression network generated from context-specific data. The weights represent Pearson correlation across samples of the same context, determining the capacity for an edge. Sources are defined as DEGs, mutated genes, drug targets or any custom gene set, while sinks are defined as genes involved in transcriptional regulation based on GO annotations [29]. Methods using heat diffusion models have the problem that highly mutated genes (hot nodes), such as TP53, propagate the heat to their neighboring genes which may not be mutated and are not biologically interesting. To overcome this issue, HotNet2 uses an insulated heat diffusion process and considers the directionality of heat flow in the identification of subnetworks. HotNet2 considers both the individual gene scores (e.g. mutation frequency) and the local network topology [30]. It has been extended with a random walk-based network clustering approach implemented in Hierarchical HotNet [31]. The latter combines network interactions and vertex scores to construct a hierarchy of high-weight, topologically close subnetworks. Hierarchical HotNet is more flexible, more robust and less computationally intensive than HotNet2.

Machine learning-based approaches score subnetworks based on their predictive performance in supervised learning. Grand Forest implements a graph-constrained random forest algorithm, extracting subnetworks of high feature importance with respect to various response variables, such as phenotype, symptom, survival, or treatment response [32]. The N2V-HC approach constructs an integrated network using known PPIs, GWAS and expression Quantitative Trait Loci (eQTL) data and employs deep representation learning on this multi-layer network. The nodes are embedded using the node2vec algorithm, based on a biased random walk, to incorporate global connectivity features in the network. Afterwards, the learned representations are subjected to hierarchical clustering. An iterative selection procedure using enrichment analysis is then applied to produce the final modules [33]. Most existing disease module mining methods rely on case-versus-control annotations. Unsupervised approaches have the advantage that they can not only return disease modules but simultaneously de novo cluster patients into subgroups. Biclustering Constrained by Networks (BiCoN) is one of the few such unsupervised approaches which is based on the Ant colony optimization algorithm. It uses a heterogeneous network of patients and genes, where genes are linked to patients via the expression data and are linked with each other via PPIs [34]. Time-course network enrichment (TiCoNE) identifies temporal response pathways by clustering genes with similar co-expression patterns. It uses as input time-series expression data and benefits from a human-augmented approach, i.e. it allows users to add, remove, merge, or split temporal patterns based on their domain knowledge. Induced subnetworks from the PPI network can then be generated from the identified gene clusters [35].

3. Gene regulatory network inference

Gene regulation is a fundamental process that influences cell fate and development, response to stimuli, and disease progression. In particular, transcription factors (TFs) regulate other genes and many methods have been developed to model these relationships as networks. Transcriptional gene regulation primarily involves the binding of transcription factors (TFs) at both promoter and enhancer regions and the physical interaction of these bound complexes via DNA looping. The problem of network inference aims to reconstruct the structure of the GRN, where a (typically directed) edge indicates an interaction between a regulator (e.g. transcription factors acting as activators or repressors) and its target gene. Network inference or “reverse-engineering” of biological networks using omics data (e.g. gene expression data) is useful for identifying genes that may influence the phenotypic changes associated with a disease of interest. Ideally, causal and direct relationships are reconstructed; however, regulatory interactions may be non-linear and complex. Reverse-engineering of GRNs remains a major challenge, as evident from large community efforts [46]. Sample sizes from biological experiments are typically small, ranging from tens to hundreds, relative to the number of variables, in the order of tens of thousands of genes or transcripts. Consequently, network inference is an underdetermined problem in which many models fit the data and an exponentially large space of networks needs to be considered [47]. Various computational GRN inference approaches have been developed, which include correlation-, information theory-, regression-based techniques, Gaussian graphical models, Boolean networks, Bayesian networks, and ordinary differential equation (ODE)-based methods. Depending on the approach, these methods could utilize either snapshot data (gene expression data sampled from a well-defined disease condition or phenotypic stage) or temporal data (samples are obtained from a series of time points). We provide an overview of these methods in Table 2.

Table 2.

Recently developed network inference tools, input data, and their core algorithmic approaches. Links to code/tools are provided in Supplementary Table 2.

Tool	Input data	Algorithmic approach	Example application	Reference
WGCNA	Snapshot expression data	Correlation	Identify differences in brain co-expression networks underlying the pathology of autism[73]	[48]
ARACNE	Snapshot expression data	Information theory	Resolve the regulatory structure of co-expression modules and identify disease drivers in post-traumatic stress disorder[74]	[50], [51]
CLR	Snapshot expression data	Information theory	Inference of miRNA co-expression network in type 2 diabetes[75]	[52]
MRNET	Snapshot expression data	Information theory	Network analysis of WNT1-regulated network in neurodegeneration[76]	[77]
GENIE3	Snapshot expression data	Regression trees	Identification of TEADs as regulators of invasive cell states in melanoma[78]	[54]
GRNBoost2	Snapshot expression data	Regression trees	Investigating the role of NKD2 in kidney fibrosis[79]	[55]
PLSNET	Snapshot expression data	Partial least squares regression	Identify new ERRα partners in breast cancer[80]	[56]
FastGGM	Snapshot expression data	Gaussian graphical model	Applied to gene expression datasets in asthma and Alzheimer’s disease[58]	[58]
BiDAG	Snapshot expression data	Bayesian network; Dynamic Bayesian network	Identify network transition structures in colorectal cancer[81]	[64]
LBN	Snapshot expression data	Bayesian network	Evaluated on DREAM3 challenge dataset and the E. coli SOS DNA repair network[65]	[65]
ATEN	Time-series expression data	Boolean network	Evaluated on Drosophila segment polarity gene regulatory network[82]	[82]
GABNI	Time-series expression data	Boolean network	Benchmarked on DREAM dataset and yeast cell cycle dataset[83]	[83]
dynGENIE3	Time-series expression data	Ordinary differential equations + Regression	Construction of GRN governing circadian clock[84]	[85]
Inferelator	Time-series expression data	Ordinary differential equations + Regression	Learning the Bacillus subtilis regulatory network[86]	[87], [88], [89]
Ma et al.	Snapshot and time-series expression data	Ordinary differential equations	Benchmarked on DREAM4 dataset and E. coli and S. cerevisiae datasets[65]	[90]
BETS	Time-series expression data	Granger causality	Predicting the transcriptional response of A549 cells to glucocorticoids[91]	[91]
SWING	Time-series expression data	Granger causality	Infer time-delayed edges in a SOS response network in E. coli following DNA damage[92]	[92]
iRafNet	Snapshot expression data; prior knowledge	Regression trees	Studying clear cell renal cell carcinoma using phosphopeptide data[93]	[94]
PostPLSR	Snapshot expression data; multi-omics data	Partial least squares regression	Studying the effects of circadian rhythm on gene expression[95]	[95]
PANDA	Snapshot expression data; prior knowledge	Message passing	Construction of sex-specific networks in chronic obstructive pulmonary disease[96]	[97]
Lemon-Tree	Snapshot expression data; multi-omics data	Bayesian network	Identifying changes in gene interactions during spontaneous migraine attack[98]	[99]
MERLIN+Prior	Snapshot expression data; prior knowledge	Bayesian network	Infer a general neural lineage network in early hindbrain and spinal cord development[100]	[101]
GRACE	Snapshot expression data; prior knowledge	Regression trees; Markov random fields	Construction of developmental GRNs in Arabidopsis thaliana and Drosophila melanogaster[102]	[102]
KiMONO	Snapshot expression data; prior knowledge	Penalized regression	Identification of host factors for COVID-19[103]	[104]
Inferelator-AMuSR	Snapshot expression data; multiple conditions	Penalized regression	Inferring shared and cell-type specific interactions in cortical interneuron development[105]	[106]
fused LASSO	Snapshot expression data; multiple conditions	Penalized regression	Construction of GRNs in early immune response to Avian influenza A viruses (IAV)[107]	[108]
GRADIS	Snapshot expression data; known TF-target interactions	Support vector machines	Evaluated on DREAM4 and DREAM5 datasets[68]	[68]
DeepSEM	Single-cell RNA sequencing (scRNA-seq) data	Deep learning	Identification of marker genes in the mouse cortex[72]	[72]
DeepDRIM	scRNA-seq data	Deep learning	Identifying genes relevant to COVID-19[70]	[70]
CNNC	scRNA-seq data	Deep learning	Evaluated on mouse embryonic stem cells, bone marrow-derived macrophages, and dendritic cells to predict new TF-target relationships[69]	[69]
GraphReg	DNA sequence data; Chromatin interaction data	Deep learning	Evaluated on ENCODE data from human cell lines and data from mouse embryonic stem cells to predict CAGE expression signals[109]	[109]
Enformer	DNA sequence data	Deep learning	Variant effect prediction[110]	[110]
Basenji	DNA sequence data	Deep learning	Identifying causal eQTLs[111]	[112]

3.1. Network inference from snapshot data

Traditional methods of constructing GRNs use correlation or mutual information as measures of edge confidence. Correlation-based methods are the most straightforward approach to infer pairwise relationships by calculating the correlation coefficient, resulting in weighted, undirected networks. Examples of correlation-based approaches include the popular weighted gene correlation network analysis (WGCNA) [48]. WGCNA constructs a correlation-based adjacency matrix, which is raised to a suitable power (ß parameter) such that the resulting network exhibits scale-free topology and ensures similar connectivity between neighboring genes. While inference using correlation-based network methods is fast, they typically produce a large number of false positives and output very dense correlation networks [49]. Information theoretic methods rely on statistical measures based on mutual information (MI), a non-linear correlation measure, to construct the networks. Popular MI-based tools include algorithms for the reconstruction of accurate cellular networks (ARACNE) [50], [51], Context Likelihood of Relatedness (CLR) [52], and minimum-redundancy network (MRNET) [53]. In general, these methods calculate pairwise MI values, followed by a pruning step to eliminate indirect interactions. MI-based methods have low computational complexity and can better detect complex, non-linear dependencies, but they can only be applied to snapshot data.

Most regression based methods formalize the GRN inference problem as a feature selection problem and construct the GRN with an ensemble strategy. A popular approach is GENIE3, which builds ensembles of regression trees to predict the expression level of each target gene using the expression levels of TFs or other genes and subsequently aggregates the results to reconstruct the final GRN [54]. GRNBoost2 and Arboreto build on the GENIE3 approach by implementing gradient boosting of the trees to improve performance and runtime [54], [55]. PLSNET is another ensemble approach that uses the partial least squares method (PLS) to select features that can predict the expression of the target genes [56].

GRNs are also often represented using Gaussian graphical models (GGM). GGMs are probabilistic models of conditional dependencies between variables and can be used to distinguish direct from indirect interactions. In a GGM, edges are defined as node pairs with non-zero partial correlation. Hence, an edge in the model indicates the dependency between two genes after removing the effects of all other genes. The GGM can be derived by calculating the inverse covariance matrix (precision matrix), with the nodes assumed to follow a multivariate normal distribution. One of the most widely used methods to estimate a GGM is the graphical LASSO, which uses L1 regularization [57]. FastGGM implements a penalized regression approach that outputs confidence intervals for each edge in the GRN [58], [59].

A Bayesian network is a probabilistic graphical model that encodes the conditional dependencies between the random variables (genes) in a directed acyclic graph (DAG) structure. The Bayesian network formalism naturally encodes causality. Learning the optimal network from data requires estimating the network structure and parameters [60]is a non-trivial task because of the considerably large space of possible graphs. Various methods have been proposed for Bayesian network structure learning, which can be generally categorized as score-based or constraint-based [60]. Score-based methods use a score function (e.g. Bayesian Dirichlet equivalence score and the Bayesian information criterion score) to evaluate the structures over the search space of possible network structures. Heuristic methods, such as hill climbing, tabu search, and simulated annealing have been proposed to search for the optimal network structures [61]. On the other hand, constraint-based methods attempt to find the skeleton of the DAG by performing conditional dependence tests among the nodes. Afterwards, edge directions are determined by resolving directional constraints on the skeleton structure. However, Bayesian network methods are limited to up to hundreds of genes and are difficult to scale to thousands of genes. The BiDAG method uses the constraint-based PC algorithm [62] to restrict the search space and generate an initial skeleton. Afterwards, it implements a Markov chain Monte Carlo method to sample the network structures from the posterior distribution [63], [64]. The local Bayesian network (LBN) method proceeds in four main steps. It first uses MI or conditional mutual information to generate a tentative skeleton structure and reduce the number of candidate regulators. Afterwards, a k-nearest neighbor algorithm is applied to decompose the network into local networks (LBNs). For each LBN, the optimal structure is determined by searching through all possible configurations. A candidate GRN is assembled by integrating all the LBNs, followed by pruning of the edges using CMI. This procedure is iterated and the networks are refined to obtain the final GRN [65]. For further reading on causal structure learning, we refer the reader to [66], [67].

Supervised machine learning approaches have also been developed for GRN inference. These require both gene expression data and a set of known regulatory interactions for predicting regulatory links between gene pairs. GRADIS first clusters samples and generates graph distance profiles from the gene expression data as features for training support vector machines to reconstruct the GRN [68]. Deep learning-based approaches have also been applied to the network inference problem using convolutional neural networks (CNNs) or variational graph autoencoders (VAEs). The convolutional neural network for coexpression (CNNC) approach uses known TF-target interactions in a supervised framework. CNNC transforms the joint expression of a gene pair into an image-like matrix, which can then be used for training a CNN [69]. DeepDRIM (deep learning-based direct regulatory interaction model) extends CNNC by considering both a target gene pair (primary image) and the gene pairs where one of the genes shows strong positive covariance to a gene that belongs to the known TF-target pairs (neighbor images). Both the primary and neighbor images are then used as inputs for training a CNN model. By incorporating neighborhood context, CNNC aims to remove false positives due to transitive interactions [70]. Recently, the Non-combinatorial Optimization via Trace Exponential and Augmented lagRangian for Structure learning (NOTEARS) algorithm has been developed, which is the first study to transform the structure learning problem from a combinatorial optimization into a continuous optimization problem as score-based learning of Bayesian networks from data [71]. This allows the use of well established numerical solvers to derive the DAG. The DAG-GNN approach adapts the NOTEARS algorithm by using a deep generative model under a VAE framework to model non-linear causal relationships. Based on the DAG-GNN formulation, DeepSEM was developed to infer GRNs from single-cell sequencing data [72]. DeepSEM implements a beta VAE and uses the weights of both the encoder and decoder functions to represent the adjacency matrix of the GRN.

3.2. Network inference from time-series data

Diseases can arise as the result of accumulated perturbations in regulatory processes that progress over time. The dynamic nature of biological phenomena can be investigated by taking “snapshots” of the system, i.e. measurements across multiple time points (e.g. through microarray or RNA-Seq experiments). The network inference methods discussed above assume static networks, which hampers the discovery of causal relationships and does not capture the temporal changes in network structure. Modeling dynamic GRNs allows for a more fine-grained investigation of molecular mechanisms and important regulators that govern these network transitions and drive topological changes over time. Various techniques have been implemented for modeling the time evolution of gene regulation, such as ODEs, Boolean networks, and dynamic Bayesian networks (DBNs).

Boolean networks describe regulatory interactions over time using Boolean variables as the states of genes and Boolean functions to determine the current gene states as a function of the previous states of other genes [113]. In a Boolean network, the expression of each gene is discretized to only “on” (expressed) or “off” (not expressed). Inferring a Boolean network corresponds to learning the Boolean functions that make up the regulatory rules. The And/Or tree ensemble (ATEN) algorithm infers a GRN from ensembles of and/or trees [82]. The MIBNI algorithm uses an MI-based feature selection step to identify potential regulators. This is followed by a subroutine that performs swapping to find optimal regulators for each target gene [114]. GABNI extends the MIBNI algorithm by further implementing a genetic algorithm to improve the set of candidate regulators and thus the dynamic consistency of the resulting Boolean network. An evaluation of Boolean methods for GRN inference and their implementations can be found in [115].

A DBN is a probabilistic graphical model for the joint distribution of random variables with observations across different time points [116]⁠. DBNs are a widely used technique for modeling GRNs using time-series data. In contrast to traditional BNs, DBNs can handle self-loops, which are abundant in biological systems. DBNs can be learned from time-series data using the methods in BN literature. Learning DBN structures remains computationally challenging because of the extremely large search space. Various greedy and heuristic methods have been developed to restrict the network topologies. However, efficient modeling with DBNs is often limited to up to hundreds of nodes. The simplest DBN uses a first-order Markov model, where the value of a variable at the current time point is conditionally dependent on the values of a set of parent variables at the previous time point only. Classical homogeneous DBN models assume that the network topology and parameters characterizing the network are constant over time. BiDAG can also infer the DBN from time-series data [81]. On the other hand, non-homogeneous DBNs provide flexibility by allowing the network parameters and/or structure to vary.

ODEs describe the rate of change of a gene’s expression levels as a function of its regulators. ODE models are a widely applied method to quantitatively describe the time evolution and regulatory dynamics of the gene expression levels. dynGENIE3 extends GENIE3 by modeling expression changes over time in an ODE. These are used as the inputs to the random forest and putative gene–gene interactions are next learned using random forest regression. A similar method uses nonlinear ODEs and gradient boosting trees [52] to infer the networks [53]. Using both snapshot and time-series data, Inferelator combines regularized regression and ODEs to model the time evolution of genes or pre-calculated gene clusters [88]. ODEs provide highly detailed models but require extensive parameterization and are computationally infeasible for genome-scale networks.

Other models that infer networks from time-series data build on Granger causality, which is based on the reasoning that if incorporating previous values of Y increases the prediction accuracy of X in an autoregression model, then Y is said to Granger-cause X. A causal relationship is then determined from the statistically significant coefficients of the model. BETS implements an elastic net autoregression model [91]. To increase robustness, the networks are inferred from bootstrapped samples from the data and stability selection is performed to identify the most frequent edges. This is combined with another bootstrapping procedure to control the false discovery rate. SWING improves on the standard pairwise Granger causality framework to simultaneously allow for multiple explanatory regulators by using user-specified sliding windows on temporally spaced observations and delay parameters to generate ensembles of training data. Potential predictors are then evaluated using supervised learning algorithms. A consensus network representing the final prediction is then aggregated from the high-confidence edges from the different windowed models [92].

The GRN inference tools discussed above typically require input from a single source or data type to reconstruct GRNs de novo and thus rely solely on the statistical properties of the data. In particular, most popular GRN inference tools utilize only gene expression data from an experiment as input.

3.3. Multi-modal and integrative network inference approaches

Recent studies are increasingly integrative and incorporate prior biological information to facilitate more biologically meaningful GRN structures (Fig. 2). Combining data from multiple modalities in a principled manner can enhance our understanding of a disease [117], [118]. Several other types of high-throughput genomics, proteomics, and metabolomics data are now being profiled over time, with studies profiling several omics levels simultaneously. Prior biological information can also be obtained from existing biomedical databases, including TF-target interactions and binding motifs, partially known networks from experimental data, DNase hypersensitivity data, ChIP-seq data, and GWAS. Therefore, the use of prior knowledge and biologically plausible assumptions with respect to the model structure can inform GRN reconstruction [119]. Various strategies that provide flexibility by allowing simultaneous analysis of multi-omics data or incorporating available prior knowledge are particularly desirable. For instance, the similarity network fusion (SNF) approach constructs a patient similarity network for each omics data type, where an edge indicates high pairwise similarity between individuals. The multiple networks are then combined into a fused network using an iterative message passing algorithm that updates the networks until they are harmonized [120]. The tool iRafNet extends the GENIE3 regression tree approach by incorporating weighted scores from different evidence layers such as knockout expression data to influence the selection of potential regulators for a gene [94]. The PostPLSR approach uses variable importance derived from partial least squares regression from time-course gene expression data and partially known relationships from pathway databases to reconstruct GRNs [95]. PANDA implements a message passing algorithm that uses available TF-motif or known protein interactions to refine GRN reconstruction [97], [121]. MERLIN+Prior constructs a prior network obtained by integrating non-expression data, including motif, knockout, and epigenomics data. The algorithm then learns a modular GRN using a Bayesian framework [101]. GRACE generates a meta-regulatory network from different biologically supported sources and filters for high-confidence edges using ensembles of Markov random fields [102]. Using a penalized regression approach, KiMONO can infer multi-level networks from any combination of omics types [104]. Lemon-Tree is a module network inference method [122] that employs a model-based Gibbs sampler [97], [120] to infer co-expression modules and subsequently finds consensus modules using a spectral clustering algorithm. It then reconstructs regulatory programs by assigning a set of regulator genes to the network modules as learned through decision trees. A probabilistic score is calculated for each resulting regulatory program, incorporating other omics data, and high-scoring programs are considered relevant to the disease of interest [99].

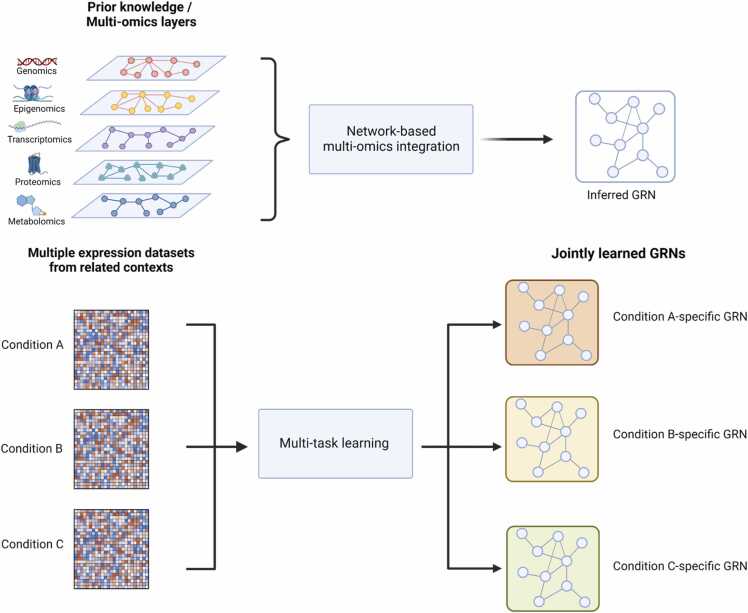
Fig. 2.

Multi-modal and integrative approaches towards network inference. Depending on the integration strategy, network-based integration methods that incorporate prior information from biomedical databases or multi-omics data can inform biologically meaningful GRN reconstruction. Other approaches exploit the similarity of data from multiple related biological conditions in multi-task learning to simultaneously infer GRNs. Created with BioRender.com.

Previous studies have shown considerable similarity in GRNs across tissues or conditions, with relatively smaller changes in local network structure driving differences in phenotypes or responses. Consequently, various methods have been developed to leverage experimental data from separate studies to improve GRN reconstruction, exploiting shared regulatory interactions across different but related biological contexts. Inferelator-AMuSR implements multi-task learning to jointly infer the GRN from multiple experiments [106]. It enforces similarity across network models using an adaptive multiple regression technique. The fused LASSO approach infers GRNs from multiple time-series or perturbation conditions and employs regularization to promote the sparsity of the coefficients of the regression predicted TF-target relationships from multiple networks constructed from each input dataset. In addition, it enforces similarity of the GRNs reconstructed from multiple experiments [108].

4. Modeling gene regulation from sequence data

Deep learning approaches have also been developed for predicting gene regulation using DNA sequence data as input. For example, Basenji applies CNNs on sequence data to predict the effects of variants on gene expression and disease risk [112]. Newer architectures are also used, including graph neural networks (GNNs) that can handle graph-structured data and have emerged as part of standard analysis toolbox in various graph-related tasks, including node classification, link prediction, and graph classification [123], [124]. GNNs work via a message passing algorithm to allow nodes in a network to exchange information. Graph attention networks are GNNs with attention, a mechanism which extracts useful context from long-range structural information [125], [126]. In the field of machine translation and natural language processing, the addition of attention layers to deep learning models significantly improved performance [127], [128]. In gene regulation, attention layers have been used to incorporate information from distal regulatory elements which has not been achieved using CNNs alone because of their limited local receptive field. For example, Enformer uses a transformer architecture which employs self-attention, thereby accurately inferring long-range enhancer-promoter interactions from up to 100 kb away from the transcription start site [110]. GraphReg predicts gene expression levels measured by Cap Analysis Gene Expression (CAGE)-seq by using CNNs to learn local representations from one-dimensional data (e.g. epigenomic data and/or sequence data) [109]. Afterwards, a graph attention network is applied to propagate the learned features over an interaction graph built using 3D chromatin data and can thus capture more distant regulatory features.

5. Differential co-expression networks

Differential co-expression (DC) represents changes in interactions between molecular components, also known as “network rewiring.” DC can occur in response to cellular stimuli, developmental stages, drug treatments, or disease states and can also occur in the absence of differential expression [129], [130], [131]. Analyzing changes in the network structure of regulatory relationships can provide more context-specific insights into the mechanisms underlying diseases. Under the premise that co-expressed genes are more likely to be co-regulated, major changes in co-expression patterns between classes may indicate changes in regulation [132], [133]. In a differential network, an edge thus represents a significant change in correlation or association strength in a pair of genes. Differential co-expression methods examine the differences in the network connectivity patterns by comparing two or more phenotypes or biological states (e.g., diseased vs. healthy individuals). This is different from disease module identification, where most methods focus on the individual genes (nodes) and typically use differentially expressed genes as starting points (seed genes). Differential co-expression analysis has been used to complement standard DE analysis [134].

A number of methods have been proposed to detect differential co-expression networks from data de novo (Table 3). Most methods use correlation as a measure of association, although others use other metrics or tests, such as information theory, GGMs, linear models, or generalized linear models. Some methods implement a network-based approach, which aims to identify pairwise changes in the strength of co-expression between genes. DGCA calculates differential correlation by z-score transformation of Pearson correlation coefficient (PCC) [77]. Information theoretic approaches include MINDy, which uses MI as a measure, and CINDy, which is based on conditional mutual information [135]. Under the GGM framework, Danaher et al. proposed the joint graphical lasso, which employs fused lasso or group lasso penalties to jointly estimate the precision matrices from multiple classes. Assuming that the two conditions have shared characteristics, this method encourages similarity between the graphical models [136]. With the key assumption that the resulting differential network is sparse, the method of Yuan et al. directly estimates the difference of the precision matrices using a penalized loss function called the D-trace loss [137].

Table 3.

Representative tools for deriving differential co-expression networks. Links to code/tools are provided in Supplementary Table 3.

Tool	Input data	Algorithmic approach	Example application	Reference
DGCA	Two conditions	Correlation	Differential connectivity analysis in myelin dysregulation in a mouse model of Alzheimer’s disease[144]	[145]
MINDY	Two conditions	Information theory	Identify modulators of B cell signaling[146]	[147]
CINDy	Two conditions	Information theory	Infer candidate upstream modulators of master regulator proteins in various cancer states[148]	[135]
Joint Graphical LASSO	Multiple conditions	Gaussian graphical model	Network analysis of gut microbiome data related to pediatric obesity[149]	[136]
Yuan et al.	Multiple conditions	Gaussian graphical model	Identification of genes involved in microsatellite stable colorectal cancers[137]	[137]
DICER	Multiple conditions	Correlation	Identification of differentially correlated gene clusters in Alzheimer’s disease[138]	[138], [142]
ALPACA	Two conditions	Differential modularity	Identification of network modules associated with glioblastoma survival[150]	[141]
Diffcoex	Multiple conditions	Correlation	Investigating altered co-expression patterns following influenza virus infection[151]	[140], [142]

Other methods implement module-based approaches and thus focus on finding groups of differentially co-expressed genes, also known as DC modules. DICER calculates a probabilistic differential co-expression score called the T-score, which is based on the Pearson correlation. The T-score is then used to identify DC clusters (a differentially co-expressed gene set) or meta-modules (pairs of gene sets with DC between phenotypes) [138]. Diffcoex first constructs a differential adjacency matrix based on correlation. Afterwards, the topological overlap measure [139] is used to derive a dissimilarity matrix prior to applying WGCNA clustering to identify the DC modules [140]. ALtered Partitions Across Community Architectures (ALPACA) is another module-based method that extracts differential subnetworks by optimizing a measure called “differential modularity,” which captures changes in network structure by comparing the density of edges in the diseased network relative to a control network [141].

A benchmarking study evaluated the performance of various differential network methods [142], indicating the need for further algorithmic improvements in handling more complex changes in co-expression structure. In addition, there is a need for the development of new methods that can better handle non-Gaussian data [143], which is abundant in biological systems.

6. Sample-specific networks

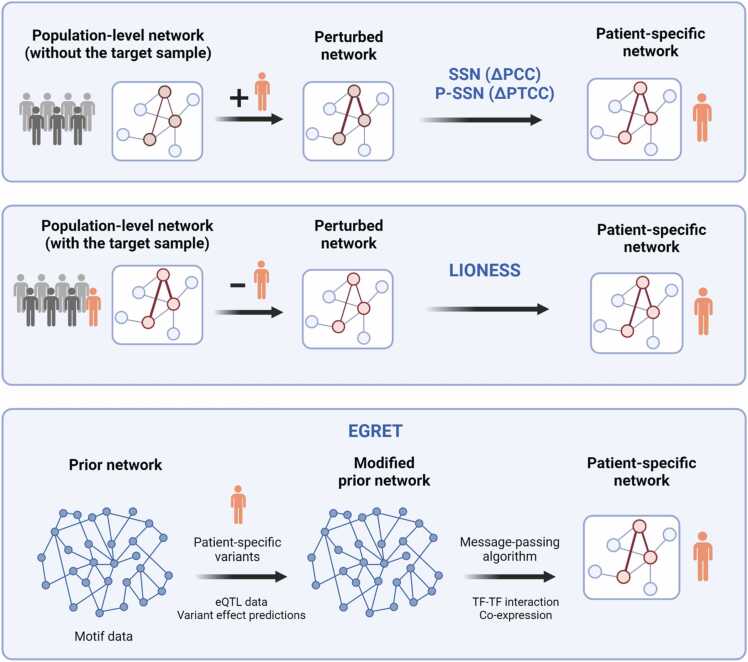
The network inference methods discussed above assume an “aggregate” network representing a phenotype of interest and are mostly aimed to discover shared disease mechanisms in a given population or dataset. As such, they do not explicitly account for patient heterogeneity. In application cases related to personalized medicine, it may be desirable to construct networks at the single-sample level, which can aid in disease characterization and development of therapies tailored for a patient or subgroup of patients. Several methods have been proposed to derive patient-specific networks from gene expression data. Representative methods include LIONESS, SSN, and P-SSN (Fig. 3). Using a perturbation strategy, dysregulated edges in the GRN that are unique to an individual can be inferred by comparison to the genotype-agnostic baseline network. The main idea behind perturbation-based inference of sample-specific networks is to compare two networks, namely, a reference network and a perturbed network. The reference network is inferred from multiple samples in the population. Depending on the method, the perturbed network is constructed by adding or removing the sample of interest. The difference between the two networks is then used to derive the sample-specific network representing the characteristics of the individual patient. The single-sample network (SSN) method calculates the change in the pairwise Pearson’s correlation coefficient values upon the addition of the sample [152]. To filter for direct interactions, the P-SSN method uses a partial correlation-based measure [153]. Linear Interpolation to Obtain Network Estimates for Single Samples (LIONESS) models the weights of the aggregate network as a linear combination of the weights of the individual sample networks. The change in the weight of an edge is attributed to the sample that was removed in generating the perturbed network. In other words, the sample-level network is considered the contribution of the individual sample to the reference network. The LIONESS approach is a framework to be used in tandem with standard network inference methods [154]. Estimating the Genetic Regulatory Effect on TFs (EGRET) is a multi-omics approach that is based on refinement of a prior network using a message-passing algorithm [155]. EGRET first constructs a prior network using motif data. A modified prior network is then derived by incorporating patient-specific genotype data, eQTLs, and variant effect predictions. Next, a message-passing algorithm is applied with co-expression and TF cooperativity data to obtain the final patient-specific network. (((Table 4))).

Fig. 3.

General principles behind methods for inferring sample-specific networks. SSN, P-SSN and LIONESS apply perturbation analysis upon the addition or removal of a particular sample from the aggregate or reference network. SSN and P-SSN estimate the sample-level networks based on correlation measures. LIONESS uses linear interpolation to derive the sample-level networks but can also be extended with alternative measures. EGRET uses a message-passing algorithm to refine a prior network using patient-specific data. ΔPCC = differential Pearson’s correlation; ΔPTCC = differential partial correlation; eQTL = expression quantitative trait loci; TF = Transcription factor. Created with BioRender.com.

Table 4.

Representative tools for deriving sample-specific networks. Links to code/tools are provided in Supplementary Table 4.

Tool	Input data	Algorithmic approach	Example application	Reference
SSN	Expression data	Network perturbation	Construction of multicellular gene network to investigating the prognostic role of macrophage–tumor cell interactions in tumor progression in gliomas[156]	[152]
P-SSN	Expression data	Network perturbation	Identify individual-specific driver genes in cancer patients using the TCGA dataset[153]	[153]
LIONESS	Expression data	Network perturbation	Infer sample-specific GRNs from 29 healthy human tissue types to study sex differences in gene expression and regulatory networks[157]	[154]
EGRET	Snapshot expression data; multi-omics data	Message passing	Construction of genotype-specific GRNs in GM12878 and K562 cell lines; construction of patient-specific networks in Crohn’s disease and coronary artery disease[155]	[155]

7. Summary and Outlook

Biological networks provide a fundamental basis for modeling the complex and dynamic nature of biological processes. The increasing availability of extensive biomedical big data has significantly improved our ability to quantify and characterize biological networks. Consequently, network theory and related concepts have become indispensable for exploring the etiology of human diseases [158] and revealing complex patterns of gene expression regulation. In particular, network enrichment and network inference have become standard methods for analyzing omics data and have significantly improved our understanding of disease development and progression.

Despite the extensive use of DNE methods, they have several shortcomings. Lazareva et al. developed a test suite to evaluate the robustness of DNE methods against network randomization. They showed that many DNE methods mostly learn from the node degree distributions rather than from the encoded biological knowledge in the edges of PPI networks [159]. By assessing the gene ontology enrichment of DNE methods on randomly permuted input data, Levi et al. questioned the context-specificity of the existing methods [24]. Since diseases with higher morbidity or mortality and their associated proteins are studied more extensively, PPI networks are subject to study bias [160]. This study bias and the fact that a large fraction of PPIs are still not discovered have been found to significantly distort networks and consequently methods used in network-based techniques that rely on PPIs [161]. The full capacity of modern computational algorithms to predict protein structures and PPIs can be used to augment our currently limited knowledge of PPIs derived from experimental settings. For instance, the protein structures output by Alphafold can be further used to predict PPIs to reduce bias and complement existing PPI networks [162].

Network inference is a classical problem in computational biology that aims to reconstruct the set of gene-gene relationships that are dominant in a phenotype of interest or how they change through time. Despite considerable progress in the past decades, network inference is far from being fully resolved and remains an active area of research, as evidenced by ongoing efforts such as the Dialogue for Reverse Engineering Assessments and Methods (DREAM) project [163]. Previous benchmarking studies have shown varying results and that no single algorithmic class consistently outperforms all other methods [164], [165]. The most suitable algorithmic approach may depend on various factors, such as the biological context being examined and the specific characteristics of the dataset. Furthermore, combining multiple network inference methods was generally found to perform better than using a single approach [46], highlighting an advantage of ensemble methods and multi-omics integration.

Earlier work on network inference focused on snapshot expression data. While these have undoubtedly advanced our knowledge on complex diseases, they provide a limited view of the underlying molecular processes. The next crucial step to understanding disease warrants new computational approaches that can more effectively incorporate and exploit the dynamic nature of biological phenomena. Time-series experimental data offer rich latent information that require more sophisticated network-based computational tools. However, recovering the network structures from temporal data at the genome scale is faced with several practical limitations. The still relatively high level of noise of current omics platforms combined with low numbers of samples and the sparsity of measured time points remain a major bottleneck. The complexity of the networks may be highly variable across phenotypes and inference approaches typically require a high number of parameters relative to the small number of available samples. In addition, the appropriate time scales for measuring disease progression are unknown or very difficult to determine in many cases. Thus, new and more efficient computational strategies are needed. As the quantity, quality, and types of temporal omics data continue to increase, we expect that network inference methods would play more important roles to accurately model disease trajectories and discover new disease drivers.

The network inference tools we described were focused on bulk transcriptomic data. Along with the development and increasing popularity of single-cell technologies, various network inference methods have been developed for single-cell transcriptomics data. Compared to bulk data, which characterizes the expression profile of an average of the cells in a sample, single-cell technology can profile up to tens of millions of individual cells and thus capture a more detailed gene regulatory landscape. However, single-cell data pose additional challenges, such as noise and zero-inflation, and thus require more tailored analysis steps. Methods for dynamic network inference from single-cell data are also an active area of research and have been especially useful for reconstructing temporal ordering of cells in multiple developmental processes. For in-depth discussion and benchmarking of network inference tools dedicated to single-cell data, we refer the reader to focused benchmarks and reviews [166], [167], [168], [169].

Multi-omics integration also represents a new challenge in the development of flexible tools that will enable researchers to more easily combine and customize their analysis or create workflows according to the nature of the biological process under study. Incorporating existing knowledge and diverse sources of information, including GWAS, molecular interaction databases (PPI, GRNs), pathway databases and literature knowledge, can further provide a more comprehensive picture of the determinants and drivers of complex diseases [170], [171]. There are now more concerted efforts to simultaneously profile several omics types using the same patient groups/samples, such as The Cancer Genome Atlas (TGCA) [172], Genotype-Tissue Expression (GTEx) [173], and ENCODE [174]. While most existing methods focus exclusively on TFs as regulators, the importance of other regulators such as microRNAs in GRN inference is increasingly recognized [175]. Nevertheless, multi-omics analysis remains a relatively underexplored area of research, considering the extensive amount of data being generated [171], [176]. Thus, we expect the development of more integrative approaches at different levels of organization, which can be much more powerful in capturing disease complexity and interplay between molecular layers.

Deep learning-based methods have also gained popularity in recent years because of their capability to handle large amounts of biological data and to achieve state-of-the-art performance in many prediction tasks in genomics. One limitation of the application of deep learning models in biology and medicine is the difficulty of obtaining mechanistic explanations behind their predictions. Nevertheless, interpretability of deep neural networks is a highly active area of research, and efforts are ongoing to systematically understand the regulatory grammar that governs gene expression regulation in various contexts [177], [178], [179].

The lack of gold standard datasets for the validation of methods in the field of computational biology is a well-known problem. Conventional validation is performed using proxy measures, such as gene set over-representation analyses against known disease genes from DisGeNET [180] or disease-associated pathways from databases such as KEGG [181], Reactome [182], and WikiPathways [183]. Competitions such as the DREAM challenges have become instrumental in harnessing the “wisdom of the crowds” to answer various computational problems in biomedicine, including challenges that address the network inference problem [184]. Importantly, they provide the community with high-quality datasets for benchmarking, including both simulated steady-state and time-series gene expression data, which can help researchers better understand mechanisms behind disease trajectories. These reference datasets have also been extensively used for systematic evaluation of newly developed algorithms against state-of-the-art algorithms and have helped avoid the “self-assessment trap” [185]. Nevertheless, our current knowledge of disease mechanisms is far from complete [159]. We can additionally improve benchmarking of GRN methods using knowledge gained from unbiased experimental methods, such as CRISPR-based perturbation screens [186], [187], [188] that allow precise manipulation of genomic sequences. Results from such studies could provide the scientific community with more context-specific methods of elucidating gene regulation [189].

Another bottleneck is the lack of mechanistic disease definitions. Diseases are largely based on phenotypes (manifested symptoms) and the clinical definitions are generally not readily harmonized with new molecular findings [14]. This can result in symptom-wise homogeneous but molecularly and mechanistically heterogeneous patient cohorts. Thus, the mechanistic profiles extracted by network-based methods, particularly the supervised ones, may not be very reliable, since the input data based on disease annotation is flawed. The databases employed for validation also use ill-defined disease terms, further propagating the problem to the validation of computational approaches.

Some of the tools reviewed here have been successfully applied in diverse disease contexts, such as diabetes, coronary heart diseases, and lung diseases [158]. Further improvements in theoretical development, tool usability, and multi-omics or multi-study integration show great promise for obtaining a more comprehensive understanding of complex diseases. We envision that the combination of enrichment, differential networks, and more focus on inference tools from time-series experiments into comprehensive and holistic analysis pipelines will help capture more detailed molecular mechanisms underlying diseases. The integration of several different types of multi-omics time-series and snapshot data sets will be instrumental to reconstruct accurate GRN models and thus obtain a more complete picture of the dynamics and complexity of disease progression. Another emerging area of research is the estimation of sample-specific gene networks. These are important for investigating heterogeneity among individuals and characterizing their specific molecular alterations or disease states. Consequently, advances in this field will enable the identification of more suitable therapeutic targets or drug combinations, representing a significant step towards precision medicine [190]. Beyond GRNs, network inference methods can also be applied in related fields such as microbiome research where networks of co-occurring taxa are already constructed borrowing concepts originally proposed for GRN inference [191].

We provided an overview of the main types of network-based methods that can be applied to study the molecular basis of diseases, their core algorithmic concepts, and some representative tools for analysis. Each type of analysis captures different aspects of the biological system. The next crucial step to understanding disease warrants new computational strategies that can more effectively exploit the dynamic nature of biological phenomena. Developing more flexible methods can fill remaining gaps and pave the way towards more accurate identification of disease mechanisms and effective drug treatments.

Funding

SS, JB and TK are grateful for financial support from REPO-TRIAL. REPO-TRIAL has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 777111. This publication reflects only the authors' view and the European Commission is not responsible for any use that may be made of the information it contains. This work was supported by the German Federal Ministry of Education and Research (BMBF) within the framework of the e:Med research and funding concept (grant 01ZX1908A) (SS, JB and ML).

CRediT authorship contribution statement

Gihanna Galindez: Investigation, Writing – original draft, Visualization, Conceptualization. Sepideh Sadegh: Investigation, Writing – original draft, Visualization, Conceptualization. Jan Baumbach: Writing – review & editing, Conceptualization. Tim Kacprowski: Writing – review & editing, Conceptualization, Supervision. Markus List: Writing – review & editing, Conceptualization, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary Table 1

Supplementary material

.