A super-Gaussian Poisson–Boltzmann model for electrostatic free energy calculation: smooth dielectric distribution for protein cavities and in both water and vacuum states

Abstract

Calculations of electrostatic potential and solvation free energy of macromolecules are essential for understanding the mechanism of many biological processes. In the classical implicit solvent Poisson–Boltzmann (PB) model, the macromolecule and water are modeled as two-dielectric media with a sharp border. However, the dielectric property of interior cavities and ion-channels is difficult to model realistically in a two-dielectric setting. In fact, the detection of water molecules in a protein cavity remains to be an experimental challenge. This introduces an uncertainty, which affects the subsequent solvation free energy calculation. In order to compensate this uncertainty, a novel super-Gaussian dielectric PB model is introduced in this work, which devices an inhomogeneous dielectric distribution to represent the compactness of atoms and characterizes empty cavities via a gap dielectric value. Moreover, the minimal molecular surface level set function is adopted so that the dielectric profile remains to be smooth when the protein is transferred from water phase to vacuum. An important feature of this new model is that as the order of super-Gaussian function approaches the infinity, the dielectric distribution reduces to a piecewise constant of the two-dielectric model. Mathematically, an effective dielectric constant analysis is introduced in this work to benchmark the dielectric model and select optimal parameter values. Computationally, a pseudo-time alternative direction implicit (ADI) algorithm is utilized for solving the super-Gaussian PB equation, which is found to be unconditionally stable in a smooth dielectric setting. Solvation free energy calculation of a Kirkwood sphere and various proteins is carried out to validate the super-Gaussian model and ADI algorithm. One macromolecule with both water filled and empty cavities is employed to demonstrate how the cavity uncertainty in protein structure can be bypassed through dielectric modeling in biomolecular electrostatic analysis.

1. Introduction

Calculations of electrostatic potential and solvation free energy of macromolecules are essential for understanding the mechanism of biological processes. However, these calculations cannot be done analytically for irregularly shaped objects, and so computational methods must be applied. There are two major approaches for solvation free energy analysis, i.e., explicit models and implicit models (Li et al. 2015). Explicit models treat water as individual molecules; on the contrary, implicit models consider solvent phase as continuum media (Che et al. 2008; Baker et al. 2001; Li et al. 2013a). Compared to explicit models, implicit models are more efficient; therefore they can handle much larger systems (Baker et al. 2001; Li et al. 2012), however, it comes with the price of losing some atomic information and having the ambiguity of how to describe the dielectric properties of the system, the solute, and the water phases.

As a partial differential equation (PDE) model for electrostatics of biomolecules, the Poisson–Boltzmann (PB) equation is a widely used implicit solvent method (Baker et al. 2001). Traditionally, a two-dielectric approach is employed in the PB model to describe the dielectric properties: a biomolecule is assigned a low dielectric constant while the surrounding water phase is considered as a high dielectric constant medium. A dielectric interface is assumed at the macromolecule-water boundary, which is usually modeled as a molecular surface. The most commonly used definitions of the macromolecule-water boundary are the Van der Waals (VDW) surface (Pang and Zhou 2013), the solvent accessible surface (SAS) (Lee and Richards 1973), and the solvent excluded surface (SES) (Richards 1977; Connolly 1983). However, these “hard sphere” molecular surface models are known to admit geometric singularities, such as cusps and self-intersecting surfaces (Bates et al. 2008).

To avoid geometric singularities associated with “hard sphere” definitions of the molecular surface, “soft sphere” models have been developed (Blinn 1982; Duncan and Olson 1993; Grant and Pickup 1995), where each atom is outlined by a Gaussian density distribution function. While dealing with multiple atoms, the summation of these Gaussian soft clouds forms a density map which generates Gaussian molecular surfaces at appropriate isosurfaces or level sets to approximate the VDW surface, SAS, or SES. The density maps based on volumes can also be generated by other smoothly decaying functions (Chen and Lu 2011) or by maximizing the Gaussian functions and then post-processing using a low-pass filtering (Giard and Macq 2010). The models based on Gaussian surfaces are particularly useful for fast and robust molecular surface mesh generations (Chen and Lu 2011; Zhang et al. 2006; Yu et al. 2008).

In most studies of Gaussian surfaces, the PB equation is still solved in a two-dielectric setting by generating an iso-surface as the dielectric boundary. Across such a sharp interface, the PB solution loses its regularity. In order to avoid accuracy reduction in numerical discretization near the interface, sophisticated interface algorithms have to be adopted for handling the dielectric jump in solving the PB equation. With rigorous interface treatments, the matched interface and boundary (MIB) method (Zhou et al. 2006; Chen et al. 2011) and the immersed interface method (IIM) (Qiao et al. 2006) can improve the accuracy significantly, but they develop complexity in the algorithm to a certain extent which reduces the computational efficiency.

Instead of using a sharp molecular surface definition, smooth or smeared molecular surfaces have also been introduced in the literature (Bates et al. 2008, 2009; Cheng et al. 2007; Zhao et al. 2013; Dai et al. 2018), in which a smooth transition is assumed in between solute and solvent domains. For instance, by using the Euler–Lagrange variation of the free energy minimization, (Bates et al. 2008, 2009) introduced a variational PDE model for molecular surface generation. Neglecting other solute-solvent interactions, this model is simplified to be the surface area minimization, and gives rise to the minimal molecular surface (MMS). Cheng et al. (2007) have employed the level set approach to minimize a free energy functional for coupling the polar-nonpolar interaction at the solvent-solute interface, and the corresponding PDE model involves contributions from electrostatic effects, pressure, Gauss and mean curvatures, and others. A phase-field variational approach has been developed in Zhao et al. (2013) to represent the solute-solvent interface via a double-well potential in the free energy functional. The convergence of the phase field free energy functionals and forces to their sharp interface limits has been rigorously proved (Dai et al. 2018). By using these smooth molecular surfaces, simple numerical methods can be employed for solving the PB equation, and complicated interface treatments are unnecessary.

Besides the free energy variational approach, another physical way to describe the solute-solvent boundary as a smooth transition layer has also been introduced in (Abrashkin et al. 2007; Koehl et al. 2009; Mengistu et al. 2009; Bohinc et al. 2017). This is achieved by incorporating the structures of water dipoles and ions into mean field modeling of the electric double layer. This introduces additional terms in the PB equation to account for interacting Langevin dipoles (Mengistu et al. 2009) or non-electrostatic type Yukawa interactions (Koehl et al. 2009). Mathematically, the generalized PB equations in these studies could be rewritten into a standard PB equation with an effective field-dependent dielectric function, which is then smoothly variant in the solvent domain (Abrashkin et al. 2007).

Besides the above mentioned PB models with two homogeneous media away from the solute-solvent boundary, heterogeneous dielectric models have also been introduced in the literature (Alexov and Gunner 1997, 1999; Nymeyer and Zhou 2008; Song 2002; Voges and Karshikoff 1998; Hu and Wei 2012; Li et al. 2013b, 2014; Chakravorty et al. 2018b), in which the dielectric function ϵ is not uniform and varies within the structure of the molecule. Physically, such an inhomogeneity, reflecting different polarizability and flexibility, is well-documented for the amino acids (Hammel 2012; Kokkinidis et al. 2012). Mathematically, the heterogeneous dielectric distribution provides an alternative means to mimic the effect of conformation changes of the macromolecule on the solvation free energy, because dielectric distributions reflect the structure-energy relations via screening of the electrostatic interactions within the solute and between the solute and solvent (Warshel and Russell 1984; Warshel et al. 2006).

This study will pay particular attention to the Gaussian dielectric PB model (Li et al. 2013b, 2014), which was developed with an aim to provide a “correct” description of the dielectric property of the macromolecule, i.e., beginning with macromolecule interior and moving toward the macromolecular surface and further into the water phase, the ability of the corresponding medium to respond to local electrostatic field constantly increases (Simonson and Perahia 1995). This dielectric model has been found to outperform the traditional two dielectric model in many biological applications, including a better agreement with experimentally measured solvation free energy of small molecules (Li et al. 2013b, 2014) and a better prediction of the pKa’s of ionizable groups against thousand experimentally measured pKa’s in various proteins (Wang et al. 2015a, b). The Gaussian dielectric model has also demonstrated the feasibility of approximating ensemble average polar solvation free energy by calculating a single macromolecular structure and without resorting to expensive molecular dynamics or Monte Carlo simulations (Chakravorty et al. 2018a).

This paper aims to extend the Gaussian PB model (Li et al. 2013b, 2014) by modeling the dielectric property of protein cavities explicitly. Cavities and channels are frequently encountered in biomolecules. The determination of dielectric values for cavities is still in its infancy for inhomogeneous models (Ng et al. 2008), because such cavity regions could be empty or filled with water molecules. Nevertheless, the detection of water molecules in a cavity remains to be an experimental challenge. This introduces an uncertainty for implicit solvent modeling. Physically, how to compensate such an uncertainty in inhomogeneous dielectric models has not been studied before. What we know are several simple principles. For example, trapped water molecules tend to interact with the surrounding atoms via either hydrogen bonds or VDW forces, and thus lose their flexibility. Consequently, the dielectric value of cavity water should be smaller in comparison with that of bulky water, while it is still larger than that of amino acids. Moreover, the size or volume of cavity plays an important role here, because it affects the rotational polarizability of confined water molecules in response to the local electrostatic field. In the Gaussian dielectric model (Li et al. 2013b, 2014), the cavity region may be characterized through the compactness of atoms. However, the dielectric value of such gap region or the maximal dielectric value ϵ_max of the macromolecule is not directly controllable, instead it is inflated by the external water dielectric value (usually taken as ϵ = 80). In order to model the dielectric property of protein cavities explicitly, we propose a super-Gaussian dielectric model in this work, in which a new parameter ϵ_gap for the cavity regions is introduced. The selection of ϵ_gap or ϵ_max could depend on cavity size and any additional information available to biologists. Moreover, the maximal dielectric value ϵ_max remains unchanged in both water or vacuum phases. Finally, this parameter also allows us to compensate the uncertainty of whether a cavity is empty or filled with water molecules in free energy calculations.

As another extension, the super-Gaussian PB model will maintain the smoothness of dielectric functions in both water and vacuum states in calculating free energies. In the Gaussian dielectric model (Li et al. 2013b, 2014), the inhomogeneous dielectric profile of the macromolecule is generated based on the water state first. Then a surface cut with an empirical iso-value is conducted to preserve the same inhomogeneous profile for the vacuum state. Consequently, the ϵ function becomes discontinuous, because outside the surface cut, ϵ = 1 is simply used for the vacuum. A modified surface cut technique has been reported recently (Chakravorty et al. 2018a), which results in a C⁰ but not C¹ continuous dielectric function in vacuum state, even though it is C^∞ continuous in water state. In the proposed model, the minimal molecular surface (MMS) (Bates et al. 2008; Tian and Zhao 2014) will be employed to represent solute and solvent regions. The main purpose of such representation is not defining a molecular surface. Instead, the MMS allows us to represent both water and vacuum states in one equation, by simply changing the exterior dielectric value to be 80 or 1. The interior dielectric profile for proteins keeps unchanged in this process. With these extensions, the new Gaussian model guarantees the dielectric functions being C^∞ continuous in both water and vacuum states.

Besides the above mentioned two extensions, there are several other differences between the Gaussian and super-Gaussian dielectric models. First, a super-Gaussian density function is employed in the new model as a “soft sphere” representation for each atom, which includes the Gaussian function as a special issue with the order m = 1. An important feature of this function is that it approaches piecewise dielectric constants of the two-dielectric model in the limit of order m going to infinity. Theoretically, the proposed super-Gaussian dielectric model bridges the gap between Gaussian and two-dielectric PB models. In practice, m = 3 or 4 achieves a good trade-off in our modeling and simulations. Second, the Gaussian model is a surface-free dielectric model (Li et al. 2013b, 2014; Chakravorty et al. 2018b), while the MMS hypersurface function is required in constructing the super-Gaussian dielectric distribution. Hence, without requiring any molecular surface definition, the Gaussian model has the potential to be applied to more general applications. Also, the super-Gaussian dielectric function needs additional computation time for setting up the MMS level set function. Fortunately, a fast algorithm is available for generating the MMS (Tian and Zhao 2014), which scales as O(N) for N being the spatial degree of freedoms. Third, the ion distribution is treated differently in both models. In the classical two-dielectric PB model, the presence of mobile ions is realized through the Debye–Huckel parameter or Debye length κ. One normally defines κ as a piecewise constant with a vanishing value in the solute region and a nonzero constant (say $\stackrel{\_}{\kappa }$) in the solvent region. In the super-Gaussian model, κ it will be defined in the same manner as the dielectric function ϵ, by using the MMS characteristic function for both solute and solvent domains. Consequently, κ will change smoothly and monotonically from zero to $\stackrel{\_}{\kappa }$. A more physical approach is proposed in the Gaussian model (Jia et al. 2017; Chakravorty et al. 2018b), in which a desolvation penalty term is introduced into the Boltzmann distribution of mobile ions. In the resulted modified PB equation, the coefficient of the nonlinear hyperbolic term will change smoothly from zero to $\stackrel{\_}{\kappa }$ in a non-monotonic manner, because the Born equation definition of desolvation penalty depends on the inhomogeneous ϵ function.

In this work, a pseudo-time alternating direction implicit (ADI) algorithm (Geng and Zhao 2013; Zhao 2014; Wilson and Zhao 2016) will be employed to solve the nonlinear PB equation of the super-Gaussian dielectric model. We note a numerical issue here relating to the smooth definition of the Debye length κ, resulting from ion distribution treatments of either Gaussian or super-Gaussian models. In particular, κ could be nonzero in certain places which belong to the solute region in the two-dielectric model, but are now in the transition layer between solute and solvent media (Zhao 2014). Therefore, the hyperbolic nonlinear term of the PB equation could take huge values at such places, so that numerical methods could be unstable (Zhao 2014). To suppress the nonlinear instability, a pseudo-time continuation approach with analytical integration of the nonlinear term has been proposed in the literature (Geng and Zhao 2013; Zhao 2014; Wilson and Zhao 2016). Based on finite difference spacial discretization, efficient alternating direction implicit (ADI) schemes have been developed for pseudo-time integration (Geng and Zhao 2013; Zhao 2014; Wilson and Zhao 2016). However, such ADI schemes could not achieve unconditional stability in treating two-dielectric PB equations. For the present super-Gaussian dielectric model and well filtered MMS representation, the pseudo-time ADI algorithm will be unconditionally stable for solving the nonlinear PB equation.

The proposed super-Gaussian dielectric PB model carries several parameters. In order to benchmark the new model and select optimal parameter values, two approaches will be considered in this paper. Mathematically, an effective dielectric constant (EDC) analysis is introduced as a simple means to assess different dielectric models. This is purely a geometrical approach that computes an averaged EDC over the entire domain either analytically or numerically, and it allows us to explore the impact of each parameter to the total dielectric function. In the other approach, comparison in electrostatic free energy is carried out for two-dielectric and super Gaussian models. We note that with a different dielectric setting, our super Gaussian results will not converge to the two-dielectric ones. However, it is useful to adjust parameters so that the new dielectric model could numerically produce energy values that are comparable to the two-dielectric model. This is particularly convenient if one wants to replace an existing two-dielectric PB solver by the proposed one in a software package. We note that the optimal parameter values produced by two approaches have some minor difference. Alternatively, the model validation could be conducted by comparing with explicit solvent molecular dynamics (MD) simulations, which, however, are quite time consuming.

The rest of the paper is organized as follows. Section 2 introduces the super-Gaussian dielectric PB model with a few parameters. An EDC analysis is proposed for determining the best fitting parameters, and the role of hypersurface function generated from MMS is discussed. In Sect. 3, the super-Gaussian PB equation is discretized by using a pseudo-time ADI algorithm. Model validation and convergence, accuracy, and stability of the ADI algorithm are experimented by calculating solvation free energy for a single atom system in Sect. 4. The proposed model and algorithm are further verified in Sect. 5, by considering various proteins. Particular attention will be paid on studying a real protein with both water-filled and empty cavities. This article ends with a brief conclusion.

2. Mathematical modeling

In this section, we will first briefly describe the existing models, including the two-dielectric Poisson–Boltzmann (PB) model and Gaussian dielectric PB model. Then, a super-Gaussian dielectric PB model will be introduced. A geometrical analysis will be employed to systematically study the influence of the adjustable parameters of the new model in various settings.

2.1. Two-dielectric Poisson–Boltzmann model

Consider a macromolecule, for example, a protein being immersed into an aqueous solvent. Define a large enough cubic domain Ω in ${\mathbb{R}}^3$ for this three dimensional (3D) solute-solvent system. In the classical two-dielectric PB model, the domain Ω is divided by a molecule surface Γ into two parts, namely the inner solute domain Ω_m and the outer solvent domain Ω_s such that Ω = Ω_m ∪ Ω_s and Ω_m ∩ Ω_s = Γ. Denote the boundary of Ω as ∂Ω. For $\overrightarrow{r}\in {\mathbb{R}}^3$, the electrostatic potential u of this system is governed by the nonlinear Poisson–Boltzmann equation and its most commonly used dimensionless form (Lu et al. 2008; Geng and Zhao 2013) is given as

$$-\nabla ·\left(ϵ\left(\overrightarrow{r}\right)\nabla u\left(\overrightarrow{r}\right)\right)+{\kappa }^2\sinh \left(u\left(\overrightarrow{r}\right)\right)={\rho }_m\left(\overrightarrow{r}\right),$$ (1)

where the singular source term is

$${\rho }_m\left(\overrightarrow{r}\right)=4\pi \frac{{e_c}^2}{k_{B}T}\sum _{j=1}^{N_m}{q}_j\delta \left(\overrightarrow{r}-{\overrightarrow{r}}_j\right).$$ (2)

On the outer boundary ∂Ω, a Dirichlet boundary condition can be assumed

$$u\left(\overrightarrow{r}\right)=\frac{{e_c}^2}{k_{B}T}\sum _{j=1}^{N_m}\frac{q_j}{{ϵ}_s\left|\overrightarrow{r}-{\overrightarrow{r}}_j\right|}{e}^{\left(-\left|\overrightarrow{r}-{\overrightarrow{r}}_j\right|\sqrt{\frac{{\overline{\kappa }}^2}{{ϵ}_s}}\right)}.$$ (3)

In the two-dielectric PB model, the dielectric function $ϵ\left(\overrightarrow{r}\right)$ is assumed to be a piecewise constant

$$ϵ\left(\overrightarrow{r}\right)=\{\begin{array}{ll}{ϵ}_m,& \overrightarrow{r}\in {\text{Ω}}_m\\ {ϵ}_s,& \overrightarrow{r}\in {\text{Ω}}_s.\end{array}$$ (4)

In the present study, we will take ϵ_m = 1 for the protein and ϵ_s = 80 for the water. Similarly, the modified Debye–Hückel parameter κ is a piecewise constant. It vanishes in Ω_m, i.e., κ = 0, while in ${\text{Ω}}_s\kappa =\overline{\kappa }$, where ${\overline{\kappa }}^2=8.486902807{\stackrel{\circ }{\text{A}}}^{-2}{I}_s$ and I_s is the ionic strength of the solvent. Here, k_B is the Boltzmann constant with k_BT = 0.5921830 kcal/mol at T = 298 K, and e_c is the fundamental charge and q_j is the partial charge for the j^th atom in the solute, centered at ${\overrightarrow{r}}_j$. Moreover, e_c and q_j have the same units and $e_c^2=33.206364\text{kcal/mol}$. The total number of atoms present in the solute macromolecule is denoted by N_m.

The energy released when the solute macromolecule is dissolved in solvent is known as the free energy of solvation. The polar component of solvation free energy can be calculated in the PB model by computing the difference between total electrostatic free energy of the macromolecule in the solvent and in the vacuum. In particular, for the two-dielectric PB model, the solvation free energy is defined as

$$\text{Δ}G=G_s-G_0=\frac{1}{2}{\int }_{\text{Ω}}{\rho }_m\left(u\left(\overrightarrow{r}\right)-u_0\left(\overrightarrow{r}\right)\right)d\overrightarrow{r}$$ (5)

where $u\left(\overrightarrow{r}\right)$ is the solution of the PB equation (1), while $u_0\left(\overrightarrow{r}\right)$ is the electrostatic potential of the macromolecule in the vacuum. The vacuum state is obtained by taking $ϵ\left(\overrightarrow{r}\right)=1$ throughout and setting the ionic strength I_s = 0. Consequently, κ = 0 in the PB equation (1) and $\overline{\kappa }=0$ in the boundary condition (3). Thus, $u_0\left(\overrightarrow{r}\right)$ is in fact the solution of a Poisson equation

$$-\text{Δ}{u}_0={\rho }_m,$$ (6)

with the same singular source (2).

2.2. Gaussian dielectric PB model

In order to overcome some inherent difficulties associated with the two-dielectric PB model, a Gaussian dielectric PB model has been proposed in Li et al. (2013b, 2014) to provide a “correct” description of the dielectric property of the macromolecule. Physically, at the atomistic level of detail, any system in molecular biophysics is made up of macromolecules immersed in water, and can be considered as a multitude of atoms: atoms of water molecules and amino acids (nucleic acids). It thus makes sense to study a smooth dielectric PB model, in which one avoids to define a solute-solvent boundary or molecular surface. Instead, an appropriate definition of the dielectric function $ϵ\left(\overrightarrow{r}\right)$ is assumed in the entire domain Ω. Moreover, it is known that beginning with the macromolecule interior and moving toward the macromolecular surface and further into the water phase, the ability of the corresponding medium to respond to the local electrostatic field constantly increases (Simonson and Perahia 1995). Hence, one should expect that $ϵ\left(\overrightarrow{r}\right)$ in the water state increases smoothly from the solute region to the solvent region. Finally, allowing $ϵ\left(\overrightarrow{r}\right)$ to be inhomogeneous gives us flexibility in modeling different polarizability of the amino acids (Hammel 2012; Kokkinidis et al. 2012), and mimicking the effect of conformation changes of the macromolecule on the solvation free energy (Warshel and Russell 1984; Warshel et al. 2006; Chakravorty et al. 2018a).

A “soft sphere” approach by introducing a density function for each atom seems to be a natural model to fulfill all of the above considerations. This motivated the development of the Gaussian dielectric PB model (Li et al. 2013b, 2014) in the water state. Suppose the density at the position $\overrightarrow{r}$ for the i^th atom is given by Grant and Pickup (1995); Grant et al. (2001); Im et al. (1998)

$$g_i\left(\overrightarrow{r}\right)=\exp \left[\frac{-{\left|\overrightarrow{r}-\overrightarrow{r_i}\right|}^2}{{\sigma }^2{R}_i^2}\right]$$ (7)

where ${\overrightarrow{r}}_i$ is the center of the i^th atom, R_i is the Van der Waals radius of the i^th atom and σ is the relative variance. Once the density for each atom is generated, the total density function for the atoms and overlapped area covered by multiple atoms is given by

$$g_0\left(\overrightarrow{r}\right)=1-\prod _{i=1}^{N_m}\left[1-g_i\left(\overrightarrow{r}\right)\right]$$ (8)

where the cross term such as g_ig_j accounts for the density of the overlap region due to the ith and jth atoms. Also the total density function ensures that the overlap region has a density higher than that generated by a single atom. The range of the function g₀ is [0, 1]. Finally, the dielectric distribution is derived as a weighted convex combination

$${ϵ}_G\left(\overrightarrow{r}\right)=g_0\left(\overrightarrow{r}\right){ϵ}_m+\left(1-g_0\left(\overrightarrow{r}\right)\right){ϵ}_s$$ (9)

where ϵ_m and ϵ_s are the dielectric constants in the molecule and water respectively. Similar to the two-dielectric model, we will take ϵ_m = 1 and ϵ_s = 80 in the present study. By simply replacing $ϵ\left(\overrightarrow{r}\right)$ in the PB equation (1) by ${ϵ}_G\left(\overrightarrow{r}\right)$, the Gaussian PB model has achieved a great success in various biophysical applications (Li et al. 2013b, 2014).

In electrostatic free energy calculations, a surface cut of ${ϵ}_G\left(\overrightarrow{r}\right)$ at an iso-value 20 is conducted to introduce a sharp boundary Γ (Li et al. 2013b, 2014). Inside Γ, the dielectric function of the vacuum state is the same as that in the water state, i.e., ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)={ϵ}_G\left(\overrightarrow{r}\right)$, while outside Γ, ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)=1$. One then solves the Poisson equation

$$-\nabla ·\left({\widetilde{ϵ}}_G\nabla u_0\left(\overrightarrow{r}\right)\right)={\rho }_m,$$ (10)

for the electrostatic potential u₀ in vacuum, and then computes the solvation free energy by (5). Note that ${\widetilde{ϵ}}_G$ is discontinuous in (10) so that various difficulties associated with the two-dielectric PB equation may not be avoided. Recently, a further modification to ${\widetilde{ϵ}}_G$ has been introduced in Chakravorty et al. (2018a), which results in a C⁰ but not C¹ continuous function.

2.3. Super-Gaussian dielectric PB model

In this paper, we propose to define the density of the ith atom as a super Gaussian function

$$g_i^s\left(\overrightarrow{r}\right)=\exp \left[-{\left(\frac{{\left|\overrightarrow{r}-{\overrightarrow{r}}_i\right|}^2}{{\sigma }^2{R}_i^2}\right)}^m\right].$$ (11)

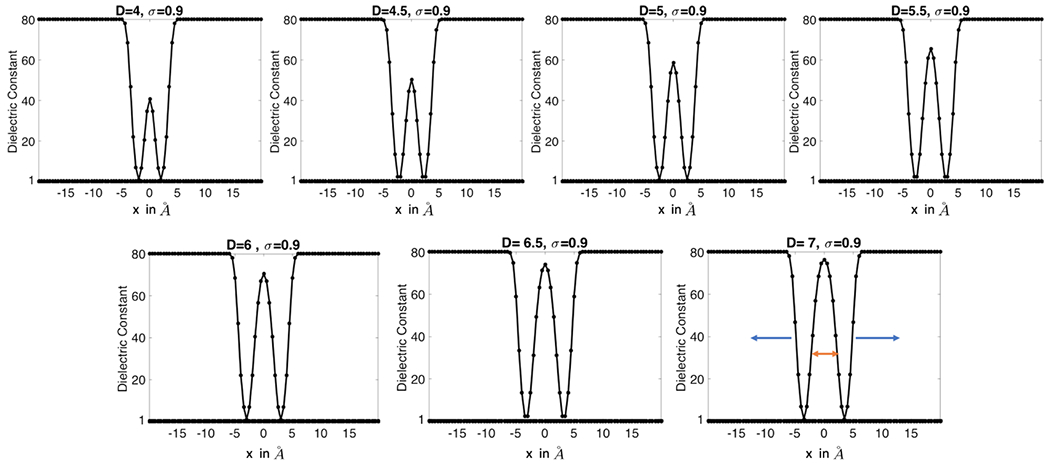
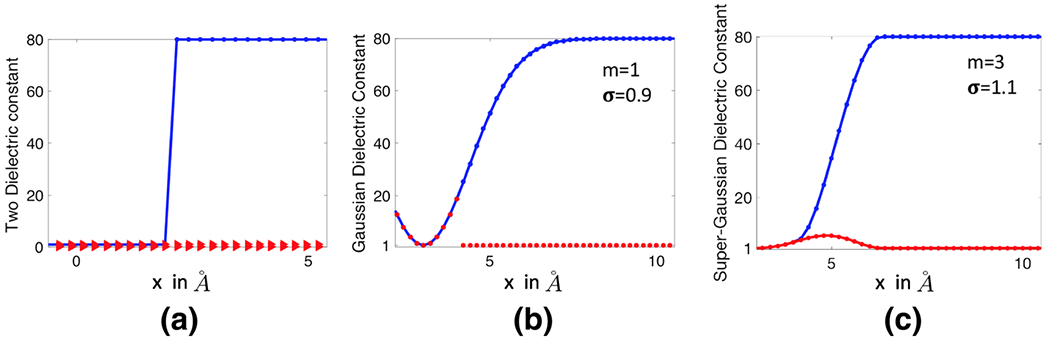
Note that with the order m = 1, $g_i^s\left(\overrightarrow{r}\right)$ becomes the original Gaussian density function $g_i\left(\overrightarrow{r}\right)$. To illustrate the idea, we first consider the dielectric distribution defined by (8), and (9) and simply replace $g_i\left(\overrightarrow{r}\right)$ by $g_i^s\left(\overrightarrow{r}\right)$. A virtual comparison of the corresponding Gaussian and super Gaussian distributions for a single atom system is depicted in Fig. 1. It can be seen that the super-Gaussian function or higher order Gaussian has a flat-top density and a rapid while smooth transition at the solute-solvent border area. As m goes to infinity, $g_i^s\left(\overrightarrow{r}\right)$ approaches to a step function that equals one inside the Van der Waals (VDW) sphere with the center ${\overrightarrow{r}}_i$ and radius R_i and equals zero outside the sphere. Consequently, the dielectric distribution shown in Fig. 1c will converge to the piecewise constant of the two-dielectric model, i.e., Eq. (4). A mathematical proof of this statement is provided in the “Appendix”. Therefore, the super Gaussian density includes both Gaussian density and piecewise constant as special cases. In practice, we will consider an order m in the range of {1, 2, …, 8}, which maintains enough smoothness when the function is sampled on a discrete grid. In Fig. 2, we depict the super Gaussian dielectric distributions for a one-atom system by using different order m and relative variance σ. The optimal selection of these parameter values will be discussed later.

Fig. 1.

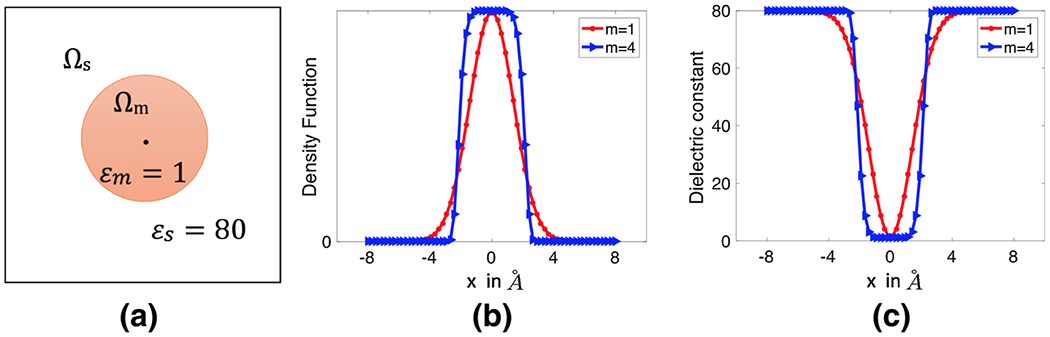
a A single atom is immersed into water, b density function of one atom for m = 1 (Gaussian), m = 4 (super-Gaussian of order 4) and c dielectric distribution of the single atom system calculated by Eq. (9) for Gaussian and super-Gaussian (order 4) densities

Fig. 2.

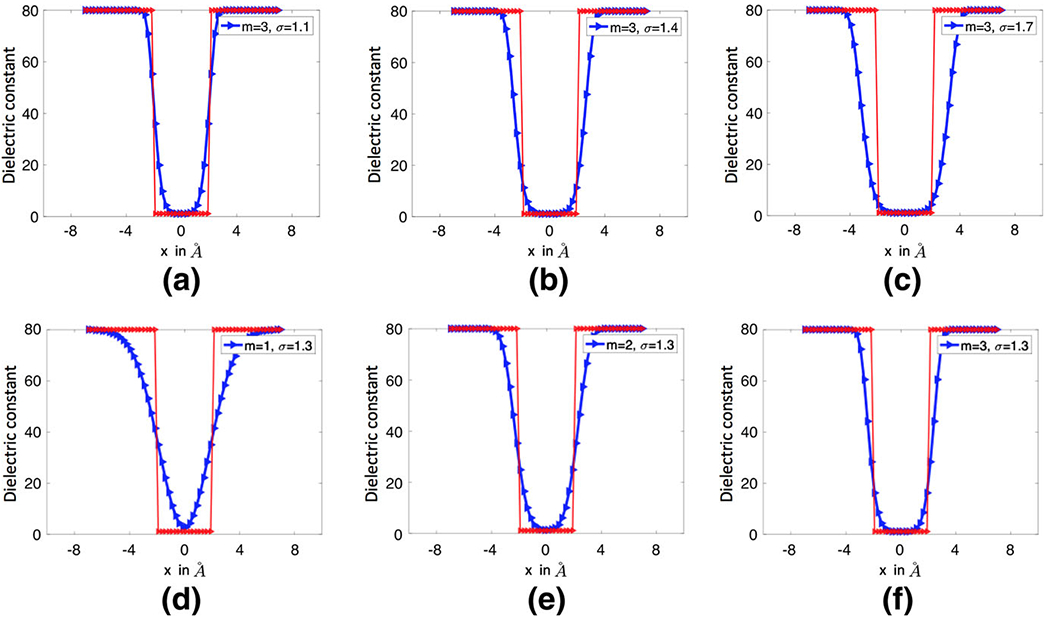
The dielectric distributions generated by the super Gaussian functions for a one-atom system. In all figures, the red line represents the piecewise constant of the two dielectric model

In order to explicitly model the dielectric properties of protein cavities, we introduce a parameter ϵ_gap to represent the maximum dielectric value of the macromolecule. In particular, we similarly define the total density function as

$$g_0^s\left(\overrightarrow{r}\right)=1-\prod _{i=1}^{N_m}\left[1-g_i^s\left(\overrightarrow{r}\right)\right].$$ (12)

A new dielectric distribution is proposed within a protein region

$${ϵ}_{in}\left(\overrightarrow{r}\right)={ϵ}_m{g}_0^s\left(\overrightarrow{r}\right)+{ϵ}_{gap}\left[1-g_0^s\left(\overrightarrow{r}\right)\right],$$ (13)

where the constants ϵ_m and ϵ_gap are defined as the reference dielectric values at the atom centers and in a gap region, respectively, with ϵ_gap > ϵ_m. By substituting (12) into (13), we have an equivalent form of ϵ_in

$${ϵ}_{in}\left(\overrightarrow{r}\right)={ϵ}_m+\left({ϵ}_{gap}-{ϵ}_m\right)\prod _{i=1}^{N_m}\left[1-g_i^s\left(\overrightarrow{r}\right)\right].$$ (14)

It is then clear that ϵ_m and ϵ_gap are, respectively, the minimal and maximal dielectric values of the protein, independent of the outside medium.

The physical idea underlying (13) or (14) is that the permittivity at a loosely packed region of a protein shall be higher than that in a densely packed region, because the former region has a higher polarization or allows a larger conformational change. In a densely packed region, the charged atoms and amino acid chains are harder to shift from their average equilibrium positions when an electric field is placed, so that the polarization or density of induced electric dipole moments is weaker. Moreover, cavities have to be taken into account in an inhomogeneous dielectric model. Crystallographic waters may be trapped inside some large cavities. The polarization of water molecules inside cavities is smaller than the bulky water molecules in a solvent due to their restricted degree of freedom, but it is still much higher than that of protein. This suggests that ϵ_m < ϵ_gap ≤ ϵ_s. An appropriate value for ϵ_gap depends on the real protein system and will be determined through analytical and numerical means in this work. Also, we will take ϵ_m = 1 and ϵ_s = 80 as in the other models.

In the super-Gaussian PB model, we propose to provide certain description of the solute and solvent domain on top of the dielectric distribution, which will eliminate the need of a surface cut operation for the vacuum state. We note that traditional molecular surfaces, including the VDW surface (Pang and Zhou 2013), the solvent accessible surface (SAS) (Lee and Richards 1973), and the solvent excluded surface (SES) (Richards 1977; Connolly 1983), could not fulfill our goal here, because the smoothness still cannot be maintained across a sharp solute-solvent interface. Instead, we propose to employ the minimal molecular surface (MMS) (Bates et al. 2008, 2009), which is defined as the unique surface that is of the smallest area and encloses all VdW balls. Physically, the MMS model is attained through the surface free energy minimization. Mathematically, the Euler–Lagrange variation of the free energy leads to a mean curvature flow partial differential equation (PDE), which can be solved by a fast algorithm developed in Tian and Zhao (2014). The numerical solution provides not only the MMS, but also a level set function or hypersurface function $S\left(\overrightarrow{r}\right)$ defining the solute and solvent regions in a smooth manner, see Fig. 3a for an illustration.

Fig. 3.

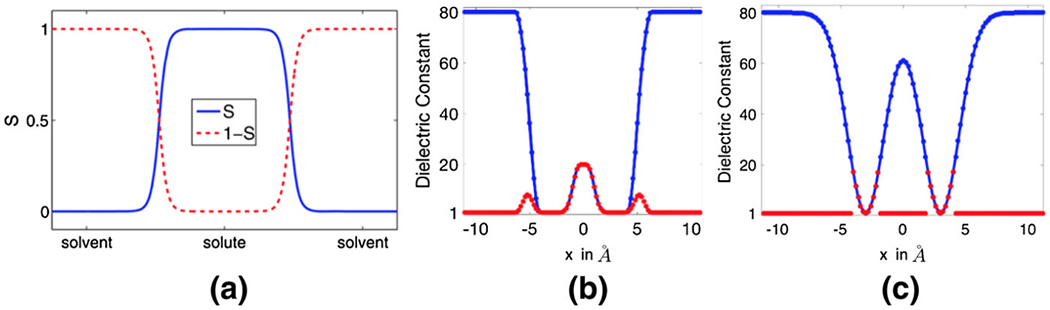
a The hypersurface functions S and (1 − S) of the solute-solvent region along a straight line. b The blue and red curves depict the dielectric function ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ of the super Gaussian model in the water and vacuum phases respectively. c The blue and red curves depict the dielectric functions ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ and ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)$ of the Gaussian model in the water and vacuum phases respectively

The hypersurface function $S\left(\overrightarrow{r}\right)$ of the MMS model (Bates et al. 2008, 2009; Tian and Zhao 2014) was originally used for representing the protein region, with S = 1 inside all VDW balls and S = 0 outside the SAS (based on a probe radius 1.5 Å). A smooth transition from one to zero is obtained through numerical PDE solution. In the proposed super Gaussian PB model, we will make use of (1 − S) to present the exterior region so that both water and vacuum phases could be modeled in one equation

$${ϵ}_{sG}\left(\overrightarrow{r}\right)=S\left(\overrightarrow{r}\right){ϵ}_{in}\left(\overrightarrow{r}\right)+\left[1-S\left(\overrightarrow{r}\right)\right]{ϵ}_{out},$$ (15)

where the constant ϵ_out determines the dielectric value far away from the protein. Note that S = 1 inside the VDW region so that inhomogeneity of the super Gaussian dielectric distribution is retained. By setting ϵ_out to be 1 or 80, one simply switches from vacuum phase to water phase.

In the proposed super Gaussian dielectric model, the PB equation is modified as

$$-\nabla ·\left({ϵ}_{sG}\nabla u\right)+\left(1-S\right){\overline{\kappa }}^2\sinh \left(u\right)=S_{{\rho }_m},$$ (16)

where we have similarly inserted the hypersurface function $S\left(\overrightarrow{r}\right)$ for both the source and nonlinear terms. Note that $\overline{\kappa }$ is a constant, not a piecewise constant in our notation. The switch off of the nonlinear term relies on (1 − S), which has some impact numerically (Zhao 2014). Similarly, the electrostatic potential u₀ in vacuum is calculated by neglecting the nonlinear term

$$-\nabla ·\left({ϵ}_{sG}\nabla u_0\right)=S_{{\rho }_m},$$ (17)

because $\overline{\kappa }=0$ now. Of course, in this Poisson equation, we shall take ϵ_out = 1 for defining ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ in (15). One can then compute the solvation free energy by (5).

In the super Gaussian model, the dielectric function ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ remains C^∞ continuous in both water and vacuum states. This is illustrated by considering a two-atoms system in Fig. 3b, in which m = 3, σ = 1.3, and ϵ_gap = 20. It can be observed that inside the solute region, ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ is identical for both water and vacuum phases. Near the solute-solvent boundary, the dielectric value produces a smooth bump, because ϵ_gap = 20 allows a large ϵ away from the center of the atom. Further away from atoms, the hypersurface function $S\left(\overrightarrow{r}\right)$ plays a dominant role so that ϵ decays to ϵ_out = 1 smoothly. For a comparison, the dielectric functions ${ϵ}_G\left(\overrightarrow{r}\right)$ and ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)$ of the Gaussian model, for water and vacuum phase respectively, are depicted in Fig. 3c. In the water phase, the maximal value of ${ϵ}_G\left(\overrightarrow{r}\right)$ is determined by ϵ_s = 80, so that it is higher than that of ${ϵ}_{s}G\left(\overrightarrow{r}\right)$. In the vacuum phase, by conducting a surface cut at 20, ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)={ϵ}_G\left(\overrightarrow{r}\right)$ inside two atoms. Nevertheless, ${\widetilde{ϵ}}_G\left(\overrightarrow{r}\right)$ is discontinuous at atom boundaries.

2.4. Effective dielectric constant analysis

In the proposed super Gaussian dielectric model, there are three adjustable parameters, i.e., the order m, the relative variance σ which determines the window width of super Gaussian distribution, and ϵ_gap which controls the maximal dielectric value of the solute. In this subsection, we will explore the impact of these parameters on the final heterogeneous dielectric function $ϵ\left(\overrightarrow{r}\right)$ and find certain means for selecting suitable values of these parameters for real applications. We are also interested in a comparison among three dielectric models, i.e., the classical two-dielectric function (4), the Gaussian dielectric distribution (9), and the super Gaussian one (15), which will be referred to as Model I, II, and III, respectively, in this subsection.

In principal, the solvation free energy calculation is an ideal means for validating dielectric PB models and calibrating parameters. For example, the solvation energies produced by the Gaussian dielectric model have been compared with experimental results for some organic small molecules (Li et al. 2013b). For large macromolecules, measurement of solvation energies is still an experimental challenge. Thus, to assess the Gaussian dielectric model for proteins, explicit solvent molecular dynamics (MD) simulations have been conducted to generate referencing solvation energies to compare with the PB results (Li et al. 2013b). We note that MD simulations are usually time consuming.

In this paper, we propose an effective dielectric constant (EDC) analysis as a simple means to assess different dielectric models. Consider some simple systems with a few atoms immersed in the water. We first generate the dielectric function $ϵ\left(\overrightarrow{r}\right)$ by a model over a certain domain Ω. We then define the effective dielectric constant as

$$\widehat{ϵ}=\frac{{\int }_{\text{Ω}}ϵ\left(\overrightarrow{r}\right)d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}},$$ (18)

which measures, in an average sense, the resistance encountered when forming an electric field in this solute-solvent system. The EDC can be calculated either analytically or numerically, and enables us to investigate the role of each parameter in the super Gaussian distribution.

To select suitable parameter values, we will benchmark the EDC of the super Gaussian model against that of the two-dielectric model, and report the relative difference between them in our studies. Note that this does not mean that we treat the two-dielectric PB model as the “correct” model to compare with. In fact, the original purpose of Gaussian type models is to improve the two-dielectric PB model. However, in practice, the two-dielectric function is still the most widely used setting for the PB equation. It thus makes sense that a new dielectric model should not deviate from the two-dielectric model too much. With the EDC analysis, we can ensure the super Gaussian model agrees with the two-dielectric model in a mean field sense. This could potentially persuade more biologists to use the new model, because more freedom is available now for modeling purpose. However, we also note that with similar EDC values, the electrostatic solvation energies produced by the two-dielectric and the super Gaussian models could still be significantly different.

In the super Gaussian model, the minimal molecular surface (MMS) is calculated by using the fast algorithm developed in Tian and Zhao (2014). Through the EDC analysis, we will choose the relative variance for the Gaussian dielectric model around the value 1, namely, σ ∈ {0.8, 0.9, …, 1.3}. When we upgrade the density function from Gaussian to super-Gaussian, the corresponding relative variance will be changed and depends on the choice of m ∈ {1, 2, …, 8}. Finally, as we consider the super-Gaussian dielectric model (ϵ_sG) for the inhomogeneous macromolecule interior, we need to decide the preference of ϵ_gap ∈ {2, 4, …, 8, 10, 20, 40, 80} for different solute-solvent system. This selection depends on the cavity inside the solute. In the two-dielectric model, the solvent excluded surface (SES) is chosen as the molecular surface defining the solute-solvent boundary, and will be calculated by using the MSMS package (Sanner et al. 1996). We refer to Bates et al. (2008) for a detailed comparison between MMS and MSMS.

2.4.1. Effective dielectric constant analysis with one atom

We first conduct the effective dielectric constant (EDC) analysis for a single atom solute-solvent system in the water phase. Consider a sphere with radius R₀ = 2 Å and center at the original. A large enough domain Ω = [−a, a]³ is chosen with a = 8 Å. See Fig. 1a for an illustration. By taking ϵ_s = 80 and ϵ_m = 1, three dielectric models are studied in this paper. By comparing the EDCs of three models, we can find the optimal values of parameter σ and m for the one atom system.

Model I: In the two-dielectric model, ${ϵ}_2\left(\overrightarrow{r}\right)$ is defined as a piecewise constant as in Eq. (4). The EDC can be calculated analytically in this case

$${\widehat{ϵ}}_2=\frac{{\int }_{\text{Ω}}{ϵ}_{2}d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{ϵ}_s{\left(2a\right)}^3-\left({ϵ}_s-{ϵ}_m\right)\left(\frac{4}{3}\pi R_0^3\right)}{{\left(2a\right)}^3}=\mathrm{79.3537.}$$ (19)

Model II: In the Gaussian dielectric model, ${ϵ}_G\left(\overrightarrow{r}\right)$ is calculated by (9). The EDC ${\widehat{ϵ}}_G$ for ϵ_G is calculated through numerical integration:

$${\widehat{ϵ}}_G=\frac{{\int }_{\text{Ω}}{ϵ}_{G}d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{\int }_{\text{Ω}}\left[{ϵ}_m{g}_0+{ϵ}_s\left(1-g_0\right)\right]d\overrightarrow{r}}{{\left(2a\right)}^3},$$ (20)

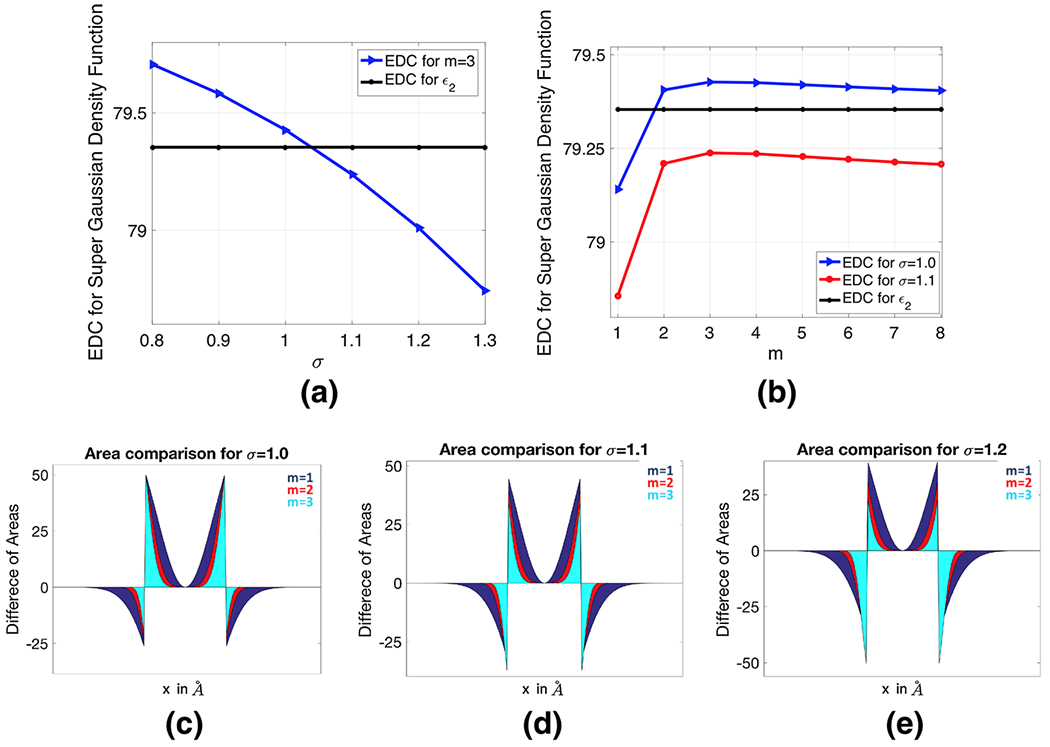
where g₀ is given by the equation (8), and ${\widehat{ϵ}}_G$ only depends on the relative variance σ. By taking σ = {0.8, 0.9, 1.0, 1.1, 1.2, 1.3}, the EDC results are reported in Fig. 4. It can be seen from Fig. 4a that out of the six discrete numbers being considered, σ = 0.9 obviously provides the best fit to ${\widehat{ϵ}}_2$. This is in excellent agreement with the existing study, in which the optimal value obtained through molecular dynamics simulations is σ = 0.93 (Chakravorty et al. 2018a). The slice plot of ${ϵ}_G\left(\overrightarrow{r}\right)$ is given in Fig. 4b for several σ values. Physically, the relative variance controls the upper half window-width of the function ϵ_G. As σ increases, the window becomes wider at the upper half section of ϵ_G which belongs to the solvent region, while has less impact to the bottom half section. Due to this broadening effect of σ, the EDC decreases as σ increases, as can be seen in Fig. 4a.

Fig. 4.

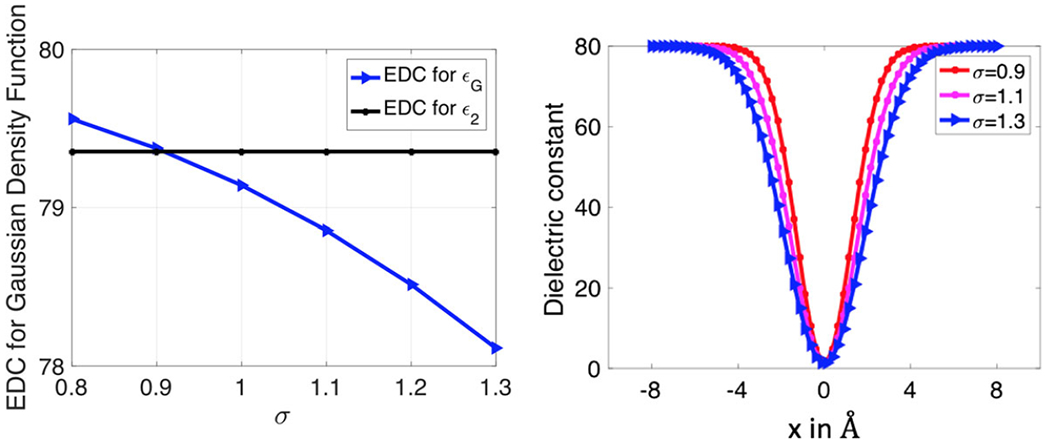
Comparison of effective dielectric constant of Gaussian dielectric model with different σ

Model III: For a comparison, we will also consider the super Gaussian function for the one-atom system. Nevertheless, we note that with only one atom, there is no cavity or gap region in the solute. Consequently, ϵ_gap is physically undefined in this system. For this reason, we will not study the actual super Gaussian dielectric model. Instead, in the Gaussian dielectric model (9), we simply replace $g_0\left(\overrightarrow{r}\right)$ by the super-Gaussian density function $g_0^s\left(\overrightarrow{r}\right)$ defined by Eq. (12). Let us denote the corresponding dielectric model as ${ϵ}_G^s$. This enables us to investigate the roles of the order m and relative variance σ in the one-atom system. Numerical integration is carried out to calculate the EDC similarly

$${\widehat{ϵ}}_G^s=\frac{{\int }_{\text{Ω}}{ϵ}_G^{s}d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{\int }_{\text{Ω}}\left[{ϵ}_m{g}_0^s+{ϵ}_s\left(1-g_0^s\right)\right]d\overrightarrow{r}}{{\left(2a\right)}^3}.$$ (21)

We first vary σ without changing m. Similarly to the previous case, it is found that ${\widehat{ϵ}}_G^s$ decreases as σ increases for a fixed m, see Fig. 5a for the case m = 3. Moreover, for a larger m, the optimal σ value becomes larger. For example, for m = 3, the optimal σ value is larger than 1 now. Next, by fixing σ, the effect of changing m is shown in Fig. 5b. It can be seen that the EDC increases quickly when m changes from 1 to 2, achieves a maximum around m = 3 or m = 4, and then declines slowly. Asymptotically, for σ = 1, the EDC of the super Gaussian density should approach to that of the two-dielectric model as m → ∞, i.e., ${\lim }_{m\to \infty }{ϵ}_G^s={ϵ}_2$. This confirms that the super Gaussian dielectric function approaches to the two-dielectric function when m goes to infinity. For σ = 1.1, the EDC curve is simply a shift of that of σ = 1.0 downwardly with the optimal orders being m = 3 or m = 4. For the other σ values, we have seen the same pattern that the EDC values for m > 4 are quite close to those of m = 3 or m = 4. Thus, in our numerical computations, we usually choose m = 3 or m = 4 with an optimized σ.

Fig. 5.

a The EDC of the super-Gaussian density function with power m = 3, b the EDC for σ = 1.0 and σ = 1.1, c–e Comparison of area differences between the compensated dielectric curves ${ϵ}_G^s\left(\overrightarrow{r}\right)-{ϵ}_2\left(\overrightarrow{r}\right)$ for σ = 1.0, 1.1, 1.2 and m = 1, 2, 3

Since the EDC values change significantly for 1 ≤ m ≤ 3, it is interesting to further compare the difference among them from a different perspective. In Fig. 5c–e, we plot the compensated dielectric curves, i.e., ${ϵ}_G^s\left(\overrightarrow{r}\right)-{ϵ}_2\left(\overrightarrow{r}\right)$, over the cross section plane y = 0. As can be seen from these figures, the compensated curves are positive inside the atom, because ${ϵ}_G^s\ge 1$ and ϵ₂ = 1. Right outside the atom boundary, ϵ₂ becomes 80, so that the compensated curves immediately drops to negative numbers. As the radius keeps increasing, ${ϵ}_G^s$ approaches 80 so that the compensated curves vanish at both ends. We note that due to the symmetry of this system, the net area obtained by integrating each compensated curve in such a two-dimensional (2D) setup essentially captures the volume difference between the EDC values for the super Gaussian and two-dielectric models. For each σ, when m becomes larger, the areas for both positive and negative regions shrink significantly. This is essentially why the EDC lines change dramatically for 1 ≤ m ≤ 3 in Fig. 5b. Comparing with the different σ values, it seems that σ = 1.1 produces more balanced net areas.

2.4.2. Effective dielectric constant analysis with four atoms

We next study a four-atom system immersed in water so that a cavity region can be formed. This enables us to explore the role of ϵ_gap in the super Gaussian model for the water phase. To this end, consider a regular tetrahedron with all sides having the same length D. Four atoms are defined by using the vertices of the tetrahedron as centers and with a radius 2 Å. By fixing the center of this tetrahedron as the origin of the coordinate, we will vary D from 4 to 7 Å. The illustrations of four atoms with D = 4 Å and D = 7 Å are shown in Figs. 7a, 8a, respectively. A large enough domain Ω = [−a, a]³ is chosen with a = 11 Å. By taking ϵ_s = 80 and ϵ_m = 1, the effective dielectric constant (EDC) in Eq. (18) is computed via numerical integration in all cases.

Fig. 7.

a Four-atom system in water solvent, where each atom-center is placed at the vertex of a regular tetrahedron of side D = 4 Å. b Effective Dielectric Constant ${\widehat{ϵ}}_{sG}$ for different m and σ with ϵ_gap = 2

Fig. 8.

a Four-atom system in water solvent, where each atom-center is placed at the vertex of a regular tetrahedron of side D = 7 Å. b Effective Dielectric Constant ${\widehat{ϵ}}_{sG}$ for different m and σ with ϵ_gap = 80. c Cross-section of ϵ_sG for the model 8(a) which contains only two atoms

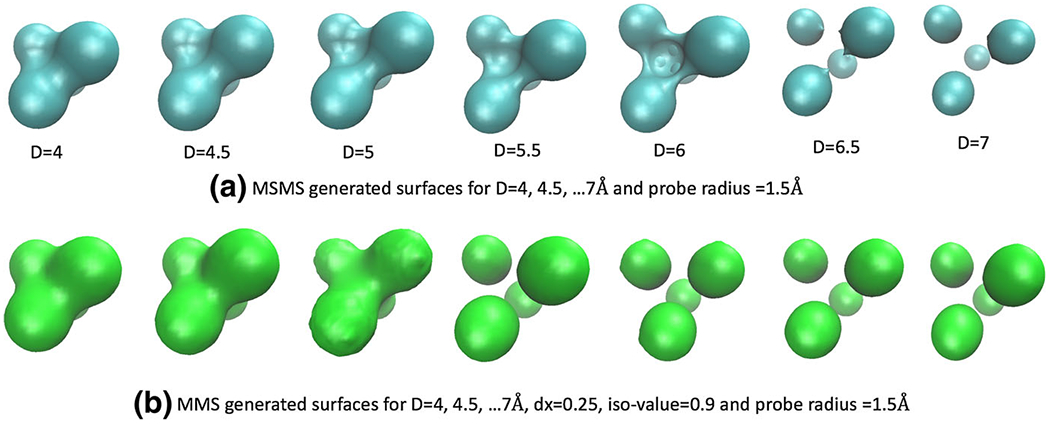
For the Gaussian dielectric model (9), ${ϵ}_G\left(\overrightarrow{r}\right)$ in the water phase is mainly determined by the positions and the radii of four atoms. For the two-dielectric model (4) and super Gaussian model (15), the dielectric function is greatly influenced by the underlying molecular surfaces. In particular, in the two-dielectric model, ${ϵ}_2\left(\overrightarrow{r}\right)=1$ inside the solvent excluded surface (SES) and ${ϵ}_2\left(\overrightarrow{r}\right)=80$ outside. The SES is generated by the MSMS package (Sanner et al. 1996) in the present study, see Fig. 6 for MSMS with different D values. It is seen that the solute domain initially becomes larger as D increases. However, as D keeps increasing, the reentry region in between the four atoms becomes smaller and smaller. Self-intersecting singularities are developed for D = 6 Å and D = 6.5 Å. When D = 7 Å, the system becomes four isolated balls, because with a probe radius 1.5, the probe sphere can freely pass the gaps between atoms. For the super Gaussian model, ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ is calculated based on the hypersurface function $S\left(\overrightarrow{r}\right)$ of the minimal molecular surface (MMS) (Tian and Zhao 2014). For a comparison, the MMS iso-surfaces with S = 0.9 at different D values are also shown in Fig. 6. A similar pattern as in the MSMS can be seen, i.e., the solute domain increases initially and then shrinks as D increases. Nevertheless, the MMS gives isolated atoms at an earlier D value, and never runs into geometrical singularities (Bates et al. 2008).

Fig. 6.

a The solvent excluded surface (SES) generated by the MSMS package for D=4, 4.5, …, 7 Å. b The minimal molecular surface (MMS) for D=4, 4.5, …, 7 Å

We first study the super Gaussian model with fixed D and ϵ_gap values. Since the hypersurface function $S\left(\overrightarrow{r}\right)$ plays an additional role in calculating dielectric distributions, the optimal m and σ results could be different from those of the one-atom system, because our previous study did not involve $S\left(\overrightarrow{r}\right)$. We consider two extreme cases, D = 4 Å and D = 7 Å, for studying m and σ.

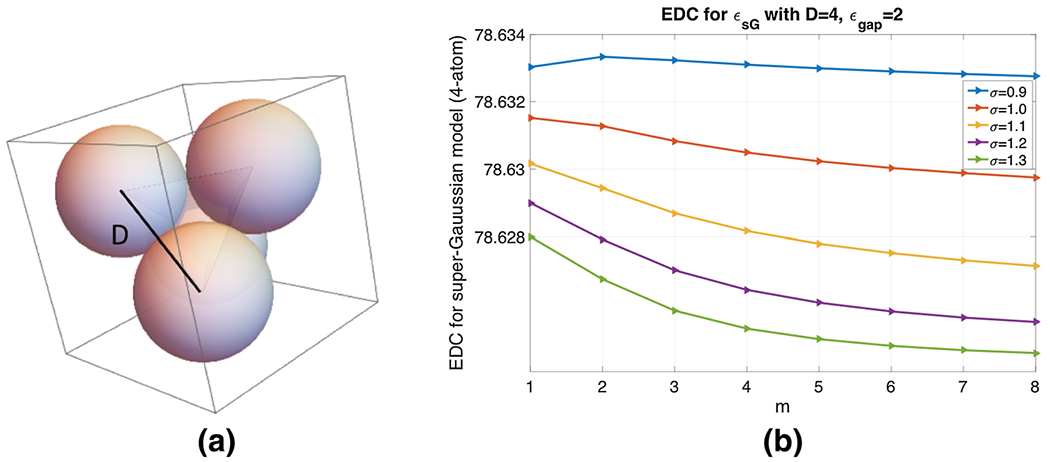
With D = 4 Å and atomic radius 2 Å, four balls are touching each other, leaving little space in between them. We thus fix ϵ_gap = 2 in this scenario, and calculate the effective dielectric constant (EDC) ${\widehat{ϵ}}_{sG}$ for σ ∈ {0.9, 1.0, …, 1.3} and m = 1, 2, …, 8, see Fig. 7b. As we have discussed for the one atom case before, with the increment of σ, the upper window part of super Gaussian function becomes wider and it reduces the EDC. We observe the same behavior in the 4-atom system too. Also, higher m values broaden the lower window-width too and it decreases the EDC ${\widehat{ϵ}}_{sG}$ of the super-Gaussian dielectric model as well. As we record the EDC, we observe very small variations in ${\widehat{ϵ}}_{sG}$ for different σ and m values, i.e., $78.626<{\widehat{ϵ}}_{sG}<78.634$. This insensitiveness indicates that the dielectric distribution is essentially dominated by the MMS hypersurface function $S\left(\overrightarrow{r}\right)$ and ϵ_gap = 2 for the current case with no cavities. In particular, the choice of ϵ_gap = 2 does not let the dielectric distribution ϵ_sG bump up inside the small room in between four atoms, see Fig. 7a. From the parameter selection point of view, we will still suggest to use m = 3 or m = 4, while any choice of σ does not make much difference for D = 4 Å.

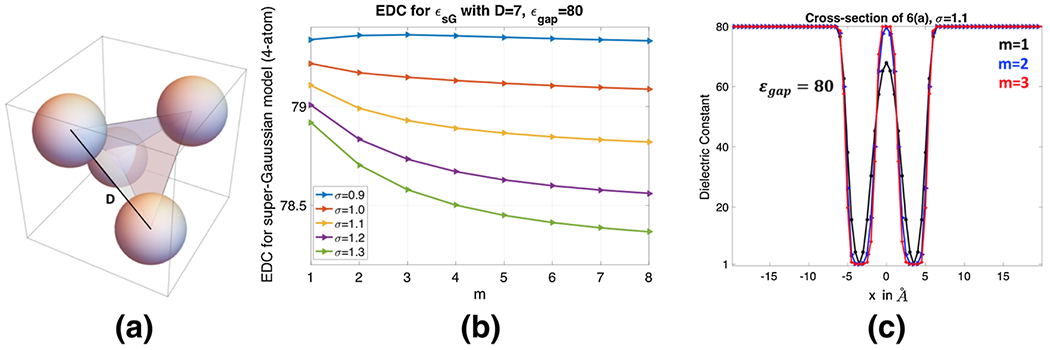
When D = 7 Å, a probe with radius 1.5 Å can freely access the interior of the four atoms. Both MSMS and MMS give isolated spheres in Fig. 6. Physically, the internal region should be treated as solvent. Thus we take ϵ_gap = 80 in the super Gaussian model, and calculate the EDC ${\widehat{ϵ}}_{sG}$ for σ ∈ {0.9, 1.0, …, 1.3} and m = 1, 2, …, 8. As can be shown in Fig. 8b, ${\widehat{ϵ}}_{sG}$ is also decaying when m or σ is large. But the range of EDC values is quite large now, i.e., from 78.3666 to 79.3623, due to ϵ_gap = 80. For a comparison, we consider the two-dielectric model whose EDC value for the present setting is calculated as ${\widehat{ϵ}}_2=79.0171$. If we choose σ = 1.0, it can be seen that ${\widehat{ϵ}}_{sG}$ could approach ${\widehat{ϵ}}_2$ when m → ∞. Again, this justifies our theory that the two-dielectric model is a limiting case of the proposed super Gaussian model as m goes to infinity. For practical computations, a finite m shall be used. For the parameter combinations shown in Fig. 8b, ${\widehat{ϵ}}_{sG}$ produces a good approximation to ${\widehat{ϵ}}_2$ when (σ, m) = (1.2, 1), (1.1, 2) or (1.1, 3). Nevertheless, for m = 1, the dielectric function actually does not reach 80 in the interior region, see Fig. 8c. Instead, associated with σ = 1.1, m = 2 or 3 would be a better choice.

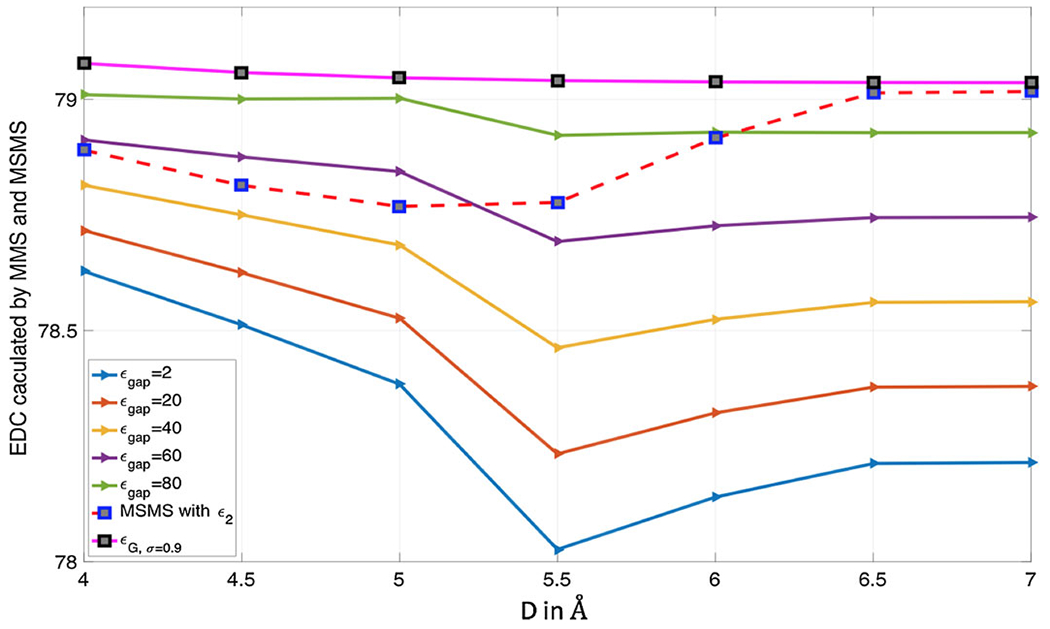
Next, we study the super Gaussian model with varying D and ϵ_gap values. As shown in the previous studies, with the presence of the hypersurface function $S\left(\overrightarrow{r}\right)$, the changes of m and σ do not alter the EDC ${\widehat{ϵ}}_{sG}$ too much, especially for compactly packed regions. Hence, we will simply fix σ = 1.1 and m = 3 in the following, which are optimal values for D = 7 Å. By considering ϵ_gap = {2, 20, 40, 60, 80}, the EDC curves of ${\widehat{ϵ}}_{sG}$ with respect to D are depicted in Fig. 9. For a comparison, the EDC results of the two-dielectric and Gaussian models are also shown in Fig. 9. Here the Gaussian results are generated with the optimal σ = 0.9.

Fig. 9.

Comparison of EDC curves for ${\widehat{ϵ}}_{sG}$ (super Gaussian model based on MMS), ${\widehat{ϵ}}_2$ (two-dielectric model based on MSMS) and ${\widehat{ϵ}}_G$ (Gaussian model)

Model I: In the two dielectric model, we have ϵ₂ = 1 within the four atoms and inside the MSMS surface in between the atoms, and ϵ₂ = 80 otherwise. The EDC ${\widehat{ϵ}}_2$ is actually determined by the total volume of the solute domain. Therefore, the change of ${\widehat{ϵ}}_2$ in Fig. 9 can be related to the volume change in Fig. 6a. In particular, as D increases from 4 to 5 Å, ${\widehat{ϵ}}_2$ becomes smaller initially and achieves a minimum around D = 5 Å. This is because the volume of solute domain becomes larger in this period. Note that the volume increment is simply because the dimension of the system is larger, while the torus surface actually becomes thinner and thinner. Thus, the volume becomes smaller later, despite of the further increment of the dimension D. Consequently, ${\widehat{ϵ}}_2$ bounces up, and reaches a constant level for D = 6.5 Å and D = 7 Å, for which the volumes are almost the same.

Model II: In the Gaussian model, the dielectric function ϵ_G defined in (9) only depends on the position and radii of the atoms, and there is no molecular surface behind it. Thus, as one can see in Fig. 9, when D increases, the EDC ${\widehat{ϵ}}_G$ is monotonically and slowly decreasing. To gain an in-depth understanding, we plot ϵ_G along a line passing two atom centers, see Fig. 10. With fixed radii, the Gaussian distributions for two atoms are unchanged as D increases. Hence, the increment of D only affects the dielectric value in between two atoms, which is higher and higher. This is why the EDC ${\widehat{ϵ}}_G$ behaves monotonically. For a very large D value, the Gaussian distribution is very close to the one for the one-atom system, for which σ = 0.9 is known to be the optimal value. Consequently, for D = 6.5 Å and D = 7 Å, ${\widehat{ϵ}}_G$ is quite close to ${\widehat{ϵ}}_2$.

Fig. 10.

Gaussian dielectric model ϵ_G with σ = 0.9 for 4-atom cross section which consists of two atoms only. D varies from 4 to 7 Å

Model III: The EDC ${\widehat{ϵ}}_{sG}$ of the super Gaussian model displays a similar pattern as ${\widehat{ϵ}}_2$ of the two-dielectric model for most ϵ_gap values except the limiting case ϵ_gap = 80. However, the pattern of ${\widehat{ϵ}}_{sG}$ is not solely determined by the volume inside the MMS isosurface, because ϵ_sG is a function of space—changing in between the minimal value ϵ_m = 1 and the maximal value ϵ_gap inside the solute domain. As Fig. 6b shows that the MMS generated isosurfaces are connected for D = 4, 4.5 and 5 (in Å). Then from D = 5.5 Å, the surfaces are disconnected and the four atoms are just isolated balls. Due to this topological change in the 4-atom system, there is a significant change in ${\widehat{ϵ}}_{sG}$ from D = 5 Å to D = 5.5 Å. Before 5.5 Å, as D increases from 4 to 5 Å, the volume of solute domain enclosed by the MMS isosurface increases, while the connecting surfaces along the edges of the tetrahedron shrink inward. This volume increment induces the decrement of ${\widehat{ϵ}}_{sG}$. It is interesting to note that ${\widehat{ϵ}}_{sG}$ keeps decreasing from D = 5 Å to D = 5.5 Å. This does not necessarily mean the isolated balls at D = 5.5 Å have larger volumes than the connected MMS region at D = 5 Å. In fact, the volume at D = 5.5 Å is still large, because four balls are much fatter than those for a bigger D value. Moreover, with a fat enough ball, ϵ_sG has the potential to approximately reach its maximum, i.e. ϵ_gap. The combining effect of volume and ϵ_sG distribution determines the minimum of ${\widehat{ϵ}}_{sG}$ in Fig. 9 for most ϵ_gap values. As D becomes even bigger, the radii of MMS balls decreases so that ${\widehat{ϵ}}_{sG}$ becomes larger. Also, for all ϵ_gap values, the EDC ${\widehat{ϵ}}_{sG}$ is almost the same for both D = 6.5 Å and D = 7 Å. For the limiting case ϵ_gap = 80, it turns out that particular MMS shape does not affect ${\widehat{ϵ}}_{sG}$, because ϵ_gap = ϵ_s = 80. Basically, ${\widehat{ϵ}}_{sG}$ just takes two values, one for a connected region and another for isolated balls.

In comparison of the EDC results of three models, we found that the Gaussian model is significantly different from the other two, because it is a surface free model. Two-dielectric and super Gaussian models share similar physics: the volume of solvent accessible region is determined by the size of the cavity in a convex manner, so that the dependence of the EDC on the cavity size is concave. Moreover, besides the MMS hypersurface function $S\left(\overrightarrow{r}\right)$, the ϵ_sG is also affected by the adjustable parameters m, σ, and ϵ_gap. If one changes m or σ, the EDC lines of ${\widehat{ϵ}}_{sG}$ in Fig. 9 will be shifted up or down, and the concave feature shall be the same. If one wishes to match ${\widehat{ϵ}}_{sG}$ with ${\widehat{ϵ}}_2$, Fig. 9 suggests that a larger ϵ_gap should be employed for a larger D. In other words, the optimal ϵ_gap depends on the size of the cavity.

2.4.3. Effective dielectric constant analysis in both water and vacuum phases

In our last EDC analysis, we consider both water and vacuum states in the solvent region. As we know, the electrostatic solvation free energy is calculated as the energy difference of the macromolecule in between the water and vacuum. Physically, the homogeneous or inhomogeneous dielectric distribution of the protein should remain unchanged in both states so that the energy difference makes sense. Consequently, the difference of $ϵ\left(\overrightarrow{r}\right)$ should not depend on a particular dielectric model for the solute, but relates to the solvent domain and property.

For the following experiments, we calculate the EDC values in both water and vacuum phases. For this purpose, we need to explicitly specify the dependence of ϵ on the solvent dielectric constant for the three models. In both two-dielectric and Gaussian models, we thus have ${ϵ}_2\left(\overrightarrow{r},{ϵ}_s\right)$ and ${ϵ}_G\left(\overrightarrow{r},{ϵ}_s\right)$, respectively, while the super Gaussian model takes the form ${ϵ}_{sG}\left(\overrightarrow{r},{ϵ}_{out}\right)$. The EDC difference is defined as

$$\text{Δ}\widehat{ϵ}=\frac{{\int }_{\text{Ω}}\left[ϵ\left(\overrightarrow{r},80\right)-ϵ\left(\overrightarrow{r},1\right)\right]d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{\int }_{\text{Ω}}ϵ\left(\overrightarrow{r},80\right)d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}-\frac{{\int }_{\text{Ω}}ϵ\left(\overrightarrow{r},1\right)d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}},$$ (22)

where ϵ ∈ {ϵ₂, ϵ_G, ϵ_sG}. We note that because one solves different PDEs, i.e., the PB equation in water phase and the Poisson equation in vacuum phase, the EDC difference may not have directly influence the electrostatic solvation free energy. Nevertheless, $\text{Δ}\widehat{ϵ}$ is still a useful quantity for investigating different dielectric models.

In Fig. 11, illustrations of three models in both states are depicted. For the two-dielectric model, ${ϵ}_2\left(\overrightarrow{r},80\right)$ is discontinuous, while ${ϵ}_2\left(\overrightarrow{r},1\right)$ is continuous because ϵ_m = 1 in the present study. If ϵ_m > 1, ${ϵ}_2\left(\overrightarrow{r},1\right)$ is discontinuous too in the vacuum. For the Gaussian dielectric model, ${ϵ}_G\left(\overrightarrow{r},80\right)$ is continuous in the water phase, but it is discontinuous in the vacuum phase, due to a surface-cut. In the proposed super Gaussian model, both ${ϵ}_{sG}\left(\overrightarrow{r},80\right)$ and ${ϵ}_{sG}\left(\overrightarrow{r},1\right)$ are continuous, respectively, in the water and vacuum states. Another thing that can be observed in Fig. 11 is that inhomogeneous solute dielectric models will impact solvent region nearby. In particular, for the Gaussian model, the dielectric values near the protein are influenced by the parameter σ in the water phase. In the super Gaussian model, such values are affected by both m and σ for both water and vacuum phases.

Fig. 11.

Dielectric models a ϵ₂: discontinuous in water phase and continuous in vacuum phase, b ϵ_G: continuous in water phase and discontinuous in vacuum phase (“surface-cut”), c ϵ_sG: continuous in both water and vacuum states

We will consider the same four atom system of the previous study. For simplicity, we test only one case with D = 7 Å for computing $\text{Δ}\widehat{ϵ}$.

Model I: In the two-dielectric model, the molecular surface is generated by the MSMS package. Since ${ϵ}_2\left(\overrightarrow{r},1\right)=1$ throughout the domain Ω, we have simply

$$\text{Δ}{\overrightarrow{ϵ}}_2=\frac{{\int }_{\text{Ω}}\left[{ϵ}_2\left(\overrightarrow{r},80\right)-1\right]d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{\int }_{\text{Ω}}{ϵ}_2\left(\overrightarrow{r},80\right)d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}-1={\widehat{ϵ}}_2-1.$$ (23)

For D = 7 Å, we have $\text{Δ}{\widehat{ϵ}}_2=78.0171$ numerically, which is exactly one unit less than the EDC ${\widehat{ϵ}}_2$ studied in the previous study.

Model II: For the Gaussian model, we consider several σ values, i.e., σ = 0.7, …, 1.3. According to (22), the EDC difference could be calculated by considering the water and vacuum phases separately. In the water phase, based on ${ϵ}_G\left(\overrightarrow{r}\right)$ given in (9), the EDC value is within (77.13635, 79.54655). In the vacuum phase, when ${ϵ}_G\left(\overrightarrow{r}\right)$ exceeds 20, a surface-cut is conducted to set dielectric constant as zero (Li et al. 2013b), see Fig. 11b. The EDC for the vacuum case is within (1.00738, 1.04756). By taking the difference, $\text{Δ}{\widehat{ϵ}}_G$ is within the range of (76.08879, 78.53918). Moreover, $\text{Δ}{\widehat{ϵ}}_G$ depends on σ significantly, see Fig. 12b. In the same figure, $\text{Δ}{\widehat{ϵ}}_2=78.0171$ is shown as a constant line. From the parameter selection point of view, this figure shows again σ = 0.9 is an optimal value for the Gaussian model. This is because with D = 7 Å, four atoms are completely separated, so that the present result is consistent with a single atom study. However, from a different perspective, the dependence of $\text{Δ}{\widehat{ϵ}}_G$ on σ indicates that the Gaussian model negatively impacts on the dielectric value in the solvent region. The inhomogeneous model here is designed for the protein and should be confined within the solute. Unfortunately, this is not the case for the Gaussian model.

Fig. 12.

a EDC difference $\text{Δ}{\widehat{ϵ}}_{sG}$ for different m ∈ {1, 2, …, 8} and σ ∈ {0.7, 0.8, …, 1.3}, b $\text{Δ}{\widehat{ϵ}}_G$ for different σ and $\text{Δ}{\widehat{ϵ}}_2$. In both the cases, D = 7 Å

Model III: In the super Gaussian model, we also fix ϵ_gap = 80 for D = 7 Å. Different parameter values are tested for m ∈ {1, 2, …, 8} and σ ∈ {0.7, 0.8, …, 1.3}. By taking ϵ_out = 80 in the water and ϵ_out = 1 in the vacuum, we note that in Eq. (15), $S\left(\overrightarrow{r}\right){ϵ}_{in}\left(\overrightarrow{r}\right)$ is simply canceled out when computing the EDC difference:

$$\text{Δ}{\widehat{ϵ}}_{sG}=\frac{{\int }_{\text{Ω}}\left[{ϵ}_{sG}\left(\overrightarrow{r},80\right)-{ϵ}_{sG}\left(\overrightarrow{r},1\right)\right]d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}=\frac{{\int }_{\text{Ω}}79\left[1-S\left(\overrightarrow{r}\right)\right]d\overrightarrow{r}}{{\int }_{\text{Ω}}d\overrightarrow{r}}.$$ (24)

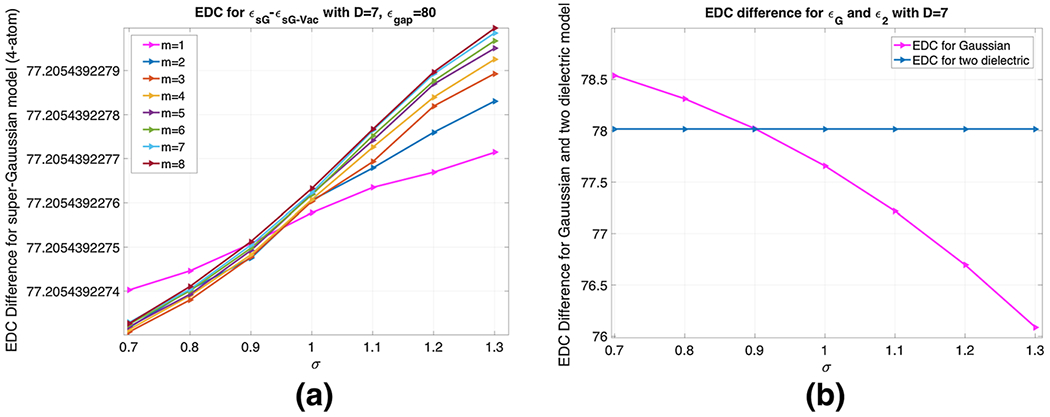
This is confirmed numerically. In Fig. 12a, $\text{Δ}{\widehat{ϵ}}_{sG}$ is plotted against σ for different m values. The vertical values change from 77.2054392274750 to 77.2054392279961, for which the difference takes place at the tenth decimal place. Thus, the EDC difference is solely dominated by the MMS hypersurface function $S\left(\overrightarrow{r}\right)$. With $S\left(\overrightarrow{r}\right)$, the impact of the super Gaussian model is confined within the solute, as shown by the present EDC analysis.

Both the two-dielectric and the super Gaussian models yield a constant $\text{Δ}\widehat{ϵ}$. But this does not mean that the change of parameter values will have no impact on electrostatic solvation free energy in the super Gaussian model. For example, a different choice of (m, σ) pair will produce a different “bump” in the vacuum case in Fig. 11c. Such a bump near solute-solvent boundary is driven by a combined mechanism: away from atom centers ϵ_in becomes larger, while away from the protein, it will damp out ϵ to one. Because ϵ_in depends on (m, σ) the height and width of the bump depend on (m, σ) too. Moreover, since different PDEs will be solved in water and vacuum phases, the electrostatic solvation free energy will rely on (m, σ) in practice.

2.4.4. Discussions

In this subsection, we have carried out an effective dielectric constant (EDC) analysis for three cases, which helps us to understand the role of each parameter, including m, σ, and ϵ_gap, in the super Gaussian dielectric function ${ϵ}_{sG}\left(\overrightarrow{r}\right)$. For the EDC difference studied in the third case, it is independent of these parameters, and just relies on the MMS hypersurface function $S\left(\overrightarrow{r}\right)$. For the first case without involving $S\left(\overrightarrow{r}\right)$, the impact of m and σ on the EDC ${\widehat{ϵ}}_{sG}$ has been identified. A comprehensive EDC analysis has been conducted for the second case, which tells us more about parameters. Basically, with a fixed ϵ_gap, optimal m and σ can be established. Moreover, due to the influence of $S\left(\overrightarrow{r}\right)$, the super Gaussian model behaves robustly with respect to m and σ, in the sense that the EDC will not change too much for different m and σ values. Furthermore, our analysis indicates that ϵ_gap, which determines the maximum of ${ϵ}_{sG}\left(\overrightarrow{r}\right)$ inside the solute, should be larger when the size or volume of the cavity increases. For proteins without cavities, we usually recommend a small value, such as ϵ_gap = 2, which does not deviate too much from ϵ_m = 1 of the two-dielectric model. On the other hand, the selection of ϵ_gap for proteins with cavities is not an easy task in practical computations. In our opinion, physical considerations have to be taken into account, so that the super Gaussian PB model can capture as many atomic details as possible in the continuum electrostatics modeling.

For proteins containing cavities and channels, one critical issue on selecting ϵ_gap is whether a cavity is empty or filled with water molecules. Trapped water molecules tend to interact with the protein via either hydrogen bonds or Van der Walls forces. As a consequence of these interactions, the water molecules are considered to lose their flexibility. Thus, the cavity water could have a smaller dielectric constant in comparison to the bulk water, but it is still larger than that of the amino acids. Moreover, the size or volume of the cavity is also important. Depending on the cavity size, confined water molecules exhibit a different ability to reorient in response to the local electrostatic field which affects their rotational polarizability. This further alters the dielectric value. Furthermore, the situation becomes more complicated in the ion channel modeling, in which the Poisson equation is used to calculate the force encountered by permanent ions. In this scenario, besides dielectric values for the protein and bulky water, one also needs to specify ϵ for water in the pore even in classical models. Physically, the dielectric value in the ion-channel shall be higher than that in regular cavities, owing to the mobility of ions. Therefore, the optimal ϵ_gap has to be determined based on a particular macromolecule, and varies for different systems. Ideally, in-depth physical investigation or biological simulation shall be carried out for selecting a proper dielectric value for cavities and pores. For instance, Brownian dynamics simulations have been conducted in Ng et al. (2008) to decide ϵ values for protein channels to be used in solving the PB equation.

3. Numerical algorithms

In this section, we discuss how to discretize the PB equation (16) and Poisson equation (17) in the proposed super Gaussian model. In solving the two-dielectric PB equation (1), special interface treatments (Zhou et al. 2006; Chen et al. 2011;Qiaoetal. 2006) are required for high order spatial discretizations, in order to handle the non-smoothness of the solution across the dielectric interface. Such a difficulty is simply bypassed in the smooth PB equation (16), because the solution now is C^∞ continuous throughout the domain. However, the nonlinearity term $\left(1-S\right){\overline{\kappa }}^2\sinh \left(u\right)$ in (16) introduces additional challenges numerically. In particular, near the solute-solution boundaries, the MMS characteristic function S is changing from one for solute to zero for solvent (see Fig. 3a for an illustration). Thus (1 − S) is not completely zero at some places for which the two-dielectric model will treat them as solute domain. If such a place happens to be close to an atom center, the magnitude of the potential u is not small then. Consequently, sinh(u) will be exponentially large. Even though (1 − S) is very close to zero, sinh(u) could still be dominant in many cases. This yields the so-called nonlinear instability, which has been observed in other smooth PB models before (Zhao 2011, 2014). In present study, we will employ the analytical treatment introduced in Zhao (2014), Geng and Zhao (2013) to overcome the nonlinear instability within a pseudo-time framework.

Consider a uniform mesh in both space and time. Without the loss of generality, we assume the grid spacing h in all x, y, and z directions to be the same. Denote the time increment as Δt. For a function u at a grid point (x_i, y_j, z_k) and time instant t_n, we denote $u_{i,j,k}^n=u\left(x_i,y_j,z_k,t_n\right)$.

3.1. Pseudo-time solution of the Poisson–Boltzmann equation

In the pseudo-time approach, a pseudo-time derivative will be added to the PB equation (Zhao 2011). Consequently, (16) becomes a time dependent PB equation

$$\frac{\partial u}{\partial t}=\nabla ·\left({ϵ}_{sG}\nabla u\right)-\left(1-S\right){\overline{\kappa }}^2\sinh \left(u\right)+S{\rho }_m,\text{in}\text{Ω},$$ (25)

with the same boundary condition (3). By using a trivial initial value u = 0, one numerically integrates (25) for a sufficiently long time period to stable state. The solution to the original nonlinear PB equation (16) is essentially recovered by the steady state solution of the pseudo-time dependent process (25).

A first order time splitting scheme (Zhao 2014; Geng and Zhao 2013) will be employed for solving (25). The time stepping of (25) over the time interval [t_n, t_n+1] can be carried out in two stages

$$\frac{\partial w}{\partial t}=-\left(1-S\right){\overline{\kappa }}^2\sinh \left(w\right),\text{with}{w}^n=u^n$$ (26)

$$\frac{\partial v}{\partial t}=\nabla ·\left({ϵ}_{sG}\nabla v\right)+S_{{\rho }_m},\text{with}{v}^n=w^{n+1}$$ (27)

We then set uⁿ⁺¹ = vⁿ⁺¹. The numerical solution uⁿ⁺¹ differs from the direct solution of (25) by an error on the order one, i.e., O(Δt). A second order time splitting has also been developed in Zhao (2014), Geng and Zhao (2013), by dividing the process into three stages.

The nonlinear sub-system (26) is integrated analytically. For the region inside VdW balls with $S\left(\overrightarrow{r}\right)=1$, we do not need to solve this equation. We will just simply set wⁿ⁺¹ = wⁿ. When $S\left(\overrightarrow{r}\right)<1$, the nonlinear term is calculated as (Zhao 2014)

$$w^{n+1}=\ln \left[\frac{\cosh \left(\frac{1}{2}\left(1-S\right){\overline{\kappa }}^2\text{Δ}t\right)+\exp \left(-w^n\right)\sinh \left(\frac{1}{2}\left(1-S\right){\overline{\kappa }}^2\text{Δ}t\right)}{\exp \left(-w^n\right)\cosh \left(\frac{1}{2}\left(1-S\right){\overline{\kappa }}^2\text{Δ}t\right)+\sinh \left(\frac{1}{2}\left(1-S\right){\overline{\kappa }}^2\text{Δ}t\right)}\right].$$ (28)

In the MMS generation, we have carefully filtered the results from the fast algorithm (Tian and Zhao 2014), so that the hypersurface function is strictly between 0 and 1, i.e., S ∈ [0, 1]. Together with (28), this guarantees that the present PB algorithm is free of nonlinear instability.

3.2. Alternating direction implicit (ADI) scheme

A Douglas–Rachford type alternating direction implicit (ADI) scheme will be applied to solve the linear diffusion equation (27). To this end, an implicit Euler spatial-temporal discretization of (27) is formulated first

$$v_{i,j,k}^{n+1}=v_{i,j,k}^n+\text{Δ}t\left({\delta }_x^2+{\delta }_y^2+{\delta }_z^2\right)v_{i,j,k}^{n+1}+\text{Δ}t{S}_{i,j,k}{Q}_{i,j,k}$$ (29)

where Q_i,j,k is the fractional charge at grid point (x_i, y_j, z_k), which is obtained by using the trilinear interpolation to distribute all charges in the charge density ρ_m. Here ${\delta }_x^2,{\delta }_y^2$ and ${\delta }_z^2$ are the central difference operators along x,y and z directions respectively,

$${\delta }_x^2{v}_{i,j,k}^n=\frac{1}{h^2}\left(ϵ\left(x_{i+1/2},y_j,z_k\right)\left(v_{i+1,j,k}^n-v_{i,j,k}^n\right)+ϵ\left(x_{i-1/2},y_j,z_k\right)\left(v_{i-1,j,k}^n-v_{i,j,k}^n\right)\right)$$

$${\delta }_y^2{v}_{i,j,k}^n=\frac{1}{h^2}\left(ϵ\left(x_i,y_{j+1/2},z_k\right)\left(v_{i,j+1,k}^n-v_{i,j,k}^n\right)+ϵ\left(x_i,y_{j-1/2},z_k\right)\left(v_{i,j-1,k}^n-v_{i,j,k}^n\right)\right)$$

$${\delta }_z^2{v}_{i,j,k}^n=\frac{1}{h^2}\left(ϵ\left(x_i,y_j,z_{k+1/2}\right)\left(v_{i,j,k+1}^n-v_{i,j,k}^n\right)+ϵ\left(x_i,y_j,z_{k-1/2}\right)\left(v_{i,j,k-1}^n-v_{i,j,k}^n\right)\right)$$

where we have dropped the subscript sG in the ϵ function for simplicity. In these finite difference discretizations, the dielectric function is needed on half grid nodes, such as ϵ(x_i+1/2, y_j, z_k). Because the MMS hypersurface function is obtained numerically, we only know S function on grid nodes, i.e., S_i,j,k = S(x_i, y_j, z_k). In the present, we will first generate ϵ_sG on (x_i, y_j, z_k) grid nodes. Then a linear interpolation at (x_i, y_j, z_k) and (x_i+1, y_j, z_k) is conducted for determining ϵ(x_i+1/2, y_j, z_k).

In the ADI scheme, instead of solving a three-dimensional (3D) linear system, (29) is solved in x, y, and z directions alternatively

$$\begin{gathered} \left(1-\text{Δ}t{\delta }_x^2\right)v_{i,j,k}^{\ast }=\left[1+\text{Δ}t\left({\delta }_y^2+{\delta }_z^2\right)\right]v_{i,j,k}^n+\text{Δ}t{S}_{i,j,k}{Q}_{i,j,k} \\ \left(1-\text{Δ}t{\delta }_y^2\right)v_{i,j,k}^{\ast \ast }=v_{i,j,k}^{\ast }-\text{Δ}t{\delta }_y^2{v}_{i,j,k}^n \\ \left(1-\text{Δ}t{\delta }_z^2\right)v_{i,j,k}^{n+1}=v_{i,j,k}^{\ast \ast }-\text{Δ}t{\delta }_z^2{v}_{i,j,k}^n \end{gathered}$$ (30)

By eliminating the intermediate solutions v* and v**, one can show that the Douglas–Rachford ADI Scheme (30) is a higher order perturbation of the implicit Euler scheme (29) (Zhao 2014). The overall temporal order is one, because both the time splitting and ADI schemes are first order accurate in time. For smooth solutions, the finite difference discretization has order two in space. Moreover, since only one-dimensional (1D) linear systems shall be solved in each stage of the ADI scheme (30) and such 1D systems are tridiagonal, the algebraic computation is very efficient based on the Thomas algorithm. The complexity of each time step is on the order of O(N), where N is the degree of freedom in all of x, y, and z directions.

We note that the same ADI scheme has been previously applied to solve the PB equation in a two-dielectric setting with a sharp interface (Geng and Zhao 2013) and in a coupled system (Zhao 2014), in which the MMS hypersurface S(x, y, z) is evolved in time as well. However, such an ADI scheme is conditionally stable for real proteins, even though the scheme is fully implicit. As to be illustrated in our numerical studies, with a C^∞ dielectric setting, the ADI scheme now becomes unconditionally stable in protein studies.

3.3. Poisson equation in the vacuum phase

For the vacuum phase, ϵ_sG is calculated by (15) with ϵ_out = 1. With inhomogeneous dielectric values inside the protein, the Poisson equation (17) cannot be solved by the fast Poisson solver as in the two-dielectric PB model. Instead of solving the Poisson equation (17) as a boundary value problem, we will solve it via a pseudo-time approach too. This is motivated by the fact that there is usually a systematic error cancellation, when one applies the same algorithm for solving the PB equation in water phase and the Poisson equation in vacuum phase (Deng et al. 2018). Thus, we rewrite the Poisson equation (17) in the vacuum phase into a time dependent one

$$\frac{\partial u_0}{\partial t}=\nabla ·\left({ϵ}_{sG}\nabla u_0\right)+S{\rho }_m,\text{in}\text{Ω.}$$ (31)

Then, the ADI discretization of (31) is exactly the same as that for Eq. (27).

However, we note that the convergence of the pseudo-time algorithm is much slower in the Poisson case in comparing with the PB case. This is probably because of the boundary condition (3). In the PB case, there is an exponential term in (3), which decays exponentially away from the protein. For the Poisson case, such decay is slow, because $\overline{\kappa }=0$ in (3) for the vacuum. Consequently, for the same domain size, the boundary data in the vacuum case is actually larger than that in the PB case. Hence, for the super-Gaussian studies with initial potential values being zero, the CPU time for solving the time dependent Poisson equation (31) is usually much larger than that for the time dependent PB equation (25).

3.4. Electrostatic free energy

After solving the time dependent PB and Poisson equations until the steady state, we denote the convergent solution, respectively, to be u(x_i, y_j, z_k) and u₀(x_i, y_j, z_k), where (x_i, y_j, z_k) is a grid node. To calculate the electrostatic free energy defined in (5), we first note that this definition is valid in super Gaussian model too, i.e.,

$$\text{Δ}G=\frac{1}{2}\underset{\text{Ω}}{\int }{\rho }_m\left(u(\overrightarrow{r})-u_0(\overrightarrow{r})\right)d\overrightarrow{r}=\frac{1}{2}\underset{\text{Ω}}{\int }S{\rho }_m\left(u(\overrightarrow{r})-u_0(\overrightarrow{r})\right)d\overrightarrow{r}.$$ (32)

This is because the charge density ρ_m is nonzero only inside the VDW atoms, for which S always equals to one. In the present study, the electrostatic free energy is calculated based on grid node values

$$\text{Δ}G=\frac{1}{2}\sum _i\sum _j\sum _k{Q}_{i,j,k}\left(u\left(x_i,y_j,z_k\right)-u_0\left(x_i,y_j,z_k\right)\right),$$ (33)

where the summation is conducted for all (i, j, k) nodes for which Q_i,j,k is nonzero, i.e., surrounding the singular charges in ρ_m. Moreover, electrostatic potentials u and u₀ are usually rescaled by a constant 0.592183 corresponding to room temperature (298 K) so that they are in units of kcal/mol/e_c.

4. Numerical validations

In this section, we will solve the PB equation on a sphere, for which an analytical solution of electrostatic free energy is available in a two-dielectric setting. This enables us to validate the proposed super Gaussian dielectric model and select model parameters, by an approach different from the EDC analysis. Numerically, we will also verify the convergence and stability of the pseudo-time ADI method.

4.1. Benchmark problem

Consider a single charge q at the center of a sphere with radius r₀. Here we take q = 1e_c and r₀ = 2 Å, and assume the center being the origin of our coordinate system. An analytical solution of electrostatic free energy ΔG is admissible if we assume a two-dielectric setting: ϵ = ϵ_m inside the sphere and ϵ = ϵ_s outside. By taking ϵ_m = 1 and ϵ_s = 80, we have

$$\begin{gathered} \text{Δ}G=-\frac{q^2}{2}\left(\frac{1}{{ϵ}_m}-\frac{1}{{ϵ}_s}\right)\frac{1}{r_0}{\text{e}}_{\text{c}}^2/\text{Å} \\ =-\frac{q^2}{2}\left(\frac{1}{{ϵ}_m}-\frac{1}{{ϵ}_s}\right)\frac{1}{r_0}\times 332.06364\text{kCal/mol} \\ =-81.9782\text{kCal/mol} \end{gathered}$$ (34)

4.2. Modal validation and parameters

In the super Gaussian model, we take ϵ_out = 80 for the water phase. Then the ADI method is employed for solving the pseudo-time PB equation (25). The computational domain is taken as Ω = [−8, 8]³. On the boundary ∂Ω, the Dirichlet boundary condition (3) is assumed in a single charge setup. By using a initial condition u = 0, Eq. (25) will be numerically integrated until the steady state. Similarly, in the vacuum state with ϵ_out = 1, the pseudo-time Poisson equation (31) will be solved by the ADI method with the corresponding boundary condition. Then, the electrostatic free energy can be computed by (33). Numerically, the same spacing is used in all three directions h = Δx = Δy = Δz. We will take h = 0.5 as in most PB computations.

In the previous section, we have discussed about the choice of m, σ and ϵ_gap through the Effective Dielectric Constant (EDC) analysis. The availability of exact free energy value for a sphere in a two-dielectric setting provides another means to examine these parameters. We note that with a different dielectric setting, our super Gaussian results will not converge to the analytical value, which is based on a two-dielectric setting. However, it makes sense to adjust parameters so that the new dielectric model could produce energy values that are comparable to the two-dielectric model. This is particularly convenient if one wants to use it to replace an existing two-dielectric PB solver in a software package. For this reason, we will simply take ϵ_gap = 2, which gives the least difference in comparing with ϵ_m = 1 within the sphere.

By considering m ∈ {1, 2, …, 8} and σ ∈ {0.9, 1.0, …, 1.3} for the super Gaussian function ϵ_sG, the steady state energies are shown in Fig. 13. The exact value −81.9782 kCal/mol is also shown for a reference. A few pairs of (m, σ) are found to produce good approximations to the two dielectric model, i.e., (1.2, 5), (1.2, 6), (1.2, 7), (1.2, 8) and (1.3, 3). Among them, we will mainly focus on m = 3 and σ = 1.3 in the following free energy calculations, to avoid using a large m.

Fig. 13.

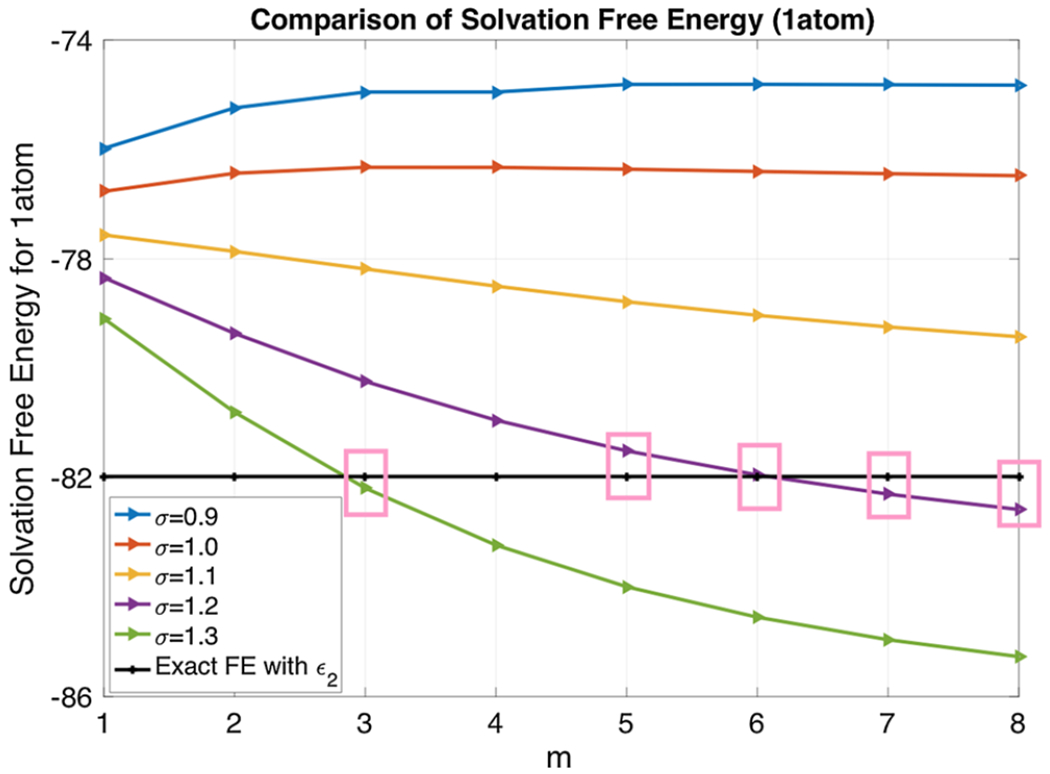
Solvation free energy (in KCal/mol) for σ ∈ {0.9, 1.0, …, 1.3} and m ∈ {1, 2, …, 8} with h = 0.5 Å

4.3. Numerical convergence and stability

By fixing m = 3, σ = 1.3, and ϵ_gap = 2, we investigate the performance of the pseudo-time ADI algorithm. By taking Δt = 0.01, we first examine the steady state convergence. The time history given in Fig. 14a shows that ΔG is increasing monotonically before the steady state is reached. The stopping criterion issue of the pseudo-time ADI algorithm has been discussed in Zhao (2014) for two-dielectric PB equation. The same stopping criteria will be adopted in the present study. In parciular, the computation will stop if either t ≥ T_e or the absolute energy difference in between two time steps is less than a tolerance TOL. For the present inhomogeneous dielectric medium, the steady state is reached fairly quick, around T_e = 5, which is consistent with the existing pseudo-time PB studies based on two-dielectric media (Zhao 2014; Geng and Zhao 2013; Wilson and Zhao 2016). We will take T_e = 10 and TOL=10⁻³ in the following studies, unless specified otherwise.

Fig. 14.

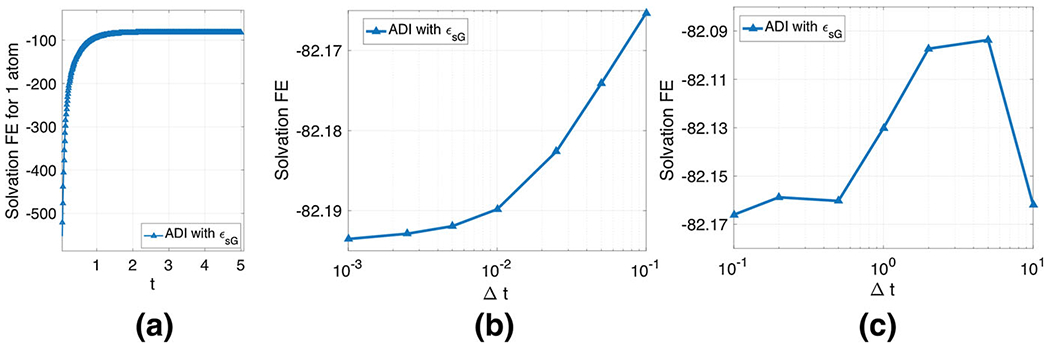
Pseudo-time ADI algorithm for one atom system. a Steady state convergence; b Temporal accuracy; c Stability. The unit of solvation free energy is KCal/mol

We next examine the temporal accuracy of the ADI algorithm. With T_e = 10, free energies are generated by using different Δt, see Fig. 14b. Obviously, as Δt becomes smaller and smaller, the free energy approaches certain limiting value. The vertical range is actually quite small. In practice, Δt = 0.01 is enough to produce a reliable energy estimate.

We finally examine the stability of the pseudo-time ADI algorithm. We note that in a two-dielectric setting, this ADI algorithm does not achieve the unconditional stability, even though it is fully implicit (Geng and Zhao 2013). In particular, to fulfill the stability requirement, one has to choose Δt ≤ h²/20 in protein studies (Geng and Zhao 2013). Because Δt is small, the resulting algorithm could be inefficient, when T_e is large. With the C^∞ continuous ϵ function in both water and vacuum states, the pseudo-time ADI algorithm is unconditionally stable in the super Gaussian model. We demonstrate this by taking some large Δt values and conduct each computation with 10, 000 time steps. As can be seen in Fig. 14c, the free energy value with a large Δt could be slightly different. Nevertheless, the ADI algorithm remains stable for any large Δt.

5. Biological application

In this section, we further explore the performance of the super Gaussian PB model and ADI algorithm by studying free energies of protein systems. We first discuss how a real protein is implemented in the super Gaussian model. Then, we test different parameter values for a particular protein. With a reasonable choice of domain and parameters, we study solvation free energies for a set of proteins. We finally consider a protein with cavities to demonstrate how cavities can be represented via inhomogeneous dielectric distributions. In all studies, a large enough computational domain Ω is assumed and a uniform mesh with h = Δx = Δy = Δz = 0.5 is adopted.

5.1. Protein structure preparation and simulation setup

We have collected a set of proteins from the RCSB protein data bank (PDB). In this collection, the proteins consist of at least 500 atoms. Usually, we download the PDB format which is a standard representation for macromolecular structure data obtained from X-ray diffraction or NMR studies. This format preserves the details of water molecules, ions, nucleic acids, ligands etc. With the aid of the PDB2PQR program from the APBS package, we extract three important data for each atom involved in the protein, i.e., centers ${\overrightarrow{r}}_i=\left(x_i,y_i,z_i\right)$, radius R_i, and partial charge q_i, for i = 1, 2, … N_m. These data are stored in two files, one with extension .xyzr which contains numerical values for ${\overrightarrow{r}}_i$ and R_i in four columns. Another file with extension .xyzq contains numerical values for ${\overrightarrow{r}}_i$ and q_i.

The density function of the super-Gaussian model defined in (11) and (12) depends on the centers and radii of all atoms. It is time-consuming if one computes the density of every atom by using the entire domain Ω. In fact, the density of the i^th atom $g_i^s\left(\overrightarrow{r}\right)$ decays quickly away from its center ${\overrightarrow{r}}_i$, so that one does not need to calculate this function in the far field. By carefully examining the numerical truncation so that it will not affect the subsequent computations, we have introduced an influence domain for each atom, which is defined as a cubic box with dimension [−d, d]³ and centered at ${\overrightarrow{r}}_i$. See Fig. 15 for an illustration. In particular, in our computations, we consider maximum relative variance σ as 1.3. The influence domain dimension depends on the radius R_i and the order of the super-Gaussian function m. An empirical function is found to be satisfactory in our computations: $d=2R_i\left(1+m^{\frac{-m}{2}}\right)$, which takes its maximum d = 4R_i at m = 1. As a monotonically decreasing function, d will be very close to its asymptotic value $\underset{m\to \infty }{\lim }2R_i\left(1+m^{\frac{-m}{2}}\right)=2R_i$ when m is large. In other words, for m = 1 (in Gaussian density function), the dimension of the influence cube is four times of the atomic radius (R_i) and as m → ∞, the cube’s dimension shrinks down to double of the radius.

Fig. 15.

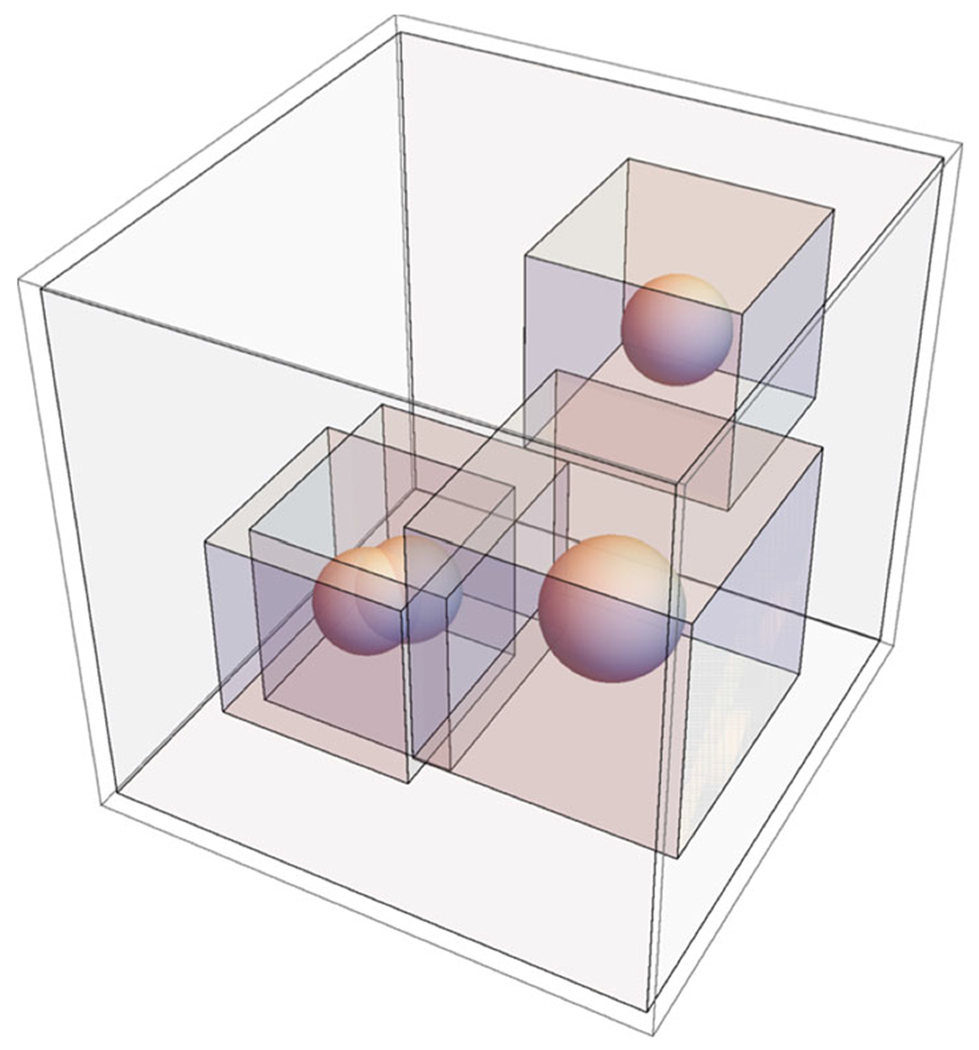
Influence domain

5.2. Solvation free energies of proteins

For studying our super Gaussian model on proteins, we first experiment the ADI algorithm with ϵ_sG on a sample protein, say 1ajj (PDB id) for different m and σ. Since 1ajj does not contain any cavity inside the molecular surface, we set ϵ_gap = 2. The performance of the pseudo-time ADI with ϵ_sG is recorded in Fig. 16. Here we considered Δt = 0.01 and T_e = 30. The solvation free energy for 1ajj at different (m, σ) values ranges from [−1457.2, −1230.6]. For a fixed σ, the increment of m from 1 to 3 gives rise to a higher energy, while the energy declines slowly as m is even larger. Numerically, the energy difference between m = 3 and m > 3 is not significant, which justifies our usual choice of m = 3. Nevertheless, the choice of σ does have a strong impact on energies, as shown in Fig. 16. Without comparing with results from other computational models, we will continue to use σ = 1.3 for simplicity.

Fig. 16.

Solvation free energy (in KCal/mol) for protein 1ajj, m ∈ {1, 2, …, 8} and σ ∈ {0.9, 1.0, …, 1.3}

We next investigate the pseudo-time ADI algorithm by fixing m = 3, σ = 1.3 and ϵ_gap = 2. We first consider the steady state convergence by using Δt = 0.01. The time-lapse data is displayed in Fig. 17a. Here the stopping criteria of the numerical computation are the same as those described in Sect. 4.3. The solvation free energy for the protein 1ajj reaches the steady state after T_e = 8. Next, for the temporal accuracy in protein 1ajj case, we consider T_e = 30 and different time steps in Fig. 17b. As Δt decreases the solvation free energy clearly approaches certain limiting value. We also experiment the stability of the pseudo-time dependent ADI scheme with ϵ_sG for the protein 1ajj. For this purpose, we take Δt ∈ {0.1, 0.25, 0.5, 1, 2, 4, 8} and T_e = 10⁴ Δt to validate stability in Fig. 17c. The result shows that the super-Gaussian ADI scheme is unconditionally stable for the protein 1ajj case. At last, we examine the spatial convergence in 17d for different h values. Again, the convergence is obvious under the limit of h goes to zero. The limiting value is of course different from the one at h = 0.5 as in other PB algorithms, but they are fairly close in the present study. So, we follow the convention in this field to choose a coarse mesh with h = 0.5 to avoid a large computational cost.

Fig. 17.

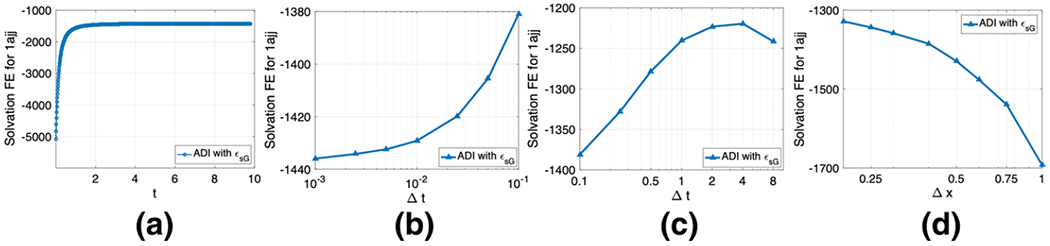
Pseudo-time ADI algorithm for the protein 1ajj. a Steady state convergence; b Temporal accuracy; c Stability; d Spatial convergence. The unit of solvation free energy is KCal/mol

Another parameter which could affect the free energy calculations is the domain size (Hage et al. 2018). We considered different domain sizes in Table 1, in which the first one is generated automatically by our PB package. Apparently, the domain size does not affect the solvation free energy calculation for the PB model with appropriate boundary conditions. Here, a large enough T_e = 30 is used so that the steady state solutions are reached in all three tested domain sizes.

Table 1.

Impact of domain-size to free energy computation for the protein 1ajj

Size of domain	Δx	Δt	ΔG in KCal/mol
[−9, 28] × [−13.5, 26] × [−19, 24]	0.5	0.01	−1428.66
[−11, 30] × [−15.5, 28] × [−21, 26]	0.5	0.01	−1428.49
[−13, 32] × [−17.5, 30] × [−23, 28]	0.5	0.01	−1428.33

We next study a set of 23 proteins with the size (number of atoms) ranging from 519 to 2809. These proteins do not contain any cavity either. Therefore, we fix ϵ_gap = 2. Regarding the (m, σ) pair, we keep (3, 1.3) in ϵ_sG. The pseudo-time dependent ADI experiment is conducted with Δt = 0.01 and T_e = 10. The free energies calculated by the super-Gaussian model are listed in Table 2. For a reference, we also show two literature results, i.e., the pseudo-time coupled nonlinear solvation (CNS) model (Zhao 2014) with $\text{Δ}t=\frac{h^2}{18}$ and h = 0.5 Å, and the two-component regularized PB (RPB) model (Geng and Zhao 2017) with h = 0.25 Å. In the CNS model (Zhao 2014), the solvation free energy including both polar and apolar parts is reported, while in the RPB model (Geng and Zhao 2017), electrostatic free energy of the two-dielectric PB equation is reported. Thus, these energy results are not necessarily close to the present ones. For example, for larger protein size, if the number of atoms exceed 2000 then the absolute energy difference between the super-Gaussian and RPB exceeds 350kcal/mol. Nevertheless, as can be observed from Fig. 18, the energies of three models are quite consistent with each other. We also note that in Fig. 18, one protein behaves significantly different from other proteins of the similar size, i.e., 1fxd. This is because this protein has the lowest total partial charge, as shown in Table 2.

Table 2.

Solvation free energy for proteins in kCal/mol

No. of atoms	PDB ID	Total partial charge	Ref. Zhao (2014)	Ref. Geng and Zhao (2017)	Present
519	1ajj	−5	−1260.6	−1139.48	−1428.66
573	2erl	−6	−919.8	−952.36	−1013.59
576	1bbl	1	−977.2	−988.40	−1186.34
596	1vii	2	−893.6	−902.31	−1031.52
648	1cbn	0	−255.5	−303.33	−398.27
667	2pde	3	−881.6	−820.97	−992.62
702	1sh1	0	−819.2	−753.99	−962.02
729	1fca	−7	−1221.8	−1204.44	−1337.86
795	1ptq	3	−869.6	−873.32	−1057.50
809	1uxc	4	−1151.7	−1139.25	−1363.33
824	1fxd	−15	−3347.0	−3321.39	−3073.39
832	1bor	−3	−928.8	−853.47	−1120.57
858	1hpt	−1	−790.4	−811.56	−1019.58
898	1bpi	6	−1283.4	−1304.37	−1450.90
903	1mbg	6	−1328.7	−1353.31	−1501.26
997	1r69	4	−1048.2	−1088.62	−1225.83
1187	1neq	4	−1710.3	−1731.71	−1991.43
1216	451c	−1	−978.5	−1025.66	−1219.22
1272	1a2s	−9	−1842.5	−1921.20	−1951.26
1435	1svr	−2	−1750.6	−1711.11	−2039.08
1478	1frd	−11	−2881.3	−2862.50	−2867.16
2065	1a63	−1	−2423.9	−2374.41	−2881.10
2809	1a7m	7	−2141.3	−2160.34	−2527.79

Fig. 18.

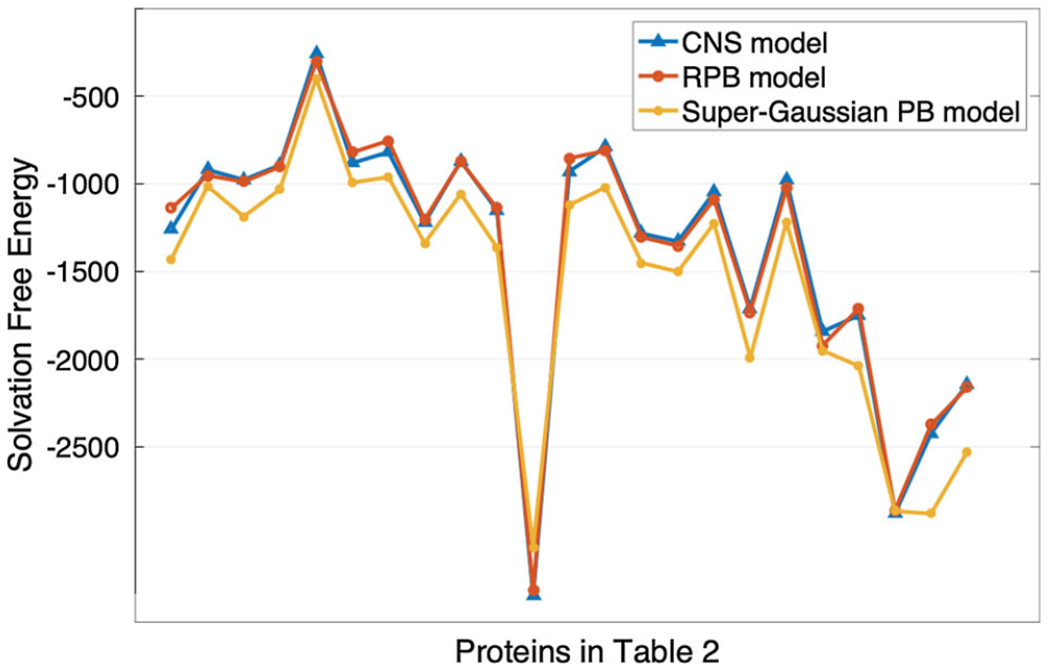
Comparing the super-Gaussian results with coupled nonlinear solvation (CNS) and regularized PB (RPB) models. Along x-axis, the proteins are listed according to the order of Table 2 and along y-axis the solvation free energies (in KCal/mol) are plotted

5.3. Protein with cavities

In this section, we investigate a protein with interior cavities and discuss how ϵ_gap should be adjusted to compensate the cavity impact on the electrostatic free energy. It is known in the literature that the cavities in protein could be filled with water molecules. Experimentally, it is very challenging to identify the water molecules inside the protein cavities with the crystallographic analysis. Computationally, these cavity water molecules play very important roles in solvation analysis. It is thus of great interest to numerically test the impact of cavity water molecules on electrostatic free energy in the present super Gaussian PB model.

In our numerical experiment, we focus on a protein IL-1β (PDB ID 2nvh), whose cavity structure has been well studied in the literature. It has been confirmed by using the electron density experiments that water molecules are present in several cavities of IL-1β (Quillin et al. 2006). In particular, there are a few cavities with volumes in the range of 16–45 ų containing a total of 6 water molecules (Quillin et al. 2006). Moreover, there is a cavity with volume 39 ų, for which electron density could not determine if water molecules exist in this cavity or not.

To study cavities with and without water molecules, we will process the protein IL-1β as illustrated in Fig. 19. We first note that in the protein preparation procedure discussed above, all water molecules will be removed in the final files, i.e., in .xyzr and .xyzq files, while all water molecules are included in the .pqr file produced by the PDB2PQR web server http://nbcr-222.ucsd.edu/pdb2pqr_2.1.1/. Furthermore, the atom IDs of six cavity water molecules are reported in David (2015). This enables us to identify these six molecules in the .pqr file and insert the corresponding hydrogen and oxygen atoms (located in the cavities) into 2nvh.xyzr and 2nvh.xyzq. These modified files will be called 2nvh-w.xyzr and 2nvh-w.xyzq. Computationally, we have generated two sets of workable files: one without water in cavities (2nvh) and another with 6 water molecules in some cavities (2nvh-w).

Fig. 19.

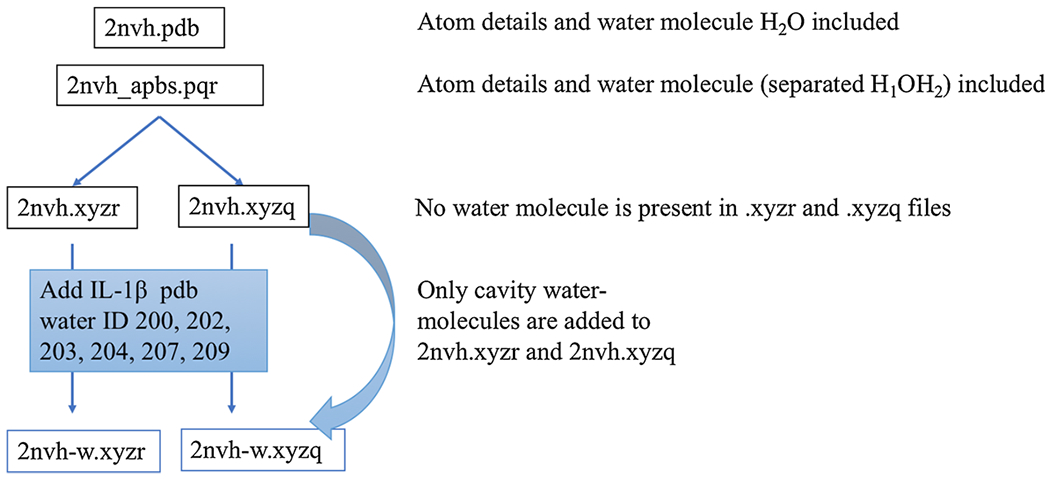
Inserting 6 water molecules in the protein IL-1β (PDB ID 2nvh)

After adding water molecules, we note that one cavity with volume 39 ų is still empty. To see this, we compare the super-Gaussian dielectric function ϵ_sG of 2nvh and 2nvh-w in Fig. 20. Here we take ϵ_gap = 7. By choosing a zoomed x-y cross section, we are able to capture three cavities of 2nvh in one contour plot (left figure). After adding water molecules, two of three cavities are filled so that ϵ values are reduced in these two locations (right figure). The cavity in the center remains unchanged in both 2nvh and 2nvh-w cases, which is the only one visible for 2nvh-w.

Fig. 20.

The super-Gaussian dielectric distribution with ϵ_gap = 7. a 2nvh, b 2nvh-w

We then study the energy difference between two structures 2nvh and 2nvh-w based on the super-Gaussian PB model. A methodical mutation analysis (Takano et al. 2003) indicates that inserting one water molecule into cavities generally produces 1–2 kcal/mol energy gain. This helps us to quantitatively examine our inhomogeneous dielectric model with cavity modeling. By using the same parameter pair (m, σ) = (3, 1.3), we first take ϵ_gap = 2. The energy gain of 2nvh-w over 2nvh is around 6 kcal/mol for inserting six water molecules, which agrees with the theoretical estimate very well.

We have further studied the energy difference for ϵ_gap = 2, 3, …, 8. Because the energy gain is on the order of a few kcal/mol, a large stopping time is chosen in the ADI algorithm so that numerical precision will not influence the present conclusion. In particular, we take T_e = 100, Δt = 0.01, and TOL = 10⁻³. Table 3 shows the energy gains of 2nvh and 2nvh-w in kcal/mol for different ϵ_gap. The idea behind this study is that we can compensate the absence of water molecules in cavities by raising the dielectric value ϵ_gap of the cavity water in the super Gaussian model. Consequently, one can represent the water molecules without physically adding them by just using a larger ϵ_gap value in the dielectric model. Indeed, as can be shown in Table 3, the energy gain becomes smaller and smaller as ϵ_gap is increased. At round ϵ_gap = 7, the difference between the solvation free energies of 2nvh and 2nvh-w is almost zero, i.e., around 0.1 kcal/mol. Our recommendation is that for proteins with cavities but one does not know if there are water molecules inside or not (such as the one shown in Fig. 20), one can model water molecules computationally by setting ϵ_gap = 7 or higher. We also believe that the magic number ϵ_gap = 7 for this example relates to the cavity size or volume. This parameter setup works well if the volume of the cavities is approximately less than or equal to 40 ų. If we have large volume cavities, we may need to increase the value of ϵ_gap.

Table 3.

Energy gain in 2nvh-w in kcal/mol

	ΔG for 2nvh	ΔG for 2nvh-w	Energy gain
Super-Gaussian
ϵgap = 2	−2718.29	−2712.59	5.70
ϵgap = 3	−2571.37	−2568.22	3.15
ϵgap = 4	−2451.26	−2448.38	2.88
ϵgap = 5	−2347.51	−2345.69	1.82
ϵgap = 6	−2256.74	−2255.82	0.92
ϵgap = 7	−2176.10	−2175.96	0.14
ϵgap = 8	−2103.60	−2104.16	−0.56
2-dielectric	−2960.40	−2957.34	3.06

For a comparison, the classical two-dielectric PB model is employed to solve 2nvh and 2nvh-w as well. The energy gain by using ϵ_m = 1 and ϵ_s = 80 is found to be 3.06 in Table 3. We note that the two-dielectric model does not have a modeling power to alter the energy gain for cavities. The use of a different ϵ_m value will affect all atoms, not just the cavity regions. This is different from the case of the super Gaussian dielectric model. In the super Gaussian case, we can change ϵ_gap for cavities without affect dielectric values of other atoms too much. This is an advantage of the super Gaussian model over the traditional PB models.

The computational costs of the super Gaussian and two-dielectric models are reported in Table 4. Here we report the CPU time for solving time-dependent Poisson equation in vacuum phase and time-dependent nonlinear PB equation in water phase, as well as the total CPU time. In general, the two-dielectric PB model is faster than the super-Gaussian model, and a few remarks are in order. First, the same pseudo-time ADI algorithm is employed in the both models for simplicity. For the super Gaussian computation, we set h = 0.5, TOL = 10⁻³, T_e = 100, and Δt = 0.01. However, for the two-dielectric setting, the ADI algorithm is conditionally stable so that a smaller Δt = 0.0025 has to be chosen. Consequently, for solving the PB equation only, the CPU time of the two-dielectric model is larger than that of the super Gaussian model. Second, we note that for the super Gaussian model, because of the smooth dielectric profile, a nonlinear instability could be experienced (Zhao 2014). That is why the pseudo-time ADI algorithm is used in the present study, which treats the nonlinear term analytically. However, a different numerical algorithm can be utilized for the two-dielectric model. In that case, the two-dielectric model could be much more efficient than super Gaussian model. Third, for the super Gaussian dielectric model, more CPU time is spend on the vacuum phase than on the water phase. As discussed previously, this should be because of the boundary condition (3). In the water phase, the potential decays exponentially away from the protein, while in the vacuum phase, such decay is much slower. Thus, it takes a long time to converge in the vacuum phase for the super Gaussian model. For two-dielectric model with ϵ_m = 1, we have ϵ = 1 throughout the domain Ω so that the FFT based fast Poisson solver can be applied. The corresponding computational cost is negligible.

Table 4.

CPU time (in hours) in free energy calculation of 2nvh and 2nvh-w

	2nvh			2nvh-w
	Poisson	PB	Total	Poisson	PB	Total
Super-Gaussian
ϵgap = 2	1.70	0.38	2.08	1.67	0.22	1.89
ϵgap = 3	1.66	0.22	1.88	1.71	0.22	1.93
ϵgap = 4	1.72	0.23	1.95	1.74	0.23	1.97
ϵgap = 5	1.79	0.22	2.01	1.68	0.24	1.92
ϵgap = 6	1.79	0.23	2.02	1.67	0.24	1.91
ϵgap = 7	1.72	0.22	1.94	1.68	0.23	1.91
ϵgap = 8	1.93	0.24	2.17	1.71	0.23	1.94
2-dielectric	0.05	1.70	1.75	0.03	1.85	1.88

6. Conclusion

In this paper, a super-Gaussian dielectric model is proposed for the electrostatic solvation free energy calculation. As an extension of the existing Gaussian dielectric Poisson–Boltzmann (PB) model, the dielectric property of protein cavity regions is modeled explicitly. Moreover, the super-Gaussian dielectric distributions are kept to be smooth when the protein is transferred from water state to vacuum state. A geometrical analysis based on the effective dielectric constant (EDC) theory is conducted to study the parameters of the super-Gaussian PB model, and compare the new model with two-dielectric and Gaussian dielectric models. Free energy calculations of a one-atom system and various proteins are carried out to validate the new model. Particular attention is paid on a protein system with multiple cavities.

Comparing with the existing models, one advantage of the super-Gaussian dielectric model is that it guarantees the ϵ function to be C^∞ continuous in both water and vacuum states in free energy computation. Computationally, a pseudo-time alternating direction implicit (ADI) algorithm is employed for solving the nonlinear PB equation of the super-Gaussian model. This ADI algorithm is fully implicit, but was found to be conditionally stable in dealing with two-dielectric media (Geng and Zhao 2013). Thanks to the smooth dielectric distributions of the super-Gaussian model, the same ADI algorithm is unconditionally stable in the present study.

Another advantage of the super-Gaussian model is an explicit definition of ϵ_gap, which opens new avenues to study proteins with internal cavities. An appropriate ϵ_gap mimics water molecules in empty cavities, because the corresponding energy will be the same as the one obtained by putting actual water molecules inside cavities. This compensate the cavity uncertainty which is commonly faced in experiments, i.e., to detect whether a particular cavity is empty or filled will water. In future studies, we plan to investigate more cavity proteins and study even large cavity size, e.g. 64–108 ų. With these studies, we hope to provide a better range of cavity water dielectric constant. Also, it is desired to establish a relation between the volume of the interior cavities and maximal dielectric constant for the cavity water molecules.

Appendix

Theorem The density function for the i^th atom is defined by

$$g_i^s(\overrightarrow{r})=\exp \left[-{\left(\frac{{\left|\overrightarrow{r}-r_i\right|}^2}{{\sigma }^2{R}_i^2}\right)}^m\right]$$

where r_i and R_i are the center and radius of the ith atom, respectively. Also, here $\overrightarrow{r}$ is the position vector, σ is the relative variance and m is the power of super-Gaussian function. Suppose σ = 1 for simplicity. Next, the total density function of a biomolecular system is defined as $g_0^s=1-\prod \left(1-g_i^s(\overrightarrow{r})\right)$ and the dielectric function of that system is modeled as

$${ϵ}_G^s={ϵ}_m{g}_0^s+{ϵ}_s\left(1-g_0^s\right).$$

Here ϵ_m and ϵ_s are the dielectric constants of the solute and solvent respectively. Then we have that $\underset{m\to \infty }{\lim }{ϵ}_G^s={ϵ}_2$ at the solute and solvent regions where ϵ₂ is the dielectric function of the classical two-dielectric model.

Proof Let us consider three cases where the position vector is either inside or outside the solute, or on the Van der Walls (VDW) molecular surface.

• Case I: There exists an atom (say ith atom) such that $\left|\overrightarrow{r}-r_i\right|<R_i$ or, $\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}<1$. In this case $\underset{m\to \infty }{\lim }{\left(\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}\right)}^{2m}=0$. Hence $\underset{m\to \infty }{\lim }\exp \left[-{\left(\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}\right)}^{2m}\right]=1$, which means $g_i^s\left(\overrightarrow{r}\right)=1$ and $g_0^s\left(\overrightarrow{r}\right)=1$. Therefore, if $\left|\overrightarrow{r}-r_i\right|<R_i$ for some i (inside the VDW surface), ${ϵ}_G^s={ϵ}_m$.

• Case II: For all atoms, we have $\left|\overrightarrow{r}-r_i\right|>R_i$ or $\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}>1$ for any i. In this case $\underset{m\to \infty }{\lim }{\left(\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}\right)}^{2m}=\infty$. So, $\underset{m\to \infty }{\lim }\exp \left[-{\left(\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}\right)}^{2m}\right]=0$, which means that $g_i^s(\overrightarrow{r})=0$ for all i. Hence $g_0^s(\overrightarrow{r})=0$. Therefore, if $\left|\overrightarrow{r}-r_i\right|>R_i$ for all i (outside the VDW surface), ${ϵ}_G^s={ϵ}_s$.

• Case III: In the last case, the position vector $\overrightarrow{r}$ has to be located on the VDW surface. Without the loss of generality, we assume that $\overrightarrow{r}$ is on the sphere boundary of the i^th atom and does not locate inside any other atoms. So, we have $\left|\overrightarrow{r}-r_i\right|=R_i$ or $\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}=1$. And, for any j ≠ i, $\left|\overrightarrow{r}-r_j\right|>R_j$. In this case $\underset{m\to \infty }{\lim }\exp \left[-{\left(\frac{\left|\overrightarrow{r}-r_i\right|}{R_i}\right)}^{2m}\right]=\frac{1}{e}$, which means $g_i^s(\overrightarrow{r})=\frac{1}{e}$. For any j ≠ i, $g_j^s(\overrightarrow{r})=0$. Hence, $g_0^s(\overrightarrow{r})=\frac{1}{e}$. Therefore, on the VDW surface, we have ${ϵ}_G^s={ϵ}_m{g}_0^s+{ϵ}_s\left(1-g_0^s\right)={ϵ}_m\frac{1}{e}+{ϵ}_s\left(1-\frac{1}{e}\right)=50.9375$ for ϵ_m = 1 and ϵ_s = 80.

In all cases, the new dielectric model converges to a two-dielectric model based on the VDW surface

$$\underset{m\to \infty }{\lim }{ϵ}_G^s(\overrightarrow{r})={ϵ}_2(\overrightarrow{r})=\{\begin{array}{ll}{ϵ}_m,& \overrightarrow{r}\text{is inside the VDW surface}\\ {ϵ}_m/e+{ϵ}_S(e-1)/e,& \overrightarrow{r}\text{is on the VDW surface}\\ {ϵ}_s,& \overrightarrow{r}\text{is outside the VDW surface.}\end{array}$$ (35)