Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 4;25(1):37–41. doi: 10.1021/acs.orglett.2c03747

High-Pressure Crystallization and Thermodynamic Stability Study on the Resolution of High-Density Enantiomers from Low-Density Racemates

Kinga Roszak 1, Andrzej Katrusiak 1,*
PMCID: PMC9841603  PMID: 36598359

Abstract

graphic file with name ol2c03747_0006.jpg

High-pressure recrystallization could be the cheapest clean method of resolving enantiomers from the racemates defying Wallach’s rule. We have investigated the effect of pressure on sodium tartrate monohydrate (NaTa·H2O), a notorious exception from Wallach’s rule: both racemic polymorphs α-dl-NaTa·H2O and β-dl-NaTa·H2O are less dense than the enantiomers. According to the mobile-equilibrium principle, such high-density enantiomorphs should spontaneously separate under high pressures. The pressure dependence of the Gibbs free energy explains the preferential crystallization of mixed enantiomers of NaTa·H2O.

For more than one and half centuries, the formation of racemates and enantiomers, as well as their resolution, has attracted general interest and today remains particularly relevant to the synthesis of pharmaceutical and natural products.1−4 The demand for pure enantiomers is continuously growing, and new efficient methods of resolving enantiomers are needed. One of the difficulties in devising new resolution methods is the lack of a general theory allowing the prediction of the crystallization mode of racemic substrates. Approximately 90% of chiral mixtures preferentially crystallize as the racemate, and the remaining 10% crystallize as the conglomerate of enantiomers.5 The often cited Wallach’s rule,6 stating that the density of racemates is higher than those of enantiomers, was based on the comparison of eight racemate–enantiomer pairs. One of them was an exception to the rule and contradicted its generality. More exceptions were found later,7,8 and it was suggested that the prevalence of racemates that are denser than enantiomers results from the bias of comparing only the compounds preferably crystallizing as racemates.9,10 The conclusion is that for the resolvable enantiomers Wallach’s rule is substantiated.9 The prevalence of racemic crystallization was associated with the larger number of possible molecular arrangements in all 230 space groups compared to enantiomers confined to the symmetry of 65 natural space groups.

Several compounds are known, for which the preference for spontaneous crystallization in the form of racemate or conglomerate of enantiomers can be altered by temperature.1−5 To the best of our knowledge, the preference for racemate and enantiomorph crystallizations so far was evidenced as a function of pressure and temperature for only 1,1′-binaphthyl.11 The high-pressure resolution of enantiomorphs would have important advantages. The pressure-induced crystallization is quick and does not require evaporation of the solvent or an increase in temperature, which chemically destabilize numerous active pharmaceutical ingredients. The pressure vessels are sealed and environmentally friendly. No costly chiral solvents or co-crystallization components are required, nor are processes of cleaning the enantiomorphic product from these technological additives. The high-pressure resolved enantiomer crystals, like those of Pasteur’s salt resolved by him manually, could be identified according to their morphology by highly efficient automatic shape recognition, chiroptical spectroscopy (e.g., vibrational and electronic circular dichroism and Raman optical activity)12 systems and sorted by pneumatic or other type of robotic automats, which today are well developed and routinely used in various technologies. Other relevant techniques of enantiomorph recognition, on the basis of the optical or NMR probing of the crystalline grains, can be envisaged.

The use of high-pressure recrystallization for resolving enantiomers that are denser than the racemates was first suggested in the 1980s,13 but the success with respect to mandelic acid14 could not be verified.7,8 At present, we analyzed the thermodynamic stability and the pressure effects on the racemate of sodium tartrate monohydrate [Na+[C4H5O6]−·H2O, hereafter NaTa·H2O (Figure 1)]. This compound notoriously defies Wallach’s rule,6 as both racemate dl-NaTa·H2O polymorphs are less dense than the enantiomers. It was suggested13,15 that according to the mobile-equilibrium principle, such high-density enantiomorphs should spontaneously separate under high pressure.

Figure 1.

Figure 1

Open in a new tab

Tartrate conformers in the NaTa·H2O enantiomorph and racemate polymorphs α and β. The thermal ellipsoids are shown at the 50% probability level.

Our X-ray diffraction studies show that up to 4.7 GPa the NaTa·H2O enantiomers remain significantly denser than the racemates, but the racemates persist to be more stable. This unexpected behavior has been rationalized by evaluating the internal energy of the structures and the pressure dependence of the Gibbs free energy controlling the preferential crystallization of mixed enantiomers in this case study on NaTa·H2O.

To better understand the role of structural and thermodynamic factors for preferential crystallization of equimolar mixtures of enantiomers, we have undertaken a high-pressure study of NaTa·H2O. The structures of enantiomers d-NaTa·H2O16 and l-NaTa·H2O17,18 as well as racemate dl-NaTa·H2O polymorphs α19 and β20,21 were determined by X-rays. Under normal conditions, the enantiomorph (orthorhombic space group P212121; Dx = 1.892 g cm–3) is by 1.5% more dense than racemate α-dl-NaTa·H2O (monoclinic space group P21/c; Dx = 1.864 g cm–3) and by 1.0% more dense than polymorph β-dl-NaTa·H2O (triclinic space group P1̅; Dx = 1.873 g cm–3). Here we show how pressure affects the course of spontaneous crystallization of dissolved dl-NaTa·H2O. Colorless crystals of d-NaTa·H2O precipitated from an equimolar d-tartaric acid (for synthesis, from Sigma-Aldrich) and sodium hydroxide (analytical grade, from Sigma-Aldrich) aqueous solution. Analogous synthesis of anhydrous dl-tartaric acid and sodium hydroxide yielded colorless prismatic crystals of dl-NaTa·H2O. To circumvent the possible persistence and nucleation of metastable forms at high pressure, single crystals of NaTa·H2O were grown in situ under isothermal and isochoric conditions in a Merrill–Bassett diamond-anvil cell (DAC).

The compression of d-NaTa·H2O and dl-NaTa·H2O forms α and β and their structures were determined by single-crystal X-ray diffraction (see the Supporting Information). High-pressure isochoric crystallizations were performed in a DAC (Figure 2). The products of recrystallizations from dl-NaTa·H2O solutions at 4.7 GPa were identified visually (Figure 2) and by single-crystal or powder X-ray diffraction. Experimental details are given in the Supporting Information.

Figure 2.

Figure 2

Open in a new tab

Isochoric growth of single crystals of (a–c) α-dl-NaTa·H2O and (d–f) β-dl-NaTa·H2O from a methanol/water mixture (2:1) at (a) 383, (b) 363, (c) and 296 K at 1.05 GPa and (d) 383, (e) 373, and (f) 296 K at 1.10 GPa. Irregular ruby chips were placed in the DAC chamber for pressure calibration.

The molecular volume of polymorph β-dl-NaTa·H2O is intermediate between those of α-dl-NaTa·H2O and d-NaTa·H2O (Figure 3). Thus, both racemate enantiomer pairs, α-dl-NaTa·H2O versus d-NaTa·H2O and β-dl-NaTa·H2O versus d-NaTa·H2O, are exempt from Wallach’s rule. The compression of the molecular volume of racemates α and β shows that above 0.4 and 0.3 GPa, respectively, their densities become higher than the ambient-pressure density of d-NaTa·H2O. However, NaTa·H2O continues to preferentially crystallize as a racemate, and single crystals of racemate α were grown up to 1.41 GPa and those of racemate β up to 1.10 GPa. Their density increased to 1.952 and 1.981 g cm–3, respectively, in both cases much higher than the density of d-NaTa·H2O at 0.10 MPa (1.892 g cm–3).

Figure 3.

Figure 3

Open in a new tab

Pressure dependence of the molecular volume (V/Z) in α-dl-NaTa·H2O (red triangles), β-dl-NaTa·H2O (blue), and d-NaTa·H2O (green). The lines represent the Birch–Murnaghan equation-of-state fits. The ΔV values are given at 0.1 MPa and 1.0 GPa.

At ∼0.50 GPa, the densities of racemates α- and β-dl-NaTa·H2O become equal. Furthermore, up to 4.70 GPa, only α-dl-NaTa·H2O was detected by X-ray powder diffraction, even when the powder was recrystallized in situ in the DAC. We also performed high-pressure recrystallizations not followed by X-ray diffraction measurements, as the α-dl, β-dl, and d forms can be distinguished by their crystal habits (Figure 2). In all of these experiments dl-NaTa·H2O preferentially crystallized in the racemic forms and no conglomerate of enantiomers was ever obtained. This behavior, that the less dense racemates spontaneously crystallize under high pressure instead of resolving into the denser conglomerate, which would reduce the pressure in the DAC chamber, appeared to be inconsistent with Le Chatelier’s principle.

In principle, the stability of phases depends on the value of Gibbs free energy G

graphic file with name ol2c03747_m001.jpg 1

where internal energy U, entropy S, and volume V depend on pressure p and temperature T. When the S changes are neglected under isothermal conditions (ΔT = 0 K), the free energy change would be equal to the work performed on the system by pressure:

graphic file with name ol2c03747_m002.jpg 2

where a superscript “o” denotes the ambient (standard) conditions and a subscript “i” denotes either the racemate (r) or enantiomers d and l (to simplify these free energy considerations, racemate polymorphs α and β have been neglected); the lower integration range of atmospheric pressure (0.1 MPa) has been rounded to 0 GPa. Equation 2 can be rewritten in the form

graphic file with name ol2c03747_m003.jpg 3

where Inline graphic. For enantiomers, it becomes

graphic file with name ol2c03747_m005.jpg 4

and for the racemate, which is a two-component mixture:

graphic file with name ol2c03747_m006.jpg 5

where R is the gas constant. The Gibbs free enthalpy of the enantiomer resolution process, ΔGs = GD – Gr can be calculated as

graphic file with name ol2c03747_m007.jpg

which can be shortened to (cf. the Supporting Information):

graphic file with name ol2c03747_m008.jpg 6

where a superscript “y” extends to the standard conditions (at y = o) to high pressure. The entropy of mixing two components, RT ln 2 = 1.706 kJ mol–1 at 296 K, is always unfavorable for the separation. The work component 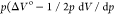Inline graphic) is negative, favoring the separation by −1.1 kJ mol–1 for α-dl-NaTa·H2O and by −2.0 kJ mol–1 for β-dl-NaTa·H2O at 1.0 GPa (Figure 4a). Component −TΔS° involving configurational entropy can be assessed from atomic displacements and interatomic interactions in the structure.22−24

Figure 4.

Figure 4

Open in a new tab

(a) Work contribution pΔV to the Gibbs free energy (eq 1) of compressed d-NaTa·H2O (green), α-dl-NaTa·H2O (red), and β-dl-NaTa·H2O (blue). (b) Calculated potential energy of Ta– conformers. (c) Electrostatic potential of Coulomb interactions (Epel) of the Na+ cation and its coordinating oxygen atom. The net atomic charges of oxygen atoms have been calculated by Gaussian25 at the B3LYP/6-311+2G(d,p) level of theory.

There are no disorder or significant differences in the amplitudes of thermal vibrations among the d-, α-dl-, and β-dl-NaTa·H2O structures; hence, the TΔS difference can be roughly estimated as a few kilojoules per mole in magnitude.

The internal energy difference ΔU° among the d-, α-dl-, and β-dl-NaTa·H2O crystals can be decomposed into (i) the energy of Ta– conformers, (ii) the energy of Coulomb interactions between Na+ and oxygen ligands, and (iii) other interactions. We have calculated the conformational component (i) of ΔU° of the Ta– anions with their torsion angles fixed to the values present in the crystal by Gaussian25 optimization at the B3LYP/6-311++G(d,p) level of theory. According to these results (Figure 4b and Figure S7), the conformer in α-dl-NaTa·H2O at 0.1 MPa is nearly 22.6 kJ mol–1 more favored than that in d-NaTa·H2O; the conformer in β-dl-NaTa·H2O is nearly 22.0 kJ mol–1 more stable than that in d-NaTa·H2O. The pressure gradually increases these differences (Figure 4b). Likewise, the energy of electrostatic forces between Na+ and its oxygen ligands in α-dl-NaTa·H2O is nearly 22.5 kJ mol–1 more favorable than in d-NaTa·H2O, and this energy difference decreases to 18 kJ mol–1 at 1.0 GPa (Figure 4c). The most favorable Na+ coordination in β-dl-NaTa·H2O remains ∼26 kJ mol–1 lower over the entire pressure range (Figure 4c). Thus, the Gibbs free energy remains by and large favorable for the racemates, despite the density of d-NaTa·H2O remaining the highest.

To correlate the density with the crystal structures, we compare the shortest intermolecular distances in the structures of α-dl-NaTa·H2O versus d-NaTa·H2O (red points) and β-dl-NaTa·H2O versus d-NaTa·H2O (blue points) in a distance–distance (d–d) plot in Figure 5.26 The d–d plot is divided into two parts by the diagonal y = x; the points representing the corresponding distances shorter in the racemates lie below the line, and those shorter in the enantiomorph lie above.

Figure 5.

Figure 5

Open in a new tab

Distance–distance (d–d) plot comparing the d-NaTa·H2O structure with those of α-dl-NaTa·H2O (red symbols) and β-dl-NaTa·H2O (blue symbols) racemates, all at 296 K and 0.1 MPa. The analogous d–d plots for the structures at 0.5 and 1.0 GPa are presented in Figures S3 and S4. The dashed line indicates equal distances. Types of contacts are differentiated by symbol shapes, as described in the legend; letter w indicates the water atoms.

The contacts shorter than 3.0 Å involve Na+ cations and their oxygen ligands, as well as H···H, H···O, and O···O contacts. There is a clear difference between the coordination of Na+ cations in the racemates and enantiomorph. In the enantiomorph, the coordination of Na+ is 8-fold and that in both racemates is 7-fold. In d-NaTa·H2O, one of the eight oxygen atoms coordinating the Na+ cation is significantly more distant, at 2.83 Å, than the other seven, all closer than 2.70 Å. In both racemates, all seven coordinating oxygen atoms are <2.70 Å from Na+, six of them are significantly closer to Na+ than those short contacts in d-NaTa·H2O, and only one in α-dl-NaTa·H2O and one in β-dl-NaTa·H2O are slightly more distant. This is consistent with the Coulomb energy calculation showing that the distribution of eight oxygen atoms around Na+ in d-NaTa·H2O is overcrowded, while the 7-fold Na+ coordination in the racemates is more energetically stable.

The shortest of the OH···O hydrogen bonds are these involving water hydrogen atoms (Hw). In β-dl-NaTa·H2O, both Ow–Hw···O hydrogen bonds are shorter than the Hw bonds in d-NaTa·H2O. In α-dl-NaTa·H2O, one of the Hw···O hydrogen bonds is slightly longer and one Hw···O bond slightly shorter than the corresponding bonds in d-NaTa·H2O. The water molecules are Hw donors in H-bonds to carboxyl groups. The next shortest hydrogen bonds in racemates α and β involve the hydroxyl groups. However, it is characteristic of d-NaTa·H2O that hydroxyl group O(3)H(31) does not form intermolecular H-bonds, but a tandem-like weak intramolecular H-bond to hydroxyl O(2)H(21). Therefore, the d-NaTa·H2O anion is strained in an unfavorable conformation, and one of its hydroxyl groups does not form short H-bonds; in the racemates, both hydroxyls are involved in short H-bonds (see the Supporting Information). Of six O···O distances shorter than 3.0 Å, four are shorter in the racemates and only two in the enantiomorph. However, in racemates, all of the relevant H···O distances are shorter and O–H···O angles are closer to 180°, which indicates energetically more favorable H-bonds. This shows that the directional intermolecular contacts are on average shorter in racemates α and β than in d-NaTa·H2O. The lower density of the racemates results from their less compact crystal packing, in a similar mode as ice is less dense than water. In other words, the shorter H-bonds between energetically more favored conformers in the racemates require some more space between structural units than the weaker H-bonds in enantiomer d-NaTa·H2O.

We can conclude that despite the significantly lower density of dl-NaTa·H2O polymorphs α and β, their high-pressure recrystallizations do not resolve the enantiomers. This strong preference for the racemates is due to the considerable internal energy contributions to the Gibbs free energy of strong directional cohesion forces and the conformational energy of Ta– anions, which are much larger than work contribution pΔV alone. It should be stressed that our case study of NaTa·H2O does not exclude the possibility of resolving some racemates into enantiomers by changing the pressure conditions of crystallizations, similarly as this can be done for a few well-known compounds resolved by varying the temperature conditions of recrystallizations.13 The work contribution is one of several components of the Gibbs free energy. We have evaluated these contributions for NaTa·H2O, which explains why in this case the density difference between enantiomers and the racemate is not sufficient for inducing the spontaneous resolution of enantiomers by high-pressure crystallization. Although several case studies of the effect of pressure on conglomerates did not achieve their transformation into racemates, either,27,28 the successful resolution by recrystallizations under either high-temperature (e.g., 1,1′-binaphthy,29 diazodicarboxylic acid,30 histidine hydrochloride,31 dilactyldiamide,32,33 and ammonium malate34,35) or low-temperature (e.g., Pasteur’s salt36 and phenylglycine sulfate37) conditions shows that the thermodynamic conditions can be decisive for the obtained resolution or racemate crystallization. Most recently, the low-density polymorphs of dl-menthol and bis-3-nitrophenyl disulfide obtained from high-pressure crystallizations38 illustrate the complex interplay between thermodynamic conditions and crystal structures. We can envision that the understanding of these relations will be employed for efficiently resolving enantiomers by manipulating the thermodynamic conditions of crystallization. This case study shows that the thermodynamic analysis is fully consistent with the in situ crystallizations of dl-NaTa·H2O under varied thermodynamic conditions.

Acknowledgments

The authors are grateful to Prof. Zofia Szafran, a professor emeritus of the Faculty of Chemistry, Adam Mickiewicz University, for her help in synthesizing dl-NaTa·H2O.

Data Availability Statement

The data underlying this study are available in the published article and its Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.orglett.2c03747.

  • Experimental procedures, density of compressed enantiomer d-NaTa·H2O and racemates α and β, crystallographic information as a function of pressure, molecular and structural information, theoretical calculations, and thermodynamics, via formula derivations from the Gibbs free energy (PDF)

The authors declare no competing financial interest.

Supplementary Material

ol2c03747_si_001.pdf (844.4KB, pdf)

References

  1. Flack H. D. Louis Pasteur’s discovery of molecular chirality and spontaneous resolution in 1848, together with a complete review of his crystallographic and chemical work. Acta Crystallogr., Sect. A 2009, 65, 371–389. 10.1107/S0108767309024088. [DOI] [PubMed] [Google Scholar]
  2. Kostyanovsky R. G. Louis Pasteur did it for us especially. Mendellev Communications 2003, 13, 85–90. 10.1070/MC2003v013n03ABEH001828. [DOI] [Google Scholar]
  3. Derewenda Z. S. On wine, chirality and crystallography. Acta Crystallogr., Sect. A 2008, 64, 246–258. 10.1107/S0108767307054293. [DOI] [PubMed] [Google Scholar]
  4. Gal J. The discovery of biological enantioselectivity: Louis Pasteur and the fermentation of tartaric acid, 1857—A review and analysis 150 yr later. Chirality 2008, 20, 5–19. 10.1002/chir.20494. [DOI] [PubMed] [Google Scholar]
  5. Eliel E. L.; Wilen S. H.; Mander L. N.. The Stereochemistry of Organic Compounds; John Wiley & Sons: New York, 1994; pp 153–464. [Google Scholar]
  6. Wallach O. Zur Kenntniss der Terpene und der ätherischen Oele. Liebigs Ann. Chem. 1895, 286, 90–118. 10.1002/jlac.18952860105. [DOI] [Google Scholar]
  7. Cai W.; Marciniak J.; Andrzejewski M.; Katrusiak A. Pressure Effect on d,l-Mandelic Acid Racemate Crystallization. J. Phys. Chem. C 2013, 117, 7279–7285. 10.1021/jp401626a. [DOI] [Google Scholar]
  8. Marciniak J.; Andrzejewski M.; Cai W.; Katrusiak A. Wallach’s Rule Enforced by Pressure in Mandelic Acid. J. Phys. Chem. C 2014, 118, 4309–4313. 10.1021/jp411738p. [DOI] [Google Scholar]
  9. Brock C. P.; Schweizer W. B.; Dunitz J. D. On the validity of Wallach’s rule: on the density and stability of racemic crystals compared with their chiral counterparts. J. Am. Chem. Soc. 1991, 113, 9811–9820. 10.1021/ja00026a015. [DOI] [Google Scholar]
  10. Friščić T.; Fábián L.; Burley J. C.; Reid D. G.; Duer M. J.; Jones W. Exploring the relationship between cocrystal stability and symmetry: is Wallach’s rule applicable to multi-component solids?. Chem. Commun. 2008, 1644–1646. 10.1039/b717532a. [DOI] [PubMed] [Google Scholar]
  11. Roszak K.; Katrusiak A. High-pressure and temperature dependence of the spontaneous resolution of 1,1′-binaphthyl enantiomers. Phys. Chem. Chem. Phys. 2018, 20, 5305–5311. 10.1039/C7CP07234A. [DOI] [PubMed] [Google Scholar]
  12. Machalska E.; Zając G.; Wierzba A.; Kapitan J.; Andruniów T.; Spiegel M.; Gryko D.; Bour P.; Barańska M. Recognition of the True and false Resonance Raman Optical Activity. Angew. Chem., Int. Ed. 2021, 60, 21205–21210. 10.1002/anie.202107600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jacques J.; Collet A.; Wilen S. H.. Enantiomers, Racemates and Resolutions; Krieger Publishing Co.: Malabar, FL, 1981; pp 23–31, 131–147, 203–207. [Google Scholar]
  14. Rietveld I. B.; Barrio M.; Tamarit J.-L.; Do B.; Céolin R. Enantiomer Resolution by Pressure Increase: Inferences from Experimental and Topological Results for the Binary Enantiomer System (R)- and (S)-Mandelic Acid. J. Phys. Chem. B 2011, 115, 14698–14703. 10.1021/jp209328d. [DOI] [PubMed] [Google Scholar]
  15. Collet A.; Vigne-Maeder F. On The Increase of The Occurrence of Spontaneous Resolution Due To The Crystallization of Racemates Under High-Pressure. New J. Chem. 1995, 19, 877–879. [Google Scholar]
  16. Zholanov G. S.; Umanskii M. M.; Varfolomeeva L. A.; Ezhkova Z. I.; Zolina Z. K. NHLiC4H406·H20, NaHC4H406·H2O and (NH4)2C4H406. Crystallogr. Rep. 1956, 1, 210. [Google Scholar]
  17. Bott R. C.; Sagatys D. S.; Lynch D. E.; Smith G.; Kennard C. H. L. Structure of sodium hydrogen (+)-tartrate monohydrate. Acta Crystallogr. Sect. C 1993, 49, 1150–1152. 10.1107/S0108270192012605. [DOI] [Google Scholar]
  18. Kubozono Y.; Hirano A.; Nagasawa S.; Maeda H.; Kashino S. Structures of Sodium Hydrogen L-Tartrate Monohydrate and Potassium Hydrogen L-Tartrate. Bull. Chem. Soc. Jpn. 1993, 66, 2166–2173. 10.1246/bcsj.66.2166. [DOI] [Google Scholar]
  19. Al-Dajani M. T. M.; Abdallah H. H.; Mohamed N.; Quah C. K.; Fun H.-K. Monoclinic polymorph of poly[aqua(μ4-hydrogen tartrato)sodium]. Acta Cystallogr., Sect. E 2010, 66, m138–m139. 10.1107/S1600536810000681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gelbrich T.; Threlfall T. L.; Hursthouse M. B. Interplay between hydrogen bonding and metal coordination in alkali metal tartrates and hydrogen tartrates. CrystEngComm 2014, 16, 6159–6169. 10.1039/C4CE00291A. [DOI] [Google Scholar]
  21. Titaeva E. K.; Somov N. V.; Portnov V. N.; Titaev D. N. Crystal structure of monobasic sodium tartrate monohydrate. Crystallography Reports 2015, 60, 72–74. 10.1134/S1063774515010265. [DOI] [Google Scholar]
  22. Madsen A.Ø.; Larsen S. Insight into Solid-State Entropy from Diffraction Data. Angew. Chem., Int. Ed. 2007, 46, 8609–8613. 10.1002/anie.200702423. [DOI] [PubMed] [Google Scholar]
  23. Madsen A.Ø.; Mattson R.; Larsen S. Understanding Thermodynamic Properties at the Molecular Level: Multiple Temperature Charge Density Study of Ribitol and Xylitol. J. Phys. Chem. A 2011, 115, 7794–7804. 10.1021/jp202411n. [DOI] [PubMed] [Google Scholar]
  24. Kofoed P. M.; Hoser A. A.; Diness F.; Capelli S. C.; Madsen A.Ø. X-ray diffraction data as a source of the vibrational free-energy contribution in polymorphic systems. IUCrJ 2019, 6, 558–571. 10.1107/S2052252519003014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; et al. Gaussian 03, rev. C.02; Gaussian, Inc.: Wallingford, CT, 2004.
  26. Dziubek K. F.; Katrusiak A. Quantitative Comparison of Structures. Z. Kristallogr. 2004, 219, 1–11. 10.1524/zkri.219.1.1.25396. [DOI] [Google Scholar]
  27. Cai W.; Katrusiak A. Enantiomeric crystallization of (±)-trans-1, 2-diaminocyclohexane under pressure. CrystEngComm 2011, 13, 6742–6746. 10.1039/c1ce05553d. [DOI] [Google Scholar]
  28. Podsiadło M.; Patyk E.; Katrusiak A. Chiral Aggregation Hierarchy in High-Pressure Resolved 2-Butanol and 2,3-Butanediol. CrystEngComm 2012, 14, 6419–6423. 10.1039/c2ce25372k. [DOI] [Google Scholar]
  29. Wilson K. R.; Pincock R. E. Thermally induced resolution of racemic 1,1’- binaphthyl in the solid state. J. Am. Chem. Soc. 1975, 97, 1474–1478. 10.1021/ja00839a033. [DOI] [Google Scholar]
  30. Labianca D. A. Resolution of (±)-4, 4’-azobis-4-cyanopentanoic acid by preferential fractional crystallization of the (+)-isomer: A chance discovery. J. Chem. Educ. 1975, 52, 156. 10.1021/ed052p156.1. [DOI] [Google Scholar]
  31. Jacques J.; Gabard J. Étude des mélanges d’antipodes optiques. III. Diagrammes de solubilité pour les divers types de racémiques. Bull. Soc. Chim. Fr. 1972, 342–350. [Google Scholar]
  32. Vièles P. Sur le dédoublement spontané de la dilactyldiamide racémique en solution aqueus. C.R. Hebd. Seances Acad. Sci. 1934, 198, 2102–2104. [Google Scholar]
  33. Vièles P. Contribution à l’ étude des acides dilactyliques. Ann. Chim. (Paris) 1935, 3, 143–225. [Google Scholar]
  34. Kenrick F. B. Die racemische umwandlung des ammoniumbimalats. Ber. Dtsch. Chem. Ges. 1897, 30, 1749–1757. 10.1002/cber.189703002108. [DOI] [Google Scholar]
  35. van’t Hoff J. H.; Dawson H. M. The racemic transformation of ammonium bimalate. Ber. Dtsch. Chem. Ges. 1898, 31, 528. 10.1002/cber.189803101110. [DOI] [Google Scholar]
  36. van’t Hoff J. H.; Goldschmidt H.; Jorissen W. P. Über die spaltung der traubensäure und das racemat von scacchi. Z. Phys. Chem. 1895, 17U, 49–61. 10.1515/zpch-1895-1704. [DOI] [Google Scholar]
  37. Suiraiwa T.; Ikawa A.; Fujimoto K.; Iwafuji K.; Kurokawa H. Racemic structure of dl-alpha phenylglycine sulfate. Nippon Kagaku Kaishi 1984, 5, 764–768. 10.1246/nikkashi.1984.764. [DOI] [Google Scholar]
  38. Sobczak S.; Ratajczyk P.; Katrusiak A. High-pressure Nucleation of Low-Density Polymorphs. Chem. - Eur. J. 2021, 27, 7069–7073. 10.1002/chem.202005121. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ol2c03747_si_001.pdf (844.4KB, pdf)

Data Availability Statement

The data underlying this study are available in the published article and its Supporting Information.

Articles from Organic Letters are provided here courtesy of American Chemical Society

RESOURCES