Abstract
A distinctive feature of this review is a critical analysis of methods and results of measurements of the optical properties of tissues in a wide spectral range from deep UV to terahertz waves. Much attention is paid to measurements of the refractive index of biological tissues and liquids, the knowledge of which is necessary for the effective application of many methods of optical imaging and diagnostics. The optical parameters of healthy and pathological tissues are presented, and the reasons for their differences are discussed, which is important for the discrimination of pathologies and the demarcation of their boundaries. When considering the interaction of terahertz radiation with tissues, the concept of an effective medium is discussed, and relaxation models of the effective optical properties of tissues are presented. Attention is drawn to the manifestation of the scattering properties of tissues in the THz range and the problems of measuring the optical properties of tissues in this range are discussed. In conclusion, a method for the dynamic analysis of the optical properties of tissues under optical clearing using an application of immersion agents is presented. The main mechanisms and technologies of optical clearing, as well as examples of the successful application for differentiation of healthy and pathological tissues, are analyzed.
1. Introduction
The measurement of tissue optical properties in a wide spectral range can be made using different techniques, which basically are classified into two main groups: the one that involves inverse simulations and the one that involves direct calculations from experimental data. For the techniques that involve inverse simulations to solve the radiation transfer equation, some computer codes, based on the Kubelka-Munk, the Monte Carlo, and the Adding-Doubling algorithms are available for immediate use or can easily be adapted to estimate the optical properties of tissues [1–7]. These algorithms usually estimate a set of two or three optical properties for a single wavelength, based on the available optical measurements that were acquired from the tissue under study, such as the refractive index (RI), the total transmittance (Tt), the total reflectance (Rt) and the collimated transmittance (Tc) [3]. With the objective of obtaining the broadband spectral optical properties of a tissue, individual simulations at discrete wavelengths within the desired spectral range are necessary, so that the estimated values can be interpolated with appropriate curves [6]. Such task is time and computer demanding, not allowing for a fast determination of the broadband spectra of tissue optical properties [8].
A faster alternative to the simulation methods, which is based on the diffusion approximation [8], is possible through direct calculations, if spectral measurements are available. Considering ex vivo tissue samples from which Tt, Rt and Tc spectra were measured, the calculation of most of the optical properties can be performed using some equations based on the diffusion approximation [8–10].
Due to a great variety of biomedical applications in the near-infrared (NIR), quantification of optical properties of tissues in this wavelength range was of great priority in the last two decades [11–17]. Time resolved techniques allowing for measuring optical properties rather fast and in backscattering mode suitable for in vivo estimations are also well-developed [18–20]. Real-time wide-field and high-quality single snapshot imaging of optical properties of tissues can be provided using a spatial frequency domain technique which principles, applications, and perspectives are discussed in literature [21–23]. All these technologies for optical properties evaluation are prospective to use in differentiation of various pathologies in ex vivo or in vivo studies, and in surgery and therapy guidance [8–10,24–32], in particular, for estimation of pigment accumulation in brain cortex [8,9] and pancreas [10] in rabbits, and colorectal cancer tissue in humans [26], for prognosis in gastroenterology [24,25], for characterization of brain tissues at the different stages of glioma development in rats [27], for differentiation of healthy and tumorous brain tissue in humans [28], for characterization of obesity in humans [29], for skin condition diagnosis in the clinical trials [30], for surgery guidance using a single-fiber diffuse reflectance spectroscopy and spatial frequency domain imaging [31], and during interstitial photodynamic therapy and photoimmunotherapy of head and neck squamous cell cancer [32].
During the past few decades, an increasing attention is paid to biomedical applications of Terahertz (THz) radiation, with the frequencies of ≈0.1–3.0 THz, or the free-space wavelengths of ≈3 mm–100 µm [33–38]. This is driven by peculiarities of THz-wave – biological tissue interactions and rapid progress in THz technology [39–44]. THz radiation is non-ionizing in nature, and, thus, low-power THz beams are reportedly harmless to living organisms [45]. THz waves are strongly absorbed by water molecules, including the tissue water in free or bound states. High content of water in majority of hydrated biological tissues limits the depth of THz wave penetration into them by hundreds or even tens of microns, depending on the electromagnetic-wave frequency and the tissue type [33,34]. On the one hand, this limits capabilities of THz diagnosis by probing only the superficial layers of hydrated biological tissues in vivo or freshly-excised tissues ex vivo, while only the reflection-mode configurations of THz measurements are reliable for such studies [46,47]. On the other hand, high sensitivity of THz radiation to tissue water makes it attractive for the label-free medical diagnosis, where water plays a role of main endogenous marker of pathology [33,34].
Сapabilities of THz spectroscopy and imaging in label-free early noninvasive, least-invasive, and intraoperative diagnosis of malignant and benign neoplasms with different nosologies and localizations [34,36,55,37,48–54], sensing of glycated tissues and blood in the context of diabetes diagnosis [56–59], determining the degree of traumatic injuries [60–63], hydration levels [64–67], and viability [68] of tissues have been vigorously explored. Along with the diagnostic applications, THz technology holds strong potential in therapeutics [45,69,70], for example, in nonthermal regulation in expression of genes associated with cancer and inflammatory diseases [71], or manipulation of cancer DNA methylation [72,73].
Thus, a critical analysis of the methods and results of measurements of the optical properties of tissues in a wide spectral range from deep-ultraviolet (UV) to the terahertz range is topical. Since knowledge of the refractive index in a wide range of wavelengths is critical for the application of many methods of optical imaging and diagnostics, much attention is paid to this parameter in the review. It is also important to present and discuss the optical properties of healthy and pathological tissues, which are used in medical diagnostics, including demarcating the boundaries of pathology. When considering the interaction of terahertz radiation with tissues, the concept of an effective medium will be used and relaxation models will be presented to determine the effective optical properties of tissues. It seems important to discuss the prospects for the method of dynamic analysis of the optical properties of tissues with optical clearing using immersion agents, including for more reliable differentiation of healthy and pathological tissues.
2. Measurement of tissue optical properties
2.1. General representations
Considering the total transmittance Tt and the total reflectance Rt spectra of a tissue-slab sample with uniform thickness (d), Eq. (1) allows the calculation of the absorption coefficient spectrum (µa(λ)) [9,10,26,74]:
| (1) |
Once µa(λ) is calculated, it can be used in a rearranged version of the Bouguer-Beer-Lambert equation [75–78] to calculate the scattering coefficient spectrum (µs(λ)), as follows:
| (2) |
There is no equation that allows the direct calculation of the reduced scattering coefficient (µ′s(λ)) from experimental measurements [9,10,74]. Due to this fact, and since its wavelength dependence in the spectral range between the deep-ultraviolet and the infrared is well described by a curve, whose equation accounts for a combination of the Rayleigh and Mie scattering regimes [5], the µ′s values at discrete wavelengths within that range can be estimated through inverse simulations and then fitted by a curve described as:
| (3) |
where a′ = µ′s(λ=500 nm), fRay is the Rayleigh scattering fraction and bMie is the exponent related to the mean size of the Mie scatterers [74]. The calculated µ′s(λ) can be combined with the µs(λ) obtained with Eq. (2) to calculate the scattering anisotropy factor (g), as follows [24]:
| (4) |
The RI of biological tissues, tissue components or optical clearing agents (OCAs) is traditionally measured at discrete wavelengths, using different instruments and methods. For tissues it can be measured using the total internal reflection method with different lasers with emission at discrete wavelengths within the range of interest [79], while for biological fluids or OCAs it can be measured using a multi-wavelength refractometer [80], or by using the minimum deviation angle method, also with different lasers at discrete wavelengths [81]. Once the RI of a tissue or fluid is measured for various wavelengths within a broad spectral range, the discrete experimental values are fitted with an appropriate dispersion curve, such as the Cauchy (Eq. (5)), the Conrady (Eq. (6)) or the Cornu (Eq. (7)) equations, which are described as follows [3,80,82–89]:
| (5) |
| (6) |
| (7) |
where A, B and C are the Cauchy, the Conrady or the Cornu parameters that are estimated during the fitting of the experimental data [79].
Once the broadband tissue dispersion is estimated from discrete measurements with one of the previous curves, a more realistic dispersion that contains the absorption contributions of tissue components can be calculated using the Kramers-Kronig (K-K) relations [10]. To proceed with this calculation, µa(λ) as calculated with Eq. (1), is first used in the following K-K relation to obtain the imaginary part of the broadband tissue dispersion (κtissue(λ)) [9,90,91]:
| (8) |
The real part of tissue dispersion (ntissue(λ)) can be calculated from κtissue(λ), using the following K-K relation [9,90,91]:
| (9) |
where Λ represents the integrating variable over the spectral range of interest and λ1 is a fixed wavelength that can be adjusted for a better vertical matching of the dispersion calculated with Eq. (9) to the dispersion that was previously obtained from experimental data with Eq. (5), Eq. (6) or Eq. (7) [9,10].
The mathematical formalism presented above allows to use the direct calculation approach to obtain the broadband optical properties of any ex vivo tissue, from which broadband Tt, Rt and Tc spectra can be measured. This approach, which only needs discrete simulated values for µ′s to be interpolated by Eq. (3), is a fast method that was already used for the evaluation of the broadband optical properties of some biological tissues [9,10,26,74]. Part of the results obtained in those studies are presented and discussed in the following subsections.
2.2. Absorption and scattering
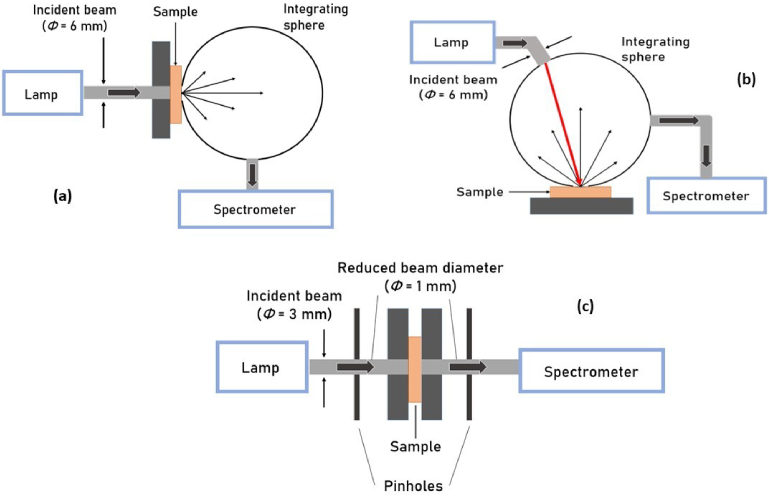
According to the direct calculation approach described above, the determination of the broadband µa and µs spectra of any particular tissue can be done through Eq. (1) and Eq. (2), provided that the Tt, Rt and Tc spectra for the same wavelength range were measured. Typical setups to perform such spectral measurements are presented in Fig. 1.
Fig. 1.
Experimental setups to measure Tt(λ) (a), Rt(λ) (b) and Tc(λ) (c). Courtesy of L. Oliveira.
In the Tt setup represented in Fig. 1(a), a pulsed high-power and broadband xenon lamp, such as the Avalight-XE-HP from Avantes™, is used to irradiate the tissue sample. The selection of such high power lamp ensures that after several reflections at the internal wall of the integrating sphere, the beam has a high signal to noise ratio, so that a reliable spectrum can be registered by the spectrometer. This lamp has an emission spectrum from 200 to 1000 nm, and its beam is delivered to the left-side of the sample through an optical fiber cable and a collimating lens, which limits the beam diameter to 6 mm. To avoid measurement contamination with the entrance of undesired light from the outside of the setup, the collimating lens is fixed inside a black plastic casing. Such casing is represented as the dark-grey rectangle on the left of the sample in Fig. 1(a). The integrating sphere used in these measurements is the AvaSphere-80-REFL from Avantes™, which has an outside cylindrical casing that perfectly fits inside the outer border of the black plastic casing on the left side of the sample. The cylindrical sphere casing and the outer border of the black plastic casing are not represented in Fig. 1(a). To perform these measurements, the tissue sample is fixed between two pinholes (ϕ = 6 mm), which are placed between the black plastic casing and the integrating sphere. The entire setup is mechanically fixed to place the sample at the sample port of the sphere without compressing it. Other methods to fix the sample at the sample port of the sphere, such as placing the sphere vertically over the sample, or through mechanically attached cuvettes are possible. With the whole setup centered with its optical axis, the beam emerging from the collimating lens irradiates the entire surface of the tissue sample, and the transmitted beam enters the integrating sphere completely. The AvaSphere-80-REFL sphere contains a baffle to shield the sample beam target area from the field of view (FOV) of the detector. Such beam that crosses the tissue sample into the inside of the integrating sphere represents the total transmitted light, which is reflected several times at the internal wall of the sphere (integration process), before being delivered to the spectrometer through another optical fiber cable [10]. The spectrometer software calculates the Tt(λ) of the tissue sample in the following way [3]:
| (10) |
where Tt-sample(λ) is the spectrum that was delivered to the spectrometer after being transmitted by the sample into the inside of the sphere and after passing through the integration process, Tt-noise(λ) is the noise spectrum that was measured with the setup in the lamp-off position and Tt-lamp(λ) is the reference spectrum of the lamp measured with the setup, but without the sample.
Considering the Rt setup represented in Fig. 1(b), the components in that setup are the same that are used in the Tt setup, but now rearranged to measure the total reflected spectrum. In this case, the light beam from the lamp enters the integrating sphere at the top, with an 8° inclination with the vertical axis of the sphere. This beam is reflected by the tissue sample into the inside of the sphere, where it will be submitted to the integration process before exiting to the spectrometer through an optical fiber cable [10]. The calculation or the Rt(λ) of the tissue sample is made by the spectrometer software in the following way [3]:
| (11) |
where Rt-sample(λ) is the spectrum that was delivered to the spectrometer after being reflected by the sample into the inside of the sphere and after passing through the integration process, Rt-noise(λ) is the noise spectrum that was measured with the setup in the lamp-off position and Rt-lamp(λ) is the reference spectrum of the lamp measured with the setup, but without the sample.
In contrast to the classical geometry of an integrating sphere, in some cases for research, for example, in vivo, a collapsible diffuse-scattering cavity of a cubic shape can be useful [92,93]. In this embodiment, the tissue sample itself or the surface of the organ can serve as one of the walls of the integrating cavity. Such a collapsible cavity also makes it possible to study the scattering properties of liquid biological materials by spraying them onto the internal walls of the cavity.
In the Tc setup, a broadband deuterium-halogen lamp, such as the Avalight-D(H)-S lamp from Avantes™, with emission between 175 and 2500 nm, is used to irradiate the tissue sample. Since in this setup the transmitted beam is directly collected after crossing a thin sample, there is no need for a high power lamp as in the measurements of Tt(λ) and Rt(λ). The beam of the Avalight-D(H)-S lamp is delivered to the left side of the sample through an optical fiber cable and a collimating lens. The collimated beam with a 3 mm diameter passes through a pinhole to decrease the beam diameter to 1 mm before irradiating the sample. On the right-side of the setup, another 1 mm pinhole collects the collimated transmitted beam to the inside of another optical fiber cable through another lens [10]. The transmitted beam is delivered to the spectrometer through the optical fiber cable, where the software calculates the Tc(λ) of the tissue sample in the following way [3]:
| (12) |
with Tc-sample(λ) representing the spectrum that was transmitted by the sample and collected by the detection optics, Tc-noise(λ) is the noise spectrum that was measured with the setup in the lamp-off position and Tc-lamp(λ) is the reference spectrum of the lamp measured with the setup, but without the sample. It should be noted that the calculated Tt(λ), Rt(λ) and Tc(λ) are characteristic of the sample and do not depend on the shape or intensity of the spectra emitted by the lamps used in these measurements, since they are normalized values (see Eqs. (11) and (12)).
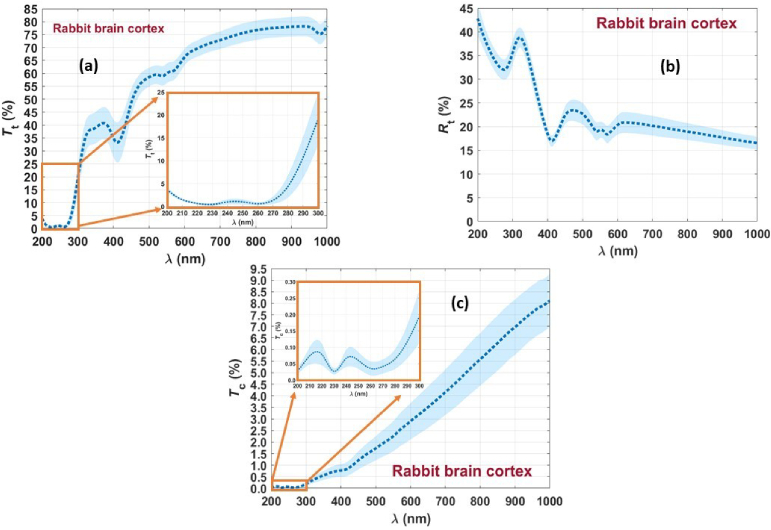
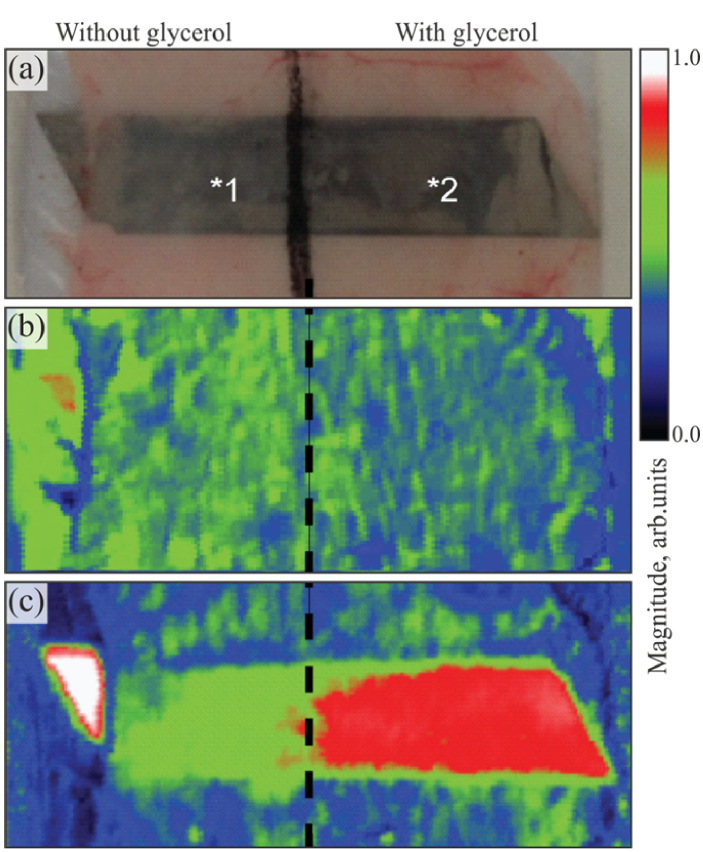
Using the setups presented in Fig. 1, several measurements were made from different tissues to calculate the µa and µs spectra of various tissues between 200 and 1000 nm. In the case of the rabbit brain cortex, 10 tissue samples were submitted to spectral measurements with all the setups presented in Fig. 1, resulting in the mean and standard deviation (SD) spectra that are presented in Fig. 2 [9]:
Fig. 2.
Mean spectra and SD of the rabbit brain cortex: Tt(λ) (a), Rt(λ) (b) and Tc(λ) (c). Figure adapted from Ref. [9], which was published under Creative Commons license, MDPI.
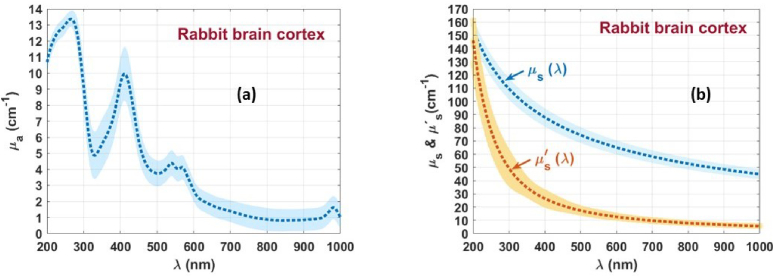
Using the individual Tt and Rt spectra that originated the graphs in Fig. 2 in Eq. (1), the 10 µa spectra for the rabbit brain cortex were calculated. By using those calculated spectra, along with the individual Tc spectra in Eq. (2), the 10 µs spectra were calculated. To obtain the µ′s spectra that correspond to the 10 tissue samples under study, inverse Adding-Doubling (IAD) simulations were performed at each 50 nm between 200 and 1000 nm. In these simulations the corresponding data from the individual Tt and Rt spectra, along with the calculated RI data [9], were used as input. The resulting set of µ′s values for each sample was fitted with a curve described by Eq. (3). Figure 3 presents the mean and SD spectra for the µa, µs and µ′s of the rabbit brain cortex [9].
Fig. 3.
Mean and SD spectra of µa(λ) (a), µs(λ) (b) and µ′s(λ) (c) of the rabbit brain cortex. Figure adapted from Ref. [9], which was published under Creative Commons license, MDPI.
The mean µa(λ) presented in Fig. 3(a) shows several absorption bands that correspond to the biological components in the brain cortex. Considering the increasing wavelength scale in that figure, the first peak in the mean µa(λ) is seen at 230 nm, which corresponds to the amino acid connections of tyrosine and tryptophan in proteins [94,95]. The brain tissues and especially the cortex contain different types of proteins, such as actin, albumin, α-tubulin, β-tubulin, neuron-specific enolase (NSE) and vimentin [96]. The occurrence of a second absorption peak at 267 nm indicates a combination of the DNA/RNA and hemoglobin bands at 260 nm and 274 nm, respectively [97]. The presence of oxygenated hemoglobin is also identified through the bands at 411 nm (Soret band) and 540/570 nm (Q bands) and the band at 980 nm indicates the presence of water [97]. The decreasing baseline observed in the µa(λ) presented in Fig. 3(a) also provides additional information. It indicates the presence of broadband absorbers, such as pigments like melanin and lipofuscin, in the brain cortex. The evaluation of the contents of such pigments will be done in section 2.4, along with the analysis of similar data for other tissues in healthy and pathological versions that presented similar baselines.
The spectra of the scattering coefficients that are presented in Fig. 3(b) also provide interesting information. The two coefficients show an exponential decreasing behavior with increasing wavelength, a dependence that is well fitted by Eq. (3) as a result of the combined Rayleigh and Mie scattering regimes that occur in biological tissues [5]. By evaluating these spectra between 200 and 1000 nm, it is possible to see that in the deep-ultraviolet µ′s(λ) ≈ µs(λ).
Similar studies have been performed with other animal and human tissues [10,26,74], where the µa(λ), µs(λ) and µ′s(λ) were calculated with the same method from the Tt, Rt and Tc spectra. The results obtained in those studies were similar to the ones presented here for the rabbit brain cortex, but since the most innovative information produced in such studies was obtained from the pigment content analysis, such results will be presented in section 2.4.
2.3. Scattering anisotropy factor
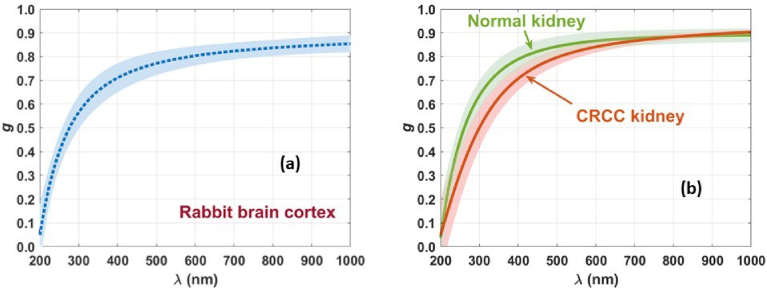
As described at the beginning of section 2, once µs(λ) and µ′s(λ) are calculated, they can be used in Eq. (4) to calculate g(λ). Using such calculation procedure, Fig. 4 presents g(λ) for the rabbit brain cortex [9], as calculated from the data in Fig. 3(b), and for the human kidney in normal and pathological (Chromophobe renal cell carcinoma – CRCC) versions [74].
Fig. 4.
Mean and SD spectra of g(λ) for the rabbit brain cortex (a), and for human normal and pathological (CRCC) kidney (b) tissues. Adapted with permission from: (a) Ref. [9], MDPI;
(b) Ref. [74], Elsevier, which were published under Creative Commons license.
All curves in Fig. 4 present the expected wavelength dependency – g increases with the wavelength due to predominant Rayleigh scattering [5,9,10,26,74,98]. In all cases represented in Fig. 4, g tends to be null close to 200 nm, increasing to nearly 0.9 at 1000 nm. Comparing between the human normal and the CRCC kidney, g(λ) provides discriminated behavior. In the case of the normal kidney, the increase in g between 200 and 350 nm is faster than the one observed for the CRCC kidney, and the linear increase for longer wavelengths (>600 nm) is higher for the CRCC kidney. Such differentiated behavior for short and long wavelengths in the CRCC tissues is certainly related to the presence of higher-dimension structures that form during cancer progression.
2.4. Healthy and pathological tissues
Pigments with broadband absorption spectra, such as melanin and lipofuscin have been reported to accumulate in biological tissues due to the aging process [99–102], but their dissimilar content in a particular tissue can be evidence of a pathology [9,26,74,103]. Both melanin and lipofuscin have a broadband absorption spectrum from the deep-UV to the NIR [10], and the combination of those spectra in appropriate proportions can be used to evaluate their contents in biological tissues, which may be correlated to the tissue aging and pathology development processes [9,26,74]. Figure 5 presents the broadband absorption spectra of melanin and lipofuscin, as retrieved from graphical data in Refs. [104] and [105], respectively.
Fig. 5.
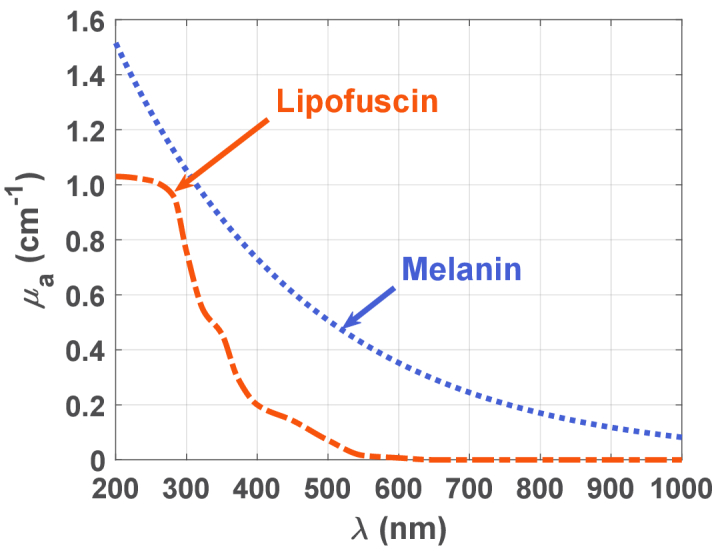
Spectral curves of µa(λ) for melanin and lipofuscin between 200 and 1000 nm. Adapted from Ref. [9], which was published under Creative Commons license, MDPI.
The curves presented in Fig. 5 show that the µa of melanin (µa-mel(λ)) decreases with increasing wavelength in the entire spectral range, while the µa of lipofuscin (µa-lip(λ)) is restricted to shorter wavelengths, presenting null values for wavelengths longer than ∼650 nm. The combination of such broadband spectra originates a decreasing baseline with increasing wavelength in the µa of various tissues, as presented in Fig. 3(a) for the rabbit brain cortex. In fact, the occurrence of such decreasing baseline in the µa(λ) of the brain cortex that is presented in Fig. 3(a) indicates that the brain cortex tissues contain these pigments [9].
Considering the brain cortex or any other tissue that presents such decreasing baseline in its µa(λ), it is possible to reconstruct it by a weighted combination of the µa-mel(λ) and the µa-lip(λ) that are presented in Fig. 5. The values of the multiplying weights can be obtained by trial-and-error until the reconstructed baseline matches the decreasing baseline that the tissue µa(λ) contains. Once the baseline reconstruction is optimized, the weights considered for the µa-mel(λ) and the µa-lip(λ) may serve as a measure of the contents of both pigments in the tissue under study. Such procedure was made in some recent studies and the retrieved pigment contents were analyzed to give information regarding the tissue aging and pathology development situation.
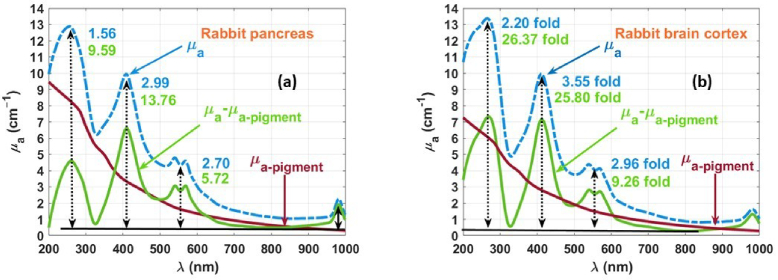
While studying the broadband optical properties of the rabbit brain cortex, the authors of Ref. [9] used the pancreas from the same animals to perform a similar study [10]. When analyzing the calculated µa(λ) of the pancreas, a similar decreasing baseline as the one observed in Fig. 3(a) was obtained. Performing a reconstruction of the baselines for the µa(λ) of the rabbit pancreas and rabbit brain cortex, these authors obtained the contents of melanin and lipofuscin in both tissues. Figure 6 presents the mean µa(λ) for these tissues, the reconstructed baselines and the µa(λ) of the tissues after subtracting the baselines.
Fig. 6.
Wavelength dependencies for µa of the rabbit pancreas (a) and rabbit brain cortex (b) before (blue-dashed line) and after (green line) subtracting the absorption of the pigments (dark-red line). Adapted with permission from: (a) Ref. [10]; (b) Ref. [9], which were published under Creative Commons license, MDPI.
A first result that is obtained with the baseline removal is that the fold-ratios calculated at the absorption bands of DNA and hemoglobin are significantly increased. As an example, the fold-ratio at the Soret band for the pancreas increased from 2.99 to 13.76. Such more realistic ratios can be considered as a measure of the contents of DNA and hemoglobin in the pancreas and brain cortex of the rabbit. The small fold-ratios presented in Fig. 6 before the baseline removal (in blue) are proof that the broadband absorption of melanin and lipofuscin was camouflaging the true content of blood and DNA in the tissues [9,10].
The graphs in Fig. 6 also show that after subtracting the reconstructed baselines, the µa(λ) of both tissues present a horizontal baseline, as it should be without the presence of the pigments. In the case of the rabbit pancreas, the reconstructed baseline (µa-pigment(λ)) was obtained as [10]:
| (13) |
The numerical values in Eq. (13) are similar one to the other, indicating that the accumulation of melanin and lipofuscin in the rabbit pancreas has occurred in approximated proportions during the aging of the pancreas tissues under study [10].
In the case of the rabbit brain cortex, the reconstructed baseline was obtained as [9]:
| (14) |
Here we see that the rabbit brain cortex contains more melanin than lipofuscin (almost 2 × more). It has been reported that lipofuscin is able to aggregate transition metals, such as iron and copper, which turn this pigment cytotoxic, leading to the oxidation of cellular components such as proteins, lipids and DNA/RNA [106]. Such cellular changes in brain tissues may be at the basis of the degeneration and death of neurons as reported in Ref. [107], and may be the primary responsible for the occurrence of stroke, Alzheimer and Parkinson diseases [108]. The excess of melanin that was obtained through Eq. (14) during the baseline reconstruction for the cortex may be associated to the neuron degeneration and death, as reported by other authors [102,103,107].
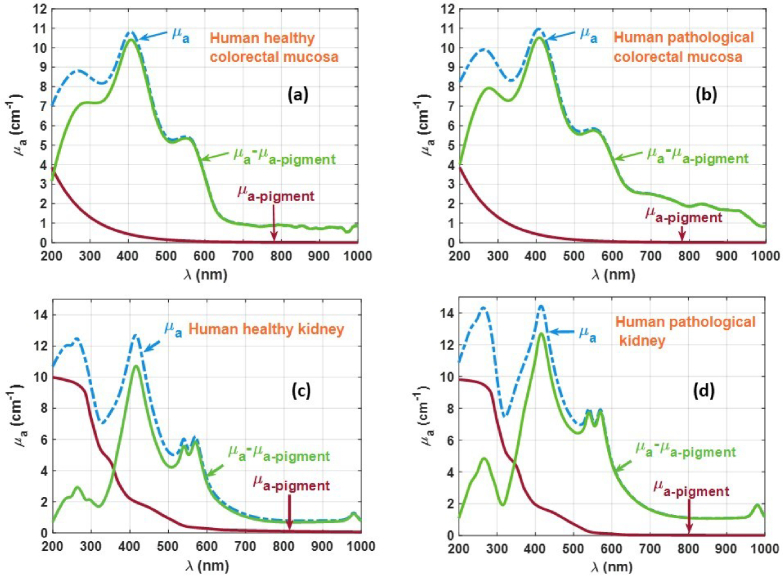
The studies that resulted in the graphs presented in Fig. 6 show that melanin and lipofuscin accumulate similarly in biological tissues as a result of the aging process, as seen in the pancreas, but differentiated accumulation of these pigments may be related to the occurrence of disease or degenerative processes, as observed for the brain cortex. With the suspicion that discriminated melanin and lipofuscin contents could also be associated with cancer diseases, the authors of Refs. [26] and [74], have used the same experimental methodology to quantify the contents of these pigments in human healthy and pathological colorectal mucosa and kidney tissues. In the case of colorectal mucosa tissues, 10 healthy samples and 10 samples with adenocarcinoma were used to measure the Tt and Rt spectra, so that the µa(λ) of both tissues could be calculated with Eq. (1) between 200 and 1000 nm [26]. The same procedure was adopted for the kidney tissues, where the pathological samples were collected from patients with a diagnosis of CRCC [74]. The baseline reconstruction for the kidney tissues was the same as described above, by combining the µa spectra of melanin and lipofuscin, as represented in Fig. 5. In the case of the colorectal mucosa, and since the study in Ref. [26] was made prior to the other studies here reported, only the absorption spectrum of lipofuscin, and as reported by Johansson [109,110] was considered in the baseline reconstruction. Although such reconstruction of the baselines for the colorectal tissues is not so accurate as the ones made for the rabbit tissues and for the human kidney tissues, it also provided differentiated results between the healthy and pathological samples. Figure 7 presents the results of those studies, including in each panel the curves for the µa(λ) of the tissue, the µa-pigment(λ) and the µa(λ) of the tissue after subtracting the baseline.
Fig. 7.
Wavelength dependencies of µa for human healthy colorectal mucosa (a), for human pathological mucosa (b), for human healthy kidney (c) and for human pathological kidney (d) before (blue-dashed line) and after (green line) subtracting the absorption of the pigments (dark-red line). Adapted with permission from: (a), (b) Ref. [26], MDPI; (c), (d) Ref. [74], Elsevier, which were published under Creative Commons license.
Although not represented in the graphs of Fig. 7, the baseline removal procedure also leaded to higher and more realistic fold-ratios at the absorption bands of DNA and hemoglobin in all tissues under study. As reported in Refs. [26] and [74], after removing the baselines, the pathological tissues were found to have more blood and DNA than the healthy tissues.
Considering the data for human colorectal mucosa tissues from the study in Ref. [26] that are presented in Fig. 7(a) and in Fig. 7(b), we see that although the absorption of melanin was not considered in the reconstruction of the baseline, it was possible to reduce the broadband contribution of lipofuscin. It is important to stress that the absorption of lipofuscin used in this study was retrieved from Ref. [110] and extended from about 475 nm to 200 nm. Such procedure is not precise, but as a first approximation, it was able to produce differentiated results between the healthy mucosa and the one with adenocarcinoma. The absorption of lipofuscin used in this study and represented in Fig. 7(a) and in Fig. 7(b) as µa-pigment(λ) is described as [26]:
| (15) |
where for the case of the healthy mucosa A equals 1, and for the case of the adenocarcinoma it equals 1.1. This means that the pathological mucosa contains 10% more lipofuscin than the healthy mucosa. Although no information about the melanin content in the healthy and pathological colorectal mucosa tissues was produced in this study, the different contents of lipofuscin seem to indicate that the content of such pigment increases with the cancer development [26].
Looking into the data for human kidney tissues that are presented in Fig. 7(c) and in Fig. 7(d), we see that by considering both the melanin and lipofuscin absorption spectra, as presented in Fig. 5 between 200 and 1000 nm, a more accurate reconstruction of the decreasing baseline is accomplished and more complete information is obtained [74]. Globally, the µa-pigment(λ) presented in the kidney graphs in Fig. 7 seem equal, but in reality they are different, since they result from different combinations of µa-mel(λ) with µa-mel(λ). For the healthy kidney, µa-pigment(λ) is described as [74]:
| (16) |
while for the CRCC kidney, µa-pigment(λ) is described as [74]:
| (17) |
Analyzing the numerical values in these equations, we see a decrease in the melanin content and an increase in the lipofuscin content from the healthy to the pathological kidney. These results seem to indicate a conversion of about 83% of melanin into lipofuscin when cancer develops, but the mechanisms of that hypothetical conversion have not been described in literature. A different explanation has been presented by Warburton et al. for the eye tissues during the formation of age-related macular degeneration (AMD) [111]. In that study, the authors refer that melanolipofuscin granules are formed as a result of AMD. Such granules consist on melanin surrounded by a lipofuscin shell, as referred by Feeney [112]. Due to the three-dimensional (3D) geometry of these granules, when light is used to perform spectroscopy measurements as those reported in Ref. [74] to obtain the spectral optical properties of the human kidney tissues, it is easier to see the response of the lipofuscin shell structure than the response of the melanin inside the shell in the calculated µa(λ) of the CRCC tissues. In face of the more precise study performed in the human kidney tissues [74], the results obtained for the human colorectal mucosa tissues can also be associated with the formation of melanolipofucin granules when cancer develops.
Considering that these results were obtained for fully developed adenocarcinoma in the colorectal tissues and for fully developed CRCC in the kidney tissues, it would be interesting to conduct similar studies using tissues in different stages of development of these or other cancer diseases. Those studies could be used to establish a relation between the content of melanolipofuscin granules and the cancer stage of development. Furthermore, if diffuse reflectance spectra could be measured from those tissues, the application of machine learning algorithms could reconstruct the µa(λ) of the tissues, allowing the analysis of the pigment contents from a minimally invasive perspective, as already performed in the study of Ref. [113].
Although in the previous sections we have reviewed the measurement of broadband spectral optical properties of biological tissues using the direct calculation method, the same evaluation in the UV range needs further exploration. In the following section we will summarize what has already been done to evaluate the optical properties of tissues in the UV range and will present some directions for further investigation.
2.5. UV wavelength range
The UV is a particular range of the electromagnetic spectrum where the optical properties of biological tissues are less studied. Various Biophotonics applications make use of this light though, and others may be developed in the future. One of the existing techniques that makes use of light in this spectral range is the fluorescence microscopy imaging with UV light stimulation. In such technique, the stimulation of specific tissue chromophores with light between 200 and 300 nm leads to the creation of fluorescence histological images with high resolution for diagnostic procedures [114]. Such procedure is fast and the generated images resemble the ones obtained with conventional haematoxylin and eosin histology techniques [114–116]. A particular study with this technique reports on the use of terbium ions as RNA labeling probes and a combination of terbium ions with DNA specific dyes to produce optical sectioning of unsliced tissues [117]. Such procedure allowed to distinguish nucleolus, nucleoplasm and cytoplasm in fluorescence images created after excitation with light between 250 and 300 nm.
Another application that makes use of UV light is the deep-UV Raman spectroscopy. Due to the combination of short wavelengths with electronic resonant enhancement with many biological molecules, the deep-UV Raman signal is several orders of magnitude stronger than the visible Raman signal. In addition, since biomolecules have a fluorescent emission spectrum that starts at 265 nm or at longer wavelengths, there is no significant fluorescent contamination in the deep-UV Raman measurements [118]. The application of deep-UV Raman spectroscopy is useful for the identification of pesticides in agricultural products, to study human bone fragility, protein structure or DNA aging and its conformity in a nucleus [119,120].
The photoacoustic imaging is another technique that allows the acquisition of ultrasound images that are generated from different tissue depths after excitation with a light source. In this technique a short-pulsed or time-modulated light is delivered to the tissue to propagate diffusively inside. Exogenous or endogenous tissue chromophores, such as DNA/RNA, oxy- and deoxy-hemoglobin, lipids or melanin absorb part of the energy from the diffused light within the tissue, creating a local temperature rise, and subsequent generation of broadband ultrasound waves in the MHz frequency range [121]. The absorption spectra of the above-mentioned endogenous chromophores are well known [97], where DNA, RNA, oxy- and deoxy-hemoglobin have absorption bands in the UV range. Melanin also has an absorption spectrum that presents increasing magnitude with decreasing wavelength within the UV range, as presented in Fig. 5. Multispectral photoacoustic imaging can be used to evaluate the content of these chromophores in a tissue through the selection of the excitation source wavelength [121], but new low-expensive lasers or light emitting diodes (LEDs) with emission at those wavelengths are necessary for clinical and healthcare application of the results already produced by the research in the field of photoacoustic imaging.
Therapeutic applications of UV light are also possible. The most common application is the use of UV light to treat or regulate skin diseases such as vitiligo, scleroderma, psoriasis or atopic dermatitis [122]. The so-called UV phototherapy works by regulation of the erythema and inflammation that occur with the above-mentioned skin conditions, and induction of pathogenic cells apoptosis in the skin. The therapeutic action of the UV light in these skin conditions is complex, consisting on simultaneous events that include trafficking of antigen cells in the skin and immediate transcriptional changes in keratinocytes, in immune cells and in pigment cells. Such set of events produce a fast transformation of the microenvironment in the skin that was exposed to UV light [122], which leads to temporary or definite control of the disease.
UV light can also be used to difficult the occurrence of melanoma in the skin. A recent study reported that the collagen and fibroblast structures in the skin degrade with the application of UV radiation [123]. The same study reported that melanomas arising at the skin area where collagen degradation has occurred become less invasive, but melanoma-associated fibroblasts can restore the melanoma invasion through the increasing of collagen synthesis. Indeed, interesting results were presented in this study, but further investigation should be done in this field to search for further mechanisms that prevent the occurrence of melanoma.
An interesting treatment application with UV light was recently reported for the SARS-CoV-2 inactivation [124]. With the emergence of the worldwide COVID-19 pandemic various research fields have developed efforts to fight this disease. Biophotonics was not an exception, and the development of a prototype that uses LED light at 275 nm was developed, tested and validated, presenting an effectiveness in the virus inactivation of 99.9% after 1 min exposure to a light dose of 83.1 J/m2 [124].
According to the discussion presented in the previous paragraphs, the measurements of the optical properties of biological tissues, tissue components and OCAs in the UV range is highly necessary for the optimization of the existing methods and development of new ones that use UV light. Some studies regarding the measurement of tissues optical properties in broad spectral range, which includes de UV, were already discussed in the previous sections. In those studies, the identification of the absorption bands of proteins at 230 nm (see Fig. 3(a)) and of DNA/RNA at 260 nm (see Fig. 6 and Fig. 7) was made. Tissues have other chromophores that present absorption bands in the UV, but the isolation of such bands from the µs spectrum of a tissue is not an easy task due to the superposition of various adjacent bands between 200 and 400 nm. Also by analyzing Fig. 3(b) we saw that at 200 nm, µs and µ′s tend to match each-other, which results in a calculated nearly null anisotropy as represented in Fig. 4.
The identification and characterization of absorption bands in the UV is useful for diagnostic procedures and for the physiological characterization of tissues, but such information can also be retrieved from measurements made during optical clearing treatments. Section 5 is dedicated to the tissue optical clearing treatments and various results regarding tissue composition and cancer discrimination that were obtained from measurements performed during optical clearing will be presented in sections 5.2 and 5.3.
3. Measurement of refractive index
3.1. Introduction
The RI is another optical property of biological tissues that needs evaluation for a broad spectral range, since tissue dispersion also provides information that can be used to characterize the RI of tissue components [125], quantify light scattering at individual wavelengths through the relative RI [126], or to differentiate pathological tissues [26,74]. There is no experimental technique that can be used to evaluate the dispersion of a tissue directly or through a direct calculation from measured spectra. Usually, the RI of tissues is measured experimentally at discrete wavelengths, using various methods [84].
3.2. Transparent tissues and bioliquids
A feature of transparent tissues and bioliquids is high, almost complete, light transmission. They include blood plasma, interstitial fluid, mucous membranes, cornea, eye lens, vitreous body and some others. To measure the refraction of such objects, all known methods can be used, such as total internal reflection, single fiber reflectance spectroscopy, and optical coherence tomography. The RI of transparent tissues and bioliquids in the visible and NIR regions is determined by water as the main component. Much attention should be paid to accuracy of measurements, since differences between objects are observed in the thousandth and ten thousandth digits. The RI of interstitial fluid is 1.3585 for a wavelength of 589 nm [125]. The most significant plasma protein is albumin. The RI of the human albumin 35 g/l at a wavelength of 589 nm is 1.3401, 55 g/l - 1.3434, when measured with a multi-wavelength Abbe refractometer [127,128]. The dispersion of the human albumin solution for the concentrations of 35 and 55 g/l in the wavelength range of 480-1550 nm can be described by the Sellmeier formulas [127,128]:
| (18) |
| (19) |
In Ref. [129], proposed a simple, reliable, and accurate method for measuring the RI of transparent liquids based on Snell's law and laser speckle correlation. The authors also demonstrated the creation of an affordable device that measures a very small change in the RI by measuring the change in the objective speckle pattern arising due to the change in laser light passing the liquid solution, which is caused by the apparent shift of a point source. An important feature of this robust method is the possibility of measuring the RI with an enough accuracy of 0.00038 with an average error of less than 4.5%. The single fiber reflectance spectroscopy method allows for obtaining data with a better accuracy of 0.2% [130].
3.3. Tissues with high absorption and scattering
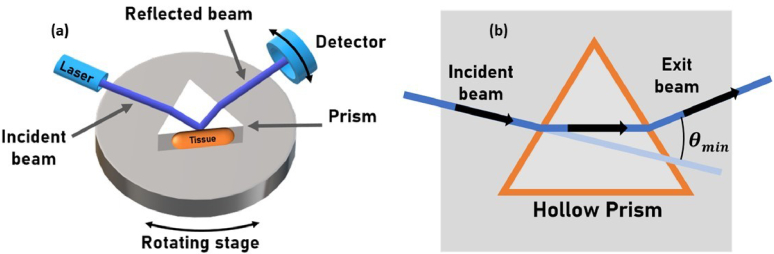
Two of the most common experimental techniques to measure the RI of tissues and fluids with high absorption and scattering, are the ones based on the total internal reflection and on the minimum deviation angle methods, respectively. Figure 8 presents the corresponding setups for these methods.
Fig. 8.
Experimental setups to measure the RI of biological tissues with the total internal reflection method (a) and to measure the RI of liquids, biological fluids and OCAs with the minimum deviation angle method (b). Courtesy of L. Oliveira.
In the total internal reflection setup (Fig. 8(a)), a laser beam enters the prism through one of its lateral surfaces, and is deviated to be reflected at the prism/tissue interface. The reflected beam exits the prism through the third prism surface, where its signal is measured by a photodetector. The reflectance of the tissue is calculated with a relation similar to Eq. (11), where the noise signal and the laser reference signal are accounted for. By varying the incidence angle of the laser beam, a reflectance curve can be represented as a function of the incidence angle [84,87]. Calculating the first derivative of such reflectance curve allows the identification of a peak that corresponds to the critical angle of reflection (θc) for the tissue at the laser wavelength. Such angle is then used in the following relation to calculate the RI of the tissue at the laser wavelength (ntissue(λ)) [131]:
| (20) |
with nprism(λ) representing the RI of the prism at the laser wavelength. Such procedure can be made with different lasers to obtain the ntissue values at different wavelengths within the spectral band of interest. After obtaining a series of ntissue values inside a broad spectral range, they can be fitted by an appropriate dispersion curve as described by Eq. (5) to (7) [87]. An improved version of the total internal reflection setup, which uses a broadband xenon lamp and a spectrometer was recently reported [132]. Such setup avoids the use of different lasers, since instead of a laser signal being measured at each angular position, a spectrum is acquired, which turns such measurement and calculation procedures faster.
Considering now the minimum deviation angle setup presented in Fig. 8(b), a hollow equilateral prism (ϕ = 60°) is constructed over a base to sustain the liquid under study. Such liquid can be the interstitial fluid of a tissue, blood or an OCA that is used to increase tissue transparency. The laser is placed into position so that, the refracted beam inside the prism is parallel to the base of the prism, as represented in Fig. 8(b). In this position, the minimum deviation angle (θmin) is the one measured on the right-side of the setup between the incident and exit beams. The calculation of the RI of the liquid under study at the laser wavelength is made according to [81]:
| (21) |
As in the case of the total internal reflection setup, this measurement procedure is made with various lasers to obtain the discrete RI values of the liquid within the spectral range of interest. These discrete values are then fitted with an appropriate dispersion curve, as described above for the biological tissues.
Whole blood plays a special role among tissues with high absorption and scattering, which is a mobile connective tissue and interacts with all kinds of other tissues. The RI of whole blood, calculated from the RIs of its main components (plasma and hemoglobin) and Gladstone–Dale relation, is 1.3632 at a wavelength of 589 nm and the dispersion follows from the selective wavelength RI measurements using multi-wavelength Abbe refractometer in the wavelength range 480-1550 nm is described by the Sellmeier formula [127]:
| (22) |
One of the most important components of blood, which determines its absorption in the visible and IR regions, is the hemoglobin. The RI of human hemoglobin solution 280 g/L is 1.3818 at a wavelength of 589 nm. The dispersion of this solution follows from the selective wavelength RI measurements using multi-wavelength Abbe refractometer in the spectral range of 480-1550 nm is described by the Sellmeier formula [133]:
| (23) |
For ex vivo muscle tissue, the RI is changed from 1.4040 to 1.3703 in the visible to NIR [84]. The RI of mouse breast tissue measured ex vivo at a wavelength of 589 nm is 1.3985, and of mouse kidney is 1.3625 at the same wavelength [134]. In the spectral range of 480-1550 nm, the RI experimental values of rat skeletal muscle, breast and kidney are described by the Sellmeier formula [84,134]:
| (24) |
| (25) |
| (26) |
The refractive indices of the epidermis and dermis of the mouse skin are 1.4254 and 1.3932 for a wavelength of 589 nm [84]. The Sellmeier formulas for these tissues for the spectral region 480-1550 nm are [84]:
| (27) |
| (28) |
The specificity of adipose tissue, which is characterized by a high content of lipids and a low content of water and blood, is its relatively high RI [80]. At a wavelength of 589 nm the RI of ex vivo abdominal fat is equal to 1.4676, 1.4740, and 1.4369 for human, porcine, and rat tissues, respectively. The differences are related to composition of triglycerides in adipose tissue. The dispersion follows from the selective wavelength RI measurements using multi-wavelength Abbe refractometer for these tissues is described by the following formulas [80]:
| (29) |
| (30) |
| (31) |
3.4. Refractive index of cells
The measurements of RI of cells allows for a deeper study and clarification of processes related to cellular metabolism, such as hydration, oxidative stress, conductivity, metabolic processes, and others [135]. The RI of cells correlates with its composition and thus can provide important information for developing various biological models and assessing the optical properties of tissues in general. Currently, all known methods for measuring cell RI can be divided into three groups. The first group includes methods that allow for determining the average RI of cells. It is assumed that the RI of a homogeneous cell suspension corresponds to the average value of the RI of cells in solution [136,137]. The second group includes methods that allow for determining the effective RI of cells. All methods of this group are united by the assumption that the RI of cells is proportional to the concentration of proteins in its composition [138]. The third group consists of methods based on creating a 3D map of RI of a single cell or a cell cluster [139–141].
The value of the RI of cells can vary for the same type of cells, depending on the presence and distribution of intracellular organelles, expression and accumulation of a specific protein, cell size and mass. However, the RI does not determine the type of cell, nor does tissue in general. The RI of a cell is affected by the thickness of the cell membrane, the size of the nucleus and organelles. In addition, experimental conditions such as temperature, chemical treatment, osmotic pressure, samples of living or fixed cells, etc. also have a marked effect on the measured values of the RI of cells.
At present, 3D tomography using RI reconstruction has become a promising research method in the field of biophotonics. The method makes it possible to study optically thick samples in a noninvasive way and without the use of chemical labeling. For example, it is possible to image blood vessels and cells, which is important for translational and clinical medicine, as well as for development of diagnostic methods based on imaging cytometry [139]. In Ref. [140] demonstrate the use of 3D Quantitative Phase Imaging to evaluate dry mass RI distribution in living and fixed cells and tissues. Changes in the RI values after the fixation process are revealed in the reconstructed phase distributions and are on the order of 10−3. The RI values decrease and the most significant losses are found in the cell nucleolus [140].
Refractometry of cells is of great importance for the development of tissue optical clearing technologies. Information about the RI of individual cells and their environment is extremely useful to select the OCA providing maximum efficiency [84].
3.5. Measuring the refractive index in a wide spectral range
The dispersion curves obtained from discrete RI values may be enough for some studies, but, as previously described, if a more realistic dispersion is necessary for a biological material or an OCA, the K-K relations (Eq. (8) and Eq. (9)) may be used to calculate it from the µa(λ).
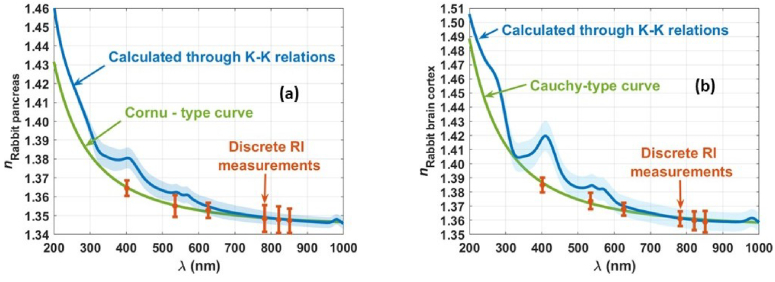
Using this experimental/calculation procedure, various studies were made to obtain the dispersions of different tissues and tissue components [84]. Figure 9 presents the calculated dispersions for the rabbit pancreas and brain cortex, obtained on two of those studies [9,79].
Fig. 9.
Experimental and calculated broadband tissue dispersion of rabbit pancreas (a) and rabbit brain cortex (b). Adapted with permission from: (a) Ref. [10]; (b) Ref. [9], which was published under Creative Commons license, MDPI.
Both graphs in Fig. 9 show a good matching between the dispersions calculated with the K-K relations and the ones calculated with the Cornu (Eq. (5)) or Cauchy (Eq. (7)) curves. Such matching is perfect for longer wavelengths, and the differences observed in the UV range for the case of the pancreas seem to indicate that due to the lack of experimental data with lasers in that range, the calculated Cornu curve is somehow imprecise at shorter wavelengths. In both cases presented in Fig. 9, the Cauchy (or Cornu) curves do not present SD, since they were calculated to fit the mean discrete RI values that resulted from experimental data [9,79]. In the case of the curves calculated through the K-K relations, SD shadows are presented, since the calculations were performed 10 times in each case using the 10 µa(λ) from each tissue [9,79]. These curves clearly present the absorption bands of hemoglobin at 411, 540/570 nm and of water at 980 nm.
3.6. Healthy and pathological tissues
The evaluation of the dispersion curves for healthy and pathological tissues also brings differentiated information, which can be used in the diagnosis of certain diseases such as cancer.
First of all, changes in the development of pathology begin with changes in the protein composition of the blood and correspondingly in the RI. In Ref. [142] shows the possibility of determining various degree of cancer development in animals associated with the difference in the dispersion of blood plasma in a wide range of waves from visible to THz [142].
The RI measurements of blood and its components can serve as the basis for the development of methods for diagnosing diabetes mellitus. In Ref. [143] shows the differences in optical properties, including RI, for glycated and non-glycated human hemoglobin fractions [143].
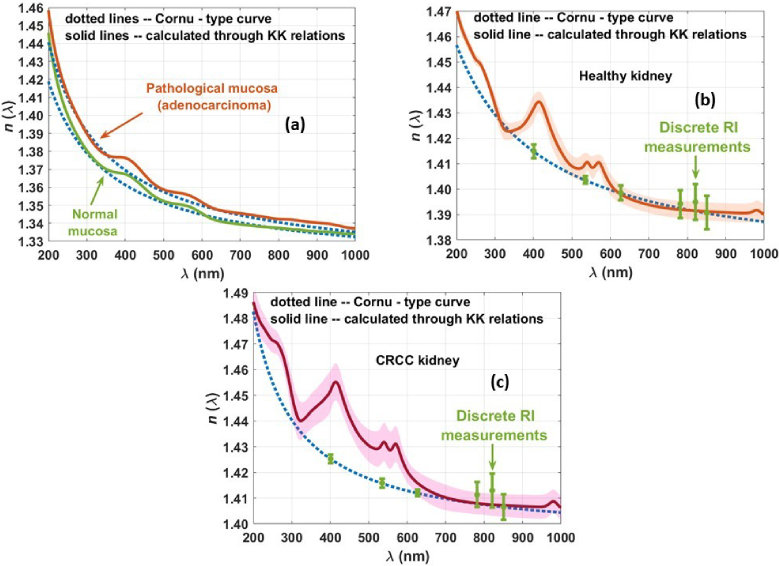
Figure 10 presents the dispersion curves for human colorectal mucosa and human kidney, both in the healthy and in the pathological (adenocarcinoma in the colorectal mucosa and CRCC in the kidney) versions [26,74].
Fig. 10.
Experimental and calculated broadband tissue dispersions of human normal and adenocarcinoma colorectal mucosa (a), human normal kidney (b) and human CRCC kidney (c). Adapted with permission from: (a) Ref. [26], MDPI; (b) and (c) Ref. [74], Elsevier, which were published under Creative Commons license.
Figure 10 shows that as in the case of the rabbit tissues presented in Fig. 9, the dispersions calculated with the K-K relations are well matched to the Cornu-type curves that were obtained from discrete RI measurements performed on colorectal mucosa and kidney tissues. Although all cases in Fig. 10 present similar results to the ones in Fig. 9, there is some important information to retain from Fig. 10 regarding both types of human tissues – the dispersions for the pathological tissues present higher values than the ones obtained for healthy tissues in the entire spectral range. According to previous studies [84,144], the human pathological colorectal mucosa has ∼5% more mobile water than the healthy mucosa and similar results may occur in the kidney. Such higher water content in the pathological tissues should originate a lower dispersion than in the healthy version of the tissues, but instead the graphs in Fig. 10 show higher dispersion curves for the pathological versions of the colorectal mucosa and the kidney. Such variations in tissue dispersion from the healthy to the pathological cases show that they do not depend on the additional mobile water in the pathological tissues. In fact, the water contribution to tissue dispersion accounts for the whole water in the tissue, which contains the mobile water and the one that is bound to the other tissue components. Since the total water content is in equilibrium between adjacent tissues, its content in the healthy and pathological tissues is the same, but when cancer develops, some of the bound water converts into mobile, as previously explained [84,144]. Considering such total water content to be equal in the two versions of the same tissue, the increase observed in the tissue dispersion from the healthy to the pathological tissues must be related to the formation of higher-dimension structures during cancer development, which increase the RI of the tissue in the entire spectral range.
The RI of tumor tissue after transplantation of alveolar liver cancer cells PC1 to rats measured using a multi-wavelength Abbe refractometer at a wavelength of 589 nm is equal to 1.3482, and for the spectral range 480-1550, the dispersion is described by the following formula [143]:
| (32) |
The RI of breast mouse tissue samples after 28 days of cancer cells 4T1 injection and kidney mouse tissue after 28 days of cell culture RenCa injection was 1.3945, and 1.3692 for wavelength of 589 nm and the RI for the range of 480-1550 nm can be calculated using the formulas [134]:
| (33) |
| (34) |
The length of the spatial autocorrelation in a small area of the tissue phase image can be used as an intrinsic cancer marker in histopathology. This parameter is sensitive to nanoscale cellular morphological changes and, therefore, may inform about carcinogenesis. In Ref. [145] demonstrate a methodology for diagnosing benign and malignant breast tissue based on highly sensitive quantitative phase imaging data obtained using spatial light interference microscopy [145].
In Ref. [146] shows the possibility of using data for RI of blood cells and their environment to select the optimal OCA in order to reduce scattering of erythrocytes and other blood cells and significantly increase the probability to detect melanoma cells [146].
The analysis of the broadband µa(λ) that was made in section 2.1 and the analysis of the broadband tissue dispersion that was made here have already provided discriminating information between healthy and pathological tissues.
4. THz waves
4.1. Effective medium theory in THz tissue optics
Consider a common approach to describe the THz-wave–tissue interactions, that relies on the effective medium theory and an assumption of the homogeneous and isotropic character of tissues at the THz-wavelength scale [33,34,36]. Due to its simplicity, this approach is conventional for THz biophotonics. As detailed in Refs. [33,34,36], such structural elements of tissues, as cell organels, separate cells and their agglomerates, microfibrils, etc. [1], are small at the scale posed by the THz wavelengths. This leads to the Rayleigh scattering of THz waves in such tissues [1] and to a conventional assumption of their homogeneous and isotropic character [33,34,36,45].
Similarly to the THz dielectric response of liquid water, water solutions and biological liquids [33], the THz response of the tissues has no resonant absorption peaks and can be described by the frequency-dependent effective complex dielectric permittivity
| (35) |
with its real ɛ’ and imaginary ɛ'‘ parts, or the frequency-dependent complex RI
| (36) |
where n≡n’ and n'‘ are its real and imaginary parts, ν is the electromagnetic-wave frequency, α is the absorption coefficient (by field) in [cm−1], and c0≈3 × 108 m/s is the speed of light in free space.
4.2. Measurement of the effective THz optical properties of tissues
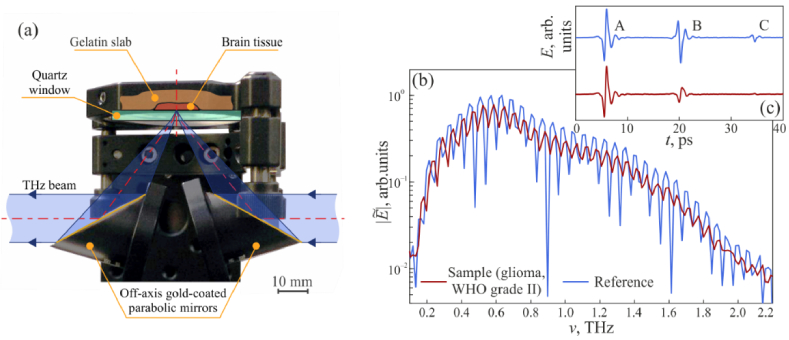
Consider representative example of tissue characterization in the THz range in the framework of the effective medium theory. For this, we discuss the results of Ref. [147], where THz pulsed spectroscopy was applied to study ex vivo the freshly-excised (hydrated) human brain gliomas of the different World Health Organization (WHO) grades, along with intact and edematous tissues of the brain. In this work, 2, 9, 4, and 11 glioma sample of the WHO Grades I, II, III, and IV, respectively, were considered. Perifocal regions of a tumor contained intact and edematous tissues. For the THz measurements, the resected tissues were fixed by gelatin slabs to preserve them from hydration / dehydration and sustain their THz response unaltered for few hours, as compared to the freshly-excised ones [148]. Hematoxylin and eosin (H&E)-stained histology was applied to confirm the initial diagnosis.
Reflection-mode THz pulsed spectrometer was used to study brain tissues [147]. The reflection-mode measurements unit is shown in Fig. 11, which is based on a pair of gold-coated off-axis parabolic mirrors and a quartz window with either air (free space) or tissues atop. The focusing mirror has the focal length of f = 50 mm and the optical diameter of D = 25 mm, which results in the diffraction-limited THz beam spot with the Airy disc radius defined by the Rayleigh limit
| (37) |
where nSiO2≈2.150 is the RI of a reference quartz window. Evidently, the spatial resolution of the focusing system and the area of tissue surface, from which the signal is collected, increase with free-space wavelength λ and decrease with frequency ν. The THz beam path is covered by the plastic housing and purged with nitrogen gas, aimed at suppressing an impact of water vapors on the measured THz data.
Fig. 11.
THz pulsed spectroscopy ex vivo of the gelatin-embedded human brain gliomas. (a) Reflection-mode THz measurement unit based on off-axis gold-coated parabolic mirrors and a reference window, atop of which the tissue specimen is handled. (b), (c) Reference Er and sample Es signals in the frequency and time domains, respectively. Reproduced from Ref. [147] published by SPIE under a Creative Commons Attribution 4.0 Unported License.
The THz RI n and absorption coefficient α (by field) were quantified in the spectral range of 0.2–1.5 THz. In Figs. 11 (b),(c), two signals of the THz-pulsed spectrometer are shown in frequency domain and time domain:
-
•
the reference one Er, reflected from a reference quartz window with a free space behind,
-
•
the sample one Es, reflected from a reference quartz window with a tissue sample behind.
They were used for reconstruction of the tissue optical properties. From Fig. 11 (c), we notice that both reference and sample waveforms are comprised of three separate wavelets – A, B, and C. Wavelets A and B correspond to THz-wave reflection from the “free space–quartz” and “quartz–tissue” (or “quartz–free space”) interfaces, respectively, while C is the satellite caused by the multiple reflection in the window. The wavelet A is equal for both reference and sample waveforms. These three wavelets form an interference pattern in the frequency domain, as shown in Fig. 11 (b).
Before the optical properties reconstruction, the apodization procedure is applied to both the reference and sample waveforms – namely, the 20-ps-width fourth-term Blackman–Harris window filter [149], centered at the peak of the wavelet B. It filters out a contribution of the wavelets A and C from the waveforms and provides the frequency-domain resolution of ≃0.05 THz. Based on the wavelet B, the frequency-domain experimental and theoretical transfer functions are defined:
| (38) |
which depend on the Fresnel reflection of s-polarized THz wave from the “quartz–tissue” (or “free space”) interface
| (39) |
Here, indexes m, k = 1, 2, and 3 correspond to the free space, quartz, and tissue, θi and θt define the angles of incidence and transmittance. Finally, complex RI of tissues is quantified via minimization of the vector error functional:
| (40) |
where |…| and φ[…] are operators allowing to extract modulus and phase of a complex value.
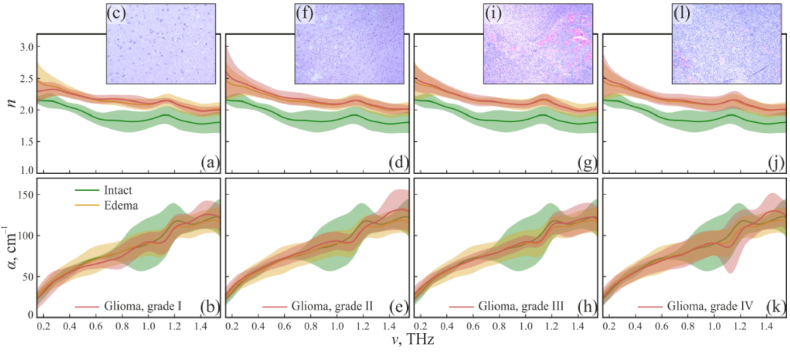
In Fig. 12, thus measured n, α-curves are shown for healthy and pathological tissues of the human brain. For each tissue specimen, reproducibility of the experimental data and fluctuations of the optical properties were examined by measuring different points of the sample surface. Mean values n, α and error bars (±2.0σ / ≈ 95% confidential intervals; σ is the SD) are shown for the intact tissues, edema, and gliomas of the WHO Grades I–IV. In complete accordance with previous studies of glioma models from animals [55,150–153], statistical difference between the THz optical properties of intact tissues and gliomas of the human brain, as well as the intact tissues and edematous tissues are evident from Fig. 12. The effective RI n of all gliomas and edematous tissues is higher than that of intact. The observed label-free contrast of several percentages agrees with the results from Ref. [153]. At the same time, the THz response of edematous tissues was found to be close to that of a tumor, and no differences between WHO Grade I–IV gliomas were found.
Fig. 12.
RI n, absorption coefficient α (by field), and representative H&E-stained histology of gelatin-embedded human brain gliomas of the different WHO grades ex vivo. (a)–(c) WHO Grade I. (d)–(f) WHO Grade II. (g)–(i) WHO Grade III. (j)–(l) WHO Grade IV (glioblastoma). Optical properties of tumors are compared with intact and edematous tissues. The error bars define a ± 2.0σ confidential interval of measurements (σ is the SD), which accounts for the optical properties variation within each tissue type. Reproduced from Ref. [147] published by SPIE under a Creative Commons Attribution 4.0 License.
The contrast between the gelatin-embedded intact tissues and gliomas is reportedly originate from the increased water content in a tumor, that is caused by its abnormal microvascularity, edema, and the presence of necrotic debris [55,154]. Other biological events, such as the increased cell density and abnormal protein content in a tumor, also contribute to the contrast, but their impact is much smaller than that of tissue water [55,154]. When using THz spectroscopy and imaging for the intraoperative delineation of glioma margins, edematous tissues may be confused with a tumor. Recently, capabilities of the THz diagnosis of traumatic brain injury were demonstrated, that relies on different water content and spatial distribution of hematoma components in normal and injured tissues [60–62]. Thus, we might expect fault positive results of THz diagnosis of brain tumor in presence of traumatic injury.
Despite the considered measurement geometry (Fig. 11 (a)) and data processing routine, other schemes of broadband THz spectroscopic measurements of hydrated tissues in vivo and ex vivo are also available, such as reflection-mode with normal incidence [47,52] or highly-sensitive total internal reflection configuration [155,156]. Furthermore, novel quantitative superresolution THz imaging modalities appears annually, in order to uncover subwavelength heterogeneity of tissues, study local distribution of the tissue optical properties over the imaging plane, as well as related THz-wave scattering effects [67,157–159]. All these methods allow to estimate the effective THz optical properties of tissues, that can play the role of physically-reasonable features for the tissue differentiation.
4.3. Relaxation models of the effective THz optical properties of tissues
The effective THz optical properties of tissue do not have any resonant features [33,34,45]. THz response of tissues is usually described by the relaxation models of complex dielectric permittivity , such as the double-Debye one [160–165] comprised of the two Debye terms
| (41) |
where ɛ∞ is a constant dielectric permittivity at a high-frequency limit, τ1, τ2 and Δɛ1, Δɛ2 are the times and contributions (magnitudes) of the “slow” and “fast” relaxators, respectively, and ω=2πν is a circular frequency. This model describes the two broad absorption bands in the loss spectrum ɛ'‘, attributed to the “slow” and “fast” relaxations of liquid water or tissue water and centered at the inverse relaxation times (2πτ1)-1, (2πτ2)-1. In turn, ɛ'-curve decreases with increasing frequency ν, with the high- and low-frequency magnitudes of ɛ∞ and ɛ∞+Δɛ1+Δɛ2, respectively. This model yields parametrization of both real ɛ’ and imaginary ɛ'‘ parts of the complex dielectric permittivity in the THz range for water and tissues using only 5 coefficients – ɛ∞, Δɛ1, Δɛ2, τ1, and τ2.
In Tab. 1, literature data on the double-Debye model parameters for water and tissues in healthy and pathological states are summarized, where intact tissues, edematous tissues and WHO Grade I–IV gliomas are also considered [165]. Such models of the effective complex dielectric permittivity of tissues can be quite useful for further research and engineering efforts in THz biophotonics, biomedical spectroscopy, and imaging. They can be applied to:
-
•
describe (analytically) the THz-wave interaction with a multilayer object using the plane-wave approximation, the Fresnel formulas, and the Bouguer–Lambert—Beer law, which is of particular importance in spectroscopic measurements of tissues.
-
•
model (numerically) the THz-wave interaction with a heterogeneous object of a complex shape using methods of computational electrodynamics or statistical Monte-Carlo approaches, which is of high importance in studies of the THz radiation transport in tissues;
-
•
apply parameters of this dielectric permittivity model as physically-reasonable principal components for the discrimination between tissues in healthy and pathological states [166].
Table 1. The parameters of the double-Debye model for water and tissues.
| # | Object | ɛ ∞ | Δɛ1 | Δɛ2 | τ1, ps | τ2, ps | Ref. |
|---|---|---|---|---|---|---|---|
| 1 | Water | 3.30 | 75.00 | 1.90 | 8.50 | 0.17 | [167] |
| 2 | 3.50 | 73.50 | 1.40 | 8.20 | 0.18 | [168] | |
| 3 | 4.10 | 72.20 | 2.50 | 10.60 | 0.18 | [160] | |
| 4 | 3.20 | 73.60 | 1.60 | 8.00 | 0.18 | [164] | |
| 5 | 3.42 | 74.16 | 1.38 | 7.87 | 0.18 | [169] | |
| 6 | Intact human skin (epidermis) in vivo | 2.89 | 20.34 | 1.74 | 3.82 | 0.11 | [166] |
| 7 | 3.00 | 56.40 | 0.60 | 10.00 | 0.20 | [160] | |
| 8 | 2.58 | 10.54 | 1.58 | 1.45 | 0.06 | [161] | |
| 9 | 2.86 | 25.70 | 1.76 | 4.80 | 0.10 | [170] | |
| 10 | 3.00 | 54.40 | 0.60 | 9.40 | 0.18 | [163] | |
| 11 | Basal cell carcinoma of the human skin ex vivo | 2.90 | 28.53 | 1.90 | 4.35 | 0.11 | [166] |
| 12 | 2.58 | 13.37 | 1.58 | 1.55 | 0.06 | [161] | |
| 13 | 3.02 | 72.25 | 1.95 | 11.02 | 0.13 | [170] | |
| 14 | Fibrous connective tissues of the human breast ex vivo | 2.10 | 72.60 | 1.80 | 10.30 | 0.07 | [164] |
| 15 | Tumor of the humor breast ex vivo | 2,50 | 73.60 | 2.80 | 9.10 | 0.08 | [164] |
| 16 | Intact tissues of the human brain ex vivo | 2.29 | 49.82 | 1.80 | 10.6 | 0.18 | [165] |
| 17 | Edematous tissues of the human brain ex vivo | 3.48 | 61.37 | 1.58 | 10.6 | 0.18 | [165] |
| 18 | WHO Grade I glioma of the human brain ex vivo | 3.29 | 50.54 | 1.93 | 10.6 | 0.18 | [165] |
| 19 | WHO Grade II glioma of the human brain ex vivo | 3.40 | 61.37 | 1.93 | 10.6 | 0.18 | [165] |
| 20 | WHO Grade III glioma of the human brain ex vivo | 3.32 | 56.32 | 2.03 | 10.6 | 0.18 | [165] |
| 21 | WHO Grade IV glioma of the human brain ex vivo | 3.30 | 58.48 | 2.00 | 10.6 | 0.18 | [165] |
Notice that the Debye kernel does not fulfill the sum rule for the oscillator strength [171–173]
| (42) |
where σ is the dynamic conductivity. Therefore, when the sum rule is applied to the Debye kernel, it predicts the infinite number of charge carriers or dipoles N underlying the dielectric response of a medium. To mitigate this problem, the double-overdamped-oscillator model was applied to describe the THz complex dielectric permittivity of biological tissues [165]. The Debye kernel and the overdamped oscillator are practically equivalent at low-frequencies ω≤(2πτi)-1, but for higher frequencies ω>(2πτi)-1 the Debye model predicts higher losses that the overdamped oscillator [165,171]. In Ref. [165], an approach for the univocal calculation of each overdamped-oscillator parameters based on the corresponding Debye kernel (and vice versa) is described.
In contrast to the Debye kernel, the overdamped oscillator appears to be more physically reasonable, since it satisfies the sum rule. Integration over the frequency ω of the dynamic conductivity σ given by each overdamped oscillator results leads to the finite value
| (43) |
where Δɛ is the overdamped oscillator strength (equal to that of the corresponding Debye relaxator), ω0 is the quasi-resonance frequency (given by restoring force), N is the number of dipoles contributing to the considered overdamped oscillator, q and m are effective charge and mass of each dipole, and ɛ0 = 8.85 × 10−12 F/m is the electric constant. We also notice other relaxation models of the complex dielectric permittivity that can be applied to describe the THz response of biological liquids and tissues; among them: the Cole-Cole [174,175], Davidson-Cole [176], Havriliak-Negami [177] and Frohlich [178] models. However, their detailed analysis is out of the scope of this review.
The two relaxation bands, described by the “slow” and “fast” Debye terms, are centered beyond or at the edges of the spectral operation range of a typical THz pulsed spectrometer [34,165]. In this way, when parametrizing the measured THz dielectric spectra by the double-Debye model, one deals with extrapolation of the experimental data. This can lead to some uncertainties, while the estimated parameters usually depend on the initial conditions and the applied fitting procedures. Methods of broadband dielectric spectroscopy, which combine backward-wave oscillator spectroscopy [179], THz pulsed spectroscopy, Fourier-transform IR spectroscopy [180], impedance measurements [181], and other techniques, can help to obtain much accurate data about the picosecond relaxation dynamics of liquid water and tissues. Despite attractiveness of such broadband measurements, they still remain quite a daunting task due to technical difficulties.
4.4. Light scattering in THz tissue optics
Despite the widespread use of the aforementioned effective medium theory in THz biophotonics, many biological objects possess mesoscale (∼λ) structural heterogeneities and, thus, manifest scattering properties in the THz range [33,34,36,45]. Evidently, for such objects, the Mie scattering effects should be taken into account while describing the THz-wave – tissue interactions in context of medical diagnostics or therapy [1,182]. Consider a few examples.
-
•
In Refs. [34,183], structural inhomogeneities of freshly-excised (hydrated) breast tissues ex vivo were studied both experimentally, using the superresolution THz microscopy, and theoretically, using methods of the Mie scattering theory. THz optical properties of separate fat cells and their agglomerates were found to differ from that of the surrounding fibrous connective tissues. Such cells form sources of the Mie scattering. Parameters of such scatterers (i.e., their scattering phase function, differential and integral cross sections, and scattering anistoropy factor) differ completely from those inherent to the Rayleigh regime [34].
-
•
In Refs. [67,154], superresolution THz microscopy revealed structural heterogeneities of intact brain tissues and glioma model 101.8 from rats ex vivo. Heterogeneities of intact tissues were attributed to the different THz dielectric response of white matter and gray matter, as well as other neurovascular structures of the brain. Heterogeneities of a tumor were due to the presence of tumoral cell accumulations, necrotic debris, hemorrhages and other factors.
-
•
In Refs. [184–187], polarization-sensitive THz imaging provided useful information for the differentiation between healthy and pathological tissues, which indirectly justifies the Mie-like THz-wave scattering in such tissues. Namely, the observed changes in THz-wave polarization cannot be described in the framework of the effective medium theory.
The discussed findings stimulate further research and development of novel approaches to describe the THz-wave–tissue interactions, that simultaneously account for the dispersion and absorption properties of tissue components, as well as geometry and organization of scatterers in tissues. This approach could rely on the radiation transfer theory and the radiation transfer equation, widely applied in the UV, VIS, and IR biophotonics [1,182,188]. Study of the scattering effects in tissues and an interplay between the THz-wave absorption and scattering phenomena remain important problem of THz biophotonics, that still remains unaddressed.
5. Tissue optical clearing
5.1. Introduction
The tissue immersion clearing technique has evolved greatly in the past 30 years, since various ex vivo and in vivo studies have been made to reduce light scattering and increase tissue transparency and light penetration depth [3,77,189–191]. Such increase in tissue transparency is obtained through three main mechanisms, commonly designated as: tissue dehydration, RI matching and protein dissociation [126,191]. These mechanisms occur during the immersion of the tissues in an OCA or in a solution that contains the OCA, and the variations they create in the tissues are time dependent. Consequently, to characterize the clearing mechanisms, kinetic measurements must be performed over the time of treatment. Section 5.2 will discuss these mechanisms and the associated measurement technology.
The kinetic measurements made during optical clearing of tissues may produce additional information regarding the physiological composition of the tissue under study, or data that can be used to discriminate pathologies [3,77]. Some examples of studies that produced such data are discussed in section 5.2. If the kinetics measurements performed during tissue clearing are made in the UV, appropriate data processing can show that the RI matching mechanism is more efficient in the UV range, where new tissue transparency windows can be artificially created [192,193]. Since proteins have their absorption bands near 230 nm, the protein dissociation rate can also be evaluated from kinetic measurements in that range. The evaluation of such rate from healthy and pathological tissues produces differentiated values that can be used for diagnostic purposes [193]. Such studies and results will be presented in section 5.3.
5.2. Mechanisms and technology
Biological tissues contain various components, such as cells, protein fibers and globules, lipid droplets and phospholipid membranes, which are distributed in a background liquid, usually designated as interstitial fluid (ISF). The same heterogeneous composition occurs within the cells, since the nucleus, mitochondria and organelles are surrounded by the cytoplasm [126,194]. Both the cytoplasm and the ISF are mainly composed by water (>90% in volume), where some minerals, proteins and salts are dissolved [3,77,195]. As a consequence of the high water content in tissue/cell fluids, which turns their RI low, a strong RI mismatch is created between those fluids and the other tissue/cell components (commonly designated as tissue scatterers) [3,196]. This RI mismatch, which can be quantified by the relative RI (m), is significantly responsible for the strong light scattering properties that tissues present [126]. By knowing the RI of tissue scatterers (nscat) and the RI of the ISF (nISF), m is calculated as [3,77,197]:
| (44) |
Usually, m is calculated at 589.6 nm [77], but due to the wavelength dependence of nscat and nISF, m will also depend on the wavelength [3,193]. At this wavelength and for a temperature of 20 °C, nISF for most tissues ranges between 1.35 and 1.37 [77], while nscat is much higher, in the range of 1.474 for collagen fibers in scleral tissues [198], or 1.530 for hydrated muscle fibers [194,199]. Considering these examples, they originate m values between 1.08 and 1.09 for the sclera and between 1.12 and 1.13 for the skeletal muscle [126]. These examples show that m always presents values higher than unity, meaning that light scattering will occur in those tissues. If m = 1 for a tissue at a particular wavelength, it means that the tissue is transparent to light at that wavelength. The magnitude of m is a measure of light scattering in biological tissues [3].
The objective of applying tissue immersion clearing treatments is to reduce light scattering inside through the approximation of nISF to nscat that leads to the increase in tissue transparency and in light penetration depth. By doing that it will be possible, as an example, to increase the contrast and the resolution in images acquired from deeper tissue layers [1,126,200,201]. The tissue immersion clearing technique has been a subject of intensive study in the last 30 years, with increasing number of publications every year [3,126,190].
The increase in nISF to approach it to nscat is achieved in this technique by replacement of the water in the tissue fluids by an OCA with higher RI, an exchange that is obtained through two fluxes – the water flux out from the tissue and the OCA flux into the interstitial or intracellular locations. These two fluxes are directly connected to the tissue dehydration and RI matching mechanisms of tissue clearing [3,126,191], and the evaluation of the diffusion properties of the OCA and water in the tissue allows the characterization of both fluxes and of the two mechanisms [191]. To explain these two clearing mechanisms, we consider an ex vivo tissue slab sample that is immersed in a solution containing an OCA. The osmotic pressure that the OCA molecules create over the tissue sample induce a fast flux of the mobile water in the ISF out from the tissue [191]. With the mobile water flowing out, the OCA molecules in the treating solution start diffusing into the tissue to replace the water that has left the ISF. Due to the fact that the OCA has a higher RI than water, closer to the RI of the tissue scatterers, such OCA diffusion into the tissue leads to the increase of the mean RI of the ISF, turning it closer to the RI of the tissue scatterers [202]. Considering this explanation, we see that the water flux out is directly connected to the tissue dehydration mechanism and the diffusion of the OCA molecules into the tissue is directly connected to the RI matching mechanism [126,191,203]. With the accumulation of the OCA molecules inside, the protein dissociation mechanism might also occur, depending on the ability of the OCA to dissociate proteins and on the amount of proteins that the tissue under study contains [126]. The reversibility of all these three mechanisms has been verified and it has been proven that they all contribute to the increase of tissue transparency [3,126].
The characterization of the tissue dehydration and the RI matching mechanisms can be made from kinetic measurements performed from tissue samples under treatment with aqueous solutions that contain different osmolarities of an OCA [3,191]. If Tc and thickness measurements performed during the clearing treatments are available, it is possible to obtain the diffusion time (τ) and the diffusion coefficient (D) for any treatment with a particular osmolarity of the OCA [191,204]. After selecting a spectral range where the tissue under study presents a linear increasing Tc in its natural state, without any absorption bands, discrete wavelengths within that range are selected to calculate the Tc kinetics during the treatment. Those kinetic curves are processed to consider only the time interval that corresponds to the initial smooth exponential increase of Tc. Such trimmed kinetic data is first displaced to have Tc = 0 at the beginning of the treatment (t = 0), and then normalized to its highest value. This way, with every kinetic dataset for the selected wavelengths varying between 0 and 1, it is possible to adjust the experimental points with a curve described by the following relation [3,126,190,191,203–205]:
| (45) |
where λi represents the wavelength that corresponds to the selected dataset of kinetic points and τi is the diffusion time that is estimated during the data fitting [126]. Since one τi value is estimated during the fitting of the data that corresponds to each of the selected wavelengths, to obtain the characterizing diffusion time for the treatment, mean and SD values are calculated from the estimated τi values. After performing these data processing tasks for all treatments, a representation of the mean τ values as a function of the OCA concentration in the treating solution is made [205]. The points in that representation are interpolated with a spline curve to show the true dependence between the two parameters. Such curve will show a minimum τ value for the highest OCA concentration used and a maximum for an intermediary concentration, which may not coincide with one of the OCA concentrations studied experimentally [203]. The minimum τ value obtained from the graphical representation corresponds to the diffusion time of water in the tissue, since the highest OCA concentration induces only the water flux in the first two minutes of treatment. The highest τ value obtained corresponds to the diffusion coefficient of the OCA in the tissue, due to the fact that for the OCA concentration that originates such maximum, the water in the solution is balanced by the mobile water in the tissue, and only the OCA flux into the tissue occurs. The identification of this maximum value also provides information about the mobile water content in the tissue, if that information is not previously available for the tissue under study [203–205]. Once the characteristic τ values for the unique OCA or water fluxes are obtained from the graphical representation, they can be combined with sample thickness (d) values obtained at the same time as the estimated τ values during the treatments with the same OCA osmolarities to calculate the corresponding D values. Such calculation is made according to the following relation [203–205]:
| (46) |
Various studies using this methodology were performed to obtain the characteristic τ and D values for water and OCAs in various tissues [3,126,190,191,203–205]. An example of those studies was recently made to characterize the optical clearing mechanisms created in skeletal muscle by gadobutrol, the active OCA in Gadovist™ [206]. Figure 13 presents the mean Tc spectrum of rabbit skeletal muscle obtained from 10 samples used in that study.
Fig. 13.

Mean Tc spectrum of the rabbit skeletal muscle. Adapted with permission from Ref. [206], which was published under Creative Commons license, Wiley.
Considering the spectral range between 600 and 800 nm in the spectrum presented in Fig. 13, we see that the rabbit skeletal muscle presents an almost linear increasing Tc with increasing wavelength. Figure 14 presents the mean Tc kinetics at discrete wavelengths within this range for the treatments performed on muscle samples with aqueous solutions containing 20%, 40% an 50% (in volume) of gadobutrol. The treatments applied to the muscle samples with each gadobutrol solution were performed 3 times to originate mean kinetics data as presented in Fig. 14.
Fig. 14.
Muscle Tc kinetics at discrete wavelengths for the treatments with aqueous solutions containing 20% (a), 40% (b) and 50% (c) of gadobutrol. Adapted with permission from Ref. [206], which was published under Creative Commons license, Wiley.
Similar kinetics graphs were calculated for the treatments with other solutions that contained gadobutrol in the concentrations between 20% and 50%. As explained in Ref. [206], the solutions used in this study were prepared by mixing Gadovist with water, but since the Gadovist already contains 50% of gadobutrol, no higher-concentrated solutions were possible to prepare.
The kinetics datasets in all treatments were processed, as described above, to have the initial smooth exponential increase variating between 0 and 1. Each of those datasets was fitted with a curve described by Eq. (45) to estimate the corresponding τ value. The mean and SD for τ that were calculated for each treatment are represented in Fig. 15 as a function of the gadobutrol concentration in the treating solution.
Fig. 15.
Mean τ as a function of gadobutrol concentration in the treating solution. Adapted with permission from Ref. [206], which was published under Creative Commons license, Wiley.
Although the solution with the highest concentration of gadobutrol used in this study had only 50% of this agent, the fitting curve in Fig. 15 was extended up to a concentration of 60% to see if a reliable τ for the water flux could be obtained. The extended curve shows that for the concentration of 60% for gadobutrol in solution, τ=58.9s. Assuming this value to be correct, and since gadobutrol is an iso-osmolar agent, which does not induce sample thickness variations [206], we can calculate D for water in these treatments through Eq. (22) as 4.30 × 10−6 cm2/s, a value that is not too different from the 3.20 × 10−6 cm2/s reported in Ref. [205] for water in muscle tissues. This result shows that by extending the spline in Fig. 15 to (a) concentration of 60%, a reasonable estimation of D for water in the skeletal muscle was obtained. The estimated τ/D values are reasonable to characterize the water flux out and the tissue dehydration mechanism.
Regarding the RI matching mechanism, Fig. 15 shows that the unique flux of gadobutrol occurs for the concentration of 40%, a concentration that is similar to the concentrations obtained in other studies for the unique OCA fluxes into skeletal muscle and other healthy tissues [132,191,203–205]. This means that the mobile water content in the skeletal muscle of the rabbit is also 60%, as obtained for those tissues [132,205]. The maximum τ value in Fig. 15 is 198.6s, which can be used in Eq. (46) to calculate the characteristic D for the gadobutrol diffusion in the muscle. As mentioned above, this agent is iso-osmolar and no sample thickness variations are expected during treatments. To confirm this, and since the solution with 40% of gadobutrol was available, three muscle samples were submitted to thickness kinetic measurements during treatment. In each of the three studies, the muscle sample was placed inside two thin glasses, with uniform thickness, and a digital micrometer was used to measure the global thickness during 30 min of treatment. At the end, the thickness of the glasses was subtracted to the measurements to obtain the sample thickness over the time of treatment. After averaging between the measurements performed in the three studies, the kinetic thickness measurements resulted in low variations, within the measuring error of the setup used. Once again considering the sample thickness to be 0.5 mm, the gadobutrol diffusion in muscle is characterized by a D of 1.28 × 10−6 cm2/s.
The method used to produce the results presented above is reliable to obtain the diffusion properties of water and OCAs in biological tissues, since it has been validated in various tissues under treatment with different OCAs [205]. As previously mentioned, such diffusion properties characterize the clearing mechanisms, but they are also useful for cryopreservation or food-industry applications, since some of the OCAs are also used in the cryopreservation of organs and sugars are sometimes added to fruits or other food products as conservation agents and sweeteners [3]. This method to obtain the diffusion properties of OCAs in tissues may also be used to discriminate pathologies. Section 5.3 discusses its application in the case of colorectal cancer, where differentiated results were obtained. The protein dissociation mechanism is not easy to study, since proteins present their absorption bands in the 200-230 nm range, as mentioned above. In the UV there are several absorption bands, which overlap each-other, and such absorption combined with a huge scattering turns it difficult to evaluate the third mechanism of optical clearing. To overcome this difficulty, a calculation method, based on kinetic measurements made from tissues during optical clearing treatment with highly concentrated glycerol solutions, was recently proposed to characterize the protein dissociation mechanism [193]. Since the measurements used in that method report to the deep-UV, such discussion and presentation of results will be made in section 5.4.
5.3. Healthy and pathological tissues
The kinetic measurements that are performed from tissues during optical clearing treatments are sometimes useful to obtain information about tissue physiology or differentiated data between healthy and pathological tissues, which can be used for diagnostic purposes.
To study and compare between the diffusion properties of glucose in human colorectal mucosa tissues in the normal and adenocarcinoma versions, the authors of Ref. [132] used the method described in the previous section. In this study, the tissue samples were collected from 15 individuals (12 men and 3 women), with ages ranging from 43 to 94, that were under treatment procedures at the Portuguese Oncology Institute of Porto (Portugal). Due to the limited glucose solubility in water, solutions containing this sugar in concentrations between 10% and 54% were used in this study to treat both versions of the tissues. Considering the Tc measurements to evaluate the τ values for glucose and water, three treatments of 30 min were made for each tissue under treatment with a particular glucose solution. After estimating the mean τ values for each treatment, the representation in Fig. 16(a) was created, where the data for normal and adenocarcinoma tissues were interpolated independently. Thickness kinetic measurements were also made from both types of tissues under treatment with particular glucose solutions to calculate the characteristic D values for water and glucose. The mean of three thickness measurements for each treatment are presented in Fig. 16(b) for the normal mucosa and in Fig. 16(c) for the adenocarcinoma tissue [132].
Fig. 16.
Mean τ as a function of glucose concentration in the treating solution (a) and mean sample thickness kinetics of the normal mucosa (b) and of the adenocarcinoma (c) for different treatments. Adapted with permission from Ref. [132], which was published under Creative Commons license, SPIE.
The graph in Fig. 16(a) shows differentiated data for the normal and pathological mucosa tissues. Looking into the maximum τ values, the normal mucosa presents this value for a concentration of 40.6%, while the adenocarcinoma presents such value for a concentration of 35.6%. This difference in the concentrations where the maxima of τ occur indicate dissimilar mobile water content in the two tissues. The normal mucosa has a mobile water content of 59.4%, while that content in the adenocarcinoma is 64.4%, 5% higher than in the normal mucosa. The maximum τ values that characterize the unique glucose flux are also different in the two tissues. For normal mucosa it is 302.4s, while for the adenocarcinoma it is 325.1s. The characteristic τ for the water flux is obtained for the concentration of 54% in the two tissues: 55.7s in the normal mucosa and 58.4s in the adenocarcinoma [132]. Although these values are a little different, they are very approximated and consistent to others obtained from other tissues in the same conditions [205].
To calculate the D values for each case, thickness kinetics measurements were made from normal mucosa samples under treatment with solutions containing 40% and 54% of glucose and from adenocarcinoma samples under treatment with solutions containing 35% and 54% of glucose. Those graphs are presented in Fig. 16(b) for the normal mucosa and in Fig. 16(c) for the adenocarcinoma. Considering all the estimated τ values above, the appropriate thickness values were retrieved at those times of treatment from the corresponding curves in Fig. 16(b) for the normal mucosa and from Fig. 16(c) for the adenocarcinoma. Using these thickness values and their corresponding τ values in Eq. (46), the various D values were calculated for glucose and water in the two tissues. The results of these calculations were: Dglucose = 5.8 × 10−7 cm2/s and DH2O = 3.3 × 10−6 cm2/s in the normal mucosa and Dglucose = 4.4 × 10−7 cm2/s and DH2O = 2.4 × 10−6 cm2/s in the pathological mucosa [132]. After obtaining differentiated τ/D values for the two tissues, we see that such information can be used to differentiate colorectal cancer. Further studies with the same method should be done in vivo using diffuse reflectance (Rd) spectral measurements to replace the Tc measurements used in the study reported in Ref. [132]. If such measurements are combined with optical coherence tomography measurements, thickness kinetics could also be acquired. After performing such evaluation in vivo and for different stages of colorectal cancer development, this technique could be applied for early detection of this disease.
5.4. UV wavelength range
The protein dissociation mechanism was initially discovered in skin tissues under treatment with glycerol using imaging methods [207], which also allowed to observe the mechanism reversibility after washing out the glycerol molecules with saline. Later the same mechanism was once again observed in skin under treatment with sugars [208,209]. As already mentioned above, due to the fact that the absorption bands of proteins are located in the deep-UV, where other absorption bands and huge scattering occur in biological tissues, the protein dissociation mechanism is difficult to detect and characterize [94,95]. Figure 13 helps in understanding this difficulty, since the Tc spectrum of the skeletal muscle in the 200-230 nm range, where the protein absorption bands occur, is practically null. With such small Tc values in the deep-UV range, any variations induced by the clearing treatments will also be small, and imperceptible. Figure 17 shows the mean time-dependence of the Tc spectrum measured from 5 samples of skeletal muscle under treatment with a solution containing 60% of glycerol.
Fig. 17.
Mean kinetics of the Tc spectrum of rabbit skeletal muscle under treatment with 60%-glycerol solution for the wavelength range between 200 and 1000 nm (a) and between 200 and 500 nm (b). Courtesy of L. Oliveira.
From the graphs in Fig. 17, we see that the magnitude of the transparency created in the muscle tissue increases with the wavelength, with the exception of the Soret band, where the increase is significantly smaller. The highest values in the created transparency are seen in the infrared, as represented in Fig. 17(a). In the deep-UV, such increase is practically null, as represented in the magnification of Fig. 17(b). Such behavior was previously observed not only for skeletal muscle, but also for other tissues, such as human gingival or normal and pathological colorectal mucosa tissues [193]. A method was recently proposed by the authors of Ref. [193] to overcome the problem of huge scattering and strong absorption in the UV region, so that the spectroscopic characterization of the protein dissociation mechanism becomes possible. According to these authors, to be able to see the small changes that occur in the deep-UV, it is necessary to calculate the time-dependent relative variations, which they designated as optical clearing efficiency (OCeff). The application of this calculation was previously used to show the creation of tissue-induced transparency windows in the deep-UV in the skeletal muscle under treatment with glycerol-water solutions [192]. In that study, it was observed that by increasing the glycerol concentration in the treating solution, the magnitude of the transparency window at 230 nm also increases, showing that by adding more glycerol molecules to the interstitial space, more proteins are dissociated. It was demonstrated in Ref. [193] that the OCeff can be calculated both from Tc or Rd spectra in a broad spectral range that includes the deep-UV. Such calculation was defined as [193]:
| (47) |
| (48) |
where Tc(λ, t) is the collimated transmittance of the tissue for wavelength λ at any time of treatment t; Tc(λ, t = 0) is the collimated transmittance at λ for the native tissue (t = 0); Rd(λ, t) is the diffuse reflectance of the tissue at λ acquired at the time of treatment t and Rd(λ, t = 0) is the diffuse reflectance of the untreated tissue at λ.
The results presented in Ref. [193] show that deep-UV transparency windows are induced by highly concentrated glycerol solutions both in human gingival and colorectal mucosa tissues. In the case of gingival tissues, 99.5% pure glycerol created a transparency window at 218 nm after a treatment of 60 min, reaching an increase of 3500%. In the human colorectal mucosa, both normal and adenocarcinoma tissues were used to look for differences in the created transparency windows and protein dissociation mechanism. These tissues (5 × each) were studied under treatment with 93% pure glycerol for 30 min. Figure 18 presents the mean kinetics for the OCeff(λ) obtained from this study for both mucosa tissues.
Fig. 18.
Kinetics for the OCeff(λ) of human normal colorectal mucosa (a) and adenocarcinoma (b) tissues. Reprinted from Ref. [193] with the permission of IEEE.
The graphs presented in Fig. 18 show that both mucosa tissues show a clearing-induced transparency window with central wavelength at 200 nm, which continues to grow over the time of treatment. The magnitude of such window in the adenocarcinoma tissue is higher than in the normal mucosa during the entire treatment, indicating that the first contains more proteins. This result is according to literature, since it has been reported that proteins accumulate in higher quantities as cancer develops [210]. Since the Deep-UV window has its peak at 200 nm, this wavelength is the one that is better associated to the protein dissociation phenomenon. Consequently, the information that can characterize the protein dissociation mechanism must be retrieved from the OCeff kinetics at that wavelength. As reported in Ref. [193], the OCeff(λ=200 nm) kinetics was analyzed, and it was verified that between 3 and 10 min of treatment a linear behavior with different inclination for both tissues occurred. The kinetics of OCeff at 200 nm is represented in Fig. 19, along with the linear fitting obtained for the normal and adenocarcinoma mucosa tissues between 3 and 10 min of treatment.
Fig. 19.
Kinetics for the OCeff(λ=200 nm) of human normal colorectal mucosa (a) and adenocarcinoma (b) tissues. Reprinted from Ref. [193] with the permission of IEEE.
Looking into the equations for the linear fittings that are represented in each panel of Fig. 19, we see that the in the case of the adenocarcinoma, a higher slope was obtained, which is about 3 × higher than in the normal mucosa. If we consider that slope to be the dissociation rate of proteins in the mucosa tissues, we can say that the treatments have dissociated 27.36 proteins per min in the normal mucosa and 79.14 proteins per min in the adenocarcinoma.
The information gathered from the graphs in Fig. 19 allowed to obtain a characterization parameter for the protein dissociation mechanism of optical clearing – the protein dissociation rate, which is differentiated between normal and pathological mucosa. Such data is highly important, since similar studies can be performed to obtain the protein dissociation rate from samples in different stages of colorectal cancer progression. Performing such studies in other types of cancer is also of interest, since the information collected in those studies, which can be obtained from minimally invasive spectroscopy measurements, like from Rd spectra, can be used to establish a relation between the protein dissociation rate and the cancer stage of development. Such relation could be used in periodic screening exams to perform an early detection of cancer and increase the life expectancy of the patient.
After analyzing the broadband spectral data, and especially in the deep-UV, that was collected from normal and diseased tissues, we see that the optical immersion clearing technique is a powerful tool to obtain diagnostic information. For this reason, further studies involving tissue clearing procedures and broadband spectroscopy measurements need to be performed, both in the tissues here discussed and in others where no information is currently available.
5.5. THz waves
The high THz-wave absorption by tissue water is a severe reason that reduces the penetration depth and corresponding applicability of THz techniques in biophotonics [33,34,36,45]. Immersion optical clearing represents a promising solution to this problem, that is rather cost effective and can be applied either ex vivo and in vivo [1,77,188,200,211,212].
This method is based on the application of specific chemical agents to a tissue, which leads to water diffusion from the tissues and agent diffusion into them. This results in substitution of free and weakly bound tissue water by an agent and provides temporal and reversible reduction of the tissue water content (tissue dehydration), RI matching, tissue shrinkage and better ordering [1,188,213]. In the VIS–IR ranges, immersion optical clearing significantly suppresses the light scattering in tissues, thanks to the achievement of tissue spatial homogeneity. Meanwhile, in the THz range, where scattering effects are not so dominating and only the tissue water strongly absorbs the THz waves, the reduction of water content is more important, leading to the increased depth of THz-wave penetration in tissues [214–216].
For example, glycerol has a much lower absorption coefficient than that of liquid water and, thus, enables reduction of the tissue THz absorption coefficient α, improvement of the THz-wave penetration in tissues and higher contrast in the THz images of tissues; see Fig. 20 [217]. One should also keep in mind that immersion optical clearing leads to a reduction of the effective RI of tissues, thus, reducing or managing the Fresnel reflectivity and corresponding Fresnel losses during the THz measurements.
Fig. 20.
Example of the THz-wave penetration depth enhancement using the immersion optical clearing, where glycerol is applied, as an immersion OCA, to a 224-µm-thick abdomen skin tissue ex vivo from a mouse. (a) A photo of the tissue specimen. (b),(c) THz pulsed images of the knife below a tissue using peak-to-peak values of the entire THz waveform or of the THz waveform part at the delays >7.5 ps, respectively. Reproduced from [217] with the permission of Optica Publishing.
For successful immersion optical clearing in the THz range, the agents, applied to tissues and temporarily changing their structure and water content, should be biocompatible and nontoxic, possess hyperosmotic status and a high diffusion coefficient, and (what even more important) have low THz absorption coefficient α (i.e., much lower than that of water). Fortunately, numerous chemicals have such a combination of physical properties, thus, demonstrating the immersion clearing potential. Among them, we notice glycerol, polyethylene glycol (PEG), propylene glycol (PG), ethylene glycol (EG), dimethyl sulfoxide (DMSO), etc. Despite they are commonly used in the VIS–IR ranges, there is a lack of data about their THz optical properties. Selection of an appropriate agents for the immersion optical clearing of tissues in the THz range is a complex task, that requires THz dielectric measurements of pure agents, their aqueous solutions, as well as biological tissues exposed to these agents [218–222].
To partially mitigate this issue, in Ref. [221], a comprehensive analysis of the common immersion OCAs in THz range was performed, aimed at the selection of optimal agents for the efficient enhancement of penetration depth of THz waves into tissues. THz pulsed spectroscopy was applied to study the optical properties of common agents in the 0.1–2.5 THz range. Using the VIS collimated transmission spectroscopy, binary diffusion coefficients D of tissue water and agent were measured using the intact rat brain tissues ex vivo. The considered agents were objectively compared using the 2D nomogram, that simultaneously account for the THz absorption coefficients α and binary diffusion coefficients D of pure agents and their aqueous solutions (Fig. 21). The results of this study demonstrate an interplay between the penetration depth enhancement and the diffusion rate of an agent, while glycerol was pointed out as somewhat optimal agent among the considered ones.
Fig. 21.
A nomogram that compares immersion OCAs and their 70% aqueous solutions, considering the experimental data of their THz absorption coefficients α (by field) at 1.0 THz and binary diffusion coefficients D (into rat brain tissues ex vivo). Mean values are shown by markers, while measurement errors – by colored areas. Reprinted from Ref. [221] with the permission of Wiley.
Finally, we notice that, along with the immersion optical clearing, compression optical clearing can be applied for the temporal local dehydration of tissue in vivo and more close packing of its components due to mechanical squeezing or stretching [189,223]. This can also improve the depth of THz-wave penetration into soft tissues in vivo. According to Ref. [223], the effective THz RI of human skin undergoes significant changes of over 10% when mechanical pressure of 1.5–3.5 N cm−2 is applied to tissues; see also [224]. Such results should be accounted for in all contact THz measurements, since they are very sensitive to the physical force applied to a subject, as well as to the occlusion effects.
6. Problem of broadband tissue measurements
Nowadays, measurements of tissues optical properties are usually carried out independently in different spectral ranges, using specific experimental tools, methods, and light – matter interaction models. In fact, in the UV, visible, and NIR ranges, a variety of the experimental techniques exist to characterize tissues (integrating-sphere spectroscopy, collimated transmission spectroscopy, diffuse light scattering spectroscopy, optical coherence tomography, etc.), while the light – tissue interactions are commonly described in the frameworks of the radiation transfer theory and the Mie scattering theory, which account for both the absorption and scattering effects [1]. In turn, in the THz domain, different modalities of pulsed or continuous-wave spectroscopy and imaging are vigorously explored and applied to study tissues. Related THz-wave – tissue interactions are usually interpreted in the frameworks of the effective medium theory and the relaxation models of tissue complex dielectric permittivity, while no method exists to study THz-wave scattering in tissues; thus, the latter is commonly neglected [33,34,36,45]. Meanwhile, we still possess quite limited knowledge on the electrodynamic response of tissues (healthy or pathological, intact or under the immersion optical clearing conditions) in the MIR, FIR, and THz bands. Thereby, bridging the gap between the high-frequency (UV–NIR) and low-frequency (FIR–THz) parts of the electromagnetic spectrum, development of the unified approaches to describe the electromagnetic-wave – tissue interactions, and studying the interplay between the absorption and scatting effects in such a broad spectral range remain challenging problems of applied physics, electrodynamics, optics, and biophotonics.
To mitigate them, broadband spectroscopic measurements of tissues are in order, that still remain a daunting task, due to the lack of appropriate experimental techniques. Indeed, nowadays, it appears to be almost impossible to simultaneously (in a real-time regime or within a realistic time interval) characterize the response of tissues in a broad UV–THz range. Quite a limited number of unique multimodal experimental approaches is capable of broadband measurements. For examples, a favorable combination of backward-wave oscillator spectroscopy, THz pulsed spectroscopy, and Fourier-transform IR spectroscopy allows to reconstruct the optical properties of an analyte in the NIR–THz range, but works mostly with solid and liquid objects, and it still to be applied to biological tissues [179,225]. Next, consider innovative approaches for broadband pulsed generation in laser gas plasma excited by femtosecond visible or NIR laser pulses [226,227]. They produce broadband pulsed radiation spanning the THz–NIR range, with the bandwidth as high as 0.1–200 THz [228,229]. Being aided by the ultrathin electrooptical detectors [230] or the interferometric (Fourier transform) measurement principles [225], such advanced emitters have a potential in the NIR–THz spectroscopy of an analyte (relying on a single measurement). At the same time, these emitters require intense (energy >1 mJ) and short (<10 fs) laser pulses to produce gas plasma, which makes them quite rare, labor intensive, and expensive. They also have poor stability, making them sub-optimal for spectroscopy. Finally, we highlight modern approaches for the supercontinuum generation (in non-linear media [231], solid waveguides [232], or hollow-core microstructured fibers [233,234]) and the broadband optical parametric generation (in bulk, periodically-poled, or microstructured non-linear media) [235]. Generally, they are capable of broadband spectral operation range (UV–MIR) and suitable for spectroscopy and pump-probe experiments [236,237], but remain rare and cumbersome, which hampers their applications in biophotonics.
Therefore, it would take considerable research and engineering efforts to make possible broadband UV–THz characterization of biological tissues. Here, we only pointed out possible technical solutions of this problem. Development of such experimental techniques will broaden our fundamental knowledge of the electrodynamic properties of tissues, as well as help us to introduce novel optical methods for the medical spectroscopy and imaging of tissues, including the multimodal ones.
7. Conclusion
The calculation of the spectral optical properties of biological tissues, namely the spectral dependence of absorption coefficient or the tissue dispersion, provides numerous information about their internal composition. By analyzing such spectra, we verify that the presence of pigments, such as melanin and lipofuscin, could be identified. The quantification of blood content can also be retrieved from such spectra, by calculating the fold ratios at the wavelengths that correspond to the main absorption bands of blood hemoglobin. By comparing such information between the healthy and pathological versions of the same tissues, differentiated pigment contents and higher blood contents were found for the diseased tissues. Although these results were obtained from measurements performed on ex vivo tissue samples, the similar analysis and results can be obtained in vivo, if diffuse reflectance spectra are used to develop the machine learning algorithms for generation of the spectra for those optical properties. One such application could be used to perform early detection of cancer.
The use of UV radiation in Biophotonics is a field that needs strong exploration. This spectral range is where biological tissues present a large number of strong absorption bands combined with a strong multiple light scattering, discourage researchers to use it. The UV radiation is cytotoxic, which is also a disadvantage, but its application to tissues in small doses and for short periods of time may be beneficial to evaluate and characterize the DNA/RNA and various types of protein connections, or even to treat pathologies. The inactivation of the COVID-19 virus was recently accomplished with UV light, as discussed above. The combination of UV spectroscopy with optical clearing treatments has also demonstrated that the dissociation of proteins occurs at different rates in healthy and pathological tissues. Further studies to evaluate such dissociation rates in different stages of cancer development need to be performed urgently to acquire precise diagnostic information that identify the stage of the pathology development through the recurrent and non-expensive screening exams for cancers that are a major concern worldwide.
Reliable experimental data for the optical properties of various tissues and their components in a wide wavelength range are required for the most complete description of the optical properties of multicomponent tissues, in particular, in in vivo studies. For example, in solving direct and inverse problems of the interaction of light beams with complexly organized tissues by using Monte Carlo statistical simulations. Section 3 describes the features of measuring the refraction of the most important tissues and their components, and presents the RI values measured for multiple laser lines and dispersion formulas for calculating the RI in the entire visible/NIR range.
Knowledge of the refraction properties of pathological tissues and blood is of particular importance for determining the interaction wavelength optimizing the penetration depth and distribution of laser radiation inside the tissue. These data are critical for choosing the operating wavelengths of pulse oximeters, for developing clinical protocols for laser treatments using interstitial heating or photodynamic therapies, etc.
Despite the aforementioned progress, THz diagnosis and therapy are still at the initial stage of their development due to a number of challenging issues. Here we particularly notice the most important of them. THz instruments still remain rare, non-ergonomic and expensive. There is a need for THz waveguides, optical fibers and fiber bundles for endoscopic measurements of hardly-accessible tissues and organs, as well as for efficient real-time THz emitters and detectors (including the 1D and 2D arrays) and superresolution optical systems. All these factors restrain transfer of THz technology to biophysical laboratory and clinical practice. As compared to the visible and IR ranges, in which the study and analysis of the optical properties of tissue have been extensively performed since the middle of the 20th century, THz biophotonics remains a novel research direction, in which much fewer data on THz-wave–tissue interactions have accumulated. Further study of the optical properties of tissue at THz frequencies, and analysis of the physical effects underlying its THz response are required in order to analyze the advantages of THz technology over other medical spectroscopy and imaging instruments.
The use of optical clearing treatments can also be beneficial to collect discriminating information for pathologies. In the studies discussed above for human colorectal mucosa tissues, the kinetic evaluation of the diffusion properties of water and glucose showed that those properties are different for the healthy and for the pathological tissues, and that the mobile water content is also higher in the diseased tissue. Even though this study was performed only with tissues that correspond to the full developed adenocarcinoma, similar studies can be performed to evaluate the diffusion properties and the mobile water content in the different stages of cancer development, in any type of cancer. Once again, by adopting a noninvasive, or minimally invasive, procedure, the measurement of diffuse reflectance spectra, combined with optimized machine learning algorithms, may be able to provide the similar discriminating information in the near future.
Improving the depth of THz-wave penetration into tissues could broaden the range of THz technology applications in malignant and benign neoplasm diagnosis. For this aim, modern methods of immersion and compression optical clearing of tissues could be adapted from the visible and IR ranges; however, the capabilities of these methods at THz frequencies have not been studied enough (see, subsection 5.5).
Notation
- THz
Terahertz
- UV
Ultraviolet
- RI
Refractive index
- NIR
Near-infrared
- OCA
Optical clearing agent
- K-K
Kramers-Kronig
- SD
Standard deviation
- IAD
Inverse Adding-Doubling
- NSE
Neuron-specific enolase
- CRCC
Chromophobe renal cell carcinoma
- AMD
age-related macular degeneration
- LED
light emitting diode
- WHO
World Health Organization
- ISF
interstitial fluid
- PEG
polyethylene glycol
- PG
propylene glycol
- EG
ethylene glycol
- DMSO
dimethyl sulfoxide
Acknowledgments
The authors are grateful to all their co-authors for published original studies, which are presented and analyzed in this review. The work of I.S.M. was supported by the Portuguese Science Foundation, grant no. FCT-UIDB/151528/2021. The work of H.F.S. and L.M.O. was supported by the Portuguese Science Foundation, grant no. FCT-UIDB/04730/2020. The work of L.E.N. on Section 3 was supported by the Russian Federation Government grant (No. 14.Z50.31.0044). The work of K.I.Z. and N.V.C. on Sections 4 and 5.5 was supported by the Russian Science Foundation, Project # 22-79-10099. The work of V.V.T. was supported by the grant under the Decree of the Government of the Russian Federation No. 220 of 09 April 2010 (Agreement No. 075-15-2021-615 of 04 June 2021).
Inês S. Martins, Hugo F. Silva, Ekaterina N. Lazareva, and Nikita V. Chernomyrdin contributed equally as executors. Kirill I. Zaytsev, Luís M. Oliveira, and Valery V. Tuchin, contributed equally as supervisors.
Funding
Fundação para a Ciência e a Tecnologia10.13039/501100001871 (FCT-UIDB/04730/2020, FCT-UIDB/151528/2021); Megagrants10.13039/501100012189 (14.Z50.31.0044); Russian Science Foundation10.13039/501100006769 (22-79-10099); Decree of the Government of the Russian Federation No. 220 of 09 April 2010 (Agreement No. 075-15-2021-615 of 04 June 2021).
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
References
- 1.Tuchin V., Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnostics , 3rd ed. (SPIE Press, 2015). [Google Scholar]
- 2.Mobley J., Vo-Dinh T., Tuchin V. V., “Optical properties of tissue,” in Biomedical Photonics Handbook , Vo-Dinh T., ed., 2nd ed. (CRC Press, 2015), pp. 23–121. [Google Scholar]
- 3.Oliveira L. M. C., Tuchin V. V., “Measurements during optical clearing,” in The Optical Clearing Method: A New Tool for Clinical Practice and Biomedical Engineering (Springer Nature, 2019), pp. 61–77. [Google Scholar]
- 4.Prahl S. A., “Inverse adding-doubling,” http://omlc.org/software/iad/.
- 5.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). 10.1088/0031-9155/58/11/R37 [DOI] [PubMed] [Google Scholar]
- 6.Bashkatov A. N., Genina E. A., Tuchin V. V., “Optical properties of skin, subcutaneous and muscle tissues: a review,” J. Innov. Opt. Health Sci. 04(01), 9–38 (2011). 10.1142/S1793545811001319 [DOI] [Google Scholar]
- 7.Lemaillet P., Cooksey C. C., Hwang J., Wabnitz H., Grosenick D., Yang L., Allen D. W., “Correction of an adding-doubling inversion algorithm for the measurement of the optical parameters of turbid media,” Biomed. Opt. Express 9(1), 55 (2018). 10.1364/BOE.9.000055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Oliveira L. R., Gonçalves T. M., Pinheiro M. R., Fernandes L. E., Martins I. S., Silva H. F., Oliveira H. P., Tuchin V. V., “Invasive and minimally invasive optical detection of pigment accumulation in brain cortex,” J. Biomed. Photonics Eng. 8(1), 010304 (2022). 10.18287/JBPE22.08.010304 [DOI] [Google Scholar]
- 9.Gonçalves T. M., Martins I. S., Silva H. F., Tuchin V. V., Oliveira L. M., “Spectral optical properties of rabbit brain cortex between 200 and 1000 nm,” Photochem 1(2), 190–208 (2021). 10.3390/photochem1020011 [DOI] [Google Scholar]
- 10.Martins I. S., Silva H. F., Tuchin V. V., Oliveira L. M., “Fast estimation of the spectral optical properties of rabbit pancreas and pigment content analysis,” Photonics 9(2), 122 (2022). 10.3390/photonics9020122 [DOI] [Google Scholar]
- 11.Troy T. L., Thennadil S. N., “Optical properties of human skin in the near infrared wavelength range of 1000 to 2200 nm,” J. Biomed. Opt. 6(2), 167 (2001). 10.1117/1.1344191 [DOI] [PubMed] [Google Scholar]
- 12.Bashkatov A. N., Genina E. A., Kochubey V. I., Tuchin V. V., “Optical properties of human skin, subcutaneous and mucous tissues in the wavelength range from 400 to 2000nm,” J. Phys. D: Appl. Phys. 38(15), 2543–2555 (2005). 10.1088/0022-3727/38/15/004 [DOI] [Google Scholar]
- 13.Sordillo L. A., Pu Y., Pratavieira S., Budansky Y., Alfano R. R., “Deep optical imaging of tissue using the second and third near-infrared spectral windows,” J. Biomed. Opt. 19(5), 056004 (2014). 10.1117/1.JBO.19.5.056004 [DOI] [PubMed] [Google Scholar]
- 14.Shi L., Sordillo L. A., Rodríguez-Contreras A., Alfano R., “Transmission in near-infrared optical windows for deep brain imaging,” J. Biophotonics 9(1-2), 38–43 (2016). 10.1002/jbio.201500192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sordillo D. C., Sordillo L. A., Sordillo P. P., Shi L., Alfano R. R., “Short wavelength infrared optical windows for evaluation of benign and malignant tissues,” J. Biomed. Opt. 22(4), 045002 (2017). 10.1117/1.JBO.22.4.045002 [DOI] [PubMed] [Google Scholar]
- 16.Golovynskyi S., Golovynska I., Stepanova L. I., Datsenko O. I., Liu L., Qu J., Ohulchanskyy T. Y., “Optical windows for head tissues in near-infrared and short-wave infrared regions: Approaching transcranial light applications,” J. Biophotonics 11(12), e201800141 (2018). 10.1002/jbio.201800141 [DOI] [PubMed] [Google Scholar]
- 17.Pu Y., Chen J., Wang W., Alfano R. R., “Basic Optical Scattering Parameter of the Brain and Prostate Tissues in the Spectral Range of 400–2400 nm,” in Neurophotonics and Biomedical Spectroscopy , Alfano R. R., Shi L., eds. (Elsevier, 2019), pp. 229–252. [Google Scholar]
- 18.Patterson M. S., Chance B., Wilson B. C., “Time resolved reflectance and transmittance for the noninvasive measurement of tissue optical properties,” Appl. Opt. 28(12), 2331 (1989). 10.1364/AO.28.002331 [DOI] [PubMed] [Google Scholar]
- 19.Lanka P., Segala A., Farina A., Konugolu Venkata Sekar S., Nisoli E., Valerio A., Taroni P., Cubeddu R., Pifferi A., “Non-invasive investigation of adipose tissue by time domain diffuse optical spectroscopy,” Biomed. Opt. Express 11(5), 2779 (2020). 10.1364/BOE.391028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Galiakhmetova D., Dremin V., Koviarov A., Stoliarov D., Ngum N., Murugesan R. C., Parri R., Sokolovski S., Rafailov E., “Ultra-short laser pulses propagation through mouse head tissues: experimental and computational study,” IEEE J. Sel. Top. Quantum Electron. 1, 7200311 (2022). 10.1109/JSTQE.2022.3214788 [DOI] [Google Scholar]
- 21.Gioux S., Mazhar A., Cuccia D. J., “Spatial frequency domain imaging in 2019: principles, applications, and perspectives,” J. Biomed. Opt. 24(07), 1 (2019). 10.1117/1.JBO.24.7.071613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Aguénounon E., Dadouche F., Uhring W., Gioux S., “Real-time optical properties and oxygenation imaging using custom parallel processing in the spatial frequency domain,” Biomed. Opt. Express 10(8), 3916 (2019). 10.1364/BOE.10.003916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Aguénounon E., Smith J. T., Al-Taher M., Diana M., Intes X., Gioux S., “Real-time, wide-field and high-quality single snapshot imaging of optical properties with profile correction using deep learning,” Biomed. Opt. Express 11(10), 5701 (2020). 10.1364/BOE.397681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bashkatov A. N., Genina E. A., Kozintseva M. D., Kochubei V. I., Gorodkov S. Y., Tuchin V. V., “Optical properties of peritoneal biological tissues in the spectral range of 350–2500 nm,” Opt. Spectrosc. 120(1), 1–8 (2016). 10.1134/S0030400X16010045 [DOI] [Google Scholar]
- 25.Bashkatov A. N., Genina E. A., Kochubey V. I., Gavrilova A. A., Kapralov S. V., Grishaev V. A., Tuchin V. V., “Optical properties of human stomach mucosa in the spectral range from 400 to 2000nm: Prognosis for gastroenterology,” Med. Laser Appl. 22(2), 95–104 (2007). 10.1016/j.mla.2007.07.003 [DOI] [Google Scholar]
- 26.Carvalho S., Carneiro I., Henrique R., Tuchin V., Oliveira L., “Lipofuscin-type pigment as a marker of colorectal cancer,” Electronics 9(11), 1805 (2020). 10.3390/electronics9111805 [DOI] [Google Scholar]
- 27.Genina E. A., Bashkatov A. N., Tuchina D. K., Dyachenko P. A., Navolokin N., Shirokov A., Khorovodov A., Terskov A., Klimova M., Mamedova A., Blokhina I., Agranovich I., Zinchenko E., Semyachkina-Glushkovskaya O. V., Tuchin V. V., “Optical properties of brain tissues at the different stages of glioma development in rats: pilot study,” Biomed. Opt. Express 10(10), 5182 (2019). 10.1364/BOE.10.005182 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shapey J., Xie Y., Nabavi E., Ebner M., Saeed S. R., Kitchen N., Dorward N., Grieve J., McEvoy A. W., Miserocchi A., Grover P., Bradford R., Lim Y., Ourselin S., Brandner S., Jaunmuktane Z., Vercauteren T., “Optical properties of human brain and tumour tissue: An ex vivo study spanning the visible range to beyond the second near-infrared window,” J. Biophotonics 15(4), e202100072 (2022). 10.1002/jbio.202100072 [DOI] [PubMed] [Google Scholar]
- 29.Rodriguez A. J., Boonya-Ananta M. T., Gonzalez M., Du Le V. N., Fine J., Palacios C., McShane M. J., Coté G. L., Ramella-Roman J. C., “Skin optical properties in the obese and their relation to body mass index: a review,” J. Biomed. Opt. 27(03), 030902 (2022). 10.1117/1.JBO.27.3.030902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Koenig A., Petitdidier N., Grateau H., Characoun S., Ghaith A., Verges S., Doutreleau S., Gharbi S., Gerbelot R., Gioux S., Dinten J.-M., “Contact, high-resolution spatial diffuse reflectance imaging system for skin condition diagnosis: a first-in-human clinical trial,” J. Biomed. Opt. 26(01), 012706 (2021). 10.1117/1.JBO.26.1.012706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tseregorodtseva P. S., Buiankin K. E., Yakimov B. P., Kamalov A. A., Budylin G. S., Shirshin E. A., “Single-fiber diffuse reflectance spectroscopy and spatial frequency domain imaging in surgery guidance: a study on optical phantoms,” Materials 14(24), 7502 (2021). 10.3390/ma14247502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gregor A., Sase S., Wagnieres G., “Optimization of the distance between cylindrical light distributors used for interstitial light delivery in biological tissues,” Photonics 9(9), 597 (2022). 10.3390/photonics9090597 [DOI] [Google Scholar]
- 33.Smolyanskaya O. A., Chernomyrdin N. V., Konovko A. A., Zaytsev K. I., Ozheredov I. A., Cherkasova O. P., Nazarov M. M., Guillet J.-P., Kozlov S. A., Kistenev Y. V., Coutaz J.-L., Mounaix P., Vaks V. L., Son J.-H., Cheon H., Wallace V. P., Feldman Y., Popov I., Yaroslavsky A. N., Shkurinov A. P., Tuchin V. V., “Terahertz biophotonics as a tool for studies of dielectric and spectral properties of biological tissues and liquids,” Prog. Quantum Electron. 62, 1–77 (2018). 10.1016/j.pquantelec.2018.10.001 [DOI] [Google Scholar]
- 34.Zaytsev K. I., Dolganova I. N., Chernomyrdin N. V, Katyba G. M., Gavdush A. A., Cherkasova O. P., Komandin G. A., Shchedrina M. A., Khodan A. N., Ponomarev D. S., Reshetov I. V., Karasik V. E., Skorobogatiy M., Kurlov V. N., Tuchin V. V, “The progress and perspectives of terahertz technology for diagnosis of neoplasms: a review,” J. Opt. 22(1), 013001 (2020). 10.1088/2040-8986/ab4dc3 [DOI] [Google Scholar]
- 35.Dolganova I. N., Aleksandrova P. V., Nikitin P. V., Alekseeva A. I., Chernomyrdin N. V., Musina G. R., Beshplav S. T., Reshetov I. V., Potapov A. A., Kurlov V. N., Tuchin V. V., Zaytsev K. I., “Capability of physically reasonable OCT-based differentiation between intact brain tissues, human brain gliomas of different WHO grades, and glioma model 101.8 from rats,” Biomed. Opt. Express 11(11), 6780 (2020). 10.1364/BOE.409692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Chernomyrdin N. V., Musina G. R., Nikitin P. V., Dolganova I. N., Kucheryavenko A. S., Alekseeva A. I., Wang Y., Xu D., Shi Q., Tuchin V. V., Zaytsev K. I., “Terahertz technology in intraoperative neurodiagnostics: A review,” Opto-Electron. Adv. 220071 (2023).
- 37.Lindley-Hatcher H., Stantchev R. I., Chen X., Hernandez-Serrano A. I., Hardwicke J., Pickwell-MacPherson E., “Real time THz imaging – opportunities and challenges for skin cancer detection,” Appl. Phys. Lett. 118(23), 230501 (2021). 10.1063/5.0055259 [DOI] [Google Scholar]
- 38.Nikitkina A. I., Bikmulina P. Y., Gafarova E. R., Kosheleva N. V., Efremov Y. M., Bezrukov E. A., Butnaru D. V., Dolganova I. N., Chernomyrdin N. V., Cherkasova O. P., Gavdush A. A., Timashev P. S., “Terahertz radiation and the skin: a review,” J. Biomed. Opt. 26(04), 043005 (2021). 10.1117/1.JBO.26.4.043005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Guerboukha H., Nallappan K., Skorobogatiy M., “Toward real-time terahertz imaging,” Adv. Opt. Photonics 10(4), 843 (2018). 10.1364/AOP.10.000843 [DOI] [Google Scholar]
- 40.Islam M. S., Cordeiro C. M. B., Franco M. A. R., Sultana J., Cruz A. L. S., Abbott D., “Terahertz optical fibers [Invited],” Opt. Express 28(11), 16089 (2020). 10.1364/OE.389999 [DOI] [PubMed] [Google Scholar]
- 41.Katyba G. M., Zaytsev K. I., Dolganova I. N., Chernomyrdin N. V., Ulitko V. E., Rossolenko S. N., Shikunova I. A., Kurlov V. N., “Sapphire waveguides and fibers for terahertz applications,” Prog. Cryst. Growth Charact. Mater. 67(3), 100523 (2021). 10.1016/j.pcrysgrow.2021.100523 [DOI] [Google Scholar]
- 42.Yachmenev A. E., Lavrukhin D. V., Glinskiy I. A., Zenchenko N. V., Goncharov Y. G., Spektor I. E., Khabibullin R. A., Otsuji T., Ponomarev D. S., “Metallic and dielectric metasurfaces in photoconductive terahertz devices: a review,” Opt. Eng. 59(06), 1 (2020). 10.1117/1.OE.59.6.061608 [DOI] [Google Scholar]
- 43.Lepeshov S., Gorodetsky A., Krasnok A., Rafailov E., Belov P., “Enhancement of terahertz photoconductive antenna operation by optical nanoantennas,” Laser Photonics Rev. 11(1), 1600199 (2017). 10.1002/lpor.201600199 [DOI] [Google Scholar]
- 44.Padmanabhan P., Boubanga-Tombet S., Fukidome H., Otsuji T., Prasankumar R. P., “A graphene-based magnetoplasmonic metasurface for actively tunable transmission and polarization rotation at terahertz frequencies,” Appl. Phys. Lett. 116(22), 221107 (2020). 10.1063/5.0006448 [DOI] [Google Scholar]
- 45.Cherkasova O. P., Serdyukov D. S., Nemova E. F., Ratushnyak A. S., Kucheryavenko A. S., Dolganova I. N., Xu G., Skorobogatiy M., Reshetov I. V., Timashev P. S., Spektor I. E., Zaytsev K. I., Tuchin V. V., “Cellular effects of terahertz waves,” J. Biomed. Opt. 26(09), 090902 (2021). 10.1117/1.JBO.26.9.090902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Parrott E. P. J., Sy S. M. Y., Blu T., Wallace V. P., Pickwell-MacPherson E., “Terahertz pulsed imaging in vivo: measurements and processing methods,” J. Biomed. Opt. 16(10), 106010 (2011). 10.1117/1.3642002 [DOI] [PubMed] [Google Scholar]
- 47.Zaytsev K. I., Gavdush A. A., Chernomyrdin N. V., Yurchenko S. O., “Highly Accurate in Vivo Terahertz Spectroscopy of Healthy Skin: Variation of Refractive Index and Absorption Coefficient Along the Human Body,” IEEE Trans. Terahertz Sci. Technol. 5(5), 817–827 (2015). 10.1109/TTHZ.2015.2460677 [DOI] [Google Scholar]
- 48.Konnikova M. R., Cherkasova O. P., Nazarov M. M., Vrazhnov D. A., Kistenev Y. V., Titov S. E., Kopeikina E. V., Shevchenko S. P., Shkurinov A. P., “Malignant and benign thyroid nodule differentiation through the analysis of blood plasma with terahertz spectroscopy,” Biomed. Opt. Express 12(2), 1020–1035 (2021). 10.1364/BOE.412715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Musina G. R., Nikitin P. V., Chernomyrdin N. V., Dolganova I. N., Gavdush A. A., Komandin G. A., Ponomarev D. S., Potapov A. A., Reshetov I. V., Tuchin V. V., Zaytsev K. I., “Prospects of terahertz technology in diagnosis of human brain tumors – A review,” J. Biomed. Photonics Eng. 6(2), 020201 (2020). 10.18287/JBPE20.06.020201 [DOI] [Google Scholar]
- 50.Woodward R. M., Wallace V. P., Pye R. J., Cole B. E., Arnone D. D., Linfield E. H., Pepper M., “Terahertz pulse imaging of ex vivo basal cell carcinoma,” J. Invest. Dermatol. 120(1), 72–78 (2003). 10.1046/j.1523-1747.2003.12013.x [DOI] [PubMed] [Google Scholar]
- 51.Wallace V. P., Fitzgerald A. J., Shankar S., Flanagan N., Pye R., Cluff J., Arnone D. D., “Terahertz pulsed imaging of basal cell carcinoma ex vivo and in vivo,” Br. J. Dermatol. 151(2), 424–432 (2004). 10.1111/j.1365-2133.2004.06129.x [DOI] [PubMed] [Google Scholar]
- 52.Zaytsev K. I., Kudrin K. G., Karasik V. E., Reshetov I. V., Yurchenko S. O., “In vivo terahertz spectroscopy of pigmentary skin nevi: Pilot study of non-invasive early diagnosis of dysplasia,” Appl. Phys. Lett. 106(5), 053702 (2015). 10.1063/1.4907350 [DOI] [Google Scholar]
- 53.Fitzgerald A. J., Wallace V. P., Jimenez-Linan M., Bobrow L., Pye R. J., Purushotham A. D., Arnone D. D., “Terahertz Pulsed Imaging of Human Breast Tumors,” Radiology 239(2), 533–540 (2006). 10.1148/radiol.2392041315 [DOI] [PubMed] [Google Scholar]
- 54.Reid C. B., Fitzgerald A., Reese G., Goldin R., Tekkis P., O’Kelly P. S., Pickwell-MacPherson E., Gibson A. P., Wallace V. P., “Terahertz pulsed imaging of freshly excised human colonic tissues,” Phys. Med. Biol. 56(14), 4333–4353 (2011). 10.1088/0031-9155/56/14/008 [DOI] [PubMed] [Google Scholar]
- 55.Oh S. J., Kim S.-H., Bin Ji Y., Jeong K., Park Y., Yang J., Park D. W., Noh S. K., Kang S.-G., Huh Y.-M., Son J.-H., Suh J.-S., “Study of freshly excised brain tissues using terahertz imaging,” Biomed. Opt. Express 5(8), 2837–2842 (2014). 10.1364/BOE.5.002837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Cherkasova O., Nazarov M., Shkurinov A., “Noninvasive blood glucose monitoring in the terahertz frequency range,” Opt. Quantum Electron. 48(3), 217 (2016). 10.1007/s11082-016-0490-5 [DOI] [Google Scholar]
- 57.Smolyanskaya O. A., Lazareva E. N., Nalegaev S. S., Petrov N. V., Zaytsev K. I., Timoshina P. A., Tuchina D. K., Toropova Y. G., Kornyushin O. V., Babenko A. Y., Guillet J. P., Tuchin V. V., “Multimodal optical diagnostics of glycated biological tissues,” Biochemistry 84(S1), 124–143 (2019). 10.1134/S0006297919140086 [DOI] [PubMed] [Google Scholar]
- 58.Hernandez-Cardoso G. G., Rojas-Landeros S. C., Alfaro-Gomez M., Hernandez-Serrano A. I., Salas-Gutierrez I., Lemus-Bedolla E., Castillo-Guzman A. R., Lopez-Lemus H. L., Castro-Camus E., “Terahertz imaging for early screening of diabetic foot syndrome: A proof of concept,” Sci. Rep. 7(1), 42124 (2017). 10.1038/srep42124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hernandez-Cardoso G. G., Amador-Medina L. F., Gutierrez-Torres G., Reyes-Reyes E. S., Benavides Martínez C. A., Cardona Espinoza C., Arce Cruz J., Salas-Gutierrez I., Murillo-Ortíz B. O., Castro-Camus E., “Terahertz imaging demonstrates its diagnostic potential and reveals a relationship between cutaneous dehydration and neuropathy for diabetic foot syndrome patients,” Sci. Rep. 12(1), 3110 (2022). 10.1038/s41598-022-06996-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhao H., Wang Y., Chen L., Shi J., Ma K., Tang L., Xu D., Yao J., Feng H., Chen T., “High-sensitivity terahertz imaging of traumatic brain injury in a rat model,” J. Biomed. Opt. 23(03), 1 (2018). 10.1117/1.JBO.23.3.036015 [DOI] [PubMed] [Google Scholar]
- 61.Shi J., Wang Y., Chen T., Xu D., Zhao H., Chen L., Yan C., Tang L., He Y., Feng H., Yao J., “Automatic evaluation of traumatic brain injury based on terahertz imaging with machine learning,” Opt. Express 26(5), 6371–6381 (2018). 10.1364/OE.26.006371 [DOI] [PubMed] [Google Scholar]
- 62.Wang Y., Wang G., Xu D., Jiang B., Ge M., Wu L., Yang C., Mu N., Wang S., Chang C., Chen T., Feng H., Yao J., “Terahertz spectroscopic diagnosis of early blast-induced traumatic brain injury in rats,” Biomed. Opt. Express 11(8), 4085–4098 (2020). 10.1364/BOE.395432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Cao Y., Huang P., Chen J., Ge W., Hou D., Zhang G., “Qualitative and quantitative detection of liver injury with terahertz time-domain spectroscopy,” Biomed. Opt. Express 11(2), 982–993 (2020). 10.1364/BOE.381660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Shchepetilnikov A. V., Zarezin A. M., Muravev V. M., Gusikhin P. A., Kukushkin I. V., “Quantitative analysis of water content and distribution in plants using terahertz imaging,” Opt. Eng. 59(06), 1 (2020). 10.1117/1.OE.59.6.061617 [DOI] [Google Scholar]
- 65.Iomdina E. N., Seliverstov S. V., Teplyakova K. O., Jani E. V., Pozdniakova V. V., Polyakova O. N., Goltsman G. N., “Terahertz scanning of the rabbit cornea with experimental UVB-induced damage: in vivo assessment of hydration and its verification,” J. Biomed. Opt. 26(04), 043010 (2021). 10.1117/1.JBO.26.4.043010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Musina G. R., Chernomyrdin N. V., Gafarova E. R., Gavdush A. A., Shpichka A. J., Komandin G. A., Anzin V. B., Grebenik E. A., Kravchik M. V., Istranova E. V., Dolganova I. N., Zaytsev K. I., Timashev P. S., “Moisture adsorption by decellularized bovine pericardium collagen matrices studied by terahertz pulsed spectroscopy and solid immersion microscopy,” Biomed. Opt. Express 12(9), 5368 (2021). 10.1364/BOE.433216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Chernomyrdin N. V., Skorobogatiy M., Gavdush A. A., Musina G. R., Katyba G. M., Komandin G. A., Khorokhorov A. M., Spektor I. E., Tuchin V. V., Zaytsev K. I., “Quantitative super-resolution solid immersion microscopy via refractive index profile reconstruction,” Optica 8(11), 1471–1480 (2021). 10.1364/OPTICA.439286 [DOI] [Google Scholar]
- 68.Bajwa N., Au J., Jarrahy R., Sung S., Fishbein M. C., Riopelle D., Ennis D. B., Aghaloo T., St. John M. A., Grundfest W. S., Taylor Z. D., “Non-invasive terahertz imaging of tissue water content for flap viability assessment,” Biomed. Opt. Express 8(1), 460–474 (2017). 10.1364/BOE.8.000460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Mattsson M.-O., Zeni O., Simko M., “Is there a biological basis for therapeutic applications of millimetre waves and THz waves?” J. Infrared, Millimeter, Terahertz Waves 39(9), 863–878 (2018). 10.1007/s10762-018-0483-5 [DOI] [Google Scholar]
- 70.Romanenko S., Begley R., Harvey A. R., Hool L., Wallace V. P., “The interaction between electromagnetic fields at megahertz, gigahertz and terahertz frequencies with cells, tissues and organisms: risks and potential,” J. R. Soc. Interface 14(137), 20170585 (2017). 10.1098/rsif.2017.0585 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Titova L. V, Ayesheshim A. K., Golubov A., Rodriguez-Juarez R., Woycicki R., Hegmann F. A., Kovalchuk O., “Intense THz pulses down-regulate genes associated with skin cancer and psoriasis: a new therapeutic avenue?” Sci. Rep. 3(1), 2363 (2013). 10.1038/srep02363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Cheon H., Paik J. H., Choi M., Yang H.-J., Son J.-H., “Detection and manipulation of methylation in blood cancer DNA using terahertz radiation,” Sci. Rep. 9(1), 6413 (2019). 10.1038/s41598-019-42855-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Cheon H., Yang H.-J., Choi M., Son J.-H., “Effective demethylation of melanoma cells using terahertz radiation,” Biomed. Opt. Express 10(10), 4931–4941 (2019). 10.1364/BOE.10.004931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Botelho A. R., Silva H. F., Martins I. S., Carneiro I. C., Carvalho S. D., Henrique R. M., Tuchin V. V., Oliveira L. M., “Fast calculation of spectral optical properties and pigment content detection in human normal and pathological kidney,” Spectrochim. Acta, Part A 286, 122002 (2023). 10.1016/j.saa.2022.122002 [DOI] [PubMed] [Google Scholar]
- 75.Chance B., Cope M., Gratton E., Ramanujam N., Tromberg B., “Phase measurement of light absorption and scatter in human tissue,” Rev. Sci. Instrum. 69(10), 3457–3481 (1998). 10.1063/1.1149123 [DOI] [Google Scholar]
- 76.Priezzhev A. V., Tuchin V. V., Shubochkin L. P., Laser Diagnostics in Biology and Medicine (Nauka, 1989). [Google Scholar]
- 77.Tuchin V. V., Optical Clearing of Tissues and Blood (SPIE Press, 2006). [Google Scholar]
- 78.Carneiro I., Carvalho S., Henrique R., Oliveira L., Tuchin V. V, “Kinetics of optical properties of colorectal muscle during optical clearing,” IEEE J. Sel. Top. Quantum Electron. 25(1), 7200608 (2018). 10.1109/JSTQE.2018.2840346 [DOI] [Google Scholar]
- 79.Martins I., Silva H., Tuchin V., Oliveira L., “Estimation of Rabbit Pancreas Dispersion Between 400 and 1000 nm,” J. Biomed. Photonics Eng. 7(2), 020303 (2021). 10.18287/JBPE21.07.020303 [DOI] [Google Scholar]
- 80.Yanina I. Y., Lazareva E. N., Tuchin V. V., “Refractive index of adipose tissue and lipid droplet measured in wide spectral and temperature ranges,” Appl. Opt. 57(17), 4839–4848 (2018). 10.1364/AO.57.004839 [DOI] [PubMed] [Google Scholar]
- 81.Singh V. K., Jaswal B. B. S., Kumar V., Prakash R., Rai P., “Application of He-Ne laser to study of the variation of refractive index of liquid solutions with the concentration,” J. Integr. Sci. Technol. 1(1), 13–18 (2013). [Google Scholar]
- 82.Giannios P., Toutouzas K. G., Matiatou M., Stasinos K., Konstadoulakis M. M., Zografos G. C., Moutzouris K., “Visible to near-infrared refractive properties of freshly-excised human-liver tissues: marking hepatic malignancies,” Sci. Rep. 6(1), 27910 (2016). 10.1038/srep27910 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Giannios P., Koutsoumpos S., Toutouzas K. G., Matiatou M., Zografos G. C., Moutzouris K., “Complex refractive index of normal and malignant human colorectal tissue in the visible and near-infrared,” J. Biophotonics 10(2), 303–310 (2017). 10.1002/jbio.201600001 [DOI] [PubMed] [Google Scholar]
- 84.Lazareva E. N., Oliveira L., Yanina I. Y., Chernomyrdin N. V., Musina G. R., Tuchina D. K., Bashkatov A. N., Zaytsev K. I., Tuchin V. V., “Refractive index measurements of tissue and blood components and OCAs in a wide spectral range,” in Handbook of Tissue Optical Clearing: New Prospects in Optical Imaging , Tuchin V. V., Zhu D., Genina E. A., eds. (CRC Press, 2022), pp. 141–166. [Google Scholar]
- 85.Carneiro I., Carvalho S., Henrique R., Oliveira L., Tuchin V., “Water content and scatterers dispersion evaluation in colorectal tissues,” J. Biomed. Photonics Eng. 3(4), 040301 (2017). 10.18287/JBPE17.03.040301 [DOI] [Google Scholar]
- 86.Carvalho S., Gueiral N., Nogueira E., Henrique R., Oliveira L., Tuchin V., “Wavelength dependence of the refractive index of human colorectal tissues: comparison between healthy mucosa and cancer,” J. Biomed. Photonics Eng. 2(4), 040307 (2016). 10.18287/JBPE16.02.040307 [DOI] [Google Scholar]
- 87.Carneiro I., Carvalho S., Henrique R., Oliveira L., Tuchin V. V, “Simple multimodal optical technique for evaluation of free/bound water and dispersion of human liver tissue,” J. Biomed. Opt. 22(12), 1 (2017). 10.1117/1.JBO.22.12.125002 [DOI] [PubMed] [Google Scholar]
- 88.Ding H., Lu J. Q., Wooden W. A., Kragel P. J., Hu X.-H., “Refractive indices of human skin tissues at eight wavelengths and estimated dispersion relations between 300 and 1600 nm,” Phys. Med. Biol. 51(6), 1479–1489 (2006). 10.1088/0031-9155/51/6/008 [DOI] [PubMed] [Google Scholar]
- 89.Matiatou M., Giannios P., Koutsoumpos S., Toutouzas K. G., Zografos G. C., Moutzouris K., “Data on the refractive index of freshly-excised human tissues in the visible and near-infrared spectral range,” Results Phys. 22, 103833 (2021). 10.1016/j.rinp.2021.103833 [DOI] [Google Scholar]
- 90.Sydoruk O., Zhernovaya O., Tuchin V., Douplik A., “Refractive index of solutions of human hemoglobin from the near-infrared to the ultraviolet range: Kramers-Kronig analysis,” J. Biomed. Opt. 17(11), 115002 (2012). 10.1117/1.JBO.17.11.115002 [DOI] [PubMed] [Google Scholar]
- 91.Gienger J., Groß H., Neukammer J., Bär M., “Determining the refractive index of human hemoglobin solutions by Kramers–Kronig relations with an improved absorption model,” Appl. Opt. 55(31), 8951–8961 (2016). 10.1364/AO.55.008951 [DOI] [PubMed] [Google Scholar]
- 92.Yu J., Zhang Y. G., Gao Q., Hu G., Zhang Z. G., Wu S. H., “Diffuse reflectivity measurement using cubic cavity,” Opt. Lett. 39(7), 1941 (2014). 10.1364/OL.39.001941 [DOI] [PubMed] [Google Scholar]
- 93.Zhou X., Yu J., Wang L., Zhang Z., “Investigating the relation between absorption and gas concentration in gas detection using a diffuse integrating cavity,” Appl. Sci. 8(9), 1630 (2018). 10.3390/app8091630 [DOI] [Google Scholar]
- 94.Fasman G. D., “Ultraviolet spectra of derivatives of cysteine, cysteine, histidine, phenylalanine, tyrosine, and tryptophan,” in Handbook of Biochemistry and Molecular Biology , Fasman G. D., ed., 3rd ed. (CRC Press, 2018). [Google Scholar]
- 95.Wetlaufer D. B., “Ultraviolet spectra Of Proteins and Amino Acids,” in Advances in Protein Chemistry (Academic Press, 1962), pp. 303–390. [Google Scholar]
- 96.Narayan R. K., Heydorn W. E., Creed G. J., Jacobowitz D. M., “Identification of major proteins in human cerebral cortex and brain tumors,” J. Protein Chem. 4(6), 375–389 (1985). 10.1007/BF01025178 [DOI] [Google Scholar]
- 97.Zhou Y., Yao J., Wang L. V., “Tutorial on photoacoustic tomography,” J. Biomed. Opt. 21(6), 061007 (2016). 10.1117/1.JBO.21.6.061007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Carneiro I., Carvalho S., Henrique R., Oliveira L., Tuchin V. V., “Measurement of optical properties of normal and pathological human liver tissue from deep-UV to NIR,” Proc. SPIE 11363, 113630G (2020). 10.1117/12.2554877 [DOI] [Google Scholar]
- 99.Hunter J. J., Morgan J. I. W., Merigan W. H., Sliney D. H., Sparrow J. R., Williams D. R., “The susceptibility of the retina to photochemical damage from visible light,” Prog. Retinal Eye Res. 31(1), 28–42 (2012). 10.1016/j.preteyeres.2011.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Gosnell M. E., Anwer A. G., Cassano J. C., Sue C. M., Goldys E. M., “Functional hyperspectral imaging captures subtle details of cell metabolism in olfactory neurosphere cells, disease-specific models of neurodegenerative disorders,” Biochim. Biophys. Acta, Mol. Cell Res. 1863(1), 56–63 (2016). 10.1016/j.bbamcr.2015.09.030 [DOI] [PubMed] [Google Scholar]
- 101.Feeney-Burns L., Hilderbrand E. S., Eldridge S., “Aging human RPE: Morphometric analysis of macular, equatorial, and peripheral cells,” Investig. Ophthalmol. Vis. Sci. 25(2), 195–200 (1984). [PubMed] [Google Scholar]
- 102.Double K. L., Dedov V. N., Fedorow H., Kettle E., Halliday G. M., Garner B., Brunk U. T., “The comparative biology of neuromelanin and lipofuscin in the human brain,” Cell. Mol. Life Sci. 65(11), 1669–1682 (2008). 10.1007/s00018-008-7581-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Moreno-García A., Kun A., Calero M., Calero O., “The neuromelanin paradox and its dual role in oxidative stress and neurodegeneration,” Antioxidants 10(1), 124 (2021). 10.3390/antiox10010124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Zonios G., Dimou A., Bassukas I., Galaris D., Tsolakidis A., Kaxiras E., “Melanin absorption spectroscopy: new method for noninvasive skin investigation and melanoma detection,” J. Biomed. Opt. 13(1), 014017 (2008). 10.1117/1.2844710 [DOI] [PubMed] [Google Scholar]
- 105.Różanowska M. B., Pawlak A., Różanowski B., “Products of docosahexaenoate oxidation as contributors to photosensitising properties of retinal lipofuscin,” Int. J. Mol. Sci. 22(7), 3525 (2021). 10.3390/ijms22073525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Höhn A., Jung T., Grimm S., Grune T., “Lipofuscin-bound iron is a major intracellular source of oxidants: Role in senescent cells,” Free Radic. Biol. Med. 48(8), 1100–1108 (2010). 10.1016/j.freeradbiomed.2010.01.030 [DOI] [PubMed] [Google Scholar]
- 107.Mattson M. P., Duan W., Pedersen W. A., Culmsee C., “Neurodegenerative disorders and ischemic brain diseases,” Apoptosis 6(1/2), 69–81 (2001). 10.1023/A:1009676112184 [DOI] [PubMed] [Google Scholar]
- 108.Jung T., Bader N., Grune T., “Lipofuscin: formation, distribution, and metabolic consequences,” Ann. N. Y. Acad. Sci. 1119(1), 97–111 (2007). 10.1196/annals.1404.008 [DOI] [PubMed] [Google Scholar]
- 109.Johansson J. D., “Spectroscopic method for determination of the absorption coefficient in brain tissue,” J. Biomed. Opt. 15(5), 057005 (2010). 10.1117/1.3495719 [DOI] [PubMed] [Google Scholar]
- 110.Johansson J. D., Wårdell K., “Intracerebral quantitative chromophore estimation from reflectance spectra captured during deep brain stimulation implantation,” J. Biophotonics 6(5), 435–445 (2013). 10.1002/jbio.201200055 [DOI] [PubMed] [Google Scholar]
- 111.Warburton S., Davis W. E., Southwick K., Xin H., Woolley A. T., Burton G. F., Thulin C. D., “Proteomic and phototoxic characterization of melanolipofuscin: correlation to disease and model for its origin,” Mol. Vis. 13, 318 (2007). [PMC free article] [PubMed] [Google Scholar]
- 112.Feeney L., “Lipofuscin and melanin of human retinal pigment epithelium. Fluorescence, enzyme cytochemical, and ultrastructural studies,” Invest. Ophthalmol. Vis. Sci. 17(7), 583–600 (1978). [PubMed] [Google Scholar]
- 113.Fernandes L., Carvalho S., Carneiro I., Henrique R., Tuchin V. V., Oliveira H. P., Oliveira L. M., “Diffuse reflectance and machine learning techniques to differentiate colorectal cancer ex vivo,” Chaos 31(5), 053118 (2021). 10.1063/5.0052088 [DOI] [PubMed] [Google Scholar]
- 114.Fereidouni F., Harmany Z. T., Tian M., Todd A., Kintner J. A., McPherson J. D., Borowsky A. D., Bishop J., Lechpammer M., Demos S. G., Levenson R., “Microscopy with ultraviolet surface excitation for rapid slide-free histology,” Nat. Biomed. Eng. 1(12), 957–966 (2017). 10.1038/s41551-017-0165-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Qorbani A., Fereidouni F., Levenson R., Lahoubi S. Y., Harmany Z. T., Todd A., Fung M. A., “Microscopy with ultraviolet surface excitation (MUSE): A novel approach to real-time inexpensive slide-free dermatopathology,” J. Cutan. Pathol. 45(7), 498–503 (2018). 10.1111/cup.13255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Yoshitake T., Giacomelli M. G., Quintana L. M., Vardeh H., Cahill L. C., Faulkner-Jones B. E., Connolly J. L., Do D., Fujimoto J. G., “Rapid histopathological imaging of skin and breast cancer surgical specimens using immersion microscopy with ultraviolet surface excitation,” Sci. Rep. 8(1), 4476 (2018). 10.1038/s41598-018-22264-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kumamoto Y., Matsumoto T., Tanaka H., Takamatsu T., “Terbium ion as RNA tag for slide-free pathology with deep-ultraviolet excitation fluorescence,” Sci. Rep. 9(1), 10745 (2019). 10.1038/s41598-019-47353-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Marble C. B., Yakovlev V. V., “Biomedical optics applications of advanced lasers and nonlinear optics,” J. Biomed. Opt. 25(04), 1 (2020). 10.1117/1.JBO.25.4.040902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Ager J. W., Nalla R. K., Breeden K. L., Ritchie R. O., “Deep-ultraviolet Raman spectroscopy study of the effect of aging on human cortical bone,” J. Biomed. Opt. 10(3), 034012 (2005). 10.1117/1.1924668 [DOI] [PubMed] [Google Scholar]
- 120.Kumamoto Y., Taguchi A., Smith N. I., Kawata S., “Deep ultraviolet resonant Raman imaging of a cell,” J. Biomed. Opt. 17(7), 0760011 (2012). 10.1117/1.JBO.17.7.076001 [DOI] [PubMed] [Google Scholar]
- 121.Kuniyil Ajith Singh M., Xia W., “Portable and affordable light source-based photoacoustic tomography,” Sensors 20(21), 6173 (2020). 10.3390/s20216173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Vieyra-Garcia P. A., Wolf P., “A deep dive into UV-based phototherapy: Mechanisms of action and emerging molecular targets in inflammation and cancer,” Pharmacol. Ther. 222, 107784 (2021). 10.1016/j.pharmthera.2020.107784 [DOI] [PubMed] [Google Scholar]
- 123.Budden T., Gaudy-Marqueste C., Porter A., Kay E., Gurung S., Earnshaw C. H., Roeck K., Craig S., Traves V., Krutmann J., Muller P., Motta L., Zanivan S., Malliri A., Furney S. J., Nagore E., Virós A., “Ultraviolet light-induced collagen degradation inhibits melanoma invasion,” Nat. Commun. 12(1), 2742 (2021). 10.1038/s41467-021-22953-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Trivellin N., Buffolo M., Onelia F., Pizzolato A., Barbato M., Orlandi V. T., Del Vecchio C., Dughiero F., Zanoni E., Meneghesso G., Crisanti A., Meneghini M., “Inactivating SARS-CoV-2 Using 275 nm UV-C LEDs through a Spherical Irradiation Box: Design, Characterization and Validation,” Materials 14(9), 2315 (2021). 10.3390/ma14092315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Gomes N., Tuchin V. V., Oliveira L. M., “UV-NIR efficiency of the refractive index matching mechanism on colorectal muscle during treatment with different glycerol osmolarities,” J. Biomed. Photonics Eng. 6(2), 3374 (2020). 10.18287/JBPE20.06.020307 [DOI] [Google Scholar]
- 126.Yu T., Zhu D., Oliveira L., Genina E. A., Bashkatov A. N., Tuchin V. V., “Tissue optical clearing mechanisms,” in Handbook of Tissue Optical Clearing , Tuchin V. V., Zhu D., Genina E. A., eds. (CRC Press, 2022), pp. 3–30. [Google Scholar]
- 127.Lazareva E., Tuchin V., “Blood refractive index modelling in the visible and near infrared spectral regions,” J. Biomed. Photonics Eng. 4(1), 010503 (2018). 10.18287/JBPE18.04.010503 [DOI] [Google Scholar]
- 128.Ermatov T., Noskov R. E., Machnev A. A., Gnusov I., Atkin V., Lazareva E. N., German S. V., Kosolobov S. S., Zatsepin T. S., Sergeeva O. V., Skibina J. S., Ginzburg P., Tuchin V. V., Lagoudakis P. G., Gorin D. A., “Multispectral sensing of biological liquids with hollow-core microstructured optical fibres,” Light: Sci. Appl. 9(1), 173 (2020). 10.1038/s41377-020-00410-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Trivedi V., Mahajan S., Joglekar M., Chhaniwal V., Zalevsky Z., Javidi B., Anand A., “3D printed hand-held refractometer based on laser speckle correlation,” Opt. Lasers Eng. 118, 7–13 (2019). 10.1016/j.optlaseng.2019.01.007 [DOI] [Google Scholar]
- 130.Zhang X. U., Faber D. J., Post A. L., van Leeuwen T. G., Sterenborg H. J. C. M., “Refractive index measurement using single fiber reflectance spectroscopy,” J. Biophotonics 12(7), e201900019 (2019). 10.1002/jbio.201900019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Liu S., Deng Z., Li J., Wang J., Huang N., “Measurement of the refractive index of whole blood and its components for a continuous spectral region,” J. Biomed. Opt. 24(03), 1 (2019). 10.1117/1.JBO.24.3.035003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Carvalho S., Gueiral N., Nogueira E., Henrique R., Oliveira L., Tuchin V. V., “Glucose diffusion in colorectal mucosa – a comparative study between normal and cancer tissues,” J. Biomed. Opt. 22(9), 091506 (2017). 10.1117/1.JBO.22.9.091506 [DOI] [PubMed] [Google Scholar]
- 133.Lazareva E. N., Tuchin V. V., “Measurement of refractive index of hemoglobin in the visible/NIR spectral range,” J. Biomed. Opt. 23(03), 1 (2018). 10.1117/1.JBO.23.3.035004 [DOI] [PubMed] [Google Scholar]
- 134.Lazareva E. N., Shushunova N. A., Tuchin V. V., Genina E. A., “Refractive properties of healthy and pathologically altered tissues of the kidney and breast measured at selected laser wavelengths in the visible and near-IR ranges,” Int. Symp. FLAMN-22 Fundam. Laser Assist. Micro– Nanotechnologies Symp. Abstr. B. 26 (2022). [Google Scholar]
- 135.Gul B., Ashraf S., Khan S., Nisar H., Ahmad I., “Cell refractive index: Models, insights, applications and future perspectives,” Photodiagn. Photodyn. Ther. 33, 102096 (2021). 10.1016/j.pdpdt.2020.102096 [DOI] [PubMed] [Google Scholar]
- 136.Zhang Q., Zhong L., Tang P., Yuan Y., Liu S., Tian J., Lu X., “Quantitative refractive index distribution of single cell by combining phase-shifting interferometry and AFM imaging,” Sci. Rep. 7(1), 2532 (2017). 10.1038/s41598-017-02797-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Liu P. Y., Chin L. K., Ser W., Chen H. F., Hsieh C.-M., Lee C.-H., Sung K.-B., Ayi T. C., Yap P. H., Liedberg B., Wang K., Bourouina T., Leprince-Wang Y., “Cell refractive index for cell biology and disease diagnosis: past, present and future,” Lab Chip 16(4), 634–644 (2016). 10.1039/C5LC01445J [DOI] [PubMed] [Google Scholar]
- 138.Song W. Z., Liu A. Q., Swaminathan S., Lim C. S., Yap P. H., Ayi T. C., “Determination of single living cell’s dry/water mass using optofluidic chip,” Appl. Phys. Lett. 91(22), 223902 (2007). 10.1063/1.2789287 [DOI] [Google Scholar]
- 139.Ledwig P., Robles F. E., “Quantitative 3D refractive index tomography of opaque samples in epi-mode,” Optica 8(1), 6–14 (2021). 10.1364/OPTICA.410135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Baczewska M., Eder K., Ketelhut S., Kemper B., Kujawińska M., “Refractive index changes of cells and cellular compartments upon paraformaldehyde fixation acquired by tomographic phase microscopy,” Cytometry, Part A 99(4), 388–398 (2021). 10.1002/cyto.a.24229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Chen X., Kandel M. E., Hu C., Lee Y. J., Popescu G., “Wolf phase tomography (WPT) of transparent structures using partially coherent illumination,” Light Sci. Appl. 9(1), 142 (2020). 10.1038/s41377-020-00379-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Nazarov M. M., Cherkasova O. P., Lazareva E. N., Bucharskaya A. B., Navolokin N. A., Tuchin V. V., Shkurinov A. P., “A complex study of the peculiarities of blood serum absorption of rats with experimental liver cancer,” Opt. Spectrosc. 126(6), 721–729 (2019). 10.1134/S0030400X19060183 [DOI] [Google Scholar]
- 143.Lazareva E. N., Zyubin A. Y., Dikht N. I., Bucharskaya A. B., Samusev I. G., Slezhkin V. A., Kochubey V. I., Tuchin V. V., “Optical Properties of Glycated and Non-Glycated Hemoglobin – Raman/Fluorescence Spectroscopy and Refractometry,” J. Biomed. Photonics Eng. 8(2), 020303 (2022). 10.18287/JBPE22.08.020303 [DOI] [Google Scholar]
- 144.Song Q. W., Ku C.-Y., Zhang C., Michalak R., “Modified critical angle method for measuring the refractive index of bio-optical materials and its application to bacteriorhodopsin,” J. Opt. Soc. Am. B 12(5), 797 (1995). 10.1364/JOSAB.12.000797 [DOI] [Google Scholar]
- 145.Takabayashi M., Majeed H., Kajdacsy-Balla A., Popescu G., “Tissue spatial correlation as cancer marker,” J. Biomed. Opt. 24(01), 1 (2019). 10.1117/1.JBO.24.1.016502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Dyachenko P. A., Dolotov L. E., Lazareva E. N., Kozlova A. A., Inozemtseva O. A., Verkhovskii R. A., Afanaseva G. A., Shushunova N. A., Tuchin V. V., Galanzha E. I., Zharov V. P., “Detection of melanoma cells in whole blood samples using spectral imaging and optical clearing,” IEEE J. Sel. Top. Quantum Electron. 27(4), 1–11 (2021). 10.1109/JSTQE.2020.3047437 [DOI] [Google Scholar]
- 147.Gavdush A. A., Chernomyrdin N. V., Malakhov K. M., Beshplav S.-I. T., Dolganova I. N., Kosyrkova A. V., Nikitin P. V., Musina G. R., Katyba G. M., Reshetov I. V., Cherkasova O. P., Komandin G. A., Karasik V. E., Potapov A. A., Tuchin V. V., Zaytsev K. I., “Terahertz spectroscopy of gelatin-embedded human brain gliomas of different grades: a road toward intraoperative THz diagnosis,” J. Biomed. Opt. 24(02), 1 (2019). 10.1117/1.JBO.24.2.027001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Fan S., Ung B., Parrott E. P. J., Pickwell-MacPherson E., “Gelatin embedding: a novel way to preserve biological samples for terahertz imaging and spectroscopy,” Phys. Med. Biol. 60(7), 2703–2713 (2015). 10.1088/0031-9155/60/7/2703 [DOI] [PubMed] [Google Scholar]
- 149.Harris F. J., “On the use of windows for harmonic analysis with the discrete Fourier transform,” Proc. IEEE 66(1), 51–83 (1978). 10.1109/PROC.1978.10837 [DOI] [Google Scholar]
- 150.Yamaguchi S., Fukushi Y., Kubota O., Itsuji T., Ouchi T., Yamamoto S., “Origin and quantification of differences between normal and tumor tissues observed by terahertz spectroscopy,” Phys. Med. Biol. 61(18), 6808–6820 (2016). 10.1088/0031-9155/61/18/6808 [DOI] [PubMed] [Google Scholar]
- 151.Meng K., Chen T., Chen T., Zhu L., Liu Q., Li Z., Li F., Zhong S., Li Z., Feng H., Zhao J., “Terahertz pulsed spectroscopy of paraffin-embedded brain glioma,” J. Biomed. Opt. 19(7), 077001 (2014). 10.1117/1.JBO.19.7.077001 [DOI] [PubMed] [Google Scholar]
- 152.Yamaguchi S., Fukushi Y., Kubota O., Itsuji T., Ouchi T., Yamamoto S., “Brain tumor imaging of rat fresh tissue using terahertz spectroscopy,” Sci. Rep. 6(1), 30124 (2016). 10.1038/srep30124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Bin Ji Y., Oh S. J., Kang S.-G., Heo J., Kim S.-H., Choi Y., Song S., Son H. Y., Kim S. H., Lee J. H., Haam S. J., Huh Y. M., Chang J. H., Joo C., Suh J.-S., “Terahertz reflectometry imaging for low and high grade gliomas,” Sci. Rep. 6(1), 36040 (2016). 10.1038/srep36040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Kucheryavenko A. S., Chernomyrdin N. V., Gavdush A. A., Alekseeva A. I., Nikitin P. V., Dolganova I. N., Karalkin P. A., Khalansky A. S., Spektor I. E., Skorobogatiy M., Tuchin V. V., Zaytsev K. I., “Terahertz dielectric spectroscopy and solid immersion microscopy of ex vivo glioma model 101.8: brain tissue heterogeneity,” Biomed. Opt. Express 12(8), 5272–5289 (2021). 10.1364/BOE.432758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Mu N., Yang C., Xu D., Wang S., Ma K., Lai Y., Guo P., Zhang S., Wang Y., Feng H., Chen T., Yao J., “Molecular pathological recognition of freshly excised human glioma using terahertz ATR spectroscopy,” Biomed. Opt. Express 13(1), 222 (2022). 10.1364/BOE.445111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Shiraga K., Ogawa Y., Suzuki T., Kondo N., Irisawa A., Imamura M., “Determination of the complex dielectric constant of an epithelial cell monolayer in the terahertz region,” Appl. Phys. Lett. 102(5), 053702 (2013). 10.1063/1.4790392 [DOI] [Google Scholar]
- 157.Chernomyrdin N. V., Skorobogatiy M., Ponomarev D. S., Bukin V. V., Tuchin V. V., Zaytsev K. I., “Terahertz solid immersion microscopy: Recent achievements and challenges,” Appl. Phys. Lett. 120(11), 110501 (2022). 10.1063/5.0085906 [DOI] [Google Scholar]
- 158.Orringer D. A., Pandian B., Niknafs Y. S., Hollon T. C., Boyle J., Lewis S., Garrard M., Hervey-Jumper S. L., Garton H. J. L., Maher C. O., Heth J. A., Sagher O., Wilkinson D. A., Snuderl M., Venneti S., Ramkissoon S. H., McFadden K. A., Fisher-Hubbard A., Lieberman A. P., Johnson T. D., Xie X. S., Trautman J. K., Freudiger C. W., Camelo-Piragua S., “Rapid intraoperative histology of unprocessed surgical specimens via fibre-laser-based stimulated Raman scattering microscopy,” Nat. Biomed. Eng. 1(2), 0027 (2017). 10.1038/s41551-016-0027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Li Z., Yan S., Zang Z., Geng G., Yang Z., Li J., Wang L., Yao C., Cui H., Chang C., Wang H., “Single cell imaging with near-field terahertz scanning microscopy,” Cell Proliferation 53(4), e12788 (2020). 10.1111/cpr.12788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Pickwell E., Cole B. E., Fitzgerald A. J., Wallace V. P., Pepper M., “Simulation of terahertz pulse propagation in biological systems,” Appl. Phys. Lett. 84(12), 2190–2192 (2004). 10.1063/1.1688448 [DOI] [Google Scholar]
- 161.Pickwell E., Fitzgerald A. J., Cole B. E., Taday P. F., Pye R. J., Ha T., Pepper M., Wallace V. P., “Simulating the response of terahertz radiation to basal cell carcinoma using ex vivo spectroscopy measurements,” J. Biomed. Opt. 10(6), 064021 (2005). 10.1117/1.2137667 [DOI] [PubMed] [Google Scholar]
- 162.Walker G. C., Berry E., Smye S. W., Zinov’ev N. N., Fitzgerald A. J., Miles R. E., Chamberlain M., Smith M. A., “Modelling the propagation of terahertz radiation through a tissue simulating phantom,” Phys. Med. Biol. 49(10), 1853–1864 (2004). 10.1088/0031-9155/49/10/002 [DOI] [PubMed] [Google Scholar]
- 163.Pickwell E., Cole B. E., Fitzgerald A. J., Pepper M., Wallace V. P., “In vivo study of human skin using pulsed terahertz radiation,” Phys. Med. Biol. 49(9), 1595–1607 (2004). 10.1088/0031-9155/49/9/001 [DOI] [PubMed] [Google Scholar]
- 164.Fitzgerald A. J., Pickwell-MacPherson E., Wallace V. P., “Use of finite difference time domain simulations and Debye theory for modelling the terahertz reflection response of normal and tumour breast tissue,” PLoS One 9(7), e99291 (2014). 10.1371/journal.pone.0099291 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Gavdush A. A., Chernomyrdin N. V., Komandin G. A., Dolganova I. N., Nikitin P. V., Musina G. R., Katyba G. M., Kucheryavenko A. S., Reshetov I. V., Potapov A. A., Tuchin V. V., Zaytsev K. I., “Terahertz dielectric spectroscopy of human brain gliomas and intact tissues ex vivo: double-Debye and double-overdamped-oscillator models of dielectric response,” Biomed. Opt. Express 12(1), 69–83 (2021). 10.1364/BOE.411025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Truong B. C. Q., Tuan H. D., Wallace V. P., Fitzgerald A. J., Nguyen H. T., “the potential of the double Debye parameters to discriminate between basal cell carcinoma and normal skin,” IEEE Trans. Terahertz Sci. Technol. 5(6), 990–998 (2015). 10.1109/TTHZ.2015.2485208 [DOI] [Google Scholar]
- 167.Ronne C., Thrane L., Astrand P.-O., Wallqvist A., Mikkelsen K. V., Keiding S. R., “Investigation of the temperature dependence of dielectric relaxation in liquid water by THz reflection spectroscopy and molecular dynamics simulation,” J. Chem. Phys. 107(14), 5319–5331 (1997). 10.1063/1.474242 [DOI] [Google Scholar]
- 168.Kindt J. T., Schmuttenmaer C. A., “Far-infrared dielectric properties of polar liquids probed by femtosecond terahertz pulse spectroscopy,” J. Phys. Chem. 100(24), 10373–10379 (1996). 10.1021/jp960141g [DOI] [Google Scholar]
- 169.Asaki M. L. T., Redondo A., Zawodzinski T. A., Taylor A. J., “Dielectric relaxation of electrolyte solutions using terahertz transmission spectroscopy,” J. Chem. Phys. 116(19), 8469–8482 (2002). 10.1063/1.1468888 [DOI] [Google Scholar]
- 170.Truong B. C. Q., Tuan Hoang Duong, Kha Ha Hoang, Nguyen H. T., “Debye parameter extraction for characterizing interaction of terahertz radiation with human skin tissue,” IEEE Trans. Biomed. Eng. 60(6), 1528–1537 (2013). 10.1109/TBME.2013.2237908 [DOI] [PubMed] [Google Scholar]
- 171.Buixaderas E., Kamba S., Petzelt J., “Lattice dynamics and central-mode phenomena in the dielectric response of ferroelectrics and related materials,” Ferroelectrics 308(1), 131–192 (2004). 10.1080/00150190490508909 [DOI] [Google Scholar]
- 172.Onodera Y., “Breakdown of Debye’s model for dielectric relaxation in high frequencies,” J. Phys. Soc. Jpn. 62(11), 4104–4107 (1993). 10.1143/JPSJ.62.4104 [DOI] [Google Scholar]
- 173.Martin P. C., “Sum Rules, Kramers-Kronig relations, and transport coefficients in charged systems,” Phys. Rev. 161(1), 143–155 (1967). 10.1103/PhysRev.161.143 [DOI] [Google Scholar]
- 174.Cole K. S., Cole R. H., “Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics,” J. Chem. Phys. 9(4), 341–351 (1941). 10.1063/1.1750906 [DOI] [Google Scholar]
- 175.Cole K. S., Cole R. H., “Dispersion and Absorption in Dielectrics II. Direct Current Characteristics,” J. Chem. Phys. 10(2), 98–105 (1942). 10.1063/1.1723677 [DOI] [Google Scholar]
- 176.Davidson D. W., “Dielectric relaxation in liquids: I. The presentation of relaxation behavior,” Can. J. Chem. 39(3), 571–594 (1961). 10.1139/v61-069 [DOI] [Google Scholar]
- 177.Havriliak S., Negami S., “A complex plane analysis of α-dispersions in some polymer systems,” J. Polym. Sci. Part C Polym. Symp. 14(1), 99–117 (1966). 10.1002/polc.5070140111 [DOI] [Google Scholar]
- 178.Fröhlich H., Theory of Dielectrics: Dielectric Constant and Dielectric Loss (Clarendon Press, 1958). [Google Scholar]
- 179.Komandin G. A., Chuchupal S. V, Lebedev S. P., Goncharov Y. G., Korolev A. F., Porodinkov O. E., Spektor I. E., Volkov A. A., “BWO Generators for Terahertz Dielectric Measurements,” IEEE Trans. Terahertz Sci. Technol. 3(4), 440–444 (2013). 10.1109/TTHZ.2013.2255914 [DOI] [Google Scholar]
- 180.Mankova A. A., Borodin A. V, Kargovsky A. V, Brandt N. N., Luo Q., Sakodynskaya I. K., Wang K., Zhao H., Chikishev A. Y., Shkurinov A. P., Zhang X.-C., “Terahertz time-domain and FTIR spectroscopic study of interaction of α-chymotrypsin and protonated tris with 18-crown-6,” Chem. Phys. Lett. 560, 55–59 (2013). 10.1016/j.cplett.2012.12.050 [DOI] [Google Scholar]
- 181.Komandin G. A., Nozdrin V. S., Gavdush A. A., Pronin A. A., Porodinkov O. E., Spektor I. E., Sigaev V. N., Mikhailov A. A., Shakhgildyan G. Y., Ulitko V. E., Abdullaev D. A., “Effect of moisture adsorption on the broadband dielectric response of SiO2-based nanoporous glass,” J. Appl. Phys. 126(22), 224303 (2019). 10.1063/1.5116790 [DOI] [Google Scholar]
- 182.Ishimaru A., Electromagnetic Wave Propagation, Radiation, and Scattering: From Fundamentals to Applications , 2nd ed. (Wiley-IEEE Press, 2017). [Google Scholar]
- 183.Chernomyrdin N. V., Kucheryavenko A. S., Kolontaeva G. S., Katyba G. M., Dolganova I. N., Karalkin P. A., Ponomarev D. S., Kurlov V. N., Reshetov I. V., Skorobogatiy M., Tuchin V. V., Zaytsev K. I., “Reflection-mode continuous-wave 0.15λ -resolution terahertz solid immersion microscopy of soft biological tissues,” Appl. Phys. Lett. 113(11), 111102 (2018). 10.1063/1.5045480 [DOI] [Google Scholar]
- 184.Joseph C. S., Patel R., Neel V. A., Giles R. H., Yaroslavsky A. N., “Imaging of ex vivo nonmelanoma skin cancers in the optical and terahertz spectral regions Optical and Terahertz skin cancers imaging,” J. Biophotonics 7(5), 295–303 (2014). 10.1002/jbio.201200111 [DOI] [PubMed] [Google Scholar]
- 185.Fan B., Neel V. A., Yaroslavsky A. N., “Multimodal imaging for nonmelanoma skin cancer margin delineation,” Lasers Surg. Med. 49(3), 319–326 (2017). 10.1002/lsm.22552 [DOI] [PubMed] [Google Scholar]
- 186.Yaroslavsky A., Joseph C., Patel R., Muzikansky A., Neel V., Giles R., “Delineating nonmelanoma skin cancer margins using terahertz and optical imaging,” J. Biomed. Photonics Eng. 3(1), 010301 (2017). 10.18287/JBPE17.03.010301 [DOI] [Google Scholar]
- 187.Doradla P., Alavi K., Joseph C. S., Giles R. H., “Detection of colon cancer by continuous-wave terahertz polarization imaging technique,” J. Biomed. Opt. 18(9), 090504 (2013). 10.1117/1.JBO.18.9.090504 [DOI] [Google Scholar]
- 188.Bashkatov A. N., Berezin K. V., Dvoretskiy K. N., Chernavina M. L., Genina E. A., Genin V. D., Kochubey V. I., “Measurement of tissue optical properties in the context of tissue optical clearing,” J. Biomed. Opt. 23(09), 1 (2018). 10.1117/1.JBO.23.9.091416 [DOI] [PubMed] [Google Scholar]
- 189.Genina E. A., Bashkatov A. N., Sinichkin Y. P., Yanina I. Y., Tuchin V. V., “Optical clearing of biological tissues: prospects of application in medical diagnostics and phototherapy,” J. Biomed. Photonics Eng. 1(1), 22–58 (2015). 10.18287/JBPE-2015-1-1-22 [DOI] [Google Scholar]
- 190.Genina E. A., Oliveira L. M. C., Bashkatov A. N., Tuchin V. V., “Optical Clearing of Biological Tissues: Prospects of Application for Multimodal Malignancy Diagnostics,” in Multimodal Optical Diagnostics of Cancer , Tuchin V. V., Popp J., Zakharov V., eds. (Springer, 2020), pp. 107–131. [Google Scholar]
- 191.Oliveira L., Carvalho M. I., Nogueira E., Tuchin V. V., “Optical clearing mechanisms characterization in muscle,” J. Innov. Opt. Health Sci. 09(05), 1650035 (2016). 10.1142/S1793545816500358 [DOI] [Google Scholar]
- 192.Carneiro I., Carvalho S., Henrique R., Oliveira L., Tuchin V., “Moving tissue spectral window to the deep-ultraviolet via optical clearing,” J. Biophotonics 12(12), e201900181 (2019). 10.1002/jbio.201900181 [DOI] [PubMed] [Google Scholar]
- 193.Carneiro I., Carvalho S., Henrique R., Selifonov A., Oliveira L., Tuchin V. V., “Enhanced ultraviolet spectroscopy by optical clearing for biomedical applications,” IEEE J. Sel. Top. Quantum Electron. 27(4), 1–8 (2021). 10.1109/JSTQE.2020.3012350 [DOI] [Google Scholar]
- 194.Oliveira L. M., Carvalho M. I., Nogueira E. M., Nogueira M. E., Tuchin V. V., “Skeletal muscle dispersion (400-1000 nm) and kinetics at optical clearing,” J. Biophotonics 11(1), e201700094 (2018). 10.1002/jbio.201700094 [DOI] [PubMed] [Google Scholar]
- 195.Oliveira L., Lage A., Pais Clemente M., Tuchin V. V., “Rat muscle opacity decrease due to the osmosis of a simple mixture,” J. Biomed. Opt. 15(5), 055004 (2010). 10.1117/1.3486539 [DOI] [PubMed] [Google Scholar]
- 196.Backman V., Gurjar R., Badizadegan K., Itzkan I., Dasari R. R., Perelman L. T., Feld M. S., “Polarized light scattering spectroscopy for quantitative measurement of epithelial cellular structures in situ,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1019–1026 (1999). 10.1109/2944.796325 [DOI] [Google Scholar]
- 197.Carneiro I., Carvalho S., Silva V., Henrique R., Oliveira L., Tuchin V. V., “Kinetics of optical properties of human colorectal tissues during optical clearing: a comparative study between normal and pathological tissues,” J. Biomed. Opt. 23(12), 1 (2018). 10.1117/1.JBO.23.12.121620 [DOI] [Google Scholar]
- 198.Bashkatov A. N., Genina E. A., Kochubey V. I., Tuchin V. V., “Estimation of wavelength dependence of refractive index of collagen fibers of scleral tissue,” Proc. SPIE 4162, 265–268 (2000). 10.1117/12.405952 [DOI] [Google Scholar]
- 199.Oliveira L., Lage A., Pais Clemente M., Tuchin V., “Optical characterization and composition of abdominal wall muscle from rat,” Opt. Lasers Eng. 47(6), 667–672 (2009). 10.1016/j.optlaseng.2008.12.005 [DOI] [Google Scholar]
- 200.Genina E. A., Bashkatov A. N., Tuchin V. V, “Tissue optical immersion clearing,” Expert Rev. Med. Devices 7(6), 825–842 (2010). 10.1586/erd.10.50 [DOI] [PubMed] [Google Scholar]
- 201.Sdobnov A. Y., Darvin M. E., Genina E. A., Bashkatov A. N., Lademann J., Tuchin V. V., “Recent progress in tissue optical clearing for spectroscopic application,” Spectrochim. Acta, Part A 197, 216–229 (2018). 10.1016/j.saa.2018.01.085 [DOI] [PubMed] [Google Scholar]
- 202.Gomes N. M., Tuchin V. V., Oliveira L. M., “Refractive index matching efficiency in colorectal mucosa treated with glycerol,” IEEE J. Sel. Top. Quantum Electron. 27(4), 1–8 (2021). 10.1109/JSTQE.2021.3050208 [DOI] [Google Scholar]
- 203.Oliveira L. M., Carvalho M. I., Nogueira E. M., Tuchin V. V, “The characteristic time of glucose diffusion measured for muscle tissue at optical clearing,” Laser Phys. 23(7), 075606 (2013). 10.1088/1054-660X/23/7/075606 [DOI] [Google Scholar]
- 204.Oliveira L. M., Carvalho M. I., Nogueira E. M., Tuchin V. V., “Diffusion characteristics of ethylene glycol in skeletal muscle,” J. Biomed. Opt. 20(5), 051019 (2014). 10.1117/1.JBO.20.5.051019 [DOI] [PubMed] [Google Scholar]
- 205.Carneiro I., Carvalho S., Henrique R., Oliveira L. M., Tuchin V. V., “A robust ex vivo method to evaluate the diffusion properties of agents in biological tissues,” J. Biophotonics 12(4), e201800333 (2019). 10.1002/jbio.201800333 [DOI] [PubMed] [Google Scholar]
- 206.Silva H. F., Martins I. S., Bogdanov A. A., Tuchin V. V., Oliveira L. M., “Characterization of optical clearing mechanisms in muscle during treatment with glycerol and gadobutrol solutions,” J. Biophotonics 1, e202200205 (2022). 10.1002/jbio.202200205 [DOI] [PubMed] [Google Scholar]
- 207.Yeh A. T., Choi B., Nelson J. S., Tromberg B. J., “Reversible dissociation of collagen in tissues,” J. Invest. Dermatol. 121(6), 1332–1335 (2003). 10.1046/j.1523-1747.2003.12634.x [DOI] [PubMed] [Google Scholar]
- 208.Hirshburg J., Choi B., Nelson J. S., Yeh A. T., “Collagen solubility correlates with skin optical clearing,” J. Biomed. Opt. 11(4), 040501 (2006). 10.1117/1.2220527 [DOI] [PubMed] [Google Scholar]
- 209.Hirshburg J., Choi B., Nelson J. S., Yeh A. T., “Correlation between collagen solubility and skin optical clearing using sugars,” Lasers Surg. Med. 39(2), 140–144 (2007). 10.1002/lsm.20417 [DOI] [PubMed] [Google Scholar]
- 210.Peña-Llopis S., Brugarolas J., “Simultaneous isolation of high-quality DNA, RNA, miRNA and proteins from tissues for genomic applications,” Nat. Protoc. 8(11), 2240–2255 (2013). 10.1038/nprot.2013.141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Zhu D., Larin K. V., Luo Q., Tuchin V. V., “Recent progress in tissue optical clearing,” Laser Photonics Rev. 7(5), 732–757 (2013). 10.1002/lpor.201200056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Tuchin V. V, “Optical clearing of tissues and blood using the immersion method,” J. Phys. D: Appl. Phys. 38(15), 2497–2518 (2005). 10.1088/0022-3727/38/15/001 [DOI] [Google Scholar]
- 213.Yanina I. Y., Nikolaev V. V., Zakharova O. A., Borisov A. V., Dvoretskiy K. N., Berezin K. V., Kochubey V. I., Kistenev Y. V., Tuchin V. V., “Measurement and modeling of the optical properties of adipose tissue in the terahertz range: aspects of disease diagnosis,” Diagnostics 12(10), 2395 (2022). 10.3390/diagnostics12102395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214.Nazarov M. M., Shkurinov A. P., Kuleshov E. A., Tuchin V. V, “Terahertz time-domain spectroscopy of biological tissues,” Quantum Electron. 38(7), 647–654 (2008). 10.1070/QE2008v038n07ABEH013851 [DOI] [Google Scholar]
- 215.Kolesnikov A. S., Kolesnikova E. A., Kolesnikova K. N., Tuchina D. K., Popov A. P., Skaptsov A. A., Nazarov M. M., Shkurinov A. P., Terentyuk A. G., Tuchin V. V, “THz monitoring of the dehydration of biological tissues affected by hyperosmotic agents,” Phys. Wave Phen. 22(3), 169–176 (2014). 10.3103/S1541308X14030029 [DOI] [Google Scholar]
- 216.Oliveira L. M., Zaytsev K., Tuchin V. V., “Improved biomedical imaging over a wide spectral range from UV to THz towards multimodality,” Proc. SPIE 11585, 20 (2020). 10.1117/12.2584999 [DOI] [Google Scholar]
- 217.Oh S. J., Kim S.-H., Jeong K., Park Y., Huh Y.-M., Son J.-H., Suh J.-S., “Measurement depth enhancement in terahertz imaging of biological tissues,” Opt. Express 21(18), 21299–21305 (2013). 10.1364/OE.21.021299 [DOI] [PubMed] [Google Scholar]
- 218.Smolyanskaya O. A., Schelkanova I. J., Kulya M. S., Odlyanitskiy E. L., Goryachev I. S., Tcypkin A. N., Grachev Y. V., Toropova Y. G., Tuchin V. V., “Glycerol dehydration of native and diabetic animal tissues studied by THz-TDS and NMR methods,” Biomed. Opt. Express 9(3), 1198–1215 (2018). 10.1364/BOE.9.001198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 219.Musina G. R., Dolganova I. N., Malakhov K. M., Gavdush A. A., Chernomyrdin N. V., Tuchina D. K., Komandin G. A., Chuchupal S. V., Cherkasova O. P., Zaytsev K. I., Tuchin V. V., “Terahertz spectroscopy of immersion optical clearing agents: DMSO, PG, EG, PEG,” Proc. SPIE 10800, 13 (2018). 10.1117/12.2324473 [DOI] [Google Scholar]
- 220.Musina G. R., Gavdush A. A., Chernomyrdin N. V., Dolganova I. N., Ulitko V. E., Cherkasova O. P., Kurlov V. N., Komandin G. A., Zhivotovskii I. V., Tuchin V. V., Zaytsev K. I., “Optical properties of hyperosmotic agents for immersion clearing of tissues in terahertz spectroscopy,” Opt. Spectrosc. 128(7), 1026–1035 (2020). 10.1134/S0030400X20070279 [DOI] [Google Scholar]
- 221.Musina G. R., Dolganova I. N., Chernomyrdin N. V., Gavdush A. A., Ulitko V. E., Cherkasova O. P., Tuchina D. K., Nikitin P. V., Alekseeva A. I., Bal N. V., Komandin G. A., Kurlov V. N., Tuchin V. V., Zaytsev K. I., “Optimal hyperosmotic agents for tissue immersion optical clearing in terahertz biophotonics,” J. Biophotonics 13(12), e202000297 (2020). 10.1002/jbio.202000297 [DOI] [PubMed] [Google Scholar]
- 222.Kim K. W., Kim H., Park J., Han J. K., Son J.-H., “Terahertz tomographic imaging of transdermal drug delivery,” IEEE Trans. Terahertz Sci. Technol. 2(1), 99–106 (2012). 10.1109/TTHZ.2011.2177175 [DOI] [Google Scholar]
- 223.Wang J., Stantchev R. I., Sun Q., Chiu T.-W., Ahuja A. T., MacPherson E. P., “THz in vivo measurements: the effects of pressure on skin reflectivity,” Biomed. Opt. Express 9(12), 6467–6476 (2018). 10.1364/BOE.9.006467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 224.Gurjarpadhye A. A., Vogt W. C., Liu Y., Rylander C. G., “Effect of localized mechanical indentation on skin water content evaluated using OCT,” Int. J. Biomed. Imaging 2011, 1 (2011). 10.1155/2011/817250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 225.Gavdush A. A., Kruczkiewicz F., Giuliano B. M., Müller B., Komandin G. A., Grassi T., Theulé P., Zaytsev K. I., Ivlev A. V., Caselli P., “Broadband spectroscopy of astrophysical ice analogues,” Astron. Astrophys. 667, A49 (2022). 10.1051/0004-6361/202244102 [DOI] [Google Scholar]
- 226.Y. E., Zhang L., Tcypkin A., Kozlov S., Zhang C., Zhang X.-C., “Broadband THz sources from gases to liquids,” Ultrafast Sci. 2021, 1–7 (2021). 10.34133/2021/9848526 [DOI] [Google Scholar]
- 227.Katyba G. M., Chizhov P. A., Kurlov V. N., Dolganova I. N., Garnov S. V., Zaytsev K. I., Bukin V. V., “THz generation by two-color laser air plasma coupled to antiresonance hollow-core sapphire waveguides: THz-wave delivery and angular distribution management,” Opt. Express 30(3), 4215 (2022). 10.1364/OE.447060 [DOI] [PubMed] [Google Scholar]
- 228.Matsubara E., Nagai M., Ashida M., “Ultrabroadband coherent electric field from far infrared to 200 THz using air plasma induced by 10 fs pulses,” Appl. Phys. Lett. 101(1), 011105 (2012). 10.1063/1.4732524 [DOI] [Google Scholar]
- 229.Zhang X. C., Shkurinov A., Zhang Y., “Extreme terahertz science,” Nat. Photonics 11(1), 16–18 (2017). 10.1038/nphoton.2016.249 [DOI] [Google Scholar]
- 230.Huber R., Brodschelm A., Tauser F., Leitenstorfer A., “Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz,” Appl. Phys. Lett. 76(22), 3191–3193 (2000). 10.1063/1.126625 [DOI] [Google Scholar]
- 231.Silva F., Austin D. R., Thai A., Baudisch M., Hemmer M., Faccio D., Couairon A., Biegert J., “Multi-octave supercontinuum generation from mid-infrared filamentation in a bulk crystal,” Nat. Commun. 3(1), 807 (2012). 10.1038/ncomms1816 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.Zhao H., Kuyken B., Clemmen S., Leo F., Subramanian A., Dhakal A., Helin P., Severi S., Brainis E., Roelkens G., Baets R., “Visible-to-near-infrared octave spanning supercontinuum generation in a silicon nitride waveguide,” Opt. Lett. 40(10), 2177 (2015). 10.1364/OL.40.002177 [DOI] [PubMed] [Google Scholar]
- 233.Dudley J. M., Genty G., Coen S., “Supercontinuum generation in photonic crystal fiber,” Rev. Mod. Phys. 78(4), 1135–1184 (2006). 10.1103/RevModPhys.78.1135 [DOI] [Google Scholar]
- 234.Skibina Y. S., Tuchin V. V, Beloglazov V. I., Shteinmaeer G., Betge I. L., Wedell R., Langhoff N., “Photonic crystal fibres in biomedical investigations,” Quantum Electron. 41(4), 284–301 (2011). 10.1070/QE2011v041n04ABEH014536 [DOI] [Google Scholar]
- 235.Levenius M., Pasiskevicius V., Laurell F., Gallo K., “Ultra-broadband optical parametric generation in periodically poled stoichiometric LiTaO3,” Opt. Express 19(5), 4121 (2011). 10.1364/OE.19.004121 [DOI] [PubMed] [Google Scholar]
- 236.Burdanova M. G., Kashtiban R. J., Zheng Y., Xiang R., Chiashi S., Woolley J. M., Staniforth M., Sakamoto-Rablah E., Xie X., Broome M., Sloan J., Anisimov A., Kauppinen E. I., Maruyama S., Lloyd-Hughes J., “Ultrafast optoelectronic processes in 1D radial van der Waals heterostructures: Carbon, Boron Nitride, and MoS2 nanotubes with coexisting excitons and highly mobile charges,” Nano Lett. 20(5), 3560–3567 (2020). 10.1021/acs.nanolett.0c00504 [DOI] [PubMed] [Google Scholar]
- 237.Burdanova M. G., Liu M., Staniforth M., Zheng Y., Xiang R., Chiashi S., Anisimov A., Kauppinen E. I., Maruyama S., Lloyd-Hughes J., “Intertube Excitonic Coupling in Nanotube Van der Waals Heterostructures,” Adv. Funct. Mater. 32(11), 2104969 (2022). 10.1002/adfm.202104969 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.