Abstract
Optical elastography offers a rich body of imaging capabilities that can serve as a bridge between organ-level medical elastography and single-molecule biophysics. We review the methodologies and recent developments in optical coherence elastography, Brillouin microscopy, optical microrheology, and photoacoustic elastography. With an outlook toward maximizing the basic science and translational clinical impact of optical elastography technologies, we discuss potential ways that these techniques can integrate not only with each other, but also with supporting technologies and capabilities in other biomedical fields. By embracing cross-modality and cross-disciplinary interactions with these parallel fields, optical elastography can greatly increase its potential to drive new discoveries in the biomedical sciences as well as the development of novel biomechanics-based clinical diagnostics and therapeutics.
1. Optical elastography in the basic sciences and clinical settings
Alteration in the mechanical properties of cells and biological tissues has emerged as not only a physical manifestation of disease, but also a physical cue that can regulate various biological processes, including both promotion and attenuation of disease [1–6]. In clinical settings, organ-level medical elastography modalities have aided the diagnostics of liver fibrosis, breast lesions, multiple sclerosis, and other disease states [7–10]. In the basic science settings, atomic force microscopy (AFM) [11] and bulk mechanical testing methods [12] have enabled fundamental research in subcellular biophysics and tissue-level biomechanics, respectively. Between these two extremes of spatial coverage, optical elastography—optical imaging approaches for mechanical characterization of biological systems—has emerged as a suite of techniques that enable access to a rich body of information with remarkable opportunities and potential for impact across the bench-to-bedside spectrum.
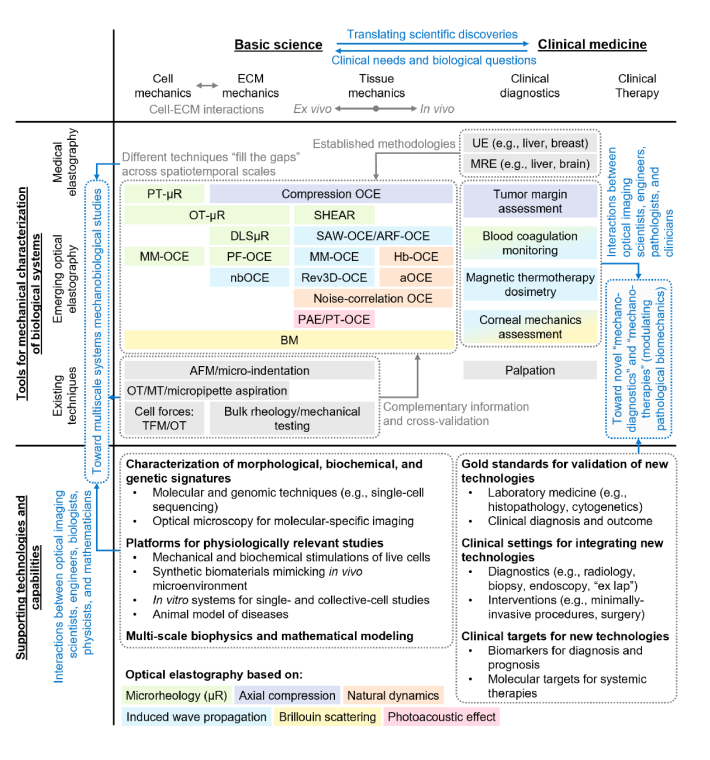
The interplay between the basic sciences and clinical medicine—unmet clinical needs informing scientific discoveries and translational research—provides a landscape for examining the capabilities of different technologies and exploring the opportunities for synergistic cross-modality and cross-disciplinary interaction (Fig. 1). Emerging optical elastography approaches are categorized by their underlying principles (box colors in Fig. 1) and positioned along the bench-to-bedside spectrum based on their demonstrated applications in basic cell, ECM, and tissue biomechanical studies as well as clinical translation. It is readily apparent that recent developments in optical coherence elastography (OCE), Brillouin microscopy (BM), optical microrheology (µR), and photoacoustic elastography (PAE) have enabled biomechanical characterization at all levels spanning cells, extracellular matrix (ECM), tissues, as well as technological advances to support clinical applications. The rapid pace of technological developments has also motivated a recent surge of studies to quantitatively characterize and understand the imaging capabilities of several modalities. Nevertheless, optical elastography does not exist as an independent entity in this bench-to-bedside landscape. Medical elastography modalities and other existing biophysical techniques (gray boxes in Fig. 1) are established resources that optical elastography can leverage in both development (e.g., for cross-validation) and applications (e.g., for supporting measurements and diagnoses). Furthermore, in order to achieve tangible biomedical impact, emerging optical elastography approaches must inevitably interact and reconcile with supporting technologies and relevant gold standards in the biomedical sciences (e.g., biomolecular techniques) and clinical medicine (e.g., current clinical workflow and standard of care).
Fig. 1.
Optical elastography in the basic sciences and clinical medicine. Box colors categorize recent developments in optical elastography by their underlying principle (see bottom of the figure). Gray boxes denote other supporting techniques outside of optical elastography. Gray text and arrows describe the roles of different techniques and how their complementary capabilities can be leveraged in the broad landscape of biomedical sciences and clinical medicine. Blue text and arrows highlight opportunities for interactions between developers and stakeholders across different modalities and disciplines toward achieving impact in the basic sciences and clinical medicine. OCE: optical coherence elastography, MM-OCE: magnetomotive OCE, PF-OCE: photonic force OCE, nbOCE: nanbomb OCE, SAW-OCE: surface acoustic wave OCE, ARF-OCE: acoustic radiation force OCE, Rev3D-OCE: reverberant 3D OCE, Hb-OCE: heartbeat OCE, aOCE: anatomical OCE, PT-OCE: photothermal OCE, µR: microrheology, PT-µR: particle-tracking µR, OT-µR: optical tweezer µR, DLSµR: dynamic light scattering µR, SHEAR: laser Speckle rHEologicAl micRoscopy, BM: Brillouin microscopy, PAE: photoacoustic elastography, UE: ultrasound elastography, MRE: magnetic resonance elastography, AFM: atomic force microscopy, OT: optical tweezer, MT: magnetic tweezer, TFM: traction force microscopy, ECM: extracellular matrix.
The objectives of this review are two-fold: 1) to highlight the body of imaging capabilities and recent developments in the field optical elastography, and 2) to draw attention to the numerous opportunities—from bench to bedside—that the field can capitalize on by engaging in cross-modality and cross-disciplinary interactions, both within and outside the field. This review is not intended to be a detailed technical description of methodologies or an appraisal of major results in the field. Rather, with an outlook toward maximizing the potential basic science and clinical impact of optical elastography, this review aims to provide a big picture overview of the main modalities and recent developments, emphasizing their current and potential future impact on fundamental mechanobiological research and translational medicine.
In Section 2 we provide a brief overview of key methodologies in optical elastography. Then, in Sections 3-6 we highlight recent developments over the past 5 years in the areas of tissue mechanics and clinical applications (Section 3), cell and ECM mechanics (Section 4), multimodal optical elastography (Section 5), and fundamental investigations of imaging capabilities (Section 6). Figures in these sections are a compilation of selected results, adapted in part from various works, and are intended to provide a big picture overview of the recent developments in each area. Readers are encouraged to peruse the original publications for further details on each topic. Lastly, in Section 7 we revisit the opportunities for interactions between optical elastography and related techniques (gray text and arrows in Fig. 1), and with scientists, engineers, and professionals in other fields (blue text and arrows in Fig. 1).
2. Overview of optical elastography methodologies
In this section, we discuss the motivating goals for technological developments in optical elastography and provide a brief overview of key methodologies that underlie major optical elastography approaches. We focus on the practical approaches that have been implemented rather than in-depth theoretical treatments and derivations of the underlying principles. An overview of relevant solid mechanics fundamentals is included to provide context for the information that is probed by each elastography approach.
2.1. Solid mechanics fundamentals of elastography
Elastography is based on the measurement of a sample response to a mechanical loading, excitation, or perturbation. The most basic form of sample response that can be measured is a displacement at each spatial location of the sample. From the displacement field u, the unitless quantity strain is often calculated. Strain is related to the applied stress via a generalized form of Hooke’s law [13]
| (1) |
where σ is the stress tensor, is the strain tensor given by εij = (∂ui/∂xj+∂uj/∂xi)/2, is the fourth-order stiffness tensor connecting stress and strain, and xi is the spatial coordinate. For a linear isotropic material, Eq. (1) takes the form
| (2) |
where K and G are the bulk and shear moduli of the material, both of which may take complex values. The first three diagonal terms in , K + 4 G/3, is also called the longitudinal modulus M. Young’s modulus E is connected to the shear and bulk moduli via E = 2 G(1+ν) and E = 3 K(1–2ν), where ν is Poisson’s ratio, defined as the ratio of transversal elongation divided by axial compression. Most tissues are nearly incompressible, and so have ν≈0.5. We also note that the shear and bulk moduli and Poisson’s ratio may be frequency dependent.
Different elastography approaches have been developed to generate images that connect in some way with components of the stiffness tensor in Eq. (1). Qualitative elastography approaches often generate images based on measured sample strain or even displacements. Quantitative approaches aim to reconstruct one or more entries in the stiffness tensor of the sample. Semi-quantitative approaches can generate images based on parameters that are related to one or more entries of the stiffness tensor. For each approach described in this review, we will highlight the relevant mechanical information that is measured and reconstructed.
2.2. Goals motivating technological developments in optical elastography
A major motivation for optical elastography has been to bridge the gap between organ-level medical elastography and single-molecule biophysical techniques. The fundamental goal for any optical elastography technique is to enable mechanical characterization at the relevant spatial and temporal scales that are ‘meaningful’ to the biological systems under study. Indeed, the technical specifics of a ‘meaningful’ mechanical characterization vary for different applications and should be defined on a case-by-case basis. For instance, a qualitative mapping of relative mechanical contrast may adequately meet the needs of some applications (e.g., mechanical contrast imaging to resolve anatomical features [14–16] or monitoring of progressive changes in tissue mechanical properties during injury repair [17]), but a quantitative measurement of absolute mechanical moduli may be essential in others (e.g., developing quantitative mechanical metrics of various breast tumor subtypes for clinical prognostic and diagnostic purposes [18–20] or characterizing complex mechanical responses of biopolymers [21,22] and cell-mediate mechanical remodeling of ECM [23–25]). Likewise, the ‘meaningful’ spatiotemporal resolution and coverage of optical elastography techniques also vary for different biological phenomena. For instance, the study of alteration in tissue mechanical properties over the course of disease progression may require sub-millimeter spatial resolution, but a large volumetric field-of-view (FOV) with days-to-weeks temporal sampling. In contrast, the study of mechanotransduction during cancer cell invasion [5,26,27] may require cellular-scale spatial resolution over a smaller FOV, but with temporal sampling on the scale of minutes-to-hours. Meanwhile, clinical applications may simultaneously require large FOV, high-speed imaging, and robustness for integration into the existing clinical workflow.
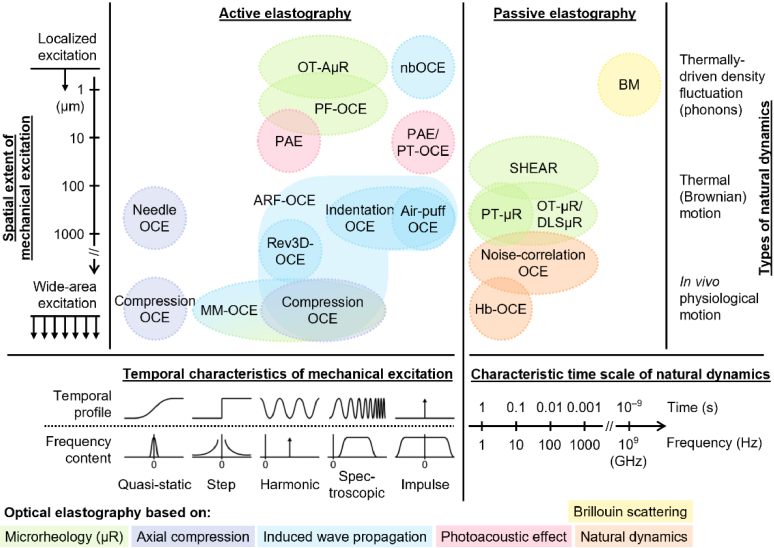
In these regards, quantification of not only linear elasticity (i.e., ‘stiffness’), but also viscoelasticity as well as nonlinear mechanics and anisotropy [13,28], has been the focus many recent developments in the field. Similarly, increasing demand in the field of mechanobiology has motivated the development of 4D (space and time) imaging capabilities to dynamically characterize various biological processes. With the on-going efforts toward clinical translation, technical advances and innovation that help streamline the clinical compatibility of optical elastography technologies are another active area of development. Figure 2 (updated from a previous review by Mulligan et al. [29]) illustrates the wide range of spatiotemporal scales and characteristics spanned by existing and emerging optical elastography techniques, including both active (i.e., externally applied mechanical loading), and passive approaches (i.e., no active mechanical excitation). The spatiotemporal scales probed by each active approach is influenced by the spatial extent (i.e., dimensions) and temporal characteristics (e.g., impulse versus continuous harmonic excitation) of the applied mechanical excitation. Similarly, the relevant spatiotemporal scales of each passive approach is determined by the nature of the naturally occurring dynamics employed for the measurement; different types of dynamics occur at different time scales (e.g., heart beats occurring at Hz versus acoustic phonons occurring at GHz regimes). Key methodologies underlying five major approaches (represented via different colors in Fig. 1 and 2) are described in the following subsections.
Fig. 2.
Classification of methodologies in optical elastography. Active approaches are characterized by the spatiotemporal characteristics of applied mechanical excitation. Passive approaches are characterized by the type and characteristic time scale of naturally occurring mechanical ‘excitation’. For further details on key methodologies utilized by different techniques, see the following sections for optical elastography based on: Section 2.3 bulk compression, Section 2.4 induced wave propagation, Section 2.5 microrheology, Section 2.6 Brillouin scattering, and Section 2.7 photoacoustic effects. For techniques based on natural dynamics, the methodologies for noise-correlation OCE and Hb-OCE are similar to those of wave-based approaches and compression OCE, respectively; both techniques are further discussed in Section 3.3.
2.3. Mechanical characterization based on bulk compression
When a material is compressed by an external load, the more compliant regions will be able to deform to a larger extent than the more rigid regions. Elastography based on quasi-static bulk compression (see Fig. 2) relies on the measurement of sample deformation map following an externally applied compression in order to infer the material mechanical properties. In practice, quasi-static bulk compression is typically achieved with a rigid plate mounted on a piezoelectric actuator [18,19,30–35]. Lubrication at the compression plate-sample interface, such that sample deformation is not impeded by friction at the contact, is another practical consideration [36].
There are several ways to measure the sample deformation. Compression PAE [33] and early implementations of compression OCE [37,38] utilize speckle tracking (via cross-correlation or digital volume correlation) between images of the sample in its compressed and uncompressed states. Nowadays, most OCE techniques utilize interferometric detection based on phase-sensitive optical coherence tomography (OCT) [30–32,39–42], which supports superior displacement sensitivity than speckle tracking. Here, the compression-induced axial displacement, uz, at each spatial voxel of the complex OCT image is obtained from the difference in its phase, Δϕ, between the compressed and uncompressed states by uz=Δϕλ0/(4πn), where λ0 and n denote the center wavelength of the OCT source and refractive index of the medium, respectively. Often, the OCT beam must interrogate the sample through a medium with different n (e.g., air, water, or ultrasound gel). In such cases, correction must be applied to Δϕ in order to isolate the displacements within the sample from the motion artifacts due to the combined effect of sample surface motion and refractive index mismatch at the sample surface-medium interface [41,42]. Readers are encouraged to peruse Section 4 of Larin and Sampson’s recent OCE review [43] for a more detailed description of the phase-sensitive OCT approach.
The ‘elastogram’ output in bulk compression elastography is typically a spatial map of uniaxial strain, εzz, given by the axial derivative of the sample displacement εzz=∂uz/∂z. In practice, εzz can be obtained via a linear regression of uz over a sliding axial window [31,32,34,44]. Recently, more sophisticated strain estimation algorithms have been implemented to obtain accurate estimation with the smallest possible window size in the presence of noise [35,45,46], which also motivated a comparative analysis of different strain estimation methods [47]. In principle, a quantitative map of the Young’s modulus E can be obtained from the strain elastogram via E=σzz/εzz according to Eq. (2), provided that the spatial map of uniaxial stress, σzz, in the sample due to the compression is known. In practice, however, the stress field is unknown and must be estimated by other means. One approach relies on measuring the deformation of a ‘stress sensing layer’—a thin layer of material with pre-characterized E that is compressed together with the sample—with the assumption that the stress field is depth-invariant [31]. This approach, called quantitative microelastography (QME), has achieved high-resolution quantitative elastograms with impressive results in the characterization of resected tumors [18,19,48,49] (see Section 3.5). Readers are encouraged to peruse a recent review by Zaitsev et al. for a two-decade perspective and recent advances in compression OCE [50].
The phase-sensitive approach described above is inherently limited to the measurement of axial (i.e., along the OCT beam propagation direction) sample displacement, and thus, calculation of strictly the uniaxial strain. More recently, in order to access other components of the full strain tensor [13] (e.g., shear strain), methods have been developed to measure transverse components of sample displacement based on computational subaperture and phase-sensitive detection [51], and reconstruction of the strain tensor from compression OCE via a close-form solution to a collection of complex cross-correlations of multiple digitally shifted images in the uncompressed and compressed states [52].
2.4. Mechanical characterization based on mechanical wave propagation
When a dynamic external load (see harmonic, spectroscopic, and impulse in Fig. 2) is applied to a spatially confined region, the deformation induced directly at the region of excitation can propagate into the surround material as mechanical waves, where a stiffer material facilitates faster propagation. By measuring the propagation speed of the induced mechanical wave, wave-based OCE approaches can quantify the material mechanical properties without the knowledge of the applied stress field. In practice, wave propagation is typically induced by dynamic excitation with an actuator-mounted shaker [15,53–55], micro-indenter [40,41,56,57], air-puff [42,58], acoustic radiation force (ARF) [44,59–63] or air-coupled ultrasound (also called acoustic micro-tapping) [64–67], and more recently, ‘explosion’ of dye-loaded nanoparticles [68–70] (see nanobomb OCE in Section 3.1). Beyond the key methodologies described below, readers are encouraged to peruse a recent review by Zvietcovich and Larin for a 10-year perspective in wave-based OCE [71], and a comparative study by Zvietcovich et al. [72] for further details on wave speed estimation methods based on different wave excitation and image acquisition schemes.
The propagation speed of the induced mechanical wave is typically measured via a time-of-flight approach. Under impulse excitation, the propagation speed of surface acoustic waves (SAW) is typically measured via a time-of-flight approach, essentially tracking the distance traveled by the sample displacement ‘pulse’ as a function of time [42,58,65]. In practice, M-mode imaging is performed at each lateral position along the wave propagation path to obtain a time-series of sample displacement uz (see Section 2.3) as a function of propagation distance, r. Then, propagation speed, c, of wave at angular frequency ω is obtained from the evolution of the wave phase, Δφ, as a function of Δr via c=ω(Δr/Δφ), where φ at the corresponding angular frequency ω is extracted from the phase angle of the temporal Fourier transform of uz [40,42,58]. (Thus, the term ‘phase velocity’ in wave-based OCE.) Although transient (impulse) OCE is typically performed in 2D (depth and 1 lateral dimension), the same methodology can be expanded to 3D measurement involving 2 lateral dimensions [67]. Furthermore, a spectroscopic 4D-OCE (3D space and frequency), implementing analysis in the spatial frequency-domain (k-space) to reconstruct wave speed at selected wave frequencies, has recently been demonstrated [60]. Other approaches to measure wave propagation speed at specific frequencies are based on harmonic excitation. Under harmonic excitation, wave propagation speed is similarly obtained from the wave phase gradient, except in this case, ω corresponds to excitation frequency and the spatial derivative of φ w.r.t. r may be extracted directly from the phase angle of the complex displacement field in both space [59] and spatial-frequency [56] domains.
Although the wave propagation speed by itself is often provided as the final output in wave-based OCE (i.e., a semi-quantitative output), a quantitative reconstruction of shear elastic modulus G can be obtained from the measured shear wave speed, cs, via G=ρcs2, where ρ denotes the mass density of the material [40]. (For an incompressible material, G and E are simply related by E = 3 G as outlined in Section 2.1). One caveat is that a pure bulk shear wave is rarely induced in practice, such that the measured c (the ‘group speed’) is not equivalent to cs [73]. For a surface (Rayleigh) wave propagating on a semi-infinite media, a simple multiplication factor of 1.049 converts the Rayleigh wave speed to cs. In bounded layered media, where highly dispersive Lamb (guided) modes typically dominate the measurements, the use of more elaborate wave models such as the Rayleigh-Lamb frequency equation [74] is required. Section 3.1 highlights recent developments in wave-based OCE that minimizes some of these complications [15,55,66,68–70,75]. Note that anisotropy (e.g., in media such as the cornea) presents additional challenges. Section 3.2 describes approaches to address the challenges posed by anisotropy and nonlinear mechanical responses of tissues. Readers are also encouraged to peruse a recent review by Kirby et al. for further details on OCE methodologies specifically pertaining to applications in ophthalmology [76].
Wave-based elastography approaches can also provide access to viscoelasticity, quantified by the frequency-dependent complex shear modulus, G*(ω)=G′(ω)+iG"(ω), instead of a single real-valued G in the linear elastic case. That is, the moduli in in Eq. (2) take complex values to account for viscous energy dissipation and are frequency-dependent. In this case, G*(ω) is given by the complex shear wave number, ks(ω), via G*(ω)=ρω2/ks2(ω), where ks(ω)=ω/cs(ω)+iαs(ω) describes the frequency-dependent shear wave speed (real part) and viscous attenuation (imaginary part) [13,29]. It is apparent that G* cannot be obtained from a single measurement of cs. One general approach is based on an a priori assumption of a rheological model (see Tables 2 and 3 in [77]), which dictates the frequency-dependent response of a material. Here, multiple measurements of cs(ω) are typically made at different frequencies, then, G*(ω) is obtained by fitting the measured frequency-dependent wave speed to the assumed model [56,58]. Alternatively, model-independent approaches based on independent measurements of both wave speed and viscous attenuation [59] or the inversion of a general wave propagation model [78] have also been demonstrated.
2.5. Mechanical characterization based on microrheological measurements
Microrheology (µR) refers to the quantification of the rheological (deformation and flow) behaviors of complex materials from the motions of micron-sized probe particles inside the material constructs. By measuring the displacements of these probe particles, either under natural (e.g., Brownian thermally-driven or cell-force-mediated) motion (passive µR) [20,24,79–85] or forced motion (active µR) [21–23,25,86–92], viscoelasticity can be quantified at the microscopic scale [93–99], providing information about the microstructure and micromechanical heterogeneity in the material constructs.
Both passive and active µR approaches are based upon the same fundamental principle: measurements of probe particle displacements as a function of time to derive the complex ‘mechanical response function’, α*(ω)=α′(ω)+iα"(ω), of the material. The difference lies in how α*(ω) is derived from the measured displacements. Under the general assumptions of thermodynamic equilibrium, incompressibility, and homogeneity (on the length scale of the probe particles), the complex shear modulus can be obtained with the Generalized Stokes-Einstein Relation (GSER) [93–99] via G*(ω) = 1/[6πaα*(ω)], where a denotes the radius of the probe particles. In practice, the displacements of probe particles can be directly detected under a conventional high-numerical aperture (NA) confocal microscope, typically equipped with a quadrant photodiode to achieve high spatiotemporal resolution [21,23,24,79,80,86–89]. However, recent techniques have also measured particle displacements based on laser speckle fluctuation dynamics [81–85] (see SHEAR in Section 3.3) and phase-sensitive OCT [22,25,90–92].
Passive µR approaches are typically implemented in two ways: particle-tracking (PT)-µR [24,79,80], where dynamics of particles in their natural environments are monitored, or optical-tweezers (OT)-based passive µR [96,97], where dynamic of an optically-trapped particle is monitored. OT-µR has the advantage of preventing any freely-diffusing particles from escaping the detection zone. In both cases, the particle dynamics are quantified by their mean-square displacement (MSD), 〈Δr2(t)〉, whose Fourier transform is related to the imaginary part of α*(ω) via 〈Δr2(ω)〉=α"(ω)[2NkBT/ω], where kB, T, and N denote the Boltzmann constant, temperature of the material, and the number of dimensions in which the MSD is tracked, respectively [96–99]. The remaining real part α′(ω) can be obtained using the Kramers-Kronig relations. Since traditional PT-µR relies on directly measuring the displacements of particles undergoing Brownian motion, it is generally applicable for fluid-like compliant materials (G < 100 Pa) [79].
Active µR approaches utilize optical micromanipulation—via OTs [21,23,86–89,92], and more recently, radiation pressure from a low-NA beam [22,25,90,91] (see Section 4.1)—to force the probe particles into an oscillatory motion (although a unidirectional translation has also been implemented [21]). In OT-based active µR (OT-AµR), a probe particle is optically trapped and forced into an oscillatory motion by oscillating the position of the trapping beam, ut. The position of the probe particle, up, is detected by another co-aligned detection beam. (In the case of [92], the cell membrane and organelles themselves are optically trapped, inducing axial membrane displacement toward the trap center that is detected via phase-sensitive OCT.) The Fourier-domain apparent ‘mechanical response function’ is obtained via A*(ω)=up(ω)/F(ω), where F(ω)=ut(ω)–up(ω) is the forcing function of the OT. A*(ω) represents the apparent response that includes the contribution of both the material viscoelasticity and the combined trap stiffness, k, of the trapping and detection beams. The actual mechanical response α*(ω) that represents the material viscoelasticity is obtained via α*(ω)=A*(ω)/[1–kA*(ω)], which compensates for the contribution k. Readers are encouraged to peruse an informative review by Bowman and Padgett [100] for further details on the theory and practical implementation of optical trapping in OT-µR.
It should be noted that a substantial portion of µR literature has been dedicated to determining the experimental conditions under which µR measurement of G*(ω) is expected to agree with that of macro-scale bulk rheometry [93–98]. This has motivated the development of multiparticle µR approach, which tends to be more robust in terms of consistency with bulk measurement [95,97,98]. However, as an optical elastography approach—with its capabilities to locally probe viscoelasticity of biological systems at the microscopic scale—we echo Squires and Mason that the so-called ‘failure’ to obtain macro-equivalent G*(ω) “does not render microrheology worthless; instead, its proper interpretation can provide additional material information that would otherwise be inaccessible to macroscopic rheometry” [98].
2.6. Mechanical characterization based on Brillouin scattering
Brownian motion is not the only thermally-driven natural dynamics exploited in optical elastography (see passive µR in Section 2.5). Thermal energy can also induce spontaneous ‘density waves’—density fluctuations comprising microscopic acoustic waves or ‘phonons’— that propagate at the speed of sound in the material. When light illuminates the material, these ‘density waves’ act as a travelling (at the speed of sound) diffraction grating that introduces a Doppler frequency shift to a small fraction of incident light that is inelastically scattered (i.e., Brillouin scattering) [101–104]. By capturing the spectrum of this spontaneous Brillouin scattering process, spontaneous BM infers high-frequency (GHz) complex longitudinal modulus, M*(ω)=M′(ω)+iM"(ω), of the material from the measured Brillouin frequency shift, νB, and linewidth, ΔB [14,17,105–113]. (Note that M = K + 4 G/3, see Eq. (2), where both K and G may take complex values and vary with frequency.) Since only a small fraction of incident light undergoes spontaneous Brillouin scattering, precise measurement of νB and ΔB typically requires a long acquisition time (on the order of tens of milliseconds to several seconds per voxel) owing to the trade-off between spectral integration time and spectral resolution [103]. Recent developments have explored stimulated BM approaches to overcome this trade-off and improve the throughput of BM without sacrificing spectral resolution [16,114–117] (see Section 4.2).
In practice, BM utilizes a monochromatic illumination source (typically in the visible to near infrared range) in an epi-illumination high-NA confocal microscope, equipped with a sub-GHz-resolution VIPA (virtually imaged phase array) spectrometer [105]. In the traditional spontaneous BM setup, a spectral line of backscattered light is acquired by VIPA at each spatial voxel and 3D imaging is accomplished by point-scanning the illumination beam [14,17,105–113]. Recently, a more rapid implementation of spontaneous BM has been demonstrated with line-scanning, where spectral lines from multiple lateral positions are acquired in parallel [108]. Each spectral line contains both the desired inelastic Brillouin scattering peaks and the ‘background’ elastic scattering peak. Several methods have been developed to improve ‘background’ suppression in VIPA-based setups [118,119]. A practical consideration when implementing BM in live biological systems is the performance trade-off between potential phototoxicity (due to weak Brillouin scattering signal requiring long integration time and high illumination dosage) and the achievable spectral, spatial, and temporal resolutions [103,104].
The measured Brillouin frequency shift νB and linewidth ΔB are respectively related to the real (elasticity) and imaginary (viscosity) parts of the longitudinal modulus via M′(ω)=ρ(νB/q)2 and M"(ω) = 2ωρΔB/q2 [101,102]. The constant q = (2n/λ)sin(θ/2) represents the scattered wavevector, where n, λ, and θ denote the refractive index of the material, wavelength of the illumination beam, and angle between the incident and scattered light, respectively. It is apparent that the knowledge of material refractive index and mass density, both of which are not readily available from the standard BM setup, is required to quantitatively derive M*(ω). However, since both M′ and M" are linearly proportional to the ratio ρ/n2, which is fairly invariant in most biological materials, the variations in n and ρ can often be neglected [16,17,106].
It is important to note that M*(ω)—measured by BM at ω∼GHz and takes values on the order of GPa—is defined by entirely different elements of the stiffness tensor in Eq. (2) than the elements that represent G*(ω), which is typically measured by OCE quasi-statically or at ω∼0.01-10 kHz and take values on the order of 0.1-1000 kPa. Whereas E and G are directly related via the Poison ratio ν, there is no universal mathematical relationship that indicates that M should be directly correlated to G [103] (it is also worth noting that typical values of K are several orders of magnitude larger than those of G, which presents a major challenge to experimentally infer G from a measurement of M). Recently, an attempt to connect BM measurements to E has been made via a multimodal BM and OCE method (see Section 5), but this approach still relies on sample-specific correlation that emerges between two independent measurements without a theoretical basis supporting the correlation [120]. The interpretation of the biophysical origin of BM measurements, as well as their relation to the more widely accepted mechanical quantities in the biomedical fields, remains an active area of development in BM [103,104].
2.7. Mechanical characterization based on thermo-mechanical effects
Thermo-mechanical effects are most well-known in optics as the underlying principle of photoacoustic (PA) imaging, which combines high-resolution optical excitation with extended-penetration-depth ultrasonic detection. PA effect refers to the generation of acoustic (pressure) waves as a result of optical absorption accompanied by nonradiative energy dissipation (i.e., heating). Under appropriate thermal and stress confinement conditions, the absorption-mediated thermal expansion of the absorber generates localized stress that acts as a pressure wave source—the so-called ‘thermoelastic expansion’ [121,122]. PA imaging forms images by detecting the generated acoustic waves via ultrasonic transducers. The spatiotemporal profile of the PA pressure is a function of the absorber geometry, excitation pulse duration, mass density, as well as the frequency-dependent speed of sound and acoustic attenuation in the material [121,122]. Thus, PA signal inherently encodes information on the mechanical properties of the materials.
Use of the PA effect in optical elastography first emerged in wave-based OCE, where laser-induced thermoelastic expansion provides an all-optical mechanism for generating surface acoustic wave (i.e., Rayleigh wave) [123,124]. Here, nanosecond-pulsed laser is focused on the surface of the sample, on which an absorber (typically blank ink) is applied. Rayleigh wave propagation is induced via absorption-mediated thermoelastic expansion at the laser focus, then, elasticity of the material is obtained by measuring the Rayleigh wave speed as described in Section 2.4. A recent study has investigated the experimental conditions under which laser-induced surface acoustic waves were generated in the desired thermoelastic regime versus the destructive ablative regime in biological tissues [125]. A cut-off laser beam energy at the onset of the ablative transition was found for samples with different absorption coefficient.
Elastography based on the PA effect has also been implemented with PA imaging [126–137]. Compared to OCE, µR, and BM, this family of techniques—referred to as PA elastography (PAE)—is relatively young, and various methodologies are still being explored. Among others, an approach based on measuring the phase delay of PA signal w.r.t. a reference harmonic excitation [126] has enabled mechanical contrast imaging via relative viscosity in various disease states [127–130,132] (see Section 3.5). Here, an intensity-modulated harmonic excitation is implemented instead of nanosecond-pulsed excitation, where the detected PA signal represents the harmonic strain response to the applied harmonic stress [126]. In a viscoelastic material, the strain response experiences a phase delay, δ, relative to the applied stress that is associated with the viscous energy dissipation in the material. This relative viscosity is quantified by the ‘loss ratio’, tanδ=G"(ω)/G′(ω), which takes the value of zero in a purely elastic material. In order to decouple elasticity and viscosity, an elasticity imaging approach based on impulse excitation, inspired by acoustic radiation force impulse (ARFI) imaging [138], has been implemented in combination with the phase delay approach [132]. Here, Young’s modulus E is obtained from the temporal profile of the PA pressure pulse, then, assuming Voigt model of linear viscoelasticity, viscosity η is obtained from the harmonic PA phase delay via tanδ=ωη/E [132]. Although a notable attempt, this approach still requires more rigorous wave analysis and reconstruction schemes to account for the influence of different wave modes and spatial variation (especially along depth) of absorption coefficient.
It should be noted that existing PAE approaches require media for coupling of US into the sample (unlike air-coupled US). Furthermore, the approaches discussed above are based on measurements of SAW, which would require that the samples are sufficiently thick to avoid guided wave modes (see Section 2.4). Other PAE approaches include measurement of PA resonance frequency (i.e., frequency of harmonic PA excitation that produces the largest PA signal amplitude) [133] and PA eigen-spectrum [136], which can be related to the material elasticity E. In another approach, multiple PA excitation wavelengths are employed to realize a multi-spectral PA elasticity tomography, where the concentration of chromophores in the sample and material bulk elastic modulus are simultaneously estimated via an iterative search based on a PA wave generation model [135].
3. Recent developments: mechanical characterization of biological tissues
In this section, we highlight recent developments in optical elastography, focusing specifically on developments related to mechanical characterization of biological tissues. The themes that have emerged over the past 5 years are: exploration of new types of wave propagation in wave-based OCE (Section 3.1), emerging approaches to characterize anisotropy (Section 3.2), development of passive elastography approaches (Section 3.3), development of handheld and minimally-invasive probes for in vivo imaging (Section 3.4), and clinical demonstration of established techniques (Section 3.5).
3.1. Expanding imaging capabilities of wave-based OCE with new types of waves
Elasticity imaging based on conventional wave-based OCE approaches are often confounded by non-shear modes of wave propagation, which complicate the estimation of shear wave speed (see Section 2.4) [73]. This complication is especially severe with the contributions of highly dispersive Lamb wave modes in layered materials such as the eye, which is one of the major application areas of OCE [76]. Another limitation of conventional wave-based OCE is the relatively lower sensitivity to mechanical contrast along the axial (depth) direction. The ability to discern depth-resolved elasticity contrast is, again, especially relevant in the eye, where different anatomical layers exhibit varying mechanical properties. In order to overcome these limitations, alternative types of mechanical waves and methods for wave generation have been explored.
Longitudinal shear waves (LSW), previously investigated theoretically and experimentally in ultrasound elastography, are a type of shear wave that propagates along the direction of its polarization. LSW has recently been exploited in OCE to improve the detection of mechanical contrast along the depth direction [54,55]. For a typical wave generation by a plate vibrating normal to the sample surface, LSW propagate axially through depth (like a compressional wave, but at the shear wave speed) and are not confined to the surface like the transversely propagating surface waves (Fig. 3(a)). Due to its propagation along depth, LSW are ideal for detecting depth-resolved elasticity contrast via the axial variation in LSW propagation speed. Zvietcovich et al. characterized the axial resolution of LSW wave speed map in a bilayer phantom to be on the order of 0.1 mm, which is not achievable by traditional transversely-propagating surface waves [55]. Another form of LSW-based OCE is nanobomb (nb)OCE [68–70]. Here, the LSW are generated via laser-induced evaporation dye-loaded nanodroplets (nanobombs). Compared to the vibrating plate, the ‘explosion’ of nanobombs generates higher-frequency (up to 9 kHz), localized, transient LSW, which makes it less susceptible to boundary conditions resulting from sample geometry. Due to the fast propagation of high-frequency LSW, nbOCE utilizes high-speed imaging with line-field low coherence interferometry [68] and MHz-rate swept-source OCT [69] for detection.
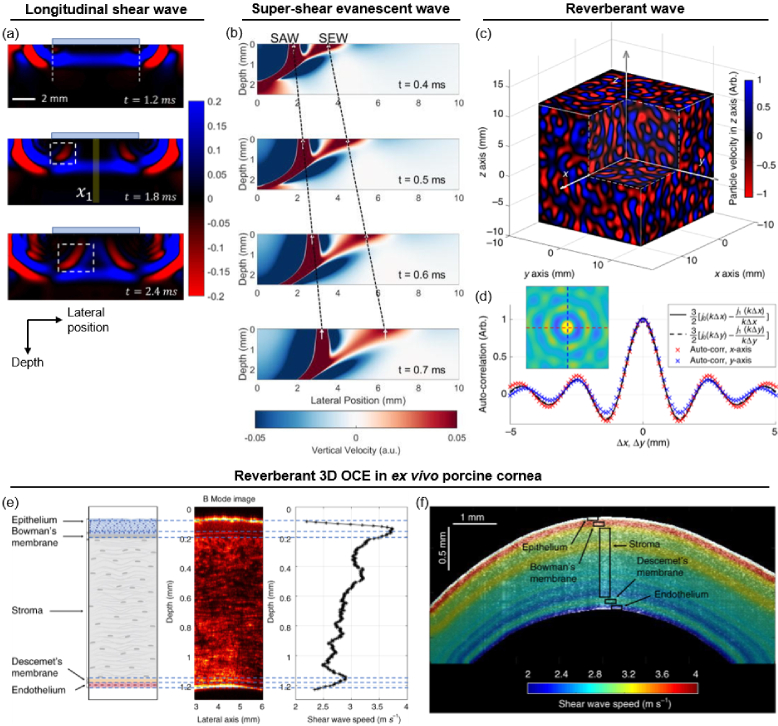
Fig. 3.
New modes of wave propagation in wave-based OCE. Simulated wave field of (a) longitudinal shear waves (LSW) propagating along depth from a vibrating plate (adapted with permission from [55] © Optica), (b) super-shear evanescent waves (SEW) propagating ahead of the surface acoustic waves (SAW) (reprinted from [75], with the permission of AIP Publishing), and (c) reverberant field produced by waves from multiple sources propagating in random directions. (d) Real-part of 2D autocorrelation map extracted from the xy-plane of reverberant field in (c). The profile cuts along x (red) and y (blue) are fit to analytical solutions (black curves) to extract the local wave number k. (e) and (f) Reverberant 3D (Rev3D)-OCE utilizes the 2D lateral autocorrelation of the reverberant wave field at each depth to reveal remarkable depth-resolved wave speed contrast in ex vivo porcine cornea. (c)–(f) Adapted by permission from Springer Nature: [15].
Super-shear evanescent waves (SEW) are another type of shear wave that has recently been explored in OCE. SEW propagate transversely along the sample surface, but at a speed faster than that of the traditional shear wave (thus, ‘super-shear’). Pitre et al. investigated the propagation of SEW from an impulse excitation by air-coupled ultrasound (Fig. 3(b)) [75]. In simulation, the propagation speed of SEW provides accurate measurements of Young’s modulus even in bounded media, where traditional shear wave speed would be confounded by the highly dispersive Rayleigh-Lamb modes.
Another type of waves that has been exploited in OCE to overcome the complications of the Lamb modes in bounded layered media is the reverberant (diffused) wave [139], produced by multiple interacting shear waves propagating in random directions (Fig. 3(c)). From the perspective of wave-based OCE, reverberant fields promote a higher proportion of shear wave propagation compared to traditional transient excitation, which predominantly produces dispersive Lamb waves in bounded media such as the cornea [15]. Zvietcovich et al. developed reverberant (Rev)3D-OCE for depth-resolved measurement of corneal elasticity, based on the analytical solutions to the autocorrelation of the reverberant fields (Fig. 3(d)) [15]. The reverberant fields were experimentally generated by eight synchronous vibrating sources on the sample surface. By analyzing the 2D en face autocorrelation of the resulting axial velocity field at each depth, depth-resolved measurement of shear wave speed in ex vivo porcine cornea was achieved with remarkable contrast between anatomical layers (Fig. 3(e) and 3(f)).
3.2. Characterizing tissue anisotropy and nonlinear mechanical responses
Biological tissues are composed of 3D network of fibrous proteins, whose architecture impacts the function of the tissue. In many tissue types such as skin, muscle, tendon, cornea, brain, and cardiac tissue, the fibril organization gives rise to anisotropic mechanical responses, as shown by UE [140–142], MRE [143] and mechanical testing [144]. Tissue anisotropy is particular of importance when considering wave-based approaches, since wave speed can vary in the same tissue depending on the propagation direction, potentially resulting in inaccurate reconstruction of moduli from 3D wave data [66]. In addition to anisotropy, biological tissues also exhibit nonlinear mechanical responses, which have been increasingly studied in clinical elastography [145,146] and biophysics [21,147–149].
The general approach to characterize anisotropy in wave-based OCE is based on measuring wave speed along different propagation directions. Wang et al. demonstrated a semi-quantitative approach to measure ‘fractional anisotropy’ in cardiac muscle [150]. Ex vivo mouse heart was mounted on a rotational stage to facilitate BM-mode scanning of air pulse-induced wave propagation along six different angular directions. It was found that infarcted cardiac tissues exhibit both lower stiffness and lower anisotropy. Zvietcovich et al. demonstrated a similar principle, but instead of measuring far-field wave propagation, ‘spatial deformation spreading’ at the region of air-pulse excitation was analyzed [151].
In order to quantify anisotropic elastic moduli from wave speed measurement, Pitre et al. developed a nearly incompressible transversely isotropic (NITI) model for characterizing tissues exhibiting transverse isotropy such as cornea and skin [152]. In this case, the stiffness tensor C in Eq. (2) requires two additional parameters to define both tensile and shear moduli and Poisson ratios corresponding to responses along and perpendicular to the axis of symmetry (typically determined by the fibril orientation in tissue). Kirby et al. utilized the NITI model to quantify G along both directions in ex vivo porcine cornea [153]. Here, the cornea was assumed have an isotropic tensile response (i.e., E is isotropic, but G is transverse isotropic), which reduced the number of additional parameters in to only one and allowed both G moduli to be obtained by fitting wave speed dispersion data to the NITI model. When the assumption of tensile isotropy cannot be made, both additional parameters in must be measured to quantify the full transverse isotropic elastic moduli. In this case, Kirby et al. employed multi-directional wave speed measurement to obtain direction-dependent wave speed anisotropy map, which was fit to the numerical simulation of the NITI model to extract transversely isotropic G moduli, Poisson ratios, and fiber orientation [154]. Applied to in vivo human skin, together with OCT angiography and polarization-sensitive OCT, this approach revealed that healed scar tissue exhibited abnormal vascularization and collagen architecture, resulting in altered elasticity and anisotropy compared to surrounding normal tissue [154].
The multi-directional measurement approach has also been explored in BM. Eltony et al. took advantage of the corneal curvature to interrogate the cornea from multiple angles as the probe beam was raster-scanned across the human eye in vivo [155]. Here, composite material models were developed to describe each corneal lamella layer (aligned collagen fibrils in gel matrix) as well as the bulk corneal stroma (multiple layers of lamellae). Microscale BM imaging across the thickness of the cornea revealed ‘ribbons’ of alternating Brillouin shift, corresponding to layers of lamellae with roughly alternating collagen fibril orientation. In vivo human cornea imaging (also see [110] in Section 3.5) showed that the microscale lamellar anisotropy translated to weak anisotropy on the macroscale in the bulk corneal stroma.
In addition to anisotropy, nonlinearity is an important consideration in most conventional mechanical testing methods since the magnitude of loading can alter the mechanical regime of biological tissues. Optical elastography, with superior displacement sensitivity of optical imaging modalities, has traditionally been able to avoid nonlinear mechanical responses by applying significantly smaller loading. However, recent studies suggest that characterizing the nonlinear behavior of tissues and biopolymers may be important in the biomechanical study of disease progression [145,146] and cell-ECM interactions [21,147–149] (see Section 4.1 for discussion of [21]). Furthermore, a combination of mathematical modeling and experimental studies have suggested that plasticity of the ECM may be an important factor in facilitating ECM remodeling by cells [156,157]. Thus, characterizing nonlinear mechanical responses, along with anisotropy, will be an important area of further development for the field of optical elastography.
3.3. Improving clinical compatibility with passive elastography of tissues
Active elastography approaches (see Fig. 2) necessitate another layer of instrumentation and measurement complexity that is associated with the externally-applied mechanical excitation. From the perspective of clinical translation, these additional complexities can significantly limit the ability to seamlessly integrate optical elastography technologies into the existing clinical workflow. This has motivated a number of passive elastography approaches that utilize naturally occurring dynamics in place of active mechanical excitation.
Noise-correlation OCE is based on time-reversal of diffuse wave fields (similar to the autocorrelation of reverberant field in Rev3D-OCE in Section 3.1), but the diffuse fields originate from naturally occurring random motion (i.e., ‘noise’) [158,159]. Nguyen et al. presented a detailed mathematical approach to extract shear wavelength (Fig. 4(b), left) from the a measurement of naturally occurring displacement fields (Fig. 4(a)) via a time-reversal approach [159]. More recently, this mathematical approach has been adopted in a full-field configuration using off-axis digital holography [158]. With the full-field acquisition, information about anisotropy can, in principle, be extracted from the 2D en face spatiotemporal correlation of the diffused fields [158]. In order to quantify elasticity from the measured shear wavelength, the knowledge of the frequency content of the naturally occurring diffused fields is needed [158]. This is an area of future development for noise-correlation OCE. Meanwhile, a similar noise-correlation algorithm has also been applied in active wave-based OCE for ultrafast elasticity imaging of single cells (called “cell quake elastography”) [160].
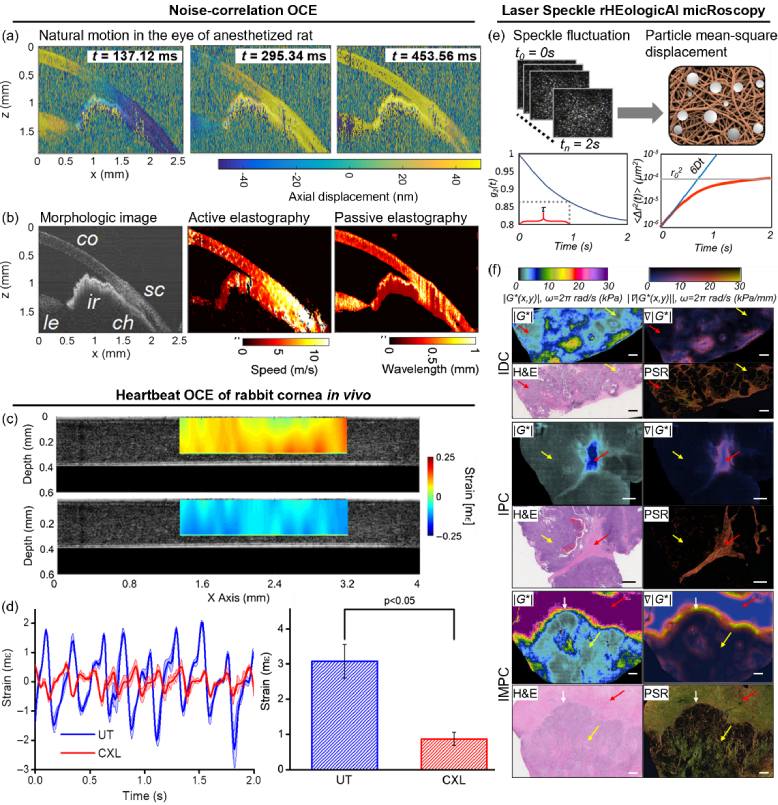
Fig. 4.
Passive optical elastography approaches. (a) Noise-correlation OCE utilizes natural motion in the sample to reconstruct the shear wavelength in the medium via time-reversal principle. (b) Passive noise-correlation OCE in the eye of an anesthetized rat produces elastogram consistent with traditional active wave-based OCE. (c) Heartbeat (Hb)-OCE measures axial strain in the cornea during cyclic compression (top) and relaxation (bottom) induced by “ocular pulses”. (d) Time-course of reconstructed corneal strain resembles the arterial pressure waveform (left), where the strain amplitude is larger in the untreated (UT) compared to the cross-linked (CXL) cornea (right). (e) Laser Speckle rHEologicAl micRoscopy (SHEAR) utilizes the fluctuation dynamics of laser speckle pattern to measure the MSD of endogenous tissue particles undergoing Brownian motion. Spatially-resolved map of shear modulus is reconstructed from the measured MSD via the GSER. (f) Maps of shear modulus magnitude, |G*|, and spatial gradient, ∇|G*|, in invasive ductal carcinoma (IDC), invasive papillary carcinoma (IPC), and invasive micropapillary carcinoma (IMPC), with corresponding H&E and picrosirius red (PSR) sections. Scale bar: 1 mm. Adapted with permission from: (a) and (b) [159], (c) and (d) [162], (e) [84] © SPIE, and (f) [20].
Heartbeat (Hb)-OCE similarly makes use of naturally occurring motion, but instead of random ‘noise’, Hb-OCE is specifically based on the physiological deformation induced in the cornea by the pulsatile arterial flow in the eye [161,162]. The variation between systolic and diastolic intraocular pressure results in the cyclical compressive strain of the cornea (Fig. 4(c)). The so-called ‘ocular pulse’ has also been exploited in ultrasound elastography [163]. To demonstrate the in vivo feasibility of Hb-OCE for the assessment of corneal elasticity, Nair et al. measured Hb-induced corneal strain in anesthetized rabbit [162]. The temporal variations of Hb-induced strain in both untreated and cross-linked corneas follow the typical arterial pressure waveform, but the stiffer cross-linked cornea expectedly exhibits significantly lower strain amplitude (Fig. 4(d)). The quantification of elasticity from the measured Hb-induced corneal strain will have to account for several factors (such as the ocular pulse amplitude, intraocular pressure, and stress in the cornea) and is an area of future development for Hb-OCE.
Laser Speckle rHEologicAl microscopy (SHEAR) is another approach that exploits naturally occurring motion in biological tissues, but instead of tissue-level displacements like in noise-correlation and Hb-OCE, SHEAR is based on µR of thermally-driven endogenous tissue particles (e.g., biomolecules, ECM proteins, cells, organelles etc.) undergoing Brownian motion [81–85]. Unlike traditional µR approaches, SHEAR is suitable for measurements in intact biological tissues since it does not require incorporating exogenous probe particles. SHEAR adopts the principle of PT-µR (see Section 2.5) but indirectly measures particle MSD from the rate of fluctuation of backscattered laser speckle pattern [84]. Here, monochromatic light illuminates the tissue, in which Brownian motion of endogenous tissue particles changes the interference pattern of backscattered light, resulting in speckle fluctuation (Fig. 4(e)). The use of laser speckle fluctuation to measure MSD (as opposed to a direct measurement of particle displacement) extends the dynamic range of SHEAR into tens of kPa range [81], several orders of magnitude higher than the typical PT-µR measurements. This has enabled quantitative mapping of shear stiffness in a cohort of 251 breast cancer specimens from 148 patients [20]. The study found that the magnitude of G*, |G*|, closely corresponded with histological features (H&E) and collagen content (picrosirius red, PSR), while spatial gradient of G*, ∇|G*|, was elevated at the tumor invasive front (Fig. 4(f)). Both |G*| and ∇|G*| were associated with breast cancer prognostic indicators based on histological subtypes, tumor grades, receptor status, and lymph node involvement.
3.4. Improving clinical compatibility with handheld and anatomical probes
Although a benchtop imaging setup may be applicable in some settings, certain clinical applications require the integration of optical elastography technologies into a more compact form factor, such as a handheld device or a minimally-invasive probes for in vivo intravascular and endoscopic imaging.
Among other imaging approaches [164], compression OCE has demonstrated potential for biomechanics-based intraoperative tumor margin assessment during tumor resection surgery. In order to streamline the integration of compression OCE into the existing surgical oncology workflow, the reduction of traditional benchtop setup into a compact handheld probe has been an active area of development in compression OCE. One of the main challenges in handheld compression OCE is motion artifact, which is exacerbated with the use of a relatively slower MEMS scanner (compared to galvanometer scanners in benchtop OCE systems) for miniaturization. Fang et al. developed a handheld QME (see Section 2.3) probe based on MEMS scanner with a custom bidirectional scanning pattern to improve the imaging speed (Fig. 5(a)) [165]. Handheld quantitative elasticity imaging was demonstrated on freshly excised mastectomy specimens. Meanwhile, compression OCE has also been integrated into a fiber-based handheld probe [166] and micro-endoscopic probe for animal study [167].
Fig. 5.
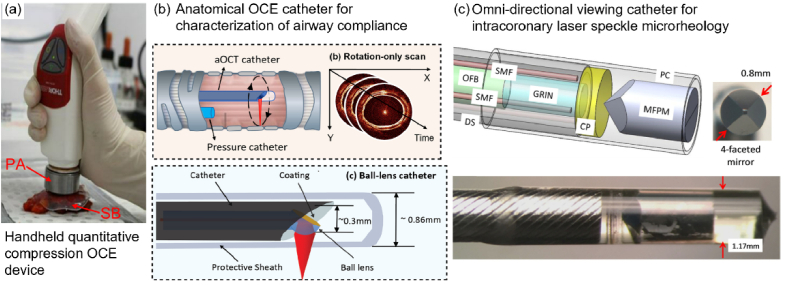
Integration of optical elastography technologies into handheld and minimally-invasive probes. (a) Handheld compression OCE device for quantitative micro-elastography of ex vivo tissue specimens. PA: PZT actuator, SB: silicone bilayer. (b) Anatomical OCE (aOCE) catheter endoscopically measure airway compliance by simultaneously capturing structural OCT image and intraluminal pressure. (c) Omni-directional viewing catheter with 4-faceted mirror for intracoronary SHEAR. OBF: optical fiber bundle, SMF: single mode fiber, GRIN: gradient index lens, MFPM: multi-faceted pyramidal mirror, DS: drive shaft, CP: circular polarizer, polycarbonate tube. Adapted with permission from: (a) [165], (b) [169], (c) [83] © Optica.
In addition to handheld devices, endoscopic and intravascular probes for in vivo mechanical characterization are other areas of active development. Bu et al. developed anatomical OCE (aOCE) for endoscopic assessment of airway compliance [168–170]. Using a combination of endoscopic OCT probe (‘aOCT’ catheter) an intraluminal pressure catheter (Fig. 5(b)), aOCE measures cross-sectional and local airway compliance from measurements of airway deformation at different induced intraluminal pressures [168,169]. A potential application of aOCE for endoscopic assessment of inhalation burn injury was demonstrated in ex vivo porcine trachea [170]. An area of future development for aOCE is to utilize physiological variation in airway pressure during respiration (instead of inducing different intraluminal pressure) for a completely passive in vivo measurement.
The assessment of atherosclerotic plaque mechanics is another major application area of optical elastography. A few established optical elastography approaches have recently begun the process of adaptation into an intracoronary probe. Wang et al. developed an omni-directional viewing catheter for intracoronary SHEAR (Fig. 5(c)) and demonstrated quantitative SHEAR measurement (see Section 3.3) in a luminal gel phantom [83]. The multi-faceted mirror enables omni-directional LS measurements around the luminal wall without the need for rotational motion of the catheter (typically implemented in intravascular OCT). Meanwhile, Qu et al. has developed a miniaturized ARF-OCE probe, but further miniaturization of the ultrasound transducer and implementation of side-viewing are still needed in order to perform in vivo intracoronary measurements [63].
3.5. Demonstrating the utility of optical elastography in clinical settings
The eventual clinical translation and adoption of optical elastography technologies hinges on establishing the clinical utility of these technologies in the clinical settings. Several established techniques including compression OCE (Section 2.3), wave-based OCE (Section 2.4), and BM (Section 2.6) have transitioned to disease-specific clinical studies following years of technological developments in the instrumentation and methodologies.
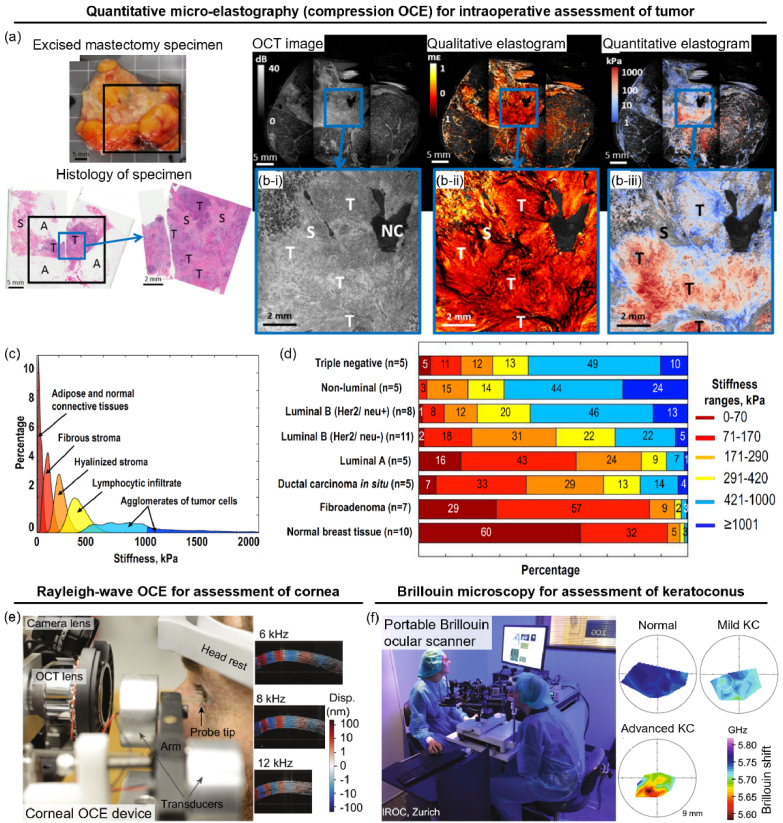
An intraoperative assessment of tumor margin based on qualitative strain elastograms from compression OCE has previously been demonstrated by Allen et al. [48]. Recently, an improvement to achieve wide-field imaging and quantitative elasticity imaging (with the QME approach, see Section 2.3) has been demonstrated (Fig. 6(a) and 6(b)) [49]. Using quantitative compression OCE, Gubarkova et al. investigated an approach to translate the obtained elastograms (i.e., Young’s modulus maps) into clinical diagnoses of tumor margin and breast cancer subtypes [18,19]. Using a detailed comparative examination of the OCE elastogram and standard histological tissue classification, ‘stiffness spectra’ can be obtained for different characteristic breast tissue components (Fig. 6(c)) [18]. Then, the obtained OCE elastograms can be segmented into different tissue components based on these stiffness spectra, which remarkably reveals distinct distributions of stiffness ranges (corresponding to different tissue components) for different breast tumor subtypes (Fig. 6(d)) [18]. Detailed visual diagnostic assessment criteria and diagnostic accuracy of this approach for distinguishing tumor versus non-tumor and determining breast cancer subtypes have been reported [19]. Taking a different approach, Hajjarian et al. performed multivariate analysis to establish that shear modulus and indices of mechanical heterogeneity measured by SHEAR (Fig. 4(f)) are associated with breast cancer prognostic indicators (see Section 3.3) [20].
Fig. 6.
Demonstration of optical elastography in clinical settings. (a) and (b) Intraoperative tumor margin assessment with compression-OCE-based quantitative micro-elastography. T: invasive tumor, S: uninvolved stroma, A: adipose, NC: non-contact. (c) Stiffness spectra of various tissue types and (d) characteristic stiffness distribution of various breast cancer subtypes obtained from correlative compression OCE elastogram and histology section. (e) First-in-human implementation of dynamic indentation-based Rayleigh-wave OCE (left), showing examples of wave displacement fields in cornea at different frequencies (right). (f) Brillouin ocular scanner (left) assessment of biomechanical heterogeneity in mild to advance keratoconus (KC) (right). Adapted with permission from: (a) and (b) [49], (c) and (d) [18] © Optica. Adapted by permission from Springer Nature: (e) [57], (f) [110].
A major clinical application area of optical elastography is the in vivo assessment of corneal elasticity. Ramier et al. demonstrated the first-in-human wave-based OCE of the cornea using dynamic indentation by a contact piezoelectric probe (Fig. 6(e)) [57]. Meanwhile, Lan et al. also demonstrated in vivo air-puff OCE in human cornea and investigated the effects of respiration and heartbeat on the OCE measurement precision and repeatability [171,172]. On the other hand, Shao et al. presented a clinical study of corneal mechanics at different stages of keratoconus (KC) with in vivo BM [110]. Analytical models and experimental investigation of the effects of corneal thickness and hydration on the measured Brillouin shift (see Section 2.6) has previously been presented to support BM measurement in the cornea [109]. It was found that the cornea exhibited increased mechanical inhomogeneity with increasing KC severity (Fig. 6(f)). Moreover, mechanical asymmetry between the left and right eye could be a promising marker for early-stage KC diagnostics [110]. In addition, given that cornea exhibits preferential fibril alignments tangential to the surface of the eye, Eltony et al. implemented angle-resolved BM with off-axis illumination to characterize the mechanical anisotropy of human cornea in vivo [155]. Notably, variations in the measured Brillouin shift—to a similar level as the changes in mild KC in [110]—was observed as a function of illumination angle owing to corneal anisotropy, suggesting that angle dependence must be considered when interpreting BM data in cornea (see Section 3.2).
Another potential clinical application area is magnetic thermotherapy dosimetry with magnetomotive (MM)-OCE. Huang et al. made use of the magnetic nanoparticles that were delivered into the tissue for magnetic thermotherapy as ‘theranostic’ probes to perform MM-OCE monitoring of the changes in tissue elasticity [173,174]. Meanwhile, PAE has also been demonstrated in various diseases including in vivo breast tumor in mouse model [127], atherosclerotic plaque [128,129], esophageal cancer [130], and liver cirrhosis [132]. The detection of liver cirrhosis based on PAE viscoelasticity imaging demonstrated by Wang et al. suggests that measurement of liver viscosity may enable distinction of liver cirrhosis from hepatitis, where conventional elasticity imaging by clinical ultrasound elastography often fails [132]. However, it should also be noted that PAE approaches (or any optical elastography approaches in general) are likely to supplement rather than replace clinical deep tissue imaging applications of medical imaging modalities such as UE and MRE.
4. Recent developments: mechanical characterization of cells and extracellular matrices
In this section, we highlight recent developments in optical elastography, focusing specifically on developments related to mechanical characterization of cells and ECM at the cellular scale. The themes that have emerged over the past 5 years are: characterization of spatiotemporal variations in ECM micromechanical properties with optical µR (Section 4.1) and subcellular-scale imaging of high-frequency biomechanics in live cells and organisms with BM (Section 4.2).
4.1. Probing extracellular matrix heterogeneities with optical microrheology
Biomechanical interactions between cells and ECM play an important role in many pathophysiological processes. The ability to probe cell-mediated dynamic spatiotemporal variations in ECM mechanical properties at the cellular scale in 3D environment has the potential to drive new mechanobiological studies in physiologically relevant settings. Optical µR approaches offer unique capability to locally probe mechanical properties of the ECM at the microscopic scale in 3D engineered cellular systems.
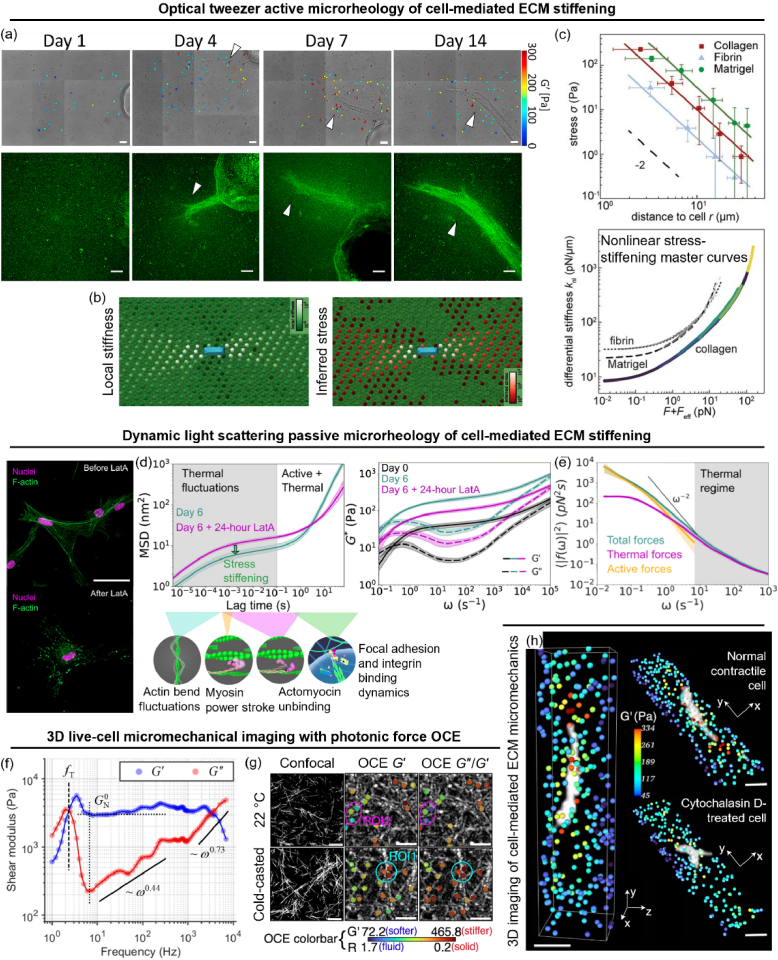
OT-AµR provides a robust method for microscopically probing the mechanical properties of biopolymer constructs (see Section 2.5). In recent years, OT-AµR has been increasingly applied in live-cell studies of cell-mediated ECM biomechanical remodeling [21,23,87,89]. With optimized instrumentation to streamline the optical alignment and measurement on each probe bead, Keating et al. performed OT-AµR in 3D collagen ECM seeded with dermal fibroblasts [87]. OT-AµR reveals that cellular contractility and proteolysis induce ECM stiffening and enhance the micromechanical heterogeneity in the pericellular space. Applying similar OT-AµR approach, Juliar et al. performed a longitudinal study of the changes in ECM mechanical properties during capillary morphogenesis (Fig. 7(a)) [23]. OT-AµR reveals that endothelial and stromal support cells collectively stiffen the ECM and create a mechanically heterogeneous microenvironment around the sprouting capillaries. Meanwhile, Staunton et al. applied OT-AµR to characterize the frequency-dependent viscoelastic responses in the cytoplasm versus the surrounding ECM, revealing that malignant cancer cells are 4-fold stiffer [89]. Combining OT-AµR with mathematical modeling, Han et al. presented a novel nonlinear stress inference microscopy (NSIM) approach to characterize the stress field exerted by cells on their microenvironment (Fig. 7(b)) [21]. NSIM reveals that the cell-generated stress field decays with a ‘rope-like’ force transmission (Fig. 7(c), top); the force can be sufficient to drive the ECM into the nonlinear regime, which can be exploited by OT-AµR to characterize the nonlinear stress-stiffening behavior of the ECM (Fig. 7(c), bottom).
Fig. 7.
Probing micromechanical heterogeneity of the ECM with optical µR. (a) OT-AµR reveals local ECM stiffening during capillary sprouting. Scale bar: 20 µm. Reprinted from [23], with permission from Elsevier. (b) Simulated stiffness (left) and inferred stress (right) in a nonlinear fiber network around a contracting cell by NSIM. (c) Cell-generated stress inferred from OT-AµR and NSIM (top). Measured stiffness and inferred stress reveal stress-stiffening behavior of the ECM (bottom). (b) and (c) Adapted with permission from [21]. (d) DLSµR measures particle MSD and ECM G* before (green) and after (purple) latrunculin A (LatA) depolymerizes F-actin cytoskeleton (confocal images). Scale bar: 50 µm. (e) Force spectra obtained from G* on day 6. Adapted with permission from [24]. (f) Spectroscopic PF-OCE reveals characteristic frequency-dependent viscoelastic responses of polyacrylamide gel. fT: transition frequency, GN°: plateau modulus, ωx: power scaling law. Adapted with permission from [22] © Optica. (g) Light-sheet PF-OCE reveals microscale viscoelasticity of collagen gels [25]. Scale bar: 20 μm. (h) 3D light-sheet PF-OCE reveals fibroblast-mediated ECM remodeling. Scale bar: 50 μm. (g) and (h) Adapted with permission from Springer Nature: [25].
Although traditional PT-µR can only support measurements in very soft materials (see Section 2.5), novel passive µR based on dynamic light scattering (DLS) has been demonstrated in biologically relevant biopolymer constructs [24,80]. Krajina et al. applied DLSµR to characterize timescale-dependent cell-mediated ECM remodeling dynamics before (Fig. 7(d), green) and after (Fig. 7(d), purple) cytoskeletal disruption. A force spectrum analysis (FSA) technique was developed to decouple the thermal (passive) versus cell-force (active) contributions to the measured ECM dynamics (Fig. 7(e)) [24]. Active cell forces (yellow) follow a power scaling law (black line) of step-like motor. Thermal forces dominate at higher frequencies (shaded region). The DLSµR-based FSA approach reveals that the emergent hybrid active and thermally-driven dynamics involve high-frequency stress-stiffening and low-frequency fluidization of the ECM.
Photonic force (PF)-OCE is a recently developed technique for 3D volumetric mechanical microscopy of biological hydrogels [22,25,90,91]. PF-OCE utilizes radiation-pressure from a low-NA beam (as opposed to a high-NA OT in OT-AµR) to harmonically ‘push’ on individual probe beads, randomly distributed over an extended depth range. Compared to OT-AµR, PF-OCE can support volumetric micromechanical imaging via beam-scanning, since it does not require serially trapping and actuating each bead [90]. Combined with a depth-resolved radiation-pressure force measurement approach [175], PF-OCE provides microrheological quantification of viscoelasticity [91], including characterizing the frequency-dependent responses of biopolymers (Fig. 7(f)) [22]. High-throughput quantitative 3D micromechanical microscopy for live-cell imaging of cell-mediated ECM remodeling has recently been demonstrated via light-sheet PF-OCE for more efficient, parallelized photonic forcing [25]. In fibrous collagen gels, light-sheet PF-OCE reveals microscopic heterogeneities in viscoelastic properties that correlate to the collagen microarchitecture (Fig. 7(g), see Fig. 2(e) in [25] for the correlative analysis). ROI1 and ROI2 indicate a stiffer solid-like and a more compliant fluid-like microenvironments, respectively. In fibroblast-seeded fibrin constructs, light-sheet PF-OCE not only shows cell-induced pericellular stiffening and heterogeneity similar to OT-AµR [21,87] (Fig. 7(h), normal contractile cell), but also provides the first quantitative time-resolved observations showing that both softening and stiffening of the pericellular ECM occurs after drug-induced (cytochalasin D) inhibition of cellular contractility, and that both types of response are correlated to the local cell-induced ECM deformation (see Fig. 3(g)–3(i) in [25]).
4.2. Imaging subcellular high-frequency biomechanics with Brillouin microscopy
A major area of development in BM has been in expanding the applications of BM to various biological systems (i.e., beyond measurements of single-cell mechanics), which has also contributed to enhancing the interpretation of BM measurements in the context of biophysical phenomena. The push to expand the applications of BM has also been accompanied by technological developments to improve speed and fidelity of the acquired Brillouin spectra, while considering practical constraints such as phototoxicity and the desired spatiotemporal as well as spectral resolution.
Zebrafish is a widely used vertebrate model organism in biological research. Its relative transparency has made zebrafish a compatible model system for biomechanical characterization by BM. Schlussler et al. applied BM to conduct an in vivo longitudinal study of zebrafish spinal cord mechanical properties during spinal cord injury repair [17]. The spinal cord exhibits lower stiffness immediately after injury due to reduced cellularity and disorganized cellular arrangement, but gradually recovers its normal stiffness over the course of repair (Fig. 8(a)). Interestingly, this study also reveals that in vivo BM measurements in live zebrafish produces different results compared to ex vivo measurements [17]. Bevilacqau et al. also performed in vivo BM measurement in live zebrafish but focused on subcellular resolution imaging of the notochord ECM (Fig. 8(b)) [14]. By implementing a more rigorous Brillouin spectral analysis (using two-Lorentzian peak fitting), sub-micron thickness of the notochord ECM could be measured (Fig. 8(c)). Notably, this study also brings attention to the consideration of spatial scales in BM, showing that the NA of the system affects the Brillouin spectrum and the contrast of the Brillouin shift maps [14]. In addition to zebrafish, BM has also been used to study the mechanical properties of murine embryo. Using OCT to provide structural guidance, Raghunathan et al. were able to identify and compare the Brillouin shift in developing heart, neural folds, and the neural tube [176].
Fig. 8.
Imaging subcellular high-frequency biomechanics with BM. (a) BM of zebrafish larvae captures mechanical changes before (3 dpf), after spinal cord injury (3+ dpf), and post-repair (4-5 dpf). Scale bar: 150 µm. dpf: days post fertilization, Sc: spinal cord, nc: notochord. Reprinted from [17], with permission from Elsevier. (b) High-resolution BM of zebrafish notochord combined with double-peak spectral fitting resolves (c) sub-micron notochord ECM thickness. Scale bar: (b) 20 µm and (c) 1 µm. d: dorsal, v: ventral, m: muscle, sh: sheath cell, vac: vacuole. (b) and (c) Adapted with permission from [14] © Optica. (d) Phase contrast (top) and BM maps (bottom) of elasticity (frequency shift, left) and viscosity (linewidth, right) in live tumor spheroid, revealing stiffer elastic center (red bars) and softer viscous outer rim (blue bars). (e) Mechanical changes in the spheroid over 2 days of chemotherapy; phase contrast (top) shows disaggregation at the outer rim by Day 2. (d) and (e) Reprinted from [111] with permission. Copyright 2019 by the American Physical Society. (f) Mechanical changes (frequency shift, ΩB) in a developing nematode (larvae stages L2, L3, L4, young adult YA, and adult A) at the organ level. High-resolution BM of an adult gonad at the subcellular level (inset) reveals nuclei and nucleoli (white and black arrowheads), cytoplasm (asterisk), uterus edge (white arrow), oocyte pushed from the spermatheca into the uterus (black arrow), and a four-cell embryo in the uterus (black diamond arrow). Adapted by permission from Springer Nature: [16].
BM has also been applied to study biopolymer constructs and engineered multicellular systems. Marquertitat et al. characterized the spatial distribution of elasticity and viscosity (via Brillouin shift and linewidth, see Section 2.6) in colorectal cancer spheroids (Fig. 8(d)), then, investigated the biomechanical changes during 5-fluorouracil chemotherapy (Fig. 8(e)) [111]. Tumor spheroids exhibit decreased stiffness (most pronounced at the rim) and increased viscosity (most pronounced at center), corresponding to the disintegration and fluidization of the spheroid construct, after 2 days of treatment. Notably, the interpretation of the GHz BM measurements is supported by the high-frequency poromechanics model (i.e., the undrained regime where fluid is trapped in the porous elastic frame, as opposed to the low-frequency drained regime where fluid is able to exude out). Meanwhile, Bailey et al. characterized viscoelasticity of gelatin hydrogels in order to investigate the role of hydration and relate the GHz Brillouin measurements to physiologically relevant low-frequency biomechanics [113].
One of the major areas of active development in BM is speed improvement via nonlinear stimulated Brillouin scattering. In standard stimulated BM, another tunable continuous wave (CW) pump laser is introduced to intersect with the illumination beam [16,114,116]. This pump laser is wavelength-swept to achieve efficient nonlinear stimulated Brillouin scattering. Stimulated BM not only reduces the acquisition time, but also provides elastic background-free Brillouin spectrum (see Section 2.6). Recently, Remer et al. presented stimulated BM with optimized acquisition speed, sensitivity and, spectral resolution [16]. The instrument can support both organ-level and subcellular-level imaging in live C. elegans, where the elasticity and viscosity contrasts reveal remarkable anatomical features (Fig. 8(f)). A variant of stimulated BM is impulsive stimulated BM, which utilizes a high-intensity broadband pulsed pump laser instead of a wavelength-swept tunable CW laser [115,117]. Stimulated BM approaches still require sophisticated illumination and collection geometries and high laser power compared to spontaneous BM. Thus, improvements in all areas of acquisition speed, phototoxicity, and simplicity of the optical setup for in vivo biomechanical measurements remain an active area of development for BM.
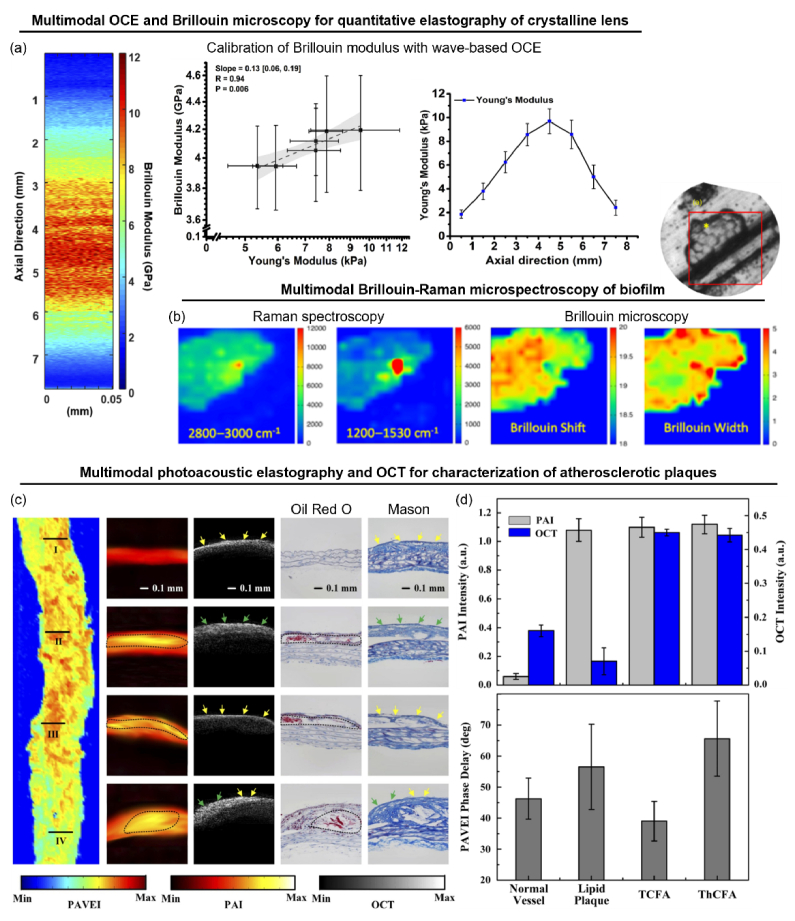
5. Recent developments: multimodal optical elastography platforms
In this section, we highlight recent developments in optical elastography, focusing specifically on multimodal imaging platforms that combine one or more optical elastography and/or other optical imaging modalities. Biological systems, both at the cellular and tissue levels, represent a complex interplay between microstructural, biomechanical, and biochemical cues. Thus, there is an increasing need to collect multiple pieces of information in order to comprehensively characterize a biological system. In addition, limitations that are inherent to individual modalities may be mitigated by synergistic combination with other modalities.
The combination of BM and wave-based OCE for depth-resolved quantification of Young’s modulus in crystalline lens demonstrated by Ambekar et al. is one such example [120]. On the one hand, BM is ideal for biomechanical imaging in transparent materials such as the crystalline lens, but the interpretation of the GPa Brillouin modulus in the terms of the more physiologically relevant biomechanical properties remains a challenge. On the other hand, wave-based OCE can quantify elasticity via the widely used Young’s or shear modulus, but measurements in transparent samples (i.e. with no significant backscattering from internal structures) can only be made on the surface since OCT relies on intrinsic scattering. Combining the two modalities, a log-log linear regression of Brillouin modulus and Young’s modulus on the crystalline lens surface (Fig. 9(a), middle) was determined from the empirical data measured by BM and wave-based OCE, respectively. Then, the 3D BM measurements (Fig. 9(a), left) were converted to Young’s modulus using the sample-specific Brillouin-to-Young’s modulus calibration (Fig. 9(a), right). As also noted in Section 2.6, this approach strictly relies on the correlation that emerges between the measured longitudinal modulus M and Young’s modulus E—two independent material moduli defining different components of the stiffness tensor — in each sample.
Fig. 9.
Multimodal optical elastography platforms. (a) 3D BM (left) and Brillouin-to-Young’s modulus calibration with wave-based OCE (middle) enables 3D elasticity imaging of crystalline lens (right). (b) BM and Raman spectroscopy enables simultaneous imaging of viscoelasticity and biochemical signatures in microbial biofilms. Regions of high Raman intensity may represent overlapping of cells and increased retention of water, which correspond to regions of low Brillouin shift (elasticity) and high Brillouin peak width (viscosity). (c) Photoacoustic viscoelasticity imaging (PAVEI), PA imaging (PAI), and OCT enables simultaneous characterization of atherosclerotic plaque relative viscosity, lipid core area (black dotted region, corroborated by Oil Red O staining), and fibrous cap thickness (yellow and green arrows for thin and thick caps, respectively, corroborated by Mason staining). (d) PAI intensity, OCT intensity, and PAVEI phase delay (relative viscosity) can distinguish different types of plaques during the progression from early-stage lipid plaque to middle-stage thin-cap fibroatheroma (TCFA) to late-stage thick-cap fibroatheroma (ThCFA) at the risk of rupture. Adapted with permission from: (a) [120], (c) and (d) [129] © Optica, (b) [177] © APS.
BM has also been combined with Raman spectroscopy in order to simultaneously obtain both mechanical and chemical information from the biological samples [177–180]. The combination with biochemical imaging modalities is particularly beneficial for BM, whose GHz mechanical measurements cannot be readily related to other widely used low-frequency moduli. Scarponi et al. related the elasticity and viscosity of microbial biofilms measured BM to the biochemical constituents inferred from Raman spectroscopy (Fig. 9(b)) [177]. Caponi et al. later applied this combined BM-Raman system to investigate the optical and acoustic contributions to the spatial resolution of BM (see Section 6) [181]. Mercatelli et al. not only combined BM with Raman spectroscopy, but also incorporated second harmonic generation (SHG) imaging to characterize the biomechanical and biochemical properties, as well as the collagen morphology in ex vivo human corneas [180]. The three modalities together offer insight into the morpho-mechano-chemical features of the cornea.
Another notable example of synergistic multimodal integration is the combination of PAE, PA imaging, and OCT for a multifunctional characterization of atherosclerotic plaques [129]. Vulnerable plaques are characterized by three hallmarks: thin fibrous cap, large necrotic and lipid core, and macrophage infiltration. Wang et al. utilized structural OCT and PA imaging to measure the fibrous cap thickness (Fig. 9(c), third column) and the lipid core size (Fig. 9(c), second column), respectively, while the macrophage infiltration was inferred from the relative viscosity measured by PAE (Fig. 9(c), first column) [129]. Demonstrated in ex vivo mouse aorta after 4-24 weeks of high-fat diet, the three pieces of information can together distinguish between normal vessel and atherosclerotic plaques at different stages of disease progression (Fig. 9(d)).
6. Recent developments: progress on understanding fundamental limits
In this section, we highlight recent developments in optical elastography, focusing specifically on the efforts to better understand the fundamental limits to the imaging capabilities of optical elastography techniques. The rapid pace of developments in the field, including the push toward multimodal combinations, has presented an increasing need to not only characterize, compare, and validate, but also understand the fundamental limits of the imaging capabilities of different techniques.
Although superior spatial resolution is one of the main advantages of optical elastography over existing medical elastography modalities, the field of optical elastography has only recently begun to rigorously investigate the spatial resolution of various establish techniques. Hepburn et al. presented an analysis of spatial resolution in compression OCE, based on a framework that accounts for the contributions of OCT imaging, elastogram reconstruction (such as the spatial dimensions of the window used to calculate strain), as well as mechanical deformation of the sample itself [34]. Based on a similar framework, Li et al. later presented a complementary analysis of elasticity sensitivity in quantitative compression OCE [36]. Using dynamic ARF-OCE as a case study, Leartprapun et al. [44] investigated the role of localized mechanical excitation on the spatial resolution of strain elastograms, in particular the long-standing conjecture in the field of elastography that more localized mechanical excitation (or loading) can enable better mechanical resolution [138,182–184]. An expanded framework for analyzing the factors that influence elastogram quality is also presented in [44]. These studies exemplify the fact that spatial resolution in elastography is both sample dependent and spatially varying (i.e., depending on mechanical properties and inhomogeneity in the material). However, recent studies so far have yet to reconcile the role of localized versus wide-area (such as in compression OCE) excitation on spatial resolution. Connecting between spatially localized excitation and bulk compression may be an area of important future investigation in the field of optical elastography.
On the other hand, Zveitcovich et al. presented a comparative study of shear wave speed estimation accuracy, spatial resolution, and CNR in various wave-based OCE approaches [72], including traditional impulse and harmonic excitation as well as a ‘crawling wave’ excitation [53]. Focusing on impulse excitation of Rayleigh waves, Kirby et al. demonstrated that spatial resolution of the reconstructed wave speed map is dependent on the bandwidth and temporal pulse width of the propagating mechanical wave [185]. Meanwhile, Pelivanov et al. investigated the accuracy of elasticity reconstruction based on the measurement of ‘group speed’ (see Section 2.4) from impulse excitation, particularly in bounded media (such as the eye) where complications arise from the presence of highly dispersive Lamb modes [73]. Notably, the reconstructed group speed map exhibits spatial heterogeneities that do not reflect the variations in mechanical properties; rather, they are artifacts that depend on the thickness of the bounded media, bandwidth and temporal profile of the propagating wave, as well as the mechanical properties of the media itself.
More attention has also been given to the fundamental limits of spatial resolution as well as the consideration of relevant spatial scales in BM [103,104]. Although BM instruments generally adopt a high-NA confocal microscope in order to acquire high-resolution images, spatial resolution of the Brillouin elasticity and viscosity maps (see Section 2.6) is also inherently dependent on the acoustic phonons. Caponi et al. investigated the optical (i.e., light scattering volume interrogated by the microscope NA) and acoustic (i.e., propagation of acoustic phonons in the material) contributions to the spatial resolution of BM, which is effectively dependent on a convolution of the two factors [181]. Notably, the acoustic contribution can lead to an unexpected outcome where a higher NA results in degraded BM spatial resolution when significant acoustic interactions occur across the interface of mechanical inhomogeneity.
Overall, the picture that has emerged from these recent studies is that spatial resolution in optical elastography cannot by universally treated as a fixed system parameter, governed solely by the optical resolution of the parent imaging modality or the image reconstruction procedure. In BM, it is the acoustic phonons rather than light that are the probe of the mechanical properties of the sample (the NA of illumination beam merely selects the range of phonons used to interrogate the material) [181]. Likewise, it is the generated sample deformation [34,36,44] or the propagating mechanical waves [72,73,185] rather than the OCT beam that probe the mechanical response of the sample in OCE. By extension, it is the generated PA pressure waves (see Section 2.7) that govern the measurement of mechanical properties in PAE. Similarly, even though the spatial sampling of optical µR is determined by the statistical distribution of the probe particles, it is the local deformation of the medium around each particle that encodes information about the mechanical properties at that location. Future developments in optical elastography should continue to elucidate the fundamental limits and factors governing the imaging capabilities of different modalities, in order to inform both technological improvements as well as the scope and optimal applications of optical elastography in both the basic sciences and clinical settings.
7. Opportunities for cross-modality and cross-disciplinary interactions
In this section, we discuss the opportunities for cross-modality and cross-disciplinary interactions both within the field of optical elastography (Section 7.1) and with other parallel fields in the basic sciences (Section 7.2) and the clinical practice (Section 7.3). These interactions, highlighted with arrows in Fig. 1, can serve as stepping-stones (from the authors’ perspective, a ‘roadmap’) for maximizing the future impact of optical elastography in both the basic sciences and clinical settings.
7.1. Cross-modality interactions to accelerate development and optimize imaging capabilities
As discussed in Section 2.2, the motivating goal for the development of emerging optical elastography techniques is to enable mechanical characterization at the relevant spatial and temporal scales for the biological systems under study. Interactions between different optical elastography modalities, as well as other existing mechanical characterization techniques, can help maximize the impact of these advances through complementary imaging capabilities, cross-modality validation, and adaptation of established techniques (see gray arrows in Fig. 1).
The synergistic combination of BM and wave-based OCE [120] highlighted in Section 5 is an example of interaction between two modalities that complement each other to overcome the limitations of each individual modality. In addition to complementing the pros and cons of different modalities, the combination of multiple emerging optical elastography techniques can also enable multiscale studies, since these techniques can provide mechanical information that spans a wide range of spatial and temporal scales (Fig. 2). For instance, live-cell imaging platform combining µR with BM could potentially enable simultaneous characterization of both cell-mediated ECM micromechanical remodeling (Section 4.1) and subcellular cell mechanics [106,107,112]. Meanwhile, combining measurements from quasi-static compression OCE, kHz harmonic/spectroscopic OCE and µR, and GHz BM could enable an unprecedented ultra-wideband characterization of biopolymer and soft tissue biomechanics. These types of measurements could help inform the development or validation of theoretical continuum mechanics models of complex biological materials. Measurements performed by different modalities can also serve as cross-validation for each other, both at the same and across different spatiotemporal scales.
Development of new/emerging optical elastography technologies can also benefit from exploiting established methodologies implemented by existing approaches. In fact, several methodologies currently utilized by various OCE approaches have been adapted from existing techniques in ultrasound and magnetic resonance elastography, such as methods for wave speed estimation [186,187] and quantification of viscoelasticity [188–190] in wave-based OCE. Among emerging optical elastography techniques, similar methodologies have also been adapted by different approaches. For instance, Rev3D-OCE [15] (Section 3.1) and cell quake elastography [160] implemented a similar autocorrelation-based reconstruction algorithm to that of passive noise-correlation OCE, despite the former two approaches being active techniques.
Along the same vein, analyzing the similarities and differences between different optical elastography methodologies may be a stimulating thought experiment that can potentially inspire new technological developments. We highlight some of these cross-modality comparisons here. Both SHEAR (Section 3.3) and BM utilize laser illumination to interrogate thermally-driven dynamics in the material, but they operate at completely different time scales. Similarly, wave-based OCE, PAE, and BM all utilize acoustic waves as the probe of mechanical properties, but they are based on different types of waves that are produced by different physical phenomena. The fundamental principle of stimulated BM is surprisingly quite similar to that of crawling-wave OCE [53] (which is in turn adapted from ultrasound elastography [191])—both are based on interference patterns produced by two counter-propagating waves (electromagnetic waves for stimulated BM and shear waves for OCE) with frequency detuned from each other. Meanwhile, both DLSµR (Section 4.1) and SHEAR utilize light scattering to measure Brownian motion of microscopic particles, but DLS operates strictly in the single scattering limit while the laser speckle pattern in SHEAR can arise from the multiple scattering regime (e.g., in scattering biological tissues).
7.2. Toward new discoveries based on elastography approaches for multiscale systems mechanobiology
Optical elastography has the potential to support new research directions and drive new discoveries in the rapidly growing field of mechanobiology [1–6]. Technologies and capabilities are continuously being developed in multiple parallel fields in order to support the study of mechanotransduction—elucidating not only molecular signaling pathways, but also biomechanical interactions between cells and ECM—in the most physiologically relevant settings. We contend that, by engaging in and supporting cross-disciplinary interactions between biologists, material scientists, biophysicists, and mathematicians, developers of optical elastography technologies can maximize the potential basic science (and ultimate clinical) impact of their innovations.
Engineered biological systems that recapitulate the range of physiologically relevant characteristics of in vivo cellular microenvironments are a cornerstone of fundamental biological studies. For the field of mechanobiology, designing biopolymers with not only physiologically-relevant, but also tunable composition, microstructure, and mechanical properties to study the onset, progression and treatment of a range of disease conditions is an active area of development. Recent progress has demonstrated hydrogels with independently controllable stiffness, microarchitecture, and composition [86,147,192,193], tunable elasticity, viscosity, and cell-adhesion-ligand density [194], as well as spatially [195] and temporally [196] varying stiffness.
In addition to engineered biomaterials and cellular systems, imaging technologies that can characterize cell morphology, migration pattern, and cell force are another important aspect in the study of biophysical cell-ECM interactions. Among others, traction force microscopy (TFM) has enabled quantitative measurements of cell-mediated ECM deformation and cell forces via noninvasive optical imaging [197–200]. In this regard, the field is increasingly shifting from isolated cell assays toward the study of collective (emergent) cellular behavior in 3D multicellular systems. Two recent examples are the study of cancer cell invasion (Fig. 10(a)) and the associated cell-mediated collagen matrix deformation (Fig. 10(b)) from cancer spheroids [201,202], and the mechanophenotypic profiling of cell forces in a multicellular cluster across different stages of the epithelial-mesenchymal transition (Fig. 10(c)) [203]. Meanwhile, organoids [204–206] and organotypic tissue-slice cultures [207] are other types of engineered multicellular systems that are particularly advantageous for genetically-controlled disease-specific studies.
Fig. 10.
Recent developments in parallel biomedical research fields that can help maximize the basic science impact of optical elastography technologies. Increasing attention has been given to the study of collective ‘emergent’ behaviors in 3D multicellular systems. 4D time-lapsed imaging of (a) invasion dynamics and (b) cell-mediated matrix deformation of co-culture adipose stromal cell (ASC) and MCF10AT1 cancer spheroid. (c) Traction force microscopy of cell-mediated matrix deformation by cellular clusters exhibiting different epithelial-to-mesenchymal mechanophenotypes. Adapted with permission from: (a) and (b) [202], (c) [203].
A significant opportunity for the field of optical elastography is to utilize these engineered biological systems during both the technological development and biological demonstration/validation stages. This can encourage cross-disciplinary collaborations with leading players in the mechanobiological fields, which will help establish the basic science applications of emerging techniques and landmark findings in mechanobiology. A key opportunity where optical elastography can drive new discoveries in the field of mechanobiology is by providing mechanical characterization of complex biological systems that is not feasible with existing mechanical testing methods or AFM. In this regard, collaboration with developers and users of TFM technologies may be a ‘low-hanging fruit’ that has the potential to reap high rewards for the field of optical elastography. Many OCE approaches may be compatible for a multimodal integration with the recent OCT-based TFM technique [202,208], while µR approaches can capitalize on the fiducial beads for TFM measurement as the probe particles. On the one hand, optical elastography can help enable a more accurate force reconstruction in TFM by providing 4D (spatiotemporal) measurements of the substrate mechanical properties, as opposed to the standard practice of using a single bulk measurement [209]. In this case, accounting for matrix anisotropy, nonlinearity, and plasticity (see Section 3.2) will be an area of concurrent development for both optical elastography and TFM. On the other hand, simultaneous live-cell imaging of cell forces, cell-mediated matrix deformation, and cell-mediated ECM micromechanical remodeling has the potential to provide unprecedented mechanobiological insights into the role of dynamic biomechanical interactions between cells and their ECM. This can lead to a better understanding of the physiological range of biomechanical properties and cell-ECM interactions, and identification of the range that is conducive to (or promotes) the onset and progression of disease.
Another active area of research in the field of mechanobiology is the development of mathematical models to describe complex biopolymer and tissue biomechanics, such as the mechanics of cross-linked fibrous polymer networks [210,211], the role of cell-induced remodeling on the mechanics of ECM constructs [212,213], and internal mechanics of tumor spheroids and solid tumors [214,215]. Computational models have also been developed to predict cell-mediated fibrous ECM remodeling [156,157,216] as well as mechanosensing and force transmission by cells [217–219]. Notably, Hall et al. combined TFM-based measurement of cell-mediated collagen matrix deformation with a nonlinear fiber network model to investigate the bi-directional biomechanical feedbacks between cells and ECM [147].
Optical elastography has the potential to help inform and validate the development of these mathematical models by providing multiscale mechanical characterization. In this context, combining measurements from multiple elastography modalities (including existing medical elastography techniques such as ultrasound and magnetic resonance elastography) in order to capture information across multiple spatial and temporal scales, as well as with other optical microscopy modalities for microstructural and biochemical imaging, could be particularly beneficial. Moreover, the comparison of experimental measurements and mathematical models could potentially improve the understanding and interpretation of the biophysical origins of the emergent mechanical properties probed by different optical elastography modality. These insights could not only help reconcile different measurements across spatiotemporal scales (such as micro- versus macroscale and low- versus high-frequency mechanics), but also help increase the biological relevance of optical elastography measurements in mechanobiology.
7.3. Toward new clinical diagnostics and therapeutics based on biomechanics
Arguably the ultimate goal for the field of elastography is to improve healthcare and contribute to a better quality of life for the patients via biomechanics-based clinical diagnostics and therapeutics. Compared to the immediate opportunities for applications in fundamental mechanobiological research, clinical translation of optical elastography technologies faces many ‘roadblocks’ to address/overcome. Developers of optical elastography technologies can more efficiently navigate this process by actively seeking cross-disciplinary interactions with clinicians, pathologists, and other stakeholders in the healthcare industry.
A crucial step toward clinical translation of emerging optical elastography technologies is to establish the clinical significance of the measured biomechanical parameters—what does a particular readout practically ‘mean’ for clinical diagnostic and therapeutic purposes? A few recent studies have already started to make strides in this direction. The clinical studies by Guberkova et al. [19] and Shao et al. [110] are two such examples (see Section 3.5). The study by Gubarkova et al., in particular, was made possible by a close collaboration with histopathologists, biologists, medical students, and surgeons. Importantly, the field of elastography can learn from previous examples of disease-specific study design for existing medical elastography modalities. Using ultrasound elastography, Wang et al. presented evidence for the hypothetical relation between tumor elasticity and drug uptake in pancreatic ductal adenocarcinoma [220]. This study also prompted a commentary by Nia et al., who brought their expertise in the mechanics of the physical tumor microenvironment to expound on the underlying biophysical phenomena that corroborated the findings [221]. Developers working on the clinical translation of optical elastography technologies may similarly benefit from interacting with those working on fundamental mechanobiological studies, especially as progress is being made to understand the role of multiscale cell and tissue biomechanics as well as the biophysical origins of emergent biomechanical properties (see Section 7.2).
In addition to the technological developments of the imaging capabilities and establishing the clinical significance of biomechanical measurements, various other application-specific factors must be considered in order to facilitate the clinical adoption of emerging optical elastography technologies. These factors are related to the ability to seamlessly integrate new technologies into the existing clinical workflow, including time, cost, space, ease-of-use, and personnel needs. Boppart et al. discusses these clinical considerations in Section 9 of a summary from the 2017 International Conference on Biophotonics [164]. Another aspect to consider among the surge of new developments, is the variability across methodologies and results, which has motivated recent efforts to understand and quantitatively characterize the imaging capabilities of different techniques (Section 6). For instance, differences of several orders of magnitude in Young’s modulus have been reported for skin by different mechanical testing methods; the discrepancies being found both across different techniques and across different implementations of the same technique [222]. For optical elastography, sources of variability in measurements may be attributed to technical limitations (e.g., failure to appropriately account for layered tissue boundary conditions and anisotropy, see Section 3.1 and 3.2) as well as the lack of standardization in the experimental implementation and reconstruction procedure, even among experiments employing the same methodologies. Thus, standardization will be an area that requires an extensive undertaking as the field of optical elastography progresses toward clinical translation. From the clinical perspective, biomechanical measurements of a particular tissue or disease state should, ideally, lead to the same clinical ‘answer’ on “any platform in any clinic, anywhere in the world” [7]. For existing medical elastography, cross-disciplinary cooperation between the medical imaging industry, academic research, and clinicians has led to the development of best practices [223] for establishing reliable biomechanical biomarkers across modalities and clinical settings [7].
In the authors’ view, these are the important steps that the field of optical elastography should set their eye on for the next decade of developments, with the eventual outlook toward bringing biomechanics-based diagnostics and therapeutic to the patients. Fortunately, as a relatively young field, optical elastography has much to learn and gain from the previous footsteps and translational pathways of existing medical elastography modalities [7–10]. The considerations discussed in this section, in addition to the technological aspects presented in the previous sections, will have practical implications on the diagnostic performance, clinical uptake, regulatory pathway, reimbursement strategy, and intellectual property (i.e., technology licensing) of emerging technologies [224]. These healthcare stakeholders will play a key role in determining not only the translational potential, but also the adoption of the technologies that will ultimately lead to clinical impact on the lives of patients.
8. Conclusion and future outlook
Optical elastography represents a diverse body of imaging methodologies, capabilities, and applications, with potential for significant impact in both the basic sciences and the clinical medicine. This review provides a methodological overview of major optical elastography approaches and presents recent developments in various areas from cell and ECM mechanics to tissue mechanics and clinical applications. The recent proliferation of new technological advances not only presents the field with numerous opportunities for application in biomedicine, but also raises the importance of understanding the fundamental imaging capabilities and the biophysical origins of biomechanical measurements made with different modalities. With the rapid rate of scientific progress in the field of mechanobiology, and the ever-emerging unmet needs in clinical medicine, a cross-modality and cross-disciplinary outlook becomes increasingly important to guide future developments and efforts in the field of optical elastography. More than ever, the field of elastography is presented with the opportunity to actively contribute to, and capitalize on, the capabilities and progress in parallel fields (such as material science, tissue engineering, biology, biophysics, and medicine) that seek to understand the role of biomechanical factors and interactions in physiological function and disease. Connecting fundamental discoveries and developments with the clinical setting will be important for the future of elastography in biomedicine. Optical elastography—uniquely positioned to close the gap between subcellular biophysics and organ-level medical imaging—has a substantial role to play in making this connection. A broadly integrated approach over the next decade and beyond will undoubtedly help to maximize the basic science and translational clinical impact not only of optical elastography, but also the parallel efforts in related fields.
Funding
National Institute of General Medical Sciences10.13039/100000057 (R01GM132823); National Science Foundation10.13039/100000001 (CAREER: CBET-1752405).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
Data availability
No data were generated or analyzed in the presented research.
References
- 1.Discher D. E., Janmey P., Wang Y. L., “Tissue cells feel and respond to the stiffness of their substrate,” Science 310(5751), 1139–1143 (2005). 10.1126/science.1116995 [DOI] [PubMed] [Google Scholar]
- 2.Paszek M. J., Zahir N., Johnson K. R., Lakins J. N., Rozenberg G. I., Gefen A., Reinhart-King C. A., Margulies S. S., Dembo M., Boettiger D., Hammer D. A., Weaver V. M., “Tensional homeostasis and the malignant phenotype,” Cancer Cell 8(3), 241–254 (2005). 10.1016/j.ccr.2005.08.010 [DOI] [PubMed] [Google Scholar]
- 3.Engler A. J., Sen S., Sweeney H. L., Discher D. E., “Matrix elasticity directs stem cell lineage specification,” Cell 126(4), 677–689 (2006). 10.1016/j.cell.2006.06.044 [DOI] [PubMed] [Google Scholar]
- 4.Eyckmans J., Boudou T., Yu X., Chen C. S., “A hitchhiker's guide to mechanobiology,” Dev. Cell 21(1), 35–47 (2011). 10.1016/j.devcel.2011.06.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wirtz D., Konstantopoulos K., Searson P. C., “The physics of cancer: the role of physical interactions and mechanical forces in metastasis,” Nat. Rev. Cancer 11(7), 512–522 (2011). 10.1038/nrc3080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lampi M. C., Reinhart-King C. A., “Targeting extracellular matrix stiffness to attenuate disease: From molecular mechanisms to clinical trials,” Sci. Transl. Med. 10(422), eaao0475 (2018). 10.1126/scitranslmed.aao0475 [DOI] [PubMed] [Google Scholar]
- 7.Ormachea J., Parker K. J., “Elastography imaging: the 30 year perspective,” Phys. Med. Biol. 65(24), 24TR06 (2020) 10.1088/1361-6560/abca00 [DOI] [PubMed] [Google Scholar]
- 8.Glaser K. J., Manduca A., Ehman R. L., “Review of MR elastography applications and recent developments,” J. Magn. Reson. Imaging 36(4), 757–774 (2012). 10.1002/jmri.23597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sigrist R. M. S., Liau J., Kaffas A. E., Chammas M. C., Willmann J. K., “Ultrasound elastography: review of techniques and clinical applications,” Theranostics 7(5), 1303–1329 (2017). 10.7150/thno.18650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lu J., Chen M., Chen Q.-H., Wu Q., Jiang J.-N., Leung T.-Y., “Elastogram: physics, clinical applications, and risks,” Maternal-Fetal Medicine 1(2), 113–122 (2019). 10.1097/FM9.0000000000000024 [DOI] [Google Scholar]
- 11.Dufrene Y. F., Ando T., Garcia R., Alsteens D., Martinez-Martin D., Engel A., Gerber C., Muller D. J., “Imaging modes of atomic force microscopy for application in molecular and cell biology,” Nat. Nanotechnol. 12(4), 295–307 (2017). 10.1038/nnano.2017.45 [DOI] [PubMed] [Google Scholar]
- 12.Wu P. H., Aroush D. R., Asnacios A., Chen W. C., Dokukin M. E., Doss B. L., Durand-Smet P., Ekpenyong A., Guck J., Guz N. V., Janmey P. A., Lee J. S. H., Moore N. M., Ott A., Poh Y. C., Ros R., Sander M., Sokolov I., Staunton J. R., Wang N., Whyte G., Wirtz D., “A comparison of methods to assess cell mechanical properties,” Nat. Methods 15(7), 491–498 (2018). 10.1038/s41592-018-0015-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carstensen E. L., Parker K. J., “Physical models of tissue in shear fields,” Ultrasound Med. Biol. 40(4), 655–674 (2014). 10.1016/j.ultrasmedbio.2013.11.001 [DOI] [PubMed] [Google Scholar]
- 14.Bevilacqua C., Sanchez-Iranzo H., Richter D., Diz-Munoz A., Prevedel R., “Imaging mechanical properties of sub-micron ECM in live zebrafish using Brillouin microscopy,” Biomed. Opt. Express 10(3), 1420–1431 (2019). 10.1364/BOE.10.001420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zvietcovich F., Pongchalee P., Meemon P., Rolland J. P., Parker K. J., “Reverberant 3D optical coherence elastography maps the elasticity of individual corneal layers,” Nat. Commun. 10(1), 4895 (2019). 10.1038/s41467-019-12803-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Remer I., Shaashoua R., Shemesh N., Ben-Zvi A., Bilenca A., “High-sensitivity and high-specificity biomechanical imaging by stimulated Brillouin scattering microscopy,” Nat. Methods 17(9), 913–916 (2020). 10.1038/s41592-020-0882-0 [DOI] [PubMed] [Google Scholar]
- 17.Schlussler R., Mollmert S., Abuhattum S., Cojoc G., Muller P., Kim K., Mockel C., Zimmermann C., Czarske J., Guck J., “Mechanical mapping of spinal cord growth and repair in living zebrafish larvae by Brillouin imaging,” Biophys. J. 115(5), 911–923 (2018). 10.1016/j.bpj.2018.07.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gubarkova E. V., Sovetsky A. A., Zaitsev V. Y., Matveyev A. L., Vorontsov D. A., Sirotkina M. A., Matveev L. A., Plekhanov A. A., Pavlova N. P., Kuznetsov S. S., Vorontsov A. Y., Zagaynova E. V., Gladkova N. D., “OCT-elastography-based optical biopsy for breast cancer delineation and express assessment of morphological/molecular subtypes,” Biomed. Opt. Express 10(5), 2244–2263 (2019). 10.1364/BOE.10.002244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gubarkova E. V., Kiseleva E. B., Sirotkina M. A., Vorontsov D. A., Achkasova K. A., Kuznetsov S. S., Yashin K. S., Matveyev A. L., Sovetsky A. A., Matveev L. A., Plekhanov A. A., Vorontsov A. Y., Zaitsev V. Y., Gladkova N. D., “Diagnostic accuracy of cross-polarization OCT and OCT-elastography for differentiation of breast cancer subtypes: comparative study,” Diagnostics 10(12), 994 (2020). 10.3390/diagnostics10120994 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hajjarian Z., Brachtel E. F., Tshikudi D. M., Nadkarni S. K., “Mapping mechanical properties of the tumor microenvironment by laser speckle rheological microscopy,” Cancer Res. 81(18), 4874–4885 (2021). 10.1158/0008-5472.CAN-20-3898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Han Y. L., Ronceray P., Xu G., Malandrino A., Kamm R. D., Lenz M., Broedersz C. P., Guo M., “Cell contraction induces long-ranged stress stiffening in the extracellular matrix,” Proc. Natl. Acad. Sci. U. S. A. 115(16), 4075–4080 (2018). 10.1073/pnas.1722619115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lin Y., Leartprapun N., Adie S. G., “Spectroscopic photonic force optical coherence elastography,” Opt. Lett. 44(19), 4897–4900 (2019). 10.1364/OL.44.004897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Juliar B. A., Keating M. T., Kong Y. P., Botvinick E. L., Putnam A. J., “Sprouting angiogenesis induces significant mechanical heterogeneities and ECM stiffening across length scales in fibrin hydrogels,” Biomaterials 162, 99–108 (2018). 10.1016/j.biomaterials.2018.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Krajina B. A., LeSavage B. L., Roth J. G., Zhu A. W., Cai P. C., Spakowitz A. J., Heilshorn S. C., “Microrheology reveals simultaneous cell-mediated matrix stiffening and fluidization that underlie breast cancer invasion,” Sci. Adv. 7(8), eabe1969 (2021). 10.1126/sciadv.abe1969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lin Y., Leartprapun N., Luo J. C., Adie S. G., “Light-sheet photonic force optical coherence elastography for high-throughput quantitative 3D micromechanical imaging,” Nat. Commun. 13(1), 3465 (2022). 10.1038/s41467-022-30995-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yu H., Mouw J. K., Weaver V. M., “Forcing form and function: biomechanical regulation of tumor evolution,” Trends Cell Biol. 21(1), 47–56 (2011). 10.1016/j.tcb.2010.08.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Labernadie A., Kato T., Brugues A., Serra-Picamal X., Derzsi S., Arwert E., Weston A., Gonzalez-Tarrago V., Elosegui-Artola A., Albertazzi L., Alcaraz J., Roca-Cusachs P., Sahai E., Trepat X., “A mechanically active heterotypic E-cadherin/N-cadherin adhesion enables fibroblasts to drive cancer cell invasion,” Nat. Cell Biol. 19(3), 224–237 (2017). 10.1038/ncb3478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Szabo T. L., Wu J., “A model for longitudinal and shear wave propagation in viscoelastic media,” J. Acoust. Soc. Am. 107(5), 2437–2446 (2000). 10.1121/1.428630 [DOI] [PubMed] [Google Scholar]
- 29.Mulligan J. A., Untracht G. R., Chandrasekaran S., Brown C. N., Adie S. G., “Emerging Approaches for High-Resolution Imaging of Tissue Biomechanics With Optical Coherence Elastography,” IEEE J. Sel. Top. Quantum Electron. 22(3), 246–265 (2016). 10.1109/JSTQE.2015.2481705 [DOI] [Google Scholar]
- 30.Kennedy B. F., McLaughlin R. A., Kennedy K. M., Chin L., Curatolo A., Tien A., Latham B., Saunders C. M., Sampson D. D., “Optical coherence micro-elastography: mechanical-contrast imaging of tissue microstructure,” Biomed. Opt. Express 5(7), 2113–2124 (2014). 10.1364/BOE.5.002113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kennedy K. M., Chin L., McLaughlin R. A., Latham B., Saunders C. M., Sampson D. D., Kennedy B. F., “Quantitative micro-elastography: imaging of tissue elasticity using compression optical coherence elastography,” Sci. Rep. 5(1), 15538 (2015). 10.1038/srep15538 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Curatolo A., Villiger M., Lorenser D., Wijesinghe P., Fritz A., Kennedy B. F., Sampson D. D., “Ultrahigh-resolution optical coherence elastography,” Opt. Lett. 41(1), 21–24 (2016). 10.1364/OL.41.000021 [DOI] [PubMed] [Google Scholar]
- 33.Hai P., Yao J., Li G., Li C., Wang L. V., “Photoacoustic elastography,” Opt. Lett. 41(4), 725–728 (2016). 10.1364/OL.41.000725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hepburn M. S., Wijesinghe P., Chin L., Kennedy B. F., “Analysis of spatial resolution in phase-sensitive compression optical coherence elastography,” Biomed. Opt. Express 10(3), 1496–1513 (2019). 10.1364/BOE.10.001496 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hepburn M. S., Wijesinghe P., Major L. G., Li J., Mowla A., Astell C., Park H. W., Hwang Y., Choi Y. S., Kennedy B. F., “Three-dimensional imaging of cell and extracellular matrix elasticity using quantitative micro-elastography,” Biomed. Opt. Express 11(2), 867–884 (2020). 10.1364/BOE.383419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Li J., Hepburn M. S., Chin L., Mowla A., Kennedy B. F., “Analysis of sensitivity in quantitative micro-elastography,” Biomed. Opt. Express 12(3), 1725–1745 (2021). 10.1364/BOE.417829 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schmitt J. M., “OCT elastography: imaging microscopic deformation and strain of tissue,” Opt. Express 3(6), 199–211 (1998). 10.1364/OE.3.000199 [DOI] [PubMed] [Google Scholar]
- 38.Nahas A., Bauer M., Roux S., Boccara A. C., “3D static elastography at the micrometer scale using Full Field OCT,” Biomed. Opt. Express 4(10), 2138–2149 (2013). 10.1364/BOE.4.002138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Adie S. G., Liang X., Kennedy B. F., John R., Sampson D. D., Boppart S. A., “Spectroscopic optical coherence elastography,” Opt. Express 18(25), 25519–25534 (2010). 10.1364/OE.18.025519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Song S., Huang Z., Nguyen T. M., Wong E., Arnal B., O’Donnell M., Wang R., “Shear modulus imaging by direct visualization of propagating shear waves with phase-sensitive optical coherence tomography,” J. Biomed. Opt. 18(12), 1 (2013). 10.1117/1.JBO.18.12.121509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Song S., Huang Z., Wang R., “Tracking mechanical wave propagation within tissue using phase-sensitive optical coherence tomography: motion artifact and its compensation,” J. Biomed. Opt. 18(12), 121505 (2013). 10.1117/1.JBO.18.12.121505 [DOI] [PubMed] [Google Scholar]
- 42.Wang S., Larin K. V., “Noncontact depth-resolved micro-scale optical coherence elastography of the cornea,” Biomed. Opt. Express 5(11), 3807–3821 (2014). 10.1364/BOE.5.003807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Larin K. V., Sampson D. D., “Optical coherence elastography - OCT at work in tissue biomechanics,” Biomed. Opt. Express 8(2), 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Leartprapun N., Iyer R. R., Mackey C. D., Adie S. G., “Spatial localization of mechanical excitation affects spatial resolution, contrast, and contrast-to-noise ratio in acoustic radiation force optical coherence elastography,” Biomed. Opt. Express 10(11), 5877–5904 (2019). 10.1364/BOE.10.005877 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zaitsev V. Y., Matveyev A. L., Matveev L. A., Gelikonov G. V., Gubarkova E. V., Gladkova N. D., Vitkin A., “Hybrid method of strain estimation in optical coherence elastography using combined sub-wavelength phase measurements and supra-pixel displacement tracking,” J. Biophotonics 9(5), 499–509 (2016). 10.1002/jbio.201500203 [DOI] [PubMed] [Google Scholar]
- 46.Matveyev A. L., Matveev L. A., Sovetsky A. A., Gelikonov G. V., Moiseev A. A., Zaitsev V. Y., “Vector method for strain estimation in phase-sensitive optical coherence elastography,” Laser Phys. Lett. 15(6), 065603 (2018). 10.1088/1612-202X/aab5e9 [DOI] [Google Scholar]
- 47.Li J., Pijewska E., Fang Q., Szkulmowski M., Kennedy B. F., “Analysis of strain estimation methods in phase-sensitive compression optical coherence elastography,” Biomed. Opt. Express 13(4), 2224–2246 (2022). 10.1364/BOE.447340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Allen W. M., Chin L., Wijesinghe P., Kirk R. W., Latham B., Sampson D. D., Saunders C. M., Kennedy B. F., “Wide-field optical coherence micro-elastography for intraoperative assessment of human breast cancer margins,” Biomed. Opt. Express 7(10), 4139–4153 (2016). 10.1364/BOE.7.004139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Allen W. M., Kennedy K. M., Fang Q., Chin L., Curatolo A., Watts L., Zilkens R., Chin S. L., Dessauvagie B. F., Latham B., Saunders C. M., Kennedy B. F., “Wide-field quantitative micro-elastography of human breast tissue,” Biomed. Opt. Express 9(3), 1082–1096 (2018). 10.1364/BOE.9.001082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zaitsev V. Y., Matveyev A. L., Matveev L. A., Sovetsky A. A., Hepburn M. S., Mowla A., Kennedy B. F., “Strain and elasticity imaging in compression optical coherence elastography: The two-decade perspective and recent advances,” J. Biophotonics 14(2), e202000257 (2021). 10.1002/jbio.202000257 [DOI] [PubMed] [Google Scholar]
- 51.Spahr H., Pfäffle C., Koch P., Sudkamp H., Hüttmann G., Hillmann D., “Interferometric detection of 3D motion using computational subapertures in optical coherence tomography,” Opt. Express 26(15), 18803–18816 (2018). 10.1364/OE.26.018803 [DOI] [PubMed] [Google Scholar]
- 52.Wijesinghe P., Chin L., Kennedy B. F., “Strain tensor imaging in compression optical coherence elastography,” IEEE J. Sel. Top. Quantum Electron. 25(1), 1–12 (2019). 10.1109/JSTQE.2018.2871596 [DOI] [Google Scholar]
- 53.Meemon P., Yao J., Chu Y. J., Zvietcovich F., Parker K. J., Rolland J. P., “Crawling wave optical coherence elastography,” Opt. Lett. 41(5), 847–850 (2016). 10.1364/OL.41.000847 [DOI] [PubMed] [Google Scholar]
- 54.Zhu J., Yu J., Qu Y., He Y., Li Y., Yang Q., Huo T., He X., Chen Z., “Coaxial excitation longitudinal shear wave measurement for quantitative elasticity assessment using phase-resolved optical coherence elastography,” Opt. Lett. 43(10), 2388–2391 (2018). 10.1364/OL.43.002388 [DOI] [PubMed] [Google Scholar]
- 55.Zvietcovich F., Ge G. R., Mestre H., Giannetto M., Nedergaard M., Rolland J. P., Parker K. J., “Longitudinal shear waves for elastic characterization of tissues in optical coherence elastography,” Biomed. Opt. Express 10(7), 3699–3718 (2019). 10.1364/BOE.10.003699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Ramier A., Tavakol B., Yun S. H., “Measuring mechanical wave speed, dispersion, and viscoelastic modulus of the cornea using optical coherence elastography,” Opt. Express 27(12), 16635–16649 (2019). 10.1364/OE.27.016635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Ramier A., Eltony A. M., Chen Y., Clouser F., Birkenfeld J. S., Watts A., Yun S. H., “In vivo measurement of shear modulus of the human cornea using optical coherence elastography,” Sci. Rep. 10(1), 17366 (2020). 10.1038/s41598-020-74383-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Han Z., Singh M., Aglyamov S. R., Liu C. H., Nair A., Raghunathan R., Wu C., Li J., Larin K. V., “Quantifying tissue viscoelasticity using optical coherence elastography and the Rayleigh wave model,” J. Biomed. Opt. 21(9), 090504 (2016). 10.1117/1.JBO.21.9.090504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Leartprapun N., Iyer R. R., Adie S. G., “Model-independent quantification of soft tissue viscoelasticity with dynamic optical coherence elastography,” Proc. SPIE 10053, 1005322 (2017). 10.1117/12.2251626 [DOI] [Google Scholar]
- 60.Liu H. C., Kijanka P., Urban M. W., “Four-dimensional (4D) phase velocity optical coherence elastography in heterogeneous materials and biological tissue,” Biomed. Opt. Express 11(7), 3795–3817 (2020). 10.1364/BOE.394835 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Qi W., Chen R., Chou L., Liu G., Zhang J., Zhou Q., Chen Z., “Phase-resolved acoustic radiation force optical coherence elastography,” J. Biomed. Opt. 17(11), 110505 (2012). 10.1117/1.JBO.17.11.110505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Qi W., Li R., Ma T., Kirk Shung K., Zhou Q., Chen Z., “Confocal acoustic radiation force optical coherence elastography using a ring ultrasonic transducer,” Appl. Phys. Lett. 104(12), 123702 (2014). 10.1063/1.4869562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Qu Y., Ma T., He Y., Yu M., Zhu J., Miao Y., Dai C., Patel P., Shung K. K., Zhou Q., Chen Z., “Miniature probe for mapping mechanical properties of vascular lesions using acoustic radiation force optical coherence elastography,” Sci. Rep. 7(1), 4731 (2017). 10.1038/s41598-017-05077-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Ambrozinski L., Pelivanov I., Song S., Yoon S. J., Li D., Gao L., Shen T. T., Wang R. K., O’Donnell M., “Air-coupled acoustic radiation force for non-contact generation of broadband mechanical waves in soft media,” Appl. Phys. Lett. 109(4), 043701 (2016). 10.1063/1.4959827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ambrozinski L., Song S., Yoon S. J., Pelivanov I., Li D., Gao L., Shen T. T., Wang R. K., O’Donnell M., “Acoustic micro-tapping for non-contact 4D imaging of tissue elasticity,” Sci. Rep. 6(1), 38967 (2016). 10.1038/srep38967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Jin Z., Khazaeinezhad R., Zhu J., Yu J., Qu Y., He Y., Li Y., Gomez Alvarez-Arenas T. E., Lu F., Chen Z., “In-vivo 3D corneal elasticity using air-coupled ultrasound optical coherence elastography,” Biomed. Opt. Express 10(12), 6272–6285 (2019). 10.1364/BOE.10.006272 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Zvietcovich F., Nair A., Ambekar Y. S., Singh M., Aglyamov S. R., Twa M. D., Larin K. V., “Confocal air-coupled ultrasonic optical coherence elastography probe for quantitative biomechanics,” Opt. Lett. 45(23), 6567–6570 (2020). 10.1364/OL.410593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Liu C. H., Nevozhay D., Schill A., Singh M., Das S., Nair A., Han Z., Aglyamov S., Larin K. V., Sokolov K. V., “Nanobomb optical coherence elastography,” Opt. Lett. 43(9), 2006–2009 (2018). 10.1364/OL.43.002006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Liu C. H., Nevozhay D., Zhang H., Das S., Schill A., Singh M., Aglyamov S., Sokolov K. V., Larin K. V., “Longitudinal elastic wave imaging using nanobomb optical coherence elastography,” Opt. Lett. 44(12), 3162–3165 (2019). 10.1364/OL.44.003162 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Boerner P., Nevozhay D., Hatamimoslehabadi M., Chawla H. S., Zvietcovich F., Aglyamov S., Larin K. V., Sokolov K. V., “Repetitive optical coherence elastography measurements with blinking nanobombs,” Biomed. Opt. Express 11(11), 6659–6673 (2020). 10.1364/BOE.401734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zvietcovich F., Larin K. V., “Wave-based optical coherence elastography: the 10-year perspective,” Prog. Biomed. Eng. 4(1), 012007 (2022). 10.1088/2516-1091/ac4512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Zvietcovich F., Rolland J. P., Yao J., Meemon P., Parker K. J., “Comparative study of shear wave-based elastography techniques in optical coherence tomography,” J. Biomed. Opt. 22(3), 035010 (2017). 10.1117/1.JBO.22.3.035010 [DOI] [PubMed] [Google Scholar]
- 73.Pelivanov I., Gao L., Pitre J., Kirby M., Song S., Li D., Shen T., Wang R., O’Donnell M., “Does group velocity always reflect elastic modulus in shear wave elastography?” J. Biomed. Opt. 24(07), 1–11 (2019). 10.1117/1.JBO.24.7.076003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Han Z., Li J., Singh M., Wu C., Liu C. H., Wang S., Idugboe R., Raghunathan R., Sudheendran N., Aglyamov S. R., Twa M. D., Larin K. V., “Quantitative methods for reconstructing tissue biomechanical properties in optical coherence elastography: a comparison study,” Phys. Med. Biol. 60(9), 3531–3547 (2015). 10.1088/0031-9155/60/9/3531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Pitre J. J., Jr., Kirby M. A., Gao L., Li D. S., Shen T., Wang R. K., O’Donnell M., Pelivanov I., “Super-shear evanescent waves for non-contact elastography of soft tissues,” Appl. Phys. Lett. 115(8), 083701 (2019). 10.1063/1.5111952 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kirby M. A., Pelivanov I., Song S., Ambrozinski L., Yoon S. J., Gao L., Li D., Shen T. T., Wang R. K., O’Donnell M., “Optical coherence elastography in ophthalmology,” J. Biomed. Opt. 22(12), 1–28 (2017). 10.1117/1.JBO.22.12.121720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Liu Y., Yasar T. K., Royston T. J., “Ultra wideband (0.5-16 kHz) MR elastography for robust shear viscoelasticity model identification,” Phys. Med. Biol. 59(24), 7717–7734 (2014). 10.1088/0031-9155/59/24/7717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Zvietcovich F., Rolland J. P., Parker K. J., “An approach to viscoelastic characterization of dispersive media by inversion of a general wave propagation model,” J. Innov. Opt. Health Sci. 10(06), 1742008 (2017). 10.1142/S1793545817420081 [DOI] [Google Scholar]
- 79.Wirtz D., “Particle-tracking microrheology of living cells: principles and applications,” Annu. Rev. Biophys. 38(1), 301–326 (2009). 10.1146/annurev.biophys.050708.133724 [DOI] [PubMed] [Google Scholar]
- 80.Krajina B. A., Tropini C., Zhu A., DiGiacomo P., Sonnenburg J. L., Heilshorn S. C., Spakowitz A. J., “Dynamic light scattering microrheology reveals multiscale viscoelasticity of polymer gels and precious biological materials,” ACS Cent. Sci. 3(12), 1294–1303 (2017). 10.1021/acscentsci.7b00449 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hajjarian Z., Nia H. T., Ahn S., Grodzinsky A. J., Jain R. K., Nadkarni S. K., “Laser Speckle Rheology for evaluating the viscoelastic properties of hydrogel scaffolds,” Sci. Rep. 6(1), 37949 (2016). 10.1038/srep37949 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Tripathi M. M., Egawa S., Wirth A. G., Tshikudi D. M., Van Cott E. M., Nadkarni S. K., “Clinical evaluation of whole blood prothrombin time (PT) and international normalized ratio (INR) using a Laser Speckle Rheology sensor,” Sci. Rep. 7(1), 9169 (2017). 10.1038/s41598-017-08693-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Wang J., Hosoda M., Tshikudi D. M., Hajjarian Z., Nadkarni S. K., “Intraluminal laser speckle rheology using an omni-directional viewing catheter,” Biomed. Opt. Express 8(1), 137–150 (2017). 10.1364/BOE.8.000137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Hajjarian Z., Nadkarni S. K., “Tutorial on laser speckle rheology: technology, applications, and opportunities,” J. Biomed. Opt. 25(05), 1 (2020). 10.1117/1.JBO.25.5.050801 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Tripathi M. M., Tshikudi D. M., Hajjarian Z., Hack D. C., Van Cott E. M., Nadkarni S. K., “Comprehensive blood coagulation profiling in patients using iCoagLab: comparison against thromboelastography,” Thromb. Haemost. 120(07), 1116–1127 (2020). 10.1055/s-0040-1712956 [DOI] [PubMed] [Google Scholar]
- 86.Kotlarchyk M. A., Shreim S. G., Alvarez-Elizondo M. B., Estrada L. C., Singh R., Valdevit L., Kniazeva E., Gratton E., Putnam A. J., Botvinick E. L., “Concentration independent modulation of local micromechanics in a fibrin gel,” PLoS One 6(5), e20201 (2011). 10.1371/journal.pone.0020201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Keating M., Kurup A., Alvarez-Elizondo M., Levine A. J., Botvinick E., “Spatial distributions of pericellular stiffness in natural extracellular matrices are dependent on cell-mediated proteolysis and contractility,” Acta Biomater. 57, 304–312 (2017). 10.1016/j.actbio.2017.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Staunton J. R., Vieira W., Fung K. L., Lake R., Devine A., Tanner K., “Mechanical properties of the tumor stromal microenvironment probed in vitro and ex vivo by in situ-calibrated optical trap-based active microrheology,” Cell Mol. Bioeng. 9(3), 398–417 (2016). 10.1007/s12195-016-0460-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Staunton J. R., So W. Y., Paul C. D., Tanner K., “High-frequency microrheology in 3D reveals mismatch between cytoskeletal and extracellular matrix mechanics,” Proc. Natl. Acad. Sci. U. S. A. 116, 14448–14455 (2019). 10.1073/pnas.1814271116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Leartprapun N., Iyer R. R., Untracht G. R., Mulligan J. A., Adie S. G., “Photonic force optical coherence elastography for three-dimensional mechanical microscopy,” Nat. Commun. 9(1), 2079 (2018). 10.1038/s41467-018-04357-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Leartprapun N., Lin Y., Adie S. G., “Microrheological quantification of viscoelastic properties with photonic force optical coherence elastography,” Opt. Express 27(16), 22615–22630 (2019). 10.1364/OE.27.022615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Sirotin M. A., Romodina M. N., Lyubin E. V., Soboleva I. V., Fedyanin A. A., “Single-cell all-optical coherence elastography with optical tweezers,” Biomed. Opt. Express 13(1), 14–25 (2022). 10.1364/BOE.444813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Mason T. G., Weitz D. A., “Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids,” Phys. Rev. Lett. 74(7), 1250–1253 (1995). 10.1103/PhysRevLett.74.1250 [DOI] [PubMed] [Google Scholar]
- 94.Mason T. G., “Estimating the viscoelastic moduli of complex fluids using the generalized Stokes–Einstein equation,” Rheol. Acta 39(4), 371–378 (2000). 10.1007/s003970000094 [DOI] [Google Scholar]
- 95.Levine A. J., Lubensky T. C., “One- and Two-Particle Microrheology,” Phys. Rev. Lett. 85(8), 1774–1777 (2000). 10.1103/PhysRevLett.85.1774 [DOI] [PubMed] [Google Scholar]
- 96.Brau R. R., Ferrer J. M., Lee H., Castro C. E., Tam B. K., Tarsa P. B., Matsudaira P., Boyce M. C., Kamm R. D., Lang M. J., “Passive and active microrheology with optical tweezers,” J. Opt. A: Pure Appl. Opt. 9(8), S103–S112 (2007). 10.1088/1464-4258/9/8/S01 [DOI] [Google Scholar]
- 97.Mizuno D., Head D. A., MacKintosh F. C., Schmidt C. F., “Active and passive microrheology in equilibrium and nonequilibrium systems,” Macromolecules 41(19), 7194–7202 (2008). 10.1021/ma801218z [DOI] [Google Scholar]
- 98.Squires T. M., Mason T. G., “Fluid Mechanics of microrheology,” Annu. Rev. Fluid. Mech. 42(1), 413–438 (2010). 10.1146/annurev-fluid-121108-145608 [DOI] [Google Scholar]
- 99.Ahmed W. W., Fodor E., Betz T., “Active cell mechanics: Measurement and theory,” Biochim. Biophys. Acta. 1853(11), 3083–3094 (2015). 10.1016/j.bbamcr.2015.05.022 [DOI] [PubMed] [Google Scholar]
- 100.Bowman R. W., Padgett M. J., “Optical trapping and binding,” Rep. Prog. Phys. 76(2), 026401 (2013). 10.1088/0034-4885/76/2/026401 [DOI] [PubMed] [Google Scholar]
- 101.Vaughan J. M., Randall J. T., “Brillouin scattering, density and elastic properties of the lens and cornea of the eye,” Nature 284(5755), 489–491 (1980). 10.1038/284489a0 [DOI] [PubMed] [Google Scholar]
- 102.Dil J. G., “Brillouin scattering in condensed matter,” Rep. Prog. Phys. 45(3), 285–334 (1982). 10.1088/0034-4885/45/3/002 [DOI] [Google Scholar]
- 103.Prevedel R., Diz-Munoz A., Ruocco G., Antonacci G., “Brillouin microscopy: an emerging tool for mechanobiology,” Nat. Methods 16(10), 969–977 (2019). 10.1038/s41592-019-0543-3 [DOI] [PubMed] [Google Scholar]
- 104.Antonacci G., Beck T., Bilenca A., Czarske J., Elsayad K., Guck J., Kim K., Krug B., Palombo F., Prevedel R., Scarcelli G., “Recent progress and current opinions in Brillouin microscopy for life science applications,” Biophys. Rev. 12(3), 615–624 (2020). 10.1007/s12551-020-00701-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Scarcelli G., Yun S. H., “Confocal Brillouin microscopy for three-dimensional mechanical imaging,” Nat. Photonics 2(1), 39–43 (2008). 10.1038/nphoton.2007.250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Scarcelli G., Polacheck W. J., Nia H. T., Patel K., Grodzinsky A. J., Kamm R. D., Yun S. H., “Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy,” Nat. Methods 12(12), 1132–1134 (2015). 10.1038/nmeth.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Antonacci G., Braakman S., “Biomechanics of subcellular structures by non-invasive Brillouin microscopy,” Sci. Rep. 6(1), 37217 (2016). 10.1038/srep37217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Zhang J., Fiore A., Yun S. H., Kim H., Scarcelli G., “Line-scanning Brillouin microscopy for rapid non-invasive mechanical imaging,” Sci. Rep. 6(1), 35398 (2016). 10.1038/srep35398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Shao P., Seiler T. G., Eltony A. M., Ramier A., Kwok S. J. J., Scarcelli G., Pineda R., II, Yun S. H., “Effects of Corneal Hydration on Brillouin Microscopy In Vivo,” Invest. Ophthalmol. Vis. Sci. 59(7), 3020–3027 (2018). 10.1167/iovs.18-24228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Shao P., Eltony A. M., Seiler T. G., Tavakol B., Pineda R., Koller T., Seiler T., Yun S. H., “Spatially-resolved Brillouin spectroscopy reveals biomechanical abnormalities in mild to advanced keratoconus in vivo,” Sci. Rep. 9(1), 7467 (2019). 10.1038/s41598-019-43811-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Margueritat J., Virgone-Carlotta A., Monnier S., Delanoe-Ayari H., Mertani H. C., Berthelot A., Martinet Q., Dagany X., Riviere C., Rieu J. P., Dehoux T., “High-frequency mechanical properties of tumors measured by Brillouin light scattering,” Phys. Rev. Lett. 122(1), 018101 (2019). 10.1103/PhysRevLett.122.018101 [DOI] [PubMed] [Google Scholar]
- 112.Nikolić M., Scarcelli G., “Long-term Brillouin imaging of live cells with reduced absorption-mediated damage at 660 nm wavelength,” Biomed. Opt. Express 10(4), 1567–1580 (2019). 10.1364/BOE.10.001567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Bailey M., Alunni-Cardinali M., Correa N., Caponi S., Holsgrove T., Barr H., Stone N., Winlove C. P., Fioretto D., Palombo F., “Viscoelastic properties of biopolymer hydrogels determined by Brillouin spectroscopy: A probe of tissue micromechanics,” Sci. Adv. 6(44), eabc1937 (2020). 10.1126/sciadv.abc1937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Ballman C. B., Thompson J. V., Traverso A. J., Meng Z., Scully M. O., Yakovlev V. V., “Stimulated Brillouin scattering microscopic imaging,” Sci. Rep. 5(1), 18139 (2016). 10.1038/srep18139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Ballmann C. W., Meng Z., Traverso A. J., Scully M. O., Yakovlev V. V., “Impulsive Brillouin microscopy,” Optica 4(1), 124 (2017). 10.1364/OPTICA.4.000124 [DOI] [Google Scholar]
- 116.Remer I., Bilenca A., “Background-free Brillouin spectroscopy in scattering media at 780 nm via stimulated Brillouin scattering,” Opt. Lett. 41(5), 926–929 (2016). 10.1364/OL.41.000926 [DOI] [PubMed] [Google Scholar]
- 117.Krug B., Koukourakis N., Czarske J. W., “Impulsive stimulated Brillouin microscopy for non-contact, fast mechanical investigations of hydrogels,” Opt. Express 27(19), 26910–26923 (2019). 10.1364/OE.27.026910 [DOI] [PubMed] [Google Scholar]
- 118.Antonacci G., “Dark-field Brillouin microscopy,” Opt. Lett. 42(7), 1432–1435 (2017). 10.1364/OL.42.001432 [DOI] [PubMed] [Google Scholar]
- 119.Fiore A., Zhang J., Shao P., Yun S. H., Scarcelli G., “High-extinction virtually imaged phased array-based Brillouin spectroscopy of turbid biological media,” Appl. Phys. Lett. 108(20), 203701 (2016). 10.1063/1.4948353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Ambekar Y. S., Singh M., Zhang J., Nair A., Aglyamov S. R., Scarcelli G., Larin K. V., “Multimodal quantitative optical elastography of the crystalline lens with optical coherence elastography and Brillouin microscopy,” Biomed. Opt. Express 11(4), 2041–2051 (2020). 10.1364/BOE.387361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Wang L. V., Hu S., “Photoacoustic Tomography: In Vivo Imaging from Organelles to Organs,” Science 335(6075), 1458–1462 (2012). 10.1126/science.1216210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Wang L. V., Gao L., “Photoacoustic microscopy and computed tomography: from bench to bedside,” Annu. Rev. Biomed. Eng. 16(1), 155–185 (2014). 10.1146/annurev-bioeng-071813-104553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Li C., Guan G., Cheng X., Huang Z., Wang R. K., “Quantitative elastography provided by surface acoustic waves measured by phase-sensitive optical coherence tomography,” Opt. Lett. 37(4), 722–724 (2012). 10.1364/OL.37.000722 [DOI] [PubMed] [Google Scholar]
- 124.Li C., Guan G., Zhang F., Nabi G., Wang R. K., Huang Z., “Laser induced surface acoustic wave combined with phase sensitive optical coherence tomography for superficial tissue characterization: a solution for practical application,” Biomed. Opt. Express 5(5), 1403–1418 (2014). 10.1364/BOE.5.001403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Das S., Schill A., Liu C. H., Aglyamov S., Larin K. V., “Laser-induced elastic wave classification: thermoelastic versus ablative regimes for all-optical elastography applications,” J. Biomed. Opt. 25(03), 1 (2020). 10.1117/1.JBO.25.3.035004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Gao G., Yang S., Xing D., “Viscoelasticity imaging of biological tissues with phase-resolved photoacoustic measurement,” Opt. Lett. 36(17), 3341–3343 (2011). 10.1364/OL.36.003341 [DOI] [PubMed] [Google Scholar]
- 127.Zhao Y., Yang S., Chen C., Xing D., “Simultaneous optical absorption and viscoelasticity imaging based on photoacoustic lock-in measurement,” Opt. Lett. 39(9), 2565–2568 (2014). 10.1364/OL.39.002565 [DOI] [PubMed] [Google Scholar]
- 128.Zhao Y., Chen C., Yang S., Xing D., “Mechanical evaluation of lipid accumulation in atherosclerotic tissues by photoacoustic viscoelasticity imaging,” Opt. Lett. 41(19), 4522–4525 (2016). 10.1364/OL.41.004522 [DOI] [PubMed] [Google Scholar]
- 129.Wang P., Chen Z., Xing D., “Multi-parameter characterization of atherosclerotic plaques based on optical coherence tomography, photoacoustic and viscoelasticity imaging,” Opt. Express 28(9), 13761–13774 (2020). 10.1364/OE.390874 [DOI] [PubMed] [Google Scholar]
- 130.Jin D., Yang F., Chen Z., Yang S., Xing D., “Biomechanical and morphological multi-parameter photoacoustic endoscope for identification of early esophageal disease,” Appl. Phys. Lett. 111(10), 103703 (2017). 10.1063/1.5001272 [DOI] [Google Scholar]
- 131.Du S., Chen Z., Xing D., “Spectral interferometric depth-resolved photoacoustic viscoelasticity imaging,” Opt. Lett. 46(7), 1724–1727 (2021). 10.1364/OL.415368 [DOI] [PubMed] [Google Scholar]
- 132.Wang Q., Shi Y., Yang F., Yang S., “Quantitative photoacoustic elasticity and viscosity imaging for cirrhosis detection,” Appl. Phys. Lett. 112(21), 211902 (2018). 10.1063/1.5021675 [DOI] [Google Scholar]
- 133.Wadamori N., “Non-restrained measurement of Young's modulus for soft tissue using a photoacoustic technique,” Appl. Phys. Lett. 105(10), 103707 (2014). 10.1063/1.4893725 [DOI] [Google Scholar]
- 134.Singh M. S., Jiang H., “Ultrasound (US) transducer of higher operating frequency detects photoacoustic (PA) signals due to the contrast in elastic property,” AIP Adv. 6(2), 025210 (2016). 10.1063/1.4942106 [DOI] [Google Scholar]
- 135.Liu Y., Yuan Z., “Multi-spectral photoacoustic elasticity tomography,” Biomed. Opt. Express 7(9), 3323–3334 (2016). 10.1364/BOE.7.003323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Gao X., Tao C., Liu X., Wang X., “Photoacoustic eigen-spectrum from light-absorbing microspheres and its application in noncontact elasticity evaluation,” Appl. Phys. Lett. 110(5), 054101 (2017). 10.1063/1.4975373 [DOI] [Google Scholar]
- 137.Singh M. S., Thomas A., “Photoacoustic elastography imaging: a review,” J. Biomed. Opt. 24(04), 1–15 (2019). 10.1117/1.JBO.24.4.040902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Nightingale K. R., Palmeri M. L., Nightingale R. W., Trahey G. E., “On the feasibility of remote palpation using acoustic radiation force,” J. Acoust. Soc. Am. 110(1), 625–634 (2001). 10.1121/1.1378344 [DOI] [PubMed] [Google Scholar]
- 139.Parker K. J., Ormachea J., Zvietcovich F., Castaneda B., “Reverberant shear wave fields and estimation of tissue properties,” Phys. Med. Biol. 62(3), 1046–1061 (2017). 10.1088/1361-6560/aa5201 [DOI] [PubMed] [Google Scholar]
- 140.Gennisson J. L., Deffieux T., Macé E., Montaldo G., Fink M., Tanter M., “Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging,” Ultrasound Med. Biol. 36(5), 789–801 (2010). 10.1016/j.ultrasmedbio.2010.02.013 [DOI] [PubMed] [Google Scholar]
- 141.Tweten D. J., Okamoto R. J., Schmidt J. L., Garbow J. R., Bayly P. V., “Estimation of material parameters from slow and fast shear waves in an incompressible, transversely isotropic material,” J. Biomech. 48(15), 4002–4009 (2015). 10.1016/j.jbiomech.2015.09.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Wang M., Byram B., Palmeri M., Rouze N., Nightingale K., “Imaging transverse isotropic properties of muscle by monitoring acoustic radiation force induced shear waves using a 2-D matrix ultrasound array,” IEEE Trans. Med. Imaging 32(9), 1671–1684 (2013). 10.1109/TMI.2013.2262948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Schmidt J. L., Tweten D. J., Benegal A. N., Walker C. H., Portnoi T. E., Okamoto R. J., Garbow J. R., Bayly P. V., “Magnetic resonance elastography of slow and fast shear waves illuminates differences in shear and tensile moduli in anisotropic tissue,” J. Biomech. 49(7), 1042–1049 (2016). 10.1016/j.jbiomech.2016.02.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Feng Y., Okamoto R. J., Namani R., Genin G. M., Bayly P. V., “Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter,” J. Mech. Behav. Biomed. Mater. 23, 117–132 (2013). 10.1016/j.jmbbm.2013.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Pagé G., Tardieu M., Gennisson J. L., Besret L., Garteiser P., Van Beers B. E., “Tumor solid stress: assessment with MR elastography under compression of patient-derived hepatocellular carcinomas and cholangiocarcinomas xenografted in mice,” Cancers 13(8), 1891 (2021). 10.3390/cancers13081891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Perepelyuk M., Chin L., Cao X., van Oosten A., Shenoy V. B., Janmey P. A., Wells R. G., “Normal and fibrotic rat livers demonstrate shear strain softening and compression stiffening: a model for soft tissue mechanics,” PLoS One 11(1), e0146588 (2016). 10.1371/journal.pone.0146588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Hall M. S., Alisafaei F., Ban E., Feng X., Hui C. Y., Shenoy V. B., Wu M., “Fibrous nonlinear elasticity enables positive mechanical feedback between cells and ECMs,” Proc. Natl. Acad. Sci. U. S. A. 113(49), 14043–14048 (2016). 10.1073/pnas.1613058113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Nam S., Hu K. H., Butte M. J., Chaudhuri O., “Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels,” Proc. Natl. Acad. Sci. U. S. A. 113(20), 5492–5497 (2016). 10.1073/pnas.1523906113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Ferruzzi J., Sun M., Gkousioudi A., Pilvar A., Roblyer D., Zhang Y., Zaman M. H., “Compressive remodeling alters fluid transport properties of collagen networks – implications for tumor growth,” Sci. Rep. 9(1), 17151 (2019). 10.1038/s41598-019-50268-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Wang S., Singh M., Tran T. T., Leach J., Aglyamov S. R., Larina I. V., Martin J. F., Larin K. V., “Biomechanical assessment of myocardial infarction using optical coherence elastography,” Biomed. Opt. Express 9(2), 728–742 (2018). 10.1364/BOE.9.000728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Zvietcovich F., Singh M., Ambekar Y. S., Aglyamov S. R., Twa M. D., Larin K. V., “Micro air-pulse spatial deformation spreading characterizes degree of anisotropy in tissues,” IEEE J. Sel. Top. Quantum Electron. 27(4), 1–10 (2021). 10.1109/JSTQE.2020.3038633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Pitre J. J., Kirby M. A., Li D. S., Shen T. T., Wang R. K., O’Donnell M., Pelivanov I., “Nearly-incompressible transverse isotropy (NITI) of cornea elasticity: model and experiments with acoustic micro-tapping OCE,” Sci. Rep. 10(1), 12983 (2020). 10.1038/s41598-020-69909-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Kirby M. A., Pitre J. J., Liou H. C., Li D. S., Wang R. K., Pelivanov I., O’Donnell M., Shen T. T., “Delineating corneal elastic anisotropy in a porcine model using noncontact OCT elastography and ex vivo mechanical tests,” Ophthalm. Sci. 1(4), 100058 (2021). 10.1016/j.xops.2021.100058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Kirby M. A., Tang P., Liou H. C., Kuriakose M., Pitre J. J., Pham T. N., Ettinger R. E., Wang R. K., O’Donnell M., Pelivanov I., “Probing elastic anisotropy of human skin in vivo with light using non-contact acoustic micro-tapping OCE and polarization sensitive OCT,” Sci. Rep. 12(1), 3963 (2022). 10.1038/s41598-022-07775-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Eltony A. M., Shao P., Yun S. H., “Measuring mechanical anisotropy of the cornea with Brillouin microscopy,” Nat. Commun. 13(1), 1354 (2022). 10.1038/s41467-022-29038-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Nam S., Lee J., Brownfield D. G., Chaudhuri O., “Viscoplasticity enables mechanical remodeling of matrix by cells,” Biophys. J. 111(10), 2296–2308 (2016). 10.1016/j.bpj.2016.10.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Ban E., Franklin J. M., Nam S., Smith L. R., Wang H., Wells R. G., Chaudhuri O., Liphardt J. T., Shenoy V. B., “Mechanisms of Plastic Deformation in Collagen Networks Induced by Cellular Forces,” Biophys. J. 114(2), 450–461 (2018). 10.1016/j.bpj.2017.11.3739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Marmin A., Catheline S., Nahas A., “Full-field passive elastography using digital holography,” Opt. Lett. 45(11), 2965–2968 (2020). 10.1364/OL.388327 [DOI] [PubMed] [Google Scholar]
- 159.Nguyen T. M., Zorgani A., Lescanne M., Boccara C., Fink M., Catheline S., “Diffuse shear wave imaging: toward passive elastography using low-frame rate spectral-domain optical coherence tomography,” J. Biomed. Opt. 21(12), 126013 (2016). 10.1117/1.JBO.21.12.126013 [DOI] [PubMed] [Google Scholar]
- 160.Grasland-Mongrain P., Zorgani A., Nakagawa S., Bernard S., Paim L. G., Fitzharris G., Catheline S., Cloutier G., “Ultrafast imaging of cell elasticity with optical microelastography,” Proc. Natl. Acad. Sci. U. S. A. 115(5), 861–866 (2018). 10.1073/pnas.1713395115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Nair A., Singh M., Aglyamov S. R., Larin K. V., “Heartbeat OCE: corneal biomechanical response to simulated heartbeat pulsation measured by optical coherence elastography,” J. Biomed. Opt. 25(05), 1–9 (2020). 10.1117/1.JBO.25.5.055001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Nair A., Singh M., Aglyamov S., Larin K. V., “Heartbeat optical coherence elastography: corneal biomechanics in vivo,” J. Biomed. Opt. 26(02), 020502 (2021). 10.1117/1.JBO.26.2.020502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Clayson K., Pavlatos E., Pan X., Sandwisch T., Ma Y., Liu J., “Ocular pulse elastography: imaging corneal biomechanical responses to simulated ocular pulse using ultrasound,” Transl. Vis. Sci. Technol. 9(1), 5 (2020). 10.1167/tvst.9.1.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Boppart S. A., Brown J. Q., Farah C. S., Kho E., Marcu L., Saunders C. M., Sterenborg H., “Label-free optical imaging technologies for rapid translation and use during intraoperative surgical and tumor margin assessment,” J. Biomed. Opt. 23(02), 1–10 (2018). 10.1117/1.JBO.23.2.021104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Fang Q., Krajancich B., Chin L., Zilkens R., Curatolo A., Frewer L., Anstie J. D., Wijesinghe P., Hall C., Dessauvagie B. F., Latham B., Saunders C. M., Kennedy B. F., “Handheld probe for quantitative micro-elastography,” Biomed. Opt. Express 10(8), 4034–4049 (2019). 10.1364/BOE.10.004034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Liu X., Zaki F. R., Wu H., Wang C., Wang Y., “Temporally and spatially adaptive Doppler analysis for robust handheld optical coherence elastography,” Biomed. Opt. Express 9(7), 3335–3353 (2018). 10.1364/BOE.9.003335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Fang Q., Curatolo A., Wijesinghe P., Yeow Y. L., Hamzah J., Noble P. B., Karnowski K., Sampson D. D., Ganss R., Kim J. K., Lee W. M., Kennedy B. F., “Ultrahigh-resolution optical coherence elastography through a micro-endoscope: towards in vivo imaging of cellular-scale mechanics,” Biomed. Opt. Express 8(11), 5127–5138 (2017). 10.1364/BOE.8.005127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Bu R., Balakrishnan S., Iftimia N., Price H., Zdanski C., Oldenburg A. L., “Airway compliance measured by anatomic optical coherence tomography,” Biomed. Opt. Express 8(4), 2195–2209 (2017). 10.1364/BOE.8.002195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Bu R., Balakrishnan S., Price H., Zdanski C., Mitran S., Oldenburg A. L., “Localized compliance measurement of the airway wall using anatomic optical coherence elastography,” Opt. Express 27(12), 16751–16766 (2019). 10.1364/OE.27.016751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Bu R., Balakrishnan S., Iftimia N., Price H., Zdanski C., Mitran S., Oldenburg A. L., “Sensing inhalation injury-associated changes in airway wall compliance by anatomic optical coherence elastography,” IEEE Trans. Biomed. Eng. 68(8), 2360–2367 (2020). 10.1109/TBME.2020.3037288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Lan G., Aglyamov S. R., Larin K. V., Twa M. D., “In vivo human corneal shear-wave optical coherence elastography,” Optom. Vis. Sci. 98(1), 58–63 (2021). 10.1097/OPX.0000000000001633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Lan G., Gu B., Larin K. V., Twa M. D., “Clinical corneal optical coherence elastography measurement precision: effect of heartbeat and respiration,” Transl. Vis. Sci. Technol. 9(5), 3 (2020). 10.1167/tvst.9.5.3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Huang P. C., Chaney E. J., Aksamitiene E., Barkalifa R., Spillman D. R., Jr., Bogan B. J., Boppart S. A., “Biomechanical sensing of in vivo magnetic nanoparticle hyperthermia-treated melanoma using magnetomotive optical coherence elastography,” Theranostics 11(12), 5620–5633 (2021). 10.7150/thno.55333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Huang P. C., Chaney E. J., Iyer R. R., Spillman D. R., Jr., Odintsov B., Sobh N. A., Boppart S. A., “Interstitial magnetic thermotherapy dosimetry based on shear wave magnetomotive optical coherence elastography,” Biomed. Opt. Express 10(2), 539–551 (2019). 10.1364/BOE.10.000539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Leartprapun N., Iyer R. R., Adie S. G., “Depth-resolved measurement of optical radiation-pressure forces with optical coherence tomography,” Opt. Express 26(3), 2410–2426 (2018). 10.1364/OE.26.002410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Raghunathan R., Zhang J., Wu C., Rippy J., Singh M., Larin K. V., Scarcelli G., “Evaluating biomechanical properties of murine embryos using Brillouin microscopy and optical coherence tomography,” J. Biomed. Opt. 22(08), 1 (2017). 10.1117/1.JBO.22.8.086013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Scarponi F., Mattana S., Corezzi S., Caponi S., Comez L., Sassi P., Morresi A., Paolantoni M., Urbanelli L., Emiliani C., Roscini L., Corte L., Cardinali G., Palombo F., Sandercock J. R., Fioretto D., “High-performance versatile setup for simultaneous brillouin-raman microspectroscopy,” Phys. Rev. X 7, 031015 (2017). 10.1103/PhysRevX.7.031015 [DOI] [Google Scholar]
- 178.Mattana S., Caponi S., Tamagnini F., Fioretto D., Palombo F., “Viscoelasticity of amyloid plaques in transgenic mouse brain studied by Brillouin microspectroscopy and correlative Raman analysis,” J. Innov. Opt. Health. Sci. 10(6), 1742001 (2017). 10.1142/S1793545817420019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Mattana S., Mattarelli M., Urbanelli L., Sagini K., Emiliani C., Serra M. D., Fioretto D., Caponi S., “Non-contact mechanical and chemical analysis of single living cells by microspectroscopic techniques,” Light: Sci. Appl. 7(2), 17139 (2018). 10.1038/lsa.2017.139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Mercatelli R., Mattana S., Capozzoli L., Ratto F., Rossi F., Pini R., Fioretto D., Pavone F. S., Caponi S., Cicchi R., “Morpho-mechanics of human collagen superstructures revealed by all-optical correlative micro-spectroscopies,” Commun. Biol. 2(1), 117 (2019). 10.1038/s42003-019-0357-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Caponi S., Fioretto D., Mattarelli M., “On the actual spatial resolution of Brillouin Imaging,” Opt. Lett. 45(5), 1063–1066 (2020). 10.1364/OL.385072 [DOI] [PubMed] [Google Scholar]
- 182.Fatemi M., Greenleaf J. F., “Vibro-acoustography: An imaging modality based on ultrasound-stimulated acoustic emission,” Proc. Natl. Acad. Sci. U. S. A. 96(12), 6603–6608 (1999). 10.1073/pnas.96.12.6603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Shih C., Huang C., Zhou Q., Shung K. K., “High-resolution acoustic-radiation-force-impulse imaging for assessing corneal sclerosis,” IEEE Trans. Med. Imaging 32(7), 1316–1324 (2013). 10.1109/TMI.2013.2256794 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Dahl J. J., “Acoustic Radiation Force Imaging,” in Emerging Imaging Technology in Medicine , Anastasio M. A., La Riviere P., eds. (CRC Press, 2013), pp. 201–220. [Google Scholar]
- 185.Kirby M. A., Zhou K., Pitre J. J., Gao L., Li D., Pelivanov I., Song S., Li C., Huang Z., Shen T., Wang R., O’Donnell M., “Spatial resolution in dynamic optical coherence elastography,” J. Biomed. Opt. 24(09), 1–16 (2019). 10.1117/1.JBO.24.9.096006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Alleyne D., Cawley P., “A two-dimensional Fourier transform method for the measurement of propagating multimode signals,” J. Acoust. Soc. Am. 89(3), 1159–1168 (1991). 10.1121/1.400530 [DOI] [Google Scholar]
- 187.Costley R. D., Berthelot Y. H., “Dispersion curve analysis of laser-generated Lamb waves,” Ultrasonics 32(4), 249–253 (1994). 10.1016/0041-624X(94)90002-7 [DOI] [Google Scholar]
- 188.Kazemirad S., Bernard S., Hybois S., Tang A., Cloutier G., “Ultrasound shear wave viscoelastography: model-independent quantification of the complex shear modulus,” IEEE Trans Ultrason Ferroelectr Freq Control 63(9), 1399–1408 (2016). 10.1109/TUFFC.2016.2583785 [DOI] [PubMed] [Google Scholar]
- 189.Nenadic I. Z., Qiang B., Urban M. W., Zhao H., Sanchez W., Greenleaf J. F., Chen S., “Attenuation measuring ultrasound shearwave elastography and in vivo application in post-transplant liver patients,” Phys. Med. Biol. 62(2), 484–500 (2017). 10.1088/1361-6560/aa4f6f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Rouze N. C., Palmeri M. L., Nightingale K. R., “An analytic, Fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources,” J. Acoust. Soc. Am. 138(2), 1012–1022 (2015). 10.1121/1.4927492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Wu Z., Hoyt K., Rubens D. J., Parker K. J., “Sonoelastographic imaging of interference patterns for estimation of shear velocity distribution in biomaterials,” J. Acoust. Soc. Am. 120(1), 535–545 (2006). 10.1121/1.2203594 [DOI] [PubMed] [Google Scholar]
- 192.Khoo A. S., Valentin T. M., Leggett S. E., Bhaskar D., Bye E. M., Benmelech S., Ip B. C., Wong I. Y., “Breast cancer cells transition from mesenchymal to amoeboid migration in tunable three-dimensional silk-collagen hydrogels,” ACS Biomater. Sci. Eng. 5(9), 4341–4354 (2019). 10.1021/acsbiomaterials.9b00519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Seo B. R., Chen X., Ling L., Song Y. H., Shimpi A. A., Choi S., Gonzalez J., Sapudom J., Wang K., Andresen Eguiluz R. C., Gourdon D., Shenoy V. B., Fischbach C., “Collagen microarchitecture mechanically controls myofibroblast differentiation,” Proc. Natl. Acad. Sci. U. S. A. 117(21), 11387–11398 (2020). 10.1073/pnas.1919394117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Chaudhuri O., Gu L., Klumpers D., Darnell M., Bencherif S. A., Weaver J. C., Huebsch N., Lee H. P., Lippens E., Duda G. N., Mooney D. J., “Hydrogels with tunable stress relaxation regulate stem cell fate and activity,” Nat. Mater. 15(3), 326–334 (2016). 10.1038/nmat4489 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Hadden W. J., Young J. L., Holle A. W., McFetridge M. L., Kim D. Y., Wijesinghe P., Taylor-Weiner H., Wen J. H., Lee A. R., Bieback K., Vo B. N., Sampson D. D., Kennedy B. F., Spatz J. P., Engler A. J., Choi Y. S., “Stem cell migration and mechanotransduction on linear stiffness gradient hydrogels,” Proc. Natl. Acad. Sci. U. S. A. 114(22), 5647–5652 (2017). 10.1073/pnas.1618239114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Ondeck M. G., Kumar A., Placone J. K., Plunkett C. M., Matte B. F., Wong K. C., Fattet L., Yang J., Engler A. J., “Dynamically stiffened matrix promotes malignant transformation of mammary epithelial cells via collective mechanical signaling,” Proc. Natl. Acad. Sci. U. S. A. 116(9), 3502–3507 (2019). 10.1073/pnas.1814204116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 197.Kraning-Rush C. M., Califano J. P., Reinhart-King C. A., “Cellular traction stresses increase with increasing metastatic potential,” PLoS One 7, 0032572 (2012). 10.1371/journal.pone.0032572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Legant W. R., Choi C. K., Miller J. S., Shao L., Gao L., Betzig E., Chen C. S., “Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions,” Proc. Natl. Acad. Sci. U. S. A. 110(3), 881–886 (2013). 10.1073/pnas.1207997110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Legant W. R., Miller J. S., Blakely B. L., Cohen D. M., Genin G. M., Chen C. S., “Measurement of mechanical tractions exerted by cells in three-dimensional matrices,” Nat. Methods 7(12), 969–971 (2010). 10.1038/nmeth.1531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Mulligan J. A., Bordeleau F., Reinhart-King C. A., Adie S. G., “Traction force microscopy for non-invasive imaging of cell forces,” in Biomechanics in Oncology , Dong C., Kuhn N., Konstantopoulos K., eds. (Springer, 2018). [Google Scholar]
- 201.Ling L., Mulligan J. A., Ouyang Y., Shimpi A. A., Williams R. M., Beeghly G. F., Hopkins B. D., Spector J. A., Adie S. G., Fischbach C., “Obesity-associated adipose stromal cells promote breast cancer invasion through direct cell contact and ECM remodeling,” Adv. Funct. Mater. 30(48), 1910650 (2020). 10.1002/adfm.201910650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Mulligan J. A., Ling L., Leartprapun N., Fischbach C., Adie S. G., “Computational 4D-OCM for label-free imaging of collective cell invasion and force-mediated deformations in collagen,” Sci. Rep. 11(1), 2814 (2021). 10.1038/s41598-021-81470-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Leggett S. E., Patel M., Valentin T. M., Gamboa L., Khoo A. S., Williams E. K., Franck C., Wong I. Y., “Mechanophenotyping of 3D multicellular clusters using displacement arrays of rendered tractions,” Proc. Natl. Acad. Sci. U. S. A. 117(11), 5655–5663 (2020). 10.1073/pnas.1918296117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204.Boj S. F., Hwang C. I., Baker L. A., Chio I. I., Engle D. D., Corbo V., Jager M., Ponz-Sarvise M., Tiriac H., Spector M. S., Gracanin A., Oni T., Yu K. H., van Boxtel R., Huch M., Rivera K. D., Wilson J. P., Feigin M. E., Ohlund D., Handly-Santana A., Ardito-Abraham C. M., Ludwig M., Elyada E., Alagesan B., Biffi G., Yordanov G. N., Delcuze B., Creighton B., Wright K., Park Y., Morsink F. H., Molenaar I. Q., Borel Rinkes I. H., Cuppen E., Hao Y., Jin Y., Nijman I. J., Iacobuzio-Donahue C., Leach S. D., Pappin D. J., Hammell M., Klimstra D. S., Basturk O., Hruban R. H., Offerhaus G. J., Vries R. G., Clevers H., Tuveson D. A., “Organoid models of human and mouse ductal pancreatic cancer,” Cell 160(1-2), 324–338 (2015). 10.1016/j.cell.2014.12.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Gjorevski N., Sachs N., Manfrin A., Giger S., Bragina M. E., Ordonez-Moran P., Clevers H., Lutolf M. P., “Designer matrices for intestinal stem cell and organoid culture,” Nature 539(7630), 560–564 (2016). 10.1038/nature20168 [DOI] [PubMed] [Google Scholar]
- 206.Tuveson D. A., Clevers H., “Cancer modeling meets human organoid technology,” Science 364(6444), 952–955 (2019). 10.1126/science.aaw6985 [DOI] [PubMed] [Google Scholar]
- 207.Liu C. J., Shamsan G. A., Akkin T., Odde D. J., “Glioma cell migration dynamics in brain tissue assessed by multimodal optical imaging,” Biophys. J. 117(7), 1179–1188 (2019). 10.1016/j.bpj.2019.08.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 208.Mulligan J. A., Feng X., Adie S. G., “Quantitative reconstruction of time-varying 3D cell forces with traction force optical coherence microscopy,” Sci. Rep. 9(1), 4086 (2019). 10.1038/s41598-019-40608-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 209.Mulligan J. A., Bordeleau F., Reinhart-King C. A., Adie S. G., “Traction force microscopy for noninvasive imaging of cell forces,” in Biomechanics in Oncology , Dong C., Zahir N., Konstantopoulos K., eds. (Springer International Publishing, 2018), pp. 319–349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210.Hadi M. F., Barocas V. H., “Microscale fiber network alignment affects macroscale failure behavior in simulated collagen tissue analogs,” J. Biomech. Eng. 135(2), 021026 (2013). 10.1115/1.4023411 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211.Zhang L., Lake S. P., Barocas V. H., Shephard M. S., Picu R. C., “Cross-linked fiber network embedded in elastic matrix,” Soft Matter 9(28), 6398–6405 (2013). 10.1039/c3sm50838b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 212.Lai V. K., Hadi M. F., Tranquillo R. T., Barocas V. H., “A multiscale approach to modeling the passive mechanical contribution of cells in tissues,” J. Biomech. Eng. 135(7), 71007 (2013). 10.1115/1.4024350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213.van Oosten A. S. G., Chen X., Chin L., Cruz K., Patteson A. E., Pogoda K., Shenoy V. B., Janmey P. A., “Emergence of tissue-like mechanics from fibrous networks confined by close-packed cells,” Nature 573(7772), 96–101 (2019). 10.1038/s41586-019-1516-5 [DOI] [PubMed] [Google Scholar]
- 214.Ciarletta P., “Buckling instability in growing tumor spheroids,” Phys. Rev. Lett. 110(15), 158102 (2013). 10.1103/PhysRevLett.110.158102 [DOI] [PubMed] [Google Scholar]
- 215.Nia H. T., Liu H., Seano G., Datta M., Jones D., Rahbari N., Incio J., Chauhan V. P., Jung K., Martin J. D., Askoxylakis V., Padera T. P., Fukumura D., Boucher Y., Hornicek F. J., Grodzinsky A. J., Baish J. W., Munn L. L., Jain R. K., “Solid stress and elastic energy as measures of tumour mechanopathology,” Nat. Biomed. Eng. 1(1), 0004 (2017). 10.1038/s41551-016-0004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216.Abhilash A. S., Baker B. M., Trappmann B., Chen C. S., Shenoy V. B., “Remodeling of fibrous extracellular matrices by contractile cells: predictions from discrete fiber network simulations,” Biophys. J. 107(8), 1829–1840 (2014). 10.1016/j.bpj.2014.08.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 217.Wang H., Abhilash A. S., Chen C. S., Wells R. G., Shenoy V. B., “Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers,” Biophys. J. 107(11), 2592–2603 (2014). 10.1016/j.bpj.2014.09.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 218.Sunyer R., Conte V., Escribano J., Elosegui-Artola A., Labernadie A., Valon L., Navajas D., García-Aznar J. M., Muñoz J. J., Roca-Cusachs P., Trepat X., “Collective cell durotaxis emerges from long-range intercellular force transmission,” Science 353(6304), 1157–1161 (2016). 10.1126/science.aaf7119 [DOI] [PubMed] [Google Scholar]
- 219.Kim M. C., Silberberg Y. R., Abeyaratne R., Kamm R. D., Asada H. H., “Computational modeling of three-dimensional ECM-rigidity sensing to guide directed cell migration,” Proc. Natl. Acad. Sci. U. S. A. 115(3), E390–E399 (2018). 10.1073/pnas.1717230115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 220.Wang H., Mislati R., Ahmed R., Vincent P., Nwabunwanne S. F., Gunn J. R., Pogue B. W., Doyley M. M., “Elastography can map the local inverse relationship between shear modulus and drug delivery within the pancreatic ductal adenocarcinoma microenvironment,” Clin. Cancer Res. 25(7), 2136–2143 (2019). 10.1158/1078-0432.CCR-18-2684 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 221.Nia H. T., Munn L. L., Jain R. K., “Mapping physical tumor microenvironment and drug delivery,” Clin. Cancer Res. 25(7), 2024–2026 (2019). 10.1158/1078-0432.CCR-18-3724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 222.Kalra A., Lowe A., Al-Jumaily A. M., “Mechanical behaviour of skin: a review,” J. Mater. Sci. Eng. 5(4), 1–7 (2016). 10.4172/2169-0022.1000254 [DOI] [Google Scholar]
- 223.Ferraioli G., “Review of liver elastography guidelines,” J. Ultrasound Med. 38(1), 9–14 (2019). 10.1002/jum.14856 [DOI] [PubMed] [Google Scholar]
- 224.Yock P. G., Zenois S., Makower J., Brinton T. J., Kumar U. N., Watkins F. T. J., Denend L., Krummel T. M., Kurihara C. Q., Biodesign: The Process of Innovating Medical Technologies (Cambridge University Press, 2015). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data were generated or analyzed in the presented research.