Length biases in single-cell RNA sequencing of pre-mRNA

Abstract

Single-cell RNA sequencing data can be modeled using Markov chains to yield genome-wide insights into transcriptional physics. However, quantitative inference with such data requires careful assessment of noise sources. We find that long pre-mRNA transcripts are over-represented in sequencing data. To explain this trend, we propose a length-based model of capture bias, which may produce false-positive observations. We solve this model and use it to find concordant parameter trends as well as systematic, mechanistically interpretable technical and biological differences in paired data sets.

Why it matters

Single-cell RNA sequencing is a method to quantify the amount of individual RNA molecules in cells. RNA reflects the extent of gene expression, which ultimately controls cell function. However, the method is imperfect, and some molecules are lost in the process. To understand the biophysics that control gene expression in the living cell, we need to produce and fit models that include both biological and technical sources of variability. Here, we show that unprocessed and mature RNA molecules exhibit counterintuitively different trends in their RNA expression and propose a mechanism of technical variability to account for these differences. This framework allows us to systematically explain differences in expression by specific physical mechanisms.

Introduction

The development of quantitative single-cell RNA sequencing (scRNA-seq) has made it increasingly tractable to fit single-molecule data to models of the RNA life cycle, thus facilitating a mechanistic view of genome-wide transcriptional regulation. Specifically, protocols with cell barcodes and unique molecular identifiers (UMIs) (1) allow for parameterization of discrete probabilistic models, with contents of cells conceptualized as draws from distributions over the nonnegative integers. When these models represent biophysical phenomena, fitting them provides information about the phenomena or about the overall plausibility of the model.

The standard framework for describing the microscopic biophysics of reactions in living cells is the chemical master equation (CME), which models mRNA counts by Markov chains that traverse a discrete state space (2,3,4). To fit biophysical parameters (the “inverse” problem of inference), one must solve the CME (the “forward” problem of prediction). This workflow requires computationally facile solutions that can be applied to thousands of genes. In mammalian and bacterial systems, the specific form of the CME is based on a random telegraph model of gene regulation, which describes a single gene locus that randomly switches between active and inactive states (2). A common simplification, supported by genome-wide fluorescence studies (5), treats the active state’s duration as vanishingly small: mRNA is produced in geometrically distributed bursts that arrive according to a Poisson process. This model can be extended to describe rather general downstream processes of splicing, degradation (6), and translation. We focus on newly available data with spliced and unspliced mRNA, which can be fit to a tractable bursting model (7), and which has seen recent use in the inference of biological dynamics from static snapshots (8,9).

A remaining barrier to the application of this classical framework for inferring the biophysics underlying scRNA-seq data is modeling of technical artifact. The sequencing process is probabilistic, and some molecules may not always be measured. Some studies attempt to “regress out” technical artifacts (10), but these methods are informal and incompatible with a discrete stochastic picture of transcription. Thus, treating both biological and technical stochasticity remains a significant lacuna in single-cell transcriptional models with no satisfactory and rigorous solutions.

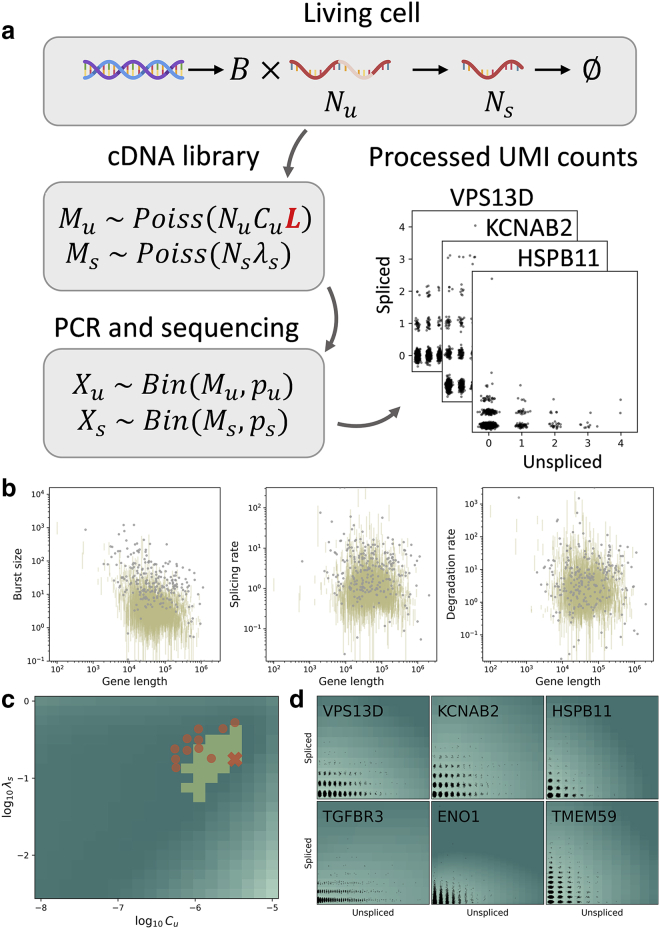
We begin by exploring the biophysical interpretability of scRNA-seq data in light of the length bias seen in pre-mRNA expression. In some data sets, average spliced mRNA counts do not seem to show a length dependence (Fig. 1 a, top), which is consistent with previous studies of UMI-based protocols (11). On the other hand, unspliced mRNA counts strongly correlate with gene length (12) (Fig. 1 a, bottom). This prompted us to investigate whether the discrepancy has biological origins and raised questions about the consequences of ignoring this bias. We find that comprehensive, integrated stochastic models of biology and experiment are mandatory for interpreting sequencing data sets and appeal to the chemistry of sequencing to propose a class of plausible models.

Figure 1.

Spliced and unspliced single-cell RNA sequencing data demonstrate counterintuitive trends in data moments and model fits. (a) Length dependence of average mRNA counts in three data sets (orange: high-expression genes; gray: discarded low-expression genes; top row: spliced RNA; bottom row: unspliced RNA). (b) Transcriptional parameter estimates without a stochastic model of sequencing demonstrate pervasive length-dependent trends (pbmc_10k_v3; gold: lower bounds on 99% confidence intervals; gray: fits rejected by statistical testing; splicing and degradation rates are reported in units of burst frequency).

Materials and methods

A model with no technical noise

To begin, we performed a naive analysis, fitting joint unspliced and spliced count data using a conventional (5,7) stochastic transcriptional model, namely a two-stage birth-death process coupled to a bursting promoter:

$$\varnothing \stackrel{k}{\to }B\times \mathcal{U}\stackrel{\beta }{\to }\mathcal{S}\stackrel{\gamma }{\to }\varnothing \text{,}$$ (1)

where $\mathcal{U}$ and $\mathcal{S}$ are unspliced and spliced mRNA species; $k$, $\beta$, and $\gamma$ are the rates of Markovian transcription, splicing, and degradation processes, respectively; and $B$ is a geometrically distributed burst size with mean $b$. We assumed the system had reached its unique steady state. The generating function solution to this system has been reported by Singh and Bokes (7).

A technical noise model

In the current section, we motivate, solve, and apply a stochastic model of sequencing that addresses technical artifacts to scRNA-seq data. We use the CME framework to derive the model from a microscopic Markov description of transcription in model definition. Finally, we report the model solution in model solution and fully describe the derivation in section S1.1.

In brief, we build a model that explicitly incorporates the stochastic sequencing steps taking place in fixed media (Fig. 2 a). Consistent with previous work on modeling pre-mRNA (8), we assume that the library construction step in the 10x sequencing workflow (1) includes molecules that have been captured at off-target binding sites. We posit that unspliced mRNA are primarily captured at internal poly(A) tracts, whereas spliced mRNA are captured at the poly(A) tail. To quantitatively model this effect, we introduce the concept of UMI “false positives”: if a molecule has sufficiently many poly(A) sites, it is likely to be captured and reverse transcribed multiple times. As a first-order approximation, we model this bias as a length-dependent capture rate. Thus, each molecule in a cell gives rise to a Poisson distribution of cDNA. The downstream sequencing and alignment steps are treated as binomial sampling from the cDNA distribution.

Figure 2.

A length-biased technical noise model produces more physically interpretable results. (a) The integrated stochastic model of transcription and sequencing, with length dependence of the library construction step indicated in red. (b) Inferred transcriptional parameters do not appear to have strong length dependence (pbmc_10k_v3; gold: lower bounds on 99% confidence intervals; gray: fits rejected by statistical testing; splicing and degradation rates are reported in units of burst frequency). (c) The sampling parameter likelihood landscape shows a single optimum (dark teal: lower, light teal: higher total Kullback-Leibler divergence between fit and data from pbmc_10k_v3; highlighted yellow region: 5% quantile region for the displayed landscape; orange cross: optimal sampling parameter fit for the displayed landscape; orange points: optimal sampling parameter fits for other analyzed v3 data sets; $C_u$: coefficient for length-dependent unspliced capture rate; ${\lambda }_s$: spliced capture rate). (d) The parameter fitting procedure successfully recapitulates empirical copy-number distributions (dark teal: lower, light teal: higher log probability mass; black points: raw data UMI counts).

Model definition

The biological processes are defined in Eq. 1. This live-cell stage yields the unobservable distribution $P\left(N_u=n_u,N_s=n_s\right):=P\left(n_u,n_s\right)$, where $N_z$ is the random variable describing true physiological counts of species $z$ and $n_z$ is the molecule count. This distribution has the probability-generating function (PGF) $G\left(g_u,g_s\right)$.

After equilibration, cDNA library construction begins, and all physiological processes halt due to cell fixation (1). Due to the possibility of multiple priming, each molecule of mRNA produces $Poisson\left(D_z\right)$ molecules of cDNA. $D_u$ is presumed to be length dependent and governed by internal priming, whereas $D_s$ is presumed to be length independent and governed by poly(A) tail priming.

Finally, amplification and sequencing take place. Unlike the library construction, these are strictly depleting processes: we suppose they cannot generate new UMIs, but they can lead to loss of UMIs. We assume the PCR amplification and product fragmentation are not substantially biased from gene to gene; further, the downstream fragments do not retain length information. Nevertheless, the overall identifiability of unspliced and mature mRNA may be different. Therefore, we suppose that each in vitro cDNA UMI gives rise to $Bernoulli\left(p_z\right)$ amplified, sequenced, and corrected in silico UMIs. The corresponding overall joint PGF takes the following form:

$$G_{X_u,X_s}\left(g_u,g_s\right)=G\left(G_{1,u}\left(G_{2,u}\left(g_u\right)\right),G_{1,s}\left(G_{2,s}\left(g_s\right)\right)\right):=H\left(g_u,g_s\right)\text{,}$$ (2)

where $G_{i,z}$ is the PGF for sampling step $i$ and species $z$. The parameters $D_z$ and $p_z$ are not independently identifiable, leading us to define net sampling rates ${\lambda }_z:=D_z{p}_z$.

We use a first-order model of length dependence ${\lambda }_u=C_{u}L$: the rate of capture of any particular molecule scales directly with its length, acting as a proxy for the number of poly(A) tracts in the molecule. Even short poly(A) sequences can be captured by the oligo(dT) primers used in sequencing (13), and the number of poly(A) sequences in a given gene is strongly correlated with length (Fig. S2). We do not directly consider the number of tracts, as the determination of appropriate length thresholds or weights is a distinct thermodynamics challenge. The spliced mRNA parameter ${\lambda }_s$ is kept constant, modeling capture at the poly(A) tail. For convenience, the model random variables and parameters are summarized in Tables S1 and S2.

Model solution

Following previous work (7), the steady-state PGF for the joint distribution of unspliced and spliced mRNA is $G\left(g_u,g_s\right)=e^{\phi \left(v_u,v_s\right)}$, where

$$\begin{array}{c}{v}_z:=g_z-1\\ \phi \left(v_u,v_s\right)=k{\int }_0^{\infty }\frac{bU}{1-bU}ds\\ f:=\frac{\beta }{\beta -\gamma }\\ U=v_{s}f{e}^{-\gamma s}+\left[v_u-v_{s}f\right]e^{-\beta s}\text{.}\end{array}$$ (3)

The PGF of a distribution under two steps of independent sampling is given in Eq. 2. Using the model assumptions outlined above, the overall PGF takes the following form:

$$H\left(g_u,g_s\right)=G\left(e^{{\lambda }_u\left(g_u-1\right)},e^{{\lambda }_s\left(g_s-1\right)}\right)\text{.}$$ (4)

The corresponding joint probability distribution $P\left(x_u,x_s\right)$ is easily computed by evaluating $g_u$ and $g_s$ around the complex unit circle and performing an inverse Fourier transform (7,14).

The moments of the model can be calculated by differentiating the PGF at $g_u=g_s=1$. We report the lower moments of the noise-free model and the full model in Table I. The full derivations are provided in section S1.2. For convenience, the definitions of the summary statistics are given in Table S3.

Table.

1Comparison of models’ lower moments

Moment	Noise-free model	Technical noise model
${\mu }_u$	$\frac{kb}{\beta }$	$\frac{{\lambda }_{u}kb}{\beta }$
${\mu }_s$	$\frac{kb}{\gamma }$	$\frac{{\lambda }_{s}kb}{\gamma }$
${\sigma }_u^2-{\mu }_u$	${\mu }_{u}b$	${\mu }_u{\lambda }_u\left(1+b\right)$
${\sigma }_s^2-{\mu }_s$	${\mu }_s\frac{b\beta }{\beta +\gamma }$	${\mu }_s{\lambda }_s\left(1+\frac{b\beta }{\beta +\gamma }\right)$
$\text{Cov}\left(u,s\right)$	$\frac{k{b}^2}{\beta +\gamma }$	$\frac{{\lambda }_u{\lambda }_{s}k{b}^2}{\beta +\gamma }$

Data processing and inference

We downloaded the human and mouse genomes from the Ensembl (15) database, computed gene lengths, and partitioned each gene’s sequence into a set of contiguous poly(A) sequences. These sequences were used to compute cumulative histograms of the number of poly(A) tracts.

The scRNA-seq processing procedure is summarized in Fig. S1 and fully described in section S4.2. We downloaded scRNA-seq reads and processed them with the kallisto|bustools workflow (16), thereby obtaining spliced and unspliced count matrices. The analyzed data sets are motivated in section S4.1 and summarized in Table S4; nine were generated by 10x Genomics, and seven were generated by the Allen Institute for Brain Science (17,18). Genes without length annotations were discarded. As shown in section S7.3, all data sets demonstrated the previously encountered (Fig. 1 a) expression bias. For each inference batch, we selected the top genes according to the number of data sets in which they passed an expression filter. We used 2,500 genes for whole-data set analyses, 3,500 for cell-type difference analysis in blood cells, and 5,000 for cell-type difference analysis in neurons.

We estimated the parameters by scanning over a grid of sampling parameters, computing the conditional maximum likelihood estimates (MLEs) of all gene-specific parameters by gradient descent, and identifying the $\left\{C_u,{\lambda }_s\right\}$ MLE. In some cases, the fits were unreliable due to the sparsity of the data, suboptimal gradient descent fits, or model misspecification. To control for these sources of error, we discarded fits that were too close to the search domain bounds. Further, we performed a chi-squared test and discarded all genes with p <0.01 and Hellinger distance >0.05 as a measure of goodness of fit with an effect size component. We estimated a lower bound on 99% confidence intervals for MLEs through the Fisher information matrix; as we omit uncertainty in $\left\{C_u,{\lambda }_s\right\}$, these intervals necessarily underestimate the error. We detail the procedure in section S4.3. The analysis was performed using the Monod 0.2.5.0 Python package (19).

Results

A model with no length bias produces implausible parameter estimates

At first glance, the rates we obtained by fitting the noise-free model to bivariate copy-number distributions seemed reasonable (Fig. 1 b; section S7.4). Two other noise models without a sequencing length bias produced qualitatively identical results (section S2). However, comparison with previous transcriptome-wide analyses suggested that the results were biophysically implausible.

We found that the inferred burst size increased with transcript length, in stark contrast with the previously observed modest inverse relationship (20). The degradation rate, normalized to burst frequency, displayed a similar positive trend. Previous studies found little to no gene length effect on burst frequency (20) and no effect on the rate of mRNA degradation (21). The latter is primarily controlled by open reading frame features rather than the length of the source gene. The decreasing splicing rates are more challenging to analyze: the splicing timescales given in the literature vary over several orders of magnitude depending on system and technology (22). However, length-based effects should be minimal, as cotranscriptional splicing is ubiquitous in mammalian cells (23,24) and widely varying intron sizes have little impact on splicing time (25).

Aside from empirical data, there are theoretical reasons to question these results: for example, the splicing rate is likely governed by spliceosome kinetics at individual introns, which is a local, rather than gene-wide, effect. Similarly, the cytoplasmic coding isoform is degraded, and its length is only weakly related to that of the parent transcript. In summary, the observed UMI counts of spliced transcripts cannot be plausibly treated the same way as those of unspliced transcripts. Such a simplification is incompatible with empirical evidence and currently accepted models.

The technical noise model produces consistent and physically interpretable results

Fitting the length-dependent Poisson technical noise model yielded transcriptional parameters (Fig. 2 b; section S7.5.2) without systematic length dependence. Therefore, we suggest that this integrated description of transcription and sequencing provides a more realistic and physically interpretable picture than available by considering the two sources of stochasticity separately.

All optima discovered by the coordinate scan procedure for the 10x v3 data sets lie within the square ${\log }_{10}{C}_u=-5.87\pm 0.40$ and ${\log }_{10}{\lambda }_s=-0.56\pm 0.32$. The Kullback-Leibler divergence (KLD) landscapes suggest that the data sets have unique optima and that the model is appropriate (Fig. 2 c; section S7.6). Furthermore, empirical joint mRNA count histograms were consistent with the fits (Fig. 2 d).

The inferred parameter distributions were consistently well fit (26) to a log normal-inverse Gaussian law (Fig. 3 a; section S7.7), although the mechanistic import of this finding is unclear. We performed a set of technical replicates, fitting distinct libraries generated from the same organism, and biological replicates, fitting libraries from multiple organisms. The results (Fig. 3 b; section S7.8) were consistent, with higher correlations among the technical replicates.

Figure 3.

The technical noise model fits can be interpreted to analyze experimental effects. (a) Inferred transcriptional parameter distributions (pbmc_10k_v3; gray: histogram of biological parameters retained after statistical testing; teal dashed line: best fit to normal-inverse Gaussian distribution; splicing and degradation rates are reported in units of burst frequency). (b) Parameter estimates from biological replicates show largely concordant inferred parameter values (conventions as in Fig. 2b). (c) 10x v2 and v3 single-cell RNA sequencing (scRNA-seq) replicates generated from a single sample demonstrate discordant RNA count distributions: the v2 data sets have lower mean values (orange dashed line: identity; black: genes). (d) The v2 data sets have higher ${\text{CV}}^2$ values (orange dashed line: identity; black: genes). (e) The v2 data sets’ distributional differences can be tentatively explained by a combination of identical biological parameters and lower technical noise parameters ($C_u$: coefficient for length-dependent unspliced capture rate; ${\lambda }_s$: spliced capture rate; colors: data set categories; intersections of grid lines indicate the sampling parameter sets evaluated in the inference process).

The technical noise model provides a framework for studying experimental effects

The obtained estimates for the technical noise parameters demonstrated limited identifiability. The data sets appeared to possess information sufficient to localize the technical noise to a coarse one-order-of-magnitude domain, but no further. When comparing multiple data sets de novo, it is challenging to attribute biases in parameter values: for example, under the current model, an apparent decrease in total RNA content may be caused by transcriptome-wide downregulation of transcription, upregulation of turnover, or decline in the sampling rates.

We can investigate the technical effects more systematically by treating replicates generated by different sequencing technologies and adopting stronger priors. We found that count data generated by the higher-efficiency v3 chemistry consistently yielded higher mean and lower noise $\left({\text{CV}}^2\right)$ levels than those generated by the older v2 chemistry (Figs. 3, c and d, and S32). We hypothesized that these differences should be appropriately attributed to technical effects, as the source tissues were similar or identical. A naive noise-free fit produced pronounced and nonphysical biases in parameter values (Fig. S33).

Imposing the belief that the underlying biological parameters should be the identical between all technical replicates and treating the results for large v3 samples as a putative ground truth, we identified the set of sampling parameters for the v2 data sets that produced the best agreement to these biological parameter values (Fig. S34; section S4.4). The resulting inferred sampling parameter optima are shown in Fig. 3 e: as expected, v2 data sets have lower sampling parameter values. These values are somewhat challenging to identify without enforcing the consistency criterion between transcriptional parameters: as shown in section S7.6, the v2 KLD landscapes are more susceptible to noise than the v3 KLD landscapes, preventing de novo inference. Although the current comparison is mostly relative, the framework provides a quantitative explanatory mechanism for the technical effect of sequencing chemistry.

Inferred biophysical parameters provide insights into the mechanistic basis of differential expression

Just as technical noise parameters provide a mechanistic route to analyzing the effect of sequencing chemistry, the biological parameters provide a principled mechanistic route to identifying genes that are differentially regulated under varying conditions. Instead of the standard descriptive approach that tests differences in average expression (10), our model can test differences in parameter values. This conceptualization provides multiple advantages. Firstly, it increases statistical power due to reliance on model-specific results rather than nonparametric limiting theorems. For example, a gene may be expressed at nearly identical average levels in two cell types but have very different distributions (12); such an effect is easier to detect using full parametric distribution fits. Secondly, our approach yields greater interpretability, as all parameters explicitly model biophysical processes. For example, a difference in average expression may be directly attributed to the modulation of specific reaction rates, as discussed in previous work using fluorescence-based measurements (5,27) and very recently applied to scRNA-seq data (19,28).

Thus far, we have tacitly assumed that cells can be described as independent and identically distributed draws from a single stationary probability distribution. This approach is consistent with previous work (29,30), as well as a foundational premise of transcriptomic analyses: cell-type differences and transient phenomena are driven by a small set of marker genes (10,18,31,32,33), whereas the rest of the transcriptome is roughly static. Therefore, we have consciously omitted intrasample heterogeneity by discarding genes that do not match the model or have particularly high or low expression.

To demonstrate the potential applications of the mechanistic approach to discovery, we separately fit the cell types present in human blood and mouse brain data sets, based on previous clustering results. Disaggregated cell-type grid fits produced technical noise parameter estimates consistent with the full data sets (Fig. S35). For simplicity, we assumed that the technical noise parameters in each cell type were identical to those of the full data set. We found that the marker gene axiom appeared to be satisfied: the matched data sets parameter values were located near the identity line, with a small number of conspicuously off-diagonal genes that included known marker genes (Fig. 4 a; section S7.10.2).

Figure 4.

The inferred biological parameters provide insight into the biophysical basis of gene expression modulation. (a) Cell types in the pbmc_10k_v3 blood cell data set show largely concordant inferred parameter values, with the conspicuous exception of marker genes (orange dashed line: identity; black: genes retained after statistical testing; orange: T cell marker genes; violet: B cell marker genes; splicing and degradation rates are reported in units of burst frequency). (b) Cell types show strong covariation in splicing and degradation rate differences, suggesting potential burst frequency modulation (conventions as in a). (c) Cell-type differences can be attributed to combination of mechanisms; marker gene differences between B and T cells appear to be most readily explained by burst frequency modulation (red line: parameter combinations that yield identical average expression levels; black: genes retained after statistical testing; orange: T cell marker genes; violet: B cell marker genes; burst frequency modulation is estimated by splicing rate modulation). (d) Differential expression analysis identifies genes that exhibit consistent intercell-type parameter modulation in Allen neuron populations (gray: parameters for genes not identified as differentially expressed by the $t$-test and a fold change criterion; light red: parameters identified as higher in the glutamatergic cell type; light teal: parameters identified as higher in the GABAergic cell type).

The parameters demonstrated patterns of comodulation. In particular, the striking high correlation between differences in $\beta /k$ and in $\gamma /k$ suggests that this modulation pattern should be properly interpreted as reflecting modulation of the burst frequency $k$ (Fig. 4 b; section S7.10.3). Using the change in $\beta /k$ as a coarse proxy for the change in $k$, we can attribute marker gene modulation to a specific transcriptional mechanism: for example, the differences between T and B cells are typically associated with modulation of the burst frequency (Fig. 4 c), as previously proposed as a primary driver for cell-type differences (20,28). However, this mechanism is far from universal in our data sets, and we generally see a combination of burst size and burst frequency modulation in cell-type differences (section S7.10.4).

We used multiple biologically independent replicates, combined with a standard $t$-test, to identify patterns of parameter modulation between glutamatergic and GABAergic cell types (section S4.5.2). The results are shown in Fig. 4 d. Most interestingly, we observed several genes that consistently exhibited transcriptional parameter modulation but exhibited approximately constant mean spliced expression between cell types (average ${\log }_2$ fold change $<1$) and would not be identifiable by standard statistical procedures. We identified burst size modulation for the genes Rnf152, Fam174a, Nin, Rgmb, Dpysl3, Bach2, Igf1r, Stx4a, and Scg3. We identified burst frequency modulation (putatively assigned due to changes in either splicing or degradation rate) for the genes Fam174a, A330023F24Rik, Socs2, Ankrd40, Slc39a11, Mblac2, Itga4, Cxxc4, Ankrd6, Ccdc136, Crtc3, Egln1, Il34, and Mid2. We visualize their distributions in a single neuronal data set in section S7.10.5: the distribution shapes demonstrate visually distinguishable differences and do not appear to suffer from significant failure to fit the data.

The identified genes largely, but not exclusively, relate to neuronal structure and development. Socs2, Igf1r, Itga4, and Dpysl3 are involved in differentiation and neurite outgrowth (34,35,36,37). Bach2 and Cxxc4 induce feedback in neuronal development, apparently to maintain differentiated status in neurons (38,39). Mid2 and Nin are associated with neural development regulation through microtubule organization (40,41). Egln1 is linked to neuronal apoptosis (42). Fam174a is involved in lipid metabolism and membrane structure (43). Rnf152 and Rgmb are broadly implicated in neural development (44,45,46). Scg3 appears to have a functional role in secretory granule biogenesis (47).

Some identified genes have less clear mechanistic connections to brain structure and function. Ankrd40 is uncharacterized and is not known to have neural functions (48), but the similar gene product Ankrd6 has an obscure neurodevelopmental role (49). Stx4a is localized on synaptic membranes (50). Slc39a11 is a zinc transporter involved in brain function (51). Mblac2 codes for an obscure protein that may have enzymatic activity (52). Ccdc136 appears to have a DNA-regulatory role (53), but may be involved in neural speech pathology (54). The role of Crtc3 in the rodent brain appears to be restricted to stress response (55). Il34 is a microglial marker; microglia have immune and regulatory functions in the brain (56). A330023F24Rik is uncharacterized.

Although these distinctions are statistically identifiable, the import and basis of cell-type differences in distribution rather than average expression is, as of yet, obscure. The mechanism may involve expression compensation previously explored using theoretical tools (4) and recently observed under DNA repair stress (57).

Discussion

We have introduced and implemented a stochastic model of intrinsic transcriptional noise that accounts for sequencing artifacts or technical noise. This model addresses an apparent overrepresentation of long unspliced mRNA in a variety of scRNA-seq data sets, and we posit that this bias is unlikely to arise biologically: fitting a simple model of mRNA production, splicing, and degradation produces parameter trends that render the fits suspect. Instead, we propose a model motivated by the chemistry of the sequencing process: each mRNA can be captured and reverse transcribed multiple times, with the possibility of such false positives growing with the length of molecule and the number of poly(A) capture sites (Fig. S2). Although Poisson models for capture have been proposed before (as outlined in section S5.1), their derivation is largely ad hoc, and their implications for the reliability of sequencing data have not been examined in detail.

We fit the proposed model to a variety of data sets and discovered that the parameter values, and thus entire mRNA distributions, are consistent for sets of technical and biological replicates. Furthermore, the parameter values themselves (Fig. S29) were concordant with previous reports. Average burst sizes in the technical noise model were in the range $\left({10}^{0.5},{10}^{1.5}\right)$ (58, 59) rather than $\left({10}^{-0.5},{10}^{0.5}\right)$ in the noise-free model (section S7.4). Degradation rates $\gamma /k$ were in the range $\left({10}^0,{10}^1\right)$, roughly consistent with fluorescence-based genome-wide results (5). Finally, the splicing rates $\beta /k$ were relatively slow and largely fell within the range $\left({10}^{-0.5},{10}^{0.5}\right)$, i.e., on the order of 100 min. This result suggests that $\beta$ is best interpreted as the rate of an abstracted, multiintron process, as a single intron takes minutes to tens of minutes to splice (22,23,25). We discuss potential refinements of this model in section S5.2.

By fitting the model to closely matched data sets, we investigated technical and biological differences between conditions. We considered the differences between 10x v2 and v3 scRNA-seq data sets and found that the lower-quality v2 data sets can be described in a biophysically consistent way by proposing lower values for the parameters describing the sequencing process. Further, we applied the model to characterize cell-type differences at the level of transcriptional parameters. Although this procedure relies on preexisting annotations and inherits their limitations, it provides a principled way to interrogate the biophysical basis of cell-type differences. With this approach, we have demonstrated the possibility for interesting discovery. For example, it is possible to identify distributional differences that are not accompanied by substantial expression changes. These differences appear to be associated with compensatory mechanisms and motivate further study of the role of noise in biophysical systems.

Author contributions

G.G. and L.P. designed the study, performed the research. and wrote the manuscript. G.G. processed the sequencing data, developed and solved the model, and implemented the statistical procedures.

Editor: Ulrike Endesfelder.

Data and code availability

https://github.com/pachterlab/GP_2021_3 contains a Python notebook that can be used to reproduce all figures. The same repository contains all scripts used to make references, quantify transcripts, and process the resulting count matrices through the inference pipeline. The raw data and all search results have been deposited in Zenodo (60).