Genetic stratification of age-dependent Parkinson’s disease risk by polygenic hazard score

Abstract

Importance:

A polygenic hazard score captures the influence of common genetic variation on age-dependent risk of Parkinson’s disease and could be clinically useful for individual risk stratification.

Objective:

To develop and validate a polygenic hazard score model in sporadic Parkinson’s disease.

Design:

Training and independent validation of a polygenic hazard score model in a genetic association study based on a Cox regression framework.

Setting:

Bioinformatic analyses of multicenter datasets from genome-wide association studies.

Participants:

A reference dataset of 11,693 Parkinson’s disease patients and 9,841 controls, a large test dataset of 5112 PD patients and 5372 controls and a small single-study validation sample of 360 patients and 160 controls.

Exposure:

Common single-nucleotide polymorphisms previously associated with Parkinson’s disease.

Main outcome:

Age at onset of Parkinson’s disease in patients or last healthy examination in controls.

Results:

A polygenic hazard score predicts onset of Parkinson’s disease. The hazard ratio was 3.78 (95% CI 3.49–4.10) when comparing the highest to the lowest risk decile. The score is combined with epidemiological data on incidence rate to estimate genetically stratified instantaneous Parkinson’s disease risk across age groups.

Conclusion and relevance:

We demonstrate the feasibility of a polygenic hazard approach in Parkinson’s disease, integrating the genetic effects on disease risk and age at onset in a single model. The approach holds promise for risk stratification in future clinical trials of disease-modifying therapies, which aim to postpone the onset of Parkinson’s disease.

Introduction

Age is the strongest known risk factor for Parkinson’s disease (PD). Consequently, a dramatic increase in PD prevalence is expected over the next decades, as a larger proportion of the population survives into old age.¹ A deeper understanding of the mechanisms linking aging to neurodegeneration and improved tools for individual risk stratification are urgently needed in order to meet this major public health challenge. Early detection and prediction through precision medicine will be increasingly important for the development of novel disease-modifying therapies in PD, as neurodegeneration is shown to start long before the onset of clinical symptoms.

Common genetic variation also accounts for a substantial proportion of variability in sporadic PD risk, with an estimated heritability of around 16–36%, based on meta-analyses of genome-wide association studies (GWAS)². A recent twin study reported 27% heritability when all age groups were included.³ Variants detected in PD GWAS have been shown to also be associated with age at onset of PD in linear regression models.^4–6 Only a few common variants have reached genome-wide significance as individual age at onset association signals, but models based on polygenic risk scores (PRS) have consistently found that a higher cumulative burden of genetic PD risk correlates with earlier onset.^7–9 Although the findings clearly overlap, association of genetic variants with disease risk and age at onset in PD have thus far only been studied as independent questions, using separate statistical frameworks.

Polygenic hazard scores (PHS) leveraging a time-to-event, or survival, framework have been successful in Alzheimer’s disease (AD) and prostate cancer, both highly age-related complex disorders.^10–12 This approach integrates association with disease risk and age at onset into a common concept, under the hypothesis that genetic variation acts as a modulator of age-dependent risk. In the present article, we apply this PHS-methodology in PD for the first time.

Although PD incidence is strongly dependent on age, some caution is warranted from the outset. Approximately 5–10% of PD cases have a monogenic etiology. Autosomal recessive disease is strongly overrepresented among early-onset cases (e.g. >40)¹³, and even patients negative for mutations in known Mendelian genes may have a different genetic architecture from the common late-onset form.⁸ In the oldest age groups, epidemiological studies have reported mixed results with respect to the trends in sporadic PD incidence.¹⁴

Using individual-level case-control genotype data from the International Parkinson’s Disease Genomics Consortium (IPDGC) with information about age of onset, we model a PHS on reference data from sporadic PD and healthy controls in the age group the age group from 40 to 75 years and validate it in two independent datasets. We further demonstrate how hazard ratios obtained using this method are directly interpretable in terms of stratified annualized incidence rates, with potential implications for clinical trial design.

Methods

All statistical analyses were performed using Matlab R2019a or R v3.6.1. Plink v1.9 was used to prepare the genetic data.

Genetic datasets

We used individual-level genotype data generated as part of previous genetic association studies by the International Parkinson’s Disease Genomics Consortium (IPDGC).⁴ Standard quality checks have been performed on site-level data before initiation of the current study, including filtering for individual and variant missingness, excess heterozygosity, relatedness, Hardy-Weinberg equilibrium, sex-check failures. All included samples were of European ancestry. Genotypes have been imputed using reference data from the Haplotype Reference Consortium before data from individual sites were combined and related samples excluded from the common dataset.

For the present study we included only samples from sites with available information on age at onset for patients or age at inclusion or last healthy examination for controls. Individuals where this age was below 40 were excluded. We selected the largest single dataset available, including 5112 PD patients and 5372 controls, as a test dataset for validation of the PHS model. Previous analyses have shown this sample size to afford high statistical power for testing of PHS in a polygenic disorder.¹⁵ The same dataset was used for replication in a 2014 PD GWAS and is available in the database of Genotypes and Phenotypes (dbGaP phs000918.v1.p1).¹⁶ Similarly, data from the Parkinson’s Progression Marker Initiative (PPMI) were reserved for independent validation.¹⁷ Remaining datasets were included in the reference dataset used to generate the PHS model. Previous studies have shown that genetic factors associated with longevity can bias allele frequencies in datasets including participants from the oldest age groups.⁴ We therefore excluded patients and controls with age above 75 from the reference dataset, which counted a total of 11,693 PD patients and 9,841 controls. Demographics are shown in Table 1, with site-specific details of the reference data in Supplementary table 1.

Table 1.

Dataset demographics

Dataset		N	Mean age (SE)	% female
Reference data (IPDGC)	PD	11693	60.8 (9.0)	0.38
	Controls	9841	59.9 (8.8)	0.53
Test data (NeuroX dbGAP)	PD	5112	62.8 (11.0)	0.43
	Controls	5372	67.0 (11.5)	0.35
PPMI	PD	360	64.5 (9.4)	0.33
	Controls	160	64.7 (9.3)	0.33

Datasets used for training, testing and additional independent validation of the polygenic hazard score model. IPDGC = International Parkinson’s Disease Genomics Consortium, PPMI = Parkinson’s Progression Marker Initiative

Training and testing the polygenic hazard model

Standard polygenic risk scores use a logistic regression framework to estimate weights for individual SNPs and treat cases and controls as permanent designations. The polygenic hazard score approach uses Cox proportional hazards models to directly estimate associations with age of onset of the disease, which may be particularly important for conditions, like Parkinson’s disease, where incidence is strongly dependent on age. The time to event for cases is the age at diagnosis, and controls are censored at age at last follow-up, allowing for the possibility that they may have developed Parkinson’s disease at an older age.

Mathematically, the polygenic hazard score is the vector product of the individual’s genotype (X_i) for n SNPs and the corresponding parameter estimates (β_i) from the Cox proportional hazards regression:

$$PH{S}_x=\sum _i^n{X}_i{\beta }_i$$

The hazard rate at time t for a given subject X_i, λ(X_i), is given by λ(X_i) = λ₀(t) exp exp (β₁X_i1 + … + β_pX_ip), where λ₀(t) is the baseline hazard rate function, β₁, …, β_p are weights optimized from the training datasets, and X_i1, …, X_ip are covariates for i-th subject. In our case, the covariates include the genotype vectors of all SNPs included in the PHS model, as well as sex and top 5 principal components of the genotype matrix.

We first used summary statistics from the largest meta-analysis of PD GWAS to date² to identify a list of single-nucleotide polymorphisms (SNPs) associated with PD risk at significance threshold of p < 1e-5. From this list, we extracted only variants with call rate > 0.95 across the individual genotype datasets, which included a total of 1532 SNPs. These SNPs were evaluated in a stepwise procedure, using a PHS to predict time to PD onset in the training dataset, applying a Cox proportional hazard model, while controlling for sex and the top five genetic principal components. In each step, the algorithm selected the SNP that maximally improved model prediction (i.e., minimizing the martingale residuals from Matlab’s “coxphfit” function) until no SNP could be included in the PHS that would further significantly improve the model (at a threshold of p < 0.01).

Having defined the model SNPs and allele weights based on the training data, we then used the same model to calculate individual PHS in the independent test dataset. We evaluated the performance of the PHS as a predictor of age-dependent PD incidence by model Z score and plotted the Kaplan-Meier estimates for PD-free survival stratified by PHS percentile ranges.

Evaluating the performance of sex-specific models

In previous studies of AD, training and testing the PHS model in sex-matched datasets has been shown to significantly improve performance¹⁸, indicating that genetic risk interacts with sex, at least for a relevant subset of common susceptibility loci. In order to evaluate this possibility in PD, we repeated the same workflow for model training and testing in male and female data separately.

Predicting population risk of PD onset

Combined with incidence rates from epidemiological studies, PHS can be used to calculate genetically stratified estimates of absolute disease risk across the age spectrum.^10,19 We defined the age-dependent baseline risk based on epidemiological incidence rates by age-group from a comprehensive 2017 report on “The Incidence and Prevalence of Parkinson’s in the UK”.²⁰ As incidence rates were reported for 5-year intervals, we let values represent the midpoint of each interval and used one-dimensional interpolation to estimate annualized incidence rates. Hazard ratios of PHS percentile strata were used to visualize the influence of polygenic risk on incidence curves and recalculate stratified “instantaneous” risk across age groups, applying sample weight correction to account for different case-control proportions in the sample sets as detailed in a previous report.¹¹

Validating the model for onset prediction in PPMI data

We further tested the accuracy of PHS stratification in the relatively small PPMI dataset of 360 PD patients and 160 controls, emulating a clinical trial cohort of premanifest individuals with a high risk of developing PD at some unknown age. PPMI participants were stratified into ten PHS decile strata and the age-dependent absolute risk for each stratum was calculated across all one-year intervals from 50 to 75. For each PHS decile we extracted the age at which the proportion of individuals having developed PD reached 25%. We defined an absolute risk reference threshold (0.005) based on the risk corresponding to the 25% prevalence age in the 5th and 6th deciles, and expected age for all other decile strata was defined as the year when the same threshold was reached. This age was then compared to the actual observed age when prevalence reached 25% in each decile stratum.¹⁰

Results

The polygenic hazard score (PHS) and model performance

The Cox stepwise regression framework identified 71 SNPs that met criteria for inclusion in the final PHS model. Among these, 65 overlapped with significant loci reported in the most recent PD meta-GWAS (Supplementary table 2). Notably, several SNPs were included from loci that have also been reported to be individually associated with age at onset, including SNCA (3 SNPs) and TMEM165 (4 SNPs). PHS showed a strong association with age-related PD incidence in the test data (Z score 17.7, beta = 0.90, SE = 0.05, p < 10e-15). Stratified Kaplan-Meier estimates are shown in Figure 1, demonstrating the effect of PHS on age at onset in the test data. At the 50% survival level, there was a difference of almost 15 years in PD onset between the individuals with the 5% highest and the 25% lowest PHS in the test dataset. The hazard ratio comparing the highest to the lowest risk decile was 3.78 (95% CI 3.49–4.10) after sample weight correction.

Figure 1.

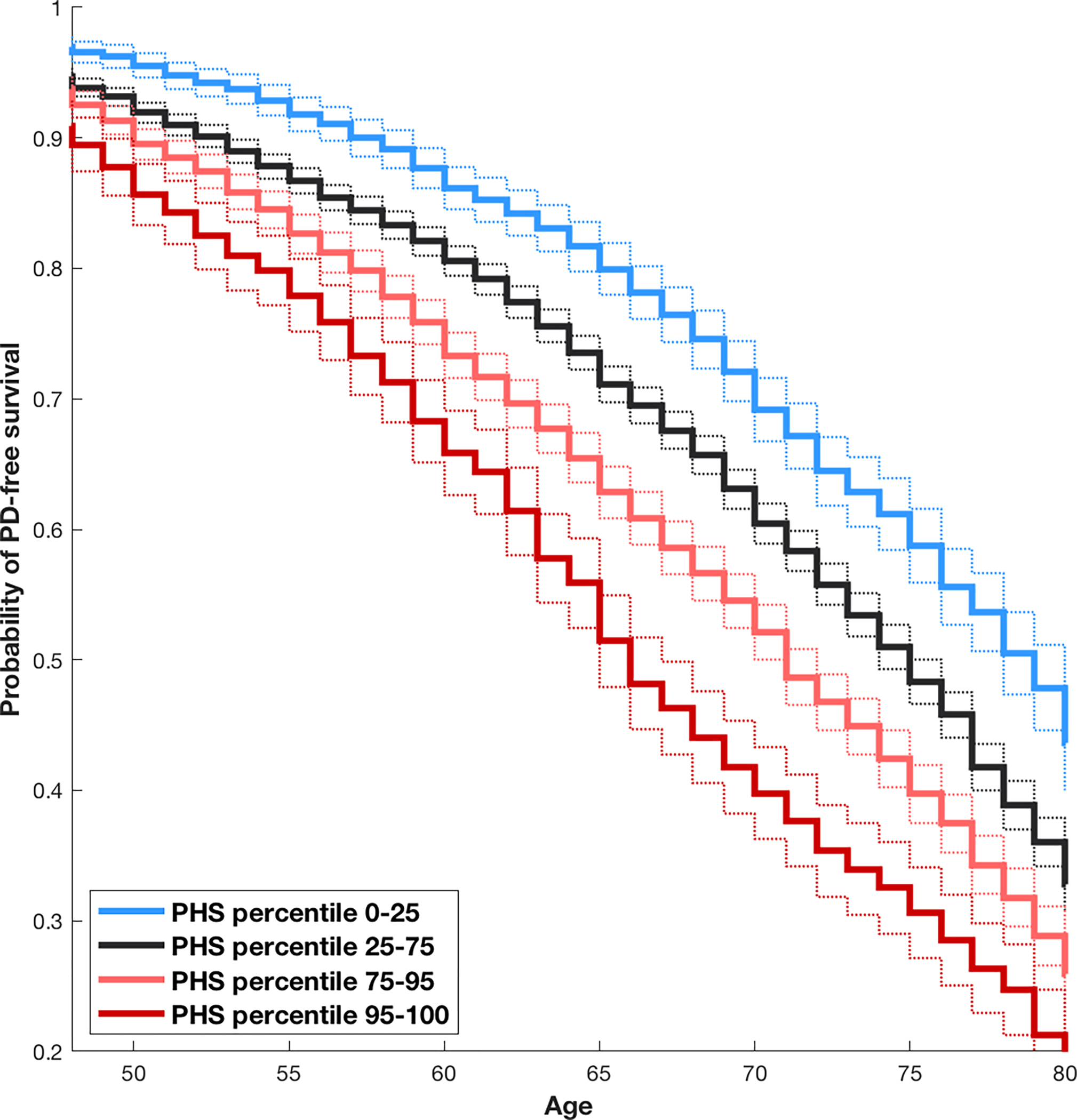
Kaplan-Meier curves for test data, stratified by PHS modeled in training data

Splitting the data into male and female subsets resulted in smaller sample size for the training (male: 7,258 PD and 4,610 controls; female 4,435 PD and 5,231 controls) and test (male: 3,297 PD and 3,061 controls; female: 1,815 and 2,311 controls) datasets. Using the same threshold (p<0.01) for SNP inclusion to the PHS model, 28 SNPs were selected for the male model and 32 SNPs for the female model. Neither model performed as well as the model combining data from both sexes (male Z score = 11.4; female Z score = 9.4). Relaxing the p-value threshold allowing more SNPs to be included did not improve the sex-specific models. Consequently, the potential benefits of a sex-specific PHS model did not outweigh the sacrifice in statistical power in our PD data.

Applying polygenic hazard scores (PHS) to population risk

Examples of estimated yearly incidence rates for different age groups recalculated for specific PHS strata are shown in Table 2. We note a more than 150-fold difference in instantaneous PD risk from the lowest risk decile in the 45–49 age group to the highest decile in the 75–79 age group. Incidence rates for selected PHS strata, estimated from hazard ratios and epidemiological data on baseline risk,²⁰ are shown in Figure 2.

Table 2.

Baseline incidence rates adjusted for polygenic hazard ratio

Age	Baseline incidence	PHS 1st decile (95% CI)	PHS 9th decile (95% CI)	PHS 10th decile (95% CI)
45–49	4	1.9 (1.8–2.0)	5.4 (5.3–5.5)	7.3 (7.0–7.5)
50–54	9.1	4.4 (4.2–4.6)	12.3 (12.0–12.5)	16.5 (15.9–17.1)
55–59	18.2	8.7 (8.3–9.1)	24.5 (24.1–25.0)	33.0 (31.8–34.2)
60–64	33.5	16.1 (15.4–16.8)	45.1 (44.3–45.9)	60.7 (58.6–63.0)
65–69	62.5	29.9 (28.5–31.2)	83.9 (82.4–85.4)	112.9 (108.9–117.1)
70–74	113.4	54.3 (51.9–56.8)	152.7 (149.9–155.5)	205.6 (198.2–213.2)
75–79	173.5	83.1 (79.5–867.0)	233.6 (229.4–237.9)	314.5 (303.3–326.1)

The table shows examples of how stratified absolute risk of Parkinson’s disease can be recalculated from baseline incidence using hazard ratio. Figures correspond to cases per 100,000 individuals in the population. Baseline incidences are from the Parkinson’s UK 2017 report on the incidence and prevalence of Parkinson's in the UK ²⁰

Figure 2.

Incidence rates for Parkinson’s disease stratified by polygenic hazard score

Onset prediction in PPMI data

Predicted and observed age at onset stratified for PHS in the PPMI data showed a clear correlation (Pearson’s r = 0.83, p = 0.0030). The results across all PHS decile strata are shown in Figure 3.

Figure 3.

Observed versus predicted age at onset in PPMI data

Discussion

We show for the first time that the PHS method can be used to estimate PHS-adjusted PD risk. Effect sizes were large enough to achieve significant validation with relatively small sample sizes, such as the PPMI study. Comparing the top and bottom PHS deciles we observed a hazard ratio of 3.78 (95% CI 3.49–4.10).

We focused our analysis on the age range from 40 to 75, demonstrating that a 71 SNP PHS model trained on the reference dataset successfully predicts empirical age at PD onset in the independent test data. The observed hazard ratio for top and bottom PHS deciles for PD is consistent with previous reports of an association between cumulative burden of genetic disease risk and age at onset in PD.^4,5,7–9 This is highly similar to previous findings in AD, where a PHS based on 31 non-APOE SNPs showed a hazard ratio of 3.34 (95% CI 2.62–4.24) between the top and bottom deciles.¹⁰

Methods that summarize the effect of many risk alleles into a polygenic score have gained increasing attention in complex genetics as ever larger GWAS datasets become available to train more powerful models.²¹ The polygenic hazard approach takes advantage of a survival analysis framework to integrate the genetic effects on disease risk and age at disease onset in a single model for age-dependent, complex disorders. A major advantage of the PHS method is that the hazard ratio is directly and intuitively interpretable as a modifier of baseline risk. We have shown how PHS can be combined with epidemiological data on incidence rates per age group in order to calculate genetically stratified estimates of instantaneous PD risk in a given population.

In AD, a sex-matched PHS was recently found to have a significantly stronger association with age at onset and other clinical outcomes than an ordinary sex-mismatched score, indicating a sex-dependent genetic architecture.¹⁸ We found no evidence of a similar sex-specific effect in PD, although we cannot exclude the possibility that a sex-matched PHS could have shown improved predictive power if the comparison was made with equal sample sizes. The lack of sex-specific effects in our study is consistent with the mostly negative sex-stratified results reported in a recent GWAS of age at onset in PD.³

Our study has some limitations. Most importantly, the model relies on assumptions that may not hold for PD at the extreme ends of the age at onset range. Early onset PD has a higher likelihood of a monogenic etiology and may have a different genetic architecture from PD with later onset also in sporadic cases. The trend for PD incidence late in life remains somewhat controversial, with conflicting results across studies. The 2017 epidemiological report from Parkinson’s UK showed a peak in annual incidence rate in the 80–84 age group, followed by a decline in the 85–89 group and even lower in individuals aged 90–94.²⁰ A similar pattern has been seen in other studies.^22,23 In contrast, a study from the Rochester Epidemiology Project, Minnesota, found increasing incidence rates all through the 9th decade of life²⁴, in line with a previous meta-analysis.¹⁴ Ascertainment challenges in the oldest age groups could plausibly contribute to these discrepancies, yet the question of a possible PD incidence peak or plateau remains currently unresolved.

We also note that determining the time of PD onset is not trivial. Subjective symptoms present insidiously, often years before the disease is diagnosed by a neurologist, and the accuracy of age at onset in large, heterogeneous datasets is likely to be low. More standardized and homogeneous criteria for determining age at onset would be expected to improve both the estimates of SNP effect sizes and the performance of the PHS. With respect to the genetic data, PHS calculation requires ethnically matched reference and test datasets. This limitation means that the model generated in our study has thus far only been validated for individuals of European ancestry. Application of a PHS derived with European ancestry data may have variable performance in individuals of other genetic ancestries, and ancestry-specific SNPs may improve performance.^25,26

Notwithstanding these limitations, our study holds promise for the future utility of polygenic hazard scores as biomarkers in PD. We anticipate clinical trials of disease-modifying therapies that aim to postpone the motor onset of PD, a context where an integrated estimate of disease risk as a function of both age and genetic profile could be an important asset for patient selection and stratification. Our validation in the PPMI dataset indicate that even with relatively small sample sizes, this type of stratification can be clinically meaningful, highlighting the clinical relevance of the current study and further efforts to optimize the polygenic hazard approach in the future.

Key points:

Question:

Is a polygenic hazard score model a useful framework to genetically stratify age-dependent risk of Parkinson’s disease?

Findings:

A polygenic hazard score predicts onset of Parkinson’s disease with a hazard ratio of 3.78 when comparing the highest to the lowest risk decile.

Meaning:

A polygenic hazard approach integrates the genetic effects on disease risk and age at onset of Parkinson’s disease in a single model, holding promise for risk stratification in future clinical trials.