On the 12th Day of Christmas, a Statistician Sent to Me . . .

Abstract

The BMJ’s statistical editors relish a quiet Christmas, so make their wish come true and pay attention to the list of common statistical faux pas presented here by Riley and colleagues

The weeks leading up to Christmas are a magical time for medical research. The impending holiday season creates a dramatic upsurge in productivity, with researchers finding time to finish off statistical analyses, draft manuscripts, and respond to reviewers’ comments. This activity leads to a plethora of submissions to journals such as The BMJ in December, so that researchers can finish the year with a sense of academic achievement and enjoy the festivities with their loved ones. Indeed, with optimism fuelled by mulled wine and mince pies, researchers may even anticipate their article’s acceptance by early January, at the end of the 12 days of Christmas.

A collective, however, works against this season of publication goodwill and cheer—a small but influential group of statisticians with very shiny noses for detail, seeking “all is right” rather than “all is bright” and emphasising no, no, no rather than ho, ho, ho. The statisticians’ core belief is that a research article is for life, not just for Christmas, and they deliver statistical reviews that promote high standards of methodological rigour and transparency. So you can imagine how busy they are during the Christmas period with its influx of submissions—even before they can eat, drink, and be merry, these individuals are working tirelessly to detect submissions with erroneous analysis methods that should be roasting on an open fire, dubious statistical interpretations as pure as yellow snow, and half-baked reporting of study details that bring zero comfort and joy. Bah humbug!

Each year The BMJ’s statistical editors review more than 500 articles. For about 30 years, the statistical team was led by Martin Gardner and Doug Altman,^{1 2} both of whom saw similarities between statisticians and the Christmas star, with the statisticians lighting a path of research integrity, promoting methodology over metrics,^{3 4} and encouraging statistical principles to “save science and the world.”⁵

To elicit the most common issues encountered during statistical peer review, an internal survey was administered to The BMJ’s statistical editors. Twelve items were identified, and each are described here. There is one item for each of the 12 days of Christmas, the period between 25 December and 5 January when the statisticians conduct their reviews in the mindset of the Grinch,⁶ but with the kind heart of Miracle On 34th Street.

Advent

Every December The BMJ’s statistical editors meet for a day, when they discuss common statistical concerns, problematic submissions (including those that slipped through the net, the so-called sin bin articles), and how to improve the review process, before unwinding at The BMJ’s Christmas party. At the meeting on 18 December 2019, the statisticians agreed that an article showcasing common statistical issues would be helpful for authors of future article submissions, and an initial set of items was discussed. When reminded about this article at subsequent Christmas meetings on 17 December 2020 and 16 December 2021, the statisticians explained that progress was being delayed, ironically because of the number of statistical reviews that needed to be prioritised in The BMJ’s system.

After further procrastination, on 28 June 2022 a potential list of items was shared among the statistical editors by email, and everyone was asked to include any further issues they regularly encountered during statistical review. The findings were collated and discussed (by email) and a final list of the most important items agreed for wider dissemination. Twelve items were selected, to match the number of days of Christmas in the well known song (and thereby increase the chance of publication in The BMJ’s Christmas issue). Sensitivity analyses, including shallow and deep learning approaches, led to the same 12 items being selected. An automated artificial intelligence algorithm quickly identified that all the statistical editors were guilty of similar statistical faux pas in some of their own research articles, and so are not whiter than snow.

The 12 days of statistical review

To help drive them home for Christmas, the 12 identified items are briefly explained. Consider them as stocking fillers for you, The BMJ reader and potential future author. Allowing for sizeable Christmas meals, digest one item each day between 25 December and 5 January and make a New Year’s resolution to follow the guidance.

On the first day of Christmas, a statistician sent to me:

Clarify the research question

Christmas is a time for reflection on the meaning of life and future expectations. Similarly, in their reviews, statisticians will often encourage authors to reflect on their research question and clarify their objectives. As an example, in an observational study, the authors may need to clarify the extent to which their research is descriptive or causal, prognostic factor identification or prediction model development, or exploratory or confirmatory. For causal research, authors may be asked to express the underlying premise (causal pathway or model), for example, in terms of a directed acyclic graph. In systematic reviews of intervention studies, authors might need to state their research question using the Population, Intervention, Comparison, and Outcome system—the PICO structure.

A related request would be to clarify the estimand—the study’s target measure for estimation.⁷ In a randomised trial, for example, the estimand is a treatment effect, but a statistician might request better definitions for the population, treatments being compared, outcomes, summary measure (eg, risk ratio or risk difference, conditional or marginal effect), and other features.^{7 8} Similarly, in a meta-analysis of randomised trials the estimand must be defined in the context of potential heterogeneity of study characteristics. In a meta-analysis of hypertension trials with different lengths of follow-up, for example, if the estimand is a treatment effect on blood pressure, clarity is needed about whether this relates to one time point (eg, one year), each of multiple time points (eg, one year and five years), or some average across a range of time points (eg, six months to two years).

On the second day of Christmas, a statistician sent to me:

Focus on estimates, confidence intervals, and clinical relevance

Just as with under-cooked turkeys being sent back so will articles that focus solely on P values and “statistical significance” to determine whether a finding is crucial. It is important to consider the estimates (eg, mean differences, risk ratios, or hazard ratios corresponding to the specified estimands from the first day of Christmas), corresponding 95% confidence intervals, and potential clinical relevance of findings. Statistical significance often does not equate to clinical significance—if, as an example, a large trial estimates a risk ratio of 0.97 and a 95% confidence interval of 0.95 to 0.99, then the treatment effect is potentially small, even though the P value is much less than 0.05. Conversely, absence of evidence does not mean evidence of absence⁹—here’s an example; if a small trial estimates a risk ratio of 0.70 and a 95% confidence interval of 0.40 to 1.10, then the magnitude of effect is still potentially large, even though the P value is greater than 0.05. Hence, the statistical editors will ask authors to clarify phrases such as “significant finding,” be less definitive when confidence intervals are wide, and consider results in the context of clinical relevance or impact. A bayesian approach may be helpful,¹⁰ to express probabilistic statements (eg, there is a probability of 0.85 that the risk ratio is <0.9).

On the third day of Christmas, a statistician sent to me:

Carefully account for missing data

Missing values occur in all types of medical research,¹¹ both for covariates and for outcomes. Authors need to not only acknowledge the completeness of their data but also to quantify and report the amount of missing data and explain how such data were handled in analyses. It is spooky how many submissions fail to do this—the ghost of Christmas articles past, present, and future.

If it transpires participants with missing data were simply excluded (ie, a complete case analysis was carried out), then authors may be asked to revise their analyses by including those participants, using an appropriate approach for imputing the missing values. A complete case analysis is rarely recommended, especially in observational research, as discarding patients usually reduces statistical power and precision to estimate relationships and may also lead to biased estimates.¹² The best approach for imputation is context specific and too nuanced for detailed interrogation here. For example, strategies for handling missing baseline values in randomised trials might include replacing with the mean value (for continuous variables), creating a separate category of a categorical predictor to indicate the presence of a missing value (ie, the missing indicator method), or multiple imputation performed separately by randomised group.^{13 14} For observational studies examining associations, mean imputation and missing indicator approaches can lead to biased results,¹⁵ and so a multiple imputation approach is often (though not always¹⁶) preferred. Under a missing at random assumption, this involves missing values being imputed (on multiple occasions to reflect the uncertainty in the imputation) conditional on the observed values of other study variables.¹⁷ When using multiple imputation, the methods used to do this need to be described, including the set of variables used in the imputation process. An introduction to multiple imputation is provided elsewhere,¹² and there are textbooks dedicated to missing data.¹⁸

On the fourth day of Christmas, a statistician sent to me:

Do not dichotomise continuous variables

Santa likes dichotomisation (you are either naughty or nice), but statisticians would be appalled if authors chose to dichotomise continuous variables, such as age and blood pressure, by splitting them into two groups defined by being above and below some arbitrary cut point, such as a systolic blood pressure of 130 mm Hg. Dichotomisation should be avoided,^{19 20} as it wastes information and is rarely justifiable compared with analysing continuous variables on their continuous scale (see the stocking filler for the fifth day of Christmas). Why should an individual with a value just below the cut point (in this instance 129 mm Hg) be considered completely different from an individual with a value just above it (131 mm Hg)? Conversely, the values for two individuals within the same group may differ greatly (let us say 131 mm Hg and 220 mm Hg) and so why should they be considered the same? In this context, dichotomisation might be considered unethical. Study participants agree to contribute their data for research on the proviso it is used appropriately; discarding information by dichotomising covariate values violates this agreement.

Dichotomisation also reduces statistical power to detect associations between a continuous covariate and the outcome,^{19 20 21} and it attenuates the predictive performance of prognostic models.²² In one example, dichotomising at the median value led to a reduction in power akin to discarding a third of the data,²³ whereas in another example, retaining the continuous scale explained 31% more outcome variability than dichotomising at the median.²⁰ Cut points also lead to data dredging and the selection of “optimal” cut points to maximise statistical significance.²¹ This leads to bias and lack of replication in new data and hinders meta-analysis because different studies adopt different cut points. Dichotomisation of continuous outcomes also reduces power and may result in misleading conclusions.^{24 25} A good example is a randomised trial in which the required sample size was reduced from 800 to 88 after the outcome (Beck score) changed from being analysed as dichotomised to being analysed on its continuous scale.²⁶

On the fifth day of Christmas, a statistician sent to me:

Consider non-linear relationships

At Christmas dinner, some family relationships are simple to handle, whereas others are more complex and require greater care. Similarly, some continuous covariates have a simple linear relationship with an outcome (perhaps after some transformation of the data, such as a natural log transformation), whereas others have a more complex non-linear relationship. A linear relationship (association) assumes that a 1 unit increase in the covariate has the same effect on the outcome across the entire range of the covariate’s values. The assumption being, for example, that the impact of a change in age from 30 to 31 years is the same as a change in age from 90 to 91 years. In contrast, a non-linear association allows the impact of a 1 unit increase in the continuous covariate to vary across the spectrum of predictor values. For example, a change in age from 30 to 31 years may have little impact on risk, whereas a change in age from 90 to 91 years may be important. The two most common approaches to non-linear modelling are cubic splines and fractional polynomials.^{27 28 29 30 31 32}

Aside from categorisation, most submissions to The BMJ only consider linear relationships. The statistical reviewers therefore may ask the researchers to consider non-linear relationships, to avoid important associations not being fully captured or even missed.³³ The study by Johannesen and colleagues is an example of non-linear relationships being examined.³⁴ The authors used restricted cubic splines to show that the association between low density lipoprotein cholesterol levels and the risk of all cause mortality is U-shaped, with low and high levels associated with an increased risk of all cause mortality in the general population of Denmark. Figure 1 illustrates the findings for the overall population, and for subgroups defined by use of lipid lowering treatment, with the relationship strongest in those not receiving treatment.

Fig 1.

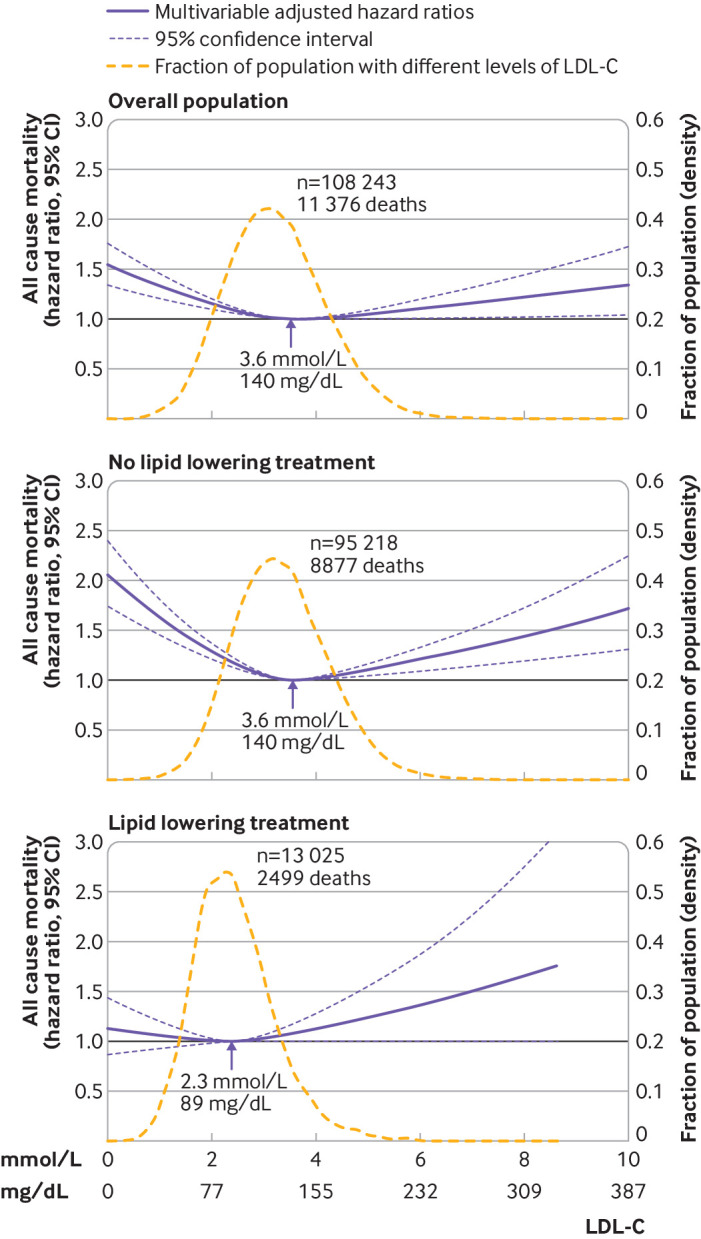
Non-linear association derived using restricted cubic splines of individuals from the Copenhagen General Population Study followed for a mean 9.4 years, from Johannesen et al.³⁴ Multivariable adjusted hazard ratios for all cause mortality are shown according to levels of low density lipoprotein cholesterol (LDL-C) on a continuous scale. 95% confidence intervals are derived from restricted cubic spline regressions with three knots. Reference lines for no association are shown at a hazard ratio of 1.0. Arrows indicate concentration of LDL-C associated with the lowest risk of all cause mortality. Analyses were adjusted for baseline age, sex, current smoking, cumulative number of cigarette pack years, systolic blood pressure, lipid lowering treatment, diabetes, cardiovascular disease, cancer, and chronic obstructive pulmonary disease

On the sixth day of Christmas, a statistician sent to me:

Quantify differences in subgroup results

Many submitted articles include results for subgroups, such as defined by sex or gender, or those who do and do not eat Brussels sprouts. A common mistake is to conclude that the results for one subgroup are different from the results of another subgroup, without actually quantifying the difference. Altman and Bland considered this eloquently,³⁵ showing treatment effect results for two subgroups, the first of which was statistically significant (risk ratio 0.67, 95% confidence interval 0.46 to 0.98; P=0.03), whereas the second was not (0.88, 0.71 to 1.08; P=0.2). A naïve interpretation is to conclude that the treatment is beneficial for the first subgroup but not for the second subgroup. However, actually comparing the results between the two subgroups reveals a wide confidence interval (ratio of risk ratios 0.76, 95% confidence interval 0.49 to 1.17; P=0.2), which suggests further research is needed before concluding a subgroup effect. A related mistake is to make conclusions about whether subgroups differ based solely on if their separate 95% confidence intervals overlap or not.³⁶ Hence, if researchers examine subgroups in their study, the statistical editors will check for quantification of differences in subgroup results, and, if not done, ask for this to be addressed. Even when genuine differences exist between subgroups, the (treatment) effect may still be important for each subgroup, and therefore this should be recognised in study conclusions.

Examining differences between subgroups is complex, and a broader topic is the modelling of interactions between (treatment) effects and covariates.³⁷ Problems include the scale used to measure the effect (eg, risk ratio or odds ratio),³⁸ ensuring subgroups are not arbitrarily defined by dichotomising a continuous covariate,³⁹ and allowing for potentially non-linear relationships (see our stocking fillers for the fourth day and fifth day of Christmas).⁴⁰

On the seventh day of Christmas, a statistician sent to me:

Consider accounting for clustering

At The BMJ’s Christmas party, the statistical editors tend to cluster in a corner, avoiding interaction and eye contact with non-statisticians whenever possible for fear of being asked to conduct a postmortem examination of rejected work. Similarly, a research study may contain data from multiple clusters, including observational studies that use e-health records from multiple hospitals or practices, cluster or multicentre randomised trials,^{41 42 43 44 45 46} and meta-analyses of individual participant data from multiple studies.⁴⁷ Sometimes the analysis does not account for this clustering, which can lead to biased results or misleading confidence intervals.^{48 49 50 51} Ignoring clustering makes a strong assumption that outcomes for individuals within different clusters are similar to each other (eg, in terms of the outcome risk), which may be difficult to justify when clusters such as hospitals or studies have different clinicians, procedures, and patient case mix.

Thus, if, in the data analysis, a submitted article ignores obvious clustering that needs to be captured or considered, the statistical editors will ask for justification of this or for a reanalysis accounting for clustering using an approach suitable for the estimand of interest (see our stocking filler for the first day of Christmas).^{52 53 54} A multilevel or mixed effects model might be recommended, for example, as this allows cluster specific baseline risks to be accounted for and enables between cluster heterogeneity in the effect of interest to be examined.

On the eighth day of Christmas, a statistician sent to me:

Interpret I² and meta-regression appropriately

Systematic reviews and meta-analyses are popular submissions to The BMJ. Most of them include the I² statistic⁵⁵ but interpret it incorrectly, which gives the statisticians a recurring nightmare before (and after) Christmas. I² describes the percentage of variability in (treatment) effect estimates that is due to between study heterogeneity rather than chance. The impact of between study heterogeneity on the summary treatment effect estimate is small if I² is close to 0%, and it is large if I² is close to 100%. A common mistake is for authors to interpret I² as a measure of the absolute amount of heterogeneity (ie, to consider I² as an estimate of the between study variance in true effects), and to erroneously use it to decide whether to use a random effects meta-analysis model. This is unwise, as I² is a relative measure and depends on the size of the within study variances of effect estimates, not just the size of the between study variance of true effects (also known as τ²). For example, if all the included studies are small, and thus within study variances of effect estimates are large, I² can be close to 0% even when the between study variance is large and important.⁵⁶ Conversely, I² may be large even when the between study variance is small and unimportant. Statistical reviews will ask authors to correct any misuse of I², and to also present the estimate of between study variance directly.

Meta-regression is often used to examine the extent to which study level covariates (eg, mean age, dose of treatment, risk of bias rating) explain between study heterogeneity, but generally the statistical editors will ask authors to interpret meta-regression results cautiously.⁵⁷ Firstly, the number of trials are often small, and then meta-regression is affected by low power to detect study level characteristics that are genuinely associated with changes in the overall treatment effect in a trial. Secondly, confounding across trials is likely, and so making causal statements about the impact of trial level covariates is best avoided. For example, those trials with a higher risk of bias might also have the highest dose or be conducted in particular countries, thus making it hard to disentangle the effect of risk of bias from the effect of dose and country. Thirdly, the trial level association of aggregated participant level covariates (eg, mean age, proportion men) with the overall treatment effect should not be used to make inferences about how values of participant level covariates (eg, age, sex, biomarker values) interact with treatment effect. Aggregation bias may lead to dramatic differences in observed relationships at the trial level from those at the participant level,^{58 59} as shown in figure 2.

Fig 2.

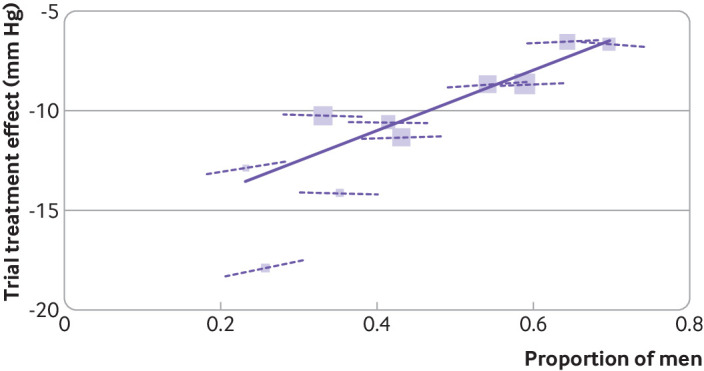
Aggregation bias when using meta-regression of study level results rather than individual participant data meta-analysis of treatment-covariate interactions. The research question was whether blood pressure lowering treatment is more effective among women than men. Evidence is shown from a meta-analysis of 10 trials of antihypertensive treatment, comparing the across trial association of treatment effect and proportion men (solid line)—which is steep and statistically significant—with participant level interactions of sex and treatment effect in each trial (dashed lines) —which are flat and neither clinically nor statistically important. This case study is based on previous work.^{47 58 60} Each block represents one trial, with block size proportional to trial size. Across trial association is denoted by gradient of solid line, derived from a meta-regression of the trial treatment effects against proportion of men, which suggests a large effect of a 15 mm Hg (95% confidence interval 8.8 to 21 mm Hg) greater reduction in systolic blood pressure in trials with only women compared with only men. However, the treatment-sex interaction based on participant level data is denoted by gradient of dashed lines within each trial, and on average these suggest only a 0.8 mm Hg (−0.5 to 2.1 mm Hg) greater treatment effect for women than for men, which is neither clinically nor statistically significant

On the ninth day of Christmas, a statistician sent to me:

Assess calibration of model predictions

Clinical prediction models estimate outcome values (for continuous outcomes) or outcome risks (for binary or time-to-event outcomes) to inform diagnosis and prognosis in individuals. Articles developing or validating prediction models often fail to fully evaluate model performance, which can have important consequences because inaccurate predictions can lead to incorrect decisions and harmful communication to patients, such as giving false reassurance or hope. For models that estimate outcome risk, predictive performance should be evaluated in terms of discrimination, calibration, and clinical utility, as described elsewhere.^{61 62 63}

However, the majority of submissions focus only on model discrimination (as quantified by, for example, the C statistic or area under the curve²⁸)—when this is done, an incomplete impression is created, just as with that unfinished 1000 piece jigsaw from last Christmas. Figure 3 shows a published calibration plot for a prediction model with a promising C statistic of 0.81, but there is clear (albeit perhaps small) miscalibration of predicted risks in the range of predicted risks between 0.05 and 0.2.⁶⁴ This miscalibration may impact the clinical utility of the model, especially if decisions, such as about treatment or monitoring strategies, are dictated by risk thresholds in that range of predicted risks, which can be investigated in a decision curve analysis.⁶⁵ Conversely, miscalibration does not necessarily indicate the model has no clinical utility, as it depends on the magnitude of miscalibration and when it occurs in relation to decision thresholds.

Fig 3.

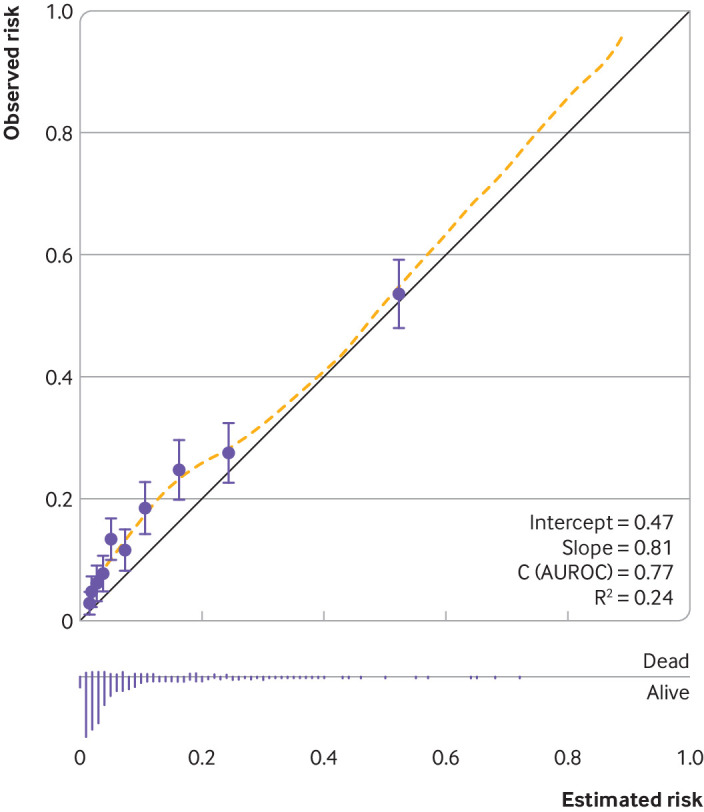
Example of a calibration plot to examine agreement between observed risks and estimated (predicted) risks from a prediction model.⁶⁴ The study developed prediction models to estimate the risk of mortality in individuals who experienced subarachnoid haemorrhage from ruptured intracranial aneurysm. Circles are estimated and observed risks grouped by 10ths of estimated risks, and the yellow dashed line is a loess smoother to capture agreement across the range of estimated risks. AUROC=area under the receiving operator characteristic

Statistical editors may also suggest that researchers of model development studies undertake a reanalysis using penalisation or shrinkage methods (eg, ridge regression, lasso, elastic net), which reduce the potential for overfitting and help improve calibration of predictions in new data.^{66 67} Penalisation methods, such as Firth’s correction,⁶⁸ can also be important in non-prediction situations (eg, randomised trials estimating treatment effects) with sparse data, as standard methods (such as logistic regression) may give biased effect estimates in this situation.⁶⁹

On the 10th day of Christmas, a statistician sent to me:

Carefully consider the variable selection approach

A common area of criticism in statistical reviews is the use of variable selection methods (eg, selection of covariates based on the statistical significance of their effects).⁷⁰ If these methods are used, statistical editors will ask authors for justification. Depending on the study, statistical editors might even suggest authors avoid these approaches entirely, just as you would that last remaining turkey sandwich on New Year’s Day. For example, variable selection methods are best avoided in prognostic factor studies, as the typical aim is to provide an unbiased estimate of how a particular factor adds prognostic value over and above other (established) prognostic factors.⁷¹ Therefore, a regression model forcing in all the existing factors is needed to examine the prognostic effect of the new factor after accounting for the effect of existing prognostic factors. Similarly, in causal research based on observational data, the choice of confounding factors to include as adjustment factors should be selected based on the causal pathway—for example, as expressed using directed acyclic graphs (with consideration of potential mediators between covariates and outcome⁷²), not statistical significance based on automated selection methods.

In the development of clinical prediction models, variable selection (through shrinkage) may be incorporated using methods such as lasso or elastic net, which start with a full model including all candidate predictors for potential inclusion. A common, but inappropriate approach is to use univariable screening, when decisions for predictor inclusion are based on P values for observed unadjusted effect estimates. This is not a sensible strategy,⁷³ as what matters is the effect of a predictor after adjustment for other predictors, because in practice the relevant predictors are used (by healthcare professionals and patients) in combination. When, for example, a prognostic model was being developed for risk of recurrent venous thromboembolism, the researchers found that the unadjusted prognostic effect of age was not statistically significant from univariable analysis but that the adjusted effect was significant and in the opposite direction from multivariable analysis.⁷⁴

On the 11th day of Christmas, a statistician sent to me:

Assess the impact of any assumptions

Everyone agrees that It’s A Wonderful Life is a Christmas movie, but whether this applies to Die Hard is debatable. Similarly, statistical editors might debate authors’ die-hard analysis assumptions, and even ask them to examine whether results change if the assumptions change (a sensitivity analysis). For example, in submitted trials with time-to-event data, such as time to recurrence or death, it is common to report the hazard ratio, assuming it is a constant over the whole follow-up period. If this assumption is not justified in an article, authors may be asked to address this—for example, by graphically presenting how the hazard ratio changes over time (perhaps based on a survival model that includes an interaction between the covariate of interest and (log) time).⁷⁵ Another example is in submissions with bayesian analyses, where prior distributions are labelled as “vague” or “non-informative” but may still be influential. In this situation, authors may be asked to demonstrate how results change when other plausible prior distributions are chosen.

On the 12th day of Christmas, a statistician sent to me:

Use reporting guidelines and avoid overinterpretation

Altman once said, “Readers should not have to infer what was probably done, they should be told explicitly. Proper methodology should be used and be seen to have been used.”⁷⁶ Incompletely reported research is indefensible and creates confusion, just as with those unlabelled presents under the Christmas tree. Readers need to know the rationale and objectives of a reported study, the study design, methods used, participant characteristics, results, certainty of evidence, research implications, and so forth. If any of these elements are missing, authors will be asked to clarify them.

Make use of reporting guidelines. They provide a checklist of items to be reported (Santa suggests checking this twice), which represent the minimum detail required to enable readers (including statistical editors) to understand the research and critically appraise its findings. Reporting guidelines are listed on The EQUATOR Network website, which maintains a comprehensive collection of guidelines and other materials related to health research reporting.⁷⁷ Table 1 shows examples, including the CONSORT statement for randomised trials⁷⁹ and the TRIPOD guideline for prediction model studies.^{80 81} The BMJ requires authors to complete the checklist within the relevant guideline (and include it with a submission), indicating on which page of the submitted manuscript each item has been reported.

Table 1.

Examples of reporting guidelines and their extensions for different study designs

Study design	Reporting guideline	Extensions available for some other common designs
Randomised trials	CONSORT (consolidated standards of reporting trials)	Cluster trials (CONSORT-Cluster), multi-arm trials, non-inferiority or equivalence trials (CONSORT non-inferiority), harms (CONSORT-HARMS), pilot and feasibility trials, adaptative designs (ACE statement), artificial intelligence (CONSORT-AI), interventions (TIDieR, template for intervention description and replication)
Observational studies	STROBE (strengthening the reporting of observational studies in epidemiology)	Genetic associations (STREGA, strengthening the reporting of genetic association studies), molecular epidemiology (STROBE-ME), infectious diseases (STROBE-ID), nutritional epidemiology (STROBE-Nut), mendelian randomisation (STROBE-MR)
Systematic reviews	PRISMA (preferred reporting items for systematic reviews and meta-analyses)	Abstracts (PRISMA-Abstracts), individual participant data (PRISMA-IPD, diagnostic test accuracy (PRISMA-DTA), harms (PRISMA-harms), network meta-analysis (PRISMA-NMA), literature searches (PRISMA-S)
Diagnostic test accuracy	STARD (standards for reporting diagnostic accuracy studies)	Abstracts (STARD-Abstracts), artificial intelligence (STARD-AI)
Prediction model studies	TRIPOD (transparent reporting of a multivariable prediction model for individual prognosis or diagnosis)	Abstracts (TRIPOD-Abstracts), individual participant data meta-analysis or clustered data (TRIPOD-Cluster),78 systematic reviews (TRIPOD-SRMA), machine learning (TRIPOD-AI)

Another common part of the statistical editors review process, related to reporting, is to query overinterpretation of findings—and even spin,⁸² such as unjustified claims of causality, generalisability of results, or immediate implications for clinical practice. Incorrect terminology is another bugbear—in particular the misuse of multivariate (rather than multivariable) to refer to a regression model with multiple covariates (variables), and the misuse of quantiles to refer to groups rather than the cut points used to create the groups (eg, deciles are the nine cut points used to create 10 equal sized groups called 10ths).⁸³

Epiphany

This list of 12 statistical issues routinely encountered during peer review of articles submitted to The BMJ will hopefully help authors of future submissions. Last Christmas statistical editors tweeted this list, but the very next day they got poor submissions anyway. This year, to save them from tears, they’ve tailored it for someone special—you, The BMJ reader.

Authors should address this list before rushing to submit papers to The BMJ next Christmas, in order to bring joy to the world by reducing the length of statistical reviews and allowing the statistical editors to spend more time with their significant (yes, pun intended) others over the festive period. If authors did adhere to this guidance, the “On the 12th Day of Christmas” song would change to the very positive “On the 12th Day of Christmas Review” with lyrics reflecting feedback from a happy statistician (perhaps join in using the song sheet in figure 4).

Fig 4.

Song sheet for “On the 12th Day of Christmas Review, a Happy Statistician sent to me . . .”

Ultimately, The BMJ wants to publish the gold not the mould, the frankincense not the makes-no-sense, and the myrrh not the urrgghh. Many other topics could have been mentioned, and for further guidance readers are directed to the BMJ Statistics Notes series (written mainly by Doug Altman and Martin Bland), the Research Methods and Reporting section of The BMJ,⁸⁴ and other overviews of common statistical mistakes.^{85 86}