Abstract
Physics-based computational models of the cardiovascular system are increasingly used to simulate hemodynamics, tissue mechanics, and physiology in evolving healthy and diseased states. While predictive models using computational fluid dynamics (CFD) originated primarily for use in surgical planning, their application now extends well beyond this purpose. In this review, we describe an increasingly wide range of modeling applications aimed at uncovering fundamental mechanisms of disease progression and development, performing model-guided design, and generating testable hypotheses to drive targeted experiments. Increasingly, models are incorporating multiple physical processes spanning a wide range of time and length scales in the heart and vasculature. With these expanded capabilities, clinical adoption of patient-specific modeling in congenital and acquired cardiovascular disease is also increasing, impacting clinical care and treatment decisions in complex congenital heart disease, coronary artery disease, vascular surgery, pulmonary artery disease, and medical device design. In support of these efforts, we discuss recent advances in modeling methodology, which are most impactful when driven by clinical needs. We describe pivotal recent developments in image processing, fluid–structure interaction, modeling under uncertainty, and reduced order modeling to enable simulations in clinically relevant timeframes. In all these areas, we argue that traditional CFD alone is insufficient to tackle increasingly complex clinical and biological problems across scales and systems. Rather, CFD should be coupled with appropriate multiscale biological, physical, and physiological models needed to produce comprehensive, impactful models of mechanobiological systems and complex clinical scenarios. With this perspective, we finally outline open problems and future challenges in the field.
I. INTRODUCTION AND CLINICAL NEED
Cardiovascular modeling and simulation methods originated to provide clinicians and surgeons with predictive modeling capabilities to aid in optimizing and personalizing patient treatment plans. Likewise, it was intended that medical device design could be accelerated by testing proposed designs in a virtual setting before they are deployed in animal or clinical studies. This was initially accomplished by adapting existing physics-based predictive simulation technology for use in the biomedical space; such methods are routinely used by the automotive, aerospace, energy, and hi-tech industries to test and optimize designs before they are built. Early pioneers in this space developed idealized, and then patient-specific, models of blood flow and initial progress was driven by close partnerships between clinicians and engineers.1–4 Adaptation of numerical technologies, such as finite element methods (FEMs), linear systems solvers, fluid–structure interaction (FSI) capabilities, and image segmentation algorithms, to biomedical problems led to rapid early growth in patient-specific modeling capabilities. However, the results of early attempts at predictive surgical planning based on “computational fluid dynamics (CFD) alone” were mixed. Indeed, this early experience laid bare the need to incorporate biological and physiological complexity that goes “beyond CFD.”
While the need for predictive treatment planning remains a primary motivation for simulation technology development, it is clearer than ever that models must account for mechanobiological response, physiologic adaptation, and patient heterogeneity across scales. Compared to traditional engineering applications, cardiovascular modeling brings a distinct set of challenges and complexities. These include anatomic structures beyond the limits of current image resolution, tissues that are mechanosensitive and adaptive, gene regulatory networks that differentially respond to mechanical stimuli, individual risk factors for disease initiation and progression, and autoregulatory systems that dynamically respond to changing conditions such as disease and exercise. Incorporating these effects across scales drives methodological developments unique to the cardiovascular setting. In addition, computational models are now proving crucial in basic scientific discovery beyond the original aims of treatment planning. As such, simulations are now being used to explain basic mechanisms of disease progression and cardiac development, settings in which mechanical forces are often instrumental but difficult to directly measure in vivo. With these deeper links between mechanical stimuli and mechanobiological response, exciting new possibilities for model-driven design are emerging.
In this review, we first briefly discuss the state of the art in patient-specific modeling capabilities, with a primary focus on core technology in image segmentation, patient-specific models, hemodynamics simulations, and fluid–structure interaction (FSI). We discuss the increasing clinical impact of this technology, with a particular focus on coronary and pulmonary applications, including congenital heart disease. Second, we describe important new modeling directions and technologies, including reduced order modeling (ROM), optimization, uncertainty quantification (UQ), multi-physics simulations, and whole heart modeling. Third, we review new and emerging capabilities at the interface of patient-specific modeling and biology, including growth and remodeling, thrombus formation, tissue engineering, and systems biology. We describe current and potential impacts of these methods to uncover fundamental mechanisms of disease progression and vascular and cardiac development. Finally, we discuss future challenges, including barriers to clinical adoption, and highlight emerging directions in tissue bioprinting and model-driven design. Before proceeding further, we briefly outline key open-source and open-data resources available to researchers in the field.
A. Open science resources
The field of cardiovascular biomechanics is fortunate to be replete with high-quality open science resources thanks to a strong culture of collaboration and sharing. Several open-source packages are available for image processing and segmentation including ITK-SNAP, 3D-Slicer, VMTK, and MITK.5–8 In the area of modeling and simulation, a complete pipeline from anatomic model construction to finite element simulation and analysis is available from SimVascular9 and Crimson,10 which both include capabilities for FSI and boundary condition coupling to physiologic lumped parameter networks (LPNs). CircAdapt provides an open-source framework to simulate reduced order models of whole body circulation and includes the ability to simulate cardiovascular structural adaptation to experienced hemodynamic loads.11 FEBio12 provides rich capabilities in continuum mechanics, soft tissues, and, more recently, flow simulation. lifex similarly offers tools to simulate multiphysics, multiscale, and multidomain problems and is particularly optimized for the simulation cardiac mechanics problems.13 General purpose solvers may also be adopted for fluid mechanics and multi-physics applications in biomechanics, including OpenFoam14 and FEniCS.15 IBAMR (https://ibamr.github.io/) also provides high-quality flow and FSI solver technology using the immersed boundary (IB) approach. OpenCARP16 is a valuable resource for single-cell and multiscale cardiac electrophysiology simulations. Open-source packages for scientific visualization are also available and include ParaView17 and VisIt.18
Open data repositories have been developed to complement simulation packages and are increasingly important to support efforts in machine learning (ML) and artificial intelligence. The vascular model repository19 (https://www.vascularmodel.com) provides approximately one hundred fifty (and growing) complete projects containing medical images, anatomic models, and simulation files that are fully compatible with the SimVascular software (Fig. 1). The Cardiac Atlas Project20 also contains multiple datasets containing cardiac images, segmented models, and accompanying tools for shape analysis, landmark detection, and motion tracking. In addition, several open-access resources exist for datasets of partial or whole-heart segmentations.21–25 These repositories are of enormous value to the medical device community in light of recent efforts by the United States Food and Drug Administration (FDA) to increasingly incorporate modeling and simulation in the device approval process.
FIG. 1.
Subset of vascular models available in the vascular model repository.
A variety of commercial packages are also available for fluid and solid mechanics, finite element, and finite volume analysis, including Ansys Fluent, COMSOL, LS-DYNA, and Abaqus. A laudable effort in the field is the Living Heart Project led by Dassault Systémes, which has fostered a growing international ecosystem of industry, academic, and governmental collaborators to develop and validate highly accurate, personalized digital human heart models.26 This group aims to establish foundational technology for cardiovascular in silico medicine in support of education and training, medical device design, testing, clinical diagnosis, and regulatory science.
II. PREDICTIVE SIMULATION METHODS
A. Anatomic model construction and image processing
Cardiovascular disease patients exhibit heterogeneity in anatomy, material properties, physiology, and genetics. Patient-specific, as opposed to idealized or population averaged, models are, thus, needed to accurately capture variable anatomy and hemodynamic conditions. The patient-specific modeling pipeline typically begins with image processing and segmentation. This is an often laborious process requiring “by hand” user segmentation and expertise in medical imaging to create accurate models. A primary method for anatomic model creation is the “path planning” approach in which centerline vessel paths are created, the vessel lumen is segmented in 2D contours normal to the paths, and the segmentations are “lofted” to create a complete 3D anatomic model. This method forms the backbone of the modeling pipeline in the SimVascular and Crimson packages and has been employed in numerous application-oriented studies.27–32 Alternative 3D segmentation approaches are also popular for model construction and are available in packages such as ITK-Snap and VMTK. Common methods include colliding fronts, region growing techniques, and active contours. Extensive reviews of available choices are found elsewhere.33
Automating the image segmentation process is crucial to enable clinical trials and studies with large patient cohorts. Currently, the substantial time required for model construction poses a major barrier to both clinical adoption and the use of modeling in large studies. While traditional approaches such as level set and thresholding methods offer some automation capabilities, these methods often require extensive parameter tuning, which largely negates any gains in efficiency.
Machine learning (ML) and convolutional neural networks (CNNs) have, thus, recently been adopted for both vascular and cardiac image segmentation with promising results. Vessel lumen regression using neural networks dramatically reduced user time for model construction in a recent study and demonstrated good accuracy, particularly in larger vessels.34,35 Uncertainties using this approach were quantified and found to be on par with user-to-user variability in by-hand image segmentation. Automated segmentation of coronary angiography images was successfully performed using the AngioNet platform with CNNs in recent work.36 Cardiac segmentation with ML, including all four heart chambers and major vessels, is also showing promise, and excellent results were recently achieved using graph neural networks with a mesh decoding module.25,37,38 ML has also been used for the automatic assessment of image quality, providing an operator-independent method of standardizing datasets for further processing, including automatic segmentation.39
B. Hemodynamics simulations and fluid–structure interaction methods
Cardiovascular modeling requires handling multiple coupled physical processes, including the interaction of fluids, solids, electrical propagation, active contraction, and transport. While simulations of flow and fluid–structure interaction are relatively well established, multi-physics models are an active area of research that will be discussed in Sec. IV B.
Unstructured mesh generation in complex anatomic models is typically performed with consideration of boundary layers, adaptation to velocity gradients, and areas of local refinement.40 Hemodynamics simulations are then carried out using computational fluid dynamics (CFD), which can be performed with a variety of numerical methods, including finite element methods (FEM) and finite volume techniques. Methods for rigid wall CFD in patient-specific models are generally well established, particularly with simple outflow boundary conditions such as resistance and Windkessel models.41,42 Even with simple boundary conditions, it is important to replicate physiologic conditions and tune parameter values to match available clinical data. Indeed, simulations can produce dramatically non-physiologic results when naive (e.g., zero pressure) boundary conditions are applied.41 More extensive physiologic models are also now routinely applied using 3D–0D approaches, in which the 3D domain is numerically coupled to an open or closed-loop lumped-parameter network (LPN) of the circulation, solved numerically.43–46 LPN models make a hydraulic analogy with electrical circuits and can include heart models, nonlinear elements, and coronary physiology. This coupling also necessitates special considerations in the linear system solution due to ill-conditioning, and custom preconditioning and bi-partitioned linear solver strategies have been developed.47,48 Backflow stabilization is often needed to avoid numerical instabilities caused by flow reversal at the model outlets.49 3D simulations have been similarly coupled to 1D models to capture wave propagation in compliant models.50,51 Reduced order modeling strategies are discussed further in Sec. IV A.
FSI is critical to capture wall deformation, wave propagation, and tissue mechanics in cardiovascular models and is increasingly well established. The arbitrary Lagrangian–Eulerian (ALE) method has been adopted for cardiovascular FSI with thick-walled vessels and variable material properties in several studies, including application to complex geometries such as cerebral aneurysms and single ventricle models.52,53 In the ALE framework, fluid–structure behavior is governed by
| (1) |
| (2) |
in the Eulerian fluid domain, where ρ is the density, χ represents the spatial coordinate with respect to a suitable reference frame moving with the domain velocity , v is the velocity, is the fluid stress tensor, and b is the body force per unit mass. The Lagrangian solid domain is governed by
| (3) |
where is the Cauchy stress in the solid domain, is the body force per unit mass in the solid domain, ρs is the density in the solid domain, and is the acceleration in the solid domain. The tractions, displacements, and velocities are constrained to match at the fluid–structure interface.
Figure 2 shows a clinical application of FSI to aortic dissection.27 This example incorporates vessel wall prestress and external tissue support, which has proven to be crucial for damping unphysical oscillations and avoiding unrealistic over-distension of pressurized models.54–56 While most FSI studies to date have used linear material models, sophisticated nonlinear models of vascular tissues based on sound experimental data are widely available in the continuum mechanics community and should be adopted to increase the realism of FSI simulations.57,58 Efficiency gains have been made with the coupled momentum method (CMM), introduced as an alternative to ALE for small deformation vascular FSI,59 and this method has been validated against in vitro experiments and widely adopted.60–64
FIG. 2.
FSI model of aortic dissection with vessel wall prestress and external tissue support. Streamlines (left) in systole (top) and diastole bottom and pressure (right). True and false lumen are clearly visible with streamlines entering the false lumen at the focal entry tear. Adapted from Ref. 27.
Key advances in FSI methodologies have been introduced recently, overcoming prior limitations of both ALE and CMM methods for vascular simulations. ALE methods traditionally employed dichotomous formulations for the fluid and solid subproblems, creating challenges and disparities in numerical schemes for modeling the coupled system. While the constitutive relations for finite elasticity were traditionally formulated in terms of the Helmholtz free energy (or strain energy), this ceases to be a proper potential in the incompressible limit, leading to ill-conditioned matrix systems. To overcome this issue, recent work of Liu et al. employed a Legendre transformation, allowing the use of Gibbs free energy to describe material behavior in both the incompressible and compressible regimes.65 In this setting, the following unified ALE description emerges, governing the conservation of mass and momentum in the fluid and the solid,
| (4) |
| (5) |
where ρ is the density, p is the pressure, is the isothermal compressibility coefficient, χ represents the spatial coordinate with respect to a suitable reference frame moving with the domain velocity , x is the spatial coordinate in the Eulerian domain, v is the velocity, is the deviatoric component of the Cauchy stress, and b is the body force per unit mass. Constitutive modeling determines the analytic forms for and to close the system. This system governs both viscous fluids and elastic solids and thus bridges the gap between methods for CFD and structural dynamics. This simplifies FSI analysis by producing a unified formulation requiring a single numerical solution strategy.
The above formulation spurred important further developments. Discretizing the nonlinear partial differential equation (PDE) system in Eqs. (4) and (5) in conjunction with the Newton–Raphson method produces a large linear system of sparse matrices, the solution of which constitutes the bulk of the computational time for simulation. A robust and efficient iterative method with nested block preconditioning was introduced to leverage the structure of the system for efficiency gains.66,67 Within the nonlinear solution procedure, a block factorization is performed for the consistent tangent matrix to decouple the kinematics from the balance laws. Within the linear solution procedure, another block factorization is performed to decouple the mass balance equation from the linear momentum balance equation. A nested block preconditioner was introduced to combine the Schur complement reduction approach with the fully coupled approach, yielding performance gains compared to standard methods in several full-scale cardiovascular examples. Further developments led to a formulation for handling viscoelasticity in finite deformation linear models.68 Improvements in the temporal accuracy for the pressure were also achieved via modifications to the generalized-α time advancement method.69
A novel reduced unified continuum (RUC) formulation was then developed for efficient vascular FSI building on the above technologies.70 In contrast to the CMM method, the underlying derivation does not require the use of a fictitious body force in the elastodynamics sub-problem, resulting in a direct reduction of the ALE method. The generalized-α method was adopted for the monolithic problem, avoiding prior issues of high-frequency oscillations. This method was formulated with a three-level nested block preconditioner which demonstrated robust performance over a wide range of physical parameters. Verification against Womersley's deformable wall theory showed excellent agreement.
The immersed boundary (IB) method, first introduced by Peskin for ventricular flow simulations,71 has also been widely adopted for FSI, particularly for cardiac geometries and heart valve simulations with large leaflet deformation and contact. The original formulation describes the momentum, viscosity, and incompressibility of the fluid–solid system in the Eulerian form and the deformations, stresses, and resultant forces of the immersed structure in Lagrangian variables. The Eulerian and Lagrangian frames are then linked using integral transforms with Dirac delta function kernels. Recent noteworthy developments in IB methodology include sharp interface and discrete immersed surface methods.72–74 Handling of incompressible solids has been improved in recent work introducing stabilization approaches for hyperelastic immersed surfaces.75 Experimental validation of these methods in artificial heart valves was successfully performed using in vitro pulse duplicators.76 Design-based models of the aortic and mitral valves provide an elegant means to obtain realistic valve models that adhere to first principles.77 Such methods have been used recently to study mitral valve hemodynamics and the effects of trabeculae in the left ventricle.78,79 Technologies and treatment strategies, including experimental and simulation methods, for aortic and mitral valve repair are further discussed in recent reviews.80–82
Many of the FSI methods described above are available in the open-source and commercial simulation suites described in Sec. I A. SimVascular supplies tools for simulating both ALE and CMM cardiovascular simulations and is also capable of assigning user-defined LPN boundary conditions. Crimson is able to simulate CMM FSI with LPN boundary conditions with ALE methods currently under development. The open-source solvers FEBio, OpenFoam, and FEniCS are also capable of solving FSI problems using implementations of the ALE methods but are less optimized for applying cardiovascular LPN boundary conditions.83,84 Open-source implementation of IB methods are available through IBAMR.
III. CLINICAL IMPACT IN ADULTS AND CHILDREN
Computational models of hemodynamics have been broadly applied to a wide range of adult and pediatric diseases spanning cerebral and abdominal aortic aneurysms, vascular surgery and endovascular devices, stroke and embolism, the thoracic aorta, and others.86–89 Models have also been instrumental in accelerating the medical device design pipeline, allowing for inexpensive design optimization prior to full-scale animal and human studies.90–93 Here, we focus primarily on two areas of clinical need in cardiovascular disease: coronary artery disease and pulmonary vascular disease. These examples illustrate the clinical impact and further motivate the need to move beyond CFD to multiscale methods incorporating mechanobiology.
A. Coronary artery hemodynamics
Perhaps the most widespread translational impact of CFD methods to date has been in the diagnostic assessment of coronary artery disease severity. Patients with ischemic vascular disease caused by atherosclerosis often undergo invasive cardiac catheterization procedures to measure fractional flow reserve (FFR), a measure of pressure drop across stenosis under hyperemic conditions. The use of FFR to guide interventional decisions (angioplasty, stenting) has been shown to significantly reduce death, myocardial infarction, and repeat revascularization in large randomized clinical trials.94,95 Technology to noninvasively assess FFR based only on computed tomography (CT) imaging, , was introduced by HeartFlow, Inc., and granted FDA approval in 2014. High-fidelity anatomic models are constructed from patient CT imaging data, and steady flow CFD simulations are performed with specialized coronary physiologic boundary conditions.61,96 Large-scale clinical trials have demonstrated superior sensitivity and specificity in diagnostic performance using computational predictions of compared to traditional imaging methods.97 Further studies in clinical efficacy showed that two-thirds of patients resulted with a different management plan when using noninvasive CFD-based analysis and a substantial reduction in unnecessary invasive and expensive catheterization laboratory procedures.98,99 This technology is currently being extended to interventional planning applications to aid clinicians in decisions on angioplasty and stent placement, particularly in patients with multiple lesions. Simulations also hold promise in surgical planning for coronary artery bypass graft (CABG) patients, and have been applied to compare competing graft configurations, including sequential, multiple and Y-shaped graft designs.100 Optimization has also been used to identify graft designs that minimize areas of low wall shear stress (WSS) and atherosclerotic plaque deposition.101,102
Patients with multi-vessel, diffuse coronary artery disease, for whom angioplasty and stenting are not recommended, typically undergo CABG surgery. Limited availability of arterial grafts necessitates the use of saphenous vein grafts (SVGs) in 95% of CABG patients.103,104 However, long-term benefits of CABG are severely limited by obstructive SVG disease, which is caused by thrombosis (early), intimal hyperplasia (intermediate), or atherosclerosis (long-term).103 Complete SVG obstruction occurs in 40%–50% of grafts within 10 yr,105,106 and recent data indicate that 25% of SVGs have severe stenosis or occlusion within 12–18 months.107 SVG failure is associated with significantly worse long-term clinical outcomes.108,109 SVG adaptation is driven by changes in mechanical stimuli that are sensed by vascular cells.110–114 CABG surgery transfers the SVGs from the low-pressure venous system to the high-pressure, high-flow arterial system (increasing pressure 20-fold and WSS fourfold), which is followed by vein arterialization.115,116 This abrupt and sustained increase in hemodynamic loads induces cellular proliferation and apoptosis, phenotypic changes, and inflammatory response, each of which are thought to contribute to vein graft maladaptation. Thus, modulating hemodynamic-induced immuno-mechano-biological responses is likely key to ensuring long-term SVG patency.117–119
Blood flow simulations have confirmed significant differences in WSS and strain when comparing arterial and venous grafts120 and have revealed correlations between WSS and SVG stenosis after CABG.121 To model SVG growth and remodeling, constrained mixture theory has been adopted, which accounts for different rates of production and removal of extracellular matrix constituents and cells within the wall.117,122 Simulations revealed that gradual, rather than abrupt, loading of SVGs following CABG might ameliorate failure risk.122 Implementation of this concept has been explored via the use of an external sheath to mechanically support vein grafts subjected to arterial pressure. Studies in animal models confirmed that external scaffolds significantly reduce neointimal hyperplasia and medial wall thickening in vein grafts after arterial bypass and can prevent vein graft dilatation.123,124 The randomized, self-controlled VEST trial of 30 human subjects undergoing multi-vessel CABG demonstrated significantly reduced neointimal hyperplasia in SVGs supported by a cobalt-chromium external stent compared to unsupported SVGs, although overall patency did not differ significantly at one year after surgery.125 Recent modeling work indicates promise of a degradable external sheath,126 which may overcome issues of inflammation observed in prior studies.
Advances in imaging methods are now enabling increasingly detailed assessment of coronary perfusion using computed tomography (CT). These measures have been demonstrated to accurately identify coronary artery disease when used in conjunction with FFR acquired with computed tomography angiography127 and show promise for increasing the accuracy of coronary CFD simulations by generating coronary tree boundary conditions based on measured perfusion zones.128
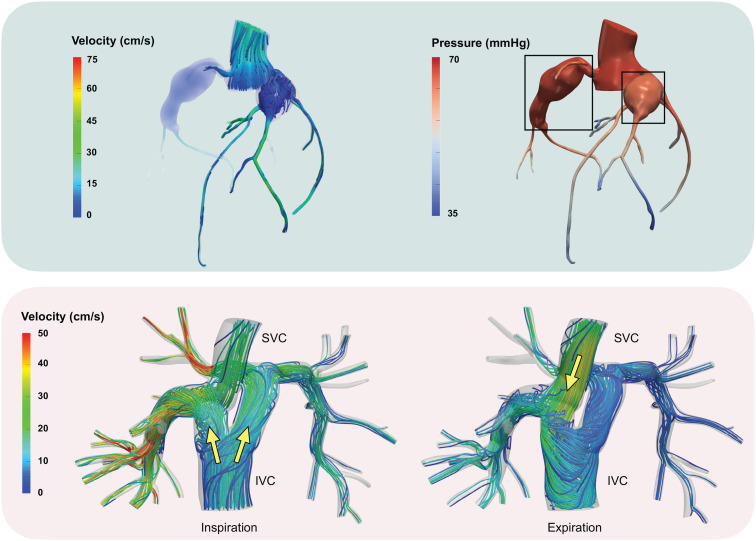
Simulations of coronary hemodynamics also show promise for treatment planning and risk stratification in pediatric cardiology. In Kawasaki disease, hemodynamic simulations have been used to improve thrombotic risk assessment for patients with coronary artery aneurysms; see, e.g., Fig. 3 (top). In these studies, high residence times and large areas of WSS in aneurysms were shown to be better indicators of thrombotic risk than purely geometric methods of risk stratification.30 In a recent computational study featuring the patient shown in Fig. 3, pressure drops across aneurysms have been shown not to be dramatic over a cohort of 15 patients.129 However, the presence of aneurysms was associated with rapid pressure drops in the distal parts of the coronary tree, which indicates an increased risk of myocardial ischemia. FSI simulations have also been applied to improve the understanding of hemodynamics in patients with anomalous origin of the coronary arteries.130
FIG. 3.
Examples of clinical applications. Top: Numerical approximation of FFR in coronary arteries with aneurysms caused by Kawasaki disease: streamlines of velocity field (left) and pressure distribution (averaged over time) in hyperemia (right). The aneurysms are marked with boxes on the right. Bottom: Y-graft Fontan model.85 During inspiration, the inferior vena cava (IVC) flow is bifurcated by the Y-graft and channeled to the pulmonary arteries. During expiration, retrograde flow in the IVC allows the superior vena cava (SVC) flow to enter the right limb of the Y-graft.
B. Pulmonary arteries and single ventricle physiology
Pulmonary vascular circulation is supplied by the right ventricle and is responsible for blood oxygenation, which occurs where the alveoli interface with the bronchial and lymphatic systems. It has a complex branched structure, with the main pulmonary artery arising from the right ventricular outflow tract, branching into left and right main pulmonary arteries, and subsequently into two lobar branches each and then segmental and sub-segmental branches. This structure generally parallels the bronchial branches with names corresponding to the associated bronchopulmonary segments. Typically, the extensive branching of the pulmonary tree allows for even distribution of blood to the alveoli interface. Pulmonary diseases, including pulmonary hypertension (PH) and congenital heart defects, that disrupt the natural flow of blood through the pulmonary arteries can lead to altered gene expression, unbalanced perfusion to the lungs, deoxygenation, adverse cardiovascular remodeling, and increased right ventricular workload. Computational modeling of blood flow has provided new insights into how pulmonary diseases disrupt normal pulmonary and cardiac function.
In pulmonary hypertension (PH), adverse growth and remodeling as well as increased ventricular workload can lead to eventual cardiac failure. However, the hemodynamics that give rise to these conditions are difficult to measure in vivo.131,132 Quantification of pulmonary artery hemodynamics using 4D MRI has shown decreased WSS, vorticity, and helicity in the main pulmonary artery of patients with PH, but the resolution limitations of 4D MRI make it unsuitable for quantifying hemodynamics in the smaller, distal branches where disease is thought to initiate.133–135 Computational simulations of the pulmonary tree can allow for detailed quantification of hemodynamics in a greater portion of the pulmonary arterial tree than is possible with current imaging techniques. Blood flow simulations showed that severe PH is associated with decreased WSS in the proximal arterial tree and increased WSS in the distal pulmonary tree, providing evidence that PH can trigger maladaptive mechanobiological responses along the entirety of the pulmonary artery tree. In addition, the oscillatory shear stress was found to be lower in the main pulmonary artery in patients with severe PH.28,136,137
It is important to carefully consider the boundary conditions for pulmonary artery simulations. While many studies have employed traction-free or constant resistance outlet conditions, distal pulmonary artery impedance significantly impacts upstream hemodynamics and is a significant predictor of pulmonary hypertension severity.138,139 To address this, the impedance of the distal pulmonary vasculature has been modeled using morphometric trees built using pulmonary scaling laws. Morphometric trees have been able to model pulmonary hypertension stemming from both arterial rarification and stiffening, showing their ability to capture in vivo trends.140 Future studies examining mechanisms of PH disease progression must account for both mechanical stimuli and biologic response at multiple scales of the pulmonary artery (PA) tree, given the disparate effects of PH in the proximal and distal tree.
Pulmonary stenosis, or narrowing of the pulmonary vessel lumen, is another significant cause of pulmonary flow disruption. Pulmonary stenosis is commonly associated with congenital heart diseases, including Williams syndrome, Alagille syndrome, and tetralogy of Fallot. In many cases, multiple stenotic lesions are present and distributed across the main and peripheral pulmonary artery branches. While correcting major lesions with a combination of stenting and balloon angioplasty has the ability to reduce pressure gradients across individual lesions, this may only lead to minor improvements in right ventricular pressures in a significant portion of patients.141–143 Computational models of the pulmonary arterial tree have shown that stenting only proximal lesions is often insufficient to reduce overall vascular resistance and thus right ventricular pressures.144 In these cases, total vascular resistance often remains high due to the remaining peripheral pulmonary lesions and distal vasculature. Detailed simulations of treatment planning scenarios may aid clinicians in identifying the most critical targets for intervention. Modeling the distal pulmonary tree using reduced order methods has also shown that pulmonary stenosis may lead to adverse downstream remodeling that may cause persistent vascular resistance increase even after universal resolution of pulmonary stenoses.145 Incorporating vascular growth and remodeling will be critical to predicting long-term PA adaptation and disease progression.
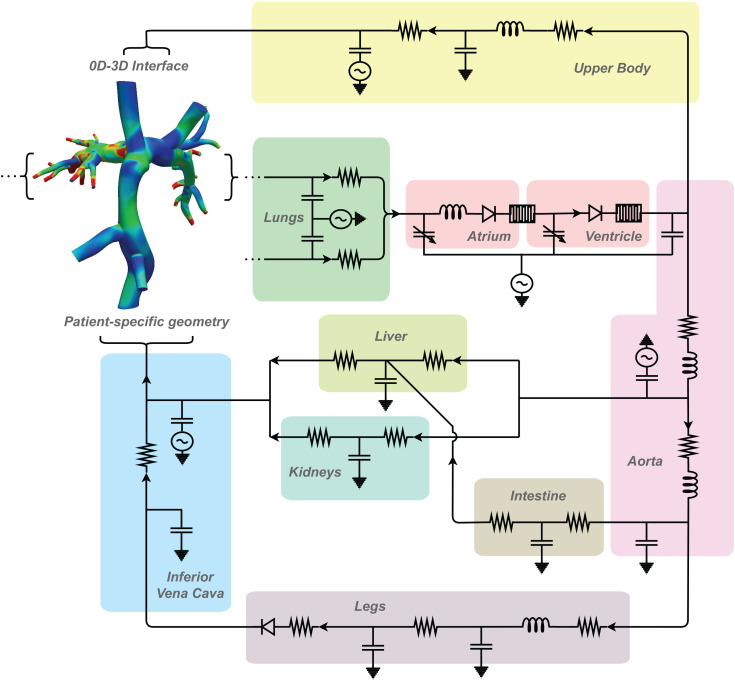
Computational modeling has also played a significant role in investigating palliation strategies for single ventricle physiology involving the pulmonary vasculature. While single ventricle physiology has numerous presentations, it is typically treated through three-stage surgical palliation that results in the Fontan physiology.146 Because single ventricle physiology affects the entire circulation, closed-loop LPNs have been an important tool in simulating the effect of modifying cavopulmonary connections in single ventricle patients (Fig. 4). Early computational studies of the Norwood operation, a version of the first stage of palliation, used LPN models of single ventricle circulation to quantify the effect of varying the arterial-pulmonary shunt size. This work showed that while larger shunts may lead to increased pulmonary flow, they can result in lower systemic oxygen delivery.147,148 The multiscale modeling approach was then employed to investigate the second stage of single ventricle palliation, the Glenn procedure, and LPNs were coupled directly to 3D models of patient-specific geometries in multiscale 0D–3D simulations.149 This allowed for the direct investigation of local hemodynamics in the cavopulmonary system and the modification of LPN parameters to model closed-loop exercise states. Closed-loop multiscale simulations have been experimentally validated against in vitro models that utilize pumps and patient-specific, 3D-printed models, with excellent results.150–152 This body of work showed that patient-specific geometries and boundary conditions could greatly impact the modeled performance of the single ventricle palliation stages and emphasized the need for high-fidelity simulations for use in surgical planning and optimization.
FIG. 4.
An example of multiscale modeling in a Fontan patient which allows for quantification of local hemodynamics and estimation of whole-body behavior in response to cavopulmonary changes. Adapted from Refs. 159 and 161.
While Fontan palliation has led to increased survival of single ventricle patients, Fontan physiology also causes elevated central venous pressure, reduced cardiac preload, and reduced pulmonary pulsatility, which bring associated morbidities such as liver fibrosis, protein losing enteropathy, arrythmia, exercise intolerance, and adverse cardiac and vascular remodeling. Because these morbidities are associated with the hemodynamic inefficiencies and elevated venous pressures of the Fontan pathway, energetics of the Fontan connection have been carefully studied as the basis for surgical optimization. At rest, simulations have shown that differences in Fontan energetics lead to a minimal difference in global circulatory physiology, including pressure–volume loops and cardiac output.153 However, differences are accentuated during exercise. Simulations have shown that increased total cavopulmonary resistance significantly decreases the ability of the Fontan circulation to increase cardiac output during exercise, and further studies showed that energy loss increases nonlinearly in the total cavopulmonary connection (TCPC) during exercise even when normalized to head loss or resistance, demonstrating the limited ability of the TCPC to accommodate exercise conditions154,155 Experiments have been performed to identify primary causes of energy loss and hemodynamic inefficiencies in the Fontan pathway. While energetics were found to be similar across the lateral tunnel and extracardiac variations of the TCPC, simulations showed that in extracardiac Fontan conduits, head-on collision of flow results in increased energy loss.2,156,157 This led to the development of an offset conduit design that prevented head-on flow collision. However, computational models of the offset conduit design showed uneven hepatic flow distribution to the pulmonary arteries. To address this issue, the bifurcated Y-graft, shown in Fig. 3 (bottom), was introduced. This improved energy loss, SVC pressure, and hepatic flow distribution compared to the offset design in computational studies that were later validated clinically.85,158 As their predictive power has grown, computational simulations continue to be used in investigations of new palliative techniques, including surgical alternatives to the first stage of palliation, such as the assisted bidirectional Glenn and models of tissue-engineered vascular grafts in the Fontan pathway.159,160
IV. EMERGING METHODOLOGIES AND APPLICATIONS
A. Reduced order modeling and uncertainty quantification
The CFD techniques discussed throughout this paper allow us to describe cardiovascular systems with an exceptional level of detail. However, this degree of accuracy is often associated with computational costs and resources incompatible with many practical scenarios. Reduced order models (ROMs) are computationally cheap alternatives to high-fidelity methods such as the finite element or finite volume methods. While high-fidelity methods often require hours or days to perform a single simulation on supercomputers, ROMs are typically associated with running times of the order of seconds or minutes and can be executed on inexpensive hardware (e.g., laptops). The dramatic increase in performance is linked to a loss in accuracy and detail, but these often remain sufficiently high for many clinical applications.
The most common ROMs in cardiovascular applications are 0D and 1D models. The former are sometimes called lumped-parameter networks or LPNs. In 0D formulations, regions of the cardiovascular system are modeled as electric circuits where the pressure drop across any two points of the model and the flow rate Q play the role of voltage and electric current, respectively. The laws governing pressure drop and flow rate Q are162
| (6) |
where R, C, and L are quantities associated with elements commonly found in electric circuits, namely, resistors, capacitors, and inductors, respectively, and and are the time derivatives of pressure and flow rate. These quantities can be expressed in terms of the geometrical and structural properties of the vessels under the assumption of a fully developed parabolic velocity profile.163,164 LPNs are often used in conjunction with 3D models to describe the effects of the downstream vasculature, for instance, using resistor-capacitor-resistor (known as RCR or Windkessel) boundary conditions.42 Moreover, 0D models have been used to model the heart, systemic, pulmonary, and coronary circulations to study congenital heart disease149,165 and coronary artery disease.166–168 The performance of 0D and 3D models has been compared in several studies, for example to estimate flow rate in cerebral artery aneurysms,169 fractional flow reserve (FFR) in coronary arteries,170 pressure drop across branch pulmonary artery stenosis,171 and pressure and flow rate distributions in a variety of different cardiovascular regions.172
In contrast to LPNs, some geometrical information from the cardiovascular model of interest is retained in 1D formulations. Here, the branches in the vessel of interest are approximated as curves (usually, the branch centerline) in 3D space and flow dynamics are described in terms of pressure and flow rate along these curves. Under the assumption of a parabolic flow profile, the 1D equations read as
| (7) |
| (8) |
where and are pressure and flow rate of blood and the area of the vessel lumen at axial location z, respectively. The kinematic viscosity ν is typically set to . System (7) and (8) needs to be complemented with a constitutive law to model the structural response of the vessel to blood flow. A popular choice is the Olufsen material model which builds on simple reduced-order linear elasticity by using an exponential relationship based on empirically fitted data.173 Reduced order 1D models can be coupled with 3D models of regions of the cardiovascular tree where higher resolution is required.51,174,175 For example, 1D models have been coupled to 3D models of regions of interest to study coronary hemodynamics.168 Due to their computational efficiency, 1D models can also be used to describe blood dynamics in all the major vessels of the cardiovascular tree.176–178 These ROMs have also been successfully employed to compute initial conditions for 3D models with the goal of reducing the number of cardiac cycles needed to reach a periodic state.179 Comparisons between 1D and 3D models have focused on the approximation of aortic flow,180–182 FFR in coronary arteries,183–185 and blood dynamics in the Circle of Willis186,187 and in the whole arterial tree.188–192 A recent study164 also found good agreement between 0D/1D and 3D results for 72 geometries taken from the Vascular Model Repository.19 Finally, some works have compared 1D results with experimental data in large networks of arteries and veins176,188,193 and in the global arterial tree.194
Other popular ROMs are data-driven, i.e., they aim to exploit past simulation results to perform future simulations more efficiently. In proper-orthogonal decomposition (POD) and reduced basis (RB) methods,195,196 for example, a small number of pressure and velocity modes is generated through singular value decomposition (SVD) from a database of high-fidelity solutions. The pressure and velocity fields are then found as linear combinations of these basis functions and, as a result, the size of the linear systems to be solved in each time step is considerably smaller than in the high-fidelity counterpart. Notable applications of the RB method to cardiovascular flow are, for example, the study of parameterized coronary artery bypass grafts and shape optimization,197–200 the solution of inverse problems to retrieve vessel structural properties,199 and the investigation of the effects of stenosis severity on flow.201 It is worth noting that other approaches not based on data-driven ROMs have been used for shape optimization in cardiovascular problems; e.g., the Surrogate Management Framework (SMF) has been successfully used to optimize the assisted bidirectional Glenn procedure160 or a Y-shaped baffle for the Fontan surgery.202 To increase the applicability POD and RB techniques to geometries not considered during the reduced basis generation, some studies have focused on decomposing vessels into multiple geometrical building blocks, each equipped with a small number of basis functions.203–205 Another promising class of data-driven techniques that has gained attention in the cardiovascular research community in recent years is physics-informed neural networks (PINNs).206 These can be trained on 1D data to derive surrogate 1D models207 or on the Navier–Stokes equations to approximate wall-shear stress from a set of sparse measurements of blood velocity and incomplete boundary conditions.208
ROMs are especially useful in many-query scenarios, namely, in cases where cardiovascular models need to be run many times for different values of parameters associated with the properties of the system. A prominent area of research requiring a great number of simulations is uncertainty quantification (UQ). Cardiovascular simulations are associated with an intrinsic level of uncertainty stemming from the challenges in setting appropriate boundary conditions, variability in material properties of vascular tissue, and uncertain vascular geometry due to operator-dependent image segmentation processes. In high-stakes situations, therefore, estimating quantities of interest via a single deterministic model evaluation is not advisable, and assigning confidence intervals and probability distributions to such quantities is of paramount importance. In UQ, this is achieved by sampling uncertain model parameters from probability distributions informed by patient data or by the literature. Specifically, in Monte Carlo (MC) approaches, the output of interest—which is generally a function of the pressure and velocity fields obtained from (expensive) 3D simulations—is evaluated for many different values of the uncertain parameters. Then, statistics on the quantities of interest are computed. This approach led to the study of the impact of geometric uncertainty on patient-specific blood flow simulations using convolutional neural networks with dropout layers for automatic segmentation.35 Similarly, sensitivity with respect to the segmentation of coronary artery vessel lumen has been estimated using anisotropic kernel regression.209 Multi-level Monte Carlo (MLMC), multi-fidelity Monte Carlo (MFMC), and multi-level multi fidelity (MLMF) estimators have been devised to alleviate the computational burden of standard MC approaches by relying on a small number of expensive high-fidelity solutions and a large number of low-fidelity ones obtained using coarse meshes, 0D and 1D ROMs, and combinations of the two, respectively.210,211 Recent efforts have also considered other UQ approaches such as Markov chain Monte Carlo (MCMC), stochastic collocation, and multi-wavelet stochastic expansion to investigate the effects of a variety of uncertain parameters on coronary flow.212,213 Another area in which a large number of cardiovascular model evaluations is required and in which, therefore, the use of ROMs becomes particularly effective, is boundary condition tuning, such as using Bayesian frameworks based on adaptive MCMC sampling.214
B. Multi-physics simulations and whole heart modeling
While the field of vascular flow simulations is relatively mature, complex clinical applications (e.g., complex congenital heart disease, cardiomyopathy, pulmonary hypertension) increasingly require the use of cardiac or coupled vascular-cardiac models. Such models bring added complexity due to their multi-physics nature.215 From a physical perspective, modeling cardiac function is a coupled problem of electrophysiology, solid mechanics, and fluid dynamics.216,217 However, the mathematical description and numerical solution of fully coupled cardiac models remains highly challenging. Current research efforts are, therefore, geared toward speeding up computations of highly detailed models218 and developing cheaper low-order models that retain physical accuracy.219–221 Depending on the clinical application, the three physical fields (electrical, solid, fluid mechanics) of the cardiac problem are coupled with varying levels of model fidelities. From a computational viewpoint, the coupling of multi-physics heart simulations can be roughly categorized by electromechanical and fluid–structure interactions, which are described below.
The electrophysiology problem solves for the transmembrane potential and is usually modeled by the monodomain or bidomain equations. For an overview of cell- and organ-scale electrophysiological models, we refer to the review of Trayanova and Rice.222 The active contraction of the cardiomyocytes has been modeled both with active stress and active strain models, whose differences are discussed by Ambrosi and Pezzuto.223 Different approaches exist to couple the electrical activation of the heart with cardiomyocyte contraction. In the weakly coupled approach,224,225 the electrical wave propagation is solved first on the undeformed cardiac geometry, typically with a finer mesh and a smaller time step than the mechanical problem, and then used as a boundary condition to calculate active mechanical contraction. The strongly coupled approach simultaneously solves the electromechanical problem, including feedback of the deformation onto the electric current flow.226 While weak coupling ignores this feedback, its approach typically offers a simpler implementation and reduced computational effort. A popular benchmark for different discretization methods in cardiac electrophysiology was proposed by Niederer et al.,227 comparing activation wavefronts in a cuboid domain. An overview of applications of whole-heart modeling to cardiac electrophysiology is given by Trayanova.228
Two popular approaches for the cardiac fluid–structure interaction are 3D–0D and 3D–3D coupling. The 3D–0D approach couples detailed models of 3D solid mechanics with 0D reduced models of fluid dynamics, modeling hemodynamics either with open-loop229 or closed-loop230,231 LPNs. 3D–0D coupled models are popular in applications focusing on myocardial mechanics, such as predicting cardiac growth and remodeling in hypertrophy with detailed microstructural solid models.232
On the other hand, studies on the influence of intracardiac blood flow on disease initiation and progression warrant a finely resolved 3D model of cardiac fluid dynamics. An excellent overview of coupling fluid-mechanics-electrophysiology was recently published by Verzicco.233 An important example of a clinical application that requires detailed models of fluid dynamics is valvular heart disease. Heart valves are thin structures undergoing large displacements while changing their status from closed to open, which makes modeling their interaction with blood flow challenging.234 Here, a popular computational method is the immersed boundary method71,235,236 which has been applied to left-heart237 and four-chamber heart models, including valves.238 In a simplified approach, the valve is implicitly represented by a resistive surface that represents the valve status, open or closed, with a 0D valve model.239,240 Another clinical application that demands resolving detailed 3D intracardiac fluid dynamics is determining the thrombogenic risk in the left atrial appendage during atrial fibrillation and the associated stroke risk.241 Here, fluid dynamics inside the left atrium can identify regions where blood flow cannot wash out the chamber sufficiently.242,243
Several open-source tools described in Sec. I A provide cardiac fluid–structure interaction capabilities. SimVascular allows for both 3D–3D and 3D–0D coupling while FEBio and lifex allow for 3D–0D coupling. CircAdapt offers a fully 0D approach to cardiac fluid–structure interaction.
C. Mechanobiology in disease and development
In recent decades, understanding the mechanisms by which the mechanical environment affects the behavior and evolution of cardiovascular structures has become increasingly central to predictive simulations. Early experiments discovered that vascular cells are sensitive to their mechanical environment and seek to maintain homeostatic stress values.244–247 This sensing is typically attributed to the extracellular matrix of endothelial and smooth muscle cells, which sense fluid shear stresses and intramural stresses, respectively. While the true mechanisms by which this sensing is translated into phenotypical expression remain under investigation, phenomenological models of mechanobiological responses have allowed for increasingly high-fidelity models of both vascular and cardiac growth and remodeling.
Early predictive models took advantage of these biological findings to create kinematic models of vascular and cardiac growth and remodeling that relied on the multiplicative decomposition of growth and elastic components of material deformation.248–250 Later frameworks of vascular growth and remodeling modeled the turnover of individual constituents in order to provide additional information about the evolving natural configuration of the vessel.251 While growth and remodeling frameworks typically work in a continuum description, recent studies have adopted a discrete fiber-based growth and remodeling framework that can provide detail on fiber structure and behavior.252
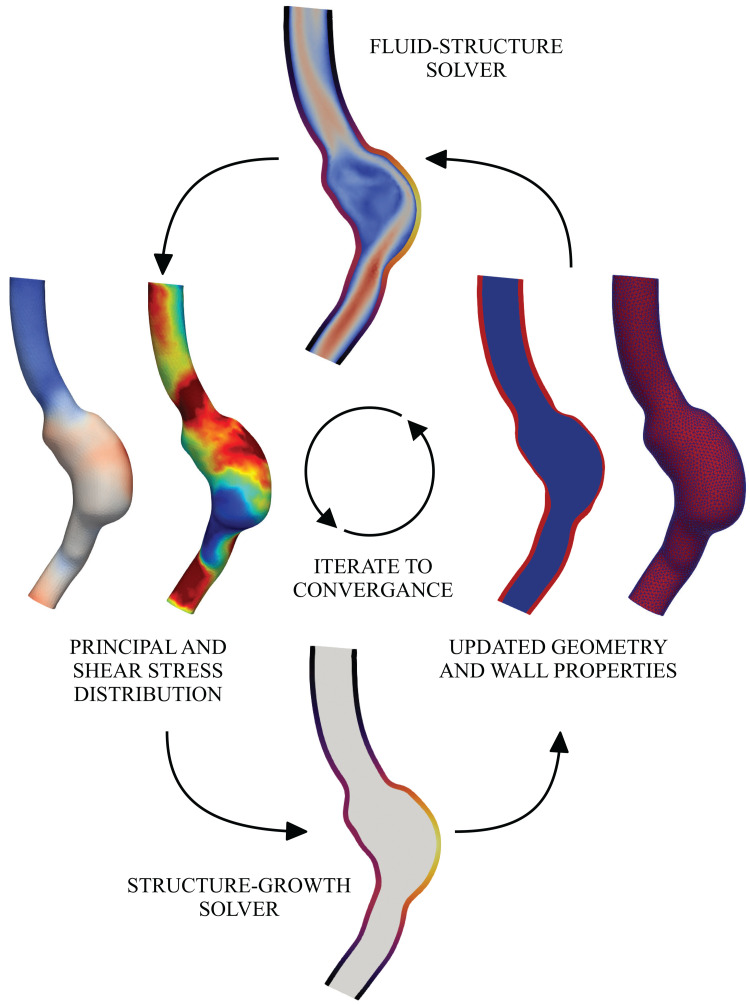
Many models of vascular growth and remodeling use reduced-order relationships to calculate the wall shear stress and intramural stress, commonly using the thin-walled cylindrical assumption to calculate intramural stress and using the assumption of Newtonian Poiseuille flow to calculate wall shear stress. Under these assumptions, growth and remodeling trends in response to hypertension, axial stretch, and increased flow have been successfully recapitulated.253,254 However, there remains a need for clinical prediction of complex, spatially resolved patient-specific growth and remodeling, which, in many cases, results in complex flow fields that do not follow such assumptions. Progress has been made toward fluid–solid-growth frameworks that allow for growth and remodeling theory to be coupled with 3D hemodynamic fields (Fig. 5).255–257
FIG. 5.
A fluid–solid-growth interaction framework, bridging different physics (fluid dynamics and solid growth) and time scales (milliseconds in fluid dynamics and days in solid growth).
Tissue engineering is an application where modeling vascular growth and constituent turnover has important clinical and design implications. Clinicians have noted the propensity of tissue-engineered vascular grafts to stenose and occlude, but in some cases such stenoses have been observed to spontaneously resolve.258,259 By expanding vascular growth and remodeling frameworks to include inflammatory response and engineered graft constituent turnover, researchers have been able to capture the evolving in vivo geometries (stenosis and subsequent resolution) exhibited by tissue-engineered vascular grafts in animal models.260
Similarly, cardiac tissue senses its mechanical environment through a mixture of extracellular matrix and internal cellular components, which are connected through focal adhesions and transmembrane integrin proteins. Unique to cardiac tissue are cardiomyocytes which are made up of sarcomeres. While myocytes themselves have a low turnover rate, sarcomeres are able to add and remove unit elements and effectively change the shape and size of a myocyte. Kinematic growth theory remains a popular model of cardiac adaption to mechanical perturbations, with the growth tensor commonly being phenomenologically modeled as a function of the stress and strain tensors. However, such models are limited in their ability to model the prestress of multiple constituents in cardiac tissue.261–263 Other models of cardiac adaption have been proposed, including those that have modeled the heart as a collection of fibers that can change in length, size, and orientation based on experienced stresses and strain,264,265 but use of full fluid–structure interaction simulations for calculation of cardiac stresses and strains in service of modeling cardiac adaption remains rare given the expense of calculating FSI in comparatively large domains. A more common approach is utilizing multiscale simulations to reduce the cardiac simulation to a purely structural problem with the fluid modeled as part of a lumped-parameter boundary system.
Mechanobiology also plays a crucial role in embryonic development, with mechanical cues influencing both normal and maladaptive cardiac formation. Experiments using zebrafish first showed the impact of fluid dynamics on cardiac development.266 Embryonic zebrafish are particularly well-suited to the study of cardiac development as they are transparent at the embryonic stage, allowing for longitudinal imaging during critical developmental stages. This has allowed researchers to quantify forces that are not otherwise measurable in the lab due to small scale or limits of imaging. Using 4D light sheet imaging and image registration, researchers have been able to quantify wall shear stresses, and oscillatory shear stress in the developing zebrafish heart help regulate the development of cardiac trabeculation, with high oscillatory shear index values correlated with upregulated endothelial Notch-related mRNA expression.267,268
Chick embryos have similarly been used to investigate developing vasculature. Methods to create computational fluid dynamics simulations of the embryonic aortic arch were developed utilizing Fluorescent dye injection, micro-CT, and Doppler velocity recordings.269 The effect of occluding various portions of the developing aorta was simulated using CFD, and a wall shear stress-based kinematic vascular growth algorithm was applied to predict the effect of flow changes on vascular growth. While purely wall shear stress-driven growth captured the qualitative trends in geometry, there was still significant variation in the quantitative growth, suggesting that additional biodynamic processes must be accounted for to simulate in vivo growth and development.270
Mechanotransduction also plays a role in the formation of thrombosis. Thrombi are formed through a combination of biochemical and biomechanical reactions that include platelet hemodynamics, platelet–platelet interaction, and platelet–wall interaction. Using patient-specific computational fluid dynamics has allowed researchers to correlate the presence of hemodynamic factors, including reduced wall shear stress and elevated residence time, to the risk of thrombosis,30 but while local hemodynamics can indicate the risk of thrombus formation, true simulation of thrombus creation and proliferation would require modeling free-body platelets and red blood cells in macroscale blood flow and a framework for tracking and applying the microscale forces experienced by activated platelets. Current frameworks have bridged the scales of this micro–macro interaction and produced simulations that couple fluid dynamics to microscopic processes that are modeled through various frameworks, including agent-based and stochastic simulations.271–274 Work in determining the relative contribution of biochemical vs biomechanical factors remains an ongoing area of research.
Although it is widely accepted that cells seek to promote tissue homeostasis in response to biochemical and biomechanical cues, the ways in which these cues translate into tissue adaption rely on the complex interaction between mechanical sensing, gene expression, and chemical cues. Work has been done toward systems biology approaches that can provide additional details to the cell signaling pathways that yield cardiovascular structural changes.275 Models of cardiac cell-signaling pathways have been coupled to finite element ventricular models to capture the effects of hypertrophy in a framework proposed by Estrada et al.276 In this framework, strain was derived from a finite element simulation of a left ventricle and used as an input into a cell-signaling model previously validated to predict changes in cell area.277 The predicted cell area was then mapped to volumetric growth which was then enforced in the finite element model via a kinematic growth formulation. The experienced strains were then updated and fed into the cell-signaling network to calculate the next growth and remodeling time step. Logic-based models of the coupled biochemical and biomechanical response in arteries have similarly shown qualitative agreement with animal models of hypertension.278 In this framework proposed by Irons et al., intramural stress and wall shear stress derived from a reduced-order simulation of a murine abdominal aorta were used as inputs into a cell-signaling network. Rather than outputting changes in cell area, the cell-signaling network was used to scale the production and degradation gains of specific constituent families, motivated by previous work that validated cell-signaling regulation of vascular composition.279 The vascular wall properties were then updated and the new geometric configuration was found using constrained mixture theory, supplying the stresses fed into the cell-signaling network at the next time step. Although more computationally expensive to scale, this framework has the benefit of tracking vascular composition and considering the relative contribution of constituent families over time. In both frameworks, additional exogenous factors were also used as inputs into the cell-signaling network, creating targets for investigating drug delivery and virtual knockout behavior at the macroscale. Current work in cell-signaling growth and remodeling has not incorporated fully 3D FSI simulations, instead relying on reduced-order simulations that do not consider the effect of a highly resolved fluid field. Coupling cell-signaling pathways to high fidelity FSI solvers is a natural evolution of the field that will allow insight into the behavior of complex, patient-specific cardiovascular geometries over time.
V. FUTURE CHALLENGES
The field of cardiovascular simulations has expanded rapidly in the past few decades, from simplified models of idealized vessels to patient-specific, multiscale simulations. Future developments in the field will continue to expand their diagnostic and predictive power.
One of the earliest applications of cardiovascular simulation was investigating the effect of surgical devices and treatment planning. However, only by moving beyond CFD to consider coupled multi-physics and mechanobiological systems will the true predictive power of simulations be realized. Fluid–solid-growth simulations are already being used to optimize proposed cardiovascular devices, and as the capabilities of such frameworks improve, it will become possible to predict hemodynamic outcomes not only at single timepoints but over days, months, and years. While previous methods of growth and remodeling have relied on reduced-order geometries or simplified boundary conditions, growth and remodeling simulations coupled to fully 3D FSI is on the near horizon. With multiscale boundary conditions, it could then be possible to use age-based scaling laws to account for closed-loop boundary condition responses to changes in local hemodynamics, furthering the predictive power of cardiovascular simulations in long-term patient settings.
As our ability to simulate such complex behavior increases, it will become increasingly necessary to provide high-fidelity parameter inputs to create patient-specific simulations. Though phenomenological drivers of cardiovascular growth remodeling are well established and widely used, most studies rely on assumed or estimated values for homeostatic targets and material properties despite observations that such values can vary significantly across patient populations.280 Increasingly mechanistic models are being developed to describe mechanobiological processes, which have the potential to be driven by patient-specific geometry, genomics, and proteomics. Careful collaboration with vascular and systems biologists will be necessary to identify patient-specific parameters of subcellular interactions. Quantifying cell-signaling parameters has historically been challenging as the complex feedback within a network can obfuscate individual reactions, and current models have relied on aggregating both biomechanical and functional evidence of pathway effects. Advances are being made in quantifying the behavior of specific regulatory pathways including, for example, studies that have quantified endothelial surface density of vascular endothelial growth factor receptors using flow cytometry in both healthy and diseased states281,282 and identifying phosphorylation pathways that critically regulate ventricular mechanical behavior using gene-targeted mice.283 These advances demonstrate tools that can be used to further the understanding of multiscale regulation and have direct application to simulation of cardiovascular diseases that are propagated at both the mechanical and cellular level. This also has the potential to expand the ability of CFD to investigate diseases such as diabetes, ischemia, and cancer where angiogenesis and vascular remodeling are intimately linked with disease progression and outcomes. The development of additional tools to identify and validate parameters will be critical for the continued development of multiscale mechanobiological modeling frameworks.
Limitations remain in creating patient-specific models of cardiovascular structures that are beneath the resolution of clinical imaging modalities. While we can utilize idealized trees and scaling laws to make estimates of distal vascular behavior, these typically rely on limited sample sizes or animal models. Validating these techniques against human data is challenging due to the inherent limitations of current imaging technologies. However, progress toward patient-specific modeling of the microvasculature could be made by incorporating experimentally measured perfusion maps to guide the growth of synthetic trees. These algorithms could further be generalized to account for more complex bifurcation patterns in vascular trees. This would allow researchers, for example, to more accurately capture blood dynamics at the capillary level, where vessels with a diameter less than are normally arranged in a web-like structure featuring loops. In the future, improved microvascular models will be used to estimate perfusion maps (in cases where these are unknown) and to set more physiological boundary conditions of large-scale models.
Given the limited precision of inputs into cardiovascular simulations, quantifying bounds on CFD-driven findings is critical to the clinical translation of simulation studies, particularly in multiscale and long-term cardiovascular simulations. Therefore, developing robust uncertainty quantification tools will be an important priority for the expansion of the translational power of computational cardiovascular medicine. Uncertainty quantification techniques rely on numerous simulations and have been shown to take great advantage of reduced order models in multi-fidelity approaches. Therefore, the development of advanced reduced order models accounting for patient-specific mechanobiology phenomena and gene regulatory networks will lead to the quantification of uncertainty associated with the long-term assessment of treatments and surgical procedures.
The field of cardiovascular modeling has expanded on traditional CFD frameworks by incorporating modeling techniques ranging from mechanobiology to electrophysiology and molecular systems biology. As computational power continues to increase exponentially, the level of detail available for patient-specific hemodynamic models will be limited only by the ability to describe multiscale interactions and to accurately identify parameters governing patient-specific behavior. Even in the absence of absolute certainty in model inputs, increasingly robust uncertainty quantification methods will allow for clinical translation of simulation results by providing well-characterized statistics on model predictions. As in silico experiments become progressively reliable and computationally efficient, we will increasingly have the ability to simulate outcomes on large cohorts of synthetic patients, paving the way toward large virtual clinical trials for FDA approval and creating new pathways for the development of cardiovascular devices and treatment methods.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the National Institutes of Health (NIH) under Award Nos. R01LM013120, R01EB029362, R01HL139976, R01HL141712, R01EB018302, K99HL161313, the National Science Foundation (NSF), American Heart Association (AHA) under Award No. 835662, Additional Ventures Foundation, the Stanford Cardiovascular Institute (CVI), Wall Center, and the Extreme Science and Engineering Discovery Environment (XSEDE) for providing the financial and computational resources that made part of the research presented in this paper possible. We also thank Dr. Baeumler, Dr. Menon, and Dr. Yang for their assistance in creating the figures reported in this paper.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Author Contributions
Erica L. Schwarz: Writing – original draft (equal); Writing – review & editing (equal). Luca Pegolotti: Writing – original draft (equal); Writing – review & editing (equal). Martin R. Pfaller: Writing – original draft (equal); Writing – review & editing (equal). Alison Marsden: Conceptualization (equal); Funding acquisition (equal); Supervision (equal); Writing – original draft (equal); Writing – review & editing (equal).
References
- 1. Migliavacca F., de Leval M. R., Dubini G., Pietrabissa R., and Fumero R., “ Computational fluid dynamic simulations of cavopulmonary connections with an extracardiac lateral conduit,” Med. Eng. Phys. 21, 187–193 (1999). 10.1016/S1350-4533(99)00042-9 [DOI] [PubMed] [Google Scholar]
- 2. Dubini G., De Leval M., Pietrabissa R., Montevecchi F. M., and Fumero R., “ A numerical fluid mechanical study of repaired congenital heart defects. Application to the total cavopulmonary connection,” J. Biomech. 29, 111–121 (1996). 10.1016/0021-9290(95)00021-6 [DOI] [PubMed] [Google Scholar]
- 3. Qiu Y. and Tarbell J. M., “ Numerical simulation of pulsatile flow in a compliant curved tube model of a coronary artery,” J. Biomech. Eng. 122, 77–85 (2000). 10.1115/1.429629 [DOI] [PubMed] [Google Scholar]
- 4. Milner J., Moore J., Rutt B., and Steinman D., “ Hemodynamics of human carotid artery bifurcations: Computational studies with models reconstructed from magnetic resonance imaging of normal subjects,” J. Vasc. Surg. 28, 143–156 (1998). 10.1016/S0741-5214(98)70210-1 [DOI] [PubMed] [Google Scholar]
- 5. Yushkevich P. A. and Gerig G., “ ITK-SNAP: An intractive medical image segmentation tool to meet the need for expert-guided segmentation of complex medical images,” IEEE Pulse 8, 54–57 (2017). 10.1109/MPUL.2017.2701493 [DOI] [PubMed] [Google Scholar]
- 6. Kikinis R., Pieper S. D., and Vosburgh K. G., “ 3D Slicer: A platform for subject-specific image analysis, visualization, and clinical support,” in Intraoperative Imaging and Image-Guided Therapy ( Springer, 2014), pp. 277–289. [Google Scholar]
- 7. Izzo R., Steinman D., Manini S., and Antiga L., “ The vascular modeling toolkit: A python library for the analysis of tubular structures in medical images,” J. Open Source Software 3, 745 (2018). 10.21105/joss.00745 [DOI] [Google Scholar]
- 8. Wolf I., Vetter M., Wegner I., Nolden M., Bottger T., Hastenteufel M., Schobinger M., Kunert T., and Meinzer H.-P., “ The medical imaging interaction toolkit (MITK): A toolkit facilitating the creation of interactive software by extending VTK and ITK,” in Medical Imaging 2004: Visualization, Image-Guided Procedures, and Display ( SPIE, 2004), Vol. 5367, pp. 16–27. [Google Scholar]
- 9. Updegrove A., Wilson N. M., Merkow J., Lan H., Marsden A. L., and Shadden S. C., “ SimVascular: An open source pipeline for cardiovascular simulation,” Ann. Biomed. Eng. 42, 525–541 (2016). 10.1007/s10439-016-1762-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Arthurs C. J., Khlebnikov R., Melville A., Marcan M., Gomez A., Dillon-Murphy D., Cuomo F., Vieira M. S., Schollenberger J., Lynch S. R., Tossas-Betancourt C., Iyer K., Hopper S., Livingston E., Youssefi P., Noorani A., Ahmed S. B., Nauta F. J. H., van Bakel T. M. J., Ahmed Y., van Bakel P. A. J., Mynard J., Achille P. D., Gharahi H., Lau K. D., Filonova V., Aguirre M., Nama N., Xiao N., Baek S., Garikipati K., Sahni O., Nordsletten D., and Figueroa C. A., “ Crimson: An open-source software framework for cardiovascular integrated modelling and simulation,” PLOS Comput. Biol. 17, e1008881 (2021). 10.1371/journal.pcbi.1008881 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Arts T., Delhaas T., Bovendeerd P., Verbeek X., and Prinzen F. W., “ Adaptation to mechanical load determines shape and properties of heart and circulation: The circadapt model,” Am. J. Physiol.-Heart Circ. Physiol. 288, H1943–H1954 (2005). 10.1152/ajpheart.00444.2004 [DOI] [PubMed] [Google Scholar]
- 12. Maas S. A., Ellis B. J., Ateshian G. A., and Weiss J. A., “ FEBio: Finite elements for biomechanics,” J. Biomech. Eng. 134, 011005 (2012). 10.1115/1.4005694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Africa P. C., “ lifex: A flexible, high performance library for the numerical solution of complex finite element problems,” arXiv:2207.14668 (2022).
- 14. Jasak H., “ OpenFOAM: Open source CFD in research and industry,” Int. J. Nav. Archit. Ocean Eng. 1, 89–94 (2009). 10.2478/IJNAOE-2013-0011 [DOI] [Google Scholar]
- 15. Logg A., Mardal K.-A., and Wells G., Automated Solution of Differential Equations by the Finite Element Method: The FEniCS Book ( Springer Science and Business Media, 2012), Vol. 84. [Google Scholar]
- 16. Plank G., Loewe A., Neic A., Augustin C., Huang Y.-L., Gsell M. A., Karabelas E., Nothstein M., Prassl A. J., Sánchez J. et al. , “ The openCARP simulation environment for cardiac electrophysiology,” Comput. Methods Programs Biomed. 208, 106223 (2021). 10.1016/j.cmpb.2021.106223 [DOI] [PubMed] [Google Scholar]
- 17. Ahrens J., Geveci B., and Law C., “ Paraview: An end-user tool for large data visualization,” The Visualization Handbook (Elsevier, 2005), p. 717. 10.1016/B978-012387582-2/50038-1 [DOI] [Google Scholar]
- 18. Childs H., Brugger E., Whitlock B., Meredith J., Ahern S., Pugmire D., Biagas K., Miller M., Harrison C., Weber G. H. et al. , “ VisIt: An end-user tool for visualizing and analyzing very large data,” High Performance Visualization: Enabling Extreme-Scale Scientific Insight ( CRC Press, 2012), pp. 357–372. 10.1201/b12985 [DOI] [Google Scholar]
- 19. Wilson N. M., Ortiz A. K., and Johnson A. B., “ The vascular model repository: A public resource of medical imaging data and blood flow simulation results,” J. Med. Devices 7, 040923 (2013). 10.1115/1.4025983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Fonseca C. G., Backhaus M., Bluemke D. A., Britten R. D., Chung J. D., Cowan B. R., Dinov I. D., Finn J. P., Hunter P. J., Kadish A. H. et al. , “ The cardiac atlas project—An imaging database for computational modeling and statistical atlases of the heart,” Bioinformatics 27, 2288–2295 (2011). 10.1093/bioinformatics/btr360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Tobon-Gomez C., Geers A. J., Peters J., Weese J., Pinto K., Karim R., Ammar M., Daoudi A., Margeta J., Sandoval Z., Stender B., Zheng Y., Zuluaga M. A., Betancur J., Ayache N., Chikh M. A., Dillenseger J.-L., Kelm B. M., Mahmoudi S., Ourselin S., Schlaefer A., Schaeffter T., Razavi R., and Rhode K. S., “ Benchmark for algorithms segmenting the left atrium from 3D CT and MRI datasets,” IEEE Trans. Med. Imaging 34, 1460–1473 (2015). 10.1109/TMI.2015.2398818 [DOI] [PubMed] [Google Scholar]
- 22. Wolterink J. M., Leiner T., de Vos B. D., Coatrieux J.-L., Kelm B. M., Kondo S., Salgado R. A., Shahzad R., Shu H., Snoeren M., Takx R. A. P., van Vliet L. J., van Walsum T., Willems T. P., Yang G., Zheng Y., Viergever M. A., and Išgum I., “ An evaluation of automatic coronary artery calcium scoring methods with cardiac CT using the orCaScore framework,” Med. Phys. 43, 2361–2373 (2016). 10.1118/1.4945696 [DOI] [PubMed] [Google Scholar]
- 23. Karim R., Blake L.-E., Inoue J., Tao Q., Jia S., Housden R. J., Bhagirath P., Duval J.-L., Varela M., Behar J. M., Cadour L., van der Geest R. J., Cochet H., Drangova M., Sermesant M., Razavi R., Aslanidi O., Rajani R., and Rhode K., “ Algorithms for left atrial wall segmentation and thickness—Evaluation on an open-source CT and MRI image database,” Med. Image Anal. 50, 36–53 (2018). 10.1016/j.media.2018.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Zhuang X., Li L., Payer C., Štern D., Urschler M., Heinrich M. P., Oster J., Wang C., Smedby Ö., Bian C., Yang X., Heng P.-A., Mortazi A., Bagci U., Yang G., Sun C., Galisot G., Ramel J.-Y., Brouard T., Tong Q., Si W., Liao X., Zeng G., Shi Z., Zheng G., Wang C., MacGillivray T., Newby D., Rhode K., Ourselin S., Mohiaddin R., Keegan J., Firmin D., and Yang G., “ Evaluation of algorithms for multi-modality whole heart segmentation: An open-access grand challenge,” Med. Image Anal. 58, 101537 (2019). 10.1016/j.media.2019.101537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Campello V. M., Gkontra P., Izquierdo C., Martin-Isla C., Sojoudi A., Full P. M., Maier-Hein K., Zhang Y., He Z., Ma J. et al. , “ Multi-centre, multi-vendor and multi-disease cardiac segmentation: The m&ms challenge,” IEEE Trans. Med. Imaging 40, 3543–3554 (2021). 10.1109/TMI.2021.3090082 [DOI] [PubMed] [Google Scholar]
- 26. Baillargeon B., Rebelo N., Fox D. D., Taylor R. L., and Kuhl E., “ The living heart project: A robust and integrative simulator for human heart function,” Eur. J. Mech.-A/Solids 48, 38–47 (2014). 10.1016/j.euromechsol.2014.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Bäumler K., Vedula V., Sailer A. M., Seo J., Chiu P., Mistelbauer G., Chan F. P., Fischbein M. P., Marsden A. L., and Fleischmann D., “ Fluid–structure interaction simulations of patient-specific aortic dissection,” Biomech. Model. Mechanobiol. 19, 1607–1628 (2020). 10.1007/s10237-020-01294-8 [DOI] [PubMed] [Google Scholar]
- 28. Yang W., Dong M., Rabinovitch M., Chan F. P., Marsden A. L., and Feinstein J. A., “ Evolution of hemodynamic forces in the pulmonary tree with progressively worsening pulmonary arterial hypertension in pediatric patients,” Biomech. Model. Mechanobiol. 18, 779–796 (2019). 10.1007/s10237-018-01114-0 [DOI] [PubMed] [Google Scholar]
- 29. Tran K., Feliciano K. B., Yang W., Schwarz E. L., Marsden A. L., Dalman R. L., and Lee J. T., “ Patient-specific changes in aortic hemodynamics is associated with thrombotic risk after fenestrated endovascular aneurysm repair with large diameter endografts,” JVS Vasc. Sci. 3, 219–231 (2022). 10.1016/j.jvssci.2022.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Gutierrez N. G., Mathew M., McCrindle B. W., Tran J. S., Kahn A. M., Burns J. C., and Marsden A. L., “ Hemodynamic variables in aneurysms are associated with thrombotic risk in children with Kawasaki disease,” Int. J. Cardiol. 281, 15–21 (2019). 10.1016/j.ijcard.2019.01.092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Taylor C. A., Hughes T. J. R., and Zarins C. K., “ Finite element modeling of blood flow in arteries,” Comput. Methods Appl. Mech. Eng. 158, 155–196 (1998). 10.1016/S0045-7825(98)80008-X [DOI] [Google Scholar]
- 32. Wilson N. M., Arko F. R., and Taylor C. A., “ Predicting changes in blood flow in patient-specific operative plans for treating aortoiliac occlusive disease,” Comput. Aided Surg. 10, 257–277 (2005). 10.3109/10929080500230445 [DOI] [PubMed] [Google Scholar]
- 33. Lesage D., Angelini E. D., Bloch I., and Funka-Lea G., “ A review of 3D vessel lumen segmentation techniques: Models, features and extraction schemes,” Med. Image Anal. 13, 819–845 (2009). 10.1016/j.media.2009.07.011 [DOI] [PubMed] [Google Scholar]
- 34. Maher G., Wilson N., and Marsden A., “ Accelerating cardiovascular model building with convolutional neural networks,” Med. Biol. Eng. Comput. 57, 2319–2335 (2019). 10.1007/s11517-019-02029-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Maher G., Parker D., Wilson N., and Marsden A., “ Neural network vessel lumen regression for automated lumen cross-section segmentation in cardiovascular image-based modeling,” Cardiovasc. Eng. Technol. 11, 621–635 (2020). 10.1007/s13239-020-00497-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Iyer K., Najarian C. P., Fattah A. A., Arthurs C. J., Soroushmehr S. M. R., Subban V., Sankardas M. A., Nadakuditi R. R., Nallamothu B. K., and Figueroa C. A., “ AngioNet: A convolutional neural network for vessel segmentation in x-ray angiography,” Sci. Rep. 11, 11, 18066 (2021). 10.1038/s41598-021-97355-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kong F. W., Wilson N., and Shadden S., “ A deep-learning approach for direct whole-heart mesh reconstruction,” Med. Image Anal. 74, 102222 (2021). 10.1016/j.media.2021.102222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Kong F. W. and Shadden S. C., “ Whole heart mesh generation for image-based computational simulations by learning free-from deformations,” in Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI), Lecture Notes in Computer Science; (Springer, 2021), Vol. 12904, pp. 550–559. [Google Scholar]
- 39. Nakanishi R., Sankaran S., Grady L., Malpeso J., Yousfi R., Osawa K., Ceponiene I., Nazarat N., Rahmani S., Kissel K. et al. , “ Automated estimation of image quality for coronary computed tomographic angiography using machine learning,” Eur. Radiol. 28, 4018–4026 (2018). 10.1007/s00330-018-5348-8 [DOI] [PubMed] [Google Scholar]
- 40. Sahni O., Jansen K., Shephard M., Taylor C., and Beall M., “ Adaptive boundary layer meshing for viscous flow simulations,” Eng. Comput. 24, 267–285 (2008). 10.1007/s00366-008-0095-0 [DOI] [Google Scholar]
- 41. Vignon-Clementel I. E., Figueroa C. A., Jansen K. E., and Taylor C. A., “ Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries,” Comput. Methods Appl. Mech. Eng. 195, 3776–3796 (2006). 10.1016/j.cma.2005.04.014 [DOI] [Google Scholar]
- 42. Vignon-Clementel I. E., Figueroa C., Jansen K., and Taylor C., “ Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries,” Comput. Methods Biomech. Biomed. Eng. 13, 625–640 (2010). 10.1080/10255840903413565 [DOI] [PubMed] [Google Scholar]
- 43. Esmaily-Moghadam M., Vignon-Clementel I., Figliola R., and Marsden A., “ A modular numerical method for implicit 0D/3D coupling in cardiovascular finite element simulations,” J. Comput. Phys. 244, 63–79 (2013). 10.1016/j.jcp.2012.07.035 [DOI] [Google Scholar]
- 44. Quarteroni A., Ragni S., and Veneziani A., “ Coupling between lumped and distributed models for blood flow problems,” Comput. Visualization Sci. 4, 111–124 (2001). 10.1007/s007910100063 [DOI] [Google Scholar]
- 45. Kim H. J., Vignon-Clementel I. E., Figueroa C. A., LaDisa J. F., Jansen K. E., Feinstein J. A., and Taylor C. A., “ On coupling a lumped parameter heart model and a three-dimensional finite element aorta model,” Ann. Biomed. Eng. 37, 2153–2169 (2009). 10.1007/s10439-009-9760-8 [DOI] [PubMed] [Google Scholar]
- 46. Kuprat A., Kabilan S., Carson J., Corley R., and Einstein D., “ A bidirectional coupling procedure applied to multiscale respiratory modeling,” J. Comput. Phys. 244, 148–167 (2013). 10.1016/j.jcp.2012.10.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Esmaily-Moghadam M., Bazilevs Y., and Marsden A. L., “ A new preconditioning technique for implicitly coupled multidomain simulations with applications to hemodynamics,” Comput. Mech. 52, 1141–1152 (2013). 10.1007/s00466-013-0868-1 [DOI] [Google Scholar]
- 48. Esmaily-Moghadam M., Bazilevs Y., and Marsden A. L., “ A bi-partitioned iterative algorithm for solving linear systems arising from incompressible flow problems,” Comput. Methods Appl. Mech. Eng. 286, 40–62 (2015). 10.1016/j.cma.2014.11.033 [DOI] [Google Scholar]
- 49. Esmaily-Moghadam M., Bazilevs Y., Hsia T.-Y., Vignon-Clementel I., and Marsden A., “ A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations,” Comput. Mech. 48, 277–291 (2011). 10.1007/s00466-011-0599-0 [DOI] [Google Scholar]
- 50. Formaggia L., Gerbeau J., Nobile F., and Quarteroni A., “ On the coupling of 3D and 1D Navier–Stokes equations for flow problems in compliant vessels,” Comput. Methods Appl. Mech. Eng. 191, 561–582 (2001). 10.1016/S0045-7825(01)00302-4 [DOI] [Google Scholar]
- 51. Blanco P., Feijóo R., and Urquiza S., “ A unified variational approach for coupling 3D–1D models and its blood flow applications,” Comput. Methods Appl. Mech. Eng. 196, 4391–4410 (2007). 10.1016/j.cma.2007.05.008 [DOI] [Google Scholar]
- 52. Long C., Hsu M., Bazilevs Y., Feinstein J., and Marsden A., “ Fluid–structure interaction simulations of the Fontan procedure using variable wall properties,” Int. J. Numer. Methods Biomed. Eng. 28, 513–527 (2012). 10.1002/cnm.1485 [DOI] [PubMed] [Google Scholar]
- 53. Bazilevs Y., Hsu M., Zhang Y., Wang W., Kvamsdal T., Hentschel S., and Isaksen J., “ Computational vascular fluid–structure interaction: Methodology and application to cerebral aneurysms,” Biomech. Model. Mechanobiol. 9, 481–498 (2010). 10.1007/s10237-010-0189-7 [DOI] [PubMed] [Google Scholar]
- 54. Hsu M. and Bazilevs Y., “ Blood vessel tissue prestress modeling for vascular fluid–structure interaction simulation,” Finite Elem. Anal. Des. 47, 593–599 (2011). 10.1016/j.finel.2010.12.015 [DOI] [Google Scholar]
- 55. Moireau P., Xiao N., Astorino M., Figueroa C. A., Chapelle D., Taylor C. A., and Gerbeau J. F., “ External tissue support and fluid–structure simulation in blood flows,” Biomech. Model. Mechanobiol. 11, 1–18 (2011). 10.1007/s10237-011-0289-z [DOI] [PubMed] [Google Scholar]
- 56. Moireau P., Bertoglio C., Xiao N., Figueroa C. A., Taylor C. A., Chapelle D., and Gerbeau J. F., “ Sequential identification of boundary support parameters in a fluid-structure vascular model using patient image data,” Biomech. Model. Mechanobiol. 12, 475–496 (2012). 10.1007/s10237-012-0418-3 [DOI] [PubMed] [Google Scholar]
- 57. Holzapfel G. A. and Weizsacker H. W., “ Biomechanical behavior of the arterial wall and its numerical characterization,” Comput. Biol. Med. 28, 377–392 (1998). 10.1016/S0010-4825(98)00022-5 [DOI] [PubMed] [Google Scholar]
- 58. Holzapfel G. A., Sommer G., Gasser C. T., and Regitnig P., “ Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling,” Am. J. Physiol.-Heart Circulatory Physiol. 289, H2048–H2058 (2005). 10.1152/ajpheart.00934.2004 [DOI] [PubMed] [Google Scholar]
- 59. Figueroa C. A., Vignon-Clementel I. E., Jansen K. E., Hughes T. J., and Taylor C. A., “ A coupled momentum method for modeling blood flow in three-dimensional deformable arteries,” Comput. Methods Appl. Mech. Eng. 195, 5685–5706 (2006). 10.1016/j.cma.2005.11.011 [DOI] [Google Scholar]
- 60. Kung E., Les A., Figueroa C., Medina F., Arcaute K., Wicker R., McConnell M., and Taylor C., “ In vitro validation of finite element analysis of blood flow in deformable models,” Ann. Biomed. Eng. 39, 1947–1960 (2011). 10.1007/s10439-011-0284-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Kim H., Jansen K., and Taylor C., “ Incorporating autoregulatory mechanisms of the cardiovascular system in three-dimensional finite element models of arterial blood flow,” Ann. Biomed. Eng. 38, 2314–2330 (2010). 10.1007/s10439-010-9992-7 [DOI] [PubMed] [Google Scholar]
- 62. LaDisa J. F., Alberto Figueroa C., Vignon-Clementel I. E., Jin Kim H., Xiao N., Ellwein L. M., Chan F. P., Feinstein J. A., and Taylor C. A., “ Computational simulations for aortic coarctation: Representative results from a sampling of patients,” J. Biomech. Eng. 133, 091008 (2011). 10.1115/1.4004996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Xiong G., Figueroa C., Xiao N., and Taylor C., “ Simulation of blood flow in deformable vessels using subject–specific geometry and spatially varying wall properties,” Int. J. Numer. Methods Biomed. Eng. 27, 1000–1016 (2011). 10.1002/cnm.1404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Tang B. T., Fonte T. A., Chan F. P., Tsao P. S., Feinstein J. A., and Taylor C. A., “ Three-dimensional hemodynamics in the human pulmonary arteries under resting and exercise conditions,” Ann. Biomed. Eng. 39, 347–358 (2011). 10.1007/s10439-010-0124-1 [DOI] [PubMed] [Google Scholar]
- 65. Liu J. and Marsden A. L., “ A unified continuum and variational multiscale formulation for fluids, solids, and fluid-structure interaction,” Comput. Methods Appl. Mech. Eng. 337, 549–597 (2018). 10.1016/j.cma.2018.03.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Liu J. and Marsden A. L., “ A robust and efficient iterative method for hyper-elastodynamics with nested block preconditioning,” J. Comput. Phys. 383, 72–93 (2019). 10.1016/j.jcp.2019.01.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Liu J., Yang W. G., Dong M., and Marsden A. L., “ The nested block preconditioning technique for the incompressible Navier–Stokes equations with emphasis on hemodynamic simulations,” Comput. Methods Appl. Mech. Eng. 367, 113122 (2020). 10.1016/j.cma.2020.113122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Liu J., Latorre M., and Marsden A. L., “ A continuum and computational framework for viscoelastodynamics. I. Finite deformation linear models,” Comput. Methods Appl. Mech. Eng. 385, 114059 (2021). 10.1016/j.cma.2021.114059 [DOI] [Google Scholar]
- 69. Liu J., Lan I. S., Tikenogullari O. Z., and Marsden A. L., “ A note on the accuracy of the generalized-alpha scheme for the incompressible Navier–Stokes equations,” Int. J. Numer. Methods Eng. 122, 638–651 (2021). 10.1002/nme.6550 [DOI] [Google Scholar]
- 70. Lan I., Liu J., Yang W., and Marsden A., “ A reduced unified continuum formulation for vascular fluid-structure interaction,” Comput. Methods Appl. Mech. Eng. 394, 114852 (2022). 10.1016/j.cma.2022.114852 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Peskin C. S., “ Numerical analysis of blood flow in the heart,” J. Comput. Phys. 25, 220–252 (1977). 10.1016/0021-9991(77)90100-0 [DOI] [Google Scholar]
- 72. Mittal R., Dong H., Bozkurttas M., Najjar F., Vargas A., and Von Loebbecke A., “ A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries,” J. Comput. Phys. 227, 4825–4852 (2008). 10.1016/j.jcp.2008.01.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Kolahdouz E. M., Bhalla A. P. S., Scotten L. N., Craven B. A., and Griffith B. E., “ A sharp interface Lagrangian-Eulerian method for rigid-body fluid-structure interaction,” J. Comput. Phys. 443, 110442 (2021). 10.1016/j.jcp.2021.110442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Kolahdouz E. M., Bhalla A. P. S., Craven B. A., and Griffith B. E., “ An immersed interface method for discrete surfaces,” J. Comput. Phys. 400, 108854 (2020). 10.1016/j.jcp.2019.07.052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Vadala-Roth B., Acharya S., Patankar N. A., Rossi S., and Griffith B. E., “ Stabilization approaches for the hyperelastic immersed boundary method for problems of large-deformation incompressible elasticity,” Comput. Methods Appl. Mech. Eng. 365, 112978 (2020). 10.1016/j.cma.2020.112978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Lee J. H., Rygg A. D., Kolahdouz E. M., Rossi S., Retta S. M., Duraiswamy N., Scotten L. N., Craven B. A., and Griffith B. E., “ Fluid-structure interaction models of bioprosthetic heart valve dynamics in an experimental pulse duplicator,” Ann. Biomed. Eng. 48, 1475–1490 (2020). 10.1007/s10439-020-02466-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Kaiser A. D., Shad R., Hiesinger W., and Marsden A. L., “ A design-based model of the aortic valve for fluid-structure interaction,” Biomech. Model. Mechanobiol. 20, 2413–2435 (2021). 10.1007/s10237-021-01516-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Kaiser A. D., McQueen D. M., and Peskin C. S., “ Modeling the mitral valve,” Int. J. Numer. Methods Biomed. Eng. 35, e3240 (2019). 10.2310/6670.2008.00083 [DOI] [PubMed] [Google Scholar]
- 79. Vedula V., Seo J.-H., Lardo A. C., and Mittal R., “ Effect of trabeculae and papillary muscles on the hemodynamics of the left ventricle,” Theor. Comput. Fluid Dyn. 30, 3–21 (2016). 10.1007/s00162-015-0349-6 [DOI] [Google Scholar]
- 80. Kheradvar A., Groves E. M., Goergen C. J., Alavi S. H., Tranquillo R., Simmons C. A., Dasi L. P., Grande-Allen K. J., Mofrad M. R. K., Falahatpisheh A., Griffith B., Baaijens F., Little S. H., and Canic S., “ Emerging trends in heart valve engineering. II. Novel and standard technologies for aortic valve replacement,” Ann. Biomed. Eng. 43, 844–857 (2015). 10.1007/s10439-014-1191-5 [DOI] [PubMed] [Google Scholar]
- 81. Kheradvar A., Groves E. M., Simmons C. A., Griffith B., Alavi S. H., Tranquillo R., Dasi L. P., Falahatpisheh A., Grande-Allen K. J., Goergen C. J., Mofrad M. R. K., Baaijens F., Canic S., and Little S. H., “ Emerging trends in heart valve engineering. III. Novel technologies for mitral valve repair and replacement,” Ann. Biomed. Eng. 43, 858–870 (2015). 10.1007/s10439-014-1129-y [DOI] [PubMed] [Google Scholar]
- 82. Kheradvar A., Groves E. M., Dasi L. P., Alavi S. H., Tranquillo R., Grande-Allen K. J., Simmons C. A., Griffith B., Falahatpisheh A., Goergen C. J., Mofrad M. R. K., Baaijens F., Little S. H., and Canic S., “ Emerging trends in heart valve engineering. I. Solutions for future,” Ann. Biomed. Eng. 43, 833–843 (2015). 10.1007/s10439-014-1209-z [DOI] [PubMed] [Google Scholar]
- 83. Shim J. J., Maas S. A., Weiss J. A., and Ateshian G. A., “ A formulation for fluid–structure interactions in FEBIO using mixture theory,” J. Biomech. Eng. 141, 051010 (2019). 10.1115/1.4043031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Tuković Ž., Karač A., Cardiff P., Jasak H., and Ivanković A., “ Openfoam finite volume solver for fluid-solid interaction,” Trans. FAMENA 42, 1–31 (2018). 10.21278/TOF.42301 [DOI] [Google Scholar]
- 85. Yang W., Chan F. P., Reddy V. M., Marsden A. L., and Feinstein J. A., “ Flow simulations and validation for the first cohort of patients undergoing the Y-graft Fontan procedure,” J. Thorac. Cardiovasc. Surg. 149, 247–255 (2015). 10.1016/j.jtcvs.2014.08.069 [DOI] [PubMed] [Google Scholar]
- 86. Les A., Shadden S., Figueroa C., Park J., Tedesco M., Herfkens R., Dalman R., and Taylor C., “ Quantification of hemodynamics in abdominal aortic aneurysms during rest and exercise using magnetic resonance imaging and computational fluid dynamics,” Ann. Biomed. Eng. 38, 1288–1313 (2010). 10.1007/s10439-010-9949-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Dabagh M., Nair P., Gounley J., Frakes D., Gonzalez L. F., and Randles A., “ Hemodynamic and morphological characteristics of a growing cerebral aneurysm,” Neurosurgical Focus 47, E13 (2019). 10.3171/2019.4.FOCUS19195 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. van de Velde L., Groot Jebbink E., Hagmeijer R., Versluis M., and Reijnen M. M., “ Computational fluid dynamics for the prediction of endograft thrombosis in the superficial femoral artery,” J. Endovasc. Ther. (published online). 10.1177/15266028221091890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89. Mukherjee D., Jani N. D., Narvid J., and Shadden S. C., “ The role of circle of Willis anatomy variations in cardio-embolic stroke: A patient-specific simulation based study,” Ann. Biomed. Eng. 46, 1128–1145 (2018). 10.1007/s10439-018-2027-5 [DOI] [PubMed] [Google Scholar]
- 90. Rodefeld M. D., Coats B., Fisher T., Giridharan G. A., Chen J., Brown J. W., and Frankel S. H., “ Cavopulmonary assist for the univentricular Fontan circulation: Von Karman viscous impeller pump,” J. Thorac. Cardiovasc. Surg. 140, 529–536 (2010). 10.1016/j.jtcvs.2010.04.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91. Malinauskas R. A., Hariharan P., Day S. W., Herbertson L. H., Buesen M., Steinseifer U., Aycock K. I., Good B. C., Deutsch S., Manning K. B. et al. , “ FDA benchmark medical device flow models for CFD validation,” ASAIO J. 63, 150–160 (2017). 10.1097/MAT.0000000000000499 [DOI] [PubMed] [Google Scholar]
- 92. Mortier P., Holzapfel G. A., De Beule M., Van Loo D., Taeymans Y., Segers P., Verdonck P., and Verhegghe B., “ A novel simulation strategy for stent insertion and deployment in curved coronary bifurcations: Comparison of three drug-eluting stents,” Ann. Biomed. Eng. 38, 88–99 (2010). 10.1007/s10439-009-9836-5 [DOI] [PubMed] [Google Scholar]
- 93. Zunino P., D'Angelo C., Petrini L., Vergara C., Capelli C., and Migliavacca F., “ Numerical simulation of drug eluting coronary stents: Mechanics, fluid dynamics and drug release,” Comput. Methods Appl. Mech. Eng. 198, 3633–3644 (2009). 10.1016/j.cma.2008.07.019 [DOI] [Google Scholar]
- 94. Tonino P. A. L., De Bruyne B., Pijls N. H. J., Siebert U., Ikeno F., van't Veer M., Klauss V., Manoharan G., Engstrom T., Oldroyd K. G., Lee P. N. V., MacCarthy P. A., Fearon W. F., and Investigators F. S., “ Fractional flow reserve versus angiography for guiding percutaneous coronary intervention,” N. Engl. J. Med. 360, 213–224 (2009). 10.1056/NEJMoa0807611 [DOI] [PubMed] [Google Scholar]
- 95. Pijls N. H. J., Fearon W. F., Tonino P. A. L., Siebert U., Ikeno F., Bornschein B., van't Veer M., Klauss V., Manoharan G., Engstrom T., Oldroyd K. G., Lee P. N. V., MacCarthy P. A., De Bruyne B., and Investigators F. S., “ Fractional flow reserve versus angiography for guiding percutaneous coronary intervention in patients with multivessel coronary artery disease 2-year follow-up of the fame (fractional flow reserve versus angiography for multivessel evaluation) study,” J. Am. College Cardiol. 56, 177–184 (2010). 10.1016/j.jacc.2010.04.012 [DOI] [PubMed] [Google Scholar]
- 96. Min J. K., Taylor C. A., Achenbach S., Koo B. K., Leipsic J., Norgaard B. L., Pijls N. J., and De Bruyne B., “ Noninvasive fractional flow reserve derived from coronary CT angiography clinical data and scientific principles,” JACC-Cardiovasc. Imaging 8, 1209–1222 (2015). 10.1016/j.jcmg.2015.08.006 [DOI] [PubMed] [Google Scholar]
- 97. Ihdayhid A. R., Norgaard B. L., Gaur S., Leipsic J., Nerlekar N., Osawa K., Miyoshi T., Jensen J. M., Kimura T., Shiomi H., Erglis A., Jegere S., Oldroyd K. G., Botker H. E., Seneviratne S. K., Achenbach S., and Ko B. S., “ Prognostic value and risk continuum of noninvasive fractional flow reserve derived from coronary CT angiography,” Radiology 292, 343–351 (2019). 10.1148/radiol.2019182264 [DOI] [PubMed] [Google Scholar]
- 98. Fairbairn T. A., Nieman K., Akasaka T., Norgaard B. L., Berman D. S., Raff G., Hurwitz-Koweek L. M., Pontone G., Kawasaki T., Sand N. P., Jensen J. M., Amano T., Poon M., Ovrehus K., Sonck J., Rabbat M., Mullen S., De Bruyne B., Rogers C., Matsuo H., Bax J. J., Leipsic J., and Patel M. R., “ Real-world clinical utility and impact on clinical decision-making of coronary computed tomography angiography-derived fractional flow reserve: Lessons from the advance registry,” Eur. Heart J. 39, 3701–3711 (2018). 10.1093/eurheartj/ehy530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Douglas P. S., De Bruyne B., Pontone G., Patel M. R., Norgaard B. L., Byrne R. A., Curzen N., Purcell I., Gutberlet M., Rioufol G., Hink U., Schuchlenz H. W., Feuchtner G., Gilard M., Andreini D., Jensen J. M., Hadamitzky M., Chiswell K., Cyr D., Wilk A., Wang F. R., Rogers C., Hlatky M. A., and Investigators P., “ 1-year outcomes of FFRCT-guided care in patients with suspected coronary disease: The platform study,” J. Am. College Cardiol. 68, 435–445 (2016). 10.1016/j.jacc.2016.05.057 [DOI] [PubMed] [Google Scholar]
- 100. Seo J., Ramachandra A. B., Boyd J., Marsden A. L., and Kahn A. M., “ Computational evaluation of venous graft geometries in coronary artery bypass surgery,” Semin. Thorac. Cardiovasc. Surg. 35, 521–532 (2021). 10.1053/j.semtcvs.2021.03.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Sankaran S. and Marsden A., “ The impact of uncertainty on shape optimization of idealized bypass graft models in unsteady flow,” Phys. Fluids 22, 121902 (2010). 10.1063/1.3529444 [DOI] [Google Scholar]
- 102. Sankaran S., Moghadam M. E., Kahn A. M., Tseng E. E., Guccione J. M., and Marsden A. L., “ Patient-specific multiscale modeling of blood flow for coronary artery bypass graft surgery,” Ann. Biomed. Eng. 40, 2228–2242 (2012). 10.1007/s10439-012-0579-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Motwani J. G. and Topol E. J., “ Aortocoronary saphenous vein graft disease—Pathogenesis, predisposition, and prevention,” Circulation 97, 916–931 (1998). 10.1161/01.CIR.97.9.916 [DOI] [PubMed] [Google Scholar]
- 104. Head S. J., Milojevic M., Taggart D. P., and Puskas J. D., “ Current practice of state-of-the-art surgical coronary revascularization,” Circulation 136, 1331–1345 (2017). 10.1161/CIRCULATIONAHA.116.022572 [DOI] [PubMed] [Google Scholar]
- 105. Sabik J. F., Lytle B. W., Blackstone E. H., Houghtaling P. L., and Cosgrove D. M., “ Comparison of saphenous vein and internal thoracic artery graft patency by coronary system,” Ann. Thorac. Surg. 79, 544–551 (2005). 10.1016/j.athoracsur.2004.07.047 [DOI] [PubMed] [Google Scholar]
- 106. Bourassa M. G., Fisher L. D., Campeau L., Gillespie M. J., McConney M., and Lespérance J., “ Long-term fate of bypass grafts: The coronary artery surgery study (CASS) and montreal heart institute experiences,” Circulation 72, V71–V78 (1985). [PubMed] [Google Scholar]
- 107. Hess C. N., Lopes R. D., Gibson C. M., Hager R., Wojdyla D. M., Englum B. R., Mack M. J., Califf R. M., Kouchoukos N. T., Peterson E. D., and Alexander J. H., “ Saphenous vein graft failure after coronary artery bypass surgery: Insights from PREVENT IV,” Circulation 130, 1445–1451 (2014). 10.1161/CIRCULATIONAHA.113.008193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Shavadia J., Norris C. M., Graham M. M., Verma S., Ali I., and Bainey K. R., “ Symptomatic graft failure and impact on clinical outcome after coronary artery bypass grafting surgery: Results from the Alberta provincial project for outcome assessment in coronary heart disease registry,” Am. Heart J. 169, 833–840 (2015). 10.1016/j.ahj.2015.02.022 [DOI] [PubMed] [Google Scholar]
- 109. Lopes R. D., Mehta R. H., Hafley G. E., Williams J. B., Mack M. J., Peterson E. D., Allen K. B., Harrington R. A., Gibson C. M., Califf R. M., Kouchoukos N. T., Ferguson T. B., and Alexander J. H., and V. Project Ex Vivo Vein Graft Engineering, “ Relationship between vein graft failure and subsequent clinical outcomes after coronary artery bypass surgery,” Circulation 125, 749–756 (2012). 10.1161/CIRCULATIONAHA.111.040311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Berceli S. A., Tran-Son-Tay R., Garbey M., and Jiang Z., “ Hemodynamically driven vein graft remodeling: A systems biology approach,” Vascular 17(Suppl. 1), S2–S9 (2009). 10.2310/6670.2008.00083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111. Zhao J., Andreasen J. J., Yang J., Rasmussen B. S., Liao D., and Gregersen H., “ Manual pressure distension of the human saphenous vein changes its biomechanical properties-implication for coronary artery bypass grafting,” J. Biomech. 40, 2268–2276 (2007). 10.1016/j.jbiomech.2006.10.014 [DOI] [PubMed] [Google Scholar]
- 112. Gusic R. J., Myung R., Petko M., Gaynor J. W., and Gooch K. J., “ Shear stress and pressure modulate saphenous vein remodeling ex vivo,” J. Biomech. 38, 1760–1769 (2005). 10.1016/j.jbiomech.2004.10.030 [DOI] [PubMed] [Google Scholar]
- 113. Krasiński Z., Biskupski P., Dzieciuchowicz Ł., Kaczmarek E., Krasińska B., Staniszewski R., Pawlaczyk K., Stanisić M., Majewski P., and Majewski W., “ The influence of elastic components of the venous wall on the biomechanical properties of different veins used for arterial reconstruction,” Eur. J. Vasc. Endovasc. Surg. 40, 224–229 (2010). 10.1016/j.ejvs.2010.04.008 [DOI] [PubMed] [Google Scholar]
- 114. Leask R. L., Butany J., Johnston K. W., Ethier C. R., and Ojha M., “ Human saphenous vein coronary artery bypass graft morphology, geometry and hemodynamics,” Ann. Biomed. Eng. 33, 301–309 (2005). 10.1007/s10439-005-1732-z [DOI] [PubMed] [Google Scholar]
- 115. Bush H. L., Jakubowski J. A., Curl G. R., Deykin D., and Nabseth D. C., “ The natural history of endothelial structure and function in arterialized vein grafts,” J. Vasc. Surg. 3, 204–215 (1986). 10.1016/0741-5214(86)90004-2 [DOI] [PubMed] [Google Scholar]
- 116. Hassantash S. A., Bikdeli B., Kalantarian S., Sadeghian M., and Afshar H., “ Pathophysiology of aortocoronary saphenous vein bypass graft disease,” Asian Cardiovasc. Thorac. Ann. 16, 331–336 (2008). 10.1177/021849230801600418 [DOI] [PubMed] [Google Scholar]
- 117. Ramachandra A., Sankaran S., Humphrey J., and Marsden A., “ Computational simulation of the adaptive capacity of vein grafts in response to increased pressure,” J. Biomech. Eng. 137, 031009 (2015). 10.1115/1.4029021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118. Latorre M. and Humphrey J. D., “ Modeling mechano-driven and immuno-mediated aortic maladaptation in hypertension,” Biomech. Model. Mechanobiol. 17, 1497–1511 (2018). 10.1007/s10237-018-1041-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Latorre M., Bersi M., and Humphrey J. D., “ Computational modeling predicts immuno-mechanical mechanisms of maladaptive aortic remodeling in hypertension,” Int. J. Eng. Sci. 141, 35–46 (2019). 10.1016/j.ijengsci.2019.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Ramachandra A., Kahn A., and Marsden A., “ Patient specific simulations reveal significant differences in mechanical stimuli in venous and arterial coronary grafts,” J. Cardiovasc. Transl. Res. 9, 279–290 (2016). 10.1007/s12265-016-9706-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Khan M. O., Tran J. S., Zhu H., Boyd J., Packard R. R. S., Karlsberg R. P., Kahn A. M., and Marsden A. L., “ Low wall shear stress is associated with saphenous vein graft stenosis in patients with coronary artery bypass grafting,” J. Cardiovasc. Transl. Res. 14, 770–781 (2020). 10.1007/s12265-020-09982-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122. Ramachandra A., Humphrey J., and Marsden A., “ Gradual loading ameliorates maladaptation in computational simulations of vein graft growth and remodeling,” J. R. Soc. Interface 14, 20160995 (2017). 10.1098/rsif.2016.0995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Sato A., Kawamoto S., Watanabe M., Suzuki Y., Takahashi G., Masaki N., Kumagai K., Saijo Y., Tabayashi K., and Saiki Y., “ A novel biodegradable external mesh stent improved long-term patency of vein grafts by inhibiting intimal-medial hyperplasia in an experimental canine model,” Gen. Thorac. Cardiovasc. Surg. 64, 1–9 (2016). 10.1007/s11748-015-0591-2 [DOI] [PubMed] [Google Scholar]
- 124. Desai M., Mirzay-Razzaz J., von Delft D., Sarkar S., Hamilton G., and Seifalian A. M., “ Inhibition of neointimal formation and hyperplasia in vein grafts by external stent/sheath,” Vasc. Med. 15, 287–297 (2010). 10.1177/1358863X10366479 [DOI] [PubMed] [Google Scholar]
- 125. Taggart D. P., Ben Gal Y., Lees B., Patel N., Webb C., Rehman S. M., Desouza A., Yadav R., De Robertis F., Dalby M., Banning A., Channon K. M., Di Mario C., and Orion E., “ A randomized trial of external stenting for saphenous vein grafts in coronary artery bypass grafting,” Ann. Thorac. Surg. 99, 2039–2045 (2015). 10.1016/j.athoracsur.2015.01.060 [DOI] [PubMed] [Google Scholar]
- 126. Ramachandra A. B., Latorre M., Szafron J. M., Marsden A. L., and Humphrey J. D., “ Vascular adaptation in the presence of external support—A modeling study,” J. Mech. Behav. Biomed. Mater. 110, 103943 (2020). 10.1016/j.jmbbm.2020.103943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. Coenen A., Rossi A., Lubbers M. M., Kurata A., Kono A. K., Chelu R. G., Segreto S., Dijkshoorn M. L., Wragg A., van Geuns R.-J. M. et al. , “ Integrating CT myocardial perfusion and CT-FFR in the work-up of coronary artery disease,” JACC: Cardiovasc. Imaging 10, 760–770 (2017). 10.1016/j.jcmg.2016.09.028 [DOI] [PubMed] [Google Scholar]
- 128. Schrauwen J. T., Coenen A., Kurata A., Wentzel J. J., van der Steen A. F., Nieman K., and Gijsen F. J., “ Functional and anatomical measures for outflow boundary conditions in atherosclerotic coronary bifurcations,” J. Biomech. 49, 2127–2134 (2016). 10.1016/j.jbiomech.2015.11.036 [DOI] [PubMed] [Google Scholar]
- 129. Menon K., Seo J., Kahn A. M., Burns J. C., and Marsden A. L., “ The risk of myocardial ischemia in patients with Kawasaki disease: Insights from patient-specific simulations of coronary hemodynamics,” medRxiv. [DOI] [PubMed]
- 130. Jiang M. X., Khan M. O., Ghobrial J., Rogers I. S., Pettersson G. B., Blackstone E. H., and Marsden A. L., “ Patient-specific fluid–structure simulations of anomalous aortic origin of right coronary arteries,” JTCVS Tech. 13, 144–162 (2022). 10.1016/j.xjtc.2022.02.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131. Dickinson M. G., Bartelds B., Borgdorff M. A., and Berger R. M., “ The role of disturbed blood flow in the development of pulmonary arterial hypertension: Lessons from preclinical animal models,” Am. J. Physiol.-Lung Cell. Mol. Physiol. 305, L1–L14 (2013). 10.1152/ajplung.00031.2013 [DOI] [PubMed] [Google Scholar]
- 132. Feinstein J. A., “ Evaluation, risk stratification, and management of pulmonary hypertension in patients with congenital heart disease,” in Proceedings of the Seminars in Thoracic and Cardiovascular Surgery: Pediatric Cardiac Surgery Annual ( Elsevier, 2009), Vol. 12, pp. 106–111. [DOI] [PubMed] [Google Scholar]
- 133. Schäfer M., Kheyfets V. O., Schroeder J. D., Dunning J., Shandas R., Buckner J. K., Browning J., Hertzberg J., Hunter K. S., and Fenster B. E., “ Main pulmonary arterial wall shear stress correlates with invasive hemodynamics and stiffness in pulmonary hypertension,” Pulm. Circ. 6, 37–45 (2016). 10.1086/685024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134. Schäfer M., Barker A. J., Kheyfets V., Stenmark K. R., Crapo J., Yeager M. E., Truong U., Buckner J. K., Fenster B. E., and Hunter K. S., “ Helicity and vorticity of pulmonary arterial flow in patients with pulmonary hypertension: Quantitative analysis of flow formations,” J. Am. Heart Assoc. 6, e007010 (2017). 10.1161/JAHA.117.007010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Barker A. J., Roldán-Alzate A., Entezari P., Shah S. J., Chesler N. C., Wieben O., Markl M., and François C. J., “ Four-dimensional flow assessment of pulmonary artery flow and wall shear stress in adult pulmonary arterial hypertension: Results from two institutions,” Magn. Reson. Med. 73, 1904–1913 (2015). 10.1002/mrm.25326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136. Dong M. L., Lan I. S., Yang W., Rabinovitch M., Feinstein J. A., and Marsden A. L., “ Computational simulation-derived hemodynamic and biomechanical properties of the pulmonary arterial tree early in the course of ventricular septal defects,” Biomech. Model. Mechanobiol. 20, 2471–2489 (2021). 10.1007/s10237-021-01519-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137. Tang B. T., Pickard S. S., Chan F. P., Tsao P. S., Taylor C. A., and Feinstein J. A., “ Wall shear stress is decreased in the pulmonary arteries of patients with pulmonary arterial hypertension: An image-based, computational fluid dynamics study,” Pulm. Circ. 2, 470–476 (2012). 10.4103/2045-8932.105035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138. Kheyfets V. O., Rios L., Smith T., Schroeder T., Mueller J., Murali S., Lasorda D., Zikos A., Spotti J., J. J. Reilly, Jr. , et al. , “ Patient-specific computational modeling of blood flow in the pulmonary arterial circulation,” Comput. Methods Programs Biomed. 120, 88–101 (2015). 10.1016/j.cmpb.2015.04.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Hunter K. S., Lee P.-F., Lanning C. J., Ivy D. D., Kirby K. S., Claussen L. R., Chan K. C., and Shandas R., “ Pulmonary vascular input impedance is a combined measure of pulmonary vascular resistance and stiffness and predicts clinical outcomes better than pulmonary vascular resistance alone in pediatric patients with pulmonary hypertension,” Am. Heart J. 155, 166–174 (2008). 10.1016/j.ahj.2007.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140. Olufsen M. S., Hill N., Vaughan G. D., Sainsbury C., and Johnson M., “ Rarefaction and blood pressure in systemic and pulmonary arteries,” J. Fluid Mech. 705, 280–305 (2012). 10.1017/jfm.2012.220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Geggel R. L., Gauvreau K., and Lock J. E., “ Balloon dilation angioplasty of peripheral pulmonary stenosis associated with williams syndrome,” Circulation 103, 2165–2170 (2001). 10.1161/01.CIR.103.17.2165 [DOI] [PubMed] [Google Scholar]
- 142. Cunningham J. W., McElhinney D. B., Gauvreau K., Bergersen L., Lacro R. V., Marshall A. C., Smoot L., and Lock J. E., “ Outcomes after primary transcatheter therapy in infants and young children with severe bilateral peripheral pulmonary artery stenosis,” Circ.: Cardiovasc. Interventions 6, 460–467 (2013). 10.1161/CIRCINTERVENTIONS.112.000061 [DOI] [PubMed] [Google Scholar]
- 143. Cobb H., Spray B., Daily J., Dossey A., and Angtuaco M. J., “ Cutting balloon angioplasty on branch pulmonary artery stenosis in pediatric patients,” Catheterization Cardiovasc. Interventions 98, 526–532 (2021). 10.1002/ccd.29803 [DOI] [PubMed] [Google Scholar]
- 144. Lan I. S., Yang W., Feinstein J. A., Kreutzer J., Collins R. T., Ma M., Adamson G. T., and Marsden A. L., “ Virtual transcatheter interventions for peripheral pulmonary artery stenosis in Williams and Alagille syndromes,” J. Am. Heart Assoc. 11, e023532 (2022). 10.1161/JAHA.121.023532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145. Spilker R. L., Feinstein J. A., Parker D. W., Reddy V. M., and Taylor C. A., “ Morphometry-based impedance boundary conditions for patient-specific modeling of blood flow in pulmonary arteries,” Ann. Biomed. Eng. 35, 546–559 (2007). 10.1007/s10439-006-9240-3 [DOI] [PubMed] [Google Scholar]
- 146. Walker S. G. and Stuth E. A., “ Single-ventricle physiology: Perioperative implications,” in Proceedings of the Seminars in Pediatric Surgery ( Elsevier, 2004), Vol. 13, pp. 188–202. [DOI] [PubMed] [Google Scholar]
- 147. Migliavacca F., Pennati G., Dubini G., Fumero R., Pietrabissa R., Urcelay G., Bove E. L., Hsia T.-Y., and de Leval M. R., “ Modeling of the Norwood circulation: Effects of shunt size, vascular resistances, and heart rate,” Am. J. Physiol.-Heart Circ. Physiol. 280, H2076–H2086 (2001). 10.1152/ajpheart.2001.280.5.H2076 [DOI] [PubMed] [Google Scholar]
- 148. Bove E. L., Migliavacca F., de Leval M. R., Balossino R., Pennati G., Lloyd T. R., Khambadkone S., Hsia T.-Y., and Dubini G., “ Use of mathematic modeling to compare and predict hemodynamic effects of the modified Blalock–Taussig and right ventricle–pulmonary artery shunts for hypoplastic left heart syndrome,” J. Thorac. Cardiovasc. Surg. 136, 312–320 (2008). 10.1016/j.jtcvs.2007.04.078 [DOI] [PubMed] [Google Scholar]
- 149. Kung E., Baretta A., Baker C., Arbia G., Biglino G., Corsini C., Schievano S., Vignon-Clementel I. E., Dubini G., Pennati G. et al. , “ Predictive modeling of the virtual Hemi-Fontan operation for second stage single ventricle palliation: Two patient-specific cases,” J. Biomech. 46, 423–429 (2013). 10.1016/j.jbiomech.2012.10.023 [DOI] [PubMed] [Google Scholar]
- 150. Biglino G., Giardini A., Baker C., Figliola R. S., Hsia T.-Y., Taylor A. M., Schievano S. et al. , “ In vitro study of the Norwood palliation: A patient-specific mock circulatory system,” ASAIO J. 58, 25–31 (2012). 10.1097/MAT.0b013e3182396847 [DOI] [PubMed] [Google Scholar]
- 151. Hang T., Giardini A., Biglino G., Conover T., and Figliola R. S., “ In vitro validation of a multiscale patient-specific Norwood palliation model,” ASAIO J. 62, 317–324 (2016). 10.1097/MAT.0000000000000336 [DOI] [PubMed] [Google Scholar]
- 152. Zhou J., Moghadam M. E., Conover T. A., Hsia T.-Y., Marsden A. L., and Figliola R. S., “ In vitro assessment of the assisted bidirectional Glenn procedure for stage one single ventricle repair,” Cardiovasc. Eng. Technol. 6, 256–267 (2015). 10.1007/s13239-015-0232-z [DOI] [PubMed] [Google Scholar]
- 153. Hsia T.-Y., Figliola R., M. of Congenital Hearts Alliance (MOCHA) Investigators, Bove E., Dorfman A., Taylor A., Giardini A., Khambadkone S., Schievano S., Hsia T.-Y. et al. , “ Multiscale modelling of single-ventricle hearts for clinical decision support: A Leducq transatlantic network of excellence,” Eur. J. Cardiothorac. Surg. 49, 365–368 (2016). 10.1093/ejcts/ezv368 [DOI] [PubMed] [Google Scholar]
- 154. Sundareswaran K. S., Pekkan K., Dasi L. P., Whitehead K., Sharma S., Kanter K. R., Fogel M. A., and Yoganathan A. P., “ The total cavopulmonary connection resistance: A significant impact on single ventricle hemodynamics at rest and exercise,” Am. J. Physiol.-Heart Circ. Physiol. 295, H2427–H2435 (2008). 10.1152/ajpheart.00628.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155. Whitehead K. K., Pekkan K., Kitajima H. D., Paridon S. M., Yoganathan A. P., and Fogel M. A., “ Nonlinear power loss during exercise in single-ventricle patients after the Fontan: Insights from computational fluid dynamics,” Circulation 116, I-165 (2007). 10.1161/CIRCULATIONAHA.106.680827 [DOI] [PubMed] [Google Scholar]
- 156. De Leval M., Dubini G., Jalali H., Pietrabissa R. et al. , “ Use of computational fluid dynamics in the design of surgical procedures: Application to the study of competitive flows in cavopulmonary connections,” J. Thorac. Cardiovasc. Surg. 111, 502–513 (1996). 10.1016/S0022-5223(96)70302-1 [DOI] [PubMed] [Google Scholar]
- 157. Dasi L. P., KrishnankuttyRema R., Kitajima H. D., Pekkan K., Sundareswaran K. S., Fogel M., Sharma S., Whitehead K., Kanter K., and Yoganathan A. P., “ Fontan hemodynamics: Importance of pulmonary artery diameter,” J. Thorac. Cardiovasc. Surg. 137, 560–564 (2009). 10.1016/j.jtcvs.2008.04.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158. Martin M. H., Feinstein J. A., Chan F. P., Marsden A. L., Yang W., and Reddy V. M., “ Technical feasibility and intermediate outcomes of using a handcrafted, area-preserving, bifurcated Y-graft modification of the Fontan procedure,” J. Thorac. Cardiovasc. Surg. 149, 239–245 (2015). 10.1016/j.jtcvs.2014.08.058 [DOI] [PubMed] [Google Scholar]
- 159. Schwarz E. L., Kelly J. M., Blum K. M., Hor K. N., Yates A. R., Zbinden J. C., Verma A., Lindsey S. E., Ramachandra A. B., Szafron J. M. et al. , “ Hemodynamic performance of tissue-engineered vascular grafts in Fontan patients,” NPJ Regener. Med. 6, 38 (2021). 10.1038/s41536-021-00148-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160. Verma A., Esmaily M., Shang J., Figliola R., Feinstein J. A., Hsia T.-Y., and Marsden A. L., “ Optimization of the assisted bidirectional Glenn procedure for first stage single ventricle repair,” World J. Pediatr. Congenital Heart Surg. 9, 157–170 (2018). 10.1177/2150135117745026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161. Kung E. O., Pennati G., Migliavacca F., Hsia T.-Y., Figliola R., Marsden A., and Giardini A., “ A simulation protocol for exercise physiology in fontan patients using a closed-loop lumped-parameter model,” J. Biomech. Eng., Trans. ASME 136, 081007 (2014). 10.1115/1.4027271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162. Westerhof N., Stergiopulos N., Noble M. I., and Westerhof B. E., Snapshots of Hemodynamics: An Aid for Clinical Research and Graduate Education ( Springer, 2010), Vol. 7. [Google Scholar]
- 163. Milišić V. and Quarteroni A., “ Analysis of lumped parameter models for blood flow simulations and their relation with 1D models,” ESAIM: Math. Model. Num. Anal. 38, 613–632 (2004). 10.1051/m2an:2004036 [DOI] [Google Scholar]
- 164. Pfaller M. R., Pham J., Verma A., Wilson N. M., Parker D. W., Yang W., and Marsden A. L., “ Automated generation of 0D and 1D reduced-order models of patient-specific blood flow,” arXiv:2111.04878 (2021). [DOI] [PMC free article] [PubMed]
- 165. Migliavacca F., Balossino R., Pennati G., Dubini G., Hsia T.-Y., de Leval M. R., and Bove E. L., “ Multiscale modelling in biofluidynamics: Application to reconstructive paediatric cardiac surgery,” J. Biomech. 39, 1010–1020 (2006). 10.1016/j.jbiomech.2005.02.021 [DOI] [PubMed] [Google Scholar]
- 166. Kim H. J., Vignon-Clementel I., Figueroa C., Jansen K., and Taylor C., “ Developing computational methods for three-dimensional finite element simulations of coronary blood flow,” Finite Elements Anal. Des. 46, 514–525 (2010). 10.1016/j.finel.2010.01.007 [DOI] [Google Scholar]
- 167. Kim H. J., Vignon-Clementel I., Coogan J., Figueroa C., Jansen K., and Taylor C., “ Patient-specific modeling of blood flow and pressure in human coronary arteries,” Ann. Biomed. Eng. 38, 3195–3209 (2010). 10.1007/s10439-010-0083-6 [DOI] [PubMed] [Google Scholar]
- 168. Grande Gutiérrez N., Sinno T., and Diamond S. L., “ A 1D–3D hybrid model of patient-specific coronary hemodynamics,” Cardiovasc. Eng. Technol. 13, 331–342 (2022). 10.1007/s13239-021-00580-5 [DOI] [PubMed] [Google Scholar]
- 169. Chnafa C., Valen-Sendstad K., Brina O., Pereira V., and Steinman D., “ Improved reduced-order modelling of cerebrovascular flow distribution by accounting for arterial bifurcation pressure drops,” J. Biomech. 51, 83–88 (2017). 10.1016/j.jbiomech.2016.12.004 [DOI] [PubMed] [Google Scholar]
- 170. Schrauwen J., Wentzel J., van der Steen A., and Gijsen F., “ Geometry-based pressure drop prediction in mildly diseased human coronary arteries,” J. Biomech. 47, 1810–1815 (2014). 10.1016/j.jbiomech.2014.03.028 [DOI] [PubMed] [Google Scholar]
- 171. Pewowaruk R., Lamers L., and Roldán-Alzate A., “ Accelerated estimation of pulmonary artery stenosis pressure gradients with distributed lumped parameter modeling vs. 3D CFD with instantaneous adaptive mesh refinement: Experimental validation in swine,” Ann. Biomed. Eng. 49, 2365–2376 (2021). 10.1007/s10439-021-02780-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172. Mirramezani M. and Shadden S. C., “ A distributed lumped parameter model of blood flow,” Ann. Biomed. Eng. 48, 2870–2886 (2020). 10.1007/s10439-020-02545-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173. Olufsen M. S., “ Structured tree outflow condition for blood flow in larger systemic arteries,” Am. J. Physiol.-Heart Circ. Physiol. 276, H257–H268 (1999). 10.1152/ajpheart.1999.276.1.H257 [DOI] [PubMed] [Google Scholar]
- 174. Blanco P. J., Pivello M., Urquiza S., and Feijóo R., “ On the potentialities of 3D–1D coupled models in hemodynamics simulations,” J. Biomech. 42, 919–930 (2009). 10.1016/j.jbiomech.2009.01.034 [DOI] [PubMed] [Google Scholar]
- 175. Blanco P. J. and Feijóo R. A., “ A 3D-1D-0D computational model for the entire cardiovascular system,” Mec. Comput. 29, 5887–5911 (2010). [Google Scholar]
- 176. Müller L. O. and Toro E. F., “ A global multiscale mathematical model for the human circulation with emphasis on the venous system,” Int. J. Numer. Methods Biomed. Eng. 30, 681–725 (2014). 10.1002/cnm.2622 [DOI] [PubMed] [Google Scholar]
- 177. Avolio A., “ Multi-branched model of the human arterial system,” Med. Biol. Eng. Comput. 18, 709–718 (1980). 10.1007/BF02441895 [DOI] [PubMed] [Google Scholar]
- 178. Zhang H., Fujiwara N., Kobayashi M., Yamada S., Liang F., Takagi S., and Oshima M., “ Development of a numerical method for patient-specific cerebral circulation using 1d–0d simulation of the entire cardiovascular system with spect data,” Ann. Biomed. Eng. 44, 2351–2363 (2016). 10.1007/s10439-015-1544-8 [DOI] [PubMed] [Google Scholar]
- 179. Pfaller M. R., Pham J., Wilson N. M., Parker D. W., and Marsden A. L., “ On the periodicity of cardiovascular fluid dynamics simulations,” Ann. Biomed. Eng. 49, 3574–3592 (2021). 10.1007/s10439-021-02796-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180. Reymond P., Crosetto P., Deparis S., Quarteroni A., and Stergiopulos N., “ Physiological simulation of blood flow in the aorta: Comparison of hemodynamic indices as predicted by 3-D FSI, 3-D rigid wall and 1-D models,” Med. Eng. Phys. 35, 784–791 (2013). 10.1016/j.medengphy.2012.08.009 [DOI] [PubMed] [Google Scholar]
- 181. Xiao N., Alastruey J., and Figueroa C. A., “ A systematic comparison between 1-D and 3-D hemodynamics in compliant arterial models,” Int. J. Numer. Methods Biomed. Eng. 30, 204–231 (2014). 10.1002/cnm.2598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182. Hasan M., Patel B., and Pradyumna S., “ Computationally efficient finite element formulation for blood flow analysis in multi-layered aorta modeled as viscoelastic material,” Int. J. Numer. Methods Eng. 122, 4313–4332 (2021). 10.1002/nme.6704 [DOI] [Google Scholar]
- 183. Boileau E., Pant S., Roobottom C., Sazonov I., Deng J., Xie X., and Nithiarasu P., “ Estimating the accuracy of a reduced-order model for the calculation of fractional flow reserve (FFR),” Int. J. Numer. Methods Biomed. Eng. 34, e2908 (2018). 10.1038/s41598-018-35344-0 [DOI] [PubMed] [Google Scholar]
- 184. Blanco P. J., Bulant C. A., Müller L. O., Talou G. D. M., Bezerra C. G., Lemos P. A., and Feijóo R. A., “ Comparison of 1D and 3D models for the estimation of fractional flow reserve,” Sci. Rep. 8, 17275 (2018). 10.1038/s41598-018-35344-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185. Müller L. O., Fossan F. E., Bråten A. T., Jørgensen A., Wiseth R., and Hellevik L. R., “ Impact of baseline coronary flow and its distribution on fractional flow reserve prediction,” Int. J. Numer. Methods Biomed. Eng. 37, e3246 (2021). 10.1002/cnm.3246 [DOI] [PubMed] [Google Scholar]
- 186. Moore S., Moorhead K., Chase J., David T., and Fink J., “ One-dimensional and three-dimensional models of cerebrovascular flow,” J. Biomech. Eng. 127, 440–449 (2005). 10.1115/1.1894350 [DOI] [PubMed] [Google Scholar]
- 187. Grinberg L., Cheever E., Anor T., Madsen J. R., and Karniadakis G., “ Modeling blood flow circulation in intracranial arterial networks: A comparative 3d/1d simulation study,” Ann. Biomed. Eng. 39, 297–309 (2011). 10.1007/s10439-010-0132-1 [DOI] [PubMed] [Google Scholar]
- 188. Reymond P., Merenda F., Perren F., Rufenacht D., and Stergiopulos N., “ Validation of a one-dimensional model of the systemic arterial tree,” Am. J. Physiol.-Heart Circ. Physiol. 297, H208–H222 (2009). 10.1152/ajpheart.00037.2009 [DOI] [PubMed] [Google Scholar]
- 189. Reymond P., Perren F., Lazeyras F., and Stergiopulos N., “ Patient-specific mean pressure drop in the systemic arterial tree, a comparison between 1-D and 3-D models,” J. Biomech. 45, 2499–2505 (2012). 10.1016/j.jbiomech.2012.07.020 [DOI] [PubMed] [Google Scholar]
- 190. Boileau E., Nithiarasu P., Blanco P. J., Müller L. O., Fossan F. E., Hellevik L. R., Donders W. P., Huberts W., Willemet M., and Alastruey J., “ A benchmark study of numerical schemes for one-dimensional arterial blood flow modelling,” Int. J. Numer. Methods Biomed. Eng. 31, e02732 (2015). 10.1002/cnm.2732 [DOI] [PubMed] [Google Scholar]
- 191. Bertaglia G., Navas-Montilla A., Valiani A., García M. I. M., Murillo J., and Caleffi V., “ Computational hemodynamics in arteries with the one-dimensional augmented fluid-structure interaction system: Viscoelastic parameters estimation and comparison with in-vivo data,” J. Biomech. 100, 109595 (2020). 10.1016/j.jbiomech.2019.109595 [DOI] [PubMed] [Google Scholar]
- 192. Blanco P. J., Müller L. O., Watanabe S. M., and Feijóo R. A., “ On the anatomical definition of arterial networks in blood flow simulations: Comparison of detailed and simplified models,” Biomech. Model. Mechanobiol. 19, 1663–1678 (2020). 10.1007/s10237-020-01298-4 [DOI] [PubMed] [Google Scholar]
- 193. Alastruey J., Khir A. W., Matthys K. S., Segers P., Sherwin S. J., Verdonck P. R., Parker K. H., and Peiró J., “ Pulse wave propagation in a model human arterial network: Assessment of 1-D visco-elastic simulations against in vitro measurements,” J. Biomech. 44, 2250–2258 (2011). 10.1016/j.jbiomech.2011.05.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194. Matthys K. S., Alastruey J., Peiró J., Khir A. W., Segers P., Verdonck P. R., Parker K. H., and Sherwin S. J., “ Pulse wave propagation in a model human arterial network: Assessment of 1-D numerical simulations against in vitro measurements,” J. Biomech. 40, 3476–3486 (2007). 10.1016/j.jbiomech.2007.05.027 [DOI] [PubMed] [Google Scholar]
- 195. Quarteroni A., Manzoni A., and Negri F., Reduced Basis Methods for Partial Differential Equations: An Introduction ( Springer, 2015), Vol. 92. [Google Scholar]
- 196. Hesthaven J. S., Rozza G., and Stamm B., Certified Reduced Basis Methods for Parametrized Partial Differential Equations ( Springer, 2016). [Google Scholar]
- 197. Ballarin F., Faggiano E., Ippolito S., Manzoni A., Quarteroni A., Rozza G., and Scrofani R., “ Fast simulations of patient-specific haemodynamics of coronary artery bypass grafts based on a POD–Galerkin method and a vascular shape parametrization,” J. Comput. Phys. 315, 609–628 (2016). 10.1016/j.jcp.2016.03.065 [DOI] [Google Scholar]
- 198. Manzoni A., Quarteroni A., and Rozza G., “ Shape optimization for viscous flows by reduced basis methods and free-form deformation,” Int. J. Numer. Methods Fluids 70, 646–670 (2012). 10.1002/fld.2712 [DOI] [Google Scholar]
- 199. Lassila T., Manzoni A., Quarteroni A., and Rozza G., “ A reduced computational and geometrical framework for inverse problems in hemodynamics,” Int. J. Numer. Methods Biomed. Eng. 29, 741–776 (2013). 10.1002/cnm.2559 [DOI] [PubMed] [Google Scholar]
- 200. Quarteroni A. and Rozza G., “ Optimal control and shape optimization of aorto-coronaric bypass anastomoses,” Math. Models Methods Appl. Sci. 13, 1801–1823 (2003). 10.1142/S0218202503003124 [DOI] [Google Scholar]
- 201. Santo N. D. and Manzoni A., “ Hyper-reduced order models for parametrized unsteady Navier–Stokes equations on domains with variable shape,” Adv. Comput. Math. 45, 2463–2501 (2019). 10.1007/s10444-019-09722-9 [DOI] [Google Scholar]
- 202. Yang W., Feinstein J. A., and Marsden A. L., “ Constrained optimization of an idealized Y-shaped baffle for the Fontan surgery at rest and exercise,” Comput. Methods Appl. Mech. Eng. 199, 2135–2149 (2010). 10.1016/j.cma.2010.03.012 [DOI] [Google Scholar]
- 203. Pegolotti L., Pfaller M. R., Marsden A. L., and Deparis S., “ Model order reduction of flow based on a modular geometrical approximation of blood vessels,” Comput. Methods Appl. Mech. Eng. 380, 113762 (2021). 10.1016/j.cma.2021.113762 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 204. Iapichino L., Quarteroni A., and Rozza G., “ A reduced basis hybrid method for the coupling of parametrized domains represented by fluidic networks,” Comput. Methods Appl. Mech. Eng. 221, 63–82 (2012). 10.1016/j.cma.2012.02.005 [DOI] [Google Scholar]
- 205. Iapichino L., Quarteroni A., and Rozza G., “ Reduced basis method and domain decomposition for elliptic problems in networks and complex parametrized geometries,” Comput. Math. Appl. 71, 408–430 (2016). 10.1016/j.camwa.2015.12.001 [DOI] [Google Scholar]
- 206. Raissi M., Perdikaris P., and Karniadakis G. E., “ Physics informed deep learning. I. Data-driven solutions of nonlinear partial differential equations,” arXiv:1711.10561 (2017).
- 207. Kissas G., Yang Y., Hwuang E., Witschey W. R., Detre J. A., and Perdikaris P., “ Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4d flow MRI data using physics-informed neural networks,” Comput. Methods Appl. Mech. Eng. 358, 112623 (2020). 10.1016/j.cma.2019.112623 [DOI] [Google Scholar]
- 208. Arzani A., Wang J.-X., and D'Souza R. M., “ Uncovering near-wall blood flow from sparse data with physics-informed neural networks,” Phys. Fluids 33, 071905 (2021). 10.1063/5.0055600 [DOI] [Google Scholar]
- 209. Sankaran S., Grady L., and Taylor C. A., “ Fast computation of hemodynamic sensitivity to lumen segmentation uncertainty,” IEEE Trans. Med. Imaging 34, 2562–2571 (2015). 10.1109/TMI.2015.2445777 [DOI] [PubMed] [Google Scholar]
- 210. Fleeter C. M., Geraci G., Schiavazzi D. E., Kahn A. M., and Marsden A. L., “ Multilevel and multifidelity uncertainty quantification for cardiovascular hemodynamics,” Comput. Methods Appl. Mech. Eng. 365, 113030 (2020). 10.1016/j.cma.2020.113030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 211. Seo J., Fleeter C., Kahn A. M., Marsden A. L., and Schiavazzi D. E., “ Multifidelity estimators for coronary circulation models under clinically informed data uncertainty,” Int. J. Uncertainty Quantif. 10, 113030 (2020). 10.1615/Int.J.UncertaintyQuantification.2020033068 [DOI] [Google Scholar]
- 212. Tran J. S., Schiavazzi D. E., Kahn A. M., and Marsden A. L., “ Uncertainty quantification of simulated biomechanical stimuli in coronary artery bypass grafts,” Comput. Methods Appl. Mech. Eng. 345, 402–428 (2019). 10.1016/j.cma.2018.10.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 213. Seo J., Schiavazzi D. E., Kahn A. M., and Marsden A. L., “ The effects of clinically-derived parametric data uncertainty in patient-specific coronary simulations with deformable walls,” Int. J. Numer. Methods Biomed. Eng. 36, e3351 (2020). 10.1002/cnm.3351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 214. Tran J. S., Schiavazzi D. E., Ramachandra A. B., Kahn A. M., and Marsden A. L., “ Automated tuning for parameter identification and uncertainty quantification in multi-scale coronary simulations,” Comput. Fluids 142, 128–138 (2017). 10.1016/j.compfluid.2016.05.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 215. Peirlinck M., Costabal F. S., Yao J., Guccione J. M., Tripathy S., Wang Y., Ozturk D., Segars P., Morrison T. M., Levine S., and Kuhl E., “ Precision medicine in human heart modeling,” Biomech. Model. Mechanobiol. 20, 803–831 (2021). 10.1007/s10237-021-01421-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 216. Quarteroni A., Lassila T., Rossi S., and Ruiz-Baier R., “ Integrated heart—Coupling multiscale and multiphysics models for the simulation of the cardiac function,” Comput. Methods Appl. Mech. Eng. 314, 345–407 (2017). 10.1016/j.cma.2016.05.031 [DOI] [Google Scholar]
- 217. Quarteroni A., Dede' L., and Manzoni A., Mathematical Modelling of the Human Cardiovascular System: Data, Numerical Approximation, Clinical Applications ( Cambridge University Press, 2019). [Google Scholar]
- 218. Richards D. F., Glosli J. N., Draeger E. W., Mirin A. A., Chan B., luc Fattebert J., Krauss W. D., Oppelstrup T., Butler C. J., Gunnels J. A., Gurev V., Kim C., Magerlein J., Reumann M., Wen H.-F., and Rice J. J., “ Towards real-time simulation of cardiac electrophysiology in a human heart at high resolution,” Comput. Methods Biomech. Biomed. Eng. 16, 802–805 (2013). 10.1080/10255842.2013.795556 [DOI] [PubMed] [Google Scholar]
- 219. Caruel M., Chabiniok R., Moireau P., Lecarpentier Y., and Chapelle D., “ Dimensional reductions of a cardiac model for effective validation and calibration,” Biomech. Model. Mechanobiol. 13, 897–914 (2013). 10.1007/s10237-013-0544-6 [DOI] [PubMed] [Google Scholar]
- 220. Pfaller M. R., Varona M. C., Lang J., Bertoglio C., and Wall W. A., “ Using parametric model order reduction for inverse analysis of large nonlinear cardiac simulations,” Int. J. Numer. Methods Biomed. Eng. 36, e3320 (2020). 10.1002/cnm.3320 [DOI] [PubMed] [Google Scholar]
- 221. Regazzoni F. and Quarteroni A., “ Accelerating the convergence to a limit cycle in 3D cardiac electromechanical simulations through a data-driven 0D emulator,” Comput. Biol. Med. 135, 104641 (2021). 10.1016/j.compbiomed.2021.104641 [DOI] [PubMed] [Google Scholar]
- 222. Trayanova N. A. and Rice J. J., “ Cardiac electromechanical models: From cell to organ,” Front. Physiol. 2, 43 (2011). 10.3389/fphys.2011.00043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 223. Ambrosi D. and Pezzuto S., “ Active stress vs. active strain in mechanobiology: Constitutive issues,” J. Elast. 107, 199–212 (2011). 10.1007/s10659-011-9351-4 [DOI] [Google Scholar]
- 224. Eriksson T., Prassl A., Plank G., and Holzapfel G., “ Influence of myocardial fiber/sheet orientations on left ventricular mechanical contraction,” Math. Mech. Solids 18, 592–606 (2013). 10.1177/1081286513485779 [DOI] [Google Scholar]
- 225. Hörmann J. M., Bertoglio C., Nagler A., Pfaller M. R., Bourier F., Hadamitzky M., Deisenhofer I., and Wall W. A., “ Multiphysics modeling of the atrial systole under standard ablation strategies,” Cardiovasc. Eng. Technol. 8, 205–218 (2017). 10.1007/s13239-017-0308-z [DOI] [PubMed] [Google Scholar]
- 226. Franzone P. C., Pavarino L. F., and Scacchi S., “ Bioelectrical effects of mechanical feedbacks in a strongly coupled cardiac electro-mechanical model,” Math. Models Methods Appl. Sci. 26, 27–57 (2015). 10.1142/S0218202516500020 [DOI] [Google Scholar]
- 227. Niederer S. A., Kerfoot E., Benson A. P., Bernabeu M. O., Bernus O., Bradley C., Cherry E. M., Clayton R., Fenton F. H., Garny A., Heidenreich E., Land S., Maleckar M., Pathmanathan P., Plank G., Rodríguez J. F., Roy I., Sachse F. B., Seemann G., Skavhaug O., and Smith N. P., “ Verification of cardiac tissue electrophysiology simulators using an n-version benchmark,” Philos. Trans. R. Soc. A: Math. Phys. Eng. Sci. 369, 4331–4351 (2011). 10.1098/rsta.2011.0139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228. Trayanova N. A., “ Whole-heart modeling,” Circ. Res. 108, 113–128 (2011). 10.1161/CIRCRESAHA.110.223610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229. Pfaller M. R., Hörmann J. M., Weigl M., Nagler A., Chabiniok R., Bertoglio C., and Wall W. A., “ The importance of the pericardium for cardiac biomechanics: From physiology to computational modeling,” Biomech. Model. Mechanobiol. 18, 503–529 (2018). 10.1007/s10237-018-1098-4 [DOI] [PubMed] [Google Scholar]
- 230. Hirschvogel M., Bassilious M., Jagschies L., Wildhirt S. M., and Gee M. W., “ A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics,” Int. J. Numer. Methods Biomed. Eng. 33, e2842 (2017). 10.1002/cnm.2842 [DOI] [PubMed] [Google Scholar]
- 231. Piersanti R., Regazzoni F., Salvador M., Corno A. F., Dede' L., Vergara C., and Quarteroni A., “ 3D-0D closed-loop model for the simulation of cardiac biventricular electromechanics,” Comput. Methods Appl. Mech. Eng. 391, 114607 (2022). 10.1016/j.cma.2022.114607 [DOI] [Google Scholar]
- 232. Sharifi H., Mann C. K., Rockward A. L., Mehri M., Mojumder J., Lee L.-C., Campbell K. S., and Wenk J. F., “ Multiscale simulations of left ventricular growth and remodeling,” Biophys. Rev. 13, 729–746 (2021). 10.1007/s12551-021-00826-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 233. Verzicco R., “ Electro-fluid-mechanics of the heart,” J. Fluid Mech. 941, P1 (2022). 10.1017/jfm.2022.272 [DOI] [Google Scholar]
- 234. Marom G., “ Numerical methods for fluid–structure interaction models of aortic valves,” Arch. Comput. Methods Eng. 22, 595–620 (2014). 10.1007/s11831-014-9133-9 [DOI] [Google Scholar]
- 235. Peskin C. S., “ Flow patterns around heart valves: A numerical method,” J. Comput. Phys. 10, 252–271 (1972). 10.1016/0021-9991(72)90065-4 [DOI] [Google Scholar]
- 236. Griffith B. E. and Patankar N. A., “ Immersed methods for fluid–structure interaction,” Annu. Rev. Fluid Mech. 52, 421–448 (2020). 10.1146/annurev-fluid-010719-060228 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237. Viola F., Meschini V., and Verzicco R., “ Fluid–structure-electrophysiology interaction (FSEI) in the left-heart: A multi-way coupled computational model,” Eur. J. Mech. -B/Fluids 79, 212–232 (2020). 10.1016/j.euromechflu.2019.09.006 [DOI] [Google Scholar]
- 238. Peskin C. S. and McQueen D. M., “ Fluid dynamics of the heart and its valves,” Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology (Prentice-Hall, 1996), pp. 309–337. [Google Scholar]
- 239. Fedele M., Faggiano E., Dedè L., and Quarteroni A., “ A patient-specific aortic valve model based on moving resistive immersed implicit surfaces,” Biomech. Model. Mechanobiol. 16, 1779–1803 (2017). 10.1007/s10237-017-0919-1 [DOI] [PubMed] [Google Scholar]
- 240. Dedè L., Menghini F., and Quarteroni A., “ Computational fluid dynamics of blood flow in an idealized left human heart,” Int. J. Numer. Methods Biomed. Eng. 37, e3287 (2019). 10.1002/cnm.3287 [DOI] [PubMed] [Google Scholar]
- 241. Masci A., Barone L., Dedè L., Fedele M., Tomasi C., Quarteroni A., and Corsi C., “ The impact of left atrium appendage morphology on stroke risk assessment in atrial fibrillation: A computational fluid dynamics study,” Front. Physiol. 9, 1938 (2019). 10.3389/fphys.2018.01938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242. Zingaro A., Dede' L., Menghini F., and Quarteroni A., “ Hemodynamics of the heart's left atrium based on a variational multiscale-LES numerical method,” Eur. J. Mech. -B/Fluids 89, 380–400 (2021). 10.1016/j.euromechflu.2021.06.014 [DOI] [Google Scholar]
- 243. Corti M., Zingaro A., Dede' L., and Quarteroni A. M., “ Impact of atrial fibrillation on left atrium haemodynamics: A computational fluid dynamics study,” arXiv:2202.10893 [physics.flu-dyn] (2022). [DOI] [PubMed]
- 244. Rodbard S., “ Vascular caliber,” Cardiology 60, 4–49 (1975). 10.1159/000169701 [DOI] [PubMed] [Google Scholar]
- 245. Kamiya A. and Togawa T., “ Adaptive regulation of wall shear stress to flow change in the canine carotid artery,” Am. J. Physiol.-Heart Circ. Physiol. 239, H14–H21 (1980). 10.1152/ajpheart.1980.239.1.H14 [DOI] [PubMed] [Google Scholar]
- 246. Lehoux S., “ Molecular mechanisms of the vascular responses to hemodynamic forces,” Biomech. Coronary Atherosclerotic Plaque 4, 49–83 (2021). 10.1016/B978-0-12-817195-0.00002-0 [DOI] [Google Scholar]
- 247. Davies P. F., “ Flow-mediated endothelial mechanotransduction,” Physiol. Rev. 75, 519–560 (1995). 10.1152/physrev.1995.75.3.519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 248. Rodriguez E. K., Hoger A., and McCulloch A. D., “ Stress-dependent finite growth in soft elastic tissues,” J. Biomech. 27, 455–467 (1994). 10.1016/0021-9290(94)90021-3 [DOI] [PubMed] [Google Scholar]
- 249. Taber L., “ A model for aortic growth based on fluid shear and fiber stresses,” J. Biomech. Eng. 120, 348–354 (1998). 10.1115/1.2798001 [DOI] [PubMed] [Google Scholar]
- 250. Himpel G., Kuhl E., Menzel A., Steinmann P. et al. , “ Computational modelling of isotropic multiplicative growth,” Comput. Model. Eng. Sci. 8, 119–134 (2005). 10.3970/cmes.2005.008.119 [DOI] [Google Scholar]
- 251. Humphrey J. and Rajagopal K., “ A constrained mixture model for growth and remodeling of soft tissues,” Math. Models Methods Appl. Sci. 12, 407–430 (2002). 10.1142/S0218202502001714 [DOI] [Google Scholar]
- 252. Mahutga R. R. and Barocas V. H., “ Investigation of pathophysiological aspects of aortic growth, remodeling, and failure using a discrete-fiber microstructural model,” J. Biomech. Eng. 142, 111007 (2020). 10.1115/1.4048031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 253. Gleason R., Taber L., and Humphrey J., “ A 2-D model of flow-induced alterations in the geometry, structure, and properties of carotid arteries,” J. Biomech. Eng. 126, 371–381 (2004). 10.1115/1.1762899 [DOI] [PubMed] [Google Scholar]
- 254. Gleason R. and Humphrey J., “ A mixture model of arterial growth and remodeling in hypertension: Altered muscle tone and tissue turnover,” J. Vasc. Res. 41, 352–363 (2004). 10.1159/000080699 [DOI] [PubMed] [Google Scholar]
- 255. Latorre M. and Humphrey J. D., “ A mechanobiologically equilibrated constrained mixture model for growth and remodeling of soft tissues,” ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 98, 2048–2071 (2018). 10.1002/zamm.201700302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 256. Figueroa C. A., Baek S., Taylor C. A., and Humphrey J. D., “ A computational framework for fluid–solid-growth modeling in cardiovascular simulations,” Comput. Methods Appl. Mech. Eng. 198, 3583–3602 (2009). 10.1016/j.cma.2008.09.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 257. Wu J. and Shadden S. C., “ Coupled simulation of hemodynamics and vascular growth and remodeling in a subject-specific geometry,” Ann. Biomed. Eng. 43, 1543–1554 (2015). 10.1007/s10439-015-1287-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258. Shin'oka T., Matsumura G., Hibino N., Naito Y., Watanabe M., Konuma T., Sakamoto T., Nagatsu M., and Kurosawa H., “ Midterm clinical result of tissue-engineered vascular autografts seeded with autologous bone marrow cells,” J. Thorac. Cardiovasc. Surg. 129, 1330–1338 (2005). 10.1016/j.jtcvs.2004.12.047 [DOI] [PubMed] [Google Scholar]
- 259. Drews J. D., Pepper V. K., Best C. A., Szafron J. M., Cheatham J. P., Yates A. R., Hor K. N., Zbinden J. C., Chang Y.-C., Mirhaidari G. J. et al. , “ Spontaneous reversal of stenosis in tissue-engineered vascular grafts,” Sci. Transl. Med. 12, eaax6919 (2020). 10.1126/scitranslmed.aax6919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 260. Szafron J., Khosravi R., Reinhardt J., Best C., Bersi M., Yi T., Breuer C., and Humphrey J., “ Immuno-driven and mechano-mediated neotissue formation in tissue engineered vascular grafts,” Ann. Biomed. Eng. 46, 1938–1950 (2018). 10.1007/s10439-018-2086-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261. Göktepe S., Abilez O. J., Parker K. K., and Kuhl E., “ A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis,” J. Theor. Biol. 265, 433–442 (2010). 10.1016/j.jtbi.2010.04.023 [DOI] [PubMed] [Google Scholar]
- 262. Kerckhoffs R. C., Omens J. H., and McCulloch A. D., “ A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload,” Mech. Res. Commun. 42, 40–50 (2012). 10.1016/j.mechrescom.2011.11.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 263. Genet M., Rausch M., Lee L. C., Choy S., Zhao X., Kassab G. S., Kozerke S., Guccione J. M., and Kuhl E., “ Heterogeneous growth-induced prestrain in the heart,” J. Biomech. 48, 2080–2089 (2015). 10.1016/j.jbiomech.2015.03.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 264. Niestrawska J. A., Augustin C. M., and Plank G., “ Computational modeling of cardiac growth and remodeling in pressure overloaded hearts–linking microstructure to organ phenotype,” Acta Biomater. 106, 34–53 (2020). 10.1016/j.actbio.2020.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 265. Gebauer A. M., Pfaller M. R., Braeu F. A., Cyron C. J., and Wall W. A., “ A homogenized constrained mixture model of cardiac growth and remodeling: Analyzing mechanobiological stability and reversal,” arXiv:2203.12615 [q-bio.TO] (2022). [DOI] [PMC free article] [PubMed]
- 266. Hove J. R., Köster R. W., Forouhar A. S., Acevedo-Bolton G., Fraser S. E., and Gharib M., “ Intracardiac fluid forces are an essential epigenetic factor for embryonic cardiogenesis,” Nature 421, 172–177 (2003). 10.1038/nature01282 [DOI] [PubMed] [Google Scholar]
- 267. Vedula V., Lee J., Xu H., Kuo C.-C. J., Hsiai T. K., and Marsden A. L., “ A method to quantify mechanobiologic forces during zebrafish cardiac development using 4-D light sheet imaging and computational modeling,” PLOS Comput. Biol. 13, e1005828 (2017). 10.1371/journal.pcbi.1005828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 268. Lee J., Vedula V., Baek K. I., Chen J., Hsu J. J., Ding Y., Chang C.-C., Kang H., Small A., Fei P. et al. , “ Spatial and temporal variations in hemodynamic forces initiate cardiac trabeculation,” JCI Insight 3, e96672 (2018). 10.1172/jci.insight.96672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 269. Wang Y., Dur O., Patrick M. J., Tinney J. P., Tobita K., Keller B. B., and Pekkan K., “ Aortic arch morphogenesis and flow modeling in the chick embryo,” Ann. Biomed. Eng. 37, 1069–1081 (2009). 10.1007/s10439-009-9682-5 [DOI] [PubMed] [Google Scholar]
- 270. Lindsey S. E., Menon P. G., Kowalski W. J., Shekhar A., Yalcin H. C., Nishimura N., Schaffer C. B., Butcher J. T., and Pekkan K., “ Growth and hemodynamics after early embryonic aortic arch occlusion,” Biomech. Model. Mechanobiol. 14, 735–751 (2015). 10.1007/s10237-014-0633-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 271. Xu Z., Chen N., Kamocka M. M., Rosen E. D., and Alber M., “ A multiscale model of thrombus development,” J. R. Soc. Interface 5, 705–722 (2008). 10.1098/rsif.2007.1202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 272. Leiderman K. and Fogelson A. L., “ Grow with the flow: A spatial–temporal model of platelet deposition and blood coagulation under flow,” Math. Med. Biol.: J. IMA 28, 47–84 (2011). 10.1093/imammb/dqq005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 273. Fogelson A. L. and Neeves K. B., “ Fluid mechanics of blood clot formation,” Annu. Rev. Fluid Mech. 47, 377 (2015). 10.1146/annurev-fluid-010814-014513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 274. Leiderman K. and Fogelson A., “ An overview of mathematical modeling of thrombus formation under flow,” Thrombosis Res. 133, S12–S14 (2014). 10.1016/j.thromres.2014.03.005 [DOI] [PubMed] [Google Scholar]
- 275. Saucerman J. J., Tan P. M., Buchholz K. S., McCulloch A. D., and Omens J. H., “ Mechanical regulation of gene expression in cardiac myocytes and fibroblasts,” Nat. Rev. Cardiol. 16, 361–378 (2019). 10.1038/s41569-019-0155-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 276. Estrada A. C., Yoshida K., Saucerman J. J., and Holmes J. W., “ A multiscale model of cardiac concentric hypertrophy incorporating both mechanical and hormonal drivers of growth,” Biomech. Model. Mechanobiol. 20, 293–307 (2021). 10.1007/s10237-020-01385-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 277. Galindo C. L., Skinner M. A., Errami M., Olson L. D., Watson D. A., Li J., McCormick J. F., McIver L. J., Kumar N. M., Pham T. Q. et al. , “ Transcriptional profile of isoproterenol-induced cardiomyopathy and comparison to exercise-induced cardiac hypertrophy and human cardiac failure,” BMC Physiol. 9, 23 (2009). 10.1186/1472-6793-9-23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 278. Irons L., Latorre M., and Humphrey J. D., “ From transcript to tissue: Multiscale modeling from cell signaling to matrix remodeling,” Ann. Biomed. Eng. 49, 1701–1715 (2021). 10.1007/s10439-020-02713-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 279. Irons L. and Humphrey J. D., “ Cell signaling model for arterial mechanobiology,” PLOS Comput. Biol. 16, e1008161 (2020). 10.1371/journal.pcbi.1008161 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 280. Ferruzzi J., Vorp D. A., and Humphrey J., “ On constitutive descriptors of the biaxial mechanical behaviour of human abdominal aorta and aneurysms,” J. R. Soc. Interface 8, 435–450 (2011). 10.1098/rsif.2010.0299 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 281. Imoukhuede P. and Popel A. S., “ Quantification and cell-to-cell variation of vascular endothelial growth factor receptors,” Exp. Cell Res. 317, 955–965 (2011). 10.1016/j.yexcr.2010.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 282. Imoukhuede P., Dokun A. O., Annex B. H., and Popel A. S., “ Endothelial cell-by-cell profiling reveals the temporal dynamics of VEGFR1 and VEGFR2 membrane localization after murine hindlimb ischemia,” Am. J. Physiol.-Heart Circ. Physiol. 304, H1085–H1093 (2013). 10.1152/ajpheart.00514.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 283. Sheikh F., Ouyang K., Campbell S. G., Lyon R. C., Chuang J., Fitzsimons D., Tangney J., Hidalgo C. G., Chung C. S., Cheng H. et al. , “ Mouse and computational models link mlc2v dephosphorylation to altered myosin kinetics in early cardiac disease,” J. Clin. Invest. 122, 1209–1221 (2012). 10.1172/JCI61134 [DOI] [PMC free article] [PubMed] [Google Scholar]