A multiple criteria approach for building a pandemic impact assessment composite indicator: The case of COVID-19 in Portugal

Abstract

The COVID-19 pandemic has caused major damage and disruption to social, economic, and health systems (among others). In addition, it has posed unprecedented challenges to public health and policy/decision-makers who have been responsible for designing and implementing measures to mitigate its strong negative impact. The Portuguese health authorities have used decision analysis techniques to assess the impact of the pandemic and implemented measures for counties, regions, or across the entire country. These decision tools have been subject to some criticism and many stakeholders requested novel approaches. In particular, those which considered the dynamic changes in the pandemic’s behaviour due to new virus variants and vaccines. A multidisciplinary team formed by researchers from the COVID-19 Committee of Instituto Superior Técnico at the University of Lisbon (CCIST analyst team) and physicians from the Crisis Office of the Portuguese Medical Association (GCOM expert team) collaborated to create a new tool to help politicians and decision-makers to fight the pandemic. This paper presents the main steps that led to the building of a pandemic impact assessment composite indicator applied to the specific case of COVID-19 in Portugal. A multiple criteria approach based on an additive multi-attribute value theory aggregation model was used to build the pandemic assessment composite indicator. The parameters of the additive model were devised based on an interactive socio-technical and co-constructive process between the CCIST and GCOM team members. The deck of cards method was the adopted technical tool to assist in the assessment the value functions as well as in the assessment of the criteria weights. The final tool was presented at a press conference and had a powerful impact on the Portuguese media and on the main health decision-making stakeholders in the country. In this paper, a completed mathematical and graphical description of this tool is presented.

1. Introduction

A pandemic leads to high damage and disruptions to social, economic, and health systems (among others) and has major implications for people’s lives throughout the world. Not only it leads to serious physical and mental health issues, but also to poverty and hunger. COVID-19, the most recent pandemic resulted in unprecedented challenges to public health and to policy/decision-makers, especially when designing and implementing measures to mitigate the pandemic’s negative impacts.

1.1. Literature review

Different countries and researchers around the world have presented tools for mitigating the impact of COVID-19. It is possible to point out two types of the literature review: on the one hand, an analysis of the tools used by other countries, and on the other hand, a review of the published literature in the field.

One of the most widely adopted tools for assessing the impact of COVID-19 has been the use of chromatic systems, especially the use of territorial units (counties, districts, municipalities, departments, provinces, regions, states, and the entire countries) risk maps. These chromatic systems assign a colour to each territorial unit, which represents the risk from the lowest to the highest level of that particular unit. The methodologies and factors considered to obtain the risk maps are slightly different from case to case, as it can be seen in the following examples:

• 1.In Spain,1 a risk flow-map is produced based on a score computed from three criteria (indicators): the daily and the cumulative incidences, and the population mobility partners. The score is used to estimate the number of cases that can be exported or imported between pairs of regions.
• 2.In Italy,2 the risk classification of each region is based on directives issued by the Ministry of Health. The risk is determined from the impact of several factors and a probability is associated with each impact level. A risk matrix (RM) is formed with different impact levels.
• 3.In France,3 a COVID-19 map was designed according to the administrative divisions (departments) to model the progression of the pandemic based on the seven-day incidence of COVID-19 per 100,000 inhabitants.
• 4.In Germany,4 the Robert Koch Institute’s coloured maps are only based on the number of COVID-19 cases and cumulative incidence (per 100,000 inhabitants) reported by each county/federal state.
• 5.In the United Kingdom (UK),5 the map indicates the seven-day case rate per 100,000 inhabitants, and like German, it is a single criterion-based assessment tool.
• 6.In the United States of America (USA),6 in particular in North Carolina, the county map considers the number of cases per 100,000 residents.
• 7.In Canada,7 the map is similar to number 6: the provinces and territories are coloured according to the number of cases over the past seven days.
• 8.In Brazil,8 the risk map is based on several factors including the number of active cases, number of tests, and lethality, which are then aggregated into two dimensions (threats and vulnerabilities); this results in a RM with several levels to build on.

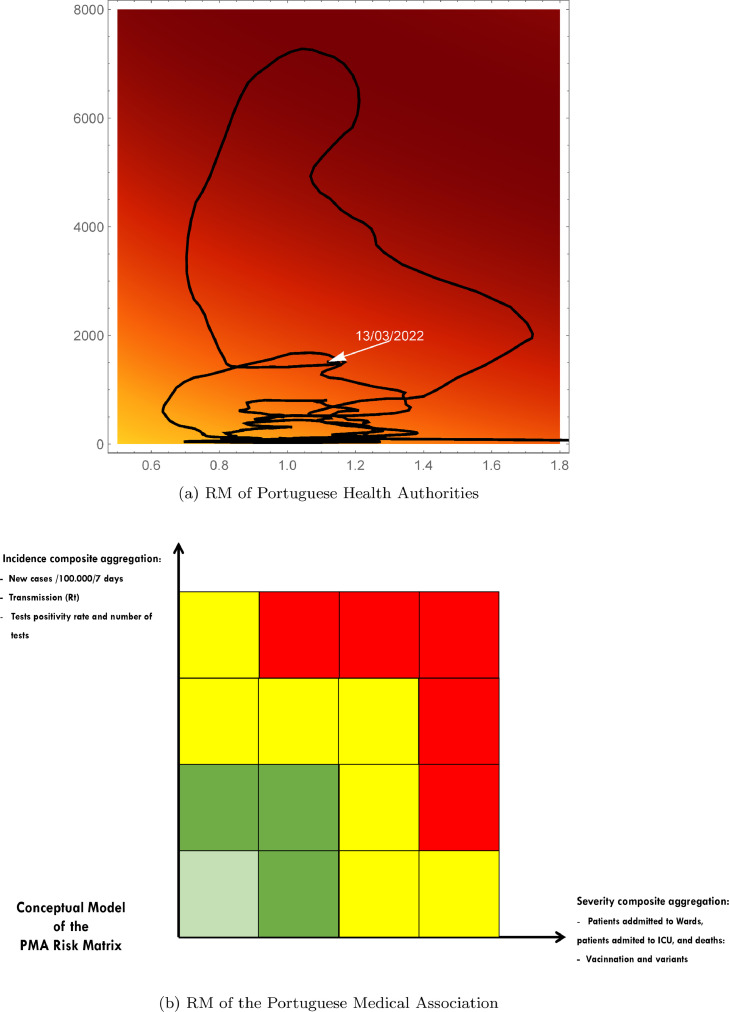
In summary, the tools presented by Brazil and Italy are closest to the one developed by the COVID-19 Crises Office of the Portuguese Medical Association (GCOM), i.e., a first step for the development of a multi-criteria decision aiding/analysis (MCDA) tool (see Fig. 6(b) in the Appendix section).

Fig. 6.

Previous RM Tools.

Although not officially adopted, a significant number of other decision support tools have been recently developed for pandemic mitigation policy-making purposes. For instance, Haghighat (2021) proposed a combined multilayer perception neural network and Markov chain approach for predicting the number of future patients and deaths in the Bushehr province, Iran. Català et al. (2021) proposed three risk indicators to estimate the status of the pandemic and applied them to the evolution of different European countries.

All these indicators quantify both the propagation and the number of estimated cases. Nelken et al. (2020) conducted a review of the different COVID-19 indicators and explore the social role of these in the pandemic from different perspectives. Hale et al. (2021) presented databases and composite indicators, which analysed the effect of policy responses on the spread of COVID-19 cases and deaths and on economic and social welfare. In their study, the composite indicators are simple formulas, which aggregate several partial indicators of a both qualitative and quantitative nature. The conversion of the qualitative nature of the scale levels by assigning numbers is highly questionable. Pang et al. (2021) carried out a study on risk environmental assessment in the Hubei province of China and put forward a composite indicator of the disaster loss for COVID-19 transmission. This indicator is based on five environmental perspectives and 38 partial indicators. Statistical and component analysis methods were used to analyse and build those indicators.

Some indicators are also related to risk, vulnerability or other impact concepts maps. Neyens et al. (2020) proposed a statistical-based method to assess the risk map of each Belgium municipality using spatial data on COVID-19 gathered from a large online survey. This study allows predicting the incidence of the disease and establishing a comparison (analysing the proportion of heterogeneity) regarding the number of confirmed cases. Li et al. (2021) presented a risk analysis of the COVID-19 infection (modelled using the classic impact $X$ probability formula) of the different regions of China, from the Wuhan region to the other 31 regions. The authors use the high-speed rail network to assess and predict the regional risk of infection of each region. Dlamini et al. (2020) proposed several risk assessment indicators for identifying the risk areas in Eswatini, Iran. The overall risk indicator uses an aggregation of socio-economic and demographic partial indicators. Sarkar & Chouhan (2021) presented a socio-environmental vulnerability indicator of the potential risk of community spread of COVID-19. The overall composite indicator was built from the four most influent socio-economic and environmental partial indicators selected through principal component analysis. It was then applied to assess the vulnerability risk of each district of India. Ghimire et al. (2021) also proposed indicators for COVID-19 risk assessment with geo-visualisation map tools applied to Nepal. The composite indicator results from a weighted-sum which considers a positive case score, a quarantined people score, a community exposure score, and a population density score.

Among the reviewed papers, three were of particular interest, two of a multi-criteria nature and one of a single criterion nature, being the last one applied to the Portuguese scenario:

• 1.Sangiorgio & Parisi (2020) presented an interesting composite indicator for the prediction of contagion risk in urban districts of the Apulia region in Italy. The indicator considers relevant socio-economic data from three perspectives: hazard, vulnerability, and exposure. Each of them comprises several dimensions that are normalised and weighted. The composite indicator is based on a factorial formula, which is calibrated through an optimisation procedure.
• 2.Shadeed & Alawna (2021) introduced a multi-criteria index for estimating vulnerability. This is based on the analytical hierarchy process method and was applied in the Governorates of Palestine. The criteria considered are the following: population, population density, elderly population, accommodation and food service activities, school students, chronic diseases, hospital beds, health insurance, and pharmacy.
• 3.Azevedo et al. (2020) presented an interesting indicator for infection risk assessment applied to each municipality on the Portuguese mainland. The indicator is based on the daily number of infected people and uses a direct block sequential simulation.

1.2. Context

Despite the relevance of these proposals for policy-making, they do not assess the impact of COVID-19 in terms of activity and severity. Building a model of the COVID-19 impact using a composite indicator is a conceptual activity that not only can provide a way of observing the evolution of the pandemic, but also be an important tool for policy-making.

In Portugal a team from the COVID-19 Crisis Office of Portuguese Medical Association (GCOM experts team) and a team from the COVID-19 Committee of Instituto Superior Técnico (CCIST analysts team), joined forces after an initial period when they worked separately to help fighting against COVID-19 to mitigate its negative impact on people’s lives.

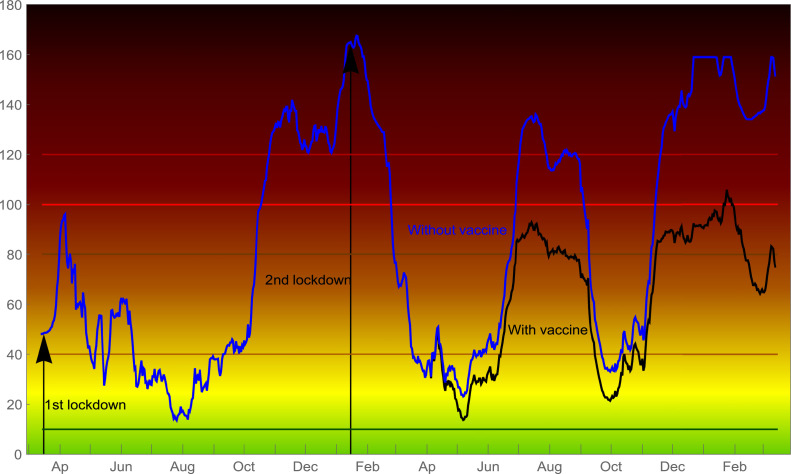
A “Risk Matrix”(RM) tool (Fig. 6(a) in the Appendix section, subsequently modified to accommodate some ad hoc rules) has been used by the Portuguese health authorities to help in the pandemic decision-making process. This tool attributes a colour coded risk status to each county. It has been target of some criticism, mainly since it is incomplete and unable to provide an adequate idea of the pandemic’s evolution in the country. RM, in this context, has a different meaning from the well-known decision aiding tool with the same name in the field of Decision Analysis. The term “matrix” is also unrelated to the mathematical concept. Here, RM is a two-dimensional (2D) referential complemented by a visual chromatic system (from light green to dark red), where one axis represents the raw data on the transmission rate ($R\left(t\right)$) and the other axis the average incidence of new positive cases over the past seven days per 100,000 inhabitants. In addition, two cut-off lines (one horizontal and one vertical) are used as criteria for separating the referential in four regions: the southwest region with the lowest risk impact; the northeast region with the highest risk impact; and, the other two regions (northwest and southeast), the ones with intermediate risk impact. The different territorial units (the counties and regions) were coloured according to this system and some measures were assigned to each colour. Overall, it is important to highlight that the concept of RM and criticism of this system in a different context (i.e., in Decision Analysis, as mentioned previously) can be seen in Cox (2008).

The RM main drawbacks can be succinctly presented as follows:

• 1.Despite the usefulness and advantages of the visual chromatic system for communication purposes, it suffers from a major pitfall, which renders very difficult to see the evolution of the pandemic over the timeline (plotting each daily situation in the referential and linking all the successive points by a line leads to a very confusing evolution curve, see Fig. 7(a) in the Appendix).
• 2.Despite the importance of the dimensions used in the referential (incidence and transmission), they are only part of the problem. Since both are related to the activity of the pandemic, more dimensions should be considered, especially those related to the severity of the pandemic.
• 3.The impact of risk does not seem to be appropriately modelled since moving from an $R\left(t\right)=0.1$ to an $R\left(t\right)=0.2$ has the same risk impact as moving from an $R\left(t\right)=0.9$ to an $R\left(t\right)=1.0$, which does not represent, in general, the feeling of the population about the impact of the transmission (the same reasoning can be applied to incidence).
• 4.There is no differentiation between the contributions of incidence and transmission to the overall risk impact; they count equally (this can be acceptable, but it is not always the case).

Fig. 7.

Validation and simulation analyses.

The CCIST team had previously presented an improved RM containing more cut-off lines than the one used by the Portuguese health authorities. It enabled a closer analysis of the situation, but still suffered from the same drawbacks as the original RM. In parallel the GCOM team also proposed an improved RM (see Fig. 6(b) in the Appendix) different from the one used by CCIST team. To overcome some of the drawbacks of the original RM, the GCOM team recommended the use of a 2D referential system that considered several indicators in both axes. This was a first important step towards an MCDA-based indicator. The two sets of dimensions (called ahead pillars) on this new RM are the “activity” and the “severity” of the pandemic. Unfortunately, the way the activity and the severity indicators were considered was questionable, and although this revised model led to a more complete and finer analysis of the problem, it also had some drawbacks (1), (3), and (4). This GCOM proposal was made public in the first week of June 2021. At the beginning of July 2021, the two teams (CCIST and GCOM), began working together to propose the composite indicator presented in this paper. This new proposal had a strong impact in Portugal, especially in the media and among health policy and decision-makers. At the end of July 2021, the RM used by the Portuguese health authorities was changed to include some ad hoc rules, based on the severity aspects of the pandemic, such as the one proposed in our pandemic assessment composite indicator (PACI).

1.3. Objectives and methodology

What was missing in the proposed RM approaches? In short, a more adequate system was needed to characterise the pandemic impact and to recommend the most suitable measures to mitigate it. Therefore, the main decision problem we faced was how to build a state indicator of the pandemic’s impact (a major objective of this paper) for a given territorial unit (country, region, county, etc.), with the purpose of assigning mitigating measures and/or recommendations for each state (the least to the most restrictive ones). This paper does not, however, present the measures for each state since this is a matter for the Portuguese health authorities, which also may evolve over the time. An essential observation is that it is essential to follow the recent evolution of the pandemic’s impact for better planning when a given territory unit moves from a given state to another one. In addition, it is extremely important to assess the impact of the Portuguese vaccination plan (another major objective of this paper). Each territorial unit is assessed on a daily basis, considering a set of criteria (also called, in our case, indicators or dimensions) grouped in two perspectives or pillars: the activity and the severity of the pandemic. This problem statement can be seen as belonging to the field of MCDA. For more details, the reader can consult Belton & Stewart (2002) and Roy (1996). In the literature, the problem is known as an ordinal classification (or sorting) MCDA problem (Doumpos, Zopounidis, 2002, Zopounidis, Doumpos, 2002). There are several ways of building a state composite (aggregation) indicator (see El Gibari et al., 2019, for a recent survey on this topic). The main MCDA approaches for designing composite indicators are the following:

• 1.Scoring-based approaches, as for example, multi-attribute utility/value theory (MAUT/MAVT) aggregation models (e.g., Dyer, 2016, Keeney, Raiffa, 1993, Tsoukiàs, Figueira, 2006), analytical hierarchy process (e.g., Saaty, 2016), fuzzy sets techniques (e.g., Dubois & Perny, 2016), and fuzzy measure-based aggregation functions (Grabisch & Labreuche, 2016).
• 2.Outranking-based approaches, as for example, Electre methods (Figueira et al., 2016), Promethee methods (Brans & De Smet, 2016), and other outranking techniques (Martel & Matarazzo, 2016).
• 3.Rule-based systems, as for example, decision rule methods (Greco et al., 2016), and verbal decision analysis (Moshkovich et al., 2016).

According to the definition of our decision problem, outranking-based methods and rule-based systems are powerful MCDA techniques for ordinal classification and could be adequate tools for building a state composite indicator (ordinal scale). However, the need to analyse the evolution of the pandemic (see the fundamental observation stated before) requires the construction of a richer scale, of a cardinal nature. It is true that outranking-based methods and rule-based systems can be adapted to produce such a cardinal scale (see, for example, Figueira et al., 2021), but this is a complex process, which is harder to explain to the main actors and the public in general. Consequently, the most suitable approach for addressing our problem was a scoring-based approach. Since the model needed to be simple enough for interaction and communication with the experts and the public in general, without losing sight of the reality it sought to represent, our study was solely focused on MAVT methods. More complex scoring-based methods were discarded. After a deeper analysis, we finally decided to keep the simple additive MAVT approach. It was suitable for modelling our problem and led to an easy communication. At this point, another question arose: how should we build the additive model? There were two possible answers:

• 1.Through a constructive learning approach (machine learning like approaches), such as UTA type methods (Siskos et al., 2016), or an adaptation of more sophisticated techniques as the GRIP method (Figueira et al., 2009) with representative functions.
• 2.Through a co-constructive socio-technical interactive process between analysts and policy/decision-makers or experts using, for example, the classical MAVT method (Keeney & Raiffa, 1993), the MACBETH method (Bana e Costa et al., 2016), or the deck of cards method (Corrente et al., 2021).

In every co-constructive socio-technical process, the analyst must be familiar with the technicalities of the method. In addition, the policy/decision-makers or experts must understand the basic questions for assessing their judgements. The improved version of the deck of cards method by Corrente et al. (2021) was found to be an adequate tool. Its adequacy comes from some important aspects: time limitation to produce a meaningful indicator, easy to be understood by the experts, easy to communicate to the general public, and easy to reproduce the calculations for a reader with an elementary background in mathematics.

In this study, we applied MAVT theory through the improved deck of cards method (DCM) (Corrente et al., 2021) to the construction of a cardinal impact assessment composite indicator of the pandemic. The objectives were two-fold: on the one hand, to observe the evolution of the pandemic as well as the impact of the vaccination plan and, on the other hand, to form a state ordinal indicator (or chromatic classification system) to give the Portuguese health authorities the possibility to associate measures and/or recommendations According to each state.

1.4. Outline of the paper

The paper is organised as follows. Section 2 introduces the basic mathematical concepts required throughout the paper. Section 3 presents the main used models to perform this study (criteria model, aggregation model, and graphical model). Section 4 displays lessons learn from practice, including the successful aspects, failures and improvements to the tool. Finally, Section 5, outlines the main conclusions and some avenues for future research.

2. Concepts, definitions, and notation

This section introduces the main concepts, definitions, and notation used throughout the paper. It comprises the criteria model basic data, the MAVT additive model, and the chromatic classification system.

2.1. Basic data

The basic data can be introduced as follows. Let, $T=\{t_1,\dots ,t_i,\dots ,t_m\}$, denote a set of actions or time periods (in general, days) used for observing the pandemic state in a given territory unit (country, region, district, etc.), and, $G=\{g_1,\dots ,g_j,\dots ,g_n\}$, denote the set of relevant criteria (our problem dimensions or indicators) identified with the experts for assessing the actions or time periods. The performance $g_j\left(t_i\right)=x_{j{t}_i}\in E_j$ represents the impact level of activity or severity over the action or time period $t_i\in T$, according to criterion $g_j$, being $E_j$ the (continuous or discrete) scale of this criterion, for $j=1,\dots ,n$. We will assume, without any loss of generality, that, for each criterion, the higher the performance level, the higher the impact on the pandemic. The set of criteria was built according to certain desirable properties (see Keeney, 1992).

2.2. The multi-attribute value theory additive model

The proposed model is a conjoint analysis model (see, for example, Bouyssou & Pirlot, 2016), more specifically an additive MAVT model. The origins of this type of models dates back to 1969, with the seminal work by H. Raiffa, published only in 2016, in Tsoukiàs & Figueira (2006), with several comments from prominent researchers in the area. For more details about the additive model see Keeney & Raiffa (1993).

Let $\succsim$ denote a comprehensive binary relation, over the actions in $T$, whose meaning is “impacts at least as much as”. Thus, an action $t^{\prime }$ is considered to impact at least as much as an action $t^{″}$, denoted $t^{\prime }\succsim t^{″}$, if and only if, the overall value of $t^{\prime }$, $v\left(t^{\prime }\right)$, is greater than or equal to the overall value of $t^{″}$, $v\left(t^{″}\right)$, i.e., $v\left(t^{\prime }\right)⩾v\left(t^{″}\right)$, where the overall value of each action is additively computed as follows:

$$v\left(t\right)=\sum _{j=1}^n{w}_j{v}_j\left(x_{jt}\right),\text{for}\text{all}t\in T$$ (1)

in which $w_j$ is the weight of criterion $g_j$, for $j=1,\dots ,n$, (assuming that ${\sum }_{j=1}^n{w}_j=1$), and $v_j\left(x_{jt}\right)$ is the value of the performance $x_{jt}$ on criterion $g_j$, for all for $j=1,\dots ,n$.

The asymmetric part of the relation, $t^{\prime }\succ t^{″}$, means that $t^{\prime }$ is considered to impact strictly more than $t^{″}$, while the symmetric of the relation, $t^{\prime }\sim t^{″}$, means that $t^{\prime }$ is considered to impact equally as $t^{″}$. The three relations $\succsim$, $\succ$, and $\sim$ are transitive.

The assessment of the value function, $v_j\left(x_{jt}\right)$, for criterion $g_j$ and each action or time period $t\in T$, is done in such a way that its value increases with an increasing of the performances level of criterion $g_j$, $j=1,\dots ,n$ (this function is a non-decreasing monotonic function). Let $t^{\prime }$ and $t^{″}$ denote two actions. The following conditions must be fulfilled:

• 1.The strict inequality $v_j\left(x_{j{t}^{\prime }}\right)>v_j\left(x_{j{t}^{″}}\right)$ holds, if and only if, the impact of performance $x_{j{t}^{\prime }}$ is considered strictly higher than the impact of performance $x_{j{t}^{″}}$, on criterion $g_j$ (it means that, $t^{\prime }$ impacts strictly more than $t^{″}$), for $j=1,\dots ,n$.
• 2.The equality $v_j\left(x_{j{t}^{\prime }}\right)=v_j\left(x_{j{t}^{″}}\right)$ holds, if and only if, the performance $x_{j{t}^{\prime }}$ impacts the same as the performance $x_{j{t}^{″}}$, on criterion $g_j$ (it means that $t^{\prime }$ impacts equally as $t^{″}$), for $j=1,\dots ,n$.

In addition, the value functions are also used for modelling the impact of the performance differences. The higher the performance difference, the higher the strength of the value function impact. Let $t^{\prime }$, $t^{″}$, $t^{″\prime }$, and $t^{″″}$ denote four actions. The following conditions must be fulfilled:

• 1.The strict inequality $v_j\left(x_{j{t}^{\prime }}\right)-v_j\left(x_{j{t}^{″}}\right)>v_j\left(x_{j{t}^{″\prime }}\right)-v_j\left(x_{j{t}^{″″}}\right)$ holds, if and only if, the strength of the impact of $x_{j{t}^{\prime }}$ over $x_{j{t}^{″}}$ is strictly higher than the strength of impact of $x_{j{t}^{″\prime }}$ over $x_{j{t}^{″″}}$, on criterion $g_j$, for $j=1,\dots ,n$.
• 2.The equality $v_j\left(x_{j{t}^{\prime }}\right)-v_j\left(x_{j{t}^{″}}\right)=v_j\left(x_{j{t}^{″\prime }}\right)-v_j\left(x_{j{t}^{″″}}\right)$ holds, if and only if, the strength of impact of $x_{j{t}^{\prime }}$ over $x_{j{t}^{″}}$ is the same to the strength of impact of $x_{j{t}^{″\prime }}$ over $x_{j{t}^{″″}}$, on criterion $g_j$, for $j=1,\dots ,n$.

In the construction of the value functions and the criteria weights we assume that the axioms of transitivity and independence hold (see Keeney & Raiffa, 1993).

2.3. Chromatic ordinal classification model

The chromatic ordinal classification model is an ordinal scale with categories and colours associated with them. Let $C=\{C_1,\dots ,C_r,\dots ,C_s\}$ denote a set of totally ordered (and pre-defined) categories, from the best $C_1$ (the lowest pandemic state impact), to the worst $C_s$ (the highest pandemic state impact): $C_1\succ \dots \succ C_r\succ \dots \succ C_s$, where $\succ$ means “impacts strictly more than”. The categories are used to define a set of states, as follows:

• –$C_1$ (green): Baseline state.
• –$C_2$ (light green): Residual state.
• –$C_3$ (yellow): Alarm state.
• –$C_4$ (orange): Alert state.
• –$C_5$ (red): Critical state.
• –$C_6$ (dark red): break state.
• –$C_7$ (dark red, darker than the previous): emergency state.

There are five fundamental states, from $C_2$ to $C_6$. It is worthy of note that the colours assigned to each state change smoothly when reaching the boundaries of the neighbouring states and that they move faster when passing from one state to the next in the upper part of the scale, (for example from $C_4$ to $C_5$), than when moving from a state to the next in the lower part of the scale, (for example from $C_2$ to $C_3$). It also goes faster from top down, i.e., in a descending way. This can be done through the way the value functions are modelled and/or the choice of the values for setting the cut-off lines with the possible definition of thresholds (see Section 3.6), for the justification.

3. Modelling aspects

This section provides the details of the three fundamental models used in our study: the criteria model, the aggregation model, and the graphical visualisation and communication model. The classification chromatic system and an illustrative example are also presented in this section.

3.1. Criteria model

A set of criteria built by the experts as the most relevant, considering the two main perspectives (called pillars) were used to characterise the pandemic, aimed to fulfil several desirable properties as stated in Keeney (1992): essential, controllable, complete, measurable, operational, decomposable, non-redundant, concise, and understandable. They were grouped as follows:

• A.
  Pillar I (ACT). Activity. This pillar was built to capture the main aspects of the COVID-19 registered or observed activity, i.e., the survival and development of the virus and its ability to still be active and cause infection in people in a given territorial unit. The following two COVID-19 activity criteria were considered to render this pillar operational.

  • 1.
    Criterion $g_1$ - Incidence (incid). The incidence (see Martcheva, 2015) is the number of new COVID-19 positive cases presented daily, $N(·)$, in the Official Health Reports. In most countries, the exact daily values vary periodically over each week. Particularly, in Portugal, the evolution of new daily cases is peaked markedly at day seven. Thus, to regularise the time series of the incidence, we consider the seven-day moving average and use this variable in our computations:

    $$g_1\left(t\right)=x_{1t}=\frac{{\displaystyle \sum _{u=t-6}^{t}N\left(u\right)}}{7}$$ (2)

    We could use the raw data directly, but that choice would introduce artificial weekly fluctuation due to weak reporting at weekends. A longer periodic average, as for example, by considering the last fourteen days would lead to a slow effect of the impact. Therefore, a seven-day average was considered the most adequate for this criterion.
  • 2.
    Criterion $g_2$ - Transmission (trans). The transmission is modelled here as the rate of change in the active cases computed from the raw data of the daily incidence, $N(·)$ (with no moving averages). With the goal of regularising these time series criterion values and smoothing the weekly fluctuations, we calculated the geometric mean over the last seven days. Our criterion is defined by the expression below:

    $$g_2\left(t\right)=x_{2t}={\left(\prod _{u=t-6}^t\frac{{\displaystyle \sum _{v=u-6}^{u}N\left(v\right)}}{{\displaystyle \sum _{v=u-7}^{u-1}N\left(v\right)}}\right)}^{\frac{1}{7}}$$ (3)

    With this formula, we have the advantage of a quicker response to the changes in incidence with respect to $R\left(t\right)$ transmission rate, the usual reproduction number of an epidemic with time. Moreover, our model has the same meaning as the $R\left(t\right)$, for $t=1$ (see Koch, 2020).
• B.
  Pillar II (SEV) - Severity. This pillar was built to capture the severity of the effects of COVID-19 on the Portuguese people, in particular on the health system. The following three COVID-19 severity criteria were considered to render this pillar operational.

  • 3.
    Criterion $g_3$ - Lethality (letha). The lethality is modelled here by considering the ratio of deaths at a given time period, $u$, over the number of new cases in the fourteen days prior. Then, by considering the accumulate number of cases, $N(·)$, and number of deaths, $O(·)$, it can be calculated by using the formula:

    $$\ell \left(t\right)=100\times \frac{O\left(t\right)-O(t-1)}{N(t-14)-N(t-15)},$$

    We hypothesise that the average time to death after the communication of the case is fourteen days. With the goal of regularising this variable and smoothing the fluctuations, we calculated a moving average of the last fourteen days for this criterion. The lethality formula used is given as follows:

    $$g_4\left(t\right)=x_{3t}=\frac{1}{14}\sum _{u=t-13}^t\ell \left(u\right).$$ (4)

    Another formula could be defined for modelling the lethality, but this one has been considered the most adequate by the experts in our case. Lethality could be modelled using a seven-day moving average formula, however the fourteen-day moving average was more adequate given that the evolution of lethality is gradual and slow and the fourteen days average regularises statistical fluctuations of the observed data.
  • 4.
    Criterion $g_4$ - Number of patients admitted to wards (wards). This criterion considers the total number of COVID-19 patients admitted to wards without counting those admitted to the intensive care unit, $H(·)$, which is raw data. The formula is thus a direct one:

    $$g_4\left(t\right)=x_{4t}=H\left(t\right)$$ (5)
  • 5.
    Criterion $g_5$ - Number of patients admitted to intensive care units (icu). Similar to the previous criterion, it counts the number of COVID-19 patients admitted to the intensive care units, $U(·)$, which is also raw data. The formula is also a direct one:

    $$g_5\left(t\right)=x_{5t}=U\left(t\right)$$ (6)

All the raw data $N(·)$, $O(·)$, $H(·)$, and $U(·)$, are available at the Direcção-Geral da Saúde (DGS) website (www.dgs.pt).

Remark 1 (Fragility Point 1

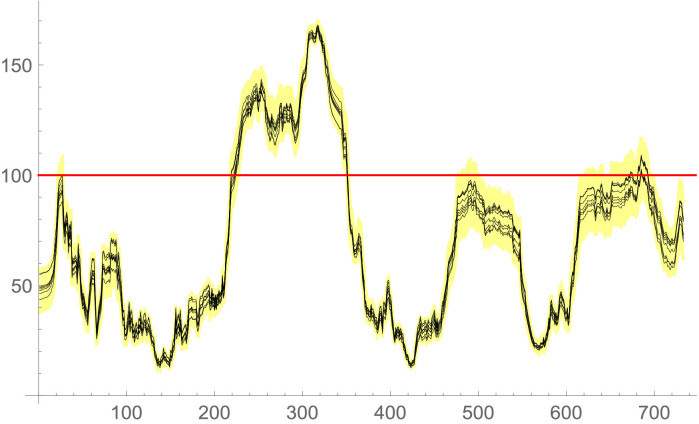
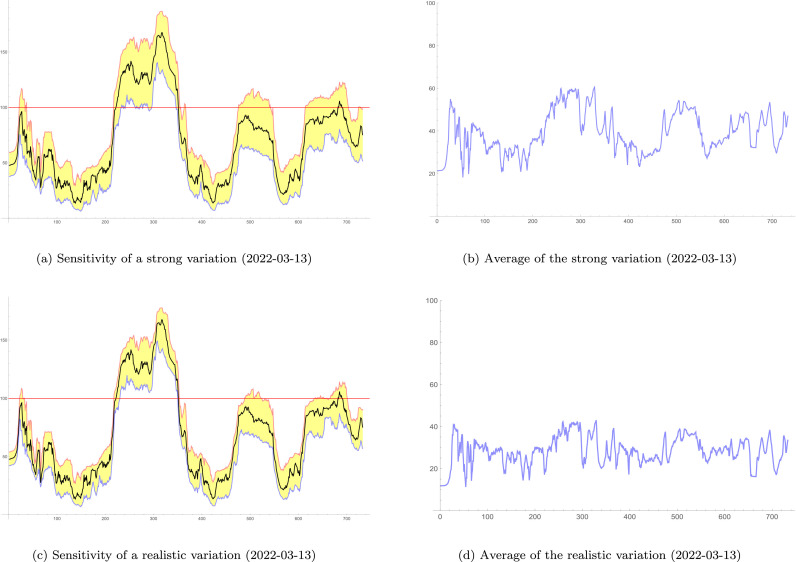
Imperfect knowledge of criteria set (seeRoy et al., 2014)) This imperfect knowledge is mainly due to the imprecision of the tools and the procedures used to determine the raw data needed for the computation of the performance levels of the three criteria (namely $N(·)$, since $O(·)$, and $U(·)$ do not suffer from significant imprecision) and also due to the arbitrariness of the formulas chosen for the three criteria ($g_1(·)$, $g_2(·)$, and $g_3(·)$). Other models could have been selected and justified. Whenever a fragility point (weakness or vulnerability) is identified, sensitivity/robustness analyses are needed to guarantee the validity of the model and confidence in the results. These sensitivity analyses will be presented in Section 4.3.

3.2. About the rationale behind the set of criteria

The building of this set of criteria followed a logic based on two fundamental principles that are somehow linked: familiarity with the problem and intelligibility. The first stems essentially from the information that the population received via the media. All Portuguese citizens are relatively well informed, and have a certain degree of in-depth knowledge of the impact of this pandemic, through two major concepts or aspects:, the activity of the pandemic and its severity. For the activity definition, two well-known key concepts by the Portuguese population are included: incidence and transmission. For severity, the concepts of mortality, bed occupancy in the wards and in the ICU are published daily in the media and are equally similarly familiar concepts to all Portuguese people. In total, there are five concepts that the Portuguese people deal with every day and therefore it is very important to consider them in a set of criteria to assess the impact of the pandemic in the country. That was also the opinion shared by the experts who were part of the team that produced the indicator. We think that the justification of the rationale behind this consideration was quite clear.

As for the principle of intelligibility, this is more closely related to the models used to operationalise each of the five concepts, then grouped into two pillars. When each of these models are presented to the population, their understanding shall be easy. Let us look at the case of incidence and the associated model. Incidence is defined as the number of positive cases detected daily (note that it is not possible to detect all the cases in a population and this number is not accurate). The direct use of this number in our indicator would imply greater fluctuation in values, since it also fluctuates throughout the week. Therefore, the incidence was chosen to be modelled using the average number of cases per week, being a model that the population finds clear and easily understandable, thus confirming the principle of intelligibility. The same philosophy was applied in the construction of the models of the other four concepts.

In summary, the rationale for the set of criteria was carried out through concepts, two of a more global scope, the pillars of disease activity and severity, and five of a more local scope, which are the basis for building operational models of the two global pillars. The consideration of additional criteria, such as the number of tests or others, would make the model more complex and in practice, it was found that these concepts did not have much influence on the perception of the impact on the pandemic, such as the ones we chose for our model

3.3. Parameters of the aggregation model and the chromatic system

This section presents the technical aspects related to the construction of the parameters of the additive aggregation model (i.e., the value functions and the weights), as well as the chromatic classification system.

The construction of the value functions (interval scales) and the weights of criteria (ratio scales) was performed using a simplified version of the Pairwise Comparison Deck of Cards Method (here called PaCo-DCM), proposed by Corrente et al. (2021). This simplified version did not consider a pairwise comparison and imprecise information leading to possible inconsistent judgements.

The origin of the DCM in MCDA dates back to the eighties, a procedure proposed by Simos (1989). This method was later revised by Figueira & Roy (2002) and used for determining the weights of criteria in outranking methods. In this revised version, Figueira & Roy (2002) mention the possibility of using the method and SRF software, proposed in the same paper, to build not only ratio scales, in general, but also to build interval scales. For another extension of the DCM and a review of its applications, see Siskos & Tsotsolas (2015). Regarding the interval scales, a first attempt to build them was proposed by Pictet & Bollinger (2008), while Bottero et al. (2018) improved the DCM method to build more general interval scales (based on the definition of at least two reference levels with a precise meaning for policy/decision-makers, users, or experts). Bottero et al. (2018) also created another extension of the construction of ratio scales for determining the capacities of the Choquet integral aggregation method. Dinis et al. (2021) made use of a tradeoff procedure for determining the weights of criteria for the additive MAVT model. The used method for computing the weights of criteria in this paper is very similar to the latter. Another recent and interesting extension of the DCM with visualisation tools was proposed by Tsotsolas et al. (2019).

3.3.1. Value functions (interval scales)

The construction of the value functions using PaCo-DCM requires the use of pairwise comparison tables. This idea was introduced into MCDA by Saaty (2016) and later adapted and improved to accommodate qualitative judgements by Bana e Costa et al. (2016).

In what follows, we will show, step-by-step, the details of the application of PaCo-DCM. In socio-technical processes, it is always important to provide key aspects of the context that enable and facilitate the evolution of these processes. It is important to note that we had a very limited time period for producing a first version of our tool (only three days) and for presenting a first prototype with meaningful results (further ten days). This was possible as we benefitted from the help of a mathematician on the CCIST team, who had also strong expertise in COVID-19 and was well very acquainted with the experts on the GCOM team. In addition, the CCIST member has substantial experience programming with Wolfram Mathematica,9 which was crucial to obtain the results of our tests and graphical tools almost instantaneously. This was a fundamental aspect for the interaction with the members of the GCOM team, comprised exclusively of physicians familiar with the fundamentals of mathematics.

We will present the main interactions between the CCIST and the GCOM teams for building together the value function of the first criterion as a socio-technical process, which considered the experts’ judgements and the technicalities of the PaCo-DCM tool. We will also present the details of all computations. Readers can easily follow how we built an interval scale with a simple, but adequate version of the PaCo-DCM.

• 1.
  The basics of PaCo-DCM for gathering and assessing the expert’s judgements. The method was introduced to the experts in a simplistic form, by explaining the meaning of the DCM used to assess their judgements via a short example. The experts were provided with two sets of cards:

  • (a)
    A very small set of labelled cards with very familiar objects (e.g., a lemon, an apple, and a mango) and that can easily be placed in preferential order (first mango, then apples, then lemon), from the best to the worst (for the sake of simplicity assume they are totally ordered, i.e., there are no ties). All experts agreed on the same ranking.
  • (b)
    A large enough set of blank cards. These blank cards are used to model the intensity or strength of preference between pairs of objects.
  • (c)
    Assume we have three objects $o_i$, $o_k$, and $o_j$. If the experts feel that the strength of preference difference between $o_i$ and $o_k$ is stronger than that between $o_k$ and $o_j$, they place more blank cards in between $o_i$ and $o_k$ than in between $o_k$ and $o_j$ (these are thus judgements for building a thermometer like scale). The experts can place as many cards as they want in between two objects and they do not need to count them, just hold them in their hands. In fact, in our case we used wooden balls instead of blank cards; this does not refute the application of the method and it is more suitable to obtain judgements from the experts, since wooden balls are easy to handle and have a better visualisation effect. Experts may always revise their judgements about the strength of preference and change the number of cards in between two objects.
  • (d)
    We then explained the experts that:

    • –
      No blank card in between two objects does not mean that the two objects have the same value, but that the difference is minimal (minimal here means equivalent to the value of the unit, a concept the experts would subsequently understand better).
    • –
      One blank card means that the difference of preference is twice the unit.
    • –
      Two blank cards means that the difference of preference is three times the unit and so on.
  • (e)
    Finally, we explained to the experts that in our case, we were modelling the strength or intensity of the pandemic impact instead of preferences, but the concept of preference was extremely useful to render the experts familiar with the concept of strength of impact and with the method.
• 2.
  (At least) two well-defined reference levels. PaCo-DCM requires the definition of two reference levels for the construction of an interval scale. These two levels must have a precise meaning for the experts. One level is typically located in the lower part of the scale and the other in the upper part of the scale. This is similar to the method proposed in Bana e Costa et al. (2016) where, in general, “neutral” and “good” reference levels are needed to build a scale, with the assignment of the values 0 and 100, respectively. In PaCo-DCM, the values of the reference levels do not need to be set at 0 and 100. Any two values can be used in PaCo-DCM for building the interval scale. In the application of the model to the pandemic situation, the two reference levels built from the interaction with the experts were the following:

  • –
    Baseline level: Incidence value equal to 0. This means that no new cases have been registered over the last seven days. It does not mean the absence of a pandemic, but only that no new cases have been observed. The value of the baseline impact level was set at $v_1\left(0\right)=0$, which is an arbitrary origin on the interval scale for the 0 preference level in the first criterion.
  • –
    Critical level: Incidence value equal to 1125. The value of the critical level was first set at 1100, but after the discussion of the subsequent step, we made a slight adjustment to 1125 and decided to set $v_1\left(1125\right)=100$, which represents the highest value before entering a critical state. Due to the number of public health physicians and contact tracing (tracking), after 900 new cases there is a saturation of resources, and the experts considered 1125 to be an adequate number to model the critical level.
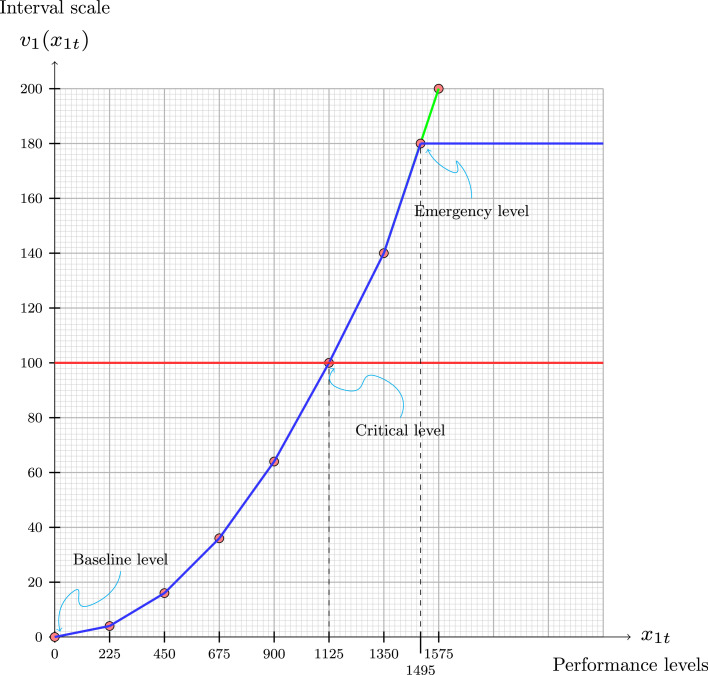
• 3.
  Setting the number of value function breakpoints. In this step, we defined alongside the experts the most adequate way of discretising, by levels, the performances of the incidence, taking into account the initial two reference levels built in the previous step, 0 and 1100. A first discussion led us to consider only values in between 0 and 2000, since higher than these values would lead to an emergency state, even 2000 seemed to be quite high. Thus, we thought to discretise the range $[0,2000]$ into six breakpoints 0, 450, 900, 1350, 1800, and 2000, but an width of 450 in between two consecutive levels was considered quite large. Finally, we decided to discretise the range in ten points, with an width of 225 between two consecutive points. The following values were finally considered with an adjustment in the last one to be consistent with the width of 225, and by considering the critical level at 1125 instead of 1100:

  $$\begin{array}{ccc}& & \left\{0\right\}\left\{225\right\}\left\{450\right\}\left\{675\right\}\left\{900\right\}\left\{1125\right\}\hfill \\ & & \left\{1350\right\}\left\{1575\right\}\left\{1800\right\}\left\{2025\right\}.\hfill \end{array}$$
• 4.
  Inserting blank cards. In this step, the experts were invited to insert blank cards in between consecutive levels; it corresponds to fill the diagonal of Table 1. This process was performed for the initial number of breakpoints (ten) and led to several adjustments resulting from the socio-technical co-constructive interaction process between experts (GCOM team) and the analysts (CCIST team). Each change was accompanied by a figure (see, for example, Fig. 1), which was an important visualisation tool for assisting the experts. The consistency tests described in the next step were also performed. After building all the value functions (Appendix) and testing them with past observations of the pandemic, the two last levels below were discarded since an emergency level was set before reaching level 1575.

  $$\begin{array}{ccc}& & \left\{0\right\}\left[0\right]\left\{225\right\}\left[2\right]\left\{450\right\}\left[4\right]\left\{675\right\}\left[6\right]\left\{900\right\}\left[8\right]\left\{1125\right\}\left[10\right]\hfill \\ & & \left\{1350\right\}\left[13\right]\left\{1575\right\}\left[11\right]\left\{1800\right\}\left[8\right]\left\{2025\right\}\hfill \end{array}$$

  However, we can observe that the number of blank cards increase until level 1575, and then it decreases. It means that the shape of the value function will move from a convex to a concave shape (it would be similar to a continuous sigmoid function). From a certain point, more new cases have almost the same impact on the pandemic as fewer new cases. We are referring to a part of the function where the situation would be out of control.
• 5.
  Testing a more sophisticated version of the method. In the PaCo-DCM method, more cells of Table 1 can be filled from the judgements provided by the experts. The time limitation and the good understanding of the method by themselves reduced the number of interactions for checking consistency judgements. Table 1 thus contains all the possible comparisons with the eight levels kept (here we are not considering the two last ones). An example of a test for assessing the impact differences between the two non-consecutive levels $\left\{900\right\}$ and $\left\{225\right\}$ was performed as follows: we placed the set of six blank cards in between $\left\{900\right\}$ and $\left\{675\right\}$, and the set of seven cards in between $\left\{675\right\}$ and $\left\{225\right\}$ (the experts do not really need to know how many cards are in between these levels, but these two numbers came from the previous interaction and were provided by the experts). Then, we placed a set of sixteen cards in between $\left\{900\right\}$ and $\left\{225\right\}$ and we asked the experts to compare the three sets of cards, asking whether they felt comfortable with the third set of sixteen cards. If not, we started by removing the blank cards, one by one. We removed blank cards until there was a set of thirteen blank cards. Then, we told the experts that thirteen cards is slightly inconsistent and showed them why. We finally, asked them whether they felt comfortable with a set of fourteen blank cards (six, in between $\left\{675\right\}$ and $\left\{900\right\}$, plus seven, in between $\left\{225\right\}$ and $\left\{675\right\}$, plus one), and they agreed. The other cells of the table can be filled by transitivity, i.e., by following the consistency condition presented in Corrente et al. (2021). The impact difference between two non-consecutive cells is determined as follows:

  $$e_{ij}=e_{ik}+e_{kj}+1\text{for}\text{all}i,k,j=1,\dots ,t\text{and}i<k<j$$ (7)

  We can see that $e_{\left\{900\right\},\left\{225\right\}}=e_{\left\{900\right\},\left\{675\right\}}+e_{\left\{675\right\},\left\{225\right\}}+1=6+7+1=14$.
• 6.
  Computations. The computation of the values of the breakpoints was done as follows:

  • –
    The values of the reference levels: $v_1\left(0\right)=0$ and $v_1\left(1125\right)=100$.
  • –
    The number of units in between them, $h=(0+1)+(2+1)+(4+1)+(6+1)+(8+1)=25$. Remember that 0 cards does not mean the same value, but that the difference is equal to the unit. Thus, we need to add one more to all the number of blank cards in between two levels.
  • –
    The value of the unit, $\alpha =(v_1\left(1125\right)-v_1\left(0\right))/h=(100-0)/25=4$. The value of the unit is equal to four points, and now the experts were able to understand better the concepts of unit and value of the unit.
  • –
    The values of the breakpoints are now easy to determine: $v_1\left(225\right)=0+4\times 1=4$, $v_1\left(450\right)=0+4\times 4=16$, and so on, for the remaining: $v_1\left(675\right)=36$, $v_1\left(900\right)=64$, $v_1\left(1125\right)=100$, $v_1\left(1350\right)=140$, $v_1\left(1575\right)=200$.
• 7.The shape of the value function. After assessing the values of the breakpoints, we can then draw a piecewise linear function as in Fig. 1. Any value within each linear piece can be obtained by linear interpolation.

  A marginal change in the lower part of the scale has less impact on the pandemic than the same marginal change in the upper part of the scale, as depicted in Fig. 1. Before reaching the emergency level, this is a convex value function, and we can observe the marginal increase in the value of the impact. Moving from 0 to 225 implies an increase in the indicator value, from 0 to 4, while moving from 1125 to 1350 implies an increase in the impact value from 100 to 140. The same number of additional units 225 in the upper part of the scale produces a much higher impact (40) than in the lowest part of the scale (only 4). It increases closer to the critical level than to the baseline level. This was a strong requirement established by the experts.

• 8.Remark. Please note that the values of the emergency/saturation levels were calculated considering Portugal’s capacity and, from a certain limit, the normal and extraordinary capacity was exceeded, and a rupture state was reached. All these values can, and should be, adjusted according to the characteristics of each country and can be revised according to the adaptations of each country. When we performed the PACI, the values for Portugal were the ones used and there was no need for further readjustment.
• 9.
  The output of the model and possible approximations. One of the outputs of the model is a piecewise linear function, whose mathematical expression can be stated as follows:

  $$v_1\left(x_{1t}\right)=\{\begin{array}{ccc}4x_{1t}/225\hfill & \text{if}& x_{1t}\in [0,225[\hfill \\ 4x_{1t}/75-8\hfill & \text{if}& x_{1t}\in [225,450[\hfill \\ 4x_{1t}/45-24\hfill & \text{if}& x_{1t}\in [450,675[\hfill \\ 28x_{1t}/225-48\hfill & \text{if}& x_{1t}\in [675,900[\hfill \\ 4x_{1t}/25-80\hfill & \text{if}& x_{1t}\in [900,1125[\hfill \\ 44x_{1t}/225-120\hfill & \text{if}& x_{1t}\in [1125,1350[\hfill \\ 52x_{1t}/225-168\hfill & \text{if}& x_{1t}\in [1350,1495[\hfill \\ 180\hfill & \text{if}& x_{1t}\in [1495,+\infty [\hfill \end{array}$$ (8)

  This particular function could be approximated by a quadratic function without losing much information, but such an approximation needs to be validated by the experts:

  $$\widetilde{v_1}\left(x_{1t}\right)=\{\begin{array}{ccc}100{(x/1125)}^2\hfill & \text{if}\hfill & x_{1t}\in [0,1125]\hfill \\ & & \\ 180\hfill & \text{if}\hfill & x_{1t}\in [1125,+\infty [.\hfill \end{array}$$

  The mean of the Euclidean distance between the functions $\widetilde{g_1}$ and $g_1$ is given by the following expression:

  $$\frac{\sqrt{{\int }_0^{+\infty }{(g_1\left(\xi \right)-\widetilde{g_1}\left(\xi \right))}^{2}d\xi }}{\sqrt{{\int }_0^{+\infty }{\left(g_1\left(\xi \right)\right)}^{2}d\xi }}=6.40389\times {10}^{-4},$$

  which is almost negligible and shows that the approximation does not lead to the loss of much information.
• 10.Missing, imprecise, and inconsistent judgements. The method described in Corrente et al. (2021) also allows us to deal with missing, imprecise, and inconsistent judgements. The inconsistency analysis is performed by using linear programming, similarly to that performed in other MCDA tools, as for example, in Mousseau et al. (2003). The team members’ experience and the way the socio-technical interaction was conducted highly helped in the information gathering process, not requiring the use of more sophisticated functionalities of the PaCo-DCM tool. Due to shortage of time, it was not possible to use all method’s functionalities, and the rise of more complex questions was limited. However, since the experts validated the results (value function and weights, in this case), there was no real need to render the dialogue more complex. This is an important issue for guaranteing the consistency of the judgements gathering process from the experts during the application of the method. In a socio-technical co-constructive process, when building the value functions and the weights, there are no true values for such parameters because there is no true reality, i.e., there are no true value functions and true weights. We used the questions that were the most adequate and accepted by the experts given the time constraints. If the time variable was not as constraint, more questions could be asked, leading to a more complex process. However, since the process was validated, there was no need to introduce additional questions. In the future we can introduce more complexity for guaranteeing even a more consistency in the whole process of gathering impact judgements. This is a socio-technical approach with some limitations inherent to all socio-technical processes because both our system and model are mental constructs.
• 11.The emergency level. After running the model for the whole set of days during the pandemic, the experts realised they could set a maximum of 180 points for this function since all the situations beyond such a point would be equally terrible and out of control. Thus, the function was truncated at level 1495, which is the first level with a value of 180. After this performance level the situation collapses and all the performance levels are considered as serious as the emergency level.

The piecewise functions for the other four criteria, as well as the number of blank cards in between consecutive levels are provided in the Appendix.

Remark 2 (Fragility Point 2

Subjectivity in building the value functions) There is some obvious subjectivity in the assessment of the value functions since the experts are not precise instruments like high tech thermometers. In addition, for example, there is no true value function for modelling the incidence; this function is a construct, which can be more or less adequate to the situation. This is another kind of fragility point in our model, which justifies the use of sensitivity analyses as it will be presented in Section 4.3.

Table 1.

Pairwise comparison table for criterion $g_1$ (incidence).

Fig. 1.

Shape of the value function for incidence.

3.3.2. Weighting coefficients (ratio scales)

The assignment of a value for each criterion weights was also performed through PaCo-DCM, but the interaction protocol with the experts and the nature of the judgements were presented in a different way. The weights are interpreted here as scaling factors or substitution rates. The dialogue with the experts was conducted as follows:

• 1.
  Building dummy situations. A set of five dummy situations (or statuses) one per criterion, representing the swings between the baseline level and the critical level were built as follows (also see Dinis et al., 2021):

  • –
    $p_1=(1125,0,0,0,0)\equiv (100,0,0,0,0)$. This situation represents the impact on the pandemic of the swing (regarding the first criterion) from the baseline level to the critical level, maintaining the remaining criteria at their baseline levels.
  • –
    $p_2=(0,1,0,0,0)\equiv (0,100,0,0,0)$. The meaning of this situation is similar to the one provided in the first situation. A transmission rate equal to one is considered adequate by the experts to represent the critical level.
  • –
    $p_3=(0,0,3.6,0,0)\equiv (0,0,100,0,0)$. The meaning of this situation is similar to the one provided for the first situation. In this situation, the experts considered that half of the maximum value of $g_3\left(t\right)$ during the pandemic in Portugal corresponds to 100 points. Thus, $\max \left\{g_3\left(t\right)\right\}=7.19148$. Consequently, 100 points correspond to the value of lethality of $3.59574\approx 3.6$.
  • –
    $p_4=(0,0,0,2500,0)\equiv (0,0,0,100,0)$. The meaning of this situation is similar to the one provided in the first situation. The 2500 represent $15\%$ of the total number of beds, which is an adequate number for defining the critical level.
  • –
    $p_5=(0,0,0,0,200)\equiv (0,0,0,0,200)$. The meaning of this situation is similar to the one provided for the first situation. The 200 beds represent $80\%$ of the difference between the current number of beds and the number of available beds before the pandemic. The experts considered this number as adequate to represent the critical level.

  The concept of swings is in line with the swing weighting technique by von Winterfeldt & Edwards (1986) and the use of two reference levels with the concepts of “neutral” and “good” by Bana e Costa et al. (2016).

• 2.
  Ranking the dummy situations with possible ties. The experts received five cards, one with each one of the previous situations and the analyst team asked them to provide a ranking of these five cards, with possible ties, according to the impact that the swings have on the pandemic. The situation(s) leading to the highest impact was (were) placed in first position, the one(s) with the second greatest impact on the second, and so on. The following ranking was proposed by the experts:

  $$\left\{p_1\right\}\{p_3,p_4,p_5\}\left\{p_2\right\}$$

  The analysts explained to the experts that the case in the first situation will receive the highest weight, the ones in the second position the second highest weight, and the situation in the last position the lowest weight.
• 3.
  Inserting blank cards. The experts were invited to insert blank cards in between consecutive positions to differentiate the role each weight (swing) would have on the pandemic impact, after telling them the meaning of swings and substitution rates. The following set of blank cards (in between brackets) was provided by the experts.

  $$\left\{p_1\right\}\left[2\right]\{p_3,p_4,p_5\}\left[3\right]\left\{p_2\right\}$$

  Similar to the value functions, a more sophisticated PaCo-DCM procedure could be used for such a purpose, but the experts felt comfortable with the information they provided.
• 4.Assessing the value of the substitution rates. This was the most difficult question for the experts. We need to establish a relation between the weight of the criterion in the first position of the ranking (incidence) and the weight of the criterion in the last position of the ranking (transmission). In PaCo-DCM, this is called the $z-$ratio that is used to build a ratio scale. After a long discussion and several attempts, the experts provided the following relation between the two weights: $z={\widehat{w}}_1/{\widehat{w}}_2=2$. We are using $\widehat{w_j}$, for the non-normalised weights of criterion $g_j$, for $j=1,\dots ,5$.
• 5.
  Calculations. The computations are similar to the ones performed for the value functions:

  • –
    The values of the non-normalised weights of the situations in the first and last positions of the ranking, i.e., ${\widehat{w}}_1=2$ and ${\widehat{w}}_2=1$.
  • –
    The number of units between them, i.e., $h=(2+1)+(3+1)=7$.
  • –
    The value of the unit, $\alpha =({\widehat{w}}_1-{\widehat{w}}_2)/h=(2-1)/7=0.14286$.
  • –
    The non-normalised weights: ${\widehat{w}}_2=1$, ${\widehat{w}}_3={\widehat{w}}_4={\widehat{w}}_5=1.42858$, and ${\widehat{w}}_1=2$.
  • –
    The normalised weights: $w_2=1/7.28574=0.13725$, $w_3=w_4=w_5=1.42858/7.28574=0.19608$, and $w_1=2/7.28574=0.27451$.
• 6.Final adjustments. After adjusting the model results to the real pandemic data and some discussions with the experts, the following weights were proposed for this model: $w_2=0.141$, $w_3=w_4=w_5=0.193$, and $w_1=0.280$.

Remark 3 (Fragility Point 3

Subjectivity in building the weights of criteria) The justification is in line with the one provided in Remark 2, which also requires the use of sensitivity analyses (see Section 4.3).

3.4. On two types of dependences between criteria

The existence of possible dependences or interactions among criteria can be a major concern and therefore was subject to some reflection before deciding to propose our criteria model (with the five criteria within two pillars) as well as our aggregation impact model (an additive model with measurable multi-criteria value functions, as the one in Dyer & Sarin, 1979). Indeed, this topic may be slippery and it can lead to nonsense or useless models, since we need to make choices to build an adequate model that fits the system. Most of the times, such choices contain some arbitrariness.

It shall be noted that in what follows we will mainly consider the dependences between pairs of criteria. Considering the dependences among more than two criteria is difficult to ascertain and to understand by both the experts and people in general.

There are several definitions of dependences between criteria; in our context we can distinguish two major categories of dependences, as described below.

• –
  One type of dependences that does not require the experts’ impact judgements. It is more technical and contains the following dependences (see Chapter 10 in Roy, 1996):

  • $a)$
    One related to the factors which directly contribute to the definition of the formulas of the criteria, or which indirectly may influence the performance levels of such criteria, called structural dependence.
  • $b)$
    Another related to the data, i.e., the possible relationship (e.g., the correlation) between the performance levels of the criteria, called statistical dependence.

  Structural and statistical dependences can be present simultaneously. It shall be noted that a statistical dependence depends on the number of periods considered relevant for testing, whether or not exists such a dependence (usually, the number of periods considered for testing the correlation between pairs of criteria); because of this aspect such a dependence may be unstable.

• –A different category of dependences requires the intervention of the experts’ judgements, being thus subjective and related to the impact aggregation model - here, this type is referred as a subjective dependence.

It is also important to notice that the structural and the statistical dependences are related to the criteria model, while the subjective dependences are related to the impact aggregation model. The existence of structural and/or statistical dependences between pairs of criteria does not imply the existence of subjective dependences between the same pairs of criteria. The latter type of dependences depends on people’s mind - it is a mental construct on how a person/expert feels the existence of a dependence between criteria and may vary from one person/expert to another.

In what follows we will provide some details about the two categories of dependences related to our criteria and impact models:

• 1.
  Structural and statistical dependences. For illustrative purposes, let us analyse our set of criteria and our data and try to identify some structural and statistical dependences that may exist.

  • (a)
    Structural dependences. In the activity pillar, both criteria transmission ($g_1$) and incidence ($g_2$) share the same common (direct and/or indirect) factors contributing to their definition. The transmission rate ($g_1$) depends directly on the number of active cases (infectious people), and indirectly on contacts (with people and/or contaminated spaces, surfaces, or objects), and on the characteristics of the virus variants, while the incidence ($g_2$) besides depending directly on the number of active cases, and indirectly on the contacts, (also depends directly) on the transmission rate itself. This shows that there is a clear structural link between transmission and incidence, which can be observed in the formula of $g_2$: the numerator inside the product is equal to 7 in $g_1$.
  • (b)
    Statistical dependences. Remember that a structural dependence does not necessarily imply the existence of a statistical dependence, and vice-versa. To check if there are dependences in our criteria model, we can compute the correlation between all pairs of criteria. These correlations values depend on the time horizon considered as relevant and can evolve over time, being thus of an unstable nature.

    • $▹$
      First, let us consider as relevant the time horizon since the beginning of the pandemic till 13 March 2022 (see Table 2 ). We can observe that despite the structural link between $g_1$ and $g_2$ there is no correlation between these two criteria performance levels. However, there is a correlation between $g_4$ and $g_5$.
    • $▹$
      Second, let us consider as relevant the time horizon associated with the last 120 days before 13 March 2022 (see Table 3 ). We can observe there is no more a correlation between $g_4$ and $g_5$, while it appears a new correlation between $g_1$ and $g_4$.
  • (c)
    Comments. To conclude, the existence of a correlation between $g_4$ and $g_5$ does not mean there is a double counting in the value of the PACI for two main reasons: $i)$ because the correlation is unstable, since it evolves over time or depends on the period considered as relevant for the computations of the correlation values, as we can observe in Tables 2 and 3, and $ii)$ because the existence of a statistical dependence does not imply the existence of a subjective dependence since they are of a different nature. Sometimes when structural and/or statistical links exist there is a tendency to use the double counting argument to justify replacing two criteria by a “dummy” one with a different unit and a meaning which is difficult for people to understand, i.e., the new criterion is no more intelligible for people (see for example, pages 225–226, in Roy, 1996, for another example and a more detailed explanation on this type of dependences).
• 2.
  Subjective dependences. This type of dependence is related to the impact model. The two conditions below are generally imposed to guarantee the existence of an additive measurable multi-criteria value function (for three or more criteria), which is the type of functions we built in our aggregation impact model. In the concepts and definitions below, we mainly followed the work by Dyer & Sarin (1979).

  • (a)
    Mutual preference (impact) independence. The criteria are mutually preference or impact independent when all the proper sets of a given set of criteria are impact independent of their complements. Consider a proper set of criteria and two different actions (time periods). These two actions have the same performance levels for the criteria belonging to the complement set. There is independence if the preference between both actions does not depend on the performance levels of the criteria belonging to the complement set. This condition guarantees that a function provides an order over the set of actions.
  • (b)
    Mutual difference independence. The criteria are mutually difference independent when all the proper sets of a given set of criteria are difference independent of their complements. A difference independence means that a preference difference between two actions, evaluated on several criteria and differing only in one of them, does not depend on the performance levels of the other criteria (Dyer, 2016). This condition guarantees the additivity of the aggregation model and captures the strength of preference (or impact, in our settings).
  • (c)
    Comments. It should be noticed that the construction of a measurable value functions requires to check not only the two previous conditions but also a condition called difference consistency, as well as some more technical assumptions (see Dyer, 2016, Dyer, Sarin, 1979)).
  • (d)
    Mutual preference (impact) independence test. Given the faced time constraints, we did not conduct any independence test with the experts. Even if we were able to make it possible, there was no guarantee that all the experts would agree on the existence of the two previous types of subjective dependences. However, and since one of the analysts was also an expert, it was reasonable to carry out some tests with him to check if there is a mutual preference (impact) independence between the criteria of the activity pillar against the criteria of the severity pillar. The performed tests used impact judgements by considering the strict impact binary relation as well as the indifference binary relation over some pairs of actions. The next example of test considers the indifference relation. This relation is denoted by the symbol “$\sim$”. We proceeded as follows with some pairs of time periods: considering a first time period performances levels (1180.3, 0.962, 3, 500, 100) and a second time period performances levels (1.000, 1000, 3, 500, 100), the analyst was asked if these two time periods were indifferent in terms of the impact, i.e., if they produce the same impact. The answer was “Yes!”, thus we made a change to the performance levels of the three criteria of pillar two and asked the same question again. The answer was again positive, i.e., (1180.3, 1.000, 6, 1000, 200) $\sim$ (1000, 1.000, 6, 1000, 200). Note that a negative answer would imply that the two first criteria would not be independent of the last three. We proceeded in the same way with different subsets of criteria and there was no hesitation, i.e., there was any doubt about the violation of mutual preference (impact) independence.
  • (e)
    Comments. This test and the assumption of independence seemed to be an acceptable working hypothesis to build our impact model. The results of our model, as well as the validation and sensitivity analyses tests confirmed that our choice was adequate. A model accommodating the possibility of having some pairs of dependent criteria would require much more complex techniques and would be very difficult to communicate to the general public.

Finally, let us point out that many elements of the models are arbitrary because they depend on the choices made by analysts and experts in a socio-technical co-constructive process. Although the pandemic system has some objective elements (as for example, the existence of the virus), most of the elements are mental constructions (as for example, the indicators provided to follow the pandemic). In addition, the model of such a system is also a mental construction. In the end, our model can be analysed to verify its suitability to model the system. Indeed, the validation and sensitivity/robustness testes showed the model was adequate: for example, when the impact is high, the model is not providing a low value. In conclusion, the validation tests and the sensitivity/robustness analyses showed that the built indicator was adequate.

Table 2.

Correlation between criteria before 13/3/2022 .

	$g_2$	$g_3$	$g_4$	$g_5$
$g_1$	0.002	$-$0.255	0.360	0.209
$g_2$		0.366	$-$0.183	$-$0.280
$g_3$			0.366	0.409
$g_4$				0.928

Table 3.

Correlation for the last 120 days before 13/3/2022 .

	$g_2$	$g_3$	$g_4$	$g_5$
$g_1$	$-$0.107	$-$0.660	0.861	0.639
$g_2$		0.407	$-$0.576	0.028
$g_3$			$-$0.768	$-$0.385
$g_4$				0.503

3.5. Illustrative example

This is an illustrative example with five actions, i.e., five different time points in the pandemic. Moment $t=0$ is four days before the press conference with the media (14 July 2021) at the Portuguese Medical Association (in Lisbon). The other moments, $t$, were set regarding the number of the days before $t=0$ and corresponds to the first lock down in Portugal (20 March 2020), one of the lowest activity and severity periods (31 July 2020), Christmas (24 December 2020), and some days after the second lock down (24 January 2021). Table 4 presents the activity as severity performance levels for the five considered criteria, according to the two pillars.

Table 4.

Performances levels for five moments of the pandemic.

$t$	Date	Pillar I (ACT)		Pillar II (SEV)
		$x_{1t}$ (incid)	$x_{2t}$ (trans)	$x_{3t}$ (letha)	$x_{4t}$ (wards)	$x_{5t}$ (icu)
$-$474	2020-03-20	194	1.301	4.160	128	41
$-$343	2020-07-31	197	0.978	1.140	340	41
$-$197	2020-12-24	3574	0.987	2.180	2348	505
$-$166	2021-01-24	12341	1.039	3.460	5375	742
0	2021-07-10	3658	1.042	0.382	488	144

From the data presented in Table 4 and by applying the previously built piecewise linear value functions, we obtained the results shown in Table 5 . The last column of this table provides the overall value of each moment of the pandemic, after applying the Model (1) formula.

Table 5.

Value functions scores for the five moments of the pandemic.

$t$	Date	Pillar I (ACT)		Pillar II (SEV)			Value
		$v_1\left(x_{1t}\right)$	$v_2\left(x_{2t}\right)$	$v_3\left(x_{3t}\right)$	$v_4\left(x_{4t}\right)$	$v_5\left(x_{5t}\right)$
		$w_1=0.280$	$w_2=0.141$	$w_3=0.193$	$w_4=0.193$	$w_5=0.193$	$v\left(t\right)$
$-$471	2020-03-20	3.441	180.00	115.571	1.0240	4.300	49.6800
$-$342	2020-07-31	3.503	60.900	31.6990	2.7200	4.300	17.0400
$-$197	2020-12-24	180.0	76.702	60.5640	89.056	180.0	124.832
$-$166	2021-01-24	180.0	180.00	96.1120	180.00	180.0	163.810
0	2021-07-10	180.0	180.00	10.6240	3.9040	52.80	88.7700

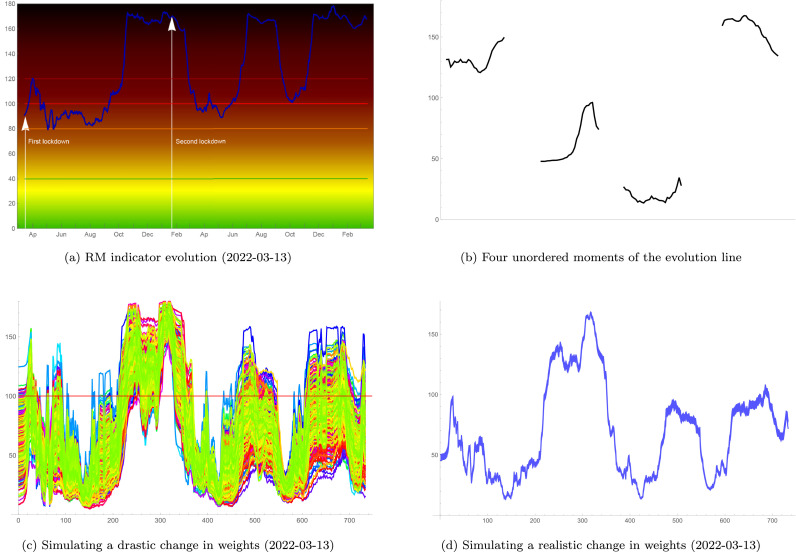
Our pandemic indicator, PACI, reached its highest value in January 2021 and the lowest in July 2020. The four first moments of this example are displayed in Fig. 7(b) (Appendix) and were used to test the experts and some anonymous people about the validity of the indicator.

3.6. Chromatic classification system (ordinal scales)

The chromatic classification system is a tool that makes use of colours for better visualising the ordinal scale built with the experts. The colours selected for our model were inspired by the ones used in the RM of the Portuguese health authorities since the Portuguese population was already familiar with them.

Five fundamental states were defined with the experts: residual, alert, alarm, critical, and break. In addition, two more states were considered at the extremes, a baseline (the very lowest one) and a saturation or emergency state (the highest). All these states are zones defined in between two consecutive levels or cut-off lines:

• –Baseline level (cut-off line value $=0$). The five performance baseline levels are presented in the following list: [0,0,0,0,0]. Each baseline level has a precise meaning for the experts. In this case, the first two mean there was no pandemic activity recorded over the last seven days, which does not mean the pandemic was extinct, but simply that no activity was registered over the past seven days. The other three values mean that there were no deaths over the last seven days and there were no hospitalised COVID-19 patients.
• –Residual level (cut-off line value $=10$). The five performance residual levels are presented in the following list: $[338,0.93,0.36,750,60]$. The experts were given this list, the values of each level on each value function, and the information on its adequacy to represent an overall value of 10. These elements were validated by the experts
• –Alert level (cut-off line value $=40$). The five performance alert levels were presented in the following list: [707,0.963,1.43,1571,126]. The discussion with the experts was performed as in the previous case.
• –Alarm level (cut-off line value $=80$). The five performance alarm levels were presented in the following list: [1000,0.989,2.89,2222,178]. The discussion with the experts was performed as in the residual and alert cases.
• –Critical level (cut-off line value $=100$). The five performance critical levels were presented in the following list: [1125,1,3.6,2500,2727,200]. As for the baseline levels, these levels are reference levels for the experts and have a particular meaning.
• –Break level (cut-off line value $=120$). The five performance break levels were presented in the following list: [1227,1.009,4.31,2727,218]. The discussion with the experts was performed as in the residual, alert, and alarm cases.
• –Emergency level (cut-off line value $=180$). The five performance saturation levels are presented in the following list: [1506,1.034,6.47,3346,268]. In this case, the experts agreed that any performance higher than the ones presented in the list will be considered as serious as the ones in the list. This corresponds to what was considered a saturation level.

The five fundamental states can be represented as shown in Fig. 4. The transition between colours or states is not necessarily abrupt.

Fig. 4.

Cumulative contribution for the PACI till 2022-03-13.

A smooth transition can be considered since the policy/decision-makers cannot make the decisions automatically, after moving to a different state. It is important to see the evolution of the pandemic over subsequent days, after definitely moving from the current to a different state and implementing new measures/recommendations. A lower and an upper threshold for each cut-off line could be considered instead of making a smooth transition.

As can also be seen in the figure, and given the way the value functions were built, whenever we move to the next state, there is less room to make the decisions, i.e., it moves faster, for example, from the alarm state to the critical state, than from the residual state to the alert state. This feature was a strong requirement of the experts. Considering their impact on the health system, the main states can be briefly defined as follows:

• –Residual: Absent or minimal pandemic activity without any impact on health structures (i.e., at the normal operating level) and without compromising the system tolerance.
• –Alert: Mild pandemic activity, still without impact on the normal activity of health structures, but reaching the usual flexibility, adaptability and safety tolerance threshold (e.g., increase in the emergency room visits and/or in the occupancy rate of hospital admissions).
• –Alarm: Moderate pandemic activity, already impacting the normal activity of health structures, with reallocation of technical and human resources and commitment to other health needs, reaching the functional reserve threshold.
• –Critical: Strong pandemic activity, already having exceeded the system’s reserve threshold, constraining the effort and the disruption in the activity of health structures allocated almost exclusively to the pandemic.
• –Break: Very strong pandemic activity and imminent collapse of health structures.

Remark 4 (Fragility Point 4

Cut-off lines subjectivity) This is in line with the previous two fragility points. The definition of the cut-off lines is subjective since they result from a co-constructive interactive process with the experts. However, defining thresholds for modelling a smooth transition between successive states can mitigate the subjectivity behind the definition of these cut-off lines.

3.7. Graphical model for visualization and communication

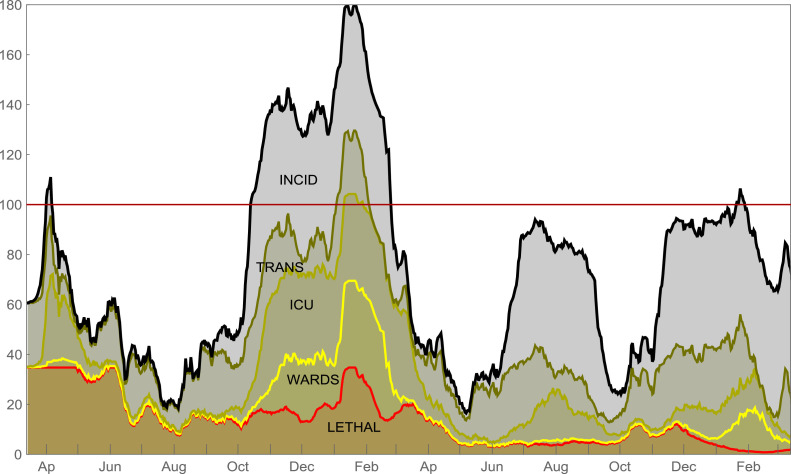
One of the main features of our model is the visualisation functionalities to enable an easy communication with the general public. Apart from other minor graphical functionalities, four types of graphical tools were developed:

• 1.A graphic which displays the evolution of the indicator behaviour with coloured states and cut-off lines to separate each state (see Fig. 3).
• 2.An animation graphical tool with the cumulative contribution of each criterion to the pandemic (see Fig. 4).
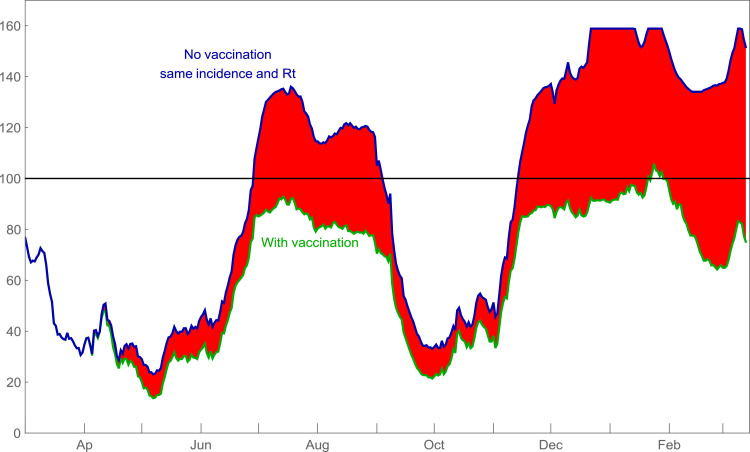
• 3.A graphical representation of the (positive) impact of the vaccination plan to mitigate the progression of the pandemic in the country (see Fig. 5).
• 4.A state chromatic line, as in Fig. 2.

Fig. 3.

Evolution of the PACI till 2022-03-13.

Fig. 5.

The vaccination impact till 2022-03-13.

Fig. 2.

Chromatic classification system.

More details on these graphical tools will be provided in the next section.

4. Results, sensitivity analyses, and simulations

This section is devoted to the implementation issues and verifications tests, results presentation, their validation, sensitivity analyses, and some final comments.

4.1. Implementation issues and verification tests

Our application was coded in the software Wolfram Mathematica, version 12.0.10 All the functionalities of the Mathematica code were checked in several small examples with particularly extreme and pathological cases. This step includes verifications on the debugging, input of criteria performance levels parameters, calculation of the criteria performance levels, calculation of the value functions and weights parameters, calculation of the comprehensive values for each time unit, all the graphical models outputs, sensitivity analyses, as well as the checking whether all the logical structure of the models was correctly represented on the computer. The entire application has been designed to translate all the three models (criteria model, MAVT aggregation model, and graphical visualization and communication model) successfully as a whole, as well as some additional functionalities for validation, simulation, and other sensitivity analyses purposes.

A Microsoft Excel version of the model was also implemented with fewer functionalities. The computations of the Excel PACI model are available for public consultation on an Instituto Superior Técnico website (indicadorcovidl9.técnico.ulisboa.pt/) and on the Portuguese Medical Association website (ordemdosmedicos.pt/iap/). This software automatically computes the daily changes in all the five criteria performance levels and the actual transmission rate, which is computed using the Robert Koch Institute formula (see Koch, 2020).

4.2. Results

The results provided information on three main aspects: the pandemic evolution, the cumulative contribution of each criterion to the evolution, and the impact of the vaccination plan. Please note that PACI can be used for forecasting if there are good prediction techniques for the raw data used in the five criteria formulas.

4.2.1. Pandemic evolution

Before running the MAVT-based model with our set of criteria, we tested it with the two RM criteria, by setting the baseline, critical, and emergency levels as we did for our PACI tool, and considering linear value functions (since moving from an $R\left(t\right)=0.1$ to an $R\left(t\right)=0.2$ has the same impact as moving from an $R\left(t\right)=0.9$ to an $R\left(t\right)=1.0$, and this is true for any location along the $R\left(t\right)$ scale; the same reasoning applies to the incidence criterion). We also considered equal weights for each criterion. For other cut-off lines we set them as in our model. The evolution line can be observed in Fig. 7(a) (Appendix). It is clear that this MAVT-based model does not adequately represent how the Portuguese people felt about the impact of the pandemic. The impact is always rather high, above the cut-off line in the alarm state. For the experts and the general public, the low impact at some points of the pandemic, as for example, in August 2020, cannot be seen clearly on this evolution line.

Figure 3 depicts the global evolution of the PACI values in Portugal, along with the cut-off lines that separate the chromatic states.

The indicator gives an intuitive human perception of the impact of the pandemic in Portugal, particularly in the four main waves. The lockdown occurred exactly during the first wave, when the PACI value was close to 50 points. The inertia of the system brought the PACI to a maximum on 6 April 2020, with 95 points. The summer of 2020 was relatively mild with minimal values of the PACI value near to 14 between 26 July and 6 August 2020. We reached intolerable values between November 2020 and January 2021. In terms of pure pandemic impact, we can see that the autumn of 2020 and the winter of 2021 corresponded to the same pandemic wave. The day of maximum impact of the pandemic in Portugal, with 167.5 points, was precisely on 21 January 2021, which preceded the reinforcement of the lockdown measures/recommendations on 22 January 2021. The sharp drop from 25 January 2021 was caused by the lockdown of 15 January 2021. This decrease was reinforced substantially from 6 February 2021, when the population started feeling the effects of closing the schools on the incidence and transmission rate values. After April 2021 and due to the vaccination effect, there was a clear detachment in the curves considering or not the new setting into account. The combined results of vaccination and non-pharmacological measures was maximal on 7 May, 2021, with 13.4 points, corresponding to the absolute minimum of the indicator since the appearance of COVID-19 in Portugal. After that date, we noticed an increase in the indicator, related to the rise of the Delta variant in the country, reaching a local maximum of 92.3 on July 9, 2021. In the absence of lockdown, after that date, there was a slow trend in the decrease of the impact, which can be related to the positive evolution of the vaccination in Portugal. With the surge in the Omicron variant, there was a strong increase in the PACI, which was related mainly to the incidence and transmissibility in late November 2021. There was a fourth pandemic wave which differed from the previous ones in terms of severity. The maximum level of the last wave was attained between 21 and 28 January 2022, when values exceeded 100 points and reached a maximum of 106.4 on 24 January.

4.2.2. Cumulative contribution of each criterion

Figure 4 shows the individual contributions of each criterion to the PACI value in Portugal.

The long term and gradual decrease in the contribution of lethality (case fatality rate, or lethal line) to the indicator is noteworthy. The contribution of this criterion increased dramatically during the January 2021 crisis. The role of the occupancy of the general number of beds for patients admitted to wards (wards line) was particularly significant during the second pandemic wave in Portugal (between October 2020 and February 2021). This partial contribution reacts strongly when the spread of the disease is out of control. It is interesting to note that the contributions of patients admitted to intensive care beds (icu line) to the PACI is significant in each pandemic wave. ICU bed occupancy grew after the increase in incidence (incid line) with a delay of $10-12$ days.

Nevertheless, the relationship between the two criteria (incidence and ICU bed occupancy) is very clear and appeared in every pandemic wave, including the last one related to the Omicron variant. Naturally, with the increment of vaccination, the relation between ICU occupancy and incidence dropped with time. In contrast to the ICU bed criterion contribution, the growth rate contribution (trans line) appeared at an early stage of each wave and was the first alarm sign of a future increase in incidence, which was natural and expected. For instance, in the first wave of 2020, the PACI was mainly due to the growth rate and the case fatality rate for the first days of the COVID-19 infection in Portugal. The same effect is clear in the second wave, in October, in the last wave before June 2021 and, finally, in the last wave.

Finally, the incidence contribution to the PACI was severe in the months between October 2020 and February 2021 and significant with the last wave, due to the Omicron variant. The softening of governmental control measures/recommendations in Portugal at Christmas 2020 occurred when the contribution of the incidence was high. The softening of measures in the last wave, in contrast, was appropriate, due to the protective effect of previous natural immunity and vaccination amongst the Portuguese population.

The introduction and the effects of the Delta variant are visible in the contribution of the incidence to the PACI in June 2021 and the effects of the Omicron variant are evident in the last pandemic wave in November 2021. Fortunately, this increase in the incidence contribution was balanced by the drop in the case fatality rate, overall number of patients admitted to wards occupancy, and number of beds for patients admitted to ICU occupancy relative to the values before the appearance of the Delta and Omicron variants and generalisation of the vaccination in Portugal.

4.2.3. The impact of vaccination

Figure 5 shows a comparison of the PACI values for actual data/parameters (lower curve) and an estimation of the indicator computed without the introduction of vaccination (upper curve). The upper curve was computed with the same observed incidence and growth rate of the actual PACI (lower curve), i.e., with the two criteria of Pillar I, but with no reduction in the severity of the disease (see the methodology described below), i.e., without the three criteria of Pillar II. The upper curve is, naturally, a lower bound estimate of the indicator without vaccination, since the immunisation process related to vaccination also affects the incidence and growth rate.

The effect of vaccination began to be measurable after 390 days, i.e., after 4 April. The method used to obtain the estimate of the indicator without vaccination consists of taking into account the original definition of the first two criteria and “frozen” the performance levels of the remaining three criteria as follows, for a given day, $d$ (after 390 days): $g_3\left(d\right)=\alpha \left({\sum }_{j=d-13}^{d}N\left(j\right)\right)/14$, $g_4\left(d\right)=\beta \left({\sum }_{j=d-6}^{d}N\left(j\right)\right)/7$, and $g_{(}d)=\lambda ({\sum }_{j=d-6}^{d}N\left(j\right))/7$, where $\alpha ={\sum }_{t=15}^{390}O\left(t\right)/{\sum }_{t=1}^{376}N\left(t\right)$, $\beta ={\sum }_{t=8}^{390}H\left(t\right)/{\sum }_{t=1}^{376}N\left(t\right)$, and $\lambda ={\sum }_{t=8}^{390}U\left(t\right)/{\sum }_{t=1}^{376}N\left(t\right)$, respectively. On day 390, there was no difference between the values of the actual PACI indicator and the values of the lower estimate PACI without vaccination.

After that date the values began to differ. It was observed a dramatic increase in the difference between the curves with time after 4 April. Naturally, since vaccination also reduced incidence and growth, after some time, more precisely on 15 July 2021, the indicator PACI began to decrease, followed immediately by the lower bound estimate of PACI without vaccination. The decoupling of severity and incidence in the last pandemic wave is noteworthy. Without vaccination, the last wave, due to the Omicron variant, could have had dramatic effects as it can be seen in the lower bound estimate of PACI without vaccination in Fig. 5.

4.3. Sensitivity analyses

Sensitivity analyses conducted in this study are in line with the definition proposed in Roy (2010), where a change in the results was observed after a (simultaneous) change in all the parameters that are affected by some fragility aspects (see Remarks 1–3). There are two major types of sensitivity analyses, one based on simulation (also called pseudo-sensitivity analysis) and another based on an exact characterisation of the effects of the changes in parameters. We detail these two types of sensitivity analyses in the following paragraphs.

4.3.1. Simulation on the weights

The fragility point of Remark 3, which is related to subjectivity when assessing the weights of criteria, is one of the most critical fragility points in practice. A simulation analysis (also called pseudo-sensitivity) is dominated by an exact sensitivity analysis, as explained in the next subsection, but it has the advantage of being able to produce a large set of lines. Their shape conveys an idea of the evolution of our indicator (just for an illustrative purpose, see the last figure in Appendix, i.e., Fig. 9, with a $\pm 5\%$ change in the weights used in the application of PACI to the Portuguese pandemic).

Fig. 9.

Simulation versus Sensitivity (2022-03-13).

In order to study the sensitivity of the results, we performed a strong change in the weights, thus enabling a variation in the range of each one, from 0 to 1 (the sum of all weights being equal to 1). A Monte Carlo simulation made this study possible. Figure 7(c) (Appendix) displays 400 lines, among the 10,000 simulations performed (the representation of more lines is time consuming and led to a software crash due to limited memory capacity). In this figure, the shape of all the lines is approximately the same. There is a drastic variation in the weights since the simulations go from an extremely unbalanced situation, where only one criterion counts for the impact on the pandemic (the one with weight equal to one), to a complete balanced situation, where all the criteria contribute equally to the impact (equal weights for all criteria). A more realistic simulation, with a perturbation of $5\%$ below the weights values elicited with PaCo-DMC (for each day) and the same $5\%$ above the elicited weights, leads to the curves (also 400) represented in Fig. 7(d). All the lines almost coincide with the shape of the curve of our PACI model. The results are quite robust for realistic variations in the weights, showing the adequate behaviour of the PACI tool.

4.3.2. Exact sensitivity analysis

The exact sensitivity analysis was performed by considering all the critical fragility points of Remarks 1–3. Changes were carried out in the data provided by the incidence, transmission, and lethality criteria (the other two were not affected by strong imprecision, i.e., the number of patients admitted to wards and the number of patients admitted to ICU are relatively precise), in the five value functions, given the subjectivity when building them, and in the weights of criteria, for the same reason as the previous one.

A first strong (direct) perturbation on all the data/parameters related to the first three criteria and the five value functions revealed: $10\%$ below and above their daily performance levels/values. As for all the criteria weights, a variation of $10\%$ enabled us to build a polyhedron in a five-dimensional space. In this polyhedron, for each day, there was a maximum and a minimum value for the indicator by using linear programming techniques. For the maximum value, we considered a $+10\%$ change in the performance levels of the first three criteria and the values of the five value functions and computed the maximum of the indicator formula over the polyhedron of the weights; this is done for each day (see the upper envelope curve in Fig. 8(a), Appendix). For computing the minimum for each day, by considering a $-10\%$ change in the performance levels of the first three criteria and values of the five value functions (see the lower envelope curve in Fig. 8(b), Appendix). The difference of the upper and lower curves is in an average of 47.12 points with a standard deviation of 11.0848 points.

Fig. 8.

sensitivity analysis.

Then, a more realistic sensitivity analysis with a $\pm 5\%$ change in the performance levels of the first three criteria and the values of the five value functions, and a similar construction of the polyhedron for the weights was performed. The results are presented in Fig. 8(c) and (d) (Appendix). The average of the difference is now 28.2366 impact points and the standard deviation is 6.9615 points.

The outline of the exact sensitivity procedure can be presented as follows:

• 1.Take a certain time unit, $t$ (e.g., a given day during the pandemic).
• 2.
  Consider the first three criteria: $g_1$, $g_2$, and $g_3$. Proceed as follows (Fragility Point 1):

  • (a)
    Consider their performance levels at time $t$: $x_{1t}$, $x_{2t}$, $x_{3t}$.
  • (b)
    Make a decrease of these levels. Let $x_{1t}^{-}$, $x_{2t}^{-}$, and $x_{3t}^{-}$, denote the new performance levels.
• 3.
  Consider all value functions: $v_1$, $v_2$, $v_3$, $v_4$, and $v_5$. Proceed as follows (Fragility Point 2):

  • (a)
    Consider their values at time $t$, tanking into account the modified performance levels of the first three criteria (as we did in the previous step) and the performance levels of the last two criteria: $v_1\left(x_{1t}^{-}\right)$, $v_2\left(x_{2t}^{-}\right)$, $v_3\left(x_{3t}^{-}\right)$, $v_4\left(x_{4t}\right)$, and $v_5\left(x_{5t}\right)$.
  • (b)
    Decrease these values. Let $v_{1t}^{-}$, $v_{2t}^{-}$, $v_{3t}^{-}$, $v_{4t}^{-}$, and $v_t^{-}$, denote the new values.
  • (c)
    (for the sake of simplicity of notation) Consider the vector, $v^{\left(t\right)-}=(v_{1t}^{-},v_{2t}^{-},v_{3t}^{-},v_{4t}^{-},v_{5t}^{-})$.
• 4.
  Consider all weights: $w_1$, $w_2$, $w_1$, $w_2$, and $w_3$. Proceed as follows (Fragility Point 3):

  • (a)
    Decrease the weights. Let $w_1^{-}$, $w_2^{-}$, $w_3^{-}$, $w_4^{-}$, and $w_5^{-}$, denote the lower bound values for the weights.
  • (b)
    Increase of the weights. Let $w_1^{+}$, $w_2^{+}$, $w_3^{+}$, $w_4^{+}$, and $w_5^{+}$, denote the upper bound values for the weights.
  • (c)
    Remark: These changes in the weights are not indexed to the time period; thus they are valid for any $t$.
  • (d)
    Construct the polyhedron of the weights, denoted by $W$, as the result of the intersection of the following constraints:

    • –
      Bounding constraints: $w_l^{-}⩽w_j⩽w_j^{+}$, for $j=1,\dots ,5$.
    • –
      Normalisation constraint: $w_1+w_2+w_3+w_4+w_5=1$.
    • –
      Consistence constraints: $0⩽w_j⩽1$, for $j=1,\dots ,5$ (these constraints avoid having negative weights with values strictly greater than one).
  • (e)
    (for the sake of simplicity of notation) Consider the vector, $w=(w_1,w_2,w_3,w_4,w_5)$. Any feasible $w$ is an element of $W$, i.e., $w\in W$.
• 5.
  Solve the following linear programming problem:

  $$v^{-}\left(t\right)=\min \{w^{\top }{v}^{\left(t\right)-}:w\in W\},$$

  where $v^{-}\left(t\right)$ is the lowest (which, in our case, corresponds to the best) value of the PACI model.
• 6.Proceed in a similar way to obtain $v^{+}\left(t\right)$, i.e., the worst value of the PACI model for time unit $t$.

4.4. Validation, adjustments, and comments

In our case, the validation consisted of presenting the actors (mainly the experts), but also some anonymous people, with the shape of the pandemic indicator and obtaining some comments to validate or do adjustments to our models. All the tests were conducted before and after performing the sensitivity analysis. However, they have more credibility after such an analysis is performed. More precisely, the following tests were performed:

• 1.In a first step, we built a figure displaying different moments of the pandemic in the country, see Fig. 7(b) (Appendix). The moments were not chronologically ordered. We asked the experts to look at the figure and tell us if they were able to identify such moments and relate them to a state of the pandemic. We selected the following moments: the beginning of the pandemic, July 2020, January 2021, and Christmas 2020. All the experts were able to easily identify all the moments. Only a slight hesitation was recorded for one expert regarding the moment related to the start of the pandemic. The team members also asked the same question to some anonymous people. We performed tests with 30 individual, mostly university administrative staff (10 individuals), students (10 individuals), and random people from the streets of Lisbon (10 individuals). They were told that the impact was represented on a scale from 0 to 180 points and an explanation on the the minimum and the maximum PACI values was given. The number of people asked to perform the validation testes was rather low. A more systematic and complete study would be important to obtain more input for validating our PACI model. When showing the four pieces of our graphic of Fig. 7(b), the lowest and the highest impact of the pandemic were easily identified, and Christmas 2020 was almost always recognised. Only the start of the pandemic led to some hesitations.
• 2.In a second step, the experts were shown the whole evolution curve since the beginning of the pandemic. They commented and justified all the moments of the pandemic and the different critical situations, i.e., the waves that occurred during the disease evolution in Portugal, namely the initial growth, the autumn and winter crisis and, finally, the surge of the Delta variant. They were also able to identify the calm situation of the spring/summer of 2020 and the relaxation of April 2021. The same exercise was also performed with the anonymous people. Most of the tests were positive, with 28 people being able to comment the initial stage, the autumn/winter crisis, and the Delta variant wave.
• 3.In a third step, we asked the experts to point out the reasons that lead to some moments of the curve and to explain the reasons behind such a behaviour in the PACI values. We also chose some particular points on the curve and asked the experts to comment and justify them. This is a different approach from the previous one, since the moments were not chosen by the experts, but by the analysts.
• 4.Finally, the experts were asked to provide some raw data characteristic of each state, run the model, and show the results. For example, the following list of performance levels $[1250,1.02,2.8,2235,$ 195] is a profile that should be considered in the critical state. After running the model, we got the value 104.2, which is within the critical state of the chromatic model. Almost all the results led to the state provided by the experts. This test led to a very slight adjustment of the weights (see point 6 of Section 3.3.2).

5. Lessons learned

This section is devoted to understanding the lessons learned from the use of the PACI since the beginning of its application for modelling the impact of COVID-19 in Portugal. We present sequentially, in the next subsections, the success features of the tool as well as its shortcomings and, finally, the aspects that can be considered for improving the PACI in the future.

5.1. Learning from pandemic assessment composite indicator successes

The successes of the PACI indicator at several levels can be summarised as follows:

• 1.Criteria model. The criteria model comprises the most relevant criteria built around the fundamental concepts followed two principles: familiarity and intelligibility, as explained in Section 3.2. Integrating more criteria would provide a more complex composite indicator, which would not add much more value as since the beginning of the pandemic none of the five criteria have been questioned revealing their acceptance and success.
• 2.Aggregation model. The additive aggregation model was also considered a success for the same reason. It was well accepted and not questioned even by the scientific community. There is, of course, room for improvement, such as considering different value functions and weights, but this was largely tested with sensitivity analysis and simulations.
• 3.Socio-technical process. The co-constructive interactive process between the group of experts and the group of analysts was also a successfully socio-technical process but, given the time constraints, this would benefit from more interaction to gain more confidence in some preference judgements. Subsection 5.4 will provide some aspects for future improvement.
• 4.Communication model. This communication model was probably one of the highest successes of our tool. Composed of three main graphical tools (the evolution graphic with the cut-off lines, the cumulative evolution graphic, and the graphic on the impact of the vaccination plan) it is very informative for the general population. We regret, however, not being able to include the forecasting capabilities of our tool for a one or two weeks’ process, which would be extremely important for the short term planning of measures and recommendations.
• 5.Sensitivity analysis and simulation tools. These two tools were of utmost important for guaranteeing confidence in the indicator. By performing drastic and realistic changes in the model parameters, we observed the effects of the indicator and have a good idea of how strong it was.
• 6.Validation tests. The validation process with experts and some individuals (a small number) was important and also a success, but it was rather brief, given the time constraints. This is an aspect that we would like to improve in the future and will be outlined in subsection 5.4.

5.2. Learning from pandemic assessment composite indicator shortcomings

The shortcomings of the PACI indicator are essentially missed opportunities given the time constraints and can be considered at several levels, as follows:

• 1.Criteria model. A possible drawback of our indicator is that despite it is an early warning indicator of future changes, due to the incidence growth rate, it does not incorporate short term forecasting of the future evolution of the pandemic. This could be included in the indicator but has some drawbacks: computation is heavy, there are computational costs, it becomes more difficult to communicate to the public, and there is a margin of error in the predictions.
• 2.Aggregation model. As it is approximately a quadratic non-linear model, the indicator reacts very quickly to an increase in the two pillars. This appears to be a drawback, i.e., when the pandemic approaches a hazardous status, the indicator increases rapidly giving little time for the authorities to react. But, in fact, this is a consequence of reality, rather than a failure of the indicator. When there is a near exponential explosion of cases, severity and transmissibility grow abruptly and the indicator reflects this behaviour. Whenever there is an increase in the indicator to moderate values, i.e., close to 40, there is a strong need for counter measures.
• 3.Socio-technical process. Despite being well accepted by the Portuguese society, the local Health Authorities did not officially change the evaluation of the pandemic in Portugal using the “RM” tool, as we explain in the conclusion of this article. The co-constructive interactive process between the group of experts and the group of analysts was also rather a successfully socio-technical process, but due to time limitations, this would have benefited from greater interaction to gain more confidence in some preference judgements. Subsection 5.4 will provide some points for future improvement.
• 4.Communication model. The communication model, despite its success, would benefit from a more adequate web-based platform, with additional graphical tools and the possibility of graphical forecasting.
• 5.Sensitivity analysis and simulation tools. These tools were the adequate, given the type of indicator designed. We cannot see any failure concerning this point.
• 6.Validation tests. The validation tests are needed for a wider application in the general public, given that the number of tests performed was rather low, as explained in the validation subsection of this paper. Also, here a web-based platform would be of utmost importance to conduct a more in-depth study related to the validation tests.

5.3. Future improvements in the pandemic assessment composite indicator

Future improvements to the PACI can be summarised as follows:

• 1.Criteria model. The PACI model makes use of incidence criteria (new cases and transmission) and severity (number of total admissions, ICU admissions and lethality) in order to streamline a limited number of easily accessible parameters, that enabled the monitoring of the social and health impact of the disease and the pandemic. The use of other indicators, such as the vaccination coverage rate, the number of tests and the percentage of positive testing, has an impact on both incidence and severity. They can be used in the future as additional criteria, but we considered that their use, in addition or replacement, did not add value to the indicator. A possible improvement would involve adding further criteria and checking their effect regarding the current version of the PACI.
• 2.Aggregation model. The value function and the weights of each indicator was established in collaboration by the two teams and according to analyses of the impact of the pandemic in the period before the development of the indicator (period of more than 12 months). Although it was not a failure, we could add more value functions and reconstruct the set of the weights (Table 1) by considering the possibility of adding more criteria, as mentioned in the previous point.
• 3.Socio-technical process. We would like to perform more interaction with experts and the population, and even test the deck of card method with the possibility of inconsistent judgements to model the impact judgements of the experts and participants in a more accurate manner.
• 4.Communication model. The improvements to the communication model are the ones mentioned in the subsection of the model failures. An interactive web-based platform would substantially benefit the general population and provide clearer information ensuring its wide availability.
• 5.Sensitivity analysis and simulation tools. This indicator was also tested in the flu epidemics prior to 2020, which confirmed the sensitivity and quality of the indicator. Due to the lack of available data, it was not possible to test the indicator in a pandemic prior to the current one, for example, in the 2009 influenza A (H1N1) pandemic. After its release in July 2021, the continuous use of the indicator led to the assessment of its reliability. The need to adjust the weights and/or the inclusion or substitution of new criteria has not been detected so far. However, it was considered that the Portuguese reality may not be replicable in other countries, so it is essential to validate the PACI in other countries and, eventually, establish different weights for different realities. This is an unquestionable point of the objectives of the dissemination of the PACI internationally.
• 6.Validation tests. The tests should also follow the ideas pointed out in the failure subsection to mitigate the less effectiveness of the current PACI tool with respect to the validation tests.

6. Conclusions

In this paper, we proposed an innovative application of a MAVT additive model for building a PACI and a chromatic ordinal classification system to assist in the management of the COVID-19 pandemic in Portugal. This indicator was built by following a socio-technical co-constructive interactive process between the CCIST and the GCMO teams, and to the best of our knowledge, it is the first MAVT model proposed to analyse the evolution of the pandemic and mitigate the impacts of COVID-19 in the world. It was designed with the particular purpose of answering several questions posed by the Portuguese population: How is the pandemic evolving in the country? In which pandemic state are we currently? What is the impact of the vaccination plan established by the government? All these questions have been answered, and our indicator had strong acceptance in Portugal. It still continues to be followed and frequently mentioned in the media, even though the Portuguese health authorities did not adopt it officially as another indicator for effective policy/decision-making.

In Portugal, pandemic-related decisions are centralised at the Ministry of Health along with the other members of the Government and with the full involvement of the Prime Minister. The Ministry of Health is responsible for two official bodies of a technical nature, the Directorate-General for Health, and the National Institute of Public Health Dr Ricardo Jorge. They monitor the pandemic activity and design the rules and guidelines to fight the pandemic and minimise its impact on health systems and on the country’s social and economic life. At the beginning of the pandemic, the National Institute of Public Health Dr Ricardo Jorge developed an RM based on the number of cases per 100,000 inhabitants at 14 days (national and regional incidence) and the transmission, $R\left(t\right)$. Before the massive vaccination campaign of the Portuguese population, this matrix was a useful tool to support measures at both a national and regional level. With vaccination, the relationship between incidence, transmission and severity was lost. For this reason, the Portuguese Medical Association and the Instituto Superior Técnico developed the PACI to better monitor activity and severity and also support decisions with coherence and greater involvement of the general public. On several occasions, Portuguese Medical Association and Instituto Superior Técnico were in touch with the Ministry of Health to provide the use of the PACI. Despite much praise for the new indicator, official authorities chose to avoid public changes to the pandemic assessment model and keep the RM already in place. The PACI was reserved for more restricted use by official bodies in monitoring the pandemic activity. This decision was also influenced by the fact that the National Institute of Public Health Dr Ricardo Jorge is an official body under the Ministry of Health and that the replacement of the RM in use could harm the collaboration between the different official bodies.

Despite the fragility points related to the data and the construction of the aggregation model itself, it has several advantages that are widely acknowledged by academics, opinion-makers, media, and Portuguese general public. Even the technicalities of the method, including computations, can be reproducible for any reader with basic mathematical knowledge. The parameters of the aggregation model can be adjusted, if justified, during the pandemic evolution. This comprises the shape of the value functions, the weights, the cut-off lines, and the reference levels, in particular the critical level (if the number of beds in intensive care increases it is normal for the critical level related to the fifth criterion to change accordingly). Also, the formulas of the criteria model can be adjusted or replaced by more suitable ones (this also implies changes in the aggregation model).

The flexibility of the PACI mode leads to several avenues for possible future research:

• –This is an open model, in the sense that it can easily accommodate the inclusion of more criteria and even more pillars to account for other points of view, as for example the economic impact of the pandemic. Other aspects, for example, the interaction effect between/among criteria are also possible, but they are more sophisticated and require adaptations in the judgement assessment techniques, such as PaCo-DCM in the case of some additional multiplicative terms (see Keeney & Raiffa, 1993). In the case of the Choquet aggregation model, PaCo-DCM could be more or less easy to adapt (see Bottero et al., 2018), but as all the value functions are between 0 and 1, it would require a re-scaling, and the identification and assessment of the capacities would not be an easy task.
• –This model can be applied to all territorial units (country, regions, counties, sets of counties, etc.) with available data and possibly with some readjustments of the critical levels of some criteria.
• –Scalability to other countries is also a possibility, but all the criteria would have to be reconsidered, as well as all the levels, in particular, the baseline critical levels, and the cut-off lines. Comparison with other countries would be of great importance in analysing the impact of different measures taken by other countries.
• –The model can be applied to other diseases, and other health problems, and even in different sectors where the building of composite indicators is important.
• –The model also has forecasting capabilities; it only needs to have good estimates of the raw data $N(·)$, $O(·)$, $H(·)$, and $U(·)$.
• –One of the most interesting avenues for future research is the use of constructive preference-learning techniques as some adaptations of the GRIP method (see Figueira et al., 2009)) for building the composite indicator. This is a kind of machine learning based tool that infers representative value functions from examples provided by the experts. After this first study, the experts now have a much better understanding of the entire issue and can easily provide a “good” set of examples for helping in the construction of the model parameters, value functions, weights, and even the cut-off lines.

Proposing the PACI was possible thanks to the collaboration between the CCIST and the GCOM teams, which continue to carry out the research proposed in the previously listed avenues for future work. In conclusion, it is important to mention that this new indicator is not necessarily a competitor for the RM as both can be used simultaneously to better inform the Portuguese health authorities when making decisions.

Appendix A

In the first part of this appendix, we provide some elements regarding the value functions for criteria, $g_2$ to $g_4$.

• 1.
  Criterion $g_2$ (Transmission - TRA̧NS). The performance levels, after discretising the scale of g2, and the blank cards inserted in between consecutive levels, are as follows:

  $$\left\{\right[0,0.92\left]\right\}\left[0\right]\{.0.96\}\left[2\right]\left\{0.98\right\}\left[4\right]\left\{1.00\right\}\left[6\right]\left\{1.02\right\}\left[8\right]\left\{1.040\right\}$$
  As in criterion $g_1$, we also used further levels to understand the evolution of the number of blank cards inserted in between consecutive levels. This was very similar to the value function for criterion $g_1$. The piecewise linear value function obtained is presented as follows:

  $$v_2\left(x_{2t}\right)=\{\begin{array}{ccc}4.34783x_2\hfill & \text{if}& x_{2t}\in [0.000,0.920[\hfill \\ 600x_{2t}-548\hfill & \text{if}& x_{2t}\in [0.920,0.940[\hfill \\ 1000x_{2t}-924\hfill & \text{if}& x_{2t}\in [0.940,0.960[\hfill \\ 1400x_{2t}-1308\hfill & \text{if}& x_{2t}\in [0.940,0.980[\hfill \\ 1800x_{2t}-1700\hfill & \text{if}& x_{2t}\in [0.980,1.000[\hfill \\ 2200x_{2t}-2100\hfill & \text{if}& x_{2t}\in [1.000,1.020[\hfill \\ 2600x_{2t}-2508\hfill & \text{if}& x_{2t}\in [1.020,1.034[\hfill \\ 180\hfill & \text{if}& x_{2t}\in [1.034,+\infty [\hfill \end{array}$$ (9)

  As in $g_1$, it also can be approximated by a quadratic function.
• 2.
  Criterion $g_3$ (Lethality - LETHA). This is a different type of value function from the ones constructed for criteria $g_1$ and $g_2$. When discretizing the scale range of criterion $g_3$ and asking the experts to add blank cards in between consecutive levels, they always considered the same number of blank cards. It means that this function is a linear function and the reason is obvious, as explained by the experts: one death is always very serious and does not depend on the place we are on the scale of this criterion, i.e., moving from one to two deaths has the same impact as moving from 49 to 50. The function can thus be presented as follows:

  $$v_3\left(x_{3t}\right)=\{\begin{array}{ccc}{\displaystyle \frac{200x_{3t}}{7.2}}\hfill & \text{if}& x_{3t}\in [0,6.48[\hfill \\ & & \\ 180\hfill & \text{if}& x_{3t}\in [6.48,+\infty [\hfill \end{array}$$ (10)

  The saturation level at 180 is used for making an upper level and limit the values of the indicator, and not because the number of deaths after a certain level has the same impact as the number of deaths leading to the saturation/emergency level. The increase in the number of deaths always has a strong impact in terms of the severity of the pandemic.
• 3.
  Criterion $g_4$ (Number of patients admitted to wards - WARDS). The scale of criterion $g_4$ is a discrete scale, which leads also to a discrete value function. The levels selected by the experts and blank cards inserted in between consecutive levels are presented below:

  $$\begin{array}{ccc}& & \left\{0\right\}\left[0\right]\left\{500\right\}\left[2\right]\left\{1000\right\}\left[4\right]\left\{1500\right\}\left[6\right]\left\{2000\right\}\left[8\right]\hfill \\ & & \left\{2500\right\}\left[10\right]\left\{3000\right\}\left[12\right]\left\{3500\right\}\hfill \end{array}$$

  The value function can be states as follows:

  $$v_4\left(x_{4t}\right)=\{\begin{array}{ccc}0.008x_{4t}\hfill & \text{if}& x_{4t}\in \{0,1,\dots ,498,499\}\hfill \\ 0.024x_{4t}-8\hfill & \text{if}& x_{4t}\in \{500,501,\dots ,999,999\}\hfill \\ 0.04x_{4t}-24\hfill & \text{if}& x_{4t}\in \{1000,1001,\dots ,1498,1499\}\hfill \\ 0.056x_{4t}-48\hfill & \text{if}& x_{4t}\in \{1500,1501,\dots ,1999,1999\}\hfill \\ 0.072x_{4t}-80\hfill & \text{if}& x_{4t}\in \{2000,2001,\dots ,2498,2499\}\hfill \\ 0.088x_{4t}-120\hfill & \text{if}& x_{4t}\in \{2500,2501,\dots ,2998,2999\}\hfill \\ 0.104x_{4t}-168\hfill & \text{if}& x_{4t}\in \{3000,3001,\dots ,3344,3345\}\hfill \\ 180\hfill & \text{if}& x_{4t}\in \{3346,3347,\dots \}\hfill \end{array}$$ (11)

  It is a discrete function, but it has the same kind of “shape” and behaviour as the functions for criteria $g_1$ and $g_2$.
• 4.
  Criterion $g_5$ (Number of patients admitted to ICU - ICU). As in the previous case, this scale is also a discrete one, which also leads to a discrete value function. The levels selected by the experts and the number of blank cards inserted in between consecutive levels are presented below:

  $$\left\{0\right\}\left[0\right]\left\{40\right\}\left[2\right]\left\{80\right\}\left[4\right]\left\{120\right\}\left[6\right]\left\{160\right\}\left[8\right]\left\{200\right\}\left[10\right]\left\{240\right\}\left[12\right]\left\{280\right\}$$

  From the previous information and useing PaCo-DCM we can derive the following function.

  $$v_5\left(x_{5t}\right)=\{\begin{array}{ccc}0.1x_{5t}\hfill & \text{if}& x_{5t}\in \{0,1,\dots ,39,40\}\hfill \\ 0.3x_{5t}-8\hfill & \text{if}& x_{5t}\in \{40,41,\dots ,78,79\}\hfill \\ 0.5x_{5t}-24\hfill & \text{if}& x_{5t}\in \{80,81,\dots ,118,119\}\hfill \\ 0.7x_{5t}-48\hfill & \text{if}& x_{5t}\in \{120,121,\dots ,158,159\}\hfill \\ 0.9x_{5t}-80\hfill & \text{if}& x_{5t}\in \{160,161,\dots ,198,199\}\hfill \\ 1.1x_{5t}-120\hfill & \text{if}& x_{5t}\in \{200,201,\dots ,238,239\}\hfill \\ 1.3x_{5t}-168\hfill & \text{if}& x_{5t}\in \{240,241,\dots ,266,267\}\hfill \\ 180\hfill & \text{if}& x_{5t}\in \{268,269,\dots \}\hfill \end{array}$$ (12)

  Its “shape” and behaviour are similar to the previous value function.