A depth-based global envelope test for comparing two groups of functions with applications to biomedical data

Abstract

Functional data are commonly observed in many emerging biomedical fields and their analysis is an exciting developing area in statistics. Numerous statistical methods, such as principal components, analysis of variance, and linear regression, have been extended to functional data. The statistical analysis of functions can be significantly improved using nonparametric and robust estimators. New ideas of depth for functional data have been proposed in recent years and can be extended to image data. They provide a way of ordering curves or images from center-outward, and of defining robust order statistics in a functional context. In this paper we develop depth-based global envelope tests for comparing two groups of functions or images. In addition to providing global P-values, the proposed envelope test can be displayed graphically and indicates the specific portion(s) of the functional data (eg, in pixels or in time) that may have led to rejection of the null hypothesis. We show in a simulation study the performance of the envelope test in terms of empirical power and size in different scenarios. The proposed depth-based global approach has good power even for small differences and is robust to outliers. The methodology introduced is applied to test whether children with normal and low birth weight have similar growth pattern. We also analyzed a brain image dataset consisting of positron emission tomography scans of severe depressed patients and healthy controls. The global envelope test was used to find and visualize differences between the two groups.

1 ∣. INTRODUCTION AND MOTIVATION

Functional data analysis is a modern and exciting area of research in statistics with direct impact in many fields. In neuroscience, for example, brain imaging tools provide us with complex collections of signals from individuals in different neurophysiological states in both healthy and diseased populations. In functional datasets each observation of the sample is an object in a high-dimensional space, such as functions or images. Statistical methods, like principal components, regression or analysis of variance have already been extended to functional and imaging data (see monographs by Ramsay and Silverman¹ and Ferraty and Vieu²). Many parametric statistical methods for analyzing functional data rely on strong assumptions and can be very sensitive to outliers. In the last two decades there has been an intensive development of different notions of data depth for functions or high-dimensional data which have been proven to be powerful nonparametric tools for analyzing functional data (eg, References 3-11). In general, a data depth is a function that measures the centrality (or outlyingness) of an observation within a population or sample. It provides a rigorous way of ranking observations from center-outward and of defining robust statistics such as the median or trimmed mean functions. These location estimators can be used as building blocks when developing robust nonparametric methods for functional data.^12-14 Also, methods for visualizing and detecting functional outliers using the notion of depth have been proposed in the literature. In this paper we develop a depth-based envelope test for comparing and visualizing differences between the medians/centers of two sample of functions or images. This is a novel approach that provides global, nonparametric and robust tests for detecting and visualizing difference between two groups of functions or images. In this paper we focus on testing difference between the groups medians although the envelope test approach could be applied for testing other hypothesis by using other functional test statistics. The proposed test does not only provides a global P-value but allows visualizing the results and indicates the portion of time points/locations that lead to rejection of the null. In addition, we show that the test is fully nonparametric and robust to outliers.

The methods proposed in this paper are applied to the analysis of two datasets. First, we focus on an early-life human growth research using the data from 1988 National Maternal and Infant Health Survey (NMIHS) and its 1991 Longitudinal Follow-up. The study included 2555 boys and 2510 girls nation-wide who were born in the United States in the calendar year of 1988 and their heights between birth and 2 years of age were measured. The height measurements were taken sporadically only when they visited a hospital and therefore a preliminary step of smoothing and estimating the growth trajectories on a common fine grid is needed before performing any depth analysis. Figure 1A displays the individual height/length paths of the children born with low (left) and normal (right) birth weights. To understand the growth patterns of low birth-weight infants (≤ 2500 g) has been a long-term research topic in epidemiology. Our goal is to test if the growth trajectories pattern of normal vs low-birth weight kids are the same using the proposed functional data depth methodology. Second, we analyzed a set of positron emission tomography (PET) brain images. The data consists of two-dimensional PET brain scans of 29 subjects with major depressive disorder and 39 healthy controls. The images represent maps of binding potential of 5- hydroxytryptamine (serotonin) 1A receptors (5-HT1A), which are thought to play an important role in the disorder. Figure 1B shows a representative image from the control group (left) and depressed group (right). The goal is to use the proposed envelope test to compare the PET brain scans of healthy controls and patients with severe depression.

FIGURE 1.

Functional and imaging data examples. (A) Scatterplot of height paths in NMIHS data; (B) Mean brain positron emission tomography image in control vs depressed groups

The rest of the paper is arranged as follows: In Section 2 we give a general overview of the main types of notions of depth introduced in the literature focusing on the modified band depth and the extremal depth. In Section 3 we propose a depth-based envelope test for comparing and visualizing differences between two groups of functions. Section 4 shows the performance and robustness of the envelope test in a simulation study where two samples of curves are generated under different scenarios. The empirical size and power of the envelope test is calibrated and compared with the standard functional rank test. This test is applied in Section 5 to the NMIHS growth data to compare growth pattern between normal and low birth weight kids. Also, the depth-based envelope test is extended to imaging data and applied to PET brain images from patients with severe depression and healthy controls.

2 ∣. GENERAL DEFINITIONS OF FUNCTIONAL DATA DEPTH: MODIFIED BAND DEPTH AND EXTREMAL DEPTH

Given a probability distribution, a statistical depth assigns to each point a real nonnegative bounded value that measures the centrality of the point with respect to its distribution. Therefore the notion of depth is a useful tool to rank observations from center-outward. Several depth definitions were originally proposed to rank multivariate data (eg, References 15-25). Liu¹⁸ and Zuo and Serfling²⁶ studied the key properties a notion of depth should satisfy, such as maximality at the center of the distribution. However, most of these depths for multivariate data are computationally intractable in high-dimensions and cannot be extended to functional data. In the last two decades new notions of depth have been proposed for functional data (eg, References 3,5-7,9,11,27-29). In addition to providing a natural and rigorous way of ranking curves, these functional depths can be used to generalize classical robust rank statistics to functional data. In this paper we focus on the modified band depth and the extremal depth introduced in Lopez-Pintado and Romo^5,6 and Narisetty and Nair,¹¹ respectively. Both of these depths can be expressed in terms of the coordinate-wise depth: the modified band depth (MBD) takes the integral (average) of the coordinate-wise simplicial depths whereas the extremal depth (ED) basically consists on comparing the infimum coordinate-wise depths. Most of the depths proposed in the literature can be expressed as an integral depth or an infimal depth. These two general types of depths are described in more detailed below.

Throughout this paper we will consider the basic unit of observation to be a general function which is defined in a subset 𝒮 of either the real line or a higher dimensional space with dimension d, taking values in a univariate space. Specifically, let $Z:𝒮\to \mathbb{R}$ be a stochastic function taking values from 𝒮 to $\mathbb{R}$, where 𝒮 is a region in ${\mathbb{R}}^d$, with probability distribution P_Z. An integral depth of a given observation z from this space is defined as:

$$FD(z,P_Z)={\int }_{𝒮}D(z(s);P_{Z(s)})ds,$$ (1)

where D(z(s); P_Z(s)) is a univariate depth for z(s) with respect to P_Z(s), the corresponding marginal distribution of Z. In other words, the functional depth is the "average" (integral) of univariate depths.

Several notions of depth proposed in the literature can be expressed as an integral depth (eg, Reference ³). The modified band depth introduced in Lopez-Pintado and Romo⁶ and later extended to images in Lopez-Pintado and Wrobel³⁰ can be expressed as an integral depth. In particular, the modified band depth measures in average for how long the function z(s) is contained in the interval (band) determined by two stochastic functions Z₁(s), Z₂(s) at each value s,

$$\text{MBD}(z,P_Z)=E({\lambda }_r[s\in 𝒮,\text{s.t.}\text{min}(Z_1(s),Z_2(s))\le z(s)\le \max (Z_1(s),Z_2(s))]),$$ (2)

where λ_r is the Lebesgue measure on 𝒮, λ, divided by the Lebesgue measure of 𝒮. For simplicity, we assume λ(𝒮) = 1. Let Z = {z₁, z₂, … , z_n} be a sample of functions, the sample version of MBD is defined as

$$\begin{gathered} {\text{MBD}}_n(z,Z)=\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i_1<i_2\le n}\lambda \{s\in 𝒮,\text{s.t.}z(s)\in \text{interval}\{z_{i_1}(s),z_{i_2}(s)\}\} \\ =\frac{1}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}\sum _{1\le i_1<i_2\le n}\lambda \{s\in 𝒮,\text{s.t.}z(s)\in \{\text{min}(z_{i_1}(s),z_{i_2}(s)),\max (z_{i_1}(s),z_{i_2}(s))\}\} \end{gathered}$$ (3)

and measures the proportion of time the function z(s) is in the band determined by z_i1 , z_i2 , averaged over all possible bands defined by pairs of functions from the sample Z.

By Fubini’s theorem one can interchange the integrals in MBD and express

$$\text{MBD}(z,P_Z)={\int }_{𝒮}\text{SD}(z(s);P_{Z(s)})ds,$$ (4)

where SD(z(s); P_z(s)) = P(z(s) ∈ interval {Z₁(s), Z₂(s)}) is the standard univariate simplicial depth of z at location s. The sample version, MBD_n, can be expressed as the integral of the sample simplicial depth. MBD_n can be computed in a very fast and efficient way using the algorithm in Sun et al.³¹ This allows its application to very high-dimensional data such as images (see Reference ³⁰). The modified band depth has also been recently extended to multivariate functions ($Z:𝒮\to {\mathbb{R}}^p$) by considering in Equation (4) the integral of the multivariate simplicial depth.⁸ Similar depths for multivariate functional data based on the multivariate halfspace depth instead of simplicial depth or weighted average of component-wise modified band depths have been proposed in the literature.^10,32

An alternative family of functional depths, denoted here as infimal depth, can be defined by taking the infimum of all the projected univariate depths instead of the average, as in

$$\text{ID}(z,P_Z)=\underset{s\in [0,1]}{\text{inf}}D(z(s);P_{Z(s)}).$$ (5)

This type of depth was introduced by Mosler³³ and its properties were established. Recently, an alternative notion of depth denoted extremal depth has been proposed based on a measure of extreme outlyingness.¹¹ It considers the cumulative distribution function of point-wise depths and it focuses on the left tail of this distribution. It is related to the infimal depth.

These notions of depth satisfy desirable properties and provide a rigorous way of ranking functions.³⁴ Robust location estimators such as median (deepest) or trimmed means can be defined. Also, those functions from the sample with low depth can be considered as potential outliers. Integral depths and infimal depths provide in general different ranking and the use of one or another depends on the research question.

The extremal depth considers the cumulative distribution function of point-wise depths and it focuses on the left tail of this distribution. Specifically, consider the point-wise depth defined as

$$D(z(s),Z)=1-\frac{\mid \sum _{i=1}^n[I\{z_i(s)<z(s)\}-I\{z_i(s)>z(s)\}]\mid }{n}.$$

and define φ_z() the d-cumultative distribution function (d-CDF) as ${\varphi }_z(r)={\int }_a^{b}I\{D(z(s),Z)\le r\}dt$ of the distinct values taken by D(z(s), Z) as s varies in 𝒮 . The extremal depth will be based on a comparison of the d-CDFs, for r near to zero, and it can be viewed as a left-tail stochastic ordering. In particular, consider two functions z and x from Z with corresponding d-CDF φ_z and φ_x and let 0 ≤ d₁ < d₂ < … < d_M ≤ 1 be the ordered elements of their combined depth levels at each s. If φ_z(d₁) > φ_x(d₁) then z is more extreme than x (z < x). If φ_x(d₁) = φ_x(d₁), we move to d₂ and make the same comparison now based on d₂. The comparison is repeated until the tie is broken and if φ_z(d_i) = φ_x(d_i) for all i = 1, … ,M, then the two functions are equivalent in terms of depth (z ≡ x). The extremal depth of a function z with respect to the sample Z = {z₁, … , z_n} is

$$\text{ED}(z,Z)=\frac{\#\{i:z\ge z_i\}}{n},$$

where z ≥ z_i if either z > z_i or z ≤ z_i. The extremal depth and modified band depth can also be extended to spatial/image data. Both, ED and MBD use a component-wise depth distributions to rank the curves. The main distinguishing features between them is that MBD considers approximately the average of the point-wise depths whereas ED uses the left-tail stochastic ordering of the depth distributions. MBD and ED provide in general different ranking and the use of one or another depends on the research question. For example, if the goal is to penalize and assign low depth to functions that are only extreme in a very short part of the domain, then infimal depths are more appropriate than integral depths. On the other hand, if we want to measure the overall depth of the function, the integral depths are better suited for this. Also, integral depths are less affected by measurement error and consequent smoothing. However, Narissety and Nair¹¹ show that the extremal depth and associated central regions satisfy some desirable properties for simultaneous confidence regions and hypothesis testing that we will discuss in the next section.

These notions of depth can only be applied to curves measured at a regular grid. However, in practice, this is rarely the case. Usually each curve from the sample is observed at sparse and unevenly spaced time points and with measurement error. Therefore, a preliminary smoothing step to evaluate all the curves at the same grid is needed. We applied a widely used functional principal components analysis (FPCA) and mixed model approach that provides ways to express functional observations from sparse data (see References 35,36). The FPCA method introduced in Yao et al³⁵ usually gives accurate estimation of the underlying true curves for sparsely observed data and that is why we choose this approach. However, alternative smoothing methods could be used and some preliminary results indicate that the envelope test is robust to the smoothing method.

3 ∣. GLOBAL NONPARAMETRIC ENVELOPE TEST

3.1 ∣. Background on depth-based permutation test for two-sample problems

MBD and the ranking it provides can be used as a building block for developing depth-based inferential statistical methods for analyzing high-dimensional data. Recently, in López-Pintado and Wrobel³⁰ we proposed new permutation tests for determining whether two groups of images come from the same distribution. In particular, we are interested in comparing the centers of both distributions. We introduced a two-sample location test based on differences in sample medians. The medians were defined as the deepest image within each group. We proposed using as test statistic: T_sum = Σ_s∈S∣T(s)∣ and T_max = max_s∈S∣T(s)∣, where $T(s)={\widehat{\mu }}_1(s)-{\widehat{\mu }}_2(s)$, and ${\widehat{\mu }}_1$ and ${\widehat{\mu }}_2$ are the deepest images in each group based on MBD. These images are evaluated at pixels or voxels s that belong to a finite domain set S. In particular, T_sum and T_max are calculated as the sum and maximum over S, respectively, of the change image defined as difference between the deepest/median image in each group. These statistics calculated for the observed data are denoted as T_obs. The distribution of the test statistics under the null hypothesis is obtained by pooling the observed images in both groups and calculating the T_perm statistic for every possible permutation of group labels. The P-value is calculated as the proportion of sampled permutations T_perm greater or equal than T_obs. This test can be computationally intensive although it is easily parallelized. Based on a simulation study we showed that these tests in the presence of outliers are more robust and powerful than standard approaches.³⁰ A main drawback of these tests is that they provide overall P-values indicating if the null hypothesis is rejected, but no indication of what values of s led to this rejection. Also, they lack graphical interpretation. To address these issues we propose a global envelope test approach based on data depth.

3.2 ∣. Depth-based envelope test

We develop global depth-based envelope tests for detecting differences between groups of functions that extend the permutation test described above . The proposed tests will provide global P-values and a graphical representation. Envelope tests are a popular tool in spatial statistics (see References 37-39). These tests graphically compare an empirical observed function T₀(s) with its simulated counterpart from the null model. The theoretical distribution of T(s) under the null is usually unknown and Monte Carlo methods are used to approximate it. The envelope test results can be displayed in a graphical manner and the method indicates the values of s that lead to rejection.

In particular, a global envelope test is a statistical test that rejects the null hypothesis if the observed T₀ is not completely inside the envelope, that is,

$${\varphi }_{\text{env}}(T_0)=I(\exists s\in S:T_0(s)\notin (T_{\text{low}}(s),T_{\text{upp}}(s))).$$ (6)

Here we propose an approach for determining the bounds T_low and T_upp such that the test in (6) has a controlled global type I error probability (α). In the context of the two-sample problem described above, let us assume we are using a functional statistic T(s) to test a null hypothesis H₀ of equal centers (medians) between two samples vs the alternative hypothesis that the medians are not equal. For example, we could consider $T(s)={\widehat{\mu }}_1(s)-{\widehat{\mu }}_2(s)$ where ${\widehat{\mu }}_i$ is the sample median observation within each group as defined in previous section. Other location estimators, such as trimmed means with different levels of trimming can also be used. The β-trimmed mean, where beta is a number between zero and one, is defined as the average of the (1-β)n deepest curves. We propose to develop depth-based approaches for building global envelope tests allowing for prior selection of a global α. This contrasts with standard methods in image data analysis where a pixel-wise test is used jointly with a multiple comparison correction. The depth-based global envelope test will not only provide an overall P-value but will help determine why the data contradicted the null hypothesis and visualize this graphically. We will consider an approach inspired by the one used in Myllymaki et al³⁹ for spatial processes. We propose to generate a sample of statistics T₁(s), … , T_r(s) from the null hypothesis by randomly permuting the joint sample as in the permutations test. Functional data depth will be used to rank the sample T_i(s), i = 0, 1, … , r from center-outward. Based on this order we will study how to determine the bounds for the envelope test defined in (6) to assure a global significance level of α.

In particular, the extremal depth described in Section 2 can be easily extended to spatial functional/image data and in what follows we will show that it has desirable properties not satisfied by other depths. Consider H a general function space and P the associated probability distribution, the (1 – α) ED central region is defined as

$$C_{1-\alpha }=\{z\in H:z_L(s)\le z(s)\le z_U(s),\text{for every}s\in S\},$$ (7)

where z_L(s) = inf {z(s) : z ∈ H, ED(z) > α} and z_U(s) = sup{z(s) : z ∈ H, ED(z) > α}. When H is the finite set of sample functions and P the empirical distribution, then C_1–α is just the convex hull determined by the sample functions with depth larger than α.

Following the ideas and assumptions in Propositions 1 and 4 in Narissety and Nair¹¹ it can be shown that the central region with level α, C_1–α, has the desirable coverage of at least 1 – α and the coverage is exactly 1 – α when the boundary of the central region does not have any mass. More concretely, define the boundary set of C_1–α as

$$\delta C_{1-\alpha }=\{z\in C_{1-\alpha }:z(s)=z_L(s)\text{or}z(s)=z_U(s),\text{for some}s\in S\}.$$

Proposition 4 in Narissety and Nair shows that

$$1-\alpha \le P[z\in C_{1-\alpha }]\le (1-\alpha )+P[z\in \delta C_{1-\alpha }].$$

If P[z ∈ δC_1–α] = 0 then the coverage is exact, P[z ∈ C_1–α] = 1 – α. This could be different from zero in finite samples if there is a curve from the sample that is equal to the upper or lower envelopes of the central region at some interval, although this probability goes to zero as n goes to infinity. This desirable property of ED central regions is based on the convexity of the depth contours (see Proposition 1 in Narissety and Nair) and it is not satisfied by other depths. For example, MBD usually has over-coverage issues, hence, the central regions will in general have coverage above 1 – α. ED central regions will be then considered/applied in simultaneous inference problems. In particular, the central region based on ED can be used to construct envelope tests. We propose applying ED to the sample test statistics T_i, i = 1, … , r simulated under the null and using the corresponding central region C_1–α as an envelope test as in (6) with T_low(s) = z_L(s) and T_upp(s) = z_U(s). If the observed statistic T₀ is not completely inside this central region we reject the null hypothesis. By construction the global type I error of this test will be α. A similar approach in a very different context was used in Myllymaki et al³⁹ where they proposed a global envelope test for spatial processes by using a r-wise ranking to order the curves. In the next section we present a simulation study to show the performance of the proposed test in different settings.

4 ∣. SIMULATION RESULTS

Simulations were run to calibrate the performance of the envelope test based on the empirical size and power under a variety of conditions. The robustness of this test was also evaluated. We simulated length trajectories that resemble characteristics of the NMIHS growth data set introduced in Section 1. Recall that the data consist on 2555 boys and 2510 girls national-wide who were born in the United States in the calendar year of 1988 and their heights between birth and 2 years of age were measured. We have filtered out the data and only considered boys with at least 5 height measurements between birth and 2 years of age. After this filter, the number of boys with normal birth weight is reduced to 873 and the number of boys with low birth weight is 269. We used functional principal component analysis (FPCA) combined with a mixed model approach introduced in Yao et al³⁵ to smooth the sparsely observed trajectories and obtain curves defined in a fine grid. The simulated data was generated from a principal components decomposition of the 873 normal birth weight trajectories. This way we ensure that the simulated data resembles the properties of the real data. The mean trajectory was subtracted from each subject and we performed FPCA on the variance covariance matrix of the centered data. In particular,

$${\mathbf{Y}}_i=c\mu +\sum _{k=1}^K{\xi }_{ik}{\psi }_k,$$ (8)

where μ represents the mean trajectory evaluated at the fine grid of dimension 25, ξ_ik are the subject-specific scores and ψ_k are the eigenfunctions. Since we want to generate functions from populations with different means we included a mean multiplier constant c. The choice of this constant will depend on the purpose of the simulation. The scores were randomly generated from a normal distribution with mean zero and variance equal to the eigenvalues, λ_k. K = 3 principal components explaining 95% of variance of the original data were retained. Table 1 shows the results of a simulation study where the envelope test was used to test differences between two groups of curves simulated from the model in (8). The proportion of times the null hypothesis (of no differences between the centers of both groups) is rejected is represented in Table 1 under different scenarios.

TABLE 1.

Envelope test and rank test (RT)

Simulation scenario	Outlier prob.	T 1	T 2	T 3	T 4	T 5	T 6	RT
Scenario 1	θ = 0	0.058	0.064	0.074	0.052	0.066	0.086	0.054
	θ = 0.05	0.062	0.100	0.068	0.078	0.134	0.694	0.084
Scenario 2	θ = 0	0.730	0.892	0.924	0.956	0.952	0.980	0.256
	θ = 0.05	0.604	0.796	0.816	0.820	0.792	0.220	0.082
Scenario 3	θ = 0	0.998	1.000	1.000	1.000	1.000	1.000	0.982
	θ = 0.05	0.992	1.000	1.000	1.000	1.000	0.086	0.612
Scenario 4	θ = 0	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	θ = 0.05	1.000	1.000	1.000	1.000	1.000	0.128	0.994
Scenario 5	θ = 0	1.000	1.000	1.000	1.000	1.000	1.000	1.000
	θ = 0.05	1.000	1.000	1.000	1.000	1.000	0.380	1.000

Notes: Results for five simulation scenarios. Numbers represent proportion of times (out of 500 iterations) a test rejected the null hypothesis that control and test subjects have the same population median. Results are based on the envelope test based on test statistics T₁, T₂, T₃, T₄, T₅ and T₆, as defined above and the RT.

For each simulation scenario we ran 500 iterations with test and control groups generated from the model in (8). The envelope test was used considering six different test statistics (T_i, i = 1, … , 6): T₁ is the difference between the sample medians and T₂, T₃, T₄, T₅, T₆ are defined as the β- trimmed means differences with trimming percentages of β =95, 90, 80, 50, 0, respectively. The β percent -trimmed mean curve were defined as the average of the 100 – β percent of deepest trajectories based on the Extremal depth ranking. Note that β = 0 corresponds to the sample mean. The number of permutations for the envelope tests was fixed at 1000 and the sample size of each group was n = 100. The simulation scenarios are outlined below.

1. Scenario 1: Control and test subjects drawn from same population, with mean multiplier set to c = 1 for both groups.

2. Scenario 2: Control and test subjects drawn from different populations, with c = 1 and c = 1.02, respectively.

3. Scenario 3: Control and test subjects drawn from different populations, with c = 1 and c = 1.04, respectively.

4. Scenario 4: Control and test subjects drawn from different populations with c = 1 and c = 1.06, respectively.

5. Scenario 5: Control and test subjects drawn from different populations with c = 1 and c = 1.08, respectively.

We repeated the simulation study randomly adding a small percentage of outliers in the control group. The contamination probability was θ = 0.05, therefore each subject had 5% chance of being an outlier. Nonoutlying observations in the control group where generated from the model in (8) with c = 1. The outliers are generated from model 8 with c = 2 and with the scores randomly generated from a normal distribution with mean zero and variance equal to two times the eigenvalues, 2 * λ_k. In Table 1 we show the simulation results with θ = 0 representing no outliers scenarios and θ = 0.05 indicating settings where outliers are included in the control group with 5% probability. Note that in scenario 1 the control and test group are simulated from the same distribution. For each simulation scenario we calculated the proportion of times a test rejected the null hypothesis that control and test subjects are coming from the same population at α level 5%. As a comparison we also included in the simulation study the results of the depth-based rank test introduced in Liu and Singh¹⁹ for multivariate data and later extended to functional data in Lopez-Pintado and Romo.⁶ For the rank test (denoted as RT), a sample of size 101 from the test group is also generated as the reference group. The simulation results are displayed in Table 1.

For scenario 1, where the control and test samples come from the same distributions, and in the case of no contamination (θ = 0), all tests rejected the null hypothesis between 5.2% and 8.6% of the time, therefore the empirical size of all the tests are slightly above the nominal size of 5%, with T₄ providing the best performance with an empirical size of 5.2%. When contamination was added in the control group (θ = 0.05) the empirical size ranks from 6.2% to 69.4%. As expected, when using difference in medians or trimmed means as test statistic in the envelope test (T₁, .., T₅), the rejection rate is still relatively low since the test is robust to outliers. However, when using the difference in means (T₆) the empirical size of the test goes up to 69% and it is inflated due to the outliers. Using the rank test the empirical size of the test is 8.4% which is slightly above the nominal size. For scenario 2 with no contamination, where there is a small difference between both groups (c = 1.02), the rank test performs very poorly with only a 25.6% empirical rejection rate (power). The best performance is obtained with the envelope test using T₆ defined as differences between means, where the rejection rate was 98%, followed closely by T₄ with a 95.6% power. However, the empirical power of T₁, difference between medians, is only 73%. In contrast, when outliers are included the power of T₆ (difference between means) goes down to 22% and the maximum power of 82% corresponds to T₄. Also, the rank test has low power in this scenario where the difference between both groups is small and there is contamination (8.2%). In Scenario 3 without contamination, all envelope tests and the rank tests have high power (above 98%), although the power of the rank test is slightly below the envelope tests. When adding contamination, all envelope tests have high power, except T₆, difference in means, that is very sensitive to the outliers and rejects the null only 8.6% of the times. Also, in this scenario with contamination, the power of the rank test goes down to 61.2%. In Scenarios 4 and 5 the patterns are very similar. In these settings, where the difference between both groups is larger, all methods have high empirical power (approximately 1) in the noncontamination settings. When the data is contaminated, all the methods except T₆ (the envelope test using difference in means as test statistic) reject the null hypothesis almost all the time. T₆ has a low empirical rejection rate (12.8% and 38%, in Scenarios 4 and 5, respectively) due to the presence of outliers. In summary, the simulation study shows that without contamination, the envelope test has in a general good performance in terms of empirical size and power and outperforms the rank test. Also, in the presence of outliers the envelope test when combined with robust test statistics based on differences in depth-based trimmed means (T₁ through T₅) outperforms T₆ (based on differences in means) and the rank test.

To further explore the performance of the envelope test, we have also considered other settings where the difference between the two groups of functions is only in a given proportion of the domain (pro) and in the rest of the domain the curves come from the same distribution. In particular, we considered pro = 40% and pro = 10%, respectively, in Tables 2 and 3. A random interval of length pro of the total domain is selected and the different scenarios in Table 1 are applied to this interval. Therefore, the two groups only differ partially in a part of the domain.

TABLE 2.

Envelope test and rank test (RT) with partial differences (pro = 40%)

Simulation scenario	Outlier Prob.	T 1	T 2	T 3	T 4	T 5	T 6	RT
Scenario 1	θ = 0	0.054	0.058	0.072	0.058	0.076	0.082	0.054
	θ = 0.05	0.058	0.106	0.074	0.094	0.130	0.684	0.084
Scenario 2	θ = 0	0.378	0.794	0.876	0.890	0.946	0.980	0.136
	θ = 0.05	0.256	0.668	0.726	0.794	0.744	0.666	0.070
Scenario 3	θ = 0	0.740	1.000	1.000	1.000	1.000	1.000	0.772
	θ = 0.05	0.674	0.996	1.000	1.000	1.000	0.668	0.374
Scenario 4	θ = 0	0.908	1.000	1.000	1.000	1.000	1.000	0.996
	θ = 0.05	0.844	1.000	1.000	1.000	1.000	0.750	0.882
Scenario 5	θ = 0	0.962	1.000	1.000	1.000	1.000	1.000	1.000
	θ = 0.05	0.906	0.996	1.000	1.000	1.000	0.900	0.988

Notes: Results for five simulation scenarios analogous to the ones described above but the differences between control and test groups are only in pro = 40% of the domain. Numbers represent proportion of times (out of 500 iterations) a test rejected the null hypothesis that control and test subjects come from the same distribution. Results are based on the envelope test based on test statistics T₁, T₂, T₃, T₄, T₅, T₆ and on the RT.

TABLE 3.

Envelope test and rank test (RT) with partial differences (pro = 10%)

Simulation scenario	Outlier prob.	T 1	T 2	T 3	T 4	T 5	T 6	RT
Scenario 1	θ = 0	0.084	0.082	0.062	0.070	0.070	0.082	0.054
	θ = 0.05	0.066	0.102	0.088	0.098	0.142	0.700	0.084
Scenario 2	θ = 0	0.174	0.572	0.718	0.756	0.876	0.966	0.044
	θ = 0.05	0.122	0.438	0.544	0.642	0.678	0.674	0.084
Scenario 3	θ = 0	0.486	0.980	0.998	1.000	1.000	1.000	0.124
	θ = 0.05	0.362	0.912	0.994	0.998	1.000	0.712	0.076
Scenario 4	θ = 0	0.67 0	0.998	1.000	1.090	1.000	1.000	0.234
	θ = 0.05	0.544	0.988	1.000	1.000	1.000	0.776	0.076
Scenario 5	θ = 0	0.750	0.996	1.000	1.000	1.000	1.000	0.338
	θ = 0.05	0.628	0.976	1.000	1.000	1.000	0.918	0.110

Notes: Results for five simulation scenarios analogous to the ones described above where the differences between control and test groups are only in pro = 10% of the domain. Numbers represent proportion of times (out of 500 iterations) a test rejected the null hypothesis that control and test subjects have the same population median. Results are based on the envelope tests based on test statistics T₁, T₂, T₃, T₄, T₅, T₆ and on the rank test RT.

The results are similar to the ones presented in Table 1. Overall, the best performance is given by the envelope test with different in trimmed means as test statistic, specially with T₄ and/or T₅. Without contamination, T₆, difference between means, also has a good performance but breaks down in the presence of outliers. The rank test performance is always inferior to the envelope test, specially when the difference between the two groups is small (in Scenarios 2 and 3).

One advantage of the global envelope test is that you can identify the significant rejection time points by looking at when the statistic function (T) goes out of the envelope. Therefore, in addition to the global type I error and power of these tests, we computed as well the false and correct detection rate, defined as the proportion of time points identified as different with the envelope test among those with no true differences and proportion of points identified as different among those with true differences, respectively. We considered the same settings as in Tables 2 and 3, where the two groups of curves differ only in a random sub-interval of length pro = 40% and pro = 10%. In all the settings we considered a 5% outlier rate. It can be seen in Table 4 that the false discovery rate is in general very low in all scenarios when using a robust test statistics based on trimmed means, such as, T₁ through T₅, and it ranges from 0.002 to 0.056. On the other hand, T₆, defined as difference in means, behaves very poorly due to the presence of outliers. In Table 5 the true discovery rate is represented for Scenarios 2 to 5. In Scenario 1 there are no points with true difference since the curves from both groups are generated from the same distribution and therefore the true discovery rate is not well defined. The true discovery rate using trimmed means test statistics (T₂ through T₅) is in general very high (between 89.6% and 100%) in Scenarios 3 to 5. For Scenario 2, where the difference between the two groups is very small, the true discovery rate goes down, as expected.

TABLE 4.

False discovery rate for the envelope test with partial differences (pro = 40% and pro = 10%)

Simulation scenario	pro	T 1	T 2	T 3	T 4	T 5	T 6
Scenario 1	pro = 40%	0.020	0.022	0.025	0.032	0.056	0.602
	pro = 10%	0.025	0.030	0.038	0.037	0.051	0.601
Scenario 2	pro = 40%	0.014	0.023	0.030	0.030	0.050	0.584
	pro = 10%	0.015	0.015	0.022	0.034	0.047	0.602
Scenario 3	pro = 40%	0.012	0.020	0.025	0.034	0.041	0.591
	pro = 10%	0.005	0.015	0.022	0.035	0.048	0.615
Scenario 4	pro = 40%	0.006	0.012	0.015	0.018	0.046	0.573
	pro = 10%	0.003	0.010	0.013	0.025	0.051	0.577
Scenario 5	pro = 40%	0.006	0.010	0.015	0.022	0.037	0.519
	pro = 10%	0.002	0.005	0.014	0.022	0.034	0.568

Notes: Results for the five simulation scenarios analogous to Tables 2 and 3, where the differences between control and test groups are in a random interval of length pro = 40% and pro = 10% of the domain. In all scenarios we are assuming a 5% outlier rate. Numbers represent false discovery rate that is defined as the proportion of points detected as different among those that are not. Results are based on the envelope test using test statistics T₁, T₂, T₃, T₄, T₅, T₆.

TABLE 5.

True discovery rate for the envelope test with partial differences (pro = 40% and pro = 10%)

Simulation scenario	pro	T 1	T 2	T 3	T 4	T 5	T 6
Scenario 2	pro = 40%	0.180	0.441	0.514	0.576	0.600	0.151
	pro = 10%	0.088	0.343	0.440	0.526	0.565	0.152
Scenario 3	pro = 40%	0.554	0.959	0.991	0.994	0.999	0.042
	pro = 10%	0.336	0.896	0.975	0.992	0.994	0.053
Scenario 4	pro = 40%	0.761	0.998	1.000	1.00 0	1.000	0.103
	pro = 10%	0.526	0.981	0.998	1.000	1.000	0.122
Scenario 5	pro = 40%	0.844	0.998	1.000	1.000	1.000	0.318
	pro = 10%	0.624	0.978	1.000	1.000	1.000	0.293

Notes: Results for the different scenarios analogous to Table 2 and 3, where the differences between control and test groups are in a random interval of length pro = 40% and pro = 10% of the domain. In all scenarios we are assuming a 5% outlier rate. Numbers represent true discovery rate defined as the proportion of points detected as different with the envelope test among those that are truly different. We excluded Scenario 1 where c = 1 since the two groups are generated from same process and therefore there are no truly different points. Results are based on the envelope test using test statistics T₁, T₂, T₃, T₄, T₅, T₆.

5 ∣. APPLICATION TO REAL DATA

5.1 ∣. Application to growth data

We have applied the proposed envelope test to the NMIHS growth data example described in Section 1. Recall that the data included 2555 boys and 2510 girls national-wide who were born in the United States in the calendar year of 1988 and their heights between birth and 2 years of age were measured. Low birth-weight infants (≤ 2500 g) were over-sampled, which constitute approximately 25% of the data. The height measurements were taken sporadically only when the children visited a hospital. Consequently, their growth paths were recorded on a set of sparse and irregularly spaced time points. We used FPCA combined with a mixed model approach to estimate individual trajectories in a common grid.^35,36

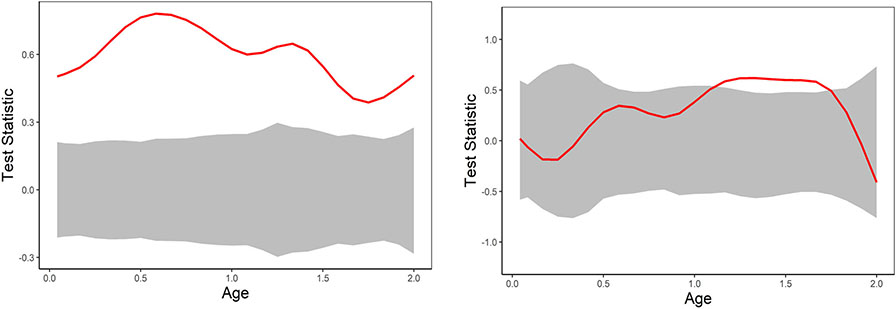
The goal is to understand the growth pattern of low birth-weight infants, and to test if it is different from normal birth-weight children. Also, within the low birth-weight kids we wanted to test if the growth pattern between boys and girls is the same. The envelope test described above (based on ED) provides not only an overall P-value, but a way of visualizing the results of the test. It also indicates the ages that lead to rejection of the null. In Figures 2 and 3 we represent the envelope test applied to this data based on 5000 statistics simulated under the null by permutations and α = 0.05. The test statistic $T(s)={\widehat{\mu }}_1(s)-{\widehat{\mu }}_2(s)$ is defined as the difference in medians (defined as the deepest functions using extremal depth) in the comparison groups. In Figure 2 we compare median height paths for normal vs low birth-weight boys and girls in the left and right panel, respectively. The observed differences is represented by a red curve and it is always above the 95% envelope indicating that normal birth-weight kids have significantly greater height than low birth-weight kids at all ages (between 0 and 2 years) although the differences decrease with age for boys and girls. In Figure 3 we are testing differences of median of height curves between boys versus girls among (a) normal birth-weight kids and (b) low birth-weight kids. As expected, for normal children the height of boys is always above girls at all considered ages since the median differences curve is always above the envelope. However, for low-birth weight kids the heights are significantly larger for boys than girls only in certain intervals of ages and by age 2 the difference is not significant.

FIGURE 2.

Envelope test for differences in medians between normal versus low birth-weight boys (left panel) and girls (right panel))

FIGURE 3.

Envelope test for differences between boys and girls among the normal-birth weight kids (left panel) and low-birth weight kids (right panel)

5.2 ∣. Application to PET brain image data

In this section we extended and applied the global depth-based envelope tests to brain image data. In particular, we are interested in testing and visualizing differences in brain PET scans between healthy controls and severe depressed patients. We will use the data described in Parsey et al to test this hypothesis. The data consists of two-dimensional PET brain images of 29 subjects with major depressive disorder and 39 healthy controls. The images represent maps of binding potential of 5- hydroxytryptamine (serotonin) 1A receptors (5-HT1A), which are thought to play an important role in the disorder. An index of the number of receptors occupied by a radioligand (called binding potential) provides a measure of the receptors availability in the brain. Using Statistical Parametric Mapping software (version SPM2), the images were coregistered to a template image in Montreal Neurological Institute standard space, resulting in a set of 68 images of 79 times 95 transaxial slices. In Figure 1B we represented the 80% trimmed mean images based on the MBD ranking in the control and depressed group. This data was recently analyzed in Lopez-Pintado and Wrobel³⁰ using MBD and a depth-based permutation test that was described in the background Section 3.1. A main drawback of these tests is that they provide overall P-values indicating if the null hypothesis is rejected but no indication of which values of s led to this rejection. The envelope tests introduced in this paper are meant to fill this gap and can be extended to image data. Based on the simulation study in previous section the performance of the envelope test using T₄ as test statistic is robust and in general outperforms other statistics T_i. In Figure 4 the envelope test based on T₄ (difference in 80%-trimmed mean) is applied to the brain PET imaging data. The global envelope test rejected the null hypothesis of no differences between control and depression disorder group fixing α = 0.05 and using 1000 permutations. In the left panel the corresponding functional test statistic is represented as a green surface and the envelope is in blue. In the right panel we represent a heatmap of the corresponding T statistic. The darker the pixels the larger the value of the T statistic measuring the difference between the location estimators. Blue and red colors indicate negative and positive differences, respectively. The pixels in gray represent the locations in the brain where the test statistic crosses the envelope, indicating significant differences between the two samples. Note that the proposed test is global and not a standard pixel-wise test, therefore there is no need to control for multiple testing.

FIGURE 4.

(A) Depth-based envelope test applied to two-sample positron emission tomography image data using T₄, defined as difference in 80%-trimmed mean (B) locations in the brain that lead to rejection of the null are represented in light gray

6 ∣. CONCLUSION

Functional data is a modern area of research in statistics. Many disciplines rely on the analysis of complex data consisting on sets of functions or images. In this paper we focus on developing robust global depth-based tests for functional data. The proposed test is fully nonparametric and is based on the envelope test ideas introduced for spatial statistics (eg, Reference ³⁸). The acceptance region of the test is constructed using depth-based central regions and controlling for global probability of type one error α. The results of the proposed envelope test can be visualized and indicate the time points/location that lead to rejection of the null. Based on a simulation study we calibrate the test and indicate its performance in terms of empirical size and power. We conclude that the envelope test outperforms the rank test in terms of power in most scenarios and is robust to outliers. We applied the envelope test to growth data from NMIHS to compare the length trajectory between normal versus low birth weight infants. We concluded that the growth pattern is different in the two groups although the differences attenuate with age. The global envelope test was also used to compare the PET brain images of healthy controls and severe depressed patients, indicating locations in the brains where these two groups of images are significantly different.

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.