Progress in Understanding Radiofrequency Heating and Burn Injuries for Safer MR Imaging

Abstract

RF electromagnetic wave exposure during MRI scans induces heat and occasionally causes burn injuries to patients. Among all the types of physical injuries that have occurred during MRI examinations, RF burn injuries are the most common ones. The number of RF burn injuries increases as the static magnetic field of MRI systems increases because higher RFs lead to higher heating. The commonly believed mechanisms of RF burn injuries are the formation of a conductive loop by the patient’s posture or cables, such as an electrocardiogram lead; however, the mechanisms of RF burn injuries that occur at the contact points, such as the bore wall and the elbow, remain unclear. A comprehensive understanding of RF heating is needed to address effective countermeasures against all RF burn injuries for safe MRI examinations. In this review, we summarize the occurrence of RF burn injury cases by categorizing RF burn injuries reported worldwide in recent decades. Safety standards and regulations governing RF heating that occurs during MRI examinations are presented, along with their theoretical and physiological backgrounds. The experimental assessment techniques for RF heating are then reviewed, and the development of numerical simulation techniques is explained. In addition, a comprehensive theoretical interpretation of RF burn injuries is presented. By including the results of recent experimental and numerical simulation studies on RF heating, this review describes the progress achieved in understanding RF heating from the standpoint of MRI burn injury prevention.

Introduction

MRI is a widely used, versatile contrast-, and radiation-free imaging modality. However, because of MRI-specific hardware characteristics, i.e., a strong static magnetic field, a fast-switching gradient magnetic field, and a RF field, accidents that harm patients can occur. The static magnetic field exerts displacement force¹ and torque² on the magnetic objects. It has been reported that a ferromagnetic gas cylinder was magnetically attracted to the scanner, causing a fatal accident.^3,4 If the time-varying magnetic field (dB/dt) and its duration are sufficient to produce an action potential across a cell, the fast-switching gradient magnetic field (which has improved new imaging techniques, such as diffusion tensor imaging⁵) stimulates the peripheral nerves^6–8 or causes heating of implantable medical devices.⁹ The RF field heats the human body (in conjunction with or without the use of medical devices) and occasionally leads to RF burn injuries.¹⁰ The frequency of these accidents is increasing with the increasing static magnetic field strength of MRI systems owing to stronger attractive displacement forces, the advent of new imaging techniques, and higher RF frequencies. Therefore, MR safety has been a concern as a medical safety issue, e.g., screening for projectile ferromagnetic objects at the walk-in stage and checking the MRI compatibility of implantable medical devices.^1,2,11–14

Several reports have surveyed accidents that occurred during MRI examinations. In the United Kingdom, the Medicines and Healthcare Products Regulatory Agency (MHRA) reported that 308 MRI accidents occurred from 1993 to 2014¹⁵, and in the United States, the Food and Drug Administration (FDA) reported that 1548 MRI accidents occurred from 2008 to 2017.¹⁶ Among these accidents, RF burn injuries were the most common, accounting for 42% and 55% of all the accidents reported by the MHRA¹⁵ and FDA,¹⁶ respectively. In addition, a survey in Japan revealed that RF burn injuries had occurred in 12% of 1319 hospitals.¹⁷ The number of RF burn injuries has increased in recent decades; the FDA reported 419 cases in 1997–2009¹⁸ and 849 cases in 2008–2017.¹⁶ This tendency may be related to the prevalence of 3T MRI because the RF heating is theoretically proportional to the square of the static magnetic field strength of MRI; the heating sensation experienced by patients increases with the increase in strength of the static magnetic field.¹⁹ Moreover, with the development of ≥ 7T MRI systems, the risk of RF burn injuries would increase. Thus, to ensure MRI safety, it is necessary to address the problem of RF burn injuries.

Focusing on RF heating during MRI examinations, this review summarize the occurrence of RF burn injuries by categorizing the RF burn injuries reported worldwide in recent decades. Safety standards and regulations governing RF heating during MRI examinations are presented, along with their theoretical and physiological backgrounds. The experimental assessment techniques used for RF heating are reviewed, and the development of numerical simulation techniques is explained. In particular, the electromagnetic characteristics of RF burn injury cases are discussed with numerical simulations, and a recent theoretical interpretation of RF burn injuries is discussed. By including the results of recent experimental and numerical simulation studies on RF heating, this review describes the progress achieved in understanding RF heating from the standpoint of MRI burn injury prevention.

RF Burn Injuries

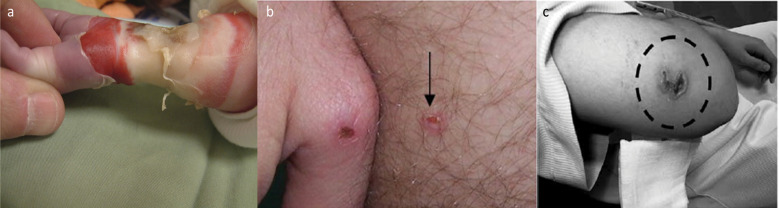
RF burn injuries (Fig. 1) are the most common MRI-related accidents, accounting for approximately half of all such accidents.^15,16 The numbers of RF burn injuries surveyed in the United States, the United Kingdom, and Japan are presented in Table 1, where RF burn occurrences are categorized as “contact with an object,” “skin-to-skin contact,” or “bore contact”.¹⁶ Some RF burn injuries were not clearly reported—particularly in surveys conducted in the United States and the United Kingdom; excluding these cases, it has been shown that RF burn injuries occur most frequently when a human body contacts an object, for example, the MR coil, monitor lead and electrode, tattoo, makeup, or dermal patch. This is followed by skin-to-skin contact, e.g., the inner thighs or calves, and bore contacts by the body’s extremities. All three countries exhibited this tendency of frequent RF burn injuries at contact points, indicating that “contact” on a human body is the key feature of RF burn injuries.

Fig. 1.

RF burn injury cases. (a) Fourth-degree burn in the right forearm and wrist, where the probe of a non-MR-compatible pulse oximeter was attached during the MRI scan; (b) third-degree burn on the skin of the right hand and pelvis 1 week after the examination; and (c) second-degree burn on the right elbow when it touched the bore wall during MRI scan. Reproduced with permission from references 159 (a), 160 (b), and 161 (c).

Table 1.

Summary of RF burn accidents from the literature

Occurrence	US16	UK15	Japan17
Contact with an object	257 (51%)	53 (58%)	79 (56%)
Skin-to-skin contact	147 (29%)	39 (42%)	49 (33%)
Bore contact	97 (19%)	0 (0%)	12 (9%)
Subtotal	501	92	140
Unclear	348	39	9
Total	849	131	149
Surveyed duration	2008–2017	1993–2014	Unknown–2010

Data from the United Kingdom and Japan were reclassified according to the categories of the United States. The percentage in parentheses shows the proportion (per subtotal) of the number of cases in each category for each country.

During an MRI scan, an RF field is applied to the conductive human body, inducing eddy currents, which leads to Joule heating. From this fundamental knowledge of electromagnetic properties, it has been determined that conductive loop formation via skin–skin contact^20,21 or body–conductive object contact, such as a conductive wire or cable attached to the patient’s skin,^22,23 is a potential cause of RF burn injuries. When a closed loop is formed on the patient’s body, it is commonly believed that the eddy currents concentrate at the skin–skin or body–conductive object contact points and induce significant local heating,²⁴ which may be intensified, in particular, for a resonant conductive loop.²⁵ This basic mechanism qualitatively explains the occurrence of RF burn injuries related to “skin-to-skin contact” and, in some instances, “contact with an object.”^15–17 Another potential mechanism of RF burn injuries is the antenna effect; the resonant length of a conductive wire functions as an antenna for induced RF electric fields, and the resonant current in the wire generates a large amount of heat.^25,26 RF burn injuries resulting from “contact with an object” that do not form a closed loop, such as an RF burn injury occurring at a contact point with an unlooped electrocardiogram cable, have been explained by the antenna effect.²⁴ In addition, safety concerns have been raised regarding patients with large tattoos, which may function as antennas.²⁷

Although conductive loop formation and the antenna effect qualitatively explain the mechanism of RF burn injuries, the mechanism of such injuries that occur at contact points without forming a loop or an antenna remains unknown; for example, when the human body contacts the bore, no loop is formed. Electromagnetically induced heat is proportional to the square of the electric field strength; Delfino et al. suggested that bore-contact RF burn injuries result from the strong electric field¹⁶ near the capacitors of the RF transmit body coil.^28–30 Thus far, the mechanisms of RF burn injuries remain insufficiently understood to prevent their occurrence.

Safety Standard

Specific absorption rate (SAR)

RF heating is quantitatively evaluated by the SAR, which is the amount of heat absorbed per unit mass of a human body. Analytically, this value is calculated for a simple homogenous sphere with radius R placed in a uniform RF magnetic field. The total heat generation P due to the RF eddy currents is³¹

$$P=\frac{\sigma D\pi {\omega }^2{B}_1^2{R}^5}{15},$$ (1)

where $\sigma$ is the electrical conductivity of the substance in the sphere; D is the duty cycle of the RF pulse, which is the rate of the RF pulse duration; $\omega$ is the angular frequency of the RF magnetic field; and B₁ is the RF magnetic pulse amplitude. By dividing Eq. 1 by the mass of the sphere, the average SAR (SAR_ave) is expressed as

$$SA{R}_{ave}=\sigma D{\omega }^2{B}_1^2{R}^2/\left(20\rho \right),$$ (2)

where $\rho$ is the density of the substance in the sphere. As indicated by Eq. 2, the SAR is proportional to the square of $\omega$ and hence to the square of the static magnetic field strength, and it tends to increase with the size of the sphere.

In MRI examinations, SAR_ave is estimated using the transmission RF power (P_trans) and the quality factor (Q value) of the RF transmit coil, with (Q_l) and without (Q_u) the subject load. P_trans, Q_l, and Q_u are automatically known to the MRI system before the scan. The whole-body SAR_ave of a patient is calculated using the following equation:³²

$$SA{R}_{ave}=\frac{P_{trans}\left(1-Q_l/Q_u\right)}{M},$$ (3)

where M is the mass of the patient. More precisely, taking into account the partial mass of a patient in an exposed area of B₁, the partial-body SAR_ave is calculated using the partial mass for M in Eq. 3. The partial mass is estimated according to the patient’s position in the MRI scanner. Moreover, using the patient’s height and weight, the patient’s body is usually modeled as a variety of homogeneous cylinders.

The upper allowable SAR values for safe MRI examinations are indicated in Standard 60601-2-33 of the International Electrotechnical Commission (IEC)³³ (Table 2). In addition to the whole-body and partial-body SAR_ave limits, the head SAR_ave limit, which corresponds to the head transmit coil, is defined. The whole-body SAR_ave limit value decided is based on environmental temperatures below 25°C; this limit value must be reduced when the environmental temperature rises. The local SAR limits in Table 2 are the values for MRI examinations using local transmit coils, which are coils other than the volume transmit coil (e.g., whole-body transmit coil and head transmit coil) and are commonly used in spectroscopic applications.³³ According to the physiological effects of static, gradient, and RF magnetic fields, the operating mode classifies the necessity of medical supervision (first-level-controlled operating mode) and approval of the investigational review board (second-level-controlled operating mode), whereas the normal operating mode is applied in clinical practice. The FDA also regulates the upper limits of whole-body and head SAR_ave for domestic clinical practice in the United States³⁴ (Table 3), while regulations in the European Union and Japan are based on the IEC standard. Although the IEC determines the limit values for averaging through 6-min imaging, the FDA’s values are averaged over a longer scan time: 10 min for head SAR_ave and 15 min for whole-body SAR_ave. The IEC also restricts the short-term SAR (any 10 s during the scan) to twice the 6-min value.

Table 2.

Safety SAR limits in the IEC standard

Operating mode	Whole-body SAR (W/kg)	Partial-body SARa (W/kg)	Head SAR (W/kg)	Local SAR (W/kg)b
				Headc	Trunk	Extremities
Normal	2	2–10	3.2	10	10	20
First-level controlled	4	4–10	3.2	20	20	40
Second-level controlled	> 4	> (4–10)	> 3.2	> 20	> 20	> 40

Averaged SARs over 6-min RF exposure. ^anormal operating mode: Partial-body SAR = 10 W/kg − (8 W/kg × exposed PATIENT mass/PATIENT mass) and first (second)-level-controlled operating mode: Partial-body SAR ≧ 10 W/kg − (6 W/kg × exposed PATIENT mass/PATIENT mass). ^bAveraged over mass of 10 g. ^cIn cases where the orbit is in the field of a small LOCAL RF TRANSMIT COIL, care should be taken to ensure that the temperature rise is limited to 1°C. SAR, specific absorption rate.

Table 3.

Safety SAR limits in the FDA guidance

Site	SAR (W/kg)	Time (min)
Whole body	4	15
Head	3.2	10

SAR, specific absorption rate.

The SAR_ave value is estimated using Eq. 3 and is displayed on the scanner console before running a scan; the scan proceeds when this value is lower than the upper limit value determined by the manufacturer. However, the displayed SAR_ave is inaccurate because Q_l and Q_u are not measured in each scan; they are assigned conservative preset values in the factory to achieve a sufficient safety margin for SAR_ave.^32,35 The displayed SAR_ave values are usually larger than the actual values;^19,36,37 however, the SAR_ave values are sometimes underestimated,^32,35 and the risk of an excessive SAR remains.

The local SAR limits, i.e., the SAR values averaged for 10-g tissue, were determined by the IEC for local transmit coils (Table 2). These limit values also lead to safety concerns in clinical scans using volume coils. However, in commercial clinical MRI systems, the local SAR cannot be monitored. Although each scan is performed when the estimated whole-body SAR_ave value is below the limit, the safety of the local SAR is not ensured due to the possibility of a local concentration of induced RF eddy currents that may cause burn injuries. Kainz pointed out this concern in preliminary and as-yet unpublished results of a phantom study: heating can result in a 48°C temperature rise in the normal operating mode of a 1.5T MRI system, with a maximum permissible whole-body SAR_ave of 2 W/kg for an insulated straight wire (20 cm) with 1-cm-long bare ends.³⁸ Therefore, a precise evaluation of the local SAR is crucial for preventing RF burn injuries.

Even with the same parameter settings in MR imaging, large variations in the displayed SAR_ave values were reported among different MRI systems,^39,40 suggesting that the displayed SAR_ave does not always guarantee the safety of MR examination. Another preliminary study indicated that large errors in the displayed SAR_ave values were observed in experiments based on the standard F2182 provided by ASTM International (see subsection “Assessment standards of RF heating due to implants”).³⁸ To avoid these errors, the root mean square of B₁⁺ (B₁⁺_rms) was introduced as a direct measurement of the RF electromagnetic field. B₁⁺ refers to the rotating component of B₁ for exciting spins, B₁^- refers to the anti-rotating component that does not function for spin excitation, and B₁^- for the receiver coil is used to represent the physical property of the MR signal, according to the mathematical formulation of a wave propagating in the opposite direction to that of the transmission wave.^41,42 B₁⁺_rms is defined as

$$B_{1rms}^{+}=\sqrt{\frac{{\int }_0^{t_x}{B}_1^{+}{\left(t\right)}^{2}dt}{t_x}},$$ (4)

where B₁⁺(t) is the RF pulse waveform at the center of a volume RF transmit coil, and t_x is the evaluation time, i.e., any 10-s period of the scan sequence used to average B₁⁺(t)² for all clinical scan sequences with various TRs.³³ Since B₁⁺(t) is designed for each pulse sequence, independent of the MR hardware, the B₁⁺_rms value is an RF exposure metric based on the scan sequences and is unaffected by variations in the MRI system. As the SAR is proportional to the square of B₁²³ and because 95% of the B₁ field in conventional quadrature excitation using volume transmit coils is homogeneous and is represented by B₁⁺,¹⁴ the SAR_ave in most clinical MR examinations using a volume transmit coil is proportional to the square of B₁⁺_rms. In addition to the displayed SAR_ave value, since 2013, it has been a requirement for B₁⁺_rms to be displayed on the scanner console.⁴³ This value is used to quantify the RF exposure heating due to implants, using the experimental relationship between B₁⁺_rms and the worst-case local SAR based on ASTM F2182 (see subsection “Assessment standards of RF heating due to implants”). The safety limit of B₁⁺_rms for an implant has been determined by implantable device manufacturers as an MR conditional value, for example, 2.0 µT at 1.5 T for a deep brain stimulation (DBS) system (Medtronic DBS system)⁴⁴ and 2.8 µT at 3 T for pacing systems (Advisa DR MRI SureScan and Advisa SR MRI sureScan).⁴⁵ Before the scan of a patient with such implants, the B₁⁺_rms of each scan displayed on the scanner console should be adjusted to lie within the safety limit by changing MRI parameters such as the TR or the echo train length. For MRI systems that cannot display B₁⁺_rms on their console, the SAR_ave of each scan for such patients is further restricted by implantable device manufacturers, e.g., ≤ 0.1 W/kg for the DBS system.⁴³ In addition to the MR conditional B₁⁺_rms values of some implants, the B₁⁺_rms limit (3.2 µT) for patients with implants under 1.5T MRI with circular volume transmission was determined in a safety imaging parameter set called the fixed parameter option: basic (FPO:B). This parameter set has other limit values for heating during MR examination: peak B₁⁺ and dB/dt values of the gradient magnetic field. The FPO:B is a set of imaging parameters for safe MR examination of patients with implantable medical devices and is used as a simple MR conditional term for labeling device products.³³

Temperature

The IEC determined the limits of the maximum temperatures of the human body during MRI examinations with regard to both core and local tissue temperatures³³ (Table 4). When the human body is exposed to an RF field, the body temperature is regulated in response to RF heating by increasing skin blood flow and sweating for heat dissipation.⁴⁶ This thermoregulation is inefficient at high heating levels, and fatal adverse effects, such as heat exhaustion and heat stroke, may occur. In one study, thermoregulation was modeled, and it was predicted that the core temperature of a lightly clothed healthy subject (37°C) could rise by 0.6°C at room temperature (24°C) during RF exposure under a whole-body SAR of 4 W/kg,⁴⁷ which is the limiting value in the first-level-controlled operating mode (Table 3). Although the body temperature rose by 0.5°C after RF exposure with a whole-body SAR of 0.1–1.6 W/kg for patients, including those with impaired thermoregulation, no adverse effects were observed.^48,49 According to these results, the international non-ionizing radiation committee of the International Radiation Protection Association (INIRC/IRPA) previously recommended limiting temperature rises due to RF exposure to 0.5°C for infants, pregnant women, and individuals with cardiocirculatory impairments, although no adverse effects were expected for temperature rises within 1°C for whole-body exposure or exposure of the head and trunk.⁵⁰ A review of thermoregulation suggested that 39°C could be a conservative threshold for thermal protection of the human body, according to evidence that there no apparent adverse effects occur below 39°C.⁵¹ Therefore, it is reasonable that the temperature limits and the limit of core temperature rise were set as 39°C and 0.5°C, respectively, for the normal operation mode to ensure patient safety.

Table 4.

Temperature safety limits in the IEC standard

Operating mode	Maximum core temperature (°C)	Maximum local tissue temperature (°C)	Rise of core temperature (°C)
Normal	39	39	0.5
First-level controlled	40	40	1

For the second-level-controlled operating mode, determining the limits is the responsibility of the investigational review board. IEC, International Electrotechnical Commission.

As the tissue damage caused by heat depends on the temperature and its duration, the thermal dose, which is the cumulative equivalent minute at 43°C (CEM43°C), has been introduced to MRI examinations.⁵² CEM43°C is the duration in minute of tissue exposure at 43°C and reflects the equivalent tissue damage caused by this thermal exposure. The cell death rate depends on the temperature and is approximated using the following equation with the temperature dependence constant (R),⁵² which differs below and above the break point of the temperature (43°C)—1/4 for T < 43°C and 1/2 for T > 43°C—according to a hyperthermia study.⁵³

$$R^{k\left(43-\mathrm{T}\right)}.$$ (5)

This equation is normalized to the cell death rate with heat exposure at 43°C, and k is a unital parameter (1/°C). The tissue temperature T(t) changes with time (t) during the MRI examination. CEM43°C is defined as

$$\mathrm{C}\mathrm{E}\mathrm{M}{43}^{\mathrm{o}}\mathrm{C}={\int }_0^{t_e}{R}^{k\left(43-\mathrm{T}\left(t\right)\right)}dt,$$ (6)

where t_e is the duration of the MRI examination. Using Eq. 6, various temperature–time histories can be translated into an equivalent number of minutes of heating at 43°C. The proposed guideline for CEM43°C is categorized into patient conditions of compromised/uncompromised thermoregulation and controlled/uncontrolled conditions of MRI examination (Table 5). Under controlled conditions, a medical doctor or a dedicated trained person should respond instantly to the heat-induced physiological stress of a patient. For patients with compromised thermoregulation under uncontrolled conditions, the limiting CEM43°C value is not defined; instead, a limiting temperature of 39°C for the normal operation mode in the IEC standard (Table 4) is adopted. To protect thermosensitive tissues, e.g., the central nervous system or eyes,⁵⁴ the conservative thermal dose is limited to 2 min of CEM43°C, even for uncompromised thermoregulation patients in regular clinical practice (uncontrolled conditions) (Table 5). Under controlled conditions, the upper thermal dose limit for these patients is 9 min of CEM43°C.

Table 5.

CEM43°C thermal dose guideline

	Compromised thermoregulationa	Uncompromised thermoregulation
Uncontrolled conditions	39℃c	2 min
Controlled conditionsb	2 min	9 min

^aAll persons with impaired systemic thermoregulation (elderly, young children, or patients with fever) or reduced local thermoregulation due to scar, edematous tissue, and nerve diseases, including diabetic neuropathies and paraplegia. ^bA medical doctor or a dedicated specifically trained person is available to respond instantly and adequately to heat-induced physiological stress and patient complaints during MR. ^cThe safety limit temperature is defined for this condition. CEM, cumulative equivalent minute.

To comply with temperature (Table 4) or CEM43°C (Table 5) guidelines, information on the temperature in the core of the human body or in each piece of tissue is required. However, no techniques are available to monitor this information during an MRI examination; hence, simulation studies on temperature mapping of various patient cases have recently been performed according to these guidelines (see “Numerical Simulation of RF Heating”).

Assessment standards of RF heating due to implants

As RF exposure heats medical implants,⁵⁵ the assessment standard for RF heating (ASTM-F2182)¹² was established for passive implants, such as hip and knee prostheses. As per this standard, the local SAR is assessed by measuring the temperature rise on or near the implant, which is immersed in a gelled saline phantom with electrical and thermal properties similar to those of the human body (see subsection “Evaluation of SAR” in “Experimental Evaluation of RF Heating”). The temperature rise produced by approximately 15 min of RF exposure is monitored with fiber-optic or fluoroptic thermometry probes. Although ASTM F2182 necessitates measurement in the worst-case configuration and orientation of the passive implant, active implantable medical devices (AIMDs), such as pacemakers which have various configurations with leads, are beyond its scope. An assessment standard for AIMDs has also been established in ISO/TS 109474:2018.¹⁴ In this standard, the RF electric field is considered for both the experiment and the simulation. This is because the RF electric field is also produced in an MR scanner during the B₁ exposure; this incident electric field is scattered by each segment of the implants (including leads), and all the scattered RF electric fields, which are mathematically formulated based on the incident electric field and the implant configuration, determine the SAR distribution.⁵⁶ This standard provides four tiers of assessment methods for local RF power deposition around an AIMD, from the simplest temperature measurement method to the rigorous simulation method. Tiers 1 and 2 are for small AIMDs, whose lengths are far shorter than the RF wavelength in the human body, i.e., electrically short AIMDs such as cochlear implants. Tiers 3 and 4 are for AIMDs with large configurations that include leads, e.g., those of a pacemaker. This four-tier approach¹⁴ is currently applicable to 1.5T MRI systems with a cylindrical bore and body coil excitation.

Experimental Evaluation of RF Heating

Evaluation of SAR

The SAR_ave of RF-exposed homogeneous phantoms can be measured using the calorimetric method provided by the National Electric Manufacturers Association.⁵⁷ This method was developed to determine the SAR_ave values of specific phantoms, which were designed to provide an RF coil loading equivalent to that of a human, by measuring the temperature rise of the phantom filler, such as an aqueous sodium chloride solution. The method requires the value of the phantom’s heat capacity, a temperature measurement system having accuracy within 0.1°C, and a long exposure time to produce a temperature rise at least 20 times larger than the error of the temperature measurement system. To assess the displayed SAR_ave on the MRI console, Stralka and Bottomley developed an RF dosimeter that monitors the true SAR_ave value of a small phantom. The loading of the dosimeter system is equivalent to that of an average human head or body. The accuracy of the monitored value was approximately 5% at 1.5 T.³² Further research improved its accuracy to 3% at 3 T by reducing the interference of the dosimetry circuitry in an MRI scanner.³⁷ The pulse energy method can be used to determine the SAR_ave either in a phantom or a human by measuring the forward and reflected RF powers at the transmit coil input and the coil power losses, that is, the Joule heat in the coil.⁵⁷ Since this method requires a complex measurement setup and an expert engineer, its implementation in clinical practice is difficult.

Local SAR measurements in the phantom are stipulated in ASTM F2182.¹² The local SAR is obtained from the initial slope of the graph of temperature changes measured with probes inserted in the ASTM phantom, using the following equation (neglecting the thermal diffusivity):

$$SAR=c_s\frac{\mathrm{\Delta }T}{\mathrm{\Delta }t},$$ (7)

where c_s is the specific heat capacity of the gel used in the phantom, and $\mathrm{\Delta }T$ is the temperature rise during time interval ( $\mathrm{\Delta }t$). The SAR can also be determined using the electric-field strength (E), based on the following equation:

$$SAR=\frac{\sigma E^2}{2\rho }.$$ (8)

The E distribution in an ASTM phantom with a straight stainless steel rod was measured using a light-emitting diode array with a phototransistor, and good congruence with the temperature rise distribution was obtained.⁵⁸

To investigate the in vivo local SAR, Katscher et al. introduced a noninvasive SAR mapping technique based on electrical properties tomography (EPT).⁵⁹ The obtained SAR map of the phantom exhibited a good correlation with that calculated from the numerical simulation. This mapping method was applied on human volunteers, and the individual SARs were mapped.⁶⁰ Although the SAR can be noninvasively mapped using this method, the obtained SAR values contain theoretical errors owing to the algorithmic limitation; i.e., the z and B₁^- components of the RF magnetic field are not accounted for. Thus, the SAR values obtained using this method tend to be lower than those obtained from numerical simulations (see “Numerical Simulation of RF Heating”); the average SAR (32%/35% for a phantom/human) and peak local SAR values of 10-g tissue (SAR_10g) (26%/27%) were lower.⁶⁰ To consider the effects of the z and B₁^- components of the RF magnetic field, a deep-learning method for predicting SAR on the basis of B₁⁺ mapping was developed. The probability of underestimating the peak local SAR was reduced from 24% (the EPT-based method) to 13%, as validated through an experiment involving MRI of volunteers at 7 T.⁶¹

Evaluation of temperature

MRI parameters, such as the proton density,⁶² relaxation times,⁶³ diffusion coefficient,⁶⁴ and proton resonance frequency (PRF),⁶⁵ change with respect to temperature. Using these properties, various MRI temperature measurement methods have been developed, and the temperatures of tissue samples^66,67 and in vivo tissues⁶⁸ have been successfully mapped. Among these methods, the PRF-based method is the most commonly used and has high precision.^69,70 The nuclear magnetic resonance phenomenon associated with the temperature dependence of the PRF (0.01 ppm/°C) was first observed in 1966,⁷¹ and the temperatures of phantom and in vivo human tissues were measured using the PRF-based method in 1995^65,72 after the advent of MRI. This method was successfully used to measure the temperature rise of phantoms due to RF exposure in various MRI systems, e.g., a saline phantom at 1.5 T and 3 T,^73,74 an aqueous cobalt phantom at 4T,⁷³ and a gelatin phantom at 7 T.⁷⁵

Temperature monitoring is crucial in high-intensity focused ultrasound (HIFU) ablation,⁷⁶ and the PRF-based method has been applied in MRI scanners implemented with the HIFU system to determine the focused temperature rise for cancer treatment.^77–80 To obtain a temperature map with high spatial and temporal resolution, a method that consecutively acquires the undersampled data of 3D imaging was developed. Using a retrospectively reconstructed temporal image set, temperature rise mapping of a rabbit thigh during HIFU heating was performed at 3 T with a temporal resolution of 2.0 s, and the temporal temperature changes were successfully mapped with a high spatial resolution.⁸¹ The temperature uncertainty of this mapping technique is approximately ± 1°C for the human brain. However, the reconstruction process requires several minutes to complete. Furthermore, by leveraging the power of computing, using graphics processing units for compressed-sensing-like imaging, a “real-time” MRI temperature mapping technique based on the PRF-based method was developed, and a 1.2-s scan time with an accuracy of ± 0.5°C for the 3D volume of a phantom was achieved.⁸²

To map the temperature rise due to RF heating, the PRF method was first applied to the forearm for 2-min RF heating in a 3T MRI.⁸³ Considering the clinical application of the PRF method, the scan time for which does not notably increase the total scan time, an asymmetric spin-echo technique⁸⁴ or compressed sensing⁸⁵ has been used to achieve fast temperature rise mapping in vivo. To monitor the whole-body temperature rise induced by RF exposure using the PRF, further development is needed for clinical practice, such as addressing the influence of motion, because the accuracy of the measured temperature is affected by human motion, e.g., that caused by respiration.⁸⁶

Numerical Simulation of RF Heating

Principal methods

To simulate RF heating, Maxwell’s equations for the electromagnetic field need to be solved. The analytical solutions can only be derived for simplified cases, such as a sphere (Eq. 2).⁸⁷ For complex cases, such as a human body, numerical simulation methods are used to approximate the solutions of Maxwell’s equations. For the numerical simulation of RF heating, the finite-difference time-domain (FDTD) method, finite integration technique (FIT), and finite element method (FEM) have mainly been used.

The FDTD method discretizes arbitrary 3D geometries using small orthogonal meshes known as Yee cells to approximate the differential forms of Maxwell’s equations.⁸⁸ This method is a time-domain method that solves Maxwell’s equations using a time integral algorithm. The time-domain method has the advantage of a shorter computation time than that of the FEM frequency-domain method mentioned below. The FDTD method shapes curved surfaces of the modeling subjects using discrete meshes and causes errors in the inhomogeneous “partial volume” mesh, such as the subdivision of curved surfaces. These errors are reduced by increasing the number of meshes, i.e., reducing the mesh size or applying extended processing;⁸⁹ however, the computation time increases, and high-performance hardware is needed. Although a mesh size of 1 mm³ is normally considered to be sufficiently small,^90,91 the number of meshes should be optimized according to the complexity of the geometries, by considering the tradeoff between accuracy and computational ability.

The FIT discretizes 3D geometries into Maxwell’s grids, determining the electric field along the side of each mesh cell and the magnetic flux crossing each mesh cell surface.⁹² This method involves both time- and frequency-domain algorithms. It has been mathematically proven that the FIT in the time domain is equivalent to the FDTD method for Cartesian grids.⁹³ The FIT can use any type of mesh that reduces the orthogonal “partial volume” mesh of the complex shape, such as a human model.⁹³ In this method, the integral form of Maxwell’s equation is first applied to each discretized Maxwell’s grid, improving the calculation efficiency for nonorthogonal grids.

The FEM is a well-known simulation method for numerically solving partial differential equations in various fields. In electromagnetic analysis, the FEM is a frequency-domain method that is disadvantageous under high frequencies, as it solves Maxwell’s equation at each frequency. The FEM typically uses tetrahedral meshes,⁹⁴ which can model complex shapes; however, it incurs higher computational costs (hardware or time) than the FDTD and FIT do.⁹⁵

Models

To simulate RF heating, computational models require precise information on the frequency-dependent electromagnetic properties of conductivity, permittivity, and permeability. The widely used phantoms in RF heating examinations, such as the ASTM phantom,¹² can be easily modeled for simulation because of their simple structure and materials. In contrast, the human body model requires detailed anatomical information and the electromagnetic properties of each tissue. The US National Library of Medicine undertook a virtual human project in 1986 and provided cross-sectional cryosection, CT, and MRI images of both males and females for scientific and medical uses.⁹⁶ From these public images, whole- and partial-body models were created for SAR simulations.^60,97–99 The electromagnetic properties of the relevant tissues are obtained from databases such as IT’IS¹⁰⁰ or the literature.^101,102 Instead of using public images, individual modeling has been performed using CT or MRI images of volunteers, e.g., a forearm model from MRI images⁸³ and anatomical heart¹⁰³ and bone models from CT images.¹⁰⁴ In particular, for general usage, MRI data acquisition of a single subject was performed, and an adult human model referred to as Norman was created.¹⁰⁵ Subsequently, a Japanese adult female model, called Naomi, was created by the same research group.¹⁰⁶ In 2010, a series of human body models—referred to as the “virtual human family”—comprising a male model (Duke), a female model (Ella), and two children models (boy: Billie and girl: Thelonious) was developed using MRI scan data from volunteers selected based on the worldwide average height and body mass index for adult models and the German statistics for children models.¹⁰⁷ This virtual family was expanded to a virtual population with the inclusion of models of both genders ranging from 3 to 84 years old, by recruiting volunteers according to the body standard of each gender and age; the 3-year-old child model was created by morphing the 5-year-old one. The spatial resolutions of all the models were improved to a minimum of 0.5 × 0.5 × 0.5 mm³ via re-segmentation.¹⁰⁸ In addition, pregnant models were developed for different pregnancy periods on the basis of a 26-year-old female model.

RF coil modeling

Various RF transmit coils have been modeled for numerical simulation, such as the transverse electromagnetic (TEM) resonator,^97,109–113 the array coil,¹¹⁴ the surface coil,^83,97,115 the saddle coil,⁹¹ and birdcage coils,^{29,30, 59, 97,98,116–134,} for field strengths ranging from 1.5 T to 9.4 T. The birdcage coil, which consists of end rings, rungs, and capacitors,^135–137 is the most widely used coil for clinical MRI. There exist three types of birdcage coils: the low-pass type with capacitors on the rungs, the high-pass type with capacitors on the rings, and the bandpass type with capacitors on both the rungs and the rings.^136,137 The number of rungs normally ranges from 8 to 32.^{121,135–137}

SAR simulation

Numerical simulations have been widely used to estimate the SARs of phantoms^{59,60,125,138} and computational human models.^60,139 Simulation results have been used as a gold standard to validate the results of experimental methods, such as EPT. In addition to validation studies, RF heating simulations have been conducted to investigate the dependence of the SAR on the RF frequency and transmit coil design, as well as on the human model (age and size), patient position, and posture in the MRI scanner.

A simulation study revealed the changes in the SAR distribution in a human head at various RF frequencies with a TEM resonator; a high SAR was observed in the fringe of the brain at 64 MHz and at the center of the brain at 340 MHz.¹¹¹ In addition, the maximal local SAR was significantly larger than the SAR_ave values in the normal operation mode (Table 2): 3–5 times the partial-body SAR_ave limit for a head model (64–400 MHz) and 10–13 times the whole-body SAR_ave limit value for a body model (64–128 MHz). Ibrahim et al. simulated the SAR of a head model for 8-, 16-, and 24-strut TEM resonators at 340 MHz;¹⁰⁹ the peak SAR was almost equivalent among the three coils, but a conspicuous inhomogeneity in B₁ was observed for the 8-strut resonators. Liu et al. compared birdcage coils with two ports (quadrature), four ports, and many sources (ideal), finding that the B₁⁺ field patterns and SAR levels simulated with two different human models were similar.⁹⁸ To achieve homogeneous RF excitation in high-tesla MRI systems, a multi-transmit mode (parallel transmit mode) that manipulates the RF currents of the body coil channels—RF shimming—has been introduced, which improved the B₁ homogeneity.¹⁴⁰ The SAR distribution is determined by the E field at each point of the imaged subject (Eq. 8), and this positional E field of the multi-transmit mode is the summation of fields that originate from each channel. The SAR distribution of this mode is calculated using the E field produced by each channel (Q-matrices) and the waveform of the RF current that flows in each channel.⁹⁹ During RF shimming, the SAR distribution (and hence the maximum local SAR) changes because the waveform of each channel is modulated to optimize the RF homogeneity; in particular, the dynamic parallel transmission modulates both the amplitude and phase of the RF waveform of each channel.⁹⁹ However, with regard to the SAR, this mode has a disadvantage: a simulation study with virtual family human models revealed that the whole-body SAR was increased by a factor of 1.6 and that the peak local SAR was increased by up to 13.4 in comparison with the standard circular polarization.¹²⁰ To reduce the SAR and improve the B₁ homogeneity in high-tesla MRI systems, a novel RF coil system concept was proposed, in which a single channel of a transmit/receive coil rapidly rotates around the subjects during the scan.¹⁴¹ A simulation of this rotating RF coil system with a head model at 7 T showed a lower SAR than that of the 8-channel parallel coil array, with an improvement in the B₁ homogeneity.¹⁴²

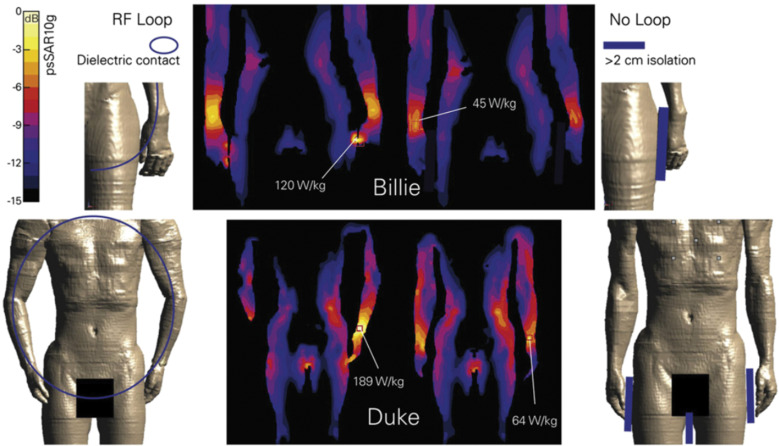
Model-dependent SAR characteristics exist as well. An SAR simulation at 1.5 T showed a lower (10–75%) peak SAR_10g in children (age 5–14 years) and a fetus (36 weeks of gestation) than in adults.¹¹⁸ Another study indicated lower peak SAR_10g values for neonate models (40 weeks of gestation) than for an adult model at 1.5 T and 3 T.¹⁴³ The human model, which was referred to as Fat because it had the largest size in the virtual family, exhibited a higher peak local SAR than Duke and Ella did, indicating that SAR depends on the coil-body proximity: if the body is closer to the coil, more energy is delivered from the nearby coil rung, particularly in the multi-transmit mode.¹²⁰ With regard to the patient position in a transmit coil, in a study involving 7T MRI, the head SAR in a head transmit coil was mapped by shifting the patient model translationally in each direction by 20 mm. The results indicated that the highest local SAR_10g varied by up to 14%, 12%, and 22% in the x-, y-, and z-directions, respectively.¹²⁷ In addition, a high local SAR_10g was observed for the models when the arm was placed near the coil rung¹¹⁹ or the end ring of the transmit coil,¹²⁹ due to the high electric field strength near the rungs and end rings. The typical arm loops in Duke and Billie significantly increased the maximal peak local SAR_10g compared with that in the unlooped postures (Fig. 2).¹¹⁸ An experimental and simulation phantom study mimicking a human arm contacting the body trunk indicated that reducing the contact areas increases the temperature rise and the peak SAR of 1-g tissue.¹⁴⁴ The same tendency was simulated using a human model with two different postures of arm–arm contacts forming closed loops. This dependence of the contact area on the SAR is understood as a concentration of the magnetically induced currents. Moreover, a correlation between the SAR and the magnetic flux in a formed loop is observed. However, electromagnetic induction remains unclear from a quantitative standpoint, and further analyses are needed.

Computational human models are sufficiently flexible to model not only healthy humans but also specific pathological models. An RF heating simulation of a brain tumor patient (the electrical properties of the tumor tissue were obtained from the results of an EPT study¹⁴⁵) at 7 T indicated a 30% local SAR increase in the tumor; the conductivity increase for the tumor was twice that for the normal tissue, which suggests a substantial local SAR for the brain-tumor patient.¹⁴⁶

Temperature simulation

The in vivo temperature has also been simulated, accounting for the thermoregulation function of humans,⁴⁶ which is analytically modeled using the Pennes’ bioheat equation model¹⁴⁷ or the discrete vessel model.¹⁴⁸ The Pennes’ bioheat equation model describes the temperature (T) change with respect to SAR due to heat transfer to perfusing blood, as follows:¹⁴⁷

$$\rho \mathrm{c}\frac{dT}{dt}=\mathrm{\nabla }\left(k\mathrm{\nabla }T\right)-{\rho }_b{c}_b{w}_b\left(T-T_{blood}\right)+Q_m+SAR\rho ,$$ (9)

where $\rho$, c, and k are the tissue density, the specific heat capacity of the tissue, and the tissue thermal conductivity, respectively. ${\rho }_b$, $c_b$, and $T_{blood}$ are the blood mass density, the blood specific heat, and the arterial temperature, respectively. $w_b$ is the blood perfusion rate. $Q_m$ is the heat generated by metabolism. The discrete vessel model considers convective heat transport due to discrete vessels by accounting for the geometrical structure of the vessels, the perfusion, and the tissue-vessel heat exchange.¹⁴⁸ The simulated temperatures of a head obtained using the different thermoregulation function models were almost identical; the maximum temperature was only 0.16°C higher for the Pennes’ bioheat equation model than for the discrete vessel model under an exposure of an averaged head SAR as 2.6 W/kg for approximately 30 min.¹²³ However, Pennes’ bioheat equations are usually used for RF heating simulations because of their simplicity, as they do not require precise anatomical information on the blood vessel network.¹²³ Using Pennes’ bioheat equations, both SAR and temperature simulations were performed for a human head model with a birdcage transmit coil at 64 MHz, a TEM, and a surface transmit coil at 300 MHz under an RF exposure of 3.2 W/kg head SAR_ave, which is the maximum allowable value in the normal operating mode.⁹⁷ Although the safety limit of the temperature rise is 0.5°C for this case (Table 4), the temperature rise in the brain tissue exceeded 1°C for the surface coil transmission, indicating that caution should be exercised when a surface transmit coil is used.

The relationship between the local SAR and the local temperature is not straightforward because of spatial differences in physiological responses, such as the augmentation of perfusion and sweating. To investigate the effects of perspiration, radiation, and perfusion on the heat transfer, a temperature simulation of the human head model was performed with and without consideration of the heat transfer.⁹⁷ The simulated temperatures in the two cases were almost identical, i.e., within 0.02°C for 30-min RF exposure of 3.0 W/kg (the maximum allowable SAR by the FDA at the time) with a head-sized TEM coil at various frequencies (64–400 MHz). This result indicates that the effect of temperature-induced physiological changes is negligible in the human head within a head-sized volume coil at various frequencies when the head SAR_ave is within the safety limit.¹¹³ In contrast, for a body-sized volume coil, simulation of whole-body RF exposure for 1 h within the FDA-specified safety limit (4 W/kg) indicated peak tissue temperatures of 60°C for the nonregulated model and 42.8°C for the thermoregulated model, which accounted for the temperature-dependent perfusion augmentation.¹²⁸ The results of the temperature simulation of a phantom using Pennes’ bioheat equations agreed with the experimental results obtained using the PRF-based method during the RF exposure of off-resonant frequency driving for heating from an adjacent circular surface coil; however, the simulation of a forearm with the same RF heating indicated a maximum temperature rise of 2°C, which is 25% higher than the experimental value.⁸³ The primary reason for this disagreement may have been the differences in the tissue electromagnetic properties between the database values for the simulation and the volunteers’ (see subsection “Validity of simulation”).

Simulation of RF heating due to implants

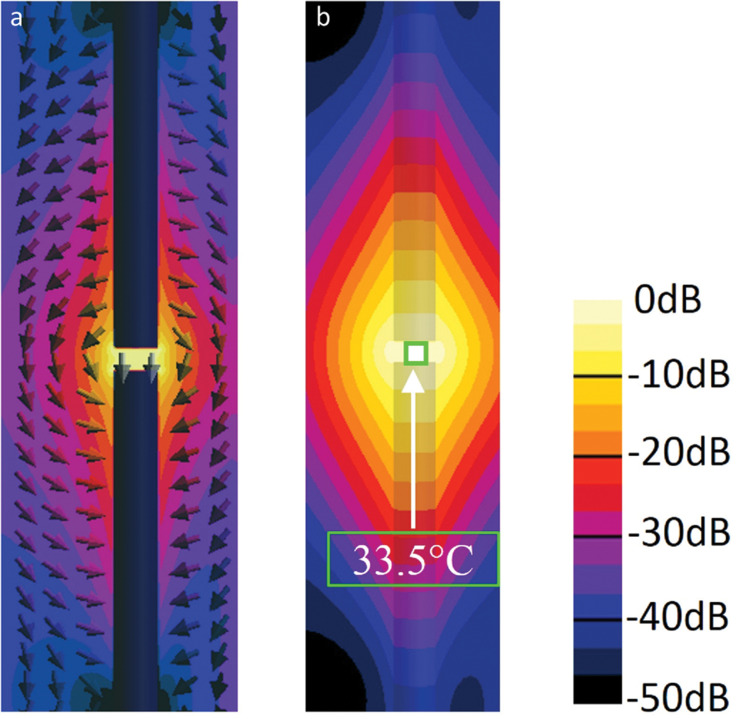
The numerical simulation method is also convenient for ensuring the MRI compatibility of implantable medical devices with regard to RF heating.¹⁴ The conventional experimental method for evaluating RF heating due to implants was introduced in ASTM F2182 (see subsection “Assessment standards of RF heating due to implants” in “Safety Standard”). Modeling of this experimental condition has revealed that the maximum SAR depends on the lengths of the implants and the positions and combination of the implants in the ASTM phantom. Liu et al. investigated how the SAR of an orthopedic fixation device (a metallic plate with four screws) changes with respect to the plate length when the plate is placed parallel to the B₀ direction in the ASTM phantom and observed the antenna effect; the SAR increased as the plate length approached the half-wavelength of the RF field in the phantom.¹²⁶ Simulation results for external fixation devices—screws, bars, and clamps that combine the screws and bars—immersed in the ASTM phantom indicated that reducing the depth from the surface of the phantom and increasing the clamp spacing increased the peak local SAR, yielding a maximum temperature rise of 59°C under permissible whole-body SAR_ave exposure (2 W/kg) in the normal operating mode for 15 min.²⁹ Muranaka et al. reported that the maximal temperature was observed on the tip of a humerus nail placed in a gel phantom where the curvature was large and the surface area was small.¹⁴⁹ Guo et al. evaluated the SAR and temperature by changing the combination of orthopedic implants (nails and plates) in the ASTM phantom; the average temperature rise in the dual-device case (two pieces of nail or plate) was 2.7 times larger than that due to a single device, suggesting that the combination of multiple implants changes RF heating significantly.¹⁵⁰ The authors also reported that when the two nails were placed 10 mm apart from each other, where a strong electric field was observed (Fig. 3), the temperature rose by 33.5°C (thick nails) and 45°C (thin nails; not shown in Fig. 3). Hence, when two implants are placed close to each other, the electric field in the gap enhances the heating.

Fig. 3.

Electric field and temperature rise distributions in the ASTM phantom with the immersed dual thick nail structure. (a) Electric field distribution and (b) temperature rise distribution for the dual 190-mm-thick nail structure oriented toward the static magnetic field direction with a 10-mm gap (highest area). The maximal temperature rise was 33.5°C (b). Reproduced with permission from reference 150.

Simulations of implants, such as aneurysm clips,¹⁵¹ cardiac stents,¹⁵² and hip prostheses,¹²² have also been performed with human models under different magnetic field strengths. A slight enhancement in the SAR surrounding an aneurysm clip has been observed; the temperature rise was up to 0.8°C at 7 T, exceeding the limit (0.5°C) when the 51.5-mm aneurysm clip was located in the right middle cerebral artery.¹⁵¹ RF heating of coronary stents under 7T MRI has also been investigated.¹⁵² Longer stents led to a higher maximal local SAR, as did a smaller angle between the electric field of the dedicated transmit coil and the long axis of the stent. By modeling a coronary stent with a cylinder, heating due to a stent in a blood vessel under RF exposure at 4.7 T was estimated in a phantom model, and a strong dependence of temperature on the blood flow was observed, i.e., 37.8°C (0% flow reduction), 42.5°C (90%), and 54.6°C (100%), indicating potentially hazardous heating of coronary stents with restenosis in MRI.¹⁵³ Even under the normal operating mode limit of whole-body SAR_ave (2 W/kg) at both 1.5 T and 3 T, the simulated local SAR close to the edge of a hip prosthesis exceeded the maximum partial-body SAR limit value. Although no safety regulation pertaining to the local SAR exists for MRI examination using a volume RF transit coil, a reduction in the transmission power for patients with this implant has been recommended.¹²²

The SAR, due to AIMDs, has also been simulated (see subsection “Assessment standards of RF heating due to implants” in “Safety Standard”). The local SAR values of DBS at 1.5 T were greater than or equal to those at 3 T, suggesting that 3T MRI should not be considered more dangerous than 1.5T MRI for patients with DBS leads.¹³² No clear rule-of-thumb for AIMD RF heating is available, and further simulation study is therefore needed.

Simulation of RF burn injuries

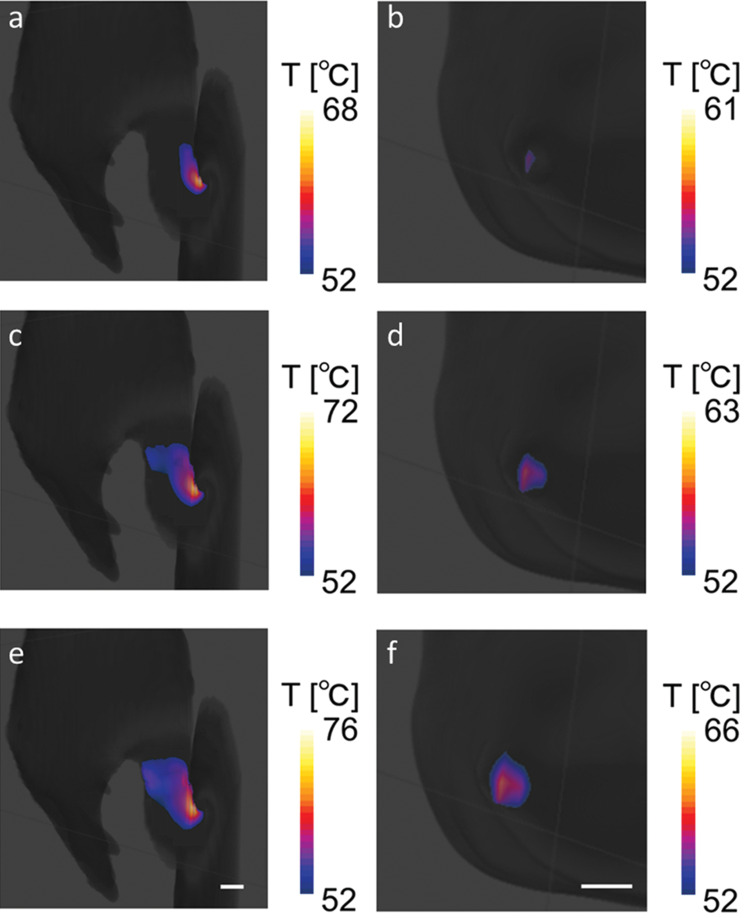
RF burn injury cases have been simulated to further understand the mechanism of such injuries from the standpoint of injury prevention. RF burn injuries occurring at the contact points (i.e., skin–skin contact between the thumb and skin of the thigh and skin–bore wall contact at the elbow) on the lateral side of the human body in an MRI scanner were modeled in silico and simulated.¹⁵⁴ The positional dependence of the local SAR on the contact points in an MRI scanner was observed; this result revealed that the local SAR peaked when the contact points were close to the end ring of the transmit coil. This positional dependence is explained by the intrinsic distribution of the electric field arising from the RF transmit coil; the electric field was remarkably strong around the edge of the transmit coil. The simulation also indicated that the highest SAR values led to a high temperature, causing burn injuries under the maximum allowable whole-body SAR_ave for the normal operating mode (Fig. 4). Simulation studies have drawn attention to the risk of RF heating in specific situations, e.g., patients with long implants¹²² or patient positions near the coil rungs and end rings.¹⁵⁴ The simulated values of the local and global SARs quantify the risks of RF heating on the basis of the SAR safety limits, and simulation of RF heating facilitates an understanding of the mechanism of RF burn injuries.

Fig. 4.

Maps of the skin surface temperature at (a and b) 3 min, (c and d) 4 min, and (e and f) 5 min for the thumb–thigh (a, c, and e) and elbow–bore wall (b, d, and f) contact cases. Temperatures above 52°C—the minimum temperature associated with a burn injury within 1 min of exposure—are mapped. The scale bar represents 10 mm. The maximum value of each color index is the maximum temperature of each mapped area (for visibility). Reproduced with permission from reference 154.

Validity of simulation

For validation, the temperature simulation results were compared with experimental results obtained using thermometry. The temperature rise in orthopedic implants placed in the ASTM phantom was simulated, and the results exhibited a good correlation with the experimental values, i.e., the differences were within 0.5°C.¹²⁶ In the simulation with Duke, small hotspots (maximum 39.8°C) were observed on the surfaces of both shoulders, and in an experiment involving a volunteer with anatomical dimensions similar to those of Duke, similar hotspots were observed within 1°C.¹²⁸

The electromagnetic properties of computable models are crucial for simulation. For the phantom study, the electromagnetic properties of the phantom composition can be easily determined. However, the tissue electromagnetic properties of humans are difficult to measure individually. The simulation uncertainties due to individual variations in electromagnetic properties have been investigated by varying the tissue electromagnetic properties by ± 10% in a human model. The uncertainty for the whole-body SAR simulation was 9%, and that for the peak local SAR simulation was 12%.¹²⁹ When the values of the tissue properties, such as the specific heat capacity or mass density, were increased by 10%, the calculated temperature changed by maximally 7%.⁸³ In addition, upon changing the specific heat capacity of tissue and blood (±10%), the metabolic heat generation rate (±20%), and the thermal conductivity of tissue (±20%), the uncertainties in the temperature rise were calculated to be 3% and 13% for the constant perfusion and thermoregulated (in which the perfusion changes with respect to the temperature) models, respectively.¹²⁸ Although the uncertainties of the constant perfusion model were less than those of the thermoregulated model, the perfusion rate properties used in the simulation were too simple to reflect actual thermoregulation, e.g., the constant perfusion rate only below the threshold temperature of 39°C.⁸³ In the larger RF power exposure simulation, a higher temperature was obtained for the constant perfusion model (60°C) than for the thermoregulated model (42.8°C).¹²⁸ Thus, the optimal thermoregulated model and tissue electromagnetic properties should be identified for accurate simulation.

Suggestions for Preventing RF Burn Injuries

Surveys in the United States, United Kingdom, and Japan have indicated that the key feature of RF burn injuries is “contact” (Table 1). The contact points where RF burns occur are classified into avoidable contacts, e.g., a calf-to-calf contact, and unavoidable ones with objects such as implants or tattoos (Table 6). An effective countermeasure to prevent RF burn injuries at avoidable contact points is avoiding contact with separation materials such as foam pads. A simulation study on skin-to-skin contacts of anatomic loop formation indicated that a 2-cm spacing significantly reduced the maximum local SAR at the contact points (Fig. 2).¹¹⁸ Although a further simulation study on the finger–thigh contact model indicated a significant reduction in the maximum local SAR with a 2-mm spacing,¹⁴⁴ the MRI guidelines provided by the MHRA recommended the use of 1–2-cm-thick foam pads to insulate the patient from cables, from the bore, and between limbs.¹⁵⁵ Therefore, the foam pads prevent RF burn injuries; however, the appropriate thicknesses and materials of the pads need to be determined. Since wetting the pad reduces the effectiveness,¹⁴⁴ the hydroscopic properties of the pad materials should be considered as well.

Table 6.

Classification of RF burn injuries and their countermeasures

Occurrence16	Contacting object	Contact type	Countermeasure/Caution
Contact with an object	Tattoo, implant, etc.	Unavoidable contact	Caution to the resonant length and positioning/direction in the scanner with respect to the RF transmit coila
	MR coil, cable, etc.	Avoidable contact	Avoid contact (using foam padb)
Skin-to-skin contact	Calf, thigh-thumb, etc.
Bore contact	Bore wall

^aThe exact countermeasures are still under investigation. ^bClothing or blankets as a form of insulation is not recommended.¹⁵⁵

For unavoidable contact with implants or tattoos,²⁷ attention should be paid to their lengths because the antenna effect increases the SAR when the length is equal to the half-wavelength. The RF wavelength is shorter inside the human body than in air because of the large permittivity of tissues. In addition to the RF wavelength, the RF electric field direction in the scanner should be considered because the electric field tangential to the implant dominantly determines the SAR.⁵⁶ In a simulation study, the highest SAR was observed when a stent was set parallel to the electric field, and the SAR decreased with an increase in the angle of the stent in the electric field direction.¹⁵² The orientation of the implant with respect to the local electric field direction inside the patient significantly affects the local SAR. The electric field distribution inside the ASTM phantom has been measured; the results indicated that the electric field in the body stem part was largely z-directional, whereas that in the shoulder, neck, and bottom parts was x-directional.⁵⁸ And significant implant heating was observed when a conductive rod was placed parallel to the measured local electric field in the ASTM phantom. When the long axes of implants or tattoos are orthogonal to the electric field, the SAR may be tolerable. However, further simulation with a computable human model is necessary.

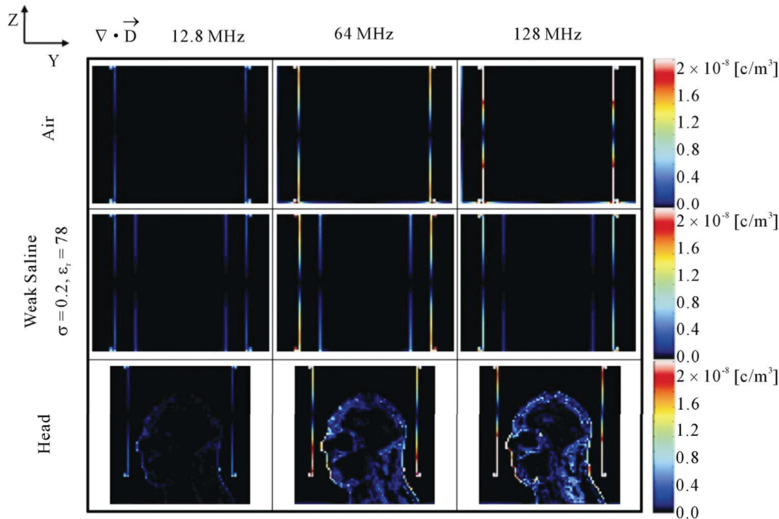
In addition, the simulation results indicated an increase in the SAR when the body approached the part of the transmit coil where the electric field was strong,^129,154 i.e., an edge or rung, depending on the coil type (e.g., high or low-pass). These results suggest a higher risk of RF burn injuries near the transmit coil. An ASTM phantom study with a straight wire (25 cm) set parallel to z-direction also revealed this tendency; when the wire in the phantom was placed close to the rung of the transmit coil, the maximum temperature rose.¹⁵⁶ The SAR at each point is determined from the electric field using Eq. 8. Based on electromagnetic analysis, the electric field is decomposed into a magnetically induced component and a conservative electric field component.¹⁵⁷ Although the former component has been considered as a major contributor to RF heating in MRI, the dominance of the latter component has been focused with increasing RF frequencies.¹⁵⁸ A conservative electric field is generated by RF alternating charged particles that are moved to the boundary of conductive substances, such as the surface of the human body or the coil.¹⁵⁸ The number of charged particles increases with the MR resonant frequency from the Maxwell’s equations, especially near the edge of the transmit coil where a strong electric field is generated (Fig. 5). Positioning that avoids such a strong electric field in the MRI scanner would reduce the risk of RF burn injuries.¹⁵⁴

Fig. 5.

Calculated volume charge density (∇⋅D) at 12.8 (first column), 64 (second column), and 128 MHz (third column) in an empty coil (first row) and a coil loaded with a weak-saline phantom (second row) and a head model (third row). Reproduced with permission from reference 158.

Conclusion

We summarized the RF burn injuries reported worldwide in recent decades and showed that “contact” on the human body is the primary cause of RF burn injuries. Even if compliance with the safety regulations pertaining to RF heating is ensured during MRI examinations, RF burn injuries occur, and the mechanism of these injuries requires further investigation. The development of numerical simulation techniques with computable human models is setting a precedent for precisely analyzing RF heating and is informing clinical practice. To prevent RF burn injuries, countermeasures and caution are recommended, focusing on avoidable or unavoidable “contact,” e.g., using foam pads to avoid “contact”; avoiding positioning the body near the RF transmit coil, where the electric field is strong; and paying attention to the antenna effect for large implants and tattoos.

Fig. 2.

Illustration of SAR enhancement for Billie and Duke, with and without an anatomical RF loop (circles on left figures). Pads (rectangles on right figures) isolated skin-to-skin contacts on the human body. All simulations were performed under the SAR safety limits for the first-level-controlled operating mode (Table 2), for the same position and slice. SAR, specific absorption rate. Reproduced with permission from reference 118.