Bi-directional Control of Synaptic Input Summation and Spike Generation by GABAergic Inputs at the Axon Initial Segment

Abstract

Differing from other subtypes of inhibitory interneuron, chandelier or axo-axonic cells form depolarizing GABAergic synapses exclusively onto the axon initial segment (AIS) of targeted pyramidal cells (PCs). However, the debate whether these AIS-GABAergic inputs produce excitation or inhibition in neuronal processing is not resolved. Using realistic NEURON modeling and electrophysiological recording of cortical layer-5 PCs, we quantitatively demonstrate that the onset-timing of AIS-GABAergic input, relative to dendritic excitatory glutamatergic inputs, determines its bi-directional regulation of the efficacy of synaptic integration and spike generation in a PC. More specifically, AIS-GABAergic inputs promote the boosting effect of voltage-activated Na⁺ channels on summed synaptic excitation when they precede glutamatergic inputs by >15 ms, while for nearly concurrent excitatory inputs, they primarily produce a shunting inhibition at the AIS. Thus, our findings offer an integrative mechanism by which AIS-targeting interneurons exert sophisticated regulation of the input-output function in targeted PCs.

Supplementary Information

The online version contains supplementary material available at 10.1007/s12264-022-00887-w.

Introduction

The chandelier cell (ChC) or axo-axonic cell has been characterized as a distinct subtype of GABAergic interneuron due to its morphology that resembles the shape of candlesticks in a chandelier [1–4]. Strings of its axon terminal buttons (cartridges) exclusively form synapses at the axon initial segment (AIS) of excitatory pyramidal cells (PCs) [3, 5]. Accumulating experimental evidence has suggested that the AIS is enriched with a tremendously high density of voltage-gated Na⁺ or K⁺ channels, which support the generation of neuronal spikes [6–10]. Moreover, as the ChC’s synapse on the AIS releases the transmitter γ-aminobutyric acid (GABA), they were initially classified as an inhibitory interneuron and thought to exert a critical gating of the spiking activity of targeted PCs. However, recent studies argue that the ChCs elicit a membrane depolarization rather than a hyperpolarization in the postsynaptic mature PCs in both neocortex [11–13] and hippocampus [14]. The latter results from a higher reversal potential of synaptic GABA action (E_GABA) caused by a high density of the Na⁺-K⁺-2Cl⁻ co-transporter NKCC1 (for importing Cl⁻) within the AIS [12]. It is worth noting that a transition of GABAergic synaptic action from initial excitation to late inhibition has been found in other subcellular compartments of most developing PCs in the first 2 postnatal weeks, a process attributed to a developmental switch of the NKCC1 to the Cl⁻ exporter K⁺-Cl⁻ co-transporter 2 (KCC2) in these compartments [15, 16]. Remarkably, synaptic inputs from a single ChC have been reported to trigger action potentials (APs) in its innervated PCs in the human cortex and the mouse amygdala [11, 17, 18]. Recently, a study using electrophysiological recordings under in vitro and in vivo-like conditions further argued that ChCs excite quiescent PCs but inhibit active PCs in cortical microcircuits, suggesting a neuronal state-dependent function of ChCs [19].

Integration of synaptic inputs is one of the basic information-processing functions of a neuron. Regarding the integration of excitatory inputs (or excitatory postsynaptic potentials, EPSPs), the classical theoretical work by Rall (1964) has proposed that EPSP summation is sub-linear within the same dendritic compartments but largely linear among different compartments [20], which has been verified experimentally in hippocampal CA1 PCs [21]. Further studies using realistic modeling proposed a two-layer computation model for EPSP summation, in which EPSPs are first summed nonlinearly at individual dendritic branches and then integrated linearly at the soma [22, 23]. The latter notion has been supported by experimental findings from recordings of hippocampal CA1 neurons in acutely-prepared rat brain slices [24, 25]. On the contrary, the integration of EPSPs and inhibitory postsynaptic potentials (IPSPs) is more complex because inhibitory GABAergic inputs can exert not only a hyperpolarization of membrane potential but also a strong shunting to excitatory currents through activated GABA_ARs [20, 26–28]. Accordingly, there is an “on-the-path” theory for the integration of inhibitory and excitatory inputs, that is, the location where inhibition is maximally effective is always on the direct path from the excitatory input location to the soma [29, 30]. These classical theoretical predictions were extensively examined in our recent experimental and modeling study [31]. In the latter work, we derived an empirical arithmetic integration rule that provides quantitative measurements for the integration of concurrent excitatory and inhibitory inputs at various dendritic locations in a PC, implementing both the hyperpolarizing and shunting actions of GABAergic input simultaneously [31]. Further studies have extended the validity of this arithmetic rule for the spatiotemporal integration of multiple excitatory and inhibitory inputs that are distributed randomly in the dendritic tree [32–34].

Although GABAergic inputs originating from cortical ChCs are generally regarded to induce excitation at the AIS of targeted PCs, it remains largely unknown how they are temporally integrated with dendritic excitatory inputs and control spike outputs. In the present study, we combined realistic NEURON stimulation [9] and electrophysiological recording from a cortical layer-5 PC to address this question quantitatively. Both the simulation and experimental results consistently suggested that AIS-specific GABAergic inputs exert a bi-directional regulation on the linearity of integration with dendritic excitatory inputs and the efficacy of spike generation, a process critically dependent on both the temporal order and onset timing between the two inputs. More specifically, depolarizing AIS-specific GABAergic inputs augment somatic excitation when they precede a dendritic EPSP by 15 ms to 50 ms, while they shunt large EPSPs when the two inputs are activated concurrently or within a narrow 10-ms window. Such timing-dependent, bi-directional actions of depolarizing GABAergic inputs at the AIS is reminiscent of the previously-reported membrane potential state-dependent effects of ChC synaptic inputs on cortical excitation [19].

Materials and Methods

NEURON Modeling Simulation

Computational simulation was performed under the NEURON Simulation Environment (v7.0) [35, 36]. A cortical layer-5 PC model with morphological and biophysical details was obtained from the MedelDB platform (http://modeldb.science/), following a previous study [9]. The morphological compartments consisted of a soma, a full dendritic tree, and an AIS (length, 57.1 μm; diameter, 2.1 μm on average) based on measurements of the reconstructed morphology of experimentally examined rat cortical neurons. The end of the AIS was followed by several cylindrical sections of myelinated internodes (length, 60 μm; diameter, 1.6 μm) and nodes of Ranvier (length, 1 μm; diameter, 1.1 μm) with a total axon length of 2.7 mm. The passive electrical properties were set as R_m = 30,000 Ω cm², C_m = 1 μF cm⁻², and R_i = 100 Ω cm, uniformly throughout all compartments, except for the myelinated axon in which the C_m was reduced to 0.02 μF cm⁻² and nodal sections possessed a 400-fold increased resting conductance. The resting membrane potential at the soma (V_rest) was set at −80 mV.

The model consisted of two major types of voltage-gated Na⁺ channel (Na_v), a high-threshold Na_v1.2 and a low-threshold Na_v1.6, with differential spatial distributions in which the Na_v1.2 channels were mainly distributed at the soma and proximal AIS and the Na_v1.6 channels were enriched at the distal AIS, based on a previous study [10]. It also consisted of three subtypes of voltage-dependent K⁺ channel, a high-voltage-activated K⁺ channel (K_v), a fast low-voltage-activated K_v1-like K⁺ channel (K_v1), and an M-type K⁺ channel (K_m) with slow activation and non-inactivation. The hyperpolarization-activated mixed cation channel I_h was also included. The kinetics and distributions of the K⁺ channels and I_h were same as that of the previous study [9]. The spatial distribution profiles for the densities of these individual ionic channels (or active conductance) across the AIS are shown in Fig. S1B. For synaptic transmission, two types of postsynaptic receptor—the AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) subtype of glutamate receptor (AMPAR) and the type A GABA receptor (GABA_AR)—were applied to the model neuron to simulate the phasic postsynaptic responses of glutamatergic and GABAergic inputs, respectively. Time constants of rise (τ_r) and decay (τ_d) for AMPARs and GABA_ARs were set at τ_rA = 0.1 ms, τ_dA = 3.4 ms and τ_rG = 0.33 ms, τ_dG = 5.6 ms, respectively, based on experimental results [35–37]. The reversal potential of GABAergic postsynaptic currents (E_GABA) at the AIS was set to −60 mV accordingly, which is consistent with the experimental measurements [12, 13], while the E_glu was generally set to 0 mV. The GABAergic input at the AIS consisted of three axonal terminal buttons located 41.4 μm, 47.1 μm, and 52.8 μm from the hillock, based on the previous experimental reports [38, 39], while the glutamatergic input was located at the shaft of the distal apical dendrite (495.6 μm from the soma).

Dynamic EPSPs and GABAergic postsynaptic potentials (GPSP_AIS) were elicited from the resting membrane state by applying the glutamatergic and GABAergic conductance (G_glu-AMPA and G_GABA) at the apical dendritic trunk and the AIS, respectively, while their summed response (Sum) was yielded by applying an EPSP and GPSP_AIS pair in one trial. Synaptic responses were all measured mainly from the soma or occasionally from the AIS (Fig. S1A). Amplitudes for individual EPSP, GPSP_AIS, and Sum were defined as the value at the time where the EPSP peaked, such that the amplitude of GPSP_AIS or Sum could slightly deviate from its own peak. The summation linearity was defined as the Sum amplitude divided by the amplitude of linearly (or arithmetically) summed responses. Blockade of a certain channel was achieved by reducing its density by 90% on the membrane in the model. In the tests of asynchronous inputs, the onset time of an EPSP was fixed at t = 0 ms while the GPSP_AIS onset timing was varied accordingly. To achieve a probabilistic spiking of the model neuron, EPSP conductance (G_glu-AMPA), varied within ±6% to mimic experimentally-recorded noisy synaptic currents (amplitude, −100 pA to 100 pA; frequency, 10 kHz), was injected into the soma to mimic in vivo-like membrane potential fluctuations. In the tests of individual time intervals between EPSP and GPSP_AIS, 400 trials were conducted to calculate a value of spike probability. The time of spike onset was defined as the time point where the potential in the rising phase of an AP reached −20 mV and spike-timing histograms were then fitted by a Gaussian function. All simulations were run in 50-μs iteration time steps at 37°C.

Cortical Slice Preparation and Electrophysiology

All animal experimental procedures were approved by the Animal Care Committee of State Key Laboratory of Cognitive Neuroscience and Learning at Beijing Normal University (IACUC-BNUNKLCNL-2016-02). The prefrontal cortical slices (350 μm thick) were prepared from Sprague-Dawley rats on postnatal days 15–20, using a vibratome (VT1200, Leica, Lelefon, Germany), and the procedure followed our previous study [31] with several modifications. Prepared slices were incubated in artificial cerebrospinal fluid (aCSF) at 34°C for 90 min before recording, allowing axon blebs to grow. After that, the slices were transferred to a recording chamber perfused with aCSF (2 mL/min; 30°C–32°C). The aCSF contained (in mmol/L) 125 NaCl, 3 KCl, 2 CaCl₂, 2 MgSO₄, 1.25 NaH₂PO₄, 1.3 sodium ascorbate, 0.6 sodium pyruvate, 26 NaHCO₃, and 11 D-glucose, and was bubbled with 95% O₂ and 5% CO₂ (pH 7.4). Simultaneous whole-cell recordings on the axonal bleb and the soma of a cortical layer-5 PC followed the procedure described in previous studies [10, 40]. In brief, recording was first made from the axonal bleb using a glass micropipette under an upright microscope (BX51WI, Olympus, Tokyo, Japan) equipped with an infrared camera (IR-1000E, DAGE-MTI, Michigan City, USA). The micropipettes were filled with an internal solution containing (in mmol/L) 145 K-gluconate, 5 KCl, 10 HEPES, 10 disodium phosphocreatine, 4 Mg₂ATP, 0.3 Na₂GTP, 0.2 EGTA, and 20 Alexa Fluor 488 (Invitrogen, Carlsbad, USA) (pH 7.3), and their resistance was 5 MΩ–8 MΩ. After the recorded neuron was filled with the fluorescent dye Alexa Fluor 488, the distance between the recorded bleb to the soma was measured. If it was within the range of 40 μm–60 μm, a second micropipette (3 MΩ–5 MΩ) recording was made from the soma of the same neuron.

Synaptic conductance injection under the dynamic-clamp mode was applied using a digitizer (1401 Power 3, CED, Cambridge, England) to elicit membrane potential responses. The rise and decay time constants for either AMPAR or GABA_AR conductance kinetics were set as the same as that used in the NEURON simulation. E_GABA and E_glu were set at −58 mV and 0 mV, which resulted in a driving force of ~12 mV for the GPSP_AIS and ~70 mV for the EPSP. Electrical signals of individual and summed membrane potential traces were recorded by an amplifier (MultiClamp 700B, Molecular Devices, San Jose, USA) under 3 kHz low-pass filtering, digitized (1401 Power3, CED, Cambridge, England) at 20 kHz, and acquired by Signal v5.08 (CED, Cambridge, England) into a computer for further analysis. Tetrodotoxin (TTX, 0.5 µmol/L) was added to the perfusion solution to block the Na_v channels. Probabilistic spiking of recorded neurons was achieved by adjusting the resting membrane potential to close to the AP threshold so that injected synaptic conductance with fixed peak amplitude could elicit spikes by chance. The value of spike probability was calculated based on 20 test trials.

Results

We first ran the NEURON model simulation for systematical quantification of the spatiotemporal integration of AIS-specific GABAergic input (GPSP_AIS) and dendritic glutamatergic inputs (EPSP_dend) at either the AIS or soma of a cortical layer-5 PC, and derived major points were then experimentally verified by neuronal recording in rat cortical slices. Such an approach allowed us to consolidate the conclusion reciprocally.

Simulation of Spatial Summation of GPSP_AIS and Dendritic EPSP

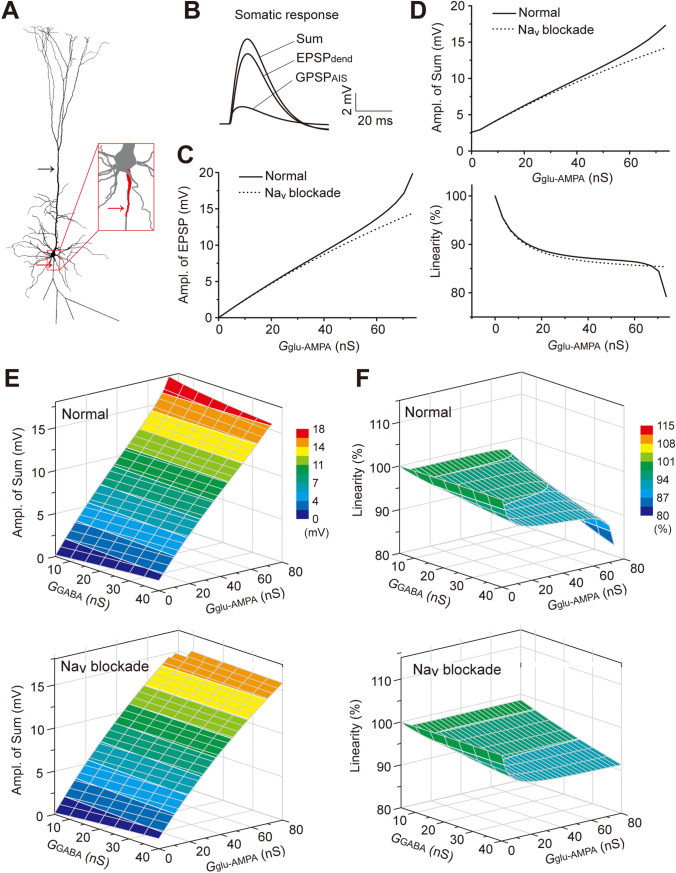
In the NEURON simulation, we implemented ChC-specific GABAergic inputs and dendritic glutamatergic inputs by delivering G_GABA conductance at the AIS and G_glu-AMPA conductance at the apical dendrites (see Materials and Methods). The resultant GPSP_AIS, EPSP_dend, and summed responses (Sum) were read out from the soma (Fig. 1A, B) or the AIS (Fig. S1). The values of V_rest and E_GABA were set at −80 mV and −60 mV, respectively, thus, the GPSP_AIS was depolarizing.

Fig. 1.

Simulation of integration of synchronous GPSP_AIS and EPSP_dend. A Morphology of a layer-5 model PC used in the NEURON simulation. Arrows indicate the locations of conductance injections for EPSPs at the apical dendrite (black arrow) and GPSPs at the AIS (red arrow). B Example membrane voltage traces of EPSP_dend, GPSP_AIS, and the Sum for their simultaneous activation, recorded from the soma. C EPSP amplitudes (Ampl.) versus conductance (G) under the Na_v intact (normal) or blockaded condition. D Changes of the Sum amplitude (upper) and summation linearity (lower) with increasing EPSP conductance under the Na_v intact or blockaded condition. E Color-coded 3D plots of the Sum amplitude for integration of synchronous GPSP_AIS and EPSP_dend induced by various conductance combinations, under the normal (upper) or Na_v blocked (lower) condition. F 3D plots for the calculated linearity for GPSP_AIS and EPSP_dend integration shown in E.

We first characterized the relationship between the somatic amplitude of EPSP_dend and its underlying G_glu-AMPA magnitude. We noted that in the simulation, there was an apparent amplification of somatic subthreshold EPSPs along with increasing G_glu-AMPA , in comparison with the arithmetic EPSPs. Such a boosting effect was absent after blocking the voltage-activated Na⁺ channels on the membrane of the soma and AIS (Fig. 1C). Further analysis showed that the boosting effect was primarily mediated by the low-threshold voltage-gated Na_v1.6 rather than the high-threshold Na_v1.2, although both subtypes were enriched at the AIS (Fig. S1C). Because the maximum amplitude of GPSP_AIS was set at ~2 mV in the simulation, little Na_v-mediated boosting was found (Fig. S1C). The apparent Na_v1.6-boosting of EPSPs is consistent with the previous experimental finding that enriched Na_v channels at the soma and AIS amplify relatively large EPSPs in cortical PCs [10, 41, 42].

We then measured the somatic integration of EPSP_dend elicited by step-increases in G_glu-AMPA with a concurrent GPSP_AIS at a fixed amplitude of ~2.5 mV. The summation linearity, defined as the ratio of the peak amplitudes of the measured Sum and the linear Sum, was used to assess the integration efficiency. The results showed that the measured Sum amplitudes were gradually amplified along with increasing G_glu-AMPA (Fig. 1D, upper), while the linearity of EPSP_dend-GPSP_AIS summation progressively decreased and showed a dramatic drop when the EPSP_dend value was close to the spike threshold (Fig. 1D, lower). Again, blocking the Na_v activity at the soma and AIS effectively suppressed the larger measured Sum and eliminated the dramatic change in the linearity (Figs 1D, S1D), suggesting a Na_v (mainly Na_v1.6)-dependent boosting effect. Such effects on the Sum and the linearity were constantly evident for integrations over a range of various GPSP_AIS and EPSP_dend amplitudes, which were largely abolished by blocking Na_v channels at the AIS (Fig. 1E, H). This set of systematic simulations suggests the presence of a boosting effect and a shunting effect simultaneously elicited by activation of AIS enriched in Na_v channels and GABA_AR, respectively.

Our previous studies have derived an empirical arithmetic rule for the dendritic integration of EPSPs and GPSPs [31–33] as follows:

Sum = EPSP + GPSP + k × EPSP × GPSP (1)

in which the non-linear component k × EPSP × GPSP depicts the shunting-inhibition component (SC) and the factor k (in the unit of mV⁻¹) reflects the SC strength. In the scenario of the somatic summation of GPSP_AIS and EPSP_dend, we found that the SC magnitudes and coefficient factor k (in negative values for depolarizing GPSP_AIS) were both substantially modulated by the Na_v-boosting effect on increased EPSP_dend (Fig. S2), and its effect on the shunting coefficient k was fitted by an exponential function (Fig. S3A). Using the calibrated k-values, we found that the somatic Sum of GPSP_AIS and EPSP_dend could still be approximated nicely by the arithmetic rule, with small errors in integrations of a range of various GPSP_AIS and EPSP_dend amplitudes (Fig. S3B, C). This result also underscores the notion that although the GABA input by ChC cells at the AIS is depolarization, its shunting effect on dendritic EPSPs still exerts an inhibition.

Timing-Dependent Bi-directional Effects of GPSP_AIS on Subthreshold Input Integration

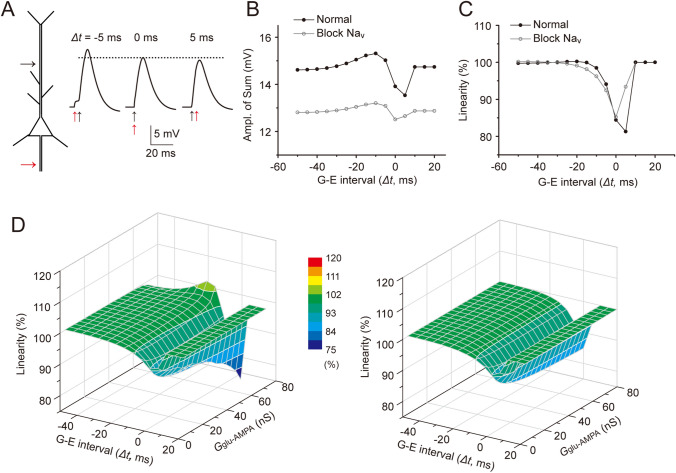
We next examined how the depolarizing GPSP_AIS integrates with asynchronous EPSP_dend at various time intervals. In the simulation, we generated GPSP_AIS at different onset timings relative to an onset time-fixed EPSP_dend and measured their summations (Fig. 2A, left). The simulation showed that, compared to the Sum of synchronized GPSP_AIS and EPSP_dend (Δt = 0 ms), the Sum amplitudes were relatively larger or smaller when a GPSP_AIS was elicited 5 ms before (Δt = −5 ms) or after (Δt = 5 ms) the EPSP_dend onset, respectively (Fig. 2A, right). Such asymmetric timing-dependence was more evident when summations were systematically measured for varied onset timing intervals (Δt: −50 to 20 ms). Specifically, the Sum amplitude gradually reached its potentiation peak when GPSP_AIS preceded the EPSP_dend by 10 ms, while it was at its suppression trough when the GPSP_AIS onset was 5 ms after the EPSP_dend (Fig. 2B). Blockade of Na_v channels substantially reduced the Sum potentiation and suppression. However, from the summation linearity plots for temporal summation, we found that the shunting inhibition was consistently apparent within a Δt window from −20 to 10 ms, despite the Na_v boosting effect (Fig. 2C).

Fig. 2.

Δt-dependent bi-directional effects of GPSP_AIS in temporal integration. A Schematic depicting the same NEURON simulation conditions as in Fig. 1A, but with varied time intervals (Δt) between the onset of GPSP_AIS and EPSP_dend, as shown by the Sum traces for two inputs with different Δt. The dotted line denotes the Sum amplitude for Δt = 0 ms. B Changes of the Sum amplitude for integration of GPSP_AIS of varying amplitudes and EPSP_dend with a fixed amplitude, under normal and Na_v blockade conditions, respectively. C Changes in calculated summation linearity from simulation shown in B. D 3D plots of the Sum amplitude versus the changed Δt and EPSP conductance under the normal (left) and Na_v blockade (right) conditions.

We further computed a complete temporal profile for the linearity of GPSP_AIS-EPSP_dend integration by varying the onset timing of GPSP_AIS (fixed at 2.5 mV) and the EPSP_dend amplitude (G_glu-AMPA) simultaneously. The linearity profile for all combinations of varied time intervals and EPSP_dend amplitudes again showed a small super-linear summation only for those higher EPSP_dend that occurred within a narrow window (Δt) of 10 ms–20 ms (Fig. 2D). On the contrary, the major part of the linearity profile exhibited a sub-linear summation, which was more evident for a higher EPSP_dend onset within a 10-ms window before the GPSP_AIS (Fig. 2D), a property resembling previously characterized shunting inhibition by GPSP [31, 33]. Again, although the super-linear summation was completely blocked by Na_v blockade, the sub-linear summation was largely maintained within a Δt from −20 to 10 ms (Fig. 2D). It is worth noting that the sub-linear peak in the temporal profile showed an accelerative diverging tendency when the concurrent G_glu-AMPA conductance was >60 ns, which yielded EPSP amplitudes close to the AP threshold (Fig. 2D).

In summary, the systematic simulations suggested that, in the process of spatiotemporal integration of GPSP_AIS and EPSP_dend at the AIS or soma, there is bi-directional regulation of the summation linearity, mediated by Na_v-boosting and GABA_AR-shunting effects. Given that GABAergic inputs at the AIS elicit membrane depolarization, they consistently exert their shunting on excitatory inputs to a substantial extent, which peaks at a time when EPSP_dend precedes GPSP_AIS by ~5 ms.

Experimental Verification of Bi-directional Regulation of Subthreshold Input Integration

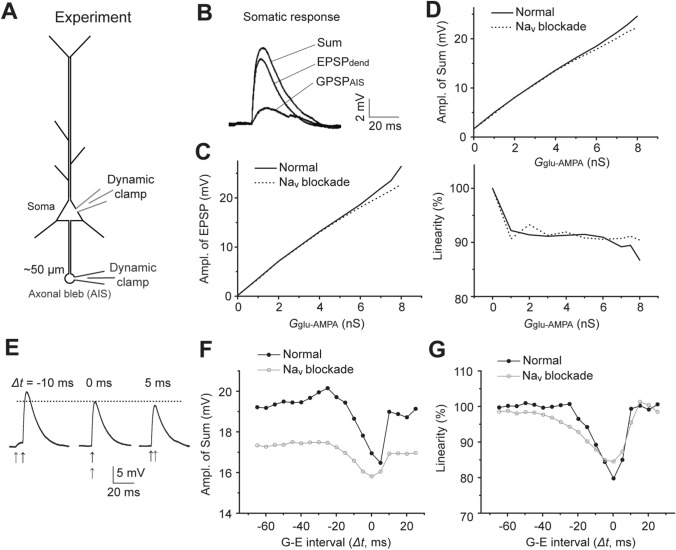
We next verified the NEURON simulation results experimentally by measuring the integration of GPSP_AIS and EPSP at the soma in recorded layer-5 PCs in rat cortical slices. As shown in Fig. 3A, simultaneous dynamic-clamp whole-cell recordings were made at the cell body and an axonal bleb ~50 µm from the soma (presumably the AIS site). The synaptic conductances G_GABA and G_glu-AMPA were injected into the axonal bleb and soma to elicit membrane depolarization of GPSP_AIS and EPSP, respectively, and the resulting GPSP_AIS, EPSP, and their Sum potentials were recorded separately (Fig. 3B; Materials and Methods).

Fig. 3.

Experimental verification of bi-directional effects of GPSP_AIS on input integration. A Schematic of the experimental electrophysiological configuration, in which simultaneous dynamic-clamp recordings were made at the soma and AIS bleb of a layer-5 cortical PC in an acutely-prepared rat brain slice. B Traces of EPSP_dend and GPSP_AIS induced by injected AMPAR and GABA_AR conductances, respectively, as well as the Sum response for their concurrent activation. Note all membrane voltages were recorded at the soma. C, D Experimental verification of the Na_v-boosting effect on EPSPs (C) and the Sum (D, upper), but reducing the linearity of concurrent EPSP_dend-GPSP_AIS summation (D, lower). E Sum traces for EPSP_dend-GPSP_AIS summation with different G-E intervals (Δt). The dotted line denotes the Sum amplitude at Δt = 0 ms. F, G Experimental tests of the bi-directional effects of GPSP_AIS on the Sum (F) and linearity (G) in the temporal summation with Δt changing from −70 ms to 30 ms.

First, we verified the Na_v-boosting effect on the somatic EPSP amplitude. Consistently, we recorded a more evident boosting effect for bigger EPSPs, which was suppressed by the application of the Na_v antagonist TTX during the recording (Fig. 3C). Accordingly, in the experiments measuring the somatic Sum of concurrent GPSP_AIS (fixed at 2.5 mV) and EPSP (with varying amplitudes), the Sum was boosted slightly by the Na_v as well (Fig. 3D). However, there was little difference in the calculated summation measured before and after TTX application, and the linearity roughly remained at ~90% in both conditions (Fig. 3D). Such sub-linear summation could be attributed to the shunting inhibition caused by AIS-GABA_AR opening since it was persistent following Na_v blockade.

We further verified how temporal shifts between GPSP_AIS and EPSP (with a fixed amplitude) affect the Sum and the summation linearity (Fig. 3E). A systematic comparison of experimental measurements before and after Na_v blockade indicated that the boosting effect was evident for the Sum amplitude for all tested GPSP_AIS-EPSP time intervals (Δt) from −60 ms to 20 ms (Fig. 3F, note the black line was consistently above the grey line). However, as shown by the Fig. 3G (black line), the temporal summation was maintained nearly linear (linearity >95%) within the Δt window from −60 ms to −25 ms, while it gradually became severely sub-linear when the GPSP_AIS onset-timing approached more closely to the EPSP, and its sub-linearity peaked when the summation of the two inputs was nearly concurrent (Δt-window: −5 ms to 5 ms). The latter sub-linearity was likely caused by shunting to synaptic excitatory currents by GPSP_AIS conductance because the shunting magnitudes critically depended on GPSP_AIS onset timings relative to the EPSP and were not affected by the Na_v blockade in the experiment (Fig. 3G, grey). Moreover, the Na_v blockade significantly widened the Δt window for apparent sub-linear summation, though the sub-linearity peak was not changed for the summations when the two inputs were nearly concurrent (Fig. 3G, grey line). These experimental findings were consistent with the simulations for GPSP_AIS-EPSP temporal summation (Fig. 2), confirming the counteracting action and sequential dominance between the Na_v-boosting effect and GABA_AR-shunting inhibition in temporal summations.

Thus, the above experimental results from recording cortical layer-5 PCs in rat brain slices confirmed the timing-dependent, bi-directional action of AIS-specific depolarizing GABAergic inputs on the integration with dendritic excitatory inputs.

Timing-Dependent Facilitation and Suppression of Spike Generation by GPSP_AIS

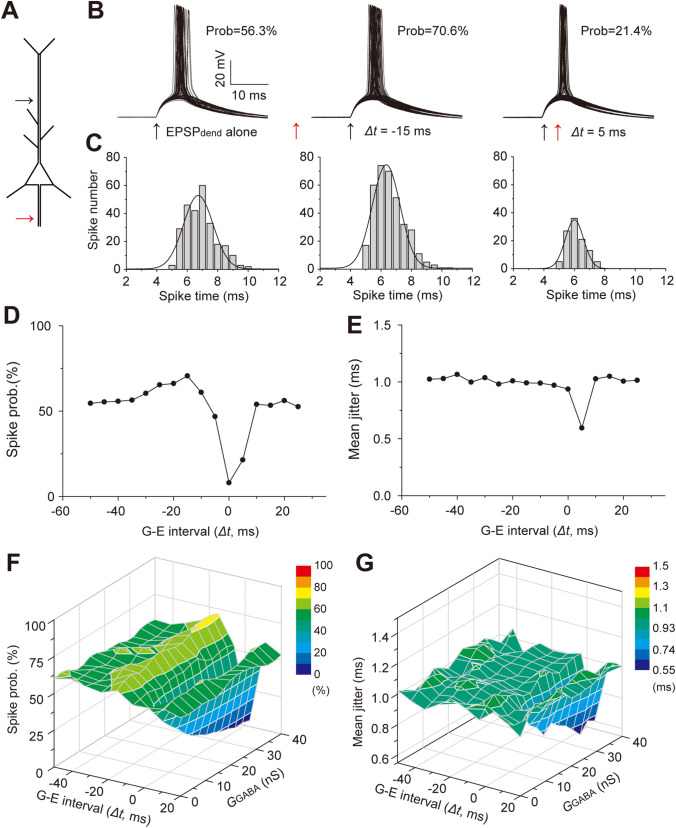
The Spatiotemporal integration of synaptic inputs determines the generation probability and pattern of output spikes. We further performed both simulation and experimental recording to examine how GPSP_AIS contributes to the spike generation of single cortical PCs, given its bi-directional impact on synaptic input summation. In the NEURON simulation, we first produced a stochastic spiking state, ~60% probability of spiking generation elicited by amplitude-varying dendritic EPSPs with their peaks close to the AP threshold, in the presence of random noise currents in the soma over time (see the Materials and Method, Fig. 4A and B–C left). Application of GPSP_AIS at a timing of 15 ms preceding dendritic EPSPs (Δt = −15 ms) slightly increased the spiking probability to ~70% (Fig. 4B, middle), but had little influence on the spike-timing precision (or jitter; Fig. 4C middle). On the contrary, GPSP_AIS delivered 5 ms after dendritic EPSPs substantially reduced the spike probability by ~40% and increased the spike-timing precision (Fig. 4B, C right). Systematically varying the GPSP_AIS delivery time from −60 ms to 30 ms relative to the dendritic EPSP timing revealed temporal profiles of the impact of GPSP_AIS (with a fixed conductance) on spike probability (Fig. 4D): within a Δt window from −40 ms to −10 ms, GPAP_AIS gradually promoted spike probability, while it strongly suppressed the spike generation when GPSP_AIS timing was nearly concurrent with dendritic EPSPs (Δt = −5 ms to 5 ms). On the contrary, GPSP_AIS significantly affected spike timing precision only when it occurred 5 ms after dendritic EPSPs (Fig. 4E). Such Δt-dependence was also fairly evident in the integration of systematically-varied amplitudes of GPSP_AIS and EPSP and more apparent suppression of spike generation was found for larger GPSP_AIS conductance (Fig. 4F, G). These simulation results indicate bi-direction regulation of dendritic EPSP-elicited spiking generation by GPSP_AIS, a cellular process highly dependent on synaptic input timing.

Fig. 4.

Simulation of timing-dependent regulation of spike generation by GPSP_AIS. A Diagram indicating activation sites of EPSP_dend (black arrow) and GPSP_AIS (red arrow) in the layer-5 PC model. B Superimposed spikes elicited by EPSP_dend alone (left) and summed responses with G-E intervals (Δt) of −15 ms (middle) and 5 ms (right), indicating spiking probability (prob.) and timing jitter. C Histograms showing the distribution of spike times (0.5 ms bins). Solid curves, Gaussian fitting. D, E Changes in spike probability (D) and spiking jitter (E) when Δt changing elicited by integration of EPSP_dend-GPSP_AIS with a fixed amplitude. F, G 3D plots of the spiking probability (F) and spiking jitter versus the changed Δt and GPSP_AIS conductance.

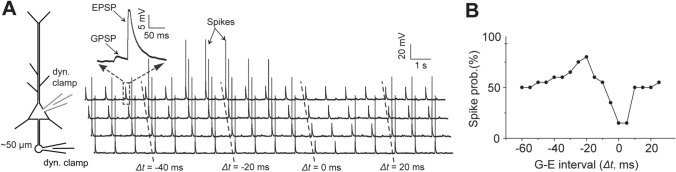
We again experimentally verified such timing-dependent bidirectional action of GPSP_AIS on spike generation using simultaneous somatic and AIS-axonal bleb recordings under the dynamic-clamp mode from a cortical layer-5 PC in the acute rat brain slice (Fig. 5A, left). Intracellular G_GABA and G_glu-AMPA conductances were injected at the AIS and the soma to elicit mimic GPSP_AIS and somatic EPSPs, respectively, at varied time intervals. Relying on intrinsic fluctuations of neuronal membrane potentials ex vivo, we initially set a probabilistic state of somatic spiking (at ~50% probability) following the integration of GPSP_AIS and somatic EPSPs separated by relatively longer intervals (Δt ≥−40 ms, GPSP_AIS preceding EPSP), and then we systematically decreased the Δt values in 5-ms steps up to Δt = +30 ms (Fig. 5A). As indicated by both the recorded spikes from a representative layer-5 PC and the quantified spiking probability, there was a clear bi-directional regulation of spike generation by GPSP_AIS in the process of subthreshold input integration transforming to all-or-none spikes: promoting the probability when GPSP_AIS preceded somatic EPSPs by −30 ms to −15 ms and suppressing the probability when GPSP_AIS occurred within a Δt window of −10 ms to +10 ms (Fig. 5). Thus, these results confirmed that depolarizing GPSP_AIS was able to exert opposite effects in the two integration windows similar to those revealed by the NEURON simulation (Fig. 4). Such timing-dependent facilitation and suppression of spike generation by GPSP_AIS are likely attributable to Na_v-boosting of subthreshold postsynaptic potentials and shunting inhibition, respectively.

Fig. 5.

Experimental test of the bi-directional effect of GPSP_AIS on spike generation. A Diagram depicting simultaneous dual dynamic-clamp recordings at the soma and AIS bleb of a layer-5 PC in a cortical slice. Four representative sweeps of recorded subthreshold membrane potentials and spikes when somatic EPSP and GPSP_AIS are introduced at different Δt. A case of GPSP_AIS preceding somatic EPSP by 40 ms is shown at higher amplification (top left). B Δt-dependent bi-directional changes in spiking probability from the recordings shown in A.

Discussion

By combining realistic computational stimulation and electrophysiological measurement, we have revealed that, in the integration with dendritic excitatory inputs, GABAergic inputs at the AIS can bi-directionally regulate the summation linearity and spike probability of single cortical PCs, although these GABAergic inputs are generally thought to be (excitatory) depolarizing [11–14, 17, 18]. The facilitation and suppression of integrative functions by GPSP_AIS are critically dependent on its onset timing relative to EPSPs and are mainly mediated by promoting the Na_v-boosting effect and producing shunting inhibition, respectively. Our findings, thus, provide an integrative mechanism by which AIS-targeting interneurons can exert timing-dependent, bidirectional regulation of neuronal input-output functions in targeted PCs.

GABAergic Depolarization Can Still Be Inhibitory Through Its Shunting Effect

There has been a debate on whether AIS-GABAergic inputs, which originate from the ChCs or axo-axonic cells, are inhibitory (hyperpolarizing) or excitatory (depolarizing) in targeted PCs. Studies using gramicidin-perforated or cell-attached recording methods, which largely preserve the normal concentration of intracellular Cl^−, reported that the ChC input depolarizes the membrane potential of cortical PC targets, an effect attributed to its E_GABA above the resting potential at the targeted AIS site [11–13]. The study by Woodruff et al. (2011) further found that the ChC inputs not only promote spike generation in targeted PCs under relatively quiescent membrane potential conditions, but also exert an inhibitory effect under in vivo-like active activity fluctuation conditions [17], suggesting a strong dependence on the ongoing membrane potential states of targeted neurons. However, a study using the completely non-invasive extracellular field recording method demonstrated a dominant hyperpolarizing action on their PC targets by GABAergic axo-axonic synapses in the hippocampus, but through an indirect action by activating intermediate PCs which, in turn, recruited other inhibitory interneurons targeting the recorded PCs [14]. Although this finding supports the direct excitatory action of AIS-specific GABAergic inputs, the inputs ultimately produce their indirect inhibition effect on other neighboring PCs via a microcircuit mechanism. Experimentally the recording with gramicidin perforation or strong extracellular field stimulation used in these studies, could inevitably affect membrane potential dynamics and E_GABA, which may also account for the different previously-reported results of GABAergic transmission in distinct subcellular compartments. However, it should be noted that most evidence supporting the excitatory action of AIS-specific GABAergic synapses in mature neural circuits has been gained from experiments under in vitro or ex vivo conditions. Neurons in the intact brain or in vivo are known to be in a high-conductance state with profound membrane potential dynamics due to the barrage of abundant active inputs, completely unlike the quiescent state of neurons in isolated brain slices [43]. Thus, it is most likely that multiple cellular factors or mechanisms are involved in determining the final outcome of AIS-specific GABAergic input, especially in the active circuits in vivo, though its synaptic action is generally thought to be depolarizing. This has demanded a quantitative elucidation of how different cellular factors, such as dynamic states of the membrane potential, input timing, and local membrane excitability control the complicated actions of AIS-GABAergic inputs on synaptic input interaction and spike generation.

The present study, combining the advantages of realistic NEURON modeling and experimental dynamic-clamp recording, largely recapitulated the physiological environment of cortical microcircuits, in order to generate stable depolarizing GABAergic responses in the AIS. In both modeling computations and experiments, we have systematically and quantitatively measured the integration of GPSP_AIS and EPSP_dend and demonstrated that, in spite of its intuitive excitatory effect, the AIS-GABAergic input exerts bi-directional control on the linearity of synaptic input integration and the efficacy of spike generation. In these sub- and supra-threshold membrane activity processes, the shunting effect of AIS-specific GABAergic synapses is a critical factor underlying the suppressive impact and imposes a stronger sub-linear reduction on larger EPSPs and further spike generation. The simulation and experimental results showed (Figs 2, 3, 4, 5) that the sub-linear shunting effect first slightly weakened subthreshold-input summation and spike generation when GPSP_AIS activation timing approached the onset of large EPSPs, but then suddenly reversed the trends of Sum responses and spiking probability into a negative direction and exerted the strongest suppression when the GPSP_AIS and EPSP onsets were simultaneous. The systematic temporal profiles for integration (Fig. 2D) and spiking probability (Fig. 4F) for varied input conductances also clearly showed a progressive transition of the bidirectional GPSP_AIS actions along with increasing EPSP conductance. More specifically, when the EPSP conductance was relatively small (e.g. <10 ns), the temporal profiles often contained only an upward phase, indicating that GPSP_AIS completely facilitated the EPSP peaks that were below the E_GABA, However, as the EPSP conductance increased, the downward phase became stronger since the EPSP peaks were above the E_GABA to enable GPSP_AIS hyperpolarizing membrane potentials. Moreover, blockade of somatic and AIS Na_v attenuated both the upward and downward peaks of the temporal integration profile when the EPSP amplitude was close to the spike threshold (Fig. 1F and 2D right), suggesting that Na_v constantly boosts the temporal integration when the Sum amplitude is large enough.

Taken together, our quantitative measurements suggest that shunting inhibition, Na_v-boosting effect, membrane potential state, and input timing are important factors that regulate the bidirectional action of AIS-GABAergic inputs in synaptic input summation and spike generation of a PC. In comparison with other subcellular compartments of a neuron, for instance, apical or basal dendrites, the AIS is a specific compartment with unique molecular assemblies such as substantially higher expression of distinct Na_v1.2 and Na_v1.6 channels and the Cl⁻ importer NKCC1 [10. 12, 13, 41]. The latter characteristics provide the molecular basis for the unique synaptic integration functions at the AIS, but not in the apical or basal dendrite.

Nonlinear Integrative Effects of Voltage-Gated Ion Channels at the AIS

Our study has also provided a systematically quantitative analysis of the contribution of Na_v-boosting to GPSP_AIS-EPSP integration. Active ionic channels, as active conductances in the dendrite, including voltage-activated Na_v and Ca²⁺ channels as well as NMDA receptors, have been reported to boost the amplitude of local EPSPs to different extents [44–47]. Similarly, highly-enriched Na_v at the AIS of cortical PCs [6–9] has also been found to amplify EPSPs propagated from the dendrites or soma [41, 42]. Consistent with this, we found the AIS-Na_v boosting effect on GPSP_AIS-EPSP integration, indicated by its super-linear amplification on both EPSP and Sum, when their magnitudes were large enough to activate a substantial number of AIS-Na_v channels (but not eliciting spikes) (Figs 1, 2). We also showed that Na_v1.6 activation within the AIS by propagated EPSP_dend almost entirely accounted for the boosting effect, while activity in the other major Na_v1.2 channel had little contribution except in the case of extremely large EPSPs (Fig. S1). Such differential contributions of these two types of Na_v channels are primarily attributable to a fact that Na_v1.6 has a relatively lower threshold activation voltage and other unique characteristics compared to Na_v1.2 [10, 48]. In addition, we also tested the effect of other voltage-dependent ion channels including three types of K⁺ channel K_v, and I_h, and found very little influence on the amplitude of both EPSPs and Sums as well as the timing- or state-dependent shunting effect of AIS-GPSPs (data not shown). However, it is notable that GPSP_AIS produced by activation of single ChCs has been reported to be capable of eliciting spikes in targeted PCs alone in the neocortex, implying its high magnitude close to the spike threshold [11]. Coincidently, GABAergic inputs tend to reside in the distal AIS region where the Na_v1.2 channels are enriched [6]. These findings imply that GPSP_AIS alone is also likely to be modulated by AIS-Na_v, and thus it is of interest to examine whether and how Na_v-boosted GPSP_AIS strengthens its bi-directional regulation of input integration and spike generation.

Applicability of the Arithmetic Integration Rule for Predicting GPSP_AIS-EPSP Summation

Our previous studies have established an arithmetic rule for the integration of excitatory glutamatergic inputs (or EPSPs) and inhibitory GABAergic inputs (or GPSPs) at the apical dendrite of a PC [31–33]. This empirical rule extracts the shunting inhibition of GABAergic inputs as a multiplicative function k × EPSP × GPSP, which well quantifies the shunting magnitude in the integration of multiple asynchronous EPSPs and GPSPs [31, 33, 34]. The coefficient factor k, reflecting the strength of shunting inhibition, is mainly determined by the location of excitatory and inhibitory inputs (more specifically by the transfer resistances between the excitatory input and the inhibitory input and the soma k_ei and k_es, respectively) and E_GABA, but is also modulated by active dendritic channels (or conductance). Given the fact of a far higher density of Na_v at the AIS and soma sites than at other subcellular sites, the Na_v modulation of k could be tremendously significant, and arithmetically fitted by an exponential function f(k, EPSP) (Fig. S2). By incorporating this additional calibration function into the EPSP-GPSP integration rule, we indeed found that the arithmetic rule still predicted the Sum well. Moreover, the applicability of the original arithmetic integration rule entails the removal of Na_v activity at the AIS and soma, indicating a significant contribution of the Na_v boosting effect to GPSP_AIS-EPSP summation. However, it is worth noting that the calibration function f(k, EPSP) may not work perfectly when EPSPs have large amplitudes close to the spike threshold. The above analysis also underscores the exceptional importance of shunting inhibition exerted by AIS-specific GABAergic inputs to somatic or dendritic EPSPs, though those inputs are depolarizing. The latter action is a primary factor that determines the negative regulation of integration linearity and spike generation.

Recent studies using more sophisticated techniques of genetic single-neuron anatomy and electrophysiology have revealed distinct input-output synaptic communication patterns of these AIS-GABAergic interneurons along the laminae [49, 50]. Together with the latter distinct neuronal connectivity, our findings of bi-directional regulation of input integration functions by these AIS- GABAergic synapses provide a synaptic basis for their unique control of the spatiotemporally specific circuit activity underlying various brain functions.

Supplementary Information

Below is the link to the electronic supplementary material.

Conflict of interest

The authors declare that they have no conflict of interest.