Abstract

Calculating accurate air–sea fluxes for polychlorinated biphenyls (PCBs) is an essential condition for evaluating their transport in the atmosphere. A three-dimensional hydrodynamic-ecosystem-PCB coupled model was developed for the northwestern Pacific Ocean to assess the air–sea fluxes of four PCBs and examine the influences of ocean currents on the fluxes. The model revealed a fine structure in the air–sea flux that is sensitive to the Kuroshio, a western boundary current with a high surface speed. Intense downward and upward fluxes (−23.6 to 44.75 ng m–2 d–1 for ∑4PCBs) can be found in the Kuroshio region south of Japan and the Kuroshio Extension east of Japan, respectively. In strong (weak) current regions, it takes ∼4 and ∼1 days (1–3 and 3–12 days) for dissolved PCBs to reach an equilibrium in scenarios where only air–sea exchange or only ocean advection is considered, respectively. In strong current regions, the ocean advection has a shorter response time than the air–sea exchange, indicating that dissolved PCBs from upstream carried by strong current can easily change the downstream concentration by disrupting the equilibrium with original air–sea exchange and induce new air–sea fluxes there. Therefore, strong western boundary currents should be correctly considered in future atmospheric transport models for PCBs.
Keywords: ocean model, seasonal variation, Kuroshio Extension, volatilization, western boundary currents
Short abstract
This article reveals the decisive role of ocean currents in the air−sea diffusion flux of PCBs, offering a suggestion for improving the atmospheric model of PCBs.
Introduction
The direction and magnitude of the air–sea diffusion flux of polychlorinated biphenyls (PCBs) depend on the concentration gradient between gaseous PCBs in the atmosphere and dissolved PCBs in water, which in turn depend on the processes influencing these concentrations.1 The oceanic biological pump, current advection, and eddy diffusion affect the distribution of PCBs in the surface ocean and therefore affect the air–sea diffusion flux. The biological pump refers to the removal of dissolved PCBs from the surface water via phytoplankton uptake, which is favorable for increasing the downward diffusion flux of PCBs from air to sea.2,3 Ocean currents bring water with different concentrations of PCBs from remote areas to a target area, thereby changing the local concentration of PCBs. Eddy diffusion usually reduces the spatial gradient of PCBs concentrations.
An accurate air–sea flux is important for evaluating the transport of PCBs in the atmosphere. Despite this fact, the ocean is usually treated as a box module in most atmospheric PCBs models, in which lateral transport by ocean currents is not considered.4−6 In addition, the western boundary currents in most oceans have widths of 100–200 km; as such, the horizontal resolution of ∼100 km or more used in the global ocean simulation of PCBs is too coarse to reproduce realistic western boundary currents.7 Therefore, the effects of such strong ocean currents on PCBs concentrations have not been fully considered in atmospheric simulations of PCBs.
The Asia-Pacific region has the largest human population and the largest manufacturing factories, thereby making it an area where PCBs are used in large quantities.8 Global ocean simulation of PCBs has estimated that approximately 30% of the total atmospheric deposition takes place in the North Pacific.7 However, most previous reports on PCBs have focused on the Atlantic Ocean, Arctic Ocean, eastern Pacific Ocean, and some coastal areas.9−11 There has likely been no field observation of PCBs in the northwestern Pacific Ocean (NWPO) since the first report in 1989/1990.12
In the NWPO, a strong western boundary current, that is, the Kuroshio, flows from low latitudes to midlatitudes, veers east at 30° N, continuously flows along the southern coast of Japan, and finally enters the open Pacific Ocean as the Kuroshio Extension (KE; Figure S1 in Supporting Information). To reproduce a more realistic current, a horizontal grid size of ∼10 km or finer is required for an ocean model.13 Some regional persistent organic pollutants (POPs) models demonstrate relatively high horizontal resolution, which is a necessary condition for resolving the fine structure in ocean currents.10,14−16 However, a constant concentration of atmospheric POPs is usually considered in such models, although this concentration is certainly nonhomogeneous in space and time owing to differences in human activities.
To obtain an accurate air–sea flux, in addition to the inclusion of spatial and temporal variations in the atmospheric POPs concentration, the ocean POPs model should also take into consideration the influence of ocean currents on POPs transport. This requires the use of a high-resolution hydrodynamic model as the framework for ocean POPs modeling. Furthermore, the presence of a biological pump effect on POPs requires full coupling of an ecosystem module in the ocean POPs model. Based on the above considerations, we established a fully coupled hydrodynamic-ecosystem-POPs model to simulate PCBs in the NWPO. We use this to examine the seasonal variation and spatial distribution of the air–sea diffusion flux of four selected PCB congeners and to clarify the regulatory effect of ocean currents on the air–sea diffusion flux.
Materials and Methods
The model domain covers the NWPO (10.5–62° N, 108–180° E, Figure S1) with a horizontal resolution of 1/12° (9.1–4.4 km) and 47 vertical levels. PCBs were simulated using three modules in this study. One is a hydrodynamic module that provides daily water temperature and current velocity in three directions, and the horizontal and vertical eddy diffusivity coefficients (see Text S1 in the Supporting Information). The second module is an ecosystem module that provides daily concentrations of phytoplankton and related biogeochemical parameters (Text S2). The third module is a PCB module that calculates the processes related to the PCB with specified boundary conditions.
PCB Module
Mass exchange and chemical degradation are the principal processes considered in this module. Mass exchange processes include advection and diffusion, biogeochemical processes, and air–sea exchange. Figure 1 illustrates a conceptual sketch of the physicochemical processes of PCBs in the NWPO. The module has a framework similar to the three-dimensional PCB model in the East China Sea.14 Compared with this,17 our PCB module contained two additional improvements. One was the inclusion of spatial and temporal variations in atmospheric PCB concentrations, as well as the inclusion of wet deposition flux of atmospheric PCBs, both of which were derived from the GEOS-Chem model.4 The other was the replacement of satellite-based chlorophyll-a with ecosystem-model-based chlorophyll-a. Because satellites only observe the surface layer, they cannot provide a vertical profile of chlorophyll-a. In addition, the product of satellite chlorophyll-a is typically updated on a weekly or monthly basis and is sometimes unavailable because of the influence of clouds. An ecosystem model can solve these two problems.
Figure 1.
Conceptual scheme of the coupled model for PCB simulation. CA is gaseous PCB in the atmosphere, CW is dissolved PCB in the water, CWP is phytoplankton-bound PCB, and CWD is detritus-bound PCB. The fields in the boxes to the right are input data for PCB simulation.
The PCBs in our module are represented by four variables, that is, gas phase (CA) in the atmosphere, dissolved phase (CW) in water, and a particle phase that contains phytoplankton-bound (CWP) and detritus-bound (CWD) PCBs in water. CA is the specified gaseous concentrations of PCBs that enter the ocean through air–sea diffusion. CWP is the sum of PCBs adsorbed by the phytoplankton surface (CWPS) and taken up by the phytoplankton matrix (CWPM).
The equations for PCBs in the ocean are given in Text S3, and the biochemical parameters and formulas for calculating biological processes are presented in Text S4 and Table S1. The primary processes are the uptake and release of PCBs by phytoplankton, mortality of phytoplankton, sinking and decomposition of detritus, and the degradation of the dissolved PCBs due to photolytic and microbial processes.
Boundary Conditions for the PCB Module
In this study, the atmosphere was the only source of PCBs in the ocean.17 Other resources, such as the most PCBs from rivers are adsorbed to particles and sink to the sediment near the river mouth. A part of them can be transported to the sea shelf but little can be transported to the open ocean. PCBs in the atmosphere enter the ocean through air–sea diffusion and wet deposition, which were treated as the surface boundary condition for the concentration of dissolved PCBs (CW) as follows:
| 1 |
where kh (m2 s–1) is the vertical eddy diffusivity coefficient, FAW (pg m–2 s–1) is the air–sea diffusion flux, and FWP is the wet deposition flux (pg m–2 s–1). The wet deposition fluxes (FWP) and gaseous concentrations (CA) of PCBs in the atmosphere were derived from the GEOS-Chem global atmospheric model,4 which was evaluated using observations available in the NWPO (Figure S2, Table S2, details are described in Text S5). The particle phase makes up only a very small fraction, while >99% for all four congeners is attributed to the gaseous diffusion,4 thus the dry deposition of the particle phase was not considered here.
The air–sea diffusion flux was calculated by following Dachs et al. (2002),
| 2 |
where H′ is the dimensionless Henry’s law constant that depends on the water temperature,18 and KAW (m s–1) is the air–sea mass transfer rate that depends on the wind speed and H′. The relevant parameters and formulas for H′ and KAW are listed in Table S3. A positive value of FAW indicates an input of PCBs from the air to the ocean, while a negative value indicates the volatilization of PCBs from the ocean to the air.
In this study, we chose four PCB congeners (CB28, CB101, CB153, and CB180) for oceanic simulation because they have substantial differences in physicochemical properties.19 Congeners with lighter molecular weights, such as CB28, are much more volatile and have a longer range transport in the atmosphere, having thus a smaller spatial concentration gradient compared to CB153, CB180. We used wind speed that was derived every 6 h from the National Centers for Environmental Projection/National Center for Atmospheric Research (NCEP/NCAR) reanalysis data to calculate the air–sea diffusion flux. At the lateral boundary, the concentrations of the dissolved, phytoplankton, and detritus phases of PCBs were set at zero. At the bottom boundary, there was no flux for any PCB phase through the sea.
Initial and Boundary Conditions and Calculation Scheme of the PCB Module
The PCB module was solved offline using the hydrodynamic and ecosystem modules. Because we only wanted to reproduce the seasonal variation in the spatial distribution of four PCB congeners in the NWPO and examine the mechanisms controlling the air–sea PCB flux, we limited our calculation to a climatological forcing base; that is, all forcings were repeated every year during the model calculations. Climatological forcing included wind speed from NCEP/NCAR every 6 h, daily ocean current velocity, and water temperature from the hydrodynamic module,20 daily phytoplankton biomass from the ecosystem module,21 monthly atmospheric PCB concentrations, and wet deposition flux of PCBs from the GEOS-Chem global atmospheric model. The average period for climatological values of PCBs ranged from 1979 to 2010, whereas that for the other variables ranged from 1993 to 2018. In the Supporting Information, we present a comparison of atmospheric PCB concentrations from GEOS-Chem and available observations.
The initial values for the concentrations of the dissolved, phytoplankton, and detritus phases of PCBs in the ocean were set at zero. Under the above climatological forcing, the model was integrated for 10 years, and the results of last year were analyzed. During the 10 years of calculation, the model results in the upper 200 m layer were almost the same in the ninth and tenth years. Hereafter, this calculation is referred to as the control-run. In addition to the control-run, sensitivity simulations were conducted to explore the role of ocean currents in the air–sea diffusion flux in the NWPO.
CB153 was reported to be the most prevalent congener in marine mammals in the NWPO22,23 and the Northern Atlantic.24 Because of its remarkable influence on ecosystems and humans, CB153, with high lipophilicity and persistence,25 was chosen as the primary objective congener for analysis in this study. We also present the simulation results for CB28, CB101, and CB180 in the Supporting Information for comparison with CB153.
Results and Discussion
Spatiotemporal Variations of CB153 in the NWPO
The simulated surface dissolved CB153 concentration in the NWPO had a mean value of 0.15 pg L–1 with a range of 0–2.16 pg L–1. The surface dissolved CB153 concentrations reported in previous studies had a range of 0.01 to 2.76 pg L–1 in the Northern Hemisphere surface ocean.9,26−29 The dissolved PCBs concentrations of the ∑3PCBs (CB28, CB101, CB153; 0–4.69 pg L–1) in December in the NWPO were lower than those in the central Pacific (3.3–8.3 pg L–1), which was attributed to the higher atmospheric PCBs concentration in the central Pacific (Table S4).
The simulated surface particulate concentrations for the individual CB153 and the total four PCB congeners (∑4PCBs) in the NWPO surface had ranges of 0–0.88 pg L–1 and 0–2.27 pg L–1, respectively. The concentrations were comparable to those observed from the North Atlantic30 (0.42 and 0.72 pg L–1), the North Sea31 (0.3–9.8 and 1.4–41.5 pg L–1), and the Baltic Sea32 (0.1–1 and 0.6–4.3 pg L–1) (Table S5). From the above comparison, we can conclude that the dissolved and particulate concentrations of PCBs on the NWPO surface given by the ocean module are within the range of known observations.
Figure 2 shows the distribution of surface-dissolved and particulate CB153 concentrations in the NWPO. The dissolved CB153 concentration displayed a general northward-increasing pattern, except for the highest value found in coastal waters around Japan and Korea from April to October (Figure 2a–d). The contour of the 0.1 pg L–1 for dissolved CB153 was located around 30° N year-round, which can be considered as the boundary of subtropical and subarctic regions. The seasonality did not coincide in the subarctic region. In the area north of 50° N, the dissolved CB153 concentration was high in January and low in July; the Okhotsk Sea presented the highest value of ∼0.5 pg L–1 in January and lowest value of <0.1 pg L–1 in July. In contrast, the concentrations in the East China Sea, Japan Sea, and the Kuroshio south of Japan were high in July and low in January; the highest value was ∼2.5 pg L–1. The gaseous CB153 concentration in the marginal sea region was particularly high in summer, when its value was approximately 15 times higher than that in winter (Figures S3, S4). The dissolved CB153 concentration in the subtropical open ocean was lower than that in marginal seas by at least 1 order of magnitude and showed little seasonal variation owing to the smaller range of seasonal variation in the water temperature and the atmospheric concentration of CB153 over the subtropical region. The details are shown in Figure S5. The spatial distribution of dissolved CB153 was consistent with that reported for the PCBs concentration inside fish.33 PCBs concentrations in skipjack tuna were reported to reflect the pollution level in the seawater from where the fish were collected. The PCBs concentrations in skipjack tuna showed high values in the marginal seas and low values in the open NWPO during 1997–2001.33
Figure 2.
Distribution of surface dissolved CB153 concentrations (pg L–1) (a–d), surface particulate CB153 concentrations (pg L–1) (e–h), and air–sea CB153 diffusion fluxes (pg m–2 s–1) (i–l) in January, April, July, and October. Positive air–sea flux is from air to sea while negative flux is from sea to air.
Particulate CB153 was concentrated in the subarctic region north of 40° N (Figure 2e–h) where it showed a higher (lower) concentration in April (July). The highest value of 0.2 pg L–1 appeared in the Okhotsk Sea in April. The distribution of particulate CB153 has a similar pattern as the phytoplankton biomass, which was also high in spring and summer in the subarctic region.21 The large phytoplankton biomass in summer did not contribute to a high concentration of particulate CB153 (Figure 2g) because the high water temperature in summer dampens PCB absorption by the phytoplankton.34
Given the large spatial variations of CB153 in seawater, the monthly mean concentrations of surface dissolved CB153 and particulate CB153 were averaged across different latitudes (20°, 30°, 40°, and 50° N) across the open NWPO (lines in Figure S1). The seasonal variation of dissolved CB153 along the 20°, 30°, and 40° N latitudes in the open NWPO was slight, but was much larger at 50° N, with a difference of 0.35 pg L–1 between winter and summer (Figure 3a). The concentration of particulate CB153 increased with latitude, and its value in the subarctic region was lower than that in the dissolved phase (Figure 3b). A peak value of 0.12 pg L–1 was observed in April.
Figure 3.

Time series for surface concentrations of dissolved CB153 (a) and particulate CB153 (b), and for air–sea diffusion fluxes (c) averaged along several latitudes across the open NWPO (lines in Figure S1). The green, cyan, magenta, and blue lines show the results at 20°, 30°, 40°, and 50° N, respectively. Positive air–sea flux is from air to sea, while negative flux is from sea to air.
Spatiotemporal Variations of Other PCB Congeners
In addition to CB153, we also conducted simulations for CB28, CB101, and CB180 (Figures S5, S6, and S7, respectively), which have diverse physicochemical properties.19 We chose CB28 for comparison with CB153 to represent two congeners spanning a broad range of volatility and hydrophobicity. The mean concentration of surface dissolved CB28 in the NWPO was 0.47 pg L–1, which was three times higher than that of CB153. The mean concentration of surface particulate CB28 was similar to that of CB153, but the highest value of CB153 (0.88 pg L–1) was approximately double that of CB28 (0.43 pg L–1). Iwata et al. reported that the observed dissolved phase of CB101 concentrations and CB(28 + 31), which was a mixture of CB28 and CB31, were 0.1–3.1 and 2–8.5 pg L–1 at several stations (Table S7). The observations were about 1–5 and 1–25 times higher than that in our model (0.1–0.7 and 0.1–0.9 pg L–1), respectively, which remained consistent with the observed higher gas phase concentrations at these stations (Table S7). The concentrations showed little spatial variations for the observed CB(28 + 31) and CB101 but showed a decreased trend from coastal region to open ocean in our simulation (Figures S5, S6). Nevertheless, the seasonal variation of dissolved CB28 at these stations in our simulation was consistent with the observation of lower concentration in summer and higher concentration in winter.
The surface distribution and monthly mean series of dissolved and particulate CB28 concentrations at several latitudes (Figures S5a–h, S8a,b) were similar to those of CB153 (Figure 2a–h, 3a,b); however, some differences were still found. The concentration of dissolved CB28 in the subarctic region was over 1.0 pg L–1, which was nearly double that of CB153. The concentration of dissolved CB28 in Japan and Korea was as high as 3.0 pg L–1, which was approximately three times higher than that of CB153. Both the gaseous concentrations and physicochemical parameters are responsible for the higher concentration of CB28 compared with that of CB153. Sensitivity experiments, in which the gaseous concentrations or the physicochemical parameters were changed to those of another congener, indicated that the difference in the gaseous concentration between these congeners had a larger influence (89%) on the dissolved concentration of CB28 than the difference of physicochemical parameters (64%). The details are shown in Figure S9.
Air–Sea Flux of CB153
Air–sea diffusion and wet deposition are the two sources of PCBs in the NWPO. Advection and eddy diffusion with the ocean outside the target area, and self-degradation of the dissolved phase, are the two sinks of PCBs in the NWPO. The daily amount of CB153 exchanged through the air–sea interface, the lateral boundary of the model domain, and the self-degradation of CB153 in the NWPO were calculated (Figure S10).
Because the wet deposition flux of CB153 is an order of magnitude smaller than the air–sea diffusion flux (Figure S11), and the air–sea diffusion flux depends on the dissolved phase concentration of CB153 in water, we examined the air–sea diffusion flux in more detail. The air–sea diffusion flux of CB153 was close to zero over the majority of the NWPO, except for the western boundary area (Figure 2i–l). In the western boundary area, the air–sea diffusion flux in the Yellow Sea, Japan Sea, and the Kuroshio region displayed remarkable downward values in April with a maximum of approximately 0.03 pg m–2 s–1 (Figure 2j). This changed to an upward flux in the summer and autumn in the Yellow Sea, southern Japan Sea, and the KE, and the maximum upward flux was as high as 0.03 pg m–2 s–1 in the KE. The upward flux indicates that these regions act as secondary sources of CB153 in air. The KE east of Japan, which possesses the strongest velocity in summer, represents the most intense volatilization region (Figure 2k).
Figure 3c shows the monthly mean air–sea diffusion flux for CB153 averaged at different latitudes (20°, 30°, 40°, and 50° N) across the open NWPO (lines in Figure S1). The flux along 40° N was close to zero in spring but demonstrated a large upward value in summer (magenta line in Figure 3c). The time series along 50° N showed a reversal of the air–sea diffusion flux direction from spring to autumn (blue line in Figure 3c). The downward flux (positive) reached its maximum in November owing to the highest gaseous concentration of CB153 in November (Figures S4, S13), whereas the upward flux (negative) reached its maximum in April. The surface dissolved CB153 exhibited a consistent response to the air–sea diffusion flux. For example, the concentration of surface dissolved CB153 was lowest along 50° N in July before the reversal of the air–sea flux direction from upward to downward, while the highest concentration along 50° N was in December because of continuous strong deposition (Figure 3a,c). More details regarding the mechanism of the air–sea diffusion flux variations will be given later.
Air–Sea Flux of Other PCB Congeners
The distribution of the air–sea diffusion flux for CB28 was similar to that for CB153. The flux in the western boundary region exhibited a large downward value in winter and spring, shifting to an upward value in the KE during summer and autumn. However, the amplitude of CB28 flux (e.g., a maximum upward flux of 0.11 pg m–2 s–1) was larger than that of CB153 (Figure S5i–l). Furthermore, there was little spatial difference in the seasonal variation of CB28. The air–sea diffusion flux along several latitudes showed large positive values in winter and small values in summer (Figure S8c).
In addition to the difference in gaseous concentrations of CB28 and CB153 in air, the discrepancy in the air–sea diffusion flux between CB28 and CB153 was also influenced by their different physicochemical properties. The air–sea mass transfer rate (KAW) in eq 2 was determined by the mass transfer coefficient in water and air, which was calculated using the Schmidt number and molecular diffusivity rates of the congeners (Table S8). A smaller Schmidt number and larger molecular diffusivity rate contributed to a larger KAW, and consequently led to a larger air–sea diffusion flux for CB28 than for CB153. A summary of modeled results of concentrations for all four PCB congeners in the surface NWPO, together with their air–sea exchange fluxes integrated yearly, is listed in Table S9.
Influence of Ocean Currents on Air–Sea Diffusion Fluxes of PCBs
Because gaseous PCBs in the atmosphere were specified in this study, the intensification of air–sea diffusion in the western boundary current area depends on the processes affecting the dissolved PCBs concentrations. Advection and diffusion are the main physical processes, while biological pump are the main biological processes responsible for modulating dissolved PCBs in water. As shown in Figure S3, the distribution of gaseous CB153 concentration was not homogeneous, and was approximately three times larger in the area south of Japan compared with that in the KE. In addition, the air–sea diffusion flux presented a band distribution but with opposing directions in these two regions in summer and autumn (Figure 2k, l). On the basis of the above facts, we infer that the ocean current affects the air–sea diffusion flux. To confirm this hypothesis, we conducted sensitivity experiments on CB28, CB101, CB153, and CB180 (Text S6).
The experiments confirmed that the Kuroshio current moved a large amount of water with lower PCBs concentrations from the upstream region to the area south of Japan, and transported water with high PCBs concentrations from the south of Japan to the KE, resulting in an intensification of downward (upward) air–sea diffusion flux in the south of Japan (the KE). The air–sea flux of CB(28 + 31) and CB101 at several stations (Table S7) were calculated using the observed paired data for air and water samples,12 which were −8.2–5.6 and −0.8–0.8 ng m–2 d–1, respectively. The simulated air–sea flux of CB101 in our model (−0.4–0.8 ng m–2 d–1) was consistent with the observation at these stations, but the simulated flux of CB28 (0–2.4 ng m–2 d–1) was 1–4 times lower compared to CB(28 + 31) in the observation. Both in observation and simulation, CB101 showed weak outgassing in some stations, while CB28 was mainly in the downward deposition, except at three stations in observation.
The simulated air–sea flux of ∑4PCBs ranged between −23.6 and 44.75 ng m–2 d–1, which was an order of magnitude larger than the air–sea flux in the central Pacific9 (−4.73 to −2.85 ng m–2 d–1) (Table S10). The strong western boundary current (the Kuroshio) in the NWPO strengthened the air–sea exchange of PCBs, whereas there were no such strong currents in the central Pacific.
To quantitatively assess the effect of the strong western boundary current on dissolved PCBs concentrations in summer (July–September) when the air–sea flux changed largely along the Kuroshio and KE, we estimated the time for the dissolved PCBs in surface water to reach equilibrium status (hereafter referred as response time) when only air–sea exchange (Case 1) or only ocean advection (Case 2) was considered (Figure 4). The temporal change rate of the dissolved concentration in the surface ocean mixed layer in Case 1 (eq 3) and Case 2 (eq 4) is as follows:
| 3 |
| 4 |
where 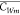 denotes the mean concentration of dissolved
PCBs in the mixed layer, hm (m) is the mixed layer depth, C* (=CA/H′) is the dissolved concentration
at equilibrium, um (m
s–1) is the mean velocity in the mixed layer and
has a value of 1 m s–1 for the Kuroshio current
in summer. We defined the mixed layer as the depth at which the temperature
is 0.2 °C less than the sea surface temperature,35 and obtained a mean summer mixed layer depth of 10 m along
the Kuroshio axis.
denotes the mean concentration of dissolved
PCBs in the mixed layer, hm (m) is the mixed layer depth, C* (=CA/H′) is the dissolved concentration
at equilibrium, um (m
s–1) is the mean velocity in the mixed layer and
has a value of 1 m s–1 for the Kuroshio current
in summer. We defined the mixed layer as the depth at which the temperature
is 0.2 °C less than the sea surface temperature,35 and obtained a mean summer mixed layer depth of 10 m along
the Kuroshio axis.
Figure 4.

Response time for dissolved PCBs to reach equilibrium in (a) scenario where only air–sea exchange was considered, (b) scenario where only ocean advection was considered.
According to the above equations, the analytical
solution for 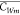 in Case 1 (eq 5) and Case 2 (eq 6) are as follows:
in Case 1 (eq 5) and Case 2 (eq 6) are as follows:
| 5 |
| 6 |
where Cu is the upstream dissolved concentration, Δx is the grid spacing in the latitudinal direction for each grid point
in the model, denoting the distance for dissolved PCBs transported
from the upstream to the target region. α and β can be
considered the response times for the local concentration 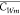 to approach C* and Cu, respectively.
to approach C* and Cu, respectively.
As shown in the “no-current” experiment, the air–sea exchange was close to equilibrium over the entire region when the current speed was zero. In the weak currents region such as the subtropical region, it took 1–3 days to reach equilibrium when only the air–sea exchange was considered (Figure 4a), while the time taken was 3–12 days in case 2 (Figure 4b). The shorter response time to the air–sea exchange means that the dissolved PCBs concentration in these region is mainly controlled by the air–sea exchange and the advection did not easily break the equilibrium of surface dissolved PCBs concentration with the air–sea exchange. In the strong western boundary current region, the response time of surface dissolved PCBs concentration was ∼4 days in case 1 (Figure 4a), whereas it decreased to 1 day in case 2 when only the ocean current was taken into account (Figure 4b). Consequently, the dissolved PCBs from upstream carried by the strong current can easily change the dissolved CB153 in the downstream because the air–sea exchange needs more time to recover it to an equilibrium status. In other words, a strong ocean current disrupts the original equilibrium in the “no current” scenario and results in significant downward and upward air–sea fluxes in the area south of Japan and the KE, respectively.
Implications
Owing to the high current speed, the Kuroshio intensified the air–sea exchange in the western boundary current region in summer by transporting large amounts of water with high PCBs concentrations downstream. The corresponding air–sea flux in the Kuroshio region is remarkable compared with that in weak current regions. Notably, strong western boundary currents exist across the globe, including the Kuroshio and East Australia Current in the Pacific, the Gulf Stream and Brazil Current in the Atlantic, the Somali and Agulhas currents in the Indian Ocean. These currents flow through coastal waters and transport high concentrations of contaminants from nearshore areas to the open ocean, which may play an important role in the global air–sea exchange of PCBs. One important implication is that the effect of western boundary currents on the air–sea diffusion flux of PCBs should be considered in atmospheric modeling of the global distribution and fate of PCBs.
Current global fate simulations for PCBs are mostly based on multimedia models, whose oceanic compartment is simplified to a box model that ignores the direct effect of ocean current advection on PCBs. Some global ocean simulations of PCBs do include the direct effect of ocean current advection on PCBs. However, these global models use a horizontal resolution of ∼100 km or more which is too coarse to represent realistic western boundary currents. These western boundary currents have a width of 100–200 km; hence, a horizontal resolution of ∼10 km is necessary to obtain a realistic velocity (∼1 m s–1) in an ocean model. Coarse resolution (∼100 km) induces a weak western boundary current in an ocean model. Therefore, the effects of western boundary currents on PCBs concentrations have not been fully considered by the global ocean simulation of PCBs.
In this study, a three-dimensional hydrodynamic-ecosystem-PCBs coupled model was developed for the northwestern Pacific Ocean to assess the air–sea diffusion fluxes of four PCB congeners and examine the influences of western boundary currents on air–sea diffusion flux. This model has a horizontal resolution of <10 km and can reproduce a realistic Kuroshio Current and its extension. The model results indicate that the Kuroshio is a necessary condition for the appearance of downward and upward fluxes of PCBs along the Kuroshio south of Japan and Kuroshio extension, respectively. We suggest that future atmospheric transport models for PCBs should include realistic western boundary currents.
Acknowledgments
We are grateful to Carey L. Friedman and Noelle Eckley Selin for providing the atmospheric PCBs data. We thank Prof. Hisato Iwata for providing the observation PCBs data. M. Yang thanks the Ministry of Education, Culture, Sports, Science and Technology, Japan (MEXT) for supporting her stay in Japan. This study was supported by a Grant-in-Aid for Scientific Research (MEXT KAKENHI, Grant No. 20KK0239).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.2c03459.
Model description supplementary section; discussion of the influence of ocean currents on air–sea exchange flux; parameters used in calculations of biological and air–sea exchange processes; observations of gaseous and oceanic concentrations; conditions of sensitivity experiments for CB153; summary of model results of surface concentrations and air–sea fluxes for four PCB congeners; additional figures as described in the text (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Lohmann R.; Dachs J.. Chapter 15 - Polychlorinated Biphenyls in the Global Ocean. In World Seas: an Environmental Evaluation, 2nd ed.; Sheppard C., Ed.; Academic Press, 2019; pp 269–282. 10.1016/B978-0-12-805052-1.00017-6. [DOI] [Google Scholar]
- Galbán-Malagón C.; Berrojalbiz N.; Ojeda M.-J.; Dachs J. The Oceanic Biological Pump Modulates the Atmospheric Transport of Persistent Organic Pollutants to the Arctic. Nat. Commun. 2012, 3 (1), 862. 10.1038/ncomms1858. [DOI] [PubMed] [Google Scholar]
- Dachs J.; Lohmann R.; Ockenden W. A.; Méjanelle L.; Eisenreich S. J.; Jones K. C. Oceanic Biogeochemical Controls on Global Dynamics of Persistent Organic Pollutants. Environ. Sci. Technol. 2002, 36 (20), 4229–4237. 10.1021/es025724k. [DOI] [PubMed] [Google Scholar]
- Friedman C. L.; Selin N. E. PCBs in the Arctic Atmosphere: Determining Important Driving Forces Using a Global Atmospheric Transport Model. Atmospheric Chemistry and Physics 2016, 16 (5), 3433–3448. 10.5194/acp-16-3433-2016. [DOI] [Google Scholar]
- Wania F. Assessing the Potential of Persistent Organic Chemicals for Long-Range Transport and Accumulation in Polar Regions. Environ. Sci. Technol. 2003, 37 (7), 1344–1351. 10.1021/es026019e. [DOI] [Google Scholar]
- MacLeod M.; Riley W. J.; Mckone T. E. Assessing the Influence of Climate Variability on Atmospheric Concentrations of Polychlorinated Biphenyls Using a Global-Scale Mass Balance Model (BETR-Global). Environ. Sci. Technol. 2005, 39 (17), 6749–6756. 10.1021/es048426r. [DOI] [PubMed] [Google Scholar]
- Wagner C. C.; Amos H. M.; Thackray C. P.; Zhang Y.; Lundgren E. W.; Forget G.; Friedman C. L.; Selin N. E.; Lohmann R.; Sunderland E. M. A Global 3-D Ocean Model for PCBs: Benchmark Compounds for Understanding the Impacts of Global Change on Neutral Persistent Organic Pollutants. Global Biogeochemical Cycles 2019, 33 (3), 469–481. 10.1029/2018GB006018. [DOI] [Google Scholar]
- Breivik K.; Sweetman A.; Pacyna J. M.; Jones K. C. Towards a Global Historical Emission Inventory for Selected PCB Congeners — A Mass Balance Approach: 3. An Update. Science of The Total Environment 2007, 377 (2), 296–307. 10.1016/j.scitotenv.2007.02.026. [DOI] [PubMed] [Google Scholar]
- Zhang L.; Lohmann R. Cycling of PCBs and HCB in the Surface Ocean-Lower Atmosphere of the Open Pacific. Environ. Sci. Technol. 2010, 44 (10), 3832–3838. 10.1021/es9039852. [DOI] [PubMed] [Google Scholar]
- Wang A.; Guo X.; Shi J.; Luo C.; Gao H. A Simulation of the Seasonal Variation of Decabromodiphenyl Ether in a Bay Adjacent to the Yellow Sea. Science of The Total Environment 2019, 664, 522–535. 10.1016/j.scitotenv.2019.01.385. [DOI] [PubMed] [Google Scholar]
- Lohmann R.; Markham E.; Klanova J.; Kukucka P.; Pribylova P.; Gong X.; Pockalny R.; Yanishevsky T.; Wagner C. C.; Sunderland E. M. Trends of Diverse POPs in Air and Water Across the Western Atlantic Ocean: Strong Gradients in the Ocean but Not in the Air. Environ. Sci. Technol. 2021, 55 (14), 9498–9507. 10.1021/acs.est.0c04611. [DOI] [PubMed] [Google Scholar]
- Iwata H.; Tanabe S.; Sakai N.; Tatsukawa R. Distribution of Persistent Organochlorines in the Oceanic Air and Surface Seawater and the Role of Ocean on Their Global Transport and Fate. Environ. Sci. Technol. 1993, 27 (6), 1080–1098. 10.1021/es00043a007. [DOI] [Google Scholar]
- Guo X.; Hukuda H.; Miyazawa Y.; Yamagata T. A Triply Nested Ocean Model for Simulating the Kuroshio—Roles of Horizontal Resolution on JEBAR. Journal of Physical Oceanography 2003, 33 (1), 146–169. . [DOI] [Google Scholar]
- Ono J.; Takahashi D.; Guo X.; Takahashi S.; Takeoka H. A Numerical Study on the Seasonal Variability of Polychlorinated Biphenyls from the Atmosphere in the East China Sea. Chemosphere 2012, 89 (4), 389–397. 10.1016/j.chemosphere.2012.05.049. [DOI] [PubMed] [Google Scholar]
- Ilyina T.; Lammel G.; Pohlmann T. Mass Budgets and Contribution of Individual Sources and Sinks to the Abundance of γ-HCH, α-HCH and PCB 153 in the North Sea. Chemosphere 2008, 72 (8), 1132–1137. 10.1016/j.chemosphere.2008.04.047. [DOI] [PubMed] [Google Scholar]
- Alekseenko E.; Thouvenin B.; Tronczyński J.; Carlotti F.; Garreau P.; Tixier C.; Baklouti M. Modeling of PCB Trophic Transfer in the Gulf of Lions; 3D Coupled Model Application. Mar. Pollut. Bull. 2018, 128, 140–155. 10.1016/j.marpolbul.2018.01.008. [DOI] [PubMed] [Google Scholar]
- Jurado E.; Zaldívar J.-M.; Marinov D.; Dachs J. Fate of Persistent Organic Pollutants in the Water Column: Does Turbulent Mixing Matter?. Mar. Pollut. Bull. 2007, 54 (4), 441–451. 10.1016/j.marpolbul.2006.11.028. [DOI] [PubMed] [Google Scholar]
- Bamford H. A.; Poster D. L.; Huie R. E.; Baker J. E. Using Extrathermodynamic Relationships To Model the Temperature Dependence of Henry’s Law Constants of 209 PCB Congeners. Environ. Sci. Technol. 2002, 36 (20), 4395–4402. 10.1021/es020599y. [DOI] [PubMed] [Google Scholar]
- Kim A. W.; Vane C. H.; Moss-Hayes V.; Engelhart S. E.; Kemp A. C. PAH, PCB, TPH and Mercury in Surface Sediments of the Delaware River Estuary and Delmarva Peninsula, USA. Mar. Pollut. Bull. 2018, 129 (2), 835–845. 10.1016/j.marpolbul.2017.10.008. [DOI] [PubMed] [Google Scholar]
- Miyazawa Y.; Varlamov S. M.; Miyama T.; Guo X.; Hihara T.; Kiyomatsu K.; Kachi M.; Kurihara Y.; Murakami H. Assimilation of High-Resolution Sea Surface Temperature Data into an Operational Nowcast/Forecast System around Japan Using a Multi-Scale Three-Dimensional Variational Scheme. Ocean Dynamics 2017, 67 (6), 713–728. 10.1007/s10236-017-1056-1. [DOI] [Google Scholar]
- Ishizu M.; Miyazawa Y.; Tsunoda T.; Guo X. Development of a Biogeochemical and Carbon Model Related to Ocean Acidification Indices with an Operational Ocean Model Product in the North Western Pacific. Sustainability 2019, 11 (9), 2677. 10.3390/su11092677. [DOI] [Google Scholar]
- Minh T. B.; Nakata H.; Watanabe M.; Tanabe S.; Miyazaki N.; Jefferson T. A.; Prudente M.; Subramanian A. Isomer-Specific Accumulation and Toxic Assessment of Polychlorinated Biphenyls, Including Coplanar Congeners, in Cetaceans from the North Pacific and Asian Coastal Waters. Arch. Environ. Contam. Toxicol. 2000, 39 (3), 398–410. 10.1007/s002440010121. [DOI] [PubMed] [Google Scholar]
- Yasunaga G.; Fujise Y. Concentration of Persistent Organic Pollutants (POPs) in Three Species of Baleen Whales in the Western North Pacific. Cetacean Population Studies 2020, 2 (1), 39–53. 10.34331/cpops.2.1_39. [DOI] [Google Scholar]
- Kleivane L.; Skaare J. U. Organochlorine Contaminants in Northeast Atlantic Minke Whales (Balaenoptera Acutorostrata). Environ. Pollut. 1998, 101 (2), 231–239. 10.1016/S0269-7491(98)00043-8. [DOI] [PubMed] [Google Scholar]
- Mackay D.; Shiu W.-Y.; Lee S. C.. Handbook of Physical-Chemical Properties and Environmental Fate for Organic Chemicals; CRC Press, 2006. [Google Scholar]
- Zhang L.; Thibodeaux L.; Jones L.; Lohmann R. Simulation of Observed PCBs and Pesticides in the Water Column during the North Atlantic Bloom Experiment. Environ. Sci. Technol. 2015, 49 (23), 13760–13767. 10.1021/acs.est.5b00223. [DOI] [PubMed] [Google Scholar]
- Gioia R.; Lohmann R.; Dachs J.; Temme C.; Lakaschus S.; Schulz-Bull D.; Hand I.; Jones K. C. Polychlorinated Biphenyls in Air and Water of the North Atlantic and Arctic Ocean. J. Geophys. Res.: Atmospheres 2008, 113 (D19), 9750. 10.1029/2007JD009750. [DOI] [Google Scholar]
- Sobek A.; Gustafsson Ö. Deep Water Masses and Sediments Are Main Compartments for Polychlorinated Biphenyls in the Arctic Ocean. Environ. Sci. Technol. 2014, 48 (12), 6719–6725. 10.1021/es500736q. [DOI] [PubMed] [Google Scholar]
- Huang Y.; Li J.; Xu Y.; Xu W.; Cheng Z.; Liu J.; Wang Y.; Tian C.; Luo C.; Zhang G. Polychlorinated Biphenyls (PCBs) and Hexachlorobenzene (HCB) in the Equatorial Indian Ocean: Temporal Trend, Continental Outflow and Air–Water Exchange. Mar. Pollut. Bull. 2014, 80 (1), 194–199. 10.1016/j.marpolbul.2014.01.007. [DOI] [PubMed] [Google Scholar]
- Schulz-Bull D. E.; Petrick G.; Bruhn R.; Duinker J. C. Chlorobiphenyls (PCB) and PAHs in Water Masses of the Northern North Atlantic. Marine Chemistry 1998, 61 (1), 101–114. 10.1016/S0304-4203(98)00010-3. [DOI] [Google Scholar]
- Schulz-Bull D. E.; Petrick G.; Duinker J. C. Polychlorinated Biphenyls in North Sea Water. Marine Chemistry 1991, 36 (1–4), 365–384. 10.1016/S0304-4203(09)90071-8. [DOI] [Google Scholar]
- Schulz-Bull D. E.; Petrick G.; Kannan N.; Duinker J. C. Distribution of Individual Chlorobiphenyls (PCB) in Solution and Suspension in the Baltic Sea. Marine Chemistry 1995, 48 (3–4), 245–270. 10.1016/0304-4203(94)00054-H. [DOI] [Google Scholar]
- Ueno D.; Takahashi S.; Tanaka H.; Subramanian A. N.; Fillmann G.; Nakata H.; Lam P. K. S.; Zheng J.; Muchtar M.; Prudente M.; Chung K. H.; Tanabe S. Global Pollution Monitoring of PCBs and Organochlorine Pesticides Using Skipjack Tuna as a Bioindicator. Arch. Environ. Contam. Toxicol. 2003, 45 (3), 378–389. 10.1007/s00244-002-0131-9. [DOI] [PubMed] [Google Scholar]
- Del Vento S.; Dachs J. Prediction of Uptake Dynamics of Persistent Organic Pollutants by Bacteria and Phytoplankton. Environ. Toxicol. Chem. 2002, 21 (10), 2099–2107. 10.1002/etc.5620211013. [DOI] [PubMed] [Google Scholar]
- Miller J. R. The Salinity Effect in a Mixed Layer Ocean Model. Journal of Physical Oceanography 1976, 6 (1), 29–35. . [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.




