Fusing 2D and 3D molecular graphs as unambiguous molecular descriptors for conformational and chiral stereoisomers

Abstract

The rapid progress of machine learning (ML) in predicting molecular properties enables high-precision predictions being routinely achieved. However, many ML models, such as conventional molecular graph, cannot differentiate stereoisomers of certain types, particularly conformational and chiral ones that share the same bonding connectivity but differ in spatial arrangement. Here, we designed a hybrid molecular graph network, Chemical Feature Fusion Network (CFFN), to address the issue by integrating planar and stereo information of molecules in an interweaved fashion. The three-dimensional (3D, i.e., stereo) modality guarantees precision and completeness by providing unabridged information, while the two-dimensional (2D, i.e., planar) modality brings in chemical intuitions as prior knowledge for guidance. The zipper-like arrangement of 2D and 3D information processing promotes cooperativity between them, and their synergy is the key to our model’s success. Experiments on various molecules or conformational datasets including a special newly created chiral molecule dataset comprised of various configurations and conformations demonstrate the superior performance of CFFN. The advantage of CFFN is even more significant in datasets made of small samples. Ablation experiments confirm that fusing 2D and 3D molecular graphs as unambiguous molecular descriptors can not only effectively distinguish molecules and their conformations, but also achieve more accurate and robust prediction of quantum chemical properties.

Introduction

Recent advances in computational power and algorithms have spawned a marriage between molecular science and computer science [1, 2]. Models based on machine learning can now make quick estimations or predictions on molecular properties [3]. Various types of machine learning (ML) methods such as convolutional neural networks [4, 5], recurrent neural networks [6, 7] and graph convolutional networks (GCNs) [8, 9] have been attempted and used in a wide range of applications, including recognition of protein structure [9], computer-assisted drug design [10] and retrosynthesis planning [11, 12]. Based on the way of molecular characterization, most existing models could be categorized into three different classes, 1D (such as SMILES), 2D (such as topological graph) or 3D (such as space atomic coordinates). Many of them could achieve excellent results in property prediction for different molecules [13, 14]. However, many adopted molecular representation methods [15] are limited in fully identifying or characterizing all molecules (Supplementary Note 1) and their possible conformations in the colorful and diverse chemical space.

Various approaches have been developed for molecular modeling. Encoding molecules as 1D vectors of text, such as simplified molecular-input line-entry system (SMILES) [16], is a convenient way to achieve molecular featurization. Molecules expressed this way could be directly fed into NLP models such as transformer [13, 14] and BERT [17, 18]. Despite the pertinent results of such models in molecular property prediction and retrosynthesis, encoding molecules as 1D text will inevitably lose the relative atomic position and adjacency information. Consequently, all models in this category fall short in analyzing molecular configurations such as cis-trans structures, let alone molecular conformations. To accurately represent adjacency information between atoms, some methods take advantage of 2D fingerprints [19] or topological graphs [20] to explicitly capture bonding information. However, they neglect 3D geometry information (stereo features) of molecules, and therefore are still unable to distinguish conformational isomers and some complicated configurational isomers including enantiomers [21]. Some 2D-structure based networks have been creatively developed to include selective 3D features of molecules such as 3D coordinates of atoms integrated spatial–temporal gated network [22], 3D graph Laplacian matrix with atoms’ soft relations [23], algebraic graph-assisted BERT model (AGBT) [3], 3DGCN [24], atom distance based 3D molecular fingerprints [3] and atomic distance and bond angel coupled to GNN [21]. While this greatly improves performances of these 2D-based networks, the lack of full 3D information prevents them from delivering satisfying results [25]. Some recent networks such as SchNet [26],s DimeNet [27] and SphereNet [28] have taken initial steps to represent complete 3D information such as Euclidean distance between atoms, bond angle and torsion angle. Explicitly including 3D information as features can indeed further enhance prediction accuracy on downstream tasks [25]. However, these approaches, which often rely entirely on extracting 3D molecular features to model, tend to need more parameters to fit the complex correlations between molecular properties and full 3D information. The ignorance of basic chemical intuitions or chemical logics hence leads such models to be hard to be trained and have giant requirements in both the perspectives of data volume and quality to achieve satisfying results.

Another drawback that limits the broad usage of ML methods is that most of them are data hungry. Real datasets in chemistry and material science are often scarce, unstructured and even full of errors [29]. Large collections of experimental data are very time-consuming and even contain a variety of unexpected inconsistencies, omissions and mistakes [30]. Mathematical theoretical calculation seems feasible but is limited by the number of atoms which complexity increases exponentially and could be prohibitively expensive [31, 32]. It is an emergent and urgent need to develop a data-efficient and error-proof ML method that is capable of delivering satisfactory results even with small and erroneous data [33] .

To address the above-mentioned challenges, a multi-modality strategy that integrates 2D and 3D molecular features is adopted. 2D molecular features contain important information such as molecular adjacency and cyclization, and are indicative of molecular chemical properties such as aromaticity. This free physical information could be used as the prior knowledge to mitigate data shortage, increase models’ generalizability [34] and facilitate the learning. A regular graph presenting such 2D molecular features makes up the planer modality. The stereo modality handles 3D features of molecules as a full connection graph. Relative atomic positions are precisely presented so the molecular conformation can be uniquely determined. It naturally distinguishes all molecular conformers and chiral molecules. This modality offers precision and completeness. To generate a non-ambiguous molecular descriptor, 2D molecular topology information (i.e. planar modality) and 3D spatial geometry information (i.e. stereo modality) are integrated organically into a single network, CFFN (Chemical Feature Fusion based Network). The 2D and 3D modalities are interweaved together in a novel zipper-like arrangement to facilitate information exchange between stereo modality and the planar modality and to extract most useful information from both modalities. CFFN not only delivers more accurate predictions on different molecules as well as conformational and chiral isomers, but also retains its accuracy when severely reducing the volume of training data or including a large amount of erroneous data.

Materials and methods

Dataset preparation

In this work, QM9, MD17 and two chiral molecular datasets are used to test the molecular property prediction performances of different models on different molecules and conformers [35]. QM9 collects many different kinds of quantum properties of its most stable conformer, and corresponding harmonic frequency, dipole moment, polarizability, energy, enthalpy and free energy of atomization for 134 k stable small organic molecules made up of C (carbon), H (hydrogen), O (oxygen), N (nitrogen) and F (fluorine) [35]. Geometry, typically of its most stable conformer, is provided [36].

MD17 is a (MD) dataset of seven molecules, including aspirin, ethanol, benzene, malonaldehyde, naphthalene, salicylic acid, toluene and uracil [37], each containing 150 k to nearly 1 M conformational geometries. The ground truth data are calculated via molecular dynamics simulations using DFT at a temperature of 500 K and in a resolution of 0.5 fs. Note that for every molecule, we only need to extract 2D information once, because the atomic and chemical bond features of different conformations of the same molecule are the same.

The first chiral dataset that consist of 3800 chiral pairs is a protein–chiral ligand binding dataset in which each enantiomer of ligand exhibits different activity in binding affinity due to the differences in 3D structural matching with the protein, sometimes known as chiral cliff in biochemistry [38].

The second home-generated chiral dataset containing 1500 chiral conformers of 1, 2-dichloro-1, 2-difluoroethane (C₂H₂F₂Cl₂) have been obtained by the ab-initio molecular dynamics simulations performed using the software package Vienna ab initio simulation package (VASP) with a canonical ensemble conducted by the algorithm of Nose [39]. These confusingly similar structures are used to throw down the gauntlet to the model.

CFFN model

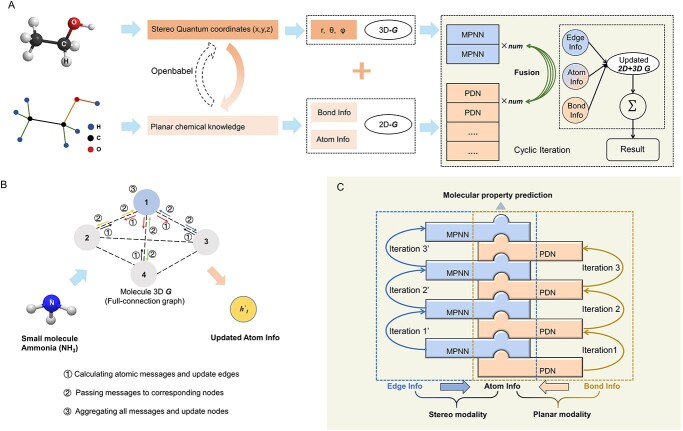
Figure 1A illustrates the basic design and overall architecture of our model. All molecules are presented as a graph-like data structure. 2D characteristics are planar (Figure 1A), carrying mostly ‘chemical’ information while 3D characteristics are stereo, carrying mostly ‘geometrical’ information. Planer modality treats 2D molecular structure as a normal molecular graph [15] and recruits Pathfinder Discovery Network (PDN) [40] to extract the chemical information encoded in it. In contrast, stereo modality handles complete 3D molecular geometry using a full connection graph [3]. Message Passing Neural Network (MPNN) is employed to extract quantum physics-related information, particularly interactions between atoms through edges, including both bonds and non-bonds.

Figure 1.

CFFN architecture. (A) Illustration of overall architecture of CFFN that integrates planar and stereo structural information for molecular property predictions. 2D and 3D information is respectively represented as common molecular graph (2D-G) and full connection graph (3D-G) including all atomic distance, angle and dihedral angle. The two types of molecular graphs are processed using PDN and MPNN networks, respectively, and fused together to form a final hybrid graph (updated 2D + 3D G), which makes final predictions toward certain molecular property. (B) Illustration of generating 3D-G using the MPNN network. Atomic information of a target atom is updated by aggregating information of all edges connecting to it, which is updated iteratively using atomic information. (C) Illustration of an interdigitated arrangement of PDN and MPNN that together forms a zipper-like structure. PDN, which processes 2D-G, and MPNN, which processes 3D-G, communicate via sharing atom information.

The planar and stereo modalities in CFFN are interdependent, cooperative and synergetic. As illustrated in Figure 1C, the two modalities share the same set of atomic information. During each stage of ML, every target atom aggregates its adjacent atomic information through the 2D network first. The updated atomic information is then introduced into the 3D network as the initial atomic information. The updated information is sent back to 2D network in the next iteration. Bond information in planar modality and edge information in stereo modality are only processed in the corresponding networks respectively, while shared atomic information serves as the passage between the two networks. In other words, the planar and stereo modalities take alternative turns in ML and exchange the ‘new knowledge’ gained during each iteration in ML. This interdigitated arrangement forms a zipper-like structure, promoting a strong cooperation and synergy between planar and stereo modalities, eventually leading to the outstanding performance of CFFN.

2D-G and 3D-G for molecular presentation

In our model, both 2D and 3D molecular features are represented using two molecular graphs, denoted as 2D-G and 3D-G, respectively. The datasets, QM9 and MD17, include the atomic coordinates, and a 3D-G is naturally generated by fully connection between atomic pairs. As for 2D-G, we convert the atomic coordinate data into ‘MOL’ files by Openbabel package [41] due to the SMILES representation is not unique for a specific molecule [42], and then get the 2D-G by Rdkit package [43]. So 2D-G and 3D-G is relatively independent in this process (Figure S1).

2D-G is a regular molecular graph, which includes atoms 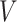, bonds 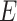, atomic features 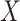and bonds’ features :

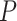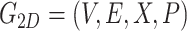(1)

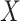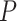where and are the one-hot code vectors containing all atomic features and bond features, respectively.

More specifically, 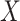is made of two parts:

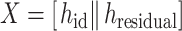(2)

where || denotes the operation of concatenation, 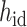is the hidden embedding of proton numbers which has 128-dimensional vectors to represent the original atomic types, and 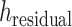is the embeddings of all residual features such as aromaticity and hybridization type. The five hybridization types and aromaticity are embedded into a five-dimensional and two-dimensional vector. In addition, there are additional three-dimensional vectors to represent atoms types as chiral centers (R/S/none), and then concatenate with .

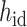Likewise, 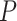includes a series indicator for whether bond is in a ring, bonding atoms and bond type:

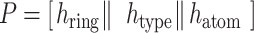(3)

Here, 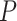is an eight-dimensional vector including whether bond is in a ring, bond type and proton number of bonding atoms which has one-dimensional, five-dimensional and two-dimensional vector respectively by one-hot encoding.

3D-G is a full connection molecular graph generated naturally by atomic coordinate from datasets that only includes the atomic types and edges between atoms.

Herein,

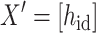(4)

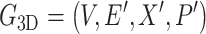(5)

Then, fusing the 2D-G and 3D-G:

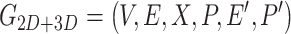(6)

where the atomic information is represented by 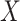from 2D-G which has more atomic information. 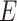represents all bond instead of bonds in the original 2D-G. And the edges information is collected from 3D-G, two additional features 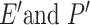correspond respectively the edge set and the 3D features of all the edges.

These 3D features in 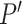about spatial distance 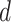, angle 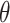and torsion φ can be calculated by:

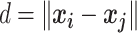(7)

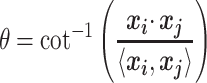(8)

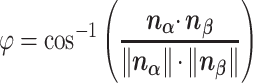(9)

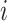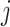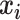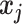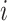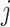where and refer to two different atoms, and indicate the coordinate vectors of atom and 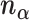, and and 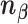correspond to the normal vectors of α and β planes (Figure S2).

These 3D features in P′ are all represented in spherical coordinates using the Spherical Radial Bessel Functions (SRBF) 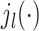and the Spherical Harmonics Bessel Functions (SHBF)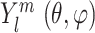, both of which are the regular solves of the Schrödinger equation (Equation 10) in spherical coordinate system:

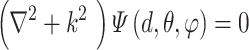(10)

where

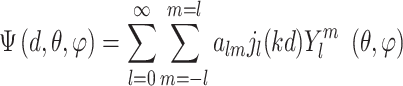(11)

where 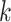is the wave number, and 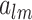is the set of coefficients regarding 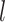and 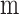, When 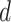exceed the cutoff value of 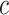[44], 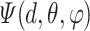is set to be zero, meaning this interaction is not taken into consideration. When assuming the atomic angular momentum 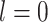and the magnetic quantum number 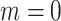in the above-mentioned Equation (12), this function can be reduced to

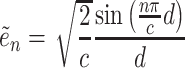(12)

where 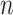is the principal quantum number. A more accurate expression can be obtained by assuming magnetic quantum number 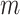to be 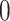and taking the atomic angular momentum 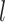into consideration. This spatial orientation information depending on 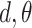can be expressed as

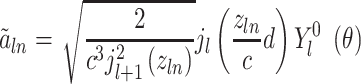(13)

Finally, to encode the full 3D information involving 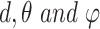an orthogonal basis [27] can be exploited using the formula:

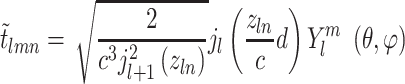(14)

where 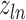denotes the 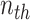root of the Bessel function of order 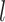. Notice here 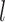∈[0, · · ·,N_SHBF − 1],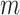∈[−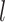, · · ·, 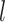] and principal quantum number 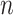∈[1, · · ·,N_SRBF] where N_SHBF and N_SRBF respectively denote the highest orders for SHBF and SRBF [28].

So far, we then initiate the 3D edge 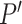by,

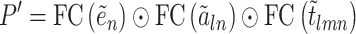(15)

where 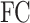corresponds to a fully connected neural network and denotes the element-wise multiplication.

PDN for processing 2D information

PDN [40] is employed to process 2D information which is superior to common GCNs [45, 46] based on our previous research. PDN pays more attention to complex and multiple bond relationships buried in a molecular as the bond difference. It is more suitable to simulate complicated chemical bonding using learned weighted adjacency matrices instead of one-hot encoding (Figure S3). It aggregates the 2D features of atoms and passes the aggregated information to their neighboring atoms with the convolution module. More specifically, PDN generates a series of weighted adjacency matrices 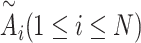based on the 2D molecular bond connections where the weights of are initialized randomly and is the number of weighted adjacency matrices. Summation of them generates an aggregated adjacency matrix 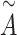as

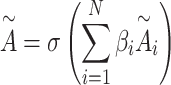(16)

where 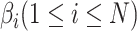is a series of trainable parameters and 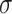is the nonlinear activation function 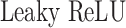[47]. The matrix 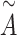is used to update 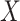in the molecular graph as

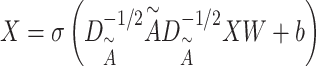(17)

where 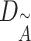is the degree of matrix 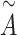, and weight matrix 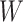and bias 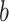are both learnable parameters in PDN.

MPNN for processing 3D information

All atoms in a molecule are connected in pairs and the connections could simulate not only chemical bonding between neighboring atoms but also non-bonding interactions such as van der Waals forces. All 3D features including Euclidean distance (r), intersection angle (θ) and torsion angle (φ) between each atom pair (Figure S1) are represented in spherical coordinates using the SRBF and the SHBF. Presenting molecules in this way naturally ensures both rotation and translation invariances of molecules.

The node and edge information are updated iteratively in the following steps. First, edge vectors representing either bond or non-bonds are updated via aggregating messages from the neighboring atoms. Second, node vectors representing atoms are updated via aggregating messages from corresponding edges and atom information is updated accordingly; then all are ready for the next iteration (Figure 1B). MPNN is employed to aggregate and update all 3D features. The message of two atoms and the corresponding edge between them is defined as

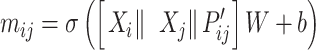(16)

where the features of atom 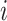and 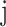and the 3D features between them 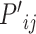are concatenated and fed into a neural network. Here 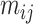is the fused message between atom 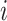and 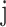, 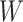is the weight matrix, and 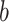is the bias in this neural network. Calculated 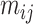is used to renew ,

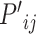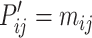(17)

and the molecular graph is updated using the fused messages for all atom pairs by,

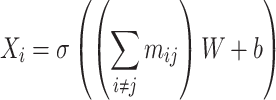(18)

In this way, atoms can update their own information by aggregating the messages from their adjacent atoms [49], and all 3D features are then fully embedded.

Zipper-like fusion process for mutual reinforcement between planar and stereo modalities

In CFFN, 2D and 3D information are arranged in an interdigitated fashion as shown in Figure 1C. We believe this zipper-like architecture is the key to the success of our model, as it promotes the mutual enforcement of 2D and 3D information processing. In the other series of experiments, we compared this method with three other approaches to integrate the information: (A) an early fusion network, (B) a late fusion network, (C) an intermediate fusion network, as shown in Figure S4. The comparison is carried using MD17 dataset and plotted in Table S9. Clearly, the zipper-like network delivers the best results, followed by the intermediate fusion network, while the early feature fusion network is the worst. While all four networks support two molecular graphs simultaneously, ensuring the consistency of information, only the zipper-like network weaved the two modalities together. The other three fusion networks simply add two modalities together without much synergy. The interdigitated arrangement of the 2D modality and the 3D modality allows the information updated in one modality to be intermediately communicated to and exploited in the other modality during information processing. The mutual reinforcement between the two modalities accumulates in each round of iteration, until satisfying performance is achieved.

In each iteration, PDN processes and updates 2D features only and passes the atomic information to MPNN to process and update 3D features. The process is repeated for 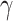times and 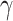is a tunable hyperparameter (Supplementary Note 3, Tables S1 and S2). In this paper, 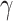is set to 4 in most cases and 8 in others. After multiple iterations, a global representation of molecular graph 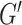is obtained by integrate multi-dimensional features,

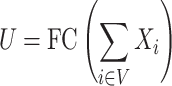(19)

This quantity can be compared with any given target molecular property.

The loss function is defined as:

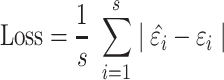(20)

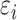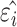The potential energy related property ε can be modeled as the combination of four parts, where and are the true and predicted values of the 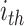sample in an energy related molecular property 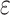, and here 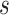indicates the total molecular sample number [50].:

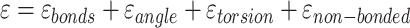(21)

Evaluation metrics

The area under the curve of receiver operating characteristic (AUC-ROC) is employed here as the evaluation metric for the classification tasks. With respect to the regression tasks, we use mean average error (MAE) for QM9 and MD17 datasets and root mean square error (RMSE) and R-squared (R²) for chiral molecules dataset. We execute six independent runs for each method and report the mean and the SD of the metrics (Supplementary Note 4).

Results

CFFN for more accurate molecular property predictions

The superiority and broad applicability of our model in predicting properties is confirmed by its performances on several datasets. First, to check our model’s ability in predicting quantum properties for molecules with various chemical configurations. Among them, QM9 is a widely used large-scale datasets, including various quantum properties of molecules. QM9 comprises calculated properties of 134 k different molecules including 6095 constitutional isomers [35]. That tabulated calculated properties, at the B3LYP/6-31G(2df, p) level of theory, for all of the small organic molecules made up of H, C, O, N and F atoms [35], together making up a subset of the GDB-17 chemical universe database in which all species contain no more than nine heavy atoms [51]. Table 1 compares the performances of our model with several advanced models. The improvement is across the board and significant, ranging from 1% to 43%, with the average around 16% compared with SphereNet. Furthermore, the absolute accuracy of CFFN approaches chemical accuracy in several key properties of many organic molecules, such as dipole moment (μ), isotropic polarizability(α), energy of LUMO (Elumo), internal energy at 0 K(U₀) and heat capacity (C_v). The performance of our model in predicting properties of molecules with various configurations is more than satisfying. Table 1 lists the basic information of these datasets and the performances of our model on them.

Table 1.

Molecular property prediction performances of several models on QM9 dataset in terms of MAE

Property	Unit	SchNet	DimeNet	SphereNet	CFFN	Targeta
μ	D	0.0802(0.0300)	0.0542(0.0029)	0.0593(0.0020)	0.0415 (0.0003)	0.1000
α	a03	0.1573(0.0100)	0.0955(0.0100)	0.1070(0.0016)	0.0613 (0.0050)	0.1000
△e	eV	0.0928(0.0080)	0.0870(0.0060)	0.0857(0.0100)	0.0741 (0.0005)	0.0430
Ehomo	eV	0.0752(0.0030)	0.0682(0.0050)	0.0460(0.0040)	0.0301 (0.0020)	0.0430
Elumo	eV	0.0589(0.0030)	0.0465(0.0030)	0.0381(0.0020)	0.0343 (0.0019)	0.0430
ZPVE	eV	0.0033(0.0030)	0.0091(0.0003)	0.0020(0.0002)	0.0019 (0.0001)	0.0012
U0	eV	0.0237(0.0030)	0.0186(0.0024)	0.0164(0.0002)	0.0151 (0.0017)	0.0430
U	eV	0.0272(0.0026)	0.0209(0.0024)	0.0187(0.0002)	0.0163 (0.0006)	/
H	eV	0.0309(0.0022)	0.0162(0.0010)	0.0165(0.0012)	0.0153 (0.0009)	/
G	eV	0.0265(0.0020)	0.0162(0.0016)	0.0174(0.0010)	0.0157 (0.0008)	/
Cv	cal mol−1 K−1	0.0769(0.0050)	0.0462(0.0030)	0.0417(0.0029)	0.0413 (0.0020)	0.0500

^aThe target accuracies are taken from [48]. SDs are in brackets. The SOTA results are shown in bold.

CFFN for accurate conformational property predictions

Atoms are not static but move constantly. However, QM9 focuses on the most stable geometry only, while a real molecule can access a very large number of three-dimensional conformations in elevated temperature above absolute zero. Particularly important ones are those formed by rotations of single bonds that could change relative positions of connected atoms or atomic groups. Since rotations of single bonds generally do not break chemical bonding, all possible conformers of a single molecule must share a same connectivity, and therefore the same 2D featurization based solely on adjacency information. This generates a synonym problem which is an intrinsic issue of using 2D-structure based networks only [52,53]. In contrast, our CFFN model, which ensures the full extraction of spatial 3D information (atomic distance, intersection angle, torsion angle) (Figures S5–S7), can naturally recognize and differentiate conformers. We expect such a model should be superior in predicting properties that are highly relevant to conformational space, such as heat capacity, C_v and free energy, G. The ability of CFFN model to handle conformations is tested on MD17, a benchmark dataset for molecules with multiple conformations. MD17 comprises several common molecules including aspirin, ethanol, malonaldehyde, naphthalene, salicylic acid, toluene and uracil. Multiple conformational geometries are calculated via DFT-based molecular dynamics simulations at a temperature of 500 K. Instead of more commonly used molecular properties such as energy, MD17 focuses on forces exerted on each conformer, which is unique for each conformation and critically important in molecular dynamics. Regarding experiments on this dataset, only a part of data is used for training: two 1000-sample subsets are used respectively for training and validation, and the rest is used for testing (Supplementary Note 3 and Table S3). The performances of our model as well as several alternative ones in predicting molecular forces are reported in Figure 2. CFFN shows excellent accuracy in predicting atomic forces of various conformers. When compared with other advanced models, CFFN achieves the lowest prediction errors. The MAEs are less than 0.364 kcal/(mol^*Å) on all seven substances tested, on average 22% better than other models (Table S4). We note that the improvement of CFFN is relatively small for a particular interesting molecule, malondialdehyde. This molecule is known to change its configuration spontaneously, i.e., tautomer in chemistry. The 2D presentation of tautomer is simply not as accurate as the 2D presentation of other common molecule such as the other six ones in this dataset. In this perspective, this observation actually further supports importance of including correct 2D structure.

Figure 2.

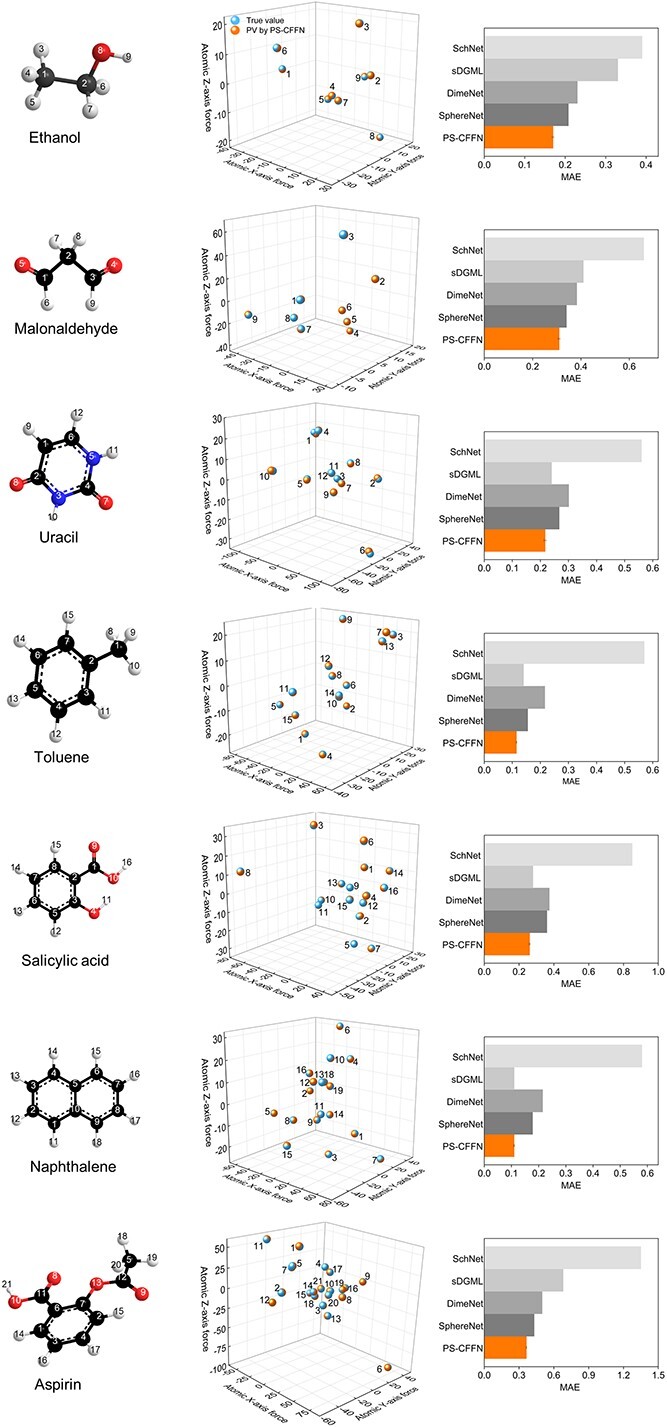
Performance comparisons of force predictions for several molecules in the MD17 dataset about predicted values of CFFN and true values and several models in terms of MAE (all units are in kcal^*mol⁻¹ Å⁻¹ and specific values are listed in Table S4).

CFFN for accurate chiral molecular property predictions

A noteworthy advantage of our model is that it naturally describes all stereoisomers of chiral molecules and their conformations. To verify this, two additional smaller datasets are also used to test our model on chiral molecules and conformations.

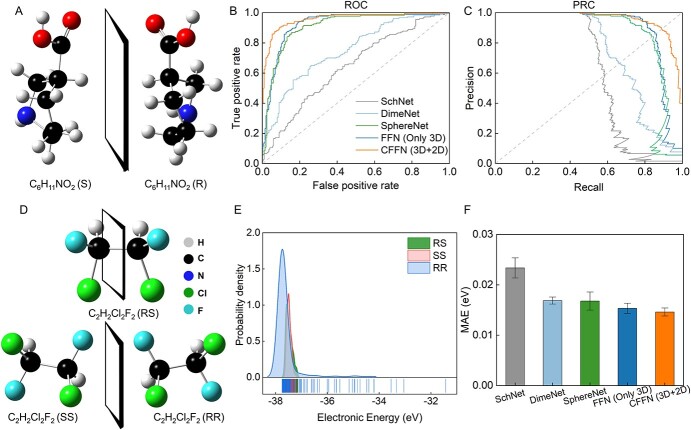
Chirality, which prevails among natural molecules due to breaking of mirror symmetry, often shows very different chemical and biochemical behaviors with their mirror counterparts [54]. Property predictions for chiral molecules are therefore of fundamental and practical importance. However, it is underexplored and challenging to predict properties of chiral molecules. Straightforward 2D molecular graphs cannot differentiate left- and right-version of enantiomers since their connectivity is identical. In our model, the 3D graph naturally distinguishes all enantiomers because stereo information is included. The effectiveness of our model is verified using a protein–chiral ligand binding dataset [38] (more details in Method) (Figure 3A). The dataset includes about 3800 chiral pairs and is divided by 8:1:1 respectively for training, verifying and testing. As shown in Figure 3B, CFFN can effectively distinguish chiral molecules with the accuracy of 92.5% and the AUC score is as high as 0.97 which is superior to all other SOTA methods. In addition, CFFN is more applicable to deal with sample imbalance (Figure 3C).

Figure 3.

Performances of CFFN model in predicting properties of chiral molecules. (A) An exemplary pair of enantiomers displaying chiral cliff. (B) ROC and (C) PRC curve of CFFN versus random classification in distinguishing enantiomeric pairs. (D) Structures of the three chiral isomers of 1, 2-dichloro-1, 2-difluoroethane (C₂H₂F₂Cl₂) and (E) corresponding energy distributions. (F) The performances of CFFN model for predicting energies of 1500 C₂H₂F₂Cl₂ configurations/conformations (500 samples for each chiral isomer). Among these three chiral isomers, RR and SS make an enantiomeric pair while RS is a meso isomer (the left and right halves are mirror images of each other).

Many molecules contain multiple chiral centers, such as 1, 2-dichloro-1, 2-difluoroethane (C₂H₂F₂Cl₂). The two symmetric chiral carbon centers in this molecule generate three stereoisomers, known as RS, SS and RR, as illustrated in Figure 3D. They have different energy distributions (Figure 3E). Notice that SS and RR make a pair of normal enantiomers, while RS is itself diastereomeric (a.k.a. meso isomer, and is non-optically active) due to existence of an inversion symmetry center. This textbook example is chosen to further challenge our model in describing multiple categories of chirality commonly seen in organic molecules (more details in Methods section). We randomly select 1200 samples as the training set and 100 samples as the validation set, and use the rest samples as the test set. As reported in Figure 3F, CFFN gained an excellent and practical prediction performance by achieving the average error accuracy of ~0.0143 eV which is on the par with chemical accuracy.

CFFN is data efficient and error proof

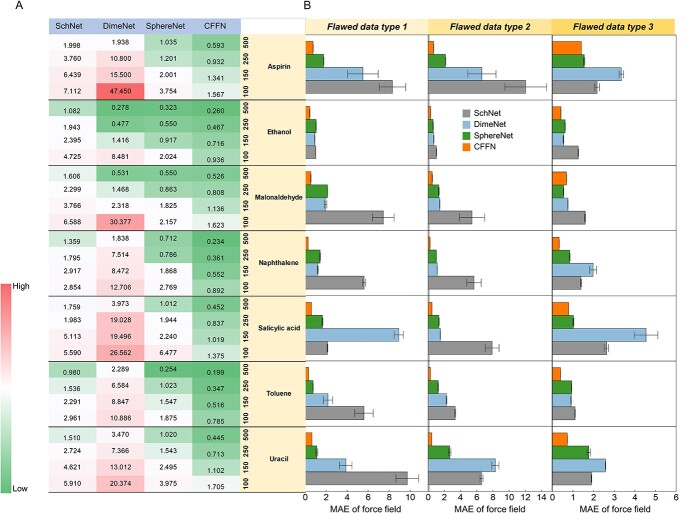
The high-fidelity datasets in chemistry is scarce. In reality, frequent mistakes, many omissions and varieties of inconsistencies are inevitable and should be considered. A data-efficient and error-proof model is essential in practice. Here we first gradually reduce the training sample size from 500 to 100 samples on MD17 dataset to simulate scenarios of small datasets. To simulate various types of data flaws in real world, we create three types of errors/omissions: missing one atomic coordinate, missing one atomic force and one inaccurate value of molecular energy. They respectively represent three common types of flaws: missing input parameters, missing target properties and inaccurate key intermediate properties (atomic force is derivative of molecular energy against atomic coordinate). In case of inaccurate key properties, we added a random noise within 1–10% of the original data. For each series, we replace 10% data of MD17 dataset with erroneous ones of one type.

As Figure 4A illustrates, CFFN is more robust and error-proofing. While the performances of all models worsen as the number of test samples decreases, CFFN deteriorates the least among all methods. For example, the MAE result of DimeNet registered an 18-fold increase on average for seven molecules while the MAE of CFFN only doubled. The results confirm that CFFN could limit the error within 1 kcal^*mol⁻¹ Å⁻¹ with only 250 samples (Table S5).

Figure 4.

Comparison of four models for seven molecules in the MD17 dataset. (A) On datasets of small samples: MAE with size of training samples reduced from 500 samples to 250, 150 and 100 samples. (B) On flawed datasets: MAE with datasets containing 10% flawed data. Three types of flaws are tested: type 1, missing one atomic coordinate; type 2, missing one atomic force; and type 3, inaccurate molecular energy. Units of MAE are in kcal^*mol⁻¹ Å⁻¹ (more details could be found in Table S5 and S6).

In addition, CFFN is more ‘poka-yoke’. As shown in Figure 4B, CFFN almost always delivers excellent performance and error tolerance for each of the three error types. One exception is observed in case of malonaldehyde with type 3 error. Malonaldehyde is a tautomer that possesses dynamic two-dimensional topology. Its 2D feature may not be as reliable or relevant to its properties as others and therefore, CFFN might have difficulties to learn more accurate relationship from 2D + 3D features. For all other molecules, CFFN has significant advantages. This indicates that CFFN is more suitable to deal with real chemical problems (Table S6).

Furthermore, various molecular conformations are also considered here and the analogous experiments were carried out on QM9. Similar conclusions were obtained. The detailed results could be found in Table S7.

Planar modality makes CFFN data efficient and error proof

To understand the effect and confirm the necessity of explicitly including 2D information, we carried out a series of ablation analyses by removing the planar modality component from CFFN. This new variant is designated as FFN (Feature Fusion Network) and serves as a comparison to its vanilla version. Certainly, adding 2D information explicitly will bring a new concern, the increase in complexity. Since all molecules live in 3D physical world, any 2D representations in whatever form are ultimately man-made notations to describe real molecules in 3D. 2D information of a molecule, in principle, should be available from its 3D information. Explicitly including 2D information on top of full 3D information inevitably increases the total number of parameters. Usually, increased complexity is disadvantageous in ML; however, we believe the opposite is true in our case of molecular featurization, and the following analyses are essential to verify the necessary of adding 2D information in our framework. Actually, 2D representations of molecules are not some random abbreviations just for convenience, they do contain some most critical and essential information about typical molecular architectures and properties (such as functional groups and aromaticity). They are languages created by some of most brilliant minds in history of chemistry and agreed upon by all chemists. Incorporating such wisdom accumulated over centuries as prior knowledge should offer ML expert guidance and therefore reduce its effective complexity. Indeed, the results of the ablation analysis in three sets of experiments undoubtedly confirm improved prediction accuracy, data efficiency and robustness of our model.

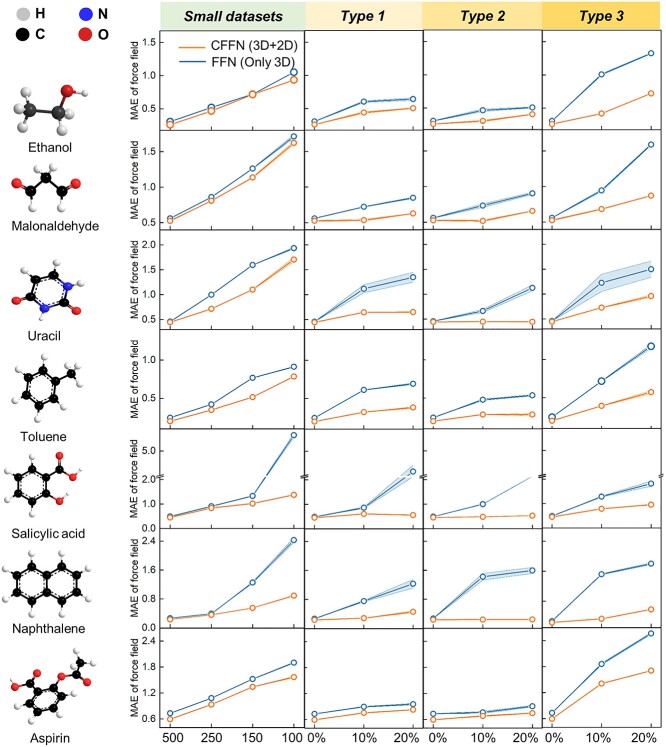
First, we compare the prediction accuracies of CFFN and FFN for all seven molecules in MD17. As seen in Figure S8, CFFN always delivers better results than its variant without explicit 2D information. The average improvement is more than 20%, with the maximum difference being 34.5%. The improvement is relatively small, ~9%, in one case of malondialdehyde. Again, we note that malondialdehyde is a tautomer and its 2D presentation might be not as accurate as others.

Incorporating prior knowledge about key properties is known to help ML even more in small datasets [55,56]. Figure 5A compares the prediction accuracies of two models with 500, 250, 150 and 100 training sets. With shrinking size of training data, both models are expected to gradually deteriorate, and they do. But interestingly, MAE of CFFN increases much slower than that of FFN. The performance gap steadily enlarges when reducing the size of training data to 250 or even 100 samples. In other words, CFFN is superior to FFN all around, and even more so with small datasets. The importance of such advantage cannot be overestimated when dealing with real experimental data. Most chemistry or material data are precious and costly, rarely available in large quantities. ML method with higher data efficiency means more extensive applications are possible in practice.

Figure 5.

Ablation analyses by removing planar information. Direct comparison of CFFN with FFN, a variant without 2D information, shows that the former is more accurate, robust, data-efficient and error-proof in different training samples (500,250,150,100 samples respectively) and flawed data proportions (10% or 20%). The baseline is 500 training samples. Three types of flaws are: type 1, missing one atomic coordinate; type 2, missing one atomic force; and type 3, inaccurate molecular energy. Units of MAE are in kcal^*mol⁻¹ Å⁻¹.

As illustrated in Figure 5B, MAEs of both models grow quickly with the increasing amount of errors/omissions, as expected. The more interesting observation is the performance gap between the two models. MAE of CFFN increases much slower than its variant, suggesting that the model become more robust and tolerate with errors/omissions. Again, we attribute this robustness to explicitly represented expert knowledge, which can regulate the model from falling into traps created by erroneous and misleading data points.

The analyses above are done on each of the seven molecules in MD17, which focuses on molecular conformations. The same experiments are carried out on QM9, which focuses on molecular configurations. As shown in Figure 6, the conclusions are similar: CFFN not only delivers more accurate predictions, but also is more adaptable to smaller sample scenarios and more tolerant for errors and omissions. Apparently, 2D network by itself is defective in the prediction of quantum properties, in line with our expectation. This could be due to the fact that these properties are closely related to 3D geometric conformation especially for stereoisomers. However, 2D information plays an indispensable role in CFFN, as elaborated early.

Figure 6.

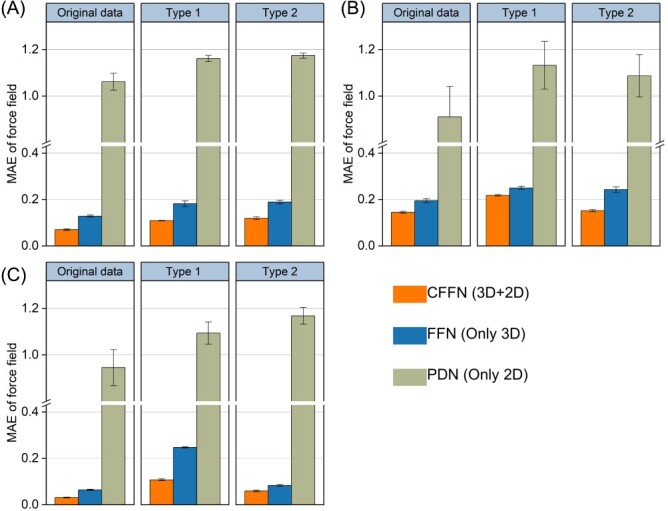
Performances of CFFN model in predicting properties of various molecules for QM9 dataset in a small training sample (10 k) set for (A) C_v, (B) △e and (C) U₀. Two types of flaws are tested: type 1, missing one atomic coordinate; and type 2, inaccurate molecular label (random error within 1–5%). Units of MAE are in kcal^*mol⁻¹ Å⁻¹.

Conclusion

The complexities of molecular structures present a great challenge to describe accurately and efficiently in ML. A multiple modality strategy is adopted to integrate chemical knowledge embedded in 2D information and molecular geometry in 3D information. A novel hybrid molecular graph is developed to fuse planar and stereo modalities in a zipper-like fashion. This interdigitated arrangement not only ensures full integration of 2D and 3D information and but also promotes synergy between them. 3D information provides full details of molecular geometry and 2D information brings in priori knowledge. Together they result in a data-efficient and error-proofing model that accurately predicts a series of physicochemical and quantum physical properties. CFFN can naturally handle all categories of isomerism commonly observed in chemistry by naturally distinguishing configurational, stereoisomeric and conformational isomers, which is one critically important but underexplored territory in molecular featurization. The versatility and accuracy of our approach make it more suitable for various downstream applications such as biosenoring, chiral separation and retrosynthesis of organic molecules. This crosstalk of modern ML technologies and traditional chemistry shows its strong vitality and potential to address some canonical chemical challenges in the foreseeable future.

Key Points

• We developed a novel network for molecule property prediction by integrating planar and stereo structures as non-ambiguous molecular descriptors in a zipper-like arrangement fashion.

• CFFN is an accurate and versatile molecular property prediction network for both conformational and chiral isomers.

• CFFN achieves high accuracies in multiple acknowledged datasets and specifically created new datasets, exceeding most state-of-the-art models.

• Using professional knowledge buried in planer modality as guidance makes CFFN be more data-efficient and error-proof.

Wenjie Du is a PhD student in the School of Software Engineering at University of Science and Technology of China. His research interests lie in deep learning and machine learning for environmental and chemical science.

Xiaoting Yang is a PhD student in the School of Computer Science and Technology at University of Science and Technology of China. His research interests include AI for chemical science.

Di Wu is a PhD student in the School of Software Engineering at University of Science and Technology of China. His research interests include deep learning, protein design, protein structure prediction and spectral analysis.

Fenfen Ma is a PhD student from Beijing Institute of Technology, China. Her research interests include molecular recognition, material structure–activity relationship analysis, lithium-sulfur battery modification and machine learning.

Baicheng Zhang is a PhD candidate from the University of Science and Technology of China. His research interests include synthesis, spectra and machine learning.

Chaochao Bao is a PhD student in the School of Software Engineering at University of Science and Technology of China. His research interests include AI for chemical science.

Yaoyuan Huo is a PhD student in the School of Chemistry and Materials Science from University of Science and Technology, China, His research interest include applying machine learning approach to different kind of molecular properties.

Jun Jiang is a professor in the School of Chemistry and Materials Science from the University of Science and Technology of China. His research interests include AI-chemistry, photochemistry, nano-electronics, electron dynamics at the surface and interface in photocatalytic systems.

Xin Chen is a professor in Suzhou Laboratory. Currently, he focuses on AI-chemistry, photochemistry, electron dynamics at the surface and interface in photocatalytic systems.

Yang Wang is a professor in the School of Computer Science and Engineering at University of Science and Technology of China. Currently, he focuses on AI-chemistry and intelligent transportation field.

Authors’ contributions

W.J. D., X.T. Y. and Y. W. designed research, W.J. D., X.T. Y., D. W., B.C. Z., F.F. M. and C.C. B. performed research, analyzed data, and W.J. D., X.T. Y., Y.W., X. C. and Y. W. wrote the paper. W.J. D., X.T.Y. and D.W. contributed equally in this work.

Funding

Project of Stable Support for Youth Team in Basic Research Field, CAS (YSBR-005); Anhui Science Foundation for Distinguished Young Scholars (No. 1908085J24); Natural Science Foundation of China (No. 62072427); Jiangsu Natural Science Foundation (No. BK20191193).

Data availability

All test result in this work are listed in SI. The CFFN code and chiral molecular dataset (1500 C₂H₂F₂Cl₂ configurations/conformations) are available in Chemical AI (https://github.com/invokerqwer/Chemical-AI).