Abstract
The brain is an information processing machine and thus naturally lends itself to be studied using computational tools based on the principles of information theory. For this reason, computational methods based on or inspired by information theory have been a cornerstone of practical and conceptual progress in neuroscience. In this Review, we address how concepts and computational tools related to information theory are spurring the development of principled theories of information processing in neural circuits and the development of influential mathematical methods for the analyses of neural population recordings. We review how these computational approaches reveal mechanisms of essential functions performed by neural circuits. These functions include efficiently encoding sensory information and facilitating the transmission of information to downstream brain areas to inform and guide behavior. Finally, we discuss how further progress and insights can be achieved, in particular by studying how competing requirements of neural encoding and readout may be optimally traded off to optimize neural information processing.
Keywords: Information theory, Efficient coding, Noise correlations, Information encoding, Information transmission, Computational tools, Spiking neural networks, Intersection information
Graphical Abstract
Highlights
-
•
We introduce computational methods to study information processing in neural circuits.
-
•
We review theories and algorithms for studying design principles for information encoding.
-
•
We review theories and algorithms for studying constraints on information transmission.
-
•
We highlight future challenges to understand tradeoffs on conflicting requirements for information processing.
1. Introduction
The brain is a highly sophisticated computing machine that processes information to produce behavior. In the words of Perkel and Bullock: “The nervous system is a communication machine and deals with information. Whereas the heart pumps blood and the lungs effect gas exchange […] the nervous system processes information.” [1]. As an information processing machine, the brain naturally lends itself to be studied with computational tools based on or inspired by the principles of information theory. These methods have played over the years a major role in the practical and conceptual progress in understanding how neurons process information to perform cognitive functions. This approach has spurred the development of principled theories of brain functions, such as the theory of how neural circuits in sensory areas of the brain may be designed to encode efficiently the natural sensory world [2], [3], [4], or how correlations between neurons shape the information encoding capabilities of neural networks [5], [6]. They have also led to the development of many influential neural recording analysis techniques that unveil the codes, computations and rules used by neurons to encode and transmit information [7], [8], [9], [10].
Here, we review how such computational methods inspired by information theory have sustained the progress in neuroscience and have influenced the study of neural information processing. In particular, we review how recent work has improved models of efficient coding towards biological plausibility (e.g., including realistic neural spiking dynamics), enabling a better comparison between mathematical models and real data as well as a clearer understanding of the computational principles of neurobiology. We also review how these computational approaches have begun to reveal how populations of neurons perform multiple functions. While earlier computational and theoretical work has focused on understanding the principles of efficient encoding of neural information [11], [12], [13], more recent work has begun to consider how the information encoded in neural activity is transmitted to downstream neural circuits and ultimately read out to inform behavior [14], [6]. In particular, we review recent computational modeling and analytical work that has begun to uncover the competing effects that correlations between neurons exert on information processing, and examine how the multiplicity of functions that a brain area needs to perform (e.g. encoding and transmission of information) may place constraints on the design of neural circuits. Finally, we discuss how recent advances in understanding the intersection of encoding and readout of information may help us formulate better theories of information processing that take into account multiple functions that neural circuits may perform.
2. Computational methods for encoding of information
A first key question is information encoding, that is, the study of how the activity of neurons or neural ensembles encodes information [15]. The study of neural encoding focuses on the information available in neural activity, without considering how it is transmitted downstream or how it is utilized to inform behavior. However, since no information can be transmitted without it first being encoded, the study of information encoding is a key prerequisite for understanding information processing in the brain. In this section, we review its theoretical foundations, focusing on theories of optimal information encoding and insights gained from the analysis of empirical neural data. In the following, we consider the information that neurons convey about features of sensory stimuli in the external world.
2.1. Efficient coding - foundations and mathematical theories
A prominent property of neural activity that has shaped studies of neural information processing is that responses of individual neurons vary substantially across repeated presentations of an identical sensory stimulus (“trials”) [7], [16]. This variability, commonly referred to as “noise” (even if in principle it can contain information), makes it challenging to understand the rules mapping external stimuli into neural spike trains. Information theory [17], the fundamental theory of communication in the presence of physical noise, has thus emerged as an appropriate framework for studying the probabilistic mapping between stimuli and neural responses [18], [19], [15], [20], [21], [22], [23].
Information theory provides a means of quantifying the amount of information that the spike trains of a neuron carry about a sensory stimulus. The mutual information between the (possibly time-varying) stimulus s(t) and the (possibly time-varying) neural response r(t) can be quantified in terms of their joint probability distribution p(s, r) and of their marginal probabilities p(s) and p(r), as follows [17], [24], [25]:
| (1) |
where the integrals are over all possible realizations of the stimulus s ∈ S and the neural response r(t) ∈ R, and the base-2 logarithm is used to measure information in units of bits. Eq. (1) is written in terms of continuous probability density functions, but it can be straightforwardly extended to discrete probability distributions. Note that continuous probability density functions are often used in theoretical models and are sometimes estimated approximately from data using, for example, kernel estimators [26], but in most cases neural information studies use discrete probabilities that are easier to sample with limited amounts of data. The neural response r(t) can either denote a spike train r(t) = ∑k δ (t − tk) or a continuous measure of neural activity (firing rate). Eq. (1) measures the divergence in the probability space between the joint distribution p(s, r) and the product of the marginal distributions of the neural activity r(t) and the stimulus s(t). If the neural activity and the stimulus are independent, this divergence equals zero, and the observation of the neural activity would not carry any information about the stimulus. Because it uses the full details of the stimulus-response probabilities, mutual information places an upper bound to the information about the stimulus that can be extracted by any decoding algorithm of neural activity [17], [24]. Note however that the mutual information is computed for a specific set of stimulus features and a specific probability distribution of stimulus values, and thus does not quantify the channel capacity of the neuron. The latter is defined as the maximum over all possible probability distributions of all stimulus features of the mutual information carried by neural activity [17], and it is difficult to determine experimentally due to the practical impossibility to test neuronal responses with all possible stimulus features and stimulus distributions. However, mutual information computed as in the above equation places a lower bound to the channel capacity of the neuron.
It has been hypothesized that specialized neural circuits dedicated to sensation have evolved to encode as much information as possible about the sensory stimuli encountered in the natural environment [3], [13], [27], [15]. This hypothesis has led to the generation of theories of efficient coding, that postulate that the properties of neurons in sensory areas are designed to maximize the information that these neurons encode about natural sensory stimuli, often with the additional hypothesis that neurons maximize information encoding in a metabolically efficient way [28], [29]. Within this framework, neural circuits are thought to be designed for efficiently encoding sensory stimuli with the statistical properties of the natural environment, with the constraint of keeping the overall neural activity level limited for metabolic efficiency. In what follows, we review foundations of theory of efficient encoding and the computational tools that this theory involves.
2.1.1. Minimizing stimulus reconstruction errors and efficient information encoding
The mutual information between stimuli and neural responses (Eq. (1)) provides a complete quantification of how well the external sensory stimuli can be reconstructed from the spike trains of a neuron. However, the information theoretic equation is complicated to solve because it includes the full probability of stimuli and neural responses and it is difficult to sample experimentally or to describe using mathematical models. This poses a major challenge for theories of efficient encoding.
Progress in this respect was made by the pioneering work of Bialek and colleagues, who studied how to mathematically reconstruct the time-varying sensory stimulus from the spike train of the movement-sensitive H1 neuron in the visual system of the fly [2]. They defined the estimated stimulus as a convolution of discrete spike times {tk} with a set of time-dependent, continuous and causal filters {w(α)(t)} as
| (2) |
where the α-th sum on the right hand side represents the α-th order expansion, so that w(1)(t) and w(2)(t) are respectively the linear and quadratic filters. The authors estimated the optimal causal filter that minimize the reconstruction error between the real stimulus s(t) and its estimate as:
| (3) |
where the integral is over the duration of the experiment. The filters are constrained to be causal, since, for biological realism, the reconstructed stimulus can only depend on the present and past values of the stimulus, but not on future values. Mathematically, this implies that the filters are non-zero only for times t > 0. Bialek and colleagues found that linear filters w(1)(t) provide a highly accurate reconstruction of the stimulus. Moreover, adding higher-order non-linear (e.g. quadratic) filters improved only marginally (by less than 5%) the reconstruction accuracy [2], [11]. By comparing the rate of information (in bits per second) that can be gained about the stimulus from the linear decoder with the rate of information obtained using the information theoretic equation, they found that the rate of information extracted with the linear convolution was close to the value obtained from Shannon’s formula (Eq. (1)). Since, as reviewed above, the Shannon information sets an upper bound on the information that can be extracted by any decoder, it means that linear decoding optimized by minimizing a quadratic reconstruction error function can extract almost as much sensory information as the information-theoretic limit in this sensory neuron. Similar findings were observed in mechanoreceptor neurons in the frog and in the cricket [11].
This result has several important implications. First, the shape and duration of the optimal filters obtained from the experimental data were similar to the post-synaptic responses of real neurons. This suggests that this type of algorithm may be implementable in the brain. Second, it suggests that efficient neural systems can be designed by replacing the complex problem of maximizing mutual information with the simpler problem of minimizing a quadratic reconstruction error, a property that will be extensively exploited in ensuing work. Indeed, finding the optimal set of filters w(α) and computing the stimulus reconstruction do not require the knowledge of the distribution of the prior p(s) or the joint distribution p(s, r), thus greatly simplifying the problem of neural encoding as posed in Eq. (1).
2.1.2. Efficient encoding of natural stimuli with artificial neural networks
The minimization of quadratic cost functions fostered the formulation of efficient coding models of receptive fields in the primary visual cortex. In a seminal work, Olshausen and Field studied how model neural networks could efficiently encode information about complex natural images [12], [30]. The stimulus was modeled as a black-and-white static natural image s(y1, y2) with spatial axes y1 and y2. They assumed that the image can be estimated as a linear superposition of basis functions wi(y1, y2):
| (4) |
where ri is the activity of the i-th neuron in the network and N is the number of neurons. The basis functions wi represent the receptive fields of visual neurons. Their hypothesis was that efficient processing of natural images with a neural network has to satisfy two requirements.
The first requirement is sparsity of neural response. It would be desirable that each image is represented by only a small number of basis functions out of a large set of available ones. In algorithmic terms, this is advantageous because of simplicity. In neural terms, this is advantageous because activation of neurons has a metabolic cost, so that activating as few neurons as possible keeps this cost low.
A second requirement is that the reconstructed image in Eq. (4) closely resembles the actual image s(y1, y2). This implies that the neural network carries high information about the natural images or, equivalently, that the network makes minimal errors in reconstructing the images. These two constraints can be formulated as the minimization of the following cost function:
| (5) |
where N is the number of neurons in the network. The first term on the right-hand side of Eq. (5) maximizes the information about the images carried by the neural activity, while the second term is a L1 regularizer which enforces sparse solutions, with the constant ν > 0 controlling the tradeoff between these two terms. The basis functions wi(y1, y2) do not need to be linearly independent, that is, some basis functions can be similar to each other and describe similar elements of the image. Yet, this does not lead to redundancy in the neural representation of images because, due to the sparsity constraint, similar basis functions are unlikely to be used in the representation of the same image. Thus, implementing efficient coding in this way maximises the information that the network carries about the stimulus and minimises redundancy between neurons.
Remarkably, the sparse linear code found by this algorithm captures well-established properties of receptive fields in the primary visual cortex (V1), such as being spatially localized and selective for the orientation and structure of the stimulus at different spatial scales, suggesting that the principle of efficient encoding has predictive power for explaining the features of real sensory neurons.
This work has inspired many successive implementations of efficient and sparse coding. Of particular interest for the present Review are studies that implemented efficient coding on biologically constrained neural networks. Zhu and Rozell [31] applied the efficient coding algorithm of Olshausen and Field on a dynamical system. Using the same cost function as in Eq. (5), they added time-dependence to the coefficient ri and constrained them to be non-negative, so that they can be interpreted as neural activity levels of neuron i, ri(t) > 0. Moreover, they interpreted the basis functions as 1-dimensional vectors , which contain all the values of pixel intensities across both spatial coordinates of the image. This interpretation allows to define the reconstructed stimulus as a positive linear combination of basis functions, i.e. (similarly as in Eq. (4) but time-dependent). The dynamical system that minimizes the cost function in Eq. (5) is given by a set of dynamical equations that describe the temporal evolution of the internal state variables Vi(t):
| (6) |
where is the dot product between the vectors and , and the function Tϑ(Vi(t)) defines how the internal state variables Vi(t) activate the i-th neuron upon reaching the threshold ϑ, then resetting its activity to a predefined value. Eq. (6) includes a leak term, the feedforward input where the image is multiplied by the neuron’s basis function , and the recurrent input .
The activity of the network aims at minimizing the cost function over time, using a fully connected neural network. Minimization of the coding error (first term in Eq. (5)) defines the structure of recurrent interaction between neurons, where the interaction between neurons i and j is inhibitory (I) if the two neurons have a similar basis function, and excitatory (E) if the basis functions of the two neurons are dissimilar [31], [4], [32]. This effectively implements competition between neurons with similar selectivity, as evidence provided by the most active neuron in favor of the exact value of its preferred stimulus ‘speaks against’, or explains away, that provided by other less active neurons preferring similar but not identical values of the stimulus, thereby leading to efficient representations of the stimulus [33], [34]. The reduction of redundancy is here enforced not only by the sparsity constraint (as in [3]), but also by a dynamical minimization of the coding error that leads to lateral inhibition between similarly tuned neurons.
The effects of explaining away the information about the stimulus are more prominent as the size of the network increases [35]. The larger the number of neurons that represent a single stimulus feature, the more likely the information about that feature is represented redundantly across neurons, as reported also with empirical data [36], [37], [38]. Selective and structured inhibition of neurons with similar feature selectivity prevents redundancy of information encoding and, therefore, keeps the code efficient. Such a neural network with efficient coding reproduces several non-classical empirical properties of receptive fields in V1 [33], [31], where activity of neurons with neighboring receptive fields modulates the response of neurons with the target receptive field, thus suggesting that dynamical efficient coding is relevant to the information processing by the neural circuits in V1 [39].
A limitation of these artificial neural network models is that they do not satisfy an important property of neural activity, that is, neurons carry information in their spiking patterns. To overcome this limitation, recent work implemented principles of efficient coding using spiking networks [4]. In these models, the cost function minimizes the distance between a time-dependent representation , and its reconstruction ,
| (7) |
where is the vector of spike trains across neurons and W is the matrix of decoding weights (analogous to the basis functions in Eq. (5)), describing the contribution of each neuron’s spikes to the representation of each stimulus feature. The model in [4] distinguishes the external stimulus from its internal representation in the neural activity. The encoding mapping between the stimulus and the internal representation is described by the matrix A (Eq. (7)). Unlike previous approaches (see Eq. (3) and (5)), the cost function in [4] imposes the minimization of the quadratic error between the desired and the reconstructed internal representation every time a spike is fired, resulting in the following cost function
| (8) |
where M is the number of stimulus features encoded by the network and ri(t) is the low-pass filtered spike train of neuron i, given by [32]. Specifically, this implies that the spike of a particular neuron at a particular time is bound to decrease the cost function. In this way, the timing of every spike is important and carries the information useful for reconstructing the internal representation .
Note also that the cost function in Eq. (8) has a linear and a quadratic regularizer. Regularizers can be implemented using linear or quadratic functions of the firing rate [4]. Linear regularizers increase the firing threshold of all neurons equally [32]. As a consequence, out of neurons with similar selectivity, those with higher threshold remain silent, while those with the lower threshold likely dominate the information encoding, leading to a sparse code. Quadratic regularizers in addition increase the amplitude of the reset current and thus affect only the neuron that recently spiked, likely preventing it from firing spikes in close temporal succession. This dynamical effect thus tends to distribute the information encoding among neurons in the network, in particular when the number of encoded stimulus features M is smaller than the number of neurons in the network N, as it is typically assumed in these settings.
This model can accurately represent multiple time-dependent stimulus features in parallel [4], and its design accounts for several computational properties of neural networks in the cerebral cortex. In particular, E and I currents in this class of networks are balanced over time [40], [41]. Moreover, the efficient spiking network implements a neural code that is distributed across the neural population [42]. We may consider that the number of features encoded by the activity of a sensory network is typically smaller than the number of neurons in the network and, as a consequence, several neurons are typically equally well suited to improve the internal representation of the stimulus through their spikes (yet the lateral inhibition prevents redundancy and keeps the code efficient). Redundancy of decoding weights allows for highly variable spiking responses on a trial-by-trial basis, while the population readout remains nearly identical [32], [43]. This makes it possible to reconcile trial-by-trial variability of spiking patterns with reliable information encoding and accurate perception.
This efficient spiking network is also robust to different sources of noise [40], compensates for neuronal loss [44], and shows broad Gaussian tuning curves as observed in experiments [45]. Such a network can be used to model state-dependent neural activity [32], [46] and can be extended to non-linear mapping between the external stimulus and the internal representation [47]. However, this type of network is not fully biologically plausible, as neurons do not obey Dale’s principle, which states that a given neuron is either excitatory or inhibitory. The recurrent interactions in the network developed from a single cost function extended from Eq. (5) are inhibitory if neurons have similar decoding weights, and excitatory if weights are dissimilar, making the same neuron send excitatory or inhibitory synaptic currents to other neurons in the network, (see Eq. (6)). Recent theoretical work has improved the biological realism of spiking network models with efficient coding. We review these models in the next section.
2.1.3. Biologically plausible spiking networks with efficient coding
Our recent work [48] extended the theory of spiking networks with efficient coding to account for the fundamental distinction of biological neuron types into excitatory (E) and inhibitory (I) neurons, as well as to endow efficient spiking models with additional properties of biological circuits, such as adaptation currents. Instead of a single cost function as in Eq. (5), we analytically developed an E-I spiking network using two cost functions, for E and I neurons respectively:
| (9) |
where NE (NI) are the number of E (I) neurons in the network, and () is the low-pass filtered spike train of an E (I) neuron with time constant (). The population read-out of the spiking activity is similar to previous models (see Eq. (7)), but here we introduced separate read-outs for the E and I populations and . The first terms on the right-hand side minimize the coding error between the desired representation and its reconstruction, while the second terms are regularizers penalizing high energy expenditure due to high firing rates [49], [50]. Good network performance is ensured when the reconstructions by E and I neurons are close to each other and close to the desired representation xm(t), which means that objectives of E and I neurons work together and do not entail a tradeoff between them.
Using Eq. (9), and assuming that a spike of an E or I neuron will be fired only if it decreases the error of the corresponding cost function, we analytically showed [48] that the optimal spiking network can be mapped onto a generalized leaky integrate-and-fire neuron (gLIF) model [51]. A gLIF model has been shown to predict well the spike times in real biological circuits [52], [53], and provides a good tradeoff between biologically detailed, computationally expensive models and simpler but analytically tractable ones. In particular, the solution to Eq. (9) yields the following equations for the membrane voltage of E and I neurons:
| (10) |
where , is the strength of spike-triggered adaptation, and b(τE, τI) > 0 is a scalar that depends on membrane time constants of E and I neurons. Synaptic currents are given by the weighted sum of presynaptic spikes , n ∈ {E, I}, and of low-pass filtered presynaptic spikes , where the spike train of E neurons is convolved with the synaptic filter. The membrane equations contain leak currents, feedforward currents to E neurons, recurrent synaptic currents between E and I neurons, spike-triggered adaptation, and hyperpolarization-induced rebound currents in E neurons [48] as the diagonal of the matrix KEE. These currents are known as the most important currents in cortical circuits [51] and their expression in [48] can be directly related to biophysical currents in cortical neurons. The optimal solution also imposes that the membrane time constant of E neurons is larger than the membrane time constant of I neurons, which is compatible with measures of biophysical time constants of pyramidal neurons and inhibitory interneurons in cortical circuits [54].
Lateral inhibition in the efficient E-I model in [48] is implemented by a fast loop of synaptic currents, E → I, I → I and I → E (connections J on Fig. 1A). Connectivity matrices implementing lateral inhibition predict that the strength of synaptic connections is proportional to the similarity in stimulus selectivity of the pre- and the postsynaptic neuron, . These synaptic currents decorrelate the activity of E neurons with similar stimulus selectivity, which has been empirically observed in primary sensory cortices [55], [56]. Moreover, such connections can be learned with biologically plausible local learning rules [57]. In the simplified network with only fast connections, neurons that receive stimulus-selective input as a feedforward current participate in network response, while other neurons remain silent (Fig. 1B).
Fig. 1.
A biologically plausible efficient spiking network that obeys Dale’s law. The network is analytically developed from two objective functions, where a quadratic coding error (implementing information maximization) and a quadratic regularizer (controlling firing rates) are minimized at every spike occurrence. The solution to the optimization problem is a generalized LIF (gLIF) neuron model. A. Schematics of the network. The set of features of the external stimulus determines the feedforward current to the network. E and I neurons are recurrently connected through structured synaptic interactions J and K. A linear population read-out computes the reconstructions and . Fast synaptic interactions (J) implement lateral inhibition between E neurons with similar selectivity through the I neurons. Slower synaptic interactions (K) implement cooperation among neurons with similar stimulus selectivity. B. Activity of a simplified E-I network with only fast synaptic interactions J. Network activity is stimulus-driven. C. Activity of the network with both fast and slower synaptic interactions J and K. The response of such a network to the stimulus is highly non-linear, and largely driven by recurrent synaptic interactions and spike-triggered adaptation.
The general and complete solution to the optimization problem in Eq. (9) also includes E → E and E → I synaptic currents that amplify activity patterns across E neurons (connections K on Fig. 1A). These currents have the dynamics of the low-pass filtered presynaptic spikes of E neurons, . Synaptic strength depends on the similarity of decoding vectors, as well as on the transformation between the stimulus and the internal representation , given by the matrix A in Eq. (7), , where I is the identity matrix. Depending on the strength and structure of these synaptic interactions, the network generates a variety of response types, controlled by the rank of synaptic connectivity matrix KEE. The rank of synaptic connectivity is here intended as the number of non-zero singular values of the connectivity matrix. With low rank of synaptic connectivity, only neurons that receive stimulus-selective input respond, while higher rank in synaptic connectivity evokes a response also in neurons that do not receive stimulus-selective input (Fig. 1C). In the latter case, it is the E → E connectivity that drives the response of these neurons and implements linear mixing of stimulus features in the neural responses.
In sum, the efficient coding theories have brought important insights into neural processing of sensory information, from linear filters that accurately reconstruct the external stimulus from the neural activity in sensory periphery, to analytically derived biologically plausible spiking neural networks of neurons.
2.2. Theory of information encoding at the population level
It is now widely accepted that many important cognitive functions do not rely on single cells, but must emerge from the interactions of large populations of neurons, either within the same neural circuits [58], [59] or across different areas of the brain [60]. Historically, theories of efficient encoding have followed the same path, first focusing on the neural encoding at the level of individual neurons and then developing further to account for the encoding properties of neural ensembles.
A prominent feature of neural population activity is the correlations between the activity of different neurons. Over the years it has become clear that these correlations have a substantial impact on the information that a neural population encodes [61], [62], [63], [5], [64]. Efficient coding theories thus have to consider also how correlations between populations of neurons contribute to the total information carried by the population. Here, we briefly review formalisms and empirical results about the impact of correlations on information coding.
A bulk of analytical work, reviewed recently in [65], has derived in a closed mathematical form how the total information carried by a population of neurons depends on the correlations between neurons. As in Eq (1), we denote the total information as I(S; R), where S is a shorthand for stimulus and R for the set of spike times fired by all neurons in the population. According to the recent systematic review of [65], the most complete closed form solution of the dependence of population information on correlations has been provided by the Information Breakdown formalism [63]. This formalism describes different ways in which correlations affect neural population information, by breaking down the information into the following components (see [63] for further details and definition of each term):
| (11) |
The linear term Ilin is the sum across neurons of the mutual information about the stimulus carried by each individual neuron. The other terms, capturing the differences between I(S; R) and Ilin, reflect the effect of correlations between neuronal responses. These correlations are traditionally conceptualized as signal correlations and noise correlations [36], [6]. Signal correlations are correlations of the trial-averaged neural responses across different stimuli, quantifying the similarity in stimulus tuning of different neurons. Noise correlations, instead, are correlations in the trial-to-trial variations of the activity of different neurons over repeated presentations of the same stimulus. Noise correlations quantify functional interactions between neurons after discounting the effect of similarities in stimulus tuning [61].
The signal similarity term Isig−sim≥ 0 quantifies the reduction of information (or increase in redundancy) due to signal correlations, present even in the absence of noise correlations. Such reduction of information occurs when neurons have partly similar stimulus tuning. Barlow’s idea of decreasing redundancy by making neurons respond to different features of the external stimuli is conceptually related to reducing the negative effect of this term by diversifying the tuning of individual neurons to different stimulus features [15].
The last two terms, Icor−ind (stimulus-independent correlation term) and Icor−dep (stimulus-dependent correlation term), quantify the effect of noise correlations in enhancing or decreasing the information content of the neuronal population. The term Icor−ind, that can be either positive or negative, quantifies the increment or decrement of information due to the relationship between signal correlation and noise correlation. This term captures mathematically the important finding of neural theory that the relative sign of signal and noise correlations is a major determinant of information encoding [5], [61]. The term Icor−ind is positive and describes synergy across neurons if signal and noise correlations have the opposite sign, while it is negative and describes redundancy if signal and noise correlations have the same sign [63]. If signal and noise correlations have the same sign, signal and noise will have a similar shape and thus overlap in population activity space more than if there were no noise correlations (compare Fig. 2A, left with Fig. 2B). In such condition, correlated variability makes a noisy fluctuation of population activity look like the signal representing a different stimulus value, and thus acts as a source of noise that cannot be eliminated [66], [5], [61]. One example is two neurons that respond vigorously to the same stimulus, and thus have a positive signal correlation, while having positively correlated variations in firing across trials to the same stimulus, and thus also have a positive noise correlation (Fig. 2A, left). Instead, if signal and noise correlations have different signs, such as a positive noise correlation for a pair of neurons that respond vigorously to different stimuli and thus have negative signal correlation, then noise correlations decrease the overlap between the response distributions to different stimuli, and therefore increase the amount of encoded information (compare Fig. 2A, right, with Fig. 2B).
Fig. 2.
Schematic of the effects of correlations in the population responses on information encoding. The cartoons illustrate the response distributions across trials of a population of two neurons to two different stimuli (blue and green ellipses). Different structure of the noise correlations and different relative configurations of the noise and signal correlations determine the effect of correlations on information encoding. A. Stimulus-independent noise correlations can decrease (left; information-limiting correlations) or increase (right; information-enhancing correlations) the amount of encoded stimulus information with respect to uncorrelated responses (panel B). Correspondingly, information-limiting (resp. -enhancing) correlations increase (resp. reduce) the overlap between the stimulus-specific response distribution with respect to uncorrelated responses. B. Same as panel A for uncorrelated population responses. C. Stimulus-dependent noise correlations, that vary in structure and/or in strength across stimuli, might provide a separate channel for stimulus information encoding (left) or even for reversing the information-limiting effect of stimulus-independent noise correlations (right).
The term Icor−dep quantifies the information added by the stimulus dependence of noise correlations. This term is non-negative and it can only contribute synergy [63]. An example of this type of coding is sketched in Fig. 2C. If noise correlations are stimulus-dependent, they can increase the information encoded in population activity by acting as an information coding mechanism complementary to the firing rates of individual neurons [67], [68], [69], [70]. Since Icor−dep adds up to the other components, the stimulus-dependent increase of the encoded information can offset the information-limiting effects of signal-noise alignment and lead to synergistic encoding of information across neurons.
The information breakdown in Eq. (11) is the most detailed breakdown of information as function of correlations, and it includes as a sub-case other types of decompositions and quantification of the effect of correlations on the information encoded by the neural population activity. For example, the sum of terms Icor−ind + Icor−dep quantifies the total effect of noise correlations on stimulus information and equals the quantity ΔInoise defined in e.g. [71]. Moreover, the sum of terms Ilin + Isig−sim quantifies the information that the population would have if all single neuron properties were the same but noise correlations were absent, and equals the quantity Ino−noise of [71]. The sum of terms Isig−sim + Icor−ind + Icor−dep equals the synergy term defined e.g. in [72]. Finally, the term Icor−dep equals the quantity ΔI introduced in [73] as an upper bound to the information that would be lost if a downstream decoder of neural population activity would ignore noise correlations.
These results have been obtained using general relationships between multivariate stochastic variables, and hold regardless of whether these correlations are expressed among activity of neurons or among other types of variables. However, most of the findings of the above general analytical calculations have been confirmed independently in models specifically made to describe the activity of populations of neurons (see e.g. [74], [75]).
2.2.1. Computational methods for testing information encoding in empirical data
An important take-home message of the above calculations is that they show that correlations can in principle increase, decrease or leave invariant the amount of information in neural activity. Which scenario is realized in a specific biological neural populations must be determined on a case-by-case basis by empirical measures. Here, we review how these issues can be addressed in empirical data using appropriate computational methods.
A first way is to apply directly the information theoretic equations described above (see e.g. in Eq. (11)) to the experimentally recorded neural activity, by numerically estimating the stimulus-response probability distributions. Numerical methods than can be used for probability estimation may include discretization of the spike trains, followed by maximum-likelihood estimators of the probability distributions [76]. This approach is very straightforward and particularly useful when considering individual neurons or small populations. In these cases the probabilities can be estimated directly, since limited sampling biases in information estimations are small and can be subtracted out [76]. Other methods include non-parametric kernel density estimators that do not require data discretization [26], [77], [78].
However, when large populations are considered, a direct calculation of information becomes unfeasible, as the size of the response space grows exponentially with the population size [76]. Due to the difficulty of adequately sampling all possible responses with the finite number of trials available in an experiment, the sampling bias becomes much larger than the true underlying information values, and it eventually becomes impossible to subtract it out [76]. A practically more feasible approach consists in decoding the activity of neural populations using cross-validated classifiers, and then quantify the total information in neural activity as mutual information in the confusion matrix [24]. In these cases, the effect of noise correlations on information encoding can be computed by comparing the information in the real, simultaneously-recorded population responses (which contain correlations between neurons) with the information computed from pseudo-population responses where noise correlations have been removed by trial shuffling (an analytical procedure to remove the effect of noise correlations by combining responses of neurons taken from different trials to a given stimulus [6]).
Although in principle correlations may have either an information-limiting or -enhancing effect, analyses of empirically recorded neural populations reported that enhancements of information by stimulus-dependent correlations are relatively rare [6]. Most studies reported information-limiting effects in empirical neural data, as shown by the fact that stimulus information encoded in a population is increased when computing it from pseudo-population responses with noise correlations removed by trial shuffling [79], [80], [81], [42], [82], [83]. This is due to the fact that, in most cases, neurons with similar stimulus tuning also have positive noise correlations [84]. The information-limiting effects of correlations become more pronounced as the population size grows, leading to a saturation of the information encoded by the population [42], [83]. This suggests that correlations place a fundamental limit on the amount of information that can be encoded by a population, even when the population size is very large. From these studies, a consensus has emerged that the most common effect of correlations in information encoding is to limit the amount of information encoded in a population [85], [66], [86].
Similarly to what described above for correlations, information theory has been applied to study whether the millisecond-precise timing of spikes is important for encoding information about external stimuli. This has been investigated by presenting different sensory stimuli, measuring the associated neural responses, and computing the amount of information about the stimuli that can be extracted from the neural responses as a function of the temporal precision of the spikes [87]. In these studies the temporal precision of spikes has been manipulated by either changing the temporal binning width used to convert spike timing sequences into sequences of bits (0 or 1, to denote absence or presence of a spike in the time bin) for information calculations, or by randomly shifting the spikes in time within a certain range (conceptually similar to the shuffling used for correlations). Using these approaches, it has been found that considerably more information is available when considering neural responses at a finer temporal scale (for example, few milliseconds precision) compared to coarser time resolutions and with respect to temporal averages of spike trains [27], [88], [89], [89], [87]. Informative temporal codes based on millisecond-precise spike timing have been found across experiments, brain areas and conditions, and are particularly prominent in earlier sensory structures and in the somatosensory and auditory systems [88], [90], [91], [92]. In the visual cortex, a temporally coarser code has been observed, encoding stimulus information on the times scales of tens to hundreds of milliseconds [8].
These findings confirm the importance of developing efficient coding theories based on models that encode information in spike times with high temporal precision, which we reviewed on theoretical grounds in earlier sections.
3. Computational methods for readout and transmission of information in the brain
While efficient coding theories have been successful in explaining properties of neurons in early sensory areas, they did not consider how much of the information encoded in their activity is transmitted to downstream areas for further computations or to inform the generation of appropriate behavioral outputs. The theory of information encoding is sufficient to describe the transmission of information if all information in neural activity is read out. However, evidence (reviewed in [6]) indicates that not all information encoded in neural activity may be read out, and thus the readout may be sup-optimal. For example, in some cases, visual features can be decoded from activity of visual cortical populations with higher precision than that of behavioral discrimination [93], proving that not all neural information is exploited for behavior. Here we therefore examine the theory and experimental evidence for how information in neural activity is read out, and then examine the implications for possible extensions of theories of efficient coding.
3.1. Biophysical computational theories of information propagation
We review theoretical studies of how features that are relevant for information encoding, such as across-neuron correlations, affect propagation of information in neural systems.
A simple mechanism by which correlations in the inputs to a neuron impact its output activity is coincidence detection [94]. A neuron fires as a coincidence detector when the time constant τm with which it integrates its inputs is much shorter than the average inter-spike interval of the input spikes. In this case, the timing of input spikes, not only the average number of input spikes received over time, determines whether the coincidence detector neuron fires. Input spikes with a larger temporal dispersion may fail to bring the readout neuron to reach the threshold for firing, but will lead to firing if received within a time window shorter than the integration time constant.
Biophysically, although the membrane time constant can be relatively large at the soma (up to τm=20 ms), the effective time constant for integration can be much shorter, down to a few ms, for various reasons. Dendrites display highly nonlinear integration properties. When synaptic inputs enter dendrites close in space and time, they can enhance the spiking output of the neuron supra-linearly [95], [96]. Moreover, background synaptic input may lower the somatic membrane resistance [97], reducing the effective value of the membrane time constant. As a result, neurons may act as coincidence detectors, firing only if they receive a number of input spikes within a short integration time window of a few milliseconds. With such coincidence detection mechanisms, correlations between the spikes in the dendritic tree would enhance the output rate of the neurons, because correlations tend to pack spikes closely in time (Fig. 3B).
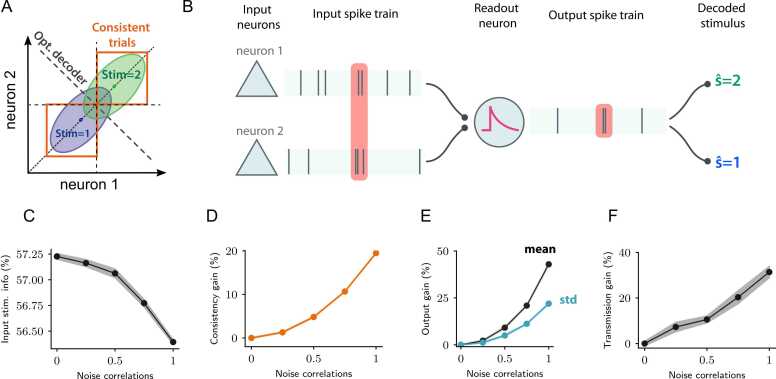
Fig. 3.
Biophysically plausible model of the effect of correlations on neural information transmission A. Schematics showing the responses of two input neurons to two distinct stimuli. The two neurons have similar tuning and positive noise correlations, resulting in information-limiting noise correlations. The dashed dark line illustrates the optimal stimulus decoder, while orange boxes indicate the fraction of trials on which stimulus information is consistent across the two neurons (i.e. the stimulus decoded from the neural activity of either neuron is the same). B. Cartoon illustrating the biophysical model of information transmission. The model consists of two input neurons generating two input spike trains whose firing is modulated by two stimuli and which have information-limiting noise correlations as in A. The input spike trains were fed to a leaky integrate-and-fire readout neuron with a short membrane time constant τm, acting as a coincidence detector. The activity of the readout neuron was then decoded to generate the decoded stimulus to quantify the information about the stimuli modulating the inputs that can be extracted from the output of the readout neuron. The readout neuron fired more often when two or more input spikes were received near-simultaneously within one integration time constant (red shaded area). C. Input stimulus information as quantified by the decoding accuracy of the stimulus from the input firing rates, as a function of input noise correlations. The stimulus information decreases with correlations (information-limiting correlations). D. Relative change (gain) of the fraction of consistent trials, on which the stimuli decoded from either neuron’s activity coincides, as a function of input noise correlations (orange boxes in panel A). E. Relative change (gain) in the mean and standard deviation of the readout firing rate as a function of input noise correlations. F. Relative change (gain) in the amount of transmitted stimulus information, defined as the ratio between output and input information, with respect to uncorrelated inputs, as a function of input noise correlations. In simulations the input rate was set to 2 Hz, the readout membrane time constant to τm = 5 ms. Values of noise correlations equal to 0 and 1 indicate uncorrelated and maximally correlated input firing rates, respectively.
However, until recently few studies have tried to connect enhanced spike rate transmission to the transmission of information. In particular, it has not been addressed whether the advantages of correlations for signal propagation can overcome their information-limiting effect. Recent work has begun to shed light on these issues. A study has proposed that information-limiting across-neuron correlations may benefit information propagation in the presence of nonlinearities in the output [98]. However, it has left open the question of identifying the biophysical conditions and mechanisms by which correlations may overcome their information-limiting effects by increasing the efficacy of information transmission.
To address these issues and analyze the tradeoff between information encoded in the input of a neuron and information transmitted by its output, we studied a biophysically plausible model of information propagation in a coincidence detector neuron [14]. The model readout neuron had two inputs and followed a leaky integrate-and-fire (LIF) dynamics with somatic voltage V(t) given by:
| (12) |
where represents the time of the k-th spike of the i-th input unit (Fig. 3A,B). The membrane time constant of the readout neuron τm was set to a small value of 5 ms. The two inputs had similar tuning to the stimulus, and exhibited positive noise correlations that reduced the stimulus information available in the inputs to the readout neuron, with respect to uncorrelated inputs (Fig. 3A,C). Despite input correlations being information-limiting, increasing correlations amplified the amount of stimulus information transmitted by the spiking output of the readout neuron (Fig. 3F). In the model, input correlations amplified both the stimulus-specific mean firing rate and its standard deviation across trials, yet the mean was amplified more than the standard deviation, resulting in a net increase of the signal-to-noise ratio (Fig. 3E).
While input correlations decreased the information encoded in the inputs, they enhanced the efficacy by which the information propagated to the spiking output of the readout neuron. Importantly, this enhancement could be strong enough to offset the decrease in information in the input activity to eventually increase the stimulus information encoded by the readout neuron [14]. Moreover, our model revealed that correlated activity amplified the transmission of stimulus information in simulation trials in which the information in the inputs was consistent across different inputs. Here, the input information is defined as consistent in a trial if the same stimulus is consistently decoded from the activity of different inputs in that trial (Fig. 3A,D).
In sum, these models suggest that the propagation of spiking activity relies on correlations. While correlations are detrimental for stimulus information encoding, they create consistency across inputs (Fig. 3A,D) which enhances stimulus information transmission, and thus improve the net information transmission.
3.2. Experimental results on information propagation
The above theoretical results beg the question of whether similar tradeoffs between the effects of correlations on information encoding and readout may be at play in vivo to support the propagation of information through multiple synaptic stages and ultimately inform the formation of accurate behavioral outputs.
Our recent study [14] investigated this question by showing that information-limiting correlations may nevertheless improve the accuracy of perceptual decisions. We recorded the simultaneous activity of a populations of neurons in mouse Posterior Parietal Cortex (PPC, an association area involved in the formation of sensory-guided decisions) during two perceptual discrimination tasks (one visual and one auditory task). In both tasks, the activity of neural populations exhibited noise correlations both across different neurons and across time. In both experiments, and as often reported, noise correlations decreased the stimulus information carried by neural population activity, as removing correlations by shuffling neural activity across trials increased stimulus information [14].
The fact that noise correlations decreased the amount of information encoded in neural activity (and thus decreased the information available to the readout for sensory discrimination) could at first sight lead us to conclude that correlations are detrimental for perceptual discrimination accuracy. However, and somehow paradoxically, we observed that noise correlations were higher in trials where the animal made correct choices, suggesting that they may instead be useful for behavior [14]. Similar findings were also reported in other studies [99], [79].
To resolve this paradox, we hypothesized that the readout of information from the neural activity in the PPC may be enhanced by consistency, similarly to the biophysical model of signal propagation described in the previous section (Fig. 3). To test this hypothesis quantitatively, we compared two distinct models of the behavioral readout of PPC neural activity. A model of behavioral readout of neural population activity is defined as a statistical model (in our case, a logistic regression model) predicting the animal’s choices in each trial from the patterns of neural population activity recorded on the same trial. The first readout model we considered predicted the animal’s choices based on the stimulus decoded from the PPC population activity. The second readout model (termed enhanced-by-consistency readout model) used an additional feature of neural activity, the consistency of information across neurons (Fig. 3D). Similarly to our definition for the computational model of biophysical propagation as described in the previous subsection, two neurons (or pools of neurons) provided consistent information on a single trial if the stimulus decoded from the activity of each of them coincided. As shown in [14], increasing the strength of information-limiting noise correlations increases the number of trials with consistent information. In the enhanced-by-consistency readout model, consistency had the effect of increasing the probability that the choice is consistent with the stimulus decoded from the neural activity. In this model, consistency amplified the behavioral readout of stimulus information. We found that in the PPC the enhanced-by-consistency behavioral readout explained more variance of the animal’s choices than the consistency-independent readout [14]. The fact that the enhanced-by-consistency model better described the behavioral readout of PPC activity suggests that propagation of information to downstream PPC targets could be facilitated by correlations in PPC activity.
The approach described above summarizes the total effect that correlations have on the downstream behavioral readout of information carried by a population. However, it did not address directly whether correlations between neurons within a network enhance the transfer of information to another specific network of neurons. A tool that may allow to test this question, when simultaneous measures of activity from different network are available, is the computation of Directed Information [100] or Transfer Entropy [101]. These are measures of information transfer between a source and a target network that have the property of being directed because, unlike mutual information, can have different values depending on which network is selected as putative source or putative target. These measures quantify mutual information between the activity of the target network at the present time and the activity of the source network at past times, conditioned on the activity of the target network at past times. The latter conditioning ensures that the measure is directional and is needed to discount the contribution to the information about the present target activity that is due to past target activity and that therefore cannot have come from the source. These measures have been applied successfully to empirical neural data, e.g. to demonstrate the behavioral relevance of information transmission [102] or the role of oscillations of neural activity in modulating information transfer [103]. However, to our knowledge, these techniques have not yet been applied to investigate whether correlations aid the transfer of information between networks.
4. Intersecting encoding and readout to understand their overall effect on behavioral discrimination accuracy
As reviewed in previous sections, certain features of neural activity may affect encoding and readout of information in conflicting ways. This raises the question of how to measure the combined effect of encoding and readout of information in the generation of appropriate behavioral choices. In other words, how can we evaluate whether a certain feature of neural activity is disadvantageous or useful for performing a certain function, such as the accurate discrimination between sensory features to perform correct choices? This is easier to address if the considered features of neural activity have the same (e.g. positive) effect on both information encoding and readout, but it is more difficult to evaluate when they have opposite effects, as in the case of correlations reviewed above.
The simplest computational way of relating neural activity to the behavioral outcome on a trial-to-trial basis would be to compute the information between neural activity and choice. This would involve using the mutual information equations (see Eq. (1)) but considering the choice expressed by the animal in each trial rather than the presented sensory stimulus. However, the presence of choice information per se would not be sufficient to conclude that the neural activity under consideration is relevant to inform choices that are appropriate to perform the tasks [104]. For example, in a perceptual discrimination task, choice information in a population of neurons may reflect the fact that neural activity contains choice signals that are unrelated to the stimulus to be discriminated, such as stimulus-unrelated internal bias toward a certain choice. Similarly, computing stimulus information only would not be sufficient to tell if such stimulus information is actually used to inform accurate behavior.
Recently, sophisticated computational methods have been developed to address these important questions. These methods are based on the idea of correlating the sensory information in neural activity (rather than just neural activity regardless of its information) with the behavioral outcome on a trial-to-trial basis. For example, a way to establish the relevance of a given neural feature for behavior consists in evaluating whether higher values of information in the neural feature correlate on a trial-by-trial basis with more accurate behavioral performance [105], [106], [99]. A rigorous information-theoretic way to quantify this intuition has been developed [9] using the concept of Intersection Information, which involves information between three variables, i.e. the stimulus (S), the choice (C), and the neural responses (R), and uses the formalism of Partial Information Decomposition (PID; Eq. (11)) to generalize information to multivariate systems [107]. Considering this set of variables, PID identifies different components contributing to the information that two source variables (e.g. R and S) carry about a third target variable (e.g. C). In particular, it disentangles the information about the target variable that is shared between the two variables from the information that is carried uniquely by one of the two source variables, and the information that is instead carried synergistically by the interaction between the two variables. Within this framework, it is natural to define as Intersection Information the part of the information between stimuli and neural activity that is shared with choice information, as this quantifies the part of stimulus information in neural activity that is relevant to forming choices [9]. As shown in [9], after eliminating artificial sources of redundancy, Intersection Information is defined in a rigorous way that satisfies a number of intuitive properties that one would assign to this measure, including being non-negative and being bounded from above by the stimulus and choice information in neural activity [9]. The Intersection Information approach is particularly convenient when addressing questions about the behavioral relevance of features of neural activity that are defined on a single-trial level. For example, it has been used to demonstrate that in somatosensory cortex, the texture information carried by millisecond-precise timing of individual spikes of single neurons has a much larger impact on perceptual discrimination than the information carried by the time-averaged spike rate of the same neurons [9], [106]. This underlies the importance of individual spikes and precise spike timing for brain function. The Intersection Information has also been used to identify sub-populations of neurons that carry information particularly relevant to perform perceptual discrimination tasks [79].
A conceptually related way to define intersection information of a given feature of neural activity has been proposed in [14]. This approach consists in fitting two types of models on data, a model of encoding (that is, the relationship between sensory stimuli and neural population responses) and a model of readout (that is, the transformation form neural activity to choice), and then to compute the behavioral performance in perceptual discrimination that would be obtained if the discrimination is based on the neural activity described by the readout and encoding models. By manipulating the statistical distribution of the neural features of interest in encoding and in readout, this approach can be used to determine the impact on behavioral accuracy of features of neural activity that are defined across ensembles of trials, such as correlations. Recent work [14] adopted this approach to estimate the impact of correlations on behavioral performance. In this work, we first determined the readout model that best explained the single-trial mouse choices based on PPC activity. This was, as reviewed in the previous subsection, an enhanced-by-consistency readout model. We used this experimentally fit behavioral readout model to simulate mouse choices in each trial, using either simultaneously recorded PPC activity (i.e. with correlations) or shuffled PPC activity to disrupt correlations. We used these simulated choices to estimate how well the mouse would have performed on the task with and without correlations. We found that better task performance was predicted when keeping correlations in PPC activity, compared to when correlations were destroyed by shuffling, suggesting that correlations were beneficial for task performance even if they decreased sensory information. This was because correlations increased encoding consistency, and consistency enhanced the conversion of sensory information into behavioral choices, despite that they limited the information about the stimulus available to the downstream readout.
The results described above were obtained from periods of the trial after the presentation of the sensory stimulus and before the mouse executed its behavioral report. Pre-choice activity has the potential to be consequential for the upcoming behavioral choice, whereas post-choice activity does not. When comparing correlations before and after choice, we found that post-choice correlations were weaker than pre-choice correlations, and were not strong enough to modulate the consistency of information [108]. Thus, PPC had strong correlations that created consistent information only before choice was executed and in trials in which correct choices were made by the mouse.
Together, these results suggest that noise correlations are consequential for the behavioral readout of information encoded in neural activity, and that correlations can promote accurate behavior by enhancing signal propagation, because a better signal propagation can offset the negative impact of correlations on encoding.
5. Discussion
We reviewed how conceptualizing the brain as an information processing machine, and using computational tools inspired by information theory to analyze brain activity, has led to major advances in understanding how networks of neurons encode information. Despite major progress, many questions remain unaddressed and call for further development of theories and computational approaches to brain functions. To stimulate future research, we here discuss how further theoretical advances may lead to a deeper understanding of neurobiology.
While the idea of efficient coding has been inspired by concepts in information theory, in practical terms, the design of efficient networks has been based on minimizing quadratic reconstruction errors [30]. This may work well with Gaussian distributions of the error signal that may be obtained from responses of peripheral sensory systems to simple stimuli, but may work less well in other cases, e.g. in the presence of higher order interactions between spikes or across neurons [109] or in the presence of non-Gaussian statistics of stimulus or neural noise. It would be thus important to extend efficient coding theories to include maximization of the full information of neural activity. Progress in this direction could be facilitated by advanced computational methods that analyze the encoding and transmission of information by neural circuits reviewed here. Importantly, these methods can be used for both the analysis of empirical neural data and of simulated responses of spiking networks. Bringing together these approaches could be useful for comparing quantitatively the information processing features of real and model neurons, as well as for testing the extent to which the optimization of simpler cost functions implies the optimization of the full Shannon information carried by neurons. The latter might not always be analytically computable, but is often computable using numerical methods in a simulated neural circuit. These simulations could be performed on a traditional computer, or alternatively on neuromorphic silicon chips [110].
So far, most research on the design of efficient neural networks has been mainly theoretical, aiming at exploring computational properties of artificial neural networks. The ability of these networks to describe information processing in real biological circuits has been limited. Recent advances have generalized the theory of efficient coding to account for biophysical constraints. In our recent work, we showed that a biologically plausible formulation of efficient coding accounted for measurable, well-established empirical properties of neurons in terms of first principles of computation [48]. Further extensions of biologically plausible efficient coding theory could be used to understand the computational principles of how and why cortical circuits drastically modulate their information coding according to the brain and behavioral states [111], [112], [113], [114]. It will be crucial for future research to capture these phenomena in terms of efficient coding and use neural network models to investigate the mechanisms supporting state-dependent changes in neural dynamics, potentially leading to insights into their computational role in information processing. We speculate that an accurate description of neural computations in these cases may require taking into account further biophysical characteristics of cortical circuits, such as different types of inhibitory neurons [115] and structured connectivity [116], [117] than the ones included in current models. Beyond the currently developed models where the objective of inhibitory neurons is formulated using the population readout, models may be developed where individual inhibitory neurons might track and predict the activity of individual excitatory neurons.
Efficient coding does not explain how neural circuits may predict future sensory signals, a computation that would have a clear benefit for forming appropriate behavioral outputs. Recent work has found that the primate retina may perform predictive encoding of motion by preferentially transmitting information that allows to optimally predict the position of visual objects in the near future [25]. This predictive code is based on selecting visual inputs with strong spatio-temporal correlations, since those are the inputs that allow prediction of the future position of visual objects. Thus, efficient and predictive coding account for partially opposing objectives of the neural code. While efficient coding tends to remove input correlations, predictive coding selects correlated inputs for further transmission and prediction of future stimuli. It would be important to extend the computation of prediction to biologically plausible cortical architectures and understand whether the objectives of predictive and efficient coding can be realized within the same neural circuit. It would be also interesting to explore this idea within models that possess the layer structure of a canonical laminar cortical microcircuit [118], [119], [120], as previous work has imputed a specialized role of computing and transmitting prediction errors to population of neurons in different layers [121].
By minimizing cost functions related to information encoding, efficient coding theories have succeeded in explaining some of the properties and computations of neurons in early sensory structures, whose function is presumably to encode information about the sensory environment. Here we reviewed the evidence that population codes support not only information encoding, but also information readout. We pointed out how multiple neural functions may place conflicting requirements on the neural code (notably on its correlation structure). In these cases, optimal neural computations need to be shaped by tradeoffs between partly conflicting objectives. In our view, a key goal for extending efficient coding theories is to develop a principled theoretical framework that accounts for trading off conflicting objectives, explaining how neural circuits balance the constraints imposed by information encoding in neural ensembles and the propagation of signals to downstream areas. This would require the mathematical formulation of a multi-objective cost function that trades off partly conflicting requirements of neural encoding and transmission. While objective functions that maximize encoding are conceptually relatively straightforward (because they relate neural activity to external sensory stimuli, which are relatively easy to manipulate) and have been implemented as reviewed above, objective functions related to activity readouts are more difficult to conceptualize and ground in empirical data. Here, we reviewed work that laid the foundations for studying the objective of information transmission with respect to readout, highlighting how the readout benefits from correlations in the input and by the single-trial consistency of information (induced by correlations) for amplifying signal propagation. This work has led to explicit analytical formulations of how the readout is shaped by correlations, which are amenable to be included in objective functions related to the information transmission. Together with careful studies of how choices can be decoded from the population activity and taking into account the functional role of neurons for the population signal [43], such studies could provide seed ideas to formulate multi-objective efficient coding theories.
We propose that such multi-objective extension of theories of efficient coding may be key to extending their success to non-sensory areas of the brain. For example, they could be used to explain whether the optimal level of correlations in one area depends on its placement along the cortical hierarchy [108] or the location in cortical laminae [122]. We speculate that for sensory cortices it may be optimal to have weak correlations to maximize information encoding, whereas association cortices might be optimized for stronger signal propagation, doing so through stronger correlations. This is because sensory cortices may need to encode all aspects of sensory stimuli, regardless for their relevance for the task at hand, thus placing more emphasis on encoding, which benefits from weaker correlations. On the other hand, cortical areas higher up in the hierarchy (for example, association areas) may prune away encoding of information of aspects of sensory stimuli not relevant to the task at hand, and thus may privilege the benefits of correlations for reliable information transmission. In higher brain areas, the cost in terms of limiting information encoding may be less damaging given the reduced requirements for encoding stimulus features. Also, cortical populations within upper or deeper layers of cortex (those that project to other areas) have stronger correlation levels [122], suggesting that the differentiation of coding properties across layers may not only relate to the information that each layer processes [121], but also to the need to amplify (by stronger correlations) the signals that are transmitted to other areas.
In this Review we have suggested the importance of adding to the studies of population coding and to theories of optimal information processing in the nervous systems multiple constraints and objectives, but we have focused on the tradeoff between the amount of encoded and transmitted information. Beyond information encoding and transmission, further relevant objectives of information maximization could include the speed (and not only the amount) of information processing. For example, correlations between neurons may contribute not only to the tradeoff between encoded and read out information, but also (in case they extend over a time range) to the speed and time scales at which information is accumulated [123]. Another important extension of this reasoning would be to consider how the tradeoffs between different constraints (including the amount of encoded and read out information) vary with the size of the neural population that encodes the stimuli. This population size is in general difficult to determine, although some studies have suggested that it is relatively small [38], [124]. Understanding better how the advantages and disadvantages of correlations for encoding and readout scale with population size would be beneficial for laying down a theoretical understanding of what could be optimal population sizes for specific neural computations.
CRediT authorship contribution statement
Veronika Koren: Conceptualization, Writing – original draft, Writing – review & editing. Giulio Bondanelli: Conceptualization, Writing – original draft, Writing – review & editing. Stefano Panzeri: Conceptualization, Writing – original draft, Writing – review & editing.
Acknowledgements
This work was supported by the NIH Brain Initiative Grants U19 NS107464, R01 NS109961, and R01 NS108410.
References
- 1.Perkel D.H., Bullock T.H. Neural coding. Neurosci Res Prog Bull. 1968;6(3):221–348. [Google Scholar]
- 2.Bialek W., Rieke F., de Ruyter van Steveninck R.R., Warland D. Reading a neural code. Science. 1991;252(5014):1854–1857. doi: 10.1126/science.2063199. [DOI] [PubMed] [Google Scholar]
- 3.Olshausen B.A., Field D.J. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381(6583):607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- 4.Boerlin M., Machens C.K., Denève S. Predictive coding of dynamical variables in balanced spiking networks. PLoS Comput Biol. 2013;9(11) doi: 10.1371/journal.pcbi.1003258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Averbeck B.B., Lee D. Effects of noise correlations on information encoding and decoding. J Neurophysiol. 2006;95(6):3633–3644. doi: 10.1152/jn.00919.2005. [DOI] [PubMed] [Google Scholar]
- 6.Panzeri S., Moroni M., Safaai H., Harvey C.D. The structures and functions of correlations in neural population codes. Nat Rev Neurosci. 2022;23(9):551–567. doi: 10.1038/s41583-022-00606-4. [DOI] [PubMed] [Google Scholar]
- 7.de Ruyter van Steveninck R.R., Lewen G.D., Strong S.P., Koberle R., Bialek W. Reproducibility and variability in neural spike trains. Science. 1997;275(5307):1805–1808. doi: 10.1126/science.275.5307.1805. [DOI] [PubMed] [Google Scholar]
- 8.Victor J.D. How the brain uses time to represent and process visual information. Brain Res. 2000;886(1–2):33–46. doi: 10.1016/s0006-8993(00)02751-7. [DOI] [PubMed] [Google Scholar]
- 9.Pica G., Piasini E., Safaai H., Runyan C., Harvey C., Diamond M., Kayser C., Fellin T., Panzeri S. In: Advances in neural information processing systems. Guyon I., Luxburg U.V., Bengio S., Wallach H., Fergus R., Vishwanathan S., Garnett R., editors. Curran Associates, Inc.; 2017. Quantifying how much sensory information in a neural code is relevant for behavior. vol. 30. [Google Scholar]
- 10.Rossi-Pool R., Zainos A., Alvarez M., Diaz-deLeon G., Romo R. A continuum of invariant sensory and behavioral-context perceptual coding in secondary somatosensory cortex. Nat Commun. 2021;12(1):2000. doi: 10.1038/s41467-021-22321-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rieke F., Warland D., Bialek W. Coding efficiency and information rates in sensory neurons. Europhys Lett. 1993;22(2):151. [Google Scholar]
- 12.Olshausen B.A., Field D.J. Natural image statistics and efficient coding. Network Comput Neural Syst. 1996;7(2):333–339. doi: 10.1088/0954-898X/7/2/014. [DOI] [PubMed] [Google Scholar]
- 13.Lewicki M.S. Efficient coding of natural sounds. Nat Neurosci. 2002;5(4):356–363. doi: 10.1038/nn831. [DOI] [PubMed] [Google Scholar]
- 14.Valente M., Pica G., Bondanelli G., Moroni M., Runyan C.A., Morcos A.S., Harvey C.D., Panzeri S. Correlations enhance the behavioral readout of neural population activity in association cortex. Nat Neurosci. 2021;24(7):975–986. doi: 10.1038/s41593-021-00845-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Barlow H.B., Rosenblith W.A. MIT Press; 1961. Possible principles underlying the transformations of sensory messages; pp. 217–234. vol. 1. [Google Scholar]
- 16.Shadlen M.N., Newsome W.T. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J Neurosci. 1998;18(10):3870–3896. doi: 10.1523/JNEUROSCI.18-10-03870.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Shannon C.E. A mathematical theory of communication. Bell Syst Tech J. 1948;27(3):379–423. [Google Scholar]
- 18.MacKay D.M., McCulloch W.S. The limiting information capacity of a neuronal link. Bull Math Biophys. 1952;14(2):127–135. [Google Scholar]
- 19.Attneave F. Some informational aspects of visual perception. Psychol Rev. 1954;61(3):183–193. doi: 10.1037/h0054663. [DOI] [PubMed] [Google Scholar]
- 20.Atick J.J., Redlich A.N. Towards a theory of early visual processing. Neural Comput. 1990;2(3):308–320. [Google Scholar]
- 21.Rieke F., Warland D., Van Steveninck R. d.R., Bialek W. MIT Press; 1999. Spikes: exploring the neural code. [Google Scholar]
- 22.Fairhall A., Shea-Brown E., Barreiro A. Information theoretic approaches to understanding circuit function. Curr Opin Neurobiol. 2012;22(4):653–659. doi: 10.1016/j.conb.2012.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Młynarski W.F., Hermundstad A.M. Efficient and adaptive sensory codes. Nat Neurosci. 2021;24(7):998–1009. doi: 10.1038/s41593-021-00846-0. [DOI] [PubMed] [Google Scholar]
- 24.Quian Quiroga R., Panzeri S. Extracting information from neuronal populations: information theory and decoding approaches. Nat Rev Neurosci. 2009;10(3):173–185. doi: 10.1038/nrn2578. [DOI] [PubMed] [Google Scholar]
- 25.Liu B., Hong A., Rieke F., Manookin M.B. Predictive encoding of motion begins in the primate retina. Nat Neurosci. 2021;24(9):1280–1291. doi: 10.1038/s41593-021-00899-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Safaai H., Onken A., Harvey C.D., Panzeri S. Information estimation using nonparametric copulas. Phys Rev E. 2018;98(5) doi: 10.1103/PhysRevE.98.053302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nemenman I., Lewen G.D., Bialek W., de Ruyter van Steveninck R.R. Neural coding of natural stimuli: information at sub-millisecond resolution. PLoS Comput Biol. 2008;4(3) doi: 10.1371/journal.pcbi.1000025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Baddeley R., Abbott L.F., Booth M.C.A., Sengpiel F., Freeman T., Wakeman E.A., Rolls E.T. Responses of neurons in primary and inferior temporal visual cortices to natural scenes. Proc R Soc Lond Ser B Biol Sci. 1997;264(1389):1775–1783. doi: 10.1098/rspb.1997.0246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levy W.B., Baxter R.A. Energy efficient neural codes. Neural Comput. 1996;8(3):531–543. doi: 10.1162/neco.1996.8.3.531. [DOI] [PubMed] [Google Scholar]
- 30.Olshausen B.A., Field D.J. Sparse coding with an overcomplete basis set: a strategy employed by v1? Vision Res. 1997;37(23):3311–3325. doi: 10.1016/s0042-6989(97)00169-7. [DOI] [PubMed] [Google Scholar]
- 31.Zhu M., Rozell C.J. Visual nonclassical receptive field effects emerge from sparse coding in a dynamical system. PLoS Comput Biol. 2013;9(8) doi: 10.1371/journal.pcbi.1003191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Koren V., Denève S. Computational account of spontaneous activity as a signature of predictive coding. PLoS Comput Biol. 2017;13(1) doi: 10.1371/journal.pcbi.1005355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lochmann T., Ernst U.A., Deneve S. Perceptual inference predicts contextual modulations of sensory responses. J Neurosci. 2012;32(12):4179–4195. doi: 10.1523/JNEUROSCI.0817-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Moreno-Bote R., Drugowitsch J. Causal inference and explaining away in a spiking network. Sci Rep. 2015;5(1):17531. doi: 10.1038/srep17531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Calaim N., Dehmelt F.A., Gonçalves P.J., Machens C.K. The geometry of robustness in spiking neural networks. Elife. 2022;11 doi: 10.7554/eLife.73276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gawne T., Richmond B. How independent are the messages carried by adjacent inferior temporal cortical neurons? J Neurosci. 1993;13(7):2758–2771. doi: 10.1523/JNEUROSCI.13-07-02758.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rolls E.T., Treves A., Tovee M.J. The representational capacity of the distributed encoding of information provided by populations of neurons in primate temporal visual cortex. Exp Brain Res. 1997;114(1):149–162. doi: 10.1007/pl00005615. [DOI] [PubMed] [Google Scholar]
- 38.Ince R.A.A., Panzeri S., Kayser C. Neural codes formed by small and temporally precise populations in auditory cortex. J Neurosci. 2013;33(46):18277–18287. doi: 10.1523/JNEUROSCI.2631-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Series P., Lorenceau J., Frégnac Y. The “silent” surround of v1 receptive fields: theory and experiments. J Physiol. 2003;97(4–6):453–474. doi: 10.1016/j.jphysparis.2004.01.023. [DOI] [PubMed] [Google Scholar]
- 40.Chalk M., Gutkin B., Deneve S. Neural oscillations as a signature of efficient coding in the presence of synaptic delays. Elife. 2016;5 doi: 10.7554/eLife.13824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Denève S., Machens C.K. Efficient codes and balanced networks. Nat Neurosci. 2016;19(3):375–382. doi: 10.1038/nn.4243. [DOI] [PubMed] [Google Scholar]
- 42.Kafashan M., Jaffe A.W., Chettih S.N., Nogueira R., Arandia-Romero I., Harvey C.D., Moreno-Bote R., Drugowitsch J. Scaling of sensory information in large neural populations shows signatures of information-limiting correlations. Nat Commun. 2021;12(1):473. doi: 10.1038/s41467-020-20722-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Koren V., Andrei A.R., Hu M., Dragoi V., Obermayer K. Reading-out task variables as a low-dimensional reconstruction of neural spike trains in single trials. PLoS One. 2019;14(10) doi: 10.1371/journal.pone.0222649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Barrett D.G., Deneve S., Machens C.K. Optimal compensation for neuron loss. Elife. 2016;5 doi: 10.7554/eLife.12454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brendel W., Bourdoukan R., Vertechi P., Machens C.K., Denéve S. Learning to represent signals spike by spike. PLoS Comput Biol. 2020;16(3) doi: 10.1371/journal.pcbi.1007692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gutierrez G.J., Denève S. Population adaptation in efficient balanced networks. ELife. 2019;8 doi: 10.7554/eLife.46926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.A. Alemi, C. Machens, S. Deneve, J.-J. Slotine, Learning nonlinear dynamics in efficient, balanced spiking networks using local plasticity rules. In: Proceedings of the AAAI conference on artificial intelligence, vol. 32, 2018.
- 48.V. Koren, S. Panzeri, Biologically plausible solutions for spiking networks with efficient coding. In: Advances in neural information processing systems, 2022 (in press). 10.48550/ARXIV.2210.07069. [DOI]
- 49.Niven J.E., Laughlin S.B. Energy limitation as a selective pressure on the evolution of sensory systems. J Exp Biol. 2008;211(11):1792–1804. doi: 10.1242/jeb.017574. [DOI] [PubMed] [Google Scholar]
- 50.Niven J.E. Neuronal energy consumption: biophysics, efficiency and evolution. Curr Opin Neurobiol. 2016;41:129–135. doi: 10.1016/j.conb.2016.09.004. [DOI] [PubMed] [Google Scholar]
- 51.Gerstner W., Kistler W.M., Naud R., Paninski L. Cambridge University Press; 2014. Neuronal dynamics: from single neurons to networks and models of cognition. [Google Scholar]
- 52.Jolivet R., Lewis T.J., Gerstner W. Generalized integrate-and-fire models of neuronal activity approximate spike trains of a detailed model to a high degree of accuracy. J Neurophysiol. 2004;92(2):959–976. doi: 10.1152/jn.00190.2004. [DOI] [PubMed] [Google Scholar]
- 53.Teeter C., Iyer R., Menon V., Gouwens N., Feng D., Berg J., Szafer A., Cain N., Zeng H., Hawrylycz M., et al. Generalized leaky integrate-and-fire models classify multiple neuron types. Nat Commun. 2018;9(1):709. doi: 10.1038/s41467-017-02717-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Tremblay R., Lee S., Rudy B. Gabaergic interneurons in the neocortex: from cellular properties to circuits. Neuron. 2016;91(2):260–292. doi: 10.1016/j.neuron.2016.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Chettih S.N., Harvey C.D. Single-neuron perturbations reveal feature-specific competition in v1. Nature. 2019;567(7748):334–340. doi: 10.1038/s41586-019-0997-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Buetfering C., Zhang Z., Pitsiani M., Smallridge J., Boven E., McElligott S., Häusser M. Behaviorally relevant decision coding in primary somatosensory cortex neurons. Nat Neurosci. 2022;25(9):1225–1236. doi: 10.1038/s41593-022-01151-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.King P.D., Zylberberg J., DeWeese M.R. Inhibitory interneurons decorrelate excitatory cells to drive sparse code formation in a spiking model of v1. J Neurosci. 2013;33(13):5475–5485. doi: 10.1523/JNEUROSCI.4188-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Yuste R. From the neuron doctrine to neural networks. Nat Rev Neurosci. 2015;16(8):487–497. doi: 10.1038/nrn3962. [DOI] [PubMed] [Google Scholar]
- 59.Saxena S., Cunningham J.P. Towards the neural population doctrine. Curr Opin Neurobiol. 2019;55:103–111. doi: 10.1016/j.conb.2019.02.002. [DOI] [PubMed] [Google Scholar]
- 60.Engel T.A., Steinmetz N.A. New perspectives on dimensionality and variability from large-scale cortical dynamics. Curr Opin Neurobiol. 2019;58:181–190. doi: 10.1016/j.conb.2019.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Averbeck B.B., Latham P.E., Pouget A. Neural correlations, population coding and computation. Nat Rev Neurosci. 2006;7(5):358–366. doi: 10.1038/nrn1888. [DOI] [PubMed] [Google Scholar]
- 62.Panzeri S., Schultz S.R., Treves A., Rolls E.T. Correlations and the encoding of information in the nervous system. Proc R Soc Lond Ser B Biol Sci. 1999;266(1423):1001–1012. doi: 10.1098/rspb.1999.0736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pola G., Thiele A., Hoffmann K., Panzeri S. An exact method to quantify the information transmitted by different mechanisms of correlational coding. Network Comput Neural Syst. 2003;14(1):35–60. doi: 10.1088/0954-898x/14/1/303. [DOI] [PubMed] [Google Scholar]
- 64.Abbott L.F., Dayan P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 1999;11(1):91–101. doi: 10.1162/089976699300016827. [DOI] [PubMed] [Google Scholar]
- 65.AzeredodaSilveira R., Rieke F. The geometry of information coding in correlated neural populations. Annu Rev Neurosci. 2021;44:403–424. doi: 10.1146/annurev-neuro-120320-082744. [DOI] [PubMed] [Google Scholar]
- 66.Moreno-Bote R., Beck J., Kanitscheider I., Pitkow X., Latham P., Pouget A. Information-limiting correlations. Nat Neurosci. 2014;17(10):1410–1417. doi: 10.1038/nn.3807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Gray C.M., König P., Engel A.K., Singer W. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 1989;338(6213):334–337. doi: 10.1038/338334a0. [DOI] [PubMed] [Google Scholar]
- 68.Decharms R.C., Merzenich M.M. Primary cortical representation of sounds by the coordination of action-potential timing. Nature. 1996;381(6583):610–613. doi: 10.1038/381610a0. [DOI] [PubMed] [Google Scholar]
- 69.Franke F., Fiscella M., Sevelev M., Roska B., Hierlemann A., daSilveira R.A. Structures of neural correlation and how they favor coding. Neuron. 2016;89(2):409–422. doi: 10.1016/j.neuron.2015.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Dan Y., Alonso J.-M., Usrey W.M., Reid R.C. Coding of visual information by precisely correlated spikes in the lateral geniculate nucleus. Nat Neurosci. 1998;1(6):501–507. doi: 10.1038/2217. [DOI] [PubMed] [Google Scholar]
- 71.Schneidman E., Bialek W., Berry M.J. Synergy, redundancy, and independence in population codes. J Neurosci. 2003;23(37):11539–11553. doi: 10.1523/JNEUROSCI.23-37-11539.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Reich D.S., Mechler F., Victor J.D. Independent and redundant information in nearby cortical neurons. Science. 2001;294(5551):2566–2568. doi: 10.1126/science.1065839. [DOI] [PubMed] [Google Scholar]
- 73.Latham P.E., Nirenberg S. Synergy, redundancy, and independence in population codes, revisited. J Neurosci. 2005;25(21):5195–5206. doi: 10.1523/JNEUROSCI.5319-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Shamir M., Sompolinsky H. Nonlinear population codes. Neural Comput. 2004;16(6):1105–1136. doi: 10.1162/089976604773717559. [DOI] [PubMed] [Google Scholar]
- 75.Josić K., Shea-Brown E., Doiron B., de la Rocha J. Stimulus-dependent correlations and population codes. Neural Comput. 2009;21(10):2774–2804. doi: 10.1162/neco.2009.10-08-879. [DOI] [PubMed] [Google Scholar]
- 76.Panzeri S., Senatore R., Montemurro M.A., Petersen R.S. Correcting for the sampling bias problem in spike train information measures. J Neurophysiol. 2007;98(3):1064–1072. doi: 10.1152/jn.00559.2007. [DOI] [PubMed] [Google Scholar]
- 77.Victor J.D. Binless strategies for estimation of information from neural data. Phys Rev E. 2002;66(5) doi: 10.1103/PhysRevE.66.051903. [DOI] [PubMed] [Google Scholar]
- 78.Kraskov A., Stögbauer H., Grassberger P. Estimating mutual information. Phys Rev E. 2004;69(6) doi: 10.1103/PhysRevE.69.066138. [DOI] [PubMed] [Google Scholar]
- 79.Francis N.A., Mukherjee S., Koçillari L., Panzeri S., Babadi B., Kanold P.O. Sequential transmission of task-relevant information in cortical neuronal networks. Cell Rep. 2022;39(9) doi: 10.1016/j.celrep.2022.110878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Koren V., Andrei A.R., Hu M., Dragoi V., Obermayer K. Pairwise synchrony and correlations depend on the structure of the population code in visual cortex. Cell Rep. 2020;33(6) doi: 10.1016/j.celrep.2020.108367. [DOI] [PubMed] [Google Scholar]
- 81.Bartolo R., Saunders R.C., Mitz A.R., Averbeck B.B. Information-limiting correlations in large neural populations. J Neurosci. 2020;40(8):1668–1678. doi: 10.1523/JNEUROSCI.2072-19.2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Montani F., Ince R.A., Senatore R., Arabzadeh E., Diamond M.E., Panzeri S. The impact of high-order interactions on the rate of synchronous discharge and information transmission in somatosensory cortex. Philos Trans R Soc A Math Phys Eng Sci. 2009;367(1901):3297–3310. doi: 10.1098/rsta.2009.0082. [DOI] [PubMed] [Google Scholar]
- 83.Rumyantsev O.I., Lecoq J.A., Hernandez O., Zhang Y., Savall J., Chrapkiewicz R., Li J., Zeng H., Ganguli S., Schnitzer M.J. Fundamental bounds on the fidelity of sensory cortical coding. Nature. 2020;580(7801):100–105. doi: 10.1038/s41586-020-2130-2. [DOI] [PubMed] [Google Scholar]
- 84.Cohen M.R., Kohn A. Measuring and interpreting neuronal correlations. Nat Neurosci. 2011;14(7):811–819. doi: 10.1038/nn.2842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Zohary E., Shadlen M.N., Newsome W.T. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature. 1994;370(6485):140–143. doi: 10.1038/370140a0. [DOI] [PubMed] [Google Scholar]
- 86.Kanitscheider I., Coen-Cagli R., Pouget A. Origin of information-limiting noise correlations. Proc Natl Acad Sci USA. 2015;112(50):E6973–E6982. doi: 10.1073/pnas.1508738112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Panzeri S., Brunel N., Logothetis N.K., Kayser C. Sensory neural codes using multiplexed temporal scales. Trends Neurosci. 2010;33(3):111–120. doi: 10.1016/j.tins.2009.12.001. [DOI] [PubMed] [Google Scholar]
- 88.Panzeri S., Petersen R.S., Schultz S.R., Lebedev M., Diamond M.E. The role of spike timing in the coding of stimulus location in rat somatosensory cortex. Neuron. 2001;29(3):769–777. doi: 10.1016/s0896-6273(01)00251-3. [DOI] [PubMed] [Google Scholar]
- 89.Tiesinga P., Fellous J.-M., Sejnowski T.J. Regulation of spike timing in visual cortical circuits. Nat Rev Neurosci. 2008;9(2):97–107. doi: 10.1038/nrn2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Jones L.M., Depireux D.A., Simons D.J., Keller A. Robust temporal coding in the trigeminal system. Science. 2004;304(5679):1986–1989. doi: 10.1126/science.1097779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Schnupp J.W., Hall T.M., Kokelaar R.F., Ahmed B. Plasticity of temporal pattern codes for vocalization stimuli in primary auditory cortex. J Neurosci. 2006;26(18):4785–4795. doi: 10.1523/JNEUROSCI.4330-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Kayser C., Logothetis N.K., Panzeri S. Millisecond encoding precision of auditory cortex neurons. Proc Natl Acad Sci. 2010;107(39):16976–16981. doi: 10.1073/pnas.1012656107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Stringer C., Michaelos M., Tsyboulski D., Lindo S.E., Pachitariu M. High-precision coding in visual cortex. Cell. 2021;184(10):2767–2778. doi: 10.1016/j.cell.2021.03.042. e15. [DOI] [PubMed] [Google Scholar]
- 94.Salinas E., Sejnowski T.J. Correlated neuronal activity and the flow of neural information. Nat Rev Neurosci. 2001;2(8):539–550. doi: 10.1038/35086012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.London M., Häusser M. Dendritic computation. Annu Rev Neurosci. 2005;28:503–532. doi: 10.1146/annurev.neuro.28.061604.135703. [DOI] [PubMed] [Google Scholar]
- 96.Polsky A., Mel B.W., Schiller J. Computational subunits in thin dendrites of pyramidal cells. Nat Neurosci. 2004;7(6):621–627. doi: 10.1038/nn1253. [DOI] [PubMed] [Google Scholar]
- 97.Koch C., Rapp M., Segev I. A brief history of time (constants) Cereb Cortex. 1996;6(2):93–101. doi: 10.1093/cercor/6.2.93. [DOI] [PubMed] [Google Scholar]
- 98.Zylberberg J., Pouget A., Latham P.E., Shea-Brown E. Robust information propagation through noisy neural circuits. PLoS Comput Biol. 2017;13(4) doi: 10.1371/journal.pcbi.1005497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Balaguer-Ballester E., Nogueira R., Abofalia J.M., Moreno-Bote R., Sanchez-Vives M.V. Representation of foreseeable choice outcomes in orbitofrontal cortex triplet-wise interactions. PLoS Comput Biol. 2020;16(6) doi: 10.1371/journal.pcbi.1007862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.J. Massey, Causality, feedback and directed information. In: Proceedings of international symposium on information theory and its applications (Institute of Electronics, Information and Communication Engineers, Tokyo)), 1990, pp.27–30.
- 101.Schreiber T. Measuring information transfer. Phys Rev Lett. 2000;85:461–464. doi: 10.1103/PhysRevLett.85.461. [DOI] [PubMed] [Google Scholar]
- 102.Campo A.T., Vázquez Y., Álvarez M., Zainos A., Rossi-Pool R., Deco G., Romo R. Feed-forward information and zero-lag synchronization in the sensory thalamocortical circuit are modulated during stimulus perception. Proc Natl Acad Sci USA. 2019;116(15):7513–7522. doi: 10.1073/pnas.1819095116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Besserve M., Lowe S.C., Logothetis N.K., Schölkopf B., Panzeri S. Shifts of gamma phase across primary visual cortical sites reflect dynamic stimulus-modulated information transfer. PLoS Biol. 2015;13(9) doi: 10.1371/journal.pbio.1002257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Panzeri S., Harvey C.D., Piasini E., Latham P.E., Fellin T. Cracking the neural code for sensory perception by combining statistics, intervention, and behavior. Neuron. 2017;93(3):491–507. doi: 10.1016/j.neuron.2016.12.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Luna R., Hernández A., Brody C.D., Romo R. Neural codes for perceptual discrimination in primary somatosensory cortex. Nat Neurosci. 2005;8(9):1210–1219. doi: 10.1038/nn1513. [DOI] [PubMed] [Google Scholar]
- 106.Zuo Y., Safaai H., Notaro G., Mazzoni A., Panzeri S., Diamond M.E. Complementary contributions of spike timing and spike rate to perceptual decisions in rat s1 and s2 cortex. Curr Biol. 2015;25(3):357–363. doi: 10.1016/j.cub.2014.11.065. [DOI] [PubMed] [Google Scholar]
- 107.P.L. Williams, R.D. Beer, Nonnegative decomposition of multivariate information (2010). 10.48550/ARXIV.1004.2515. [DOI]
- 108.Runyan C.A., Piasini E., Panzeri S., Harvey C.D. Distinct timescales of population coding across cortex. Nature. 2017;548(7665):92–96. doi: 10.1038/nature23020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Ohiorhenuan I.E., Mechler F., Purpura K.P., Schmid A.M., Hu Q., Victor J.D. Sparse coding and high-order correlations in fine-scale cortical networks. Nature. 2010;466(7306):617–621. doi: 10.1038/nature09178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.J. Büchel, J. Kakon, M. Perez, G. Indiveri, Implementing efficient balanced networks with mixed-signal spike-based learning circuits. In: 2021 IEEE international symposium on circuits and systems (ISCAS), IEEE, 2021, pp. 1–5.
- 111.Luczak A., McNaughton B.L., Harris K.D. Packet-based communication in the cortex. Nat Rev Neurosci. 2015;16(12):745–755. doi: 10.1038/nrn4026. [DOI] [PubMed] [Google Scholar]
- 112.Zerlaut Y., Zucca S., Panzeri S., Fellin T. The spectrum of asynchronous dynamics in spiking networks as a model for the diversity of non-rhythmic waking states in the neocortex. Cell Rep. 2019;27(4):1119–1132. doi: 10.1016/j.celrep.2019.03.102. e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.van Kempen J., Gieselmann M.A., Boyd M., Steinmetz N.A., Moore T., Engel T.A., Thiele A. Top-down coordination of local cortical state during selective attention. Neuron. 2021;109(5):894–904. doi: 10.1016/j.neuron.2020.12.013. e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Shi Y.-L., Steinmetz N.A., Moore T., Boahen K., Engel T.A. Cortical state dynamics and selective attention define the spatial pattern of correlated variability in neocortex. Nat Commun. 2022;13(1):44. doi: 10.1038/s41467-021-27724-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Yu J., Hu H., Agmon A., Svoboda K. Recruitment of gabaergic interneurons in the barrel cortex during active tactile behavior. Neuron. 2019;104(2):412–427. doi: 10.1016/j.neuron.2019.07.027. e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Lee W.-C.A., Bonin V., Reed M., Graham B.J., Hood G., Glattfelder K., Reid R.C. Anatomy and function of an excitatory network in the visual cortex. Nature. 2016;532(7599):370–374. doi: 10.1038/nature17192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.A.T. Kuan, G. Bondanelli, L.N. Driscoll, J. Han, M. Kim, D.G. Hildebrand, B.J. Graham, L.A. Thomas, S. Panzeri, C.D. Harvey, et al., Synaptic wiring motifs in posterior parietal cortex support decision-making, bioRxiv (2022). [DOI] [PMC free article] [PubMed]
- 118.Douglas R.J., Martin K.A., Whitteridge D. A canonical microcircuit for neocortex. Neural Comput. 1989;1(4):480–488. [Google Scholar]
- 119.Douglas R.J., Martin K.A. A functional microcircuit for cat visual cortex. J Physiol. 1991;440(1):735–769. doi: 10.1113/jphysiol.1991.sp018733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Douglas R.J., Martin K.A. Neuronal circuits of the neucortex. Annu Rev Neurosci. 2004;27(1):419–451. doi: 10.1146/annurev.neuro.27.070203.144152. [DOI] [PubMed] [Google Scholar]
- 121.Bastos A.M., Usrey W.M., Adams R.A., Mangun G.R., Fries P., Friston K.J. Canonical microcircuits for predictive coding. Neuron. 2012;76(4):695–711. doi: 10.1016/j.neuron.2012.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Hansen B.J., Chelaru M.I., Dragoi V. Correlated variability in laminar cortical circuits. Neuron. 2012;76(3):590–602. doi: 10.1016/j.neuron.2012.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Zariwala H., Kepecs A., Uchida N., Hirokawa J., Mainen Z. The limits of deliberation in a perceptual decision task. Neuron. 2013;78(2):339–351. doi: 10.1016/j.neuron.2013.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Bathellier B., Ushakova L., Rumpel S. Discrete neocortical dynamics predict behavioral categorization of sounds. Neuron. 2012;76(2):435–449. doi: 10.1016/j.neuron.2012.07.008. [DOI] [PubMed] [Google Scholar]