Data-driven color augmentation for H&E stained images in computational pathology

Niccolò Marini; Sebastian Otalora; Marek Wodzinski; Selene Tomassini; Aldo Franco Dragoni; Stephane Marchand-Maillet; Juan Pedro Dominguez Morales; Lourdes Duran-Lopez; Simona Vatrano; Henning Müller; Manfredo Atzori

doi:10.1016/j.jpi.2022.100183

. 2023 Jan 3;14:100183. doi: 10.1016/j.jpi.2022.100183

Data-driven color augmentation for H&E stained images in computational pathology

Niccolò Marini ^a,^b,^⁎, Sebastian Otalora ^c, Marek Wodzinski ^a,^d, Selene Tomassini ^e, Aldo Franco Dragoni ^e, Stephane Marchand-Maillet ^b, Juan Pedro Dominguez Morales ^f,^g, Lourdes Duran-Lopez ^f,^g, Simona Vatrano ^h, Henning Müller ^a,ⁱ, Manfredo Atzori ^a,^j

PMCID: PMC9852546 PMID: 36687531

Abstract

Computational pathology targets the automatic analysis of Whole Slide Images (WSI). WSIs are high-resolution digitized histopathology images, stained with chemical reagents to highlight specific tissue structures and scanned via whole slide scanners. The application of different parameters during WSI acquisition may lead to stain color heterogeneity, especially considering samples collected from several medical centers. Dealing with stain color heterogeneity often limits the robustness of methods developed to analyze WSIs, in particular Convolutional Neural Networks (CNN), the state-of-the-art algorithm for most computational pathology tasks. Stain color heterogeneity is still an unsolved problem, although several methods have been developed to alleviate it, such as Hue-Saturation-Contrast (HSC) color augmentation and stain augmentation methods. The goal of this paper is to present Data-Driven Color Augmentation (DDCA), a method to improve the efficiency of color augmentation methods by increasing the reliability of the samples used for training computational pathology models. During CNN training, a database including over 2 million H&E color variations collected from private and public datasets is used as a reference to discard augmented data with color distributions that do not correspond to realistic data. DDCA is applied to HSC color augmentation, stain augmentation and H&E-adversarial networks in colon and prostate cancer classification tasks. DDCA is then compared with 11 state-of-the-art baseline methods to handle color heterogeneity, showing that it can substantially improve classification performance on unseen data including heterogeneous color variations.

Keywords: Color augmentation, Deep learning, Computational pathology, Stain variability, Digital pathology, Histopathology

Introduction

Dealing with stain color heterogeneity is still one of the main challenges in the computational pathology domain.1, 2, 3, 4, 5, 6, 7

Stain color heterogeneity involves variations of colors within whole slide images (WSI),³^,⁶^,⁸ high-resolution digitized histopathology images.⁹ Histopathology is the gold-standard for the analysis of tissue samples,¹⁰^,¹¹ aiming to identify particular structures that may lead to the diagnosis of diseases, such as cancer. Stain color heterogeneity is a consequence of the inconsistencies of the procedures involved in the acquisition of WSIs.12, 13, 14, 15, 16 The acquisition of WSIs is composed of a sequence of procedures, including tissue preparation, tissue staining, and tissue scanning. Tissue preparation includes the tissue cutting (splitting of tissue specimen, removed from the patient, into slices or sections) and tissue fixation (a technique to apply chemicals to preserve tissue components and structure). Samples are usually cut with an automatic sectioning machine, but usually the thickness may not be uniform¹⁷ (around 3–5 μm) across laboratories, in particular when the tissue size is rather large; several fixatives including different chemical solutions were developed for the fixation, each one reacting differently with tissue specimen¹⁸ and therefore introducing inconsistent results across laboratories. Tissue staining involves the application of chemicals reagents to the tissue sample¹⁹ to highlight structures of the tissue that are transparent otherwise.20, 21, 22 The goal of stains is to absorb light, so that it is possible to observe structures within the tissue that otherwise would be transparent white.²² Usually, the reagents include concentrations of Hematoxylin & Eosin (H&E). Hematoxylin is responsible for the blue shades of cellular nuclei, while Eosin is responsible for the pink shades of extracellular structures. Several formulations of both hematoxylin and eosin are available,²³^,²⁴ leading to concentrations of H&E that are not standardized and may be inconsistent across different laboratories. Furthermore, the exposition to light, during tissue storing, may fade the stains.²² Tissue scanning involves the capture of images at high-resolution, creating a digital file.²⁵ Whole slide scanners are the hardware developed for tissue scanning. Currently, whole slide scanners are developed with peculiar properties, raw materials, manufacturing techniques, and setups that are not consistent across vendors.²^,¹⁷^,²⁶^,²⁷ In particular, the temperature⁸ impacts the reagents used to stain and to fix the tissue and the light acquired²⁷ influences the scanner response to the color. The color variation of a tissue depends on the light absorbed by stains,²² that are influenced by all steps in the WSI acquisition. Therefore, different acquisition parameters lead to different color variations. While the acquisition parameters are usually consistent within a single laboratory (despite small possible errors in the tissue cutting, tissue fixation, tissue staining, and small variations in the environmental conditions) they vary across medical centers.²^,³ For example, a medical center usually prepares the reagents to stain images with the same concentrations of H&E and can use a single whole slide scanner to scan the images, leading usually to a small variability in terms of acquisition procedures. Therefore, the inconsistency in WSIs acquisition usually is a problem related to multi-center data acquisition.⁶^,⁷^,²⁸

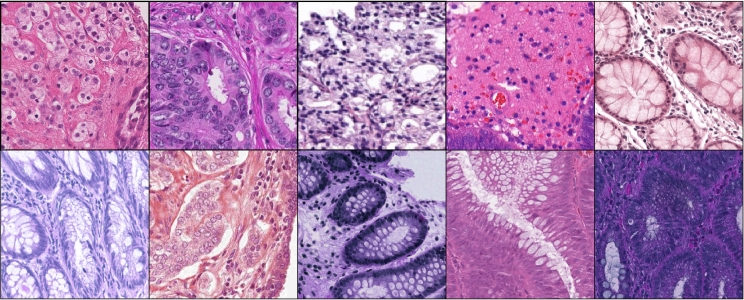
Fig. 1 shows an example of heterogeneous stain colors.

Dealing with stain color heterogeneity is still a challenge for the development of computational pathology algorithms.²^,³^,⁶^,¹²^,²⁹

Computational pathology is a domain involving the development of automatic algorithms to analyze WSIs,¹^,¹¹^,³⁰ such as the classification or segmentation of images. Currently, several algorithms developed to analyze WSIs are based on deep learning algorithms,¹ such as convolutional neural networks (CNN), which are the state-of-the-art algorithm for most WSI classification and segmentation tasks. Despite the high performance reached by CNNs, stain color heterogeneity between train and test images still limits the development of computational pathology algorithms, hindering their capability to generalize on heterogeneous data. CNNs trained on data acquired with a defined set of acquisition parameters (i.e., the H&E concentrations and the whole slide scanner adopted in a medical center) usually do not generalize well³ (i.e., they show poor performance) when tested on new data acquired with very different conditions. This problem limits the development of robust CNNs that can generalize well when tested on data including unseen stain color variations. This challenge is one of the limitations that prevent the adoption of computational pathology algorithms in clinical practice.¹^,³¹

Several algorithms and techniques have been developed to increase the robustness and the generalization of CNNs. The algorithms developed to alleviate the effects of stain heterogeneity on CNNs training mainly target modifications of input data at pixel-level,³^,²²^,²⁷ such as data normalization and color augmentation; or the application of training strategies aiming to induce specific properties at the feature-level,²^,⁶^,⁷^,¹² such as the invariance to the domain where the images are collected or to the image color variations.

Color normalization and color augmentation are methods working at pixel-level. In both cases, the methods modify the raw pixels of input data during CNN training. Color normalization¹⁵^,¹⁶^,²²^,²⁷^,³²^,³³ transforms the original image to match the stain of an image used as a template. Traditional color normalization approaches²²^,²⁷^,³⁴ match the stain matrix²² (or stain vector) from input data with the RGB components from a template sample. The stain matrix includes the RGB components of the light wavelength absorbed during the scanning for each stain component (H&E), according to Macenko et al.,²² that describes the color variation of the tissue and that can vary according to several factors (such as the H&E composition used to stain the image, the tissue thickness, the whole slide scanner used). More recently, the normalization problem is tackled with style-transfer methods based on deep learning approaches.³²^,³³ Data augmentation performs a random perturbation on the input-image,³^,²⁹^,³⁵ aiming to create a color variation in the data. Hue-Saturation-Contrast (HSC) color augmentation includes techniques perturbing parameters related to color (i.e., hue, saturation, and contrast), while stain color augmentation includes techniques perturbing parameters related to the stain matrices. Color augmentation methods usually show higher performance than color normalization ones.³

Adversarial CNN training strategies are usually adopted in feature-level algorithms.²^,⁶^,⁷ These algorithms are multi-task algorithms: the CNN is trained to optimize the main task (e.g., classification of images) and a secondary task related to desirable characteristics. Domain-adversarial networks⁶^,⁷^,¹² work under the assumption that images collected from the same medical center (or domain) present the same staining characteristics, being acquired with the same set of acquisition parameters. During the training of the CNN, the secondary task of the network is to predict the domain where the image was collected, allowing to learn domain-invariant features. The domain-adversarial assumption is generalized by H&E-adversarial CNNs²: the network is trained to directly predict the stain matrices of input data as a secondary task. H&E-adversarial CNNs relax the constraint related to domain-adversarial networks, in the case where the definition of the domain may be fuzzy (e.g., too strict if every single patient is considered as a domain or too broad if a medical center is considered as a domain), forcing the network to directly learn features invariant to the color variation (i.e., stain matrices).

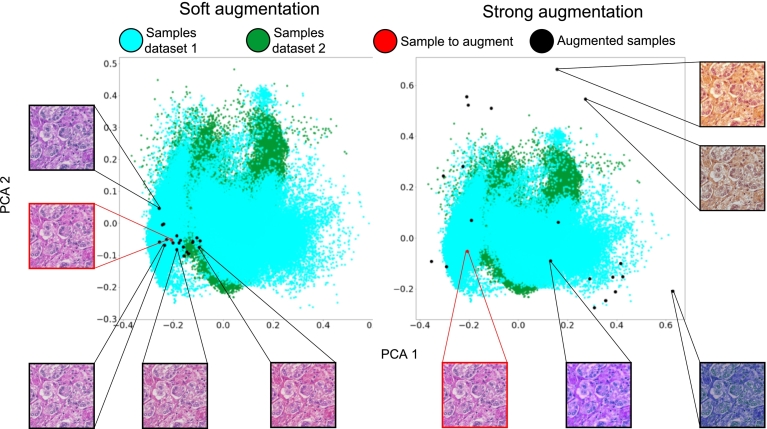
Despite the variety of solutions, the domain still shows several limitations linked to the tuning of algorithm parameters, especially in color augmentation techniques: small color perturbations may link to augmented data including similar stains to the original data, while large color perturbations may lead to augmented data including color artifacts. In this context, color artifacts include color variations that are not present in clinical practice, representing a problem for the training of CNNs. Fig. 2 shows some examples of the problems related to the tuning of color augmentation algorithms. In the left part of Fig. 2, the color perturbation applied to input data is too soft, leading to augmented samples that are very similar to the original image in terms of stain variations. In the right part of Fig. 2, the color perturbation is too strong, leading to augmented samples that include artifacts in terms of stain variations (such as dark and yellow shades).

Fig. 2 — Problems related to color augmentation parameters: on the left, small color perturbations lead to similar color variations (soft augmentation); while on the left, strong color perturbations lead to artifacts, such as yellowish or dark stains (strong augmentation). Blue and green dots represent color variations collected from clinical practice (from 2 different datasets, to show the stain heterogeneity); the red dot represents the sample to augment; black dots represent augmented versions of the sample. The samples are projected in a bi-dimensional space via Principal Component Analysis (PCA).

This paper proposes Data-Driven Color Augmentation (DDCA), a novel color augmentation method to train CNNs that avoids the generation of color artifacts during data augmentation, removing the need for tuning color augmentation algorithms.

DDCA aims to improve the efficiency of color augmentation methods by increasing the reliability of the samples used for training computational pathology models. DDCA exploits the increasing amount of available WSIs from private and public sources to build a database including millions of stain matrices, representing color variations. During CNN training, the method compares the stain matrix of augmented samples with the color variations collected in the database, discarding the ones corresponding to unrealistic color variations. DDCA is applied to HSC color augmentation, stain augmentation, and H&E-adversarial networks and compared with over 10 baseline algorithms developed to target stain color heterogeneity.

The method is tested on the classification of colon and prostate images, considering unseen data collected from heterogeneous medical sources. Colon and prostate cancers are 2 of the most common cancers worldwide.³⁶^,³⁷ One of the most important findings related to colon cancer is the presence of malignant glands and polyps (small agglomerations of cells) within colon WSIs.³⁸ The presence of malignant glands is also important for the diagnosis of prostate cancers: the Gleason grading system assesses the characteristics of glands to evaluate the aggressiveness of the tumor.³⁹ The rest of the paper is organized as follows: Section “Methods and Material” describes the CCDA method, the data used to evaluate it, including the datasets composition and the preprocessing, the description of other baselines to handle stain color heterogeneity, and the training strategy; Section “Results” presents a quantitative assessment of the method; Section “Discussion” presents a qualitative evaluation of the results obtained; “Conclusions” draws some conclusions.

Methods and materials

Data-driven color augmentation method

The paper proposes Data-Driven Color Augmentation (DDCA), a color augmentation method to avoid the generation of color variations including artifacts during the training of deep learning models.

Color variations are described by the composition of Hematoxylin and Eosin used to stain an image. The stain matrix (representing the color variation) is a 2x3 matrix including the RGB components of the light wavelength absorbed by Hematoxylin and Eosin stains, estimated using the Macenko et al.²² method.

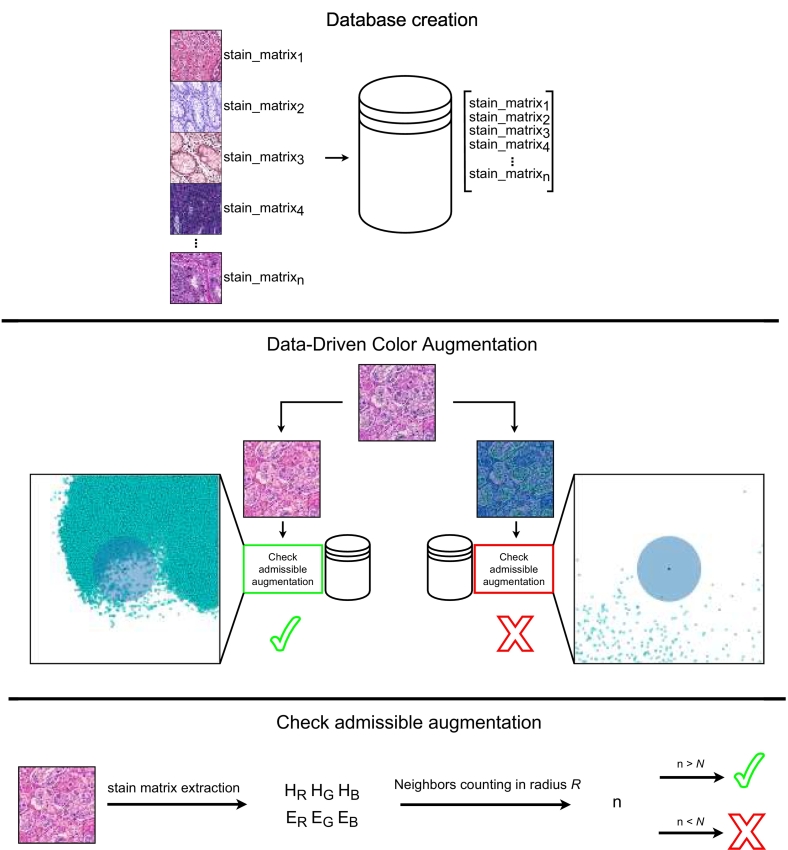
Fig. 3 summarizes the method operations. At training time, color augmentation is applied to input data to generate augmented samples including new color variations.

DDCA evaluates the quality of augmented color variations, labeling a sample as admissible or inadmissible. Only admissible samples are used to train the model, while inadmissible ones are discarded. The evaluation compares the similarity of the color variation from the augmented samples with color variations collected from clinical practice (private and public WSIs) and collected in a database, under the assumption that data collected from many medical sources are heterogeneous in terms of stain and allow to describe the color variations included in clinical practice. The similarity is evaluated considering 2 parameters: R (radius) and N (neighbors). R is the Euclidean distance within which 2 samples are considered similar. N is the minimum number of samples that must be located nearer (i.e., at a distance less than R) to the augmented sample to detect a similarity. The latter parameter is adopted to prevent potential outliers among admissible samples to have an impact on data augmentation. Therefore, the color variation of an augmented sample A is considered admissible only if it is near to more than N admissible samples. Furthermore, DDCA limits the need for the tuning of color algorithms. The tuning aims to generate valuable augmented samples that can describe the heterogenous stain variations in clinical practice. However, as shown in Fig. 2, small perturbations of original data limit the artifacts but lead to small variability in terms of color. In contrast, large perturbations lead to high variability but create a large number of artifacts. DDCA can be applied to any method involving color augmentation of input data, such as HSC color augmentation or stain augmentation, or in combination with training strategies, such as domain-invariant and H&E-invariant CNNs.

Data

Two heterogeneous sets of data are used to develop and test the method proposed in the paper.

The first set includes heterogeneous samples collected for training and testing a CNN. Data come from several medical sources, guaranteeing high variability in terms of color to test the capability of the CNN to generalize on heterogeneous unseen data. The CNN is trained to classify colon and prostate images at patch-level. For both use cases, the images are paired with pixel-wise annotations, done manually by trained pathologists. In both use cases, the training schema involves 3 partitions: training, validation, and testing partition. Training and validation partitions include patches from 2 medical sources, while the testing partition includes patches from independent medical sources and from the same 2 medical sources used during training. The colon data partition includes images collected from 7 medical sources: AOEC,²^,⁴⁰ Radboudumc.²^,⁴⁰ AIDA.⁴¹ GlaS⁴² (Gland Segmentation in Colon Histology Images Challenge), CRC⁴³ (ColoRectal Cancer Tissue Phenotyping), UNITOPATHO.⁴⁴ and CAMEL⁴⁵ datasets. The images are WSIs (AOEC, Radboudumc, AIDA) and cropped sections of WSIs (GlaS, CRC, UNITOPATHO, and CAMEL). Images from AOEC and Radboudumc are used to train and evaluate algorithms (using separate and independent subsets of data), while images from the other datasets are only used to evaluate the capability of the method to generalize on data collected from independent sources. The heterogeneity of medical sources is reflected in the annotations including several classes, mapped to cancer, dysplasia, and normal.

Table 1 summarizes the composition of the colon dataset.

Table 1.

Composition of the colon dataset. The colon dataset includes patches annotated as Cancer, Dysplasia, or Normal. Patches from AOEC and Radboudumc are used to train, validate, and test the method, while patches from AIDA, GlaS, CRC, UNITOPATHO, and CAMEL are used as external sources to test the capability of the method to generalize on data collected from independent sources.

Colon data
Source	Cancer	Dysplasia	Normal	Total
Training partition
AOEC	4059	13 170	3402	20 631
Radboudumc	2995	2498	1304	6797
Total training	7054	15 668	4706	27 428

Validation partition
AOEC	844	4005	78	4927
Radboudumc	643	707	365	1715
Total validation	1487	4714	443	6642

Internal testing partition
AOEC	1255	6137	373	7765
Radboudumc	792	337	329	1458
Total internal testing	2047	6474	702	9223

External testing partition
AIDA	7881	3296	31 859	43 036
GlaS	450	0	210	660
CRC	1507	0	1144	2651
UNITOPATHO	0	13 326	2182	21 551
CAMEL	0	12 083	7795	27 787
Total external testing	9838	28 705	43 190	81 733

Open in a new tab

The prostate data partition includes images collected from 6 medical sources: TMAZ⁴⁶ (Tissue MicroArray Zurich), SICAPv2,⁴⁷ Gleason challenge,⁴⁸ Diagset,⁴⁹ Valme,⁵⁰^,⁵¹ and PANDA challenge⁵² datasets. The images are WSIs (SICAPv2, Diagset, Valme, and PANDA challenge) and tissue microarray (TMAZ and Gleason). Images from TMAZ and SICAPv2 are used to train and evaluate algorithms (using separate and independent subsets of data), while images from the other datasets are only used to evaluate the capability of the method to generalize on data collected from independent sources. The classes chosen to train the CNN are benign, Gleason pattern 3 (GP3), Gleason pattern 4 (GP4), and Gleason pattern 5 (GP5).

Table 2 summarizes the composition of the prostate cancer dataset.

Table 2.

Composition of the prostate dataset. The prostate dataset includes patches annotated as Benign, Gleason Pattern 3 (GP3), Gleason Pattern 4 (GP4), and Gleason Pattern 5 (GP5). Patches from TMAZ and SICAPv2 are used to train, validate, and test the method, while patches from Gleason challenge, Diagset, Valme, and PANDA are used as external sources to test the capability of the method to generalize on data collected from independent sources.

Prostate data
Source	Benign	GP3	GP4	GP5	Total
Training partition
TMAZ	2010	5992	4472	2766	15 240
SICAPv2	9432	6499	2250	2011	20 192
Total training	11 442	12 491	6722	4777	35 432

Validation partition
TMAZ	1350	1352	831	457	4927
SICAPv2	604	819	302	210	1935
Total validation	1954	2171	1133	667	6862

Internal testing partition
TMAZ	127	1602	2121	387	4237
SICAPv2	1033	3466	427	546	5427
Total internal testing	1160	5068	2548	933	9709

External testing partition
Gleason challenge	1080	2431	3649	100	7260
Diagset	8783	1243	4334	696	15 056
Valme	13 652	3026	5510	800	22 988
PANDA	10 189	20 000	20 000	8014	58 203
Total external testing	33 704	26 700	33 493	9610	103 507

Open in a new tab

The second set includes data collected to create the database of color variations, from private and public sources.

The goal of this set is to describe the variability of colors in clinical practice, therefore it includes data (H&E matrices) collected from heterogeneous sources: TCGA platform (datasets including several tissues, from 123 centers), ExaMode colon data (AOEC and Radboudumc), Camelyon⁵³ (4 centers), Clinic, Puerta del Mar, and CAD⁶⁴. Images collected from TCGA platform are Formalin Fixed Paraffin Embedded (FFPE) tissue samples. The database includes over 2 million H&E matrices evaluated using Macenko et al. method.²² From each WSI, the patches are densely extracted at magnification 10x, leading to over 8 million samples. WSIs may vary in terms of tissue size, leading to a larger number of patches extracted from larger images (such as TCGA) and therefore to a larger number of H&E matrices extracted from those images. Since patches from the same image may share the same matrices, the database may include several entries with the same values. Several entries may represent a problem during the evaluation of augment sample neighbors, since the matrices will be counted several times, even if they represent the same color variation, creating a bias. The problem becomes increasingly serious as the number of matrices that share the same value increases. To avoid any kind of bias, introduced by image size, the database is filtered: all double H&E matrix entries are removed.

Table 3 summarizes the composition of the database.

Table 3.

Composition of the database including H&E color variations. Color variations are collected from several heterogeneous sources to represent the variability in clinical practice. From each center the variations are filtered, to avoid the possible introduction of biases due to the repetition of the same variation in the database.

Source	Number H&E matrices	Number WSIs	Number patches	Number medical centers
TCGA	646 332	951	2 835 516	123
ExaMode⁴⁰^,⁵⁴	985 147	5390	3 983 025	2
Camelyon⁵³	219 743	454	520 660	4
Puerta del Mar	132 863	138	272 276	1
Clinic	50 871	225	114 725	1
CAD⁶⁴	71 495	1085	350 407	1
Total	2 106 451	8243	8 076 609	132

Open in a new tab

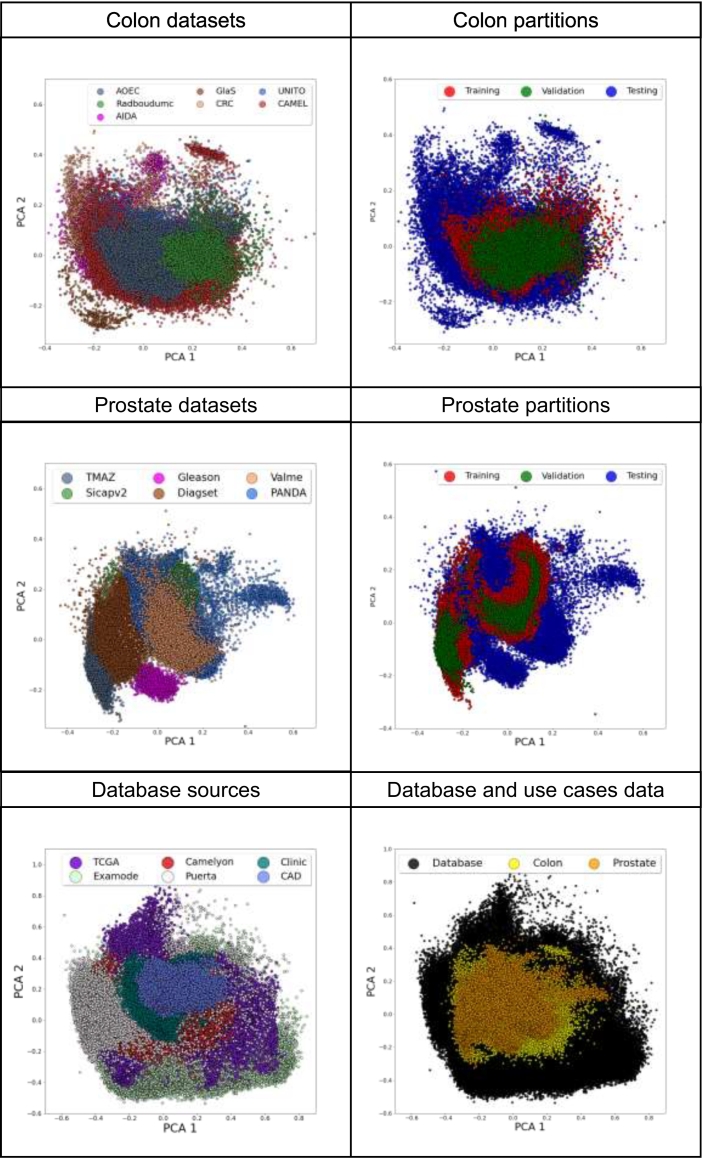
Fig. 4 highlights the color variability of data, considering the colon data (first row), the prostate data (second row) and the data included in the database (third row). For each subfigure, the 6-dimensional H&E matrices corresponding to the patches are projected on a bi-dimensional space using the Principal Component Analysis (PCA).

Data pre-processing

WSIs are split into smaller sub-regions. Image splitting is required due to hardware constraints¹: WSIs may be very large in terms of size and modern graphics processing units (GPU) may face difficulties to handle an entire WSI.

Image splitting involves the generation of subregions, called patches, selected from valuable regions. Patches must be consistent in terms of pixel size and magnification (optical resolution); however, patch generation strategy varies across different types of images (WSIs, cropped sections, and TMAs). WSIs (AOEC, Radboudumc, AIDA, colon data; SICAPv2, Diagset, Valme, PANDA, prostate data) are split in a grid, without any stride, and densely sampled, using Multi_Scale_Tools python library.⁵⁵ During the extraction, patches are resized to 224x224 pixels. The grid building may vary according to setup parameters (such as the wanted magnification), as follows:

ps : mw = ps’ : mh

where ps represents the wanted patch size, mw represents the wanted magnification level, ps’ represents the size of the patches in the highest magnification level available (mh). While the patch size is the same for both tissues (224×224 pixels), the magnification is different between the colon and prostate. Patches from colon images are extracted at magnification 10x,⁴⁰ so that a patch can include enough tissue with glands. On the other hand, patches from prostate images are extracted with a size of 750×750 pixels⁴⁶^,⁵⁶ at magnification 40× and resized to 224×224 pixels, so that a patch can include both glands and stroma. The parameters are different among use cases. Colon image parameters are: ps equal to 224 (patch size is 224×224 pixels) and mw equal to 10 (patches must be at magnification 10×). Prostate image parameters are: ps equal to 224 (patch size is 224×224 pixels), ps’ and mh (patches must be extracted 750×750 pixels in size from magnification 40×). Cropped sections (GlaS, CRC, UNITO and CAMEL, colon data) are split in a grid and densely extracted, using the same setup presented for WSIs. However, the grid is built with a few pixels of variable stride (20 in CRC, 2 in GlaS, 5 in UNITO and CAMEL), aiming to avoid high similarity between patches. Tissue Micro Arrays (TMAs) (TMAZ and Gleason challenge, prostate data) are not split in a grid. Due to the small size of TMAs (3’100 × 3’100 for TMAZ, 5000 × 5000 for Gleason), 30 patches are randomly generated from each TMA core, using the same setup hereby presented. Patches are selected from valuable regions to discard uninformative tissue or image background. In the case of data used to train and evaluate the method, patches are selected from annotated regions. WSIs and TMAs are paired with a tissue mask including pixel-wise annotations of different classes, made by pathologists. Cropped sections come without any pixel-wise annotation. However, cropped sections are very small in size, therefore the patches inherit the label assigned to the whole cropped section. In the case of data used to create the color variation database, patches are selected from regions including tissue (generated using the HistoQC tool⁵⁷).

Baselines

The paper presents a comparison between the proposed DDCA method and other baseline algorithms developed to train robust CNNs on unseen data including high color variations. The algorithms performance is evaluated on the classification of histopathology patches, using Cohen’s κ-score⁵⁸ as metric. Furthermore, the Wilcoxon Rank-Sum test⁵⁹ is performed to verify that the difference in the performance reached by the methods is statistically significant, setting the statistical level of significance P at .05.

DDCA method is applied to HSC color augmentation (HSC DDCA), stain augmentation (Stain DDCA), and H&E-adversarial CNN methods (Data-driven HSC color augmentation and H&E-adversarial CNN). The algorithms chosen as baselines include: no strategy to handle color variability, grayscale normalization, color normalization, HSC color augmentation, stain augmentation, domain-adversarial CNNs, and H&E-invariant CNNs. Every algorithm is evaluated on the internal test partition (including unseen patches coming from the same sources used to train and validate the CNN), on the external test partition (including data coming from independent data sources than the ones used to train), and on the combination of both. The method including no strategy to handle color variability does not apply any color modification to input data. Grayscale normalization involves the transformation of input data (both during training and testing) to grayscale images, instead of RGB. Color normalization algorithms include Macenko et al.²² method, StainGAN,³³ and StainNet³². Macenko et al. is a traditional approach to normalize color, while StainGAN and StainNet are based on deep learning GANs (Generative Adversarial Networks). For both the colon and prostate, the image used as a stain template is randomly selected. StainGAN and StainNet are both pre-trained to normalize images among different domains (in this case, only 2 domains). HSC color augmentation algorithm³^,²⁹ involves the perturbation of input data modifying the contrast, saturation, and hue of input images. Two setups are presented: in the first one, the parameters related to the perturbations are tuned to have meaningful color variations (Tuned HSC color augmentation), while in the second one, strong perturbations are applied (Strong HSC color augmentation).

Stain augmentation algorithm involves the perturbation of H&E matrix, using 2 parameters, σ₁ and σ₂. Both parameters identify a range within the stain matrix can be perturbed: for each component of the vector, a float value [-σ, σ] is randomly generated and summed to the original color variation. Also in this case, 2 setups are presented to show the effects of stain augmentation with tuned parameters (tuned stain augmentation) and with strong perturbations (strong stain augmentation). The domain-adversarial CNN is a multitask network predicting the patches class (as the main task) and the domain where they are collected (as a secondary task), proposed by Otalora et al.,¹² Ren et al.,⁶ Lafarge et al.⁷ In this case, only 2 domains are used during the training (the 2 centers selected as the training set). H&E-adversarial CNN is a multitask network predicting the classes of input patches (main task) and regressing their stain matrices (as a secondary task), proposed by Marini et al.² The κ-score measures the agreement (and reliability) between annotations. The metric is commonly adopted in histopathology, to evaluate the performance of pathologists in data annotation tasks. When κ-score is adopted in computation pathology tasks, the prediction of a model is compared with the ground truth made by pathologists. A κ-score equal to 1 shows a complete agreement between the annotators, while a κ-score equal to -1 shows a complete disagreement. The random agreement between annotators is a κ-score equal to 0, since the metric is normalized to the agreement obtained by chance.

The Wilcoxon-Rank Sum is a statistical test to evaluate if 2 probabilistic populations present the same distribution (the null hypothesis). If the hypothesis is tested negative, the P-value obtained is lower than .05, while the hypothesis is rejected to be tested negative if the P-value is greater than .05. In this paper, the 10 repetitions of the CCDA methods are compared with the 10 repetitions of the baseline algorithm reaching the highest performance, to test if the improvement obtained by CCDA methods is statistically significant.

Training strategy & parameters

The strategy adopted to train and set the hyperparameters is the same for both the DDCA method and the baseline algorithms chosen for comparison.

The CNN backbone chosen for the method and the baseline algorithms is a DenseNet121 pre-trained on ImageNet.⁶⁰ The Densenet backbone it is chosen since it has proven to be effective in many histopathology tasks⁶¹ when compared with other architectures. For each patch (224×224×3 in size), the convolutional backbone outputs a vector with 1024 features. Between the feature vector and the classifier, another fully connected layer is introduced, including 128 features. All the parameters within the network are trainable. For each of the algorithms presented, the CNN is trained 10 times, reporting the average and the standard deviation. This procedure is necessary to alleviate the undesired effects introduced by the stochastic gradient descent optimizer adopted during the model optimization. For each method, the choice of the hyper-parameters is driven by the grid search algorithm.⁶² The grid search finds the optimal configuration (in this case, the one reaching the lowest loss function in the validation partition) of the CNN hyperparameters. The grid search is used for both general parameters (such as the learning rate) and for specific parameters related to an algorithm (such as the σ in the stain augmentation). The general parameters involved in the grid search algorithm are the optimizer (Adam identified as optimal; Adam and SGD tested); the learning rate (10⁻³ identified as optimal; 10⁻², 10⁻³, 10⁻⁴, 10⁻⁵ tested); the decay rate (0 identified as optimal; 10⁻², 10⁻³, 10⁻⁴, 10⁻⁴ tested); the number of epochs (after 15 epochs the CNN loss function no longer decreases), and the number of nodes in the intermediate layer of the CNN (128 identified as optimal; 64,128, 256, 512 tested). The specific parameters of the algorithms involved in the grid search algorithm are the σ₁ and σ₂ of stain augmentation algorithm (for both parameters 0.2 is identified as optimal for the tuned implementation for both parameters; for both parameters 0.7 is identified as optimal for the strong implementation for both parameters); the shift values for the hue of HSC color augmentation (between −15 and 8 for colon data; between −9 and 9 for prostate data); the shift values for the saturation of HSC color augmentation (between −20 and 10 for colon data; between −25 and 25 for prostate data); the shift of brightness value for HSC color augmentation (between −8 and 8 for colon data; between −10 and 10 for prostate data); the lambda parameter for the domain-adversarial CNN (0.5 identified as optimal); the lambda parameter for the H&E-adversarial CNN (0.5 identified as optimal); the radius R and the neighbors N for the DDCA method presented in the paper (0.05 identified as optimal for R; 10 identified as optimal for N). The effects introduced by unbalanced classes within datasets are alleviated using a class-wise data augmentation strategy during the training. The operations applied are 90–180–270 degrees rotations and flipping, implemented with Albumentations library.⁶³

Results

The Data-Driven Color Augmentation methods improve the performance of a CNN compared with other methods developed to handle stain color variability, showing more robust performance on colon and prostate image classification, in both internal and external test partitions.

Colon data include 7 heterogeneous datasets annotated with cancer, dysplasia, and normal classes. Data are aggregated in the internal test partition (AOEC and Radboudumc), external test partition (AIDA, GlaS, CRC, UNITO, and CAMEL), and the test partition (including the combination of internal and external partitions). DDCA is applied with 3 setups: HSC DDCA (Data-Driven color augmentation applied to HSC color augmentation), Stain DDCA (Data-Driven color augmentation applied to stain augmentation), and DDCA combined with H&E-adversarial CNN.

The performance of the methods on colon data are summarized in Table 4, Table 5.

Table 4.

Classification performance on the colon test partitions, considering 7 datasets. The performance is reported considering the κ-score (average and standard deviation) of every method tested. Statistically significant results (considering the best method among DDCA and the best method among baselines) are marked with (*).

Dataset/Method	AOEC	Radboudumc	AIDA	GlaS	CRC	UNITO	CAMEL
No strategy	0.551 ± 0.055	0.796 ± 0.021	0.523 ± 0.071	0.098 ± 0.126	0.527 ± 0.097	0.075 ± 0.102	0.108 ± 0.099
Grayscale normalization	0.582 ± 0.025	0.769 ± 0.033	0.601 ± 0.038	0.129 ± 0.083	0.320 ± 0.172	0.148 ± 0.064	0.276 ± 0.108
Macenko color normalization	0.578 ± 0.033	0.762 ± 0.057	0.557 ± 0.035	0.221 ± 0.101	0.602 ± 0.044	0.046 ± 0.081	0.229 ± 0.147
StainGAN	0.418 ± 0.101	0.579 ± 0.238	0.502 ± 0.060	0.187 ± 0.098	0.579 ± 0.071	0.175 ± 0.044	0.262 ± 0.091
StainNET	0.531 ± 0.054	0.566 ± 0.147	0.362 ± 0.118	0.238 ± 0.095	0.337 ± 0.107	0.073 ± 0.102	0.176 ± 0.148
Tuned HSC color augmentation	0.551 ± 0.057	0.768 ± 0.031	0.566 ± 0.042	0.198 ± 0.136	0.494 ± 0.156	0.130 ± 0.050	0.189 ± 0.163
Strong HSC color augmentation	0.337 ± 0.180	0.500 ± 0.272	0.416 ± 0.192	0.064 ± 0.105	0.132 ± 0.177	0.086± 0.075	0.157 ± 0.142
Tuned stain augmentation	0.588 ± 0.038	0.765 ± 0.032	0.521 ± 0.066	0.355 ± 0.110	0.510 ± 0.124	0.110 ± 0.077	0.281 ± 0.098
Strong stain augmentation	0.601 ± 0.037	0.772 ± 0.040	0.508 ± 0.109	0.236 ± 0.146	0.498 ± 0.139	0.179 ± 0.066	0.188 ± 0.089
Domain-adversarial CNN	0.553 ± 0.070	0.695 ± 0.060	0.566 ± 0.067	0.346 ± 0.174	0.331 ± 0.197	0.120 ± 0.089	0.279 ± 0.118
H&E-adversarial CNN	0.592 ± 0.035	0.776 ± 0.030	0.602 ± 0.041	0.343 ± 0.123	0.480 ± 0.160	0.123 ± 0.074	0.214 ± 0.111
HSC DDCA	0.601 ± 0.033	0.768 ± 0.032	0.625 ± 0.039	0.258 ± 0.138	0.558 ± 0.159	0.189 ± 0.091	0.417 ± 0.092*
Stain DDCA	0.580 ± 0.056	0.758 ± 0.047	0.584 ± 0.052	0.242 ± 0.108	0.539 ± 0.187	0.158 ± 0.063	0.296 ± 0.140
HSC DDCA combined with H&E-adversarial CNN	0.626 ± 0.018	0.821 ± 0.032*	0.630 ± 0.054	0.252 ± 0.127	0.662 ± 0.049*	0.208 ± 0.031	0.406 ± 0.065

Open in a new tab

Table 5.

Aggregated results on colon data, considering the internal data partition (AOEC and Radboudumc), the external data (AIDA, GlaS, CRC, UNITO, and CAMEL) and the whole test partition. The table reports the results as the average performance for the datasets included in a partition (Dataset aggregation) and as the performance on a partition (Sample aggregation).

	Dataset aggregation			Sample aggregation
Dataset/Method	Internal test partition	External test partition	Test partition	Internal test partition	External test partition	Test partition
No strategy	0.674 ± 0.042	0.267 ± 0.101	0.382 ± 0.088	0.644 ± 0.036	0.424 ± 0.074	0.453 ± 0.075
Grayscale normalization	0.675 ± 0.029	0.294 ± 0.103	0.403 ± 0.089	0.663 ± 0.043	0.485 ± 0.040	0.518 ± 0.039
Macenko color normalization	0.670 ± 0.046	0.331 ± 0.091	0.428 ± 0.081	0.650 ± 0.036	0.493 ± 0.037	0.520 ± 0.034
StainGAN	0.530 ± 0.183	0.341 ± 0.075	0.395 ± 0.117	0.528 ± 0.115	0.464 ± 0.053	0.347 ± 0.106
StainNET	0.548 ± 0.111	0.238 ± 0.116	0.327 ± 0.051	0.558 ± 0.077	0.312 ± 0.105	0.487 ± 0.051
Tuned HSC color augmentation	0.660 ± 0.046	0.316 ± 0.122	0.414 ± 0.105	0.636 ± 0.031	0.488 ± 0.049	0.518 ± 0.046
Strong HSC color augmentation	0.419 ± 0.231	0.170 ± 0.145	0.241 ± 0.174	0.383 ± 0.199	0.288 ± 0.139	0.321 ± 0.142
Tuned stain augmentation	0.676 ± 0.035	0.356 ± 0.097	0.447 ± 0.084	0.656 ± 0.033	0.479 ± 0.061	0.509 ± 0.055
Strong stain augmentation	0.687 ± 0.039	0.322 ± 0.114	0.427 ± 0.099	0.667 ± 0.036	0.455 ± 0.096	0.483 ± 0.092
Domain-adversarial CNN	0.624 ± 0.065	0.328 ± 0.138	0.413 ± 0.122	0.608 ± 0.057	0.477 ± 0.048	0.507 ± 0.048
H&E-adversarial CNN	0.677 ± 0.038	0.353 ± 0.109	0.446 ± 0.094	0.655 ± 0.035	0.514 ± 0.066	0.542 ± 0.063
HSC DDCA	0.683 ± 0.033	0.410 ± 0.113	0.488 ± 0.097	0.661 ± 0.033	0.571 ± 0.033*	0.601 ± 0.030*
Stain DDCA	0.669 ± 0.051	0.364 ± 0.121	0.451± 0.106	0.648 ± 0.040	0.525 ± 0.040	0.553 ± 0.037
HSC DDCA combined with H&E-adversarial CNN	0.723 ± 0.027	0.432 ± 0.073	0.515 ± 0.063	0.697 ± 0.024*	0.560 ± 0.033	0.594 ± 0.032

Open in a new tab

Specifically, Table 4 shows the performance of the methods for each dataset. DDCA outperforms the baseline methods in all datasets, except in GlaS. HSC DDCA combined with H&E-adversarial CNN reaches the highest performance for all datasets, except for GlaS and CAMEL (where HSC DDCA reaches the highest performance). Furthermore, the difference in performance is statistically significant on Radboudumc, CRC and UNITO datasets. Table 5 shows the aggregated performance of the methods on internal, external, and test partitions. The performance is aggregated at dataset- and sample-level. The dataset-level aggregation aims to alleviate the effect that the size of datasets may have on the global results. For each method, the average of the performance reached for each dataset is reported, combined with the average of the standard deviations. HSC DDCA combined with H&E-adversarial CNN allows reaching the highest performance in the internal and the test partition (κ-score = 0.626 ± 0.018 and κ-score = 0.515 ± 0.063, respectively), while HSC DDCA reaches the highest performance in the external partition (κ-score = 0.410 ± 0.113). The sample-level aggregation aims to show the performance of the methods on a dataset including highly heterogeneous images collected from several sources. For each partition, the DDCA method reaches the highest performance: in the internal partition, HSC DDCA combined with H&E-adversarial CNN allows to reach the highest performance (κ-score = 0.697 ± 0.024), while in the external and the test partitions, HSC DDCA reaches the highest performance (κ-score = 0.571 ± 0.033 and κ-score = 0.601 ± 0.030, respectively). The difference in performance is statistically-significant respect to all the partitions. Prostate data include 6 heterogeneous datasets annotated with benign, GP3, GP4, and GP5 classes. Data are aggregated in the internal test partition (TMAZ and SICAPv2), external test partition (Gleason, Diagset, Valme, and PANDA), and the test partition (including the combination of internal and external partitions).

The performance of the methods on prostate data are summarized in Table 6, Table 7.

Table 6.

Classification performance on the prostate test partitions, considering 6 datasets. The performance is reported considering the κ -score (average and standard deviation) of every method tested. Statistically significant results (considering the best method among DDCA and the best method among baselines) are marked with (*).

Dataset/Method	TMAZ	SICAPv2	Gleason	Diagset	Valme	PANDA
No strategy	0.568 ± 0.044	0.715 ± 0.040	0.262± 0.149	0.122 ± 0.060	0.276 ± 0.098	0.263 ± 0.072
Grayscale normalization	0.526 ± 0.039	0.704 ± 0.051	0.509 ± 0.039	0.252 ± 0.074	0.326 ± 0.085	0.406 ± 0.038
Macenko color normalization	0.463 ± 0.079	0.738 ± 0.048	0.448 ± 0.070	0.266 ± 0.133	0.407 ± 0.065	0.444 ± 0.080
StainGAN	0.497 ± 0.088	0.630 ± 0.083	0.235 ± 0.145	0.358 ± 0.072	0.256 ± 0.109	0.341 ± 0.185
StainNET	0.489 ± 0.084	0.662 ± 0.097	0.350 ± 0.099	0.445 ± 0.079	0.374 ± 0.053	0.467 ± 0.063
Tuned HSC color augmentation	0.546 ± 0.034	0.736 ± 0.058	0.494 ± 0.039	0.439 ± 0.077	0.427 ± 0.091	0.414 ± 0.081
Strong HSC color augmentation	0.221 ± 0.147	0.571 ± 0.202	0.298 ± 0.198	0.260 ± 0.078	0.238 ± 0.071	0.327 ± 0.116
Tuned stain augmentation	0.528 ± 0.044	0.701 ± 0.076	0.304 ± 0.089	0.265 ± 0.074	0.305 ± 0.060	0.373 ± 0.047
Strong stain augmentation	0.550 ± 0.047	0.744 ± 0.045	0.295 ± 0.114	0.192 ± 0.072	0.297 ± 0.069	0.374 ± 0.085
Domain-adversarial CNN	0.451 ± 0.101	0.695 ± 0.060	0.409 ± 0.087	0.392 ± 0.101	0.392 ± 0.054	0.387 ± 0.127
H&E-adversarial CNN	0.581 ± 0.026	0.736 ± 0.054	0.516 ± 0.040	0.449 ± 0.072	0.442 ± 0.052	0.450 ± 0.067
Data-driven HSC color augmentation	0.572 ± 0.034	0.717 ± 0.048	0.563 ± 0.047*	0.505 ± 0.086	0.467 ± 0.043	0.492 ± 0.061
Data-driven stain augmentation	0.545 ± 0.068	0.734 ± 0.049	0.538 ± 0.051	0.367 ± 0.059	0.457 ± 0.067	0.500 ± 0.029
Data-driven HSC color augmentation and H&E-adversarial CNN	0.562 ± 0.045	0.744 ± 0.036	0.541 ± 0.043	0.480 ± 0.041	0.413 ± 0.036	0.476 ± 0.042

Open in a new tab

Table 7.

Aggregated results on prostate data, considering the internal data partition (TMAZ and SICAPv2), the external data (Gleason, Diagset, Valme, and PANDA) and the whole test partition. The table reports the results as the average performance for the datasets included in a partition (Dataset aggregation) and as the performance on a partition (Sample aggregation).

	Dataset aggregation			Sample aggregation
Dataset/Method	Internal test partition	External test partition	Test partition	Internal test partition	External test partition	Test partition
No strategy	0.641± 0.042	0.240 ± 0.116	0.374 ± 0.098	0.713 ± 0.026	0.233 ± 0.078	0.263 ± 0.072
Grayscale normalization	0.615 ± 0.046	0.374 ± 0.063	0.454 ± 0.057	0.694 ± 0.032	0.320 ± 0.050	0.348 ± 0.046
Macenko color normalization	0.597 ± 0.073	0.391 ± 0.091	0.460 ± 0.085	0.680 ± 0.066	0.392 ± 0.040	0.413 ± 0.040
StainGAN	0.554 ± 0.114	0.290 ± 0.137	0.378 ± 0.129	0.633 ± 0.065	0.303 ± 0.172	0.331 ± 0.156
StainNET	0.576 ± 0.090	0.409 ± 0.076	0.465 ± 0.081	0.650 ± 0.078	0.447 ± 0.058	0.463 ± 0.053
Tuned HSC color augmentation	0.641 ± 0.048	0.444 ± 0.075	0.510 ± 0.067	0.720 ± 0.041	0.446 ± 0.070	0.467 ± 0.066
Strong HSC color augmentation	0.397± 0.176	0.280 ± 0.126	0.319 ± 0.145	0.402 ± 0.200	0.262 ± 0.067	0.273 ± 0.074
Tuned stain augmentation	0.615 ± 0.062	0.312 ± 0.069	0.412 ± 0.067	0.690 ± 0.038	0.334 ± 0.055	0.361 ± 0.051
Strong stain augmentation	0.647 ± 0.046	0.290 ± 0.087	0.409 ± 0.076	0.721 ± 0.037	0.292 ± 0.087	0.324 ± 0.081
Domain-adversarial CNN	0.573 ± 0.083	0.395 ± 0.096	0.455 ± 0.092	0.650 ± 0.071	0.413 ± 0.118	0.432 ± 0.110
H&E-adversarial CNN	0.659 ± 0.035	0.464 ± 0.059	0.529 ± 0.054	0.725 ± 0.035	0.477 ± 0.045	0.496 ± 0.041
Data-driven HSC color augmentation	0.647 ± 0.041	0.507 ± 0.062	0.553 ± 0.056	0.714 ± 0.028	0.508 ± 0.037	0.524 ± 0.033
Data-driven stain augmentation	0.639 ± 0.059	0.465 ± 0.053	0.523 ± 0.055	0.714 ± 0.047	0.469 ± 0.042	0.487 ± 0.036
Data-driven HSC color augmentation and H&E-adversarial CNN	0.653 ± 0.041	0.477 ± 0.041	0.536 ± 0.041	0.730 ± 0.033	0.472 ± 0.027	0.491 ± 0.023

Open in a new tab

Table 6 shows the performance of the methods for each dataset. DDCA outperforms the baseline methods in all datasets, except in TMAZ. HSC DDCA reaches the highest performance in Gleason, Diagset, and Valme; stain DDCA reaches the highest performance in PANDA; HSC DDCA combined with H&E-adversarial CNN reaches the highest performance in SICAPv2. The difference in performance is statistically significant only on Diagset dataset.

Table 7 shows the aggregated performance of the methods on internal, external, and test partitions. At dataset-level, HSC DDCA reaches the highest performance in external and test partitions (κ-score = 0.507 ± 0.062 and κ-score = 0.553 ± 0.056, respectively). At sample-level, DDCA reaches the highest performance: in the internal partition, HSC DDCA combined with H&E-adversarial CNN allows reaching the highest performance (κ-score = 0.730 ± 0.033), while in the external and the test partitions, HSC DDCA reaches the highest performance (respectively κ-score = 0.508 ± 0.037 and κ-score = 0.524 ± 0.033). The difference in performance is not statistically significant respect to all the partitions.

Discussion

The DDCA method outperforms other state-of-the-art methods developed to handle the stain color variability across histopathology images, showing the capability to develop CNNs that generalize on heterogeneous data.

Currently, stain color variability may represent a problem for the training of convolutional neural networks (CNN): CNNs trained on data including with a defined set of color variations usually do not generalize well (i.e., they show poor performance) when tested on new data including very different color variations. Among the methods developed to tackle this problem, currently color augmentation and adversarial CNN represent the state-of-the-art algorithm. However, color augmentation requires the user to tune some parameters (i.e., the perturbation to apply) in order to avoid any color artifacts. The parameter tuning is not trivial, therefore the color augmentation algorithm may easily be ineffective, risking the model to overfit on the only color variations seen during the training. The method presented in the paper is built to limit the noise introduced by unacceptable color variations during CNN training, which can hinder the learning process of a data-driven algorithm. During augmentation, strong perturbations are applied to the data, in order to cover the widest possible color variation spectrum, discarding samples including unacceptable color variations. The presented method, when applied to well-known approaches such as color augmentation and domain-adversarial CNNs allows to obtain higher performance on unseen heterogeneous data (considering both colon and prostate data) compared to other state-of-the-art baselines. In both colon and prostate use cases, methods to handle WSI color variations are tested on several heterogeneous datasets, aggregated (at database- and sample-level) on 3 partitions: the internal test partition, including data collected from the same sources used to train and validate the CNNs, the external test partition, including data collected from independent external medical sources, and the test partition, including both the internal and the external partitions. While the performance obtained by the DDCA method on the internal partition is comparable (even if slightly higher) with the one obtained by the baseline methods, the performance obtained by the DDCA method on the external partition is higher than the one from the baseline methods. On colon data, HSC DDCA and HSC DDCA combined with H&E-adversarial CNNs reach the highest performance on the external partitions, considering the aggregation at dataset-level. The result indicates that the method is the one reaching the highest performance on most datasets. The performance on single datasets confirms the hypothesis: DDCA reaches the highest performance on 4 datasets out of 7 (in 2 other datasets the highest performance is reached by Data-driven HSC color augmentation method). On prostate data, DDCA reaches the highest performance on the external partition, considering the aggregation at dataset-level. Also for the prostate use case, results indicate that the method is the one reaching the highest performance on most of datasets: the method reaches the highest performance on 4 datasets out of 6 (in another datasets, the highest performance is reached by HSC DDCA combined with H&E-adversarial CNNs). The results reached on external datasets, for both colon and prostate data, suggest that the method can generalize on unseen heterogeneous data. The generalization of the DDCA method is confirmed considering the performance on the external partition and on the whole test partition, aggregated at sample-level. Sample-level aggregation allows to create a dataset including patches collected from multiple sources, simulating a scenario where data are highly heterogeneous. In both the use cases, the highest performance is reached by HSC DDCA, confirming the hypothesis (the method generalizes on unseen heterogeneous data). The improved generalization power can be explained by the data-driven augmentation mechanism. DDCA aims to limit the generation of artifacts during data augmentation, filtering the input-data noise introduced by artifacts on color variations, allowing to only use augmented samples that are considered admissible. The criterion of admissibility involves the comparison between the stain matrix of augmented samples and a database of color variations, collected from hundreds of medical sources. The criterion allows to generate only augmented samples with color variations included in clinical practice, under the hypothesis that these color variations included in the database are acceptable. This aspect may also help to explain the similar performance obtained on the internal partition: the color variations are usually homogeneous among the same medical center, leading to training, validation, and test partitions including similar color variations. Therefore, the method does not allow to improve the performance, in contrast to what happens on the external partition, where the DDCA method outperforms other state-of-the-art baselines. The overhead introduced from the comparison varies considering the algorithm parameters (the neighbors N and the radius R) and the augmentation parameters. Large values of neighbors N and small values of radius R leads to a higher number of discarded patches, as well as the application of large perturbation. However, the overhead introduced by the criterion does not affect the algorithm performance in terms of time, since a single epoch lasts a few minutes (around 7 and 10, respectively without and with the DDCA method, considering the parameters adopted in this paper). The nature of the method alleviates another problem related to augmentation methods: the tuning of parameters. Fig. 2 shows possible effects related to augmentation parameter tuning. Augmented samples may include color variations that are very similar to the original input data (small perturbations) or color artifacts (strong perturbations). Since there are no deterministic solutions to tune the parameters, usually the choice of the values is empirically made. On the other hand, the DDCA method removes this problem: the augmentation will generate only admissible stain matrices and therefore acceptable color variations, discarding color artifacts. Therefore, it is possible to apply large ranges of perturbations to the input images, that usually lead to artifacts, without any drawback. This fact is particularly clear when comparing the performance of HSC DDCA and stain DDCA with, respectively, tuned HSC color augmentation and tuned stain augmentation. Considering both the performance aggregated at sample-level (or even the single datasets), the DDCA method reaches dramatically higher performance on both use cases. On colon data, HSC DDCA reaches κ-score = 0.571 ± 0.033, while tuned HSC color augmentation reaches κ-score = 0.488 ± 0.049; stain DDCA reaches κ-score = 0.525 ± 0.040, while tuned stain augmentation reaches κ-score = 0.479 ± 0.061. On prostate data, HSC DDCA reaches κ-score = 0.508 ± 0.037, while tuned HSC color augmentation reaches κ-score = 0.446 ± 0.070; stain DDCA reaches κ-score = 0.469 ± 0.042, while tuned stain augmentation reaches κ-score = 0.334 ± 0.055. This difference in performance can be identified also evaluating the performance on the single datasets (Table 5 and Table 7). The method is designed to work on original input data, even if it can be combined with methods working at feature-level (as shown in HSC DDCA combined with H&E-adversarial CNNs). Therefore, the method can be applied also in weakly supervised contexts, where it is not always possible to apply feature-level methods to handle color heterogeneity, such as Multiple Instance Learning or Visual Transformers, since usually the hardware does not have enough GPU memory. This implication is not trivial: the method shows dramatically higher performance when compared only with the pixel-level baseline methods (both augmentations or normalization). Therefore, DDCA may help to increase the performance reached in weakly supervised contexts.

Conclusion

The paper presents Data-Driven Color Augmentation, a novel simple but effective method that can be applied to color augmentation methods, helping to build more accurate CNNs that better generalize on data including heterogeneous color variations. The method is based on reasonable assumptions about the realistic color variations of H&E images. The method is used during data augmentation: the stain matrix of an augmented sample is compared with the color variations collected from heterogeneous sources, discarding artifacts (color variations dissimilar from the ones available in clinical practice). The method is tested on 2 cases, colon and prostate histopathology image classification, and compared with several baselines, showing robust performance and outperforming other state-of-the-art baselines with statistical significance when tested on unseen new data. The code to implement the methods and the database including color variations (with the methods to expand the database with new data) is released on Github (https://github.com/ilmaro8/Data_Driven_Color_Augmentation) acceptance.

Declaration of Interests

The authors declare that there are no competing interests.

Acknowledgments

This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement No. 825292 (ExaMode, {htttp://www.examode.eu/}).

References

1.Morales S., Engan K., Naranjo V. Artificial intelligence in computational pathology – challenges and future directions. Digital Signal Process. 2021;119 doi: 10.1016/j.dsp.2021.103196. [DOI] [Google Scholar]
2.Marini N., Atzori M., Otálora S., Marchand-Maillet S., Müller H. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops. 2021. H&E-adversarial network: a convolutional neural network to learn stain-invariant features through hematoxylin & eosin regression; pp. 601–610. [Google Scholar]
3.Tellez D, Litjens G, Bándi P, et al. Quantifying the Effects of Data Augmentation and Stain Color Normalization in Convolutional Neural Networks for Computational Pathology. [DOI] [PubMed]
4.Khan A., Janowczyk A., Müller F., et al. Impact of scanner variability on lymph node segmentation in computational pathology. J Pathol Inform. 2022:100127. doi: 10.1016/j.jpi.2022.100127. Published online July 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Litjens G., Ciompi F., van der Laak J. A decade of GigaScience: the challenges of gigapixel pathology images. GigaScience. 2022;11:giac056. doi: 10.1093/gigascience/giac056. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Ren J., Hacihaliloglu I., Singer E.A., Foran D.J., Qi X. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2018. Adversarial domain adaptation for classification of prostate histopathology whole-slide images; pp. 201–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Lafarge M.W., Pluim J.P.W., Eppenhof K.A.J., Veta M. Learning domain-invariant representations of histological images. Front Med. 2019:6. doi: 10.3389/fmed.2019.00162. Accessed August 25, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Clarke E.L., Treanor D. Colour in digital pathology: a review. Histopathology. 2017;70(2):153–163. doi: 10.1111/his.13079. [DOI] [PubMed] [Google Scholar]
9.Pantanowitz L., Valenstein P.N., Evans A.J., et al. Review of the current state of whole slide imaging in pathology. J Pathol Inform. 2011;2(1):36. doi: 10.4103/2153-3539.83746. [DOI] [PMC free article] [PubMed] [Google Scholar]
10.Gurcan M.N., Boucheron L.E., Can A., Madabhushi A., Rajpoot N.M., Yener B. Histopathological image analysis: a review. IEEE Rev Biomed Eng. 2009 doi: 10.1109/RBME.2009.2034865. Published online. [DOI] [PMC free article] [PubMed] [Google Scholar]
11.van der Laak J., Litjens G., Ciompi F. Deep learning in histopathology: the path to the clinic. Nat Med. 2021;27(5):775–784. doi: 10.1038/s41591-021-01343-4. [DOI] [PubMed] [Google Scholar]
12.Otálora S., Atzori M., Andrearczyk V., Khan A., Müller H. Staining invariant features for improving generalization of deep convolutional neural networks in computational pathology. Front Bioeng Biotechnol. 2019;7(AUG):198. doi: 10.3389/FBIOE.2019.00198/BIBTEX. [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Hou L., Agarwal A., Samaras D., Kurc T.M., Gupta R.R., Saltz J.H. 2019. Robust Histopathology Image Analysis: To Label or To Synthesize? pp. 8533–8542.https://openaccess.thecvf.com/content_CVPR_2019/html/Hou_Robust_Histopathology_Image_Analysis_To_Label_or_to_Synthesize_CVPR_2019_paper.html Accessed August 25, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Khan A., Atzori M., Otálora S., Andrearczyk V., Müller H. Medical Imaging 2020: Digital Pathology. Vol 11320. SPIE; 2020. Generalizing convolution neural networks on stain color heterogeneous data for computational pathology; pp. 173–186. [DOI] [Google Scholar]
15.Cong C., Liu S., Di Ieva A., Pagnucco M., Berkovsky S., Song Y. Colour adaptive generative networks for stain normalisation of histopathology images. Med Image Anal. 2022:102580. doi: 10.1016/j.media.2022.102580. Published online August 27. [DOI] [PubMed] [Google Scholar]
16.Ciompi F., Geessink O., Bejnordi B.E., et al. 2017. The importance of stain normalization in colorectal tissue classification with convolutional networks. Published online May 23. [DOI] [Google Scholar]
17.Inoue T., Yagi Y. Color standardization and optimization in whole slide imaging. Clin Diagn Pathol. 2020;4(1) doi: 10.15761/cdp.1000139. [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Howat W.J., Wilson B.A. Tissue fixation and the effect of molecular fixatives on downstream staining procedures. Methods. 2014;70(1):12–19. doi: 10.1016/j.ymeth.2014.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Alturkistani H.A., Tashkandi F.M., Mohammedsaleh Z.M. Histological stains: a literature review and case study. Glob J Health Sci. 2015;8(3):72–79. doi: 10.5539/gjhs.v8n3p72. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Chan J.K.C. The wonderful colors of the hematoxylin–eosin stain in diagnostic surgical pathology. Int J Surg Pathol. 2014;22(1):12–32. doi: 10.1177/1066896913517939. [DOI] [PubMed] [Google Scholar]
21.Fischer A.H., Jacobson K.A., Rose J., Zeller R. Hematoxylin and eosin staining of tissueand cell sections. Cold Spring Harbor Protocols. 2008;3(5) doi: 10.1101/pdb.prot4986. [DOI] [Google Scholar]
22.Macenko M., Niethammer M., Marron J.S., et al. Proceedings - 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, ISBI 2009. 2009. A method for normalizing histology slides for quantitative analysis. [DOI] [Google Scholar]
23.Feldman A.T., Wolfe D. In: Histopathology: Methods and Protocols. Methods in Molecular Biology. Day C.E., editor. Springer; 2014. Tissue processing and hematoxylin and eosin staining; pp. 31–43. [DOI] [PubMed] [Google Scholar]
24.Bancroft J.D., Layton C. In: Bancroft’s Theory and Practice of Histological Techniques. 7th ed. Suvarna S.K., Layton C., Bancroft J.D., editors. Churchill Livingstone; 2013. 10 - The hematoxylins and eosin; pp. 173–186. [DOI] [Google Scholar]
25.Hanna M.G., Reuter V.E., Ardon O., et al. Validation of a digital pathology system including remote review during the COVID-19 pandemic. Mod Patholgy. 2020;33(11):2115–2127. doi: 10.1038/s41379-020-0601-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Cheng W.C., Saleheen F., Badano A. Assessing color performance of whole-slide imaging scanners for digital pathology. Color Res Appl. 2019;44(3):322–334. doi: 10.1002/col.22365. [DOI] [Google Scholar]
27.Vahadane A., Peng T., Sethi A., et al. Structure-preserving color normalization and sparse stain separation for histological images. IEEE Trans Med Imaging. 2016;35(8):1962–1971. doi: 10.1109/TMI.2016.2529665. [DOI] [PubMed] [Google Scholar]
28.Stacke K., Eilertsen G., Unger J., Lundstrom C. Measuring domain shift for deep learning in histopathology. IEEE J Biomed Health Inform. 2021;25(2):325–336. doi: 10.1109/JBHI.2020.3032060. [DOI] [PubMed] [Google Scholar]
29.Otálora S., Marini N., Podareanu D., et al. Stainlib: a python library for augmentation and normalization of histopathology H&E images. Bioinformatics. 2022 doi: 10.1101/2022.05.17.492245. [DOI] [Google Scholar]
30.Campanella G., Hanna M.G., Geneslaw L., et al. Clinical-grade computational pathology using weakly supervised deep learning on whole slide images. Nat Med. 2019;25(8):1301–1309. doi: 10.1038/s41591-019-0508-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Janowczyk A., Madabhushi A. Deep learning for digital pathology image analysis: a comprehensive tutorial with selected use cases. J Pathol Inform. 2016;7(1):29. doi: 10.4103/2153-3539.186902. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Kang H., Luo D., Feng W., et al. StainNet: a fast and robust stain normalization network. Front Med. 2021:8. doi: 10.3389/fmed.2021.746307. Accessed August 26, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Shaban M.T., Baur C., Navab N., Albarqouni S. StainGAN: Stain Style Transfer for Digital Histological Images. 2018. http://arxiv.org/abs/1804.01601 Published online April 4. Accessed August 26, 2022.
34.Reinhard E., Adhikhmin M., Gooch B., Shirley P. Color transfer between images. IEEE Comput Graphics Appl. 2001;21(5):34–41. doi: 10.1109/38.946629. [DOI] [Google Scholar]
35.Faryna K., van der Laak J., Litjens G. Tailoring automated data augmentation to H&E-stained histopathology. 2022. https://openreview.net/forum?id=JrBfXaoxbA2 Accessed September 5, 2022. [DOI] [PubMed]
36.Rahib L., Wehner M.R., Matrisian L.M., Nead K.T. Estimated projection of US cancer incidence and death to 2040. JAMA Netw Open. 2021;4(4) doi: 10.1001/jamanetworkopen.2021.4708. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Rawla P. Epidemiology of prostate cancer. World J Oncol. 2019;10(2):63–89. doi: 10.14740/wjon1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Benson A.B., Venook A.P., Al-Hawary M.M., et al. NCCN guidelines insights: colon cancer, version 2.2018. J Natl Compr Canc Netw. 2018;16(4):359–369. doi: 10.6004/jnccn.2018.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Current Perspectives on the Gleason Grading of Prostate Cancer | Archives of Pathology & Laboratory Medicine. 2022. https://meridian.allenpress.com/aplm/article/133/11/1810/460670/Current-Perspectives-on-the-Gleason-Grading-of Accessed August 26. [DOI] [PubMed]
40.Marini N., Marchesin S., Otálora S., et al. Unleashing the potential of digital pathology data by training computer-aided diagnosis models without human annotations. npj Digit Med. 2022;5(1):1–18. doi: 10.1038/s41746-022-00635-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Stadler C.B., Lindvall M., Lundström C., et al. Proactive construction of an annotated imaging database for artificial intelligence training. J Digit Imag. 2020;34(1):105–115. doi: 10.1007/S10278-020-00384-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Sirinukunwattana K., Snead D.R.J., Rajpoot N.M. A stochastic polygons model for glandular structures in colon histology images. IEEE Trans Med Imag. 2015;34(11):2366–2378. doi: 10.1109/TMI.2015.2433900. [DOI] [PubMed] [Google Scholar]
43.Awan R., Sirinukunwattana K., Epstein D., et al. Glandular morphometrics for objective grading of colorectal adenocarcinoma histology images. Scient Rep. 2017;7(1):2220–2243. doi: 10.1038/s41598-017-16516-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Barbano C.A., Perlo D., Tartaglione E., et al. 2021. UniToPatho, a labeled histopathological dataset for colorectal polyps classification and adenoma dysplasia grading; pp. 76–80. Published online January. [DOI] [Google Scholar]
45.Xu G., Song Z., Sun Z., et al. 2019. CAMEL: A Weakly Supervised Learning Framework for Histopathology Image Segmentation. Published online August 28. [DOI] [Google Scholar]
46.Arvaniti E., Fricker K.S., Moret M., et al. Automated Gleason grading of prostate cancer tissue microarrays via deep learning. Scient Rep. 2018;8(1):12054. doi: 10.1038/s41598-018-30535-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Silva-Rodríguez J., Colomer A., Sales M.A., Molina R., Naranjo V. Going deeper through the Gleason scoring scale: an automatic end-to-end system for histology prostate grading and cribriform pattern detection. Comput Methods Prog Biomed. 2020;195 doi: 10.1016/j.cmpb.2020.105637. [DOI] [PubMed] [Google Scholar]
48.Karimi D., Nir G., Fazli L., Black P.C., Goldenberg L., Salcudean S.E. Deep learning-based gleason grading of prostate cancer from histopathology images—role of multiscale decision aggregation and data augmentation. IEEE J Biomed Health Inform. 2020;24(5):1413–1426. doi: 10.1109/JBHI.2019.2944643. [DOI] [PubMed] [Google Scholar]
49.Koziarski M., Cyganek B., Olborski B., et al. 2021. DiagSet: a dataset for prostate cancer histopathological image classification. Published online May 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Duran-Lopez L., Dominguez-Morales J.P., Rios-Navarro A., et al. Performance evaluation of deep learning-based prostate cancer screening methods in histopathological images: measuring the impact of the model’s complexity on its processing speed. Sensors. 2021;21(4):1122. doi: 10.3390/s21041122. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Duran-Lopez L., Dominguez-Morales J.P., Conde-Martin A.F., Vicente-Diaz S., Linares-Barranco A. PROMETEO: a CNN-based computer-aided diagnosis system for WSI prostate cancer detection. IEEE Access. 2020;8:128613–128628. doi: 10.1109/ACCESS.2020.3008868. [DOI] [Google Scholar]
52.Bulten W., Kartasalo K., Chen P.H.C., et al. Artificial intelligence for diagnosis and Gleason grading of prostate cancer: the PANDA challenge. Nat Med. 2022;28(1):154–163. doi: 10.1038/s41591-021-01620-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Litjens G., Bandi P., Ehteshami Bejnordi B., et al. 1399 H&E-stained sentinel lymph node sections of breast cancer patients: the CAMELYON dataset. GigaScience. 2018;7(6):giy065. doi: 10.1093/gigascience/giy065. [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Marchesin S., Giachelle F., Marini N., et al. Empowering digital pathology applications through explainable knowledge extraction tools. J Pathol Inform. 2022;13 doi: 10.1016/j.jpi.2022.100139. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Marini N., Otálora S., Podareanu D., et al. Multi_scale_tools: a python library to exploit multi-scale whole slide images. Front Comput Sci. 2021;0:68. doi: 10.3389/FCOMP.2021.684521. [DOI] [Google Scholar]
56.Marini N., Otálora S., Müller H., Atzori M. Semi-supervised training of deep convolutional neural networks with heterogeneous data and few local annotations: an experiment on prostate histopathology image classification. Med Image Anal. 2021;73 doi: 10.1016/J.MEDIA.2021.102165. [DOI] [PubMed] [Google Scholar]
57.Janowczyk A., Zuo R., Gilmore H., Feldman M., Madabhushi A. HistoQC: an open-source quality control tool for digital pathology slides. JCO Clin Cancer Inform. 2019;3:1–7. doi: 10.1200/CCI.18.00157. [DOI] [PMC free article] [PubMed] [Google Scholar]
58.McHugh M.L. Interrater reliability: the kappa statistic. Biochem Med. 2012;22:276–282. [PMC free article] [PubMed] [Google Scholar]
59.Wilcoxon F. Individual comparisons by ranking methods. Biomet Bull. 1945;1(6):80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]
60.Deng J., Dong W., Socher R., Li L.J., Li K., Fei-Fei L. 2009 IEEE Conference on Computer Vision and Pattern Recognition. 2009. ImageNet: a large-scale hierarchical image database; pp. 248–255. [DOI] [Google Scholar]
61.Mormont R., Geurts P., Marée R. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) 2018. Comparison of deep transfer learning strategies for digital pathology; pp. 2343–234309. [DOI] [Google Scholar]
62.Ten C.D. quick tips for machine learning in computational biology. BioData Mining. 2017;10(1):35. doi: 10.1186/s13040-017-0155-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Buslaev A., Parinov A., Khvedchenya E., Iglovikov V.I., Kalinin A.A. 2018. Albumentations: fast and flexible image augmentations. ArXiv e-prints. Published online. [Google Scholar]
64.Oliveira S.P., Neto P.C., Fraga J., et al. CAD systems for colorectal cancer from WSI are still not ready for clinical acceptance. Sci Rep. 2021;11:14358. doi: 10.1038/s41598-021-93746-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0005] 1.Morales S., Engan K., Naranjo V. Artificial intelligence in computational pathology – challenges and future directions. Digital Signal Process. 2021;119 doi: 10.1016/j.dsp.2021.103196. [DOI] [Google Scholar]

[bb0010] 2.Marini N., Atzori M., Otálora S., Marchand-Maillet S., Müller H. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops. 2021. H&E-adversarial network: a convolutional neural network to learn stain-invariant features through hematoxylin & eosin regression; pp. 601–610. [Google Scholar]

[bb0015] 3.Tellez D, Litjens G, Bándi P, et al. Quantifying the Effects of Data Augmentation and Stain Color Normalization in Convolutional Neural Networks for Computational Pathology. [DOI] [PubMed]

[bb0020] 4.Khan A., Janowczyk A., Müller F., et al. Impact of scanner variability on lymph node segmentation in computational pathology. J Pathol Inform. 2022:100127. doi: 10.1016/j.jpi.2022.100127. Published online July 25. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0025] 5.Litjens G., Ciompi F., van der Laak J. A decade of GigaScience: the challenges of gigapixel pathology images. GigaScience. 2022;11:giac056. doi: 10.1093/gigascience/giac056. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0030] 6.Ren J., Hacihaliloglu I., Singer E.A., Foran D.J., Qi X. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2018. Adversarial domain adaptation for classification of prostate histopathology whole-slide images; pp. 201–209. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0035] 7.Lafarge M.W., Pluim J.P.W., Eppenhof K.A.J., Veta M. Learning domain-invariant representations of histological images. Front Med. 2019:6. doi: 10.3389/fmed.2019.00162. Accessed August 25, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0040] 8.Clarke E.L., Treanor D. Colour in digital pathology: a review. Histopathology. 2017;70(2):153–163. doi: 10.1111/his.13079. [DOI] [PubMed] [Google Scholar]

[bb0045] 9.Pantanowitz L., Valenstein P.N., Evans A.J., et al. Review of the current state of whole slide imaging in pathology. J Pathol Inform. 2011;2(1):36. doi: 10.4103/2153-3539.83746. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0050] 10.Gurcan M.N., Boucheron L.E., Can A., Madabhushi A., Rajpoot N.M., Yener B. Histopathological image analysis: a review. IEEE Rev Biomed Eng. 2009 doi: 10.1109/RBME.2009.2034865. Published online. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0055] 11.van der Laak J., Litjens G., Ciompi F. Deep learning in histopathology: the path to the clinic. Nat Med. 2021;27(5):775–784. doi: 10.1038/s41591-021-01343-4. [DOI] [PubMed] [Google Scholar]

[bb0060] 12.Otálora S., Atzori M., Andrearczyk V., Khan A., Müller H. Staining invariant features for improving generalization of deep convolutional neural networks in computational pathology. Front Bioeng Biotechnol. 2019;7(AUG):198. doi: 10.3389/FBIOE.2019.00198/BIBTEX. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0065] 13.Hou L., Agarwal A., Samaras D., Kurc T.M., Gupta R.R., Saltz J.H. 2019. Robust Histopathology Image Analysis: To Label or To Synthesize? pp. 8533–8542.https://openaccess.thecvf.com/content_CVPR_2019/html/Hou_Robust_Histopathology_Image_Analysis_To_Label_or_to_Synthesize_CVPR_2019_paper.html Accessed August 25, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0070] 14.Khan A., Atzori M., Otálora S., Andrearczyk V., Müller H. Medical Imaging 2020: Digital Pathology. Vol 11320. SPIE; 2020. Generalizing convolution neural networks on stain color heterogeneous data for computational pathology; pp. 173–186. [DOI] [Google Scholar]

[bb0075] 15.Cong C., Liu S., Di Ieva A., Pagnucco M., Berkovsky S., Song Y. Colour adaptive generative networks for stain normalisation of histopathology images. Med Image Anal. 2022:102580. doi: 10.1016/j.media.2022.102580. Published online August 27. [DOI] [PubMed] [Google Scholar]

[bb0080] 16.Ciompi F., Geessink O., Bejnordi B.E., et al. 2017. The importance of stain normalization in colorectal tissue classification with convolutional networks. Published online May 23. [DOI] [Google Scholar]

[bb0085] 17.Inoue T., Yagi Y. Color standardization and optimization in whole slide imaging. Clin Diagn Pathol. 2020;4(1) doi: 10.15761/cdp.1000139. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0090] 18.Howat W.J., Wilson B.A. Tissue fixation and the effect of molecular fixatives on downstream staining procedures. Methods. 2014;70(1):12–19. doi: 10.1016/j.ymeth.2014.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0095] 19.Alturkistani H.A., Tashkandi F.M., Mohammedsaleh Z.M. Histological stains: a literature review and case study. Glob J Health Sci. 2015;8(3):72–79. doi: 10.5539/gjhs.v8n3p72. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0100] 20.Chan J.K.C. The wonderful colors of the hematoxylin–eosin stain in diagnostic surgical pathology. Int J Surg Pathol. 2014;22(1):12–32. doi: 10.1177/1066896913517939. [DOI] [PubMed] [Google Scholar]

[bb0105] 21.Fischer A.H., Jacobson K.A., Rose J., Zeller R. Hematoxylin and eosin staining of tissueand cell sections. Cold Spring Harbor Protocols. 2008;3(5) doi: 10.1101/pdb.prot4986. [DOI] [Google Scholar]

[bb0110] 22.Macenko M., Niethammer M., Marron J.S., et al. Proceedings - 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, ISBI 2009. 2009. A method for normalizing histology slides for quantitative analysis. [DOI] [Google Scholar]

[bb0115] 23.Feldman A.T., Wolfe D. In: Histopathology: Methods and Protocols. Methods in Molecular Biology. Day C.E., editor. Springer; 2014. Tissue processing and hematoxylin and eosin staining; pp. 31–43. [DOI] [PubMed] [Google Scholar]

[bb0120] 24.Bancroft J.D., Layton C. In: Bancroft’s Theory and Practice of Histological Techniques. 7th ed. Suvarna S.K., Layton C., Bancroft J.D., editors. Churchill Livingstone; 2013. 10 - The hematoxylins and eosin; pp. 173–186. [DOI] [Google Scholar]

[bb0125] 25.Hanna M.G., Reuter V.E., Ardon O., et al. Validation of a digital pathology system including remote review during the COVID-19 pandemic. Mod Patholgy. 2020;33(11):2115–2127. doi: 10.1038/s41379-020-0601-5. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0130] 26.Cheng W.C., Saleheen F., Badano A. Assessing color performance of whole-slide imaging scanners for digital pathology. Color Res Appl. 2019;44(3):322–334. doi: 10.1002/col.22365. [DOI] [Google Scholar]

[bb0135] 27.Vahadane A., Peng T., Sethi A., et al. Structure-preserving color normalization and sparse stain separation for histological images. IEEE Trans Med Imaging. 2016;35(8):1962–1971. doi: 10.1109/TMI.2016.2529665. [DOI] [PubMed] [Google Scholar]

[bb0140] 28.Stacke K., Eilertsen G., Unger J., Lundstrom C. Measuring domain shift for deep learning in histopathology. IEEE J Biomed Health Inform. 2021;25(2):325–336. doi: 10.1109/JBHI.2020.3032060. [DOI] [PubMed] [Google Scholar]

[bb0145] 29.Otálora S., Marini N., Podareanu D., et al. Stainlib: a python library for augmentation and normalization of histopathology H&E images. Bioinformatics. 2022 doi: 10.1101/2022.05.17.492245. [DOI] [Google Scholar]

[bb0150] 30.Campanella G., Hanna M.G., Geneslaw L., et al. Clinical-grade computational pathology using weakly supervised deep learning on whole slide images. Nat Med. 2019;25(8):1301–1309. doi: 10.1038/s41591-019-0508-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0155] 31.Janowczyk A., Madabhushi A. Deep learning for digital pathology image analysis: a comprehensive tutorial with selected use cases. J Pathol Inform. 2016;7(1):29. doi: 10.4103/2153-3539.186902. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0160] 32.Kang H., Luo D., Feng W., et al. StainNet: a fast and robust stain normalization network. Front Med. 2021:8. doi: 10.3389/fmed.2021.746307. Accessed August 26, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0165] 33.Shaban M.T., Baur C., Navab N., Albarqouni S. StainGAN: Stain Style Transfer for Digital Histological Images. 2018. http://arxiv.org/abs/1804.01601 Published online April 4. Accessed August 26, 2022.

[bb0170] 34.Reinhard E., Adhikhmin M., Gooch B., Shirley P. Color transfer between images. IEEE Comput Graphics Appl. 2001;21(5):34–41. doi: 10.1109/38.946629. [DOI] [Google Scholar]

[bb0175] 35.Faryna K., van der Laak J., Litjens G. Tailoring automated data augmentation to H&E-stained histopathology. 2022. https://openreview.net/forum?id=JrBfXaoxbA2 Accessed September 5, 2022. [DOI] [PubMed]

[bb0180] 36.Rahib L., Wehner M.R., Matrisian L.M., Nead K.T. Estimated projection of US cancer incidence and death to 2040. JAMA Netw Open. 2021;4(4) doi: 10.1001/jamanetworkopen.2021.4708. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0185] 37.Rawla P. Epidemiology of prostate cancer. World J Oncol. 2019;10(2):63–89. doi: 10.14740/wjon1191. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0190] 38.Benson A.B., Venook A.P., Al-Hawary M.M., et al. NCCN guidelines insights: colon cancer, version 2.2018. J Natl Compr Canc Netw. 2018;16(4):359–369. doi: 10.6004/jnccn.2018.0021. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0195] 39.Current Perspectives on the Gleason Grading of Prostate Cancer | Archives of Pathology & Laboratory Medicine. 2022. https://meridian.allenpress.com/aplm/article/133/11/1810/460670/Current-Perspectives-on-the-Gleason-Grading-of Accessed August 26. [DOI] [PubMed]

[bb0200] 40.Marini N., Marchesin S., Otálora S., et al. Unleashing the potential of digital pathology data by training computer-aided diagnosis models without human annotations. npj Digit Med. 2022;5(1):1–18. doi: 10.1038/s41746-022-00635-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0205] 41.Stadler C.B., Lindvall M., Lundström C., et al. Proactive construction of an annotated imaging database for artificial intelligence training. J Digit Imag. 2020;34(1):105–115. doi: 10.1007/S10278-020-00384-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0210] 42.Sirinukunwattana K., Snead D.R.J., Rajpoot N.M. A stochastic polygons model for glandular structures in colon histology images. IEEE Trans Med Imag. 2015;34(11):2366–2378. doi: 10.1109/TMI.2015.2433900. [DOI] [PubMed] [Google Scholar]

[bb0215] 43.Awan R., Sirinukunwattana K., Epstein D., et al. Glandular morphometrics for objective grading of colorectal adenocarcinoma histology images. Scient Rep. 2017;7(1):2220–2243. doi: 10.1038/s41598-017-16516-w. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0220] 44.Barbano C.A., Perlo D., Tartaglione E., et al. 2021. UniToPatho, a labeled histopathological dataset for colorectal polyps classification and adenoma dysplasia grading; pp. 76–80. Published online January. [DOI] [Google Scholar]

[bb0225] 45.Xu G., Song Z., Sun Z., et al. 2019. CAMEL: A Weakly Supervised Learning Framework for Histopathology Image Segmentation. Published online August 28. [DOI] [Google Scholar]

[bb0230] 46.Arvaniti E., Fricker K.S., Moret M., et al. Automated Gleason grading of prostate cancer tissue microarrays via deep learning. Scient Rep. 2018;8(1):12054. doi: 10.1038/s41598-018-30535-1. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0235] 47.Silva-Rodríguez J., Colomer A., Sales M.A., Molina R., Naranjo V. Going deeper through the Gleason scoring scale: an automatic end-to-end system for histology prostate grading and cribriform pattern detection. Comput Methods Prog Biomed. 2020;195 doi: 10.1016/j.cmpb.2020.105637. [DOI] [PubMed] [Google Scholar]

[bb0240] 48.Karimi D., Nir G., Fazli L., Black P.C., Goldenberg L., Salcudean S.E. Deep learning-based gleason grading of prostate cancer from histopathology images—role of multiscale decision aggregation and data augmentation. IEEE J Biomed Health Inform. 2020;24(5):1413–1426. doi: 10.1109/JBHI.2019.2944643. [DOI] [PubMed] [Google Scholar]

[bb0245] 49.Koziarski M., Cyganek B., Olborski B., et al. 2021. DiagSet: a dataset for prostate cancer histopathological image classification. Published online May 9. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0250] 50.Duran-Lopez L., Dominguez-Morales J.P., Rios-Navarro A., et al. Performance evaluation of deep learning-based prostate cancer screening methods in histopathological images: measuring the impact of the model’s complexity on its processing speed. Sensors. 2021;21(4):1122. doi: 10.3390/s21041122. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0255] 51.Duran-Lopez L., Dominguez-Morales J.P., Conde-Martin A.F., Vicente-Diaz S., Linares-Barranco A. PROMETEO: a CNN-based computer-aided diagnosis system for WSI prostate cancer detection. IEEE Access. 2020;8:128613–128628. doi: 10.1109/ACCESS.2020.3008868. [DOI] [Google Scholar]

[bb0260] 52.Bulten W., Kartasalo K., Chen P.H.C., et al. Artificial intelligence for diagnosis and Gleason grading of prostate cancer: the PANDA challenge. Nat Med. 2022;28(1):154–163. doi: 10.1038/s41591-021-01620-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0265] 53.Litjens G., Bandi P., Ehteshami Bejnordi B., et al. 1399 H&E-stained sentinel lymph node sections of breast cancer patients: the CAMELYON dataset. GigaScience. 2018;7(6):giy065. doi: 10.1093/gigascience/giy065. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0270] 54.Marchesin S., Giachelle F., Marini N., et al. Empowering digital pathology applications through explainable knowledge extraction tools. J Pathol Inform. 2022;13 doi: 10.1016/j.jpi.2022.100139. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0275] 55.Marini N., Otálora S., Podareanu D., et al. Multi_scale_tools: a python library to exploit multi-scale whole slide images. Front Comput Sci. 2021;0:68. doi: 10.3389/FCOMP.2021.684521. [DOI] [Google Scholar]

[bb0280] 56.Marini N., Otálora S., Müller H., Atzori M. Semi-supervised training of deep convolutional neural networks with heterogeneous data and few local annotations: an experiment on prostate histopathology image classification. Med Image Anal. 2021;73 doi: 10.1016/J.MEDIA.2021.102165. [DOI] [PubMed] [Google Scholar]

[bb0285] 57.Janowczyk A., Zuo R., Gilmore H., Feldman M., Madabhushi A. HistoQC: an open-source quality control tool for digital pathology slides. JCO Clin Cancer Inform. 2019;3:1–7. doi: 10.1200/CCI.18.00157. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0290] 58.McHugh M.L. Interrater reliability: the kappa statistic. Biochem Med. 2012;22:276–282. [PMC free article] [PubMed] [Google Scholar]

[bb0295] 59.Wilcoxon F. Individual comparisons by ranking methods. Biomet Bull. 1945;1(6):80–83. doi: 10.2307/3001968. [DOI] [Google Scholar]

[bb0300] 60.Deng J., Dong W., Socher R., Li L.J., Li K., Fei-Fei L. 2009 IEEE Conference on Computer Vision and Pattern Recognition. 2009. ImageNet: a large-scale hierarchical image database; pp. 248–255. [DOI] [Google Scholar]

[bb0305] 61.Mormont R., Geurts P., Marée R. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW) 2018. Comparison of deep transfer learning strategies for digital pathology; pp. 2343–234309. [DOI] [Google Scholar]

[bb0310] 62.Ten C.D. quick tips for machine learning in computational biology. BioData Mining. 2017;10(1):35. doi: 10.1186/s13040-017-0155-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bb0315] 63.Buslaev A., Parinov A., Khvedchenya E., Iglovikov V.I., Kalinin A.A. 2018. Albumentations: fast and flexible image augmentations. ArXiv e-prints. Published online. [Google Scholar]

[bib316] 64.Oliveira S.P., Neto P.C., Fraga J., et al. CAD systems for colorectal cancer from WSI are still not ready for clinical acceptance. Sci Rep. 2021;11:14358. doi: 10.1038/s41598-021-93746-z. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Data-driven color augmentation for H&E stained images in computational pathology

Niccolò Marini

Sebastian Otalora

Marek Wodzinski

Selene Tomassini

Aldo Franco Dragoni

Stephane Marchand-Maillet

Juan Pedro Dominguez Morales

Lourdes Duran-Lopez

Simona Vatrano

Henning Müller

Manfredo Atzori

Abstract

Introduction

Fig. 1.

Fig. 2.

Methods and materials

Data-driven color augmentation method

Fig. 3.

Data

Table 1.

Table 2.

Table 3.

Fig. 4.

Data pre-processing

Baselines

Training strategy & parameters

Results

Table 4.

Table 5.

Table 6.

Table 7.

Discussion

Conclusion

Declaration of Interests

Acknowledgments

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases