Acoustic Micro-Tapping Optical Coherence Elastography to Quantify Corneal Collagen Cross-Linking

Abstract

Purpose

To evaluate changes in the anisotropic elastic properties of ex vivo human cornea treated with ultraviolet cross-linking (CXL) using noncontact acoustic micro-tapping optical coherence elastography (AμT-OCE).

Design

Acoustic micro-tapping OCE was performed on normal and CXL human donor cornea in an ex vivo laboratory study.

Subjects

Normal human donor cornea (n = 22) divided into 4 subgroups. All samples were stored in optisol.

Methods

Elastic properties (in-plane Young’s, E, and out-of-plane, G, shear modulus) of normal and ultraviolet CXL–treated human corneas were quantified using noncontact AμT-OCE. A nearly incompressible transverse isotropic model was used to reconstruct moduli from AμT-OCE data. Independently, cornea elastic moduli were also measured with destructive mechanical tests (tensile extensometry and shear rheometry).

Main Outcome Measures

Corneal elastic moduli (in-plane Young’s modulus, E, in-plane, μ, and out-of-plane, G, shear moduli) can be evaluated in both normal and CXL treated tissues, as well as monitored during the CXL procedure using noncontact AμT-OCE.

Results

Cross-linking induced a significant increase in both in-plane and out-of-plane elastic moduli in human cornea. The statistical mean in the paired study (presurgery and postsurgery, n = 7) of the in-plane Young’s modulus, $E=3\mu$, increased from 19 MPa to 43 MPa, while the out-of-plane shear modulus, G, increased from 188 kPa to 673 kPa. Mechanical tests in a separate subgroup support CXL-induced cornea moduli changes and generally agree with noncontact AμT-OCE measurements.

Conclusions

The human cornea is a highly anisotropic material where in-plane mechanical properties are very different from those out-of-plane. Noncontact AμT-OCE can measure changes in the anisotropic elastic properties in human cornea as a result of ultraviolet CXL.

The unique structure and organization of the collagen matrix within the cornea helps preserve shape and maintain transparency. Most corneal collagen is type I, containing fibrils within the stroma that run the entire plane and connect with fibrils in the limbus or sclera.¹ Collagen fibrils are more tightly packed in the anterior portion compared to the posterior but are generally arranged within the stroma in 200–300 stacked sheets (1–2 μm thick) referred to as lamellae.² The fibrils lie within a protein rich, hydrated proteoglycan mesh.^3,4 It is well established that the complex micronetwork of collagen bundles contributes to macroscale deformation and stability linked to functional vision. In pathologies affecting the cornea, microstructural changes in the collagen fibers and proteoglycan-rich fluid of the stroma alter the cornea’s macroscale biomechanical response to intraocular pressure⁵ (IOP) and can result in corneal shape changes and degraded visual acuity.6, 7, 8

In degenerative corneal diseases such as keratoconus, local changes in mechanical properties result in a bulging conical shape associated with vision loss.^7,9 Keratoconus is commonly treated with collagen cross-linking (CXL), a procedure reported to delay ectasia progression by increasing stiffness via ultraviolet (UV) light–induced cross-links in stromal collagen soaked in riboflavin (RF). While CXL can halt disease progression by greatly reducing the number of required keratoplasties,¹⁰ the specific relationships between enhanced CXL and mechanical stabilization in UV-CXL remain speculative,¹¹ and both long-term and immediate outcomes remain unpredictable for individual patients.

Due to these uncertainties, a personalized biomechanical model predicting postsurgical corneal shape and function is needed to improve CXL outcomes. Personalized biomechanical models of the cornea can be generated if (i) cornea shape and thickness are mapped and (ii) corneal elastic moduli are known.

There are numerous clinical tools available to assess corneal shape, yet there are currently none that can accurately measure low-strain corneal elastic moduli presurgery, intrasurgery, and postsurgery in a nondestructive, noninvasive manner. While technologies based on tonometry (e.g., Ocular Response Analyzer, Dynamic Scheimpflug Analyzer) have shown some success in correlating biomechanical estimates with disease progression,^12,13 these methods rely on a number of novel metrics that indirectly assess elastic moduli responsible for corneal deformation.14, 15, 16, 17, 18 Specifically, both use a relatively high-pressure, widely distributed air-puff to deform the cornea and measure its response. While an ocular response analyzer has been used in multiple CXL studies in vivo, the one-dimensional nature of the system has resulted in poor sensitivity in detecting differences between CXL and control groups, where several studies described stabilized disease progression but found no change in the novel biomechanics-related metrics of corneal hysteresis or corneal resistance factor.^19,20 Additionally, tonometry-based techniques often require a non-trivial IOP correction in finite element simulations^14,21 and use a simplified isotropic mechanical model, leading to high variability depending on experimental conditions.

Recently, optical coherence elastography (OCE) has measured corneal stiffness at various length scales while simultaneously mapping shape in a single non-invasive measurement.²² Contact-based OCE techniques have demonstrated potential to detect biomechanical differences between keratoconic and healthy corneas in vivo.²³ However, direct contact with the cornea is not ideal for clinical translation and cannot be performed during the CXL procedure.

Advances in both the sensitivity and imaging rate of phase-sensitive OCT have led to noncontact imaging systems that track propagating elastic waves launched by noncontact low-amplitude (less than a micrometer displacement) excitation.^24,25 Assuming an appropriate corneal mechanical model, dynamic OCE can measure in near real-time both the shape and biomechanical changes resulting from keratoconus and CXL surgery, with the potential for elastic moduli mapping at high spatial resolution.26, 27, 28, 29

Until recently, the existing body of literature did not present a clear picture on the appropriate elastic model for human cornea. Common models assumed an incompressible, isotropic, and linear elastic material to describe corneal deformation, where a single parameter, the Young’s modulus ($E$, or equivalently the shear modulus $\mu =E/3$), defined elasticity. However, the in-plane collagen arrangement in the cornea leads to an anisotropic biomechanical response,³⁰ that is, corneal in-plane elastic properties are different from those out-of-plane, which suggests that the cornea more closely resembles a transverse isotropic material. As a result, up to 3 orders of magnitude differences have been reported from mechanical tests between the in-plane Young’s modulus and the out-of-plane shear modulus, depending on the method used.30, 31, 32, 33 Consequently, corneal elastic moduli obtained with isotropic models are highly inconsistent, greatly depend on the measurement technique and cannot be used to predict corneal deformation.^32,34, 35, 36, 37, 38, 39, 40, 41, 42 Because the anisotropic cornea cannot be characterized with a single elastic modulus, more appropriate models are required.

Recently, a model of a nearly incompressible transversely isotropic (NITI) medium was proposed based on corneal tissue microstructure.³⁰ It has been used to measure elastic anisotropy (i.e., in-plane, $\mu$, and out-of-plane, G, shear moduli) in porcine cornea using noncontact acoustic micro-tapping OCE (AμT-OCE). Notably, AμT-OCE is the only reported method that can quantify both $\mu$ (and therefore $E=3\mu$) and $G$ simultaneously in a noninvasive, noncontact manner.⁴³ This is critical for in vivo studies of human corneal physiology and pathophysiology.

In this study, the NITI model was used to compute anisotropic mechanical moduli ($E$ and $G$) from elastic wave fields generated and detected using AμT-OCE in both ex vivo untreated human donor corneas and in samples subject to RF/UV collagen CXL at physiologically relevant controlled pressures. Mechanical moduli were then directly measured in a subgroup of the same samples using destructive mechanical methods that loaded tissue in tension (in the plane of stromal fibers in tensile extensometry) and in shear (between the lamellar sheets in shear rheometry) to independently quantify $E$ and $G$. We show that the human cornea is highly anisotropic, and thus, current isotropic models cannot predict corneal deformation under load.

Corneal mechanical anisotropy was also probed using AμT-OCE on a set of samples before undergoing CXL and immediately after the procedure, as well as on a set of samples scanned during CXL, to both demonstrate potential in-line monitoring of corneal stiffness intraoperatively and understand the range of cornea moduli changes induced by CXL. The noncontact nature of AμT-OCE makes it promising to study corneal disease progression through objective measurements of corneal moduli. Indeed, it can play a critical role in optimizing CXL treatment of progressive keratoconus.

Methods

Cornea Preparation

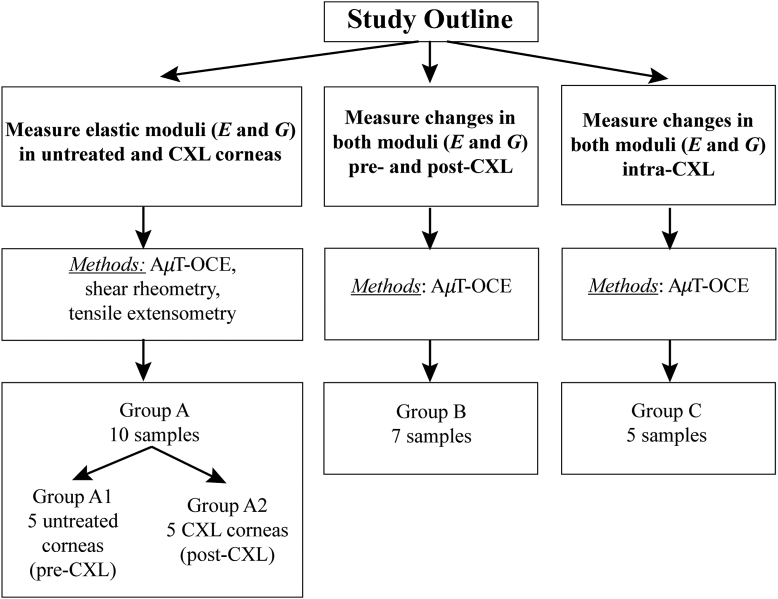
A total of 22 human corneal-scleral rings stored in Optisol (Chiron Ophthalmics) were secured through both the University of Utah Lion’s Eye Bank and CorneaGen. Exclusion parameters included tissue over 2 months from enucleation, progressive corneal disease, and visual corneal damage. Such broad exclusion criteria were necessary to obtain research samples and resulted in a wide range of both ages and times between enucleation and analysis. Corneas were placed into 3 groups (groups A, B, and C) for different experiments based on their availability (Fig. 1). The study adhered to the tenants in the Declaration of Helsinki and institutional review board/ethics committee approval was obtained.

Figure 1.

Schematic of the 3 different experiments performed and the corresponding number of samples in each group. AμT = acoustic micro-tapping; CXL = cross–linking; OCE = optical coherence elastography.

In group A, 10 samples were subject to both noncontact AμT-OCE and destructive mechanical testing (shear rheometry and tensile extensometry) to determine mechanical moduli in both normal and CXL corneas. The results were obtained using different methods to justify the use of the NITI model (described later) in human cornea. All samples were removed from solution upon acquisition and fitted to an artificial anterior chamber (Barron, CorzaMedical) connected via the inlet port to a bath filled with balanced saline solution (BSS). The outlet port was closed to induce hydrostatic pressure along the anterior corneal surface. The bath could be raised and lowered relative to the cornea surface (according to a height previously calibrated using a digital hydrostatic pressure sensor) to control the IOP over a range of 5 mmHg–20 mmHg, depending on the group under study. Each sample was inflated to a desired pressure for 5 minutes, over which a single drop of BSS was applied to prevent corneal dehydration. Corneal hydration was previously validated using this method, where a 50-μL dropper was used to apply BSS to the cornea every 5 minutes, and the thickness remained unchanged.

Corneas in group A were selected as untreated (group A1, n = 5) and cross-linked (group A2, n = 5) based on their availability. The average age of the untreated group (A1) was 53 $\pm$ 5 years and the samples were tested on average 31 $\pm$ 18 days from preservation. In the CXL group (A2), the average age was 29 $\pm$ 10 years and the samples were tested on average 15 $\pm$ 5 days from preservation.

In group A1, each cornea was scanned with AμT-OCE at physiologically relevant pressures (5, 10, 15, and 20 mmHg). Immediately following AμT-OCE scanning, each sample was transported in a BSS-damped cloth for parallel-plate rheometry at room temperature before being sectioned into strips approximately 6 mm wide and transported for tensile testing.

In group A2, all samples were inflated to 15 mmHg and then subjected to a CXL procedure following the Dresden protocol prior to being scanned with AμT-OCE at pressures from 5 mmHg to 20 mmHg. Following CXL, corneas were transported for mechanical testing. Groups A1 and A2 independently demonstrated corneal anisotropy in both untreated cornea and those that underwent CXL.

In group B, n = 7 cornea were inflated to 15 mmHg and mechanical moduli were measured on the same sample using noncontact AμT-OCE before and after CXL. The average age was 51 $\pm$ 17 years, and samples were scanned on average 30 $\pm$ 5 days from preservation. Group B provided a paired analysis of biomechanical changes on the same samples resulting from the CXL procedure.

In group C, n = 5 cornea were inflated to 15 mmHg and mechanical moduli were measured using AμT-OCE preoperatively, intraoperatively, and following CXL. The average age was 62 $\pm$ 8 years and samples were scanned on average 31 $\pm$ 15 days from preservation. Group C helped determine how quickly biomechanical changes occurred in each cornea during CXL.

Collagen CXL Procedure

The CXL procedure followed the widely adopted Dresden protocol.^44,45 A 0.1% RF solution in 20% dextran was first prepared using 500 000 weight dextran (Alfa Aesar) in isotonic saline. Before applying this solution, the epithelium was debrided using a blunt knife. Next, a 50-μL drop of RF solution was placed on the cornea every 2 minutes over a total duration of 30 minutes. After RF loading, each cornea was exposed to 3 mW/cm² of 370 nm UV light for 30 minutes. Riboflavin solution was reapplied every 5 minutes during the 30-minute irradiation period.

For the samples in group A2 (CXL group), a baseline AμT-OCE scan was taken prior to and post epithelial debridement. The preepithelial and postepithelial debridement measurements showed no statistical difference. As such, the postepithelial debridement scan was used as the “pre-CXL” data set. For samples in group B, (pre-CXL and post-CXL), the pre-CXL scan was taken immediately following epithelium removal and prior to applying RF/dextran. All corneas were then scanned following 30 minutes of RF/dextran solution exposure and 30-minute UV light exposure.

Cornea samples in group C were used to explore the rate of changes in cornea mechanical moduli during UV irradiation. In this experiment, a baseline scan was taken prior to and following epithelial debridement. As with group A, preepithelial and postepithelial debridement measurements showed no statistical difference, and the postepithelial debridement scan was considered the initial untreated data set. Then, a 50-μL drop of 0.1% RF in 20% dextran solution was placed on each cornea every 2 minutes for 30 minutes. Excess solution was removed, and a post-RF scan was taken. The cornea was then exposed to 3 mW/cm² of 370 nm UV light for 30 minutes, and drops were continued every 5 minutes during irradiation. Excess solution was removed from the tissue surface and the cornea was scanned every 90 seconds during the 30-minute UV exposure. Following UV exposure, 5 post-CXL scans were performed.

NITI Model of Corneal Elasticity

To account for cornea collagen microstructure consisting of thin layers (lamellas) primarily oriented in-plane of the stroma, the macroscopic stress-strain relationship in the cornea for small deformations is described by Hook’s law in a NITI material, taking the form (in Voigt notation)⁴³:

$$\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\sigma }_{zz}\\ {\tau }_{yz}\\ {\tau }_{xz}\\ {\tau }_{xy}\end{array}\right]=\left[\begin{array}{cccccc}\lambda +2\mu & \lambda & \lambda & & & \\ \lambda & \lambda +2\mu & \lambda & & & \\ \lambda & \lambda & \lambda +\delta & & & \\ & & & G& & \\ & & & & G& \\ & & & & & \mu \end{array}\right]\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\gamma }_{yz}\\ {\gamma }_{xz}\\ {\gamma }_{xy}\end{array}\right]$$ (1)

where ${\sigma }_{ij}$ denotes engineering stress, ${\epsilon }_{ij}$ denotes engineering strain, ${\tau }_{ij}$ denotes shear stresses, ${\gamma }_{ij}$ = 2 ${\epsilon }_{ij}$ denotes shear strains, and the subscripts $x$, $y$, and $z$ refer to standard Cartesian axes. Thus, there are 4 independent elastic constants, $\lambda$, $\delta$, $G$, and $\mu$, defining the cornea’s elasticity matrix. Because the cornea is nearly incompressible, the longitudinal modulus, $\lambda$, does not influence deformation. $G$ and $\mu$ represent out-of-plane and in-plane shear moduli, respectively, whose magnitudes were shown to differ in corneal tissue. Indeed, several studies (including OCE,^30,43 and mechanical testing^31,32,46) have reported the out-of-plane shear modulus, $G$, to be on the order of tens of kPa, whereas the in-plane shear modulus, $\mu$, to be on the order of MPa.^40,43

The in-plane Young’s modulus

$$E_T=3\mu +\frac{\mu \delta }{4\mu +\delta }$$ (2)

is defined by $\mu$ and delta (associated to the tensile anisotropy), but does not depend on $G$. In the studies by Kirby et al,^43,47 we showed that

$$-2\mu <\delta <0$$ (3)

to obey cornea symmetry but highlight that $\delta$ cannot be extracted from guided wave propagation. Fortunately, constraints on $\delta$ limit the range of the in-plane Young’s modulus to

$$2\mu <E_T<3\mu \text{.}$$ (4)

Here, we assume that

$$E=E_T\cong 3\mu \text{,}$$ (5)

producing slight overestimates of actual values. Note that due to strong corneal anisotropy, $\delta$ likely varies little between corneas in a population. The exact relationship between $\mu$ and $E$ can be clarified with tensile testing and is the focus of future studies. Even with this approximation (Eq. (5)), the elastic moduli $E$ and $G$ can fully characterize small corneal deformations.

AμT OCE

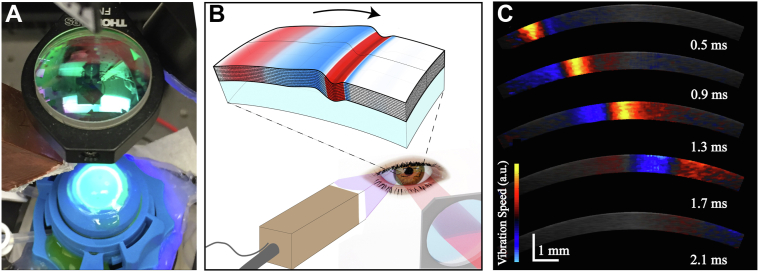
Elastic moduli of human cornea were quantified using wave fields of guided mechanical waves generated and measured with a phase-sensitive spectral-domain OCT system combined with an air-coupled AμT ultrasound transducer. The OCT system used polarization-maintaining optical fibers and components, as previously described in detail.⁴³

To generate and track propagating elastic waves, the OCT system operated in M-B mode, in which a sequence of 512 A-scans were repeated at the same location, (referred to as an M-scan). A trigger signal was sent to a function generator at the beginning of each M-scan to direct a 100-μs-long chirped (1 MHz–1.1 MHz) waveform to an air-coupled piezoelectric transducer (AμT source) with a matching layer, providing a temporally localized and spatially focused acoustic “push.”²⁶ The acoustic force created a localized displacement (hundreds of nanometers in amplitude) at the cornea’s surface. The pulse/M-scan sequence was captured at 256 spatial locations across the imaging plane to create a three-dimensional volume (z, x, t). A complete M-B scan consisted of 1024 depth × 256 lateral locations × 512 temporal frames (captured at a functional 46 kHz frame rate) with an effective imaging range of 1.5 mm × 10 mm x 11 ms (axial × lateral × temporal). Each scan took ∼3 seconds to acquire and save. Note that the OCT scanning range of 10 mm in the lateral direction was partially shaded (∼1.5 mm from the first scan location) by the AμT-OCE transducer.

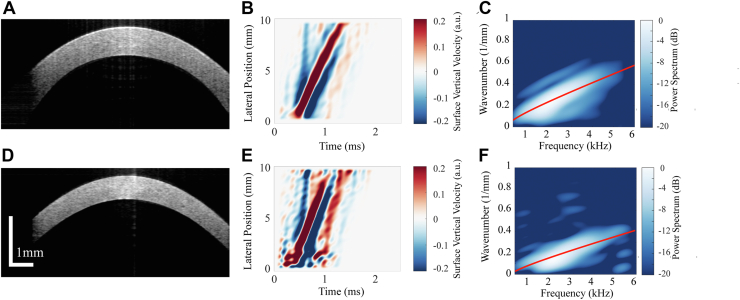
The resulting three-dimensional data set was used to reconstruct central corneal structure pre-CXL and post-CXL, as well as track propagating mechanical waves in the cornea following AμT excitation (Fig. 2). The central corneal thickness pre-CXL and post-CXL was calculated from the OCT structural image after correcting for the cornea’s refractive index (assumed to be 1.38) (Fig. 3A, D). The OCT-measured local particle axial vibration velocity ($v_z\left(x,z,t\right))$ was obtained from the optical phase difference $\Delta {\phi }_{opt}\left(x,z,t\right)$ between 2 consecutive A-line scans at each location.²⁵ Surface vibrations were detected using automatic segmentation of the anterior surface based on an edge detection algorithm. One half of a Gaussian window (HWHM = 90 μm, weight decreasing with depth) was applied as a weighted-average to phase data in the anterior 183 μm of the cornea, resulting in robust sampling of the vertical displacement for propagating guided elastic waves along the air-tissue boundary. Guided wave signals in the cornea recorded at different time moments were combined to form a wave field (Fig. 3B, E).

Figure 2.

(A) Acoustic micro-tapping optical coherence elastography imaging system with cornea inflated via artificial anterior chamber undergoing cross-linking treatment. (B) Schematic of mechanical wave propagation within the cornea. (C) Snapshots of elastic transients detected at different time instants using phase-sensitive OCT.

Figure 3.

Central cornea cross-section and automatic segmentation to determine the surface location and thickness (A) pre-cross-linking (CXL) and (D) post-CXL. Wave fields of propagating guided waves in the same cornea (B) pre-CXL and (E) post-CXL tracked over ∼8.5 mm of corneal tissue. Best-fit solution to the dispersion equation (based on a unique combination of elastic moduli, $E$ and $G$, displayed in red) on top of the measured waveform in the two-dimensional Fourier spectrum for the corresponding cornea (C) pre- and (F) post-CXL.

A temporal super Gaussian filter ($SG$) that followed the maximum vibration velocity of the wave-field $t_m^{wf}\left(x\right)$ at each discrete position $x$, was then applied:

$$SG\left(t\right)=\exp \left[-{\left(\frac{1}{2}{\left(\frac{t-t_m^{wf}\left(x\right)}{{\sigma }_t}\right)}^2\right)}^2\right]\left(6\right)$$

with ${\sigma }_t$ = 0.5 ms. Equation 6 acted as a moving temporal window around the peak of the space-time (x-t) plot to remove any unwanted reverberations around the main elastic wave mode, as can be seen in Figure 3B, E. A two-dimensional Fourier transform was computed to describe wavefields in the frequency-wavenumber (f-k) domain (Fig. 3C, F).

A solution to the equation for guided wave propagation in the NITI material³⁰ was found that most closely matched the experimental f-k spectrum using an iterative routine that converged on a best-fit of the dispersion relation. By varying both the in-plane ($\mu$, assuming tensile isotropy where $\mu =E/3$) and out-of-plane, $G$, shear moduli and using the corneal thickness, h, as a constant, a dispersion relation that closely matched experimental data was determined (see Supplemental Methods 1, 2 for details on the fitting routine). In all samples, the wave energy was mainly contained within the A₀ mode^22,30 and fit to a theoretical solution of the A₀ mode assuming a linear-elastic NITI material.

Due to the nature of the weighted fitting routine, residuals are not generated, making traditional confidence interval methods difficult to apply. As such, asymmetrical error bars corresponding to uncertainties in $E$ and $G$ for each cornea (due to both model and data error) are described in Supplemental Methods 2. All cases that produced a poor fit quality (detailed in Supplemental Methods 3) were omitted.

Destructive Biomechanical Testing

Following AμT-OCE, subgroups A1 and A2 were subject to mechanical testing under tensile and shear loading.

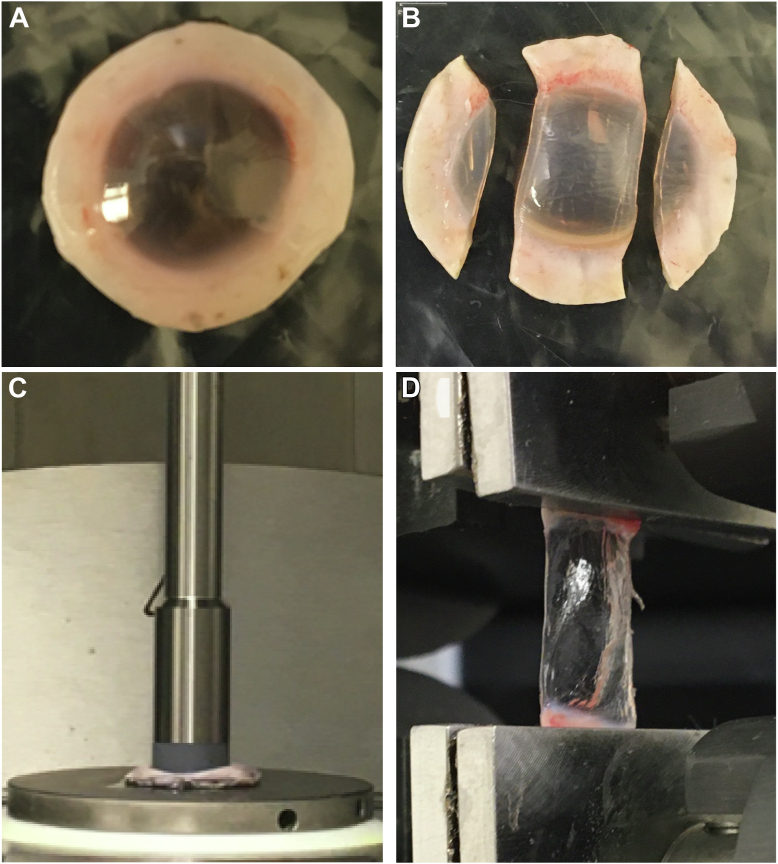
The frequency-dependent shear behavior of a subset of corneal buttons was measured using a rheometer (Anton Paar MCR 301 Physica, Fig. 4A) over a range of 0.16–16 Hz using a 5 N compressive preload and a peak shear strain of ∼0.1%. Rheometry produced estimates of the frequency-dependent storage ($G^{\prime }\left(\omega \right)$) and loss ($G^{″}\left(\omega \right)$) components, corresponding to the real and imaginary parts of the modulus $G$.

Figure 4.

(A) Cornea buttons prepared and (C) loaded in parallel-plate rheometry to measure out-of-plane shear modulus, $G$. (B) Cornea strips prepared and (D) clamped during extension testing to determine in-plane Young’s modulus, $E$.

Each sample was then cut into strips for tensile testing and pneumatically clamped (2752-005 BioPuls submersible pneumatic grips, 250 N max load) to the edge of the cornea (Fig. 4B). A 50 mN pre-load was applied and each sample was stretched at 2 mm/min (Instron model 5543) up to either 10% strain, 10 N load, or corneal breakage (whichever occurred first). Two load-unload cycles were performed to precondition the tissue, followed by 3 rounds of force-elongation followed by relaxation. The force-elongation measurement was converted to stress-strain according to sample geometry. A second order exponential was fit using 3 sets of raw data to determine the stress-strain curve. The in-plane Young’s modulus, $E$, was defined as the tangential slope of the stress-strain curve. Consequently, extension testing provided a value for the strain-dependent Young’s modulus, $E$, up to 10% strain.

Results

Elasticity Changes with IOP in Untreated and CXL Cornea

Corneal Thickness

The mean thickness of all samples in group A is presented in Table 1 for all tests. The CXL group (A2) was statistically thinner (P < 0.05) than the untreated group (A1) at all pressures tested with OCE and during rheometry. Corneal thickness in AμT-OCE was determined by OCT imaging; in rheometry – via parallel plate separation; and in extension testing – using a digital micrometer. Note that the OCE setup placed the cornea under inflating forces and assumed a refractive index; rheometry required a flattening of the cornea and was insensitive to differences in the central and peripheral thickness; and the digital micrometer required hand tuning.

Table 1.

Corneal Thickness for Each Testing Condition

Mean Thickness [μm] (± Standard Deviation)
	OCE				Rheometry	Extension Testing
	5 mmHg	10 mmHg	15 mmHg	20 mmHg
Group A1 (Untreated)	839 (± 230)	821 (± 219)	825 (± 260)	816 (± 259)	852 (± 94)	781 (± 161)
Group A2 (CXL)	630 (± 114)	633 (± 120)	631 (± 123)	633 (± 128)	654 (± 107)	645 (± 129)

CXL = cross-linking; OCE = optical coherence elastography.

Because OCE enabled measurements in cornea inflated to different IOP, a general (but not statistically significant) decrease in thickness was measured as pressure increased in the untreated group. Inflation induced thickness changes were not corrected for in rheometry and extension testing due to limitations in the experimental setup.

Out-Of-Plane Shear Modulus, G

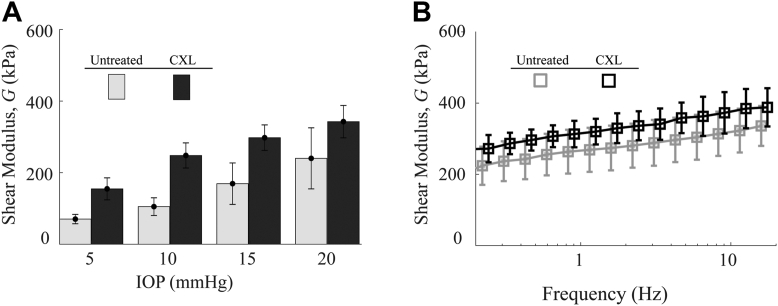
In the “untreated” group (A1), the OCE-determined out-of-plane shear modulus, $G$, for each sample is shown in Figure 5A. The statistical mean and standard deviation of the moduli between samples was 70 kPa ($\pm$ 29 kPa) at 5 mmHg, 105 kPa ($\pm$ 55 kPa) at 10mmHg, 169 kPa ($\pm$ 129 kPa) at 15 mmHg, and 240 kPa ($\pm$ 191 kPa) at 20 mmHg. In the “CXL” group A2, the OCE-measured out-of-plane shear moduli, $G$, are also shown in Figure 5A, where the statistical mean and standard deviation of the moduli were 151 kPa ($\pm$ 67 kPa) at 5 mmHg, 242 kPa ($\pm$ 76 kPa) at 10 mmHg, 290 kPa ($\pm$ 78 kPa) at 15 mmHg, and 334 kPa ($\pm$ 99 kPa) at 20 mmHg.

Figure 5.

(A) Out-of-plane shear modulus, $G$, in untreated (A1) and cross-linkng (CXL) (A2) cornea groups measured with acoustic micro-tapping optical coherence elastography at intraocular pressures (IOPs) from 5–20 mmHg, respectively. (B) Shear storage modulus, $G$, measured with parallel plate rheometry for untreated (A1) and CXL (A2) cornea groups.

A relative change of modulus, $G$, with increasing IOP for both untreated and CXL groups can be seen, where the mean shear modulus, $G$, increased at 20 mmHg (relative to the value at 5 mmHg) by a factor of 3.4 in the normal group compared with 2.2 in the CXL group.

Mechanical measurements using parallel-plate rheometry are shown in Figure 5B for both untreated and CXL corneas. In untreated samples, the statistical mean and standard deviation of the moduli between samples were 201 kPa (± 55 kPa) at 0.16 Hz and 336 kPa (± 56 kPa) at 16 Hz. For the CXL group, the statistical mean and standard deviation were 270 kPa ($\pm$ 34 kPa) at 0.16 Hz and 388 kPa ($\pm$ 54 kPa) at 16 Hz. Rheometry measurements lie within the range of OCE-determined modulus, $G$.

Individual results from each cornea have been included in Supplemental Methods 4. Note that OCE measured values in individual corneas generally tracked with rheometry measurements. Uncertainty intervals and detailed exclusion criterion can also be found in Supplemental Methods 2 and 3.

Optical coherence elastography-measured values of $G$ were statistically different (P < 0.05) between untreated and CXL groups at 5 mmHg and 10 mmHg, but not at 15 mmHg (P = 0.11) and 20 mmHg (P = 0.36). The means of rheometery results were not statistically different between groups at any frequency.

In-Plane Young’s Modulus, E

Acoustic micro-tapping-OCE experiments simultaneously evaluated in-plane, $\mu$, and out-of-plane, $G$, shear moduli. The modulus $\mu$ could then be converted to the in-plane Young’s modulus ($E=3\mu )$.^28,45 Note that E cannot be determined from rheometry measurements. We used tensile extensometry to compare E with that determined from AμT-OCE.

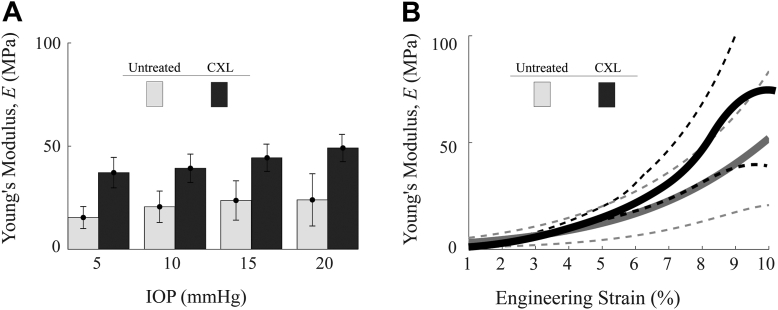
In the untreated group (A1), the OCE-measured in-plane Young’s modulus, $E$, for each sample is shown in Figure 6A. The statistical mean and standard deviation of the moduli between samples were 15 MPa ($\pm$ 5 MPa) at 5mmHg, 21 MPa ($\pm$ 8 MPa) at 10 mmHg, 24 MPa ($\pm$ 9 MPa) at 15 mmHg, and 24 MPa ($\pm$ 13 MPa) at 20 mmHg. In the CXL group (A2), each of the in-plane Young’s moduli, $E$, is also shown in Figure 6A, where the statistical mean and standard deviation of the moduli between samples were 37 MPa ($\pm$ 7 MPa) at 5 mmHg, 39 MPa ($\pm$ 7 MPa) at 10 mmHg, 44 MPa ($\pm$ 6 MPa) at 15 mmHg, and 47 MPa ($\pm$ 7 MPa) at 20 mmHg.

Figure 6.

(A) In-plane Young’s modulus, $E$, in untreated group (A1) and cross-linking (CXL) group (A2) measured with coustic micro-tapping optical coherence elastography at intraocular pressures (IOPs) from 5–20 mmHg. (B) Strain-dependent Young’s moduli measured via extension testing up to 10% strain in untreated group (A1) and CXL group (A2). E was determined via extension testing to 10% strain, or where visible tissue damage occurred. The dashed lines correspond with ± 1 standard deviation. Individual tests can be found in the Supplemental Methods.

Relative changes in Young’s modulus with IOP were smaller for CXL corneas than for untreated ones, where Young’s modulus for untreated corneas increased by a factor of 1.6 with an increase in IOP from 5 mmHg to 20 mmHg and $E$ increased by ∼1.3 for CXL cornea.

The in-plane Young’s modulus determined by extension testing at 1%–10% strains following dissection of the samples is shown in Figure 6B, where the statistical mean and standard deviation at 1% strain were 3.2 MPa ($\pm$ 2.2 MPa) and at 10% strain were 51 MPa ($\pm$ 31 MPa). In the CXL group (A2), the in-plane Young’s modulus determined by extension testing at 1%–10% strains is also shown in Figure 6B where the statistical mean at 1% strain was 2.9 MPa ($\pm$ 0.9 MPa). The high strain modulus was either at 10% strain, or at the inflection point before structural damage occurred. The high strain modulus in the CXL group was 74 MPa ($\pm$ 50 MPa). Samples in the CXL group demonstrated significant tissue damage at higher strains and required more force to extend.

Optical coherence elastography-measured values of $E$ were statistically different between groups at all pressures (P < 0.1 for IOP of 5 mmHg to 20 mmHg, respectively). The means of the best fit curve of the strain dependent tangential modulus were not statistically different across all strains. Uncertainty intervals and individual results from each cornea have also been included in Supplemental Methods 4.

The independent subgroup study suggests that in general, (i) both moduli $(G$ and $E$) could be measured in ex vivo human cornea using the NITI model in untreated and CXL treated samples and (ii) OCE measurements generally agree with mechanical tests. Thus, the effect of CXL on corneal elasticity can be explored in more detail without direct comparison to mechanical tests. This result also suggests that OCE can monitor elasticity changes throughout the entire treatment cycle, including untreated corneas pre-CXL, intra-CXL, and post-CXL.

Additionally, the results suggest that one-to-one comparison before and after CXL is required to better understand the effect of CXL. Such scans can measure CXL-induced changes for each individual cornea rather than relying on group comparison between untreated and treated samples. Analyzing results for every cornea independently should greatly reduce the effect of population variability of corneal properties, which is key to developing personalized models of the eye for optimal surgery planning. Results on ex vivo preliminary studies are considered in the sub-sections below.

Independent Monitoring of Corneal Moduli Pre- and Post-CXL

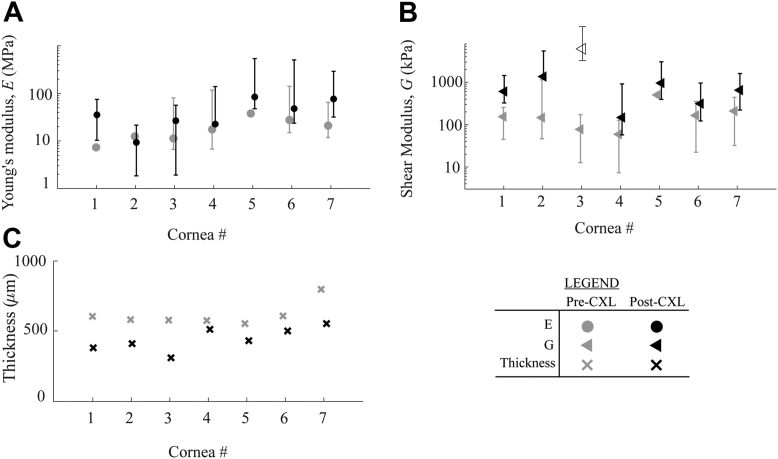
Results for each sample in group B, where moduli were quantified immediately before and after CXL, can be seen in Figure 7A, B. Clearly, changes induced by CXL vary from cornea to cornea, suggesting that individual treatment plans may be required to reach desired moduli outcomes.

Figure 7.

Cross-linking (CXL)-induced differences in (A) in-plane Young’s modulus, $E$, and (B) out-of-plane shear modulus, $G$, for cornea in group B. Error bars correspond with uncertainty intervals described in the Supplemental Methods. Note that in one sample (cornea #3) all 5 scans demonstrated high uncertainty in $G$ following CXL, thus the value is displayed as an “open” triangle and omitted from analysis of the means. (C) Thickness for each individual cornea pre- and post-CXL.

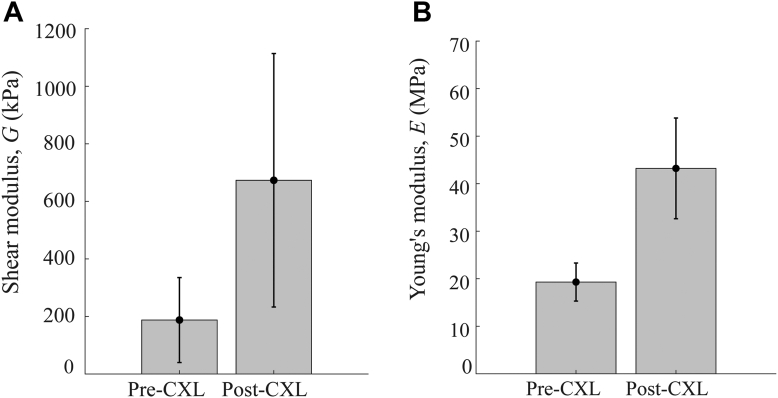
The statistical mean (standard deviation) of $E$ changed from 19 MPa ($\pm$ 4 MPa) to 43 MPa ($\pm$ 11 MPa) and the shear modulus, $G$, from 188 kPa ($\pm$ 148 kPa) to 673 kPa ($\pm$ 440 kPa) (see Fig. 8). Note that in cornea #3, (post-CXL), (Fig. 7B), all 5 repeat scans demonstrated high uncertainty in $G$. As such, its value was omitted from the calculation of mean values.

Figure 8.

The mean and standard deviation in (A) $G$ and (B) $E$ prior to and following ultraviolet cross-linking (CXL) in n = 5 samples.

While both moduli increased following UV exposure in RF/dextran-soaked cornea, the average change in in-plane Young’s modulus, $E$, was approximately double (2.3), whereas the out-of-plane shear modulus $G$ changed by > 3 times (3.6). Notably, both E and $G$ increased for all samples following CXL.

Both E and G had significantly different stiffening responses to CXL, where statistical significance (P < 0.05) was determined using a 2-tailed t test where the null hypothesis was no difference between the means in the pre-CXL and post-CXL values. The P value for $G$ was 0.03 and for E was 0.02, indicating a significant stiffening response in both moduli.

The central corneal thickness following epithelium removal was calculated from the OCT structural image pre-CXL and post-CXL. The measured thickness pre-CXL was 577 μm ($\pm$ 58 μm) and reduced to 450 μm ($\pm$ 80 μm) post-CXL. The measured thickness was also statistically different in the samples following CXL (P = 0.001).

Evaluation of Both Corneal Moduli during CXL Procedure

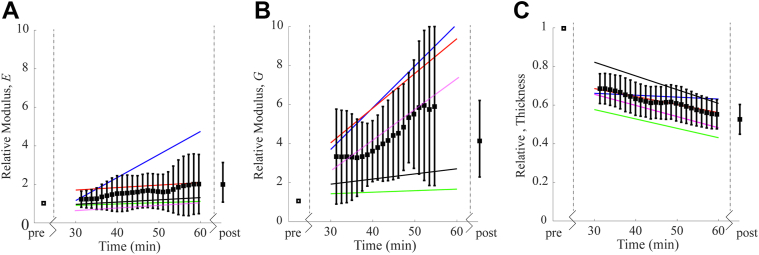
To demonstrate the ability of AμT-OCE to directly quantify corneal biomechanics intraoperatively, $E$, $G$, and thickness were measured in group C every 90 seconds during the procedure. A moving average on both the output value and uncertainty intervals was performed over 4.5 minutes (the full data set has been included in the Supplemental Materials). The mean and standard deviation of the relative modulus (i.e., modulus at any time normalized to the modulus pre-CXL) can be seen in Figure 9, along with a linear fit (over time) to highlight individual changes in $G$, $E$, and central cornea thickness with CXL. While both moduli increased with UV exposure, $E$ changed on average by about 2 times (from 15 MPa [$\pm$ 4 MPa] to 31 MPa [$\pm$ 6 MPa]), whereas $G$ changed by approximately 4 times (from 107 kPa [$\pm$ 26 kPa] to 421 kPa [$\pm$ 110 kPa]) following CXL. Both moduli changed significantly (P < 0.01) between pre-CXL and post-CXL values. Each cornea changed stiffness and thickness at a slightly different rate. Non-negligible stiffening also occurred from the RF/dextran alone within the first 30 minutes. Note that 2 of the corneas resulted in a poor fit for $G$ over the last 6 minutes. Four of the 5 samples provided sufficient fit for $G$ in the scans taken immediately following CXL.

Figure 9.

(A) Young’s Modulus E and (B) Shear Modulus G, relative to the pre-cross-linking (CXL) value; (C) central cornea thickness relative to the pre-CXL value. Black markers are the mean and standard deviation of the relative changes between the n = 5 samples. The solid colored lines represent a linear best-fit of the relative change from each individual cornea. For 2 of the corneas, the fit for $G$ was very poor over the last 6 minutes, so the values have been omitted from the displayed average. The post-CXL average includes 4 corneas.

The cornea progressively thinned during CXL. The measured thickness pre-CXL and post-CXL was 560 μm ($\pm$ 70 μm) and 340 μm ($\pm$ 20μm), respectively. Combined elasticity and thickness changes during CXL will have significant impact on both the overall corneal stiffness and potential refractive changes. Although this experiment required a slight modification of the Food and Drug Administration–approved Dresden protocol (i.e., removal of RF/dextran from the corneal surface prior to each scan), the results indicate that AμT-OCE can potentially monitor treatment progression.

Discussion

Mechanical anisotropy was confirmed in ex vivo human cornea, where the in-plane tensile (Young’s) modulus, $E$, was on average multiple orders of magnitude larger than the out-of-plane shear modulus, $G$. Similar to porcine cornea,⁴³ the results of group A suggest that human cornea can be approximated as an NITI material. Using the NITI model to describe corneal deformation plays a key role in explaining the order(s) of magnitude difference in corneal stiffness estimates extracted from shear- and tensile-based mechanical measurements.

Guided elastic wave propagation mixes fundamental modes, allowing $E$ and $G$ to be measured simultaneously in the cornea.³⁰ As shown previously for strongly anisotropic materials, a change in $E/\mu$ results in a small, but detectable change in A₀-mode dispersion, particularly in the low frequency region (where the wavelength is long compared to the thickness). As such, the wave velocity is roughly dominated by the shear modulus, $G$, and applying an isotropic model to fit the same recorded waveforms of guided mechanical waves would lead to a rough approximation of $G$, not $E$ or $\mu$. In this case, Young’s modulus, $E\text{,}$ calculated using the expression $E=3G$ (as done previously48, 49, 50) would be highly underestimated compared to the correct relationship of $E$ with $\mu$. Such an underestimated $E$ modulus used in prediction models would produce an inaccurate estimate of cornea stiffness, its deformation, and would fail to evaluate clinical procedure outcomes, including that for CXL.

To better understand the limitations in quantifying moduli, a method to determine uncertainty intervals in OCE-measured modulus was presented in Supplemental Methods 2 using a goodness-of-fit routine that compared the $A_0$ structure for different values of $E$, and $G$, independently. As demonstrated previously, the $A_0$ mode is increasingly insensitive to changes in $E$ as the degree of mechanical anisotropy increases ($E$ >> $G$).³⁰ This suggests that when $E$ is much larger than $G$, it can be very difficult to accurately determine $E$ for typical signal to noise ratios achieved with OCE. Signal averaging or multichannel scanning may be used to improve signal to noise ratio and enable more accurate determination of $E$ but can be difficult to perform in vivo. To predict refractive changes and model the cornea as a curved lens system, both $G$ and $E$ are required, yet, a remaining question is the precision needed to measure a change in $E$ corresponding to a physical change in corneal shape. Static models are required to answer this question and remain an area of future interest.

The results of Group A suggest that AμT-OCE can quantify both $G$ and $E$, with less certainty around $E$ (Supplemental Methods 2). Although $E$ in the NITI model can have a high degree of uncertainty, analyzing guided wave propagation remains the only noncontact, nondestructive method reported to date to estimate in-plane tensile stiffness.

While elastic moduli measured via OCE and mechanical methods in this study generally agree, there are subtle experimental differences that make it difficult to quantitatively compare values between methods. For example, an artificial anterior chamber was used to inflate corneal samples, providing additional boundary conditions in the lateral direction limiting the propagation distance of the guided wave over the cornea, that differ from those of both in vivo and destructive ex vivo settings. While probing tissue inflated via an artificial anterior chamber is more like cornea loading in vivo, mechanical boundary conditions are markedly different from those for whole-globe samples. Together with AμT excitation, it can lead to modifications in the low-frequency region of the f-k spectrum, worsening fitting accuracy. Additionally, to facilitate extension testing, a portion of the sclera was left on each sample during rheometry, which was shown to induce a measurable increase in the apparent modulus $G$.⁴³ Sample transportation, time limitations, and measurement precision also contributed to differences in measured thickness between OCE and destructive methods, potentially influencing final quantitative moduli values.

In Group B, both the out-of-plane shear modulus, $G$, and in-plane Young’s modulus, E, increased significantly following cross-link formation. The measured increase in both $G$ and E suggests that CXL strengthened the tensile and flexural response, as well as the ability of the cornea to resist shearing forces. The measured increases in $G$ and $E$ of approximately 4-fold and 2-fold, respectively, generally agreed with values previously reported. For example, Marbini et al.⁵¹ and Del Buey et al.⁵² reported a post-CXL increase in corneal Young’s modulus, E, by a factor of ∼1.5–2 in the 7%–10% strain range, while Wollensak et al³⁶ report an increase by a factor of 4.5 (1.3 MPa-5.9 MPa at 6% strain) in human cornea tested via strip extension within 1 hour of enucleation. The results of this study are also consistent with Aslanides et al.,⁴¹ who reported an increase as high as 20-fold in the shear modulus G in porcine cornea following CXL (as measured using a parallel-plate scheme) and Sondergaard et al.⁴² who reported a general 2 to 5-fold increase in $G$ in human cornea under 5% compressive strain, where samples were probed using a parallel plate arrangement to provide a translational shear (as opposed to rotational).

Following UV-CXL, the out-of-plane shear modulus, $G$, and the in-plane Young’s modulus, $E$, increased from untreated values by different multiples. Specifically, the shear modulus, $G$, (most likely related to the proteoglycan mesh and interlamellar connectivity) changed almost 4 times in CXL corneas compared to untreated corneas, whereas the tensile modulus, $E$, changed only about 2 times. This result suggests that CXL changes elastic properties of the connective tissue mesh between the lamellar sheets in addition to that of fibers, making the connective tissue or proteoglycan mesh apparently “stickier.” The effect of the connective matrix on mechanical stability is well known in different material science and engineering areas, where fibers embedded in a composite material can produce almost equivalent tensile properties as the fibers, with shear properties independently defined by the connective matrix. Consistent with this effect, the in-plane tensile properties of CXL cornea increased relatively less than the apparent connectivity between fibers.

To date, the specific relationship between corneal microstructure and macrostructure with shape and focusing power remains speculative. Based on the NITI model, it can be hypothesized that a loss in lamellar interconnectivity or degradation of the proteoglycan host-mesh would produce a higher degree of lamellar slippage while degradation in fiber strength along its axis would produce reduced tensile strength and a corresponding change in shape. In keratoconus progression, it has been shown that reduced interlamellar branching can be found in the anterior portion that corresponds to a measurable reduction in tensile modulus.⁵³ Reduced biomechanical stability due to lamellar slippage and collagen degradation has been suggested as a potential mechanism behind disease progression^8,54, 55, 56 but remains difficult to monitor in a clinical setting. Still, studies of micro and macro biomechanical and biochemical stability of the cornea following CXL are required to better understand both short- and long-term effects on refractive changes.

Due to difficulties in acquiring human research tissue, all samples were scanned once the viable donor period had passed (over 1–2 weeks following enucleation). As such, biomechanical changes due to tissue necrosis and swelling may have occurred in samples prior to testing. Note that the apparent corneal stiffness (both E and G) for different hydration levels has been explored in detail using numerous animal models.^31,33,42,57, 58, 59 In the present study, CXL via the mock Dresden protocol induced a change in thickness from approximately 577 μm to 450 μm, and a measured doubling of the Young’s modulus. The doubling in tensile modulus was greater than what would be expected due to swelling alone. As previously reported, the shear modulus G appeared less sensitive to hydration compared to the tensile modulus. In the samples tested in group B, we measured a 3-fold increase in the shear modulus G; again, a change unlikely to result from thinning alone.

While carefully accounting for swelling in all samples remains an area of future study, the degree to which swelling alone, versus CXL alone, changes mechanical properties remains unclear. Of course, it remains likely that the reported differences in stiffness were due to a combination of simultaneous CXL and thinning. Because the present study sought to demonstrate that noncontact OCE can quantify changes induced in corneas undergoing a procedure similar to a clinical protocol, it does not measure the effect of CXL alone. Instead, a tool to measure expected changes during and following CXL is presented. Note that the measured differences in thickness generally agree with what has been reported elsewhere in both in vivo and ex vivo studies using a similar CXL procedure.^33,60, 61, 62

Ideally, real-time monitoring of corneal stiffness during CXL would enable immediate feedback on procedure progression. In this study (group C), we noted different rates of stiffening for individual corneas. We also note that there was a measurable difference in both moduli and thickness following the application of the RF/dextran solution. Simply soaking the cornea in dextran can result in a measurable change in corneal thickness and stiffness,³³ consistent with pre-CXL and pre-UV measurements in group C. As corneas were exposed to UV illumination, OCE could measure the overall effect of the mock CXL procedure (from both RF/dextran soaking and UV illumination) in the Dresden protocol. If the effects of both total stiffening and the rate of stiffening induced by RF/dextran and UV illumination need to be explored independently, further studies are required.

Because research tissue was difficult to acquire, the inclusion of older aged samples (Supplemental Methods 5), may have resulted in generally higher moduli.⁶³ In fact, corneas from eye-banks tend to be from older donors, which makes it difficult to study samples from the age groups that most commonly present progressing keratoconus (i.e., age groups most likely to undergo CXL).⁶⁴ One issue that remains a limitation in this study, for example, is that the mean age in group A1 was approximately 24 years greater than A2, suggesting that the pretreatment moduli may be skewed toward higher values in group A1. Still, the younger tissues (group A2) demonstrated a relatively higher modulus post-CXL than the older (A2) samples. Note that groups B and C were closer in age to group A1, and older than the age where keratoconus most commonly presents. Due to a host of microstructural differences and unique CXL behaviors between human and animal models,^36,37,65, 66, 67, 68 even older human samples can provide valuable information and help demonstrate the potential for in vivo human use. Difficulties acquiring human tissues for research are not unique and have been previously recognized as a limiting factor in acquiring sufficient sample sizes.^64,66,68

While the moduli quantified with AμT-OCE are generally consistent with both literature and mechanical testing, the proposed method has several limitations. One is that depth-dependent moduli cannot be measured using an approach based on guided mechanical waves and, consequently, the measurements most likely correspond to depth-averaged values of corneal moduli. It has been shown that CXL is most dramatic in the anterior portion of the cornea,⁶⁶ which contains a complex fiber arrangement that likely determines most of its flexural (tensile) strength. It has also been shown that the relative increase in $G$ is much greater in the anterior portion of the cornea.³¹ Thus, if there was a significant increase in anterior CXL, much of the stroma may still be susceptible to interlamellar slippage. Exploring the importance of depth-resolved changes, as well as the interplay between moduli and IOP, remain directions of future interest.

Treatment success in CXL is currently defined by secondary measures such as corneal shape and refractive power changes over time.⁶⁹ To truly optimize outcomes, elastic moduli maps in cornea before and after surgery could evaluate individual stiffness correction requirements and monitor whether the required correction had been reached. As focal biomechanical weakening in the cone can occur in progressive keratoconus, localized biomechanical mapping is more likely to provide the information needed to develop a personalized model for each individual cornea suitable for screening, surgical planning, and treatment monitoring. Because elastic moduli maps may be combined with topography measurements provided by ophthalmic systems, topographic and mechanical changes would not only provide potentially important diagnostic information but may also be used to monitor localized CXL treatments. Although OCT can provide micron-scale resolution in tracking mechanical waves, the resultant OCE resolution in mapping mechanical properties across the cornea is lower.^28,29 Cornea is a bounded material and, therefore, guided mechanical waves further degrade the resolution in mapping moduli. While high-resolution images of local group velocity have been demonstrated in three-dimensional corneal sections,²⁶ local mapping of elastic moduli has not yet been demonstrated. Methods improving spatial resolution in dynamic OCE measurements of bounded material (such as the cornea) are currently under investigation, and the demonstration of spatially resolved maps of cornea mechanical moduli is a subject of future studies.

The standard Dresden protocol involves a 30 minute corneal exposure to 370 nm UV radiation at an irradiance of 3 mW/cm² following RF/dextran saturation.⁴⁵ Several other protocols have been proposed which reduce exposure time. For example, accelerated CXL uses higher irradiance UV-A (longest wavelengths of the UV spectrum) to shorten the time needed to deliver the equivalent total energy dose.¹⁷ While different protocols have demonstrated varying degrees of stiffening based on the time of UV irradiance,⁴⁰ their translation remains limited and cannot be personalized without quantitative measurements of corneal elasticity, which is critical in guiding CXL treatment and predicting outcomes.

Finally, we note that thickness remains an important parameter in determining whether or not to perform CXL based on the hypothesis that RF serves as both a CXL agent and a means to protect the posterior segment of the eye from UV radiation.70, 71, 72, 73, 74, 75, 76, 77 While analytical models describing RF loading, UV light exposure, and polymerization have been used to determine safety limits and predict surgical outcomes, current treatment parameters are designed assuming that a large majority of the UV light is absorbed or scattered in the anterior 250 to 350 μm of the corneal stroma in all patients. Thus, a minimum stromal thickness of 400 μm is required to protect corneal endothelium and deeper ocular structures.⁷⁵ This approach often excludes advanced keratoconus patients. We hypothesize that OCE can be used to design patient-specific procedures balancing the benefit between UV radiation time and desired biomechanical stabilization, opening the possibility for optimized CXL treatment of even advanced keratoconus patients.

In this study, we demonstrate the potential of AμT-OCE to monitor stiffening and thinning of the cornea intraoperatively, with varying rates of change in $E$ and $G$. Although we demonstrated the potential to quantify both elastic moduli noninvasively using a noncontact near real-time procedure, it is important to note that results obtained in ex vivo studies (such as the one reported herein) may not fully correspond to changes expected in in vivo corneas using the same protocol. Given the favorable ectasia-stabilizing results with cornea CXL therapy, efforts aimed at optimizing the procedure’s treatment time, intraoperative and postoperative comfort, and efficacy remain an area of focus.

Conclusions

Corneal CXL is increasingly being used clinically to biomechanically stabilize the cornea in vision degrading diseases such as keratoconus or post-laser-assisted in situ keratomileusis ectasia. While clinical outcomes are largely positive, there remains a gap in both understanding the mechanisms behind corneal stabilization and providing clinicians feedback on how those mechanisms may relate to disease progression and treatment plans.

In this study, AμT-OCE quantified changes in both the in-plane Young’s modulus, $E$, and out-of-plane shear modulus, $G$, of human donor cornea due to UV induced CXL in a noncontact, nondestructive manner. The results demonstrated a significantly different stiffening response in both $E$ and $G$, where $G$ experienced a larger relative increase from the CXL procedure. This suggests that while CXL strengthened the tensile and flexural strength of the tissue, the ability of the cornea to resist shearing forces was more dramatically altered by the procedure.

Acoustic micro-tapping OCE provides a unique noninvasive and noncontact tool that can monitor and evaluate corneal elasticity, including changes induced by CXL. Cross-linking-induced changes in mechanical anisotropy likely carry diagnostic and prognostic information that warrant future studies.

Manuscript no. XOPS-D-22-00197