A Complete Picture of Cation Dynamics in Hybrid Perovskite Materials from Solid-State NMR Spectroscopy

Abstract

The organic cations in hybrid organic–inorganic perovskites rotate rapidly inside the cuboctahedral cavities formed by the inorganic lattice, influencing optoelectronic properties. Here, we provide a complete quantitative picture of cation dynamics for formamidinium-based perovskites and mixed-cation compositions, which are the most widely used and promising absorber layers for perovskite solar cells today. We use ²H and ¹⁴N quadrupolar solid-state NMR relaxometry under magic-angle spinning to determine the activation energy (E_a) and correlation time (τ_c) at room temperature for rotation about each principal axis of a series of organic cations. Specifically, we investigate methylammonium (MA⁺), formamidinium (FA⁺), and guanidinium (GUA⁺) cations in current state-of-the-art single- and multi-cation perovskite compositions. We find that MA⁺, FA⁺, and GUA⁺ all have at least one component of rotation that occurs on the picosecond timescale at room temperature, with MA⁺ and GUA⁺ also exhibiting faster and slower components, respectively. The cation dynamics depend on the symmetry of the inorganic lattice but are found to be insensitive to the degree of cation substitution. In particular, the FA⁺ rotation is invariant across all compositions studied here, when sufficiently above the phase transition temperature. We further identify an unusual relaxation mechanism for the ²H of MA⁺ in mechanosynthesized FA_xMA_1–xPbI₃, which was found to result from physical diffusion to paramagnetic defects. This precise picture of cation dynamics will enable better understanding of the relationship between the organic cations and the optoelectronic properties of perovskites, guiding the design principles for more efficient perovskite solar cells in the future.

Introduction

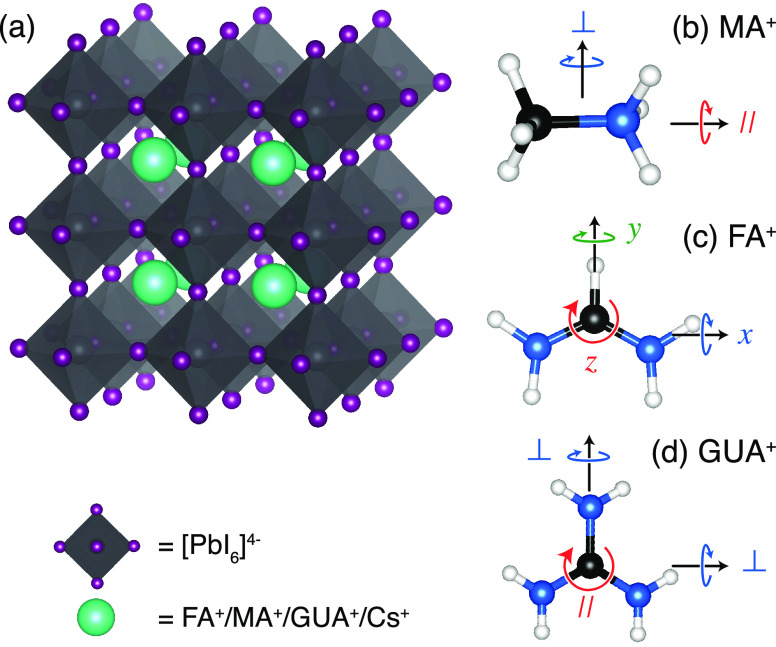
Hybrid organic–inorganic perovskite materials have drawn significant attention owing to their pertinent optoelectronic properties for use in solar cells and LEDs.¹⁻³ Notably, the power conversion efficiencies (PCEs) of perovskite solar cells have already exceeded 25%,^4,5 rivaling conventional solar cell technologies at a lower cost.⁶⁻⁸ These materials adopt the ABX₃ perovskite crystal structure, where A⁺ is a monovalent cation—primarily methylammonium (MA⁺, CH₃NH₃⁺), formamidinium [FA⁺, CH(NH₂)₂⁺], guanidinium [GUA⁺, C(NH₂)₃⁺], and/or Cs⁺—that resides in the cuboctahedral cavity formed by corner-sharing lead halide octahedra (I^–, Br^–, and Cl^–) as illustrated schematically in Figure 1a.⁹⁻¹⁵ The best-performing devices today use double-^4,16−21 or triple-cation compositions²² with a mixture of different A-site cations, which increases the PCE^4,21,23,24 and stability^4,21,25,26 as compared to their single-cation analogues.

Figure 1.

Perovskite crystal structure (a) and principal axes of rotation for the most commonly employed cations: (b) methylammonium (MA⁺), (c) formamidinium (FA⁺), and (d) guanidinium (GUA⁺). H, C, and N atoms are represented by white, black, and blue balls, respectively.

These materials exhibit a variety of complex atomic-level motions spanning a wide range of frequencies. This includes ion migration on long timescales (milliseconds to hours),^27,28 low energy polar (optical) vibrational modes of the metal-halide sublattice (up to ps),^29,30 and reorientation of the A-site cation within the cuboctahedral cavities of the inorganic lattice on a similar timescale (∼0.1–1 ps).³¹⁻³⁴ These multi-timescale structural dynamics affect key electronic properties such as exciton binding energies and charge-carrier mobilities.^14,35−41 The rotation of the A-site cation is particularly important because it has also been shown to be linked with key phenomena such as efficient charge separation,⁴² tolerance to intrinsic point defects,⁴³ and dynamic splitting of band extrema.⁴⁴

Consequently, MA⁺ cation dynamics have been widely explored through a range of techniques including quasi-elastic and inelastic neutron scattering,⁴⁵⁻⁴⁹ dielectric spectroscopy,²⁷ millimeter-wave spectroscopy,⁵⁰ two-dimensional infrared spectroscopy,^51,52 and NMR spectroscopy.^31,53−56 The MA⁺ cation dynamics have been further found to correlate strongly with the crystallographic perovskite phase evolution.⁹ Among these techniques, NMR relaxometry and linewidth analysis have proved to be sensitive probes of both the nature and the rate of motion.^{31,53−55,57} Notably, ²H and ¹⁴N quadrupolar relaxation measurements performed under static conditions have been used to determine the correlation times about each of the two unique principal axes of the MA⁺ ion.⁵⁴

In contrast, there has been much less focus on the dynamics of the FA⁺ cation, despite it being the most widely used in optoelectronic applications.^4,58 Experimental studies using two-dimensional infrared spectroscopy⁵⁹ and low temperature neutron scattering⁶⁰ rely heavily on molecular dynamic simulations to aid interpretation. ¹H NMR relaxometry^32,61 and ¹⁴N linewidth analysis⁵³ have been used to study FA⁺ dynamics but with simple motional models that rely on a series of assumptions (Bloembergen–Purcell–Pound theory and model free analysis) and that yield only a single correlation time, while FA⁺ motion is notably characterized by rotational rates about three distinct principal axes. Device-relevant multi-cation systems introduce additional experimental complexity. As a result, a complete picture of the dynamics in FAPbI₃ and mixed-cation perovskites is lacking.

Here, we use variable temperature, multi-nuclear ²H and ¹⁴N NMR relaxometry under magic angle spinning (MAS) to determine the rotational rates and activation energies for each distinct axis of FA⁺, MA⁺, and GUA⁺ in a series of contemporary multi-cation perovskite compositions. MAS critically facilitates the study of lower symmetry cations and mixtures. We discover noticeably faster rotational dynamics for MA⁺ in mixed FA⁺/MA⁺ compositions, whereas the FA⁺ dynamics are essentially unaffected. In contrast, we find that the addition of Cs⁺ into the FA⁺ matrix does change the FA⁺ motion at room temperature significantly, largely because of changes in the phase transition temperature. Further, extending the approach to a mixed GUA⁺/MA⁺ perovskite, we find that MA⁺ rotation is again faster than in MAPbI₃ and that surprisingly GUA⁺ also exhibits fast picosecond rotation, despite its bulky nature.

Results

Symmetry and Phase Transitions of FAPbI₃

²H and ¹⁴N are quadrupolar nuclei (I = 1) which yield NMR spectra that are very sensitive to the local symmetry.^62,63 To perform deuterium NMR measurements, deuterated FAPbI₃ was synthesized using d-FAI and d₄-FAI, with substitution of the CH and NH₂ hydrogens, respectively. Figure 2a,b shows the ²H MAS spectra of d-FAPbI₃ and d₄-FAPbI₃ at room temperature in the metastable, cubic black phase (α, Pm3̅m). d-FAPbI₃ shows one peak at 8.5 ppm, as expected (inset, Figure 2a), whereas two isotropic shifts are observed for d₄-FAPbI₃, corresponding to the two inequivalent deuterons arising from restricted rotation of the C–N bond, as also seen by solution NMR.⁶⁴ These can be assigned in the fully deuterated d₅-FAPbI₃ sample using a ²H–²H EXSY experiment on the basis of their proximity to the CD deuteron (Figure S1).

Figure 2.

Single pulse solid-state ²H MAS NMR spectra in the cubic phase of d-FAPbI₃ (a) and d₄-FAPbI₃ (b). The insets show a zoom of the isotropic resonances and the resolved peaks of the two ND₂ deuterons. ²H MAS NMR spectra in the tetragonal phase (at 260 K) of d-FAPbI₃ (c) and d₄-FAPbI₃ (d). Hahn-echo detected ¹⁴N MAS NMR spectra of d-FAPbI₃ (e). The inset shows a zoom of the central peak. All spectra were recorded at 5 kHz MAS; further experimental details are given in the Supporting Information.

Figure 2e shows the ¹⁴N MAS spectrum at room temperature, where the quadrupolar coupling results in a spinning sideband manifold spanning a full-width at half-maximum of ∼20 kHz, which can be approximately fitted using a Czjzek model⁶⁵ (Figure S2), with an average C_Q of 27 kHz. This narrow width compared to the ¹⁴N quadrupolar coupling constant (C_Q) for FA⁺ of ∼2.7 MHz in the absence of any motion indicates that the cation undergoes almost, but not quite, isotropic reorientation, as expected at room temperature in the cubic cavity.⁵³

The residual anisotropy is also visible as low-intensity spinning sidebands in the ²H spectra (Figure S3), but the anisotropy is smaller for CD and the trans ND₂ deuteron than for the cis deuteron. This indicates that the anisotropy predominantly arises from preferred orientation of the x- and z-axes (using the axis scheme shown in Figure 1c); i.e., the S_xx and S_zz components of the order tensor are larger than the S_yy term, although the residual orientational order is very small, with |S| on the order of 0.01. The similarity of the anisotropies for CD and the parallel ND₂ further corroborates the assignment of the ND₂ deuterons since they have similar orientations within the molecule (noting that quadrupolar coupling is invariant to a 180° rotation).

Black FAPbI₃ is known to undergo a phase transition at ∼285 K from the cubic phase to the tetragonal phase (β, P4/mbm).^66,67 This reduction in symmetry is clearly observed in the ²H spectrum, which shows a significantly broader sideband manifold at 260 K (Figure 2c,d). This is associated with a distribution of quadrupolar coupling tensors corresponding to a distribution of motions with different orientational anisotropies. Due to the larger quadrupolar moment of ¹⁴N, the ¹⁴N spectrum becomes challenging to measure with conventional techniques in the β phase because the quadrupolar pattern becomes very broad.⁶¹

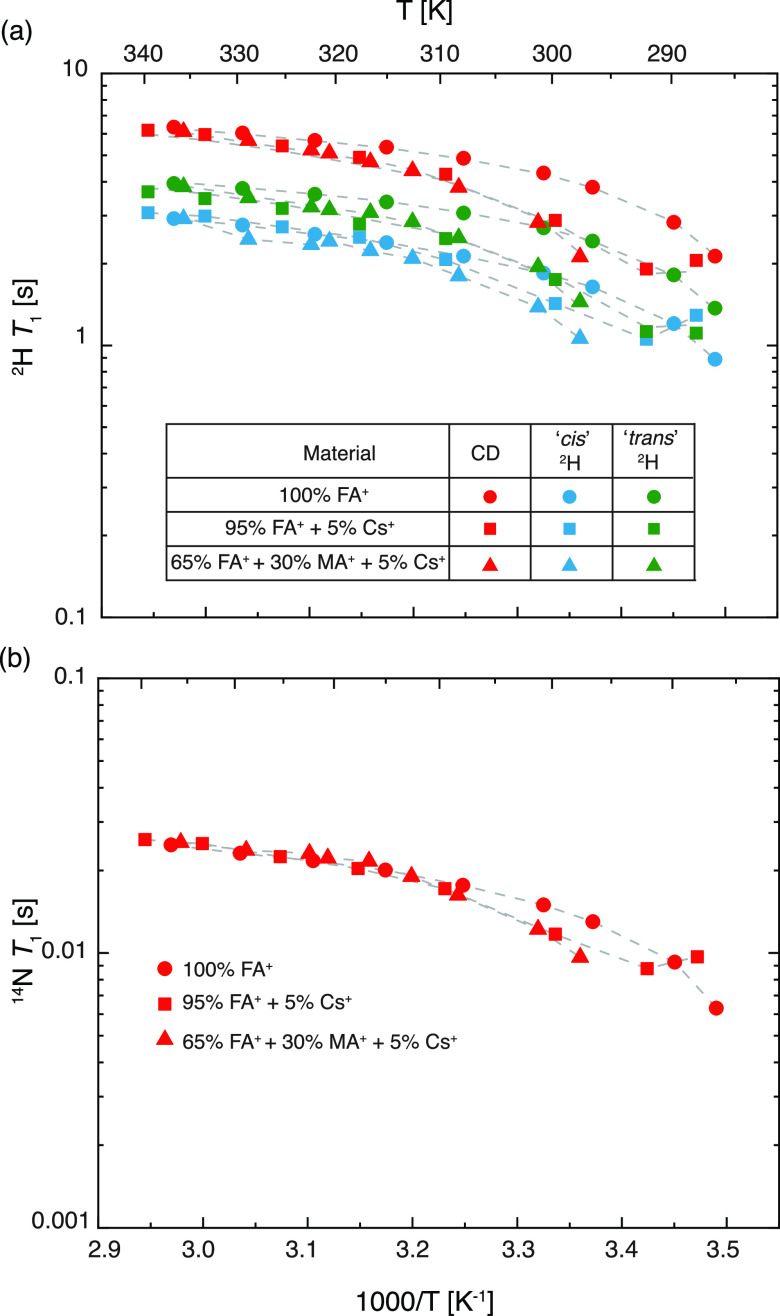
Motion on a similar timescale to the nuclear Larmor frequency (∼10⁸ Hz) induces longitudinal nuclear spin relaxation (T₁). ²H and ¹⁴N T₁ relaxation times are pertinent probes to investigate rotation as they depend upon the orientation of the electric field gradient (EFG) tensor with respect to the principal axes of rotation and can therefore differentiate the correlation times about different axes. Figure 3 shows the measured ²H and ¹⁴N T₁ constants for FAPbI₃, which are observed to decrease with decreasing temperature, indicating that the cation rotation is in the so-called fast motion regime (faster than the Larmor frequency). As the characteristic timescale of the rotational motion slows down at lower temperatures, it becomes closer to the Larmor frequency and induces relaxation more effectively. Superimposed on this general trend, we observe discontinuities at 285 K corresponding to the α ↔ β first-order phase transition. In the following, we analyze the NMR relaxometry data in depth, exploiting the sensitivity of the T₁ relaxation to motion on this timescale to extract a detailed picture of the cation dynamics.

Figure 3.

Measured ²H and ¹⁴N longitudinal relaxation time constants (T₁) of black FAPbI₃ as a function of temperature. The discontinuities in the T₁ behavior are indicative of the crystallographic phase transition of the material. Experimental details are given in the Supporting Information.

Rotational Dynamics in FAPbI₃

In order to extract motional rates from the relaxation data, a motional model is required. Here, we use the rotational diffusion model of Huntress⁶⁸ in which the orientation of the molecule is assumed to change randomly, resulting in overall rotational diffusion, analogously to the random translation that results in overall translational diffusion. This rotational diffusion is characterized by rotational diffusion constants (D_i) about the three principal axes of the molecule, which are in turn related to angular correlation times about the corresponding axes by D = 1/(6τ_c).⁶⁸ When the principal axes are not equivalent by symmetry, the rotational diffusion rates about these axes are different. Note that, even with different rotational rates about the three axes, this rotational diffusion model assumes an isotropic orientational distribution.⁶⁸ Although as discussed above the orientation of FA⁺ in FAPbI₃ is not quite isotropic, the very small residual orientational order would be a negligibly minor correction to the model. We note that the rotational diffusion model has previously been applied to MAPbI₃ in the tetragonal phase, which has a much larger residual orientational order.⁵⁴

Quadrupolar T₁ relaxation depends on the rotational diffusion rate about each axis, the size of the quadrupolar coupling, and the orientation of the quadrupolar coupling tensor with respect to the principal axes of the rotational diffusion tensor. Expressions for quadrupolar relaxation under rotational diffusion have been derived by Huntress;⁶⁸ in the case of the planar FA⁺ cation, the ²H relaxation is given by

1

where C_Q is the quadrupolar coupling constant in units of Hz, η is the quadrupolar asymmetry, ϕ is the angle between the EFG principal axis V_zz^2H (along the deuterium bond), and the x-axis of the diffusion tensor. For ¹⁴N, where the principal component of the EFG tensor is perpendicular to the plane, T₁ is given by

2

where ϕ′ is the angle between V_xx^14N and the x-axis of the diffusion tensor.

The quadrupolar parameters used here for the ²H and ¹⁴N nuclei in FA⁺ are given in Table 1 (see also Figure S18). It is the quadrupolar coupling constant in the absence of motion that dictates the quadrupolar relaxation, and to measure this experimentally, all motion must be frozen out. However, in FAPbI₃, even at ∼100 K, the motion is not completely arrested (see Figure S4). To counter this, we measured the ²H quadrupolar couplings in d-FAI and d₄-FAI at 100 K (Figures S5 and S6) and use those values as proxies. The ¹⁴N quadrupolar coupling is challenging to measure due to the large width of the quadrupolar pattern. Therefore, we have used the value calculated from density functional theory by Kubicki et al. of 2.7 MHz.⁵³ We note that Mozur et al. calculated a C_Q of 2.8 MHz in FAPbBr₃,⁶¹ and we have calculated C_Q = 2.4 MHz in FACl; therefore, we estimate an uncertainty of ∼0.2 MHz.

Table 1. Nuclear Quadrupolar Tensor Parameters for FA⁺.

Nucleus	CQ (MHz)	η	ϕ (deg)
14N	2.7 ± 0.2	0.26	55.5
2H-CD	0.165 ± 0.005	0.16	90
2H ND2-trans	0.207 ± 0.005	0.17	–84.2
2H ND2-cis	0.207 ± 0.005	0.17	32.8

To extract the rotational rates about the three axes, the T₁ constants of all three deuterons and ¹⁴N must be combined; therefore, we measured these for perdeuterated d₅-FAPbI₃ (Figure 4a). As the cubic α-FAPbI₃ phase is the most relevant to photovoltaic applications, we focus on the temperature range 290–340 K. At each temperature, the four T₁ constants were combined to give D_x, D_y, and D_z using the above equations (Figure 4b). The resulting T₁ constants (dashed lines in Figure 4a) match the experimental data extremely well, lending confidence in the model. The determined rotational diffusion constants show an Arrhenius dependence above 305 K, below which deviation is observed due to the nearby first-order phase transition^32,66,67 (cf. Figure 3). Arrhenius analysis gives the activation energies (E_a) about each axis independently (Table 2). Using the relation D = 1/(6τ_c), the correlation time about each axis was calculated at 298 K (Table 2) from the data shown in Figure 4b; note that due to non-Arrhenius behavior near the phase transition, the correlation time was interpolated directly from the adjacent data, not taken from the Arrhenius analysis. The motion about all three axes is on the picosecond timescale, with the fastest rotation about the x-axis, as predicted by Fabini et al. using molecular dynamics simulations⁶¹ and in line with the relative moments of inertia I_x < I_y < I_z.(69)

Figure 4.

d₅-FAPbI₃ NMR relaxometry and rotational diffusion rates. (a) Three ²H and one ¹⁴N T₁ constants measured as a function of temperature in the cubic phase. Dashed lines indicate the fit to the rotational diffusion model. (b) Arrhenius plot of the rotational diffusion constants derived from (a). Dashed lines indicate fits to the Arrhenius behavior. Only the five highest temperature points were considered in the Arrhenius fits as the phase transition at ∼285 K causes deviation from Arrhenius behavior.

Table 2. Activation Energy (E_a) and Correlation Time at 298 K (τ_c) Determined Here for Rotation about Each Axis of FA⁺ in FAPbI₃ Using the Axis System Shown in Figure 1.

Axis	Ea (meV)	τc (ps), 298 K
x	62 ± 17	0.38 ± 0.08
y	130 ± 16	1.05 ± 0.24
z	99 ± 26	1.3 ± 0.5

FA⁺ Dynamics in Cs⁺-Alloyed Perovskite Compositions

Alloying FAPbI₃ with a small amount of Cs⁺ is the best strategy to date to suppress the detrimental processes of ion migration and light-induced phase segregation in mixed-halide perovskites, which limit device performance and lifetimes.^{25,58,70−74} In order to assess the changes in the FA⁺ dynamics on Cs⁺ substitution, d₅-FAPbI₃ was substituted with 5% Cs⁺ as confirmed by ¹³³Cs MAS NMR⁷⁵ (Figure S7). Compared to pristine FAPbI₃, we note that the phase transition temperature was raised to 300 K, consistent with prior work.⁶⁶ The ²H T₁ is shorter for the Cs⁺/FA⁺ composition around room temperature, indicating that the motion is slower due to the vicinity of the phase transition (Figures 4 and S27, Table S2). However, at higher temperatures, the T₁ time constants for FAPbI₃ and Cs_0.05FA_0.95PbI₃ are the same within error, suggesting that there is no significant change in the energy landscape for the FA⁺ rotation (Figure S26).

Further alloying with MA⁺ to yield a triple-cation composition²² does not significantly change the experimental FA⁺T₁ values (Figure 5). We conclude that FA⁺ dynamics are similar in the single-, double-, and triple-cation compositions.

Figure 5.

FA⁺ dynamics in Cs-alloyed perovskite compositions. Experimentally measured (a) ²H and (b) ¹⁴N T₁ as a function of inverse temperature. Dashed lines represent fitted T₁ values using the rotational diffusion model.

FA⁺ Dynamics in FA⁺/MA⁺ Perovskites

To explore the effect of MA⁺ doping on the cation dynamics directly, we synthesized deuterated FA_xMA_1–xPbI₃ perovskite compositions. First, we determine the FA⁺ dynamics. As shown in Figure 6a, all four deuterium signals are resolvable, allowing all the necessary ²H and ¹⁴N T₁ constants to be measured. The ¹⁴N sideband manifold of FA⁺ is broader than in pure FAPbI₃ (Figure S8) because MA⁺ substitution breaks the local cubic symmetry. The ¹⁴N sideband manifold of MA⁺ is narrower than that of FA⁺ due to the smaller C_Q of the former, but still broader than the isotropic signal observed in the cubic phase of pure MAPbI₃ due to the presence of FA⁺. As shown in Figure 6b,c, the ²H and ¹⁴N relaxation times for FA⁺ are largely unchanged as the composition is changed to include up to 40% MA⁺, indicating that the FA⁺ cation dynamics in the cubic phase are essentially unaltered by MA⁺ substitution (see Figures S24 and S25). Unlike for Cs⁺ doping, there is little change in the α ↔ β phase transition temperature for FAPbI₃ upon MA⁺ substitution.^60,76

Figure 6.

FA⁺ dynamics in FA_xMA_1–xPbI₃ perovskite compositions. (a) Single pulse solid-state ²H MAS NMR spectra of the cubic phase of FA_0.70MA_0.30PbI₃. The MA⁺ peak shows J-coupling of ¹J(²H–¹⁴N) = 8.25 Hz. The deconvolution of all four sites is shown below the spectrum. Experimentally measured (b) ²H and (c) ¹⁴N T₁ as a function of inverse temperature and as a function of x in FA_xMA_1–xPbI₃.

MA⁺ Dynamics in FA/MA Perovskites

Having analyzed the FA⁺ dynamics in mixed compositions, we now turn to MA⁺. Surprisingly, mechanosynthesized FA_0.7MA_0.3PbI₃ exhibits a maximum in the ²H T₁ at 310 K (Figure 7). As discussed above, the cations are rotating faster than the Larmor frequency , and this fast-motion limit is characterized by a T₁ that increases with increasing temperature. However, above 310 K, T₁ decreases. This intriguing effect is consistently observed across different batches and different FA⁺/MA⁺ compositions (Figures S9–S12).

Figure 7.

²H relaxation times (T₁) of MA⁺ in FA_xMA_1–xPbI₃ prepared using either mechanosynthesis or a solution-based high-purity protocol as described in the text.

T₁ maxima have previously been observed for ¹H, ¹³C, and ¹⁵N in pure MAPbI₃ and were ascribed to the contribution of spin–rotation relaxation, which becomes more efficient at high temperatures.⁵⁷ However, since the spin–rotational relaxation rate is proportional to the square of the nuclear magnetic moment, protons on the MA⁺ which are subject to the same rotation should relax = 42 times faster than deuterium spins.⁷⁷ Contrary to this, we observed that MA⁺¹H relaxation is slower than ²H relaxation, even after accounting for the equilibration of T₁ by fast spin-diffusion between MA⁺ and FA⁺ moieties (Figures S13 and S14). This clearly rules out an appreciable contribution of spin–rotation to the ²H T₁.

Alternatively, the T₁ maximum could be caused by a separate slow-motion process that becomes dominant above 310 K, since in the slow-motion regime, T₁ decreases with increasing temperature. This can be readily checked by testing the expected T₁ ∝ ω₀² field dependence of a slow-motion process.⁷⁸ However, the measured ²H T₁ constants at 21.1 and 11.7 T are essentially identical (Figure S15). Therefore, a slow-motion contribution to the ²H T₁ can also be ruled out.

To propose a mechanism for the ²H T₁ maximum, we consider that the measured ¹H relaxation times in solids are often limited by ¹H–¹H spin diffusion to relaxation sinks such as paramagnetic impurities, which cause rapid relaxation of nearby protons.^79,80 We find this to be the case for mechanosynthesized MAPbI₃, for which the ¹H T₁ can be increased by deuteration to suppress ¹H–¹H spin diffusion (Figure S14). Furthermore, above the T₁ maximum, the ²H T₁ varies somewhat between samples and over time (Figures S10–S12), suggesting the role of defects or impurities. Although ²H–²H spin diffusion is very slow (owing to the lower gyromagnetic ratio and lower concentration), physical diffusion of MA⁺ and/or H⁺ is well known in the literature and could potentially cause a similar effect. At higher temperatures, physical diffusion becomes faster, so that a deuteron would encounter a paramagnetic defect more quickly, on average, resulting in a shorter relaxation time. We note that this proposed mechanism would be field independent, because although the diffusion is slower than the Larmor frequency, it is not the spectral density of motion driving the relaxation, but rather it is the interaction with paramagnetic defects. To test this hypothesis, we prepared a high-purity sample by solution processing (see the Experimental Section in the Supporting Information) with a lower concentration of paramagnetic relaxation sinks as evidenced by the longer ¹H T₁ (Figure S17). At lower temperatures, the ²H T₁ constants of the two samples are the same (Figure 7), but the high-purity sample does not exhibit a T₁ maximum and the T₁ increases monotonically with temperature. This corroborates the proposed mechanism of physical diffusion to paramagnetic defects for the ²H T₁ maximum in the mechanosynthesized sample. See Note S1 for further discussion of this effect.

Having removed the unusual ²H T₁ maximum, the ²H T₁ of the high purity mixed FA⁺/MA⁺ sample is now induced purely by quadrupolar relaxation and can be used as a straightforward reporter of dynamics. We measured the ²H and ¹⁴N T₁ as a function of temperature and compared them with pristine MAPbI₃, as shown in Figure 8. Note that in MA⁺, the ¹⁴N T₁ only depends upon the motion of the C–N bond (caused by the perpendicular rotation illustrated in Figure 1b) as the EFG tensor is axially symmetric along the C–N bond and invariant to the C₃-rotation (Figure S18), whereas the ²H T₁ is induced by both parallel and perpendicular rotations.⁵⁴ Unlike the FA⁺ motion, which was unaffected by MA⁺ substitution, we observed that both the ²H T₁ and ¹⁴N T₁ of MA⁺ in FA_0.78MA_0.22PbI₃ are higher than in pristine MAPbI₃. In order to extract the rates about both axes, we applied the rotational diffusion model, using the equations of Bernard et al.⁵⁴ (see Table S1 and eqs S1, S2). As shown in Figure 8, the rotational diffusional model reproduces very well the experimental data. The activation energies from Arrhenius analysis and the correlation times at 298 K are shown in Table 3 for each axis. The parallel (C₃) rotation rate is unchanged for MA⁺ in the mixed sample and, as previously found by Bernard et al. for pure MAPbI₃, appears to be an essentially unactivated process. This shows that in both materials, the parallel rotation of MA⁺ is unhindered. Since the perpendicular rotation can be determined from the ¹⁴N T₁ alone (and the ¹⁴N relaxation is too fast to be affected by paramagnetic defects as observed above for ²H), this was measured for all the mechanosynthesized compositions (Table 3). We find that while the activation energy for the perpendicular rotation of MA⁺ is similar for pure MAPbI₃ and MA_xFA_1–xPbI₃, the motion is faster by a factor of ∼2 when MA⁺ is substituted into FAPbI₃, with τ_c (298 K) changing from 1.95 to ∼1.0 ps. Furthermore, the correlation time is found to be independent of the MA⁺ concentration up to 40% MA⁺.

Figure 8.

Experimentally measured (a) ²H and (b) ¹⁴N T₁ constants as a function of inverse temperature in MAPbI₃ and high-purity FA_0.78MA_0.22PbI₃. Dashed lines indicate fits to the rotational diffusion model.

Table 3. Dynamic Parameters of MA⁺ in MA_xFA_1–xPbI₃.

Material	Ea (meV)	τc (ps), 298 K
MAPbI3	⊥: 156 ± 7	⊥: 1.95 ± 0.04
	∥: ∼0	∥: 0.15 ± 0.04
FA0.78MA0.22PbI3(high-purity)	⊥: 141 ± 10	⊥: 1.06 ± 0.03
	∥: ∼0	∥: 0.16 ± 0.03
FA0.90MA0.10PbI3 (mechanosynthesis)		⊥: 0.96 ± 0.02
FA0.80MA0.20PbI3 (mechanosynthesis)		⊥: 0.98 ± 0.01
FA0.70MA0.30PbI3 (mechanosynthesis)		⊥: 0.99 ± 0.02
FA0.60MA0.40PbI3 (mechanosynthesis)		⊥: 1.10 ± 0.02

MA⁺ and GUA⁺ Dynamics in MA_xGUA_1–xPbI₃

Incorporation of the GUA⁺ ion in the MAPbI₃ perovskite has been shown to provide improved performance, specifically long charge-carrier lifetimes,⁸¹ high open-circuit voltage,^81,82 efficient charge transfer,⁸³ and increased stability.¹¹ This may be related to the absence of dipole moment in GUA⁺, which has been suggested computationally to minimize the hysteresis in perovskite solar cells caused by cation motion.⁸⁴

Here, we investigated the GUA⁺ and MA⁺ dynamics for the MA_0.75GUA_0.25PbI₃ composition. Although the room temperature phase of MAPbI₃ is tetragonal, substitution with the GUA⁺ ion has been shown to decrease the phase transition temperature from 326 to 280 K for 20% GUA⁺. However, despite the global cubic symmetry at room temperature, substitution with GUA⁺ breaks the local symmetry, resulting in orientational anisotropy for both MA⁺ and GUA⁺. This anisotropy can clearly be seen from the large residual quadrupolar coupling in the ²H and ¹⁴N spectra (Figures S19 and S20). Nevertheless, the signals from GUA⁺ and MA⁺ can be distinguished in both the ²H and ¹⁴N NMR spectra (Figure S21). Due to the considerable residual ¹⁴N quadrupolar coupling for GUA⁺, it is challenging to saturate the spectrum in order to measure the ¹⁴N T₁. Therefore, we used a long phase-modulated pulse to saturate the broad ¹⁴N pattern⁸⁵ (details in the Supporting Information).

Figure 9a shows the experimentally measured ²H and ¹⁴N T₁ relaxation times of MA⁺ as a function of temperature in the room temperature phase. The T₁ behavior is consistent with the expected MA⁺ motion in the fast motion limit. Applying the rotational diffusion model to this relaxation data, we found that, similar to mixed MA⁺/FA⁺ compositions, the MA⁺ parallel motion remains unactivated and at a similar rate upon GUA⁺ substitution as in the pure MA⁺ formulation (Table 4). The perpendicular motion also has a similar activation energy barrier as in MAPbI₃ (Table 4); however, again we found that the correlation time for the perpendicular motion at 298 K becomes faster with GUA⁺ doping, as observed for MA⁺ in the MA⁺/FA⁺ compositions.

Figure 9.

²H and ¹⁴N T₁ constants of (a) MA⁺ and (b) GUA⁺ as a function of inverse temperature in MA_0.75GUA_0.25PbI₃ at 20 kHz MAS. Dashed lines indicate fits to the rotational diffusion model.

Table 4. Dynamic Parameters of MA⁺ and GUA⁺ in MA_xGUA_1–xPbI₃.

Material	Ea (meV)	τc (ps), 298 K
MAPbI3	⊥: 156 ± 7	⊥: 1.95 ± 0.04
	∥: ∼0	∥: 0.15 ± 0.04
MA0.75GUA0.25PbI3	⊥: 168 ± 11	⊥: 1.32 ± 0.03
	∥: ∼0	∥: 0.25 ± 0.03
MA0.75GUA0.25PbI3	⊥: 121 ± 30	⊥: 1.27 ± 0.08
	∥: —	∥: 14 ± 8

Now we consider the motion of the guanidinium cation. GUA⁺ is characterized by two distinct principal axes (Figure 1d) owing to the C₃ symmetry. The ¹⁴N and ²H quadrupolar relaxation constants are determined by the rotation about these axes according to

3

4

where C_Q is the quadrupolar coupling constant in units of Hz, and η is the quadrupolar asymmetry. The GUA⁺ quadrupolar parameters used here are shown in Table 5.

Table 5. Nuclear Quadrupolar Tensor Parameters for GUA⁺.

Nucleus	CQ (MHz)	η
14Na	3.5 ± 0.3	0.4
2Hb	0.20 ± 0.01	0.14

^aAveraged from nuclear quadrupole resonance experiments on different guanidinium salts.⁸⁶

^bExperimental values for guanidinium chloride.⁸⁷

Figure 9b shows the ²H and ¹⁴N T₁ relaxation data along with fits to the rotational diffusion model of eqs 3 and 4. The resulting activation energies and correlation times at 298 K are shown in Table 4. We find that the perpendicular rotation is on the picosecond timescale, which is similar to the other cations considered above. The parallel motion is slower than the perpendicular motion, which is consistent with the larger moment of inertia. However, we note that the parallel motion determined by this model is extremely sensitive to the input parameters, in particular the experimentally measured ¹⁴N T₁ and the value of the static ¹⁴N C_Q, which are both associated with large uncertainties. As discussed above, the ¹⁴N spectrum of GUA⁺ has a very broad pattern, resulting in a low signal-to-noise ratio and difficulties in accurately measuring T₁. Moreover, the ¹⁴N static C_Q parameters are averaged from experimental nuclear quadrupole resonance studies for different guanidinium compounds, which could change to some degree in this sample. Consequently, there is a large uncertainty in the parallel correlation time at room temperature, and it was not possible to determine an activation energy for the parallel motion.

Discussion

In summary, we have experimentally determined the rotational rates about each axis in FA⁺, MA⁺, and GUA⁺ for different perovskite compositions (Figure 10).

Figure 10.

Comparison of experimentally measured rotational correlation times at room temperature for MA⁺, FA⁺, and GUA⁺ cations in the various iodoplumbate perovskite compositions studied in this work. The corresponding activation energies are shown in Figure S22.

Despite these observed differences in rotation about the internal axes, there is at least one component of rotation for all three cations on the picosecond timescale. This similar timescale of the motion is surprising given the differences in dipole moment (GUA⁺: 0 D, FA⁺: 0.2 D, and MA⁺: 2.3 D),⁴² effective ionic radius (GUA⁺: 278 pm, FA⁺: 253 pm, and MA⁺: 217 pm),^88,89 and lattice parameters (Table S3). The fastest motion we observe is the C₃ parallel rotation of MA⁺ (τ_c = 0.16 ± 0.03 ps), which is consistent with it having the smallest moment of inertia and the apparent absence of any energy barrier to rotation. The slowest motion is the C₃ parallel rotation of GUA⁺ (τ_c = 15 ± 8 ps), which is consistent with it having the largest moment of inertia, although we note the large error associated with this value.

Fabini et al.³² also noted the similarity of the rotational rates of MA⁺ and FA⁺, based on a single correlation time determined from ¹H NMR relaxometry. However, their values (8 and 7 ps for FA⁺ and MA⁺ at room temperature, respectively) were significantly larger than those determined using ²H and ¹⁴N relaxometry here (and by Bernard et al.⁵⁴ for MAPbI₃). We propose that while this reflects the same physical phenomenon, i.e., the similarity of the rotational dynamics, the numerical discrepancy may arise from considering a single correlation time or the challenges in applying BPP theory away from the T₁ minimum.⁹⁰

Here, we note that we have analyzed our data using an anisotropic rotational diffusion model, which corresponds to an isotropic continuum of possible cation orientations but with different rotational rates about each axis. This is in line with MD simulations of MA⁺ rotation in MAPbI₃.⁹¹ In contrast, Chen et al. reported that a C₃⊗C₄ jump model, combining threefold jumps about the parallel axis and fourfold jumps about the perpendicular axis (Figure 1b), was a better fit to their neutron scattering data than an isotropic rotational model⁴⁷ (a C₃⊗O model with octahedral perpendicular jumps also gave indistinguishable results in the cubic phase). Based on the completely averaged ²H and ¹⁴N quadrupolar tensors in the experimental spectra of MAPbI₃ in the cubic phase, the perpendicular motion must have cubic or higher symmetry, but it is not possible to distinguish between octahedral jumps or rotational diffusion on this basis. To compare, we modeled the ²H and ¹⁴N T₁ relaxation of MA⁺ in MAPbI₃ at 330 K using a jump model, as implemented in the Express software package.⁹² However, this yielded an unphysical correlation time for the C₃ jumps of 0.008 ps (see Note S2). Therefore, we conclude that the rotational diffusion model is a better fit to the experimental data. Nevertheless, at the current level of our analysis, we cannot discount a preferred orientation of the cations within the cage during rotational diffusion, if this preferred orientation has cubic symmetry.

To utilize ²H NMR relaxometry, (partially) deuterated cations were used in this work, and it is important to note that the greater moment of inertia will result in slower cation rotation.⁴⁶ This effect is the greatest for the C₃ (parallel) rotation of MA⁺, since the moment of inertia is entirely determined by the hydrogens, whereas the effect is significantly smaller for the perpendicular MA⁺ rotation and for the other cations. The increase in moment of inertia is also mitigated here by the use of relatively low deuteration, typically ∼20%. Changes in the phase transition temperatures⁹³ and coupling to the inorganic lattice^46,94 have been observed in other hybrid perovskites on deuteration; however, since here we focus on the dynamics in the cubic phase near room temperature, this is not expected to have a significant effect. In particular, we note that there is no observable difference in the ²H T₁ constants for two different levels of deuteration in MAPbI₃, to within the accuracy of the measurements (Figure S16), suggesting that any isotope effect is small. We believe that the trends we identify here are directly relevant to the fully protonated analogues used in photovoltaic devices.

Kubicki et al. previously reported that the MA⁺ and FA⁺ dynamics in FA_0.67MA_0.33PbI₃ are the same as in MAPbI₃ and FAPbI₃, respectively.⁵³ However, the correlation times deduced for MA⁺ were 2–3 orders of magnitude longer than those determined here and by Bernard et al.⁵⁴ We ascribe this discrepancy to difficulties in relating measured ¹⁴N linewidths to the motionally induced T₂ relaxation in their model-free analysis.

Considering the different compositions together, consistently it appears that cation substitution does not directly affect the cation dynamics. Both the FA⁺ and MA⁺ dynamics are unchanged throughout the mixed FA_xMA_1–xPbI₃ compositions studied, up to x = 40%. Similarly, the FA⁺ dynamics in FA⁺/Cs⁺ and FA⁺/MA⁺/Cs⁺ are unchanged from pure FAPbI₃, when sufficiently above the phase transition temperature. This implies that the cation dynamics (for these cations) are insensitive to both direct and indirect cation–cation interactions, perhaps due to the picosecond timescale of the rotation, as well as to minor changes in lattice parameters on substitution. The invariance of the FA⁺ dynamics across different compositions aligns with the unchanged favorable optoelectronic properties compared to pristine FAPbI₃.

In contrast, the cation dynamics are affected by the underlying symmetry of the inorganic lattice. The rotational rates of FA⁺ are suppressed in the vicinity of the cubic/tetragonal phase transition, and therefore, the increase in the phase transition temperature on Cs⁺ substitution causes changes in the room temperature dynamics.⁶⁶ Furthermore, we find that the perpendicular rotation of MA⁺ is faster at room temperature in cubic FA⁺/MA⁺ and MA⁺/GUA⁺ compositions, as compared to tetragonal MAPbI₃. Given that most device-relevant perovskite compositions possess this faster perpendicular rotation of MA⁺, we speculate that it might be linked with improved optoelectronic properties of the material.

Conclusions

We developed a protocol to experimentally determine the activation energies (E_a) and correlation times (τ_c) for rotation about each principal axis of the formamidinium ion (FA⁺) separately, by measuring all the ²H and ¹⁴N T₁ relaxation constants as a function of temperature and applying a rotational diffusional model.

We then extended this method to study state-of-the-art multi-cation FA⁺/Cs⁺, FA⁺/MA⁺, FA⁺/MA⁺/Cs⁺, and MA⁺/GUA⁺ compositions. We find that in all cases, there is at least one component of rotation for all three cations on the picosecond timescale at room temperature. MA⁺ also has a faster component (0.1 ps), and GUA⁺ also has a slower component (∼10 ps).

Notably, the observed motion is sensitive to the symmetry of the inorganic lattice but not directly to the degree of substitution. In particular, the FA⁺ dynamics were found to be unchanged in all samples, except for slower rotation at room temperature upon Cs⁺ substitution due to the higher phase-transition temperature. However, the perpendicular rotation of MA⁺ is approximately a factor of two faster at room temperature in cubic FA_xMA_1–xPbI₃, as compared to tetragonal MAPbI₃.

Surprisingly, we found that for mechanosynthesized FA_xMA_1–xPbI₃, the ²H relaxation of MA⁺ is dominated at high temperatures by physical diffusion to paramagnetic defects. This phenomenon could be used in future to study ion migration and the formation of paramagnetic defects. Importantly, high-purity solution-processed samples did not exhibit this effect.

Having demonstrated this relaxometry methodology for MA⁺, FA⁺, and GUA⁺, we note that it can be readily extended to understand the dynamics of other relevant cations used in hybrid perovskites, such as dimethylammonium (DMA⁺)⁹⁵⁻⁹⁷ and methylenediammonium (MDA⁺).^58,98 We further highlight that by understanding the FA⁺ cation dynamics, we were recently able to mitigate the detrimental ¹H relaxation by deuteration and enable dynamic nuclear polarization experiments that show the structure of a surface coating on a single thin film.⁹⁹ Overall, the complete picture of the cation dynamics presented here will help reveal the underlying causes of the beneficial optoelectronic properties seen in some hybrid perovskite formulations and thereby aid the design of perovskite solar cells with higher efficiencies in the future.

Data Availability Statement

All data presented here (raw NMR and XRD data) can be accessed at the following DOI: 10.5281/zenodo.7317848 and is available under the CC-BY-4.0 (Creative Commons Attribution-ShareAlike 4.0 International) license.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.2c10149.

• Experimental details, fitting analysis, and supplementary figures and notes (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.