Is There a Male-Breadwinner Norm? The Hazards of Inferring Preferences from Marriage Market Outcomes

Abstract

This paper argues that distributions of spousal earnings gaps provide no identifying information for the male breadwinner norm, nor such a norm’s consequences for gender inequality. First, we show that simple marital matching models—without norm-related assumptions—closely replicate U.S. distributions of wife-husband earnings gaps. Second, we show that the discontinuity in this distribution as wives start to out-earn husbands reflects not breadwinner norms, but rather a point mass of equal-earning couples. We conclude by arguing that the point mass may also threaten other tests of the male breadwinner hypothesis, and proposing several robustness checks that future research should utilize.

I. Introduction

Married women tend to be shorter, younger, and lower-earning than their husbands. Do these patterns reflect efficient sorting of people into couples? Or, are they driven by societal practices that may inhibit economic efficiency? Social scientists analyzing these questions have often used observed matching patterns to infer social norms about what constitutes an ideal marriage. Some studies identify a “male taller” norm from the fact that fewer wives are taller than their husbands than would be predicted by random sorting (e.g. Gillis and Avis 1980; Stulp et al. 2013; Belot and Fidrmuc 2010; Sohn 2015). Others evaluate the “male breadwinner” hypothesis—which posits that a socially acceptable marriage is one in which the husband is the main income earner—by applying a similar approach to distributions of spousal earnings differences (e.g. Winkler 1998; Brennan, Barnett and Gareis 2001; Raley, Mattingly and Bianchi 2006).

Recently, Bertrand, Kamenica and Pan (2015) proposed a novel assessment of the male breadwinner hypothesis, based on analysis of spouses who earn close to equal amounts. Bertrand, Kamenica and Pan (hereafter BKP) examined the U.S. distribution of the share of total spousal income earned by the wife. They reported a cliff-like drop—a discontinuity—in this distribution just beyond 0.5: the point at which wife and husband earn the same amount. BKP asserted that “standard economic models of the marriage market cannot account for this pattern” (p. 571). Instead, they argued that the data reflect the presence of a male breadwinner norm: i.e. a prevailing social norm that induces couples to avoid a situation in which a wife out-earns her husband. BKP’s discontinuity result has become a cornerstone reference in the economics literature on marriage: as of July 15, 2020, the work had been cited nearly 700 times.

In this paper, we offer a critique on the practice of inferring social norms regarding an attribute from that attribute’s observed distribution in marriage. We critique both the standard approach of comparing the observed distribution to a hypothetical one based on random sorting, as well as BKP’s test for a discontinuity across the equal-attribute threshold. We argue that little, if anything, can be learned about social norms from these approaches.

Our critique of the standard approach rests on the classic economic model of marriage introduced by Becker (1973). We show that this model generates matching patterns that suggest social norms of husbands being taller and earning more than their wives, even when individuals prefer the reverse. Taking the example of height, we show that a broad class of loss functions for deviation from the social norm generates positive assortative matching on height in equilibrium, regardless of what the norm dictates about the ideal spousal height difference (including the absence of any norm). Positive assortative matching together with the prevailing gender gap in height results in an equilibrium in which few husbands are shorter than their wives—even if husbands strictly prefer to be shorter than their wives. In an empirical application to spousal earnings data drawn from the 2000 U.S. Census, we show that two different assortative matching models—neither of which imposes explicit preferences for husbands to out-earn wives—succeed in reproducing the observed (and highly skewed) distribution of wives’ relative income. These exercises illustrate that a naive interpretation of marital matching patterns may produce incorrect inferences about underlying preferences.

BKP’s “pointwise” approach obviates this critique. That is, although the Beckerian marriage model broadly matches the observed distribution of wives’ relative income, it fails to generate the discontinuous cliff across the 0.5 threshold. This appears to lend support to BKP’s conclusion that a marriage model featuring a male breadwinner norm is necessary to explain the data.

However, we show that BKP’s approach does not hold up to econometric scrutiny. One feature of U.S. spousal earnings data—fully acknowledged and reported by BKP—is the presence of a small share of couples earning exactly identical incomes. This generates a point mass in the distribution of the wives’ relative income at exactly 0.5. BKP’s main result is based on testing for a discontinuity just to the right of 0.5—consistent with testing for a social norm that the wife should not earn strictly more than her husband. Using the same data source,¹ we first replicate BKP’s result. Then, when we test for a discontinuity just to the left of 0.5, we find evidence of a sharp gain in probability mass. This sharp gain in mass as one moves from left of 0.5 to 0.5 could be interpreted as evidence for a social norm that the wife should not earn strictly less than her husband. Thus, the data appear consistent with two nearly opposite social norms.

We show that the point mass of equal-earning couples is responsible for these apparently contradictory results: omitting these couples eliminates the estimated discontinuities. Moreover, we argue that the point mass does not likely reflect male breadwinner norms. Instead, it could be generated by small search frictions in the marriage market, or when the gains from marriage for some potential couples are driven by a joint business venture. In sum, we submit that no feature of the observed distribution of wives’ relative income, broad or pointwise, offers definitive information about the male breadwinner norm.

Considering these observations, what can be learned about male breadwinner norms and their effects on household behavior? We conclude the paper with a discussion on this subject. Instead of an approach based solely on spousal earnings distributions, we favor an approach that considers the relationship between spousal earnings and other household variables. BKP explore this approach (to the authors’ credit): additional analyses in their paper found that, all else constant, when a wife out-earned her husband she became likelier to work fewer hours in the future and to perform more household chores. Additionally, the marriage became likelier to end in divorce. However, we show that our critique of BKP’s relative income discontinuity may also apply to these analyses. We propose some robustness checks to mitigate this possibility. Ultimately, we recommend that future evaluations of the male breadwinner hypothesis combine the pointwise evaluation (augmented with our robustness checks) with the more “holistic” evaluations undertaken by sociologists. We briefly review this literature in the next section before returning to it in our concluding synthesis.

II. Related Literature

Our study is related to several pieces of literature in economics and sociology. Our theoretical critique reprises a common theme within the literature on matching models, which is that matching patterns alone are insufficient to identify marital preferences (e.g. Echenique et al. 2013; Chiappori and Salanié 2016). Identification of how observed individual attributes affect the marital surplus has been eased by a class of structural models that impose restrictive assumptions on unobserved tastes (e.g. Choo and Siow 2006; Galichon and Salanié 2017; Dupuy and Galichon 2014; Chiappori, Salanié and Weiss 2017). With these assumptions in place, marital sorting patterns become sufficient to identify returns to individual attributes in marriage. We instead analyze how spousal attribute gaps affect the marital surplus. When social norms dictate an ideal attribute gap, we show that individual attributes exhibit strong complementarity (and hence positive assortativeness) within marriage, regardless of what is the ideal attribute gap. Thus, the strong degrees of positive assortative matching on height, earnings and age that exist in the data appear particularly uninformative about male-taller, male-breadwinner or male-older norms.

Our empirical analysis of spousal earnings data integrates two strands of work on the earnings patterns of dual-earning couples. Raley, Mattingly and Bianchi (2006) documented that as the earnings distributions of women and men converged between 1970 and 2001, the share of wives earning between 40 and 60 percent of household income rose considerably. (See also Oppenheimer 1997, Winkler 1998.) This development is consistent with our positive assortative matching models, which emphasize the importance of prevailing earnings distributions, rather than social norms, in determining the distribution of wives’ relative income. Regarding dual-earning couples who earn close to the same amount, two contemporary studies also probe the robustness of BKP’s discontinuity result. Hederos and Stenberg (2019) found, in Swedish administrative income data, that the existence of a similar point mass of equal-earning couples also explained the discontinuity result. Zinovyeva and Tverdostup (2018) found the point mass in Finnish data and argued that it resulted from a tendency of spouses to start a business together or co-work at the same establishment. The earlier studies of Winkler, McBride and Andrews (2005) and Winslow-Bowe (2006) reported that many female-breadwinner households in the U.S. are transitory rather than persistent arrangements: wives who slightly out-earned their husbands in one year tended not to do so over the long-run.

As mentioned above, a rich literature in sociology has also sought to evaluate the male breadwinner hypothesis. In contrast to the pointwise analysis of BKP—i.e. an analysis of variation in marital outcomes exactly at the equal-earning threshold—this literature holistically analyzes the joint distribution of spousal earnings, divorce hazards and time allocation. Moreover, in contrast to BKP,² this literature has not documented a consistently gendered relationship between male breadwinner status and these outcomes. For example, Sayer and Bianchi (2000) found a positive relationship between wives’ relative incomes and divorce hazards in U.S. data, but also that this relationship disappeared when controls for marital quality were added. This pattern may indicate reverse causality: in anticipation of divorce, wives in unhappy marriages may invest more in their earnings potential (e.g. Johnson and Skinner 1986). Killewald (2016) found husbands’ full-time employment status (in all marriage cohorts considered) and wives’ contribution to housework (only in marriages formed before 1975) to be strong negative predictors of divorce, with earnings playing no role in divorce conditional on time use variables. Schwartz and Gonalons-Pons (2016) found a slight negative relationship between the wife’s relative income and the divorce hazard in marriages formed after 1989, and only a marginally significant positive relationship for 1970s and 80s marital cohorts.

Regarding time allocation, Bianchi et al. (2000) found a negative linear relationship between the wife’s relative income and her housework time (as well as the gender gap in housework) in U.S. data. Bittman et al. (2003) found a U-shaped relationship in Australia: after breaching the equal-earnings threshold, further increases in the wife’s relative income translated into greater gender gaps in housework. Subsequent work, however, critiqued these findings: Gupta (2007) and Killewald and Gough (2010) found strong (and non-linear) relationships between wives’ absolute income and their time spent in housework, and no significant relationship between relative income and housework after controlling carefully for absolute income. More recent literature (Raley, Mattingly and Bianchi 2012; Hook 2017; Horne et al. 2018) also failed to find a significant relationship between a wife’s relative income and her housework time (in absolute terms as well as relative to her husband). Perhaps the clearest prima facie evidence of normative behavior comes from the fact that after conditioning on earnings and work time, wives perform more housework on average than husbands.³ Some patterns in the data also suggest that husbands reduce (or at least fail to increase) their housework time as they become more economically dependent on their wives (e.g. Brines 1994; Chesley and Flood 2017).

III. Applying Becker’s Theory of Marriage to the Study of Social Norms

We found our study of social norms on Gary Becker’s economic theory of marriage (Becker 1973; 1981). To start, consider a man m and a woman f who are considering marriage. We assume they marry if and if only if it makes both better off compared to alternatives. Denote the “output” of the marriage by Z_mf. Assume output can be divided

$$Z_{mf}=m_{mf}+f_{mf},$$ (1)

where m_mf indicates what man m consumes when married to woman f. That is, it is possible for men to make offers to potential wives (and women to make offers to potential husbands) of some division of output.

Suppose there are multiple men and multiple women considering marriage. Becker showed that a competitive equilibrium in this marriage market will be the set of assignments that maximizes the sum of output across all marriages. The proof relies on a standard argument about the Pareto optimality of competitive markets. If an existing set of pairings does not maximize total output, then there must exist at least two couples who could switch partners and increase total output. Because output is transferable, it is possible to distribute the total output gains from the switch such that everyone is made better off.

Becker applied this result to the case of sorting on some trait A, where we will consider woman f to have a trait value A_f and man m to have trait value A_m. We characterize marital output as a function of the values of A for each partner: Z_mf = Z(A_m,A_f). Becker showed that the marriage market equilibrium will consist of positive assortative matching on A if

$$\frac{{\partial }^{2}Z\left(A_m,A_f\right)}{\partial A_m\partial A_f}>0$$ (2)

and negative assortative matching if the cross-partial is negative. If, for example, having a better-educated husband raises the impact of the wife’s education on marital output, then we will tend to see positive assortative matching on education. We draw on this well-known result below.

A. Illustrative Model of Sorting on Height

We build up to our key point with a very simple model of marital sorting on height. Denote female height by H_f and male height by H_m. Suppose there are two women: f₁ is 60 inches tall and f₂ is 66 inches tall. There are two men: m₁ is 66 inches tall and m₂ is 72 inches tall. Thus, there are two possible pairings: (f₁m₁,f₂m₂), which is positive assortative matching on height, and (f₁m₂,f₂m₁), which is negative assortative matching on height.

Assume that people get utility from their individual consumption and some bonus that comes from being married. The gains from marriage take the very simple form of some bonus K (representing, say, economies of scale in consumption or benefits of household public goods) that is offset by a quadratic loss in the deviation of the given spousal height difference from the social norm.

Consider three alternative social norms: a 6^” male-taller norm, an equal-heights norm, and a 6^” female-taller norm:

$$Z\left(H_m,H_f\right)=K-{\left(H_m-H_f-6\right)}^2[\text{Male}\text{taller}\text{norm}]$$

$$Z\left(H_m,H_f\right)=K-{\left(H_m-H_f\right)}^2[\text{Equal}\text{heights}\text{norm}]$$

$$Z\left(H_m,H_f\right)=K-{\left(H_f-H_m-6\right)}^2[\text{Female}\text{taller}\text{norm}]$$

It is trivial to show that a 6^” male-taller norm will give rise to positive assortative matching on height in equilibrium, as this yields two marriages in perfect compliance with the norm. Notice, however, that positive assortative matching will also prevail in the case of an equal-heights norm. This is because, even though the alternate sorting yields one couple in perfect compliance with the norm (the short man and tall woman), the other couple has a height difference of 12^” and produces a total loss of 144. The positive sorting assignment yields a lower total loss of 36 + 36 = 72, since each couple is 6^” from the ideal height difference. Therefore, positive sorting is the competitive equilibrium.⁴ The same is true in the case of a 6^” female-taller norm: negative sorting creates a total loss of 36 + 324 = 360, while positive sorting creates a total loss of 144 + 144 = 288. Hence, all 3 social norms are consistent with the same competitive equilibrium: positive assortative matching.

B. A More General Model of Marital Matching

This non-identifiability of social norms regarding height generalizes to cases with large numbers of women and men covering a broad range of heights.

Proposition 1.

Consider a population with N men and N women, and assume the following marital surplus function:

$$Z\left(H_m,H_f\right)=K-\lambda \left(g_{mf}\right)$$ (3)

where the male-female height gap g_mf = H_m − H_f. If λ is (strictly) convex in g, then strict positive sorting on height is a (the unique) marriage market equilibrium.

Proof.

Note that $\frac{{\partial }^{2}Z\left(H_m,H_f\right)}{\partial H_m\partial H_f}={\lambda }^{\prime \prime }(g)>0$ by strict convexity of λ. Thus the payoff function satisfies condition (2), and so strict positive sorting on height is the unique marriage market equilibrium. If λ is merely convex, then, starting from strict positive sorting, no exchanges of partners can be made that strictly increase total marital output. Hence, such a sorting is an equilibrium.□

This result establishes that positive sorting on height can be consistent with both male-taller and female-taller norms, as well without any explicit norms at all. Whatever the ideal spousal height gap may be, convex losses for deviating from the ideal implies that spousal heights are complementary in the marital output function, creating a tendency for positive sorting to arise in equilibrium. The next result illustrates that if there is a gender gap in the attribute distributions, as is the case for height and for earnings, the equilibrium implied by positive sorting is highly skewed in nature.

Proposition 2.

Consider a population with N men and N women, and assume the marital surplus function is given by Equation 3. If the male height distribution exhibits first order stochastic dominance (FOSD) over the female distribution,⁵ then there exists a marriage market equilibrium in which no wives are taller than their husbands. Moreover, if the loss function exhibits strict convexity, this equilibrium is unique.

Proof.

By Proposition 1, a marriage market equilibrium characterized by strict positive sorting on height exists, and is unique if the loss function is strictly convex in the height gap. In a strict positive sorting equilibrium, the spouses of each couple have heights of identical rank in their respective distributions. Therefore, by the FOSD assumption, the husband is taller than the wife in each couple.□

These results have important implications for the study of social norms in marriage. To the extent that society has preferences about the ideal height, age or earnings gap between spouses, competitive forces operating within the marriage market will push the equilibrium toward perfect rank-order sorting on these traits. And if men in the marriage market tend to be taller, older or higher-earning than comparable women, positive assortative matching leads to a situation in which the large majority of wives are shorter, younger or lower-earning than their husband—suggesting a male-taller, male-older or male-breadwinner norm when one may not exist.⁶

It is important to note that the results depend on the convexity of the loss function. With this structure, the competitive equilibrium is not generally the one which maximizes the number of couples in perfect compliance with the social norm—–it is instead one in which many couples may deviate from the norm by small amounts, but few couples deviate by large amounts. Note that increasing marginal losses from deviating from the social norm is isomorphic to diminishing marginal returns from greater adherence to the social norm. Social welfare is thus maximized when this commodity (level of adherence to the norm), is distributed as equally as possible in the population. Such a situation is realized by positive assortative matching.

Note also that the convex structure nests “kinked” loss functions (Fisman et al. 2006). For example, a structure in which households are indifferent when the husband is taller (shorter) than the wife, but face a loss increasing in the amount by which the husband is shorter (taller) than the wife, is also consistent with strict positive assortative matching on height in equilibrium. (Although, because kinked loss functions are not necessarily strictly convex, such an equilibrium may not be unique).

C. Extensions of the Model

Propositions 1 and 2 predict an equilibrium in which no wives are taller than their husbands (or, analogously, no wives earn more than their husbands). This result is clearly counterfactual. Several factors are presumably at work in actual marriage markets—–couples do not match on a single trait, there are search frictions, there is not perfectly transferable utility, etc. We consider some of these issues below.

Sorting on multiple attributes.

If the economic gains to marriage depend on attributes other than height, then the distribution of height gaps in marriage will clearly depend on how these attributes are correlated with height in the population.

As an example, suppose there is an additional attribute X that enters the marital output function:

$$Z_{mf}=Z\left(X_m,X_f,H_m,H_f\right)=K\left(X_m,X_f\right)-\lambda \left(g_{mf}\right)$$ (4)

Suppose that X is positively correlated with H and that $\frac{{\partial }^{2}Z\left(X_m,X_f\right)}{\partial X_m\partial X_f}>0$. Thus, K satisfies sufficient condition (2) for positive assortative matching on X in equilibrium, while λ generates positive assortative matching on H by Proposition 1. It is impossible to know without further assumptions whether the prevailing equilibrium will consist of positive sorting on X, on H, or on some function of X and H. However, given that X and H are positively correlated in the population, some degree of positive sorting on H must exist in equilibrium. Therefore, given a significant gender gap in H, this model still predicts that an equilibrium in which few wives are taller than their husbands is consistent with a variety of social preferences over the spousal height gap. There could also be no social preferences regarding height whatsoever—–λ could be constant—–yet the positive correlation between X and H would still lead to an equilibrium making it look as if a male-taller norm exists.⁷

The work of Mansour and McKinnish (2014) illustrates subtle sorting patterns when individuals care about multiple attributes. Mansour and McKinnish observed that couples in which the husband is significantly older than the wife tend to be negatively selected on education and earning potential. They argued that this pattern results from the fact that higher-earning individuals tend to locate in marriage markets with more similarlyaged individuals. That is, the preponderance of “husband-significantly-older” couples among relatively low-earning individuals may have little to do with a husband-significantly-older norm in this population.

Non-transferable marital surplus.

The Becker model assumes that the gains from marriage are fully transferable between spouses. In this setup, the allocation of marriages and the transfers are determined in equilibrium as prospective partners make binding agreements in the marriage market. If the division of the marital surplus cannot be negotiated in the marriage market, the market clears on the basis of what prospective partners expect to obtain from bargaining within marriage.⁸ Pollak (2019) notes that such a setup is consistent with using the Gale-Shapley framework (Gale and Shapley 1962) rather than Becker’s framework to analyze the marital equilibrium.

When the marital surplus is fully non-transferable, equilibrium marital outcomes may have the potential to offer some identifying information about the underlying social norm. For example, if the ideal is for husbands to be two inches taller than wives, we might expect to see a point mass at two inches in the height gap distribution. Though such an allocation would likely result in some very tall men matching with some very short women, the impossibility of credible side payments prevents these individuals from attracting more suitable partners.

This situation strikes us as unrealistic. For example, consider the man who is just taller than the male partner of the tallest woman. This man would be forced to match with one of the shortest women and realize a very low marital surplus. He stands to gain a tremendous amount from matching with the tallest woman, and the total marital surplus of her marriage would shrink only very slightly from matching with him. Thus, even a modest degree of credible divisibility of the marital surplus might inspire a reshuffling of partners in this context.⁹ The resulting equilibrium would blend elements of positive sorting with a cluster of couples with height gaps near 2 inches. Its exact nature would depend not just on preferences but on the prevailing height distributions and market size (i.e. the availability of close partner substitutes), the efficacy of the transfer technology, and the presence of search frictions in the market.

D. Application to Analysis of Spousal Height Differences

Two recent studies of spousal height differences illustrate our point about the difficulty of inferring preferences from equilibrium matches. Stulp et al. (2013) analyzed the distribution of height differences among couples in the United Kingdom’s Millennium Cohort Study. They compared the actual distribution of height differences to hypothetical distributions based on random matching, drawing several inferences based on this comparison. Table 1 presents their data, divided into bins of 5 cm (2 inch) height differences. A key observation is that the actual distribution has fewer women who are taller than their husbands than would occur through random matching. The authors argue that this is consistent with a “male-taller” norm. They also interpret the data as supporting a “male-not-too-tall” norm, since there are fewer men who are more than 25 cm taller than their wives than would occur through random matching.

Table 1.

Spousal Height Differences, UK Millennium Cohort Study

Husband height minus wife height (cm)	Proportion in:		Ratio of actual to random
	actual distribution	random distribution
< −10	0.6%	1.3%	0.47
−10 to −5	1.5%	2.6%	0.58
−5 to 0	1.9%	2.5%	0.77
0 to 5	8.5%	8.7%	0.97
5 to 10	16.3%	14.5%	1.12
10 to 15	21.3%	19.2%	1.11
15 to 20	20.7%	19.7%	1.05
20 to 25	15.3%	15.8%	0.97
25 to 30	8.8%	9.4%	0.94
30 to 35	3.7%	4.2%	0.87
> 35	1.4%	2.1%	0.66

Notes: Data taken from Table 1 of Stulp et al. (2013).

It is easy to see that the data are consistent with other social norms as well. These include what might be called a “wife-not-too-short” norm or a “heights-not-too-different” norm. In fact, a better way to describe the norm implied by Table 1 might be a norm to keep the difference in heights between husbands and wives close to the overall average difference in heights between men and women in the population. The three bins closest to the actual average height difference of 14.1 cm (5.5 inches) are the bins that occur more frequently in the actual distribution than in the random matching distribution. The bins with the height differences farthest from 14.1 cm are the bins that occur with the lowest frequency relative to random matching. Sohn (2015) found similar sorting patterns in Indonesia: spousal height gaps closest to the mean gap occurred more frequently in the observed data than in hypothetical random sortings, while those furthest away from the mean occurred less frequently. Notice that this is exactly what will happen if there is a tendency for positive assortative matching on height, as this pushes the equilibrium toward an outcome in which the height gap is uniform across all marriages. Thus, it is likely that a wide variety of underlying preferences could produce these observed distributions of spousal height gaps.

IV. The Skewed Distribution of Spousal Earnings Differences in the U.S. does not Imply a Male Breadwinner Norm

We apply the above insights to an investigation of earnings differences between spouses, where, like height, a persistent gender gap also exists. As gender gaps in wages and hours worked have shrunk throughout the late 20th century, the proportion of wives earning similar to or more than their husbands has risen (Winkler 1998; Raley, Mattingly and Bianchi 2006). However, this proportion remains small (Bertrand, Kamenica and Pan 2015), and the gender gap in earnings remains substantial (Blau and Kahn 2017). A tendency for positive sorting combined with this gender gap would lead to a skewed marriage market equilibrium in which most husbands out-earn their wives—even if there is no social norm dictating this outcome.

Our approach is to simulate marriage market equilibria using observed earnings in U.S. Census data and simple matching processes. Following the literature on dual-earning couples, we summarize spousal earnings differences by plotting the distribution of the share of the couple’s total earnings that was earned by the wife—or the wife’s relative income. Thus, 0.01 indicates that the wife earned 1 percent of the couple’s total earnings, and 1.0 indicates that she earned all of it. 0.5 represents a couple in which wife and husband earned equal amounts. These exercises illustrate that simple matching models, which do not include any specific preference about the husband earning more than the wife, can reproduce the observed distribution of wives’ relative income.

A. Empirical distributions of spousal earnings differences

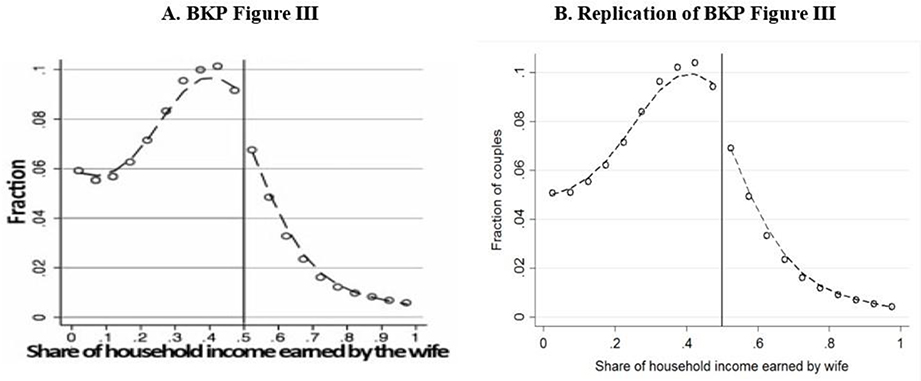
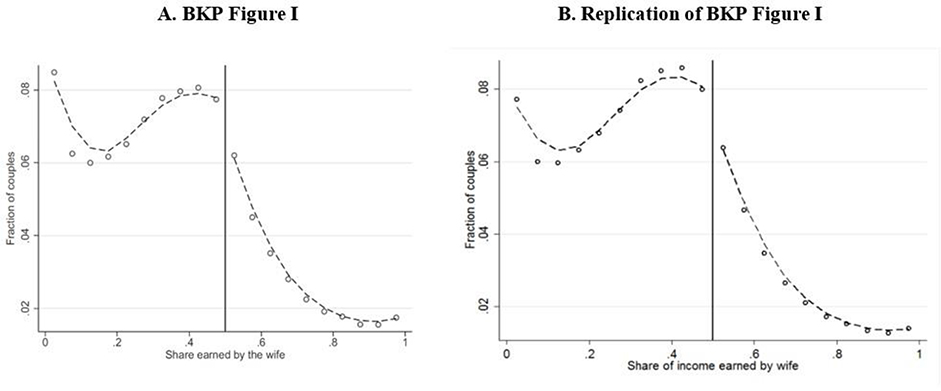
We begin with a sample of men and women drawn from the 5 percent sample of the 2000 U.S. Census (Ruggles et al. 2015). Following BKP, we restrict the sample to couples ages 18–65 and process earned income variables following the procedure outlined in that paper’s main text and appendix. We keep only couples in which both spouses report positive earnings. Figure 1 displays two 20-bin histograms of the distribution of the share of total earnings earned by the wife: the one published in BKP and our replication. As in BKP, we apply a local linear smoother to the histogram bins, allowing for a break in the smoothed distribution at 0.5. The two distributions are almost identical, and both display a substantial reduction in probability mass to the right of 0.5.¹⁰

Figure 1. Distributions of Gender Relative Income in the 2000 U.S. Census.

Notes: Graph A is a screenshot of Figure III of Bertrand, Kamenica and Pan (2015). Graph B is our replication. Each graph is based on a sample of dual-earning married couples in which both husband and wife are between 18 and 65 years of age. Each graph plots a 20-bin histogram of the distribution, across couples, of the share of total household income that was earned by the wife. The dashed lines depict the lowess smoother applied to each histogram, allowing for a break at 0.5.

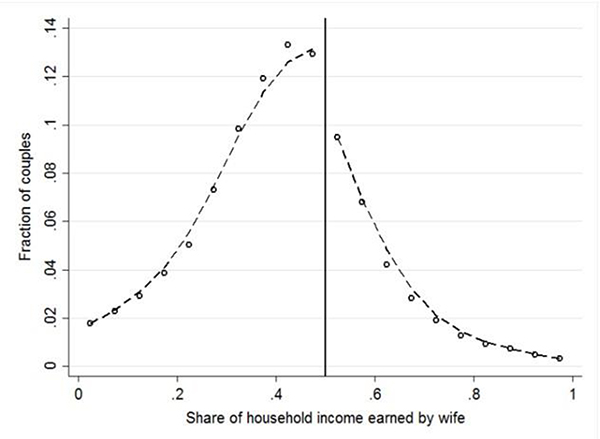
Our simulation exercises restrict the sample to relatively young couples (aged 18–40) without children. Our final sample consists of 109,569 dual-earning couples. Figure 2 plots the sample distribution of the wife’s share of total earnings. The main difference between this distribution and that in Figure 1 is that there is less mass below 0.25, which likely reflects the impact of specialization after childbearing.¹¹ Our simple simulations are not set up to handle the dynamic considerations of fertility and its effect on the wife’s labor supply and earning potential. Nonetheless, imposing this sample restriction does not change the fact that most of the distribution lies to the left of 50 percent (where the wife earns less than the husband), and the probability mass drops sharply as one moves to the right of 50 percent. These are the stylized facts we attempt to replicate in the following exercises.

Figure 2. Distribution of Gender Relative Income in the 2000 U.S. Census: Couples aged 18–40 without children.

Notes: The sample includes dual-earning married couples who do not have children and where both husband and wife are between 18 and 40 years of age. The figure plots a 20-bin histogram of the distribution, across couples, of the share of total household income that was earned by the wife. The dashed lines depict the lowess smoother applied to the histogram, allowing for a break at 0.5.

B. Simulated Distributions

Random matching of couples.

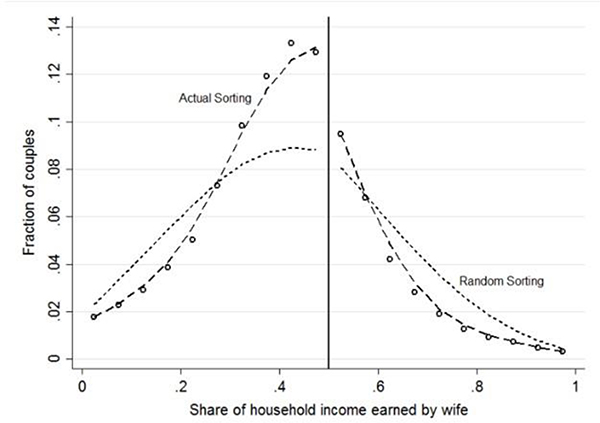
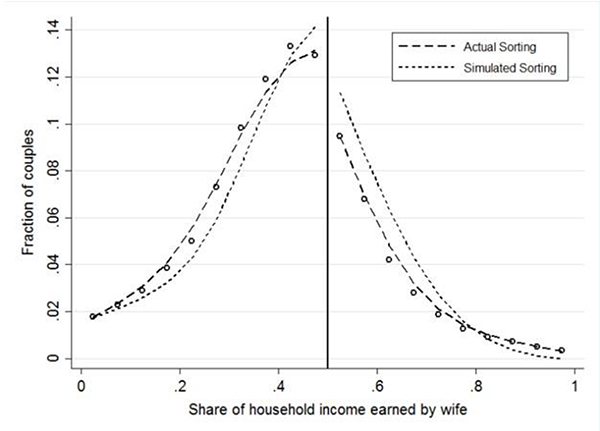
Figure 3 displays a smoothed distribution of the wife’s share of total earnings based on random matching, again allowing for a break at 0.50, overlaid on the observed distribution. Like the observed distribution, the distribution generated by random matching contains a mode around 0.42 and a drop-off in mass to the right of that point. Moreover, significantly fewer wives slightly out-earn their husbands than vice versa; the point of equal earnings (0.50) corresponds to the 70th percentile of the distribution. This benchmark exercise demonstrates that the prevailing male and female earnings distributions exert a strong influence on spousal earnings differences.

Figure 3. Distributions of Gender Relative Income in the 2000 U.S. Census: Actual and Random Sorting.

Notes: The sample is the same as in Figure 2. The figure plots a 20-bin histogram of the actual distribution of the wife’s share of total spousal earnings (“Actual Sorting”), and a 20-bin histogram of a simulated distribution based on random sorting of couples (“Random Sorting”). The dashed lines represent the lowess smoother applied to each histogram on either side of 0.5.

Notice that Figure 3 follows a similar pattern to the distribution of height differences shown in Table 1. The bins in Figure 3 that occur more frequently in the actual distribution than in the distribution with random matching are those closest to 0.42, the average wife’s share of total earnings. (Although Figure 3 is in shares rather than differences, the pattern would look similar if plotted in absolute or proportional income differences.) A key feature is that the actual distribution is pushed toward the mean earnings difference and away from extremes, exactly as in our simple theoretical examples.

Positive assortative matching on potential earnings.

We take male and female earnings as observed in our sample (denoted as $Y_i^m$ for male i and $Y_i^f$ for female i). We create couples by rank-order-matching individuals not according to observed earnings, but rather observed earnings perturbed with noise. That is, for each individual i of gender g we assign

$$W_i^g=Y_i^g+u_i,$$ (5)

where u is normally distributed white noise, and pair up males and females according to their ranks of W. This is consistent with at least two interpretations. One interpretation is that couples are perfectly sorted on permanent earning potential and the white noise represents transitory earnings shocks realized after marriage. A second is that men and women care about other characteristics as well as earnings, or that assortative matching on earnings is imperfect, for example due to the presence of search frictions. Under the latter interpretation, equilibrium sorting on observed earnings plus noise is the reduced form of a more complicated matching process.

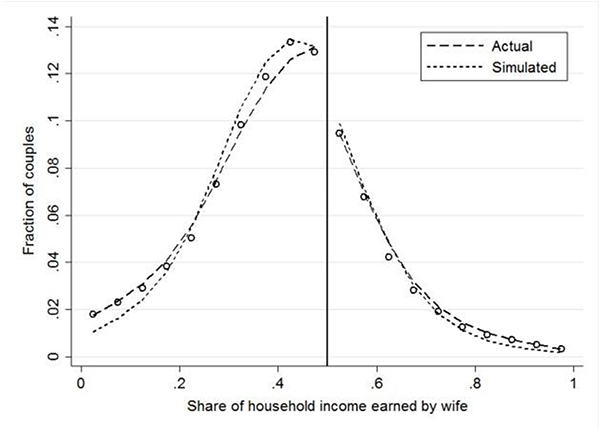
Figure 4 displays the distribution of the wife’s share of total earnings, simulated from this simple model, overlaid on the actual distribution.¹² The simulated distribution is very similar to the actual distribution: it exhibits a sharp drop in mass across the 50 percent threshold and contains few couples in which the wife out-earns her husband.¹³ Thus, given the gender gap in earnings distributions, the observed distribution of spousal earnings differences is largely consistent with positive assortative matching on earnings. As the previous section indicates, this matching is consistent with a wide variety of underlying preferences. It could be based on a desire for equality in spousal earnings, a preference for wives to earn more than their husbands, or economic gains from marriage related to household public goods¹⁴ (i.e. with no explicit preference for equal or unequal spousal earnings).

Figure 4. Distributions of Gender Relative Income in the 2000 U.S. Census: Actual Sorting and Simulated Sorting with Exogenous Earnings.

Notes: The sample is the same as in Figure 2. The figure plots a 20-bin histogram of the actual distribution of the wife’s share of total spousal earnings (“Actual Sorting”), and a 20-bin histogram of a simulated distribution based on assortative matching of couples on observed income plus noise (“Simulated Sorting”). See Section IV.B for further detail on the simulation. The dashed lines represent the lowess smoother applied to each histogram on either side of 0.5.

Positive assortative matching on potential earnings with endogenous labor supply.

One shortcoming of the previous exercise is that it treats the observed distributions of men’s and women’s earnings as fixed attributes, determined outside of the household. Yet, a literature dating back to Becker (1981) argues that household incentives, such as gains from specialization, influence spousal labor supply choices. Moreover, BKP argue that social norms themselves may influence how many hours a wife chooses to work in the market: if she is at risk of outearning her husband in a full-time job, she may work fewer hours. To address this shortcoming, we endogenize the wife’s earnings via a simple labor supply model—that does not assume an explicit male breadwinner norm—and explore the model’s predictions about the distribution of spousal earnings differences.

We assume that, for a given male m and female f, the match output function is given by

$$Z_{mf}=Z\left(Y_m,Y_f,P_f\right)=\frac{c_{mf}^{1-\gamma }}{1-\gamma }-\psi P_f,$$ (6)

with C_mf = 0.61(Y_m + Y_fP_f); where C is household consumption of a composite good, Y_m and Yf denote each spouse’s permanent income, Pf is the wife’s labor supply decision (constrained to be in the unit interval), γ is the coefficient of relative risk aversion, and ψ is the disutility incurred by the household if the wife works.¹⁵ This specification of household utility has been used in recent work investigating determinants of wives’ labor supply (e.g. Attanasio et al., 2008). It assumes household consumption is a public good with congestion: 0.61 is a McClements scale calibration capturing consumption economies of scale. In this setup, where spouses consume an indivisible public good, positive sorting on permanent earnings occurs in marriage market equilibrium so long as each member’s permanent earnings positively affects match output (Becker 1973; 1981). It is trivial to show that this holds here.

After marriage, the household takes household potential income as given and chooses the wife’s labor supply P_f ∈ [0,1] to maximize the above utility function.¹⁶ With an interior solution, the household will choose

$$P_f^{*}=\frac{\frac{1}{0.61}\cdot {\left(\frac{\psi }{0.61\cdot Y_f}\right)}^{\frac{-1}{\gamma }}-Y_m}{Y_f}.$$ (7)

If $P_f^{*}$ lies outside of the unit interval, the appropriate corner solution applies.

We calibrate the model by imposing γ = 1.5, following Attanasio, Low and Sánchez-Marcos (2008). We assume log-normally distributed potential earnings and allow the work disutility parameter, ψ, to be heterogeneous in the population and negatively correlated with Y_f. In total there are 8 remaining parameters, which we calibrate by targeting 8 moments in our observed data: the means and standard deviations of male and female log observed income, the observed mean gender earnings ratio conditional on earning positive income, the observed mean gender earnings ratio conditional on full-time work (defined in the data as at least 1600 hours worked in the last calendar year; defined in the model as $P_f^{*}>0.95$), the female employment rate (defined in the data as the share of wives working positive hours in the last calendar year), and the female full-time employment rate. We do not target any moment related to marital matching or spousal earnings differences, as doing so would threaten the external validity of our inferences.

Table 2 summarizes the calibration. Overall the model does a good job of replicating the targets in the data. With the calibrated model we simulate the distribution of the wife’s share of total spousal earnings (Figure 5). The simulated distribution again matches the actual distribution quite closely, delivering a sharp drop in probability mass at the 0.50 threshold.

Table 2.

Model Calibration

Parameter	Symbol	Calibrated value
Mean, male log earnings	μm	10.350
Std dev, male log earnings	σm	0.750
Mean, female log potential earnings	μf	10.160
Std dev, female log potential earnings	σm	0.700
Mean, disutility of work	ψ	0.002
Std dev, disutility of work	σψ	0.001
Earnings-disutility correlation, females	ρ	−0.400
Std dev, transitory earnings shock (1000s)	μu	13.000
Targets in the data	Data	Model
Mean, male log earnings	10.350	10.350
Std dev, male log earnings	0.750	0.750
Mean, female log earnings	10.000	9.980
Std dev, female log earnings	0.870	0.870
Gender earnings ratio, all	0.740	0.710
Gender earnings ratio, full-timers only	0.800	0.790
Labor force-participation rate, females	0.880	0.910
Full-time employment rate, females	0.670	0.670

Notes: Calibration of model discussed in Section IV.B.

Figure 5. Distributions of Gender Relative Income in the 2000 U.S. Census: Actual Sorting and Simulated Sorting with Endogenous Earnings.

Notes: The sample is the same as in Figure 2. The figure plots a 20-bin histogram of the actual distribution of the wife’s share of total spousal earnings (“Actual Sorting”), and a 20-bin histogram of a simulated distribution based on assortative matching of couples on potential income plus noise (“Simulated Sorting”)—and in which the wife’s observed earnings are endogenized via a neoclassical labor supply decision. See Section IV.B for further detail on the simulation. The dashed lines represent the lowess smoother applied to each histogram on either side of 0.5.

V. Discontinuity or Point Mass? Assessing Alternative Evidence for a Male Breadwinner Norm

The above evidence suggests that social scientists wishing to test the importance of social norms need to find strategies beyond interpreting skewed distributions of spousal attributes. The challenge in doing so makes the discontinuity found by BKP at the equal-earnings threshold a compelling addition to the literature. The logic behind BKP’s discontinuity test runs as follows. Suppose we observe the distribution of the share of total spousal earnings that was earned by the wife in the neighborhood of 0.50. Suppose we find that this distribution exhibits a sharp change in probability mass at the 0.50 threshold—that is, there are far fewer wives barely outearning their husbands than husbands barely out-earning their wives. Because standard models of the marriage market, involving agents optimizing continuous utility functions, should not generate discontinuous equilibrium distributions, such a finding suggests the existence of a utility penalty that applies if and only if the wife out-earns the husband.

BKP estimated a discontinuous drop-off in probability mass across the equal-earnings threshold in a variety of Census samples. However, inference is complicated by the fact that earnings are not precisely measured in Census survey data. Mis-measurement occurs for several reasons. First, earnings are reported, rather than measured directly. (Moreover, earnings for both spouses are typically reported by one household member.) Second, earnings are imputed for individuals who do not answer earnings questions, and the earnings of high-earning individuals are top-coded at a common value. Third, reported earnings are rounded by the U.S. Census Bureau in public-use samples, usually to the nearest thousand. These issues create a large point mass of couples with identical earnings. Even after employing several procedures to adjust the data, BKP still found that around 3 percent of dual-earning Census couples have identical earnings. (We corroborate this finding.)

To overcome these limitations, BKP also assembled a sample of administrative earnings records from the Social Security Administration (SSA). These data have been linked to a household survey (the Survey of Income and Program Participation, or SIPP) which allows couples to be identified.¹⁷ In this administrative data sample, the point mass of equal-earning couples still exists but is much smaller: only around one quarter of one percent of all dual-earning couples earn identical incomes. BKP obtained a similar discontinuity result in this sample.

Without the point mass, the straightforward way to implement BKP’s procedure would be to test for a discontinuity in the distribution exactly at 0.50, and interpret the finding of a significant drop-off in the density function as evidence for a social norm that the wife should not out-earn her husband. The presence of the point mass presents a challenge, which BKP acknowledge in footnote 7 of their paper. To circumvent this problem, they tested for a discontinuity just to the right of 0.50. One might interpret this treatment of the data as a test for whether there is a social norm dictating that a wife should not strictly out-earn her husband. Their finding of a significant drop-off in the density function to the right of 0.50, combined with the presence of the point mass of equal earners, might suggest that couples manipulate their earnings on the margin to comply with such a social norm.

This treatment of the data seems sensible a priori, but the existence of the mass point violates one of the assumptions required by the discontinuity test, namely, that the distribution is continuous everywhere except possibly at the supposed breakpoint (McCrary 2008). Like a non-parametric regression discontinuity design, the test involves local linear smoothing of a finely-binned histogram on either side of the supposed breakpoint, and asymptotic inference is based on the size of the bins shrinking to zero at the correct rate as the number of observations increases to infinity. In BKP’s application of the test, for a small bin size, the bin immediately before the breakpoint will (by containing the point mass) be taller than the bin immediately after the breakpoint. This could exert undue influence on the discontinuity estimate, especially if a small bin size and bandwidth is used to perform the test.

A. Gauging the Robustness of BKP’s Discontinuity Test Results

To investigate the sensitivity of the discontinuity test to the presence of the point mass, we replicate BKP’s SIPP-SSA data sample and analysis. BKP constructed a sample of earnings data for all dual-earning couples aged 18 to 65 observed in the first year they were in the SIPP panel. They considered SIPP panels 1990 through 2004. We construct a sample according to the same conditions but include the 1984 and 2008 SIPP panels as well, which were available in the 2018 version of the SIPP-SSA data product. We obtain a sample of around 83,000 couples—about 9,500 more than in BKP’s sample. Despite using a slightly different sample, the resultant distribution of the wife’s share of total spousal earnings is virtually identical to BKP’s, as illustrated in Figure 6.

Figure 6. Distributions of Gender Relative Income in U.S. Administrative Record Sample.

Notes: Graph A is a screenshot of Figure I of Bertrand, Kamenica and Pan (2015). The data underlying this graph are administrative income data from the SIPP-SSA Gold Standard File covering the 1990 to 2004 SIPP panels. Graph B is our replication. We use the latest version of the Gold Standard File, which includes the 1984 and 2008 SIPP panels as well. The sample in each graph includes all dual-earning couples aged 18 to 65, with income information taken from the first year the couple was observed in the SIPP panel. See Section V for further discussion. Each graph plots 20-bin histograms of the observed distribution of the wife’s share of total spousal earnings. The dashed lines represent the lowess smoother applied to each histogram on either side of 0.5.

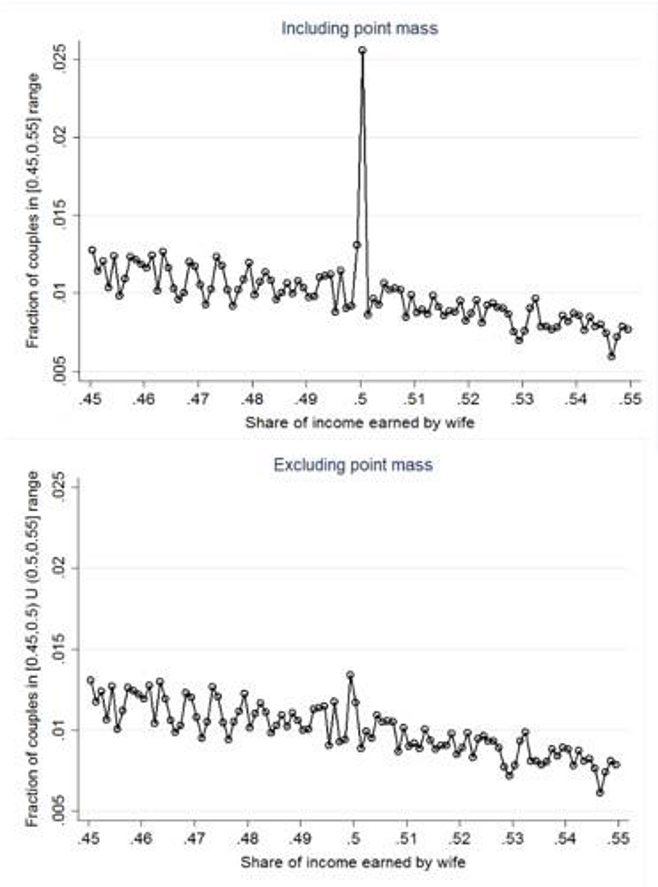
In our replicated sample, 0.21 percent of all dual-earning couples earn identical incomes, compared to 0.26 percent in BKP’s sample. To see the impact of this mass point on the distribution, Figure 7 zooms in on the portion of the distribution between 45 and 55 percent, displaying histograms with a very small bin size of 0.001 (about the size used in the discontinuity tests). The top histogram retains the mass point, while the bottom histogram removes it. The two histograms look very different: the top one exhibits a large spike right at 0.50, while the bottom one does not. Moreover, though the data are noisy for such a small bin size, the histogram that drops the point mass does not look particularly discontinuous at 0.50. These illustrations suggest that the point mass may exert an undue influence on the discontinuity estimates.

Figure 7. Distributions of Gender Relative Income in U.S. Administrative Record Data: Couples who Earn Close to the Same Incomes.

Notes: The sample is the same as in graph B of Figure 6, but is restricted to couples in which the wife earns between 45 and 55 percent of total income. The graph in the top panel retains the point mass of couples earning identical incomes; the graph in the bottom panel excludes it. The bin size used in both graphs is .001; each graph contains 100 bins.

Using our sample we perform 3 different versions of the McCrary (2008) discontinuity test, based on three different treatments of the point mass: keeping the point mass and testing for a discontinuity at .500001, keeping the point mass and testing for a discontinuity at .499999, and deleting the point mass and testing for a discontinuity exactly at 0.50. For each version we use 4 different sets of tuning parameters. McCrary’s test procedure involves an algorithm which automatically chooses a bin size for the histogram and a bandwidth within which to apply the local linear smoother to the histogram. McCrary (2008) recommends using a smaller bandwidth than the automatically-selected one (around half the size) to conduct robust asymptotic inference. We consider the automatically selected bandwidth, which in this case is around .084; and then bandwidths of .045, .023, and .011. The last bandwidth may be too narrow for optimal statistical inference, but using successively smaller bandwidths allows us to gauge the sensitivity of the test to the presence of the point mass (which becomes increasingly dominant as the bandwidth shrinks).

Table 3 reports the discontinuity estimates, which equal the estimated log increase in the height of the density function as one travels from just to the left of the supposed breakpoint to just to the right. A negative number thus indicates a sharp drop and a positive number indicates a sharp gain. The first version of the test replicates BKP’s choice of retaining the point mass of couples and testing for a discontinuity just to the right of 50 percent (.500001). With the standard bandwidth and bin size, we estimate that the density function drops by a statistically significant 12.4 percent across the threshold. This is very similar to BKP’s reported estimate of a 12.3 percent drop in their very similar sample (reported on p. 576). Observe that as the bandwidth shrinks, the estimate of the sharp drop rises in magnitude, such that with the smallest bandwidth we estimate a 57.5 percent drop—over 4 times as large as the first estimate. This suggests that the point estimates are sensitive to the existence of the point mass.

Table 3.

Different Treatments of the Point Mass Produce Different Discontinuity Estimates

		Hypothesized Breakpoint:
Bandwidth	Bin size	.500001	.499999	.5 (omit point mass)
.084	.0016	−.124*** (.031)	.064** (.031)	−.034 (.032)
.045	.0016	−.184*** (.040)	.129*** (.040)	−.031 (.043)
.023	.0016	−.310*** (.055)	.240*** (.055)	−.040 (.061)
.011	.0005	−.575*** (.078)	.451*** (.081)	−.078 (.091)

Notes: Sample of spousal earnings data taken from the SIPP-SSA Gold Standard Files. See Section V for discussion of the sample. The first reported bandwidth and bin size correspond to those automatically selected by the McCrary (2008) test algorithm. McCrary (2008) recommends using a small bandwidth than the automatically selected one, as is done in the second thru fourth rows. Point estimates report the change in log height of the density function as one travels from just left of the hypothesized breakpoint to just right of it. Asymptotic standard errors reported below coefficient estimates in parentheses; standard statistical significance legend used.

When we retain the point mass and test for a discontinuity just to the left of 50 percent, we find the exact opposite result: the density function jumps discontinuously upward. Once again, the estimate starts out reasonably small (6.4 percent) and becomes very large (45.1 percent) as the bandwidth shrinks. The finding of a sharp increase in the distribution at 50 percent suggests that couples manipulate earnings to avoid a situation in which the wife earns strictly less than her husband. Put another way, the data appear consistent with a social norm dictating that a wife should earn at least as much as her husband. This is nearly opposite to the social norm dictating that a wife should not earn strictly more than her husband, which is supported by the first version of the results.

The third column of results derives from deleting the point mass and testing for a discontinuity exactly at 50 percent. Two features stand out. First, while the estimates are negative, they are no longer statistically significant–—moreover, the estimate based on the standard bandwidth is close to estimates generated by performing the test with the standard bandwidth on our simulated data. Second, the estimates do not rise appreciably in magnitude or statistical significance as the bandwidth shrinks, likely because the point mass is no longer present. Therefore, if we ignore the one quarter of one percent of couples earning identical incomes, the conclusion that the observed distribution of spousal earnings differences could be consistent with a variety of underlying social preferences (including no explicit social norm) is supported by the data. A related conclusion is that while BKP’s discontinuity test eschews the theoretical critique of the literature we levied in Section III, it does not produce robust empirical results, given the point mass of couples earning identical incomes.

B. A Further Inquiry into the Point Mass

Considering these conclusions, it is worth exploring why the point mass exists in the first place, and what it means to remove it from the sample. For example, the existence of the point mass could indicate a social preference, in the population or a certain sub-population, for strict equality of spousal earnings. Further exploration of the 2000 Census data reveals the following facts about the couples who report identical earnings in comparison to the full sample.^{18 19}First, couples who report identical earnings are almost six times more likely to both be self-employed than couples who report different earnings (13.0 percent versus 2.3 percent). Among couples in which husband and wife indicate being self-employed in the same occupation and industry (a likely indicator of running a family business), 34 percent report identical incomes. (These couples represent 0.18 percent of the full sample of couples.) Since income from a family business can be allocated in any way between husband and wife on tax returns, this suggests that one source of identical incomes is couples choosing to divide family business income equally for income tax purposes.²⁰

In addition, there are couples in which the husband and wife do appear to earn identical salary incomes. Couples reporting that husband and wife both earn wages (i.e., are not selfemployed) and report identical earnings, occupations, and industries (suggesting that they are likely to have identical jobs) constitute 0.34 percent of the sample. Elementary, middle school, and secondary teachers make up 18.9 percent of this group, by far the largest occupation. Taken together, the group of self-employed and salaried couples with identical incomes, occupations, and industries constitute 0.52 (= 0.18 + 0.34) percent of all couples. Some of these are presumably “false positives,” given the fact that Census data are self-reported and rounded. But this suggests that it is not difficult to account for the 0.2–0.3 percent of couples with identical earnings in the administrative data. (Indeed, Zinovyeva and Tverdostup 2018 found that coworking spouses could account for the entire point mass of equal-earning couples in Finnish data.)

Our interpretation of these cases is that they do not provide much information about a social norm related to husbands earning more than wives. They could constitute evidence for an equal-earning norm in a subset of the population. Alternatively, they could indicate frictions in the marriage market which lead a disproportionate share of equal-earning individuals to marry, for example, because they met through work. That is, there could be a small utility loss for the husband not out-earning his wife which is outweighed by the search cost of finding a more suitable partner. For example, McKinnish (2007) and Mansour and McKinnish (2018) found evidence that the workplace plays an important role in marital sorting and dissolution, consistent with the search-friction paradigm. It could also be the case that some individuals pair up because they desire to go into business together—that is, for a small subset of potential couples, the gains from marriage are driven by joint business ventures.

VI. Discussion

Our paper demonstrates the difficulty of identifying social norms regarding a given attribute from how people sort themselves into married couples based on that attribute. Marital sorting on an attribute is affected by preferences, but also by the underlying distributions of attributes. If men are taller or higher-earning than women on average, preferences which lead to positive assortative matching will produce equilibria in which it is unusual for women to be taller or higher-earning than their husbands. Even a preference for men to earn less than their wives can lead to positive assortative matching and, consequently, an equilibrium in which men tend to earn more than their wives. Simple models of positive assortative matching—that impose no explicit assumption about the male breadwinner norm—generate distributions of wives’ relative income that closely resemble the observed distribution. The one feature these models cannot reproduce is the cliff-like drop in probability mass to the right of the equal-earning threshold. However, this discontinuity is uninformative, since it is the result of a point mass of equal-earning couples—a point mass that we argue is not indicative of male breadwinner norms. No feature of the observed distribution of wives’ relative income, broad or pointwise, appears to offer information about the male breadwinner norm.

In light of this critique, we offer a short discussion on what we believe are best practices for studying the male breadwinner norm and its effects on household behaviors. As recognized by literature on matching models (e.g. Chiappori and Salanié 2016), identification of marital preferences is eased when one observes marital sorting patterns in conjunction with other indicators of the marital surplus (and its division between spouses). Thus, instead of an approach based solely on spousal earnings distributions, we favor an approach that considers the relationship between spousal earnings and other household outcomes. BKP explore this approach: some additional analyses in their paper found that when a wife out-earned her husband, she became likelier to work fewer hours in the future and to perform more household chores.²¹ Additionally, the marriage became likelier to end in divorce. These analyses suggest that when a wife out-earns her husband, marital output is lowered, the terms of marriage shift away from her, or both—consistent with the male breadwinner hypothesis.

Compelling as these analyses appear, they may also be threatened by our critique of BKP’s relative income discontinuity. This is because BKP compare situations in which a wife out-earns her husband to situations in which she does not, conditional on a rich set of controls for absolute and relative income. These include controls for cubic polynomials in both spouses’ earnings; the wife’s relative income; and the difference between the wife and husband’s earnings rank in their respective distributions. (See Tables II, III, V, VI and VII of their paper.) Holding these variables constant—or even just holding the wife’s relative income constant—residual variation in the event that a wife out-earns her husband occurs exactly at the equal-earning threshold. That is, BKP effectively compare marriages in which the wife earns the same as her husband to marriages in which the wife earns slightly more.

As we have seen, survey and administrative data contain a point mass of equal-earning couples who tend to work the exact same job or own a business together. It is unlikely that these couples are the same (in every respect except male breadwinner status) as couples working in different occupations. For example, it could be that the small share of couples reporting equal earnings in a given year subscribe to egalitarian values and marital stability (Murray-Close and Heggeness 2018). Indeed, the joint ownership of a business may itself be a source of marital stability. It could also be the case that, as joint business owners, such couples are more skilled in (or tolerant of) outsourcing their housework tasks to the market. In addition, among couples working in different occupations, the wife slightly out-earning her husband in given year likely reflects transitory shocks rather than a stable arrangement (Winslow-Bowe, 2006; Winkler et al., 2005). Put differently: the higher divorce probability and more gendered division of housework seen in marriages in which the wife barely out-earns the husband could reflect idiosyncratic features of equal-earning couples rather than a prevailing male breadwinner norm.

One way to handle these concerns issue is to control for couple fixed effects in a longitudinal analysis. However, families are not fixed entities (e.g. Bumpass 1990): family businesses dissolve, careers change, and gender divisions of tasks may also change for reasons other than compliance with a male breadwinner norm. We recommend that “pointwise” evaluations of the male breadwinner hypothesis at the equal-earning threshold—both cross-sectional and longitudinal—adopt a series of robustness checks. These include: i) re-defining the independent variable as the wife earning equal to or greater than her husband (instead of just looking at whether the wife strictly out-earns her husband); ii) excluding observations in which wife and husband report identical incomes; iii) adding finely-grained occupation controls, or a control for the husband and wife working in the same occupation; and iv) controlling for source of income (i.e. if business income makes up all of or a majority of the couple’s total income). If these alternative specifications still show that when a wife out-earns her husband, she takes up more housework, reduces her labor supply, and becomes likelier to trigger a divorce, then we would feel more confident assigning a male breadwinner norm explanation to the data.

Overall, we recommend that researchers seeking to evaluate the male breadwinner hypothesis combine this pointwise approach—augmented with our robustness checks—with the more “holistic” approach taken by the sociological literature. (See above discussion in Section II.) There may be important information conferred by the entire joint distribution of wives’ relative income and household outcomes that the pointwise approach misses. In particular, as the share of wives persistently out-earning their husbands grows, it may be increasingly important to analyze co-variation between household outcomes and the wife’s relative income beyond the equal-earning threshold. That is, couples may not just care about whether a wife out-earns her husband, but by how much she out-earns him. As neither approach offers bulletproof causal identification, and each approach elicits different potential effects of the male breadwinner norm, researchers should utilize both approaches and take care in interpreting the results.

Inquiries into the existence and potential consequences of male breadwinner norms are likely to continue to be an active area of research. We believe this research will be more convincing if researchers are sensitive to the challenges of identifying social norms from observed marriage market outcomes, and to the tendency of certain couples to earn equal incomes.

Appendix

Table A1.

Distributions of Gender Relative Income in 2000 Census: Including versus Excluding Business Income

	Including biz earnings		Excluding biz earnings
	All	Dual-earners	All	Dual-earners
0	.228	—	.244	—
0+ to .10	.072	.099	.062	.092
.10+ to .20	.082	.113	.074	.109
.20+ to .30	.108	.148	.100	.148
.30+ to .40	.139	.191	.133	.196
.40+ to .50	.153	.211	.148	.218
.50+ to .60	.096	.132	.091	.135
.60+ to .70	.040	.055	.037	.054
.70+ to .80	.020	.027	.017	.026
.80+ to .90	.011	.016	.010	.014
.90+ to 1−	.007	.009	.006	.009
1	.044	—	.078	—

Notes: Sample of married couples taken from the 2000 Census in which both husband and wife are between 18 and 65 years of age, and with positive total earnings. Columns 2 and 4 restrict the sample to dual-earning couples. Columns 3 and 4 exclude business income.