Automating Hair Loss Labels for Universally Scoring Alopecia From Images

Key Points

Question

Can a single algorithm automatically quantitate the extent of hair loss in several different types of alopecia (eg, alopecia areata, central centrifugal centripetal alopecia, female-pattern baldness)?

Findings

In this research study to create a new algorithmic quantification system for all hair loss, first, it is shown that there is a correlation between existing scoring systems and the underlying hair loss percentage, and second, a new algorithm to quantify hair loss from images of scarring and nonscarring alopecia is presented. Third, this study demonstrates how this algorithm can measure the percentage of hair loss at every location on the scalp and predict hair loss scores tailored to specific subtypes; in images from 404 participants, this automated hair loss percentage showed more than 92% segmentation accuracy and predicted scores with errors comparable to human annotators.

Meaning

The presented algorithm quantifies hair loss from photographic images independent of alopecia type.

Abstract

Importance

Clinical estimation of hair density has an important role in assessing and tracking the severity and progression of alopecia, yet to the authors’ knowledge, no automation currently exists for this process. While some algorithms have been developed to assess alopecia presence on a binary level, their scope has been limited by focusing on a re-creation of the Severity of Alopecia Tool (SALT) score for alopecia areata (AA). Yet hair density loss is common to all alopecia forms, and an evaluation of that loss is used in established scoring systems for androgenetic alopecia (AGA), central centrifugal cicatricial alopecia (CCCA), and many more.

Objective

To develop and validate a new model, HairComb, to automatically compute the percentage hair loss from images regardless of alopecia subtype.

Design, Setting, and Participants

In this research study to create a new algorithmic quantification system for all hair loss, computational imaging analysis and algorithm design using retrospective image data collection were performed. This was a multicenter study, where images were collected at the Children’s Hospital of Philadelphia, University of Pennsylvania (Penn), and via a Penn Dermatology web interface. Images were collected from 2015 to 2021, and they were analyzed from 2019 to 2021.

Main Outcomes and Measures

Scoring systems correlation analysis was measured by linear and logarithmic regressions. Algorithm performance was evaluated using image segmentation accuracy, density probability regression error, and average percentage hair loss error for labeled images, and Pearson correlation for manual scores.

Results

There were 404 participants aged 2 years and older that were used for designing and validating HairComb. Scoring systems correlation analysis was performed for 250 participants (70.4% female; mean age, 35.3 years): 75 AGA, 66 AA, 50 CCCA, 27 other alopecia diagnoses (frontal fibrosing alopecia, lichen planopilaris, telogen effluvium, etc), and 32 unaffected scalps without alopecia. Scoring systems showed strong correlations with underlying percentage hair loss, with coefficient of determination R² values of 0.793 and 0.804 with respect to log of percentage hair loss. Using HairComb, 92% accuracy, 5% regression error, 7% hair loss difference, and predicted scores with errors comparable to annotators were achieved.

Conclusions and Relevance

In this research study,it is shown that an algorithm quantitating percentage hair loss may be applied to all forms of alopecia. A generalizable automated assessment of hair loss would provide a way to standardize measurements of hair loss across a range of conditions.

This research study develops and validates a new model, HairComb, to automatically compute the percentage of hair loss from images regardless of alopecia subtype.

Introduction

Alopecia, or hair loss, is experienced in some form by most people during their lifetime. The condition manifests itself through a wide variety of patterns and etiologies. For example, female-pattern hair loss (FPHL) is a nonscarring hair loss due to follicular miniaturization that affects 30 million women in the US¹; alopecia areata (AA) is an autoimmune disease with a lifetime incidence of 2%²; and central centrifugal cicatricial alopecia (CCCA) is a scarring alopecia that has been estimated to affect up to 15% of women of African descent.^3,4,5,6 Underlying these disparate forms of alopecia is a common link: a change in hair density that tracks with the progression of the condition.^7,8 Thus, both in the clinic and in clinical trials, hair density is commonly used by dermatologists and other specialists to monitor the progression of hair loss, either directly as a stand-alone hair loss metric or in the context of a visual scale.

Since the 1950s, a multitude of scales have been proposed and established to help quantify, diagnose, and track the stages of hair density loss.⁹ Designed to be used by clinicians during visual inspection, these scales consist of visual references focusing on gradual decreases in hair density,^{10,11,12,13,14} binary distinctions between normal and alopecic areas (ie, areas of lower hair density),^15,16,17 or a combination of the 2.^{18,19,20,21,22,23} The assessed areas are then used to either directly quantify hair loss or to evaluate the location, shape, and pattern of involvement.

The dermatology community conceptualizes each alopecia scale as a distinct tool, only to be applied in the context of 1 specific form of alopecia. For example, both the Severity of Alopecia Tool (SALT) score¹⁶ and its refinement, the Alopecia Density and Extent (ALODEX) score,²⁰ are almost exclusively used for AA, even though both scales function as a direct measure of percentage hair loss—a metric with applicability to all alopecias. Even recently developed algorithms to automate the computation of the overall percentage of scalp area affected have been designed exclusively for 1 diagnosis (AA).^24,25 Furthermore, scales that use gradual densities usually only divide severity levels into a few degrees (3 on average) due to the challenges of gauging alopecia extent by eye. A tool that could automate hair loss measurement in such a way that correlates closely with existing clinical scales would greatly diminish the time needed to assess the degree of hair loss and would do so in a more consistent and standardized manner.

In this article, we propose that a single quantification system that measures percentage hair loss would be useful across different types of hair loss. First, we demonstrate that given the same viewing conditions, a strong correlation can be found between distinct alopecia scoring systems and the underlying percentage hair loss. We then present a new automated algorithm, HairComb, to extract percentage hair loss information from images at every point of the scalp and show its applicability, as a tool on its own or as a first step for automating existing scoring systems.

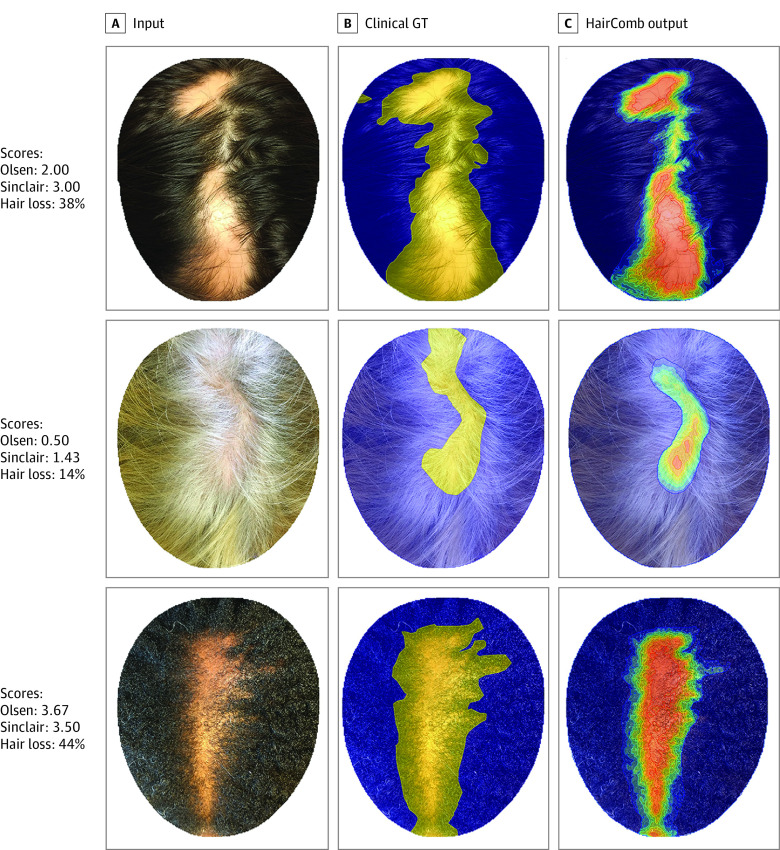
In particular, we focus on 3 commonly used scoring systems: SALT score for AA,¹⁶ Sinclair 5-point mid-scalp clinical visual analog scale for FPHL,²³ and Olsen Top Extent Scale for CCCA.¹⁹ While many other scales for types of alopecia exist, we selected these scales because each derives their values from visual examination of the (same) crown region of the head and have been clinically validated for grading photographs. Shown in Figure 1A are images of 3 types of alopecia (AA, FPHL, and CCCA), each scored according to the 3 scoring systems. These scales serve different purposes and have value independent of alopecia type: the SALT score, or percentage hair loss, gives an overall alopecia assessment; the Sinclair score focuses on the extent of the widening of the central part; and Olsen shifts the attention to the loss in the more pronounced area (anterior or vertex). Results from our proposed algorithm (Figure 1C) quantitate the distribution of local hair loss probability at every pixel and can be applied to any alopecia subtype.

Figure 1. Rethinking Alopecia Scores Motivation.

Alopecia scoring systems have been traditionally designed and clinically validated for only 1 type of alopecia (eg, in A, from top to bottom, AA, alopecia areata; FPHL, female-pattern hair loss; and CCCA, central centrifugal cicatricial alopecia). Here, we score each image with the Olsen CCCA scale, the Sinclair scale for FPHL, and percentage hair loss—a proxy for the Severity of Alopecia Tool (SALT) score for AA, derived from the manually annotated labels shown in B, where blue is normal hair density, and yellow, areas of alopecia. Each scale provides value: percentage hair loss gives an overall alopecia assessment; Sinclair focuses on the extent of the widening of the part; and Olsen shifts the attention to the loss in the more pronounced area (anterior or vertex). In C, we show the output distribution of local hair loss probability at every pixel (from red, 100% alopecia, to blue, 100% normal density) computed by our new algorithm, HairComb. GT indicates ground truth.

Validating our method on images taken from 404 participants, we demonstrate that we can quantitate percentage hair loss over the entire scalp and predict scores with a high degree of accuracy, independent of alopecia type.

Methods

Data Sets

To design HairComb, we used an alopecia image data set of 1605 images taken from 404 participants. Of this set, 1484 images were taken from 293 participants seen within the dermatology clinics of the Children’s Hospital of Philadelphia and the Hospital of the University of Pennsylvania (Penn) (Table). Scalp images were captured and standardized following guidelines defined by the SALT score¹⁶ and its pediatric adaptation²⁶: for each participant, up to 4 views of the head (top, back, and lateral) were taken per time point. For the alopecia top scores analysis and automation, we added an additional 121 top (crown) view only images from 111 participants enrolled via Penn Dermatology’s alopecia monitoring interface, Trichy (Figure 2).²⁷ While the first group of images was taken entirely in the dermatology clinics, the Trichy set consisted of a mixture of sources from both patients with alopecia and from the general population. Complete image acquisition and preprocessing details are in included in eMethods 1 in the Supplement.²⁸ This study was approved by the hospitals’ respective institutional review boards and followed the CLEAR Derm Consensus Guidelines for evaluation of image-based artificial intelligence reports in dermatology.²⁹ A mix of written and oral informed consent was obtained from all participants. Images were collected from 2015 to 2021, and they were analyzed from 2019 to 2021.

Table. Patient Characteristics for HairComb Data Set^a.

	No. (%)
Diagnosis
No.	293
AA	210 (71.7)
AGA	18 (6.1)
CCCA	39 (13.3)
Other	24 (8.2)
Unaffected scalp (no alopecia)	2 (0.7)
Hair color
No.	293
Bald	26 (9.0)
Grey	8 (2.7)
Blonde	49 (16.7)
Red	10 (3.4)
Brown	93 (31.7)
Black	102 (34.8)
Mixed (partially dyed)	5 (1.7)
Skin tone
No.	293
Light	164 (56.0)
Medium	69 (23.5)
Dark	60 (20.5)
Hair texture
No.	293
Bald	37 (12.6)
Straight	96 (32.8)
Relaxed	23 (7.9)
Wavy	81 (27.6)
Curly	24 (8.2)
Tightly coiled	32 (10.9)

Abbreviations: AA, alopecia areata; AGA, androgenetic alopecia; CCCA, central centrifugal cicatricial alopecia.

^a Percent of patients for each alopecia diagnosis, hair color, skin tone, and texture type are reported. Light, medium, and dark skin tones are similar to Fitzpatrick skin types I-II, III-IV, and V-VI, and were determined by observing the patients in the clinics. Additionally, 6% of the 293 patients had additional hair styling (braids, locs, etc) that altered the overall texture appearance (eFigure 5 in the Supplement) and 12% required pins to expose areas of interest (eFigure 6 in the Supplement).

Figure 2. Trichy, a New Web-Based Clinical Tool for Quantifying Hair Loss and Computing Alopecia Scores.

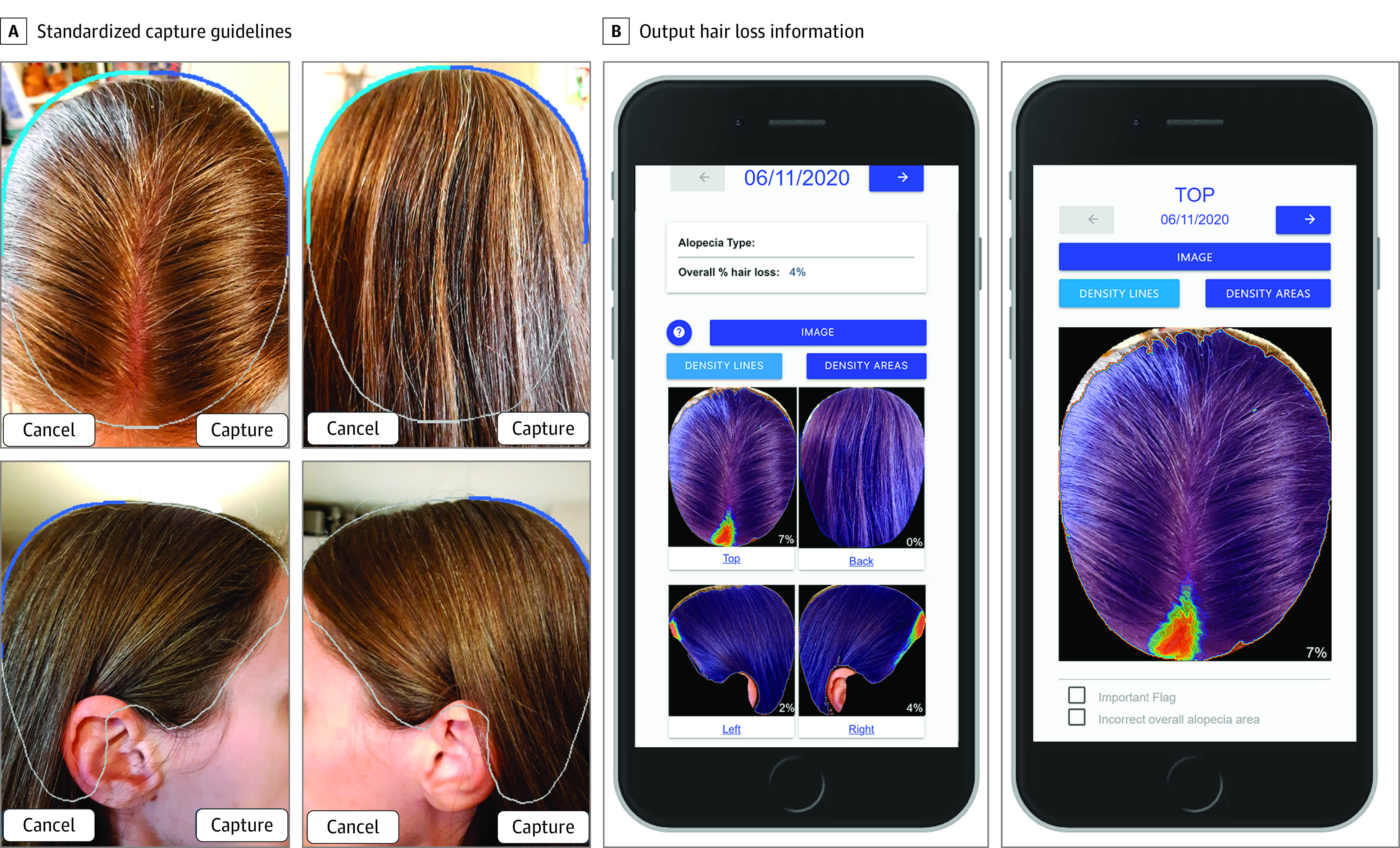
The interface guides the user with image capture guidelines that are adjusted for age and then returns the quantified alopecia (in this case, a probable mild case of telogen effluvium toward the front) in a couple of seconds. Note how background that is accidentally captured within the guidelines is correctly excluded by the algorithm.

Labeling Alopecia Images

To minimize human measurement error^30,31 and to have a baseline that provided exact information as to the location of the alopecia, we manually outlined normal vs abnormal hair density areas (ie, normal vs alopecia regions) on the images, allowing us to obtain an initial set of coarse-level alopecia (discrete) labels C. From these labels, we automatically counted the number of pixels in the regions affected by alopecia vs the overall scalp area to extract a baseline, or ground-truth (GT), for the percentage of scalp area affected (Π^GT_C). To increase the granularity of the hair loss information, we then created fine-level hair (continuous) labels F in a semisupervised way by using a classic closed-form matting algorithm³² to extract a probability map of whether each pixel belonged to either hair or skin. Input to the algorithm consisted of images that had been annotated by 4 researchers to provide hard constraints as to which pixels should be considered hair or skin. Note, both C and F carry important alopecia information: C encodes whether a pixel displays hair loss, considering the relative hair density of the entire scalp (as the annotators estimated a baseline normal hair density for each participant against which potentially abnormal areas were compared); F, on the other hand, encodes hair density information at every pixel independent of the participants’ baseline density. To show that F is a good proxy for local hair density, we computed Pearson correlation between F and C for varying image patch sizes over the 1484 image set.

Scoring Systems Analysis

We then used all 283 top (crown) view images (162 clinical dermatology images and 121 Trichy images) from 250 unique participants for the scoring system comparison. Multiple photos from a single patient were included if the photos were taken at different time points and had visually distinct alopecia. The photos were then classified by diagnosis: 81 androgenetic alopecia (AGA)/FPHL, 83 AA, 52 CCCA, 32 other alopecia diagnoses (discoid lupus, frontal fibrosing alopecia, lichen planopilaris, telogen effluvium, and others), and 35 nonalopecia (healthy) scalps (eTable 1 in the Supplement).

For Olsen and Sinclair scales, 3 independent raters scored each of the images using the photographic references provided in the original papers (eFigure 1 in the Supplement). For a measure of the SALT score, we used the manually outlined C labels to automatically calculate Π^GT_C (ie, the percentage of alopecia pixels over the top scalp). The SALT score is calculated independently for each of its 4 head views, so we used only the top view for comparison to the other 2 scales.

We assessed interrater reliability by calculating an Intraclass Correlation Coefficient (ICC),³³ as well as separate ICCs for the images classified as AGA/FPHL, AA, CCCA, and other diagnoses. The 3 raters’ Olsen and Sinclair scores were separately averaged, leaving us with a final set of 2 manually calculated scores for each image. These scores were then checked for correlation against each other and against the percentage affected area Π^GT_C. To assess correlation, we performed linear regressions pairwise yielding R² values. Two-tailed test statistical significance was set at P < .05.

HairComb Network

HairComb is a convolutional neural network (CNN) that combines overall hair pattern and pixel-level hair density information starting from a single image as input. HairComb learned both F and C labels by running 2 parallel encoder-decoder branches based on the implementation of the UNet³⁴ and ResNet50³⁵ architectures in TensorFlow 2.1.0³⁶: (1) a segmentation branch (ResNet) to encode the overall hair loss information learning from coarse-grained labels C; (2) a regression branch (UNet) to estimate local hair probability learning from the fine-grained labels F. The final output is computed by updating normal and background regions in F to match those of C. The resulting output HairComb label, H, provides a percentage hair loss at every pixel, ie, a hair density measure adjusted by the person’s overall hair density at baseline. The output H can then be visualized as a contour plot for a qualitative evaluation. Complete details of the network’s architecture and implementation are included in the eMethods 4 in the Supplement.^37,38,39 Alopecia visual characteristics spanned the full spectrum of hair texture, skin tones, and hair colors. The Table includes details for all patients in the data set, and eFigure 2 in the Supplement visualizes all image pairs of hair color vs skin tone combinations used for training and testing the algorithm.

We evaluated the performance of our network for the separate branches in terms of segmentation accuracy (percentage of correctly labeled pixels with respect to coarse labels C), regression error (average difference between predicted and GT pixel value with respect to fine labels F), as well as change in percentage hair loss ΔΠ for an indirect measure of SALT score error. The output label H allows extraction of a wide variety of hair loss information, such as density distribution across the scalp, largest area of involvement, and average density, which can then be used to build data models to predict other alopecia scores that rely on the underlying hair density loss information. To conclude, we show how to use the outputs to create simple prediction models for both Sinclair and Olsen scores (eMethods 5 in the Supplement), which could be refined in the future given larger data sets.

Results

Scoring Systems Analysis

For the Olsen and Sinclair scores, intraclass correlations (ICCs) calculated were 0.965 (95% CI, 0.919-0.981) and 0.980 (95% CI, 0.975-0.984), respectively (eTable 2 in the Supplement). Manual scores using all 3 scoring systems revealed strong correlations between the Olsen and Sinclair scores and the percentage hair loss (Π^GT_C). Linear regression models of Olsen vs Sinclair, Olsen vs Π^GT_C, and Sinclair vs Π^GT_C, showed a true linear relationship between Olsen and Sinclair and an exponential relationship between each score and Π^GT_C (Figure 3). By a natural log transformation of the (1 + Π^GT_C) values ln(Π^GT_C) before repeating the linear regression analysis of Sinclair and Olsen vs ln(Π^GT_C), we found R² of 0.793 for Sinclair vs ln(Π^GT_C) and R² of 0.809 for Olsen vs ln(Π^GT_C). Olsen vs Sinclair (Figure 3A) resulted in an R² of 0.963 suggesting that the Olsen and Sinclair scales encode almost identical information, and that roughly 80% of the variance in information encoded by those scales can be explained using ln(Π^GT_C).^40,41

Figure 3. Scoring Systems Analysis.

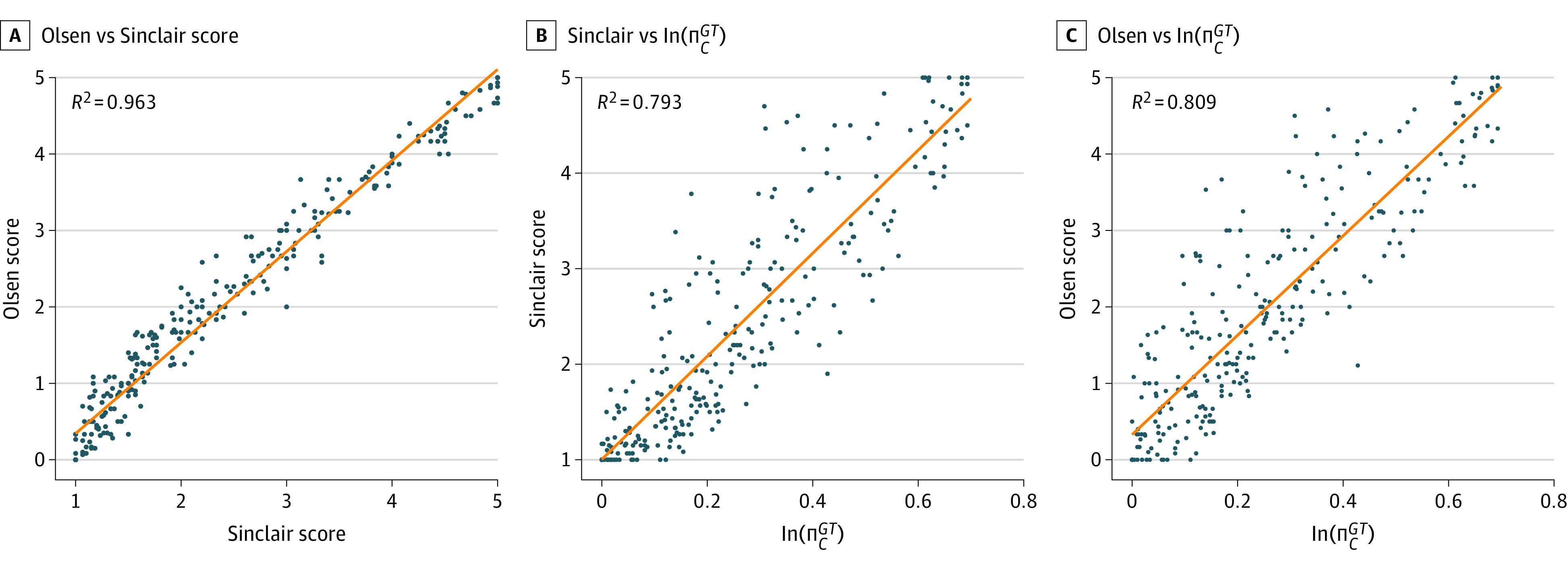
In each plot, we show results of pairwise correlations between the manually annotated scores (blue dots) of Olsen, Sinclair, and percentage affected area ln(Π^GT_C): A, Olsen vs Sinclair; B, Olsen vs ln(Π^GT_C); C, Sinclair vs ln(Π^GT_C). Olsen and Sinclair scores are taken as the average of the raters’ 3 scores, while ln(Π^GT_C) is computed automatically from C. As visible in the plots, a clear linear correlation (orange line) exists between Olsen and Sinclair (A), and strong logarithmic correlations are revealed for both in relation to the underlying percentage loss (B and C).

HairComb Results and Applications

Sample qualitative HairComb results are shown in Figure 4. For each top-view input images divided by alopecia types, the original input, the corresponding ground-truth (GT) labels (C and F), and the final output labels H, smoothed and discretized at 10% intervals for visualization are shown. For each set, manual (clinical) Olsen and Sinclair scores together with percentage affected area (loss) derived from the manually annotated labels C (in black) and the automated scores from the presented algorithms (in blue) are shown. As seen in these examples, the model performs well on a variety of hair and alopecia appearances. More qualitative results are shown in eFigure 3 in the Supplement. To show the correlation between F and C, Pearson coefficients of 0.7, 0.74, 0.75, 0.77, and 0.8 for image patches of 2, 4, 8, 16, and 32 square pixels, respectively, were obtained. Values above 0.7 indicate a strong positive linear relationship through a firm linear rule⁴¹ providing evidence that the hair probability maps provided by F could indeed be used to complement the information in C.

Figure 4. Sample Qualitative HairComb Results.

For each top-view input image, we show (1) the input image; (2) coarse-level (ground-truth, GT) labels C; (3) fine-level GT labels F; and (4) automated output HairComb labels H, ie, continuous hair loss percentage at every pixel that takes into account each individual’s normal density at baseline. Images are divided in sets of alopecia types: AA, alopecia areata (A); AGA, androgenetic alopecia/FPHL, female-pattern hair loss (B); CCCA, central centrifugal cicatricial alopecia (C); and other (D). For each set, we show manual (clinical) Olsen and Sinclair scores together with percentage affected area (loss) derived from the manually annotated labels C (in black) and the predicted scores from the presented algorithms (in blue). Note that the percentage loss is computed over the detected scalp: obstructing objects such as hands, pins, and other objects, are correctly detected and excluded from the overall head area.

Quantitatively, evaluating HairComb on the entire multiview set, 92% segmentation accuracy and 5% regression error (ΔR) were obtained. eFigure 4 in the Supplement visualizes these metrics in terms of image distribution, showing that more than 85% of the images have more than 85% accuracy, and more than 80% of the images have less than 7% regression error. The overall average absolute error (ΔΠ), ie, the percentage affected area difference between automated and manual scores, indirectly measuring the SALT score error, was 7%. Finally, using HairComb outputs as inputs to 2 support vector machine prediction models trained using features extracted from the manual scoring (eMethods 5 in the Supplement), overall average scoring error between automated and manual to be 0.48 for Sinclair and 0.60 for Olsen were calculated. For comparison, the human interrater average Sinclair and Olsen errors were 0.20 and 0.35, respectively (recall that Olsen has score ranges 0-5 and Sinclair 1-5). Final automated scores vs the manual scores on the same set of images, using only the top-view images that were not included in any models’ training set, showed a very strong agreement between manual and automated scores with linear correlations of 0.87 and 0.90 for Olsen and Sinclair scores, respectively.

Discussion

HairComb quantitates percentage hair loss at every pixel starting with an image of the scalp. The data set used for training included a variety of hair textures and colors so that HairComb quantified hair without the need for additional input such as hair color by the user. As HairComb extracts the percentage hair loss at every pixel, it most closely automates the ALODEX score and can be binarized to retrieve the SALT score over the entire scalp, when given the complete 4 views, or the percentage affected area for individual views. An absolute error of 7% in automated percentage affected area places HairComb in the same range as the state-of-the-art SALT score algorithm presented by Lee et al.²⁵ HairComb, however, goes beyond computing an overall percentage hair loss for each image and instead outputs the percentage hair loss at every point of the scalp within each image. Additionally, the strong correlation shown by both Olsen and Sinclair scores with percentage affected areas suggests that having an automated measure of hair loss at every point of the scalp could also be used to refine or create new measures for CCCA and FPHL, similarly to how ALODEX was created to refine the granularity of SALT.

Finally, HairComb was designed to extract hair loss information independent of alopecia subtype and thus can be equally applied to any alopecia, as long as the hair is properly combed and alopecia area exposed. In the Supplement (eDiscussion in the Supplement), we include guidelines on how to prepare and take images of different alopecia types, including how to style the hair and image the scalp (eTable 4 and 5, eFigures 5 and 6 in the Supplement). While many other scales for alopecias exist, this study focused on analyzing scoring systems for AA, FPHL, and CCCA because they had been clinically validated for grading 2-dimensional photographs that could be also recreated for computational image analysis. Moving toward 3-dimensional scalp visualizations⁴² will enable expanding this work to other alopecia scoring systems.

Limitations

While the algorithm is designed to correctly exclude obstructing objects such as hands, pins, and other objects, it is limited by what is visible in the image: if the underlying hair loss is entirely obstructed, then the hair loss will remain undetected. The hair would have to be repositioned, for example, with the help of pins or swab handles, to expose the area of loss before taking its image (eFigures 5 and 6 in the Supplement). If the original forehead hairline is no longer visible, eg, in patients with frontal fibrosing alopecia, the algorithm will simply treat forehead skin as scalp area (and the output densities can be used for measuring changes over time). If a series of images is required to expose all the hair loss, eg, in the case of patterned thinning where multiple parts may be needed, HairComb would only output the densities visible in each image (which could then be integrated by the clinician). Future refinements to address these issues could include adding interactive user input (eg, manually drawing the original hairline on an image) to correctly delineate the forehead or moving to 3D⁴² to integrate outputs from multiple images across the scalp automatically.

Conclusions

In this research study, we first demonstrated that 3 distinct alopecia scoring systems encode similar information, that this information is approximated by a measure of percentage hair loss, and that an automated algorithm quantifying this percentage hair loss may be designed and applied independent of alopecia subtype. We then presented a new computational algorithm, HairComb, to extract a measure of hair loss from images and validated its use both as a self-standing tool for any alopecia subtype as well as to automate 2 alopecia-specific photographic scoring systems by building prediction models for each one. In 404 participants, automated hair loss percentage showed more than 92% segmentation accuracy and errors comparable to human annotators. In the future, we hope to make progress toward a more accessible system for scoring alopecia by making our online interface Trichy publicly available, especially to populations with limited access to a dermatologist, providing anyone with a method to quantify and track alopecia in a reliable and standardized way.

Supplement.

eMethods 1. Dataset and labeling

eMethods 2. Olsen’s CCCA and Sinclair’s FPHL scoring systems

eMethods 3. Scoring systems analysis

eMethods 4. HairComb algorithm design

eMethods 5. An application: building Olsen and Sinclair prediction models

eDiscussion. Image taking guidelines

eTable 1. Demographics of Study Sample for Scoring Systems Correlations

eTable 2. ICC Values Reported Overall by Score and by Diagnosis

eTable 3. Olsen and Sinclair prediction model quantitative evaluation

eTable 4. Hair styling instructions for different alopecia types

eTable 5. Guidelines for image taking using standardized views

eFigure 1. Established photographic scoring systems for AA, FPHL, and CCCA

eFigure 2. Skin tone vs. hair color combinations for HairComb

eFigure 3. Sample qualitative results on multi-view images

eFigure 4. Image distributions vs. HairComb network output metrics

eFigure 5. Hair styling examples included in Trichy for AA and CCCA

eFigure 6. Sample hair preparation for photographing alopecia under longer hair