Digital twin demonstrates significance of biomechanical growth control in liver regeneration after partial hepatectomy

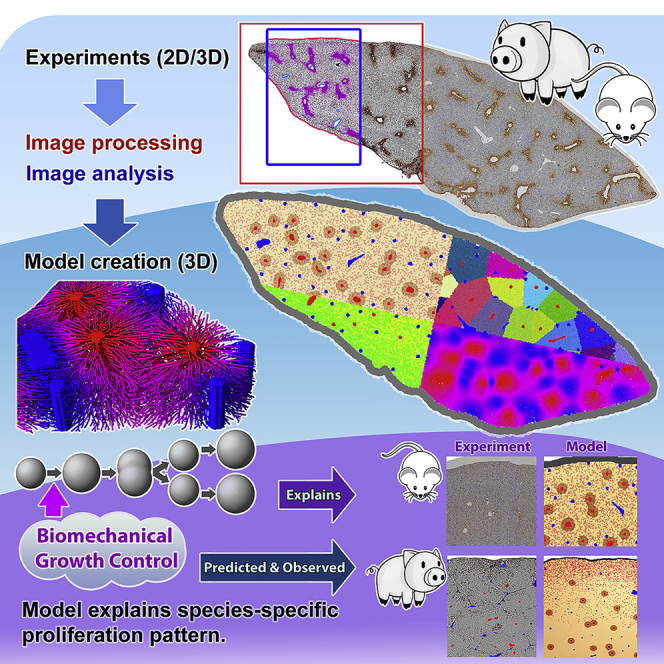
Summary

Partial liver removal is an important therapy option for liver cancer. In most patients within a few weeks, the liver is able to fully regenerate. In some patients, however, regeneration fails with often severe consequences. To better understand the control mechanisms of liver regeneration, experiments in mice were performed, guiding the creation of a spatiotemporal 3D model of the regenerating liver. The model represents cells and blood vessels within an entire liver lobe, a macroscopic liver subunit. The model could reproduce the experimental data only if a biomechanical growth control (BGC)-mechanism, inhibiting cell cycle entrance at high compression, was taken into account and predicted that BGC may act as a short-range growth inhibitor minimizing the number of proliferating neighbor cells of a proliferating cell, generating a checkerboard-like proliferation pattern. Model-predicted cell proliferation patterns in pigs and mice were found experimentally. The results underpin the importance of biomechanical aspects in liver growth control.

Graphical abstract

Highlights

• •First agent-based, organ-scale spatiotemporal 3D model of liver regeneration
• •Biomechanical cell-cycle control can explain regeneration after partial hepatectomy
• •Biomechanical cell-cycle control can act as a short-range proliferation inhibitor
• •Liver regeneration model calibrated with mouse data predicts proliferation in pig

Tissue engineering; Mathematical biosciences; Systems biology

Introduction

Due to its exposure to toxic compounds, the liver evolutionary acquired an extraordinary capacity for self-renewal (Häussinger, 2011). The high regeneration capacity allows the partial surgical removal of the organ, partial hepatectomy (PHx), as a therapy of neoplasms, intrahepatic gallstones, or cysts, whereby the remnant liver regenerates its mass within three to 10 days, depending on the species. However, the precise mechanisms and underlying principles controlling liver regeneration are still not fully understood and in some patients, the regeneration process following PHx fails.

The liver consists of repetitive functional and anatomical building blocks, so-called liver lobules. A human liver consists of about a million lobules, while a mouse liver comprises only several thousand lobules. Blood from the intestine reaches the liver via the portal vein. Moreover, it is supplied by arterial blood from the liver artery. Both, blood from the portal vein and from arterial vein branches reach the periphery of the liver lobules, from where it is drained through a network of micro-vessels, named sinusoids, toward the central vein located in the center of the lobule. Liver lobules of the mouse have mean diameters of about 500 micrometers perpendicular to the orientation of the central vein. In mice, the liver lobules are organized into five lobes, each encapsulated by a layer of connective tissue, the Glisson capsule. Liver regeneration after PHx is characterized by a massive increase in cell mass followed by a remodeling phase. During the mass recovery phase that was addressed in the present study, the remaining lobe grows until the entire liver has reached its original mass. In the common case where entire lobes are resected, this means that the original number of lobes is not restored. During the growth phase, proliferating hepatocytes within each remaining lobe have to push their neighboring cells to generate space for the daughter cells. In principle, this may lead to an increase in pressure and unphysiological compression. If 66% of the liver mass is resected (2/3 PHx), the remaining lobes have to increase their volume by a factor of three. Under the simplifying assumption that liver lobes are spherical, an increase of 66% in volume corresponds to an increase of the lobe diameter to 3^1/3 of its original value, corresponding to 44%. This increase occurs against the resistance of the Glisson capsule. This means that proliferating cells in the interior of a lobe need to generate a net force that is high enough to cause a net displacement of the lobe border by about 44% of the lobe diameter.

The situation is conceptually reminiscent of recent experiments of growing multicellular spheroids in elastic alginate capsules (Alessandri et al., 2013). Here, multicellular spheroids growing within elastic alginate capsules reduce their expansion speed significantly when they touch the capsule demonstrating influence of mechanical stress on cell cycle progression. Comparing the remaining speed of expansion and the mechanical resistance of the alginate capsule, it was possible to infer the influence of mechanical stress on individual cell cycle progression (van Liedekerke et al., 2019). Mechanical stress on cells has been observed to affect cell cycle progression in various situations (Helmlinger et al., 1997; Cheng et al., 2009; Fritsch et al., 2010; Delarue et al., 2014; Mills et al., 2014), and it may impact on tissue form (Ingber, 2005; Shraiman, 2005; Ambrosi et al., 2012; Etournay et al., 2015; Irvine and Shraiman, 2017; Smeets et al., 2020). The findings inspired numerous model approaches (Chen et al., 2001; Ambrosi and Preziosi, 2009; Basan et al., 2009; Byrne and Drasdo, 2009; van Liedekerke et al., 2015; Almet et al., 2020).

The above observations raise the question of whether mechanical stress may build up in the liver lobe as a consequence of the growth during regeneration after PHx and whether this may critically influence the regeneration process. A potentially liver-specific role of mechanical stress is supported by recent findings on the possible and confirmed roles of the YAP protein and its homolog transcriptional co-activator with PDZ-binding motif, TAZ (also named WWTR1), in the regulation of liver regeneration, in particular of liver size (Michalopoulos, 2017). YAP/TAZ are downstream effectors of the Hippo pathway, which is affected for example by cell adhesion and polarity. The Hippo pathway is thought to be active during homeostasis, associated with high levels of the phosphorylation of YAP in the cytoplasm and low levels of YAP in the nucleus, while if Hippo is “OFF,” YAP is translocating into the nucleus promoting expression of TEAD-associated genes causing proliferation, anti-apoptosis, and so forth (Patel et al., 2017). Overexpression of YAP resulted in liver overgrowth and can promote the formation of hepatocellular carcinoma (HCC) (Manmadhan and Ehmer, 2019). At the same time, YAP has also been demonstrated to be a mechanosensitive protein (Elosegui-Artola et al., 2017) i.e., it integrates chemical and mechanical signals (Guo and Zhao, 2013).

To address the question of the possible role of mechanical stress in liver regeneration after PHx, we here developed a computational model by studying the growth of a single lobe down to the level of micro-architecture. The model was parameterized from biological experiments after ⅔ PHx and a cell-based model of liver regeneration after intoxication by carbon tetrachloride (Hoehme et al., 2010). Cell-based (also named “agent-based” or “individual-cell”- or “single-cell”-based) models attract increasing interest to mimic multicellular processes (Anderson et al., 2007; Schlüter et al., 2015; van Liedekerke et al., 2015; Bookholt et al., 2016; Kulawik et al., 2017; Karolak et al., 2018; Metzcar et al., 2019) as they represent a direct approach of systems as single-cell resolution and permit to straightforwardly include intracellular mechanisms (Holzhütter et al., 2012; Robertson-Tessi et al., 2015; Jagiella et al., 2016; Chamseddine and Rejniak, 2020). Such models display each individual hepatocyte in a virtual liver lobule constructed from confocal laser scanning micrographs and hence represent the micro-architecture of liver tissue (Drasdo et al., 2014).

Recently, significant effort has been made toward mathematical models on blood or lymph flow, molecular transport, metabolism, or signaling in liver (Debbaut et al., 2012; König et al., 2012; Schliess et al., 2014; Siggers et al., 2014; Ricken et al., 2015; Schwen et al., 2015; Ghallab et al., 2016; Audebert et al., 2017; Meyer et al., 2017; Berndt et al., 2018; Cordes et al., 2018; Dasgupta et al., 2018; Vartak et al., 2020). These models consider the lobule level within schematic, regular hexagonal geometries, or within compartment models without spatial representation of microarchitecture. The present model focuses on cells as individual basic modeling units organized in space in a realistic tissue microarchitecture and can hence be regarded as an in-silico abstracted copy of the real system.

In this study, we developed a cell-based model of liver regeneration after PHx that comprises an entire lobe consisting of numerous lobules (Figures 1 and 2). In the first step, the model was used to explain liver regeneration in mouse (Figures 1A and 2). Besides cell kinetic parameters the model addresses biomechanical aspects. In particular, the possible role of a biomechanical growth control on cell cycle progression, thereafter abbreviated as BGC was investigated. In the next step, the model was extrapolated from mouse to pig by the re-adjustment of the model parameters (Figure 1B). The underlying question was whether the model could help in an extrapolation from mouse to humans. Livers from pigs were studied, because their size is in the same order of magnitude as that of humans, while liver of mice are about three orders of magnitude smaller (Figure S1). Moreover, it is difficult to obtain human liver tissue at defined periods after PHx, while such material is available from pigs.

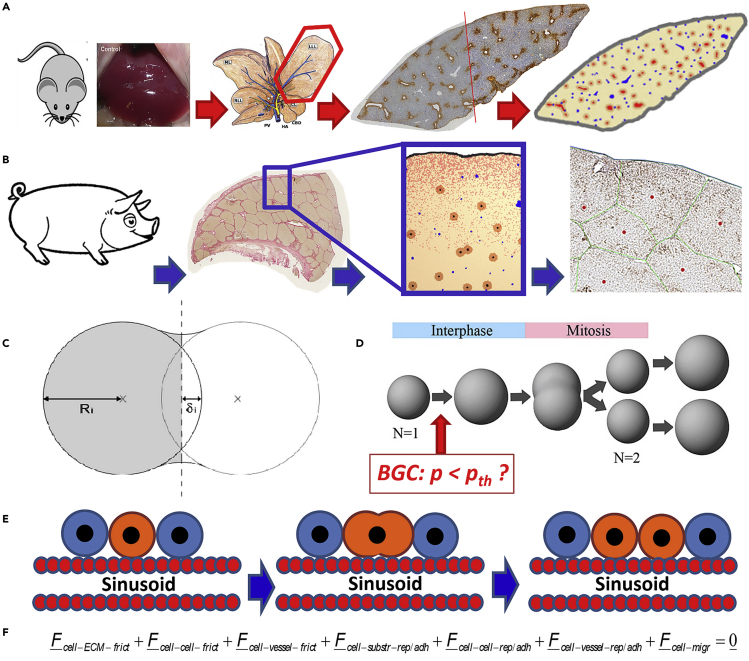
Figure 1.

Main components of the biophysical cell-based computational model and workflow of the article

(A) Experimental data from the regeneration of liver lobules after partial hepatectomy in mice (removing part of the liver) have been used to calibrate a quantitative computational cell-based model of liver regeneration by a pipeline of imaging, image processing, and model development and simulation.

(B) The computational model has been recalibrated with experimental data from pig and predictive simulations been performed on the regeneration scenario of a piece of pig tissue that includes the Glisson capsule. The simulated prediction has been confronted with a pilot experiment.

(C) shows a sketch of two interacting cells for the definition of the indention δ and cell radius R _i used to calculate the cell-cell interaction force. Each cell’s movement is calculated from all forces on that cell including active forces due to migration.

(D) shows the implementation of cell growth in the interface by radius increase until cell volume doubled, and division by splitting. Biomechanical Growth Control (BGC) assumes that a cell does not enter the cell cycle if the pressure exerted on it exceeds a certain threshold value p_th, while in absence of BGC such a constrained is absent. (2D sketch shown for simplicity; the model is 3D.).

(E) Dividing cells align along the closest sinusoid, a mechanism we had named “HSA” (Hoehme et al., 2010).

(F) The dynamics of cells have been simulated by solving a force balance equation for each cell and for each vessel element. Vessels have been mimicked in 3D as a chain of spheres connected by springs (details in text). The force balance equation for each cell includes friction forces between cells and extracellular matrix (including the Glisson capsule), among cells, of cells with vessel elements, as well as adhesion and repulsion forces between cells and substrate (here the Glisson capsule enclosing the liver lobe), among cells, and between cells and vessel elements, and finally an active force to mimic cell migration. Force balance for translational movement is complemented by cell rotations for which a Monte Carlo simulation scheme based on the total interaction energy for the entire system has been used.

Figure 2.

Construction of a computational single-cell-based model from two whole slide scans of a liver lobe by an image processing and analysis chain

(A) PCNA stained micrograph of a mouse liver lobe.

(B) A neighboring slice stained for glutamine synthetase (GS).

(C) Intermediate step in which the contrast of the micrographs was enhanced by contrast-limited adaptive histogram equalization (CLAHE). The localization of the capsule (red outline) and of larger vessels (blue/cyan) was determined. The effect of CLAHE is illustrated within the red rectangle in (B). GS permits distinguishing between central veins and portal veins or arteries. Each central vein of a liver lobule is circumvented by GS-positive hepatocytes. The green coloring shows the GS staining of (B) used to identify the central veins among the larger vessels in the image (red in (D)).

(E–G) Growth simulation of a liver lobe. Time series of proliferating and growing lobe. (E) t = 0 days, (F) t = 2 days, (G) t = 5 days.

(H–J) Exemplary 3D models automatically constructed from the dataset (A). (H-J) only differ in the height that is extrapolated from (A) (H: 3D with a height of 4 cell layers, I: 3D with a height of 10 cell layers). In (H–J) model cells were omitted to reveal the sinusoidal network. The coloring of the network in (H–J) illustrates the predicted oxygen concentration within the sinusoids (blue = high concentration in the portal field, red = low concentration near the central veins). All simulations were carried out for the whole lobe but only half of the lobe was visualized. (J) Magnified sinusoidal network within the lobe model. The sinusoids were not directly reconstructed from bright-field micrographs but are based on the statistical data obtained from the corresponding three-dimensional volume datasets obtained by confocal fluorescence microscopy (Hoehme et al., 2010).

Results

Preparation of experimental data by image processing and -analysis

In conceptual analogy with the analysis of the regeneration process after CCl₄-induced damage (Hoehme et al., 2010; Drasdo et al., 2014) we defined several process parameters to characterize the regeneration process to set up and parameterize a predictive mathematical model of liver regeneration after partial hepatectomy (PHx). The process parameters were chosen for regeneration after PHx were (i) the cell size (PPi), (ii) the lobule size (PPii), (iii) the lobe size (PPiii), and (iv) the proliferation pattern (PPiv) (Figure 3 and Table S1 in the supplement). This information was extracted from histological tissue slides of mouse liver tissue. The data were then used to parameterize the model.

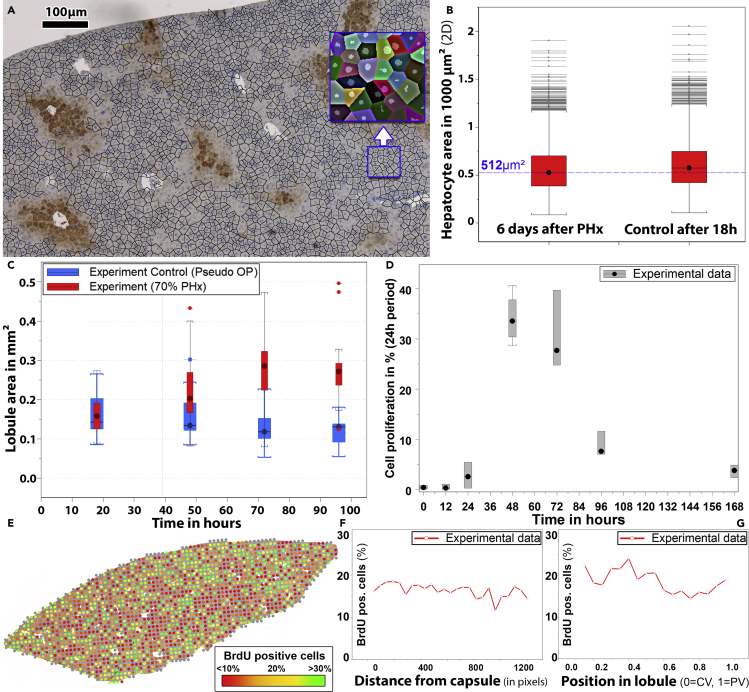
Figure 3.

Experimental parameters in regenerating liver tissue of mice

(A) Representative DAPI and GS-stained bright-field micrograph.

(B) A number of similar micrographs were used to study cell size distributions during regeneration after PHx. The blue line represents the model = 512 μm².

(C) Lobule size in control mice (blue) and mice that underwent PHx (red). The area of the lobules increased during regeneration by a factor of approximately two. Accordingly, the volume increased by about a factor of 3 as expected after 2/3 hepatectomy.

(D) Kinetics of proliferation.

(E) Bright-field micrograph with overlaid proliferation quantification averaged for square-shaped regions of 100 × 100 μm (one dot per region) within the lobe micrograph. The color of the dots represents the average fraction of proliferating cells within the corresponding region (green: >30% proliferating cells, red: <10% proliferating cells).

(F and G) Distribution of BrdU-positive cells as a measure for proliferation within (F) the lobe, (G) the individual lobules.

Hepatocyte size

First, possible changes in the hepatocyte size during regeneration were studied (Figure 3A). We analyzed tissue consisting of more than 10⁵ cells and observed that the average hepatocyte size and size distribution underwent no major changes in the early phase (until 6 days) of the regeneration (Figure 3B). In this phase, the remnant liver lobes grew until the original liver mass was almost recovered. This suggests that the increase in the volume of the liver lobe occurred mainly by the proliferation of hepatocytes that divide and grow until they reach their original size, and not by the size increase of remaining hepatocytes. Hence, we assumed in our model that the average size of hepatocytes does not change during the regeneration process.

Lobule size

For the determination of possible changes in lobule size during the regeneration process first GS-stained bright-field micrographs were analyzed to determine the positions of central and portal veins. The size of the lobules was then automatically calculated from these locations. The exact calculation of the three-dimensional shape and volume of individual lobules was not possible on the basis of two-dimensional micrographs but the distribution of lobule areas in the cutting plane could be used to robustly estimate the growth of the lobules in 3D. The size of the liver lobules during the first 4 days after PHx increased significantly, whereby the difference in lobule area on days 3 and 4 was negligible. The experimentally obtained lobule area increase explained almost the entire regeneration of the liver mass after PHx i.e., after reducing the liver mass to ∼33% of its original value (Figure 3C); in case the lobe would grow isotopically, such an area growth until 96 h would account for 82-94% of mass recovery. An implication of this observation, together with the finding that the cell size remained unchanged, was that it was proliferation and not the volume increase of existing hepatocytes that led to the growth of the liver remnant after PHx. While the majority of liver mass growth occurs by an increase in the size of the existing lobules, the remodeling phase, which can take weeks to months and is not the subject of this article, is characterized by a remodeling of the liver tissue microarchitecture to restore its original microarchitecture as much as this is possible, start by vessel sprouting (Figure S5).

Kinetics of proliferation

As a further process parameter, the percentage of proliferating cells in the entire lobe was experimentally determined at 12, 24, 48, 72, 96, and 168 h after PHx (Figure 3D). The strongest proliferation occurred on days 2 and 3 followed by a decrease. This temporal proliferation pattern was reminiscent of the cell proliferation pattern after CCl₄-induced pericentral damage, which also increases significantly on day 2 and drops on day 4 (Hoehme et al., 2010).

Spatial distribution of proliferation

In the next step, the spatiotemporal distribution of proliferation during the regeneration process was quantified to further parameterize the model. For this, whole slide scans of mouse lobes stained with BrdU or PCNA and GS were analyzed. After identifying the hepatocyte nuclei, an intensity-based threshold was used to decide whether a cell nucleus is BrdU (or PCNA) positive or not (both BrdU and PCNA were used to stain proliferating cells). By combining this data with information about the localization of the central veins in the lobe (based on the GS staining) we were able to quantify the spatial proliferation pattern (A) within the lobe in relation to the closest distance of proliferating cells to the Glisson capsule, and (B) within the lobules in relation to the distance to the closest central vein and portal field. A homogeneously and isotopically distributed proliferation both within the lobe and within the individual lobules was obtained (Figures 3E–3G). In three-dimensional cell aggregates embedded in a homogeneous material such a distribution of proliferation events would be likely to generate an expansion with is largely conserving the overall lobe shape (but not its volume). However, the vascular network generates a scaffold that may break isotropy and homogeneity and hence may lead to deviations of growth maintaining a geometrically similar shape. Moreover, structures neighboring the liver may impact the cell shape, as supported by findings of the impact of external confining geometries on the shape of a growing cell aggregate (Drasdo and Hoehme, 2012). The PHx data did not permit quantifying asymmetries.

In summary, the data of regeneration after ⅔ PHx suggested that the liver recovers most of its mass within 4 days by mainly increasing each lobule by cell proliferation, as the average hepatocyte size and the size distribution does not change. The proliferation of hepatocytes peaked at days 2 and 3 after PHx and was approximately homogeneously distributed over lobes and lobules.

Modeling approach

Before reporting on the results of the model simulations below a list of the key model assumptions is given, at the lobule level by A-x, x enumerates the assumption, and the lobe level by B-x. Detailed descriptions and equations can be found in the SI.

• (A)
  Lobule level:

  • (A-1)
    An individual agent-“center”-based model (CBM) has been used, which approximates a cell in G0, G1, S, an G2 - phase by a sphere, and during mitosis by a dumb-bell (Figure 2D), assuming that these approximate shapes represent the region in space that the cell occupies with overwhelming probability. A dumb-bell is composed of two spheres at a distance of zero when the cell enters into the mitosis phase, and a distance equal to the cell diameter right before division when it splits into two daughter cells. The CBM approximates physical forces between two interacting spherical cells by forces between their centers. In the dumb-bell phase the CBM represents the forces between the closest dumb-bell-spheres of two interacting cells (Figure 2C). The central interaction force between two cells or a cell and an extracellular structure (e.g. the Glisson capsule) integrates compression, deformation, and adhesion forces. The applied force model is the Johnson-Kendal-Roberts (JKR)-force model for homogeneous elastic sticky spheres (SI). Forces are calculated pairwise. Two versions of this model are considered: (i) the original pairwise force, (ii) a modified force, that corrects the JKR force with decreasing distance of the cell-cell center by the effect of volume compression forces (SI). This correction has been computed by comparison to a high-resolution cell model that mimics cell shape in great detail at the expense of significantly longer simulation times [50]. Polarity is taken into account by labeling certain regions on the cell surface that are decorated with cell adhesion molecules by associating to each cell a polarity axis, and an opening angle labeling the adhesive cell surface within an area around the polarity axis.
  • (A-2)
    Cell movement is mimicked as a consequence of force balance (Figure 2F). In the force balance equation, all forces are summed up. For a cell, these are inertia forces, cell-ECM-, cell-sinusoid (sinusoids are liver capillaries)-and cell-cell friction forces, the JKR-forces (s. A-1) between cells, between each cell and the substrate (including the Glisson capsule), each cell and the sinusoids, and an active force for cell migration.
  • (A-3)
    The active cell migration term includes uniform random micro-motility and a directed term by chemotaxis. The chemotaxis term became active only in presence of a local morphogen gradient. Morphogen sources located in the Glisson capsule were one option that was tested to explain the expansion of the liver lobe during regeneration after PHx, and to explain the closure of the central lesion after drug-induced damage in the SI.
  • (A-4)
    Both, polarity and dumb-bell shape break spherical symmetry. As a consequence, an orientation change of a cell in most cases leads to a new state with either higher or lower potential energy. This was mimicked by a Monte Carlo simulation, which evaluates orientation changes based on their accompanying change of energy. We chose this algorithm over equations for the torque for each cell, as the latter is algorithmically much more tedious, and more computationally expensive.
  • (A-5)
    In the cell cycle, a cell first doubles its volume in phases G1, S, G2, then deforms in M-phase into a dumb-bell, which increases its axis until the cell slits into two equally large spheres. The volume of each sphere after this split is half of the volume of the cell before it enters the mitosis phase.
  • The decision of whether it enters the cell cycle i.e., of whether it remains at its size after division or crosses the restriction point to commit to the cell cycle depends on (A5a) an intrinsic cell cycle entrance rate, and (A5b) on the pressure exerted on the cell at the moment it has been selected to enter the cell cycle. Only if this pressure does not exceed a certain threshold value p_th, then the cell is finally entering the cell cycle. This second control step is referred to for simplicity as “Biomechanical Growth Control” (BGC). The formal setting of p_th, to infinity corresponds to the absence of BGC as in that case the cell once selected in step (A5a) is always committing to the cell cycle.
  • A “pressure” was computed by the sum of the cell-cell (or cell-Glisson-capsule) contact pressures.
  • (A-6)
    Cell deformation from a spherical into a dumb-bell shape during mitosis is favored to occur along the closest sinusoid, a mechanism, previously introduced as hepatocyte-sinusoid-alignment (HSA) (Hoehme et al., 2010).
  • (A-7)
    The sinusoids are modeled as chains of small connected spheres, connected to form a capillary network and anchored in the portal veins and the central vein. This description permitted us to simulate the sinusoidal network by an equation of motion for each small sphere in conceptual analogy with the hepatocytes, only missing out the active motion term.
  • (A-8)
    As the model is parameterized in terms of measurable parameters, the physiological range of their numerical values was estimated and the best agreement searched for (more details, SI).
• (B)
  Lobe level:

  • (B-1)
    A model lobe was directly constructed from lobe images by (1) identifying Glisson capsule, portal, and central veins in these images, and then fitting a computed sinusoidal network into each lobule within the lobe such that the network links each central vein with the portal veins within the same lobule. The construction algorithm takes into account geometry and topology of sinusoidal networks by sampling from lobule data obtained from image analysis. One could think of directly replacing each hepatocyte in the whole-slide image with a model hepatocyte, which was not possible because the CBM gives only an approximate cell shape (A-1). Using a higher-resolution model as a “deformable cell model” (DCM) would have been too computationally expensive to permit the simulation of a liver lobe (van Liedekerke et al., 2020).
  • (B-2)
    The Glisson capsule is a construct of vertices linked by linear springs. This description permitted the simulation of the Glisson capsule by an equation of motion for each vertex in analogy with sinusoids.

The BGC enters the cell cycle progression model assumption (A5, A5b) and expresses in our model the condition that a cell does not commit to the cell cycle if the pressure on it exceeds a certain critical threshold value. BGC influences the displacement of cells as well as the spatial-temporal growth pattern at the tissue level. E.g. at a given lobe size proliferation increases the pressure, hence to remain below the critical threshold value, either the cell proliferation must not be accompanied by a volume increase of the cells and its offspring (meaning the average cell volume shrinks with time), or the lobe volume needs to expand proportionally to the increase in the number of cells. The possible consequences are in the next step simulated for realistic parameter combinations and directly compared to experimental data. (Possible molecular players for model assumptions A5a, b are elaborated in the discussion section.)

Simulation of the regenerating liver lobe

The next step was to study whether the experimental observations could consistently be explained in a spatial-temporal computational model that resolved cell scale (Figures 1C–1F). The model represented each hepatocyte as an individual modeling unit parameterized by measurable biomechanical and biokinetic parameters. Furthermore, the model included sinusoids, and central as well as portal vessels. Each model hepatocyte was able to move, grow and divide. Movement of a hepatocyte in the model was a consequence of forces exerted on the hepatocyte, by other hepatocytes, by the sinusoids, and by extracellular material, as well as of hepatocyte micro-motility represented as an active force in the equation simulating hepatocyte movement (Figure 1F). Sinusoids were mimicked as elastic chains anchored in the central and portal veins. Other cell types have not been explicitly represented. At the lobule scale, the model largely corresponded to the experimentally validated model of the regenerating liver lobule after the administration of the hepatotoxic compound CCl₄ (Hoehme et al., 2010) (Figure S2). As the PHx experiments have been executed in the same animal model as previously the experiments on CCl₄-induced damage, we varied only those cell-and sinusoid model parameters at the lobule scale, that were observed or expected to change, as in particular the spatial-temporal cell cycle progression pattern, the size of the sinusoidal network, and the lobule size. These parameters were varied within physiological meaningful ranges (the model parameters and ranges are denoted in Table S2 in the supplement). At the lobe scale, the model represented a longitudinal section through an entire liver lobe with all its lobules and included the Glisson capsule (Figure 4C). The thickness of the section was varied in the simulations to identify the minimum lobe thickness at which the simulation results no longer depended on that parameter (Figure S3). We assumed that proliferation is stopped as soon as the original mass of the liver has been restored (at a lobule area of ∼0.3 mm²). For the control curve, mice underwent a pseudo surgery whereby no part of the liver was removed (Figure 3C). In the model, the proliferation rate in homeostasis was chosen to be 0.001 per day according to (Michalopoulos and DeFrances, 1997).

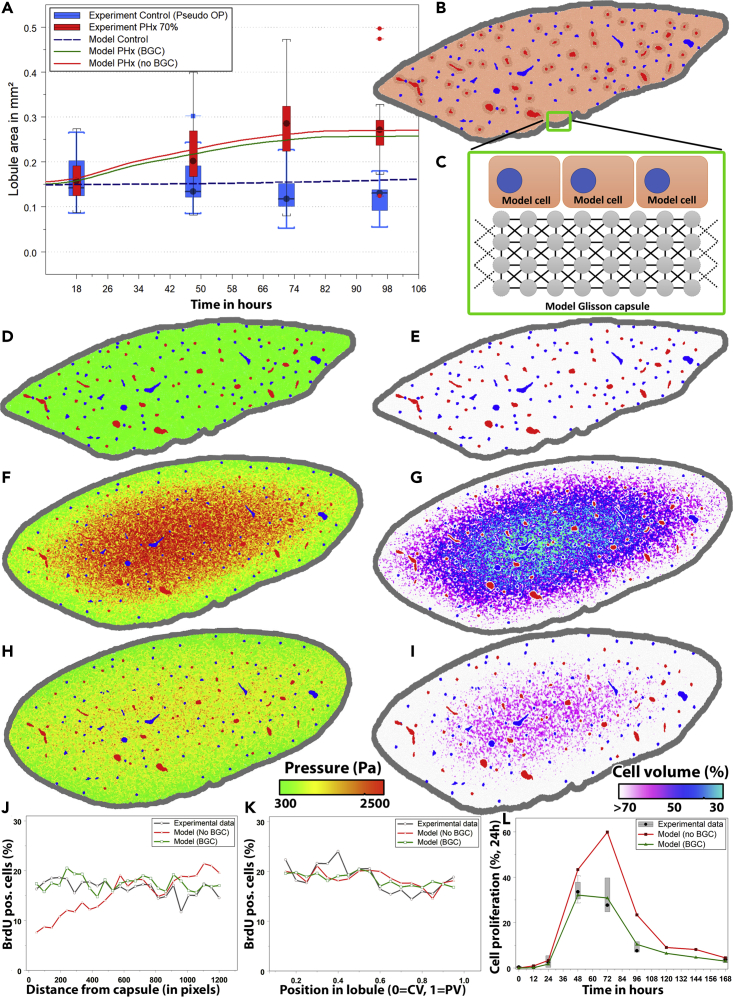
Figure 4.

Simulated liver lobule regeneration scenarios

(A) Increase in liver lobule size comparing the model simulation to experimental data.

(B) Model lobe architecture at t = 0 days (model initial state).

(C–E) (C) Illustration of the model of the Glisson capsule (D) pressure and (E) cell volume visualization at t = 0.

(F and G) (F) Pressure and (G) cell volume visualization at t = 4 days without BGC.

(H and I) (H) Pressure and (I) cell volume visualization at t = 4 days with BGC enabled. Cell volume predictions were based on Voronoi space subdivision in the lobe model. Red = central veins, Blue = portal veins. Cell volume coloring: White: Cell volume of more than 70% of an isolated (uncompressed) cell, magenta: 50%, blue: 40%, cyan: 30% (see legend). Without BGC, the model shows unrealistically small cell volumes within the lobe. Pressure coloring: Green = Low pressure, Yellow = Intermediate, Red = High pressure. The compression in presence of BGC (H and I) is lower than in absence of BGC. Note also that in simulations with and without BGC the lobule shape is approximately conserved (i.e., mathematically “similar”) during lobe growth (compare E-G, E-I), while the borders are rounded off likely by the smoothing effect of the Glisson capsule. (J) Number of BrdU-positive cells by distance from capsule or (K) by position in lobule. (L) Cell proliferation per day by time after PHx.

Simulation of liver regeneration in absence of biomechanical growth control

As liver lobule regeneration after an overdose of CCl₄, which induces pericentral necrosis (Hoehme et al., 2010), could be explained without assuming BGC, we first studied whether the data on liver lobe regeneration after PHx could be explained in the absence of BGC. Simulation of the volume of an entire liver lobe was not feasible in a reasonable time. Therefore, we studied a slice of a certain thickness of an entire liver lobe using the whole slide bright-field scan (Figure 2A) as a starting scenario. Central and portal vessels were identified and the internal lobule structure was obtained by a published algorithm to generate statistically representative liver lobules (Hoehme et al., 2010) (Figures 2J, S2A, and S2B). The hepatocytes were inserted in between the vessels. The remaining fit parameter was the cell cycle entrance rate, which was varied until the average lobule size in the simulation matched that of the experiment (Figure 4A). To exclude artifacts by a too small slide thickness, we repeated the simulation procedure with different thickness values (Figure S3A). For slides with a thickness corresponding to four or more cells the results of the simulation became independent of the slide thickness.

Cell cycle entrance in absence of BGC was mimicked by randomly selecting cells at a certain rate k for cell cycle entrance as explained in assumptions A5a, b assuming that each cell entering the candidate phase enters the cell cycle (formally setting the pressure threshold $p_{th}\to \infty$ in A5b).

However, for a cell cycle entrance rate that was large enough to reproduce the recovery of liver lobule size in absence of BGC, the cell volume decreased to 40% of the volume in a relaxed state (Figure 4G). This finding was in disagreement with experimental observations of unchanged average cell size (Figure 3B). Occupation of the Disse space by the hepatocytes would not be able to account for an average reduction of area per nucleus by 40% as the Disse space with a diameter of about 0.5 μm is much too small to provide sufficient volume for the proliferating cells. Compression of the simulated hepatocytes resulted from the high pressure in the interior of the lobule (Figure 4F), which built up as a consequence of hepatocyte proliferation and could not be relaxed sufficiently fast by pushing the cells toward the borders and by expanding the lobe. A consequence of compression was that the growth rate necessary to expand the lobule within the experimentally observed time period (Figure 4A) needed to be larger than the experimentally observed growth rate (Figure 4L) in order to compensate for the decrease in volume due to compression. Moreover, as cells in the lobe center were much more compressed than those in the periphery of the lobe, the density of proliferation events was predicted to be higher in the lobe center than the lobe periphery (Figure 4K). Such a compression was experimentally not observed. It might be possible that endothelial cell proliferation is delayed in comparison with hepatocyte proliferation. In this case, the sinusoids would have to be stretched and get narrower i.e., the diameter of the sinusoids could be reduced. In the extreme case where the blood inside the sinusoids would give no resistance, this could increase the volume available for hepatocytes up to about 13%, which is insufficient to compensate for the 60% volume reduction observed in the simulations. Hence, we concluded that cell cycle progression in regeneration after PHx must be controlled by a mechanism that inhibits the build-up of too high pressure and too high-volume compression.

Simulation of liver regeneration with simulation in presence of biomechanical growth control

In the next step, biomechanical control of cell cycle progression was included in the model to study if this mechanism allowed to avoid unphysiological cell compressions and consistently explain the experimental data. With BGC, now only those cells that experienced a pressure p below the inhibitory threshold p_th (Figure 1D) entered the cell cycle. p_th was chosen of the order of a few hundreds of Pascals (Figures 2F, 2G, and 4H). In contrast, without BGC (formally equivalent to setting p_th→∞) every cell was able to enter the cell cycle independent of the pressure it experienced. Hence in presence of BGC the cell cycle entrance is controlled by two parameters, an intrinsic proliferation rate k (cf. A5a), and the pressure threshold p_th (cf. A5b). k determines the rate at which a cell enters a "candidate phase," p_th whether a cell in the candidate phase enters the cell cycle i.e., gets a "GO." The model does not specify the molecular origin of the processes. However, a possible origin for entering the candidate phase might be the receipt of growth signals that are required but not sufficient for the cell to commit to the cell cycle, while a possible origin for the second decision process might be related to mechanotransduction as a negative regulator. The proliferating index quantifies the fraction of proliferating cells. Hence the proliferative index is controlled by both intrinsic proliferating rate and pressure threshold. Cell divisions and local re-arrangements lead to stochastic fluctuations of the local pressure. For a given pressure threshold p_th the chance that the local pressure on a cell in the candidate phase is smaller than the pressure threshold, increases with the number of cells in the candidate phase. This number increases with k. If k=0, no cell enters the cell cycle.

The model with BGC was able to correctly simulate the experimentally observed growth kinetics of the lobules (Figure 4A) and the cell proliferation kinetics (Figures 4J–4L) simultaneously in the same simulation. Moreover, the cell compression turned out to be significantly reduced (Figure 4I). BGC ensured that forces emerging from volume increase through cell growth and division in the interior of the lobe do not increase to unrealistically large values. Also, the cell proliferation events were independent of their distance to the Glisson capsule (Figure 4J) and from their absolute position in the lobule (Figures 4J and 4K), in agreement with experimental data. Moreover, the volume of the remnant liver has to increase by a factor of 3 after ⅔ hepatectomy. Assuming that the hepatocyte population size is proportional to the liver volume and an approximately equal expansion of a lobe in each coordinate direction, the hepatocyte population in a cross-section of the lobe should increase by a factor of about 3^2/3 ≈ 2.08. In our simulations, this was reached after about 3 days in mice indicating that the deviation of the lobule area after 3 days from a factor of ∼2.08 might be caused by a compression of the lobules that relax only slowly.

Increasing the mitotic index within a given unit of time by an increase of the probability of a cell to start proliferating (the experimentally found values is 0.5, see Figure S1) within 24 h (this defines the intrinsic proliferation rate) increased the lobe size (Figures S1B–S1D), but also led to short-wavelength undulations at the Glisson capsule. This is reminiscent of buckling instability (Drasdo, 2000). Choosing the pressure threshold too small resulted in the inhibition of cell cycle progression already at low pressure and confinement of cell proliferation to a zone close to the Glisson capsule. This is found to decrease the regeneration velocity hence the lobules at the same time point after PHx too small (Figures S1G and S1H). Both the intrinsic proliferation rate and the pressure threshold are model fit parameters that have to be calibrated so that the mitotic index in the simulation matches that in the experimental data at realistic cell compression.

A cell that is circumvented by many proliferating, growing neighbor cells is more likely to be under large compressive stress than a cell with no proliferating neighbor cell, and is hence unlikely to enter the cell cycle itself (Figure 5D). Consequently, BGC should favor local arrangements where a proliferating cell has only a small number of proliferating neighbor cells (Figure 5D). This was indeed confirmed by the simulations, where at the cellular resolution the model predicted a characteristic checkerboard pattern (Figure 5B). This markedly differed from the pattern obtained if the same total number of cells in that slice entered the cell cycle randomly with equal probability independently of their neighbors, where local accumulations of proliferating cells were observed (Figure 5A).

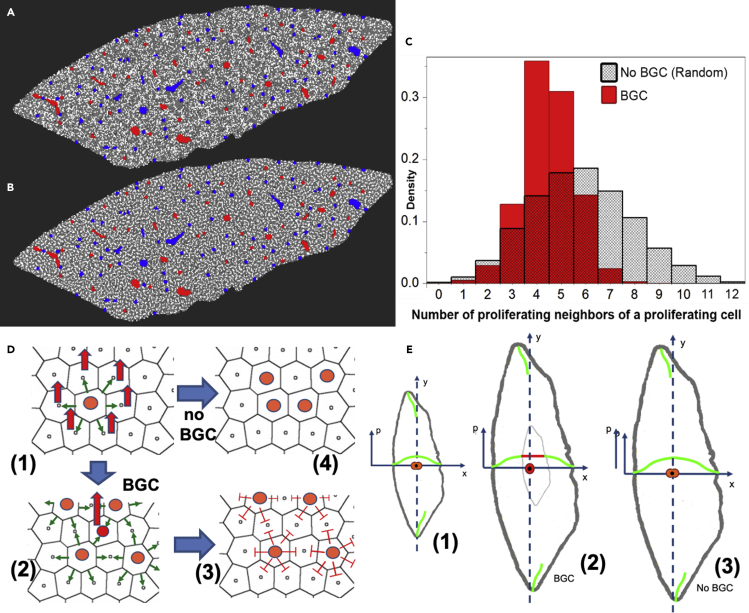
Figure 5.

Simulated spatial cell proliferation pattern in case cells enter the cell cycle

(A–C) (A) randomly (proliferating cells in white) and (B) in the presence of BGC at time t = 3d (C) Corresponding frequency histograms for the number of proliferating cells in the vicinity of a proliferating cell for BGC (pressure-based) control of cell cycle entrance and for random entrance.

(D) Illustration of mechanism. A cell entering the cell cycle (orange in (D, (1))) increases its volume (green arrows) hence increasing the pressure in its neighbor cells (indicated by the red arrows) and itself. In the presence of BGC, a cell (red in (D, (2))) surrounded by proliferating cells (orange in (D, (2))) experiences a high pressure, that, if the pressure exceeds a threshold value p_th, will inhibit this cell to also enter the cell cycle. As a consequence, BGC acts as an inhibitor neighbor cell of proliferating cells favoring distance between proliferating cells (D, (3)). The result is a checkerboard-like proliferation pattern as in (B). With no BGC, cells would enter the cell cycle randomly, which can lead to locally much higher-pressure peaks (and compression forces) (D, (4)), resulting in the situation as in (A).

(E) For sufficiently small liver lobules (E, (1)) the overall pressure can still remain under the threshold pressure of BGC (indicated by the green curves) hence all cells can divide, though inhibiting local pressure peaks by forming a checkerboard-like pattern at the cell scale, as the pressure can be released by the shift of the lobule border. A central dividing cell (orange in the center of the lobule in (E, (1))) can enter the cell cycle and push its neighbor cells toward the border, resulting after some time in a small displacement of the cells right at the Glisson capsule and release of the pressure at the position of the central dividing cell. The pressure is smallest at the lobe border (indicated by the green curves in (E)), as only by the expansion of the Glisson capsule, the lobe can gain volume. Beyond a certain lobule size the pressure release is not fast enough anymore (indicated by the light gray zone in which the red curve indicates the threshold pressure at which no cell cycle progression occurs anymore), hence a zone in the interior occurs in which the pressure gets so high that BGC does not permit proliferations anymore (indicated by the red cell in (E, (2)), unless each cell division would be balanced by a cell death event (which is not observed in liver regeneration). Without BGC, cell divisions would continue (E, (3)) leading to further increase in pressure, which is not observed. (Note that (E) is a schematic representation; in the simulations, the lobule shape during the regeneration simulation is approximately conserved (geometrically “similar”) with rounded-off borders probably arising by the smoothing effect of the Glisson capsule (see Figures 2 and 4)).

In order to quantify this observation, we calculated the average fraction of proliferating cells in the vicinity of a proliferating cell f_PP as well as the histogram of the number of proliferating cells neighboring a proliferating cell in both cases (Figure 5C). We find that BGC indeed reduces the average fraction of proliferating cells in the vicinity of a proliferating cell to f_PP = 0.2418 versus f_PP = 0.3068 in the case of cell cycle entrance by pure chance, i.e., in the absence of BGC.

To see whether the difference of ∼0.06 is small or significant, we searched in the next step for the theoretically smallest and largest values of f_PP for that mitotic index of 0.3 algorithmically, and find the algorithmic minimum at f_PP = 0.2211, and the maximum at 0.3205.

Hence the minimal and maximal values for f_PP, are close to the algorithmically found extremes with and without BGC. Consistent with this finding, we verified algorithmically that BGC maximizes the number of non-proliferating cells of a proliferating cell, kept the average fraction of proliferating cells in the vicinity of a non-proliferating cell low, and the average fraction of non-proliferating cells in the vicinity of a non-proliferating cell high (Table 1). In addition to f_PP, the histogram depicting the number of proliferating neighbor cells of proliferating cells was measured in the presence and absence of BGC. It showed a peak at a lower number for BGC than for random cell cycle entrance, and that BGC inhibited too many neighboring cells of a proliferating cell to enter the cell cycle (Figure 5C).

Table 1.

Average fraction of (non)-proliferation cells in the vicinity of other (non)-proliferating cells

	Average fraction of proliferating cells in the vicinity of a proliferating cell	Average fraction of non-proliferating cells in the vicinity of a proliferating cell	Average fraction of proliferating cells in the vicinity of a non-proliferating cell	Average fraction of non-proliferating cells in the vicinity of a non-proliferating cell
Random (uniform) distribution Figures 5A/5C	0.3068	0.6932	0.3076	0.6923
Biomechanical growth control Figures 5B/5D	0.2418	0.7582	0.3352	0.6649
Heuristic min.	0.2211	0.7789	0.3527	0.6473

The next question was whether one would be able to identify such a checkerboard-like pattern in BrdU-stained images, as BrdU, staining S-phase only, was used to analyze the proliferation kinetics (Figure 4D). For this purpose, the BrdU-staining was simulated in the same simulations that had led to Figures 5A and 5B and—similar to Figure 5C the histograms of neighborhoods were computed. However, significant differences in the number of proliferating neighbors of proliferating cell histograms between random and BGC-controlled cell proliferation for BrdU-stained cells could not be found (Figure S4), likely, as the difference in absolute numbers between random and BGC-controlled cell proliferation was too small.

We used a generated pressure-limited 2D cut through the mouse lobe with an initial cell number of 26368. The number of proliferating cells in both cases was 8102 (=30.73%) at t = 2 days. The simulation with pressure limitation (BGC) was now perfectly matching the experimental data (e.g. Figure 4). The difference with and without BGC was now visible in numbers and population (see Figure 5C).

To challenge our regeneration model, we further studied how the interface fraction that a hepatocyte shares with the sinusoids develops during regeneration. In ref (Hoehme et al., 2010) we used this parameter to quantify the spatial organization of hepatocytes after drug-induced liver damage, which guided us toward hepatocyte-sinusoid alignment (Figure 2E) as a guiding order mechanism in that process. A large interface facilitates the exchange of metabolites and hence should promote liver function. During the first days of regeneration, almost no neo-vascularization is observed suggesting that the hepatocyte-sinusoid interface should decrease. This model prediction could be validated by comparison with data until day 4, when neo-vascularization starts, which is not considered in the model (Figure S6).

In conclusion, the model of a regenerating liver lobe including BGC was able to consistently explain the experimental data and predicted a checkerboard pattern of cell proliferation that is characterized by avoiding local clusters of neighboring proliferating cells.

Alternative mechanisms to biomechanical growth control?

A further question was if possible alternative mechanisms could relax the proliferative stress. One hypothesis could be a mechanism that amplifies the migration of cells toward the Glisson capsule. For example, diffusive signals entering the liver from the Glisson capsule might have made cells migrate actively toward the Glisson capsule thereby relaxing cell compression.

We tested this hypothesis assuming forces of up to ∼30 nN as this is in the range of physiologically meaningful migration forces (van Liedekerke et al., 2020). However, a significant relaxation permitting lobe growth without unrealistic cell compression in absence of BGC could not be found (Figure S3). This indicated that for realistic force values, a directed migration was insufficient to ensure physiologic regeneration after PHx in absence of BGC.

Moreover, we tested different resistances against cell compression by smaller or larger repulsion forces as cells approach each other but also this could not account for the experimental data.

Role of biomechanical growth control in regeneration after CCl₄-induced liver damage?

As BGC seems to be necessary to explain liver regeneration after PHx, we next asked the question of its effect on liver regeneration after CCl₄-induced damage given in the previously created model of the liver lobule regeneration process after an overdose of CCl₄ BGC (Hoehme et al., 2010). In order to study if BGC might modify the results and conclusions of that article, all three different hypotheses of that study were now re-simulated with BGC. It was found that BGC had no effect on the finally identified mechanisms of regeneration (denoted as model 3), while significantly impacting the mechanism underlying model 1 and moderately changing the results of model 2 (Figure S2).

In conclusion, a biomechanically based cell cycle progression control mechanism (BGC) inhibits the buildup of large pressure and local accumulation of proliferating cells. BGC is compatible with both regeneration of liver after CCl₄-induced pericentral damage and after partial hepatectomy.

Model prediction of an inhomogeneous proliferation pattern in pig

In the next step, it was studied whether the model for regeneration after PHx in mouse, after reparameterization with architectural data from pig liver, could describe regeneration after PHx in pig. A pig liver lobe is much larger than a mouse liver lobe hence the absolute displacement of cells close to the Glisson capsule necessary to recover the liver mass that need to be caused by hepatocytes dividing inside the lobe is significantly larger in pig than in mouse i.e., a cell in the center of the lobe has to shift much more tissue to generate space to adopt its original volume after division. The question was, whether this would affect the spatial regeneration pattern.

The choice of pig liver was motivated by its weight that is about the same as the liver weight of human liver, such that pig liver might be considered as a template for the translation from mouse to human (Figure S6). A doubling of the weight of the remnant liver during the regeneration after PHx in mice takes approximately 2 days while in humans the same doubling of weight takes about 7 days (Fausto, 2000; Taub, 2004). At the same time, the size of the individual hepatocytes is largely the same in different species (Watanabe et al., 1978) and the general liver architecture is largely similar. Differences are mainly in the size and number of the lobules. The reasons for the experimentally observed differences in regeneration velocity are still poorly understood.

In order to construct a predictive model for pig on the basis of the presented mouse lobe model, we re-parameterized our computational mouse model based on bright-field and confocal laser scanning micrographs of pig. Image analysis of pig liver lobes stained with Sirius Red for collagen in the portal field (Figure S6A) showed that pig liver lobules are approximately 8 times larger in the area compared to mouse lobules (Figure S6C) while the volume of the individual hepatocytes is largely similar. Different from mouse lobules, pig lobules are enclosed each by septae of connective tissue. Moreover, the microarchitecture of pig lobules might slightly differ compared to mouse lobules but our tissue samples were insufficient for a thorough statistical quantification of these differences. However, the precise lobule architecture did not seem to play a critical role in simulations of regeneration after PHx in mouse, which is why it was here assumed that the architecture is largely the same for pig than for mouse (Table S1).

The data displayed in Table S1 were used to construct liver lobules for pig. However, simulations of an entire pig liver lobe turned out to be not amenable to computer simulations due to the lobe size, which is why only a part of the pig lobe was simulated wherein the lobules were encapsulated by an elastic capsule (Top of Figures 6B and 6C). Moreover, in x-direction periodic boundary conditions were used (i.e., the cells moving out at the right border in Figure 6B and 6C would enter on the left border and vice-versa) and a hard, impermeable border taking into account the vertical lobe symmetry at the bottom of the simulation domain of Figures 6B and 6C was implemented. To verify that considering such a slice does not generate artifacts, simulations with the mouse lobe model using a similar stripe geometry were performed. If the partition was chosen to be large enough (with an edge length of larger than approx. 2-3 lobules) the results were the same as for a full lobe model.

Figure 6.

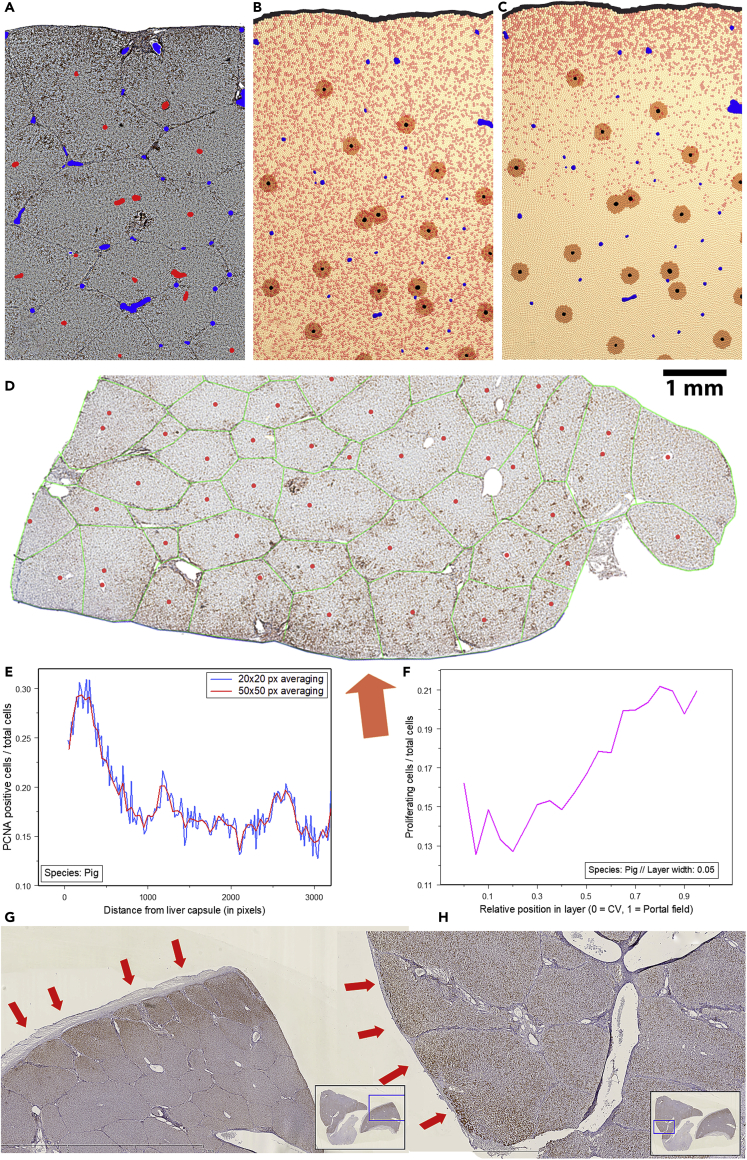
Simulated and experimentally found proliferation pattern in a pilot experiment in pig

(A) Bright-field micrograph of pig liver t = 2 days after PHx (Red = Central veins detected by image processing and analysis, Blue = portal veins; height of sample: 3.5 mm, width: 2.5 mm).

(B) Predicted proliferation scenario in pig during first proliferation wave (t = 1 day) and C) after t = 2 days.

(D) PCNA stained micrograph (whole slide scan) of a part of a pig liver 14 days after PHx. Proliferation is mainly localized near the Glisson capsule (orange arrow).

(E) (Lower left) Quantification of proliferation within the lobe in relation to the distance to the Glisson capsule.

(F) Quantification of proliferation within the lobule shows increased periportal proliferation. (G and H) Proliferation pattern in further pig livers (2 days after PHx). This experimental data also indicates possible increased proliferation near the Glisson capsule (orange/red arrows).

Besides the differences in the architectural parameters depicted in Table S1 for the regenerating pig liver sample the same model parameters as for the regenerating mouse lobe used (e.g. the proliferation inhibition threshold was chosen for pig as for mouse in Figures 2 and 4 (p_th = 300 Pa)). This was based on the assumptions that evolutionary cell level parameters and mechanisms should not largely differ between mouse and pig.

The result of the simulation in pig shows initially a homogeneous isotropic proliferation pattern as in mouse (Figure 6B), while after the first round of proliferation (from around day 2 on) the model predicts the establishment of a proliferation gradient, which is a marked difference from regeneration in mouse (Figure 6C). In the latter phase, the proliferation was predicted to be most pronounced in the vicinity of the Glisson capsule (Figure 6C).

This effect could be explained by the BGC mechanism that inhibited cell cycle progression in case of a locally too large pressure (Figure 5E). As pig lobes are much larger than mouse lobes, the force of growing and dividing cells in the interior of a pig lobe within the simulation was not sufficient anymore to maintain the same degree of cell cycle progression as close to the Glisson capsule. This line of argument is supported by the observation in computed parameter sensitivity analyses for the regenerating mouse lobe that the proliferation of cells located in the lobe center was inhibited when the pressure threshold is too low (Figure S1H). At the same time, the partial cell cycle progression inhibition in the interior of the pig lobe resulted in a decrease of the overall mitotic index compared to mouse, which might explain a slower regeneration after PHx in pig than in mouse. I.e., assuming the same pressure threshold as in mice (p_th = 300 Pa) in the much larger livers such as those of pigs or humans (Figure S6B) the volume fraction wherein the pressure would be predicted to be above the pressure threshold at which cells are able to enter the cell cycle (e.g. lower tissue region in Figure 6C) significantly increased, resulting in an overall slower regeneration after PHx in those larger species compared to smaller species. The time until the liver mass is restored can be approximately estimated from the growth of a lobe slice or part of it.

This hypothesis was tested in a pilot analysis against experimental data in a single pig so far. For this purpose, PCNA-stained micrographs of pig livers (whole slide scans) were studied. The staining patterns indeed suggested the possible existence of a gradient of proliferation with highest proliferation close to the Glisson capsule, as it was predicted by the model (Figures 6E–6H). Moreover, the existence of such a gradient can be considered an important indicator for the validity of our hypothesis of a biomechanical growth control (BGC).

However, the current findings cannot yet be considered as final proof of this theory as other reasons for the experimentally observed gradient of proliferation could not be excluded.

Discussion

In this study, we have developed a computational model that was able to quantitatively explain spatial-temporal data on the regeneration of the liver after partial hepatectomy (PHx) in mouse occurring by the growth of the remnant non-dissected lobules until the liver mass prior to dissection had been recovered. The model in this work thereby addressed the first of two regeneration phases. This first phase is the mass recovery phase of a few days in which the lobules inside each lobe grow until the total mass of all lobes reaches the mass prior to PHx, which in case of resection of entire lobes means that the liver after regeneration from PHx does not restore the original number of lobes. In the second phase not considered here, the tissue micro-architecture is remodeled accompanied by neovascularization toward recovery of the original interface fraction of exchange area between hepatocytes and sinusoids (Figure S5). The interface fraction may contribute to liver function in that a greater exchange area may facilitate the exchange of molecules between blood and hepatocytes.

The computational model (of this first regeneration phase) considered a four cells thick tissue slice of an entire lobe at the resolution of an individual hepatocyte. Besides the individual hepatocytes, the model considered the sinusoidal network, central and portal veins. Hepatocytes were mimicked as homogeneous elastic sticky spheres capable of movement, growth, and division. The model was built upon an earlier model of regeneration after pericentral damage of the liver lobule induced by a hepatotoxic compound (Hoehme et al., 2010) but underwent some important modifications. To ensure compatibility between our liver lobe model with the previously published liver lobule model, aiming prospectively at a full virtual liver model, most model parameters were kept from that lobule-scale model. The repulsive force between cells and cells and capsule mimicking the resistance of a cell to compression was modified based on recent findings in multicellular spheroids growing against the mechanical resistance of an elastic alginate capsule, because this case might be considered similar as a growing population of hepatocytes expanding a lobe against the mechanical resistance of the Glisson capsule (van Liedekerke et al., 2020).

In presence of a biomechanical growth control (BGC) that has not been considered in the model of the regenerating liver lobule after CCl₄-induced peri-central lobular damage (Hoehme et al., 2010), the model was able to explain the experimentally found doubling of liver lobule size, the proliferation kinetics and the spatial pattern of proliferating cells. At the end of the mass recovery, the overall lobe shape was largely conserved but rounded off by the effect of the Glisson capsule. BGC assumes cells are only able to progress in the cell cycle if the pressure on them is below a certain threshold. This is consistent with the growth function found in (van Liedekerke et al., 2020). In the model, BGC was a “gate-keeper mechanism” deciding on whether a cell commits to the cell cycle (assumption A-5b) after it was previously selected as a candidate to “wait at the gate” (A-5a). Such a candidate selection may at the molecular level be realized by HGF and EGF, which are known for their key mitogenic signaling function in hepatocyte division after PHx or acute CCl4-induced damage (Michalopoulos, 2010).

In absence of BGC the repulsive forces between the cells are insufficient to guarantee a sufficiently fast expansion of the Glisson capsule unless the proliferation is set so high, that the cells reveal unrealistic compressions. Even assuming directed migration of the hepatocytes toward the Glisson capsule turned out for realistic magnitudes of forces to be insufficient to avoid occurring of such unrealistic compressions. In presence of BGC the compressions were significantly reduced. Interestingly, BGC caused a checkerboard-like proliferation pattern indicating that BGC minimized for each proliferating cell the number of its proliferating neighbor cells. This observation suggests that BGC results in a spatial pattern of cell proliferation reminiscent of what is known from activator-inhibitor mechanisms with short range activator and long-range inhibitors (Meinhardt, 1982). This prediction shall be studied in future experiments.

The same model was then tested for pig liver that is much larger than mouse liver. For this purpose, the architectural values of the model have been adapted to values obtained by image analysis in pig. For pig liver the model predicted that cell proliferation after the first wave of proliferation should be most pronounced close to the Glisson capsule, while in mouse liver, proliferation was homogeneous isotropic over the liver lobe during the entire regeneration period. This finding provided another testable model prediction.

A first pilot experiment indicates that this prediction might be correct even though a careful study with more pigs would be necessary to validate this prediction. The cause of the difference in the proliferation pattern for small and large liver lobes is that interior proliferating cells in large lobes have to shift much more material in order to generate space for division than this is the case in small liver lobes. This leads to the buildup of a pressure gradient with highest pressure values in the center of the lobe and lowest pressure values close to the Glisson capsule. BGC limits the pressure value in the lobe interior but does not avoid the gradient at the border.

The presence of a pressure gradient with lowest pressure at the border is a generic feature unless the Glisson capsule is so stiff, that no expansion of the lobe by cell division would be possible anymore (Figure 5E). This can be seen by considering the two hypothetical limits of infinitely stiff versus soft Glisson capsule. In the theoretical limit where the Glisson capsule would be infinitely stiff, the pressure would be homogeneous and isotropic with no gradient (as in a pressure cooker). Due to the inextensibility of the capsule in that case either no net change of the cell population size can occur, or the cells would have to shrink, or to occupy space normally taken by sinusoids or ECM. This limit does not apply in the regenerating liver after PHx. The other hypothetical limit is that with infinitely soft (or no) Glisson capsule. In that case, the cells close to the Glisson capsule behave almost as cells at an interface to a liquid medium hence a pressure gradient develops with low pressure at the border and increasing pressure toward the interior. This behavior is reminiscent of growing 3D spheroids and monolayers where a proliferating layer forms, which in monolayers is by construction not nutrient-controlled, and in multicellular spheroids is not nutrient controlled if sufficient nutrients are available (Drasdo & Hoehme, 2005, 2012; Byrne and Drasdo, 2009). The case of the regenerating liver must be closer to the latter case.

We concluded that the Glisson capsule can be expanded by the proliferation of the enclosed cell population only if the stiffness of the capsule is sufficiently moderate. In this case a pressure gradient forms (Figure 5E). The gradient is more pronounced, the lower is the stiffness of the Glisson capsule. If the pressure (or compression, as in (van Liedekerke et al., 2020)) remains on average over the entire lobe below the threshold values at which cell cycle progression would be inhibited, cell proliferation is homogeneous and isotropic. This could be the case in mouse. If at some region in the lobe interior the pressure is larger than the threshold value, regions with more (border) and less (interior) cell proliferation form. In this case the growth is slower than in the former case. This could be the case in pig. If, as in mouse, cells proliferate homogeneously and isotropically in the lobe one might expect exponential growth of the cell population enclosed by the Glisson capsule, but this is unlikely to be detectable as (1) only a fraction of cells enter the cell cycle and as (2) the lobe only increases its cell population size by a factor of roughly three, (3) the Glisson capsule still provides a resistance that might depend on the degree of its extension, and (4) the density of cells might slightly increase.

Still, it is possible that we might have under-or overestimated the mechanical resistance of the Glisson capsule, or the threshold pressure for proliferation, which is not precisely known. However, in the case of a stiffer capsule, the results are unaltered as long as the threshold pressure is larger than the pressure that forms inside the lobe. If the latter is not the case, elevating the pressure threshold would again result in homogeneous, isotropic growth (Figure S1).

We here did not consider the possibility that the Glisson capsule itself grows. Long-term one would certainly expect that remodeling of the capsule after or during the expansion of the lobe would relax the tensile stress in the Glisson capsule, and might even put it to zero i.e., as if there were no Glisson capsule. This, however, would not be expected to alter the conclusion of this work as even in the total absence of a Glisson capsule stress would build up in the interior of the lobule and compress cells un-physiologically in absence of BGC as can be seen by comparison with simulations of growing monolayers or multicellular spheroids, where an enclosing capsule does not exist and where the diameters are of the same order of magnitude as for a mouse lobe.

Besides regeneration of a liver lobe after partial hepatectomy BGC is compatible with the regeneration of a peri-central CCl₄-induced damage as we finally demonstrated by simulations of this process in presence of BGC. BGC is fully compatible with active migration toward the central necrosis and hepatocyte-sinusoid-alignment during that regeneration process (SI). Hence the conclusions of earlier work (Hoehme et al., 2010) remain unaltered.

Limitations of the study

The model did not specify the molecular alphabet of BGC (assumption A-5b), but a possible candidate could be through YAP/TAZ-activation/de-activation. Upon the application of a mechanical force on a cell in an appropriate manner, YAP protein has been shown to enter the nucleus, where it can interact with transcription factors such as TEADs, activate gene transcription and thus promote cell proliferation, inhibit apoptosis, and regulate cell differentiation (Patel et al., 2017). YAP activation resulting in cell proliferation has also been observed in cells plated and low density, while once confluence was reached, YAP was shuttled out of the nucleus and proliferation ceased (Patel et al., 2017; Aragona et al. 2013). While confluence may be attributed to cell-cell and cell-substrate contact involving cadherins and integrins, confluence in cell cultures can be accompanied by cells being pushed out of the monolayer indicating non-negligible mechanical pressure i.e., compressive stress, on cells in the monolayer interior (Galle et al., 2005) that may be sensed by the cytoskeleton and other cell organelles. This raises the question of whether YAP may not also be able to directly sense compressive stress via the cytoskeleton. The possible role of YAP is further supported by observations on its involvement in liver regeneration after PHx (Michalopoulos, 2017; Patel et al., 2017), by the formation as well as the control of hepatocellular carcinoma by modulating YAP activation (Moya et al., 2019), as well as in its association with F-actin (Patel et al., 2017). Moreover, a possible regulatory of YAP in regeneration after PHx has recently been attributed to pressure alterations emerging from a bile canaliculi network expansion as a response to compensate for the overload of bile acid after PHx (Meyer et al., 2020). However, also other mechanotransduction mechanisms may be involved here (Martino et al., 2018), hence the predictions in this work may be challenged by molecular perturbation experiments addressing those different pathways. For example, if the key regulator involved in BGC were YAP (and associated control proteins such as F-acting-capping/severing proteins Cofilin, CapZ, and Gelsolin (Dupont et al., 2011; Aragona et al., 2013)), the effect of overexpressing YAP or blocking Hippo by, for example, knockdown of MST-1/2 should be similar as reducing the threshold pressure p_th, which is compatible with the observation that both, upregulation of YAP in liver and reducing p_th in the computational model after PHx both lead to hepatomegaly ((Patel et al., 2017) and Figure S1). The latter line of argument is further supported by simulations of proliferating cell populations competing for space: if the pressure threshold is lower in one than in the other (competing) cell population, the former outcompetes the latter (Drasdo and Hoehme, 2012), which is reminiscent of the observation by (Moya et al., 2019), that overexpression of YAP in cells circumventing a primary liver tumors may trigger regression of the tumor.

The model prediction for pig could be confirmed in a pilot experiment but further experiments with more pigs would be necessary to validate this prediction.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
5-Bromo-2′-deoxyuridine (BrdU, raised in rat)	AbD Serotec	MCA2060; RRID: AB_323427
Glutamine synthetase (GS, raised in rabbit)	Abcam	ab49873; RRID: AB_880241
Glutamine synthetase (GS, raised in rabbit)	Sigma	G2781, RRID: AB_259853
Proliferating cell nuclear antigen (PCNA, raised in rabbit)	Abcam	ab2426; RRID: AB_303062
HRP Peroxidase-conjugated streptavidin	Dianova	016-030-084; RRID: AB_2337238
Biotin-SP-Affinipure Goat anti-Rat IgG	Dianova	112-065-167; RRID: AB_2338179
Biotin-SP-Affinipure Goat anti-Rabbit IgG	Dianova	111-065-144; RRID: AB_2337965
Experimental models: Organisms/strains
Male C57BL/6N mice	Charles River, Sulzfeld, Germany	N/A
Female German Landrace pigs	(Lehr- und Versuchsgut, Oberholz, Veterinary Medical Faculty, University Leipzig, Germany)	N/A
Software and algorithms
TiQuant 1.4	(Friebel et al., 2015, 2022)	https://www.hoehme.com/Software/TiQuant
CellSys 7.1	(Hoehme and Drasdo, 2010)	https://www.hoehme.com/Software/CellSys

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Dirk Drasdo (dirk.drasdo@inria.fr) or alternatively by Stefan Hoehme (hoehme@uni-leipzig.de).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

Mice

The mice used in this study were maintained according to European (Directive, 2010/63/EU) and Germna guidelines for the care and safe use of experimental animals. The animal experiments were approved by the Landesdirektion Saxony. Male C57BL/6N mice, 11–14 weeks old (Charles River, Sulzfeld, Germany) were used.

Pigs

Commercially available, female German Landrace pigs (Lehr-und Versuchsgut, Oberholz, Leipzig Germany), 2–3 weeks old, were allocated randomly into 2 groups (untreated 0 and 1 day after liver resection; from (Bauer et al., 2008). The study was approved by the local Institutional Animal Use Committee (Regierungspräsidium, Leipzig, Germany).

Method details

Mouse Experiments

The mice were fed ad libitum with Ssniff R/M-H, 10 mm standard diet (Ssniff, Soest, Germany). A precise vessel-oriented, parenchyma-preserving surgical technique was used for 70% partial hepatectomy, using a modification of the technique described by (Madrahimov et al., 2006) for rats. All surgical interventions were performed under inhalation of 2% isoflurane mixed with an oxygen flow of 0.3 L/min (isoflurane vaporizer, Sigma Delta, UK) in S1 operation room. The procedure started with a laparotomy via a transverse abdominal incision. The whole liver was well exposed by elevating the xiphoid process. Skin and muscle were fixed by retractors, and the small bowel was moved out to the left side of the abdomen and covered with saline soaked gauze. The liver was freed from the falciform ligament and triangular ligamentum. The liver lobes were positioned so that hilum of left lateral lobe (LLL) and median lobe (ML) were clearly visible. All subsequent steps were performed using a stereo microscope with a 10× magnification. A ligature (6–0 silk) was applied loosely to the pedicle of LLL. The ligature was tightened keeping a distance of about 3 mm from the cava while the LLL remained in its anatomical position and the lobe resected. Next, cholecystectomy was performed after double ligating the cystic duct and cystic artery using a 7-0 prolene suture. For resection of the median lobe, a virtual line was drawn between the left side of the cava and the gallbladder. The clamp was placed, roughly perpendicular to the surface of the left median lobe (LML), about 3 mm lateral to this line and the left median lobe removed. Proximal to the clamp, a piercing suture was positioned according to vascular anatomy to ligate the left median hepatic vein and the clamp removed. Then, the right median lobe (RML) was clamped in similar way. After resection, two piercing sutures were placed to ligate the right and median hepatic vein as well as the arterial and portal supply. Finally, the abdomen was irrigated with warm saline solution and closed with a 2-layer running suture (6-0 prolene). At the end of anesthesia, animals were able to recover on a heating pad. Temgesic (0.05 mg/kg) was applied subcutaneously after operation and at an interval of 12 h in next 3 days. Animals were monitored daily for body weight development and activity using a scoring system according to (Gentleman et al., 2004). Briefly, mice with normal activity, physiological position, no jaundice, and no signs of bleeding were regarded as healthy (+++); animals showing a weaker activity, hunched back position and/or signs of jaundice or bleeding were regarded as weak (++); and animals with no spontaneous activity and lying position and signs of jaundice or bleeding were regarded as severely ill (+). After the specified period of time the mice were sacrificed by neck dislocation. The abdominal cavity was immediately opened and the whole liver was carefully excised without damaging the liver capsule. The two larger parts of about 1 cm3 in size were used for immunohistochemical analysis. For the preparation of vibratome slices one of them was collected in 4% paraformaldehyde (Sigma, Munich, Germany) and penetrated for 48 h at room temperature and then stored in PBS at 4°C until further use. The latter part of the liver was embedded into paraffin. For this purpose, it was transferred to paraffin embedding cassettes (Carl-Roth, Karlsruhe, Germany) and stored in 4% paraformaldehyde for 48 h at 4°C. Formalin-fixed liver tissue was washed in PBS for 48 h, dehydrated through an ethanol gradient (four times 5 min in 70%, 90 and 95% ethanol, respectively, followed by three times in 100% ethanol). Subsequently, tissue specimens were incubated four times in xylene (Carl-Roth, Karlsruhe, Germany) and incubated overnight in xylene/paraffin (1:1) at 60°C. Afterward, tissue specimens were incubated twice in 60°C paraffin for 3 h, followed by embedding in paraffin.

Slices of 5 μm were prepared using a microtome (Microm, Walldorf, Germany) mounted onto SuperfrostPlus slides, and heated for 20 min at 60°C. The immunostaining protocol is fully described by (Hammad et al., 2014). Briefly, sections were then deparaffinized by five times washing in Rotihistol (Carl-Roth, Karlsruhe, Germany) for 5 min each, followed by hydration through a descending ethanol gradient (100%, 95%, 90%, and 70% ethanol for 5 min each) and 5 min in PBS. During the next step the sections were boiled twice in a microwave oven for 7 min in 0.01M citrate buffer (Carl-Roth, Karlsruhe, Germany; pH 6.0). Endogenous peroxidase was blocked by 30 min incubation in a solution of 7.5% H₂O₂ in methanol at room temperature. All further incubations were performed in a humidified chamber. Unspecific binding sites were blocked by 3% BSA/0.1% TweenR20 using 100 μL per section. Subsequently, endogenous biotin and avidin were blocked using a commercially available kit (Avidin-/Biotin-Blocking-Kit, Vector Lab., Burlingame, USA) according to the manufacturer’s instructions. Leaving out a washing step the blocking solution was dripped off carefully and the primary antibodies (rat-anti-BrdU, Serotec, Dusseldorf, Germany; 1:25; rabbit anti-GS, Sigma Aldrich, 1:4000) were incubated on the tissue section for 1 h at room temperature. Before proceeding with the next incubation step the slides were washed three times 5 min in PBS. Biotinylated secondary antibodies (Dianova, Hamburg, Germany; raised in goat, 1:250 diluted) were chosen to detect the primary antibodies. After 1 h incubation at room temperature the slices were washed again for three times 5 min in PBS. Streptavidin-horseraddish-peroxidase (Dianova, Hamburg, Germany; 1:500 diluted) was incubated on the tissue sections for 1 h at room temperature. After three times 5 min washing in PBS the slices were incubated for 5 min at room temperature with DAB (Dako, Glostrup, Denmark) freshly prepared according to the manufacturer’s instructions. Following this the slides were rinsed for 10 min under tap-water and then counter stained using Mayer’s hemalum (Merck, Darmstadt, Germany) for 90 s. Again, the slides were rinsed for 10 min under tap-water and then dehydrated using the graded ethanol series (70%, 90%, 95%, and 100% for 90 s each) and four times 90 s of Rotihistol. Using Entellan (Merck, Darmstadt, Germany) the slides were mounted and stored in the dark at room temperature until further analysis. Screening of DAB-stained slices was done using a conventional brightfield microscope (Olympus BX41). Images were acquired and organized using cell software (Olympus).

Porcine experiments

Paraffin blocks were obtained and sliced as described in previous section (mouse experiments). Then picro-sirius red staining of porcine liver tissue were performed according to (Hammad et al., 2017). IHC using Proliferating cell nuclear antigen (PCNA) was performed using antibody raised in rabbit (1:100) using similar protocols in mouse section. Screening of DAB-stained slices was done using a conventional brightfield microscope (Olympus BX41). Images were acquired and organized using cell software (Olympus).

Image analysis

At the liver lobule level, we analyzed confocal volume datasets of high resolution (2048 ∗ 2048 pixels in xy-plane) and 10x-20x magnification such that more than one individual lobule could be studied. At the lobe level, stained whole slide scans were analyzed (Figure 1A). In order to quantify the microarchitecture of groups of lobules, we used an improved variant of the image processing and analysis chain that was established in (Hoehme et al., 2010) (for further details also refer to the extensive supplemental information in the supplement of (Hoehme et al., 2010). For example, we now used contrast limited adaptive histogram equalization (CLAHE) as elaborated in (Zuiderveld, 2000) to more efficiently increase and equalize the contrast in the volume datasets without too strong amplification of noise (Figure 1B, red rectangle). By analyzing groups of lobules, we were for example able to obtain a better understanding of the architecture of the sinusoidal blood vessels in the portal field. In addition to the quantification of the three-dimensional architecture of groups of lobules, we also obtained information on the lobe level by additionally analyzing whole slide scans of mouse liver lobes. These data allowed us to (1) quantify the proliferation during regeneration after partial hepatectomy and (2) automatically construct a three-dimensional cell-based model of a whole liver lobe.

Cell size analysis

Possible changes of the hepatocyte size during the regeneration were analyzed using bright field micrographs of control mice (18 h after a pseudo surgery) and of mice 6 days after PHx that were i.a. stained using DAPI. After improving the micrographs using the image processing and-analysis chain described above, we used a marker-controlled watershed segmentation algorithm as in (Meyer, 2005) to determine the position of the cell nuclei. The centers of the cell nuclei were then interpreted as Voronoi sites. The corresponding Voronoi diagram (Figure 3A) gives a good approximation of the cell area per nucleus in the cutting plane of the micrograph. Despite this information cannot be used to determine the exact cell volume or cell shape of individual cells in 3D, it can, however, be used as a first estimate for the cell size distributions for different time points during PHx and detect possible size changes. Knowing the relation between cell area in 2D sections and 3D reconstructions from confocal micrographs (Hoehme et al., 2010), an approximation for the volume per nucleus was inferred from the measured cell area. A more detailed analysis would have required here membrane and nucleus staining to separate between mono- and bi-nucleated cells. In the following we refer to the area per nucleus as “cell area” and to the volume per nucleus as “cell volume”, which is strictly correct in case of mono-nucleated cells.

Lobule size analysis

Using a similar approach as for the cell size analysis, we studied possible changes in lobule size during the regeneration process. We analyzed GS-stained bright field micrographs by a partially manual procedure. While the position of the central vein of each lobule could be automatically determined by an OTSU threshold segmentation of the pericentral GS staining (as described above), the complex shape of some lobules in the two-dimensional cutting plane required a manual assessment of the localization of the corresponding portal veins. The size of the lobules was then automatically calculated from these locations by obtaining the area within the convex hull (Brown, 1979) of the obtained points. Similar to the previous section, the exact calculation of the three-dimensional shape and volume of individual lobules is not possible based on two-dimensional micrographs but the distribution of lobule areas in the cutting plane can be used to robustly estimate the growth of the lobules in 3D. We studied the area of the liver lobules during the first 4 days after PHx (Figure 3C) and found that their size increases significantly. An immediate implication of this finding, together with the finding that the cell area per nucleus remains unchanged, is that it is proliferation and not increase in volume per nucleus (which in the case of only mononuclear cells would correspond to the cell volume) that leads to the growth of the liver remnant after PHx. Note, that if the first wave of proliferations were by bi-nucleated cells that divide into two mononucleated cells by cytoplasmic division, the lobule volume would not significantly increase. Thus proliferation (growth and division) is necessary to increase the lobule volume.

Distribution of proliferation

In a next step, we quantified proliferation during the regeneration process to further parameterize our model. We analyzed whole slide scans of mouse lobes that were stained with BrdU/PCNA and GS. After identifying the hepatocyte nuclei within the images using a marker-controlled watershed segmentation algorithm as in (Meyer, 2005), we used an OTSU threshold to decide whether a cell nucleus is BrdU (or PCNA) positive or not. By combining this data with information about the localization of the central veins in the lobe (based on the GS staining), we were able to quantify proliferation (A) within the lobe e.g. in relation to the distance of proliferating cells to the Glisson capsule and (B) within the lobules e.g. in relation to the distances to the central vein and the portal field. Interestingly, for mouse we found a homogeneously distributed proliferation both within the lobe and within the individual lobules.

Model description

Model at the liver lobule level

At the lobular level, we closely follow the model description in (Hoehme et al., 2018), with some modifications based on (van Liedekerke et al., 2020). Parameters are given in Table S2 in supplement.

(A-1) hepatocyte cell shape and physical forces

Hepatocytes in 3D culture adopt an almost perfect spherical shape (supplement in (Hoehme et al., 2010)). In in vivo tissues visualized by confocal micrographs, hepatocytes adopt shapes reminiscent of densely packed deformed spheres (Hoehme et al., 2010). Therefore, we assumed that hepatocytes can be modeled as homogeneous, isotropic elastic, adhesive, intrinsically spherical, and moderately deformable objects capable of migration, growth, division and death. Hepatocyte-hepatocyte and hepatocyte-blood vessel interaction forces were mimicked by the Johnson-Kendall-Roberts (JKR) (Drasdo and Hoehme, 2005), which could be shown by (Chu et al., 2005) to apply to living cells if compression and pulling of one cell with respect to the other cell is sufficiently fast. It shows a hysteresis behavior depending on whether the two cells approach each other or are pulled apart. For example, cohering cells when pulled apart still cohere beyond the distance at which they came into contact when they were approached. However, upon strong compression the JKR force underestimates the resistance of cells (van Liedekerke et al., 2015). This can be balanced by phenomenologically upregulation of the Young modulus with decreasing cell-cell distance (van Liedekerke et al., 2020). We considered simulations with and without this correction.

Hepatocytes are polar, the distribution of their cell adhesion molecules is not isotropic. We represented hepatocyte polarity by assuming that the contacts are constrained to certain regions of the hepatocyte surface. As a consequence, the force depends on the overlap of the cell surface regions where adhesive molecules are located in. In case the contact area of any of two cells in contact do not contain adhesion molecules the cohesion force is zero.

Mathematically, this was expressed as follows:

The JKR-force $F_{ij}^{JKR}=\left|{\underset{\_}{F}}_{ij}^{JKR}\left(d_{ij}\right)\right|$ where $d_{ij}$ is the distance between the centers of two interacting spheres i and j that was calculated from two implicit equations (Figure 1C):

$${\delta }_{ij}=\frac{a_{ij}^2}{{\tilde{R}}_{ij}}-\sqrt{\frac{2\pi {\hat{\gamma }}_{ij}{a}_{ij}}{{\tilde{E}}_{ij}}}$$

$$a_{ij}^3=\frac{3{\tilde{R}}_{ij}}{4{\tilde{E}}_{ij}}\left[F_{ij}^{JKR}+3\pi {\hat{\gamma }}_{ij}{\tilde{R}}_{ij}+\sqrt{6\pi {\hat{\gamma }}_{ij}{\tilde{R}}_{ij}{F}_{ij}^{JKR}+{\left(3\pi {\hat{\gamma }}_{ij}{\tilde{R}}_{ij}\right)}^2}\right]$$

where $a_{ij}$ is the contact radius. The effective radius ${\tilde{R}}_{ij}$ in this equation is defined by ${\tilde{R}}_{ij}^{-1}=R_i^{-1}+R_j^{-1}$, where $R_i$ is the radius of cell i. $d_{ij}=R_i+R_j-{\delta }_{ij}$ is the distance between the centers of model cell i and cell j, where ${\delta }_{ij}={\delta }_i+{\delta }_j$ is the sum of the deformations of each cell (upon compression it is the overlap of the two spheres) along the axis linking the centers of these cells. ${\tilde{E}}_{ij}$ is the composite Young modulus defined by $E_{ij}^{-1}=\left(1-v_i^2\right)E_i^{-1}+\left(1-v_j^2\right)E_j^{-1}$. ${\nu }_i$ is the Poisson ratio of cell i. We approximated ${\hat{\gamma }}_{ij}\approx {\rho }_m^{ij}{W}_s$ where ${\rho }_m^{ij}$ is the density of surface adhesion molecules acting in the contact area and $W_s$ is the energy of a single bond. The second equation could not be solved explicitly for $F_{ij}^{JKR}\left(d_{ij}\right)$ if $\hat{\gamma }>0$. It was solved first to obtain $a_{ij}\left(F_{ij}^{JKR}\right)$. The value of $a_{ij}$ was then inserted into the first equation to give ${\delta }_{ij}\left(F_{ij}\right)$, and via $d_{ij}=R_i+R_j-{\delta }_{ij}$, $d_{ij}\left(F_{ij}\right)$. $F_{ij}^{JKR}\left(d_{ij}\right)$ could be obtained by plotting $F_{ij}^{JKR}\left(d_{ij}\right)$ vs $d_{ij}$. Different from previous communications we here also studied the effects of cell compression forces upon large compression, which we approximated by choosing $E_i$ as a function that increases with decreasing distance $d_{ij}$ in the equation for ${\tilde{E}}_{ij}$, $E_i\to E_i\left(1+\alpha {{\delta }_{ij}}^4\right)$. Such a function captures the observations made in simulations within a computational high-resolution cell model to correct the JKR-force at high volume compressions (van Liedekerke et al., 2020). This was necessary, as the JKR-force is based on pairwise interactions between cells, which remains a reasonable approximation for more than two interaction cells only if volume compressions remain moderate.

For polar cells, the cell adhesion molecules were assumed to be localized in specific membrane regions, that were defined with regard to a polarity axis of a cell. The effect of polarity on the interaction force was modeled by replacing the membrane density of adhesion molecules ${\rho }_m\to {\rho }_m{A}_{ij}^{adh}\left({\psi }_{ij}\right)/A_{ij}$, in which case only adhesion is downscaled. Here, $A_{ij}^{adh}\left({\psi }_{ij}\right)$ is the area of the overlapping regions that were able to form the adhesive contact within the contact area $A_{ij}\approx \pi a_{ij}\ge A_{ij}^{adh}\left({\psi }_{ij}\right)$. This approximation results in a reduced adhesion force if the overlap area of the membrane regions of neighboring cells carrying the adhesion molecules is smaller than the physical contact area.

In general the density of adhesion molecules on the surface of the two interacting cells differs (Ramis-Conde et al., 2008; Ramis-Conde and Drasdo, 2012), so that ${\rho }_m^{ij}$ has to be calculated from the density of cell adhesion molecules on the surface of each individual cell (or, more general, of a cell i and its interaction object X). We here assumed for simplicity that all surface adhesion molecules in the contact region of a cell and its interacting object (e.g. another cell or sinusoid) were saturated. In this case the density of formed bonds behaves approximately as ${\rho }_m^{iX}\propto \min \left({\rho }_i,{\rho }_X\right)$. Here ${\rho }_i$ is the density of surface adhesion molecules of cell i, ${\rho }_X$ the density of surface adhesion molecules of object X. We further assumed that the density of adhesion molecules in the cell surface was the same for each cell. However, for the simulations of regeneration the assumptions of saturated bonds in contact zone and the same density of adhesion molecules are not critical, as the cells are compressed due to proliferation so cell-cell contacts not under tensile stress.

(A-2) equation of motion for cells

Migration of hepatocytes had been calculated using one equation of motion for each hepatocyte. An equation of motion permits to calculate the change of position of an object (here a hepatocyte) with time. It is obtained by denoting all forces acting on the object, including active force contributions as for example a contribution due to cell micro-motility.

Knowing the velocity v and the current position r permits to calculate the new position of the object from $dr/dt=\underset{\_}{v}$, emerging from solving force balance.

Mathematically, the equation of motion for the cell i reads:

$$m_i\frac{d{\underset{\_}{v}}_i}{dt}+{{\overline{\overline{\varsigma }}}_i}_{ECM}^{CECM}{\underset{\_}{v}}_i\left(t\right)=\sum _{jNNi}{{\overline{\overline{\varsigma }}}_{ij}}^{CC}\left({\underset{\_}{v}}_j\left(t\right)-{\underset{\_}{v}}_i\left(t\right)\right)+\sum _{jNNi}{\underset{\_}{F}}_{ij}^{CC}+\sum _i{\underset{\_}{F}}_{iECM}$$

$$+\sum _{jNNi}{{\overline{\overline{\varsigma }}}_{ij}}^{CS}\left({\underset{\_}{w}}_j\left(t\right)-{\underset{\_}{v}}_i\left(t\right)\right)+\sum _{jNNi}{\underset{\_}{F}}_{ij}^{CS}+\sum _i{\underset{\_}{F}}_i^{active,C}$$ (Equation 1)

${\underset{\_}{v}}_i\left(t\right)$ is the velocity of hepatocyte i. In the first sum, j denotes all neighbor cells of cell i, in the second sum, j denotes all sinusoidal elements interacting with cell i. The first term on the lhs. denotes inertia, the second cell-ECM friction. The first term on the rhs. of the equation denotes cell-cell friction, the second cell-cell adhesion and repulsion forces, the third cell-substrate adhesion and repulsion forces, the fourth term cell-sinusoidal friction, the fifth term cell-sinusoidal adhesion and repulsion forces, and the last term the cell micro-motility i.e., an active movement (migration) term.

Within tissues the friction between cells and the extracellular matrix components, and between cells and the sinusoids is large such that the inertia term, the first term in Equation 1, can be neglected and be set to zero. ${\overline{\overline{\varsigma }}}_{iX}^k$ denotes the friction tensor (here a 3 × 3 matrix) describing the friction of hepatocytes i and j (for X=j, k=CC), or cells i and sinusoids (for X=j, k=CS), or hepatocytes and ECM (for X=ECM, k=CECM). The friction tensor may be decomposed into a perpendicular and parallel component:

${\overline{\overline{\varsigma }}}_{iX}^k={\gamma }_{\perp }^{k,iX}\left({\underset{\_}{u}}_{iX}⨂{\underset{\_}{u}}_{iX}\right)+{\gamma }_{\parallel }^{k,iX}\left(\overline{\overline{I}}-{\underset{\_}{u}}_{iX}⨂{\underset{\_}{u}}_{iX}\right)$. Here, ${\underset{\_}{u}}_{iX}=\left(r_X-r_i\right)/\left|r_X-r_i\right|$ with $r_i$ denoting the position of cell i, and “$⨂$” denoting the dyadic product. ${\underset{\_}{F}}_{iX}$ denotes the JKR-force between cells i and j (for X=j, k=CC) as well as between cell i and substrate (for X=s enumerating sinusoidal elements, k=CS). $\overline{\overline{I}}$ is the unity matrix (here a 3 × 3 matrix with “1” on the diagonal and “0” on the off-diagonals). ${\gamma }_{\perp }^{k,iX}$ , ${\gamma }_{\parallel }^{k,iX}$ are the perpendicular and parallel friction coefficients, respectively, between elements i and X, whereby k = CC, CS, CECM, … denotes the nature of the involved elements. This becomes more apparent when multiplying the friction tensor by the difference in velocity between cell i and object X, $\Delta {\underset{\_}{v}}_{iX}={\underset{\_}{v}}_X-{\underset{\_}{v}}_i$,

$${\overline{\overline{\varsigma }}}_{iX}^k\Delta {\underset{\_}{v}}_i={\gamma }_{\perp }^{k,iX}\left({\underset{\_}{u}}_{iX}⨂{\underset{\_}{u}}_{iX}\right)\Delta {\underset{\_}{v}}_{ij}+{\gamma }_{\parallel }^{k,iX}\left(\overline{\overline{I}}-{\underset{\_}{u}}_{iX}⨂{\underset{\_}{u}}_{iX}\right)\Delta {\underset{\_}{v}}_{iX}={\gamma }_{\perp }^{k,iX}{\underset{\_}{u}}_{iX}\left({\underset{\_}{u}}_{iX}\Delta {\underset{\_}{v}}_{iX}\right)+{\gamma }_{\parallel }^{k,iX}(\overline{\overline{I}}\Delta {\underset{\_}{v}}_{iX}-{\underset{\_}{u}}_{iX}{\underset{\_}{(u}}_{iX}\Delta {\underset{\_}{v}}_{iX}))$$

The first term on the rhs. specifies the friction perpendicular to the direction of movement difference (e.g. if a cell moves against a sinusoid), the second term on the rhs. the tangential friction (e.g. if a cell moves along a sinusoid).

${\underset{\_}{F}}_i^{active,H}$ denotes the active movement force by migration and is denoted in assumption A-3.

The model assumes ${\overline{\overline{\varsigma }}}_{iECM}={\gamma }^{CECM}\overline{\overline{I}}$ i.e., isotropic friction with the extracellular matrix in the space of Disse.

Generally, the perpendicular and parallel friction coefficients, ${\gamma }_{\perp }^{k,iX}$, ${\gamma }_{\parallel }^{k,iX}$ is different for each type of interaction (k=CC, CS, CECM), and depend on the mechanisms of friction. For example, for adhesion-controlled cell-cell friction one might expect ${\gamma }_{\parallel }^{k,ij}=A_{ij}^{adh}{\rho }_{ij}^m{\zeta }_{\parallel }^k$ with k=CC. I.e., friction basically depends on the shared contact area decorated with adhesive bonds, the density of adhesive bonds formed, and an unknown coefficient that characterizes the strength of friction between two cells, ${\zeta }_{\parallel }^{CC}$.

The density of surface adhesion molecules and friction coefficient were lumped together by setting ${\gamma }_{\parallel }^{k,iX}=A_{ij}^{adh}{\xi }_{\parallel }^k$ with ${\xi }_{\parallel }^k={\rho }_{ij}^m{\zeta }_{\parallel }^k$ and ${\gamma }_{\perp }^{k,iX}=A_{ij}^{adh}{\xi }_{\perp }^k$ with ${\xi }_{\perp }^k={\rho }_{ij}^m{\zeta }_{\perp }^k$. Moreover, we chose ${\xi }_{\perp }^k={\xi }_{\parallel }^k\equiv {\xi }^k$ with k=CC, CS, CECM.

(A-3) cell migration

Cells migrate actively. In the absence of morphogen gradients active cell micro-motility was assumed to be random and isotropic (uniform).

In the presence of a morphogen gradient, the cells were assumed to actively move up the gradient by chemotaxis hence in that case migration was directed in accordance with the finding in (Hoehme et al., 2010).

In this work we tested alternatively the hypothesis that cells during migration move toward the Glisson capsule enclosing the liver lobe.

Formally, active cell movement (migration) was mimicked by ${\underset{\_}{F}}_i^{active,H}=\chi \underset{\_}{\nabla }c+\sqrt{2D{\gamma }^2}{\underset{\_}{\eta }}_i\left(t\right)$.

${\underset{\_}{\eta }}_i\left(t\right)$ denotes a Gaussian-distributed random variable with average $⟨{\underset{\_}{\eta }}_i\left(t\right)⟩=0$ and autocorrelation $⟨{\eta }_{mi}\left(t^{\prime }\right){\eta }_{nj}\left(t\right)⟩={\delta }_{ij}\delta \left(t^{\prime }-t\right)$ (m, n = x, y, z denote the coordinate direction; i, j are the hepatocyte indices). Here, $⟨\underset{\_}{X}⟩$ denotes the expectation value obtained by averaging the random variable $\underset{\_}{X}$ over many of its realizations. As each component of $\underset{\_}{\eta }$ is Gaussian distributed, each realization is sampled from a Gaussian distribution. D is the cell diffusion constant and assumed to be a scalar, $\chi$ is the chemotaxis coefficient, c(r,t) the morphogen concentration secreted by the cells dying from damage by CCl₄ or from the Glisson capsule as one model hypothesis we tested. The same result can be obtained if a cell at an interface to the Glisson capsule or a necrotic zone moves in a way that it escapes regions with high cell density (Hoehme et al., 2010). In (Hoehme et al., 2010) also a pressure-based migration mechanism had been established, that for the results presented in this work yielded the same outcome and is therefore not detailed in this work.

(A-4) cell orientation changes

Cell orientation changes can be modeled by an optimization process based on the energy change occurring if the cell orientation changes (Drasdo et al., 2007), or an equation for the angular momentum (Drasdo and Hoehme, 2005). The energy can be calculated from the forces by integration of the energy over the path. The energy-based method is much easier to evaluate and leads to equivalent results, which is why we used it here. Fundamentally, orientation changes were assumed to be driven by energy minimization for which we used the Metropolis algorithm (Drasdo and Hoehme, 2005). In the Metropolis algorithm a trial step (here: a small rotation) was performed, and subsequently it was evaluated whether this step was accepted, or rejected (in which case the step is taken back). The change of total energy of the whole cell configuration was used to evaluate the step. As the orientation change of a hepatocyte only affects the next and maybe next-next neighbors, only those neighbors needed to be considered.

In mathematical terms, to calculate the orientation change of a cell, within each time interval $\Delta t$ for each hepatocyte a rotation trial around three space-fixed axes by angles $\delta {\beta }_i$ with i = 1, 2, 3, $\delta {\omega }_i\in [0,\delta {\omega }_{\mathit{max}})$, with $\delta {\omega }_{\mathit{max}}\ll \pi /2$ was performed, using the algorithm of Barker and Watts (explained in (Drasdo et al., 2007)). The energy was calculated by integration of the equation ${\underset{\_}{F}}_{ij}=-\partial V_{ij}/\partial {\underset{\_}{r}}_i$ where only the JKR-force contributions were considered. The energy difference is then calculated from $\Delta V_{ij}\left(t\right)=V_{ij}\left(t+\Delta t\right)-V_{ij}\left(t\right)$ and the probability that a step was accepted was calculated using $p=\min \left(1,e^{-\Delta V_{ij}/F_T}\right)$ where $F_T$ ≈10⁻¹⁶J is a reference energy (comparable to the k_bT in fluids or gases were k_b is the Boltzmann factor, T the temperature).

(A-5) cell cycle progression & division

During G₁, S, and G₂-phase (interphase) we assumed that a cell doubled its volume, and then deformed into a dumb-bell at constant volume until division (Figure 1D).

Different from (Hoehme et al., 2010) we studied the effect of pressure-inhibited cell cycle progression (BGC) by assuming that a hepatocyte i does not re-enter the cell cycle if the pressure exerted on it overcomes a threshold value.

The decision of whether a hepatocyte of a regenerating liver lobule enters into the cell cycle was now made in two steps:

A5(a): Sampling of candidate cells for cell cycle entrance. For this prior to start of the simulation a cell cycle entrance rate k and a fixed time step $\Delta t$ are fixed such that $N_{\mathit{max}}\mathrm{k}\Delta t\ll 1$ for the maximal cell population number $N=N_{\mathit{max}}$ that might be reached in the simulation. Then, at any time step $\Delta t$ it is calculated whether in that time interval a cell enters the cell cycle by (1.) choosing a uniformly distributed random number $\zeta \in [\mathrm{0,1})$ and (2.) determining if $\zeta <Nk\Delta t$ for the actual cell population size N. If the latter conditions apply, one cell out of the N cells is picked at random and marked as a candidate cell for cell cycle entrance. The chosen process determines a Poisson process, however, small modifications reducing noise may be chosen (Drasdo et al., 2007) without expecting major differences.

A5(b): Permitting a candidate cell to enter the cell cycle if the mechanical pressure $p_i$ (for cell i) on it was below a threshold value p_th (Figure 1D). If condition (A5(b)) i.e., p_i<p_th was not met, the cell did not enter the cell cycle. Absence of BGC was modeled formally by setting the threshold pressure to infinity ($p_{th}\to \infty$), presence of BGC by choosing the pressure threshold to smaller values.

Note here that pressure is closely related to volume by the cell compressibility. We expect therefore that a volume threshold would have led to the same qualitative scenarios.

Mathematically, during interphase, a cell increased its volume by increasing its radius R in small steps $\Delta R\ll R$ until it had doubled its initial “intrinsic” volume to $V_{\mathit{DIV}}={2V}_{INIT}$, where $V_{INIT}$ was its volume immediately after cell division (Figure 1D). Here, the intrinsic volume V_i of a model cell i was approximated by $V_i\left(R_i\right)=4\pi R_i^3/3$. If $V_i=V_{\mathit{DIV}}$ (hence $R_{\mathit{DIV}}$ ≈1.26 R) the model cell i deformed into a dumbbell at constant volume in mitosis (Figure 1D). Subsequently, it divided into two daughter cells of radius R. The duration T of the cell cycle was stochastic, sampled from a Gaussian distribution with expectation value $\tau$ and variance $\Delta \tau =2h$ additionally cropping outside the interval $T\in \left[\tau -\Delta \tau ,\tau +\Delta \tau \right]$

Pressure was defined by the simplified measure $p_i=\frac{{\sum }_j\left({\underset{\_}{F}}_{ij}^{CX}{\underset{\_}{u}}_{ij}\right)}{A_{ij}}$. Here, ${\underset{\_}{F}}_{ij}^{CX}$ denotes the interaction force between a cell i and object j (X denotes an object which can be a cell or a piece of the sinusoid, see A-8), ${\underset{\_}{u}}_{ij}$ the normal vector pointing from cell i to object j, $A_{ij}$ the interface between cell i and object j. Compression is related with a positive pressure, traction with a negative pressure. An alternative, more sophisticated way to associate a pressure to each cell would have been using the virial stress tensor (van Liedekerke et al., 2020). Its trace is the homeostatic pressure. A cell volume could then be associated with the stress by using the relation $\frac{d{p}_i}{d{V}_i}=-\frac{K_i}{V_i}$, whereby $p_i$ is pressure on the cell, $V_i$ the cell volume, and $K_i=\frac{E_i}{3\left(1-2{\nu }_i\right)}$ the compression modulus of cell i. However, the pressure values emerging from this measure and the simpler one in this paper behave proportionally (van Liedekerke et al., 2015).

(A-6) cell orientation during division

In agreement with the findings in liver regeneration after CCl₄ induced liver damage, we assumed that hepatocytes divide along the closest sinusoid (named HSA, hepatocyte-sinusoid alignment, Figure 1E) (Hoehme et al., 2010).

(A-7) sinusoids (blood micro vessels)

The model only considered sinusoids and hepatocytes, the main constituents in a liver lobule. Other cell types such as hepatic stellate cells, Kupffer cells or externally invading macrophages were neglected as these were not needed to explain the principle of regeneration of liver mass and architecture after CCl₄-induced liver damage.

Sinusoids were mimicked as a chain of spheres with a radius equivalent to that obtained by inscribing spheres into vessel segmentations within full volume datasets reconstructed from confocal laser scanning images. Neighbor spheres were pairwise linked by linear springs whereby the spring constant was chosen to reproduce a certain range of Young moduli.

In mathematical terms, each of the sinusoidal spherical elements was assumed to interact with the hepatocytes by a JKR-force (${\underset{\_}{F}}_{ij}=\underset{\_}{F}\left(d_{ij},{\psi }_{ij}\right)$). The forces among sinusoidal elements was approximated by linear elastic springs. ${\underset{\_}{F}}_{kl}^S=\frac{k{l}_0}{A}\times \left(\frac{l_{kl}^S}{l_0}-1\right){\underset{\_}{u}}_{kl}$ with k, l being spheres on the chain connected by a spring denotes the force of sinusoidal element l on sinusoidal element k, $A=\pi r_{kl}^S$ is the sinusoid element intersection area with $r_{kl}^S$ being the radius of the sinusoid element connecting points k and l (in (Hoehme et al., 2010) we used a constant sinusoid radius, see Table S1). l₀ is the spring rest length, $l_{kl}^S$ the actual length. The spring and geometrical parameters can be related to the (elastic) Young modulus by setting $E^S=\frac{k{l}_0}{A}$. The Young modulus is one model parameter. ${\underset{\_}{u}}_{kl}$ is the unit vector pointing from the center of sinusoidal object k to sinusoidal object l.

Movement of the sinusoids is modeled by an equation of motion for each of the sinusoidal spheroid elements using the same type of equation as in for the hepatocytes except for sinusoid we missed out an active motion (migration) force.

Sinusoids in the model were anchored in the central vein, and in the portal veins.

(A-8) reference parameters

All parameters in the model defined above have either a direct biophysical or a bio-kinetic interpretation, and in principle could be determined experimentally. Thus, the physiologically meaningful parameter range for each of the parameters could be estimated. As reference parameters (Table S2) we used the parameter set, for which we had found the best agreement between model simulations and experimental data in regeneration after CCl₄-induced peri-central liver lobule damage in the mouse model (Hoehme et al., 2010). This set of parameters was found by simulated parameter sensitivity analysis varying each model parameter within its physiologically meaningful range, followed by direct comparison of the model simulation outcome with experimental results. By this sensitivity analysis that could be embedded in a general model identification strategy (Drasdo et al., 2014) we were able to rule out model mechanisms that were insufficient in explaining the biological data, and identify the minimal model and its parameters for which the experimental findings could be quantitatively explained.

Effect of biomechanical growth control on liver regeneration after drug-induced damage

The “final” virtual liver twin model should consistently reproduce the findings of former sub-models. Accordingly, we studied the effect of the BGC (assumption A-5b) on liver regeneration after drug-induced pericentral damage happening at the level of each individual liver lobule (Hoehme et al., 2010).

The question was whether BGC, not assumed in the validated model by (Hoehme et al., 2010) where we had studied liver regeneration after intoxication with CCl₄, would modify the conclusions in that reference. In that model, intoxication by CCl₄ leads to a pericentral necrotic lesion, that is then closed within a regeneration process taking about one week to restore the liver mass and 2 weeks to restore liver microarchitecture. The final model obtained (here referred to as (sub-) model 3) out of three alternative models studied in (Hoehme et al., 2010) corresponds to the model detailed in “Material and Methods”, except that BGC was not considered in any of the three models, and that the repulsive forces at large compression were smaller. In each of the models we had directly used the experimentally determined spatial-temporal proliferation pattern after CCl₄ administration as a model input by sampling from the spatial-temporal distribution of BrdU-positive cells to select cells that enter the cell cycle in the computer simulation. The question of this section is to evaluate if including BGC would have modified the results and conclusion of the model of liver regeneration after CCl₄ administration, which could be critical as that model formed the basis of the model at the lobe scale in this work.

First, we briefly summarize how we quantitatively compared them to data and the three models 1–3, before we present the simulation simulations with the updated versions of the models that include BGC.

Process parameters: In order to evaluate the agreement of the results of each submodel with the experimental findings, we had considered three "process" parameters (PPs, (Hoehme et al., 2010; Drasdo et al., 2014)) that we equally measured in experimental images as in the spatial multicellular tissue configurations, namely, (i) the number of hepatocytes per lobule area (PP1), (ii) the area of the necrotic lesion (PP2) and (iii) the hepatocyte-sinusoid interface area fraction (PP3) as a measure for the regeneration of liver lobule microarchitecture. Within a simulated sensitivity analysis, we had varied each model parameter within its physiological range to identify the best possible match between that model and the data. The physiological range could well be identified as the model was parameterized by measurable, meaningful biophysical and bio-kinetic parameters (Drasdo et al., 2014).

Models: In “(sub-)model 1” we had assumed that micro-motility and cell division are both isotropic. This model was not able to close the necrotic peri-central lesion within the experimentally observed regeneration time (i.e. the process parameter "necrotic area", PP2 did not drop to zero in time) but it was able to regenerate the number of cells per lobule (process parameter PP1) by generating a population of strongly compressed hepatocytes at the lobule periphery. In an improved “(sub-)model 2”, we had considered directed cell migration modeled as biased micro-motility in the direction of the necrotic lesion. Even though this model was able to explain the restoration of the liver cell number (PP1) and the closure of the necrotic lesion (PP2) within the experimentally measured time, it could not explain the regeneration of liver architecture (PP3). Only a further improved “(sub-)model 3” in which a novel mechanism, HSA, the alignment of hepatocytes along local sinusoidal vessels after cell division had been introduced (Figure 1E), was able to explain the experimentally observed regeneration process i.e., all parameters PP1-PP3. In order to ensure that all physiological parameters would be captured, a simulated sensitivity analysis has been pursued, varying each model parameter within its physiological range and quantifying the deviation of each process parameter PP1-PP3 between data and simulation.

To compute the potential impact of BGC-based cell cycle entrance on those results, we re-simulated all (sub-)models 1–3 in (Hoehme et al., 2010) now including the pressure-based cell cycle progression mechanism BGC as explained in (A5(B)) i.e., we first use the experimental proliferation pattern to pick cells as candidates for cell cycle progression (A5(A)), and then choose those cells to enter the cell cycle for which the pressure is below a threshold value (A5(B)). Vice-versa, cell cycle entrance was inhibited if the local pressure overcame a critical threshold. Consequently, re-running the simulations with model 1 extended by a pressure-controlled growth inhibition removed unphysiological compression of hepatocytes (cf. Figures S2B with S2A). However, as a consequence model 1 was then not be able anymore to retain the experimentally observed time development of the hepatocyte population within each lobule (PP1, Figure S2C, red line) as approximately two-thirds of all proliferation events were suppressed (Figure S2E). Increasing the number of cells chosen under step (A5(A)) as candidates in model 1 would not have much changed the fraction of cells entering the cell cycle as those would be rejected due to the too high pressure in the second step (A5(B)) so the too small number of cell cycle progression events for (sub-)model 1 cannot be balanced by an increase of candidates under step (A5(A)).

Adding the pressure-controlled growth inhibition to (sub-)models 2 and 3 had almost no effect on the regeneration kinetics since a non-physiological compression was already avoided due to active cell migration toward the necrotic lesion (Figures S2C and S2D). In both model variants, the introduction of a pressure-controlled growth inhibition suppressed only a minor fraction of proliferation events (Figure S2E, model 2: ∼6%, model 3: ∼3%). In our simulations presented here, we focused only on PP1 as in this parameter where the differences showed up.

Model at the liver lobe level

(B-1) lobe model construction by image processing and -analysis

The model of the liver lobe represented a larger portion of liver tissue composed of many liver lobules enclosed by an elastic capsule. Each lobule was modeled as described in the previous section. The sinusoidal network of the individual lobules was generated by a novel species-dependent extension of the vessel generator that was previously introduced in (Hoehme et al., 2010). This extension was used to create an interconnected sinusoidal network for an arbitrary number of lobules thereby constituting either an entire model liver lobe (Figure 2) or a representative part of it that fully represented the network statistics of in vivo sinusoidal networks (Figure S2A and S2B).

We parameterized the liver lobe model by quantifying experimental liver lobe micrographs, segmenting all central veins, and portal veins or hepatic arteries using them as base points for an approximation of liver lobule shape as described in (Friebel et al., 2015). The model construction algorithm used two neighboring whole slide scans of liver lobes (Figure 2), one reference slide as the basis for the reconstruction and the other providing complementary information. The reference slide could for example have been stained for proliferating cells using PCNA (Figure 2A), while the second slide could have been stained for glutamine synthetase (GS) to permit distinguishing between central and portal vessels (Figure 2B). In principle, the algorithm also works with only one single GS-stained slide, but we found that two neighboring slides, one GS-stained and other not GS-stained generally produce better results due to the easier cell nuclei segmentation of non-GS-stained hepatocytes. In a first step the whole slide scans were preprocessed using the improved image processing chain to prepare the following analysis e.g. by improving the contrast of the scans using CLAHE (Figure 2B, red rectangle). In the next step, the two slides were rigidly registered thus merging the information from the GS staining into the first base slide (Figure 2C, green).

Utilizing this information, we determine whether a larger vessel should be considered a central vein or a part of a portal triad by the area of GS-positive tissue in its vicinity. We found that the complex three-dimensional architecture of the liver vascular system may lead to configurations where such decision was very hard if not impossible to take with certainty on the basis of two-dimensional images. A solution would be to use three-dimensional imaging for the entire lobe, which was not available. Alternatively, in these cases, manual adjustments of experts would then be required. In most situations, however, central veins can be robustly and automatically distinguished from portal veins and arteries.

In a next step, we quantified the cell nuclei using a marker-controlled watershed segmentation algorithm as in (Meyer, 2005). We calculated the positions of the corresponding hepatocytes as centers of the Voronoi cells of the Voronoi diagram that could be constructed using the centers of the segmented cell nuclei as Voronoi sites.

Since a lobe model integrating an entire lobe volume would be too computation-time intense, we considered a slice of a lobe (Figure 2D) and varied the thickness in the simulations to test at which thickness the simulation results became independent of the slice thickness. We used a linear extrapolation of 2D information to 3D and studied thicknesses of the model liver lobe of one (Figure 2D), two, four, and 10 hepatocyte diameters (Figure S3A).

(B-2) glisson capsule

Additionally, the liver lobe model represents the Glisson capsule by a system of springs whereby the spring constant was varied to represent different resistances effectively mimicking an elastic layer around the model lobe (Figure 4C). An intensity-based OTSU segmentation identified the shape of the lobe which was assumed to represent the position of the Glisson capsule (Figure 2C, red) that generally encapsulates the whole lobe: In a mathematical model on the scale of a lobe, the mechanical impact of the Glisson capsule (E(Capsule) ≈ 400 kPa, (Carter et al., 2000)) may be significant and thus must be taken into account. Using the obtained information on (1) the shape of the lobe (B-2) and its capsule, (2) the position, shape and type of the larger vessels within the lobe, and (3) the position of the cells within the lobe (B-1), we are able to automatically construct a corresponding cell-based model that reflects all of these aspects (Figures 2D–2J).

Published: January 20, 2023

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •All software code used in this study is available in binary form upon request by Stefan Hoehme (hoehme@uni-leipzig.de).
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.