Nucleotide addition and cleavage by RNA polymerase II: Coordination of two catalytic reactions using a single active site

Abstract

RNA polymerase II (Pol II) incorporates complementary ribonucleotides into the growing RNA chain one at a time via the nucleotide addition cycle. The nucleotide addition cycle, however, is prone to misincorporation of noncomplementary nucleotides. Thus, to ensure transcriptional fidelity, Pol II backtracks and then cleaves the misincorporated nucleotides. These two reverse reactions, nucleotide addition and cleavage, are catalyzed in the same active site of Pol II, which is different from DNA polymerases or other endonucleases. Recently, substantial progress has been made to understand how Pol II effectively performs its dual role in the same active site. Our review highlights these recent studies and provides an overall model of the catalytic mechanisms of Pol II. In particular, RNA extension follows the two-metal-ion mechanism, and several Pol II residues play important roles to facilitate the catalysis. In sharp contrast, the cleavage reaction is independent of any Pol II residues. Interestingly, Pol II relies on its residues to recognize the misincorporated nucleotides during the backtracking process, prior to cleavage. In this way, Pol II efficiently compartmentalizes its two distinct catalytic functions using the same active site. Lastly, we also discuss a new perspective on the potential third Mg²⁺ in the nucleotide addition and intrinsic cleavage reactions.

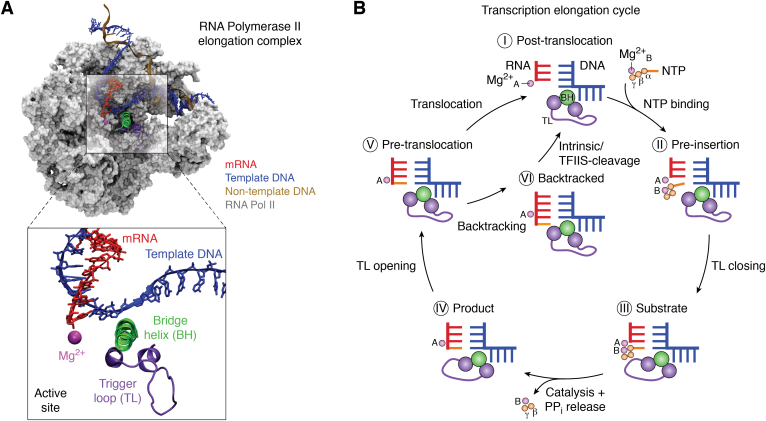
RNA polymerase II (Pol II) is a multisubunit enzyme that synthesizes messenger RNA and regulatory RNAs from a DNA template in eukaryotes. Pol II consists of key motifs that are crucial for the nucleotide addition cycle (NAC), including the trigger loop (TL) and bridge helix (BH) (Fig. 1A) (1, 2). Each NAC of Pol II consists of multiple steps (Fig. 1B) that involves several conformational changes of TL and BH. Starting from the pretranslocation state, Pol II translocates one base pair forward along the template DNA strand to reach the posttranslocation state. Then, nucleotide triphosphate (NTP), alongside an Mg²⁺ (Mg_B) ion, binds to the empty active site. This step is followed by the folding of the TL to stabilize the substrate in the active site. Cognate NTP is then incorporated into the nascent RNA and is facilitated by 2 Mg ions (Mg_A and Mg_B), generating pyrophosphate (PPi) as a by-product. Next, PPi is released alongside Mg_B from the Pol II active site, and the TL unfolds such that the cycle returns to the pretranslocation state. The NAC repeats until Pol II encounters the termination signal. During the elongation process, mismatched or noncognate NTP may be occasionally incorporated into the nascent RNA. If noncognate NTP is incorporated, the forward translocation is compromised, and instead, Pol II backtracks one base pair along the template DNA strand and a short 3′-terminal RNA transcript containing the mis-incorporated nucleotide is removed either by intrinsic cleavage or transcription elongation factor IIS (TFIIS)-assisted cleavage.

Figure 1.

RNA Pol II elongation complex and nucleotide addition cycle.A, overview of the Pol II elongation complex. The trigger loop (purple) and bridge helix (green) are the key motifs involved in the nucleotide addition cycle. Pol II, RNA, and the template DNA are shown in gray, red, and blue, respectively. Mg²⁺ is shown as a magenta sphere. B, the nucleotide addition cycle and proofreading scheme of Pol II. Panel A and B are reproduced with permission from ref. 2. Copyright 2018 Elsevier. NTP, nucleotide triphosphate; Pol II, RNA polymerase II.

Both the nucleotide addition and cleavage reactions have been suggested to follow the universal two-metal-ion reaction mechanism. The two-metal-ion catalytic mechanism was first proposed by T. Steitz and J. Steitz for the 3′-5′ exonuclease activity of bacterial DNA polymerase (3, 4, 5). Based on the crystal structure of the cleaving DNA polymerase, two divalent ions ∼3.8 Å apart were observed in the active site, forming a complex with the scissile phosphate. The scissile phosphate bond is positioned in between the two divalent ions. Metal ion A was suggested to help form the nucleophile OH⁻ to attack the phosphor atom of the scissile phosphate group. Upon the first nucleophilic attack, both metal ions were proposed to stabilize the pentacovalent transition state by coordination with the scissile phosphate oxygen atoms. Then, metal ion B was suggested to help the leaving 3′O⁻ ion.

Pol II utilizes the same active site to perform both nucleotide addition and intrinsic cleavage. Similar to the exonuclease activity of DNA polymerase (6), two Mg²⁺ ions are required for the chemical reactions, which also form a complex with the scissile phosphate, or the phosphate to be added in intrinsic cleavage or nucleotide addition, respectively. However, the general acid and base that activate the attacking nucleophile and protonate the reaction product are enzyme specific (7).

Alongside X-ray crystallography and biochemical experiments, quantum mechanics (QM) calculation is a powerful tool that can elucidate the mechanisms of different chemical reactions. QM calculations consider electronic degrees of freedom and can be used to examine the catalysis and cleavage steps of Pol II. However, QM calculations are too computationally demanding when simulating the entire Pol II (around 50,000 atoms). Thus, the QM/molecular mechanics (MM) method, a hybrid of QM and MM, is often employed to study the chemical reactions of large biological complexes. In the QM/MM method, a small part of the system (e.g., the active site) is simulated with QM (8), while the rest of the system is modeled with classical molecular mechanics methods. QM/MM simulations can elucidate the atomistic mechanism and the energy barrier of chemical reactions.

In this article, we review the detailed mechanisms of the nucleotide addition and cleavage reactions that occur at the same active site in Pol II. We particularly highlight the recent works that examine the roles of Pol II residues in both reaction mechanisms. First, we review several computational and experimental studies to elucidate the catalytic mechanisms of the nucleotide addition reaction of Pol II and the mechanism of PPi release. Next, we review the studies that elucidate the molecular dynamics (MD) of Pol II’s backtracking upon misincorporation and the catalytic mechanisms of the intrinsic and TFIIS-aided cleavage of Pol II. We also discuss the potential role of the third Mg²⁺ ion during the nucleotide addition and intrinsic cleavage of Pol II. Finally, we discuss the dual role of Pol II in catalyzing two distinct chemical reactions (i.e., nucleotide addition and cleavage) using the same active site.

Catalytic mechanisms of nucleotide addition by pol II

Upon binding of NTP to the active site, TL of Pol II needs to be folded to close the active site and stabilize the bound NTP to proceed to the catalysis step. Specifically, residue L1081 forms hydrophobic interactions with the base of NTP, and H1085 interacts with the phosphate of NTP (9, 10). These interactions are important to position the NTP in the correct geometry for catalysis. To catalyze the reaction, both Mg²⁺ ions coordinate with the phosphate oxygen of NTP, aspartic acid residues of Pol II, and the 3′OH of the terminal RNA (11). It is suggested that Mg_A ion coordinate with the 3′OH of RNA and an oxygen atom of P_α on the NTP to keep the distance between the attacking 3′O⁻ ion and P_α within the range for catalysis (12).

The folding of TL and correct geometry of active site is selective for cognate NTP which ensure high fidelity of the RNA elongation process. MD simulations show that only cognate NTP can stabilize the interactions between TL residues and NTP as well as the correct geometry in the active site (12). On the other hand, when noncognate NTP is in the active site, the interactions are disrupted which may lead to opening of unfolding of TL or expulsion of NTP. The distance between 3′OH of RNA and the P_α increases beyond the range for catalysis when noncognate NTP is in the active site. This observation is in line with single-molecule FRET experiment of another multisubunit RNA polymerase (RNAP), Escherichia coli RNAP, that monitors the folding of TL in the presence of either cognate or noncognate NTPs (13). When cognate NTP is added to the elongation complex, TL generally adopts a folded conformation. Conversely, when only noncognate NTP is added, TL remains in the unfolded conformation.

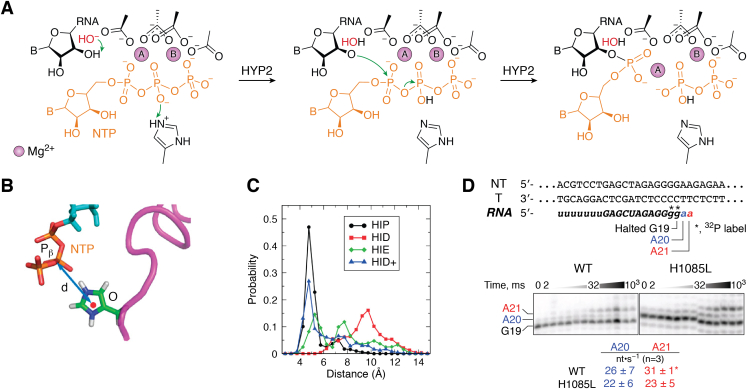
For the nucleotide addition reaction by Pol II to occur, the 3′ OH of the terminal RNA (OH_RNA) must be deprotonated to perform a nucleophilic attack toward the P_α atom on the NTP, resulting in the protonation of PPi. The nucleotide addition reaction mechanism was studied using QM calculations based on density functional theory (14). In this study, the free energy barrier of four proposed nucleotide addition reaction mechanisms was calculated. In the first pathway (HYP1), the phosphate oxygen α of the NTP acts as a general base to deprotonate OH_RNA, which is followed by the nucleophilic attack of the P_α and protonation of the PPi by the protonated phosphate oxygen α. The other three pathways differ in the general base that deprotonates the OH_RNA, while the general acid that protonates the leaving PPi remains the same, i.e., the protonated H1085 (HIP) of the TL. Histidine is absolutely conserved at the H1085 position (in Pol II) in all cellular RNAPs, which suggests its importance to the chemical reactions in RNAPs. In addition, when TL is folded, H1085 is within the spatial range to act as general acid in the reaction. The general bases for the three pathways are (i) an OH⁻ ion (HYP2), (ii) an Mg_A-coordinated OH⁻ (HYP3), and (iii) D485 (HYP4). Based on the density functional theory calculations, HYP2 has the lowest energy barrier of the rate limiting step compared to the other proposed mechanisms (Fig. 2A). The low energy barrier of HYP2 is mostly contributed by the deprotonation of OH_RNA by external OH^- prior to the nucleophilic attack. This result also suggests that the HIP plays an important role as general acid to protonate the leaving PPi in the nucleotide addition reaction. However, the protonation of the PPi via H1085 is not the rate limiting step for any of the proposed mechanisms. Thus, HIP is not exclusively relevant to HYP2 and can act as general acid regardless of the reaction mechanism.

Figure 2.

The role of conserved residue, H1085, during the nucleotide addition reaction in Pol II is proposed via experimental and computational methods.A, the proposed reaction mechanism of nucleotide addition which has the lowest energy barrier based on quantum mechanics calculations. An external hydroxide ion acts as the nucleophile that deprotonates the 3′ OH of RNA, which is followed by the protonation of the leaving pyrophosphate group. B, the distance between H1085 and P_β of NTP was calculated. C, Only protonated H1085 (HIP) can stabilize the NTP in the active site, as shown by the small distance between HIP and P_β of NTP. HID and HIE are H1085 with hydrogen on the delta and epsilon nitrogen of the imidazole ring, respectively. HID+ is HID with a +1 net charge. D, the rate of the single nucleotide addition assay was measured for both the WT and H1085L Pol II. The mutant H1085L does not significantly affect the nucleotide addition rate. Panel A is reproduced with permission from ref 14. Copyright 2011 American Chemical Society. Panel B and C are reproduced with permission from ref 9. National Academy of Sciences, 2010. Panel D is reproduced with permission from ref 19. Copyright 2021 American Chemical Society. NTP, nucleotide triphosphate; Pol II, RNA polymerase II.

An MD simulation study has also shown that when the TL is folded, L1081 and H1085 interact with the NTP substrate (9). In addition, only the HIP can stabilize the NTP in the active site, which is shown by the small distance between HIP and NTP (Fig. 2, B and C). This further suggests that H1085 plays a functional role in facilitating nucleotide addition, either by stabilizing the NTP in the catalytically active conformation or directly serving as the general acid during catalysis.

The importance of H1085 in PoI II catalysis is well-established in experimental work. Previous structural studies from the Kornberg lab revealed direct interactions between H1085 and the NTP substrate when the TL is in a closed conformation (10). Furthermore, the Kaplan lab found that several H1085 variants (A/N/D/F) were lethal, mutations to K/R/W/Y caused severe growth defects, and mutations to Q caused a slight growth defect (7, 15, 16, 17). Strikingly, H1085Y, a mutant that closely mimics the histidine residue, reduces the nucleotide addition rate by an order of magnitude (7). Similarly, the Thomm lab found that when the homologous histidine (H87) in the TL of Pyrococcus furiosus RNAP is mutated into alanine, the nucleotide addition rate reduces by an order of magnitude, and there is a 2-fold decrease in substrate binding (18). On the other hand, among many of the H1085 mutants reported, the H1085L mutant is found to be surprisingly healthy (17). Recently, Landick et al. found that this mutant (H1085L) only slightly reduces the single nucleotide addition rate (Fig. 2D) (19). It is not fully understood why H1085L only has a modest effect, whereas the other mutants have much more severe defects. It is also unclear why H1085F is lethal, whereas H1085Y is viable. We anticipate that multiple factors may contribute to the complicated TL mutant patterns: (a) As pointed out by Landick et al. (19), H1085 may have a structural role to facilitate the formation of the catalytically active conformation and stabilize the cognate substrate at a position poised for reaction. Certain mutants (such as H1085A) may compromise this role; (b) The proton transfer to PPi may require the involvement of the side chain of a TL residue and/or solvent water. While the polar side chains of WT H1085 (imidazole side chain) and viable polar mutants (such as the 4-hydroxyl group of H1085Y and the amide group of H1085Q) may be involved in the proton transfer to PPi, the proton transfer step can also be mediated by solvent water in the hydrophobic H1085L mutant (viable). In contrast, for other nonviable hydrophobic mutants, such as H1085F, the solvent water may be completely excluded by the aromatic bulky side chains and thus compromise the proton transfer step and subsequent PPi release (these findings may explain why H1085Y and H1085L are viable, whereas H1085F is not); (c). It is also possible that the H1085 mutants have distinct effects on the dynamics of TL folding and therefore change its contribution in Pol II catalysis (residue of 1085) or the rate-limiting steps. Nevertheless, further studies are needed to explore this direction.

Furthermore, time-resolved X-ray crystallography has shown the involvement of a third divalent metal in the nucleotide addition reaction of DNA polymerase (20). Specifically, upon the formation of the DNA product and breakage of PPi from the P_α, an Mg²⁺ was shown to bind to newly formed DNA product and the leaving the PPi ion. The third Mg²⁺ was speculated to coordinate with the transition state, between the O_α and O_β, after the nucleophilic attack to the P_α, which will help to overcome the high energy barrier of the product formation (20). A computational study using the QM/MM free energy calculations have shown that the presence of third Mg²⁺ during the catalysis stabilizes and lowering the energy of the product state via electrostatic interaction with the leaving PPi (21). Yet, it is still unclear whether the third metal ion is involved in the catalysis reaction or simply stabilizes the product to help the exit of PPi. Considering that the conformation of the active site of DNA polymerase and RNAP are highly conserved, further studies to confirm the involvement of the third metal ion to the nucleotide addition reaction of RNAPs would be worthwhile.

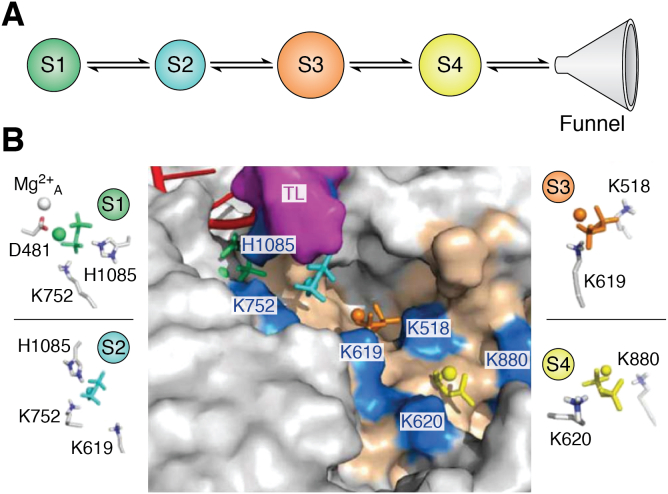
Upon addition of NTP into the nascent RNA, PPi is generated as a by-product. PPi alongside MgB must leave the active site to provide enough space for the next incoming NTP. To study the PPi release pathway, Huang et al. employ Markov State Models (MSMs) constructed based on MD simulations (22). MD simulations are a computational method that can estimate the movement of biological molecules in atomic resolution. Although powerful, it is challenging to simulate large biological complexes, such as Pol II, at biologically relevant timescales (μs to ms) due to technological limitations and unfeasible computational times. MSMs can predict the slow timescale dynamics based on short MD simulations, which can be performed in parallel (23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47). MSMs model the dynamics processes estimated from Markovian or Memoryless transitions between metastable states, meaning that the transition to the next state only depends on the current state and is independent of the previous transitions. Importantly, MSMs built from MD simulations can elucidate atomistic mechanisms and the dynamics of functional conformational changes (36, 48, 49, 50, 51, 52, 53), such as the release of PPi (22, 54).

MSMs were constructed to study the dynamic process of the (Ppi-Mg)²⁻ ion leaving the active site to enter the bulk solvent through the secondary channel of Pol II. MSMs identify four metastable states (State S1-S4, Fig. 3) during PPi release, and the transition from State S1 to S4 occurs at ∼1.5μs. (Ppi-Mg)²⁻ was shown to “hop” between several positively charged residues along the secondary channel. In State S1, (Ppi-Mg)²⁻ forms a salt bridge interaction with the HIP residue on the TL in the active site (Fig. 3B). This interaction is crucial for the release of (Ppi-Mg)²⁻ from the active site as a simulation with the mutant, H1085F, shows that (Ppi-Mg)²⁻ is stable in the active site and thus has less of a tendency to be released. This step is followed by a series of salt-bridge interactions between lysine residues in the secondary channel. Importantly, the interaction between (Ppi-Mg)²⁻ and H1085 during PPi release may increase the flexibility of the TL, leading to the TL unfolding and preparing Pol II for the next NAC.

Figure 3.

MSM elucidated the molecular mechanism of PPi release from the active site after the nucleotide addition reaction.A, MSMs identify four metastable states for the release of (PPi-Mg)²⁻ from the active site into the bulk solvent (S1-S4). B, the representative structures of each metastable state. This figure is reproduced with permission from ref 22. Copyright 2012 American Chemical Society. MSMs, Markov State Models.

Molecular mechanisms of pol II’s backtracking and cleavage

If a noncognate nucleotide is incorporated into the nascent RNA, Pol II can backtrack (i.e., perform backward translocation on the RNA–DNA hybrid) and then cleave a short piece of the 3′-end of the RNA transcript which contains the misincorporated nucleotide either via intrinsic or TFIIS-aided cleavage (55). Upon backtracking, Pol II cleaves the phosphodiester bond between the -1 and +1 position and releases dinucleotides (or a longer piece of RNA) at the 3′ terminal of the nascent RNA. As a result, the Pol II complex is reactivated to generate a new posttranslocation state (step VI, Fig. 1B). It has been suggested that the cleavage also follows the two-metal-ions mechanism, requiring two Mg²⁺ (MgA and MgB) to be positioned in the active site to form a complex with the scissile phosphate of the backtracked RNA.

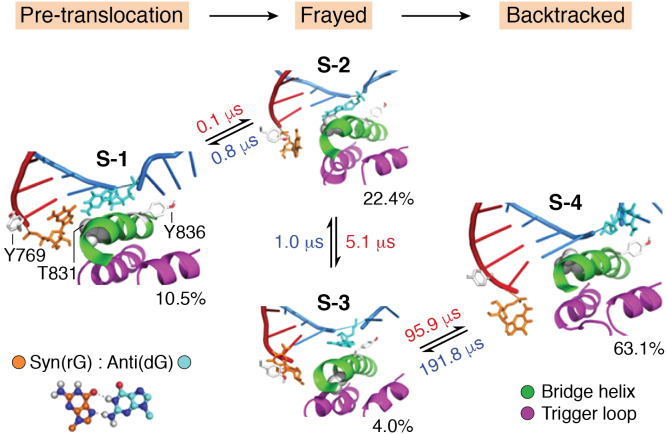
Using MSMs, four metastable states of the backtracking process were identified, showing the stepwise mechanism of the backtracking process (State S-1 to S-4, Fig. 4) (56). In this mechanism, the misincorporated RNA first frays from the active site (S-1 → S-2 → S-3, Fig. 4), after which the backtracking of the template and nontemplate DNA by one basepair takes place (S-3→S-4, Fig. 4). During the transition from S-1 to S-2, the T831 residue on the BH acts as a sensing probe that examines the stability of the DNA–RNA pair in the active site. Misincorporated RNA forms less stable hydrogen bonds with the template DNA and thus tends to fray and transition to the frayed state (S-2 and S-3, Fig. 4). The role of T831 is validated by a mutagenesis experiment, where a significantly slower cleavage rate is observed for T831A compared to the wildtype Pol II.

Figure 4.

MSM identified four metastable states for the backtracking of misincorporated RNA by one base pair in Pol II (S-1 to S-4). The representative structure for each metastable state is shown. This figure is reproduced with permission from ref 56. Copyright 2016 Springer Nature. MSM, Markov State Model.

Upon backtracking, Pol II removes the downstream terminal RNA nucleotides via either intrinsic cleavage or TFIIS-assisted cleavage. Similar to other two-metal-ion reaction mechanisms, the cleavage reaction also requires a general base to activate the attacking nucleophile and a general acid to protonate the by-product. Pol II residues (H1085) or the nucleobase of terminal RNA have been suggested to act as a general base. Yet, a recent biochemical study has shown that the mutation of H1085 to leucine, a nonpolar residue, does not affect the cleavage rate, which indicates that H1085 does not serve as a general base during cleavage (19).

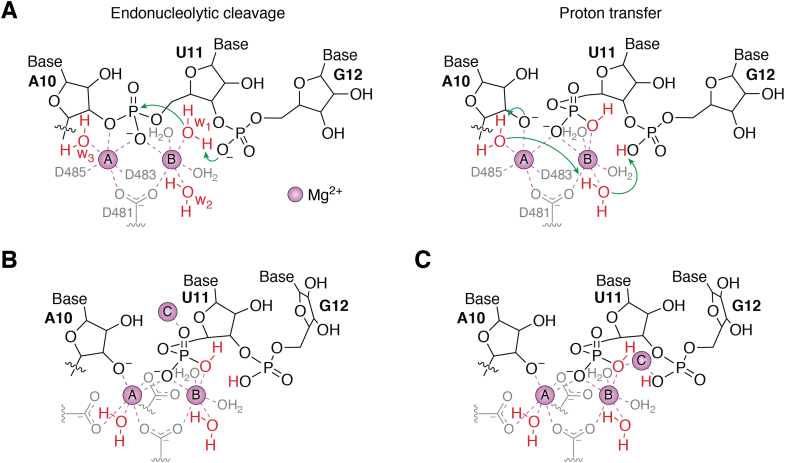
QM/MM-MD simulations coupled with biochemical experiments have also been performed to examine the reaction mechanism of intrinsic cleavage (57). Based on the QM/MM calculation, the phosphate oxygen of the backtracked RNA (Rp-O of G12, Fig. 5A) acts as a general base to activate the active site water molecule and generate a hydroxide (OH⁻) ion which acts as the attacking nucleophile. The OH⁻ ion attacks the phosphate bond between A10 and U11 of the nascent RNA (Fig. 5A), which leads to the cleavage of the terminal dinucleotide of RNA (U11 and G12). The next step is the protonation of the newly formed terminal O3⁻. QM/MM simulations show that a water molecule in the active site acts as a general acid to protonate the terminal O3⁻, which is followed by a series of proton transfers to recover the water molecules in the active site.

Figure 5.

QM/MM-MD simulations showed that the intrinsic cleavage reaction does not involve any Pol II residues.A, the proposed reaction mechanism of intrinsic cleavage of Pol II. B and C, modeled Mg_C ion upon intrinsic cleavage in Pol II, which is positioned on the (B) cleaved phosphate and (C) near the general base Rp-O of G12. This figure is reproduced from ref 57. Copyright 2019 Springer Nature. Pol II, RNA polymerase II.

The role of Rp-O as a general base is validated by two sets of experiments. The first experiment measures the cleavage rate of the elongation complexes with two kinds of RNA, 3′-5′ and 2′-5′ phosphodiester linkages between U11 and G12. The 2′-5′ linkage between the 0 and −1 sites causes the RNA at site 0 to be further away from the active site and discourages its participation in the cleavage reaction. The rate of the 2′-5′ linked RNA indeed was shown to be 14 times slower than the wildtype, 3′-5′ linked RNA. The second experiment measures the cleavage rate when G12 possesses a thiol-substituted phosphate oxygen. The substitution of the oxygen atom with sulfur creates two stereoisomers of the terminal RNA, R_p-S and S_p-S. It was hypothesized that R_p-S would reduce the tendency of the terminal RNA to attack a water molecule. R_p-S was indeed shown to have a 3-fold reduction in cleavage rate, while S_p-S only minimally affected the cleavage rate. This result further confirms the role of R_p-O as the general base in the intrinsic cleavage reaction. To test whether the G12 nucleobase can act as a general base, the cleavage rate of the elongation complex with an RNA scaffold containing a 7-deaza-guanine (substitution at N7 to C) at the G12 position was measured and shown to not affect the cleavage rate. This result indicates that the nucleobase of the backtracked RNA does not act as a general base. Lastly, it has been suggested that a Pol II residue, protonated D485, may act as a general acid during proton transfer. However, based on MD simulations, a protonated D485 cannot stabilize the active site. The role of H1085 residue to the cleavage reactions has also been examined via a recent biochemical experiment. The mutation of H1085 to leucine, which is nonpolar and cannot participate in proton transfer, does not affect the rate of the cleavage reaction (19). This result further supports the hypothesis that Pol II residues are not involved in the proton transfer of the cleavage reaction.

A third Mg²⁺ ion has been speculated to facilitate the cleavage of the RNA by Ribonuclease H (58). Another study has also observed that a third Mg²⁺ may lower the activation barrier in the nucleotide addition reaction of DNA Pol ƞ (20, 59) as well as DNA pol β (60). Indeed, structural modeling shows that there is enough space for the third Mg²⁺ in the active site (Fig. 5, B and C). Experimental results have also shown that an increase in Mg²⁺ concentration increases the k_cat of intrinsic cleavage in N7-modified terminal guanine, supporting the participation of the third Mg²⁺ in cleavage. Furthermore, the introduction of the third Mg²⁺ may further facilitate the deprotonation of the attacking nucleophile by increasing the pK_a of the R_p-O of backtracked RNA (Fig. 5C). However, the introduction of the third Mg²⁺ only causes minimal rearrangement of the RNA active site and residues and is thus unlikely to alter the previously proposed mechanism.

For longer backtracked RNA, TFIIS is required to reactivate the arrested Pol II state. TFIIS has also been shown to accelerate the cleavage reaction by one order of magnitude compared with intrinsic cleavage (61). Based on the crystal structure of a Pol II elongation complex with TFIIS bound, TFIIS binds through the secondary channel (pore and funnel) of Pol II and extends to the active site of Pol II (62). TFIIS reactivates Pol II by displacing the backtracked RNA in the secondary channel and facilitates the cleavage of the RNA (63). It has been suggested that residues D290-E291 of TFIIS’s domain III may coordinate with and stabilize Mg_B. In addition, residue R287 on TFIIS may further stabilize the transition state.

Conclusions

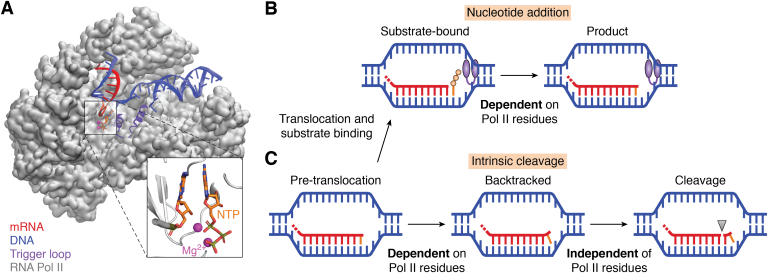
Unlike DNA polymerases or ribonuclease H, Pol II catalyzes both nucleotide addition and intrinsic cleavage (corresponding to the formation and breaking of the phosphodiester bond, respectively) in the same active site. In this article, we review recent progress in elucidating how Pol II performs this dual-function role via a single active site. We present an overall model of Pol II’s catalytic mechanisms for both reactions (Fig. 6). On one hand, Pol II catalyzes the nucleotide addition following a two-metal-ion mechanism. Several TL residues play important roles in facilitating this reaction (Fig. 6B). For example, the HIP may help the protonation of the leaving PPi in the nucleotide addition reaction. In addition, L1081 aligns the incoming NTP base to stabilize the catalytically active conformation. On the other hand, the phosphate Rp-oxygen of RNA serves as the general base in the intrinsic cleavage reaction, and none of the Pol II residues is directly involved in the reaction. (Fig. 6C). To recognize misincorporations, Pol II utilizes the conformational change of backtracking, which only occurs when Pol II encounters mis-incorporated nucleotides. In this article, we review recent computational and experimental studies to elucidate catalytic mechanisms of the nucleotide addition reaction of Pol II, the mechanism of PPi release, the MD of Pol II’s backtracking upon misincorporation, and the catalytic mechanisms of the intrinsic and TFIIS-aided cleavage of Pol II. As a new perspective, we discuss the potential involvement of a third metal ion to nucleotide addition and cleavage reactions. These studies provide mechanistic insights into how Pol II catalyzes two distinct chemical reactions (i.e., nucleotide addition and cleavage) using a single active site and the universal two-metal-ion mechanism.

Figure 6.

A cartoon scheme illustrating how Pol II catalyzes two opposite reactions using a single active site.A, the Pol II elongation complex (PDB ID: 2E2H). The colors represent the following, gray: Pol II, red: mRNA, blue: DNA, purple: trigger loop (TL), orange: NTP, magenta: Mg2+ ions. The inset figure displays the catalytically active conformation of Pol II’s active site for the nucleotide addition reaction. B, the nucleotide addition reaction adds the substrate NTP to the growing RNA chain. This chemical reaction relies on several Pol II residues on the TL domain (e.g., H1085 and L1081). C, if mismatched nucleotides are incorporated, Pol II probes the misincorporation via its bridge helix residue (T831) and enables backtracking. The backtracked nucleotides will be subsequently cleaved, and none of the Pol II residues directly involves in the cleavage reaction. NTP, nucleotide triphosphate; Pol II, RNA polymerase II.

Conflict of interest

The authors declare that they have no conflicts of interest with the contents of this article.

Edited by Patrick Sung