Modeling net energy partition patterns of growing–finishing pigs using nonlinear regression and artificial neural networks

Abstract

The objectives of this study were to evaluate the net energy (NE) partition patterns of growing–finishing pigs at different growing stages and to develop the corresponding prediction models using nonlinear regression (NLR) and artificial neural networks (ANN). Twenty-four pigs with an initial body weight (BW) of ~30 kg were kept in metabolic cages and fed ad libitum and were moved into six respiration chambers in turns until ~90 kg. The NE partition patterns, i.e., NE for maintenance (NEm), NE retained as protein (NE_p), and NE retained as lipid (NE_l), were calculated based on indirect calorimetry and nitrogen balance techniques. The energy balance data collected through the animal trial was then randomly split into a training data set containing 75% of the samples and a testing data set containing the remaining 25% of the samples. The NLR models and a series of ANN models were established on the training data set to predict the metabolizable energy intake, NE intake, NEm, NE_p, and NE_l of pigs. The best-fitted ANN models were selected by 5-fold cross-validation in the training data set. The prediction performance of the best-fitted NLR and ANN models were compared on the testing data set. The results showed that the average NE intakes of pigs were 17.71, 23.25, 24.56, and 28.96 MJ/d in 30 to 45 kg, 45 to 60 kg, 60 to 75 kg, and 75 to 90 kg, respectively. The NEm and NE_l (MJ/d) kept increasing as BW increased from 30 kg to 90 kg, while the NE_p increased to its maximum value and then kept in a certain range of 4.64 to 4.88 MJ/d. The proportion of NEm for pigs at 30 to 90 kg stayed within the range of 42.0% to 48.6%, while the proportion of NE_l kept increasing. For the prediction models built based on the animal trial, ANN models exhibited better performance than NLR models for all the target outputs. In conclusion, NE partition patterns changed in different growth stages of pigs, and ANN models are more flexible and powerful than NLR models in predicting the NE partition patterns of growing–finishing pigs.

This study provides a clear understanding of net energy (NE) utilization in pigs and finds that the NE intake and NE partition patterns were greater compared with those reported previously, indicating the increased NE requirements of modern pig breeds. This study has also applied and compared the corresponding nonlinear regression models and artificial neural networks models.

Introduction

Energy is one of the most important nutrients, which accounts for nearly 60% to 70% of the total animal feeding cost (Pirgozliev and Rose, 1999; Noblet et al., 2004). Adequate energy supplementation in diets is the prerequisite for efficient growth and high carcass quality of animals. The most commonly used energy systems in swine nutrition for describing the energy values in feedstuff as well as the energy requirements of pigs include digestible energy, metabolizable energy (ME), and net energy (NE), among which NE is the most refined system because it considers the heat increment (HI) (Noblet and van Milgen, 2004).

Based on the factorial approach, NE intake could be partitioned into energy for basic functions (i.e., NE for maintenance, defined as NE_m) and energy retained in the body (i.e., NE retained as protein or lipid, defined as NE_p and NE_l, respectively) (Noblet and Henry, 1993). However, due to the high cost of NE measurement, most previous studies have reported the energy partition patterns of pigs on the ME basis with the following model:

$${\displaystyle \begin{array}{l}{\displaystyle ME=M{E}_m+1/k_p\times P_d+1/k_l\times L_d}\end{array}}$$

among which ME_m, k_p, and k_l represent ME for maintenance, coefficient of protein, and lipid deposition on the ME basis, P_d and L_d represent the protein deposition and lipid deposition. Only a few studies reported the directly measured NE_m or reported the calculated NE partition patterns of growing pigs using a stable NE/ME ratio (Noblet, 2007). Thus, evaluating the NE partition patterns of growing–finishing pigs at different growing stages based on scientific-designed animal trials and then developing the corresponding prediction models may provide a clearer understanding of energy utilization in pigs, and could help to develop suitable feeding strategies to improve the growth performance and carcass traits of pigs (Tess et al., 1984).

Regression is the most widely used mathematical tool to depict the relationships between two variables in swine nutrition research, and it is well known that the predictive accuracy could be greatly affected by the model types (Li et al., 2019). Machine learning models, e.g., artificial neural networks (ANN), have been applied to animal nutrition research within the last 20 yr. With the advent of big data in recent years, the ANN and machine learning realms have reinvigorated these models, which have demonstrated their advantages in dealing with big data collected from various sensors installed in modern farms. The latest relevant studies have demonstrated the promising prediction performance of ANN models, especially in handling a large number of variables with complex relationships (Dallago et al., 2019; Fu et al., 2020). However, to our knowledge, little literature has focused on the application of ANN models to swine energy partition patterns.

Therefore, the objectives of this study were to evaluate the NE partition patterns (including NE_m, NE_p, and NE_l) of growing–finishing pigs fed ad libitum at different growth stages, and to develop the corresponding prediction models using nonlinear regression (NLR) and ANN.

Materials and Methods

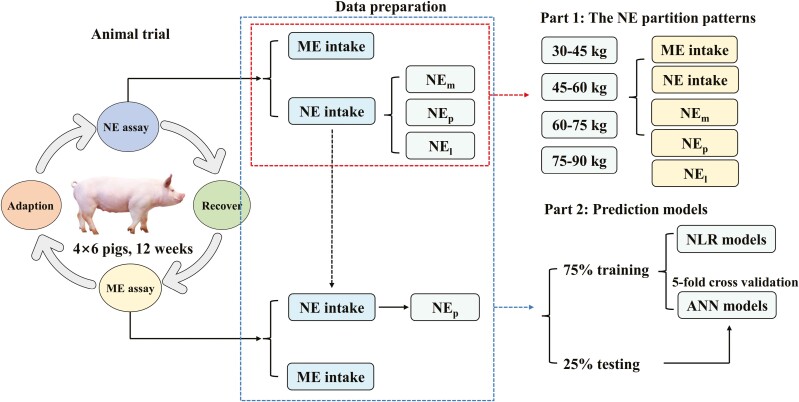
The general scheme of this study is outlined in Figure 1. All experimental protocols including animal care and use were approved by the Institutional Animal Care and Use Committee of China Agricultural University (Beijing, China).

Figure 1.

The general scheme of this study. Firstly, 24 pigs were used and took turns into the net energy (NE) assay and metabolic energy (ME) assay. Secondly, data were handled to obtain NE intake, NE for maintenance (NE_m), NE retained as protein (NE_p), and NE retained as lipid (NE_l). Thirdly, data from the NE assay were divided into four groups based on their body weight and used to evaluate the NE partition patterns of growing–finishing pigs. Finally, data of the NE assay and the ME assay were mixed and randomly split into a training data set containing 75% samples and a testing data set containing the remaining samples. The best-fitted nonlinear regression (NLR) models and artificial neural networks (ANN) models were generated on the training data set and were further compared on the testing data set.

Equipment

In the current study, six open-circuit respiration chambers with a volume of approximately 7.8 m³ were used, and the construction of these chambers was based on a design described by van Milgen et al. (van Milgen et al., 1997). Details on the open-circuit respiration chambers and indirect calorimetry (IC) method were reported by Zhang et al. (2014) and van Milgen et al. (1997), respectively. Gas was extracted continuously from the respiration chamber by a vacuum pump. The respiration chamber was air-conditioned to maintain a constant temperature and humidity using an air conditioner and a heater. Temperature and atmospheric pressure in the chamber were measured and calibrated to the standard temperature and pressure (0 °C and 101 kPa) before quantifying the extraction rate. The O₂ concentration was measured with a paramagnetic differential analyzer (Oxymat 6E; Siemens, Munich, Germany), whereas CO₂ and CH₄ concentrations were measured with infrared analyzers (Ultramat 6E; Siemens, Munich, Germany). Before utilization, the analyzers were standardized and calibrated by applying a series of prepared standard gases to span the measurement range of sensors. The analyzers had a measuring range of 19.5% to 21% for O₂, 0% to 1% for CO₂, and 0% to 0.1% for CH₄ with a sensitivity of 0.2% within the range. The gas extraction rate was measured by a mass flow meter (Alicat, Tucson, AZ). Two respiration chambers shared one analyzer system. Gas concentrations in the chamber were measured at 5-min intervals.

Animals, diets, experimental design, and procedures

The animal trial was conducted at FengNing Swine Research Unit of China Agricultural University (Academician Workstation in Chengdejiuyun Agricultural and Livestock Co., Ltd, Hebei Province, China). To mimic the practical feeding conditions, two commercial corn-soybean meal diets used in the swine research unit were adopted in this research to feed pigs at two different growth stages (30 to 60 kg and 60 to 90 kg), respectively, which meet the nutrient requirements of pigs reported in Nutrient Requirements of Swine in China (Li et al., 2020) (Table 1). Twenty-four growing (Duroc × Landrace × Yorkshire, 34.4 ± 2.6 kg) barrows were used to eliminate the impact of gender and breeds on energy partition, which were randomly divided into four batches and took turns into six IC chambers, with 1 pig per chamber at each time. The period from one batch of pigs entering the IC chambers to the same batch of pigs reentering the chambers was defined as one experimental cycle which lasted 4 wk: diet and cages adaptation for the first week, NE measurement in the IC chambers for the second week, the recovery period after moving out of the IC chambers for the third week, and ME measurement in the metabolic cages outside chambers for the fourth week. Under such arrangement, the NE partition data of one batch of pigs (through NE assay in IC chambers) and the ME partition data of another batch of pigs (through ME assay in metabolic cages) were collected simultaneously each week. The whole animal trial lasted for 12 consecutive weeks using the same facility and similar experimental conditions and procedures.

Table 1.

Ingredients and nutrient compositions of the experimental diets used in the animal trial (as-fed basis)¹

Items	30–60 kg	60–90 kg
Corn	74.68	76.82
Soybean meal	22.00	20.00
Dicalcium phosphate	0.90	0.80
Limestone	0.75	0.75
Sodium chloride	0.35	0.35
Premix2	0.50	0.50
Lys-HCl	0.36	0.36
DL-Met	0.13	0.11
L-Thr	0.17	0.16
L-Trp	0.05	0.05
L-Val	0.11	0.10
Total	100.00	100.00
Calculated values3
ME, MJ/kg	13.64	13.67
NE, MJ/kg	10.27	10.33
CP	16.65	15.88
SID Lys	1.00	0.95
SID AA/SID Lys
Met	0.36	0.35
Thr	0.65	0.65
Trp	0.20	0.20
Val	0.70	0.70
Ile	0.55	0.55
Met + Cys	0.60	0.60

¹All the dietary nutrient concentrations were calculated based on the nutrient compositions of ingredients published in Nutrient Requirements of Swine in China.

²Premix provided the following quantities per kilogram of diets: vitamin A as retinyl acetate, 8,250 IU; vitamin D₃ as cholecalciferol, 825 IU; vitamin E as DL-alpha-tocopheryl acetate, 40 IU; vitamin K₃ as menadione nicotinamide bisulfite, 4 mg; vitamin B₁₂, 25 μg; riboflavin, 5 mg; pantothenic acid as DL-calcium pantothenate, 15 mg; niacin, 35 mg; choline chloride, 600 mg; folacin, 2 mg; thiamin as thiamin mononitrate, 1 mg; pyridoxine as pyridoxine hydrochloride, 2 mg; biotin, 4 mg; Mn as MnO, 25 mg; Fe as FeSO₄·H₂O, 80 mg; Zn as ZnSO₄, 100 mg; Cu as CuSO₄·5H₂O, 50 mg; I as KI, 0.5 mg; Se as Na₂SeO₃, 0.15 mg.

³CP, crude protein; NE, net energy; ME, metabolic energy; SID, standardized ileal digestible.

Specifically, data including NE intake and NE partition (NE_m, NE_p, and NE_l) could be gained through the NE assay. The fasting heat production (FHP) was considered equal to NE_m in this research because the 8-h measurement was performed at night when pigs were sleeping, during which the heat production (HP) caused by physical activity could be ignored (Tess et al., 1984; van Milgen et al., 2000). The retained energy (RE) as protein and lipid (defined as RE_p and RE_l, respectively) was used to estimate NE_p and NE_l, respectively. In addition, data including NE intake and NE_p could also be gained through the ME assay, with the NE value of the diet calculated from the NE assay, and feed intake and N balance data collected from the ME assay. The information of the data set from the NE assay and ME assay are available in Supplementary Tables S1 and S2.

The NE assay

Each batch of six pigs stayed individually in the IC chambers for 7 d in one experimental cycle for the NE assay, with day 1 for adaptation, day 2 to day 6 for daily O₂ consumption and CO₂ and CH₄ production measurement, and day 7 for FHP measurement. To ensure pigs were fed ad libitum, excessive feed and water were given to pigs in the airtight IC chambers. During day 2 to day 6, total feces and urine samples were collected once daily for determination of energy and N in feces and urine, and feed refusals and spillage were collected once daily and subsequently dried and weighted to calculate the feed intake. On day 7, pigs fasted, total urine samples were collected, and gas exchanges were measured during the lasted 8 h from 22:30 (day 7) to 06:30 (day 8) to calculate FHP. During this period, pigs are generally sleeping and the heat generated from activities was ignored, so the value of FHP was considered as NE_m. Moreover, pigs were weighed on day 2 and day 6. Collected feces were weighted daily and stored at −20 °C. Urine was collected in plastic containers containing 50 mL of 6 N HCl to minimize N losses, and the volume was determined daily, and a 10% daily aliquot was stored at −20 °C. For the IC chamber settings, the temperature was maintained at 22 °C in the fed state (day 2 to day 6), the relative humidity was controlled at 70%, and a 10-h lighting schedule was used.

The ME assay

Each batch of 6 pigs stayed individually in the metabolic cages outside the IC chambers for 7 d in one experimental cycle for the ME assay, with day 1 to day 2 for adaption, and day 3 to day 7 for total feces and urine collection (twice daily at 8:00 h and 16:00 h). Pigs were weighed at the beginning and the end of the assay and were fed ad libitum. Feces and urine samples as well as feed refusals and spillage were collected, weighed, and stored as described in the NE assay. The feed intake of each pig in each turn can be calculated. The room temperature and relative humidity were set the same as those in the NE assay.

Chemical analyses, calculation, and data set preparation

All the feed, feces, and urine samples collected from the NE assay and the ME assay were prepared and analyzed following the same procedure with two replicates. Before chemical analysis, fecal samples were oven-dried for 72 h at 65 °C and were ground through a 1-mm screen, while urine samples were thawed and pooled separately for each pig. The dry matter (DM) content of feed and feces samples was determined by drying 5 g of samples in a forced-air oven (model GZX-9140 MBE; Boxun Company, Shanghai, China) at 105 °C to a constant weight (method 934.01; AOAC, 2006). The gross energy (GE) contents in the feed, feces, and urine samples were determined using an isoperibol calorimeter (Parr 6300 Calorimeter, Moline, IL) with benzoic acid as a standard. The N contents in the feed, feces, and urine samples were determined following the standard procedure (method 984.13; AOAC, 2006).

The ME intake was calculated as the difference between GE intake and GE losses in feces, urine, and methane (Adeola, 2001). Energy loss in methane was calculated using the conversion factor 39.54 kJ/L (Brouwer, 1965). Total heat production (THP) was calculated on daily basis from gas exchanges using the equation reported by Brouwer (1965):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{H}\mathrm{P}(\mathrm{k}\mathrm{J})=16.18\times {\mathrm{O}}_2(\mathrm{L})+5.02\times \mathrm{C}{\mathrm{O}}_2(\mathrm{L})2.17}\\ \times \mathrm{C}{\mathrm{H}}_4(\mathrm{L})5.99\times \mathrm{N}(\mathrm{U}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{N},\mathrm{g})\end{array}}$$

FHP was also calculated using the same equation, but the 8-h HP was extrapolated to a 24-h period to base production for the same period as for the calculation of THP. The RE was calculated as the difference between ME intake and average HP. The NE intake was calculated as the sum of FHP and RE, and the NE value of the diet was calculated as the NE intake divided by the average feed intake. Energy retained as protein (NE_p) was calculated as N retention (g) × 6.25 × 23.86 (kJ/g) (Chwalibog et al., 2005), and NE_l was calculated as the difference between RE and NE_p (Labussière et al., 2009). Nitrogen retention was calculated as the difference between N intake and N losses in feces and urine (Noblet et al., 1994). L_d (g/d) was calculated as NE_l divided by the conversion factor of 39.6 kJ/g.

Data set was built to contain ME intake, NE intake, THP, RE, NE_m, NE_p, NE_l, P_d, and L_d of each pig and pig information was collected through the NE assay, and each pig was considered as an observation. To better understand the energy partition patterns, NE_m, NE_p, and NE_l were presented in three forms with different units: on a daily basis (MJ/d), metabolic body weight (BW) basis (MJ/kg BW^0.6·d⁻¹), or as percentages of NE intake (%). The whole data set was then divided into four subsets based on growth stages of pigs with ~15 kg BW as a stage gap: earlier growing stage (30 to ~45 kg BW), later growing stage (45 to ~60 kg BW), earlier finishing stage (60 to ~75 kg BW), and later finishing stage (75 to ~90 kg BW). Additionally, six observations were discarded because of gas leakage of the IC chambers, and 10 observations were deleted due to failure in fecal samples collection caused by diarrhea. As a result, 59 observations from the NE assay and 61 observations from the ME assay remained in the database.

Moreover, ME intake, NE intake, NE_p, and P_d could also be obtained from the ME assay and were combined with those gained from the NE assay in the same data set to develop the prediction models. The whole data set was randomly split into a training data set containing 75% samples for the best-fitted model selection and a testing data set containing the remaining 25% samples for model comparison. In the analysis of ANN models, the training data set (75%) was then divided into a new training data set and the validation data set by using a 5-fold cross-validation.

Statistical analyses

The normality of the data was tested using the Shapiro–Wilk test, and outliers were detected using the UNIVARIATE procedure of SAS 9.4 (SAS Institute Inc., Carry, NC). Data were then analyzed using the MIXED procedure of SAS 9.4. The statistical model included the growth stage as the only fixed effect and the IC chamber as the random effect. Multiple comparisons were performed with the Tukey–Kramer test as adjustment. P-value of <0.05 was set as the threshold for significance.

Analysis of NLR models

NLR model analysis

The NLR models on ME intake of pigs have been well studied; thus, the most widely used Bridge function (Bridges et al., 1986): y = a × {1 − exp [−exp(b) × BW^c]}, was adapted to fit the ME intake and NE intake data in this study. Consider that NRC (2012) used the cubic equation (y = a + b × BW + c × BW² + d × BW³) to predict P_d and L_d. Our pilot study showed that the newly introduced variable (NE intake) could greatly increase the accuracy of RE prediction, so the NE intake and BW and their quadratic and cubic terms were included as candidate input variables to predict NE_m, NE_p, and NE_l using NLR models, and stepwise regression was conducted for further variables selection. The Nonlinear and Fit Model procedures of JMP Pro 14.0 (SAS Institute Inc., Carry, NC) were used to establish the NLR models. The stop limit of iteration was set at 1,000. For stepwise regression, the mixed direction and P-value threshold stopping rules were chosen, and the criteria for variables entered and removed from the model were set at a probability of 0.05. Models with the minimized root mean square error (RMSE) were identified as the best-fitted regression model (Littell, 2002).

Analysis of NLR models

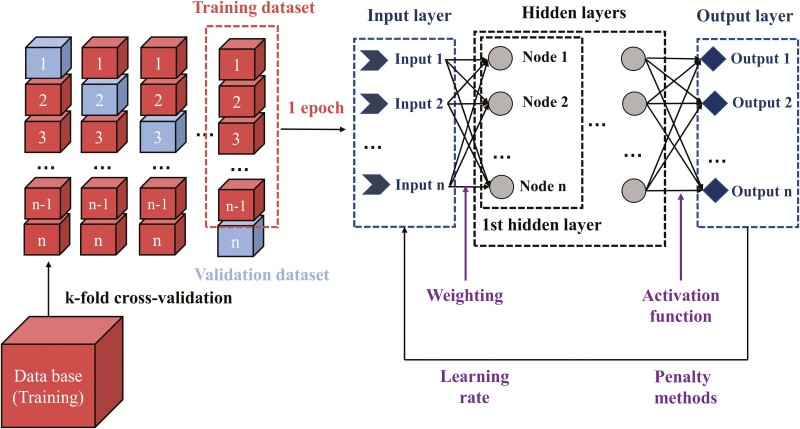
ANN is an information-processing paradigm inspired by the way the brain processes information. The architecture and hyperparameters of ANN were shown in Figure 2. Cross-validation is a data resampling method to tune model parameters, which can assess the generalization ability of predictive models and to prevent overfitting (Duda et al., 2001). Thus, the k-fold cross-validation procedure in JMP Pro 14.0 was applied to tune the hyperparameters in the ANN models. One epoch was defined as all the training data entering ANN once and greater epochs allow the neural network to more fully explore the relationships between the data. The main components of an ANN model include an input layer, a series of hidden layers and an output layer (Shafi et al., 2006). The input layer is connected to the hidden layer, and then connected to the output layer, representing the handling direction of the raw input information. The information of each input was multiplied by their weight and computed the sum, then fed to a neuron (node), and the same procedure is adopted to the next hidden layers. The last hidden layer applies an activation function to process the information to the output layer (Margenot et al., 2020). The number of hidden layers in ANN is dependent on the complexity of the relationships between inputs and target outputs. More hidden layers would increase the chance of obtaining local minima during the training phase but contribute to a more unstable gradient. Huang (2003) stated that an ANN model with two hidden layers can learn the data with any desired precision; thus, only the ANN models with one and two hidden layers were analyzed in this study. The use of penalty methods prevents ANN overfitting and increases the predictive ability of the model. The learning rate is related to the update of weighting, with learning rate close to 1 resulting in faster convergence on a final model, but also a higher tendency to overfit data. All of the above parameters could affect the predictive power of the ANN model. Therefore, the grid search method was employed for tuning the hyperparameters of the ANN model. The candidate hyperparameters were: hidden layers (range: 1 to 2), nodes in hidden layers (1 to 10), activation functions (hyperbolic tangent function, $\tanh (x)=\frac{e^{2x}-1}{e^{2x}+1}$; Gaussian function, $RB(x)=e^{-x^2}$), learning rate (0.01, 0.1), penalty method (squared and weight decay), and epochs (200, 400, 600, 800, and 1,000). Totally, 4,000 candidate ANN architectures were generated by the grid search method using JMP Pro 14.0 (SAS Institute Inc., Carry, NC), and the above hyperparameters were tuned using the Neural Network procedure in JMP Pro 14.0. The 5-fold cross-validation procedure was used in the training phase. The training data set (75%) was divided into a new training data set and validation data set in ANN analysis. The averaged RMSE of validation data was recorded to select the optimal ANN hyperparameters. The model with the minimized RMSE in the validation set was considered to be the best-fitted ANN model.

Figure 2.

The architecture and hyperparameters of artificial neural networks (ANN). Cross-validation was used to resampling the data set and to prevent overfitting. The information of each input was multiplied by their weight and computed the sum, then fed to a neuron (node), and the same procedure is adopted to the next hidden layers. The last hidden layer applies an activation function to process the information to the output layer. The penalty method and learning rate are related to adjusting the weights of the inputs after one iteration.

To ensure the unbiased comparison between NLR and ANN, the input variables in ANN models were fixed to the same as the NLR models. The BW and its quadratic and cubic terms were used as the input variables for ME intake and NE intake prediction, while the BW, NE intake, and their quadratic and cubic terms were used as the input variables for NE_m, NE_p, and NE_l prediction. Before establishing the ANN models, all data would be normalized to get prediction errors with step sizes and update systematic weights (Li et al., 2019). Therefore, data sets in the current study were normalized using the min-max approach, and the output variables were re-normalized using the minimal and maximal values of the data.

Comparison and evaluation of NLR and ANN models

Comparison between NLR models and ANN models: predicted values gained through the best-fitted NLR models and ANN models based on the training data set were recorded, and used to calculate the RMSE, R², and concordance correlation coefficients (CCC). A lower RMSE is considered to be more accurate while a higher R² is considered to be more precise. The CCC represents both accuracy and precision of the model and a higher CCC value means this model is more accurate and precise (Tedeschi, 2006). The comparison and evaluation of NLR and ANN models were the same as Wang et al. (2022). Simplify, predicted values were also gained through the two models based on the testing data set (25% of the whole data set, data normalization was performed when using the ANN model for prediction). The observed vs. predicted plots were generated, and the following linear equation was obtained in each plot: y = a + bx, where x refers to the observed values, and y refers to the predicted values. The plot with a slope closer to 1 represents a better prediction performance of the corresponding model in the testing phase. In addition, the RMSE, mean absolute error (MAE), and mean relative error (MRE) were calculated based on the observed values and predicted values. The prediction models with less RMSE, MAE, and MRE were considered as better prediction accuracy in the testing phase.

Results

NE partition patterns of growing–finishing pigs

The averaged ME intake and NE intake of pigs fed ad libitum increased as BW increased (P < 0.01), which were 21.75 and 17.71, 29.40 and 23.25, 30.73 and 24.56, and 35.88 and 28.96 MJ/d at 30 to 45 kg, 45 to 60 kg, 60 to 75 kg and 75 to 90 kg, respectively (Table 2). Moreover, the THP and RE in MJ/d also increased as BW increased (P < 0.01) but revealed no differences when expressed as MJ/kg BW^0.6·d⁻¹ (P > 0.05). The P_d of pigs at 30 to 45 kg was lower than that at 45to- 60 kg, and the L_d of pigs at 60 to 90 kg was greater than that at 30 to 45 kg (P < 0.01). Efficiency of NE/ME was 81.42%, 79.13%, 80.07%, and 80.53% at 30 to 45 kg, 45 to 60 kg, 60 to 75 kg, and 75 to 90 kg, respectively, with no difference among the four stages that were set manually based on data sets (P > 0.05).

Table 2.

The energy balance and NE partition patterns of growing–finishing pigs in different growth stages¹

Items	30–45 kg	45–60 kg	60–75 kg	75–90 kg	SEM	P-value
n	12	16	14	17
Energy balance
ME intake, MJ/d	21.75c	29.40b	30.73b	35.88a	0.85	<0.01
NE intake, MJ/d	17.71c	23.25b	24.56b	28.96a	0.69	<0.01
THP, MJ/d	12.55c	16.01b	16.44b	19.49a	0.40	<0.01
RE, MJ/d	9.20b	13.39a	14.29a	16.38a	0.59	<0.01
ME intake, MJ/kg BW0.6·d−1	2.40	2.56	2.35	2.44	0.04	0.36
NE intake, MJ/kg BW0.6·d−1	1.95	2.02	1.88	1.97	0.04	0.58
THP, MJ/kg BW0.6·d−1	1.39	1.4	1.26	1.32	0.02	0.06
RE, MJ/kg BW0.6·d−1	1.01	1.16	1.10	1.11	0.04	0.64
NE/ME, %	81.42	79.13	80.07	80.53	0.48	0.41
Growth
Pd, g/d	169b	204a	195ab	201ab	4.52	0.03
Ld, g/d	131a	215ab	243b	293b	13.5	<0.01
NE partition
NEm, MJ/d	8.51c	9.86b	10.23b	12.57a	0.26	<0.01
NEp, MJ/d	4.03b	4.88a	4.64ab	4.80ab	0.11	0.03
NEl, MJ/d	5.17b	8.52ab	9.64a	11.58a	0.53	<0.01
NEm, MJ/kg BW0.6·d−1	0.94a	0.86ab	0.78b	0.85ab	0.01	<0.01
NEp, MJ/kg BW0.6·d−1	0.44a	0.42a	0.36b	0.33b	0.01	<0.01
NEl, MJ/kg BW0.6·d−1	0.57	0.74	0.74	0.79	0.04	0.20
NEm, % of NE intake	48.6	43.6	42.0	44.7	1.10	0.24
NEp, % of NE intake	22.8a	21.3ab	18.9bc	16.7c	0.47	<0.01
NEl, % of NE intake	28.7b	35.1ab	38.5a	39.1a	1.31	0.03

¹ME, metabolic energy; NE, net energy; NE_m, NE for maintenance; NE_p, NE retained as protein; NE_l, NE retained as lipid; P_d, protein deposition; L_d, lipid deposition; RE, retained energy; THP, total heat production; k, ME/NE × 100.

^a–cMeans within a row with different superscripts differ (P < 0.05).

For the partition patterns of NE (Table 2), both NE_m and NE_l increased as BW increased, and pigs at 45 to 60 kg showed the greatest NE_p value when expressed as MJ/d (P < 0.01). When expressed on a metabolic BW basis (MJ/kg BW^0.6·d⁻¹), pigs at 30 to 45 kg showed greater NE_m than those at 60 to 75 kg (P < 0.01), while NE_p decreased with BW raised (P < 0.01), and NE_l revealed no difference among the four growth stages (P > 0.05). When expressed as proportions to NE intake, NE_m maintained in a range of 42.0% to 48.6% in all growth stages (P > 0.05), and the NE_p proportion decreased while the NE_l proportion increased as BW grew (P < 0.05).

Development and comparison of the NLR models and ANN models

The best-fitted NLR models for predicting ME intake and NE intake were 76.66 × {1 − exp[−exp(−3.397) × BW^0.6820]} and 65.74 × {1 − exp[−exp (−3.445) × BW^0.6543]}, respectively (Table 3). For NE_m prediction, the NLR model with BW³ as the only predictor exhibited the smallest RMSE, among which BW³ had a positive effect on NE_m. For NE_p prediction, the NLR model with BW³, NE intake, and NE intake³ as predictors showed the smallest RMSE, among which BW³ and NE intake³ had negative effects while NE intake had a positive effect on NE_p. For NE_l prediction, the NLR model with BW³ and NE intake² as predictors demonstrated the smallest RMSE, among which BW³ had a negative effect while NE intake² had a positive effect on NE_l.

Table 3.

The best-fitted nonlinear regression models generated on the training data set^1,2

Items, MJ/d	Nonlinear regression models	RMSE
ME intake	y = 76.66 × {1 − exp [−exp(−3.397) × BW0.6820]}	4.64
NE intake	y = 65.74 × {1 − exp [−exp(−3.445) × BW0.6543]}	4.24
NEm	y = 8.173 + 5.965 × 10−6 × BW3	1.26
NEp	y = 0.6343 − 6.364 × 10−7 × BW3 + 0.2133 × NE intake − 6.239 × 10−5 × NE intake3	0.63
NEl	y = 0.2731 − 3.976 × 10−6 × BW3 + 1.672 × 10−2 × NE intake2	1.50

¹The training data for predicting ME intake, NE intake, and NE_p were obtained from NE assay and ME assay, but the training data for predicting NE_m and NE_l were obtained only from NE assay.

²ME, metabolic energy; NE, net energy; NE_m, NE for maintenance; NE_p, NE retained as protein; NE_l, NE retained as lipid; RMSE, root mean square error.

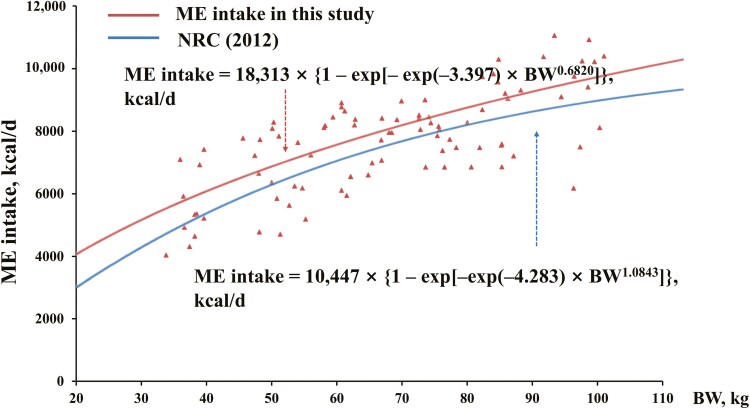
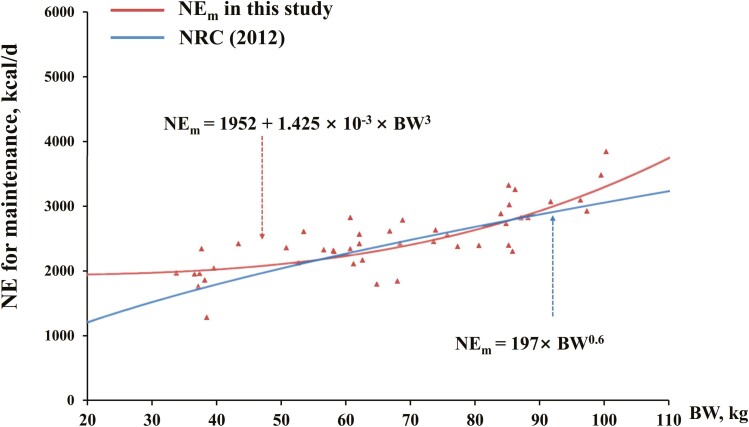
The NLR models developed in the current study for ME intake and NE_m prediction were compared with those available in NRC (2012) using a curve plot (Figures 3 and 4). The predicted ME intake values using our NLR models were 600 to 900 kcal/d greater than those using models reported by NRC (2012). The predicted NE_m values using our NLR models were also greater than those using models reported by NRC (2012) for pigs at 20 to 50 kg, with the gap narrowed when BW increased in this BW range.

Figure 3.

The predicted metabolic energy (ME) intake using best-fitted nonlinear regression (NLR) model in this research vs. NRC (2012).

Figure 4.

The predicted NE for maintenance (NE_m) using the best-fitted nonlinear regression (NLR) model in this research vs. NRC.

The best ANN models with the optimal hyperparameters were selected by grid search using a 5-fold cross-validation (Table 4). All the best-fitted ANN models for predicting ME intake, NE intake, NE_m, NE_p, and NE_l were those using the Gaussian function and penalty method of weighted decay. The best-fitted ANN models for predicting ME intake and NE_l contained 1 hidden layer with 3 and 5 nodes, respectively. The best-fitted ANN model for predicting NE intake, NE_m, and NE_p contained 2 hidden layers with 3, 3, and 2 nodes in the first hidden layer and 4, 4, and 4 nodes in the last hidden layer, respectively. Except for the learning rate of NE intake which is 0.01, the optimal learning rate of all the other predictors is 0.1. The optimal epochs for ME intake, NE intake, NE_m, NE_p, and NE_l predictions were 600, 800, 600, 600, and 1,000, respectively.

Table 4.

The optimal hyperparameters selected by grid search in trainng phase^1,2

Items3	Candidate hyperparameters4	ME intake, MJ/d	NE intake, MJ/d	NEm, MJ/d	NEp, MJ/d	NEl, MJ/d
Layer	1, 2	1	2	2	2	1
Nodes	1–10	3	3, 4	3, 4	2, 4	5
Activation	TanH, Gaussian	Gaussian	Gaussian	Gaussian	Gaussian	Gaussian
Learning rate	0.1, 0.01	0.1	0.01	0.1	0.1	0.1
Penalty methods	Squred, weighted decay	Weighted decay	Weighted decay	Weighted decay	Weighted decay	Weighted decay
Epoch	200, 400, 600, 800, 1,000	600	800	600	600	1,000

¹Artificial neural networks (ANN) models were developed on a training set originating from 75% of the whole training data set. In the training of ANN models, the training data were divided into a new training data set and a validation data set by using the 5-fold cross-validation procedure.

²The averaged root mean square error (RMSE) of the validation data set was used to select the optimal ANN hyperparameters. The model with the minimized RMSE in the validation set was considered to be the best-fitted ANN model.

³ME, metabolic energy; NE, net energy; NE_m, NE for maintenance; NE_p, NE retained as protein; NE_l, NE retained as lipid.

⁴A total of 4,000 candidate ANN models were generated by the grid search method.

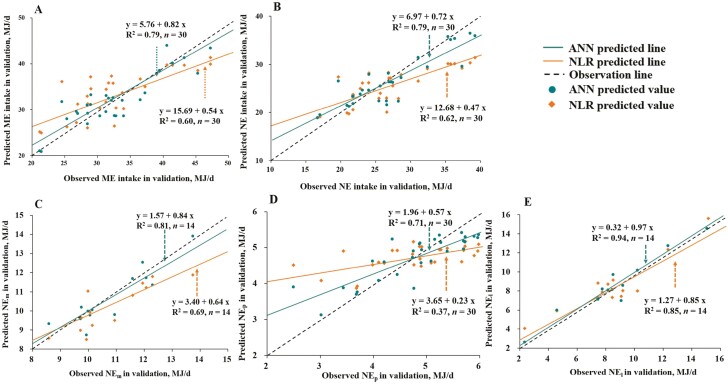
On the training data set, the best-fitted ANN models showed lower RMSE and greater R² and CCC than the best-fitted NLR models in all five parameters (ME intake, NE intake, NE_m, NE_p, and NE_l) prediction compared with NLR models (Table 5). Moreover, both the NLR model and ANN model exhibited the poorest performance for NE_p prediction but revealed the greatest accuracy in NE_l prediction.

Table 5.

The comparison between nonlinear regression (NLR) models and artificial neural networks (ANN) models in the training phase^1,2

Items, MJ/d	n	RMSE		R 2		CCC
		NLR	ANN	NLR	ANN	NLR	ANN
ME intake	90	4.90	3.61	0.50	0.69	0.65	0.74
NE intake	90	3.74	2.94	0.49	0.74	0.66	0.81
NEm	45	1.23	0.70	0.64	0.86	0.78	0.90
NEp	90	0.61	0.41	0.29	0.72	0.46	0.79
NEl	45	1.45	0.36	0.88	0.97	0.94	0.98

¹The RMSE, R², and CCC were calculated using the predicted value and observed value in the whole training data set.

²CCC, concordance correlation coefficients; RMSE, root mean square error; ME, metabolic energy; NE, net energy; NE_m, NE for maintenance; NE_p, NE retained as protein; NE_l, NE retained as lipid.

On the testing data set, the best-fitted ANN models showed slopes closer to 1 in the observed vs. predicted plots than the best-fitted NLR models in all five parameters prediction, implying the superiority of ANN models over NLR models again (Figure 5A–E). Meanwhile, the corresponding slopes of lines for NE_l prediction of both models were the closest to 1, while those for NE_p prediction of both models were the farthest to 1, indicating that NE_p prediction had the lowest accuracy in all five parameters. In addition, the best-fitted ANN models exhibited approximately 25% to 38% smaller MAE values compared to the best-fitted NLR models in all five parameters prediction (Table 6). In ANN models, the RMSE of ME intake and NE intake in the testing phase were similar to the training phase. The RMSE of NE_m in the testing phase was lower than in the training phase while NE_p and NE_l were opposite. This indicates no overfitting occurs in ANN models except a slight overfitting in NE_l.

Figure 5.

Relationship between the observed vs. the predicted (A) metabolic energy (ME) intake, (B) net energy (NE) intake, (C) NE for maintenance (NE_m), (D) NE retained as protein (NE_p), and (E) NE retained as lipid (NE_l) from the best-fitted models using testing data set. The best-fitted models were the nonlinear regression (NLR) and artificial neural networks (ANN) models generated in training. Thirty observations in the testing data set were used in ME intake, NE intake, and NE_p while 14 observations in the testing data set were used in NE_m and NE_l. Each plot represents a sample with an observed value or predicted value from prediction models.

Table 6.

The MAE and MRE of nonlinear regression models and artificial neural networks (ANN) models in testing phase^1,2

Items, MJ/d	n	RMSE		MAE		MRE
		Regression	ANN	Regression	ANN	Regression	ANN
ME intake	30	4.46	3.23	3.56	2.64	11.39	7.99
NE intake	30	4.24	2.95	3.47	2.15	12.45	8.30
NEm	14	0.67	0.45	0.82	0.52	7.75	5.19
NEp	30	0.74	0.51	0.6	0.39	14.02	8.80
NEl	14	0.78	0.58	0.93	0.63	15.21	8.11

¹The RMSE, MAE, and MRE were calculated using the predicted value and observed value in the testing data set which was not used to establish the prediction models.

²RMSE, root mean square error; MAE, mean absolute error; MRE, mean relative error; NE, net energy, NE_m, NE for maintenance; NE_p, NE retained as protein; NE_l, NE retained as lipid.

Based on the defined ANN models in the current study, a Microsoft Excel application (named Pig_NE_Partition_ANN calculator) was developed as an efficient and user-friendly tool to share our results with readers who might be interested to duplicate the results or predict a new output (ME intake, NE intake, NE_m, NE_p, and NE_l for pigs at growing–finishing stages) using ANN models (Figure 6). The only required input information was the BW (kg). This spreadsheet is accessible via the Supplementary Materials.

Figure 6.

The Microsoft Excel application (named Pig_NE_Partition_ANN calculator) developed to predict metabolizable energy (ME) intake, net energy (NE) intake, NE for maintenance (NE_m), NE retained as protein (NE_p), and NE retained as lipid (NE_l) for pigs at growing–finishing stages based on artificial neural networks (ANN) models.

Discussion

NE partition patterns of growing–finishing pigs

One of the most important findings of this article is using the scientific approach to determine the NE partition patterns of 30 to 90 kg pigs. The NE can simplify divided into two parts, HP and energy retained in the body (RE). In the current study, the THP of pigs tended to increase as BW grew, which may be due to the increased energy intake in later growth stages, and higher energy intake could strengthen the thermal effects of feeding (de Lange et al., 2006; Labussière et al., 2011). The average THP value (1.34 MJ/kg BW^0.6·d⁻¹) during the whole growing–finishing phase was close to the value (1.39 MJ/kg BW^0.6·d⁻¹) reported by Zhang et al. (2014). The RE usually can be evaluated by the comparative slaughter technology (CST) and IC methods. The CST method, specifically, refers to slaughtering different pigs in a group at the beginning and end of the trial, and then physically dividing the carcass into bone, muscle, and fat. The P_d and L_d can be calculated by the differences in muscle and lipid weight between the beginning and the end of the trial, then the RE can be calculated by multiplying P_d and L_d by their corresponding energy values (Quiniou et al., 1995). Even though the measurement of RE using either the CST or IC method is considerable, it should be noted there is a risk to produce inaccurate HP and RE values using the IC method. The RE obtained from the CST method may be lower than that from the IC method, which is induced by the discrepancy in environmental conditions, pig behaviors, and thermoregulatory demand between the respiration chambers and the housing conditions, leading to systematically lower energy expenditure and greater RE using the IC method (Noblet et al., 2021). The RE values of growing pigs (1.01 and 1.16 MJ/kg BW^0.6·d⁻¹ for 30 to 45 kg and 45 to 60 kg, respectively) reported in the current study were in accordance with the results of Lyu et al. (2018), who also use the IC method (1.08 MJ/kg BW^0.6·d⁻¹ for growing pigs). Besides, Quiniou et al. (1995) reported an average RE value of 14.49 MJ/d for three breeds of pigs ranging from 45 to 100 kg using the CST method, which was also similar to the average value in this study (14.69 MJ/d for pigs at 45 to 90 kg). Moreover, as to the k value (i.e., NE/ME), the standard range should be between 0.70 to 0.80 for pigs (Noblet et al., 1994; van Milgen et al., 2001). Even though different measurement methods were used, the k values in this study and in Lyu et al. (2018) were close to those reported by Just et al. (Just, 1982). The similar RE and k values obtained in the current study using the IC method to those obtained using the CST method indicated the reliability of our data, as well as the negligibility of HP caused by physical activity in FHP measurement in this study.

The NE_m proportion does not change greatly during the growth period of 30 to 90 kg in pigs. This part of the NE may be preferentially retained by the organism to ensure the survival of the animal. It also reminds us that regardless of the growth stage, roughly 40% to 50% of the NE will be used to generate heat that cannot be converted into products. Usually, the NE_m value of pigs could be measured using the calorimetry method or regression method (Close and Mount, 1975). Zhang et al. (2014) reported that the NE_m values were 758 and 732 kJ/kg BW^0.6·d⁻¹ for pigs at the growing and finishing stages using the regression method, respectively, which were all lower than the values measured in the current study using IC method. The regression method usually sets various dietary energy levels, with some groups below the energy requirement, which then could underestimate the NE_m value. The greater NE_m value using IC method in this study could also be attributed to the greater energy intake that can increase the basal metabolic rate and the HI of pigs, and the fasting process that may generate excessive physical activity and greater NE_m measurement. The HI would eventually result in reduced feed intake, even when the animal is in its thermoneutral range. Furthermore, agreeing with Zhang et al. (2014) and van Milgen et al. (1998), we observed decreased NE_m values on the metabolic BW basis with increased BW, which could be explained by the declined P_d rate in finishing pigs considering that muscle mass and visceral organ are the main contributors to HP in pigs. Thus, it is also reasonable that we observed the greatest percentage of NE_m (48.6%) in pigs at 30 to 45 kg, when the pigs contained the highest proportion of muscle mass and visceral organ.

Differing from NE_m, NE_p, and NE_l are dynamic in the NE partition patterns throughout the growth phase. Whittemore and Fawcett (1976) proposed that the relationship between energy intake and P_d comprised an initial ascending linear component and a plateau representing the animal’s maximal rate of protein deposition (P_dmax). It was also reported that P_d was affected by energy intake rather than pig’s BW (Quiniou et al., 1995; Sandberg et al., 2005). Therefore, P_d would increase as energy intake ascends at the initial growth stage of pigs until the maximum rate of P_d is reached, which is called P_dmax. Then P_d keeps stabilized in the later growth stages of pigs. The P_dmax value observed in the current study was 204 g/d, with L_dmax value of 293 g/d, which were slightly different from those reported by Quiniou et al. (1996) especially for P_d (P_dmax = 170 g/d and L_dmax = 290 g/d), indicating that the P_d potential of modern pig breeds was greater compared with those two decades ago. It is reasonable because modern pig breeds have been genetically improved to achieve a faster growth rate and greater lean meat deposition, thus leading to changes in patterns of body deposition as well as energy partition. Even though the changed genetic potential, the increment of P_d and NE_p in the current study mainly came from the increased NE intake, which would deposit as lipid in later growth stages after pigs reached their P_dmax, leading to increased NE_l proportion and decreased NE_p proportion as pigs grow. It should be pointed out that during the later stage of growth, more NE would deposit as a lipid. Therefore, energy concentrations in diets fed to pigs in the late growth stage should be paid special attention to, which would directly affect the meat quality.

Development and comparison of the NLR models and ANN models

The development of mathematical models for NE partition is necessary because the NE values of many commonly used feed ingredients have been evaluated recently (Li et al., 2017, 2018; Lyu et al., 2018). It is the prerequisite to use the same energy system to describe the available energy value in feed ingredients and energy utilization of pigs to achieve precision diet formulation. The starting point of simulation models to predict animal growth was using fewer parameters, which is easier for understanding and utilization (Wellock et al., 2004). As a result, the simple cubic regression function with BW as the only predictor has been adapted for P_d and L_d prediction previously. Thus, NE intake was also introduced into the above cubic NLR model for NE_m, NE_p, and NE_l prediction, just as reported by van Milgen et al. (2000) and has achieved better prediction accuracy.

The predicted ME intake and NE_m values using NLR models generated in this study were greater than those reported in NRC (2012), which were summarized from different pieces of literature a decade or two ago, and may be greatly influenced by systematic errors caused by different experimental conditions. For example, the variation in diet formulations would result in different protein intakes, which are highly related to the loss of NE as nitrogen (contained in NE_m) and voluntary feed intake. Even though an increase in NE requirement and NE_m of modern pig breeds could still be observed compared to previous pig breeds, and that the heavier muscle mass and visceral organs weights in modern pig breeds were the main contributors to the greater energy demand (Tess et al., 1984; Kerr et al., 1995; Rhule, 1996; Schiavon et al., 2018).

The learning ability of ANN models is highly determined by their architecture, such as the number of hidden layers, neurons in the hidden layer, activation functions, momentum term, epochs, and learning rate (Cross et al., 2018). Insufficient numbers of neurons could limit the learning capacity of ANN (Kumar, 2005). However, excess numbers of neurons may lead to overfitting (SubbaNarasimha et al., 2020). In agreement with previous studies which stated that the number of neurons in the hidden layers should be between the input numbers and output numbers (Blum, 1992; Boger and Guterman, 1997), the neurons of the best-fitted ANN models developed in the current study followed this principle. All the selected epochs in 5 prediction models were at least 600, which can be explained by that the greater epochs provided more opportunities for the ANN model to fully understand the relationships between the inputs and outputs. Furthermore, the activation function is also an imperative hyper-parameter in ANN, which empowers ANN to learn and recognize complex mapping from data. TanH function is continuous and differentiable, and it is symmetric around the origin. So, it is preferable in most cases considering it has gradients that are not restricted to vary in a certain direction and also, it is zero-cantered (Sharma et al., 2017). The Gaussian function is also a universal approximator in ANN models and can be used for approximation of any continuous function with given accuracy, but the main problem is the number of Gaussian functions required for approximation. Karlik and Olgac (2011) compared five conventional differentiable and monotonic functions and stated that the TanH function performed better recognition accuracy than Gaussian function. However, ANN models with Gaussian function developed in this study were observed to be more powerful than those with TanH function in all five parameters prediction, which could be explained by the limited numbers of input variables in this research, making only one Gaussian function enough, not like the situation in other comparative studies with more input variables that had a complex relationship with output variables (Shymkovych et al., 2021). Due to the strong learning abilities of ANN models, overfitting often occurs, but not in the current study, which could be attributed to the cross-validation, the larger learning rate, and the use of the penalty method. When we decayed the learning rate, parameter update takes a smaller step toward the minimum loss function and easier to locally optimal solutions (Jacobs, 1988). However, the lower learning rate increases the computing time and the risk of overfitting. The penalty method is introduced to prevent overfitting; thus, the tuning process may prefer a larger learning rate.

On both the training data set and the testing data set, ANN models exhibited more flexibility and accuracy than NLR models in this study. Similar results have been reported by previous studies conducted on other species (Dallago et al., 2019; Fu et al., 2020; Margenot et al., 2020). The superiority of ANN over the regression model is mainly because the regression model requires a pre-assumption relationship (linear or nonlinear) between input variables and target variables, which greatly limits its flexibility in prediction (Hanrahan, 2011). The existing associations between input and output variables may not follow the pre-assumption of regression model, especially in animals, which is a dynamic physiology system and can change at any time (Wang et al., 2022). On the contrary, ANN models do not need to make assumptions between inputs and outputs, alternatively, it uses neurons to weight the input and employ activations to transform to approximate the actual values (Adamczyk et al., 2016). Moreover, Margenot et al. (2020) stated that the architecture selection can improve the accuracy of ANN models. Based on the fact that the hyperparameters were carefully selected by the grid search method, the architecture selection can interpret part of the greater accuracy of ANN than NLR models. Fu et al. (2020) reported that the precision improved nearly 70% when using ANN models compared to regression models, while we only observed a smaller improvement in this study, which may be due to two main reasons. Firstly, Fu et al. (2020) used simple linear regression methods, which usually had much lower prediction accuracy. Secondly, large-scaled comparisons between those two models have illustrated that the ANN models would greatly outperform the regression models when using relatively large data sets (n > 20,000), while the opposite pattern occurred for small data sets. The data set used in this study was relatively small (n = 45 or 90) and cannot exhibit the full advantages of ANN to capture the complex relationship between inputs and outputs. With more reliable data collected using sensors installed in modern farms, the model parameters can be updated, thus greatly improving model applicability. It should also be highlighted that the ANN models did not always perform better than regression models, especially in the data set with skewed distribution or introducing extra variables (Duliba, 1991; SubbaNarasimha et al., 2020).

Among the five parameters predicted in the current study, NE_p was the variable with the highest predictive error in both two models. Similarly, Tess et al. (1984) found P_d suffered more from measurement error than any other body composition of pigs, especially at heavier weights. To achieve better prediction on NE_p, more accurate data are needed, and introducing extra relevant variables is also helpful even though this is hardly achieved. The utilization of a better predictive method such as ANN can reduce the predictive error more easily, as revealed in this study, encouraging future ANN applications in swine nutrition. In addition, the developed Microsoft Excel application containing trained results and connection weight matrices could also greatly help to share the developed ANN models in the current study. The representative, normality, and homogeneity of data for modeling need to be checked in advance to avoid overfitting, because the run mode of ANN is to obtain a local optimal solution rather than a global optimal solution (Ghorbani et al., 2016).

Even though we have used the animal trial data to build the most accurate and precise NLR and ANN models, there were still some limitations that can not be ignored. The ANN model was labeled “black box,” which means the inputs and outputs are known, but the connections among them are unknown (Jacobs et al., 2022). If we want a more concise and more easily understandable model, then its accuracy must be surrendered. However, we believe that this kind of model has even more serious consequences. For example, Gauthier et al. (2022) applied simple regression equations to predict the litter growth as well as the standardized ileal digestible Lys requirements of lactating sows. Even though the regression models are simple and understandable, the precision was poor with an R² of 0.12, which may result in Lys deficiency in half of the lactating sows. Another inevitable limitation is that we built a data set in a standardized condition (i.e., same breeds, sexes, temperatures, and the same metabolic cages), which limits our models being applied to various and complex conditions. The breeds, sexes, temperatures, and feeding conditions were all important factors that would affect energy intake and partition patterns (Renaudeau et al., 2006; Noblet et al., 2021; Zhang et al., 2021) and the data would produce great variation if these variables were not controlled. Extremely variable data can greatly increase the difficulty of developing a prediction model and decrease the accuracy of the model. Therefore, data on NE partition patterns under special breeds, sexes, and different feeding conditions can also be collected to update model parameters. Such an operation would increase the adaptability of the model and reduce the effort of rebuilding new models.

Similarly to the decision support system built by Institut National de la Recherche Agronomique (van Milgen et al., 2007; Dourmad et al., 2008), our models could be used to predict the ideal dietary energy concentrations according to the BW, feed intake, and the targeted body composition (P_d and L_d) of pigs. Furthermore, with the automatic feeding equipments, e.g., an auto-blend feedline system (Gauthier et al., 2022), the dietary energy concentrations could be achieved by blending high-energy and low-energy diets, which can greatly contribute to feed waste control, manure emission reduction, and carcass quality regulation, and finally promote the realization of precision feeding in growing–finishing pigs.

Conclusions

The NE intake and NE partition patterns are influenced by the growth stages of growing–finishing pigs. The NE_m and NE_l (MJ/d) kept increasing as BW increased from 30 kg to 90 kg, while the NE_p increased to its maximum value and then kept in a certain range of 4.64 to 4.88 MJ/d which aligns with previous studies. The proportion of NE_m for pigs at 30 to 90 kg kept in the range of 42.0% to 48.6%, while the proportion of NE_l kept increasing. The NE intake, NE_m, and NE_p measured were greater compared with those reported previously, indicating the increased NE requirements for the specific breeds used in this study. The ANN models were more accurate and precise than NLR models in NE partition pattern prediction. However, considering the difficulties of establishing an ANN model with appropriate architecture, more concise and easier-to-understand regression models using BW and energy intake as inputs were also recommended. The prediction models of NE partition pattern shows great potential for precision feeding in the future.

Glossary

Abbreviations

ANN

artificial neural networks

BW

body weight

CCC

concordance correlation coefficients

CST

comparative slaughter technology

FHP

fasting heat production

GE

gross energy

HI

heat increment

HP

heat production

L_d

lipid deposition

IC

indirect calorimetry

MAE

mean absolute error

MRE

mean relative error

ME

metabolizable energy

NE

net energy

NE_m

net energy for maintenance

NE_l

net energy retained as lipid

NE_p

net energy retained as protein

NLR

nonlinear regression

P_d

protein deposition

Pdmax

maximal rate of protein deposition

RE

retained energy

RMSE

root mean square error

THP

total heat production

Conflict of Interest Statement

The authors declare no real or perceived conflicts of interest.

Ethics Statement

All experimental protocols including animal care and use were approved by the Institutional Animal Care and Use Committee of China Agricultural University (Beijing, China, protocol code: AW9111202-1-3 and 21 June 2020).

Data Availability Statement

The original data used to support the findings of this study are available in the Supplementary Materials.