Undermatching Is a Consequence of Policy Compression

Abstract

The matching law describes the tendency of agents to match the ratio of choices allocated to the ratio of rewards received when choosing among multiple options (Herrnstein, 1961). Perfect matching, however, is infrequently observed. Instead, agents tend to undermatch or bias choices toward the poorer option. Overmatching, or the tendency to bias choices toward the richer option, is rarely observed. Despite the ubiquity of undermatching, it has received an inadequate normative justification. Here, we assume agents not only seek to maximize reward, but also seek to minimize cognitive cost, which we formalize as policy complexity (the mutual information between actions and states of the environment). Policy complexity measures the extent to which the policy of an agent is state dependent. Our theory states that capacity-constrained agents (i.e., agents that must compress their policies to reduce complexity) can only undermatch or perfectly match, but not overmatch, consistent with the empirical evidence. Moreover, using mouse behavioral data (male), we validate a novel prediction about which task conditions exaggerate undermatching. Finally, in patients with Parkinson's disease (male and female), we argue that a reduction in undermatching with higher dopamine levels is consistent with an increased policy complexity.

SIGNIFICANCE STATEMENT The matching law describes the tendency of agents to match the ratio of choices allocated to different options to the ratio of reward received. For example, if option a yields twice as much reward as option b, matching states that agents will choose option a twice as much. However, agents typically undermatch: they choose the poorer option more frequently than expected. Here, we assume that agents seek to simultaneously maximize reward and minimize the complexity of their action policies. We show that this theory explains when and why undermatching occurs. Neurally, we show that policy complexity, and by extension undermatching, is controlled by tonic dopamine, consistent with other evidence that dopamine plays an important role in cognitive resource allocation.

Introduction

Over half a century ago, Richard Herrnstein discovered an orderly relationship between choices and rewards (Herrnstein, 1961), which he termed “matching” behavior. Herrnstein's matching law describes the tendency of animals to “match” the ratio of choices allocated to the ratio of reward received when choosing among multiple options. For two options, matching is defined by the following:

$$\frac{C_{\text{a}}}{C_{\text{a}}+C_{\text{b}}}=\frac{R_{\text{a}}}{R_{\text{a}}+R_{\text{b}}}\text{and}\frac{C_{\text{b}}}{C_{\text{a}}+C_{\text{yb}}}=\frac{R_{\text{b}}}{R_{\text{a}}+R_{\text{b}}},$$

where C_a is the number of choices allocated to option a and R_a is the number of rewards obtained from option a. The matching law describes choice behavior fairly accurately in a number of animals, including pigeons (Herrnstein, 1961; de Villiers and Herrnstein, 1976; Baum, 1979; Mazur, 1981; Villarreal et al., 2019), mice (Gallistel et al., 2007; Fonseca et al., 2015; Bari et al., 2019), rats (Graft et al., 1977; Gallistel, 1994; Belke and Belliveau, 2001; Gallistel et al., 2001; Lee et al., 2017), monkeys (Anderson et al., 2002; Sugrue et al., 2004; Lau and Glimcher, 2005; Kubanek and Snyder, 2015; Tsutsui et al., 2016; Soltani et al., 2021), and humans (Schroeder and Holland, 1969; Pierce and Epling, 1983; Beardsley and McDowell, 1992; Savastano and Fantino, 1994; Vullings and Madelain, 2018; Cero and Falligant, 2020). A closer look reveals systematic deviations from matching in many of these articles, which we expand on below.

Perfect matching, however, is only seen infrequently. Theoretically, animals can deviate from perfect matching by undermatching, biasing choices toward the poorer option, or by overmatching, biasing choices toward the richer option (Baum, 1974). Empirically, animals systematically undermatch (Baum, 1974; Myers and Myers, 1977; Baum, 1979; Wearden and Burgess, 1982). Overmatching is rarely observed. This systematic bias toward undermatching has received a number of explanations, including mistuned learning rules (Loewenstein and Seung, 2006; Loewenstein, 2008), procedural variation in tasks (Baum, 1979; Williams, 1985), the inability to detect the richer stimulus/action (Baum, 1974), behavioral bursts (Wearden, 1983), poor credit assignment (Trepka et al., 2021), inappropriate choice stochasticity (Trepka et al., 2021), noise in neural mechanisms of decision-making (Soltani et al., 2006), synaptic plasticity rules (Iigaya and Fusi, 2013), belief in environmental volatility (Saito et al., 2014), and optimal decision-making under uncertainty (Iigaya et al., 2019). Here, we extend a framework with broad explanatory power to provide a normative rationale for undermatching and furnish novel predictions that we test.

We begin with the premise that agents seek to simultaneously maximize reward and minimize some measure of cognitive cost, which we formalize as policy complexity, the mutual information between states and actions (Parush et al., 2011; Gershman, 2020; Lai and Gershman, 2021). The policy $\pi (a|s)$ corresponds to the probabilistic mapping between environment states (s) and actions (a). Because policy complexity is a lower bound on the number of bits needed to store a policy in memory, more complex policies necessitate more bits. If the optimal policy exceeds the memory capacity of an agent, then it will need to “compress” its policy by reducing complexity. In this article, we argue that undermatching is a consequence of policy compression.

We first extend the notion of policy complexity to describe matching behavior. We find that agents should only perfectly match or undermatch, but never overmatch, since overmatching requires more memory than perfect matching and yields less reward. We validate a novel prediction that capacity-constrained agents should increase undermatching on task variants that demand greater policy complexity for perfect matching behavior. We then test an implication of the hypothesis that tonic dopamine signals average reward (Niv et al., 2007) and thereby controls the allocation of cognitive effort (Mikhael et al., 2021). When tonic dopamine is higher, individuals should adopt higher policy complexity, as if their capacity limit had effectively increased. We find evidence for this hypothesis using data from patients with Parkinson's disease performing a dynamic foraging task on and off dopaminergic medication (Rutledge et al., 2009): undermatching was reduced on medication compared with off medication. Together, our results support a policy compression account of undermatching.

Materials and Methods

Behavioral data.

We reanalyzed data from mice (Bari et al., 2019) and human subjects (Rutledge et al., 2009) performing a dynamic foraging task (differences between the mouse and human versions of the task are detailed below). In this task, subjects chose between two options, each of which delivered reward probabilistically. The “base” reward probabilities of each option remained fixed within a given block, and changed between blocks. Block transitions were uncued. A key feature of the dynamic foraging task was the baiting rule, which stipulated that the longer an agent has abstained from choosing a particular option, the greater the probability of reward on that option. Stated another way, if the unchosen option would have been rewarded, the reward was delivered the next time that option was chosen. The baiting rule was designed to mimic ecological conditions, where abstaining from a foraging option will allow that option to replenish reward. Mathematically, the baiting probability took the following form:

$$P_a=1-{\left(1-p_a\right)}^{t_a+1},$$

where p_a is the base reward probability for option a, t_a is the number of consecutive choices since that option was last chosen, and P_a is the probability of reward when the agent next chooses that option (Fig. 1A, illustration). The baiting rule applies to both datasets.

Figure 1.

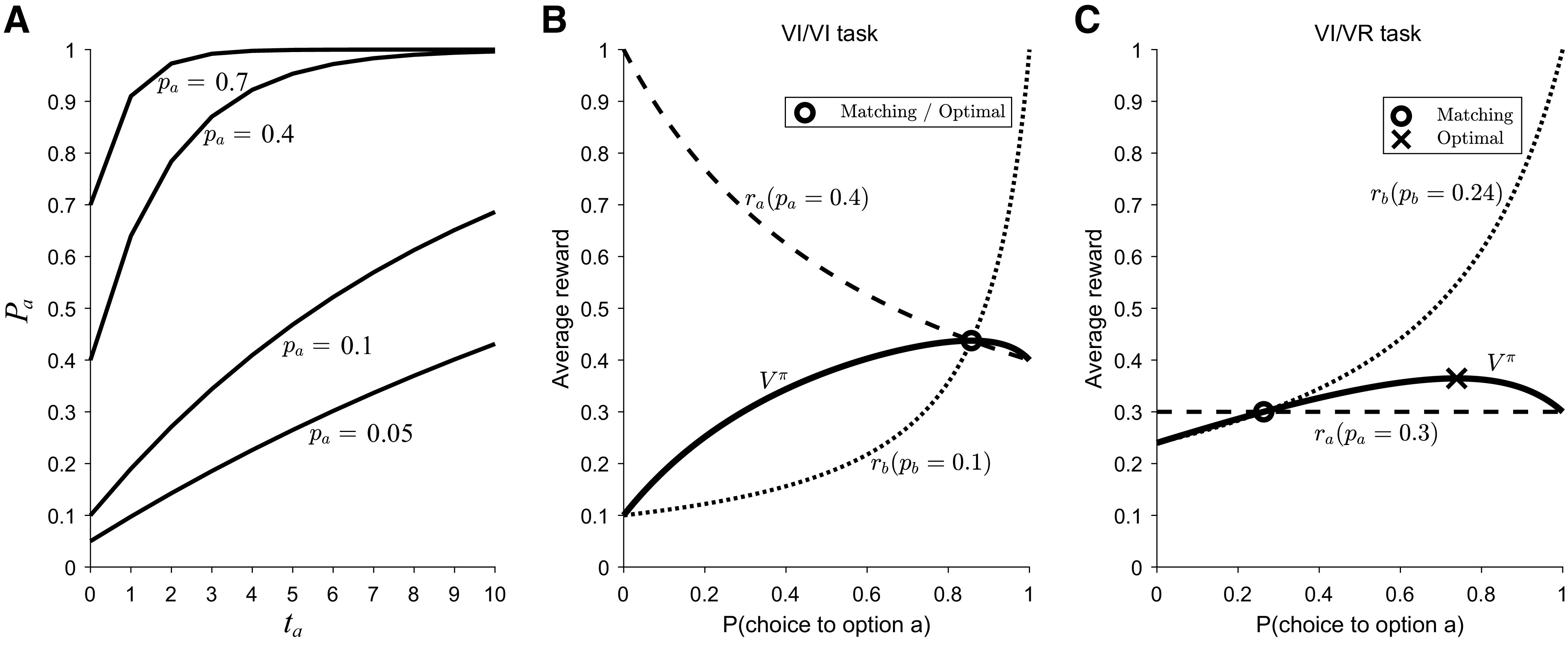
Geometric representation of matching behavior in different task conditions. A, The baiting rule for four different values of p_a (base reward probabilities). The x-axis is t_a, the number of consecutive choices since that option was last chosen, and the y-axis is p_a, the probability of reward. Here, P_a ∈ {0.05, 0.1, 0.4, 0.7}. Adapted from Huh et al. (2009). B, In VI/VI tasks, where both options use the “baiting” rule, matching emerges as the optimal probabilistic policy. Matching occurs where r_a = r_b (hence they match). C, VI/VR tasks allow us to disambiguate whether animals match or whether they approximate the optimal probabilistic solution. In these task variants, one option (here, option b) follows a VI schedule (i.e., programmed with the baiting rule) and the other option (here, option a) follows a VR schedule (standard probabilistic reward delivery). The matching policy (where r_a = r_b) differs from the optimal probabilistic policy. Adapted from Bari and Cohen (2021).

In the mouse dynamic foraging task, male C57BL/6J mice (age range, 6–20 weeks; catalog #000664, The Jackson Laboratory) were surgically implanted with a head plate in preparation for head fixation. After recovery, these animals were water restricted and habituated. Cues were delivered in the form of odors via a custom-made olfactometer (Cohen et al., 2012). Animals received one of two cues, selected pseudorandomly on each trial, for 0.5 s. The first odor (presented on 95% of trials) was a “go cue,” after which mice made a leftward or rightward lick toward a custom-built “lick port.” The second odor (presented on 5% of trials) was a “no-go cue.” Licks after this cue were neither rewarded nor punished. If a lick was emitted within 1.5 s of cue onset, reward was delivered probabilistically. Intertrial intervals (ITIs) were drawn from an exponential distribution with a rate parameter of 0.3, with a maximum of 30 s. This resulted in a flat ITI hazard function, ensuring that expectation about the start of the next trial did not increase over time (Luce, 1986). The mean ITI was 7.1 s. Miss trials (go cue trials with no response) were rare (<1% of all trials). To minimize spontaneous licking, we enforced a 1 s no-lick window before odor delivery. Licks within this window were punished with a new randomly generated ITI, followed by a 2.5 s no-lick window.

We included data from three task variants. In the “40/10” task variant, the base reward probabilities switched between {0.4/0.1} (corresponding to base reward probabilities for the left and right option) and {0.1/0.4}. This corresponds to a task with two possible states. A similar logic applied to the “40/5” task variant. In the “multiple probability” task variant, the base reward probabilities were chosen from the set {0.4/0.05, 0.3857/0.0643, 0.3375/0.1125, 0.225/0.225, 0.1125/0.3375, 0.0643/0.3857, 0.05/0.4}, which corresponds to a task with seven possible states. We included 30 mice total, 10 of which performed the 40/10 task for 236 total sessions, 17 of which performed the 40/5 task for 325 total sessions, and 9 of which performed the multiple probability task for 70 sessions. Animals completed 121–830 trials per session, with a median of 362. Block lengths were drawn from a uniform distribution that spanned a maximum range of 40–100 trials. For full details, we refer readers to the study Bari et al. (2019).

In the human dynamic foraging task, subjects performed a similar task with the following four possible states: {0.257/0.043, 0.225/0.075, 0.075/0.225, 0.043/0.257}. This dataset included 26 healthy young subjects (14 females, 12 males), 26 healthy elderly control subjects (12 females, 14 males), and 26 patients with idiopathic Parkinson's disease (12 females, 14 males) who performed the task both off and on dopaminergic medications (order counterbalanced across patients). During “off-medication” sessions, patients withheld taking all dopaminergic medications for at least 10 h (mean, 14.4 h). During “on-medication” sessions, patients were tested an average of 1.6 h after receiving dopaminergic medications. All subjects were prescribed l-DOPA, and the majority (n = 17) were also taking a D₂ receptor agonist (pramipexole, pergolide, or ropinirole). Patients had scores of 2 or 2.5 on the Hoehn–Yahr scale of motor function, indicating that they were in mild to moderate stages of the disease (Hoehn and MD, 1967). Subjects were trained by reading task instructions and answering five multiple-choice questions to ensure they had a basic understanding of the task. They then completed five separate blocks of 40 trials (for a total of 200 trials) with base reward probabilities fixed within each block. On each trial, subjects chose a red or green stimulus. After each block, subjects were given feedback about which option was the richer option. After training, subjects performed 800 trials in 10 blocks of 70–90 trials. Subjects had unlimited time to make each choice, but typically completed 800 trials within 30 min. We excluded one patient with Parkinson's disease who did not complete all trials on an on-medication session. For full details, we refer readers to Rutledge et al. (2009).

Theoretical framework.

We model an agent that can take actions (denoted by a) and visit states (denoted by s). Agents learn a policy $\pi (a|s)$, a probabilistic mapping from states to actions. Technically, states are defined as a representation of the information needed to predict reward (Sutton and Barto, 2018). Based on this definition, the correct state for the dynamic foraging task would need to include more information than what we have included in our specification of task states given earlier. Specifically, task states correspond to the different baiting probabilities that appear repeatedly in the task, switching after a random number of trials. Because the task state is not directly observable by the agent, the state representation would need to include the sufficient statistics for the posterior probability distribution over the task state. In addition, it would need to include t_a, the number of consecutive choices since option a was last chosen. These requirements significantly complicate the analysis of the optimal policy; moreover, it is doubtful that mice and humans keep accurate track of all this information at the same time.

Our model is predicated on the assumption that subjects represent a simpler state representation consisting only of the task state. Although the task state is in fact unobservable, we restrict our analysis to behavior during “steady state” (after the first 20 trials postswitch), during which time it is plausible that subjects have relatively little task state uncertainty. This was empirically chosen, as 20 trials is sufficient to exclude behavior that has not yet reached steady state (Rutledge et al., 2009, their Fig. 3B; Bari et al., 2019, their Fig. 1D). The assumption that subjects neglect t_a (i.e., that they either do not track their choice history or do not use it in their state representation) is more drastic, but it is nevertheless common in many models of matching, and has some empirical support (Nevin, 1969, 1979; Heyman, 1979), though the evidence is equivocal (Shimp, 1966; Silberberg et al., 1978). Further evidence against response counting is discussed later. In summary, we assume that agents represent the task state (number of pairs of base probabilities) and ignore the baiting rule.

Policy complexity is the mutual information between states and actions, as follows:

$$I^{\pi }(S;A)=\sum _{s}P(s)\sum _a\pi (a|s)\log \frac{\pi (a|s)}{P(a)},$$

where $P(a)=\sum _{s}P(s)\pi (a|s)$ is the marginal action probability. A key assumption underlying our formulation of the optimal policy is that agents are capacity constrained (i.e., there is an upper bound, C, on policy complexity). Stated another way, agents must compress the optimal policy if they lack the memory resources to store it. We therefore define a joint optimization problem where agents seeks to maximize reward subject to a capacity constraint. We define the optimal policy as follows:

$${\pi }^{*}=\underset{\pi }{\text{arg}\max }{V}^{\pi },\mathrm{subject\; to}{I}^{\pi }(S;A)\le C,$$

where V^π is the value (average reward) under policy π. Note that we allow the agent to ignore unnecessary information to maximize reward, so more information can never corrupt performance. This does not mean that an agent discards task-irrelevant information from storage entirely, simply that this information is not used to generate the optimal policy.

The value is given by the following:

$$V^{\pi }=\sum _{s}P(s)\sum _a\pi (a|s)Q^{\pi }(s,a),$$

where Q^π(s, a) is the average reward for taking action a in state s.

For the dynamic foraging task, the expected reward for choosing action a is obtained by marginalizing over t_a:

$$\begin{array}{l}{Q}^{\pi }(s,a)=\pi (a|s)\sum _{t_a=0}^{\infty }{\left[1-\pi (a|s)\right]}^{t_a}\left[1-{\left(1-p_a\right)}^{t_a+1}\right]\\ =\frac{p_a}{\pi (a|s)+p_a\left[1-\pi (a|s)\right]}.\end{array}$$

We will sometimes use the shorthand r_a to denote the expected reward for choosing action a. Because task states and actions are both marginally equiprobable, we assume in our analyses that P(s) = 1/N (where N is the number of task states) and P(a) = 1/2.

Data analysis.

Following convention, we defined undermatching by fitting the following function

$${\log }_2\left(\frac{C_{\text{a}}}{C_{\text{b}}}\right)=a·{\log }_2\left(\frac{R_{\text{a}}}{R_{\text{b}}}\right)+b,$$

where C_a, C_b, R_a, and R_b correspond to the total choices and rewards in an individual block. We report a, where a = 1 is perfect matching, a < 1 is undermatching, and a > 1 is overmatching (Baum, 1974). In calculating ${\log }_2\left(\frac{R_{\text{a}}}{R_{\text{b}}}\right)$, we excluded blocks with R_a = 0 or R_b = 0. For both mouse and human datasets, we excluded trials 1–20 following each block transition to allow behavior to stabilize.

To construct the empirical reward–complexity curves, in both datasets, we computed the average reward and mutual information between states and actions for each session. We estimated mutual information by computing the empirical action frequencies for each state for each session. Although there are numerous methods for computing mutual information, we found that using the empirical action frequencies for each state gave reasonably good performance, likely given the large number of trials, limited states, and limited number of actions in each state.

To determine the effect of policy complexity on false alarm rates for the mouse dataset, we calculated a logistic regression predicting false alarm as a function of policy complexity. To determine the effect of dopaminergic medications on perseveration, we calculated the following logistic regression for the Parkinson's disease dataset, as follows:

$$\log \left(\frac{P(c_r(t))}{1-P(c_r(t))}\right)=\sum _{i=1}^5{\beta }_i^r(r_r(t-i)-r_g(t-i))+{\beta }^c{c}_r(t-1)+{\beta }_0,$$

where c_r(t) = 1 for a choice to the red target and 0 for a choice to the green target, r_r(t) = 1 if the red target delivered reward and 0 otherwise, r_g(t) = 1 if the green target delivered reward, and 0 otherwise. We included an interaction term indicating whether data were from the on-medication versus off-medication sessions, and report β^C for this interaction, which quantifies how perseveration (the tendency to repeat the same choice) changes as a function of dopaminergic medication.

In performing all paired and unpaired statistical tests, we first performed a Lilliefors test, which tests the null hypothesis that the data are normally distributed. In all cases, the null hypothesis was rejected, and we subsequently performed nonparametric testing, either the Wilcoxon rank-sum test (for independent samples) or the Wilcoxon signed-rank test (for paired samples).

Data availability.

All code and data to reproduce the analyses in this article can be obtained at https://github.com/bilalbari3/undermatching_compression.

Results

Matching is an optimal probabilistic policy in variable-interval/variable-interval tasks

To understand how policy compression leads to undermatching, we must first understand matching behavior, the task conditions that generate matching behavior, and what matching implies about state representations of the brain. We have developed a number of these arguments previously and repeat them here for clarity (Bari and Cohen, 2021).

Task conditions are critical for observing matching behavior. Most studies use “variable interval” (VI) reward schedules. In these tasks, reward is available at an option after a variable number of choices has been made (in discrete choice tasks). Once the requisite number of choices has been made, that option is “baited,” guaranteeing reward delivery when it is next chosen. The reward is not physically present, but will be delivered when that option is next chosen. The baiting rule takes the form shown in Equation 2. To gain an intuition, if the probability of reward on the unchosen option increases the longer it has been left unchosen, it makes sense to occasionally probe it to harvest-baited rewards. The logic of this task rule is to mimic harvesting conditions where abstaining from a resource allows that resource to replenish. Concretely, imagine $p_a=0.1,p_b=0.4$ and the animal repeatedly chooses option b. On the first trial, P_a = 0.1 and P_b = 0.4. After option b is chosen once, P_a ∼ 0.19. After option b is chosen twice in a row, now P_a ∼ 0.27. As this continues, P_a approaches 1. After option a is chosen, P_a then resets to 0.1 and P_b = 0.64 since it has not been chosen for one trial. Figure 1A demonstrates the baiting rule for different values of p_a.

In tasks where both options follow VI reward schedules (so-called VI/VI tasks), matching is the optimal probabilistic policy for state representations that ignore t_a (Eq. 2). Rewriting Equation 1, matching occurs when $\frac{R_{\text{a}}}{C_{\text{a}}}\text{=}\frac{R_{\text{b}}}{C_{\text{b}}}$. This simply states that matching occurs when the expected reward obtained from each option is equal. Figure 1B provides a geometric intuition for matching, which occurs when r_a and r_b cross one another (in this case, when π_a ∼ 0.86). A normative explanation is therefore that matching behavior is the best probabilistic behavior animals can exhibit to harvest reward.

Matching is generally a suboptimal probabilistic policy and implies animals are unaware of baiting

A key insight into understanding why matching behavior arises came from the study by Sakai and Fukai (2008b). To implement the optimal probabilistic policy, an agent needs to understand how adjusting the parameters of its policy changes behavior (a relatively easy problem) and how changing this policy modifies the environment (a much harder problem). If an agent ignores the change in the environment, then matching behavior emerges. In other words, matching occurs because agents ignore the baiting rule (i.e., behave as if their actions do not change reward probabilities). Because of this, generally speaking, matching is not the optimal probabilistic policy.

In VI/VI tasks, matching fortuitously corresponds to the optimal probabilistic policy, and we therefore cannot use this task to conclude whether agents are aware of the baiting rule. The critical test is an experiment in which matching is not the optimal strategy. For example, if one option follows a VI schedule (i.e., programmed with the baiting rule) the other follows a variable-ratio (VR) schedule (i.e., standard probabilistic reward delivery), then matching will harvest suboptimal rewards, as shown in Figure 1C.

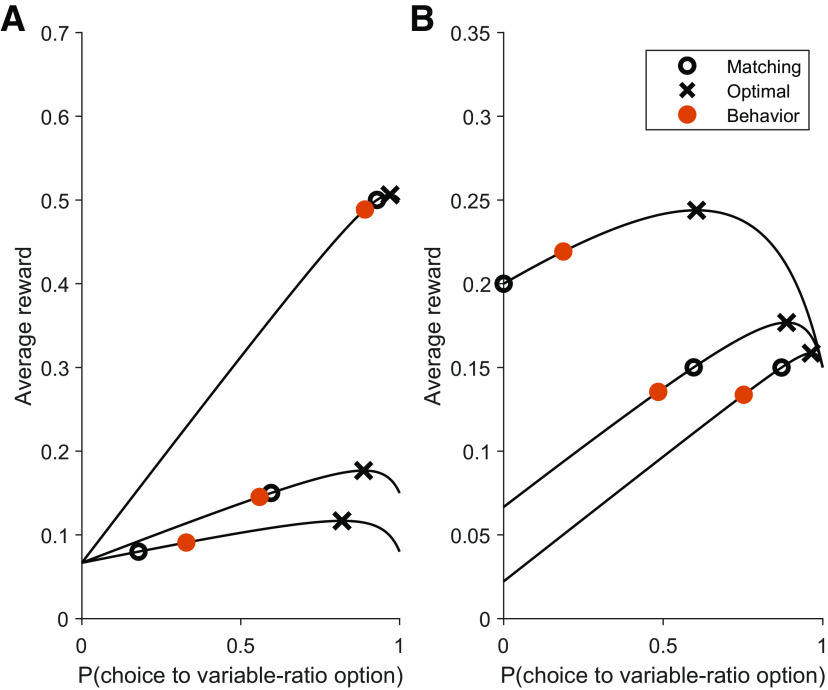
Figure 2 demonstrates a telling set of experiments from the study by Williams (1985), which is reanalyzed here. Rats performed 6 different VI/VR task variants, each summarized with one line (three on the left plot, three on the right plot). Each black line here is V^π for each task. In each task variant, rats more closely approximate the matching solution than the maximizing solution, and in fact demonstrate a significant degree of undermatching (choice probabilities are closer to 50% than would be expected from perfect matching). The finding that animals match instead of maximize has been replicated numerous times (Herrnstein and Heyman, 1979; Mazur, 1981; Vyse and Belke, 1992), including in humans (Savastano and Fantino, 1994).

Figure 2.

Rats are systematically biased toward undermatching instead of the optimal probabilistic policy. A, In the study by Williams (1985), rats performed 6 different VI/VR task variants. Each black line demonstrates V^π for each task variant. Overlaid on each V^π line are X symbols for the optimal solution, O symbols for the matching solution, and filled orange circles for the empirical behavior. Rats were consistently closer to matching than to maximizing, and demonstrated a significant degree of undermatching. Because a choice of the VI option resulted in a 6 s time-out, we approximated the reward probability of the VI option by 6/τ, where τ is the mean reward time under the VI schedule. The schedules are defined as follows, where each number corresponds to p_i, the base reward probability. VI/VR, from top to bottom: (0.07, 0.5), (0.07, 0.15), (0.07, 0.08). B, VI/VR, from top to bottom: (0.2, 0.15), (0.07, 0.15), (0.02, 0.15).

We briefly note that periodic switching policies (i.e., sample the other option every n choices) are the global optimal policies in VI/VI tasks (Houston and McNamara, 1981). These are more difficult for an agent to implement, as it requires tracking choice history (i.e., tracking t_a in Eq. 2), which necessitates a much larger state representation. In the case of p_a = 0.4 and p_b = 0.1, the optimal policy is to alternate selecting option a six times and option b once (when P_b ∼ 0.52). If these policies are used, they should be easy to diagnose, since stay duration distributions will be bimodal. Across a variety of species, stay duration distributions remain unimodal (Gallistel et al., 2001; Sugrue et al., 2004; Bari et al., 2019). This constitutes further evidence against models based on response counting (as discussed earlier).

Empirically, the finding that animals behave as if they are unaware of changes in environmental statistics may explain why most models of matching behavior do not account for the baiting rule. Examples include melioration (Herrnstein and Vaughan, 1980), local matching (Sugrue et al., 2004), logistic regression (Lau and Glimcher, 2005; Tsutsui et al., 2016), and models with covariance-based update rules like those underlying direct actor and actor critic agents (Loewenstein and Seung, 2006). We are aware of one study that models the baiting rule (Huh et al., 2009), though this model failed to explain behavioral data better than Q-learning in any of 31 mice in the study by Bari et al. (2019).

In summary, because of the complexity of the baiting rules underlying VI/VI tasks, animals behave as if they are unaware of the baiting rule because of the following: (1) they do not adopt the optimal probabilistic policies in VI/VR tasks; (2) they do not adopt deterministic policies in VI/VI tasks; (3) their behavior is better fit by models that ignore the baiting rule; and (4) successful models of matching typically ignore the baiting rule. Instead, animals seem to behave in these tasks as if their actions do not change the reward probabilities.

Policy compression only allows for perfect matching or undermatching and excludes overmatching

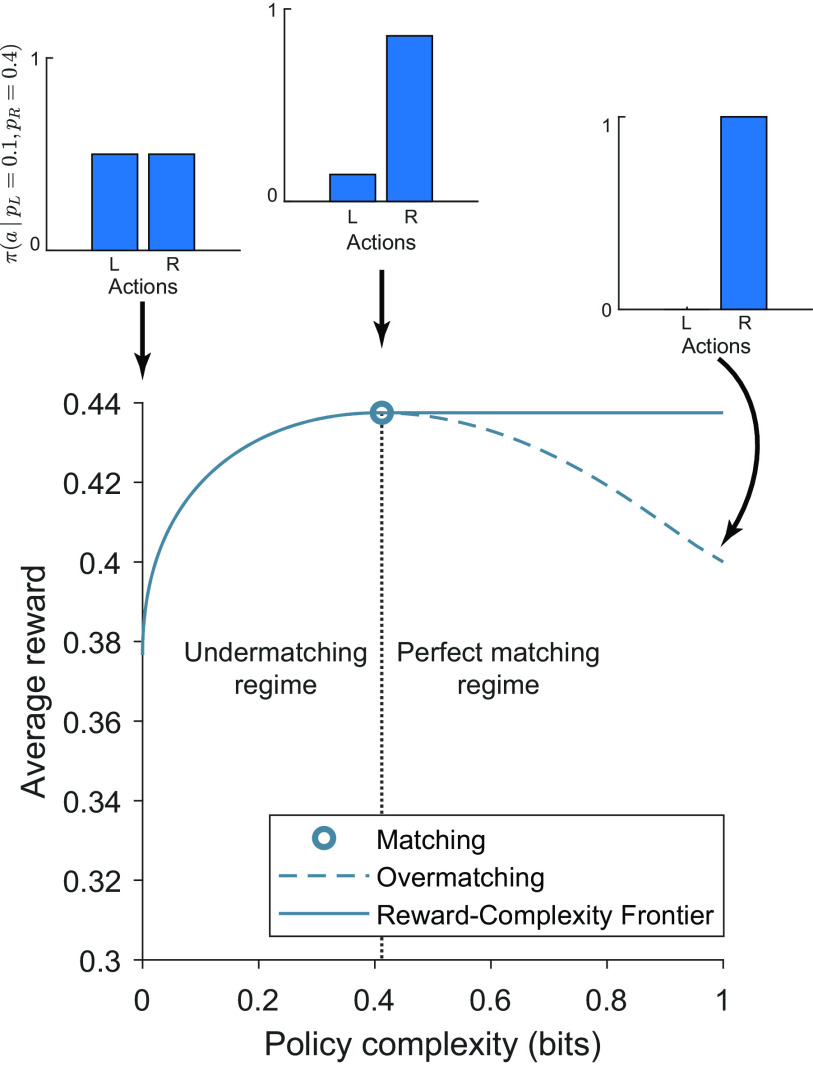
We now apply the notion of policy compression to matching behavior. Figure 3 shows the reward–complexity frontier for the 40/10 task variant in Bari et al. (2019). In this task, mice chose between two options, each following a variable-interval schedule. One option gave reward with a base probability of p_a = 0.4 and the other option gave reward with p_b = 0.1. These alternated every 40–100 trials and the transitions were uncued to the mice. Using the arguments we developed above, we assume the brain believes the world consists of the following two states: $s_1:p_a=0.4,p_b=0.1$ or $s_2:p_a=0.1,p_b=0.4$. That is, we ignore the baiting rule in generating these state representations.

Figure 3.

Policy compression allows for perfect matching or undermatching, but not overmatching. Under the assumption that agents are unaware of the baiting rule, the optimal reward–complexity curve is a monotonically nondecreasing function. At policy complexities below perfect matching, agents exhibit undermatching, biasing choice the poorer option (see inset for policy at policy complexity = 0 bits). At an intermediate policy complexity, agents exhibit perfect matching, harvesting optimal reward. At high levels of policy complexity, agents continue to exhibit perfect matching. Agents with sufficiently high capacity above matching are capable of exhibiting overmatching, shown by the dashed line (see inset at policy complexity = 1 bit). However, agents with sufficiently high capacity can compress their policies and increase their reward rates by adopting a perfect matching policy. Therefore, policy compression disallows overmatching.

Under this assumption, the reward–complexity frontier is a monotonically nondecreasing function. Each point on the frontier corresponds to a reward-maximizing policy under a particular policy complexity constraint. The frontier achieves a maximum at policy complexity equal to and exceeding the matching solution (Fig. 3). Lower-complexity policies correspond to undermatching (choosing the poorer option more often than prescribed by matching). More complex policies correspond to overmatching (choosing the richer option more often). However, overmatching yields less reward than matching with a higher cognitive cost. We posit that the brain optimizes its policy under a complexity constraint, thereby generating matching behavior.

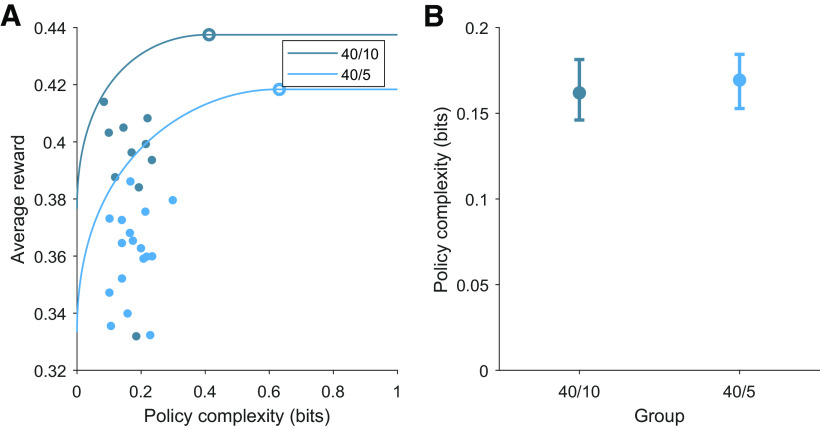
Mice operate near the optimal reward–complexity frontier and undermatch in a manner predicted by policy compression

Applying the policy compression framework to mouse behavior (Fig. 4A), as expected, we find that mice are capacity constrained (Fig. 5A). Moreover, they operate near the optimal frontier, which suggests that they are close to optimally balancing reward and complexity. We additionally find that policy complexity does not appreciably change across task variants (Fig. 5B), suggesting a constant resource constraint, which we have observed in prior applications of policy complexity (Gershman and Lai, 2021).

Figure 4.

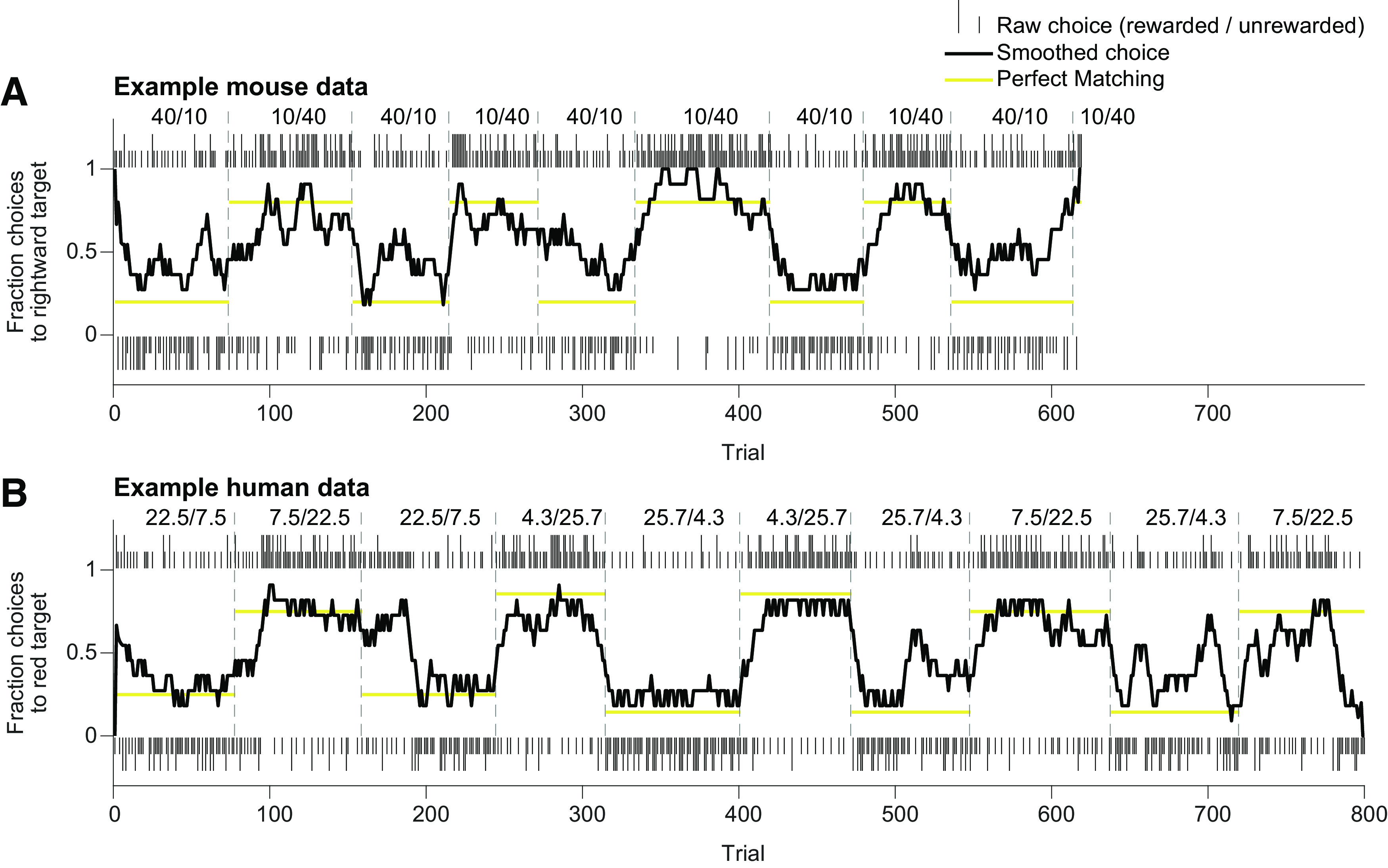
Raw mouse and human behavioral data. A, Example mouse behavior in the “40/10” task variant. Tall (rewarded) and short (unrewarded) ticks correspond to leftward (below) and rightward (above) choices on individual trials. Dashed lines denote unsigned block transitions. Choices were smoothed with an 11-trial boxcar filter. Gold lines correspond to perfect matching behavior. Numbers indicate base reward probabilities for leftward and rightward choices. B, Example human behavior. Ticks correspond to green target (below) and red target (above) choices on individual trials. Numbers indicate base reward probabilities for green and red target choices.

Figure 5.

Mice exhibit capacity-constrained policies near the optimal reward–complexity frontier. A, Optimal and empirical reward–complexity curves for mice performing the 40/10 and 40/5 task variants in the study by Bari et al. (2019). In each task variant, mice are capacity constrained (policy complexity below optimal) and operate near the optimal reward–complexity frontier. Open circles denotes matching behavior. Filled circles denote individual mice. B, Policy complexity in each task condition. Data are the median ± 95% bootstrapped CI. Wilcoxon rank-sum test, p = 0.18.

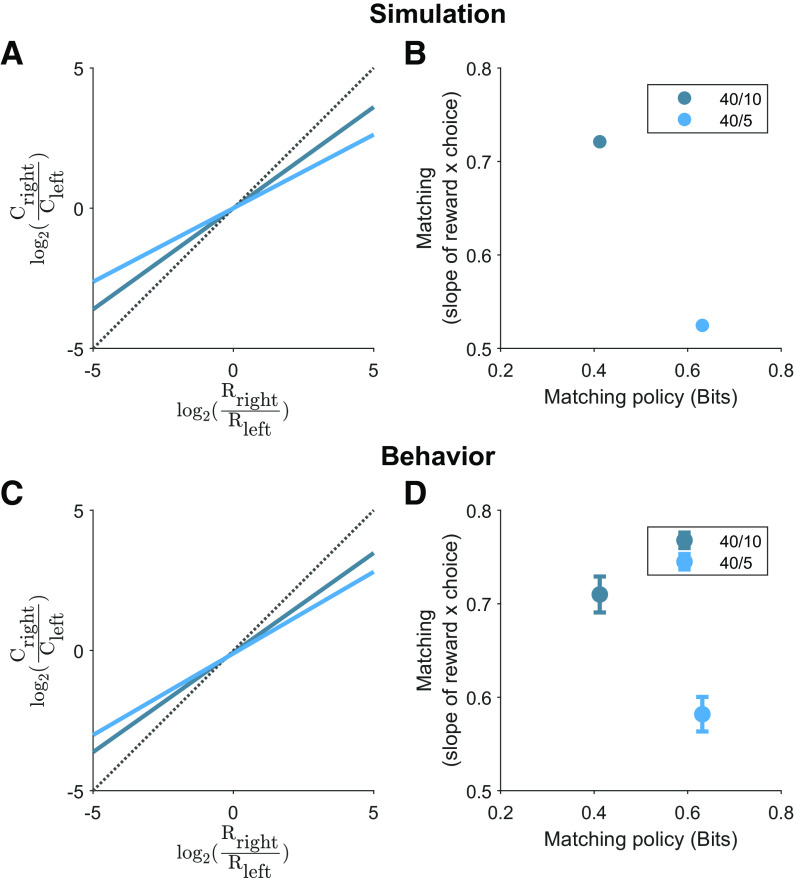
Policy compression makes a prediction about the degree of undermatching capacity-constrained animals should exhibit in different task variants. Undermatching should become exaggerated under reward schedules that demand more complex policies for matching behavior (Fig. 6A,B). In Figure 5A, the 40/10 reward schedule demands the fewest bits for matching behavior and the 40/5 reward schedule demands more. As an alternative prediction, one might instead predict greater overmatching for the 40/5 reward schedule, as the higher-probability side is easier to discriminate and mice may therefore perseverate on that side. We find that the policy compression prediction is borne out, with mice exhibiting significantly greater undermatching on the 40/5 schedule relative to the 40/10 schedule (Fig. 6C,D).

Figure 6.

Mice exhibit greater undermatching in task variants that demand greater policy complexity. A, Simulation of a policy at a capacity constraint of 0.19 bits. The log-choice ratio is plotted as a function of log-reward ratio. Dotted line corresponds to unity. B, Theoretical matching slopes as a function of the policy complexity for perfect matching. C, Log-choice ratio as a function of log-reward ratio for the 40/10 (slope = 0.710) and 40/5 (slope = 0.582) task variants. Each colored line is the best fit and dotted line corresponds to unity. D, Empirical matching slopes (least-squares estimate ± 95% CI) for each task variant. 95% CIs: 0.691–0.729 for 40/10 task variant; 0.563–0.600 for 40/5 task variant. These data are significantly different as the 95% CI bands do not overlap.

We tested several other predictions of policy complexity. First, given the relationship between cognitive effort and inhibitory control (van der Wel and van Steenbergen, 2018), we predicted sessions with greater policy complexity would be associated with a decreased false alarm rate. In this dataset, 5% of all trials were “no-go” trials, and a response was neither rewarded nor punished. We indeed found evidence that increased policy complexity was associated with improved inhibitory control, as there was a significant negative association between the two using logistic regression (β = −1.4, p < 0.005). Second, policy complexity predicts that increasing cognitive load (in our framework, an increased number of states) should reduce policy complexity or force a fixed complexity to be distributed across more states, which should cause actions to become more stochastic (Lai and Gershman, 2021). We compared behavior in our 40/10 and 40/5 tasks (two states) to a “multiple probability” variant with seven states. As predicted, the conditional entropy (randomness of behavior in each state) increased with an increased number of states (median conditional entropy [95% bootstrapped confidence intervals (CIs)] for two states [0.794 (0.783–0.805)] and seven states [0.871 (0.849–0.899)].

Dopaminergic medication increases capacity limits on memory

Having determined that undermatching and capacity constraint are related, we next sought to determine the neural basis underlying this capacity constraint. We have argued previously that tonic dopamine controls the precision of state representations, with greater precision accessible at a greater cognitive cost (Mikhael et al., 2021). Greater precision implies increased mutual information between states and actions, since states are represented with higher fidelity. We therefore hypothesized that tonic dopamine may modulate policy complexity, which in matching tasks would alter the degree of undermatching. Although the literature is scarce, there is some extant data to argue that pharmacologic manipulations of dopamine have the expected effect on undermatching (Soto et al., 2014; Lie et al., 2016). To address this question, we reanalyzed data from human subjects performing a dynamic foraging task, similar to the mice (Rutledge et al., 2009). Four groups of subjects (young controls, elderly controls, patients with Parkinson's disease off dopaminergic medications, and patients with Parkinson's disease on dopaminergic medications) performed a VI/VI task, similar to the mice above (Fig. 4B). In this task, each option followed a VI schedule, with reward probabilities alternating among the following four task states: s₁ : {0.075, 0.225}, s₂ : {0.043, 0.257}, s₃ : {0.225, 0.075}, s₄ : {0.257, 0.043}. Subjects performed 800 trials with uncued transitions between blocks of 70–90 trials.

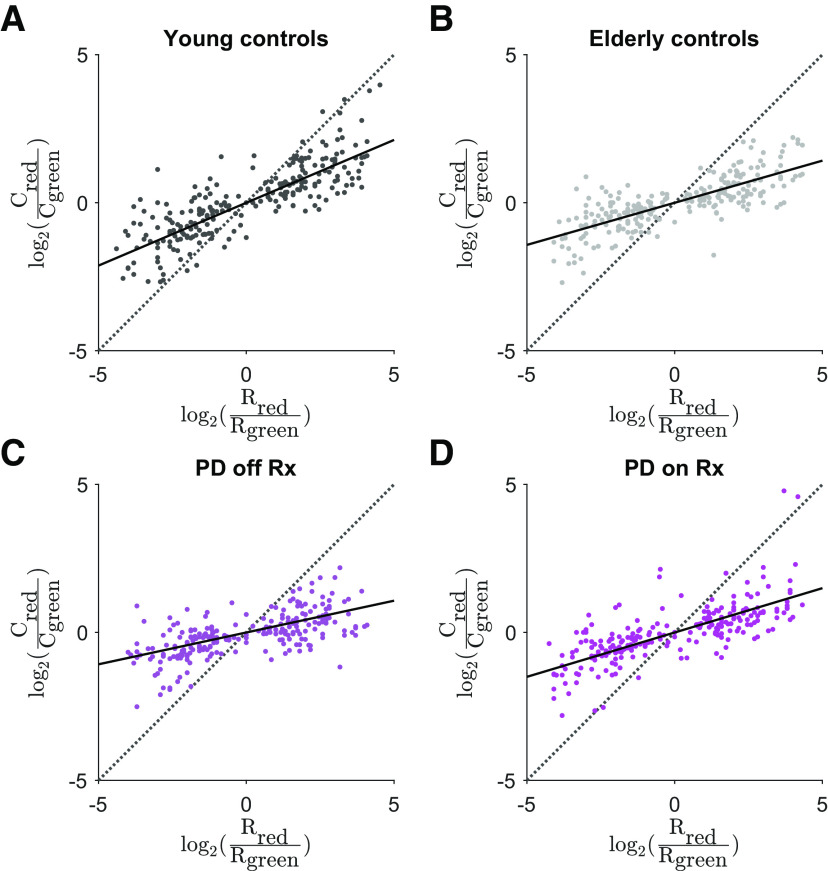
First, we confirmed that all groups demonstrated a significant degree of undermatching in this task (Fig. 7). Young control subjects exhibited significantly less undermatching than elderly control subjects (Fig. 8A). Interestingly, patients with Parkinson's disease off dopaminergic medications exhibited significantly greater undermatching than on sessions when they received dopaminergic medications (Fig. 8A), due partly to an increase in policy complexity (Fig. 8B). On a subject-by-subject basis, the patients with Parkinson's disease who demonstrated the greatest increase in policy complexity also exhibited the least degree of undermatching. If dopaminergic medications increase policy complexity, we additionally predicted that they should decrease perseveration (Gershman, 2020). Consistent with the study by Rutledge et al. (2009), we indeed found evidence in support of this effect, as Parkinson's disease subjects became less perseverative on dopaminergic medications (logistic regression: β = – 0.23, p < 0.005).

Figure 7.

Human subjects exhibit undermatching in a dynamic foraging task. A, Log-choice ratio as a function of log-reward ratio for young control subjects. Slope = 0.424. B, Log-choice ratio as a function of log-reward ratio for elderly control subjects. Slope = 0.285. C, Log-choice ratio as a function of log-reward ratio for patients with Parkinson's disease off dopaminergic medications. Slope = 0.215. D, Log-choice ratio as a function of log-reward ratio for patients with Parkinson's disease on dopaminergic medications. Slope = 0.300. In all panels, the black solid line corresponds to the best fit line and the dotted line corresponds to unity.

Figure 8.

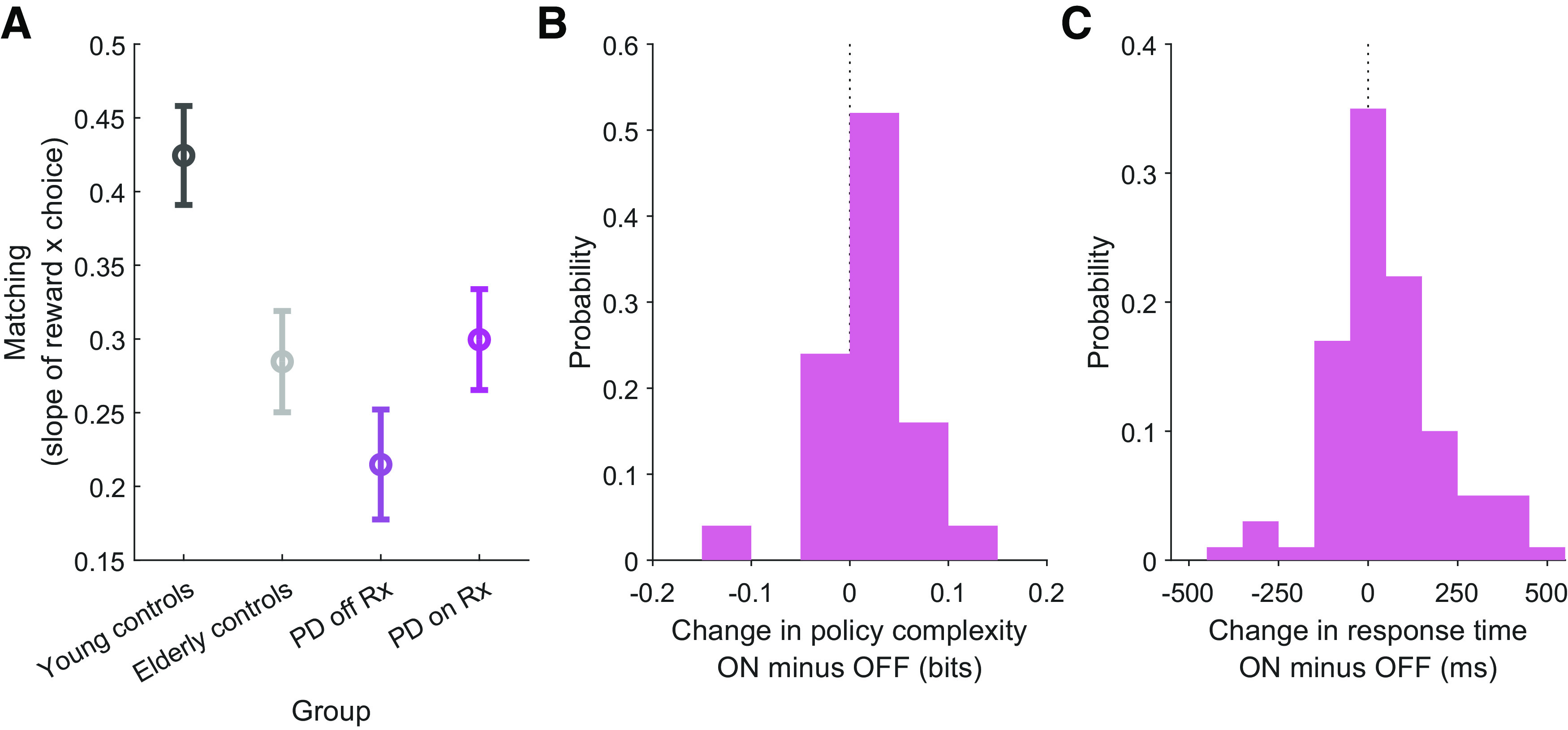
Dopaminergic medications increase policy complexity and reduce undermatching in Parkinson's patients. A, Matching slope for each group (least-squares estimate ± 95% CI). Young control subjects: 0.424 (0.391–0.458); elderly control subjects: 0.285 (0.250–0.319); patients with Parkinson's disease off dopaminergic medications: 0.215 (0.178–0.252); patients with Parkinson's disease on dopaminergic medications: 0.300 (0.265–0.334). The two Parkinson's disease groups, our groups of interest, are significantly different, since the 95% CI bands do not overlap. B, Change in policy complexity on dopaminergic medication minus off dopaminergic medication for the Parkinson's disease group. Medians are significantly different between groups (Wilcoxon signed-rank test, p < 0.05). C, Change in response times on dopaminergic medication minus off dopaminergic medication for the Parkinson's disease group. Medians are significantly different between groups (Wilcoxon signed-rank test, p < 0.01).

The policy compression framework additionally makes the prediction that more complex policies should result in slower response times, since this necessitates more bits that the brain must inspect to find a coded state (Lai and Gershman, 2021). This is a counterintuitive prediction for patients with Parkinson's disease, since bradykinesia is a defining feature of the condition that is improved with dopaminergic medications. We find that, indeed, the policy compression prediction is borne out: dopaminergic medications slow down response times for patients with Parkinson's disease (Fig. 8C).

Discussion

Decades of observations in the matching literature demonstrate a consistent bias toward undermatching, but its origin has been mysterious. Our main contribution is to show that undermatching can arise from policy compression: under some assumptions about state representation, maximizing reward subject to a limit on policy complexity implies undermatching or perfect matching, never overmatching. Our theory makes the prediction that capacity-constrained agents should undermatch more on task variants that require greater policy complexity for perfect matching behavior, which we confirmed using analyses of existing data. Finally, we showed that dopaminergic medications reduce undermatching in patients with Parkinson's disease, in part by increasing policy complexity.

We did not develop policy compression to explain undermatching, but rather found that it naturally explains undermatching in addition to other phenomena. Policy compression has broad explanatory power and has been used to explain softmax policies (Parush et al., 2011), perseveration (Gershman, 2020), reward insensitivity (Gershman and Lai, 2021), response times (this article; Lai et al., 2022), action chunking (Lai et al., 2022), and state chunking (Lai and Gershman, 2021).

We argue that overmatching should never be observed for an agent maximizing reward under a capacity constraint. Overmatching, however, has been obtained in task variants that impose a strong cost for switching actions (Aparicio, 2001). These task variants do not pose any substantial problems for our theory. They alter both the state representation that agents must use, as agents must store the last action to determine whether switching is warranted, and the calculation of expected reward V^π, which should include the cost of switching. We leave a more systematic treatment of this hypothesis to future work.

Our formulation of the optimal reward–complexity curve assumes that agents ignore the baiting rule (meaning they do not response count) and that they represent the state as the task state (number of pairs of base reward probabilities). These are the same assumptions used by Sakai and Fukai (2008b), who developed a theoretical framework that made it clear how these assumptions lead to matching behavior, even when other similar policies would be optimal (Figs. 1C, 2). Similar bounded rationality arguments were developed by Loewenstein and Seung (2006), who approached the problem from the perspective of synaptic plasticity rules. They proved that any synaptic plasticity rule driven by the covariance between reward and neural activity guarantees matching behavior. They further demonstrated that optimal behavior requires maintaining a memory of covariance between reward and neural activity over a long (potentially infinite) timescale. In their framework, ignoring this long-timescale memory results in matching behavior. Sakai and Fukai (2008b) in fact relate this synaptic plasticity view of matching to their own theory in the discussion. Our framing of matching behavior for VI tasks can be viewed as the framing of matching behavior for an infinite capacity agent by Sakai and Fukai (2008b). We extend their framework by invoking a limit on this capacity.

Our model is normative in the sense that it describes undermatching as an optimal solution to a constrained optimization problem. Our model relies on assumptions about state representation that are not veridical but nonetheless empirically plausible. As such, it does not predict the globally optimal solution, consistent with the empirical evidence. Our assumptions about the state representation yield a monotonic nondecreasing reward–complexity function (Fig. 3). These assumptions are by no means unique to our theory and in fact underlie a number of theories of matching and undermatching (Soltani et al., 2006; Sakai and Fukai, 2008a; Saito et al., 2014). Our contribution is not in using these assumptions, which we laid out explicitly for clarity, but in applying the notion of compression to matching behavior. With a more complete state definition that includes response counting (Fig. 1A), the reward–complexity curve should be monotonically increasing, and the policy with the greatest mutual information between states and actions would yield the greatest reward. In fact, baiting can be learned, but requires explicit training (Tunney and Shanks, 2002), and to our knowledge has not been observed simply with lengthy practice. While biological agents clearly do not possess the full state representation necessary to optimize reward in matching tasks, overtrained agents often alternate choices somewhat, which requires a representation of past choice (Lau and Glimcher, 2005; Bari et al., 2019). Although alternation appears to be a minor component of behavior, it is one that emerges with training, and it is unclear how agents learn this augmented state representation.

Our model makes the prediction that in a one-state task (e.g., base reward probabilities remain fixed within a session), perfect matching should emerge because policy complexity is 0. Given the relative dearth of perfect matching in the literature, this might appear to be a fundamental flaw of our model, since we claim to offer a general explanation for why undermatching occurs (including in one-state tasks). However, an important aspect of our model is the assumption that animals assume a generative model of the environment that is mismatched to the true generative process. A number of previous models (Courville et al., 2006; Yu and Cohen, 2008) have explained sequential dependencies in behavior as arising from the assumption that there is sequential structure in the environment. This is a reasonable assumption in many natural environments, but is an incorrect assumption in particular experimental tasks such as the ones considered in this article. If animals assume sequential dependencies, then they are not modeling the task as a single state, even under conditions where the reward contingencies are stable. This line of reasoning is consistent with existing data. First, perfect matching tends to be observed in studies with significant session-to-session stability in reward probabilities (Herrnstein, 1961; Baum and Rachlin, 1969), consistent with the idea that the assumption of instability has to be overridden by extensive training. Second, a transition from a long period of stability to a new set of reward probabilities is associated with increased undermatching (Mazur, 1995; Gallistel et al., 2001), consistent with the idea that such transitions cue the animal to construct multiple states. The idea that undermatching may be a consequence of nonveridical state representations is not unique to our theory and is the basis of several other explanations for undermatching (Saito et al., 2014; Iigaya et al., 2019).

We make no claims about the particular algorithms for optimizing the reward–complexity trade-off. One mechanistic model proposed to underlie undermatching introduces noise in a biophysical model of matching and predicts that increased noise leads to increased undermatching (Soltani et al., 2006). Interestingly, introducing noise (e.g., in state representations) would degrade the mutual information between states and actions, forcing a capacity constraint. However, noise by itself does not constitute a mechanistic model of policy complexity, since it does not guarantee that the resulting policy lies on the optimal reward–complexity frontier. The development of policy complexity process models remains an active area of research (Gershman and Lai, 2021; Lai et al., 2022).

We reported the unexpected and counterintuitive finding that dopaminergic medications slowed down response times in patients with Parkinson's disease. Clinically, dopaminergic medications are used to improve bradykinesia. How do we reconcile these findings? One view is that our task isolated a cognitive aspect of movement. Response times have long been known to increase with the number of choices (Hick, 1952). In the framework of policy compression, this arises because the number of bits needed to encode a policy increases with the number of choices in simple response selection tasks, and therefore more bits need to be decoded to produce a response, which takes more time (Lai and Gershman, 2021). Because our human task was a fairly straightforward computer-based assay with simple motor requirements, we believe we isolated the effect of policy complexity on response time. Bradykinesia, on the other hand, is typically assessed using a battery of tests that attempt to isolate movement speed independent of sophisticated decision-making (e.g., rapid alternating movements of the hands, leg agility, rising from a chair, gait). Since subjects were tested ∼14 h off dopaminergic medications, our effects were likely largely driven by levodopa (half-life, 1.5–2 h) and minimally affected by D₂ receptor agonists like pramipexole and ropinirole (half-life range, 6–12 h), which were likely still at therapeutic concentrations (e.g., Lexicomp; https://online.lexi.com/lco/action/home). We further found that dopaminergic medications reduced undermatching. This is consistent with a rational inattention account of tonic dopamine (Mikhael et al., 2021), in which high tonic dopamine increases the precision of task parameters and, by extension, state representations. Increased precision of state representations implies increased mutual information between states and actions, which is consistent with increased policy complexity.

In conclusion, we have argued that undermatching arises from the imperative to compress policies by reducing their information-theoretic complexity. This insight was consistent across different tasks and species. Our model also made nontrivial predictions about response time and the effects of dopaminergic medications, which we confirmed empirically. Our findings join a range of other observations (Lai and Gershman, 2021), suggesting that capacity limits play an important role in determining the structure of choice behavior.