Multi-mitigation strategies in medical supplies for epidemic outbreaks

Abstract

The outbreak of Coronavirus disease 2019 (COVID-19) highlights the importance of sufficient medical supplies stockpiling at the pre-event stage. In contrast, the potential disadvantages of maintaining adequate items at strategic locations (i.e., reserves) are considerable inventory-related costs. Unpredicted demand leads to a high degree of uncertainty. Efforts to mitigate the uncertainty should rely not only on prepositioning supplies at reserves but also on integrating various channels of medical materials. This paper proposes multi-mitigation strategies in medical supplies to ensure uninterrupted supply for hospitals and significant savings by introducing two-type suppliers, reserving and manufacturing suppliers. Thus, each hospital with uncertain demand is enabled to be served by various channels during pandemics: prepositioning in reserves, backups served by reserving suppliers, and medical commodities produced by manufacturing suppliers. Stochasticity is also incorporated into the raw materials available to produce. This research aims to develop an emergency response application that integrates preparedness action (reserve location, inventory level, and contract supplier's selection) with post-event operations (allocating medical materials from various channels). We formulate a two-stage stochastic mixed integer program to determine prepositioning strategy, including two-type suppliers' selection, and post-event allocation of multiple sources. A branch-and-Benders-cut method is developed for this problem and significantly outperforms both the classical Benders decomposition and Gurobi in the solution time. Different-sized test instances also verify the robustness of the proposed method. Based on a realistic and typical case study (inspired by the COVID-19 pandemic in Wuhan, China), significant savings, an increase in inventory utilization and an increase in demand fulfilment are obtained by our approach.

1. Introduction

Medical supplies, including drugs and medical protective equipment, play a crucial role in decreasing morbidity and mortality during pandemics. Inadequate preparations may severely delay epidemic control and entail irreparable life losses. The attack of the Coronavirus disease 2019 (COVID-19) in Wuhan, China, showed this characteristic. The production comes to an abrupt halt around the Spring Festival, and insufficient stored medical materials put lives at risk from the new coronavirus. As a result of inadequate preparations, medical supplies were scarce in the early stage of the COVID-19 epidemic, leading to the continuous strikes of the subsequent crisis. The media reported that several hospitals even appealed donations of protective equipment for frontline workers fighting COVID-19 since the regular inventory of strategic locations (i.e., reserves) had exhausted rapidly.

Coincidentally, when the first wave was tapering, the government of India had not planned for a second wave and assumed the worst in advance: oxygen, antiviral drugs and other medical supplies stockpiled were not sufficient and manufacturing capacity failed to ramp up. Then India became the worst COVID-19 surge in the world [1]. Surge demand caused by epidemics has a lower arrival rate but higher demand volume per arrival [2], even lasting for a long time. It seems to be not enough to rely solely on the inventory of reserves.

On the other hand, the potential disadvantages of maintaining adequate items at reserves are considerable inventory-related costs [3], and even substantial waste in the absence of an outbreak, as the emergency has low-frequency characteristics. Due to their fixed use-by date, especially perishable products (even masks and gloves), expiration problems make stockpilers challenging. For example, Australia dumped expired materials worth $200 million into landfills [4]. Clearly, unpredicted demand leads to a high degree of uncertainty. Thereby, an effective inventory strategy for medical supplies is concerned. If the supply chain of medical resources is broken, insufficient materials may accelerate the spread of the epidemic and lead to irreparable losses. It highlights the importance of resilience in the medical resources supply chain. In this regard, a key issue is to increase the resilience of the medical supply chain and balance appropriateness against the adequacy of medical supplies. Determining prepositioning strategy to satisfy surgent demand while avoiding inventory surplus as much as possible is the motivation of this work. Efforts to seek the balance should not only rely on prepositioning supplies at reserves, but integrate various sources of relief materials as well.

Unpredicted demand for medical supplies leads to a high degree of uncertainty. This paper introduces several supply strategies to mitigate or deal with uncertainty. Specifically, the supply strategies include materials prepositioned in reserves, backups served by reserving suppliers, and medical commodities produced by manufacturing suppliers. We denote these various supply channels as multi-mitigation strategies. In terms of prepositioning in reserves, we explicitly consider materials stored in municipal (local) and regional reserves for emergencies, which involve location problems and stocking levels. Apart from locations and sizes, administrative duties are fundamental differences between municipal reserves and regional reserves. Each municipal reserve covers a subset of hospitals assigned to it in advance, whereas regional reserves cover all hospitals. Typically, municipal reserves improve the quick response, especially in metropolitan areas. Contract suppliers in multi-mitigation strategies play a critical role in simultaneously ensuring uninterrupted supply and maintaining relatively lower inventory levels. More specifically, there are two typical store options except for prepositioning in reserves: one is backups from the reserving supplier (RS), and the other is medical commodities provided by the manufacturing supplier (MS). The former is undertaken by some pharmaceutical companies with a regular and high stocking level, and they prioritize medical supplies to hospitals as soon as an emergency occurs. And the latter is being conducted by enterprises with government approval, which are able to make the rapid adjustment to their facilities and turn to produce masks, protective suits, and other products for the fight against the pandemic. Whether prepositioning physical supplies (end products) is the fundamental difference between MSs and RSs. Typically, MSs keep production capacity and stock semi-finished products, while RSs store finished products. The two-type suppliers are responsive to surging demand after epidemic strikes, whereas both needs to be paid subsidies for potential public service in advance. In addition, China's emergency supplies reserve system involves physical supplies offered by both strategic reserves and RSs, and production capacity provided by MSs. Multi-mitigation strategies align with the emergency supplies reserve system of China.

Unlike most rescue supplies for natural disasters, such as tents, medical supplies tend to have a short shelf life and are mostly disposable. Some of them have higher requirements for storage environments. It indicates mass storage is not economical. The perishability of medical supplies and the uncertain duration of a health disaster highlights the necessity of considering production capacity in epidemic outbreaks. Procurement from RSs and stocked commodities in reserves are near-term channels since it gets finished products immediately, compared with the production of MS. Whereas the production of MS is resilient against long-term needs. Different from short-duration emergencies such as natural disasters, health disasters such as epidemic outbreaks are of uncertain duration. If the duration is short, the physical reserves from near-term channels are sufficient. If the duration is long, only considering near-term supply channels suggests that a large number of medical materials need to be stocked in advance to cope with the surge in demand. It is not economical for the strategic reserve and RS, and there is a risk of overdue waste. It highlights the necessity of production provided by MS, which can alleviate the risk of excess medical materials on the one hand and improve the capacity for securing the supply on the other.

Furthermore, COVID-19 brings challenges in raw materials procurement and logistics, which lead to production limitations (“Securing critical raw materials supply is key to the response to COVID-19 | [5]. We incorporate a real-life issue: MS's production may be disrupted since the pandemic acts as a trigger for the lack of raw materials. In this paper, raw materials refer to the components required to further process semi-finished products, such as melt-blown fabric for surgical masks. One of our contributions is regarding MS's production as one of the various sources to powerfully mitigate the high uncertainty in demand and increase the resilience of medical supply.

In this study, we formulate the problem as a two-stage stochastic mixed integer program, and propose an exact algorithm based on the classical Benders decomposition (BD) method incorporating a branch-and-cut framework, namely branch-and-Benders-cut (B&BC). This solution approach builds a single search tree and generates valid cuts for the integer solutions encountered inside the tree, attaining the same optimal solution as BD [6]. The classical BD solves a master problem to integer optimality multiple times, whereas the B&BC method only once.

In summary, our research contributes to the existing literature in the following ways.

• (1)We propose multi-mitigation strategies in medical supplies involving two-type contract suppliers, namely MS and RS. Multi-mitigation strategies ensure uninterrupted supply and significant savings in terms of unfulfilled demand penalty cost and handling cost associated with the expiration problem. We explicitly take raw materials available for MS into account. A two-stage stochastic mixed integer program is formulated to determine prepositioning strategy, including the selection of two-type suppliers and post-event allocation of multiple sources.
• (2)We develop an exact algorithm, the B&BC method, for solving this problem and compare its performance with the classical BD and Gurobi. We observe that the B&BC method significantly outperforms both the classical BD and Gurobi in the solution time, which is somehow more robust against input data and occupies less memory.
• (3)We design numerical experiments based on a realistic and typical case study in Wuhan, China, to demonstrate the effectiveness of multi-mitigation strategies and the proposed model.

In the remainder of this paper, Section 2 reviews the relevant literature, with an emphasis on the location and allocation problem, and then Section 3 formally describes a two-stage stochastic mixed integer program for the problem and discusses its various versions. Section 4 develops the B&BC solution approach for solving the problem. We test the formulation and the solution approach for application using a realistic and typical case study in Wuhan in Section 5. Finally, this paper's conclusions and managerial implications and suggestions for future research are summarized in Section 6.

2. Literature review

This work explicitly concentrates on the preposition of medical supplies, which make a lot of difference in preventing and controlling the epidemic. Prepositioning is related to two considerations, the location of reserves where supplies and assets are to be placed on the preparedness action side, and the allocation of the supplies to the demand point on the post-event operations side [7]. Both aspects are closely integrated with the location and allocation (LA) problem. LA determines the number, location and size of facilities that economically supply the given demand nodes with commodities. Recently, Ref. [8] devised three different LA models and deployed them on the real distribution network, and the parameters involved in LA models are all deterministic. Research on LA also incorporates parametric uncertainties [9]. used a novel robust possibilistic programming approach to design an organ transplant supply chain deemed LA under uncertain shipment times. Our work combines LA-related decisions (i.e., location of strategic reserves, decisions on stocking levels for multiple medical supplies and allocation of those supplies to demand points after an event), with two-type supplier selection and uncertainty about demand and raw materials available to produce. Survival of pre-positioned stocks is also included. Specifically, two-type suppliers, RS and MS, contribute to the uninterrupted supply and lower inventory levels of reserves.

Prepositioning strategy of responding to emergencies is a series of highly complex problems, where the challenge is, as briefly mentioned by Ref. [10]; the presence of uncertainty, which cannot be ignored or simplified. Uncertainty entails the risk of a shortage associated with irreparable losses or a surplus related to potential waste. For the uncertainty challenge, Refs. [11,12] developed robust algorithms to predict the COVID-19 pandemic and help policymakers plan for resource allocation. There are increasing and various studies concentrating on facility locations and inventory management in the pre-event stage to efficiently and effectively tackle uncertainties [13]. integrated facility locations with stocking decisions of multiple commodities to deal with demand uncertainty. They evaluated the unsatisfied demands and unused materials with the objective of the stochastic mixed integer program to seek the balance between demand fulfilment and inventory [14]. incorporated uncertainty in facility damage and casualty losses, and determined the location and capacities of regional distribution centres. Based on this work [15], allowed various trips between facilities and demand nodes to utilize the remaining survivability time, as well as minimize deprivation costs [16]. combined backup services with facility locations to minimize the distance and operating cost of facilities [17]. involved various uncertainties in facility damage, casualty by severity, and travel time to capture earthquake magnitude-specific features [18]. designed a new two-echelon pre-disaster relief network for rare disasters and included the uncertainty in demand [19,20]. studied the prepositioning problem in the context of earthquakes. They allowed network restoration efforts after the disaster to repair vulnerable roads and ensure the timely delivery of relief items [21]. incorporated vehicle routing in the post-disaster phase. Interested readers can refer to Refs. [7,22] for a recent and comprehensive review of prepositioning strategy. Most prepositioning or LA studies involve general natural disasters [13,[23], [24], [25], [26]], or a specific type, such as flood (Rodríguez-Espíndola et al., 2018), hurricane [27,28] and earthquake [[29], [30], [31], [32]], rather than health disasters.

A handful of studies have incorporated supplier selection into prepositioning strategy in recent three years. Our work is closely related to the research of [33]; which proposed a stochastic program to make decisions on supplier selection, facility location and inventory, but they did not involve multiple commodities. Ref. [34] described a two-period option contract accounting for supplier selection and inventory prepositioning as a two-stage stochastic programming formulation. Ref. [35] integrated the perishability of items and mobility of relief facilities with a pharmaceutical relief chain composed of suppliers, warehouses, mobile pharmacies, hospitals and affected areas. Maintaining small stockpiles in the reserves may not meet the overwhelming demand caused by emergencies. In contrast, a high stocking level entails considerable inventory-related costs and potential expiration problems. Integrating contract suppliers' selection into the prepositioning policy balances uninterrupted supply with relatively lower inventory levels. Following this trend, we combine the contract suppliers’ selection with the preparedness action.

Although a few existing studies consider backup supplier (similar to reserving suppliers in this paper) selection in the preparedness operations for natural disasters [33,34,36], they do not incorporate the production capacity of suppliers, which is the key to tackling uncertain duration derived from epidemic outbreaks. As Ref. [37] described, the major differences between health disasters and natural disasters are long-term disruption and increasing propagation. The shock of a natural disaster is often one-off and highly localized in a particular region. The production cycle of materials is even longer than the duration of these disasters. Demand for relief items caused by a natural disaster with a short duration may not require a long-term supply served by MS, which tends to satisfy fully by physical stores offered by reserves or served by RSs. However, health disasters, such as epidemic outbreaks, are of uncertain duration. The uncertainty in duration poses a challenge for physical reserves offered by reserves or served by RSs: a higher risk of overdue waste. Hence, pandemics highlight the importance of incorporating manufacturers' production into resource management, which is a practical approach to mitigate the risk from uncertain demand and struggle against long-term needs. Besides the suppliers considered in existing literature (i.e., RS in this paper), this work also takes the production of the manufacturer (i.e., MS in this paper) into account. Moreover, a pandemic may induce uncertainty of MSs' output due to a lack of raw materials availability, and we also take the uncertainty into account.

From the perspective of the solution approach, the existing studies have developed heuristic algorithms (such as the differential evolution algorithm, see Ref. [23] to obtain an approximate solution or employ a commercial solver [26,33,35] to solve the problem to optimality. As Ref. [38] mentioned, high-quality solutions should be obtained within a reasonable time from the mathematical models to support the decision-making process in disaster management. However, instances with larger sizes could not be solved to optimality within a reasonable runtime by the solver. Heuristic algorithms proposed by existing studies do not provide any guarantee of the solution quality. The high level of uncertainty in data with questionable solution quality can lead to fatally wrong decisions [20]. It is difficult to speed up the solution process while maintaining the accuracy of the solution.

BD has been successfully employed to solve mixed integer programs of optimization problems, such as logistics network planning [39], supply chain networks design [40,41], and assembly line balancing [42,43]. The classical BD is usually presented for two-stage stochastic optimization models (e.g., Refs. [[44], [45], [46]]). Ref. [47] applied the classical BD to solve the emergency supply planning problem, which combines emergency supply prepositioning and transportation planning. However, the time required for this solution approach increases rapidly with the size of the problem. It also takes up excessive memory. In this paper, we develop an advanced exact algorithm, the B&BC method, which exploits Benders decomposition to generate violated cuts and add to the current model globally. This method occupies less memory and significantly outperforms both the classical BD and Gurobi in the solution time.

3. Problem formulation

3.1. Problem description

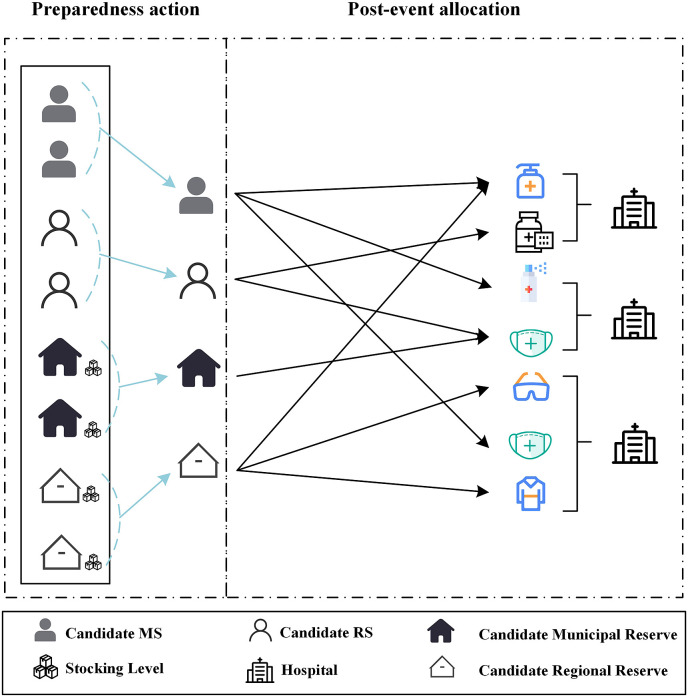
There are $\left|D\right|$ hospitals (i.e., demand nodes) whose demand for medical supplies is random during an epidemic in a certain area. There are various channels to serve hospitals: $\left|C\right|$ candidate municipal reserves, $\left|Z\right|$ candidate regional reserves, $\left|H\right|$ candidate MSs, and $\left|E\right|$ candidate RSs. Each channel is subject to capacity or random raw materials restrictions, and it associates with related costs. Fig. 1 shows the supply strategy. To minimize the total cost, the decisions to be made are as follows.

• (1)Where to set up two-type reserves.
• (2)Inventory level at opened reserves.
• (3)Contract suppliers' selection.
• (4)Distribution of medical supplies from various channels.

Fig. 1.

Multi-mitigation strategies in medical supplies.

3.2. Problem analysis

Before the pandemic strikes (i.e., the first stage), decisions on the location and stocking level of both municipal and regional reserves, as well as contract suppliers selection, should be determined in the presence of uncertainty about future realization. Typically, the municipal reserve should be setup to undertake an immediate supply of medical materials for hospitals. To describe the actual situation, each demand node in this paper will be assigned to at least one open municipal reserve, where various commodities are prepositioned in response to potential events. While the municipal reserve cannot serve the hospital, which is unassigned to it. Opened regional reserves and selected contract suppliers can be employed to cover all demand nodes. In addition, MS and RS provide hospitals with different medical commodities during pandemics. Both the municipal and regional reserves have fixed opening costs. The selection of MSs and RSs results in subsidies. Stocking levels of multiple supplies incur acquisition costs.

In the aftermath of an epidemic outbreak, demand is accurately known. There are several recourse actions based on the first-stage decisions and a specific scenario to cover demand: allocation from the assigned municipal reserves, medical supplies transferred from open regional reserves, backups served by selected RS and medical commodities produced by MS. If demand for a particular commodity cannot be met, it leads to the penalty cost associated with the shortage. Moreover, unused stocks in a single scenario result in additional handling costs, corresponding to spoilage costs or rotation costs [13]. Specifically, unused materials have no value after they expire and spoilage costs are incurred. Unused stocks near their expiration date need to be transferred and replaced with new items, and it causes rotation costs.

We formulate a two-stage stochastic program, taking uncertain demand into account. Furthermore, stochasticity is also considered for the raw materials available to produce. The production of medical products is subject to the limitation of raw materials offered to MS, whereas the raw materials supplies are uncertain.

In the first stage, the decisions to be made are related to the location of reserves, assignment of demand nodes and selection of suppliers, as well as stocking decisions for various materials. Nevertheless, the second stage (recourse) decisions involve the allocation of multiple sources in response to specific scenario events. The objective function of the optimization model is to minimize the total cost involving the opening cost of reserves, the acquisition cost of medical materials, subsidies of suppliers and recourse costs. Recourse cost is a function of a specific scenario and the first stage decisions, which have several terms: distribution cost, transferring cost, service cost, penalty cost caused by unmet demand, and handling cost resulting from unused stocks.

The assumptions that we make are itemized as follows.

• (1)The production lead time of MS is short relative to the epidemic outbreaks, and it can be ignored.
• (2)Medical supplies from different channels are transferred to hospitals directly.
• (3)The probability distribution of the random variables is known and derived from historical data.
• (4)All of the medical commodities produced by MS are available to serve hospitals.

3.3. Mathematics models

We introduce some notions used for the sets, indices, parameters, random variables and decision variables of the formulation.

3.3.1. Sets

• $C$: set of candidate municipal reserves.

• $Z$: set of candidate regional reserves.

• $D$: set of hospitals, i.e., demand points.

• $H$: set of candidate MSs.

• $E$: set of candidate RSs.

• $G$: set of commodities.

3.3.2. Indices

• $j_c\in C$: index of candidate municipal reserves.

• $j_z\in Z$: index of candidate regional reserves.

• $i\in D$: index of hospitals.

• $h\in H$: index of candidate MS.

• $e\in E$: index of candidate RS.

• $g\in G$: index of commodities.

3.3.3. Parameters

• $a_{j_c},a_{j_z}$: maximum available capacity of municipal reserve $j_c$ or regional reserves $j_z$.

• $o_g$: unit space requirement for commodity $g$.

• ${\eta }_g$: unit acquisition cost of commodity $g$.

• $f_{j_c},f_{j_z}$: fixed cost of municipal reserve $j_c$ or regional reserves $j_z$ incurred by opening and operating facility.

• $d_{i{j}_{c}g}^1$: transportation cost for per unit commodity $g$ from municipal reserve $j_c$ to hospital $i$.

• $d_{i{j}_{z}g}^2$: transportation cost for per unit commodity $g$ from regional reserve $j_z$ to hospital $i$.

• $m_e$: subsidies for RS $e$, which is the one-time payment cost when signing the contract.

• $n_h$: subsidies for MS $h$, which is the one-time payment cost when signing the contract.

• ${\alpha }_{ieg}$: unit service cost for commodity $g$ provided for hospital $i$ by RS $e$.

• ${\beta }_{ihg}$: unit service cost for commodity $g$ provided for hospital $i$ by MS $h$.

• $k_{ig}$: unit penalty cost incurred by hospital's unmet demand for commodity $g$.

• ${\psi }_{eg}$: capacity of RS $e$ for commodity $g$.

• $l_g$: unit handling cost for unused commodity $g$.

• ${\upsilon }_g$: amount of raw materials consumed by per unit commodity $g$, i.e., raw materials productivity.

• $M$: a large number.

3.3.4. Random symbols

• $\mathrm{\Omega }$: set of random scenarios.

• $\omega \in \mathrm{\Omega }$: random scenario.

• $q_{ig}\left(\omega \right)$: hospital's demand for commodity $g$ under scenario $\omega$.

• ${\chi }_h\left(\omega \right)$: number of raw materials available to produce medical products by MS $h$ under scenario $\omega$.

• $\mathit{\xi }\left(\omega \right)$: vector of the random variables.

• Note that we obtain a vector by piecing together the stochastic components of second-stage data $\mathit{\xi }\left(\omega \right)$. A single random scenario $\omega$ influences all components of $\mathit{\xi }$.

3.3.5. Decision variables

The first stage decision variables are as follows.

• $r_{j_{c}g},r_{j_{z}g}\in {\mathbb{R}}^{+}$: stocking levels for commodity $g$ at municipal reserve $j_c$ or regional reserves $j_z$.

• $x_{j_c},x_{j_z}\in \mathbb{B}$: 1 if municipal reserve $j_c$ or regional reserves $j_z$ is opened, 0 otherwise.

• $y_h\in \mathbb{B}$: 1 if MS $h$ is chosen, 0 otherwise.

• $v_e\in \mathbb{B}$: 1 if RS $e$ is selected, 0 otherwise.

• $z_{i{j}_c}\in \mathbb{B}$: 1 if municipal reserve $j$ covers hospital $i$, 0 otherwise.

The second stage decision variables are as follows.

• $t{p}_{i{j}_{c}g}\left(\omega \right)$: amount of commodity $g$ transported from municipal reserve $j_c$ to hospital $i$ under scenario $\omega$.

• $t{b}_{i{j}_{z}g}\left(\omega \right)$: amount of commodity $g$ transferred from regional reserve $j_z$ to hospital $i$ under scenario $\omega$.

• $p{c}_{ihg}\left(\omega \right)$: amount of commodity $g$ provided to hospital $i$ by MS $h$ under scenario $\omega$.

• $c{r}_{ieg}\left(\omega \right)$: amount of commodity $g$ provided to hospital $i$ by RS $e$ under scenario $\omega$.

• $s{c}_{ig}\left(\omega \right)$: amount of unmet demand for commodity $g$ at hospital $i$ under scenario $\omega$.

• $u{r}_{j_{c}g}\left(\omega \right),u{r}_{j_{z}g}\left(\omega \right)$: amount of unused commodity $g$ at municipal reserve $j_c$ or regional reserves $j_z$ under scenario $\omega$.

• ${\phi }_{hg}\left(\omega \right)$: amount of commodity $g$ produced by MS $h$ under scenario $\omega$.

• $\mathbf{u}\left(\omega \right)=\left(t{p}_{i{j}_{c}g}\left(\omega \right),t{b}_{i{j}_{z}g}\left(\omega \right),p{c}_{ihg}\left(\omega \right),{\phi }_{hg}\left(\omega \right),c{r}_{ieg}\left(\omega \right),s{c}_{ig}\left(\omega \right),u{r}_{j_{c}g}\left(\omega \right),u{r}_{j_{z}g}\left(\omega \right)\right)$: vector of the second-stage decisions.

3.3.6. Formulations

$$\min \sum _{j_c\in C}{f}_{j_c}{x}_{j_c}+\sum _{j_z\in Z}{f}_{j_z}{x}_{j_z}+\sum _{h\in H}{y}_h{n}_h+\sum _{e\in E}{v}_e{m}_e+\sum _{j_c\in C}\sum _{g\in G}{\eta }_g{r}_{j_{c}g}+\sum _{j_z\in Z}\sum _{g\in G}{\eta }_g{r}_{j_{z}g}+\mathcal{Q}\left(r,v,y,x,z\right)\text{,}$$ (1)

$$\text{s.t.}\sum _{j_c\in C}{z}_{i{j}_c}\ge 1,\forall i\in D\text{,}$$ (2)

$$z_{i{j}_c}\le x_{j_c},\forall j_c\in C,i\in D\text{,}$$ (3)

$$\sum _{g\in G}{o}_g{r}_{j_{c}g}\le a_{j_c}{x}_{j_c},\forall j_c\in C\text{,}$$ (4)

$$\sum _{g\in G}{o}_g{r}_{j_{z}g}\le a_{j_z}{x}_{j_z},\forall j_z\in Z\text{,}$$ (5)

$$x_{j_c},x_{j_z}\in \mathbb{B},\forall j_c\in C,j_z\in Z\text{,}$$ (6)

$$y_h\in \mathbb{B},\forall h\in H\text{,}$$ (7)

$$v_e\in \mathbb{B},\forall e\in E\text{,}$$ (8)

$$z_{i{j}_c}\in \mathbb{B},\forall i\in D,j_c\in C\text{,}$$ (9)

$$r_{j_{c}g},r_{j_{z}g}\ge 0,\forall j_c\in C,j_z\in Z,g\in G\text{.}$$ (10)

The expected recourse function $\mathcal{Q}\left(r,v,y,x,z\right)=E_{\mathit{\xi }}\left[Q\left(r,v,y,x,z,\mathit{\xi }\left(\omega \right)\right)\right]$, where for each $\omega \in \mathrm{\Omega }$.

$$Q\left(r,v,y,x,\xi \left(\omega \right)\right)={\min }_{\mathbf{u}\left(\omega \right)}\sum _{h\in H}\sum _{i\in D}\sum _{g\in G}{\beta }_{ihg}p{c}_{ihg}\left(\omega \right)+\sum _{e\in E}\sum _{i\in D}\sum _{g\in G}{\alpha }_{ieg}c{r}_{ieg}\left(\omega \right)+\sum _{i\in D}\sum _{g\in G}{k}_{ig}s{c}_{ig}\left(\omega \right)+\sum _{i\in D}\sum _{j_c\in C}\sum _{g\in G}{d}_{i{j}_{c}g}^{1}t{p}_{i{j}_{c}g}\left(\omega \right)+\sum _{i\in D}\sum _{j_z\in Z}\sum _{g\in G}{d}_{i{j}_{z}g}^{2}t{b}_{i{j}_{z}g}\left(\omega \right)+\sum _{j_c\in C}\sum _{g\in G}{l}_{j_c}u{r}_{j_{c}g}\left(\omega \right)+\sum _{j_z\in Z}\sum _{g\in G}{l}_{j_{\mathrm{z}}}u{r}_{j_{z}g}\left(\omega \right)\text{,}$$ (11)

$$\sum _{h\in H}p{c}_{ihg}\left(\omega \right)+\sum _{e\in E}c{r}_{ieg}\left(\omega \right)+s{c}_{ig}\left(\omega \right)+\sum _{j_z\in Z}t{b}_{i{j}_{z}g}\left(\omega \right)+\sum _{j_c\in C}t{p}_{i{j}_{c}g}\left(\omega \right)\ge q_{ig}\left(\omega \right),\forall i\in D,g\in G\text{,}$$ (12)

$$\sum _{i\in D}c{r}_{ieg}\left(\omega \right)\le {\psi }_{eg}{v}_e,\forall e\in E,g\in G\text{,}$$ (13)

$$\sum _{g\in G}{\upsilon }_g{\phi }_{hg}\left(\omega \right)\le {\chi }_h\left(\omega \right)y_h,\forall h\in H\text{,}$$ (14)

$$\sum _{i\in D}p{c}_{ihg}\left(\omega \right)\le {\phi }_{hg}\left(\omega \right),\forall h\in H,g\in G\text{,}$$ (15)

$$\sum _{i\in D}t{p}_{i{j}_{c}g}\left(\omega \right)+u{r}_{j_{c}g}\left(\omega \right)=r_{j_{c}g},\forall j_c\in C,g\in G\text{,}$$ (16)

$$\sum _{i\in D}t{b}_{i{j}_{z}g}\left(\omega \right)+u{r}_{j_{z}g}\left(\omega \right)=r_{j_{z}g},\forall j_z\in Z,g\in G\text{,}$$ (17)

$$t{p}_{i{j}_{c}g}\left(\omega \right)\le M{z}_{i{j}_c},\forall j_c\in C,i\in D,g\in G\text{,}$$ (18)

$$p{c}_{ihg}\left(\omega \right)\ge 0,\forall i\in D,h\in H,g\in G\text{,}$$ (19)

$$c{r}_{ieg}\left(\omega \right)\ge 0,\forall i\in D,e\in E,g\in G\text{,}$$ (20)

$${\phi }_{hg}\left(\omega \right)\ge 0,\forall h\in H,g\in G\text{,}$$ (21)

$$u{r}_{j_{c}g}\left(\omega \right),u{r}_{j_{z}g}\left(\omega \right)\ge 0,\forall j_c\in C,j_z\in Z,g\in G\text{,}$$ (22)

$$t{b}_{i{j}_{z}g}\left(\omega \right)\ge 0,\forall j_z\in Z,i\in D,g\in G\text{,}$$ (23)

$$t{p}_{i{j}_{c}g}\left(\omega \right)\ge 0,\forall j_c\in C,i\in D,g\in G\text{,}$$ (24)

$$s{c}_{ig}\left(\omega \right)\ge 0,\forall i\in D,g\in G\text{.}$$ (25)

Objective (1) evaluates the total costs, consisting of fixed cost and acquisition cost of two-type reserves, subsidies for contract suppliers, and the expected cost of the second-stage problem. Constraints (2) ensure that one or more municipal reserves cover each hospital. Constraints (3) guarantee that a municipal reserve serves a hospital only if the municipal reserve is made available. Constraints (4)–(5) ensure that the capacity of each reserve is not exceeded. Constraints (6)–(10) are variable specification constraints.

The objective (11) of the recourse problem (i.e., the second-stage problem) minimizes the cost of a single scenario caused by recourse actions in dealing with uncertainty, including distribution of municipal reserves, transfer from open regional reserves, medical commodities produced by MSs, backup supplies served by RSs, shortage and unused stocks. Constraints (12) ensure the total amount of medical supplies received by each hospital must satisfy its demand if there is no shortage. Constraints (13) specify that RS's capacity is not exceeded if the RS is selected. Constraints (14)–(15) state that raw materials available for MS's limit production during an epidemic outbreak, so output sent to hospitals is also restricted. Constraints (16)–(17) represent that the unused materials plus the allocation to hospitals equal the stocking level of municipal and regional reserves, respectively. Constraints (18) imply that a hospital receives supplies from the municipal reserve that covers it. Constraints (19)–(25) enforce the nonnegativity restrictions on the decision variables.

Assuming that uncertainties can be modelled by a finite set of scenarios $S$ with corresponding probabilities $p_s\left(s\in S\right)$, we can derive an equivalent stochastic mixed integer program (SMIP) by expanding out the scenario-specific constraints (details of the model are provided in Appendix A), which can be solved by solver directly. That is, replace $\omega$ in scenario-specific decision variables with a superscript $s\in S$. To be specific, the second-stage decisions $p{c}_{ihg}\left(\omega \right)$, $c{r}_{ieg}\left(\omega \right)$, $t{b}_{i{j}_{z}g}\left(\omega \right)$, $t{p}_{i{j}_{c}g}\left(\omega \right)$, ${\phi }_{hg}\left(\omega \right)$, $s{c}_{ig}\left(\omega \right)$, $u{r}_{j_{c}g}\left(\omega \right)$ and $u{r}_{j_{z}g}\left(\omega \right)$ become $p{c}_{ihg}^s$, $c{r}_{ieg}^s$, $t{b}_{i{j}_{z}g}^s$, $t{p}_{i{j}_{c}g}^s$, ${\phi }_{hg}^s$, $s{c}_{ig}^s$, $u{r}_{j_{c}g}^s$ and $u{r}_{j_{z}g}^s$, respectively. Convert random variables $q_{ig}\left(\omega \right)$ and ${\chi }_h\left(\omega \right)$ into $q_{ig}^s$ and ${\chi }_h^s$, respectively.

When shortage (i.e., unsatisfied demand) is not allowed, we have $s{c}_{ig}\left(\omega \right)=0$, and constraints (12) reduce to

$$\sum _{h\in H}p{c}_{ihg}\left(\omega \right)+\sum _{e\in E}c{r}_{ieg}\left(\omega \right)+\sum _{j_z\in Z}t{b}_{i{j}_{z}g}\left(\omega \right)+\sum _{j_c\in C}t{p}_{i{j}_{c}g}\left(\omega \right)\ge q_{ig}\left(\omega \right)\text{.}$$

When the various mitigation strategies reduce to a single mitigation strategy - only transferring from reserves is allowed, we can eliminate decision variables $p{c}_{ihg}\left(\omega \right)$, $c{r}_{ieg}\left(\omega \right)$ and ${\phi }_{hg}\left(\omega \right)$, eliminate constraints (13)–(15) and (19)–(21), as well as reduce constraints (12) to $s{c}_{ig}\left(\omega \right)+\sum _{j_z\in Z}t{b}_{i{j}_{z}g}\left(\omega \right)+\sum _{j_c\in C}t{p}_{i{j}_{c}g}\left(\omega \right)\ge q_{ig}\left(\omega \right)$.

Replacing random variables (i.e., hospitals' demand and amount of raw materials available to MS) with their expected value leads to a deterministic mixed integer program (DMIP), that is, decisions on location and stocking level, and contract suppliers, are made under deterministic demand and raw materials available to produce. The details of the formulation are described in Appendix B.

4. Branch-and-benders-cut method

The extra dimension imposed by the scenario set results in large-sized SMIP, even for small instances. The existing relevant studies (e.g. Refs. [33,48], which are similar to our research, used an industrial solver to solve the problems without considering MS. However, those instances with larger sizes (involving MSs’ selection, multiple commodities, more scenarios, etc.) may not be solved to optimality by a solver in a reasonable runtime. Hence, developing an advanced solution algorithm is essential to solving large-scale problems in a shorter solution time. It motivates us to develop the B&BC method. In this section, we introduce a B&BC method for solving SMIP, which allows us to add Benders cuts as needed during a single branch-and-cut process. In the B&BC method, a single search tree (i.e., branch-and-bound tree) is built, and the cuts are generated inside the tree using separation procedures that find violated feasibility or optimality cuts according to the subproblem [49,50].

On the other hand, the classical BD is usually presented for two-stage stochastic optimization models (e.g., Refs. [[44], [45], [46], [47]]; etc.). The main idea of the classical BD is to decompose the original SMIP into two problems: a master problem (MP) and a subproblem (SP), which are iteratively solved to guide the search process and generate the violated cuts, respectively. Specifically, the MP is a relaxation of the original minimization problem and provides lower bounds on this problem. The SP is obtained by reformulating the original problem concerning noncomplicated variables (continuous variables) and returns upper bounds. At each iteration, the MP is solved to optimality by a MIP solver, and considerable time may be spent revisiting candidate solutions that have been eliminated in previous iterations [6].

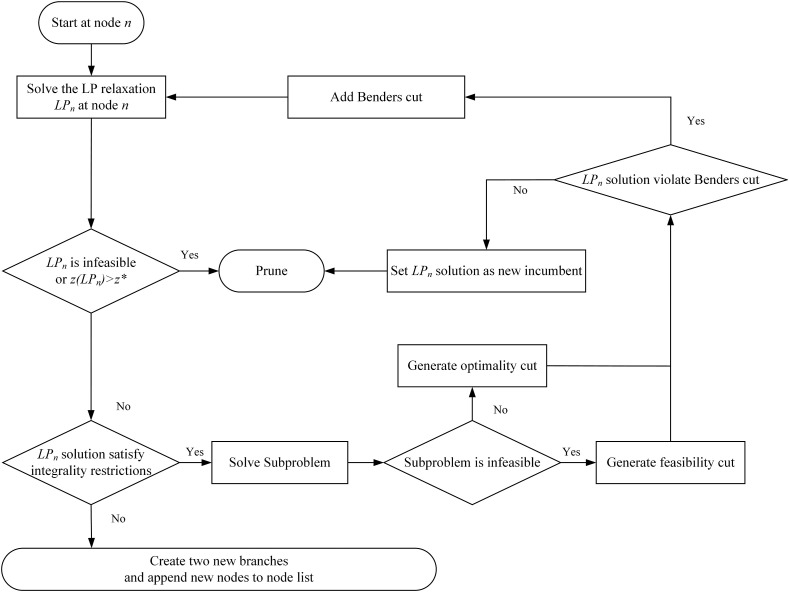
Fig. 2 provides a flowchart of the B&BC method specifying how the separation procedures work at each node of the branch-and-bound tree. We start by solving the linear programming relaxation (LP-relaxation, $L{P}_n$) of the current node $n$. Note that each node refers to a linear program. If $L{P}_n$ is infeasible or the optimal objective function $obj\left(L{P}_n\right)$ is greater than the upper bound $ob{j}^{*}$, which corresponds to the incumbent solution, fathom the current node. Otherwise, check the integrality restrictions. If a restriction is violated, perform branching schemes, i.e., add a constraint to the current model $L{P}_n$ to enforce the branching rule, create two new branches (nodes) and add them to the node list. Otherwise, an integer and feasible solution is obtained and updates the incumbent. We call the separation mechanisms of SP based on the solution of $L{P}_n$. If the SP is feasible, the dual values (i.e., extreme point) for the SP are retrieved directly by the commercial solvers. If the SP is infeasible, which signifies that the dual of SP is unbounded, extreme rays of the dual of an infeasible linear program can also be retrieved through solvers. Then we take the associated cut from the dual of SP and add the valid cut globally to the search tree to remove non-optimal solution or infeasible (fractional) solution. It is worth noting that we allow the industrial solver to automatically determine a node to explore and select a branch variable, and these strategies are not included in Fig. 2.

Fig. 2.

Flowchart of B&BC method at each node of the branch-and-bound tree.

Furthermore, in this problem, the SP can be modelled as follows (Since the constraints and decisions associated with municipal and regional reserves are similar, to be more intuitive, we all use the same index $j$ to represent reserves.).

$$\min \sum _{j\in C\cup Z}\sum _{g\in G}{\eta }_g{r}_{jg}+\sum _{s\in S}{p}_s(\sum _{h\in H}\sum _{i\in D}\sum _{g\in G}{\beta }_{ihg}p{c}_{ihg}^s+\sum _{e\in E}\sum _{i\in D}\sum _{g\in G}{\alpha }_{ieg}c{r}_{ieg}^s+\sum _{i\in D}\sum _{g\in G}{k}_{ig}s{c}_{ig}^s$$

$$+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}{d}_{ijg}^{1}t{p}_{ijg}^s+\sum _{i\in D}\sum _{j\in Z}\sum _{g\in G}{d}_{ijg}^{2}t{b}_{ijg}^s+\sum _{j\in C\cup Z}\sum _{g\in G}{l}_{j}u{r}_{jg}^s)\text{,}$$ (26)

$$\mathrm{s}.\mathrm{t}.\sum _{g\in G}{o}_g{r}_{jg}\le a_j{x}_j^{*},\forall j\in C\cup Z\text{,}$$ (27)

$$\sum _{h\in H}p{c}_{ihg}^s+\sum _{e\in E}c{r}_{ieg}^s+s{c}_{ig}^s+\sum _{j\in Z}t{b}_{ijg}^s+\sum _{j\in C}t{p}_{ijg}^s\ge q_{ig}^s,\forall i\in D,g\in G,s\in S\text{,}$$ (28)

$$\sum _{i\in D}c{r}_{ieg}^s\le {\psi }_{eg}{v}_e^{*},\forall e\in E,g\in G,s\in S\text{,}$$ (29)

$$\sum _{g\in G}{\upsilon }_g{\phi }_{hg}^s\le {\chi }_h^s{y}_h^{*},\forall h\in H,s\in S\text{,}$$ (30)

$$\sum _{i\in D}p{c}_{ihg}^s\le {\phi }_{hg}^s,\forall h\in H,g\in G,s\in S\text{,}$$ (31)

$$\sum _{i\in D}t{p}_{ijg}^s+u{r}_{jg}^s=r_{jg},\forall j\in C,g\in G,s\in S\text{,}$$ (32)

$$\sum _{i\in D}t{b}_{ijg}^s+u{r}_{jg}^s=r_{jg},\forall j\in Z,g\in G,s\in S\text{,}$$ (33)

$$t{p}_{ijg}^s\le M{z}_{ij}^{*},\forall i\in D,j\in C,g\in G,s\in S\text{,}$$ (34)

$$r_{jg}\ge 0,\forall j\in C\cup Z,g\in G\text{,}$$ (35)

$$u{r}_{jg}^s\ge 0,\forall j\in C\cup Z,g\in G,s\in S\text{,}$$ (36)

$$t{b}_{ijg}^s\ge 0,\forall j\in Z,i\in D,g\in G,s\in S\text{,}$$ (37)

$$t{p}_{ijg}^s\ge 0,\forall j\in C,i\in D,g\in G,s\in S\text{,}$$ (38)

$$p{c}_{ihg}^s\ge 0,\forall i\in D,h\in H,g\in G,s\in S\text{,}$$ (39)

$$c{r}_{ieg}^s\ge 0,\forall i\in D,e\in E,g\in G,s\in S\text{,}$$ (40)

$${\phi }_{hg}^s\ge 0,\forall h\in H,g\in G,s\in S\text{,}$$ (41)

$$s{c}_{ig}^s\ge 0,\forall i\in D,g\in G,s\in S\text{,}$$ (42)

where $x_j^{*}$, $v_e^{*}$, $y_h^{*}$ and $z_{ij}^{*}$ are derived from the current node in the branch-and-bound tree for the first-stage binary variables $x_j$, $v_e$, $y_h$ and $z_{ij}$, which satisfies the integrality requirement.

The dual variables set related to constraints of the SP are denoted as follows.

• ${\kappa }_j,j\in C\cup Z$: dual variables corresponding to the constraints (27).

• ${\varsigma }_{ig}^s,i\in D,g\in G,s\in S$: dual variables corresponding to the constraints (28).

• ${\delta }_{eg}^s,e\in E,g\in G,s\in S$: dual variables corresponding to the constraints (29).

• ${\gamma }_h^s,h\in H,s\in S$: dual variables corresponding to the constraints (30).

• ${\Phi }_{hg}^s,h\in H,g\in G,s\in S$: dual variables corresponding to the constraints (31).

• ${\lambda }_{jg}^s,j\in C,g\in G,s\in S$: dual variables corresponding to the constraints (32).

• ${\mu }_{jg}^s,j\in Z,g\in G,s\in S$: dual variables corresponding to the constraints (33).

• ${\vartheta }_{ijg}^s,i\in D,j\in C,g\in G,s\in S$: dual variables corresponding to the constraints (34).

We set $M=\max \left\{a_j,j\in C\right\}$.

The objective function of the dual form of the SP can be written as follows.

$$\sum _{j\in C\cup Z}{\kappa }_j{a}_j{x}_j^{*}+\sum _{i\in D}\sum _{g\in G}\sum _{s\in S}{\varsigma }_{ig}^s{q}_{ig}^s+\sum _{e\in E}\sum _{g\in G}\sum _{s\in S}{\delta }_{eg}^s{\psi }_{eg}{v}_e^{*}+\sum _{h\in H}\sum _{s\in S}{\gamma }_h^s{\chi }_h^s{y}_h^{*}+\sum _{h\in H}\sum _{g\in G}\sum _{s\in S}{\phi }_{hg}^s{\Phi }_{hg}^s$$

$$+\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}{\lambda }_{jg}^s{r}_{jg}+\sum _{j\in Z}\sum _{g\in G}\sum _{s\in S}{\mu }_{jg}^s{r}_{jg}+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}M{z}_{ij}^{*}{\vartheta }_{ijg}^s\text{.}$$ (43)

According to (43), we can obtain two types of Benders cuts: feasibility cut (44) and optimality cut (45).

$$\sum _{j\in C\cup Z}{\kappa }_j{a}_j{x}_j^{*}+\sum _{i\in D}\sum _{g\in G}\sum _{s\in S}{\varsigma }_{ig}^s{q}_{ig}^s+\sum _{e\in E}\sum _{g\in G}\sum _{s\in S}{\delta }_{eg}^s{\psi }_{eg}{v}_e^{*}+\sum _{h\in H}\sum _{s\in S}{\gamma }_h^s{\chi }_h^s{y}_h^{*}+\sum _{h\in H}\sum _{g\in G}\sum _{s\in S}{\phi }_{hg}^s{\Phi }_{hg}^s$$

$$+\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}{\lambda }_{jg}^s{r}_{jg}+\sum _{j\in Z}\sum _{g\in G}\sum _{s\in S}{\mu }_{jg}^s{r}_{jg}+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}M{z}_{ij}^{*}{\vartheta }_{ijg}^s\le 0\text{,}$$ (44)

$$\theta \ge \sum _{j\in C\cup Z}{\kappa }_j{a}_j{x}_j^{*}+\sum _{i\in D}\sum _{g\in G}\sum _{s\in S}{\varsigma }_{ig}^s{q}_{ig}^s+\sum _{e\in E}\sum _{g\in G}\sum _{s\in S}{\delta }_{eg}^s{\psi }_{eg}{v}_e^{*}+\sum _{h\in H}\sum _{s\in S}{\gamma }_h^s{\chi }_h^s{y}_h^{*}+\sum _{h\in H}\sum _{g\in G}\sum _{s\in S}{\phi }_{hg}^s{\Phi }_{hg}^s+\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}{\lambda }_{jg}^s{r}_{jg}+\sum _{j\in Z}\sum _{g\in G}\sum _{s\in S}{\mu }_{jg}^s{r}_{jg}+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}\sum _{s\in S}M{z}_{ij}^{*}{\vartheta }_{ijg}^s\text{.}$$ (45)

The CP of each node can be formulated as follows.

$$\left(\mathrm{C}\mathrm{P}\right)\min \sum _{j\in C\cup Z}{f}_j{x}_j+\sum _{h\in H}{y}_h{n}_h+\sum _{e\in E}{v}_e{m}_e+\theta \text{.}$$ (46)

Subject to: Constraints (A.2)-(A.3), (A.12)-(A.15),

Feasibility cut (44),

Optimality cut (45),

$$\theta \in \mathbb{R}\text{.}$$ (47)

We employ the result of CP to update the upper and lower bound are obtained by taking the smallest optimal objective value for an LP-relaxation among all current branch-and-bound nodes. The B&BC method is implemented using callback functions available to check violated inequalities from the LP solution and the feasibility of primal solutions [51].

5. Numerical experiments

In this section, a realistic case study focusing on preparedness for the COVID-19 pandemic threat in Wuhan, China, serves to illustrate our investigation. As of February 29, 2020, there are three types of hospitals to effectively control the spread of COVID-19 in Wuhan, including 46 government-designated hospitals, 16 Fangcang shelter hospitals and 2 emergency specialty field hospitals (Huoshenshan and Leishenshan Hospital). Among them, the designated hospitals and specialty field hospitals were used to cure patients in severe or critical conditions; Fangcang shelter hospitals were built as makeshift hospitals to treat mildly infected people.

5.1. Experimental settings

We select these 64 hospitals as demand nodes. For simplicity, we assume their locations are known before the assignment to potential municipal reserves.

Conventionally, reserves for responding to pandemic strikes are generally used to store four types of medical supplies: disinfection supplies such as 84 disinfectants, medical alcohol, etc.; medical equipment such as ventilators, thermometers, and ECG monitors, etc.; prevention and control drugs such as Chloroquine phosphate, Arbidol, etc.; and protective supplies such as medical protective suit, gloves, surgical masks, etc. Among them, medical equipment is not disposable consumable; for example, the lifespan of the ventilator is up to 7 years. Therefore, medical equipment is not included in this paper, and the typical medical supplies we consider are listed as follows.

• (1)Prevention and control drugs: Oseltamivir, Arbidol.
• (2)Disinfection supplies: medical alcohol, hand sanitizer.
• (3)Protective materials: surgical masks, protective suits, and safety goggles.

The number of beds and bed-to-care ratios (which indicate the number of medical staff per bed, for example, the bed-to-care ratio of 1:1.2 demonstrates that the number of medical staff per ten beds is twelve) depends on the type of demand nodes. Specifically, the number of medical staff in shelter hospitals is less for treating mild patients. In contrast, in designated hospitals and emergency specialty field hospitals, the number is higher for treating severe patients (in Table 1 ).

Table 1.

Bed-to-care ratio of different demand node categories.

Demand node category	Bed-to-care ratio
Designated hospitals	1:1.2–1.5
Shelter hospitals	1:0.2–0.5
Temporary special hospitals	1: 0.9–1.2

Notes: each bed needs 5L medical alcohol, 4 Hand sanitizer, 0.5 boxes of Arbidol (only for patients), 1.22 boxes of Oseltamivir (only for patients), 1.2 safety goggles (only for medical crew), 2 sets of protective suit (only for medical crew), 24 surgical masks within a certain period of time during a critical health crisis [52].

To generate a specific instance, we introduce the following symbols to describe the experimental settings.

$S=\left\{S_1,S_2,S_3,S_4\right\}$: the scenario set $S$ is divided into four subsets based on the emergency response ratings of a health crisis (ERRHC) in China. In the four-level rating system, i.e., critical ($s\in S_1$), major ($s\in S_2$), situational ($s\in S_1$) and general ($s\in S_4$) [53], the first is the most urgent and severe, like COVID-19, while the fourth is the lowest level. Generally, a critical health crisis with a small chance of happening brings severe negative impacts. Enhance risk awareness and properly overweighting these low probability, high consequence events in the policymaking process can reduce the risk. We overweight the critical health crisis by assuming $\left|S_1\right|:\left|S_2\right|:\left|S_3\right|:\left|S_4\right|=1:1:1:1$, and take it as a base case.

$b{n}_i$: number of beds in hospital $i$ (details are provided in Appendix C), which is available from the Wuhan Municipal Health Commission's official website [54,55].

$b{o}_{S_k},k=1,\cdots ,4$: occupancy rate of beds under the scenario element in subset $S_k$, which can be employed to characterize the ERRHC.

$b{c}_i$: number of medical staff assigned to per bed in hospital $i$, which can be computed by the bed-to-care ratio of hospital $i$ associated with the categories of demand node.

${\zeta }_g$: number of commodity $g$ per bed, per patient, or per medical staff.

We partition the commodities set $G$ into three subsets $G=\left\{G_1,G_2,G_3\right\}$. $G_1$ contains Arbidol and Oseltamivir, which are only utilized by patients; protective suits and safety goggles constitute $G_2$, which are only consumed by the medical crew; $G_3$ is made up of the rest and applies to both patients and medical staff. Particularly, the demand for the commodities in $G_1$ is calculated based on the number of beds; the needs for the commodities in $G_2$ are computed according to the number of medical staff per bed; the demand for commodities in $G_3$ is estimated by the sum of the number of beds and medical staff per bed.

${\hat{q}}_{ig}^{S_k}$: estimated demand for commodity $g$ under scenario subset $S_k$ at the hospital $i$, which is roughly calculated based on its number of beds, patients, and medical staff, i.e., ${\hat{q}}_{ig}^{S_k}=\{\begin{array}{l}{\zeta }_g\times b{n}_i\times b{o}_{S_k},g\in G_1,\\ {\zeta }_g\times b{n}_i\times b{o}_{S_k}\times b{c}_i,g\in G_2,\\ {\zeta }_g\times b{n}_i\times b{o}_{S_k}\times \left(1+b{c}_i\right),g\in G_3.\end{array}$.

We employ ${\hat{q}}_{ig}^{S_k}$ to generate each hospital's demand for commodity $g$ under each scenario $s$ (i.e., $q_{ig}^s$) based on Poisson distribution.

Further, the number of scenarios is set to be 60, which refers to varying demands and raw materials in the case study. We set $b{o}_{S_1}=1$, $b{o}_{S_2}=0.5$, $b{o}_{S_3}=0.2$, and $b{o}_{S_4}=0.05$, that is, the bed utilization rate during the most severe pandemic (ERRHC Level 1) is 100%. The probability of each scenario's occurrence $p_s=1/\left|S\right|$, where the number of scenarios $\left|S\right|$ can be viewed as the sample extracted randomly from historical data, so the probability of each scenario is the same.

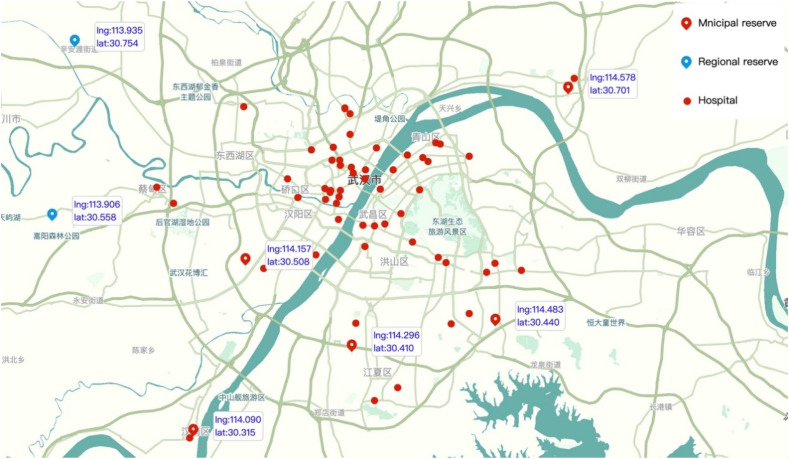
According to the geographical conditions and other factors, the municipal reserves of medical supplies are set in Jiangxia District, Dongxihu District, Hannan District and Caidian District, and the regional reserves are set in Xinzhou District and Caidian District. As shown in Fig. 3 , there are two candidate regional reserves with a fixed cost of 2 million RMB and five candidate municipal reserves with 1 million RMB.

Fig. 3.

Candidate reserves and partial hospital locations.

We set the number of candidate MSs as 5, whose subsidies are generated from the discrete uniform distribution [$1\times 10^6$, $3\times 10^6$]. Note that the most severe health crises, such as COVID-19, may bring challenges in raw materials procurement and logistics, and lead to production limitations. For this reason, we generate random variables ${\chi }_h^s$, for $s\in S_1$ corresponding to the raw materials available to produce from the discrete uniform distribution of [$5\times 10^4$, $2\times 10^5$], and each ${\chi }_h^s$, for $s\in S_2,S_3,S_4$ is drawn uniformly from [$2\times 10^5$, $5\times 10^5$]. To simplify the experiments, we set ${\upsilon }_g=1,\forall g\in G$.

The subsidies of 5 candidate RSs are generated from the discrete uniform distribution [$1\times 10^6$, $3\times 10^6$], and the maximum capacity for various materials is generated from the discrete uniform distribution [$5\times 10^4$, $2\times 10^5$].

According to Ref. [13]; the available area of supplies roughly estimated in the municipal reserve is 25m ², and the area of the regional reserve is 36m ². The distance data associated with transportation costs from reserves to each demand node is derived from Baidu Map. Table 2 lists relatively realistic unit cost intervals of medical supplies used to generate unit acquisition cost randomly and the quantity stored per square meter of the reserve.

Table 2.

Unit acquisition cost and quantity of supplies per square meter.

Index	Supplies category	Unit cost interval for acquisition	Quantity
1	Medical alcohol	[5,10]	200L
2	Hand sanitizer	[5,10]	2400 bottles
3	Surgical mask	[1,5]	$3\times 10^4$
4	Safety goggles	[35,80]	4000
5	Protective suit	[40,120]	500
6	Arbidol	[20,50]	$1.5\times 10^5$
7	Oseltamivir	[20,60]	$1.5\times 10^5$

We refer to Ref. [13] to set the unit cost. Each commodity's unit handling cost and unit-mile transportation cost are set to 25% and 0.1% of its acquisition cost, respectively. The unit penalty cost for unfulfilled demand is assumed to be ten times its purchase price. The unit service cost paid to MSs and RSs is assumed to be 2 times and 2.5 times its purchase price, respectively. As a primary focus of our research is studying the impact of multi-mitigation strategies, we assume that the unit penalty cost and the unit service cost paid to contract suppliers of all the hospitals are the same or similar to simplify the experiments.

5.2. Performance of solution approach

In this part, we report the results of computational experiments to evaluate the performance of the B&BC method.

5.2.1. Experimental setup

We construct test instances based on the realistic case study described in Section 5.1 to evaluate the performance of the B&BC method, including different problem sizes with the number of medical supplies ranging from 2 to 7 (randomly selected from those supplies mentioned above), the number of demand nodes from 10 to 64 (randomly selected from those hospitals mentioned above), and the number of scenarios from 40 to 100. Table 3 reports the size of the 27 random test data (P1–P27).

Table 3.

Size of test instances.

No.	Sizea	# int. var.	# cont. var.	# constr.	No.	Sizea	# int. var.	# cont. var.	# constr.
P1	2-10-40	67	15374	6427	P15	4-30-100	167	220828	79487
P2	2-10-60	67	23054	9607	P16	4-64-40	337	186268	64751
P3	2-10-100	67	38414	15967	P17	4-64-60	337	279388	96931
P4	2-30-40	167	44174	16147	P18	4-64-100	337	465628	161291
P5	2-30-60	167	66254	24127	P19	7-10-40	67	53809	21827
P6	2-30-100	167	110414	40087	P20	7-10-60	67	80689	32707
P7	2-64-40	337	93134	32671	P21	7-10-100	67	134449	54467
P8	2-64-60	337	139694	48811	P22	7-30-40	167	154609	55547
P9	2-64-100	337	232814	81091	P23	7-30-60	167	231889	83227
P10	4-10-40	67	30748	12587	P24	7-30-100	167	386449	138587
P11	4-10-60	67	46108	18847	P25	7-64-40	337	325969	112871
P12	4-10-100	67	76828	31367	P26	7-64-60	337	488929	169111
P13	4-30-40	167	88348	31907	P27	7-64-100	337	814849	281591
P14	4-30-60	167	132508	47767

Notes: # int. var. Represents the number of integer variables; # cont. var. means the number of continuous variables; # constr. indicates the number of constraints.

^aThe first, second, and last numbers embody the number of commodities, demand points and scenarios.

For each data set, we generate 20 instances separately and record the minimum, maximum and average runtime. We have implemented the data generation and SMIP formulations in Python 3.8, which are solved by calling the commercial solver Gurobi 9.1.0. All Benders cuts of the B&BC method are added to the problem using the Callback procedures. We set the “InfUnbdInfo” parameter as 1 to query the unbounded ray and the “LazyConstraints” as 1 to add Benders cuts through a callback. The stopping criteria were either the run time exceeding the time limit of 3600 s or optimal solutions obtained. Except stated otherwise, we use the default values in Gurobi. It is worth noting that this allows Gurobi to automatically determine which child node is explored first in the search process. All experiments are conducted on a laptop with Intel Core i5 at 2.3 GHz and 8 GB memory using macOS 11.2.

5.2.2. Results

We compare the B&BC method with the BD algorithm and Gurobi in Table 4 . We observe that the B&BC method significantly outperforms both the classical BD and Gurobi in the solution time. As expected, the B&BC with a single search tree has better performance in average solution time than Gurobi (with only one exception: the smallest sized instance, i.e., P1), and the classical BD (with only two exceptions: P1 and P2). For the different instances with the same number of binary variables, we see that the advantages of the B&BC method in terms of solution time are becoming more prominent, with the increase in the number of scenarios. For example, P7′s average solution time gained from the B&BC method is one-fifth of Gurobi's runtime, and 71% of classical BD's runtime. While for P9 with 100 scenarios, the average solution time of the B&BC method is one-third of the classical BD algorithm's, and one-tenth of Gurobi's.

Table 4.

Comparison among Gurobi, BD algorithm and B&BC method: CPU time.

No.	Gurobi			BD method			B&BC
	Min	Max	Avg.	Min	Max	Avg.	Min	Max	Avg.
P1	0.64	16.15	4.89	2.59	7.94	4.08	3.29	7.60	5.20
P2	5.10	41.39	14.90	4.81	10.28	6.37	5.54	11.91	7.59
P3	8.04	105.77	30.25	9.55	23.56	12.12	9.42	17.52	11.83
P4	12.12	257.14	75.44	10.30	25.47	15.59	10.07	23.68	15.08
P5	16.64	503.32	108.55	15.92	30.16	22.41	14.78	30.73	20.85
P6	45.07	1119.17	343.62	27.20	166.74	51.89	26.92	72.98	42.89
P7	25.88	1114.36	194.13	24.69	126.91	53.98	20.17	55.64	38.45
P8	86.44	981.98	285.85	42.92	166.92	89.41	33.36	79.55	53.43
P9	72.59	2943.24	1006.13	71.88	376.97	167.83	60.01	125.14	92.90
P10	10.04	61.68	27.02	8.03	28.82	14.11	8.40	24.70	13.98
P11	15.19	180.61	51.09	13.27	32.53	18.17	12.43	28.48	18.05
P12	28.85	298.53	120.63	23.02	63.14	37.69	21.13	51.57	36.55
P13	31.58	737.88	219.44	34.53	100.78	61.59	25.73	66.93	52.94
P14	76.54	2849.49	594.64	43.18	145.02	83.33	36.12	88.62	66.57
P15	222.83	3191.62	1257.81	61.37	351.54	163.22	53.90	192.04	107.65
P16	85.54	1413.52	315.99	88.28	316.03	185.75	83.91	177.34	109.09
P17	87.47	3247.33	724.19	109.83	444.79	274.81	83.26	373.23	181.62
P18	230.13	2561.23	1163.77	319.37	1427.74	734.97	221.92	485.41	332.47
P19	27.86	104.98	52.33	19.48	53.61	30.47	19.92	41.84	29.91
P20	33.82	266.83	113.05	34.21	58.00	44.02	29.60	50.36	42.40
P21	118.95	737.19	310.02	53.42	102.58	81.19	50.28	93.69	71.95
P22	111.02	384.36	229.06	84.88	437.61	190.82	85.86	202.53	135.39
P23	178.82	1192.57	491.34	201.56	499.92	312.26	129.54	306.91	192.54
P24	560.31	2366.39	1242.19	294.98	1198.07	612.95	224.06	571.64	354.12
P25	168.89	1032.06	295.07	212.49	433.27	325.52	142.75	308.19	196.95
P26	279.66	2136.29	634.88	417.20	1872.57	855.95	252.65	730.51	427.15
P27	793.02	>3600	2094.19	868.62	2753.56	1473.49	346.00	699.67	553.97

Note: The term “>3600” represents the solution method terminated at 3600 s without attaining an optimal solution.

Further, as the problem size increases, the runtime differences among these solution approaches grow. Notably, for large-sized problems, the B&BC method has an evident advantage, which even halved the solution time of the classical BD (see the runtime of P26-27 in Table 4). In contrast, Gurobi cannot solve the large-sized problem optimally within a time limit of 3600 s (e.g., see the runtime of P27 in Table 4). The classical BD algorithm solves the SMIP by building and discarding complete branch-and-bound trees, which is time-consuming. Unlike the classical BD, the B&BC method adds Benders cuts as needed during a single branch-and-cut process. It exploits many integer feasible solutions, which are potentially optimal for the current node. Hence, the optimal solution time is considerably reduced.

5.2.3. Robustness analysis

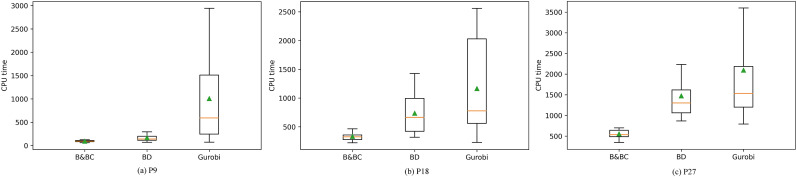
In Section 5.2.2, Table 4 reports three solution approaches' minimum and maximum runtime. It should be noted that the B&BC method seems to be somehow more robust (the gap between the minimum and the maximum solution time is always the smallest). It inspired us to investigate the robustness of the proposed solution approach in this part. For this purpose, the solution time of three solution approaches for problems with a larger number of integer variables, i.e., P9, P18, and P27, are summarized to illustrate the variability in Fig. 4 (without outliers). Note that each box in Fig. 4 shows the values of the first quartile, the median, and the third quartile, respectively, and the triangle point marks the mean value.

Fig. 4.

CPU time of B&BC method, classical BD and Gurobi.

CPU time of these three solution approaches increases with an increase in the number of commodities (from 2 to 7). However, the gap in CPU time's mean values between the B&BC method and classical BD is more significant, when the number of commodities increases. The box length signifies the variability of 20 instances of the problem, which is employed to capture the robustness of the solution approach. In Fig. 4(a), we observe that for P9 the length of the “B&BC” box is much shorter than the “BD” box and “Gurobi” box. Fig. 4 (b) and (c) show a similar pattern in the boxplots of P18 and P27. We see that changes in the test data of the same problem size seem to influence the performance of the B&BC method slightly, compared with the classical BD and Gurobi, which indicates that the B&BC method is more robust against input data.

5.2.4. Space complexity analysis

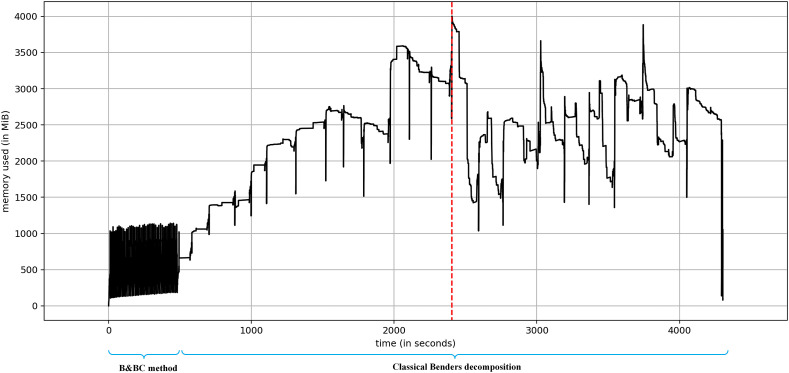
In this part, we use the case study mentioned in Section 5.1 to examine the space complexity of the B&BC method and classical BD. Note that the case study is a replication of P27. A memory profiler is employed to evaluate the size of work memory used by algorithms, which estimates the space complexity of the algorithms. Fig. 5 reflects the memory usage of two solution approaches when implementing the algorithm procedure. The horizontal axis is CPU time, and the vertical axis is memory usage (1MiB = 1.04 Megabytes). We note that the process of the B&BC method with less solution time occupies less memory than the classical BD.

Fig. 5.

Memory usage of the B&BC method and classical BD.

Moreover, the memory usage of the B&BC method remains stable. It indicates that the classical BD can lead to memory overflow for large-sized instances. Managing the Benders cuts derived from various search trees increases memory consumption.

5.3. Comparison between SMIP and DMIP

In this section, we use the case study described in Section 5.1 to discuss the different model versions. The experimental results are summarized in Table 5, Table 6 .

Table 5.

SMIP vs. DMIP: binary decision variables in the first stage.

	# Municipal Reserve	# Regional Reserve	# MSs	# RSs
SMIP	1	1	2	3
DMIP	1	2	1	1
Diff. (%)	0%	100%	−50%	−67%

Table 6.

SMIP vs DMIP: cost.

		SMIP		DMIP		Diff. (%)
		Cost (RMB)	Percentage	Cost (RMB)	Percentage
1st-stage Cost	Fixed Cost	3.00E+06	4.523%	5.00E+06	4.944%	66.67%
	Subsidies	8.20E+06	12.368%	2.15E+06	2.129%	−73.76%
	Acquisition Cost	1.07E+07	16.156%	2.37E+07	23.441%	121.22%
Recourse cost	Transportation Cost	6.60E+04	0.100%	1.06E+05	0.104%	59.95%
	Handling Cost	3.27E+03	0.005%	1.31E+04	0.013%	301.60%
	Serve Cost1	1.87E+07	28.156%	9.53E+06	9.423%	−48.97%
	Serve Cost2	2.57E+07	38.692%	1.50E+07	14.804%	−41.66%
	Penalty Cost	0	0.000%	4.57E+07	45.141%	–
Total Cost		6.63E+07		1.01E+08		52.47%

Note: Serve Cost¹ and Serve Cost² represent the service cost paid to MS and RS in the second stage, respectively.

To illustrate the difference in the two formulations' results, we first study the number of open reserves and selected contract suppliers in SMIP and DMIP (Table 5). Note that the “Diff” row shows the percentage differences in binary decision variables derived from the two models. We then make a detailed comparison of the two programs related to cost (Table 6). We observe that DMIP, regardless of uncertainties, may open the same reserves as compared to SMIP. But one additional regional reserve will be established to respond to epidemic strikes in DMIP. Instead, SMIP may result in more selected contract suppliers. More contract suppliers are somehow robust against the risk of expiration and regarded as recourse actions in dealing with uncertain demand.

In Table 6, we provide the results on the first-stage cost and recourse cost in detail, by evaluating the optimal solutions of the two models. Note that the “Diff” column presents the percentage differences in various costs derived from the two models. In DMIP, penalty cost induced by stockout accounts for nearly 45.14% of the total cost, while there is no shortage in SMIP. Medical supplies are essential to preventing and controlling pandemics, and the shortage will cause huge losses.

We observe that SMIP significantly improves over DMIP in penalty cost but at the expense of increasing subsidies and service costs paid to suppliers. However, the total cost of DMIP is about 1.52 times as much as that of SMIP. Service costs paid to contract suppliers in the aftermath of the epidemic attack occupy 66.85% of SMIP's total cost, implying that contract suppliers play a significant part when stocks are insufficient. While that account for only 24.22% of DMIP's, signifying that more stored medical supplies need to be fulfilled the demand in a few scenarios, which potentially entail a higher stocking level and acquisition costs (121.22% higher than that of SMIP), even more handling cost (301.6% higher than that of SMIP). These results clearly illustrate the benefit of SMIP, which can be solved within a reasonable solution time of 471.69 s by the B&BC method.

Note that, as discussed in Section 3.3, eliminating the decision variables $s{c}_{ig}^s$ and reducing constraints (12) to $\sum _{h\in H}p{c}_{ihg}^s+\sum _{e\in E}c{r}_{ieg}^s+\sum _{j_z\in Z}t{b}_{i{j}_{z}g}^s+\sum _{j_c\in C}t{p}_{i{j}_{c}g}^s\ge q_{ig}^s$, leads to a stochastic program without stockout. An important finding is that replacing random variables with their expected value most likely causes the deterministic version to be infeasible. This observation further suggests that the DMIP ignoring the uncertainty results in a shortage to a large extent.

5.4. Comparison between single-mitigation strategy and multi-mitigation strategies

In this subsection, we study the impact of multi-mitigation strategies under stochastic conditions. Using the case study, we computationally assess the multi-mitigation strategies and single-mitigation strategy in medical supplies. This is inspired by the actual situation in Wuhan during the COVID-19 pandemic outbreak. In the early stage, hospitals’ demand for medical supplies was almost exclusively satisfied by the inventory of reserves.

As described in Section 3.3, the single-mitigation strategy suggests that only transportation from reserves is allowed when an epidemic breaks out. Table 7 provides the single-mitigation model costs involving the fixed cost of reserves, the acquisition cost of medical materials, and recourse costs (i.e., cost for allocation of stored medical materials, holding and penalty cost). The “Diff” column shows the percentage difference in the various costs relative to the proposed model.

Table 7.

Multi-mitigation vs single-mitigation: cost.

	Single-mitigation		Diff. (%)
	Cost (RMB)	Percentage
Fixed Cost	8.00E+06	4.39%	166.67%
Acquisition Cost	4.10E+07	22.46%	282.35%
Transportation Cost	1.80E+05	0.10%	173.17%
Handling Cost	4.46E+04	0.02%	1263.41%
Penalty Cost	1.33E+08	73.03%	–
Total Cost	1.82E+08	–	175.05%

We observe that one more regional reserve and three more municipal reserves are decided to open, and the total cost concerning the decisions is about 2.75 times that of the multi-mitigation cost. The single-mitigation results in costly penalties, accounting for almost 73.03% of the total cost, indicating unfulfilled demand under a wide range of scenarios.

We further compare the handling cost induced by unused materials, which can be employed to evaluate expiration risk. The handling cost is 13.63 times as much as the multi-mitigation, indicating that it may generate waste under a few scenarios. Moreover, maintaining adequate commodities in reserves has to face expiration problems since there is no steady demand. In contrast, a low stocking level cannot cover a surge in demand and further trigger significant losses.

It implies that only the inventory of reserves is allowed to meet the demand, which will result in a severe shortage, even if there is excess inventory. It aligns with the actual situation. If multi-mitigation strategies were adopted during the outbreak, out-of-stocks would be avoided while inventory levels would not be high. The multi-mitigation strategies are a highly effective approach to overcome this challenge by maximizing resource utilization and minimizing losses. These results clearly reveal that medical supplies from various channels should be combined with prepositioning strategy.

5.5. Benefit of considering manufacturing suppliers

A few published works capture supplier selection or procurement [23,33,56] in prepositioning policy, which is the same as or similar to RS in this paper. We integrate the MS's selection into the first-stage decisions. Using this case study, we compare the results of the proposed model with that of the existing studies, which exclude MS (SMIP-EMS), by two measures: inventory utilization and unfulfilled demand proportion.

On the inventory utilization side, surplus inventory (unused materials) associated with potential waste of both models mainly occurs in $s\in S_3\cup S_4$, the scenario subsets with less demand. We introduce the inventory utilization $I{U}_{g{S}_k}$ of various medical supplies under different scenario subsets, which can be computed as follows:

$$I{U}_{g{S}_k}=\left(\sum _{j\in C\cup Z}{r}_{jg}-\sum _{j\in C\cup Z}\sum _{s\in S_k}u{r}_{jg}^s/\left|S_k\right|\right)/\sum _{j\in C\cup Z}{r}_{jg},\forall g=\mathrm{1,2},...,7;k=\mathrm{3,4}\text{.}$$

The possible unmet demand often occurs in the scenarios with higher demand (i.e., $s\in S_1$), we denote unfulfilled demand proportion in the scenario subset $S_k$ as $UD{P}_{g{S}_k}$ to capture the demand fulfilment of medical supplies, and it is calculated as

$$UD{P}_{g{S}_k}=\sum _{s\in S_k}\sum _{i\in D}s{c}_{ig}^s/\sum _{s\in S_k}\sum _{i\in D}{q}_{ig}^s,k=1;g=1,...,7\text{.}$$

The two measures comparison is illustrated in Table 8 . We observe that except hand sanitizer (g = 2), for all $g\in G$, the corresponding $I{U}_{g{S}_3}$ and $I{U}_{g{S}_4}$ obtained from SMIP are greater than or equal to those obtained from SMIP-EMS. Despite SMIP results in a slightly lower inventory utilization of hand sanitizer, the unfulfilled demand proportion of this commodity is 0. However, the unfulfilled demand proportion of hand sanitizer $UD{P}_{2S_1}$ in SMIP-EMS is 3.23%, indicating that 3.23% of demands for hand sanitizer would be improved by taking MS into consideration. We note that RSs and MSs provide approximately 94.97% of hand sanitizer under the scenario $s\in S_1$ to cover the demand in SMIP. Additionally, SMIP-EMS exploits RSs to cover 88.65% of the demand for the commodity. In other words, SMIP improves demand fulfilment at the expense of a few surplus inventories. Compared to SMIP, SMIP-EMS may trigger the inadequateness of certain medical supplies, such as hand sanitizer, during the most severe pandemic (i.e., $s\in S_1$), like COVID-19. The shortage of medical commodities may cause irreparable harm to the public and impede control and prevention. SMIP achieves a reduction of 5.61% in total cost compared to SMIP-EMS. Though the gap of the total cost between SMIP and SMIP-EMS is small, the results illustrate that regarding MS as one of the various sources can mitigate the high uncertainty in demand powerfully, by improving demand fulfilment and inventory utilization. The multi-mitigation strategies set up "redundant" reserves and suppliers, which are capable of preventing sudden surges in demand from causing supply interruptions. From this perspective, while demand can be satisfied as much as possible, supply resilience has also increased.

Table 8.

SMIP vs SMIP-EMS: inventory utilization and unfulfilled demand proportion.

Commodity Index	$I{U}_{g{S}_k}$				$UD{P}_{g{S}_k}$
	S3		S4		S1
	SMIP-EMS	SMIP	SMIP-EMS	SMIP	SMIP-EMS	SMIP
1	99.80%	99.96%	97.51%	97.68%	0	0
2	99.99%	99.98%	90.98%	99.76%	3.23%	0
3	99.96%	99.99%	82.42%	82.46%	0	0
4	100%	100%	100%	100%	0	0
5	100%	100%	100%	100%	0	0
6	100%	100%	100%	100%	0	0
7	91.04%	99.93%	80.22%	82.46%	0	0

5.6. Benefit of considering uncertainty in raw materials available to produce

The COVID-19 pandemic incredibly brings challenges in raw materials procurement and logistics struggles, leading to severely disrupted production. We include the stochasticity of raw materials offered to MS and study its effect. Observe that replacing the random variables ${\chi }_h^s$ with their expected values ${\bar{\chi }}_h$ leads to a stochastic mixed integer program with deterministic raw materials available to produce (the demand for medical supplies is still uncertain). We denote the corresponding model as SMIP-DRL. This subsection provides a comparison between SMIP and SMIP-DRL to illustrate the benefit of considering uncertainty in raw materials.

Decisions on the location of reserves gained from these two models are the same. However, SMIP results in two MSs and three RSs, and SMIP-DRL selects three MSs and two RSs. Compared with SMIP-DRL, SMIP, considering the uncertainty in raw materials, makes more rational and conservative decisions (one more RS and one less MS) on contract suppliers’ selection. Although the first-stage decisions are not exactly the same, the gap between their objective values is tiny, only 2.24%. And the gap between the costs in the pre-event stage is only 7.64%.

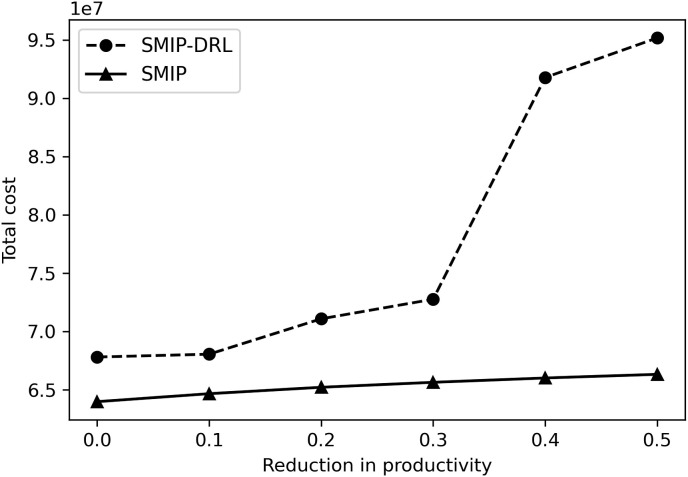
Next, we provide a sensitivity study on ${\upsilon }_g$, which is termed as raw materials productivity, to reveal the benefits of considering uncertainty in raw materials available to produce. We denote a coefficient of variation as $\tau$, to vary the parameter ${\upsilon }_g$ by replacing it with ${\upsilon }_g\left(1-\tau \right)$. Note that an increase in the coefficient of variation $\tau$ results in a productivity reduction. We vary $\tau$ from 0 to 0.5 and plot the objectives of the two models in Fig. 6 . It is evident that the increase in $\tau$ from 0 to 0.5 causes a 50% reduction in raw materials productivity. The objective of the SMIP model changes very little, only 3.66% and the objective of the SMIP-DRL model ignoring the uncertainty of raw materials varies greatly, about 28.75%. When $\tau =0$ and the productivity ${\upsilon }_g=1$, the gap of the total cost between SMIP and SMIP-DRL is only 2.24%. We observe that when ${\upsilon }_g\in \left[\mathrm{0.9,1}\right]$, the gap between the optimal objectives of the two models is small and the corresponding curve is relatively stable. It indicates that whether to consider the uncertainty in raw materials available to produce has little influence on the solution, and this uncertainty can be ignored. When $\tau =0.5$ and ${\upsilon }_g=0.5$, the gap in the total cost between SMIP and SMIP-DRL reaches 48.74%. It indicates that accounting for the uncertainty results in significant savings in terms of cost, especially when the productivity of MS is low. The government and other relevant departments should make decisions based on the production capacity of MS (not just the cost). When MS's production capacity is low or fluctuates greatly due to epidemic outbreaks, incorporating the stochasticity of raw materials into resource management can make a more reasonable choice. For MS, it is necessary to open up more raw materials supply channels to ensure the supply during the epidemic strikes.

Fig. 6.

Impact of productivity on the objective: SMIP vs SMIP-DRL.

6. Conclusion and outlook

6.1. Summary

In this paper, we study multi-mitigation strategies in medical supplies to ensure uninterrupted supply and significant savings by introducing two-type suppliers, reserving suppliers and manufacturing suppliers. Thus, each hospital with uncertain demand is enabled to be served by various channels during pandemics: prepositioning in reserves, backups served by reserving suppliers, and medical commodities produced by manufacturing suppliers. Uncertainty in raw materials available for the manufacturing suppliers is also included. We formulate the problem as a two-stage stochastic mixed integer program to determine prepositioning strategy and post-event allocation of multiple channels.

Accordingly, we develop an exact algorithm branch-and-Benders-cut method for solving this problem which utilizes the special structure of the stochastic programs. A series of test instances show that the proposed method outperforms both Gurobi and classical Benders decomposition in solution time. The robustness test is also included and shows the branch-and-Benders-cut method is somehow more robust against input data. We further compare the space complexity of the branch-and-Benders-cut method with classical Benders decomposition. We note that the branch-and-Benders-cut method occupies less memory since it builds a single search tree.

A realistic case study based on the COVID-19 pandemic in Wuhan is investigated, demonstrating the benefits of our approach. We analyze the stochastic and deterministic versions and observe that the stochastic program is robust against uncertainties resulting from epidemic strikes. More contract suppliers will be selected to support adequate supplies in the stochastic program. Compared to the single-mitigation strategy (only inventory is allowed to satisfy demand), the multi-mitigation strategies result in significant savings in terms of unsatisfied demand penalty cost and handling cost (1263.41%) associated with the expiration problem. Furthermore, we explore the benefit of considering manufacturing suppliers by inventory utilization and unfulfilled demand proportion. Considering manufacturing suppliers entails an improvement of the demand fulfilment rate (or a reduction in unfulfilled demand proportion) and relatively greater inventory utilization. Finally, we perform a sensitivity study on raw materials productivity, to reveal the benefits of considering uncertainty in raw materials available to produce. This work studies the prepositioning strategy with COVID-19 as an example. Our proposed methodology is applicable not only to COVID-19 but also to other related contexts, especially for health disasters with uncertain duration.

6.2. Managerial implications

This work enables government agencies and humanitarian organizations to effectively support decision-making within a reasonable time when the pandemic strikes. We explain our findings on the numerical experiments.

• (1)Medical supplies from various channels, i.e., regular inventory of reserves, backups served by reserving suppliers, and medical commodities produced by manufacturing suppliers, should be combined with a prepositioning strategy to balance uninterrupted supply with relatively lower stocking levels. Significantly, in the context of an epidemic outbreak with uncertain duration, the production of MS mitigates the risk from uncertain demand and struggles against long-term needs.
• (2)When the production capacity of MS is high, the uncertainty in raw materials available to produce has little effect on the results and can be ignored. When the MS's production capacity is low or fluctuates greatly due to epidemic outbreaks, incorporating the stochasticity of raw materials into resource management can make a more reasonable choice.
• (3)For MS, it is necessary to open up more raw materials supply channels to ensure the supply during the epidemic strikes.

6.3. Limitations and future research

Future work is needed to tackle some limitations in our research. For example, multiple time periods need to be further involved. More details of the options contract, such as the number of medical commodities offered by contract suppliers, should be further determined before epidemic outbreaks. From the algorithm's perspective, it would be of interest to tighten the lower bound of CP and develop hybrid methods combining exact and metaheuristic strategies to obtain tighter upper bounds.

Authorship contribution statement

Yuwei Zhang: Software, Methodology, Writing - original draft. Zhenping Li: Methodology, Supervision. Yuwei Zhao: Writing - review & editing, Software.

Declaration of competing interest

No potential conflict of interest was reported by the author(s).

Biographies

Yuwei Zhang received a Ph.D. degree in management science and engineering from the Capital University of Economics and Business, China, in 2022. Her research interests include integer programming and stochastic programming.

Zhenping Li was born in Shandong, China. She received the Ph.D. degree from the Academy of Mathematics and Systems Science, Chinese Academy of Sciences, in 2004. She is currently a Professor with the School of Information, Beijing Wuzi University. Her research interests include operations research and management science, logistics optimization, and intelligent algorithm.

Yuwei Zhao received the M.S. degree in logistics engineering from Beijing Wuzi University, China, in 2020. She is currently pursuing the Ph.D. degree in management science and engineering with the Beijing University of Chemical Technology, China. Her research interests include traffic optimization, logistics optimization and optimization algorithm.

Appendix A. Equivalent Mixed Integer Programming Model

In order to be more intuitive, we all use the same index $j$ to represent reserves.

$$\min \sum _{j\in C\cup Z}{f}_j{x}_j+\sum _{h\in H}{y}_h{n}_h+\sum _{e\in E}{v}_e{m}_e+\sum _{j\in C\cup Z}\sum _{g\in G}{\eta }_g{r}_{jg}+\sum _{s\in S}{p}_s(\sum _{h\in H}\sum _{i\in D}\sum _{g\in G}{\beta }_{ihg}p{c}_{ihg}^s+\sum _{e\in E}\sum _{i\in D}\sum _{g\in G}{\alpha }_{ieg}c{r}_{ieg}^s$$

$$+\sum _{i\in D}\sum _{g\in G}{k}_{ig}s{c}_{ig}^s+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}{d}_{ijg}^{1}t{p}_{ijg}^s+\sum _{i\in D}\sum _{j\in Z}\sum _{g\in G}{d}_{ijg}^{2}t{b}_{ijg}^s+\sum _{j\in C\cup Z}\sum _{g\in G}{l}_{j}u{r}_{jg}^s)\text{,}$$ (A.1)

$$\text{s.t.}\sum _{j\in C}{z}_{ij}\ge 1,\forall i\in D\text{,}$$ (A.2)

$$z_{ij}\le x_j,\forall j\in C,i\in D\text{,}$$ (A.3)

$$\sum _{g\in G}{o}_g{r}_{jg}\le a_j{x}_j,\forall j\in C\cup Z\text{,}$$ (A.4)

$$\sum _{h\in H}p{c}_{ihg}^s+\sum _{e\in E}c{r}_{ieg}^s+s{c}_{ig}^s+\sum _{j\in Z}t{b}_{ijg}^s+\sum _{j\in C}t{p}_{ijg}^s\ge q_{ig}^s,\forall i\in D,g\in G,s\in S\text{,}$$ (A.5)

$$\sum _{i\in D}c{r}_{ieg}^s\le {\psi }_{eg}{v}_e,\forall e\in E,g\in G,s\in S\text{,}$$ (A.6)

$$\sum _{g\in G}{\upsilon }_g{\phi }_{hg}^s\le {\chi }_h^s{y}_h,\forall h\in H,s\in S\text{,}$$ (A.7)

$$\sum _{i\in D}p{c}_{ihg}^s\le {\phi }_{hg}^s,\forall h\in H,g\in G,s\in S\text{,}$$ (A.8)

$$\sum _{i\in D}t{p}_{ijg}^s+u{r}_{jg}^s=r_{jg},\forall j\in C,g\in G,s\in S\text{,}$$ (A.9)

$$\sum _{i\in D}t{b}_{ijg}^s+u{r}_{jg}^s=r_{jg},\forall j\in Z,g\in G,s\in S\text{,}$$ (A.10)

$$t{p}_{ijg}^s\le M{z}_{ij},\forall i\in D,j\in C,g\in G,s\in S\text{,}$$ (A.11)

$$x_j\in \mathbb{B},\forall j\in C\cup Z\text{,}$$ (A.12)

$$y_h\in \mathbb{B},\forall h\in H\text{,}$$ (A.13)

$$v_e\in \mathbb{B},\forall e\in E\text{,}$$ (A.14)

$$z_{ij}\in \mathbb{B},\forall i\in D,j\in C\text{,}$$ (A.15)

$$r_{jg}\ge 0,\forall j\in C\cup Z,g\in G\text{,}$$ (A.16)

$$u{r}_{jg}^s\ge 0,\forall j\in C\cup Z,g\in G,s\in S\text{,}$$ (A.17)

$$t{b}_{ijg}^s\ge 0,\forall j\in Z,i\in D,g\in G,s\in S\text{,}$$ (A.18)

$$t{p}_{ijg}^s\ge 0,\forall j\in C,i\in D,g\in G,s\in S\text{,}$$ (A.19)

$$p{c}_{ihg}^s\ge 0,\forall i\in D,h\in H,g\in G,s\in S\text{,}$$ (A.20)

$$c{r}_{ieg}^s\ge 0,\forall i\in D,e\in E,g\in G,s\in S\text{,}$$ (A.21)

$${\phi }_{hg}^s\ge 0,\forall h\in H,g\in G,s\in S\text{,}$$ (A.22)

$$s{c}_{ig}^s\ge 0,\forall i\in D,g\in G,s\in S\text{.}$$ (A.23)

Appendix B. Deterministic Mixed Integer Program

By dropping superscript $s$ in the second-stage problem and replacing all random variables with their expected value, we obtain a deterministic model called the expected value problem (EV).

${\bar{q}}_{ig}$: expected value of hospital $i$'s demand for commodity $g$.

${\bar{\chi }}_h$: expected amount of raw materials used to produce medical products by MS $h$.

In order to be more intuitive, we all use the same index $j$ to represent reserves.

The deterministic mixed integer program is formulated as follows.

$$\min \sum _{j\in C\cup Z}{f}_j{x}_j+\sum _{h\in H}{y}_h{n}_h+\sum _{e\in E}{v}_e{m}_e+\sum _{j\in C\cup Z}\sum _{g\in G}{\eta }_g{r}_{jg}+\sum _{h\in H}\sum _{i\in D}\sum _{g\in G}{\beta }_{ihg}p{c}_{ihg}+\sum _{e\in E}\sum _{i\in D}\sum _{g\in G}{\alpha }_{ieg}c{r}_{ieg}$$

$$+\sum _{i\in D}\sum _{g\in G}{k}_{ig}s{c}_{ig}+\sum _{i\in D}\sum _{j\in C}\sum _{g\in G}{d}_{ijg}^{1}t{p}_{ijg}+\sum _{i\in D}\sum _{j\in Z}\sum _{g\in G}{d}_{ijg}^{2}t{b}_{ijg}+\sum _{j\in C\cup Z}\sum _{g\in G}{l}_{j}u{r}_{jg}\text{,}$$ (B.1)

$$\text{s.t.}\sum _{j\in C}{z}_{ij}\ge 1,\forall i\in D\text{,}$$ (B.2)

$$z_{ij}\le x_j,\forall j\in C,i\in D\text{,}$$ (B.3)

$$\sum _{g\in G}{o}_g{r}_{jg}\le a_j{x}_j,\forall j\in C\cup Z\text{,}$$ (B.4)

$$\sum _{h\in H}p{c}_{ihg}+\sum _{e\in E}c{r}_{ieg}+s{c}_{ig}+\sum _{j\in Z}t{b}_{ijg}+\sum _{j\in C}t{p}_{ijg}\ge {\bar{q}}_{ig},\forall i\in D,g\in G\text{,}$$ (B.5)

$$\sum _{i\in D}c{r}_{ieg}\le {\psi }_{eg}{v}_e,\forall e\in E,g\in G\text{,}$$ (B.6)

$$\sum _{g\in G}{\upsilon }_g{\phi }_{hg}\le {\bar{\chi }}_h{y}_h,\forall h\in H\text{,}$$ (B.7)

$$\sum _{i\in D}p{c}_{ihg}\le {\phi }_{hg},\forall h\in H,g\in G\text{,}$$ (B.8)

$$\sum _{i\in D}t{p}_{ijg}+u{r}_{jg}=r_{jg},\forall j\in C,g\in G\text{,}$$ (B.9)

$$\sum _{i\in D}t{b}_{ijg}+u{r}_{jg}=r_{jg},\forall j\in Z,g\in G\text{,}$$ (B.10)

$$t{p}_{ijg}\le M{z}_{ij},\forall i\in D,j\in C,g\in G\text{,}$$ (B.11)

$$x_j\in \mathbb{B},\forall j\in C\text{,}$$ (B.12)

$$y_h\in \mathbb{B},\forall h\in H\text{,}$$ (B.13)

$$v_e\in \mathbb{B},\forall e\in E\text{,}$$ (B.14)

$$z_{ij}\in \mathbb{B},\forall i\in D,j\in C\text{,}$$ (B.15)

$$r_{jg}\ge 0,\forall j\in C\cup Z,g\in G\text{,}$$ (B.16)

$$u{r}_{jg}\ge 0,\forall j\in C\cup Z,g\in G\text{,}$$ (B.17)

$$t{b}_{ijg}\ge 0,\forall j\in Z,i\in D,g\in G\text{,}$$ (B.18)

$$t{p}_{ijg}\ge 0,\forall j\in C,i\in D,g\in G\text{,}$$ (B.19)

$$p{c}_{ihg}\ge 0,\forall i\in D,h\in H,g\in G\text{,}$$ (B.20)

$$c{r}_{ieg}\ge 0,\forall i\in D,e\in E,g\in G\text{,}$$ (B.21)

$${\phi }_{hg}\ge 0,\forall h\in H,g\in G\text{,}$$ (B.22)

$$s{c}_{ig}\ge 0,\forall i\in D,g\in G\text{.}$$ (B.23)

An optimization problem corresponding to a specific scenario is employed to calculate expected costs. The objective and constraints are similar to the stochastic model (9)–(23), except that the variables $x_j$, $z_{ij}$, $y_h$, $v_e$ and $r_{jg}$ in the second stage problem are fixed to EV's optimal solution denoted as ${\hat{x}}_j$, ${\hat{z}}_{ij}$, ${\hat{y}}_h$, ${\hat{v}}_e$ and ${\hat{r}}_{jg}$, respectively.

Appendix C. Demand node Information

Hospital category	Hospital name	# Beds
Government-designated hospital	Jinyintan Hospital	684
	Pulmonary Hospital	322
	Hankou Hospital	378
	Wuchang Hospital	504
	Wuhan Fifth Hospital	420
	Wuhan Seventh Hospital	268
	Wuhan Ninth Hospital	793
	Municipal Red Cross Hospital	404
	Wuhan Fourth Hospital (Western Hospital)	619
	The Second Hospital of Wuhan Iron and Steel Corporation	207
	Central Hospital (Houhu District)	510
	Wuhan Third Hospital (Optical Valley Campus)	600
	Tongji Hospital (Sino-French New City Branch)	1050
	Union Hospital Tongji Medical College Huazhong University of Science and Technology	810
	Hubei General Hospital	800
	Hubei Provincial Hospital of Integrated Chinese & Western Medicine	950
	Tianyou Hospital	400
	Wuhan Sixth Hospital	500
	Hubei Provincial Hospital of Traditional Chinese Medicine	400
	Wuhan 672 Hospital	305
	Wuhan Hospital of Traditional Chinese Medicine Hospital	411
	Jiangxia District Traditional Chinese Medicine Hospital	260
	Xinzhou District Traditional Chinese Medicine Hospital	300
	Wuhan Zijing Hospital	288
	Hannan District Traditional Chinese Medicine Hospital	26
	Caidian District Maternal and Child Health Hospital	610
	PLA Central Theater General Hospital	240
	Wuhan Children's Hospital	262
	Tongji Hospital (Optical Valley Branch)	828
	Wuhan Eighth Hospital	255
	Xincheng Hospital	89
	Yangluo District, Provincial Third People's Hospital	135
	Wuhan Asia Heart General Hospital	451
	Wuhan First Hospital	1000
	Hubei Provincial Hospital of Traditional Chinese Medicine (Optical Valley Branch)	430
	Tongji Hospital (Main Hospital Area)	1026
	Union Hospital Tongji Medical College Huazhong University of Science and Technology (Tumor Center)	808
	Provincial Third People's Hospital	240
	General Hospital of Wuhan Iron and Steel Corporation	235
	Wuhan Hospital for Special Care	260
	Zhongnan Hospital	262
	Wuhan Third Hospital	600
	Wuhan Fourth Hospital	59
	General Hospital of the Yangtze River Shipping	300
	Liyuan Hospital	233
	Maternal and Child Health Care Hospital	800
Fangcang shelter hospitals	Hubei Provincial Party School Fangcang Hospital	932
	Dongxihu Fangcang Shelter Hospital	1461
	Huangpi No 1 High School	200
	Jiang'an Fangcang Hospital	1000
	Jianghan Fangcang Hospital	1564
	Qiaokou District Fangcang Hospital	200
	Wuhan Sports Center	682
	Hannan District Fangcang Hospital	960
	Wuhan Sports University	960
	Hanyang Fangcang Hospital	960
	Wuchang Fangcang Hospital	784
	Fangcang Hospital of Jianghan Economic Development Zone	682
	Qingshan District Hospital	388
	China Optics Valley Convention & Exhibition Center	850
	Optics Valley Rihai Fangcang Hospital	3690
	Jiangxia Fangcang Hospital	400
Specialty field hospitals	Huoshenshan Hospital	1000
	Leishenshan Hospital	1600

Data availability

No data was used for the research described in the article.