SUMMARY
Single-cell Hi-C (scHi-C) technologies can probe three-dimensional (3D) genome structures in individual cells. However, existing scHi-C analysis methods are hindered by the data quality and complex 3D genome patterns. The lack of computational scalability and interpretability poses further challenges for large-scale analysis. Here, we introduce Fast-Higashi, an ultrafast and interpretable method based on tensor decomposition and partial random walk with restart, enabling joint identification of cell identities and chromatin meta-interactions from sparse scHi-C data. Extensive evaluations demonstrate the advantage of Fast-Higashi over existing methods, leading to improved delineation of rare cell types and continuous developmental trajectories. Fast-Higashi can directly identify 3D genome features that define distinct cell types and help elucidate cell type-specific connections between genome structure and function. Moreover, Fast-Higashi can generalize to incorporate other single-cell omics data. Fast-Higashi provides a highly efficient and interpretable scHi-C analysis solution that is applicable to a broad range of biological contexts.
eTOC paragraph
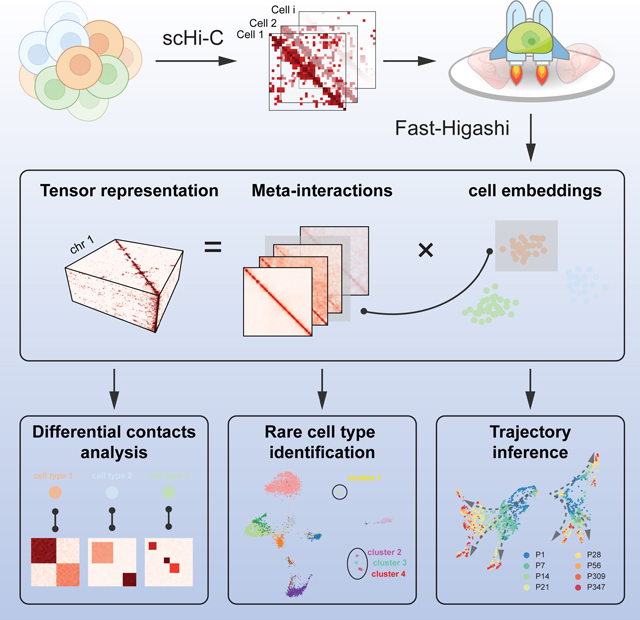
A new computational framework called Fast-Higashi enables efficient and effective analysis of single-cell Hi-C data to unveil distinct cell types and identify cell type-specific 3D genome features.
Graphical Abstract
INTRODUCTION
The advent of high-throughput whole-genome mapping methods for the three-dimensional (3D) genome organization such as Hi-C (Lieberman-Aiden et al., 2009) has revealed distinct features of chromatin folding in various scales within the cell nucleus, including A/B compartments (Lieberman-Aiden et al., 2009), subcompartments (Rao et al., 2014; Xiong and Ma, 2019), topologically associating domains (TADs) (Dixon et al., 2012; Nora et al., 2012), and chromatin loops (Rao et al., 2014). These multiscale 3D genome features collectively contribute to vital genome functions such as transcription (Zheng and Xie, 2019; Kempfer and Pombo, 2020). However, the variation of 3D genome features and their functional significance in single cells remain poorly understood (Misteli, 2020; Zhou et al., 2021). The recent advances of single-cell Hi-C (scHi-C) technologies have provided us with unprecedented opportunities to probe chromatin interactions at single-cell resolution, from a few cells of given cell types (Ramani et al., 2017; Nagano et al., 2017; Kim et al., 2020; Li et al., 2019) to thousands of cells from complex tissues (Tan et al., 2021; Lee et al., 2019; Liu et al., 2021). These new technologies and datasets have the promise to unveil the connections between genome structure and function in single cells for a wide range of biological contexts in health and disease (Zhou et al., 2021).
However, the complexity of scHi-C data has created significant analysis challenges. Computational methods HiCRep/MDS (Liu et al., 2018), scHiCluster (Zhou et al., 2019), LDA (Kim et al., 2020), and the more recent deep learning based methods 3DVI (Zheng et al., 2021) and Higashi (Zhang et al., 2022) have been developed for the embedding and imputation of the sparse scHi-C data. These existing methods, however, cannot (i) effectively infer informative embeddings for the delineation of rare cell types in complex tissues, (ii) directly identify critical chromatin organizations related to cell type-specific genome functions, and (iii) efficiently operate on large-scale datasets with limited memory resources. It remains an open question on how to develop effective computational methods that can identify rare cell types in complex tissues in an interpretable manner with high scalability, key to understanding the interplay among chromatin organization, genome functions, and cellular phenotypes.
The recent scHi-C embedding method scHiCluster (Zhou et al., 2019) uses linear convolution and random walk with restart to impute the sparse contact maps and applies principal component analysis (PCA) on the imputed maps. This requires the storage of all imputed dense maps in the memory, drastically limiting its application to datasets with a large number of cells at high resolution. More recently, deep learning based scHi-C analysis methods have been proposed, including 3DVI (Zheng et al., 2021) based on a deep generative model and our recent work Higashi (Zhang et al., 2022) that uses a hypergraph neural network architecture (Zhang et al., 2020). Both methods suggest better embedding results with Higashi being the first scHi-C embedding approach to demonstrate that the complex neuron subtypes in human prefrontal cortex can be revealed by chromatin conformation only. However, due to the computation-intensive nature of neural networks, the scalability of both methods has much room for improvement for large-scale datasets. For 3DVI, individual variational autoencoders are trained for each genomic distance and each chromosome, leading to thousands of deep neural network models to be trained. For Higashi, since the model treats each contact of scHi-C data as individual samples, it takes a long time to fully iterate over the dataset or to train the model till convergence. Crucially, methods for improving the interpretability of the embeddings for scHi-C data are particularly lacking, limiting our understanding of 3D genome structure-function connections for a diverse set of cellular phenotypes.
Here, we develop Fast-Higashi, an interpretable and scalable framework for embedding and integrative analysis of scHi-C data. We propose a concept for single-cell 3D genome analysis, called “meta-interactions” (analogous to the definition of metagenes in scRNA-seq analysis (Welch et al., 2019)), to improve the model interpretability. Our proposed Fast-Higashi algorithm jointly produces embeddings and meta-interactions for a given scHi-C dataset. Applications to various scHi-C datasets of complex tissues demonstrate that Fast-Higashi has overall comparable or even better embeddings than existing methods but is much faster than neural-network based methods (>40x faster than 3DVI and >9x faster than Higashi), enabling ultrafast delineation of cell subtypes or rare cell types in different biological contexts. Moreover, Fast-Higashi is able to infer critical chromatin meta-interactions that define cell types with strong connections to cell type-specific gene transcription. Fast-Higashi is the fastest and most scalable method for large-scale scHi-C data analysis to date.
RESULTS
Overview of Fast-Higashi
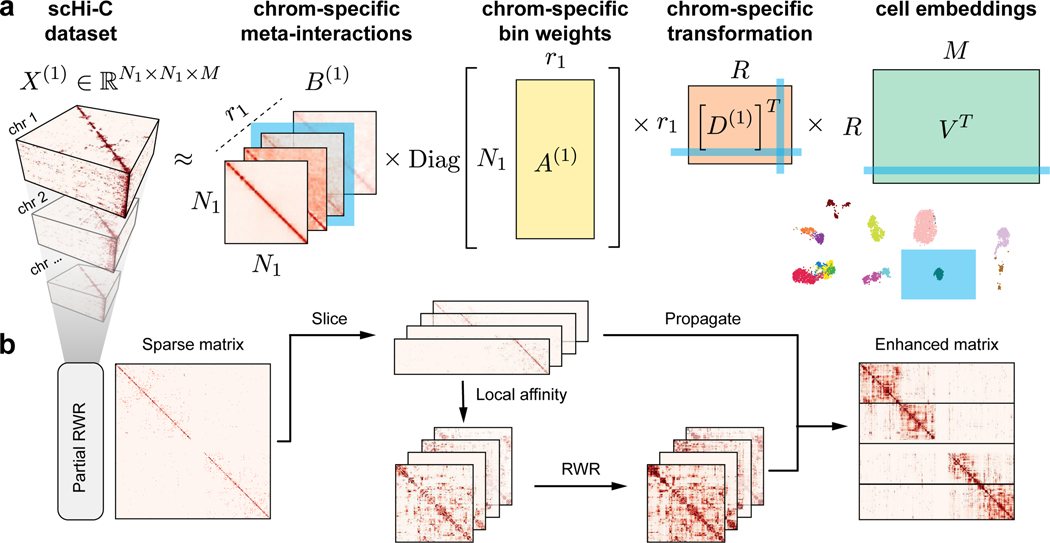
Fig. 1a illustrates the overall architecture of Fast-Higashi, which is an interpretable model for scHi-C analysis. In Fast-Higashi, scHi-C contact maps from different chromosomes are represented as multiple three-way tensors. Then a tensor decomposition model is utilized and generalized to simultaneously model these 3-way tensors that share only a single dimension (single cells). The tensor decomposition model takes the tensor representation of scHi-C data as input and decomposes the tensors into multiple factor matrices (Fig. 1a) to jointly infer cell embeddings as well as meta-interactions. These meta-interactions manifest the aggregated patterns of chromatin interactions, which are analogous to the concept of metagenes in scRNA-seq analysis. Each meta-interaction corresponds directly to a specific dimensions of the cell embeddings, providing a direct solution to interpret the association between embedding results and 3D genome features. We derived the mini-batch optimization procedure for the tensor decomposition model such that it can efficiently model tensors with drastically different sizes and effectively scale to scHi-C datasets with a large number of cells or at high resolutions. To mitigate the sparseness of the scHi-C contact maps while keeping the advantages of mini-batch training, we proposed a partial random walk with restart algorithm (Partial RWR, Fig. 1b) that efficiently imputes the sparse scHi-C contact maps before passing them to the tensor decomposition model. The detailed descriptions of the tensor decomposition model, the Partial RWR module, and the optimization procedures are in STAR Methods.
Figure 1: Overview of Fast-Higashi.
a. Workflow of the Fast-Higashi algorithm. Given an input scHi-C dataset of k chromosomes, Fast-Higashi models it as k 3-way tensors. The tensor of chromosome c is denoted by X(c), where the first two dimensions correspond to genomic bins and the last dimension corresponds to the single cells. Fast-Higashi then decomposes the tensors X(c) into four factors: a set of meta-interactions (B(c)), a genomic bin weights indicating importance for each bin (A(c)), a cell embedding matrix V that is shared across all chromosomes, and a chromosome-specific transformation matrix D(c) that transforms the shared cell embeddings into chromosome-specific ones. b. Workflow of the partial random walk with restart (Partial RWR) algorithm. The Partial RWR is integrated into the Fast-Higashi framework. When calculating the decomposed factors for frontal slices of the tensor X(c), the corresponding slices would be imputed through Partial RWR first. The imputation process includes the calculation of local affinity, standard RWR algorithm, and information propagation using both sliced tensor and the RWR imputed affinity matrix.
Fast-Higashi achieves accurate and fast embedding of scHi-C data
We systematically evaluated the performance of Fast-Higashi for generating embedding vectors for various scHi-C datasets. To demonstrate the effectiveness of Fast-Higashi for delineating subtle cell-to-cell variability of 3D genome features, we applied it to three recent scHi-C datasets of complex tissues at 500Kb resolution. These datasets include the (Tan et al., 2021) dataset, the (Lee et al., 2019) dataset, and the (Liu et al., 2021) dataset (see STAR Methods for data processing). We evaluated the performance of Fast-Higashi and baselines under various evaluation metrics including: (1) the modularity score, (2) the adjusted rand index (ARI) and adjusted mutual information (AMI) scores, and (3) the Micro-F1 and Macro-F1 scores (see STAR Methods for details). We made direct comparisons of Fast-Higashi against three scHi-C embedding methods, including two very recently developed scHi-C embedding methods, Higashi (Zhang et al., 2022) and 3DVI (Zheng et al., 2021) as well as scHiCluster (Zhou et al., 2019) (which has been updated recently). It has been suggested that the updated scHiCluster can distinguish neuron subtypes better on the Lee et al. dataset while the earlier version of scHiCluster cannot achieve (Lee et al., 2019; Zhang et al., 2022).
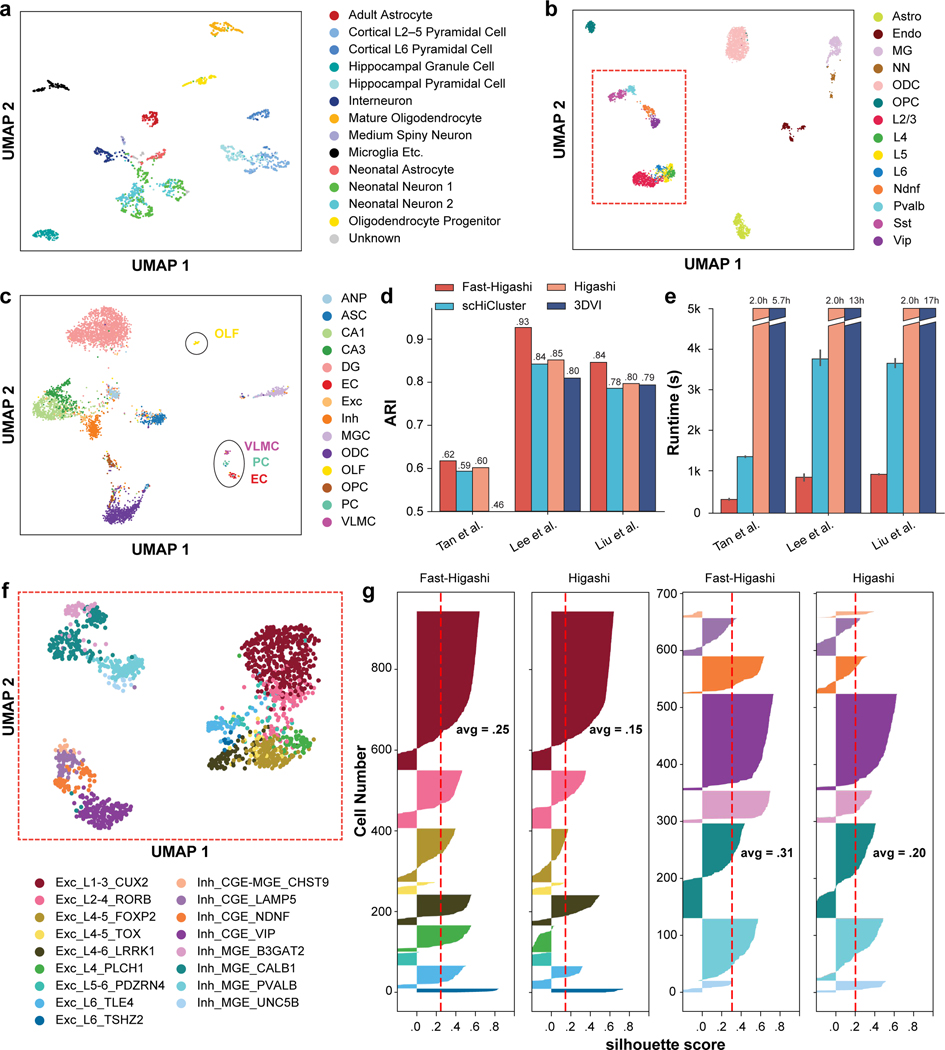
As shown in Fig. 2a-c, the UMAP visualizations of the Fast-Higashi embeddings on these three datasets show clear clustering patterns consistently corresponding to the annotated cell types. Notably, we observed several major advantages of the Fast-Higashi embeddings compared to other methods. On the Lee et al. dataset of the human prefrontal cortex, based on the UMAP visualization of the embedding results, Fast-Higashi can resolve the differences among neuron subtypes clearly, separating all Pvalb, Sst, Vip, Ndnf, L2–3, L4, L5, and L6 neuron subtypes and showing more detailed structures within some cell types (Fig. 2b, marked in red box). To the best of our knowledge, this is the first time that excitatory neurons of different layers can be separated by using chromatin interaction information only. As a comparison (Fig. S1), the embeddings from Higashi and scHiCluster, while separating most of the neuron subtypes, have much weaker capability to distinguish excitatory neurons of different layers. The embeddings of 3DVI separate neurons into two categories, excitatory neurons and inhibitory neurons, lacking the ability for more refined cell type delineation. Moreover, the embeddings from both scHiCluster and 3DVI show obvious batch effects (Fig. S1).
Figure 2: Evaluation of Fast-Higashi for generating embeddings for scHi-C data.
a. UMAP visualization of the Fast-Higashi embeddings for the (Tan et al., 2021) dataset (GEO:GSE162511). See also Fig. S7. b. UMAP visualization of the Fast-Higashi embeddings for the (Lee et al., 2019) dataset (GEO:GSE130711). Cells in the red box are neuron cells. c. UMAP visualization of the Fast-Higashi embeddings for the (Liu et al., 2021) dataset (GEO:GSE156683). See also Fig. S2. d. Quantitative evaluation based on adjusted rand index (ARI) scores of the Louvain clustering results for each scHi-C embedding methods. See also Fig. S3. e. Runtime of different embedding methods across different datasets. f. UMAP visualization of the Fast-Higashi embeddings for the neuron cells in the Lee et al. dataset (cells in the red box in (b)). Cell type information is from (Luo et al., 2022). See also Fig. S1. g. Quality of the embeddings for the neuron cells in the Lee et al. dataset measured as silhouette coefficients for neuron subtypes. See also Fig. S4. All cell type abbreviations are consistent with the data source.
On the Liu et al. dataset of the mouse hippocampus, we again observed Fast-Higashi’s clear advantage over other methods. Fast-Higashi is the only method that can separate CA3 cells from CA1 cells, and successfully identify small clusters of VLMC, PC, and EC cells, while all other methods (except Higashi) cannot (Fig. 2c and Fig. S2).
All these observations are supported by our quantitative results, where Fast-Higashi consistently achieves the highest or second best scores across all metrics of all three datasets (Fig. 2d and Fig. S3). We repeated the evaluation on two sci-Hi-C datasets with relatively lower coverage and/or a smaller number of cells and reached similar conclusions (see STAR Methods for details).
In addition, we assessed the runtime of all scHi-C embedding methods. As shown in Fig. 2e, Fast-Higashi is much faster than all existing scHi-C embedding methods, especially the neural-network based methods (>40x faster than 3DVI and >9x faster than Higashi on the scHi-C datasets used for benchmarking). The runtime of Higashi mostly depends on its number of training epochs and is almost constant for datasets with more than 1000 cells.
Together, these results demonstrate that Fast-Higashi achieves the state-of-the-art performance for scHi-C embeddings with an ultrafast computational efficiency.
Fast-Higashi enables the identification of rare cell types in complex tissues
In addition to the global evaluation on how well the Fast-Higashi embeddings correspond to the annotated cell types from the original datasets, we also sought to demonstrate that Fast-Higashi has unique capabilities to further improve the annotation of rare cell types in complex tissues.
We first visualized the Fast-Higashi embeddings of the neuron cells in the (Lee et al., 2019) dataset using the UMAP projection (Fig. 2f). We obtained a new cell type annotation from (Luo et al., 2022), where the methylation profiles of the Lee et al. dataset were jointly embedded with single-cell methylation profiles from snmC-seq, snmCT-seq, and snmC2T-seq on human prefrontal cortex to annotate cell types. This joint analysis allows the characterization of neuron subtypes in the Lee et al. dataset at a much more refined resolution. Based on the UMAP visualization, we observed that the smaller clusters within the same cell type (red box in Fig. 2b) can in fact be delineated into more detailed cell subtypes. For instance, the two finer clusters of Sst in Fig. 2b correspond to the CALB1 and B3GAT2 cell subtypes in Fig. 2f. By comparing with the UMAP visualization of other embedding methods (Fig. S1 last row), we found that Fast-Higashi has the best ability to distinguish neuron subtypes, especially for the excitatory neurons. For inhibitory neurons, both Fast-Higashi and Higashi perform well and are the only two methods that can identify a smaller cluster of the UNC5B type (Fig. S1 last row). To further support these observations, we also evaluated each method’s ability of separating neuron subtypes on the Lee et al. dataset through silhouette score analysis (Fig. 2g and Fig. S4). Consistent with our observations based on the UMAP visualization, Fast-Higashi achieves the highest average silhouette score on the neuron subtypes.
We next systematically evaluated the robustness of Fast-Higashi’s ability of identifying rare cell types, by simulating scHi-C dataset with different coverage. Specifically, we downsampled the contact pairs from the Lee et al. dataset to 10% to 50% of the original dataset and applied Fast-Higashi and Higashi, two models with strongest performance on these simulated datasets. As demonstrated by the UMAP visualizations in Fig. S5, Fast-Higashi is more robust to the coverage of the dataset than Higashi, showing clearer clustering patterns that correspond to the cell types. The quantitative evaluation (Fig. S6) further supports this observation.
Additionally, we applied Fast-Higashi to the Tan et al. dataset of the developing mouse brain. Fast-Higashi is able to separate most of the cell types marked from the data source (Fig. 2a). As compared to the existing scHi-C embedding methods, Fast-Higashi preserves the local trajectory of the time course better (Fig. S7). In addition, we found two small clusters within the interneuron cell types and two separate clusters of neonatal neurons that do not correspond to the original Neonatal Neuron 1/2 labels from the dataset. These patterns are absent from the embeddings of other existing embedding methods except Higashi (Fig. S7). With the observation on the Lee et al. dataset that the small clusters within a cell type could reflect more refined subtypes, we believe that this could also be the case for the Tan et al. dataset. Detailed results will be discussed in a later section.
Taken together, these results confirm the unique capability of Fast-Higashi for identifying rare cell types or subtypes based on scHi-C data only.
Fast-Higashi effectively captures cell-type specific 3D genome structures
We then sought to demonstrate that the meta-interactions captured by Fast-Higashi reflect the cell type-specific 3D genome features and can be used to interpret the generated embeddings. As a proof-of-principle, we first analyzed the meta-interactions of chromosome 1 for the (Kim et al., 2020) dataset. In this section, we mainly focus on the 4 cell types with enough cell numbers, including GM12878, H1ESC, HAP1, and HFFc6. We first visualized the single cell loadings of these meta-interactions (chromosome-specific embeddings). As shown in Fig. 3a, each cell type has its preferred set of meta-interactions. Note that due to the utilization of SVD (singular value decomposition) for solving the meta-interaction during the optimization process (see STAR Methods), the first meta-interaction (sorted by the singular value during the SVD process) would correspond to the general contact patterns of all cells within the scHi-C data. This is consistent with the observation that for all cells, their loadings of the first meta-interaction (marked as “1st MI” in Fig. 3a) are large and similar across all cell types. For all other meta-interactions, they represent how the cell type-specific 3D genome features deviate from the population interaction patterns. To validate this, we aggregated the cell type-specific meta-interactions weighted by the average single cell loadings and made comparisons to the differential contact patterns calculated from the bulk Hi-C. Specifically, we first calculated a “common bulk Hi-C” as the average of the bulk Hi-C of the same four cell types. Then for each cell type we calculated the differential contact patterns as the difference between the bulk Hi-C of that cell type and the “common bulk Hi-C”. As shown in Fig. 3b, the differential contact patterns calculated using the bulk Hi-C share similar patterns to the aggregated cell type-specific meta-interactions. This observation is consistent with the phenomenon that the Spearman correlations between cell type specific meta-interactions and the corresponding differential contact map is the highest (Fig. 3c).
Figure 3: Analysis of the chromatin meta-interactions generated by Fast-Higashi.
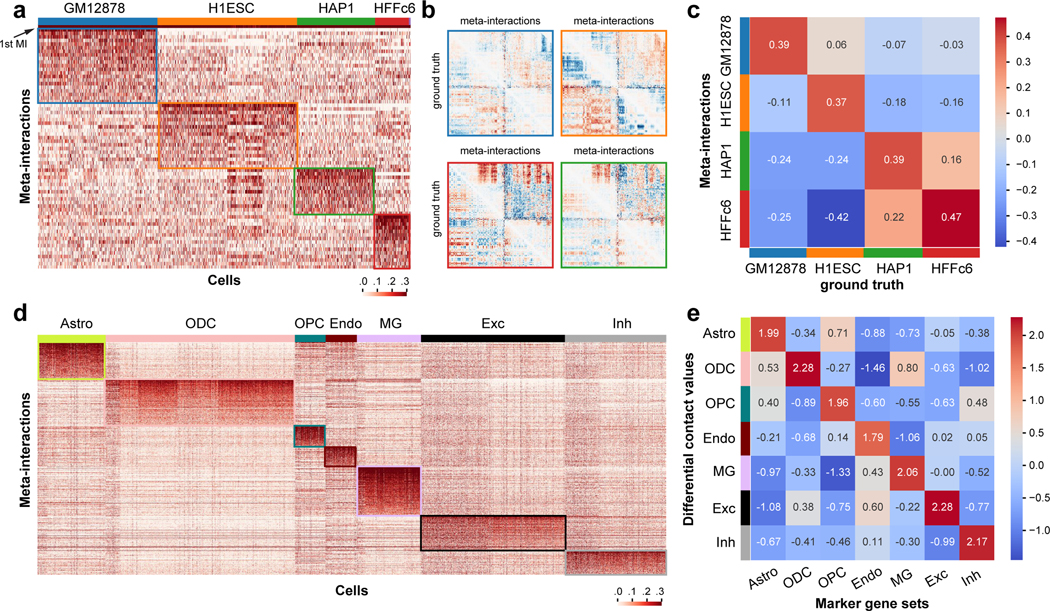
a. Heatmap of the single cell loadings for each meta-interaction of chromosome 1 for the (Kim et al., 2020) dataset. b. Visualization of the differential contact maps generated based on meta-interactions and those generated based on bulk Hi-C (marked with “ground truth”). Border color matches the cell type color in (a). c. Spearman correlation between differential contact maps generated based on meta-interactions and those generated based on bulk Hi-C (marked with “ground truth”). d. Heatmap of the single cell loadings for each meta-interaction of the whole genome for the (Lee et al., 2019) dataset. e. Mean differential contact values of the lists of cell type marker genes averaged for each cell type. The mean differential contact values are calculated using the corresponding meta-interactions as the summation of values for each bin in the meta-interaction contact map. For each cell type, the top 200 marker genes were identified using Seurat (Stuart et al., 2019).
Next, we analyzed the meta-interactions of a scHi-C dataset on complex tissues, i.e., the (Lee et al., 2019) dataset. Fig. 3d shows the single cell loadings of the whole genome meta-interactions for this dataset. We again can observe a clear preference of meta-interaction sets for different cell types. To confirm that these cell type-specific meta-interactions manifest cell type-specific 3D genome features that are functionally relevant, we calculated the differential contact values for each bin given a specific set of meta-interactions. We first aggregated the meta-interactions for a specific cell type by the average single cell loadings, leading to one meta-interaction map of size N × N for each chromosome of one cell type. We then calculated the differential contact values by summing over the column of this meta-interaction map, representing the overall deviation of a genomic bin from its population-level pattern. By comparing to the marker genes called from scRNA-seq (Hawrylycz et al., 2012; Hodge et al., 2019), we found that there is a strong positive correlation between the differential contact values and the expressions of the marker genes (Fig. 3e).
These results demonstrate that the meta-interactions from Fast-Higashi effectively capture the cell type-specific 3D genome features that are relevant to cell type-specific gene regulation. The meta-interactions from Fast-Higashi can be used to associate the embedding results to a specific region of the scHi-C contact map, pointing to further investigation of differential 3D chromatin contact patterns of various cell types in complex tissues.
Fast-Higashi unveils single-cell 3D genome features in developing mouse brain
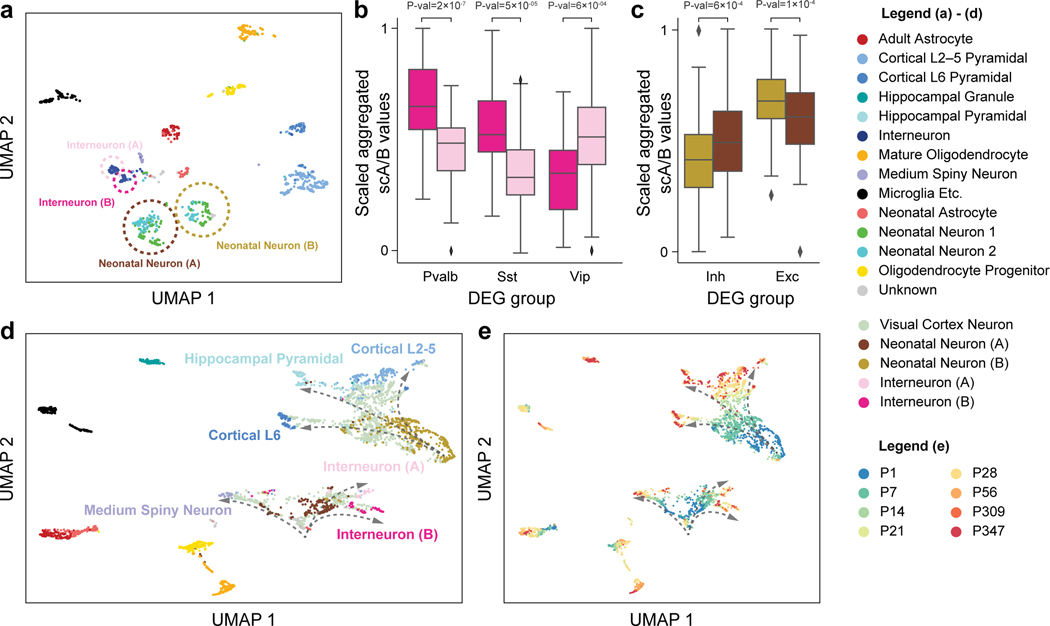
As discussed above, we applied Fast-Higashi to a scHi-C dataset of developing mouse brain, i.e., the (Tan et al., 2021) dataset, and observed local clusters of cells within the two annotated cell types in the UMAP visualization (Fig. 2a). We postulated that these local clusters could potentially be subtypes not captured by other scHi-C embedding methods as well as the original data source. To demonstrate that Fast-Higashi can delineate finer scale cell types and uncover developmental trajectories, we first obtained Fast-Higashi embeddings for all cortex cells and annotated the observed small clusters as Interneuron (A), Interneuron (B), Neonatal Neuron (A), and Neonatal Neuron (B) (Fig. 4a).
Figure 4: Application of Fast-Higashi to the (Tan et al., 2021) scHi-C dataset of the mouse developing brain for more detailed identification of cell types and developmental trajectories.
a. UMAP visualization of the Fast-Higashi embeddings for the cortex cells in the Tan et al. dataset (GEO:GSE162511). Cell subtypes identified by Fast-Higashi are highlighted with circles and texts. b. Distribution of the scaled aggregated single-cell A/B values for interneuron (A) and interneuron (B) subtypes identified by Fast-Higashi. For better visualization, the aggregated single-cell A/B values are linearly scaled to the range from 0 to 1 for each differentially expressed gene (DEG) group. c. Distribution of the scaled aggregated single-cell A/B values for Neonatal Neuron (A) and Neonatal Neuron (B) subtypes identified by Fast-Higashi. The scaling is the same as in panel (b). d-e. UMAP visualization of the joint Fast-Higashi embeddings of visual cortex, cortex, and hippocampus scHi-C datasets in (Tan et al., 2021) (GEO:GSE162511). The potential developmental trajectories from neonatal neurons to fully mature neurons are marked by dashed arrows. Note that here (d) is colored with cell type labels and (e) is colored with ages of the mouse.
We sought to confirm our refined cell type labels of neonatal neurons and interneurons (highlighted with circles in Fig. 4a) by scA/B values in the gene bodies of marker genes. The marker genes were obtained from (Tan et al., 2021), which were calculated using Seurat (Stuart et al., 2019) on the MALBACDT of the developing mouse brain. We quantified the A/B compartments of a set of differentially expressed genes (DEGs) by the aggregated scA/B value (see STAR Methods). Previous studies reported the existence of global correlations between the scA/B values and the gene expression level within the same cell type (Su et al., 2020) and across different cell types in complex tissues (Tan et al., 2021; Zhang et al., 2022). In particular, genes with higher scA/B values are more likely to be highly expressed. We found that the aggregated scA/B value of the marker genes of Pvalb and Sst is significantly higher in Interneuron (B) as compared to Interneuron (A) and the marker genes of Vip show the opposite trend (Fig. 4b). These results suggest that the DEGs of Pvalb and Sst neurons are expressed at a higher level in Interneuron (B) than in Interneuron (A) and that the DEGs of Vip neurons exhibit the opposite behavior, indicating that Interneuron (A) and (B) are more likely to be Vip and Pvalb/Sst, respectively. Similarly, the aggregated scA/B value of the marker genes of neonatal inhibitory neurons is higher in Neonatal Neuron (A) and the aggregated scA/B value of the marker genes of neonatal excitatory neurons is higher in Neonatal Neuron (B) (Fig. 4c), indicating the Neonatal Neuron (A) and (B) are neonatal inhibitory neurons and neonatal excitatory neurons, respectively. Meanwhile, the aggregated scA/B values of neonatal excitatory neurons do not show different distributions (P>0.2) between the Neonatal Neuron 1 and 2 in the original annotations from (Tan et al., 2021), confirming that our annotations are indeed a refinement. Collectively, we again demonstrate the advantage of Fast-Higashi in identifying finer cell types.
To further validate our refined subtype annotation, we jointly embed the cortex and hippocampus dataset of Tan et al. with another dataset of the visual cortex of developing mouse brain (Tan et al., 2021). The cortex and hippocampus dataset consists of cells from mice at 6 ages: P1, P7, P28, P56, P309, and P347, while the visual cortex dataset includes cells of mice at ages P7, P14, P21, and P28, which covers the critical development period from P7 to P28 that was missed in the original dataset. When we applied Fast-Higashi to the union of these datasets, it recovered the complex developmental trajectories of inhibitory neurons and excitatory neurons. Specifically, in the UMAP visualization (Fig. 4d), a portion of the cells from the visual cortex dataset (light green) connect Neonatal Neuron (A) (Inhibitory neonatal neurons) to the 3 mature inhibitory neuronal types: Interneuron (A) (Vip), Interneuron (B) (Pvalb/Sst), and Medium Spiny Neuron. Similarly, a different set of visual cortex cells connect Neonatal Neuron (B) (Excitatory neonatal neuroins) to the multiple excitatory neuronal types: Cortical L2–5, Cortical L6, and Hippocampal Pyramidal. Since the Neonatal Neuron (A) and Neonatal Neuron (B) are primarily composed of P1/7 cells, and the 6 mature neuronal types consist of almost only P28 or older cells, placing the P14∼28 cells between P1/7 cells and P28+ cells is consistent with the developmental process. Moreover, along the inferred developmental branches (Fig. 4e (curved arrows)), cells are indeed ordered by the mouse ages, strongly supporting the ability of Fast-Higashi in recovering trajectory from scHi-C datasets. As a comparison, we included the results of scHiCluster (see Fig. S8). Although cells are ordered by mouse age in the embedding space of scHiCluster, we found that inhibitory neurons and excitatory neurons are not separated and scHiCluster cannot delineate two distinct developmental trajectories of inhibitory neurons and excitatory neurons.
In summary, using the (Tan et al., 2021) dataset, we have demonstrated the clear advantages of Fast-Higashi in unveiling finer cell types over existing methods as well as the unique ability of Fast-Higashi to characterize the cell-to-cell variability of 3D genome features along complex biological processes.
DISCUSSION
In this work, we developed Fast-Higashi, an ultrafast and interpretable framework for scHi-C data analysis. Our generalization from core-PARAFAC2 to Fast-Higashi not only leverages its strong scalability, but also enables joint and interpretable modeling of meta-interactions and cell embeddings. The development and incorporation of the Partial RWR algorithm further improve the performance of Fast-Higashi with negligible impact to the scalability. Evaluations of Fast-Higashi using a wide range of real scHi-C datasets have demonstrated its effectiveness and scalability for inferring informative cell embeddings, enabling the delineation of rare cell types and the reconstruction of developmental trajectories. Besides, as a proof-of-principle, we identified cell type-specific meta-interactions that are related to cell type-specific gene transcription. Together, we have demonstrated the effectiveness, scalability, and interpretability of our method Fast-Higashi.
By using its predecessor Higashi (Zhang et al., 2022) as a direct baseline to compare, we demonstrated the superior scalability of Fast-Higashi to data size, robustness to data quality, and effectiveness in generating informative cell embeddings that facilitate rare cell type identification. Moreover, the unique scheme of meta-interactions allows direct analysis of cell type-specific 3D genome features that correspond to the embedding results. Even though Fast-Higashi has superior effectiveness and interpretability for scHi-C analysis, we note that Fast-Higashi is not developed to replace Higashi (Zhang et al., 2022). For instance, Fast-Higashi uses a random-walk-with-restart based method for imputing the sparse contact maps, which is efficient but also has limited imputation power. As demonstrated in (Zhang et al., 2022), the accurate imputation empowered by hypergraph representation learning is key to unveiling some important 3D genome features related to cell type-specific gene regulation. On the other hand, the underlying relationship between the tensor representation and the hypergraph representation of scHi-C data makes Fast-Higashi in some way a quasi-linear version of Higashi and can thus be used to initialize the Higashi model. As a proof-of-principle, we found that the Fast-Higashi initialized Higashi model can indeed achieve even better performance than any of these two methods (Fig. S9). As one of the future directions, we plan to integrate Fast-Higashi into the Higashi software suite, providing a more flexible and comprehensive framework for scHi-C analysis.
Fast-Higashi can be further enhanced by incorporating multimodal single-cell omics data, such as single-cell RNA-seq data and single-cell methylome data. Jointly modeling of co-assayed scHi-C data and other multimodal data has the potential to further improve cell embeddings and to establish connections between different modalities. Fast-Higashi may also be applied to study DNA-RNA interactions in single cells (Takei et al., 2021).
The continued development of scHi-C related technologies is expected to expand rapidly in the coming years. Fast-Higashi has the potential to become an essential method in the toolbox of single-cell 3D epigenomic analysis to greatly enhance the integrative investigation of 3D genome organization, genome functions, and cellular phenotypes at single-cell resolution for a wide range of biological applications.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact:
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Jian Ma (jianma@cs.cmu.edu)
Materials Availability:
This study did not generate new materials or reagents.
Data and Code Availability:
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
All original code has been deposited at https://github.com/ma-compbio/Fast-Higashi, and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and virus strains | ||
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Critical commercial assays | ||
| Deposited data | ||
| sn-m3c-seq dataset of human prefrontal cortex | Lee et al., 2019 | GEO:GSE130711 |
| sn-m3c-seq dataset of mouse hippocampus | Liu et al., 2021 | GEO:GSE156683 |
| Dip-C dataset of developing mouse brain | Tan et al., 2021 | GEO:GSE162511 |
| sci-Hi-C dataset of 4 cell lines (GM12878, HAP1, HeLa, K562) | Ramani et al., 2017 | GEO:GSE84920 |
| sci-Hi-C dataset of 5 cell lines (GM12878, H1ESC, HAP1, HFFc6, IMR90) | Kim et al., 2020 | 4DN Data Portal: 4DNES4D5MWEZ, 4DNESUE2NSGS, 4DNESIKGI39T, 4DNES1BK1RMQ, and 4DNESTVIP977 |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and algorithms | ||
| Fast-Higashi | This paper | DOI: 10.5281/zenodo.7023632 |
| Other | ||
METHOD DETAILS
The design of Fast-Higashi is based on a tensor decomposition model, called core-PARAFAC2 (Van Benthem et al., 2020), and is generalized to simultaneously model multiple 3-way tensors that share only a single dimension (single cells). The core-PARAFAC2 model is usually used to analyze multimodal data where observations may not be aligned along one of its modes. A concrete example in other applications is the electronic health records that contain multimodal phenotypes of multiple patients at various time points. Because a particular disease stage may begin at different time points and may have varying lengths across patients, a critical difficulty is that it is hard to align observations of different patients along the temporal dimension. Similarly, in scHi-C contact maps, TAD-like structures usually have varying sizes and boundaries in different genomic bins, obscuring the direct alignment of genomic bins. Therefore, we have developed Fast-Higashi based on core-PARAFAC2 to address this issue. In the following sections, we first introduce how Fast-Higashi performs tensor decomposition on the scHi-C datasets assuming that contact maps of only one chromosome are present. We discuss next how we generalize to multi-chromosome cases. We then derive the optimization procedure and introduce the partial random walk with restart (Partial RWR) module to address the sparseness of single-cell Hi-C dataset efficiently.
Problem formulation of the Fast-Higashi model
For a scHi-C dataset, let denote the set of chromosomes. We formulate a collection of scHi-C contact maps of chromosome as a 3-way tensor, denoted by , where Nc is the number of genomic loci (also denoted as genomic bins) in chromosome c, Lc is the number of features at each bin, and M is the number of cells in this dataset. In principle, Lc need not be equal to Nc because, for example, we may use different resolutions for genomic bins along the two dimensions and even include additional epigenomic features. However, for convenience, here we only consider contact maps and use the same resolution for both dimensions. We assume that follows a 3-way core-PARAFAC2 model which includes: (1) a 3-way tensor of meta-interactions; (2) a matrix of bin weights indicating importance for each bin in every meta-interaction; (3) a chromosome-specific transformation matrix ; and (4) an orthogonal matrix that contains cell embeddings and is shared across all chromosomes, where and R are hyperparameters, representing the dimensions of the chromosome-specific cell embedding and shared cell embedding.
We first introduce the cell-wise form of our model. As shown in Fig. 1a, the -th slice of along the last dimension, denoted by , is the -th single-cell contact map, and we assume that it can be approximated by the weighted sum of meta-interactions:
| (1) |
where is a matrix of i.i.d. Gaussian noises with zero mean and arbitrary variance. Since V is the cell embedding matrix shared across all chromosomes, right multiplying V by the chromosome-specific transformation matrix projects V to another space, which we term the chromosome-specific embedding space. The chromosome-specific embeddings directly quantify the contribution of each meta-interaction to single-cell contact maps, i.e., the overall weight of the k-th meta-interaction in cell is equal to . Additionally, we also assume that bins in a meta-interaction may have different weights, i.e., the weight of bin i in the k-th meta-interaction is . Together, the weight of the k-th meta-interaction at the i-th bin in cell is equal to the product of (1) the meta-interaction weight in the chromosome-specific embedding of cell and (2) the bin weight in the bin weight matrix, i.e., .
To simplify the optimization problem, we introduce an alternative bin-wise form of this model (Kiers et al., 1999). Let be the i-th slice along the first dimension of , i.e., the features of the i-th bin across all cells, and we use similar notations for other tensors. We assume that has the following decomposition:
| (2) |
where is a noise matrix. Since the noise is assumed to follow i.i.d. Gaussian distributions, the optimal set of parameters is the solution to the following optimization problem:
| (3) |
Additional constraints for uniqueness
Now we introduce additional constraints to address the uniqueness issue of Eqn. 3 and to improve the ability of Fast-Higashi to capture critical topological patterns in single-cell Hi-C contact maps.
Without loss of generality, we show the uniqueness issue on a dataset with only one chromosome, denoted by c. Let be one optimal solution to Eqn. 3. Then for any and is also an optimal solution to Eqn. 3, implying the non-uniqueness. To address this, we impose constraints on the Gram matrices of that,
| (4) |
where is constant over i. This is equivalent to requiring that can be transformed to each other by left multiplying an orthogonal matrix, i.e., a rotation along the feature dimension. Note that is not determined a priori and is optimized during inference. Similarly, for any , solution is also equivalent to , implying the non-uniqueness. To address this, we require V to be orthogonal. The scaling of tensors , , and also leads to non-uniqueness and is addressed in Eqn. 11.
These constraints enable Fast-Higashi to be less prune to noise and allow Fast-Higashi capture critical topological patterns from single-cell Hi-C contact maps. A concrete example is the TAD-like structure where the number of interactions within this region is expected to be higher but also non-uniform, in that, the near-diagonal elements usually include more interactions. The characteristics of a TAD-like structure cause the boundaries of this TAD-like structure to be the same for all bins in it but cause the location of the peak to vary across these bins. This indicates that it is impossible to directly find a pattern that fits more than one bin in this TAD-like structure. However, since we allow bin-specific rotations along the feature dimension, these rotations potentially can keep the boundary unchanged and redistribute the contacts among the features of each bin, allowing the shift of the peak. Matrices A(c) are designed to capture the other bin-to-bin variability in scHi-C datasets. For example, bins usually have varying accessibility, which leads to different row sums in single-cell contact maps, and even in bins from one TAD-like structure. This variability is expected to be biologically meaningful and cannot be corrected by normalization. In Fast-Higashi, the bin weight matrix will capture this variability. In addition, a single bin may also show cell type-specific accessibility, which is expected to be reflected as variation across meta-interactions in Fast-Higashi. In Fast-Higashi, these bin-specific and cell type-specific characteristics will be captured in the bin weight matrix so that (1) any two bins may have different scaling factors in one meta-interaction and (2) one bin may have different scaling factors in any two meta-interactions. Therefore, these constraints retain the ability of capturing critical structures but also reduce the parameter spaces of Fast-Higashi, making it more robust to tolerate noise.
Efficient parameter inference in Fast-Higashi
Here we show key steps in the derivation of a coordinate descent optimization procedure (summarized in Algorithm 1) for the optimization problem in Eqn. 3. We also introduce necessary tricks for a GPU-compatible algorithm.
Reformulation of the optimization problem
To simplify the optimization, we express as where is orthogonal, and . Both and are model parameters and are optimized during inference. The relation between in Eqn. 4 and is . With this reformulation, the optimization problem in Eqn. 3 can be rewritten as
| (5) |
Derivation for the optimal solution of and
Now we derive the optimal value of given the rest parameters. For the sake of simplicity, let be and the optimization of can be simplified as follows:
| (6) |
| (7) |
where the second to last equality is true because holds for any orthogonal matrix U. Since is orthogonal, the solution to this optimization has a closed form. Specifically, let the SVD of be , and the optimal solution of is . Note that, the optimal value of different frontal slices of can be solved in parallel.
The closed form of can be derived similarly. Let , and then
| (8) |
which implies where is the SVD of .
Derivation for the optimal solution of , , and
Next, we derive the optimization of , and . Since and V are orthogonal, we can simplify the optimization in Eqn. 5 to
| (9) |
After we stack the -by-R matrices to create a 3-way tensor , the optimization becomes:
| (10) |
which is exactly the PARAFAC model and , , and can be solved by alternative least square (ALS) (Bro, 1997). To guarantee the uniqueness of the solution, we include an additional constraint that controls the scaling of the three factors:
| (11) |
Mini-batch optimization
To improve the scalability of the method, we implemented the optimization of U(c) in a batch-wise manner. For a typical human scHi-C dataset of 10,000 cells, if we set the resolution to 500Kb, the 3-way dense tensor of chromosome 1 that is ready for tensor operations takes up to 6GB GPU RAM, which leaves inadequate RAM for subsequent computations on GPU. To utilize the computation power of GPU, we divide and into batches along the first dimension, and update all the frontal slices of from this batch in parallel using GPU. To minimize the data transfer amount between CPU and GPU, we compute the for the optimization of V in Eqn. 8 before we remove the copy of this batch from GPU. Since is much smaller than Nc in practice, the entire tensor fits in the GPU. Besides, we store these 3-way tensors in the COO format and transfer each batch of slices into GPU in the form of sparse COO tensors, which minimizes the data transfer as well as CPU memory usage. Hence, our method is optimized for GPU with limited RAM and data transfer rate to utilize its computation power and accelerate the overall running time.
Algorithm 1.
Optimization procedure for Fast-Higashi
| 1: | for chromosome c do |
| 2: | Initialize to be full of one |
| 3: | Initialize to be the identity matrix |
| 4: | Flatten the first two dimensions of , denote its right singular vectors by |
| 5: | end for |
| 6: | Concatenate all along the rank dimension, and initialize V as its top R left singular vectors |
| 7: | Initialize as for every chromosome c |
| 8: | for do |
| 9: | Update the value of by its closed form for each chromosome c |
| 10: | Update the value of V by its closed form |
| 11: | Update , , by alternative least square (ALS) until convergence for chromosome c |
| 12: | end for |
Initialization of the Fast-Higashi model
Here we provide efficient initialization of model parameters based on their interpretations (Algorithm 1). We initialize the matrix to be full of one and the square matrix to be the identity matrix, for each chromosome. For chromosome c, we find the SVD of the single-cell contact maps of chromosome c and keep the top right singular vectors which are the initial cell embeddings of chromosome c. To aggregate information from multiple chromosomes, we concatenate the initial cell embeddings from all chromosomes and find its SVD. We initialize the meta embedding V to be one of the orthogonal matrix and ’s to contain the rest components in the SVD.
Embedded partial random walk with restart (Partial RWR)
To mitigate the sparseness of the scHi-C contact maps, we sought to incorporate the random walk with restart (RWR) data imputation method (Zhou et al., 2019) into the Fast-Higashi framework. However, direct utilization of RWR before the tensor decomposition process is not desirable. The RWR imputed contact maps are usually much denser than the original contact map, leading to much higher memory consumption for storing the results and lower computational efficiency for transforming data format between sparse matrices to dense tensors as well as data transferring between GPU and CPU. Our solution is to integrate the RWR process during the optimization process of tensor decomposition and compute the RWR imputation batch by batch. The challenge for this design is that, as mentioned in the above section, the batch of the tensor decomposition optimization process is defined at the frontal slice of the tensor (Eqn. 3), i.e., the genomic bins, while the normal RWR requires the input of a complete graph adjacency matrix. To utilize RWR in our framework, here we propose the partial random walk with restart (Partial RWR) algorithm. The procedures of this algorithm are shown in Fig. 1b, which consists of the following steps: For simplicity, in this section, we use to represent the tensor representation of scHi-C contact maps of one chromosome. First, we fetch a small batch of the tensor along the first dimension, where bs represents the batch size. Then, based on this small batch of tensor, we calculate the local affinity matrix of bins within this batch for each cell based on dot-product similarity:
| (12) |
After that, the standard RWR algorithm is applied to these local affinity matrices:
| (13) |
where , and is the restart probability in the RWR algorithm. We denote the converged results of the RWR algorithm as and use it as the weight to propagate the information from the original batch of the tensor
| (14) |
Finally, we use as the imputed results and pass it to the tensor decomposition optimization procedure. Our analysis showed that partial RWR can approximate the imputation of standard RWR well even with small batch sizes (see later section for details. In this work, we use batch size 64 to keep the balance between accuracy and computational efficiency.
Data processing
We used several publicly available single-cell Hi-C datasets in this work. We refer to them as (Lee et al., 2019) (GEO: GSE130711), (Liu et al., 2021) (GEO: GSE156683), (Tan et al., 2021) (GEO: GSE162511), (Ramani et al., 2017) (GEO: GSE84920), (Kim et al., 2020) (4DN Data Portal: 4DNES4D5MWEZ, 4DNESUE2NSGS, 4DNESIKGI39T, 4DNES1BK1RMQ, and 4DNESTVIP977).
For all datasets except the Kim et al. dataset, we downloaded the contact pairs file from the corresponding GEO repository and transformed them into sparse contact maps at a given resolution (1Mb for the Ramani et al. dataset, 500Kb for the Lee et al., Liu et al., and Tan et al. datasets). For the Kim et al. dataset, we downloaded the FASTQ files from 4DN data portal and used the recommended processing pipeline (https://github.com/VRam142/combinatorialHiC).
Benchmarking scHi-C embedding methods
In this work, we mainly compared Fast-Higashi against three existing scHi-C embedding methods: Higashi (Zhang et al., 2022), scHiCluster (Zhou et al., 2019), and 3DVI (Zheng et al., 2021) in terms of the quality of the generated embeddings and the runtime. We kept the embedding dimensions as the recommended ones for each method. The default hyper-parameters of Fast-Higashi sets R as 64, and rc as 0.6Nc. But due to the orthogonal property of V, one can always set R as a large enough number, and then use only the top-k dimensions. The final dimension number k can be determined using methods developed for selecting the number of principal components for scRNA-seq analysis (Hao et al., 2021). For methods that allow selecting the maximum genomic distance to be considered, we set it to be 100Mb for all methods. We evaluated the embeddings generated by different methods under various evaluation metrics including: (1) Modularity score between the generated embeddings and the reference cell type label, (2) Adjusted rand index (ARI) and adjusted mutual information (AMI) score between the louvain clustering results and reference cell type label. Because the embeddings from different methods may reach the best clustering results at different combinations of parameters of Louvain clustering, we did a grid search for the number of neighbors and resolution parameters of the Louvain clustering for each method. The top 5 best clustering results for each method were kept and averaged as the final results. (3) We trained a logistic regression model using 10% of the cells and predicted the cell type for the rest 90% of cells. The Micro-F1 and Macro-F1 scores between the predicted cell type and reference ones were used to quantify the performance.
For the runtime analysis, all methods require different input formats and methods including 3DVI and Higashi can choose to only generate embeddings skipping the process of imputing sparse contact maps. To make a fair comparison, the runtime of all methods was calculated without the time of data processing, including transforming the scHi-C data into the format of a hypergraph in Higashi and reformatting the sparse contact maps into bands in 3DVI. For 3DVI and Higashi, we turned off the imputation function in the program and only used them to generate embeddings. For all methods, we added multiprocessing when possible even the multiprocessing was not originally implemented in some of the methods. Specifically, we parallelized the linear convolution and the random walk with restart algorithm of scHiCluster across all cells. We also parallelized 3DVI across different chromosomes, allowing the program to make full utilization of the GPUs. All methods were tested on a Linux machine with 1 NVIDIA RTX 2080 Ti GPU card, a 16-core Intel Xeon Silver 4110 CPU, and 252GB memory. All methods were set to use GPU when supported.
Aggregated single-cell A/B value
We developed the aggregated single-cell A/B value to collectively quantify the chromatin conformation at multiple loci in one cell. We calculated the scA/B value of every 500Kb genomic locus in single cells following the method proposed in (Tan et al., 2021). We defined the scA/B value of one gene as the average of the scA/B values of the genomic loci spanned by that gene. Although Higashi software includes an algorithm to to calculate scA/B values based on its embeddings and imputations, to avoid potential analysis bias, we instead used the more orthogonal method from (Tan et al., 2021). It is worth noting that in/Volumes/GoogleDrive/My Drive/mywork/Ruochi.FastHigashi/CellSystems-0830/latex/refs.bib (Tan et al., 2021), by using the calculated scA/B values as embeddings, the observed refined clustering results in Fast-Higashi embeddings do not exist. To summarize the behavior of a group of genes, we defined the aggregated scA/B value of these genes in one cell as the average scA/B value across all genes in that cell. To systematically assess the differential expression of a group of genes between two sets of cells, we examined the difference in the distribution of aggregated scA/B value of these genes between the two sets of cells by t-test.
Evaluation for Partial RWR
To evaluate how the Partial RWR algorithm would perform for sparse data imputation compared to the original RWR algorithm, we tested the impact of batch size on chromosome 1 of the (Lee et al., 2019) dataset at 500Kb resolution. Specifically, we applied Partial RWR of different batch sizes and RWR on the sparse contact maps and then calculated Pearson and Spearman correlation scores between the imputed results from the Partial RWR and the standard RWR. As expected, both similarity measurements increase with the batch size (Fig. S10). We also observed that even for a relatively small batch size, such as 32 or 64, the correlation score already surpasses 0.9.
To evaluate how the Partial RWR algorithm would improve the performance of Fast-Higashi under scHi-C datasets with various coverage, we compared the embeddings generated by Fast-Higashi with and without Partial RWR for the (Lee et al., 2019) dataset at 500Kb resolution with different downsample rate. As shown in Fig. S5 and Fig. S6, Partial RWR consistently improves the ability of Fast-Higashi to delineate cell types on complex tissues over all downsampling rate. The improvement is more profound when applying Fast-Higashi to a dataset with smaller coverage. Moreover, Fast-Higashi without Partial RWR can still outperform the original Higashi algorithm, further demonstrating the robustness of Fast-Higashi.
Evaluation on sci-Hi-C datasets
To further demonstrate that Fast-Higashi can work with scHi-C datasets with relatively lower coverage with a simpler cell type composition, we applied it to two sci-Hi-C datasets at 1Mb resolution: the (Ramani et al., 2017) dataset and the (Kim et al., 2020) dataset (Fig. S11). On these two relatively simpler datasets, all four embedding methods performed well based on the quantitative evaluation (Fig. S3). In terms of identifying cell types with a relatively small number of cells, Fast-Higashi and Higashi perform the best for the Ramani et al. dataset, where the GM12878 cells form into a small cluster. 3DVI performs the best on the Kim et al. dataset, where the IMR90 cells are clustered into a corner of the HFFc6 cell cluster.
In addition, we assessed the runtime of all scHi-C embedding methods on these two datasets. As shown in Fig. S12, Fast-Higashi is much faster than all existing scHi-C embedding methods.
QUANTIFICATION AND STATISTICAL ANALYSIS
The statistical tests were carried out using the SciPy package (version 1.5.3) in python.
Supplementary Material
Highlights.
Fast-Higashi models single-cell Hi-C data using tensor decomposition.
It is a highly efficient and interpretable method for single-cell Hi-C data analysis.
It delineates cell types and reconstructs biological trajectories.
It identifies cell type-specific 3D genome features based on single-cell Hi-C data.
Box 1. PROGRESS AND POTENTIAL.
Progress:
The emerging single-cell Hi-C (scHi-C) technologies provide us with an unprecedented opportunity to probe the 3D genome organization by detecting genome-wide chromatin interactions in individual cells. However, there are critical analysis challenges for scHi-C data. Existing computational methods for scHi-C data often cannot: (i) effectively infer informative cell embeddings for the delineation of rare cell types in complex tissues, (ii) directly identify important 3D chromatin features related to cell type-specific genome functions, and (iii) efficiently operate on large-scale datasets with limited memory resources.
Our proposed method Fast-Higashi improves the scHi-C analysis by addressing these three challenges directly. We propose a concept for single-cell 3D genome analysis, called chromatin “meta-interactions”, representing combinations of chromatin interactions that can serve as informative signatures to identify cell types. The key conceptual advance of Fast-Higashi is to jointly identify cell identities and chromatin meta-interactions, providing an effective and interpretable solution for scHi-C analysis. To achieve the goal, we leverage a tensor decomposition model called core-PARAFAC2 that can efficiently model tensors with drastically different sizes and effectively scale to scHi-C datasets with a large number of cells or at high resolutions.
Our extensive evaluations using the available scHi-C datasets have demonstrated the advantage of Fast-Higashi over existing methods, leading to improved delineation of rare cell types and better reconstruction of developmental trajectories. The inferred meta-interactions directly connect the embedding results to cell type-specific chromatin structures that are correlated with cell type-specific transcriptional activities.
Potential:
Fast-Higashi shows superior efficiency, effectiveness, and interpretability for scHi-C analysis compared to its predecessor Higashi, but Fast-Higashi is not developed to replace Higashi. Crucially, the underlying relationship between tensor representation (in Fast-Higashi) and the hypergraph representation (in Higashi) of scHi-C data allows Fast-Higashi to hot-initialize the Higashi model. As demonstrated in the paper, the integration of Fast-Higashi and Higashi can achieve even better performance. Moreover, Fast-Higashi can be extended to incorporate co-assayed scHi-C data and other multimodal data, with the potential to further improve cell embeddings and to establish connections between different modalities.
With the upcoming scHi-C datasets of larger number of cells on complex tissues, Fast-Higashi has the potential to become an essential method for large-scale single-cell 3D epigenomic studies. Our method provides a unique solution to the integrative analysis of 3D genome organization, genome functions, and cellular phenotypes at single-cell resolution for a wide range of biological applications.
ACKNOWLEDGEMENTS
This work was supported by the National Institutes of Health Common Fund 4D Nucleome Program grant UM1HG011593 (J.M.) and the National Institutes of Health grants R01HG007352 (J.M.) and R01HG012303 (J.M.). J.M. is additionally supported by a Guggenheim Fellowship from the John Simon Guggenheim Memorial Foundation.
Footnotes
DECLARATION OF INTERESTS
J.M. is on the Advisory Board of Cell Systems. The other authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bro R. (1997). PARAFAC. tutorial and applications. Chemometrics and Intelligent Laboratory Systems, 38(2):149–171. [Google Scholar]
- Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, and Ren B. (2012). Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature, 485(7398):376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hao Y, Hao S, Andersen-Nissen E, Mauck III WM, Zheng S, Butler A, Lee MJ, Wilk AJ, Darby C, Zager M, et al. (2021). Integrated analysis of multimodal single-cell data. Cell, 184(13):3573–3587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawrylycz MJ, Lein ES, Guillozet-Bongaarts AL, Shen EH, Ng L, Miller JA, Van De Lagemaat LN, Smith KA, Ebbert A, Riley ZL, et al. (2012). An anatomically comprehensive atlas of the adult human brain transcriptome. Nature, 489(7416):391–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodge RD, Bakken TE, Miller JA, Smith KA, Barkan ER, Graybuck LT, Close JL, Long B, Johansen N, Penn O, et al. (2019). Conserved cell types with divergent features in human versus mouse cortex. Nature, 573(7772):61–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kempfer R. and Pombo A. (2020). Methods for mapping 3D chromosome architecture. Nature Reviews Genetics, 21(4):207–226. [DOI] [PubMed] [Google Scholar]
- Kiers HA, Ten Berge JM, and Bro R. (1999). PARAFAC2âĂŤ–Part I. A direct fitting algorithm for the PARAFAC2 model. Journal of Chemometrics: A Journal of the Chemometrics Society, 13(34):275–294. [Google Scholar]
- Kim H-J, Yardımcı GG, Bonora G, Ramani V, Liu J, Qiu R, Lee C, Hesson J, Ware CB, Shendure J, et al. (2020). Capturing cell type-specific chromatin compartment patterns by applying topic modeling to single-cell Hi-C data. PLoS Computational Biology, 16(9):e1008173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D-S., Luo C., Zhou J., Chandran S., Rivkin A., Bartlett A., Nery JR., Fitzpatrick C., OâĂŹ-Conno C., Dixon JR., et al. (2019). Simultaneous profiling of 3D genome structure and DNA methylation in single human cells. Nature Methods, 16(10):999–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Liu Y, Zhang Y, Kubo N, Yu M, Fang R, Kellis M, and Ren B. (2019). Joint profiling of DNA methylation and chromatin architecture in single cells. Nature Methods, 16(10):991–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E, Van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. (2009). Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science, 326(5950):289–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Zhou J, Tian W, Luo C, Bartlett A, Aldridge A, Lucero J, Osteen JK, Nery JR, Chen H, et al. (2021). DNA methylation atlas of the mouse brain at single-cell resolution. Nature, 598(7879):120–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Lin D, Yardımcı GG, and Noble WS (2018). Unsupervised embedding of single-cell Hi-C data. Bioinformatics, 34(13):i96–i104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo C, Liu H, Xie F, Armand EJ, Siletti K, Bakken TE, Fang R, Doyle WI, Stuart T, Hodge RD, et al. (2022). Single nucleus multi-omics identifies human cortical cell regulatory genome diversity. Cell Genomics, 2(3):100107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misteli T. (2020). The self-organizing genome: Principles of genome architecture and function. Cell, (1):28–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagano T, Lubling Y, Várnai C, Dudley C, Leung W, Baran Y, Cohen NM, Wingett S, Fraser P, and Tanay A. (2017). Cell-cycle dynamics of chromosomal organization at single-cell resolution. Nature, 547(7661):61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nora EP, Lajoie BR, Schulz EG, Giorgetti L, Okamoto I, Servant N, Piolot T, van Berkum NL, Meisig J, Sedat J, et al. (2012). Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature, 485(7398):381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramani V, Deng X, Qiu R, Gunderson KL, Steemers FJ, Disteche CM, Noble WS, Duan Z, and Shendure J. (2017). Massively multiplex single-cell Hi-C. Nature Methods, 14(3):263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. (2014). A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell, 159(7):1665–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart T, Butler A, Hoffman P, Hafemeister C, Papalexi E, Mauck III WM, Hao Y, Stoeckius M, Smibert P, and Satija R. (2019). Comprehensive integration of single-cell data. Cell, 177(7):1888–1902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su J-H, Zheng P, Kinrot SS, Bintu B, and Zhuang X. (2020). Genome-scale imaging of the 3D organization and transcriptional activity of chromatin. Cell, 182(6):1641–1659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takei Y, Zheng S, Yun J, Shah S, Pierson N, White J, Schindler S, Tischbirek CH, Yuan G-C, and Cai L. (2021). Single-cell nuclear architecture across cell types in the mouse brain. Science, 374(6567):586–594. [DOI] [PubMed] [Google Scholar]
- Tan L., Ma W., Wu H., Zheng Y., Xing D., Chen R., Li X., Daley N., Deisseroth K., and Xie XS. (2021). Changes in genome architecture and transcriptional dynamics progress independently of sensory experience during post-natal brain development. Cell, 184(3):741–758. [DOI] [PubMed] [Google Scholar]
- Van Benthem MH, Keller TJ, Gillispie GD, and DeJong SA (2020). Getting to the core of PARAFAC2, a nonnegative approach. Chemometrics and Intelligent Laboratory Systems, 206:104127. [Google Scholar]
- Welch JD, Kozareva V, Ferreira A, Vanderburg C, Martin C, and Macosko EZ (2019). Single-cell multi-omic integration compares and contrasts features of brain cell identity. Cell, 177(7):1873–1887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiong K. and Ma J. (2019). Revealing Hi-C subcompartments by imputing inter-chromosomal chromatin interactions. Nature Communications, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Zhou T, and Ma J. (2022). Multiscale and integrative single-cell Hi-C analysis with higashi. Nature biotechnology, 40(2):254–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang R, Zou Y, and Ma J. (2020). Hyper-SAGNN: a self-attention based graph neural network for hypergraphs. In International Conference on Learning Representations (ICLR). [Google Scholar]
- Zheng H. and Xie W. (2019). The role of 3D genome organization in development and cell differentiation. Nature Reviews Molecular Cell Biology, page 1. [DOI] [PubMed] [Google Scholar]
- Zheng Y, Shen S, and Keles S. (2021). Normalization and de-noising of single-cell Hi-C data with BandNorm and 3DVI. bioRxiv. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Ma J, Chen Y, Cheng C, Bao B, Peng J, Sejnowski TJ, Dixon JR, and Ecker JR (2019). Robust single-cell Hi-C clustering by convolution-and random-walk–based imputation. Proceedings of the National Academy of Sciences, 116(28):14011–14018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou T, Zhang R, and Ma J. (2021). The 3D genome structure of single cells. Annual Review of Biomedical Data Science, 4. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This paper analyzes existing, publicly available data. These accession numbers for the datasets are listed in the key resources table.
All original code has been deposited at https://github.com/ma-compbio/Fast-Higashi, and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
Key resources table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and virus strains | ||
| Biological samples | ||
| Chemicals, peptides, and recombinant proteins | ||
| Critical commercial assays | ||
| Deposited data | ||
| sn-m3c-seq dataset of human prefrontal cortex | Lee et al., 2019 | GEO:GSE130711 |
| sn-m3c-seq dataset of mouse hippocampus | Liu et al., 2021 | GEO:GSE156683 |
| Dip-C dataset of developing mouse brain | Tan et al., 2021 | GEO:GSE162511 |
| sci-Hi-C dataset of 4 cell lines (GM12878, HAP1, HeLa, K562) | Ramani et al., 2017 | GEO:GSE84920 |
| sci-Hi-C dataset of 5 cell lines (GM12878, H1ESC, HAP1, HFFc6, IMR90) | Kim et al., 2020 | 4DN Data Portal: 4DNES4D5MWEZ, 4DNESUE2NSGS, 4DNESIKGI39T, 4DNES1BK1RMQ, and 4DNESTVIP977 |
| Experimental models: Cell lines | ||
| Experimental models: Organisms/strains | ||
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and algorithms | ||
| Fast-Higashi | This paper | DOI: 10.5281/zenodo.7023632 |
| Other | ||