Abstract
Iterative reconstruction has demonstrated superior performance in medical imaging under compressed, sparse, and limited-view sensing scenarios. However, iterative reconstruction algorithms are slow to converge and rely heavily on hand-crafted parameters to achieve good performance. Many iterations are usually required to reconstruct a high-quality image, which is computationally expensive due to repeated evaluations of the physical model. While learned iterative reconstruction approaches such as model-based learning (MBLr) can reduce the number of iterations through convolutional neural networks, it still requires repeated evaluations of the physical models at each iteration. Therefore, the goal of this study is to develop a Fast Iterative Reconstruction (FIRe) algorithm that incorporates a learned physical model into the learned iterative reconstruction scheme to further reduce the reconstruction time while maintaining robust reconstruction performance. We also propose an efficient training scheme for FIRe, which releases the enormous memory footprint required by learned iterative reconstruction methods through the concept of recursive training. The results of our proposed method demonstrate comparable reconstruction performance to learned iterative reconstruction methods with a 9x reduction in computation time and a 620x reduction in computation time compared to variational reconstruction.
Keywords: Photoacoustic tomography, Iterative algorithm, Deep learning, Image reconstruction, Learned forward operator, Neural operator
1. Introduction
Photoacoustic tomography (PAT) imaging is a promising non-invasive hybrid imaging modality that combines the advantages of optical and ultrasound imaging [1]. The intrinsic mechanism of the photoacoustic effect allows functional imaging through the distinct spectroscopic specificity of endogenous chromophores in vivo [2]. PAT has shown great potential for preclinical research in small-animal whole-body imaging, for instance, mapping the microvasculature network and studying the resting state functional connectivity of the mouse brain [3], [4], [5]. More recently, it has been applied to human imaging such as functional human brain imaging, diagnosis of cardiovascular disease, cancer detection and staging, and image-guided surgery [6], [7], [8], [9], [10], [11], [12].
In PAT, the imaging system aims to recover the initial pressure distribution from a collection of time-resolved acoustic pressure waves generated by the tissue medium excited by laser pulses on a nanosecond timescale [13]. In vasculature imaging, hemoglobin is commonly excited by the optical wavelength ranging from visible to near-infrared (NIR) spectrum [1]. The irradiated tissue undergoes thermoelastic expansion by converting the absorbed light energy into thermal energy. The tissue medium subsequently turns into a relaxation state and produces the resulting acoustic pressure waves that propagate throughout the entire space. Ultimately, these acoustic pressure waves are recorded by the transducers arranged in arbitrary geometry (e.g., planar-view system [14] and hemispherical array-based system [15]) or by mechanically scanned detector [16]. These time-resolved signals can be used to reconstruct the initial pressure source, i.e., local concentration of light-absorbing chromophores, using analytical solutions, numerical methods, and variational approaches [17], [18], [19].
Conventional reconstruction methods (e.g., universal/filter backprojection [20], [21] and time-reversal reconstruction [22]) involve solving single wave equations, and thereby reconstruction is dramatically faster. However, these methods are feasible only when the sensing configuration is robust. Under the more realistic imaging scenarios (e.g., sparse, limited view, and compressed sensing), which are often encountered in biomedical applications, variational and iterative reconstruction outperform the conventional methods at the cost of computational time [23]. To break through the computational burden inherent in variational and iterative reconstruction, the medical imaging community now resorts to powerful computational techniques based on machine learning [24], [25], [26]. In photoacoustic imaging, an intuitive approach to increase the image quality is fitting the acquired sensor data directly to the neural network and obtaining the reconstruction output [27]. However, neural networks typically suffer from difficulties in handling the transformation between time-series sensor data and spatial domain image data and thus are prone to overfitting to training data [28]. To avoid the domain transformation problem, input data to the neural network can be kept in the spatial domain by a single inversion step carried out by a fast conventional reconstruction method [29]. Nonetheless, this approach limits the information that the neural network can use after simple inversion from time-series sensor data, as a result, more expressive neural network architectures may be required [30], [31]. An alternative to overcome this problem is to use a hybrid architecture that considers both time-series sensor data and initial inversion images as input to the neural network [32]. In addition, preprocessing techniques that preserve channel information by encoding measured time-series sensor data for each transducer provide more useful information that can be exploited by neural networks. [28], [33]. The above methods are defined as purely data-driven methods, where the reconstruction performance of the model depends only on the information from the data. Reconstructing high-quality images usually requires a large amount of training data, and the generalization and robustness of the model are not as good as variational and iterative reconstruction methods. More recently, the learned iterative reconstruction method has been introduced to address this challenge [34], [35], [36], [37], [38], [39], [40]. The general idea of this technique is to integrate variational and iterative reconstruction methods into a deep learning framework to provide higher model performance in terms of generalizability and robustness while reducing reconstruction time. Although computational time has been reduced by the learned iterative reconstruction approach, the tedious process involving repeated simulations of a physical model is still a requirement for each iteration. To further reduce the computational time for the proposed learned iterative reconstruction, instead of integrating conventional numerical solvers into a learned iterative reconstruction approach, we propose to leverage learned physical models.
Solving complex partial differential equations (PDEs) by machine learning has become a paradigm change in understanding physical models in science and engineering [41]. Two reasons make it a fascinating choice of studying physical models. First, it models underlying physical systems without requiring extensive prior knowledge of a corresponding field. Second, solving complex PDEs through machine learning enables efficient simulations of real-world problems on large scale. Examples of this approach include solutions for molecular dynamics [42] and turbulent flows [43]. There are four categories of machine-learning frameworks that have been used for solving PDEs: finite-dimensional operators, neural finite element models (neural-FEM), neural operators, and Fourier neural operators (FNO) [44]. The finite-dimensional operators are parameterized by a deep convolutional neural network mapping between finite-dimensional Euclidean spaces. However, mesh-dependent properties of these approaches restrict the new solution to query only at specific spatial resolutions, geometries, and discretization corresponding to the training data. Such approaches require neural networks to be modified and retrained for different levels of resolution and discretization. Likewise, the neural-FEM models are designed for only one specific instance of the PDE; thus, the neural network needs to be retrained to solve for a different set of function coefficients. In addition, these approaches are limited to the well-study physical system where the underlying PDE is fully understood. In contrast, the neural operators, known as infinite-dimensional operators, characterize as mesh-free nature and only need to train once for any different spatial resolution and discretization. These approaches share the same parameters and network architecture among different underlying functional data. Moreover, neural operators require no knowledge of the underlying PDE, suitable to the field in which formulation of the governing PDE for fundamental physical systems remains elusive. Similarly, the FNO has the same characteristics as the above-mentioned neural operators. It learns a mapping between infinite dimensional spaces from a finite collection, and the trained network can be used to query the solution in any spatial resolution and dimension without network retraining and architecture modification. Compared to the neural operators, the cost of evaluating the integration operator is reduced by parameterizing the integral kernel directly in Fourier space. In addition to gaining significant improvement in the computational time, the FNO exhibits superior performance and is robust to noise in applications for solving Bayesian inverse problems without any accuracy degradation [44].
In this study, we replace the conventional numeric solvers of the photoacoustic wave equation with the FNO in a learned iterative reconstruction pipeline where the forward and downstream inverse problems are solved iteratively, thereby reducing computational costs through a more expressive model. To the best of our knowledge, this is the first paper that integrates learned physical models into learned iterative reconstruction in medical image reconstruction specifically for PAT reconstruction. Since applications that require repeated evaluations of PDEs can greatly benefit from the reduced computation time of deep learning, we choose an FNO designed specifically for PDE solvers along with its state-of-the-art performance as the backbone of our proposed methods.
2. Methods
2.1. Photoacoustic signal generation
Time-resolved signals acquired by ultrasound receivers can mathematically represent the initial pressure distribution at a point by the following equation
| (1) |
where is the Gruneisen coefficient, a dimensionless thermodynamic constant measuring the conversion efficiency from thermal energy to pressure. It can be further defined by , where is the thermal coefficient of volume expansion, is the mass density, is the specific heat capacity at constant volume, is the isothermal compressibility. For soft tissue, is approximately 5 × 10−10 Pa−1 and is around 4 × 10−4 K−1 [45]. is the absorbed optical energy distribution defined by the product of the local absorption coefficient and the optical fluence where itself is governed by the absorption coefficient , scattering coefficients , and anistropy factor .
The equation defined above for the initial pressure distribution can be rewritten as
| (2) |
Here, Gruneisen coefficient is usually assumed to be spatially invariant among different tissue mediums. Hence, the image contrast of the initial pressure distribution is proportional to the product of the absorption coefficient and optical fluence rate. In PAT imaging, since the laser pulse duration is less than the thermal confinement time and stress confinement time, the thermal diffusion and volume expansion of the absorber are negligible [46].
2.2. Conventional solvers for the acoustic wave equation
Well-established physical model in medical imaging plays a critical role in the design of imaging devices prior to the production stages and clinical trial deployment. It provides a comprehensive study of different parameters that interactively affect the simulation of measurement and, in turn, the downstream image reconstruction task. Furthermore, reconstruction methods such as variational reconstruction and iterative reconstruction approximate the true solution by explicitly performing a forward operator to repeatedly evaluate the predicted measurements [47]. Consequently, high-quality images reconstructed from these methods require an accurate forward operator resulting in extreme computational demands.
In photoacoustic imaging, the common methods for constructing the forward model of photoacoustic wave propagation include finite element method [48], finite difference method [49], and pseudospectral and k-space model [50]. The finite element method aims at finding unknown coefficients for defined N-dimensional basis functions and gives a solution by a linear combination of the N-dimensional functions based on the calculated coefficients [51]. Its flexibility in choosing basis functions improves efficiency through coefficients calculated from sparse matrix equations and allows for heterogeneities of any shape. In contrast, the finite difference method tackles the derivative in the PDEs by the differences. Generally, a large number of points are required to better estimate the gradient field by fitting a higher-order polynomial. Compared to the finite element method, the finite difference method is less flexible due to the restriction in the use of regular computational mesh. The disadvantage is that the finite element and finite difference methods require about 10 mesh points per wavelength to represent the field accurately, and small timesteps are usually required to avoid numerical dispersion, limiting the capability to be used in high-frequency and large-scale applications for photoacoustic imaging.
To address these limitations, the pseudospectral and k-space model was introduced [50], which can significantly reduce the number of nodes needed in finite element and finite difference methods by fitting a Fourier series to all data on each line in the mesh. The nature of the Fourier transforms results in a pseudospectral approach that requires only two nodes per wavelength to describe a wave. The gradient can simply be calculated by the Fast Fourier Transform (FFT) followed by its inverse. In addition, the k-space model is more suitable for biomedical photoacoustic imaging applications involving the modeling of large-scale high-frequency photoacoustic waves at larger timesteps in the case of acoustically heterogeneous mediums [51]. Although the pseudospectral and k-space model alleviates the computational burden required by finite element and finite difference methods, they are still not fast enough to achieve real-time reconstruction when incorporated with variational and iterative reconstruction, which is largely due to an inherent trade-off between accuracy and computational time of the model.
2.3. Learned physical model for acoustic wave equation
The feasibility of using machine learning for solving acoustic wave equations has been demonstrated in [52]. Inspired by [52], the FNO was adapted as the PDE solver for modeling acoustic wave propagation due to its superior performance. Here, training data for the FNO is generated using the k-wave toolbox [53] which computes the acoustic wave simulation through the pseudospectral and k-space model. The simulation parameters are the same as following data generation section, in which the computational grid was 128 × 128 with a grid spacing of 100 micrometers. The medium was assumed as non-absorptive and homogeneous with a speed of sound of 1540 m/s and a density of 1000 kg/m3. The time step for the simulations was 38.96 ns per step for 302 steps. The input to the FNO was simply the initial pressure distribution at time equal to 0, reconstructed either from the initial inversion or the artifact-contaminated images generated from the learned iterative reconstruction at each iteration. Consequently, conventional solvers can be excluded from the following reconstruction pipeline to reduce computation time. Given the initial pressure distribution , the FNO can accurately infer full spatiotemporal solutions for all timesteps.
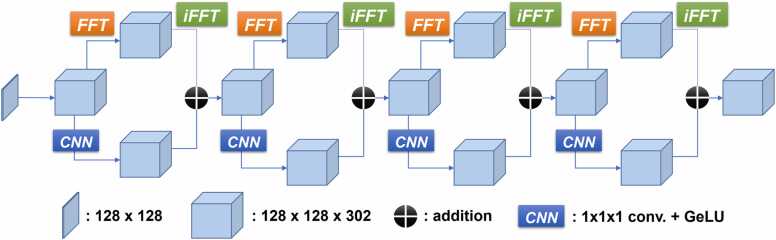
The architecture of FNO shown in Fig. 1 begins with converting the inputs (e.g., initial pressure distribution ) to a higher dimension. The dimensionality of these latent representations is determined by a hyperparameter termed channels. These N-channel latent representations then iteratively update the features through four Fourier layers. Each Fourier layer learns a global feature representation in spectral space by performing the Fourier transform and its inverse. The features learned in the spectral space can be truncated by another hyperparameter, a regularization parameter, termed modes. In biomedical photoacoustic imaging, the acquired signals predominantly contain high-frequency components throughout the simulation processes; thus, we retain all the modes without any spectral truncation. Spectral truncation can result in smoothing of acoustic waves, resulting in an inaccurate collection of measured time-series sensor data, which in turn affects downstream reconstruction pipelines. In addition to learning global feature representations, the convolutional neural network is also used to learn the local features for detailed edges and shapes. These iterative updates can be expressed as follows
| (3) |
where is a non-linear activation function, is a linear transformation, is a kernel integral operator directly parameterized in Fourier space by Fourier transform , and features learned in the Fourier space are inversed to spatial space by its inverse . After the iterative updates, the updated features are then projected back to the desired dimensions corresponding to the acoustic wave equation simulation.
Fig. 1.
Architecture of Fourier neural operator for acoustic wave simulation.
2.4. Variational reconstruction
Variational reconstruction has been identified as a method of solving the ill-posed problem for the signals acquired in the compressed and sub-Nyquist manner [54]. Furthermore, it also demonstrated superior performance in limited-view angle tomographic image reconstruction [55]. The variational approach aims at approximating the true solution by solving the optimization problem and can be defined as
| (4) |
Here, is the measured time-series signal. denotes a forward operator. represents the regularization functional encoding a-priori knowledge about the solution and is used to penalize the unwanted features. The weighting factor determines the impact of the regularization. The fidelity term measures the difference between acquired time-series signals and the predicted signals evaluated by the known forward operator. This optimization problem can be solved iteratively through a proximal gradient descent scheme. Although introducing the regularization functional can increase the generalizability of the model performance and avoid overfitting by penalizing the unfeasible features, inappropriate choice of the regularization functional and weighting factor potentially leads to poor reconstruction and the need of many iterations for a model to converge.
The popular regularization in medical imaging reconstruction includes the Tikhonov regularization [56] and total variation regularization [54]. Among them, total variation is widespread use for recovering noise-contaminated images under the restricted imaging configuration. Compared to Tikhonov regularization which measures the l2 norm of , total variation is a non-smooth and edge-preserving technique characterized by removing the unimportant features with spatial sparsity constraints through the l1 penalization on the gradient field of .
2.5. Learned iterative reconstruction
Learned iterative reconstruction aims at solving the same optimization problem in variational reconstruction methods. However, instead of using proximal gradient descent to find the true solution of the reconstructed image, the neural network replaces conventional methods to solve the optimization problem. It has been shown the state-of-the-art performance in medical imaging reconstruction [24]. Compared to the variational reconstruction, the handcrafted parameters (e.g., step size, regularization function, and the weighting factor of the regularization function) are implicitly learned from the data in the training phase. Hauptmann et al. proposed an iteratively learning strategy for PAT reconstruction termed deep gradient descent (DGD) or learned gradient scheme (LGS) [57]. The reconstruction pipeline is illustrated in Fig. 2a and can be mathematically expressed as
| (5) |
Fig. 2.
Block diagram of the iterative reconstruction algorithm at ith iteration. (a) Model-based learning (MBLr) (b) Fast Iterative Reconstruction (FIRe).
Here, is the measured time-series signal. denotes a forward operator. represents an adjoint operator. shown in Fig. 3a is the convolutional neural network parameterized at th iteration. The initial pressure distribution is computed by the adjoint reconstruction on the acquired sensor data . In each iteration, the reconstructed images from the previous iteration and the computed gradient information are served as a pair of inputs to the neural network. Then, the objective function of this optimization problem can be formulated as
| (6) |
Fig. 3.
Convolutional neural network for (a) Model-based learning (MBLr) and (b) Fast Iterative Reconstruction (FIRe).
Here, denotes the ground truth image. Unlike the end-to-end training scheme, this training strategy unrolls the entire model into multiple iterations and computes the objective function in each iteration, thereby, the parameters of the convolutional neural network are updated based on its current iteration. Ideally, an end-to-end training scheme potentially can offer better reconstruction performance by being evaluated on a single objective function for whole iterations. However, this training strategy is not feasible for PAT image reconstruction. The main reason is that the end-to-end training strategy for PAT requires excessive memory footprint and expensive computation costs during the processes requiring repetitive evaluations of forward and adjoint operators. In other words, training one epoch with the N iterations necessitates 2 N times of simulations on each training data, making the training impractical. Hence, this inherent characteristic prevents the end-to-end training strategy to be exploited in PAT image reconstruction.
2.6. Fast iterative reconstruction
Compared to variational reconstruction which generally requires a large number of iterations to converge, learned iterative reconstruction can reconstruct high-quality images with a small number of iterations. Although there has been a substantial improvement in the learned iterative reconstruction approach, evaluating the physical models at each iteration is an indispensable process. To release the computational burden, we propose the Fast Iterative Reconstruction (FIRe) exploiting the learned physical model. Instead of using pseudo-spectral and k-space models for solving time-domain photoacoustic wave propagation in the learned iterative reconstruction, the FNO is used as the learned forward operator to further reduce the computational time required by the conventional methods. In addition, gradient information originally computed by the adjoint operator in the learned iterative reconstruction is then replaced by the pixel-interpolation [28], resulting in N channels of gradient maps. Pixel interpolation is an operation that converts time-series sensor data into channel-specific pressure maps based on the assumption of the speed of sound and a known computational grid. Here, N is determined by the number of sensors. Pixel-interpolation, which is a delayed data for each channel, provides more information without background artifacts, and deep neural network can suppress unwanted signals channel-wise during training phase. Nonetheless, backprojection collapses the channel dimension which leads to the reconstructed images contaminated with severe artifact especially in the sparse-sensing and limited-viewed scenarios, and this poor reconstructed image will directly influence the subsequent iterations sequentially, resulting in more iterations to converge. The comparison of the reconstruction performance for the MBLr using adjoint and pixel-interpolation respectively is shown in supplementary Fig. A.1, observing that pixel-interpolation as the reconstruction operator performs better than the adjoint operator after five iterations in both PSNR and SSIM metrics. The block diagram of the proposed method is illustrated in Fig. 2b. Similar to (5) and (6), the reconstruction process can be expressed as
| (7) |
and objective function can be written as
| (8) |
Here, the initial pressure distribution is acquired by simple backprojection from measured time-series signal. The forward operator is parameterized based on the FNO framework at th iteration, and represents a pixel-interpolated operation.
The training scheme is similar to learned iterative reconstruction using an iteratively adjusting manner, in which the reconstruction model is unrolled to multiple iterations, and parameters are updated based on its current objective function. In FIRe, the architecture of the reconstruction model (CNN) shown in Fig. 3b is similar to the model used in the DGD, with a small adjustment to the gradient input where it constitutes the channels of the gradient map. In addition to the reconstruction model, the learned forward operator is trained iteratively as well. Specifically, the learned forward operator at th iteration is trained on the artifact-contaminated images generated from the reconstruction model at th iteration. The reconstruction model is then trained on the combination of reconstructed images and the gradients estimated from a current learned forward operator followed by a pixel-interpolated operation. Therefore, N iterations of FIRe generate 2 N of models.
To reduce the memory footprint, herein, we propose the lightweight training scheme and reconstruction pipeline built on FIRe, termed two-stage FIRe (2S-FIRe). The illustration of the training scheme of 2S-FIRe is shown in Fig. 4. In the first iteration of 2S-FIRe, the training of the learned forward operator and reconstruction model is identical to the training scheme of the FIRe. Starting from the second iteration, reconstructed images from all previous iterations excluding the initialization are aggregated for the training of the learned forward operator and reconstruction model. Here, models in the first iteration are not used for following iterations as a result of the task in the first iteration involving the removal of the server artifact background. Another consideration is that features in the initialization does not contain the unrealistic features that generate from the subsequent reconstruction models; it only contains the artifact arising from the backprojection. Conversely, the later iterations gradually update the reconstruction in a fine-tuning manner. In the reconstruction pipeline, the same learned forward operator and reconstruction model are reused for each iteration to evaluate the simulation and reconstruction, respectively, resulting in a closed-form reconstruction model. Thereby, the output of the model is served as the input itself, and only four models including two learned forward operators and two reconstruction models are used for the entire reconstruction pipeline. The reconstruction process after the first iteration can be expressed mathematically as
| (9) |
and objective function can be written as
| (10) |
Fig. 4.
Block diagram of two-stage fast iterative reconstruction (2S-FIRe).
This recursive training scheme allows trained models to be reused for every iteration. Therefore, increasing the number of iterations for reconstruction does not increase the use of number of the models. The memory footprint for 2S-FIRe is primarily based on the number of time steps compared to FIRe. On the other hand, the memory footprint in the FIRe is proportional to both the number of iterations and times steps.
2.7. Deep learning implementation
The experimental platform is based on Windows 10 64-bit operating system, Intel i9–10980XE CPU, 256 GB memory, and two NVIDIA RTX A5000 (each with 24 GB memory). All proposed and established deep neural networks are implemented in Python 3.9 with an open-source deep-learning library (Pytorch 1.12.1).
FNO is trained using the Adam optimizer, and parameters are updated based on the mean squared error (MSE) loss for 1000 epochs. Additionally, the learning rate is decreased by 0.5 every 100 epochs starting from 10e−3. The batch size of 1 is used for training the FNO. As for the training of CNN for both FIRe and 2S-FIRe, Adam optimizer is used, and parameters are update based on the MSE for 1000 epochs. Besides, the learning rate is decreased by 0.5 every 100 epochs starting from 10e−4. The batch size of 8 is used for training CNN.
3. Results and discussion
3.1. Data generation
Synthetic vasculature was generated from a simple vasculature phantom provided by the k-Wave toolbox [53], a well-established photoacoustic wave simulation software. The diversity of the synthetic vasculature was increased by superimposing a different number of transformed synthetic vasculature phantoms by some augmentation techniques (e.g., rotation, translation, scaling, and shearing). As a result, a dataset containing 750 images of synthetic vasculature was used for training purposes. In addition, in vivo mouse brain vasculature was used for evaluating the model reconstruction performance in terms of generalizability. Here, in vivo mouse brain was acquired by contrast-enhanced micro-CT, providing high-resolution volumetric data with fine vasculature [58]. This volumetric mouse brain vasculature was then processed into 2D images by performing a Frangi vesselness filter to extract the vessel-like features in the 3D volume, followed by simple thresholding to remove the remaining background. Subsequently, maximum intensity projections (MIPs) were applied to randomly selected sub-volumes. To maximize the preservation of realistic mouse brain vascular features, advanced augmentation techniques were not performed on the generated mouse brain MIPs. Consequently, a dataset containing 300 images of mouse brain vasculature was generated.
In the simulation process, brain both synthetic vasculature and mouse vasculature were defined inside the computational grid of 128 × 128, and the grid spacing was 100 micrometers. The medium was assumed as non-absorptive and homogeneous with a speed of sound of 1540 m/s and a density of 1000 kg/m3. The time step for the simulations was 38.96 ns per step for 302 steps. The photoacoustic signals were simulated in a sparse sensor configuration, with 32 sensors evenly distributed on a circle with a 6.3 mm radius. The simulated signals were backprojected into the initial pressure distribution contaminated with the severe artifact. All models were then trained in a supervised manner where backprojected synthetic vasculature images served as inputs and generated synthetic vasculature images served as the ground truth.
3.2. FNO forward simulation
A visual comparison of the k-Wave (ground truth) and FNO forward simulations for photoacoustic wave propagation on an instance of mouse brain vasculature at selected time steps are shown in Fig. 5 and its corresponding full-time series wave propagation video is attached. The error distributions suggest that a little nuance difference is measured between k-Wave and FNO simulations. The color in red indicates that the simulation of FNO does not fully recover the intensity of the photoacoustic waves generated by the k-Wave in the defined computational grid. Conversely, the color in blue indicates that FNO's simulations accidentally introduce false-positive photoacoustic waves. Although FNO simulations accidentally introduce slight false-positive photoacoustic waves at selected time steps, they do not randomly generate artifacts in the context of the defined computational grid, but instead, enhance the wavefront of the mouse brain vasculature. Consequently, sampled time-series sensor data may result in reconstructed images having a slightly stronger intensity than the actual imaged targets. In summary, the simulation between k-Wave and FNO cannot visually distinguish the difference.
Fig. 5.
Visual comparison of the ground truth (upper row) using k-Wave and FNO networks (middle row) at 1, 26, 51, 76, and 101 timesteps to simulate photoacoustic wave propagation for an example image of the mouse brain vasculature. Error maps between ground truth and FNO simulation are shown in bottom row.
The FNO-based simulations are quantitatively compared to k-Wave simulations with root mean square error (RMSE) measured at different iterations in Fig. 6. This finding demonstrates that the error of FNO simulations is inversely proportional to the timesteps. Furthermore, FNO simulations of the initial distribution for the first iteration exhibit larger errors compared to all subsequent iterations. In addition, the FNO simulation for subsequent iterations (from second to fifth) shows similar errors. These findings strongly support the proposed 2S-FIRe, which separates the learned iterative reconstruction using learned physical models into two stages. Since the task in the first iteration usually involves the removal of severe background artifacts, the subsequent iterations gradually update the reconstructed images in a fine-tuning manner.
Fig. 6.
RMSE of the time-series sensor data between k-Wave and FNO simulation on the unseen mouse brain vasculature dataset. FNO_0: FNO is used for simulated photoacoustic wave propagation for the initial pressure distribution. FNO_1 to FNO_4 is used to simulate the following iterations.
3.3. Mouse brain vasculature reconstruction
Models trained on synthetic vasculature are evaluated for generalizability by reconstruction on the out-of-domain mouse brain vasculature data. Fig. 7 quantitively shows the reconstruction performance of the models on the unseen mouse brain vasculature over five iterations under the sparse sensing configuration scenario. After the five iterations, FIRe reaches an SSIM of 0.928 ± 0.024 and a PSNR of 28.918 ± 1.938. 2S-FIRe reaches an SSIM of 0.921 ± 0.025 and a PSNR of 28.055 ± 1.624. MBLr achieves an SSIM of 0.936 ± 0.024 and a PSNR of 29.573 ± 2.054. Compared to the learned iterative reconstruction methods (MBLr, 2S-FIRe, and FIRe), the single-step post-processing method based on the U-Net has an SSIM of 0.709 ± 0.051 and a PSNR of 22.628 ± 1.588. This experiment demonstrates that all learned iterative reconstruction methods outperform the single-step post-processing method. Furthermore, there is no significant difference between learned iterative reconstruction methods.
Fig. 7.
Comparison of the model reconstruction performance on the unseen mouse brain vasculature under sparse sensing configuration. Left: SSIM is used as the metric for the comparison. Right: PSNR is used as the metric for the comparison. MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction. U-Net: single-step post-processing.
The reconstruction time of different models shown in Table 1 is evaluated on an average of 300 instances. U-Net as a single-step post-processing method executes the fastest reconstruction time with 5 ms. Learned iterative reconstruction method using MBLr with 5 iterations executes a reconstruction time of 4.69 s. In addition, FIRe and 2S-FIRe with 5 iterations perform a reconstruction time of 510 ms. TV variational reconstruction with 50 iterations performs a reconstruction with 316 s.
Table 1.
Reconstruction speed of different methods.
| MBLr | FIRe | 2S-FIRe | TV | U-Net |
|---|---|---|---|---|
| 4.69 s | 510 ms | 510 ms | 316 s | 5 ms |
MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction.TV: total variation. U-Net: single-step post-processing.
A visual comparison of an instance of the mouse brain vasculature is shown in Fig. 8. U-Net as a single-step post-processing method fails to reconstruct the fine vasculature while MLBr and 2S-FIRe reconstruct successfully. FIRe also captures the fine vasculature but is slightly dull compared to the MBLr and 2S-FIRe. Although the TV result demonstrates the capability of reconstructing the fine vasculature, it is contaminated by random artifacts distributed in the background. The bottom row of Fig. 8 shows the error distribution between ground truth and reconstruction in the mouse brain vasculature. The color in red indicates the reconstruction does not capture the vasculature as it should have been in the original ground truth. Conversely, the color in blue indicates the reconstruction accidentally introduces false-positive vasculature. Compared with all other learned iterative methods, the error distribution of the U-Net reconstruction shows worse results as can be seen in darker red and blue regions. Among the learned iterative reconstruction methods, the error distribution of MBLr reconstruction is slightly better than 2S-FIRe and FIRe. In addition, the learned iterative reconstruction methods are less prone to introducing false-positive vasculature than single-step post-processing reconstruction with U-Net.
Fig. 8.
Visualization of photoacoustic image reconstruction on unseen mouse brain vasculature in different models under sparse sensing configuration scenario. Green arrows point out the details of the fine vasculature reconstructed in the different models. MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction. TV: total variation. U-Net: single-step post-processing. BP: backprojection.
The robustness of the models is then evaluated on the noise-added mouse brain vasculature data in Fig. 9. Here, the mouse brain vasculature sensor data is introduced Gaussian noise with a 15 dB signal-to-noise ratio (SNR). After the five iterations, FIRe reaches an SSIM of 0.901 ± 0.028 and a PSNR of 28.037 ± 1.971. 2S-FIRe reaches an SSIM of 0.915 ± 0.026 and a PSNR of 27.850 ± 1.638. MBLr achieves an SSIM of 0.907 ± 0.033 and a PSNR of 28.695 ± 2.090. The single-step post-processing method based on the U-Net has an SSIM of 0.699 ± 0.051 and a PSNR of 22.562 ± 1.593. Among the learned iterative reconstruction methods, 2S-FIRe performs the best reconstruction in SSIM, with the mean SSIM only slightly decreasing from 0.921 to 0.915. In contrast, MBLr and FIRe perform in mean SSIM with a drop from 0.936 to 0.907 and 0.928–0.901, respectively. In terms of PSNR, MBLr performs the best compared to all other reconstruction methods.
Fig. 9.
Comparison of the model reconstruction performance on the noise introducing mouse brain vasculature under sparse sensing configuration. Left: SSIM is used as the metric for the comparison. Right: PSNR is used as the metric for the comparison. MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction. U-Net: single-step post-processing.
To further investigate the robustness of the models, different levels of Gaussian noise were introduced into the collected sensor data, ranging from 6 dB to 30 dB SNR in 3 dB increments. Fig. 10 demonstrates the reconstruction performance of the models under different levels of noise on the unseen mouse brain vasculature data. In addition, the evaluation of model performance based on SSIM and PSNR metrics is quantitatively shown in Table 2 and Table 3, respectively.2S-FIRe shows the greatest robustness in SSIM as the collected sensor data is contaminated by the severe Gaussian noise at 6, 9, and 15 dB. In contrast, MBLr exhibits the greatest robustness in PSNR at all levels of noise. When the acquired signal involves severe distortion at lower SNR, the reconstruction performance of 2S-FIRe is better than the MBLr in terms of the SSIM metric, indicating that 2S-FIRe is shown to be more tolerant to signal distortion when evaluated using local metrics. In contrast, MBLr performs better than the 2S-FIRe when evaluated using the global metric (PSNR). Iterative reconstruction schemes are already known for their robustness and generalizability [34]–[40]. The robustness of the proposed FIRe and 2S-FIRe reconstructions can be attributed in part to the generalizability of FNO networks. A test performed using a smaller 64×64×151 FNO model indicated that when trained using vasculature data, FNOs were able to match forward photoacoustic wave propagation results obtained using K-Wave toolbox even when the tests were performed using non-biological initial pressure sources such as a Shepp-Logan phantom and Mason-M logo (supplementary Fig. A.2.). These results were promising and provided evidence that the trained FNO network was generalizable to other initial photoacoustic sources not in the training data. Inclusion of a more diverse and larger training dataset can further improve the generalizability of the FNO network.
Fig. 10.
Model performance evaluated on mouse brain vasculature under different levels of noise. Left panel: SSIM is used as a metric for different levels of noise. Right panel: PSNR is used as a metric for different levels of noise. MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction. TV: total variation. U-Net: single-step post-processing.
Table 2.
Evaluation of model performance on the mouse brain vasculature in ssim metrics at different noise levels.
| MBLr | FIRe | 2S-FIRe | TV | U-Net | |
|---|---|---|---|---|---|
| 6 dB SNR | 0.736 ± 0.048 | 0.788 ± 0.038 | 0.797 ± 0.047 | 0.515 ± 0.031 | 0.432 ± 0.049 |
| 9 dB SNR | 0.831 ± 0.044 | 0.847 ± 0.033 | 0.853 ± 0.039 | 0.583 ± 0.032 | 0.559 ± 0.049 |
| 12 dB SNR | 0.887 ± 0.037 | 0.886 ± 0.030 | 0.886 ± 0.033 | 0.635 ± 0.034 | 0.636 ± 0.052 |
| 15 dB SNR | 0.907 ± 0.033 | 0.901 ± 0.028 | 0.915 ± 0.026 | 0.660 ± 0.034 | 0.699 ± 0.051 |
| 18 dB SNR | 0.926 ± 0.027 | 0.918 ± 0.026 | 0.912 ± 0.027 | 0.698 ± 0.035 | 0.692 ± 0.052 |
| 21 dB SNR | 0.931 ± 0.025 | 0.923 ± 0.025 | 0.916 ± 0.026 | 0.712 ± 0.036 | 0.701 ± 0.051 |
| 24 dB SNR | 0.934 ± 0.024 | 0.926 ± 0.024 | 0.919 ± 0.025 | 0.720 ± 0.036 | 0.705 ± 0.051 |
| 27 dB SNR | 0.935 ± 0.024 | 0.927 ± 0.024 | 0.920 ± 0.025 | 0.724 ± 0.036 | 0.708 ± 0.051 |
| 30 dB SNR | 0.936 ± 0.024 | 0.928 ± 0.024 | 0.920 ± 0.025 | 0.726 ± 0.037 | 0.708 ± 0.051 |
| - | 0.936 ± 0.024 | 0.928 ± 0.024 | 0.921 ± 0.025 | 0.729 ± 0.037 | 0.709 ± 0.051 |
MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction.TV: total variation. U-Net: single-step post-processing. -: no noise included in collected sensor data.
Table 3.
Evaluation of model performance on the mouse brain vasculature in psnr metrics at different noise levels.
| MBLr | FIRe | 2S-FIRe | TV | U-Net | |
|---|---|---|---|---|---|
| 6 dB SNR | 25.568 ± 1.999 | 25.236 ± 2.012 | 25.012 ± 1.831 | 23.204 ± 1.762 | 20.854 ± 1.599 |
| 9 dB SNR | 27.180 ± 2.065 | 26.624 ± 1.998 | 26.170 ± 1.723 | 24.552 ± 1.791 | 21.724 ± 1.619 |
| 12 dB SNR | 28.243 ± 2.091 | 27.614 ± 1.963 | 26.970 ± 1.683 | 25.483 ± 1.789 | 22.184 ± 1.606 |
| 15 dB SNR | 28.695 ± 2.090 | 28.037 ± 1.971 | 27.850 ± 1.638 | 25.911 ± 1.810 | 22.562 ± 1.593 |
| 18 dB SNR | 29.211 ± 2.080 | 28.565 ± 1.964 | 27.743 ± 1.645 | 26.468 ± 1.818 | 22.515 ± 1.594 |
| 21 dB SNR | 29.397 ± 2.066 | 28.740 ± 1.938 | 27.895 ± 1.637 | 26.681 ± 1.824 | 22.580 ± 1.591 |
| 24 dB SNR | 29.481 ± 2.050 | 28.834 ± 1.934 | 27.976 ± 1.618 | 26.776 ± 1.825 | 22.602 ± 1.585 |
| 27 dB SNR | 29.528 ± 2.055 | 28.884 ± 1.933 | 28.011 ± 1.627 | 26.830 ± 1.823 | 22.615 ± 1.587 |
| 30 dB SNR | 29.554 ± 2.048 | 28.911 ± 1.932 | 28.034 ± 1.626 | 26.862 ± 1.822 | 22.624 ± 1.589 |
| - | 29.573 ± 2.054 | 28.918 ± 1.938 | 28.055 ± 1.624 | 26.887 ± 1.824 | 22.628 ± 1.588 |
MBLr: model-based learning. FIRe: fast iterative reconstruction. 2S-FIRe: two-stage fast iterative reconstruction.TV: total variation. U-Net: single-step post-processing. -: no noise included in collected sensor data.
4. Conclusion
In this research, we propose novel photoacoustic image reconstruction methods incorporating learned physical models for photoacoustic wave simulation into an established MBLr framework. Furthermore, we propose a lightweight reconstruction pipeline (2S-FIRe) to reduce the memory footprint required in FIRe. Our proposed methods demonstrate comparable performance to the state-of-the-art MBLr approach. Furthermore, leveraging the learned physical model reduces the computational time by a 9x factor compared to the MBLr and a 620x factor compared to the TV variational reconstruction method. Using learned forward operators for learning-based iterative reconstruction is still in the early stage of research. Here, we provide a comprehensive study of the use of learned physical models in learned iterative inverse problems. Moreover, incorporating the learned physical models exhibits stronger robustness and reconstruction performance when the image is contaminated with more severe noise.
Although our proposed methods can reduce computational time, the training time is much longer than the MBLr and TV variational reconstruction methods. In the future, developing the methodology to reduce the training time of the learned physical models can benefit our proposed methods to be used in a higher number of iterations for image reconstruction, taking full advantage of the essence of learned iterative reconstruction methods. Although the proposed methods are built for photoacoustic image reconstruction, the concept of the frameworks can be generalized to other imaging modalities which require repeatedly solving forward and backward simulations.
Funding sources
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Declaration of competing interest
The authors declare that there are no conflicts of interest.
Acknowledgment
Ko-Tsung Hsu would like to acknowledge Steven Guan and Parag V. Chitnis for their substantial guidance and advice on this study. Ko-Tsung Hsu is responsible for all experiments and for writing the manuscript, edited by Steven Guan and Parag V. Chitnis. The authors acknowledge the source code for Fourier neural operator available at https://github.com/zongyi-li/fourier_neural_operator.
Biographies

Ko-Tsung Hsu is currently a Ph.D. candidate at George Mason University in the Bioengineering Department. He received a B.S. in Biotechnology from Ming Chuan University, and M.S. in Bioinformatics and Computational Biology from George Mason University. His current research field focuses on the development of machine learning framework for healthcare and medical imaging solutions.

Steven Guan received his Ph.D. degree at George Mason University in the Bioengineering Department. He received a B.S. in chemical engineering, B.A. in physics, and M.S. in biomedical engineering from the University of Virginia. He worked as a senior data scientist for the MITRE corporation to support various government agencies. His primary research interests are in applying deep learning techniques for medical imaging problems such as classification, segmentation, and reconstruction.

Parag V. Chitnis is an Associate Professor in the Department of Bioengineering at George Mason University (GMU). He received a B.S. degree in engineering physics and mathematics from the West Virginia Wesleyan College, Buckhannon, WV, in 2000. He received M.S. and Ph.D. degrees in mechanical engineering from Boston University in 2002 and 2006, respectively. His dissertation focused on experimental studies of acoustic shock waves for therapeutic applications. After a two-year postdoctoral fellowship at Boston University involving a study of bubble dynamics, Dr. Chitnis joined Riverside Research as a Staff Scientist in 2008, where he pursued research in high-frequency ultrasound and photoacoustic imaging. Dr. Chitnis joined the Bioengineering department at GMU as a tenure-track faculty in 2014 and was promoted to Associate Professor with tenure in 2020. In 2017, he was nominated for and selected as the State Finalist for the Outstanding Faculty Award (Rising Star Category). With funding support from DARPA, DoD, NSF, NIH, and CIT-CRCF, Dr. Chitnis leads a multidisciplinary team that pursues research in wearable sensors, therapeutic ultrasound and localized drug delivery, photoacoustic neuro-imaging, and deep-learning strategies for photoacoustic tomography. He also serves as an Associate Editor for Ultrasonic Imaging, and reviewer on NIH and NSF grant panels.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.pacs.2023.100452.
Contributor Information
Ko-Tsung Hsu, Email: khsu5@gmu.edu.
Steven Guan, Email: sguan2@gmu.edu.
Parag V. Chitnis, Email: pchitnis@gmu.edu.
Appendix A. Supplementary material
Supplementary material
.
Supplementary material
.
Data Availability
Data will be made available on request.
References
- 1.Beard P. Biomedical photoacoustic imaging. Interface Focus. 2011;vol. 1(4) doi: 10.1098/rsfs.2011.0028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhang H.F., Maslov K., Stoica G., Wang L.V. Functional photoacoustic microscopy for high-resolution and noninvasive in vivo imaging. Nat. Biotechnol. 2006;vol. 24(7) doi: 10.1038/nbt1220. [DOI] [PubMed] [Google Scholar]
- 3.Xia J., Wang L.V. Small-animal whole-body photoacoustic tomography: a review. IEEE Trans. Biomed. Eng. 2014;vol. 61(5):1380–1389. doi: 10.1109/TBME.2013.2283507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang P., et al. High-resolution deep functional imaging of the whole mouse brain by photoacoustic computed tomography in vivo. J. Biophotonics. 2018;vol. 11(1) doi: 10.1002/jbio.201700024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nasiriavanaki M., Xia J., Wan H., Bauer A.Q., Culver J.P., Wang L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. 2014;vol. 111(1):21–26. doi: 10.1073/pnas.1311868111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Na S., Wang L.V., Wang L.V. “Photoacoustic computed tomography for functional human brain imaging [Invited. Biomed. Opt. Express. 2021;vol. 12(7):4056–4083. doi: 10.1364/BOE.423707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu M., Awasthi N., Rad N.M., Pluim J.P.W., Lopata R.G.P. Advanced ultrasound and photoacoustic imaging in cardiology. Sensors. 2021;vol. 21(23):7947. doi: 10.3390/s21237947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mehrmohammadi M., Yoon S.J., Yeager D., Emelianov S.Y. Photoacoustic imaging for cancer detection and staging. Curr. Mol. Imaging. 2013;vol. 2(1):89–105. doi: 10.2174/2211555211302010010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Han S.H. Review of photoacoustic imaging for imaging-guided spinal surgery. Neurospine. 2018;vol. 15(4):306–322. doi: 10.14245/ns.1836206.103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lediju Bell M.A., Shubert J. Photoacoustic-based visual servoing of a needle tip. Sci. Rep. 2018;vol. 8(1) doi: 10.1038/s41598-018-33931-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wu Y., et al. System-level optimization in spectroscopic photoacoustic imaging of prostate cancer. Photoacoustics. 2022;vol. 27 doi: 10.1016/j.pacs.2022.100378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Najafzadeh E., Ghadiri H., Alimohamadi M., Farnia P., Mehrmohammadi M., Ahmadian A. Application of multi-wavelength technique for photoacoustic imaging to delineate tumor margins during maximum-safe resection of glioma: a preliminary simulation study. J. Clin. Neurosci. 2019;vol. 70:242–246. doi: 10.1016/j.jocn.2019.08.040. [DOI] [PubMed] [Google Scholar]
- 13.Fan Y., Mandelis A., Spirou G., Alex Vitkin I. Development of a laser photothermoacoustic frequency-swept system for subsurface imaging: theory and experiment. J. Acoust. Soc. Am. 2004;vol. 116(6) doi: 10.1121/1.1819393. [DOI] [PubMed] [Google Scholar]
- 14.Nyayapathi N., et al. Dual scan mammoscope (DSM)—a new portable photoacoustic breast imaging system with scanning in craniocaudal plane. IEEE Trans. Biomed. Eng. 2020;vol. 67(5) doi: 10.1109/TBME.2019.2936088. [DOI] [PubMed] [Google Scholar]
- 15.Nyayapathi N., Xia J. Photoacoustic imaging of breast cancer: a mini review of system design and image features. J. Biomed. Opt. 2019;vol. 24(12) doi: 10.1117/1.JBO.24.12.121911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gao S., et al. Compact and low-cost acoustic-resolution photoacoustic microscopy based on delta configuration actuator. 2020 IEEE Int. Ultrason. Symp. . (IUS) 2020:1–4. doi: 10.1109/IUS46767.2020.9251640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li S., Montcel B., Liu W., Vray D. Analytical model of optical fluence inside multiple cylindrical inhomogeneities embedded in an otherwise homogeneous turbid medium for quantitative photoacoustic imaging. Opt. Express. 2014;vol. 22(17):20500–20514. doi: 10.1364/OE.22.020500. [DOI] [PubMed] [Google Scholar]
- 18.Huang C., Wang K., Schoonover R.W., Wang L.V., Anastasio M.A. Joint reconstruction of absorbed optical energy density and sound speed distributions in photoacoustic computed tomography: a numerical investigation. IEEE Trans. Comput. Imaging. 2016;vol. 2(2):136–149. doi: 10.1109/TCI.2016.2523427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hammernik K., Pock T., Nuster R. Variational photoacoustic image reconstruction with spatially resolved projection data. Photons Ultrasound.: Imaging Sens. 2017. 2017;vol. 10064:500–503. doi: 10.1117/12.2254863. [DOI] [Google Scholar]
- 20.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;vol. 71(1) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 21.Zeng L., Da X., Gu H., Yang D., Yang S., Xiang L. High antinoise photoacoustic tomography based on a modified filtered backprojection algorithm with combination wavelet. Med. Phys. 2007;vol. 34(2) doi: 10.1118/1.2426406. [DOI] [PubMed] [Google Scholar]
- 22.Bossy E., et al. Time reversal of photoacoustic waves. Appl. Phys. Lett. 2006;vol. 89(18) doi: 10.1063/1.2382732. [DOI] [Google Scholar]
- 23.Najafzadeh E., et al. Photoacoustic image improvement based on a combination of sparse coding and filtering. J. Biomed. Opt. . 2020;vol. 25(10) doi: 10.1117/1.JBO.25.10.106001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hauptmann A., Cox B. Deep Learning in Photoacoustic Tomography: Current approaches and future directions. J. Biomed. Opt. 2020;vol. 25(11) doi: 10.1117/1.JBO.25.11.112903. [DOI] [Google Scholar]
- 25.Zeng G., et al. A review on deep learning MRI reconstruction without fully sampled k-space. BMC Med. Imaging. 2021;vol. 21(1):195. doi: 10.1186/s12880-021-00727-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.DiSpirito A., Vu T., Pramanik M., Yao J. Sounding out the hidden data: a concise review of deep learning in photoacoustic imaging. Exp. Biol. Med. 2021;vol. 246(12):1355–1367. doi: 10.1177/15353702211000310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Allman D., Reiter A., Bell M.A.L. Photoacoustic source detection and reflection artifact removal enabled by deep learning. IEEE Trans. Med. Imaging. 2018;vol. 37(6):1464–1477. doi: 10.1109/TMI.2018.2829662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Guan S., Khan A.A., Sikdar S., Chitnis P.V. Limited view and sparse photoacoustic tomography for neuroimaging with deep learning. Sci. Rep. 2020;vol. 10(1):8510. doi: 10.1038/s41598-020-65235-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Antholzer S., Haltmeier M., Schwab J. Deep learning for photoacoustic tomography from sparse data. Inverse Probl. Sci. Eng. 2019;vol. 27(7) doi: 10.1080/17415977.2018.1518444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hsu K.-T., Guan S., Chitnis P.V. Comparing deep learning frameworks for photoacoustic tomography image reconstruction. Photoacoustics. 2021;vol. 23 doi: 10.1016/j.pacs.2021.100271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Guan S., Khan A., Sikdar S., Chitnis P.V. Fully dense UNet for 2D sparse photoacoustic tomography artifact removal. IEEE J. Biomed. Health Inform. 2020;vol. 24(2) doi: 10.1109/JBHI.2019.2912935. [DOI] [PubMed] [Google Scholar]
- 32.H. Lan, D. Jiang, C. Yang, and F. Gao, Y-Net: A Hybrid Deep Learning Reconstruction Framework for Photoacoustic Imaging in vivo, ArXiv190800975 Cs Eess, Aug. 2019, Accessed: May 29, 2020. [Online]. Available: http://arxiv.org/abs/1908.00975.
- 33.Kim M., Jeng G.-S., Pelivanov I., O’Donnell M. Deep-learning image reconstruction for real-time photoacoustic system. IEEE Trans. Med. Imaging. 2020;vol. 39(11):3379–3390. doi: 10.1109/TMI.2020.2993835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.A. Kofler, M. Haltmeier, T. Schaeffter, and C. Kolbitsch, An End-To-End-Trainable Iterative Network Architecture for Accelerated Radial Multi-Coil 2D Cine MR Image Reconstruction, ArXiv210200783 Cs Eess, Feb. 2021, Accessed: Feb. 07, 2021. [Online]. Available: http://arxiv.org/abs/2102.00783. [DOI] [PubMed]
- 35.Hosseini S.A.H., Yaman B., Moeller S., Hong M., Akçakaya M. Dense recurrent neural networks for accelerated MRI: history-cognizant unrolling of optimization algorithms. IEEE J. Sel. Top. Signal Process. 2020;vol. 14(6):1280–1291. doi: 10.1109/JSTSP.2020.3003170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu J., Sun Y., Eldeniz C., Gan W., An H., Kamilov U.S. RARE: image reconstruction using deep priors learned without ground truth. IEEE J. Sel. Top. Signal Process. 2020;vol. 14(6):1088–1099. doi: 10.1109/JSTSP.2020.2998402. [DOI] [Google Scholar]
- 37.Yang Y., Sun J., Li H., Xu Z. ADMM-CSNet: a deep learning approach for image compressive sensing. IEEE Trans. Pattern Anal. Mach. Intell. 2020;vol. 42(3):521–538. doi: 10.1109/TPAMI.2018.2883941. [DOI] [PubMed] [Google Scholar]
- 38.Adler J., Öktem O. Learned primal-dual reconstruction. IEEE Trans. Med. Imaging. 2018;vol. 37(6):1322–1332. doi: 10.1109/TMI.2018.2799231. [DOI] [PubMed] [Google Scholar]
- 39.Hauptmann A., Adler J., Arridge S., Öktem O. Multi-scale learned iterative reconstruction. IEEE Trans. Comput. Imaging. 2020;vol. 6:843–856. doi: 10.1109/TCI.2020.2990299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.R. Barbano, Z. Kereta, A. Hauptmann, S.R. Arridge, and B. Jin, Unsupervised Knowledge-Transfer for Learned Image Reconstruction, ArXiv210702572 Cs Eess, Jul. 2021, Accessed: Jul. 13, 2021. [Online]. Available: http://arxiv.org/abs/2107.02572.
- 41.Kovachki N., et al. Neural operator: learning maps between function spaces. arXiv. 2021 doi: 10.48550/arXiv.2108.08481. [DOI] [Google Scholar]
- 42.V.G. Satorras, E. Hoogeboom, and M. Welling, E(n) Equivariant Graph Neural Networks. arXiv, Feb. 16, 2022. Accessed: Jul. 30, 2022. [Online]. Available: http://arxiv.org/abs/2102.09844.
- 43.R. Wang, K. Kashinath, M. Mustafa, A. Albert, and R. Yu, Towards Physics-informed Deep Learning for Turbulent Flow Prediction. arXiv, Jun. 13, 2020. Accessed: Jul. 30, 2022. [Online]. Available: http://arxiv.org/abs/1911.08655.
- 44.Z. Li et al., Fourier Neural Operator for Parametric Partial Differential Equations, ArXiv201008895 Cs Math, Oct. 2020, Accessed: Feb. 22, 2021. [Online]. Available: http://arxiv.org/abs/2010.08895.
- 45.Xia J., Yao J., Wang L.V. Photoacoustic tomography: principles and advances. Electromagn. Waves Camb. Mass. 2014;vol. 147:1–22. doi: 10.2528/pier14032303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang L.V. Tutorial on photoacoustic microscopy and computed tomography. IEEE J. Sel. Top. Quantum Electron. 2008;vol. 14(1):171–179. doi: 10.1109/JSTQE.2007.913398. [DOI] [Google Scholar]
- 47.Arridge S.R., Betcke M.M., Cox B.T., Lucka F., Treeby B.E. On the adjoint operator in photoacoustic tomography. Inverse Probl. 2016;vol. 32(11) doi: 10.1088/0266-5611/32/11/115012. [DOI] [Google Scholar]
- 48.Baumann B., Wolff M., Kost B., Groninga H. Finite element calculation of photoacoustic signals. Appl. Opt. 2007;vol. 46(7):1120. doi: 10.1364/AO.46.001120. [DOI] [PubMed] [Google Scholar]
- 49.Sheu Y.-L., Li P.-C. Simulations of photoacoustic wave propagation using a finite-difference time-domain method with Berenger’s perfectly matched layers. J. Acoust. Soc. Am. . 2008;vol. 124(6):3471–3480. doi: 10.1121/1.3003087. [DOI] [PubMed] [Google Scholar]
- 50.Treeby B.E., Jaros J., Rendell A.P., Cox B.T. Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using a k-space pseudospectral method. J. Acoust. Soc. Am. 2012;vol. 131(6):4324–4336. doi: 10.1121/1.4712021. [DOI] [PubMed] [Google Scholar]
- 51.Cox B.T., Kara S., Arridge S.R., Beard P.C. k-space propagation models for acoustically heterogeneous media: Application to biomedical photoacoustics. J. Acoust. Soc. Am. 2007;vol. 121(6):3453–3464. doi: 10.1121/1.2717409. [DOI] [PubMed] [Google Scholar]
- 52.S. Guan, K.-T. Hsu, and P.V. Chitnis, Fourier Neural Operator Networks: A Fast and General Solver for the Photoacoustic Wave Equation, p. 14.
- 53.Treeby B.E., Cox B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010;vol. 15(2) doi: 10.1117/1.3360308. [DOI] [PubMed] [Google Scholar]
- 54.Arridge S., et al. Accelerated high-resolution photoacoustic tomography via compressed sensing. Phys. Med. Biol. 2016;vol. 61(24):8908–8940. doi: 10.1088/1361-6560/61/24/8908. [DOI] [PubMed] [Google Scholar]
- 55.Velikina J., Leng S., Chen G.-H. Limited view angle tomographic image reconstruction via total variation minimization. Med. Imaging 2007: Phys. Med. Imaging. 2007;vol. 6510:709–720. doi: 10.1117/12.713750. [DOI] [Google Scholar]
- 56.Gutta S., Kalva S.K., Pramanik M., Yalavarthy P.K. Accelerated image reconstruction using extrapolated Tikhonov filtering for photoacoustic tomography. Med. Phys. 2018 doi: 10.1002/mp.13023. [DOI] [PubMed] [Google Scholar]
- 57.Hauptmann A., et al. Model-based learning for accelerated, limited-view 3-D photoacoustic tomography. IEEE Trans. Med. Imaging. 2018;vol. 37(6):1382–1393. doi: 10.1109/TMI.2018.2820382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Dorr A., Sled J.G., Kabani N. Three-dimensional cerebral vasculature of the CBA mouse brain: A magnetic resonance imaging and micro computed tomography study. NeuroImage. 2007;vol. 35(4) doi: 10.1016/j.neuroimage.2006.12.040. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material
Supplementary material
Data Availability Statement
Data will be made available on request.