Abstract
Purpose:
Myocardial perfusion imaging (MPI) using single-photon emission computed tomography (SPECT) is widely applied for the diagnosis of cardiovascular diseases. In clinical practice, the long scanning procedures and acquisition time might induce patient anxiety and discomfort, motion artifacts, and misalignments between SPECT and computed tomography (CT). Reducing the number of projection angles provides a solution that results in a shorter scanning time. However, fewer projection angles might cause lower reconstruction accuracy, higher noise level, and reconstruction artifacts due to reduced angular sampling. We developed a deep-learning-based approach for high-quality SPECT image reconstruction using sparsely-sampled projections.
Methods:
We proposed a novel deep-learning-based dual-domain sinogram synthesis (DuDoSS) method to recover full-view projections from sparsely-sampled projections of cardiac SPECT. DuDoSS utilized the SPECT images predicted in the image domain as guidance to generate synthetic full-view projections in the sinogram domain. The synthetic projections were then reconstructed into non-attenuation-corrected (NAC) and attenuation-corrected (AC) SPECT images for voxel-wise and segment-wise quantitative evaluations in terms of normalized mean square error (NMSE) and absolute percent error (APE). Previous deep-learning-based approaches including direct sinogram generation (Direct Sino2Sino) and direct image prediction (Direct Img2Img) were tested in this study for comparison. The dataset used in this study included a total of 500 anonymized clinical stress-state MPI studies acquired on a GE NM/CT 850 scanner with 60 projection angles following the injection of 99mTc-tetrofosmin.
Results:
Our proposed DuDoSS generated more consistent synthetic projections and SPECT images with the ground truth than other approaches. The average voxel-wise NMSE between the synthetic projections by DuDoSS and the ground-truth full-view projections was 2.08 ± 0.81%, as compared to 2.21 ± 0.86% (p < 0.001) by Direct Sino2Sino. The averaged voxel-wise NMSE between the AC SPECT images by DuDoSS and the ground-truth AC SPECT images was 1.63 ± 0.72%, as compared to 1.84 ± 0.79% (p < 0.001) by Direct Sino2Sino and 1.90 ± 0.66% (p < 0.001) by Direct Img2Img. The averaged segment-wise APE between the AC SPECT images by DuDoSS and the ground-truth AC SPECT images was 3.87 ± 3.23%, as compared to 3.95 ± 3.21% (p = 0.023) by Direct Img2Img and 4.46 ± 3.58% (p < 0.001) by Direct Sino2Sino.
Conclusions:
Our proposed DuDoSS is feasible to generate accurate synthetic full-view projections from sparsely-sampled projections for cardiac SPECT. The synthetic projections and reconstructed SPECT images generated from DuDoSS are more consistent with the ground-truth full-view projections and SPECT images than other approaches. DuDoSS can potentially enable fast data acquisition of cardiac SPECT.
Keywords: Deep learning, synthetic projections, cardiac SPECT, myocardial perfusion imaging
1. INTRODUCTION
Myocardial perfusion imaging (MPI) using single-photon emission computed tomography (SPECT) is the most widely performed nuclear cardiology exam that allows sensitive detection, localization, and risk stratification of ischemic heart disease.1–3 In clinical practice, cardiac SPECT imaging using rotational scanners generally involves detectors rotating around the chest in a step-and-shoot protocol to acquire the projection data. The long scanning procedures and acquisition time present challenges that hinder efficient and accurate clinical exams. First, patients undergoing complex imaging examinations such as hybrid SPECT-CT might experience anxiety and discomfort due to the long scanning time.4 This will increase the likelihood of noncompliance during the imaging procedures, leading to suboptimal scans and inaccurate reports.5, 6 Second, body motion during a long scanning time might cause motion artifacts and further affect the diagnostic accuracy.7–9 Voluntary or involuntary body motions during the data acquisition procedure might cause significant displacements of hearts or other organs, which will cause misregistration of projection data. Excessive movements may require repeated scans with additional radiation exposure to patients. Third, SPECT and CT images are acquired sequentially and the displacements of the patient body during the long acquisition time might lead to misalignment of SPECT and CT scans, thus creating attenuation correction artifacts.10–12 Last, SPECT imaging in a large volume clinical lab requires efficiency of imaging.13, 14 Therefore, shorter imaging times could increase the patient throughput in a busy lab.
Reducing the number of projection angles provides a solution that results in a shorter scanning time. However, fewer projection angles can lead to lower reconstruction accuracy, higher noise level, and severe artifacts due to the reduced angular sampling.15–17 Thus, compensating the image quality degradation under the premise of sparsely-sampled projections is an important topic to investigate. Sparse-view image reconstruction is a widely explored application in CT.18, 19 The evolving deep learning techniques has provided solutions to this important topic in CT.20–24 However, the sparse-view sinogram recovery or sinogram inpainting in PET and SPECT is still under explored. Prior conventional works in sinogram inpainting and synthesis of PET and SPECT included sparse presentation-based methods that applied dictionary learning for sparse representation and data recovery of PET sinogram,25–27 compressive sensing-based methods based on wavelet-domain total variation minimization to recover missing data in PET acquisition,28 and model-based reconstruction methods that combined the estimation maximization algorithm with mixed region and voxel image representation,29 etc. For deep-learning-based methods, U-Net30 was applied to inpaint the missing data in the sinogram of whole-body PET in a previous study.31 The experiment was implemented in the sinogram domain, in which the defective sinogram was input to U-Net to predict the intact sinogram. In another study, ResNet32 was applied to generate synthesis projections from half-time or sparse-view sampled projections of cardiac SPECT, which was implemented in sinogram domain.33 Another study implemented the PET sinogram recovery in either sinogram domain or image domain, in which the defective sinogram or the PET image was input to U-Net to predict the complete sinogram or image.34 A novel deep learning framework LU-Net combining Long Short-Term Memory network (LSTM)35 and U-Net was proposed for the sparse-view SPECT sinogram synthesis.36 Due to the embedded LSTM modules, the LU-Net has a larger receptive field since it can exploit the projection data in both neighboring and distant view angles.
A recent method named convolutional U-Net-shaped synthetic intermediate projections (CUSIP) generated synthetic projections (120 angles) from sparsely-sampled projections (30 angles) for 177Lu SPECT images.37 In CUSIP, three separate neural networks were independently trained to predict three sets of 30 intermediate projections, which were then combined with the input sparsely-sampled projections to generate the predicted full-view projections (120 angles). However, this method predicted each set of projections separately, which did not incorporate the 3D spatial information of image volumes into neural networks.
The aforementioned deep learning methods were implemented in either image or sinogram domain, and none of them has combined the information of both image and sinogram domains for the sparse-view sinogram recovery of PET or SPECT. The dual-domain strategy has widely used in many fields of medical imaging including reconstruction,38, 39 CT metal artifact reduction,40, 41 segmentation,42, 43 image synthesis,44, 45 etc., but it has not been investigated in the sparse-view sinogram recovery of PET or SPECT yet. In this study, we proposed a deep-learning-based Dual-Domain Sinogram Synthesis (DuDoSS) method to predict the synthetic full-view projections from sparsely-sampled projections of cardiac SPECT.
2. MATERIALS AND METHODS
2.1. Study datasets
The dataset used in this study included a total of 500 anonymized clinical stress SPECT MPI studies acquired on a GE NM/CT 850 scanner with 60 projection angles. The projection data were acquired using a step-and-shoot protocol over 360 degrees with a parallel head (H-mode) configuration. The patient studies were anonymized and exported from the clinical PACS using the AI Accelerator (Visage Imaging, Inc., San Diego, CA). One-day stress-only low-dose protocol was used with the mean administered dose of 15 mCi 99mTc-tetrofosmin. Among the 500 patient studies, 250, 100, 150 were used for training, validation, and testing, respectively. The patient information including gender, age, height, weight, and BMI distribution are listed in Table 1.
TABLE 1.
The gender, age, height, weight, and BMI distribution of the enrolled patients.
| Patient Information | Age (year) | Height (m) | Weight (kg) | BMI | |
|---|---|---|---|---|---|
| Training Data (132 M, 118 F)a |
Range | 34 – 94 | 1.42 – 1.90 | 44.50 – 150.1 | 16.35 – 49.98 |
| Mean ± Std. | 64.79 ± 11.35 | 1.69 ± 0.11 | 87.09 ± 19.08 | 30.66 ± 6.16 | |
| Validation Data (50 M, 50 F) |
Range | 39 – 96 | 1.45 – 1.93 | 42.20 – 159.2 | 17.69 – 49.14 |
| Mean ± Std. | 63.37 ± 11.91 | 1.67 ± 0.12 | 88.89 ± 21.00 | 31.67 ± 6.21 | |
| Testing Data (86 M, 64 F) |
Range | 37 – 94 | 1.42 – 1.93 | 19.10 – 160.7 | 17.66 – 46.63 |
| Mean ± Std. | 67.90 ± 12.31 | 1.69 ± 0.11 | 84.34 ± 21.23 | 29.49 ± 5.71 | |
M stands for male and F stands for female.
Clinical imaging with the GE NM/CT 850 involves full-view projections with a dimension of 64×64×60 and a voxel size of 6.8×6.8×6.8 mm3 acquired in a photopeak window (126.5 – 154.5 keV). The CT-derived attenuation maps were all manually checked and registered with SPECT images by technologists at Yale Nuclear Cardiology Clinic using GE’s ACQC package.
2.2. Image preprocessing and reconstructions
To reduce the number of projection angles, the 60 angles were evenly divided into four sparsely-sampled sub-datasets. Each sub-dataset with a dimension of 64×64×15 consisted of 15 projections. The four sub-datasets were formed by selecting every first, second, third, and fourth projections of the full-view 60 projections, which were labeled as Angles 1, 2, 3, and 4. In the CUSIP approach,37 Angle 1 was used as the input to three individual U-Nets with different trainable parameters to predict Angles 2, 3, and 4 independently. In our DuDoSS approach, the input Angle 1 was zero-padded into the dimension of 64×64×60 and then used as the input to the networks.
The sparsely-sampled (64×64×15) or full-view (64×64×60) projections were reconstructed into SPECT images (64×64×64) using Maximum-Likelihood Expectation-Maximization (MLEM, 120 iterations, no scatter correction) and Butterworth filter (cutoff frequency = 0.37 cm−1, order = 7). Non-attenuation-corrected (NAC) and AC SPECT images were reconstructed without or with the incorporation of the CT-derived attenuation maps, respectively.
Analyzing the specific regions of interest (ROI) is quite important for medical imaging. However, in cardiac SPECT, the tracer distributions outside the cardiac regions, especially at the abdomen, are sometimes extremely high, which might affect the quantitative evaluations of hearts. Thus, we cropped 32 slices out of the original 64 slices along the z axis of the full-view projections, to include the cardiac regions and exclude the background signals. The size of the full-view projections was cropped from 64×64×60 into 64×32×60. Similarly, the size of the SPECT images was cropped from 64×64×64 into 64×64×32. In our experiment, we utilized the cropped projections and images for the network training, testing, and quantitative evaluations, to reduce the effect of the background signals.
2.3. Overview of DuDoSS
Figure 1 shows the diagram of our proposed DuDoSS approach. The general principle was utilizing the predicted full-view images as guidance to generate the synthetic full-view projections. The overall workflow included image-domain prediction using an image-domain networks ImgNet, domain transitions using a forward-projection operator, and sinogram-domain generation using a sinogram-domain networks SinoNet.
FIGURE 1.
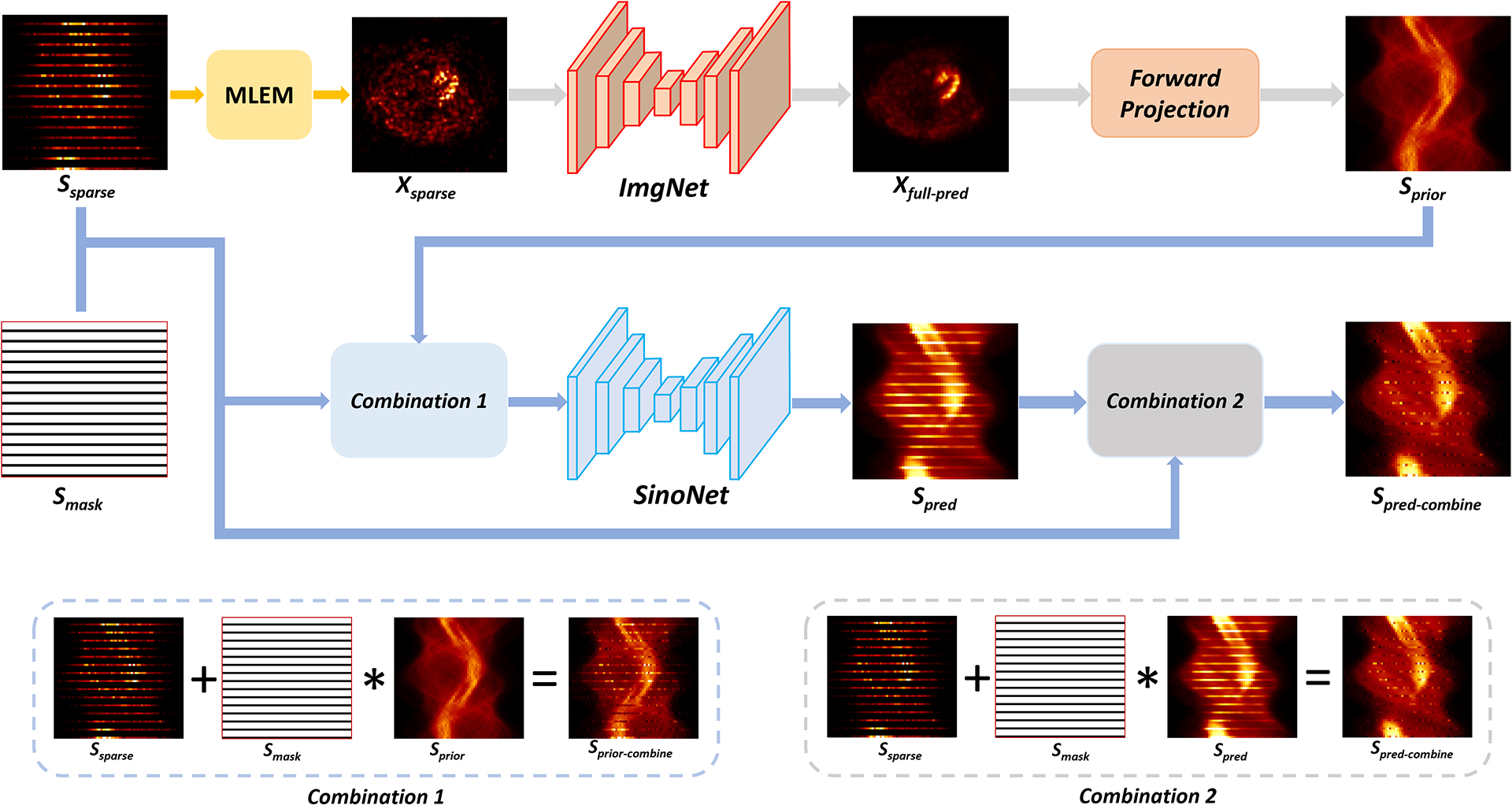
Diagram of DuDoSS. Xsparse reconstructed using sparsely-sampled projections Ssparse was input to the ImgNet to predict the full-view SPECT image Xfull−pred. Then, Xfull−pred was forward-projected to generate a prior full-view projections Sprior, which were then combined with the ground-truth acquired Angle 1 to obtain Sprior−combine. Next, Sprior−combine was input to the SinoNet to generate the predicted sinogram Spred. Finally, Spred was combined with the ground-truth acquired Angle 1 to output the combined projections Spred−combine.
First, the zero-padded sparsely-sampled projections Ssparse were reconstructed into a sparsely-reconstructed image Xsparse using MLEM. In the image domain, Xsparse was input to ImgNet to generate the predicted full-view image Xfull−pred, formulated as:
| (1) |
where fImg denoted the image prediction using ImgNet. L1 loss is a robust mean-based measurement that does not over-penalize significant errors nor tolerate subtle errors. Thus, to optimize ImgNet, we employed L1 loss to minimize the difference between Xfull−pred and Xfull which was reconstructed using the ground-truth full-view projections, formulated as:
| (2) |
where ℒImg denoted the image-domain loss. Then, the predicted Xfull−pred was forward-projected to generate the prior full-view projections Sprior, formulated as:
| (3) |
where 𝒫 referred to the forward-projection operator. Sprior was utilized as a prior estimate of the ground-truth full-view projections Sfull. Then, Angle 1 of Sprior was replaced by the ground-truth acquired Angle 1 in a combination module to further improve the accuracy of the projections, formulated as:
| (4) |
where * denoted the element-wise multiplications. Sprior−combine referred to the combined projections. Smask was a binary mask with value 0 in Angle 1 and value 1 at Angles 2, 3, and 4.
Next, in the sinogram domain, Sprior−combine was input to SinoNet to generate the synthetic full-view projections Spred, formulated as:
| (5) |
where fSino referred to the sinogram generation using SinoNet. Finally, Angle 1 of Spred was replaced by the ground-truth acquired Angle 1 in a combination module to further improve the accuracy of the synthetic projections, formulated as:
| (6) |
To optimize SinoNet, we employed L1 loss to minimize the difference between Spred−combine and the ground-truth full-few projections Sfull, formulated as
| (7) |
where ℒSino denoted the sinogram-domain loss.
In our study, we jointly trained the ImgNet and SinoNet in an end-to-end manner and the total objective loss function is formulated as
| (8) |
In this workflow, both ImgNet and SinoNet were Dual-Squeeze-and-Excitation Residual Dense Network (DuRDN) which was proposed in one of our previous works and showed superior performance than U-Net in some image transformation tasks.46 DuRDN was built using Residual Dense Blocks (RDB) and Dual Squeeze-and-Excitation (DuSE) self-attention modules. RDB effectively extract the image information using densely-connected structures and global residual connections. DuSE encouraged the networks to recalibrate both channel-wise and spatial features such that more accurate and relevant feature maps can be learned.
2.4. Experiments
In our experiment, the original full-view projections and the SPECT images reconstructed using the original full-view projections were considered as the ground truth. The CUSIP approach was tested as the benchmark in this study, labeled as CUSIP. Alternatively, we implemented another CUSIP by replacing the U-Net by DuRDN, which was labeled as CUSIP-DuRDN.
We tested two additional ablation study groups, labeled as Direct Sino2Sino and Direct Img2Img. The detailed schematics of Direct Sino2Sino and Direct Img2Img are presented in Section 1 of Supplementary Materials. The Direct Sino2Sino was implemented only in the sinogram domain. The zero-padded sparse-view projections Ssparse were input to the SinoNet to predict the synthetic full-view projections Spred, with the ground-truth full-view projections Sfull as targets. Then, Angle 1 of Spred was replaced by ground-truth Angle 1 to produce Spred−combine for the reconstruction of the predicted full-view SPECT image. Direct Img2Img was implemented only in the image domain, without any intermediate step of synthetic projections. The SPECT image Xsparse reconstructed using Ssparse was input to the ImgNet to directly generate the predicted full-view image Xfull−pred, with the ground-truth full-view image Xfull as targets.
2.5. Network training
All the hyperparameters including learning rates, learning rate decay rates, batch sizes, have been optimized to maximize the performance for each testing group after repeated experiments. To maintain the spatial integrity of the sinogram, we did not implement patch-based strategies and the entire image volumes were used as input and output in this study.
In the CUSIP, CUSIP-DuRDN, and Direct Sino2Sino group, U-Net or DuRDN were trained for 600 epochs with a learning rate of 5×10−4, a batch size of 4, and an Adam optimizer (exponential decay rates β1 = 0.5, β2 = 0.999). A learning rate decay policy with a step size of 1 and a decay rate of 0.99 was employed to avoid overfitting.47 In the Direct Img2Img group, the learning rate was 5×10−4, and other hyperparameters were the same as above. In our proposed DuDoSS, the learning rates of ImgNet and SinoNet were 1×10−5 and 1×10−4 respectively. The other parameters were the same as above.
The numbers of trainable parameters in CUSIP, CUSIP-DuRDN, Direct Sino2Sino, Direct Img2Img, and DuDoSS were respectively about 2 m, 2.5 m, 2.5 m, 2.5 m, and 5 m (m: million). DuDoSS contained the most trainable parameters because it had two end-to-end connected networks. The consumed memories during the training process of CUSIP, CUSIP-DuRDN, Direct Sino2Sino, Direct Img2Img, and DuDoSS were about 3 GB, 4 GB, 7 GB, 7.5 GB, and 12 GB (GB: gigabytes). Under the same hardware support of the NVIDIA Quadro RTX 8000 graphic card, the training time of CUSIP was about 4 hours for each angle and 12 hours in total, and the training time of CUSIP-DuRDN was about 7 hours for each angle and 21 hours in total. The total training time of Direct Sino2Sino, Direct Img2Img, and DuDoSS were 9 hours, 10 hours, and 16 hours, respectively. CUSIP-DuRDN group consumed the longest training time to converge. For every testing group, the testing time of each case was shorter than 0.1 second, which was a reasonable inference time for clinical practice.
2.6. Voxel-wise quantitative evaluations
The voxel-wise quantitative evaluation metrics used in this study included normalized mean square error (NMSE), normalized mean absolute error (NMAE), structural similarity (SSIM),48 and peak signal-to-noise ratio (PSNR). NMSE, NMAE, PSNR are defined as:
| (9) |
| (10) |
| (11) |
where Xi and Yi are the ith voxels of the predicted image and ground-truth image. N is the total number of voxels of the image volume. Max(Y) is the maximum voxel value of the ground-truth image. SSIM is defined as:
| (12) |
where C1 = (K1 × R)2 and C2 = (K2 × R)2 are constants to stabilize the ratios. R stands for dynamic range of pixel values. Usually, we set K1 = 0.01 and K2 = 0.03. μX and μY are the means of Y and X. and are the variances of Y and X. σYX is the covariance of Y and X.
The calculation of NMSE/NMAE/PSNR/SSIM should be restricted within the region containing the patient heart to eliminate the influence of background signals or artifacts. Thus, we generated binary image masks by thresholding to restrict quantitative evaluations within the voxels of the patient heart. Then, we applied forward projection of the binary image masks to generate the binary sinogram masks that restrict the quantitative evaluations within the cardiac sinogram regions. The images or sinograms were element-wise multiplied with the binary image or sinogram masks before the quantitative evaluations using NMSE/NMAE/PSNR/SSIM. The sample binary masks for quantitative evaluations of images and sinograms are provided in Section 2 of Supplementary Materials.
The synthetic projections were compared with the ground-truth full-view projections. The SPECT images reconstructed with the synthetic projections are compared with the images reconstructed with the ground-truth full-view projections. Both AC and NAC SPECT images were involved in the voxel-wise quantitative evaluations.
2.7. Segment-wise quantitative evaluations
To specifically quantify the myocardial perfusion intensities, standard 17-segment polar maps were generated for qualitative and quantitative evaluations of the NAC and AC SPECT images.49 The mean values of segments were measured using the Carimas Software50 for computing the segment-wise absolute percent error (APE) and percent error (PE) defined as:
| (13) |
| (14) |
where Predi and ACi represent the mean values of the ith segment in the polar maps of the predicted and ground-truth SPECT images.
2.8. Statistical analysis
For statistical analysis, two-tailed paired t-tests with a significance level of 0.05 was performed based on the above quantification metrics between two testing groups. P-values lower than 0.05 represented a significant difference of the quantification metrics between the two testing groups.
3. RESULTS
3.1. Synthetic projections
Figure 2 shows representative synthetic full-view projections. It can be observed that CUSIP and CUSIP-DuRDN under-estimated the intensities of the synthetic projections. Based on error maps of the synthetic projections, Direct Sino2Sino generated more consistent synthetic projections than the above two groups. DuDoSS provided the most consistent projections compared with the ground-truth full-view projections. Table 2 lists the voxel-wise quantitative evaluations of the synthetic projections in terms of NMSE, NMAE, SSIM, and PSNR for the 150 testing patient studies. CUSIP-DuRDN showed more accurate prediction results than CUSIP, demonstrating the superiority of DuRDN to U-Net. Direct Sino2Sino was more accurate than the above two groups. DuDoSS showed the lowest errors among all the testing groups. The significant p-values further validated that DuDoSS produced more accurate synthetic projections relative to the other groups. In addition, to test the influence of loss functions on the accuracy of the synthetic sinograms by DuDoSS, we implemented several ablation DuDoSS groups supervised by different loss functions. The results demonstrated that L1 loss was currently the most simple but effective loss function in this study, which are presented in Section 3 of the Supplementary Materials.
FIGURE 2.

Sample synthetic projections of the slice crossing the center of the patient heart. The error maps between the synthetic and ground-truth full-view projections are shown in the second row. CUSIP and CUSIP-DuRDN show obvious under-estimations of the synthetic projections. DuDoSS outputs the most consistent projections with the ground truth full-view projections compared with other testing groups. Errors between the predicted and ground-truth projections are denoted with white arrows.
TABLE 2.
Voxel-wise quantitative evaluations of the synthetic projections of the 150 testing patient studies.
| Testing Groups | NMSE (×10−2) | NMAE (×10−2) | SSIM | PSNR | P-valuea |
|---|---|---|---|---|---|
| CUSIP | 2.53 ± 1.04 | 10.91 ± 1.26 | 0.979 ± 0.072 | 35.11 ± 4.08 | – |
| CUSIP-DuRDN | 2.17 ± 0.84 | 10.23 ± 1.59 | 0.980 ± 0.075 | 35.82 ± 4.44 | < 0.001* |
| Direct Sino2Sino | 1.80 ± 0.82 | 9.22 ± 1.58 | 0.983 ± 0.068 | 36.71 ± 4.35 | < 0.001* |
| DuDoSS (proposed) | 1.65 ± 0.72 | 8.95 ± 1.56 | 0.984 ± 0.067 | 37.09 ± 4.51 | < 0.001* |
Two-tailed paired t-test of NMSE between the current and previous group in the table.
Refers to significant difference with a significance level of 0.05.
Figure 3 provides an example of synthetic projections at three consecutive Angles 2, 3, 4. In Angles 2, 3, and 4, CUSIP and CUSIP-DuRDN both showed obvious under-estimations of the projection intensity, especially at the cardiac regions. In contrast, Direct Sino2Sino yielded more consistent projections than the above two groups. DuDoSS yielded the most consistent projections with ground truth in all 3 projection angles. In addition, Table 3 lists the quantitative evaluations of the synthetic projections at Angles 2, 3, and 4 for the 150 testing patient studies. At each projection angle, it can be observed that Direct Sino2Sino yielded more accurate projections than CUSIP and CUSIP-DuRDN. DuDoSS provided the most accurate predictions at each angle. DuDoSS predicted significantly more accurate projections than other groups in Angles 2, 3, and 4 based on the significant p-values.
FIGURE 3.
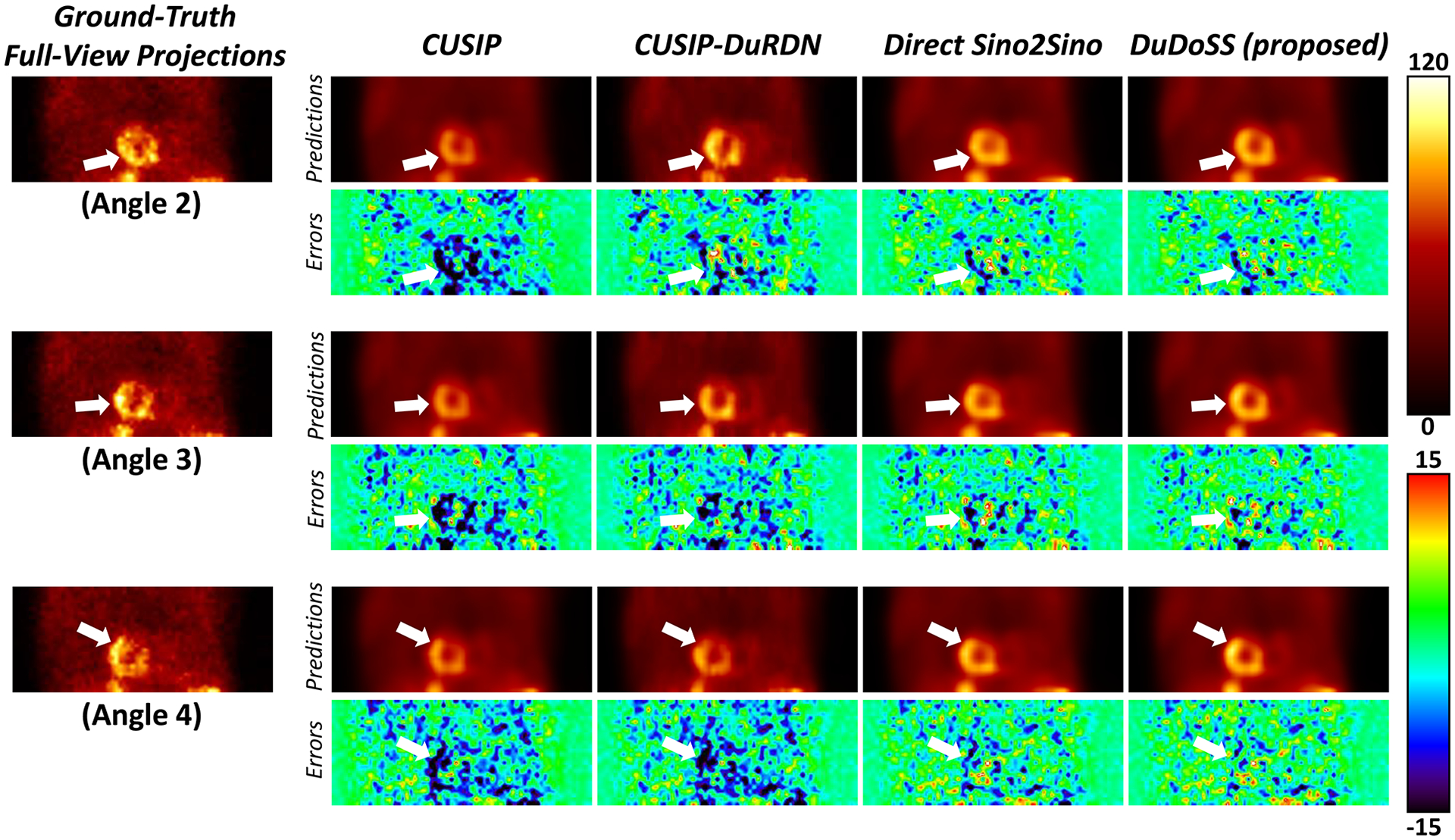
Sample synthetic projections at three consecutive Angles 2, 3, 4. The error maps between the synthetic and ground-truth corresponding projections are shown below each image. CUSIP and CUSP-DuRDN show obvious under-estimations in all angles, especially at the central cardiac regions. DuDoSS predicts the most consistent projections in all Angles 2, 3, and 4 compared with the ground-truth projections. Errors between the predicted and ground-truth projections are denoted with white arrows.
TABLE 3.
Quantitative evaluations of synthetic projections at Angle 2, 3, and 4 respectively of the 150 testing patient studies.
| Testing Groups | Projection Angle 2 | Projection Angle 3 | Projection Angle 4 | |||
|---|---|---|---|---|---|---|
| NMSE (×10−2) | P-valuea | NMSE (×10−2) | P-valuea | NMSE (×10−2) | P-valuea | |
| CUSIP | 3.57 ± 1.26 | – | 3.29 ± 1.63 | – | 3.23 ± 1.38 | – |
| CUSIP-DuRDN | 2.89 ± 1.08 | < 0.001* | 2.93 ± 1.36 | < 0.001* | 2.86 ± 1.06 | < 0.001* |
| Direct Sino2Sino | 2.25 ± 1.02 | < 0.001* | 2.47 ± 1.32 | < 0.001* | 2.46 ± 1.13 | < 0.001* |
| DuDoSS (proposed) | 2.18 ± 0.96 | 0.004* | 2.22 ± 1.05 | < 0.001* | 2.20 ± 1.03 | < 0.001* |
Two-tailed paired t-test of NMSE between the current and previous group in the table.
Refers to significant difference with a significance level of 0.05.
3.2. Reconstructed SPECT images
The synthetic projections from CUSIP, CUSIP-DuRDN, Direct Sino2Sino, and DuDoSS were reconstructed into NAC and AC SPECT images using MLEM. Direct Img2Img predicted full-view SPECT images from sparsely-sampled SPECT images directly. Sample NAC and AC SPECT images are shown in Figure 4. The reconstructed NAC or AC images by CUSIP and CUSIP-DuRDN showed obvious under-estimations of the myocardial perfusion intensities due to the under-estimations of synthetic projections as presented in Figure 3. Direct Img2Img showed slightly more visually consistent NAC and AC images with ground truth than Direct Sino2Sino. In contrast, DuDoSS showed the most consistent NAC and AC SPECT images with the ground-truth full-view SPECT images.
FIGURE 4.
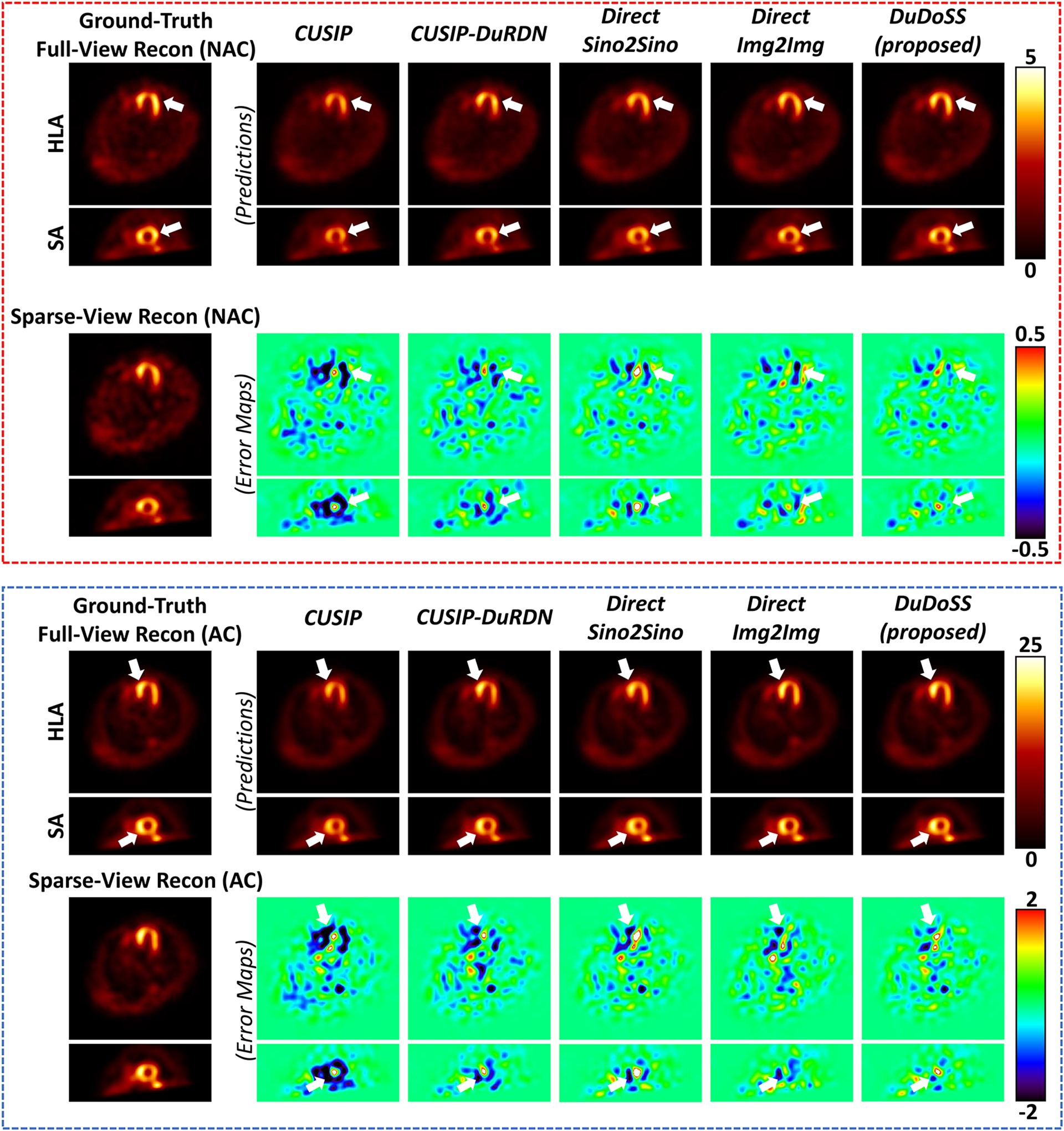
Sample NAC and AC SPECT images and corresponding error maps shown in the horizontal long axis (HLA) and the short axis (SA) views. The NAC SPECT images are shown in the top red dash box, and the AC SPECT images are shown in the bottom blue dash box. DuDoSS outputs the most consistent NAC and AC SPECT images with the ground-truth full-view SPECT images. Errors between the predicted and ground-truth SPECT images are denoted with white arrows.
To better quantify the myocardial perfusion intensities of the NAC and AC SPECT images, we plotted the circumferential count profiles of myocardial perfusion intensities for representative NAC and AC SPECT images as shown in Figure 5. The detailed implementation of the circumferential profiles is presented in Section 4 of Supplementary Materials. It can be observed that the profiles from DuDoSS were the most consistent with those of the ground truth for both the NAC and AC SPECT images. In contrast, the profiles of CUSIP were even worse than those from Sparse-View baseline due to the significant under-estimations of myocardial perfusion intensities in the cardiac regions.
FIGURE 5.
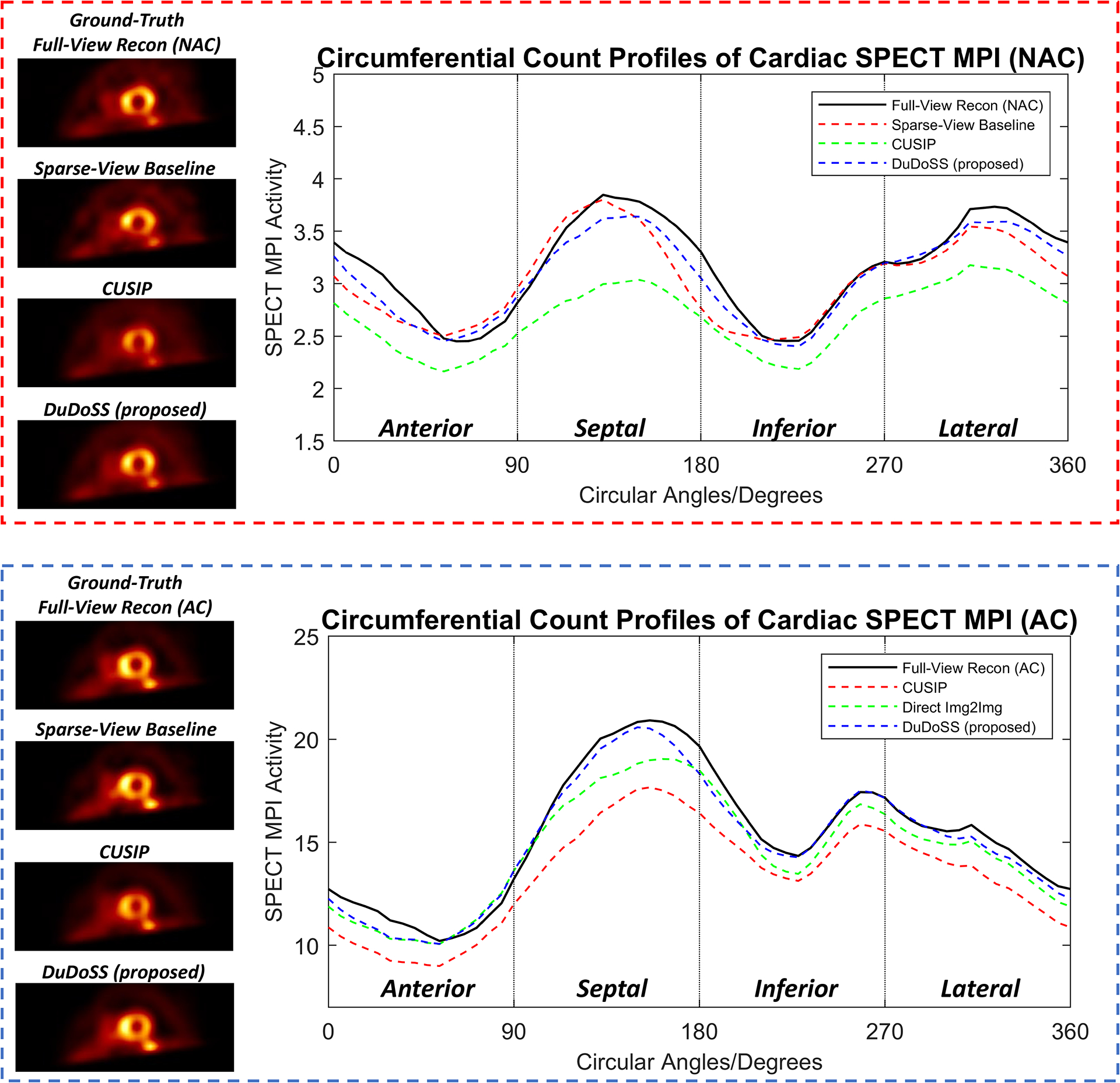
Circumferential count profiles of myocardial perfusion intensities of sample NAC and AC SPECT images in the SA view. The profiles of NAC and AC images are shown in the top red dash box and the bottom blue dash box. DuDoSS outputs the most consistent profiles with those of the ground-truth Full-View Recon, while CUSIP shows the highest prediction errors.
The voxel-wise quantitative evaluations of the reconstructed NAC and AC SPECT images of the 150 patient studies are provided in Tables 4 and 5. In both NAC and AC images, CUSIP produced the highest voxel-wise errors, followed by CUSIP-DuRDN. Direct Sino2Sino showed better results than Direct Img2Img, and our DuDoSS showed more consistent results than other testing groups. DuDoSS showed statistically more accurate results relative to the other testing groups based on the significant p-values.
TABLE 4.
Quantitative evaluations of the reconstructed NAC SPECT images of the 150 testing patient studies.
| Testing Groups | NMSE (×10−2) | NMAE (×10−2) | SSIM | PSNR | p-valuea |
|---|---|---|---|---|---|
| Sparse-View Baseline | 2.51 ± 1.58 | 12.73 ± 2.77 | 0.9948 ± 0.0020 | 38.81 ± 2.86 | – |
| CUSIP | 2.54 ± 1.13 | 13.31 ± 2.19 | 0.9938 ± 0.0015 | 38.51 ± 2.02 | – |
| CUSIP-DuRDN | 1.64 ± 0.77 | 10.41 ± 2.10 | 0.9958 ± 0.0014 | 40.49 ± 2.28 | < 0.001* |
| Direct Img2Img | 1.53 ± 1.05 | 9.77 ± 2.69 | 0.9965 ± 0.0014 | 41.00 ± 1.82 | 0.154 |
| Direct Sino2Sino | 1.33 ± 0.81 | 9.17 ± 2.25 | 0.9967 ± 0.0013 | 41.54 ± 2.23 | 0.003* |
| DuDoSS (proposed) | 1.07 ± 0.67 | 8.29 ± 1.84 | 0.9974 ± 0.0010 | 42.45 ± 2.55 | < 0.001* |
Two-tailed paired t-test of NMSE between the current and previous group in the table.
Refers to significant difference with a significance level of 0.05.
TABLE 5.
Quantitative evaluations of the reconstructed AC SPECT images of the 150 testing patient studies.
| Testing Groups | NMSE (×10−2) | NMAE (×10−2) | SSIM | PSNR | P-valuea |
|---|---|---|---|---|---|
| Sparse-View Baseline | 1.53 ± 0.72 | 9.84 ± 1.98 | 0.9966 ± 0.0011 | 41.16 ± 2.91 | – |
| CUSIP | 2.50 ± 1.03 | 12.99 ± 1.92 | 0.9938 ± 0.0013 | 38.89 ± 2.01 | – |
| CUSIP-DuRDN | 1.68 ± 0.86 | 10.20 ± 1.98 | 0.9958 ± 0.0014 | 40.72 ± 2.24 | < 0.001* |
| Direct Img2Img | 1.37 ± 0.80 | 9.02 ± 2.03 | 0.9967 ± 0.0012 | 41.71 ± 2.20 | 0.090 |
| Direct Sino2Sino | 1.28 ± 0.48 | 8.99 ± 1.61 | 0.9969 ± 0.0011 | 41.81 ± 2.41 | < 0.001* |
| DuDoSS (proposed) | 1.16 ± 0.71 | 8.30 ± 1.79 | 0.9973 ± 0.0011 | 42.43 ± 2.50 | < 0.001* |
Two-tailed paired t-test of NMSE between the current and previous group in the table.
Refers to significant difference with a significance level of 0.05.
3.3. Polar maps of SPECT images
Figure 6 shows the 17-segment polar maps from representative NAC and AC SPECT images. The segment intensities of polar maps by CUSIP and CUSIP-DuRDN were under-estimated compared with the ground-truth polar maps of the full-view SPECT images. Direct Sino2Sino and Direct Img2Img produced more consistent polar maps with ground truth than the above two groups, in which the Direct Img2Img appeared slightly better. In contrast, the polar maps of DuDoSS showed polar maps that were more consistent with the ground truth than other testing groups.
FIGURE 6.
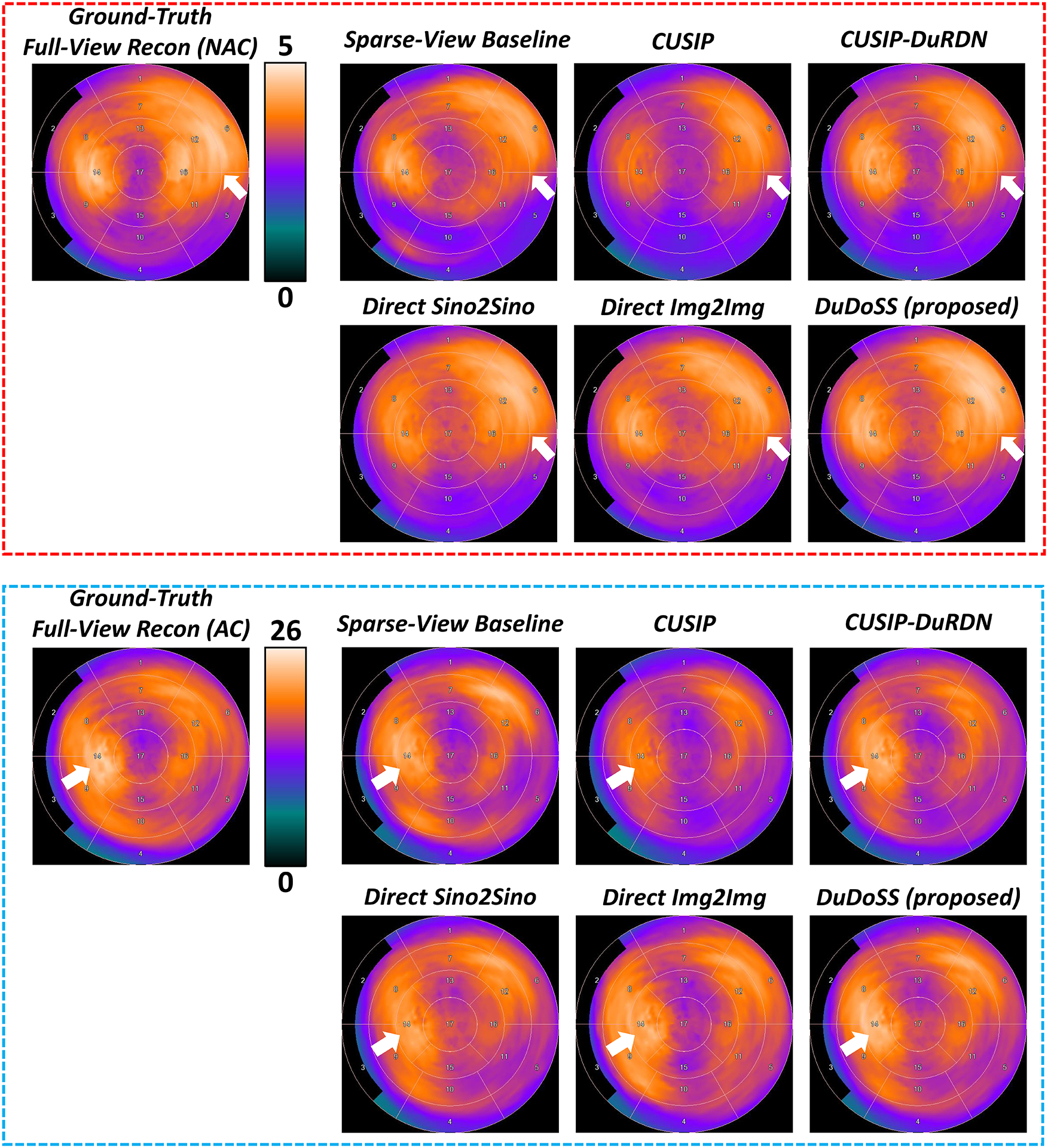
Standard 17-segment polar maps of sample NAC and AC SPECT images. The polar maps of the NAC SPECT images are shown in the top red dash box, and the polar maps of the AC SPECT images are shown in the bottom blue dash box. DuDoSS outputs the most consistent polar maps with the ground-truth polar maps of both NAC and AC SPECT images. Errors between the predicted and ground-truth polar maps are denoted with white arrows.
Figure 7 shows the correlation maps of the polar map segments between the predicted and the ground-truth full-view SPECT images of the 150 testing patient studies. For the segments of both NAC and AC images, the distributions of the correlation points using CUSIP deviated from the identity line, which produced the highest segment-wise errors. Direct Sino2Sino also showed slight deviations from the line of identity. The point distributions from Sparse-View Baseline were more dispersed than other groups. In contrast, point distributions of DuDoSS were the most concentrated along the identity line, which suggested that DuDoSS outputs the most consistent polar maps with the ground truth.
FIGURE 7.
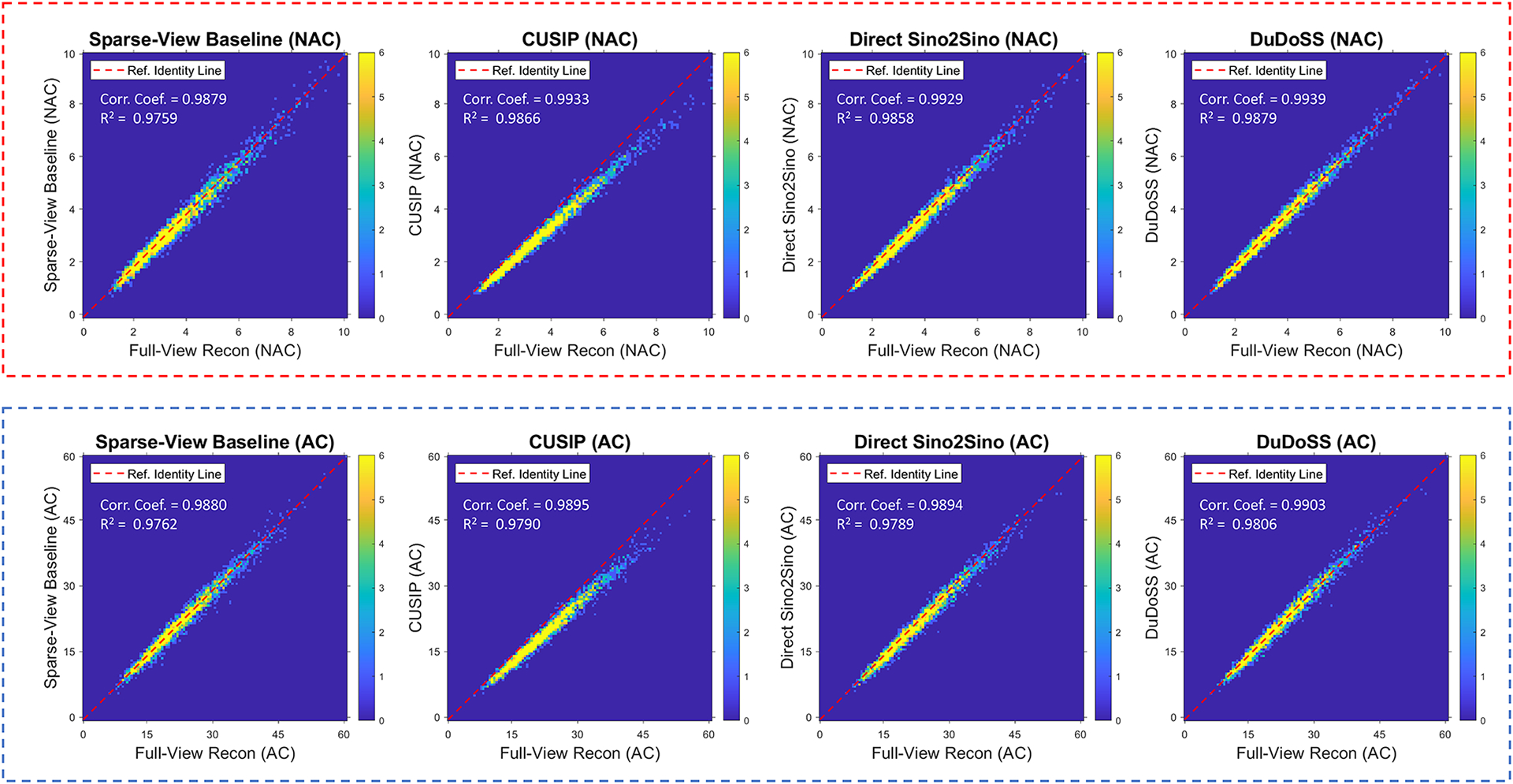
Correlation maps of the polar map segments between the predicted and the ground-truth full-view NAC and AC SPECT images of the 150 testing patient studies. The top red dash box and the bottom blue dash box show the NAC and AC SPECT images respectively. The red dash line in each figure represents the identity line (y = x). The distributions of correlation points in CUSIP deviate away from the identity line. The correlation points in DuDoSS concentrate most densely along the identity line. The correlation coefficients (Corr. Coef.) and coefficients of determination (R2) are shown at top left side of each plot.
Figure 8 displays the Bland-Altman plots of segment PE between the predicted and ground-truth full-view NAC and AC SPECT images from the 150 patient studies tested. In the polar maps of both NAC and AC images, the PE distributions of CUSIP were obviously lower than 0, leading to higher segment-wise errors. The PE distributions of Sparse-View Baseline were more dispersed than other testing groups. In contrast, the PE distributions of DuDoSS concentrated more densely around 0, showing lower quantification errors than other groups.
FIGURE 8.
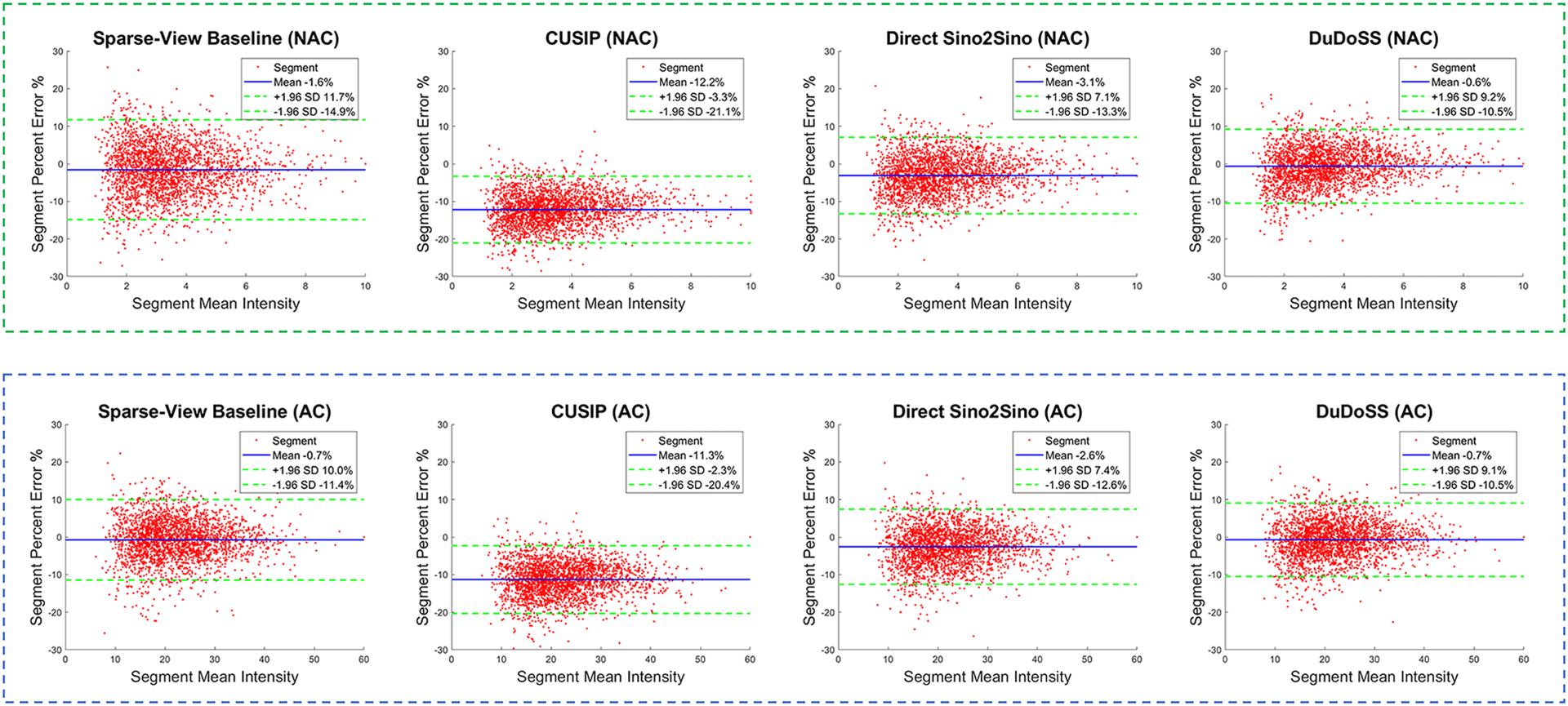
Bland-Altman plots of segment PE between the predicted and the ground-truth full-view NAC and AC SPECT images of the 150 testing patient studies. In each plot, the mean errors are denoted with blue solid lines, and the 97.5% confidence interval (±1.96 standard deviations) are denoted as green dash lines. In both NAC and AC images, the errors of CUSIP obviously deviate from the center line y = 0, which leads to much higher absolute errors than other groups. In contrast, the error of DuDoSS concentrates more densely along y = 0, showing lower segment-wise errors than other groups.
Table 6 lists the segment-wise quantitative evaluations of the polar maps in terms of the APE from the 150 patient studies used for testing. CUSIP and CUSIP-DuRDN showed the highest errors. Direct Img2Img showed slightly better performance than Direct Sino2Sino, which was consistent with the SPECT images shown in Figure 4 and polar maps shown in Figure 6. Our DuDoSS yielded the most accurate polar maps compared with other testing groups. The significant p-values further showed that DuDoSS were statistically more accurate than the other testing groups.
TABLE 6.
Quantitative evaluations of the polar map segments of the 150 testing patients.
| Testing Groups | NAC SPECT Images | AC SPECT Images | ||
|---|---|---|---|---|
| APE (×10−2) | P-valuea | APE (×10−2) | P-valuea | |
| Sparse-View Baseline | 5.45 ± 4.35 | – | 5.19 ± 4.58 | – |
| CUSIP | 12.23 ± 4.46 | – | 11.35 ± 4.52 | – |
| CUSIP-DuRDN | 6.41 ± 4.23 | < 0.001* | 5.97 ± 4.15 | < 0.001* |
| Direct Sino2Sino | 4.79 ± 3.69 | < 0.001* | 4.46 ± 3.58 | < 0.001* |
| Direct Img2Img | 4.34 ± 3.50 | < 0.001* | 3.95 ± 3.21 | < 0.001* |
| DuDoSS (proposed) | 3.92 ± 3.20 | < 0.001* | 3.87 ± 3.23 | 0.023* |
Two-tailed paired t-test of APE between the current and previous group.
Refers to significant difference with a significance level of 0.05.
4. DISCUSSION
We have established a novel deep-learning-based algorithm DuDoSS to generate synthetic full-view projections from sparsely sampled projections of cardiac SPECT. The prior image predicted in the image domain was forward-projected and utilized as guidance for the generation of synthetic full-view projections in the sinogram domain. For data consistency, the Sprior−combine was combined with Angle 1 of the Ssparse and Angles 2–4 of the Sprior. The Sprior provided a prior coarse estimation of Angles 2–4 in the target sinogram Sfull. Thus, the Sprior−combine contained the information of both the ground-truth Angle 1 and the prior estimation of Angles 2–4. The prior estimation of Angles 2–4 enabled the input Sprior−combine to be closer to the target Sfull, and thus enabled the SinoNet to be easier to predict a more accurate synthetic sinogram. In contrast, it was more challenging for the Direct Sino2Sino to estimate the Sfull since the input of Direct Sino2Sino contains only zero values at Angles 2–4 and thus was further away from the target Sfull. The synthetic projections generated with DuDoSS were the most consistent with the ground-truth full-view projections compared to the other groups. The CUSIP approach predicted the projections in Angles 2, 3, and 4 separately using three separate neural networks. In this way, the inter-angle spatial information of image volumes was not fully incorporated into the networks. In DuDoSS, Angles 1, 2, 3, and 4 were all concatenated into the dimension of 64×64×60. Thus, the inter-angle spatial information of Angles 2, 3, and 4 was fully incorporated, which yielded a higher prediction accuracy. If the proposed DuDoSS are deployed in clinical practice, theoretically the SPECT scanning time can be reduced to about only 25% of that using the conventional full-view scanning since only one fourth of the angles are used. This scanning time can be potentially further reduced if sparser projections are scanned. In addition, the time of generating synthetic projections using DuDoSS is neglectable, less than 100 ms for each patient. Even though the total scanning time can be largely reduced, extensive validation of DuDoSS in real clinical scenario should be performed before this technique is translated into clinical applications.
A good performance was previously reported for CUSIP in the sinogram synthesis of whole-body 177Lu SPECT37. However, CUSIP did not yield favorable results for 99mTc-tetrofosmin cardiac SPECT images in our study. The observed inconsistency in performance of CUSIP might be related to difference in the whole-body and cardiac imaging protocols, tracer types, data noise level, etc.
It can be noticed that the MLEM algorithm is derived based on Poisson distributed data,51, 52 but the synthetic projections in our study are not strictly Poisson distributed. The MLEM algorithm can sometimes be used when the data is not strictly Poisson distributed.53 In addition, the proposed DuDoSS method in this paper focuses on synthetic projection generations instead of image reconstructions. Based on the properties of the synthetic projections, more appropriate algorithms, such as Maximum a Posteriori (MAP)54 and Penalized Weighted Least-Squared (PWLS),55 could be applied depending on user’s preference.
However, using MLEM reconstruction on non-Poisson synthetic data could still be a major limitation of this study. Investigating other networks and loss functions to maintain Poisson distribution should be pursued in future studies. For example, adding a convolutional module, such as the variational autoencoder (VAE),56 could be a promising solution to amend the statistical properties of the synthetic sinograms. The statistical properties of the synthetic sinograms can be extracted and encoded at the bottleneck latent space of VAE, which can be then modified to satisfy the conditions of the Poisson distribution. This might address the non-Poisson issue and be the next promising research direction to explore.
The complexity of DuDoSS compared with other approaches cannot be ignored. Two neural networks were concatenated in an end-to-end manner to enable the information transition from the image domain to the sinogram domain. Although the total training time of DuDoSS was shorter than CUSIP-DuRDN, implementing DuDoSS still consumed more memories. How to simplify the overall architectures of DuDoSS while keeping the original performance will be a meaningful algorithm-optimization topic to explore in the future. A potential solution is to reduce the number of convolutional layers in DuRDN or replace the DuRDN with other simpler but efficient modules like ResNet.32 Another solution could be based on the weight-shared strategy.57 The weights of some structures in ImgNet and SinoNet that have similar functions can be shared with each other. For example, the weights of the input encoding layer of ImgNet can be reused in the SinoNet to reduce the total amount of parameters in the whole framework.
The image noise level was another important factor in this study. In Figure 3, the noise levels of the synthetic projections were lower than the ground-truth projections. A style-transferring convolutional module could be incorporated into the overall workflow to adjust the noise level to make the noise level of the synthetic projections more consistent. This might be a promising research direction to explore in the future. In addition, incorporating the statistical properties of the synthetic projections could be another promising research direction to further improve the prediction accuracy. A potential solution is developing additional convolutional modules to extract and represent the Poisson statistical properties of the synthetic sinograms. Then, the extracted statistical properties can be further regularized by KL-divergence or related loss functions, to further improve the network performance.
5. CONCLUSIONS
Our proposed DuDoSS approach was demonstrated to be an effective approach to generate accurate synthetic projections from sparsely-sampled projections of cardiac SPECT. The synthetic projections by DuDoSS were the most consistent with the ground-truth full-view projections when compared to previous approaches. The reconstructed NAC and AC SPECT images using the synthetic projections generated by DuDoSS showed the lowest voxel-wise and segment-wise errors. DuDoSS demonstrated good performance in the sparse-view cardiac SPECT reconstruction and can potentially enable fast data acquisition of cardiac SPECT.
Supplementary Material
Acknowledgements
This work is supported by NIH grant R01HL154345.
Footnotes
CONFLICT OF INTEREST
The authors have no conflicts to disclose.
DATA AVAILABILITY STATEMENTS
The data that supports the findings of this study area available from the corresponding author upon reasonable request and approval of Yale University.
REFERENCES
- 1.Danad I, Raijmakers PG, Driessen RS, Leipsic J, Raju R, Naoum C et al. Comparison of coronary CT angiography, SPECT, PET, and hybrid imaging for diagnosis of ischemic heart disease determined by fractional flow reserve. JAMA cardiology 2017;2:1100–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gimelli A, Rossi G, Landi P, Marzullo P, Iervasi G, L’abbate A et al. Stress/rest myocardial perfusion abnormalities by gated SPECT: still the best predictor of cardiac events in stable ischemic heart disease. Journal of Nuclear Medicine 2009;50:546–53. [DOI] [PubMed] [Google Scholar]
- 3.Nishimura T, Nakajima K, Kusuoka H, Yamashina A, Nishimura S. Prognostic study of risk stratification among Japanese patients with ischemic heart disease using gated myocardial perfusion SPECT: J-ACCESS study. European journal of nuclear medicine and molecular imaging 2008;35:319–28. [DOI] [PubMed] [Google Scholar]
- 4.Nightingale JM, Murphy FJ, Blakeley C. ‘I thought it was just an x-ray’: a qualitative investigation of patient experiences in cardiac SPECT-CT imaging. Nuclear medicine communications 2012;33:246–54. [DOI] [PubMed] [Google Scholar]
- 5.Loeken K, Steine S, Sandvik L, Laerum E. A new instrument to measure patient satisfaction with mammography: validity, reliability, and discriminatory power. Medical care 1997:731–41. [DOI] [PubMed] [Google Scholar]
- 6.Murphy F Understanding the humanistic interaction with medical imaging technology. Radiography 2001;7:193–201. [Google Scholar]
- 7.Agarwal V, DePuey EG. Myocardial perfusion SPECT horizontal motion artifact. Journal of Nuclear Cardiology 2014;21:1260–5. [DOI] [PubMed] [Google Scholar]
- 8.Botvinick EH, Zhu Y, O’Connell WJ, Dae MW. A quantitative assessment of patient motion and its effect on myocardial perfusion SPECT images. Journal of Nuclear Medicine 1993;34:303–10. [PubMed] [Google Scholar]
- 9.Fitzgerald J, Danias PG. Effect of motion on cardiac SPECT imaging: recognition and motion correction. Journal of Nuclear Cardiology 2001;8:701–6. [DOI] [PubMed] [Google Scholar]
- 10.Goetze S, Brown TL, Lavely WC, Zhang Z, Bengel FM. Attenuation correction in myocardial perfusion SPECT/CT: effects of misregistration and value of reregistration. Journal of Nuclear Medicine 2007;48:1090–5. [DOI] [PubMed] [Google Scholar]
- 11.Goetze S, Wahl RL. Prevalence of misregistration between SPECT and CT for attenuation-corrected myocardial perfusion SPECT. Journal of nuclear cardiology 2007;14:200–6. [DOI] [PubMed] [Google Scholar]
- 12.Saleki L, Ghafarian P, Bitarafan-Rajabi A, Yaghoobi N, Fallahi B, Ay MR. The influence of misregistration between CT and SPECT images on the accuracy of CT-based attenuation correction of cardiac SPECT/CT imaging: Phantom and clinical studies. Iranian Journal of Nuclear Medicine 2019;27:63–72. [Google Scholar]
- 13.Bateman TM. Advantages and disadvantages of PET and SPECT in a busy clinical practice. Journal of Nuclear Cardiology 2012;19:3–11. [DOI] [PubMed] [Google Scholar]
- 14.Heller GV. Practical issues regarding the incorporation of PET into a busy SPECT practice. Journal of Nuclear Cardiology 2012;19:12–8. [DOI] [PubMed] [Google Scholar]
- 15.Niu S, Gao Y, Bian Z, Huang J, Chen W, Yu G et al. Sparse-view x-ray CT reconstruction via total generalized variation regularization. Physics in Medicine & Biology 2014;59:2997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xie S, Zheng X, Chen Y, Xie L, Liu J, Zhang Y et al. Artifact removal using improved GoogLeNet for sparse-view CT reconstruction. Scientific reports 2018;8:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu Z, Wahid K, Babyn P, Cooper D, Pratt I, Carter Y. Improved compressed sensing-based algorithm for sparse-view CT image reconstruction. Computational and mathematical methods in medicine 2013;2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kudo H, Suzuki T, Rashed EA. Image reconstruction for sparse-view CT and interior CT—introduction to compressed sensing and differentiated backprojection. Quantitative imaging in medicine and surgery 2013;3:147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xu C, Yang B, Guo F, Zheng W, Poignet P. Sparse-view CBCT reconstruction via weighted Schatten p-norm minimization. Optics Express 2020;28:35469–82. [DOI] [PubMed] [Google Scholar]
- 20.Han Y, Ye JC. Framing U-Net via deep convolutional framelets: Application to sparse-view CT. IEEE transactions on medical imaging 2018;37:1418–29. [DOI] [PubMed] [Google Scholar]
- 21.Zhang Z, Liang X, Dong X, Xie Y, Cao G. A sparse-view CT reconstruction method based on combination of DenseNet and deconvolution. IEEE transactions on medical imaging 2018;37:1407–17. [DOI] [PubMed] [Google Scholar]
- 22.Zhou B, Chen X, Zhou SK, Duncan JS, Liu C. DuDoDR-Net: Dual-Domain Data Consistent Recurrent Network for Simultaneous Sparse View and Metal Artifact Reduction in Computed Tomography. Medical Image Analysis 2021:102289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zang G, Idoughi R, Li R, Wonka P, Heidrich W. IntraTomo: Self-supervised Learning-based Tomography via Sinogram Synthesis and Prediction. Proceedings of the IEEE/CVF International Conference on Computer Vision; 2021. p. 1960–70. [Google Scholar]
- 24.Zhou B, Zhou SK, Duncan JS, Liu C. Limited view tomographic reconstruction using a cascaded residual dense spatial-channel attention network with projection data fidelity layer. IEEE transactions on medical imaging 2021;40:1792–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Shojaeilangari S, Schmidtlein CR, Rahmim A, Ay MR. Recovery of missing data in partial geometry PET scanners: Compensation in projection space vs image space. Medical physics 2018;45:5437–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Valiollahzadeh S, Clark JW, Mawlawi O. Dictionary learning for data recovery in positron emission tomography. Physics in Medicine & Biology 2015;60:5853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen S, Liu H, Shi P, Chen Y. Sparse representation and dictionary learning penalized image reconstruction for positron emission tomography. Physics in Medicine & Biology 2015;60:807. [DOI] [PubMed] [Google Scholar]
- 28.Valiollahzadeh S, Clark JW Jr, Mawlawi O. Using compressive sensing to recover images from PET scanners with partial detector rings. Medical physics 2015;42:121–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xu J, Tsui BM. Interior and sparse-view image reconstruction using a mixed region and voxel-based ML-EM algorithm. IEEE Transactions on Nuclear Science 2012;59:1997–2007. [Google Scholar]
- 30.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical image computing and computer-assisted intervention; 2015. p. 234–41. [Google Scholar]
- 31.Whiteley W, Gregor J. CNN-based PET sinogram repair to mitigate defective block detectors. Physics in Medicine & Biology 2019;64:235017. [DOI] [PubMed] [Google Scholar]
- 32.He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition; 2016. p. 770–8. [Google Scholar]
- 33.Shiri I, AmirMozafari Sabet K, Arabi H, Pourkeshavarz M, Teimourian B, Ay MR et al. Standard SPECT myocardial perfusion estimation from half-time acquisitions using deep convolutional residual neural networks. Journal of Nuclear Cardiology 2020:1–19. [DOI] [PubMed] [Google Scholar]
- 34.Amirrashedi M, Sarkar S, Ghadiri H, Ghafarian P, Zaidi H, Ay MR. A Deep Neural Network To Recover Missing Data In Small Animal Pet Imaging: Comparison Between Sinogram-And Image-Domain Implementations. 2021 IEEE 18th International Symposium on Biomedical Imaging (ISBI); 2021. p. 1365–8. [Google Scholar]
- 35.Greff K, Srivastava RK, Koutník J, Steunebrink BR, Schmidhuber J. LSTM: A search space odyssey. IEEE transactions on neural networks and learning systems 2016;28:2222–32. [DOI] [PubMed] [Google Scholar]
- 36.Li S, Ye W, Li F. LU-Net: combining LSTM and U-Net for sinogram synthesis in sparse-view SPECT reconstruction. Mathematical Biosciences and Engineering 2022;19:4320–40. [DOI] [PubMed] [Google Scholar]
- 37.Rydén T, Van Essen M, Marin I, Svensson J, Bernhardt P. Deep-learning generation of synthetic intermediate projections improves 177Lu SPECT images reconstructed with sparsely acquired projections. Journal of Nuclear Medicine 2021;62:528–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Souza R, Lebel RM, Frayne R. A hybrid, dual domain, cascade of convolutional neural networks for magnetic resonance image reconstruction. International Conference on Medical Imaging with Deep Learning; 2019. p. 437–46. [Google Scholar]
- 39.Zhou B, Zhou SK. DuDoRNet: learning a dual-domain recurrent network for fast MRI reconstruction with deep T1 prior. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2020. p. 4273–82. [Google Scholar]
- 40.Lyu Y, Fu J, Peng C, Zhou SK. U-DuDoNet: Unpaired dual-domain network for CT metal artifact reduction. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2021. p. 296–306. [Google Scholar]
- 41.Wang H, Li Y, Zhang H, Chen J, Ma K, Meng D et al. InDuDoNet: An interpretable dual domain network for ct metal artifact reduction. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2021. p. 107–18. [Google Scholar]
- 42.Bian X, Luo X, Wang C, Liu W, Lin X. DDA-Net: Unsupervised cross-modality medical image segmentation via dual domain adaptation. Computer Methods and Programs in Biomedicine 2022;213:106531. [DOI] [PubMed] [Google Scholar]
- 43.Li K, Wang S, Yu L, Heng PA. Dual-teacher++: Exploiting intra-domain and inter-domain knowledge with reliable transfer for cardiac segmentation. IEEE Transactions on Medical Imaging 2020;40:2771–82. [DOI] [PubMed] [Google Scholar]
- 44.Wang T, Lei Y, Fu Y, Wynne JF, Curran WJ, Liu T et al. A review on medical imaging synthesis using deep learning and its clinical applications. Journal of applied clinical medical physics 2021;22:11–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang Y, Cheng J-Z, Xiang L, Yap P-T, Shen D. Dual-domain cascaded regression for synthesizing 7T from 3T MRI. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2018. p. 410–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chen X, Zhou B, Shi L, Liu H, Pang Y, Wang R et al. CT-free attenuation correction for dedicated cardiac SPECT using a 3D dual squeeze-and-excitation residual dense network. Journal of Nuclear Cardiology 2021:1–16. [DOI] [PubMed] [Google Scholar]
- 47.You K, Long M, Wang J, Jordan MI. How does learning rate decay help modern neural networks? arXiv preprint arXiv:190801878 2019. [Google Scholar]
- 48.Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 2004;13:600–12. [DOI] [PubMed] [Google Scholar]
- 49.Pereztol-Valdés O, Candell-Riera J, Santana-Boado C, Angel J, Aguadé-Bruix S, Castell-Conesa J et al. Correspondence between left ventricular 17 myocardial segments and coronary arteries. European heart journal 2005;26:2637–43. [DOI] [PubMed] [Google Scholar]
- 50.Nesterov SV, Han C, Mäki M, Kajander S, Naum AG, Helenius H et al. Myocardial perfusion quantitation with 15 O-labelled water PET: high reproducibility of the new cardiac analysis software (Carimas™). European journal of nuclear medicine and molecular imaging 2009;36:1594–602. [DOI] [PubMed] [Google Scholar]
- 51.Lange K, Carson R. EM reconstruction algorithms for emission and transmission tomography. J Comput Assist Tomogr 1984;8:306–16. [PubMed] [Google Scholar]
- 52.Shepp LA, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE transactions on medical imaging 1982;1:113–22. [DOI] [PubMed] [Google Scholar]
- 53.Nuyts J, Michel C, Dupont P. Maximum-likelihood expectation-maximization reconstruction of sinograms with arbitrary noise distribution using NEC-transformations. IEEE transactions on medical imaging 2001;20:365–75. [DOI] [PubMed] [Google Scholar]
- 54.Levitan E, Herman GT. A maximum a posteriori probability expectation maximization algorithm for image reconstruction in emission tomography. IEEE transactions on medical imaging 1987;6:185–92. [DOI] [PubMed] [Google Scholar]
- 55.Fessler JA. Penalized weighted least-squares image reconstruction for positron emission tomography. IEEE transactions on medical imaging 1994;13:290–300. [DOI] [PubMed] [Google Scholar]
- 56.Pu Y, Gan Z, Henao R, Yuan X, Li C, Stevens A et al. Variational autoencoder for deep learning of images, labels and captions. Advances in neural information processing systems 2016;29. [Google Scholar]
- 57.Takahashi R, Matsubara T, Uehara K. A novel weight-shared multi-stage CNN for scale robustness. IEEE Transactions on Circuits and Systems for Video Technology 2018;29:1090–101. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that supports the findings of this study area available from the corresponding author upon reasonable request and approval of Yale University.


