Prioritizing Small Sets of Molecules for Synthesis through in‐silico Tools: A Comparison of Common Ranking Methods

Abstract

Prioritizing molecules for synthesis is a key role of computational methods within medicinal chemistry. Multiple tools exist for ranking molecules, from the cheap and popular molecular docking methods to more computationally expensive molecular‐dynamics (MD)‐based methods. It is often questioned whether the accuracy of the more rigorous methods justifies the higher computational cost and associated calculation time. Here, we compared the performance on ranking the binding of small molecules for seven scoring functions from five docking programs, one end‐point method (MM/GBSA), and two MD‐based free energy methods (PMX, FEP+). We investigated 16 pharmaceutically relevant targets with a total of 423 known binders. The performance of docking methods for ligand ranking was strongly system dependent. We observed that MD‐based methods predominantly outperformed docking algorithms and MM/GBSA calculations. Based on our results, we recommend the application of MD‐based free energy methods for prioritization of molecules for synthesis in lead optimization, whenever feasible.

Multiple physics‐based methods exist for ranking compounds using their predicted affinity. We probed the ranking ability of these methods against sixteen pharmaceutically relevant targets with a total of 423 known binders. Our results show that, despite system dependency, MD‐based free energy methods should be used for prioritization whenever feasible.

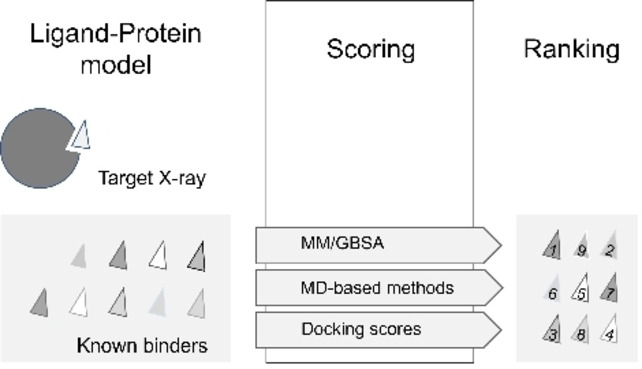
Introduction

In drug discovery, optimizing a molecule to become a clinical candidate takes several years. While the binding affinity of the molecule to the target protein is not the only optimization parameter, it is a necessary pre‐requisite to arrive at an efficacious drug molecule. In each of the many optimization cycles, the number of design proposals is typically much larger than the number of molecules (compounds) that can be synthesized in the lab. Prioritizing the most promising molecules for synthesis is therefore a crucial step in drug discovery project work.

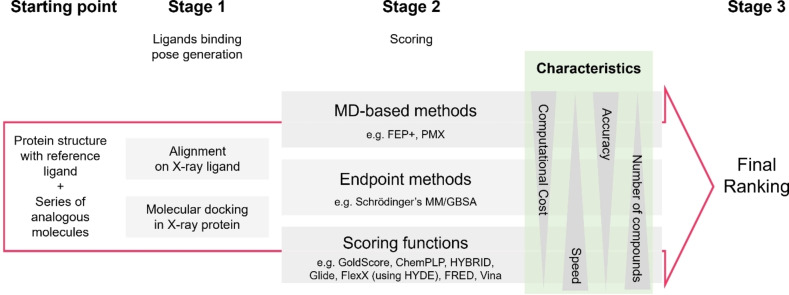
Nowadays, computational methods have become indispensable in supporting this important task. ^[1] A range of different methods to support the selection of compounds are available. However, the choice of method involves a trade‐off between speed and accuracy (Figure 1). For projects with a known three‐dimensional structure of the protein target, docking has evolved to a popular approach widely applied in industry today. ^[2] Due to its low computational cost, molecular docking is a powerful tool for screening very large libraries up to millions of compounds ^[3] to achieve an enrichment of actives or filter out binders from non‐binders respectively.

Figure 1.

Generalized workflow for the ranking of smaller compound sets.

The basic principle of docking was developed decades ago ^[4] and involves two steps in general: (1) search in a predefined space (e. g. the binding site of the protein) for different potential binding poses (conformations and orientations) and (2) evaluate the potential binding of each ligand with a pose from the first step (assigning a numerical value referred to as the score, which preferably would correlate with the binding free energy). Both stages have used several simplifications to optimize for efficiency. These simplifications allow docking to be efficient in structure‐based virtual screening campaigns and applicable to typical library sizes of millions of compounds at a reasonable cost. While simplified docking algorithms allow for fast pose generation and scoring, their accuracy is impaired by several approximations such as omitting degrees of freedom important to rigorously describe entropic contributions of the ligand and protein (e. g. protein reorganization), and de‐solvation effects. ^[5] Despite those limitations and due to the robustness and ease of use, docking is often also applied for prioritizing smaller sets (typically <100) of compounds for synthesis in lead optimization based on their docking scores.

Post‐processing of docking results provides an alternative to using the docking scoring function to rank compounds (Figure 1). Such methods include the molecular mechanics combined with the generalized Born surface area approach (MM/GBSA). ^[6] MM/GBSA can significantly improve the success rate for some targets, albeit with large system dependency. ^[7] Compared to docking, MM/GBSA has a more physical representation of the protein‐ligand binding problem. It takes into account not only the bound but also the unbound states as well as implicit solvation. Representative structures of the two states are either generated by molecular dynamics simulations or energy minimization as implemented in the Schrödinger Suite (Prime, Schrödinger, LLC, New York, NY, 2021 and Prime MM‐GBSA node ^[8] ). As an end‐state method, MM/GBSA focuses more on enthalpic than entropic changes. Especially for systems where entropic contributions play a major role, the accuracy required for ligand ranking in lead optimization is largely hampered by these approximations.

Molecular‐dynamics (MD)‐based methods for calculating protein‐ligand binding free energies are more computationally demanding than docking methods but have the most rigorous representation of the underlying physics of the protein‐ligand complex systems, at least within a given energy model. They make use of a physics‐based model Hamiltonian, a representative conformational ensemble obtained through extensive sampling, and a free energy estimator derived from statistical mechanics. ^[9] Often, these are referred to as ‘alchemical’ or ‘FEP’ (Free Energy Perturbation) methods. MD‐based methods in principle account for the full range of entropic and enthalpic contributions relevant for accurate binding free energy estimates. Sufficiency in sampling and the accuracy of the molecular mechanics force field are among the crucial determinants for successful application of relative binding free energy calculations (RBFEs). ^[10]

The improved usability, efficiency, and performance of MD‐based (FEP) methods lead to increased adoption of RBFE calculations using MD simulation within industry. ^[11] In drug discovery project teams, this often raises the question whether their accuracy justifies the higher computational cost, compared to faster and less complex docking approaches. However, comparative studies on the performance of docking with or without post‐processing algorithms and MD‐based methods are only available anecdotally for few or single targets. ^[12] A systematic comparison on a larger data set of multiple, pharmaceutically relevant targets is yet to be reported.

In this work, we evaluated the ligand ranking performance of multiple docking algorithms (GOLD ^[13] , Glide ^[14] , FlexX ^[15] , OEDocking (FRED ^[16] , HYBRID ^[17] ), AutoDock Vina ^[18] ), the single snapshot end‐point method MM/GBSA for docking refinement, and more expensive MD‐based free energy methods on a large publicly available protein‐ligand test set of which subsets were used in several RBFE studies published recently.[ ^11b , ¹⁹ ] The two MD‐based free energy methods we included in this work were FEP+[ ^12b , ^19b , ²⁰ ] implemented in the Schrödinger software suite and PMX ^[21] (a non‐equilibrium switching method implemented with GROMACS and pmx). Both methods have shown robustness and good accuracy in predicting binding free energies for ligand ranking.[ ^11b , ^19b , ^19e ] All FEP+ and PMX results discussed in this study were retrieved from previously published literature.[ ^11b , ^19e , ²² ]

Docking methods were compared using the lowest energy pose the methods generated, instead of comparing scoring functions against a single consistent reference pose. This was to compare how methods performed to reflect a realistic use case within medicinal chemistry projects. For extensive work done in the past decades on benchmarking the performance of docking algorithms for pose prediction and ranking (enrichment of actives) we refer the reader to prior work. ^[23] Here, we consider sets of active ligands only. Focusing only on actives facilitated the comparison to the recently published RBFE results mentioned above. We see a high practical value of our study as an aid to medicinal and computational chemists working on drug discovery projects with the need to prioritize molecules for synthesis.

Results and Discussion

In this study, we wanted to test whether the accuracy of MD‐based methods for ligand ranking justifies the higher cost in MD‐based methods (FEP+/PMX) compared to docking methods, across a range of pharmaceutically relevant targets. We also sought to determine whether MD‐based methods were worth the extra investment and whether commercial methods outperform the non‐commercial alternatives. For completeness, we also include results from MM/GBSA calculations. MM/GBSA calculations were a post‐processing of the Glide docked poses to refine docking scores. We were interested in how much this re‐scoring improves ligand ranking compared to the original results from Glide docking scores. In the main text, we evaluate the ranking abilities of all methods through the Kendall's τ coefficient analysis across all targets and for each target individually. ^[24] This is followed by a comparison of each method‘s ability to, for three randomly selected ligands for a given target, correctly rank the random ligands and identify the most potent ligand in the set, known as high‐ and low‐level success rate of ligand ranking analysis. This type of analysis enabled us to better compare between targets. Further confusion matrix‐based analysis can be found within the supporting information.

Docking programs are able to generate binding poses which are close to reference structures

The first, and most important, stage of ligand ranking is to accurately generate the protein‐ligand binding pose. The binding pose prediction capabilities of docking programs have been extensively studied previously[ ^23k , ^23l , ^23y , ^23ac , ²⁵ ] and are not the focus of this study. However, we briefly investigated the ability of each algorithm to recreate a co‐crystallized pose – to enable us to interpret the differences in ranking ability. It is important to reiterate that both MM/GBSA and MD‐based free energy methods are seen as post‐processing of either docked, or even aligned, poses and not studied with regards to pose prediction.

In this work, we investigated 16 pharmaceutically relevant targets with a total of 423 known binders used in recent benchmarks of binding free energy calculations.[ ^11b , ^19b , ^19e , ^22a ] More information on the data set is given in the Experimental Section.

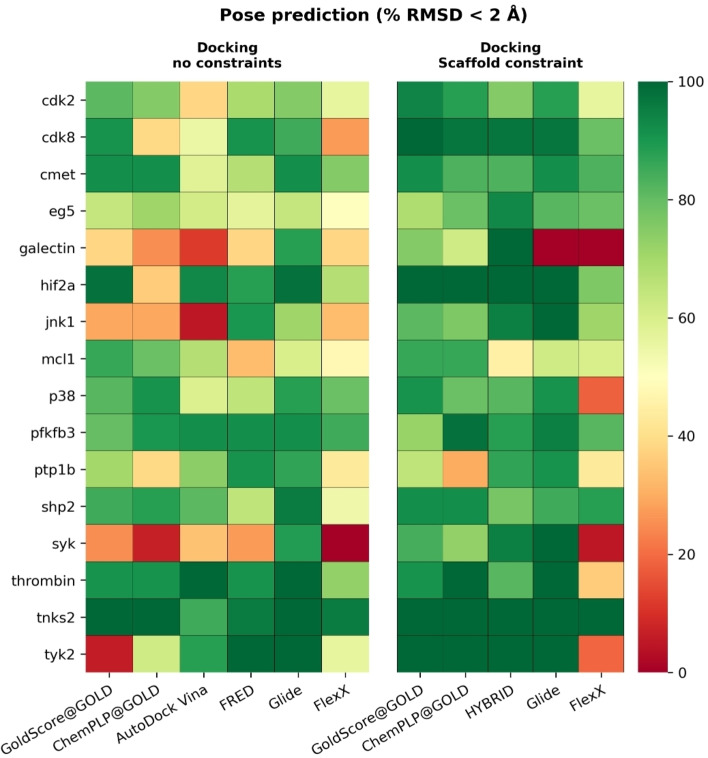
Six docking algorithms were used for non‐constrained docking: Glide, GoldScore@GOLD, FRED, ChemPLP@GOLD, AutoDock Vina, and FlexX. Five algorithms were used that employed constraints: Glide, GoldScore@GOLD, HYBRID, ChemPLP@GOLD and FlexX. Constraints can be used to ‘guide’ the docking results and a common use case is where a similar ligand has already been co‐crystallized and can be used to bias the docking result towards this pose. For each docking algorithm in our study, the top scoring pose for each of the 423 compounds for 16 targets was used to compute heavy‐atom root‐mean‐squared deviation (RMSD) values from the reference co‐crystallized ligand structures (see Experimental Section). The results are summarized in Figure 2. For each docking algorithm, green cells indicated a higher percentage (closer to 100 %) of the docked poses that were within the 2 Å cut‐off and vice versa for red cells.

Figure 2.

The percentage of compounds for which the top scored docked pose was found within 2 Å of the crystal structure for all targets. Docking programs are able to generate binding poses which are close to reference structures for most targets.

In Figure 2 we show, for all targets, at least one non‐constrained docking algorithm could predict a pose within 2 Å of the reference structure for more than 60 % of compounds. None of the non‐constrained docking algorithms could get over 50 % of the docked poses within 2 Å of the reference structure for the full set of targets. The performance varied between different targets.

As expected, docking algorithms that used scaffold constraints had, in general, better performance than non‐constrained docking algorithms. This high degree of success is partially due to the compounds in the dataset sharing a high structural similarity with the co‐crystallized ligand in each target system.

In some cases of reduced performance in constrained docking pose predictions, the observation can be explained by how the constraints were set up. The determination of the ligand‘s common core substructure in Glide and FlexX is automated, while the common core had to be determined manually for constrained docking with GOLD. Special care has to be taken when using automatic determination of the common core for ligands that contain symmetrical fragments. In such cases, automatic determination of the common core can result in poses which flip the structure over, rotating it around any symmetrical part, especially when there is additional functional symmetry when considering the whole structure of the ligand. This can result in binding modes which are essentially opposite of what they ought to be. This highlights the importance of manually inspecting the binding poses after docking, before proceeding with further post‐processing. Such inspection can incorporate additional information, such as existing knowledge on compound structure activity relationships (SAR).

Binding free energies calculated by MD‐based methods show better rank correlations with experimentally measured binding free energies than docking scores

To assess the performance of ranking compounds for all docking, MM/GBSA and MD‐based methods, averaged Kendall's τ coefficient values were computed (perfect ranking agreement when τ=1) across all targets. Experimental values were converted from reported affinity measurements (IC₅₀ or K_d to the binding free energy ΔG in kcal ⋅ mol⁻¹). The results are summarized in Table 1. Note that MM/GBSA, as used here, is a post‐processing algorithm for the refinement of docking results and involves no molecular dynamics. In this work, poses from Glide (constrained/non‐constrained) were used in MM/GBSA calculations. We grouped MM/GBSA results with results from docking algorithms in tables and figures in this manuscript, even though we considered MM/GBSA as an end‐point method instead of a docking method. Reported values for FEP+ and PMX are based on calculated RBFEs retrieved from previously published sources [11b, 19e, 22a] and [22b], respectively (see also Experimental Section).

Table 1.

Averaged Kendall's τ coefficient values across all targets for each method. Uncertainties were estimated using standard deviations.

Type	Methods[a]	Kendall's τ coefficient
non‐constrained docking	ChemPLP	0.2±0.2
	GoldScore	0.3±0.2
	Glide	0.1±0.2
	FlexX	0.0±0.3
	FRED	0.1±0.2
	AutoDock Vina	0.1±0.3
	MM/GBSA*	0.3±0.3
constrained docking	ChemPLP	0.3±0.3
	GoldScore	0.3±0.1
	Glide	0.1±0.3
	FlexX	0.1±0.3
	HYBRID	0.1±0.3
	MM/GBSA*	0.2±0.3
MD‐based	FEP+	0.6±0.2
	PMX	0.4±0.2

[a] * indicates that the Glide docking was used to generate the initial coordinates before pre‐processing.

Docking scores had a relatively poor correlation with experimental binding free energies whereas MD‐based free energy methods showed better performance. This trend of poor correlation between docking scores and experimental results is consistent with that observed in a previous benchmark study by Warren et al. (2006) where they found no strong correlation for any scoring function. ^[23y] Here, MM/GBSA outperformed some docking algorithms (AutoDock Vina, Glide, FlexX, FRED, HYBRID) but had similar or worse performance than the best docking method in this case (GOLD). MD‐based methods have a more detailed representation of the underlying physics of the protein‐ligand complex system compared to MM/GBSA and docking scores. This is in line with our observation that MD‐based methods (especially FEP+) had the best performance in this case.

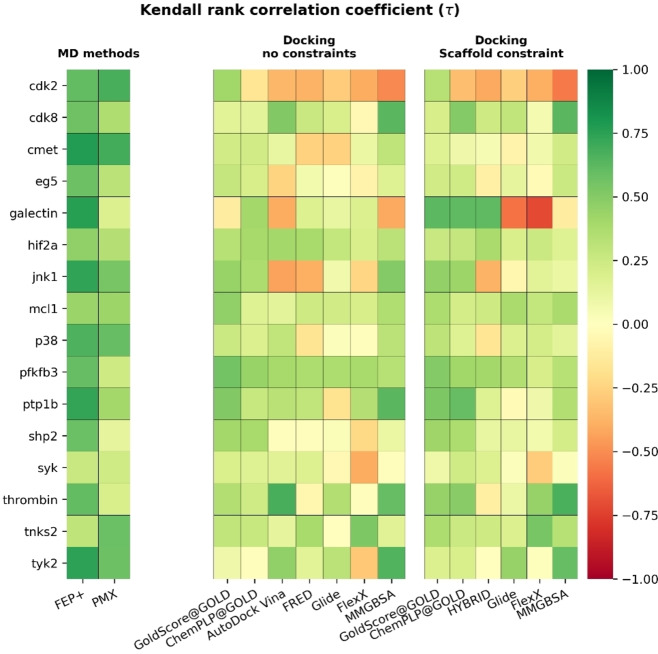
The error bars for Kendall's τ values in Table 1 are large (>0.2), indicating varied performance across these targets for each method. Additionally, we computed Kendall's τ values separately for each target in order to assess performance of ranking ligands for each method. Figures S3–S33 show the results with the RMSD value of each ligand, with Figure 3 as an example. In most targets, at least one of the MD‐based free energy methods (FEP+ or PMX) had the highest Kendall's τ value among all methods. FEP+ typically outperformed PMX. The most prominent reasons for the better performance of FEP+ may be the different sampling protocol of the MD engines (free energy perturbations with Hamiltonian replica exchange versus non‐equilibrium switching) and the force field parameters (OPLS3e (with custom parameters) versus Open Force Field 1.0 “Parsley” for the ligands and Amber99sb*ILDN for the protein).

Figure 3.

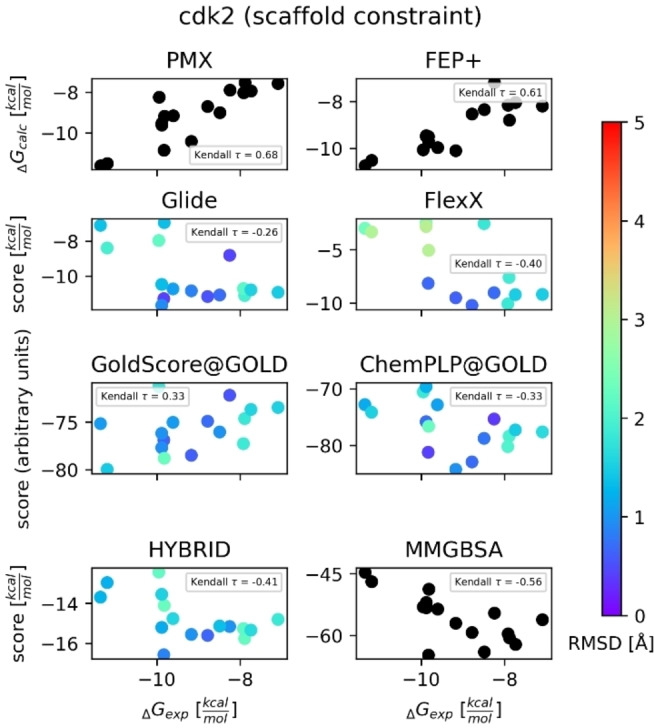
Scatter plot of predicted binding free energies/docking scores vs. experimental binding free energies for cdk2. Results for non‐constrained docking algorithms are shown here. The color map shows RMSD (Å) of each compound (we did not compute RMSD values for MD‐based methods (PMX, FEP+) and MM/GBSA calculations since it is not applicable to these methods). FEP+ and PMX results were retrieved from Refs. [11b] and [22b], respectively. The relative free energy differences were converted into free energy differences with Arsenic. ^[27]

We observed a few exceptions where docking or MM/GBSA yielded higher Kendall's τ values than MD‐based free energy methods. However, the differences to the best performing MD‐based method were mostly marginal. Non‐constrained docking algorithms got the highest Kendall's τ value among all methods in mcl1 (Kendall's τ=0.46 (GoldScore) versus Kendall's τ=0.43 (FEP+); Figure S14) and thrombin (Kendall's τ=0.67 (AutoDock Vina) versus Kendall's τ=0.60 (FEP+); S17). MM/GBSA results of cdk8 had the highest Kendall's τ value (Kendall's τ=0.63 (MM/GBSA) versus Kendall's τ=0.56 (FEP+)) as shown in Figures S10 and Figure S26. There are also a few targets (4 for non‐constrained and 4 for constrained docking) in which we saw docking algorithms and/or MM/GBSA results yielding higher Kendall's τ values than one of the MD‐based free energy methods (Figures S5, S6, S8, S9, S18, S19, S21, S24).

The observation for those targets could indicate potential issues frequently encountered in simulations, such as non‐converged simulations (finite sampling), approximations coming from the force field or finite size of the simulation box, and inappropriate preparation of the starting structures (e. g. poor or incorrect selection of tautomeric and charge states and/or ligand poses). ^[26] The mcl1 ligand data set exhibits several meta‐substituted phenyl rings which can indicate a potentially strong dependence on the starting structure. Further investigations by the authors of the corresponding published binding free energy study ^[22b] are ongoing and will be part of a separate publication. A small dynamic range as in the case of thrombin (1.7 kcal/mol) poses a particular challenge for ranking methods. The detailed investigation for all particular examples mentioned is beyond the scope of the current study.

To estimate the uncertainties of the computed Kendall's τ values for each target, we performed 10000 rounds of bootstrapping (sampled with replacement) for docking scores/predicted binding free energies from each method across all targets. The mean values from bootstrapping are reported in Figure 4. It was remarkable that FEP+ had a Kendall's τ value larger than 0.5 in 12/16 systems.

Figure 4.

Kendall's rank correlation coefficient (τ) for all tested methods across all targets. Mean values of each target after 10000 rounds of bootstrapping are reported. MD‐based methods get a higher Kendall's rank correlation coefficient than docking methods in most targets. FEP+ and PMX data based on results published in Refs. [11b, 19e, 22a] and [22b], respectively.

Reflecting on the docked ligand RMSDs shown in Figure 2 can help partially elucidate some of the poor correlations for docking methods in Figure 4. For example, in galectin both constrained Glide and FlexX algorithms failed to recreate the crystallographic poses across the ligand series. So it is not surprising that the series is poorly ranked by constrained docking. The lower correlation for non‐constrained docking in galectin and jnk1 can also be partially explained by the poorer docked poses. The opposite case can also be seen in our study, where syk shows a larger deviation from the crystallographic poses while still showing a slight positive correlation across most non‐constrained docking methods.

Among all tested docking algorithms with scaffold constraints, GOLD with ChemPLP and GoldScore scoring functions had the best performance and at least one of these scoring functions got the highest Kendall's τ values for 12 targets. Among non‐constrained docking, GOLD with GoldScore had the best performance and got the highest Kendall's τ values in 8 targets.

Compared to docking algorithms, MM/GBSA got higher Kendall's τ values for 6 targets with both constrained and non‐constrained docking, respectively. In addition, the performance of docking algorithms and MM/GBSA again varied between different targets and none of them could consistently return good results in all targets. The Kendall's τ analysis compares ligand series of different sizes. Therefore, we sought to better compare methods through two further analyses. The first was how well each method could rank three random ligands within the dataset (known as the high‐level success of each method). The second was how well each method could identify the most potent ligand amongst a set of three randomly selected ligands (known as the low‐level success of each method).

MD‐based methods outperform docking algorithms and MM/GBSA in both high‐ and low‐level success rate

Some of the smaller protein‐target sets lead to a lower statistical significance, based on the number of data points and the dynamic range (affinity range). Particularly for targets like galectin and thrombin, which suffer from a very low number of data points (8 and 11, respectively) and low dynamic ranges (2.7 and 1.7 kcal ⋅ mol⁻¹). Given the experimental (0.64 kcal ⋅ mol⁻¹ for affinity measurements ^[28] ) and calculation errors (typically larger than 1.0 kcal ⋅ mol⁻¹ for MD‐based methods) the low dynamic ranges render data points within this dataset indistinguishable by docking, MM/GBSA or MD‐based methods. ^[29]

To better account for the different number of data points per target, we sought another measure to assess the ligand‐ranking performance of the different methods under investigation. This was achieved through the determination of high‐ and low‐level success rates. Here we used three different, randomly picked ligands for each target. The low‐level ranking success rate tells how many times the most potent ligand in this random set was also evaluated as the best by the program. The high‐level ranking success rate indicates how many times the combination of three ligands were ranked correctly relative to one another.

The overall success rate of each method was evaluated by averaging across all targets. The mean values and standard deviations were reported in Table 2. On average, all methods performed better than a random assignment. Success rates for FEP+ and PMX were calculated based on results published in Refs. [11b, 19e, 22a] and [22b], respectively. In general, MD‐based methods (FEP+, PMX) yielded higher success rates than docking algorithms and MM/GBSA, indicating a better performance of ranking ligands using calculated binding free energies. Among constrained docking algorithms, GoldScore and ChemPLP had better performance than other algorithms and MM/GBSA calculations. Better performance of GOLD with constrained docking might be related to the fact that the common core had to be determined manually. This resulted in more reliable determination of the common core in cases where ligands exhibited functional symmetry and contained symmetrical fragments. FlexX on the other hand, did not offer an option for manual determination of the common core between the ligand to dock and the reference structure (co‐crystallized ligand).

Table 2.

Success rate (%) of docking algorithms and MD‐based methods. Reported values are averaged across all targets (without bootstrapping). Uncertainties are estimated using standard deviations. Success rates for FEP+ and PMX were calculated based on results published in Refs. [11b, 19e, 22a] and [22b], respectively.

Type	Methods[a]	High level [%]	Low level [%]
non‐constrained docking	ChemPLP	27±7	47±11
	GoldScore	31±10	52±13
	Glide	20±9	37±12
	FlexX	19±12	34±17
	FRED	21±10	36±14
	AutoDock Vina	25±16	42±19
	MM/GBSA*	31±16	49±21
constrained docking	ChemPLP	33±11	51±15
	GoldScore	33±8	54±10
	Glide	21±11	40±12
	FlexX	23±11	37±18
	HYBRID	23±11	37±16
	MM/GBSA*	30±15	47±18
MD‐based methods	FEP+	52±13	70±10
	PMX	37±14	57±12

[a] * indicates that the Glide docking was used to generate the initial coordinates before post‐processing.

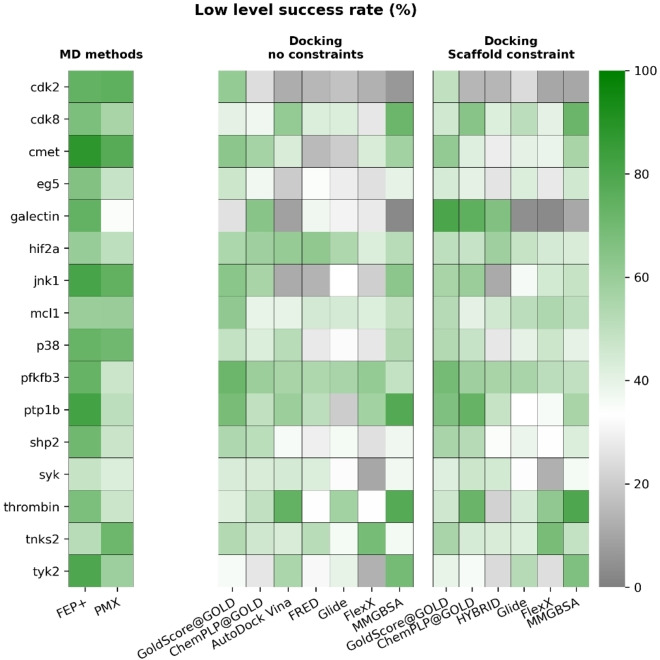
We then checked performance of these methods in each target. The results are summarized in Figures 5 and 6 (uncertainties are shown in Figure S35 and S36).

Figure 5.

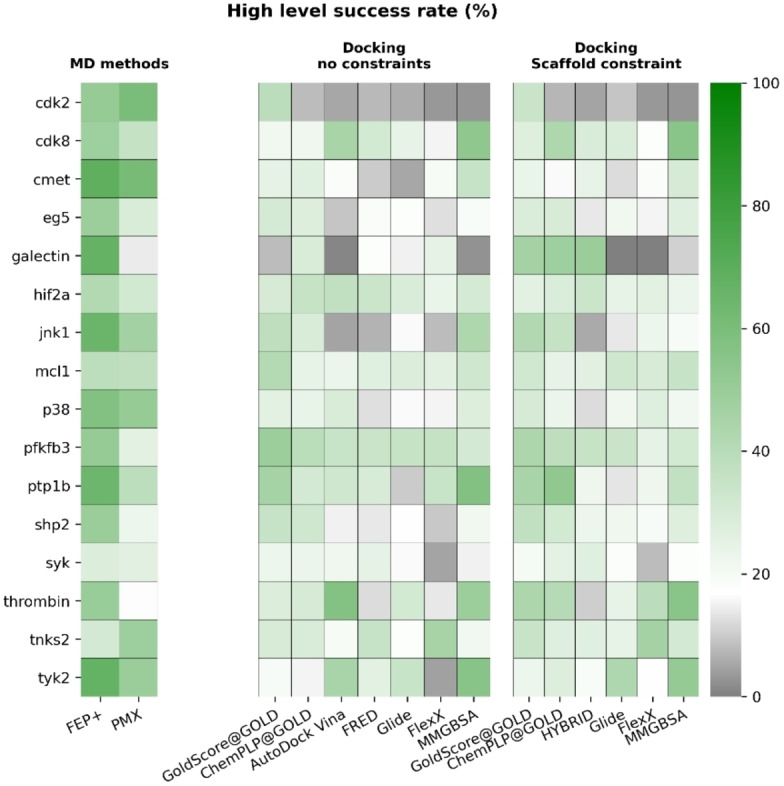
High‐level success rate for all docking algorithms across all targets. This is the rate of correctly ranking three randomly selected ligands for a given target. Mean values of each target after 10000 rounds of bootstrapping are reported. Success rates for FEP+ and PMX were calculated based on results published in Refs. [11b, 19e, 22a] and [22b], respectively. MD‐based methods have higher high‐level success rates than docking algorithms for most targets. The grey scale indicates a success rate worse than a random guess (16.67 %) and the green scale indicates a success rate better than a random guess.

Figure 6.

Low‐level success rate for all docking algorithms across all targets. This is the rate of correctly identifying the most potent ligand in a set of three randomly selected ligands for a given target. Mean values of each target after 10000 rounds of bootstrapping are reported. Success rates for FEP+ and PMX were calculated based on results published in Refs. [11b, 19e, 22a] and [22b], respectively. MD‐based methods have higher low‐level success rates than docking algorithms for most targets. The grey scale indicates a success rate worse than a random guess (33.33 %) and the green scale indicates a success rate better than a random guess.

Similar to the results in Kendall's τ analysis, MD‐based methods again outperformed docking algorithms and MM/GBSA for most targets. We also observed exceptions as we did in Kendall's τ results and summarized them in Tables S3, S4. MM/GBSA outperformed constrained docking algorithms in 4 targets (high‐level success) and 4 targets (low‐level success). Compared to non‐constrained docking algorithms, MM/GBSA had a better performance in 6 targets for both high‐ and low‐level success rates. We also compared docking algorithms for their performance and summarized the results in Table S5. Overall, GOLD with GoldScore had the best performance in both constrained and non‐constrained docking for both high‐ and low‐level success rates.

Interestingly, our results showed that MM/GBSA calculations had similar performance as the best docking algorithm judged by both Kendall's τ and high/low‐level success rates (also in confusion matrix analysis, which can be found in the SI) and outperformed other docking algorithms. For the majority of systems, MM/GBSA improved the correlation to experimental results of the non‐constrained Glide docking results. This result implies that post‐processing Glide results with relatively cheap MM/GBSA calculations will often improve the ranking of a set of compounds. However, as suggested by previous studies and confirmed in this work, the performance of MM/GBSA calculations and docking scores are system dependent. ^[7] It is also known that MM/GBSA calculated binding free energies are sensitive to many parameters (e. g., force field, dielectric constant, protein‐ligand conformation, and, when dynamics is used in these calculations (as is common in other implementations) the amount and type of dynamics employed). Since the focus of this work was not a thorough comparison between MM/GBSA calculations and docking methods, we did not explore the impact of the many parameters of MM/GBSA in the current work.

Conclusion

The main focus of this work was assessing ligand ranking abilities of commonly used docking and MD‐based free energy methods. Overall, MD‐based free energy methods (PMX and FEP+) predominantly outperformed docking methods and showed considerably less system dependency for the investigated targets. Our results suggest the more expensive MD‐based algorithms should be the methods of choice when it comes to prioritization of (smaller) ligand sets for synthesis in lead optimization. For an example on the use of machine learning to expand the applicability of MD‐based free energy methods to larger ligand sets we refer to Ref. [30]. In contrast to docking, MD‐based free energy methods provide a full description of the underlying statistical thermodynamics. They include conformational sampling of both ligand and protein as well as an explicit treatment of solvation degrees of freedom. This leads to a more accurate estimation of binding free energies. However, in lead optimization, docking will likely remain a powerful tool for system preparation or pre‐filtering large virtual chemical spaces. Docking is also a key component in recent developments of automatized holistic workflows combining docking, MD‐based binding affinity estimation and machine learning.[ ³⁰ , ³¹ ]

Experimental Section

Selected docking algorithms and MD simulations

We evaluated five docking programs (GOLD ^[13] , Glide ^[14] , FlexX ^[15] , OEDocking (FRED ^[16] , HYBRID ^[17] ), AutoDock Vina ^[18] ), an end‐point method (MM/GBSA calculation ^[8] based on docked poses from Glide), and two MD simulation‐based free energy calculation methods (FEP+[ ^12b , ^19b , ²⁰ ] (in the Schrodinger software suite) and PMX ^[21] (non‐equilibrium switching method implemented in GROMACS and pmx)). Both MD simulation‐based methods have been successful in predicting ligand binding free energies in previous work.[ ^19b , ^19d , ^19e , ^20a , ^20b , ³² ]

System selection

We selected 16 target protein structures with 423 ligands (Table 3) from the reference dataset (protein‐ligand benchmark: https://zenodo.org/record/5679599) ^[33] which were used in several relative binding free energy benchmark studies.[ ^11b , ^19a , ^19b , ^19c , ^19e ]

Table 3.

Targets studied in this work.

Target label	Protein	PDB ID	Ligands
cdk2	Cyclin‐dependent kinase 2	1H1Q	16
cdk8	Cyclin‐dependent kinase 8	5HNB	33
cmet	Hepatocyte growth factor receptor	4R1Y	12
Eg5	Kinesin‐like protein kif11	3 L9H	28
galectin	Galectin‐3	5E89	8
hif2a	Endothelial pas domain‐containing protein 1	5TBM	42
jnk1	Mitogen‐activated protein kinase 8	2GMX	21
mcl1	Induced myeloid leukaemia cell differentiation protein	4HW3	42
p38	Mitogen‐activated protein kinase 14	3FLY	34
pfkfb3	Fructose‐2,6‐bisphosphatase 3	6HVI	40
ptp1b	Protein tyrosine phosphatase 1B	2QBS	23
shp2	Tyrosine‐protein phosphatase non‐receptor type 11	5EHR	26
syk	Tyrosine‐protein kinase syk	4PV0	44
thrombin	Thrombin light chain	2ZFF	11
tnks2	Tankyrase‐2	4UI5	27
tyk2	Non‐receptor tyrosine‐protein kinase tyk2	4GIH	16

This study examines only active compounds and their relative ranking, rather than focusing on an enrichment of actives (picking active compounds out of a library containing both actives and inactives). That is, all of the compounds studied here are binders, without any decoys, and share high structural similarity (common scaffold) within each series of the protein target. Focusing on active compounds only enabled the comparison to data from recent benchmarks of binding free energy calculations.[ ^11b , ^19b , ^19e , ^22a ] This test set reflects typical use cases for compound prioritization within a congeneric series as performed during lead optimization in industry.

Protein preparation

The protein structures were prepared for molecular docking studies from the original published structures for each target from the reference dataset ^[33] (PDB ID in Table 1), which allowed for selection of key water molecules. The structures were downloaded from the Protein Data Bank (https://www.rcsb.org) and aligned to the structures in the reference dataset, in order to calculate the RMSD between the docking solution pose and the reference ligand binding pose contained in the reference dataset ^[33] . The following targets from the reference dataset were eliminated in this present study:

• Ros1 was eliminated as the original crystal structure that was used for the preparation of the protein in the reference dataset was not published.

• Pde2 was eliminated as there was no common substructure between the co‐crystallized ligand and the ligand series being docked.

• Pde10 was removed, as despite the high sequence similarity between human and rat, we only wanted to inspect targets where an identical sequence was used throughout all models and assays.

• The Base structures were excluded as the docking model setups, accounting for a more basic pH, might have required manual adaptation and this was beyond our generalizable preparation workflows at pH 7.4.

The PDB structures were aligned to the benchmark set input structures using the Maestro ^[34] structalign command in the terminal. The structures were aligned by chain A in all cases but thrombin, which contained the relevant binding site in chain H. The PDB ID and the alignment RMSD (as output from the structalign algorithm) for every target are provided in Table S1. The aligned protein structures were used directly as the input for docking with FlexX, since it required no prior receptor preparation. The protein preparation step (including the selection of water molecules) was one part of the docking process (https://www.biosolveit.de/wp‐content/uploads/2021/01/FlexX.pdf).

For all the other docking programs, only the protein chain containing the binding site was used. We removed the remaining chains along with cofactors, ions, and ligands which were distanced more than 6 Å away from the atoms of the crystal ligand. The following preparation procedure was done using the Protein Preparation Workflow (beta). ^[35] N‐acetyl (NCA) and N‐methyl amide (NMA) groups were added to uncapped N and C termini. Bond orders were assigned to all bonds in the structures, including the use of SMILES from the Chemical Component Dictionary database for known het groups ^[34] . Missing loops were rebuilt using Prime.[ ^35c , ³⁶ ] The protonation states of the ligands were generated with Epik at pH 7.4±2.0. Missing side chains and atoms were corrected. If the crystal structure contained any multiple alternate residue structures, only the position with the highest occupancy was considered. All hydrogen atoms in the crystal structure were deleted first and then were added explicitly to the whole complex structure by the program. Water molecules beyond 5 Å from the ligand were deleted, remaining waters were examined for possible interactions or clashes with the ligands being docked (see below).

The hydrogen‐bonding network was optimized, and any water molecules that did not form any clear hydrogen‐bonds with both the protein and the co‐crystallized ligand were deleted. For the chosen targets, there was a recognizable common core between the structure of the co‐crystallized ligand and respective ligands in the protein‐ligand benchmark set. In some cases a water molecule formed interactions with the substructure of the crystal ligand that was differing between the ligands of the benchmark set. If such water molecules were expected to be displaced by the docked ligands, they were only considered when docking with GOLD, as it was the only program that can displace the waters during docking. The final structures were minimized within the root‐mean‐square deviation (RMSD) 0.3 Å constraint using the Protein Preparation Workflow (beta). ^[35]

Since the protein preparation step is a part of the docking algorithm of FlexX, the protein structures (e. g., protonation states, water molecules) prepared by FlexX were expected to be different from those prepared by Protein Preparation Workflow (see above). Since this is how FlexX was designed, the difference here is inevitable and we did not introduce any human bias in this preparation step.

Using CORINA to prepare ligand 3D conformers

We used the ligand conformations in the reference dataset ^[33] and standardized the bond lengths and angles using CORINA 4.3.0 ^[37] to prevent any bias. 3D coordinates were used as the basis of the determination of the stereochemistry, using the option ‐d 3dst. Since we aimed at a direct comparison to the published results from MD‐based free energy calculations, we applied the same tautomers and charge states as in the reference dataset. ^[33]

GOLD

GOLD (Genetic Optimization for Ligand Docking, v2020.3.0) uses a genetic algorithm to sample possible ligand conformations. Docking was performed with the “gold_auto” command. After the use of the CORINA 3D structure generator, ligands were converted from a SD format to a mol2 format. The atom types and bond orders were assigned appropriately during this process with utility programs gold_utils ‐convert and check_mol2. ^[13]

Water molecules forming interactions with the part of the crystal ligand that was differing between the ligands being docked were set as displaceable by the ligand, and rotation and translation within the maximum radius (2 Å) was used to optimize their position. Using the GOLD algorithm for water displacement and translation has consistently shown improved results in our dataset when compared to not considering these water molecules (data not shown). For water molecules that were forming H‐bonds with the substructure common to all the ligands and the crystal ligand, only rotation was used to optimize the binding (they were considered the same way as an e. g. hydroxy group of threonine).

We used the same general settings for docking with GOLD for all targets. The binding site was defined by whole residues reaching within the 6.0 Å radius (default) of the co‐crystallized ligand, and the cavity detection algorithm ^[38] was used to restrict the binding site to concave parts of the protein surface. All H‐bond donors/acceptors were set to be treated as solvent accessible by GOLD, to enable solvent accessibility of backbone carbonyls.

The formation of intramolecular hydrogen bonds was disabled, otherwise the highest ligand flexibility settings were used: flipping of ring corners, ^[39] amides, and pyramidal nitrogens was enabled, and all planar nitrogens and protonated carboxylic acid groups have been selected as rotatable. Default torsion angle distributions were enabled to bias the search towards the ligand torsion‐angle values commonly observed in crystal structures, and rotatable bonds were post‐processed. The genetic algorithm was set to “very flexible”.

We enabled generation of diverse solutions and internal ligand energy offset. Ten poses were generated for each ligand. Only the top‐ranked ligand pose was saved. We disabled early termination of the genetic algorithm. For scaffold constrained docking, the maximal common substructure to all ligands and the crystal ligand was determined manually for each target. This common substructure pose was extracted from the co‐crystallized ligand pose, docking was then performed using the default constraint weight (5.0).

The choice of the GOLD scoring function was made based on the evaluation of the pose prediction performance on our dataset (RMSD values from redocking the crystal ligand, data not shown). GoldScore (the original GOLD scoring function) and ChemPLP (the default scoring function for GOLD version 5.1 and later) performed much better in this respect.

KNIME workflows

The MM/GBSA calculations, and docking with both FlexX and Glide were performed using KNIME workflows, ^[40] using the official nodes issued by the providers of the docking software. KNIME workflows were also used for the direct collection, analysis, and post‐processing of the docking results of FlexX, Glide, and GOLD. The RMSD node ^[8] was used to calculate RMSDs between the docked poses and the reference ligand pose from the dataset.

FlexX

The Docking (FlexX) node from BioSolveIT (https://www.biosolveit.com/KNIME) ^[41] was used to generate a maximum of 10 FlexX docking poses per ligand (default). This node requires SDF and PDB format for ligand and protein input files. The CORINA standardized molecule library of ligand conformations and the crystal ligand were imported using the SDF reader nodes with the “Extract molecule name” option enabled. The crystal ligand structures were used to define the binding site (input port 1), just as well as the template pose when the docking was done with the common substructure constraint (input port 3). The protein structure was imported with the PDB Reader node ^[8] .

The resulting poses from docking were input in the Affinity Calculator (HYDE) ^[41] node along with the protein structure and the crystal ligand structure as the reference for the binding site definition. The HYDE affinity calculator was used to optimize the FlexX‐generated poses, estimate their upper affinity limits, and label the intramolecular clashes, the intermolecular clashes, and the torsion qualities of the docked poses. If any of these attributes was labelled as unfavorable by HYDE scorer (“red”), the respective pose was filtered out with the Rule‐based Row Filter node. The optimal pose per ligand was determined by grouping the poses by the molecule name, and with a Group By node aggregating the lowest Upper Affinity (K_i ) Limit value [nM] of them as determined by HYDE scorer. HYDE‐optimized pose with the lowest Upper Affinity Limit value was extracted with the “Inner Join” mode option of the Joiner node. The binding free energy (ΔG) was calculated using ΔG=RT ln(K_i ).

Glide and MM/GBSA calculations

Glide docking was performed using the Glide Ligand Docking node. ^[8] The Glide Grid Generation node ^[8] was used to create the glide grid from the prepared protein‐ligand complex. Ligands were not re‐prepared for docking using LigPrep (in the Schrodinger software suite). This was to allow the protonation states and bond orders from the reference dataset ^[33] to be kept unchanged.

MM/GBSA calculations were done with the Prime MM‐GBSA node, ^[8] using the conformations resulting from the scaffold‐constrained and non‐constrained Glide docking runs as the input.

OEDocking (FRED, HYBRID)

The performance of a rigid docking algorithm – OEDocking – was also evaluated in this work. Since the ligand conformation is fixed in a rigid docking process, it is more efficient than flexible docking since less conformational space is sampled during docking.

Both FRED ^[16] and HYBRID ^[17] programs in the OEDocking Toolkit 4.0.0.2 (OpenEye Scientific Software) were evaluated using the dataset. Both programs use Chemgauss4, a scoring function developed based on Chemgauss3 ^[16] with improved recognition of hydrogen bond networks, for the final refinement of the docked poses. FRED and HYBRID programs differ in the initial exhaustive searching phase where FRED uses Chemgauss3 but HYBRID uses the Chemical Gaussian Overlay (CGO). CGO is a ligand‐based scoring function and considers the similarity of the shape and 3D arrangement of chemical features between the ligands to dock and the reference ligand (bound ligand in the reference structure from the dataset). Thus, docked poses from HYBRID are expected to be closer to the reference structure. In this work, we considered FRED to be non‐constrained docking and HYBRID as constrained docking.

OMEGA ^[42] 4.0.1.2 in OEToolkits was used to generate conformers for ligands with all default parameters. The docking volume (active site) was automatically determined by the program based on the input protein‐ligand bound complex structure from procedures described in the protein preparation section (using the MakeReceptor function). Both FRED and HYBRID were performed using default settings except a maximum of 10 docked poses were generated for each ligand. To retain crystallographic water molecules in the receptor, the MakeReceptor GUI app in the OEDocking Toolkit was used when creating the receptors used in docking.

AutoDock Vina

AutoDock Vina ^[18] (v1.1.2) is a free docking program which is an evolution of AutoDock 4. ^[43] It implements a more efficient scoring function than AutoDock 4, while still maintaining a comparable level of accuracy. ^[18]

The search space (a cubic docking box) was defined using the center of mass of the ligand in the reference structure. The size of the box was automatically determined using algorithms based on a previous study, ^[44] which performed a systematic analysis of the effect of the box size on docking using AutoDock Vina and showed that an optimal box size should be 2.9 times larger than the radius of gyration of a docking compound. The protein structures, which were prepared using the procedures described in the previous section on protein preparation, were used as the receptor input. The top scoring ligand conformers from OEDocking (HYBRID) were used as the input ligand conformations for AutoDock Vina. Unlike in rigid docking (FRED and HYBRID), AutoDock Vina allows ligand conformations to change during docking process. For AutoDock Vina we used the top scoring ligand conformers from HYBRID as input, which is similar to the protocol we used in a previous study. ^[45] Default settings in the scripts provided in AutoDock Tools ^[43a] were used to prepare receptors and ligands, with the exception that the crystallographic water molecules were retained in the receptors (the default is to remove them). The exhaustiveness was set to 40, which controls how many times AutoDock Vina repeated the calculations with different randomizations for a ligand. 10 docked poses were saved out for each ligand. Single point energy calculations (the score_only flag) were performed on the best docked pose to get higher resolution of the scores (5 decimals) for ranking analysis.

Non‐equilibrium free energy calculations using pmx and GROMACS (PMX)

The results using a non‐equilibrium workflow based on GROMACS and pmx, ^[21] were retrieved from published sources. ^[22b] These published results originate from the same calculation workflow as in a previous study, ^[19e] but employing the Parsley forcefield (v1.0.0) parameters for the ligands. ^[46] The alchemical perturbations and the input structures were used in these calculations as available in the reference dataset. ^[33] The analysis workflow used for analyzing the calculations is available in Ref. [22b]. The final free energy differences were calculated from the combined relative free energy differences with Arsenic. ^[27]

Free energy perturbation using FEP+

The results using Schrodinger FEP+ ^[19b] were retrieved from published sources, where the calculation results can be found.[ ^11b , ^19e , ^22a ] These calculations used the same input structures as available in the reference dataset as well as the same alchemical perturbations. ^[33] The results for targets cdk2, galectin, jnk1, mcl1, p38, ptp1b, thrombin and tyk2 were retrieved from reference [19e]. Reference [11b] is the source of the results of targets cdk8, cmet, eg5, hif2a, pfkfb3, shp2, syk, and tnks2. Again, the relative free energy differences were converted into free energy differences with Arsenic. ^[27]

Evaluate performance of bound conformation predictions

To compare performance of these docking methods for binding pose predictions, we computed the root‐mean‐square‐distance (RMSD) of the top scored docked pose of each ligand and the reference structure with symmetry adjustments (e. g., flipping of a phenyl ring does not yield an artificially high RMSD). Each ligand was aligned to the available protein‐ligand complex crystal structure for each target and was used as the reference structure in binding pose assessment. We calculated the percentage of ligands of which the RMSD are within 2 Å for each target and used them to compare different docking methods.

Evaluate performance of ligand ranking

We performed multiple analyses to compare the predictive performance of the methods studied (docking methods, MM/GBSA calculations and MD‐based methods) with respect to ligand ranking. First, we computed Kendall's τ (with perfect ranking agreement when τ=1) for each target separately and the overall dataset. Kendall's τ is especially suited as a metric to assess pairwise ligand ranking performance. We also calculated both low‐ and high‐level success of ligand ranking as defined as follows: for three different randomly picked ligands of a target, the low‐level ranking success rate tells how many times the most potent ligand was also evaluated as the best by the program; while the high‐level ranking success rate indicates how many times the combination of three ligands were ranked correctly (from the worst to the best). To assess uncertainties, we performed 10000 bootstrapping trials by randomly selecting half of the compounds for each target. A further performance analysis using a confusion matrix can be found in the supporting information.

Conflict of interest

J.P.B., H.B., C.D.C., J.M., and K.M. are employees of Bayer AG. Furthermore, K.M. and C.D.C. are shareholders of Bayer AG. D.F.H. is an employee of Janssen. D.L.M. is a member of the Scientific Advisory Board of OpenEye Scientific Software and an Open Science Fellow with Roivant.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Breznik M., Ge Y., Bluck J. P., Briem H., Hahn D. F., Christ C. D., Mortier J., Mobley D. L., Meier K., ChemMedChem 2023, 18, e202200425.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.