Self-supervised graph representation learning integrates multiple molecular networks and decodes gene-disease relationships

Summary

Leveraging molecular networks to discover disease-relevant modules is a long-standing challenge. With the accumulation of interactomes, there is a pressing need for powerful computational approaches to handle the inevitable noise and context-specific nature of biological networks. Here, we introduce Graphene, a two-step self-supervised representation learning framework tailored to concisely integrate multiple molecular networks and adapted to gene functional analysis via downstream re-training. In practice, we first leverage GNN (graph neural network) pre-training techniques to obtain initial node embeddings followed by re-training Graphene using a graph attention architecture, achieving superior performance over competing methods for pathway gene recovery, disease gene reprioritization, and comorbidity prediction. Graphene successfully recapitulates tissue-specific gene expression across disease spectrum and demonstrates shared heritability of common mental disorders. Graphene can be updated with new interactomes or other omics features. Graphene holds promise to decipher gene function under network context and refine GWAS (genome-wide association study) hits and offers mechanistic insights via decoding diseases from genome to networks to phenotypes.

Highlights

• •Integrating multiple molecular networks to improve signal-to-noise ratio
• •Self-supervised representation learning at both node level and context level
• •Task-specific re-training using graph attention network converges efficiently
• •Achieves superior performance to refine disease gene reprioritization

The bigger picture

With the recent progress of high-throughput experimental techniques, physical interactions and functional associations of genes and proteins are accumulating into multiple molecular networks. Effective integration of these networks and extraction of biological insight remains a long-standing challenge. The two-step GNN (graph neural network) approach (Graphene) introduced here offers a self-supervised solution and validates its utility in a range of disease gene sets.

Integrating multiple molecular networks is essential to decipher gene function under specific biological context, refine GWAS (genome-wide association study) hits, and offer mechanistic insights via decoding diseases from genome to networks to phenotypes. In this paper, Graphene is introduced as a self-supervised learning framework to aggregate information from biological networks.

Introduction

Diseases or traits involve molecules interacting within cellular networks and pathways under certain biological contexts. Understanding functional interdependencies of genes and proteins can provide a system-level view of how genetic alterations dysregulate relevant pathways or biological processes, and further lead to disease phenotypes.¹ A classical insight behind network biology is that genes or proteins presenting similar topological neighborhood patterns are more likely to be correlated, which enables knowledge refinement for known molecules and property inference for unknown ones through “guilt by association” principle. There has been a recent community benchmark effort to evaluate disease module discovery methods on various network configurations.² A network-based method has been utilized to reprioritize statistical signals from disease-focused genome-wide association studies (GWAS). For example, the NetWAS³ framework leverages tissue-specific networks in combination with marginally significant GWAS hits as input for deploying a machine learning model to rank candidate genes. The NAGA⁴ framework harnessed a compositive molecular network to implement a propagation approach to boost GWAS results for eight diseases. iRIGs⁵ reprioritized schizophrenia (SCZ) GWAS genes by using a Bayesian framework to integrate multi-omics data and a protein-protein interaction (PPI) network. Buphamalai et al.⁶ constructed a multiplex network organized into hierarchical layers spanning different omics levels and revealed that rare diseases also exhibit network signatures similar to complex diseases through propagation-based algorithms.⁷ A comprehensive review⁸ of network-based disease gene prioritization categorizes existing computational efforts into three major classes, including network diffusion methods, traditional machine learning methods with handcrafted features, and graph representation learning methods. Notably, Set2Gaussian⁹ embeds gene sets as a multivariate Gaussian distribution in low-dimensional space based on genes’ proximity in the PPI network, manifesting stronger expressive power over traditional network diffusion methods.

The utilities of these network methods strongly rely on the quality and coverage of available molecular networks. Recent advances in high-throughput experimental platforms and computational techniques have enabled characterizing heterogeneous genome-scale networks, including physical interactions (for example, PPI,¹⁰ signaling, and regulatory networks) and functional associations (for example, gene co-expression, genetic dependencies, co-evolution, and phylogenetic patterns). Huang et al.¹¹ systematically evaluated 21 human interaction networks covering various types of interactions, concluding that ConsensusPathDB,¹² GIANT¹³ (now available as Humanbase), and STRING¹⁰ perform best to recover disease gene sets and the larger network as a whole outweighs the drawbacks of potential false positives, and recurrent but nuanced signals can be amplified. Picart et al.¹⁴ also emphasized the merit of introducing a larger network. The ever-growing repositories of interactomes require developing methods to combine these networks while simultaneously tackling inherent noise and incompleteness among them. Huang et al. pioneered a parsimonious composite network (PCNet)¹¹ with high efficiency. Mashup¹⁵ leverages random walks with restart (RWR)¹⁶ for each network, then optimizes a consistent dimension reduction function to derive compact network integration as low-dimensional vectors for each gene or protein to be plugged into downstream functional tasks. Several other methods have been proposed to integrate multiple networks. Gao et al.¹⁷ used multi-view representation learning to cluster network data. Ma et al.¹⁸ adopted matrix decomposition to integrate heterogeneous networks. Lin et al.¹⁹ combined node2vec²⁰ and matrix factorization to analyze cancer attributed networks. DeepMNE-CNN²¹ developed a semi-supervised autoencoder method to integrate RWR-derived embeddings from multiple networks and predict gene function using convolutional network.

Graph neural network (GNN) has recently emerged to incorporate graph structures into a deep learning framework.²² To represent genes as nodes and their interactions as edges, GNN naturally captures the interdependent relationships of comprised molecules within networks, and node embeddings are learned by iteratively updating the information aggregated from its adjacent neighbors. According to the different ways with which GNN propagates information, the architectures of GNN include graph convolutional networks (GCNs),²³ GraphSAGE,²⁴ GAT,²⁵ GIN,²⁶ etc. In recent years, GNN had demonstrated effectiveness in biologically related tasks, such as drug-target interactions²⁷ and disease identification.²⁸ For example, EMOGI²⁹ leverages GCNs to integrate topologic features from PPI networks with multi-omics pan-cancer data to propose novel cancer genes. Furthermore, multimodal GNNs incorporating more than one type of node enables multi-relational link prediction. Decagon³⁰ constructed a heterogeneous gene-drug network to predict polypharmacy side effects via decoding links between drug pairs.

Self-supervised learning (SSL) has recently provided a promising paradigm toward human-level intelligence and achieved great success in the domains of natural language processing and computer vision, such as BERT,³¹ SimCLR,³² and MAE.³³ SSL firstly pre-trains a model on a well-designed pretext task, then fine-tunes it on a specific downstream task of interest. Biology networks contain tremendous intrinsic information, and applying SSL to network biology shows promise to directly learn from interacted biological molecules. Due to the non-Euclidean data structure, graph SSL has several particular characteristics for which pre-training can be implemented at the level of individual nodes and entire graphs to derive useful local and global representations simultaneously.³⁴ A recent review article³⁵ divided the pre-training task into four categories, including generative, contrastive, and auxiliary property-based, as well as their hybridizations. Avoiding negative generalizability during knowledge transfer from pre-training task to downstream objectives is the key consideration for self-supervised graph representation learning.³⁶

Inspired by the recent progress of self-supervised GNN,³⁴ we propose Graphene, a two-step graph representation learning method for gene function analysis. We first integrate multiple molecular networks and then pre-train a GCN to derive initialized embeddings for each gene or protein. Then we re-train the network via GAT model architecture and achieve state-of-the-art performance to recover pathway and disease genes. The integration is simply done through taking the unions of edges derived from different networks after aligning the nodes’ identities (see methods). The generalizability of gene embeddings learned from GWAS hits is directly tested by another two independently curated disease gene sets (DisGeNET³⁷ and UK Biobank³⁸) without further model training. Tissue-specific patterns are recapitulated for a broad range of diseases. Reprioritized genes show biologically relevant functional enrichment in related pathways. We also show that attention weights between gene nodes learned from the GAT network offer natural hints on regulatory relationships. Shared gene modules are identified among several common psychiatric disorders, offering functional evidence and recapitulating previous mechanistic insights. In brief, we demonstrate that pre-training GNN on molecular networks in a self-supervised manner provides strategic adaptability to a series of downstream tasks, including pathway gene recovery, disease gene prioritization, module identification, and comorbidity validation. Prioritizing disease-related markers can also benefit from explicitly adding disease nodes. For example, Zhang et al.³⁹ integrated a microRNA network and disease phenotype network to prioritize disease relevant microRNA. In the comorbidity prediction task, we also demonstrate how to incorporate disease nodes to build a heterogeneous GNN, followed by adding a decoder function and re-training the network, which achieves superior accuracy.

Results

Overview of Graphene

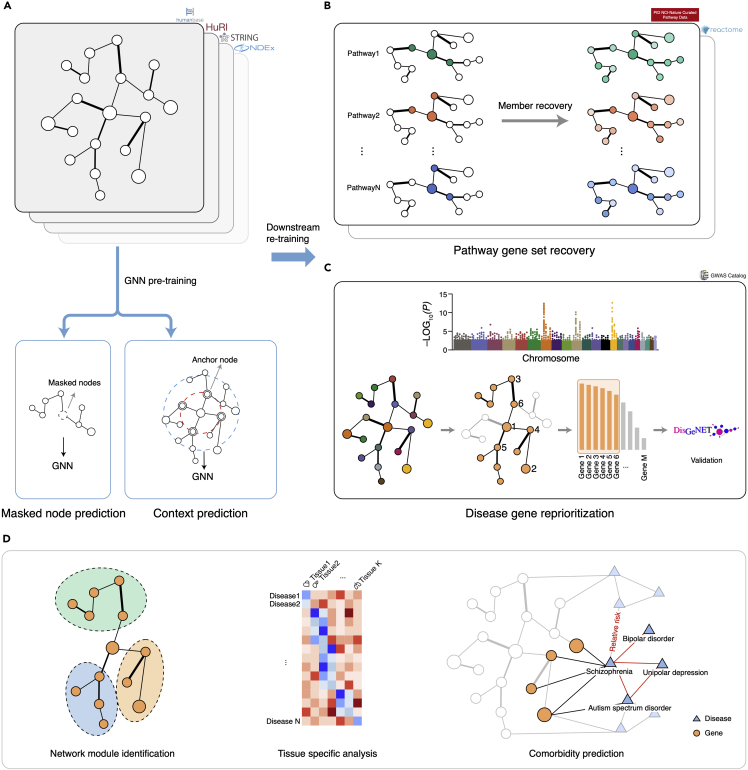
As shown in Figure 1A, we use four molecular networks to pre-train Graphene, including 142 tissue-specific gene networks from Humanbase, a PPI network from STRING (9606 v11), a recently released systematic proteome-wide reference, namely the Human Reference Interactome (HuRI),⁴⁰ and a well-integrated composite network, PCNet. These networks are combined by unifying their edges and nodes (see methods and all network datasets in Table S1) and result in a giant network comprising 19,324 gene nodes and 16,142,804 interconnected edges. We adopt node recovery and context-prediction as two pretext tasks for Graphene pre-training³⁴ (methods). In particular, we randomly mask 15% of nodes and predict the identifications of masked nodes from transformation of neighborhood representations, defined as a multi-class classification problem through cross-entropy loss. For context prediction, the k-hop neighborhood contains all nodes that are k-hops away from the center node. Nodes shared between the neighborhood and the context graph are referred to as context anchor nodes, providing the connectivity information between the neighborhood and context graphs. Then negative sampling⁴¹ is used to jointly learn both neighborhood and context graph-derived embeddings, casting it as a binary classification problem whether particular context graph and neighborhood belong to the same center node or not. These two auxiliary tasks enable the integration of four molecular networks in a self-supervised manner. We consider GCN and GAT as two pre-training GNN architectures to aggregate neighborhood features. In our experiments of model pre-training, we find that GCN produces more flexible embeddings than GAT, which is beneficial to the downstream re-training process. Embedding size is set as 100. The number of layers for GCN is set as 5. We use one Tesla V100 GPU and draw lessons from the previous report³⁴ to pre-train Graphene for 100 epochs in around 150 h. The downstream tasks of disease gene reprioritization and gene set member identification can be completed in about 300 s (1,000 epochs) on a Quadro RTX 6000 GPU (Table S2), which is much more efficient than other competing methods.

Figure 1.

Overview of Graphene workflow

(A) Graphene pre-training includes two pretext tasks, i.e., masked node recovery and context prediction. Four molecular networks are used for self-supervised learning, including HumanBase, STRING (9606 v11), HuRI, and PCNet; nodes stand for genes or proteins, edges stand for the presence of connections between genes in a specific network.

(B) Graphene re-training for gene set member recovery as downstream task. NCI and Reactome are used for pathway gene set recovery.

(C) Graphene re-training for disease gene reprioritization. GWAS signals are used for re-training and DisGeNET dataset is used as independent test set.

(D) Functional analysis include module identification, tissue specificity analysis, and comorbidity prediction. Disease nodes are introduced into Graphene to construct bipartite network. Edges between disease pairs stand for relative risks.

At the downstream re-training stage, we borrow all pre-trained node embedding as model initialization and adopt two to three GAT layers to drive node embeddings for downstream tasks due to GAT’s faster convergence speed (see Table S2) during re-training. These node representations are then fed into one multiple-perceptron classification layer to predict node labels. We use Reactome⁴² and NCI⁴³ as validation datasets for membership recovery task of pathway gene sets (Figure 1B). Only half of the nodes’ pathway labels are kept for training, and the remaining members are recovered for each pathway. We use the GWAS Catalog⁴⁴ dataset, composed of 202 common diseases, as a training set for the task of disease-gene reprioritization (Figure 1C). It is noted that the re-training process of the disease gene prioritization task is different from the pathway member recovery setting in aspects of train-validation ratio and mask split (methods). Then DisGeNET and UK Biobank (171 aligned disease nomenclatures with GWAS for DisGeNET and 81 diseases for UK Biobank) are used as hold-out test set without further model training for independent cross-dataset evaluation. The re-ranked genes by Graphene can then be used for disease-relevant function module identification and tissue specificity analysis. We also construct a heterogeneous graph via explicitly adding disease nodes to explore the comorbidity relationship between disease pairs, where a decoder function is introduced to predict the edge labels between two disease nodes (Figure 1D). Detailed model architectures for each stage can be found in Figure S1, and illustrations of Graphene implementation can be found in the methods.

Graphene improves member identification for the pathway gene set

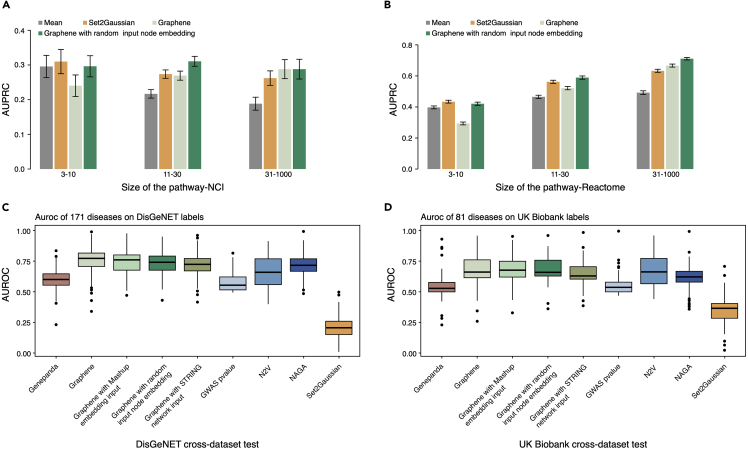
Publicly available pathway gene sets related to certain biological processes contain abundant noise due to the inherent nature of high-throughput experiments. We first sought to assess whether re-training Graphene could accurately denoise and recover pathway gene sets. Initialized with pre-trained embeddings, we use a two-layer GAT architecture followed by one classification layer to learn domain-specific representations for Reactome and NCI pathway gene sets. We adopt the same train-test ratio for Set2Gaussian where only half of those membership labels are used in the re-training stage. Evaluated on an NCI dataset using the same metric (mean area under the precision recall curve [mean AUPRC]), Graphene outperforms Set2Gaussian and the simple mean pooling method across all three levels of pathway sets (mean AUPRC = 0.29, 0.31, and 0.29 for small (3–10), medium (11–30), and large (31–1,000), respectively) (Figure 2A). For the purpose of comparison, we also use random initial input embeddings to train Graphene with the same model architecture and obtain inferior performance. Detailed comparison results can be found in Table S3. For the Reactome dataset, Graphene achieves mean an AUPRC of 0.58 and 0.69 for medium (11–30) and large (31–1,000) sets (Figure 2B), outperforming Set2Gaussian. Graphene’s GNN architecture effectively propagates information across the graph and facilitates knowledge transfer using a two-step training strategy. This task is run with five repetitions (Figure S5).

Figure 2.

Graphene achieves superior performance in pathway gene set recovery and disease gene reprioritization

(A and B) Application of Graphene downstream re-training for pathway gene set member recovery (NCI [A], Reactome [B]) in comparison with Set2Gaussian, Graphene with random input node embeddings, and mean pooling. Boxplot shows the comparison of area under precision recall curve (AUPRC). Error bars represent the 95% confidence interval.

(C) Comparison of AUROC results on 171 diseases from DisGeNET dataset among nine methods (Graphene, Graphene with Mashup embedding input, Graphene with random input node embedding, Graphene with STRING network input, GWAS p value, NAGA, Set2Gaussian, and GenePanda, N2V).

(D) Comparison of AUROC results on 81 diseases from UK Biobank dataset among nine methods (Graphene, Graphene with Mashup embedding input, Graphene with random input node embedding, Graphene with STRING network input, GWAS p value, NAGA, Set2Gaussian, and GenePanda, N2V). In the boxplot, the center line and box limits denote the median and upper/lower quartiles, respectively. 1.5× interquartile ranges are displayed as whiskers.

Graphene achieves superior performance for disease gene reprioritization with tissue specificity

As potential disease genes converge on interacting molecules in functional networks, we next apply Graphene to GWAS hits to examine how integration of multiple networks and pre-training can benefit decoding gene-disease relationships. We collect association signals for 202 diseases downloaded from the GWAS Catalog and leverage 60% of labels to re-train Graphene on the disease gene recovery task, which is compatible with canonical GWAS workflow. NAGA,⁴ which uses RWR as its propagation scheme, together with GenePanda⁴⁵ and N2V,²⁰ are chosen as benchmark methods. NAGA reported stronger performance over other network-based methods, including NetWAS³ and GWAB.⁴⁶ To keep consistent with NAGA, we use the DisGeNET dataset as independent evaluation. In other words, we train, validate on GWAS Catalog disease gene sets, and test on the DisGeNET dataset. DisGeNET is a comprehensive source from expert curations, GWAS catalogs, animal models, and scientific literature, and developed to support mechanistic studies on human diseases. Like the settings in NAGA, we use the area under the receiver operating characteristic curve (AUROC) as an evaluation metric. Graphene achieves a mean AUROC of 0.76, outperforms NAGA (mean AUROC = 0.71), GenePanda (mean AUROC = 0.59), and N2V (mean AUROC = 0.67) (Figure 2C). Graphene initialized with Mashup embeddings ranked second for the DisGeNET task. Set2Gaussinan (mean AUROC = 0.2) is specifically developed on pathway-level gene sets and its low-dimensional embedding cannot effectively transfer to the disease domain. AUROC results of Graphene for all DisGeNET diseases can be found in Figure S2. In addition, we use UK Biobank summary statistics to check whether the result of GWAS-trained Graphene will generalize to other independent gene-disease association databases. The results show that all four different settings of Graphene exhibit better performance (mean AUROC = 0.68, 0.67, 0.65, and 0.67) than the other four methods, i.e., GWAS (p = 0.55), GenePanda (p = 0.54), NAGA (p = 0.62), and Set2Gaussian (p = 0.34). N2V also achieves a relatively high mean AUROC (p = 0.66), which is comparable with Graphene (Figure 2D). We also show that original GWAS p values cannot compete with a network-based denoising method to recover UK Biobank associations. Notably, NAGA, N2V, and GenePanda can only evaluate one disease at a time, whereas Graphene can test on all diseases in a batch-wise manner. The validation on 202 GWAS diseases is repeated 5 times during downstream re-training, as shown in Figure S5. We also train Graphene on a single network, i.e., STRING (which is the largest of the four individual networks that Graphene has integrated), to illustrate how integrating multiple networks rather than using single input can benefit disease gene prioritization task.¹⁴ DisGeNET and UK Biobank results are shown in Figures 2C and 2D, respectively (Graphene with STRING network input).

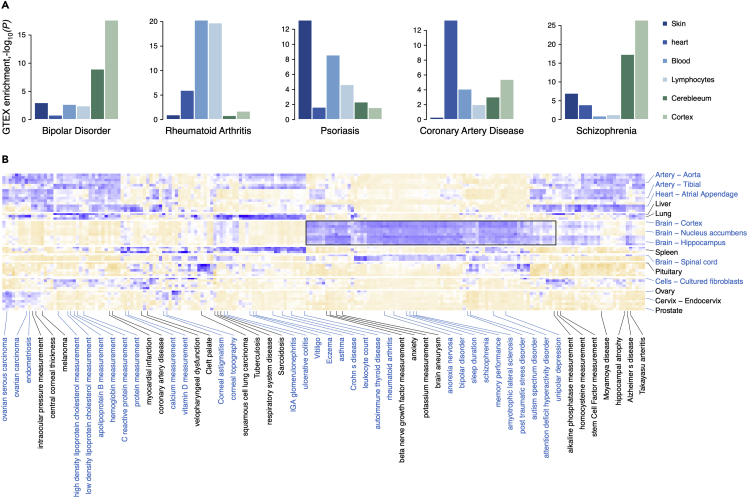
We then investigate whether top prioritized genes for a given disease (TPGs) identified by Graphene can reveal tissue specificity in network wiring for relevant diseases. We use expression data from the Genotype-Tissue Expression (GTEx) project⁴⁷ and adopt Jensen-Shannon (JS) divergence⁴⁸ to measure the tissue specificity of each gene in each tissue. By implementing one-sided Wilcoxon rank-sum test and Bonferroni correction, we test the significance levels of tissue specificity for 300 TPGs against last-ranked 1,000 genes after Graphene reprioritization on GWAS hits. Taking five common diseases as examples (Figure 3A), we show that 300 TPGs of BIP and SCZ have significantly enriched expression level in brain tissues (p_adjusted = 2.2 × 10⁻¹⁸ for BIP, 3.4 × 10⁻²⁷ for SCZ in cortex; p_adjusted = 5.4 × 10⁻¹⁰ for BIP, 1.9 × 10⁻¹⁹ for SCZ in the spinal cord) compared with other tissue types. The 300 TPGs of rheumatoid arthritis are observed to exhibit an enriched expression pattern in blood (p_adjusted = 4.6 × 10⁻²¹) and lymphocytes (p_adjusted = 1.7 × 10⁻²⁰) over other unrelated tissue types, such as the cerebellum (p_adjusted = 0.15) and skin (p_adjusted = 0.1). Also, 300 TPGs show expression enrichment in heart tissue (p_adjusted = 3.1 × 10⁻¹⁴) for coronary artery disease and in skin tissue (p_adjusted = 3.9 × 10⁻¹³) for psoriasis.

Figure 3.

Tissue specificity of top prioritized genes identified by Graphene

(A) Tissue specificity of genes reprioritized by Graphene from GWAS hits. Tissue enrichment scores of five diseases on six different tissue types are plotted for illustration. Details of computing tissue enrichment score are described in methods.

(B) Tissue specificity of genes reprioritized by Graphene on 202 GWAS diseases across 53 tissues in GTEx. Deep blue represents top predicted risk genes highly expressed in corresponding tissues. Wilcoxon rank-sum test is adopted using 300 TPGs and 1,000 last-ranked background genes predicted by Graphene. TPGs, top prioritized genes.

The overall heatmap shows clear tissue enrichment differences among various diseases (Figure 3B). Particularly, TPGs of mental diseases are enriched in brain-related tissues. For comparison, original disease-gene mappings from the GWAS Catalog are used as baseline, which present no clear clustering pattern (Figure S3). Although the Humanbase network is incorporated during the Graphene pre-training stage, the tissue information is not explicitly included in the training process. Re-training on GWAS hits can guide the network in recovering tissue specificity. In brief, Graphene effectively denoises the GWAS signals validated by the above observations regarding disease-relevant tissue specificity. In this case, Graphene provides a convenient way to reprioritize GWAS risk genes through injecting molecular network topology derived from graph representation learning.

Graphene effectively characterizes functional enrichment pattern of prioritized disease-associated genes

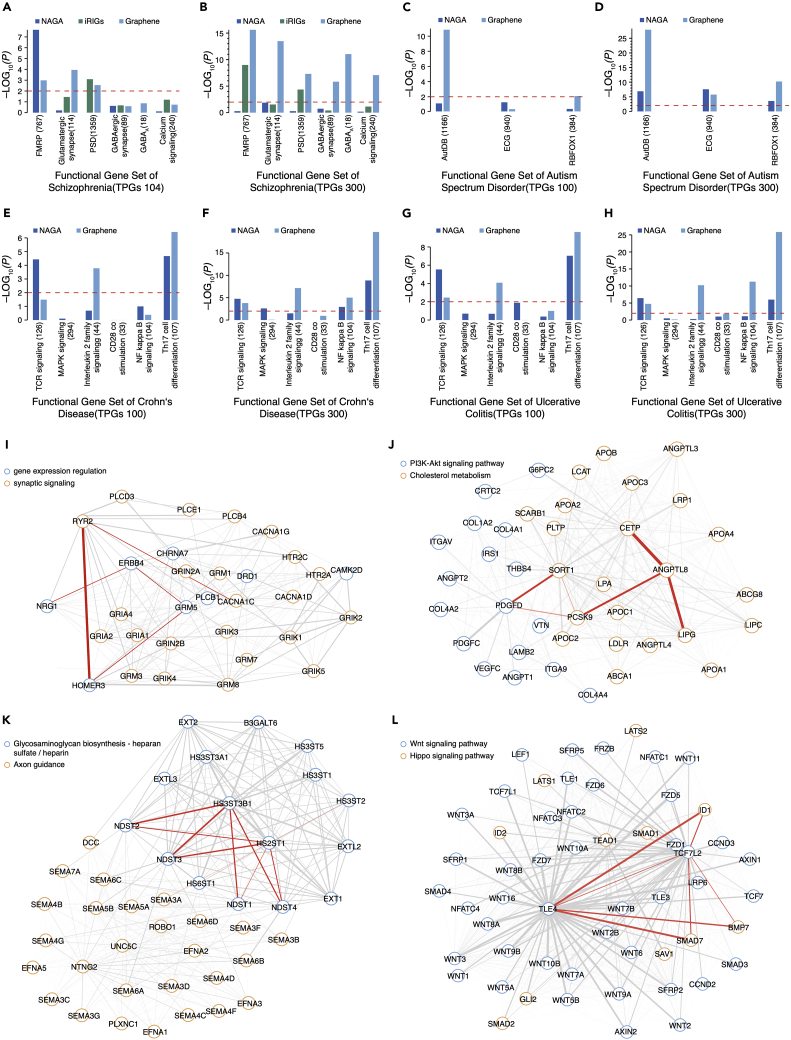
Dysregulated genes underlying diseases are frequently involved in context-specific biological processes. We further evaluate how TPGs uncover functional modules via gene set enrichment analysis (GSEA). Schizophrenia (SCZ) and autism spectrum disorder (ASD) are both complex mental disorders, representing paradigmatic challenge to illuminate disease biology. iRIGs jointly models multi-omics data for each gene together with their network-based interactions to prioritize GWAS risk loci and assess several gene sets, which have been widely and repeatedly implicated in SCZ. We choose six functional gene sets to evaluate the quality of Graphene TPGs against 104 high-confidence risk genes (HRGs) by iRIGs and NAGA results. Functional gene set includes fragile X mental retardation protein (FMRP) targets⁴⁹ (n = 767), postsynaptic density (PSD) proteins⁵⁰ (n = 1,359), GABA_A receptor complex,⁵¹ and another 3 KEGG pathways,⁵² i.e., calcium signaling pathway⁵³ (n = 240), glutamatergic synapse⁵⁴ (n = 114), and GABAergic synapse (n = 89) (see methods). When using 300 TPGs, Graphene recovers far more significantly enriched signals than an equal number of genes ranked by NAGA and iRIGs HRGs in all 6 gene sets (Figure 4B) (p_adjusted = 2.4 × 10⁻¹⁶ for FMRP, p_adjusted = 4.9 × 10⁻⁸ for PSD; p_adjusted = 9.1 × 10⁻¹² for GABA_A; p_adjusted = 8.4 × 10⁻⁸ for calcium signaling, p_adjusted = 3.3 × 10⁻¹⁴ for glutamatergic synapse, and p_adjusted = 1.5 × 10⁻⁶ for GABAergic synapse). Enrichment results using 104 Graphene TPGs outperforms equal numbers of genes prioritized by NAGA in all gene sets and surpasses iRIGs HRGs except for the FMRP gene set (Figure 4A). In addition, we analyzed the ASD scenario in 3 ASD-relevant gene sets (Figure 4D). Using the top-ranked 300 genes, Graphene achieves more significant enrichment than NAGA in the target gene set of RBFOX1 RNA binding protein⁵⁵ (n = 384, p_adjusted = 2.4 × 10⁻¹¹) and the gene set from the AutDB database⁵⁶ (n = 1,166, p_adjusted = 4.9 × 10⁻²⁹), while exhibiting slightly weaker signals in evolutionarily constrained genes (ECGs)⁵⁷ (n = 940, p_adjusted = 7.1 × 10⁻⁷). However, when we test 100 TPGs, Graphene still shows enrichment signals in AutDB (n = 1,166, p_adjusted = 1.2 × 10⁻¹¹) and RBFOX1 (n = 384, p_adjusted = 6.6 × 10⁻³), while the top 100 genes identified by NAGA fail to reach significance level (Figure 4C). To further validate whether Graphene-derived gene sets can identify enriched biological insights as in other curated knowledgebase or populational studies, we evaluate TPGs of two types of inflammatory bowel disease (IBD) (ulcerative colitis and Crohn disease) identified by Graphene on six previously reported pathways related to immune system signal transduction and T cell activation^42,58 (methods). We demonstrate that 100 TPGs of Graphene signals are significantly enriched (p < 0.01) in Th17 cell differentiation pathway and interleukin-2 family signaling pathway, and 300 TPGs of Graphene further recapitulate enriched signals in NF-κB signaling and TCR signaling pathways (Figures 4E–4H).

Figure 4.

Graphene identifies functional enrichment pattern of mental disorders and discovers relevant molecular interactions

(A and B) Enrichment of 104 TPGs and 300 TPGs identified by Graphene in six schizophrenia (SCZ)-related functional gene sets in comparison with equal number of genes ranked by iRIGs and NAGA.

(C and D) Enrichment of 100 TPGs and 300 TPGs identified by Graphene in three autism spectrum disorder (ASD) relevant functional gene sets in comparison with equal numbers of genes ranked by NAGA.

(E–H) Enrichment of 100 TPGs and 300 TPGs identified by Graphene on six IBD (ulcerative colitis, Crohn disease) relevant gene sets in comparison with equal numbers of genes ranked by NAGA.

(I–L) Attention weights extracted from 300 Graphene TPGs of four different diseases exhibit important molecular interactions within functional pathways. (I) SCZ, (J) coronary artery disease, (K) hippocampal atrophy, (L) alopecia.

It is essential to translate GWAS hits to uncover underlying biological mechanisms. EMOGI adapts a layer-wise relevance propagation (LRP) rule⁵⁹ to the GCN network to calculate importance scores of PPI partners. Graphene uses the GAT network for downstream functional analysis, so we utilize attention weights to extract important gene-gene interactions under certain disease contexts. For illustration purpose, we check part of 300 SCZ TPGs identified by Graphene that are enriched in glutamatergic synapse and calcium signaling pathways. Two main Gene Ontology (GO) terms, synaptic signaling and gene expression regulation, emerge as key modules. Visualized by the width of the edges scaling with the attention weights for the Graphene model (Figure 4I), we take the following examples to illustrate several important interactions, highlighted in red. RYR2 encodes ryanodine receptor protein of the calcium channel and calcium release is triggered by its activation of the L-type calcium channel CACNA1C.^60,61 Among all RYR proteins widely expressed in the cerebellum and hippocampus (RYR1, RYR2, and RYR3), RYR2 is the most abundant.^61,62 HOMER3 encodes a PSD scaffolding protein that binds and crosslinks to cytoplasmic regions of GRM5, and RYR2⁶³ assists surface receptors to couple with intracellular calcium release. SCZ GWAS hits on ERBB4 and GRM5 loci were discovered by Greenwood et al.⁶⁴ In addition, NRG1 encodes a membrane glycoprotein that mediates cell-cell signaling, and its receptor ERBB4⁶⁵ is found to be expressed in GABAergic neurons.^66,67 All prioritized genes connected by attention weights can be found in Figure S4. We show large attention weights representing strong interconnections naturally provide insights about underlying regulatory or interplay mechanisms of complex mental diseases and equip the Graphene model with certain interpretability. To better illustrate the potential utilities of attention weights, we add examples for another three diseases, shown in Figures 4J–4L. Identified TPGs of coronary artery disease are enriched in “cholesterol metabolism” and “PI3K-Akt signaling pathway” (Figure 4J). Sortilin (SORT1) might bind components of the platelet-derived growth factor,⁶⁸ whose function can be enhanced by PCSK9.⁶⁹ SORT1 is a high-affinity sorting receptor for PCSK9.⁷⁰ PathCards⁷¹ and GWAS⁷² also show correlations among ANGPTL8, CETP, and LIPG. For hippocampal atrophy’s TPGs, two major pathways identified by attention weights are “lycosaminoglycan biosynthesis-heparan sulfate/heparin” and “axon guidance” (Figure 4K). Heparan sulfate is reported to be related to hippocampal atrophy⁷³ and its synthesis and modification involve NDST1-4, the HS3ST family, and HS2ST1. NDST enzymes may affect the potential functional relation between NDSTs and HS2ST1.^74,75 In addition, HS3ST and NDST have very similar sulfotransferase domain.⁷⁶ Studies show that semaphorin-3a (Sema3a)-induced axonal growth cone collapse depends on HS3ST, indicating that activities of the semaphorin family rely on HS modifications.^77,78,79 TPGs of alopecia mainly cluster into two pathways termed the “Wnt signaling pathway” and the “Hippo signaling pathway” (Figure 4L). A previous study indicated that Wnt/β-catenin and Hippo signaling pathways played important roles in hair follicle regeneration⁸⁰ and development of alopecia.⁸¹ TLE4 is involved in the negative regulation of the canonical Wnt signaling pathway. It can suppress Smad7 and activate the expression of bone morphogenetic protein (BMP) signaling, and enhance and sustain the upregulation of the endogenous ID1 gene induced by BMP7.⁸² Through interacting with TCF7L2, the co-repressor TLEs repress transactivation.⁸³ The TCF/LEF family interacts with Smad families to coordinate the transcription of target genes,⁸⁴ while it may repress BMP/SMAD signaling with elevated expression of BMP signaling targets, such as Id1, Id2, and Id3.⁸⁵

Graphene discovers both shared heritability and distinct genetic underpinnings of multiple psychiatric disorders

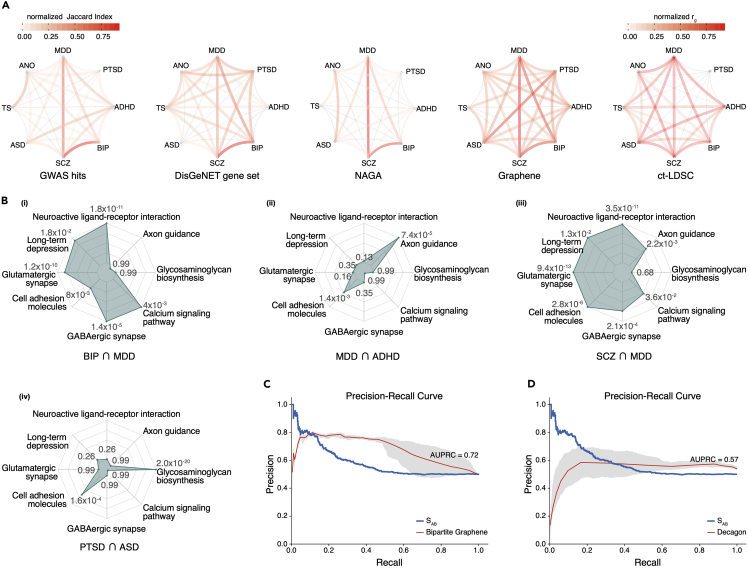
Mental disorders usually share similar symptoms with epidemiological comorbidity, posing difficulties for diagnosis and treatments.⁸⁶ Illuminating genetic underpinnings can provide evidence about intercorrelated psychopathology and raise the need to refine current clinical psychiatric diagnostics. We investigate whether Graphene TPGs of eight common mental diseases can reveal their genetic intercorrelations. Following CC-GWAS⁸⁷ definition, we measure the pairing correlation of every two diseases via computing the normalized Jaccard Index of their prioritized gene set (100–500 min-max normalization for each disease). We also leverage similar methods to compare the correlation results obtained from original GWAS hits, DisGeNET, and NAGA. The values of normalized genetic correlation (defined as the r_g value) computed by cross-trait LD score regression (ct-LDSC)⁸⁸ are directly retrieved from the CC-GWAS paper.⁸⁷ We compare different correlation patterns derived from all these strategies (Figure 5A). Overall, ct-LDSC and Graphene exhibit stronger intercorrelations among these mental disorders compared with original GWAS hits, NAGA, and DisGeNET. Considering two closely related depressive disorders as an example, i.e., unipolar depression (MDD) and BIP, their GWAS hits correlation (0.32) is much lower than ct-LDSC (0.5), DisGeNET (0.76), and Graphene (0.94), again demonstrating the importance to refine GWAS signals. We extract the overlapping Graphene TPGs for BIP and MDD (overlapping genes include KCND2, RIMS1, KCNA4, and RGS8) and implement GSEA on eight mental illness-relevant KEGG pathways (Figure 5B-i). We observe that these genes have functional enrichment in neuroactive ligand-receptor interaction (p_adjusted = 1.8 × 10⁻¹¹), glutamatergic synapse (p_adjusted = 1.2 × 10⁻¹⁰), and GABAergic synapse (p_adjusted = 1.4 × 10⁻⁵). Moreover, both Graphene (0.54) and ct-LDSC (0.49) report higher correlation between ASD and MDD against GWAS (0.15), NAGA (0.26), and DisGeNET (0.06). A similar trend is also observed between anorexia nervosa (ANO) and SCZ, where GWAS (0.05), DisGeNET (0.2), and NAGA (0.05) show relatively lower correlation than ct-LDSC (0.37) and Graphene (0.31). SCZ and MDD are identified as strongly correlated disease pairs among all approaches, their overlapping Graphene TPGs (including CTNNA3, HLA-G, CSRNP3, GRIN2B, and RELN) manifest functional enrichment in seven KEGG pathways (Figure 5B-iii), including neuroactive ligand-receptor interaction (p_adjusted = 3.5 × 10⁻¹¹), glutamatergic synapse (p_adjusted = 9.4 × 10⁻¹³), GABAergic synapse (p_adjusted = 2.1 × 10⁻⁴), calcium signaling (p_adjusted = 3.6 × 10⁻²), axon guidance (p_adjusted = 2.2 × 10⁻³), cell adhesion molecules (p_adjusted = 2.8 × 10⁻⁶), and long-term depression (p_adjusted = 1.3 × 10⁻²). For MDD and ADHD, their overlapping Graphene TPGs (including NALCN, NRXN3, NRG3, and LRP1B) are enriched in axon guidance (p_adjusted = 7.4 × 10⁻⁵) and cell adhesion molecules (p_adjusted = 1.4 × 10⁻³) (Figure 5B-ii). Another interesting discovery from Graphene is the relatively stronger correlation between post-traumatic stress disorder (PTSD) and ASD, and their overlapping Graphene TPGs (including CBLN4, BRINP1, and GLCE) are enriched in glycosaminoglycan biosynthesis (p_adjusted = 2.0 × 10⁻²⁰) and cell adhesion molecules (p_adjusted = 1.6 × 10⁻⁴) (Figure 5B-iv). Brinp1 has been reported to be associated with both ASD⁸⁹ and PTSD.⁹⁰ Several cognitive and behavioral mechanisms might be shared between PTSD and ASD, such as increased rumination, cognitive rigidity, avoidance, anger, and aggression. Understanding the shared genetics can help explore the common mechanisms underlying paired mental disorders. Correlation values of each disease pair extracted by the above five methods are listed in Tables S4–S8. Considering ct-LDSC derived scores as gold standard, we also calculate the Spearman correlation coefficients of all paired similarities extracted by Graphene, NAGA, GWAS, and DisGeNet with ct-LDSC (PTSD is not included in ct-LDSC), and the result (Table S9) shows that Graphene and NAGA denoise the underlying signals and achieve more similarly shared genetics with ct-LDSC than GWAS and DisGeNet.

Figure 5.

Graphene identifies strongly shared heritability of mental illnesses and boosts performance for comorbidity prediction

(A) Comparison plot of genetic correlations among eight mental diseases identified by original GWAS hits, DisGeNET gene sets, ct-LDSC correlation score, NAGA, and Graphene. The gradational color between disease pairs represents normalized Jaccard Index except ct-LDSC. Eight mental diseases include unipolar depression (MDD), post-traumatic stress disorder (PTSD), attention deficit hyperactivity disorder (ADHD), bipolar disorder (BIP), schizophrenia (SCZ), autism spectrum disorder (ASD), Tourette syndrome (TS), and anorexia nervosa (ANO).

(B) Functional enrichment score of overlapping Graphene TPGs for four disease pairs (BIP and MDD, MDD and ADHD, SCZ and MDD, and PTSD and ASD). Eight KEGG pathways associated with mental disorders were used for evaluation.

(C) Precision-recall (PR) curve of Bipartite Graphene for comorbidity prediction in comparison with original disease separation score (s_AB).

(D) PR curve of Decagon for comorbidity prediction in comparison with disease separation score (s_AB). Ten-fold cross validation is implemented for (C) and (D).

As opposed to the shared genetic correlation, we also investigate whether the genetic differences between two diseases can reveal their distinct parthenogenesis mechanisms. CC-GWAS⁸⁷ leverages allele frequency differences to identify differential genetic components between cases of two disorders. We also check the non-overlapping TPGs between two diseases identified by Graphene. For ANO versus Tourette syndrome (TS) and SCZ against TS, POU3F2^91,92 encodes neural transcription factors involved in neuronal differentiation. For SCZ against MDD, KCNV1⁹³ encodes a member of the potassium voltage-gated channel subfamily V as an essential function in the brain. For SCZ against TS, NFIB⁹⁴ is a transcriptional activator, essential for neuron axon genesis and other CNS. All overlapping and non-overlapping genes between the aforementioned mental disease pairs can be found in Tables S10 and S11, respectively.

Leveraging heterogeneous graph to re-train Graphene enables comorbidity prediction of disease pairs

All the above disease-gene association analyses are based on homogeneous GNNs, where only the gene node presents, and diseases are used as node attributes or labels. Constructing a multimodal graph where two or more types of nodes exist, more diverse inter-node relationships can be modeled. Decagon builds a bipartite graph to represent protein-drug interactions and model polypharmacy side effects as edges between paired drug nodes. Inspired by Decagon, we further introduce disease node into Graphene to model comorbidity relationship as links between disease nodes. Disease-associated genes or proteins interacting with each other tend to cluster into neighborhood structure as disease modules. If two diseases partially share overlapping modules, the local perturbation of functional pathways of one disease can lead to similar disruption in another, displaying as shared clinical and pathobiological features. Menche et al.⁹⁵ integrated disease-gene annotations from Online Mendelian Inheritance in Man (OMIM)⁹⁶ and GWAS data from the Phenotype-Genotype Integrator database (PheGenI),⁹⁷ obtaining 299 diseases and 3,173 associated genes, and used 30 million individuals aged 65 and older to determine relative risk (RR) for each disease pair as comorbidity metric. They also developed a network-based separation measurement of a disease pair defined as s_AB by comparing the shortest distances between proteins within each disease based on their constructed interactome, which is a network of 13,460 protein nodes and 141,296 links. They found that s_AB can be used as a metric to discriminate the degree of RR between disease pair (RR ≥ 10 for s_AB < 0 versus random expectation of RR ≈ 1 for s_AB > 0, see methods). Akram et al.⁹⁸ developed a weighted geometric embedding algorithm on this dataset and predicted comorbidity with performance of AUROC = 0.76 at threshold RR = 1 in a supervised manner. To test the decoder utility of bipartite Graphene to predict RR, we reconstruct Graphene through adding the same 299 disease nodes, re-training on the same gene-disease associations data, and training Graphene on paired disease RR values as edge labels in 10-fold cross validation setting. Similar training procedures are implemented for Decagon architecture. As shown in Figure 5C, Bipartite Graphene achieves a mean AUPRC of 0.72 and a mean AUROC of 0.79 (training for 20 epochs), significantly surpassing Decagon (mean AUPRC = 0.57, mean AUROC = 0.67 for 30 epochs of training, Figure 5D). Graphene’s GAT decoder and pre-training setting show stronger performance to predict disease separation than Decagon’s end-to-end supervised training with GCN decoder.

Discussion

We present Graphene, an integrative GNN framework to decode gene function under network-defined context. Graphene integrates multiple interactome networks from heterogeneous sources via a graph SSL approach. Then the informative gene embeddings are used as model initialization to infer functional properties of genes or proteins. We successfully demonstrate the wide applicability of Graphene in pathway gene recovery, disease-gene reprioritization, module identification, and comorbidity prediction. Several benchmark experiments have been performed to validate substantial improvements of Graphene over previous methods in each application.

The parameters sharing the scheme of pre-training GCN allow Graphene to encode both node attributes and its diverse neighborhood or context, leading to stronger expressive power over traditional network diffusion-based methods. During the re-training stage, GAT architecture guides Graphene to search task-specific connectivity patterns across the network and reprioritize all genes with fast convergence speed. We have shown that the emerging pre-training and re-training paradigm in deep learning community can be applied to complex biological networks and effectively transfer knowledge to downstream functional analysis. In this paper, we only implement node-level pre-training, and we plan to incorporate a graph-level pre-training task as a supplement to further capture global-level representations.

We also showcase that Graphene can re-rank GWAS hits and validate superior disease gene recovery performance on an independent hold-out DisGeNET dataset. Population-wide GWAS have identified a large number of disease-associated loci with genome-wide significance, although only contributing small amount of the heritability. There is an ongoing debate whether GWAS hits can reveal disease etiology and imply therapeutic targets; in particular, most signals do not match with core genes. The “Omnigenic” model¹ has been raised to explain those genomic regions that fell below statistical significance for association increase disease susceptibility through cumulative weak effects in relevant tissues. These weak effects are broadly distributed across network modules and function together in certain biological processes, pathways, and more complex networks. Indeed, disease genes are not scattered randomly but organized into disease-specific modules. Therefore, molecular networks can serve as functional map to refine GWAS hits, re-rank risk genes and guide the discovery of additional candidate genes. Developing a powerful network-based method based on large-scale, cross-tissue interactome datasets is essential to understand pathophysiological processes. Although we only use generic networks as integration inputs where tissue or context labels are not explicitly incorporated into Graphene during both pre-training and downstream re-training process, we recapitulate tissue specificity of reprioritized GWAS signals based on the GTEx dataset. In the future, we expect explicitly incorporating multi-view labels during network integration of GNN pre-training can equip the model with tissue awareness and further boost learning effectiveness. As an ever greater number of biological interactome are mapped, the Graphene framework presented here is easily expandable by adding newly discovered networks into the GNN model and is thereby adaptable to various functional analysis.

We showcase TPGs identified by Graphene revealing stronger functional enrichment in SCZ- and ASD-relevant pathways over previous methods. We also demonstrate certain model interpretability by extracting significant gene-gene attention weights from the GAT network to pinpoint important gene-wise interaction partners. Moreover, Graphene provides genetic underpinnings of shared heritability among eight common mental disorders by investigating their overlapping TPGs. The non-overlapping TPGs also offer some hints regarding distinct pathogenesis mechanisms between disease pairs. By adding disease nodes into Graphene to build a heterogeneous bipartite network, Graphene achieves excellent performance for comorbidity prediction via link prediction. Due to the fact that 299 diseases used for evaluation are far fewer than the number of genes, learning effective disease-disease edge embedding is non-trivial. Our GAT decoder outperforms Decagon’s GCN decoder, again demonstrating the importance of GNN architecture choices at different stages.

In the absence of a gold standard disease gene set, Graphene serves as a ready-to-use tool to refine any novel GWAS findings and retrieve candidate genes for detailed follow-up investigation. Since GWAS are based on population-level genotype-phenotype information, which is different from those networks used as input to Graphene, we foresee our tool can offer orthogonal evidence to discover biologically relevant modules and elucidate underlying disease mechanisms. Based on the robustness for gene prioritization, Graphene can also be extended to develop target gene panels for diagnosis of inherited disease or risk evaluation panel for complex traits. In addition, for a cohort where individual-level omics data are available, Graphene can concatenate variant information and other multi-omics features together with pre-trained gene embeddings, as in EMOGI,²⁹ and enable patient-level disease classification during the downstream re-training stage, thus providing a potential analysis tool for applications in precision medicine. Considering recent progress in applying graph SSL for information retrieval and recommendation system, we plan to further explore causal inference-based learned GNN to interpret large biological networks in the future.

Experimental procedures

Resource availability

Lead contact

Meng Yang, yangmeng1@mgi-tech.com.

Materials availability

This study did not generate new unique reagents.

Methods

In this work, we first design two auxiliary tasks to pre-train GNN to integrate four molecular networks and re-train the network for downstream investigations, including pathway gene set recovery, disease gene reprioritization, and other functional studies. In the following sections, we describe each of the proposed components in details.

Pre-training the GNN

Sources of pre-training molecular networks

We combine four different sources of networks freely accessible to build a single network for pre-training. We assign the presence of edge connection between two nodes as long as there exists interaction in any single network. HumanBase, as a tissue-specific gene network, is built on a collection of datasets covering thousands of experiments from 14,000 distinct publications. Incorporating HumanBase might help inject tissue specificity into our combined network and we download 142 gold standard tissue networks from Humanbase (https://hb.flatironinstitute.org/download). The tissue label is not explicitly included. We download STRING9606 v11 (https://string-db.org), which contains experimentally derived protein-protein interactions through literature curation, scientific text mining, calculation from genomic features, and other model organisms. We also collected 52,548 connections from the Human Reference Interactome (HuRI) (http://www.interactome-atlas.org/download), which is a systematic proteome-wide reference that links genomic variation to phenotypic outcomes. In addition, PCnet itself is a composite network that can boost performance and serves as supplementary to the other three networks, and 2,610,605 connections were downloaded from the Network Data Exchange (NDEx) database (http://www.ndexbio.org). We convert each network to a set of tuples, and each tuple consists of two nodes, interconnected by an edge between them. The node ID of each node is Entrez ID. We then take the union of four sets to generate a unified network of 19,324 gene nodes and 16,142,804 edges. The edges are equally weighted.

Model structure for pre-training

A schematic diagram of model architectures can be found in Figure S1 and we illustrate in formula form below. Our graph was denoted by G = {V, E} with N nodes v_i∈V, edges (v_i, v_j)∈E, a binary adjacency matrix A∈A^N×N. We randomly initialized node feature vector matrix X_vi for v_i∈V as the input to GNN:

$$X_{v_i}=Embedding\left(V,embedsize\right),$$ (Equation 1)

where X_vi ∈R^1×De, where D_e represents the embedding size. Node representations were updated at each layer by:

$$H^{\left(l+1\right)}=\sigma \left(\tilde{D}-\frac{1}{2}\tilde{A}\tilde{D}-\frac{1}{2}{H}^{\left(l\right)}{W}^{\left(l\right)}\right),$$ (Equation 2)

where à= A + I_N is the adjacency matrix of the graph G, I_N is the identity matrix, D is a trainable weight matrix. The equation adopts ReLU activation (σ(·)) with a certain number of hidden units. We devised two pre-training auxiliary tasks, context prediction and masked node recovery, as follows.

Context prediction

We performed this task by negatively sampling neighborhood and context representations. The above node update scheme provided us with neighborhood representation $h_{v_i}^k$ of center node v_i. Furthermore, we defined context representation $c_{v_i}^G$ by calculating the mean sum of representations of anchor nodes v_j∈A_anchor that are k hops adjacent to the center node:

$$c_{v_i}^G=MEAN\left(\sum _{v_j\in A_{anchor}}{h}_{v_j}^k\right).$$ (Equation 3)

With these two representations, the learning objective of Context Prediction was a binary classification of whether a particular neighborhood $h_{v_i}^k$ of v_i and a particular context $c_{v_j}^G$ of v_j belong to the same node:

$$y^{\text{'}}=\sigma \left(h_{v_i}^{\left(k\right)T}{c}_{v_j}^G\right)=\{\begin{array}{l}0\left(i\ne j\right)\\ 1\left(i=j\right)\end{array},$$ (Equation 4)

where σ(·) is a sigmoid function. During training, we chose either a positive pair of $h_{v_i}^k$ and $c_{v_j}^G$ (i = j) or a random negative pair (i ≠ j) with positive/negative sampling ratio 1:1, and we used binary cross entropy loss:

$${\mathcal{L}}_c=-y\log \left(y^{\prime }\right)-\left(1-y\right)\log \left(1-y^{\prime }\right).$$ (Equation 5)

Node prediction

We cast the masked node recovery as a classification task. We masked the node and let the pre-train model predict those nodes. First, we masked a node in the graph by replacing its node embedding with a mask embedding. Second, we applied a pre-training graph model to obtain a corresponding node hidden state $h_{v_i}^{\left(k\right)}$, which is consistent with Equation 2. Finally, we applied FC (fully connected layer) on $h_{v_i}^{\left(k\right)}$ to predict the node:

$$p_{v_i}^{node}=softmax\left(W^{node}\cdot h_{v_i}^{\left(k\right)}+b^{node}\right).$$ (Equation 6)

$p_{v_i}^{node}$∈ R^N is a vector that represents the probability of each node. W^node is weight matrix and b^node donates the bias matrix. We use cross entropy loss to optimize the entire pre-train model:

$${\mathcal{L}}_{NodeMask-v_i}=-\log \left(p_{v_i}^{node}\left[i\right]\right).$$ (Equation 7)

As the ground truth label is a one-hot vector, the cross entropy loss can be simplified to the above format. $p_{v_i}^{node}\left[i\right]$ indicates the i-th item in vector p_vi.

Re-training for pathway gene set recovery

Sources of pathway gene sets

Two widely used public gene sets were considered in this task, i.e., the National Cancer Institute Pathway Interaction Database (NCI) and The Reactome Knowledgebase (Reactome). We downloaded all 211 NCI pathways from NDEx (http://www.ndexbio.org) composed of human molecular signaling, regulatory events, and key cellular processes. Reactome is a free and open source database of biological pathways in intermediary metabolism, signaling, innate and adapted immunity, transcriptional regulation, apoptosis, and various diseases. We downloaded the Reactome Pathways Gene Set file, which contained 2,408 sets (https://reactome.org/download-data). We removed those pathways containing fewer than 3 genes and finally obtained a Reactome label file of 2,035 pathways.

Sources of disease gene sets

Disease-gene associations for re-training are downloaded from GWAS Catalog v1.0.2 (https://www.ebi.ac.uk/gwas/docs/file-downloads), which is a publicly available resource of GWAS. We obtained 3,954 diseases grouped by mapped traits with gene p < 5 ×10⁻⁵. To unify the nomenclature with downstream DisGeNET datasets, we chose diseases/traits that have identical names in DisGeNET (https://www.disgenet.org/downloads) and deleted those traits/diseases with associated genes less than 30 and we finally obtained 202 traits/GWAS disease. Most of these 202 chosen diseases were among the most common disorders cataloged in both GWAS and DisGeNET, and 171 of them have curated gene lists in DisGeNET (for detailed IDs, see Figure S2). A total of 171 DisGeNET gene sets was used as a hold-out test set for disease gene reprioritization.

Model structure for gene set member recovery

For each database above, suppose we had M gene sets and each set corresponded to N human genes. We arranged these datasets into a target matrix S = {s_ij}_M×N, where s_ij is a binary value indicating whether the gene v_j was the member of i-th gene set. Our aim was to predict the presence possibility of gene v_j in a given gene set m_i. The proposed downstream re-training of the GNN model consists of three modules: the embedding layer, the GAT layers, and the classification layer. Input gene embeddings were extracted from the above pre-trained network.

The pre-trained node embeddings can be represented as H = {h₁, h₂, …, h_N}, where h_i ∈R^K and K represent embedding size. The embedding layer accepts graph node embeddings as initializations. Each node embedding is represented as a K-dimensional vector and the weights are initialized by our pre-trained node embeddings, i.e., the i-th node embedding is h_i. Then we map these node embeddings into F-dimensional vectors through a fully connected layer:

$$H^{emb}=f\left(W^{emb}\cdot H+b^{emb}\right)=\left\{h_1^{emb},h_2^{emb},\cdots ,h_N^{emb}\right\}.$$ (Equation 8)

Here, $h_i^{emb}$ ∈R^F is the output embedding, W^emb∈R^F×K is weight matrix, b^emb∈R^F is the bias vector, and H^emb∈R^N×F represents the output of embedding layer.

Then, the GAT layers take the output from the embedding layer H^emb as input and aggregate the node information through a graph structure. We use the following formula to obtain the edge weight α_ij between nodes v_i and v_j:

$${\alpha }_{ij}=\frac{\exp \left(\text{LeakyReLU}\left({\alpha }^{⊺}\left[W^{GAT}{h}_i^{emb}\parallel W^{GAT}{h}_j^{emb}\right]\right)\right)}{{\sum }_{l\in O_i}\exp \left(\text{LeakyReLU}\left({\alpha }^{⊺}\left[W^{GAT}{h}_i^{emb}\parallel W^{GAT}{h}_l^{emb}\right]\right)\right)}.$$ (Equation 9)

W^GAT∈R^F′×F is a weight matrix applied to every node transforming the dimensionality from F to F′, a ∈R^2F′ is a learnable vector. We applied LeakyReLU as the activation function. O_i is the set of the neighboring nodes close to v_i in graph G. With weight α_ij, we can obtain the final output feature of every node produced by the GAT layer:

$$h_i^{GAT}=\prod _{t=1}^T\sigma \left(\sum _{j\in O_i}{\alpha }_{ij}^t{W}_t{h}_j^{emb}\right).$$ (Equation 10)

We employed the multi-head attention mechanism, where T is the number of heads and ∏ represents concatenation. W^t, t = 1, · · ·, T is a weight matrix and σ is a nonlinearity activation function. $h_i^{GAT}$ ∈R^{T F ′} is the produced vector for node v_i. The output of the GAT layer is H^GAT = {$h_1^{GAT}$, $h_2^{GAT}$, …, $h_N^{GAT}$}.

Then the classification layer takes H^GAT as input and derives final classification. This layer applies average pooling to H^GAT over all heads and then uses the sigmoid function for classification:

$$h_i^{out}=sigmoid\left(\frac{1}{T}\sum _{t=1}^T\sum _{j\in O_i}{\alpha }_{ij}^t{W}_t^{out}{h}_j^{GAT}\right),$$ (Equation 11)

where W^out_t ∈R^{M ×T F ′}, t = 1, · · ·, T, and M is the number of gene sets. $h_i^{out}$ ∈R^M is the output probability vector of node v_i. The output of the classification layer can be represented as a matrix H^out = [$h_1^{out}$, $h_2^{out}$, …, $h_N^{out}$] ∈R ^N×M. Each element $H_{ij}^{out}$ in this matrix means the probability of the gene v_i is the member of gene set j. Then we can use the binary cross entropy loss to optimize the full network:

$${\mathcal{L}}_{GenSet}=\sum _{i=1}^N\sum _{j=1}^M-s_{ij}\log H_{ij}^{out}-\left(1-s_{ij}\right)\log \left(1-H_{ij}^{out}\right).$$ (Equation 12)

During the re-training stage, we randomly masked the labels of half of all nodes and used the other half as a training set to enforce the model to predict the probabilities of all genes.

We used the same model architecture as described above for gene set member recovery. The embedding layer also takes pre-trained node embeddings H as input, and the GAT layer employs G_gg as the graph. The output of the classification layer represents the importance probability of the gene v_j to disease d_i. We used the binary cross entropy as loss function to train the model, given the ground-truth label matrix D = {d_ij}^Q×N.

Disease comorbidity prediction

Source of disease-disease comorbidity and disease-gene associations

For this task we adopted RR (from 0 to <9,000) of disease-disease comorbidity for each pair of diseases that were determined using the disease history records of 30 million individuals aged 65 years or older (U.S. Medicare). There were 6,269 disease pairs with comorbidity value RR ≥ 1 as positive pair and the rest were negative. For convenience of comparison, we used the disease-gene associations through integrating OMIM (www.ncbi.nlm.nih.gov/omim) and GWAS (www.ncbi.nlm.nih.gov/gap/PheGenI), using a p value cutoff of 5 × 10⁻⁸.

Bipartite model structure for disease comorbidity prediction

We constructed Bipartite Graphene by replacing GCN layer of Decagon model’s decoder with a GAT layer. In addition to gene-gene graph G and disease-gene association matrix D, a disease-disease relationship matrix C was required. Disease-disease relationships were calculated by the Jaccard Index between those 299 diseases chosen above. Then, we learned hidden states of each node from their neighborhood consisting of heterogeneous node types. Finally, we made predictions between two nodes via an edge decoding function. Then comorbidity can be considered as links between two disease nodes. We trained a model to learn the relationships between disease pairs and then predicted those test links in 10-fold cross validation. Formally, the Bipartite Graphene model takes the following form:

$$h_{i,x}^{BGAT}=\sum _l\sum _{j\in O_i^l}{u}_{i,j}{W}_l^x{z}_{j,x}+W_{b_{i,s}}^x{z}_{i,x},z_{i,x+1}=\varnothing \left(h_{i,x}\right).$$ (Equation 13)

z_i,x∈ R^ux represents the hidden state of node v_i in the x-th GAT layer. $h_{i,x}^{BGAT}$ is the feature vector that aggregates information from v_i’s neighborhoods, l is the type of node links, and O^l_i is the neighborhood set of node v_i with regard to type l. $W_l^x$ and $W_{b_{i,s}}^x$, are the weight matrices at layer x, and b_i is the type of the node. u_i,j is a normalization constant, which can be formulated as $u_{i,j}=1/\sqrt{\left|Q_i\right|\cdot \left|Q_j\right|}$. φ indicates the activation function ReLU.

Since we have different types of nodes and links, the computation of the graph propagation can vary according to different types of the neighborhood. We used GAT architecture to aggregate and propagate node representation z_i,x into the node representation z_i,x+1 for the next layer. The final representation of node v_i is z_i,x, where x is the number of GAT layers. For the edge decoding model, the probability of a link between disease j and disease i can be described as:

$$P\left(d_i,d_j\right)=\sigma \left(z_{d_{i,X}}^{⊺}{W}_c{z}_{d_{j,X}}\right).$$ (Equation 14)

z_di,X is disease node representation for d_i, z_dj,X is disease node representation for d_j. W_c is the weight matrix to capture the relationships between disease pairs. σ is the sigmoid function, so P (d_i, d_j) will be a real value within range (0, 1) indicating the co-occurrence coefficient between d_i and d_j.

During the training stage, we select edges where c_ij≥0.9 are positive samples, and recorded the index (i, j) into the positive set S_p. For negative samples, we still employ negative sampling given a positive edge c_ij, we randomly sampled one negative edge c_ir, where c_ir < 0.9, and recorded the sampled negative index (i, r) into the negative set S_n. The training objective is thus:

$${\mathcal{L}}_{Comorbid}=\sum _{\left(i,j\right)\in S_p\cup S_n}-c_{ij}\log P\left(d_i,d_j\right)-\left(1-c_{ij}\right)\log \left(1-P\left(d_i,d_j\right)\right).$$ (Equation 15)

Experimental setting and hyperparameters choice

The dimensionality of pre-trained node embeddings K is set to 100. For the gene set member recovery task, the dimensionality of the embedding layer output is set to 256. The number of heads T is 8, the number of GAT layers is 2. The output representation dimensionality of each head in the first GAT layer is 128. We set the learning rate to 1e⁻³. During the pathway gene set recovery experiments, we followed the setting of Set2Gaussian to retrieve 50% of the gene set members as test data and used the remaining 50% as the training data. For the disease gene reprioritization task, we randomly masked 40% of the associations for disease-gene matrix D as test set and used the other 60% of data for training. We set the attention dropout to 0.3, and the learning rate to 5e⁻³. The hidden size of the GAT layer is 128 per head. We train the model for 7,100 epochs. For comorbidity prediction, we randomly hid 10% of edges of the comorbid disease matrix C as test set and used the remaining 90% as the training set (10-fold cross validation). We trained the bipartite Graphene model for 20 epochs (30 epochs for Decagon), with batch size of 512 and learning rate of 1e⁻³. The threshold of the input relative risk is 1.0.

GSEA

GSEApy (https://github.com/zqfang/GSEApy) API was used for enrichment analysis, where the p value was computed using the hypergeometric test and the p_adjusted value using the Benjamini-Hochberg method for correction. The p_adjusted value was reported. The following gene sets were included for SCZ: FMRP targets, PSD genes, GABA_A receptor, calcium signaling, and glutamatergic synapse of KEGG. ASD related gene sets include database AutDB, ECGs, and targets of RBFOX1. In downstream analysis of disease gene prioritization, the following KEGG pathways were used for correlation analysis for eight mental disorders: Neuroactive ligand-receptor interaction, long-term depression, glutamatergic synapse, cell adhesion molecules, GABAergic synapse, calcium signaling pathway, glycosaminoglycan biosynthesis, and axon guidance. For two IBDs, i.e., ulcerative colitis and Crohn disease, we chose three pathways involved in immune system and signal transduction (mitogen-activated protein kinase) signaling, NF-κB signaling, Th17 cell differentiation) from KEGG (https://www.genome.jp/kegg/pathway.html) and we chose another three pathways of T cell activation (TCR signaling, CD28 co-stimulation, interleukin-2 family signaling) from Reactome.

Tissue specificity analysis

For the tissue-specificity analysis, we downloaded gene-level TPM (transcripts per kilobase million) data containing 53 tissues from GTEx portal (https://www.gtexportal.org/home/datasets) and adopted the JS divergence to measure the tissue specificity of each gene in each tissue. JS divergence is an entropy measurement that quantifies the similarity between a gene’s expression pattern e and an extreme pattern where a gene is expressed in only one tissue e^t, and their JS divergence to be

$$JS\left(e,e^t\right)=H\left(\frac{e+e^t}{2}\right)-\frac{H\left(e\right)+H\left(e^t\right)}{2},$$ (Equation 16)

where the entropy of a discrete probability distribution is denoted as H:

$$e=\left(e_1,e_2\cdots e_n\right),0\le e_i\le 1and\sum _{i=1}^n{e}_i=1$$

$$e^t=\left(e_1^t,e_2^t\cdots e_n^t\right)and{e}_i^t=\{\begin{array}{l}0,\left(i\ne t\right)\hfill \\ 1,\left(i=t\right)\hfill \end{array}$$ (Equation 17)

$$H\left(p\right)=-\sum _{i=1}^n{e}_i\log \left(e_i\right).$$

The distance between two tissue expression patterns, e and e^t is defined as:

$$J{S}_{dist\left(e,e^t\right)}=\sqrt{JS\left(e,e^t\right)}.$$ (Equation 18)

Then the tissue-specific expression pattern of gene e with respect to tissue t can be defined as

$$J{S}_{sp}\left(\text{e}|t\right)=1-J{S}_{dist}\left(e,e^t\right).$$ (Equation 19)

Finally, Wilcoxon rank-sum test was adopted to calculate the overall expression pattern of genes relating to one disease.

Gene classification according to GO annotation

In the task of SCZ disease module identification (Figure S4), we devised a way of classifying module genes according to GO annotation. Like other mental diseases, the following functions played important roles: gene expression regulation: GO:0010468, GO:0032774, GO:0051252; synaptic signaling: GO:0099536, GO:0007154, GO:0023052, GO:0005737, GO:0007267; ion transport: GO:0006811, GO:0006810; cytoskeleton organization: GO:0070507, GO:0032886, GO:0000226, GO:0007010, GO:0006996; nervous system development: GO:0048854, GO:0009887, GO:0007399, GO:0050877, and so on. Each function class contains a certain amount of GO annotations. We classified a gene by searching the GO annotation hierarchy tree and see if the gene itself has any annotation belonging to a certain function or if any close ancestor of it does.

TPGs chosen for Jaccard Index calculation among eight mental disorders

The number of TPGs used for Jaccard Index calculation of eight mental disorders was chosen according to their GWAS association genes in training, and then normalized to a range from 100 to 500 (min-max normalization).

Published: December 6, 2022

Data and code availability

All datasets in this study were published previously, and their availabilities are described in Table S1. Graphene is written in Python using the Pytorch library. The source code has been deposited at Zenodo under the https://doi.org/10.5281/zenodo.7233857.