Abstract
The consequences of any extreme event can deteriorate any system at all levels: socially, economically, and operationally. The COVID-19 pandemic, caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), provides a good example of the tremendous impact that can be produced by such extreme events. To effectively measure and mitigate the impact of the COVID-19 pandemic and relaunch the Moroccan economy, policymakers need to determine which sectors have been most impacted. Due to the high level of uncertainty and complexity surrounding this health crisis, this study first develops a new technique for dealing with decision problems under uncertainty using exclusive-or (XOR) logic, called the XOR-analytic network process (XOR-ANP). Then, the proposed technique is adopted to assess the impact of COVID-19 on seven relevant sectors (tourism, transport, industrial, financial, agriculture, education, and healthcare) by considering social, operational, and economic dimensions. The key findings show that COVID-19 has a significant impact on Moroccan’s tourism, healthcare, and transport sectors, with respect to social-economic and operational dimensions by 30.99%, 21.81%, and 17.88%, respectively. These results indicate that most of the United Nations Sustainable Development Goals for 2030, such as “Healthy Lives”, “Decent Work” and “Economic Growth” have been severely impacted, thus, assistance and recovery are urgently needed.
Keywords: Multiple criteria analysis, XOR analytic hierarchy process, XOR analytic network process, COVID-19, Sectorial impact
1. Introduction
Extreme events and their consequences are among the most challenging phenomena of the modern age and demand urgent interest from the scientific community. Albeverio et al. (2010) define extreme events as events that are rare, exceptional, catastrophic, and surprising and which occur within a limited space and time, by chance or necessity (or through a combination of both). The consequences of any extreme event, such as COVID-19, are severe, unpredictable, and usually facilitate the transmission of financial shocks across the market and multiple sectors. After several months of fighting the pandemic, many countries have started to slowly transition to recovering from COVID-19, and policymakers in these countries require reliable decision support systems. The main challenge is that the literature related to the transition between the response to the pandemic and the recovery phase is relatively scarce (Gupta et al., 2020). By setting efficient policies, governments will be able to plan relevant strategies that go far beyond prevention, such as increasing hospital capacity, strengthening medical staff recruitment, investing in medical equipment, improving social aids, etc. Policymakers must put in place successful social and economic policies to fight against the disease from different perspectives. Recently, many countries and regions with governance mechanisms have announced the development and implementation of various programs aiming to guide economic recovery. In these situations, governments are required to take effective measures that reduce the negative impacts of the pandemic. Thus, their first task is to assess the current situation and determine where support and intervention are needed. From this perspective naturally arise the questions: which sectors have been most affected by the COVID-19 pandemic, and which sectors should receive priority for support and recovery?
The main challenge for decision-makers (DMs) is that there are no forecasts, indices, or projections that can reliably help to answer questions related to the impact of the COVID-19 pandemic. The majority of the existing studies are focused on the earth sciences and natural hazards such as earthquakes and tsunamis (see, e.g., Albeverio et al., 2010). In this context, the extreme value theory and extreme value analyses remain the most used techniques to estimate the likelihood of the extreme events. This type of analyses mainly rely on statistical methods and probability theory (Benstock & Cegla, 2017). However, one of the most known barriers and limitations of using this statistical techniques is the availability of historical data. As alternatives the qualitative methods such as Delphi and the qualitative risk assessment matrix, which are constructed based on expert judgments, could be very beneficial (Keeney et al., 2011). In many situations, we need experts’ opinions to guide us and reduce the spread of misinformation. Expert judgments are an important asset to many decision-making problems and have been studied in various fields (Werner et al., 2017). They are essential and widely used in the design and management of large or complex systems. Such projects are often essentially unique, so there is very limited experience regarding the performance of their components. It is natural then to rely on expert judgments, especially in situations such as COVID-19 where historical data is scarce or absent. In general, the most difficult decisions are those where the consequences are subject to substantial uncertainty. Although experts are valuable sources of information and knowledge, experience and global events have proven that they can also be wrong due to the high level of uncertainty (Ayyub, 2001). Since uncertainty is viewed as a lack of information, when seeking to reduce its impact, experts often try to provide a large amount of information to enrich their analysis, rather than explaining their opinions in a determined or crisp way. For example, when experts are asked how long it will be until an effective vaccine for COVID-19 is available, the most common answer has so far been something along the lines of, “If everything goes well, a vaccine may be available in either the coming months or next year”. The experts prefer to use exclusive-or (XOR) logic, “or”, to express their judgments about the time of availability, saying: “coming months or next year”. Due to a lack of information, experts do not know precisely when an efficient vaccine will be available; consequently, they are forced to express their preferences using XOR logic to reduce uncertainty.
Recently, Hocine and Kouaissah (2020) have developed a new technique for dealing with decision-making problems under uncertainty using XOR logic called XOR analytic hierarchy process (XOR-AHP). Conceptually, XOR is an uncertain logic that describes a situation in which there is only one choice between two or more competitive actions, and neither is strong enough to overcome the others. Unlike classical logic, which requires a deep understanding of a system, exact equations, and precise numeric values, XOR logic offers a more free way of thinking, which allows complex systems to be modeled using a higher level of abstraction originating from our knowledge and experience. In contrast to existing uncertainty theories, the XOR analysis framework provides an intuitive and natural way to model imprecise and uncertain decision-making problems. The use of XOR analysis, at least in some cases, is the natural, simplest, and best representation of imprecision and uncertainty. In particular, it does not require assumptions such as lower and upper bound values, types of distributions, and fuzzy membership functions. For example, when experts are asked to assess the relative impact of COVID-19 on the tourism and agriculture sectors in terms of operation level, using a numerical scale ranging from 1 (equal) to 9 (extremely more impact), it is very difficult for them to provide an exact estimated value. Experts are forced to express their estimations using XOR logic, for example: “On an operational level, the tourism sector is more impacted than the agriculture sector, by 5 or 6 times”. Mathematically, we can express the expert’s statement as follows: 5 XOR 6. Thus, problems featuring these characteristics should be modeled using an XOR framework, as suggested in Hocine and Kouaissah (2020). Obviously, in the XOR-AHP model, the criteria are assumed to be independent. However, since many decision problems include the interaction and dependency of top-level elements on down-level elements, they cannot be ordered hierarchically (see, e.g., May et al., 2013, Saaty, 2006, Saaty and Vargas, 2013). It is well known that problems in many fields, such as telecommunications, energy, and economics, have strong correlations and dependencies in their companions and structures that are not compatible with linear modelization. For example, in the context of COVID-19, if we want to evaluate the multisectoral impact of COVID-19 with respect to some dimensions or criteria, such as economic and social, then these dimensions are generally correlated with and dependent on each other. In this regard, the analytic network process (ANP) method (Saaty, 2001) allows the dependencies (or feedbacks) to be modeled realistically, and the results yield more accurate outputs. Dependencies can arise between any of the elements in the decision problem, such as alternatives, criteria, sub-criteria, and the goal (Mu et al., 2020). For instance, dependencies in the alternatives can arise between the different sectors — such as the transport and tourism sectors — where there is a strong correlation between them. This means that the model no longer has a linear structure as in the analytic hierarchy process (AHP) methodology. To tackle this problem, this study aims to develop a new model called the XOR-analytic network process (XOR-ANP). The proposed model contributes to the literature and is distinct from previously presented models for the following reasons:
-
•
It generalizes the XOR-AHP formulation so it can be applied as an efficient tool in many real-life decision-making problems where the interactions among the decision elements lead to a network system. This contribution provides more flexibility and reality in dealing with real scenarios, especially extreme events such as the COVID-19 pandemic.
-
•
Given the complexity of the problem and uncertainty surrounding COVID-19, this model provides the ability to deal with uncertainty, especially when DMs are hesitant or reluctant in expressing their judgments. In addition, the proposed XOR-ANP model allows incorporation of DMs preferences by using three types of XOR matrices: optimistic, pessimistic, and neutral. These contributions play an important role in supporting DMs and are suitable for many real-world scenarios.
-
•
It contributes to the COVID-19 literature from an operational research perspective, considering a real-world scenario of determining the Moroccan economic sectors most impacted by COVID-19 to assist policymakers in mitigating the effects of the pandemic and prioritizing interventions aimed at relaunching the Moroccan economy.
The rest of this paper is organized as follows. Section 2 formulates the XOR-ANP technique. Section 3 applies the developed XOR-ANP technique to detect the sectorial impact of COVID-19 in Morocco. Finally, our conclusions and suggestions for future work are presented in Section 4.
2. XOR analytic network process (XOR-ANP) technique
2.1. Backgrounds
The ANP and its linear version, the AHP, are general techniques of measurement (Saaty & Vargas, 2013). These two methods were developed by Thomas Saaty and his colleagues through a series of studies that began in the early 1970s and are still attracting the attention of many researchers (see, e.g., Aguaron et al., 2021, Harker and Vargas, 1987, Ishizaka et al., 2012, Rezaei and Ortt, 2013). Due to their simplicity, solid theoretical foundation, and user support software packages, these two techniques have become one of the most widely used methods in operations research/management science (Ho and Ma, 2018, Ishizaka and Nemery, 2013, Saaty and Vargas, 2013). Chronologically, the AHP method appeared first to deal with linear systems. Later, the ANP was proposed to relieve the fundamental restrictions related to the linear hierarchical structure. Many decision problems cannot be modeled hierarchically due to the interactions and dependence between their elements. Thus, the main idea behind the development of this technique was to avoid the assumption of independence among the decision-making elements of the standard AHP.
Methodologically, the ANP is very similar to the AHP: pairwise comparisons are still key to running the necessary computations to generate the priority vectors, and are carried out for all the components of the network system (i.e., nodes and clusters). Through this process, the DM’s preferences are converted from linguistic expressions to numerical values using a numerical 1–9 scale. The priority vectors derived from the pairwise comparisons are used to fill the columns (or blocks) of a new matrix called the supermatrix. The main role of this supermatrix is to synthesize the raw priority vectors obtained from the pairwise comparisons, which is considered as one of the distinguished features of the ANP method. To obtain the weighted supermatrix, the primary (or unweighted) supermatrix must first be transformed into a matrix whose columns each sum to unity, known as a stochastic matrix. Next, to generate the overall priority vectors, the limit supermatrix is created by raising the weighted supermatrix to the power of , where is an arbitrarily large number. This step helps to capture the transmission of influence along all possible paths of the supermatrix. Finally, the element with the largest overall priority is the best option. For more details about the theoretical background, mathematical concepts, and best practice of the ANP methodology, see, for example, Mu et al. (2020) and Saaty and Vargas (2013).
“When a DM is uncertain about his preferences, what effect can this uncertainty have on the final decision?” This question was raised by Saaty and Vargas (1987) to highlight the uncertainty issue in the AHP framework. In this study, the authors classify the uncertainty related to AHP into two categories: uncertainty about the occurrence of events, and uncertainty about the range of judgments used to express preferences. The first is related to external uncertainty, which is uncontrollable by the DM, while the second is due to internal uncertainty, which represents a lack of information available to the DM. Many efforts have been made to tackle this issue and three main streams of research have been proposed on fuzzy, interval, and probability theories (see Saaty and Vargas, 1987, Salo and Hämäläinen, 1995, Van Laarhoven and Pedrycz, 1983). In this context, analysts often select the most suitable technique that overcomes their problems. For instance, interval ANP is generally used to cope with rounding and measurement errors. Although it is generally accepted that random variables are handled through stochastic processes and probability theory, consensus fails on whether historical data is sufficient, which is required for formulating probabilistic distribution (see Kirkwood, 1992). Unfortunately, in some situations such as COVID-19, historical data is not sufficiently available or is absent, and uncertainty may come from linguistic sources. Under these circumstances, fuzzy ANP could be adopted, where fuzzy numbers capture the input data of pairwise comparisons. However, since fuzzy numbers are represented by possibility distributions, the issue of overlapping may arise, rendering it difficult to rank these fuzzy numbers. Even when ordering a set of single fuzzy numbers, the defuzzification procedure could result in the loss of some information contained in the original data. It can be argued that no technique is superior to the others in all cases; all techniques have their advantages and limitations, and the choice of the right technique should be directed by the analysis.
The importance of the proper treatment of uncertainties is growing: the consequences of inadequate treatments are very costly in social, economic, and environmental terms. Ongoing global changes create fundamentally new scientific problems that require new concepts, methods, and tools. In real-life decision problems related to extreme events such as COVID-19, sufficient observations do not exist, it is very difficult to secure necessary data or conduct experiments, and the learning-by-doing process may be very expensive, dangerous, or simply impossible. In this context, XOR logic serves the purpose well and captures experts’ hesitancy and uncertainty with the ANP methods. Thus, the main distinguishing characteristic of the XOR-ANP technique is its capability to overcome many limitations of other uncertain ANP methods (e.g., the overlapping problem, an infinite number of possibilities within the interval boundaries, and difficulty in comparison and ranking) and offer many advantages (e.g., incorporating DM preferences). For example, given the XOR judgment, 3 XOR 4 XOR 5, the XOR logic function, in this case, aims to select the most suitable judgment from among the three potential candidates ‘3’ or ‘4’ or ‘5’ that will achieve consistency with the DM’s preferences. Another potential advantage of using the XOR logic function is that it can consider more preferences from the DM, i.e., the optimistic and pessimistic situations (see, e.g., Hocine and Kouaissah, 2020, Kouaissah and Hocine, 2022). Furthermore, XOR could be used to model and represent the preferences of a large number of actors whose preferences may concur or diverge on a particular choice. To the authors’ knowledge, these concepts cannot be formulated by the current ANP approaches.
To cope with uncertainty in the COVID-19 context, the fuzzy ANP, stochastic ANP, and interval ANP could be useful tool if certain conditions hold. For instance, in fuzzy ANP, to use this approach in the context of Covid-19, it is necessary to have enough time to convert expert preferences’ into an appropriate fuzzy membership function (triangular, trapezoidal, or others) which is a difficult task to perform. The linguistic expressions such as “the impact could be approximate to 5 or between 6 and 7” should be converted to an equivalent membership function through an appropriate scale or an interval scale. Then through a complex process of arithmetic transformation, the weight vector must be generated. To avoid this complexity and pri-assumptions, the use of XOR-ANP seems very suitable since it fits well the reality in the preferences elicitation process of expert judgments. In other words, there is no need to convert the expert judgment to an equivalent fuzzy membership function or split it into two bounded values.
2.2. XOR analytic network process (XOR-ANP) modeling
According to Saaty and Vargas (2013), the ANP method can be employed with the following three main principles: (i) decomposition of the decision problem in a network system; (ii) measurement and priority vectors estimation; and (iii) synthesis.
2.2.1. Decomposition of the decision problem in a network system
This process involves structuring the decision problem into a network system through identifying its main clusters, elements, and dependencies between and within clusters (see, e.g., Fig. 1). For example, in a network, it is not necessary to specify levels as in a hierarchy model with a linear top–down structure without feedback from lower to higher levels. In general, three types of clusters could exist in the ANP methodology: a source cluster (C1) with no arcs into the cluster, an intermediate cluster (C2) with arcs into and out of the cluster, and a sink cluster (C3) with arcs only into the cluster. These clusters have dependencies and interactions with other clusters, such as the one between C1 and C4 (outer dependence). A cluster of elements also has a loop if its elements depend on each other, resulting in dependence known as inner dependence (Fig. 1).
Fig. 1.
Types of components in a network.
2.2.2. Measurement and priority vectors estimation
Let be a cluster of the network, with , and let be the total number of clusters in the network. Assume that cluster has elements, denoted by . Following the XOR-AHP methodology, the estimated priority vectors of a given set of elements from a cluster on any other element in the network can be generated through the following steps (Hocine & Kouaissah, 2020):
Step 1: Construction of XOR pairwise comparison
The main idea behind this step is conversion of the verbal comparisons to numerical values based on a discrete scale ranging from 1 to 9, as reported in Table 1. Mathematically, the XOR pairwise matrix should respect some properties as follows.
Table 1.
Fundamental ratio scale to measure the impact.
| Scales | Definition |
|---|---|
| 1 | Equal impact |
| 3 | Moderate impact |
| 5 | Strong impact |
| 7 | Very strong impact |
| 9 | Extreme impact |
| 2, 4, 6, 8 | Intermediate values |
Property 1
Matrix is an XOR comparison matrix if
(2.1) where represents the degree of preference of th criterion to th criterion.
Property 2
Matrix is an XOR comparison matrix if a priority vector exists which satisfies and the following equalities hold:
where . Then,
(2.2)
Property 3
An XOR comparison matrix is positive reciprocal if , and for all . Consequently, Matrix (2.1) can be rewritten as follows:
(2.3)
Step 2: Incorporate decision-makers’ preferences
According to Hocine and Kouaissah (2020), the XOR comparison matrix corresponding to real-world scenarios assumes one and only one of three directions: (i) optimistic (positive), (ii) pessimistic (negative), and (iii) neutral (no direction is provided).
Definition 1
Matrix is an optimistic XOR comparison matrix if , is a pessimistic XOR comparison matrix if , or is a neutral XOR comparison matrix if does not follow any mandatory direction (max or min) for all .
Step 3: Estimate the priority vectors
Priority vector is the keystone of generating the ranking solutions. To obtain the priority vector from an XOR matrix, a mathematical programming model called the XOR weighting technique (XOR-W) is formulated as follows (Hocine & Kouaissah, 2020):
| (2.4) |
| (2.5) |
| (2.6) |
| (2.7) |
| (2.8) |
| (2.9) |
where and , is the maximum deviation, is the element of an preference matrix (2.3) giving the relative import of the th criterion considered against the th criterion, is the derived weight given to the th criterion, is the function of XOR judgment logic, and is a binary variable. The objective function (Eq. (2.4)) guarantees that the maximum deviations of the inconsistencies of the XOR comparison matrix, as well as the undesirable deviations and from the aspiration level are minimized. Eq. (2.5) defines a hyperplane in the -dimensional priority space. Eq. (2.6) represents the DM’s preferences, where is a psychological parameter that gauges optimism/pessimism assessment and ranges from 0 to 1, as shown in Table 2. Eq. (2.7) allows inconsistency to be controlled. Eq. (2.8) guarantees that only one evaluation will be selected for the th and th pairwise comparisons, which is the most appropriate evaluation among the potential evaluations that will achieve the highest level of DM consistency. Eq. (2.9) satisfies the normalization condition and ensures the derivation of a positive priority vector.
Table 2.
Scales for optimism/pessimism.
| Scale for cost criteria | Scale for benefit criteria | Definition |
|---|---|---|
| 0 | 1 | Optimistic |
| 0.2 | 0.8 | Moderately optimistic |
| 0.5 | 0.5 | Neutral |
| 0.8 | 0.2 | Moderately pessimistic |
| 1 | 0 | Pessimistic |
Step 4: Check the consistency
Once judgments have been conducted, it is important to double-check the consistency of decisions. The consistency ratio (CR) is a useful tool for determining how consistent a pairwise comparison is.
Property 4
An XOR pairwise matrix is consistent if transitivity and reciprocity and for all . rules are respected.
The consistency level of pairwise judgments is measured by calculating a consistency ratio (CR). The following formula is used in this calculation:
| (2.10) |
where is the optimal solution of the XOR-W program and CI is the consistency index, determined based on Table 3 (Rezaei, 2015).
Table 3.
Consistency Index (CI) table.
| Scale | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Consistency Index (CI) | 0.00 | 0.44 | 1.00 | 1.63 | 2.30 | 3.00 | 3.73 | 4.47 | 5.23 |
It is clear that CR takes values between interval [0,1]. Therefore, the most consistent is the nearest to 0.
2.2.3. Synthesis
After accomplishing all the necessary pairwise comparisons, the obtained priority vectors will organize into a special matrix, called the supermatrix. This supermatrix represents the flow of influence either from a cluster to itself or from a cluster to another cluster in the network. Since the dependencies and influences in real-life decision problems come in different varieties and combinations, Saaty and Vargas (2013) present some potential structures and their supermatrix, including hierarchy, holarchy, suparchy, intarchy, etc. The mathematical form of the supermatrix can be represented as follows:
| (2.11) |
where is called a block of the supermatrix which represents a principal priority vector of the influence (or importance) of the elements in the th component of the network on an element in the th component. Some of its entries may be zero corresponding to those elements that have no influence. The generic format of the block can be written as follow:
| (2.12) |
Then, by converting all column sums to unity exactly, the weighted supermatrix is formed (or called a stochastic matrix). This process is similar to the idea of a Markov chain, which ensures that the number of all state probabilities equals 1. Next, we raise the weighted supermatrix to limit powers to get the global priority vectors as follows:
| (2.13) |
In case the supermatrix has the effect of cyclicity, the Cesaro sum can be used to obtain the average priority as follows:
| (2.14) |
3. Sectorial assessment of COVID-19 impact through XOR-ANP technique
3.1. Background
Viruses have significant potential to become dangerous and life-threatening and cause irreparable losses to human beings. Hardly does the world learn to cope with one strain of virus when another emerges and poses a threat to the human well-being. Such a situation has occurred with the emergence of a new strain of SARS-CoV-2 that has not been previously known in human history (see Arthi and Parman, 2020, Peckham, 2020). On March 11, 2020, the WHO declared COVID-19 a public health emergency and pandemic (WHO, 2020). By end of March 2020, COVID-19 had spread quickly around the globe; at the time of this writing, over 60 million people had been infected with the virus and it had caused over 1.5 million deaths. One of the most dangerous aspects of COVID-19 is that people carrying the virus may spread the virus to others before or without showing symptoms; its basic reproduction number has been estimated between 1.4 and 5.7, i.e., each infected person in turn infects an average of up to 5.7 people. Fig. 2 shows the worldwide spread of COVID-19. Like the rest of the world, Morocco has been affected by the COVID-19 pandemic. The virus was confirmed to have spread to Morocco on March 2, 2020, when the first COVID-19 case was confirmed in Casablanca. As the outbreak widened in Morocco, the government called for an emergency, stay-in-home order and intensified various restrictions such as closing borders and social distancing. By end of November 2020, Morocco had reported more than 335,000 confirmed cases and more than 5,500 deaths. Note that due to the rapid spread and evolution of COVID-19, this representation corresponds to 2020 data and may not updated (visit the WHO website for updated information).
Fig. 2.
World map of confirmed COVID-19 cases, December 2020 (Our World in Data, 2020).
Screenshot from Our World In Data website: original data derived from Johns Hopkins University CSSE, The Centers for Disease Control and Prevention, New York Times, CNBC.
3.2. Multidimensional network impact of COVID-19 in Moroccan sectors: An overview
As COVID-19 spread across Morocco, its impact increased and began to appear in all aspects of life. For example, the Moroccan office of the high commissioner for planning claims that the growth forecast for 2020 will be dramatically reduced and that the pandemic may cause one of the most severe recessions to hit Morocco over the last three decades. Ample evidence suggests that the pandemic has had a significant impact on financial planning and the budget deficit and, consequently, may force the government to adopt austerity policies. According to the World Bank (2020), it is estimated that the overall budget deficit will deteriorate by approximately 7% of GDP by the end of 2020. As a result, Morocco’s external debt could reach 73% of GDP, its highest level in decades. For instance, in the tourism sector, which is crucial to the Moroccan economy (generating around 500,000 direct jobs and around 2.5 million total jobs including indirect jobs OECD, 2020), the national tourism confederation estimates significant losses of $3.6 billion in terms of tourism turnover and $1.5 billion of lost turnover for the hotels industry. More than 500,000 employees and 8,500 firms, including hotels, travel agencies, and tourist transportation companies are at risk, according to the same confederation. Another sector that has experienced a negative impact is transportation; according to the international air transport association (IATA, 2020), the pandemic could trigger losses of around 4.9 million passengers and a shortfall of $728 million in Morocco. Given the fact that the healthcare sector is at front-line or the epicenter of this pandemic, most hospitals, private and public, have witnessed a remarkable increase in demand and even reached their capacity. In the education sector, the Moroccan government announced the closure of schools and universities, leading to the organization of online classes via internet platforms or television channels. To support the financial sector and facilitate access to credit, the Central Bank lowered the key interest rate by 25 basis points, to 2%. For agriculture sector that contributes about 13% of GDP and provides about 38% of national employment, policy-makers revise their strategy to promote and release Green Morocco Plan for 2030 (HCP, 2020). On a similar vein, Morocco has recently introduced a new industrial policy known as the Industrial Acceleration Plan which aims to increase industrial sector competitiveness and diversification. There have also been minor interventions at the governmental and institutional levels aimed at supporting and relaunching the economy (for more details see OECD, 2020 report). The impact of the pandemic has left governments and policymakers counting mounting costs and wondering what recovery could look like. In this context, the design of an efficient policy for recovery and economic relaunch is a high priority and requires taking all economic sectors into consideration.
A salient feature of extreme event problems is the complexity and interdependence of their components. Generally, this complexity arises from the interaction and interdependence of one or several elements with the other elements. This feature is clear from the impact of COVID-19. For example, the tourism sector depends on the transport sector and other resources. Education likewise depends on transport. The result is a complex network with varying dependencies. In an attempt to determine the effect of COVID-19 on the economy, in this study, we focus on seven specific primary economic sectors, as defined by the High Commission for Planning (HCP): (1) industrial, (2) tourism, (3) agriculture, (4) transport, (5) financial, (6) healthcare, and (7) education. According to HCP which is the Moroccan national statistics office, these sectors contribute to more than 90% of national GDP and are linked to each others in several ways (HCP, 2020). After determining the most important specific economic sectors that have been impacted by COVID-19, we proceed with the evaluation process by ascertaining the different aspects of impact. The social, operational, and economic dimensions are the main criteria chosen for measuring the level of this impact. These criteria are generally used to evaluate the performance of any nation economic system and thus allow us to capture the real impact of COVID-19 from different perspectives.
3.3. Modeling
This section applies the XOR-ANP method described in Section 2 to determine the economic sectors most impacted by COVID-19 in Morocco. The main steps of the XOR-ANP model are as follows: define the clusters and elements, incorporate the DM’s preferences (optimistic, pessimistic, and control the consistency preferences), build the XOR comparison matrix, generate priority vectors, construct the supermatrices (unweighted, weighted, and limited) and, finally, obtain the overall ranking. A typical ANP structure is shown in Fig. 3, where the goal of the decision problem is to detect the most impacted sector among seven sectors based on three dimensions or criteria. This means that we will have three clusters: (1) cluster of goal; (2) cluster of alternatives with seven nodes (i.e., agriculture, industrial, transport, tourism, financial, healthcare, and education), and (3) cluster of criteria with three nodes (social, economic, and operational).
Fig. 3.
COVID-19 XOR-ANP diagram.
To proceed with the XOR-ANP technique, the supermatrix should be determined. This means a series of pairwise comparison matrices are required. To fill these matrices, 120 experts from different sectors are interviewed (about 15 experts from each economic sector). These experts occupy highly specialized tasks at ministerial departments. These matrices reflect the evaluation process of each option over another option based on a fundamental scale ranging from 1 to 9 that captures the verbal expressions of experts and DMs. The necessary pairwise comparisons required to fill the supermatrix are: (i) comparisons of the criteria with respect to goals, (ii) criteria with respect to other criteria, (iii) alternatives with respect to each criterion, and (iv) the criteria with respect to the alternatives. First, we start with comparisons of the criteria with respect to the goal. To accomplish this, the following question is asked: “With respect to the goal of selecting the most impacted sector, which criterion is more important in detecting the impact and by how much?” The related pairwise comparison is illustrated in Table 4. The estimated priority vector is used as an input in the goal node block of the supermatrix.
Table 4.
XOR pairwise comparison for the three adopted dimensions.
| Soc. | Social | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1 | 3 |
| Econ. | 1 | 1 | 3XOR4 |
| Oper. | 1/3 | 1/3XOR1/4 | 1 |
| CR = 0 and | |||
Then, we move to the comparison of criteria with respect to the criteria. The main aim to this evaluation is to capture the relative importance of the criteria when another dependent criterion has already been evaluated. To achieve this aim, the following question is asked: “If your goal is to select the most impacted sector and you know that you are evaluating them against social, which other criterion, operational or economic, would be most important and by how much?” The related pairwise comparisons are illustrated in Table 5, Table 6, Table 7. The estimated priority vectors are used as inputs in the criteria cluster blocks of the supermatrix.
Table 5.
XOR pairwise comparison with respect to the social level.
| Social | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1/2 | 1/6 |
| Econ. | 2 | 1 | 1/3 |
| Oper. | 6 | 3 | 1 |
| CR = 0 | |||
Table 6.
XOR pairwise comparison with respect to the economic level.
| Econ. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1 | 1/9 |
| Econ. | 1 | 1 | 1/9 |
| Oper. | 9 | 9 | 1 |
| CR = 0 | |||
Table 7.
XOR pairwise comparison with respect to the operational level.
| Oper. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1 | 3 |
| Econ. | 1 | 1 | 3 |
| Oper. | 1/3 | 1/3 | 1 |
| CR = 0 | |||
Next, we evaluate the pairwise comparisons of alternatives with respect to the criteria. The mechanism for filling these matrices is performed through the following question: “If your goal is to select the most impacted sector, how much is a certain sector impacted over another sector with respect to a particular criterion?” For example, to fill the comparison matrix (see Table 10), the experts are asked to give their estimate about how much more the tourism sector has been impacted than the industrial sector with respect to the social dimension. Due to the high cognitive effort needed to generate the right judgements, a lack of information, and the rapid evolution of the situation, an expert may not be entirely sure of the precise values of his or her judgments. Experts frequently have multiple preferences and are hesitant and irresolute of which to choose; they articulate them using XOR logic. For example, according to available data and reports, the tourism sector may be impacted by 6 XOR 7 times more than the industrial sector, according to the social level. Then, we fill the cell (4, 1) with 6 XOR 7. The same reasoning holds for determining the impact of sectors according to each criterion, and related XOR pairwise comparison matrices are presented in Table 8, Table 9, Table 10. The obtained priority vectors are used as inputs in related blocks of the supermatrix.
Table 10.
XOR pairwise comparison for determining the degree of COVID-19 impact for each sector with respect to the social level.
| Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Educ. | |
|---|---|---|---|---|---|---|---|
| Agri. | 1 | 1/3XOR1/4 | 1/4XOR1/5 XOR1/6 | 1/5 | 1/3 | 1/5 | 1/3 |
| Ind. | 3 XOR 4 | 1 | 1/5 | 1/6 | 3 | 1/4 | 2 |
| Trans. | 4XOR5XOR6 | 5 | 1 | 1/2 | 5 | 3 | 4 |
| Tour. | 5 | 6 | 2 | 1 | 7 | 3XOR4 | 3 |
| Fin. | 3 | 1/3 | 1/5 | 1/7 | 1 | 1/3 | 4 |
| Health. | 5 | 4 | 1/3 | 1/3XOR1/4 | 3 | 1 | 3 |
| Edu. | 3 | 1/2 | 1/4 | 1/3 | 1/4 | 1/3 | 1 |
| CR = 0.0159 and | |||||||
Table 8.
XOR pairwise comparison for determining the degree of COVID-19 impact for each sector with respect to the economic level.
| Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Educ. | |
|---|---|---|---|---|---|---|---|
| Agr. | 1 | 1/4 | 1/5 | 1/6 XOR1/7 | 1/3 | 1 | 1/2 |
| Ind. | 4 | 1 | 1/3 | 1/5 | 3 | 5 | 4 |
| Trans. | 5 | 3 | 1 | 1/3 | 4 | 6 | 5 |
| Tour. | 6 XOR7 | 5 | 3 | 1 | 4XOR5 | 6XOR7 | 7 |
| Fin. | 3 | 1/3 | 1/4 | 1/4XOR1/5 | 1 | 4 | 4 |
| Health. | 1 | 1/5 | 1/6 | 1/6XOR1/7 | 1/4 | 1 | 1 |
| Educ. | 2 | 1/4 | 1/5 | 1/7 | 1/4 | 1 | 1 |
| CR = 0.0115 and | |||||||
Table 9.
XOR pairwise comparison for determining the degree of COVID-19 impact for each sector with respect to the operational level.
| Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Educ. | |
|---|---|---|---|---|---|---|---|
| Agri. | 1 | 1/5 | 1/6 | 1/7 | 1/4 | 1/7 XOR1/8 | 1/4 |
| Ind. | 5 | 1 | 1/5 | 1/6 | 1/3 | 1/6 | 1/5 |
| Trans. | 6 | 5 | 1 | 1/2 | 6 | 1/3 | 4 |
| Tour. | 7 | 6 | 2 | 1 | 4 | 1/2 XOR1/3 | 5 |
| Fin. | 4 | 3 | 1/6 | 1/4 | 1 | 1/6 | 1/4 |
| Health. | 7XOR8 | 6 | 3 | 2XOR3 | 6 | 1 | 6 |
| Educ. | 4 | 5 | 1/4 | 1/5 | 4 | 1/6 | 1 |
| CR = 0.0089 and | |||||||
One of the main challenges in the evaluation process is the high uncertainty existing in the problem. This uncertainty produces a complex state of contradiction between optimism and pessimism. The rapidly changing situation and the amount of information being received creates optimistic and pessimistic views. Over the past few months, much information has supported our hopes and occasionally verified our fears. For example, are we optimistic or pessimistic about recovering quickly from the impact of COVID-19? Optimism and pessimism refer to positive and negative future expectations, respectively (Hocine & Kouaissah, 2020). These positive or negative expectations affect the evaluation process of experts in evaluating the impact of COVID-19 on a certain sector with respect to another sector. For example, say an expert is asked to provide his estimation of the impact of COVID-19 on the transport sector over the agriculture sector with respect the social dimension and responds with 4 XOR 5 XOR 6; however, he also notes that, according to the available data, indicators, and reports, the pessimism state is high and the expected impact is deeper in the transportation sector and may reach level 6. The related pairwise comparisons are reported in Table 11.
Table 11.
XOR pairwise comparison for each criterion with respect to the agriculture sector.
| Agri. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 6 | 6 |
| Econ. | 1/6 | 1 | 1 |
| Oper. | 1/6 | 1 | 1 |
| CR = 0 | |||
Finally, to finish filling the supermatrix, the pairwise comparisons of criteria with respect to the alternatives are required. These comparisons capture the relative importance of the alternatives when another dependent alternative is already known. The mechanism for filling these matrices is performed through the following question: “If your goal is to select the most impacted sector and you know that the agriculture sector is also in the evaluation cluster, which other sectors are the most impacted?” The related pairwise comparisons are reported in Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17. The obtained priority vectors will be used as inputs in related blocks of the supermatrix.
Table 12.
XOR pairwise comparison for each criterion with respect to the industrial sector.
| Ind. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1 | 1/5 |
| Econ. | 1 | 1 | 1/5 |
| Oper. | 5 | 5 | 1 |
| CR = 0 | |||
Table 13.
XOR pairwise comparison for each criterion with respect to the transport sector.
| Trans. | Soc. | Econ. | Operat. |
|---|---|---|---|
| Soc. | 1 | 2 | 1/4 |
| Econ. | 1/2 | 1 | 1/4 |
| Oper. | 4 | 4 | 1 |
| CR = 0.0281 | |||
Table 14.
XOR pairwise comparison for each criterion with respect to the tourism sector.
| Tour. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1/6 | 1/2 |
| Econ. | 6 | 1 | 3 |
| Oper. | 2 | 1/3 | 1 |
| CR = 0 | |||
Table 15.
XOR pairwise comparison for each criterion with respect to the financial sector.
| Fin. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 1/8 | 1/2 |
| Econ. | 8 | 1 | 4 |
| Oper. | 2 | 1/4 | 1 |
| CR = 0 | |||
Table 16.
XOR pairwise comparison for each criterion with respect to the healthcare sector.
| Health. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 6 | 6 |
| Econ. | 1/6 | 1 | 1 |
| Oper. | 1/6 | 1 | 1 |
| CR = 0 | |||
Table 17.
XOR pairwise comparison for each criterion with respect to the education sector.
| Educ. | Soc. | Econ. | Oper. |
|---|---|---|---|
| Soc. | 1 | 9 | 3 |
| Econ. | 1/9 | 1 | 1/6 |
| Oper. | 1/3 | 6 | 1 |
| CR = 0.0056 | |||
After acquiring data, the XOR-W technique is used to derive the necessary priority vectors for all pairwise comparisons. Using the software Lingo (Schrage, 2015),1 the objectives function, CR, and binary variables, are reported for each pairwise comparison (see Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18). We noticed that the results of CR were very consistent. Based on the binary variable set, the XOR function output for each judgment is as follows: , , , , , , , , and . The XOR function of the Agriculture/Transport comparison clearly produced its minimum value, meaning that the DM’s pessimistic situation was achieved. Then, a supermatrix is constructed using the obtained priority vectors for the previous pairwise comparisons, as shown in Table 18.
Table 18.
Unweighted supermatrix.
| Goal | Soc. | Econ. | Oper. | Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Edu. | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Soc. | 0.4286 | 0.1111 | 0.0909 | 0.4286 | 0.7500 | 0.1429 | 0.2069 | 0.1111 | 0.0909 | 0.3273 | 0.6743 |
| Econ. | 0.4286 | 0.2222 | 0.0909 | 0.4286 | 0.1250 | 0.1428 | 0.1494 | 0.6667 | 0.7273 | 0.0909 | 0.0716 |
| Oper. | 0.1428 | 0.6667 | 0.8182 | 0.1428 | 0.1250 | 0.7143 | 0.6437 | 0.2222 | 0.1818 | 0.5818 | 0.2541 |
| Agri. | 0.0000 | 0.0857 | 0.0691 | 0.0512 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Ind. | 0.0000 | 0.0923 | 0.1056 | 0.0557 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Trans. | 0.0000 | 0.2127 | 0.1877 | 0.1536 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tour. | 0.0000 | 0.3062 | 0.4342 | 0.2272 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Fin. | 0.0000 | 0.0904 | 0.0782 | 0.0596 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Health. | 0.0000 | 0.1305 | 0.0626 | 0.3743 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Edu. | 0.0000 | 0.0822 | 0.0626 | 0.0784 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Next, the weighted supermatrix is obtained by ensuring all columns sum up to unity, as shown in Table 19. These calculations must be done for every column to obtain the normalized supermatrix (or so-called a stochastic matrix). Finally, the limited super matrix can be calculated in order to select and rank the most impacted sector. The limited supermatrix is obtained by raising it to the th power until the columns stabilize and become identical in each block. The limiting power of the supermatrix is reached at the 15th stage (see Table 20).
Table 19.
Weighted supermatrix (also called a stochastic matrix).
| Goal | Soc. | Econ. | Oper. | Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Edu. | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Soc. | 0.4286 | 0.0555 | 0.0455 | 0.2143 | 0.7500 | 0.1429 | 0.2069 | 0.1111 | 0.0909 | 0.3273 | 0.6743 |
| Econ. | 0.4286 | 0.1111 | 0.0455 | 0.2143 | 0.1250 | 0.1428 | 0.1494 | 0.6667 | 0.7273 | 0.0909 | 0.0716 |
| Oper. | 0.1428 | 0.3333 | 0.4091 | 0.0714 | 0.1250 | 0.7143 | 0.6437 | 0.2222 | 0.1818 | 0.5818 | 0.2541 |
| Agri. | 0.0000 | 0.0428 | 0.0345 | 0.0255 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Ind. | 0.0000 | 0.0462 | 0.0528 | 0.0279 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Trans. | 0.0000 | 0.1064 | 0.0938 | 0.0768 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Tour. | 0.0000 | 0.1531 | 0.2171 | 0.1136 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Fin. | 0.0000 | 0.0452 | 0.0391 | 0.0298 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Health. | 0.0000 | 0.0653 | 0.0313 | 0.1872 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Edu. | 0.0000 | 0.0411 | 0.0313 | 0.0392 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Table 20.
Limit supermatrix.
| Goal | Soc. | Econ. | Oper. | Agri. | Ind. | Trans. | Tour. | Fin. | Health. | Edu. | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Goal | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| Soc. | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 | 0.1688 |
| Econ. | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 | 0.2018 |
| Oper. | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 | 0.2961 |
| Agri. | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 | 0.0218 |
| Ind. | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 | 0.0267 |
| Trans. | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 | 0.0596 |
| Tour. | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 | 0.1033 |
| Fin. | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 | 0.0243 |
| Health. | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 | 0.0727 |
| Edu. | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 | 0.0249 |
3.4. Results, discussion, and comparison
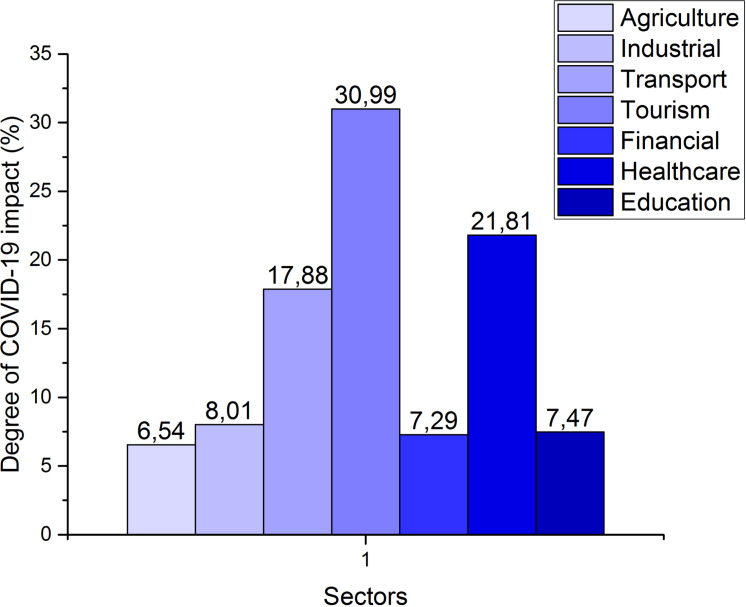
One of the key objectives of this study is to assess the impact of the COVID-19 pandemic on Moroccan performance at the social, economic, and operational levels, sector by sector. This information could be extremely useful to policymakers in terms of prioritizing impacted sectors for intervention and funding, thus contributing to the well-being of the Moroccan region. According to the obtained results, especially Fig. 4, Fig. 5, the tourism, healthcare, and transport sectors were the most impacted by COVID-19, with 30.99%, 21.81%, and 17.88% respectively. These results indicate that the third and the eighth sustainable development goals (SDG) of the United Nations (UN) agenda for 2030, “Healthy Lives” and “Decent Work”, have strongly impacted Morocco due to the pandemic crisis. These three sectors have a deep effect on the social, operational, and economic levels, where it is clear that the operational level has received the highest impact of 44.41%. This reflects the vital role that these sectors play in the Moroccan economy. The high impact observed on the operational level is essentially due to the direct role of the healthcare sector in fighting against the pandemic. For instance, Moroccan private health sector has not had a great response while public health system has borne most of the expenses. We can also observe that the financial, education, industrial, and agriculture sectors have received relatively less impact from COVID-19, with 7.29%, 7.47%, 8.01%, and 6.54% respectively. This could be explained by the fact that these sectors are in the second line in fighting against the pandemic.
Fig. 4.
Global sectorial impact of COVID-19.
Fig. 5.
The local dimensions impact of COVID-19.
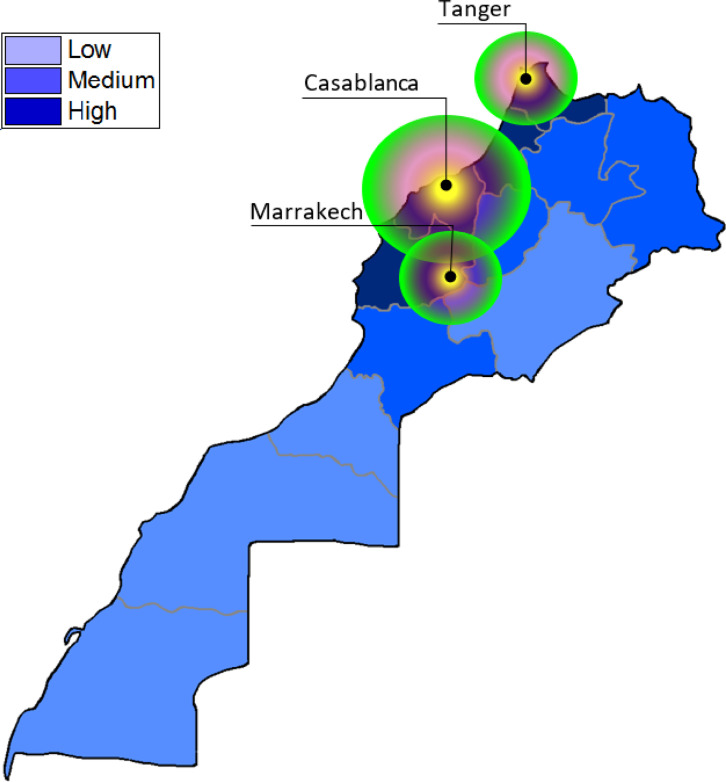
Fig. 6 depicts how the COVID-19 pandemic quickly took on a regional dimension, which was expressed not only in the contagion’s geography but also in the government’s response to contain the side effect of the pandemic. The three most impacted regions not only conglomerate Moroccan population but also concentrate most Moroccan economic activities. Furthermore, Fig. 6 can be used as a visual tool to link the spatial Moroccan impact from the global to regional or local perspectives. For instance, it shows how Moroccan cities like Casablanca and Tanger have suffered economically as a result of their high population density. Despite the fact that Casablanca region was the epicenter of the health crisis, Marrakech region has paid the highest economic and social price for the lockdown steps due to its high dependency to tourism activities. Current unemployment figure estimates for 2020 show the Casablanca region set to lose around 4.3% of its jobs, while Marrakech region is projected to lose approximately 6%. This would not only be an economic disaster, also risks destabilizing fragile social conditions in many Moroccan regions.
Fig. 6.
Spatial Moroccan impact of COVID-19.
The usefulness of this study is to determine the sectorial impact levels of the pandemic and the implications for social, economic, and operational performance. This could be of great help to policymakers looking to prioritize the most impacted sectors in terms of intervention and financing. The design of new policies for recovery, economic growth, and support of the SDGs is key to emergence from this critical state. First, we need to develop innovative methods to collect and filter data. Data management in times of crisis has tremendous importance for informing and supporting policymakers. However, the lack of data and information available during the pandemic in Morocco makes it more difficult to assess the impact. After obtaining the necessary data and information, we need to analyze and understand the impact of the crisis on the various sectors and design economic and social policies in response. For example, due to the high correlation between the transport and tourism industry, governments and industry have to focus their efforts on lifting travel restrictions, applying new health protocols for safe travel, restoring traveler confidence, and stimulating demand with new safety and cleanliness labels for the sector. In this regard, tourist information applications and domestic tourism promotion initiatives can be beneficial. Once borders start reopening, the tourism industry will start to recover and the government must support it by preparing short and long-term tourism recovery plans, rebuilding destinations, and rethinking the tourism sector. This may both assist in the sector’s recovery and strengthen it in the long term, particularly in regions and cities where the sector supports many jobs and businesses. Investing in transportation infrastructure is crucial for economic recovery and job creation. The government must strike a balance between building a more connected urban network between the north and south regions. This is especially beneficial for the healthcare sector to avoid major bottlenecks and for a successful vaccination campaign against COVID-19. For the industry sector, the government has to provide quick financial support to small and medium enterprises in terms of direct capital injections or subsidiaries such as loans, taxes relief, and promoting new investments. Since the agriculture sector has been slightly impacted by this pandemic and its contribution to Moroccan GDP, it has an outsized impact on the overall economic growth. In this scenario, the adoption of technology-enabled systems seems to be quite ambitious for making the agriculture sector more resilient and responsive to COVID-19 consequences. While for the education sector, the government is urged to intensify e-learning methods, develop new platforms, increase school’s infrastructure, and implement learning recovery programs. Moreover, investing in private and other public sectors and services during and after the crisis is also a good strategy for long-term and sustainable recovery.
Finally, following our discussion in Section 2, we compare under certain assumptions our results against the XOR-AHP, interval ANP, and fuzzy ANP techniques that share certain theoretical similarities with our model. It can be argued that each method has benefits and drawbacks, and none consistently outperforms the others in all situations. Although the primary goal of this paper is not to conduct a comparative study between the uncertain AHP/ANP techniques, however, having an overview of the diverse output solutions of these techniques is always beneficial to the DMs and readers. Performing a feasible and fair comparison is a difficult task due to the mathematical structure, pre-assumptions, and optimization process of each technique. Thus, the following assumptions have been adopted. For interval ANP, the upper and lower values of each interval evaluation are the min and max values of each XOR evaluation. The triangular membership function is considered for fuzzy ANP (see, Mikhailov, 2004). It is worth noting that the selected interval ANP and fuzzy ANP techniques are typically mathematical programming-based methods. In this context, Mikhailov’s (Mikhailov, 2004) and Wang and Chin’s (Wang & Chin, 2011) models have been chosen to derive the priority vectors from interval ANP and fuzzy ANP respectively. Under these assumptions and using Lingo (Schrage, 2015), the obtained solutions are reported in Table 21 and plotted in Fig. 7, Fig. 8.
Fig. 7.
The local dimensions impact of COVID-19 obtained from different techniques.
Fig. 8.
Global sectorial impact of COVID-19 obtained from different techniques.
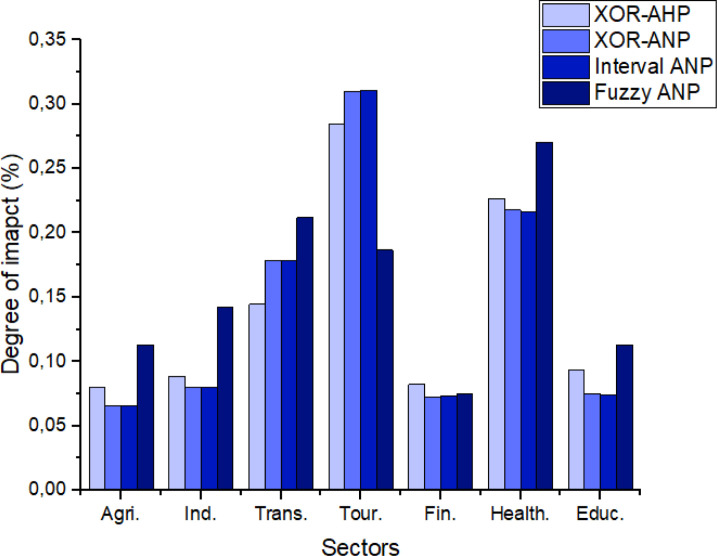
From these results, we observe that the solutions obtained from the XOR-AHP technique are very different from those produced by the XOR-ANP, interval ANP, and fuzzy ANP methods. This is mainly because of causality between decision elements (criteria and sectors) in pairwise comparison matrices (see Fig. 7). Moreover, we observe that the solutions generated by the XOR-AHP, XOR-ANP, and interval ANP are generally homogeneous with slight differences in the degree of impact. This is typically due to the similarity between the mathematical programming of these techniques. For the degree of impact, we observe many changesets, especially for fuzzy ANP. For example, the health sector has received the highest impact followed by transport and tourism with 27.06%, 21.18%, and 18.68% respectively (see Table 21 and Fig. 8). These results could be explained by the structure of the membership function in transforming the judgment into a crisp weight. We conclude that these benchmarking techniques, based on different assumptions, require different information for their applications and, thus, normally yield slightly different results than the proposed method.
Table 21.
Global sectorial impact of COVID-19 obtained from different techniques.
| Decision problem | Models |
|||
|---|---|---|---|---|
| XOR-AHP | XOR-ANP | Interval ANP | Fuzzy ANP | |
| Soc. | 42.86% | 25.32% | 25,54% | 28,57% |
| Econ. | 42.86% | 30.27% | 30,54% | 26,50% |
| Oper. | 14.29% | 44.14% | 43,93% | 44,93% |
| Agri. | 8.00% | 6.54% | 6,58% | 11,31% |
| Ind. | 8.86% | 8.01% | 8,02% | 14,27% |
| Trans. | 14.45% | 17.88% | 17,89% | 21,18% |
| Tour. | 28.47% | 30.99% | 31,07% | 18,68% |
| Fin. | 8.26% | 7.29% | 7,31% | 7,50% |
| Health. | 22.64% | 21.81% | 21,67% | 27,06% |
| Educ. | 9.34% | 7.47% | 7,45% | 11,31% |
4. Conclusion
COVID-19 has been the matter of the moment from the day it was declared a pandemic, it has led to the termination of economic activities globally. Scientists and policymakers across continents are joining forces for innovative tie-ups in response: pharmaceutical giants and medical start-ups are working together to develop efficient vaccines and policymakers in all countries are setting policies to relaunch the economy. Morocco has taken a good path in fighting against the COVID-19 pandemic. Despite the ongoing efforts, many questions remain unanswered. What is the right policy to relaunch the economy? The process of economic recovery is complex, with many stages. The most interesting question that arises: what sectors have been most impacted by COVID-19 and require priority in intervention from the central government? This is the main motivation behind this study. However, due to the lack of information and a high level of uncertainty, decision support becomes very challenging and requires more advanced techniques. In this study, first, we develop a new technique for dealing with uncertainty and complexity called XOR-ANP. The main benefit to using this technique is its ability to deal with uncertainty stemming from hesitation or reluctance and the flexibility to incorporate the DM’s preferences by using three types of XOR matrices: optimistic, pessimistic, and neutral. Moreover, to contribute to the COVID-19 literature from an operational research perspective, the developed XOR-ANP technique is adopted to determine the economic sectors most impacted by COVID-19 to assist policymakers in mitigating the impact of the pandemic and prioritizing their interventions to relaunch the Moroccan economy. The results show that tourism and transport are the most impacted sectors, followed by healthcare. Based on these results, the government needs to give high priority to these sectors by helping them to overcome the present crisis. Finally, since the COVID-19 pandemic has affected the entire globe, we can simulate the proposed study on other countries, such as Italy and Algeria, to see which sectors have been the most impacted there and helps to learn the main reasons why certain countries may respond better than others. The proposed XOR-ANP model can also be easily applied to a variety of different research fields, such as renewable energy, banking and portfolio selection, and healthcare planning.
CRediT authorship contribution statement
Amin Hocine: Conceptualization, Methodology, Software, Data curation, Writing – original draft. Noureddine Kouaissah: Conceptualization, Methodology, Software, Data curation, Writing – original draft, Reviewing and editing. Sergio Ortobelli Lozza: Conceptualization, Methodology, Formal analysis, Validation, Reviewing and editing.
Footnotes
Lingo codes are available on the following GitHub repository: https://github.com/XOR-ANP-CAIE/XOR-ANP.
Data availability
No data was used for the research described in the article.
References
- Aguaron J., Escobar M.T., Moreno-Jiménez J.M. Reducing inconsistency measured by the geometric consistency index in the analytic hierarchy process. European Journal of Operational Research. 2021;288(2):576–583. [Google Scholar]
- Albeverio S., Jentsch V., Kantz H. The frontiers collection. Springer; 2010. Extreme events in nature and society. Softcover reprint of hardcover 1st ed. 2006 ed. [Google Scholar]
- Arthi V., Parman J. Disease, downturns, and wellbeing: Economic history and the long-run impacts of COVID-19. Explorations in Economic History. 2020 doi: 10.1016/j.eeh.2020.101381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayyub B.M. 1st ed. CRC Press; 2001. Elicitation of expert opinions for uncertainty and risks. [Google Scholar]
- Benstock D., Cegla F. Extreme value analysis (EVA) of inspection data and its uncertainties. NDT & E International. 2017;87:68–77. [Google Scholar]
- Our World in Data . 2020. Covid-19 (CSSE) at johns hopkins universit. https://ourworldindata.org/covid-cases. (Last Accessed April 2021) [Google Scholar]
- Gupta S., Starr M.K., Zanjirani Farahani R., Asgari N. Pandemics/epidemics: Challenges and opportunities for operations management research. Manufacturing and Service Operations Management. 2020:1523–4614. [Google Scholar]
- Harker P.T., Vargas L.G. The theory of ratio scale estimation: Saaty’s analytic hierarchy process. Management Science. 1987;33(11):1383–1403. [Google Scholar]
- Ho W., Ma X. The state-of-the-art integrations and applications of the analytic hierarchy process. European Journal of Operational Research. 2018;267(2):399–414. [Google Scholar]
- Hocine A., Kouaissah N. XOR analytic hierarchy process and its application in the renewable energy sector. Omega. 2020;97 [Google Scholar]
- IATA (International Air Transport Association) 2020. Updates COVID-19 financial impacts-relief measures needed. IATA. https://www.iata.org/en/pressroom/pr/2020-03-05-01/. (Last Accessed March 2021) [Google Scholar]
- Ishizaka A., Nemery P. 1st ed. Wiley; 2013. Multi-criteria decision analysis: methods and software. [Google Scholar]
- Ishizaka A., Pearman C., Nemery P. AHPSort: An AHP-based method for sorting problems. International Journal of Production Research. 2012;50(17):4767–4784. [Google Scholar]
- Keeney S., McKenna H., Hasson F. 1st ed. Wiley-Blackwell; 2011. He Delphi technique in nursing and health research. [Google Scholar]
- Kirkwood C.W. Estimating the impact of uncertainty on a deterministic multiattribute evaluation. Management Science. 1992;38(6):819–826. [Google Scholar]
- Kouaissah N., Hocine A. Vol. 207. 2022. XOR data envelopment analysis and its application to renewable energy sector. (Expert systems with applications). [DOI] [Google Scholar]
- May J.H., Shang J., Tjader Y.C., Vargas L.G. A new methodology for sensitivity and stability analysis of analytic network models. European Journal of Operational Research. 2013;224(1):180–188. [Google Scholar]
- Mikhailov L. A fuzzy approach to deriving priorities from interval pairwise comparison judgements. European Journal of Operational Research. 2004;159(3):687–704. [Google Scholar]
- Mu E., Cooper O., Peasley M. Best practices in analytic network process studies. Expert Systems with Applications. 2020;159 [Google Scholar]
- OECD . 2020. The COVID-19 crisi in Morocco. https://www.oecd.org/mena/competitiveness/The-Covid-19-Crisis-in-Morocco.pdf. [Google Scholar]
- Peckham R. COVID-19 and the anti-lessons of history. The Lancet. 2020;395(10227):850–852. doi: 10.1016/S0140-6736(20)30468-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HCP (High Commission for Planning) 2020. Hcp publications. https://www.hcp.ma/downloads/. (Last Accessed March 2021) [Google Scholar]
- Rezaei J. Best-worst multi-criteria decision-making method. Omega. 2015;53:49–57. [Google Scholar]
- Rezaei J., Ortt R. Multi-criteria supplier segmentation using a fuzzy preference relations based AHP. European Journal of Operational Research. 2013;225(1):75–84. [Google Scholar]
- Saaty T.L. 2nd ed. Rws Pubns; 2001. The analytic network process: Decision making with dependence and feedback. [Google Scholar]
- Saaty T.L. Rank from comparisons and from ratings in the analytic hierarchy/network processes. European Journal of Operational Research. 2006;168(2):557–570. [Google Scholar]
- Saaty T.L., Vargas L.G. Uncertainty and rank order in the analytic hierarchy process. European Journal of Operational Research. 1987;32(1):107–117. [Google Scholar]
- Saaty T.L., Vargas L.G. 2nd ed. Springer; 2013. Decision making with the analytic network process: Economic, political, social and technological applications with benefits, opportunities, costs and … research & management science (195) 2013 ed. [Google Scholar]
- Salo A.A., Hämäläinen R.P. Preference programming through approximate ratio comparisons. European Journal of Operational Research. 1995;82(3):458–475. [Google Scholar]
- Schrage L. Lindo Systems Inc; Chicago: 2015. Optimization modeling with LINGO. [Google Scholar]
- Van Laarhoven P.J.M., Pedrycz W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets and Systems. 1983;11(1–3):229–241. [Google Scholar]
- Wang Y.M., Chin K.S. Fuzzy analytic hierarchy process: A logarithmic fuzzy preference programming methodology. International Journal of Approximate Reasoning. 2011;52(4):541–553. [Google Scholar]
- Werner C., Bedford T., Cooke R.M., Hanea A.M., Morales-Nápoles O. Expert judgement for dependence in probabilistic modelling: A systematic literature review and future research directions. European Journal of Operational Research. 2017;258(3):801–819. [Google Scholar]
- WHO . 2020. WHO director-general’s opening remarks at the media briefing on COVID - 11 March. https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-mediabriefing-on-covid-19. (Accessed 18 December 2020) [Google Scholar]
- World Bank . 2020. The World Bank in Morocco. https://www.worldbank.org/en/country/morocco/overview. (Last Accessed April 2021) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.