A methodology to design, develop, and evaluate machine learning models for predicting dropout in school systems: the case of Chile

Abstract

School dropout is a structural problem which permanently penalizes students and society in areas such as low qualification jobs, higher poverty levels and lower life expectancy, lower pensions, and higher economic burden for governments. Given these high consequences and the surge of the problem due to COVID-19 pandemic, in this paper we propose a methodology to design, develop, and evaluate a machine learning model for predicting dropout in school systems. In this methodology, we introduce necessary steps to develop a robust model to estimate the individual risk of each student to drop out of school. As advancement from previous research, this proposal focuses on analyzing individual trajectories of students, incorporating the student situation at school, family, among other levels, changes, and accumulation of events to predict dropout. Following the methodology, we create a model for the Chilean case based on data available mostly through administrative data from the educational system, and according to known factors associated with school dropout. Our results are better than those from previous research with a relevant sample size, with a predictive capability 20% higher for the actual dropout cases. Also, in contrast to previous work, the including non-individual dimensions results in a substantive contribution to the prediction of leaving school. We also illustrate applications of the model for Chilean case to support public policy decision making such as profiling schools for qualitative studies of pedagogic practices, profiling students’ dropout trajectories and simulating scenarios.

Introduction

School failure has a central place in educational systems due to its enduring effects on students. This happens when the school system fails to ensure that students reach certain levels of schooling, experiencing grade repetition and temporary or definitive dropout from school (OECD, 2020). This results in adults with low qualifications or students who do not complete their schooling at the secondary level.

School failure has moved from a vision that sees school dropout as a problem associated with the students’ —attributing responsibility to them— to one that understands it as an expression of a systemic problem where school system and society are also responsible (OECD, 2010).

Impact of school failure and its impact on students

As evidence states, school dropout permanently penalizes students and the whole society in aspects such as:

• Low qualification jobs, lower skills to face the labor world and lower productivity (Gil et al., 2019; Lee-St John et al., 2018; Sahin et al., 2016) and higher unemployment (Lee-St John et al., 2018; Sahin et al., 2016).

• Lower income (Lee-St John et al., 2018), higher poverty level and lower life expectancy (Sahin et al., 2016),

• Lower pensions (Dussaillant, 2017) and higher economic burden to the State for social protection concepts (Höfter, 2006; Levin et al., 2012).

• Higher crime rates (Lee-St John et al., 2018; Sahin et al., 2016), lower social cohesion and citizen participation (Sahin et al., 2016).

• Lower economic growth and − in social terms − lower tax payments (Gil et al., 2019; Lee-St John et al., 2018).

Dropping out in the world

School failure is a structural problem in most societies. In OECD, the average percentage of adults between 25 and 64 years old whose maximum level of education is lower secondary OECD is 27% and Chile is slightly above with 35%. However, many other countries such as Colombia, Mexico, and Spain report higher dropout rates (OECD, 2020), as shown in Fig. 1.

Fig. 1.

Lower secondary as higher level attained for 25–64-year-old adults, showing differences by gender. Own elaboration based on OECD (2020) data

Additionally, due to COVID-19 pandemic, about 24 million learners, from pre-primary to university level, are at risk of not returning to school following the education disruption (UNESCO, 2020). For this, societies must address proactively all the drivers of educational exclusion to strengthen the resilience of education systems in the face of this crisis (UNESCO, 2020).

Risk factors for school dropout

The causes of dropout are associated with the students, their family, the school, educational system, and elements of the context or social environment where they are (Boniolo & Najmias, 2018; Weybright et al., 2017). Since this is a gradual and cumulative process, some indicators warn of this disengagement risk even from early in the school trajectory (Boniolo & Najmias, 2018). We can classify these risk factors at:

• Individual level: such as school repetition and overage (Boniolo & Najmias, 2018; Hirakawa & Taniguchi, 2021), school attendance (Hirakawa & Taniguchi, 2021; Sahin et al., 2016), academic performance (Hirakawa & Taniguchi, 2021) and specific learning needs (Gil et al., 2019). Socioemotional factors are also included, like attitudes towards learning (Hirakawa & Taniguchi, 2021; Sahin et al., 2016; Zaff et al., 2017), non-academic problematic behaviors (Weybright et al., 2017) and school mobility (Sahin et al., 2016). As well as sociodemographic factors, such as gender, ethnicity, and nationality (Hirakawa & Taniguchi, 2021; Lee-St John et al., 2018).

• Family level: such as socioeconomic status and parental involvement (Adelman et al., 2018; Boniolo & Najmias, 2018; Lee-St John et al., 2018; Sahin et al., 2016).

• School level: its characteristics, socioeconomic and sociocultural composition (Hirakawa & Taniguchi, 2021), its resources (Dussaillant, 2017; Ecker-Lyster & Niileksela, 2016), the relationship between students and teachers (Gil et al., 2019) and participation in school activities (Gil et al., 2019).

• Extra-school level considers community factors, e.g., the geographic location of residences, families and the condition of their housing, access to playgrounds, green areas, or “urbanity” (Zaff et al., 2017), having a network of high-achieving and aspirational peers (Hirakawa & Taniguchi, 2021). And it also includes contextual factors, understood as potential “pull factors” that incentivize early job attachment (Kattan & Székely, 2017).

Predictive models for school dropout based on machine learning

Machine Learning is a discipline that employs algorithms to automate tasks like classification and regression. Algorithms learn from known datasets (training sample) to estimate the true value of a target variable using predictor variables. To evaluate the performance of these results, they are contrasted with the real values in out-of- sample data (test or validation sample) (Sorensen, 2019).

A meta-analysis on academic literature and case studies on machine learning applications to predict dropout between 2013 and 2017 found that algorithms such as neural networks or decision trees are mainly used for the dropout prediction as a binary classification exercise on the dropout/non-dropout dichotomy (Mduma et al., 2019).

For predicting school dropout, researchers chose algorithms from the family of decision trees such as CART (Jena & Dehuri, 2020), and decision trees ensembles (Bentéjac et al., 2021). Sorensen (2019) elaborated a decision tree model to estimate, considering records in students’ last year of primary education, dropout in the secondary level predicting 63.3% of actual dropout cases using only academic and individual factors.

Similar dropout prediction models have been used to develop Early Warning Systems (EWS). These systems allow decision makers to identify in time students at risk of dropping out, to react to this notification and, eventually, to help potential dropouts to continue with their learning processes at different levels (Lee & Chung, 2019).

The main difficulty in large-scale dropout prediction is related to the severe imbalance of the phenomenon (Lee & Chung, 2019). Therefore, it is necessary to apply corrections, choosing an adequate model performance evaluation metrics and selecting a machine learning algorithm whose flexibility allows overfitting reduction (Lee & Chung, 2019; Sansone, 2019).

Purpose and structure of this article

Given the high consequences and impact of school dropout and the surge of the problem due the school closure during COVID pandemic (Khan & Ahmed, 2021; Pereira de Souza et al., 2020), our objective is to develop a methodology to design, develop, and evaluate a machine learning model for predicting dropout in school system. The aim of this methodology is supporting and guiding models’ development by practitioners and policy makers, − specially from Latin American and African countries (UNESCO, 2020) where the student dropout is higher than other regions − to implement national or subnational Early Warning Systems (EWS) to identify student with higher risk of abandoning their studies.

This methodology produces necessary steps to develop a robust model to estimate the individual risk of each student to drop out of school, generating applications to support public policy decision making. As advancement from previous research, this proposal focuses on analyzing individual trajectories of students, incorporating the student situation at multiple levels (school, family, among others), and changes and accumulation of events to predict dropout. In this way, we shift the computational from the machine learning model to the trajectories’ calculation, what is, a one-time development comparing to multiple trainings of models. Since machine learning model are less transparent (Sorensen, 2019) in this paper we provide a reliable option to explain results and how they depend on the context.

We develop a model for the Chilean educational system to illustrate a practical case, which is relevant for three reasons. First, reduction of school dropout has been a policy for the last decade; second, data quality permits sophisticated analysis for machine learning approach; and finally, Chile is a medium income country, therefore this experience could be useful for similar countries or others with less development level.

This paper is structured as follows. In Section 2, we present the methodology defining the dimensions of robustness and describing every step to develop a predictive model. In Section 3, we address the model development for the Chilean education system presenting the main results. In Section 4, we present public policy applications, to end discussing the implications of this methodology in Section 5.

A methodology for predicting school dropout using machine learning

The aim of this methodology is to produce a robust model to estimate the individual student risk for dropping out of school, to answer the research question stated in Section 1.5. A robust model is one which fulfill the following criteria (Studer et al., 2021):

• Has good general performance in the chosen metrics, allowing practical use in the context of application.

• Is stable: the performance doesn’t depend on assumptions, imputed data, creation of training and test samples and has good general avoiding under and overfitting.

• Is computational effective: has reasonable computational times for training and prediction, depending on the context of application.

• Is easy to maintain, requiring the minimum variables to predict results, allowing to obtain data, and creating every case straightforward for training and predicting purposes.

• Its explanations are consistent with the dominion of the model. The variables’ importance and its variance explanations are consistent with literature about the topic.

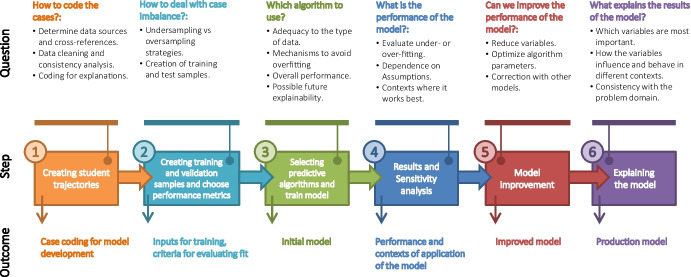
The methodology comprises the following steps, as they are shown in Fig. 2.

Fig. 2.

Steps of the proposed methodology for design, development and evaluating a machine learning model for predicting dropout. Each step answers specific questions about model robustness and produces an outcome for the next phase

In the following subsections, we will describe every step.

Step 1: Creating student trajectories

We define as the objective of the model to predict the first time where students leave their school (regular dropout) to avoid consequences stated in Section 1.1. Therefore, every case should be codified to train the algorithm. Contemplating the risk factors identified previously (Section 1.3), we propose to codify each student’s history in the school system through a continuous range of years in a single vector of data. This is because each trajectory comprises the student situation at multiple levels (school, family, among others), and changes and accumulation of events are relevant to predict dropout (Kattan & Székely, 2017). Thus, we can identify clearly both dropping out and protective factors throughout the educational cycle after 12 years.

Every case should be labeled as dropout (1, positive class) or not (0, negative class) to use binary classification. Since we can verify in the data if they in a given year ($i$) are not enrolled in any school in the next year ($i+1$). In that case, we label that student as a dropout in year $i$.

Several datasets should be considered to incorporate dropout factors at individual, family, school, and extra school levels. This will facilitate an explanation of the model in step 6. How many variables associated with these factors will depend on the availability and reliability of data in the school system, being the most important challenge to face in the first place.

To reduce errors, data should be carefully cleaned. If there are several sources of data, we should perform several consistency analyses to ensure reliability of data: e.g., consistency of date of birth, sex, enrollment in schools in each year through the period analyzed. If there is some data that cannot be found, and we need to impute it (e.g., results of surveys of income and education of parents to create a socioeconomic status), we need to analyze the impact of chosen imputation methods on results in step 4.

Step 2: Creating training and test samples and choose performance metrics

For this kind of problems were there are a temporal prediction, we will not use a traditional sample construction which divide all the cases in a proportion such as 80% for training and 20% for testing. In this instance, we have dropouts until year $t$, and we need to predict if a given students will leave school at year $t+1$. Therefore, the sample and testing samples will follow the same logic (Sorensen, 2019).

Dropping out is a phenomenon naturally imbalanced since significantly fewer students abandon school than graduate. Thus, specific solutions for training unbalanced data should be used (Mduma et al., 2019). Two options to deal with the imbalance are undersampling the majority class (non-dropouts) or oversampling the minority class (dropouts).

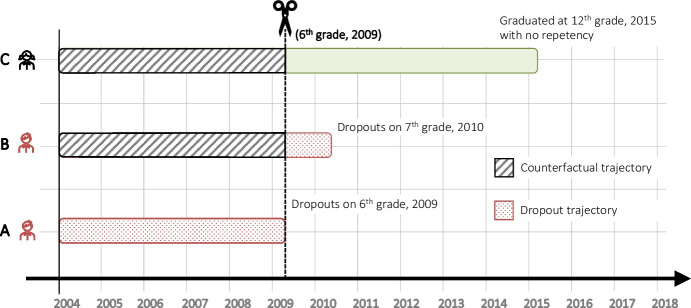
Since each case codifies a student trajectory, we propose to create the training and test samples as follows. To include in the training sample cases to compare the variables from trajectories that lead to regular dropouts with those that don’t, we create a set of counterfactual trajectories for each student who drops out. For each student who drops out in a grade-year ($i,m$), we generate trajectories belonging to students of the same cohort1 who don’t drop out or do at a later grade-year ($i+j,m+n$) with $j\ge 0,n\ge 1$. Hence, all these trajectories were abbreviated multiple times based on their counterfactual similarity (evaluated by year and grade reached) of a dropout case (see Fig. 3).

Fig. 3.

Example of two counterfactual trajectories for student A, who begins primary education in 2004 and dropouts in 6^th grade in 2009. Since students B and C (which also began education in 2004) graduate, or dropout in a higher grade and year, their counterfactual trajectories are calculated to the same grade and year of student A

Subsequently, we will create a training sample until a year $t$ considering all the dropouts at year $i$ ($i\le t$) plus a random undersampling of the total counterfactual trajectories, creating a sample where dropout cases have higher proportion than the natural prevalence of the phenomenon, e.g., 30%, 40% or 50%. Additionally, some stratification criteria to subsample contrafactual trajectories can be used also based on some variables such as grade, sex, socioeconomic status, or schools’ categories to ensure their representativity. The impact of these stratification procedures on results should be also tested on step 4.

For the test sample, all the trajectories which should be on school in a year $t+1$ are included to measure the performance of the model prediction. Test sample remains unbalanced.

Imbalanced models should be also evaluated with appropriate performance metrics. We consider the following performance metrics for binary classification:

• Recall: is the class hit rate with respect to the total number of real cases belonging to that class. The false negative rate is 1 − recall. Minimizing false negatives, it ensures students could potentially drop out are detected.

• Precision: is the class hit rate with respect to the total number of predictions for a class. The false positive rate is 1 − precision.

• Sensitivity: Recall of the positive class in a binary classifier.

• Specificity: Recall of the negative class in a binary classifier.

• F1 score: Harmonic mean between the precision and the recall of a class, in this case, the positive one.

To balance results of true positive and negative rates, we use the geometric mean between the sensitivity and specificity (GM Score) to measure performance in the test sample (Márquez-Vera et al., 2016). Also, we consider the recall and precision of both classes, and the F1 score of the positive class (Mduma et al., 2019).

Step 3: Selecting predictive algorithms and train model

In the third step, we choose an algorithm to train the model. There are several algorithms to create the model such as Decision Trees and its ensembles, SVM machines, neural networks between others (Şara et al., 2015). However, international experiences in the application of machine learning for the prediction of school dropout strongly suggest the use of decision tree ensemble algorithms since:

• They are better suited to deal with both continuous and categorical variables (Jena & Dehuri, 2020).

• They have shown a robust performance in exercises of a similar nature (Lee & Chung, 2019; Sansone, 2019; Sorensen, 2019).

• Ensemble decision trees use strategies to avoid overfitting (Bentéjac et al., 2021).

In this regard, there are a set of decision trees with gradient boosting ensembles such as eXtreme Gradient Boosting (XGBoost) (Chen & Guestrin, 2016), Light Gradient Boosting Machine (LightGBM) (Ke et al., 2017) and Categorical Boosting (CatBoost) (Prokhorenkova et al., 2019).

Step 4: Results and sensitivity analysis

The performance obtained with the test sample, should be carefully analyzed to discard under or overfitting. Overfitting occurs where performance is very good with the training sample but bad with test sample, and underfitting when performance is bad in both samples (Dos Santos et al., 2009).

In previous steps, several imputing methods and assumptions were made, and the quality of the obtained trajectories may vary. Other decisions include how stratified random undersampling methods were used to create the training sample. Impact of these assumptions on the stability of the results should be tested.

Also, model could have better results in some contexts, for example in some levels or categories of schools (e.g., public vs private, urban vs rural). These contexts can determine the limitations of the model or where could be used with more confidence.

Step 5: Model improvement

As outcome from step 4, we obtained an initial model. If such a model has good results in terms of performance the question which arises is: can we refine our model making it easy to maintain and with better computer performance in the training and predicting tasks? Producing a model easy to main means reducing the quantity of variables involved, finding a subset which enables us to make predictions at the same level of performance metric. Less variables will reduce both the effort to create the trajectories for the training and simplify obtaining data for prediction.

There are at least three algorithms to discard and determine relevance of each variable in estimating results:

• Naïve Recursive Feature Elimination (RFE): eliminates variables recursively until the minimum number that maximizes the performance of the model (given an objective function) is obtained (Misra & Yadav, 2020). In this case, we propose to use the GM score as an objective function (see Section 2.2).

• Boruta: evaluates the importance of each variable with respect to a permuted version of it to determine its relevance (Kursa et al., 2010).

• Shap RFE: is a modified version of RFE that identifies more robustly the importance of each variable using SHAP (see Section 2.6) (Lundberg et al., 2019; Sharma et al., 2020).

Alternatively, each machine learning algorithm has some parameters (hyperparameters) which can affect both performance results and computation time to train the model. There are optimization hyperparameters algorithms based on brute force, Bayesian statistics, genetic algorithms, among others. In the present work, we consider two of them:

• Tree Parzen Estimator (TPE): is a semi-random optimization algorithm improving performance by analyzing the history of parameters already used, seeking the optimization of a loss function based on Parzen Estimators (Bergstra et al., 2011).

• Population Based Training (PBT): is an evolutionary mechanism where generations of hyperparameter configurations are created. Then, PBT evaluates their performance and selects the best ones, creating a new generation of configurations with changes with respect to previous one, repeating the process until algorithm stops after a given number of iterations, or no improvement appears (Jaderberg et al., 2017).

A last option for model improvement is using a corrective model to decrease the false positive rate after variable reduction and hyperparameters optimization. Reducing false positive rate decreases students identified wrongly as possible leavers. For this, a second model is trained with true positives and false positives results of previous years. Thus, to correct the original model to predict dropping out on $t+1$, the corrective model is trained until year $t-1$. These two models are applied successively and if both agree that students are positive cases, then the overall results are positive as shown in Fig. 4.

Fig. 4.

Improvement of the optimized model created in step 4, using a second corrective model

Step 6: Explaining the model

For the public accountability, no discrimination and transparency criteria in decision making where automatic systems are involved should be fulfilled (Buenadicha et al., 2019). Algorithmic discrimination refers where discrimination occurring in real world is reproduced in data environments, e.g., by gender or ethnic. Algorithm transparency refers to data they collect, how they manage it, how they analyze it, with whom they share it, what decisions are made based on it and based on what factors.

Therefore, after the best model is obtained, an explanatory model to understand how the model makes its predictions should be created. We propose using SHAP (SHapley Additive exPlanations) (Lundberg et al., 2019), because this method allows us to estimate the contribution of each variable to individual predictions in a robust, consistent, and locally accurate way (Lundberg et al., 2018). It uses an optimized procedure for tree-based algorithms allowing interpreting and debugging the resultant model (Sharma et al., 2020; Yoshida, 2020).

Thus, the output of this explanatory model is the probability decomposed into the specific contribution of each variable. Hence, all variable contributions for a given student sums his/her probability of dropping out. Using this method, students and schools can be profiled based on the contribution of each variable in the final probability of dropout (Section 4).

Using proposed methodology to Chilean education system

For better understanding of the model development, we first present an overview of the Chilean education system (Section 3.1). From Section 3.2 to 3.7, we develop a model for the Chilean case.

Overview of Chilean education system

In Chile, compulsory education lasts 12 years. Grades 1^st to 8^th are for primary education and grades 9^th to 12^th are for secondary education, with three cycles: first cycle (1^st – 4^th grade), second cycle (5^th – 8^th grades) and third cycle (9^th – 12^th grades).

In the early 1980s, Chile implemented a school choice system, introducing a per- student subsidy mechanism (voucher scheme). The per-student subsidy is the same for public and private schools meant to cover the school’s operating costs. Students can attend the school of their choice without administrative boundaries restrictions. This policy was supposed to stimulate competition between schools to attract and retain students, leading to improved efficiency and higher quality educational services (Ladd & Fiske, 2020).

There are mainly three school categories of schools2: a) public schools, funded by the per-student subsidy paid by the state and run by each of 345 municipalities, b) private-voucher schools, funded by the per-student subsidy paid by the state and operated by the private sector, and c) private fee- paying schools, financed solely by fees paid by parents, and run by the private sector (Ladd & Fiske, 2020).

An ongoing system-wide reform in public school education calls for de-municipalization of the public-school sector. This creates 70 new Local Education Services (LES) between 2018 and 2025, consolidating administration of schools formerly under mayoral control (Anderson et al., 2021). These 70 LES respond to a new agency responsibility for public schools: The Directorate of Public Education.

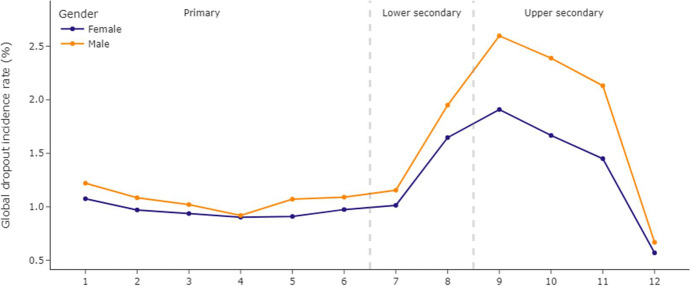
Figure 5 shows global dropout incidence rate. The highest one appears when students transit from primary to secondary education.

Fig. 5.

Global dropout per level in 2019, showing differences by gender. Grades are shown according to International Standard Classification of Education (UNESCO, 2012). Source: Own Elaboration based on Chilean Ministry of Education open data

Students can enroll in adult education, which accepts over 15-year-olds to primary or over 17-years-olds to secondary education. Since also they can enroll in more than one grade per year, this is a de facto alternative to avoid regular dropout. National evidence shows enrollment in this modality increases at higher grades. In 2019, 57,130 students left regular education to adult modality. In contrast, only 36,230 students dropped out the same year.

Step 1: Creating student trajectories

With the available datasets, we created student trajectories as an analyzable artifact. This consists of three procedures to produce a single observation summarizing a time ordered sequence of each student's transit from the first grade of regular primary education to the last reported period. These procedures are: 1) Dataset collection, 2) Determining student sequences; and 3) summarizing sequences into trajectories.

Datasets collection

In previous works on measuring and predicting school dropout, the data were collected from surveys and using administrative sources to obtain longitudinal data. For example, Sorensen (2019) and Lee and Chung (2019) used data from administrative and secondary sources to identify and quantify variables associated with students' situations.

We chose to use administrative data, obtained from secondary sources collected, organized, and published by Ministry of Education (MINEDUC) since 2004 in its open data platform, and to a lesser extent, from data related to the Education Quality Measurement System (SIMCE3) census tests as well as the parents and students’ surveys made available by the Agency for Quality in Education (AQE) for research purposes (Table 1).

Table 1.

Dataset used to develop predictive models

Dataset	Description
School enrollment (internal version)	Enrollment reported by schools. This internal version contains some additional information from MINEDUC (e.g., pregnancies, home address, among others) provided within NDA agreement
Final academic status	Academic performance, e.g., attendance and GPA, and descriptive data of students, provided by MINEDUC
Deceased students	Students who died before completing their school education. Provided by MINEDUC
School graduates	Students who completed compulsory education each year, either by regular or alternative means, and the pathway by which they graduated
SIMCE standardized test results	Performance achieved on SIMCE census tests (by grades and subjects). These results are in scores and by learning standards categorized for each subject as insufficient, basic, adequate. Datasets provided by AQE
Parents and students’ surveys	Parents and students’ surveys collected with the SIMCE test, provided by AQE
Schools	Information on schools and results in the National Performance Evaluation Systema (NPES) in score 0 to 100%
Index of School Performance (ISP)	Index of School Performance to monitor the improvement on time of each school (Valenzuela & Allende, 2014)
PSS Law allowances	Preferential School Subsidy (PSS). Law classifies students in two categories (preferential and priority ones), increasing the voucher amount depending on this classification. Schools must agree to enroll students from lower socioeconomic statuses to receive this extra voucher. These datasets identify the students in preferential and priority categories
Personal and Social Development Indicators scores (PSDI)	Indicators for measuring the quality of education in non-academic aspects, specifically: self-esteem and school motivation, school climate, participation and citizenship formation, and hygiene and healthy living habits
JUNAEB programs	JUNAEB is an agency of the State Administration, responsible for managing state resources to ensure that children and young Chileans in conditions of biopsychosocial vulnerability enter, remain, and succeed in the Educational System. Programs implemented by JUNAEB, designed to retain students into schools: Skills for Life I and II, and School Retention Support Program
Rurality index	Level of rurality of a location: from urban to rural areas. Own elaboration based on 1) distance to urban areas, 2) population density and 3) land use classification
LES territories	Provisional territorial definition of all the LES (in operation or not). One LES is composed of several municipalities belonging to the same region. Provided by the Directorate of Public Education

^aAvailable at: https://sned.mineduc.cl/

In these datasets, all students are identified anonymously by masking their National Identification Number (Masked ID or MID). Thus, individual data can be cross-referenced, and we can trace the trajectories of every student.

Using administrative data for assembling student trajectories is a great opportunity to identify trends and patterns that lead to dropout. Still, some limitations need to be considered. Mainly the exclusion of certain factors identified as relevant in the literature, but difficult to measure or non-existent in administrative data, like, e.g., contextual factors or non-academic problem behaviors.

When we consolidated all this data, we found several inconsistencies through the years, such as implausible birth years, data inconsistencies for the same student, gender discrepancies, academic statuses reported without enrollments and vice versa, students skipping grades, students graduated on a non-final grade and mismatches on the grade reported in SIMCE/PDSI datasets.

To address these problems, these situations were operationalized to subsequently assess the consistency of the reported history for each student (see Table 2).

Table 2.

Definition of criteria for selection of enrollment-performance records

Priority	Criterion
1	There is a unique pair of enrollment-academic status
2	The school and grades are the same as the previous year
3	The final situation of the students is either approved or reproved (different to retire or transfer)
4	There was a change of school within the year
5	The greatest number of the following sub-criteria are met: Of all pairs, it is the lowest numbered teaching modality code, it is the lowest numbered grade available, the grade reported in the enrollment is less than or equal to the academic status grade. Teaching modality code identifies the characteristics of a grade: primary or secondary, its target audience (children and youth, adults, or people with disabilities and/or disorders), and its orientation (vocational, scientific humanist, among others)
6	A random pair is selected

Determining students’ sequences

We generate sequence tables composed of time-ordered series, for each student, where the student's situation is described with respect to their trajectory: enrollment status, dropout incidence, among others. For each student in the sequence table, we calculate new variables relevant to the model such as changes of grade, changes of school between or within the same year and grade repetitions. The procedure is as follows:

1. We standardized the available information on enrollment and academic status. These operate as articulating axes of the sequences to allow traceability. Then, we completed them by assigning data from other sources.

2. We assigned each student to a cohort from the first available period (2004).

3. After cohort assignment, the base sequences are created with enrollment and academic status of the students, matching enrollment-academic status pairs available for each year and MID. When there is no either enrollment or academic status, fictitious enrollment and academic status data are created by duplicating the available case and filling in the unavailable columns with missing values.

4. When there is more than one enrollment or academic status, we define the following criteria to identify the unique enrollment- academic status pair to represent the period within the sequence (Table 2).

After performing the above procedure, it was possible to trace the sequences of each student in the cohorts from the year 2004, obtaining sequence tables. However, it was only possible to create trajectories for students entering the first year of primary education in 2004 and, therefore, the number of students per year whose trajectory is feasible increases each successive year and stabilizes after 12 years, when the students of the 2004 cohort reached their last grade.

Even after 12 years, it is not possible to create the trajectory of all students because it is not possible to identify their cohort of origin, which occurs, for example, in the case of foreigners who do not start school in the national system, however, a traceability rate of 96.4% is achieved.

Summarizing sequences into student trajectories

Given the amount of data available, we opted for traditional supervised machine learning methods to generate the predictive model over larger scale alternatives traditionally used in forecasting exercises, such as models based on neural networks. This is because such models work with training samples larger than those available, and they have lower interpretability.

Then, we reduced the sequence tables of each student to a single observation describing their passage through school education. To this end, we generate a student trajectory, adding variables created from grouping the sequences table, summarizing the student's final situation, their most frequent values in some variables (for instance, number of public schools attended) and other elements related to risk factors identified in the literature. The socioeconomic status is included in the family level risk factor, and it was calculated as the mean of the standardized declared household income and the maximum standardized parental schooling. In this case, a multilevel imputation was performed to deal with the high number of missing cases. Additionally, we included other sequence descriptors, allowing us to capture relevant milestones of the trajectory summarized, such as the last year or grade reached.

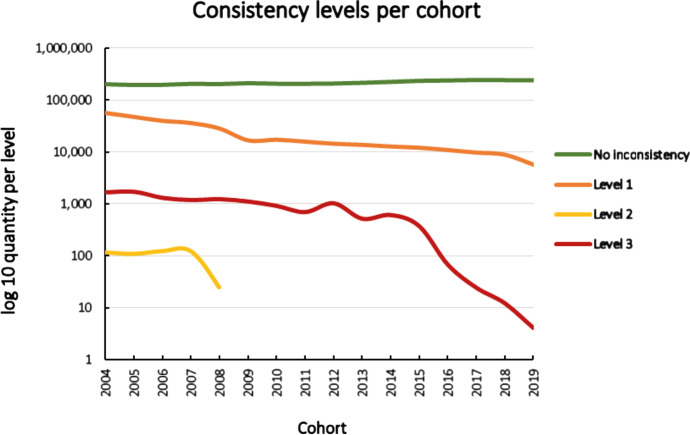
Since the original raw data contains inconsistencies resulting from the data collection procedures, we create a score to evaluate the quality of the trajectories and analyze the consequences of considering s with lower consistency. We define 15 inconsistency indicators in 3 levels: from the data reported on enrollment and performance (10 indicators, level 1), from datasets provided by MINEDUC (2 indicators, level 2) and from data reported by other sources (3 indicators, level 3) (complete criteria are available in Table 9 in Appendix A). The consistency score was normalized with mean 0 and standard deviation 1, the distribution per cohort is shown in Fig. 6.

Fig. 6.

Inconsistencies per cohort. Every color line represents an inconsistency level that increases by severity. The consistency of the student trajectories by cohort has gradually improved in the last 10 years making levels two or three infrequent. Values are in log₁₀ scale

Each trajectory operationalizes regular dropout, which is where a student enrolled in some grade for children and youth on year $t$ is either enrolled in adult education or out of the school system on year $t+1$. We also include consistency descriptors to control and evaluate the quality with which the trajectories are calculated with the procedure described in Section 2.3. Thus, 111 variables were considered and grouped according to its type (Table 3), including SIMCE and IDPS ones. Complete variable descriptions are available in Appendix B.

Table 3.

Variables count by type

Type of variables	Number of variables
Risk factors
Individual	40
Family	3
School	33
Extra-scholar	6
Others
Consistency	5
Trajectory descriptors	24
Total	111

Using administrative data limits the availability of contextual or family variables compared to more readily available individual and school data. At the end, we generated 3,847,469 student trajectories.

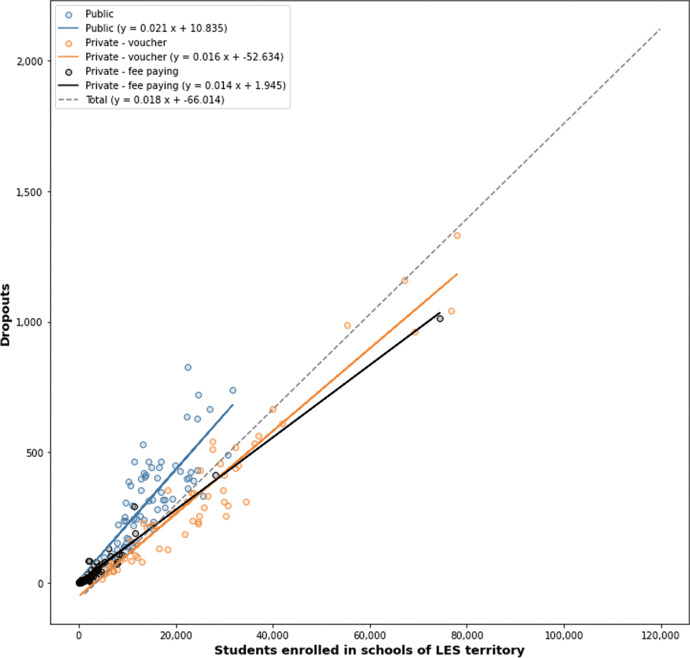
Using these trajectories, a first visual exploratory analysis allows us to recognize differences of performance on dropout of the different schools on LES territories, by school dependency and total school enrollment (Fig. 7). As Fig. 7 shows, there are territories with performance worse than regression predicted and should be the focus of public policies.

Fig. 7.

Regression models built based on students’ trajectories by total enrollment in school categories. Several public schools on LES territories underperform. The private-voucher schools in the same territory have better results with greater enrollment

Step 2: Training and test samples and performance metrics

As we explained in Section 2.2, we create a training and test sample with trajectories until 2018, and 2019 respectively.

The training sample was created with data until 2018. This sample is imbalanced since contains 3,847,469 trajectories of which 345,874 (8.9%) lead to dropout, with an imbalance ratio of 10.12. To deal with this problem, as it is proposed in Section 2.2, we create contrafactual trajectories for students who drop out. We opted for a stratified subsampling using four variables: gender, category of the last school, last year and registered grade. This reduced the negative class from 26,793,262 counterfactuals to 345,874, amount equal to the number of dropouts. Therefore, the training sample has 691.748 cases, with an imbalance ratio of 1.

The test sample uses all student trajectories that reached 2019 and were (or not) dropouts in 2020, totaling 2,802,156 trajectories of which 47,632 (1.7%) lead to dropout with an imbalance ratio of 57.82. There is no intersection between training and test samples since their variables were constructed until different years. We will report recall and precision for each class, looking for better performance in GM and F1 scores. Given the sample sizes, it is unnecessary to use cross validation.

Step 3: Selecting predictive algorithms

We produced machine learning models using a basic decision tree algorithm as the simplest model and then we also tried 3 decision tree ensemble algorithms with gradient boosting: XGBoost, LightGBM and CatBoost (see Section 2.3 for justification). We trained and tested them using the samples created in the previous section.

Step 4: Results and Sensitivity analysis

The results of the four algorithms on the test sample considering 103 variables without missing data (excluding SIMCE and PSDI scores) are shown in Table 4.

Table 4.

Results for trained models using decision tree-based algorithms

Algorithm	Class 0 (Staying)		Class 1 (Drops out)		GM Score	F1 score	Training time (s)
	Recall	Precision	Recall	Precision
Decision Tree classifier	0.7995	0.9959	0.8112	0.0654	0.8053	0.1210	70.70
XGBoost	0.9391	0.9967	0.8201	0.1888	0.8776	0.3069	284.82
LightGBM	0.9317	0.9970	0.8397	0.1754	0.8845	0.2902	67.18
CatBoost	0.9211	0.9972	0.8488	0.1569	0.8842	0.2645	407.24

The performance of the tree algorithms with gradient boosting is superior to the classic CART decision tree. LightGBM is slightly superior to CatBoost in GM score. This indicates that while the CatBoost model achieves better performance in terms of recall for class 1 (which means fewer false negatives), it also has a higher false positive rate. Hereafter, the LightGBM model will be referenced as the base model.

Stability of performance on trajectories consistency, training sample creation and SIMCE and PDSI scores

Several models were also trained considering the internal consistency score of each trajectory. We concluded that it is necessary to consider all cases since less consistent trajectories also indicate a higher prevalence of dropout and discarding them does affect the final performance of the model.

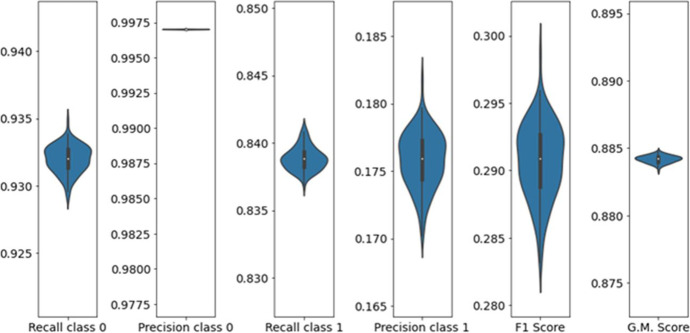
The stability of the performance was evaluated for 100 random different samples of contrafactual trajectories. The greater variation was just 0.014 for the F1-score, as can be seen in Fig. 8.

Fig. 8.

Distribution and range of model performance results in multiple training samples

Variables related to performance on SIMCE tests and PDSI scores were also considered. but their contribution to the performance of the model was very low compared to the cost of obtaining these datasets and the high amount of missing data.

Performance in different grades, schools’ categories, and sizes

Since the base model is stable in trajectory consistency, random choice of counterfactuals and, SIMCE and PDSI variables did not introduce significant performance improvements, we finally address the question of how the base model performs in different contexts, defined by combinations of grades and school categories, thinking in its practical use (Table 5).

Table 5.

Results of LightGBM model in different grades and schools’ categories

Grades	School category	Class 0 (Staying)		Class 1 (Drops out)		GM Score	F1 score
		Recall	Precision	Recall	Precision
Cycle 1 (1st – 4th grades)	Public	0.9364	0.9981	0.8525	0.1387	0.8935	0.2386
	Private voucher	0.9223	0.9979	0.7309	0.0627	0.8210	0.1155
	Private fee paying	0.8742	0.9927	0.6048	0.0726	0.7272	0.1296
Cycle 2 (5th – 8th grades)	Public	0.9444	0.9975	0.8202	0.1609	0.8801	0.2690
	Private voucher	0.9377	0.9979	0.7596	0.0923	0.8440	0.1646
	Private fee paying	0.8984	0.9934	0.5110	0.0578	0.6776	0.1039
Primary (1st – 8th grades)	Public	0.9404	0.9978	0.8358	0.1492	0.8865	0.2532
	Private voucher	0.9297	0.9979	0.7458	0.0755	0.8327	0.1371
	Private fee paying	0.8854	0.9930	0.5680	0.0666	0.7092	0.1192
Secondary (Cycle 3): (9th – 12th grades)	Public	0.9361	0.9953	0.9058	0.4018	0.9208	0.5567
	Private voucher	0.9372	0.9969	0.8939	0.2819	0.9153	0.4286
	Private fee paying	0.9486	0.9949	0.6689	0.1601	0.7966	0.2584
7th – 12th grades	Public	0.9342	0.9957	0.8885	0.3298	0.9110	0.4810
	Private voucher	0.9374	0.9970	0.8708	0.2343	0.9035	0.3692
	Private fee paying	0.9385	0.9944	0.6143	0.1212	0.7593	0.2025

Performance tends to improve at higher grades (where the natural prevalence of dropping out in Chile is higher, as Fig. 5 shows) and in public schools (as shown in Fig. 7), with the best performance in secondary for public schools, and the worst relative performance in primary education in the private fee-paying sector. Despite that, these results are better than those from previous research with a relevant sample size (Lee & Chung, 2019), and a predictive capability 20% higher for the actual dropout cases, also considering the advantage of addressing the problem of classroom imbalance.

If we analyze the classification error of this model based on school size, public and private voucher schools follow the same patterns. Figure 9 shows the results for public schools, where error is minimal for false negative rates of any school size and false positive rates decreasing for large schools from 500 students.

Fig. 9.

False negative rates (left) and false positive rates (right) by public school size for secondary and 7^th to 12^th grade

Step 5: Model improvement

To determine the relevance of each variable in estimating each student’s dropout probability and because the naïve version of RFE has problems in dealing with noise from irrelevant variables, we used two feature selection methods (see Section 2.5): 1) first using Boruta and then applying naïve RFE and 2) applying ShapRFE. Both approaches proved more effective than using naïve RFE, which discarded only 64 of the 103 original variables in contrast to the proposed methods which discarded 83 and 87 respectively. In Table 6, we compare the performance of the three models with 103, 30 and 26 variables.

Table 6.

Performance of the model with selected variables

Method	Total Variables	Class 0 (Staying)		Class 1 (Drops out)		GM Score	F1 score	Training time (s)
		Recall	Precision	Recall	Precision
None	103	0.9317	0.9970	0.8397	0.1754	0.8845	0.2902	67.18
Boruta plus naïve RFE	30	0.9304	0.9970	0.8368	0.1721	0.8824	0.2880	19.21
Shap RFE	26	0.9344	0.9970	0.8368	0.1798	0.8842	0.2960	16.84

Both methods allowed to create simpler and more efficient models maintaining performance. Table 7 shows the contribution of the variables selected by the two previous methods by its type (as in Table 3), considering two values: 1) the aggregated contribution, which is the sum of the importance of each variable in the set, and 2) the average contribution, which is the aggregated contribution divided by the number of variables per type. The contributions of only the 26 relevant variables per type are depicted in Appendix B.

Table 7.

Contribution of variables by type for selection approaches

Type of variable	Total Number	Boruta plus naïve RFE			Shap RFE
		Relevant variables	Aggregated contribution	Average contribution	Relevant variables	Aggregated contribution	Average contribution
Risk factor
Individual	34	12	0.4137	0.0345	13	0.4325	0.0333
Family	3	1	0.0151	0.0151	1	0.0177	0.0177
School	32	9	0.1059	0.0118	5	0.0978	0.0196
Extra scholar	5	0	0	0	0	0	0
Other
Consistency	5	0	0	0	0	0	0
Trajectory descriptors	24	8	0.1488	0.0186	7	0.1472	0.021
Total	103	30			26

Individual level factors made the greatest contribution, consistent with literature. School factors and trajectories’ descriptors are also relevant in both approaches. Therefore, in contrast to previous work, the inclusion of non-individual dimensions results in a substantive contribution to the prediction of school dropout.

Since our final model is just trained in 16 s on a desktop computer (Table 6) and it takes less than 1 s to predict 2.8 million cases, we considered this a reasonable performance, and we did not optimize the hyperparameters of the LightGBM algorithm.

Finally, we generated a corrective model using the procedure described in Section 2.5. For that, we took the 26 variables and identified true and false positives until 2018. False positives were codified as 0 and true positives as 1. The results of the correction are shown in Table 8.

Table 8.

Results after applying a corrective model. See Table 5 for comparison

Grades	School category	Class 0 (Staying)		Class 1 (Drops out)		GM Score	F1 score
		Recall	Precision	Recall	Precision
Secondary (Cycle 3): (9th – 12th grades)	Public	0.9487 ↑	0.9941	0.8814 ↓	0.4489 ↑	0.9145 ↓	0.5948 ↑
	Private voucher	0.9459 ↑	0.9965	0.8779 ↓	0.3091 ↑	0.9112	0.4572 ↑
7th – 12th grades	Public	0.9467 ↑	0.9948	0.8631 ↓	0.3711 ↑	0.9039	0.5190 ↑
	Private voucher	0.9467 ↑	0.9966	0.8539 ↓	0.2605 ↑	0.8991 ↓	0.3992 ↑

↑↓ increase/decrease at the second decimal number.

In all grades and school categories, recall scores for class 0, precision scores for class 1 and all the F1 scores improved to the minimal detriment of recall scores for class 1. In terms of absolute quantities, for secondary education in public schools, false positives diminished from 6.1% to 4.9% and for private voucher schools came from 6.16% to 5.15%. In the case of 7^th – 12^th grades, the reduction was from 6.35% to 5.25% in public schools, and from 6.1% to 5.19% in private voucher schools.

Step 6: Explaining the model

The SHAP method decomposes each individual probability prediction into the specific contribution of each variable. Thus, all variable contributions for a given student sums their probability of dropping out. SHAP values were computed from the initial model without the false positive correction. Figure 10 shows the contribution of each variable of the final model for two cases, one where the model predicts a high probability (0.99) and other a lower one (0.01).

Fig. 10.

Individual variable contribution for two cases using SHAP values. SHAP values per variable for a student with low dropout probability (0.01) are shown in green, while SHAP values for a student with high dropout probability (0.99) are shown in red

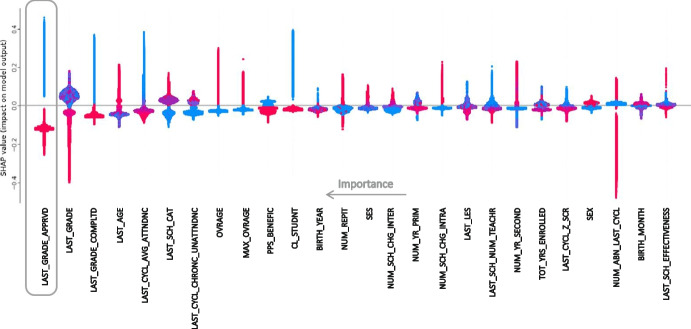
Figure 11 shows the individual contribution of each variable selected for the final model with 26 variables for all 2019 cases.

Fig. 11.

Beeswarm plot for final model. Every point shows the impact of each variable in a dropout prediction per student in the 2019 test sample. The colors denote the value of the variable in its own scale (high values in red, low ones in blue). Absolute mean contributions to predictions are ordered from left (higher) to right (lower). Variable codes are in Appendix B

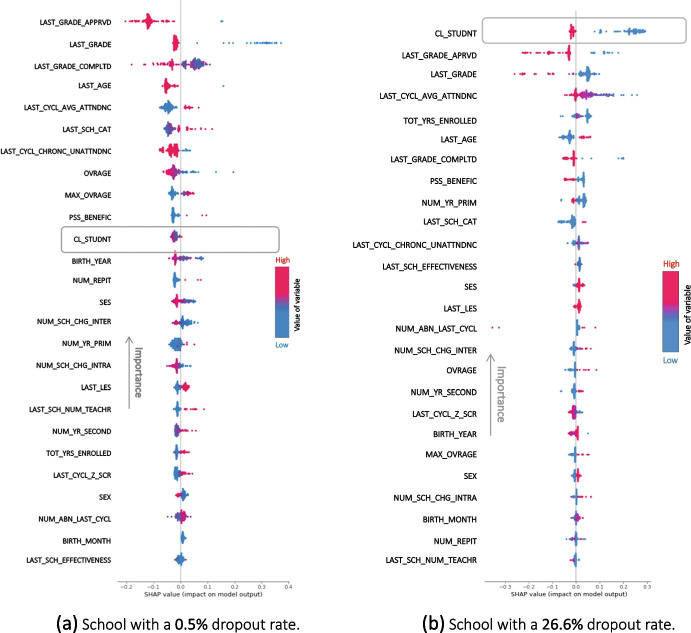
For example, LAST_GRADE_APPRVD is a binary variable indicating if a student passed (1) or not (0) their last year at school. Figure 11 shows us two things: 1) LAST_GRADE_APPRVD is the most important variable in predicting dropping out and, 2) in all the cases lower LAST_GRADE_APPRVD values (0, shown in blue) have a positive contribution while higher values (1, shown in red) have negative contribution to dropping out probability. This analysis can be repeated for each school, allowing to identify the most important variables for dropout at local level. For example, the school on Fig. 12a has a 0.5% dropout rate while the school on Fig. 12b) has a 26.6% dropout rate. Variable importance ranks are different between schools and contribute in different ways.

Fig. 12.

Beeswarm profiles of two schools with different dropout rates. The colors denote the value of the variable in its own scale (high values in red, low ones in blue). The school on the left (a) has a dropout rate of 0.5% while the school on the right (b) has 26.6%. Absolute mean contributions to predictions are ordered from above (higher) to below (lower). Variable codes are in Appendix B

Further implications for public policy will be discussed on Section 4.1.

Public policy applications

The straightforward application of this model is developing an EWS. But as it was stated in Section 1.5, we can also envision other applications of these models for decision and public policy making. These are: profiling schools for qualitative studies of pedagogic practices, profiling students’ dropout trajectories and simulating scenarios.

Profiling schools for qualitative studies of pedagogic practices

As it was stated in Section 2.6, model explanations allow to guide further qualitative research about pedagogic practices. Results of the explained model can guide qualitative studies in schools. For example, the variable CL_STUDENT is a binary one indicating if a student is Chilean (1) or not (0) (see Appendix B). As general results of the test sample show (Fig. 11), being foreign student increases your chance of dropping out. If we analyze a school with a low rate of dropout (Fig. 12a), it is indifferent if a student is Chilean or not since the contribution of the variable to the dropout probability is negative. However, in the school of Fig. 12b, CL_STUDENT is the variable with most importance and being foreign has a positive contribution. Therefore, pedagogic practices with foreign students can be investigated further in both schools, and the question which arises is: what are the pedagogic practices that can be replicated (school a) or avoided (school b) in similar contexts?

Additionally, any significant difference in the quantities of dropouts expected at school or LES level could be indicative of changes in local policies for school retention with better or worse results.

Profiling students’ dropout trajectories

In second place, since SHAP values for every variable are continuous, we used clustering algorithms to identify typologies of trajectories leading to dropout. We used the 39,844 true positives’ SHAP values calculated for the year 2019 in a clustering model.

SHAP values were rescaled to adjust them to a range between -1 and 1, preserving the directionality of the predictions, but normalizing the different impact level of every variable. Since the excessive dimensionality of the data (26 variables), we used UMAP (McInnes et al., 2020) to reduce the information to only two. From this, 20 clusters were found using DBSCAN (Ester et al., 1996). The detailed characterization of clusters based on the original domain of each variable can be found in Table 10 in Appendix.

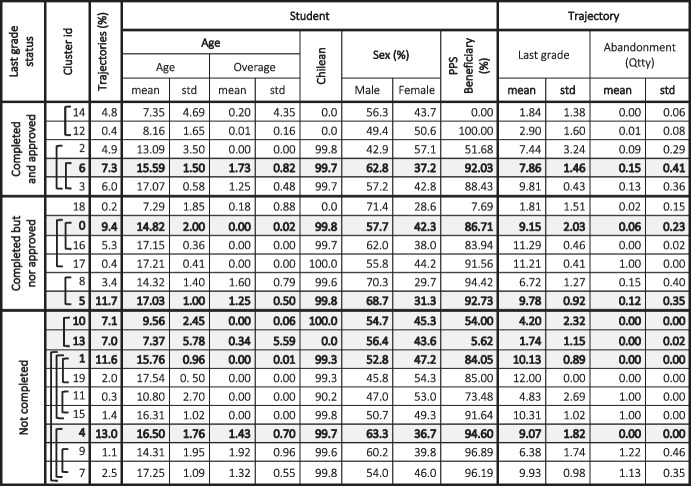
There are 3 main categories of trajectories: 1) where students completed and approved their last level (23.5%); 2) where students completed their last level but did not approve (30.4%), and 3) where students did not complete last level (46.1%). As Fig. 13 shows, within these 3 categories there are also subcategories based on just 5 variables: student is Chilean (CL_STUDNT), PPS beneficiary (PPS_BENFNC), Overage (OVRAGE), Last grade on school (LAST_GRADE) and Number of abandonments in the last cycle (NUM_ABN_LAST_CYCL). Category 1 has 5 clusters; Category 2 has 6 clusters and Category 3 has 9 clusters.

Fig. 13.

Typology of trajectories based on the clustering model. Every square indicates a division by the variable indicated. Bifurcation to left is to lesser values and to the right to greater values

The 67% of the students’ trajectories are concentrated just in seven clusters (Table 9): one of category 1 (cluster 6), two of category 2 (clusters 0 and 5) and four of category 3 (clusters 1,4,10 and 13). In these clusters predominates the school categories, grade and sex expected according to incidence of the phenomenon (see Figs. 5 and 7). They have the following characteristics (from greater to lesser trajectories) according to variables in Table 12 in Appendix C:

• Cluster 4 (13.0%): Last grade not completed, mainly students in 9^th grade, almost only Chileans, with averages: SES of 0.22, attendance in last cycle of 82.13%, z score of − 0.99, repetition of 2.1, changes of schools of 2.47 and last school effectiveness of 41.96%.

• Cluster 5 (11.7%): Last grade completed but nor approved, mainly students in 9^th and 10^th grade, almost only Chileans, with averages: SES of 0.24, attendance in last cycle of 75.7%, z score of − 1.64, repetition of 2.87, changes of schools of 2.51, last school effectiveness of 43.42%.

• Cluster 1 (11.6%): Last grade not completed, mainly students in 10^th and 11^th grade, almost only Chileans, with averages SES of 0.31, attendance in last cycle of 85.37%, z score of − 0.63, repetition of 0.55, changes of schools of 2.09, last school effectiveness of 45.57%.

• Cluster 0 (9.4%): Last grade completed but nor approved, mainly students in 9^th grade, almost only Chileans, with averages: SES of 0.29, attendance in last cycle of 74.52%, z score of − 1.66, repetition of 1.56, change of schools of 1.91, last school effectiveness of 46.26%.

• Cluster 6 (7.3%): Completed and approved, mainly students in 7^th and 8^th grade, almost only Chileans, with averages: SES of 0.25, attendance in last cycle of 85.35%, z score of − 0.88, repetition of 2.20, change of schools of 2.42, last school effectiveness of 43.51%.

• Cluster 10 (7.1%): Last grade not completed, mainly students in 4^th grade, only Chileans, with averages: SES of 0.47, attendance in last cycle of 88.53, z score of − 0.08, repetition of 0.16, change of schools of 0.59, last school effectiveness of 50%.

• Cluster 13 (7.0%): Last grade not completed, only foreigners in 1^st and 2^nd grade, almost only Chileans, with averages: SES of 0.33, attendance in last cycle of 92.56%, z score of + 0.05, repetition of 0.03, change of schools of 0.08, last school effectiveness of 45.26%.

Table 9.

Clusters in the five variables identified (CL_STUDNT, PPS_BENFNC, OVRAGE, LAST_GRADE and NUM_ABN_LAST_CYCL). Age and sex were added for reference. Clusters marked on grey are the one which concentrate 67% of the trajectories

In all these clusters, the last schools were predominant public except in clusters 0 (48.6% voucher vs 42.7% public schools), 1 (44.5% voucher vs 44.2% public schools) and 10 (45.6% voucher vs 32.7% public schools). Apparently, the clustering model grouped in Cluster 13, all trajectories of foreign students which changed their identity number from a provisional to the official one. This causes an abnormal incidence of dropout in first and second grades since these trajectories were truncated by an administrative anomaly.

As Sansone (2019) verified, the heterogeneity of students at risk of dropping out through this kind of unsupervised learning, allowing to identify subpopulations among students and, thus, to design programs appropriate to each group, understanding both their peculiarities and key factors associated with their situation, so that policymakers could benefit from exploiting this to customize the treatment of each cluster of students.

Simulating scenarios: External shocks

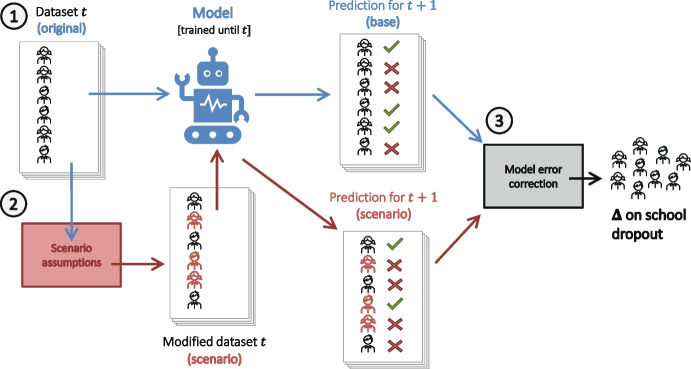
In third place, predictive models can be used to evaluate impact in dropping out of external shocks, such as an economic recession, natural catastrophe, or a pandemic.

In this case, we present a simulation of the effect of a pandemic such as the COVID-19 in the increase of dropping out following the methodology described on Fig. 14. The shock is created by applying scenario assumptions which alter the input data (scenario data), and the results of the model are compared in a base case (unchanged data) with the scenario data. Since we know the prediction error of the model (see Tables 5 and 8), we can correct final quantities to avoid overestimation.

Fig. 14.

Procedure for simulating a scenario using the predictive model. In stage 1, the prediction is created as business usual (base). In step 2, the original dataset is altered according to the scenario assumptions, creating a modified dataset which is used for prediction (scenario). In step 3, since the error of prediction is known, the results are corrected using that generating a difference on dropout

For illustrative purposes, we analyzed the effect of diminishing attendance in the marginal increase of dropout. If we assume that all variables behave the same as 2019 where students attended in person and we just correct replace individual LAST_CYCL_AVG_ATTNDNC variable by a fixed factor, we obtain results shown in Fig. 15.

Fig. 15.

Results of a simulating of decreasing attendance by a given factor in additional dropouts. Note that factor a zero factor conduces to repetition, but not necessarily to dropout

On first semester of 2022, monthly attendance data from Mineduc shows that it is approximately 9% lower (equivalent to a factor of 0.91) in average compared to 2018 and 2019, for either public or private voucher schools. Therefore, without any intervention and this tendency remains and does not worsen, the simulation estimates 10,501 additional dropouts at end of the year 2022.

Discussion

In this paper, we proposed a methodology to design, develop, and evaluate a predictive model for regular school dropout using: 1) individual student trajectories as individual cases; 2) procedures for creating training and test samples, and choosing performance metrics considering class imbalance; 3) machine learning algorithms for this kind of problems; 4) sensitivity analyses to test dependency of results on previous assumptions, and determine contexts where the model works better; 5) methods to reduce variables improving maintenance and reducing false positives, and; 6) explanatory techniques to calculate the individual contribution of each variable to dropout probability.

Following the methodology, we develop a model for the Chilean case (Section 3) based on data available mostly through administrative data from the educational system, and according to known factors associated with school dropout. Our results are better than those from previous research with a relevant sample size (Lee & Chung, 2019), with a predictive capability 20% higher for the actual dropout cases. Also, in contrast to previous work, the inclusion of non-individual dimensions results in a substantive contribution to the prediction of leaving school. Contrary to Sorensen (2019), who found better results using SVM, Gradient based boosting decision trees worked best for us. Therefore, the importance of trying different algorithms in step 3.

Long-term policies can be devised to manage risk factors, such as academic lag, for reducing that prevalence in future cohorts of students. At school level, the model can identify students with higher dropout risk requiring support and protection strategies to ensure positive school trajectories. For example, those who have recently repeated, have high levels of absenteeism, have accumulated more than one repetition and are over-aged. In Chile, this is exacerbated when the student is male, migrant or has started his education overseas. Results show that these efforts will have greater impact in public schools, with lower socioeconomic levels from secondary education. As can be seen, these are all indicators that are easy to construct at school level. Also, in the case of Chile, these analyses will be useful for the Directorate of Public Education to understand the challenges of the territories that will become part of new public education soon.

The major contributions of this study are:

• As Sorensen (2019) states, machine learning is less transparent and technological demanding. However, techniques like SHAP proposed in this paper provides a reliable option to explain results and how they depend on the context. Cloud computing infrastructure also reduces significantly computational cost, but, in our case, it was not necessary. This is because the burden of computational cost is shifted from the machine learning model to the trajectories’ calculation, what is, a one-time development comparing to multiple trainings of models.

• The public policy applications envisioned in Section 4, to inform public policies such as profiling schools for qualitative studies of pedagogic practices, profiling students’ dropout trajectories and simulating the impact of events such as pandemics or natural disasters. Simulations estimate the decreasing/increasing of dropout, providing information for calculating the return of investment of public policies on school retention.

Some limitations of this study are that the administrative nature of the available data limits the possibility of transforming the prediction into concrete action and, at the same time, gives a constrained vision of the school trajectory. In addition, since certain data are hard to obtain, it is difficult to assess their potential contribution to the predictive value.

For the Chilean dropout prediction, future work includes developing a model for predicting dropout within the same year. This was not actually possible with public data available since attendance and grades of students are not reported monthly. Another challenge is adapting the model for years 2020 and 2021 where students received mostly remote classes during COVID-19 pandemic. Attendance was measured differently (if students attended at least one online class at day) and curriculum was shortened and adapted to circumstances. Therefore, the continuity of measurement in attendance and school performance broke and they should be considered as additional and separated variables in the model. Additionally, the pandemic had an impact on socio-economic status because of parents' unemployment or death and until today there is not an actualized income data since SIMCE test and surveys were suspended in 2020 and 2021.

School failure was a diminishing problem, but the pandemic of COVID-19 will push the poorest students outside the system, especially women. Therefore, developing EWS systems with evidence-based strategies at school and territorial level should be carried out, to prevent children from abandoning their studies. The methodology proposed comprises the necessary steps to develop models with high predictive power if proper data is available.

We expect that the methodology and case presented in this article helps practitioners and public decision makers to create their own models to predict school failure, but also motivates them to capture, clean and systematize data to allow developing such kinds of systems.

Appendix A

Table 10

Table 10.

Criteria used to score each student trajectory consistency

Source of inconsistency	Importance	Criteria
1. From data provided by enrollment and/or final academic status datasets	Mild (Level 1)	• Some implausible birth date is reported • More than two birth dates reported • More than 2 enrollments in a year • More than 2 final academic statuses in a year
	Moderate (Level 2)	• There are skipped grades in regular education • Birth dates in enrollment and performance datasets are different • Sex in enrollment and final academic status are different • Overages are greater than seven in some years
	Severe (Level 3)	• An enrollment was imputed • A final status was imputed
2. From data available on MINEDUC's open data platform	Moderate (Level 2)	• Student completed secondary education when they are still enrolled on a non-final grade
	Severe (Level 3)	• School without a name
3. From data reported by other agencies	Severe (Level 3)	• Grade in SIMCE test(s) is(are) different to the grade reported either in enrollment or final status dataset in the same year • Grade in PSDI is different to the grade reported either in enrollment or final status dataset in the same year • Income is reported in a different grade from either enrollment or final status datasets in the same year

Appendix B List of variables used and their significance in the final model

Table 11

Table 11.

(Only codes and contributions for the most relevant variables are shown)

Type of variables	Code (most relevant)	Description	Importance (most relevant)
Individual level	LAST_GRADE_APPRVD	Last grade was reported as approved	0.12744
	LAST_GRADE_COMPLTD	Last grade was reported as completed	0.04987
	LAST_CYCL_AVG_ATTNDNC	Average attendance rate in the last available cycle	0.03785
	LAST_AGE	Final age in trajectory (up to the last enrolled year)	0.04035
	LAST_CYCL_CHRONC_UNATTNDNC	Number of chronic absences in the last available cycle	0.03062
	BIRTH_YEAR	Student's year of birth	0.01987
	OVRAGE	Over-age in the last available year	0.02892
	NUM_REPIT	Total number of grade repetitions	0.01876
	CL_STUDNT	Student is Chilean	0.02181
	MAX_OVRAGE	Maximum over age reported in the trajectory	0.02236
	LAST_CYCL_Z_SCR	Standardized average for the last available cycle	0.01317
	SEX	Student's gender	0.01214
	BIRTH_MONTH	Month of student's birth	0.00933
		Number of municipalities in which the student attended education
		Student's ethnicity
		Initial age in the trajectory
		Student was in school integration
		Type of school integration reported (last)
		Student is foreign
		Student is naturalized
		Student was pregnant
		Number of different schools attended
		Number of different municipalities where a student resided
		Number of different Local Education Services (LES) territories where the student studied (even if the LES is not active). See Section 2.1
		Number of different LES territories where the student resided (even if the LES is not active). See Section 2.1
		Student changed school
		Student changed municipality of the school
		Student changed municipality of residence
		Number of years in special groups
		Number of years in school integration
		Number of dropouts in children and youth education
		Total average attendance
		Total standardized performance
		Total periods of chronic non-attendance
		Learning standard category in last SIMCE reading comprehension
		Learning standard category in last SIMCE in mathematics
		Learning standard category in the last SIMCE in natural sciences
		Learning standard category in the last SIMCE in social sciences
		Last PSDI in dimension Academic Self-Esteem and School Motivation
		Last PSDI in dimension Healthy Life Habits
Family level	SES	Calculated socioeconomic status	0.01776
		Priority student according to PPS criteria during any year
		Preferential student according to PPS criteria during any year
School level	LAST_SCH_CAT	Last school category (see Section 2.1)	0.03771
	PPS_BENEFIC	Student benefiting from PPS law	0.02218
	LAST_SCH_NUM_TEACHRS	Number of teachers from the last school	0.01478
	LAST_LES	Local Education Service of last school (see Section 2.1)	0.01568
	LAST_SCH_EFFECTIVENESS	NPES Effectiveness index for last school	0.00746
		Category of last school
		NPES Improvement index for last school
		Number of years in which the student was enrolled in a private fee-paying school
		Municipality of the last school
		Most frequent school
		Most frequent study municipality
		Most frequent region of study
		Most frequent LES territory of study
		Most frequent school category
		Category of most frequent school
		Last school
		Index of last school performance
		Region of last school
		Teacher turnover at the last school
		NPES Equality index for last school
		NPES Integration index for last school
		NPES Improvement index for the last school
		NPES Initiative index for the last school
		NPES index for last school
		Number of years in which the student was enrolled in a public school
		Number of years in which the student was enrolled in a private charter school
		Number of years in which the student was enrolled in a school with delegated administration (public school)
		Assigned to the 'Skills for Life I' program (JUNAEB) in some period
		Number of periods in the 'Skills for Life I' program (JUNAEB)
		Assigned to 'Skills for Life II' program (JUNAEB) in any period
		Number of periods in the 'Skills for Life II' program (JUNAEB)
		Assigned to the former School Retention Support Program (JUNAEB) in any period
		Last PSDI in dimension School climate of coexistence
Extra scholar level		Most frequent school is rural
		Rurality index of the most frequent school
		Last school is rural according to MINEDUC classification
		Rurality index of last school
		Number of rural schools in which academic status is recorded
		Last PSDI in dimension Participation and citizenship formation
Consistency		Number of enrollments reconstructed in the trajectory
		Number of final statuses reconstructed in the trajectory
		Maximum number of enrollments reported in a year
		Maximum number of final statuses reported in a year
		Consistence score for the trajectory
Trajectory descriptors	LAST_GRADE	Maximum grade of the trajectory where the student was registered	0.05998
	TOT_YRS_ENROLLED	Total enrollments registered	0.01338
	NUM_SCH_CHG_INTER	Total number of periods in which there was a change of school between years	0.01763
	NUM_SCH_CHG_INTRA	Total number of periods in which there was a change of school within a year	0.01573
	NUM_YR_SECONDRY	Number of years in secondary education	0.01414
	NUM_ABN_LAST_CYCL	Number of dropouts from regular education in the last available cycle	0.01047
	NUM_YR_PRIMRY	Number of years of elementary education	0.01582
		Last year when a student was registered
		Cohort of the student
		Most frequent municipality of residence of the student
		Most frequent region of residence
		Most frequent LES of residence
		Last reported cycle
		Student was in scientific-humanistic secondary education in the last grade
		Student was in technical-professional secondary education at the last grade
		Student was in artistic secondary education at the last grade
		Number of years in scientific-humanistic secondary school education
		Number of years in technical-professional secondary education
		Number of years in artistic secondary education
		Student was enrolled in elementary school
		Number of periods in elementary school
		Student changed school from 6th grade onwards from a basic school
		Number of changes due to school closure
		Number of dropouts in regular education

Appendix C

Table 12

Table 12.

Clusters description

Cluster	STUDENT
	AGE & BIRTH DATE										CHILEAN		SEX
	AGE		YEAR		MONTH		OVERAGE		MAX OVERAGE
	mean	std	mean	std	mean	std	mean	std	mean	std	Yes	No	Male	Female
0	14.82	2.00	2003.54	2.03	7.07	3.39	0.00	0.02	0.02	0.16	99.8%	0.2%	57.7%	42.3%
1	15.76	0.96	2002.66	1.05	6.82	3.46	0.00	0.01	0.02	0.17	99.3%	0.7%	52.8%	47.2%
2	13.09	3.50	2005.28	3.61	7.05	3.36	0.00	0.00	0.00	0.07	99.8%	0.2%	42.9%	57.1%
3	17.07	0.58	2001.48	0.68	6.37	3.43	1.25	0.48	1.27	0.50	99.7%	0.3%	57.2%	42.8%
4	16.50	1.76	2002.07	1.79	6.30	3.42	1.43	0.70	1.47	0.72	99.7%	0.3%	63.3%	36.7%
5	17.03	1.00	2001.57	1.04	6.13	3.44	1.25	0.50	1.27	0.51	99.8%	0.2%	68.7%	31.3%
6	15.59	1.50	2002.89	1.56	6.72	3.45	1.73	0.82	1.76	0.82	99.7%	0.3%	62.8%	37.2%
7	17.25	1.09	2001.31	1.17	6.29	3.42	1.32	0.55	1.34	0.57	99.8%	0.2%	54.0%	46.0%
8	14.32	1.40	2004.22	1.44	6.41	3.38	1.60	0.79	1.63	0.79	99.6%	0.4%	70.3%	29.7%
9	14.31	1.95	2004.22	1.96	6.44	3.56	1.92	0.96	1.94	0.95	99.6%	0.4%	60.2%	39.8%
10	9.56	2.45	2008.92	2.51	6.56	3.50	0.00	0.06	0.01	0.13	100.0%	0.0%	54.7%	45.3%
11	10.80	2.70	2007.58	2.87	6.73	3.58	0.00	0.00	0.02	0.12	90.2%	9.8%	47.0%	53.0%
12	8.16	1.65	2010.34	1.62	6.60	3.33	0.01	0.16	0.01	0.16	0.0%	100.0%	49.4%	50.6%
13	7.37	5.78	2011.11	5.75	6.66	3.53	0.34	5.59	0.39	5.96	0.0%	100.0%	56.4%	43.6%
14	7.35	4.69	2011.15	4.67	6.48	3.48	0.20	4.35	0.20	4.35	0.0%	100.0%	56.3%	43.7%
15	16.31	1.02	2002.08	1.09	6.81	3.56	0.00	0.00	0.00	0.04	99.8%	0.2%	50.7%	49.3%
16	17.15	0.36	2001.25	0.58	6.95	3.51	0.00	0.00	0.01	0.10	99.7%	0.3%	62.0%	38.0%
17	17.21	0.41	2001.25	0.62	6.31	3.64	0.00	0.00	0.02	0.24	100.0%	0.0%	55.8%	44.2%
18	7.29	1.85	2011.22	1.91	6.52	3.26	0.18	0.88	0.18	0.88	0.0%	100.0%	71.4%	28.6%
19	17.54	0.50	2000.88	0.64	6.93	3.41	0.00	0.00	0.00	0.05	99.3%	0.8%	45.8%	54.3%

Cluster	FAMILY				TRAJECTORY
	PPS BENEFICIARY		SES		ATTENDANCE LAST CYCLE				LAST_LEVEL				REPETITION
					LAST CYCLE		CRONIC UNATTENDANCE		LEVEL		APPROVED	COMPLETED
	Yes	No	mean	std	mean	std	mean	std	mean	std			mean	std
0	86.71%	13.29%	0.29	0.21	74.52	18.05	1.59	0.99	9.15	2.03	0	1	1.56	0.55
1	84.05%	15.95%	0.31	0.24	85.37	12.47	0.84	0.88	10.13	0.89	0	0	0.55	0.56
2	51.68%	48.32%	0.52	0.32	76.78	12.72	1.97	0.98	7.44	3.24	1	1	0.43	0.52
3	88.43%	11.57%	0.30	0.21	80.39	11.47	1.86	0.89	9.81	0.43	1	1	1.87	0.73
4	94.60%	5.40%	0.22	0.17	82.13	14.13	1.34	1.30	9.07	1.82	0	0	2.10	0.88
5	92.73%	7.27%	0.24	0.18	75.70	17.17	1.67	1.16	9.78	0.92	0	1	2.87	0.74
6	92.03%	7.97%	0.25	0.20	85.35	11.15	2.19	1.88	7.86	1.46	1	1	2.20	1.00
7	96.19%	3.81%	0.20	0.16	81.00	15.26	1.07	1.07	9.93	0.98	0	0	1.05	0.72
8	94.42%	5.58%	0.23	0.17	76.11	15.47	2.75	1.54	6.72	1.27	0	1	3.14	0.97
9	96.89%	3.11%	0.19	0.15	75.33	15.66	2.05	1.33	6.38	1.74	0	0	1.42	0.99
10	54.00%	46.00%	0.47	0.31	88.53	10.04	0.73	0.98	4.20	2.32	0	0	0.16	0.39
11	73.48%	26.52%	0.30	0.23	83.84	12.87	1.06	0.96	4.83	2.69	0	0	0.02	0.12
12	100.00%	0.00%	0.28	0.12	89.71	8.67	0.78	0.96	2.90	1.60	1	1	0.05	0.22
13	5.62%	94.38%	0.33	0.23	92.56	5.87	0.17	0.46	1.74	1.15	0	0	0.03	0.17
14	0.00%	100.00%	0.36	0.26	90.50	8.37	0.52	0.69	1.84	1.38	1	1	0.02	0.14
15	91.64%	8.36%	0.27	0.19	84.72	11.96	0.86	0.89	10.31	1.02	0	0	0.02	0.15
16	83.94%	16.06%	0.32	0.22	83.81	10.37	2.10	1.36	11.29	0.46	0	1	1.82	0.42
17	91.56%	8.44%	0.29	0.20	77.51	12.69	2.22	0.98	11.21	0.41	0	1	1.01	0.08
18	7.69%	92.31%	0.30	0.21	71.69	24.92	0.89	0.66	1.81	1.51	0	1	1.03	0.18
19	85.00%	15.00%	0.28	0.22	85.08	9.17	1.90	1.21	12.00	0.00	0	0	0.45	0.50

Cluster	TRAJECTORY
	ZSCORE		CHANGE OF SCHOOLS				LEVEL YEARS				Abandonment (Qtty)		ENROLLMENTS (Qtty)
			INTER YEAR		INTRA-YEAR		PRIMARY		SECONDARY
	mean	std	mean	std	mean	std	mean	std	mean	std	mean	std	mean	std
0	-1.66	0.82	1.91	1.38	0.52	0.82	7.93	1.40	1.83	1.09	0.06	0.23	9.77	2.00
1	-0.63	0.82	2.09	1.40	0.59	0.86	8.31	0.47	2.39	1.00	0.00	0.00	10.69	0.97
2	-0.56	0.90	1.74	1.57	0.56	0.85	6.62	2.55	1.35	1.35	0.09	0.29	7.97	3.59
3	-0.85	0.66	2.69	1.60	0.75	0.95	9.25	0.90	2.64	0.95	0.13	0.36	11.90	0.64
4	-0.99	0.87	2.47	1.57	0.67	0.94	9.29	1.27	1.99	1.62	0.00	0.00	11.27	1.90
5	-1.64	0.73	2.51	1.51	0.55	0.84	9.29	0.86	2.56	1.28	0.12	0.35	11.85	1.04
6	-0.88	0.67	2.22	1.57	0.74	1.00	9.86	1.47	0.48	0.99	0.15	0.41	10.33	1.65
7	-0.74	0.89	3.18	1.64	0.81	1.04	8.60	0.66	3.54	1.22	1.13	0.35	12.14	1.11
8	-1.59	0.65	1.98	1.54	0.66	0.95	9.08	1.52	0.00	0.00	0.15	0.40	9.08	1.52
9	-1.03	0.76	2.67	1.56	1.02	1.14	9.10	2.00	0.00	0.00	1.22	0.46	9.10	2.00
10	-0.08	0.83	0.59	0.96	0.27	0.61	4.36	2.47	0.00	0.00	0.00	0.00	4.36	2.47
11	-0.29	0.70	1.86	1.41	0.67	0.95	5.80	2.70	0.00	0.00	1.00	0.00	5.80	2.70
12	0.29	0.85	0.26	0.59	0.10	0.34	2.96	1.61	0.00	0.00	0.01	0.08	2.96	1.61
13	0.05	0.57	0.08	0.30	0.06	0.25	1.76	1.14	0.00	0.06	0.00	0.02	1.77	1.15
14	0.29	0.84	0.10	0.35	0.06	0.25	1.85	1.34	0.01	0.14	0.00	0.06	1.86	1.39
15	-0.32	0.60	2.68	1.38	0.71	0.89	8.00	0.04	3.32	1.02	1.00	0.00	11.31	1.02
16	-1.30	0.56	2.09	1.50	0.44	0.74	8.37	0.49	3.76	0.57	0.00	0.02	12.14	0.34
17	-1.11	0.59	2.94	1.62	0.60	0.91	8.00	0.00	4.21	0.41	1.00	0.00	12.21	0.41
18	-1.82	1.17	0.16	0.37	0.12	0.39	1.84	1.49	0.01	0.10	0.02	0.15	1.85	1.54
19	-0.60	0.65	2.16	1.54	0.53	0.84	8.21	0.41	4.26	0.44	0.00	0.00	12.47	0.50

Cluster	LAST SCHOOL								DROPOUT PROBABILITY
	SCHOOL CATEGORY				SCHOOL SIZE (Qtty Teachers)		SCHOOL EFFECTIVENESS (score)
	Voucher	Public	Adm	Private	mean	std	mean	std	mean	std
0	48.6%	42.7%	6.0%	2.7%	28.17	15.94	46.26	10.22	0.84	0.11
1	44.5%	44.2%	5.8%	5.5%	29.48	15.86	45.57	10.35	0.99	0.00
2	52.3%	20.0%	1.7%	25.9%	21.19	13.17	50.28	11.36	0.64	0.10
3	40.8%	51.0%	5.1%	3.1%	28.06	14.98	43.39	9.10	0.82	0.10
4	34.0%	57.9%	7.2%	0.9%	25.49	14.97	41.96	8.20	1.00	0.00
5	38.0%	52.5%	8.5%	1.0%	30.44	15.00	43.42	8.86	0.97	0.02
6	41.8%	55.2%	0.9%	2.2%	15.62	9.94	43.51	8.66	0.83	0.13
7	33.3%	59.9%	6.4%	0.4%	28.12	13.18	39.76	6.63	0.98	0.02
8	46.2%	52.9%	0.2%	0.7%	14.89	7.08	43.78	8.40	0.96	0.03
9	37.6%	61.6%	0.0%	0.9%	12.27	6.32	41.14	7.58	0.98	0.03
10	45.6%	32.7%	0.0%	21.7%	15.87	8.66	50.00	10.15	0.99	0.00
11	45.5%	52.3%	0.8%	1.5%	13.05	9.21	43.62	9.60	0.85	0.05
12	36.1%	63.3%	0.0%	0.6%	13.86	5.67	45.60	8.17	0.77	0.09
13	32.7%	59.9%	0.0%	7.4%	13.90	7.49	45.26	8.38	1.00	0.00
14	28.8%	60.5%	0.0%	10.7%	14.73	8.61	45.30	7.64	0.90	0.06
15	41.6%	49.3%	8.0%	1.0%	27.71	13.59	41.71	7.96	0.95	0.04
16	47.2%	43.9%	5.7%	3.2%	30.24	15.92	47.32	10.63	0.97	0.01
17	42.2%	49.4%	7.1%	1.3%	30.16	15.16	43.26	9.09	0.98	0.01
18	33.0%	62.6%	1.1%	3.3%	14.05	8.92	46.00	8.46	0.89	0.07
19	41.8%	48.1%	6.5%	3.6%	29.30	15.58	45.36	9.96	1.00	0.00

Funding

We thank the support from ANID/PIA/Basal Funds for Centers of Excellence FB0003 and ANID-FONDEF IT17I0006 grants.

Data availability

Specially thanks to the Center of Studies from the Ministry of Education, Agency of Quality of Education and JUNJI for providing special datasets to develop the model.

The data that support the findings of this study are available from Ministry of Education – Open data platform, but restrictions apply to the availability of these data, which were used under licence for the current study, and so are not publicly available. Data are however available from the authors upon reasonable request and with permission of Ministry of Education, Agency of Quality of Education and/or JUNJI.

Declarations

Competing interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.