Abstract
A strained Ge quantum well, grown on a SiGe/Si virtual substrate and hosting two electrostatically defined hole spin qubits, is nondestructively investigated by synchrotron-based scanning X-ray diffraction microscopy to determine all its Bravais lattice parameters. This allows rendering the three-dimensional spatial dependence of the six strain tensor components with a lateral resolution of approximately 50 nm. Two different spatial scales governing the strain field fluctuations in proximity of the qubits are observed at <100 nm and >1 μm, respectively. The short-ranged fluctuations have a typical bandwidth of 2 × 10–4 and can be quantitatively linked to the compressive stressing action of the metal electrodes defining the qubits. By finite element mechanical simulations, it is estimated that this strain fluctuation is increased up to 6 × 10–4 at cryogenic temperature. The longer-ranged fluctuations are of the 10–3 order and are associated with misfit dislocations in the plastically relaxed virtual substrate. From this, energy variations of the light and heavy-hole energy maxima of the order of several 100 μeV and 1 meV are calculated for electrodes and dislocations, respectively. These insights over material-related inhomogeneities may feed into further modeling for optimization and design of large-scale quantum processors manufactured using the mainstream Si-based microelectronics technology.
Keywords: lattice strain, synchrotron, X-ray diffraction, quantum computing, silicon germanium, thermomechanical FEM simulation
1. Introduction
The development of a fault-tolerant universal quantum computer will require the integration of millions of qubits.1 This long-term requirement has motivated research into silicon quantum dot (QD) spin qubits, which are compatible with the transistor process flow in advanced semiconductor manufacturing and have long coherence time.2,3 While most efforts have been focused on electron spin qubits, hole spins in planar germanium have rapidly emerged as a promising platform for scaling to large quantum processors,4 due to several advantageous properties. The high mobility in strained Ge/SiGe heterostructures ensures a low-disorder qubit environment;5,6 the light effective mass gives rise to large orbital splitting, and the absence of valley degeneracy improves the qubit state isolation,7 easing quantum operation, while the inherent strong spin–orbit coupling allows for fast and local qubit driving.8 Furthermore, Ge qubits may also benefit from advanced semiconductor manufacturing by introduction into an industrial-scale foundry process.9 Indeed, recent progress with planar Ge qubits includes full operation of a 2 × 2 spin qubit array,10 single-triplet qubits at low magnetic fields,11 and simultaneous qubit driving at the fault-tolerant threshold.12
To increase the qubit count, quantum-dot crossbars are envisioned, eventually interconnected by coherent links and having a shared gate control.13 This, in turn, requires a high degree of spatial homogeneity of the potential landscape in the active region of the semiconductor material. Recent progress in this direction includes the demonstration of a germanium crossbar where the shared control of plunger and barrier gates enables the definition of 16 QDs with similar occupancy and addressable interdot coupling.14
In large-scale spin qubit quantum processors,
the homogeneity of
the confining potential landscape may be influenced by irregularities
in the shape of the nanofabricated metallic electrodes, which define
and control the QD. However, attention should be equally paid to local
energy variations due to inhomogeneities in the semicondutor material,
especially in strained quantum wells (QWs), such as fluctuations of
the lattice deformation,15 which are described
by the spatially dependent strain tensor 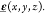 Indeed, the strain tensor may
be affected
by local defects, such as bunches of misfit dislocations (MD).16 These strain fluctuations, occurring over a
spatial scale in excess of 1 μm, related to the misfit dislocation
network present in heteroepitaxial systems,17,18 could challenge the uniformity of the energy landscape experienced
by a large array of qubits and, consequently, shared gate control
architectures.
Indeed, the strain tensor may
be affected
by local defects, such as bunches of misfit dislocations (MD).16 These strain fluctuations, occurring over a
spatial scale in excess of 1 μm, related to the misfit dislocation
network present in heteroepitaxial systems,17,18 could challenge the uniformity of the energy landscape experienced
by a large array of qubits and, consequently, shared gate control
architectures.
Furthermore, a stressing action over smaller length scales may arise from the metal contacts in the gate stack,20,21 which control the QD confining potential. Strain inhomogeneities with a length scale of ∼100 nm were reported in gate-defined electron QDs in Si/SiGe heterostructures. This kind of strain fluctuation was found to induce a spatially varying potential-energy landscape in the Si QW layer with a peak-to-peak amplitude of 1.4 meV.22 In Si-MOS systems, where the electron gas is accumulated directly below the metal gate stack, lattice deformation from metal electrodes may even induce the formation of QDs below the metal electrodes in the absence of an electrical bias.21 Therefore, the possible spatial variation of the strain landscapes should be measured, ideally with resolution matching the QD sizes and taking into account in the design of qubit crossbars.
Spatial characterization of strain in heteroepitaxial layers using scanning X-ray diffraction microscopy (SXDM) has progressed significantly in the past decade. In 2012, Evans et al. investigated the lattice distortions in a Si/Si0.7Ge0.3 heterostructure for electron spin qubits by mapping projections of the reciprocal space map (RSM) of the 004 Bragg reflection of the Si QW layer.15 An improved version of the SXDM technique was introduced in 2014,23 and soon after, Zoellner et al. showed that by combining two SXDM data sets, acquired for the 004 and 113 Bragg reflections, the contributions of lattice tilt, in-plane, and vertical strain to the scattering vector can be individually quantified in epitaxial Si0.3Ge0.7 layers.16 Finally, in 2022, Richter et al. utilized SXDM data sets from three asymmetric Bragg reflections to measure the local variations of the strain tensor induced by composition fluctuations and the presence of dislocations in a patterned InxGa1–xN double layer.24
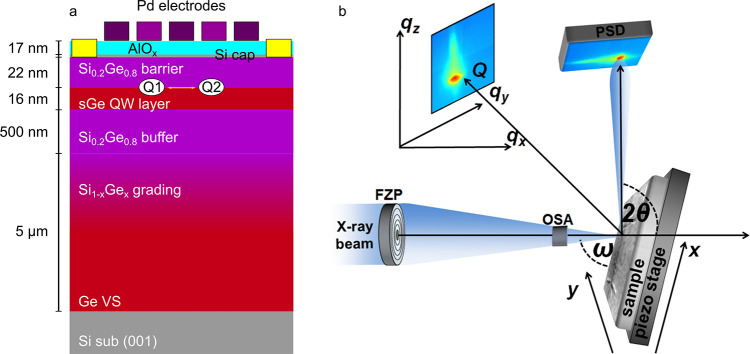
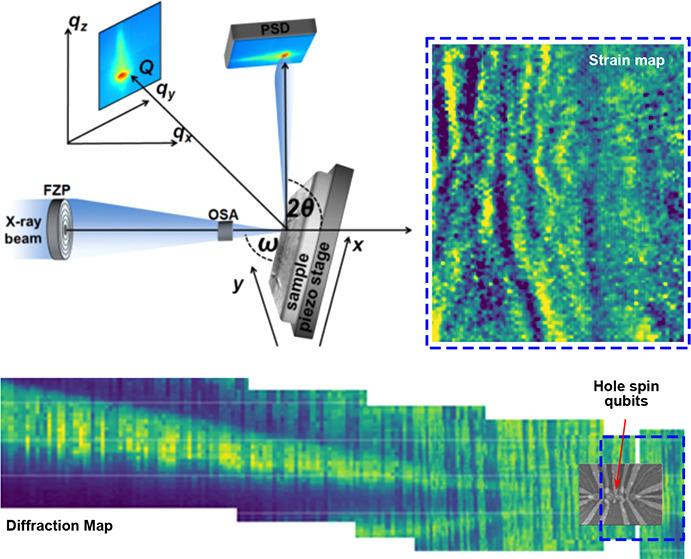
In this work, we use the state-of-the-art SXDM technique to fully measure the spatial dependence of the strain tensor in the lattice of a Ge QW layer hosting a functional quantum processor. This is the exact same device employed for the demonstration of fast two-qubit logic with holes in germanium.19 In this device, the cross-section of which is shown in Figure 1a, two QD qubits Q1 and Q2 are defined by applying voltages to a set of metal electrodes, to laterally confine holes in the single (s)Ge QW layer. A detailed description of the electronic properties of the device and its qubits is given by Hendrickx et al.19
Figure 1.
(a) Schematic cross section of the heterostructure and device gate layer stacks.19 (b) Experimental setup of the scanning X-ray diffraction microscopy measurement.
We use the experimental setup at the beamline ID01/ESRF (Figure 1b) and acquire diffraction
maps for three different asymmetric Bragg reflections to achieve the
two-dimensional SXDM mapping of 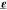 in the QW layer within the device area
with a lateral resolution of ∼50 nm. We make use of the increased
flux of the X-ray beam after the extremely bright source (EBS) upgrade
to the ESRF storage ring,25 enabling us
to observe the diffraction from the 16 nm thin Ge QW layer even with
this small spot size. We analyze the room temperature SXDM measurements
using Fourier transform band filtering to disentangle the contribution
to the lattice distortion brought by the metal electrodes (short spatial
scale) and by the dislocation field (longer scale). We compare the
electrode-induced strain at room temperature (RT) with numerical results
obtained from finite element calculations (COMSOL MultiPhysics) and
use this modeling to extrapolate the electrode-induced strain at cryogenic
temperature. The induced strain is enhanced at low temperature (LT)
by the additional compressive stress caused by the mismatch of the
thermal expansion existing between the metal electrodes and the QW
stack. Finally, we have performed band-structure simulations, taking
into account all the components of the strain tensor, and estimated
the resulting band-edge energy fluctuations in the QW layer in proximity
of the qubits.
in the QW layer within the device area
with a lateral resolution of ∼50 nm. We make use of the increased
flux of the X-ray beam after the extremely bright source (EBS) upgrade
to the ESRF storage ring,25 enabling us
to observe the diffraction from the 16 nm thin Ge QW layer even with
this small spot size. We analyze the room temperature SXDM measurements
using Fourier transform band filtering to disentangle the contribution
to the lattice distortion brought by the metal electrodes (short spatial
scale) and by the dislocation field (longer scale). We compare the
electrode-induced strain at room temperature (RT) with numerical results
obtained from finite element calculations (COMSOL MultiPhysics) and
use this modeling to extrapolate the electrode-induced strain at cryogenic
temperature. The induced strain is enhanced at low temperature (LT)
by the additional compressive stress caused by the mismatch of the
thermal expansion existing between the metal electrodes and the QW
stack. Finally, we have performed band-structure simulations, taking
into account all the components of the strain tensor, and estimated
the resulting band-edge energy fluctuations in the QW layer in proximity
of the qubits.
2. Results and Discussion
First, we discuss the analysis procedure leading to the calculation of the position-dependent strain tensor from the knowledge of the lattice parameters in the sGe QW layer which, in turn, we obtained from the SXDM diffraction maps.
In Figure 2, we
show an exemplary RSM acquired at a given location of the SXDM map.
The most intense peaks (in green) originate from the underlying Ge/Si(001)
section of the virtual substrate (VS) and the Si0.2Ge0.8 buffer. These two intense peaks are connected by a continuous
diffraction signal originating from the Si1–xGex in the linearly reverse-graded VS portion
(see Figure 1a). The
diffraction signal from the pseudomorphic Ge QW layer can be individuated
along Qz, just below
the Si0.2Ge0.8 buffer signal, at the same in-plane
momentum transfers 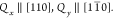
Figure 2.
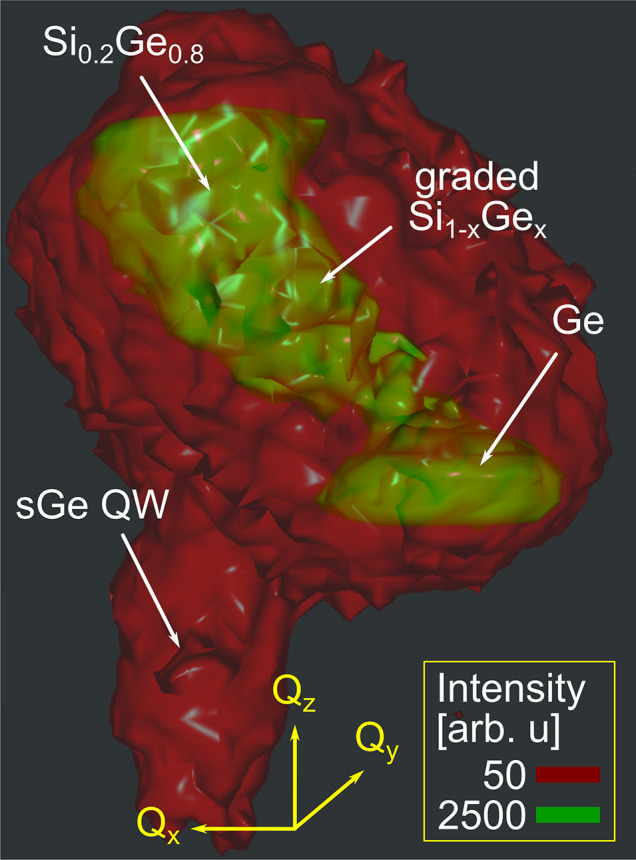
Isosurface plot of the 3D reciprocal space map around the 335 Bragg reflection of the heterostructure. The relative intensities for the isosurfaces are described in the legend.
We point out that the possibility to isolate the QW layer contribution in a reliable way is given by the improved brilliance of the X-ray beam after the EBS upgrade that allowed us to record the signal from the thin QW layer with reasonable intensity, enabling a thorough analysis of its lattice inhomogeneities. This enables a tomographic characterization of the sample lattice, since, in the laterally resolved SXDM maps, we elaborate only the signal originating from the depth of the QW layer.
2.1. X-ray Diffraction Maps
After fitting
the position of the QW layer peak in the 3D reciprocal space map at
every (x,y) point on the map, we
obtain laterally resolved spatial maps of the three components Qx, Qy, and Qz of the scattering vector 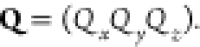 The data processing
and peak fitting procedure
employed to determine the local Q from the raw data are
described in the data analysis section in the Supporting Information. In Figure 3, the map of the total length of the scattering
vector Q = |Q| is shown for the three
reflections
The data processing
and peak fitting procedure
employed to determine the local Q from the raw data are
described in the data analysis section in the Supporting Information. In Figure 3, the map of the total length of the scattering
vector Q = |Q| is shown for the three
reflections 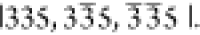 Due to drift of the sample
during the measurement,
the maps of Q for the three different Bragg reflections
cover areas slightly shifted with respect to each other. In the following
analysis, only the area covered by all three data sets is considered
(red boxes in Figure 3).
Due to drift of the sample
during the measurement,
the maps of Q for the three different Bragg reflections
cover areas slightly shifted with respect to each other. In the following
analysis, only the area covered by all three data sets is considered
(red boxes in Figure 3).
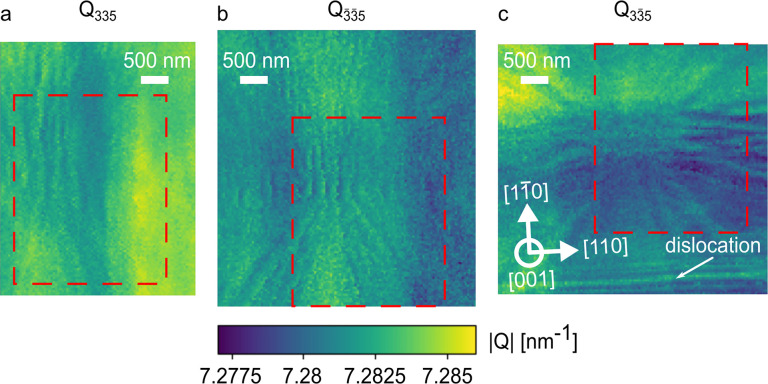
Figure 3.
Maps for the length of the scattering vector Q from
the Ge QW layer in the vicinity of the qubits: (a) diffraction
map for the 335 reflection; (b) 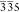 diffraction
map; (c) 33̅5 diffraction
map. The direction of the lattice planes is described by the white
arrows. The area on the sample which is covered by all three reflections
and thus suitable for calculation of the full strain tensor is outlined
by the red dashed box.
diffraction
map; (c) 33̅5 diffraction
map. The direction of the lattice planes is described by the white
arrows. The area on the sample which is covered by all three reflections
and thus suitable for calculation of the full strain tensor is outlined
by the red dashed box.
We notice that the maps
of the 335 and 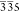 reflections
do not appear identical, as
would be expected for two opposite asymmetric reflections, if the
lattice was deformed by only normal instead of asymmetric strain.
The difference of the local lengths of the scattering vectors between
335 and
reflections
do not appear identical, as
would be expected for two opposite asymmetric reflections, if the
lattice was deformed by only normal instead of asymmetric strain.
The difference of the local lengths of the scattering vectors between
335 and 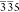 is attributed
to local shear strains. This
is an indication of the power of the SXDM technique and its ability
to resolve the shear deformation in a crystalline lattice with nanoscale
spatial resolution, which cannot be achieved by other methods to the
knowledge of the authors.
is attributed
to local shear strains. This
is an indication of the power of the SXDM technique and its ability
to resolve the shear deformation in a crystalline lattice with nanoscale
spatial resolution, which cannot be achieved by other methods to the
knowledge of the authors.
Also, we observe a relatively narrow, sharp line in the 33̅5 reflection that we attribute to the lattice deformation around a misfit dislocation (MD), the region of which is not covered in the maps of the other two reflections. The small width in real space of this feature, compared to the long-ranged modulations stemming from the MD-network providing plastic relaxation of the virtual substrate, suggests that it is a misfit segment of a dislocation loop located close to the QW layer (the threading segment is not observed within the map).26
As such, we believe that the presence of this MD is associated with the onset of the plastic relaxation of the QW layer, which is close to its critical thickness.27 Alternatively, the MD could be located close to the interface between the top SiGe barrier and the Ge QW or at the interface between the top SiGe barrier and the only 2 nm thin, but highly strained Si cap. Its orientation and slipping plane match that for MDs in the (Si)Ge/Si(001) system, which typically run parallel to ⟨110⟩ directions within the interface,28 allowing us to determine the precise orientation of the lattice planes within the SXDM maps.
2.2. Strain Tensor
From the three diffraction
maps, we calculate the six lattice parameters 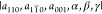 by a procedure described in the data analysis
section in the Supporting Information.
Together, the six parameters provide a complete description of the
lattice distortion relative to a reference lattice which, in our analysis
of the QW layer, is represented by the Ge diamond lattice with a lattice
constant of a0 = 5.6578 Å.29 To calculate the strain tensor, we define an
orthogonal reference system setting x̂ and ŷ along the [110] and
by a procedure described in the data analysis
section in the Supporting Information.
Together, the six parameters provide a complete description of the
lattice distortion relative to a reference lattice which, in our analysis
of the QW layer, is represented by the Ge diamond lattice with a lattice
constant of a0 = 5.6578 Å.29 To calculate the strain tensor, we define an
orthogonal reference system setting x̂ and ŷ along the [110] and 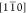 crystallographic axes. With this choice, ẑ is parallel to the [001] axis, and following Schlenker
et al.,30 one finds
crystallographic axes. With this choice, ẑ is parallel to the [001] axis, and following Schlenker
et al.,30 one finds
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
2.3. Strain Fluctuations in the Ge QW Layer
In Figure 4a, we show the scanning electron microscopy (SEM) image of the double qubit device under analysis. For our further discussion, we have labeled the different electrodes appearing in the top half of the SEM image (e1–e5). In Figure 4b, we show a typical strain map, here that of the εzz component, as derived from SXDM data. Here the inner region of the device, i.e., the area depicted in panel a, is bounded by the dashed blue box. The strain field landscape appears to be modulated at two different length scales: a short one, of a few tens of nanometers, governing the abrupt, short-range strain changes in the areas covered by electrodes and a longer one, on the 1 μm scale, which is associated with strain gradients that we attribute to the presence of misfit dislocations in the underlying plastically relaxed layers.16
Figure 4.
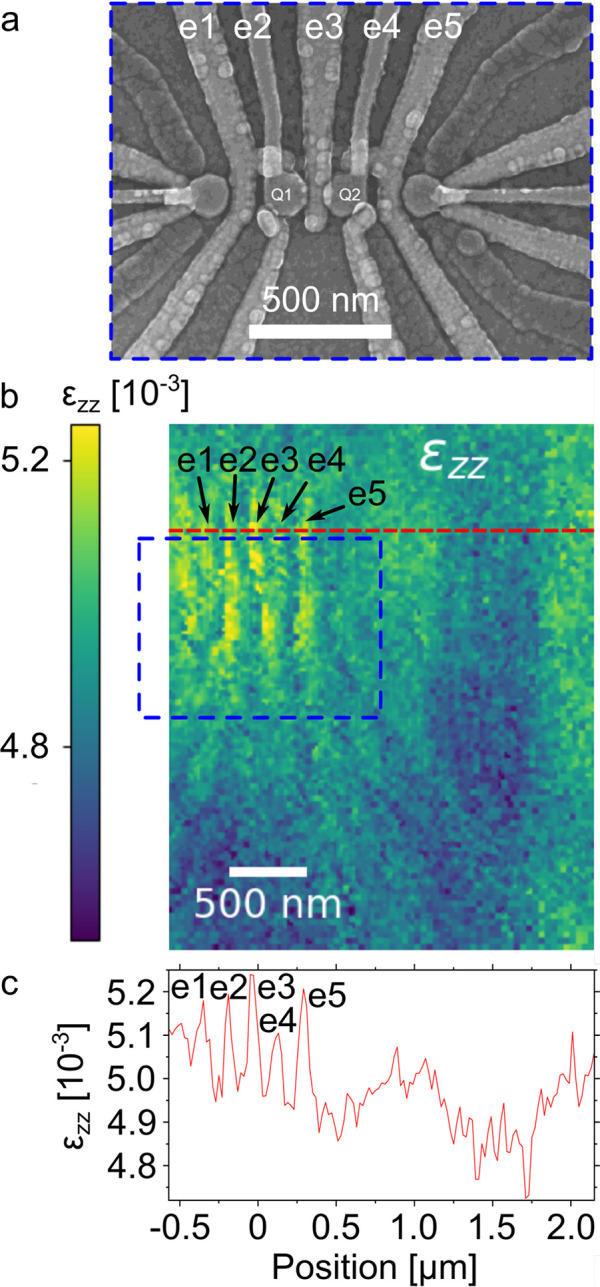
SEM image, εzz strain map, and strain line profile. (a) Top view SEM image of the qubit device. The QDs housing the two qubits are labeled with Q1, Q2 and the electrodes for qubit control with e1–e5. (b) Map of the εzz strain. The area in the blue box is the region shown in the SEM image. (c) Profile along the red line in (b).
The perturbation to the strain field εzz component associated with the e1–e5 electrodes is clearly visible on the left side on panel c, with steep and narrow (on the 100 nm scale) increase of the strain field with a magnitude of few 10–4 units. This short-scale fluctuation is superimposed to the long-range contribution (over a scale of approximately 1 μm) by the MD networks located in the plastically relaxed VS. The MD network causes fluctuations of both strain and composition,16 resulting in a modulation of the local lattice constant in the SiGe at the bottom interface of the Ge QW layer.
The length scale of this modulation corresponds to the distance of the MD network to the interface, which is at least the 500 nm thickness of the Si0.2Ge0.8 buffer layer, for which strain and composition maps of are provided in the Supporting Information.
Thus, we conclude that the strain fluctuations caused by the electrodes and the strain/composition fluctuations in the underlayer take place on very different length scales, of approximately 100 nm vs >500 nm lateral extent. Therefore, we are able to univocally distinguish between them based on their spatial frequencies.
We now concentrate on the electrode-driven strain modulation of the QW layer. To this purpose, we have applied a Fourier bandpass filter to all six strain component maps to remove the long-range fluctuations induced by crystal defects present in the underlying virtual substrate (the unfiltered maps are available in Figure S3).
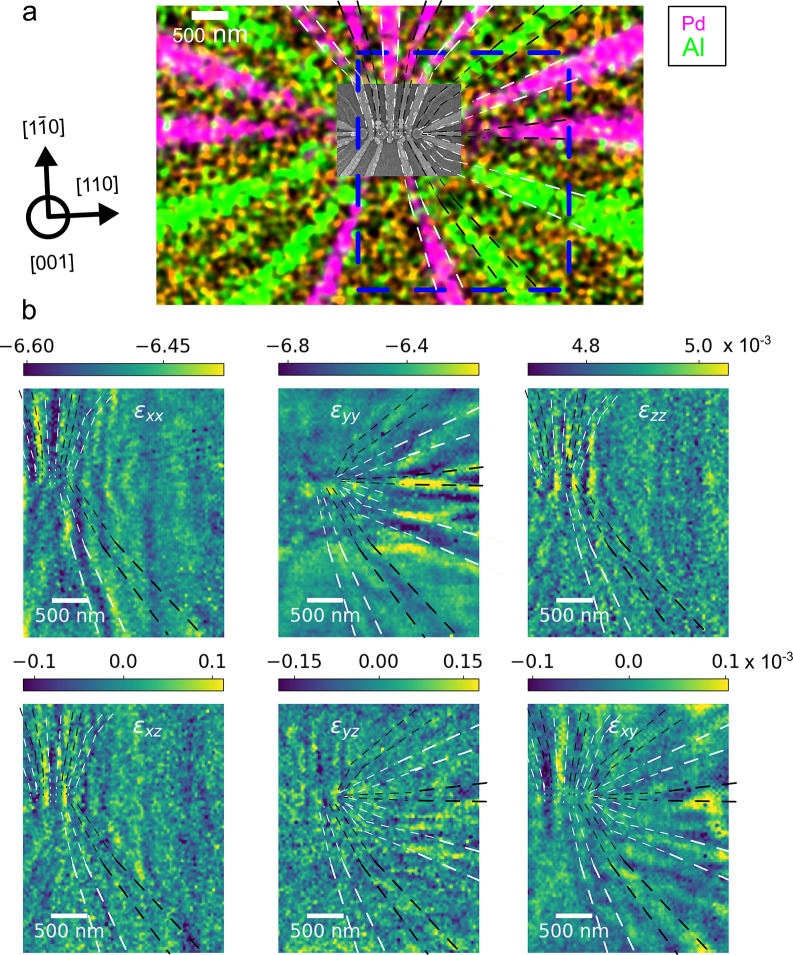
Filtered images are presented in Figure 5 together with the SEM image of Figure 4a, here overlaid to an energy-dispersive X-ray (EDX) spectroscopy map of the Pd and Al signal, stemming from the electrodes, which we use as a reference framework for our further analysis (Figure 5a).
Figure 5.
SXDM strain maps for the effect of the metal electrodes. (a) Map of the EDX signals for the electrode materials overlaid with the SEM image. The blue box outlines the area covered by the SXDM strain maps. The black arrows describe the orientation of the lattice planes within the maps. (b) Maps of all six strain tensor components after application of a Fourier high-pass filter. The dashed black and white lines in each map outline the positions of the electrodes which have a visible effect on the respective strain component. The color bars describe the local strains in multiples of 10–3.
The comparison of the SEM/EDX images and the filtered strain maps enables us to univocally link the local short-range features in the strain maps to each of the individual electrodes, since the imprint of the device is apparent in the maps. The strain field in the Ge QW layer beneath a metal stripe strongly depends on its lateral size, chemical composition, and orientation. Consequently, electrodes oriented along different directions are characterized by different visibility in the six SXDM maps.
The average in-plane biaxial strain in the Ge QW layer is approximately −6.5 × 10–3, resulting from the sum of the heteroepitaxial strain due to the lattice mismatch between the Ge QW and the SiGe buffer layer, and the thermal strain which stems from the difference in the coefficient of thermal expansion existing between the Ge-rich epi-layers and the Si substrate.31
Directly underneath an electrode, we generally observe a decrease of approximately (1–2) × 10–4 in one or both of the in-plane diagonal strain components εxx or εyy. The details of this perturbation to the purely biaxial strain field vary for the individual electrodes and depend on their orientation. Electrodes running mostly along one of the {110} planes cause a modulation in either εxx or εyy, while electrodes running diagonal to the {110} planes affect both components.
In line with the compressive deformation, induced below the central region of the electrode, near its edges we generally observe a corresponding increase of the in-plane diagonal strains, with comparable magnitude of (1–2) × 10–4.
If the lattice becomes compressed along the in-plane directions in a given location, generally at the same spot the lattice stretches in the out-of-plane direction, since, in Ge, the system tends to preserve the Bravais cell volume. Therefore, also the εzz strain component, whose average value is again controlled by the lattice mismatch with the buffer layer, is locally affected by electrodes. Directly underneath an electrode, we generally observe a magnitude of this strain perturbation of approximately (1–2) × 10–4, a value close to the one observed for the in-plane diagonal components, but opposite in sign.
Likewise, beside an electrode, where the in-plane perturbation of the strains are more tensile, a compressive effect on εzz is observed.
Under biaxial stress condition with no stress along the surface normal, which is typically assumed for extended epitaxial layers studied with large X-ray beams, the relation between in-plane and out-of-plane strain is linear and described by the Poisson ratio. To check the validity of this assumption for our case, we calculated spatial maps of the stress tensor from the strain measurements, finding non-negligible local values for σzz in the vicinity of the device (see Figure S6). Thus, we conclude that within the qubit device, the biaxial stress model is not entirely valid and more complex relations between εxx, εyy, and εzz need to be considered.
In line with the consideration above, we can observe a clear “footprint” of the device structure also in the maps of the shear strains described by the off-diagonal components of the strain tensor (which are identically zero in the purely biaxial strain condition).
In absolute terms, the shear strains are smaller than the normal strains by at least 2 orders of magnitude. However, they undergo local changes around the electrodes on a magnitude of approximately (1–2) × 10–4.
The out-of-plane shear component
εxz varies mainly across the electrodes
oriented in 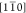 direction; thus its map appears qualitatively
similar to that of εxx. Accordingly,
εyz is modulated by electrodes running
along [110] and therefore shows similarities to εyy. The in-plane shear εxy shows the imprint of all electrodes independent of their orientation.
Importantly, we observe that the changes of the shear strains induced
by the electrodes are within the same order of magnitude of the perturbation
induced by the electrodes on the diagonal components of the strain
tensor and thus cannot be neglected in the modeling of the local properties
of the QW layer.
direction; thus its map appears qualitatively
similar to that of εxx. Accordingly,
εyz is modulated by electrodes running
along [110] and therefore shows similarities to εyy. The in-plane shear εxy shows the imprint of all electrodes independent of their orientation.
Importantly, we observe that the changes of the shear strains induced
by the electrodes are within the same order of magnitude of the perturbation
induced by the electrodes on the diagonal components of the strain
tensor and thus cannot be neglected in the modeling of the local properties
of the QW layer.
2.4. Thermomechanical Deformation Induced by the Electrodes
We now discuss the origin of the strain induced by the electrodes. The internal stress of a metallic thin film, deposited onto a substrate at a given temperature, is comprised of intrinsic and extrinsic (thermal) stress.20 Consequently, the electrode itself acts as a stressor for the underlying lattice. The intrinsic stress in the metal layer is due to the deposition process and it is influenced by different process parameters, such as the metal growth rate and the actual temperature of the metal during fabrication, which is very difficult to know due to the localized heating effect of the ion beam used for deposition. This can lead to different metal crystallite sizes, orientations, and coalescence, parameters that are very difficult to control at the nanometer scale and that, ultimately, control the intrinsic metal stress. Furthermore, when the metal cools down from its deposition temperature, the electrode accumulates additional stress due to the mismatch of the coefficient of thermal expansion (CTE) existing between the metal and the semiconductor/oxide substrate (see Table 1). Since the metals (Pd and Al) contract more than the semiconductor layers, the (Si)Ge lattice beneath the electrodes experiences additional compressive, lateral stress. It follows that the resulting deformation in these regions, already clearly visible in the present experimental data for the Ge QW layer at T = 300 K, is expected to be enhanced when cooling down to cryogenic temperatures. To emphasize this point we notice that the operation temperature for any qubit device to date is in the mK regime. Therefore, to achieve a better understanding of the impact of the strain fluctuations on the electronic properties of semiconductor qubit devices, we have developed a numerical approach to extrapolate our RT measurements to the cryogenic regime.
Table 1. Linear Thermal Expansion Coefficient (CTE) at Standard Conditions (T ≈ 300 K) for the Materials in the Hole Spin Qubit Device.
For this purpose, the mechanical properties of the (Si)Ge semiconductor structure and the metal regions have been modeled by FEM simulations using the COMSOL Multiphysics suite.
We note that the device had already been cooled down to approximately 20 mK when its quantum properties were characterized prior to the SXDM measurements.19 Thus, additional cryogenic cycling starting from the state in which the strain maps were taken is likely to cause only elastic deformation, as we assume in the simulations.
As a first step, we have calibrated the COMSOL RT simulation using the SXDM data, since it is very difficult to accurately determine the initial stress condition of the metal induced by the deposition process.
Subsequently, we have used the obtained stress as initial condition for the extrapolation of the strain field of the electrode/semiconductor system at T = 1 K (details are given in the thermomechanical simulation section of the Supporting Information).
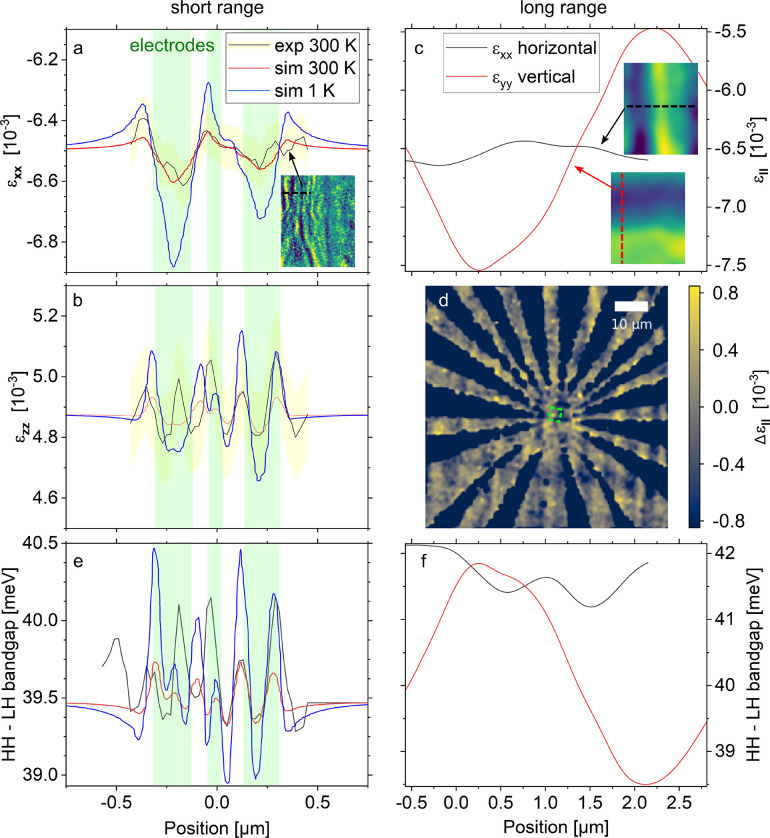
In Figure 6a, we plot the numerical values of εxx, calculated at T = 300 K and T = 1 K, along with experimental curves obtained from the average of several adjacent line cuts across three electrodes, evidenced in the inset where the Fourier-filtered εxx strain map of Figure 5 is displayed. The out-of-plane strain εzz obtained along the same line is shown in Figure 6b (all other strain component profiles are reported in Figure S12).
Figure 6.
(a) Experimental and simulated profiles of the εxx strain from the electrodes along the dashed line in the inset (εxx map). The extent of the three electrodes in the simulation is shaded in green, the experimental 3σ confidence interval in yellow. (b) Experimental and simulated profiles of εzz along the same line. (c) Profiles of εxx and εyy (maps shown in the insets) including only the long-ranged gradients. (d) Map of relative variations of the in-plane strain determined from Raman shift mapping. The green dashed box approximately indicates the area covered by SXDM. (e) Profiles of the bandgap between the heavy hole (HH) and light hole (LH) bands along the cut in (a) and (b). (f) Profiles of the HH–LH bandgap along the two cuts in (c).
In both cases, we plot the 3σ confidence interval band for the experimental data, as evaluated by propagating the SXDM measurement errors (light yellow bands, see data analysis section in the Supporting Information for details). The light green vertical bands indicate the position and lateral width of the investigated electrodes.
There is a general agreement, within the confidence interval band, between the entire SDXM measured strain profile and the simulated one at T = 300 K, when we set an intrinsic stress value of 90 MPa for the electrodes in the COMSOL simulation. We point out that this value has been selected by minimizing the difference between experimental and simulation data simultaneously for all the six strain components.
We notice that, in line with our previous observation of the compressive stressing action of the metal stripes, there are minima in εxx directly underneath the first and third electrodes and maxima at their sides, resulting in “V” shaped strain profiles. However, due to the proximity of the electrodes to each other, their strain fields overlap. Consequently, we do not see the valley of the “V” shape for the middle electrode due to the convolution of the three profiles.
This implies that the somehow naive description of the electrodes we used in the simulations, i.e., as homogeneous trapezoidal metal layers, is adequate enough to capture the physics of the electrode-induced strain fluctuations. Nonetheless, we reckon that the modeling could be further improved, thence the agreement between experiments and simulations, by a deeper knowledge of the actual electrode structure. Indeed, real metal stripes fabricated by e-beam lithography commonly show local irregularities of thickness, grain boundaries, and nonvertical sidewalls. Furthermore, segmentation of the electrodes is likely to occur due to the presence of boundaries or other inhomogeneities, leading to local stress modulations.
For what concerns the strain profiles extrapolated for LT, depicted in Figure 6a,b, we see a clear increase of the strain induced into the QW layer, brought about by the thermal mismatch with the electrode. By cooling down the sample, the peak-to-valley fluctuation under the electrodes increases by almost a factor of 3, with εxx spanning approximately 2 × 10–4 at RT and 6 × 10–4 at 1 K, while εzz fluctuations at this temperature extend to 3 × 10–4.
2.5. Large-Scale Strain Fields
After discussion
of the short-scale strain fluctuations induced by the electrodes,
we now investigate the effect of the plastic relaxation of the virtual
substrate/buffer on the lattice of the Ge QW layer. In the unfiltered
SXDM strain maps (Figures 4b and S3) and in the Raman strain
map in Figure 6d, we
observe a long-ranged gradient of εxx (εyy) along the [110] (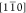 ) crystallographic axis. We attribute these
gradual changes in the Ge QW layer lattice strain, occurring over
a length scale of the order of 1 μm, to two interdependent effects.
First, the misfit dislocation bunches in the virtual substrate, oriented
along the [110] and
) crystallographic axis. We attribute these
gradual changes in the Ge QW layer lattice strain, occurring over
a length scale of the order of 1 μm, to two interdependent effects.
First, the misfit dislocation bunches in the virtual substrate, oriented
along the [110] and 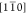 directions,28,37 generate local
lattice distortions that propagate upward into the QW layer.38 Second, these lattice fluctuations are also
driving local variations of the Ge content in the SiGe buffer,16 which, in turn, induce a spatial variation of
the in-plane lattice parameter of the coherent QW epilayer.39 The characteristic strain fields caused by the
misfit dislocation network tend to average out at large thicknesses
of the virtual substrate and are the root cause of the appearance
of the cross hatch pattern in semiconductor heterostructures.40,41
directions,28,37 generate local
lattice distortions that propagate upward into the QW layer.38 Second, these lattice fluctuations are also
driving local variations of the Ge content in the SiGe buffer,16 which, in turn, induce a spatial variation of
the in-plane lattice parameter of the coherent QW epilayer.39 The characteristic strain fields caused by the
misfit dislocation network tend to average out at large thicknesses
of the virtual substrate and are the root cause of the appearance
of the cross hatch pattern in semiconductor heterostructures.40,41
Observing the exemplary line-cuts of εxx and εyy obtained along [110]
and 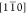 (see Figure 6c),
excluding short-ranged fluctuations by a Fourier
low-pass filter, we notice that the magnitudes of the gradients for
the two in-plane strains are very different in the two profiles, with
approximately Δεxx = 3 ×
10–4 and Δεyy = 2 × 10–3. The latter value is significantly
larger than those associated with the electrodes. Since misfit bunches
running along
(see Figure 6c),
excluding short-ranged fluctuations by a Fourier
low-pass filter, we notice that the magnitudes of the gradients for
the two in-plane strains are very different in the two profiles, with
approximately Δεxx = 3 ×
10–4 and Δεyy = 2 × 10–3. The latter value is significantly
larger than those associated with the electrodes. Since misfit bunches
running along 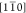 ([110]) mainly influence the εxx (εyy)
strain component, we attribute the difference in the observed bandwidth
of the black and red curves in Figure 6c to the stochastic nature of the dislocation-bunching
phenomenon and to the limited area explored by the SXDM technique,
of only a few μm2.
([110]) mainly influence the εxx (εyy)
strain component, we attribute the difference in the observed bandwidth
of the black and red curves in Figure 6c to the stochastic nature of the dislocation-bunching
phenomenon and to the limited area explored by the SXDM technique,
of only a few μm2.
2.6. Band Energy Level Simulations
In order to evaluate the impact of electrodes and dislocations on the qubit energy landscape, we have calculated the strain-dependent valence band edge profiles in the Ge layer along the same cuts of the SXDM maps displayed in Figure 6a,c. Due to the small values of the strain perturbation, we expect that the QW confinement energy remains practically unaltered, and consequently, the variation in the valence subbands is mainly controlled by the fluctuation of the band edges in the strained Ge heavy hole (HH) and light hole (LH) band edge levels. To assess the spatial variation of these quantities, we have diagonalized the bulk 6 × 6 Luttinger–Khon Hamiltonian,42,43 at the Γ point of Brillouin’s zone, including the strain contribution described by the six independent elements of ε through the Bir–Pikus perturbative approach.44 To account for the possible impact of the strain on the qubit operation, we have plotted in Figure 6 the behavior of the HH–LH energy difference, since this energy separation determines key properties of the two-dimensional hole gas such as the effective mass, g-factor, and spin–orbit coupling strength45 and, in turn, may influence spin qubit properties such as Rabi frequencies and coherence times.4 In detail, in Figure 6e,f we show the HH–LH band edge gap calculated at RT using the experimental and simulated strain profiles obtained for the cuts shown in Figure 6a and Figure 6c, respectively (the individual energy profiles for the HH and LH band edges are shown in Figure S13). The two plots have been obtained considering the short- and long-scale contribution to the strain fluctuation, respectively.
Furthermore, in panel e LT data, calculated using the input strain predicted by FEM simulations, are also reported. At RT, the electrode stress induces a variation of the HH–LH gap of several hundreds of μeV, while this value is calculated to increase to up to ∼1.5 meV when the sample is cooled to cryogenic temperatures.
As expected, owing to the larger bandwidth of the strain fluctuation induced by the extended defect network, greater HH–LH energy gap variations, of the order of few meV, have been calculated when considering the spatial range characteristic of the perturbation induced by the plastically relaxed virtual substrate.
3. Conclusion
We gave insights on the origin and degree of local strain fluctuations in Ge QWs that host gate-defined QD qubits. The strains exerted are large enough to possibly affect the local potential in functional devices. Aiming at an improved homogeneity, they represent an important optimization parameter for the material growth and electrode fabrication of QD spin qubit arrays. We have shown how the short-scale contribution to the strain fluctuations, which originates from the metal electrodes, corresponds to variations of the HH and LH band edge profiles of the order of 1 meV in the Ge QW at LT, while the relative HH–LH energy gap varies by up to 1.5 meV. We believe that these values are useful to improve the description of interacting qubits, since such perturbation may influence different scattering rates. We notice also that typical charging energies in QDs hosting a few electrons or holes are at the same scale. These fluctuations clearly do not prohibit the functionality of this few-qubit device, since successful operation of two qubits has been demonstrated on it.19 However, future designs envision arrays featuring many qubits, which will require QDs that are not only functional individually but also homogeneous in their electronic properties. Our findings predict both the confining potential in the QDs and the state separation energy for the qubits will suffer from nonuniformity due to the strain modulations. Moreover, since we have shown that the lattice distortion at the device operation temperature is enhanced by the thermal mismatch between the metallic and semiconductor materials, our results suggest, in line with ref (21), that this potentially detrimental effect can be suppressed by the adoption of polysilicon gates, featuring a much smaller thermal mismatch with (Si)Ge, which have been already implemented in CMOS-foundry processes to contact high-performance Ge devices.46 Nonetheless, the strain originating from different electrodes sharing the same geometry and composition appears to be fairly reproducible. Consequently, their impact can be considered in a systematic manner and exploited for the optimization of the qubit performance. In fact, a detailed knowledge of the lattice at the sub-100 nm scale is an important tool for the design of quantum devices based on semiconductor heterostructures, since it allows us to include the effect of strain modulations on the potential landscape felt by the electrical charges. The diagnostic capability here demonstrated will be even more relevant when large array of qubits will be manufactured on large areas, where the strain fluctuation induced by the extended defects originating in the plastic relaxation will be dominating.
Where the MD-related gradients are concerned, it is clear that they do not inhibit the functionality of the two qubits. However, they may pose a challenge for the operation of larger arrays with multiple qubits set further apart from each other. Indeed, the relatively large band edge energy fluctuation induced by the presence of the MD network imposes consideration of the spatial frequency of the cross hatch pattern associated with the defective plastically relaxed VS,40 as a key optimization parameter for further improvement of the hole-based spin qubit technology. As a matter of fact, it is well-known that in reverse-graded VS, a decrease of the Si content in the buffer underneath the QW layer entails a sparser MD network for the same degree of relaxation. This suggests a route for the realization of larger areas in the QW layer which are unaffected by MDs and therefore homogeneous in strain, capable of hosting a larger number of physical qubits. Furthermore, the presence of a dense MD network induces a local thickness and composition fluctuation at the top dielectric/SiGe barrier interface.47 This would lead to a local fluctuation of the oxide properties, impacting the qubit performances. It is worth mentioning that a reduction of the Si content in the SiGe buffer layer and the QW barrier from 0.2 down to 0.1 is not critical to achieve carrier confinement at cryogenic temperature while at the same time this leads to record values of the hole mobility, mainly due to the improved quality of the Ge/SiGe heterointerface. The hole mobility, which is reported for this specific device as μ > 5 × 105 cm–2V–1s–1,19 is influenced by different mechanisms, in particular interface roughness scattering that in turn is influenced by the strain distribution.48
Moreover, the effect of local inhomogeneities in the crystal lattice, which may be studied by SXDM as demonstrated in this work, is of possible interest in other material platforms for housing spin qubits, such as III–V compound semiconductors49 and different approaches to quantum computing, in particular superconducting qubits.50
Our results highlight the importance of ”strain noise”, beyond the well-known charge noise, for the development of large qubit arrays capable of error correction schemes. SXDM offers a non-destructive means to study the strain landscape around quantum devices in various epitaxial material systems, in particular ultrathin strained layers, thus providing a starting point for the development of accurate theoretical models to design optimized and homogeneous many-qubit arrays.
4. Experimental Section
4.1. Sample Fabrication
The epitaxial layer stack (Figure 1a) was grown on a commercial 100 mm Si wafer by reduced pressure chemical vapor deposition (RP-CVD) and comprises a plastically relaxed Ge virtual substrate, a linear-graded Si1–xGex layer, a Si0.2Ge0.8 buffer with a thickness of 500 nm, a 16 nm fully strained Ge QW layer, a 22 nm thick Si0.2Ge0.8 barrier, and a sacrificial Si cap (<2 nm).5 The key elements of the device fabrication comprise: ohmic contacts (20 nm Al layer), gate dielectric (17 nm Al2O3 by atomic layer deposition at 300 °C), first layer of gates (40 nm Ti/Pd layer), second dielectric layer (17 nm Al2O3), and second layer of overlapping gates (40 nm Ti/Pd layer). Further details of device fabrication can be found in ref (8).
4.2. X-ray Nanoprobe Setup
The measurements were carried out at ID01/ESRF with a beam focused onto the sample surface by a Fresnel zone plate (FZP),51 while an order sorting aperture (OSA) blocked out the higher diffraction orders from the FZP. An X-ray energy of 9.3 keV was chosen to measure Bragg reflections from the {3 3 5} family with a steep incidence–grazing exit geometry (see Figure 1b). This setup ensures a shallow penetration depth of the X-rays and thus high sensitivity for the QW layer, which is located close to the sample surface, while maintaining a small beam footprint on the sample. The improved brilliance after the EBS upgrade provides a symmetric (circular) beam spot and enables a reciprocal space mapping of the 3 3 5 Bragg peak from the 16 nm QW layer within an exposure time of 30 ms. The spot size d of the X-ray beam, which limits the lateral resolution, was determined by ptychographic reconstruction prior to the measurement and found as d < 30 nm.52
4.3. Raman Measurement
Mapping of the Raman shift was performed with a μ-focus Renishaw InVia, employing a laser for excitation with a wavelength of 532 nm and a focal spot size of approximately 500 nm. To generate a map of the Raman shift, the sample was scanned with a lateral step size of 200 nm and a spectrum recorded at each frame.
4.4. Thermomechanical and Band Edge Simulations
The thermomechanical simulations were performed by means of COMSOL Multi-Physics software exploiting the Solid Mechanics module. The room temperature strain has been estimated assuming the presence of an initial stress in the metallic gate, before relaxation. Additionally, in order to predict the behavior of the elastic deformations at cryogenic temperatures, the contribution of the CTE mismatch has been included, by means of the Thermal Expansion node in the Solid Mechanics module of COMSOL MultiPhysics. The strain-dependent band edge profiles were numerically extracted as a result of the diagonalization of the 6 × 6 Luttinger–Kohn Hamiltonian, following the Bir–Pikus perturbative approach. The Bir–Pikus deformation potentials and the spin–orbit split-off energy are from ref (53).
Acknowledgments
We acknowledge the European Synchrotron Radiation Facility for provision of synchrotron radiation facilities, and we thank the staff for assistance in using beamline ID01. From the Leibniz Institute for Crystal Growth, the authors thank Dr. M. Albrecht for useful discussions regarding the strain landscape in plastically relaxed SiGe layers and Dr. K.-P. Gradwohl for proofreading the manuscript. The authors thank C. David and F. Koch from Paul Scherrer Institut for developing and fabricating the Fresnel zone plates employed to focus the beam for the measurements at ID01. This research was financially supported by the Leibniz associations “High-Definition Crystalline Silicon–Germanium Structures for Quantum Circuits” project (SiGeQuant, Project K124/2018), the European Union and its Horizon 2020 framework program (Grant FETFLAG-05-2020) as part of the project “Quantum Large Scale Integration in Silicon” (QLSI, Grant 951852), and the German Federal Ministry of Education and Research within the frame of the project “Halbleiter-Quantenprozessor mit Shuttlingbasierter Skalierbarer Architektur” (QUASAR, Grant FKZ 13N15654).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.2c17395.
Description of SXDM data treatment and analysis; as-measured maps of the strains and lattice rotations in the Ge QW layer; histograms of the strains from SXDM and Raman; strain and composition maps of the SiGe buffer layer; description and discussion of the local stress tensor and stress maps; details on the thermomechanical FEM simulation; simulated profiles of all strain tensor components; AFM image of the cross hatch pattern; characterization of the X-ray nanoprobe by ptychographic reconstruction (PDF)
Author Contributions
A.S., N.W.H, M.Ve., and G.S. made the heterostructures and the qubit device. C.R. and M.H.Z. conceived the synchrotron experiment. C.C-W., C.R., and M.H.Z. participated in the measurements and analyzed the experimental data. E.Z. and T.U.S. were local contacts at ID01/ESRF. I.Z. and C.L.M. performed FEM simulations of the mechanical properties. M.Vi. carried out band structure simulations and supervised the overall theoretical efforts. A.A.C-W. carried out Raman and AFM mapping. J.K. recorded EDX images. C.C-W., G.C., and M.Vi. wrote the manuscript with input from all the other authors. M.Vi, C.R., and G.C. supervised the formal analysis. W.M.K., F.R., and G.C. coordinated the work.
The authors declare no competing financial interest.
Supplementary Material
References
- Campbell E. T.; Terhal B. M.; Vuillot C. Roads towards Fault-tolerant Universal Quantum Computation. Nature 2017, 549, 172–179. 10.1038/nature23460. [DOI] [PubMed] [Google Scholar]
- Chatterjee A.; Stevenson P.; De Franceschi S.; Morello A.; de Leon N. P.; Kuemmeth F. Semiconductor Qubits in Practice. Nat. Rev. Phys. 2021, 3, 157–177. 10.1038/s42254-021-00283-9. [DOI] [Google Scholar]
- Zwerver A. M. J.; et al. Qubits made by Advanced Semiconductor Manufacturing. Nat. Electronics 2022, 5, 184–190. 10.1038/s41928-022-00727-9. [DOI] [Google Scholar]
- Scappucci G.; Kloeffel C.; Zwanenburg F. A.; Loss D.; Myronov M.; Zhang J.-J.; De Franceschi S.; Katsaros G.; Veldhorst M. The Germanium Quantum Information Route. Nat. Rev. Mater. 2021, 6, 926–943. 10.1038/s41578-020-00262-z. [DOI] [Google Scholar]
- Sammak A.; Sabbagh D.; Hendrickx N. W.; Lodari M.; Paquelet Wuetz B.; Tosato A.; Yeoh L.; Bollani M.; Virgilio M.; Schubert M. A.; Zaumseil P.; Capellini G.; Veldhorst M.; Scappucci G. Shallow and Undoped Germanium Quantum Wells: A Playground for Spin and Hybrid Quantum Technology. Adv. Funct. Mater. 2019, 29, 1807613. 10.1002/adfm.201807613. [DOI] [Google Scholar]
- Lodari M.; Hendrickx N. W.; Lawrie W. I. L.; Hsiao T.-K.; Vandersypen L. M. K.; Sammak A.; Veldhorst M.; Scappucci G. Low Percolation Density and Charge Noise with Holes in Germanium. Mater. Quantum Technol. 2021, 1, 011002. 10.1088/2633-4356/abcd82. [DOI] [Google Scholar]
- Lodari M.; Tosato A.; Sabbagh D.; Schubert M. A.; Capellini G.; Sammak A.; Veldhorst M.; Scappucci G. Light Effective Hole Mass in Undoped Ge/SiGe Quantum Wells. Phys. Rev. B 2019, 100, 041304. 10.1103/PhysRevB.100.041304. [DOI] [Google Scholar]
- Hendrickx N. W.; Lawrie W. I. L.; Petit L.; Sammak A.; Scappucci G.; Veldhorst M. A Single-Hole Spin Qubit. Nat. Commun. 2020, 11, 3478. 10.1038/s41467-020-17211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pillarisetty R. Academic and Industry Research Progress in Germanium Nanodevices. Nature 2011, 479, 324–328. 10.1038/nature10678. [DOI] [PubMed] [Google Scholar]
- Hendrickx N. W.; Lawrie W. I. L.; Russ M.; van Riggelen F.; de Snoo S. L.; Schouten R. N.; Sammak A.; Scappucci G.; Veldhorst M. A Four-qubit Germanium Quantum Processor. Nature 2021, 591, 580–585. 10.1038/s41586-021-03332-6. [DOI] [PubMed] [Google Scholar]
- Jirovec D.; et al. A Singlet-Triplet Hole Spin Qubit in Planar Ge. Nat. Mater. 2021, 20, 1106–1112. 10.1038/s41563-021-01022-2. [DOI] [PubMed] [Google Scholar]
- Lawrie W. I. L.; Russ M.; van Riggelen F.; Hendrickx N. W.; de Snoo S. L.; Sammak A.; Scappucci G.; Veldhorst M. Simultaneous Driving of Semiconductor Spin Qubits at the Fault-Tolerant Threshold. arXiv 2021, 2109.07837.(https://arxiv.org/abs/2109.07837) 10.48550/arXiv.2109.07837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandersypen L.; Bluhm H.; Clarke J.; Dzurak A.; Ishihara R.; Morello A.; Reilly D.; Schreiber L.; Veldhorst M. Interfacing Spin Qubits in Quantum Dots and Donors - Hot, Dense, and Coherent. npj Quantum Inf. 2017, 3, 34. 10.1038/s41534-017-0038-y. [DOI] [Google Scholar]
- Borsoi F.; Hendrickx N. W.; John V.; Motz S.; van Riggelen F.; Sammak A.; de Snoo S. L.; Scappucci G.; Veldhorst M. Shared Control of a 16 Semiconductor Quantum Dot Crossbar Array. arXiv 2022, 2209.06609.(https://arxiv.org/abs/2209.06609). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans P. G.; Savage D. E.; Prance J. R.; Simmons C. B.; Lagally M. G.; Coppersmith S. N.; Eriksson M. A.; Schülli T. U. Nanoscale Distortions of Si Quantum Wells in Si/SiGe Quantum-Electronic Heterostructures. Adv. Mater. 2012, 24, 5217–5221. 10.1002/adma.201201833. [DOI] [PubMed] [Google Scholar]
- Zoellner M. H.; Richard M.-I.; Chahine G. A.; Zaumseil P.; Reich C.; Capellini G.; Montalenti F.; Marzegalli A.; Xie Y.-H.; Schülli T. U.; Häberlen M.; Storck P.; Schroeder T. Imaging Structure and Composition Homogeneity of 300 mm SiGe Virtual Substrates for Advanced CMOS Applications by Scanning X-ray Diffraction Microscopy. ACS Appl. Mater. Interfaces 2015, 7, 9031–9037. 10.1021/am508968b. [DOI] [PubMed] [Google Scholar]
- Albrecht M.; Christiansen S.; Michler J.; Dorsch W.; Strunk H. P.; Hansson P. O.; Bauser E. Surface Ripples, Crosshatch Pattern, and Dislocation Formation: Cooperating Mechanisms in Lattice Mismatch Relaxation. Appl. Phys. Lett. 1995, 67, 1232–1234. 10.1063/1.115017. [DOI] [Google Scholar]
- Marshall M. C.; Phillips D. F.; Turner M. J.; Ku M. J. H.; Zhou T.; Delegan N.; Heremans F. J.; Holt M. V.; Walsworth R. L. Scanning X-Ray Diffraction Microscopy for Diamond Quantum Sensing. Phys. Rev. Appl. 2021, 16, 054032. 10.1103/PhysRevApplied.16.054032. [DOI] [Google Scholar]
- Hendrickx N.; Franke D.; Sammak A.; Scappucci G.; Veldhorst M. Fast Two-qubit Logic with Holes in Germanium. Nature 2020, 577, 487–491. 10.1038/s41586-019-1919-3. [DOI] [PubMed] [Google Scholar]
- Ohring M. In Materials Science of Thin Films, 2nd ed.; Ohring M., Ed.; Academic Press: San Diego, CA, 2002; pp 711–781. [Google Scholar]
- Thorbeck T.; Zimmerman N. M. Formation of Strain-induced Quantum Dots in Gated Semiconductor Nanostructures. AIP Advances 2015, 5, 087107. 10.1063/1.4928320. [DOI] [Google Scholar]
- Park J.; Ahn Y.; Tilka J. A.; Sampson K. C.; Savage D. E.; Prance J. R.; Simmons C. B.; Lagally M. G.; Coppersmith S. N.; Eriksson M. A.; Holt M. V.; Evans P. G. Electrode-Stress-Induced Nanoscale Disorder in Si Quantum Electronic Devices. APL Mater. 2016, 4, 066102. 10.1063/1.4954054. [DOI] [Google Scholar]
- Chahine G. A.; Richard M.-I.; Homs-Regojo R. A.; Tran-Caliste T. N.; Carbone D.; Jacques V. L. R.; Grifone R.; Boesecke P.; Katzer J.; Costina I.; Djazouli H.; Schroeder T.; Schulli T. U. Imaging of Strain and Lattice Orientation by Quick Scanning X-ray Microscopy Combined with Three-Dimensional Reciprocal Space Mapping. J. Appl. Crystallogr. 2014, 47, 762–769. 10.1107/S1600576714004506. [DOI] [Google Scholar]
- Richter C.; Kaganer V. M.; Even A.; Dussaigne A.; Ferret P.; Barbier F.; Le Vaillant Y.-M.; Schülli T. U. Nanoscale Mapping of the Full Strain Tensor, Rotation and Composition in Partially Relaxed InxGa1–xN Layers by Scanning X-ray Diffraction Microscopy. Phys. Rev. Appl. 2022, 18, 064015. 10.1103/PhysRevApplied.18.064015. [DOI] [Google Scholar]
- Revol J.-L.; Berkvens P.; Bouteille J.-F.; Carmignani N.; Carver L.; Chavanne J.; Chaize J.; Ewald F.; Franchi A.; Hardy L.. ESRF- EBS: Implementation, Performance and Restart of User Operation. Proceedings of IPAC’21, 2021.
- Bolkhovityanov Y. B.; Sokolov L. Ge-on-Si Films Obtained by Epitaxial Growing: Edge Dislocations and their Participation in Plastic Relaxation. Semicond. Sci. Technol. 2012, 27, 043001. 10.1088/0268-1242/27/4/043001. [DOI] [Google Scholar]
- Wang G.Investigation on SiGe Selective Epitaxy for Source and Drain Engineering in 22 nm CMOS Technology Node and Beyond; Springer, 2019; pp 23–48. [Google Scholar]
- Becker L.; Storck P.; Schulz T.; Zoellner M. H.; Di Gaspare L.; Rovaris F.; Marzegalli A.; Montalenti F.; De Seta M.; Capellini G.; Schwalb G.; Schroeder T.; Albrecht M. Controlling the Relaxation Mechanism of low Strain Si1–xGex/Si(001) Layers and Reducing the Threading Dislocation Density by Providing a Preexisting Dislocation Source. J. Appl. Phys. 2020, 128, 215305. 10.1063/5.0032454. [DOI] [Google Scholar]
- Dismukes J. P.; Ekstrom L.; Paff R. J. Lattice Parameter and Density in Germanium-Silicon Alloys. J. Phys. Chem. 1964, 68, 3021–3027. 10.1021/j100792a049. [DOI] [Google Scholar]
- Schlenker J. L.; Gibbs G. V.; Boisen J. M. B. Strain-Tensor Components Expressed in Terms of Lattice Parameters. Acta Crystallogr. 1978, A34, 52–54. 10.1107/S0567739478000108. [DOI] [Google Scholar]
- Capellini G.; De Seta M.; Zaumseil P.; Kozlowski G.; Schroeder T. High Temperature X-ray Diffraction Measurements on Ge/Si(001) Heterostructures: A Study on the Residual Tensile Strain. J. Appl. Phys. 2012, 111, 073518. 10.1063/1.3702443. [DOI] [Google Scholar]
- Arblaster J. W. Crystallographic Properties of Palladium. Platinum Metals Review 2012, 56, 181–189. 10.1595/147106712X646113. [DOI] [Google Scholar]
- Middelmann T.; Walkov A.; Bartl G.; Schödel R. Thermal Expansion Coefficient of Single Crystal Silicon from 7 to 293 K. Phys. Rev. B 2015, 92, 174113. 10.1103/PhysRevB.92.174113. [DOI] [Google Scholar]
- Slack G. A.; Bartram S. F. Thermal Expansion of some Diamondlike Crystals. J. Appl. Phys. 1975, 46, 89–98. 10.1063/1.321373. [DOI] [Google Scholar]
- Schaffler F. In Properties of Advanced Semiconductor Materials: GaN, AlN, InN, BN, SiC, SiGe; Levinshtein M. E, Rumyantsev S. L., Shur M. S., Eds.; John Wiley and Sons, Inc., 2001; pp 149–188. [Google Scholar]
- Schauer A. Thermal Expansion, Grueneisen Parameter, and Temperature Dependence of Lattice Vibration Frequencies of Aluminum Oxide. Can. J. Phys. 1965, 43, 523–531. 10.1139/p65-049. [DOI] [Google Scholar]
- Chen H.; Li Y. K.; Peng C. S.; Liu H. F.; Liu Y. L.; Huang Q.; Zhou J. M.; Xue Q.-K. Crosshatching on a SiGe Film Grown on a Si(001) Substrate studied by Raman Mapping and Atomic Force Microscopy. Phys. Rev. B 2002, 65, 233303. 10.1103/PhysRevB.65.233303. [DOI] [Google Scholar]
- Rovaris F.; Zoellner M. H.; Zaumseil P.; Schubert M. A.; Marzegalli A.; Di Gaspare L.; De Seta M.; Schroeder T.; Storck P.; Schwalb G.; Richter C.; Schülli T. U.; Capellini G.; Montalenti F. Misfit-Dislocation Distributions in Heteroepitaxy: From Mesoscale Measurements to Individual Defects and back. Phys. Rev. Appl. 2018, 10, 054067. 10.1103/PhysRevApplied.10.054067. [DOI] [Google Scholar]
- Richard M.-I.; Zoellner M. H.; Chahine G. A.; Zaumseil P.; Capellini G.; Haeberlen M.; Storck P.; Schuelli T. U.; Schroeder T. Structural Mapping of Functional Ge Layers Grown on Graded SiGe Buffers for sub-10 nm CMOS Applications Using Advanced X-ray Nanodiffraction. ACS Appl. Mater. Interfaces 2015, 7, 26696–26700. 10.1021/acsami.5b08645. [DOI] [PubMed] [Google Scholar]
- Eastman D. E.; Stagarescu C. B.; Xu G.; Mooney P. M.; Jordan-Sweet J. L.; Lai B.; Cai Z. Observation of Columnar Microstructure in Step-Graded Si1–xGex/Si Films Using High-Resolution X-Ray Microdiffraction. Phys. Rev. Lett. 2002, 88, 156101. 10.1103/PhysRevLett.88.156101. [DOI] [PubMed] [Google Scholar]
- Rovaris F.; Zoellner M. H.; Zaumseil P.; Marzegalli A.; Di Gaspare L.; De Seta M.; Schroeder T.; Storck P.; Schwalb G.; Capellini G.; Montalenti F. Dynamics of Crosshatch Patterns in Heteroepitaxy. Phys. Rev. B 2019, 100, 085307. 10.1103/PhysRevB.100.085307. [DOI] [Google Scholar]
- Luttinger J. M.; Kohn W. Motion of Electrons and Holes in Perturbed Periodic Fields. Phys. Rev. 1955, 97, 869–883. 10.1103/PhysRev.97.869. [DOI] [Google Scholar]
- Luttinger J. M. Quantum Theory of Cyclotron Resonance in Semiconductors: General Theory. Phys. Rev. 1956, 102, 1030–1041. 10.1103/PhysRev.102.1030. [DOI] [Google Scholar]
- Bir G. L.; Pikus G. E.. Symmetry and Strain-Induced Effects in Semiconductors; Wiley: New York, 1974; Vol. 484. [Google Scholar]
- Del Vecchio P.; Lodari M.; Sammak A.; Scappucci G.; Moutanabbir O. Vanishing Zeeman Energy in a Two-Dimensional Hole Gas. Phys. Rev. B 2020, 102, 115304. 10.1103/PhysRevB.102.115304. [DOI] [Google Scholar]
- Lischke S.; Peczek A.; Morgan J. S.; Sun K.; Steckler D.; Yamamoto Y.; Korndörfer F.; Mai C.; Marschmeyer S.; Fraschke M.; Krüger A.; Beling A.; Zimmermann L. Ultra-fast Germanium Photodiode with 3-dB Bandwidth of 265 GHz. Nat. Photonics 2021, 15, 925–931. 10.1038/s41566-021-00893-w. [DOI] [Google Scholar]
- Olsen S. H.; O'Neill A. G.; Norris D. J.; Cullis A. G.; Woods N. J.; Zhang J.; Fobelets K.; Kemhadjian H. A. Strained Si/SiGe n-channel MOSFETs: Impact of Cross-hatching on Device Performance. Semicond. Sci. Technol. 2002, 17, 655–661. 10.1088/0268-1242/17/7/303. [DOI] [Google Scholar]
- Lodari M.; Kong O.; Rendell M.; Tosato A.; Sammak A.; Veldhorst M.; Hamilton A. R.; Scappucci G. Lightly Strained Germanium Quantum Wells with Hole Mobility exceeding one Million. Appl. Phys. Lett. 2022, 120, 122104. 10.1063/5.0083161. [DOI] [Google Scholar]
- Pateras A.; Park J.; Ahn Y.; Tilka J. A.; Holt M. V.; Reichl C.; Wegscheider W.; Baart T. A.; Dehollain J. P.; Mukhopadhyay U.; et al. Mesoscopic Elastic Distortions in GaAs Quantum Dot Heterostructures. Nano Lett. 2018, 18, 2780–2786. 10.1021/acs.nanolett.7b04603. [DOI] [PubMed] [Google Scholar]
- Murray C. E. Material Matters in Superconducting Qubits. Materials Science and Engineering: R: Reports 2021, 146, 100646. 10.1016/j.mser.2021.100646. [DOI] [Google Scholar]
- Leake S. J.; Chahine G. A.; Djazouli H.; Zhou T.; Richter C.; Hilhorst J.; Petit L.; Richard M.-I.; Morawe C.; Barrett R.; Zhang L.; Homs-Regojo R. A.; Favre-Nicolin V.; Boesecke P.; Schulli T. U. The Nanodiffraction Beamline ID01/ESRF: a Microscope for Imaging Strain and Structure. J. Synchrotron Radiat. 2019, 26, 571–584. 10.1107/S160057751900078X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer F. X-ray ptychography. Nat. Photonics 2018, 12, 9–17. 10.1038/s41566-017-0072-5. [DOI] [Google Scholar]
- Van de Walle C. G. Band Lineups and Deformation Potentials in the Model-solid Theory. Phys. Rev. B 1989, 39, 1871–1883. 10.1103/PhysRevB.39.1871. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.