Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jan 6;127(2):468–476. doi: 10.1021/acs.jpca.2c07693

Linking the Interatomic Exchange-Correlation Energy to Experimental J-Coupling Constants

Ibon Alkorta †, Paul L A Popelier ‡,*
PMCID: PMC9869393  PMID: 36608277

Abstract

graphic file with name jp2c07693_0006.jpg

The main aim of the current work is to find an experimental connection to the interatomic exchange-correlation energy as defined by the energy decomposition method Interacting Quantum Atoms (IQA). A suitable candidate as (essentially) experimental quantity is the nuclear magnetic resonance (NMR) J-coupling constant denoted 3J(H,H′), which a number of previous studies showed to correlate well with QTAIM’s delocalization index (DI), which is essentially a bond order. Inspired by Karplus equations, here, we investigate correlations between 3J(H,H′) and a relevant dihedral angle in six simple initial compounds of the shape H3C-YHn (Y = C, N, O, Si, P, and S), N-methylacetamide (as prototype of the peptide bond), and five peptide-capped amino acids (Gly, Ala, Val, Ile, and Leu) because of the protein direction of the force field FFLUX. In conclusion, except for methanol, the inter-hydrogen exchange-correlation energy Vxc(H,H′) makes the best contact with experiment, through 3J(H,H′), when multiplied with the internuclear distance RHH′.

1. Introduction

Energy decomposition analysis1 remains a vital activity of theoretical chemistry, serving as a tool to interpret a wealth of chemical phenomena. While its roots go back about half a century,2 new methods continue to be added to the current plethora of energy partitioning schemes. Many of them are actually variations on older schemes in an attempt to overcome some of their shortcomings. However, a quantum topological energy partitioning called Interacting Quantum Atoms (IQA)3 presents a departure from the central ideas behind the more traditional but still popular energy decomposition methods. IQA is inspired by an earlier topological energy partitioning,4 which works for systems that are not stationary points on a potential energy surface. In contrast, the original virial partitioning,5 which is at the heart of the Quantum Theory of Atoms in Molecules (QTAIM),6,7 could only be applied to systems with vanishing forces on their nuclei. Moreover, IQA does not invoke artificial wave functions (e.g., non-Pauli) as a reference state.

IQA offers an atomistic picture of how energy is distributed, whether in a single molecule or in a molecular assembly. It provides this localized information by partitioning the total energy in intra-atomic energy contributions and interatomic ones. Besides localizing energy, IQA also delivers insight in terms of the physical type of energy that underpins any chemical phenomenon. Indeed, IQA’s interatomic energy includes the electrostatic interaction energy between any two atoms, and both the exchange energy and electron correlation energy.8 The intra-atomic energy consists of the atomic kinetic energy as well as the electrostatic, exchange, and correlation energy. Equipped with the capacity to provide both (atomic) location and energy type, IQA can determine the degree of covalency in a hydrogen bond, for example. Very recently, the quantum topological approach was shown9 to provide a real space alternative of magnetic spin coupling, one that focuses on the role of electron delocalization and one that overcomes the limitations of the orbital approach.

A question that presents itself, perhaps even imposingly, is if any of IQA’s energy contributions make contact with experiment. This question is useful in force field design, in particular, for the force field FFLUX,10,11 which is based on IQA. Of course, force fields are tasked to predict12 properties of condensed matter, for example, the self-diffusion coefficient of liquid water at various temperatures. It is clear that force fields make contact with experiments at a high level (e.g., heat capacity of constant pressure) but it would be nice to know if they also do so at a lower level (e.g., interatomic exchange energy). This may be important as a test of the soundness of the energy contributions that make up the force field. In particular, we are interested to know if the interatomic exchange-correlation energy (which is dominated by the exchange energy) can be brought in correspondence with a measurable quantity.

Interpretational quantum chemistry also benefits from the establishment of a link between the experiment and calculated atomic energy. For example, the exchange energy between two vicinal (i.e., 1,4) hydrogen atoms in staggered ethane is larger13 in magnitude when they are in a trans relationship as opposed to in a gauche one. This so-called “trans effect” (for convenience) appears counterintuitive because the hydrogens are farther away from each other while in a trans configuration. However, in that work,13 the trans effect was repeatedly observed in other saturated hydrocarbons, all calculated at the Hartree–Fock level of theory, which already covers exchange. It is tempting to find support for this computationally established fact from the measured J-coupling, also called indirect nuclear spin–spin coupling constant in full. In the case of vicinal hydrogens (protons), the relevant J-coupling is 3J(H,H′).

This (scalar) coupling constant quantifies the splitting of NMR resonance energies due to the coupling of nuclear spins, in this case, those of two protons separated by three bonds. Although any value of 3J(H,H′) is expressed in Hertz (Hz or s–1), J-coupling is really an energy but for a proportionality factor. In order to produce this splitting energy, J is multiplied by Planck’s constant (in SI units of J s) and the respective spin quantum numbers (dimensionless, e.g., 1/2 for a proton) of the two interacting nuclei. The well-known Karplus equation14 then offers an empirical expression, usually in the form of a heavily truncated Fourier series, that relates 3J(H,H′) to the H–A–B–H dihedral angle governing the HH interaction. In the particular case of ethane (A and B are carbon atoms), J reaches a local maximum when the dihedral angle is 180°, exactly when the two hydrogens are trans to each other. Thus, by observation, there is a potential link between the behavior of a through-space quantum topological exchange energy, Vx(H,H′), and a measured quantity, 3J(H,H′).

Already in 1996, Bader et al. observed,15 within the context of QTAIM, that a measure of Fermi-hole density delocalization between two vicinal hydrogens (denoted F(H,H′)) correlates very well with the coupling constant 3J(H,H′), both following the same Karplus equation. The Fermi hole is a consequence of the Pauli exclusion principle, which states that no two electrons with the same spin can occupy the same point in space. To understand the Fermi hole, let us fix an electron of a given spin at a fixed position. There will thus be a decrease in the probability of finding another electron with the same spin relative to this given electron. The Fermi hole is a distribution function that quantifies16 this decrease relative to an uncorrelated pair density. As an electron moves through space, it carries with it a Fermi hole as “no go zone” of an ever-changing degree and shape. Returning to F(H,H′), it is curious that this quantity does not adopt the dimension of energy but rather that of a delocalization index (DI), which is often identified with a bond order, and which is derived from F(A,B) values. The DI represents the number of electrons exchanged or shared between two given atoms.17 The DI has also been used as a measure of the bond order18−22 and the average value between para atoms in six-membered rings has been used to characterize the aromaticity of these rings.23 Referring for the mathematical details to the mature literature,24,25 we just summarize here that F(H,H′) is calculated as a double sum of products over atomic overlap integrals. The latter are denoted Sji(ΩH)Sij(ΩH′) and defined in Section 2, where the indices i and j refer to spin orbitals, and ΩA to the volume of atom A over which the orbitals are integrated. Being aware, at this point, of this stub of a formula is important to understand the following argument.

The observation that NJ(A,B) (which is more general than 3J(H,H′)) is proportional26 to doubly summed products of overlap integrals can be rationalized by going back to McConnell’s formula27 published in 1956. His equation, which is also given and discussed in detail elsewhere,25 is based on the valid assumption that the dominant term (out of three terms) in the J-coupling Hamiltonian28,29 is the Fermi contact (FC) term. This term consists of the magnetic interaction between the nuclear spin and the electron spin, which is much larger than the direct interaction between two nuclear spins. The FC interaction is the magnetic interaction between an electron and an atomic nucleus when the electron is at the nucleus. This is why elaborate basis sets with excellent core-electron flexibility are important for accurate calculations of the J-coupling. The FC offers a mechanism25 to transmit the presence of the spin of one nucleus to that of another nucleus. Indeed, the spin magnetic moment of nucleus A polarizes the spin density of the electrons in its immediate neighborhood, which leads to a small excess of oppositely polarized electron spin density. This information is then transmitted to the vicinity of another nucleus B via the mechanism of electron exchange. This fact is compatible with the appearance of exchange terms (i.e., atomic overlap integrals) in McConnell’s formula. However, to be more precise, this is only true if the density at the proton parallels the increase of the density within the volume of the hydrogen atom. As a result, one can prove that NJ(A,B) will depend linearly on 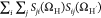Inline graphic and thus on the DI or bond order.

Matta et al.25 computationally verified the validity of the last statement for 3J(H,H′) in a small series of polyaromatic compounds as well as for a handful of saturated hydrocarbons. At first glance, this result is expected, following the reasoning starting with McConnell’s equation, because the atomic volume of the hydrogen atom is primarily described by spherically symmetric s-functions. However, it will then come as a surprise that 3J(F,F′) also depends30 linearly on the respective DI for 29 fluorinated aromatics, spanning a J-coupling range of 85 Hz. Indeed, one would expect the approximate link with Sji(ΩF)Sij(ΩF′) to fail for non-hydrogen atoms due to the presence of basis functions with nonzero angular momentum, which increase31 the contribution to the J-coupling due to terms other than the FC term. Still, these authors phenomenologically showed that the correlation even holds with oxygen atoms intervening between the coupled fluorine atoms (although not in compounds with crowded fluorine atoms).

Finding a successful correlation between experimental NJ(H,H′) (with N = 1,2,3,4,...) values and the corresponding DIs for heteroaromatics containing oxygen (as well as nitrogen, sulfur, and selenium) is unique to the QTAIM partitioning. Mandado et al. have shown32 that the alternative partitioning method of Mulliken is useless (in their words) since no correlation was found for the original set of polybenzoids of Matta et al.25 when extended with 5- and 6-membered heteroaromatics. The Hirshfeld partitioning scheme fares better than that of Mulliken but shows the reduced correlation for hydrogens placed in the presence of electronegative atoms. That work32 justifies the current study’s use of the QTAIM partitioning when studying (doubly peptide-) capped amino acids, compounds of interest to the development of FFLUX. It is worth reflecting for a moment on how an ab initio program is able to provide J-coupling, localized between two atoms, without ever invoking a partitioning method. The integrals in McConnell’s original formula are calculated over all space, yet they allow themselves to be approximated by integrals over the finite volume of quantum topological atoms. Even the atomic weight factor of Hirshfeld’s partitioning corroborates the somehow natural localization that characterizes J values.

Using QTAIM, more successful correlations33 have been obtained since the pioneering work mentioned above: B3LYP34 calculations on seven 9-substituted anthracene derivatives confirmed linear correlations between the DI and both vicinal (3J) as well as long-range (4J) proton–proton coupling constants, respectively. Furthermore, an MCSCF study of hydrogen dissociation in protonated benzene shows that a larger QTAIM CH delocalization index implies35 a larger CH J-coupling. Another QTAIM B3LYP study showed36 an accurate correlation between the HH DI and HH J-coupling of a highly investigated, bioactive diterpenoid. Finally, a striking similarity was found37 between the variation of the J-coupling with the intermolecular distance in noncovalent interactions and the same type of plot for the Laplacian of the electron density at the intermolecular bond critical point.

It is against the extensive background outlined above that we now investigate, for the first time to the best of our knowledge, if there is a correlation between the coupling constant 3J(H,H′) and the interatomic exchange-correlation energy Vxc(H,H′). Although we will investigate this matter in the above phenomenological tradition of this type of calculations, we start by reviewing the established theoretical link between Vxc(H,H′) and DI(H,H′). This link will help in interpreting the observed results.

2. Theoretical Background

2.1. Exchange Energy and Delocalization Index

The IQA method is the most used topological energy partitioning method (see ref (38) for an alternative) to divide the total electronic energy of a system into intra-atomic and interatomic contributions,

2.1. 1

where A and B label different (quantum topological) atoms. The interatomic energy can be further partitioned into contributions associated with nuclei (n) and electrons (e) in each atom:

2.1. 2

where a vertical match between subscript and superscript tells which entities (n or e) interact. Finally, the electron–electron potential energy VeeAB can be even further partitioned into a Coulombic, exchange, and correlation term:

2.1. 3

where the (alternatively written) exchange term Vx(A,B) provides information on the degree of covalent bonding between A and B.

As we will work with B3LYP wave functions, the interatomic exchange energy is written in terms of Kohn–Sham (KS) orbitals ψiKS, by following the template of (closed-shell in our case) Hartree–Fock theory:

2.1. 4

where the KS orbitals simply replace the Hartree–Fock orbitals and the two consecutive 3D integrals constitute a 6D integral over the volumes of atom A and B. The subscript X emphasizes that, formally, we extract only the exchange part from the exchange-correlation energy. We should and will actually write Vxc(A,B) and also mention that the total molecular energy can be sufficiently accurately recovered by the first ever DFT-IQA partitioning scheme proposed39 a few years ago. In eq 4, R = RB – RA represents the internuclear vector while RB and RA are the respective nuclear position vectors of nucleus B and A. The vectors r1 and r2 describe the electron density in the volumes of atom A and B, respectively. It should be noted that the magnitude of the compound vector appearing in the denominator, |R + r2 – r1|, is the distance between two infinitesimal pieces of electron density, one in A and one in B. Rewriting eq 4 using the overlap function Sij(r) = ψiKS(r)ψjKS(r) leads to

2.1. 5

Following a derivation published40 in 2007, a Taylor expansion of |R + r2 – r1|–1 and subsequent use of an addition theorem for regular spherical harmonics (Rlm(r)) factorize the electronic (r1 and r2) and nuclear coordinates (R) as follows:

2.1. 6

where we call Qlmij(Ω) exchange (multipole) moments in analogy with the electrostatic multipole moments Qlm(Ω), which depend on the electron density rather than a product of two orbitals; this is why they lack an imprint of the orbitals i and j. The exchange moments are defined by

2.1. 7

Equation 7 can now be truncated to the first term only, by setting l = m = 0 and using the fact that R00(r) = 1 and T00,00(r) = 1,

2.1. 8

where R is the internuclear distance. It is pleasing to spot the similarity between eq 8 and qAqB/R, which expresses the electrostatic interaction between two point charges q. Both equations result from a truncated multipolar expansion of an energy that actually depends on an electron density or an exchange density. For our purpose, it is important to connect eq 8 with the DI, which is defined as

2.1. 9

where

2.1. 10

Substituting eq 9 into eq 8 yields the equation that is central to this paper:

2.1. 11

A study40 of the convergence behavior showed that this equation is quite a good approximation, unless A and B are very close, such as in a 1,2 relation, in which case the expansion typically diverges. However, as a successful example of convergence, eq 11 returns an approximate exchange energy of −4.8 kJ/mol for two hydrogen atoms interacting in a trans relation in acrolein, being 3.1 Å away from each other, while their exact exchange energy is −4.0 kJ/mol. However, many atoms separated by more than 3.5 to 4 Å reveal that the approximation at the heart of eq 11 holds within 0.1 kJ/mol. As a result, one expects the expression DI(A,B) = 2RAB|Vxc(A,B)| to hold quite well, which is important to interpret the observed results.

2.2. J-Coupling Constants

Among the different relationships that correlate structural characteristics with NMR parameters, the Karplus equation is widely used. This equation relates 3J(A,B) with the value of the dihedral angle (A–X–Y–B), θ. The equation was originally developed for H–H J-couplings, 3J(H,H′), but later extended to other nuclei.41−43 The Karplus equation can be written as eq 12 or eq 13, where we use eq 12 in this work,

2.2. 12
2.2. 13

It should be noted that Karplus published another paper44 four years after his original one, partially motivated by some criticism on the limitation of this theory. He analyzed the effect of the substituent’s electronegativity and the dependence on the bond angle and bond length, but the latter turned out to be of minor relevance.43 It is known that J-couplings associated with the backbones of peptides and proteins are actually functions of both the φ and ψ dihedral angles rather than simply φ or ψ, but for our purpose, this insight is not crucial. Interpolations45 obtained from thousands of geometries over a two-dimensional dihedral angle grid can be used to more accurately determine peptide and protein structures from NMR measurements in solution. Finally, we point out43 that measured J-couplings are actually a time average of instantaneous values over a time scale of milliseconds. In the static approach, one uses an individual structure that represents the averaged dihedral angles. The motional averaging effects are automatically included in the adjusted coefficients during the parameterization process.

3. Materials and Computational Details

In their assessment, against the experiment, of using DFT, CCSD, and MCSCF for the calculation of J-couplings in ethane, methanol, and methylamine, Pecul and Helgaker concluded46 that B3LYP34 performs well for geminal 2J(H,H′) and 2J(C,H) couplings but tends to slightly overestimate the vicinal 3J(H,H′) couplings, although B3LYP is sufficiently accurate for most purposes. Thus, we employed the B3LYP functional in combination with different basis sets in the calculation of 3J(H,H′) for ethane in order to select the most adequate basis set against the experiment. Ethane has been measured under various conditions, and hence, a range of five experimental values was reported47 spanning 7.992 and 8.005 Hz. The results for CH3CH3, CH3NH2, and CH3OH have been gathered in Table S1 of the Supporting Information (SI). The IGLO-III basis set48 provides the value (7.88 Hz) closest to the experiment for ethane for all eight basis sets considered, by only ∼0.1 Hz. The reliability of this basis set is confirmed by comparing the experimental and calculated values of 3J(H,H′) in CH3OH (Exp49 = 5.535 Hz, Calc = 5.82 Hz) and CH3NH2 (Exp50 = 7.0 Hz, Calc = 7.00 Hz). Consequently, the geometries of the energy minima of all systems were obtained at the B3LYP/IGLO-III level and a rotational energy profile was generated by changing the H–C–Y–H angle in increments of 15° and then reoptimizing the rest of the geometrical parameters. The minima of the capped glycine, alanine, valine, leucine, and isoleucine were taken from a previous study where the potential energy surface was explored for 20 natural amino acids.51 The 3J(H,H′) values were calculated at the B3LYP/IGLO-III level of theory. All calculations were carried out with the GAUSSIAN09 program,52 while DI and Vxc values were calculated with the AIMAll program53 using the B3LYP wavefunction by a method that makes IQA compatible39 with this functional.

We explored the correlation between 3J(H,H′) and two quantities, DI and Vxc, between the two hydrogens of interest in a set of six simple molecules: CH3CH3, CH3NH2, CH3OH and their period-3 semi-counterparts, CH3SiH3, CH3PH2, and CH3SH, summarized as H3C-YHn (where Y = C, N, O, Si, P, or S with n = 1, 2, or 3 depending on element Y). In addition, we have calculated correlations for N-methylacetamide (NMA), which is a prototype molecule representing the peptide bond in proteins. Increments of 15° in the HN–N–Cα–Hα dihedral angle of NMA were used to control the scanning of its energy profile. Finally, we also calculated the correlations for five capped amino acids (Gly, Ala, Val, Leu, and Ile) in their local energy minima and along φ dihedral energy profiles54 centered on the global energy minimum. First, the ψ dihedral angle of the global minimum was frozen, and then, the φ dihedral angle was rotated by 15° increments between −180° and +180°, resulting in 24 = [180 – (−180)]/15 geometries, additionally to the global minimum. The 24 geometries were then relaxed through geometry optimization, keeping both the φ and ψ dihedral angles frozen. Figure 1 shows the HN–N–Cα–Hα dihedral angle in NMA and alanine as a representative of the five capped amino acids.

Figure 1.

Figure 1

Open in a new tab

Labeling of the HN–N–Cα–Hα dihedral angle that is varied in the calculation of 3J(HN,Hα) in NMA (left) and alanine (right). It should be noted that this dihedral angle is labeled as θ throughout the paper and the SI for convenience.

4. Results and Discussion

The calculated 3J(H,H′) values for the H3C-YHn series and NMA as well as the corresponding DI(H,H′) and Vxc(H,H′) values have been gathered in Table S2 of the SI. The 3J(H,H′) values fit nicely to Karplus equations showing coefficients of determination, R2, with values larger than 0.98 for all the H3C-YHn molecules (Table S3). In the case of the capped amino acids (glycine, alanine, valine, leucine, and isoleucine), two sets of 3J(HN,Hα) values are considered. One set consists of J-couplings from the dihedral φ scan, centered on the global minimum for each of the five amino acids, and a second set incorporates the previous values plus those of all the reported local energy minima.51 For all 5 amino acids, the fitting of the dihedral scan values provides better statistics (R2 > 0.95) than when all the minima are included (R2 > 0.93). It should be noted that because 3J(H,H′) is dominated by the FC term, similar correlations are found for FC as a function of the dihedral angle. Indeed, Table S4 confirms linear relationships between the total 3J(H,H′) and the FC term, showing a slope very close to 1.0, intercepts close to 0.0, and R2 values larger than 0.998.

The calculated 3J(HN,Hα) values for NMA and the five amino acids can be clustered in two groups. The first group comprises NMA, Gly, and Ile, which show values of 3J for |θ| = 180° around 12 Hz while the systems in the second group (Ala, Val, and Leu) show values around 8 Hz for the same angles. The fitted Karplus equations based on our calculated J-coupling values and the two Karplus equations reported based on experimental studies show a reasonable agreement, as can be concluded from Figure 2. It should be noted that this figure plots the “scan” equations listed in the second part of Table S3. The agreement is encouraging especially considering that the experimental values correspond to average values of all the amino acids and the fact that the Karplus equation is affected by the substituents55 and the side-chain conformation.56 It should be noted that what we refer to here as experimental J-coupling values are actually calculated from two equations (eq 1 and eq 2 in Figure 2) obtained by an ensemble fitting method applied to two different proteins, the details of which can be found in the top two entries of Table 5.7 of ref (43).

Figure 2.

Figure 2

Open in a new tab

3J(HN,Hα) for NMA, Gly, Ala, Val, Ile, and Leu as a function of the dihedral angle θ (specified in Figure 1), fitted to either values calculated in this work or fitted to experimental data.43

The use of a single Karplus equation to fit all the calculated J-coupling values for NMA and the amino acids together (259 points) provides a much smaller R2 value (0.88, Table S3) due to the scattering of values in the amino acids previously mentioned in the data set.

The correlations between 3J(HN,Hα) and the corresponding FC term are excellent (R2 = 0.999) for NMA, Gly, and Ile (Table S4). However, for Ala, Val, and Leu, the R2 decreases to 0.94. However, after separating the data in two intervals of the dihedral angle (|θ| > 90° and |θ| < 90°), excellent correlations are again found. Table S4 also shows plots of Ala, Val, and Leu where the contribution of the FC term to the total 3J(H,H′) coupling constant is larger if |θ| < 90° than if |θ| > 90°.

Table 1 shows Karplus-like relationships between Vxc and the relevant dihedral angle θ with good correlation (R2 > 0.93) even when all the values for NMA and the amino acids are considered together (R2 = 0.937). Table S5 shows Karplus-like relationships between DI and θ with excellent correlation (R2 > 0.97) holding out very well even when all the values for NMA and the amino acids are considered together again (R2 = 0.98). In all cases, the largest 3J(H,H) and DI values are associated with a dihedral angle of 180°. For Vxc, the largest absolute value is found at 0° for CH3-YHn, with Y = C, Si, P, and S and all the amino acids while it is at 180° for Y = N and O, and for NMA.

Table 1. Karplus-Like Relationships between Vxc (kJ/mol) and the Dihedral Angle, θ, which Is HN–N–Cα–Hα or H–C–Y–H.

system fitted equation [x = cosθ] R2
CH3-CH3 Vxc = −1.327x2 – 0.172x – 0.216 0.998
CH3-NH2 Vxc = −0.941x2 + 0.034x – 0.169 0.991
CH3-OH Vxc = −0.717x2 + 0.087x – 0.113 0.9995
CH3-SiH3 Vxc = −0.9890x2 – 0.148x – 0.334 0.987
CH3-PH2 Vxc = −1.433x2 – 0.351x – 0.365 0.939
CH3-SH Vxc = −1.300x2 – 0.260x – 0.246 0.979
NMA Vxc = −0.623x2 + 0.0846x – 0.129 0.994
Gly (scan + min) Vxc = −0.682x2 + 0.043x – 0.102 0.960
Ala (scan + min) Vxc = −0.718x2 – 0.053x – 0.147 0.970
Val (scan + min) Vxc = −0.796x2 – 0.043x – 0.089 0.969
Ile (scan + min) Vxc = −0.764x2 – 0.041x – 0.102 0.959
Leu (scan + Min) Vxc = −0.694x2 – 0.030x – 0.139 0.983
All-AA + NMA Vxc = −0.734x2 – 0.015x – 0.110 0.937
Open in a new tab

The linear correlation between 3J(H,H′) and DI shows good R2 values for DI (R2 > 0.9) while for Vxc, the results are more variable, with R2 values between 0.5 and 0.99. However, the behavior of Vxc and DI as a function of the J-couplings shows that the data points are separated in two different trends depending on the value of θ. Figure 3 illustrates this effect for ethane while Figure S1 shows this for all other compounds. Those configurations with |θ| < 90° show larger values of Vxc and DI than those with |θ| > 90° for a given 3J(H,H) value. The two fitted lines converge (i.e., intersect) for the smaller values of 3J(H,H′), which are associated with a θ value of about 90°. The differences between the two subsets in the Vxc and DI parameters very much depend on the molecule, being maximal for the Vxc values of CH3-SiH3, while in the same molecule, the values of DI almost fully coincide (i.e., the angle between the two fitted lines collapses to nearly zero (Figure S1)).

Figure 3.

Figure 3

Open in a new tab

DI (top left), Vxc (kJ/mol) (top right), and VxcR (kJ/mol Å) (bottom) as a function of J (Hz) in ethane. The values are separated in two groups based on the values of the dihedral angle θ.

The splitting of the values in two linear correlations (Figure 3) can be understood if the normalized values (between 0 and 1) of the three properties are plotted simultaneously (see Figure 4 for ethane). The largest normalized values for J and DI in ethane correspond to θ = 180° (−180°). The normalized values of these two properties perfectly overlap in the range of values of |θ| > 90°. However, this is not the case for |θ| < 90°. Consequently, the same linear correlations cannot hold for both |θ| > 90° and |θ| < 90°. The absolute value of Vxc is the largest at θ = 0°, and for |θ| < 90°, its normalized values are larger than those of J while the opposite is true for |θ| > 90°. The correlation of normalized |Vxc| versus J should have a slope larger than 1.0 for |θ| < 90° and one smaller than 1.0 for |θ| > 90°. Similar results are obtained when the FC term is used versus DI and Vxc (Figure S2).

Figure 4.

Figure 4

Open in a new tab

Normalized values (between 0 and 1) of 3J(H,H), DI, and −Vxc for ethane.

Because, according to eq 11, the DI is approximately proportional to VxcR (where R is the internuclear distance), the correlation between VxcR and 3J(H,H) was checked in the whole range of angles. Table 2 allows a full comparison between fits of 3J(H,H′) against DI, Vxc or VxcR for all 12 compounds. The first important observation is that the fits to VxcR give (mostly substantially) higher R2 values than those to Vxc for all compounds except one. The exception is CH3OH where the correlation of Vxc (R2 = 0.991) barely beats that of VxcR (R2 = 0.983). Second, the correlations of VxcR with 3J(H,H) shows larger R2 values than those between DI and 3J(H,H) in 4 of the 6 small compounds. The two exceptions are CH3-SiH3 and CH3-PH2, while for CH3-CH3, the fits are almost identical (0.978 and 0.973). Thirdly and importantly, in the set of NMA with the amino acids, VxcR is the best single descriptor with R2 values between 0.95 and 0.99. The fact that fits to DI are always the worst (and sometimes markedly so) shows that the rationale offered by eq 11 cannot be taken for granted. In particular, the worst DI correlations are found for Ala, Val, and Leu, which were identified earlier in the subset for which the correlation between 3J(HN,Hα) and the FC term was worse than that for the other subset of NMA, Gly, and Ile.

Table 2. Coefficient of Determination, R2, of the Regression of 3J(H,H′) against DI, Vxc, and VxcR.

system DI Vxc VxcR
CH3-CH3 0.978 0.828 0.973
CH3-NH2 0.916 0.965 0.993
CH3-OH 0.902 0.991 0.983
CH3-SiH3 0.997 0.521 0.786
CH3-PH2 0.980 0.678 0.913
CH3-SH 0.940 0.804 0.965
NMA 0.918 0.941 0.992
Gly 0.934 0.909 0.981
Ala 0.784 0.920 0.964
Val 0.779 0.889 0.948
Ile 0.931 0.708 0.958
Leu 0.752 0.868 0.941
Open in a new tab

5. Conclusions

The IQA method is a relatively new addition to energy decomposition analysis. It mandatorily operates at the atomic level because it adopts the quantum topological atom defined by the Quantum Theory of Atoms in Molecules (QTAIM). IQA is at the basis of the force field FFLUX while its various atomistic energy contributions provide chemical insight (e.g., the origin of the rotation barrier in biphenyl). The main aim of the current work is to find an experimental connection to IQA’s interatomic exchange-correlation energy Vxc(A,B). A suitable candidate as (essentially) experimental quantity is the NMR J-coupling constant denoted 3J(H,H′), which a number of previous studies showed to correlate well with QTAIM’s the DI, which is essentially a bond order.

Inspired by Karplus equations, here, we investigate correlations between 3J(H,H′) and a relevant dihedral angle in six simple initial compounds of the shape H3C-YHn (Y = C, N, O, Si, P, and S), N-methylacetamide (as a prototype of the peptide bond), and five peptide-capped amino acids (Gly, Ala, Val, Ile, and Leu) because of the protein direction of FFLUX. In order to test the reliability of the chosen level of theory (B3LYP/IGLO-III), the 3J(H,H′) values of ethane, methylamine, and methanol were calculated and confirmed to be close to the experiment. Furthermore, nicely fitted Karplus equations of 3J(H,H′) emerged for all 12 compounds in the whole range of the relevant dihedral angle. Because the Fermi contact term is typically the dominant contribution to 3J(H,H), similar excellent correlations are found except for Ala, Val, and Leu. However, when values are separated in two groups, depending on the dihedral angle (|θ| > 90° and |θ| < 90°), their correlations also become excellent (R2 > 0.999).

Finally, we observed that, for NMA and all five amino acids, the correlations between 3J(H,H′) and VxcR (where R is the internuclear distance) are always stronger than those with DI. Looking at all 12 systems, correlations between 3J(H,H′) and Vxc can be excellent (R2 > 0.91) but only for five systems. In conclusion, except for methanol, the inter-hydrogen exchange-correlation energy Vxc(H,H′) makes the best contact with the experiment, through 3J(H,H′), when multiplied with the internuclear distance RHH′. However, the three types of plot, 3J(H,H′) against DI, Vxc, or VxcR, each indicate that the fit improves if two lines are fitted instead of one, based on the value of the dihedral angle, |θ| > 90° or |θ| < 90°.

Looking at the future, such experimental reassurance may boost the newly proposed Relative Energy Gradient (REG) method,57 which computes chemical insight. For example, REG resolved58 the controversy surrounding the origin of the planar torsional energy barrier in biphenyl. The knowledge that the interatomic exchange-correlation energy has a link with experiment bolsters REG’s findings. For example, if REG ranks the exchange-correlation energy of the O···H hydrogen bond interaction in a classic water dimer configuration as five times weaker than its electrostatic counterpart, then the current work may lend this finding credibility. After all, J-couplings have been known to be associated with purely covalent bonds since the 1950s, but four decades later, direct evidence emerged59 for the presence of J-couplings between magnetically active nuclei on both sides of the hydrogen bond.

Acknowledgments

This work was carried out with financial support from the Ministerio de Ciencia, Innovación y Universidades (PID2021-125207NB-C32) and Comunidad de Madrid (P2018/EMT-4329 AIRTEC-CM). Gratitude is due to the CTI (CSIC) for their continued computational support. P.L.A.P. acknowledges the EPSRC for funding through the award of an Established Career Fellowship (grant EP/K005472).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpca.2c07693.

  • Table S1. Average value of 3J(H,H′) (Hz) calculated at the B3LYP computational level with eight different basis sets; Table S2. 3J(H,H′) (Hz), DI, Vxc (kJ/mol) for H3C-YHn, Y = C, N, O, Si, P, and S and N-methylacetamide (NMA) as a function of the dihedral angle (°) H–C–Y–H or HN–N–Cα–Hα (NMA); Table S3. Fitted Karplus equations for 3J(H,H′); Table S4. Linear relationship between 3J(H,H′) and the Fermi contact (FC) term (Hz); Table S5. Karplus-like relationships between DI and the dihedral angle, θ; Figure S1. 3J(H,H′) as a function of DI and Vxc; and Figure S2. FC term (Hz) as a function of DI and Vxc (PDF)

The authors declare no competing financial interest.

Supplementary Material

jp2c07693_si_001.pdf (2.1MB, pdf)

References

  1. Phipps M. J. S.; Fox T.; Tautermann C. S.; Skylaris C.-K. Energy decomposition analysis approaches and their evaluation on prototypical protein–drug interaction patterns. Chem. Soc. Rev. 2015, 44, 3177. 10.1039/C4CS00375F. [DOI] [PubMed] [Google Scholar]
  2. Kitaura K.; Morokuma K. A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation. Int. J. Quantum Chem. 1976, 10, 325. 10.1002/qua.560100211. [DOI] [Google Scholar]
  3. Blanco M. A.; Martín Pendás A.; Francisco E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theor. Comput. 2005, 1, 1096. 10.1021/ct0501093. [DOI] [PubMed] [Google Scholar]
  4. Popelier P. L. A.; Kosov D. S. Atom-atom partitioning of intramolecular and intermolecular Coulomb energy. J. Chem. Phys. 2001, 114, 6539. 10.1063/1.1356013. [DOI] [Google Scholar]
  5. Bader R. F. W.; Beddall P. M. Virial Field Relationship for Molecular Charge Distributions and the Spatial Partitioning of Molecular Properties. J. Chem. Phys. 1972, 56, 3320. 10.1063/1.1677699. [DOI] [Google Scholar]
  6. Bader R. F. W.Atoms in Molecules. A Quantum Theory; Oxford Univ. Press: Oxford, Great Britain, 1990. [Google Scholar]
  7. Popelier P. L. A.Atoms in Molecules. An Introduction; Pearson Education: London, Great Britain, 2000. [Google Scholar]
  8. Silva A. F.; Duarte L. J.; Popelier P. L. A. Contributions of IQA electron correlation in understanding the chemical bond and non-covalent interactions. Struct. Chem 2020, 31, 507. 10.1007/s11224-020-01495-y. [DOI] [Google Scholar]
  9. Martín Pendás A.; Francisco E. Questioning the orbital picture of magnetic spin coupling: a real space alternative. Phys. Chem. Chem. Phys. 2022, 24, 639. 10.1039/D1CP03485E. [DOI] [PubMed] [Google Scholar]
  10. Popelier P. L. A. Molecular Simulation by Knowledgeable Quantum Atoms. Phys. Scr. 2016, 91, 033007 10.1088/0031-8949/91/3/033007. [DOI] [Google Scholar]
  11. Popelier P. L. A. QCTFF: On the Construction of a Novel Protein Force Field. Int. J. Quantum Chem. 2015, 115, 1005. 10.1002/qua.24900. [DOI] [Google Scholar]
  12. Symons B. C. B.; Popelier P. L. A. Application of quantum chemical topology force field FFLUX to condensed matter simulations: liquid water. J. Chem. Theory Comput. 2022, 18, 5577–5588. 10.1021/acs.jctc.2c00311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Garcia-Revilla M.; Francisco E.; Popelier P. L. A.; Martin Pendas A. Domain-averaged exchange correlation energies as a physical underpinning for chemical graphs. ChemPhysChem 2013, 14, 1211. 10.1002/cphc.201300092. [DOI] [PubMed] [Google Scholar]
  14. Karplus M. Contact Electron-Spin Coupling of Nuclear Magnetic Moments. J. Chem. Phys. 1959, 30, 11. 10.1063/1.1729860. [DOI] [Google Scholar]
  15. Bader R. F. W.; Streitwieser A.; Neuhaus A.; Laidig K. E.; Speers P. Electron delocalization and the Fermi hole. J. Am. Chem. Soc. 1996, 118, 4959. 10.1021/ja953563x. [DOI] [Google Scholar]
  16. McWeeny R. Some Recent Advances in Density Matrix Theory Rev. Mod. Phys. 1960, 32, 335. 10.1103/RevModPhys.32.335. [DOI] [Google Scholar]
  17. Fradera X.; Austen M. A.; Bader R. F. W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304. 10.1021/jp983362q. [DOI] [Google Scholar]
  18. Outeiral C.; Vincent M. A.; Martin Pendas A.; Popelier P. L. A. Revitalizing the concept of bond order through delocalization measures in real space. Chem. Sci. 2018, 9, 5517. 10.1039/C8SC01338A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Matito E.; Poater J.; Solà M.; Duran M.; Salvador P. Comparison of the AIM Delocalization Index and the Mayer and Fuzzy Atom Bond Orders. J. Phys. Chem. A 2005, 109, 9904. 10.1021/jp0538464. [DOI] [PubMed] [Google Scholar]
  20. García-Revilla M.; Popelier P. L. A.; Francisco E.; Martín-Pendás A. Nature of chemical interactions from the profiles of electron delocalization indices. J. Chem. Theory Comput. 2011, 7, 1704. 10.1021/ct2001842. [DOI] [PubMed] [Google Scholar]
  21. Matta C. F.; Hernandez-Trujillo J. Bonding in polycyclic aromatic hydrocarbons in terms of the electron density and of electron delocalization. J. Phys. Chem. A 2003, 107, 7496. 10.1021/jp034952d. [DOI] [Google Scholar]
  22. Matta C. F.; Hernández-Trujillo J. Bonding in Polycyclic Aromatic Hydrocarbons in Terms of the Electron Density and of Electron Delocalization. J. Phys. Chem. A 2005, 109, 10798. 10.1021/jp055864r. [DOI] [Google Scholar]
  23. Poater J.; Fradera X.; Duran M.; Sola M. The delocalization index as an electronic aromaticity criterion: Application to a series of planar polycyclic aromatic hydrocarbons. Chem. – Eur. J. 2003, 9, 400. 10.1002/chem.200390041. [DOI] [PubMed] [Google Scholar]
  24. Bader R. F. W.; Stephens M. E. Spatial Localization of the Electronic Pair and Number Distributions in Molecules. J. Am. Chem. Soc. 1975, 97, 7391. 10.1021/ja00859a001. [DOI] [Google Scholar]
  25. Matta C. F.; Hernández-Trujillo J.; Bader R. F. W. Proton Spin–Spin Coupling and Electron Delocalization. J. Phys. Chem. A 2002, 106, 7369. 10.1021/jp020514f. [DOI] [Google Scholar]
  26. Matta C. F.; Arabi A. A. Electron-density descriptors as predictors in quantitative structure–activity/property relationships and drug design. Future Med. Chem 2011, 3, 969. 10.4155/fmc.11.65. [DOI] [PubMed] [Google Scholar]
  27. McConnell H. M. Molecular Orbital Approximation to Electron Coupled Interaction between Nuclear Spin. J. Chem. Phys. 1956, 24, 460. 10.1063/1.1742498. [DOI] [Google Scholar]
  28. Ramsey N. F. Electron Coupled Interactions between Nuclear Spins in Molecules. Phys. Rev. 1953, 91, 303. 10.1103/PhysRev.91.303. [DOI] [Google Scholar]
  29. Cremer D.; Gräfenstein J. Calculation and analysis of NMR spin–spin coupling constants. Phys. Chem. Chem. Phys. 2007, 9, 2791. 10.1039/B700737J. [DOI] [PubMed] [Google Scholar]
  30. Castillo N.; Matta C. F.; Boyd R. J. Fluorine–Fluorine Spin–Spin Coupling Constants in Aromatic Compounds: Correlations with the Delocalization Index and with the Internuclear Separation. J. Chem. Inf. Model. 2005, 45, 354. 10.1021/ci0497051. [DOI] [PubMed] [Google Scholar]
  31. Barone V.; Peralta J. E.; Contreras R. H.; Snyder J. P. DFT Calculation of NMR JFF Spin-Spin Coupling Constants in Fluorinated Pyridines. J. Phys. Chem. A 2002, 106, 5607. 10.1021/jp020212d. [DOI] [Google Scholar]
  32. Mandado M.; Blockhuys F.; Alsenoy C. V. On the applicability of QTAIM, Hirshfeld and Mulliken delocalisation indices as a measure of proton spin–spin coupling in aromatic compounds. Chem. Phys. Lett. 2006, 430, 454. 10.1016/j.cplett.2006.09.037. [DOI] [Google Scholar]
  33. Sánchez-Mendoza E.; Hernández-Trujillo J.; del Río-Portilla F. Experimental and Theoretical Analysis of Vicinal and Long-Range Proton–Proton Coupling Constants for Anthracene Derivatives. J. Phys. Chem. A 2007, 111, 8264. 10.1021/jp073564z. [DOI] [PubMed] [Google Scholar]
  34. Becke A. D. Density-Functional Thermochemistry. 3. the Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648. 10.1063/1.464913. [DOI] [Google Scholar]
  35. Garcia-Revilla M.; Hernandez-Trujillo J. Energetic and electron density analysis of hydrogen dissociation of protonated benzene. Phys. Chem. Chem. Phys. 2009, 11, 8425. 10.1039/B906961E. [DOI] [PubMed] [Google Scholar]
  36. Soares B. A.; Firme C. L.; Maciel M. A. M.; Kaiser C. R.; Schilling E.; Bortoluzzi A. J. Experimental and NMR theoretical methodology applied to geometric analysis of the bioactive clerodane trans-dehydrocrotonin. J. Braz. Chem. Soc. 2014, 25, 629. 10.5935/0103-5053.20140010. [DOI] [Google Scholar]
  37. Del Bene J. E.; Alkorta I.; Elguero J. Halogen Bonding Involving CO and CS with Carbon as the Electron Donor. Molecules 2017, 22, 1955. 10.3390/molecules22111955. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Darley M. G.; Popelier P. L. A. Role of short-range electrostatics in torsional potentials. J. Phys. Chem. A 2008, 112, 12954. 10.1021/jp803271w. [DOI] [PubMed] [Google Scholar]
  39. Maxwell P.; Martín Pendás A.; Popelier P. L. A. Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory. Phys. Chem. Chem. Phys. 2016, 18, 20986. 10.1039/c5cp07021j. [DOI] [PubMed] [Google Scholar]
  40. Rafat M.; Popelier P. L. A. In Quantum Theory of Atoms in Molecules; Matta C. F., Boyd R. J., Eds.; Wiley-VCH: Weinheim, Germany, 2007; Vol. 5; p 121. [Google Scholar]
  41. Grimmer C. D.; Slabber C. A. Conformational analysis: 3JHCOC and 3JHCCC Karplus relationships for methylene 1H nuclei. Magn. Res. Chem. 2015, 53, 590. 10.1002/mrc.4264. [DOI] [PubMed] [Google Scholar]
  42. Coxon B. In Advances in Carbohydrate Chemistry and Biochemistry; Derek H., Ed.; Academic Press, 2009; vol 62; p 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Salvador P. In Annual Reports on NMR Spectroscopy; Graham A. W., Ed.; Academic Press: 2014; vol 81; p 185. [Google Scholar]
  44. Karplus M. Vicinal Proton Coupling in Nuclear Magnetic Resonance. J. Am. Chem. Soc. 1963, 85, 2870. 10.1021/ja00901a059. [DOI] [Google Scholar]
  45. Salvador P.; Tsai I.-H.; Dannenberg J. J. J-coupling constants for a trialanine peptide as a function of dihedral angles calculated by density functional theory over the full Ramachandran space. Phys. Chem. Chem. Phys. 2011, 13, 17484. 10.1039/C1CP20520J. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Pecul M.; Helgaker T. The Spin–Spin Coupling Constants in Ethane, Methanol and Methylamine: A Comparison of DFT, MCSCF and CCSD Results. Int. J. Mol. Sci. 2003, 4, 143. 10.3390/i4030143. [DOI] [Google Scholar]
  47. Kaski J.; Lantto P.; Vaara J.; Jokisaari J. Experimental and Theoretical ab Initio Study of the 13C–13C Spin–Spin Coupling and 1H and 13C Shielding Tensors in Ethane, Ethene, and Ethyne. J. Am. Chem. Soc. 1998, 120, 3993. 10.1021/ja972936m. [DOI] [Google Scholar]
  48. Huzinaga S. Gaussian-Type Functions for Polyatomic Systems I. J. Chem. Phys. 1965, 42, 1293. 10.1063/1.1696113. [DOI] [Google Scholar]
  49. Kupka T. Complete basis set prediction of methanol isotropic nuclear magnetic shieldings and indirect nuclear spin–spin coupling constants (SSCC) using polarization-consistent and XZP basis sets and B3LYP and BHandH density functionals. Magn. Res. Chem. 2009, 47, 674. 10.1002/mrc.2448. [DOI] [PubMed] [Google Scholar]
  50. Wielogórska E.; Makulski W.; Koźmiński W.; Jackowski K. 15N, 13C and 1H nuclear magnetic shielding and spin–spin coupling in gaseous 15N-enriched methylamine. J. Mol. Struct. 2004, 704, 305. 10.1016/j.molstruc.2003.11.062. [DOI] [Google Scholar]
  51. Yuan Y.; Mills M. J. L.; Popelier P. L. A.; Jensen F. Comprehensive Analysis of Energy Minima of the 20 Natural Amino Acids. J. Phys. Chem. A 2014, 118, 7876–7891. 10.1021/jp503460m. [DOI] [PubMed] [Google Scholar]
  52. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M. J.; Heyd J.; Brothers E. N.; Kudin K. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A. P.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam N. J.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas Ö.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  53. Keith T. A. TK Gristmill Software: Overland Park KS, USA, Version 15.05.18, p (aim. tkgristmill.com).
  54. Maxwell P. I.; Popelier P. L. A. Unfavorable Regions in the Ramachandran Plot: Is It Really Steric Hindrance? The Interacting Quantum Atoms Perspective. J. Comput. Chem. 2017, 38, 2459. 10.1002/jcc.24904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Schmidt J. M. Asymmetric Karplus curves for the protein side-chain 3 J couplings. J. Biomol. NMR 2007, 37, 287. 10.1007/s10858-006-9140-8. [DOI] [PubMed] [Google Scholar]
  56. Pérez C.; Löhr F.; Rüterjans H.; Schmidt J. M. Self-Consistent Karplus Parametrization of 3J Couplings Depending on the Polypeptide Side-Chain Torsion χ1. J. Am. Chem. Soc. 2001, 123, 7081. 10.1021/ja003724j. [DOI] [PubMed] [Google Scholar]
  57. Thacker J. C. R.; Vincent M. A.; Popelier P. L. A. Using the Relative Energy Gradient Method with Interacting Quantum Atoms to Determine the Reaction Mechanism and Catalytic Effects in the Peptide Hydrolysis in HIV-1 Protease. Chem. – Eur. J. 2018, 14, 11200. 10.1002/chem.201802035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Popelier P. L. A.; Maxwell P. I.; Thacker J. C. R.; Alkorta I. A Relative Energy Gradient (REG) study of the planar and perpendicular torsional energy barriers in biphenyl. Theor. Chem. Acc. 2019, 138, 12. 10.1007/s00214-018-2383-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Blake P. R.; Park J.-B.; Adams M. W. W.; Summers M. F. Novel observation of NH-S(Cys) hydrogen-bond-mediated scalar coupling in cadmium-113 substituted rubredoxin from Pyrococcus furiosus. J. Am. Chem. Soc. 1992, 114, 4931. 10.1021/ja00038a084. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c07693_si_001.pdf (2.1MB, pdf)

Articles from The Journal of Physical Chemistry. a are provided here courtesy of American Chemical Society

RESOURCES