Effect of disturbances in neuronal calcium and IP3 dynamics on β-amyloid production and degradation

Abstract

Overproduction and accumulation of β-amyloid and its improper clearance can cause neurotoxicity leading to Alzheimer’s disease. The production and degradation of β-amyloid depend on the calcium ([Ca²⁺]) and IP3 dynamics in the nerve cells. Thus, there is a need to understand the impacts of disturbances in the processes of [Ca²⁺] and IP3 dynamics on β-amyloid production and its degradation. Here, a model is proposed to investigate the role of [Ca²⁺] and IP3 dynamics on β-amyloid production and degradation. The problem is formulated in terms of the initial boundary value problem involving the system of two reaction–diffusion equations respectively for [Ca²⁺] and IP3 in the nerve cell. The solution is obtained by employing the Finite element approach. The numerical results are used to analyze the impact of various mechanisms of calcium and IP3 dynamics on β-amyloid production and degradation in a neuron cell. The results indicate that disturbances in any of the constitutive processes of interdependent calcium and IP3 dynamics like source influx, buffering, serca pump, and IP3 dynamics, etc. can cause dynamic changes in β-amyloid production and degradation, which in turn can be the cause of neurotoxicity and neuronal disorders like Alzheimer’s disease. Thus, the relationships obtained by the proposed model among various mechanisms can be useful in addressing the challenges of identifying specific constitutive processes causing neuronal disorders like Alzheimer’s disease, etc., and developing the framework for their diagnosis and treatment.

Introduction

The deposition of high concentrations of β-amyloid (Aβ) in neuron cells is reported to be the major causative factors for Alzheimer’s disease. It is well established that Aβ is neurotoxic and its accumulation leads to neuronal loss in the brain. This disease process involves the degeneration of synapses and neurons due to the plaques formed in the brain regions. Also, various research workers in the past have noticed that disturbances in calcium dynamics are associated with the neuro degenerative process.

Hodgkin and Huxley (1952) studied the behavior of membrane current and its significance in other processes in the nerve cell. Crank (1979) examined the diffusion process and measurement of the diffusion coefficient in various media. Llinas (1979) studied the action of calcium conductance as dendritic spiking and synaptic transmission in the cell. The presynaptic diffusion model of calcium distant from the membrane with the significant role of the surface pump, influx, and cytoplasmic binding for the transmitter release in the cell has been discussed by Fogelson and Zucker (1985). Ahmed and Connor (1988) studied the kinetic properties and impact of buffer in the regulatory processes of calcium in a neuron cell. Bootman and Berridge (1995) explained the elemental events associated with calcium signaling. Wagner and Keizer (1994); Smith (1996); Smith et al. (1996) devised the calcium diffusion model that incorporates and validates the buffer for calcium channels. Egelman and Montague (1999) studied the dependence of calcium oscillation on the biologically relevant parameters as diffusion coefficient, the geometrical structure of elements, etc. in the nerve cell. The functions of ER in different aspects of [Ca²⁺] signaling in the nerve cell have been discussed by Verkhratsky (2002). The disturbances in the calcium concentration are seen because of the high concentration of slow buffers in a neuron cell (Falcke 2003). Sneyd et al. (2003) developed the mathematical model of calcium signaling that incorporates the ryanodine receptor and IP3R receptor in the acinar cell. Brini et al. (2014) discussed the contribution of calcium signaling in neuronal disorders like Huntington's, Familial hemiplegic migraine, and Alzheimer's diseases. In recent times, various researchers have studied the calcium signaling in the diverse cells such as myocyte (Pathak and Adlakha 2015, 2016), astrocyte (Jha and Adlakha 2014, 2015), neuron cell (Tewari et al. 2008, 2010, 2011, 2012; Tripathi and Adlakha 2011; Jha and Adlakha 2014), Oocyte (Panday et al. 2013; Naik et al. 2015, 2016, 2019), fibroblast cell (Kotwani et al. 2012, 2014), hepatocyte cell (Jagtap et al. 2018), acinar (Manhas et al. 2014, 2014), etc. using analytical and numerical approaches. Tewari et al. (2010, 2011) have examined the calcium diffusion model incorporating the excess buffer and Na⁺ ions in the nerve cell. Jha and Adlakha (2014, 2015) discussed the influences of diffusion, VGCC, and buffer on the calcium signaling in astrocyte. The serca pump, leak, and buffer have notable impacts on the calcium distribution in the myocyte cell (Pathak and Adlakha 2015, 2016). The significance of various parameters like buffer, source influx on calcium distribution in fibroblast cells has been discussed by Kotwani et al. (2014). Panday and Pardasani (2013) discussed the advection–diffusion model of calcium involving buffer, Na⁺/Ca²⁺ exchanger, and serca pump in the Oocyte cell. The spatiotemporal calcium distribution model in the Oocytes has been examined by Naik et al. (2015, 2016, 2019). The impacts of buffer on the calcium signaling in hepatocyte cell has been examined by Jagtap and Adlakha (2018). The mechanisms of calcium regulation have been studied by Naik (2020) using the finite element procedure in T-lymphocytes. A reaction–diffusion equation-based model of spatiotemporal calcium dynamics has been simulated using the combination of finite difference and finite element procedure by Naik and Zu (2020) T-lymphocyte cell. Thus, FEM is a good option for performing such studies in various human cells.

Michell (1975) hypothesized a relationship between the catabolism of PIP₂ and elevated intracellular calcium. Berridge and Irvine (1984) identified the IP3 as a second messenger to mobilize the calcium, particularly from the endoplasmic reticulum. The negative and positive feedbacks for calcium release depend on the IP3R gated channels in the range of cytoplasmic calcium in the cell (Bezprozvanny et al. 1991). The range of messenger actions of [Ca2 +] and IP3 based on the diffusion coefficients of calcium and IP3 in the Oocytes has been investigated by Allbritton et al. (1992). Keizer and Young (1993) studied the calcium fluctuations which depend on the inhibition and activation of IP3R in the ER. Li and Rinzel (1994) analyzed two variables model for calcium fluctuations in ER membrane. Falcke et al. (2000) examined the calcium dynamics with IP₃ and chaotic behavior from the interaction of slower calcium and fast voltage dynamics in the nerve cells. Wagner et al. (2004) examined the bistability of [Ca²⁺] and IP₃, which is achieved by the calcium-feedback on the calcium-dependent IP3 generation and IP3-mediated calcium release in Oocytes.

The primary amino acid sequence of Aβ was found in amyloid plaques and extracellular deposits (Glenner and Wong 1984). The Accumulation of Aβ peptides is the result of proteolytic cleavage of an amyloid precursor protein (APP) (Bloom 2014). Chen et al. (2017) discussed the structure, biological function, and toxicity of Aβ in a neuron cell and the curative developments and strategies for treating Alzheimer’s disease. Demuro et al. (2005) examined the role of calcium in the dysfunction and death of the cell through the amyloid-induced toxicity mechanism. Bezprozvanny and Mattson (2008) examined that the calcium influx is influenced by Aβ by affecting the membrane-associated oxidative stress in the nerve cell. Emilsson et al. (2006) discussed the changes in proteins and genes level associated with calcium signaling in the nerve cell that is found in Alzheimer’s disease patients. The neuron cell undergoes degenerative changes with Aβ accumulation in APP mutant mice, referring the Aβ neurotoxicity due to involvement of calcium (Meyer-Luehmann et al. 2008). Pierrot et al. (2004) explained the composition and toxicity of Aβ with AD-related mutations in the nerve cells which increase by increment in basal calcium concentration. Aβ promotes an increase in [Ca2 +] and which in turn increases Aβ levels, generating a positive feedback loop, leading to disease development (Bojarski et al. 2008).

Manhas and Pardasani (2014) studied the IP3 dependent disturbances in calcium distribution in the acinar cell. Recently, the coupled dynamics of calcium and IP₃ have been studied in the myocyte cell (Singh and Adlakha 2019a, b, 2020) and hepatocyte cell (Jagtap and Adlakha 2019), using different numerical approaches. Very few researchers attempted to study the temporal interdependence of calcium and IP₃ in neuron cell. But no attempt is noticed to study interdependent [Ca²⁺] and IP3 dynamics regulating the β-amyloid production and degradation.

The objective of this present work is to examine the interdependent calcium and IP₃ dynamics regulating the production and degradation of Aβ in a neuron cell. The FEM has been used to get the results and, the consequences of various variables on coupled dynamics of calcium and IP₃ dynamics and their effects on production and degradation of Aβ in neuron cells have been examined.

Mathematical formulation

Incorporating the buffer concentration in the model given by Wagner et al. (2004), and the [Ca2 +] dynamics involving IP₃ can be expressed in a neuron cell as,

$$\frac{\partial \left[{\text{Ca}}^{2+}\right]}{\partial \text{t}}={\text{D}}_{\text{Ca}}\frac{{\partial }^2\left[{\text{Ca}}^{2+}\right]}{\partial {\text{x}}^2}+\left(\frac{{\text{J}}_{\text{IPR}}-{\text{J}}_{\text{SERCA}}{\text{+ J}}_{\text{LEAK}}}{{\text{F}}_{\text{C}}}\right)-{\text{K}}^{+}{\left[\text{B}\right]}_{\infty }\left(\left[{\text{Ca}}^{2+}\right]-{\left[{\text{Ca}}^{2+}\right]}_{\infty }\right),$$ 1

Here, the steady-state calcium and buffer concentrations are denoted by [Ca²⁺]_∞, and [B]_∞, respectively. The diffusion coefficients of [Ca²⁺] and Buffer association rate are represented by D_Ca, and K⁺, respectively. The time and position variables are represented by ‘t’ and ‘x’, respectively.

Here IP₃ dynamics involving [Ca²⁺] given by Wagner et al. (2004) is employed and therefore the calcium dependent IP3 dynamics can be expressed in a neuron cell as,

$$\frac{\partial \left[{\text{IP}}_3\right]}{\partial \text{t}}={\text{D}}_{\text{i}}\frac{{\partial }^2\left[{\text{IP}}_3\right]}{\partial {\text{x}}^2}+\frac{{\text{J}}_{\text{production}}-\mathrm{\lambda }\left({\text{J}}_{\text{kinase}}{\text{+ J}}_{\text{phosphatase}}\right)}{{\text{F}}_{\text{c}}},$$ 2

where the diffusion coefficient of IP₃ is represented by Di.

The various influx and outflux terms of Eqs. (1 and 2) are expressed in the “Appendix”.

Initial conditions

The initial conditions for [Ca²⁺] and IP₃ are given by Dupont et al. (2000) and Brown et al. (2008) are employed here and are as given below,

$${\left[{\text{Ca}}^{2+}\right]}_{\text{t}=0}=0.1\mathrm{\mu }\text{M}.$$ 3

$${\left[{\text{IP}}_3\right]}_{\text{t = 0}}=0\text{.16}\mathrm{\mu }\text{M}.$$ 4

Boundary conditions

The appropriate boundary condition for [Ca²⁺] is given by Brown et al. (2008), as mentioned below,

$$\underset{\text{x}\to 0}{lim}\left(-{\text{D}}_{\text{c}}\frac{\partial \left[{\text{Ca}}^{2+}\right]}{\partial \text{x}}\right)=\sigma ,$$ 5

where source amplitude is denoted by σ.

At the boundary distant from the source, [Ca²⁺] attains the value 0.1 µM, i.e. its background concentration,

$$\underset{x\to 5}{lim}\left[{\text{Ca}}^{2+}\right]={\left[{\text{Ca}}^{2+}\right]}_{\infty }=0\text{.1}\mathrm{\mu }\text{M}.$$ 6

Also, for IP₃ dynamics, the boundary conditions given by Brown et al. (2008) are employed in the present study and given by,

$$\underset{x\to 5}{lim}\left[{\text{IP}}_3\right]=0\text{.16}.$$ 7

$$\underset{x\to 0}{lim}\left[{\text{IP}}_3\right]=3\mathrm{\mu }\text{M},\text{t}>0;$$ 8

The Aβ dynamics is given by (De Caluwé and Dupont 2013) as,

$$\frac{\partial A\beta }{\partial t}=\left({\text{V}}_{A\beta }+{\text{J}}_{A\beta }-{\text{J}}_{DA\beta }\right),$$ 9

The fluxes of Aβ production and degradation is defined by (De Caluwé and Dupont 2013) as,

$${\text{J}}_{A\beta }={\text{V}}_{\alpha }\left(\frac{{[{\text{Ca}}^{2+}]}^2}{K_{\alpha }^2+{[{\text{Ca}}^{2+}]}^2}\right),$$ 10

$${\text{J}}_{DA\beta }={\text{K}}_{11}A\beta ,$$ 11

where the maximal rate of production of Aβ by calcium and half-saturation constant are denoted by V_α, and K_α, respectively. V_Aβ is the constant production rate of β-amyloid, and K₁₁ is the degradation rate constant of β-amyloid. Initially the β-amyloid maintains its concentration at 0 μM in the cell. The solution is obtained by employing the finite element approach and its procedure is given in “Appendix”.

Results and discussion

The parameters and their numerical values employed in the present study are shown in Table 1.

Table 1.

Various parameters with numerical values and unit (Wagner et al. (2004); De Caluwé and Dupont (2013))

Symbols	Values	Symbols	Values
VIPR	8.5 s−1	KIP3	0.15 μM
Kserca	0.4 μM	Vserca	0.65 μM/s
VLeak	0.01 s−1	KAc	0.8 μM
Kinh	1.8 µM	k+	1.5 µM−1 s−1
DCa	16 µm2s−1	Di	283 µm2s−1
VProduction	0.075 µMs−1	KProduction	0.4 µM
V1	0.001 µMs−1	V2	0.005 µMs−1
Vph	0.02 µMs−1	λ	30
FC	0.83	FE	0.17
Vα	0.05 nMs−1	Kα	0.12 µM
K11	0.01 s−1	VAβ	0.0065 nMs−1

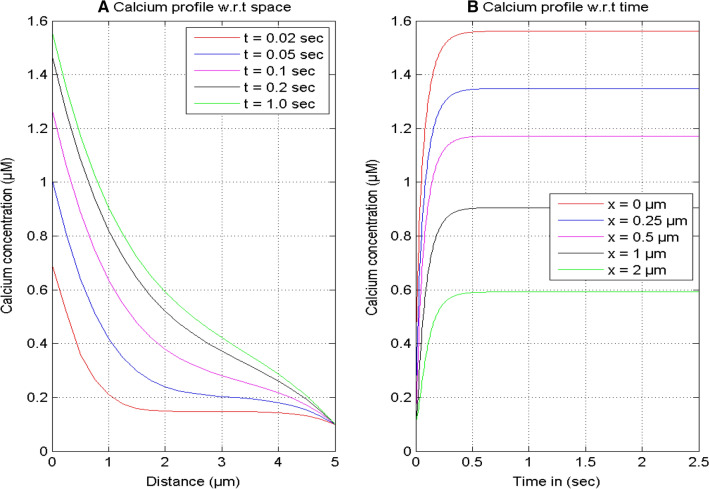
Figure 1 exhibits the spatial and temporal [Ca²⁺] distributions profile at different instants of time and positions in a neuron cell. It is noticed in Fig. 1A that the [Ca²⁺] concentration is high close to the source since the source channel releases a sufficient amount of calcium ions in the cell. The spatial calcium profile decreases on moving away from x = 0 μm to 5 μm and attains to the minimum concentration of calcium (0.1 μM) in the cell. The reasons for the reduction of the spatial calcium concentration are the extrusion of [Ca²⁺] from the cytosol by the serca pump, the free [Ca²⁺] bound by buffer, and the diffusion of calcium from the source to the other ends of the nerve cell. In Fig. 1B, it is seen that the temporal [Ca²⁺] distributions profile increases with time for different positions x = 0, 0.25, 0.5, 1.0, and 2.0 μm since the [Ca²⁺] concentration starts to release with the opening of the source channel and calcium concentration is elevated in the cytosol. The temporal calcium profile achieved the equilibrium state at the same time of 0.5 s for different positions in the cell.

Fig. 1.

Calcium concentration profile at various instances of time and positions for [B] = 5 μM and σ = 15 pA

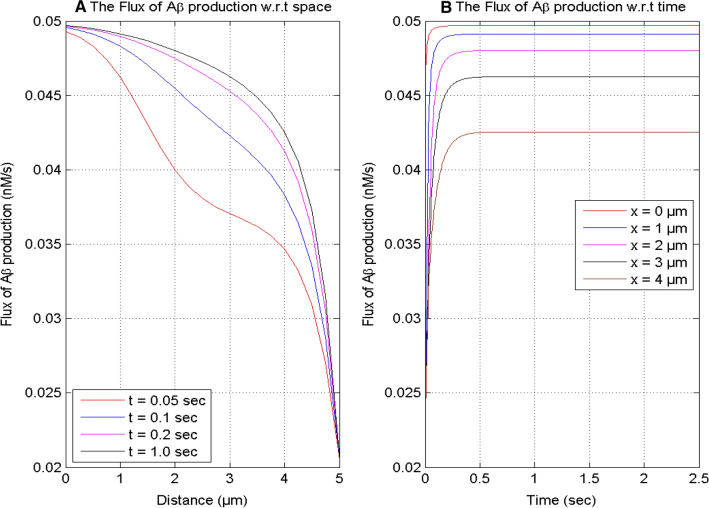
Figure 2 displays the production of β-amyloid corresponding to calcium concentration at different times and positions in the nerve cell. It is seen in Figs. 1A and 2A that the spatial profiles of calcium and the flux of β-amyloid production achieve their peak value near the source and decrease on moving away from x = 0 to x = 5 μm for different instants of time in the cell. This implies that elevated calcium concentration leads to the higher production of β-amyloid in the cell. The nonlinear behavior of β-amyloid production also changes with time in Fig. 2A in response to change in nonlinear behavior of calcium concentration profile in Fig. 1A. This change in nonlinear behavior is attributed to the increase in β-amyloid levels by the accumulation of these molecules with the passage of time. The main cause of this accumulation is the elevation in the production of β-amyloid due to increase in calcium concentration in the cell. Figures 1B and 2B show that the temporal profiles of calcium and the production of β-amyloid increase with time at different positions. But the flux of production of β-amyloid achieves the steady-state at various instants of time for various positions in a neuron cell. The time required to achieve equilibrium state of the flux of β-amyloid production increases with the distance from the source.

Fig. 2.

The flux of β-amyloid (Aβ) production for different points of time and positions for [B] = 5 μM and σ = 15 pA

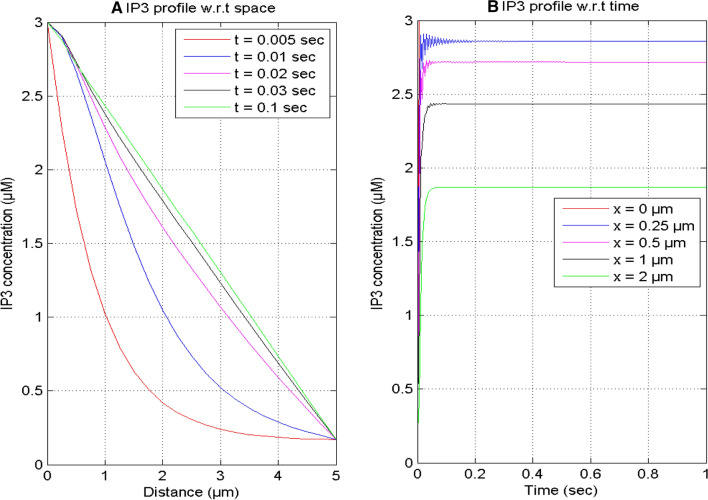
Figure 3 displays the spatial and temporal profiles of IP3 concentration at various instants of time and positions in a neuron cell. In Fig. 3A, it is noticed that the spatial profile of IP3 decreases from the boundary x = 0 μm to 5 μm and achieves the background concentration (0.16 μM) in the cell. The IP3 molecules bind near the IP3R and attain the boundary concentration of 3 μM at x = 0 μm for different instants of time t = 0.005, 0.01, 0.02, 0.03, and 0.1 s in the nerve cell. Initially, the IP3 concentration profile is nonlinear, and this nonlinearity decreases with the passage of time and becomes almost linear after some time due to the equilibrium being achieved among the various processes of IP3 dynamics. Figure 3B exhibits the temporal profile of IP3 concentration which increases with time for different positions x = 0, 0.25, 0.5, 1, and 2 μm, because the IP3 stores bind to the IP3R and discharge the calcium ions from ER to the cytosol in a neuron cell. The IP3 concentration shows the oscillatory behavior near the source because of a mismatch among the regulatory processes of IP3 dynamics in the cell.

Fig. 3.

IP3 concentration profile at various points of time and positions for [B] = 5 μM and σ = 15 pA

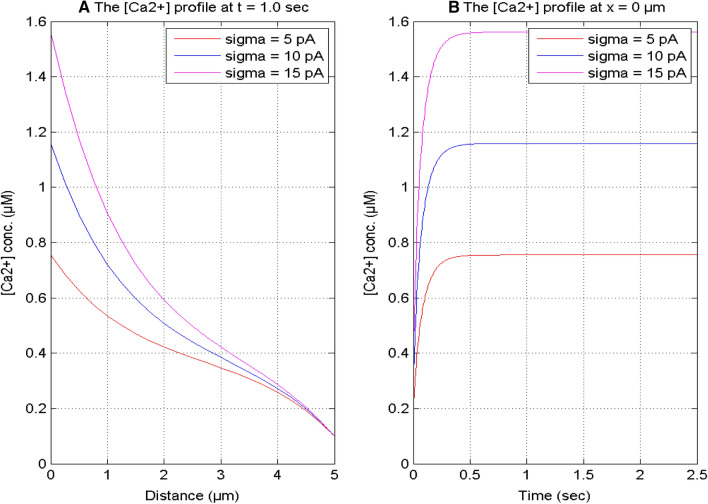
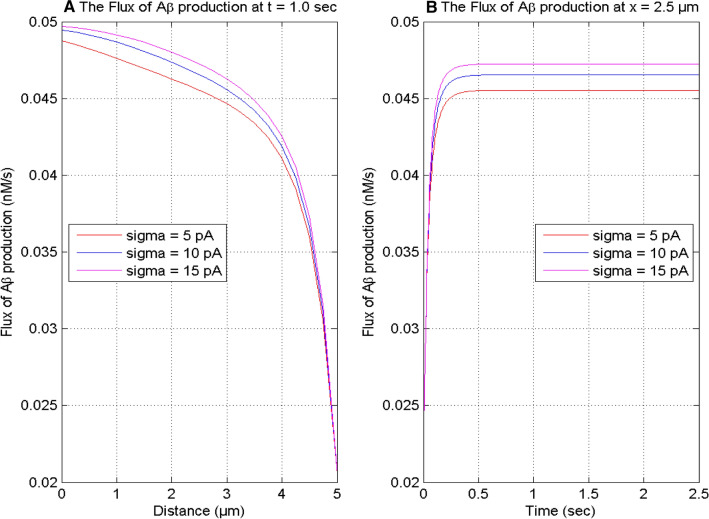
Figure 4 exhibits the spatial and temporal [Ca²⁺] concentration profiles at time t = 1.0 s and position x = 0 μm for different values of source influx in a neuron cell. The spatial calcium concentration profile attains the maximum value at x = 0 μm for varying source influx from 5 to 15 pA in the cell. When the value of source influx increases from 5 to 15 pA, the calcium concentration also increases. The required calcium concentration can be accomplished by increasing or decreasing the source influx in the nerve cell.

Fig. 4.

[Ca2 +] profile for distinct

source influx (σ) at t = 1.0 s and x = 0 μm for [B] = 5 μM

Figure 5 displays the influence of the source influx of calcium on the spatial and temporal profiles of the flux of β-amyloid production at various instants of time and positions in the nerve cell. In Figs. 4 and 5, it is seen that the [Ca²⁺] profile and the flux of β-amyloid production increase with the increase in the source influx of calcium from 5 to 15 pA in the cell. Thus, the source influx of calcium is a key mechanism for lowering or increasing the calcium-dependent production of β-amyloid in the cell.

Fig. 5.

The flux of production of β-amyloid (Aβ) at t = 1.0 s and x = 2.5 μm for [B] = 5 μM

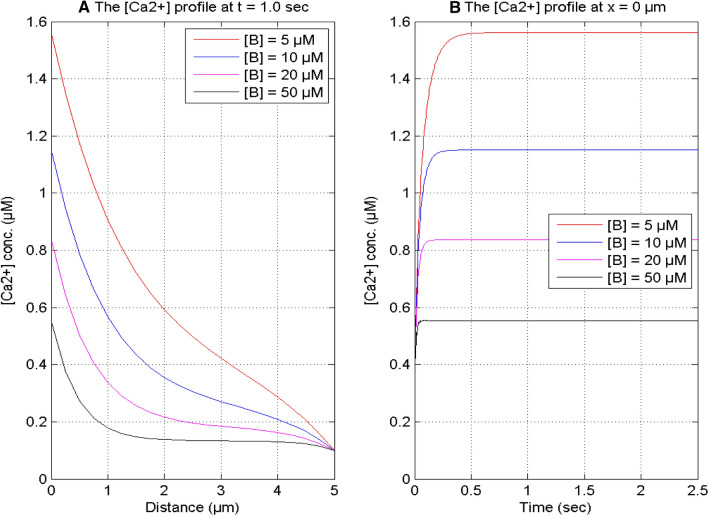
Figure 6 exhibits the impact of buffer on the [Ca²⁺] concentration for various instants of time and positions in the nerve cell. It is noticed in Fig. 6A that the spatial calcium distribution profile reduces with the increase in the values of buffer from [B] = 5 μM to 50 μM in the cell, since the buffer concentration binds additional calcium ions and decreases the free calcium availability in the nerve cell. Also, the spatial calcium concentration profile decreases from x = 0 to 5 μm for different buffers and attains the minimum concentration of calcium (0.1 μM) in a neuron cell. It is noticed in Fig. 6B that the temporal profile of [Ca²⁺] elevates with time and attains the steady-state earlier for the higher value of buffer in the cell.

Fig. 6.

Calcium distributions at the time t = 1.0 s and x = 0 μm with different buffer concentrations and σ = 15 pA

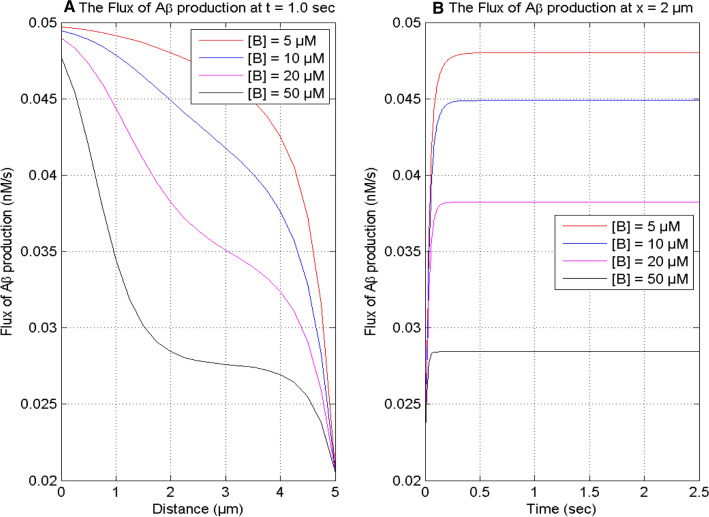
Figure 7 displays the spatial and temporal profiles of the flux of β-amyloid production at t = 1.0 s and x = 2 μm, respectively, in the nerve cell for different values of buffers. Figures 6A and 7A exhibit that the spatial profiles of calcium concentration and the flux of β-amyloid production decrease with the increase in the buffer concentration from 5 to 50 μM in the cell. The nonlinear behavior of the flux of β-amyloid production changes with the change in buffer concentration. For high values of buffer, the behavior of the curve is highly nonlinear exhibiting a concave shape due to imbalances among the regulatory processes caused by very high values of buffer in the cell. This nonlinearity decreases with the decrease in buffer concentration and after a certain threshold the decrease in buffer concentration causes the change in the nonlinear behavior of the curves approaching convex shape caused by the increasing calcium concentration due to a decrease in the buffering process. The temporal profile of the flux of β-amyloid production increases with time and achieves the steady-state earlier for the higher value of the buffer in the cell. Thus, the buffer influences the production of β-amyloid through the calcium signaling in the cell.

Fig. 7.

The flux of production of β-amyloid (Aβ) for time t = 1.0 s and position x = 2 μm for σ = 15 pA

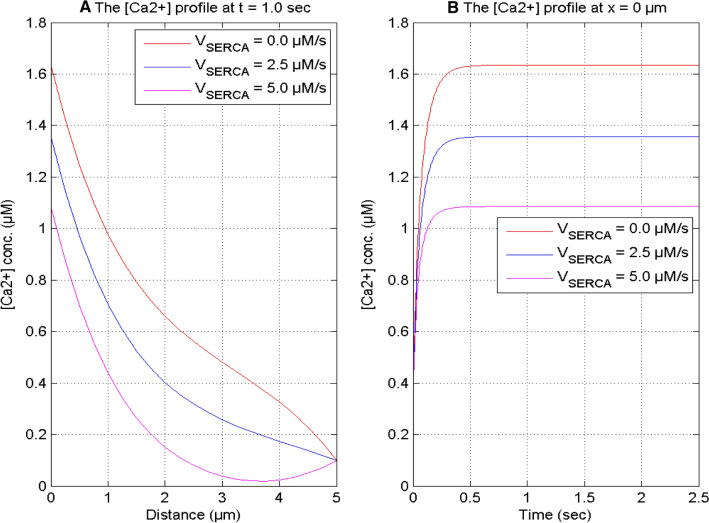
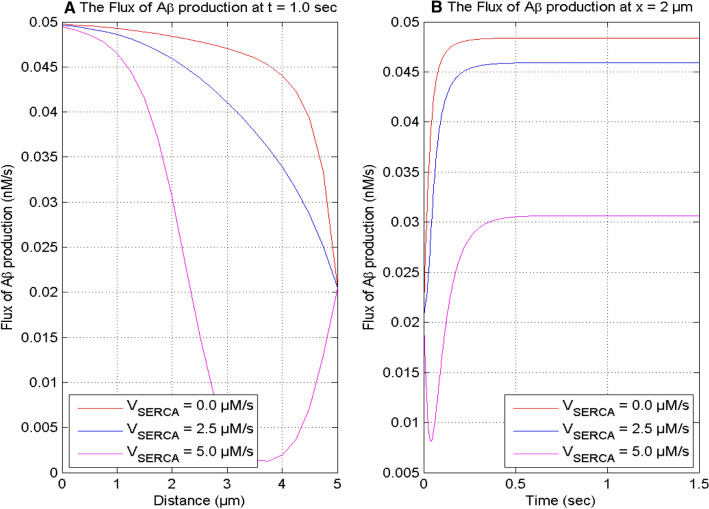
Figure 8 exhibits the impact of the constant rate of the serca pump on the calcium concentration at time t = 1.0 s and position x = 0 μm for in a neuron cell. With the increase in serca pump rate from V_SERCA = 0 to 5 μM/sec, the spatial and temporal calcium profiles decrease since the extrusion of [Ca²⁺] from the cytosol to the ER by the serca pump in a neuron cell. The calcium distribution achieves a high value when the serca pump is absent or stops functioning in the cell.

Fig. 8.

[Ca²⁺] profile at t = 1.0 s and x = 0 μm for different Serca pump rate and [B] = 5 μM and σ = 15 pA

The serca pump rate influences the production of β-amyloid (Aβ) through the interdependent calcium and IP3 signaling in the nerve cell. In Figs. 8 and 9, it is observed that the calcium profiles and the flux of production of β-amyloid decrease with the increase in the serca pump rate in a neuron cell. Also, the temporal profiles of calcium and the flux of β-amyloid production increase with time. The temporal profile of the flux of Aβ production achieves the steady-state at different instants of time for different values of the serca pump rate in the cell.

Fig. 9.

The flux of production of β-amyloid (Aβ) at t = 1.0 s and x = 2 μm for [B] = 5 μM and σ = 15 pA

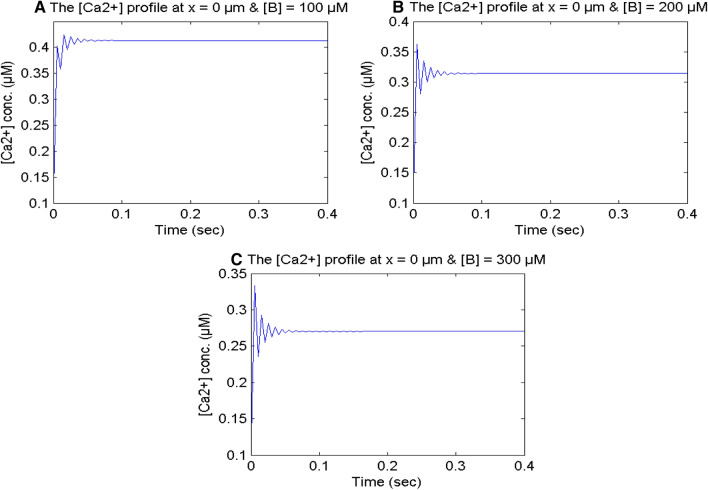
Figure 10 exhibits the calcium concentration at x = 0 μm for higher buffer values from [B] = 100 to 300 μM in a neuron cell. The fluctuations in the temporal calcium profile are seen in the initial time for higher buffer values in the cell. Since buffer fixes the calcium ions and lowers the [Ca²⁺] concentration in the cell, the other processes try to enhance the [Ca²⁺] concentration in the cell. The calcium profile achieves the steady-state inspite of oscillations. This implies that the calcium control mechanism tries to balance and neutralize the disturbances caused by the different processes in the cell to some extent and minimize the effects of these disturbances on calcium dynamics in the cell.

Fig. 10.

[Ca²⁺] profile at x = 0 μm for different buffer concentrations for σ = 15 pA

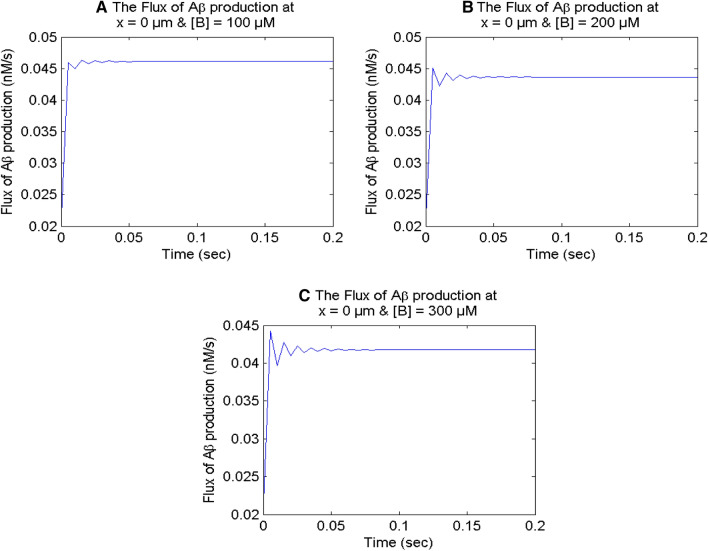
Figure 11 displays the impact of a higher buffer on the flux of β-amyloid (Aβ) through calcium signaling at x = 0 μm in a neuron cell. The fluctuations are also observed in temporal profiles of the flux of Aβ for higher buffer values in Fig. 11 as noticed in Fig. 10 for calcium profile in the nerve cell.

Fig. 11.

The flux of β-amyloid (Aβ) production at x = 0 μm for different buffer concentrations for σ = 15 pA

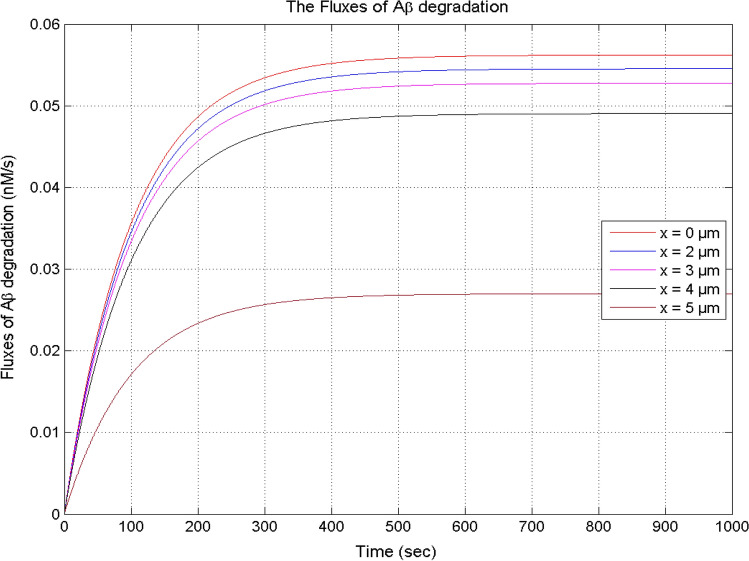
Figure 12 exhibits the effects of interdependent dynamics of calcium and IP3 on the degradation of β-amyloid for different positions in the neurons. In Fig. 1, it is noticed that the temporal [Ca²⁺] concentration increases with time for different positions, and the flux of β-amyloid degradation also increases with time in the cell. The flux of β-amyloid degradation decreases with distance from the position x = 0 μm to 5 μm. The temporal flux of β-amyloid degradation achieves the steady-state at the same time in the cell.

Fig. 12.

The flux of β-amyloid (Aβ) degradation at different positions for [B] = 5 μM, and σ = 15 pA

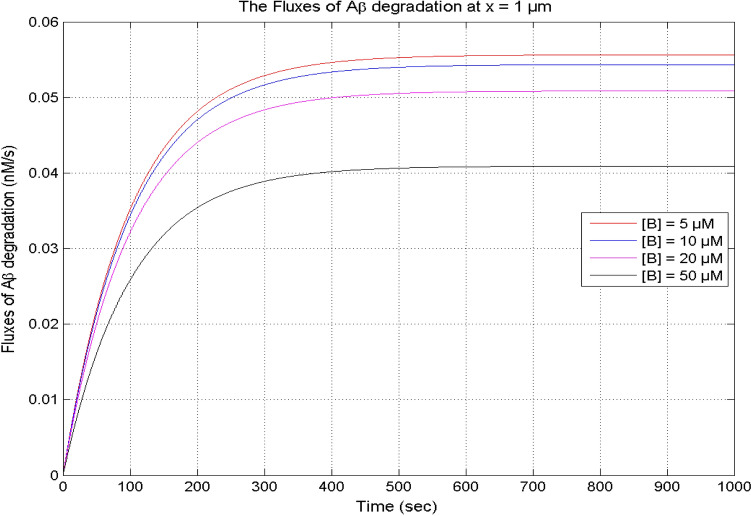
Figure 13 exhibits the temporal profile of the flux of β-amyloid degradation at x = 1 μm for various buffer concentrations from 5 to 50 μM in a neuron cell. In Figs. 6A and 13, it is noticed that the temporal profiles of calcium and the flux of the β-amyloid degradation are lower with the increase in the buffer concentration in a neuron cell. Thus, the buffer controls the β-amyloid degradation through the calcium signaling in the cell.

Fig. 13.

The flux of β-amyloid (Aβ) degradation at x = 1 μm for different buffer concentrations, and σ = 15 pA

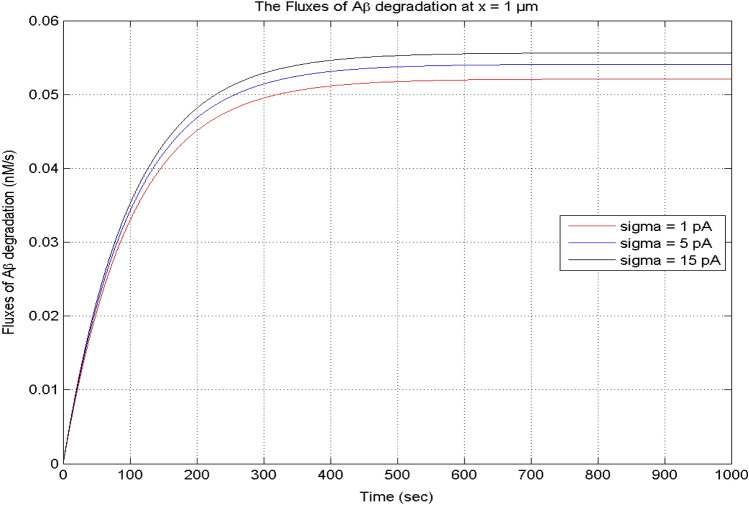
The source influx of calcium plays a crucial function in maintaining the required [Ca²⁺] level in the nerve cell. In Fig. 14, it is noticed that the temporal profile of β-amyloid degradation flux elevates with time for various values of calcium source influx. When the [Ca²⁺] source influx increases from 1 to 15 pA, the flux of β-amyloid degradation also increases in the cell. The calcium-dependent flux of β-amyloid degradation attains the equilibrium state at the same time for different source influx values of calcium in a neuron cell.

Fig. 14.

The flux of β-amyloid (Aβ) degradation at x = 1 μm for different calcium

source influxes, and [B] = 5 μM

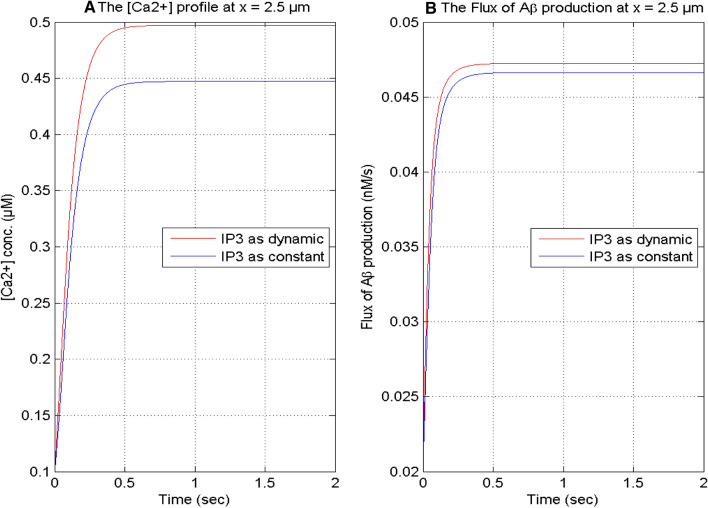
Figure 15 exhibits the temporal profiles of calcium and calcium-dependent β-amyloid production flux for IP3 as dynamic and IP3 as constant in a neuron cell. The IP3 as dynamic can regulate the [Ca2 +] at a higher level in the cell because when the IP3 is constant, then calcium concentration is lower than the calcium concentration obtained by taking IP3 as dynamic. The temporal profile of β-amyloid production flux is also influenced by the variation in IP3 as constant and dynamics through calcium signaling. The flux of β-amyloid production is more elevated with IP3 as dynamics than β-amyloid production flux with IP3 as constant in the cell.

Fig. 15.

The calcium concentration and the flux of β-amyloid (Aβ) production with IP3 as dynamic and IP3 as constant (1 μM) at x = 2.5 μm for [B] = 5 μM, and σ = 15 pA

For the time t = 0.1, 0.5, 1.0, and 2.0 s, the accuracy of the model for calcium is 99.76%, 99.916656%, 99.910415%, and 99.910425% respectively and for IP3 dynamics, the accuracy is 99.87%., 99.94008%, 99.97488%, and 99.9929333% respectively. Thus the maximum error % and minimum accuracy for this model are 0.24% and 99.76%, respectively. The grid sensitivity is negligible; this implies that the solution is grid independent (Tables 2 and 3).

Table 3.

Error analysis of IP3 concentration profile at x = 0.25 μm

Time (s)	N = 20 elements	N = 40 elements	Error	Error %
t = 0.1	2.87343286538522	2.86988114612419	0.0036	0.13
t = 0.5	2.85908272565951	2.85753010502270	0.0016	0.05992
t = 1.0	2.85845932581781	2.85774146645704	0.00071786	0.025120
t = 2.0	2.85839852910731	2.85819654838843	0.00020198	0.0070667

Table 2.

Error analysis of [Ca2 +] concentration profile at x = 0 μm

Time (s)	N = 20 elements	N = 40 elements	Error	Error %
t = 0.1	1.270271285548480	1.267294607162714	0.003	0.24
t = 0.5	1.558454937495950	1.559797388658348	0.0013	0.083344
t = 1.0	1.561578411926424	1.562931157676452	0.0014	0.089585
t = 2.0	1.56159028586953	1.56294304372431	0.0014	0.089575

The [Ca²⁺] and IP₃ concentration profiles were obtained for the various values of the parameter, for [B] = 0 μM, and σ = 2.46 pA for the calcium concentration profile, and the boundary concentration of IP3 dynamics as 0.5 μM at x = 0 μm, are compared with earlier published results of Wagner et al. (2004) at time t = 50 s, and results are found in a good agreement as shown in Table 4. However, no experiment results are available for further validation of obtained results.

Table 4.

[Ca²⁺] and IP₃ concentration profiles compared with Wagner et al. (2004) at t = 50 s

Distance (μm)	[Ca2+] concentration Wagner et al. (2004)	[Ca2+] concentration (present results)	IP3 concentration Wagner et al. (2004)	IP3 concentration (present results)
x = 0 μm	1.35000000000000	1.34981836731882	0.5000000000000	0.500000000000
x = 1 μm	1.19311237093306	1.19298936853484	0.431787347314089	0.431787350767981
x = 2 μm	1.01615701363841	1.01607655910625	0.363691491730167	0.363691496147387
x = 3 μm	0.795857981478569	0.795809556080343	0.295702455054905	0.295702458806600
x = 4 μm	0.503271331553076	0.503248604412665	0.227809391393345	0.227809393499215
x = 5 μm	0.100000000000000	0.100000000000000	0.160000000000	0.160000000000

To perform stability analysis, the spectral radius was calculated and the system is said to be stable if the spectral radius is less than or equal to unity (Öziş et al. 2003). In our case, the spectral radius was 0.9851, which is less than unity. Thus the finite element solution in the present condition is stable.

Conclusion

A model is framed and employed effectively to study the disturbances in interdependent calcium and IP3 dynamics on β-amyloid production and degradation in a neuron cell. The disturbances in interdependent calcium and IP3 can be caused by the dysfunction of processes like source influx, buffer, and serca pump. Therefore, high values of source influx and serca pump rate and low and high values of buffer were considered due to some disorder in these processes. A notable effect of these disturbances was seen on the calcium and IP3 dynamics as well as on the production and degradation of β-amyloid. The following novel conclusions were made by analyzing the results obtained.

• i.The high values of source influx can cause an elevation in calcium and IP3 concentration profiles, which in turn elevates the production and degradation of β-amyloid. The increased influx of calcium is associated with Familial Hemiplegic Migraine (FHM), Huntington, and Alzheimer’s disease (Brini et al. 2014).
• ii.The low values of serca pump rate can cause an elevation in calcium and IP3 concentration profiles, which in turn elevates the production and degradation of β-amyloid. The altered ER function is associated with Alzheimer’s disease, which may be caused by the altered serca pump capacity (Brini et al. 2014). The low levels of cellular ATP can cause the reduced function of the ATP-dependent serca pump, which in turn causes an elevation in free calcium in the case of Alzheimer’s disease (Bojarski et al. 2008).
• iii.The low values of the buffer can be the cause of high levels of calcium and IP3 concentration in neuron cells, which in turn can cause the higher flux of β-amyloid production and degradation. The decrease in buffering capacity is associated with Huntington’s, Amyotrophic Lateral Sclerosis (ALS), and Cerebellar Ataxia (Brini et al. 2014). The low buffering capacity of calbindin D (Bojarski et al. 2008) is found to be associated with aging and neurodegenerative diseases (Bojarski et al. 2008) like Alzheimer’s etc.
• iv.The high values of the buffer can be the cause of low levels of calcium and IP3 concentration leading to the decrease in the flux of β-amyloid production and degradation. Also, high values of the buffer can cause mismatches among the levels of regulatory processes, which lead to oscillations in calcium and β-amyloid production. The most important proteins are the EF hand proteins and C2 proteins, which perform the function of buffering. CaM (Brini et al. 2014) belongs to the category of EF hand proteins and is found in high concentrations (up to 100 μM), which can cause dysfunction in calcium homeostasis.
• v.The elevations in IP3 levels can result in an elevation of calcium concentration and β-amyloid production. The increased IP3 sensitivity is associated with Cerebellar Ataxia (Brini et al. 2014).

Thus, it can be concluded that disturbances in various constitutive processes of calcium and IP3 dynamics can result in altered β-amyloid production and degradation, which can lead to various neuronal disorders. The lower levels of buffering capacity, reduced function of serca pump, high levels of source influx, and variations in IP3 levels can cause elevations in free calcium levels and β-amyloid production, which is the cause of Alzheimer’s in the case where there is mismatch between β-amyloid production and its degradation and β-amyloid metabolism.

The results agree with the biological facts. The finite element simulation approach is quite effective in the present study.

Any disturbances in the interdependence of calcium and IP3 dynamics can result in dysfunction leading to neurological disorders. The model gives us insights of the constitutive processes of calcium and IP3 dynamics causing elevations in β-amyloid production, which in turn is a cause of neurotoxicity resulting in Alzheimer’s disease. The results indicate the challenge of identifying the appropriate constitutive process of calcium and IP3 dynamics, which is the main cause of the altered β-amyloid production in Alzheimer’s disease patients. Thus, there are many questions still to be answered. However, the results obtained about the relationships of constitute processes of calcium and IP3 dynamics with β-amyloid production and degradation can be useful in addressing the above challenges. The information generated from the model can be useful for the development of diagnostics and treatment protocols for neuronal disorders like Alzheimer’s etc. The major novel outcomes of the present study are that the results of the proposed model give us a clear understanding of specific constitutive processes, which on being disturbed by any cause can lead to diseases like Alzheimer’s, Familial Hemiplegic Migraine (FHM), Huntington’s, Amyotrophic Lateral Sclerosis (ALS), Cerebellar Ataxia, etc.

Appendix:Summary of the model equations

The different fluxes of Eq. (1) are provided by Wagner et al. (2004),

$${\text{J}}_{\text{IPR}}{\text{= V}}_{\text{IPR}}{\text{m}}^3{\text{h}}^3\left({\left[{\text{Ca}}^{2+}\right]}_{\text{ER}}-\left[{\text{Ca}}^{2+}\right]\right),$$ 12

$${\text{J}}_{\text{SERCA}}{\text{= V}}_{\text{SERCA}}\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^2}{{\left[{\text{Ca}}^{2+}\right]}^2{\text{+ K}}_{\text{SERCA}}^2}\right),$$ 13

$${\text{J}}_{\text{LEAK}}{\text{= V}}_{\text{LEAK}}\left({\left[{\text{Ca}}^{2+}\right]}_{\text{ER}}-\left[{\text{Ca}}^{2+}\right]\right),$$ 14

where the flux of leak, IP3 receptor, and serca pump is denoted by J_LEAK, J_IPR, and J_SERCA. The flux rate constant of IP₃R and leak are denoted by V_IPR and V_LEAK, respectively. V_SERCA and K_SERCA are the maximum rate constant and Michaelis constant for serca pump, respectively.

Here the terms m and h are provided by Li and Rinzel (1994),

$$\text{m =}\left(\frac{{\text{[IP}}_3]}{{\text{[IP}}_3{\text{] + K}}_{\text{IP3}}}\right)\left(\frac{\left[{\text{Ca}}^{2+}\right]}{\left[{\text{Ca}}^{2+}\right]{\text{+ K}}_{\text{Ac}}}\right),$$ 15

$$\text{h =}\frac{{\text{K}}_{\text{Inh}}}{{\text{K}}_{\text{Inh}}+\left[{\text{Ca}}^{2+}\right]},$$ 16

where K_IP3, K_Ac, and K_inh are the dissociation constant of the binding position of activating IP₃, activating [Ca²⁺] and inhibiting [Ca²⁺], sequentially.

The production of IP₃ depends on calcium is provided by Wagner et al. (2004) is mentioned below:

$${\text{J}}_{\text{production}}{\text{= V}}_{\text{production}}\left(\frac{{\left[{\text{Ca}}^{2+}\right]}^2}{{\left[{\text{Ca}}^{2+}\right]}^2{\text{+ K}}_{\text{production}}^2}\right),$$ 17

where The IP₃ production flux term is denoted by J_Production. The maximum IP₃ production rate and Michaelis constant concerning calcium activation are expressed by V_Production and K_Production, respectively.

The IP₃ degradation by J_Kinase and J_phosphatase are given by Sims and Allbrittont (1998) and Bugrim et al. (2003) are shown below:

$${\text{J}}_{\text{kinase}}=\left(1-\zeta \right){\text{V}}_1\left(\frac{\left[{\text{IP}}_3\right]}{\left[{\text{IP}}_3\right]+2.5}\right)+\zeta {\text{V}}_2\left(\frac{\left[{\text{IP}}_3\right]}{\left[{\text{IP}}_3\right]+0.5}\right),$$ 18

$${\text{J}}_{\text{phosphatase}}{\text{= V}}_{\text{ph}}\left(\frac{\left[{\text{IP}}_3\right]}{\left[{\text{IP}}_3\right]+30}\right),$$ 19

$$\zeta =\left(\frac{\left[{\text{Ca}}^{2+}\right]}{\left[{\text{Ca}}^{2+}\right]+0.39}\right),$$ 20

Also, the maximum rate constant for low calcium (3-kinase), high calcium (3-kinase), and phosphatase are V₁, V₂, and V_ph, respectively. The degradation rate is estimated by an adjustable parameter, (λ = 30) (Wagner et al. 2004). The [Ca²⁺]_ER may be eliminated by employing the conservation relationship of the total cellular calcium concentration,

$${\text{[Ca2 + ]}}_{\text{T}}{\text{= F}}_{\text{E}}{\text{[Ca2 + ]}}_{\text{ER}}{\text{+ F}}_{\text{C}}{\text{[Ca2 + ]}}_{\text{C}},$$

The shape function of [Ca²⁺] and IP₃, for each element is taken as,

$${\text{u}}_1^{\text{(e)}}{\text{= q}}_{11}^{\text{(e)}}{\text{+ q}}_{12}^{\text{(e)}}\text{x,}$$ 21

$${\text{u}}_2^{\text{(e)}}{\text{= q}}_{21}^{\text{(e)}}{\text{+ q}}_{22}^{\text{(e)}}\text{x,}$$ 22

$${\text{u}}_1^{\text{(e)}}{\text{= S}}^{\text{T}}{\text{q}}_1^{\text{(e)}}{\text{, u}}_2^{\text{(e)}}{\text{= S}}^{\text{T}}{\text{q}}_2^{\text{(e)}},$$ 23

$${\text{S}}^{\text{T}}=[\begin{array}{cc}1& \text{x}\end{array}{\text{], q}}_1^{{\text{(e)}}^{\text{T}}}=[\begin{array}{cc}{\text{q}}_{11}^{\text{(e)}}& {\text{q}}_{12}^{\text{(e)}}\end{array}{\text{], q}}_2^{{\text{(e)}}^{\text{T}}}=[\begin{array}{cc}{\text{q}}_{21}^{\text{(e)}}& {\text{q}}_{22}^{\text{(e)}}\end{array}],$$ 24

Putting the nodal conditions in Eq. (23), we get

$${\overline{\text{u}}}_1^{(\text{e})}={\text{S}}^{(\text{e})}{\text{q}}_1^{(\text{e})},{\overline{\text{u}}}_2={\text{S}}^{(\text{e})}{\text{q}}_2^{(\text{e})},$$ 25

where

$${\overline{\text{u}}}_1^{\text{(e)}}=\left[\begin{array}{c}{\text{u}}_{\text{1i}}\\ {\text{u}}_{\text{1j}}\end{array}\right],{\overline{\text{u}}}_2^{\text{(e)}}=\left[\begin{array}{c}{\text{u}}_{\text{2i}}\\ {\text{u}}_{\text{2j}}\end{array}\right],\text{and}{\text{S}}^{\text{(e)}}=\left[\begin{array}{cc}1& {\text{x}}_{\text{i}}\\ 1& {\text{x}}_{\text{j}}\end{array}\right],$$ 26

By the Eq. (25), we get

$${\text{q}}_1^{\text{(e)}}{\text{= R}}^{\text{(e)}}{\overline{\text{u}}}_1^{\text{(e)}}{\text{, q}}_2^{\text{(e)}}{\text{= R}}^{\text{(e)}}{\overline{\text{u}}}_2^{\text{(e)}},$$ 27

And

$${\text{R}}^{\text{(e)}}{\text{= S}}^{{\text{(e)}}^{-1}},$$ 28

Putting ${\text{q}}_1^{\text{(e)}}$ and ${\text{q}}_2^{\text{(e)}}$ using Eq. (27) in (23), we obtain

$${\text{u}}_1^{\text{(e)}}{\text{= S}}^{\text{T}}{\text{R}}^{\text{(e)}}{\overline{\text{u}}}_1^{\text{(e)}}{\text{, u}}_2^{\text{(e)}}{\text{= S}}^{\text{T}}{\text{R}}^{\text{(e)}}{\overline{\text{u}}}_2^{\text{(e)}},$$ 29

Discretized form of Eq. (1 & 7) is given by,

The integral ${\text{I}}_1^{\text{(e)}}$ and ${\text{I}}_2^{\text{(e)}}$ can be expressed in this formation

$${\text{I}}_1^{\text{(e)}}{\text{= I}}_{\text{a11}}^{\text{(e)}}-{\text{I}}_{\text{a12}}^{\text{(e)}}{\text{+ I}}_{\text{a13}}^{\text{(e)}}-{\text{I}}_{\text{a14}}^{\text{(e)}}{\text{+ I}}_{\text{a15}}^{\text{(e)}}-{\text{I}}_{\text{a16}}^{\text{(e)}}-{\text{I}}_{\text{a17}}^{\text{(e)}},$$ 30

where

$${\text{I}}_{\text{a11}}^{\text{(e)}}=\underset{x_i}{\overset{x_j}{\int }}\left\{{\left(\frac{\partial {\text{u}}_1^{\text{(e)}}}{\partial \text{x}}\right)}^2\right\}\text{dx},$$ 31

$${\text{I}}_{\text{a12}}^{\text{(e)}}=\frac{\text{d}}{\text{dt}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[\frac{{\text{(u}}_1^{\text{(e)}})}{{\text{D}}_{\text{Ca}}}\right]\text{dx},$$ 32

$${\text{I}}_{\text{a13}}^{\text{(e)}}=\frac{{\text{V}}_{\text{IPR}}}{{\text{D}}_{\text{ca}}{\text{F}}_{\text{c}}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[{\alpha u}_1^{\text{(e)}}+{\beta u}_2^{\text{(e)}}+\mathrm{\gamma }\right]\text{dx},$$ 33

$${\text{I}}_{\text{a}14}^{(\text{e})}=\frac{{\text{V}}_{\text{SERCA}}}{{\text{D}}_{\text{ca}}{\text{F}}_{\text{c}}}\underset{{\text{x}}_i}{\overset{{\text{x}}_j}{\int }}\left[\kappa {\text{u}}_1^{(\text{e})}+\eta \right]\text{dx},$$ 34

$${\text{I}}_{\text{a15}}^{\text{(e)}}=\frac{{\text{V}}_{\text{LEAK}}}{{\text{D}}_{\text{ca}}{\text{F}}_{\text{c}}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[{\text{[Ca}}^{2+}{]}_{\text{ER}}{\text{- u}}_1^{\text{(e)}}\right]\text{dx},$$ 35

$${\text{I}}_{\text{a16}}^{\text{(e)}}=\frac{{\text{K}}^{+}}{{\text{D}}_{\text{ca}}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[{\text{u}}_1^{\text{(e)}}-{\text{[Ca}}^{2+}{]}_{\infty }\right]\text{dx},$$ 36

$${\text{I}}_{\text{a17}}^{\text{(e)}}{\text{= f}}^{\text{(e)}}{\frac{\mathrm{\sigma }}{{\text{D}}_{\text{ca}}}}_{\text{x = 0}},$$ 37

$${\text{I}}_2^{\text{(e)}}{\text{= I}}_{\text{a21}}^{\text{(e)}}-{\text{I}}_{\text{a22}}^{\text{(e)}}{\text{+ I}}_{\text{a23}}^{\text{(e)}}-{\text{I}}_{\text{a24}}^{\text{(e)}},$$ 38

$${\text{I}}_{\text{a21}}^{\text{(e)}}=\underset{x_i}{\overset{x_j}{\int }}\left\{{\left(\frac{\partial {\text{u}}_2^{\text{(e)}}}{\partial \text{x}}\right)}^2\right\}\text{dx},$$ 39

$${\text{I}}_{\text{a22}}^{\text{(e)}}=\frac{\text{d}}{\text{dt}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[\frac{{\text{u}}_2^{\text{(e)}}}{{\text{D}}_{\text{i}}}\right]\text{dx},$$ 40

$${\text{I}}_{\text{a23}}^{\text{(e)}}=\frac{{\text{V}}_{\text{PROD}}}{{\text{D}}_{\text{i}}{\text{F}}_{\text{c}}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[{\mathrm{\mu }u}_1^{\text{(e)}}+\mathrm{\tau }\right]\text{dx},$$ 41

$${\text{I}}_{\text{a2}4}^{(\text{e})}=\frac{\lambda }{{\text{F}}_{\text{c}}{\text{D}}_{\text{i}}}\underset{{\text{x}}_{\text{i}}}{\overset{{\text{x}}_{\text{j}}}{\int }}\left[\delta {\text{u}}_1^{(\text{e})}+\xi {\text{u}}_1^{(\text{e})}+\omega )\right]dx,$$ 42

The different parameters $\alpha ,{\beta }_1,\gamma ,\kappa ,\eta ,\mu ,\tau ,\delta ,\xi ,\text{and},\omega$ are obtained by the linearization of nonlinear interdependent calcium and IP3 dynamics. The equations are analyzed and boundary conditions are included to give the following system of equations.

$$\frac{{\text{dI}}_1}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}=\sum _{\text{e = 1}}^{\text{N}}{\overline{\text{Q}}}^{\text{(e)}}\frac{{\text{dI}}_1^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}\text{Q}{\overline{\text{Q}}}^{{\text{(e)}}^{\text{T}}}=0,$$ 43

$$\frac{{\text{dI}}_2}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}=\sum _{\text{e = 1}}^{\text{N}}{\overline{\text{Q}}}^{\text{(e)}}\frac{{\text{dI}}_2^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}{\overline{\text{Q}}}^{{\text{(e)}}^{\text{T}}}=0,$$ 44

where

$${\overline{\text{Q}}}^{\text{(e)}}=\left[\begin{array}{cc}\begin{array}{c}0\\ \begin{array}{c}.\\ \begin{array}{c}0\\ 1\\ \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}.\\ 0\end{array}\end{array}\end{array}\end{array}\end{array}& \begin{array}{c}0\\ \begin{array}{c}.\\ \begin{array}{c}0\\ 0\\ \begin{array}{c}\begin{array}{c}1\\ 0\end{array}\\ \begin{array}{c}.\\ 0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right]\text{and}\overline{\text{u}}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\text{u}}_{1_1}\\ {\text{u}}_{1_2}\end{array}\\ {\text{u}}_{1_3}\end{array}\\ \begin{array}{c}.\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ {\text{u}}_{1_{19}}\end{array}\\ {\text{u}}_{1_{20}}\end{array}\\ {\text{u}}_{1_{21}}\end{array}\end{array}\end{array}\right],{\overline{\text{u}}}_2=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\text{u}}_{2_1}\\ {\text{u}}_{2_2}\end{array}\\ {\text{u}}_{2_3}\end{array}\\ \begin{array}{c}.\\ \begin{array}{c}\begin{array}{c}\begin{array}{c}.\\ {\text{u}}_{2_{19}}\end{array}\\ {\text{u}}_{2_{20}}\end{array}\\ {\text{u}}_{2_{21}}\end{array}\end{array}\end{array}\right],$$ 45

$$\frac{{\text{dI}}_1^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}=\frac{{\text{dI}}_{\text{a11}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}+\frac{\text{d}}{\text{dt}}\frac{{\text{dI}}_{\text{a12}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}+\frac{{\text{dI}}_{\text{a13}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}+\frac{{\text{dI}}_{\text{a14}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}-\frac{{\text{dI}}_{\text{a15}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}}-\frac{{\text{dI}}_{\text{a16}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_1^{\text{(e)}}},$$ 46

$$\frac{{\text{dI}}_2^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}=\frac{{\text{dI}}_{\text{a21}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}+\frac{\text{d}}{\text{dt}}\frac{{\text{dI}}_{\text{a22}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}+\frac{{\text{dI}}_{\text{a23}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}}-\frac{{\text{dI}}_{\text{a24}}^{\text{(e)}}}{\text{d}{\overline{\text{u}}}_2^{\text{(e)}}},$$ 47

$${\left[\text{A}\right]}_{42\times 42}\left[\begin{array}{c}{\left[\frac{\partial {\overline{\text{u}}}_1}{\partial \text{t}}\right]}_{21\times 1}\\ {\left[\frac{\partial {\overline{\text{u}}}_2}{\partial \text{t}}\right]}_{21\times 1}\end{array}\right]+{\left[\text{B}\right]}_{42\times 42}\left[\begin{array}{c}{\left[{\overline{\text{u}}}_1\right]}_{21\times 1}\\ {\left[{\overline{\text{u}}}_2\right]}_{21\times 1}\end{array}\right]={[\text{F}]}_{42\times 1}.$$ 48

Here, the system matrices are A and B with the system vectors F. The Crank–Nicolson method which is numerically stable is applied to solve the time derivate in FEM.

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.